1. Introduction
In many African countries, the relationships between wildlife and rural people are complex. Wildlife can be a source of food and income, yet living with wildlife imposes significant costs on rural communities, which have been documented extensively elsewhere (e.g., Thirgood et al., Reference Thirgood, Woodroffe, Rabinowitz, Woodroffe, Thirgood and Rabinowitz2005). A range of community-based conservation and development programs have attempted to improve the incentives for wildlife conservation by rural residents, such as community-based natural resource management (CBNRM) programs (e.g., Borgerhoff Mulder and Coppolillo, Reference Borgerhoff Mulder and Coppolillo2005). These programs were intended to reduce human–wildlife conflict and to encourage wildlife and habitat conservation by providing (semi-subsistence) rural communities with wildlife user rights. In Botswana, rural residents were expected to benefit financially from wildlife conservation by entering into joint venture partnerships with wildlife-based tourism operators or by selling the photographic or hunting rights to wildlife on community land to tourism operators, and by gaining employment and training from the tourism industry. Ultimately, the government of Botswana expected CBNRM programs to increase wildlife conservation by rural communities, increase revenues for the wildlife-based tourism industry, and increase income and employment for rural communities (e.g., Ministry of Environment, Wildlife and Tourism, 2007).
Unfortunately, CBNRM programs have consistently underperformed, both in Botswana and in other African countries (e.g., Haller et al., Reference Haller, Galvin, Meroka, Alca and Alvarez2008). A principal reason is the lack of direct financial incentives to protect wildlife at the individual level (Pienaar et al., Reference Pienaar, Jarvis and Larson2013). Rather, revenues from wildlife are often spent on projects that are intended to benefit the community (e.g., the construction of a community hall, the purchase of a tractor to plow fields or training programs for only a few community members) and in payments to the community-based organization (or Trust) that runs the CBNRM program. At the individual level where decisions to poach wildlife, destroy predators or degrade habitat are made, the opportunity costs of conservation are direct and immediate,Footnote 1 whereas the prospective individual benefit from conservation is weak and uncertain. From an economic perspective, the policy design problem thus is twofold: institutional mechanisms must provide direct rewards for decisions to conserve wildlife, and information is needed on how large wildlife conservation incentives should be and whether such incentives are fiscally feasible.Footnote 2
This paper addresses the second of these two policy design issues, providing information on rural residents' willingness to accept wildlife conservation jobs. Our purposes are: (a) to develop and implement a straightforward, yet rigorous, method of identifying the amounts of money that rural Botswana residents require to work in several key conservation activities that reduce human–wildlife conflict or help improve wildlife habitat and numbers; (b) to introduce a generalization of standard models of the value of time, which is a central concept when considering inducements to work; and (c) to provide empirical estimates of willingness to accept payment by rural Batswana for employment in conservation jobs.
To do these things, we develop a model of labor supply and reservation wages for these jobs that identifies both people's marginal money values of working in wildlife conservation and their opportunity costs of time spent working (which we refer to generically as the shadow value of time, or svt). The conditional indirect utility function used in our analysis is more general than that used in standard discrete choice analysis, which is a special case that can be tested for in our framework. It provides an explanation for how the svt varies with a person's economic constraints and their choice of time worked, which does not currently exist in the literature, as standard models of the svt imply that it is independent of income and time spent working. This implication is counter-intuitive, as one might expect that, as a person's income increases, or as the amount of time an individual spends working increases, the opportunity cost of time will also increase. Thus, our paper contributes both to the development economics literature by developing and estimating a model of rural African labor supply and reservation wages for conservation work, and to the literature on valuing time, which is important to applications in the areas of home production (e.g., Gronau, Reference Gronau1973), labor supply (Becker, Reference Becker1965; Heckman, Reference Heckman1974), outdoor recreation demand (Knetsch, Reference Knetsch1964; Bockstael et al., Reference Bockstael, Strand and Hanemann1987) and transportation mode choice (DeSerpa, Reference DeSerpa1971; Jara-Díaz and Guevara, Reference Jara-Díaz and Guevara2003).
Section 2 introduces the choice experiment data on willingness to work in wildlife conservation. Section 3 develops the analytical framework used to assess labor supply and reservation wages for working in wildlife conservation in rural Botswana. Section 4 presents the empirical estimates of the model and a discussion of the results. Section 5 concludes.
2. Data
The data used in this analysis come from a household survey conducted in five CBNRM programs in Botswana during 2007, to collect information about how these programs could be restructured such that rural community members would actively engage in wildlife conservation. The survey underwent extensive pre-testing, using focus groups and one-on-one sessions in the design phase, as well as a field pretest. In addition, there was extensive consultation with village and Trust authorities, to gain cooperation for our survey effort. After completing a basic census of households in each village visited, stratified random sampling was used to select households to be surveyed based on the gender of the household head, the tribe to which the household belongs, and the income and assets of the household.Footnote 3 In total, 499 surveys were completed in 13 villages between April and September 2007. The response rate was 92 per cent.
Table 1 provides information on the main criteria used to select the five CBNRM programs surveyed, which involved their location, village size and tribal compositions, and economic benefits and types of tourism provided. The Chobe Enclave Conservation Trust, Okavango Community Trust and Sankuyo Tshwaragano Management Trust received relatively large wildlife tourism revenues in 2006 (the most proximate date to our survey work), which provided direct and indirect employment to CBNRM members and other economic benefits. In contrast, the Molema and Nqwaa Khobe Xeya Trusts received little or no economic benefit from wildlife tourism. Incomes for surveyed households are relatively low in several CBNRM programs.
Table 1. Characteristics of the community-based natural resource management trusts
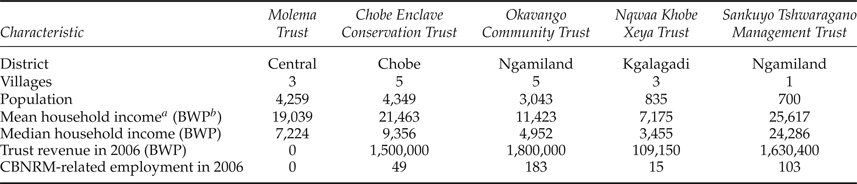
Notes: a Estimates from our survey. b Botswana currency (Pula). Exchange rate: BWP5.67 = US$1 in 2007; BWP9.11 = US$1 in 2014.
Source: Schuster (Reference Schuster2007).
Table 2 provides information on how households in the five CBNRM programs allocate their time among agricultural and household activities, and employment in tourism and other sectors. Typically, households in the surveyed villages are highly dependent on agricultural production and remittances to meet their consumption needs. With the exception of the Nqwaa Khobe Xeya Trust, most residents engage in some agricultural production. A point to take away from table 2 is that there is considerable excess labor supply: depending on the village, from 49 to 91 per cent of household adult time is spent in these activities, leaving a substantial amount of available time for employment in wildlife conservation or other job opportunities. The figures in table 2 are percentages of ‘full-time equivalent’ work, which is based on the normal full-time employment year, which is 49 weeks of work at 45–48 hours per week (Government of Botswana, 2012).
Table 2. Percentage of ‘full employment equivalent’ allocated to jobs and activities by adult household members, a by activity and village
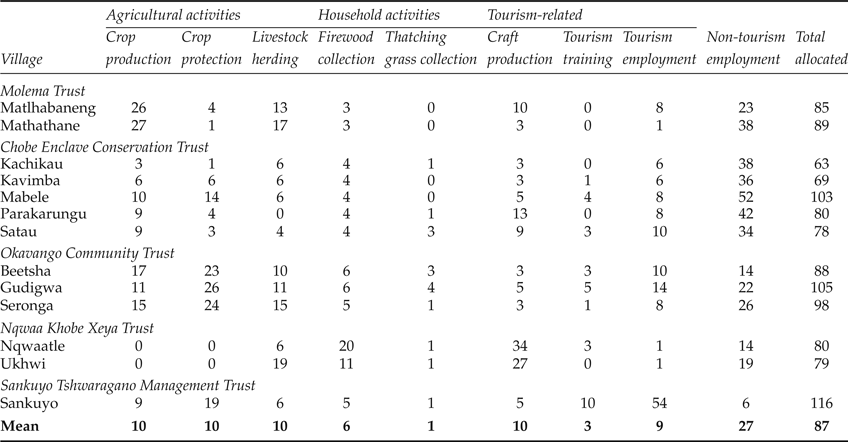
Notes: a Those of age 14 years or above.
The percentages presented in this table assume a 40-hour working week, but full-time employees may also work a 48-hour week. Based on our discussions with survey respondents and other village members, the 48-hour working week is typical for a full-time employee. As such, the percentages shown in this table likely overestimate the percentage of full employment equivalent time allocated to each task.
Given low household incomes, the cost of living with wildlife and excess labor supply, households would benefit from wage-based conservation employment. Such employment would allow them to meet their consumption needs and would provide tangible benefits from wildlife conservation.
2.1. Willingness to accept wildlife conservation employment
As part of the household survey, contingent behavior questions were used to elicit respondents' willingness to work part-time in local jobs related to wildlife and habitat management and protection of crops and domestic animals from wildlife damage. Contingent behavior is a stated preference technique that asks people what they would do in a particular scenario. Asking people what they would do, instead of what they would pay (as in contingent valuation), may be less subject to strategic biases because there is not necessarily a clear connection between an action and a monetary outcome.
Seven different activities were proposed to survey respondents, with two (building fences and building kraals, which are livestock pens or corrals) having both a public and a private orientation, for a total of nine distinct jobs: building crop fences for individual households or for the community; patrolling fields at night against crop pests; herding livestock; building livestock kraals for individual households or for the community; anti-poaching enforcement; wildlife monitoring; and revegetation of wildlife habitat. Individual respondents were asked about four to six of these jobs. Using the Adelman 29 orthogonal design, 15 different combinations of the conservation tasks were included in the surveys.
The jobs were offered to respondents with differing wages and days per month of work, along with detailed descriptions of what the jobs entailed.Footnote 4 The stated purposes of the jobs were to reduce human–wildlife conflict by reducing crop raiding and livestock predation by wildlife; and to increase wildlife stocks by reducing poaching and improving the quality of habitat.
The jobs offered were selected based both on what is understood about protecting crops and property from wildlife, as well as their familiarity to rural residents and required skill levels, which were identified through the pretesting process. The rationales for the jobs evaluated are as follows. Constructing fences and patrolling fields at night should reduce opportunistic raiding of crops by both wildlife and livestock (Osborn and Hill, Reference Osborn, Hill, Woodroffe, Thirgood and Rabinowitz2005) and increase expected crop harvests. Constructing kraals and active herding of livestock away from areas in which carnivores are likely to be present should reduce livestock depredation, which is integral to increasing tolerance for carnivores (e.g., Quigley and Herrero, Reference Quigley, Herrero, Woodroffe, Thirgood and Rabinowitz2005). Improved protection of crops and livestock must be combined with antipoaching enforcement to prevent the illegal killing of wildlife, either for consumptive purposes or as retribution for crop raiding and livestock depredation.Footnote 5 Community involvement in wildlife monitoring would supplement government monitoring and improve community understanding of how wildlife stocks change over time, and the linkages between human activities, wildlife stocks and the financial and non-financial benefits of conserving wildlife. Revegetation is required to improve the quantity and quality of wildlife habitat to increase wildlife stocks.
3. The analytical framework
Respondents were offered the conservation jobs described above on different economic terms (both the daily wage and the number of days per month to be worked). We hypothesized that respondents derive utility or disutility from different conservation jobs, depending on cultural norms, risk involved and the effort required to perform the job. Each respondent was given a description of a job, including the daily and monthly wage and days per month to be worked, and was asked for a simple yes-no response to the question, ‘Will you accept this job?’ Thus the response data are dichotomous choices. These are generally viewed as less likely to be biased than multiple-bounded response data (Alberini, Reference Alberini1995) or more cognitively challenging questions (Hoehn and Randall, Reference Hoehn and Randall1987; Freeman, Reference Freeman2003), but are inherently less precise since one obtains only a lower or upper bound on the reservation wage (i.e., the minimum wage required to induce the respondent to accept the job under the terms offered).
Each respondent evaluated from four to six different conservation jobs, being instructed in each case to consider each job against the baseline of not working in a conservation job. Respondents were instructed that each job was to be considered separately, with any other job they might have previously accepted being unavailable (to ensure that each job was considered with the same status quo reference conditions). Each contingent behavior question included a detailed description of the conservation job to be performed, the number of days per month it was to be performed, the number of years the job would last, and the daily and monthly wage to be received. The order in which jobs were asked about was varied randomly across the sample, as were wages and days of work offered. The job durations were one, three and five years, with intensity levels of three, five, seven and 10 days per month; and wages offered ranged from 18 to 192 Botswana pula (BWP) per day (US$2.70–28.79 per day in 2005 US$).
We assume that people's responses reflect their best choices when they consider the economic and non-economic characteristics of a job, relative to the utility they receive without working.Footnote 6 The conditional indirect utility for respondent i evaluating job j, is
where U ij is the systematic part of the utility of job j, and ε ij is an associated random error. The systematic part of the utility consists of four parts. The function U(c j , D ij ) is a linear function expressing the utility (or disutility) of working in job j, which may depend on the number of days spent working, D ij , which is predetermined in our application, as well as the job's other characteristics c j . That is, the utility of working in job j may have both time-varying and time-invariant components. The term T i − t ij · D ij is respondent i's discretionary time if the job is accepted, since t ij · D ij days must be allocated to the job from total available time T i Footnote 7 (where t ij is the unit time price of working in the conservation job j that requires D ij time). Similarly, E i + w ij · D ij is individual i's discretionary income after adding earnings from the job w ij · D ij to status quo income E i (where w ij is the daily wage for conservation job j).
These first three terms of U ij are standard in discrete choice models representing problems involving time and money tradeoffs. The fourth term, the cross-product of discretionary time and discretionary money, distinguishes the svt we use from other models in the literature. This term explains how the svt changes as the variables defining the constraints on time and money change. It satisfies the two-constraint requirements for the svt identified by Larson and Shaikh (Reference Larson and Shaikh2004), and results in predictions of the effects of resource constraint levels (time and money budgets) that correspond to the conditions developed by Weber (Reference Weber2005). Based on the model described by equation (1), the marginal utility of time is
while the marginal utility of money isFootnote 8
and the resulting svt is
Thus, the svt varies with person i's non-wage income E i , available time T i , and the amount of time D ij spent working in job j, along with the time and money prices of work (t ij and w ij , respectively).
In contrast, the standard discrete choice model, which contains only the first three terms of equation (1), produces a constant svt:
which is the special case of equation (4) where γ = 0. Thus, whether a person's choices are better explained by a varying or a constant svt is testable.
Although not written specifically to emphasize this point, the model in (1) is perfectly capable of representing choices by farm households where there is agricultural production, and consumption of some or all of that production. Essentially, (1) is the result of a sequential optimization of a standard farm-household model (e.g., Singh et al., Reference Singh, Squire and Strauss1986; Jacoby, Reference Jacoby1993; Skoufias, Reference Skoufias1994), with variables other than the choice of working in a conservation job optimized first, leaving only the decision as to whether or not to accept conservation job j. The marginal utilities of time and money reflect the optimized values of time spent in all other household/farm activities, and of the income resulting from those optimal choices. Choices of agricultural production and other household activities adjust optimally as new opportunities such as conservation employment are accepted.
Given the specification of the conditional indirect utility when person i accepts job j in equation (1), the conditional indirect utility when the job is not accepted (and D ij = 0) is
With equation (1) representing the utility if person i accepts job j and equation (6) representing the utility if it is declined, and taking the time price of working to be 1,Footnote 9 the probability that the respondent will accept the job (i.e., offer a Yes response) is
where Δε ij ≡ ε i0 − ε ij is the difference in errors and
is the utility difference between having the job and not having the job. The probability corresponding to No responses is 1 − P(Yes).
To account for the possibility that errors within our panel data set are correlated and heteroskedastic, which would violate classical assumptions, we specify the estimation errors as the combination of independent individual-specific and question-specific errors, each of which is distributed normally. That is, the error difference is Δε ij ≡ ε i + u ij , where ε i ~ N(0,σ 2 ) is the individual-specific component which varies only across respondents, and u ij ~ N(0, 1) varies within and across respondents. In addition, E(ε i · u jk )=E(u ij · u kl )=0 for all i, j, k, and l, and E(ε i · ε ik )=0 for k ≠ i. With this structure, if σ ≠ 0, the errors are, in general, correlated for a given respondent i (that is, conditional on i). Her responses j and k have cov(Δε ij , Δε ik ) ≡ E[(σ · ε i +u ij ) · (σ · ε i + u ik )]=σ 2 · ε i 2 , which is nonzero for all nonzero ε i . Across respondents, the errors are in general heteroskedastic, since for response j by respondent i, var(Δε ij ) ≡ E[(σ · ε i + u ij ) 2 ]=σ 2 ·ε i 2 + 1, while for response l by respondent k, it is var(Δε kl ) ≡ E[(σ · ε k +u kl ) 2 ] = σ 2 · ε k 2 +1, which in general are different. We estimate the scale factor σ to test whether errors are correlated and/or heteroskedastic.Footnote 10
Given the probability statement in (7), utility difference from (8), and the error structure, when σ = 0 the probability of observing a Yes response by person i regarding job j is the standard probit structure,
while the probability of observing a No response is Pr(No ij ) = Φ (−ΔU ij ), where Φ (·) is the cdf of the standard normal distribution. The log-likelihood of observing the sample pattern of Yes and No responses is
where A ij is an indicator variable taking the value one if respondent i was asked about job j and zero otherwise, and I ij is an indicator variable taking the value one for Yes responses and zero for No responses.
To correct for the possible violation of classical error assumptions when σ ≠ 0, we first run the model in (10), and calculate the empirical mean error for each respondent and use this estimate as an instrument in the model. For person i, the mean error component is
![]() $\hat{\varepsilon}_{i} =\sum\nolimits_{j}^{n_{i}} {E\lpar \Delta \hat{\varepsilon}_{ij}\rpar }/n_{i}$
, where (using results on conditional expectations of the standard normal distribution)
$\hat{\varepsilon}_{i} =\sum\nolimits_{j}^{n_{i}} {E\lpar \Delta \hat{\varepsilon}_{ij}\rpar }/n_{i}$
, where (using results on conditional expectations of the standard normal distribution)
![]() $E\lpar \Delta \hat{\varepsilon}_{ij}\rpar =\phi \lpar -X_{ij} \cdot \hat{\beta}\rpar /[ 1-\Phi \lpar -X_{ij} \cdot \hat{\beta}\rpar ] $
for a Yes response and
$E\lpar \Delta \hat{\varepsilon}_{ij}\rpar =\phi \lpar -X_{ij} \cdot \hat{\beta}\rpar /[ 1-\Phi \lpar -X_{ij} \cdot \hat{\beta}\rpar ] $
for a Yes response and
![]() $E\lpar \Delta \hat{\varepsilon}_{ij}\rpar =-\phi \lpar -X_{ij} \cdot \hat{\beta}\rpar /\Phi\lpar -X_{ij} \cdot \hat{\beta}\rpar $
for a No response. In these conditional expectations, X
ij
and
$E\lpar \Delta \hat{\varepsilon}_{ij}\rpar =-\phi \lpar -X_{ij} \cdot \hat{\beta}\rpar /\Phi\lpar -X_{ij} \cdot \hat{\beta}\rpar $
for a No response. In these conditional expectations, X
ij
and
![]() ${\hat{\beta}}$
are the variables and estimated parameter vector from equation (8), respectively. With the instrument
${\hat{\beta}}$
are the variables and estimated parameter vector from equation (8), respectively. With the instrument
![]() $\hat{\varepsilon}_{i}$
, equation (8) becomes
$\hat{\varepsilon}_{i}$
, equation (8) becomes
which asymptotically satisfies the classical assumptions for the probit discrete choice model. Estimation proceeds as before with equation (8′) replacing (8).
3.1. Reservation wages
The reservation wage,
![]() $w_{ij}^{r}$
, is defined as the minimum wage person i would accept to supply a given amount of labor in job j, and is defined implicitly by the utility difference in (8) being zero, i.e., by
$w_{ij}^{r}$
, is defined as the minimum wage person i would accept to supply a given amount of labor in job j, and is defined implicitly by the utility difference in (8) being zero, i.e., by
 $$\eqalign{ & U\lpar {\bf c}_{\bf j} \comma \; D_{ij} \rpar +D_{ij} \cr & \quad \cdot \lcub {-\mu_0 \cdot t_{ij} +\lambda_0 \cdot w_{ij}^r +\gamma \cdot [ {\lpar {T_i -t_{ij} \cdot D_{ij} } \rpar \cdot w_{ij}^r -t_{ij} \cdot E_i } ] } \rcub \equiv 0.} $$
$$\eqalign{ & U\lpar {\bf c}_{\bf j} \comma \; D_{ij} \rpar +D_{ij} \cr & \quad \cdot \lcub {-\mu_0 \cdot t_{ij} +\lambda_0 \cdot w_{ij}^r +\gamma \cdot [ {\lpar {T_i -t_{ij} \cdot D_{ij} } \rpar \cdot w_{ij}^r -t_{ij} \cdot E_i } ] } \rcub \equiv 0.} $$
This can be solved explicitly for
which is person i's inverse labor supply function for job j, expressing the minimum wage required for different levels of labor required, D ij .
Equation (12), explaining the reservation wage function in a discrete choice model where the respondent chooses either working for a specified number of days D ij or working zero days, takes an intuitive form, especially when compared to the first-order condition from a continuous-choice version of the problem (i.e., when days worked is a choice variable). The terms μ 0 + γ · (E i + 0.5 · D ij ) and λ 0 + γ · (T i − 0.5· D ij ) are the marginal utilities of time and money, respectively, when days worked is 0.5· D ij , that is, the mean of the two options from which the respondent can choose (D ij and zero). The term U(c j , D ij )/D ij is the mean per-day (dis)utility of working in the job. It is also the discrete marginal utility of working, that is, the incremental change in utility (ΔU ≡ U(c j , D ij ) − 0) for the incremental change in days (ΔD ≡ D ij − 0) between the two options; thus the discrete marginal utility of work is MU = ΔU/ΔD = U(c j , D ij )/D ij . When MU is monetized by dividing through by the marginal utility of money, the discrete marginal value of work, MV = MU/[λ 0 +γ · (T i − 0.5· D ij )], is the result. We refer to this as the ‘value of work time’ in the empirical section.
With these interpretations, the reservation wage in the discrete choice model (equation (12)) can also be written as
that is, the reservation wage equals the opportunity cost of time (svt) at mean days worked, multiplied by the total amount of time required to deliver this number of days, less the monetary value of any utility received. Thus, people who like a job (with MV ij > 0) require a lower wage for that job than those who do not like or are neutral about it.
The decomposition in equation (13) also emerges from continuous choice models, which in this case would mean days worked is chosen optimally. To see this, if equation (1) were optimized with respect to D ij , the first-order condition would be
which can be rewritten as
and solving for the (reservation) wage function,
which has the same form and content as the discrete version in equation (13), aside from the minor differences in translating concepts from the discrete to the continuous case. In both cases, the reservation wage is the svt applied to the total time required for the activity, with adjustment for the monetary value of utility or disutility from the activity. A novel aspect of our model and empirical work is that we provide estimates of both the svt and the marginal value of work as constituent elements of the reservation wage.
4. Estimation results
To complete the estimation model, a functional form must be chosen for the marginal (dis)utility of work and the svt, and specific variables entering the model must be articulated. With respect to the utility from work, aside from the detailed qualitative description provided to each respondent about the jobs they were asked about and what they involved, there are no quantitative measures of how they differed other than the wage and number of days required. We therefore estimate different parameters for each job, whose utilities vary with characteristics of the individuals. We assume the utility of work is both linear in parameters and consists of a fixed and a time-varying component. Both the fixed and time-varying components are allowed to vary with gender (a dummy variable taking the value one for females and zero for males), and there are two dimensions to the time-varying component, the duration of the job (the total days to be worked, D) and its intensity (the number of days per month worked, DM). Thus the utility of working in job j for person i is
The other part of conditional indirect utility to be specified is the svt, which has the parameters μ 0(s), λ 0(s), and γ(s), written as functions of covariates s. Each of these can be functions of any covariates that do not enter the constraints that define the svt. One can incorporate observed or unobserved heterogeneity by allowing the parameters of conditional indirect utility to vary across the sample. We focus on observed heterogeneity, in order to better understand how the svt might vary with peoples' observable characteristics.Footnote 11
Combining equation (12) with equation (17), the general form of the estimated model is
 $$\eqalign{w_{ij}^r &=-\displaystyle{{\lpar \alpha_{j0} +\alpha_{j1} \cdot {gender}_i \rpar /D_{ij} +\lpar \alpha_{j2} +\alpha_{j3} \cdot {gender}_i\rpar} \over {\lpar {\lambda_0 \lpar {{\bf s}}\rpar +\gamma \lpar {{\bf s}}\rpar \cdot \lpar {T_i -0.5\cdot D_{ij} } \rpar } \rpar }}\cr &\quad +t_{ij} \cdot \displaystyle{{\mu_0 \lpar {{\bf s}}\rpar +\gamma \lpar {{\bf s}}\rpar \cdot \lpar E_i +0.5\cdot D_{ij} \rpar } \over {\lambda_0 \lpar {{\bf s}}\rpar +\gamma \lpar {{\bf s}}\rpar \cdot \lpar {T_i -0.5\cdot D_{ij}}\rpar }}\comma \; }$$
$$\eqalign{w_{ij}^r &=-\displaystyle{{\lpar \alpha_{j0} +\alpha_{j1} \cdot {gender}_i \rpar /D_{ij} +\lpar \alpha_{j2} +\alpha_{j3} \cdot {gender}_i\rpar} \over {\lpar {\lambda_0 \lpar {{\bf s}}\rpar +\gamma \lpar {{\bf s}}\rpar \cdot \lpar {T_i -0.5\cdot D_{ij} } \rpar } \rpar }}\cr &\quad +t_{ij} \cdot \displaystyle{{\mu_0 \lpar {{\bf s}}\rpar +\gamma \lpar {{\bf s}}\rpar \cdot \lpar E_i +0.5\cdot D_{ij} \rpar } \over {\lambda_0 \lpar {{\bf s}}\rpar +\gamma \lpar {{\bf s}}\rpar \cdot \lpar {T_i -0.5\cdot D_{ij}}\rpar }}\comma \; }$$
and the explanatory variables used to allow μ 0 (s), λ 0 (s), and γ (s) to vary are: gender; age of the respondent (entering quadratically); the ratio of female adults to total adults in the household (femp); whether the household took measures to protect its crops against wildlife damage (Crop Protection); and whether the household received any government assistance (Gov't Assistance). In addition, there are three dummy variables representing the CBNRM programs that respondents were members of: Molema Trust (Molema), Chobe Enclave Conservation Trust (Chobe), and Okavango Community Trust (Okavango).Footnote 12 The baseline Trusts defined when all these dummy variables are zero are the Nqwaa Khobe Xeya and Sankuyo Tshwarangano Management Trusts. These variables proved to be the most significant from the pool of variables explored and provided the best fit of the data.
The model selection process was a simple specification search, since there was little in the way of a priori information to suggest which variables would be most appropriate. In such circumstances it is sensible to use model selection criteria in arriving at a final model. Starting with a large pool of variables and reducing the size of the pool based on each covariate's marginal contribution to the log-likelihood, we used the Akaike Information Criterion (AICc, adjusted for sample size) and the Bayesian Information Criterion (BIC) as guides to selecting a final model (Akaike, Reference Akaike1974; Schwarz, Reference Schwarz1978).
It is worth noting that some restrictions are required for parameter identification in equation (18). For example, if the term μ 0(s) were specified with constant terms for men and women [i.e., as μ 0(s) = μ 00 + μ 01 · gender + μ 1 (s)], the terms μ 00 and μ 01 could not be estimated as they are confounded with α j2 and α j3, respectively, in equation (18).Footnote 13 In our application, we normalize μ 00 =μ 01 = 0 and estimate α j2 and α j3. We return to this point later when discussing the marginal values of working and svts implied by the estimated reservation wages.
Summary statistics for the variables entering the utility difference and reservation wage are presented in table 3. In total, 305 females and 194 males were surveyed,Footnote 14 and the median age for respondents was 36 years. The median gross annual income for the household was BWP10,780 (US$1,609) and the median annual endowment of time for adult members of the household was 1,095 days. The median proportion of female adults in the household was 0.5, although the mean measure was somewhat higher at 0.6. The number of surveys completed per trust varied from 24 (Sankuyo Tshwaragano Management) to 179 (Chobe Enclave Conservation Trust). The number of days per month of employment for the conservation jobs ranged from 1 to 10, with a median of 5. The offered wage ranged from BWP18 (US$2.70) to BWP192 (US$28.79) per day, with a mean of 60.
Table 3. Summary statistics for key variables in the conservation jobs choice models
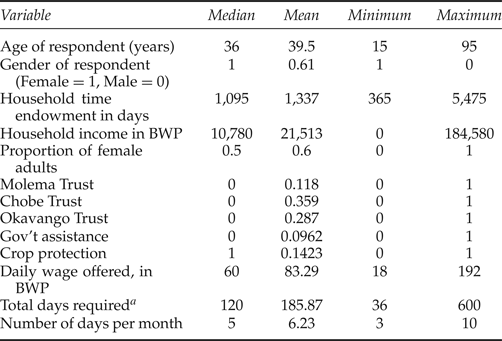
Notes: a In a job lasting from one to five years.
Results of maximizing the likelihood function in equation (10) with heteroskedasticity and correlation accounted for are presented in table 4. Because the AICc and BIC model selection criteria gave different indications as to what the best final model is, a range of models are presented in table 4. The first and third models are those that minimize the AICc (with 30 parameters) and the BIC (with 15 parameters). The second model is an intermediate model with a benchmark based on Student's t-statistics all being significant at the 5 per cent level (with 27 parameters). The minimum AICc and 5 per cent significance models were quite similar qualitatively, with the same signs and similar magnitudes on all coefficients in both models. The minimum BIC model, which had just under half the number of parameters of the 5 per cent significance model, also had the same signs on all variables common with the other two models, although differences in magnitudes were greater.
Table 4. Parameter estimates for the job choices models
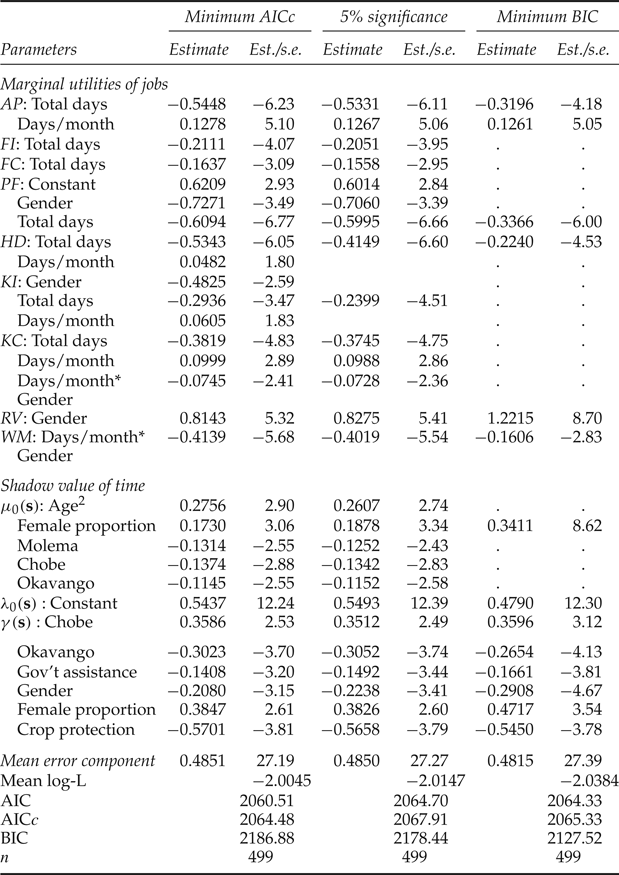
There were a number of regularities in the features of all three models. First, the marginal utilities of work all decreased with the duration (total number of days to be worked) and increased with the intensity (days per month) of the job. Women uniformly had lower utilities of time worked, with the exception of revegetation, which is widely understood to be ‘women's work’ and is also, based on debriefings with respondents, felt to convey external benefits to the community through improvement of the surrounding area vegetation (e.g., improved livestock grazing, and increased firewood, thatching grass and edible veld products).
Regarding the parameters of the value of time, there were broad similarities among all three models. The constant term of the marginal utility of money (λ 0) was modeled as a constant, so all of its variation was due to variations in the cross-product term γ(s). All terms in γ(s) were significant at the 2 per cent level (two-tailed) in all three models, which indicates that the svt varies with money income, time available, the wage offered, and number of days worked. Chi-square tests of the hypothesis that the parameters in γ(s) are jointly zero strongly indicated rejection of this hypothesis. This is evidence that our generalized model of the value of time offers a significant improvement in statistical fit, compared with the standard models.
4.1. Reservation wages and values of time
To see the implications of these models for reservation wages and values of time, the minimum AICc and 5 per cent significance models were used to generate reservation wages. These models were used because the minimum BIC model pruned the number of parameters in the model so severely that variables that were highly significant, based on Student's t-values, were excluded in arriving at the minimum BIC model. Given that the minimum AICc is often judged to be superior to the minimum BIC as a model selection criterion (e.g., Burnham and Anderson, Reference Burnham and Anderson2002, Reference Burnham and Anderson2004), and our focus on the covariates that, in our application, help explain the reservation wages and values of time, it seemed appropriate to use the models with more covariates.Footnote 15
The reservation wages and svts are determined from the parameter estimates in table 4, using equation (18). We assume that people would not pay to accept jobs, i.e., reservation wages are non-negative; if equation (18) predicts a negative reservation wage, the true value is taken to be zero. The other expectation is that for the range of days that can be worked, a person's svt is non-negative, which is implied by the setup of the model. Since each respondent evaluated several jobs with numbers of different days worked, their svts implied by each job vary, although they are linked by the commonality of the parameters in the svt function.
The requirement of non-negative svts can be ensured without loss of generality because of the normalization of the parameter μ
00 (which is the constant term in the svt) to zero in estimation. By defining μ
00i
and α
2ji
for each person i such that
![]() $\mu_{00i} +\alpha_{2ji} =\hat{\alpha}_{2j}$
(where
$\mu_{00i} +\alpha_{2ji} =\hat{\alpha}_{2j}$
(where
![]() $\hat{\alpha}_{2j}$
is the estimate of α
2j
in equation (18)), increases in μ
00i
(and corresponding decreases in α
2ji
) simultaneously increase all of the svts and marginal values of working for that person. So when any svt for a person is negative with the original normalization μ
00i
= 0, another normalization consistent with the model's parameter estimates can be found with μ
00i
≠ 0 such that all svts are non-negative. Our approach is to choose the smallest value of μ
00i
that results in non-negative svts for individuals i who had one or more negative predicted svt from equation (18).
$\hat{\alpha}_{2j}$
is the estimate of α
2j
in equation (18)), increases in μ
00i
(and corresponding decreases in α
2ji
) simultaneously increase all of the svts and marginal values of working for that person. So when any svt for a person is negative with the original normalization μ
00i
= 0, another normalization consistent with the model's parameter estimates can be found with μ
00i
≠ 0 such that all svts are non-negative. Our approach is to choose the smallest value of μ
00i
that results in non-negative svts for individuals i who had one or more negative predicted svt from equation (18).
Table 5 presents the sample estimates of mean reservation wages, marginal values of working, and svts for each job, along with the standard deviations of the sample mean estimates.Footnote 16 There are several interesting features to this comparison. The first point to note is that the mean daily svts (which measure the value of opportunities foregone by accepting a conservation job) are low, on average, for both men and women (means in the range of BWP8–12 for men, and BWP17–21 for women). This is consistent with the relatively scarce formal employment opportunities in the vicinity of most Trust villages and the excess household labor capacity indicated by table 2.Footnote 17 The trend of higher svts for women is consistent with the fact that in most households women have more responsibilities for child-rearing, meal preparation, cleaning, collecting firewood and veld products, and tending smallstock and the fields.
Table 5. Sample estimates of reservation wages (w r ), marginal values of time spent working (MV), and shadow values of time (svt) for wildlife conservation jobs (in 2014 BWP)
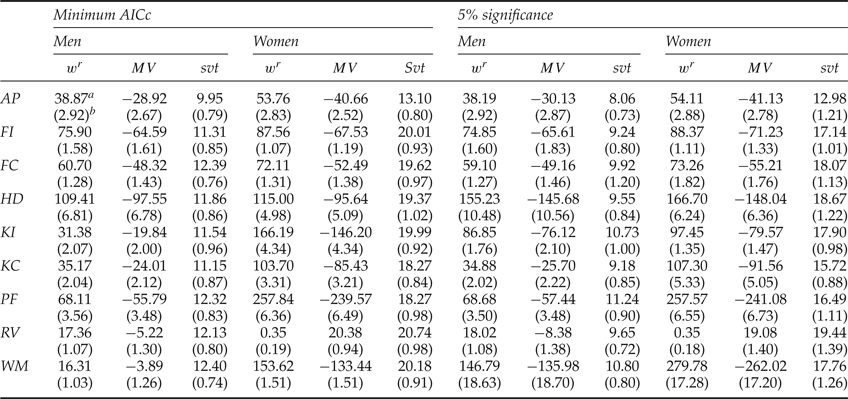
Notes: a BWP per day. Exchange rate in October 2014 was US$1 = BWP9.11. b Standard error of the sample mean in parentheses.
For men, the highest reservation wages are required for patrolling fields, herding livestock, and building fences and kraals, consistent with respondents' views that these jobs are more strenuous than others. For women, reservation wages are highest for patrolling fields, wildlife monitoring, herding animals and building kraals. These wages are consistent with female respondents' comments that these tasks are physically demanding, dangerous, culturally inappropriate for women to perform, or some combination thereof.
At the other extreme is the revegetation job, for which reservation wages are low, reflecting that respondents find this job less onerous or, in the case of women, slightly ‘enjoyable’. The reservation wages of BWP1 for women and BWP17–18 for men for this job are consistent with actual experience in Botswana, as the central government periodically hires community members for revegetation jobs, for approximately BWP10 per day, as part of its drought relief efforts, and it is most commonly performed by women.
The one job for which reservation wages seem unexpectedly low is anti-poaching enforcement. Analysis of this job is somewhat problematic because it seems that many community members in villages across Botswana still engage in some poaching and snaring of problem animals, although minimal data are available to confirm or refute this hypothesis (e.g., Saum Reference Saum and Haller2010). From discussions with community members, it was clear that they know that poaching occurs, is illegal, carries high penalties, and that they should vilify poachers. But these professed attitudes may not reflect community members' true opinion of poaching, especially since respondents complained that there is too much wildlife in nearby areas.Footnote 18
5. Conclusions
This paper provides a straightforward and rigorous approach to part of the puzzle of improving the performance of community-based natural resource management programs. A significant failing of these programs has been the inability to deliver adequate incentives for the villagers who live with wildlife to conserve and protect wildlife habitats. A key issue is what is required to induce village residents to perform conservation-related and protective activities with respect to the wildlife populations in their vicinity. There are few, if any, more direct linkages between conservation of wildlife and wildlife-based benefits than to pay people directly to conserve and protect against wildlife damages. A key question is how much must be paid to attract workers to conservation jobs whose purpose is to protect wildlife and their habitat.
To help fill this gap, this paper has developed and implemented a model of reservation wages and inverse labor supply for wildlife conservation jobs in rural Botswana. The model we develop to determine rural residents' willingness to accept work in conservation jobs is novel in several respects. It generalizes the functional form of commonly used discrete choice models so that the opportunity cost, or shadow value, of time varies explicitly with economic variables such as household income, time available, days worked, and the respondent's wage. This is achieved through a simple extension of the standard linear-in-discretionary budgets model, which nests the standard model and also satisfies the theoretical requirements for models in which the svt varies with budgets and prices. We also show how, in the discrete choice setting, the reservation wage can be decomposed into the sum of the marginal value of work and the opportunity cost of time spent working (the svt), which is an analog to the standard condition from continuous choice models.
When applied to data collected from members of five wildlife conservation Trusts from Botswana, the model with generalized value of time performed better than the standard discrete choice model, which explicitly assumes that the svt is a constant for each person. Not surprisingly, given the relative scarcity of economic opportunity in many Trust villages and indications that households have surplus time available for formal work, the shadow values of time were low overall, although higher for women than for men. Conservation jobs that involve hard work, danger or both generate considerable disutility to workers, which, when monetized, explains a significant share of reservation wages. Overall, the mean reservation wages varied from BWP1 to BWP18 (approximately US$0.10–2 in 2014) per day for revegetation, a familiar job considered generally easy to perform and which has auxiliary benefits to the village, to BWP280 (about US$31) per day for women asked to patrol fields at night to deter wildlife.
We identify a number of areas for further work. First, our analysis is limited insofar as we do not formally include discounting, although some jobs offered employment for up to a five-year period. While discount rates are relatively low in underdeveloped areas such as rural Botswana, a fuller model would incorporate time preferences into the reservation wages model. Secondly, we assume the utility parameters are fixed, in consideration of our rich data set and a desire to learn more about the roles that individual characteristics play in conservation job choice. An alternative would be a random parameters model that would sacrifice information about specific demographic influences to learn more about the distributions of key parameters. Finally, it must be emphasized that while an understanding of the economic responses of rural Botswanans to conservation job opportunities is a necessary part of re-orienting CBNRM programs, it is by no means sufficient. An ultimately successful policy requires a design that takes into account the cultural and historical realities and sensitivities of the prospective employees, so that policies actually work and meaningful improvements to their welfare and to conservation outcomes can be realized. We recognize that these fundamentally important considerations, which are beyond our scope, are not addressed here.









