The closing aria of Georg Philipp Telemann's cantata for Pentecost Zischet nur, stechet, ihr feurigen Zungen (twv1:1732) contains striking metric irregularities (Figure 1). Over the course of the aria's one hundred bars, the time signature switches between 3/8 and 2/4 twenty-four times. These changes are perplexing for several reasons: perhaps most fundamentally, it is far from obvious how the 2/4 bars should be performed. Should they have the same duration as a 3/8 bar, yielding a duplet effect? Or should the quaver pulse remain constant, giving rise to bars of unequal length? Even more puzzlingly, there is little in the aria's text that warrants the unsettling effect created by so many changes of metre: ‘Der Himmel ist nicht ohne Sterne / Und Gottes Geist nicht ohne Trost’ (Heaven is not without stars, / And God's Spirit is not without comfort). This is not to suggest that such irregularity does not fit the text – on the contrary, the shifts to 2/4 are consistently aligned with important words – but rather that the text alone fails to account for the use of mixed metre here. We are, therefore, dealing with rather a different situation from the famous ‘mad scene’ in Handel's Orlando, wherein the irregular metre can be linked directly to – and is thus justified by – the composer's desire to depict the protagonist's deteriorating mental state. In ‘Der Himmel’, Telemann appears to be mixing metres as if the technique were quite normal. Yet, at least according to the present state of knowledge, such a practice is decidedly odd. Understandably, we tend to think of eighteenth-century music as rather regular, certainly as far as notated metre is concerned. To be sure, composers often played with the idea of different-sounding metres emerging from passages in a single time signature. Danuta Mirka has analysed this very phenomenon in the chamber music of Mozart and Haydn. Yet Mirka argues that, for these composers and their contemporaries, mixed metre lay beyond the realm of compositional possibility:
In the eighteenth century, the constancy of notated metre was taken for granted equally by composers and listeners. Virtually every piece or movement was written with one time signature maintained from the beginning to the end. Exceptions to this rule occur only in movements preceded by a slow introduction, which normally differs from the following main part of a movement not only in tempo but in metre as well.Footnote 1
Likewise, in a recent study of early modern musical time, one of Roger Grant's key findings is that integrated metrical changes emerged as a viable option only at the end of the eighteenth century, following a shift in theoretical conceptions of metre. Grant's earliest examples of notated mixed metre include passages from Mozart's Die Entführung aus dem Serail (1782) and Beethoven's ‘Eroica’ Symphony (1803–1804).Footnote 2 Both Mirka and Grant reach their conclusions primarily through readings of eighteenth-century metric theory, in which changes such as Telemann's either go unmentioned or are explicitly forbidden.

Figure 1 Georg Philipp Telemann, ‘Der Himmel ist nicht ohne Sterne’, Zischet nur, stechet, ihr feurigen Zungen, twv1:1732, bars 1–24, from Harmonischer Gottes-Dienst (Hamburg, 1725–1726), 316–317. Bayerische Staatsbibliothek, Munich, 2 Liturg. 431 k-1, 378–379 urn:nbn:de:bvb:12-bsb10496490-4, https://reader.digitale-sammlungen.de/resolve/display/bsb10496490.html. Used by permission. The text reads ‘Der Himmel ist nicht ohne Sterne, / Und Gottes Geist nicht ohne Trost’ (Heaven is not without stars, / And God's Spirit is not without comfort)
In light of this, we might expect Telemann's aria to be an isolated quirk – perhaps a one-off experiment with limited reach that can teach us very little about the broader eighteenth-century musical landscape. In truth, the situation is quite the opposite. This aria was included in the composer's first – and perhaps most successful – published cantata cycle, the Harmonischer Gottes-Dienst of 1725–1726. The impressive spread of this cycle's surviving prints across northern Europe supports Johann Ernst Bach's 1758 claim that ‘one can barely find a Protestant church in Germany where Telemann's cantata cycles are not performed’.Footnote 3 Judging by the extant manuscript sources, Zischet nur, stechet, ihr feurigen Zungen was one of the most frequently copied cantatas of the Harmonischer Gottes-Dienst; one copy was made in Copenhagen in as late as 1822, nearly a century after the cycle's initial publication.Footnote 4 These cantatas were also a source of inspiration for Telemann's good friend Handel. As John H. Roberts has shown, Handel ‘mined Harmonischer Gottes-Dienst with extraordinary persistence’ from around 1727 to 1751.Footnote 5 A third of the collection's 144 arias can be linked with one or more of Handel's compositions, making it Telemann's most borrowed-from publication.Footnote 6 Although Handel did not borrow from ‘Der Himmel’, the cantata as a whole did not escape his notice: its opening aria is reworked as ‘Come Nembo che fugge col vento’ in the 1737 version of Il trionfo del Tempo e della Verità.Footnote 7
Clearly, the metre changes of ‘Der Himmel’ were played, heard and copied out by many eighteenth-century musicians. Perhaps this should not surprise us, given the high regard in which Telemann's works were held. What is surprising, however, is the abundance of additional examples of mixed metre from the first two thirds of the eighteenth century. In Telemann's output alone, this feature is found in over fifty compositions. Alongside those works, comparable techniques are employed in a handful of pieces by his German contemporaries Fux, Fasch, Graupner and Stölzel, and in three keyboard sonatas by Domenico Scarlatti (k315, 419 and 502). In addition to ‘Der Himmel’, another sixteen of Telemann's mixed-metre works appeared in popular publications during the composer's lifetime and enjoyed similarly wide dissemination. As with ‘Der Himmel’, one rarely gets a sense that metric irregularity in these pieces is ‘justified’ in any obvious way by textual or programmatic concerns. Again, this is not to suggest that eighteenth-century examples of mixed metre are lacking in dramatic, communicative or illustrative function – indeed, the opposite is almost always true. Yet if all of the eighteenth-century composers listed above had used this technique only for moments of extreme drama (such as in Handel's Orlando), little further explanation would be required beyond stating simply that extraordinary circumstances call for extraordinary musical techniques. The fact that these composers did not exclusively (or even primarily) use mixed metre for dramatic extremes suggests that something more far-reaching is at play. Eighteenth-century mixed metre is – despite what the theorists say – not as exceptional as we have previously thought.
The substantial repertory of mixed-metre pieces by Telemann and his contemporaries reveals a hitherto unrecognized diversity of eighteenth-century metric techniques. Crucially, however, these works are not united solely by metric peculiarity. Rather, such pieces can be grouped according to their notated contents, compositional function and connections with other aspects of eighteenth-century music-making. These groupings yield valuable clues about the origins of various temporal techniques and help to explain why composers deploy mixed metre. By identifying trends across this repertory, it is possible to clarify ambiguous notational features of eighteenth-century mixed metre and thus shed light on how a piece like ‘Der Himmel’ might have been performed. More significantly, these pieces by Telemann and his contemporaries challenge us to rethink our wider narratives concerning metric practices in the eighteenth century. At a most basic level, this article demonstrates that the intermixing of time signatures was part of the eighteenth-century compositional toolkit well before its better-documented uses by Mozart and Beethoven. This fact reminds us, however, that theorists alone cannot illuminate contemporary conceptions of metre, nor is the relationship between eighteenth-century theory and practice straightforward. In so far as music can ‘make time audible’ (to quote Susanne Langer), it is perhaps the sonorities themselves which could tell us the most about how musical temporalities were understood by eighteenth-century musicians.Footnote 8 Lacking access to eighteenth-century sounds, we can do our best to reconstruct parts of this soundscape from written scores (for this enterprise, eighteenth-century theory is, of course, vital). Yet there are also musical sonorities which scores can barely hint at, such as improvised practices and oral or ‘folk’ traditions. For Dean Sutcliffe, Scarlatti's metre changes point towards such traditions: they show the composer ‘straining towards something . . . that is quite beyond the comprehension of the world of high art’, thus offering a rare glimpse into entire domains of eighteenth-century music-making which never made it onto the written page.Footnote 9 Likewise, the pieces under consideration here remind us not only of a diversity of notated practices beyond the statements of music theorists, but also of those practices which now are lost to us.
Throughout this article I use the term ‘mixed metre’ in a rather specific sense. While there are several ways in which eighteenth-century composers can effect a change of metre, my discussion is restricted to those changes which are both notated and ‘integrated’.Footnote 10 I have borrowed the latter term from Grant's notion of the ‘integrated metric shift’, which he defines as ‘a change in metre without a concurrent change or break in the texture, tempo, or overall character of the music’.Footnote 11 Like Grant, I am interested in cases where musical continuity is maintained across a change in metre. Excluded, therefore, are those that take place between distinct parts of a piece (such as the different sections of a French overture or da capo aria) or any that occur in conjunction with a new tempo direction. Unlike Grant, however, I also set aside those shifts that take place at a hypermetrical level, as well as those where the mixed metre does not occur simultaneously for all members of the ensemble (as is the case in Grant's aforementioned Mozart example, in which the metric mixing only affects one singer). My focus is on changes in the duration of the written-out bar across all parts (often, but not always, accompanied by a new time signature). In other words, I am interested in cases where neighbouring bars contain different amounts of notated musical time, just as we saw in ‘Der Himmel’. Whether these different notated amounts always corresponded to audible changes in bar duration in eighteenth-century performance is one of the central questions explored in this article and, of course, has important implications for how we might interpret pieces like ‘Der Himmel’ today. But why have I defined mixed metre so restrictively? First, it is precisely this sort of change (that is, notated and integrated) that is currently overlooked in studies of eighteenth-century metre. Second, this narrower definition is borne out in the writings and compositions of eighteenth-century musicians. As we shall see, changes of metre within a single time signature (such as those studied by Mirka) were, at this time, conceptualized differently from those involving notated changes in bar length.
EIGHTEENTH-CENTURY METRIC THEORIES
Before exploring the mixed-metre repertory, we should consider the extent to which changes such as those found in ‘Der Himmel’ posed difficulties for eighteenth-century theorists. Besides yielding some terms and concepts that will be needed to help us grapple with Telemann's mixed-metre compositions, this exercise provides a useful overview of the shifting landscape of eighteenth-century metric theory. It is a well-established narrative that the long eighteenth century witnessed a move from motion-oriented theories of metre (invoking Aristotelian understandings of time) to more abstract and absolute ones (in line with Newtonian understandings of time). This was first argued by Wilhelm Seidel in 1975 and has recently been expanded upon by William Caplin, Roger Grant and Tomas McAuley.Footnote 12 As Grant shows, the ‘Aristotelian’ approach – in which the visceral action of beating time constituted metre itself – was, broadly speaking, prevalent until around the time of Johann Mattheson's Der Vollkommene Capellmeister (1739).Footnote 13 The ‘Newtonian’ approach, often referred to as the Akzenttheorie, emerged in the early 1770s in the writings of Johann Georg Sulzer, Johann Philipp Kirnberger and Johann Abraham Peter Schulz.Footnote 14 These latter authors defined metre as the pattern arising from regular accents applied to an imagined stream of equally spaced pulses.
While, for simplicity, I refer to these two approaches as ‘Aristotelian’ and ‘Newtonian’, we should remember that neither was really a coherent ‘school’. As far as mixed metre is concerned, however, the key difference between the two approaches lies in how each relates whole bars to their constituent parts. For earlier writers, the bar (tactus) was always bipartite, consisting of the downstroke (thesis) and the upstroke (arsis). This was true even for triple (known as ‘unequal’) metre, in which case the duration of the downstroke was double that of the upstroke. This distinction between ‘equal’ and ‘unequal’ meant that duple and triple metres did not simply comprise a different quantity of the same interchangeable building-blocks. Instead, they possessed a fundamentally different quality – each was a different genus of time. Mattheson makes his position on this quite clear. He explains that ‘each segment of the measure has only two parts and no more’ and warns that ‘those who seek four parts in an even, and three in an uneven mensuration’ will find ‘nothing but confusion’.Footnote 15 Christopher Hasty uses the term ‘givenness’ to describe how, for Mattheson, the whole tactus is a pre-existing entity (a ‘given’) which does not derive from its parts but rather constitutes them.Footnote 16 By contrast, the authors of the Akzenttheorie constructed the bar (Takt) from an infinite stream of identical beats (Taktteile). Placing an accent on every second Taktteil would therefore yield duple metre, on every third, triple, and so on: the Taktteile of any one time signature were equivalent to those of another. Thus while Mattheson and his predecessors understood the thesis and arsis of duple metre to be qualitatively different from those of triple metre, the Akzenttheorie conceptualized all metres with the same bottom numeral as different quantities cut from the same cloth. This has significant implications for the viability of mixed metre. Unlike older theories, the Akzenttheorie does seem to allow for certain kinds of metric mixing. Because Taktteile are interchangeable, we might imagine that, under this theoretical regime, metre changes could take place simply through selecting a different pattern of Taktteile to receive an accent. The earlier metric paradigm had no equivalent mechanism for achieving such shifts.
Hidden within this difference, however, is a deeper similarity between the Aristotelian and Newtonian approaches. Hasty observes that the ‘givenness’ attached to Mattheson's tactus does not entirely disappear in later theories. Rather, in the Akzenttheorie, this ‘givenness’ is displaced to the level of the pulse or Taktteile. Footnote 17 In other words, just as how, for Mattheson, the pre-existing measure logically precedes its parts, so too, for Kirnberger's circle, the pre-existing equal pulses logically precede the bars that they form, and are thus also a ‘given’. The ‘givenness’ of Taktteile is what prevents the mixing of metres with different denominators (such as we find in ‘Der Himmel’) from being neatly explicable within the Akzenttheorie. If anything, the Akzenttheorie appears even less well-equipped to explain multi-denominator mixed metre than older models. It is important to note, however, that the shift from Aristotelian to Newtonian metric theories was neither swift nor tidy. Nearly thirty years prior to the first formulations of Akzenttheorie, Mattheson lamented the fact that physical motion was no longer an adequate explanation for the phenomenon of metre:
Once, one said, and wrote happily for the world: Takt is nothing other than a raising and lowering of the hand. Oh! What beautiful ideas must this not give those who want to know what sort of a thing a Takt is. It was still better than nothing.Footnote 18
Grant connects this drifting apart of metre and motion to a mid-eighteenth-century theoretical phenomenon that he terms a ‘multiplicity of measures’. With motion no longer able to capture metre's true nature, theorists – anxious to maintain their conceptual grasp on musical time – turned to notation. This is manifest in the extensive inventories of notated metres and their associated tempos, affects and characteristic rhythmic profiles found in many theoretical treatises of the time, and it is in this context that Telemann and his contemporaries operate.Footnote 19 Yet the changes in ‘Der Himmel’ sit still less comfortably within this paradigm of metric specificity; Grant's ‘integrated metric shifts’ are impossible if each time signature possesses a distinct tempo and character. The only sort of change congruent with the ‘multiplicity of measures’ involves tempo and metre shifting together, as in Francois Couperin's ‘La Coquéterie’ from his ‘Les Dominos’ of 1722 (Figure 2).

Figure 2 François Couperin, ‘La Coquéterie’, from ‘Les Dominos’, from Troisième livre de pièces de clavecin (Paris: Boivin, 1722), 12. Bibliothèque du Conservatoire de Paris, L-3982 (3), 12, https://gallica.bnf.fr/ark:/12148/btv1b9083215k
THEORETICAL PERSPECTIVES ON MIXED METRE
Beyond these broader theoretical approaches, eighteenth-century writers do occasionally discuss metric irregularity, though they have more to say about quintuple and septuple time than about the intermixing of more commonplace metres. This is surprising, given that quintuple and septuple time seem virtually non-existent in eighteenth-century music.Footnote 20 From Johann Walther's Praecepta (1708) to Sulzer's Allgemeine Theorie der schönen Künste (1771–1774), quintuple and septuple metres are almost universally rejected as unnatural, obsolete and unpleasant.Footnote 21 Perhaps the most disparaging of eighteenth-century commentaries is that by Friedrich Wilhelm Marpurg, who argues that
Alle diese vermeinte neue Tactarten sind nichts anders, als eine Vermischung des schon bekannten geraden und ungeraden Tacts . . . [die] beständig einander abwechseln; und wie nimmt das Gehör diese beständige Abwechselung an? Mit dem außersten Verdruß und Widerwillen.Footnote 22
All of these supposedly new metres are nothing more than a mixture of the already known equal and unequal tactus . . . constantly alternating with one another. And how does the ear receive these constant changes? With the utmost frustration and reluctance.
Marpurg's understanding of quintuple and septuple time as asymmetrical compound metres suggests some degree of conceptual overlap with mixed metre. Knowing their views on quintuple and septuple metres, eighteenth-century writers might have responded to the changes in ‘Der Himmel’ in similar ways. We may also infer theoretical perspectives on mixed metre from the emphasis most writers place on regularity as a fundamental property of well-formed music. For many theorists, it was not enough for a piece to be written in a regular metre; the regularity had also to be rendered audible through constant articulation of beats and subdivisions. Writing in 1752, Joseph Riepel argued that ‘in music, motion must be continuously heard’ and therefore that ‘when one or more voices rest, the others must move’.Footnote 23 While Heinrich Christoph Koch likewise recommended increased bass movement ‘if the melody . . . does not preserve the accepted metre perceptibly enough’, he did permit occasional breaks in the rhythmic flow as a special effect, provided the listener was ‘not confused through any contrasting motion’.Footnote 24 Yet again, ‘Der Himmel’ falls foul of theory. When the flow of quaver pulses is interrupted by crotchets, the changes of metre (regardless of whether they yield duplet effects or changes in bar length) prevent the listener from ‘thinking along’ in 3/8.
In the form of metric irregularity most commonly addressed in eighteenth-century theory, the changes are not notated with new time signatures or changing bar lengths. Known as imbroglio, the practice is defined by Koch as comprising ‘those phrases in which a contrary meter is inserted’ and is described approvingly by mid- to late eighteenth-century theorists.Footnote 25 Riepel illustrates imbroglio with examples of 4/4 arising from within 3/4 and 3/4 arising from 2/4 (Example 1).Footnote 26 Noteworthy here is that Riepel's metre changes occur through the repetition of melodic and rhythmic units of a length matching the new metre. Mirka refers to such repetition as ‘parallelism’, which takes advantage of the fact that listeners are predisposed to align repeating patterns with metric accent, an essential feature of imbroglio.Footnote 27 The most frequently encountered form of the device involves shifts to duple metre within a triple-time context. Daniel Gottlob Türk illustrates this kind of imbroglio with an excerpt from Hasse's oratorio I pellegrini al sepolcro di Nostro Signore (1742) and rewrites the passage with a change of time signature to explain the resulting sonic effect (Example 2).Footnote 28 The shortest possible form of duple-within-triple imbroglio takes place over just two bars: I refer to this as an ‘imbroglio hemiola’. Although we now use the word ‘hemiola’ for a host of apparently similar metric techniques, they are never discussed under the umbrella of a single term in eighteenth-century theory.Footnote 29 Exemplifying our modern approach, Richard Cohn defines hemiolas as occurring ‘when a span of time is trisected in place of an expected bisection’.Footnote 30 Tidy as such definitions are, however, they risk obscuring the variety of hemiola-like practices at play in eighteenth-century music. This becomes apparent when we consider a particularly interesting metric phenomenon, found in the works of Telemann and his contemporaries, wherein a triple-metre passage contains written-out bars of doubled length. Due to its notated changes of bar length, I call the technique a ‘mixed-metre hemiola’. Although, like imbroglio, these mixed-metre hemiolas appear in eighteenth-century theory amongst permissible exceptions to metric regularity, they are not classed as imbroglio. An aria from Handel's Tamerlano illustrates the technique, which, according to Kirnberger, is formed when ‘two measures are joined so that they become one’ (Example 3).Footnote 31 Koch likewise understands the mixed-metre hemiola as an expanded version of the bars surrounding it. Citing a chorus from Carl Heinrich Graun's Der Tod Jesu (1755; Example 4), he explains that ‘the value of the Taktteile in one measure is doubled for the sake of a graver and more emphatic expression’.Footnote 32

Examples 1a and 1b Examples of imbroglio from Joseph Riepel's Theory of Metric and Tonal Order: Phrase and Form. A Translation of His ‘Anfangsgründe zur Musicalischen Setzkunst’, Chapters 1 and 2 (1752/54, 1755), trans. John Walter Hill (Hillsdale, NY: Pendragon, 2014), 32

Examples 2a and 2b Johann Adolph Hasse, ‘Pellegrino è l'uomo in terra’, I pellegrini al sepolcro di Nostro Signore (1742), bars 83–86, as cited in Daniel Gottlob Türk, Klavierschule (Leipzig: Schwickert, 1789), 93–94

Example 3 George Frideric Handel, ‘No, che sei tanto costante’, Tamerlano (1724), bars 1–6, as cited in Johann Philipp Kirnberger, The Art of Strict Musical Composition, trans. David Beach and Jurgen Thym (New Haven: Yale University Press, 1982), 213

Example 4 Carl Heinrich Graun, ‘Freut euch alle, ihr frommen’, Der Tod Jesu, bars 15–22, as cited in Heinrich Christoph Koch, Musikalisches Lexikon (Frankfurt am Main: August Hermann der Jüngere, 1802), 1277–1280
Particularly in triple time, imbroglio techniques can yield similar sonic outcomes to notated mixed metre (the line between imbroglio hemiolas and mixed-metre hemiolas appears especially thin). Türk's renotating of Hasse's chorus exemplifies this, since the same music is ‘spelled’ both as imbroglio (Example 2a) and as mixed metre, with a written-out change in time signature (Example 2b). Crucially, however, in eighteenth-century theory and practice these two kinds of metric irregularity receive distinct treatment. There seem to be three reasons for this. First, imbroglio necessarily involves a regrouping of Taktteile through parallelism, whereas notated mixed metre has no such requirement. Imbroglio's reliance on parallelism means that its bar-by-bar contents tend to differ from those of mixed metre, as is apparent from a comparison of the previous four examples. While Riepel's and Hasse's passages (Examples 1 and 2) generate metrical shifts through repeating patterns, those of Handel and Graun (Examples 3 and 4) do so through forceful articulation of the new metre's Taktteile. Of course, nothing prevents notated mixed metre from containing parallelism, just as there is no reason why imbroglio should not be notated with time-signature changes. None the less, examples of either are practically non-existent in eighteenth-century music.Footnote 33 Second, imbroglio always ‘resolves’ after some number of bars. This means it is always possible for a listener – stubbornly, in the face of conflicting accents – to continue counting in the original metre and eventually become resynchronized with the sounding downbeats. Imbroglio passages are therefore restricted to certain lengths relating to the lowest common multiple of the two time signatures. Notated mixed metre can, conversely, last for any duration (including durations which preclude metric ‘resolution’). In such cases, a listener attempting to count along in the original metre might end up displaced for the remainder of the piece. Again, there is nothing stopping composers from writing metre changes which occupy lengths of time congruent with the prevailing metre. Yet aside from mixed-metre hemiolas (which take up precisely two ordinary bars), such congruency is absent from the mixed-metre repertoire. Thirdly, imbroglio always involves the regrouping of Taktteile of equal duration, whereas notated mixed metre allows for the introduction of time signatures with different denominators as well as numerators. Therefore, while all forms of imbroglio are congruent with late eighteenth-century metric theory, only certain kinds of notated mixed metre are.
The differences between imbroglio and mixed metre are encapsulated in Telemann's keyboard overture twv32:9, wherein the two forms of metric irregularity are juxtaposed. As Example 5a shows, a mixed-metre hemiola articulated through ‘brute-force’ homorhythm is immediately followed by an imbroglio hemiola created via rhythmic/melodic parallelism. Following Türk, we could renotate this passage to show the changes of time signature that a listener would hear (Example 5b): first to a single a bar of 3/2 (the mixed-metre hemiola doubles the value of the Taktteile), then to three bars of 2/4 (the imbroglio hemiola regroups the Taktteile into pairs). While it is tempting describe both changes simply as ‘hemiolas’, eighteenth-century theorists and composers seem to have viewed the two techniques as distinct. This means that theoretical discussions of imbroglio cannot, unfortunately, tell us much about eighteenth-century views on notated mixed metre. As the following section shows, however, it is the mixed-metre hemiolas that hold the key to understanding the strange changes of time signature in ‘Der Himmel’ and other works like it.

Examples 5a and 5b Georg Philipp Telemann, Overture V, twv32:9, bars 25–33: (a) transcribed and (b) renotated by Paul Newton-Jackson from Telemann, VI Ouverturen (Nuremberg: Balthasar Schmid, c1740), 13
FOUR CATEGORIES OF EIGHTEENTH-CENTURY MIXED METRE
Telemann and his contemporaries employ mixed metre across virtually all the compositional forms of their day, from solo keyboard pieces to works for large instrumental ensemble, from sacred cantatas to opera. I divide this repertory into four categories: recitative-type, declamatory-type, dance-type and experimental. Since there is scant room in eighteenth-century theory for notated mixed metre, my four categories are necessarily a modern invention, constructed as a tool for navigating this complex metric landscape. Accordingly, some pieces belong to more than one category, while others threaten to destabilize the enterprise entirely. The function of these categories is not to provide neat classifications for every instance of eighteenth-century mixed metre. Rather, they reveal lineages in metric practice that might otherwise be hidden from us. These lineages are suggested not only through shared habits of notation across the repertory, but also through the ways in which different pieces respond to shared musical concerns. Beyond demonstrating the richness of eighteenth-century metric invention, my four categories show that the mixed-metre repertory is more than just a cluster of quirks. While such compositions are often fascinatingly inexplicable, some types can be explained as arising from the innovative extension of more widespread eighteenth-century techniques into new metric territory. In this sense, many works in this repertory represent particularly creative solutions to common issues facing eighteenth-century composers.
1 Recitative-Type
Encompassing metre changes in recitative and arioso, recitative-type is probably the most familiar kind of eighteenth-century mixed metre, owing to its well-known use in French music from Lully onwards. Despite this, modern studies of eighteenth-century metre exclude recitative, probably on account of its ostensibly ‘unmeasured’ status. Yet, as I will show, mixed-metre recitative can disturb notions of a firm boundary between measured and unmeasured music. This category hosts great diversity; Telemann's uses of the technique range from one-off changes in secco recitative to multiple changes in sections scored for full chorus and multi-instrument accompaniment. The common factor in recitative-type mixed metre is its function as a more flexible approach to text setting. Mid-recitative changes of metre are a way of ensuring that rhymes, pauses and important syllables can be notated with appropriate emphasis even when the prose is highly irregular. Telemann makes this clear in his 1751 correspondence with Graun, in which he justifies changes of time signature within recitative as ‘a means to make the words more flowing without lengthening certain notes to fill up the spaces’.Footnote 34 Some justification was clearly called for, since German writers seem almost unanimous in condemning the practice. Johann Adolf Scheibe viewed such changes as an unnecessary complication, while Marpurg saw them as outdated and at odds with the ‘good symmetrical rhythms of today's music’.Footnote 35 Graun voiced similar objections in his letters to Telemann, wherein he appealed to naturalness and simplicity in rejecting recitative-type mixed metre. Believing that ‘one must not create any unnatural difficulties without important reasons’, Graun argued that time-signature changes in recitative were a troublesome burden for singers and accompanists.Footnote 36 In response, Telemann assured Graun that ‘the metre changes cause the French no difficulties at all; everything flows like champagne’. Telemann also drew on his own experience as evidence that this kind of recitative posed no challenge to German musicians either, declaring that even his ‘by no means witch-like orchestra did not pull any faces’ when performing his 1746 Matthäus-Passion (twv5:31), a piece saturated with recitative-type metrical changes.Footnote 37 Whereas Graun had a strong preference for Italian recitative, Telemann was more equivocal. In line with his philosophy of ‘mixed taste’, Telemann saw neither style as superior, but instead celebrated the coexistence of both as enlarging a composer's expressive options.
In fact, it appears that Graun took issue mainly with the notational irregularity, rather than with the sonic result. Peter Czornyj argues that Telemann's recitative-type metre changes are ‘essentially inaudible, and worry only the critical eye’.Footnote 38 While he is right to point out that neither Italian nor French recitative was sung completely ‘in time’, it does not follow that the differences between the two are solely notational. In reality, French recitative was probably sung more metrically than its Italian cousin. In Das Neu-eröffnete Orchestre (1713) Mattheson commented wryly that ‘if beauty is to change time signature five to six times per line and sing the recitative to the beat, then the French have victory here’, and his observation that French aria and recitative were too similar-sounding might have stemmed from the fact that the latter retains a sense of pulse. (‘Wenn das aber eine Schönheit ist, den Tact in einer Zeile 5.6. mahl zu verändern, und den Recitatif nach der battut zu singen: so haben die Franzosen den Sieg hierinn . . . gleich wie ihre Arien fast den Recitativen ähnlich lauten; so sollte mancher auch ihre Recitativen für Liedermäßig halten’.)Footnote 39 French-style recitative more often features accompanying instruments and has a greater degree of bass movement than its Italian counterpart, further suggesting a more measured approach to its performance. Accordingly, we should not rule out the possibility that recitative-type changes of metre may, in some cases, have been heard as such. Even if the changes themselves (that is to say, the downbeats) were not audible, listeners would likely have been aware that pulses were being grouped and regrouped in irregular patterns. At times Telemann appears to leverage this audible irregularity for expressive effect. At the point in his 1746 Matthäus-Passion when Judas greets Jesus with a kiss, the time signature undergoes a shift from 4/4 to 6/8 while the bass line moves in rhythmic unison with the disciple's arioso salutation (Example 6). By means of this change – rendered audible through repeated sautillant rhythms – Telemann seems to lend Judas's greeting a duplicitous and mocking tone. Here, rather than functioning as a neutral container for text, mixed metre allows the composer to insert a brief fragment of ‘measuredness’. Given the rarity of compound time signatures in French-style recitative, the bar of 6/8 seems carefully chosen for its affect and characteristic rhythms – perhaps, in this moment, Telemann is aligned with the mid-century theoretical paradigm of metric specificity discussed by Grant.Footnote 40 Elsewhere, however, Telemann's recitative-type metre changes, while audible, have little to do with textual meaning. An accompagnato passage from the oratorio Die Auferstehung und Himmelfahrt Jesu of 1760 (twv6:6) contains shifts between 3/4, 4/4 and 5/4 which, although lacking any clear dramatic function, cannot help but be heard metrically owing to the consistent pulsing of quaver beats (Example 7). This shows that even in cases when the music is more measured than not, Telemann required no special textual justification to adjust metrical containers. In such cases, mixed metre enables Telemann to simulate the flexibility of secco recitative in passages where the addition of accompanying instruments might otherwise reassert an inexpressive regularity. Putting it another way, these recitative-type changes help to create a middle ground between recitative and aria, in which the former's declamatory sensitivity is combined with the latter's instrumental colour and rhythmic interest.

Example 6 Telemann, ‘Und als er noch redete’, Matthäus-Passion (1746), twv5:31, bars 12–16, ed. Felix Schröder (Heidelberg: Willy Müller, 1976)

Example 7 Telemann, ‘Dort seh ich aus den Toren Jerusalems’, Die Auferstehung und Himmelfahrt Jesu (1760), twv6:6, bars 29–34, ed. Ralph-Jürgen Reipsch (Kassel: Bärenreiter, 1997). The abbreviations ‘st.’ (‘stark’, strong or loud) and ‘gel.’ (‘gelinde’, soft or quiet) are part of a unique tendency, seen in works from the 1730s onwards, for Telemann to replace the usual Italian dynamic, expression or tempo markings with their German-language equivalents
Telemann scholar Ute Poetzsch has argued that such pieces demonstrate the composer's inventive adaptation of a technique that most eighteenth-century commentators dismissed as having little value outside of French language and taste.Footnote 41 Even more significant, however, is the way these pieces problematize the very idea of ‘metric music’, reminding us that the line we draw between measured and unmeasured is an artificial one. Indeed, Telemann's recitative-type pieces prompt us to recall the many early modern works straddling the boundary between metric and non-metric. Claudio Monteverdi's Lamento della Ninfa, ostensibly a piece of measured music, opens with a directive that singers proceed ‘according to the tempo of the affections, not that of the hand’ (‘cantato a tempo del'affetto del animo, & non a quello della mano’), while some of J. S. Bach's recitatives contain the instruction ‘a battuta’.Footnote 42 Historians of musical time cannot afford to cordon off so-called unmeasured music, but instead should consider a piece's ‘measuredness’ within a spectrum of expressive options (with, say, unmeasured keyboard preludes at one end, and military marches at the other). Given that many instances of mixed-metre recitative and arioso seem closer to arias in terms of ‘measuredness’ than they are to unmeasured preludes, recitative-type mixed metre surely has much still to tell us about the inner workings of eighteenth-century musical time.
2 Declamatory-Type
Moving further towards the measured end of the spectrum, this category encompasses arias in which time-signature changes emphasize or accommodate important words. A defining characteristic is the one-off nature of the changes; these pieces feature a single bar (or pair of bars) in a foreign metre which is always attached to a certain word or phrase. If a declamatory-type piece contains multiple shifts to a foreign time signature, it will be because the text associated with the shift has been repeated. Declamatory-type mixed metre is exemplified by the aria ‘Laßt mir den letzten Streich nur geben’ from Telemann's opera Emma und Eginhard (1728). Here the hero Eginhard awaits his seemingly imminent death, declaring that to sacrifice oneself for love's sake is to die without regret. The shift (from 3/4 to 2/4) occurs in the final two bars of the B section, allowing Telemann to lend a speech-like accentuation to these words without having arbitrarily to lengthen syllables or add rests (Example 8). Like most declamatory-type examples, therefore, his metrical change carries out similar text-setting work to those in French-style recitative and arioso.Footnote 43

Example 8 Telemann, ‘Laß mir den letzten Streich nur geben’, Emma und Eginhard (1728), twv21:25, bars 101–113, ed. Wolfgang Hirschmann (Kassel: Bärenreiter, 2000)
We can also link Telemann's declamatory-type mixed metre with a common eighteenth-century practice, described by Koch, of breaking the metric flow in response to important words. Koch cites a cantata by Christian Scheinpflug as a case where, ‘for special reasons, the accepted metrical motion is . . . interrupted on purpose’ (Example 9). Koch rightly observes that ‘the beginner can, without difficulty, explain the reasons for this from the contents of the poetry’: Scheinpflug has illustrated the repeated ‘langen, langen’ with aptly drawn-out notes.Footnote 44 This technique is not restricted to word-painting, however. Koch explains that such interruptions take many forms (even appearing in instrumental music), and thus can occur independently of textual content. Similar metric interruptions to Scheinpflug's are found in Christoph Graupner's cantata Müssiggehn bringt keine Krone (gwv1117/20; Example 10). Similarly to Scheinpflug, Graupner sets the word ‘längst’ to the expanded rhythms of a mixed-metre hemiola. Here, however, the sense of length arises not through interruptions to the flow of crotchet beats (since these continue unabated), but through a metric deceleration (reinforced through a concurrent slowing-down of text declamation and harmonic change). Reading this excerpt through the lens of the Akzenttheorie, the continuo's crotchet Taktteile in 3/4 become Taktglieder (subdivisions) in 3/2, while the soprano articulates the doubled Taktteile in minims. Rather ingeniously, Graupner has brought his text to life with an unexpected metric shift, yet he embeds this within rhythmic regularity, thus maintaining forward motion. Given the widespread nature of the ‘interruption’ technique described by Koch, it makes sense to view declamatory-type changes as a close relative of this tactic. Such a suggestion does not ‘normalize’ declamatory-type mixed metre (nor should it diminish its compelling aural effect), but rather reveals it as a particularly imaginative and open-minded application of a commonly used eighteenth-century technique.

Example 9 Christian Scheinpflug, extract from an unknown cantata, as cited in Heinrich Christoph Koch, Introductory Essay on Composition: The Mechanical Rules of Melody, Sections 3 and 4, trans. Nancy Kovaleff Baker (New Haven: Yale University Press, 1983), 76

Example 10 Christoph Graupner, ‘Die Seligkeit ist zwar schon längst erworben’, Müssiggehn bringt keine Krone, gwv1117/20, bars 1–6. Universtitäts- und Landesbibliothek Darmstadt Mus-Ms-428-03
Beyond Telemann's output, I am aware of only two pieces that contain declamatory-type mixed metre, both by Graupner. The piece excerpted in Example 10 also contains a shift to 4/4 in its final bars, as does the aria ‘Tief gebückt’ from Mein Herz schwimmt in Blut (gwv1152/12b). In the latter, a change from 3/4 to 4/4 occurs at the end of the aria's A section, lending a compelling directness to the final three syllables of the phrase ‘Lieg ich, liebster Gott, vor dir’ (Example 11). Both Graupner examples are remarkably similar to Telemann's Emma und Eginhard aria; given that both composers were familiar with each other's work, it seems likely that one was influenced by the other. While a precise origin for declamatory-type mixed metre seems elusive, we can perhaps view the category as a result of the convergence of two fairly common kinds of eighteenth-century metric irregularity. On the one hand, the flexibility afforded by French-style recitative is extended into the domain of the aria, while on the other, well-established methods of metric interruption are expanded creatively to encompass changes of time signature.

Example 11 Graupner, ‘Tief gebückt’, Mein Herz schwimmt in Blut, gwv1152/12b, bars 22–28. Universtitäts- und Landesbibliothek Darmstadt Mus-Ms-420-21
3 Dance-Type
Like declamatory-type pieces, examples in this category lie at the ‘measured’ end of the metric spectrum and are always set in one prevailing metre, within which changes lasting for (usually) a single bar are embedded. This category owes its name to a link with the choreography and rhythmic profile of the passepied, a dance that was well known for its rhythmic tricks. Mattheson described the passepied as frivolous and inconstant, while Kirnberger noted its tendency to contain ‘joined measures’.Footnote 45 Indeed, the hemiola rhythm (in the modern sense) was physically inscribed into the passepied's choreography: based on a four-step sequence, the dance's steps fall on the first, third, fourth and fifth beats of a six-beat pattern.Footnote 46 Hemiolas within a passepied might therefore be understood as the temporary foregrounding of an alternative metrical measuring that had existed ‘beneath the surface’ all along. This link with the physicality of dance enabled composers of dance-type pieces to insert bars which abandon the prevailing metre entirely, often through articulating the beats of the latent double measure in rhythmic unison. This gives rise to the phenomenon I have already referred to as the mixed-metre hemiola. These are, however, only the most tame variety of dance-type mixed metre. As Steven Zohn has pointed out, one of Telemann's most exciting and disruptive metrical shifts takes place in the passepied from the overture-suite twv55:B10.Footnote 47 Here the mixed-metre hemiola is split across a repeat, giving rise to an apparent 2/4 bar, the missing beat of which is only ‘resolved’ at the end of the phrase (Figure 3). Until the first repeat is reached, there is no way for a listener to know whether the opening bar is in 2/4 or whether it constitutes the final two beats of a 3/4 bar. This is more important than it may at first seem, for here we have a clear example of something which sounds like a 2/4 bar appearing within a piece in 3/8. From this we can glean a vital clue as to how the mixed metre in ‘Der Himmel’ (Figure 1) might have sounded in eighteenth-century practice. If the changes in ‘Der Himmel’ are performed in such a way that quaver equivalence is maintained between 3/8 and 2/4, they give rise to a remarkably similar aural effect to the split hemiolas of twv55:B10, a resemblance strengthened by the fact that the ‘odd bars out’ in both pieces consist solely of homorhythmic crotchet beats.

Figure 3 Telemann, Passepied 1, from Overture-Suite in B flat major, twv55:B10, oboe 1 part. Sächsische Landesbibliothek - Staats- und Universitäts-Bibliothek Dresden, Mus.2392-N-11, 21, https://digital.slub-dresden.de/werkansicht/dlf/53157/1/
The aural knife-edge between 2/4 and 3/4 in twv55:B10 raises the possibility that, in the minds of eighteenth-century musicians, there is little separating the passepied's split hemiolas from the time-signature changes of ‘Der Himmel’, provided that quaver equivalence is maintained in the latter. More broadly, this suggests that mixed-metre hemiolas such as those in twv32:9 (see Example 5) might share a lineage – via the split hemiolas of twv55:B10 – with the 2/4 bars of ‘Der Himmel’. Counterintuitively, then, these latter three pieces appear more closely related to one another than mixed-metre hemiolas are to their imbroglio counterparts. Figure 4 sums up the proposed connections between the different kinds of dance-type mixed metre. Understanding these relationships allows us to interpret a rather ambiguous notation that frequently crops up in Telemann's dance-type pieces. In several handwritten (or hand-engraved) sources, passepied-style movements contain bars of two crotchets annotated with a small numeral ‘2’ (Figure 5).Footnote 48 Wherever such bars occur, all parts are in rhythmic unison, and so there are no contextual hints as to how the speed of these notes might relate to the tempo of the surrounding 3/8 bars. The confusion arising from this ambiguity is evident in recent performances. Early-music group Musica Alta Ripa perform the ‘duplet’ bars in the passepied from the overture-suite twv55:g8 as 2/4 bars in which the quaver pulse remains constant; conversely, Concerto Antico interpret these bars as literal duplets, thus preserving a bar-equals-bar relation.Footnote 49 The interpretative consensus varies from piece to piece: all modern renditions of the passepied from the solo partita twv41:B1 preserve the quaver-equals-quaver relation, while identically notated bars in the trio sonata twv42:A4 are always performed as duplets.Footnote 50
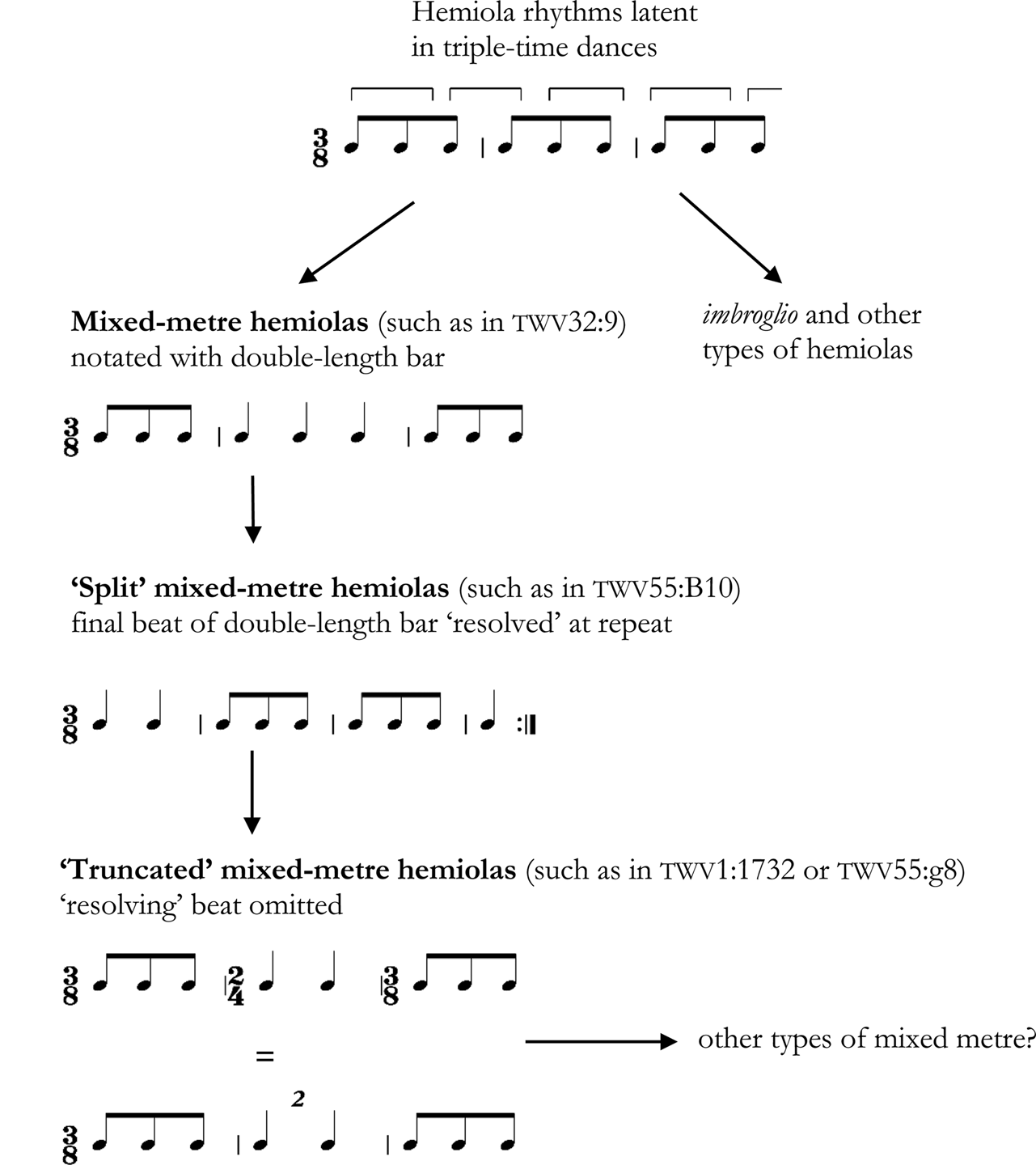
Figure 4 Some probable lineages and relationships within the ‘hemiola family’ of metric irregularity

Figure 5 Telemann, Passepied, from Overture-Suite in G minor, twv55:g8, violin 1 part, bars 1–24. Sächsische Landesbibliothek - Staats- und Universitäts-Bibliothek Dresden, Mus.2392-O-41, 4, https://digital.slub-dresden.de/werkansicht/dlf/15407/1/
On the basis of the close aural link between mixed-metre hemiolas and embedded 2/4 bars (exemplified by twv55:B10), and on account of the frequent appearance of this ‘duplet notation’ in passepieds, I draw two conclusions. First, that the duplet notation is shorthand for – and is therefore equivalent to – a spelled-out change of time signature to 2/4. Second, embedded 2/4 bars in 3/8 time (such as those in ‘Der Himmel’) are probably intended to be played in such a way as to maintain a constant quaver pulse, thus yielding what I refer to as ‘truncated hemiolas’. The split hemiolas of twv55:B10 show that apparent 2/4 bars are quite at home in 3/8 time. Moreover, the idea of a bar formed from two dotted-quaver beats (the aural result of treating duplet notation literally) is irreconcilable with the choreography of the passepied. The numeral ‘2’ therefore does nothing to alter the written rhythms: rather than acting as a duplet, this annotation seems to function as a signpost for performers, alerting them to metric irregularity.Footnote 51 Perhaps the most compelling evidence for interpreting duplet notation in this way is found in the aria ‘Mein Herz kennt kein Mitleid mehr’ from Telemann's early opera Germanicus. In Michael Maul's edition, the final bars of the B section contain a hemiola notated across the barline (Example 12).Footnote 52 In the manuscript parts, however, this passage is written as a mixed-metre hemiola with identical duplet notation to that which is found two bars earlier (see Figure 6). Within the space of a few bars, duplet notation appears both within a stand-alone bar of two crotchets, as well as in the last two crotchet beats of a mixed-metre hemiola. This strongly suggests that the notes annotated with a ‘2’ should keep their full length, and further confirms the close relationship between mixed-metre hemiolas and interpolated 2/4 bars like those in ‘Der Himmel’. The Germanicus example also demonstrates that editors must take care to represent eighteenth-century metric irregularity in such a way as to preserve important notational information. The final bars of Maul's edition suggest a rather different pattern and weight of accents than are indicated in the manuscript parts, in which both syllables of ‘meine’ are clearly intended to be emphasized in the same way when the word is heard for the second time.

Figure 6 Telemann, ‘Mein Herz kennt kein Mitleid mehr’, Germanicus, voice part, bars 47–51. Universitätsbibliothek Johann Christian Senckenberg, Frankfurt am Main, Ms.Ff.Mus. 1587, fol. 6v, http://sammlungen.ub.uni-frankfurt.de/telemann/content/titleinfo/4730993. Used by permission

Example 12 Telemann, ‘Mein Herz kennt kein Mitleid mehr’, Germanicus, bars 44–52, ed. Michael Maul (Beeskow: Ortus, 2010)
While dance-type mixed metre is particularly well represented in Telemann's oeuvre, it is occasionally used by his contemporaries. A famous example is the aria ‘Bel piacere’ from Handel's Agrippina (1709), which mixes 2/4 and 3/8 (Example 13). This aria is especially interesting on account of its paired 2/4 bars, a technique found only once in Telemann's output (in the A section of the same Germanicus aria discussed above). Ellwood Derr has even suggested that Telemann must have used ‘Bel piacere’ as a model when he came to compose ‘Der Himmel’.Footnote 53 This only makes sense, however, if we regard such changes as exceptional. Knowing now that mixed metre is widespread across Telemann's output, it is equally probable that Handel borrowed from one of Telemann's early works. The likelihood of this increases if we account for George Buelow's observation that, since ‘eighty-five per cent of [Agrippina's] arias are traceable directly to another source . . . one can say without fear of exaggeration that the entire opera was in a sense borrowed, and that we lack only the ability now to identify sources for the remaining arias’.Footnote 54 If Handel did borrow the changes of metre in ‘Bel piacere’ from Telemann, it may well have been from one of the latter's many lost Leipzig-period operas.

Example 13 Handel, ‘Bel piacere’, Agrippina (1709), violin and voice parts, bars 9–30, ed. John E. Sawyer (Kassel: Bärenreiter, 2013)
To uncover the origins of dance-type mixed metre we must again turn to French practice. Describing how he acquired his Gallic taste, Telemann explained that while employed in Sorau (1705–1709) he studied the orchestral works of ‘Lully, Campra and other good authors’.Footnote 55 Ian Payne has revealed the fruits of this study, manifest in a constellation of borrowings from the works of French and Francophile composers.Footnote 56 That Telemann was intimately familiar with the music of this generation suggests that their output is a good place to seek precedents for dance-type changes of metre. Although I have yet to find any truncated hemiolas in the works of Telemann's French models, there are many examples of ‘ordinary’ mixed-metre hemiolas by André Campra and André Destouches: a passepied from the latter's Omphale contains similar mixed-metre hemiolas to those found in Telemann's overture-suite of the same name (twv55:e8). The Lullist Johann Sigismund Kusser (John Sigismond Cousser) employs both ‘split’ and ‘whole’ mixed-metre hemiolas in a passepied from his collection Festin des Muses (1700), confirming that the metric tricks of twv55:B10 are not Telemann's own invention (Example 14). Most intriguing of all, however, are two instrumental pieces by Fux from around the turn of the century: a ‘contredanse’ from the trio partita k327 and a passepied from the overture-suite in D major, n4. While, like many of Telemann's mixed-metre works, the contredanse mixes 3/8 with 2/4, the passepied creates (presumably) the same aural effect by combining 3/4 and 2/2 (Example 15). As Fux was almost twenty years Telemann's senior, it seems almost certain that the truncated hemiola did not originate with Telemann. Although Telemann was certainly influenced by Fux – Payne refers to Telemann's borrowings from the Austrian as ‘the most explicit, complex and skillful piece of transformative imitation yet discovered’ – none of Telemann's dance-type pieces combine 3/4 and 2/2, and none employs rests in the embedded duple bars as Fux's passepied does.Footnote 57 Despite this, the sonic result of Fux's notation seems identical to that of Telemann's truncated-hemiola dance-type pieces, especially since the latter often articulate mixed-metre bars with short vertical strokes (détaché) which, in French practice, denote the equivalent of a foreshortening owing to a rest.Footnote 58 These notational differences raise the possibility that Fux and Telemann independently committed to paper a metric practice that existed primarily outside written traditions: truncated hemiolas may even have arisen from practices of extemporized dance accompaniment as one of many metric variants associated with the playful passepied. Thus while Telemann by no means invented dance-type metre changes, he clearly had a special affinity for them, for he wrote far more examples than any other composer. And, although dance-type examples also appear in cantatas by Fasch and Stölzel, Telemann and Handel appear to be the first composers to have extended this sort of mixed metre, originally a dance technique, into the realm of vocal composition.Footnote 59

Example 14 Johann Sigismund Kusser (John Sigismond Cousser), ‘Autre passepied’, Ouverture I, bars 1–6. Transcribed from a c1900 manuscript copy of Kusser's Festin des Muses (1700), Staatsbibliothek zu Berlin – Preußischer Kulturbesitz, Mus.ms. 4245, 17

Example 15 Johann Joseph Fux, ‘Trio: passepied’, Overture-Suite in D major, N4 (c1700), ed. Klaus Winkler (Stuttgart: Carus, 2007)
4 Experimental
In one sense, this category is a catch-all, containing pieces that do not fit neatly within the preceding types. Experimental works do, however, share a tendency toward the bizarre. Perhaps the most fascinating of Telemann's mixed-metre pieces, they are also the most difficult to fathom. In experimental works, Telemann stretches (and sometimes breaks) the boundaries of metric coherence and explores the sonic effects of highly unusual combinations: many such pieces cannot be heard in terms of one prevailing metre. The strangeness of experimental mixed metre is epitomized in the penultimate movement of the trio twv42:a3. As Figure 7 shows, there are an equal number of bars of 6/8 and 4/4. Neither time signature dominates, and the listener is prevented from settling into one or the other. For Zohn, this extraordinary irregularity ‘recalls Telemann's fondness for metrical ambiguity in his passepieds’.Footnote 60 Indeed, like Telemann's passepieds, this movement contains two instances of duplet notation, both appearing in the first half of 6/8 bars. Unsurprisingly, twv42:a3 has given rise to radically different modern interpretations. While the ensemble Le Petit Bruit maintain a consistent quaver pulse across the alternations in time signature, they perform only the first instance of duplet notation as a literal duplet.Footnote 61 In contrast, Thomas Indermühle and Claudio Brizi treat the crotchets of 4/4 as equal to the dotted crotchets of 6/8, whilst performing both duplet pairs literally.Footnote 62 It is far from clear what the ‘right’ answer here might be, even if such a thing exists. By tentative analogy with dance-type mixed metre, my inclination is towards a reading which, like that of Le Petit Bruit, preserves the quaver pulse between 4/4 and 6/8 but which, unlike either ensemble, gives all duplet crotchets their full value (effectively transforming the affected 6/8 bars into 7/8 bars).

Figure 7 Telemann, Vivace, from Suite V, twv42:a3, obbligato keyboard, from 6 Concerts et 6 Suites, two volumes (Hamburg, c1734), volume 2, 28. Bibliothèque nationale de France, Département de la Musique, K-8285, page 67, https://gallica.bnf.fr/ark:/12148/btv1b90815276
Amongst Telemann's non-recitative mixed-metre pieces, there are very few cases where note duration does not remain constant across a change in time signature. One example, though, is the song ‘Redlichkeit’ from the pedagogical collection Singe-, Spiel- und Generalbaßübungen (c1743–1744), which contains shifts from 4/4 to 3/2 and 3/1 (the latter through a mixed-metre hemiola) (Figure 8). Wherever 4/4 changes to 3/2, the average note value more than doubles, suggesting that crotchets in 4/4 correspond (at least) to minims in 3/2. Similar tempo relations are required in several of Telemann's mixed-metre recitatives – perhaps ‘Redlichkeit’ is intended to be sung as quasi-recitative. The notational ambiguities of twv42:a3 and ‘Redlichkeit’ raise an interesting question: would eighteenth-century players have known how Telemann intended these pieces to be performed? Two thirds of Telemann's experimental pieces are found in publications catering for amateur musicians; the aforementioned Singe-, Spiel- und Generalbaßübungen and the serial Der getreue Musikmeister. Czornyj points to Graun's lack of familiarity with the tempo relations required to perform French-style recitative. If a professional musician like Graun was unaware of a relatively commonplace aspect of eighteenth-century practice, how can we expect amateurs to have known the ‘correct’ interpretation of far more obscure notations? Given that Singe-, Spiel- und Generalbaßübungen is an explicitly pedagogical collection, and that each song is accompanied by a written ‘lesson’ on figured-bass realization, it is perplexing that Telemann explains neither the tempo relations in ‘Redlichkeit’ nor the duplet notation in songs 13 and 22, nor even the utterly bewildering sequence of changes in song 42 (Figure 9). If there is any truth to the idea of unwritten mixed-metre traditions, then perhaps Telemann's performers already had some idea of how these pieces were supposed to sound and could use this to decipher the ambiguous notation. If not, Telemann's published pieces of this kind were probably just as much of a puzzle to his subscribers as they are to us.Footnote 63

Figure 8 Telemann, ‘Redlichkeit’, twv25:45, from Singe- Spiel- und Generalbaßübungen (Hamburg, c1733–1734), No. 7. Det Kongelige Bibliotek, Copenhagen (DK-Kk), mu 6510.0533. Used by permission

Figure 9 Telemann, ‘Freundschaft’, twv25:79, from Singe- Spiel- und Generalbaßübungen, No. 42. Det Kongelige Bibliotek, Copenhagen (DK-Kk), mu 6510.0533. Used by permission
Mixed metre, especially of the types outlined above, must be acknowledged as a viable – albeit rarely written-down – expressive option available to eighteenth-century musicians. Unfortunately, however, we know almost nothing about how players and listeners might have received the mixed-metre compositions of Telemann and his contemporaries. As noted earlier, modern scholars have been similarly silent on this repertory: on the rare occasion that mixed-metre pieces are discussed, there is a tendency to explain unusual metric characteristics solely in terms of the text. Martina Janitzek views the spectacular declamatory-type shifts between 6/8 and 4/4 in ‘Mich tröstet die Hoffnung’ from Der geduldige Socrates as symbolizing the protagonist's indecisiveness.Footnote 64 For Anne-Marie Clostermann, the dance-type metre changes in ‘Die Dankbarkeit’ from Miriways (twv21:24) illustrate a character's duplicity.Footnote 65 These text-oriented interpretations of mixed metre can certainly deepen our understanding of specific works – indeed, there is much work to be done exploring how composers used mixed metre for dramatic effect or to engender particular kinds of listening experiences. Yet a series of one-off analyses cannot tell the full story. Only by engaging with mixed-metre pieces as a repertory can we allow them to challenge and inflect our understandings of eighteenth-century metric practice.
Even if this repertory cannot be brought within the fold of any one theoretical approach, it still has a great deal to tell us about the relationship between eighteenth-century theory and practice. Grant proposes that integrated metric shifts were ‘an outgrowth of metre's conceptual divorce from the tempo giusto relationships that had once bound it intimately with character and tempo’.Footnote 66 In doing so, Grant seemingly frames metric theory as a permissive force, in which each conceptual advance unleashes new creative opportunities. He writes, for example, that ‘when Kirnberger described metre as an activity of the mind . . . he was also admitting the theoretical possibility of an irregular or changing application of that activity’.Footnote 67 This notion of practice being led by theory is borne out in Grant's examples of integrated metric shifts, even the earliest of which were written well after the first formulations of the Akzenttheorie. The idea of such a relationship between theory and practice is certainly complicated by the sizeable repertory of pre-Akzenttheorie mixed-metre pieces unearthed here, especially since only a small subset of integrated metric shifts (those involving equal Taktteile) are neatly explicable within late eighteenth-century metric theory. Grant's model, in which broader conceptual shifts drive stylistic change, is, however, a welcome counterbalance to the tendency in twentieth-century writing to view the Akzenttheorie solely as a response to musical developments. As Tomas McAuley points out, authors of Carl Dahlhaus's generation tended to argue that, ‘faced with the wonders of contemporary Viennese music, . . . contemporary thinkers were compelled to transform their conceptions of the art’.Footnote 68 In stark contrast to Grant, William Caplin asserts simply that ‘when compositional styles change, theorists respond’.Footnote 69 It is tempting to take this latter angle regarding Telemann's relationship with contemporary theory. In such a narrative, the composer is a rule-breaking revolutionary, surrounded by conservatively minded pedants who, at best, struggle to keep up with compositional developments and, at worst, attempt to ban all forms of expression contrary to their world view. It is certainly true that Telemann demonstrates a greater-than-average appetite for unusual metric combinations, many of which challenge contemporary theoretical conceptions of metre. Such an appetite fits well with Telemann's broader compositional approach, in which – as Wolfgang Hirschmann puts it – his music often ‘gains all its expressive qualities from the subtle arrangement and spacing of what we might call “pure sound”’.Footnote 70
Yet while Telemann's mixed-metre works reveal a composer deeply interested in exploring unorthodox dispositions of sound in time, to suggest that he operated against – or in spite of – theoretical thought would do a disservice to the aims of eighteenth-century theorists. Rather than attempting to provide an all-encompassing theory of music, these writers sought to provide practical and aesthetically sound guidelines which musicians could then supplement with experience. The concepts of experience and taste are crucial to readings of eighteenth-century music theory, as shown in the fact that while theorists tended to be hostile to metric irregularity as a general concept, they would often respond positively to specific examples. Discussing the mixed-metre hemiola in Handel's Tamerlano, Kirnberger seems uninterested in accommodating the technique within his broader theory of metre. Rather, he explained that ‘all great masters make such exceptions, but they do it with deliberation’.Footnote 71 Likewise, Koch admitted that such anomalies come in so many varieties that ‘they cannot be classed in definite precise types’, but ‘the justification for such exceptions . . . is for the most part easier felt than explained’.Footnote 72 It is telling that the only eighteenth-century writers to express approval for quintuple metre do so in response to specific pieces: in his Dictionnaire de Musique Jean-Jacques Rousseau cites a ‘well-cadenced air’ (‘un chant très bien cadencé’) in 5/4 time, and Charles Burney views the 5/8 bars in Handel Orlando as ‘admirable’.Footnote 73 By their own admission, theorists’ statements will never be enough to reconstruct the diversity of approaches to metre in the eighteenth century. Scholars of eighteenth-century musical time must also account for the actions (both notated and otherwise) of practising musicians. Furthermore, we should remember that our modern distinction between theorist and composer is rather artificial: many of the ‘theorists’ cited here were employed primarily as composers. Telemann is a particularly interesting case: his publications often contained prefaces in a theoretical or pedagogical vein, he exchanged letters with Walther, Mattheson and Scheibe, and he was an active member of Lorenz Mizler's Correspondirende Societät der Musicalischen Wissenschaften (Corresponding Society for the Musical Sciences). At the same time, however, Telemann distanced himself from theoretical pedantry and received wisdom, especially in his autobiographies, in which he portrayed himself as a self-taught free spirit. Keith Chapin characterizes Telemann's aesthetic stance as a ‘productive mix’ of ‘independence, innovation and respect for tradition’; this is the outlook of a composer who maintained a close yet critical dialogue with music theory throughout his life.Footnote 74 Accordingly, we cannot separate Telemann the composer from eighteenth-century theoretical discussions: his compositions and writings alike are entangled in wider webs of music theory and criticism. This is especially true for ideas concerning musical time, the nature of which was contested and reformulated during Telemann's lifetime.
In a far-reaching critique of Karol Berger's 2008 book Bach's Cycle, Mozart's Arrow: An Essay on the Origins of Musical Modernity, Bettina Varwig warns of narratives ‘so broadly conceived that all musical and historical specifics readily slip into place’.Footnote 75 Perhaps more so than Berger's proposed shift from circular to linear notions of musical time, the idea of a transition from Aristotelian to Newtonian metric theories is well grounded in eighteenth-century writings. This does not, however, guarantee that conclusions reached at the level of theory and philosophy are applicable to the day-to-day realities of eighteenth-century music-making. The overwhelming volume and diversity of musical source materials from this time ensure that broad claims are equally easy to back up, complicate or contradict with well-chosen examples. Accordingly, there is little utility in harnessing the contents of the mixed-metre repertory to support or refute the narratives set out by Seidel, Caplin and Grant. These pieces are, however, a compelling reminder of the tangled relationships between theory and practice: they highlight the problems that arise when findings in the domain of the former are assumed to apply to the latter. Eighteenth-century metric practice is much more diverse and complicated than we have imagined: seemingly exceptional mixed-metre techniques are widespread, while familiar hemiola devices are rendered strange and multifarious. That these findings emerge largely from Telemann's output should remind us of the valuable lessons to be learnt from exploring works beyond the traditional canon: we surely have much still to discover.



























