1 Introduction
Much of the design process is accomplished by teams rather than individuals (Paulus, Dzindolet & Kohn Reference Paulus, Dzindolet, Kohn and Mumford2011). During design, there often arise situations in which members of a team have different opinions, yet a group decision must still be made (Dwarakanath & Wallace Reference Dwarakanath and Wallace1995). Unfortunately, a proof by Arrow indicates that there is no method for aggregating group preferences that will always satisfy a small number of ‘fair’ conditions (Arrow Reference Arrow1950). The work presented in this paper used an empirical approach that evaluates several methods for aggregating group preference. The objective was to identify methods for aggregating individual preferences that have a high likelihood of being fair in practice, by conducting numerical simulations using real preference data.
A broad debate within the engineering design literature has attempted to assess whether or not Arrow’s theorem applies to engineering design (Reich Reference Reich2010). Hazelrigg (Reference Hazelrigg1996, Reference Hazelrigg1999, Reference Hazelrigg2010) and Franssen (Reference Franssen2005) have espoused the view that Arrow’s theorem applies to all problems with multiple criteria or multiple decision makers. In contrast, Scott & Antonsson (Reference Scott and Antonsson1999) have adopted the stance that engineering design is a case of multi-criterion decision making, and that the aggregation of multiple criteria is fundamentally different from the aggregation of individual preferences, thus distancing engineering design from considerations of Arrow’s theorem. The current work adopts the point of view that social choice principles primarily relate to the decisions that aggregate designers’ preferences in the early stages of engineering design, serving to guide the early search for solutions.
It is undeniable that there do exist cases for which design can be framed as multi-criterion decision making (Scott & Antonsson Reference Scott and Antonsson1999; Yeo, Mak & Balon Reference Yeo, Mak and Balon2004). In such situations, design quality can be quantified with respect to an agreed-upon reference point and scale, which allows solution concepts to be objectively compared between individuals. In essence, the multi-criterion aspect of the decision problem becomes more important than the team aspect, negating the need to consider Arrow’s theorem. However, in the earlier part of design, the problem itself is still being defined, and there are often differing opinions on the relevant objectives, the methods for quantifying them, and their relative importance. These perceptual gaps describe differences in opinion that may exist within, but especially across, disciplines (Weingart et al. Reference Weingart, Neider and Schriesheim2005; Cagan & Vogel Reference Cagan and Vogel2012). Because all individuals do not necessarily agree upon evaluation criteria, the team aspect of the decision problem becomes superior to the multi-criterion aspect. Therefore, group decisions at this stage necessarily fall within the realm of social choice. For these situations, Arrow’s theorem does apply to the creation of group preferences, but does not necessarily preclude the formation of a fair group ranking in all situations. Rather, Arrow’s theorem states that there is no procedure for creating a group ranking that will always offer fair results. Maximization of the perceived fairness of decisions has the potential to enhance innovation (Janssen Reference Janssen2000) and collaborative problem-solving (Li, Bingham & Umphress Reference Li, Bingham and Umphress2007).
The process of recognizing and negotiating perceptual gaps allows a team to resolve differences of preference while simultaneously deepening their understanding of the product space. Once the team reaches agreement regarding the relevant evaluation criteria, the team based aspect of the decision problem becomes subordinate to the multi-criterion aspect, and Arrow’s theorem no longer applies. It is important to note that this work is only relevant to the early parts of the design process in which Arrow’s theorem applies.
In cases that take the form of social choice, there exist methods for computing a group ranking from the preferences of individuals. These methods are generally referred to as aggregation functions. These are simply functions that take as input a set of individual rankings, and return a single group ranking. Although aggregation functions may be simple in form, the aggregation of individual preferences is not a trivial task. Consider three individuals who must decide on a group ranking over three alternatives (
![]() $A$
,
$A$
,
![]() $B$
, and
$B$
, and
![]() $C$
). Their set of individual preferences, also known as a preference profile, is as follows. Individual 1 has the ranking
$C$
). Their set of individual preferences, also known as a preference profile, is as follows. Individual 1 has the ranking
![]() $A\succ B\succ C$
, individual 2 has the ranking
$A\succ B\succ C$
, individual 2 has the ranking
![]() $B\succ C\succ A$
, and individual 3 has the ranking
$B\succ C\succ A$
, and individual 3 has the ranking
![]() $C\succ A\succ B$
. This specific preference profile, brought to the attention of the engineering design community by Saari, is commonly known as the Condorcet paradox (de Condorcet Reference de Condorcet1785; Saari & Sieberg Reference Saari and Sieberg2004). One method that can be used to develop the required group ranking is the pairwise majority rule. The pairwise majority rule would be implemented as follows. A majority of voters prefer
$C\succ A\succ B$
. This specific preference profile, brought to the attention of the engineering design community by Saari, is commonly known as the Condorcet paradox (de Condorcet Reference de Condorcet1785; Saari & Sieberg Reference Saari and Sieberg2004). One method that can be used to develop the required group ranking is the pairwise majority rule. The pairwise majority rule would be implemented as follows. A majority of voters prefer
![]() $A$
to
$A$
to
![]() $B$
; therefore, the group should also prefer
$B$
; therefore, the group should also prefer
![]() $A$
to
$A$
to
![]() $B$
. A majority of voters also prefer
$B$
. A majority of voters also prefer
![]() $B$
to
$B$
to
![]() $C$
, so the group should also reflect this preference. Finally, a majority of voters prefer
$C$
, so the group should also reflect this preference. Finally, a majority of voters prefer
![]() $C$
to
$C$
to
![]() $A$
, so the group should prefer
$A$
, so the group should prefer
![]() $C$
to
$C$
to
![]() $A$
. In summary, the group should simultaneously prefer
$A$
. In summary, the group should simultaneously prefer
![]() $A$
to
$A$
to
![]() $B$
,
$B$
,
![]() $B$
to
$B$
to
![]() $C$
, and
$C$
, and
![]() $C$
to
$C$
to
![]() $A$
. This cyclic group preference structure violates the property of transitivity, and provides no rational basis upon which to make a decision. Motivated by this paradox, Arrow proved that no aggregation function can always satisfy a small set of fair and reasonable conditions (Arrow Reference Arrow1950).
$A$
. This cyclic group preference structure violates the property of transitivity, and provides no rational basis upon which to make a decision. Motivated by this paradox, Arrow proved that no aggregation function can always satisfy a small set of fair and reasonable conditions (Arrow Reference Arrow1950).
In addition, it is sometimes possible for a sole individual to strategically modify the preferences that they share in order to alter the outcome of the aggregation procedure. This action is known as strategic voting, and is also examined in this work. An aggregation function is susceptible to strategic voting if an individual can achieve a more preferred group ranking by misreporting their own preferences. If a rule cannot be manipulated via strategic voting it is called strategy-proof. Although strategic voting is typically considered to be malicious in nature, we propose that this is not necessarily the case in engineering design. For instance, an individual may have a strongly held belief that a certain design solution is superior to other alternatives. A rational designer would have nothing personal invested in this solution; rather, they would advocate for it because the achievement of a high-quality solution benefits the whole team. Now, imagine a situation in which this individual can take one of two courses of action: report their preferences truly and allow the team to select an alternative that they see as inferior, or report their preferences incorrectly and guide the team towards a solution that they see as superior. Acting in the best interest of the team, a rational designer must choose the second option. This course of action is chosen for the good of the team, and is devoid of malicious intent. This is an assumption made in this work, and may not always be the case.
This work examined Arrow’s theorem and strategic voting using a combination of numerical simulations and actual preference elicitation. First, experiential conjoint analysis was used to query real preferences for a class of products (Tovares, Cagan & Boatwright Reference Tovares, Cagan and Boatwright2014). Then, using these empirical preferences, simulated voting scenarios were constructed and analysed to determine the probability with which certain aggregation functions (namely plurality, veto, Borda, instant runoff voting, and Copeland) violate specific conditions of Arrow’s theorem. In addition, randomly generated individual preference profiles were explored to provide a baseline against which to compare the collected empirical data. The probability of susceptibility to strategic voting was also evaluated within the simulated voting scenarios. Finally, we identified the aggregation function that is most likely to provide results that are strategy-proof and fair (in accordance with Arrow’s theorem).
Section 2 provides relevant background that pertains to social choice theory, the role of social choice in design, and approaches to modelling preference. Section 3 introduces the methodology used here to evaluate strategy-proofness and fairness, and Section 4 presents the results of these evaluations (with respect to both empirical and random preference profiles). Sections 5 and 6 present further discussion of the results as well as outlining limitations and avenues for future work. An appendix provides detailed results for each aggregation function addressed in this work.
2 Background
2.1 Social choice theory and Arrow’s theorem
Social choice theory is broadly concerned with the aggregation of different perspectives and can be partitioned into a number of different task types (Sen Reference Sen1977). One of these task types is committee decision, or voting (Sen Reference Sen1977). The task consists of transforming the preferences of the individuals in a group into a single preference structure that is indicative of the constituent preferences of the group. Arrow proved a theorem stating that no aggregation function can always satisfy a small number of reasonable conditions. The conditions constituting Arrow’s theorem are stated as follows (Arrow Reference Arrow1950; Nisan et al. Reference Nisan2007).
-
(1) Unrestricted domain: The aggregation function is defined for preference profiles with any number of voters, any number of alternatives, and any composition of individual rankings over alternatives.
-
(2) Unanimity: If all individuals prefer
 $x$
to
$x$
to
 $y$
, then the group ranking must also prefer
$y$
, then the group ranking must also prefer
 $x$
to
$x$
to
 $y$
.
$y$
. -
(3) Independence of irrelevant alternatives: The group preference between alternatives
 $x$
and
$x$
and
 $y$
must depend solely on individual preferences between
$y$
must depend solely on individual preferences between
 $x$
and
$x$
and
 $y$
.
$y$
. -
(4) Citizen sovereignty: There exists a preference profile that can make any alternative a winner.
-
(5) Non-dictatorship: The aggregation function does not simply return a specific individual’s ranking.
The independence of irrelevant alternatives (IIA) condition is often criticized as being overly restrictive (Luce & Raiffa Reference Luce and Raiffa1957). Less restrictive versions of this IIA condition have been proposed. One alternative is local independence of irrelevant alternatives, which only considers the effect of removing the first and last candidates on the group ranking (Young Reference Young1995). Despite such criticism, other work has demonstrated impossibility results similar to that of Arrow that do not depend upon an IIA condition (Seidenfeld, Kadane & Schervish Reference Seidenfeld, Kadane and Schervish1989).
Another common axiom in social choice theory is strategy-proofness. An aggregation function is only strategy-proof if it is impossible for an individual to achieve a more preferred outcome by misrepresenting their own preferences. It is known that no deterministic aggregation function is perfectly strategy-proof (Satterthwaite Reference Satterthwaite1975; Gibbard Reference Gibbard1977). Complete information on all individuals’ preferences is necessary to compute a dependable strategic voting solution (Bartholdi, Tovey & Trick Reference Bartholdi, Tovey and Trick1989). Because design teams can be composed of a small number of individuals who are familiar with one another’s preferences (Wegner Reference Wegner1987), it is possible that an individual would be capable of collecting the information necessary to vote strategically. This behaviour has not been demonstrated in design teams, but there is both theoretical (Austen-Smith & Banks Reference Austen-Smith and Banks1996) and empirical (Ladha, Miller & Oppenheimer Reference Ladha, Miller and Oppenheimer2003) evidence of strategic voting in trial juries, which are decision-making teams that can be similar in size to design teams. The adoption of an aggregation function that is likely to be strategy-proof could provide peace of mind for design teams that operate in defense-related, safety-critical, or other sensitive domains.
A large number of aggregation functions exist, and they have been analysed extensively with respect to many different axioms (Nurmi Reference Nurmi, Felsenthal and Machover2012). Methods for analysing aggregation methods include mathematical proofs as well as an array of geometric methods (Saari Reference Saari2011). This work utilizes a computational simulation based approach for the ease of incorporating empirically measured preferences into the analysis.
2.2 The role of social choice in engineering design
The role of social choice theory in engineering design (specifically with respect to Arrow’s theorem) is a subject of debate (Reich Reference Reich2010). Some researchers have adopted the viewpoint that Arrow’s theorem applies to all decision problems with either multiple criteria or multiple decision makers (Hazelrigg Reference Hazelrigg1999; Franssen Reference Franssen2005). It is possible that such generalizations are too broad in scope (Keeney Reference Keeney2009). In contrast, work by Scott & Antonsson (Reference Scott and Antonsson1999) argued that engineering design involves the aggregation of criteria rather than individual preferences, and that this fundamental difference means that Arrow’s theorem does not directly apply.
Still other work takes a fine-grained approach by demonstrating that specific design decision tools can be useful despite potential issues with Arrow’s theorem. For instance, work by Dym, Wood & Scott (Reference Dym, Wood and Scott2002) demonstrated that although the Borda aggregation function fails the IIA condition, the failures rarely affect the most preferred alternatives. They concluded that Arrow’s theorem might pose a considerable theoretical problem, but the practical implications are less than dire (Dym et al. Reference Dym, Wood and Scott2002). Additional research has also utilized the Borda aggregation function for parameter selection within an optimization schema, despite possible theoretical failures of IIA (Kaldate et al. Reference Kaldate2006). Work by See & Lewis (Reference See and Lewis2006) proposed Group-HEIM, a structured method for making group decisions that attempts to avoid severe theoretical failures and excessive complexity. Frey et al. (Reference Frey2009) conducted a set of computational simulations to support the use of the Pugh controlled convergence method, with Hazelrigg (Reference Hazelrigg2010) and Frey et al. (Reference Frey2010) later arguing alternative views on the performance of this approach.
Recent work has recognized a need for more clarity in the discussion of design decision methods. Work by Katsikopoulos (Reference Katsikopoulos2009) discussed how a dichotomy of coherence and correspondence can be used to structure the discussion. Coherence is used to mean the internal consistency of a method, while correspondence refers to the external performance of a method. This contrast between consistency and correspondence is similar in many ways to the contrast between scientism and praxis proposed by Reich (Reference Reich1994). Katsikopoulos (Reference Katsikopoulos2009) proposes that the arguments put forth by Franssen (Reference Franssen2005) are based on coherence, while the arguments of Scott & Antonsson (Reference Scott and Antonsson1999) are rooted in the rhetoric of correspondence. The work presented in this paper focuses on coherence – no external measure of performance is made.
In addition to the coherence/correspondence dichotomy, Jacobs, van de Poel & Osseweijer (Reference Jacobs, van de Poel and Osseweijer2014) recognized several additional issues that cloud the discussion. These additional issues are the need for researchers to indicate whether they are addressing the aggregation of individuals’ preference or of performance metrics, and the need to express what sort of information researchers assume is available for an aggregation procedure (specifically with respect to measurability and comparability) (Jacobs et al. Reference Jacobs, van de Poel and Osseweijer2014). With respect to the first issue raised by Jacobs et al., this work addresses the aggregation of preferences expressed by individuals, not the aggregation of disparate performance criteria. Regarding the second issue, an assumption of this work is that only individually expressed ranking data are available for an aggregation procedure. Because we focus on the early stages of conceptual design, this is the most accessible information for an aggregation procedure.
2.3 Modelling preference
Capturing and modelling preference is an active area of research in the engineering design community, and has seen significant growth over the past decade (Petiot & Grognet Reference Petiot and Grognet2006; Orsborn, Cagan & Boatwright Reference Orsborn, Cagan and Boatwright2009; Hoyle & Chen Reference Hoyle and Chen2011; Kelly et al. Reference Kelly2011; Reid, Macdonald & Du Reference Reid, Macdonald and Du2013; Sylcott, Cagan & Tabibnia Reference Sylcott, Cagan and Tabibnia2013; Tovares et al. Reference Tovares, Cagan and Boatwright2014; Goucher-Lambert & Cagan Reference Goucher-Lambert and Cagan2015). In particular, conjoint and discrete choice analyses (Train Reference Train2003) have been popular choices, due to the ability of these methods to allow for decomposition of a product into a set of discrete or continuous attributes, from which a mathematical model of preferences for these attributes can then be determined using a number of techniques.
This work utilized experiential conjoint analysis to empirically determine individual preferences across a product space (Luce & Tukey Reference Luce and Tukey1964; Green Reference Green1974; Green & Wind Reference Green and Wind1975). Conjoint analysis has been widely used in engineering design research. Data are typically collected through a survey in which participants are asked to rate, rank, or choose between different offerings composed of varying combinations of researcher-specified product attributes. Each attribute is described by multiple levels, which represent the variability in the parameter being investigated. Levels of different attributes are varied based on standard design of experiment techniques. Participant response data can be used to determine preference weights for each attribute and level that was tested during the experiment. A mathematical representation can then be created to describe preference for every design within the design space under investigation. A main effects model assumes that attributes are linearly independent (which is generally not true). However, this modelling approach, which is utilized in this work, has been shown to accurately represent individual preferences (Tovares et al. Reference Tovares, Cagan and Boatwright2014).
The representation of the product attributes in conjoint analysis has traditionally been limited to descriptive text. However, recent developments have expanded upon conjoint analysis by utilizing more complex forms of attributes. Orsborn et al. (Reference Orsborn, Cagan and Boatwright2009) introduced an extension of conjoint analysis, termed visual conjoint analysis, which can derive utility functions based upon preference for continuous aesthetic attributes (seen in 2D in that work), resulting in preference that can be extrapolated to any point within the continuous design space explored. In that work, Bezier curves were used to parameterize various sport utility vehicles (SUVs) and determine optimal SUV forms outside of the original design space. Several researchers have further explored visual conjoint methods. Sylcott et al. (Reference Sylcott, Cagan and Tabibnia2013) used a visual conjoint process to examine preference for car forms. These data were then combined with functional preference data in a meta-conjoint approach. Kelly et al. (Reference Kelly2011) developed a separate approach to determine the most preferred shape of a bottle within an engineering optimization framework.
Beyond visual conjoint analysis, Tovares et al. (Reference Tovares, Cagan and Boatwright2014) developed experiential conjoint analysis based upon experience based preference judgments (touching, manipulating, etc.), where again preference could be extrapolated to any point within the design space. The ability of preference to be accurately modelled under this framework was demonstrated using a virtual reality based task in which participants were asked to adjust control locations for a truck dashboard layout. Additionally, ceramic 3D printed drinking mugs were used to demonstrate the applicability of the experiential conjoint methodology to physical product experiences. We used experiential conjoint analysis to model individuals’ preferences in this work. This mathematical model of preference allowed us to computationally simulate a large number of design-related social choice scenarios.
3 Methods
This work employed a three-step approach that combined user studies and computational modelling. This approach bears some similarity to that employed by Olewnik & Lewis (Reference Olewnik and Lewis2005, Reference Olewnik and Lewis2008) to study design decision support tools. First, individual preferences for different variations of a parameterized drinking mug were measured through experiential conjoint methodology. Second, the results of the conjoint study were used to generate a distribution of personal utility functions. Finally, this distribution was used to simulate the utility functions of individuals in a design team, and thus test the performance of five aggregation functions. These functions were analysed to assess how often they fulfilled Arrow’s conditions, and how often they were strategy-proof.
3.1 Experiential conjoint study
3.1.1 Stimulus
For this analysis, 3D printed ceramic drinking mugs were used as a stimulus to determine individual preferences (Tovares et al.
Reference Tovares, Cagan and Boatwright2014). The mugs were 3D printed in accordance with a pre-defined experimental design. Three continuous attributes, each represented by three levels, were chosen to decompose the product: height (75 mm, 95 mm, and 115 mm), base width (40 mm, 60 mm, 80 mm), and handle curvature (three Bezier curves, each defined by three points). The three levels that were chosen to describe the drinking mugs created a diverse design space of 27 (
![]() $3^{3}$
) candidate designs.
$3^{3}$
) candidate designs.
In addition to the wide range of forms achieved through traditional design of experiments techniques, the physical representation of the stimulus provided an opportunity by which additional characteristics of each design could be explored. Participants interacted with the ceramic mugs by touching, holding, and manipulating them during their preference evaluations. Therefore, participants were able to infer and evaluate additional attributes of the mugs (e.g. ergonomics, weight, and capacity) during the experiential conjoint study. These additional attributes could then be tacitly incorporated into their preference judgments.
3.1.2 Participants
Participants for the empirical portion of the experiment were recruited through two undergraduate courses at Carnegie Mellon University, and were compensated with course credit for their participation. In total, 51 participants completed the 25-minute study.
3.1.3 Experimental design
The study was conducted in two parts. In the first part of the study, each participant was asked to independently rate 22 ceramic drinking mugs on a scale from 1 (least appealing) to 10 (most appealing). Participants were presented with one of two random orders of drinking mugs. Of the 22 ceramic drinking mugs rated during the study, nine mugs were used as a question set to estimate the model parameters, seven were used as holdouts to validate the model performance, and the remainder were used as calibration for the participants to become adjusted to the rating task. Additionally, participants were asked to rate two identical mugs, making it possible to measure participants’ self-consistency. If a participant’s ratings for these two mugs differed by more than 1 point, data from that participant were disregarded.
In order to determine the size of the question set, as well as the specific design alternatives included within this set, the D-efficiency criterion was used (Kuhfeld Reference Kuhfeld2010). The D-efficiency is one method for ensuring that the balance (attribute levels appearing equally) and orthogonality (pairs of attributes appearing equally) of the design are maximized. The experimental design selected for this experiment represented design with the highest D-efficiency other than a full-factorial experimental design. The full factorial was not used because it was deemed to be too large for the experimental setup employed in this work.
In the second part of the study, participants performed a ranking task. Participants were asked to individually rank four drinking mug designs in order from most appealing to least appealing. The designs chosen for this task are shown in Table 1. Within this set of designs, every level of every attribute appears at least once, thus representing significant variety. This allowed the participants’ explicit ranking to be compared with the ranking predicted through conjoint analysis.
Table 1. The subset of the mug design space used for the individual ranking task

3.2 Generating preference profiles
Experiential conjoint analysis was used to build utility functions for every study participant. The nine-question D-efficiency maximizing question set was used to estimate the preference function parameters for every individual. A Gaussian distribution was then used to describe the distribution of parameters of these individualized utility functions, and drawing parameter vectors from this distribution made it possible to build unique empirically based preference profiles. The process of building a preference profile from the Gaussian parameter distribution is illustrated in Figure 2, and explained in more detail in this section. Drawing from an empirically developed distribution produced preference combinations that were likely to occur in reality. Merely generating all possible preference combinations, or building preference profiles from random orderings, would have no such link to real preferences.
Using the ratings data collected from study participants, the attribute preference weights,
![]() $\unicode[STIX]{x1D6FC}$
, were solved for using ordinary least squares regression:
$\unicode[STIX]{x1D6FC}$
, were solved for using ordinary least squares regression:
Here, X is the coded design matrix, and y is the vector containing ratings for each design alternative provided by the survey participants. Taking advantage of the continuous nature of the attributes employed in this study, differentiable quadratic utility functions were used to model preference. Quadratic utility functions were chosen to allow for maxima that were not corner solutions, and to remain consistent with prior work (Orsborn et al. Reference Orsborn, Cagan and Boatwright2009; Tovares et al. Reference Tovares, Cagan and Boatwright2014). The form of this model is shown in equation (2):
In equation (2), the variable
![]() $u_{r,q}$
denotes the total utility, u, for the
$u_{r,q}$
denotes the total utility, u, for the
![]() $r\text{th}$
participant and
$r\text{th}$
participant and
![]() $q\text{th}$
design alternative. The calculation of the total utility requires the uncoded design matrix, X, and the individual attribute preference weights,
$q\text{th}$
design alternative. The calculation of the total utility requires the uncoded design matrix, X, and the individual attribute preference weights,
![]() $\unicode[STIX]{x1D6FC}$
. The quality of the individual utility functions was validated using the mean absolute error (MAE) criterion:
$\unicode[STIX]{x1D6FC}$
. The quality of the individual utility functions was validated using the mean absolute error (MAE) criterion:
The MAE compares the predicted ratings,
![]() $s_{j,\text{pred}}$
, with the observed ratings,
$s_{j,\text{pred}}$
, with the observed ratings,
![]() $s_{j,\text{obs}}$
, for each design alternative in the holdout set by summing the absolute difference between these two values, and then dividing by the number of holdout alternatives,
$s_{j,\text{obs}}$
, for each design alternative in the holdout set by summing the absolute difference between these two values, and then dividing by the number of holdout alternatives,
![]() $J$
. The holdout set was used to validate the model due to the fact that these ratings did not contribute to the formation of the parameter estimates.
$J$
. The holdout set was used to validate the model due to the fact that these ratings did not contribute to the formation of the parameter estimates.
As part of the conjoint approach, utility function coefficients were computed for each individual using equation (1). Figure 1 shows the empirical probability density function of each coefficient from the conjoint study performed as part of this work. The numbers shown next to the coefficient names are the mean value and standard error. The empirical probability density function is approximately normally distributed, indicating that our treatment of the data using a Gaussian model is appropriate.
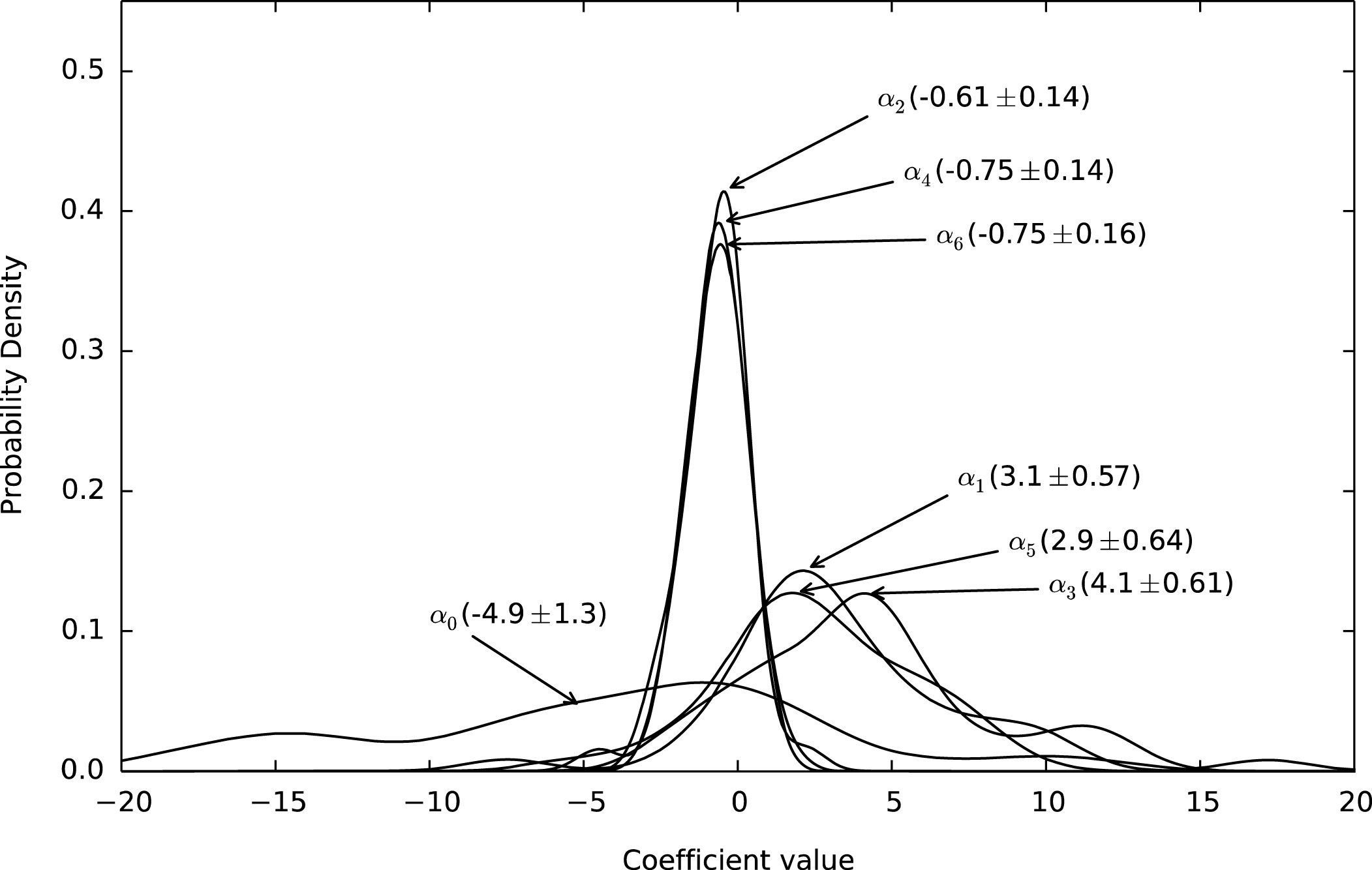
Figure 1. Distribution of preference weights.
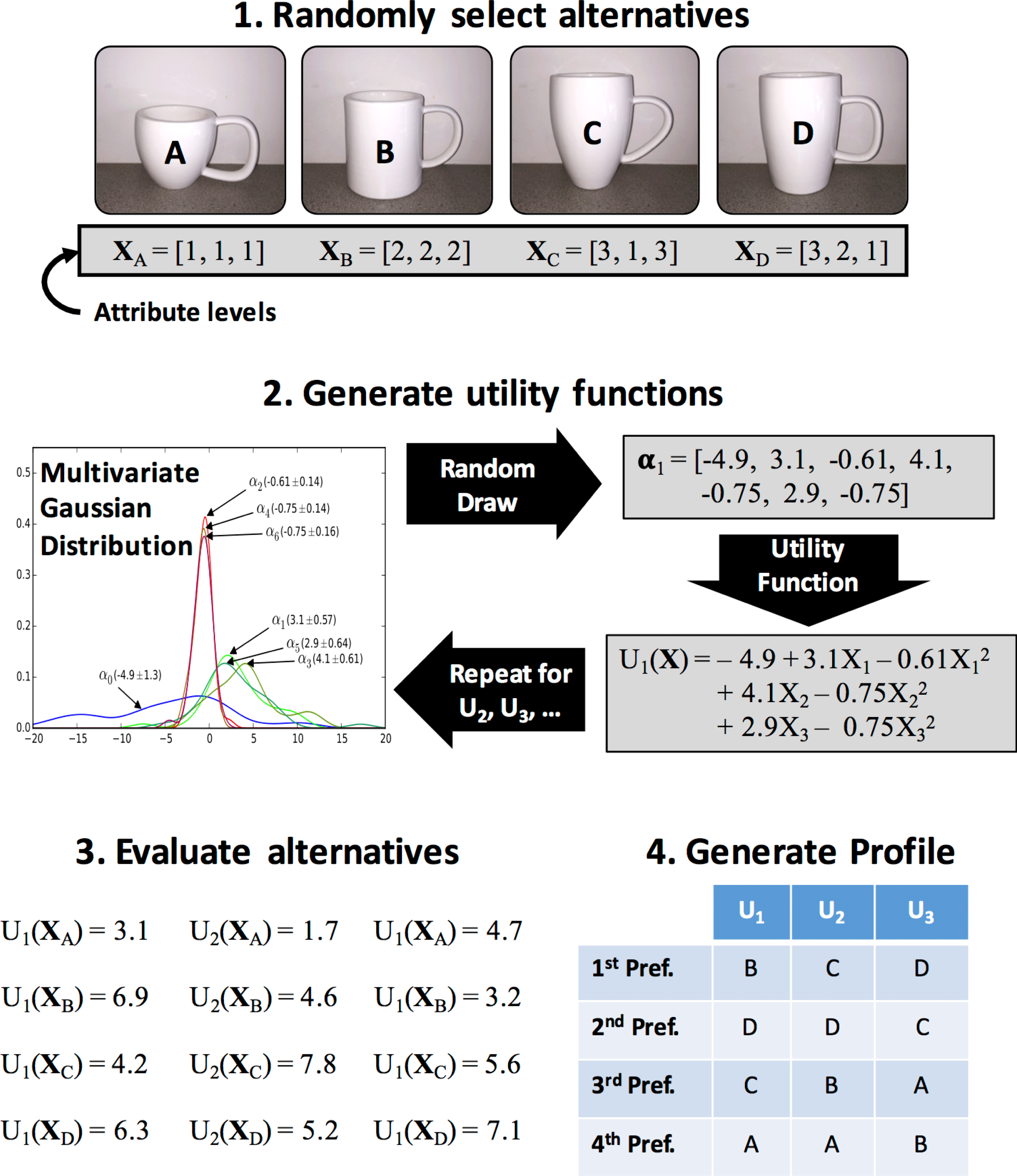
Figure 2. Example of empirical preference profile generation for four alternatives and three individuals.
It should be noted that the distributions in Figure 1 are only one-dimensional projections of the true multivariate distribution. The coefficient
![]() $\unicode[STIX]{x1D6FC}_{0}$
is an intercept term in equation (2), the coefficients
$\unicode[STIX]{x1D6FC}_{0}$
is an intercept term in equation (2), the coefficients
![]() $\unicode[STIX]{x1D6FC}_{1}$
,
$\unicode[STIX]{x1D6FC}_{1}$
,
![]() $\unicode[STIX]{x1D6FC}_{3}$
, and
$\unicode[STIX]{x1D6FC}_{3}$
, and
![]() $\unicode[STIX]{x1D6FC}_{5}$
correspond to linear terms, and the coefficients
$\unicode[STIX]{x1D6FC}_{5}$
correspond to linear terms, and the coefficients
![]() $\unicode[STIX]{x1D6FC}_{2}$
,
$\unicode[STIX]{x1D6FC}_{2}$
,
![]() $\unicode[STIX]{x1D6FC}_{4}$
, and
$\unicode[STIX]{x1D6FC}_{4}$
, and
![]() $\unicode[STIX]{x1D6FC}_{6}$
correspond to quadratic terms. The linear terms are positive on average, while the average quadratic terms are negative. Therefore, an average utility function should be increasing (due to the positive linear term) and concave down (due to the negative quadratic term). However, the variance around the mean coefficient values (see Figure 1) allows for substantial variation from these average coefficient values.
$\unicode[STIX]{x1D6FC}_{6}$
correspond to quadratic terms. The linear terms are positive on average, while the average quadratic terms are negative. Therefore, an average utility function should be increasing (due to the positive linear term) and concave down (due to the negative quadratic term). However, the variance around the mean coefficient values (see Figure 1) allows for substantial variation from these average coefficient values.
In order to generate unique preference profiles, a multivariate Gaussian distribution was first fitted to the set of utility function coefficients. Then, taking a random draw from this multivariate distribution (accounting for covariance) created a unique vector. This vector contained coefficients for a unique utility function, with a functional form as provided in equation (2). The utility function defined by this vector was then used to calculate a utility for each of
![]() $m$
randomly selected design alternatives. Using these utilities, the alternatives were ranked in order of decreasing utility, and this ranking was added to the preference profile. Figure 2 shows an example of the generation of a preference profile with four alternatives and three simulated individuals.
$m$
randomly selected design alternatives. Using these utilities, the alternatives were ranked in order of decreasing utility, and this ranking was added to the preference profile. Figure 2 shows an example of the generation of a preference profile with four alternatives and three simulated individuals.
The process of generating coefficient vectors, creating utility functions, and ranking alternatives was repeated
![]() $n$
times, thus building an
$n$
times, thus building an
![]() $n$
-individual/
$n$
-individual/
![]() $m$
-alternative preference profile. This methodology enabled the construction of empirical preference profiles with any number of individuals (
$m$
-alternative preference profile. This methodology enabled the construction of empirical preference profiles with any number of individuals (
![]() $n$
) and any number of design alternatives (
$n$
) and any number of design alternatives (
![]() $m$
). Since these preference profiles were generated from the unimodal preference distribution (see Figure 1), some implicit agreement between individuals was expected.
$m$
). Since these preference profiles were generated from the unimodal preference distribution (see Figure 1), some implicit agreement between individuals was expected.
The procedure for constructing empirical preference profiles was compared with a second procedure for constructing purely random preference profiles. In this second procedure, a list of
![]() $m$
alternatives was shuffled to create a random ranking. This shuffling process was repeated
$m$
alternatives was shuffled to create a random ranking. This shuffling process was repeated
![]() $n$
times, thus building an
$n$
times, thus building an
![]() $n$
-individual/
$n$
-individual/
![]() $m$
-alternative preference profile. Because the preference profiles generated through this procedure were purely random, they were expected to show lower levels of implicit agreement than the empirical preference profiles.
$m$
-alternative preference profile. Because the preference profiles generated through this procedure were purely random, they were expected to show lower levels of implicit agreement than the empirical preference profiles.
3.3 Aggregation functions, Arrow’s conditions, and strategic voting
Aggregation functions provide a method for building a group ranking from a preference profile. For an aggregation function and a given preference profile, Arrow’s conditions could be evaluated, and whether or not the group ranking was strategy-proof could be determined. By performing this analysis for many different preference profiles and the same aggregation function, it was possible to estimate the probability that the function would satisfy Arrow’s conditions, and the probability that the result was strategy-proof.
Exhaustive evaluation of every possible preference scenario would provide a ‘true’ evaluation of the performance of a given voting rule. However, this would also exact a large computational burden. For
![]() $m$
alternatives there are
$m$
alternatives there are
![]() $m!$
possible individual orderings of those alternatives. Since a preference profile with
$m!$
possible individual orderings of those alternatives. Since a preference profile with
![]() $n$
individuals is an
$n$
individuals is an
![]() $n$
-multisubset of the possible individual orderings, there are
$n$
-multisubset of the possible individual orderings, there are
![]() $(\begin{smallmatrix}m!+n-1\\ n\end{smallmatrix})$
unique arrangements (Pemmaraju & Skiena Reference Pemmaraju and Skiena2003) for an
$(\begin{smallmatrix}m!+n-1\\ n\end{smallmatrix})$
unique arrangements (Pemmaraju & Skiena Reference Pemmaraju and Skiena2003) for an
![]() $n$
-individual/
$n$
-individual/
![]() $m$
-alternative preference profile. As a concrete example, even a five-individual/five-alternative preference profile has over 200 million arrangements. Thus, the sampling approach adopted in this work is a reasonable computational expedient.
$m$
-alternative preference profile. As a concrete example, even a five-individual/five-alternative preference profile has over 200 million arrangements. Thus, the sampling approach adopted in this work is a reasonable computational expedient.
3.3.1 Aggregation functions
Five aggregation functions were evaluated as part of this work. These included three positional scoring functions (plurality, veto, and Borda), and two multi-step functions (instant runoff voting and Copeland). These functions were selected because they are well-studied in the social choice and voting theory literature, offer variety in terms of the information that must be provided by individuals, and vary in terms of the complexity of computing a group ranking. A positional scoring rule is defined by a scoring vector
![]() $s$
of length
$s$
of length
![]() $m$
, where
$m$
, where
![]() $m$
is the number of alternatives. Each voter allots
$m$
is the number of alternatives. Each voter allots
![]() $s_{k}$
points to their
$s_{k}$
points to their
![]() $k\text{th}$
most preferred alternative. To establish a group ranking, the number of points scored by each individual is counted. The group ranking is simply a ranking of alternatives in order of most points scored. The scoring vectors for the plurality, veto, and Borda functions are
$k\text{th}$
most preferred alternative. To establish a group ranking, the number of points scored by each individual is counted. The group ranking is simply a ranking of alternatives in order of most points scored. The scoring vectors for the plurality, veto, and Borda functions are
![]() $[1,0,\ldots ,0,0]$
,
$[1,0,\ldots ,0,0]$
,
![]() $[1,1,\ldots ,1,0]$
, and
$[1,1,\ldots ,1,0]$
, and
![]() $[m-1,m-2,\ldots ,1,0]$
respectively.
$[m-1,m-2,\ldots ,1,0]$
respectively.
The two multi-step aggregation functions used in this work both use the plurality function. The instant runoff voting (IRV) function is composed of
![]() $m$
rounds. In each round, the plurality function is applied, and the alternative with the least points is removed from the alternative set. The next round begins with the updated set of alternatives. This continues until only a single alternative remains. The group ranking is defined by the order in which alternatives are removed from contention. The Copeland aggregation function performs a plurality vote between every pair of alternatives. For every pairwise election that an alternative wins, it receives one point. For every loss, it loses one point. The group preference is then a ranking of alternatives in order of net points earned.
$m$
rounds. In each round, the plurality function is applied, and the alternative with the least points is removed from the alternative set. The next round begins with the updated set of alternatives. This continues until only a single alternative remains. The group ranking is defined by the order in which alternatives are removed from contention. The Copeland aggregation function performs a plurality vote between every pair of alternatives. For every pairwise election that an alternative wins, it receives one point. For every loss, it loses one point. The group preference is then a ranking of alternatives in order of net points earned.
3.3.2 Analysis of Arrow’s conditions
Let a preference scenario be a combination of a specific preference profile and an aggregation function. The aggregation function uses the preference profile to produce a group ranking. For any preference scenario, it is possible to check whether or not Arrow’s conditions are satisfied. The unrestricted domain condition was addressed by generating preference profiles that included different numbers of alternatives and team members, as well as individual preference rankings. The non-dictatorship and citizen-sovereignty conditions are dependent only on the aggregation function, and were satisfied by the aggregation functions chosen for this work. The conditions of unanimity and IIA are dependent upon the specific preference scenario. The unanimity condition was checked by first finding the pairwise preferences that were shared by all individuals. If these unanimous preferences were also found in the group preference, then the preference scenario satisfied the condition. The IIA condition was assessed using a removal procedure and an inclusion procedure. The removal procedure consisted of first computing the group ranking for the original preference profile. Then, a subset of alternatives was removed from the original set of alternatives. The preference profile was updated according to individuals’ utility functions, and a new group ranking was computed. If the relative position of original (or remaining) alternatives in the new group ranking was unchanged from that in the original ranking, then the preference scenario satisfied the IIA condition. This was repeated for every possible subset of alternatives in the original set. The inclusion procedure was similar, but additional alternatives were added. Specifically, every remaining alternative in the mug design space was added individually to the preference scenario, and the effect of its inclusion assessed.
Further, we define a concept of conditional Arrow fairness. A preference scenario exhibits conditional Arrow fairness if it satisfies the conditions of unanimity and IIA, and if the aggregation function satisfies the conditions of non-dictatorship and citizen sovereignty. This concept is conditional upon Arrow’s first condition (unrestricted domain) because it is checked using preference profiles with a specific number of alternatives and individuals. However, by generating and checking many profiles, the probability with which a given aggregation function satisfies conditional Arrow fairness can be estimated. This probability serves as an indication of an aggregation function’s ability to come close to consistently satisfying Arrow’s conditions. As will be shown empirically, our measure of conditional Arrow fairness is empirically limited by the measurement of IIA satisfaction.
3.3.3 Analysis of strategy-proofness
Perfect knowledge of the preferences of all individuals is often necessary to compute a dependable strategic voting solution (Bartholdi et al.
Reference Bartholdi, Tovey and Trick1989). Individuals who work frequently with the same team can become familiar with one another’s preferences (Wegner Reference Wegner1987). If an individual develops sufficient familiarity with their team-mates’ preferences, strategic voting becomes a real possibility. Therefore, every preference scenario was assessed to determine whether a single individual could strategically alter the outcome. This assessment was accomplished by sequentially modifying the preferences of a given individual to discover a successful strategy, if one existed. The process was continued until a manipulation was discovered, or until all possible individual preference orderings were evaluated (a total of
![]() $m!$
orderings, where
$m!$
orderings, where
![]() $m$
is the number of alternatives). A successful strategy is a modification in an individual’s preferences that would result in a more preferred group ranking for that individual. This process was repeated separately for every individual. If a successful strategy was not found, then the preference scenario was deemed to be strategy-proof. For
$m$
is the number of alternatives). A successful strategy is a modification in an individual’s preferences that would result in a more preferred group ranking for that individual. This process was repeated separately for every individual. If a successful strategy was not found, then the preference scenario was deemed to be strategy-proof. For
![]() $m$
alternatives, there are
$m$
alternatives, there are
![]() $m!$
possible individual orderings of those alternatives. Therefore, designation of an
$m!$
possible individual orderings of those alternatives. Therefore, designation of an
![]() $n$
-individual/
$n$
-individual/
![]() $m$
-alternative preference scenario as strategy-proof required the evaluation of
$m$
-alternative preference scenario as strategy-proof required the evaluation of
![]() $n\cdot m!$
modified versions of the preference scenario. Because this study was limited to a maximum of six alternatives, this was not a computational burden. It should be noted that there exist algorithms that can efficiently compute strategic voting solutions for some classes of voting rules (Bartholdi et al.
Reference Bartholdi, Tovey and Trick1989).
$n\cdot m!$
modified versions of the preference scenario. Because this study was limited to a maximum of six alternatives, this was not a computational burden. It should be noted that there exist algorithms that can efficiently compute strategic voting solutions for some classes of voting rules (Bartholdi et al.
Reference Bartholdi, Tovey and Trick1989).
4 Results
Before presenting the results of the empirical simulations, the results of simulations using random preference profiles will be provided. Random preference profiles were used as a worst-case scenario for the formation of group preference, because the random preference profiles in this work were likely to show more variance in preferences than what would be observed from real-world data. This provided a good basis for comparison with the empirical results. For both random and empirical preference profiles, aggregation functions were compared using preference profiles with varying numbers of individuals (from three to 15) and alternatives (from three to six).
4.1 Random preference profiles
In this section of the analysis, all preference profiles were composed of randomly generated rankings of design alternatives (with no input from the conjoint analysis). Conditional Arrow fairness and strategy-proofness were evaluated using 1000 random preference profiles for every combination of number of individuals (from three to 15) and number of alternatives (from three to six). Table 2 shows the mean results from this analysis, averaged across all preference profiles.
Table 2. Average results for random individuals
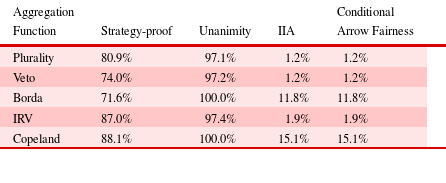
Strategy-proofness ranged from approximately 70% for the Borda function to almost 90% for the Copeland and IRV functions. Only low levels of conditional Arrow fairness were achieved with random preference profiles: the Borda function and Copeland function had probabilities of conditional Arrow fairness that exceeded 10%, but every other function fell below 2%. The Copeland function achieved both the highest probability of conditional Arrow fairness and the highest probability of strategy-proofness. Figure 3 shows the dependence of the Copeland function’s characteristics on the number of individuals and the number of alternatives in the preference profile. Similar plots for the other aggregation functions are provided in Appendix A.
In Figure 3(a), the contours indicate the probability of conditional Arrow fairness, and in Figure 3(b), the contours indicate the probability of strategy-proofness. For every grid point in the plot, 1000 random preference profiles were created and analysed.

Figure 3. Copeland function characteristics (random preference profiles).
An examination of the contour plots in Figure 3 indicates that decreasing the number of alternatives increased the probability of both conditional Arrow fairness and strategy-proofness. Furthermore, despite the fact that the Copeland function was fairly strategy-proof for most cases, the highest probability of conditional Arrow fairness was only slightly greater than 30%. These results can be considered to be indicative of a worst-case scenario.
4.2 Empirical preference profiles
Here, results are presented that depend upon the empirical data generated from the experiential conjoint survey. The quality of the ratings provided during the conjoint study was ensured through a two-step process. First, a duplicate rating task was included in the experiment for which the provided rating had to be within 1 point for the two identical designs. Data from 15 participants were omitted due to failure to meet the minimum accuracy requirements for this duplicate task. Second, the MAE was calculated to ensure that the model predicted accurate ratings for the survey respondents. The mean model MAE was
![]() $1.17\pm 0.59$
, which is commensurate with the MAE of the experiential conjoint model developed by Tovares et al. (Reference Tovares, Cagan and Boatwright2014).
$1.17\pm 0.59$
, which is commensurate with the MAE of the experiential conjoint model developed by Tovares et al. (Reference Tovares, Cagan and Boatwright2014).
It should be recalled that conjoint analysis was used to create a probability distribution of utility functions, and that this distribution was used to create unique empirical preference profiles. Therefore, some preference relations were much more probable than others, resulting in preference profiles that were likely to show some level of tacit agreement between individuals. Namely, preference relations defined by draws near the mean of the distribution would be more common than those defined by draws from the tails. It should be noted that while using the empirical distribution modified the probability with which certain preference relations were generated, it did not restrict the range of possible preference relations. Thus, Arrow’s condition of unrestricted domain was still respected.
Conditional Arrow fairness and strategy-proofness were evaluated using 1000 empirically generated preference profiles for every combination of number of individuals (from three to 15) and number of alternatives (from three to six). Table 3 shows the mean results of this analysis, averaged across all preference profiles.
Table 3. Average results for empirical individuals
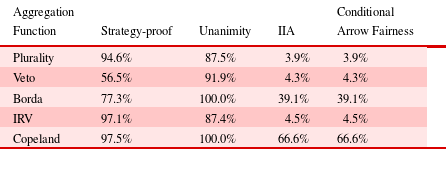
The IRV and Copeland aggregation functions were strategy-proof in more than 95% of preference profiles. In contrast, the veto rule offered the worst performance, since only slightly more than half of the preference profiles were strategy-proof. Conditional Arrow fairness was an even starker criterion for differentiating the aggregation functions. Plurality, veto, and IRV provided conditional Arrow fairness in less than 5% of preference profiles. Borda was slightly better at approximately 40%, and Copeland was the best, providing conditional Arrow fairness in more than 65% of preference profiles. For the criteria of strategy-proofness and conditional Arrow fairness, Copeland was once again clearly better than the other aggregation functions. Figure 4 shows the dependence of the Copeland function characteristics on the number of individuals and the number of alternatives in the preference profile. Similar plots for the other aggregation functions are provided in Appendix A.
In Figure 4(a), the contours indicate the probability of conditional Arrow fairness, and in Figure 4(b), the contours indicate the probability of strategy-proofness. Once again, every grid point represents the average of 1000 simulated preference scenarios.
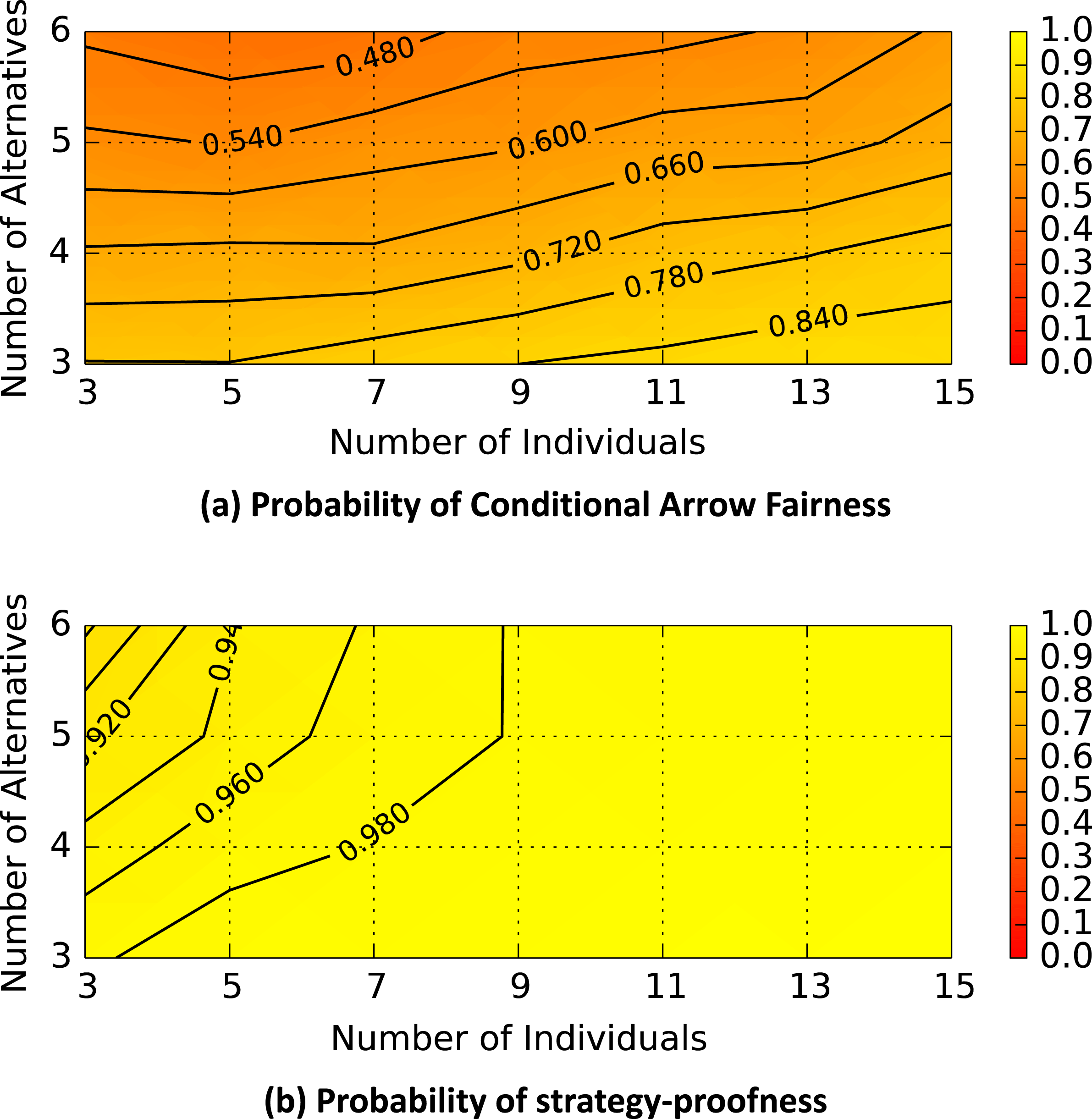
Figure 4. Copeland function characteristics (empirical preference profiles).
The probability of conditional Arrow fairness, shown in Figure 4(a), appears to be primarily a function of the number of alternatives (with fewer alternatives resulting in a higher probability). The probability of strategy-proofness, shown in Figure 4(b), is a function of both the number of individuals and the number of alternatives. The probability of strategy-proofness appears to asymptotically approach 100% for a large number of individuals and a small number of alternatives. It should be noted that the Copeland function is well above 90% strategy-proof for most of the preference profiles explored in this analysis.
Table 4. Comparison of group preference from utility function and ranking data.

The results that have been discussed thus far were predicated upon the utility functions developed through ratings based conjoint analysis. For that reason, participants in the conjoint study were also asked to explicitly rank a subset of four designs (the same four designs as shown in Table 1). This allowed for direct comparison between the group ranking predicted by the utility functions and the group ranking computed from the rankings provided by study participants. This was accomplished by applying an aggregation function to the individual rankings obtained directly by participants, thus creating a single group ranking. Table 4 shows the group rankings predicted from the conjoint utility functions, the group rankings computed directly from the ranking task data, and the Kendall’s tau statistic relating the two rankings. Any differences between the two aggregate rankings are underlined. Most aggregation functions (plurality, Borda, IRV, and Copeland) returned an aggregate utility based ranking that was in perfect agreement with the aggregate empirical ranking. The sole exception was the veto aggregation function, which displayed disagreement amongst the top two alternatives. The veto aggregation function was the only function explored in this work that directly counted votes against the least preferred alternatives. All other functions counted, in some way, votes that support various alternatives. Therefore, this result could indicate that voting in support of design alternatives more firmly resolves a group preference structure.
5 Discussion
This work used both empirical preference profiles (generated from experiential conjoint study results) and uniform random preference profiles. Uniform random preference profiles served as a worst-case scenario for the formation of group preference, because it was unlikely that individuals would display much agreement. In more realistic preference profiles that were based on conjoint data, it was likely that individuals would agree on at least some preference judgements. A detailed analysis using both random and empirical preference profiles was performed with varying numbers of individuals and alternatives (Tables 2 and 3).
For both uniform random and empirical preference profiles, the Copeland aggregation function displayed the highest probability of conditional Arrow fairness, and of being strategy-proof. When the number of alternatives was small relative to the number of individuals, the probability of satisfying conditional Arrow fairness exceeded 80%, and the probability of strategy-proofness exceeded 98% (see Figure 4). However, for uniform random preference profiles, the probability that the Copeland function would fail conditional Arrow fairness rose above 90% when the number of alternatives was large (see Figure 3(a)).
Work by others has recommended the Borda aggregation function for use in design decision-making (Dym et al. Reference Dym, Wood and Scott2002). The current work showed that the Borda aggregation function can provide a high probability of conditional Arrow fairness (above 50% for some preference profiles). However, the Borda aggregation function provided low strategy-proofness relative to other aggregation functions. This drawback was recognized by Jean-Charles de Borda himself, who proclaimed that his scheme ‘is intended only for honest men’ (Black et al. Reference Black1958). Within the context of the current work, the Copeland function was preferable to Borda in terms of both conditional Arrow fairness and strategy-proofness.
Although some aggregation functions offered a high probability of conditional Arrow fairness, unfair results were still possible. This possibility warrants a discussion of the practical implications of a failure of conditional Arrow fairness, which may result from a failure of either IIA or unanimity. A failure of unanimity indicates that all individuals in a preference profile ranked
![]() $x$
over
$x$
over
![]() $y$
, but the group ranking did not. This is not always an egregious fault. Assume that a group is trying to select their most preferred alternative from the set
$y$
, but the group ranking did not. This is not always an egregious fault. Assume that a group is trying to select their most preferred alternative from the set
![]() $\{a,b,c,x,y\}$
and all members of a group prefer alternative
$\{a,b,c,x,y\}$
and all members of a group prefer alternative
![]() $x$
to alternative
$x$
to alternative
![]() $y$
. If the final group ranking is
$y$
. If the final group ranking is
![]() $a\succ b\succ c\succ y\succ x$
, the failure of unanimity is relatively harmless. However, if the final group ranking is
$a\succ b\succ c\succ y\succ x$
, the failure of unanimity is relatively harmless. However, if the final group ranking is
![]() $y\succ x\succ a\succ b\succ c$
, the failure of unanimity is much more serious.
$y\succ x\succ a\succ b\succ c$
, the failure of unanimity is much more serious.
A failure of IIA is more likely than a failure of unanimity (see Tables 2 and 3). In fact, failures of IIA were responsible for limiting the total probability of conditional Arrow fairness in all cases in this work. This was not surprising, as the IIA condition (as stated in Arrow’s theorem) is often criticized as being an overly restrictive axiom (Luce & Raiffa Reference Luce and Raiffa1957; Young Reference Young1995). An IIA failure means that adding (or removing) an alternative from the preference profile changes the relative ranking of the original (or remaining) alternatives. Consider a situation in which the group ranking is
![]() $a\succ b\succ c$
$a\succ b\succ c$
![]() $\succ d$
, but the addition of alternative
$\succ d$
, but the addition of alternative
![]() $x$
changes the group ranking to
$x$
changes the group ranking to
![]() $a\succ b\succ d\succ x\succ c$
. The relative ranking of alternatives
$a\succ b\succ d\succ x\succ c$
. The relative ranking of alternatives
![]() $c$
and
$c$
and
![]() $d$
has changed. If the purpose of the construction of the group ranking is to select the most preferred alternative, then this failure of IIA is inconsequential. However, if the purpose of the ranking is to eliminate the least preferred alternative, the result is more troublesome. These examples illustrate the fact that the importance of any failure of conditional Arrow fairness is highly context-dependent. However, the utilization of an aggregation function that has a high probability of conditional Arrow fairness provides protection against both trivial and serious failures of these conditions. By structuring decisions so that the number of individuals is much larger than the number of alternatives, the Copeland function can achieve a high probability of conditional Arrow fairness (over 80% in this case), thus protecting against failures of IIA and unanimity in the majority of situations.
$d$
has changed. If the purpose of the construction of the group ranking is to select the most preferred alternative, then this failure of IIA is inconsequential. However, if the purpose of the ranking is to eliminate the least preferred alternative, the result is more troublesome. These examples illustrate the fact that the importance of any failure of conditional Arrow fairness is highly context-dependent. However, the utilization of an aggregation function that has a high probability of conditional Arrow fairness provides protection against both trivial and serious failures of these conditions. By structuring decisions so that the number of individuals is much larger than the number of alternatives, the Copeland function can achieve a high probability of conditional Arrow fairness (over 80% in this case), thus protecting against failures of IIA and unanimity in the majority of situations.
In this work, empirical preference profiles were generated from a unimodal distribution of preference weights, resulting in some implicit agreement between individuals in the preference profile. In contrast, random preference profiles were generated from random shuffles of the available alternatives, and thus show negligible implicit agreement. These two cases can be thought of as two points sampled along a spectrum of implicit agreement. The current results support a possible correlation between aggregation function performance (probability of conditional Arrow fairness and strategy-proofness) and implicit agreement. Through the process of convergence, members of a design team build agreement regarding the representation and goals of a design problem (Dong, Hill & Agogino Reference Dong, Hill and Agogino2004; Fu, Cagan & Kotovsky Reference Fu, Cagan and Kotovsky2010). This process should also lead to alignment of preferences, and increase implicit agreement. Here, preference profiles with stronger implicit agreement (empirically derived) produced fair results with a higher probability than preference profiles with lower implicit agreement (random). By ascertaining the implicit agreement within a preference profile, it may be possible to then infer the probability of conditional Arrow fairness. Future work in engineering design should explore metrics for quantifying and tracking the level of implicit agreement within a team, as well as exploring the relationship between implicit agreement and the performance of aggregation functions.
Several trends were robust across different levels of implicit agreement. These included the relative probability of conditional Arrow fairness (in decreasing order: Copeland, Borda, IRV, veto, plurality), the relative probability of strategy-proofness (in decreasing order: Copeland, IRV, plurality, veto, Borda), the positive correlation between number of individuals and conditional Arrow fairness, and the positive correlation between number of individuals and strategy-proofness.
These robust results can be applied directly to decision making in team based design. It is often necessary for design teams to rank design alternatives, usually to narrow down the number of alternatives before continuing work. Late in the design process (for instance, detail design), it may be possible to create a ranking based entirely on quantifiable performance characteristics. However, early in the design process (for instance, during conceptual design), it is not realistic to quantify the performance of solution concepts. Therefore, a ranking must be built from the individual preferences of design team members. Individuals’ rankings over design alternatives may vary enough that the group ranking is not immediately obvious, so it is important to use a structured aggregation procedure. The application of the Copeland function in such a situation would allow the team to form a group ranking that is more likely to have fair characteristics. The result would also have a higher likelihood of strategy-proofness, meaning that team members would have no incentive to provide anything but their true ranking over the alternatives.
Further, the results of this work indicate that the beneficial properties of the Copeland function can be amplified by structuring decision scenarios so that the number of alternatives is small relative to the number of design team members. This finding might be implemented in practice by dividing a conceptual design team into smaller sub-teams, and instructing every sub-team to collaboratively generate a single concept. The team could then reconvene, share concepts, and utilize the Copeland method to make a group decision. This and other approaches should be evaluated in future research.
The stimulus addressed in this work was a traditional drinking mug, which effectively elicited preferences used in the simulations conducted in this work. However, there are distinct differences between a drinking mug and many of the complex technology-driven products that design teams commonly address. Specifically, a more complex product would have the potential to force more difficult trade-offs between form, function, and cost. If the way in which trade-offs are addressed is fairly consistent across individuals, then the results of a group decision could be similar to the empirical preference scenarios developed in this work. However, difficult trade-offs could also have a divisive effect if individuals disagree on the relative importance of objectives. This would lead to lower implicit agreement within the preference profile, and therefore lower conditional Arrow fairness. Although this work explored only one example stimulus, the results of this study can serve as a reference point for future research in this area with different and more complex stimuli.
It should also be noted that the methodology employed in this paper did not model the discussions and negotiations that are often a part of team based design. Such communication within a team can result over time in a unanimous decision, in which case aggregation of preferences is not necessary. However, it is often the case that a team does not have sufficient time to reach a unanimous state, or discussion leads to an impasse in which members of the team are no longer willing to compromise on their preferences. In cases like these, preference aggregation functions are necessary, and our work indicates that the Copeland function offers more fair and strategy-proof decisions.
6 Conclusions
This work took an empirical approach to examine several methods for combining individual preferences into a group preference. Each of these methods, referred to in this work as aggregation functions, was analysed in terms of strategy-proofness and conditional Arrow fairness. The objective was to identify the aggregation function with the highest probability of being fair and robust to manipulation in practice. Of the aggregation functions explored in this work, the Copeland function offered the highest probability of conditional Arrow fairness as well as the highest probability of strategy-proofness. This indicates that it is likely to return a fair result in practice, and that individuals would thus have no incentive to provide anything but their true preference for the alternatives. This result was true for both empirical preference profiles and randomly generated preference profiles (which offer a worst-case scenario for forming a group preference). The Copeland function could be applied to a variety of domains, including the aggregation of preferences from user surveys and decision-making during the design process.
The simulations in this work (based on both random and empirical preference profiles) largely agree with theoretical results from the literature. For instance, the empirical assessments of the Borda aggregation function demonstrate its ability to produce Arrow-fair outcomes for approximately 50% of empirical preference profiles (Dym et al. Reference Dym, Wood and Scott2002), but also show that it is less strategy-proof than other functions (Black et al. Reference Black1958). These results also echo the general sentiment that the IIA criterion is over-restrictive (Luce & Raiffa Reference Luce and Raiffa1957; Young Reference Young1995). This was also shown to be the limiting factor behind the measure of conditional Arrow fairness in this work (Tables 2 and 3).
Future work should extend this analysis to a larger set of aggregation functions, and explore the efficacy of the Copeland function in more difficult and longitudinal design contexts, such as those involving technology based products with higher complexity. Future work should also validate methods for structuring decisions so that the number of alternatives is small relative to the number of design team members, thus ensuring higher conditional Arrow fairness. In addition, this work only measured the probability of strategy-proofness. Therefore, future work should ascertain how easily individuals can recognize and exploit lapses in strategy-proofness.
Acknowledgments
The authors would like to thank Dr. Teddy Seidenfeld and Dr. Michael Scott for their suggestions and guidance regarding this work. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under grant DGE125252, the National Science Foundation under grant CMMI1233864, and the United States Air Force Office of Scientific Research under grant FA9550-16-1-0049. A previous version of this paper was published in the proceedings of the International Conference on Engineering Design (McComb, Goucher-Lambert & Cagan Reference McComb, Goucher-Lambert and Cagan2015).
Appendix A
Figure 5 shows aggregation function characteristics for random preference profiles and Figure 6 shows aggregation function characteristics for empirical preference profiles.
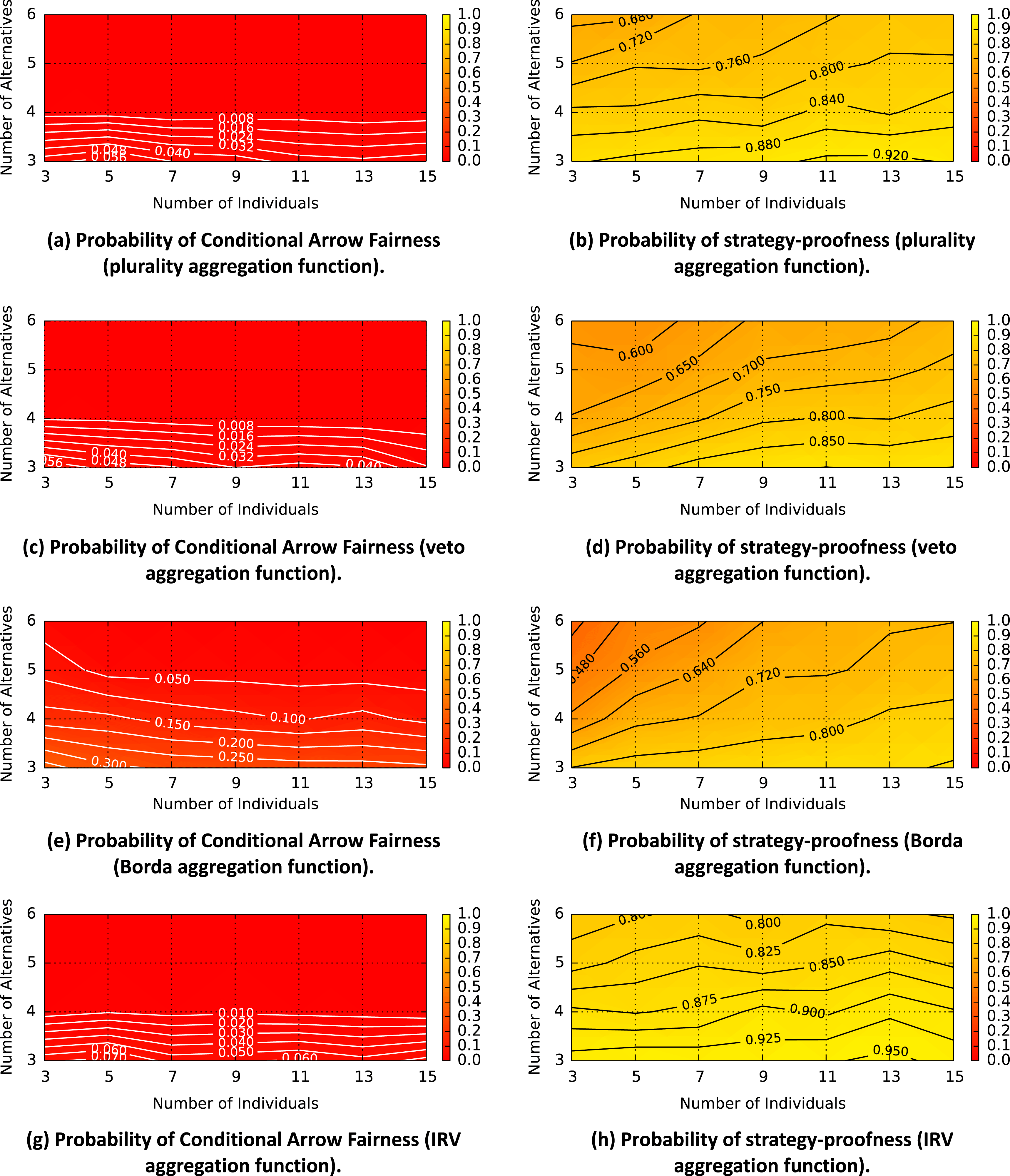
Figure 5. Aggregation function characteristics for random preference profiles.

Figure 6. Aggregation function characteristics for empirical preference profiles.












