Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-25T19:32:37.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Zariski closures of images of algebraic subsets under the uniformization map on finite-volume quotients of the complex unit ball

Part of: Diophantine approximation, transcendental number theory Geometric convexity Global differential geometry Cycles and subschemes

Published online by Cambridge University Press:  19 September 2019

Ngaiming Mok
Ngaiming Mok*
Affiliation:
Department of Mathematics, The University of Hong Kong, Pokfulam, Hong Kong email nmok@hku.hk
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the analogue of the Ax–Lindemann–Weierstrass theorem for not necessarily arithmetic lattices of the automorphism group of the complex unit ball 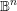$\mathbb{B}^{n}$ using methods of several complex variables, algebraic geometry and Kähler geometry. Consider a torsion-free lattice 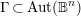$\unicode[STIX]{x1D6E4}\,\subset \,\text{Aut}(\mathbb{B}^{n})$ and the associated uniformization map 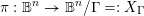$\unicode[STIX]{x1D70B}:\mathbb{B}^{n}\rightarrow \mathbb{B}^{n}/\unicode[STIX]{x1D6E4}=:X_{\unicode[STIX]{x1D6E4}}$. Given an algebraic subset 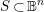$S\,\subset \,\mathbb{B}^{n}$ and writing 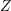$Z$ for the Zariski closure of 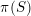$\unicode[STIX]{x1D70B}(S)$ in 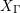$X_{\unicode[STIX]{x1D6E4}}$ (which is equipped with a canonical quasi-projective structure), in some precise sense we realize 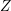$Z$ as a variety uniruled by images of algebraic subsets under the uniformization map, and study the asymptotic geometry of an irreducible component 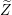$\widetilde{Z}$ of 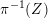$\unicode[STIX]{x1D70B}^{-1}(Z)$ as 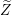$\widetilde{Z}$ exits the boundary 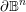$\unicode[STIX]{x2202}\mathbb{B}^{n}$ by exploiting the strict pseudoconvexity of 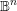$\mathbb{B}^{n}$, culminating in the proof that 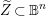$\widetilde{Z}\,\subset \,\mathbb{B}^{n}$ is totally geodesic. Our methodology sets the stage for tackling problems in functional transcendence theory for arbitrary lattices of 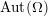$\text{ Aut}(\unicode[STIX]{x1D6FA})$ for (possibly reducible) bounded symmetric domains 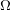$\unicode[STIX]{x1D6FA}$.

Keywords

bounded symmetric domainuniformizationChow spacefoliationKähler metricasymptotic geometrystrictly pseudoconvex domains

MSC classification

Primary: 11J81: Transcendence (general theory) 14C05: Parametrization (Chow and Hilbert schemes) 32F32: Analytical consequences of geometric convexity (vanishing theorems, etc.) 53C55: Hermitian and Kählerian manifolds
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 11 , November 2019 , pp. 2129 - 2149
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partially supported by the GRF 17301518 of the HKRGC, Hong Kong.

References

Baily, W. L. and Borel, A., Compactification of arithmetic quotients of bounded symmetric domains , Ann. of Math. (2) 84 (1966), 442–528.Google Scholar
Chow, W.-L. and van der Waerden, B. L., Zur algebraische Geometrie IX , Math. Ann. 113 (1937), 692–704.Google Scholar
Grauert, H., Peternell, T. and Remmert, R., Several complex variables VII, sheaf-theoretical methods in complex analysis, Encyclopedia of Mathematical Sciences, vol. 7 (Springer, Berlin, Heidelberg, 1994).Google Scholar
Klembeck, P. F., Kähler metrics of negative curvature, the Bergman metric near the boundary, and the Kobayashi metric on smooth bounded strictly pseudoconvex sets , Indiana Univ. Math. J. 27 (1978), 275–282.Google Scholar
Klingler, B., Ullmo, E. and Yafaev, A., The hyperbolic Ax–Lindemann–Weierstrass conjecture , Publ. Math. Inst. Hautes Études Sci. 123 (2016), 333–360.Google Scholar
Margulis, G. A., Arithmeticity of the irreducible lattices in the semisimple groups of rank greater than 1 , Invent. Math. 76 (1984), 93–120.Google Scholar
Mok, N., Metric rigidity theorems on Hermitian locally symmetric manifolds, Series in Pure Mathematics, vol. 6 (World Scientific, Singapore, 1989).Google Scholar
Mok, N., On the Zariski closure of a germ of totally geodesic complex submanifold on a subvariety of a complex hyperbolic space form of finite volume , in Complex analysis, Trends in Mathematics, eds Ebenfelt, P. et al. (Birkhäuser, Basel, 2010), 279–300.Google Scholar
Mok, N., Projective-algebraicity of minimal compactifications of complex-hyperbolic space forms of finite volume , in Perspectives in analysis, geometry, topology, Progress in Mathematics, vol. 296 (Birkhäuser, Boston, MA, 2012), 331–354.Google Scholar
Mok, N., Extension of germs of holomorphic isometries up to normalizing constants with respect to the Bergman metric , J. Eur. Math. Soc. (JEMS) 14 (2012), 1617–1656.Google Scholar
Mok, N., Pila, J. and Tsimerman, J., Ax-Schanuel for Shimura varieties , Ann. of Math. (2) 189 (2019), 945–978.Google Scholar
Mok, N. and Zhang, Y., Rigidity of pairs of rational homogeneous spaces of Picard number 1 and analytic continuation of geometric substructures on uniruled projective manifolds , J. Differential Geom. 112 (2019), 263–345.Google Scholar
Mok, N. and Zhong, J.-Q., Compactifying complete Kähler–Einstein manifolds of finite topological type and bounded curvature , Ann. of Math. (2) 129 (1989), 427–470.Google Scholar
Pila, J., O-minimality and the André-Oort conjecture for ℂ n , Ann. of Math. (2) 173 (2011), 1779–1840.Google Scholar
Pila, J. and Tsimerman, J., Ax-Lindemann for 𝓐g , Ann. of Math. (2) 179 (2014), 659–681.Google Scholar
Pila, J. and Zannier, U., Rational points in periodic analytic sets and the Manin-Mumford conjecture , Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 19 (2008), 149–162.Google Scholar
Satake, I., On compactifications of the quotient spaces for arithmetically defined discontinuous groups , Ann. of Math. (2) 72 (1960), 555–580.Google Scholar
Siu, Y.-T. and Yau, S.-T., Compactification of negatively curved complete Kähler manifolds of finite volume , in Seminar on differential geometry, Annals of Mathematics Studies, vol. 102, ed. Yau, S.-T. (Princeton University Press, Princeton, NJ, 1982), 363–380.Google Scholar
Ullmo, E. and Yafaev, A., Hyperbolic Ax-Lindemann theorem in the cocompact case , Duke Math. J. 163 (2014), 433–463.Google Scholar
Wolf, J. A., Fine structure of Hermitian symmetric spaces , in Symmetric spaces, Pure and Applied Mathematics, vol. 8 (Dekker, New York, 1972), 271–357.Google Scholar