Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-18T11:09:32.161Z Has data issue: false hasContentIssue false
  • English
  • Français

Wiles defect for Hecke algebras that are not complete intersections

Part of: Discontinuous groups and automorphic forms Arithmetic rings and other special rings Theory of modules and ideals

Published online by Cambridge University Press:  16 August 2021

Gebhard Böckle ,
Chandrashekhar B. Khare  and
Jeffrey Manning
Gebhard Böckle
Affiliation:
Interdisciplinary Center for Scientific Computing, Universität Heidelberg, INF 205, 69120Heidelberg, Germanygebhard.boeckle@iwr.uni-heidelberg.de
Chandrashekhar B. Khare
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA90095-1555, USAshekhar@math.ucla.edu
Jeffrey Manning
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA90095-1555, USAjmanning@math.ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In his work on modularity theorems, Wiles proved a numerical criterion for a map of rings $R\to T$ to be an isomorphism of complete intersections. He used this to show that certain deformation rings and Hecke algebras associated to a mod $p$ Galois representation at non-minimal level are isomorphic and complete intersections, provided the same is true at minimal level. In this paper we study Hecke algebras acting on cohomology of Shimura curves arising from maximal orders in indefinite quaternion algebras over the rationals localized at a semistable irreducible mod $p$ Galois representation $\bar {\rho }$. 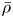If $\bar {\rho }$ is scalar at some primes dividing the discriminant of the quaternion algebra, then the Hecke algebra is still isomorphic to the deformation ring, but is not a complete intersection, or even Gorenstein, so the Wiles numerical criterion cannot apply. We consider a weight-2 newform 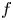$f$ which contributes to the cohomology of the Shimura curve and gives rise to an augmentation 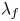$\lambda _f$ of the Hecke algebra. We quantify the failure of the Wiles numerical criterion at 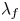$\lambda _f$ by computing the associated Wiles defect purely in terms of the local behavior at primes dividing the discriminant of the global Galois representation 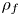$\rho _f$ which 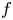$f$ gives rise to by the Eichler–Shimura construction. One of the main tools used in the proof is Taylor–Wiles–Kisin patching.

Keywords

wiles defectmodularity theoremCohen–Macaulay

MSC classification

Primary: 11F80: Galois representations
Secondary: 13C99: None of the above, but in this section 13F99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 9 , September 2021 , pp. 2046 - 2088
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, P., Deformations of polarized automorphic Galois representations and adjoint Selmer groups, Duke Math. J. 165 (2016), 2407–2460.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179 (2014), 501–609; MR 3152941.CrossRefGoogle Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi–Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci. 47 (2011), 29–98; MR 2827723.CrossRefGoogle Scholar
Bruns, W. and Vetter, U., Determinantal rings, Lecture Notes in Mathematics, vol. 1327 (Springer, Berlin, 1988); MR 953963.CrossRefGoogle Scholar
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V. and Shin, S. W., Patching and the $p$-adic local Langlands correspondence, Camb. J. Math. 4 (2016), 197–287; MR 3529394.CrossRefGoogle Scholar
Carayol, H., Formes modulaires et représentations galoisiennes à valeurs dans un anneau local complet, in p-adic monodromy and the Birch and Swinnerton-Dyer conjecture (Boston, MA, 1991), Contemporary Mathematics, vol. 165 (American Mathematical Society, Providence, RI, 1994), 213–237; MR 1279611.CrossRefGoogle Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some $l$-adic lifts of automorphic mod $l$Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181, with Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras; MR 2470687.CrossRefGoogle Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat's last theorem, in Elliptic curves, modular forms & Fermat's last theorem (Hong Kong, 1993) (International Press, Cambridge, MA, 1997), 2–140; MR 1605752.Google Scholar
Diamond, F., The Taylor–Wiles construction and multiplicity one, Invent. Math. 128 (1997), 379–391; MR 1440309.CrossRefGoogle Scholar
Diamond, F. and Ribet, K., $\ell$-adic deformations and Wiles's ‘main conjecture’, in Modular forms and Fermat's last theorem (Boston, MA, 1995) (Springer, New York, 1997), 357–371; MR 1638487.CrossRefGoogle Scholar
Diamond, F. and Taylor, R., Lifting modular mod $l$representations, Duke Math. J. 74 (1994), 253–269; MR 1272977.CrossRefGoogle Scholar
Diamond, F. and Taylor, R., Nonoptimal levels of mod $l$modular representations, Invent. Math. 115 (1994), 435–462; MR 1262939.CrossRefGoogle Scholar
Edixhoven, B., The weight in Serre's conjectures on modular forms, Invent. Math. 109 (1992), 563–594; MR 1176206.CrossRefGoogle Scholar
Eisenbud, D., Commutative algebra, Graduate Texts in Mathematics, vol. 150 (Springer, New York, 1995), with a view toward algebraic geometry; MR 1322960.CrossRefGoogle Scholar
Emerton, M., Gee, T. and Savitt, D., Lattices in the cohomology of Shimura curves, Invent. Math. 200 (2015), 1–96; MR 3323575.CrossRefGoogle Scholar
Fakhruddin, N., Khare, C. and Patrikis, S., Relative deformation theory and lifting irreducible Galois representations, Duke Math.J., to appear. Preprint (2019), arXiv:1904.02374.Google Scholar
Fujiwara, K., Galois deformations and arithmetic geometry of Shimura varieties, International Congress of Mathematicians, vol. II (European Mathematical Society, Zürich, 2006), 347–371; MR 2275601.Google Scholar
Hamblen, S. and Ramakrishna, R., Deformations of certain reducible Galois representations. II, Amer. J. Math. 130 (2008), 913–944; MR 2427004.CrossRefGoogle Scholar
Helm, D., On maps between modular Jacobians and Jacobians of Shimura curves, Israel J. Math. 160 (2007), 61–117; MR 2342491.CrossRefGoogle Scholar
Hida, H., Congruence of cusp forms and special values of their zeta functions, Invent. Math. 63 (1981), 225–261; MR 610538.CrossRefGoogle Scholar
Hida, H., On congruence divisors of cusp forms as factors of the special values of their zeta functions, Invent. Math. 64 (1981), 221–262; MR 629471.CrossRefGoogle Scholar
Khare, C., On isomorphisms between deformation rings and Hecke rings, Invent. Math. 154(1) (2003), 199–222, with an appendix by Gebhard Böckle; MR 2004460.CrossRefGoogle Scholar
Khare, C. and Wintenberger, J.-P., Serre's modularity conjecture. I, Invent. Math. 178 (2009), 485–504; MR 2551763 (2010k:11087).CrossRefGoogle Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity, Ann. of Math. (2) 170 (2009), 1085–1180; MR 2600871.CrossRefGoogle Scholar
Lenstra, H. W. Jr., Complete intersections and Gorenstein rings, in Elliptic curves, modular forms, & Fermat's last theorem (Hong Kong, 1993), Series in Number Theory, vol. I International Press, Cambridge, MA, 1995, 99–109; MR 1363497.Google Scholar
The LMFDB Collaboration, The l-functions and modular forms database, 2019, http://www.lmfdb.org [online; accessed 8 September 2019].Google Scholar
Manning, J., Patching and multiplicity $2^k$for Shimura curves, Algebra Number Theory 15 (2021), 387–434.CrossRefGoogle Scholar
Mazur, B., A brief introduction to the work of Haruzo Hida (2012), http://www.math.harvard.edu/mazur/papers/Hida.August11.pdf.Google Scholar
Mazur, B. and Tate, J., Refined conjectures of the ‘Birch and Swinnerton-Dyer type’, Duke Math. J. 54 (1987), 711–750; MR 899413.CrossRefGoogle Scholar
Ribet, K. A., Congruence relations between modular forms, in Proceedings of the International Congress of Mathematicians, vols. 1, 2 (Warsaw, 1983) (PWN, Warsaw, 1984), 503–514; MR 804706.Google Scholar
Ribet, K. A., On modular representations of ${\rm Gal}(\bar {\textbf {Q}}/\textbf {Q})$arising from modular forms, Invent. Math. 100 (1990), 431–476; MR 1047143.CrossRefGoogle Scholar
Ribet, K. A., Multiplicities of Galois representations in Jacobians of Shimura curves, in Festschrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part II (Ramat Aviv, 1989), Israel Mathematical Conference Proceedings, vol. 3 (Weizmann, Jerusalem, 1990), 221–236; MR 1159117.Google Scholar
Ribet, K. A. and Takahashi, S., Parametrizations of elliptic curves by Shimura curves and by classical modular curves, Proc. Natl. Acad. Sci. USA 94(21) (1997), 11110–11114, Elliptic curves and modular forms (Washington, DC, 1996); MR 1491967.CrossRefGoogle ScholarPubMed
Shotton, J., Local deformation rings for ${\rm GL_2}$and a Breuil–Mézard conjecture when $\ell \ne p$, Algebra Number Theory 10 (2016), 1437–1475; MR 3554238.CrossRefGoogle Scholar
Shotton, J., The Breuil–Mézard conjecture when $l\neq p$, Duke Math. J. 167 (2018), 603–678; MR 3769675.CrossRefGoogle Scholar
Silverman, J. H., Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 151 (Springer, New York, 1994); MR 1312368.CrossRefGoogle Scholar
Snowden, A., Singularities of ordinary deformation rings, Math. Z. 288 (2018), 759–781; MR 3778977.CrossRefGoogle Scholar
The Stacks Project Authors, Stacks project (2019), http://stacks.math.columbia.edu.Google Scholar
Taylor, R., Automorphy for some $l$-adic lifts of automorphic mod $l$Galois representations. II, Publ. Math. Inst. Hautes Études Sci. 108 (2008) 183–239; MR 2470688.CrossRefGoogle Scholar
Thorne, J. A., Automorphy of some residually dihedral Galois representations, Math. Ann. 364 (2016), 589–648; MR 3451399.CrossRefGoogle Scholar
Tilouine, J. and Urban, E., Integral period relations and congruences, Preprint (2018), arXiv:1811.11166.Google Scholar
Watanabe, K.-I., Ishikawa, T., Tachibana, S. and Otsuka, K., On tensor products of Gorenstein rings, J. Math. Kyoto Univ. 9 (1969), 413–423; MR 257062.Google Scholar
Wiles, A., Modular elliptic curves and Fermat's last theorem, Ann. of Math. (2) 141 (1995), 443–551; MR 1333035.CrossRefGoogle Scholar