Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-07T13:13:36.310Z Has data issue: false hasContentIssue false
  • English
  • Français

A twisted topological trace formula for Hecke operators and liftings from symplectic to general linear groups

Part of: Classical Topics in Algebraic Topology Forms and linear algebraic groups Linear algebraic groups and related topics Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  09 November 2011

Uwe Weselmann
Uwe Weselmann*
Affiliation:
Mathematisches Institut, Im Neuenheimer Feld 288, D-69121 Heidelberg, Germany (email: weselman@mathi.uni-heidelberg.de)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For the locally symmetric space X attached to an arithmetic subgroup of an algebraic group G of ℚ-rank r, we construct a compact manifold 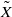by gluing together 2r copies of the Borel–Serre compactification of X. We apply the classical Lefschetz fixed point formula to 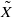and get formulas for the traces of Hecke operators ℋ acting on the cohomology of X. We allow twistings of ℋ by outer automorphisms η of G. We stabilize this topological trace formula and compare it with the corresponding formula for an endoscopic group of the pair (G,η) . As an application, we deduce a weak lifting theorem for the lifting of automorphic representations from Siegel modular groups to general linear groups.

Keywords

Borel–Serre compactificationLefschetz fixed point formulaHecke operatorstrace formulastabilizationendoscopic groupliftcohomology of arithmetic groupssymplectic groupSiegel modular variety

MSC classification

Secondary: 11F75: Cohomology of arithmetic groups 55M20: Fixed points and coincidences 11E72: Galois cohomology of linear algebraic groups 11F23: Relations with algebraic geometry and topology 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms 20G10: Cohomology theory 57S30: Discontinuous groups of transformations
Type
Research Article
Information
Compositio Mathematica , Volume 148 , Issue 1 , January 2012 , pp. 65 - 120
Copyright
Copyright © Foundation Compositio Mathematica 2011

References

[Art88]Arthur, J., The invariant trace formula II. Global theory, J. Amer. Math. Soc. 1 (1988), 501–554.CrossRefGoogle Scholar
[Bal01]Ballmann, J., Berechnung der Kottwitz–Shelstad-Transferfaktoren für unverzweigte Tori in nicht zusammenhängenden reduktiven Gruppen, Dissertation, University of Mannheim (2001), http://bibserv7.bib.uni-mannheim.de/madoc/volltexte/2002/38/.Google Scholar
[BGS85]Ballmann, W., Gromov, M. and Schroeder, V., Manifolds of nonpositive curvature, Progress in Mathematics, vol. 61 (Birkhäuser, Boston–Basel–Stuttgart, 1985).CrossRefGoogle Scholar
[BWW02]Ballmann, J., Weissauer, R. and Weselmann, U., Remarks on the fundamental lemma for stable twisted endoscopy of classical groups, Manuskripte der Forschergruppe Arithmetik, vol. 7 (Universities of Mannheim and Heidelberg, 2002).Google Scholar
[Bew85]Bewersdorff, J., Eine Lefschetzsche Fixpunktformel für Hecke-Operatoren, Bonner Mathematische Schriften, vol. 164 (University of Bonn, 1985).Google Scholar
[Bor91]Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126 (Springer, Berlin–Heidelberg–New York, 1991).CrossRefGoogle Scholar
[BS73]Borel, A. and Serre, J. P., Corners and arithmetic groups, Comment. Math. Helv. 73 (1973), 436–491.CrossRefGoogle Scholar
[Bor98]Borovoi, M. V., Abelian Galois cohomology of reductive groups, Mem. Amer. Math. Soc. 626 (1998).Google Scholar
[Fli96]Flicker, Y. F., On the symmetric square. Unit elements, Pacific J. Math. 175 (1996), 507–526.CrossRefGoogle Scholar
[Fli99]Flicker, Y. F., Matching of orbital integrals on GL(4) and GSp(2), Mem. Amer. Math. Soc. 137 (1999).Google Scholar
[Fli05]Flicker, Y. F., Automorphic forms and Shimura varieties of PGSp(2) (World Scientific, Singapore, 2005).CrossRefGoogle Scholar
[Fra98]Franke, J., Harmonic analysis in weighted L 2-spaces, Ann. Sci. Éc. Norm. Supér. 31 (1998), 181–279.CrossRefGoogle Scholar
[God62/63]Godement, R., Domaines fondamentaux des groupes arithmétiques, Sémin. Bourbaki (1962/63), exp. 257.Google Scholar
[GHM94]Goresky, M., Harder, G. and MacPherson, R., Weighted cohomology, Invent. Math. 116 (1994), 139–213.CrossRefGoogle Scholar
[GKM97]Goresky, M., Kottwitz, R. and MacPherson, R., Discrete series characters and the Lefschetz formula for Hecke operators, Duke Math. J. 89 (1997), 477–554.CrossRefGoogle Scholar
[GKM98]Goresky, M., Kottwitz, R. and MacPherson, R., Correction to ‘Discrete series characters and the Lefschetz formula for Hecke operators’, Duke Math. J. 92 (1998), 665–666.CrossRefGoogle Scholar
[GM92]Goresky, M. and MacPherson, R., Lefschetz numbers of Hecke correspondences, in The zeta functions of Picard modular surfaces, eds Langlands, R. P. and Ramakrishnan, D. (Centre de Recherche Mathématiques, Montréal, 1992), 465–478.Google Scholar
[GM93]Goresky, M. and MacPherson, R., Local contribution to the Lefschetz fixed point formula, Invent. Math. 111 (1993), 1–33.CrossRefGoogle Scholar
[GM03]Goresky, M. and MacPherson, R., The topological trace formula, J. Reine Angew. Math. 560 (2003), 77–150.Google Scholar
[GT99]Goresky, M. and Tai, Y.-S., Toroidal and reductive Borel–Serre compactifications of locally symmetric spaces, Amer. J. Math. 121 (1999), 1095–1151.CrossRefGoogle Scholar
[Hal94]Hales, Th., The twisted endoscopy of GL(4) and GL(5): transfer of Shalika germs, Duke Math. J. 76 (1994), 595–632.CrossRefGoogle Scholar
[Hal95]Hales, Th., On the fundamental lemma for standard endoscopy: reduction to the unit element, Canad. J. Math. 47 (1995), 974–994.CrossRefGoogle Scholar
[Har71]Harder, G., A Gauss–Bonnet formula for discrete arithmetically defined groups, Ann. Sci. Éc. Norm. Supér. (4) (1971), 409–455.CrossRefGoogle Scholar
[Har93]Harder, G., Eisensteinkohomologie und die Konstruktion gemischter Motive, Lecture Notes in Mathematics, vol. 1562 (Springer, Berlin, 1993).CrossRefGoogle Scholar
[Har95]Harder, G., Five notes on the topological trace formula and its applications (1995), unpublished manuscript, Bonn.Google Scholar
[Hel62]Helgason, , Differential geometry and symmetric spaces, Pure and Applied Mathematics, vol. 12 (Academic Press, New York, 1962).Google Scholar
[Hum72]Humphreys, J. E., Introduction to Lie algebras and representation theory, Graduate Texts in Mathematics, vol. 9 (Springer, New York, 1972).CrossRefGoogle Scholar
[Kos61]Kostant, B., Lie algebra cohomology and the generalized Borel–Weil theorem, Ann. of Math. (2) 74 (1961), 329–387.CrossRefGoogle Scholar
[Kot83]Kottwitz, R., Sign changes in harmonic analysis on reductive groups, Trans. Amer. Math. Soc. 278 (1983), 289–297.CrossRefGoogle Scholar
[Kot88]Kottwitz, R., Tamagawa numbers, Ann. of Math. (2) 127 (1988), 629–646.CrossRefGoogle Scholar
[KS99]Kottwitz, R. and Shelstad, D., Foundations of twisted endoscopy, Astérisque 255 (1999).Google Scholar
[KS72]Kuga, M. and Sampson, J. H., A coincidence formula for locally symmetric spaces, Amer. J. Math. 94 (1972), 486–500.CrossRefGoogle Scholar
[LS78]Lee, R. and Szczarba, R. H., On the torsion in K 4(ℤ) and K 5(ℤ), Duke Math. J. 45 (1978), 101–129.CrossRefGoogle Scholar
[Leu96]Leuzinger, E., On the Gauss–Bonnet formula for locally symmetric spaces of noncompact type, Enseign. Math. II. Sér. 42 (1996), 201–214.Google Scholar
[Ngo10]Ngô, B. C., Le lemme fondamental pour les algêbres de Lie, Publ. Math. Inst. Hautes Études Sci. 111 (2010), 1–271.CrossRefGoogle Scholar
[Osh78]Oshima, T., A realization of Riemannian symmetric spaces, J. Math. Soc. Japan 30 (1978), 117–132.CrossRefGoogle Scholar
[Roh90]Rohlfs, J., Lefschetz numbers for arithmetic groups, in Cohomology of arithmetic groups and automorphic forms: Proceedings of a Conference held in Luminy/Marseille, France, May 22–27 1989, Lecture Notes in Mathematics, vol. 1447 (Springer, New York, 1990), 303–313.CrossRefGoogle Scholar
[RS93]Rohlfs, J. and Speh, B., Lefschetz numbers and twisted stabilized orbital integrals, Math. Ann. 296 (1993), 191–214.CrossRefGoogle Scholar
[San81]Sansuc, J.-J., Groupe de Brauer et arithmétique des groupes algébriques linéaires sur un corps de nombres, J. Reine Angew. Math. 327 (1981), 12–80.Google Scholar
[She79]Shelstad, D., Characters and inner forms of a quasi-split group over ℝ, Compositio Math. 39 (1979), 11–45.Google Scholar
[Ste68]Steinberg, R., Endomorphisms of algebraic groups, Mem. Amer. Math. Soc. 80 (1968).Google Scholar
[Wal97]Waldspurger, J.-L., Le lemme fondamental implique le transfert, Compositio Math. 105 (1997), 153–236.CrossRefGoogle Scholar
[Wal06]Waldspurger, J.-L., Endoscopie et changement de caractéristique, J. Inst. Math. Jussieu 5 (2006), 423–525.CrossRefGoogle Scholar
[Wal08]Waldspurger, J.-L., L’endoscopie tordue n’est pas si tordue, Mem. Amer. Math. Soc. 908 (2008).Google Scholar
[Wei06]Weissauer, R., Spectral approximation of twisted local κ-orbital integrals, Preprint (2006).Google Scholar
[Wei08]Weissauer, R., A remark on the existence of Whittaker models for L-packets of automorphic representations of GSp(4), in Modular forms on Schiermonnikoog. Based on the conference on Modular Forms, Schiermonnikoog, Netherlands, October 2006, eds Edixhoven, B.et al. (Cambridge University Press, Cambridge, 2008), 285–310.Google Scholar
[Wei09]Weissauer, R., Endoscopy for GSp(4) and the cohomology of Siegel modular threefolds, Lecture Notes in Mathematics, vol. 1968 (Springer, Heidelberg–Berlin, 2009).CrossRefGoogle Scholar
[Wen01]Wendt, R., Weyl’s character formula for non-connected Lie groups and orbital theory for twisted affine Lie algebras, J. Funct. Anal. 180 (2001), 31–65.CrossRefGoogle Scholar