Article contents
Shifted generic cohomology
Published online by Cambridge University Press: 07 August 2013
Abstract
The idea that the cohomology of finite groups might be fruitfully approached via the cohomology of ambient semisimple algebraic groups was first shown to be viable in the papers [E. Cline, B. Parshall, and L. Scott, Cohomology of finite groups of Lie type, I, Publ. Math. Inst. Hautes Études Sci. 45 (1975), 169–191] and [E. Cline, B. Parshall, L. Scott and W. van der Kallen, Rational and generic cohomology, Invent. Math. 39 (1977), 143–163]. The second paper introduced, through a limiting process, the notion of generic cohomology, as an intermediary between finite Chevalley group and algebraic group cohomology. The present paper shows that, for irreducible modules as coefficients, the limits can be eliminated in all but finitely many cases. These exceptional cases depend only on the root system and cohomological degree. In fact, we show that, for sufficiently large  $r$, depending only on the root system and
$r$, depending only on the root system and 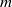 $m$, and not on the prime
$m$, and not on the prime 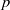 $p$ or the irreducible module
$p$ or the irreducible module 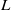 $L$, there are isomorphisms
$L$, there are isomorphisms 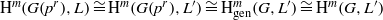 ${\mathrm{H} }^{m} (G({p}^{r} ), L)\cong {\mathrm{H} }^{m} (G({p}^{r} ), {L}^{\prime } )\cong { \mathrm{H} }_{\mathrm{gen} }^{m} (G, {L}^{\prime } )\cong {\mathrm{H} }^{m} (G, {L}^{\prime } )$, where the subscript ‘gen’ refers to generic cohomology and
${\mathrm{H} }^{m} (G({p}^{r} ), L)\cong {\mathrm{H} }^{m} (G({p}^{r} ), {L}^{\prime } )\cong { \mathrm{H} }_{\mathrm{gen} }^{m} (G, {L}^{\prime } )\cong {\mathrm{H} }^{m} (G, {L}^{\prime } )$, where the subscript ‘gen’ refers to generic cohomology and 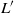 ${L}^{\prime } $ is a constructibly determined irreducible ‘shift’ of the (arbitrary) irreducible module
${L}^{\prime } $ is a constructibly determined irreducible ‘shift’ of the (arbitrary) irreducible module 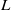 $L$ for the finite Chevalley group
$L$ for the finite Chevalley group 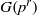 $G({p}^{r} )$. By a famous theorem of Steinberg, both
$G({p}^{r} )$. By a famous theorem of Steinberg, both 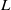 $L$ and
$L$ and 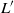 ${L}^{\prime } $ extend to irreducible modules for the ambient algebraic group
${L}^{\prime } $ extend to irreducible modules for the ambient algebraic group 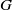 $G$ with
$G$ with 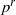 ${p}^{r} $-restricted highest weights. This leads to the notion of a module or weight being ‘shifted
${p}^{r} $-restricted highest weights. This leads to the notion of a module or weight being ‘shifted 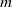 $m$-generic’, and thus to the title of this paper. Our approach is based on questions raised by the third author in [D. I. Stewart, The second cohomology of simple
$m$-generic’, and thus to the title of this paper. Our approach is based on questions raised by the third author in [D. I. Stewart, The second cohomology of simple 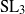 ${\mathrm{SL} }_{3} $-modules, Comm. Algebra 40 (2012), 4702–4716], which we answer here in the cohomology cases. We obtain many additional results, often with formulations in the more general context of
${\mathrm{SL} }_{3} $-modules, Comm. Algebra 40 (2012), 4702–4716], which we answer here in the cohomology cases. We obtain many additional results, often with formulations in the more general context of 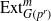 ${ \mathrm{Ext} }_{G({p}^{r} )}^{m} $ with irreducible coefficients.
${ \mathrm{Ext} }_{G({p}^{r} )}^{m} $ with irreducible coefficients.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2013
References
- 7
- Cited by


