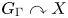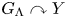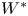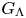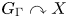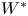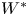Introduction
A main goal in measured group theory, initiated by work of Dye [Reference DyeDye59], is to classify measure-preserving group actions on standard probability spaces up to orbit equivalence, i.e. up to the existence of a measure space isomorphism sending orbits to orbits. More generally, we are interested in stable orbit equivalence of actions of countable groups, defined as follows: two free, ergodic, measure-preserving actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ by Borel automorphisms on standard probability spaces are stably orbit equivalent (SOE) if there exist positive measure Borel subsets
$H\curvearrowright Y$ by Borel automorphisms on standard probability spaces are stably orbit equivalent (SOE) if there exist positive measure Borel subsets ![]() $U\subseteq X$ and
$U\subseteq X$ and ![]() $V\subseteq Y$, and a measure-scaling isomorphism
$V\subseteq Y$, and a measure-scaling isomorphism ![]() $f:U\to V$, such that for every
$f:U\to V$, such that for every ![]() $x\in U$, one has
$x\in U$, one has ![]() $f((G\cdot x)\cap U)=(H\cdot f(x))\cap V$.
$f((G\cdot x)\cap U)=(H\cdot f(x))\cap V$.
A first striking result in this theory was the proof by Ornstein and Weiss [Reference Ornstein and WeissOW80], building on Dye's work, that any two free, ergodic, probability measure-preserving actions of countably infinite amenable groups are orbit equivalent.
Later, Gaboriau used the notion of cost (introduced by Levitt in [Reference LevittLev95]) to distinguish actions of free groups of different ranks [Reference GaboriauGab00], and showed that ![]() $\ell ^2$-Betti numbers also provide useful invariants for the classification [Reference GaboriauGab02].
$\ell ^2$-Betti numbers also provide useful invariants for the classification [Reference GaboriauGab02].
In contrast to the Ornstein–Weiss theorem exhibiting a wide class of groups that are indistinguishable from the viewpoint of orbit equivalence, several strong rigidity results have then been obtained for various classes of groups, such as higher-rank lattices (Furman [Reference FurmanFur99a, Reference FurmanFur99b]), mapping class groups (Kida [Reference KidaKid10, Reference KidaKid08]) and related groups (e.g. [Reference Chifan and KidaCK15]), certain large-type Artin groups [Reference Horbez and HuangHH20] or ![]() $\mathrm {Out}(F_N)$ with
$\mathrm {Out}(F_N)$ with ![]() $N\ge 3$ (as proved by Guirardel and the first named author in [Reference Guirardel and HorbezGH21]). Interestingly, negative curvature features of the groups under consideration are often key ingredients in the proofs of orbit equivalence rigidity of their ergodic actions.
$N\ge 3$ (as proved by Guirardel and the first named author in [Reference Guirardel and HorbezGH21]). Interestingly, negative curvature features of the groups under consideration are often key ingredients in the proofs of orbit equivalence rigidity of their ergodic actions.
Other rigidity phenomena were discovered by Monod and Shalom [Reference Monod and ShalomMS06], who proved superrigidity-type results for irreducible actions of direct products of free groups, or more generally of direct products ![]() $G_1\times \dots \times G_k$, with
$G_1\times \dots \times G_k$, with ![]() $k\ge 2$, where
$k\ge 2$, where ![]() $\mathrm {H}^2_{\mathrm {b}}(G_i,\ell ^2(G_i))\neq 0$ for every
$\mathrm {H}^2_{\mathrm {b}}(G_i,\ell ^2(G_i))\neq 0$ for every ![]() $i\in \{1,\dots,k\}$ (this condition on the bounded cohomology can be viewed as an analytical form of negative curvature). The crucial irreducibility assumption means that every factor
$i\in \{1,\dots,k\}$ (this condition on the bounded cohomology can be viewed as an analytical form of negative curvature). The crucial irreducibility assumption means that every factor ![]() $G_i$ acts ergodically on
$G_i$ acts ergodically on ![]() $X$.
$X$.
In yet another direction, Popa obtained orbit equivalence rigidity results for Bernoulli actions of all property (T) groups [Reference PopaPop06b], and all nonamenable groups that split as direct products or have an infinite center [Reference PopaPop08]; these results were obtained in the framework of Popa's deformation/rigidity theory, and their proofs exploit a specific property of Bernoulli actions called malleability, rather than geometric properties of the acting group.
In [Reference Horbez and HuangHH22], we started to investigate the class of right-angled Artin groups from the viewpoint of measured group theory. These groups are of basic importance (see e.g. [Reference CharneyCha07, Reference WiseWis12]) and have a very simple definition: given a finite simple graph ![]() $\Gamma$ (i.e. with no loop-edge and no multiple edges between two vertices), the right-angled Artin group
$\Gamma$ (i.e. with no loop-edge and no multiple edges between two vertices), the right-angled Artin group ![]() $G_\Gamma$ is defined by the following presentation: it has one generator per vertex of
$G_\Gamma$ is defined by the following presentation: it has one generator per vertex of ![]() $\Gamma$, and relations are given by commutation of any two generators whose associated vertices are joined by an edge.
$\Gamma$, and relations are given by commutation of any two generators whose associated vertices are joined by an edge.
On the rigidity side, we proved in [Reference Horbez and HuangHH22] that if two right-angled Artin groups ![]() $G_\Gamma,G_\Lambda$ with finite outer automorphism groups admit free, ergodic, measure-preserving actions on standard probability spaces which are orbit equivalent, or merely SOE (equivalently, if the groups are measure equivalent), then
$G_\Gamma,G_\Lambda$ with finite outer automorphism groups admit free, ergodic, measure-preserving actions on standard probability spaces which are orbit equivalent, or merely SOE (equivalently, if the groups are measure equivalent), then ![]() $G_\Gamma$ and
$G_\Gamma$ and ![]() $G_\Lambda$ are isomorphic. However, rigidity fails beyond this context: given any right-angled Artin group
$G_\Lambda$ are isomorphic. However, rigidity fails beyond this context: given any right-angled Artin group ![]() $G_\Gamma$, and any group
$G_\Gamma$, and any group ![]() $H$ which is a graph product of countably infinite amenable groups over the same graph
$H$ which is a graph product of countably infinite amenable groups over the same graph ![]() $\Gamma$, we can build free, ergodic, probability measure-preserving actions of
$\Gamma$, we can build free, ergodic, probability measure-preserving actions of ![]() $G_\Gamma$ and
$G_\Gamma$ and ![]() $H$ which are orbit equivalent [Reference Horbez and HuangHH22, Proposition 4.2]. In fact, our proof of [Reference Horbez and HuangHH22, Proposition 4.2] shows that starting from any action
$H$ which are orbit equivalent [Reference Horbez and HuangHH22, Proposition 4.2]. In fact, our proof of [Reference Horbez and HuangHH22, Proposition 4.2] shows that starting from any action ![]() $G_\Gamma \curvearrowright Z$ as above, we can find a blown-up action
$G_\Gamma \curvearrowright Z$ as above, we can find a blown-up action ![]() $G_\Gamma \curvearrowright \hat {Z}$ (i.e. coming with a
$G_\Gamma \curvearrowright \hat {Z}$ (i.e. coming with a ![]() $G_\Gamma$-equivariant map
$G_\Gamma$-equivariant map ![]() $\hat {Z}\to Z$) which fails to be superrigid for orbit equivalence. We can also build two actions of
$\hat {Z}\to Z$) which fails to be superrigid for orbit equivalence. We can also build two actions of ![]() $G_\Gamma$ which are orbit equivalent but not conjugate [Reference Horbez and HuangHH22, Remark 4.4].
$G_\Gamma$ which are orbit equivalent but not conjugate [Reference Horbez and HuangHH22, Remark 4.4].
The goal of the present paper is to show that rigidity can be achieved if one restricts to a certain class of actions satisfying more restrictive ergodicity conditions, as in the following definition.
Definition 1 Let ![]() $G$ be a right-angled Artin group. A free, probability measure-preserving action of
$G$ be a right-angled Artin group. A free, probability measure-preserving action of ![]() $G$ on a standard probability space
$G$ on a standard probability space ![]() $X$ is irreducible if there exist a finite simple graph
$X$ is irreducible if there exist a finite simple graph ![]() $\Gamma$ and an isomorphism between
$\Gamma$ and an isomorphism between ![]() $G$ and the right-angled Artin group
$G$ and the right-angled Artin group ![]() $G_\Gamma$ such that, through this isomorphism, every standard generator of
$G_\Gamma$ such that, through this isomorphism, every standard generator of ![]() $G_\Gamma$ (associated to a vertex of
$G_\Gamma$ (associated to a vertex of ![]() $\Gamma$) acts ergodically on
$\Gamma$) acts ergodically on ![]() $X$.
$X$.
The above definition is a natural extension of Monod and Shalom's irreducibility condition to the context of right-angled Artin groups (and could be naturally extended to graph products). Examples of irreducible actions of right-angled Artin groups include Bernoulli actions (considered in Theorem 3) and Gaussian actions associated to mixing orthogonal representations (introduced by Connes and Weiss in [Reference Connes and WeissCW80], see also [Reference Peterson and SinclairPS12, § 2.1] for a detailed study). To build other examples, one can start with a discrete and faithful representation of a right-angled Artin group into ![]() $\mathrm {SL}(n,\mathbb {R})$ or even
$\mathrm {SL}(n,\mathbb {R})$ or even ![]() $\mathrm {SL}(n,\mathbb {Z})$ (see [Reference WangWan07] for examples). Using this embedding in
$\mathrm {SL}(n,\mathbb {Z})$ (see [Reference WangWan07] for examples). Using this embedding in ![]() $\mathrm {SL}(n,\mathbb {R})$, one can then consider the restriction of a mixing action of a closed subgroup of
$\mathrm {SL}(n,\mathbb {R})$, one can then consider the restriction of a mixing action of a closed subgroup of ![]() $\mathrm {SL}(n,\mathbb {R})$ on a homogeneous space, coming from the Howe–Moore theorem [Reference Howe and MooreHM79], see e.g. [Reference BekkaBek18, Corollary 2.5]. Our main theorem is the following.
$\mathrm {SL}(n,\mathbb {R})$ on a homogeneous space, coming from the Howe–Moore theorem [Reference Howe and MooreHM79], see e.g. [Reference BekkaBek18, Corollary 2.5]. Our main theorem is the following.
Theorem 1 Let ![]() $G$ and
$G$ and ![]() $H$ be two one-ended right-angled Artin groups with trivial center. Let
$H$ be two one-ended right-angled Artin groups with trivial center. Let ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ be two free irreducible measure-preserving actions by Borel automorphisms on standard probability spaces.
$H\curvearrowright Y$ be two free irreducible measure-preserving actions by Borel automorphisms on standard probability spaces.
If the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are SOE (or merely stably
$H\curvearrowright Y$ are SOE (or merely stably ![]() $W^*$-equivalentFootnote 1), then they are conjugate, i.e. there exist a group isomorphism
$W^*$-equivalentFootnote 1), then they are conjugate, i.e. there exist a group isomorphism ![]() $\alpha :G\to H$ and a measure space isomorphism
$\alpha :G\to H$ and a measure space isomorphism ![]() $f:X\to Y$ such that for every
$f:X\to Y$ such that for every ![]() $g\in G$ and almost every
$g\in G$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $f(gx)=\alpha (g)f(x)$.
$f(gx)=\alpha (g)f(x)$.
Theorem 1 covers a much larger class of right-angled Artin groups than our previous work [Reference Horbez and HuangHH22], including many examples with infinite outer automorphism group.
For example, it applies to all right-angled Artin groups whose defining graph is a tree of diameter at least three, which are usually less rigid from other viewpoints (for instance, they are all quasi-isometric [Reference Behrstock and NeumannBN08], and the problem of their measure equivalence classification is open). In addition, in contrast to our previous work (and to other measure equivalence rigidity statements in the literature, such as [Reference KidaKid10, Reference Horbez and HuangHH20, Reference Guirardel and HorbezGH21]), our proof of Theorem 1 does not rely on a combinatorial rigidity statement for a curve graph analogue [Reference Kim and KoberdaKK14] associated to the right-angled Artin group. Instead, rigidity comes from the combination of a local argument (untwisting the orbit equivalence cocycle to a group homomorphism inside a vertex group), and a propagation argument where the commutation relations play a central role. The irreducibility assumption is crucial in both steps. The first step relies on a new orbit equivalence invariant of right-angled Artin groups (compared with [Reference Horbez and HuangHH22]), namely, the orbit equivalence relation remembers the maximal join subgroups of ![]() $G$ and
$G$ and ![]() $H$; this is important as it enables us to apply the results of Monod and Shalom in these local subgroups as a crucial step of the proof.
$H$; this is important as it enables us to apply the results of Monod and Shalom in these local subgroups as a crucial step of the proof.
As explained previously, counterexamples without the irreducibility assumption were given in [Reference Horbez and HuangHH22, § 4.1]. Counterexamples when the groups are infinitely ended already arise in the context of free groups. Indeed, Bowen proved in [Reference BowenBow11a] that all nontrivial Bernoulli shifts of a given finitely generated free group are orbit equivalent; more generally, if ![]() $G=A_1\ast \dots \ast A_n$ and
$G=A_1\ast \dots \ast A_n$ and ![]() $G'=A'_1\ast \dots \ast A'_n$ are two free products of amenable groups with the same number of factors, then all Bernoulli shifts of
$G'=A'_1\ast \dots \ast A'_n$ are two free products of amenable groups with the same number of factors, then all Bernoulli shifts of ![]() $G$ and
$G$ and ![]() $G'$ are orbit equivalent. In these contexts, the Bernoulli shifts are completely classified up to conjugation by the entropy of their base space [Reference BowenBow10b, Reference BowenBow10a], yielding a one-parameter family of orbit equivalent pairwise nonconjugate actions. He also proved that all nontrivial Bernoulli shifts of finitely generated nonabelian free groups (possibly of different ranks) are SOE [Reference BowenBow11b], although, as already mentioned, the work of Gaboriau ensures that they are not orbit equivalent when the ranks of the acting groups are different, by comparing their costs [Reference GaboriauGab00]. This is in sharp contrast with our Theorem 1, where SOE irreducible actions are automatically orbit equivalent and, in fact, even conjugate.
$G'$ are orbit equivalent. In these contexts, the Bernoulli shifts are completely classified up to conjugation by the entropy of their base space [Reference BowenBow10b, Reference BowenBow10a], yielding a one-parameter family of orbit equivalent pairwise nonconjugate actions. He also proved that all nontrivial Bernoulli shifts of finitely generated nonabelian free groups (possibly of different ranks) are SOE [Reference BowenBow11b], although, as already mentioned, the work of Gaboriau ensures that they are not orbit equivalent when the ranks of the acting groups are different, by comparing their costs [Reference GaboriauGab00]. This is in sharp contrast with our Theorem 1, where SOE irreducible actions are automatically orbit equivalent and, in fact, even conjugate.
We mention that in the context of right-angled Artin groups, the stable ![]() $W^*$-rigidity statement in Theorem 1 is a consequence of the stable orbit equivalence rigidity statement, using that the corresponding von Neumann algebras have a unique virtual Cartan subalgebra up to unitary conjugacy. Uniqueness of the virtual Cartan subalgebra up to unitary conjugacy was proved in a groundbreaking work of Popa and Vaes [Reference Popa and VaesPV14, Theorem 1.2 and Remark 1.3] for all free, ergodic, probability measure-preserving actions of groups satisfying Ozawa and Popa's property
$W^*$-rigidity statement in Theorem 1 is a consequence of the stable orbit equivalence rigidity statement, using that the corresponding von Neumann algebras have a unique virtual Cartan subalgebra up to unitary conjugacy. Uniqueness of the virtual Cartan subalgebra up to unitary conjugacy was proved in a groundbreaking work of Popa and Vaes [Reference Popa and VaesPV14, Theorem 1.2 and Remark 1.3] for all free, ergodic, probability measure-preserving actions of groups satisfying Ozawa and Popa's property ![]() $(\mathrm {HH})^+$; the fact that right-angled Artin groups satisfy this property was established by Ozawa and Popa in [Reference Ozawa and PopaOP10, Theorem 2.3(5)]. See also [Reference Horbez and HuangHH22, Corollary 3.20] for a more detailed explanation, and recent work of Chifan and Kunnawalkam Elayavalli for the more general case of graph products [Reference Chifan and Kunnawalkam ElayavalliCKE21].
$(\mathrm {HH})^+$; the fact that right-angled Artin groups satisfy this property was established by Ozawa and Popa in [Reference Ozawa and PopaOP10, Theorem 2.3(5)]. See also [Reference Horbez and HuangHH22, Corollary 3.20] for a more detailed explanation, and recent work of Chifan and Kunnawalkam Elayavalli for the more general case of graph products [Reference Chifan and Kunnawalkam ElayavalliCKE21].
We also mention that we actually obtain a slightly stronger statement than Theorem 1, namely: every stable orbit equivalence between the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ has compression 1 (see § 2.1 for definitions, and Propositions 6.1 and 6.2 for our precise statements). In particular, the fundamental group of the equivalence relation
$H\curvearrowright Y$ has compression 1 (see § 2.1 for definitions, and Propositions 6.1 and 6.2 for our precise statements). In particular, the fundamental group of the equivalence relation ![]() $\mathcal {R}$ associated to the action
$\mathcal {R}$ associated to the action ![]() $G\curvearrowright X$ (i.e. the subgroup of
$G\curvearrowright X$ (i.e. the subgroup of ![]() $\mathbb {R}_+^*$ consisting of all
$\mathbb {R}_+^*$ consisting of all ![]() $t>0$ such that
$t>0$ such that ![]() $\mathcal {R}$ is isomorphic to the amplification
$\mathcal {R}$ is isomorphic to the amplification ![]() $\mathcal {R}^t$) is trivial. Note that the class of one-ended right-angled Artin groups with trivial center contains groups whose
$\mathcal {R}^t$) is trivial. Note that the class of one-ended right-angled Artin groups with trivial center contains groups whose ![]() $\ell ^2$-Betti numbers all vanish (e.g. all right-angled Artin groups whose defining graph is a tree of diameter at least three, see [Reference Davis and LearyDL03]), and for these triviality of the fundamental group does not follow from Gaboriau's proportionality principle [Reference GaboriauGab02]. As a consequence, the fundamental group of the group measure space von Neumann algebra
$\ell ^2$-Betti numbers all vanish (e.g. all right-angled Artin groups whose defining graph is a tree of diameter at least three, see [Reference Davis and LearyDL03]), and for these triviality of the fundamental group does not follow from Gaboriau's proportionality principle [Reference GaboriauGab02]. As a consequence, the fundamental group of the group measure space von Neumann algebra ![]() $L^\infty (X)\rtimes G$ (defined by Murray and von Neumann in [Reference Murray and von NeumannMvN36, Reference Murray and von NeumannMvN43] as the subgroup of
$L^\infty (X)\rtimes G$ (defined by Murray and von Neumann in [Reference Murray and von NeumannMvN36, Reference Murray and von NeumannMvN43] as the subgroup of ![]() $\mathbb {R}_+^*$ consisting of all
$\mathbb {R}_+^*$ consisting of all ![]() $t>0$ such that
$t>0$ such that ![]() $L^\infty (X)\rtimes G$ is isomorphic to the amplification
$L^\infty (X)\rtimes G$ is isomorphic to the amplification ![]() $(L^\infty (X)\rtimes G)^t$) is also trivial. Indeed, this again follows from the analogous result for
$(L^\infty (X)\rtimes G)^t$) is also trivial. Indeed, this again follows from the analogous result for ![]() $\mathcal {R}$ precisely because
$\mathcal {R}$ precisely because ![]() $L^\infty (X)\rtimes G$ has a unique Cartan subalgebra; this reduction is at the heart of many remarkable results in deformation/rigidity theory [Reference PopaPop06a].
$L^\infty (X)\rtimes G$ has a unique Cartan subalgebra; this reduction is at the heart of many remarkable results in deformation/rigidity theory [Reference PopaPop06a].
Using general techniques from measured group theory, developed in successive works of Furman [Reference FurmanFur99b], Monod and Shalom [Reference Monod and ShalomMS06] and Kida [Reference KidaKid08], Theorem 1 yields a superrigidity theorem within the class of mildly mixing group actions. Recall that an action of a countable group ![]() $G$ on a standard probability space
$G$ on a standard probability space ![]() $X$ is mildly mixing if for every nonsingular properly ergodic action of
$X$ is mildly mixing if for every nonsingular properly ergodic action of ![]() $G$ on a standard probability measure space
$G$ on a standard probability measure space ![]() $Y$, the diagonal
$Y$, the diagonal ![]() $G$-action on
$G$-action on ![]() $X\times Y$ is ergodic. Recall also that two measure-preserving actions
$X\times Y$ is ergodic. Recall also that two measure-preserving actions ![]() $G_1\curvearrowright X_1$ and
$G_1\curvearrowright X_1$ and ![]() $G_2\curvearrowright X_2$ of countable groups on standard probability spaces are virtually conjugate if there exist short exact sequences
$G_2\curvearrowright X_2$ of countable groups on standard probability spaces are virtually conjugate if there exist short exact sequences ![]() $1\to F_i\to G_i\to \bar {G}_i\to 1$ with
$1\to F_i\to G_i\to \bar {G}_i\to 1$ with ![]() $F_i$ finite, finite-index subgroups
$F_i$ finite, finite-index subgroups ![]() $\bar {G}_i^0\subseteq \bar {G}_i$, and conjugate actions
$\bar {G}_i^0\subseteq \bar {G}_i$, and conjugate actions ![]() $\bar {G}^0_i\curvearrowright X'_i$ (through an isomorphism between
$\bar {G}^0_i\curvearrowright X'_i$ (through an isomorphism between ![]() $\bar {G}_1^0$ and
$\bar {G}_1^0$ and ![]() $\bar {G}_2^0$) such that for every
$\bar {G}_2^0$) such that for every ![]() $i\in \{1,2\}$, the action
$i\in \{1,2\}$, the action ![]() $\bar {G}_i\curvearrowright X_i/F_i$ is induced from
$\bar {G}_i\curvearrowright X_i/F_i$ is induced from ![]() $\bar {G}_i^0\curvearrowright X'_i$ as in [Reference KidaKid08, Definition 2.1].
$\bar {G}_i^0\curvearrowright X'_i$ as in [Reference KidaKid08, Definition 2.1].
Theorem 2 Let ![]() $G$ be a one-ended right-angled Artin group with trivial center. Let
$G$ be a one-ended right-angled Artin group with trivial center. Let ![]() $G\curvearrowright X$ be a free, irreducible, measure-preserving action of
$G\curvearrowright X$ be a free, irreducible, measure-preserving action of ![]() $G$ on a standard probability space
$G$ on a standard probability space ![]() $X$. Let
$X$. Let ![]() $H$ be a countable group, and let
$H$ be a countable group, and let ![]() $H\curvearrowright Y$ be a mildly mixing, free, measure-preserving action of
$H\curvearrowright Y$ be a mildly mixing, free, measure-preserving action of ![]() $H$ on a standard probability space
$H$ on a standard probability space ![]() $Y$.
$Y$.
If the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are SOE (or merely stably
$H\curvearrowright Y$ are SOE (or merely stably ![]() $W^*$-equivalent), then they are virtually conjugate.
$W^*$-equivalent), then they are virtually conjugate.
In the specific case of nontrivial Bernoulli actions of ![]() $G$ (i.e. of the form
$G$ (i.e. of the form ![]() $G\curvearrowright X_0^G$, where
$G\curvearrowright X_0^G$, where ![]() $X_0$ is a standard probability space not reduced to a single atom, and the action is by shift), an even stronger conclusion holds, which does not require any mildly mixing assumption on the
$X_0$ is a standard probability space not reduced to a single atom, and the action is by shift), an even stronger conclusion holds, which does not require any mildly mixing assumption on the ![]() $H$-action. By exploiting works of Popa [Reference PopaPop08] and of Ioana et al. [Reference Ioana, Popa and VaesIPV13], we reach the following statement.
$H$-action. By exploiting works of Popa [Reference PopaPop08] and of Ioana et al. [Reference Ioana, Popa and VaesIPV13], we reach the following statement.
Theorem 3 Let ![]() $G$ be an ICC countable group, which admits a finite generating set
$G$ be an ICC countable group, which admits a finite generating set ![]() $S=\{s_1,\dots,s_k\}$ made of infinite-order elements, such that for every
$S=\{s_1,\dots,s_k\}$ made of infinite-order elements, such that for every ![]() $i\in \{1,\dots,k-1\}$, the elements
$i\in \{1,\dots,k-1\}$, the elements ![]() $s_i$ and
$s_i$ and ![]() $s_{i+1}$ commute, and
$s_{i+1}$ commute, and ![]() $s_1$ has a nonamenable centralizer in
$s_1$ has a nonamenable centralizer in ![]() $G$.
$G$.
Let ![]() $G\curvearrowright X$ be a nontrivial Bernoulli action of
$G\curvearrowright X$ be a nontrivial Bernoulli action of ![]() $G$. Let
$G$. Let ![]() $H$ be a countable group, and let
$H$ be a countable group, and let ![]() $H\curvearrowright Y$ be a free, ergodic, measure-preserving action of
$H\curvearrowright Y$ be a free, ergodic, measure-preserving action of ![]() $H$ on a standard probability space
$H$ on a standard probability space ![]() $Y$.
$Y$.
If the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are orbit equivalent (or merely
$H\curvearrowright Y$ are orbit equivalent (or merely ![]() $W^*$-equivalent), then they are conjugate.
$W^*$-equivalent), then they are conjugate.
This applies to all one-ended nonabelian right-angled Artin groups: in fact, in this case, using the uniqueness of the virtual Cartan subalgebra up to unitary conjugacy, we also obtain that if the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are stably
$H\curvearrowright Y$ are stably ![]() $W^*$-equivalent, then they are virtually conjugate. The above theorem also applies to many (non-right-angled) Artin groups and to most mapping class groups of finite-type orientable surfaces. Let us also mention that the
$W^*$-equivalent, then they are virtually conjugate. The above theorem also applies to many (non-right-angled) Artin groups and to most mapping class groups of finite-type orientable surfaces. Let us also mention that the ![]() $W^*$-superrigidity of Bernoulli actions of countable ICC property (T) groups was proved by Ioana in [Reference IoanaIoa11]. It is conjectured that Bernoulli actions of nonamenable groups with vanishing first
$W^*$-superrigidity of Bernoulli actions of countable ICC property (T) groups was proved by Ioana in [Reference IoanaIoa11]. It is conjectured that Bernoulli actions of nonamenable groups with vanishing first ![]() $\ell ^2$-Betti number should always be
$\ell ^2$-Betti number should always be ![]() $W^*$-superrigid. This conjecture is a consequence of the combination of two conjectures of Popa, see [Reference PopaPop13, pp. 2 and 4] and [Reference IoanaIoa18, Problems III and IV]. Theorem 3 provides new classes of groups that verify this conjecture.
$W^*$-superrigid. This conjecture is a consequence of the combination of two conjectures of Popa, see [Reference PopaPop13, pp. 2 and 4] and [Reference IoanaIoa18, Problems III and IV]. Theorem 3 provides new classes of groups that verify this conjecture.
Let us conclude this introduction by presenting the main steps of our proof of Theorem 1. We have a cocycle ![]() $c:G\times X\to H$, given by the stable orbit equivalence of the actions. We first observe that it is enough to find a standard generator
$c:G\times X\to H$, given by the stable orbit equivalence of the actions. We first observe that it is enough to find a standard generator ![]() $s$ of
$s$ of ![]() $G$ such that, after replacing
$G$ such that, after replacing ![]() $c$ by a cohomologous cocycle (of the form
$c$ by a cohomologous cocycle (of the form ![]() $c'(g,x)=\varphi (gx)c(g,x)\varphi (x)^{-1}$ for some measurable map
$c'(g,x)=\varphi (gx)c(g,x)\varphi (x)^{-1}$ for some measurable map ![]() $\varphi :X\to H$), the map
$\varphi :X\to H$), the map ![]() $c_{|\langle s\rangle \times X}$ is almost everywhere constant. Indeed, a propagation argument, using that
$c_{|\langle s\rangle \times X}$ is almost everywhere constant. Indeed, a propagation argument, using that ![]() $s$ is part of a generating set of
$s$ is part of a generating set of ![]() $G$ with the property that two consecutive elements commute, then shows that
$G$ with the property that two consecutive elements commute, then shows that ![]() $c$ is cohomologous to a group homomorphism (and likewise for the given cocycle
$c$ is cohomologous to a group homomorphism (and likewise for the given cocycle ![]() $H\times Y\to G$), from which the conclusion follows. This propagation argument is presented in § 4.
$H\times Y\to G$), from which the conclusion follows. This propagation argument is presented in § 4.
The first step towards the above goal is to use the techniques from our previous work [Reference Horbez and HuangHH22] to ‘recognize’ certain natural subgroups of ![]() $G$ and
$G$ and ![]() $H$ from the orbit equivalence relation coming from their actions. More precisely, we prove that there exist maximal join parabolic subgroups
$H$ from the orbit equivalence relation coming from their actions. More precisely, we prove that there exist maximal join parabolic subgroups ![]() $P\subseteq G$ and
$P\subseteq G$ and ![]() $Q\subseteq H$ (i.e. decomposing as a nontrivial product), and positive measure Borel subsets
$Q\subseteq H$ (i.e. decomposing as a nontrivial product), and positive measure Borel subsets ![]() $U\subseteq X$ and
$U\subseteq X$ and ![]() $V\subseteq Y$, such that after identifying
$V\subseteq Y$, such that after identifying ![]() $U$ and
$U$ and ![]() $V$ through a measure-scaling isomorphism, the intersections of the
$V$ through a measure-scaling isomorphism, the intersections of the ![]() $P$-orbits with
$P$-orbits with ![]() $U$ coincide with the intersections of the
$U$ coincide with the intersections of the ![]() $Q$-orbits with
$Q$-orbits with ![]() $V$.
$V$.
If ![]() $P$ and
$P$ and ![]() $Q$ have trivial center, then we can directly apply Monod and Shalom's rigidity theorem [Reference Monod and ShalomMS06, Theorem 2.17] regarding actions of direct products of groups in the class
$Q$ have trivial center, then we can directly apply Monod and Shalom's rigidity theorem [Reference Monod and ShalomMS06, Theorem 2.17] regarding actions of direct products of groups in the class ![]() $\mathcal {C}_{\mathrm {reg}}$ to obtain the desired conclusion.
$\mathcal {C}_{\mathrm {reg}}$ to obtain the desired conclusion.
The most difficult case is when all maximal join parabolic subgroups of ![]() $G$ have nontrivial center. This often happens in fact: for instance, if the underlying graph of
$G$ have nontrivial center. This often happens in fact: for instance, if the underlying graph of ![]() $G$ is triangle-free and square-free, then the maximal join parabolic subgroups are exactly the star subgroups, isomorphic to
$G$ is triangle-free and square-free, then the maximal join parabolic subgroups are exactly the star subgroups, isomorphic to ![]() $\mathbb {Z}\times F_n$. In this case, a simple combinatorial argument enables us to find two maximal join parabolic subgroups
$\mathbb {Z}\times F_n$. In this case, a simple combinatorial argument enables us to find two maximal join parabolic subgroups ![]() $P_1,P_2\subseteq G$ with commuting centers. Using techniques from [Reference Horbez and HuangHH22], we are able to show that the orbits of the subgroups
$P_1,P_2\subseteq G$ with commuting centers. Using techniques from [Reference Horbez and HuangHH22], we are able to show that the orbits of the subgroups ![]() $P_i$, restricted to some positive measure Borel subset
$P_i$, restricted to some positive measure Borel subset ![]() $U$, coincide with the orbits (restricted to some
$U$, coincide with the orbits (restricted to some ![]() $V$) of two maximal join parabolic subgroups
$V$) of two maximal join parabolic subgroups ![]() $Q_1,Q_2\subseteq H$ with commuting centers. As the centers
$Q_1,Q_2\subseteq H$ with commuting centers. As the centers ![]() $A_1,A_2$ of
$A_1,A_2$ of ![]() $P_1,P_2$ act ergodically (and likewise for the centers
$P_1,P_2$ act ergodically (and likewise for the centers ![]() $B_1,B_2$ of
$B_1,B_2$ of ![]() $Q_1,Q_2$), we can then apply another rigidity theorem due to Monod and Shalom [Reference Monod and ShalomMS06] to derive that for every
$Q_1,Q_2$), we can then apply another rigidity theorem due to Monod and Shalom [Reference Monod and ShalomMS06] to derive that for every ![]() $i\in \{1,2\}$, the cocycle
$i\in \{1,2\}$, the cocycle ![]() $c$ is cohomologous to a cocycle
$c$ is cohomologous to a cocycle ![]() $c_i$ that induces a group isomorphism between the quotients
$c_i$ that induces a group isomorphism between the quotients ![]() $P_i/A_i$ and
$P_i/A_i$ and ![]() $Q_i/B_i$. Informally, this means that our cocycle
$Q_i/B_i$. Informally, this means that our cocycle ![]() $c_i$ is only controlled up to an ambiguity in the central direction. However, by comparing the ambiguities given by
$c_i$ is only controlled up to an ambiguity in the central direction. However, by comparing the ambiguities given by ![]() $c_1$ and
$c_1$ and ![]() $c_2$, we manage to cancel them and prove that
$c_2$, we manage to cancel them and prove that ![]() $c$ is actually cohomologous to a group homomorphism on
$c$ is actually cohomologous to a group homomorphism on ![]() $A_i$. As explained previously, this is enough to conclude our proof.
$A_i$. As explained previously, this is enough to conclude our proof.
1. Right-angled Artin groups and combinatorial lemmas
Given a finite simple graph ![]() $\Gamma$, the right-angled Artin group
$\Gamma$, the right-angled Artin group ![]() $G_\Gamma$ is the group defined by the following presentation:
$G_\Gamma$ is the group defined by the following presentation:
![]() $G_\Gamma =\langle V\Gamma \mid [v,w]=1$ if
$G_\Gamma =\langle V\Gamma \mid [v,w]=1$ if ![]() $v$ and
$v$ and ![]() $w$ are joined by an edge
$w$ are joined by an edge![]() $\rangle$.
$\rangle$.
The images in ![]() $G_\Gamma$ of the vertices of
$G_\Gamma$ of the vertices of ![]() $\Gamma$ form the standard generating set of
$\Gamma$ form the standard generating set of ![]() $G_\Gamma$. A full subgraph of
$G_\Gamma$. A full subgraph of ![]() $\Gamma$ is a subgraph
$\Gamma$ is a subgraph ![]() $\Lambda \subseteq \Gamma$ such that two vertices of
$\Lambda \subseteq \Gamma$ such that two vertices of ![]() $\Lambda$ are adjacent in
$\Lambda$ are adjacent in ![]() $\Lambda$ if and only if they are adjacent in
$\Lambda$ if and only if they are adjacent in ![]() $\Gamma$. Any full subgraph
$\Gamma$. Any full subgraph ![]() $\Lambda \subseteq \Gamma$ induces an injective homomorphism
$\Lambda \subseteq \Gamma$ induces an injective homomorphism ![]() $G_{\Lambda }\hookrightarrow G_{\Gamma }$ (sending the standard generating set of
$G_{\Lambda }\hookrightarrow G_{\Gamma }$ (sending the standard generating set of ![]() $G_\Lambda$ to a subset of the standard generating set of
$G_\Lambda$ to a subset of the standard generating set of ![]() $G_\Gamma$), whose image is called a standard subgroup of
$G_\Gamma$), whose image is called a standard subgroup of ![]() $G_{\Gamma }$. Conjugates of standard subgroups are called parabolic subgroups of
$G_{\Gamma }$. Conjugates of standard subgroups are called parabolic subgroups of ![]() $G_\Gamma$.
$G_\Gamma$.
It is known that if ![]() $gG_{\Lambda _1}g^{-1}\subseteq G_{\Lambda _2}$ for some full subgraphs
$gG_{\Lambda _1}g^{-1}\subseteq G_{\Lambda _2}$ for some full subgraphs ![]() $\Lambda _1,\Lambda _2$ of
$\Lambda _1,\Lambda _2$ of ![]() $\Gamma$, then
$\Gamma$, then ![]() $\Lambda _1\subseteq \Lambda _2$ and there exists
$\Lambda _1\subseteq \Lambda _2$ and there exists ![]() $h\in G_{\Lambda _2}$ such that
$h\in G_{\Lambda _2}$ such that ![]() $hG_{\Lambda _1}h^{-1}=gG_{\Lambda _1}g^{-1}$ (this follows from [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2]). Thus, the parabolic subgroup
$hG_{\Lambda _1}h^{-1}=gG_{\Lambda _1}g^{-1}$ (this follows from [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2]). Thus, the parabolic subgroup ![]() $gG_{\Lambda _1}g^{-1}$ of
$gG_{\Lambda _1}g^{-1}$ of ![]() $G_\Gamma$ is also a parabolic subgroup of
$G_\Gamma$ is also a parabolic subgroup of ![]() $G_{\Lambda _2}$.
$G_{\Lambda _2}$.
For a full subgraph ![]() $\Lambda \subseteq \Gamma$, define
$\Lambda \subseteq \Gamma$, define ![]() $\Lambda ^\perp$ to be the full subgraph spanned by all vertices in
$\Lambda ^\perp$ to be the full subgraph spanned by all vertices in ![]() $V\Gamma \setminus V\Lambda$ that are adjacent to all vertices of
$V\Gamma \setminus V\Lambda$ that are adjacent to all vertices of ![]() $\Lambda$. Let now
$\Lambda$. Let now ![]() $P=gG_{\Lambda }g^{-1}$ be a parabolic subgroup. We define
$P=gG_{\Lambda }g^{-1}$ be a parabolic subgroup. We define ![]() $P^\perp =gG_{\Lambda ^\perp }g^{-1}$. This is well-defined: if we can write the parabolic subgroup
$P^\perp =gG_{\Lambda ^\perp }g^{-1}$. This is well-defined: if we can write the parabolic subgroup ![]() $P$ in two different ways
$P$ in two different ways ![]() $gG_{\Lambda }g^{-1}$ and
$gG_{\Lambda }g^{-1}$ and ![]() $hG_{\Lambda '}h^{-1}$, then [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2] implies that
$hG_{\Lambda '}h^{-1}$, then [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2] implies that ![]() $\Lambda =\Lambda '$ and
$\Lambda =\Lambda '$ and ![]() $gG_{\Lambda ^\perp }g^{-1}=hG_{\Lambda ^\perp }h^{-1}$.
$gG_{\Lambda ^\perp }g^{-1}=hG_{\Lambda ^\perp }h^{-1}$.
Lemma 1.1 (Charney, Crisp and Vogtmann [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2])
Let ![]() $P\subseteq G_\Gamma$ be a para- bolic subgroup. Then the normalizer of
$P\subseteq G_\Gamma$ be a para- bolic subgroup. Then the normalizer of ![]() $P$ in
$P$ in ![]() $G_{\Gamma }$ is
$G_{\Gamma }$ is ![]() $P\times P^\perp$.
$P\times P^\perp$.
Many properties of ![]() $G_\Gamma$ can be read from its defining graph
$G_\Gamma$ can be read from its defining graph ![]() $\Gamma$. For instance,
$\Gamma$. For instance, ![]() $G_\Gamma$ is one-ended if and only if
$G_\Gamma$ is one-ended if and only if ![]() $\Gamma$ is connected, and
$\Gamma$ is connected, and ![]() $G_\Gamma$ has trivial center if and only if no vertex of
$G_\Gamma$ has trivial center if and only if no vertex of ![]() $\Gamma$ is connected to every other vertex.
$\Gamma$ is connected to every other vertex.
For any full subgraph ![]() $\Lambda \subseteq \Gamma$, there is a retraction
$\Lambda \subseteq \Gamma$, there is a retraction ![]() $r_\Lambda :G_{\Gamma }\to G_{\Lambda }$ defined by sending every element of the standard generating set corresponding to a vertex in
$r_\Lambda :G_{\Gamma }\to G_{\Lambda }$ defined by sending every element of the standard generating set corresponding to a vertex in ![]() $V\Gamma \setminus V\Lambda$ to the identity element. Hence, for any parabolic subgroup
$V\Gamma \setminus V\Lambda$ to the identity element. Hence, for any parabolic subgroup ![]() $P=gG_{\Lambda }g^{-1}$ of
$P=gG_{\Lambda }g^{-1}$ of ![]() $G_{\Gamma }$, we have a (uniquely well-defined) retraction
$G_{\Gamma }$, we have a (uniquely well-defined) retraction ![]() $r_P:G_{\Gamma }\to P$, defined by letting
$r_P:G_{\Gamma }\to P$, defined by letting ![]() $r_P(gsg^{-1})=gr_\Lambda (s)g^{-1}$ for every standard generator
$r_P(gsg^{-1})=gr_\Lambda (s)g^{-1}$ for every standard generator ![]() $s$ of
$s$ of ![]() $G_\Gamma$.
$G_\Gamma$.
A join subgraph ![]() $\Lambda$ of
$\Lambda$ of ![]() $\Gamma$ is a full subgraph which admits a join decomposition
$\Gamma$ is a full subgraph which admits a join decomposition ![]() $\Lambda =\Lambda _1\circ \Lambda _2$ (i.e. every vertex of
$\Lambda =\Lambda _1\circ \Lambda _2$ (i.e. every vertex of ![]() $\Lambda _1$ is adjacent to every vertex of
$\Lambda _1$ is adjacent to every vertex of ![]() $\Lambda _2$) with
$\Lambda _2$) with ![]() $\Lambda _i\neq \emptyset$ for every
$\Lambda _i\neq \emptyset$ for every ![]() $i\in \{1,2\}$. A maximal join subgraph is a join subgraph which is not properly contained in another join subgraph.
$i\in \{1,2\}$. A maximal join subgraph is a join subgraph which is not properly contained in another join subgraph.
A (maximal) join parabolic subgroup is a parabolic subgroup of the form ![]() $gG_{\Lambda }g^{-1}$ where
$gG_{\Lambda }g^{-1}$ where ![]() $\Lambda$ is a (maximal) join subgraph of
$\Lambda$ is a (maximal) join subgraph of ![]() $\Gamma$.
$\Gamma$.
The clique factor of a graph ![]() $\Lambda$ is the maximal complete subgraph appearing in a join decomposition of
$\Lambda$ is the maximal complete subgraph appearing in a join decomposition of ![]() $\Lambda$.
$\Lambda$.
Lemma 1.2 Let ![]() $G=G_\Gamma$ be a right-angled Artin group, let
$G=G_\Gamma$ be a right-angled Artin group, let ![]() $P$ be a join parabolic subgroup of
$P$ be a join parabolic subgroup of ![]() $G$, and let
$G$, and let ![]() $S\subseteq P$ be a parabolic subgroup. Then
$S\subseteq P$ be a parabolic subgroup. Then ![]() $S\times S^{\perp }$ is a join parabolic subgroup.
$S\times S^{\perp }$ is a join parabolic subgroup.
Proof. Let ![]() $\Lambda \subseteq \Gamma$ be a full subgraph such that
$\Lambda \subseteq \Gamma$ be a full subgraph such that ![]() $P$ is conjugate to
$P$ is conjugate to ![]() $G_\Lambda$; the subgraph
$G_\Lambda$; the subgraph ![]() $\Lambda$ decomposes nontrivially as a join
$\Lambda$ decomposes nontrivially as a join ![]() $\Lambda =\Lambda _1\circ \Lambda _2$. Then
$\Lambda =\Lambda _1\circ \Lambda _2$. Then ![]() $S$ is conjugate to
$S$ is conjugate to ![]() $G_\Upsilon$ for some full subgraph
$G_\Upsilon$ for some full subgraph ![]() $\Upsilon$ of
$\Upsilon$ of ![]() $\Lambda$ (as follows from [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2]). If
$\Lambda$ (as follows from [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2]). If ![]() $\Upsilon \subseteq \Lambda _i$ for some
$\Upsilon \subseteq \Lambda _i$ for some ![]() $i\in \{1,2\}$, then
$i\in \{1,2\}$, then ![]() $\Upsilon ^{\perp }$ contains
$\Upsilon ^{\perp }$ contains ![]() $\Lambda _{3-i}$, so
$\Lambda _{3-i}$, so ![]() $S\times S^{\perp }$ is a join parabolic subgroup. Otherwise
$S\times S^{\perp }$ is a join parabolic subgroup. Otherwise ![]() $\Upsilon$ decomposes nontrivially as a join, and
$\Upsilon$ decomposes nontrivially as a join, and ![]() $S$ itself is a join parabolic subgroup (and, therefore, so is
$S$ itself is a join parabolic subgroup (and, therefore, so is ![]() $S\times S^{\perp }$).
$S\times S^{\perp }$).
Lemma 1.3 Let ![]() $G=G_\Gamma$ be a nonabelian right-angled Artin group with connected defining graph. Then no maximal join parabolic subgroup is abelian.
$G=G_\Gamma$ be a nonabelian right-angled Artin group with connected defining graph. Then no maximal join parabolic subgroup is abelian.
Proof. Let ![]() $\Omega \subseteq \Gamma$ be a maximal join subgraph, and assume towards a contradiction that
$\Omega \subseteq \Gamma$ be a maximal join subgraph, and assume towards a contradiction that ![]() $\Omega$ is a clique. As
$\Omega$ is a clique. As ![]() $G$ is nonabelian and
$G$ is nonabelian and ![]() $\Gamma$ is connected, we can find a vertex
$\Gamma$ is connected, we can find a vertex ![]() $v\in V\Omega$ which is joined by an edge to a vertex
$v\in V\Omega$ which is joined by an edge to a vertex ![]() $u\notin V\Omega$. In particular,
$u\notin V\Omega$. In particular, ![]() $v\circ v^{\perp }$ is a join subgraph of
$v\circ v^{\perp }$ is a join subgraph of ![]() $\Gamma$ which properly contains
$\Gamma$ which properly contains ![]() $\Omega$, contradicting the maximality of
$\Omega$, contradicting the maximality of ![]() $\Omega$.
$\Omega$.
The following basic combinatorial lemma will be crucial for the general structure of the proof of our main theorems: two different arguments will be used in the paper, depending on whether ![]() $G_\Gamma$ satisfies the first or second conclusion below.
$G_\Gamma$ satisfies the first or second conclusion below.
Lemma 1.4 Let ![]() $G=G_\Gamma$ be a one-ended right-angled Artin group with trivial center. Then either
$G=G_\Gamma$ be a one-ended right-angled Artin group with trivial center. Then either ![]() $G$ contains a maximal join parabolic subgroup with trivial center or otherwise
$G$ contains a maximal join parabolic subgroup with trivial center or otherwise ![]() $G$ contains two distinct nonabelian maximal join parabolic subgroups whose centers commute.
$G$ contains two distinct nonabelian maximal join parabolic subgroups whose centers commute.
Proof. We assume that every maximal join parabolic subgroup of ![]() $G$ has a nontrivial center, and prove that the second conclusion of the lemma holds. Let
$G$ has a nontrivial center, and prove that the second conclusion of the lemma holds. Let ![]() $\Omega$ be a maximal join subgraph in
$\Omega$ be a maximal join subgraph in ![]() $\Gamma$, with clique factor
$\Gamma$, with clique factor ![]() $\Omega _1$. As
$\Omega _1$. As ![]() $G$ has trivial center and
$G$ has trivial center and ![]() $\Gamma$ is connected (because
$\Gamma$ is connected (because ![]() $G$ is one-ended), there is a vertex
$G$ is one-ended), there is a vertex ![]() $v\in V\Omega$ such that
$v\in V\Omega$ such that ![]() $v$ is adjacent to a vertex
$v$ is adjacent to a vertex ![]() $u$ outside
$u$ outside ![]() $\Omega$. Let
$\Omega$. Let ![]() $\Lambda$ be a maximal join subgraph containing
$\Lambda$ be a maximal join subgraph containing ![]() $v\circ v^\perp$. Then
$v\circ v^\perp$. Then ![]() $\Omega _1\subsetneq v\circ v^\perp \subseteq \Lambda$ and
$\Omega _1\subsetneq v\circ v^\perp \subseteq \Lambda$ and ![]() $\Omega \neq \Lambda$ (as
$\Omega \neq \Lambda$ (as ![]() $u\in V\Lambda$). By Lemma 1.3, the parabolic subgroups
$u\in V\Lambda$). By Lemma 1.3, the parabolic subgroups ![]() $G_\Omega$ and
$G_\Omega$ and ![]() $G_\Lambda$ are nonabelian. Finally, letting
$G_\Lambda$ are nonabelian. Finally, letting ![]() $\Lambda _1$ be the clique factor of
$\Lambda _1$ be the clique factor of ![]() $\Lambda$, the group
$\Lambda$, the group ![]() $G_{\Lambda _1}$ commutes with
$G_{\Lambda _1}$ commutes with ![]() $G_{v\circ v^{\perp }}$, in particular
$G_{v\circ v^{\perp }}$, in particular ![]() $G_{\Lambda _1}$ and
$G_{\Lambda _1}$ and ![]() $G_{\Omega _1}$ commute.
$G_{\Omega _1}$ commute.
Lemma 1.5 Let ![]() $G=G_{\Gamma }$ be a right-angled Artin group, and let
$G=G_{\Gamma }$ be a right-angled Artin group, and let ![]() $P_1,P_2\subseteq G$ be two distinct maximal join parabolic subgroups. For every
$P_1,P_2\subseteq G$ be two distinct maximal join parabolic subgroups. For every ![]() $i\in \{1,2\}$, let
$i\in \{1,2\}$, let ![]() $Z_i$ be the center of
$Z_i$ be the center of ![]() $P_i$.
$P_i$.
Then ![]() $Z_1\cap Z_2=\{1\}$. In particular, if
$Z_1\cap Z_2=\{1\}$. In particular, if ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ commute, then
$Z_2$ commute, then ![]() $Z_1\subseteq Z_2^{\perp }$ and
$Z_1\subseteq Z_2^{\perp }$ and ![]() $Z_2\subseteq Z_1^{\perp }$.
$Z_2\subseteq Z_1^{\perp }$.
Proof. For every ![]() $i\in \{1,2\}$, the subgroup
$i\in \{1,2\}$, the subgroup ![]() $Z_i$ is a parabolic subgroup of
$Z_i$ is a parabolic subgroup of ![]() $G$, so
$G$, so ![]() $Z_1\cap Z_2$ is a parabolic subgroup of
$Z_1\cap Z_2$ is a parabolic subgroup of ![]() $G$ by [Reference Duncan, Kazachkov and RemeslennikovDKR07, Proposition 2.6]. Let
$G$ by [Reference Duncan, Kazachkov and RemeslennikovDKR07, Proposition 2.6]. Let ![]() $Z=Z_1\cap Z_2$, and assume towards a contradiction that
$Z=Z_1\cap Z_2$, and assume towards a contradiction that ![]() $Z\neq \{1\}$. Then
$Z\neq \{1\}$. Then ![]() $P=Z\times Z^{\perp }$ is a join parabolic subgroup of
$P=Z\times Z^{\perp }$ is a join parabolic subgroup of ![]() $G$ which contains
$G$ which contains ![]() $P_1$ and
$P_1$ and ![]() $P_2$. By maximality, we have
$P_2$. By maximality, we have ![]() $P_1=P_2=P$, a contradiction.
$P_1=P_2=P$, a contradiction.
We now prove the last assertion of the lemma, so assume that ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ commute. Then
$Z_2$ commute. Then ![]() $Z_2$ is a parabolic subgroup of
$Z_2$ is a parabolic subgroup of ![]() $G$ contained in
$G$ contained in ![]() $Z_1\times Z_1^{\perp }$, so it is a parabolic subgroup of
$Z_1\times Z_1^{\perp }$, so it is a parabolic subgroup of ![]() $Z_1\times Z_1^{\perp }$ (as can be derived from [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2(2)]). However, [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2(2)] also ensures that parabolic subgroups of
$Z_1\times Z_1^{\perp }$ (as can be derived from [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2(2)]). However, [Reference Charney, Crisp and VogtmannCCV07, Proposition 2.2(2)] also ensures that parabolic subgroups of ![]() $Z_1\times Z_1^{\perp }$ are of the form
$Z_1\times Z_1^{\perp }$ are of the form ![]() $A\times B$, where
$A\times B$, where ![]() $A$ is a parabolic subgroup of
$A$ is a parabolic subgroup of ![]() $Z_1$ and
$Z_1$ and ![]() $B$ is a parabolic subgroup of
$B$ is a parabolic subgroup of ![]() $Z_1^{\perp }$. As
$Z_1^{\perp }$. As ![]() $Z_2\cap Z_1=\{1\}$, it follows that
$Z_2\cap Z_1=\{1\}$, it follows that ![]() $Z_2\subseteq Z_1^{\perp }$. The fact that
$Z_2\subseteq Z_1^{\perp }$. The fact that ![]() $Z_2\subseteq Z_1^{\perp }$ follows by symmetry.
$Z_2\subseteq Z_1^{\perp }$ follows by symmetry.
Recall that a countable group ![]() $G$ is ICC (standing for infinite conjugacy classes) if the conjugacy class of every nontrivial element of
$G$ is ICC (standing for infinite conjugacy classes) if the conjugacy class of every nontrivial element of ![]() $G$ is infinite.
$G$ is infinite.
Lemma 1.6 Every right-angled Artin group with trivial center is ICC.
Proof. Let ![]() $G$ be a right-angled Artin group with trivial center, with defining graph
$G$ be a right-angled Artin group with trivial center, with defining graph ![]() $\Gamma$, and let
$\Gamma$, and let ![]() $\Gamma =\Gamma _1\circ \cdots \circ \Gamma _{k}$ be a join decomposition of
$\Gamma =\Gamma _1\circ \cdots \circ \Gamma _{k}$ be a join decomposition of ![]() $\Gamma$ into factors which does not allow any further nontrivial join decomposition. Then each
$\Gamma$ into factors which does not allow any further nontrivial join decomposition. Then each ![]() $G_{\Gamma _i}$ has trivial center. It suffices to prove that each
$G_{\Gamma _i}$ has trivial center. It suffices to prove that each ![]() $G_{\Gamma _i}$ is ICC. Note that
$G_{\Gamma _i}$ is ICC. Note that ![]() $G_{\Gamma _i}$ is acylindrically hyperbolic in the sense of [Reference OsinOsi16]: the case when
$G_{\Gamma _i}$ is acylindrically hyperbolic in the sense of [Reference OsinOsi16]: the case when ![]() $\Gamma _i$ is connected follows from [Reference Kim and KoberdaKK14, Theorem 30], or alternatively from the combination of [Reference SistoSis18, Reference OsinOsi16], and the case when
$\Gamma _i$ is connected follows from [Reference Kim and KoberdaKK14, Theorem 30], or alternatively from the combination of [Reference SistoSis18, Reference OsinOsi16], and the case when ![]() $\Gamma _i$ is disconnected follows from the fact that
$\Gamma _i$ is disconnected follows from the fact that ![]() $G_{\Gamma _i}$ splits nontrivially as a free product. Hence,
$G_{\Gamma _i}$ splits nontrivially as a free product. Hence, ![]() $G_{\Gamma _i}$ is ICC by [Reference Dahmani, Guirardel and OsinDGO17, Theorem 2.35].
$G_{\Gamma _i}$ is ICC by [Reference Dahmani, Guirardel and OsinDGO17, Theorem 2.35].
2. Background on stable orbit equivalence and measured groupoids
This section reviews material regarding stable orbit equivalence, cocycles and measured groupoids. A familiar reader can directly skip to the next section.
2.1 Stable orbit equivalence and cocycles
A standard Borel space is a measurable space ![]() $X$ which is isomorphic to a Polish topological space (i.e. separable and completely metrizable) equipped with its Borel
$X$ which is isomorphic to a Polish topological space (i.e. separable and completely metrizable) equipped with its Borel ![]() $\sigma$-algebra. By a standard probability space we mean a standard Borel space equipped with a Borel measure
$\sigma$-algebra. By a standard probability space we mean a standard Borel space equipped with a Borel measure ![]() $\mu$ such that
$\mu$ such that ![]() $\mu (X)=1$. In this paper, all actions of countable groups on standard Borel spaces are assumed to be by Borel automorphisms. Given a standard probability space
$\mu (X)=1$. In this paper, all actions of countable groups on standard Borel spaces are assumed to be by Borel automorphisms. Given a standard probability space ![]() $(X,\mu )$ and a Borel subset
$(X,\mu )$ and a Borel subset ![]() $A\subseteq X$ of positive measure, we denote by
$A\subseteq X$ of positive measure, we denote by ![]() $\mu _A$ the Borel probability measure on
$\mu _A$ the Borel probability measure on ![]() $A$ defined by renormalizing
$A$ defined by renormalizing ![]() $\mu _{|A}$.
$\mu _{|A}$.
Let ![]() $G$ and
$G$ and ![]() $H$ be two countable groups, and assume we have a measure-preserving
$H$ be two countable groups, and assume we have a measure-preserving ![]() $G$-action on a standard probability space
$G$-action on a standard probability space ![]() $X$. A measurable map
$X$. A measurable map ![]() $c:G\times X\to H$ is a cocycle if for every
$c:G\times X\to H$ is a cocycle if for every ![]() $g,g'\in G$ and almost every
$g,g'\in G$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c(gg',x)=c(g,g'x)c(g',x)$. The cocycle
$c(gg',x)=c(g,g'x)c(g',x)$. The cocycle ![]() $c$ is strict if this relation holds for all
$c$ is strict if this relation holds for all ![]() $g,g'\in G$ and all
$g,g'\in G$ and all ![]() $x\in X$. As
$x\in X$. As ![]() $G$ is countable, there always exists a
$G$ is countable, there always exists a ![]() $G$-invariant conull Borel subset
$G$-invariant conull Borel subset ![]() $X^*\subseteq X$ such that
$X^*\subseteq X$ such that ![]() $c_{|G\times X^*}$ is a strict cocycle. Two cocycles
$c_{|G\times X^*}$ is a strict cocycle. Two cocycles ![]() $c,c':G\times X\to H$ are cohomologous if there exists a measurable map
$c,c':G\times X\to H$ are cohomologous if there exists a measurable map ![]() $\varphi :X\to H$ such that for all
$\varphi :X\to H$ such that for all ![]() $g\in G$ and almost every
$g\in G$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c'(g,x)=\varphi (gx)c(g,x)\varphi (x)^{-1}$.
$c'(g,x)=\varphi (gx)c(g,x)\varphi (x)^{-1}$.
We now briefly review the notion of SOE group actions, and refer the reader to [Reference FurmanFur99b] for more information. Let ![]() $G\curvearrowright (X,\mu )$ and
$G\curvearrowright (X,\mu )$ and ![]() $H\curvearrowright (Y,\nu )$ be two free, ergodic, measure-preserving actions on standard probability spaces. A stable orbit equivalence between
$H\curvearrowright (Y,\nu )$ be two free, ergodic, measure-preserving actions on standard probability spaces. A stable orbit equivalence between ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ is a measure space isomorphism
$H\curvearrowright Y$ is a measure space isomorphism ![]() $f:(U,\mu _U)\to (V,\nu _V)$, where
$f:(U,\mu _U)\to (V,\nu _V)$, where ![]() $U\subseteq X$ and
$U\subseteq X$ and ![]() $V\subseteq Y$ are positive measure Borel subsets, such that
$V\subseteq Y$ are positive measure Borel subsets, such that ![]() $f((G\cdot x)\cap U)=(H\cdot f(x))\cap V$ for almost every
$f((G\cdot x)\cap U)=(H\cdot f(x))\cap V$ for almost every ![]() $x\in U$. The compression constant of
$x\in U$. The compression constant of ![]() $f$ is defined as
$f$ is defined as ![]() $\kappa (f)=\nu (V)/\mu (U)$. Following the exposition from [Reference VaesVae07, § 4], we say that a cocycle
$\kappa (f)=\nu (V)/\mu (U)$. Following the exposition from [Reference VaesVae07, § 4], we say that a cocycle ![]() $c:G\times X\to H$ is an SOE cocycle associated to
$c:G\times X\to H$ is an SOE cocycle associated to ![]() $f$ if there exists a measurable map
$f$ if there exists a measurable map ![]() $p:X\to U$, with
$p:X\to U$, with ![]() $p(x)\in G\cdot x$ for almost every
$p(x)\in G\cdot x$ for almost every ![]() $x\in X$, such that for almost every
$x\in X$, such that for almost every ![]() $x\in X$,
$x\in X$, ![]() $c(g,x)$ is the unique element
$c(g,x)$ is the unique element ![]() $h\in H$ such that
$h\in H$ such that ![]() $f\circ p(g\cdot x)=h \cdot (f\circ p(x))$ (uniqueness comes from freeness of the
$f\circ p(g\cdot x)=h \cdot (f\circ p(x))$ (uniqueness comes from freeness of the ![]() $H$-action). An SOE cocycle associated to
$H$-action). An SOE cocycle associated to ![]() $f$ always exists by ergodicity of the
$f$ always exists by ergodicity of the ![]() $G$-action (i.e. we can always find a map
$G$-action (i.e. we can always find a map ![]() $p$ as above), and any two such cocycles (corresponding to different choices of
$p$ as above), and any two such cocycles (corresponding to different choices of ![]() $p$) are cohomologous. Note that we can always choose
$p$) are cohomologous. Note that we can always choose ![]() $p$ as above such that
$p$ as above such that ![]() $p_{|U}=\mathrm {id}_U$. The two actions
$p_{|U}=\mathrm {id}_U$. The two actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are SOE if there exists a stable orbit equivalence between them; they are orbit equivalent if it can be chosen with
$H\curvearrowright Y$ are SOE if there exists a stable orbit equivalence between them; they are orbit equivalent if it can be chosen with ![]() $U=X$ and
$U=X$ and ![]() $V=Y$. We mention that two free, ergodic, measure-preserving actions on standard probability spaces are orbit equivalent if and only if there is a stable orbit equivalence between them whose compression constant is equal to one, see [Reference FurmanFur99b, Proposition 2.7].
$V=Y$. We mention that two free, ergodic, measure-preserving actions on standard probability spaces are orbit equivalent if and only if there is a stable orbit equivalence between them whose compression constant is equal to one, see [Reference FurmanFur99b, Proposition 2.7].
In the above situation, observe that if ![]() $A\subseteq G$ and
$A\subseteq G$ and ![]() $B\subseteq H$ are subgroups acting ergodically on
$B\subseteq H$ are subgroups acting ergodically on ![]() $X,Y$, and satisfy
$X,Y$, and satisfy ![]() $f((A\cdot x)\cap U)=(B\cdot f(x))\cap V$, then an SOE cocycle associated to
$f((A\cdot x)\cap U)=(B\cdot f(x))\cap V$, then an SOE cocycle associated to ![]() $f$ can always be chosen so that
$f$ can always be chosen so that ![]() $c_{|A\times X}$ is an SOE cocycle associated to
$c_{|A\times X}$ is an SOE cocycle associated to ![]() $f$, viewed as a stable orbit equivalence between the actions
$f$, viewed as a stable orbit equivalence between the actions ![]() $A\curvearrowright X$ and
$A\curvearrowright X$ and ![]() $B\curvearrowright Y$ (in particular,
$B\curvearrowright Y$ (in particular, ![]() $c(A\times X^*)\subseteq B$ for some conull Borel subset
$c(A\times X^*)\subseteq B$ for some conull Borel subset ![]() $X^*\subseteq X$). Indeed, this is proved by choosing the map
$X^*\subseteq X$). Indeed, this is proved by choosing the map ![]() $p$ so that
$p$ so that ![]() $p(x)\in A\cdot x$ for almost every
$p(x)\in A\cdot x$ for almost every ![]() $x\in X$.
$x\in X$.
2.2 Background on measured groupoids
The arguments in § 5 rely on earlier work of the first two named authors [Reference Horbez and HuangHH22], which is phrased in the language of measured groupoids. In this section we offer a quick review and refer the reader to [Reference Anantharaman-DelarocheAD13, § 2.1], [Reference KidaKid09] or [Reference Guirardel and HorbezGH21, § 3] for more detailed treatments. It is possible to skip this section for now and come back to it when reading § 5.
A discrete Borel groupoid is a standard Borel space ![]() $\mathcal {G}$ equipped with two Borel maps
$\mathcal {G}$ equipped with two Borel maps ![]() $s,r:\mathcal {G}\to X$ towards a standard Borel space
$s,r:\mathcal {G}\to X$ towards a standard Borel space ![]() $X$ whose fibers are at most countable, and coming with a measurable (partially defined) composition law, a measurable inverse map, and a unit element
$X$ whose fibers are at most countable, and coming with a measurable (partially defined) composition law, a measurable inverse map, and a unit element ![]() $e_x$ per
$e_x$ per ![]() $x\in X$. The space
$x\in X$. The space ![]() $X$ is called the base space of the groupoid, and we think of an element
$X$ is called the base space of the groupoid, and we think of an element ![]() $g\in \mathcal {G}$ as being an arrow whose source
$g\in \mathcal {G}$ as being an arrow whose source ![]() $s(g)$ and range
$s(g)$ and range ![]() $r(g)$ both belong to
$r(g)$ both belong to ![]() $X$ (composition of two arrows
$X$ (composition of two arrows ![]() $g_1g_2$ makes sense when
$g_1g_2$ makes sense when ![]() $s(g_1)=r(g_2)$). A bisection of
$s(g_1)=r(g_2)$). A bisection of ![]() $\mathcal {G}$ is a Borel subset
$\mathcal {G}$ is a Borel subset ![]() $B\subseteq \mathcal {G}$ such that
$B\subseteq \mathcal {G}$ such that ![]() $s_{|B}$ and
$s_{|B}$ and ![]() $r_{|B}$ are injective; it thus defines a Borel isomorphism between two Borel subsets of
$r_{|B}$ are injective; it thus defines a Borel isomorphism between two Borel subsets of ![]() $X$ (see [Reference KechrisKec95, Corollary 15.2]). A theorem of Lusin and Novikov (see [Reference KechrisKec95, Theorem 18.10]) ensures that any discrete Borel groupoid is covered by countably many pairwise disjoint bisections. A measured groupoid is a discrete Borel groupoid
$X$ (see [Reference KechrisKec95, Corollary 15.2]). A theorem of Lusin and Novikov (see [Reference KechrisKec95, Theorem 18.10]) ensures that any discrete Borel groupoid is covered by countably many pairwise disjoint bisections. A measured groupoid is a discrete Borel groupoid ![]() $\mathcal {G}$ whose base space
$\mathcal {G}$ whose base space ![]() $X$ comes equipped with a quasi-invariant finite Borel measure
$X$ comes equipped with a quasi-invariant finite Borel measure ![]() $\mu$, i.e. for every bisection
$\mu$, i.e. for every bisection ![]() $B\subseteq \mathcal {G}$, one has
$B\subseteq \mathcal {G}$, one has ![]() $\mu (s(B))=0$ if and only if
$\mu (s(B))=0$ if and only if ![]() $\mu (r(B))=0$. A measured groupoid
$\mu (r(B))=0$. A measured groupoid ![]() $\mathcal {G}$ is trivial if
$\mathcal {G}$ is trivial if ![]() $\mathcal {G}=\{e_x|x\in X\}$. On the other hand,
$\mathcal {G}=\{e_x|x\in X\}$. On the other hand, ![]() $\mathcal {G}$ is of infinite type if for every Borel subset
$\mathcal {G}$ is of infinite type if for every Borel subset ![]() $U\subseteq X$ of positive measure, and almost every
$U\subseteq X$ of positive measure, and almost every ![]() $x\in U$, there are infinitely many elements
$x\in U$, there are infinitely many elements ![]() $g\in \mathcal {G}$ with
$g\in \mathcal {G}$ with ![]() $s(g)=x$ and
$s(g)=x$ and ![]() $r(g)\in U$.
$r(g)\in U$.
In the present paper, the most important example of a measured groupoid is the following. Let ![]() $G$ be a countable group which acts on a standard finite measure space
$G$ be a countable group which acts on a standard finite measure space ![]() $X$ by Borel automorphisms in a measure-preserving way (or merely by preserving the measure class). Then
$X$ by Borel automorphisms in a measure-preserving way (or merely by preserving the measure class). Then ![]() $G\times X$ is naturally a measured groupoid over
$G\times X$ is naturally a measured groupoid over ![]() $X$, with
$X$, with ![]() $s(g,x)=x$ and
$s(g,x)=x$ and ![]() $r(g,x)=gx$. This groupoid is denoted by
$r(g,x)=gx$. This groupoid is denoted by ![]() $G\ltimes X$.
$G\ltimes X$.
Let now ![]() $\mathcal {G}, X$ and
$\mathcal {G}, X$ and ![]() $\mu$ be as above. Every Borel subset
$\mu$ be as above. Every Borel subset ![]() $\mathcal {H}\subseteq \mathcal {G}$ which is stable under composition and inversion, and contains all unit elements
$\mathcal {H}\subseteq \mathcal {G}$ which is stable under composition and inversion, and contains all unit elements ![]() $e_x$, has the structure of a discrete Borel groupoid over
$e_x$, has the structure of a discrete Borel groupoid over ![]() $X$, for which
$X$, for which ![]() $\mu$ is quasi-invariant; we say that
$\mu$ is quasi-invariant; we say that ![]() $\mathcal {H}$ is a measured subgroupoid of
$\mathcal {H}$ is a measured subgroupoid of ![]() $\mathcal {G}$. Given two measured subgroupoids
$\mathcal {G}$. Given two measured subgroupoids ![]() $\mathcal {H}_1,\mathcal {H}_2\subseteq \mathcal {G}$, we denote by
$\mathcal {H}_1,\mathcal {H}_2\subseteq \mathcal {G}$, we denote by ![]() $\langle \mathcal {H}_1,\mathcal {H}_2\rangle$ the subgroupoid generated by
$\langle \mathcal {H}_1,\mathcal {H}_2\rangle$ the subgroupoid generated by ![]() $\mathcal {H}_1$ and
$\mathcal {H}_1$ and ![]() $\mathcal {H}_2$, defined as the smallest measured subgroupoid of
$\mathcal {H}_2$, defined as the smallest measured subgroupoid of ![]() $\mathcal {G}$ that contains
$\mathcal {G}$ that contains ![]() $\mathcal {H}_1$ and
$\mathcal {H}_1$ and ![]() $\mathcal {H}_2$; equivalently, this is the measured subgroupoid of
$\mathcal {H}_2$; equivalently, this is the measured subgroupoid of ![]() $\mathcal {G}$ made of all elements that are finite compositions of elements of
$\mathcal {G}$ made of all elements that are finite compositions of elements of ![]() $\mathcal {H}_1$ and
$\mathcal {H}_1$ and ![]() $\mathcal {H}_2$. Given any Borel subset
$\mathcal {H}_2$. Given any Borel subset ![]() $U\subseteq X$, the restriction
$U\subseteq X$, the restriction ![]() $\mathcal {G}_{|U}=\{g\in \mathcal {G}|s(g),r(g)\in U\}$ is naturally a measured groupoid over
$\mathcal {G}_{|U}=\{g\in \mathcal {G}|s(g),r(g)\in U\}$ is naturally a measured groupoid over ![]() $U$, with quasi-invariant measure
$U$, with quasi-invariant measure ![]() $\mu _{|U}$.
$\mu _{|U}$.
Given a countable group ![]() $G$, a strict cocycle
$G$, a strict cocycle ![]() $\rho :\mathcal {G}\to G$ is a Borel map such that for all
$\rho :\mathcal {G}\to G$ is a Borel map such that for all ![]() $g_1,g_2\in \mathcal {G}$ satisfying
$g_1,g_2\in \mathcal {G}$ satisfying ![]() $s(g_1)=r(g_2)$ (so that
$s(g_1)=r(g_2)$ (so that ![]() $g_1g_2$ is well-defined), one has
$g_1g_2$ is well-defined), one has ![]() $\rho (g_1g_2)=\rho (g_1)\rho (g_2)$. Its kernel is
$\rho (g_1g_2)=\rho (g_1)\rho (g_2)$. Its kernel is ![]() $\{g\in \mathcal {G}|\rho (g)=1\}$, a measured subgroupoid of
$\{g\in \mathcal {G}|\rho (g)=1\}$, a measured subgroupoid of ![]() $\mathcal {G}$. A strict cocycle
$\mathcal {G}$. A strict cocycle ![]() $\rho :\mathcal {G}\to G$ is action-type (as in [Reference Guirardel and HorbezGH21, Definition 3.20]) if it has trivial kernel, and for every infinite subgroup
$\rho :\mathcal {G}\to G$ is action-type (as in [Reference Guirardel and HorbezGH21, Definition 3.20]) if it has trivial kernel, and for every infinite subgroup ![]() $H\subseteq G$, the subgroupoid
$H\subseteq G$, the subgroupoid ![]() $\rho ^{-1}(H)$ is of infinite type. The following example is crucial: if
$\rho ^{-1}(H)$ is of infinite type. The following example is crucial: if ![]() $G$ acts on a standard finite measure space
$G$ acts on a standard finite measure space ![]() $X$ by Borel automorphisms in a measure-preserving way, then the natural cocycle
$X$ by Borel automorphisms in a measure-preserving way, then the natural cocycle ![]() $G\ltimes X\to G$ is action-type [Reference KidaKid09, Proposition 2.26].
$G\ltimes X\to G$ is action-type [Reference KidaKid09, Proposition 2.26].
Let now ![]() $\mathcal {H}$ and
$\mathcal {H}$ and ![]() $\mathcal {H}'$ be two measured subgroupoids of
$\mathcal {H}'$ be two measured subgroupoids of ![]() $\mathcal {G}$. The subgroupoid
$\mathcal {G}$. The subgroupoid ![]() $\mathcal {H}'$ is stably contained in
$\mathcal {H}'$ is stably contained in ![]() $\mathcal {H}$ (respectively, stably equal to
$\mathcal {H}$ (respectively, stably equal to ![]() $\mathcal {H}$) if there exist a conull Borel subset
$\mathcal {H}$) if there exist a conull Borel subset ![]() $X^*\subseteq X$ and a partition
$X^*\subseteq X$ and a partition ![]() $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every ![]() $i\in I$, one has
$i\in I$, one has ![]() $\mathcal {H}'_{|X_i}\subseteq \mathcal {H}_{|X_i}$ (respectively,
$\mathcal {H}'_{|X_i}\subseteq \mathcal {H}_{|X_i}$ (respectively, ![]() $\mathcal {H}'_{|X_i}=\mathcal {H}_{|X_i}$).
$\mathcal {H}'_{|X_i}=\mathcal {H}_{|X_i}$).
The subgroupoid ![]() $\mathcal {H}$ is normalized by
$\mathcal {H}$ is normalized by ![]() $\mathcal {H}'$ if there exists a conull Borel subset
$\mathcal {H}'$ if there exists a conull Borel subset ![]() $X^*\subseteq X$ such that
$X^*\subseteq X$ such that ![]() $\mathcal {H}'_{|X^*}$ can be covered by at most countably many bisections
$\mathcal {H}'_{|X^*}$ can be covered by at most countably many bisections ![]() $B_n$ in such a way that for every
$B_n$ in such a way that for every ![]() $n$, every
$n$, every ![]() $g_1,g_2\in B_n$, and every
$g_1,g_2\in B_n$, and every ![]() $h\in \mathcal {H}'_{|X^*}$ such that
$h\in \mathcal {H}'_{|X^*}$ such that ![]() $g_2hg_1^{-1}$ is well-defined, one has
$g_2hg_1^{-1}$ is well-defined, one has ![]() $h\in \mathcal {H}$ if and only if
$h\in \mathcal {H}$ if and only if ![]() $g_2hg_1^{-1}\in \mathcal {H}$. Here is an example: if
$g_2hg_1^{-1}\in \mathcal {H}$. Here is an example: if ![]() $\mathcal {G}$ comes equipped with a cocycle
$\mathcal {G}$ comes equipped with a cocycle ![]() $\rho :\mathcal {G}\to G$ towards a countable group, and if
$\rho :\mathcal {G}\to G$ towards a countable group, and if ![]() $H,H'\subseteq G$ are two subgroups such that
$H,H'\subseteq G$ are two subgroups such that ![]() $H$ is normalized by
$H$ is normalized by ![]() $H'$, then
$H'$, then ![]() $\rho ^{-1}(H)$ is normalized by
$\rho ^{-1}(H)$ is normalized by ![]() $\rho ^{-1}(H')$. The subgroupoid
$\rho ^{-1}(H')$. The subgroupoid ![]() $\mathcal {H}$ is stably normalized by
$\mathcal {H}$ is stably normalized by ![]() $\mathcal {H}'$ if there exists a partition
$\mathcal {H}'$ if there exists a partition ![]() $X=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every
$X=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every ![]() $i\in \mathbb {N}$, the groupoid
$i\in \mathbb {N}$, the groupoid ![]() $\mathcal {H}_{|X_i}$ is normalized by
$\mathcal {H}_{|X_i}$ is normalized by ![]() $\mathcal {H}'_{|X_i}$.
$\mathcal {H}'_{|X_i}$.
We refer to [Reference KidaKid09] for the notion of amenability of a measured groupoid, and only record a few properties we will need. Amenability of measured groupoids is stable under passing to subgroupoids and taking restrictions, and under stabilization in the following sense: if there exist a conull Borel subset ![]() $X^*\subseteq X$ and a partition
$X^*\subseteq X$ and a partition ![]() $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every ![]() $i\in I$, the groupoid
$i\in I$, the groupoid ![]() $\mathcal {G}_{|X_i}$ is amenable, then
$\mathcal {G}_{|X_i}$ is amenable, then ![]() $\mathcal {G}$ is amenable (see [Reference Guirardel and HorbezGH21, Definition 3.33 and Remark 3.34]). If
$\mathcal {G}$ is amenable (see [Reference Guirardel and HorbezGH21, Definition 3.33 and Remark 3.34]). If ![]() $\rho :\mathcal {G}\to G$ is a strict cocycle with trivial kernel towards a countable group
$\rho :\mathcal {G}\to G$ is a strict cocycle with trivial kernel towards a countable group ![]() $G$, and if
$G$, and if ![]() $A\subseteq G$ is amenable, then
$A\subseteq G$ is amenable, then ![]() $\rho ^{-1}(A)$ is amenable (see, e.g., [Reference Guirardel and HorbezGH21, Corollary 3.39]).
$\rho ^{-1}(A)$ is amenable (see, e.g., [Reference Guirardel and HorbezGH21, Corollary 3.39]).
A measured groupoid ![]() $\mathcal {G}$ over a standard finite measure space
$\mathcal {G}$ over a standard finite measure space ![]() $X$ is everywhere nonamenable if for every Borel subset
$X$ is everywhere nonamenable if for every Borel subset ![]() $U\subseteq X$ of positive measure, the restricted groupoid
$U\subseteq X$ of positive measure, the restricted groupoid ![]() $\mathcal {G}_{|U}$ is nonamenable. The following fact is crucial: if
$\mathcal {G}_{|U}$ is nonamenable. The following fact is crucial: if ![]() $\rho :\mathcal {G}\to G$ is a strict action-type cocycle towards a countable group
$\rho :\mathcal {G}\to G$ is a strict action-type cocycle towards a countable group ![]() $G$, and if
$G$, and if ![]() $G$ contains a nonabelian free subgroup, then
$G$ contains a nonabelian free subgroup, then ![]() $\mathcal {G}$ is everywhere nonamenable [Reference KidaKid10, Lemma 3.20] (compare also [Reference Horbez and HuangHH22, Remark 3.3]).
$\mathcal {G}$ is everywhere nonamenable [Reference KidaKid10, Lemma 3.20] (compare also [Reference Horbez and HuangHH22, Remark 3.3]).
3. Monod and Shalom's rigidity theorems
3.1 Quotient by a normal subgroup
The following lemma is extracted from the work of Monod and Shalom [Reference Monod and ShalomMS06]. Its proof comes from [Reference Monod and ShalomMS06, p. 862]; we recall it here for the convenience of the reader.
Lemma 3.1 (Monod and Shalom [Reference Monod and ShalomMS06])
Let ![]() $G,H$ be countable groups, and let
$G,H$ be countable groups, and let ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ be free ergodic measure-preserving actions on standard probability spaces. Assume that they are SOE, let
$H\curvearrowright Y$ be free ergodic measure-preserving actions on standard probability spaces. Assume that they are SOE, let ![]() $f:U\to V$ be a stable orbit equivalence between them (where
$f:U\to V$ be a stable orbit equivalence between them (where ![]() $U\subseteq X$ and
$U\subseteq X$ and ![]() $V\subseteq Y$ are positive measure Borel subsets), and let
$V\subseteq Y$ are positive measure Borel subsets), and let ![]() $c:G\times X\to H$ be an SOE cocycle associated to
$c:G\times X\to H$ be an SOE cocycle associated to ![]() $f$.
$f$.
Let ![]() $A\unlhd G$ and
$A\unlhd G$ and ![]() $B\unlhd H$ be normal subgroups acting ergodically on
$B\unlhd H$ be normal subgroups acting ergodically on ![]() $X,Y$, and assume that for every
$X,Y$, and assume that for every ![]() $x\in U$, one has
$x\in U$, one has ![]() $f((A\cdot x)\cap U)= (B\cdot f(x))\cap V$.
$f((A\cdot x)\cap U)= (B\cdot f(x))\cap V$.
Then there exist a group isomorphism ![]() $\alpha :G/A\to H/B$ and a measurable map
$\alpha :G/A\to H/B$ and a measurable map ![]() $\varphi :X\to H$ with
$\varphi :X\to H$ with ![]() $\varphi (x)=e$ for every
$\varphi (x)=e$ for every ![]() $x\in U$, such that for every
$x\in U$, such that for every ![]() $g\in G$ and almost every
$g\in G$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $\varphi (gx) c(g,x)\varphi (x)^{-1}\in \alpha (gA)$.
$\varphi (gx) c(g,x)\varphi (x)^{-1}\in \alpha (gA)$.
Proof. As observed in § 2.1, up to replacing ![]() $c$ by a cohomologous cocycle, and
$c$ by a cohomologous cocycle, and ![]() $X$ by a conull
$X$ by a conull ![]() $G$-invariant Borel subset, we can (and do) assume that
$G$-invariant Borel subset, we can (and do) assume that ![]() $c(A\times X)\subseteq B$. Likewise, up to replacing
$c(A\times X)\subseteq B$. Likewise, up to replacing ![]() $Y$ by a conull
$Y$ by a conull ![]() $H$-invariant subset, we can choose an SOE cocycle
$H$-invariant subset, we can choose an SOE cocycle ![]() $c':H\times Y\to G$ associated to the stable orbit equivalence
$c':H\times Y\to G$ associated to the stable orbit equivalence ![]() $f^{-1}:V\to U$ between
$f^{-1}:V\to U$ between ![]() $H\curvearrowright Y$ and
$H\curvearrowright Y$ and ![]() $G\curvearrowright X$, so that
$G\curvearrowright X$, so that ![]() $c'(B\times Y)\subseteq A$.
$c'(B\times Y)\subseteq A$.
Let ![]() $\Sigma =X\times H$, equipped with the measure-preserving action of
$\Sigma =X\times H$, equipped with the measure-preserving action of ![]() $G\times H$ given by
$G\times H$ given by ![]() $(g,h)\cdot (x,k)= (gx,c(g,x)kh^{-1})$. Letting
$(g,h)\cdot (x,k)= (gx,c(g,x)kh^{-1})$. Letting ![]() $X_e=X\times \{e\}$ (which is a fundamental domain for the
$X_e=X\times \{e\}$ (which is a fundamental domain for the ![]() $H$-action on
$H$-action on ![]() $\Sigma$), we observe that
$\Sigma$), we observe that ![]() $A X_e\subseteq B X_e$, so
$A X_e\subseteq B X_e$, so ![]() $A B X_e=BAX_e\subseteq B BX_e= BX_e$, thus
$A B X_e=BAX_e\subseteq B BX_e= BX_e$, thus ![]() $BX_e$ is invariant under
$BX_e$ is invariant under ![]() $A\times B$. In addition, from the ergodicity of the
$A\times B$. In addition, from the ergodicity of the ![]() $A$-action on
$A$-action on ![]() $X$, we deduce that the action of
$X$, we deduce that the action of ![]() $A\times B$ on
$A\times B$ on ![]() $BX_e$ is ergodic. Moreover, for every
$BX_e$ is ergodic. Moreover, for every ![]() $h\in H$, we have
$h\in H$, we have ![]() $hBX_e=BX_e$ if and only if
$hBX_e=BX_e$ if and only if ![]() $h\in B$, and otherwise
$h\in B$, and otherwise ![]() $hBX_e\cap BX_e=\emptyset$. In addition, the union of all
$hBX_e\cap BX_e=\emptyset$. In addition, the union of all ![]() $H$-translates of
$H$-translates of ![]() $BX_e$ cover
$BX_e$ cover ![]() $\Sigma$. This proves that
$\Sigma$. This proves that ![]() $\bar {H}=H/B$ acts simply transitively on the space
$\bar {H}=H/B$ acts simply transitively on the space ![]() $\bar \Sigma$ of ergodic components of the action of
$\bar \Sigma$ of ergodic components of the action of ![]() $A\times B$ on
$A\times B$ on ![]() $\Sigma$.
$\Sigma$.
By [Reference FurmanFur99b, Theorem 3.3], the space ![]() $\Sigma$ is measurably isomorphic to
$\Sigma$ is measurably isomorphic to ![]() $Y\times G$, equipped with the measure-preserving action of
$Y\times G$, equipped with the measure-preserving action of ![]() $G\times H$ given by
$G\times H$ given by ![]() $(g,h)\cdot (y,k)=(hy,c'(h,y)kg^{-1})$. A symmetric argument then shows that
$(g,h)\cdot (y,k)=(hy,c'(h,y)kg^{-1})$. A symmetric argument then shows that ![]() $\bar {G}=G/A$ also acts simply transitively on
$\bar {G}=G/A$ also acts simply transitively on ![]() $\bar {\Sigma }$.
$\bar {\Sigma }$.
Therefore, there exist an isomorphism ![]() $\alpha :\bar {G}\to \bar {H}$, and a measurable isomorphism
$\alpha :\bar {G}\to \bar {H}$, and a measurable isomorphism ![]() $\bar {\Sigma }\approx \bar {H}$ sending
$\bar {\Sigma }\approx \bar {H}$ sending ![]() $BX_e$ to
$BX_e$ to ![]() $e$, such that the action of
$e$, such that the action of ![]() $\bar {G}\times \bar {H}$ on
$\bar {G}\times \bar {H}$ on ![]() $\bar {\Sigma }$ is given by
$\bar {\Sigma }$ is given by ![]() $(\bar {g},\bar {h})\cdot \bar {k}=\alpha (\bar {g})\bar {k}\bar {h}^{-1}$ through this identification. We also have a
$(\bar {g},\bar {h})\cdot \bar {k}=\alpha (\bar {g})\bar {k}\bar {h}^{-1}$ through this identification. We also have a ![]() $(G\times H)$-equivariant Borel map
$(G\times H)$-equivariant Borel map ![]() $\Phi :\Sigma \to \bar {H}$ (sending
$\Phi :\Sigma \to \bar {H}$ (sending ![]() $BX_e$ to
$BX_e$ to ![]() $e$).
$e$).
The equivariance of ![]() $\Phi$ shows that for all
$\Phi$ shows that for all ![]() $g\in G$ and almost every
$g\in G$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $\Phi (g(x,e))=\alpha (\bar {g})$, i.e.
$\Phi (g(x,e))=\alpha (\bar {g})$, i.e. ![]() $\Phi (gx,c(g,x))=\alpha (\bar {g})$. Letting
$\Phi (gx,c(g,x))=\alpha (\bar {g})$. Letting ![]() $h\in H$ be such that
$h\in H$ be such that ![]() $\alpha (\bar {g})=\bar {h}$, we deduce that
$\alpha (\bar {g})=\bar {h}$, we deduce that ![]() $\Phi (gx,c(g,x)h^{-1})=e$. This shows that
$\Phi (gx,c(g,x)h^{-1})=e$. This shows that ![]() $c(g,x)h^{-1}\in B$, i.e.
$c(g,x)h^{-1}\in B$, i.e. ![]() $c(g,x)\in \alpha (gA)$, as desired.
$c(g,x)\in \alpha (gA)$, as desired.
3.2 Direct products
Following [Reference Monod and ShalomMS06, Notation 1.2], we let ![]() $\mathcal {C}_{\mathrm {reg}}$ be the class of all countable groups
$\mathcal {C}_{\mathrm {reg}}$ be the class of all countable groups ![]() $\Gamma$ such that
$\Gamma$ such that ![]() $\mathrm {H}^2_{\mathrm {b}}(\Gamma,\ell ^2(\Gamma ))\neq 0$. By [Reference Chatterji, Fernós and IozziCFI16, Corollary 1.8], every nonabelian right-angled Artin group which does not split nontrivially as a direct product belongs to the class
$\mathrm {H}^2_{\mathrm {b}}(\Gamma,\ell ^2(\Gamma ))\neq 0$. By [Reference Chatterji, Fernós and IozziCFI16, Corollary 1.8], every nonabelian right-angled Artin group which does not split nontrivially as a direct product belongs to the class ![]() $\mathcal {C}_{\mathrm {reg}}$ (this also follows from [Reference HamenstädtHam08, Reference Hull and OsinHO13] and the fact that these groups are acylindrically hyperbolic, see [Reference Kim and KoberdaKK14] or [Reference SistoSis18, Reference OsinOsi16]).
$\mathcal {C}_{\mathrm {reg}}$ (this also follows from [Reference HamenstädtHam08, Reference Hull and OsinHO13] and the fact that these groups are acylindrically hyperbolic, see [Reference Kim and KoberdaKK14] or [Reference SistoSis18, Reference OsinOsi16]).
Theorem 3.2 (Monod and Shalom [Reference Monod and ShalomMS06, Theorem 2.17])
Let ![]() $m,n\ge 2$, and let
$m,n\ge 2$, and let ![]() $G_1,\dots,G_m$ and
$G_1,\dots,G_m$ and ![]() $H_1,\dots,H_n$ be torsion-free countable groups in
$H_1,\dots,H_n$ be torsion-free countable groups in ![]() $\mathcal {C}_{\mathrm {reg}}$. Let
$\mathcal {C}_{\mathrm {reg}}$. Let ![]() $G=G_1\times \dots \times G_m$ and
$G=G_1\times \dots \times G_m$ and ![]() $H=H_1\times \dots \times H_n$.
$H=H_1\times \dots \times H_n$.
Let ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ be two free, ergodic, measure-preserving actions on standard probability spaces. Assume that all groups
$H\curvearrowright Y$ be two free, ergodic, measure-preserving actions on standard probability spaces. Assume that all groups ![]() $G_i$ act ergodically on
$G_i$ act ergodically on ![]() $X$, and all groups
$X$, and all groups ![]() $H_j$ act ergodically on
$H_j$ act ergodically on ![]() $Y$, and the actions are SOE (via a stable orbit equivalence
$Y$, and the actions are SOE (via a stable orbit equivalence ![]() $f:U\to V$).
$f:U\to V$).
Then ![]() $\kappa (f)=1$, the actions
$\kappa (f)=1$, the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are conjugate through a group isomorphism between
$H\curvearrowright Y$ are conjugate through a group isomorphism between ![]() $G$ and
$G$ and ![]() $H$, and every SOE cocycle
$H$, and every SOE cocycle ![]() $G\times X\to H$ is cohomologous to a group isomorphism.
$G\times X\to H$ is cohomologous to a group isomorphism.
4. Exploiting chain-commuting generating sets
We start with an elementary lemma.
Lemma 4.1 Let ![]() $G$ and
$G$ and ![]() $H$ be groups, with
$H$ be groups, with ![]() $G$ countable. Let
$G$ countable. Let ![]() $G\curvearrowright X$ be a measure-preserving
$G\curvearrowright X$ be a measure-preserving ![]() $G$-action on a standard probability space
$G$-action on a standard probability space ![]() $X$, and let
$X$, and let ![]() $c:G\times X\to H$ be a cocycle. Let
$c:G\times X\to H$ be a cocycle. Let ![]() $S\subseteq G$ be a generating set for
$S\subseteq G$ be a generating set for ![]() $G$. Assume that there exists a conull Borel subset
$G$. Assume that there exists a conull Borel subset ![]() $X^*\subseteq X$ such that for every
$X^*\subseteq X$ such that for every ![]() $s\in S$, the value of
$s\in S$, the value of ![]() $c(s,\cdot )_{|X^*}$ is constant.
$c(s,\cdot )_{|X^*}$ is constant.
Then there exists a group homomorphism ![]() $\alpha :G\to H$ such that for every
$\alpha :G\to H$ such that for every ![]() $g\in G$ and almost every
$g\in G$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c(g,x)=\alpha (g)$.
$c(g,x)=\alpha (g)$.
Proof. The fact that ![]() $c(g,\cdot )$ is almost everywhere constant follows from the same fact for
$c(g,\cdot )$ is almost everywhere constant follows from the same fact for ![]() $g\in S$ together with our assumption that
$g\in S$ together with our assumption that ![]() $S$ generates
$S$ generates ![]() $G$. Letting
$G$. Letting ![]() $\alpha :G\to H$ be defined by sending
$\alpha :G\to H$ be defined by sending ![]() $g$ to the essential value of
$g$ to the essential value of ![]() $c(g,\cdot )$, the fact that
$c(g,\cdot )$, the fact that ![]() $c$ is a cocycle implies that
$c$ is a cocycle implies that ![]() $\alpha$ is a homomorphism, completing the proof.
$\alpha$ is a homomorphism, completing the proof.
A generating set ![]() $S$ of a group
$S$ of a group ![]() $G$ is chain-commuting if the graph whose vertex set is
$G$ is chain-commuting if the graph whose vertex set is ![]() $S$, with one edge between two vertices if the corresponding elements of
$S$, with one edge between two vertices if the corresponding elements of ![]() $G$ commute, is connected. Note that a group
$G$ commute, is connected. Note that a group ![]() $G$ has a finite chain-commuting generating set if and only if it is a quotient of a one-ended right-angled Artin group (defined over a finite simple graph
$G$ has a finite chain-commuting generating set if and only if it is a quotient of a one-ended right-angled Artin group (defined over a finite simple graph ![]() $\Gamma$). Interestingly, having a finite chain-commuting generating set whose elements have infinite order is a condition that has already been successfully exploited in various contexts in measured group theory: for instance, Gaboriau proved in [Reference GaboriauGab00, Critères VI.24] that it forces all free probability measure-preserving actions of
$\Gamma$). Interestingly, having a finite chain-commuting generating set whose elements have infinite order is a condition that has already been successfully exploited in various contexts in measured group theory: for instance, Gaboriau proved in [Reference GaboriauGab00, Critères VI.24] that it forces all free probability measure-preserving actions of ![]() $G$ to have cost
$G$ to have cost ![]() $1$; see also [Reference Abert, Gelander and NikolovAGN17] for a more recent use.
$1$; see also [Reference Abert, Gelander and NikolovAGN17] for a more recent use.
We say that a group ![]() $H$ has the root-conjugation property if for every
$H$ has the root-conjugation property if for every ![]() $h_1,h_2\in H$ and every integer
$h_1,h_2\in H$ and every integer ![]() $k>0$, if
$k>0$, if ![]() $h_1$ commutes with
$h_1$ commutes with ![]() $h_2^k$, then
$h_2^k$, then ![]() $h_1$ commutes with
$h_1$ commutes with ![]() $h_2$.
$h_2$.
Lemma 4.2 Let ![]() $G$ and
$G$ and ![]() $H$ be countable groups. Assume that
$H$ be countable groups. Assume that ![]() $H$ satisfies the root-conjugation property. Let
$H$ satisfies the root-conjugation property. Let ![]() $G\curvearrowright X$ be a measure-preserving
$G\curvearrowright X$ be a measure-preserving ![]() $G$-action on a standard probability space
$G$-action on a standard probability space ![]() $X$, and let
$X$, and let ![]() $c:G\times X\to H$ be a cocycle. Let
$c:G\times X\to H$ be a cocycle. Let ![]() $S$ be a generating set of
$S$ be a generating set of ![]() $G$. Assume that:
$G$. Assume that:
(i)
 $S$ is chain-commuting;
$S$ is chain-commuting;(ii) every element of
 $S$ acts ergodically on
$S$ acts ergodically on  $X$; and
$X$; and(iii) there exist
 $s\in S$ and a conull Borel subset
$s\in S$ and a conull Borel subset  $X^*\subseteq X$ such that
$X^*\subseteq X$ such that  $c(s,\cdot )_{|X^*}$ is constant.
$c(s,\cdot )_{|X^*}$ is constant.
Then there exists a group homomorphism ![]() $\alpha :G\to H$ such that for every
$\alpha :G\to H$ such that for every ![]() $g\in G$ and almost every
$g\in G$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c(g,x)=\alpha (g)$.
$c(g,x)=\alpha (g)$.
Proof. Let ![]() $s\in S$ be as in assertion (iii) and denote by
$s\in S$ be as in assertion (iii) and denote by ![]() $\beta _s$ the constant value of
$\beta _s$ the constant value of ![]() $c(s,\cdot )$ on
$c(s,\cdot )$ on ![]() $X^*$. We claim that for every
$X^*$. We claim that for every ![]() $u\in S$ which commutes with
$u\in S$ which commutes with ![]() $s$, the value
$s$, the value ![]() $c(u,\cdot )$ is constant on a conull Borel subset of
$c(u,\cdot )$ is constant on a conull Borel subset of ![]() $X$. As
$X$. As ![]() $S$ is chain-commuting, arguing inductively will then ensure that the same is true for all
$S$ is chain-commuting, arguing inductively will then ensure that the same is true for all ![]() $u\in S$, and as
$u\in S$, and as ![]() $G$ is countable the conull Borel subset of
$G$ is countable the conull Borel subset of ![]() $X$ can be chosen independent of
$X$ can be chosen independent of ![]() $u$. The conclusion will then follow from Lemma 4.1.
$u$. The conclusion will then follow from Lemma 4.1.
We now prove the above claim. Up to replacing ![]() $X^*$ by a further conull Borel subset (which we can assume to be
$X^*$ by a further conull Borel subset (which we can assume to be ![]() $G$-invariant), we assume that the cocycle
$G$-invariant), we assume that the cocycle ![]() $c$ is strict. Let
$c$ is strict. Let ![]() $X^*=\sqcup _{i\in I}X_i$ be a partition into at most countably many Borel subsets such that for each
$X^*=\sqcup _{i\in I}X_i$ be a partition into at most countably many Borel subsets such that for each ![]() $i$, the value of
$i$, the value of ![]() $c(u,\cdot )$ is constant when restricted to
$c(u,\cdot )$ is constant when restricted to ![]() $X_i$: we denote it by
$X_i$: we denote it by ![]() $\alpha _i$. Let
$\alpha _i$. Let ![]() $i,j\in I$ be such that
$i,j\in I$ be such that ![]() $X_i$ and
$X_i$ and ![]() $X_j$ have positive measure (possibly with
$X_j$ have positive measure (possibly with ![]() $i=j$). As
$i=j$). As ![]() $s$ acts ergodically on
$s$ acts ergodically on ![]() $X$, there exist an integer
$X$, there exist an integer ![]() $k_{i,j}\neq 0$ and
$k_{i,j}\neq 0$ and ![]() $x\in X_i$ such that
$x\in X_i$ such that ![]() $s^{k_{i,j}}x\in X_j$. As
$s^{k_{i,j}}x\in X_j$. As ![]() $u$ and
$u$ and ![]() $s^{k_{i,j}}$ commute, we have
$s^{k_{i,j}}$ commute, we have ![]() $c(us^{k_{i,j}},x)=c(s^{k_{i,j}}u,x)$. Thus,
$c(us^{k_{i,j}},x)=c(s^{k_{i,j}}u,x)$. Thus, ![]() $c(u,s^{k_{i,j}}x)c(s^{k_{i,j}},x)=c(s^{k_{i,j}},ux)c(u,x)$, in other words
$c(u,s^{k_{i,j}}x)c(s^{k_{i,j}},x)=c(s^{k_{i,j}},ux)c(u,x)$, in other words
Letting ![]() $i=j$, we see that
$i=j$, we see that ![]() $\alpha _i$ commutes with
$\alpha _i$ commutes with ![]() $\beta _s^{k_{i,j}}$. By the root-conjugation property, it follows that
$\beta _s^{k_{i,j}}$. By the root-conjugation property, it follows that ![]() $\alpha _i$ and
$\alpha _i$ and ![]() $\beta _s$ commute. Using (1) again with
$\beta _s$ commute. Using (1) again with ![]() $i,j$ arbitrary, we see that
$i,j$ arbitrary, we see that ![]() $\alpha _i=\alpha _j$ whenever both
$\alpha _i=\alpha _j$ whenever both ![]() $X_i$ and
$X_i$ and ![]() $X_j$ have positive measure. In other words, the value
$X_j$ have positive measure. In other words, the value ![]() $c(u,\cdot )$ is almost everywhere constant.
$c(u,\cdot )$ is almost everywhere constant.
In the present paper, Lemma 4.2 will be applied to the setting of right-angled Artin groups in the following way.
Lemma 4.3 Let ![]() $G,H$ be two right-angled Artin groups, with
$G,H$ be two right-angled Artin groups, with ![]() $G$ one-ended. Let
$G$ one-ended. Let ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ be two free, ergodic, measure-preserving actions on standard probability spaces, and assume that there is a stable orbit equivalence
$H\curvearrowright Y$ be two free, ergodic, measure-preserving actions on standard probability spaces, and assume that there is a stable orbit equivalence ![]() $f$ between
$f$ between ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$, with compression constant
$H\curvearrowright Y$, with compression constant ![]() $\kappa (f)\ge 1$. Assume that
$\kappa (f)\ge 1$. Assume that ![]() $G\curvearrowright X$ is irreducible, and let
$G\curvearrowright X$ is irreducible, and let ![]() $S$ be a standard generating set of
$S$ be a standard generating set of ![]() $G$ (given by an isomorphism to some
$G$ (given by an isomorphism to some ![]() $G_\Gamma$) such that all elements of
$G_\Gamma$) such that all elements of ![]() $S$ act ergodically on
$S$ act ergodically on ![]() $X$. Let
$X$. Let ![]() $c:G\times X\to H$ be an SOE cocycle associated to
$c:G\times X\to H$ be an SOE cocycle associated to ![]() $f$.
$f$.
If ![]() $c$ is cohomologous to a cocycle
$c$ is cohomologous to a cocycle ![]() $c'$ for which there exists
$c'$ for which there exists ![]() $s\in S$ such that
$s\in S$ such that ![]() $c'(s,\cdot )$ is almost everywhere constant, then
$c'(s,\cdot )$ is almost everywhere constant, then ![]() $\kappa (f)=1$, the cocycle
$\kappa (f)=1$, the cocycle ![]() $c$ is cohomologous to a group isomorphism
$c$ is cohomologous to a group isomorphism ![]() $\alpha :G\to H$, and the actions are conjugate through
$\alpha :G\to H$, and the actions are conjugate through ![]() $\alpha$.
$\alpha$.
Proof. Right-angled Artin groups have the root-conjugation property, as follows from [Reference MinasyanMin12, Lemma 6.3]. In addition, the standard generating set ![]() $S$ of
$S$ of ![]() $G$ is chain-commuting (because
$G$ is chain-commuting (because ![]() $G$ is one-ended, i.e. its defining graph
$G$ is one-ended, i.e. its defining graph ![]() $\Gamma$ is connected), and by assumption every element of
$\Gamma$ is connected), and by assumption every element of ![]() $S$ acts ergodically on
$S$ acts ergodically on ![]() $X$. Lemma 4.2 therefore implies that
$X$. Lemma 4.2 therefore implies that ![]() $c$ is cohomologous to a group homomorphism
$c$ is cohomologous to a group homomorphism ![]() $\alpha :G\to H$. As
$\alpha :G\to H$. As ![]() $G$ is torsion-free, it follows from [Reference VaesVae07, Lemma 4.7] that
$G$ is torsion-free, it follows from [Reference VaesVae07, Lemma 4.7] that ![]() $\alpha$ is injective,
$\alpha$ is injective, ![]() $\alpha (G)$ has finite index in
$\alpha (G)$ has finite index in ![]() $H$, the action
$H$, the action ![]() $H\curvearrowright Y$ is conjugate to the action induced from
$H\curvearrowright Y$ is conjugate to the action induced from ![]() $G\curvearrowright X$, and
$G\curvearrowright X$, and ![]() $\kappa (f)={1}/{[H:\alpha (G)]}$. As
$\kappa (f)={1}/{[H:\alpha (G)]}$. As ![]() $\kappa (f)\ge 1$, we deduce that
$\kappa (f)\ge 1$, we deduce that ![]() $[H:\alpha (G)]=1$ (in particular,
$[H:\alpha (G)]=1$ (in particular, ![]() $\alpha$ is a group isomorphism) and [Reference VaesVae07, Lemma 4.7] ensures that the actions
$\alpha$ is a group isomorphism) and [Reference VaesVae07, Lemma 4.7] ensures that the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are conjugate through
$H\curvearrowright Y$ are conjugate through ![]() $\alpha$.
$\alpha$.
5. Recognition lemmas
5.1 Review of parabolic supports
The following notion was introduced in [Reference Horbez and HuangHH22, § 3.3]. Let ![]() $\mathcal {G}$ be a measured groupoid over a standard finite measure space
$\mathcal {G}$ be a measured groupoid over a standard finite measure space ![]() $X$, equipped with a strict cocycle
$X$, equipped with a strict cocycle ![]() $\rho :\mathcal {G}\to G$, where
$\rho :\mathcal {G}\to G$, where ![]() $G$ is a right-angled Artin group. Fix an identification
$G$ is a right-angled Artin group. Fix an identification ![]() $G=G_\Gamma$, and let
$G=G_\Gamma$, and let ![]() $\mathbb {P}$ be the set of all parabolic subgroups of
$\mathbb {P}$ be the set of all parabolic subgroups of ![]() $G$ with respect to this identification. Given
$G$ with respect to this identification. Given ![]() $P\in \mathbb {P}$, we say that
$P\in \mathbb {P}$, we say that ![]() $(\mathcal {G},\rho )$ is tightly
$(\mathcal {G},\rho )$ is tightly ![]() $P$-supported if:
$P$-supported if:
(i) there exists a conull Borel subset
 $X^*\subseteq X$ such that
$X^*\subseteq X$ such that  $\rho (\mathcal {G}_{|X^*})\subseteq P$; and
$\rho (\mathcal {G}_{|X^*})\subseteq P$; and(ii) for every parabolic subgroup
 $Q\subsetneq P$ and every Borel subset
$Q\subsetneq P$ and every Borel subset  $U\subseteq X$ of positive measure, one has
$U\subseteq X$ of positive measure, one has  $\rho (\mathcal {G}_{|U})\nsubseteq Q$.
$\rho (\mathcal {G}_{|U})\nsubseteq Q$.
A parabolic subgroup ![]() $P$ such that
$P$ such that ![]() $(\mathcal {G},\rho )$ is tightly
$(\mathcal {G},\rho )$ is tightly ![]() $P$-supported, if it exists, is unique. The following lemma records the contents of [Reference Horbez and HuangHH22, Lemma 3.7 and Remark 3.9].
$P$-supported, if it exists, is unique. The following lemma records the contents of [Reference Horbez and HuangHH22, Lemma 3.7 and Remark 3.9].
Lemma 5.1 Let ![]() $G=G_\Gamma$ be a right-angled Artin group, let
$G=G_\Gamma$ be a right-angled Artin group, let ![]() $\mathcal {G}$ be a measured groupoid over a standard finite measure space
$\mathcal {G}$ be a measured groupoid over a standard finite measure space ![]() $X$, and let
$X$, and let ![]() $\rho :\mathcal {G}\to G$ be a strict cocycle.
$\rho :\mathcal {G}\to G$ be a strict cocycle.
Then there exists a partition ![]() $X=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets, and for every
$X=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets, and for every ![]() $i\in I$, a parabolic subgroup
$i\in I$, a parabolic subgroup ![]() $P_i$, such that
$P_i$, such that ![]() $(\mathcal {G}_{|X_i},\rho )$ is tightly
$(\mathcal {G}_{|X_i},\rho )$ is tightly ![]() $P_i$-supported.
$P_i$-supported.
The following is a consequence of Lemma 1.1 and [Reference Horbez and HuangHH22, Lemma 3.8 and Remark 3.9].
Lemma 5.2 Let ![]() $G=G_\Gamma$ be a right-angled Artin group, let
$G=G_\Gamma$ be a right-angled Artin group, let ![]() $\mathcal {G}$ be a measured groupoid over a standard finite measure space
$\mathcal {G}$ be a measured groupoid over a standard finite measure space ![]() $X$, and let
$X$, and let ![]() $\rho :\mathcal {G}\to G$ be a strict cocycle. Let
$\rho :\mathcal {G}\to G$ be a strict cocycle. Let ![]() $\mathcal {H}$ and
$\mathcal {H}$ and ![]() $\mathcal {H}'$ be two measured subgroupoids of
$\mathcal {H}'$ be two measured subgroupoids of ![]() $\mathcal {G}$. Assume that
$\mathcal {G}$. Assume that ![]() $(\mathcal {H},\rho )$ is tightly
$(\mathcal {H},\rho )$ is tightly ![]() $P$-supported for a parabolic subgroup
$P$-supported for a parabolic subgroup ![]() $P$. Assume also that
$P$. Assume also that ![]() $\mathcal {H}$ is normalized by
$\mathcal {H}$ is normalized by ![]() $\mathcal {H}'$.
$\mathcal {H}'$.
Then there exists a conull Borel subset ![]() $X^*\subseteq X$ such that
$X^*\subseteq X$ such that ![]() $\rho (\mathcal {H}'_{|X^*})\subseteq P\times P^\perp$.
$\rho (\mathcal {H}'_{|X^*})\subseteq P\times P^\perp$.
We now establish a lemma which essentially follows from [Reference Horbez and HuangHH22].
Lemma 5.3 Let ![]() $G=G_\Gamma$ be a right-angled Artin group. Let
$G=G_\Gamma$ be a right-angled Artin group. Let ![]() $\mathcal {G}$ be a measured groupoid over a standard finite measure space
$\mathcal {G}$ be a measured groupoid over a standard finite measure space ![]() $X$ and let
$X$ and let ![]() $\rho :\mathcal {G}\to G$ be a strict cocycle with trivial kernel. Let
$\rho :\mathcal {G}\to G$ be a strict cocycle with trivial kernel. Let ![]() $\mathcal {H}$ be a measured subgroupoid of
$\mathcal {H}$ be a measured subgroupoid of ![]() $\mathcal {G}$. Assume that
$\mathcal {G}$. Assume that ![]() $\mathcal {H}$ is everywhere nonamenable and stably normalizes an amenable subgroupoid
$\mathcal {H}$ is everywhere nonamenable and stably normalizes an amenable subgroupoid ![]() $\mathcal {A}$.
$\mathcal {A}$.
Then there exist a conull Borel subset ![]() $X^*\subseteq X$, a partition
$X^*\subseteq X$, a partition ![]() $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets of positive measure, and for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets of positive measure, and for every ![]() $i\in I$, a parabolic subgroup
$i\in I$, a parabolic subgroup ![]() $P_i$ such that:
$P_i$ such that:
(i)
 $\mathcal {A}_{|X_i}\subseteq \rho ^{-1}(P_i)_{|X_i}$;
$\mathcal {A}_{|X_i}\subseteq \rho ^{-1}(P_i)_{|X_i}$;(ii)
 $\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i\times P_i^{\perp })_{|X_i}$;
$\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i\times P_i^{\perp })_{|X_i}$;(iii)
 $(\mathcal {H}\cap \rho ^{-1}(P_i))_{|X_i}$ is amenable;
$(\mathcal {H}\cap \rho ^{-1}(P_i))_{|X_i}$ is amenable;(iv)
 $P_i^{\perp }$ is nonabelian.
$P_i^{\perp }$ is nonabelian.
Proof. Consider a partition ![]() $X=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every
$X=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every ![]() $i\in I$, there exists a parabolic subgroup
$i\in I$, there exists a parabolic subgroup ![]() $P_i$ such that
$P_i$ such that ![]() $(\mathcal {A}_{|X_i},\rho )$ is tightly
$(\mathcal {A}_{|X_i},\rho )$ is tightly ![]() $P_i$-supported (given by Lemma 5.1). As
$P_i$-supported (given by Lemma 5.1). As ![]() $\mathcal {A}$ is stably normalized by
$\mathcal {A}$ is stably normalized by ![]() $\mathcal {H}$, Lemma 5.2 ensures that up to replacing
$\mathcal {H}$, Lemma 5.2 ensures that up to replacing ![]() $X$ by a conull Borel subset and refining the above partition, we can assume that
$X$ by a conull Borel subset and refining the above partition, we can assume that ![]() $\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i\times P_i^{\perp })_{|X_i}$ for every
$\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i\times P_i^{\perp })_{|X_i}$ for every ![]() $i\in I$. As
$i\in I$. As ![]() $\mathcal {A}$ is stably normalized by
$\mathcal {A}$ is stably normalized by ![]() $\mathcal {H}$ which is everywhere nonamenable, and as
$\mathcal {H}$ which is everywhere nonamenable, and as ![]() $\rho$ has trivial kernel, it follows from [Reference Horbez and HuangHH22, Lemma 3.10] that
$\rho$ has trivial kernel, it follows from [Reference Horbez and HuangHH22, Lemma 3.10] that ![]() $P_i^\perp$ is nonamenable, and
$P_i^\perp$ is nonamenable, and ![]() $(\mathcal {H}\cap \rho ^{-1}(P_i))_{|X_i}$ is amenable.
$(\mathcal {H}\cap \rho ^{-1}(P_i))_{|X_i}$ is amenable.
5.2 Recognizing maximal join parabolic subgroupoids
Given an equivalence relation arising from a probability measure-preserving action of a right-angled Artin group, the following lemma will enable us to recognize subrelations arising from restricting the action to a maximal join parabolic subgroup. Its proof is based on the techniques developed in our previous work [Reference Horbez and HuangHH22].
Lemma 5.4 Let ![]() $G$ be a one-ended nonabelian right-angled Artin group. Let
$G$ be a one-ended nonabelian right-angled Artin group. Let ![]() $\mathcal {G}$ be a measured groupoid over a standard finite measure space
$\mathcal {G}$ be a measured groupoid over a standard finite measure space ![]() $X$, coming with a strict action-type cocycle
$X$, coming with a strict action-type cocycle ![]() $\rho :\mathcal {G}\to G$. Let
$\rho :\mathcal {G}\to G$. Let ![]() $\mathcal {H}$ be a measured subgroupoid of
$\mathcal {H}$ be a measured subgroupoid of ![]() $\mathcal {G}$. Then the following assertions are equivalent.
$\mathcal {G}$. Then the following assertions are equivalent.
(i) There exist a conull Borel subset
 $X^*\subseteq X$ and a partition
$X^*\subseteq X$ and a partition  $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every  $i\in I$, there exists a maximal join parabolic subgroup
$i\in I$, there exists a maximal join parabolic subgroup  $P_i$ such that
$P_i$ such that  $\mathcal {H}_{|X_i}=\rho ^{-1}(P_i)_{|X_i}$.
$\mathcal {H}_{|X_i}=\rho ^{-1}(P_i)_{|X_i}$.(ii) The following properties hold.
(a) The subgroupoid
 $\mathcal {H}$ contains two subgroupoids
$\mathcal {H}$ contains two subgroupoids  $\mathcal {A},\mathcal {N}$, where
$\mathcal {A},\mathcal {N}$, where  $\mathcal {A}$ is amenable, of infinite type, and stably normalized by
$\mathcal {A}$ is amenable, of infinite type, and stably normalized by  $\mathcal {N}$, and
$\mathcal {N}$, and  $\mathcal {N}$ is everywhere nonamenable and stably normalized by
$\mathcal {N}$ is everywhere nonamenable and stably normalized by  $\mathcal {H}$.
$\mathcal {H}$.(b) Whenever
 $\mathcal {H}'$ is another measured subgroupoid of
$\mathcal {H}'$ is another measured subgroupoid of  $\mathcal {G}$ satisfying property (a), if
$\mathcal {G}$ satisfying property (a), if  $\mathcal {H}$ is stably contained in
$\mathcal {H}$ is stably contained in  $\mathcal {H}'$, then they are stably equal.
$\mathcal {H}'$, then they are stably equal.
Proof. In this proof, we fix an identification between ![]() $G$ and
$G$ and ![]() $G_\Gamma$; parabolic subgroups of
$G_\Gamma$; parabolic subgroups of ![]() $G$ are understood with respect to this identification.
$G$ are understood with respect to this identification.
We first prove that assertion (i) implies property (ii)(a). For every ![]() $i\in I$, the group
$i\in I$, the group ![]() $P_i$ is nonabelian (Lemma 1.3); hence,
$P_i$ is nonabelian (Lemma 1.3); hence, ![]() $P_i$ splits as a direct product
$P_i$ splits as a direct product ![]() $P_i=M_i\times N_i$, where
$P_i=M_i\times N_i$, where ![]() $M_i$ and
$M_i$ and ![]() $N_i$ are infinite parabolic subgroups, and at least one of them (say
$N_i$ are infinite parabolic subgroups, and at least one of them (say ![]() $N_i$) is nonabelian. Therefore,
$N_i$) is nonabelian. Therefore, ![]() $N_i$ contains a nonabelian free subgroup. Choose an infinite cyclic subgroup
$N_i$ contains a nonabelian free subgroup. Choose an infinite cyclic subgroup ![]() $A_i\subseteq M_i$. Then
$A_i\subseteq M_i$. Then ![]() $A_i$ commutes with
$A_i$ commutes with ![]() $N_i$. The conclusion follows by letting
$N_i$. The conclusion follows by letting ![]() $\mathcal {A}$ be a measured subgroupoid of
$\mathcal {A}$ be a measured subgroupoid of ![]() $\mathcal {G}$ such that for every
$\mathcal {G}$ such that for every ![]() $i\in I$, one has
$i\in I$, one has ![]() $\mathcal {A}_{|X_i}=\rho ^{-1}(A_i)_{|X_i}$, and letting
$\mathcal {A}_{|X_i}=\rho ^{-1}(A_i)_{|X_i}$, and letting ![]() $\mathcal {N}$ be such that for every
$\mathcal {N}$ be such that for every ![]() $i\in I$, one has
$i\in I$, one has ![]() $\mathcal {N}_{|X_i}=\rho ^{-1}(N_i)_{|X_i}$.
$\mathcal {N}_{|X_i}=\rho ^{-1}(N_i)_{|X_i}$.
We now claim that if a measured subgroupoid ![]() $\mathcal {H}\subseteq \mathcal {G}$ satisfies property (ii)(a), then there exist a conull Borel subset
$\mathcal {H}\subseteq \mathcal {G}$ satisfies property (ii)(a), then there exist a conull Borel subset ![]() $X^*\subseteq X$, a Borel partition
$X^*\subseteq X$, a Borel partition ![]() $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets, and for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets, and for every ![]() $i\in I$, a join parabolic subgroup
$i\in I$, a join parabolic subgroup ![]() $P_i\subseteq G$ such that
$P_i\subseteq G$ such that ![]() $\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i)_{|X_i}$. Once we prove the claim, we explain in the last paragraphs why this suffices to establish the lemma.
$\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i)_{|X_i}$. Once we prove the claim, we explain in the last paragraphs why this suffices to establish the lemma.
By Lemma 5.3, there exists a conull Borel subset ![]() $X^*\subseteq X$ and a partition
$X^*\subseteq X$ and a partition ![]() $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every ![]() $i\in I$, there exists a parabolic subgroup
$i\in I$, there exists a parabolic subgroup ![]() $R_i$ with
$R_i$ with ![]() $R_i^{\perp }$ nonabelian, such that
$R_i^{\perp }$ nonabelian, such that ![]() $\rho (\mathcal {A}_{|X_i})\subseteq R_i$ and
$\rho (\mathcal {A}_{|X_i})\subseteq R_i$ and ![]() $\rho (\mathcal {N}_{|X_i})\subseteq R_i\times R_i^\perp$. Note that
$\rho (\mathcal {N}_{|X_i})\subseteq R_i\times R_i^\perp$. Note that ![]() $R_i$ is nontrivial because
$R_i$ is nontrivial because ![]() $\mathcal {A}$ is of infinite type and
$\mathcal {A}$ is of infinite type and ![]() $\rho$ has trivial kernel. In particular,
$\rho$ has trivial kernel. In particular, ![]() $R_i\times R_i^{\perp }$ is a join parabolic subgroup.
$R_i\times R_i^{\perp }$ is a join parabolic subgroup.
Up to a further partition, for every ![]() $i\in I$, there exists a nontrivial parabolic subgroup
$i\in I$, there exists a nontrivial parabolic subgroup ![]() $S_i\subseteq R_i\times R_i^{\perp }$ such that
$S_i\subseteq R_i\times R_i^{\perp }$ such that ![]() $(\mathcal {N}_{|X_i},\rho )$ is tightly
$(\mathcal {N}_{|X_i},\rho )$ is tightly ![]() $S_i$-supported (Lemma 5.1). As
$S_i$-supported (Lemma 5.1). As ![]() $\mathcal {N}$ is stably normalized by
$\mathcal {N}$ is stably normalized by ![]() $\mathcal {H}$, up to a further partition and restriction to a further conull Borel subset of
$\mathcal {H}$, up to a further partition and restriction to a further conull Borel subset of ![]() $X$, we can assume that
$X$, we can assume that ![]() $\rho (\mathcal {H}_{|X_i})\subseteq S_i\times S_i^{\perp }$ by Lemma 5.2. Lemma 1.2 ensures that
$\rho (\mathcal {H}_{|X_i})\subseteq S_i\times S_i^{\perp }$ by Lemma 5.2. Lemma 1.2 ensures that ![]() $S_i\times S_i^{\perp }$ is a join parabolic subgroup, which proves our claim.
$S_i\times S_i^{\perp }$ is a join parabolic subgroup, which proves our claim.
We have already proved that assertion (i) implies property (ii)(a). To see that assertion (i) implies property (ii)(b), let ![]() $\mathcal {H}$ be a measured subgroupoid as in assertion (i) (coming with a partition
$\mathcal {H}$ be a measured subgroupoid as in assertion (i) (coming with a partition ![]() $X^*=\sqcup _{i\in I}X_i$ and maximal join parabolic subgroups
$X^*=\sqcup _{i\in I}X_i$ and maximal join parabolic subgroups ![]() $P_i$), and let
$P_i$), and let ![]() $\mathcal {H}'$ be as in property (ii)(b). The above claim ensures that up to passing to a further conull Borel subset and refining the above partition, we can assume that for every
$\mathcal {H}'$ be as in property (ii)(b). The above claim ensures that up to passing to a further conull Borel subset and refining the above partition, we can assume that for every ![]() $i\in I$, there exists a join parabolic subgroup
$i\in I$, there exists a join parabolic subgroup ![]() $Q_i$ such that
$Q_i$ such that ![]() $\mathcal {H}'_{|X_i}\subseteq \rho ^{-1}(Q_i)_{|X_i}$. As
$\mathcal {H}'_{|X_i}\subseteq \rho ^{-1}(Q_i)_{|X_i}$. As ![]() $\mathcal {H}$ is stably contained in
$\mathcal {H}$ is stably contained in ![]() $\mathcal {H}'$ and
$\mathcal {H}'$ and ![]() $\rho$ is action-type, we deduce that every element of
$\rho$ is action-type, we deduce that every element of ![]() $P_i$ has a power contained in
$P_i$ has a power contained in ![]() $Q_i$, and therefore
$Q_i$, and therefore ![]() $P_i\subseteq Q_i$ by [Reference MinasyanMin12, Lemma 6.4]. By maximality of
$P_i\subseteq Q_i$ by [Reference MinasyanMin12, Lemma 6.4]. By maximality of ![]() $P_i$, we have
$P_i$, we have ![]() $P_i=Q_i$, from which it follows that
$P_i=Q_i$, from which it follows that ![]() $\mathcal {H}'$ is stably contained in
$\mathcal {H}'$ is stably contained in ![]() $\mathcal {H}$, proving property (ii)(b).
$\mathcal {H}$, proving property (ii)(b).
We finally prove that assertion (ii) implies assertion (i), so let ![]() $\mathcal {H}$ be as in assertion (ii). The above claim shows that there exists a Borel partition
$\mathcal {H}$ be as in assertion (ii). The above claim shows that there exists a Borel partition ![]() $X^*=\sqcup _{i\in I}X_i$ of a conull Borel subset into at most countably many subsets such that for every
$X^*=\sqcup _{i\in I}X_i$ of a conull Borel subset into at most countably many subsets such that for every ![]() $i\in I$,
$i\in I$, ![]() $\rho (\mathcal {H}_{|X_i})$ is contained in a join parabolic subgroup
$\rho (\mathcal {H}_{|X_i})$ is contained in a join parabolic subgroup ![]() $P_i$. The maximality assumption (ii)(b) together with the implication
$P_i$. The maximality assumption (ii)(b) together with the implication ![]() $\rm (i)\Rightarrow (ii)(a)$ implies that
$\rm (i)\Rightarrow (ii)(a)$ implies that ![]() $P_i$ is maximal whenever
$P_i$ is maximal whenever ![]() $X_i$ has positive measure. Indeed, if
$X_i$ has positive measure. Indeed, if ![]() $P_i$ is contained in a join parabolic subgroup
$P_i$ is contained in a join parabolic subgroup ![]() $P'_i$, then
$P'_i$, then ![]() $\rho ^{-1}(P_i)_{|X_i}\subseteq \rho ^{-1}(P'_i)_{|X_i}$, so these two subgroupoids would have to be stably equal. As
$\rho ^{-1}(P_i)_{|X_i}\subseteq \rho ^{-1}(P'_i)_{|X_i}$, so these two subgroupoids would have to be stably equal. As ![]() $\rho$ is action-type, this implies that every element of
$\rho$ is action-type, this implies that every element of ![]() $P'_i$ has a power contained in
$P'_i$ has a power contained in ![]() $P_i$. By [Reference MinasyanMin12, Lemma 6.4], it follows that
$P_i$. By [Reference MinasyanMin12, Lemma 6.4], it follows that ![]() $P_i=P'_i$, which proves the maximality of
$P_i=P'_i$, which proves the maximality of ![]() $P_i$. Using again the maximality assumption, after passing to a conull subset and a countable partition, we have
$P_i$. Using again the maximality assumption, after passing to a conull subset and a countable partition, we have ![]() $\mathcal {H}_{|X_i}=\rho ^{-1}(P_i)_{|X_i}$.
$\mathcal {H}_{|X_i}=\rho ^{-1}(P_i)_{|X_i}$.
A subgroupoid ![]() $\mathcal {H}$ satisfying one of the equivalent conclusions of Lemma 5.4 will be called a maximal join subgroupoid of
$\mathcal {H}$ satisfying one of the equivalent conclusions of Lemma 5.4 will be called a maximal join subgroupoid of ![]() $\mathcal {G}$. Lemma 5.4 ensures that this notion does not depend on the choice of an action-type cocycle from
$\mathcal {G}$. Lemma 5.4 ensures that this notion does not depend on the choice of an action-type cocycle from ![]() $\mathcal {G}$ towards a one-ended nonabelian right-angled Artin group. Note that the partition that arises in the first assertion of Lemma 5.4 is not unique (for instance, one can always pass to a further partition), so it is not determined by the pair
$\mathcal {G}$ towards a one-ended nonabelian right-angled Artin group. Note that the partition that arises in the first assertion of Lemma 5.4 is not unique (for instance, one can always pass to a further partition), so it is not determined by the pair ![]() $(\mathcal {H},\rho )$ in any way. However, the map sending any point
$(\mathcal {H},\rho )$ in any way. However, the map sending any point ![]() $x\in Y_i$ to the parabolic subgroup
$x\in Y_i$ to the parabolic subgroup ![]() $P_i$ is determined completely, up to changing its value on a null set. We call it the parabolic map of
$P_i$ is determined completely, up to changing its value on a null set. We call it the parabolic map of ![]() $(\mathcal {H},\rho )$. We insist that, while being a maximal join parabolic subgroup is a notion that is independent of the action-type cocycle
$(\mathcal {H},\rho )$. We insist that, while being a maximal join parabolic subgroup is a notion that is independent of the action-type cocycle ![]() $\rho$, the parabolic map does depend on
$\rho$, the parabolic map does depend on ![]() $\rho$.
$\rho$.
5.3 Recognizing the center of a right-angled Artin group
Lemma 5.5 Let ![]() $G$ be a right-angled Artin group, and let
$G$ be a right-angled Artin group, and let ![]() $Z$ be the center of
$Z$ be the center of ![]() $G$. Let
$G$. Let ![]() $\mathcal {G}$ be a measured groupoid over a standard finite measure space
$\mathcal {G}$ be a measured groupoid over a standard finite measure space ![]() $X$, coming with a strict action-type cocycle
$X$, coming with a strict action-type cocycle ![]() $\rho :\mathcal {G}\to G$. Let
$\rho :\mathcal {G}\to G$. Let ![]() $\mathcal {H}\subseteq \mathcal {G}$ be a measured subgroupoid. Then the following statements are equivalent.
$\mathcal {H}\subseteq \mathcal {G}$ be a measured subgroupoid. Then the following statements are equivalent.
(i) There exist a conull Borel subset
 $X^*\subseteq X$ and a partition
$X^*\subseteq X$ and a partition  $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets such that for every  $i\in I$, one has
$i\in I$, one has  $\mathcal {H}_{|X_i}=\rho ^{-1}(Z)_{|X_i}$.
$\mathcal {H}_{|X_i}=\rho ^{-1}(Z)_{|X_i}$.(ii) The following properties hold:
(a) the subgroupoid
 $\mathcal {H}$ is amenable and stably normalized by
$\mathcal {H}$ is amenable and stably normalized by  $\mathcal {G}$;
$\mathcal {G}$;(b) if
 $\mathcal {H}'\subseteq \mathcal {G}$ is another measured subgroupoid of
$\mathcal {H}'\subseteq \mathcal {G}$ is another measured subgroupoid of  $\mathcal {G}$ that satisfies property (a), and if
$\mathcal {G}$ that satisfies property (a), and if  $\mathcal {H}$ is stably contained in
$\mathcal {H}$ is stably contained in  $\mathcal {H}'$, then
$\mathcal {H}'$, then  $\mathcal {H}$ is stably equal to
$\mathcal {H}$ is stably equal to  $\mathcal {H}'$.
$\mathcal {H}'$.
A central subgroupoid of ![]() $\mathcal {G}$ is a subgroupoid
$\mathcal {G}$ is a subgroupoid ![]() $\mathcal {H}$ satisfying one of the equivalent conclusions of Lemma 5.5. In the context of Lemma 5.5, if a central subgroupoid
$\mathcal {H}$ satisfying one of the equivalent conclusions of Lemma 5.5. In the context of Lemma 5.5, if a central subgroupoid ![]() $\mathcal {H}$ is not stably trivial, then
$\mathcal {H}$ is not stably trivial, then ![]() $Z$ is infinite. The main point of Lemma 5.5 is that the notion of central subgroupoid is independent of the choice of an action-type cocycle from
$Z$ is infinite. The main point of Lemma 5.5 is that the notion of central subgroupoid is independent of the choice of an action-type cocycle from ![]() $\mathcal {G}$ towards a right-angled Artin group.
$\mathcal {G}$ towards a right-angled Artin group.
Proof. The lemma is clear when ![]() $G$ is abelian, so we assume otherwise. In particular,
$G$ is abelian, so we assume otherwise. In particular, ![]() $\mathcal {G}$ is everywhere nonamenable. As usual, we fix an identification between
$\mathcal {G}$ is everywhere nonamenable. As usual, we fix an identification between ![]() $G$ and
$G$ and ![]() $G_\Gamma$; parabolic subgroups are understood with respect to this identification.
$G_\Gamma$; parabolic subgroups are understood with respect to this identification.
We first observe that statement (i) implies property (ii)(a). Indeed, if ![]() $\mathcal {H}$ is a subgroupoid as in statement (i), then amenability of
$\mathcal {H}$ is a subgroupoid as in statement (i), then amenability of ![]() $Z$ ensures that
$Z$ ensures that ![]() $\mathcal {H}$ is amenable (using that
$\mathcal {H}$ is amenable (using that ![]() $\rho$ has trivial kernel), and the fact that
$\rho$ has trivial kernel), and the fact that ![]() $Z$ is normal in
$Z$ is normal in ![]() $G$ ensures that
$G$ ensures that ![]() $\mathcal {H}$ is stably normalized by
$\mathcal {H}$ is stably normalized by ![]() $\mathcal {G}$.
$\mathcal {G}$.
We now claim that if ![]() $\mathcal {H}$ satisfies property (ii)(a), then there exists a partition
$\mathcal {H}$ satisfies property (ii)(a), then there exists a partition ![]() $X^*=\sqcup _{i\in I}X_i$ of a conull Borel subset
$X^*=\sqcup _{i\in I}X_i$ of a conull Borel subset ![]() $X^*\subseteq X$ into at most countably many Borel subsets such that for every
$X^*\subseteq X$ into at most countably many Borel subsets such that for every ![]() $i\in I$, one has
$i\in I$, one has ![]() $\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(Z)_{|X_i}$. Together with the maximality assertion (ii)(b) and the fact that a subgroupoid as in statement (i) satisfies property (ii)(a), this will show that
$\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(Z)_{|X_i}$. Together with the maximality assertion (ii)(b) and the fact that a subgroupoid as in statement (i) satisfies property (ii)(a), this will show that ![]() $\rm (ii)\Rightarrow (i)$. This claim will also prove that every subgroupoid as in statement (i) is stably maximal with respect to property (ii)(a), showing that
$\rm (ii)\Rightarrow (i)$. This claim will also prove that every subgroupoid as in statement (i) is stably maximal with respect to property (ii)(a), showing that ![]() $\rm (i)\Rightarrow (ii)$.
$\rm (i)\Rightarrow (ii)$.
We are thus left with proving the above claim. By Lemma 5.3, there exist a conull Borel subset ![]() $X^*\subseteq X$, a partition
$X^*\subseteq X$, a partition ![]() $X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets, and for every
$X^*=\sqcup _{i\in I}X_i$ into at most countably many Borel subsets, and for every ![]() $i\in I$, a parabolic subgroup
$i\in I$, a parabolic subgroup ![]() $P_i\subseteq G$ (with respect to the chosen standard generating set), such that:
$P_i\subseteq G$ (with respect to the chosen standard generating set), such that:
(i)
 $\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i)_{|X_i}$,
$\mathcal {H}_{|X_i}\subseteq \rho ^{-1}(P_i)_{|X_i}$,(ii)
 $\mathcal {G}_{|X_i}\subseteq \rho ^{-1}(P_i\times P_i^{\perp })_{|X_i}$,
$\mathcal {G}_{|X_i}\subseteq \rho ^{-1}(P_i\times P_i^{\perp })_{|X_i}$,(iii)
 $\rho ^{-1}(P_i)_{|X_i}$ is amenable.
$\rho ^{-1}(P_i)_{|X_i}$ is amenable.
As ![]() $\rho$ is action-type, the second point implies that every element of
$\rho$ is action-type, the second point implies that every element of ![]() $G$ has a power contained in
$G$ has a power contained in ![]() $P_i\times P_i^{\perp }$, which, in turn, implies that
$P_i\times P_i^{\perp }$, which, in turn, implies that ![]() $G=P_i\times P_i^{\perp }$ by [Reference MinasyanMin12, Lemma 6.4]. As
$G=P_i\times P_i^{\perp }$ by [Reference MinasyanMin12, Lemma 6.4]. As ![]() $\rho$ is action-type and
$\rho$ is action-type and ![]() $\rho ^{-1}(P_i)_{|X_i}$ is amenable, the parabolic subgroup
$\rho ^{-1}(P_i)_{|X_i}$ is amenable, the parabolic subgroup ![]() $P_i$ does not contain any nonabelian free subgroup, so it is abelian. These two facts together imply that
$P_i$ does not contain any nonabelian free subgroup, so it is abelian. These two facts together imply that ![]() $P_i\subseteq Z$, and the first point above completes our proof.
$P_i\subseteq Z$, and the first point above completes our proof.
Corollary 5.6 Let ![]() $G_1,G_2$ be two right-angled Artin groups. Assume that there exists a measured groupoid
$G_1,G_2$ be two right-angled Artin groups. Assume that there exists a measured groupoid ![]() $\mathcal {G}$ which admits two action-type cocycles
$\mathcal {G}$ which admits two action-type cocycles ![]() $\rho _1:\mathcal {G}\to G_1$ and
$\rho _1:\mathcal {G}\to G_1$ and ![]() $\rho _2:\mathcal {G}\to G_2$.
$\rho _2:\mathcal {G}\to G_2$.
If ![]() $G_1$ has trivial center, then
$G_1$ has trivial center, then ![]() $G_2$ has trivial center.
$G_2$ has trivial center.
Proof. We prove the contrapositive statement, so assume that the center ![]() $Z_2$ of
$Z_2$ of ![]() $G_2$ is nontrivial. Then
$G_2$ is nontrivial. Then ![]() $\mathcal {Z}=\rho _2^{-1}(Z_2)$ is a subgroupoid of
$\mathcal {Z}=\rho _2^{-1}(Z_2)$ is a subgroupoid of ![]() $\mathcal {G}$ of infinite type which satisfies assertion 2 from Lemma 5.5 (by using the implication
$\mathcal {G}$ of infinite type which satisfies assertion 2 from Lemma 5.5 (by using the implication ![]() $\rm (i)\Rightarrow (ii)$ of that lemma, applied to the cocycle
$\rm (i)\Rightarrow (ii)$ of that lemma, applied to the cocycle ![]() $\rho _2$). Using now the implication
$\rho _2$). Using now the implication ![]() $\rm (ii)\Rightarrow (i)$ from Lemma 5.5, applied to the cocycle
$\rm (ii)\Rightarrow (i)$ from Lemma 5.5, applied to the cocycle ![]() $\rho _1$, we deduce that there exists a Borel subset
$\rho _1$, we deduce that there exists a Borel subset ![]() $U\subseteq Y$ of positive measure such that
$U\subseteq Y$ of positive measure such that ![]() $\rho _1(\mathcal {Z}_{|U})$ is contained in the center
$\rho _1(\mathcal {Z}_{|U})$ is contained in the center ![]() $Z_1$ of
$Z_1$ of ![]() $G_1$. As
$G_1$. As ![]() $\rho _1$ has trivial kernel and
$\rho _1$ has trivial kernel and ![]() $\mathcal {Z}$ is of infinite type, this implies that
$\mathcal {Z}$ is of infinite type, this implies that ![]() $Z_1$ is nontrivial.
$Z_1$ is nontrivial.
5.4 Recognizing commuting centers
Lemma 5.7 Let ![]() $G$ be a one-ended nonabelian right-angled Artin group. Let
$G$ be a one-ended nonabelian right-angled Artin group. Let ![]() $\mathcal {G}$ be a measured groupoid over a standard probability space
$\mathcal {G}$ be a measured groupoid over a standard probability space ![]() $X$, and let
$X$, and let ![]() $\rho :\mathcal {G}\to G$ be a strict action-type cocycle. Let
$\rho :\mathcal {G}\to G$ be a strict action-type cocycle. Let ![]() $\mathcal {H},\mathcal {H}'$ be two maximal join parabolic subgroupoids of
$\mathcal {H},\mathcal {H}'$ be two maximal join parabolic subgroupoids of ![]() $\mathcal {G}$. Let
$\mathcal {G}$. Let ![]() $X^*\subseteq X$ be a conull Borel subset, and
$X^*\subseteq X$ be a conull Borel subset, and ![]() $X^*=\sqcup _{i\in I}X_i$ be a partition into at most countably many Borel subsets, such that for every
$X^*=\sqcup _{i\in I}X_i$ be a partition into at most countably many Borel subsets, such that for every ![]() $i\in I$, there exist parabolic subgroups
$i\in I$, there exist parabolic subgroups ![]() $P_i,P'_i$ of
$P_i,P'_i$ of ![]() $G$ such that
$G$ such that ![]() $\mathcal {H}_{|X_i}=\rho ^{-1}(P_i)_{|X_i}$ and
$\mathcal {H}_{|X_i}=\rho ^{-1}(P_i)_{|X_i}$ and ![]() $\mathcal {H}'_{|X_i}=\rho ^{-1}(P'_i)_{|X_i}$. Then for every
$\mathcal {H}'_{|X_i}=\rho ^{-1}(P'_i)_{|X_i}$. Then for every ![]() $i\in I$ such that
$i\in I$ such that ![]() $X_i$ has positive measure, the following assertions are equivalent.
$X_i$ has positive measure, the following assertions are equivalent.
(i) The centers of
 $P_i$ and
$P_i$ and  $P'_i$ commute.
$P'_i$ commute.(ii) Given any central subgroupoids
 $\mathcal {Z}_i\subseteq \mathcal {H}_{|X_i}$ and
$\mathcal {Z}_i\subseteq \mathcal {H}_{|X_i}$ and  $\mathcal {Z}'_i\subseteq \mathcal {H}'_{|X_i}$ and any Borel subset
$\mathcal {Z}'_i\subseteq \mathcal {H}'_{|X_i}$ and any Borel subset  $U\subseteq X_i$ of positive measure, there exists a Borel subset
$U\subseteq X_i$ of positive measure, there exists a Borel subset  $V\subseteq U$ of positive measure such that
$V\subseteq U$ of positive measure such that  $\langle (\mathcal {Z}_i)_{|V},(\mathcal {Z}'_i)_{|V}\rangle$ is amenable.
$\langle (\mathcal {Z}_i)_{|V},(\mathcal {Z}'_i)_{|V}\rangle$ is amenable.
In the following, when two maximal join parabolic subgroupoids of ![]() $\mathcal {G}$ satisfy one of the equivalent conditions of Lemma 5.7 for every
$\mathcal {G}$ satisfy one of the equivalent conditions of Lemma 5.7 for every ![]() $i\in I$, we say that they are center-commuting (note that this notion does not depend of the choice of a partition as in the statement).
$i\in I$, we say that they are center-commuting (note that this notion does not depend of the choice of a partition as in the statement).
Proof. Let ![]() $i\in I$ be such that
$i\in I$ be such that ![]() $X_i$ has positive measure, and let
$X_i$ has positive measure, and let ![]() $C_i,C'_i$ be the respective centers of
$C_i,C'_i$ be the respective centers of ![]() $P_i,P'_i$. Let
$P_i,P'_i$. Let ![]() $\hat {\mathcal {Z}}_i=\rho ^{-1}(C_i)_{|X_i}$ and
$\hat {\mathcal {Z}}_i=\rho ^{-1}(C_i)_{|X_i}$ and ![]() $\hat {\mathcal {Z}}'_i=\rho ^{-1}(C'_i)_{|X_i}$. Note that
$\hat {\mathcal {Z}}'_i=\rho ^{-1}(C'_i)_{|X_i}$. Note that ![]() $\mathcal {H}_{|X_i}$ and
$\mathcal {H}_{|X_i}$ and ![]() $\mathcal {H}'_{|X_i}$ admit strict action-type cocycles towards
$\mathcal {H}'_{|X_i}$ admit strict action-type cocycles towards ![]() $P_i,$ and
$P_i,$ and ![]() $P'_i$, respectively. Therefore, Lemma 5.5 ensures that
$P'_i$, respectively. Therefore, Lemma 5.5 ensures that ![]() $\hat {\mathcal {Z}}_i$ and
$\hat {\mathcal {Z}}_i$ and ![]() $\hat {\mathcal {Z}}'_i$ are central subgroupoids of
$\hat {\mathcal {Z}}'_i$ are central subgroupoids of ![]() $\mathcal {H}_{|X_i}$ and
$\mathcal {H}_{|X_i}$ and ![]() $\mathcal {H}'_{|X_i}$, respectively, and, conversely, every central subgroupoid of
$\mathcal {H}'_{|X_i}$, respectively, and, conversely, every central subgroupoid of ![]() $\mathcal {H}_{|X_i}$ or
$\mathcal {H}_{|X_i}$ or ![]() $\mathcal {H}'_{|X_i}$ is stably equal to
$\mathcal {H}'_{|X_i}$ is stably equal to ![]() $\hat {\mathcal {Z}}_i$ or
$\hat {\mathcal {Z}}_i$ or ![]() $\hat {\mathcal {Z}}'_i$, respectively.
$\hat {\mathcal {Z}}'_i$, respectively.
Assuming that assertion (i) holds, the group ![]() $\langle C_i,C'_i\rangle$ is abelian. Let
$\langle C_i,C'_i\rangle$ is abelian. Let ![]() $\mathcal {Z}_i$ and
$\mathcal {Z}_i$ and ![]() $\mathcal {Z}'_i$ be central subgroupoids of
$\mathcal {Z}'_i$ be central subgroupoids of ![]() $\mathcal {H}_{|X_i}$ and
$\mathcal {H}_{|X_i}$ and ![]() $\mathcal {H}'_{|X_i}$, respectively. Let
$\mathcal {H}'_{|X_i}$, respectively. Let ![]() $U\subseteq X_i$ be a Borel subset of positive measure, and let
$U\subseteq X_i$ be a Borel subset of positive measure, and let ![]() $V\subseteq U$ be a Borel subset of positive measure such that
$V\subseteq U$ be a Borel subset of positive measure such that ![]() $(\mathcal {Z}_i)_{|V}=(\hat {\mathcal {Z}}_i)_{|V}$ and
$(\mathcal {Z}_i)_{|V}=(\hat {\mathcal {Z}}_i)_{|V}$ and ![]() $(\mathcal {Z}'_i)_{|V}=(\hat {\mathcal {Z}}'_i)_{|V}$. Then
$(\mathcal {Z}'_i)_{|V}=(\hat {\mathcal {Z}}'_i)_{|V}$. Then ![]() $\langle (\mathcal {Z}_i)_{|V},(\mathcal {Z}'_i)_{|V}\rangle \subseteq \rho ^{-1}(\langle C_i,C'_i\rangle )_{|V}$ is amenable (as
$\langle (\mathcal {Z}_i)_{|V},(\mathcal {Z}'_i)_{|V}\rangle \subseteq \rho ^{-1}(\langle C_i,C'_i\rangle )_{|V}$ is amenable (as ![]() $\rho$ has trivial kernel). It follows that assertion (ii) holds.
$\rho$ has trivial kernel). It follows that assertion (ii) holds.
Assuming that assertion (i) fails, there exist infinite cyclic subgroups ![]() $A_i\subseteq C_i$ and
$A_i\subseteq C_i$ and ![]() $A'_i\subseteq C'_i$ that together generate a rank-two free group: this follows, for instance, from [Reference Kim and KoberdaKK14, Theorem 44]. Let
$A'_i\subseteq C'_i$ that together generate a rank-two free group: this follows, for instance, from [Reference Kim and KoberdaKK14, Theorem 44]. Let ![]() $V\subseteq X_i$ be any Borel subset of positive measure. It follows from [Reference KidaKid10, Lemma 3.20] that
$V\subseteq X_i$ be any Borel subset of positive measure. It follows from [Reference KidaKid10, Lemma 3.20] that ![]() $\langle \rho ^{-1}(A_i)_{|V},\rho ^{-1}(A'_i)_{|V}\rangle$ is nonamenable. Therefore,
$\langle \rho ^{-1}(A_i)_{|V},\rho ^{-1}(A'_i)_{|V}\rangle$ is nonamenable. Therefore, ![]() $\langle (\hat {\mathcal {Z}}_i)_{|V},(\hat {\mathcal {Z}}'_i)_{|V}\rangle$ is nonamenable, showing that assertion (ii) fails.
$\langle (\hat {\mathcal {Z}}_i)_{|V},(\hat {\mathcal {Z}}'_i)_{|V}\rangle$ is nonamenable, showing that assertion (ii) fails.
6. Strong rigidity
In this section, we prove Theorem 1. As explained in the introduction, the ![]() $W^*$-rigidity statement follows from the orbit equivalence rigidity statement via [Reference Popa and VaesPV14, Theorem 1.2 and Remark 1.3], see the argument in the proof of [Reference Horbez and HuangHH22, Corollary 3.20] for details. We therefore focus on the orbit equivalence rigidity statement. Our proof distinguishes two cases, regarding whether or not
$W^*$-rigidity statement follows from the orbit equivalence rigidity statement via [Reference Popa and VaesPV14, Theorem 1.2 and Remark 1.3], see the argument in the proof of [Reference Horbez and HuangHH22, Corollary 3.20] for details. We therefore focus on the orbit equivalence rigidity statement. Our proof distinguishes two cases, regarding whether or not ![]() $G$ contains a maximal join parabolic subgroup with trivial center. Theorem 1 is the combination of Propositions 6.1 and 6.2 below.
$G$ contains a maximal join parabolic subgroup with trivial center. Theorem 1 is the combination of Propositions 6.1 and 6.2 below.
6.1 The case where some maximal join parabolic subgroup has trivial center
We first prove Theorem 1 in the case where ![]() $G$ contains a maximal join parabolic subgroup with trivial center.
$G$ contains a maximal join parabolic subgroup with trivial center.
Proposition 6.1 Let ![]() $G,H$ be two one-ended right-angled Artin groups. Assume that some maximal join parabolic subgroup of
$G,H$ be two one-ended right-angled Artin groups. Assume that some maximal join parabolic subgroup of ![]() $G$ has trivial center.
$G$ has trivial center.
Let ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ be two free, irreducible, measure-preserving actions on standard probability spaces. If the actions
$H\curvearrowright Y$ be two free, irreducible, measure-preserving actions on standard probability spaces. If the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are SOE (through a stable orbit equivalence
$H\curvearrowright Y$ are SOE (through a stable orbit equivalence ![]() $f:U\to V$ between positive measure Borel subsets
$f:U\to V$ between positive measure Borel subsets ![]() $U\subseteq X$ and
$U\subseteq X$ and ![]() $V\subseteq Y$), then
$V\subseteq Y$), then ![]() $\kappa (f)=1$, any SOE cocycle associated to
$\kappa (f)=1$, any SOE cocycle associated to ![]() $f$ is cohomologous to a group isomorphism, and the actions are actually conjugate through a group isomorphism
$f$ is cohomologous to a group isomorphism, and the actions are actually conjugate through a group isomorphism ![]() $\alpha :G\to H$.
$\alpha :G\to H$.
Proof. Throughout the proof, we always identify ![]() $G,H$ with right-angled Artin groups
$G,H$ with right-angled Artin groups ![]() $G_\Gamma,G_\Lambda$, in such a way that through these identifications, all standard generators act ergodically on
$G_\Gamma,G_\Lambda$, in such a way that through these identifications, all standard generators act ergodically on ![]() $X,Y$. All parabolic subgroups will be understood with respect to these identifications.
$X,Y$. All parabolic subgroups will be understood with respect to these identifications.
The groupoid ![]() $\mathcal {G}=(G\ltimes X)_{|U}$ is naturally isomorphic (via
$\mathcal {G}=(G\ltimes X)_{|U}$ is naturally isomorphic (via ![]() $f$) to
$f$) to ![]() $(H\ltimes Y)_{|V}$ (after renormalizing the measures on
$(H\ltimes Y)_{|V}$ (after renormalizing the measures on ![]() $U$ and
$U$ and ![]() $V$). Thus,
$V$). Thus, ![]() $\mathcal {G}$ comes equipped with two action-type cocycles
$\mathcal {G}$ comes equipped with two action-type cocycles ![]() $\rho _G:\mathcal {G}\to G$ and
$\rho _G:\mathcal {G}\to G$ and ![]() $\rho _H:\mathcal {G}\to H$.
$\rho _H:\mathcal {G}\to H$.
Let ![]() $P\subseteq G$ be a maximal join parabolic subgroup with trivial center, and let
$P\subseteq G$ be a maximal join parabolic subgroup with trivial center, and let ![]() $\mathcal {P}=\rho _G^{-1}(P)$. Then
$\mathcal {P}=\rho _G^{-1}(P)$. Then ![]() $\mathcal {P}$ satisfies assertion (ii) from Lemma 5.4, as it follows from applying this lemma to the cocycle
$\mathcal {P}$ satisfies assertion (ii) from Lemma 5.4, as it follows from applying this lemma to the cocycle ![]() $\rho _G$. Using now the implication
$\rho _G$. Using now the implication ![]() $\rm (ii)\Rightarrow (i)$ from Lemma 5.4, applied to the cocycle
$\rm (ii)\Rightarrow (i)$ from Lemma 5.4, applied to the cocycle ![]() $\rho _H$, we see that
$\rho _H$, we see that ![]() $\mathcal {P}$ also satisfies assertion (i) with respect to
$\mathcal {P}$ also satisfies assertion (i) with respect to ![]() $\rho _H$. In particular, there exist a Borel subset
$\rho _H$. In particular, there exist a Borel subset ![]() $W\subseteq U$ of positive measure and a maximal join parabolic subgroup
$W\subseteq U$ of positive measure and a maximal join parabolic subgroup ![]() $Q\subseteq H$ such that
$Q\subseteq H$ such that ![]() $\mathcal {P}_{|W}=\rho _H^{-1}(Q)_{|f(W)}$. In particular,
$\mathcal {P}_{|W}=\rho _H^{-1}(Q)_{|f(W)}$. In particular, ![]() $\mathcal {P}_{|W}$ comes equipped with two action-type cocycles towards
$\mathcal {P}_{|W}$ comes equipped with two action-type cocycles towards ![]() $P$ and
$P$ and ![]() $Q$. As
$Q$. As ![]() $P$ has trivial center, Corollary 5.6 ensures that
$P$ has trivial center, Corollary 5.6 ensures that ![]() $Q$ also has trivial center.
$Q$ also has trivial center.
Let ![]() $c:G\times X\to H$ be an SOE cocycle associated to
$c:G\times X\to H$ be an SOE cocycle associated to ![]() $f_{|W}$. Note that
$f_{|W}$. Note that ![]() $c$ is also an SOE cocycle associated to
$c$ is also an SOE cocycle associated to ![]() $f$, and any two such cocycles are cohomologous. Thus, if we prove that
$f$, and any two such cocycles are cohomologous. Thus, if we prove that ![]() $c$ is cohomologous to a group isomorphism, then the same is true of any SOE cocycle associated to
$c$ is cohomologous to a group isomorphism, then the same is true of any SOE cocycle associated to ![]() $f$. Note also that
$f$. Note also that ![]() $\kappa (f_{|W})=\kappa (f)$.
$\kappa (f_{|W})=\kappa (f)$.
The actions ![]() $P\curvearrowright X$ and
$P\curvearrowright X$ and ![]() $Q\curvearrowright Y$ are ergodic (by our irreducibility assumption), and the above ensures that for almost every
$Q\curvearrowright Y$ are ergodic (by our irreducibility assumption), and the above ensures that for almost every ![]() $x\in W$, one has
$x\in W$, one has ![]() $f((P\cdot x)\cap W)=(Q\cdot f(x))\cap f(W)$. Thus,
$f((P\cdot x)\cap W)=(Q\cdot f(x))\cap f(W)$. Thus, ![]() $c$ is cohomologous to a cocycle
$c$ is cohomologous to a cocycle ![]() $c'$ such that
$c'$ such that ![]() $c'_{|P\times X}$ is an SOE cocycle associated to
$c'_{|P\times X}$ is an SOE cocycle associated to ![]() $f_{|W}$ for the stable orbit equivalence between
$f_{|W}$ for the stable orbit equivalence between ![]() $P\curvearrowright X$ and
$P\curvearrowright X$ and ![]() $Q\curvearrowright Y$ (in particular
$Q\curvearrowright Y$ (in particular ![]() $c'(P\times X^*)\subseteq Q$ for some conull Borel subset
$c'(P\times X^*)\subseteq Q$ for some conull Borel subset ![]() $X^*\subseteq X$). The groups
$X^*\subseteq X$). The groups ![]() $P$ and
$P$ and ![]() $Q$ are join parabolic subgroups with trivial center, so they split as direct products
$Q$ are join parabolic subgroups with trivial center, so they split as direct products ![]() $P=P_{1}\times \dots \times P_{k}$ and
$P=P_{1}\times \dots \times P_{k}$ and ![]() $Q=Q_1\times \dots \times Q_\ell$ of at least two nonabelian parabolic subgroups that do not admit any nontrivial product decomposition. All subgroups
$Q=Q_1\times \dots \times Q_\ell$ of at least two nonabelian parabolic subgroups that do not admit any nontrivial product decomposition. All subgroups ![]() $P_i$ and
$P_i$ and ![]() $Q_j$ belong to Monod and Shalom's class
$Q_j$ belong to Monod and Shalom's class ![]() $\mathcal {C}_{\mathrm {reg}}$, so Theorem 3.2 ensures that
$\mathcal {C}_{\mathrm {reg}}$, so Theorem 3.2 ensures that ![]() $\kappa (f_{|W})=1$ (so
$\kappa (f_{|W})=1$ (so ![]() $\kappa (f)=1$) and that
$\kappa (f)=1$) and that ![]() $c'_{|P\times X}$ is cohomologous to a group isomorphism
$c'_{|P\times X}$ is cohomologous to a group isomorphism ![]() $\alpha :P\to Q$. As
$\alpha :P\to Q$. As ![]() $P$ contains a conjugate of a standard generator of
$P$ contains a conjugate of a standard generator of ![]() $G$, Lemma 4.3 ensures that
$G$, Lemma 4.3 ensures that ![]() $c$ is cohomologous to a group isomorphism
$c$ is cohomologous to a group isomorphism ![]() $\alpha :G\to H$, and the actions
$\alpha :G\to H$, and the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are conjugate through
$H\curvearrowright Y$ are conjugate through ![]() $\alpha$. As already mentioned in the previous paragraph, this is enough to conclude.
$\alpha$. As already mentioned in the previous paragraph, this is enough to conclude.
6.2 The case where every maximal join parabolic subgroup has a nontrivial center
We now prove Theorem 1 when every maximal join parabolic subgroup of ![]() $G$ has a nontrivial center.
$G$ has a nontrivial center.
Proposition 6.2 Let ![]() $G,H$ be two one-ended right-angled Artin groups with trivial center. Assume that every maximal join parabolic subgroup of
$G,H$ be two one-ended right-angled Artin groups with trivial center. Assume that every maximal join parabolic subgroup of ![]() $G$ has a nontrivial center.
$G$ has a nontrivial center.
Let ![]() $G\curvearrowright (X,\mu )$ and
$G\curvearrowright (X,\mu )$ and ![]() $H\curvearrowright (Y,\nu )$ be two free, irreducible, measure-preserving actions on standard probability spaces. If the actions
$H\curvearrowright (Y,\nu )$ be two free, irreducible, measure-preserving actions on standard probability spaces. If the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are SOE (through a stable orbit equivalence
$H\curvearrowright Y$ are SOE (through a stable orbit equivalence ![]() $f:U\to V$ between positive measure Borel subsets
$f:U\to V$ between positive measure Borel subsets ![]() $U\subseteq X$ and
$U\subseteq X$ and ![]() $V\subseteq Y\!$), then
$V\subseteq Y\!$), then ![]() $\kappa (f)=1$, every SOE cocycle associated to
$\kappa (f)=1$, every SOE cocycle associated to ![]() $f$ is cohomologous to a group isomorphism, and the actions are actually conjugate through a group isomorphism
$f$ is cohomologous to a group isomorphism, and the actions are actually conjugate through a group isomorphism ![]() $\alpha :G\to H$.
$\alpha :G\to H$.
Proof. As in our previous proof, we always identify ![]() $G,H$ with right-angled Artin groups
$G,H$ with right-angled Artin groups ![]() $G_\Gamma,G_\Lambda$, in such a way that through these identifications, all standard generators act ergodically on
$G_\Gamma,G_\Lambda$, in such a way that through these identifications, all standard generators act ergodically on ![]() $X,Y$. All parabolic subgroups will be understood with respect to these identifications.
$X,Y$. All parabolic subgroups will be understood with respect to these identifications.
Up to exchanging the roles of ![]() $G$ and
$G$ and ![]() $H$, we assume without loss of generality that
$H$, we assume without loss of generality that ![]() $\kappa (f)\ge 1$. Let
$\kappa (f)\ge 1$. Let ![]() $\mathcal {G}=(G\ltimes X)_{|U}$, which is naturally isomorphic (through
$\mathcal {G}=(G\ltimes X)_{|U}$, which is naturally isomorphic (through ![]() $f$) to
$f$) to ![]() $(H\ltimes Y)_{|V}$ (after renormalizing the measures on
$(H\ltimes Y)_{|V}$ (after renormalizing the measures on ![]() $U$ and
$U$ and ![]() $V$). Then
$V$). Then ![]() $\mathcal {G}$ comes equipped with two action-type cocycles
$\mathcal {G}$ comes equipped with two action-type cocycles ![]() $\rho _G:\mathcal {G}\to G$ and
$\rho _G:\mathcal {G}\to G$ and ![]() $\rho _H:\mathcal {G}\to H$.
$\rho _H:\mathcal {G}\to H$.
Lemma 1.4 ensures that there exist two distinct maximal join parabolic subgroups ![]() $P_1,P_2\subseteq G$, whose centers
$P_1,P_2\subseteq G$, whose centers ![]() $A_1,A_2$ are infinite and commute, and by Lemma 1.5 we have
$A_1,A_2$ are infinite and commute, and by Lemma 1.5 we have ![]() $A_1\cap A_2=\{1\}$.
$A_1\cap A_2=\{1\}$.
For every ![]() $i\in \{1,2\}$, let
$i\in \{1,2\}$, let ![]() $\mathcal {P}_i=\rho _G^{-1}(P_i)$ and
$\mathcal {P}_i=\rho _G^{-1}(P_i)$ and ![]() $\mathcal {A}_i=\rho _G^{-1}(A_i)$. Then
$\mathcal {A}_i=\rho _G^{-1}(A_i)$. Then ![]() $\mathcal {P}_1$ and
$\mathcal {P}_1$ and ![]() $\mathcal {P}_2$ are two maximal join subgroupoids of
$\mathcal {P}_2$ are two maximal join subgroupoids of ![]() $\mathcal {G}$ which contain a central subgroupoid of infinite type, and are center-commuting. Using Lemmas 5.4 and 5.7, we can therefore find two distinct maximal join parabolic subgroups
$\mathcal {G}$ which contain a central subgroupoid of infinite type, and are center-commuting. Using Lemmas 5.4 and 5.7, we can therefore find two distinct maximal join parabolic subgroups ![]() $Q_1,Q_2\subseteq H$ with commuting infinite centers
$Q_1,Q_2\subseteq H$ with commuting infinite centers ![]() $B_1,B_2$, and a Borel subset
$B_1,B_2$, and a Borel subset ![]() $W\subseteq U$ of positive measure, such that for every
$W\subseteq U$ of positive measure, such that for every ![]() $i\in \{1,2\}$, one has
$i\in \{1,2\}$, one has ![]() $(\mathcal {P}_i)_{|W}=\rho _H^{-1}(Q_i)_{|f(W)}$. In addition, Lemma 5.5 implies that up to replacing
$(\mathcal {P}_i)_{|W}=\rho _H^{-1}(Q_i)_{|f(W)}$. In addition, Lemma 5.5 implies that up to replacing ![]() $W$ by a positive measure Borel subset, we can assume that
$W$ by a positive measure Borel subset, we can assume that ![]() $(\mathcal {A}_i)_{|W}=\rho _H^{-1}(B_i)_{|f(W)}$ for every
$(\mathcal {A}_i)_{|W}=\rho _H^{-1}(B_i)_{|f(W)}$ for every ![]() $i\in \{1,2\}$.
$i\in \{1,2\}$.
Let ![]() $c:G\times X\to H$ be an SOE cocycle associated to
$c:G\times X\to H$ be an SOE cocycle associated to ![]() $f_{|W}$. Up to replacing
$f_{|W}$. Up to replacing ![]() $X$ by a conull invariant Borel subset, we can (and do) assume that
$X$ by a conull invariant Borel subset, we can (and do) assume that ![]() $c$ is chosen so that whenever
$c$ is chosen so that whenever ![]() $(g,x)\in G\times X$ satisfies
$(g,x)\in G\times X$ satisfies ![]() $x,gx\in W$, then
$x,gx\in W$, then ![]() $c(g,x)$ is the unique element
$c(g,x)$ is the unique element ![]() $h\in H$ so that
$h\in H$ so that ![]() $f(gx)=hf(x)$. We prove that
$f(gx)=hf(x)$. We prove that ![]() $c$ is cohomologous to a cocycle
$c$ is cohomologous to a cocycle ![]() $c'$ for which there exists a standard generator
$c'$ for which there exists a standard generator ![]() $s\in G$ such that
$s\in G$ such that ![]() $c'(s,\cdot )$ is almost everywhere constant. This will be enough to conclude the proof of our proposition in view of Lemma 4.3 (after observing that
$c'(s,\cdot )$ is almost everywhere constant. This will be enough to conclude the proof of our proposition in view of Lemma 4.3 (after observing that ![]() $c$ is also an SOE cocycle associated to
$c$ is also an SOE cocycle associated to ![]() $f$, and
$f$, and ![]() $\kappa (f_{|W})=\kappa (f)$).
$\kappa (f_{|W})=\kappa (f)$).
For ![]() $i\in \{1,2\}$, we have
$i\in \{1,2\}$, we have ![]() $(\mathcal {P}_i)_{|W}=\rho _H^{-1}(Q_i)_{|f(W)}$, and
$(\mathcal {P}_i)_{|W}=\rho _H^{-1}(Q_i)_{|f(W)}$, and ![]() $P_i,Q_i$ act ergodically on
$P_i,Q_i$ act ergodically on ![]() $X,Y$ by assumption. Thus,
$X,Y$ by assumption. Thus, ![]() $c$ is cohomologous to a cocycle
$c$ is cohomologous to a cocycle ![]() $c_i$ such that
$c_i$ such that ![]() $(c_i)_{|P_i\times X}$ is an SOE cocycle associated to
$(c_i)_{|P_i\times X}$ is an SOE cocycle associated to ![]() $f_{|W}$ for the stable orbit equivalence between
$f_{|W}$ for the stable orbit equivalence between ![]() $P_i\curvearrowright X$ and
$P_i\curvearrowright X$ and ![]() $Q_i\curvearrowright Y$, and such that
$Q_i\curvearrowright Y$, and such that ![]() $c$ and
$c$ and ![]() $c_i$ coincide on all pairs
$c_i$ coincide on all pairs ![]() $(g,x)$ with
$(g,x)$ with ![]() $x,gx\in W$.
$x,gx\in W$.
By Lemma 3.1 (applied to the ambient groups ![]() $P_i,Q_i$ and to the normal subgroups
$P_i,Q_i$ and to the normal subgroups ![]() $A_i,B_i$), for every
$A_i,B_i$), for every ![]() $i\in \{1,2\}$, up to replacing
$i\in \{1,2\}$, up to replacing ![]() $c_i$ by a cohomologous cocycle and replacing
$c_i$ by a cohomologous cocycle and replacing ![]() $X$ by a conull
$X$ by a conull ![]() $G$-invariant and
$G$-invariant and ![]() $H$-invariant Borel subset, we can assume that the following hold:
$H$-invariant Borel subset, we can assume that the following hold:
(i) there is a group isomorphism
 $\bar {\alpha }_i:P_i/A_i\to Q_i/B_i$ satisfying that for every
$\bar {\alpha }_i:P_i/A_i\to Q_i/B_i$ satisfying that for every  $g\in P_i$ and every
$g\in P_i$ and every  $x\in X$, one has
$x\in X$, one has  $c_i(g,x)\in \bar {\alpha }_i(gA_i)$ and in particular,
$c_i(g,x)\in \bar {\alpha }_i(gA_i)$ and in particular,  $c_i(A_i\times X)\subseteq B_i$;
$c_i(A_i\times X)\subseteq B_i$;(ii)
 $c_i$ coincides with
$c_i$ coincides with  $c$ on all pairs
$c$ on all pairs  $(g,x)$ with
$(g,x)$ with  $x,gx\in W$.
$x,gx\in W$.
Let ![]() $r_i:Q_i=B_i\times B_i^{\perp }\to B_i^{\perp }$ be the retraction, and let
$r_i:Q_i=B_i\times B_i^{\perp }\to B_i^{\perp }$ be the retraction, and let ![]() $c'_i:A_i^{\perp }\times X\to B_i^{\perp }$ be the cocycle defined as
$c'_i:A_i^{\perp }\times X\to B_i^{\perp }$ be the cocycle defined as ![]() $c'_i=(r_i\circ c_i)_{|A_i^{\perp }\times X}$. There are isomorphisms
$c'_i=(r_i\circ c_i)_{|A_i^{\perp }\times X}$. There are isomorphisms ![]() $P_i/A_i\to A_i^{\perp }$ and
$P_i/A_i\to A_i^{\perp }$ and ![]() $Q_i/B_i\to B_i^{\perp }$ (coming from choosing the unique lift). Through these identifications
$Q_i/B_i\to B_i^{\perp }$ (coming from choosing the unique lift). Through these identifications ![]() $\bar {\alpha }_i$ yields an isomorphism
$\bar {\alpha }_i$ yields an isomorphism ![]() $\alpha _i:A_i^{\perp }\to B_i^{\perp }$ such that for every
$\alpha _i:A_i^{\perp }\to B_i^{\perp }$ such that for every ![]() $g\in A_i^{\perp }$ and every
$g\in A_i^{\perp }$ and every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c'_i(g,x)=\alpha _i(g)$.
$c'_i(g,x)=\alpha _i(g)$.
Recall from Lemma 1.5 that for every ![]() $i\in \{1,2\}$, we have
$i\in \{1,2\}$, we have ![]() $A_{3-i}\subseteq A_i^{\perp }$ and
$A_{3-i}\subseteq A_i^{\perp }$ and ![]() $B_{3-i}\subseteq B_i^{\perp }$. We now prove that for every
$B_{3-i}\subseteq B_i^{\perp }$. We now prove that for every ![]() $i\in \{1,2\}$, the isomorphism
$i\in \{1,2\}$, the isomorphism ![]() $\alpha _i$ restricts to an isomorphism between
$\alpha _i$ restricts to an isomorphism between ![]() $A_{3-i}$ and
$A_{3-i}$ and ![]() $B_{3-i}$. By symmetry, it suffices prove it for
$B_{3-i}$. By symmetry, it suffices prove it for ![]() $i=2$. By Poincaré recurrence, for every
$i=2$. By Poincaré recurrence, for every ![]() $g\in A_1$, there exist an integer
$g\in A_1$, there exist an integer ![]() $n>0$ and
$n>0$ and ![]() $x\in W$ such that
$x\in W$ such that ![]() $g^nx\in W$. Then
$g^nx\in W$. Then ![]() $c_2(g^n,x)=c_1(g^n,x)$ (they are both equal to
$c_2(g^n,x)=c_1(g^n,x)$ (they are both equal to ![]() $c(g^n,x)$), and these belong to
$c(g^n,x)$), and these belong to ![]() $B_1$, which is contained in
$B_1$, which is contained in ![]() $B_2^{\perp }$. In particular,
$B_2^{\perp }$. In particular, ![]() $c_2(g^n,x)=c'_2(g^n,x)$, which, in turn, equals
$c_2(g^n,x)=c'_2(g^n,x)$, which, in turn, equals ![]() $\alpha _2(g)^n$ by the above. Thus,
$\alpha _2(g)^n$ by the above. Thus, ![]() $\alpha _2(g)^n\in B_1$, and therefore
$\alpha _2(g)^n\in B_1$, and therefore ![]() $\alpha _2(g)\in B_1$ by [Reference MinasyanMin12, Lemma 6.4]. Thus,
$\alpha _2(g)\in B_1$ by [Reference MinasyanMin12, Lemma 6.4]. Thus, ![]() $\alpha _2(A_1)\subseteq B_1$. We now show that actually
$\alpha _2(A_1)\subseteq B_1$. We now show that actually ![]() $\alpha _2(A_1)=B_1$. Take
$\alpha _2(A_1)=B_1$. Take ![]() $h\in B_1$. Then there exist an integer
$h\in B_1$. Then there exist an integer ![]() $m>0$ and
$m>0$ and ![]() $y\in f(W)$ such that
$y\in f(W)$ such that ![]() $h^my\in f(W)$. As the actions
$h^my\in f(W)$. As the actions ![]() $A_1\curvearrowright X$ and
$A_1\curvearrowright X$ and ![]() $B_1\curvearrowright Y$ induce (via
$B_1\curvearrowright Y$ induce (via ![]() $f$) the same orbit equivalence relation on
$f$) the same orbit equivalence relation on ![]() $W$, there exists
$W$, there exists ![]() $g\in A_1$ such that
$g\in A_1$ such that ![]() $c_1(g,y)=c_2(g,y)=h^m$. As
$c_1(g,y)=c_2(g,y)=h^m$. As ![]() $h^m\in B_1\subseteq B_2^{\perp }$, we have
$h^m\in B_1\subseteq B_2^{\perp }$, we have ![]() $c_2(g,y)=c'_2(g,y)$, so
$c_2(g,y)=c'_2(g,y)$, so ![]() $\alpha _2(g)=h^m$. As
$\alpha _2(g)=h^m$. As ![]() $\alpha _2:A_2^\perp \to B_2^\perp$ is an isomorphism, there also exists
$\alpha _2:A_2^\perp \to B_2^\perp$ is an isomorphism, there also exists ![]() $g_0\in A_2^\perp$ such that
$g_0\in A_2^\perp$ such that ![]() $\alpha _2(g_0)=h$, hence
$\alpha _2(g_0)=h$, hence ![]() $g^m_0=g\in A_1$. It follows that
$g^m_0=g\in A_1$. It follows that ![]() $g_0\in A_1$ by [Reference MinasyanMin12, Lemma 6.4]. This proves that
$g_0\in A_1$ by [Reference MinasyanMin12, Lemma 6.4]. This proves that ![]() $\alpha _2$ restricts to an isomorphism between
$\alpha _2$ restricts to an isomorphism between ![]() $A_1$ and
$A_1$ and ![]() $B_1$, as desired.
$B_1$, as desired.
For every ![]() $i\in \{1,2\}$, we can therefore extend
$i\in \{1,2\}$, we can therefore extend ![]() $\alpha _i$ on
$\alpha _i$ on ![]() $A_i$ by defining
$A_i$ by defining ![]() $(\alpha _i)_{|A_i}=(\alpha _{3-i})_{|A_i}$ (in particular,
$(\alpha _i)_{|A_i}=(\alpha _{3-i})_{|A_i}$ (in particular, ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\alpha _2$ coincide on
$\alpha _2$ coincide on ![]() $\langle A_1,A_2\rangle$). This yields an isomorphism
$\langle A_1,A_2\rangle$). This yields an isomorphism ![]() $\alpha _i:P_i\to Q_i$ such that for every
$\alpha _i:P_i\to Q_i$ such that for every ![]() $g\in A_i\cup A_i^{\perp }$ and every
$g\in A_i\cup A_i^{\perp }$ and every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c_i(g,x)\in \alpha _i(g)B_i$. Now, using the cocycle relation and the fact that every element of
$c_i(g,x)\in \alpha _i(g)B_i$. Now, using the cocycle relation and the fact that every element of ![]() $P_i$ is a product of the form
$P_i$ is a product of the form ![]() $hk$ with
$hk$ with ![]() $h\in A_i$ and
$h\in A_i$ and ![]() $k\in A_i^{\perp }$, we see that
$k\in A_i^{\perp }$, we see that ![]() $c_i(g,x)\in \alpha _i(g)B_i$ for every
$c_i(g,x)\in \alpha _i(g)B_i$ for every ![]() $g\in P_i$ and almost every
$g\in P_i$ and almost every ![]() $x\in X$.
$x\in X$.
Altogether, these show that, for every ![]() $i\in \{1,2\}$, we have a measurable map
$i\in \{1,2\}$, we have a measurable map ![]() $\varphi _i:X\to H$ and a measurable map
$\varphi _i:X\to H$ and a measurable map ![]() $\kappa _i:P_i\times X\to B_i$ such that for every
$\kappa _i:P_i\times X\to B_i$ such that for every ![]() $g\in P_i$ and almost every
$g\in P_i$ and almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c(g,x)=\varphi _i(gx)\alpha _i(g)\kappa _i(g,x)\varphi _i(x)^{-1}$. Up to replacing
$c(g,x)=\varphi _i(gx)\alpha _i(g)\kappa _i(g,x)\varphi _i(x)^{-1}$. Up to replacing ![]() $X$ by a conull
$X$ by a conull ![]() $G$-invariant Borel subset, we assume that these relations hold for every
$G$-invariant Borel subset, we assume that these relations hold for every ![]() $g\in G$ and every
$g\in G$ and every ![]() $x\in X$. Let
$x\in X$. Let ![]() $X=\sqcup _{j\in J}X_j$ be a partition into at most countably many Borel subsets such that for every
$X=\sqcup _{j\in J}X_j$ be a partition into at most countably many Borel subsets such that for every ![]() $j\in J$, the maps
$j\in J$, the maps ![]() $\varphi _1,\varphi _2$ have constant values
$\varphi _1,\varphi _2$ have constant values ![]() $\gamma _{1,j},\gamma _{2,j}$ when restricted to
$\gamma _{1,j},\gamma _{2,j}$ when restricted to ![]() $X_j$.
$X_j$.
Let ![]() $g\in A_1$ be a nontrivial element. By Poincaré recurrence, for every
$g\in A_1$ be a nontrivial element. By Poincaré recurrence, for every ![]() $j\in J$ such that
$j\in J$ such that ![]() $X_j$ has positive measure, there exist an integer
$X_j$ has positive measure, there exist an integer ![]() $k_j>0$ and
$k_j>0$ and ![]() $x\in X_j$ such that
$x\in X_j$ such that ![]() $g^{k_j}x\in X_j$. By observing that
$g^{k_j}x\in X_j$. By observing that ![]() $A_1\subseteq P_1\cap P_2$, we can then write
$A_1\subseteq P_1\cap P_2$, we can then write
where ![]() $\alpha _1(g)^{k_j}=\alpha _2(g)^{k_j}$ belongs to
$\alpha _1(g)^{k_j}=\alpha _2(g)^{k_j}$ belongs to ![]() $B_1\subseteq B_2^{\perp }$, and
$B_1\subseteq B_2^{\perp }$, and ![]() $\kappa _1(g^{k_j},x)\in B_1$ and
$\kappa _1(g^{k_j},x)\in B_1$ and ![]() $\kappa _2(g^{k_j},x)\in B_2$. Let
$\kappa _2(g^{k_j},x)\in B_2$. Let ![]() $r_2:H\to B_2$ be the retraction as in § 1. As
$r_2:H\to B_2$ be the retraction as in § 1. As ![]() $B_1\subseteq B_2^{\perp }$, we have
$B_1\subseteq B_2^{\perp }$, we have ![]() $r_2(B_1)=\{1\}$. By applying
$r_2(B_1)=\{1\}$. By applying ![]() $r_2$ to the above equation, we deduce that
$r_2$ to the above equation, we deduce that ![]() $\kappa _2(g^{k_j},x)$ is trivial. Now applying
$\kappa _2(g^{k_j},x)$ is trivial. Now applying ![]() $r_1:H\to B_1$ to the above equation, and using the fact that
$r_1:H\to B_1$ to the above equation, and using the fact that ![]() $\alpha _1(g)=\alpha _2(g)$ and
$\alpha _1(g)=\alpha _2(g)$ and ![]() $B_1$ is abelian, we deduce that
$B_1$ is abelian, we deduce that ![]() $\kappa _1(g^{k_j},x)$ is trivial. Therefore,
$\kappa _1(g^{k_j},x)$ is trivial. Therefore, ![]() $\gamma _{1,j}^{-1}\gamma _{2,j}$ commutes with
$\gamma _{1,j}^{-1}\gamma _{2,j}$ commutes with ![]() $\alpha _1(g)^{k_j}$.
$\alpha _1(g)^{k_j}$.
We claim that the centralizer ![]() $Z$ of
$Z$ of ![]() $\alpha _1(g)^{k_j}$ is a join parabolic subgroup. Indeed, let
$\alpha _1(g)^{k_j}$ is a join parabolic subgroup. Indeed, let ![]() $C_1\subseteq B_1$ be the smallest parabolic subgroup that contains
$C_1\subseteq B_1$ be the smallest parabolic subgroup that contains ![]() $\alpha _1(g)^{k_j}$. As
$\alpha _1(g)^{k_j}$. As ![]() $B_1$ (whence
$B_1$ (whence ![]() $C_1$) is abelian, we have
$C_1$) is abelian, we have ![]() $Z=C_1\times C_1^{\perp }$. In addition
$Z=C_1\times C_1^{\perp }$. In addition ![]() $C_1$ is nontrivial (because
$C_1$ is nontrivial (because ![]() $g$ is nontrivial), and
$g$ is nontrivial), and ![]() $C_1^\perp$ is also nontrivial because it contains
$C_1^\perp$ is also nontrivial because it contains ![]() $B_1^{\perp }$. This proves our claim. As
$B_1^{\perp }$. This proves our claim. As ![]() $Z$ contains
$Z$ contains ![]() $Q_1=B_1\times B_1^{\perp }$, it follows that
$Q_1=B_1\times B_1^{\perp }$, it follows that ![]() $Z=Q_1$ by the maximality of
$Z=Q_1$ by the maximality of ![]() $Q_1$ as a join parabolic subgroup.
$Q_1$ as a join parabolic subgroup.
This proves that for almost every ![]() $x\in X$, one has
$x\in X$, one has ![]() $\varphi _2(x)=\varphi _1(x)\eta _1(x)\mu _1(x)$, where
$\varphi _2(x)=\varphi _1(x)\eta _1(x)\mu _1(x)$, where ![]() $\eta _1(x)\in B_1$ and
$\eta _1(x)\in B_1$ and ![]() $\mu _1(x)\in B_1^{\perp }$. Now, for every
$\mu _1(x)\in B_1^{\perp }$. Now, for every ![]() $g\in A_1$ and every
$g\in A_1$ and every ![]() $x\in X$, one has
$x\in X$, one has
 \begin{align*} c(g,x)&=\varphi_1(gx)\alpha_1(g)\kappa_1(g,x)\varphi_1(x)^{-1}\\ & =\varphi_1(gx)\eta_1(gx)\mu_1(gx)\alpha_1(g)\kappa_2(g,x)\mu_1(x)^{-1}\eta_1(x)^{-1}\varphi_1(x)^{-1}, \end{align*}
\begin{align*} c(g,x)&=\varphi_1(gx)\alpha_1(g)\kappa_1(g,x)\varphi_1(x)^{-1}\\ & =\varphi_1(gx)\eta_1(gx)\mu_1(gx)\alpha_1(g)\kappa_2(g,x)\mu_1(x)^{-1}\eta_1(x)^{-1}\varphi_1(x)^{-1}, \end{align*}
and, therefore,
Retracting to ![]() $B_1$ yields
$B_1$ yields
and, therefore,
This proves that there exists a measurable map ![]() $\psi :X\to H$ and a homomorphism
$\psi :X\to H$ and a homomorphism ![]() $\alpha _1:A_1\to H$ such that for every
$\alpha _1:A_1\to H$ such that for every ![]() $g\in A_1$ and every
$g\in A_1$ and every ![]() $x\in X$, one has
$x\in X$, one has ![]() $c(g,x)=\psi (gx)\alpha _1(g)\psi (x)^{-1}$, which concludes our proof.
$c(g,x)=\psi (gx)\alpha _1(g)\psi (x)^{-1}$, which concludes our proof.
7. Superrigidity
In this section, we derive Theorem 2 from Theorem 1, using general techniques developed in prior works of Furman [Reference FurmanFur99b], Monod and Shalom [Reference Monod and ShalomMS06] and Kida [Reference KidaKid08].
Let ![]() $G$ be a countable group, and let
$G$ be a countable group, and let ![]() $\mathcal {F}$ be a collection of subgroups of
$\mathcal {F}$ be a collection of subgroups of ![]() $G$. One says that a free, ergodic, measure-preserving action of
$G$. One says that a free, ergodic, measure-preserving action of ![]() $G$ on a standard probability space
$G$ on a standard probability space ![]() $X$ is
$X$ is ![]() $\mathcal {F}$-ergodic if every subgroup in
$\mathcal {F}$-ergodic if every subgroup in ![]() $\mathcal {F}$ acts ergodically on
$\mathcal {F}$ acts ergodically on ![]() $X$. In our setting, an irreducible action of a right-angled Artin group is an action which is
$X$. In our setting, an irreducible action of a right-angled Artin group is an action which is ![]() $\mathcal {F}$-ergodic with respect to the collection of all cyclic subgroups associated to a standard generating set
$\mathcal {F}$-ergodic with respect to the collection of all cyclic subgroups associated to a standard generating set ![]() $\mathcal {F}$.
$\mathcal {F}$.
One says that ![]() $(G,\mathcal {F})$ is strongly cocycle-rigid if given any two SOE
$(G,\mathcal {F})$ is strongly cocycle-rigid if given any two SOE ![]() $\mathcal {F}$-ergodic free, ergodic, measure-preserving actions
$\mathcal {F}$-ergodic free, ergodic, measure-preserving actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $G\curvearrowright Y$ on standard probability spaces, any SOE cocycle
$G\curvearrowright Y$ on standard probability spaces, any SOE cocycle ![]() $c:G\times X\to G$ is cohomologous to a group isomorphism
$c:G\times X\to G$ is cohomologous to a group isomorphism ![]() $\alpha :G\to G$. Note that Propositions 6.1 and 6.2 imply that if
$\alpha :G\to G$. Note that Propositions 6.1 and 6.2 imply that if ![]() $G$ is a one-ended right-angled Artin group with trivial center, and if
$G$ is a one-ended right-angled Artin group with trivial center, and if ![]() $\mathcal {F}$ is the set of all cyclic subgroups associated to standard generators of
$\mathcal {F}$ is the set of all cyclic subgroups associated to standard generators of ![]() $G$ (under an isomorphism between
$G$ (under an isomorphism between ![]() $G$ and some
$G$ and some ![]() $G_\Gamma$), then
$G_\Gamma$), then ![]() $(G,\mathcal {F})$ is strongly cocycle-rigid.
$(G,\mathcal {F})$ is strongly cocycle-rigid.
Recall that a free, ergodic, measure-preserving action of a countable group ![]() $G$ on a standard probability space
$G$ on a standard probability space ![]() $(X,\mu )$ is mildly mixing if for every Borel subset
$(X,\mu )$ is mildly mixing if for every Borel subset ![]() $A\subseteq X$, and every sequence
$A\subseteq X$, and every sequence ![]() $(g_n)_{n\in \mathbb {N}}\in G^{\mathbb {N}}$ made of pairwise distinct elements, either
$(g_n)_{n\in \mathbb {N}}\in G^{\mathbb {N}}$ made of pairwise distinct elements, either ![]() $A$ is null or conull, or else
$A$ is null or conull, or else ![]() $\liminf _{n\to \infty }\mu (g_nA\Delta A)>0$. This is equivalent to requiring that for every nonsingular properly ergodic action of
$\liminf _{n\to \infty }\mu (g_nA\Delta A)>0$. This is equivalent to requiring that for every nonsingular properly ergodic action of ![]() $G$ on a standard probability measure space
$G$ on a standard probability measure space ![]() $Y$, the diagonal
$Y$, the diagonal ![]() $G$-action on
$G$-action on ![]() $X\times Y$ is ergodic [Reference Schmidt and WaltersSW82]. Every mildly mixing
$X\times Y$ is ergodic [Reference Schmidt and WaltersSW82]. Every mildly mixing ![]() $G$-action is
$G$-action is ![]() $\mathcal {F}$-ergodic, taking for
$\mathcal {F}$-ergodic, taking for ![]() $\mathcal {F}$ the collection of all infinite subgroups of
$\mathcal {F}$ the collection of all infinite subgroups of ![]() $G$.
$G$.
Theorem 7.1 Let ![]() $G$ be an ICC countable group, and let
$G$ be an ICC countable group, and let ![]() $\mathcal {F}$ be a collection of infinite subgroups of
$\mathcal {F}$ be a collection of infinite subgroups of ![]() $G$. Assume that
$G$. Assume that ![]() $(G,\mathcal {F})$ is strongly cocycle-rigid. Let
$(G,\mathcal {F})$ is strongly cocycle-rigid. Let ![]() $H$ be a countable group. Let
$H$ be a countable group. Let ![]() $X,Y$ be standard probability spaces, let
$X,Y$ be standard probability spaces, let ![]() $G\curvearrowright X$ be an
$G\curvearrowright X$ be an ![]() $\mathcal {F}$-ergodic free, ergodic, measure-preserving
$\mathcal {F}$-ergodic free, ergodic, measure-preserving ![]() $G$-action, and let
$G$-action, and let ![]() $H\curvearrowright Y$ be a free, measure-preserving, mildly mixing
$H\curvearrowright Y$ be a free, measure-preserving, mildly mixing ![]() $H$-action.
$H$-action.
If the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are SOE, then they are virtually conjugate.
$H\curvearrowright Y$ are SOE, then they are virtually conjugate.
Proof. By [Reference FurmanFur99b, Theorem 3.3], there exists a standard measure space ![]() $\Sigma$ equipped with a measure-preserving action of
$\Sigma$ equipped with a measure-preserving action of ![]() $G\times H$ such that the
$G\times H$ such that the ![]() $G$-action on
$G$-action on ![]() $X$ is isomorphic to the
$X$ is isomorphic to the ![]() $G$-action on
$G$-action on ![]() $H\backslash \Sigma$, and the
$H\backslash \Sigma$, and the ![]() $H$-action on
$H$-action on ![]() $Y$ is isomorphic to the
$Y$ is isomorphic to the ![]() $H$-action on
$H$-action on ![]() $G\backslash \Sigma$ (the space
$G\backslash \Sigma$ (the space ![]() $\Sigma$ is a measure equivalence coupling between
$\Sigma$ is a measure equivalence coupling between ![]() $G$ and
$G$ and ![]() $H$ in the sense of [Reference GromovGro93, 0.5.E]). Let
$H$ in the sense of [Reference GromovGro93, 0.5.E]). Let ![]() $\Omega$ be the self measure equivalence coupling of
$\Omega$ be the self measure equivalence coupling of ![]() $G$ defined by
$G$ defined by ![]() $\Omega =\Sigma \times _{H}H\times _{H}\check {\Sigma }$ (see [Reference FurmanFur99a, § 2] for definitions). By definition,
$\Omega =\Sigma \times _{H}H\times _{H}\check {\Sigma }$ (see [Reference FurmanFur99a, § 2] for definitions). By definition, ![]() $\Omega$ comes equipped with a measure-preserving action of
$\Omega$ comes equipped with a measure-preserving action of ![]() $G\times G$; for notational simplicity, we let
$G\times G$; for notational simplicity, we let ![]() $G_{\ell }=G\times \{1\}$ and
$G_{\ell }=G\times \{1\}$ and ![]() $G_r=\{1\}\times G$. As the
$G_r=\{1\}\times G$. As the ![]() $H$-action on
$H$-action on ![]() $Y$ is mildly mixing, [Reference Monod and ShalomMS06, Lemma 6.5] ensures that the actions of
$Y$ is mildly mixing, [Reference Monod and ShalomMS06, Lemma 6.5] ensures that the actions of ![]() $G_\ell$ on
$G_\ell$ on ![]() $G_r\backslash \Omega$, and of
$G_r\backslash \Omega$, and of ![]() $G_r$ on
$G_r$ on ![]() $G_\ell \backslash \Omega$, are ergodic and
$G_\ell \backslash \Omega$, are ergodic and ![]() $\mathcal {F}$-ergodic. In addition, the essential freeness of the
$\mathcal {F}$-ergodic. In addition, the essential freeness of the ![]() $G$-action on
$G$-action on ![]() $H\backslash \Sigma$ ensures that the actions of
$H\backslash \Sigma$ ensures that the actions of ![]() $G_\ell$ on
$G_\ell$ on ![]() $G_r\backslash \Omega$ and of
$G_r\backslash \Omega$ and of ![]() $G_r$ on
$G_r$ on ![]() $G_\ell \backslash \Omega$ are essentially free.
$G_\ell \backslash \Omega$ are essentially free.
We now claim that there exist a Borel map ![]() $\Phi :\Omega \to G$ and an automorphism
$\Phi :\Omega \to G$ and an automorphism ![]() $\rho :G\to G$ such that
$\rho :G\to G$ such that ![]() $\Phi$ is
$\Phi$ is ![]() $\rho$-twisted equivariant, i.e.
$\rho$-twisted equivariant, i.e. ![]() $\Phi$ is
$\Phi$ is ![]() $(G\times G)$-equivariant when
$(G\times G)$-equivariant when ![]() $G$ is equipped with the action of
$G$ is equipped with the action of ![]() $G\times G$ given by
$G\times G$ given by ![]() $(g_1,g_2)\cdot g=\rho (g_1)gg_2^{-1}$. Let
$(g_1,g_2)\cdot g=\rho (g_1)gg_2^{-1}$. Let ![]() $Z\subseteq \Omega$ be a fundamental domain for the action of
$Z\subseteq \Omega$ be a fundamental domain for the action of ![]() $G_r$. By identifying
$G_r$. By identifying ![]() $Z$ with
$Z$ with ![]() $G_r\backslash \Omega$, we get an essentially free, ergodic,
$G_r\backslash \Omega$, we get an essentially free, ergodic, ![]() $\mathcal {F}$-ergodic, measure-preserving action of
$\mathcal {F}$-ergodic, measure-preserving action of ![]() $G_\ell$ on
$G_\ell$ on ![]() $Z$. It follows from [Reference FurmanFur99b, Lemma 3.2] that there exist an SOE cocycle
$Z$. It follows from [Reference FurmanFur99b, Lemma 3.2] that there exist an SOE cocycle ![]() $c:G_\ell \times Z\to G_r$ and a
$c:G_\ell \times Z\to G_r$ and a ![]() $(G_\ell \times G_r)$-equivariant Borel isomorphism
$(G_\ell \times G_r)$-equivariant Borel isomorphism ![]() $\Omega \to Z\times G_r$, where the action of
$\Omega \to Z\times G_r$, where the action of ![]() $G_\ell \times G_r$ on
$G_\ell \times G_r$ on ![]() $Z\times G_r$ is given by
$Z\times G_r$ is given by ![]() $(g_1,g_2)\cdot (z,g)=(g_1z,c(g_1,z)gg_2^{-1})$. As the actions of
$(g_1,g_2)\cdot (z,g)=(g_1z,c(g_1,z)gg_2^{-1})$. As the actions of ![]() $G$ on
$G$ on ![]() $G_\ell \backslash \Omega$ and
$G_\ell \backslash \Omega$ and ![]() $G_r\backslash \Omega$ are
$G_r\backslash \Omega$ are ![]() $\mathcal {F}$-ergodic, and
$\mathcal {F}$-ergodic, and ![]() $(G,\mathcal {F})$ is strongly cocycle-rigid, the cocycle
$(G,\mathcal {F})$ is strongly cocycle-rigid, the cocycle ![]() $c$ is cohomologous to a group isomorphism, i.e. there exist a group isomorphism
$c$ is cohomologous to a group isomorphism, i.e. there exist a group isomorphism ![]() $\rho :G_\ell \to G_r$ and a measurable map
$\rho :G_\ell \to G_r$ and a measurable map ![]() $\varphi :Z\to G_r$ such that for every
$\varphi :Z\to G_r$ such that for every ![]() $g_1\in G_\ell$ and almost every
$g_1\in G_\ell$ and almost every ![]() $z\in Z$, one has
$z\in Z$, one has ![]() $c(g_1,z)=\varphi (g_1z)\rho (g_1)\varphi (z)^{-1}$. We define
$c(g_1,z)=\varphi (g_1z)\rho (g_1)\varphi (z)^{-1}$. We define ![]() $\Phi (z,g)=\varphi (z)^{-1}g$. Then the equivariance is verified as follows:
$\Phi (z,g)=\varphi (z)^{-1}g$. Then the equivariance is verified as follows: ![]() $\Phi ((g_1,g_2)\cdot (z,g))=\Phi (g_1z,c(g_1,z)gg_2^{-1})$
$\Phi ((g_1,g_2)\cdot (z,g))=\Phi (g_1z,c(g_1,z)gg_2^{-1})$ ![]() $=\rho (g_1)\varphi (z)^{-1}gg_2^{-1}=(g_1,g_2)\cdot \Phi (g,z)$. This proves our claim.
$=\rho (g_1)\varphi (z)^{-1}gg_2^{-1}=(g_1,g_2)\cdot \Phi (g,z)$. This proves our claim.
We can thus apply [Reference KidaKid10, Theorem 6.1] (or the reasoning on [Reference Monod and ShalomMS06, pp. 865–867]) to obtain a homomorphism ![]() $\alpha :H\to G$ with finite kernel and finite-index image, and an almost
$\alpha :H\to G$ with finite kernel and finite-index image, and an almost ![]() $(G\times H)$-equivariant Borel map
$(G\times H)$-equivariant Borel map ![]() $\Sigma \to G$, where the action of
$\Sigma \to G$, where the action of ![]() $G\times H$ on
$G\times H$ on ![]() $G$ is via
$G$ is via ![]() $(g,h)\cdot g'=gg'\alpha (h)^{-1}$. The conclusion then follows from [Reference FurmanFur11, Lemma 4.18] (alternatively, see the argument from the proof of [Reference KidaKid08, Theorem 1.1]).
$(g,h)\cdot g'=gg'\alpha (h)^{-1}$. The conclusion then follows from [Reference FurmanFur11, Lemma 4.18] (alternatively, see the argument from the proof of [Reference KidaKid08, Theorem 1.1]).
We can now complete the proof of Theorem 2 from the introduction.
Proof of Theorem 2 By definition of irreducibility of the ![]() $G$-action on
$G$-action on ![]() $X$, there exists an isomorphism between a right-angled Artin group
$X$, there exists an isomorphism between a right-angled Artin group ![]() $G_\Gamma$ and
$G_\Gamma$ and ![]() $G$ such that, letting
$G$ such that, letting ![]() $\mathcal {F}$ be the set of all cyclic subgroups of
$\mathcal {F}$ be the set of all cyclic subgroups of ![]() $G$ generated by the images (under this identification) of the standard generators of
$G$ generated by the images (under this identification) of the standard generators of ![]() $G_\Gamma$, the
$G_\Gamma$, the ![]() $G$-action on
$G$-action on ![]() $X$ is
$X$ is ![]() $\mathcal {F}$-ergodic. Propositions 6.1 and 6.2 ensure that
$\mathcal {F}$-ergodic. Propositions 6.1 and 6.2 ensure that ![]() $(G,\mathcal {F})$ is strongly cocycle-rigid. In addition
$(G,\mathcal {F})$ is strongly cocycle-rigid. In addition ![]() $G$ is ICC (Lemma 1.6). Thus, Theorem 7.1 applies and yields the orbit equivalence superrigidity statement. The
$G$ is ICC (Lemma 1.6). Thus, Theorem 7.1 applies and yields the orbit equivalence superrigidity statement. The ![]() $W^*$-superrigidity statement follows because
$W^*$-superrigidity statement follows because ![]() $L^\infty (X)\rtimes G$ contains a unique virtual Cartan subalgebra up to unitary conjugacy (by [Reference Popa and VaesPV14, Theorem 1.2 and Remark 1.3], see also the proof of [Reference Horbez and HuangHH22, Corollary 3.20]).
$L^\infty (X)\rtimes G$ contains a unique virtual Cartan subalgebra up to unitary conjugacy (by [Reference Popa and VaesPV14, Theorem 1.2 and Remark 1.3], see also the proof of [Reference Horbez and HuangHH22, Corollary 3.20]).
8.  $W^*$-rigidity results for Bernoulli actions
$W^*$-rigidity results for Bernoulli actions
In this final section, we establish the ![]() $W^*$-rigidity theorem given in Theorem 3 of the introduction of the paper. We first recall a cocycle superrigidity theorem due to Popa.
$W^*$-rigidity theorem given in Theorem 3 of the introduction of the paper. We first recall a cocycle superrigidity theorem due to Popa.
Theorem 8.1 (Popa [Reference PopaPop08, Theorem 1.1])
Let ![]() $G$ be a countable group that admits a chain of infinite subgroups
$G$ be a countable group that admits a chain of infinite subgroups ![]() $G_0\subseteq G_1\subseteq \dots \subseteq G_n=G$ such that:
$G_0\subseteq G_1\subseteq \dots \subseteq G_n=G$ such that:
(i) for every
 $k\in \{1,\dots,n\}$, the set of all
$k\in \{1,\dots,n\}$, the set of all  $g\in G_k$ with
$g\in G_k$ with  $|gG_{k-1}g^{-1}\cap G_{k-1}|=\infty$ generates
$|gG_{k-1}g^{-1}\cap G_{k-1}|=\infty$ generates  $G_k$; and
$G_k$; and(ii) the centralizer of
 $G_0$ in
$G_0$ in  $G$ is nonamenable.
$G$ is nonamenable.
Let ![]() $G\curvearrowright X$ be a nontrivial Bernoulli action, and let
$G\curvearrowright X$ be a nontrivial Bernoulli action, and let ![]() $H$ be any countable group. Then any cocycle
$H$ be any countable group. Then any cocycle ![]() $c:G\times X\to H$ is cohomologous to a group homomorphism.
$c:G\times X\to H$ is cohomologous to a group homomorphism.
Note that in the terminology from [Reference PopaPop08], our assumption precisely says that ![]() $G_0$ is wq-normal in
$G_0$ is wq-normal in ![]() $G$.
$G$.
In particular, if a free, ergodic, probability measure-preserving action ![]() $H\curvearrowright Y$ on a standard probability space
$H\curvearrowright Y$ on a standard probability space ![]() $Y$ is orbit equivalent to
$Y$ is orbit equivalent to ![]() $G\curvearrowright X$ and if
$G\curvearrowright X$ and if ![]() $G$ has no finite nontrivial normal subgroup, then the two actions are conjugate. Likewise, if
$G$ has no finite nontrivial normal subgroup, then the two actions are conjugate. Likewise, if ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are SOE, then they are, in fact, virtually conjugate.
$H\curvearrowright Y$ are SOE, then they are, in fact, virtually conjugate.
Theorem 8.1 applies to every countable group ![]() $G$ which has a finite chain-commuting generating set
$G$ which has a finite chain-commuting generating set ![]() $S$ whose elements all have infinite order, and such that
$S$ whose elements all have infinite order, and such that ![]() $S$ contains an element
$S$ contains an element ![]() $s_0$ with nonamenable centralizer in
$s_0$ with nonamenable centralizer in ![]() $G$. Indeed, this is proved by writing
$G$. Indeed, this is proved by writing ![]() $S=\{s_0,\dots,s_n\}$ in such a way that
$S=\{s_0,\dots,s_n\}$ in such a way that ![]() $s_i$ and
$s_i$ and ![]() $s_{i+1}$ commute for all
$s_{i+1}$ commute for all ![]() $i\in \{0,\dots,n-1\}$, letting
$i\in \{0,\dots,n-1\}$, letting ![]() $G_0=\langle s_0\rangle$, and letting
$G_0=\langle s_0\rangle$, and letting ![]() $G_i=\langle G_{i-1},s_i\rangle$ for every
$G_i=\langle G_{i-1},s_i\rangle$ for every ![]() $i\in \{1,\dots,n\}$. In particular, it applies to all one-ended nonabelian right-angled Artin groups. For these,
$i\in \{1,\dots,n\}$. In particular, it applies to all one-ended nonabelian right-angled Artin groups. For these, ![]() $W^*$-superrigidity of all nontrivial Bernoulli actions then follows from the uniqueness of the virtual Cartan subalgebra of
$W^*$-superrigidity of all nontrivial Bernoulli actions then follows from the uniqueness of the virtual Cartan subalgebra of ![]() $L^\infty (X)\rtimes G$ up to unitary conjugacy. We now present another approach to
$L^\infty (X)\rtimes G$ up to unitary conjugacy. We now present another approach to ![]() $W^*$-superrigidity which bypasses Cartan-rigidity (thereby providing new examples), which is a slight variation on [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] (whose notation we now follow for convenience). A free, ergodic, measure-preserving action
$W^*$-superrigidity which bypasses Cartan-rigidity (thereby providing new examples), which is a slight variation on [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] (whose notation we now follow for convenience). A free, ergodic, measure-preserving action ![]() $G\curvearrowright X$ of a countable group on a standard probability space is
$G\curvearrowright X$ of a countable group on a standard probability space is ![]() $W^*$-superrigid if for every other free, ergodic, measure-preserving action
$W^*$-superrigid if for every other free, ergodic, measure-preserving action ![]() $H\curvearrowright Y$, if
$H\curvearrowright Y$, if ![]() $L^\infty (X)\rtimes G\approx L^\infty (Y)\rtimes H$, then the actions
$L^\infty (X)\rtimes G\approx L^\infty (Y)\rtimes H$, then the actions ![]() $G\curvearrowright X$ and
$G\curvearrowright X$ and ![]() $H\curvearrowright Y$ are conjugate.
$H\curvearrowright Y$ are conjugate.
Theorem 8.2 [Reference Ioana, Popa and VaesIPV13]
Let ![]() $\Gamma$ be an ICC countable group that admits a chain of infinite subgroups
$\Gamma$ be an ICC countable group that admits a chain of infinite subgroups ![]() $\Gamma _0\subseteq \Gamma _1\subseteq \cdots \subseteq \Gamma _n=\Gamma$ such that for every
$\Gamma _0\subseteq \Gamma _1\subseteq \cdots \subseteq \Gamma _n=\Gamma$ such that for every ![]() $k\in \{1,\dots,n\}$, the set of all
$k\in \{1,\dots,n\}$, the set of all ![]() $g\in \Gamma _k$ with
$g\in \Gamma _k$ with ![]() $|g\Gamma _{k-1}g^{-1}\cap \Gamma _{k-1}|=\infty$ generates
$|g\Gamma _{k-1}g^{-1}\cap \Gamma _{k-1}|=\infty$ generates ![]() $\Gamma _k$, and the centralizer of
$\Gamma _k$, and the centralizer of ![]() $\Gamma _0$ in
$\Gamma _0$ in ![]() $\Gamma$ is nonamenable.
$\Gamma$ is nonamenable.
Then every nontrivial Bernoulli action of ![]() $\Gamma$ is
$\Gamma$ is ![]() $W^*$-superrigid.
$W^*$-superrigid.
Proof. We assume the notation from the proof of [Reference Ioana, Popa and VaesIPV13, Theorem 10.1]. Let ![]() $\Gamma \curvearrowright X$ be a nontrivial Bernoulli action, denote
$\Gamma \curvearrowright X$ be a nontrivial Bernoulli action, denote ![]() $M=L^{\infty }(X)\rtimes \Gamma$ and endow
$M=L^{\infty }(X)\rtimes \Gamma$ and endow ![]() $M$ with its canonical trace
$M$ with its canonical trace ![]() $\tau$ and the associated
$\tau$ and the associated ![]() $2$-norm,
$2$-norm, ![]() $\|\cdot \|_2$. Let
$\|\cdot \|_2$. Let ![]() $\pi :L^{\infty }(Y)\rtimes \Lambda \rightarrow M$ be a
$\pi :L^{\infty }(Y)\rtimes \Lambda \rightarrow M$ be a ![]() $*$-isomorphism, for some free, ergodic, measure-preserving action
$*$-isomorphism, for some free, ergodic, measure-preserving action ![]() $\Lambda \curvearrowright Y$ of a countable group on a standard probability space. Identify
$\Lambda \curvearrowright Y$ of a countable group on a standard probability space. Identify ![]() $M=L^{\infty }(Y)\rtimes \Lambda$ via
$M=L^{\infty }(Y)\rtimes \Lambda$ via ![]() $\pi$. Let
$\pi$. Let ![]() $\Delta :M\rightarrow M\overline {\otimes }M$ be the unital
$\Delta :M\rightarrow M\overline {\otimes }M$ be the unital ![]() $*$-homomorphism given by
$*$-homomorphism given by ![]() $\Delta (bv_s)=bv_s\otimes v_s$, for every
$\Delta (bv_s)=bv_s\otimes v_s$, for every ![]() $b\in L^\infty (Y)$ and
$b\in L^\infty (Y)$ and ![]() $s\in \Lambda$ (see [Reference Popa and VaesPV10]). Here,
$s\in \Lambda$ (see [Reference Popa and VaesPV10]). Here, ![]() $(v_s)_{s\in \Lambda }$ denote the canonical unitaries used to define
$(v_s)_{s\in \Lambda }$ denote the canonical unitaries used to define ![]() $L^\infty (Y)\rtimes \Lambda$.
$L^\infty (Y)\rtimes \Lambda$.
In the following, we also denote by ![]() $(u_g)_{g\in \Gamma }$ the canonical unitaries used to define
$(u_g)_{g\in \Gamma }$ the canonical unitaries used to define ![]() $L^\infty (X)\rtimes \Gamma$ and by
$L^\infty (X)\rtimes \Gamma$ and by ![]() $(\sigma _g)_{g\in \Gamma }$ the Bernoulli action of
$(\sigma _g)_{g\in \Gamma }$ the Bernoulli action of ![]() $\Gamma$ on
$\Gamma$ on ![]() $L^\infty (X)$. In addition, we use the notation
$L^\infty (X)$. In addition, we use the notation ![]() $A\prec B$, for von Neumann subalgebras
$A\prec B$, for von Neumann subalgebras ![]() $A,B\subset M\overline {\otimes }M$, to mean that a corner of
$A,B\subset M\overline {\otimes }M$, to mean that a corner of ![]() $A$ embeds into
$A$ embeds into ![]() $B$ inside
$B$ inside ![]() $M\overline {\otimes }M$ in the sense of Popa [Reference PopaPop06b] (see also [Reference Ioana, Popa and VaesIPV13, Definition 2.1]).
$M\overline {\otimes }M$ in the sense of Popa [Reference PopaPop06b] (see also [Reference Ioana, Popa and VaesIPV13, Definition 2.1]).
As the action ![]() $\Gamma \curvearrowright X$ satisfies Popa's cocycle superrigidity theorem (Theorem 8.1 above), the proof of [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] shows that in order to derive the conclusion we only need to justify the following.
$\Gamma \curvearrowright X$ satisfies Popa's cocycle superrigidity theorem (Theorem 8.1 above), the proof of [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] shows that in order to derive the conclusion we only need to justify the following.
Step 1. There exists a unitary ![]() $v\in M\overline {\otimes }M$ such that
$v\in M\overline {\otimes }M$ such that ![]() $v\Delta (\text {L}\Gamma )v^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$.
$v\Delta (\text {L}\Gamma )v^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$.
Denote by ![]() $P$ the quasi-normalizer of
$P$ the quasi-normalizer of ![]() $\Delta (\text {L}\Gamma _0)$ inside
$\Delta (\text {L}\Gamma _0)$ inside ![]() $M\overline {\otimes }M$. Since the centralizer
$M\overline {\otimes }M$. Since the centralizer ![]() $C$ of
$C$ of ![]() $\Gamma _0$ in
$\Gamma _0$ in ![]() $\Gamma$ is nonamenable,
$\Gamma$ is nonamenable, ![]() $\text {L}C$ has no amenable direct summand. By [Reference Ioana, Popa and VaesIPV13, Lemma 10.2(5)] we get that
$\text {L}C$ has no amenable direct summand. By [Reference Ioana, Popa and VaesIPV13, Lemma 10.2(5)] we get that ![]() $\Delta (\text {L}C)$ is strongly nonamenable relative to
$\Delta (\text {L}C)$ is strongly nonamenable relative to ![]() $M\otimes 1$ and
$M\otimes 1$ and ![]() $1\otimes M$, and that
$1\otimes M$, and that ![]() $\Delta (\text {L}C)\nprec M\overline {\otimes }\text {L}^{\infty }(X)$ and
$\Delta (\text {L}C)\nprec M\overline {\otimes }\text {L}^{\infty }(X)$ and ![]() $\Delta (\text {L}C)\nprec \text {L}^{\infty }(X)\overline {\otimes }M$. Using that
$\Delta (\text {L}C)\nprec \text {L}^{\infty }(X)\overline {\otimes }M$. Using that ![]() $\Delta (\text {L}C)\subset P$, we derive that
$\Delta (\text {L}C)\subset P$, we derive that ![]() $P\nprec M\overline {\otimes }\text {L}^{\infty }(X)$ and
$P\nprec M\overline {\otimes }\text {L}^{\infty }(X)$ and ![]() $P\nprec \text {L}^{\infty }(X)\overline {\otimes }M$. The rest of Step 1 in the proof of [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] now applies to show the existence of a unitary
$P\nprec \text {L}^{\infty }(X)\overline {\otimes }M$. The rest of Step 1 in the proof of [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] now applies to show the existence of a unitary ![]() $v\in M\overline {\otimes }M$ such that
$v\in M\overline {\otimes }M$ such that ![]() $vPv^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$. Thus, we have
$vPv^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$. Thus, we have ![]() $v\Delta (\text {L}\Gamma _0)v^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$.
$v\Delta (\text {L}\Gamma _0)v^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$.
We prove by induction that ![]() $P_k:=v\Delta (\text {L}\Gamma _k)v^*$ is contained in
$P_k:=v\Delta (\text {L}\Gamma _k)v^*$ is contained in ![]() $\text {L}\Gamma \overline {\otimes }\text {L}\Gamma$ for all
$\text {L}\Gamma \overline {\otimes }\text {L}\Gamma$ for all ![]() $k\in \{0,\dots,n\}$. Assume that
$k\in \{0,\dots,n\}$. Assume that ![]() $P_k\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$ for some
$P_k\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$ for some ![]() $k$ with
$k$ with ![]() $0\leq k\leq n-1$. Let
$0\leq k\leq n-1$. Let ![]() $g\in \Gamma _{k+1}$ such that
$g\in \Gamma _{k+1}$ such that ![]() $\Sigma :=g\Gamma _k g^{-1}\cap \Gamma _k$ is infinite and denote
$\Sigma :=g\Gamma _k g^{-1}\cap \Gamma _k$ is infinite and denote ![]() $R=v\Delta (\text {L}\Sigma )v^*$. As
$R=v\Delta (\text {L}\Sigma )v^*$. As ![]() $\Sigma \subset \Gamma _k$ we have that
$\Sigma \subset \Gamma _k$ we have that ![]() $R\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$. As
$R\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$. As ![]() $\Sigma$ is infinite, Step 1 in the proof of [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] shows that
$\Sigma$ is infinite, Step 1 in the proof of [Reference Ioana, Popa and VaesIPV13, Theorem 10.1] shows that ![]() $R\nprec M\otimes 1$ and
$R\nprec M\otimes 1$ and ![]() $R\nprec 1\otimes M$. We continue with the following claim.
$R\nprec 1\otimes M$. We continue with the following claim.
Claim The inclusion ![]() $\text {L}\Gamma \overline {\otimes }\text {L}\Gamma \subset M\overline {\otimes }M$ is weakly mixing through
$\text {L}\Gamma \overline {\otimes }\text {L}\Gamma \subset M\overline {\otimes }M$ is weakly mixing through ![]() $R$ in the sense of [Reference Popa and VaesPV08, Definition 6.13].
$R$ in the sense of [Reference Popa and VaesPV08, Definition 6.13].
Proof of the claim As ![]() $R\nprec M\otimes 1$ and
$R\nprec M\otimes 1$ and ![]() $R\nprec 1\otimes M$, by Fact 1 in the proof of [Reference Ioana, Peterson and PopaIPP08, Theorem 4.3] there is a sequence
$R\nprec 1\otimes M$, by Fact 1 in the proof of [Reference Ioana, Peterson and PopaIPP08, Theorem 4.3] there is a sequence ![]() $u_n\in \mathcal {U}(R)$ such that for all
$u_n\in \mathcal {U}(R)$ such that for all ![]() $a,b\in M\overline {\otimes }M$, we have
$a,b\in M\overline {\otimes }M$, we have ![]() $\|E_{M\otimes 1}(au_nb)\|_2\rightarrow 0$ and
$\|E_{M\otimes 1}(au_nb)\|_2\rightarrow 0$ and ![]() $\|E_{1\otimes M}(au_nb)\|_2\rightarrow 0$. As
$\|E_{1\otimes M}(au_nb)\|_2\rightarrow 0$. As ![]() $R\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$, we can write
$R\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$, we can write ![]() $u_n=\sum _{g,h\in \Gamma }c_{g,h}^n(u_g\otimes u_h)$, where the coefficients
$u_n=\sum _{g,h\in \Gamma }c_{g,h}^n(u_g\otimes u_h)$, where the coefficients ![]() $c_{g,h}^n\in \mathbb {C}$ for every
$c_{g,h}^n\in \mathbb {C}$ for every ![]() $g,h\in \Gamma$ satisfy
$g,h\in \Gamma$ satisfy ![]() $\sum _{g,h\in \Gamma }|c_{g,h}^n|^2=\|u_n\|_2^2=1$. If
$\sum _{g,h\in \Gamma }|c_{g,h}^n|^2=\|u_n\|_2^2=1$. If ![]() $g\in \Gamma$, then
$g\in \Gamma$, then ![]() $\text {E}_{1\otimes M}(u_n(u_g^*\otimes 1))=1\otimes (\sum _{h\in \Gamma }c_{g,h}^nu_h)$ and so
$\text {E}_{1\otimes M}(u_n(u_g^*\otimes 1))=1\otimes (\sum _{h\in \Gamma }c_{g,h}^nu_h)$ and so ![]() $\sum _{h\in \Gamma }|c_{g,h}^n|^2=\|E_{1\otimes M}(u_n(u_g^*\otimes 1))\|_2^2\rightarrow 0$. Similarly,
$\sum _{h\in \Gamma }|c_{g,h}^n|^2=\|E_{1\otimes M}(u_n(u_g^*\otimes 1))\|_2^2\rightarrow 0$. Similarly, ![]() $\sum _{g\in \Gamma }|c_{g,h}^n|^2\rightarrow 0$, for every
$\sum _{g\in \Gamma }|c_{g,h}^n|^2\rightarrow 0$, for every ![]() $h\in \Gamma$.
$h\in \Gamma$.
We show that
which by [Reference Popa and VaesPV08, Definition 6.13] implies the above claim. Let ![]() $(\text {L}^\infty (X))_1$ be the operator norm unit ball of
$(\text {L}^\infty (X))_1$ be the operator norm unit ball of ![]() $\text {L}^\infty (X)$, i.e. the set of
$\text {L}^\infty (X)$, i.e. the set of ![]() $a\in \text {L}^\infty (X)$ with
$a\in \text {L}^\infty (X)$ with ![]() $\|a\|\leq 1$. Then the linear span of
$\|a\|\leq 1$. Then the linear span of ![]() $\{(u_g\otimes u_h)(a\otimes b)\mid g,h\in \Gamma, a,b\in (\text {L}^{\infty }(X))_1, \tau (a)\tau (b)=0\}$ is
$\{(u_g\otimes u_h)(a\otimes b)\mid g,h\in \Gamma, a,b\in (\text {L}^{\infty }(X))_1, \tau (a)\tau (b)=0\}$ is ![]() $\|\cdot \|_2$-dense in
$\|\cdot \|_2$-dense in ![]() $(M\overline {\otimes }M)\ominus (\text {L}\Gamma \overline {\otimes }\text {L}\Gamma )$ and the linear span of
$(M\overline {\otimes }M)\ominus (\text {L}\Gamma \overline {\otimes }\text {L}\Gamma )$ and the linear span of ![]() $\{(c\otimes d)(u_k\otimes u_l)\mid k,l\in \Gamma, c,d\in (\text {L}^{\infty }(X))_1\}$ is
$\{(c\otimes d)(u_k\otimes u_l)\mid k,l\in \Gamma, c,d\in (\text {L}^{\infty }(X))_1\}$ is ![]() $\|\cdot \|_2$-dense in
$\|\cdot \|_2$-dense in ![]() $M\overline {\otimes }M$. As
$M\overline {\otimes }M$. As ![]() $\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }$ is
$\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }$ is ![]() $\text {L}\Gamma \overline {\otimes }\text {L}\Gamma$-bimodular, for every
$\text {L}\Gamma \overline {\otimes }\text {L}\Gamma$-bimodular, for every ![]() $v,w\in \text {L}(\Gamma )\overline {\otimes }\text {L}(\Gamma )$ and
$v,w\in \text {L}(\Gamma )\overline {\otimes }\text {L}(\Gamma )$ and ![]() $a,b,c,d\in \text {L}^\infty (X)$, we have
$a,b,c,d\in \text {L}^\infty (X)$, we have ![]() $\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(v(a\otimes b)u_n(c\otimes d)w)=v\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }((a\otimes b)u_n(c\otimes d))w$. By combining the last two facts we see that it suffices to prove the displayed convergence for every
$\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(v(a\otimes b)u_n(c\otimes d)w)=v\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }((a\otimes b)u_n(c\otimes d))w$. By combining the last two facts we see that it suffices to prove the displayed convergence for every ![]() $x$ and
$x$ and ![]() $y$ of the form
$y$ of the form ![]() $x=a\otimes b,y=c\otimes d$, where
$x=a\otimes b,y=c\otimes d$, where ![]() $a,b,c,d\in (\text {L}^\infty (X))_1$ are such that
$a,b,c,d\in (\text {L}^\infty (X))_1$ are such that ![]() $\tau (a)\tau (b)=0$.
$\tau (a)\tau (b)=0$.
Assume that ![]() $\tau (a)=0$ because the case
$\tau (a)=0$ because the case ![]() $\tau (b)=0$ is similar. Let
$\tau (b)=0$ is similar. Let ![]() $\varepsilon >0$. For every
$\varepsilon >0$. For every ![]() $n$ we have
$n$ we have ![]() $\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(xu_ny) =\sum _{g,h\in \Gamma }c_{g,h}^n\tau (a\sigma _g(c))\tau (b\sigma _h(d))(u_g\otimes u_h)$ and, thus,
$\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(xu_ny) =\sum _{g,h\in \Gamma }c_{g,h}^n\tau (a\sigma _g(c))\tau (b\sigma _h(d))(u_g\otimes u_h)$ and, thus,
As the Bernoulli action ![]() $(\sigma _g)_{g\in \Gamma }$ is mixing and
$(\sigma _g)_{g\in \Gamma }$ is mixing and ![]() $\tau (a)=0$, we can find a finite set
$\tau (a)=0$, we can find a finite set ![]() $F\subset \Gamma$ such that
$F\subset \Gamma$ such that ![]() $|\tau (a\sigma _g(c))|\leq \varepsilon$, for every
$|\tau (a\sigma _g(c))|\leq \varepsilon$, for every ![]() $g\in \Gamma \setminus F$. Since
$g\in \Gamma \setminus F$. Since ![]() $a,b,c,d\in (\text {L}^\infty (X))_1$ we also have that
$a,b,c,d\in (\text {L}^\infty (X))_1$ we also have that ![]() $|\tau (a\sigma _g(c))|\leq 1$ and
$|\tau (a\sigma _g(c))|\leq 1$ and ![]() $|\tau (b\sigma _h(d))|\leq 1$, for every
$|\tau (b\sigma _h(d))|\leq 1$, for every ![]() $g,h\in \Gamma$. Altogether, we obtain
$g,h\in \Gamma$. Altogether, we obtain
As ![]() $\sum _{h\in \Gamma }|c_{g,h}^n|^2\rightarrow 0$, for every
$\sum _{h\in \Gamma }|c_{g,h}^n|^2\rightarrow 0$, for every ![]() $g\in F$, and
$g\in F$, and ![]() $\sum _{g\in \Gamma \setminus F,h\in \Gamma }|c_{g,h}^n|^2\leq \sum _{g,h\in \Gamma }|c_{g,h}^n|^2=1$, it follows that
$\sum _{g\in \Gamma \setminus F,h\in \Gamma }|c_{g,h}^n|^2\leq \sum _{g,h\in \Gamma }|c_{g,h}^n|^2=1$, it follows that ![]() $\limsup _n\|\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(xu_ny)\|_2^2\leq \varepsilon ^2.$ Since this holds for every
$\limsup _n\|\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(xu_ny)\|_2^2\leq \varepsilon ^2.$ Since this holds for every ![]() $\varepsilon >0$, we conclude that
$\varepsilon >0$, we conclude that ![]() $\|\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(xu_ny)\|_2\rightarrow 0$, which proves the above claim.
$\|\text {E}_{\text {L}\Gamma \overline {\otimes }\text {L}\Gamma }(xu_ny)\|_2\rightarrow 0$, which proves the above claim.
We can now complete the proof of Theorem 8.2. As ![]() $\Sigma g\subset g\Gamma _k$, we get that
$\Sigma g\subset g\Gamma _k$, we get that ![]() $R(v\Delta (u_g)v^*)\subset (v\Delta (u_g)v^*)P_k\subset (v\Delta (u_g)v^*)(\text {L}\Gamma \overline {\otimes }\text {L}\Gamma )$. Using the claim, a weak mixing technique due to Popa (see [Reference Popa and VaesPV08, Proposition 6.14]) implies that
$R(v\Delta (u_g)v^*)\subset (v\Delta (u_g)v^*)P_k\subset (v\Delta (u_g)v^*)(\text {L}\Gamma \overline {\otimes }\text {L}\Gamma )$. Using the claim, a weak mixing technique due to Popa (see [Reference Popa and VaesPV08, Proposition 6.14]) implies that ![]() $v\Delta (u_g)v^*\in \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$, for every
$v\Delta (u_g)v^*\in \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$, for every ![]() $g\in \Gamma _{k+1}$ such that
$g\in \Gamma _{k+1}$ such that ![]() $\Sigma :=g\Gamma _k g^{-1}\cap \Gamma _k$ is infinite. As the set of such
$\Sigma :=g\Gamma _k g^{-1}\cap \Gamma _k$ is infinite. As the set of such ![]() $g\in \Gamma _{k+1}$ generates
$g\in \Gamma _{k+1}$ generates ![]() $\Gamma _{k+1}$ we conclude that
$\Gamma _{k+1}$ we conclude that ![]() $P_{k+1}\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$.
$P_{k+1}\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$.
For ![]() $k=n$, we get that
$k=n$, we get that ![]() $v\Delta (\text {L}\Gamma )v^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$, which finishes the proof.
$v\Delta (\text {L}\Gamma )v^*\subset \text {L}\Gamma \overline {\otimes }\text {L}\Gamma$, which finishes the proof.
As previously, we record the following consequence, which is Theorem 3 from the introduction.
Corollary 8.3 Let ![]() $G$ be an ICC countable group. Assume that
$G$ be an ICC countable group. Assume that ![]() $G$ has a finite chain-commuting generating set consisting of infinite-order elements, one of which has nonamenable centralizer in
$G$ has a finite chain-commuting generating set consisting of infinite-order elements, one of which has nonamenable centralizer in ![]() $G$.
$G$.
Then every nontrivial Bernoulli action of ![]() $G$ is
$G$ is ![]() $W^*$-superrigid.
$W^*$-superrigid.
Corollary 8.4 Let ![]() $S=S_{g,n}$ be a surface obtained from a closed orientable surface of genus
$S=S_{g,n}$ be a surface obtained from a closed orientable surface of genus ![]() $g$ by removing
$g$ by removing ![]() $n$ points. Assume that
$n$ points. Assume that ![]() $3g+n-5\ge 0$.
$3g+n-5\ge 0$.
Then every nontrivial Bernoulli action of the mapping class group ![]() $\mathrm {Mod}(S_{g,n})$ is
$\mathrm {Mod}(S_{g,n})$ is ![]() $W^*$-superrigid.
$W^*$-superrigid.
Proof. The fact that mapping class groups are ICC was proved by Kida in [Reference KidaKid10, Theorem 2.9]. The fact that they admit chain-commuting generating sets as in Corollary 8.3 follows, for instance, from [Reference Labruère and ParisLP01, Corollary 2.11] when ![]() $g\ge 1$, and from [Reference WajnrybWaj99, Lemma 23] when
$g\ge 1$, and from [Reference WajnrybWaj99, Lemma 23] when ![]() $g=0$ (note that each element
$g=0$ (note that each element ![]() $h$ in the generating set is either a Dehn twist or a braid twist, so its centralizer is nonamenable by considering mapping classes supported on a subsurface which is disjoint from the support of
$h$ in the generating set is either a Dehn twist or a braid twist, so its centralizer is nonamenable by considering mapping classes supported on a subsurface which is disjoint from the support of ![]() $h$). The conclusion thus follows from Corollary 8.3.
$h$). The conclusion thus follows from Corollary 8.3.
Recall that given a finite, labeled, simple graph ![]() $\Gamma$, where every edge is labeled by an integer at least
$\Gamma$, where every edge is labeled by an integer at least ![]() $2$, the Artin group
$2$, the Artin group ![]() $G_\Gamma$ with defining graph
$G_\Gamma$ with defining graph ![]() $\Gamma$ is the group defined by the following presentation: it has one generator per vertex of
$\Gamma$ is the group defined by the following presentation: it has one generator per vertex of ![]() $\Gamma$, with a relation
$\Gamma$, with a relation ![]() $uvu\dots =vuv\dots$ (with
$uvu\dots =vuv\dots$ (with ![]() $n$ letters on each side) whenever the vertices
$n$ letters on each side) whenever the vertices ![]() $u,v$ are joined by an edge labeled
$u,v$ are joined by an edge labeled ![]() $n$ in
$n$ in ![]() $\Gamma$. Whenever
$\Gamma$. Whenever ![]() $\Lambda \subseteq \Gamma$ is a full subgraph (i.e. two vertices of
$\Lambda \subseteq \Gamma$ is a full subgraph (i.e. two vertices of ![]() $\Lambda$ are adjacent in
$\Lambda$ are adjacent in ![]() $\Lambda$ if and only if they are adjacent in
$\Lambda$ if and only if they are adjacent in ![]() $\Gamma$) with the induced labeling, then the natural homomorphism
$\Gamma$) with the induced labeling, then the natural homomorphism ![]() $G_\Lambda \to G_\Gamma$ induced by the inclusion
$G_\Lambda \to G_\Gamma$ induced by the inclusion ![]() $\Lambda \hookrightarrow \Gamma$ is injective [Reference van der LekvdL83].
$\Lambda \hookrightarrow \Gamma$ is injective [Reference van der LekvdL83].
Corollary 8.5 Let ![]() $G$ be a one-ended ICC Artin group. Then every nontrivial Bernoulli action of
$G$ be a one-ended ICC Artin group. Then every nontrivial Bernoulli action of ![]() $G$ is
$G$ is ![]() $W^*$-superrigid.
$W^*$-superrigid.
Many classes of Artin groups are known to be ICC. For instance, this is satisfied whenever ![]() $G$ is acylindrically hyperbolic and has no nontrivial finite normal subgroup [Reference Dahmani, Guirardel and OsinDGO17, Theorem 2.35]. See e.g. [Reference CalvezCal22] and the references therein for the current status of known results regarding acylindrical hyperbolicity of Artin groups. The lack of nontrivial finite normal subgroup would follow from the
$G$ is acylindrically hyperbolic and has no nontrivial finite normal subgroup [Reference Dahmani, Guirardel and OsinDGO17, Theorem 2.35]. See e.g. [Reference CalvezCal22] and the references therein for the current status of known results regarding acylindrical hyperbolicity of Artin groups. The lack of nontrivial finite normal subgroup would follow from the ![]() $K(\pi,1)$-conjecture for Artin groups, see [Reference Godelle and ParisGP12, Reference ParisPar14] for surveys of known cases and [Reference Paolini and SalvettiPS21] for the most recent developments. Combining these references, we see that all Artin groups with trivial center and connected defining graph that are either of Euclidean type, two-dimensional, or of type FC, are ICC and satisfy Corollary 8.5.
$K(\pi,1)$-conjecture for Artin groups, see [Reference Godelle and ParisGP12, Reference ParisPar14] for surveys of known cases and [Reference Paolini and SalvettiPS21] for the most recent developments. Combining these references, we see that all Artin groups with trivial center and connected defining graph that are either of Euclidean type, two-dimensional, or of type FC, are ICC and satisfy Corollary 8.5.
Proof. Write ![]() $G=G_\Gamma$ for some finite labeled simple graph
$G=G_\Gamma$ for some finite labeled simple graph ![]() $\Gamma$. Note that
$\Gamma$. Note that ![]() $G$ being one-ended implies that
$G$ being one-ended implies that ![]() $\Gamma$ is connected (otherwise
$\Gamma$ is connected (otherwise ![]() $G$ is a free product).
$G$ is a free product).
If all edges of ![]() $G$ are labeled by
$G$ are labeled by ![]() $2$, then
$2$, then ![]() $G$ is a right-angled Artin group. In this case
$G$ is a right-angled Artin group. In this case ![]() $\Gamma$ is not a clique (otherwise
$\Gamma$ is not a clique (otherwise ![]() $G$ is free abelian, whence not ICC). Thus, the standard generating set is a chain-commuting generating set such that one generator has a nonamenable centralizer, and the conclusion follows from Corollary 8.3.
$G$ is free abelian, whence not ICC). Thus, the standard generating set is a chain-commuting generating set such that one generator has a nonamenable centralizer, and the conclusion follows from Corollary 8.3.
We now assume that ![]() $\Gamma$ has at least one edge with label at least
$\Gamma$ has at least one edge with label at least ![]() $3$. Whenever
$3$. Whenever ![]() $e\subseteq \Gamma$ is an edge with label at least
$e\subseteq \Gamma$ is an edge with label at least ![]() $3$, the edge group
$3$, the edge group ![]() $G_e$ is nonamenable and has an infinite cyclic center
$G_e$ is nonamenable and has an infinite cyclic center ![]() $Z_e$, see [Reference CrispCri05, § 2]. The generating set
$Z_e$, see [Reference CrispCri05, § 2]. The generating set ![]() $S$ of
$S$ of ![]() $G$ consisting of the generators associated to the vertices of
$G$ consisting of the generators associated to the vertices of ![]() $\Gamma$, together with a generator of
$\Gamma$, together with a generator of ![]() $Z_e$ for every edge
$Z_e$ for every edge ![]() $e$ with label at least
$e$ with label at least ![]() $3$, satisfies the assumption of Corollary 8.3, so the conclusion follows.
$3$, satisfies the assumption of Corollary 8.3, so the conclusion follows.
Acknowledgements
We thank the referees for their careful reading of our manuscript. The first named author acknowledges support from the Agence Nationale de la Recherche under Grant ANR-16-CE40-0006 DAGGER.