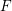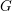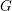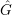Introduction
The study of harmonic functions on trees has a long history. In the early 1960s Dynkin and Malyutov [Reference Dynkin and MalyutovDM61] considered nearest-neighbor random walks on free groups and obtained an analogue of the Poisson formula for them by identifying the Martin boundary of such a group with the space of ends of its Cayley graph. This result was then generalized by a number of authors, among others by Cartier [Reference CartierCar72], who considered nearest-neighbor, but not necessarily homogeneous, random walks on trees. Finite-range random walks were subsequently studied by Derriennic [Reference DerriennicDer75] in the homogeneous case and by Picardello and Woess [Reference Picardello and WoessPW87] in general. In both cases the result was the same as before: the Martin boundary of a tree coincides with its space of ends. This was later generalized to hyperbolic graphs by Ancona [Reference AnconaAnc88] who considered finite-range random walks on such graphs and showed that (under mild assumptions) the corresponding Martin boundaries coincide with the Gromov boundaries. A related result was also obtained by Kaimanovich [Reference KaimanovichKai00] who studied only bounded harmonic functions on hyperbolic groups but went beyond finite-range random walks.
The natural quantum analogues of free groups are the duals of free quantum groups of Van Daele and Wang [Reference Van Daele and WangVDW96]. An interpretation of these duals as vertices of some quantum trees was proposed by Vergnioux [Reference VergniouxVer05], and an analogue of the end compactification was defined by Vaes and Vergnioux [Reference Vaes and VergniouxVV07] in the free orthogonal case and by Vaes and Vander Vennet in the free unitary case [Reference Vaes and Vander VennetVVV10]. The duals of free orthogonal quantum groups behave in many respects like the group
$\mathbb{Z}$
, so the corresponding tree has valency
$2$
, but the quantum boundary is less trivial than this analogy might suggest; for example, for the dual of
$\text{SU}_{q}(2)$
(
$q\neq \pm 1$
) it is the Podleś quantum sphere
$S_{q}^{2}$
. An identification of the quantum Poisson and Martin boundaries with the quantum spaces of ends was obtained in [Reference IzumiIzu02, Reference Neshveyev and TusetNT04, Reference Vaes and VergniouxVV07]; see also the earlier paper by Biane [Reference BianeBia94] on the dual of
$\text{SU}(2)$
, which to a great extent motivated the development of the quantum theory.
The duals of free unitary quantum groups behave more like the free group with two generators. In this case Vaes and Vander Vennet showed [Reference Vaes and Vander VennetVVV10] that the Poisson boundary is isomorphic to the quantum boundary they defined, or more precisely, that the von Neumann algebra of bounded harmonic functions is isomorphic to the von Neumann algebra generated by the C
$^{\ast }$
-algebra of continuous functions on the boundary in the GNS-representation defined by a particular state. Classically this would mean a computation of the Martin boundary as a measure space rather than as a topological space, where the measure is defined as the hitting distribution of the random walk. The goal of the present paper is to show that the Martin boundary of the dual of a free unitary quantum group does coincide with the boundary defined in [Reference Vaes and Vander VennetVVV10] topologically, that is, we have an equality of C
$^{\ast }$
-algebras.
It should be added that a precise relation between quantum Poisson and Martin boundaries has not been established. It was shown in [Reference Neshveyev and TusetNT04] that for the dual of
$\text{SU}_{q}(2)$
the computation of the Martin boundary allows one to easily identify the Poisson boundary as well. This was also recently confirmed in [Reference JordansJor17] by a different argument, and the same is true for the duals of free orthogonal quantum groups. But a general result of this sort is not available yet, so we cannot claim that our result automatically covers the computation of the Poisson boundary in [Reference Vaes and Vander VennetVVV10].
If one wants to compute the Martin boundary of the dual a free unitary quantum group
$G=A_{u}(F)$
, it is natural to try to follow the strategy used in [Reference Vaes and VergniouxVV07] in the free orthogonal case. However, this requires more precise information on the Green functions of particular classical random walks on trees than seems to be available. We propose a different approach, which also reduces the computation to a classical problem (and works equally well in the free orthogonal case). The idea is that by considering the spectral subspaces of
$\ell ^{\infty }({\hat{G}})$
with respect to the adjoint action of
$G$
, we see that a quantum random walk is determined by a collection of operators on the
$\ell ^{2}$
-spaces of branches of the classical tree
$\operatorname{Irr}(G)$
. It turns out that the matrix coefficients of any two such operators corresponding to the common branch of definition are exponentially small perturbations of each other (with respect to the distance to the root of
$\operatorname{Irr}(G)$
). Our main technical result roughly says that the corresponding classical Green functions all have the same asymptotics at infinity. While this is probably not surprising, we point out that the tree
$\operatorname{Irr}(G)$
has exponential growth, so it is not immediately obvious that even an exponentially small perturbation is enough to compensate for this growth.
1 Preliminaries
1.1 Compact and discrete quantum groups
In this section we recall the basic notions related to compact and discrete quantum groups; see, for example, [Reference Neshveyev and TusetNT13] for more details.
A compact quantum group
$G$
is given by a unital C
$^{\ast }$
-algebra
$C(G)$
and a unital
$\ast$
-homomorphism
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}:C(G)\rightarrow C(G)\otimes C(G)\end{eqnarray}$$
such that
$(\unicode[STIX]{x1D6E5}\otimes \unicode[STIX]{x1D704})\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D6E5})\unicode[STIX]{x1D6E5}$
and the spaces
$(C(G)\otimes 1)\unicode[STIX]{x1D6E5}(C(G))$
and
$(1\otimes C(G))\unicode[STIX]{x1D6E5}(C(G))$
are dense in
$C(G)\otimes C(G)$
.
A finite-dimensional unitary representation of
$G$
is a pair
$(U,H_{U})$
consisting of a finite-dimensional Hilbert space
$H_{U}$
and a unitary element
$U\in B(H_{U})\otimes C(G)$
such that
$\unicode[STIX]{x1D6E5}(U)=U_{12}U_{13}$
. The tensor product of two representations
$U$
and
$V$
is defined by
$$\begin{eqnarray}U\otimes V=U_{13}V_{23}\in B(H_{U})\otimes B(H_{V})\otimes C(G).\end{eqnarray}$$
With this tensor product, the finite-dimensional unitary representations of
$G$
form a C
$^{\ast }$
-tensor category
$\operatorname{Rep}G$
.
The space
$\mathbb{C}[G]$
of matrix coefficients of all finite-dimensional unitary representations of
$G$
is a Hopf
$\ast$
-algebra with comultiplication
$\unicode[STIX]{x1D6E5}$
and antipode
$S$
such that
$(\unicode[STIX]{x1D704}\otimes S)(U)=U^{\ast }$
for all
$U\in \operatorname{Rep}G$
. The dual space
${\mathcal{U}}(G)=\mathbb{C}[G]^{\ast }$
is a
$\ast$
-algebra with multiplication dual to
$\unicode[STIX]{x1D6E5}$
, so that
$\unicode[STIX]{x1D714}\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D714}\otimes \unicode[STIX]{x1D702})\unicode[STIX]{x1D6E5}$
, and involution
$\unicode[STIX]{x1D714}^{\ast }=\bar{\unicode[STIX]{x1D714}}S$
, where
$\bar{\unicode[STIX]{x1D714}}(a)=\overline{\unicode[STIX]{x1D714}(a^{\ast })}$
. This is by definition the algebra of all (unbounded) functions on the dual discrete quantum group
$\unicode[STIX]{x1D6E4}={\hat{G}}$
.
More concretely,
${\mathcal{U}}(G)$
can be described as follows. For every
$U\in \operatorname{Rep}G$
we have a
$\ast$
-representation
$\unicode[STIX]{x1D70B}_{U}:{\mathcal{U}}(G)\rightarrow B(H_{U})$
defined by
$\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D714})=(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(U)$
. Consider the set
$I=\operatorname{Irr}(G)$
of isomorphism classes of irreducible unitary representations of
$G$
. For every
$s\in I$
choose a representative
$U_{s}$
. We write
$\unicode[STIX]{x1D70B}_{s}$
,
$H_{s}$
, etc., instead of
$\unicode[STIX]{x1D70B}_{U_{s}}$
,
$H_{U_{s}}$
. Then the collection of representations
$(\unicode[STIX]{x1D70B}_{s})_{s\in I}$
defines a
$\ast$
-isomorphism
${\mathcal{U}}(G)\cong \prod _{s\in I}B(H_{s})$
. The subalgebra
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})\subset {\mathcal{U}}(G)$
corresponding to
$\ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s})$
under this isomorphism is, by definition, the algebra of bounded functions on
$\unicode[STIX]{x1D6E4}$
. We will not distinguish between the algebras
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
and
$\ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s})$
. We will also consider the subalgebras
$$\begin{eqnarray}c_{0}(\unicode[STIX]{x1D6E4})=c_{0}\text{-}\bigoplus _{s\in I}B(H_{s})\quad \text{and}\quad c_{c}(\unicode[STIX]{x1D6E4})=\bigoplus _{s\in I}B(H_{s})\end{eqnarray}$$
of functions vanishing at infinity and of finitely supported functions, respectively.
By duality the product on
$\mathbb{C}[G]$
defines a comultiplication
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D6E5}}:{\mathcal{U}}(G)\rightarrow {\mathcal{U}}(G\times G):=(\mathbb{C}[G]\otimes \mathbb{C}[G])^{\ast }\cong \mathop{\prod }_{s,t\in I}B(H_{s})\otimes B(H_{t}).\end{eqnarray}$$
By restriction it gives a map
$\hat{\unicode[STIX]{x1D6E5}}:\ell ^{\infty }(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4})\,\bar{\otimes }\,\ell ^{\infty }(\unicode[STIX]{x1D6E4}).$
The antipode
$S$
on
$\mathbb{C}[G]$
defines an antipode
${\hat{S}}$
on
${\mathcal{U}}(G)$
by
${\hat{S}}(\unicode[STIX]{x1D714})=\unicode[STIX]{x1D714}S$
. There exists a unique element
$\unicode[STIX]{x1D70C}\in {\mathcal{U}}(G)$
, called the Woronowicz character, such that
$\unicode[STIX]{x1D70C}$
is positive, invertible,
${\hat{S}}^{2}=\operatorname{Ad}\unicode[STIX]{x1D70C}$
and
$\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}))=\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{-1}))$
for all
$U\in \operatorname{Rep}G$
. It also has the property
$\hat{\unicode[STIX]{x1D6E5}}(\unicode[STIX]{x1D70C})=\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D70C}$
justifying the name ‘character’. The number
$\operatorname{Tr}(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}))$
is called the quantum dimension of
$U$
and denoted by
$\dim _{q}(U)$
. We will write
$\dim _{q}(s)$
instead of
$\dim _{q}(U_{s})$
.
The element
$\unicode[STIX]{x1D70C}$
allows one to define a canonical duality functor on
$\operatorname{Rep}G$
. Namely, given a finite-dimensional unitary representation
$U$
of
$G$
, the conjugate representation is defined by
$$\begin{eqnarray}\bar{U}=(j(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{1/2}))\otimes 1)(j\otimes \unicode[STIX]{x1D704})(U^{\ast })(j(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{-1/2}))\otimes 1)\in B(\bar{H}_{U})\otimes C(G),\end{eqnarray}$$
where
$\bar{H}_{U}$
is the complex conjugate Hilbert space to
$H_{U}$
and
$j$
is the canonical
$\ast$
-anti-isomorphism
$B(H_{U})\rightarrow B(\bar{H}_{U})$
,
$j(T)\bar{\unicode[STIX]{x1D709}}=\overline{T^{\ast }\unicode[STIX]{x1D709}}$
. Note that the element
$U^{c}=(j\otimes \unicode[STIX]{x1D704})(U^{\ast })$
already satisfies
$(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D6E5})(U^{c})=U_{12}^{c}U_{13}^{c}$
, and the additional conjugation by
$j(\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{1/2}))\otimes 1$
is needed only to make this element unitary.
The object
$\bar{U}$
is conjugate to
$U$
in
$\operatorname{Rep}G$
, meaning that there exist morphisms
$R_{U}:\unicode[STIX]{x1D7D9}\rightarrow \bar{U}\otimes U$
and
$\bar{R}_{U}:\unicode[STIX]{x1D7D9}\rightarrow U\otimes \bar{U}$
, where
$\unicode[STIX]{x1D7D9}$
is the trivial representation of
$G$
on the one-dimensional space
$\mathbb{C}$
, solving the conjugate equations: the compositions
$$\begin{eqnarray}U\xrightarrow[{}]{\unicode[STIX]{x1D704}\otimes R_{U}}U\otimes \bar{U}\otimes U\xrightarrow[{}]{\bar{R}_{U}^{\ast }\otimes \unicode[STIX]{x1D704}}U\quad \text{and}\quad \bar{U}\xrightarrow[{}]{\unicode[STIX]{x1D704}\otimes \bar{R}_{U}}\bar{U}\otimes U\otimes \bar{U}\xrightarrow[{}]{R_{U}^{\ast }\otimes \unicode[STIX]{x1D704}}\bar{U}\end{eqnarray}$$
are the identity morphisms. Using the Woronowicz character
$\unicode[STIX]{x1D70C}$
, we can define such morphisms by
$$\begin{eqnarray}R_{U}(1)=\mathop{\sum }_{i}\bar{\unicode[STIX]{x1D709}}_{i}\otimes \unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{-1/2})\unicode[STIX]{x1D709}_{i},\quad \bar{R}_{U}(1)=\mathop{\sum }_{i}\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C}^{1/2})\unicode[STIX]{x1D709}_{i}\otimes \bar{\unicode[STIX]{x1D709}}_{i},\end{eqnarray}$$
where
$\{{\unicode[STIX]{x1D709}_{i}\}}_{i}$
is an orthonormal basis in
$H_{U}$
. The pair
$(R_{U},\bar{R}_{U})$
is standard, meaning that
$\Vert R_{U}\Vert =\Vert \bar{R}_{U}\Vert$
and the product
$\Vert R_{U}\Vert \,\Vert \bar{R}_{U}\Vert$
is minimal among all possible solutions of the conjugate equations for
$U$
and
$\bar{U}$
. Note that
$\Vert R_{U}\Vert =\Vert \bar{R}_{U}\Vert =\dim _{q}(U)^{1/2}$
.
1.2 Quantum random walks
We now recall the main concepts of the boundary theory of quantum random walks; see [Reference IzumiIzu02, Reference Neshveyev and TusetNT04].
For every
$s\in I=\operatorname{Irr}(G)$
, consider the state
$\unicode[STIX]{x1D719}_{s}$
on
$B(H_{s})$
defined by
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{s}=\frac{\operatorname{Tr}(\cdot \,\unicode[STIX]{x1D70B}_{s}(\unicode[STIX]{x1D70C}^{-1}))}{\dim _{q}(s)}.\end{eqnarray}$$
This is a unique state invariant under the left action of
$G$
on
$B(H_{s})$
given by
$$\begin{eqnarray}B(H_{s})\rightarrow C(G)\otimes B(H_{s}),\quad T\mapsto (U_{s})_{21}^{\ast }(1\otimes T)(U_{s})_{21}.\end{eqnarray}$$
Taken together, these actions define the left adjoint action of
$G$
on
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
.
Consider now a probability measure
$\unicode[STIX]{x1D707}$
on
$I$
and define a normal state
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
on
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
by
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}=\mathop{\sum }_{s\in I}\unicode[STIX]{x1D707}(s)\unicode[STIX]{x1D719}_{s}.\end{eqnarray}$$
Consider the corresponding convolution Markov operator
$P_{\unicode[STIX]{x1D707}}$
on
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
:
$$\begin{eqnarray}P_{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D704})\hat{\unicode[STIX]{x1D6E5}}.\end{eqnarray}$$
This operator commutes with the left adjoint action of
$G$
and the right action by translations of
$\unicode[STIX]{x1D6E4}$
on
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, which is defined by
$\hat{\unicode[STIX]{x1D6E5}}$
. We therefore say that
$P_{\unicode[STIX]{x1D707}}$
defines a
$G$
-
$\unicode[STIX]{x1D6E4}$
-invariant quantum random walk on
$\unicode[STIX]{x1D6E4}$
.
By the
$G$
-equivariance, the operator
$P_{\unicode[STIX]{x1D707}}$
preserves the center
$\ell ^{\infty }(I)$
of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, hence it defines a classical random walk on the set
$I$
with transition probabilities
$p_{\unicode[STIX]{x1D707}}(s,t)$
such that
$$\begin{eqnarray}P_{\unicode[STIX]{x1D707}}(I_{t})I_{s}=p_{\unicode[STIX]{x1D707}}(s,t)I_{s},\end{eqnarray}$$
where
$I_{s}$
denotes the unit of
$B(H_{s})\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. Explicitly, the transition probabilities are given by
$$\begin{eqnarray}p_{\unicode[STIX]{x1D707}}(s,t)=\mathop{\sum }_{r\in I}\unicode[STIX]{x1D707}(r)m_{rs}^{t}\frac{\dim _{q}(t)}{\dim _{q}(r)\dim _{q}(s)},\end{eqnarray}$$
where
$m_{rs}^{t}$
is the multiplicity of
$U_{t}$
in
$U_{r}\otimes U_{s}$
. We will only be interested in the case where this classical random walk is irreducible and transient. The irreducibility assumption means that, given
$s,t$
, there exist
$s_{0}=s,s_{1},\ldots ,s_{n}=t$
such that
$p_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots p_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n})>0$
. Equivalently, every representation
$U_{t}$
is a subrepresentation of
$U_{r_{1}}\otimes \cdots \otimes U_{r_{n}}$
for some
$r_{1},\ldots ,r_{n}\in \operatorname{supp}\unicode[STIX]{x1D707}$
. In this case we also say that the measure
$\unicode[STIX]{x1D707}$
and the state
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
are generating. The assumption of transience means that the sum of all such products
$p_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots p_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n})$
(with
$s_{0}=s$
and
$s_{n}=t$
) is finite for all
$s,t\in I$
. In this case we also say that
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D707}}$
and
$\unicode[STIX]{x1D707}$
are transient. Similarly to [Reference Derriennic and Guivarc’hDG73], it can be shown that, assuming irreducibility, the random walk is transient if the quantum dimension function is non-amenable; in particular, when
$\unicode[STIX]{x1D6E4}$
is either non-amenable or non-Kac (recall that the latter means that
$\unicode[STIX]{x1D70C}\neq 1$
). We will prove a related result more useful for our purposes in Lemma 4.1 below.
Assuming irreducibility and transience, the Green kernel is defined as the completely positive map
$$\begin{eqnarray}G_{\unicode[STIX]{x1D707}}:c_{c}(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4}),\quad G_{\unicode[STIX]{x1D707}}(a)=\mathop{\sum }_{n=0}^{\infty }P_{\unicode[STIX]{x1D707}}^{n}(a),\end{eqnarray}$$
and then the Martin kernel is defined as the map
$$\begin{eqnarray}K_{\unicode[STIX]{x1D707}}:c_{c}(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4}),\quad K_{\unicode[STIX]{x1D707}}(a)=G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}G_{\unicode[STIX]{x1D707}}(a),\end{eqnarray}$$
where
$e\in I$
is the point corresponding to the trivial representation
$\unicode[STIX]{x1D7D9}$
. We remark that the element
$G_{\unicode[STIX]{x1D707}}(I_{e})$
is a strictly positive scalar in every matrix block
$B(H_{s})$
, so
$G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}$
is a well-defined, but possibly unbounded, function on
$I$
. The elements
$K_{\unicode[STIX]{x1D707}}(a)=G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}G_{\unicode[STIX]{x1D707}}(a)$
are, however, bounded. Furthermore, if
$a\in c_{c}(\unicode[STIX]{x1D6E4})$
is positive and non-zero, then
$K_{\unicode[STIX]{x1D707}}(a)$
is a positive invertible element of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
.
We have an involution
$s\mapsto \bar{s}$
on
$I$
defined by
$\bar{U}_{s}\cong U_{\bar{s}}$
. For every probability measure
$\unicode[STIX]{x1D707}$
on
$I$
, we define a new probability measure
$\check{\unicode[STIX]{x1D707}}$
on
$I$
by
$\check{\unicode[STIX]{x1D707}}(s)=\unicode[STIX]{x1D707}(\bar{s})$
. The corresponding transition probabilities satisfy
$$\begin{eqnarray}p_{\check{\unicode[STIX]{x1D707}}}(s,t)=\frac{\dim _{q}(t)^{2}}{\dim _{q}(s)^{2}}p_{\unicode[STIX]{x1D707}}(t,s).\end{eqnarray}$$
It follows that
$\check{\unicode[STIX]{x1D707}}$
is generating and transient if and only if
$\unicode[STIX]{x1D707}$
has the same properties.
Finally, given a generating transient probability measure
$\unicode[STIX]{x1D707}$
, the Martin compactification of
$\unicode[STIX]{x1D6E4}$
is defined as the C
$^{\ast }$
-subalgebra
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
generated by
$K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))$
and
$c_{c}(\unicode[STIX]{x1D6E4})$
. This C
$^{\ast }$
-algebra is invariant under the left adjoint action of
$G$
and the right action of
$\unicode[STIX]{x1D6E4}$
by translations. The Martin boundary is defined by
$C(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{M,\unicode[STIX]{x1D707}})=C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})/c_{0}(\unicode[STIX]{x1D6E4})$
.
1.3 Module categories and categorical random walks
To every C
$^{\ast }$
-algebra
$A$
equipped with a left action of
$G$
one can associate the category of equivariant finitely generated Hilbert modules. We will need this only for unital C
$^{\ast }$
-subalgebras
$A\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, equipped with the action given by the restriction of the adjoint action, in which case this category has the following concrete description [Reference Neshveyev and YamashitaNY14, § 4].
For
$U,V\in \operatorname{Rep}G$
, consider the subspace
$$\begin{eqnarray}\displaystyle {\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V) & := & \displaystyle \ell ^{\infty }\text{-}\bigoplus _{s\in I}\operatorname{Hom}_{G}(H_{s}\otimes H_{U},H_{s}\otimes H_{V})\nonumber\\ \displaystyle & \subset & \displaystyle \ell ^{\infty }\text{-}\bigoplus _{s\in I}B(H_{s}\otimes H_{U},H_{s}\otimes H_{V})=\ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V}),\nonumber\end{eqnarray}$$
and define
${\mathcal{D}}_{A}(U,V)$
as the intersection of this space with
$A\otimes B(H_{U},H_{V})$
. We can then define a new category
${\mathcal{D}}_{A}$
with the same objects as in
$\operatorname{Rep}G$
, but with the morphism spaces
${\mathcal{D}}_{A}(U,V)$
. (To be more precise, we also need to complete
${\mathcal{D}}_{A}$
with respect to subobjects, but whether we do this or not is not going to play any role in this paper.) The category
$\operatorname{Rep}G$
can be considered as a (non-full) subcategory of
${\mathcal{D}}_{A}$
, if we identify a morphism
$T:H_{U}\rightarrow H_{V}$
in
$\operatorname{Rep}G$
with the collection of morphisms
$\unicode[STIX]{x1D704}_{s}\otimes T:H_{s}\otimes H_{U}\rightarrow H_{s}\otimes H_{V}$
. Furthermore, the functors of tensoring on the right by objects of
$\operatorname{Rep}G$
define on
${\mathcal{D}}_{A}$
the structure of a right
$(\operatorname{Rep}G)$
-module category.
The morphism spaces
${\mathcal{D}}_{A}(U,V)$
are completely determined by the spaces of the form
${\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U)$
thanks to the Frobenius reciprocity isomorphisms
$$\begin{eqnarray}{\mathcal{D}}_{A}(U,V)\cong {\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},V\otimes \bar{U}),\quad T\mapsto (T\otimes \unicode[STIX]{x1D704}_{\bar{U}})\bar{R}_{U}.\end{eqnarray}$$
By decomposing
$V\otimes \bar{U}$
into irreducibles we see that
${\mathcal{D}}_{A}$
is completely determined already by the spaces
${\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
,
$s\in I$
.
The
$G$
-C
$^{\ast }$
-algebra
$A$
can be easily reconstructed from the morphism spaces
${\mathcal{D}}_{A}(U,V)$
: the elements of the form
$(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(T)$
, where
$T\in {\mathcal{D}}_{A}(U,V)\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V})$
and
$\unicode[STIX]{x1D714}\in B(H_{U},H_{V})^{\ast }$
, span a dense
$\ast$
-subalgebra of
$A$
. By the previous paragraph it is clear that it suffices to take
$T\in {\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
,
$s\in I$
. For each
$s\in I$
, the linear span of elements of the form
$(\unicode[STIX]{x1D704}\otimes \unicode[STIX]{x1D714})(T)$
, with
$T\in {\mathcal{D}}_{A}(\unicode[STIX]{x1D7D9},U_{s})$
and
$\unicode[STIX]{x1D714}\in B(H_{e},H_{e}\otimes H_{s})^{\ast }=H_{s}^{\ast }$
, is nothing other than the spectral subspace of
$A$
corresponding to
$\bar{U}_{s}$
.
Assume now that we are given a probability measure
$\unicode[STIX]{x1D707}$
on
$I$
and consider the corresponding Markov operator
$P_{\unicode[STIX]{x1D707}}$
on
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. Since
$P_{\unicode[STIX]{x1D707}}$
commutes with left adjoint action of
$G$
, the operator
$P_{\unicode[STIX]{x1D707}}\otimes \unicode[STIX]{x1D704}$
is well defined on
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V)\subset \ell ^{\infty }(\unicode[STIX]{x1D6E4})\otimes B(H_{U},H_{V})$
. We will denote this operator by
$P_{\unicode[STIX]{x1D707}}$
again. This operator can be described in purely categorical terms as follows.
The space
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V)$
can be identified with the space
$\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
of bounded natural transformations between the functors
$\unicode[STIX]{x1D704}\otimes U$
and
$\unicode[STIX]{x1D704}\otimes V$
on
$\operatorname{Rep}G$
, that is, uniformly bounded collections
$(\unicode[STIX]{x1D702}_{W})_{W}$
of morphisms
$\unicode[STIX]{x1D702}_{W}:W\otimes U\rightarrow W\otimes V$
that are natural in
$W$
, since any such collection is completely determined by the morphisms
$\unicode[STIX]{x1D702}_{s}=\unicode[STIX]{x1D702}_{U_{s}}$
. For every
$s\in I$
, we have a contraction
$P_{s}$
on
$\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
defined by
$$\begin{eqnarray}P_{s}(\unicode[STIX]{x1D702})_{W}=(\text{tr}_{s}\,\otimes \,\unicode[STIX]{x1D704})(\unicode[STIX]{x1D702}_{U_{s}\otimes W}).\end{eqnarray}$$
where
$\text{tr}_{s}\,\otimes \,\unicode[STIX]{x1D704}$
denotes the normalized categorical partial trace
$\operatorname{Mor}(U_{s}\otimes X,U_{s}\otimes Y)\rightarrow \operatorname{Mor}(X,Y)$
defined by
$$\begin{eqnarray}(\text{tr}_{s}\,\otimes \,\unicode[STIX]{x1D704})(T)=\dim _{q}(s)^{-1}(R_{s}^{\ast }\otimes \unicode[STIX]{x1D704}_{Y})(\unicode[STIX]{x1D704}_{\bar{s}}\otimes T)(R_{s}\otimes \unicode[STIX]{x1D704}_{X}),\end{eqnarray}$$
and where
$(R_{s},\bar{R}_{s})$
is a standard solution of the conjugate equations for
$U_{s}$
and
$U_{\bar{s}}$
. Then
$$\begin{eqnarray}P_{\unicode[STIX]{x1D707}}=\mathop{\sum }_{s\in I}\unicode[STIX]{x1D707}(s)P_{s}.\end{eqnarray}$$
This leads to the following categorical description of the Martin compactification
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
in [Reference JordansJor17]; see also [Reference Neshveyev and YamashitaNY17] for the initial motivation and [Reference De Rijdt and Vander VennetDRVV10] for a precursor of this picture.
Consider the subspace
$\operatorname{Nat}_{c}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)\subset \operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes U,\unicode[STIX]{x1D704}\otimes V)$
consisting of all natural transformations
$\unicode[STIX]{x1D702}$
such that
$\unicode[STIX]{x1D702}_{s}=0$
for all but finitely many
$s$
. In other words, we consider the subspace
$$\begin{eqnarray}{\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(U,V):=\bigoplus _{s\in I}\operatorname{Hom}_{G}(H_{s}\otimes H_{U},H_{s}\otimes H_{V})\subset \ell ^{\infty }\text{-}\bigoplus _{s\in I}\operatorname{Hom}_{G}(H_{s}\otimes H_{U},H_{s}\otimes H_{V}).\end{eqnarray}$$
We have well-defined maps
$$\begin{eqnarray}K_{\unicode[STIX]{x1D707}}:{\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(U,V)\rightarrow {\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(U,V),\quad K_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D702})=G_{\unicode[STIX]{x1D707}}(I_{e})^{-1}G_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D702}),\end{eqnarray}$$
where
$G_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D702})=\sum _{n=0}^{\infty }P_{\unicode[STIX]{x1D707}}^{n}(\unicode[STIX]{x1D702})$
. Then
${\mathcal{D}}_{C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})}$
is the smallest C
$^{\ast }$
-subcategory of
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}$
containing
$\operatorname{Rep}G$
,
${\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}$
and all morphisms of the form
$K_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702})$
, where
$\unicode[STIX]{x1D702}$
is a morphism in
${\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}$
. Again using (4), we see that it suffices to take
$\unicode[STIX]{x1D702}\in {\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(\unicode[STIX]{x1D7D9},U_{s})$
,
$s\in I$
.
Note that the previous paragraph does not really add any new information on
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
. What we are basically saying is that in computing
$K_{\check{\unicode[STIX]{x1D707}}}:c_{c}(\unicode[STIX]{x1D6E4})\rightarrow \ell ^{\infty }(\unicode[STIX]{x1D6E4})$
it suffices to consider elements
$a$
lying in spectral subspaces of
$c_{c}(\unicode[STIX]{x1D6E4})$
(with respect to the left adjoint action of
$G$
) corresponding to
$U_{s}$
, and then
$K_{\check{\unicode[STIX]{x1D707}}}(a)$
is again an element of the spectral subspace of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
corresponding to
$U_{s}$
. But this is clear, since
$c_{c}(\unicode[STIX]{x1D6E4})$
is the direct sum of its spectral subspaces and the operator
$P_{\unicode[STIX]{x1D707}}$
is
$G$
-equivariant. Nevertheless, working with the spaces
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D7D9},U_{s})$
is more convenient than with the spectral subspaces, and the interpretation of elements of
${\mathcal{D}}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D7D9},U_{s})$
as natural transformations between certain functors makes some computations more transparent.
1.4 Free unitary quantum groups
In this section we recall some properties of free unitary quantum groups introduced in [Reference Van Daele and WangVDW96] and studied in detail in [Reference BanicaBan97].
Fix a natural number
$n\geqslant 2$
and a matrix
$F\in \operatorname{GL}_{n}(\mathbb{C})$
such that
$\operatorname{Tr}(F^{\ast }F)=\operatorname{Tr}((F^{\ast }F)^{-1})$
. The compact free unitary quantum group
$A_{u}(F)$
is defined as the universal unital C
$^{\ast }$
-algebra with generators
$u_{ij}$
,
$1\leqslant i,j\leqslant n$
, such that the matrices
$U=(u_{ij})_{i,j}$
and
$FU^{c}F^{-1}$
are unitary, where
$U^{c}=(u_{ij}^{\ast })_{i,j}$
, equipped with the comultiplication
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(u_{ij})=\mathop{\sum }_{k=1}^{n}u_{ik}\otimes u_{kj}.\end{eqnarray}$$
Therefore
$U$
defines a unitary representation of the quantum group
$A_{u}(F)$
on the
$n$
-dimensional Hilbert space, called the fundamental representation.
The set
$I$
of isomorphism classes of irreducible representations of
$A_{u}(F)$
is the free monoid on letters
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
, with
$\unicode[STIX]{x1D6FC}$
corresponding to
$U$
. The involution
$s\mapsto \bar{s}$
is the anti-automorphism of the monoid defined by
$\bar{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FD}$
and
$\bar{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FC}$
.
From now on we will use the conventions of [Reference Vaes and Vander VennetVVV10] in that we write
$x$
instead of
$U_{x}$
for
$x\in I$
whenever convenient. The fusion rules for the representations of
$A_{u}(F)$
are given by
$$\begin{eqnarray}x\otimes y\cong \bigoplus _{z\in I:x=x_{0}z,y=\bar{z}y_{0}}x_{0}y_{0}.\end{eqnarray}$$
Therefore if the last letter of
$x$
is the same as the first letter of
$y$
, then
$U_{x}\otimes U_{y}$
is irreducible and isomorphic to
$U_{xy}$
. In this case we write
$xy=x\otimes y$
.
The Woronowicz character
$\unicode[STIX]{x1D70C}$
of
$A_{u}(F)$
is determined by the property
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{U}(\unicode[STIX]{x1D70C})=(F^{\ast }F)^{t}\quad (\text{the transpose of}~F^{\ast }F).\end{eqnarray}$$
Clearly,
$\dim _{q}(\unicode[STIX]{x1D6FC})=\operatorname{Tr}(F^{\ast }F)\geqslant n$
, and the equality holds if and only if
$F$
is unitary. Let
$q\in (0,1]$
be such that
$$\begin{eqnarray}\operatorname{Tr}(F^{\ast }F)=q+q^{-1}.\end{eqnarray}$$
Then
$q=1$
if and only if
$F$
is a unitary
$2\times 2$
matrix.
An element
$x\in I$
is said to be indecomposable if there are only trivial decompositions
$x=y\otimes z$
, that is, we must have
$y=e$
or
$z=e$
. Equivalently,
$x$
is an alternating product of
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
. Every word
$x\in I$
can be written as
$x_{1}\otimes \cdots \otimes x_{n}$
, where
$x_{1},\ldots ,x_{n}$
are indecomposable. Then
$$\begin{eqnarray}\dim _{q}(x)=\mathop{\prod }_{i=1}^{n}[|x_{i}|+1]_{q},\end{eqnarray}$$
where
$|x_{i}|$
denotes the length of
$x_{i}$
and
$\displaystyle [n]_{q}=(q^{n}-q^{-n})/(q-q^{-1})$
.
2 Topological boundary of the dual of
$A_{u}(F)$
Consider a free unitary quantum group
$G=A_{u}(F)$
, with
$F$
not a unitary
$2\times 2$
matrix. Recall that this assumption means that the number
$q\in (0,1]$
defined by (5) is strictly less than
$1$
. Denote by
$\unicode[STIX]{x1D6E4}$
the dual discrete quantum group.
As we discussed in § 1.4, the set
$I$
of isomorphism classes of irreducible representations of
$G$
is a free monoid on letters
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
. The empty word is denoted by
$e$
. Consider the tree with vertex set
$I$
such that different elements
$x$
and
$y$
of
$I$
are connected by an edge if and only if one of them is obtained from the other by adding (or removing) one letter on the left. Denote by
$\bar{I}$
the corresponding end compactification of
$I$
. The elements of
$\bar{I}$
are words in
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
that are either finite or infinite on the left, and the boundary
$\unicode[STIX]{x2202}I=\bar{I}\setminus I$
is the set of infinite words. The algebra
$C(\bar{I})$
of continuous functions on
$\bar{I}$
can be identified with the algebra of functions
$f\in \ell ^{\infty }(I)$
such that
$$\begin{eqnarray}|f(yx)-f(x)|\rightarrow 0~\text{as}~x\rightarrow \infty ,~\text{uniformly in}~y\in I.\end{eqnarray}$$
In [Reference Vaes and Vander VennetVVV10], Vaes and Vander Vennet extended this construction to
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
as follows. (More precisely, they consider words infinite on the right, while in order to be consistent with our conventions, we consider words infinite on the left.)
For all
$x,y\in I$
, fix an isometry
$V(xy,x\otimes y)\in \operatorname{Mor}(xy,x\otimes y)$
. Define ucp maps
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{yx,x}:B(H_{x})\rightarrow B(H_{yx})\quad T\mapsto V(yx,y\otimes x)^{\ast }(1\otimes T)V(yx,y\otimes x).\end{eqnarray}$$
They do not depend on any choices. Define
$$\begin{eqnarray}{\mathcal{B}}=\{a\in \ell ^{\infty }(\unicode[STIX]{x1D6E4}):\Vert a_{yx}-\unicode[STIX]{x1D713}_{yx,x}(a_{x})\Vert \rightarrow 0~\text{as}~x\rightarrow \infty ,~\text{uniformly in}~y\in I\}.\end{eqnarray}$$
By [Reference Vaes and Vander VennetVVV10, Theorem 3.2], this is a unital C
$^{\ast }$
-subalgebra of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
containing
$c_{0}(\unicode[STIX]{x1D6E4})$
. It can therefore be considered as the algebra of continuous functions on a compactification of
$\unicode[STIX]{x1D6E4}$
. The (non-commutative) algebra of continuous functions on the corresponding boundary is defined by
${\mathcal{B}}_{\infty }={\mathcal{B}}/c_{0}(\unicode[STIX]{x1D6E4})$
. The left adjoint action of
$G$
and the right action by translations of
$\unicode[STIX]{x1D6E4}$
on
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
define actions of
$G$
and
$\unicode[STIX]{x1D6E4}$
on
${\mathcal{B}}$
and
${\mathcal{B}}_{\infty }$
.
If we view
${\mathcal{B}}$
only as a
$G$
-C
$^{\ast }$
-algebra, then from our discussion in § 1.3 we immediately get the following result.
Proposition 2.1. Consider the module category
${\mathcal{D}}_{{\mathcal{B}}}$
associated with the left action of
$G$
on
${\mathcal{B}}$
. Then, for all
$U,V\in \operatorname{Rep}G$
, the morphism space
${\mathcal{D}}_{{\mathcal{B}}}(U,V)$
consists of all elements
$$\begin{eqnarray}T\in \ell ^{\infty }\text{-}\bigoplus _{x\in I}\operatorname{Hom}_{G}(H_{x}\otimes H_{U},H_{x}\otimes H_{V})\end{eqnarray}$$
such that
$\Vert T_{yx}-(V(yx,y\otimes x)^{\ast }\otimes \unicode[STIX]{x1D704}_{V})(\unicode[STIX]{x1D704}_{y}\otimes T_{x})(V(yx,y\otimes x)\otimes \unicode[STIX]{x1D704}_{U})\Vert \rightarrow 0$
as
$x\rightarrow \infty$
, uniformly in
$y\in I$
.
In order to get a better understanding of the morphism spaces
${\mathcal{D}}_{{\mathcal{B}}}(U,V)$
we will now make a particular choice of representations
$U_{x}$
and isometries
$V(z,x\otimes y)\in \operatorname{Mor}(z,x\otimes y)$
for all
$z\prec x\otimes y$
; cf. [Reference Vaes and VergniouxVV07, Appendix].
Fix representatives
$U_{\unicode[STIX]{x1D6FC}}$
and
$U_{\unicode[STIX]{x1D6FD}}$
of
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
. All other representatives
$U_{x}$
we construct as follows. If
$x=x_{1}\cdots x_{n}\in I$
, with
$x_{i}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for all
$i$
, then, since
$\operatorname{Mor}(x,x_{1}\otimes \cdots \otimes x_{n})$
is one-dimensional,
$H_{x_{1}}\otimes \cdots \otimes H_{x_{n}}$
contains a unique invariant subspace on which
$U_{x_{1}}\otimes \cdots \otimes U_{x_{n}}$
is irreducible of class
$x$
. We take this subspace as
$H_{x}$
and define
$U_{x}$
as the restriction of
$U_{x_{1}}\otimes \cdots \otimes U_{x_{n}}$
to
$H_{x}$
. Denote by
$p_{x}$
the projection in
$B(H_{x_{1}}\otimes \cdots \otimes H_{x_{n}})$
with image
$H_{x}$
.
Note that the fusion rules and our choice of representatives imply that
$H_{xy}$
is a subspace of
$H_{x}\otimes H_{y}$
. We take the embedding map
$H_{xy}\rightarrow H_{x}\otimes H_{y}$
as
$V(xy,x\otimes y)$
. Then
$V(xy,x\otimes y)^{\ast }$
coincides with the projection
$p_{xy}^{x\otimes y}:=p_{xy}|_{H_{x}\otimes H_{y}}$
.
Next, viewing
$U_{\unicode[STIX]{x1D6FD}}$
as the dual of
$U_{\unicode[STIX]{x1D6FC}}$
, fix a standard solution
$(R_{\unicode[STIX]{x1D6FC}},\bar{R}_{\unicode[STIX]{x1D6FC}})$
of the conjugate equations for
$U_{\unicode[STIX]{x1D6FC}}$
. Put
$R_{\unicode[STIX]{x1D6FD}}=\bar{R}_{\unicode[STIX]{x1D6FC}}$
and
$\bar{R}_{\unicode[STIX]{x1D6FD}}=R_{\unicode[STIX]{x1D6FC}}$
. Assume now that
$x=x_{1}\cdots x_{n}$
and
$y=y_{1}\cdots y_{m}$
, with
$x_{i},y_{j}\in \{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}\}$
for all
$i$
and
$j$
, and assume that
$z$
is a subrepresentation of
$x\otimes y$
, so
$z=x_{1}\cdots x_{n-k}\,y_{k+1}\cdots y_{m}$
for some
$k$
and
$x_{n-i}=\bar{y}_{i+1}$
for
$i=0,\ldots ,k-1$
. We then define an operator
$\tilde{V}(z,x\otimes y):H_{z}\rightarrow H_{x}\otimes H_{y}$
by
$$\begin{eqnarray}\tilde{V}(z,x\otimes y)=(p_{x}\otimes p_{y})(\unicode[STIX]{x1D704}^{\otimes (n-1)}\otimes \bar{R}_{x_{n-k+1}}\otimes \unicode[STIX]{x1D704}^{\otimes (m-1)})\ldots (\unicode[STIX]{x1D704}^{\otimes (n-k)}\otimes \bar{R}_{x_{n}}\otimes \unicode[STIX]{x1D704}^{\otimes (m-k)}).\end{eqnarray}$$
This can also be described as follows. Our fixed standard solutions
$(R_{\unicode[STIX]{x1D6FC}},\bar{R}_{\unicode[STIX]{x1D6FC}})$
and
$(R_{\unicode[STIX]{x1D6FD}},\bar{R}_{\unicode[STIX]{x1D6FD}})=(\bar{R}_{\unicode[STIX]{x1D6FC}},R_{\unicode[STIX]{x1D6FC}})$
of the conjugate equations allow us to construct standard solutions of the conjugate equations for tensor products of
$U_{\unicode[STIX]{x1D6FC}}$
and
$U_{\unicode[STIX]{x1D6FD}}$
. By restriction we then get standard solutions
$(R_{x},\bar{R}_{x})$
of the conjugate equations for all
$x\in I$
. By construction, we have
$(R_{\bar{x}},\bar{R}_{\bar{x}})=(\bar{R}_{x},R_{x})$
and
$$\begin{eqnarray}R_{xy}=(p_{\bar{y}\bar{x}}^{\bar{y}\otimes \bar{x}}\otimes p_{xy}^{x\otimes y})(\unicode[STIX]{x1D704}_{\bar{y}}\otimes R_{x}\otimes \unicode[STIX]{x1D704}_{y})R_{y},\quad \bar{R}_{xy}=(p_{xy}^{x\otimes y}\otimes p_{\bar{y}\bar{x}}^{\bar{y}\otimes \bar{x}})(\unicode[STIX]{x1D704}_{x}\otimes \bar{R}_{y}\otimes \unicode[STIX]{x1D704}_{\bar{x}})\bar{R}_{x}.\end{eqnarray}$$
Then the morphism
$\tilde{V}(z,x\otimes y)$
for
$x=sv$
,
$y=\bar{v}t$
and
$z=st$
is given by
$$\begin{eqnarray}\tilde{V}(st,sv\otimes \bar{v}t)=(p_{sv}^{s\otimes v}\otimes p_{\bar{v}t}^{\bar{v}\otimes t})(\unicode[STIX]{x1D704}_{s}\otimes \bar{R}_{v}\otimes \unicode[STIX]{x1D704}_{t})V(st,s\otimes t).\end{eqnarray}$$
Since
$\tilde{V}(st,sv\otimes \bar{v}t)$
is an element of
$\operatorname{Mor}(st,sv\otimes \bar{v}t)$
, it must be isometric up to a scalar factor.
Lemma 2.2. There is a constant
$c>0$
depending only on
$q$
such that
$$\begin{eqnarray}\dim _{q}(v)^{1/2}\geqslant \Vert \tilde{V}(st,sv\otimes \bar{v}t)\Vert \geqslant c\dim _{q}(v)^{1/2}\end{eqnarray}$$
for all
$v,s,t\in I$
.
Proof. The first inequality is an immediate consequence of (9), since
$\Vert \bar{R}_{v}\Vert =\dim _{q}(v)^{1/2}$
.
The second inequality can be deduced from an analogous result for
$\text{SU}_{-q}(2)$
using arguments similar to those in [Reference Vaes and Vander VennetVVV10, Reference Vander VennetVan08]. Namely, we proceed as follows.
We first reduce the proof to a particular case. If
$v=v_{1}\otimes v_{2}$
, then, using that
$\bar{R}_{v}=(\unicode[STIX]{x1D704}_{v_{1}}\otimes \bar{R}_{v_{2}}\otimes \unicode[STIX]{x1D704}_{\bar{v}_{1}})\bar{R}_{v_{1}}$
by (8) and that
$p_{sv}^{s\otimes v}=p_{sv_{1}}^{s\otimes v_{1}}\otimes \unicode[STIX]{x1D704}_{v_{2}}$
,
$p_{\bar{v}t}^{\bar{v}\otimes t}=\unicode[STIX]{x1D704}_{\bar{v}_{2}}\otimes p_{\bar{v}_{1}t}^{\bar{v}_{1}\otimes t}$
, we see that
$$\begin{eqnarray}\Vert \tilde{V}(st,sv\otimes \bar{v}t)\Vert =\dim _{q}(v_{2})^{1/2}\Vert \tilde{V}(st,sv_{1}\otimes \bar{v}_{1}t)\Vert .\end{eqnarray}$$
We may therefore assume that
$v$
is indecomposable. We also assume that
$v\neq e$
, since
$\tilde{V}(st,s\otimes t)=V(st,s\otimes t)$
is isometric by definition.
Next, write
$sv$
as
$s_{1}\otimes s_{2}v$
, with
$s_{2}v$
indecomposable. Assume first that
$s_{2}=e$
. Then
$$\begin{eqnarray}\tilde{V}(st,sv\otimes \bar{v}t)=(\unicode[STIX]{x1D704}_{s}\otimes \unicode[STIX]{x1D704}_{v}\otimes p_{\bar{v}t}^{\bar{v}\otimes t})(\unicode[STIX]{x1D704}_{s}\otimes \bar{R}_{v}\otimes \unicode[STIX]{x1D704}_{t})V(st,s\otimes t),\end{eqnarray}$$
hence
$$\begin{eqnarray}\tilde{V}(st,sv\otimes \bar{v}t)^{\ast }\tilde{V}(st,sv\otimes \bar{v}t)=V(st,s\otimes t)^{\ast }(\unicode[STIX]{x1D704}_{s}\otimes (\operatorname{Tr}_{\bar{v}}\otimes \unicode[STIX]{x1D704})(p_{\bar{v}t}^{\bar{v}\otimes t}))V(st,s\otimes t),\end{eqnarray}$$
where
$\operatorname{Tr}_{\bar{v}}$
denotes the categorical trace. The morphism
$(\operatorname{Tr}_{\bar{v}}\otimes \unicode[STIX]{x1D704})(p_{\bar{v}t}^{\bar{v}\otimes t})$
is a scalar multiple of
$\unicode[STIX]{x1D704}_{t}$
, and, applying
$\operatorname{Tr}_{t}$
, we see that this scalar is
$\dim _{q}(\bar{v}t)/\text{dim}_{q}(t)$
. It follows that
$$\begin{eqnarray}\Vert \tilde{V}(st,sv\otimes \bar{v}t)\Vert =\frac{\dim _{q}(\bar{v}t)^{1/2}}{\dim _{q}(t)^{1/2}}.\end{eqnarray}$$
From (6) it is easy to see that this quantity is not smaller than
$c\dim _{q}(v)^{1/2}$
for a constant
$c$
depending only on
$q$
; cf. [Reference Vaes and VergniouxVV07, (5)].
Assume now that
$s_{2}\neq e$
. Then
$st=s_{1}\otimes s_{2}t$
and
$\tilde{V}(st,sv\otimes \bar{v}t)=\unicode[STIX]{x1D704}_{s_{1}}\otimes \tilde{V}(s_{2}t,s_{2}v\otimes \bar{v}t)$
. We see that in this case the computation reduces to the case where
$s_{1}=e$
, that is, we may assume that
$sv$
is indecomposable. In a similar way we reduce the computation to the case where
$\bar{v}t$
is indecomposable as well, so we assume that all three elements
$sv$
,
$v\bar{v}$
and
$\bar{v}t$
are indecomposable (and
$v\neq e$
). In other words,
$sv\bar{v}t$
equals
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\cdots \,$
or
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\cdots \,$
. But in this case the computation of the norm of
$\tilde{V}(st,sv\otimes \bar{v}t)$
is equivalent to a similar computation for
$\text{SU}_{-q}(2)$
(see [Reference Vander VennetVan08, Lemma 8.7.2]), which gives
$$\begin{eqnarray}\Vert \tilde{V}(st,sv\otimes \bar{v}t)\Vert =\left[\frac{|s|+|t|+|v|+1}{|v|}\right]_{q}^{1/2}\left[\frac{|s|+|v|}{|v|}\right]_{q}^{-1/2}\left[\frac{|t|+|v|}{|v|}\right]_{q}^{-1/2}\end{eqnarray}$$
(see [Reference Vaes and VergniouxVV07, (7.3)]), where
$[\begin{smallmatrix}n\\ k\end{smallmatrix}]_{q}$
denote the
$q$
-binomial coefficients. Using that
$$\begin{eqnarray}\left[\frac{n}{k}\right]_{q}=q^{-k(n-k)}\mathop{\prod }_{i=0}^{k-1}\frac{1-q^{2(n-i)}}{1-q^{2(k-i)}},\end{eqnarray}$$
we easily deduce that
$\Vert \tilde{V}(st,sv\otimes \bar{v}t)\Vert \geqslant c[|v|+1]_{q}^{1/2}=c\dim _{q}(v)^{1/2}$
for a constant
$c>0$
depending only on
$q$
; cf. [Reference Vaes and VergniouxVV07, Lemma 8.5].◻
In particular, the morphisms
$\tilde{V}(z,x\otimes y)$
are non-zero, so we can define isometries
$$\begin{eqnarray}V(z,x\otimes y)=\frac{\tilde{V}(z,x\otimes y)}{\Vert \tilde{V}(z,x\otimes y)\Vert }.\end{eqnarray}$$
The following result will play a crucial role in our computations. Note that it does not depend on the particular choice of isometries
$V(z,x\otimes y)$
.
Proposition 2.3 ([Reference Vaes and Vander VennetVVV10, Lemma A.1], [Reference Vander VennetVan08, Lemma 8.7.3]).
There is a constant
$C$
depending only on
$q$
such that
$$\begin{eqnarray}\displaystyle \Vert (\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))p_{uz}^{u\otimes z}-(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))\Vert & {\leqslant} & \displaystyle Cq^{(|z|+|x|-|y|)/2},\nonumber\\ \displaystyle \Vert (V(z,x\otimes y)\otimes \unicode[STIX]{x1D704}_{u})p_{zu}^{z\otimes u}-(\unicode[STIX]{x1D704}_{y}\otimes p_{yu}^{y\otimes u})(V(z,x\otimes y)\otimes \unicode[STIX]{x1D704}_{u})\Vert & {\leqslant} & \displaystyle Cq^{(|z|+|y|-|x|)/2},\nonumber\end{eqnarray}$$
for all
$u,x,y,z\in I$
such that
$z\prec x\otimes y$
.
For our particular choice of
$V(z,x\otimes y)$
this implies the following estimates. (In fact, it is not difficult to see that these estimates are equivalent to the ones above, but with different constants.)
Corollary 2.4. There is a constant
$C$
depending only on
$q$
such that
$$\begin{eqnarray}\displaystyle \Vert V(uz,ux\otimes y)p_{uz}^{u\otimes z}-(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))\Vert & {\leqslant} & \displaystyle Cq^{(|z|+|x|-|y|)/2},\nonumber\\ \displaystyle \Vert V(zu,x\otimes yu)p_{zu}^{z\otimes u}-(\unicode[STIX]{x1D704}_{x}\otimes p_{yu}^{y\otimes u})(V(z,x\otimes y)\otimes \unicode[STIX]{x1D704}_{u})\Vert & {\leqslant} & \displaystyle Cq^{(|z|+|y|-|x|)/2},\nonumber\end{eqnarray}$$
for all
$u,x,y,z\in I$
such that
$z\prec x\otimes y$
.
Proof. By construction we have
$$\begin{eqnarray}\tilde{V}(uz,ux\otimes y)p_{uz}^{u\otimes z}=(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes \tilde{V}(z,x\otimes y))p_{uz}^{u\otimes z},\end{eqnarray}$$
hence
$$\begin{eqnarray}\Vert \tilde{V}(z,x\otimes y)\Vert ^{-1}\tilde{V}(uz,ux\otimes y)p_{uz}^{u\otimes z}=(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))p_{uz}^{u\otimes z},\end{eqnarray}$$
so in particular
$$\begin{eqnarray}\Vert \tilde{V}(z,x\otimes y)\Vert ^{-1}\Vert \tilde{V}(uz,ux\otimes y)\Vert =\Vert (p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))p_{uz}^{u\otimes z}\Vert .\end{eqnarray}$$
Therefore in order to prove the first inequality in the formulation it suffices to show that the last norm is close to
$1$
up to
$C^{\prime }q^{(|z|+|x|-|y|)/2}$
for some constant
$C^{\prime }$
, and that
$$\begin{eqnarray}(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))p_{uz}^{u\otimes z}\end{eqnarray}$$
is close to
$(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))$
up to
$C^{\prime }q^{(|z|+|x|-|y|)/2}$
. But this is indeed the case by the previous proposition, since
$(\unicode[STIX]{x1D704}_{u}\otimes V(z,x\otimes y))p_{uz}^{u\otimes z}$
is an isometry on
$H_{uz}$
. The second inequality is proved in a similar way.◻
We can now get a description of the morphism spaces
${\mathcal{D}}_{{\mathcal{B}}}(e,y)$
. If
$y$
is not of the form
$\bar{z}z$
,
$z\in I$
, then
$\operatorname{Mor}(x,x\otimes y)=0$
for all
$x$
, so
${\mathcal{D}}_{{\mathcal{B}}}(e,y)=0$
. If
$y=\bar{z}z$
, then
$x\prec x\otimes y$
precisely for
$x$
of the form
$uz$
,
$u\in I$
. Denote by
$\unicode[STIX]{x1D6FA}_{y}$
the set of all such
$x$
. It forms a branch of the tree
$I$
and its closure
$\bar{\unicode[STIX]{x1D6FA}}_{y}$
in
$\bar{I}$
is a clopen subset.
Corollary 2.5. Fix
$y\in I$
of the form
$\bar{z}z$
. Define an element
$T=(T_{x})_{x}\in \ell ^{\infty }\text{-}\bigoplus _{x\in I}\operatorname{Mor}(x,x\otimes y)$
by
$$\begin{eqnarray}T_{x}=\left\{\begin{array}{@{}ll@{}}V(x,x\otimes y)\quad & \text{if}~~x\in \unicode[STIX]{x1D6FA}_{y},\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Then
${\mathcal{D}}_{{\mathcal{B}}}(e,y)=C(\bar{\unicode[STIX]{x1D6FA}}_{y})T$
.
Proof. By Proposition 2.1, in order to show that
$T\in {\mathcal{D}}_{{\mathcal{B}}}(e,y)$
we have to prove that
$$\begin{eqnarray}\Vert T_{ux}-(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes T_{x})V(ux,u\otimes x)\Vert \rightarrow 0\end{eqnarray}$$
as
$x\rightarrow \infty$
, uniformly in
$u\in I$
. But this is true by the previous corollary. Next, if
$S\in {\mathcal{D}}_{{\mathcal{B}}}(e,y)$
, then
$S=fT$
for a function
$f\in \ell ^{\infty }(\unicode[STIX]{x1D6FA}_{y})$
such that
$|f(ux)-f(x)|\rightarrow 0$
as
$x\rightarrow \infty$
in
$\unicode[STIX]{x1D6FA}_{y}$
, uniformly in
$u\in I$
. But this means precisely that
$f\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
.◻
Later we will also need the following estimate.
Corollary 2.6. There is a constant
$C$
depending only on
$q$
such that
$$\begin{eqnarray}\Vert (V(ux,uv\otimes \bar{v}x)\otimes \unicode[STIX]{x1D704}_{y})V(ux,ux\otimes y)-(\unicode[STIX]{x1D704}_{uv}\otimes V(\bar{v}x,\bar{v}x\otimes y))V(ux,uv\otimes \bar{v}x)\Vert \leqslant Cq^{|x|-|y|/2}\end{eqnarray}$$
for all
$u,v,x,y\in I$
such that
$x\prec x\otimes y$
.
Proof. Using Corollary 2.4, we see that up to an operator of norm
${\leqslant}Cq^{|x|-|y|/2}$
the morphism
$$\begin{eqnarray}(V(ux,uv\otimes \bar{v}x)\otimes \unicode[STIX]{x1D704}_{y})V(ux,ux\otimes y)p_{ux}^{u\otimes x}\end{eqnarray}$$
equals
$(V(ux,uv\otimes \bar{v}x)\otimes \unicode[STIX]{x1D704}_{y})(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(x,x\otimes y))p_{ux}^{u\otimes x}$
. By (9), the latter operator equals
$$\begin{eqnarray}\Vert \tilde{V}(ux,uv\otimes \bar{v}x)\Vert ^{-1}(p_{uv}^{u\otimes v}\otimes p_{\bar{v}x}^{\bar{v}\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes \bar{R}_{v}\otimes \unicode[STIX]{x1D704}_{x}\otimes \unicode[STIX]{x1D704}_{y})(p_{ux}^{u\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(x,x\otimes y))p_{ux}^{u\otimes x}.\end{eqnarray}$$
By Proposition 2.3, this, in turn, equals
$$\begin{eqnarray}\displaystyle & & \displaystyle \Vert \tilde{V}(ux,uv\otimes \bar{v}x)\Vert ^{-1}(p_{uv}^{u\otimes v}\otimes p_{\bar{v}x}^{\bar{v}\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes \bar{R}_{v}\otimes \unicode[STIX]{x1D704}_{x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes V(x,x\otimes y))p_{ux}^{u\otimes x}\nonumber\\ \displaystyle & & \displaystyle \qquad =\Vert \tilde{V}(ux,uv\otimes \bar{v}x)\Vert ^{-1}(p_{uv}^{u\otimes v}\otimes p_{\bar{v}x}^{\bar{v}\otimes x}\otimes \unicode[STIX]{x1D704}_{y})(\unicode[STIX]{x1D704}_{u}\otimes \bar{R}_{v}\otimes V(x,x\otimes y))p_{ux}^{u\otimes x}\end{eqnarray}$$
up to an operator of norm not greater than
$$\begin{eqnarray}C\frac{\Vert \bar{R}_{v}\Vert }{\Vert \tilde{V}(ux,uv\otimes \bar{v}x)\Vert }q^{|x|-|y|/2}=C\frac{\dim _{q}(v)^{1/2}}{\Vert \tilde{V}(ux,uv\otimes \bar{v}x)\Vert }q^{|x|-|y|/2}.\end{eqnarray}$$
The last quantity is not greater than
$Cc^{-1}q^{|x|-|y|/2}$
, where
$c$
is the constant from Lemma 2.2.
In a similar way one checks that the right-hand side of (10) equals
$$\begin{eqnarray}(\unicode[STIX]{x1D704}_{uv}\otimes V(\bar{v}x,\bar{v}x\otimes y))V(ux,uv\otimes \bar{v}x)p_{ux}^{u\otimes x}\end{eqnarray}$$
up to an operator of norm not greater than
$Cq^{|x|-|y|/2}+Cc^{-1}q^{|x|-|y|/2}$
, where
$C$
is from Proposition 2.3 and
$c$
is from Lemma 2.2.◻
3 Identification of the Martin boundary
The following theorem is our main result.
Theorem 3.1. Consider a free unitary quantum group
$G=A_{u}(F)$
, with
$F$
not a unitary
$2\times 2$
matrix, and a generating finitely supported probability measure
$\unicode[STIX]{x1D707}$
on
$I=\operatorname{Irr}(G)$
. Then the Martin compactification
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
of the discrete quantum group
$\unicode[STIX]{x1D6E4}={\hat{G}}$
with respect to the quantum random walk defined by
$\unicode[STIX]{x1D707}$
coincides with the compactification
${\mathcal{B}}$
defined in (7). It follows that the Martin boundary
$C(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E4}_{M,\unicode[STIX]{x1D707}})$
coincides with
${\mathcal{B}}_{\infty }$
.
In order to simplify the notation, let us denote the Martin compactification
$C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
by
${\mathcal{M}}$
. Since both
${\mathcal{M}}$
and
${\mathcal{B}}$
are
$G$
-C
$^{\ast }$
-subalgebras of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, with the actions of
$G$
coming from the left adjoint action of
$G$
on
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
, by the discussion in § 1.3 in order to show that they coincide it suffices to check that
${\mathcal{D}}_{{\mathcal{M}}}(e,y)={\mathcal{D}}_{{\mathcal{B}}}(e,y)$
for all
$y\in I$
.
Consider first
$y=e$
. Then, by definition,
${\mathcal{D}}_{{\mathcal{B}}}(e,e)$
coincides with
$C(\bar{I})$
considered as a subalgebra of the center
$\ell ^{\infty }(I)$
of
$\ell ^{\infty }(\unicode[STIX]{x1D6E4})$
. On the other hand,
${\mathcal{D}}_{{\mathcal{M}}}(e,e)$
contains the algebra of continuous functions on the Martin compactification of
$I$
defined by the Markov operator with transition probabilities
$p_{\unicode[STIX]{x1D707}}(s,t)$
defined by (1). More precisely, denoting by
$P$
this Markov operator and by
$G_{P}$
the corresponding classical Green kernel,
$$\begin{eqnarray}G_{P}(s,t)=\mathop{\sum }_{n=0}^{\infty }p_{\unicode[STIX]{x1D707}}^{(n)}(s,t)=\unicode[STIX]{x1D6FF}_{st}+\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{s=s_{0},s_{1},\ldots ,s_{n}=t}p_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots p_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n}),\end{eqnarray}$$
in view of (3) we have
$$\begin{eqnarray}G_{\check{\unicode[STIX]{x1D707}}}(I_{s})I_{t}=\frac{\dim _{q}(s)^{2}}{\dim _{q}(t)^{2}}G_{P}(s,t).\end{eqnarray}$$
Therefore, denoting by
$K_{P}$
the classical Martin kernel,
$\displaystyle K_{P}(s,t)=G_{P}(s,t)/G_{P}(e,t)$
, we see that the function
$K_{P}(s,\cdot )\in \ell ^{\infty }(I)$
differs from
$K_{\check{\unicode[STIX]{x1D707}}}(I_{s})$
only by a scalar factor:
$$\begin{eqnarray}K_{\check{\unicode[STIX]{x1D707}}}(I_{s})=\dim _{q}(s)^{2}K_{P}(s,\cdot ).\end{eqnarray}$$
Hence the C
$^{\ast }$
-algebra generated by
$c_{c}(I)\subset c_{c}(\unicode[STIX]{x1D6E4})$
and the elements
$K_{\check{\unicode[STIX]{x1D707}}}(I_{s})$
,
$s\in I$
, coincides with the algebra of continuous functions on the Martin compactification of
$I$
. (Note that this does not yet exclude the possibility that
${\mathcal{D}}_{{\mathcal{M}}}(e,e)={\mathcal{M}}\cap \ell ^{\infty }(I)$
is a strictly larger algebra.) By a result of Picardello and Woess [Reference Picardello and WoessPW87] (see also [Reference WoessWoe00, Corollary 26.14] or [Reference WoessWoe00, Theorem 27.1]), the Martin compactification of
$I$
coincides with the end compactification
$\bar{I}$
. It is checked in [Reference Vaes and Vander VennetVVV10, § 2] that this result can indeed be applied in our case, since the transition probabilities
$p_{\unicode[STIX]{x1D707}}(s,t)$
satisfy the following properties.
– The spectral radius
$\lim _{n}p_{\unicode[STIX]{x1D707}}^{(n)}(s,s)^{1/n}$
of the random walk is strictly less than
$1$
(see also Remark 4.2 below).– The random walk has bounded range: there is
$S\in \mathbb{N}$
such that
$p_{\unicode[STIX]{x1D707}}(s,t)=0$
whenever
$d(s,t)>S$
,– The random walk is uniformly irreducible (in the sense used in [Reference WoessWoe00]): there are
$\unicode[STIX]{x1D700}_{0}>0$
and
$K\in \mathbb{N}$
such that for any
$s,t\in I$
with
$d(s,t)=1$
we have
$p_{\unicode[STIX]{x1D707}}^{(k)}(s,t)\geqslant \unicode[STIX]{x1D700}_{0}$
for some
$k\leqslant K$
.
We thus have
$$\begin{eqnarray}{\mathcal{D}}_{{\mathcal{B}}}(e,e)=C(\bar{I})=C^{\ast }(c_{c}(I),K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(I)))\subset {\mathcal{D}}_{{\mathcal{M}}}(e,e).\end{eqnarray}$$
Assume next
$y=\bar{z}z$
for some
$z\neq e$
. Then, by Corollary 2.5, we have
${\mathcal{D}}_{{\mathcal{B}}}(e,y)=C(\bar{\unicode[STIX]{x1D6FA}}_{y})T$
, where
$T_{x}=V(x,x\otimes y)$
for
$x\in \unicode[STIX]{x1D6FA}_{y}$
. For every
$t\in \unicode[STIX]{x1D6FA}_{y}$
define
$\unicode[STIX]{x1D702}^{(t)}\in {\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(e,y)=\operatorname{Nat}_{c}(\unicode[STIX]{x1D704},\unicode[STIX]{x1D704}\otimes y)$
by
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{s}^{(t)}=\left\{\begin{array}{@{}ll@{}}V(t,t\otimes y)\quad & \text{if}~s=t,\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Define numbers
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
for
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
by
$$\begin{eqnarray}P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}=\check{q}_{\unicode[STIX]{x1D707}}(s,t)V(s,s\otimes y).\end{eqnarray}$$
Motivated by (3), we then put
$$\begin{eqnarray}q_{\unicode[STIX]{x1D707}}(s,t)=\frac{\dim _{q}(t)^{2}}{\dim _{q}(s)^{2}}\,\check{q}_{\unicode[STIX]{x1D707}}(t,s).\end{eqnarray}$$
Lemma 3.2. The numbers
$q_{\unicode[STIX]{x1D707}}(s,t)$
are real and
$|q_{\unicode[STIX]{x1D707}}(s,t)|\leqslant p_{\unicode[STIX]{x1D707}}(s,t)$
for all
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
.
Proof. Equivalently, we have to show that the numbers
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
are real and
$|\check{q}_{\unicode[STIX]{x1D707}}(s,t)|\leqslant p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.
Since
$\check{\unicode[STIX]{x1D707}}$
is a convex combination of point masses, it suffices to consider
$\check{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FF}_{u}$
. Fix
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
. We may assume that
$t\prec u\otimes s$
, as otherwise
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)=p_{\check{\unicode[STIX]{x1D707}}}(s,t)=0$
. Then, with
$\unicode[STIX]{x1D702}^{(t)}$
given by (12),
$$\begin{eqnarray}P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}=(\text{tr}_{u}\,\otimes \,\unicode[STIX]{x1D704})(\unicode[STIX]{x1D702}_{u\otimes s}^{(t)})=(\text{tr}_{u}\,\otimes \,\unicode[STIX]{x1D704})((V(t,u\otimes s)\otimes \unicode[STIX]{x1D704}_{y})V(t,t\otimes y)V(t,u\otimes s)^{\ast }),\end{eqnarray}$$
and hence
$$\begin{eqnarray}\check{q}_{\unicode[STIX]{x1D707}}(s,t)=\operatorname{tr}_{u\otimes s}((\unicode[STIX]{x1D704}_{u}\otimes V(s,s\otimes y)^{\ast })(V(t,u\otimes s)\otimes \unicode[STIX]{x1D704}_{y})V(t,t\otimes y)V(t,u\otimes s)^{\ast }).\end{eqnarray}$$
Somewhat informally, the statement that
$\check{q}_{\unicode[STIX]{x1D707}}(s,t)$
is real follows now from the fact that in order to compute the above trace we need only to use that
$R_{\unicode[STIX]{x1D6FC}}$
and
$\bar{R}_{\unicode[STIX]{x1D6FC}}$
solve the conjugate equations and satisfy
$R_{\unicode[STIX]{x1D6FC}}^{\ast }R_{\unicode[STIX]{x1D6FC}}=q+q^{-1}=\bar{R}_{\unicode[STIX]{x1D6FC}}^{\ast }\bar{R}_{\unicode[STIX]{x1D6FC}}$
, and all these relations involve only real numbers. This can be formalized, for example, as follows. We can choose orthonormal bases
$(e_{i})_{i}$
of
$H_{\unicode[STIX]{x1D6FC}}$
and
$(f_{i})_{i}$
of
$H_{\unicode[STIX]{x1D6FD}}$
such that
$$\begin{eqnarray}R_{\unicode[STIX]{x1D6FC}}(1)=\mathop{\sum }_{i}\unicode[STIX]{x1D706}_{i}f_{i}\otimes e_{i}\quad \text{and}\quad \bar{R}_{\unicode[STIX]{x1D6FC}}(1)=\mathop{\sum }_{i}\unicode[STIX]{x1D706}_{i}^{-1}e_{i}\otimes f_{i}\end{eqnarray}$$
for some
$\unicode[STIX]{x1D706}_{i}>0$
(with
$\sum _{i}\unicode[STIX]{x1D706}_{i}^{2}=\sum _{i}\unicode[STIX]{x1D706}_{i}^{-2}=q+q^{-1}$
). Then the real linear spans of these bases define real forms of
$H_{\unicode[STIX]{x1D6FC}}$
and
$H_{\unicode[STIX]{x1D6FD}}$
. Taking tensor products of these forms, we get a real form of
$H_{x_{1}}\otimes \cdots \otimes H_{x_{n}}$
for every word
$x=x_{1}\cdots x_{n}$
in
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
. Since
$H_{x}$
is the orthogonal complement of the images of operators of the form
$\unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}\otimes R_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}\otimes \bar{R}_{\unicode[STIX]{x1D6FC}}\otimes \unicode[STIX]{x1D704}\otimes \cdots \otimes \unicode[STIX]{x1D704}$
, which respect the real forms of the tensor products, we then also get a real form of
$H_{x}$
. Now, in computing the right-hand side of (13) we may work only with the real forms of all the spaces involved, hence the result must be real.
In order to prove the second statement of the lemma, note that we also have
$|\check{q}_{\unicode[STIX]{x1D707}}(s,t)|=\Vert P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}\Vert$
. Consider the map
$P_{\check{\unicode[STIX]{x1D707}}}$
on
$\operatorname{Nat}_{b}(\unicode[STIX]{x1D704}\otimes (e\oplus y),\unicode[STIX]{x1D704}\otimes (e\oplus y))\cong \ell ^{\infty }\text{-}\bigoplus _{x}\operatorname{End}(x\otimes (e\oplus y))$
. Then, by restricting it to the block corresponding to
$t$
and by projecting the image onto the block corresponding to
$s$
, we get a completely positive map
$P_{st}:\operatorname{End}(t\otimes (e\oplus y))\rightarrow \operatorname{End}(s\otimes (e\oplus y))$
. By definition, this map, being divided by
$p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
, becomes unital. Hence
$\Vert P_{st}\Vert =p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
. Viewing
$V(t,t\otimes y)$
as the element
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}0 & 0\\ V(t,t\otimes y) & 0\end{array}\right)\in \operatorname{End}(t\otimes (e\oplus y)),\end{eqnarray}$$
we conclude that
$\Vert P_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(t)})_{s}\Vert \leqslant \Vert P_{st}\Vert =p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.◻
Denote by
$Q$
the matrix
$(q_{\unicode[STIX]{x1D707}}(s,t))_{s,t\in \unicode[STIX]{x1D6FA}_{y}}$
. We can define the ‘Green kernel’
$$\begin{eqnarray}G_{Q}(s,t)=\unicode[STIX]{x1D6FF}_{st}+\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{s=s_{0},s_{1},\ldots ,s_{n}=t}q_{\unicode[STIX]{x1D707}}(s_{0},s_{1})\cdots q_{\unicode[STIX]{x1D707}}(s_{n-1},s_{n}).\end{eqnarray}$$
Then
$$\begin{eqnarray}G_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(s)})_{t}=\frac{\dim _{q}(s)^{2}}{\dim _{q}(t)^{2}}G_{Q}(s,t)V(t,t\otimes y).\end{eqnarray}$$
Therefore if we let
$\displaystyle K_{Q}(s,t)=G_{Q}(s,t)/G_{P}(e,t)$
, then
$$\begin{eqnarray}K_{\check{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D702}^{(s)})=\dim _{q}(s)^{2}K_{Q}(s,\cdot )T,\end{eqnarray}$$
with
$T$
as in Corollary 2.5. We thus need to understand the behavior of the functions
$K_{Q}(s,\cdot )$
at infinity. As we will see, this behavior is not that different from that of
$K_{P}(s,\cdot )$
. The starting point is the following estimate.
Lemma 3.3. There is a constant
$C$
(depending on
$q$
,
$|y|$
and the support of
$\unicode[STIX]{x1D707}$
) such that
$$\begin{eqnarray}|q_{\unicode[STIX]{x1D707}}(s,t)-p_{\unicode[STIX]{x1D707}}(s,t)|\leqslant Cq^{|s|}\end{eqnarray}$$
for all
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
.
Proof. Recall that
$p_{\unicode[STIX]{x1D707}}(s,t)=0$
if
$d(s,t)>S$
, and then
$q_{\unicode[STIX]{x1D707}}(s,t)=0$
as well, so we could equally well use
$q^{|t|}$
instead of
$q^{|s|}$
in the formulation. Using (6), it is also easy to see that the ratios
$\dim _{q}(s)/\text{dim}_{q}(t)$
are bounded when
$d(s,t)\leqslant S$
. It follows that the statement of the lemma is equivalent to the existence of
$C^{\prime }$
such that
$|\check{q}_{\unicode[STIX]{x1D707}}(s,t)-p_{\check{\unicode[STIX]{x1D707}}}(s,t)|\leqslant C^{\prime }q^{|s|}$
.
Similarly to the proof of the previous lemma, we may assume that
$\check{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FF}_{u}$
and consider
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
such that
$t\prec u\otimes s$
. We may also assume that
$|s|-|u|\geqslant |y|/2$
, as there are only finitely many pairs
$(s,t)$
as above not satisfying this condition. Then
$u=u_{0}v$
,
$s=\bar{v}s_{0}$
and
$t=u_{0}s_{0}$
for some
$s_{0},u_{0},v\in I$
. Since
$|s_{0}|=|s|-|v|\geqslant |s|-|u|\geqslant |y|/2$
, we have
$s_{0}\prec s_{0}\otimes y$
. By (13) we have
$$\begin{eqnarray}\check{q}_{\unicode[STIX]{x1D707}}(s,t)=\operatorname{tr}_{u\otimes s}((\unicode[STIX]{x1D704}_{u_{0}v}\otimes V(\bar{v}s_{0},\bar{v}s_{0}\otimes y)^{\ast })(V(u_{0}s_{0},u_{0}v\otimes \bar{v}s_{0})\otimes \unicode[STIX]{x1D704}_{y})V(u_{0}s_{0},u_{0}s_{0}\otimes y)V(t,u\otimes s)^{\ast }).\end{eqnarray}$$
By Corollary 2.6 the last expression is close to
$$\begin{eqnarray}\operatorname{tr}_{u\otimes s}(V(u_{0}s_{0},u_{0}v\otimes \bar{v}s_{0})V(t,u\otimes s)^{\ast })=\operatorname{tr}_{u\otimes s}(V(t,u\otimes s)V(t,u\otimes s)^{\ast })=\frac{\dim _{q}(t)}{\dim _{q}(u)\dim _{q}(s)}\end{eqnarray}$$
up to
$Cq^{|s_{0}|-|y|/2}\leqslant Cq^{|s|-|u|-|y|/2}$
. By (2), the quantity on the right is exactly
$p_{\check{\unicode[STIX]{x1D707}}}(s,t)$
.◻
From this we will deduce in the next section the following result.
Proposition 3.4. For every
$s\in \unicode[STIX]{x1D6FA}_{y}$
, the function
$\displaystyle K_{Q}(s,\cdot )=G_{Q}(s,\cdot )/G_{P}(e,\cdot )$
on
$\unicode[STIX]{x1D6FA}_{y}$
extends to a continuous function on
$\bar{\unicode[STIX]{x1D6FA}}_{y}\subset \bar{I}$
.
By (14), this already shows that
$$\begin{eqnarray}K_{\check{\unicode[STIX]{x1D707}}}({\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(e,y))\subset C(\bar{\unicode[STIX]{x1D6FA}}_{y})T={\mathcal{D}}_{{\mathcal{B}}}(e,y).\end{eqnarray}$$
As opposed to the functions
$K_{P}(s,\cdot )$
, it may happen that the functions
$K_{Q}(s,\cdot )$
vanish at some points of the boundary of
$\unicode[STIX]{x1D6FA}_{y}$
. Nevertheless we have the following result, whose proof we also postpone till the next section.
Proposition 3.5. For every point
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
, we have
$K_{Q}(s,t_{\infty })>0$
for all
$s$
sufficiently close to
$t_{\infty }$
.
It is now easy to complete the proof of the equality
${\mathcal{M}}={\mathcal{B}}$
.
Proof of Theorem 3.1.
By (11), (15) and our discussion at the end of § 1.3, we can already conclude that
$K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))\subset {\mathcal{B}}$
. Hence
${\mathcal{M}}\subset {\mathcal{B}}$
, since we also have
$c_{0}(\unicode[STIX]{x1D6E4})\subset {\mathcal{B}}$
.
Furthermore,
${\mathcal{D}}_{{\mathcal{M}}}(e,y)$
is a bimodule over
${\mathcal{D}}_{{\mathcal{M}}}(e,e)$
and by (11) we know that
${\mathcal{D}}_{{\mathcal{M}}}(e,e)\supset C(\bar{I})$
. Using Proposition 3.5, for every function
$f\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
we can find
$s_{1},\ldots ,s_{n}\in \unicode[STIX]{x1D6FA}_{y}$
and
$g_{1},\ldots ,g_{n}\in C(\bar{\unicode[STIX]{x1D6FA}}_{y})$
such that
$f(t_{\infty })=\sum _{i}g_{i}(t_{\infty })K_{Q}(s_{i},t_{\infty })$
for all
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. In view of (14) this shows that, with
$T$
as in Corollary 2.5, we have
$$\begin{eqnarray}{\mathcal{D}}_{{\mathcal{B}}}(e,y)=C(\bar{\unicode[STIX]{x1D6FA}}_{y})T\subset C(\bar{I})K_{\check{\unicode[STIX]{x1D707}}}({\mathcal{D}}_{\unicode[STIX]{x1D6E4},c}(e,y))+c_{0}(I)T.\end{eqnarray}$$
Hence
${\mathcal{D}}_{{\mathcal{B}}}(e,y)\subset {\mathcal{D}}_{{\mathcal{M}}}(e,y)$
and therefore
${\mathcal{B}}\subset {\mathcal{M}}$
.◻
Remark 3.6. The equality
${\mathcal{M}}={\mathcal{B}}$
and (16) imply that the space
$C(\bar{I})K_{\check{\unicode[STIX]{x1D707}}}(c_{c}(\unicode[STIX]{x1D6E4}))+c_{0}(\unicode[STIX]{x1D6E4})$
is dense in
${\mathcal{B}}=C(\bar{\unicode[STIX]{x1D6E4}}_{M,\unicode[STIX]{x1D707}})$
.
4 Estimates of the Green kernels
In this section we will prove Propositions 3.4 and 3.5. We thus fix a generating probability measure
$\unicode[STIX]{x1D707}$
, a point
$y\in I$
of the form
$\bar{z}z$
,
$z\neq e$
, and consider the set
$\unicode[STIX]{x1D6FA}_{y}\subset I$
of words of the form
$uz$
. In order to simplify the notation we denote the transition probabilities
$p_{\unicode[STIX]{x1D707}}(s,t)$
by
$p(s,t)$
.
In the previous section we introduced the numbers
$q_{\unicode[STIX]{x1D707}}(s,t)$
,
$s,t\in \unicode[STIX]{x1D6FA}_{y}$
, which we now denote simply by
$q(s,t)$
. The only information we will need about them is that, by Lemmas 3.2 and 3.3, they are real and
$$\begin{eqnarray}|q(s,t)|\leqslant p(s,t)\quad \text{and}\quad |q(s,t)-p(s,t)|\leqslant Cq^{|s|}\quad \text{for all }s,t\in \unicode[STIX]{x1D6FA}_{y}.\end{eqnarray}$$
Denote by
$P$
and
$Q$
the matrices
$(p(s,t))_{s,t\in I}$
and
$(q(s,t))_{s,t\in \unicode[STIX]{x1D6FA}_{y}}$
.
The space
$c_{c}(I)$
can be completed to two different Hilbert spaces, depending on the inner product we choose. Denote by
$\ell ^{2}(I)$
the completion of
$c_{c}(I)$
with respect to the inner product
$(\cdot ,\cdot )$
corresponding to the counting measure:
$(f,g)=\sum _{x\in I}f(x)\overline{g(x)}$
. Denote by
$\ell ^{2}(I,m)$
the completion of
$c_{c}(I)$
with respect to the inner product corresponding to the ‘Haar measure’
$m$
given by
$m(x)=\dim _{q}(x)^{2}$
:
$(f,g)_{m}=\sum _{x\in I}\,m(x)\,f(x)\overline{g(x)}$
. For any
$f\in c_{c}(I)$
and
$s\in I$
, we have
$$\begin{eqnarray}(f,\unicode[STIX]{x1D6FF}_{s})=m(s)^{-1}(f,\unicode[STIX]{x1D6FF}_{s})_{m}.\end{eqnarray}$$
Lemma 4.1. The operator
$P$
on
$c_{c}(I)$
extends to a bounded operator on
$\ell ^{2}(I,m)$
of norm
$\unicode[STIX]{x1D706}<1$
. The operator
$Q$
on
$c_{c}(\unicode[STIX]{x1D6FA}_{y})$
extends to a bounded operator on
$\ell ^{2}(\unicode[STIX]{x1D6FA}_{y},m)$
of norm not greater than
$\unicode[STIX]{x1D706}$
.
Proof. Denote by
$\dim _{\text{min}}$
the dimension function on the finite-dimensional representations of our quantum group
$G=A_{u}(F)$
obtained by letting
$q=1$
in formula (6).
As can be easily seen from (2), the unitary operator
$\ell ^{2}(I,m)\rightarrow \ell ^{2}(I)$
,
$\unicode[STIX]{x1D6FF}_{s}\mapsto \dim _{q}(s)\unicode[STIX]{x1D6FF}_{s}$
, transforms the operator
$P$
into the operator
$$\begin{eqnarray}\mathop{\sum }_{r\in I}\frac{\unicode[STIX]{x1D707}(r)}{\dim _{q}(r)}\unicode[STIX]{x1D706}_{r},\end{eqnarray}$$
where
$\unicode[STIX]{x1D706}_{r}$
is the operator of multiplication by
$r$
on the fusion algebra
$\mathbb{C}[I]$
of
$G$
(which we identify with
$c_{c}(I)$
as a space). By [Reference Neshveyev and TusetNT13, Lemma 2.7.3], the operator
$\unicode[STIX]{x1D706}_{r}$
on
$\ell ^{2}(I)$
is bounded, of norm not greater than
$\dim _{\text{min}}(r)$
. Therefore
$$\begin{eqnarray}\unicode[STIX]{x1D706}\leqslant \mathop{\sum }_{r\in I}\unicode[STIX]{x1D707}(r)\frac{\dim _{\text{min}}(r)}{\dim _{q}(r)}<1,\end{eqnarray}$$
since
$\dim _{\text{min}}(r)<\dim _{q}(r)$
for all
$r\neq e$
.
The second statement of the lemma follows from (17), since we get
$$\begin{eqnarray}|(Qf,g)_{m}|\leqslant (P|f|,|g|)_{m}\end{eqnarray}$$
for all
$f,g\in c_{c}(\unicode[STIX]{x1D6FA}_{y})$
.◻
Remark 4.2. Note that by (18) we have
$$\begin{eqnarray}p^{(n)}(s,t)=(P^{n}\unicode[STIX]{x1D6FF}_{t},\unicode[STIX]{x1D6FF}_{s})=m(s)^{-1}(P^{n}\unicode[STIX]{x1D6FF}_{t},\unicode[STIX]{x1D6FF}_{s})_{m}.\end{eqnarray}$$
From this we see that the spectral radius of the random walk defined by
$P$
is not greater than
$\unicode[STIX]{x1D706}$
. This (already mentioned) fact that the spectral radius of the random walk is strictly less than one is actually enough for the results below, but since the inequality
$\Vert P\Vert <1$
slightly simplifies the arguments, we will use it.
For
$x\in I$
, let us introduce the following subset of
$I$
:
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{x}=\{ux:u\in I\}.\end{eqnarray}$$
We will have to consider the substochastic matrices
$P_{\unicode[STIX]{x1D6E5}_{x}}=(p(s,t))_{s,t\in \unicode[STIX]{x1D6E5}_{x}}$
and the corresponding Green kernels, which we denote by
$G_{P,\unicode[STIX]{x1D6E5}_{x}}$
. For
$x\in \unicode[STIX]{x1D6FA}_{y}$
, we similarly define
$Q_{\unicode[STIX]{x1D6E5}_{x}}$
and
$G_{Q,\unicode[STIX]{x1D6E5}_{x}}$
.
The Green kernels
$G_{P,\unicode[STIX]{x1D6E5}_{x}}$
satisfy the following uniform version of Harnack’s inequality.
Lemma 4.3. There exists
$\unicode[STIX]{x1D6FF}\in (0,1)$
such that
$$\begin{eqnarray}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant \unicode[STIX]{x1D6FF}^{-d(s,v)}G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)\quad \text{and}\quad G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant \unicode[STIX]{x1D6FF}^{-d(t,v)}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,v)\end{eqnarray}$$
for all
$x\in I$
and
$v,s,t\in \unicode[STIX]{x1D6E5}_{x}$
.
Proof. As we already mentioned in the previous section, the random walk defined by
$P$
is uniformly irreducible. In fact, the following slightly stronger property (also called uniform irreducibility in [Reference Picardello and WoessPW87]) is shown in [Reference Vaes and Vander VennetVVV10, § 2]. There exist
$K\in \mathbb{N}$
and
$\unicode[STIX]{x1D6FF}_{0}>0$
such that:
–
$p(s,t)\geqslant \unicode[STIX]{x1D6FF}_{0}$
whenever
$p(s,t)>0$
;– for any
$s,t\in I$
with
$d(s,t)=1$
we have
$p^{(k)}(s,t)>0$
for some
$k\leqslant K$
.
In particular, given
$s,t\in I$
with
$d(s,t)=1$
, there are points
$x_{0}=s,x_{1},\ldots ,x_{k}=t$
,
$k\leqslant K$
, such that
$p(x_{i},x_{i+1})\geqslant \unicode[STIX]{x1D6FF}_{0}$
for all
$i=0,\ldots ,k-1$
. But then we also have
$p(x_{i}x,x_{i+1}x)\geqslant \unicode[STIX]{x1D6FF}_{0}$
for any
$x\in I$
. That is, the same constants
$K$
and
$\unicode[STIX]{x1D6FF}_{0}$
work for
$P_{\unicode[STIX]{x1D6E5}_{x}}$
. This implies the lemma; specifically, we can take
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{0}^{K}$
.◻
The most important property of the Green kernels of random walks on trees (shared also by random walks on hyperbolic graphs, where it is much more difficult to prove [Reference AnconaAnc88]) is their almost multiplicativity along geodesics. We will need the following uniform version of this property, cf. [Reference Izumi, Neshveyev and OkayasuINO08, Proposition 2.1].
For
$s,t\in I$
, we denote by
$[s,t]$
the unique geodesic segment between
$s$
and
$t$
.
Lemma 4.4. There exists a constant
$C_{1}>0$
such that
$$\begin{eqnarray}\frac{1}{C_{1}}\,G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,v)G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)\leqslant G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant C_{1}\,G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,v)G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)\end{eqnarray}$$
for all
$x\in I$
,
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
and
$v\in [s,t]$
.
Proof. The first inequality is true, with
$C_{1}=(1-\unicode[STIX]{x1D70C})^{-1}$
, for any irreducible random walk with spectral radius
$\unicode[STIX]{x1D70C}<1$
. Namely, we have
$$\begin{eqnarray}\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,v)}{G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,v)}G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)\leqslant G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t),\end{eqnarray}$$
since the expression on the left is the sum of
$p(s_{0},s_{1})\cdots p(s_{n-1},s_{n})$
over all paths
$(s=s_{0},s_{1},\ldots ,s_{n}=t)$
in
$\unicode[STIX]{x1D6E5}_{x}$
that pass through
$v$
. As
$G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,v)\leqslant G_{P}(v,v)\leqslant (1-\unicode[STIX]{x1D706})^{-1}$
by Remark 4.2, we can take
$C_{1}=(1-\unicode[STIX]{x1D706})^{-1}$
.
For the second inequality, take
$x\in I$
,
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
and
$v\in [s,t]$
. Then any path from
$s$
to
$t$
in
$\unicode[STIX]{x1D6E5}_{x}$
contributing to
$G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)$
must pass through the set
$A=\unicode[STIX]{x1D6E5}_{x}\cap B_{S}(v)$
, where
$B_{S}(v)$
is the open ball of radius
$S$
with center
$v$
. (Recall that
$S\in \mathbb{N}$
is such that
$p(u,w)=0$
whenever
$d(u,w)>S$
.) It follows that
$$\begin{eqnarray}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant \mathop{\sum }_{u\in A}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t).\end{eqnarray}$$
By Lemma 4.3, for every
$u\in A$
, we have
$$\begin{eqnarray}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)\leqslant \unicode[STIX]{x1D6FF}^{-2(S-1)}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,v)G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t).\end{eqnarray}$$
Since the number of vertices in
$B_{S}(v)$
is not greater than
$3\cdot 2^{S-1}-2$
, we thus see that for the second inequality in the formulation of the lemma we can take
$C_{1}=3(2/\unicode[STIX]{x1D6FF}^{2})^{S-1}$
.◻
We are now ready to prove the following key estimate.
Lemma 4.5. There is a constant
$C_{2}$
such that
$$\begin{eqnarray}|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\leqslant C_{2}q^{|x|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\end{eqnarray}$$
for all
$x\in \unicode[STIX]{x1D6FA}_{y}$
and
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
.
Proof. By (19) we have
$G_{P}(s,t)=m(s)^{-1}((1-P)^{-1}\unicode[STIX]{x1D6FF}_{t},\unicode[STIX]{x1D6FF}_{s})_{m}$
. Similarly,
$$\begin{eqnarray}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)=m(s)^{-1}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\unicode[STIX]{x1D6FF}_{t},\unicode[STIX]{x1D6FF}_{s})_{m}\quad \text{and}\quad G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)=m(s)^{-1}((1-Q_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\unicode[STIX]{x1D6FF}_{t},\unicode[STIX]{x1D6FF}_{s})_{m}.\end{eqnarray}$$
Define functions
$\tilde{\unicode[STIX]{x1D6FF}}_{u}=\unicode[STIX]{x1D6FF}_{u}/\sqrt{m(u)}$
for
$u\in I$
. Then we can write
$$\begin{eqnarray}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)=\frac{\sqrt{m(t)}}{\sqrt{m(s)}}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{t},\tilde{\unicode[STIX]{x1D6FF}}_{s})_{m}\quad \text{and}\quad G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)=\frac{\sqrt{m(t)}}{\sqrt{m(s)}}((1-Q_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{t},\tilde{\unicode[STIX]{x1D6FF}}_{s})_{m}.\end{eqnarray}$$
From this we get
$$\begin{eqnarray}|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|=\frac{\sqrt{m(t)}}{\sqrt{m(s)}}|((1-Q_{\unicode[STIX]{x1D6E5}_{x}})^{-1}(Q_{\unicode[STIX]{x1D6E5}_{x}}-P_{\unicode[STIX]{x1D6E5}_{x}})(1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{t},\tilde{\unicode[STIX]{x1D6FF}}_{s})_{m}|.\end{eqnarray}$$
Since
$\{{\tilde{\unicode[STIX]{x1D6FF}}_{u}\}}_{u\in \unicode[STIX]{x1D6E5}_{x}}$
is an orthonormal basis in
$\ell ^{2}(\unicode[STIX]{x1D6E5}_{x},m)$
, the scalar product in the expression above equals
$$\begin{eqnarray}\mathop{\sum }_{u,v\in \unicode[STIX]{x1D6E5}_{x}}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{t},\tilde{\unicode[STIX]{x1D6FF}}_{v})_{m}((Q_{\unicode[STIX]{x1D6E5}_{x}}-P_{\unicode[STIX]{x1D6E5}_{x}})\tilde{\unicode[STIX]{x1D6FF}}_{v},\tilde{\unicode[STIX]{x1D6FF}}_{u})_{m}((1-Q_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{u},\tilde{\unicode[STIX]{x1D6FF}}_{s})_{m}.\end{eqnarray}$$
It follows that
$$\begin{eqnarray}\displaystyle & & \displaystyle |G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\nonumber\\ \displaystyle & & \displaystyle \qquad \leqslant \frac{\sqrt{m(t)}}{\sqrt{m(s)}}\mathop{\sum }_{u,v\in \unicode[STIX]{x1D6E5}_{x}}|((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{t},\tilde{\unicode[STIX]{x1D6FF}}_{v})_{m}((Q_{\unicode[STIX]{x1D6E5}_{x}}-P_{\unicode[STIX]{x1D6E5}_{x}})\tilde{\unicode[STIX]{x1D6FF}}_{v},\tilde{\unicode[STIX]{x1D6FF}}_{u})_{m}((1-Q_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{u},\tilde{\unicode[STIX]{x1D6FF}}_{s})_{m}|\nonumber\\ \displaystyle & & \displaystyle \qquad =\mathop{\sum }_{u,v\in \unicode[STIX]{x1D6E5}_{x}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)\,|q(u,v)-p(u,v)|\,|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,u)|.\nonumber\end{eqnarray}$$
By (17) we have
$|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,u)|\leqslant G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)$
and
$|q(u,v)-p(u,v)|\leqslant Cq^{|u|}$
. Since we also have
$q(u,v)=p(u,v)=0$
if
$d(u,v)>S$
, we conclude that
$$\begin{eqnarray}|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\leqslant C\mathop{\sum }_{\substack{ u,v\in \unicode[STIX]{x1D6E5}_{x}: \\ d(u,v)\leqslant S}}q^{|u|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t).\end{eqnarray}$$
Applying Lemma 4.3, we then get
$$\begin{eqnarray}|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\leqslant 3\biggl(\frac{2}{\unicode[STIX]{x1D6FF}}\biggr)^{S}C\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{|u|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t),\end{eqnarray}$$
where we used again that every closed ball of radius
$S$
contains not more than
$3\cdot 2^{S}-2$
vertices.
In order to estimate the above expression, for every
$u\in \unicode[STIX]{x1D6E5}_{x}$
denote by
$u^{\prime }$
the point on the geodesic
$[s,t]$
closest to
$u$
. Then
$u^{\prime }\in [u,s]\cap [u,t]$
, so by Lemma 4.4 we have
$$\begin{eqnarray}\displaystyle G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t) & {\leqslant} & \displaystyle C_{1}^{2}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,u^{\prime })G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime })G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },t)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C_{1}^{3}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime }),\end{eqnarray}$$
and hence
$$\begin{eqnarray}|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\leqslant 3\biggl(\frac{2}{\unicode[STIX]{x1D6FF}}\biggr)^{S}C\,C_{1}^{3}\,G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{|u|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime }).\end{eqnarray}$$
It remains to estimate the sum in the above expression on the right. Observe that if
$u^{\prime }\neq x^{\prime }$
(where
$x^{\prime }\in [s,t]$
is the vertex closest to
$x$
), then
$$\begin{eqnarray}|u|\geqslant |u^{\prime }|=|x^{\prime }|+d(u^{\prime },x^{\prime })\geqslant |x|+d(u^{\prime },x^{\prime }).\end{eqnarray}$$
If
$u^{\prime }=x^{\prime }$
, then the inequality
$|u|\geqslant |x|+d(u^{\prime },x^{\prime })$
is obvious. See Figure 1 illustrating these two cases.
Figure 1. Possible positions of the closest point on the geodesic.
It follows that
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{|u|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime }) & {\leqslant} & \displaystyle q^{|x|}\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}q^{d(u^{\prime },x^{\prime })}G_{P,\unicode[STIX]{x1D6E5}_{x}}(u^{\prime },u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,u^{\prime })\nonumber\\ \displaystyle & {\leqslant} & \displaystyle q^{|x|}\mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}\mathop{\sum }_{w\in [s,t]}q^{d(w,x^{\prime })}G_{P,\unicode[STIX]{x1D6E5}_{x}}(w,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,w).\end{eqnarray}$$
Next, for every
$w\in [s,t]$
, we have
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{x}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(w,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,w) & = & \displaystyle \mathop{\sum }_{u\in \unicode[STIX]{x1D6E5}_{w}}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{u},\tilde{\unicode[STIX]{x1D6FF}}_{w})_{m}((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-1}\tilde{\unicode[STIX]{x1D6FF}}_{w},\tilde{\unicode[STIX]{x1D6FF}}_{u})_{m}\nonumber\\ \displaystyle & = & \displaystyle ((1-P_{\unicode[STIX]{x1D6E5}_{x}})^{-2}\tilde{\unicode[STIX]{x1D6FF}}_{w},\tilde{\unicode[STIX]{x1D6FF}}_{w})_{m}\leqslant (1-\unicode[STIX]{x1D706})^{-2}.\end{eqnarray}$$
We also have
$$\begin{eqnarray}\mathop{\sum }_{w\in [s,t]}q^{d(w,x^{\prime })}<2(1+q+q^{2}+\cdots \,)=2(1-q)^{-1}.\end{eqnarray}$$
Combining (22)–(24), we get from (21) that
$$\begin{eqnarray}|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\leqslant 6\biggl(\frac{2}{\unicode[STIX]{x1D6FF}}\biggr)^{S}\frac{C\,C_{1}^{3}}{(1-\unicode[STIX]{x1D706})^{2}(1-q)}\,q^{|x|}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t),\end{eqnarray}$$
and we are done.◻
Proof of Proposition 3.4.
Fix
$s\in \unicode[STIX]{x1D6FA}_{y}$
and
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. We have to show that as
$t\rightarrow t_{\infty }$
the numbers
$\displaystyle K_{Q}(s,t)=G_{Q}(s,t)/G_{P}(e,t)$
converge to a finite limit.
Fix
$\unicode[STIX]{x1D700}>0$
. By Lemma 4.5 there exists
$x\in \unicode[STIX]{x1D6FA}_{y}$
such that
$s\not \in \unicode[STIX]{x1D6E5}_{x}$
,
$t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{x}\cap \unicode[STIX]{x2202}I$
and
$$\begin{eqnarray}|G_{Q,\unicode[STIX]{x1D6E5}_{x}}(u,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)|\leqslant \unicode[STIX]{x1D700}\,G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)\quad \text{for all }u,t\in \unicode[STIX]{x1D6E5}_{x}.\end{eqnarray}$$
Take
$t\in \unicode[STIX]{x1D6E5}_{x}$
. Then
$x\in [s,t]$
, so, similarly to the proof of Lemma 4.4, every path from
$s$
to
$t$
in
$I$
contributing to
$G_{P}(s,t)$
must pass through the set
$A=\unicode[STIX]{x1D6E5}_{x}\cap B_{S}(x)$
and there is a well-defined moment when it leaves
$I\setminus \unicode[STIX]{x1D6E5}_{x}$
and enters
$A$
for the last time. It follows that if for
$u\in A$
we put
$$\begin{eqnarray}M_{P}(s,u)=\mathop{\sum }_{n=1}^{\infty }\mathop{\sum }_{\substack{ s=s_{0},s_{1},\ldots ,s_{n}=u: \\ s_{n-1\not \in \unicode[STIX]{x1D6E5}_{x}}}}p(s_{0},s_{1})\cdots p(s_{n-1},s_{n}),\end{eqnarray}$$
then
$$\begin{eqnarray}G_{P}(s,t)=\mathop{\sum }_{u\in A}M_{P}(s,u)G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t).\end{eqnarray}$$
We can similarly define
$M_{Q}(s,u)$
and get a decomposition of
$G_{Q}(s,t)$
. Then, for any
$t,t^{\prime }\in \unicode[STIX]{x1D6E5}_{x}$
, we have
$$\begin{eqnarray}\displaystyle |K_{Q}(s,t)-K_{Q}(s,t^{\prime })| & = & \displaystyle \biggl|\mathop{\sum }_{u\in A}\frac{M_{Q}(s,u)G_{Q,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\mathop{\sum }_{u\in A}\frac{M_{Q}(s,u)G_{Q,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D700}\mathop{\sum }_{u\in A}\frac{|M_{Q}(s,u)|G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}+\unicode[STIX]{x1D700}\mathop{\sum }_{u\in A}\frac{|M_{Q}(s,u)|G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{u\in A}|M_{Q}(s,u)|\biggl|\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \unicode[STIX]{x1D700}(K_{P}(s,t)+K_{P}(s,t^{\prime }))+\mathop{\sum }_{u\in A}|M_{Q}(s,u)|\biggl|\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|,\nonumber\end{eqnarray}$$
where we used that
$|M_{Q}(s,u)|\leqslant M_{P}(s,u)$
by (17). If we could prove that the sum above converges to zero as
$t,t^{\prime }\rightarrow t_{\infty }$
, then we would get
$$\begin{eqnarray}\limsup _{t,t^{\prime }\rightarrow t_{\infty }}|K_{Q}(s,t)-K_{Q}(s,t^{\prime })|\leqslant 2\unicode[STIX]{x1D700}\,K_{P}(s,t_{\infty }),\end{eqnarray}$$
and since
$\unicode[STIX]{x1D700}$
could be taken arbitrarily small, we would be able to conclude that the numbers
$K_{Q}(s,t)$
converge to a finite limit as
$t\rightarrow t_{\infty }$
.
Therefore it remains to show that for every
$u\in A$
we have
$$\begin{eqnarray}\lim _{t,t^{\prime }\rightarrow t_{\infty }}\biggl|\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}{G_{P}(e,t)}-\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}{G_{P}(e,t^{\prime })}\biggr|=0.\end{eqnarray}$$
Again using (25), but now applied to
$G_{P}(e,t)$
, we can rewrite this as
$$\begin{eqnarray}\lim _{t,t^{\prime }\rightarrow t_{\infty }}\biggl|\biggl(\mathop{\sum }_{v\in A}M_{P}(e,v)\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t)}{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t)}\biggr)^{-1}-\biggl(\mathop{\sum }_{v\in A}M_{P}(e,v)\frac{G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,t^{\prime })}{G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,t^{\prime })}\biggr)^{-1}\biggr|=0.\end{eqnarray}$$
In order to prove this, it suffices to show that for all
$u,v\in A$
the function
$G_{P,\unicode[STIX]{x1D6E5}_{x}}(v,\cdot )/G_{P,\unicode[STIX]{x1D6E5}_{x}}(u,\cdot )$
on
$\unicode[STIX]{x1D6E5}_{x}$
extends to a non-vanishing continuous function on
$\bar{\unicode[STIX]{x1D6E5}}_{x}\subset \bar{I}$
. But this is indeed true, since this function is nothing else than the Martin kernel of the random walk on the tree
$\unicode[STIX]{x1D6E5}_{x}$
defined by the matrix
$P_{\unicode[STIX]{x1D6E5}_{x}}$
. Although this matrix is only substochastic, it still satisfies the assumptions of [Reference WoessWoe00, Corollary 26.14] or [Reference WoessWoe00, Theorem 27.1], as we essentially discussed in the proof of Lemma 4.3. So the same arguments as in [Reference WoessWoe00] show that the Martin compactification of
$\unicode[STIX]{x1D6E5}_{x}$
with respect to
$P_{\unicode[STIX]{x1D6E5}_{x}}$
coincides with the end compactification, which is
$\bar{\unicode[STIX]{x1D6E5}}_{x}$
.◻
Proof of Proposition 3.5.
Fix
$t_{\infty }\in \bar{\unicode[STIX]{x1D6FA}}_{y}\cap \unicode[STIX]{x2202}I$
. By Lemma 4.5 we can find
$x\in \unicode[STIX]{x1D6FA}_{y}$
such that
$t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{x}$
and
$$\begin{eqnarray}G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)\geqslant {\textstyle \frac{1}{2}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\quad \text{for all }s,t\in \unicode[STIX]{x1D6E5}_{x}.\end{eqnarray}$$
Suppose next that we can find
$u\in \unicode[STIX]{x1D6E5}_{x}$
such that
$t_{\infty }\in \bar{\unicode[STIX]{x1D6E5}}_{u}$
and
$$\begin{eqnarray}G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant {\textstyle \frac{1}{4}}G_{P}(s,t)\quad \text{for all }s,t\in \unicode[STIX]{x1D6E5}_{u}.\end{eqnarray}$$
Then, by (17),
$$\begin{eqnarray}|G_{Q}(s,t)-G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)|\leqslant G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant {\textstyle \frac{1}{4}}G_{P}(s,t)\leqslant {\textstyle \frac{1}{3}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant {\textstyle \frac{2}{3}}G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t),\end{eqnarray}$$
whence
$$\begin{eqnarray}G_{Q}(s,t)\geqslant {\textstyle \frac{1}{3}}G_{Q,\unicode[STIX]{x1D6E5}_{x}}(s,t)\geqslant {\textstyle \frac{1}{6}}G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\geqslant {\textstyle \frac{1}{8}}G_{P}(s,t),\end{eqnarray}$$
and therefore
$$\begin{eqnarray}K_{Q}(s,t_{\infty })\geqslant {\textstyle \frac{1}{8}}K_{P}(s,t_{\infty })>0\quad \text{for all }s\in \unicode[STIX]{x1D6E5}_{u}.\end{eqnarray}$$
Therefore it remains to find
$u$
such that (26) is satisfied.
For
$s,t\in \unicode[STIX]{x1D6E5}_{x}$
, similarly to the proof of Lemma 4.4, the paths from
$s$
to
$t$
contributing to
$G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)$
must pass through the set
$A=B_{S}(x)\cap \unicode[STIX]{x1D6E5}_{x}$
of cardinality
$2^{S}-1$
. It follows that
$$\begin{eqnarray}G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant \mathop{\sum }_{v\in A}G_{P}(s,v)G_{P}(v,t),\end{eqnarray}$$
and, using Lemma 4.3, we get
$$\begin{eqnarray}G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant \biggl(\frac{2}{\unicode[STIX]{x1D6FF}^{2}}\biggr)^{S}G_{P}(s,x)G_{P}(x,t).\end{eqnarray}$$
Now take any
$u\in \unicode[STIX]{x1D6E5}_{x}$
and assume that
$s,t\in \unicode[STIX]{x1D6E5}_{u}$
. Let
$v$
be the point on
$[s,t]$
closest to
$u$
, or equivalently, to
$x$
. Then
$v\in [s,x]\cap [t,x]$
, so, similarly to (20), we have
$$\begin{eqnarray}G_{P}(s,x)G_{P}(x,t)\leqslant C_{1}^{3}G_{P}(s,t)G_{P}(x,v)G_{P}(v,x).\end{eqnarray}$$
Hence
$$\begin{eqnarray}G_{P}(s,t)-G_{P,\unicode[STIX]{x1D6E5}_{x}}(s,t)\leqslant \biggl(\frac{2}{\unicode[STIX]{x1D6FF}^{2}}\biggr)^{S}C_{1}^{3}G_{P}(s,t)G_{P}(x,v)G_{P}(v,x).\end{eqnarray}$$
Therefore for (26) to be satisfied it suffices to have
$$\begin{eqnarray}G_{P}(x,v)G_{P}(v,x)\leqslant \frac{1}{4C_{1}^{3}}\biggl(\frac{\unicode[STIX]{x1D6FF}^{2}}{2}\biggr)^{S}\end{eqnarray}$$
for all
$v\in \unicode[STIX]{x1D6E5}_{u}$
. But, similarly to (23),
$$\begin{eqnarray}\mathop{\sum }_{v\in I}G_{P}(x,v)G_{P}(v,x)\leqslant (1-\unicode[STIX]{x1D706})^{-2}<\infty ,\end{eqnarray}$$
so (27) is true for all but finitely many
$v$
in
$I$
.◻
Remark 4.6. Essentially the same proof shows that actually
$K_{Q}(s,t_{\infty })/K_{P}(s,t_{\infty })\rightarrow 1$
as
$s\rightarrow t_{\infty }$
.
Acknowledgements
Part of the research leading to this article was carried out during the authors’ visit to the Texas A&M University. The authors are grateful to Michael Brannan, Ken Dykema, Guoliang Yu and the staff of the university for their hospitality.
