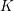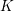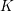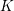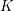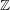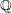1 Statement of results
We generalise methods of Poonen [Reference PoonenPoo09] and Koenigsmann [Reference KoenigsmannKoe16] to prove the following theorem.
Theorem. Let
![]() $K$
be a global field, i.e. a number field or a function field in one variable over a finite field, and
$K$
be a global field, i.e. a number field or a function field in one variable over a finite field, and
![]() $n>0$
a positive integer. Then the set
$n>0$
a positive integer. Then the set
is diophantine.
As usual, a subset
![]() $A\subseteq K^{n}$
is called diophantine if there exist
$A\subseteq K^{n}$
is called diophantine if there exist
![]() $m\geqslant 0$
and a polynomial
$m\geqslant 0$
and a polynomial
![]() $F\in K[X_{1},\ldots ,X_{n},Y_{1},\ldots ,Y_{m}]$
such that
$F\in K[X_{1},\ldots ,X_{n},Y_{1},\ldots ,Y_{m}]$
such that
Equivalently, diophantine subsets of
![]() $K^{n}$
are exactly those that are definable by an existential first-order formula (with parameters) in the language of rings (equivalently, a positive existential first-order formula), and we will frequently adopt this viewpoint, in particular when seeking uniformity between different fields.
$K^{n}$
are exactly those that are definable by an existential first-order formula (with parameters) in the language of rings (equivalently, a positive existential first-order formula), and we will frequently adopt this viewpoint, in particular when seeking uniformity between different fields.
In the theorem, the construction of the polynomial
![]() $F$
, or equivalently the defining first-order formula, is explicit in principle, although we have not taken care to optimise the number of variables (quantifiers) necessary.
$F$
, or equivalently the defining first-order formula, is explicit in principle, although we have not taken care to optimise the number of variables (quantifiers) necessary.
As an immediate corollary to the theorem we obtain the following.
Corollary. For every global field
![]() $K$
and
$K$
and
![]() $n>0$
, the set of non-
$n>0$
, the set of non-
![]() $n$
th powers in
$n$
th powers in
![]() $K$
is diophantine.
$K$
is diophantine.
This was previously proven in [Reference Colliot-Thélène and Van GeelCVG15] in the case of a number field. We can also translate the theorem into the terminology of mathematical logic.
Corollary. Let
![]() $K$
be a global field and
$K$
be a global field and
![]() $K^{\ast \ast }\supseteq K^{\ast }$
any two fields which are both elementary extensions of
$K^{\ast \ast }\supseteq K^{\ast }$
any two fields which are both elementary extensions of
![]() $K$
. Then
$K$
. Then
![]() $K^{\ast }$
is relatively algebraically closed in
$K^{\ast }$
is relatively algebraically closed in
![]() $K^{\ast \ast }$
.
$K^{\ast \ast }$
.
This answers [Reference KoenigsmannKoe16, Question 25]. A simple model-theoretic argument yields the following statement on irreducibility.
Corollary. Let
![]() $K$
be a global field. There exists a diophantine criterion for a polynomial over
$K$
be a global field. There exists a diophantine criterion for a polynomial over
![]() $K$
in an arbitrary number of variables to be irreducible. More formally, fix
$K$
in an arbitrary number of variables to be irreducible. More formally, fix
![]() $r,d\geqslant 0$
. Then the set
$r,d\geqslant 0$
. Then the set
is diophantine.
2 Preliminaries on central simple algebras
In this section, we extend the methods pioneered in [Reference PoonenPoo09] from quaternion algebras over
![]() $\mathbb{Q}$
to general central simple algebras of prime degree over global fields. We assume the reader to be familiar with the theory of central simple algebras; see for instance [Reference Gille and SzamuelyGS06] for an introduction.
$\mathbb{Q}$
to general central simple algebras of prime degree over global fields. We assume the reader to be familiar with the theory of central simple algebras; see for instance [Reference Gille and SzamuelyGS06] for an introduction.
Let
![]() $F$
be a field and
$F$
be a field and
![]() $A$
a (finite-dimensional) central simple algebra over
$A$
a (finite-dimensional) central simple algebra over
![]() $F$
. Define
$F$
. Define
where
![]() $\text{Trd}$
and
$\text{Trd}$
and
![]() $\text{Nrd}$
are the reduced trace and norm, respectively.
$\text{Nrd}$
are the reduced trace and norm, respectively.
Proposition 2.1. Let
![]() $L$
be a global field and
$L$
be a global field and
![]() $A$
a central simple algebra over
$A$
a central simple algebra over
![]() $L$
of prime degree
$L$
of prime degree
![]() $l$
. Then
$l$
. Then
This proposition is well known for
![]() $\operatorname{char}L\neq 2$
and
$\operatorname{char}L\neq 2$
and
![]() $l=2$
(the proof in this case can rely on the Hasse principle for quadratic forms), and this case has been exploited for first-order definitions of
$l=2$
(the proof in this case can rely on the Hasse principle for quadratic forms), and this case has been exploited for first-order definitions of
![]() $\mathbb{Z}$
in
$\mathbb{Z}$
in
![]() $\mathbb{Q}$
(and more generally for rings of integers in number fields, see [Reference ParkPar13], since adapted to global fields of odd characteristic, see [Reference Eisenträger and MorrisonEM16]). For the proof in the general case we quote two lemmas from the theory of central simple algebras.
$\mathbb{Q}$
(and more generally for rings of integers in number fields, see [Reference ParkPar13], since adapted to global fields of odd characteristic, see [Reference Eisenträger and MorrisonEM16]). For the proof in the general case we quote two lemmas from the theory of central simple algebras.
Lemma 2.2 [Reference JacobsonJac09, Theorem 4.12].
Let
![]() $D$
be a central division algebra of degree
$D$
be a central division algebra of degree
![]() $n$
over a field
$n$
over a field
![]() $F$
, and let
$F$
, and let
![]() $F^{\prime }$
be a field of degree
$F^{\prime }$
be a field of degree
![]() $n$
over
$n$
over
![]() $F$
. Then
$F$
. Then
![]() $F^{\prime }$
splits
$F^{\prime }$
splits
![]() $D$
if and only if
$D$
if and only if
![]() $F^{\prime }$
can be embedded into
$F^{\prime }$
can be embedded into
![]() $D$
over
$D$
over
![]() $F$
(i.e. there is a subalgebra of
$F$
(i.e. there is a subalgebra of
![]() $D$
isomorphic to
$D$
isomorphic to
![]() $F^{\prime }$
over
$F^{\prime }$
over
![]() $F$
).
$F$
).
Lemma 2.3 [Reference Gille and SzamuelyGS06, Proposition 2.6.3].
Let
![]() $A/F$
be a central simple algebra of degree
$A/F$
be a central simple algebra of degree
![]() $n$
and
$n$
and
![]() $x\in A$
. If
$x\in A$
. If
![]() $F^{\prime }\subseteq A$
is commutative subalgebra which contains
$F^{\prime }\subseteq A$
is commutative subalgebra which contains
![]() $x$
and is a degree
$x$
and is a degree
![]() $n$
field extension of
$n$
field extension of
![]() $F$
, then
$F$
, then
![]() $\text{Nrd}(x)=\operatorname{N}_{F^{\prime }/F}(x)$
and
$\text{Nrd}(x)=\operatorname{N}_{F^{\prime }/F}(x)$
and
![]() $\text{Trd}(x)=\text{Tr}_{F^{\prime }/F}(x)$
. In particular, if
$\text{Trd}(x)=\text{Tr}_{F^{\prime }/F}(x)$
. In particular, if
![]() $n$
is prime and
$n$
is prime and
![]() $A$
is a division algebra, then
$A$
is a division algebra, then
![]() $\text{Nrd}(x)=x^{n}$
and
$\text{Nrd}(x)=x^{n}$
and
![]() $\text{Trd}(x)=nx$
if
$\text{Trd}(x)=nx$
if
![]() $x\in F$
and otherwise
$x\in F$
and otherwise
![]() $\text{Nrd}(x)=\operatorname{N}_{F(x)/F}(x)$
and
$\text{Nrd}(x)=\operatorname{N}_{F(x)/F}(x)$
and
![]() $\text{Trd}(x)=\text{Tr}_{F(x)/F}(x)$
.
$\text{Trd}(x)=\text{Tr}_{F(x)/F}(x)$
.
We write
![]() $F(x)$
for the smallest subalgebra of
$F(x)$
for the smallest subalgebra of
![]() $A$
containing
$A$
containing
![]() $F$
and
$F$
and
![]() $x$
; under the assumption that
$x$
; under the assumption that
![]() $A$
is a division algebra of prime degree
$A$
is a division algebra of prime degree
![]() $n$
,
$n$
,
![]() $F(x)$
is necessarily a commutative division algebra, i.e. a field. Then the degree
$F(x)$
is necessarily a commutative division algebra, i.e. a field. Then the degree
![]() $[F(x):F]$
is either
$[F(x):F]$
is either
![]() $1$
or
$1$
or
![]() $n$
, since
$n$
, since
![]() $A$
is a (left)
$A$
is a (left)
![]() $F(x)$
-vector space and
$F(x)$
-vector space and
![]() $n^{2}=\dim _{F}A=\dim _{F(x)}A\cdot [F(x):F]$
(cf. the usual tower law for field extensions).
$n^{2}=\dim _{F}A=\dim _{F(x)}A\cdot [F(x):F]$
(cf. the usual tower law for field extensions).
Lastly, we need the following easy consequence of Krasner’s lemma.
Lemma 2.4. Let
![]() $l$
be a prime number,
$l$
be a prime number,
![]() $L$
a global field,
$L$
a global field,
![]() $a\in L$
, and
$a\in L$
, and
![]() $v_{1},\ldots ,v_{r}$
places of
$v_{1},\ldots ,v_{r}$
places of
![]() $L$
. For each
$L$
. For each
![]() $i$
, let
$i$
, let
![]() $f_{i}\in L_{v_{i}}[X]$
be a monic irreducible polynomial of degree
$f_{i}\in L_{v_{i}}[X]$
be a monic irreducible polynomial of degree
![]() $l$
with constant coefficient
$l$
with constant coefficient
![]() $(-1)^{l}$
and
$(-1)^{l}$
and
![]() $X^{l-1}$
-coefficient
$X^{l-1}$
-coefficient
![]() $-a$
. Then there exists a monic irreducible polynomial
$-a$
. Then there exists a monic irreducible polynomial
![]() $f\in L[X]$
of degree
$f\in L[X]$
of degree
![]() $l$
with constant coefficient
$l$
with constant coefficient
![]() $(-1)^{l}$
and
$(-1)^{l}$
and
![]() $X^{l-1}$
-coefficient
$X^{l-1}$
-coefficient
![]() $-a$
such that
$-a$
such that
![]() $L_{v_{i}}[X]/(f)\cong L_{v_{i}}[X]/(f_{i})$
, i.e. the completion above
$L_{v_{i}}[X]/(f)\cong L_{v_{i}}[X]/(f_{i})$
, i.e. the completion above
![]() $v_{i}$
of the global field
$v_{i}$
of the global field
![]() $L[X]/(f)$
is unique and given by
$L[X]/(f)$
is unique and given by
![]() $L_{v_{i}}[X]/(f_{i})$
.
$L_{v_{i}}[X]/(f_{i})$
.
Proof. Each
![]() $f_{i}$
must automatically be separable, otherwise we would have to have
$f_{i}$
must automatically be separable, otherwise we would have to have
![]() $l=\operatorname{char}L$
,
$l=\operatorname{char}L$
,
![]() $f_{i}=X^{l}+(-1)^{l}$
, but then
$f_{i}=X^{l}+(-1)^{l}$
, but then
![]() $f_{i}$
would be reducible.
$f_{i}$
would be reducible.
If the coefficients of
![]() $f$
are
$f$
are
![]() $v_{1}$
-adically sufficiently close to those of
$v_{1}$
-adically sufficiently close to those of
![]() $f_{1}$
, then
$f_{1}$
, then
![]() $f$
is irreducible in
$f$
is irreducible in
![]() $L_{v_{1}}[X]$
and therefore in
$L_{v_{1}}[X]$
and therefore in
![]() $L[X]$
, and additionally
$L[X]$
, and additionally
![]() $L_{v_{1}}[X]/(f)\cong L_{v_{1}}[X]/(f_{1})$
: this is a standard consequence of Krasner’s lemma, see e.g. [Reference JacobsonJac09, Exercise 9.8.7]; see also [Reference Neukirch, Schmidt and WingbergNSW08, Lemma 8.1.6 and proof of Proposition 8.1.5]. (For archimedean places
$L_{v_{1}}[X]/(f)\cong L_{v_{1}}[X]/(f_{1})$
: this is a standard consequence of Krasner’s lemma, see e.g. [Reference JacobsonJac09, Exercise 9.8.7]; see also [Reference Neukirch, Schmidt and WingbergNSW08, Lemma 8.1.6 and proof of Proposition 8.1.5]. (For archimedean places
![]() $v_{i}$
, the statement is easily checked separately.)
$v_{i}$
, the statement is easily checked separately.)
By weak approximation, we can choose the coefficients of
![]() $f$
to
$f$
to
![]() $v_{i}$
-adically approximate the coefficients of
$v_{i}$
-adically approximate the coefficients of
![]() $f_{i}$
arbitrarily well simultaneously for all
$f_{i}$
arbitrarily well simultaneously for all
![]() $i$
.◻
$i$
.◻
Proof of Proposition 2.1.
This is a local–global principle. Note that there is nothing to show if
![]() $A$
is isomorphic to the algebra of
$A$
is isomorphic to the algebra of
![]() $l\times l$
-matrices over
$l\times l$
-matrices over
![]() $L$
since the set on both sides is just
$L$
since the set on both sides is just
![]() $L$
in this case. So let us assume that
$L$
in this case. So let us assume that
![]() $A$
is non-split over
$A$
is non-split over
![]() $L$
; hence, since
$L$
; hence, since
![]() $A$
has prime degree over
$A$
has prime degree over
![]() $L$
,
$L$
,
![]() $A$
is a division algebra by Wedderburn’s theorem (see e.g. [Reference Gille and SzamuelyGS06, Theorem 2.1.3]). The inclusion
$A$
is a division algebra by Wedderburn’s theorem (see e.g. [Reference Gille and SzamuelyGS06, Theorem 2.1.3]). The inclusion
![]() $\subseteq$
is clear. For the other inclusion, consider an element
$\subseteq$
is clear. For the other inclusion, consider an element
![]() $a\in L$
of the right-hand side. We want to show that
$a\in L$
of the right-hand side. We want to show that
![]() $a\in S(A/L)$
, i.e. that there exists
$a\in S(A/L)$
, i.e. that there exists
![]() $x\in A$
with
$x\in A$
with
![]() $\operatorname{Nrd}(x)=1$
and
$\operatorname{Nrd}(x)=1$
and
![]() $\operatorname{Trd}(x)=a$
. Let
$\operatorname{Trd}(x)=a$
. Let
![]() $v_{1},\ldots ,v_{r}$
be the ramified places of
$v_{1},\ldots ,v_{r}$
be the ramified places of
![]() $A$
. (The local condition is trivial at all other places.) For each
$A$
. (The local condition is trivial at all other places.) For each
![]() $v_{i}$
there exists an element
$v_{i}$
there exists an element
![]() $x_{i}\in A\otimes L_{v_{i}}$
of reduced norm
$x_{i}\in A\otimes L_{v_{i}}$
of reduced norm
![]() $1$
and reduced trace
$1$
and reduced trace
![]() $a$
. We can disregard the case where
$a$
. We can disregard the case where
![]() $x_{i}$
is in the centre
$x_{i}$
is in the centre
![]() $L_{v_{i}}$
, as the norm condition then forces
$L_{v_{i}}$
, as the norm condition then forces
![]() $x_{i}^{l}=1$
, and if
$x_{i}^{l}=1$
, and if
![]() $l\neq \operatorname{char}L$
, then the trace condition forces
$l\neq \operatorname{char}L$
, then the trace condition forces
![]() $x_{i}=a/l\in L$
, or if
$x_{i}=a/l\in L$
, or if
![]() $l=\operatorname{char}L$
, then
$l=\operatorname{char}L$
, then
![]() $x_{i}=1\in L$
; in either case we are done globally.
$x_{i}=1\in L$
; in either case we are done globally.
Assume therefore that
![]() $x_{i}\not \in L_{v_{i}}$
, so
$x_{i}\not \in L_{v_{i}}$
, so
![]() $L_{v_{i}}(x_{i})/L_{v_{i}}$
is a field extension of degree
$L_{v_{i}}(x_{i})/L_{v_{i}}$
is a field extension of degree
![]() $l$
which splits
$l$
which splits
![]() $A\otimes L_{v_{i}}$
(by Lemma 2.2), with
$A\otimes L_{v_{i}}$
(by Lemma 2.2), with
![]() $\operatorname{N}_{L_{v_{i}}(x)/L_{v_{i}}}(x)=1$
and
$\operatorname{N}_{L_{v_{i}}(x)/L_{v_{i}}}(x)=1$
and
![]() $\text{Tr}_{L_{v_{i}}(x)/L_{v_{i}}}(x)=a$
(by Lemma 2.3). Write
$\text{Tr}_{L_{v_{i}}(x)/L_{v_{i}}}(x)=a$
(by Lemma 2.3). Write
![]() $f_{i}\in L_{v_{i}}[X]$
for the minimal polynomial of
$f_{i}\in L_{v_{i}}[X]$
for the minimal polynomial of
![]() $x_{i}$
; it is a monic irreducible polynomial of degree
$x_{i}$
; it is a monic irreducible polynomial of degree
![]() $l$
with constant coefficient
$l$
with constant coefficient
![]() $(-1)^{l}$
and
$(-1)^{l}$
and
![]() $X^{l-1}$
-coefficient
$X^{l-1}$
-coefficient
![]() $-a$
for reasons of norm and trace.
$-a$
for reasons of norm and trace.
Let
![]() $f\in L[X]$
be a polynomial as in Lemma 2.4, so
$f\in L[X]$
be a polynomial as in Lemma 2.4, so
![]() $L^{\prime }=L[X]/(f)$
is a degree
$L^{\prime }=L[X]/(f)$
is a degree
![]() $l$
field extension of
$l$
field extension of
![]() $L$
with completions
$L$
with completions
![]() $L_{v_{i}}[X]/(f_{i})\cong L_{v_{i}}(x_{i})$
above each
$L_{v_{i}}[X]/(f_{i})\cong L_{v_{i}}(x_{i})$
above each
![]() $v_{i}$
. The element
$v_{i}$
. The element
![]() $\overline{X}\in L^{\prime }$
has minimal polynomial
$\overline{X}\in L^{\prime }$
has minimal polynomial
![]() $f$
, hence
$f$
, hence
![]() $\operatorname{N}_{L^{\prime }/L}(\overline{X})=1$
and
$\operatorname{N}_{L^{\prime }/L}(\overline{X})=1$
and
![]() $\text{Tr}_{L^{\prime }/L}(\overline{X})=a$
. The field
$\text{Tr}_{L^{\prime }/L}(\overline{X})=a$
. The field
![]() $L^{\prime }$
splits
$L^{\prime }$
splits
![]() $A$
by the Hasse–Brauer–Noether theorem since it splits
$A$
by the Hasse–Brauer–Noether theorem since it splits
![]() $A$
everywhere locally, so
$A$
everywhere locally, so
![]() $L^{\prime }$
embeds into
$L^{\prime }$
embeds into
![]() $A$
by Lemma 2.2, and the image of
$A$
by Lemma 2.2, and the image of
![]() $\overline{X}$
under this embedding has reduced norm
$\overline{X}$
under this embedding has reduced norm
![]() $1$
and reduced trace
$1$
and reduced trace
![]() $a$
by Lemma 2.3.◻
$a$
by Lemma 2.3.◻
The idea behind this proof is already present in [Reference EisenträgerEis05, Theorem 3.1].
Next we investigate the local conditions
![]() $S(A/L_{v})$
. For a finite field
$S(A/L_{v})$
. For a finite field
![]() $\mathbb{F}$
, define
$\mathbb{F}$
, define
where we write
![]() $\mathbb{F}^{(l)}$
for the extension field of
$\mathbb{F}^{(l)}$
for the extension field of
![]() $\mathbb{F}$
of degree
$\mathbb{F}$
of degree
![]() $l$
(unique up to isomorphism).
$l$
(unique up to isomorphism).
The following is essentially [Reference PoonenPoo09, Lemma 2.1].
Lemma 2.5. Let
![]() $A/F$
be a central simple algebra of prime degree
$A/F$
be a central simple algebra of prime degree
![]() $l$
over a local field.
$l$
over a local field.
(i) If
 $A$
is split, then
$A$
is split, then
 $S(A/F)=F$
.
$S(A/F)=F$
.(ii) If
 $A$
is a division algebra, then for all irreducible monic polynomials
$A$
is a division algebra, then for all irreducible monic polynomials
 $X^{l}+a_{l-1}X^{l-1}+\cdots +a_{0}$
with constant coefficient
$X^{l}+a_{l-1}X^{l-1}+\cdots +a_{0}$
with constant coefficient
 $a_{0}=(-1)^{l}$
we have
$a_{0}=(-1)^{l}$
we have
 $-a_{l-1}\in S(A/F)$
.
$-a_{l-1}\in S(A/F)$
.(iii) If
 $A$
is a division algebra and
$A$
is a division algebra and
 $F$
is non-archimedean, then
$F$
is non-archimedean, then
 ${\mathcal{O}}\supseteq S(A/F)\supseteq \operatorname{res}^{-1}(U_{l}(\mathbb{F}))$
, where
${\mathcal{O}}\supseteq S(A/F)\supseteq \operatorname{res}^{-1}(U_{l}(\mathbb{F}))$
, where
 ${\mathcal{O}}$
is the valuation ring,
${\mathcal{O}}$
is the valuation ring,
 $\mathbb{F}$
is the residue field, and
$\mathbb{F}$
is the residue field, and
 $\operatorname{res}:{\mathcal{O}}\rightarrow \mathbb{F}$
is the residue map.
$\operatorname{res}:{\mathcal{O}}\rightarrow \mathbb{F}$
is the residue map.
Proof. In the split case, reduced norm and trace coincide with the usual matrix determinant and trace, and all monic polynomials of degree
![]() $l$
do occur as characteristic polynomials.
$l$
do occur as characteristic polynomials.
For the second point, every monic irreducible polynomial
![]() $f$
generates a field extension
$f$
generates a field extension
![]() $F[x]/(f)$
, and every such field extension splits
$F[x]/(f)$
, and every such field extension splits
![]() $A$
by the theory of central simple algebras over local fields (see e.g. [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.1.4]). Hence, by Lemma 2.2,
$A$
by the theory of central simple algebras over local fields (see e.g. [Reference Neukirch, Schmidt and WingbergNSW08, Corollary 7.1.4]). Hence, by Lemma 2.2,
![]() $F[x]/(f)$
embeds into
$F[x]/(f)$
embeds into
![]() $A$
, and then
$A$
, and then
![]() $-a_{l-1}\in S(A/F)$
by Lemma 2.3, where
$-a_{l-1}\in S(A/F)$
by Lemma 2.3, where
![]() $a_{l-1}$
is the coefficient of
$a_{l-1}$
is the coefficient of
![]() $X^{l-1}$
in
$X^{l-1}$
in
![]() $f$
.
$f$
.
For the case of a division algebra over a non-archimedean local field, let
![]() $x\in A$
with
$x\in A$
with
![]() $\text{Nrd}(x)=1$
. Then by Lemma 2.3
$\text{Nrd}(x)=1$
. Then by Lemma 2.3
![]() $\operatorname{N}_{F(x)/F}(x)^{l}=1$
, so
$\operatorname{N}_{F(x)/F}(x)^{l}=1$
, so
![]() $x$
is contained in the valuation ring of the local field
$x$
is contained in the valuation ring of the local field
![]() $F(x)$
, therefore integral over
$F(x)$
, therefore integral over
![]() ${\mathcal{O}}$
and hence has integral trace. This proves
${\mathcal{O}}$
and hence has integral trace. This proves
![]() $S(A/F)\subseteq {\mathcal{O}}$
. For the other inclusion, if
$S(A/F)\subseteq {\mathcal{O}}$
. For the other inclusion, if
![]() $\overline{a}\in U_{l}(\mathbb{F})$
then there exists a monic irreducible polynomial
$\overline{a}\in U_{l}(\mathbb{F})$
then there exists a monic irreducible polynomial
![]() $\overline{f}=X^{n}+\overline{a_{l-1}}X^{l-1}+\cdots +\overline{a_{0}}\in \mathbb{F}[X]$
with
$\overline{f}=X^{n}+\overline{a_{l-1}}X^{l-1}+\cdots +\overline{a_{0}}\in \mathbb{F}[X]$
with
![]() $\overline{a_{l-1}}=-\overline{a}$
and
$\overline{a_{l-1}}=-\overline{a}$
and
![]() $\overline{a_{0}}=(-1)^{l}$
. Any lift of
$\overline{a_{0}}=(-1)^{l}$
. Any lift of
![]() $\overline{f}$
to
$\overline{f}$
to
![]() $F[X]$
is irreducible over
$F[X]$
is irreducible over
![]() $F$
(because it generates an unramified extension of degree
$F$
(because it generates an unramified extension of degree
![]() $l$
), hence any lift
$l$
), hence any lift
![]() $a\in {\mathcal{O}}$
of
$a\in {\mathcal{O}}$
of
![]() $\overline{a}$
is in
$\overline{a}$
is in
![]() $S(A/F)$
by the second point.◻
$S(A/F)$
by the second point.◻
We can now give a satisfactory statement on
![]() $S(A/F)$
in the non-split local case.
$S(A/F)$
in the non-split local case.
Proposition 2.6. Let
![]() $A/F$
be a central division algebra of prime degree
$A/F$
be a central division algebra of prime degree
![]() $l$
over a non-archimedean local field.
$l$
over a non-archimedean local field.
(i) If
 $l>2$
, then
$l>2$
, then
 $S(A/F)$
is equal to the valuation ring
$S(A/F)$
is equal to the valuation ring
 ${\mathcal{O}}$
of
${\mathcal{O}}$
of
 $F$
.
$F$
.(ii) If
 $l=2$
, write
$l=2$
, write
 $V(A/F)$
for the topological interior of
$V(A/F)$
for the topological interior of
 $S(A/F)$
. We then have
$S(A/F)$
. We then have
 $V(A/F)-V(A/F)={\mathcal{O}}$
, where
$V(A/F)-V(A/F)={\mathcal{O}}$
, where
 $V(A/F)-V(A/F)$
is the set of differences of two elements of
$V(A/F)-V(A/F)$
is the set of differences of two elements of
 $V(A/F)$
.
$V(A/F)$
.
For the proof of the first point, it suffices to prove the following lemma.
Lemma 2.7. For
![]() $l>2$
and an arbitrary finite field
$l>2$
and an arbitrary finite field
![]() $\mathbb{F}$
, we have
$\mathbb{F}$
, we have
![]() $U_{l}(\mathbb{F})=\mathbb{F}$
.
$U_{l}(\mathbb{F})=\mathbb{F}$
.
Proof. This result is equivalent to showing that for any given
![]() $a\in \mathbb{F}$
, there exists a monic irreducible polynomial
$a\in \mathbb{F}$
, there exists a monic irreducible polynomial
![]() $f\in \mathbb{F}[X]$
of degree
$f\in \mathbb{F}[X]$
of degree
![]() $l$
with
$l$
with
![]() $X^{l-1}$
-coefficient
$X^{l-1}$
-coefficient
![]() $-a$
and constant coefficient
$-a$
and constant coefficient
![]() $-1$
. Let us write
$-1$
. Let us write
![]() $q$
for the cardinality of
$q$
for the cardinality of
![]() $\mathbb{F}$
. If
$\mathbb{F}$
. If
![]() $l>5$
, or
$l>5$
, or
![]() $l=5$
and
$l=5$
and
![]() $q>9$
, the result follows from Theorem 2.8 below. The remaining cases for
$q>9$
, the result follows from Theorem 2.8 below. The remaining cases for
![]() $l=5$
we check by hand.
$l=5$
we check by hand.
It remains to consider the case
![]() $l=3$
. If a polynomial
$l=3$
. If a polynomial
![]() $f_{b}=X^{3}-aX^{2}+bX-1$
is not irreducible, it must be divisible by
$f_{b}=X^{3}-aX^{2}+bX-1$
is not irreducible, it must be divisible by
![]() $X-c$
for some
$X-c$
for some
![]() $c\in \mathbb{F}^{\times }$
. However, for each
$c\in \mathbb{F}^{\times }$
. However, for each
![]() $c$
there exists exactly one
$c$
there exists exactly one
![]() $f_{b}$
divisible by
$f_{b}$
divisible by
![]() $X-c$
. By counting, there exists an
$X-c$
. By counting, there exists an
![]() $f_{b}$
which is not divisible by any
$f_{b}$
which is not divisible by any
![]() $X-c$
and therefore irreducible.◻
$X-c$
and therefore irreducible.◻
Theorem 2.8. Let
![]() $\mathbb{F}$
be a finite field of cardinality
$\mathbb{F}$
be a finite field of cardinality
![]() $q$
and
$q$
and
![]() $n>0$
.
$n>0$
.
(i) If
 $n\geqslant 5$
and
$n\geqslant 5$
and
 $q>\big((n+1)/2\big)^{2}$
, there exists a monic irreducible polynomial of degree
$q>\big((n+1)/2\big)^{2}$
, there exists a monic irreducible polynomial of degree
 $n$
over
$n$
over
 $\mathbb{F}$
with any given non-zero constant coefficient and given
$\mathbb{F}$
with any given non-zero constant coefficient and given
 $X^{n-1}$
-coefficient.
$X^{n-1}$
-coefficient.(ii) If
 $n\geqslant 6$
, the same is true without assumption on
$n\geqslant 6$
, the same is true without assumption on
 $q$
.
$q$
.
Proof. These are [Reference CohenCoh05, Corollaries 2.2 and 2.3].◻
Proof of Proposition 2.6.
For
![]() $l>2$
, the claim follows from the third part of Lemmas 2.5 and 2.7, so let us consider
$l>2$
, the claim follows from the third part of Lemmas 2.5 and 2.7, so let us consider
![]() $l=2$
. Write
$l=2$
. Write
![]() $\mathbb{F}$
for the residue field of
$\mathbb{F}$
for the residue field of
![]() $F$
and pick a uniformiser
$F$
and pick a uniformiser
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
For
![]() $a\in 2+\unicode[STIX]{x1D70B}+\unicode[STIX]{x1D70B}^{2}{\mathcal{O}}$
, the polynomial
$a\in 2+\unicode[STIX]{x1D70B}+\unicode[STIX]{x1D70B}^{2}{\mathcal{O}}$
, the polynomial
![]() $f=X^{2}-aX+1$
is irreducible, since
$f=X^{2}-aX+1$
is irreducible, since
![]() $f(X+1)=X^{2}-(a-2)X+(2-a)$
is irreducible by Eisenstein’s criterion. Hence, by the second point of Lemma 2.5, we have
$f(X+1)=X^{2}-(a-2)X+(2-a)$
is irreducible by Eisenstein’s criterion. Hence, by the second point of Lemma 2.5, we have
![]() $2+\unicode[STIX]{x1D70B}+\unicode[STIX]{x1D70B}^{2}{\mathcal{O}}\subseteq S(A/F)$
, so
$2+\unicode[STIX]{x1D70B}+\unicode[STIX]{x1D70B}^{2}{\mathcal{O}}\subseteq S(A/F)$
, so
![]() $V(A/F)$
contains the element
$V(A/F)$
contains the element
![]() $b=2+\unicode[STIX]{x1D70B}$
; likewise
$b=2+\unicode[STIX]{x1D70B}$
; likewise
![]() $-b\in V(A/F)$
by passing from
$-b\in V(A/F)$
by passing from
![]() $f$
to
$f$
to
![]() $f(-X)$
. Furthermore, we also have
$f(-X)$
. Furthermore, we also have
![]() $V(A/F)\supseteq \operatorname{res}^{-1}(U_{2}(\mathbb{F}))$
by Lemma 2.5 since the right-hand side is open.
$V(A/F)\supseteq \operatorname{res}^{-1}(U_{2}(\mathbb{F}))$
by Lemma 2.5 since the right-hand side is open.
If
![]() $\mathbb{F}$
has cardinality greater than
$\mathbb{F}$
has cardinality greater than
![]() $11$
, then
$11$
, then
![]() $U_{2}(\mathbb{F})-U_{2}(\mathbb{F})=\mathbb{F}$
by [Reference PoonenPoo09, Lemma 2.3]. We can check exhaustively that for the remaining finite fields we have
$U_{2}(\mathbb{F})-U_{2}(\mathbb{F})=\mathbb{F}$
by [Reference PoonenPoo09, Lemma 2.3]. We can check exhaustively that for the remaining finite fields we have
![]() $(U_{2}(\mathbb{F})\cup \{2,-2\})-U_{2}(\mathbb{F})=\mathbb{F}$
. Hence
$(U_{2}(\mathbb{F})\cup \{2,-2\})-U_{2}(\mathbb{F})=\mathbb{F}$
. Hence
This proof is adapted from the proof of Proposition 2.3 in [Reference ParkPar13]. A modification is necessary because the set
![]() $V_{v}$
constructed there fails to be contained in the interior of
$V_{v}$
constructed there fails to be contained in the interior of
![]() $S(A/F)$
, interfering with the application of approximation theorems later on.
$S(A/F)$
, interfering with the application of approximation theorems later on.
For a central simple algebra
![]() $A$
of prime degree
$A$
of prime degree
![]() $l$
over a global field
$l$
over a global field
![]() $L$
, we define
$L$
, we define
![]() $T(A/L)=S(A/L)$
if
$T(A/L)=S(A/L)$
if
![]() $l>2$
and
$l>2$
and
![]() $T(A/L)=S(A/L)-S(A/L)$
(the set of pairwise differences of elements of
$T(A/L)=S(A/L)-S(A/L)$
(the set of pairwise differences of elements of
![]() $S$
) if
$S$
) if
![]() $l=2$
.
$l=2$
.
Proposition 2.9. If
![]() $A/L$
splits at all real places of
$A/L$
splits at all real places of
![]() $L$
(which is always the case if
$L$
(which is always the case if
![]() $l\neq 2$
or
$l\neq 2$
or
![]() $L$
is a global function field), then
$L$
is a global function field), then
where
![]() $\unicode[STIX]{x1D6E5}_{A/L}$
is the finite set of places of
$\unicode[STIX]{x1D6E5}_{A/L}$
is the finite set of places of
![]() $L$
at which
$L$
at which
![]() $A/L$
does not split.
$A/L$
does not split.
Proof. For
![]() $l>2$
, this is immediate from Propositions 2.1 and 2.6, so consider the case
$l>2$
, this is immediate from Propositions 2.1 and 2.6, so consider the case
![]() $l=2$
. The inclusion
$l=2$
. The inclusion
![]() $\subseteq$
is clear from Proposition 2.1 and Lemma 2.5, so let
$\subseteq$
is clear from Proposition 2.1 and Lemma 2.5, so let
![]() $x\in \bigcap _{\mathfrak{q}\in \unicode[STIX]{x1D6E5}_{A/L}}{\mathcal{O}}_{\mathfrak{q}}\cap L$
. For each
$x\in \bigcap _{\mathfrak{q}\in \unicode[STIX]{x1D6E5}_{A/L}}{\mathcal{O}}_{\mathfrak{q}}\cap L$
. For each
![]() $\mathfrak{q}\in \unicode[STIX]{x1D6E5}_{A/L}$
we have
$\mathfrak{q}\in \unicode[STIX]{x1D6E5}_{A/L}$
we have
![]() $x\in {\mathcal{O}}_{\mathfrak{q}}=V(A/L_{\mathfrak{q}})-V(A/L_{\mathfrak{q}})$
according to Proposition 2.6, so pick
$x\in {\mathcal{O}}_{\mathfrak{q}}=V(A/L_{\mathfrak{q}})-V(A/L_{\mathfrak{q}})$
according to Proposition 2.6, so pick
![]() $a_{\mathfrak{q}}\in V(A/L_{\mathfrak{q}})$
such that
$a_{\mathfrak{q}}\in V(A/L_{\mathfrak{q}})$
such that
![]() $x+a_{\mathfrak{q}}\in V(A/L_{\mathfrak{q}})$
. Since
$x+a_{\mathfrak{q}}\in V(A/L_{\mathfrak{q}})$
. Since
![]() $\unicode[STIX]{x1D6E5}_{A/L}$
is finite and the
$\unicode[STIX]{x1D6E5}_{A/L}$
is finite and the
![]() $V(A/L_{\mathfrak{q}})$
are open, we can use weak approximation to find
$V(A/L_{\mathfrak{q}})$
are open, we can use weak approximation to find
![]() $a\in L$
such that
$a\in L$
such that
![]() $a,x+a\in V(A/L_{\mathfrak{q}})\subseteq S(A/L_{\mathfrak{q}})$
for all
$a,x+a\in V(A/L_{\mathfrak{q}})\subseteq S(A/L_{\mathfrak{q}})$
for all
![]() $\mathfrak{q}\in \unicode[STIX]{x1D6E5}(A/L)$
, hence
$\mathfrak{q}\in \unicode[STIX]{x1D6E5}(A/L)$
, hence
![]() $a,x+a\in S(A/L)$
by Proposition 2.1 and therefore
$a,x+a\in S(A/L)$
by Proposition 2.1 and therefore
![]() $x\in T(A/L)$
.◻
$x\in T(A/L)$
.◻
For later use, we also record the following fact.
Proposition 2.10. Assume
![]() $K$
is global field of characteristic
$K$
is global field of characteristic
![]() $p>0$
and
$p>0$
and
![]() $L/K$
is a finite inseparable extension. Then any central simple algebra
$L/K$
is a finite inseparable extension. Then any central simple algebra
![]() $A/K$
of degree
$A/K$
of degree
![]() $p$
is split by
$p$
is split by
![]() $L$
.
$L$
.
Proof. By replacing
![]() $K$
with the maximal separable subextension of
$K$
with the maximal separable subextension of
![]() $L/K$
, we may assume that
$L/K$
, we may assume that
![]() $L/K$
is a purely inseparable proper extension. Since
$L/K$
is a purely inseparable proper extension. Since
![]() $[K^{1/p}:K]=p$
, we now necessarily have
$[K^{1/p}:K]=p$
, we now necessarily have
![]() $L\supset K^{1/p}$
. Hence, the result follows from Lemma 2.11 below.◻
$L\supset K^{1/p}$
. Hence, the result follows from Lemma 2.11 below.◻
Lemma 2.11 [Reference JacobsonJac96, Theorem 4.1.8].
Let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $p>0$
and
$p>0$
and
![]() $A/F$
be a central simple algebra of degree
$A/F$
be a central simple algebra of degree
![]() $p$
. Then
$p$
. Then
![]() $A$
is split by the field
$A$
is split by the field
![]() $F^{1/p}$
.
$F^{1/p}$
.
2.1 First-order definability
For what is to follow we will need that
![]() $S(A/F)$
is existentially first-order definable (in the language of rings) in terms of structure constants of
$S(A/F)$
is existentially first-order definable (in the language of rings) in terms of structure constants of
![]() $A$
, i.e.
$A$
, i.e.
![]() $S(A/F)$
needs to be diophantine uniformly over central simple algebras of some prime degree
$S(A/F)$
needs to be diophantine uniformly over central simple algebras of some prime degree
![]() $l$
and uniformly over base fields. (Recall that structure constants with respect to a basis
$l$
and uniformly over base fields. (Recall that structure constants with respect to a basis
![]() $(X_{i})_{1\leqslant i\leqslant l^{2}}$
of
$(X_{i})_{1\leqslant i\leqslant l^{2}}$
of
![]() $A/F$
are the constants
$A/F$
are the constants
![]() $(a_{ijk})_{1\leqslant i,j,k\leqslant l^{2}}$
in
$(a_{ijk})_{1\leqslant i,j,k\leqslant l^{2}}$
in
![]() $F$
such that
$F$
such that
![]() $X_{i}\cdot X_{j}=\sum _{k}a_{ijk}X_{k}$
.) It suffices to prove the following lemma.
$X_{i}\cdot X_{j}=\sum _{k}a_{ijk}X_{k}$
.) It suffices to prove the following lemma.
Lemma 2.12. The functions
![]() $\text{Trd}$
and
$\text{Trd}$
and
![]() $\text{Nrd}$
are uniformly quantifier-freely definable, i.e. for fixed
$\text{Nrd}$
are uniformly quantifier-freely definable, i.e. for fixed
![]() $l$
there exists a quantifier-free first-order formula
$l$
there exists a quantifier-free first-order formula
![]() $\unicode[STIX]{x1D70F}$
in
$\unicode[STIX]{x1D70F}$
in
![]() $l^{6}+l^{2}+1$
variables such that if
$l^{6}+l^{2}+1$
variables such that if
![]() $F$
is a field,
$F$
is a field,
![]() $(a_{ijk})_{1\leqslant i,j,k\leqslant l^{2}}$
are structure constants of a central simple algebra
$(a_{ijk})_{1\leqslant i,j,k\leqslant l^{2}}$
are structure constants of a central simple algebra
![]() $A/F$
,
$A/F$
,
![]() $(b_{i})_{1\leqslant i\leqslant l^{2}}$
is the basis expansion of an element
$(b_{i})_{1\leqslant i\leqslant l^{2}}$
is the basis expansion of an element
![]() $x\in A$
, and
$x\in A$
, and
![]() $c\in F$
is arbitrary, then
$c\in F$
is arbitrary, then
![]() $F\models \unicode[STIX]{x1D70F}(\overline{a},\overline{b},c)$
if and only if
$F\models \unicode[STIX]{x1D70F}(\overline{a},\overline{b},c)$
if and only if
![]() $c=\text{Trd}(x)$
, and there is likewise such a formula for
$c=\text{Trd}(x)$
, and there is likewise such a formula for
![]() $\text{Nrd}$
in place of
$\text{Nrd}$
in place of
![]() $\text{Trd}$
.
$\text{Trd}$
.
Proof. If
![]() $(a_{ijk})$
are the structure constants of
$(a_{ijk})$
are the structure constants of
![]() $M_{l\times l}$
in the standard basis (i.e. the basis given by matrices with a single entry equal to
$M_{l\times l}$
in the standard basis (i.e. the basis given by matrices with a single entry equal to
![]() $1$
and all other entries
$1$
and all other entries
![]() $0$
), then the elements
$0$
), then the elements
![]() $(b_{i})$
are precisely the entries of the matrix
$(b_{i})$
are precisely the entries of the matrix
![]() $x\in M_{l\times l}$
, and hence reduced norm and trace, which agree with matrix determinant and trace, are given by polynomial functions of the
$x\in M_{l\times l}$
, and hence reduced norm and trace, which agree with matrix determinant and trace, are given by polynomial functions of the
![]() $b_{i}$
.
$b_{i}$
.
If
![]() $F$
is algebraically closed, then any central simple algebra of degree
$F$
is algebraically closed, then any central simple algebra of degree
![]() $l$
is isomorphic to
$l$
is isomorphic to
![]() $M_{l\times l}$
, i.e. there exists a base change matrix that transforms the situation to the previous one. Hence we can find an existential formula
$M_{l\times l}$
, i.e. there exists a base change matrix that transforms the situation to the previous one. Hence we can find an existential formula
![]() $\unicode[STIX]{x1D70F}$
that works over algebraically closed fields: it asserts the existence of a base change transforming the
$\unicode[STIX]{x1D70F}$
that works over algebraically closed fields: it asserts the existence of a base change transforming the
![]() $a_{ijk}$
into the structure constants with respect to the standard basis, and
$a_{ijk}$
into the structure constants with respect to the standard basis, and
![]() $c$
being the right polynomial function of the (transformed)
$c$
being the right polynomial function of the (transformed)
![]() $b_{i}$
. By quantifier elimination, we can replace
$b_{i}$
. By quantifier elimination, we can replace
![]() $\unicode[STIX]{x1D70F}$
by a quantifier-free formula which is equivalent over algebraically closed fields.
$\unicode[STIX]{x1D70F}$
by a quantifier-free formula which is equivalent over algebraically closed fields.
This formula
![]() $\unicode[STIX]{x1D70F}$
in fact works for all fields. For this it suffices to note that
$\unicode[STIX]{x1D70F}$
in fact works for all fields. For this it suffices to note that
![]() $\text{Trd}_{A/F}(x)=\text{Trd}_{A\otimes \overline{F}/\overline{F}}(x\otimes 1)$
and likewise for the reduced norm, and
$\text{Trd}_{A/F}(x)=\text{Trd}_{A\otimes \overline{F}/\overline{F}}(x\otimes 1)$
and likewise for the reduced norm, and
![]() $F\models \unicode[STIX]{x1D70F}(\overline{a},\overline{b},c)$
if and only if
$F\models \unicode[STIX]{x1D70F}(\overline{a},\overline{b},c)$
if and only if
![]() $\overline{F}\models \unicode[STIX]{x1D70F}(\overline{a},\overline{b},c)$
since
$\overline{F}\models \unicode[STIX]{x1D70F}(\overline{a},\overline{b},c)$
since
![]() $\unicode[STIX]{x1D70F}$
is quantifier-free.◻
$\unicode[STIX]{x1D70F}$
is quantifier-free.◻
Consequently, the set
![]() $T(A/L)$
is existentially first-order definable, uniformly over
$T(A/L)$
is existentially first-order definable, uniformly over
![]() $A$
of some fixed prime degree
$A$
of some fixed prime degree
![]() $l$
and global fields
$l$
and global fields
![]() $L$
. We can even require the defining formula to be positive and existential, since an inequality
$L$
. We can even require the defining formula to be positive and existential, since an inequality
![]() $x\neq 0$
may always be replaced by the equivalent
$x\neq 0$
may always be replaced by the equivalent
![]() $\exists y(x\cdot y=1)$
.
$\exists y(x\cdot y=1)$
.
Corollary 2.13. For any finite place
![]() $\mathfrak{p}$
of a global field
$\mathfrak{p}$
of a global field
![]() $K$
, the ring
$K$
, the ring
![]() ${\mathcal{O}}_{\mathfrak{p}}\cap K$
is diophantine in
${\mathcal{O}}_{\mathfrak{p}}\cap K$
is diophantine in
![]() $K$
.
$K$
.
Proof. Take a prime number
![]() $l$
, e.g.
$l$
, e.g.
![]() $l=2$
, and pick two central simple algebras
$l=2$
, and pick two central simple algebras
![]() $A,A^{\prime }/K$
of degree
$A,A^{\prime }/K$
of degree
![]() $l$
splitting at all real places of
$l$
splitting at all real places of
![]() $K$
and such that
$K$
and such that
![]() $\unicode[STIX]{x1D6E5}_{A/K}\cap \unicode[STIX]{x1D6E5}_{A^{\prime }/K}=\{\mathfrak{p}\}$
. This is always possible by the characterisation of the Brauer group of global fields by Hasse invariants, see [Reference Neukirch, Schmidt and WingbergNSW08, Theorem 8.1.17]. Then
$\unicode[STIX]{x1D6E5}_{A/K}\cap \unicode[STIX]{x1D6E5}_{A^{\prime }/K}=\{\mathfrak{p}\}$
. This is always possible by the characterisation of the Brauer group of global fields by Hasse invariants, see [Reference Neukirch, Schmidt and WingbergNSW08, Theorem 8.1.17]. Then
![]() $T(A/K)+T(A^{\prime }/K)={\mathcal{O}}_{\mathfrak{p}}\cap K$
, and this is positively existentially definable in
$T(A/K)+T(A^{\prime }/K)={\mathcal{O}}_{\mathfrak{p}}\cap K$
, and this is positively existentially definable in
![]() $K$
with parameters.◻
$K$
with parameters.◻
Of course, this result is far from new: see, for instance, [Reference ShlapentokhShl94, Theorem 4.4]. The proof is essentially the same as [Reference PoonenPoo09, Remark 2.6].
For later use, we also spell out a definability result for cyclic algebras. Recall that for a field
![]() $F$
and a cyclic extension
$F$
and a cyclic extension
![]() $M/F$
of degree
$M/F$
of degree
![]() $l$
with a generator
$l$
with a generator
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $\operatorname{Gal}(M/F)$
and an element
$\operatorname{Gal}(M/F)$
and an element
![]() $a\in F$
the cyclic algebra
$a\in F$
the cyclic algebra
![]() $(M,\unicode[STIX]{x1D70E},a)$
is the
$(M,\unicode[STIX]{x1D70E},a)$
is the
![]() $F$
-algebra generated by
$F$
-algebra generated by
![]() $M$
and an element
$M$
and an element
![]() $y$
subject to the relations
$y$
subject to the relations
![]() $y^{l}=a$
and
$y^{l}=a$
and
![]() $xy=y\unicode[STIX]{x1D70E}(x)$
for all
$xy=y\unicode[STIX]{x1D70E}(x)$
for all
![]() $x\in M$
. It is central simple of degree
$x\in M$
. It is central simple of degree
![]() $l$
.
$l$
.
Lemma 2.14. Let
![]() $K$
be a global field and
$K$
be a global field and
![]() $M/K$
a cyclic extension of prime degree
$M/K$
a cyclic extension of prime degree
![]() $l$
with a generator
$l$
with a generator
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $\operatorname{Gal}(M/K)$
. Then there is a positive existential formula
$\operatorname{Gal}(M/K)$
. Then there is a positive existential formula
![]() $\unicode[STIX]{x1D711}_{M,\unicode[STIX]{x1D70E}}(a,x)$
in the language of rings, with parameters from
$\unicode[STIX]{x1D711}_{M,\unicode[STIX]{x1D70E}}(a,x)$
in the language of rings, with parameters from
![]() $K$
, such that in any finite extension
$K$
, such that in any finite extension
![]() $L/K$
and for any
$L/K$
and for any
![]() $a\in K$
the formula
$a\in K$
the formula
![]() $\unicode[STIX]{x1D711}_{M,\unicode[STIX]{x1D70E}}(a,\cdot )$
defines the set
$\unicode[STIX]{x1D711}_{M,\unicode[STIX]{x1D70E}}(a,\cdot )$
defines the set
![]() $T((M,\unicode[STIX]{x1D70E},a)\otimes _{K}L/L)$
.
$T((M,\unicode[STIX]{x1D70E},a)\otimes _{K}L/L)$
.
Proof. Fixing an irreducible polynomial over
![]() $K$
with splitting field
$K$
with splitting field
![]() $M$
, we can write structure constants for
$M$
, we can write structure constants for
![]() $(M,\unicode[STIX]{x1D70E},a)$
as polynomial expressions in
$(M,\unicode[STIX]{x1D70E},a)$
as polynomial expressions in
![]() $a$
with parameters from
$a$
with parameters from
![]() $K$
. These are then also structure constants for
$K$
. These are then also structure constants for
![]() $(M,\unicode[STIX]{x1D70E},a)\otimes _{K}L/L$
. Now we can use the positive existential definition of
$(M,\unicode[STIX]{x1D70E},a)\otimes _{K}L/L$
. Now we can use the positive existential definition of
![]() $T$
.◻
$T$
.◻
3 An interlude in class field theory
Fix a global field
![]() $K$
and
$K$
and
![]() $n>1$
. Also fix a prime
$n>1$
. Also fix a prime
![]() $l\mid n$
for this section.
$l\mid n$
for this section.
The entirety of this section is rather technical; we set up the necessary machinery from class field theory, notably describing certain ideal groups
![]() $I_{\mathfrak{m}}$
and
$I_{\mathfrak{m}}$
and
![]() $H$
as well as field extensions
$H$
as well as field extensions
![]() $M_{i}/K$
, which is needed for our main proofs in the next section, in particular the central Proposition 4.5.
$M_{i}/K$
, which is needed for our main proofs in the next section, in particular the central Proposition 4.5.
Let us fix some notation. Write
![]() $\unicode[STIX]{x1D6F4}$
for the set of places of
$\unicode[STIX]{x1D6F4}$
for the set of places of
![]() $K$
. If
$K$
. If
![]() $K$
is a number field, write
$K$
is a number field, write
![]() $\unicode[STIX]{x1D6F4}_{\infty }\subset \unicode[STIX]{x1D6F4}$
for the set of archimedean places. If
$\unicode[STIX]{x1D6F4}_{\infty }\subset \unicode[STIX]{x1D6F4}$
for the set of archimedean places. If
![]() $K$
is a global function field, arbitrarily fix
$K$
is a global function field, arbitrarily fix
![]() $\unicode[STIX]{x1D6F4}_{\infty }$
to be any finite non-empty subset of
$\unicode[STIX]{x1D6F4}_{\infty }$
to be any finite non-empty subset of
![]() $\unicode[STIX]{x1D6F4}$
. In either case, we call
$\unicode[STIX]{x1D6F4}$
. In either case, we call
![]() $\unicode[STIX]{x1D6F4}_{\infty }$
the set of places at infinity.
$\unicode[STIX]{x1D6F4}_{\infty }$
the set of places at infinity.
Let
![]() ${\mathcal{O}}_{K}$
be the ring of elements of
${\mathcal{O}}_{K}$
be the ring of elements of
![]() $K$
integral at each place in
$K$
integral at each place in
![]() $\unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
; this is a Dedekind domain, and the prime ideals of
$\unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
; this is a Dedekind domain, and the prime ideals of
![]() ${\mathcal{O}}_{K}$
are in bijection to places in
${\mathcal{O}}_{K}$
are in bijection to places in
![]() $\unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
. This ring is the usual ring of integers in the number field case. In the case of function fields,
$\unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
. This ring is the usual ring of integers in the number field case. In the case of function fields,
![]() ${\mathcal{O}}_{K}$
depends on the choice of
${\mathcal{O}}_{K}$
depends on the choice of
![]() $\unicode[STIX]{x1D6F4}_{\infty }$
.
$\unicode[STIX]{x1D6F4}_{\infty }$
.
Write
![]() $I_{{\mathcal{O}}_{K}}$
for the group of fractional ideals of
$I_{{\mathcal{O}}_{K}}$
for the group of fractional ideals of
![]() ${\mathcal{O}}_{K}$
,
${\mathcal{O}}_{K}$
,
![]() $P_{{\mathcal{O}}_{K}}$
for the subgroup of principal fractional ideals, and
$P_{{\mathcal{O}}_{K}}$
for the subgroup of principal fractional ideals, and
![]() $\operatorname{Cl}({\mathcal{O}}_{K})=I_{{\mathcal{O}}_{K}}/P_{{\mathcal{O}}_{K}}$
. In the number field case, this is the usual ideal class group and well known to be finite. In the function field case, this is not the usual divisor class group, since we are ignoring the places at infinity, but rather the
$\operatorname{Cl}({\mathcal{O}}_{K})=I_{{\mathcal{O}}_{K}}/P_{{\mathcal{O}}_{K}}$
. In the number field case, this is the usual ideal class group and well known to be finite. In the function field case, this is not the usual divisor class group, since we are ignoring the places at infinity, but rather the
![]() $\unicode[STIX]{x1D6F4}_{\infty }$
-class group in the sense of [Reference RosenRos02, ch. 14], essentially the divisor class group modulo the classes of prime divisors at infinity. It is finite by [Reference RosenRos02, Corollary 2 to Proposition 14.1].
$\unicode[STIX]{x1D6F4}_{\infty }$
-class group in the sense of [Reference RosenRos02, ch. 14], essentially the divisor class group modulo the classes of prime divisors at infinity. It is finite by [Reference RosenRos02, Corollary 2 to Proposition 14.1].
We now fix some field extensions of
![]() $K$
for later use. Choose
$K$
for later use. Choose
![]() $k$
such that
$k$
such that
![]() $l^{k}>|\operatorname{Cl}({\mathcal{O}}_{K})|\cdot n!$
. Find an abelian extension
$l^{k}>|\operatorname{Cl}({\mathcal{O}}_{K})|\cdot n!$
. Find an abelian extension
![]() $M/K$
with Galois group
$M/K$
with Galois group
![]() $\operatorname{Gal}(M/K)\cong (\mathbb{Z}/l\mathbb{Z})^{k}$
and such that
$\operatorname{Gal}(M/K)\cong (\mathbb{Z}/l\mathbb{Z})^{k}$
and such that
![]() $M/K$
is completely split at all infinite places.
$M/K$
is completely split at all infinite places.
Lemma 3.1. For any choice of
![]() $k$
we can find such
$k$
we can find such
![]() $M$
.
$M$
.
Proof. This follows from existence theorems in class field theory, e.g. the general version of the Grunwald–Wang theorem [Reference Neukirch, Schmidt and WingbergNSW08, Theorem 9.2.8]. (Note that we are never in what is called the ‘special case’ there, since we are looking for an abelian extension whose Galois group has prime exponent.)
It is not hard to give an explicit argument in the present situation, using (the totally real part of) cyclotomic extensions in the number field case, and the analogous Carlitz module construction (see [Reference RosenRos02, ch. 12]) over a suitable subfield
![]() $\mathbb{F}_{p}(T)\subseteq K$
in the function field case.◻
$\mathbb{F}_{p}(T)\subseteq K$
in the function field case.◻
Remark 3.2. This choice of a distinguished abelian extension of
![]() $K$
is already present in previous papers, in the special case
$K$
is already present in previous papers, in the special case
![]() $l=k=2$
; most notably in [Reference ParkPar13, §3.3], a field extension
$l=k=2$
; most notably in [Reference ParkPar13, §3.3], a field extension
![]() $K(\sqrt{a},\sqrt{b})/K$
is chosen. Likewise, the modulus
$K(\sqrt{a},\sqrt{b})/K$
is chosen. Likewise, the modulus
![]() $8$
which appears throughout [Reference KoenigsmannKoe16] can be retrospectively explained by an implicit choice of field extension
$8$
which appears throughout [Reference KoenigsmannKoe16] can be retrospectively explained by an implicit choice of field extension
![]() $\mathbb{Q}(\sqrt{2},\sqrt{-1})/\mathbb{Q}$
. The paper [Reference Eisenträger and MorrisonEM16] independently from us transfers some of the ideas of [Reference ParkPar13] to the setting of global function fields. Note however that in our situation the analogy between function fields and number fields is more direct: we do not have to impose the condition that
$\mathbb{Q}(\sqrt{2},\sqrt{-1})/\mathbb{Q}$
. The paper [Reference Eisenträger and MorrisonEM16] independently from us transfers some of the ideas of [Reference ParkPar13] to the setting of global function fields. Note however that in our situation the analogy between function fields and number fields is more direct: we do not have to impose the condition that
![]() $M$
be linearly disjoint from the Hilbert class field of
$M$
be linearly disjoint from the Hilbert class field of
![]() $K$
as in (the proof of) [Reference ParkPar13, Lemma 3.19], a condition that [Reference Eisenträger and MorrisonEM16] changes in the function field situation.
$K$
as in (the proof of) [Reference ParkPar13, Lemma 3.19], a condition that [Reference Eisenträger and MorrisonEM16] changes in the function field situation.
Let us write
![]() $I_{\mathfrak{m}}\leqslant I_{{\mathcal{O}}_{K}}$
for the set of fractional ideals of
$I_{\mathfrak{m}}\leqslant I_{{\mathcal{O}}_{K}}$
for the set of fractional ideals of
![]() ${\mathcal{O}}_{K}$
in which none of the prime ideals ramified in
${\mathcal{O}}_{K}$
in which none of the prime ideals ramified in
![]() $M/K$
occur in numerator or denominator. Then we obtain the well-known Artin map
$M/K$
occur in numerator or denominator. Then we obtain the well-known Artin map
as the unique homomorphism sending an unramified prime ideal to its Frobenius element. (In the function field case, note that since all infinite places are completely split in
![]() $M/K$
, this map is induced by the Artin map on divisors.) Write
$M/K$
, this map is induced by the Artin map on divisors.) Write
![]() $H<I_{\mathfrak{m}}$
for the kernel of this map.
$H<I_{\mathfrak{m}}$
for the kernel of this map.
By the Chebotarev density theorem, the set of prime ideals (excluding those at infinity and ramified ones) mapping to a given element of
![]() $\operatorname{Gal}(M/K)$
, i.e. in a given coset in
$\operatorname{Gal}(M/K)$
, i.e. in a given coset in
![]() $I_{m}/H$
, has density
$I_{m}/H$
, has density
![]() $1/|\operatorname{Gal}(M/K)|=1/|I_{\mathfrak{m}}/H|=l^{-k}$
. (Throughout, it does not matter whether we choose natural or Dirichlet density.)
$1/|\operatorname{Gal}(M/K)|=1/|I_{\mathfrak{m}}/H|=l^{-k}$
. (Throughout, it does not matter whether we choose natural or Dirichlet density.)
By class field theory (see e.g. [Reference LangLan70, X, §2] for number fields and [Reference RosenRos02, Theorem 9.23] for function fields), there exists a modulus or cycle
![]() $\mathfrak{m}=\sum _{\mathfrak{p}}n_{\mathfrak{p}}\mathfrak{p}$
, a formal sum of places of
$\mathfrak{m}=\sum _{\mathfrak{p}}n_{\mathfrak{p}}\mathfrak{p}$
, a formal sum of places of
![]() $K$
ramified in
$K$
ramified in
![]() $M$
with
$M$
with
![]() $n_{\mathfrak{p}}\geqslant 0$
, such that
$n_{\mathfrak{p}}\geqslant 0$
, such that
![]() $H$
contains the subgroup
$H$
contains the subgroup
![]() $P_{\mathfrak{m}}=\{(a):a\in U_{\mathfrak{m}}\}$
, where
$P_{\mathfrak{m}}=\{(a):a\in U_{\mathfrak{m}}\}$
, where
The quotient group
![]() $I_{\mathfrak{m}}/P_{\mathfrak{m}}$
, a generalised ideal class group, is finite.
$I_{\mathfrak{m}}/P_{\mathfrak{m}}$
, a generalised ideal class group, is finite.
Now choose subextensions
![]() $M_{1},\ldots ,M_{k}$
with
$M_{1},\ldots ,M_{k}$
with
![]() $\operatorname{Gal}(M_{i}/K)\cong \mathbb{Z}/l\mathbb{Z}$
such that
$\operatorname{Gal}(M_{i}/K)\cong \mathbb{Z}/l\mathbb{Z}$
such that
![]() $M$
is the composite of the
$M$
is the composite of the
![]() $M_{i}$
. Furthermore, fix a generator
$M_{i}$
. Furthermore, fix a generator
![]() $\unicode[STIX]{x1D70E}_{i}$
of
$\unicode[STIX]{x1D70E}_{i}$
of
![]() $\operatorname{Gal}(M_{i}/K)$
for each
$\operatorname{Gal}(M_{i}/K)$
for each
![]() $i$
.
$i$
.
The rest of this section consists of two lemmas needed in the proof of Proposition 4.5.
Lemma 3.3. Let
![]() $a\in K^{\times }$
such that
$a\in K^{\times }$
such that
![]() $(a)\in I_{\mathfrak{m}}$
and
$(a)\in I_{\mathfrak{m}}$
and
![]() $(a)\not \in H$
. Then there exist a place
$(a)\not \in H$
. Then there exist a place
![]() $\mathfrak{p}\not \in \unicode[STIX]{x1D6F4}_{\infty }$
and an
$\mathfrak{p}\not \in \unicode[STIX]{x1D6F4}_{\infty }$
and an
![]() $M_{i}$
such that the algebra
$M_{i}$
such that the algebra
![]() $(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
is not split at
$(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
is not split at
![]() $\mathfrak{p}$
, and
$\mathfrak{p}$
, and
![]() $a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
.
$a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
.
Proof. The fractional ideal
![]() $(a)$
of
$(a)$
of
![]() ${\mathcal{O}}_{K}$
factors as a product of prime ideals of
${\mathcal{O}}_{K}$
factors as a product of prime ideals of
![]() $K$
unramified in
$K$
unramified in
![]() $M$
and not in
$M$
and not in
![]() $\unicode[STIX]{x1D6F4}_{\infty }$
. The group
$\unicode[STIX]{x1D6F4}_{\infty }$
. The group
![]() $I_{\mathfrak{m}}/H\cong \operatorname{Gal}(M/K)\cong (\mathbb{Z}/l\mathbb{Z})^{k}$
has exponent
$I_{\mathfrak{m}}/H\cong \operatorname{Gal}(M/K)\cong (\mathbb{Z}/l\mathbb{Z})^{k}$
has exponent
![]() $l$
, hence there exists a prime ideal
$l$
, hence there exists a prime ideal
![]() $\mathfrak{p}\not \in H$
that occurs in
$\mathfrak{p}\not \in H$
that occurs in
![]() $(a)$
with multiplicity not divisible by
$(a)$
with multiplicity not divisible by
![]() $l$
since
$l$
since
![]() $(a)\not \in H$
.
$(a)\not \in H$
.
The prime
![]() $\mathfrak{p}$
is not completely split in
$\mathfrak{p}$
is not completely split in
![]() $M$
since
$M$
since
![]() $\mathfrak{p}\not \in H$
, so there exists some
$\mathfrak{p}\not \in H$
, so there exists some
![]() $M_{i}$
in which
$M_{i}$
in which
![]() $\mathfrak{p}$
is inert, i.e. the local extension
$\mathfrak{p}$
is inert, i.e. the local extension
![]() $M_{i}K_{\mathfrak{p}}/K_{\mathfrak{p}}$
is unramified of degree
$M_{i}K_{\mathfrak{p}}/K_{\mathfrak{p}}$
is unramified of degree
![]() $l$
. Therefore the group of local norms
$l$
. Therefore the group of local norms
![]() $\operatorname{N}_{M_{i}K_{\mathfrak{p}}/K_{\mathfrak{p}}}((M_{i}K_{\mathfrak{p}})^{\times })\subseteq K_{\mathfrak{p}}^{\times }$
consists of the elements of
$\operatorname{N}_{M_{i}K_{\mathfrak{p}}/K_{\mathfrak{p}}}((M_{i}K_{\mathfrak{p}})^{\times })\subseteq K_{\mathfrak{p}}^{\times }$
consists of the elements of
![]() $l$
-divisible valuation; thus
$l$
-divisible valuation; thus
![]() $a$
is not a local norm and therefore
$a$
is not a local norm and therefore
![]() $(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
is not split at
$(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
is not split at
![]() $\mathfrak{p}$
.◻
$\mathfrak{p}$
.◻
Lemma 3.4. Let
![]() $P\subset \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
be a set of places of density at least
$P\subset \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
be a set of places of density at least
![]() $1/n!$
. Then there exists
$1/n!$
. Then there exists
![]() $a\in K^{\times }$
such that
$a\in K^{\times }$
such that
![]() $(a)\in I_{\mathfrak{m}}$
,
$(a)\in I_{\mathfrak{m}}$
,
![]() $(a)\not \in H$
and all places
$(a)\not \in H$
and all places
![]() $\mathfrak{p}\in \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
with
$\mathfrak{p}\in \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
with
![]() $a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
are in
$a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
are in
![]() $P$
.
$P$
.
Proof. We may remove the finitely many places ramified in
![]() $M/K$
from
$M/K$
from
![]() $P$
without affecting the hypotheses.
$P$
without affecting the hypotheses.
The set
![]() $P$
has density at least
$P$
has density at least
![]() $1/n!>|\operatorname{Cl}({\mathcal{O}}_{K})|/|I_{\mathfrak{m}}/H|$
. Since the set of prime ideals in each coset in
$1/n!>|\operatorname{Cl}({\mathcal{O}}_{K})|/|I_{\mathfrak{m}}/H|$
. Since the set of prime ideals in each coset in
![]() $I_{\mathfrak{m}}/H$
has density
$I_{\mathfrak{m}}/H$
has density
![]() $1/|I_{\mathfrak{m}}/H|$
as noted above,
$1/|I_{\mathfrak{m}}/H|$
as noted above,
![]() $P$
contains prime ideals from at least
$P$
contains prime ideals from at least
![]() $|\operatorname{Cl}({\mathcal{O}}_{K})|+1$
different cosets; thus we may pick
$|\operatorname{Cl}({\mathcal{O}}_{K})|+1$
different cosets; thus we may pick
![]() $\mathfrak{p},\mathfrak{p}^{\prime }\in P$
in different classes in
$\mathfrak{p},\mathfrak{p}^{\prime }\in P$
in different classes in
![]() $I_{\mathfrak{m}}/H$
and in the same class in
$I_{\mathfrak{m}}/H$
and in the same class in
![]() $\operatorname{Cl}({\mathcal{O}}_{K})$
.
$\operatorname{Cl}({\mathcal{O}}_{K})$
.
Now
![]() $\mathfrak{p}{\mathfrak{p}^{\prime }}^{-1}$
is a principal fractional ideal of
$\mathfrak{p}{\mathfrak{p}^{\prime }}^{-1}$
is a principal fractional ideal of
![]() ${\mathcal{O}}_{K}$
; pick a generator
${\mathcal{O}}_{K}$
; pick a generator
![]() $a$
. By construction, this generator satisfies all of the requirements.◻
$a$
. By construction, this generator satisfies all of the requirements.◻
4 A diophantine criterion for proper extensions of global fields
In this section we find an existential sentence that distinguishes the fixed global field
![]() $K$
from its finite extensions of degree
$K$
from its finite extensions of degree
![]() $n$
, see Theorem 4.8.
$n$
, see Theorem 4.8.
Definition 4.1. Let
![]() $L/K$
be an extension of degree
$L/K$
be an extension of degree
![]() $n$
and
$n$
and
![]() $l\mid n$
a prime number. A prime ideal
$l\mid n$
a prime number. A prime ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $K$
is
$K$
is
![]() $l$
-good (for
$l$
-good (for
![]() $L$
) if it is unramified in
$L$
) if it is unramified in
![]() $L$
and for all prime ideals
$L$
and for all prime ideals
![]() $\mathfrak{q}$
of
$\mathfrak{q}$
of
![]() $L$
above
$L$
above
![]() $\mathfrak{p}$
the inertia degree
$\mathfrak{p}$
the inertia degree
![]() $[{\mathcal{O}}_{L}/\mathfrak{q}:{\mathcal{O}}_{K}/\mathfrak{p}]$
is divisible by
$[{\mathcal{O}}_{L}/\mathfrak{q}:{\mathcal{O}}_{K}/\mathfrak{p}]$
is divisible by
![]() $l$
.
$l$
.
The prime number
![]() $l\mid n$
is admissible (for
$l\mid n$
is admissible (for
![]() $L$
) if either:
$L$
) if either:
(i)
 $L/K$
is separable and the set of
$L/K$
is separable and the set of
 $l$
-good prime ideals of
$l$
-good prime ideals of
 $K$
has density at least
$K$
has density at least
 $1/n!$
; or
$1/n!$
; or(ii)
 $L/K$
is inseparable and
$L/K$
is inseparable and
 $l=\operatorname{char}K$
.
$l=\operatorname{char}K$
.
Lemma 4.2. For every
![]() $L/K$
of degree
$L/K$
of degree
![]() $n$
there exists an admissible
$n$
there exists an admissible
![]() $l\mid n$
.
$l\mid n$
.
Proof. If
![]() $L/K$
is inseparable, then by basic field theory
$L/K$
is inseparable, then by basic field theory
![]() $\operatorname{char}K\mid n$
, so
$\operatorname{char}K\mid n$
, so
![]() $l=\operatorname{char}K$
is admissible. Let us now assume that
$l=\operatorname{char}K$
is admissible. Let us now assume that
![]() $L/K$
is separable.
$L/K$
is separable.
Let
![]() $L^{\prime }/K$
be the Galois hull of
$L^{\prime }/K$
be the Galois hull of
![]() $L/K$
,
$L/K$
,
![]() $G=\operatorname{Gal}(L^{\prime }/K)$
,
$G=\operatorname{Gal}(L^{\prime }/K)$
,
![]() $H=\operatorname{Gal}(L^{\prime }/L)\gneqq G$
. Then
$H=\operatorname{Gal}(L^{\prime }/L)\gneqq G$
. Then
![]() $|G|\leqslant n!$
. Let
$|G|\leqslant n!$
. Let
![]() $g\in G$
of prime power order
$g\in G$
of prime power order
![]() $l^{r}$
with
$l^{r}$
with
![]() $l\mid n$
such that no conjugate of
$l\mid n$
such that no conjugate of
![]() $g$
is in
$g$
is in
![]() $H$
. Existence of such
$H$
. Existence of such
![]() $g$
is assured by Theorem 4.3 below: an element
$g$
is assured by Theorem 4.3 below: an element
![]() $g$
has no conjugate in
$g$
has no conjugate in
![]() $H$
if and only if
$H$
if and only if
![]() $g$
has no fixed point in the left-multiplication action of
$g$
has no fixed point in the left-multiplication action of
![]() $G$
on
$G$
on
![]() $\unicode[STIX]{x1D6FA}=G/H$
. If
$\unicode[STIX]{x1D6FA}=G/H$
. If
![]() $\mathfrak{q}$
is a prime ideal of
$\mathfrak{q}$
is a prime ideal of
![]() $L^{\prime }$
above an unramified ideal
$L^{\prime }$
above an unramified ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $K$
such that
$K$
such that
![]() $\operatorname{Frob}(\mathfrak{q}/\mathfrak{p})$
is conjugate to
$\operatorname{Frob}(\mathfrak{q}/\mathfrak{p})$
is conjugate to
![]() $g$
, then the inertia degree
$g$
, then the inertia degree
![]() $f(\mathfrak{q}/\mathfrak{p})$
is equal to
$f(\mathfrak{q}/\mathfrak{p})$
is equal to
![]() $\operatorname{ord}(g)=l^{r}$
, so for
$\operatorname{ord}(g)=l^{r}$
, so for
![]() $\mathfrak{q}^{\prime }=\mathfrak{q}\cap L$
we have
$\mathfrak{q}^{\prime }=\mathfrak{q}\cap L$
we have
![]() $f(\mathfrak{q}^{\prime }/\mathfrak{p})\neq 1$
since
$f(\mathfrak{q}^{\prime }/\mathfrak{p})\neq 1$
since
![]() $\operatorname{Frob}(\mathfrak{q}/\mathfrak{p})\not \in H$
, and
$\operatorname{Frob}(\mathfrak{q}/\mathfrak{p})\not \in H$
, and
![]() $f(\mathfrak{q}^{\prime }/\mathfrak{p})\mid l^{r}$
, hence
$f(\mathfrak{q}^{\prime }/\mathfrak{p})\mid l^{r}$
, hence
![]() $l\mid f(\mathfrak{q}^{\prime }/\mathfrak{p})$
. The set of such prime ideals
$l\mid f(\mathfrak{q}^{\prime }/\mathfrak{p})$
. The set of such prime ideals
![]() $\mathfrak{p}$
has density at least
$\mathfrak{p}$
has density at least
![]() $1/n!$
by the Chebotarev density theorem.◻
$1/n!$
by the Chebotarev density theorem.◻
Theorem 4.3 (Fein–Kantor–Schacher).
Let
![]() $G$
be a finite group acting transitively on a set
$G$
be a finite group acting transitively on a set
![]() $\unicode[STIX]{x1D6FA}$
with
$\unicode[STIX]{x1D6FA}$
with
![]() $|\unicode[STIX]{x1D6FA}|>1$
. Then there exists an element
$|\unicode[STIX]{x1D6FA}|>1$
. Then there exists an element
![]() $g\in G$
of prime power order
$g\in G$
of prime power order
![]() $l^{r}$
, with
$l^{r}$
, with
![]() $l\mid |\unicode[STIX]{x1D6FA}|$
, acting without fixed points on
$l\mid |\unicode[STIX]{x1D6FA}|$
, acting without fixed points on
![]() $\unicode[STIX]{x1D6FA}$
.
$\unicode[STIX]{x1D6FA}$
.
Remark 4.4. The paper [Reference Fein, Kantor and SchacherFKS81], in which this theorem was first proved, used it for a similar purpose as we do: classifying relative Brauer groups
![]() $\operatorname{Br}(L/K)$
of global fields. There appears to be no known proof of this theorem that does not use the classification of finite simple groups.
$\operatorname{Br}(L/K)$
of global fields. There appears to be no known proof of this theorem that does not use the classification of finite simple groups.
Proposition 4.5. For a global field
![]() $L/K$
consider the following statement, which we call
$L/K$
consider the following statement, which we call
![]() $(\dagger )_{L/K}^{l}$
.
$(\dagger )_{L/K}^{l}$
.
![]()
Then this statement is false for
![]() $L=K$
, and it is true if
$L=K$
, and it is true if
![]() $L/K$
is an extension of degree
$L/K$
is an extension of degree
![]() $n$
with
$n$
with
![]() $l$
admissible.
$l$
admissible.
Proof. Let us first consider the case
![]() $L=K$
, and assume there were
$L=K$
, and assume there were
![]() $a$
as in the statement. By Lemma 3.3 there exist an
$a$
as in the statement. By Lemma 3.3 there exist an
![]() $M_{i}$
and a place
$M_{i}$
and a place
![]() $\mathfrak{p}\not \in \unicode[STIX]{x1D6F4}_{\infty }$
such that the algebra
$\mathfrak{p}\not \in \unicode[STIX]{x1D6F4}_{\infty }$
such that the algebra
![]() $(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
is not split at
$(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
is not split at
![]() $\mathfrak{p}$
and
$\mathfrak{p}$
and
![]() $a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
. Hence
$a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
. Hence
![]() $a\not \in T((M_{i},\unicode[STIX]{x1D70E}_{i},a))^{\times }$
by Proposition 2.9 in contradiction to our assumption on
$a\not \in T((M_{i},\unicode[STIX]{x1D70E}_{i},a))^{\times }$
by Proposition 2.9 in contradiction to our assumption on
![]() $a$
.
$a$
.
Now consider the case of a proper extension
![]() $L/K$
of degree
$L/K$
of degree
![]() $n$
with
$n$
with
![]() $l$
admissible. If
$l$
admissible. If
![]() $L/K$
is inseparable and
$L/K$
is inseparable and
![]() $l=\operatorname{char}K$
, then Proposition 2.10 implies that all algebras
$l=\operatorname{char}K$
, then Proposition 2.10 implies that all algebras
![]() $(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
are split over
$(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
are split over
![]() $L$
, so any choice of
$L$
, so any choice of
![]() $a$
will do as long as
$a$
will do as long as
![]() $(a)\in I_{\mathfrak{m}}$
,
$(a)\in I_{\mathfrak{m}}$
,
![]() $(a)\not \in H$
. Such
$(a)\not \in H$
. Such
![]() $a$
is afforded by Lemma 3.4.
$a$
is afforded by Lemma 3.4.
If
![]() $L/K$
is separable, let
$L/K$
is separable, let
![]() $P\subseteq \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
be the set of
$P\subseteq \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
be the set of
![]() $l$
-good primes; it has density at least
$l$
-good primes; it has density at least
![]() $1/n!$
. Therefore Lemma 3.4 is applicable, so we obtain
$1/n!$
. Therefore Lemma 3.4 is applicable, so we obtain
![]() $a\in K^{\times }$
such that
$a\in K^{\times }$
such that
![]() $(a)\in I_{\mathfrak{m}}$
,
$(a)\in I_{\mathfrak{m}}$
,
![]() $(a)\not \in H$
and all places
$(a)\not \in H$
and all places
![]() $\mathfrak{p}\in \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
such that
$\mathfrak{p}\in \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
such that
![]() $a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
are in
$a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
are in
![]() $P$
. We claim that
$P$
. We claim that
![]() $a$
is as desired, so we must show that
$a$
is as desired, so we must show that
for all
![]() $i$
. The algebras
$i$
. The algebras
![]() $(M_{i},\unicode[STIX]{x1D70E}_{i},a)\otimes _{K}L$
split at all infinite places of
$(M_{i},\unicode[STIX]{x1D70E}_{i},a)\otimes _{K}L$
split at all infinite places of
![]() $L$
by construction of the
$L$
by construction of the
![]() $M_{i}$
, so by Proposition 2.9 it suffices to show that they split at all primes
$M_{i}$
, so by Proposition 2.9 it suffices to show that they split at all primes
![]() $\mathfrak{q}$
of
$\mathfrak{q}$
of
![]() $L$
above primes
$L$
above primes
![]() $\mathfrak{p}\in \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
with
$\mathfrak{p}\in \unicode[STIX]{x1D6F4}\setminus \unicode[STIX]{x1D6F4}_{\infty }$
with
![]() $a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
. But all those
$a\not \in {\mathcal{O}}_{\mathfrak{p}}^{\times }$
. But all those
![]() $\mathfrak{p}$
are
$\mathfrak{p}$
are
![]() $l$
-good, so
$l$
-good, so
![]() $l\mid [L_{\mathfrak{q}}:K_{\mathfrak{p}}]$
and hence
$l\mid [L_{\mathfrak{q}}:K_{\mathfrak{p}}]$
and hence
![]() $L_{\mathfrak{q}}$
does split all
$L_{\mathfrak{q}}$
does split all
![]() $(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
by the theory of central simple algebras over local fields.◻
$(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
by the theory of central simple algebras over local fields.◻
Remark 4.6. The element
![]() $a$
in the statement
$a$
in the statement
![]() $(\dagger )_{L/K}^{l}$
can be multiplied by an arbitrary element of
$(\dagger )_{L/K}^{l}$
can be multiplied by an arbitrary element of
![]() ${\mathcal{O}}_{K}^{\times }$
, i.e. the statement is really one about the principal ideal
${\mathcal{O}}_{K}^{\times }$
, i.e. the statement is really one about the principal ideal
![]() $(a)$
. To see this, observe that
$(a)$
. To see this, observe that
![]() $T$
is invariant under multiplication by
$T$
is invariant under multiplication by
![]() ${\mathcal{O}}_{K}^{\times }$
, and the local splitting behaviour of
${\mathcal{O}}_{K}^{\times }$
, and the local splitting behaviour of
![]() $(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
at a prime
$(M_{i},\unicode[STIX]{x1D70E}_{i},a)$
at a prime
![]() $\mathfrak{p}$
unramified in
$\mathfrak{p}$
unramified in
![]() $M/K$
only depends on the valuation
$M/K$
only depends on the valuation
![]() $v_{\mathfrak{p}}(a)$
, since the local norm group contains the local unit group for unramified extensions.
$v_{\mathfrak{p}}(a)$
, since the local norm group contains the local unit group for unramified extensions.
For each class of ideals in the set
![]() $(I_{\mathfrak{m}}/P_{\mathfrak{m}})\setminus (H/P_{\mathfrak{m}})$
that contains a principal (fractional) ideal, fix a representative principal ideal
$(I_{\mathfrak{m}}/P_{\mathfrak{m}})\setminus (H/P_{\mathfrak{m}})$
that contains a principal (fractional) ideal, fix a representative principal ideal
![]() $(a_{j})$
and a generator
$(a_{j})$
and a generator
![]() $a_{j}\in K^{\times }$
thereof. This is a finite list since
$a_{j}\in K^{\times }$
thereof. This is a finite list since
![]() $I_{\mathfrak{m}}/P_{\mathfrak{m}}$
is finite. Thus every principal ideal in
$I_{\mathfrak{m}}/P_{\mathfrak{m}}$
is finite. Thus every principal ideal in
![]() $I_{\mathfrak{m}}\setminus H$
has the form
$I_{\mathfrak{m}}\setminus H$
has the form
![]() $(a_{j}b)$
for some
$(a_{j}b)$
for some
![]() $b\in U_{\mathfrak{m}}$
and one of the
$b\in U_{\mathfrak{m}}$
and one of the
![]() $a_{j}$
. Therefore, by Remark 4.6, we may rephrase the statement
$a_{j}$
. Therefore, by Remark 4.6, we may rephrase the statement
![]() $(\dagger )_{L/K}^{l}$
as follows.
$(\dagger )_{L/K}^{l}$
as follows.
For some
![]() $a_{j}$
, there exists a
$a_{j}$
, there exists a
![]() $b\in U_{\mathfrak{m}}$
such that for all
$b\in U_{\mathfrak{m}}$
such that for all
![]() $i$
we have
$i$
we have
This statement is of a very specific form; in fact, we will show that is equivalent to a certain system of polynomial equations
![]() $G_{r}(x_{1},\ldots ,x_{s},y_{1},\ldots ,y_{t})=0$
having a solution in
$G_{r}(x_{1},\ldots ,x_{s},y_{1},\ldots ,y_{t})=0$
having a solution in
![]() $K^{s}\times L^{t}$
. We again adopt the viewpoint of first-order logic in phrasing and proving this expressibility result.
$K^{s}\times L^{t}$
. We again adopt the viewpoint of first-order logic in phrasing and proving this expressibility result.
Lemma 4.7. Consider the first-order language of pairs of rings, i.e. with signature
![]() $(+,\cdot ,0,1,U)$
, where
$(+,\cdot ,0,1,U)$
, where
![]() $U$
is a unary predicate for a distinguished subring. There exists a positive existential sentence
$U$
is a unary predicate for a distinguished subring. There exists a positive existential sentence
![]() $\unicode[STIX]{x1D713}_{K,n,l}$
in this language, with parameters from
$\unicode[STIX]{x1D713}_{K,n,l}$
in this language, with parameters from
![]() $K$
, such that the condition
$K$
, such that the condition
![]() $(\dagger )_{L/K}^{l}$
from Proposition 4.5 is expressed precisely by
$(\dagger )_{L/K}^{l}$
from Proposition 4.5 is expressed precisely by
![]() $(L,K)\models \unicode[STIX]{x1D713}_{K,n,l}$
.
$(L,K)\models \unicode[STIX]{x1D713}_{K,n,l}$
.
Proof. We use the equivalent form of
![]() $(\dagger )_{L/K}^{l}$
introduced above. This statement is straightforwardly written as
$(\dagger )_{L/K}^{l}$
introduced above. This statement is straightforwardly written as
where
![]() $b\in U_{\mathfrak{m}}$
can be phrased as a positive existential statement since
$b\in U_{\mathfrak{m}}$
can be phrased as a positive existential statement since
![]() $U_{\mathfrak{m}}$
is a diophantine subset of
$U_{\mathfrak{m}}$
is a diophantine subset of
![]() $K$
by Corollary 2.13, and
$K$
by Corollary 2.13, and
![]() $a_{j}b\in T((M_{i},\unicode[STIX]{x1D70E}_{i},a_{j}b))$
can likewise be expressed by Lemma 2.14.◻
$a_{j}b\in T((M_{i},\unicode[STIX]{x1D70E}_{i},a_{j}b))$
can likewise be expressed by Lemma 2.14.◻
Theorem 4.8. There exists a positive existential sentence
![]() $\unicode[STIX]{x1D713}_{K,n}$
in the language of pairs of rings, with parameters from
$\unicode[STIX]{x1D713}_{K,n}$
in the language of pairs of rings, with parameters from
![]() $K$
, such that
$K$
, such that
![]() $(K,K)\models \neg \unicode[STIX]{x1D713}_{K,n}$
, but
$(K,K)\models \neg \unicode[STIX]{x1D713}_{K,n}$
, but
![]() $(L,K)\models \unicode[STIX]{x1D713}_{K,n}$
for all extensions
$(L,K)\models \unicode[STIX]{x1D713}_{K,n}$
for all extensions
![]() $L/K$
of degree
$L/K$
of degree
![]() $n$
.
$n$
.
5 Proof of the main results
Lemma 5.1. Let
![]() $f\in K[X]$
be monic of degree
$f\in K[X]$
be monic of degree
![]() $n>1$
, so
$n>1$
, so
![]() $K[X]/(f)$
is a ring into which
$K[X]/(f)$
is a ring into which
![]() $K$
embeds canonically. Then
$K$
embeds canonically. Then
![]() $f$
has no root in
$f$
has no root in
![]() $K$
if and only if either
$K$
if and only if either
![]() $(K[X]/(f),K)\models \unicode[STIX]{x1D713}_{K,n}$
or
$(K[X]/(f),K)\models \unicode[STIX]{x1D713}_{K,n}$
or
![]() $f$
factors as
$f$
factors as
![]() $f=g\cdot h$
with
$f=g\cdot h$
with
![]() $g,h\in K[X]$
of degree
$g,h\in K[X]$
of degree
![]() ${<}n-1$
with both
${<}n-1$
with both
![]() $g$
and
$g$
and
![]() $h$
not having a root in
$h$
not having a root in
![]() $K$
.
$K$
.
Proof. Assume that
![]() $f$
has a root
$f$
has a root
![]() $x\in K$
. Then
$x\in K$
. Then
![]() $K[X]/(X-x)\cong K$
is a homomorphic image of
$K[X]/(X-x)\cong K$
is a homomorphic image of
![]() $K[X]/(f)$
preserving
$K[X]/(f)$
preserving
![]() $K$
. Since
$K$
. Since
![]() $(K,K)\models \neg \unicode[STIX]{x1D713}_{K,n}$
by Theorem 4.8, we obtain
$(K,K)\models \neg \unicode[STIX]{x1D713}_{K,n}$
by Theorem 4.8, we obtain
![]() $(K[X]/(f),K)\not \models \unicode[STIX]{x1D713}_{K,n}$
, since truth of positive existential sentences is preserved under taking homomorphic images. Furthermore
$(K[X]/(f),K)\not \models \unicode[STIX]{x1D713}_{K,n}$
, since truth of positive existential sentences is preserved under taking homomorphic images. Furthermore
![]() $f$
cannot factor as a product of two polynomials in
$f$
cannot factor as a product of two polynomials in
![]() $K[X]$
without roots in
$K[X]$
without roots in
![]() $K$
.
$K$
.
For the converse direction, assume that
![]() $f$
has no root in
$f$
has no root in
![]() $K$
. Then either
$K$
. Then either
![]() $f$
can be written as a product of two polynomials in
$f$
can be written as a product of two polynomials in
![]() $K[X]$
without roots (and therefore each of degree
$K[X]$
without roots (and therefore each of degree
![]() ${>}1$
), or
${>}1$
), or
![]() $f$
is irreducible. In the latter case
$f$
is irreducible. In the latter case
![]() $K[X]/(f)$
is a field of degree
$K[X]/(f)$
is a field of degree
![]() $n$
over
$n$
over
![]() $K$
, so
$K$
, so
![]() $(K[X]/(f),K)\models \unicode[STIX]{x1D713}_{K,n}$
by Theorem 4.8.◻
$(K[X]/(f),K)\models \unicode[STIX]{x1D713}_{K,n}$
by Theorem 4.8.◻
Now we can prove our main theorem.
Theorem 5.2. There exists an existential first-order formula
![]() $\unicode[STIX]{x1D711}_{K,n}(a_{0},\ldots ,a_{n-1})$
in the language of rings, with parameters in
$\unicode[STIX]{x1D711}_{K,n}(a_{0},\ldots ,a_{n-1})$
in the language of rings, with parameters in
![]() $K$
, such that
$K$
, such that
![]() $K\models \unicode[STIX]{x1D711}_{K,n}(a_{0},\ldots ,a_{n-1})$
if and only if the polynomial
$K\models \unicode[STIX]{x1D711}_{K,n}(a_{0},\ldots ,a_{n-1})$
if and only if the polynomial
![]() $f=X^{n}+a_{n-1}X^{n-1}+\cdots +a_{0}$
has no root in
$f=X^{n}+a_{n-1}X^{n-1}+\cdots +a_{0}$
has no root in
![]() $K$
.
$K$
.
Proof. We translate the equivalent statement from Lemma 5.1. Note that
![]() $(K[X]/(f),K)$
, as a structure in the language of pairs of rings, is quantifier-freely definable in
$(K[X]/(f),K)$
, as a structure in the language of pairs of rings, is quantifier-freely definable in
![]() $K$
, since elements of
$K$
, since elements of
![]() $K[X]/(f)$
correspond in a straightforward way to
$K[X]/(f)$
correspond in a straightforward way to
![]() $n$
-tuples of elements of
$n$
-tuples of elements of
![]() $K$
, and the definitions of addition, multiplication, and the distinguished subset
$K$
, and the definitions of addition, multiplication, and the distinguished subset
![]() $K$
are immediate.
$K$
are immediate.
Hence we obtain
![]() $\unicode[STIX]{x1D711}_{K,2}(a_{0},a_{1})$
by rewriting
$\unicode[STIX]{x1D711}_{K,2}(a_{0},a_{1})$
by rewriting
![]() $\big(K[X]/(X^{2}+a_{1}X+a_{0}),K\big)\models \unicode[STIX]{x1D713}_{K,2}$
as a statement about
$\big(K[X]/(X^{2}+a_{1}X+a_{0}),K\big)\models \unicode[STIX]{x1D713}_{K,2}$
as a statement about
![]() $K$
and similarly
$K$
and similarly
![]() $\unicode[STIX]{x1D711}_{K,3}(a_{0},a_{1},a_{2})$
, since polynomials of degree at most
$\unicode[STIX]{x1D711}_{K,3}(a_{0},a_{1},a_{2})$
, since polynomials of degree at most
![]() $3$
cannot factor as polynomials of smaller degrees without roots. For
$3$
cannot factor as polynomials of smaller degrees without roots. For
![]() $\unicode[STIX]{x1D711}_{K,4}$
, we have to allow for the possibility of a reducible polynomial of degree
$\unicode[STIX]{x1D711}_{K,4}$
, we have to allow for the possibility of a reducible polynomial of degree
![]() $4$
without roots, so we rewrite the statement
$4$
without roots, so we rewrite the statement
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle ((K[X]/(X^{4}+a_{3}X^{3}+X^{2}a_{2}+Xa_{1}+x_{0}),K)\models \unicode[STIX]{x1D713}_{K,4})\vee \nonumber\\ \displaystyle & & \displaystyle \displaystyle \exists b_{0},b_{1},c_{0},c_{1}(X^{4}+a_{3}X^{3}+a_{2}X^{2}+a_{1}X+a_{0}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =(X^{2}+b_{1}X+b_{0})(X^{2}+c_{1}X+c_{0})\wedge \unicode[STIX]{x1D711}_{K,2}(b_{0},b_{1})\wedge \unicode[STIX]{x1D711}_{K,2}(c_{0},c_{1}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle ((K[X]/(X^{4}+a_{3}X^{3}+X^{2}a_{2}+Xa_{1}+x_{0}),K)\models \unicode[STIX]{x1D713}_{K,4})\vee \nonumber\\ \displaystyle & & \displaystyle \displaystyle \exists b_{0},b_{1},c_{0},c_{1}(X^{4}+a_{3}X^{3}+a_{2}X^{2}+a_{1}X+a_{0}\nonumber\\ \displaystyle & & \displaystyle \displaystyle =(X^{2}+b_{1}X+b_{0})(X^{2}+c_{1}X+c_{0})\wedge \unicode[STIX]{x1D711}_{K,2}(b_{0},b_{1})\wedge \unicode[STIX]{x1D711}_{K,2}(c_{0},c_{1}))\nonumber\end{eqnarray}$$
as a first-order statement about
![]() $K$
to obtain
$K$
to obtain
![]() $\unicode[STIX]{x1D711}_{K,4}$
; this is again correct by Lemma 5.1. Inductively, we can construct
$\unicode[STIX]{x1D711}_{K,4}$
; this is again correct by Lemma 5.1. Inductively, we can construct
![]() $\unicode[STIX]{x1D711}_{K,n}$
in this manner for all
$\unicode[STIX]{x1D711}_{K,n}$
in this manner for all
![]() $n$
.◻
$n$
.◻
Corollary 5.3. Let
![]() $K^{\ast \ast }\supseteq K^{\ast }$
be any two fields which are both elementary extensions of
$K^{\ast \ast }\supseteq K^{\ast }$
be any two fields which are both elementary extensions of
![]() $K$
. Then
$K$
. Then
![]() $K^{\ast }$
is relatively algebraically closed in
$K^{\ast }$
is relatively algebraically closed in
![]() $K^{\ast \ast }$
.
$K^{\ast \ast }$
.
Proof. Theorem 5.2 is also true in
![]() $K^{\ast }$
and
$K^{\ast }$
and
![]() $K^{\ast \ast }$
, with the same formulae
$K^{\ast \ast }$
, with the same formulae
![]() $\unicode[STIX]{x1D711}_{K,n}$
, by first-order transfer. Let
$\unicode[STIX]{x1D711}_{K,n}$
, by first-order transfer. Let
![]() $f=X^{n}+a_{n-1}X^{n-1}+\cdots a_{0}\in K^{\ast }[X]$
be a polynomial without a root in
$f=X^{n}+a_{n-1}X^{n-1}+\cdots a_{0}\in K^{\ast }[X]$
be a polynomial without a root in
![]() $K^{\ast }$
. Then
$K^{\ast }$
. Then
![]() $K^{\ast }\models \unicode[STIX]{x1D711}_{K,n}(\mathbf{a})$
, therefore
$K^{\ast }\models \unicode[STIX]{x1D711}_{K,n}(\mathbf{a})$
, therefore
![]() $K^{\ast \ast }\models \unicode[STIX]{x1D711}_{K,n}(\mathbf{a})$
(since
$K^{\ast \ast }\models \unicode[STIX]{x1D711}_{K,n}(\mathbf{a})$
(since
![]() $\unicode[STIX]{x1D711}_{K,n}$
is an existential formula), whence
$\unicode[STIX]{x1D711}_{K,n}$
is an existential formula), whence
![]() $f$
does not have a root in
$f$
does not have a root in
![]() $K^{\ast \ast }$
either.◻
$K^{\ast \ast }$
either.◻
Corollary 5.4. There exists a diophantine criterion for a polynomial over
![]() $K$
in an arbitrary number of variables to be irreducible.
$K$
in an arbitrary number of variables to be irreducible.
Proof. Irreducibility is expressible by a universal first-order formula, since
![]() $f$
being irreducible means that for all pairs of polynomials of smaller total degree,
$f$
being irreducible means that for all pairs of polynomials of smaller total degree,
![]() $f$
is not equal to their product. By the Łoś–Tarski preservation theorem of model theory [Reference HodgesHod97, Corollary 5.4.5], this property is expressible by an existential first-order formula with parameters if and only if for every
$f$
is not equal to their product. By the Łoś–Tarski preservation theorem of model theory [Reference HodgesHod97, Corollary 5.4.5], this property is expressible by an existential first-order formula with parameters if and only if for every
![]() $K^{\ast \ast }\supseteq K^{\ast }$
with
$K^{\ast \ast }\supseteq K^{\ast }$
with
![]() $K^{\ast \ast },K^{\ast }\succcurlyeq K$
every irreducible polynomial over
$K^{\ast \ast },K^{\ast }\succcurlyeq K$
every irreducible polynomial over
![]() $K^{\ast }$
remains irreducible over
$K^{\ast }$
remains irreducible over
![]() $K^{\ast \ast }$
.
$K^{\ast \ast }$
.
We shall now show that this condition follows from relative algebraic closedness. Consider an irreducible polynomial
![]() $f\in K^{\ast }[\mathbf{X}]$
, and assume without loss of generality (after affine change of coordinates and rescaling) that
$f\in K^{\ast }[\mathbf{X}]$
, and assume without loss of generality (after affine change of coordinates and rescaling) that
![]() $f$
has constant coefficient
$f$
has constant coefficient
![]() $1$
. Then
$1$
. Then
![]() $f$
factors into irreducible factors
$f$
factors into irreducible factors
![]() $f_{1},\ldots ,f_{n}\in \overline{K^{\ast }}[\mathbf{X}]$
, each with constant coefficient
$f_{1},\ldots ,f_{n}\in \overline{K^{\ast }}[\mathbf{X}]$
, each with constant coefficient
![]() $1$
, and these factors remain irreducible in
$1$
, and these factors remain irreducible in
![]() $\overline{K^{\ast \ast }}[\mathbf{X}]$
. If
$\overline{K^{\ast \ast }}[\mathbf{X}]$
. If
![]() $f$
factors non-trivially as
$f$
factors non-trivially as
![]() $g\cdot h$
in
$g\cdot h$
in
![]() $K^{\ast \ast }[\mathbf{X}]$
, we may assume after rescaling that both
$K^{\ast \ast }[\mathbf{X}]$
, we may assume after rescaling that both
![]() $g$
and
$g$
and
![]() $h$
have constant coefficient
$h$
have constant coefficient
![]() $1$
, so
$1$
, so
![]() $g,h$
can be factored into products of the
$g,h$
can be factored into products of the
![]() $f_{i}$
in
$f_{i}$
in
![]() $\overline{K^{\ast \ast }}[\mathbf{X}]$
since this is a unique factorisation domain. But then the coefficients of
$\overline{K^{\ast \ast }}[\mathbf{X}]$
since this is a unique factorisation domain. But then the coefficients of
![]() $g$
and
$g$
and
![]() $h$
are both in
$h$
are both in
![]() $\overline{K^{\ast }}$
and in
$\overline{K^{\ast }}$
and in
![]() $K^{\ast \ast }$
, so they are in
$K^{\ast \ast }$
, so they are in
![]() $K^{\ast }$
, contradicting
$K^{\ast }$
, contradicting
![]() $f$
being irreducible.◻
$f$
being irreducible.◻
Acknowledgement
I would like to thank my PhD supervisor, Jochen Koenigsmann, for helpful discussions on the subject of this paper and comments on the exposition.