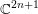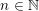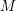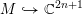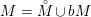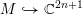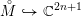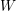1 Introduction and main results
Let
![]() $W$
be a complex manifold of odd dimension
$W$
be a complex manifold of odd dimension
 $2n+1\geqslant 3$
. A holomorphic vector subbundle
$2n+1\geqslant 3$
. A holomorphic vector subbundle
 $\mathscr{L}\subset TW$
of complex codimension one in the tangent bundle
$\mathscr{L}\subset TW$
of complex codimension one in the tangent bundle
![]() $TW$
defines a holomorphic contact structure on
$TW$
defines a holomorphic contact structure on
![]() $W$
if every point
$W$
if every point
![]() $p\in W$
admits an open neighborhood
$p\in W$
admits an open neighborhood
![]() $U\subset W$
such that
$U\subset W$
such that
 $\mathscr{L}|_{U}=\ker \unicode[STIX]{x1D70F}$
is defined by a holomorphic
$\mathscr{L}|_{U}=\ker \unicode[STIX]{x1D70F}$
is defined by a holomorphic
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D70F}$
on
$\unicode[STIX]{x1D70F}$
on
![]() $U$
satisfying
$U$
satisfying
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}\wedge (d\unicode[STIX]{x1D70F})^{n}=\unicode[STIX]{x1D70F}\wedge d\unicode[STIX]{x1D70F}\,\wedge \stackrel{n\text{ times}}{\cdots }\wedge \,d\unicode[STIX]{x1D70F}\neq 0\quad \text{everywhere on }U.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}\wedge (d\unicode[STIX]{x1D70F})^{n}=\unicode[STIX]{x1D70F}\wedge d\unicode[STIX]{x1D70F}\,\wedge \stackrel{n\text{ times}}{\cdots }\wedge \,d\unicode[STIX]{x1D70F}\neq 0\quad \text{everywhere on }U.\end{eqnarray}$$
This nondegeneracy condition depends only on the subbundle
![]() $\mathscr{L}$
and not on the particular choice of the local defining
$\mathscr{L}$
and not on the particular choice of the local defining
![]() $1$
-form. The pair
$1$
-form. The pair
![]() $(W,\mathscr{L})$
is called a complex contact manifold. When
$(W,\mathscr{L})$
is called a complex contact manifold. When
 $\mathscr{L}=\ker \unicode[STIX]{x1D70F}$
for a globally defined holomorphic
$\mathscr{L}=\ker \unicode[STIX]{x1D70F}$
for a globally defined holomorphic
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D70F}$
on
$\unicode[STIX]{x1D70F}$
on
![]() $W$
, we shall write
$W$
, we shall write
![]() $(W,\unicode[STIX]{x1D70F})$
instead of
$(W,\unicode[STIX]{x1D70F})$
instead of
![]() $(W,\mathscr{L})$
. A contact subbundle
$(W,\mathscr{L})$
. A contact subbundle
![]() $\mathscr{L}$
is maximally nonintegrable, meaning that it has no integral complex submanifolds (i.e., tangent to
$\mathscr{L}$
is maximally nonintegrable, meaning that it has no integral complex submanifolds (i.e., tangent to
![]() $\mathscr{L}$
) of dimension greater than
$\mathscr{L}$
) of dimension greater than
![]() $n$
. In fact, local holomorphic vector fields tangent to
$n$
. In fact, local holomorphic vector fields tangent to
![]() $\mathscr{L}$
, along with their first-order commutators, span
$\mathscr{L}$
, along with their first-order commutators, span
![]() $TW$
at every point. Although the geometry of smooth contact manifolds is a classical subject with a large literature devoted to it (we refer e.g. to Geiges’ surveys [Reference GeigesGei08, Reference GeigesGei12] and the references therein), many important questions remain open in the holomorphic case.
$TW$
at every point. Although the geometry of smooth contact manifolds is a classical subject with a large literature devoted to it (we refer e.g. to Geiges’ surveys [Reference GeigesGei08, Reference GeigesGei12] and the references therein), many important questions remain open in the holomorphic case.
The most basic example of a complex contact manifold is the complex Euclidean space
![]() $\mathbb{C}^{2n+1}$
endowed with the standard holomorphic contact form
$\mathbb{C}^{2n+1}$
endowed with the standard holomorphic contact form
 $$\begin{eqnarray}\unicode[STIX]{x1D702}=dz+\mathop{\sum }_{j=1}^{n}x_{j}\,dy_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}=dz+\mathop{\sum }_{j=1}^{n}x_{j}\,dy_{j}.\end{eqnarray}$$
Here,
 $(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
denote the complex coordinates on
$(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
denote the complex coordinates on
![]() $\mathbb{C}^{2n+1}$
. By Darboux’s theorem (see Theorem A.2 in the Appendix A), every complex contact manifold
$\mathbb{C}^{2n+1}$
. By Darboux’s theorem (see Theorem A.2 in the Appendix A), every complex contact manifold
 $(W^{2n+1},\mathscr{L})$
is locally contactomorphic to
$(W^{2n+1},\mathscr{L})$
is locally contactomorphic to
 $(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
, meaning that in a neighborhood of any point
$(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
, meaning that in a neighborhood of any point
![]() $p\in W$
there are local holomorphic coordinates
$p\in W$
there are local holomorphic coordinates
 $(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
in which
$(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
in which
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
.
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
.
Let
![]() $(W,\mathscr{L})$
be a complex contact manifold of dimension
$(W,\mathscr{L})$
be a complex contact manifold of dimension
![]() $2n+1$
. A holomorphic map
$2n+1$
. A holomorphic map
 $F:M\rightarrow W$
from a complex manifold
$F:M\rightarrow W$
from a complex manifold
![]() $M$
is said to be
$M$
is said to be
![]() $\mathscr{L}$
-Legendrian if
$\mathscr{L}$
-Legendrian if
 $$\begin{eqnarray}dF_{p}(T_{p}M)\subset \mathscr{L}_{F(p)}\text{ holds for all points }p\in M.\end{eqnarray}$$
$$\begin{eqnarray}dF_{p}(T_{p}M)\subset \mathscr{L}_{F(p)}\text{ holds for all points }p\in M.\end{eqnarray}$$
If
 $\mathscr{L}=\ker \unicode[STIX]{x1D70F}$
for a contact
$\mathscr{L}=\ker \unicode[STIX]{x1D70F}$
for a contact
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D70F}$
, then the above condition is equivalent to
$\unicode[STIX]{x1D70F}$
, then the above condition is equivalent to
 $$\begin{eqnarray}F^{\ast }\unicode[STIX]{x1D70F}=0.\end{eqnarray}$$
$$\begin{eqnarray}F^{\ast }\unicode[STIX]{x1D70F}=0.\end{eqnarray}$$
This condition is independent of the local parametrization of
![]() $M$
and hence can be treated in local holomorphic coordinates on
$M$
and hence can be treated in local holomorphic coordinates on
![]() $M$
. If
$M$
. If
![]() $F$
is nondegenerate (i.e., an immersion at a generic point of
$F$
is nondegenerate (i.e., an immersion at a generic point of
![]() $M$
), then
$M$
), then
 $\dim _{\mathbb{C}}M\leqslant n$
since
$\dim _{\mathbb{C}}M\leqslant n$
since
![]() $\mathscr{L}$
is maximally nonintegrable. (When
$\mathscr{L}$
is maximally nonintegrable. (When
 $\dim M<n$
, such maps are often referred to as isotropic; we prefer to use the term Legendrian even in this subcritical case.) The case when
$\dim M<n$
, such maps are often referred to as isotropic; we prefer to use the term Legendrian even in this subcritical case.) The case when
![]() $M$
is compact and
$M$
is compact and
![]() $W$
is the projective space
$W$
is the projective space
![]() $\mathbb{CP}^{2n+1}$
, endowed with the contact form obtained by projectivizing the standard symplectic form of
$\mathbb{CP}^{2n+1}$
, endowed with the contact form obtained by projectivizing the standard symplectic form of
![]() $\mathbb{C}^{2n+2}$
(see § 2.1), has been a major focus of interest in the theory. An important result in this subject is that every compact Riemann surface embeds as a complex Legendrian curve in
$\mathbb{C}^{2n+2}$
(see § 2.1), has been a major focus of interest in the theory. An important result in this subject is that every compact Riemann surface embeds as a complex Legendrian curve in
![]() $\mathbb{CP}^{3}$
(see Bryant [Reference BryantBry82, Theorem G] and Segre [Reference SegreSeg26]). On the other hand, when
$\mathbb{CP}^{3}$
(see Bryant [Reference BryantBry82, Theorem G] and Segre [Reference SegreSeg26]). On the other hand, when
![]() $M$
is an open Riemann surface, an
$M$
is an open Riemann surface, an
![]() $\mathscr{L}$
-Legendrian holomorphic map
$\mathscr{L}$
-Legendrian holomorphic map
 $F:M\rightarrow W$
is called an
$F:M\rightarrow W$
is called an
![]() $\mathscr{L}$
-Legendrian curve; if
$\mathscr{L}$
-Legendrian curve; if
 $(W,\mathscr{L})=(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
then we shall just say that
$(W,\mathscr{L})=(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
then we shall just say that
![]() $F$
is a Legendrian curve in
$F$
is a Legendrian curve in
![]() $\mathbb{C}^{2n+1}$
. The latter are complex analogues of real Legendrian curves in
$\mathbb{C}^{2n+1}$
. The latter are complex analogues of real Legendrian curves in
![]() $\mathbb{R}^{2n+1}$
which play a major role in differential geometry.
$\mathbb{R}^{2n+1}$
which play a major role in differential geometry.
The aim of this paper is a systematic investigation of holomorphic Legendrian curves in
![]() $\mathbb{C}^{2n+1}$
for any
$\mathbb{C}^{2n+1}$
for any
![]() $n\in \mathbb{N}$
. In particular, we settle some general questions raised by Alarcón and Forstnerič in [Reference Alarcón and ForstneričAF14, p. 740], as well as a couple of other well-known open problems in the theory. Moreover, as we shall see later in this introduction, our results also find applications to holomorphic Legendrian curves in an arbitrary complex contact manifold.
$n\in \mathbb{N}$
. In particular, we settle some general questions raised by Alarcón and Forstnerič in [Reference Alarcón and ForstneričAF14, p. 740], as well as a couple of other well-known open problems in the theory. Moreover, as we shall see later in this introduction, our results also find applications to holomorphic Legendrian curves in an arbitrary complex contact manifold.
The following first main result of the paper concerns the existence of properly embedded Legendrian curves in the standard contact manifold
 $(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
.
$(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
.
Theorem 1.1 (Runge approximation by proper Legendrian embeddings).
Let
![]() $M$
be an open Riemann surface and
$M$
be an open Riemann surface and
 $K\subset M$
be a smoothly bounded compact domain in
$K\subset M$
be a smoothly bounded compact domain in
![]() $M$
whose complement has no relatively compact connected components. Then every holomorphic Legendrian curve
$M$
whose complement has no relatively compact connected components. Then every holomorphic Legendrian curve
 $F:K\rightarrow \mathbb{C}^{2n+1}$
$F:K\rightarrow \mathbb{C}^{2n+1}$
![]() $(n\in \mathbb{N})$
can be approximated as closely as desired in the
$(n\in \mathbb{N})$
can be approximated as closely as desired in the
![]() $\mathscr{C}^{1}(K)$
-topology by proper holomorphic Legendrian embeddings
$\mathscr{C}^{1}(K)$
-topology by proper holomorphic Legendrian embeddings
 $\widetilde{F}:M{\hookrightarrow}\mathbb{C}^{2n+1}$
. Furthermore, given a pair of indices
$\widetilde{F}:M{\hookrightarrow}\mathbb{C}^{2n+1}$
. Furthermore, given a pair of indices
 $\{i,j\}\subset \{1,2,\ldots ,2n+1\}$
with
$\{i,j\}\subset \{1,2,\ldots ,2n+1\}$
with
![]() $i\neq j$
, we may choose
$i\neq j$
, we may choose
 $\widetilde{F}=(\widetilde{F}_{1},\widetilde{F}_{2},\ldots ,\widetilde{F}_{2n+1})$
as above such that
$\widetilde{F}=(\widetilde{F}_{1},\widetilde{F}_{2},\ldots ,\widetilde{F}_{2n+1})$
as above such that
 $(\widetilde{F}_{i},\widetilde{F}_{j}):M\rightarrow \mathbb{C}^{2}$
is a proper map.
$(\widetilde{F}_{i},\widetilde{F}_{j}):M\rightarrow \mathbb{C}^{2}$
is a proper map.
Theorem 1.1 shows in particular that every open Riemann surface properly embeds into
![]() $\mathbb{C}^{3}$
as a complex Legendrian curve. This result, which is analogous to Bryant’s embedding theorem for compact Riemann surfaces as complex Legendrian curves in
$\mathbb{C}^{3}$
as a complex Legendrian curve. This result, which is analogous to Bryant’s embedding theorem for compact Riemann surfaces as complex Legendrian curves in
![]() $\mathbb{CP}^{3}$
(see [Reference BryantBry82, Theorem G] and [Reference SegreSeg26]), has been a long-standing open problem in complex contact geometry.
$\mathbb{CP}^{3}$
(see [Reference BryantBry82, Theorem G] and [Reference SegreSeg26]), has been a long-standing open problem in complex contact geometry.
Theorem 1.1 is a particular case of Theorem 5.1, where the latter result also ensures approximation of Mergelyan type on certain admissible subsets (see § 4 for definitions and preliminary results). The key ingredients in the proof of Theorem 5.1 are a Mergelyan theorem for Legendrian curves (see Lemma 4.3) and a general position theorem ensuring that every holomorphic Legendrian curve
 $K\rightarrow \mathbb{C}^{2n+1}$
, where
$K\rightarrow \mathbb{C}^{2n+1}$
, where
![]() $K$
is as in Theorem 1.1, may be approximated in the
$K$
is as in Theorem 1.1, may be approximated in the
![]() $\mathscr{C}^{1}(K)$
-topology by holomorphic Legendrian embeddings
$\mathscr{C}^{1}(K)$
-topology by holomorphic Legendrian embeddings
 $K{\hookrightarrow}\mathbb{C}^{2n+1}$
(see Lemma 4.4). The methods of proof exploit the classical Runge and Mergelyan approximation theorems for holomorphic functions on open Riemann surfaces and the construction of period-dominating sprays of Legendrian curves. Further, to ensure the general position result, we use the classical proof of the transversality theorem due to Abraham [Reference AbrahamAbr63]. Similar techniques have been developed by the authors in the theories of minimal surfaces in the real Euclidean space
$K{\hookrightarrow}\mathbb{C}^{2n+1}$
(see Lemma 4.4). The methods of proof exploit the classical Runge and Mergelyan approximation theorems for holomorphic functions on open Riemann surfaces and the construction of period-dominating sprays of Legendrian curves. Further, to ensure the general position result, we use the classical proof of the transversality theorem due to Abraham [Reference AbrahamAbr63]. Similar techniques have been developed by the authors in the theories of minimal surfaces in the real Euclidean space
![]() $\mathbb{R}^{N}$
$\mathbb{R}^{N}$
 $(N\geqslant 3)$
, null holomorphic curves in
$(N\geqslant 3)$
, null holomorphic curves in
![]() $\mathbb{C}^{N}$
, and, more generally, holomorphic immersions of open Riemann surfaces into
$\mathbb{C}^{N}$
, and, more generally, holomorphic immersions of open Riemann surfaces into
![]() $\mathbb{C}^{N}$
which are directed by Oka conical subvarieties (see [Reference Alarcón and LópezAL12, Reference Alarcón and LópezAL13, Reference Alarcón and LópezAL14, Reference Alarcón and ForstneričAF14, Reference Alarcón and LópezAL15, Reference Alarcón, Forstnerič and LópezAFL16c, Reference Alarcón, Forstnerič and LópezAFL16b, Reference Alarcón, Forstnerič and LópezAFL16a] and the references therein). The main difference here is that the holomorphic distribution controlling Legendrian curves depends on the base point, and this requires a novel approach. Finally, with Lemmas 4.3 and 4.4 in hand, Theorem 5.1 follows by a standard recursive argument.
$\mathbb{C}^{N}$
which are directed by Oka conical subvarieties (see [Reference Alarcón and LópezAL12, Reference Alarcón and LópezAL13, Reference Alarcón and LópezAL14, Reference Alarcón and ForstneričAF14, Reference Alarcón and LópezAL15, Reference Alarcón, Forstnerič and LópezAFL16c, Reference Alarcón, Forstnerič and LópezAFL16b, Reference Alarcón, Forstnerič and LópezAFL16a] and the references therein). The main difference here is that the holomorphic distribution controlling Legendrian curves depends on the base point, and this requires a novel approach. Finally, with Lemmas 4.3 and 4.4 in hand, Theorem 5.1 follows by a standard recursive argument.
Our second main theorem concerns the existence of complete bounded Legendrian curves with Jordan boundaries in the contact manifold
 $(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
(cf. (1.1)) for any
$(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
(cf. (1.1)) for any
![]() $n\in \mathbb{N}$
.
$n\in \mathbb{N}$
.
Theorem 1.2 (Complete Legendrian curves with Jordan boundaries).
Let
![]() $M$
be a compact bordered Riemann surface with nonempty boundary
$M$
be a compact bordered Riemann surface with nonempty boundary
![]() $bM$
. Every Legendrian curve
$bM$
. Every Legendrian curve
 $F:M\rightarrow \mathbb{C}^{2n+1}$
$F:M\rightarrow \mathbb{C}^{2n+1}$
![]() $(n\in \mathbb{N})$
of class
$(n\in \mathbb{N})$
of class
![]() $\mathscr{A}^{1}(M)$
can be approximated uniformly on
$\mathscr{A}^{1}(M)$
can be approximated uniformly on
![]() $M$
by continuous injective maps
$M$
by continuous injective maps
 $\widetilde{F}:M{\hookrightarrow}\mathbb{C}^{2n+1}$
whose restriction to the interior
$\widetilde{F}:M{\hookrightarrow}\mathbb{C}^{2n+1}$
whose restriction to the interior
 ${M\unicode[STIX]{x0030A}}=M\setminus bM$
is a complete holomorphic Legendrian embedding
${M\unicode[STIX]{x0030A}}=M\setminus bM$
is a complete holomorphic Legendrian embedding
 ${M\unicode[STIX]{x0030A}}{\hookrightarrow}\mathbb{C}^{2n+1}$
.
${M\unicode[STIX]{x0030A}}{\hookrightarrow}\mathbb{C}^{2n+1}$
.
Recall that a compact bordered Riemann surface is the same thing as a smoothly bounded compact domain in an open Riemann surface (see § 2.2 for a precise definition). An immersion
 $\unicode[STIX]{x1D711}:R\rightarrow \mathbb{C}^{N}$
of a smooth open surface
$\unicode[STIX]{x1D711}:R\rightarrow \mathbb{C}^{N}$
of a smooth open surface
![]() $R$
into
$R$
into
![]() $\mathbb{C}^{N}$
is said to be complete if the Riemannian metric on
$\mathbb{C}^{N}$
is said to be complete if the Riemannian metric on
![]() $R$
induced by the Euclidean metric of
$R$
induced by the Euclidean metric of
![]() $\mathbb{C}^{N}$
via
$\mathbb{C}^{N}$
via
![]() $\unicode[STIX]{x1D711}$
is complete.
$\unicode[STIX]{x1D711}$
is complete.
The existence of complete bounded holomorphic Legendrian curves in
![]() $\mathbb{C}^{2n+1}$
for any
$\mathbb{C}^{2n+1}$
for any
![]() $n\in \mathbb{N}$
is derived from Theorem 1.2; this settles the question posed by Martín et al. [Reference Martín, Umehara and YamadaMUY14, p. 314]. Theorem 1.2 is also connected to the problem, raised by Yang in 1977 (see [Reference YangYan77a, Question II] and [Reference YangYan77b]), about the existence of complete bounded immersed or embedded complex submanifolds of a complex Euclidean space. For recent advances and a history of this problem, we refer to the papers by Alarcón and Forstnerič [Reference Alarcón and ForstneričAF13], Alarcón and López [Reference Alarcón and LópezAL16], Globevnik [Reference GlobevnikGlo15], and Alarcón et al. [Reference Alarcón, Globevnik and LópezAGL16].
$n\in \mathbb{N}$
is derived from Theorem 1.2; this settles the question posed by Martín et al. [Reference Martín, Umehara and YamadaMUY14, p. 314]. Theorem 1.2 is also connected to the problem, raised by Yang in 1977 (see [Reference YangYan77a, Question II] and [Reference YangYan77b]), about the existence of complete bounded immersed or embedded complex submanifolds of a complex Euclidean space. For recent advances and a history of this problem, we refer to the papers by Alarcón and Forstnerič [Reference Alarcón and ForstneričAF13], Alarcón and López [Reference Alarcón and LópezAL16], Globevnik [Reference GlobevnikGlo15], and Alarcón et al. [Reference Alarcón, Globevnik and LópezAGL16].
The proof of Theorem 1.2 requires, in addition to the above mentioned approximation and desingularization results given by Lemmas 4.3 and 4.4, to approximately solve certain Riemann–Hilbert type boundary value problems for Legendrian curves in
![]() $\mathbb{C}^{2n+1}$
; see Lemma 3.2 and Theorem 3.3.
$\mathbb{C}^{2n+1}$
; see Lemma 3.2 and Theorem 3.3.
The analogues of Theorem 1.2 have already been established for complex curves in
![]() $\mathbb{C}^{k}$
$\mathbb{C}^{k}$
![]() $(k\geqslant 2)$
, minimal surfaces in
$(k\geqslant 2)$
, minimal surfaces in
![]() $\mathbb{R}^{N}$
$\mathbb{R}^{N}$
 $(N\geqslant 3)$
, and null holomorphic curves in
$(N\geqslant 3)$
, and null holomorphic curves in
![]() $\mathbb{C}^{N}$
$\mathbb{C}^{N}$
 $(N\geqslant 3)$
; see Alarcón et al. [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, Theorems 1.1 and 1.6] and also [Reference Alarcón and ForstneričAF15, Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15a] where approximate solutions to Riemann–Hilbert problems for minimal surfaces and null curves are provided. With the Mergelyan theorem, the desingularization theorem, and the Riemann–Hilbert method for Legendrian curves in hand, the proof of Theorem 1.2 is an adaptation of [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, proof of Theorem 1.1]. For this reason, and with simplicity of exposition in mind, we provide the details only in the case when
$(N\geqslant 3)$
; see Alarcón et al. [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, Theorems 1.1 and 1.6] and also [Reference Alarcón and ForstneričAF15, Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15a] where approximate solutions to Riemann–Hilbert problems for minimal surfaces and null curves are provided. With the Mergelyan theorem, the desingularization theorem, and the Riemann–Hilbert method for Legendrian curves in hand, the proof of Theorem 1.2 is an adaptation of [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, proof of Theorem 1.1]. For this reason, and with simplicity of exposition in mind, we provide the details only in the case when
![]() $M$
is the closed unit disk
$M$
is the closed unit disk
![]() $\overline{\mathbb{D}}\subset \mathbb{C}$
(see Theorem 6.2); the proof of the general case is a simple adaptation of this special case as in the cited works. An important ingredient in the proof is the observation that almost every affine complex hyperplane of
$\overline{\mathbb{D}}\subset \mathbb{C}$
(see Theorem 6.2); the proof of the general case is a simple adaptation of this special case as in the cited works. An important ingredient in the proof is the observation that almost every affine complex hyperplane of
![]() $\mathbb{C}^{2n+1}$
contains properly embedded Legendrian curves
$\mathbb{C}^{2n+1}$
contains properly embedded Legendrian curves
 $\mathbb{C}{\hookrightarrow}\mathbb{C}^{2n+1}$
passing through any given point in the hyperplane (see Proposition 6.1).
$\mathbb{C}{\hookrightarrow}\mathbb{C}^{2n+1}$
passing through any given point in the hyperplane (see Proposition 6.1).
As a consequence of Theorem 1.2 and Darboux’s theorem for complex contact manifolds (see Theorem A.2), we obtain the following existence result for complete, relatively compact, Legendrian curves in an arbitrary complex contact manifold.
Corollary 1.3. Let
![]() $(W,\mathscr{L})$
be a complex contact manifold. Given any compact bordered Riemann surface
$(W,\mathscr{L})$
be a complex contact manifold. Given any compact bordered Riemann surface
![]() $M$
, there exists a continuous injective map
$M$
, there exists a continuous injective map
 $M{\hookrightarrow}W$
whose restriction to
$M{\hookrightarrow}W$
whose restriction to
![]() ${M\unicode[STIX]{x0030A}}$
is a holomorphic Legendrian embedding that is complete with respect to every Riemannian metric on
${M\unicode[STIX]{x0030A}}$
is a holomorphic Legendrian embedding that is complete with respect to every Riemannian metric on
![]() $W$
.
$W$
.
Proof. Let
 $\dim W=2n+1\geqslant 3$
. By Darboux’s theorem (see Theorem A.2), every point of
$\dim W=2n+1\geqslant 3$
. By Darboux’s theorem (see Theorem A.2), every point of
![]() $W$
has a neighborhood
$W$
has a neighborhood
![]() $U\subset W$
and holomorphic coordinates
$U\subset W$
and holomorphic coordinates
 $\unicode[STIX]{x1D6F7}=(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
on
$\unicode[STIX]{x1D6F7}=(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
on
![]() $U$
such that
$U$
such that
 $\mathscr{L}|_{U}=\ker \unicode[STIX]{x1D6F7}^{\ast }(\unicode[STIX]{x1D702})$
, where
$\mathscr{L}|_{U}=\ker \unicode[STIX]{x1D6F7}^{\ast }(\unicode[STIX]{x1D702})$
, where
![]() $\unicode[STIX]{x1D702}$
is the standard contact form given by (1.1). Let
$\unicode[STIX]{x1D702}$
is the standard contact form given by (1.1). Let
![]() $V\Subset U$
be a relatively compact domain. Theorem 1.2 provides a continuous injective map
$V\Subset U$
be a relatively compact domain. Theorem 1.2 provides a continuous injective map
 $F_{0}:M\rightarrow \unicode[STIX]{x1D6F7}(V)\subset \mathbb{C}^{2n+1}$
whose restriction to
$F_{0}:M\rightarrow \unicode[STIX]{x1D6F7}(V)\subset \mathbb{C}^{2n+1}$
whose restriction to
![]() ${M\unicode[STIX]{x0030A}}$
is a holomorphic
${M\unicode[STIX]{x0030A}}$
is a holomorphic
![]() $\unicode[STIX]{x1D702}$
-Legendrian embedding which is complete with respect to the Euclidean metric
$\unicode[STIX]{x1D702}$
-Legendrian embedding which is complete with respect to the Euclidean metric
 $g_{0}:=|dz|^{2}+\sum _{j=1}^{n}(|dx_{j}|^{2}+|\,dy_{j}|^{2})$
on
$g_{0}:=|dz|^{2}+\sum _{j=1}^{n}(|dx_{j}|^{2}+|\,dy_{j}|^{2})$
on
![]() $\mathbb{C}^{2n+1}$
. As a consequence,
$\mathbb{C}^{2n+1}$
. As a consequence,
 $F:=\unicode[STIX]{x1D6F7}^{-1}\circ F_{0}:M\rightarrow W$
is
$F:=\unicode[STIX]{x1D6F7}^{-1}\circ F_{0}:M\rightarrow W$
is
![]() $\mathscr{L}$
-Legendrian. Further, since
$\mathscr{L}$
-Legendrian. Further, since
![]() $\overline{V}$
is compact, the restriction to
$\overline{V}$
is compact, the restriction to
![]() $V$
of any Riemannian metric
$V$
of any Riemannian metric
![]() $g$
on
$g$
on
![]() $W$
is comparable to
$W$
is comparable to
 $\unicode[STIX]{x1D6F7}^{\ast }(g_{0}|_{\unicode[STIX]{x1D6F7}(V)})$
, and hence,
$\unicode[STIX]{x1D6F7}^{\ast }(g_{0}|_{\unicode[STIX]{x1D6F7}(V)})$
, and hence,
![]() $F|_{{M\unicode[STIX]{x0030A}}}$
is complete with respect to any such
$F|_{{M\unicode[STIX]{x0030A}}}$
is complete with respect to any such
![]() $g$
. This completes the proof.◻
$g$
. This completes the proof.◻
The paper includes an Appendix A in which we collect some results concerning holomorphic contact and symplectic forms and structures; in particular, the Darboux theorems. These results are well known in the real case, but their complex analogues do not seem easily available in the literature. The proofs in the holomorphic case follow those for the smooth case rather closely, and we do not claim any originality on them.
Our results open several natural new questions and possible directions of future investigation. Explicitly, we pose the following problems.
Problem 1.4. Assume that
![]() $W$
is a complex manifold of dimension
$W$
is a complex manifold of dimension
![]() $n\geqslant 4$
and
$n\geqslant 4$
and
 $\mathscr{L}\subset TW$
is a completely nonintegrable holomorphic subbundle of dimension
$\mathscr{L}\subset TW$
is a completely nonintegrable holomorphic subbundle of dimension
![]() $m$
with
$m$
with
 $2\leqslant m\leqslant n-2$
(i.e., the repeated commutators of holomorphic vector fields tangent to
$2\leqslant m\leqslant n-2$
(i.e., the repeated commutators of holomorphic vector fields tangent to
![]() $\mathscr{L}$
span
$\mathscr{L}$
span
![]() $TW$
). Does Corollary 1.3 hold in this setting, i.e., does every bordered Riemann surface admit a bounded complete holomorphic map (immersion, embedding) to
$TW$
). Does Corollary 1.3 hold in this setting, i.e., does every bordered Riemann surface admit a bounded complete holomorphic map (immersion, embedding) to
![]() $W$
which is tangent to
$W$
which is tangent to
![]() $\mathscr{L}$
?
$\mathscr{L}$
?
Problem 1.5. It has recently been shown by the second named author that for any
![]() $n\geqslant 3$
there exists a holomorphic contact structure on
$n\geqslant 3$
there exists a holomorphic contact structure on
![]() $\mathbb{C}^{2n+1}$
which is Kobayashi hyperbolic, and in particular is not globally contactomorphic to the standard one (see [Reference ForstneričFor17]). Are there infinitely many, or perhaps even uncountable many pairwise nonequivalent complex contact structures on
$\mathbb{C}^{2n+1}$
which is Kobayashi hyperbolic, and in particular is not globally contactomorphic to the standard one (see [Reference ForstneričFor17]). Are there infinitely many, or perhaps even uncountable many pairwise nonequivalent complex contact structures on
![]() $\mathbb{C}^{3}$
? (Eliashberg showed that on
$\mathbb{C}^{3}$
? (Eliashberg showed that on
![]() $\mathbb{R}^{3}$
there exist countably many different isotopy classes of smooth contact structures [Reference EliashbergEli89, Reference EliashbergEli93].)
$\mathbb{R}^{3}$
there exist countably many different isotopy classes of smooth contact structures [Reference EliashbergEli89, Reference EliashbergEli93].)
Problem 1.6. Does the analogue of Theorem 1.1 hold for maps of bordered Riemann surfaces into an arbitrary Stein contact manifold
![]() $(W,\mathscr{L})$
?
$(W,\mathscr{L})$
?
An even more ambitious problem is to develop methods for constructing higher-dimensional complex Legendrian submanifolds in complex contact manifolds. (We refer to Landsberg and Manivel [Reference Landsberg and ManivelLM07] for examples of compact Legendrian submanifolds in the projective space
![]() $\mathbb{CP}^{2n+1}$
endowed with the standard contact structure.) One of the main questions in this direction is the following.
$\mathbb{CP}^{2n+1}$
endowed with the standard contact structure.) One of the main questions in this direction is the following.
Problem 1.7. Let
![]() $X^{n}$
be an
$X^{n}$
be an
![]() $n$
-dimensional Stein manifold for some
$n$
-dimensional Stein manifold for some
![]() $n>1$
. (Recall that
$n>1$
. (Recall that
![]() $1$
-dimensional Stein manifolds are open Riemann surfaces.) Does
$1$
-dimensional Stein manifolds are open Riemann surfaces.) Does
![]() $X$
admit a proper holomorphic contact map (immersion, embedding) into to the standard complex contact manifold
$X$
admit a proper holomorphic contact map (immersion, embedding) into to the standard complex contact manifold
 $(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
?
$(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
?
2 Preliminaries
2.1 The standard holomorphic contact structure on
 $\mathbb{C}^{2n+1}$
$\mathbb{C}^{2n+1}$
Let
![]() $\unicode[STIX]{x1D702}$
denote the contact form (1.1) on the Euclidean space
$\unicode[STIX]{x1D702}$
denote the contact form (1.1) on the Euclidean space
![]() $\mathbb{C}^{2n+1}$
for some
$\mathbb{C}^{2n+1}$
for some
![]() $n\in \mathbb{N}$
. Its differential
$n\in \mathbb{N}$
. Its differential
 $$\begin{eqnarray}d\unicode[STIX]{x1D702}=\mathop{\sum }_{j=1}^{n}dx_{j}\wedge dy_{j}\end{eqnarray}$$
$$\begin{eqnarray}d\unicode[STIX]{x1D702}=\mathop{\sum }_{j=1}^{n}dx_{j}\wedge dy_{j}\end{eqnarray}$$
is the standard holomorphic symplectic form on
 $\mathbb{C}_{x_{1},y_{1},\ldots ,x_{n},y_{n}}^{2n}$
, and
$\mathbb{C}_{x_{1},y_{1},\ldots ,x_{n},y_{n}}^{2n}$
, and
 $$\begin{eqnarray}\unicode[STIX]{x1D702}\wedge (d\unicode[STIX]{x1D702})^{n}=n!\,dx_{1}\wedge dy_{1}\wedge \cdots \wedge dx_{n}\wedge dy_{n}\wedge dz\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}\wedge (d\unicode[STIX]{x1D702})^{n}=n!\,dx_{1}\wedge dy_{1}\wedge \cdots \wedge dx_{n}\wedge dy_{n}\wedge dz\end{eqnarray}$$
is a multiple of the standard holomorphic volume form on
![]() $\mathbb{C}^{2n+1}$
. Note that
$\mathbb{C}^{2n+1}$
. Note that
 $(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
is contactomorphic to the restriction of the holomorphic contact structure
$(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
is contactomorphic to the restriction of the holomorphic contact structure
![]() $\mathscr{L}$
on the projective space
$\mathscr{L}$
on the projective space
![]() $\mathbb{CP}^{2n+1}$
obtained by projectivizing the standard symplectic holomorphic structure
$\mathbb{CP}^{2n+1}$
obtained by projectivizing the standard symplectic holomorphic structure
 $(\mathbb{C}^{2n+2},\unicode[STIX]{x1D6FC})$
given by the symplectic form
$(\mathbb{C}^{2n+2},\unicode[STIX]{x1D6FC})$
given by the symplectic form
 $\unicode[STIX]{x1D6FC}=\sum _{i=0}^{n}dx_{i}\wedge dy_{i}$
. Explicitly, for every complex line
$\unicode[STIX]{x1D6FC}=\sum _{i=0}^{n}dx_{i}\wedge dy_{i}$
. Explicitly, for every complex line
 $\mathbb{C}v\subset \mathbb{C}^{2n+2}$
representing a point
$\mathbb{C}v\subset \mathbb{C}^{2n+2}$
representing a point
 $[v]\in \mathbb{CP}^{2n+1}$
we let
$[v]\in \mathbb{CP}^{2n+1}$
we let
 $\mathscr{L}_{v}=\{[w]\in \mathbb{CP}^{2n+1}:\langle \unicode[STIX]{x1D6FC},v\wedge w\rangle =0\}$
.
$\mathscr{L}_{v}=\{[w]\in \mathbb{CP}^{2n+1}:\langle \unicode[STIX]{x1D6FC},v\wedge w\rangle =0\}$
.
Let us write
 $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{j}=\unicode[STIX]{x2202}_{x_{j}}$
and similarly for the other coordinates on
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}x_{j}=\unicode[STIX]{x2202}_{x_{j}}$
and similarly for the other coordinates on
![]() $\mathbb{C}^{2n+1}$
. Note that
$\mathbb{C}^{2n+1}$
. Note that
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
is a trivial bundle that is spanned at each point by the holomorphic vector fields
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
is a trivial bundle that is spanned at each point by the holomorphic vector fields
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{x_{j}},\quad \unicode[STIX]{x2202}_{y_{j}}-x_{j}\unicode[STIX]{x2202}_{z},\quad j=1,\ldots ,n.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{x_{j}},\quad \unicode[STIX]{x2202}_{y_{j}}-x_{j}\unicode[STIX]{x2202}_{z},\quad j=1,\ldots ,n.\end{eqnarray}$$
Furthermore, we have that
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D702},\unicode[STIX]{x2202}_{z}\rangle =1\quad \text{and}\quad \unicode[STIX]{x2202}_{z}\rfloor d\unicode[STIX]{x1D702}=0\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D702},\unicode[STIX]{x2202}_{z}\rangle =1\quad \text{and}\quad \unicode[STIX]{x2202}_{z}\rfloor d\unicode[STIX]{x1D702}=0\end{eqnarray}$$
where
![]() $\rfloor$
denotes the interior product:
$\rfloor$
denotes the interior product:
 $$\begin{eqnarray}\langle \unicode[STIX]{x2202}_{z}\rfloor d\unicode[STIX]{x1D702},V\rangle =\langle d\unicode[STIX]{x1D702},\unicode[STIX]{x2202}_{z}\wedge V\rangle \quad \text{for any vector field }V.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x2202}_{z}\rfloor d\unicode[STIX]{x1D702},V\rangle =\langle d\unicode[STIX]{x1D702},\unicode[STIX]{x2202}_{z}\wedge V\rangle \quad \text{for any vector field }V.\end{eqnarray}$$
Hence,
![]() $\unicode[STIX]{x2202}_{z}$
is the Reeb vector field of the contact manifold
$\unicode[STIX]{x2202}_{z}$
is the Reeb vector field of the contact manifold
 $(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
(cf. (A.5)). On
$(\mathbb{C}^{2n+1},\unicode[STIX]{x1D702})$
(cf. (A.5)). On
![]() $\mathbb{C}^{3}$
with complex coordinates
$\mathbb{C}^{3}$
with complex coordinates
![]() $x,y,z$
we have
$x,y,z$
we have
 $$\begin{eqnarray}\unicode[STIX]{x1D702}=dz+x\,dy,\quad \unicode[STIX]{x1D702}\wedge d\unicode[STIX]{x1D702}=dx\wedge dy\wedge dz.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}=dz+x\,dy,\quad \unicode[STIX]{x1D702}\wedge d\unicode[STIX]{x1D702}=dx\wedge dy\wedge dz.\end{eqnarray}$$
The projection
 $(x,y,z)\mapsto (y,z)$
is called the front projection and
$(x,y,z)\mapsto (y,z)$
is called the front projection and
 $(x,y,z)\mapsto (x,y)$
is the Lagrange projection.
$(x,y,z)\mapsto (x,y)$
is the Lagrange projection.
Note that the holomorphic distribution
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}\subset T\mathbb{C}^{2n+1}$
is completely noninvolutive. In fact, we have that
$\mathscr{L}=\ker \unicode[STIX]{x1D702}\subset T\mathbb{C}^{2n+1}$
is completely noninvolutive. In fact, we have that
 $[\unicode[STIX]{x2202}_{x_{j}},\unicode[STIX]{x2202}_{y_{j}}-x_{j}\unicode[STIX]{x2202}_{z}]=-\unicode[STIX]{x2202}_{z}$
and the vector fields (2.1) together with
$[\unicode[STIX]{x2202}_{x_{j}},\unicode[STIX]{x2202}_{y_{j}}-x_{j}\unicode[STIX]{x2202}_{z}]=-\unicode[STIX]{x2202}_{z}$
and the vector fields (2.1) together with
![]() $\unicode[STIX]{x2202}_{z}$
clearly span
$\unicode[STIX]{x2202}_{z}$
clearly span
![]() $T\mathbb{C}^{2n+1}$
. It follows that the real and imaginary parts of these vector fields, along with their commutators, span
$T\mathbb{C}^{2n+1}$
. It follows that the real and imaginary parts of these vector fields, along with their commutators, span
![]() $T\mathbb{C}^{2n+1}$
over
$T\mathbb{C}^{2n+1}$
over
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
The following observation will be important at several points of our argumentation.
Remark 2.1. For each
 $j\in \{1,\ldots ,n\}$
, the holomorphic automorphism of
$j\in \{1,\ldots ,n\}$
, the holomorphic automorphism of
![]() $\mathbb{C}^{2n+1}$
given by
$\mathbb{C}^{2n+1}$
given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}(x_{1},y_{1},\ldots ,x_{n},y_{n},z)=(x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}(x_{1},y_{1},\ldots ,x_{n},y_{n},z)=(x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z^{\prime }),\end{eqnarray}$$
where
 $(x_{j}^{\prime },y_{j}^{\prime })=(x_{j},-y_{j})$
,
$(x_{j}^{\prime },y_{j}^{\prime })=(x_{j},-y_{j})$
,
 $(x_{i}^{\prime },y_{i}^{\prime })=(x_{i},y_{i})$
for all
$(x_{i}^{\prime },y_{i}^{\prime })=(x_{i},y_{i})$
for all
![]() $i\neq j$
, and
$i\neq j$
, and
 $z^{\prime }=z+x_{j}y_{j}$
, is an involution satisfying
$z^{\prime }=z+x_{j}y_{j}$
, is an involution satisfying
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}^{\ast }\unicode[STIX]{x1D702}=dz+y_{j}\,dx_{j}+\mathop{\sum }_{i\neq j}x_{i}\,dy_{i}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{j}^{\ast }\unicode[STIX]{x1D702}=dz+y_{j}\,dx_{j}+\mathop{\sum }_{i\neq j}x_{i}\,dy_{i}.\end{eqnarray}$$
More precisely, setting
 $\unicode[STIX]{x1D702}_{j}=dz+y_{j}\,dx_{j}+\sum _{i\neq j}x_{i}\,dy_{i}$
, we have
$\unicode[STIX]{x1D702}_{j}=dz+y_{j}\,dx_{j}+\sum _{i\neq j}x_{i}\,dy_{i}$
, we have
 $\unicode[STIX]{x1D6F7}_{j}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{j}$
, and hence the contact manifolds
$\unicode[STIX]{x1D6F7}_{j}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{j}$
, and hence the contact manifolds
 $(\mathbb{C}^{2n+1},\ker \unicode[STIX]{x1D702})$
and
$(\mathbb{C}^{2n+1},\ker \unicode[STIX]{x1D702})$
and
 $(\mathbb{C}^{2n+1},\ker \unicode[STIX]{x1D702}_{j})$
are contactomorphic and
$(\mathbb{C}^{2n+1},\ker \unicode[STIX]{x1D702}_{j})$
are contactomorphic and
![]() $\unicode[STIX]{x1D6F7}_{j}$
is a contactomorphism between them. In particular,
$\unicode[STIX]{x1D6F7}_{j}$
is a contactomorphism between them. In particular,
![]() $\unicode[STIX]{x1D6F7}_{j}$
maps
$\unicode[STIX]{x1D6F7}_{j}$
maps
![]() $\unicode[STIX]{x1D702}$
-Legendrian curves to
$\unicode[STIX]{x1D702}$
-Legendrian curves to
![]() $\unicode[STIX]{x1D702}_{j}$
-Legendrian curves and vice versa. Thus, the role of the variables
$\unicode[STIX]{x1D702}_{j}$
-Legendrian curves and vice versa. Thus, the role of the variables
![]() $x_{j}$
and
$x_{j}$
and
![]() $y_{j}$
can be interchanged in many arguments.
$y_{j}$
can be interchanged in many arguments.
2.2 Riemann surfaces and mapping spaces
For
![]() $n\in \mathbb{N}$
we denote by
$n\in \mathbb{N}$
we denote by
![]() $|\cdot |$
the Euclidean norm in
$|\cdot |$
the Euclidean norm in
![]() $\mathbb{C}^{n}$
. Given a topological space
$\mathbb{C}^{n}$
. Given a topological space
![]() $L$
and a map
$L$
and a map
 $f:L\rightarrow \mathbb{C}^{n}$
we denote by
$f:L\rightarrow \mathbb{C}^{n}$
we denote by
 $\Vert f\Vert _{0,L}:=\sup \{|f(u)|:u\in L\}$
the supremum norm of
$\Vert f\Vert _{0,L}:=\sup \{|f(u)|:u\in L\}$
the supremum norm of
![]() $f$
.
$f$
.
Let
![]() $M$
be an open Riemann surface. Given a subset
$M$
be an open Riemann surface. Given a subset
 $K\subset M$
, we denote by
$K\subset M$
, we denote by
![]() $\mathscr{O}(K)$
the algebra of all holomorphic functions on open neighborhoods of
$\mathscr{O}(K)$
the algebra of all holomorphic functions on open neighborhoods of
![]() $K$
in
$K$
in
![]() $M$
, where we identify any pair of functions which agree on some neighborhood of
$M$
, where we identify any pair of functions which agree on some neighborhood of
![]() $K$
. In particular,
$K$
. In particular,
![]() $\mathscr{O}(M)$
denotes the algebra of all holomorphic functions
$\mathscr{O}(M)$
denotes the algebra of all holomorphic functions
 $M\rightarrow \mathbb{C}$
.
$M\rightarrow \mathbb{C}$
.
If
![]() $K$
is a smoothly bounded compact domain in
$K$
is a smoothly bounded compact domain in
![]() $M$
and
$M$
and
 $r\in \mathbb{Z}_{+}=\{0,1,2,\ldots \}$
, we denote by
$r\in \mathbb{Z}_{+}=\{0,1,2,\ldots \}$
, we denote by
![]() $\mathscr{C}^{r}(K)$
the algebra of all
$\mathscr{C}^{r}(K)$
the algebra of all
![]() $r$
times continuously differentiable complex-valued functions on
$r$
times continuously differentiable complex-valued functions on
![]() $K$
and by
$K$
and by
![]() $\mathscr{A}^{r}(K)$
the subalgebra of
$\mathscr{A}^{r}(K)$
the subalgebra of
![]() $\mathscr{C}^{r}(M)$
consisting of all functions that are holomorphic in the interior
$\mathscr{C}^{r}(M)$
consisting of all functions that are holomorphic in the interior
 ${K\unicode[STIX]{x0030A}}=K\setminus bK$
. We denote by
${K\unicode[STIX]{x0030A}}=K\setminus bK$
. We denote by
![]() $||f||_{r,K}$
the standard
$||f||_{r,K}$
the standard
![]() $\mathscr{C}^{r}$
norm of a function
$\mathscr{C}^{r}$
norm of a function
 $f\in \mathscr{C}^{r}(K)$
, where the derivatives are measured with respect to a Riemannian metric on
$f\in \mathscr{C}^{r}(K)$
, where the derivatives are measured with respect to a Riemannian metric on
![]() $M$
; the precise choice of the metric will not be important for our purposes. We shall use the same notation for maps
$M$
; the precise choice of the metric will not be important for our purposes. We shall use the same notation for maps
 $f=(f_{1},\ldots ,f_{n}):K\rightarrow \mathbb{C}^{n}$
with
$f=(f_{1},\ldots ,f_{n}):K\rightarrow \mathbb{C}^{n}$
with
 $f_{j}\in \mathscr{C}^{r}(K)$
for
$f_{j}\in \mathscr{C}^{r}(K)$
for
 $j=1,\ldots ,n$
.
$j=1,\ldots ,n$
.
A compact bordered Riemann surface is a compact Riemann surface
![]() $M$
with nonempty boundary
$M$
with nonempty boundary
 $\emptyset \neq bM\subset M$
consisting of finitely many pairwise disjoint smooth Jordan curves. The interior
$\emptyset \neq bM\subset M$
consisting of finitely many pairwise disjoint smooth Jordan curves. The interior
 ${M\unicode[STIX]{x0030A}}=M\setminus bM$
of such
${M\unicode[STIX]{x0030A}}=M\setminus bM$
of such
![]() $M$
is called a bordered Riemann surface. It is classical that every compact bordered Riemann surface
$M$
is called a bordered Riemann surface. It is classical that every compact bordered Riemann surface
![]() $M$
is diffeomorphic to a smoothly bounded compact domain in an open Riemann surface
$M$
is diffeomorphic to a smoothly bounded compact domain in an open Riemann surface
![]() $\widehat{M}$
, and so the function spaces
$\widehat{M}$
, and so the function spaces
 $\mathscr{A}^{r}(M)$
,
$\mathscr{A}^{r}(M)$
,
![]() $r\in \mathbb{Z}_{+}$
, are defined as above.
$r\in \mathbb{Z}_{+}$
, are defined as above.
2.3 Sprays of holomorphic maps
We shall frequently use the notion of a holomorphic spray of maps
 $X\rightarrow Y$
between a pair of complex manifolds. This is simply a holomorphic map
$X\rightarrow Y$
between a pair of complex manifolds. This is simply a holomorphic map
 $F:X\times W\rightarrow Y$
, where
$F:X\times W\rightarrow Y$
, where
![]() $W$
is a connected domain in a Euclidean space
$W$
is a connected domain in a Euclidean space
![]() $\mathbb{C}^{N}$
containing the origin. We often consider
$\mathbb{C}^{N}$
containing the origin. We often consider
 $F_{w}=F(\cdot ,w):X\rightarrow Y$
as a family of holomorphic maps depending holomorphically on the parameter
$F_{w}=F(\cdot ,w):X\rightarrow Y$
as a family of holomorphic maps depending holomorphically on the parameter
![]() $w\in W$
. The map
$w\in W$
. The map
 $F_{0}=F(\cdot ,0)$
is called the core of the spray. The spray is said to be dominating at a point
$F_{0}=F(\cdot ,0)$
is called the core of the spray. The spray is said to be dominating at a point
![]() $x\in X$
if the map
$x\in X$
if the map
 $w\mapsto F(x,w)\in Y$
has maximal rank equal to
$w\mapsto F(x,w)\in Y$
has maximal rank equal to
![]() $\dim Y$
at
$\dim Y$
at
![]() $w=0$
; if this holds at every point of
$w=0$
; if this holds at every point of
![]() $X$
then the spray is said to be dominating (on
$X$
then the spray is said to be dominating (on
![]() $X$
).
$X$
).
Sprays are a useful tool in linearization problems. In particular, in this paper we use period dominating sprays in order to control periods of holomorphic maps from Riemann surfaces in approximation problems; see (3.7) where this notion is first introduced. For a more complete information on holomorphic sprays and their applications we refer the reader to [Reference ForstneričFor11].
3 The Riemann–Hilbert method for Legendrian curves
We shall write
 $\mathbb{D}=\{\unicode[STIX]{x1D701}\in \mathbb{C}:|\unicode[STIX]{x1D701}|<1\}$
and
$\mathbb{D}=\{\unicode[STIX]{x1D701}\in \mathbb{C}:|\unicode[STIX]{x1D701}|<1\}$
and
 $\mathbb{T}=b\mathbb{D}=\{\unicode[STIX]{x1D701}\in \mathbb{C}:|\unicode[STIX]{x1D701}|=1\}$
.
$\mathbb{T}=b\mathbb{D}=\{\unicode[STIX]{x1D701}\in \mathbb{C}:|\unicode[STIX]{x1D701}|=1\}$
.
Lemma 3.1. For every holomorphic disk
 $F=(x,y,z):\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
the map
$F=(x,y,z):\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
the map
 $$\begin{eqnarray}\widetilde{F}(\unicode[STIX]{x1D701})=\biggl(x(\unicode[STIX]{x1D701}),y(\unicode[STIX]{x1D701}),z(\unicode[STIX]{x1D701})-\int _{0}^{\unicode[STIX]{x1D701}}F^{\ast }\unicode[STIX]{x1D702}\biggr),\quad \unicode[STIX]{x1D701}\in \mathbb{D}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{F}(\unicode[STIX]{x1D701})=\biggl(x(\unicode[STIX]{x1D701}),y(\unicode[STIX]{x1D701}),z(\unicode[STIX]{x1D701})-\int _{0}^{\unicode[STIX]{x1D701}}F^{\ast }\unicode[STIX]{x1D702}\biggr),\quad \unicode[STIX]{x1D701}\in \mathbb{D}\end{eqnarray}$$
is a holomorphic Legendrian disk. In particular, for every holomorphic disk
 $F:\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
there exists a Legendrian disk
$F:\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
there exists a Legendrian disk
 $\widetilde{F}:\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
satisfying
$\widetilde{F}:\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
satisfying
 $$\begin{eqnarray}||\widetilde{F}-F||_{0,\mathbb{D}}\leqslant \sup _{|\unicode[STIX]{x1D701}|<1}\biggl|\int _{0}^{\unicode[STIX]{x1D701}}F^{\ast }\unicode[STIX]{x1D702}\biggr|.\end{eqnarray}$$
$$\begin{eqnarray}||\widetilde{F}-F||_{0,\mathbb{D}}\leqslant \sup _{|\unicode[STIX]{x1D701}|<1}\biggl|\int _{0}^{\unicode[STIX]{x1D701}}F^{\ast }\unicode[STIX]{x1D702}\biggr|.\end{eqnarray}$$
Proof. We have
 $(\widetilde{F}^{\ast }\unicode[STIX]{x1D702})(\unicode[STIX]{x1D701})=z^{\prime }(\unicode[STIX]{x1D701})\,d\unicode[STIX]{x1D701}-(F^{\ast }\unicode[STIX]{x1D702})(\unicode[STIX]{x1D701})+\sum _{j=1}^{n}x_{j}(\unicode[STIX]{x1D701})y_{j}^{\prime }(\unicode[STIX]{x1D701})\,d\unicode[STIX]{x1D701}=0.$
◻
$(\widetilde{F}^{\ast }\unicode[STIX]{x1D702})(\unicode[STIX]{x1D701})=z^{\prime }(\unicode[STIX]{x1D701})\,d\unicode[STIX]{x1D701}-(F^{\ast }\unicode[STIX]{x1D702})(\unicode[STIX]{x1D701})+\sum _{j=1}^{n}x_{j}(\unicode[STIX]{x1D701})y_{j}^{\prime }(\unicode[STIX]{x1D701})\,d\unicode[STIX]{x1D701}=0.$
◻
The following lemma provides approximate solutions to the Riemann–Hilbert problem for holomorphic Legendrian disks.
Lemma 3.2. Assume that
 $f=(x,y,z):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
is a holomorphic Legendrian disk of class
$f=(x,y,z):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
is a holomorphic Legendrian disk of class
![]() $\mathscr{A}^{1}(\mathbb{D})$
, and for every
$\mathscr{A}^{1}(\mathbb{D})$
, and for every
![]() $u\in \mathbb{T}$
the map
$u\in \mathbb{T}$
the map
 $$\begin{eqnarray}\overline{\mathbb{D}}\ni v\longmapsto F(u,v)=(X(u,v),Y(u,v),Z(u,v))\in \mathbb{C}^{2n+1}\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbb{D}}\ni v\longmapsto F(u,v)=(X(u,v),Y(u,v),Z(u,v))\in \mathbb{C}^{2n+1}\end{eqnarray}$$
is a Legendrian disk of class
![]() $\mathscr{A}^{1}(\mathbb{D})$
depending continuously on
$\mathscr{A}^{1}(\mathbb{D})$
depending continuously on
![]() $u\in \mathbb{T}$
and such that
$u\in \mathbb{T}$
and such that
 $F(u,0)=f(u)$
holds for all
$F(u,0)=f(u)$
holds for all
![]() $u\in \mathbb{T}$
. Given numbers
$u\in \mathbb{T}$
. Given numbers
![]() $\unicode[STIX]{x1D716}>0$
and
$\unicode[STIX]{x1D716}>0$
and
 $0<\unicode[STIX]{x1D70C}_{0}<1$
, there exist a number
$0<\unicode[STIX]{x1D70C}_{0}<1$
, there exist a number
 $\unicode[STIX]{x1D70C}^{\prime }\in [\unicode[STIX]{x1D70C}_{0},1)$
and a holomorphic Legendrian disk
$\unicode[STIX]{x1D70C}^{\prime }\in [\unicode[STIX]{x1D70C}_{0},1)$
and a holomorphic Legendrian disk
 $G:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
such that
$G:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
such that
 $G(0)=f(0)$
and the following conditions hold:
$G(0)=f(0)$
and the following conditions hold:
-
(i)
 $\sup \{|G(u)-f(u)|:|u|\leqslant \unicode[STIX]{x1D70C}^{\prime }\}<\unicode[STIX]{x1D716}$
;
$\sup \{|G(u)-f(u)|:|u|\leqslant \unicode[STIX]{x1D70C}^{\prime }\}<\unicode[STIX]{x1D716}$
; -
(ii)
 $\text{dist}(G(u),F(u,\mathbb{T}))<\unicode[STIX]{x1D716}$
for all
$\text{dist}(G(u),F(u,\mathbb{T}))<\unicode[STIX]{x1D716}$
for all
 $u\in \mathbb{T}$
; and
$u\in \mathbb{T}$
; and -
(iii)
 $\text{dist}(G(\unicode[STIX]{x1D70C}u),F(u,\overline{\mathbb{D}}))<\unicode[STIX]{x1D716}$
for all
$\text{dist}(G(\unicode[STIX]{x1D70C}u),F(u,\overline{\mathbb{D}}))<\unicode[STIX]{x1D716}$
for all
 $u\in \mathbb{T}$
and all
$u\in \mathbb{T}$
and all
 $\unicode[STIX]{x1D70C}\in [\unicode[STIX]{x1D70C}^{\prime },1)$
.
$\unicode[STIX]{x1D70C}\in [\unicode[STIX]{x1D70C}^{\prime },1)$
.
If in addition
![]() $I$
is a proper closed segment in the circle
$I$
is a proper closed segment in the circle
![]() $\mathbb{T}$
and
$\mathbb{T}$
and
 $F(u,v)=f(u)$
for all
$F(u,v)=f(u)$
for all
 $u\in \mathbb{T}\setminus I$
and
$u\in \mathbb{T}\setminus I$
and
![]() $v\in \overline{\mathbb{D}}$
, then for every open neighborhood
$v\in \overline{\mathbb{D}}$
, then for every open neighborhood
![]() $U$
of
$U$
of
![]() $I$
in
$I$
in
![]() $\overline{\mathbb{D}}$
we may choose
$\overline{\mathbb{D}}$
we may choose
![]() $G$
as above such that it also satisfies the following condition:
$G$
as above such that it also satisfies the following condition:
-
(iv)
 $G$
is
$G$
is
 $\unicode[STIX]{x1D716}$
-close to
$\unicode[STIX]{x1D716}$
-close to
 $f$
in the
$f$
in the
 $\mathscr{C}^{1}$
topology on
$\mathscr{C}^{1}$
topology on
 $\overline{\mathbb{D}}\setminus U$
.
$\overline{\mathbb{D}}\setminus U$
.
Proof. For simplicity of notation we shall consider the case
![]() $n=1$
; the same proof will apply also for
$n=1$
; the same proof will apply also for
![]() $n>1$
.
$n>1$
.
Since we are looking for Legendrian disks
 $G:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
satisfying certain approximate conditions in relationship to
$G:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
satisfying certain approximate conditions in relationship to
![]() $f$
and
$f$
and
![]() $F$
, we may assume by approximation that all our holomorphic Legendrian disks are defined on a fixed open neighborhood of
$F$
, we may assume by approximation that all our holomorphic Legendrian disks are defined on a fixed open neighborhood of
![]() $\overline{\mathbb{D}}$
. Indeed, for
$\overline{\mathbb{D}}$
. Indeed, for
![]() $f$
just use Mergelyan’s approximation for
$f$
just use Mergelyan’s approximation for
![]() $x$
and
$x$
and
![]() $y$
and define
$y$
and define
![]() $z$
in a neighborhood of
$z$
in a neighborhood of
![]() $\overline{\mathbb{D}}$
accordingly; for the boundary disks proceed likewise but using the parametric version of Megelyan’s theorem. For
$\overline{\mathbb{D}}$
accordingly; for the boundary disks proceed likewise but using the parametric version of Megelyan’s theorem. For
 $(u,v)\in \mathbb{T}\times \overline{\mathbb{D}}$
we have
$(u,v)\in \mathbb{T}\times \overline{\mathbb{D}}$
we have
 $$\begin{eqnarray}\displaystyle X(u,v) & = & \displaystyle \mathop{\sum }_{j\geqslant 0}a_{j}(u)v^{j},\nonumber\\ \displaystyle Y(u,v) & = & \displaystyle \mathop{\sum }_{k\geqslant 0}b_{k}(u)v^{k},\nonumber\\ \displaystyle Z(u,v) & = & \displaystyle \mathop{\sum }_{n\geqslant 0}c_{n}(u)v^{n},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X(u,v) & = & \displaystyle \mathop{\sum }_{j\geqslant 0}a_{j}(u)v^{j},\nonumber\\ \displaystyle Y(u,v) & = & \displaystyle \mathop{\sum }_{k\geqslant 0}b_{k}(u)v^{k},\nonumber\\ \displaystyle Z(u,v) & = & \displaystyle \mathop{\sum }_{n\geqslant 0}c_{n}(u)v^{n},\nonumber\end{eqnarray}$$
where the coefficients
![]() $a_{j}$
,
$a_{j}$
,
![]() $b_{k}$
, and
$b_{k}$
, and
![]() $c_{n}$
are continuous functions of
$c_{n}$
are continuous functions of
![]() $u\in \mathbb{T}$
and we have
$u\in \mathbb{T}$
and we have
 $$\begin{eqnarray}a_{0}(u)=x(u),\quad b_{0}(u)=y(u),\quad c_{0}(u)=z(u).\end{eqnarray}$$
$$\begin{eqnarray}a_{0}(u)=x(u),\quad b_{0}(u)=y(u),\quad c_{0}(u)=z(u).\end{eqnarray}$$
The Legendrian condition for the map
 $v\mapsto F(u,v)$
(with a fixed
$v\mapsto F(u,v)$
(with a fixed
![]() $u\in \mathbb{T}$
) says that
$u\in \mathbb{T}$
) says that
 $Z_{v}+XY_{v}=0$
, where the subscript denotes the partial derivative with respect to the indicated variable. From the power series expansions for
$Z_{v}+XY_{v}=0$
, where the subscript denotes the partial derivative with respect to the indicated variable. From the power series expansions for
![]() $X$
and
$X$
and
![]() $Y$
we obtain
$Y$
we obtain
 $$\begin{eqnarray}XY_{v}=\mathop{\sum }_{j\geqslant 0}a_{j}v^{j}\cdot \mathop{\sum }_{k\geqslant 1}b_{k}kv^{k-1}=\mathop{\sum }_{n\geqslant 1}\biggl(\mathop{\sum }_{j+k=n}ka_{j}b_{k}\biggr)v^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}XY_{v}=\mathop{\sum }_{j\geqslant 0}a_{j}v^{j}\cdot \mathop{\sum }_{k\geqslant 1}b_{k}kv^{k-1}=\mathop{\sum }_{n\geqslant 1}\biggl(\mathop{\sum }_{j+k=n}ka_{j}b_{k}\biggr)v^{n-1}.\end{eqnarray}$$
Comparison with
 $$\begin{eqnarray}Z_{v}=\mathop{\sum }_{n\geqslant 1}c_{n}nv^{n-1}\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}=\mathop{\sum }_{n\geqslant 1}c_{n}nv^{n-1}\end{eqnarray}$$
gives the equations
 $$\begin{eqnarray}c_{n}=-\frac{1}{n}\mathop{\sum }_{j+k=n}ka_{j}b_{k},\quad n=1,2,\ldots .\end{eqnarray}$$
$$\begin{eqnarray}c_{n}=-\frac{1}{n}\mathop{\sum }_{j+k=n}ka_{j}b_{k},\quad n=1,2,\ldots .\end{eqnarray}$$
By approximation we may assume that there are only finitely many nonzero coefficients
![]() $a_{j}$
,
$a_{j}$
,
![]() $b_{k}$
and hence
$b_{k}$
and hence
![]() $c_{n}$
, i.e., the Legendrian curves
$c_{n}$
, i.e., the Legendrian curves
 $v\mapsto F(u,v)$
are polynomial in
$v\mapsto F(u,v)$
are polynomial in
![]() $v\in \mathbb{C}$
of bounded degree independent of
$v\in \mathbb{C}$
of bounded degree independent of
![]() $u\in \mathbb{T}$
. Furthermore, we may approximate each of the coefficients
$u\in \mathbb{T}$
. Furthermore, we may approximate each of the coefficients
![]() $a_{j}$
and
$a_{j}$
and
![]() $b_{k}$
(which are continuous functions on
$b_{k}$
(which are continuous functions on
![]() $\mathbb{T}$
) by a rational function with the only pole at
$\mathbb{T}$
) by a rational function with the only pole at
![]() $0$
. In view of the above formulas for the coefficients
$0$
. In view of the above formulas for the coefficients
![]() $c_{n}$
of
$c_{n}$
of
![]() $Z$
these also become rational functions on
$Z$
these also become rational functions on
![]() $\mathbb{C}$
with the only pole at
$\mathbb{C}$
with the only pole at
![]() $0$
. We denote the resulting functions and maps by the same letters. Note that this gives a family of polynomial Legendrian curves
$0$
. We denote the resulting functions and maps by the same letters. Note that this gives a family of polynomial Legendrian curves
 $F(u,\cdot )=(X(u,\cdot ),Y(u,\cdot ),Z(u,\cdot )):\mathbb{C}\rightarrow \mathbb{C}^{3}$
for
$F(u,\cdot )=(X(u,\cdot ),Y(u,\cdot ),Z(u,\cdot )):\mathbb{C}\rightarrow \mathbb{C}^{3}$
for
 $u\in \mathbb{C}\setminus \{0\}$
which are Laurent polynomials in the variable
$u\in \mathbb{C}\setminus \{0\}$
which are Laurent polynomials in the variable
![]() $u$
. In particular, we have that
$u$
. In particular, we have that
 $$\begin{eqnarray}Z_{v}(u,v)+X(u,v)Y_{v}(v,u)=0,\quad u\in \mathbb{C}\setminus \{0\},~v\in \mathbb{C}.\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}(u,v)+X(u,v)Y_{v}(v,u)=0,\quad u\in \mathbb{C}\setminus \{0\},~v\in \mathbb{C}.\end{eqnarray}$$
Let
![]() $N_{0}$
be the biggest degree of pole of any of these coefficients at
$N_{0}$
be the biggest degree of pole of any of these coefficients at
![]() $0$
. For any
$0$
. For any
![]() $N\in \mathbb{N}$
with
$N\in \mathbb{N}$
with
 $N>N_{0}$
the map
$N>N_{0}$
the map
 $F_{N}:\mathbb{C}\rightarrow \mathbb{C}^{3}$
given by
$F_{N}:\mathbb{C}\rightarrow \mathbb{C}^{3}$
given by
 $$\begin{eqnarray}F_{N}(u)=(X_{N}(u),Y_{N}(u),Z_{N}(u)):=F(u,u^{N})=(X(u,u^{N}),Y(u,u^{N}),Z(u,u^{N}))\end{eqnarray}$$
$$\begin{eqnarray}F_{N}(u)=(X_{N}(u),Y_{N}(u),Z_{N}(u)):=F(u,u^{N})=(X(u,u^{N}),Y(u,u^{N}),Z(u,u^{N}))\end{eqnarray}$$
is a holomorphic polynomial with
 $F_{N}(0)=f(0)$
. It is well known that for sufficiently big
$F_{N}(0)=f(0)$
. It is well known that for sufficiently big
![]() $N\in \mathbb{N}$
the map
$N\in \mathbb{N}$
the map
![]() $F_{N}$
satisfies properties (i)–(iv) in the lemma (see e.g. [Reference Drinovec Drnovšek and ForstneričDF12, Lemma 3.1]).
$F_{N}$
satisfies properties (i)–(iv) in the lemma (see e.g. [Reference Drinovec Drnovšek and ForstneričDF12, Lemma 3.1]).
Although the maps
![]() $F_{N}$
obtained in this way need not be Legendrian, we shall now show that for all sufficiently big
$F_{N}$
obtained in this way need not be Legendrian, we shall now show that for all sufficiently big
![]() $N\in \mathbb{N}$
the map
$N\in \mathbb{N}$
the map
![]() $F_{N}$
is as close as desired uniformly on
$F_{N}$
is as close as desired uniformly on
![]() $\overline{\mathbb{D}}$
to a Legendrian disk
$\overline{\mathbb{D}}$
to a Legendrian disk
 $G=G_{N}=(X_{N},Y_{N},\widetilde{Z}_{N}):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
of the form given by Lemma 3.1; this will complete the proof. To this end we estimate the expression
$G=G_{N}=(X_{N},Y_{N},\widetilde{Z}_{N}):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
of the form given by Lemma 3.1; this will complete the proof. To this end we estimate the expression
 $$\begin{eqnarray}F_{N}^{\ast }\unicode[STIX]{x1D702}=dZ_{N}+X_{N}\,dY_{N}.\end{eqnarray}$$
$$\begin{eqnarray}F_{N}^{\ast }\unicode[STIX]{x1D702}=dZ_{N}+X_{N}\,dY_{N}.\end{eqnarray}$$
We have that
 $$\begin{eqnarray}\displaystyle \frac{d}{du}Z(u,u^{N}) & = & \displaystyle Z_{u}(u,u^{N})+Z_{v}(u,u^{N})Nu^{N-1},\nonumber\\ \displaystyle X(u,u^{N})\frac{d}{du}Y(u,u^{N}) & = & \displaystyle X(u,u^{N})(Y_{u}(u,u^{N})+Y_{v}(u,u^{N})Nu^{N-1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{d}{du}Z(u,u^{N}) & = & \displaystyle Z_{u}(u,u^{N})+Z_{v}(u,u^{N})Nu^{N-1},\nonumber\\ \displaystyle X(u,u^{N})\frac{d}{du}Y(u,u^{N}) & = & \displaystyle X(u,u^{N})(Y_{u}(u,u^{N})+Y_{v}(u,u^{N})Nu^{N-1}).\nonumber\end{eqnarray}$$
By adding these two equations and taking into account the condition
 $Z_{v}+XY_{v}=0$
for the Legendrian disk
$Z_{v}+XY_{v}=0$
for the Legendrian disk
 $v\mapsto F(u,v)$
we obtain
$v\mapsto F(u,v)$
we obtain
 $$\begin{eqnarray}F_{N}^{\ast }\unicode[STIX]{x1D702}/du=Z_{u}+Z_{v}Nu^{N-1}+XY_{u}+XY_{v}Nu^{N-1}=Z_{u}+XY_{u}.\end{eqnarray}$$
$$\begin{eqnarray}F_{N}^{\ast }\unicode[STIX]{x1D702}/du=Z_{u}+Z_{v}Nu^{N-1}+XY_{u}+XY_{v}Nu^{N-1}=Z_{u}+XY_{u}.\end{eqnarray}$$
From the power series expansions of
 $F=(X,Y,Z)$
we get
$F=(X,Y,Z)$
we get
 $$\begin{eqnarray}\displaystyle (Z_{u}+XY_{u})(u,u^{N}) & = & \displaystyle \mathop{\sum }_{n\geqslant 0}c_{n}^{\prime }(u)u^{nN}+\mathop{\sum }_{j\geqslant 0}a_{j}(u)u^{jN}\,\,\cdot \mathop{\sum }_{k\geqslant 0}b_{k}^{\prime }(u)u^{kN}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n\geqslant 1}\biggl(c_{n}^{\prime }(u)+\mathop{\sum }_{j+k=n}a_{j}(u)b_{k}^{\prime }(u)\biggr)u^{nN}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (Z_{u}+XY_{u})(u,u^{N}) & = & \displaystyle \mathop{\sum }_{n\geqslant 0}c_{n}^{\prime }(u)u^{nN}+\mathop{\sum }_{j\geqslant 0}a_{j}(u)u^{jN}\,\,\cdot \mathop{\sum }_{k\geqslant 0}b_{k}^{\prime }(u)u^{kN}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n\geqslant 1}\biggl(c_{n}^{\prime }(u)+\mathop{\sum }_{j+k=n}a_{j}(u)b_{k}^{\prime }(u)\biggr)u^{nN}.\nonumber\end{eqnarray}$$
The term with
![]() $n=0$
in the above sum equals
$n=0$
in the above sum equals
 $c_{0}^{\prime }+a_{0}b_{0}^{\prime }=z^{\prime }+xy^{\prime }=0$
since the curve
$c_{0}^{\prime }+a_{0}b_{0}^{\prime }=z^{\prime }+xy^{\prime }=0$
since the curve
 $f=(x,y,z)$
is Legendrian, and hence it drops out from the sum.
$f=(x,y,z)$
is Legendrian, and hence it drops out from the sum.
Recall that each of the coefficients
![]() $a_{j}$
,
$a_{j}$
,
![]() $b_{k}$
and
$b_{k}$
and
![]() $c_{n}$
is Laurent polynomial of the form
$c_{n}$
is Laurent polynomial of the form
 $P(u,1/u)$
where
$P(u,1/u)$
where
![]() $P$
is a holomorphic polynomial on
$P$
is a holomorphic polynomial on
![]() $\mathbb{C}^{2}$
. The same is then true for their derivatives, and hence for the coefficients
$\mathbb{C}^{2}$
. The same is then true for their derivatives, and hence for the coefficients
 $c_{n}^{\prime }+\sum _{j+k=n}a_{j}b_{k}^{\prime }$
in the above expansion of
$c_{n}^{\prime }+\sum _{j+k=n}a_{j}b_{k}^{\prime }$
in the above expansion of
 $Z_{u}+XY_{u}$
. Let
$Z_{u}+XY_{u}$
. Let
![]() $N_{1}$
be the maximal power of
$N_{1}$
be the maximal power of
![]() $1/u$
that appears in any of these finitely many coefficients. If
$1/u$
that appears in any of these finitely many coefficients. If
 $N\geqslant N_{1}$
then the function
$N\geqslant N_{1}$
then the function
 $(Z_{u}+XY_{u})(u,u^{N})$
is a polynomial in
$(Z_{u}+XY_{u})(u,u^{N})$
is a polynomial in
![]() $u$
whose lowest order term is
$u$
whose lowest order term is
![]() $u^{N-N_{1}}$
or higher. Note that
$u^{N-N_{1}}$
or higher. Note that
 $\int _{0}^{\unicode[STIX]{x1D701}}u^{N-N_{1}}\,du=\unicode[STIX]{x1D701}^{N-N_{1}+1}/(N-N_{1}+1)$
which converges to zero uniformly on the disk
$\int _{0}^{\unicode[STIX]{x1D701}}u^{N-N_{1}}\,du=\unicode[STIX]{x1D701}^{N-N_{1}+1}/(N-N_{1}+1)$
which converges to zero uniformly on the disk
![]() $|\unicode[STIX]{x1D701}|\leqslant 1$
when
$|\unicode[STIX]{x1D701}|\leqslant 1$
when
 $N\rightarrow \infty$
. Since we have finitely many such terms in the sum, it follows that the integral
$N\rightarrow \infty$
. Since we have finitely many such terms in the sum, it follows that the integral
 $$\begin{eqnarray}\int _{0}^{\unicode[STIX]{x1D701}}F_{N}^{\ast }\unicode[STIX]{x1D702}=\int _{0}^{\unicode[STIX]{x1D701}}(Z_{u}+XY_{u})(u,u^{N})\,du\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{\unicode[STIX]{x1D701}}F_{N}^{\ast }\unicode[STIX]{x1D702}=\int _{0}^{\unicode[STIX]{x1D701}}(Z_{u}+XY_{u})(u,u^{N})\,du\end{eqnarray}$$
converges to zero uniformly on
![]() $\overline{\mathbb{D}}$
as
$\overline{\mathbb{D}}$
as
 $N\rightarrow +\infty$
. Furthermore, if the last assumption in the lemma holds then we can perform the same construction on a somewhat bigger compact simply connected domain
$N\rightarrow +\infty$
. Furthermore, if the last assumption in the lemma holds then we can perform the same construction on a somewhat bigger compact simply connected domain
![]() $D\subset \mathbb{C}$
containing the disk
$D\subset \mathbb{C}$
containing the disk
![]() $\overline{\mathbb{D}}$
such that
$\overline{\mathbb{D}}$
such that
![]() $I\subset bD$
and
$I\subset bD$
and
 $\overline{\mathbb{D}}\setminus U\subset {D\unicode[STIX]{x0030A}}$
; the
$\overline{\mathbb{D}}\setminus U\subset {D\unicode[STIX]{x0030A}}$
; the
![]() $\mathscr{C}^{0}$
-estimate on
$\mathscr{C}^{0}$
-estimate on
![]() $D\cong \overline{\mathbb{D}}$
then yields
$D\cong \overline{\mathbb{D}}$
then yields
![]() $\mathscr{C}^{1}$
estimate on
$\mathscr{C}^{1}$
estimate on
![]() $\overline{\mathbb{D}}\setminus U$
in view of the Cauchy estimates. Finally, setting
$\overline{\mathbb{D}}\setminus U$
in view of the Cauchy estimates. Finally, setting
 $\widetilde{Z}_{N}(\unicode[STIX]{x1D701})=Z_{N}(\unicode[STIX]{x1D701})-\int _{0}^{\unicode[STIX]{x1D701}}F_{N}^{\ast }\unicode[STIX]{x1D702}$
(cf. Lemma 3.1) gives a sequence of holomorphic Legendrian maps
$\widetilde{Z}_{N}(\unicode[STIX]{x1D701})=Z_{N}(\unicode[STIX]{x1D701})-\int _{0}^{\unicode[STIX]{x1D701}}F_{N}^{\ast }\unicode[STIX]{x1D702}$
(cf. Lemma 3.1) gives a sequence of holomorphic Legendrian maps
 $G_{N}=(X_{N},Y_{N},\widetilde{Z}_{N}):\mathbb{C}\rightarrow \mathbb{C}^{3}$
satisfying the conclusion of Lemma 3.2.◻
$G_{N}=(X_{N},Y_{N},\widetilde{Z}_{N}):\mathbb{C}\rightarrow \mathbb{C}^{3}$
satisfying the conclusion of Lemma 3.2.◻
We now prove the analogous result for any bordered Riemann surface.
Theorem 3.3. Assume that
![]() $M$
is a compact bordered Riemann surface,
$M$
is a compact bordered Riemann surface,
 $I\subset bM$
is an arc which is not a boundary component of
$I\subset bM$
is an arc which is not a boundary component of
![]() $M$
,
$M$
,
 $f=(x,y,z):M\rightarrow \mathbb{C}^{2n+1}$
is a Legendrian map of class
$f=(x,y,z):M\rightarrow \mathbb{C}^{2n+1}$
is a Legendrian map of class
![]() $\mathscr{A}^{1}(M)$
, and for every point
$\mathscr{A}^{1}(M)$
, and for every point
 $u\in bM$
the map
$u\in bM$
the map
 $$\begin{eqnarray}\overline{\mathbb{D}}\ni v\longmapsto F(u,v)=(X(u,v),Y(u,v),Z(u,v))\in \mathbb{C}^{2n+1}\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbb{D}}\ni v\longmapsto F(u,v)=(X(u,v),Y(u,v),Z(u,v))\in \mathbb{C}^{2n+1}\end{eqnarray}$$
is a Legendrian disk of class
![]() $\mathscr{A}^{1}(\mathbb{D})$
, depending continuously on
$\mathscr{A}^{1}(\mathbb{D})$
, depending continuously on
 $u\in bM$
, such that
$u\in bM$
, such that
 $F(u,0)=f(u)$
for all
$F(u,0)=f(u)$
for all
 $u\in bM$
and
$u\in bM$
and
 $F(u,v)=f(u)$
for all
$F(u,v)=f(u)$
for all
 $u\in bM\setminus I$
and
$u\in bM\setminus I$
and
![]() $v\in \overline{\mathbb{D}}$
. Given a number
$v\in \overline{\mathbb{D}}$
. Given a number
![]() $\unicode[STIX]{x1D716}>0$
and a neighborhood
$\unicode[STIX]{x1D716}>0$
and a neighborhood
![]() $U\subset M$
of the arc
$U\subset M$
of the arc
![]() $I$
, there exist a holomorphic Legendrian map
$I$
, there exist a holomorphic Legendrian map
 $H:M\rightarrow \mathbb{C}^{2n+1}$
and a neighborhood
$H:M\rightarrow \mathbb{C}^{2n+1}$
and a neighborhood
![]() $V\Subset U$
of
$V\Subset U$
of
![]() $I$
with a smooth retraction
$I$
with a smooth retraction
 $\unicode[STIX]{x1D70C}:V\rightarrow V\cap bM$
such that the following conditions hold:
$\unicode[STIX]{x1D70C}:V\rightarrow V\cap bM$
such that the following conditions hold:
-
(i)
 $\sup \{|H(u)-f(u)|:u\in M\setminus V\}<\unicode[STIX]{x1D716}$
;
$\sup \{|H(u)-f(u)|:u\in M\setminus V\}<\unicode[STIX]{x1D716}$
; -
(ii)
 $\text{dist}(H(u),F(u,\mathbb{T}))<\unicode[STIX]{x1D716}$
for all
$\text{dist}(H(u),F(u,\mathbb{T}))<\unicode[STIX]{x1D716}$
for all
 $u\in bM$
; and
$u\in bM$
; and -
(iii)
 $\text{dist}(H(u),F(\unicode[STIX]{x1D70C}(u),\overline{\mathbb{D}}))<\unicode[STIX]{x1D716}$
for all
$\text{dist}(H(u),F(\unicode[STIX]{x1D70C}(u),\overline{\mathbb{D}}))<\unicode[STIX]{x1D716}$
for all
 $u\in V$
.
$u\in V$
.
Proof. For simplicity of notation we consider the case
![]() $n=1$
; the same proof applies in general by considering
$n=1$
; the same proof applies in general by considering
![]() $x$
and
$x$
and
![]() $y$
as vector-valued functions and writing
$y$
as vector-valued functions and writing
 $x\,dy=\sum _{i=1}^{n}x_{i}\,dy_{i}$
.
$x\,dy=\sum _{i=1}^{n}x_{i}\,dy_{i}$
.
We may assume that
![]() $M$
is connected. Choose a smoothly bounded simply connected domain
$M$
is connected. Choose a smoothly bounded simply connected domain
![]() $D\subset U$
(a disk) such that
$D\subset U$
(a disk) such that
![]() $D$
is a neighborhood of the closed arc
$D$
is a neighborhood of the closed arc
![]() $I$
. By denting
$I$
. By denting
![]() $bM$
slightly inward along a neighborhood of
$bM$
slightly inward along a neighborhood of
![]() $I$
we can find a smoothly bounded compact domain
$I$
we can find a smoothly bounded compact domain
 $M^{\prime }\subset M$
such that
$M^{\prime }\subset M$
such that
 $M=M^{\prime }\cup D$
and the following separation condition holds:
$M=M^{\prime }\cup D$
and the following separation condition holds:
 $$\begin{eqnarray}\overline{M^{\prime }\setminus D}\cap \overline{D\setminus M^{\prime }}=\emptyset .\end{eqnarray}$$
$$\begin{eqnarray}\overline{M^{\prime }\setminus D}\cap \overline{D\setminus M^{\prime }}=\emptyset .\end{eqnarray}$$
Thus,
 $(M^{\prime },D)$
is a Cartan pair (cf. [Reference ForstneričFor11, Definition 5.7.1]).
$(M^{\prime },D)$
is a Cartan pair (cf. [Reference ForstneričFor11, Definition 5.7.1]).
Let
 $C_{1},\ldots ,C_{\ell }\subset {M\unicode[STIX]{x0030A}}^{\prime }$
be closed curves forming a basis of the homology group
$C_{1},\ldots ,C_{\ell }\subset {M\unicode[STIX]{x0030A}}^{\prime }$
be closed curves forming a basis of the homology group
 $H_{1}(M^{\prime };\mathbb{Z})\cong H_{1}(M;\mathbb{Z})=\mathbb{Z}^{\ell }$
such that the union
$H_{1}(M^{\prime };\mathbb{Z})\cong H_{1}(M;\mathbb{Z})=\mathbb{Z}^{\ell }$
such that the union
 $\bigcup _{j=1}^{\ell }C_{j}$
is Runge in
$\bigcup _{j=1}^{\ell }C_{j}$
is Runge in
![]() $M$
. Consider the period map
$M$
. Consider the period map
 $$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):\mathscr{A}^{1}(M)^{2}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):\mathscr{A}^{1}(M)^{2}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
whose
![]() $j\text{th}$
component equals
$j\text{th}$
component equals
 $$\begin{eqnarray}{\mathcal{P}}_{j}(x,y)=\int _{C_{j}}x\,dy,\quad x,y\in \mathscr{A}^{1}(M).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{j}(x,y)=\int _{C_{j}}x\,dy,\quad x,y\in \mathscr{A}^{1}(M).\end{eqnarray}$$
Note that
 ${\mathcal{P}}(x,y)=0$
if and only if the 1-form
${\mathcal{P}}(x,y)=0$
if and only if the 1-form
![]() $x\,dy$
is exact, and this holds if and only if
$x\,dy$
is exact, and this holds if and only if
![]() $(x,y)$
is the Lagrange projection of a Legendrian curve
$(x,y)$
is the Lagrange projection of a Legendrian curve
 $f=(x,y,z):M\rightarrow \mathbb{C}^{3}$
.
$f=(x,y,z):M\rightarrow \mathbb{C}^{3}$
.
We shall first assume that the second component
![]() $y$
of
$y$
of
![]() $f$
is not constant; then
$f$
is not constant; then
![]() $y|_{C_{j}}$
is not constant for any
$y|_{C_{j}}$
is not constant for any
 $j=1,\ldots ,\ell$
by the identity principle. By the Runge property of
$j=1,\ldots ,\ell$
by the identity principle. By the Runge property of
 $\bigcup _{j=1}^{\ell }C_{j}$
there exist holomorphic functions
$\bigcup _{j=1}^{\ell }C_{j}$
there exist holomorphic functions
 $g_{1},\ldots ,g_{\ell }$
on
$g_{1},\ldots ,g_{\ell }$
on
![]() $M$
such that for every
$M$
such that for every
 $j,k=1,\ldots ,\ell$
the number
$j,k=1,\ldots ,\ell$
the number
 $\int _{C_{j}}g_{k}\,dy\approx \unicode[STIX]{x1D6FF}_{j,k}$
is close to
$\int _{C_{j}}g_{k}\,dy\approx \unicode[STIX]{x1D6FF}_{j,k}$
is close to
![]() $1$
if
$1$
if
![]() $j=k$
and to
$j=k$
and to
![]() $0$
if
$0$
if
![]() $j\neq k$
. (Here,
$j\neq k$
. (Here,
![]() $\unicode[STIX]{x1D6FF}_{j,k}$
is the Kronecker symbol. We first construct smooth functions
$\unicode[STIX]{x1D6FF}_{j,k}$
is the Kronecker symbol. We first construct smooth functions
![]() $g_{k}$
on
$g_{k}$
on
 $\bigcup _{j=1}^{\ell }C_{j}$
such that
$\bigcup _{j=1}^{\ell }C_{j}$
such that
 $\int _{C_{j}}g_{k}\,dy=\unicode[STIX]{x1D6FF}_{j,k}$
and then use Mergelyan’s theorem to approximate them by holomorphic functions on
$\int _{C_{j}}g_{k}\,dy=\unicode[STIX]{x1D6FF}_{j,k}$
and then use Mergelyan’s theorem to approximate them by holomorphic functions on
![]() $M$
.) Let
$M$
.) Let
 $\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{\ell })\in \mathbb{C}^{\ell }$
. Consider the function
$\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{\ell })\in \mathbb{C}^{\ell }$
. Consider the function
 $\widetilde{x}:M\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
given by
$\widetilde{x}:M\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
given by
 $$\begin{eqnarray}\widetilde{x}(u,\unicode[STIX]{x1D701})=x(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in M,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{x}(u,\unicode[STIX]{x1D701})=x(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in M,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
Note that for all
 $j,k\in \{1,\ldots ,\ell \}$
we have
$j,k\in \{1,\ldots ,\ell \}$
we have
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{k}}\bigg|_{\unicode[STIX]{x1D701}=0}\int _{C_{j}}\widetilde{x}(\cdot ,\unicode[STIX]{x1D701})\,dy=\int _{C_{j}}g_{k}\,dy\approx \unicode[STIX]{x1D6FF}_{j,k}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{k}}\bigg|_{\unicode[STIX]{x1D701}=0}\int _{C_{j}}\widetilde{x}(\cdot ,\unicode[STIX]{x1D701})\,dy=\int _{C_{j}}g_{k}\,dy\approx \unicode[STIX]{x1D6FF}_{j,k}.\end{eqnarray}$$
If the above approximations are close enough then
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\bigg|_{\unicode[STIX]{x1D701}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y):\mathbb{C}^{\ell }\longrightarrow \mathbb{C}^{\ell }~\text{is an isomorphism}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\bigg|_{\unicode[STIX]{x1D701}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y):\mathbb{C}^{\ell }\longrightarrow \mathbb{C}^{\ell }~\text{is an isomorphism}.\end{eqnarray}$$
If this holds, then the map (3.5) is called a period dominating holomorphic spray with the core
 $\widetilde{x}(\cdot ,0)=x$
.
$\widetilde{x}(\cdot ,0)=x$
.
Assume now that
 $(x,y)\in \mathscr{A}^{1}(M)^{2}$
is the Lagrange projection of the given Legendrian map
$(x,y)\in \mathscr{A}^{1}(M)^{2}$
is the Lagrange projection of the given Legendrian map
 $f=(x,y,z):M\rightarrow \mathbb{C}^{3}$
; hence
$f=(x,y,z):M\rightarrow \mathbb{C}^{3}$
; hence
 ${\mathcal{P}}(x,y)=0$
. By the inverse function theorem there is a ball
${\mathcal{P}}(x,y)=0$
. By the inverse function theorem there is a ball
 $r\mathbb{B}\subset \mathbb{C}^{\ell }$
around the origin such that the map
$r\mathbb{B}\subset \mathbb{C}^{\ell }$
around the origin such that the map
 $r\mathbb{B}\ni \unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y)\in \mathbb{C}^{\ell }$
is biholomorphic onto its image (a neighborhood of
$r\mathbb{B}\ni \unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y)\in \mathbb{C}^{\ell }$
is biholomorphic onto its image (a neighborhood of
![]() $0\in \mathbb{C}^{\ell }$
). Fix a point
$0\in \mathbb{C}^{\ell }$
). Fix a point
![]() $u_{0}\in D$
and consider the function
$u_{0}\in D$
and consider the function
 $\widetilde{z}:D\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
of class
$\widetilde{z}:D\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
of class
 $\mathscr{A}^{1}(D\times \mathbb{C}^{\ell })$
given by
$\mathscr{A}^{1}(D\times \mathbb{C}^{\ell })$
given by
 $$\begin{eqnarray}\widetilde{z}(u,\unicode[STIX]{x1D701})=z(u_{0})-\int _{u_{0}}^{u}\widetilde{x}(\cdot ,\unicode[STIX]{x1D701})\,dy,\quad u\in D,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{z}(u,\unicode[STIX]{x1D701})=z(u_{0})-\int _{u_{0}}^{u}\widetilde{x}(\cdot ,\unicode[STIX]{x1D701})\,dy,\quad u\in D,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
Recall that
![]() $z$
is the third component of the Legendrian map
$z$
is the third component of the Legendrian map
 $f=(x,y,z):M\rightarrow \mathbb{C}^{3}$
and the integral is taken over any path in the disk
$f=(x,y,z):M\rightarrow \mathbb{C}^{3}$
and the integral is taken over any path in the disk
![]() $D$
. Note that
$D$
. Note that
 $\widetilde{z}(\cdot ,0)=z|_{D}$
since
$\widetilde{z}(\cdot ,0)=z|_{D}$
since
 $\widetilde{x}(\cdot ,0)=x$
and
$\widetilde{x}(\cdot ,0)=x$
and
 $dz=-x\,dy$
. Let
$dz=-x\,dy$
. Let
 $\widetilde{f}:D\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}^{3}$
be the family of Legendrian disks
$\widetilde{f}:D\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}^{3}$
be the family of Legendrian disks
 $$\begin{eqnarray}D\ni u\mapsto \widetilde{f}(u,\unicode[STIX]{x1D701})=(\widetilde{x}(u,\unicode[STIX]{x1D701}),y(u),\widetilde{z}(u,\unicode[STIX]{x1D701}))\in \mathbb{C}^{3}\end{eqnarray}$$
$$\begin{eqnarray}D\ni u\mapsto \widetilde{f}(u,\unicode[STIX]{x1D701})=(\widetilde{x}(u,\unicode[STIX]{x1D701}),y(u),\widetilde{z}(u,\unicode[STIX]{x1D701}))\in \mathbb{C}^{3}\end{eqnarray}$$
depending holomorphically on
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
. (The second component
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
. (The second component
![]() $y$
is independent of the parameter
$y$
is independent of the parameter
![]() $\unicode[STIX]{x1D701}$
.) Note that
$\unicode[STIX]{x1D701}$
.) Note that
 $\widetilde{f}(u,0)=f(u)$
for
$\widetilde{f}(u,0)=f(u)$
for
![]() $u\in D$
.
$u\in D$
.
For each point
 $u\in bD\cap bM$
and for every
$u\in bD\cap bM$
and for every
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
we let
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
we let
 $$\begin{eqnarray}\overline{\mathbb{D}}\ni v\mapsto \widetilde{F}(u,v,\unicode[STIX]{x1D701})=(\widetilde{X}(u,v,\unicode[STIX]{x1D701}),\widetilde{Y}(u,v,\unicode[STIX]{x1D701}),\widetilde{Z}(u,v,\unicode[STIX]{x1D701}))\in \mathbb{C}^{3}\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbb{D}}\ni v\mapsto \widetilde{F}(u,v,\unicode[STIX]{x1D701})=(\widetilde{X}(u,v,\unicode[STIX]{x1D701}),\widetilde{Y}(u,v,\unicode[STIX]{x1D701}),\widetilde{Z}(u,v,\unicode[STIX]{x1D701}))\in \mathbb{C}^{3}\end{eqnarray}$$
be the Legendrian disk of class
![]() $\mathscr{A}^{1}(\mathbb{D})$
given by
$\mathscr{A}^{1}(\mathbb{D})$
given by
 $$\begin{eqnarray}\displaystyle \widetilde{X}(u,v,\unicode[STIX]{x1D701}) & = & \displaystyle X(u,v)+\widetilde{x}(u,\unicode[STIX]{x1D701})-x(u),\nonumber\\ \displaystyle \widetilde{Y}(u,v,\unicode[STIX]{x1D701}) & = & \displaystyle Y(u,v),\nonumber\\ \displaystyle \widetilde{Z}(u,v,\unicode[STIX]{x1D701}) & = & \displaystyle \widetilde{z}(u,\unicode[STIX]{x1D701})-\int _{t=0}^{t=v}\widetilde{X}(u,t,\unicode[STIX]{x1D701})\,d\widetilde{Y}(u,t).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{X}(u,v,\unicode[STIX]{x1D701}) & = & \displaystyle X(u,v)+\widetilde{x}(u,\unicode[STIX]{x1D701})-x(u),\nonumber\\ \displaystyle \widetilde{Y}(u,v,\unicode[STIX]{x1D701}) & = & \displaystyle Y(u,v),\nonumber\\ \displaystyle \widetilde{Z}(u,v,\unicode[STIX]{x1D701}) & = & \displaystyle \widetilde{z}(u,\unicode[STIX]{x1D701})-\int _{t=0}^{t=v}\widetilde{X}(u,t,\unicode[STIX]{x1D701})\,d\widetilde{Y}(u,t).\nonumber\end{eqnarray}$$
When
![]() $\unicode[STIX]{x1D701}=0$
, we have
$\unicode[STIX]{x1D701}=0$
, we have
 $\widetilde{X}(u,v,0)=X(u,v)$
,
$\widetilde{X}(u,v,0)=X(u,v)$
,
 $\widetilde{Y}(u,v,0)=Y(u,v)$
and hence
$\widetilde{Y}(u,v,0)=Y(u,v)$
and hence
 $$\begin{eqnarray}\widetilde{Z}(u,v,0)=z(u)-\int _{0}^{v}X(u,\cdot )\,dY(u,\cdot )=Z(u,v),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(u,v,0)=z(u)-\int _{0}^{v}X(u,\cdot )\,dY(u,\cdot )=Z(u,v),\end{eqnarray}$$
so we see that
 $\widetilde{F}(u,v,0)=F(u,v)$
is the given Legendrian disk in the theorem. Furthermore, setting
$\widetilde{F}(u,v,0)=F(u,v)$
is the given Legendrian disk in the theorem. Furthermore, setting
![]() $v=0$
we have
$v=0$
we have
 $$\begin{eqnarray}\widetilde{F}(u,0,\unicode[STIX]{x1D701})=\widetilde{f}(u,\unicode[STIX]{x1D701}),\quad u\in bD\cap bM,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{F}(u,0,\unicode[STIX]{x1D701})=\widetilde{f}(u,\unicode[STIX]{x1D701}),\quad u\in bD\cap bM,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
Finally, for every point
 $u\in bD\cap bM\setminus I$
and for all
$u\in bD\cap bM\setminus I$
and for all
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
we have
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
we have
 $$\begin{eqnarray}\widetilde{F}(u,v,\unicode[STIX]{x1D701})=\widetilde{F}(u,0,\unicode[STIX]{x1D701})=\widetilde{f}(u,\unicode[STIX]{x1D701}),\quad v\in \overline{\mathbb{D}},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{F}(u,v,\unicode[STIX]{x1D701})=\widetilde{F}(u,0,\unicode[STIX]{x1D701})=\widetilde{f}(u,\unicode[STIX]{x1D701}),\quad v\in \overline{\mathbb{D}},\end{eqnarray}$$
so
 $\widetilde{F}(u,\cdot ,\unicode[STIX]{x1D701})$
is the constant disk. We extend
$\widetilde{F}(u,\cdot ,\unicode[STIX]{x1D701})$
is the constant disk. We extend
![]() $\widetilde{F}$
to all points
$\widetilde{F}$
to all points
![]() $u\in bD$
by setting
$u\in bD$
by setting
 $$\begin{eqnarray}\widetilde{F}(u,v,\unicode[STIX]{x1D701})=\widetilde{f}(u,\unicode[STIX]{x1D701})\quad \text{for all }u\in bD\setminus I,v\in \overline{\mathbb{D}}\text{ and }\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{F}(u,v,\unicode[STIX]{x1D701})=\widetilde{f}(u,\unicode[STIX]{x1D701})\quad \text{for all }u\in bD\setminus I,v\in \overline{\mathbb{D}}\text{ and }\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
Note that
 $\widetilde{f}(\cdot ,\unicode[STIX]{x1D701}):D\rightarrow \mathbb{C}^{3}$
and
$\widetilde{f}(\cdot ,\unicode[STIX]{x1D701}):D\rightarrow \mathbb{C}^{3}$
and
 $\widetilde{F}(u,\cdot ,\unicode[STIX]{x1D701}):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
are families of holomorphic Legendrian maps, depending continuously on
$\widetilde{F}(u,\cdot ,\unicode[STIX]{x1D701}):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
are families of holomorphic Legendrian maps, depending continuously on
![]() $u\in bD$
(this only pertains to
$u\in bD$
(this only pertains to
![]() $\widetilde{F}$
) and holomorphically on
$\widetilde{F}$
) and holomorphically on
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, which satisfy the assumptions of Lemma 3.2 on the disk
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, which satisfy the assumptions of Lemma 3.2 on the disk
![]() $D\cong \overline{\mathbb{D}}$
. Hence there is a family of Legendrian disks
$D\cong \overline{\mathbb{D}}$
. Hence there is a family of Legendrian disks
 $\widetilde{G}(\cdot ,\unicode[STIX]{x1D701}):D\rightarrow \mathbb{C}^{3}$
satisfying the approximation conditions in Lemma 3.2 with respect to the central Legendrian disk
$\widetilde{G}(\cdot ,\unicode[STIX]{x1D701}):D\rightarrow \mathbb{C}^{3}$
satisfying the approximation conditions in Lemma 3.2 with respect to the central Legendrian disk
![]() $\widetilde{f}(\cdot ,\unicode[STIX]{x1D701})$
and the family of Legendrian disks
$\widetilde{f}(\cdot ,\unicode[STIX]{x1D701})$
and the family of Legendrian disks
 $\widetilde{F}(u,\cdot ,\unicode[STIX]{x1D701})$
over the boundary point
$\widetilde{F}(u,\cdot ,\unicode[STIX]{x1D701})$
over the boundary point
![]() $u\in bD$
. It is easily seen from the proof of Lemma 3.2 that the family
$u\in bD$
. It is easily seen from the proof of Lemma 3.2 that the family
![]() $\widetilde{G}(\cdot ,\unicode[STIX]{x1D701})$
may be chosen to depend holomorphically on
$\widetilde{G}(\cdot ,\unicode[STIX]{x1D701})$
may be chosen to depend holomorphically on
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, and the estimates in the lemma can be made uniform for all points
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, and the estimates in the lemma can be made uniform for all points
![]() $\unicode[STIX]{x1D701}$
in any given bounded domain in
$\unicode[STIX]{x1D701}$
in any given bounded domain in
![]() $\mathbb{C}^{\ell }$
, in particular, on the ball
$\mathbb{C}^{\ell }$
, in particular, on the ball
 $r\mathbb{B}\subset \mathbb{C}^{\ell }$
.
$r\mathbb{B}\subset \mathbb{C}^{\ell }$
.
Let
 $V\subset D\setminus M^{\prime }$
be a small neighborhood of the arc
$V\subset D\setminus M^{\prime }$
be a small neighborhood of the arc
![]() $I\subset bD$
. By condition (iv) in Lemma 3.2 we may assume that
$I\subset bD$
. By condition (iv) in Lemma 3.2 we may assume that
![]() $\widetilde{G}(\cdot ,\unicode[STIX]{x1D701})$
is as close as desired to
$\widetilde{G}(\cdot ,\unicode[STIX]{x1D701})$
is as close as desired to
![]() $\widetilde{f}(\cdot ,\unicode[STIX]{x1D701})$
in the
$\widetilde{f}(\cdot ,\unicode[STIX]{x1D701})$
in the
![]() $\mathscr{C}^{1}$
norm on the set
$\mathscr{C}^{1}$
norm on the set
![]() $D\setminus V$
, and hence on
$D\setminus V$
, and hence on
 $M^{\prime }\cap D\subset D\setminus V$
. In particular, given
$M^{\prime }\cap D\subset D\setminus V$
. In particular, given
![]() $\unicode[STIX]{x1D6FF}>0$
we may assume that
$\unicode[STIX]{x1D6FF}>0$
we may assume that
 $$\begin{eqnarray}||\widetilde{G}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{f}(\cdot ,\unicode[STIX]{x1D701})||_{1,M^{\prime }\cap D}<\unicode[STIX]{x1D6FF},\quad \unicode[STIX]{x1D701}\in r\mathbb{B}.\end{eqnarray}$$
$$\begin{eqnarray}||\widetilde{G}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{f}(\cdot ,\unicode[STIX]{x1D701})||_{1,M^{\prime }\cap D}<\unicode[STIX]{x1D6FF},\quad \unicode[STIX]{x1D701}\in r\mathbb{B}.\end{eqnarray}$$
We shall write
 $\widetilde{G}=(\widetilde{G}_{1},\widetilde{G}_{2},\widetilde{G}_{3})$
.
$\widetilde{G}=(\widetilde{G}_{1},\widetilde{G}_{2},\widetilde{G}_{3})$
.
Recall that the first component of
![]() $\widetilde{f}$
(see (3.8)) is the function
$\widetilde{f}$
(see (3.8)) is the function
![]() $\widetilde{x}$
(cf. (3.5)) which is defined on all of
$\widetilde{x}$
(cf. (3.5)) which is defined on all of
![]() $M$
. By solving a Cousin-I problem with bounds on the Cartan pair
$M$
. By solving a Cousin-I problem with bounds on the Cartan pair
 $(M^{\prime },D)$
we glue
$(M^{\prime },D)$
we glue
![]() $\widetilde{x}$
and
$\widetilde{x}$
and
![]() $\widetilde{G}_{1}$
and obtain a function
$\widetilde{G}_{1}$
and obtain a function
 $H_{1}(\cdot ,\unicode[STIX]{x1D701}):M\rightarrow \mathbb{C}$
of class
$H_{1}(\cdot ,\unicode[STIX]{x1D701}):M\rightarrow \mathbb{C}$
of class
![]() $\mathscr{A}^{1}(M)$
, holomorphic in
$\mathscr{A}^{1}(M)$
, holomorphic in
![]() $\unicode[STIX]{x1D701}$
, such that for all
$\unicode[STIX]{x1D701}$
, such that for all
![]() $\unicode[STIX]{x1D701}\in r\mathbb{B}$
we have
$\unicode[STIX]{x1D701}\in r\mathbb{B}$
we have
 $$\begin{eqnarray}||H_{1}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{x}(\cdot ,\unicode[STIX]{x1D701})||_{1,M^{\prime }}<C\unicode[STIX]{x1D6FF},\quad ||H_{1}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{G}_{1}(\cdot ,\unicode[STIX]{x1D701})||_{1,D}<C\unicode[STIX]{x1D6FF},\end{eqnarray}$$
$$\begin{eqnarray}||H_{1}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{x}(\cdot ,\unicode[STIX]{x1D701})||_{1,M^{\prime }}<C\unicode[STIX]{x1D6FF},\quad ||H_{1}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{G}_{1}(\cdot ,\unicode[STIX]{x1D701})||_{1,D}<C\unicode[STIX]{x1D6FF},\end{eqnarray}$$
where the constant
![]() $C$
only depends on the Cartan pair
$C$
only depends on the Cartan pair
 $(M^{\prime },D)$
. This is accomplished by first patching the two functions smoothly, using the separation condition (3.3), and then correcting the
$(M^{\prime },D)$
. This is accomplished by first patching the two functions smoothly, using the separation condition (3.3), and then correcting the
![]() $\mathscr{C}^{1}$
-small error by solving the
$\mathscr{C}^{1}$
-small error by solving the
![]() $\overline{\unicode[STIX]{x2202}}$
-equation with
$\overline{\unicode[STIX]{x2202}}$
-equation with
![]() $\mathscr{C}^{1}$
-estimates on the bordered Riemann surface
$\mathscr{C}^{1}$
-estimates on the bordered Riemann surface
![]() $M$
. The variable
$M$
. The variable
![]() $\unicode[STIX]{x1D701}$
is treated as a parameter. This is standard; see e.g. [Reference ForstneričFor11, proof of Lemma 8.5.2] and use
$\unicode[STIX]{x1D701}$
is treated as a parameter. This is standard; see e.g. [Reference ForstneričFor11, proof of Lemma 8.5.2] and use
![]() $\mathscr{C}^{1}$
estimates instead of
$\mathscr{C}^{1}$
estimates instead of
![]() $\mathscr{C}^{0}$
estimates.
$\mathscr{C}^{0}$
estimates.
Likewise, we can glue the second component
 $\widetilde{y}=y\in \mathscr{A}^{1}(M)$
of
$\widetilde{y}=y\in \mathscr{A}^{1}(M)$
of
![]() $\widetilde{f}$
with the function
$\widetilde{f}$
with the function
 $\widetilde{G}_{2}(\cdot ,\unicode[STIX]{x1D701})$
into a function
$\widetilde{G}_{2}(\cdot ,\unicode[STIX]{x1D701})$
into a function
 $H_{2}(\cdot ,\unicode[STIX]{x1D701}):M\rightarrow \mathbb{C}$
of class
$H_{2}(\cdot ,\unicode[STIX]{x1D701}):M\rightarrow \mathbb{C}$
of class
![]() $\mathscr{A}^{1}(M)$
, holomorphic in
$\mathscr{A}^{1}(M)$
, holomorphic in
![]() $\unicode[STIX]{x1D701}$
, such that for all
$\unicode[STIX]{x1D701}$
, such that for all
![]() $\unicode[STIX]{x1D701}\in r\mathbb{B}$
we have the estimates
$\unicode[STIX]{x1D701}\in r\mathbb{B}$
we have the estimates
 $$\begin{eqnarray}||H_{2}(\cdot ,\unicode[STIX]{x1D701})-y||_{1,M^{\prime }}<C\unicode[STIX]{x1D6FF},\quad ||H_{2}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{G}_{2}(\cdot ,\unicode[STIX]{x1D701})||_{1,D}<C\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
$$\begin{eqnarray}||H_{2}(\cdot ,\unicode[STIX]{x1D701})-y||_{1,M^{\prime }}<C\unicode[STIX]{x1D6FF},\quad ||H_{2}(\cdot ,\unicode[STIX]{x1D701})-\widetilde{G}_{2}(\cdot ,\unicode[STIX]{x1D701})||_{1,D}<C\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
From the above estimates on
![]() $M^{\prime }$
and the fact that
$M^{\prime }$
and the fact that
 $\bigcup _{j=1}^{\ell }C_{j}\subset M^{\prime }$
it follows that the period map
$\bigcup _{j=1}^{\ell }C_{j}\subset M^{\prime }$
it follows that the period map
 $\unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(H_{1}(\cdot ,\unicode[STIX]{x1D701}),H_{2}(\cdot ,\unicode[STIX]{x1D701}))$
(cf. (3.4)) approximates the biholomorphic period map
$\unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(H_{1}(\cdot ,\unicode[STIX]{x1D701}),H_{2}(\cdot ,\unicode[STIX]{x1D701}))$
(cf. (3.4)) approximates the biholomorphic period map
 $\unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,\unicode[STIX]{x1D701}))$
uniformly on the ball
$\unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,\unicode[STIX]{x1D701}))$
uniformly on the ball
![]() $\unicode[STIX]{x1D701}\in r\mathbb{B}$
. Assuming that
$\unicode[STIX]{x1D701}\in r\mathbb{B}$
. Assuming that
![]() $\unicode[STIX]{x1D6FF}>0$
is chosen small enough, it follows that there is a point
$\unicode[STIX]{x1D6FF}>0$
is chosen small enough, it follows that there is a point
![]() $\unicode[STIX]{x1D701}^{\prime }\in r\mathbb{B}$
near the origin such that
$\unicode[STIX]{x1D701}^{\prime }\in r\mathbb{B}$
near the origin such that
 $$\begin{eqnarray}{\mathcal{P}}(H_{1}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),H_{2}(\cdot ,\unicode[STIX]{x1D701}^{\prime }))=0.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}(H_{1}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),H_{2}(\cdot ,\unicode[STIX]{x1D701}^{\prime }))=0.\end{eqnarray}$$
For this value of
![]() $\unicode[STIX]{x1D701}^{\prime }$
we obtain a Legendrian curve
$\unicode[STIX]{x1D701}^{\prime }$
we obtain a Legendrian curve
 $$\begin{eqnarray}H=(H_{1}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),H_{2}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),H_{3}):M\rightarrow \mathbb{C}^{3}\end{eqnarray}$$
$$\begin{eqnarray}H=(H_{1}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),H_{2}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),H_{3}):M\rightarrow \mathbb{C}^{3}\end{eqnarray}$$
whose third component equals
 $$\begin{eqnarray}H_{3}(u)=z(u_{0})-\int _{u_{0}}^{u}H_{1}(\cdot ,\unicode[STIX]{x1D701}^{\prime })\,dH_{2}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),\quad u\in M.\end{eqnarray}$$
$$\begin{eqnarray}H_{3}(u)=z(u_{0})-\int _{u_{0}}^{u}H_{1}(\cdot ,\unicode[STIX]{x1D701}^{\prime })\,dH_{2}(\cdot ,\unicode[STIX]{x1D701}^{\prime }),\quad u\in M.\end{eqnarray}$$
The integral is independent of the choice of the path in
![]() $M$
since by (3.9) all the periods over closed curves in
$M$
since by (3.9) all the periods over closed curves in
![]() $M$
vanish. (Note however that we do not get a Legendrian curve for parameter values
$M$
vanish. (Note however that we do not get a Legendrian curve for parameter values
![]() $\unicode[STIX]{x1D701}\neq \unicode[STIX]{x1D701}^{\prime }$
since the period condition (3.9) fails.) It follows from the construction that
$\unicode[STIX]{x1D701}\neq \unicode[STIX]{x1D701}^{\prime }$
since the period condition (3.9) fails.) It follows from the construction that
![]() $H$
satisfies the conclusion of Theorem 3.3 provided that the approximations made in the proof were close enough. This completes the proof under the assumption that the second component
$H$
satisfies the conclusion of Theorem 3.3 provided that the approximations made in the proof were close enough. This completes the proof under the assumption that the second component
![]() $y$
of
$y$
of
![]() $f$
is nonconstant.
$f$
is nonconstant.
Assume now that
![]() $y=y_{0}$
is constant. If the first component
$y=y_{0}$
is constant. If the first component
![]() $x$
is nonconstant, we consider a spray of the form (3.5) over the second component:
$x$
is nonconstant, we consider a spray of the form (3.5) over the second component:
 $$\begin{eqnarray}\widetilde{y}(p,\unicode[STIX]{x1D701})=y_{0}+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(p),\quad p\in M,~\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{\ell })\in \mathbb{C}^{\ell },\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{y}(p,\unicode[STIX]{x1D701})=y_{0}+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(p),\quad p\in M,~\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{\ell })\in \mathbb{C}^{\ell },\end{eqnarray}$$
where the functions
 $g_{1},\ldots ,g_{\ell }\in \mathscr{O}(M)$
are chosen such that
$g_{1},\ldots ,g_{\ell }\in \mathscr{O}(M)$
are chosen such that
 $$\begin{eqnarray}\int _{C_{j}}x\,dg_{k}=-\!\int _{C_{j}}g_{k}\,dx\approx \unicode[STIX]{x1D6FF}_{j,k}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{C_{j}}x\,dg_{k}=-\!\int _{C_{j}}g_{k}\,dx\approx \unicode[STIX]{x1D6FF}_{j,k}.\end{eqnarray}$$
This ensures that the period map
 $\unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(x,\widetilde{y}(\cdot ,\unicode[STIX]{x1D701}))$
has maximal rank at
$\unicode[STIX]{x1D701}\mapsto {\mathcal{P}}(x,\widetilde{y}(\cdot ,\unicode[STIX]{x1D701}))$
has maximal rank at
![]() $\unicode[STIX]{x1D701}=0$
, so we can proceed as before, keeping the component
$\unicode[STIX]{x1D701}=0$
, so we can proceed as before, keeping the component
![]() $x$
fixed during the proof.
$x$
fixed during the proof.
Finally, if
![]() $x=x_{0}$
and
$x=x_{0}$
and
![]() $y=y_{0}$
are both constant, then any perturbation of either
$y=y_{0}$
are both constant, then any perturbation of either
![]() $x$
or
$x$
or
![]() $y$
integrates to a Legendrian curve which brings us back to the second case considered above. Of course we must also adjust the Legendrian disks
$y$
integrates to a Legendrian curve which brings us back to the second case considered above. Of course we must also adjust the Legendrian disks
![]() $F(u,\cdot )$
$F(u,\cdot )$
 $(u\in bM)$
accordingly so that the condition
$(u\in bM)$
accordingly so that the condition
 $F(u,0)=f(u)$
is satisfied.◻
$F(u,0)=f(u)$
is satisfied.◻
4 Mergelyan approximation by embedded Legendrian curves
In this section we prove an approximation result of Runge–Mergelyan type for Legendrian curves by holomorphic Legendrian embeddings; see Lemma 4.4 below. This is an important step in the proof of Theorem 5.1 given in the following section.
Recall that a compact set
![]() $K$
in a complex manifold
$K$
in a complex manifold
![]() $M$
is said to be
$M$
is said to be
![]() $\mathscr{O}(M)$
-convex, or holomorphically convex, or Runge in
$\mathscr{O}(M)$
-convex, or holomorphically convex, or Runge in
![]() $M$
, if for every point
$M$
, if for every point
 $p\in M\setminus K$
there exists
$p\in M\setminus K$
there exists
 $f\in \mathscr{O}(M)$
with
$f\in \mathscr{O}(M)$
with
 $|f(p)|>\max _{K}|f|$
. If
$|f(p)|>\max _{K}|f|$
. If
![]() $M$
is an open Riemann surface, then a compact subset
$M$
is an open Riemann surface, then a compact subset
 $K\subset M$
is Runge if and only if
$K\subset M$
is Runge if and only if
![]() $M\setminus K$
has no relatively compact connected components in
$M\setminus K$
has no relatively compact connected components in
![]() $M$
.
$M$
.
Definition 4.1. A compact subset
![]() $S$
of an open Riemann surface
$S$
of an open Riemann surface
![]() $M$
is said to be admissible if
$M$
is said to be admissible if
 $S=K\cup \unicode[STIX]{x1D6E4}$
, where
$S=K\cup \unicode[STIX]{x1D6E4}$
, where
 $K=\bigcup \overline{D}_{j}$
is a union of finitely many pairwise disjoint, compact, smoothly bounded domains
$K=\bigcup \overline{D}_{j}$
is a union of finitely many pairwise disjoint, compact, smoothly bounded domains
![]() $\overline{D}_{j}$
in
$\overline{D}_{j}$
in
![]() $M$
and
$M$
and
 $\unicode[STIX]{x1D6E4}=\bigcup \unicode[STIX]{x1D6E4}_{i}$
is a union of finitely many pairwise disjoint smooth arcs or closed curves that intersect
$\unicode[STIX]{x1D6E4}=\bigcup \unicode[STIX]{x1D6E4}_{i}$
is a union of finitely many pairwise disjoint smooth arcs or closed curves that intersect
![]() $K$
only in their endpoints (or not at all), and such that their intersections with the boundary
$K$
only in their endpoints (or not at all), and such that their intersections with the boundary
![]() $bK$
are transverse. Note that
$bK$
are transverse. Note that
![]() ${S\unicode[STIX]{x0030A}}={K\unicode[STIX]{x0030A}}$
.
${S\unicode[STIX]{x0030A}}={K\unicode[STIX]{x0030A}}$
.
Given an admissible set
 $S=K\cup \unicode[STIX]{x1D6E4}\subset M$
, we shall use the notation
$S=K\cup \unicode[STIX]{x1D6E4}\subset M$
, we shall use the notation
 $$\begin{eqnarray}\mathscr{A}^{r}(S)=\{f\in \mathscr{C}^{r}(S):f|_{{K\unicode[STIX]{x0030A}}}\in \mathscr{O}({K\unicode[STIX]{x0030A}})\},\quad r\in \mathbb{Z}_{+}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{A}^{r}(S)=\{f\in \mathscr{C}^{r}(S):f|_{{K\unicode[STIX]{x0030A}}}\in \mathscr{O}({K\unicode[STIX]{x0030A}})\},\quad r\in \mathbb{Z}_{+}.\end{eqnarray}$$
The natural topology on
 $\mathscr{A}^{r}(S)\subset \mathscr{C}^{r}(S)$
coincides with the
$\mathscr{A}^{r}(S)\subset \mathscr{C}^{r}(S)$
coincides with the
![]() $\mathscr{C}^{r}(K)$
topology on the subset
$\mathscr{C}^{r}(K)$
topology on the subset
![]() $K$
, while on each of the arcs
$K$
, while on each of the arcs
![]() $\unicode[STIX]{x1D6E4}_{i}\subset \unicode[STIX]{x1D6E4}$
we use the
$\unicode[STIX]{x1D6E4}_{i}\subset \unicode[STIX]{x1D6E4}$
we use the
![]() $\mathscr{C}^{r}$
-norm of the function measured with respect to a fixed regular parametrization of
$\mathscr{C}^{r}$
-norm of the function measured with respect to a fixed regular parametrization of
![]() $\unicode[STIX]{x1D6E4}_{i}$
. Note that an admissible set
$\unicode[STIX]{x1D6E4}_{i}$
. Note that an admissible set
![]() $S$
is Runge in
$S$
is Runge in
![]() $M$
if and only if the inclusion map
$M$
if and only if the inclusion map
 $S{\hookrightarrow}M$
induces an injective homomorphism
$S{\hookrightarrow}M$
induces an injective homomorphism
 $H_{1}(S;\mathbb{Z}){\hookrightarrow}H_{1}(M;\mathbb{Z})$
of the first homology groups. If that is the case, the classical Mergelyan approximation theorem (see [Reference MergelyanMer51]) ensures that every function
$H_{1}(S;\mathbb{Z}){\hookrightarrow}H_{1}(M;\mathbb{Z})$
of the first homology groups. If that is the case, the classical Mergelyan approximation theorem (see [Reference MergelyanMer51]) ensures that every function
 $f\in \mathscr{A}^{r}(S)$
$f\in \mathscr{A}^{r}(S)$
 $(r\in \mathbb{Z}_{+})$
can be approximated in the
$(r\in \mathbb{Z}_{+})$
can be approximated in the
![]() $\mathscr{C}^{r}(S)$
-topology by functions holomorphic on
$\mathscr{C}^{r}(S)$
-topology by functions holomorphic on
![]() $M$
. When there is no place for ambiguity, we shall simply write
$M$
. When there is no place for ambiguity, we shall simply write
![]() $\mathscr{A}^{r}(S)$
for
$\mathscr{A}^{r}(S)$
for
 $\mathscr{A}^{r}(S)^{n}$
,
$\mathscr{A}^{r}(S)^{n}$
,
![]() $n\in \mathbb{N}$
.
$n\in \mathbb{N}$
.
Let
 $f:S\rightarrow \mathbb{C}$
be a function of class
$f:S\rightarrow \mathbb{C}$
be a function of class
![]() $\mathscr{A}^{1}(S)$
. Fix a holomorphic
$\mathscr{A}^{1}(S)$
. Fix a holomorphic
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D703}$
vanishing nowhere on
$\unicode[STIX]{x1D703}$
vanishing nowhere on
![]() $M$
and consider the continuous map
$M$
and consider the continuous map
 $\widehat{f}:S\rightarrow \mathbb{C}$
given by:
$\widehat{f}:S\rightarrow \mathbb{C}$
given by:
-
–
 $\widehat{f}=df/\unicode[STIX]{x1D703}$
on
$\widehat{f}=df/\unicode[STIX]{x1D703}$
on
 ${K\unicode[STIX]{x0030A}}$
;
${K\unicode[STIX]{x0030A}}$
; -
–
 $\widehat{f}(\unicode[STIX]{x1D6FC}(t))=(f\circ \unicode[STIX]{x1D6FC})^{\prime }(t)/\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FC}(t),\dot{\unicode[STIX]{x1D6FC}}(t))$
for any smooth regular path
$\widehat{f}(\unicode[STIX]{x1D6FC}(t))=(f\circ \unicode[STIX]{x1D6FC})^{\prime }(t)/\unicode[STIX]{x1D703}(\unicode[STIX]{x1D6FC}(t),\dot{\unicode[STIX]{x1D6FC}}(t))$
for any smooth regular path
 $\unicode[STIX]{x1D6FC}$
in
$\unicode[STIX]{x1D6FC}$
in
 $M$
parametrizing a connected component
$M$
parametrizing a connected component
 $\unicode[STIX]{x1D6E4}_{i}$
of
$\unicode[STIX]{x1D6E4}_{i}$
of
 $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Clearly,
![]() $\widehat{f}$
is a well-defined map of class
$\widehat{f}$
is a well-defined map of class
![]() $\mathscr{A}^{0}(S)$
. By definition, we set
$\mathscr{A}^{0}(S)$
. By definition, we set
 $$\begin{eqnarray}df:=\widehat{f}\unicode[STIX]{x1D703},\quad f\in \mathscr{A}^{1}(S).\end{eqnarray}$$
$$\begin{eqnarray}df:=\widehat{f}\unicode[STIX]{x1D703},\quad f\in \mathscr{A}^{1}(S).\end{eqnarray}$$
Obviously,
![]() $\widehat{f}$
depends on the choice of
$\widehat{f}$
depends on the choice of
![]() $\unicode[STIX]{x1D703}$
but
$\unicode[STIX]{x1D703}$
but
![]() $df$
does not. If
$df$
does not. If
 $f\in \mathscr{O}(S)$
then
$f\in \mathscr{O}(S)$
then
![]() $df$
(4.2) agrees with the restriction of the exterior differential of
$df$
(4.2) agrees with the restriction of the exterior differential of
![]() $f$
to the points of
$f$
to the points of
![]() $S$
, i.e.,
$S$
, i.e.,
 $d(f|_{S})=(df)|_{S}$
. Conversely, every pair
$d(f|_{S})=(df)|_{S}$
. Conversely, every pair
![]() $(\unicode[STIX]{x1D703},\widehat{f})$
, where
$(\unicode[STIX]{x1D703},\widehat{f})$
, where
![]() $\unicode[STIX]{x1D703}$
is a holomorphic
$\unicode[STIX]{x1D703}$
is a holomorphic
![]() $1$
-form vanishing nowhere on
$1$
-form vanishing nowhere on
![]() $M$
and
$M$
and
 $\widehat{f}:S\rightarrow \mathbb{C}$
is a function of class
$\widehat{f}:S\rightarrow \mathbb{C}$
is a function of class
![]() $\mathscr{A}^{0}(S)$
such that
$\mathscr{A}^{0}(S)$
such that
 $\int _{\unicode[STIX]{x1D6FE}}\widehat{f}\unicode[STIX]{x1D703}=0$
for all closed curves
$\int _{\unicode[STIX]{x1D6FE}}\widehat{f}\unicode[STIX]{x1D703}=0$
for all closed curves
![]() $\unicode[STIX]{x1D6FE}\subset S$
, determines a function
$\unicode[STIX]{x1D6FE}\subset S$
, determines a function
 $f:S\rightarrow \mathbb{C}$
of class
$f:S\rightarrow \mathbb{C}$
of class
![]() $\mathscr{A}^{1}(S)$
, with
$\mathscr{A}^{1}(S)$
, with
 $df=\widehat{f}\unicode[STIX]{x1D703}$
, by the formula
$df=\widehat{f}\unicode[STIX]{x1D703}$
, by the formula
 $$\begin{eqnarray}f(p)=\int ^{p}\widehat{f}\unicode[STIX]{x1D703},\quad p\in S.\end{eqnarray}$$
$$\begin{eqnarray}f(p)=\int ^{p}\widehat{f}\unicode[STIX]{x1D703},\quad p\in S.\end{eqnarray}$$
Definition 4.2. Let
 $S=K\cup \unicode[STIX]{x1D6E4}$
be a compact admissible set in an open Riemann surface
$S=K\cup \unicode[STIX]{x1D6E4}$
be a compact admissible set in an open Riemann surface
![]() $M$
. A map
$M$
. A map
 $f=(x_{1},y_{1},\ldots ,x_{n},y_{n},z):S\rightarrow \mathbb{C}^{2n+1}$
of class
$f=(x_{1},y_{1},\ldots ,x_{n},y_{n},z):S\rightarrow \mathbb{C}^{2n+1}$
of class
![]() $\mathscr{A}^{1}(S)$
is a generalized Legendrian curve if
$\mathscr{A}^{1}(S)$
is a generalized Legendrian curve if
 $f^{\ast }\unicode[STIX]{x1D702}=0$
, where
$f^{\ast }\unicode[STIX]{x1D702}=0$
, where
![]() $\unicode[STIX]{x1D702}$
is the standard contact form (1.1); that is to say, if
$\unicode[STIX]{x1D702}$
is the standard contact form (1.1); that is to say, if
 $$\begin{eqnarray}dz+\mathop{\sum }_{j=1}^{n}x_{j}\,dy_{j}=0\quad \text{everywhere on }S.\end{eqnarray}$$
$$\begin{eqnarray}dz+\mathop{\sum }_{j=1}^{n}x_{j}\,dy_{j}=0\quad \text{everywhere on }S.\end{eqnarray}$$
As a preliminary step in the proof of Lemma 4.4, we show the following approximation result which will be very useful in subsequent applications.
Lemma 4.3. Let
 $S=K\cup \unicode[STIX]{x1D6E4}$
be an admissible subset in an open connected Riemann surface
$S=K\cup \unicode[STIX]{x1D6E4}$
be an admissible subset in an open connected Riemann surface
![]() $R$
(see Definition 4.1) such that
$R$
(see Definition 4.1) such that
![]() $S$
is a deformation retract of
$S$
is a deformation retract of
![]() $R$
, and let
$R$
, and let
 $f=(x_{1},y_{1},\ldots ,x_{n},y_{n},z):S\rightarrow \mathbb{C}^{2n+1}$
be a generalized Legendrian curve (see Definition 4.2). Then
$f=(x_{1},y_{1},\ldots ,x_{n},y_{n},z):S\rightarrow \mathbb{C}^{2n+1}$
be a generalized Legendrian curve (see Definition 4.2). Then
![]() $f$
may be approximated in the
$f$
may be approximated in the
![]() $\mathscr{C}^{1}(S)$
-topology by holomorphic Legendrian curves
$\mathscr{C}^{1}(S)$
-topology by holomorphic Legendrian curves
 $\widetilde{f}:R\rightarrow \mathbb{C}^{2n+1}$
such that
$\widetilde{f}:R\rightarrow \mathbb{C}^{2n+1}$
such that
![]() $\widetilde{f}$
has no constant component function.
$\widetilde{f}$
has no constant component function.
Furthermore, assume that for some
 $\unicode[STIX]{x1D70E}\in \{1,\ldots ,2n+1\}$
the following hold.
$\unicode[STIX]{x1D70E}\in \{1,\ldots ,2n+1\}$
the following hold.
-
(i) The
 $\unicode[STIX]{x1D70E}\text{th}$
component of
$\unicode[STIX]{x1D70E}\text{th}$
component of
 $f$
is nonconstant and holomorphic on
$f$
is nonconstant and holomorphic on
 $R$
.
$R$
. -
(ii) If
 $\unicode[STIX]{x1D70E}=2n+1$
then there is
$\unicode[STIX]{x1D70E}=2n+1$
then there is
 $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
 $x_{i}$
and
$x_{i}$
and
 $y_{i}$
are not constant on any component of
$y_{i}$
are not constant on any component of
 $K$
,
$K$
,
 $x_{i}$
has no zeros in
$x_{i}$
has no zeros in
 $\unicode[STIX]{x1D6E4}$
, and
$\unicode[STIX]{x1D6E4}$
, and
 $y_{i}$
has no critical points in
$y_{i}$
has no critical points in
 $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Then the approximating Legendrian curves
 $\widetilde{f}:R\rightarrow \mathbb{C}^{2n+1}$
can be chosen such that the
$\widetilde{f}:R\rightarrow \mathbb{C}^{2n+1}$
can be chosen such that the
![]() $\unicode[STIX]{x1D70E}\text{th}$
component of
$\unicode[STIX]{x1D70E}\text{th}$
component of
![]() $\widetilde{f}$
agrees with the
$\widetilde{f}$
agrees with the
![]() $\unicode[STIX]{x1D70E}\text{th}$
component of
$\unicode[STIX]{x1D70E}\text{th}$
component of
![]() $f$
.
$f$
.
Proof. Since
![]() $S$
is a deformation retract of
$S$
is a deformation retract of
![]() $R$
, we have that
$R$
, we have that
![]() $R$
is of finite topological type and
$R$
is of finite topological type and
![]() $S$
is connected and Runge in
$S$
is connected and Runge in
![]() $R$
. Without loss of generality, we can assume that
$R$
. Without loss of generality, we can assume that
![]() $K\neq \emptyset$
. Indeed, otherwise
$K\neq \emptyset$
. Indeed, otherwise
![]() $S=\unicode[STIX]{x1D6E4}$
consists of a single closed curve or Jordan arc. Then we choose a small smoothly bounded close disk
$S=\unicode[STIX]{x1D6E4}$
consists of a single closed curve or Jordan arc. Then we choose a small smoothly bounded close disk
![]() $K$
in
$K$
in
![]() $R$
such that
$R$
such that
 $S^{\prime }=K\cup \unicode[STIX]{x1D6E4}$
is admissible and connected, and
$S^{\prime }=K\cup \unicode[STIX]{x1D6E4}$
is admissible and connected, and
![]() $K\cap S$
is a single Jordan arc. Approximating
$K\cap S$
is a single Jordan arc. Approximating
![]() $f$
by a generalized Legendrian curve
$f$
by a generalized Legendrian curve
 $S^{\prime }\rightarrow \mathbb{C}^{2n+1}$
reduces the proof to the case when
$S^{\prime }\rightarrow \mathbb{C}^{2n+1}$
reduces the proof to the case when
![]() $K\neq \emptyset$
.
$K\neq \emptyset$
.
Assume as we may that
![]() $K\neq \emptyset$
. It follows that every component of
$K\neq \emptyset$
. It follows that every component of
![]() $\unicode[STIX]{x1D6E4}$
(hence of
$\unicode[STIX]{x1D6E4}$
(hence of
![]() $S$
) meets
$S$
) meets
![]() $K$
. Let
$K$
. Let
 $C_{1},\ldots ,C_{\ell }\subset S$
be closed curves forming a basis of the homology group
$C_{1},\ldots ,C_{\ell }\subset S$
be closed curves forming a basis of the homology group
 $H_{1}(S;\mathbb{Z})\,=\,\mathbb{Z}^{\ell }$
$H_{1}(S;\mathbb{Z})\,=\,\mathbb{Z}^{\ell }$
 $(\ell \in \mathbb{Z}_{+})$
such that the union
$(\ell \in \mathbb{Z}_{+})$
such that the union
 $\bigcup _{k=1}^{\ell }C_{k}$
is Runge in
$\bigcup _{k=1}^{\ell }C_{k}$
is Runge in
![]() $R$
. By our assumptions on
$R$
. By our assumptions on
![]() $S$
, we may ensure that each curve
$S$
, we may ensure that each curve
![]() $C_{k}$
,
$C_{k}$
,
 $k=1,\ldots ,\ell$
, contains a subarc
$k=1,\ldots ,\ell$
, contains a subarc
![]() $\widetilde{C}_{k}$
lying in
$\widetilde{C}_{k}$
lying in
![]() ${K\unicode[STIX]{x0030A}}$
.
${K\unicode[STIX]{x0030A}}$
.
The argument at the end of the proof of Theorem 3.3 and Remark 2.1 enable us to assume without loss of generality that
![]() $y_{1}$
is not constant on any component of
$y_{1}$
is not constant on any component of
![]() $K$
. Let
$K$
. Let
 $$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):\mathscr{A}^{1}(S)^{2n}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):\mathscr{A}^{1}(S)^{2n}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
be the period map (3.4) with the components
 $$\begin{eqnarray}{\mathcal{P}}_{k}(g_{1},h_{1},\ldots ,g_{n},h_{n})=\int _{C_{k}}\mathop{\sum }_{j=1}^{n}g_{j}\,dh_{j},\quad k=1,\ldots ,\ell .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{k}(g_{1},h_{1},\ldots ,g_{n},h_{n})=\int _{C_{k}}\mathop{\sum }_{j=1}^{n}g_{j}\,dh_{j},\quad k=1,\ldots ,\ell .\end{eqnarray}$$
Let us construct a spray
 $\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}):S\rightarrow \mathbb{C}$
of the form
$\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}):S\rightarrow \mathbb{C}$
of the form
 $$\begin{eqnarray}\widetilde{x}_{1}(u,\unicode[STIX]{x1D701})=x_{1}(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in S,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell },\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{x}_{1}(u,\unicode[STIX]{x1D701})=x_{1}(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in S,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell },\end{eqnarray}$$
(cf. (3.5)) with the core
 $\widetilde{x}_{1}(\cdot ,0)=x_{1}$
(the first component of
$\widetilde{x}_{1}(\cdot ,0)=x_{1}$
(the first component of
![]() $f$
), depending holomorphically on
$f$
), depending holomorphically on
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, such that the
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, such that the
![]() $\unicode[STIX]{x1D701}$
-derivative of the period map
$\unicode[STIX]{x1D701}$
-derivative of the period map
 ${\mathcal{P}}(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),y_{1},\ldots ,x_{n},y_{n})$
at
${\mathcal{P}}(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),y_{1},\ldots ,x_{n},y_{n})$
at
![]() $\unicode[STIX]{x1D701}=0$
is an isomorphism (cf. (3.7)). We proceed as follows. Since
$\unicode[STIX]{x1D701}=0$
is an isomorphism (cf. (3.7)). We proceed as follows. Since
![]() $y_{1}$
is holomorphic and nonconstant on each component of
$y_{1}$
is holomorphic and nonconstant on each component of
![]() $K$
, we may first construct smooth functions
$K$
, we may first construct smooth functions
![]() $g_{k}$
on
$g_{k}$
on
![]() $C$
, with support on
$C$
, with support on
 $\widetilde{C}_{k}\subset {K\unicode[STIX]{x0030A}}$
, defining the spray
$\widetilde{C}_{k}\subset {K\unicode[STIX]{x0030A}}$
, defining the spray
![]() $\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})$
on
$\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})$
on
![]() $C$
and then, by Mergelyan theorem, assume that each
$C$
and then, by Mergelyan theorem, assume that each
![]() $g_{k}$
is holomorphic on
$g_{k}$
is holomorphic on
![]() $R$
(recall that
$R$
(recall that
![]() $C$
is Runge in
$C$
is Runge in
![]() $R$
). This ensures the existence of the desired spray on
$R$
). This ensures the existence of the desired spray on
![]() $S$
, the domain of definition of
$S$
, the domain of definition of
![]() $x_{1}$
.
$x_{1}$
.
Next, we approximate
 $(x_{1},y_{1},\ldots ,x_{n},y_{n})\in \mathscr{A}^{1}(S)^{2n}$
in the
$(x_{1},y_{1},\ldots ,x_{n},y_{n})\in \mathscr{A}^{1}(S)^{2n}$
in the
![]() $\mathscr{C}^{1}(S)$
-norm by a holomorphic map
$\mathscr{C}^{1}(S)$
-norm by a holomorphic map
 $(x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })\in \mathscr{O}(R)^{2n}$
such that
$(x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })\in \mathscr{O}(R)^{2n}$
such that
 $\sum _{j=1}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }$
does not vanish everywhere on
$\sum _{j=1}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }$
does not vanish everywhere on
![]() $R$
and all the component functions
$R$
and all the component functions
 $x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime }$
are nonconstant. For that, recall that
$x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime }$
are nonconstant. For that, recall that
![]() $S$
is Runge in
$S$
is Runge in
![]() $R$
and apply Mergelyan approximation with jet-interpolation. Let
$R$
and apply Mergelyan approximation with jet-interpolation. Let
 $\widetilde{x}_{1}^{\prime }:R\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
be the spray (4.3) obtained by replacing the core
$\widetilde{x}_{1}^{\prime }:R\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
be the spray (4.3) obtained by replacing the core
![]() $x_{1}$
by
$x_{1}$
by
![]() $x_{1}^{\prime }$
:
$x_{1}^{\prime }$
:
 $$\begin{eqnarray}\widetilde{x}_{1}^{\prime }(u,\unicode[STIX]{x1D701})=x_{1}^{\prime }(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in R,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{x}_{1}^{\prime }(u,\unicode[STIX]{x1D701})=x_{1}^{\prime }(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in R,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
If the approximations are close enough, then the period map
 ${\mathcal{P}}(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })$
is so close to
${\mathcal{P}}(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })$
is so close to
 ${\mathcal{P}}(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),y_{1},\ldots ,x_{n},y_{n})$
that there is a point
${\mathcal{P}}(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),y_{1},\ldots ,x_{n},y_{n})$
that there is a point
![]() $\unicode[STIX]{x1D701}^{\prime }\in \mathbb{C}^{\ell }$
close to
$\unicode[STIX]{x1D701}^{\prime }\in \mathbb{C}^{\ell }$
close to
![]() $0$
for which
$0$
for which
 $$\begin{eqnarray}{\mathcal{P}}(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })=0.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })=0.\end{eqnarray}$$
This means that
 $\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime })\,dy_{1}^{\prime }+\sum _{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }$
is an exact holomorphic
$\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime })\,dy_{1}^{\prime }+\sum _{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }$
is an exact holomorphic
![]() $1$
-form on
$1$
-form on
![]() $R$
. Pick an initial point
$R$
. Pick an initial point
![]() $u_{0}\in {K\unicode[STIX]{x0030A}}$
and define the holomorphic function
$u_{0}\in {K\unicode[STIX]{x0030A}}$
and define the holomorphic function
 $z^{\prime }\in \mathscr{O}(R)$
by
$z^{\prime }\in \mathscr{O}(R)$
by
 $$\begin{eqnarray}z^{\prime }(u)=z(u_{0})-\int _{u_{0}}^{u}\biggl(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime })\,dy_{1}^{\prime }+\mathop{\sum }_{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }\biggr),\quad u\in R.\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime }(u)=z(u_{0})-\int _{u_{0}}^{u}\biggl(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime })\,dy_{1}^{\prime }+\mathop{\sum }_{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }\biggr),\quad u\in R.\end{eqnarray}$$
Clearly, the map
 $\widetilde{f}=(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z^{\prime }):R\rightarrow \mathbb{C}^{2n+1}$
is then a holomorphic Legendrian curve approximating
$\widetilde{f}=(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z^{\prime }):R\rightarrow \mathbb{C}^{2n+1}$
is then a holomorphic Legendrian curve approximating
![]() $f$
in the
$f$
in the
![]() $\mathscr{C}^{1}(S)$
-topology and having no constant component function provided that
$\mathscr{C}^{1}(S)$
-topology and having no constant component function provided that
![]() $\unicode[STIX]{x1D701}^{\prime }$
is close enough to
$\unicode[STIX]{x1D701}^{\prime }$
is close enough to
![]() $0\in \mathbb{C}^{\ell }$
. This proves the first part of the lemma.
$0\in \mathbb{C}^{\ell }$
. This proves the first part of the lemma.
For the second part, let
 $\unicode[STIX]{x1D70E}\in \{1,\ldots ,2n+1\}$
and assume that conditions (i) and (ii) hold. By Remark 2.1 we may assume that
$\unicode[STIX]{x1D70E}\in \{1,\ldots ,2n+1\}$
and assume that conditions (i) and (ii) hold. By Remark 2.1 we may assume that
 $\unicode[STIX]{x1D70E}\in \{2,2n+1\}$
.
$\unicode[STIX]{x1D70E}\in \{2,2n+1\}$
.
Case 1: Assume that
![]() $\unicode[STIX]{x1D70E}=2$
. In this case, the argument above works with the only difference that when approximating
$\unicode[STIX]{x1D70E}=2$
. In this case, the argument above works with the only difference that when approximating
 $(x_{1},y_{1},\ldots ,x_{n},y_{n})\in \mathscr{A}^{1}(S)^{2n}$
in the
$(x_{1},y_{1},\ldots ,x_{n},y_{n})\in \mathscr{A}^{1}(S)^{2n}$
in the
![]() $\mathscr{C}^{1}(S)$
-norm by a holomorphic map
$\mathscr{C}^{1}(S)$
-norm by a holomorphic map
 $(x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })\in \mathscr{O}(R)^{2n}$
, we choose
$(x_{1}^{\prime },y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })\in \mathscr{O}(R)^{2n}$
, we choose
![]() $y_{1}^{\prime }=y_{1}$
. Take into account that, in this case,
$y_{1}^{\prime }=y_{1}$
. Take into account that, in this case,
![]() $y_{1}$
is holomorphic and nonconstant on
$y_{1}$
is holomorphic and nonconstant on
![]() $R$
by assumption (i), and so neither the argument at the end of the proof of Theorem 3.3 nor Remark 2.1 are required.
$R$
by assumption (i), and so neither the argument at the end of the proof of Theorem 3.3 nor Remark 2.1 are required.
Case 2: Assume that
 $\unicode[STIX]{x1D70E}=2n+1$
. By condition (ii) and Remark 2.1 we may assume that
$\unicode[STIX]{x1D70E}=2n+1$
. By condition (ii) and Remark 2.1 we may assume that
![]() $x_{1}$
and
$x_{1}$
and
![]() $y_{1}$
are not constant on any component of
$y_{1}$
are not constant on any component of
![]() $K$
,
$K$
,
![]() $x_{1}$
has no zeros in
$x_{1}$
has no zeros in
![]() $\unicode[STIX]{x1D6E4}$
, and
$\unicode[STIX]{x1D6E4}$
, and
![]() $y_{1}$
has no critical points in
$y_{1}$
has no critical points in
![]() $\unicode[STIX]{x1D6E4}$
. Denote by
$\unicode[STIX]{x1D6E4}$
. Denote by
![]() ${\mho}$
the subset of
${\mho}$
the subset of
 $\mathscr{A}^{1}(S)^{2n}$
consisting of those maps
$\mathscr{A}^{1}(S)^{2n}$
consisting of those maps
 $(a_{1},a_{2},b_{2},\ldots ,a_{n},b_{n},w):S\rightarrow \mathbb{C}^{2n}$
(note that
$(a_{1},a_{2},b_{2},\ldots ,a_{n},b_{n},w):S\rightarrow \mathbb{C}^{2n}$
(note that
![]() $b_{1}$
is omitted) such that, for some (and hence for any) holomorphic
$b_{1}$
is omitted) such that, for some (and hence for any) holomorphic
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D703}$
vanishing nowhere on
$\unicode[STIX]{x1D703}$
vanishing nowhere on
![]() $R$
, the map
$R$
, the map
 $$\begin{eqnarray}\frac{1}{a_{1}\unicode[STIX]{x1D703}}\biggl(dw+\mathop{\sum }_{j=2}^{n}a_{j}\,db_{j}\biggr):S\rightarrow \mathbb{C}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{a_{1}\unicode[STIX]{x1D703}}\biggl(dw+\mathop{\sum }_{j=2}^{n}a_{j}\,db_{j}\biggr):S\rightarrow \mathbb{C}\end{eqnarray}$$
is well defined and of class
![]() $\mathscr{A}^{0}(S)$
(see (4.1) and (4.2)). The fact that
$\mathscr{A}^{0}(S)$
(see (4.1) and (4.2)). The fact that
![]() $f$
is a generalized Legendrian curve implies that
$f$
is a generalized Legendrian curve implies that
 $(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
. Consider the period map
$(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
. Consider the period map
 $$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):{\mho}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):{\mho}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
with the components
 $$\begin{eqnarray}{\mathcal{P}}_{k}(a_{1},a_{2},b_{2},\ldots ,a_{n},b_{n},w)=\int _{C_{k}}\frac{1}{a_{1}}\biggl(dw+\mathop{\sum }_{j=2}^{n}a_{j}\,db_{j}\biggr),\quad k=1,\ldots ,\ell .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{k}(a_{1},a_{2},b_{2},\ldots ,a_{n},b_{n},w)=\int _{C_{k}}\frac{1}{a_{1}}\biggl(dw+\mathop{\sum }_{j=2}^{n}a_{j}\,db_{j}\biggr),\quad k=1,\ldots ,\ell .\end{eqnarray}$$
We shall now construct a spray
 $\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}):S\rightarrow \mathbb{C}$
of the form
$\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}):S\rightarrow \mathbb{C}$
of the form
 $$\begin{eqnarray}\widetilde{x}_{1}(u,\unicode[STIX]{x1D701})=x_{1}(u)e^{\mathop{\sum }_{l=1}^{\ell }\unicode[STIX]{x1D701}_{l}\,g_{l}(u)},\quad u\in S,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell },\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{x}_{1}(u,\unicode[STIX]{x1D701})=x_{1}(u)e^{\mathop{\sum }_{l=1}^{\ell }\unicode[STIX]{x1D701}_{l}\,g_{l}(u)},\quad u\in S,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell },\end{eqnarray}$$
where
 $g_{l}\in \mathscr{O}(R)$
for all
$g_{l}\in \mathscr{O}(R)$
for all
 $l\in \{1,\ldots ,\ell \}$
, with the core
$l\in \{1,\ldots ,\ell \}$
, with the core
 $\widetilde{x}_{1}(\cdot ,0)=x_{1}$
, depending holomorphically on
$\widetilde{x}_{1}(\cdot ,0)=x_{1}$
, depending holomorphically on
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, such that the
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
, such that the
![]() $\unicode[STIX]{x1D701}$
-derivative of the period map
$\unicode[STIX]{x1D701}$
-derivative of the period map
 ${\mathcal{P}}(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),x_{2},y_{2},\ldots ,x_{n},y_{n},z)$
at
${\mathcal{P}}(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),x_{2},y_{2},\ldots ,x_{n},y_{n},z)$
at
![]() $\unicode[STIX]{x1D701}=0$
is an isomorphism. (Note that
$\unicode[STIX]{x1D701}=0$
is an isomorphism. (Note that
 $(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
for all
$(\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701}),x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
for all
![]() $\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
since
$\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }$
since
 $(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
and
$(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
and
 $e^{\sum _{l=1}^{\ell }\unicode[STIX]{x1D701}_{l}g_{l}}$
has no zeros.) We proceed as follows. Note that, for such a spray,
$e^{\sum _{l=1}^{\ell }\unicode[STIX]{x1D701}_{l}g_{l}}$
has no zeros.) We proceed as follows. Note that, for such a spray,
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{l}}\biggr|_{\unicode[STIX]{x1D701}=0}\int _{C_{k}}\frac{1}{\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}\,dy_{j}\biggr)=-\!\int _{C_{k}}\frac{g_{l}}{x_{1}}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}\,dy_{j}\biggr)=\int _{C_{k}}g_{l}\,dy_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}_{l}}\biggr|_{\unicode[STIX]{x1D701}=0}\int _{C_{k}}\frac{1}{\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}\,dy_{j}\biggr)=-\!\int _{C_{k}}\frac{g_{l}}{x_{1}}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}\,dy_{j}\biggr)=\int _{C_{k}}g_{l}\,dy_{1}.\end{eqnarray}$$
As above, since
 $\widetilde{C}_{k}\subset {K\unicode[STIX]{x0030A}}$
and
$\widetilde{C}_{k}\subset {K\unicode[STIX]{x0030A}}$
and
![]() $y_{1}$
is holomorphic and nonconstant on every component of
$y_{1}$
is holomorphic and nonconstant on every component of
![]() $K$
, we may first construct smooth functions
$K$
, we may first construct smooth functions
![]() $g_{l}$
on
$g_{l}$
on
![]() $C$
, with support on
$C$
, with support on
![]() $\widetilde{C}_{k}$
, defining the spray
$\widetilde{C}_{k}$
, defining the spray
![]() $\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})$
on
$\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})$
on
![]() $C$
, such that
$C$
, such that
 $$\begin{eqnarray}\int _{C_{k}}g_{l}\,dy_{1}\approx \unicode[STIX]{x1D6FF}_{l,k}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{C_{k}}g_{l}\,dy_{1}\approx \unicode[STIX]{x1D6FF}_{l,k}.\end{eqnarray}$$
(Recall that
![]() $\unicode[STIX]{x1D6FF}_{l,k}$
is the Kronecker symbol.) By the Mergelyan theorem, we may assume that each
$\unicode[STIX]{x1D6FF}_{l,k}$
is the Kronecker symbol.) By the Mergelyan theorem, we may assume that each
![]() $g_{l}$
is holomorphic on
$g_{l}$
is holomorphic on
![]() $R$
. As above, this guarantees the existence of the desired spray
$R$
. As above, this guarantees the existence of the desired spray
![]() $\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})$
on
$\widetilde{x}_{1}(\cdot ,\unicode[STIX]{x1D701})$
on
![]() $S$
. We next approximate
$S$
. We next approximate
 $(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n})\in \mathscr{A}^{1}(S)^{2n-1}$
in the
$(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n})\in \mathscr{A}^{1}(S)^{2n-1}$
in the
![]() $\mathscr{C}^{1}(S)$
-norm by a holomorphic map
$\mathscr{C}^{1}(S)$
-norm by a holomorphic map
 $(x_{1}^{\prime },x_{2}^{\prime },y_{2}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })\in \mathscr{O}(R)^{2n-1}$
such that the following hold.
$(x_{1}^{\prime },x_{2}^{\prime },y_{2}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime })\in \mathscr{O}(R)^{2n-1}$
such that the following hold.
-
(a) Each component function
 $x_{1}^{\prime },x_{2}^{\prime },y_{2}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime }$
is nonconstant.
$x_{1}^{\prime },x_{2}^{\prime },y_{2}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime }$
is nonconstant. -
(b) The zeros of
 $x_{1}^{\prime }$
in
$x_{1}^{\prime }$
in
 $R$
are those of
$R$
are those of
 $x_{1}$
in
$x_{1}$
in
 $S$
(which lie in
$S$
(which lie in
 $K$
, see assumption (ii)), with the same order; in particular,
$K$
, see assumption (ii)), with the same order; in particular,
 $x_{1}^{\prime }$
has no zeros in
$x_{1}^{\prime }$
has no zeros in
 $R\setminus K$
.
$R\setminus K$
. -
(c) The
 $1$
-form
$1$
-form
 $dz+\sum _{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }$
does not vanish identically on
$dz+\sum _{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }$
does not vanish identically on
 $R$
, but it does vanish at the zeros of
$R$
, but it does vanish at the zeros of
 $dz+\sum _{j=2}^{n}x_{j}\,dy_{j}=-x_{1}\,dy_{1}$
in
$dz+\sum _{j=2}^{n}x_{j}\,dy_{j}=-x_{1}\,dy_{1}$
in
 $K$
, with the same order. (Observe that, by assumption (ii),
$K$
, with the same order. (Observe that, by assumption (ii),
 $x_{1}\,dy_{1}$
does not vanish identically on
$x_{1}\,dy_{1}$
does not vanish identically on
 $K$
and has no zeros in
$K$
and has no zeros in
 $\unicode[STIX]{x1D6E4}$
.)
$\unicode[STIX]{x1D6E4}$
.)
To ensure these conditions we make use of Mergelyan approximation with jet interpolation.
Let
 $\widetilde{x}_{1}^{\prime }:R\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
be the spray (4.5) obtained by replacing the core
$\widetilde{x}_{1}^{\prime }:R\times \mathbb{C}^{\ell }\rightarrow \mathbb{C}$
be the spray (4.5) obtained by replacing the core
![]() $x_{1}$
by
$x_{1}$
by
![]() $x_{1}^{\prime }$
:
$x_{1}^{\prime }$
:
 $$\begin{eqnarray}\widetilde{x}_{1}^{\prime }(u,\unicode[STIX]{x1D701})=x_{1}^{\prime }(u)e^{\mathop{\sum }_{l=1}^{\ell }\unicode[STIX]{x1D701}_{l}\,g_{l}(u)},\quad u\in R,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{x}_{1}^{\prime }(u,\unicode[STIX]{x1D701})=x_{1}^{\prime }(u)e^{\mathop{\sum }_{l=1}^{\ell }\unicode[STIX]{x1D701}_{l}\,g_{l}(u)},\quad u\in R,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
Since
 $(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
, conditions (b) and (c) above guarantee that
$(x_{1},x_{2},y_{2},\ldots ,x_{n},y_{n},z)\in {\mho}$
, conditions (b) and (c) above guarantee that
 $$\begin{eqnarray}\frac{1}{\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701})}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }\biggr)\quad \text{is holomorphic on }R\text{ for all }\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701})}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }\biggr)\quad \text{is holomorphic on }R\text{ for all }\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
As above, if the approximations are close enough, there is a point
![]() $\unicode[STIX]{x1D701}^{\prime }\in \mathbb{C}^{\ell }$
close to
$\unicode[STIX]{x1D701}^{\prime }\in \mathbb{C}^{\ell }$
close to
![]() $0$
for which
$0$
for which
 ${\mathcal{P}}(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),x_{2}^{\prime },y_{2}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z)=0$
. Thus, choosing an initial point
${\mathcal{P}}(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),x_{2}^{\prime },y_{2}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z)=0$
. Thus, choosing an initial point
![]() $u_{0}\in {K\unicode[STIX]{x0030A}}$
and defining
$u_{0}\in {K\unicode[STIX]{x0030A}}$
and defining
 $$\begin{eqnarray}y_{1}^{\prime }(u)=y_{1}(u_{0})-\int _{u_{0}}^{u}\frac{1}{\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime })}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }\biggr),\quad u\in R,\end{eqnarray}$$
$$\begin{eqnarray}y_{1}^{\prime }(u)=y_{1}(u_{0})-\int _{u_{0}}^{u}\frac{1}{\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime })}\biggl(dz+\mathop{\sum }_{j=2}^{n}x_{j}^{\prime }\,dy_{j}^{\prime }\biggr),\quad u\in R,\end{eqnarray}$$
it follows from (4.7) that
 $y_{1}^{\prime }:R\rightarrow \mathbb{C}$
is holomorphic and, in view of conditions (a) and (c), the map
$y_{1}^{\prime }:R\rightarrow \mathbb{C}$
is holomorphic and, in view of conditions (a) and (c), the map
 $$\begin{eqnarray}\widetilde{f}=(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z):R\rightarrow \mathbb{C}^{2n+1}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{f}=(\widetilde{x}_{1}^{\prime }(\cdot ,\unicode[STIX]{x1D701}^{\prime }),y_{1}^{\prime },\ldots ,x_{n}^{\prime },y_{n}^{\prime },z):R\rightarrow \mathbb{C}^{2n+1}\end{eqnarray}$$
is a holomorphic Legendrian curve satisfying the conclusion of the lemma, provided that the approximations are sufficiently close. ◻
Lemma 4.4. Let
![]() $M$
be a compact bordered Riemann surface. Every Legendrian curve
$M$
be a compact bordered Riemann surface. Every Legendrian curve
 $f:M\rightarrow \mathbb{C}^{2n+1}$
$f:M\rightarrow \mathbb{C}^{2n+1}$
![]() $(n\in \mathbb{N})$
of class
$(n\in \mathbb{N})$
of class
![]() $\mathscr{A}^{1}(M)$
may be approximated in the
$\mathscr{A}^{1}(M)$
may be approximated in the
![]() $\mathscr{C}^{1}(M)$
-topology by Legendrian embeddings
$\mathscr{C}^{1}(M)$
-topology by Legendrian embeddings
 $\widetilde{f}:M{\hookrightarrow}\mathbb{C}^{2n+1}$
of class
$\widetilde{f}:M{\hookrightarrow}\mathbb{C}^{2n+1}$
of class
 $\mathscr{A}^{1}(M)$
having no constant component function.
$\mathscr{A}^{1}(M)$
having no constant component function.
Proof. We assume that
![]() $n=1$
; the same proof applies in general. We may also assume without loss of generality that
$n=1$
; the same proof applies in general. We may also assume without loss of generality that
![]() $M$
is connected.
$M$
is connected.
Let
![]() $R$
be an open Riemann surface containing
$R$
be an open Riemann surface containing
![]() $M$
as a smoothly bounded compact domain which is a deformation retract of
$M$
as a smoothly bounded compact domain which is a deformation retract of
![]() $R$
. By Lemma 4.3 we may assume that
$R$
. By Lemma 4.3 we may assume that
![]() $f$
is a holomorphic Legendrian curve on
$f$
is a holomorphic Legendrian curve on
![]() $R$
having no constant component function. Write
$R$
having no constant component function. Write
 $f=(x,y,z):R\rightarrow \mathbb{C}^{3}$
.
$f=(x,y,z):R\rightarrow \mathbb{C}^{3}$
.
The proof will proceed in two steps. In the first step we shall approximate
![]() $f$
in the
$f$
in the
![]() $\mathscr{C}^{1}(M)$
-topology by a Legendrian immersion
$\mathscr{C}^{1}(M)$
-topology by a Legendrian immersion
 $R\rightarrow \mathbb{C}^{3}$
whose
$R\rightarrow \mathbb{C}^{3}$
whose
![]() $(x,y)$
-projection is an immersion
$(x,y)$
-projection is an immersion
 $R\rightarrow \mathbb{C}^{2}$
. In the second step we shall show how to remove double points on
$R\rightarrow \mathbb{C}^{2}$
. In the second step we shall show how to remove double points on
![]() $M$
of the new Legendrian immersion and hence obtain a Legendrian embedding
$M$
of the new Legendrian immersion and hence obtain a Legendrian embedding
 $M{\hookrightarrow}\mathbb{C}^{3}$
. If the approximation in both steps is close enough then the resulting Legendrian embedding will have no constant component function.
$M{\hookrightarrow}\mathbb{C}^{3}$
. If the approximation in both steps is close enough then the resulting Legendrian embedding will have no constant component function.
Let
 $C_{1},\ldots ,C_{\ell }\subset {M\unicode[STIX]{x0030A}}$
be closed curves forming a basis of the homology group
$C_{1},\ldots ,C_{\ell }\subset {M\unicode[STIX]{x0030A}}$
be closed curves forming a basis of the homology group
 $H_{1}(M;\mathbb{Z})=\mathbb{Z}^{\ell }$
such that the union
$H_{1}(M;\mathbb{Z})=\mathbb{Z}^{\ell }$
such that the union
 $\bigcup _{k=1}^{\ell }C_{k}$
is Runge in
$\bigcup _{k=1}^{\ell }C_{k}$
is Runge in
![]() ${M\unicode[STIX]{x0030A}}$
, hence in
${M\unicode[STIX]{x0030A}}$
, hence in
![]() $R$
. Let
$R$
. Let
 $$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):\mathscr{A}^{1}(M)^{2}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}=({\mathcal{P}}_{1},\ldots ,{\mathcal{P}}_{\ell }):\mathscr{A}^{1}(M)^{2}\rightarrow \mathbb{C}^{\ell }\end{eqnarray}$$
be the period map (3.4) with the components
 $$\begin{eqnarray}{\mathcal{P}}_{k}(g,h)=\int _{C_{k}}g\,dh,\quad g,\,h\in \mathscr{A}^{1}(M),~k=1,\ldots ,\ell .\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}_{k}(g,h)=\int _{C_{k}}g\,dh,\quad g,\,h\in \mathscr{A}^{1}(M),~k=1,\ldots ,\ell .\end{eqnarray}$$
For the first step of the proof, let
 $u_{1},u_{2},\ldots$
be the zeros of
$u_{1},u_{2},\ldots$
be the zeros of
![]() $dy$
in
$dy$
in
![]() $R$
. We shall approximate
$R$
. We shall approximate
![]() $x$
in the
$x$
in the
![]() $\mathscr{C}^{1}(M)$
-norm by a function
$\mathscr{C}^{1}(M)$
-norm by a function
 $x^{\prime }\in \mathscr{O}(R)$
such that
$x^{\prime }\in \mathscr{O}(R)$
such that
 $$\begin{eqnarray}dx^{\prime }(u_{j})\neq 0\quad \text{for }j=1,2,\ldots \quad \text{and}\quad {\mathcal{P}}(x^{\prime },y)=0.\end{eqnarray}$$
$$\begin{eqnarray}dx^{\prime }(u_{j})\neq 0\quad \text{for }j=1,2,\ldots \quad \text{and}\quad {\mathcal{P}}(x^{\prime },y)=0.\end{eqnarray}$$
The first condition ensures that the map
 $(x^{\prime },y):R\rightarrow \mathbb{C}^{2}$
is an immersion, and the second one that
$(x^{\prime },y):R\rightarrow \mathbb{C}^{2}$
is an immersion, and the second one that
![]() $x^{\prime }\,dy$
is an exact
$x^{\prime }\,dy$
is an exact
![]() $1$
-form on
$1$
-form on
![]() $R$
. Choosing an initial point
$R$
. Choosing an initial point
 $u_{0}\in M$
and setting
$u_{0}\in M$
and setting
 $$\begin{eqnarray}z^{\prime }(u)=z(u_{0})-\int _{u_{0}}^{u}x^{\prime }\,dy,\quad u\in R\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime }(u)=z(u_{0})-\int _{u_{0}}^{u}x^{\prime }\,dy,\quad u\in R\end{eqnarray}$$
we shall obtain a desired Legendrian immersion
 $f^{\prime }=(x^{\prime },y,z^{\prime }):R\rightarrow \mathbb{C}^{3}$
.
$f^{\prime }=(x^{\prime },y,z^{\prime }):R\rightarrow \mathbb{C}^{3}$
.
We now explain how to find the function
 $x^{\prime }\in \mathscr{O}(R)$
satisfying (4.8). Choose a function
$x^{\prime }\in \mathscr{O}(R)$
satisfying (4.8). Choose a function
 $h\in \mathscr{O}(R)$
such that for every
$h\in \mathscr{O}(R)$
such that for every
 $j=1,2,\ldots$
we have
$j=1,2,\ldots$
we have
 $dh(u_{j})=0$
if
$dh(u_{j})=0$
if
 $dx(u_{j})\neq 0$
and
$dx(u_{j})\neq 0$
and
 $dh(u_{j})\neq 0$
if
$dh(u_{j})\neq 0$
if
 $dx(u_{j})=0$
; the existence of such a function is ensured, for instance, by the theorem of Gunning and Narasimhan (see [Reference Gunning and NarasimhanGN67]). Then, for every
$dx(u_{j})=0$
; the existence of such a function is ensured, for instance, by the theorem of Gunning and Narasimhan (see [Reference Gunning and NarasimhanGN67]). Then, for every
 $\unicode[STIX]{x1D6FF}\in \mathbb{C}\setminus \{0\}$
the function
$\unicode[STIX]{x1D6FF}\in \mathbb{C}\setminus \{0\}$
the function
 $x_{\unicode[STIX]{x1D6FF}}:=x+\unicode[STIX]{x1D6FF}h\in \mathscr{O}(R)$
satisfies
$x_{\unicode[STIX]{x1D6FF}}:=x+\unicode[STIX]{x1D6FF}h\in \mathscr{O}(R)$
satisfies
 $$\begin{eqnarray}dx_{\unicode[STIX]{x1D6FF}}(u_{j})\neq 0,\quad j=1,2,\ldots .\end{eqnarray}$$
$$\begin{eqnarray}dx_{\unicode[STIX]{x1D6FF}}(u_{j})\neq 0,\quad j=1,2,\ldots .\end{eqnarray}$$
Hence,
 $(x_{\unicode[STIX]{x1D6FF}},y):R\rightarrow \mathbb{C}^{2}$
is an immersion. We need to correct
$(x_{\unicode[STIX]{x1D6FF}},y):R\rightarrow \mathbb{C}^{2}$
is an immersion. We need to correct
![]() $x_{\unicode[STIX]{x1D6FF}}$
in order to achieve the period vanishing condition in (4.8). To this end, choose the curves
$x_{\unicode[STIX]{x1D6FF}}$
in order to achieve the period vanishing condition in (4.8). To this end, choose the curves
 $C_{1},\ldots ,C_{\ell }$
above such that
$C_{1},\ldots ,C_{\ell }$
above such that
 $C:=\bigcup _{k=1}^{\ell }C_{k}$
does not contain any of the critical points
$C:=\bigcup _{k=1}^{\ell }C_{k}$
does not contain any of the critical points
 $u_{1},u_{2},\ldots$
of
$u_{1},u_{2},\ldots$
of
![]() $y$
. Let
$y$
. Let
 $\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}):R\rightarrow \mathbb{C}(\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell })$
be the spray (3.5) with the core
$\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}):R\rightarrow \mathbb{C}(\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell })$
be the spray (3.5) with the core
 $\widetilde{x}(\cdot ,0)=x$
, where the functions
$\widetilde{x}(\cdot ,0)=x$
, where the functions
 $g_{k}\in \mathscr{O}(R)$
are chosen such that the derivative of the period map
$g_{k}\in \mathscr{O}(R)$
are chosen such that the derivative of the period map
 ${\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y)$
at
${\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y)$
at
![]() $\unicode[STIX]{x1D701}=0$
(see (3.7)) is an isomorphism and
$\unicode[STIX]{x1D701}=0$
(see (3.7)) is an isomorphism and
 $dg_{k}(u_{j})=0$
for all
$dg_{k}(u_{j})=0$
for all
 $k=1,2,\ldots ,\ell$
and
$k=1,2,\ldots ,\ell$
and
 $j=1,2,\ldots .$
Let
$j=1,2,\ldots .$
Let
 $\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}):R\rightarrow \mathbb{C}$
be the holomorphic spray
$\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}):R\rightarrow \mathbb{C}$
be the holomorphic spray
 $$\begin{eqnarray}\widetilde{x}_{\unicode[STIX]{x1D6FF}}(u,\unicode[STIX]{x1D701})=x_{\unicode[STIX]{x1D6FF}}(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in R,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{x}_{\unicode[STIX]{x1D6FF}}(u,\unicode[STIX]{x1D701})=x_{\unicode[STIX]{x1D6FF}}(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\quad u\in R,~\unicode[STIX]{x1D701}\in \mathbb{C}^{\ell }.\end{eqnarray}$$
If
![]() $x_{\unicode[STIX]{x1D6FF}}$
is sufficiently close to
$x_{\unicode[STIX]{x1D6FF}}$
is sufficiently close to
![]() $x$
on the compact set
$x$
on the compact set
![]() $C$
(which can be achieved by choosing
$C$
(which can be achieved by choosing
![]() $|\unicode[STIX]{x1D6FF}|>0$
small enough), then the period map
$|\unicode[STIX]{x1D6FF}|>0$
small enough), then the period map
 ${\mathcal{P}}(\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}),y)$
is close to
${\mathcal{P}}(\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}),y)$
is close to
 ${\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y)$
. If the approximation is close enough, the implicit function theorem furnishes a point
${\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D701}),y)$
. If the approximation is close enough, the implicit function theorem furnishes a point
![]() $\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}}\in \mathbb{C}^{\ell }$
near
$\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}}\in \mathbb{C}^{\ell }$
near
![]() $0$
such that
$0$
such that
 ${\mathcal{P}}(\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}}),y)=0$
and
${\mathcal{P}}(\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}}),y)=0$
and
 $\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}}=0$
. Fix such
$\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}}=0$
. Fix such
![]() $\unicode[STIX]{x1D6FF}$
and set
$\unicode[STIX]{x1D6FF}$
and set
 $x^{\prime }=\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}})\in \mathscr{O}(R)$
; hence the
$x^{\prime }=\widetilde{x}_{\unicode[STIX]{x1D6FF}}(\cdot ,\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FF}})\in \mathscr{O}(R)$
; hence the
![]() $1$
-form
$1$
-form
![]() $x^{\prime }\,dy$
is exact on
$x^{\prime }\,dy$
is exact on
![]() $R$
. Since
$R$
. Since
 $dg_{k}(u_{j})=0$
, we also have that
$dg_{k}(u_{j})=0$
, we also have that
 $dx^{\prime }(u_{j})=dx_{\unicode[STIX]{x1D6FF}}(u_{j})\neq 0$
for all
$dx^{\prime }(u_{j})=dx_{\unicode[STIX]{x1D6FF}}(u_{j})\neq 0$
for all
 $j=1,2,\ldots$
(cf. (4.10)), so
$j=1,2,\ldots$
(cf. (4.10)), so
 $(x^{\prime },y):R\rightarrow \mathbb{C}^{2}$
is an immersion. Finally, defining the function
$(x^{\prime },y):R\rightarrow \mathbb{C}^{2}$
is an immersion. Finally, defining the function
 $z^{\prime }\in \mathscr{O}(R)$
by (4.9) we obtain a Legendrian immersion
$z^{\prime }\in \mathscr{O}(R)$
by (4.9) we obtain a Legendrian immersion
 $f^{\prime }=(x^{\prime },y,z^{\prime }):R\rightarrow \mathbb{C}^{3}$
which approximates
$f^{\prime }=(x^{\prime },y,z^{\prime }):R\rightarrow \mathbb{C}^{3}$
which approximates
![]() $f$
in the
$f$
in the
![]() $\mathscr{C}^{1}(M)$
-norm. This concludes the first step of the proof.
$\mathscr{C}^{1}(M)$
-norm. This concludes the first step of the proof.
It remains to show that a holomorphic Legendrian immersion
 $f:M\rightarrow \mathbb{C}^{3}$
can be approximated in the
$f:M\rightarrow \mathbb{C}^{3}$
can be approximated in the
![]() $\mathscr{C}^{1}(M)$
-norm by holomorphic Legendrian embeddings
$\mathscr{C}^{1}(M)$
-norm by holomorphic Legendrian embeddings
 $\widetilde{f}:M\rightarrow \mathbb{C}^{3}$
. We shall follow the idea in [Reference Alarcón, Forstnerič and LópezAFL16c, proof of Theorem 4.1] where the analogous result was shown for holomorphic null curves in
$\widetilde{f}:M\rightarrow \mathbb{C}^{3}$
. We shall follow the idea in [Reference Alarcón, Forstnerič and LópezAFL16c, proof of Theorem 4.1] where the analogous result was shown for holomorphic null curves in
![]() $\mathbb{C}^{n}$
for
$\mathbb{C}^{n}$
for
![]() $n\geqslant 3$
; a similar idea was also used in [Reference Alarcón and ForstneričAF14, proof of Theorem 2.4] to find conformal minimal embeddings of open Riemann surfaces into
$n\geqslant 3$
; a similar idea was also used in [Reference Alarcón and ForstneričAF14, proof of Theorem 2.4] to find conformal minimal embeddings of open Riemann surfaces into
![]() $\mathbb{R}^{n}$
for any
$\mathbb{R}^{n}$
for any
![]() $n\geqslant 5$
.
$n\geqslant 5$
.
To a map
 $f:M\rightarrow \mathbb{C}^{3}$
we associate the difference map
$f:M\rightarrow \mathbb{C}^{3}$
we associate the difference map
 $\unicode[STIX]{x1D6FF}f:M\times M\rightarrow \mathbb{C}^{3}$
defined by
$\unicode[STIX]{x1D6FF}f:M\times M\rightarrow \mathbb{C}^{3}$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}f(u,v)=f(v)-f(u),\quad u,v\in M.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}f(u,v)=f(v)-f(u),\quad u,v\in M.\end{eqnarray}$$
Clearly,
![]() $f$
is injective if and only if
$f$
is injective if and only if
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FF}f)^{-1}(0)=D_{M}:=\{(u,u):u\in M\}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FF}f)^{-1}(0)=D_{M}:=\{(u,u):u\in M\}.\end{eqnarray}$$
Assuming that
![]() $f$
is an immersion, there is an open neighborhood
$f$
is an immersion, there is an open neighborhood
 $U\subset M\times M$
of the diagonal
$U\subset M\times M$
of the diagonal
![]() $D_{M}$
such that
$D_{M}$
such that
![]() $\unicode[STIX]{x1D6FF}f$
does not assume the value
$\unicode[STIX]{x1D6FF}f$
does not assume the value
![]() $0\in \mathbb{C}^{3}$
on
$0\in \mathbb{C}^{3}$
on
![]() $\overline{U}\setminus D_{M}$
.
$\overline{U}\setminus D_{M}$
.
Assume that
 $f:M\rightarrow \mathbb{C}^{3}$
is a holomorphic Legendrian immersion. We shall approximate
$f:M\rightarrow \mathbb{C}^{3}$
is a holomorphic Legendrian immersion. We shall approximate
![]() $f$
in the
$f$
in the
![]() $\mathscr{C}^{1}(M)$
-norm by a holomorphic Legendrian immersion
$\mathscr{C}^{1}(M)$
-norm by a holomorphic Legendrian immersion
 $\widetilde{f}:M\rightarrow \mathbb{C}^{3}$
whose difference map
$\widetilde{f}:M\rightarrow \mathbb{C}^{3}$
whose difference map
![]() $\unicode[STIX]{x1D6FF}\widetilde{f}$
is transverse to the origin
$\unicode[STIX]{x1D6FF}\widetilde{f}$
is transverse to the origin
![]() $0\in \mathbb{C}^{3}$
on
$0\in \mathbb{C}^{3}$
on
 $M\times M\setminus U$
. Since
$M\times M\setminus U$
. Since
 $\dim M\times M=2<3=\dim \mathbb{C}^{3}$
, this will imply that
$\dim M\times M=2<3=\dim \mathbb{C}^{3}$
, this will imply that
![]() $\unicode[STIX]{x1D6FF}\widetilde{f}$
does not assume the value zero on
$\unicode[STIX]{x1D6FF}\widetilde{f}$
does not assume the value zero on
 $M\times M\setminus U$
, so
$M\times M\setminus U$
, so
 $\widetilde{f}(u)\neq \widetilde{f}(v)$
if
$\widetilde{f}(u)\neq \widetilde{f}(v)$
if
 $(u,v)\in M\times M\setminus U$
. If on the other hand
$(u,v)\in M\times M\setminus U$
. If on the other hand
 $(u,v)\in U\setminus D_{M}$
, then
$(u,v)\in U\setminus D_{M}$
, then
 $\widetilde{f}(u)\neq \widetilde{f}(v)$
provided that
$\widetilde{f}(u)\neq \widetilde{f}(v)$
provided that
![]() $\widetilde{f}$
is close enough to
$\widetilde{f}$
is close enough to
![]() $f$
; hence the map
$f$
; hence the map
![]() $\widetilde{f}$
is an embedding.
$\widetilde{f}$
is an embedding.
To find such
![]() $\widetilde{f}$
, it suffices to construct a holomorphic map
$\widetilde{f}$
, it suffices to construct a holomorphic map
 $H:M\times \mathbb{C}^{N}\rightarrow \mathbb{C}^{3}$
for some big integer
$H:M\times \mathbb{C}^{N}\rightarrow \mathbb{C}^{3}$
for some big integer
![]() $N\in \mathbb{N}$
satisfying the following properties for some
$N\in \mathbb{N}$
satisfying the following properties for some
![]() $r>0$
.
$r>0$
.
-
(a)
 $H(\cdot ,0)=f$
.
$H(\cdot ,0)=f$
. -
(b) The map
 $H(\cdot ,\unicode[STIX]{x1D709}):M\rightarrow \mathbb{C}^{3}$
is a holomorphic Legendrian immersion for every
$H(\cdot ,\unicode[STIX]{x1D709}):M\rightarrow \mathbb{C}^{3}$
is a holomorphic Legendrian immersion for every
 $\unicode[STIX]{x1D709}\in r\mathbb{B}$
, where
$\unicode[STIX]{x1D709}\in r\mathbb{B}$
, where
 $\mathbb{B}$
is the unit ball in
$\mathbb{B}$
is the unit ball in
 $\mathbb{C}^{N}$
.
$\mathbb{C}^{N}$
. -
(c) The difference map
 $\unicode[STIX]{x1D6FF}H:M\times M\times r\mathbb{B}\rightarrow \mathbb{C}^{3}$
, defined by is a submersive family of maps on
$\unicode[STIX]{x1D6FF}H:M\times M\times r\mathbb{B}\rightarrow \mathbb{C}^{3}$
, defined by is a submersive family of maps on $$\begin{eqnarray}\unicode[STIX]{x1D6FF}H(u,v,\unicode[STIX]{x1D709})=H(v,\unicode[STIX]{x1D709})-H(u,\unicode[STIX]{x1D709}),\quad u,\,v\in M,~\unicode[STIX]{x1D709}\in r\mathbb{B},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}H(u,v,\unicode[STIX]{x1D709})=H(v,\unicode[STIX]{x1D709})-H(u,\unicode[STIX]{x1D709}),\quad u,\,v\in M,~\unicode[STIX]{x1D709}\in r\mathbb{B},\end{eqnarray}$$
 $M\times M\setminus U$
, in the sense that (4.11)
$M\times M\setminus U$
, in the sense that (4.11) $$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}H(u,v,\unicode[STIX]{x1D709}):\mathbb{C}^{N}\rightarrow \mathbb{C}^{3}~\text{is surjective for every }(u,v)\in M\times M\setminus U.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}H(u,v,\unicode[STIX]{x1D709}):\mathbb{C}^{N}\rightarrow \mathbb{C}^{3}~\text{is surjective for every }(u,v)\in M\times M\setminus U.\end{eqnarray}$$
Assume for a moment that such
![]() $H$
exists. By compactness of
$H$
exists. By compactness of
 $M\times M\setminus U$
it follows from (4.11) that the partial differential
$M\times M\setminus U$
it follows from (4.11) that the partial differential
![]() $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D6FF}H)$
is surjective on
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D6FF}H)$
is surjective on
 $(M\times M\setminus U)\times r^{\prime }\mathbb{B}$
for some
$(M\times M\setminus U)\times r^{\prime }\mathbb{B}$
for some
 $0<r^{\prime }\leqslant r$
. Hence the map
$0<r^{\prime }\leqslant r$
. Hence the map
 $\unicode[STIX]{x1D6FF}H:(M\times M\setminus U)\times r^{\prime }\mathbb{B}\rightarrow \mathbb{C}^{3}$
is transverse to any submanifold of
$\unicode[STIX]{x1D6FF}H:(M\times M\setminus U)\times r^{\prime }\mathbb{B}\rightarrow \mathbb{C}^{3}$
is transverse to any submanifold of
![]() $\mathbb{C}^{3}$
, in particular, to the origin
$\mathbb{C}^{3}$
, in particular, to the origin
![]() $0\in \mathbb{C}^{3}$
. By Abraham’s reduction to Sard’s theorem [Reference AbrahamAbr63] (see also [Reference ForstneričFor11, § 7.8] and the references therein for the holomorphic case) it follows that for a generic choice of
$0\in \mathbb{C}^{3}$
. By Abraham’s reduction to Sard’s theorem [Reference AbrahamAbr63] (see also [Reference ForstneričFor11, § 7.8] and the references therein for the holomorphic case) it follows that for a generic choice of
![]() $\unicode[STIX]{x1D709}\in r^{\prime }\mathbb{B}$
the difference map
$\unicode[STIX]{x1D709}\in r^{\prime }\mathbb{B}$
the difference map
 $\unicode[STIX]{x1D6FF}H(\cdot ,\cdot ,\unicode[STIX]{x1D709})$
is transverse to
$\unicode[STIX]{x1D6FF}H(\cdot ,\cdot ,\unicode[STIX]{x1D709})$
is transverse to
![]() $0\in \mathbb{C}^{3}$
on
$0\in \mathbb{C}^{3}$
on
 $M\times M\setminus U$
, and hence it omits the value
$M\times M\setminus U$
, and hence it omits the value
![]() $0$
by dimension reasons. Choosing
$0$
by dimension reasons. Choosing
![]() $\unicode[STIX]{x1D709}$
sufficiently close to
$\unicode[STIX]{x1D709}$
sufficiently close to
![]() $0\in \mathbb{C}^{N}$
we obtain a holomorphic Legendrian embedding
$0\in \mathbb{C}^{N}$
we obtain a holomorphic Legendrian embedding
 $\widetilde{f}=H(\cdot ,\unicode[STIX]{x1D709}):M\rightarrow \mathbb{C}^{3}$
close to
$\widetilde{f}=H(\cdot ,\unicode[STIX]{x1D709}):M\rightarrow \mathbb{C}^{3}$
close to
![]() $f$
in the
$f$
in the
![]() $\mathscr{C}^{1}(M)$
-norm.
$\mathscr{C}^{1}(M)$
-norm.
The main point is to find for any given point
 $(p,q)\in M\times M\setminus U$
a spray
$(p,q)\in M\times M\setminus U$
a spray
![]() $H$
as above, with
$H$
as above, with
![]() $N=3$
, such that (4.11) holds at
$N=3$
, such that (4.11) holds at
 $(u,v)=(p,q)$
. Since the submersivity of the differential is an open condition and
$(u,v)=(p,q)$
. Since the submersivity of the differential is an open condition and
 $M\times M\setminus U$
is compact, we obtain a spray
$M\times M\setminus U$
is compact, we obtain a spray
![]() $H$
that is submersive at all points of
$H$
that is submersive at all points of
 $M\times M\setminus U$
by composing finitely many such sprays as explained in [Reference Alarcón, Forstnerič and LópezAFL16c, proof of Theorem 4.1] or [Reference Alarcón and ForstneričAF14, proof of Theorem 2.4].
$M\times M\setminus U$
by composing finitely many such sprays as explained in [Reference Alarcón, Forstnerič and LópezAFL16c, proof of Theorem 4.1] or [Reference Alarcón and ForstneričAF14, proof of Theorem 2.4].
Fix a pair of distinct points
![]() $p\neq q$
in
$p\neq q$
in
![]() $M$
. Choose a smooth embedded arc
$M$
. Choose a smooth embedded arc
![]() $E\subset M$
connecting
$E\subset M$
connecting
![]() $p$
to
$p$
to
![]() $q$
. As above, there exist smooth closed curves
$q$
. As above, there exist smooth closed curves
 $C_{1},\ldots ,C_{\ell }\subset M$
forming a basis of the homology group
$C_{1},\ldots ,C_{\ell }\subset M$
forming a basis of the homology group
 $H_{1}(M;\mathbb{Z})=\mathbb{Z}^{\ell }$
such that
$H_{1}(M;\mathbb{Z})=\mathbb{Z}^{\ell }$
such that
 $(\bigcup _{k=1}^{\ell }C_{k})\cap E=\emptyset$
and
$(\bigcup _{k=1}^{\ell }C_{k})\cap E=\emptyset$
and
 $(\bigcup _{k=1}^{\ell }C_{k})\cup E$
is Runge in
$(\bigcup _{k=1}^{\ell }C_{k})\cup E$
is Runge in
![]() $M$
. Given a number
$M$
. Given a number
![]() $\unicode[STIX]{x1D707}>0$
, we choose holomorphic functions
$\unicode[STIX]{x1D707}>0$
, we choose holomorphic functions
 $g_{1},\ldots ,g_{\ell },h_{1},h_{2}\in \mathscr{O}(M)$
satisfying the following conditions:
$g_{1},\ldots ,g_{\ell },h_{1},h_{2}\in \mathscr{O}(M)$
satisfying the following conditions:
-
(i)
 $\int _{C_{j}}g_{k}\,dy\approx \unicode[STIX]{x1D6FF}_{j,k}~\text{for all}~j,k=1,\ldots ,\ell$
;
$\int _{C_{j}}g_{k}\,dy\approx \unicode[STIX]{x1D6FF}_{j,k}~\text{for all}~j,k=1,\ldots ,\ell$
; -
(ii)
 $|g_{k}(u)|<1$
for all
$|g_{k}(u)|<1$
for all
 $u\in E$
and
$u\in E$
and
 $k=1,\ldots ,\ell$
;
$k=1,\ldots ,\ell$
; -
(iii)
 $h_{1}(p)=0$
,
$h_{1}(p)=0$
,
 $h_{1}(q)=1$
,
$h_{1}(q)=1$
,
 $h_{2}(p)=h_{2}(q)=0$
;
$h_{2}(p)=h_{2}(q)=0$
; -
(iv)
 $\int _{E}h_{2}\,dy=-1$
;
$\int _{E}h_{2}\,dy=-1$
; -
(v)
 $|h_{j}(u)|<\unicode[STIX]{x1D707}$
and
$|h_{j}(u)|<\unicode[STIX]{x1D707}$
and
 $|dh_{j}(u)|<\unicode[STIX]{x1D707}$
for all
$|dh_{j}(u)|<\unicode[STIX]{x1D707}$
for all
 $u\in \bigcup _{k=1}^{\ell }C_{k}$
and
$u\in \bigcup _{k=1}^{\ell }C_{k}$
and
 $j=1,2$
.
$j=1,2$
.
Functions with these properties are easily found by first constructing suitable smooth functions on the curves
 $(\bigcup _{k=1}^{\ell }C_{k})\cup E$
and applying Mergelyan’s approximation theorem.
$(\bigcup _{k=1}^{\ell }C_{k})\cup E$
and applying Mergelyan’s approximation theorem.
Let
 $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})\in \mathbb{C}^{3}$
and
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3})\in \mathbb{C}^{3}$
and
 $\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{\ell })\in \mathbb{C}^{\ell }$
. Consider the following sprays of holomorphic functions of
$\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{\ell })\in \mathbb{C}^{\ell }$
. Consider the following sprays of holomorphic functions of
![]() $u\in M$
:
$u\in M$
:
 $$\begin{eqnarray}\displaystyle \widetilde{x}(u,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}) & = & \displaystyle x(u)+\unicode[STIX]{x1D709}_{1}h_{1}(u)+\unicode[STIX]{x1D709}_{3}h_{2}(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{x}(u,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}) & = & \displaystyle x(u)+\unicode[STIX]{x1D709}_{1}h_{1}(u)+\unicode[STIX]{x1D709}_{3}h_{2}(u)+\mathop{\sum }_{k=1}^{\ell }\unicode[STIX]{x1D701}_{k}\,g_{k}(u),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \widetilde{y}(u,\unicode[STIX]{x1D709}) & = & \displaystyle y(u)+\unicode[STIX]{x1D709}_{2}h_{1}(u).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{y}(u,\unicode[STIX]{x1D709}) & = & \displaystyle y(u)+\unicode[STIX]{x1D709}_{2}h_{1}(u).\end{eqnarray}$$
Note that
 $\widetilde{x}(u,0,0)=x(u)$
and
$\widetilde{x}(u,0,0)=x(u)$
and
 $\widetilde{y}(u,0)=y(u)$
. Condition (i) ensures that
$\widetilde{y}(u,0)=y(u)$
. Condition (i) ensures that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\bigg|_{\unicode[STIX]{x1D701}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,0,\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,0)):\mathbb{C}^{\ell }\longrightarrow \mathbb{C}^{\ell }\text{ is an isomorphism}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\bigg|_{\unicode[STIX]{x1D701}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,0,\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,0)):\mathbb{C}^{\ell }\longrightarrow \mathbb{C}^{\ell }\text{ is an isomorphism}.\end{eqnarray}$$
Therefore, by the implicit function theorem, the period vanishing equation
 $$\begin{eqnarray}{\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,\unicode[STIX]{x1D709}))=\biggl(\int _{C_{k}}\widetilde{x}(\cdot ,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})\,d\widetilde{y}(\cdot ,\unicode[STIX]{x1D709})\biggr)_{k=1,\ldots ,\ell }=0\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,\unicode[STIX]{x1D709}))=\biggl(\int _{C_{k}}\widetilde{x}(\cdot ,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701})\,d\widetilde{y}(\cdot ,\unicode[STIX]{x1D709})\biggr)_{k=1,\ldots ,\ell }=0\end{eqnarray}$$
(which holds at
![]() $\unicode[STIX]{x1D709}=0$
and
$\unicode[STIX]{x1D709}=0$
and
![]() $\unicode[STIX]{x1D701}=0$
) can be solved in the form
$\unicode[STIX]{x1D701}=0$
) can be solved in the form
 $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})$
, where
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})$
, where
![]() $\unicode[STIX]{x1D70C}$
is a holomorphic map from a neighborhood of
$\unicode[STIX]{x1D70C}$
is a holomorphic map from a neighborhood of
![]() $0\in \mathbb{C}^{3}$
to a neighborhood of
$0\in \mathbb{C}^{3}$
to a neighborhood of
![]() $0\in \mathbb{C}^{\ell }$
with
$0\in \mathbb{C}^{\ell }$
with
 $\unicode[STIX]{x1D70C}(0)=0$
. We must estimate the differential
$\unicode[STIX]{x1D70C}(0)=0$
. We must estimate the differential
![]() $d\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})$
at
$d\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})$
at
![]() $\unicode[STIX]{x1D709}=0$
. Differentiating (4.14) gives in view of
$\unicode[STIX]{x1D709}=0$
. Differentiating (4.14) gives in view of
 $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})$
and the chain rule that
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})$
and the chain rule that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\biggr|_{\unicode[STIX]{x1D701}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,0,\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,0))\cdot d\unicode[STIX]{x1D70C}(0)=-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D709},0),\widetilde{y}(\cdot ,\unicode[STIX]{x1D709})).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D701}}\biggr|_{\unicode[STIX]{x1D701}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,0,\unicode[STIX]{x1D701}),\widetilde{y}(\cdot ,0))\cdot d\unicode[STIX]{x1D70C}(0)=-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}{\mathcal{P}}(\widetilde{x}(\cdot ,\unicode[STIX]{x1D709},0),\widetilde{y}(\cdot ,\unicode[STIX]{x1D709})).\end{eqnarray}$$
From (4.12), (4.13) and condition (v) on
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
we see that the right-hand side of the above equation is of size
$h_{2}$
we see that the right-hand side of the above equation is of size
![]() $O(\unicode[STIX]{x1D707})$
. Indeed, its components are integrals over the curves
$O(\unicode[STIX]{x1D707})$
. Indeed, its components are integrals over the curves
 $C_{1},\ldots ,C_{\ell }$
of terms which involve at least one of the functions
$C_{1},\ldots ,C_{\ell }$
of terms which involve at least one of the functions
![]() $h_{1},h_{2}$
or
$h_{1},h_{2}$
or
![]() $dh_{1}$
; these are of size
$dh_{1}$
; these are of size
![]() $O(\unicode[STIX]{x1D707})$
by condition (v). Since the first term on the left-hand side is close to the identity, we get
$O(\unicode[STIX]{x1D707})$
by condition (v). Since the first term on the left-hand side is close to the identity, we get
 $$\begin{eqnarray}|d\unicode[STIX]{x1D70C}(0)|=O(\unicode[STIX]{x1D707}).\end{eqnarray}$$
$$\begin{eqnarray}|d\unicode[STIX]{x1D70C}(0)|=O(\unicode[STIX]{x1D707}).\end{eqnarray}$$
Define the holomorphic spray
![]() $\widetilde{z}(\cdot ,\unicode[STIX]{x1D709})$
with the core
$\widetilde{z}(\cdot ,\unicode[STIX]{x1D709})$
with the core
 $\widetilde{z}(\cdot ,0)=z$
on
$\widetilde{z}(\cdot ,0)=z$
on
![]() $M$
by
$M$
by
 $$\begin{eqnarray}\widetilde{z}(u,\unicode[STIX]{x1D709})=z(p)-\int _{t=p}^{t=u}\widetilde{x}(t,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709}))\,d\widetilde{y}(t,\unicode[STIX]{x1D709}),\quad u\in M.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{z}(u,\unicode[STIX]{x1D709})=z(p)-\int _{t=p}^{t=u}\widetilde{x}(t,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709}))\,d\widetilde{y}(t,\unicode[STIX]{x1D709}),\quad u\in M.\end{eqnarray}$$
Note that the integral is independent of the choice of the path from
![]() $p$
to
$p$
to
![]() $u$
. It follows that the spray
$u$
. It follows that the spray
 $H(\cdot ,\unicode[STIX]{x1D709}):M\rightarrow \mathbb{C}^{3}$
defined by
$H(\cdot ,\unicode[STIX]{x1D709}):M\rightarrow \mathbb{C}^{3}$
defined by
 $$\begin{eqnarray}H(u,\unicode[STIX]{x1D709})=(\widetilde{x}(u,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})),\widetilde{y}(u,\unicode[STIX]{x1D709}),\widetilde{z}(u,\unicode[STIX]{x1D709})),\quad u\in M,\end{eqnarray}$$
$$\begin{eqnarray}H(u,\unicode[STIX]{x1D709})=(\widetilde{x}(u,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})),\widetilde{y}(u,\unicode[STIX]{x1D709}),\widetilde{z}(u,\unicode[STIX]{x1D709})),\quad u\in M,\end{eqnarray}$$
consists of Legendrian maps and is holomorphic with respect to
![]() $\unicode[STIX]{x1D709}\in \mathbb{C}^{3}$
near the origin. Obviously,
$\unicode[STIX]{x1D709}\in \mathbb{C}^{3}$
near the origin. Obviously,
![]() $H$
satisfies properties (a) and (b). It remains to see that it also satisfies property (c), i.e.,
$H$
satisfies properties (a) and (b). It remains to see that it also satisfies property (c), i.e.,
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}H(p,q,\unicode[STIX]{x1D709}):\mathbb{C}^{3}\rightarrow \mathbb{C}^{3}\text{ is an isomorphism}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}H(p,q,\unicode[STIX]{x1D709}):\mathbb{C}^{3}\rightarrow \mathbb{C}^{3}\text{ is an isomorphism}.\end{eqnarray}$$
Condition (iii) on
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
implies that
$h_{2}$
implies that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\unicode[STIX]{x1D6FF}\widetilde{x}(p,q,\unicode[STIX]{x1D709},0)=(1,0,0),\quad \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\unicode[STIX]{x1D6FF}\widetilde{y}(p,q,\unicode[STIX]{x1D709},0)=(0,1,0).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\unicode[STIX]{x1D6FF}\widetilde{x}(p,q,\unicode[STIX]{x1D709},0)=(1,0,0),\quad \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\unicode[STIX]{x1D6FF}\widetilde{y}(p,q,\unicode[STIX]{x1D709},0)=(0,1,0).\end{eqnarray}$$
We claim that the following estimates hold:
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}\widetilde{x}(p,q,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})) & = & \displaystyle (1,0,0)+O(\unicode[STIX]{x1D707}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}\widetilde{x}(p,q,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})) & = & \displaystyle (1,0,0)+O(\unicode[STIX]{x1D707}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}\widetilde{y}(p,q,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})) & = & \displaystyle (0,1,0)+O(\unicode[STIX]{x1D707}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}\biggr|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}\widetilde{y}(p,q,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709})) & = & \displaystyle (0,1,0)+O(\unicode[STIX]{x1D707}),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{3}}\biggr|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}\widetilde{z}(p,q,\unicode[STIX]{x1D709}) & = & \displaystyle 1+O(\unicode[STIX]{x1D707}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{3}}\biggr|_{\unicode[STIX]{x1D709}=0}\,\unicode[STIX]{x1D6FF}\widetilde{z}(p,q,\unicode[STIX]{x1D709}) & = & \displaystyle 1+O(\unicode[STIX]{x1D707}).\end{eqnarray}$$
The first two follow directly from the definitions of
![]() $\widetilde{x}$
and
$\widetilde{x}$
and
![]() $\widetilde{y}$
(see (4.12) and (4.13)) and taking into account (4.15) and (4.18). To get (4.21), note that (4.16) implies
$\widetilde{y}$
(see (4.12) and (4.13)) and taking into account (4.15) and (4.18). To get (4.21), note that (4.16) implies
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}\widetilde{z}(p,q,\unicode[STIX]{x1D709})=-\!\int _{t=p}^{t=q}\widetilde{x}(t,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709}))\,d\widetilde{y}(t,\unicode[STIX]{x1D709})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}\widetilde{z}(p,q,\unicode[STIX]{x1D709})=-\!\int _{t=p}^{t=q}\widetilde{x}(t,\unicode[STIX]{x1D709},\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D709}))\,d\widetilde{y}(t,\unicode[STIX]{x1D709})\end{eqnarray}$$
where the integral is taken over the arc
![]() $E$
. From conditions (ii), (iv), (4.12), (4.13) and (4.15) we infer that
$E$
. From conditions (ii), (iv), (4.12), (4.13) and (4.15) we infer that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{3}}\biggr|_{\unicode[STIX]{x1D709}=0}\unicode[STIX]{x1D6FF}\widetilde{z}(p,q,\unicode[STIX]{x1D709})=-\!\int _{E}h_{2}\,dy-\int _{E}\mathop{\sum }_{k=1}^{\ell }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{k}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{3}}(0)\,g_{k}\,dy=1+O(\unicode[STIX]{x1D707})\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{3}}\biggr|_{\unicode[STIX]{x1D709}=0}\unicode[STIX]{x1D6FF}\widetilde{z}(p,q,\unicode[STIX]{x1D709})=-\!\int _{E}h_{2}\,dy-\int _{E}\mathop{\sum }_{k=1}^{\ell }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}_{k}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}_{3}}(0)\,g_{k}\,dy=1+O(\unicode[STIX]{x1D707})\end{eqnarray}$$
which establishes (4.21). Choosing the constant
![]() $\unicode[STIX]{x1D707}>0$
small enough, we see from (4.19), (4.20) and (4.21) that (4.17) holds. By what has been said before, this shows that
$\unicode[STIX]{x1D707}>0$
small enough, we see from (4.19), (4.20) and (4.21) that (4.17) holds. By what has been said before, this shows that
![]() $f$
can be approximated on
$f$
can be approximated on
![]() $M$
by Legendrian embeddings.◻
$M$
by Legendrian embeddings.◻
5 Approximation by proper holomorphic Legendrian embeddings
Given
![]() $n\in \mathbb{N}$
and
$n\in \mathbb{N}$
and
 $\unicode[STIX]{x1D70E}\in \{1,\ldots ,n\}$
we denote by
$\unicode[STIX]{x1D70E}\in \{1,\ldots ,n\}$
we denote by
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}:\mathbb{C}^{n}\rightarrow \mathbb{C}$
the coordinate projection
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}:\mathbb{C}^{n}\rightarrow \mathbb{C}$
the coordinate projection
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(z_{1},\ldots ,z_{n})=z_{\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(z_{1},\ldots ,z_{n})=z_{\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
If
![]() $n>1$
and
$n>1$
and
 $\unicode[STIX]{x1D70D}\in \{1,\ldots ,n\}\setminus \{\unicode[STIX]{x1D70E}\}$
, we write
$\unicode[STIX]{x1D70D}\in \{1,\ldots ,n\}\setminus \{\unicode[STIX]{x1D70E}\}$
, we write
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}}=(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}):\mathbb{C}^{n}\rightarrow \mathbb{C}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}}=(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}):\mathbb{C}^{n}\rightarrow \mathbb{C}^{2}.\end{eqnarray}$$
In this section we prove the following main theorem of the paper.
Theorem 5.1. Let
 $S=K\cup \unicode[STIX]{x1D6E4}$
be an admissible subset in an open connected Riemann surface
$S=K\cup \unicode[STIX]{x1D6E4}$
be an admissible subset in an open connected Riemann surface
![]() $R$
(see Definition 4.1), and let
$R$
(see Definition 4.1), and let
 $f:S\rightarrow \mathbb{C}^{2n+1}$
be a generalized Legendrian curve (see Definition 4.2). Also choose two distinct numbers
$f:S\rightarrow \mathbb{C}^{2n+1}$
be a generalized Legendrian curve (see Definition 4.2). Also choose two distinct numbers
 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\in \{1,\ldots ,2n+1\}$
. Then
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\in \{1,\ldots ,2n+1\}$
. Then
![]() $f$
may be approximated in the
$f$
may be approximated in the
![]() $\mathscr{C}^{1}(S)$
-topology by holomorphic Legendrian embeddings
$\mathscr{C}^{1}(S)$
-topology by holomorphic Legendrian embeddings
 $\widetilde{f}:R{\hookrightarrow}\mathbb{C}^{2n+1}$
such that the projection
$\widetilde{f}:R{\hookrightarrow}\mathbb{C}^{2n+1}$
such that the projection
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}}\circ f:R\rightarrow \mathbb{C}^{2}$
is a proper map.
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}}\circ f:R\rightarrow \mathbb{C}^{2}$
is a proper map.
The next result will be the key to obtain the properness condition in Theorem 5.1.
Lemma 5.2. Let
![]() $M_{1}$
and
$M_{1}$
and
![]() $M_{2}$
be smoothly bounded compact domains in an open Riemann surface
$M_{2}$
be smoothly bounded compact domains in an open Riemann surface
![]() $R$
such that
$R$
such that
 $M_{1}\subset {M\unicode[STIX]{x0030A}}_{2}$
and
$M_{1}\subset {M\unicode[STIX]{x0030A}}_{2}$
and
![]() $M_{1}$
is a strong deformation retract of
$M_{1}$
is a strong deformation retract of
![]() $M_{2}$
. Choose two distinct numbers
$M_{2}$
. Choose two distinct numbers
 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\in \{1,\ldots ,2n+1\}$
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\in \{1,\ldots ,2n+1\}$
![]() $(n\in \mathbb{N})$
, let
$(n\in \mathbb{N})$
, let
 $f:M_{1}\rightarrow \mathbb{C}^{2n+1}$
be a Legendrian curve of class
$f:M_{1}\rightarrow \mathbb{C}^{2n+1}$
be a Legendrian curve of class
 $\mathscr{A}^{1}(M_{1})$
, and assume that
$\mathscr{A}^{1}(M_{1})$
, and assume that
 $$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f|\}>\unicode[STIX]{x1D707}\quad \text{on }bM_{1}\end{eqnarray}$$
$$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f|\}>\unicode[STIX]{x1D707}\quad \text{on }bM_{1}\end{eqnarray}$$
for some
![]() $\unicode[STIX]{x1D707}>0$
. Then
$\unicode[STIX]{x1D707}>0$
. Then
![]() $f$
may be approximated in the
$f$
may be approximated in the
 $\mathscr{C}^{1}(M_{1})$
-topology by holomorphic Legendrian embeddings
$\mathscr{C}^{1}(M_{1})$
-topology by holomorphic Legendrian embeddings
 $\widetilde{f}:M_{2}\rightarrow \mathbb{C}^{2n+1}$
enjoying the following properties:
$\widetilde{f}:M_{2}\rightarrow \mathbb{C}^{2n+1}$
enjoying the following properties:
-
(i)
 $\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}+1$
on
$\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}+1$
on
 $bM_{2}$
;
$bM_{2}$
; -
(ii)
 $\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}$
on
$\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}$
on
 $M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
.
$M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
.
Proof. Let
 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k}$
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{k}$
![]() $(k\in \mathbb{N})$
be pairwise disjoint smooth Jordan curves which are the connected components of
$(k\in \mathbb{N})$
be pairwise disjoint smooth Jordan curves which are the connected components of
![]() $bM_{1}$
. Likewise, let
$bM_{1}$
. Likewise, let
 $\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{k}$
be the pairwise disjoint smooth Jordan curves in
$\unicode[STIX]{x1D6FD}_{1},\ldots ,\unicode[STIX]{x1D6FD}_{k}$
be the pairwise disjoint smooth Jordan curves in
![]() $bM_{2}$
, labeled so that
$bM_{2}$
, labeled so that
![]() $M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
consists of
$M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
consists of
![]() $k$
closed annuli
$k$
closed annuli
 $A_{1},\ldots ,A_{k}$
with boundaries
$A_{1},\ldots ,A_{k}$
with boundaries
 $bA_{l}=\unicode[STIX]{x1D6FC}_{l}\cup \unicode[STIX]{x1D6FD}_{l}$
,
$bA_{l}=\unicode[STIX]{x1D6FC}_{l}\cup \unicode[STIX]{x1D6FD}_{l}$
,
 $l=1,\ldots ,k$
; take into account that
$l=1,\ldots ,k$
; take into account that
![]() $M_{1}$
is a strong deformation retract of
$M_{1}$
is a strong deformation retract of
![]() $M_{2}$
. Since
$M_{2}$
. Since
 $\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f|\}>\unicode[STIX]{x1D707}$
on
$\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f|\}>\unicode[STIX]{x1D707}$
on
![]() $bM_{1}$
(cf. (5.1)), there exist an integer
$bM_{1}$
(cf. (5.1)), there exist an integer
![]() $m\geqslant 2$
and compact connected subarcs
$m\geqslant 2$
and compact connected subarcs
 $\{\unicode[STIX]{x1D6FC}_{l,a}:a\in \mathbb{Z}_{m}=\mathbb{Z}/m\mathbb{Z}\}$
of
$\{\unicode[STIX]{x1D6FC}_{l,a}:a\in \mathbb{Z}_{m}=\mathbb{Z}/m\mathbb{Z}\}$
of
![]() $\unicode[STIX]{x1D6FC}_{l}$
for
$\unicode[STIX]{x1D6FC}_{l}$
for
 $l=1,\ldots ,k$
such that the following conditions hold.
$l=1,\ldots ,k$
such that the following conditions hold.
-
(A1)
 $\bigcup _{a\in \mathbb{Z}_{m}}\unicode[STIX]{x1D6FC}_{l,a}=\unicode[STIX]{x1D6FC}_{l}$
.
$\bigcup _{a\in \mathbb{Z}_{m}}\unicode[STIX]{x1D6FC}_{l,a}=\unicode[STIX]{x1D6FC}_{l}$
. -
(A2) The arcs
 $\unicode[STIX]{x1D6FC}_{l,a-1}$
and
$\unicode[STIX]{x1D6FC}_{l,a-1}$
and
 $\unicode[STIX]{x1D6FC}_{l,a}$
meet at a point
$\unicode[STIX]{x1D6FC}_{l,a}$
meet at a point
 $p_{l,a}$
and are otherwise disjoint for all
$p_{l,a}$
and are otherwise disjoint for all
 $a\in \mathbb{Z}_{m}$
, whereas
$a\in \mathbb{Z}_{m}$
, whereas
 $\unicode[STIX]{x1D6FC}_{l,a}\cap \unicode[STIX]{x1D6FC}_{l,a^{\prime }}=\emptyset$
provided that
$\unicode[STIX]{x1D6FC}_{l,a}\cap \unicode[STIX]{x1D6FC}_{l,a^{\prime }}=\emptyset$
provided that
 $a^{\prime }\notin \{a-1,a,a+1\}\subset \mathbb{Z}_{m}$
.
$a^{\prime }\notin \{a-1,a,a+1\}\subset \mathbb{Z}_{m}$
. -
(A3) The set
 $I:=\{1,\ldots ,k\}\times \mathbb{Z}_{m}$
splits into two disjoint subsets
$I:=\{1,\ldots ,k\}\times \mathbb{Z}_{m}$
splits into two disjoint subsets
 $I_{\unicode[STIX]{x1D70E}}$
and
$I_{\unicode[STIX]{x1D70E}}$
and
 $I_{\unicode[STIX]{x1D70D}}$
such that (Either of the sets
$I_{\unicode[STIX]{x1D70D}}$
such that (Either of the sets $$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{c}\circ f|>\unicode[STIX]{x1D707}\text{ on }\unicode[STIX]{x1D6FC}_{l,a}\text{ for all }(l,a)\in I_{c},c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{c}\circ f|>\unicode[STIX]{x1D707}\text{ on }\unicode[STIX]{x1D6FC}_{l,a}\text{ for all }(l,a)\in I_{c},c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}.\end{eqnarray}$$
 $I_{\unicode[STIX]{x1D70E}}$
or
$I_{\unicode[STIX]{x1D70E}}$
or
 $I_{\unicode[STIX]{x1D70D}}$
could be empty.)
$I_{\unicode[STIX]{x1D70D}}$
could be empty.)
Choose a family of pairwise disjoint smooth Jordan arcs
 $\unicode[STIX]{x1D6FE}_{l,a}\subset M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
,
$\unicode[STIX]{x1D6FE}_{l,a}\subset M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
,
 $(l,a)\in I$
, such that
$(l,a)\in I$
, such that
 $p_{l,a}\in bM_{1}$
is an endpoint of
$p_{l,a}\in bM_{1}$
is an endpoint of
![]() $\unicode[STIX]{x1D6FE}_{l,a}$
, the other endpoint of
$\unicode[STIX]{x1D6FE}_{l,a}$
, the other endpoint of
![]() $\unicode[STIX]{x1D6FE}_{l,a}$
, which will be called
$\unicode[STIX]{x1D6FE}_{l,a}$
, which will be called
![]() $q_{l,a}$
, lies in
$q_{l,a}$
, lies in
![]() $bM_{2}$
, and
$bM_{2}$
, and
 $\unicode[STIX]{x1D6FE}_{l,a}\setminus \{p_{l,a},q_{l,a}\}\subset {M\unicode[STIX]{x0030A}}_{2}\setminus M_{1}$
. Moreover, we choose the arcs
$\unicode[STIX]{x1D6FE}_{l,a}\setminus \{p_{l,a},q_{l,a}\}\subset {M\unicode[STIX]{x0030A}}_{2}\setminus M_{1}$
. Moreover, we choose the arcs
 $\unicode[STIX]{x1D6FE}_{l,a}\subset M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
for
$\unicode[STIX]{x1D6FE}_{l,a}\subset M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
for
 $(l,a)\in I$
such that the set
$(l,a)\in I$
such that the set
 $$\begin{eqnarray}S:=M_{1}\cup \biggl(\mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6FE}_{l,a}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}S:=M_{1}\cup \biggl(\mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6FE}_{l,a}\biggr)\end{eqnarray}$$
is admissible in
![]() $R$
(see Definition 4.1). Note that the set
$R$
(see Definition 4.1). Note that the set
 $A_{l}\setminus (\unicode[STIX]{x1D6FC}_{l}\cup \unicode[STIX]{x1D6FD}_{l}\cup (\bigcup _{a\in \mathbb{Z}_{m}}\unicode[STIX]{x1D6FE}_{l,a}))$
consists of
$A_{l}\setminus (\unicode[STIX]{x1D6FC}_{l}\cup \unicode[STIX]{x1D6FD}_{l}\cup (\bigcup _{a\in \mathbb{Z}_{m}}\unicode[STIX]{x1D6FE}_{l,a}))$
consists of
![]() $m$
pairwise disjoint open disks; we denote by
$m$
pairwise disjoint open disks; we denote by
![]() $\unicode[STIX]{x1D6FA}_{l,a}$
the one whose closure contains
$\unicode[STIX]{x1D6FA}_{l,a}$
the one whose closure contains
![]() $\unicode[STIX]{x1D6FC}_{l,a}$
,
$\unicode[STIX]{x1D6FC}_{l,a}$
,
 $(l,a)\in I$
. We also set
$(l,a)\in I$
. We also set
 $\unicode[STIX]{x1D6FD}_{l,a}:=\unicode[STIX]{x1D6FD}_{l}\cap \overline{\unicode[STIX]{x1D6FA}}_{l,a}$
for all
$\unicode[STIX]{x1D6FD}_{l,a}:=\unicode[STIX]{x1D6FD}_{l}\cap \overline{\unicode[STIX]{x1D6FA}}_{l,a}$
for all
 $(l,a)\in I$
, and hence
$(l,a)\in I$
, and hence
![]() $\unicode[STIX]{x1D6FA}_{l,a}$
is bounded by the arcs
$\unicode[STIX]{x1D6FA}_{l,a}$
is bounded by the arcs
![]() $\unicode[STIX]{x1D6FC}_{l,a}$
,
$\unicode[STIX]{x1D6FC}_{l,a}$
,
![]() $\unicode[STIX]{x1D6FE}_{l,a}$
,
$\unicode[STIX]{x1D6FE}_{l,a}$
,
![]() $\unicode[STIX]{x1D6FE}_{l,a+1}$
, and
$\unicode[STIX]{x1D6FE}_{l,a+1}$
, and
![]() $\unicode[STIX]{x1D6FD}_{l,a}$
. (See Figure 5.1.)
$\unicode[STIX]{x1D6FD}_{l,a}$
. (See Figure 5.1.)

Figure 5.1. Sets in the proof of Lemma 5.2.
In the first step we extend the map
 $f:M_{1}\rightarrow \mathbb{C}^{2n+1}$
to a generalized Legendrian curve
$f:M_{1}\rightarrow \mathbb{C}^{2n+1}$
to a generalized Legendrian curve
 $\widehat{g}:S\rightarrow \mathbb{C}^{2n+1}$
(see Definition 4.2) such that:
$\widehat{g}:S\rightarrow \mathbb{C}^{2n+1}$
(see Definition 4.2) such that:
-
–
 $|\unicode[STIX]{x1D70B}_{c}\circ \widehat{g}|>\unicode[STIX]{x1D707}$
on
$|\unicode[STIX]{x1D70B}_{c}\circ \widehat{g}|>\unicode[STIX]{x1D707}$
on
 $\unicode[STIX]{x1D6FE}_{l,a}\cup \unicode[STIX]{x1D6FC}_{l,a}\cup \unicode[STIX]{x1D6FE}_{l,a+1}$
for all
$\unicode[STIX]{x1D6FE}_{l,a}\cup \unicode[STIX]{x1D6FC}_{l,a}\cup \unicode[STIX]{x1D6FE}_{l,a+1}$
for all
 $(l,a)\in I_{c}$
,
$(l,a)\in I_{c}$
,
 $c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
;
$c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
; -
–
 $\min \{|\unicode[STIX]{x1D70B}_{c}(\widehat{g}(q_{l,a}))|,|\unicode[STIX]{x1D70B}_{c}(\widehat{g}(q_{l,a+1}))|\}>\unicode[STIX]{x1D707}+1$
for all
$\min \{|\unicode[STIX]{x1D70B}_{c}(\widehat{g}(q_{l,a}))|,|\unicode[STIX]{x1D70B}_{c}(\widehat{g}(q_{l,a+1}))|\}>\unicode[STIX]{x1D707}+1$
for all
 $(l,a)\in I_{c}$
,
$(l,a)\in I_{c}$
,
 $c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
.
$c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
.
To construct such extensions we just use property (A3) and the fact that every compact path in
![]() $\mathbb{C}^{2n+1}$
may be uniformly approximated by Legendrian paths (see Theorem A.6). Lemma 4.3 then provides a holomorphic Legendrian curve
$\mathbb{C}^{2n+1}$
may be uniformly approximated by Legendrian paths (see Theorem A.6). Lemma 4.3 then provides a holomorphic Legendrian curve
 $g:M_{2}\rightarrow \mathbb{C}^{2n+1}$
with no constant component function and satisfying the following conditions:
$g:M_{2}\rightarrow \mathbb{C}^{2n+1}$
with no constant component function and satisfying the following conditions:
-
(B1) the map
 $g$
approximates
$g$
approximates
 $f$
in the
$f$
in the
 $\mathscr{C}^{1}(M_{1})$
-topology;
$\mathscr{C}^{1}(M_{1})$
-topology; -
(B2)
 $|\unicode[STIX]{x1D70B}_{c}\circ g|>\unicode[STIX]{x1D707}$
on
$|\unicode[STIX]{x1D70B}_{c}\circ g|>\unicode[STIX]{x1D707}$
on
 $\unicode[STIX]{x1D6FE}_{l,a}\cup \unicode[STIX]{x1D6FC}_{l,a}\cup \unicode[STIX]{x1D6FE}_{l,a+1}$
for all
$\unicode[STIX]{x1D6FE}_{l,a}\cup \unicode[STIX]{x1D6FC}_{l,a}\cup \unicode[STIX]{x1D6FE}_{l,a+1}$
for all
 $(l,a)\in I_{c}$
,
$(l,a)\in I_{c}$
,
 $c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
;
$c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
; -
(B3)
 $\min \{|\unicode[STIX]{x1D70B}_{c}(g(q_{l,a}))|,|\unicode[STIX]{x1D70B}_{c}(g(q_{l,a+1}))|\}>\unicode[STIX]{x1D707}+1$
for all
$\min \{|\unicode[STIX]{x1D70B}_{c}(g(q_{l,a}))|,|\unicode[STIX]{x1D70B}_{c}(g(q_{l,a+1}))|\}>\unicode[STIX]{x1D707}+1$
for all
 $(l,a)\in I_{c}$
,
$(l,a)\in I_{c}$
,
 $c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
.
$c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
.
Let
 $\unicode[STIX]{x1D6FA}\subset M_{2}$
be a compact domain meeting the following requirements.
$\unicode[STIX]{x1D6FA}\subset M_{2}$
be a compact domain meeting the following requirements.
-
–
 $S\subset \unicode[STIX]{x1D6FA}$
and
$S\subset \unicode[STIX]{x1D6FA}$
and
 $S\cap b\unicode[STIX]{x1D6FA}=\{q_{l,a}:(l,a)\in I\}$
.
$S\cap b\unicode[STIX]{x1D6FA}=\{q_{l,a}:(l,a)\in I\}$
. -
– The set
 $b\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x1D6FD}_{l}$
consists of
$b\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x1D6FD}_{l}$
consists of
 $m$
pairwise disjoint compact arcs
$m$
pairwise disjoint compact arcs
 $\{\unicode[STIX]{x1D706}_{l,a}:a\in \mathbb{Z}_{m}\}$
such that
$\{\unicode[STIX]{x1D706}_{l,a}:a\in \mathbb{Z}_{m}\}$
such that
 $\unicode[STIX]{x1D706}_{l,a}\subset \unicode[STIX]{x1D6FD}_{l,a-1}\cup \unicode[STIX]{x1D6FD}_{l,a}$
and
$\unicode[STIX]{x1D706}_{l,a}\subset \unicode[STIX]{x1D6FD}_{l,a-1}\cup \unicode[STIX]{x1D6FD}_{l,a}$
and
 $q_{l,a}$
is in the relative interior of
$q_{l,a}$
is in the relative interior of
 $\unicode[STIX]{x1D706}_{l,a}$
for all
$\unicode[STIX]{x1D706}_{l,a}$
for all
 $a\in \mathbb{Z}_{m}$
,
$a\in \mathbb{Z}_{m}$
,
 $l=1,\ldots ,k$
.
$l=1,\ldots ,k$
. -
– The set
 $\overline{A_{l}\setminus \unicode[STIX]{x1D6FA}}$
consists of
$\overline{A_{l}\setminus \unicode[STIX]{x1D6FA}}$
consists of
 $m$
pairwise disjoint, smoothly bounded, simply connected compact domains
$m$
pairwise disjoint, smoothly bounded, simply connected compact domains
 $\unicode[STIX]{x1D6F6}_{l,a}$
,
$\unicode[STIX]{x1D6F6}_{l,a}$
,
 $a\in \mathbb{Z}_{m}$
,
$a\in \mathbb{Z}_{m}$
,
 $l=1,\ldots ,k$
. Up to relabeling, we assume that
$l=1,\ldots ,k$
. Up to relabeling, we assume that
 $\unicode[STIX]{x1D6F6}_{l,a}\subset \overline{\unicode[STIX]{x1D6FA}}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}\subset \overline{\unicode[STIX]{x1D6FA}}_{l,a}$
for all
 $(l,a)\in I$
. Note that
$(l,a)\in I$
. Note that
 $\unicode[STIX]{x1D6F6}_{l,a}\cap (\unicode[STIX]{x1D6FE}_{l,a}\cup \unicode[STIX]{x1D6FC}_{l,a}\cup \unicode[STIX]{x1D6FE}_{l,a+1})=\emptyset$
.
$\unicode[STIX]{x1D6F6}_{l,a}\cap (\unicode[STIX]{x1D6FE}_{l,a}\cup \unicode[STIX]{x1D6FC}_{l,a}\cup \unicode[STIX]{x1D6FE}_{l,a+1})=\emptyset$
.
Furthermore, in view of properties (B2) and (B3), continuity of
![]() $g$
enables us to choose
$g$
enables us to choose
![]() $\unicode[STIX]{x1D6FA}$
sufficiently close to
$\unicode[STIX]{x1D6FA}$
sufficiently close to
![]() $S$
such that the following properties hold:
$S$
such that the following properties hold:
-
(C1)
 $|\unicode[STIX]{x1D70B}_{c}\circ g|>\unicode[STIX]{x1D707}$
on
$|\unicode[STIX]{x1D70B}_{c}\circ g|>\unicode[STIX]{x1D707}$
on
 $\overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
for all
$\overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
for all
 $(l,a)\in I_{c}$
,
$(l,a)\in I_{c}$
,
 $c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
;
$c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
; -
(C2)
 $|\unicode[STIX]{x1D70B}_{c}\circ g|>\unicode[STIX]{x1D707}+1$
on
$|\unicode[STIX]{x1D70B}_{c}\circ g|>\unicode[STIX]{x1D707}+1$
on
 $(\unicode[STIX]{x1D706}_{l,a}\cup \unicode[STIX]{x1D706}_{l,a+1})\cap \unicode[STIX]{x1D6FD}_{l,a}$
for all
$(\unicode[STIX]{x1D706}_{l,a}\cup \unicode[STIX]{x1D706}_{l,a+1})\cap \unicode[STIX]{x1D6FD}_{l,a}$
for all
 $(l,a)\in I_{c}$
,
$(l,a)\in I_{c}$
,
 $c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
.
$c\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
.
Assume that
![]() $I_{\unicode[STIX]{x1D70E}}\neq \emptyset$
; otherwise
$I_{\unicode[STIX]{x1D70E}}\neq \emptyset$
; otherwise
 $I_{\unicode[STIX]{x1D70D}}=I\neq \emptyset$
and we reason in a symmetric way. For each
$I_{\unicode[STIX]{x1D70D}}=I\neq \emptyset$
and we reason in a symmetric way. For each
 $(l,a)\in I_{\unicode[STIX]{x1D70E}}$
pick an arc
$(l,a)\in I_{\unicode[STIX]{x1D70E}}$
pick an arc
 $\unicode[STIX]{x1D6FF}_{l,a}\subset \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
with an endpoint in the relative interior of
$\unicode[STIX]{x1D6FF}_{l,a}\subset \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
with an endpoint in the relative interior of
![]() $\unicode[STIX]{x1D6FC}_{l,a}$
, the other endpoint in
$\unicode[STIX]{x1D6FC}_{l,a}$
, the other endpoint in
 $\unicode[STIX]{x1D6F6}_{l,a}\setminus \unicode[STIX]{x1D6FD}_{l,a}$
, and otherwise disjoint from
$\unicode[STIX]{x1D6F6}_{l,a}\setminus \unicode[STIX]{x1D6FD}_{l,a}$
, and otherwise disjoint from
 $\unicode[STIX]{x1D6F6}_{l,a}\cup b\overline{\unicode[STIX]{x1D6FA}}_{l,a}$
. (See Figure 5.1.) Moreover, we choose the family of arcs
$\unicode[STIX]{x1D6F6}_{l,a}\cup b\overline{\unicode[STIX]{x1D6FA}}_{l,a}$
. (See Figure 5.1.) Moreover, we choose the family of arcs
![]() $\unicode[STIX]{x1D6FF}_{l,a}$
,
$\unicode[STIX]{x1D6FF}_{l,a}$
,
 $(l,a)\in I_{\unicode[STIX]{x1D70E}}$
, such that the set
$(l,a)\in I_{\unicode[STIX]{x1D70E}}$
, such that the set
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D70E}}:=S\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a}\biggr)~\text{is admissible in }R\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D70E}}:=S\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a}\biggr)~\text{is admissible in }R\end{eqnarray}$$
(see (5.2)) and
 $$\begin{eqnarray}\text{no component function of }g\text{ has a zero or a critical point in }\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}.\end{eqnarray}$$
$$\begin{eqnarray}\text{no component function of }g\text{ has a zero or a critical point in }\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}.\end{eqnarray}$$
The latter condition is easy to fulfil since
![]() $g$
is holomorphic and has no constant component function. Notice that
$g$
is holomorphic and has no constant component function. Notice that
 $S_{\unicode[STIX]{x1D70E}}\subset M_{2}$
is a deformation retract of
$S_{\unicode[STIX]{x1D70E}}\subset M_{2}$
is a deformation retract of
![]() $M_{2}$
. Set
$M_{2}$
. Set
 $$\begin{eqnarray}K_{\unicode[STIX]{x1D70E}}:=\overline{{S\unicode[STIX]{x0030A}}_{\unicode[STIX]{x1D70E}}},\quad \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70E}}:=\overline{S_{\unicode[STIX]{x1D70E}}\setminus K_{\unicode[STIX]{x1D70E}}}=\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}\end{eqnarray}$$
$$\begin{eqnarray}K_{\unicode[STIX]{x1D70E}}:=\overline{{S\unicode[STIX]{x0030A}}_{\unicode[STIX]{x1D70E}}},\quad \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70E}}:=\overline{S_{\unicode[STIX]{x1D70E}}\setminus K_{\unicode[STIX]{x1D70E}}}=\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}\end{eqnarray}$$
(cf. Definition 4.1). Let us prove the following claim.
Claim 5.3. There exists a generalized Legendrian curve
 $\widetilde{h}_{\unicode[STIX]{x1D70E}}:S_{\unicode[STIX]{x1D70E}}\rightarrow \mathbb{C}^{2n+1}$
satisfying the following properties:
$\widetilde{h}_{\unicode[STIX]{x1D70E}}:S_{\unicode[STIX]{x1D70E}}\rightarrow \mathbb{C}^{2n+1}$
satisfying the following properties:
-
(D1)
 $\widetilde{h}_{\unicode[STIX]{x1D70E}}=g$
on
$\widetilde{h}_{\unicode[STIX]{x1D70E}}=g$
on
 $S\cup (\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
;
$S\cup (\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
; -
(D2)
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ g|_{S_{\unicode[STIX]{x1D70E}}}$
;
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ g|_{S_{\unicode[STIX]{x1D70E}}}$
; -
(D3)
 $|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}|>\unicode[STIX]{x1D707}+1$
on
$|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{\unicode[STIX]{x1D70E}}$
;
$(l,a)\in I_{\unicode[STIX]{x1D70E}}$
; -
(D4) if
 $\unicode[STIX]{x1D70E}=2n+1$
, then
$\unicode[STIX]{x1D70E}=2n+1$
, then
 $\unicode[STIX]{x1D70B}_{1}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
and
$\unicode[STIX]{x1D70B}_{1}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
and
 $\unicode[STIX]{x1D70B}_{2}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
are constant on no component of
$\unicode[STIX]{x1D70B}_{2}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
are constant on no component of
 $K_{\unicode[STIX]{x1D70E}}$
,
$K_{\unicode[STIX]{x1D70E}}$
,
 $\unicode[STIX]{x1D70B}_{1}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
has no zeros in
$\unicode[STIX]{x1D70B}_{1}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
has no zeros in
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70E}}$
, and
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70E}}$
, and
 $\unicode[STIX]{x1D70B}_{2}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
has no critical points in
$\unicode[STIX]{x1D70B}_{2}\circ \widetilde{h}_{\unicode[STIX]{x1D70E}}$
has no critical points in
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70E}}$
.
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70E}}$
.
Proof. If
 $2n+1\notin \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
then, by Remark 2.1, we may assume that
$2n+1\notin \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\}$
then, by Remark 2.1, we may assume that
![]() $\unicode[STIX]{x1D70E}=1$
; note that the transformation in that remark preserves the norm of the first
$\unicode[STIX]{x1D70E}=1$
; note that the transformation in that remark preserves the norm of the first
![]() $2n$
components. Thus, it suffices to discuss the cases
$2n$
components. Thus, it suffices to discuss the cases
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})\in \{1\}\times \{1,\ldots ,2n\}$
and
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})\in \{1\}\times \{1,\ldots ,2n\}$
and
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})\in (\{1,2\}\times \{2n+1\})\cup (\{2n+1\}\times \{1,2\})$
. Write
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})\in (\{1,2\}\times \{2n+1\})\cup (\{2n+1\}\times \{1,2\})$
. Write
 $g=(a_{1},b_{1},\ldots ,a_{n},b_{n},w)$
.
$g=(a_{1},b_{1},\ldots ,a_{n},b_{n},w)$
.
Case 1:
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})\in \{1\}\times \{1,\ldots ,2n\}$
. Let
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})\in \{1\}\times \{1,\ldots ,2n\}$
. Let
 $g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
be any map of class
$g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
be any map of class
![]() $\mathscr{A}^{1}(S_{1})$
(see (4.1)) satisfying the following conditions:
$\mathscr{A}^{1}(S_{1})$
(see (4.1)) satisfying the following conditions:
-
(a)
 $g^{\prime }=g$
on
$g^{\prime }=g$
on
 $S\cup (\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
;
$S\cup (\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
; -
(b)
 $a_{1}^{\prime }=a_{1}|_{S_{1}}$
;
$a_{1}^{\prime }=a_{1}|_{S_{1}}$
; -
(c)
 $|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ g^{\prime }|>\unicode[STIX]{x1D707}+1$
on
$|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ g^{\prime }|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{1}$
.
$(l,a)\in I_{1}$
.
The existence of such a map is trivial. In principle,
![]() $g^{\prime }$
does not need to be Legendrian. Choose an initial point
$g^{\prime }$
does not need to be Legendrian. Choose an initial point
 $u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
$u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
 $w^{\prime \prime }:S_{1}\rightarrow \mathbb{C}$
by
$w^{\prime \prime }:S_{1}\rightarrow \mathbb{C}$
by
 $w^{\prime \prime }=w^{\prime }=w$
on
$w^{\prime \prime }=w^{\prime }=w$
on
 $S\cup (\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
and
$S\cup (\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
and
 $$\begin{eqnarray}w^{\prime \prime }(u)=w(u_{0})-\int _{u_{0}}^{u}\mathop{\sum }_{j=1}^{n}a_{j}^{\prime }\,db_{j}^{\prime },\quad u\in S_{1}.\end{eqnarray}$$
$$\begin{eqnarray}w^{\prime \prime }(u)=w(u_{0})-\int _{u_{0}}^{u}\mathop{\sum }_{j=1}^{n}a_{j}^{\prime }\,db_{j}^{\prime },\quad u\in S_{1}.\end{eqnarray}$$
Conditions (a) and (b), together with the facts that
![]() $g$
is a Legendrian curve and the set
$g$
is a Legendrian curve and the set
 $$\begin{eqnarray}S_{1}\bigg\backslash\biggl(S\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a}\biggr)\biggr)=\mathop{\bigcup }_{(l,a)\in I_{1}}\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a}\end{eqnarray}$$
$$\begin{eqnarray}S_{1}\bigg\backslash\biggl(S\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a}\biggr)\biggr)=\mathop{\bigcup }_{(l,a)\in I_{1}}\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a}\end{eqnarray}$$
is simply connected, ensure that
![]() $w^{\prime \prime }$
is well defined and of class
$w^{\prime \prime }$
is well defined and of class
![]() $\mathscr{A}^{1}(S_{1})$
. Thus, conditions (a), (b), and (c) guarantee that the map
$\mathscr{A}^{1}(S_{1})$
. Thus, conditions (a), (b), and (c) guarantee that the map
 $\widetilde{h}_{1}:=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime \prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
is a generalized Legendrian curve satisfying properties (D1), (D2), and (D3). Property (D4) is vacuous in this case.
$\widetilde{h}_{1}:=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime \prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
is a generalized Legendrian curve satisfying properties (D1), (D2), and (D3). Property (D4) is vacuous in this case.
Case 2:
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(1,2n+1)$
. Choose any map
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(1,2n+1)$
. Choose any map
 $g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
of class
$g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
of class
![]() $\mathscr{A}^{1}(S_{1})$
with the following properties:
$\mathscr{A}^{1}(S_{1})$
with the following properties:
-
(a)
 $g^{\prime }=g$
on
$g^{\prime }=g$
on
 $S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
;
$S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
; -
(b)
 $a_{1}^{\prime }=a_{1}|_{S_{1}}$
;
$a_{1}^{\prime }=a_{1}|_{S_{1}}$
; -
(c)
 $|w^{\prime }|>\unicode[STIX]{x1D707}+1$
on
$|w^{\prime }|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{1}$
;
$(l,a)\in I_{1}$
; -
(d)
 $dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
vanishes nowhere on
$dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
vanishes nowhere on
 $\bigcup _{(l,a)\in I_{1}}\unicode[STIX]{x1D6FF}_{l,a}$
and its zeros on
$\bigcup _{(l,a)\in I_{1}}\unicode[STIX]{x1D6FF}_{l,a}$
and its zeros on
 $\bigcup _{(l,a)\in I_{1}}\unicode[STIX]{x1D6F6}_{l,a}$
are those of
$\bigcup _{(l,a)\in I_{1}}\unicode[STIX]{x1D6F6}_{l,a}$
are those of
 $a_{1}^{\prime }=a_{1}$
, with the same order.
$a_{1}^{\prime }=a_{1}$
, with the same order.
The existence of such
![]() $g^{\prime }$
is clear; for property (d) take into account (5.4). Now choose an initial point
$g^{\prime }$
is clear; for property (d) take into account (5.4). Now choose an initial point
 $u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
$u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
 $b_{1}^{\prime \prime }:S_{1}\rightarrow \mathbb{C}$
by
$b_{1}^{\prime \prime }:S_{1}\rightarrow \mathbb{C}$
by
 $b_{1}^{\prime \prime }=b_{1}^{\prime }=b_{1}$
on
$b_{1}^{\prime \prime }=b_{1}^{\prime }=b_{1}$
on
 $S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
and
$S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
and
 $$\begin{eqnarray}b_{1}^{\prime \prime }(u)=b_{1}(u_{0})-\int _{u_{0}}^{u}\frac{dw^{\prime }+\mathop{\sum }_{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }}{a_{1}^{\prime }},\quad u\in S_{1};\end{eqnarray}$$
$$\begin{eqnarray}b_{1}^{\prime \prime }(u)=b_{1}(u_{0})-\int _{u_{0}}^{u}\frac{dw^{\prime }+\mathop{\sum }_{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }}{a_{1}^{\prime }},\quad u\in S_{1};\end{eqnarray}$$
recall that, by (5.4) and property (b),
![]() $a_{1}^{\prime }$
has no zeros in
$a_{1}^{\prime }$
has no zeros in
 $\bigcup _{(l,a)\in I_{1}}\unicode[STIX]{x1D6FF}_{l,a}$
. It follows that the map
$\bigcup _{(l,a)\in I_{1}}\unicode[STIX]{x1D6FF}_{l,a}$
. It follows that the map
 $\widetilde{h}_{1}:=(a_{1}^{\prime },b_{1}^{\prime \prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
is a generalized Legendrian curve satisfying properties (D1), (D2), and (D3); property (D4) is again vacuous.
$\widetilde{h}_{1}:=(a_{1}^{\prime },b_{1}^{\prime \prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{1}\rightarrow \mathbb{C}^{2n+1}$
is a generalized Legendrian curve satisfying properties (D1), (D2), and (D3); property (D4) is again vacuous.
Case 3:
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(2,2n+1)$
. Choose any map
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(2,2n+1)$
. Choose any map
 $g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2}\rightarrow \mathbb{C}^{2n+1}$
of class
$g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2}\rightarrow \mathbb{C}^{2n+1}$
of class
![]() $\mathscr{A}^{1}(S_{2})$
enjoying the following properties:
$\mathscr{A}^{1}(S_{2})$
enjoying the following properties:
-
(a)
 $g^{\prime }=g$
on
$g^{\prime }=g$
on
 $S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
;
$S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
; -
(b)
 $b_{1}^{\prime }=b_{1}|_{S_{2}}$
;
$b_{1}^{\prime }=b_{1}|_{S_{2}}$
; -
(c)
 $|w^{\prime }|>\unicode[STIX]{x1D707}+1$
on
$|w^{\prime }|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{2}$
;
$(l,a)\in I_{2}$
; -
(d)
 $dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
vanishes nowhere on
$dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
vanishes nowhere on
 $\bigcup _{(l,a)\in I_{2}}\unicode[STIX]{x1D6FF}_{l,a}$
and its zeros on
$\bigcup _{(l,a)\in I_{2}}\unicode[STIX]{x1D6FF}_{l,a}$
and its zeros on
 $\bigcup _{(l,a)\in I_{2}}\unicode[STIX]{x1D6F6}_{l,a}$
are those of
$\bigcup _{(l,a)\in I_{2}}\unicode[STIX]{x1D6F6}_{l,a}$
are those of
 $db_{1}^{\prime }=db_{1}$
, with the same order.
$db_{1}^{\prime }=db_{1}$
, with the same order.
Now choose an initial point
 $u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
$u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
 $a_{1}^{\prime \prime }:S_{2}\rightarrow \mathbb{C}$
by
$a_{1}^{\prime \prime }:S_{2}\rightarrow \mathbb{C}$
by
 $a_{1}^{\prime \prime }=a_{1}^{\prime }=a_{1}$
on
$a_{1}^{\prime \prime }=a_{1}^{\prime }=a_{1}$
on
 $S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
and
$S\cup (\bigcup _{(l,a)\in I_{2n+1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
and
 $$\begin{eqnarray}a_{1}^{\prime \prime }(u)=-\frac{dw^{\prime }+\mathop{\sum }_{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }}{db_{1}^{\prime }},\quad u\in S_{1}.\end{eqnarray}$$
$$\begin{eqnarray}a_{1}^{\prime \prime }(u)=-\frac{dw^{\prime }+\mathop{\sum }_{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }}{db_{1}^{\prime }},\quad u\in S_{1}.\end{eqnarray}$$
The map
 $\widetilde{h}_{2}:=(a_{1}^{\prime \prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2}\rightarrow \mathbb{C}^{2n+1}$
is a generalized Legendrian curve satisfying Claim 5.3.
$\widetilde{h}_{2}:=(a_{1}^{\prime \prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2}\rightarrow \mathbb{C}^{2n+1}$
is a generalized Legendrian curve satisfying Claim 5.3.
Case 4:
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(2n+1,1)$
. Pick a map
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(2n+1,1)$
. Pick a map
 $g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
of class
$g^{\prime }=(a_{1}^{\prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
of class
 $\mathscr{A}^{1}(S_{2n+1})$
meeting the following requirements:
$\mathscr{A}^{1}(S_{2n+1})$
meeting the following requirements:
-
(a)
 $g^{\prime }=g$
on
$g^{\prime }=g$
on
 $S\cup (\bigcup _{(l,a)\in I_{1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
;
$S\cup (\bigcup _{(l,a)\in I_{1}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
; -
(b)
 $w^{\prime }=w|_{S_{2n+1}}$
;
$w^{\prime }=w|_{S_{2n+1}}$
; -
(c)
 $|a_{1}^{\prime }|>\unicode[STIX]{x1D707}+1$
on
$|a_{1}^{\prime }|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{2n+1}$
and
$(l,a)\in I_{2n+1}$
and
 $a_{1}^{\prime }$
vanishes nowhere on
$a_{1}^{\prime }$
vanishes nowhere on
 $\bigcup _{(l,a)\in I_{2n+1}}(\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a})$
;
$\bigcup _{(l,a)\in I_{2n+1}}(\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a})$
; -
(d)
 $dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
has no zeros on
$dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
has no zeros on
 $\bigcup _{(l,a)\in I_{2n+1}}\unicode[STIX]{x1D6FF}_{l,a}$
.
$\bigcup _{(l,a)\in I_{2n+1}}\unicode[STIX]{x1D6FF}_{l,a}$
.
Also, pick an initial point
 $u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
$u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
 $b_{1}^{\prime \prime }:S_{2n+1}\rightarrow \mathbb{C}$
as in Case 2. Thus, the map
$b_{1}^{\prime \prime }:S_{2n+1}\rightarrow \mathbb{C}$
as in Case 2. Thus, the map
 $\widetilde{h}_{2n+1}:=(a_{1}^{\prime },b_{1}^{\prime \prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
satisfies the claim. Notice that requirements (c) and (d) imply property (D4).
$\widetilde{h}_{2n+1}:=(a_{1}^{\prime },b_{1}^{\prime \prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
satisfies the claim. Notice that requirements (c) and (d) imply property (D4).
Case 5:
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(2n+1,2)$
. Take a map
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D})=(2n+1,2)$
. Take a map
 $g^{\prime }:S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
of class
$g^{\prime }:S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
of class
 $\mathscr{A}^{1}(S_{2n+1})$
meeting the following requirements:
$\mathscr{A}^{1}(S_{2n+1})$
meeting the following requirements:
-
(a)
 $g^{\prime }=g$
on
$g^{\prime }=g$
on
 $S\cup (\bigcup _{(l,a)\in I_{2}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
;
$S\cup (\bigcup _{(l,a)\in I_{2}}\overline{\unicode[STIX]{x1D6FA}}_{l,a})$
; -
(b)
 $w^{\prime }=w|_{S_{2n+1}}$
;
$w^{\prime }=w|_{S_{2n+1}}$
; -
(c)
 $|b_{1}^{\prime }|>\unicode[STIX]{x1D707}+1$
on
$|b_{1}^{\prime }|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{2n+1}$
and
$(l,a)\in I_{2n+1}$
and
 $db_{1}^{\prime }$
vanishes nowhere on
$db_{1}^{\prime }$
vanishes nowhere on
 $\bigcup _{(l,a)\in I_{2n+1}}(\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a})$
;
$\bigcup _{(l,a)\in I_{2n+1}}(\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a})$
; -
(d)
 $dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
has no zeros on
$dw^{\prime }+\sum _{j=2}^{n}a_{j}^{\prime }\,db_{j}^{\prime }$
has no zeros on
 $\bigcup _{(l,a)\in I_{2n+1}}\unicode[STIX]{x1D6FF}_{l,a}$
.
$\bigcup _{(l,a)\in I_{2n+1}}\unicode[STIX]{x1D6FF}_{l,a}$
.
Fix a point
 $u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
$u_{0}\in {M\unicode[STIX]{x0030A}}_{1}$
and define
 $a_{1}^{\prime \prime }:S_{2n+1}\rightarrow \mathbb{C}$
as in Case 3. Again, the map
$a_{1}^{\prime \prime }:S_{2n+1}\rightarrow \mathbb{C}$
as in Case 3. Again, the map
 $\widetilde{h}_{2n+1}:=$
$\widetilde{h}_{2n+1}:=$
 $(a_{1}^{\prime \prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
meets all the requirements. As in the previous case, requirements (c) and (d) ensure property (D4).◻
$(a_{1}^{\prime \prime },b_{1}^{\prime },\ldots ,a_{n}^{\prime },b_{n}^{\prime },w^{\prime }):S_{2n+1}\rightarrow \mathbb{C}^{2n+1}$
meets all the requirements. As in the previous case, requirements (c) and (d) ensure property (D4).◻
With Claim 5.3 in hand, and since
![]() $g$
has no constant component function, we may apply Lemmas 4.3 and 4.4 to obtain a holomorphic Legendrian embedding
$g$
has no constant component function, we may apply Lemmas 4.3 and 4.4 to obtain a holomorphic Legendrian embedding
 $h_{\unicode[STIX]{x1D70E}}:M_{2}{\hookrightarrow}\mathbb{C}^{2n+1}$
with the following properties:
$h_{\unicode[STIX]{x1D70E}}:M_{2}{\hookrightarrow}\mathbb{C}^{2n+1}$
with the following properties:
-
(E1)
 $h_{\unicode[STIX]{x1D70E}}$
approximates
$h_{\unicode[STIX]{x1D70E}}$
approximates
 $\widetilde{h}_{\unicode[STIX]{x1D70E}}$
in the
$\widetilde{h}_{\unicode[STIX]{x1D70E}}$
in the
 $\mathscr{C}^{1}(S_{\unicode[STIX]{x1D70E}})$
-topology;
$\mathscr{C}^{1}(S_{\unicode[STIX]{x1D70E}})$
-topology; -
(E2)
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ h_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ g$
.
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ h_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ g$
.
Thus, in view of properties (D3) and (D1), if the approximation in property (E1) is close enough, we have that:
-
(E3)
 $|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ h_{\unicode[STIX]{x1D70E}}|>\unicode[STIX]{x1D707}+1$
on
$|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ h_{\unicode[STIX]{x1D70E}}|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{\unicode[STIX]{x1D70E}}$
;
$(l,a)\in I_{\unicode[STIX]{x1D70E}}$
;
-
(E4)
 $h_{\unicode[STIX]{x1D70E}}$
has no constant component function.
$h_{\unicode[STIX]{x1D70E}}$
has no constant component function.
We claim that if
![]() $I_{\unicode[STIX]{x1D70D}}=\emptyset$
, then
$I_{\unicode[STIX]{x1D70D}}=\emptyset$
, then
![]() $\widetilde{f}:=h_{\unicode[STIX]{x1D70E}}$
satisfies the conclusion of Lemma 5.2. Indeed, properties (B1) and (E1) ensure that
$\widetilde{f}:=h_{\unicode[STIX]{x1D70E}}$
satisfies the conclusion of Lemma 5.2. Indeed, properties (B1) and (E1) ensure that
![]() $\widetilde{f}$
approximates
$\widetilde{f}$
approximates
![]() $f$
in the
$f$
in the
 $\mathscr{C}^{1}(M_{1})$
-topology. If on the other hand
$\mathscr{C}^{1}(M_{1})$
-topology. If on the other hand
![]() $I_{\unicode[STIX]{x1D70D}}=\emptyset$
, then
$I_{\unicode[STIX]{x1D70D}}=\emptyset$
, then
![]() $I_{\unicode[STIX]{x1D70E}}=I$
and hence
$I_{\unicode[STIX]{x1D70E}}=I$
and hence
 $$\begin{eqnarray}bM_{2}\subset \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6F6}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D706}_{l,a}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}bM_{2}\subset \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6F6}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D706}_{l,a}\biggr)\end{eqnarray}$$
and
 $$\begin{eqnarray}M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}=\biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6F6}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}=\biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6F6}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}\biggr).\end{eqnarray}$$
Thus, properties (C2), (E2), and (E3) give condition (i), whereas properties (C1), (E2), and (E3) guarantee condition (ii).
Assume now that
![]() $I_{\unicode[STIX]{x1D70D}}\neq \emptyset$
. As above, for each
$I_{\unicode[STIX]{x1D70D}}\neq \emptyset$
. As above, for each
 $(l,a)\in I_{\unicode[STIX]{x1D70D}}$
, we take an arc
$(l,a)\in I_{\unicode[STIX]{x1D70D}}$
, we take an arc
 $\unicode[STIX]{x1D6FF}_{l,a}\subset \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
with an endpoint in the relative interior of
$\unicode[STIX]{x1D6FF}_{l,a}\subset \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
with an endpoint in the relative interior of
![]() $\unicode[STIX]{x1D6FC}_{l,a}$
, the other endpoint in
$\unicode[STIX]{x1D6FC}_{l,a}$
, the other endpoint in
 $\unicode[STIX]{x1D6F6}_{l,a}\setminus \unicode[STIX]{x1D6FD}_{l,a}$
, and otherwise disjoint from
$\unicode[STIX]{x1D6F6}_{l,a}\setminus \unicode[STIX]{x1D6FD}_{l,a}$
, and otherwise disjoint from
 $\unicode[STIX]{x1D6F6}_{l,a}\cup b\overline{\unicode[STIX]{x1D6FA}}_{l,a}$
, such that the set
$\unicode[STIX]{x1D6F6}_{l,a}\cup b\overline{\unicode[STIX]{x1D6FA}}_{l,a}$
, such that the set
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D70D}}:=S\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D70D}}:=S\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\overline{\unicode[STIX]{x1D6FA}}_{l,a}\biggr)\cup \biggl(\mathop{\bigcup }_{(l,a)\in I_{\unicode[STIX]{x1D70D}}}\unicode[STIX]{x1D6FF}_{l,a}\cup \unicode[STIX]{x1D6F6}_{l,a}\biggr)\end{eqnarray}$$
is admissible in
![]() $R$
and no component function of
$R$
and no component function of
![]() $h_{\unicode[STIX]{x1D70E}}$
has a zero or a critical point in
$h_{\unicode[STIX]{x1D70E}}$
has a zero or a critical point in
 $\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}$
. Reasoning as above, in a symmetric way, we may construct a holomorphic Legendrian embedding
$\bigcup _{(l,a)\in I_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D6FF}_{l,a}$
. Reasoning as above, in a symmetric way, we may construct a holomorphic Legendrian embedding
 $h_{\unicode[STIX]{x1D70D}}:M_{2}\rightarrow \mathbb{C}^{2n+1}$
enjoying the following properties:
$h_{\unicode[STIX]{x1D70D}}:M_{2}\rightarrow \mathbb{C}^{2n+1}$
enjoying the following properties:
-
(F1)
 $h_{\unicode[STIX]{x1D70D}}$
approximates
$h_{\unicode[STIX]{x1D70D}}$
approximates
 $h_{\unicode[STIX]{x1D70E}}$
in the
$h_{\unicode[STIX]{x1D70E}}$
in the
 $\mathscr{C}^{1}(S_{\unicode[STIX]{x1D70D}})$
-topology;
$\mathscr{C}^{1}(S_{\unicode[STIX]{x1D70D}})$
-topology; -
(F2)
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ h_{\unicode[STIX]{x1D70D}}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ h_{\unicode[STIX]{x1D70E}}$
;
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ h_{\unicode[STIX]{x1D70D}}=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ h_{\unicode[STIX]{x1D70E}}$
; -
(F3)
 $|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ h_{\unicode[STIX]{x1D70D}}|>\unicode[STIX]{x1D707}+1$
on
$|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ h_{\unicode[STIX]{x1D70D}}|>\unicode[STIX]{x1D707}+1$
on
 $\unicode[STIX]{x1D6F6}_{l,a}$
for all
$\unicode[STIX]{x1D6F6}_{l,a}$
for all
 $(l,a)\in I_{\unicode[STIX]{x1D70D}}$
.
$(l,a)\in I_{\unicode[STIX]{x1D70D}}$
.
We claim that, if the approximations in properties (B1), (D1), (E1), and (F1) are close enough, the Legendrian curve
 $\widetilde{f}:=h_{\unicode[STIX]{x1D70D}}:M_{2}\rightarrow \mathbb{C}^{2n+1}$
satisfies the conclusion of the lemma. Indeed, the mentioned properties ensure that
$\widetilde{f}:=h_{\unicode[STIX]{x1D70D}}:M_{2}\rightarrow \mathbb{C}^{2n+1}$
satisfies the conclusion of the lemma. Indeed, the mentioned properties ensure that
![]() $\widetilde{f}$
approximates
$\widetilde{f}$
approximates
![]() $f$
in the
$f$
in the
 $\mathscr{C}^{1}(M_{1})$
-topology. It remains to check conditions (i) and (ii). Let
$\mathscr{C}^{1}(M_{1})$
-topology. It remains to check conditions (i) and (ii). Let
 $p\in M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
. If
$p\in M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1}$
. If
 $p\in \unicode[STIX]{x1D6F6}_{l,a}$
for some
$p\in \unicode[STIX]{x1D6F6}_{l,a}$
for some
 $(l,a)\in I_{\unicode[STIX]{x1D70E}}$
, we have
$(l,a)\in I_{\unicode[STIX]{x1D70E}}$
, we have
 $$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(\widetilde{f}(p))|\stackrel{\text{(F1)}}{{\approx}}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(h_{\unicode[STIX]{x1D70E}}(p))|\stackrel{\text{(E3)}}{{>}}\unicode[STIX]{x1D707}+1,\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(\widetilde{f}(p))|\stackrel{\text{(F1)}}{{\approx}}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(h_{\unicode[STIX]{x1D70E}}(p))|\stackrel{\text{(E3)}}{{>}}\unicode[STIX]{x1D707}+1,\end{eqnarray}$$
and together with property (F3) we infer that
 $$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}+1\quad \text{on }\mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6F6}_{l,a}.\end{eqnarray}$$
$$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}+1\quad \text{on }\mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6F6}_{l,a}.\end{eqnarray}$$
On the other hand, if
 $p\in \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
for some
$p\in \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
for some
 $(l,a)\in I_{\unicode[STIX]{x1D70E}}$
, we have
$(l,a)\in I_{\unicode[STIX]{x1D70E}}$
, we have
 $$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(\widetilde{f}(p))|\stackrel{\text{(F1)}}{{\approx}}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(h_{\unicode[STIX]{x1D70E}}(p))|\stackrel{\text{(E2)}}{=}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(g(p))|,\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(\widetilde{f}(p))|\stackrel{\text{(F1)}}{{\approx}}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(h_{\unicode[STIX]{x1D70E}}(p))|\stackrel{\text{(E2)}}{=}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}(g(p))|,\end{eqnarray}$$
whereas if
 $p\in \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
for some
$p\in \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}}$
for some
 $(l,a)\in I_{\unicode[STIX]{x1D70D}}$
, then
$(l,a)\in I_{\unicode[STIX]{x1D70D}}$
, then
 $$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(\widetilde{f}(p))|\stackrel{\text{(F2)}}{=}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(h_{\unicode[STIX]{x1D70E}}(p))|\stackrel{\text{(E1),(D1)}}{{\approx}}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(g(p))|.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(\widetilde{f}(p))|\stackrel{\text{(F2)}}{=}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(h_{\unicode[STIX]{x1D70E}}(p))|\stackrel{\text{(E1),(D1)}}{{\approx}}|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}(g(p))|.\end{eqnarray}$$
So, the estimates (5.6) and (5.7) together with the inequalities (5.5), (C1), and (C2), and the facts that
 $$\begin{eqnarray}\displaystyle bM_{2} & = & \displaystyle \mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6FD}_{l,a}\subset \mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6F6}_{l,a}\cup (\unicode[STIX]{x1D6FD}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}),\nonumber\\ \displaystyle M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1} & = & \displaystyle \mathop{\bigcup }_{(l,a)\in I}\overline{\unicode[STIX]{x1D6FA}}_{l,a}=\mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6F6}_{l,a}\cup \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle bM_{2} & = & \displaystyle \mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6FD}_{l,a}\subset \mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6F6}_{l,a}\cup (\unicode[STIX]{x1D6FD}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}),\nonumber\\ \displaystyle M_{2}\setminus {M\unicode[STIX]{x0030A}}_{1} & = & \displaystyle \mathop{\bigcup }_{(l,a)\in I}\overline{\unicode[STIX]{x1D6FA}}_{l,a}=\mathop{\bigcup }_{(l,a)\in I}\unicode[STIX]{x1D6F6}_{l,a}\cup \overline{\unicode[STIX]{x1D6FA}_{l,a}\setminus \unicode[STIX]{x1D6F6}_{l,a}},\nonumber\end{eqnarray}$$
guarantee conditions (i) and (ii). This concludes the proof. ◻
Proof of Theorem 5.1.
Up to adding suitable arcs to the admissible set
![]() $S$
and extending
$S$
and extending
![]() $f$
to a generalized Legendrian curve in the arising admissible set (see Theorem A.6), we may assume that
$f$
to a generalized Legendrian curve in the arising admissible set (see Theorem A.6), we may assume that
![]() $S$
is connected. As in the proof of Lemma 4.3, we may also assume that
$S$
is connected. As in the proof of Lemma 4.3, we may also assume that
![]() $K\neq \emptyset$
.
$K\neq \emptyset$
.
Let
 $M_{0}\subset R$
be a smoothly bounded compact connected domain such that
$M_{0}\subset R$
be a smoothly bounded compact connected domain such that
 $S\subset {M\unicode[STIX]{x0030A}}_{0}$
and
$S\subset {M\unicode[STIX]{x0030A}}_{0}$
and
![]() $S$
is a strong deformation retract of
$S$
is a strong deformation retract of
![]() $M_{0}$
. By Lemmas 4.3 and 4.4,
$M_{0}$
. By Lemmas 4.3 and 4.4,
![]() $f$
can be approximated in the
$f$
can be approximated in the
![]() $\mathscr{C}^{1}(S)$
-topology by a holomorphic Legendrian embedding
$\mathscr{C}^{1}(S)$
-topology by a holomorphic Legendrian embedding
 $f_{0}:M_{0}\rightarrow \mathbb{C}^{2n+1}$
. Moreover, up to a slight deformation of
$f_{0}:M_{0}\rightarrow \mathbb{C}^{2n+1}$
. Moreover, up to a slight deformation of
![]() $f_{0}$
, we may assume that
$f_{0}$
, we may assume that
 $\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{0}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{0}|\}>\unicode[STIX]{x1D707}$
on
$\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{0}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{0}|\}>\unicode[STIX]{x1D707}$
on
![]() $bM_{0}$
for some constant
$bM_{0}$
for some constant
![]() $\unicode[STIX]{x1D707}>0$
.
$\unicode[STIX]{x1D707}>0$
.
Let
 $M_{0}\Subset M_{1}\Subset M_{2}\Subset \cdots \,$
be a sequence of smoothly bounded compact connected Runge domains in
$M_{0}\Subset M_{1}\Subset M_{2}\Subset \cdots \,$
be a sequence of smoothly bounded compact connected Runge domains in
![]() $R$
such that:
$R$
such that:
-
–
 $\bigcup _{k\geqslant 0}M_{k}=R$
;
$\bigcup _{k\geqslant 0}M_{k}=R$
; -
– the Euler characteristic
 $\unicode[STIX]{x1D712}(M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1})\in \{0,-1\}$
for all
$\unicode[STIX]{x1D712}(M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1})\in \{0,-1\}$
for all
 $k\in \mathbb{N}$
.
$k\in \mathbb{N}$
.
Let us construct a sequence
 $\{f_{k}:M_{k}\rightarrow \mathbb{C}^{2n+1}\}_{k\in \mathbb{N}}$
of Legendrian embeddings meeting the following requirements for every
$\{f_{k}:M_{k}\rightarrow \mathbb{C}^{2n+1}\}_{k\in \mathbb{N}}$
of Legendrian embeddings meeting the following requirements for every
 $k=1,2,\ldots :$
$k=1,2,\ldots :$
-
 $(\text{i}_{k})$
$(\text{i}_{k})$
-
 $f_{k}$
approximates
$f_{k}$
approximates
 $f_{k-1}$
uniformly on
$f_{k-1}$
uniformly on
 $M_{k-1}$
;
$M_{k-1}$
; -
 $(\text{ii}_{k})$
$(\text{ii}_{k})$
-
 $\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{k}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{k}|\}>\unicode[STIX]{x1D707}+k$
on
$\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{k}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{k}|\}>\unicode[STIX]{x1D707}+k$
on
 $bM_{k}$
;
$bM_{k}$
; -
 $(\text{iii}_{k})$
$(\text{iii}_{k})$
-
 $\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{k}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{k}|\}>\unicode[STIX]{x1D707}+k-1$
on
$\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{k}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{k}|\}>\unicode[STIX]{x1D707}+k-1$
on
 $M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1}$
.
$M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1}$
.
We reason in a recursive way. Observe that
 $f_{0}:M_{0}\rightarrow \mathbb{C}^{2n+1}$
satisfies condition (ii
$f_{0}:M_{0}\rightarrow \mathbb{C}^{2n+1}$
satisfies condition (ii
![]() $_{0}$
), whereas the conditions (i
$_{0}$
), whereas the conditions (i
![]() $_{0}$
) and (iii
$_{0}$
) and (iii
![]() $_{0}$
) are vacuous. Assume we have found
$_{0}$
) are vacuous. Assume we have found
 $f_{0},\ldots ,f_{k-1}$
satisfying the above properties, and let us construct the next map
$f_{0},\ldots ,f_{k-1}$
satisfying the above properties, and let us construct the next map
![]() $f_{k}$
.
$f_{k}$
.
If
 $\unicode[STIX]{x1D712}(M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1})=0$
, then
$\unicode[STIX]{x1D712}(M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1})=0$
, then
![]() $M_{k-1}$
is a strong retract deformation of
$M_{k-1}$
is a strong retract deformation of
![]() $M_{k}$
. Lemma 5.2 applied to
$M_{k}$
. Lemma 5.2 applied to
![]() $M_{k-1}$
,
$M_{k-1}$
,
![]() $M_{k}$
,
$M_{k}$
,
 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\in \{1,\ldots ,2n+1\}$
,
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}\in \{1,\ldots ,2n+1\}$
,
 $\unicode[STIX]{x1D707}+k-1$
, and
$\unicode[STIX]{x1D707}+k-1$
, and
 $f_{k-1}:M_{k-1}\rightarrow \mathbb{C}^{2n+1}$
provides a holomorphic Legendrian embedding
$f_{k-1}:M_{k-1}\rightarrow \mathbb{C}^{2n+1}$
provides a holomorphic Legendrian embedding
 $f_{k}:M_{k}{\hookrightarrow}\mathbb{C}^{2n+1}$
enjoying the desired properties (i
$f_{k}:M_{k}{\hookrightarrow}\mathbb{C}^{2n+1}$
enjoying the desired properties (i
![]() $_{k}$
), (ii
$_{k}$
), (ii
![]() $_{k}$
), and (iii
$_{k}$
), and (iii
![]() $_{k}$
).
$_{k}$
).
If
 $\unicode[STIX]{x1D712}(M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1})=-1$
, there is a Jordan arc
$\unicode[STIX]{x1D712}(M_{k}\setminus {M\unicode[STIX]{x0030A}}_{k-1})=-1$
, there is a Jordan arc
 $\unicode[STIX]{x1D6FC}\subset {M\unicode[STIX]{x0030A}}_{k}$
with the endpoints in
$\unicode[STIX]{x1D6FC}\subset {M\unicode[STIX]{x0030A}}_{k}$
with the endpoints in
![]() $bM_{k-1}$
and otherwise disjoint from
$bM_{k-1}$
and otherwise disjoint from
![]() $M_{k-1}$
, such that
$M_{k-1}$
, such that
 $S^{\prime }:=M_{k-1}\cup \unicode[STIX]{x1D6FC}$
is an admissible subset of
$S^{\prime }:=M_{k-1}\cup \unicode[STIX]{x1D6FC}$
is an admissible subset of
![]() $R$
and a strong deformation retract of
$R$
and a strong deformation retract of
![]() $M_{k}$
. By Theorem A.6 we may extend
$M_{k}$
. By Theorem A.6 we may extend
![]() $f_{k-1}$
to a generalized Legendrian map
$f_{k-1}$
to a generalized Legendrian map
 $f_{k-1}^{\prime }:S^{\prime }\rightarrow \mathbb{C}^{2n+1}$
satisfying
$f_{k-1}^{\prime }:S^{\prime }\rightarrow \mathbb{C}^{2n+1}$
satisfying
 $$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{k-1}^{\prime }|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{k-1}^{\prime }|\}>\unicode[STIX]{x1D707}+k-1\quad \text{on }\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
$$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ f_{k-1}^{\prime }|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ f_{k-1}^{\prime }|\}>\unicode[STIX]{x1D707}+k-1\quad \text{on }\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
By Lemmas 4.3 and 4.4 we can approximate
![]() $f_{k-1}^{\prime }$
in the
$f_{k-1}^{\prime }$
in the
![]() ${\mathcal{C}}^{1}(S^{\prime })$
-topology by a holomorphic Legendrian embedding
${\mathcal{C}}^{1}(S^{\prime })$
-topology by a holomorphic Legendrian embedding
 $\widetilde{f}_{k-1}:M_{k}\rightarrow \mathbb{C}^{n+1}$
. If the approximation is close enough, there is a smoothly bounded compact domain
$\widetilde{f}_{k-1}:M_{k}\rightarrow \mathbb{C}^{n+1}$
. If the approximation is close enough, there is a smoothly bounded compact domain
![]() $M_{k-1}^{\prime }$
such that
$M_{k-1}^{\prime }$
such that
 $S^{\prime }\subset {M\unicode[STIX]{x0030A}}_{k-1}^{\prime }\subset M_{k-1}^{\prime }\subset {M\unicode[STIX]{x0030A}}_{k}$
,
$S^{\prime }\subset {M\unicode[STIX]{x0030A}}_{k-1}^{\prime }\subset M_{k-1}^{\prime }\subset {M\unicode[STIX]{x0030A}}_{k}$
,
![]() $M_{k-1}^{\prime }$
is a deformation retract of
$M_{k-1}^{\prime }$
is a deformation retract of
![]() $M_{k}$
, and
$M_{k}$
, and
 $$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}_{k-1}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}_{k-1}|\}>\unicode[STIX]{x1D707}+k-1\quad \text{on }M_{k-1}^{\prime }\setminus {M\unicode[STIX]{x0030A}}_{k-1}.\end{eqnarray}$$
$$\begin{eqnarray}\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}_{k-1}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}_{k-1}|\}>\unicode[STIX]{x1D707}+k-1\quad \text{on }M_{k-1}^{\prime }\setminus {M\unicode[STIX]{x0030A}}_{k-1}.\end{eqnarray}$$
This reduces the proof to the previous case. This closes the induction.
If the approximations in condition (i
![]() $_{k}$
) are close enough, the sequence of Legendrian embeddings
$_{k}$
) are close enough, the sequence of Legendrian embeddings
 $\{f_{k}:M_{k}{\hookrightarrow}\mathbb{C}^{2n+1}\}_{k\in \mathbb{N}}$
converges uniformly on compacts in
$\{f_{k}:M_{k}{\hookrightarrow}\mathbb{C}^{2n+1}\}_{k\in \mathbb{N}}$
converges uniformly on compacts in
![]() $R$
to a holomorphic Legendrian embedding
$R$
to a holomorphic Legendrian embedding
 $\widetilde{f}:R{\hookrightarrow}\mathbb{C}^{2n+1}$
. Condition (i
$\widetilde{f}:R{\hookrightarrow}\mathbb{C}^{2n+1}$
. Condition (i
![]() $_{k}$
) for
$_{k}$
) for
![]() $k\in \mathbb{Z}_{+}$
ensures that
$k\in \mathbb{Z}_{+}$
ensures that
![]() $\widetilde{f}|_{S}$
approximates
$\widetilde{f}|_{S}$
approximates
![]() $f_{0}$
, and hence
$f_{0}$
, and hence
![]() $f$
, in the
$f$
, in the
![]() $\mathscr{C}^{1}(S)$
-topology. Finally,
$\mathscr{C}^{1}(S)$
-topology. Finally,
 $\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}+k$
on
$\max \{|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}}\circ \widetilde{f}|,|\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70D}}\circ \widetilde{f}|\}>\unicode[STIX]{x1D707}+k$
on
![]() $R\setminus M_{k}$
for all
$R\setminus M_{k}$
for all
![]() $k$
provided that the approximations in condition (i
$k$
provided that the approximations in condition (i
![]() $_{j}$
) are sufficiently close; take into account conditions (ii
$_{j}$
) are sufficiently close; take into account conditions (ii
![]() $_{j}$
) and (iii
$_{j}$
) and (iii
![]() $_{j}$
),
$_{j}$
),
![]() $j\in \mathbb{N}$
. In particular,
$j\in \mathbb{N}$
. In particular,
 $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}}\circ \widetilde{f}:R\rightarrow \mathbb{C}^{2}$
is a proper map.
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70D}}\circ \widetilde{f}:R\rightarrow \mathbb{C}^{2}$
is a proper map.
This concludes the proof of Theorem 5.1. ◻
6 Complete holomorphic Legendrian curves with Jordan boundaries
In this section we prove Theorem 1.2 in the introduction. For simplicity of exposition we shall prove the theorem in the particular case when the source compact bordered Riemann surface
![]() $M$
is the closed unit disk
$M$
is the closed unit disk
![]() $\overline{\mathbb{D}}\subset \mathbb{C}$
(see Theorem 6.2 below). We point out that the same proof applies in the general case; for that one simply uses Theorem 3.3 (the Riemann–Hilbert problem for holomorphic Legendrian curves normalized by any given bordered Riemann surface) as opposed to Lemma 3.2 (the Riemann–Hilbert problem for holomorphic Legendrian disks). We leave the details to the interested reader and refer to [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, § 4] where complete details are given for any bordered Riemann surface
$\overline{\mathbb{D}}\subset \mathbb{C}$
(see Theorem 6.2 below). We point out that the same proof applies in the general case; for that one simply uses Theorem 3.3 (the Riemann–Hilbert problem for holomorphic Legendrian curves normalized by any given bordered Riemann surface) as opposed to Lemma 3.2 (the Riemann–Hilbert problem for holomorphic Legendrian disks). We leave the details to the interested reader and refer to [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, § 4] where complete details are given for any bordered Riemann surface
![]() $M$
in a geometrically similar situation of conformal minimal immersions and holomorphic null curves.
$M$
in a geometrically similar situation of conformal minimal immersions and holomorphic null curves.
We begin by pointing out the existence of a large family of Legendrian curves which are contained in certain complex affine hyperplanes of
![]() $\mathbb{C}^{2n+1}$
. These curves will be crucial in the subsequent construction.
$\mathbb{C}^{2n+1}$
. These curves will be crucial in the subsequent construction.
Proposition 6.1. Let
 $(a_{1},b_{1},\ldots ,a_{n},b_{n})\in \mathbb{C}^{2n}$
$(a_{1},b_{1},\ldots ,a_{n},b_{n})\in \mathbb{C}^{2n}$
![]() $(n\in \mathbb{N})$
be such that
$(n\in \mathbb{N})$
be such that
 $a_{1}\cdots a_{n}\neq 0$
and denote by
$a_{1}\cdots a_{n}\neq 0$
and denote by
 $\unicode[STIX]{x1D6F1}\subset \mathbb{C}^{2n+1}$
the complex vectorial hyperplane
$\unicode[STIX]{x1D6F1}\subset \mathbb{C}^{2n+1}$
the complex vectorial hyperplane
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:=\biggl\{(x_{1},y_{1},\ldots ,x_{n},y_{n},z)\in \mathbb{C}^{2n+1}:z+\mathop{\sum }_{j=1}^{n}(a_{j}x_{j}+b_{j}y_{j})=0\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:=\biggl\{(x_{1},y_{1},\ldots ,x_{n},y_{n},z)\in \mathbb{C}^{2n+1}:z+\mathop{\sum }_{j=1}^{n}(a_{j}x_{j}+b_{j}y_{j})=0\biggr\}.\end{eqnarray}$$
Given a point
 $p_{0}=(x_{0,1},y_{0,1},\ldots ,x_{0,n},y_{0,n},z_{0})\in \mathbb{C}^{2n+1}$
, the map
$p_{0}=(x_{0,1},y_{0,1},\ldots ,x_{0,n},y_{0,n},z_{0})\in \mathbb{C}^{2n+1}$
, the map
 $$\begin{eqnarray}\mathbb{C}\ni \unicode[STIX]{x1D701}\mapsto \unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D701})=(X_{1}(\unicode[STIX]{x1D701}),Y_{1}(\unicode[STIX]{x1D701}),\ldots ,X_{n}(\unicode[STIX]{x1D701}),Y_{n}(\unicode[STIX]{x1D701}),Z(\unicode[STIX]{x1D701}))\in \mathbb{C}^{2n+1}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}\ni \unicode[STIX]{x1D701}\mapsto \unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D701})=(X_{1}(\unicode[STIX]{x1D701}),Y_{1}(\unicode[STIX]{x1D701}),\ldots ,X_{n}(\unicode[STIX]{x1D701}),Y_{n}(\unicode[STIX]{x1D701}),Z(\unicode[STIX]{x1D701}))\in \mathbb{C}^{2n+1}\end{eqnarray}$$
defined by
 $$\begin{eqnarray}\displaystyle Y_{j}(\unicode[STIX]{x1D701}) & = & \displaystyle y_{0,j}+\unicode[STIX]{x1D701},\nonumber\\ \displaystyle X_{j}(\unicode[STIX]{x1D701}) & = & \displaystyle \frac{x_{0,j}-b_{j}}{e^{y_{0,j}/a_{j}}}e^{Y_{j}(\unicode[STIX]{x1D701})/a_{j}}+b_{j},\nonumber\\ \displaystyle Z(\unicode[STIX]{x1D701}) & = & \displaystyle z_{0}+\mathop{\sum }_{j=1}^{n}(a_{j}x_{0,j}+b_{j}y_{0,j}-a_{j}X_{j}(\unicode[STIX]{x1D701})-b_{j}Y_{j}(\unicode[STIX]{x1D701})),\quad j=1,\ldots ,n,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Y_{j}(\unicode[STIX]{x1D701}) & = & \displaystyle y_{0,j}+\unicode[STIX]{x1D701},\nonumber\\ \displaystyle X_{j}(\unicode[STIX]{x1D701}) & = & \displaystyle \frac{x_{0,j}-b_{j}}{e^{y_{0,j}/a_{j}}}e^{Y_{j}(\unicode[STIX]{x1D701})/a_{j}}+b_{j},\nonumber\\ \displaystyle Z(\unicode[STIX]{x1D701}) & = & \displaystyle z_{0}+\mathop{\sum }_{j=1}^{n}(a_{j}x_{0,j}+b_{j}y_{0,j}-a_{j}X_{j}(\unicode[STIX]{x1D701})-b_{j}Y_{j}(\unicode[STIX]{x1D701})),\quad j=1,\ldots ,n,\nonumber\end{eqnarray}$$
is a proper holomorphic Legendrian embedding
 $\mathbb{C}{\hookrightarrow}\mathbb{C}^{2n+1}$
such that
$\mathbb{C}{\hookrightarrow}\mathbb{C}^{2n+1}$
such that
 $\unicode[STIX]{x1D6F9}(0)=p_{0}$
and
$\unicode[STIX]{x1D6F9}(0)=p_{0}$
and
 $\unicode[STIX]{x1D6F9}(\mathbb{C})\subset p_{0}+\unicode[STIX]{x1D6F1}$
. Moreover,
$\unicode[STIX]{x1D6F9}(\mathbb{C})\subset p_{0}+\unicode[STIX]{x1D6F1}$
. Moreover,
![]() $\unicode[STIX]{x1D6F9}$
depends holomorphically on
$\unicode[STIX]{x1D6F9}$
depends holomorphically on
 $p_{0}\in \mathbb{C}^{2n+1}$
.
$p_{0}\in \mathbb{C}^{2n+1}$
.
Proof. Obviously,
![]() $\unicode[STIX]{x1D6F9}$
is holomorphic and depends holomorphically on
$\unicode[STIX]{x1D6F9}$
is holomorphic and depends holomorphically on
 $p_{0}\in \mathbb{C}^{2n+1}$
. A trivial computation shows that
$p_{0}\in \mathbb{C}^{2n+1}$
. A trivial computation shows that
 $dZ_{j}+\sum _{j=1}^{n}X_{j}\,dY_{j}=0$
everywhere on
$dZ_{j}+\sum _{j=1}^{n}X_{j}\,dY_{j}=0$
everywhere on
![]() $\mathbb{C}$
and so
$\mathbb{C}$
and so
![]() $\unicode[STIX]{x1D6F9}$
is Legendrian. Further,
$\unicode[STIX]{x1D6F9}$
is Legendrian. Further,
 $Y_{j}:\mathbb{C}\rightarrow \mathbb{C}$
is a proper (linear) embedding for each
$Y_{j}:\mathbb{C}\rightarrow \mathbb{C}$
is a proper (linear) embedding for each
 $j\in \{1,\ldots ,n\}$
and hence
$j\in \{1,\ldots ,n\}$
and hence
![]() $\unicode[STIX]{x1D6F9}$
is a proper embedding as well. Finally, the facts that
$\unicode[STIX]{x1D6F9}$
is a proper embedding as well. Finally, the facts that
 $\unicode[STIX]{x1D6F9}(0)=p_{0}$
and
$\unicode[STIX]{x1D6F9}(0)=p_{0}$
and
 $\unicode[STIX]{x1D6F9}(\mathbb{C})\subset p_{0}+\unicode[STIX]{x1D6F1}$
can be checked by direct computation.◻
$\unicode[STIX]{x1D6F9}(\mathbb{C})\subset p_{0}+\unicode[STIX]{x1D6F1}$
can be checked by direct computation.◻
A holomorphic disk
 $f:\mathbb{D}\rightarrow \mathbb{C}^{N}$
$f:\mathbb{D}\rightarrow \mathbb{C}^{N}$
 $(N\in \mathbb{N})$
is said to be complete if for any path
$(N\in \mathbb{N})$
is said to be complete if for any path
 $\unicode[STIX]{x1D6FE}:[0,1)\rightarrow \mathbb{D}$
with
$\unicode[STIX]{x1D6FE}:[0,1)\rightarrow \mathbb{D}$
with
 $\lim _{t\rightarrow 1}|\unicode[STIX]{x1D6FE}(t)|=1$
the path
$\lim _{t\rightarrow 1}|\unicode[STIX]{x1D6FE}(t)|=1$
the path
 $f\circ \unicode[STIX]{x1D6FE}:[0,1)\rightarrow \mathbb{C}^{N}$
has infinite length. Equivalently, denoting by
$f\circ \unicode[STIX]{x1D6FE}:[0,1)\rightarrow \mathbb{C}^{N}$
has infinite length. Equivalently, denoting by
![]() $ds^{2}$
the Euclidean metric on
$ds^{2}$
the Euclidean metric on
![]() $\mathbb{C}^{N}$
, the pull-back
$\mathbb{C}^{N}$
, the pull-back
![]() $f^{\ast }ds^{2}$
is a complete metric on
$f^{\ast }ds^{2}$
is a complete metric on
![]() $\mathbb{D}$
.
$\mathbb{D}$
.
If
 $f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{N}$
is an immersion of class
$f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{N}$
is an immersion of class
![]() $\mathscr{A}^{1}(\overline{\mathbb{D}})$
, we denote by
$\mathscr{A}^{1}(\overline{\mathbb{D}})$
, we denote by
 $\text{dist}_{f}:\overline{\mathbb{D}}\times \overline{\mathbb{D}}\rightarrow \mathbb{R}$
the distance on
$\text{dist}_{f}:\overline{\mathbb{D}}\times \overline{\mathbb{D}}\rightarrow \mathbb{R}$
the distance on
![]() $\overline{\mathbb{D}}$
associated to the Riemannian metric
$\overline{\mathbb{D}}$
associated to the Riemannian metric
![]() $f^{\ast }ds^{2}$
.
$f^{\ast }ds^{2}$
.
The following is the main result in this section.
Theorem 6.2. Every Legendrian curve
 $f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
$f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
![]() $(n\in \mathbb{N})$
of class
$(n\in \mathbb{N})$
of class
![]() $\mathscr{A}^{1}(\overline{\mathbb{D}})$
may be approximated uniformly on
$\mathscr{A}^{1}(\overline{\mathbb{D}})$
may be approximated uniformly on
![]() $\overline{\mathbb{D}}$
by continuous injective maps
$\overline{\mathbb{D}}$
by continuous injective maps
 $\widetilde{f}:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
such that
$\widetilde{f}:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
such that
 $\widetilde{f}|_{\mathbb{D}}:\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
is a complete holomorphic Legendrian embedding.
$\widetilde{f}|_{\mathbb{D}}:\mathbb{D}\rightarrow \mathbb{C}^{2n+1}$
is a complete holomorphic Legendrian embedding.
Recall that
 $\mathbb{T}=b\overline{\mathbb{D}}=\{\unicode[STIX]{x1D701}\in \mathbb{C}:|\unicode[STIX]{x1D701}|=1\}$
. Most of the technical part in the proof of Theorem 6.2 is provided by the following lemma.
$\mathbb{T}=b\overline{\mathbb{D}}=\{\unicode[STIX]{x1D701}\in \mathbb{C}:|\unicode[STIX]{x1D701}|=1\}$
. Most of the technical part in the proof of Theorem 6.2 is provided by the following lemma.
Lemma 6.3. Let
 $f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
$f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
![]() $(n\in \mathbb{N})$
be a Legendrian immersion of class
$(n\in \mathbb{N})$
be a Legendrian immersion of class
![]() $\mathscr{A}^{1}(\overline{\mathbb{D}})$
,
$\mathscr{A}^{1}(\overline{\mathbb{D}})$
,
 $\mathfrak{Y}:\mathbb{T}\rightarrow \mathbb{C}^{2n+1}$
be a smooth map, and
$\mathfrak{Y}:\mathbb{T}\rightarrow \mathbb{C}^{2n+1}$
be a smooth map, and
![]() $\unicode[STIX]{x1D6FF}>0$
and
$\unicode[STIX]{x1D6FF}>0$
and
![]() $d>0$
be numbers such that the following conditions hold:
$d>0$
be numbers such that the following conditions hold:
-
(i)
 $\Vert f-\mathfrak{Y}\Vert _{0,\mathbb{T}}<\unicode[STIX]{x1D6FF}$
;
$\Vert f-\mathfrak{Y}\Vert _{0,\mathbb{T}}<\unicode[STIX]{x1D6FF}$
; -
(ii)
 $\text{dist}_{f}(0,\mathbb{T})>d$
.
$\text{dist}_{f}(0,\mathbb{T})>d$
.
Given
![]() $\unicode[STIX]{x1D707}>0$
,
$\unicode[STIX]{x1D707}>0$
,
![]() $f$
may be approximated uniformly on compacts in
$f$
may be approximated uniformly on compacts in
![]() $\mathbb{D}$
by Legendrian embeddings
$\mathbb{D}$
by Legendrian embeddings
 $\widetilde{f}:\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{2n+1}$
of class
$\widetilde{f}:\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{2n+1}$
of class
![]() $\mathscr{O}(\overline{\mathbb{D}})$
satisfying the following properties:
$\mathscr{O}(\overline{\mathbb{D}})$
satisfying the following properties:
-
(I)
 $\Vert \widetilde{f}-\mathfrak{Y}\Vert _{0,\mathbb{T}}<\sqrt{\unicode[STIX]{x1D6FF}^{2}+\unicode[STIX]{x1D707}^{2}}$
;
$\Vert \widetilde{f}-\mathfrak{Y}\Vert _{0,\mathbb{T}}<\sqrt{\unicode[STIX]{x1D6FF}^{2}+\unicode[STIX]{x1D707}^{2}}$
; -
(II)
 $\text{dist}_{\widetilde{f}}(0,\mathbb{T})>d+\unicode[STIX]{x1D707}$
.
$\text{dist}_{\widetilde{f}}(0,\mathbb{T})>d+\unicode[STIX]{x1D707}$
.
Proof. We assume that
![]() $n=1$
; the same proof applies in general.
$n=1$
; the same proof applies in general.
Choose numbers
![]() $\unicode[STIX]{x1D716}_{0}>0$
and
$\unicode[STIX]{x1D716}_{0}>0$
and
 $0<r_{0}<1$
. To prove the lemma it suffices to find a Legendrian embedding
$0<r_{0}<1$
. To prove the lemma it suffices to find a Legendrian embedding
 $\widetilde{f}:\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{3}$
of class
$\widetilde{f}:\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{3}$
of class
![]() $\mathscr{O}(\overline{\mathbb{D}})$
satisfying properties (I), (II), and
$\mathscr{O}(\overline{\mathbb{D}})$
satisfying properties (I), (II), and
 $\Vert \widetilde{f}-f\Vert _{0,r_{0}\overline{\mathbb{D}}}<\unicode[STIX]{x1D716}_{0}$
.
$\Vert \widetilde{f}-f\Vert _{0,r_{0}\overline{\mathbb{D}}}<\unicode[STIX]{x1D716}_{0}$
.
Write
 $f=(f_{1},f_{2},f_{3})$
and
$f=(f_{1},f_{2},f_{3})$
and
 $\mathfrak{Y}=(\mathfrak{Y}_{1},\mathfrak{Y}_{2},\mathfrak{Y}_{3})$
. By condition (ii) and up to enlarging
$\mathfrak{Y}=(\mathfrak{Y}_{1},\mathfrak{Y}_{2},\mathfrak{Y}_{3})$
. By condition (ii) and up to enlarging
![]() $r_{0}<1$
if necessary, there is a number
$r_{0}<1$
if necessary, there is a number
![]() $d_{0}$
such that
$d_{0}$
such that
 $$\begin{eqnarray}\text{dist}_{f}(0,r_{0}\mathbb{T})>d_{0}>d.\end{eqnarray}$$
$$\begin{eqnarray}\text{dist}_{f}(0,r_{0}\mathbb{T})>d_{0}>d.\end{eqnarray}$$
Set
 $g=(g_{1},g_{2},g_{3}):=f-\mathfrak{Y}:\mathbb{T}\rightarrow \mathbb{C}^{3}$
and, up to slightly deforming
$g=(g_{1},g_{2},g_{3}):=f-\mathfrak{Y}:\mathbb{T}\rightarrow \mathbb{C}^{3}$
and, up to slightly deforming
![]() $\mathfrak{Y}$
, assume that
$\mathfrak{Y}$
, assume that
 $$\begin{eqnarray}g_{1}g_{3}:\mathbb{T}\rightarrow \mathbb{C}\text{ has no zeros}.\end{eqnarray}$$
$$\begin{eqnarray}g_{1}g_{3}:\mathbb{T}\rightarrow \mathbb{C}\text{ has no zeros}.\end{eqnarray}$$
By dimension reasons, this can be achieved without loss of generality. In particular,
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{3}$
(and hence
$g_{3}$
(and hence
![]() $g$
) vanish nowhere on
$g$
) vanish nowhere on
![]() $\mathbb{T}$
. Further, condition (i) gives a number
$\mathbb{T}$
. Further, condition (i) gives a number
![]() $\unicode[STIX]{x1D6FF}_{0}$
such that
$\unicode[STIX]{x1D6FF}_{0}$
such that
 $$\begin{eqnarray}\Vert f-\mathfrak{Y}\Vert _{0,\mathbb{T}}<\unicode[STIX]{x1D6FF}_{0}<\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert f-\mathfrak{Y}\Vert _{0,\mathbb{T}}<\unicode[STIX]{x1D6FF}_{0}<\unicode[STIX]{x1D6FF}.\end{eqnarray}$$
Pick a number
![]() $\unicode[STIX]{x1D716}>0$
which will be specified later. Let
$\unicode[STIX]{x1D716}>0$
which will be specified later. Let
![]() $m\in \mathbb{N}$
be a large enough integer such that, setting
$m\in \mathbb{N}$
be a large enough integer such that, setting
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{j}:=\biggl\{e^{i2\unicode[STIX]{x1D70B}t}:t\in \biggl[\frac{j-1}{m},\frac{j}{m}\biggr]\biggr\}\subset \mathbb{T},\quad j\in \mathbb{Z}_{m},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{j}:=\biggl\{e^{i2\unicode[STIX]{x1D70B}t}:t\in \biggl[\frac{j-1}{m},\frac{j}{m}\biggr]\biggr\}\subset \mathbb{T},\quad j\in \mathbb{Z}_{m},\end{eqnarray}$$
the following estimates are satisfied for all
 $u,u^{\prime }\in \unicode[STIX]{x1D6FC}_{j}$
and
$u,u^{\prime }\in \unicode[STIX]{x1D6FC}_{j}$
and
![]() $j\in \mathbb{Z}_{m}$
:
$j\in \mathbb{Z}_{m}$
:
 $$\begin{eqnarray}|f(u)-f(u^{\prime })|<\unicode[STIX]{x1D716},\quad |f(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0},\quad |\mathfrak{Y}(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D716}.\end{eqnarray}$$
$$\begin{eqnarray}|f(u)-f(u^{\prime })|<\unicode[STIX]{x1D716},\quad |f(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0},\quad |\mathfrak{Y}(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D716}.\end{eqnarray}$$
Such
![]() $m$
exists in view of (6.3) and continuity of
$m$
exists in view of (6.3) and continuity of
![]() $f$
and
$f$
and
![]() $\mathfrak{Y}$
. For every
$\mathfrak{Y}$
. For every
![]() $j\in \mathbb{Z}_{m}$
we set
$j\in \mathbb{Z}_{m}$
we set
 $$\begin{eqnarray}u_{j}:=e^{i2\unicode[STIX]{x1D70B}(j/m)};\end{eqnarray}$$
$$\begin{eqnarray}u_{j}:=e^{i2\unicode[STIX]{x1D70B}(j/m)};\end{eqnarray}$$
hence
![]() $u_{j-1}$
and
$u_{j-1}$
and
![]() $u_{j}$
are the endpoints of the arc
$u_{j}$
are the endpoints of the arc
![]() $\unicode[STIX]{x1D6FC}_{j}\subset \mathbb{T}$
.
$\unicode[STIX]{x1D6FC}_{j}\subset \mathbb{T}$
.
Given
 $w\in \mathbb{C}^{3}\setminus \{0\}$
we denote by
$w\in \mathbb{C}^{3}\setminus \{0\}$
we denote by
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{w}:\mathbb{C}^{3}\rightarrow \mathbb{C}w=\{\unicode[STIX]{x1D701}w:\unicode[STIX]{x1D701}\in \mathbb{C}\}\subset \mathbb{C}^{3}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{w}:\mathbb{C}^{3}\rightarrow \mathbb{C}w=\{\unicode[STIX]{x1D701}w:\unicode[STIX]{x1D701}\in \mathbb{C}\}\subset \mathbb{C}^{3}\end{eqnarray}$$
the Hermitian orthogonal projection onto the complex line
![]() $\mathbb{C}w$
. The proof of the lemma consists of two different deformation procedures. The first one is provided by the following.
$\mathbb{C}w$
. The proof of the lemma consists of two different deformation procedures. The first one is provided by the following.
Claim 6.4. Let
![]() $\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF}_{0},r_{0}$
and
$\unicode[STIX]{x1D716},\unicode[STIX]{x1D6FF}_{0},r_{0}$
and
![]() $\unicode[STIX]{x1D707}$
be as above. For any
$\unicode[STIX]{x1D707}$
be as above. For any
![]() $\unicode[STIX]{x1D716}^{\prime }>0$
there exists a Legendrian embedding
$\unicode[STIX]{x1D716}^{\prime }>0$
there exists a Legendrian embedding
 $F=(F_{1},F_{2},F_{3}):\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{3}$
of class
$F=(F_{1},F_{2},F_{3}):\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{3}$
of class
![]() $\mathscr{O}(\overline{\mathbb{D}})$
satisfying the following conditions:
$\mathscr{O}(\overline{\mathbb{D}})$
satisfying the following conditions:
-
(A1)
 $\Vert F-f\Vert _{1,r_{0}\overline{\mathbb{D}}}<\unicode[STIX]{x1D716}^{\prime }$
;
$\Vert F-f\Vert _{1,r_{0}\overline{\mathbb{D}}}<\unicode[STIX]{x1D716}^{\prime }$
; -
(A2)
 $|F(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
$|F(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
 $|F(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
$|F(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
 $u,u^{\prime }\in \unicode[STIX]{x1D6FC}_{j}$
and
$u,u^{\prime }\in \unicode[STIX]{x1D6FC}_{j}$
and
 $j\in \mathbb{Z}_{m}$
;
$j\in \mathbb{Z}_{m}$
; -
(A3) setting
 $G=(G_{1},G_{2},G_{3}):=F-\mathfrak{Y}:\mathbb{T}\rightarrow \mathbb{C}^{3}$
, the function
$G=(G_{1},G_{2},G_{3}):=F-\mathfrak{Y}:\mathbb{T}\rightarrow \mathbb{C}^{3}$
, the function
 $G_{1}G_{3}:\mathbb{T}\rightarrow \mathbb{C}$
has no zeros;
$G_{1}G_{3}:\mathbb{T}\rightarrow \mathbb{C}$
has no zeros; -
(A4) if
 $\unicode[STIX]{x1D6FE}\subset \mathbb{D}$
is an arc with the initial point in
$\unicode[STIX]{x1D6FE}\subset \mathbb{D}$
is an arc with the initial point in
 $r_{0}\overline{\mathbb{D}}$
and the final point
$r_{0}\overline{\mathbb{D}}$
and the final point
 $u_{j}\in \mathbb{T}$
(see (6.5)) for some
$u_{j}\in \mathbb{T}$
(see (6.5)) for some
 $j\in \mathbb{Z}_{m}$
, and if
$j\in \mathbb{Z}_{m}$
, and if
 $\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
$\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
 $\unicode[STIX]{x1D6FE}$
by Borel measurable subsets, then
$\unicode[STIX]{x1D6FE}$
by Borel measurable subsets, then  $$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(F(J_{a})))>2\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(F(J_{a})))>2\unicode[STIX]{x1D707}.\end{eqnarray}$$
Proof. For every
![]() $j\in \mathbb{Z}_{m}$
, let
$j\in \mathbb{Z}_{m}$
, let
![]() $u_{j}\in \mathbb{T}$
be given by (6.5) and set
$u_{j}\in \mathbb{T}$
be given by (6.5) and set
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{j}:=\{tu_{j}:t\in [1,2]\}\subset \mathbb{C}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{j}:=\{tu_{j}:t\in [1,2]\}\subset \mathbb{C}.\end{eqnarray}$$
In
![]() $\mathbb{C}$
we consider the admissible subset
$\mathbb{C}$
we consider the admissible subset
 $$\begin{eqnarray}S:=\overline{\mathbb{D}}\cup \biggl(\mathop{\bigcup }_{j\in \mathbb{Z}_{m}}\unicode[STIX]{x1D6FE}_{j}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}S:=\overline{\mathbb{D}}\cup \biggl(\mathop{\bigcup }_{j\in \mathbb{Z}_{m}}\unicode[STIX]{x1D6FE}_{j}\biggr).\end{eqnarray}$$
Choose a number
![]() $c>0$
to be specified later. Let
$c>0$
to be specified later. Let
 $\widetilde{h}=(\widetilde{h}_{1},\widetilde{h}_{2},\widetilde{h}_{3}):S\rightarrow \mathbb{C}^{3}$
be a generalized Legendrian curve satisfying the following requirements:
$\widetilde{h}=(\widetilde{h}_{1},\widetilde{h}_{2},\widetilde{h}_{3}):S\rightarrow \mathbb{C}^{3}$
be a generalized Legendrian curve satisfying the following requirements:
-
(a1)
 $\widetilde{h}=f$
on
$\widetilde{h}=f$
on
 $\overline{\mathbb{D}}$
;
$\overline{\mathbb{D}}$
; -
(a2)
 $|\widetilde{h}(u)-f(u_{j})|<c$
for all
$|\widetilde{h}(u)-f(u_{j})|<c$
for all
 $u\in \unicode[STIX]{x1D6FE}_{j}$
,
$u\in \unicode[STIX]{x1D6FE}_{j}$
,
 $j\in \mathbb{Z}_{m}$
;
$j\in \mathbb{Z}_{m}$
; -
(a3)
 $(\widetilde{h}_{1}(u)-\mathfrak{Y}_{1}(u_{j}))(\widetilde{h}_{3}(u)-\mathfrak{Y}_{3}(u_{j}))\neq 0$
for all
$(\widetilde{h}_{1}(u)-\mathfrak{Y}_{1}(u_{j}))(\widetilde{h}_{3}(u)-\mathfrak{Y}_{3}(u_{j}))\neq 0$
for all
 $u\in \unicode[STIX]{x1D6FE}_{j}$
,
$u\in \unicode[STIX]{x1D6FE}_{j}$
,
 $j\in \mathbb{Z}_{m}$
;
$j\in \mathbb{Z}_{m}$
; -
(a4) if
 $\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
$\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
 $\unicode[STIX]{x1D6FE}_{j}$
,
$\unicode[STIX]{x1D6FE}_{j}$
,
 $j\in \mathbb{Z}_{m}$
, by Borel measurable subsets, then
$j\in \mathbb{Z}_{m}$
, by Borel measurable subsets, then  $$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{g(u_{a})}(\widetilde{h}(J_{a})))>2\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{g(u_{a})}(\widetilde{h}(J_{a})))>2\unicode[STIX]{x1D707}.\end{eqnarray}$$
The existence of such
![]() $\widetilde{h}$
is ensured by (6.2), (6.4), and the fact that every compact path in
$\widetilde{h}$
is ensured by (6.2), (6.4), and the fact that every compact path in
![]() $\mathbb{C}^{3}$
may be uniformly approximated by Legendrian paths (see Theorem A.6). Indeed, by (6.2) we have that
$\mathbb{C}^{3}$
may be uniformly approximated by Legendrian paths (see Theorem A.6). Indeed, by (6.2) we have that
 $g(u_{j})\neq 0$
for all
$g(u_{j})\neq 0$
for all
![]() $j\in \mathbb{Z}_{m}$
and hence there is
$j\in \mathbb{Z}_{m}$
and hence there is
 $w_{0}\in \mathbb{C}^{3}$
such that
$w_{0}\in \mathbb{C}^{3}$
such that
 $\langle w_{0},g(u_{j})\rangle \neq 0$
for all
$\langle w_{0},g(u_{j})\rangle \neq 0$
for all
![]() $j\in \mathbb{Z}_{m}$
. (For instance,
$j\in \mathbb{Z}_{m}$
. (For instance,
 $w_{0}=(1,0,0)$
or
$w_{0}=(1,0,0)$
or
 $w_{0}=(0,0,1)$
meet this requirement since
$w_{0}=(0,0,1)$
meet this requirement since
 $g_{1}(u_{j})g_{3}(u_{j})\neq 0$
for all
$g_{1}(u_{j})g_{3}(u_{j})\neq 0$
for all
![]() $j\in \mathbb{Z}_{m}$
.) Thus, it suffices to define
$j\in \mathbb{Z}_{m}$
.) Thus, it suffices to define
![]() $\widetilde{h}$
on each arc
$\widetilde{h}$
on each arc
![]() $\unicode[STIX]{x1D6FE}_{j}$
as a Legendrian path which is highly oscillating in the direction of
$\unicode[STIX]{x1D6FE}_{j}$
as a Legendrian path which is highly oscillating in the direction of
![]() $w_{0}$
(which ensures condition (a4)) but with very small diameter in
$w_{0}$
(which ensures condition (a4)) but with very small diameter in
![]() $\mathbb{C}^{3}$
(which guarantees conditions (a2) and (a3); take into account (6.2) for the latter). Choosing
$\mathbb{C}^{3}$
(which guarantees conditions (a2) and (a3); take into account (6.2) for the latter). Choosing
![]() $c>0$
sufficiently small, (6.4) and condition (a2) give that
$c>0$
sufficiently small, (6.4) and condition (a2) give that
-
(a5)
 $|\widetilde{h}(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
$|\widetilde{h}(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
 $|\widetilde{h}(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
$|\widetilde{h}(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
 $(u,u^{\prime })\in (\unicode[STIX]{x1D6FE}_{j-1}\cup \unicode[STIX]{x1D6FC}_{j}\cup \unicode[STIX]{x1D6FE}_{j})\times \unicode[STIX]{x1D6FC}_{j}$
,
$(u,u^{\prime })\in (\unicode[STIX]{x1D6FE}_{j-1}\cup \unicode[STIX]{x1D6FC}_{j}\cup \unicode[STIX]{x1D6FE}_{j})\times \unicode[STIX]{x1D6FC}_{j}$
,
 $j\in \mathbb{Z}_{m}$
.
$j\in \mathbb{Z}_{m}$
.
By Lemmas 4.3 and 4.4 we may approximate
![]() $\widetilde{h}$
in the
$\widetilde{h}$
in the
![]() $\mathscr{C}^{1}(S)$
-topology by Legendrian embeddings
$\mathscr{C}^{1}(S)$
-topology by Legendrian embeddings
 $h=(h_{1},h_{2},h_{3}):3\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{2n+1}$
. If the approximation of
$h=(h_{1},h_{2},h_{3}):3\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{2n+1}$
. If the approximation of
![]() $\widetilde{h}$
by
$\widetilde{h}$
by
![]() $h$
is close enough, conditions (a4) and (a5) guarantee the existence of numbers
$h$
is close enough, conditions (a4) and (a5) guarantee the existence of numbers
 $$\begin{eqnarray}0<\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D706}^{\prime }<\unicode[STIX]{x1D706}<\unicode[STIX]{x1D70C}<1-r_{0}\end{eqnarray}$$
$$\begin{eqnarray}0<\unicode[STIX]{x1D70F}<\unicode[STIX]{x1D706}^{\prime }<\unicode[STIX]{x1D706}<\unicode[STIX]{x1D70C}<1-r_{0}\end{eqnarray}$$
such that the following properties are satisfied (see Figure 6.1):
-
(b1)
 $(\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cap \overline{\mathbb{D}}\subset u_{j}+\unicode[STIX]{x1D706}^{\prime }\overline{\mathbb{D}}$
,
$(\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cap \overline{\mathbb{D}}\subset u_{j}+\unicode[STIX]{x1D706}^{\prime }\overline{\mathbb{D}}$
,
 $j\in \mathbb{Z}_{m}$
;
$j\in \mathbb{Z}_{m}$
; -
(b2)
 $((\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}}))\cap ((\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{i}+\unicode[STIX]{x1D706}\overline{\mathbb{D}}))=\emptyset$
for all
$((\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}}))\cap ((\unicode[STIX]{x1D6FE}_{i}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{i}+\unicode[STIX]{x1D706}\overline{\mathbb{D}}))=\emptyset$
for all
 $i\neq j\in \mathbb{Z}_{m}$
;
$i\neq j\in \mathbb{Z}_{m}$
; -
(b3)
 $|h(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
$|h(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
 $|h(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
$|h(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
 $(u,u^{\prime })\in ((\unicode[STIX]{x1D6FE}_{j-1}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{j-1}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup \unicode[STIX]{x1D6FC}_{j}\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}}))\times \unicode[STIX]{x1D6FC}_{j}$
,
$(u,u^{\prime })\in ((\unicode[STIX]{x1D6FE}_{j-1}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{j-1}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup \unicode[STIX]{x1D6FC}_{j}\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})\cup (u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}}))\times \unicode[STIX]{x1D6FC}_{j}$
,
 $j\in \mathbb{Z}_{m}$
;
$j\in \mathbb{Z}_{m}$
; -
(b4)
 $(h_{1}(u)-\mathfrak{Y}_{1}(u^{\prime }))(h_{3}(u)-\mathfrak{Y}_{3}(u^{\prime }))\neq 0$
for all
$(h_{1}(u)-\mathfrak{Y}_{1}(u^{\prime }))(h_{3}(u)-\mathfrak{Y}_{3}(u^{\prime }))\neq 0$
for all
 $(u,u^{\prime })\in ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}}))\times ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cap \mathbb{T})$
,
$(u,u^{\prime })\in ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}}))\times ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cap \mathbb{T})$
,
 $j\in \mathbb{Z}_{m}$
;
$j\in \mathbb{Z}_{m}$
; -
(b5) if
 $\unicode[STIX]{x1D6FE}_{j}^{\prime }\subset (u_{j}+\unicode[STIX]{x1D706}\mathbb{D})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})$
is an arc with the initial point in
$\unicode[STIX]{x1D6FE}_{j}^{\prime }\subset (u_{j}+\unicode[STIX]{x1D706}\mathbb{D})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})$
is an arc with the initial point in
 $u_{j}+\unicode[STIX]{x1D706}\mathbb{D}$
and the final point
$u_{j}+\unicode[STIX]{x1D706}\mathbb{D}$
and the final point
 $2u_{j}$
, and if
$2u_{j}$
, and if
 $\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
$\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
 $\unicode[STIX]{x1D6FE}_{j}^{\prime }$
,
$\unicode[STIX]{x1D6FE}_{j}^{\prime }$
,
 $j\in \mathbb{Z}_{m}$
, by Borel measurable subsets, then
$j\in \mathbb{Z}_{m}$
, by Borel measurable subsets, then  $$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{g(u_{a})}(h(J_{a})))>2\unicode[STIX]{x1D707};\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{g(u_{a})}(h(J_{a})))>2\unicode[STIX]{x1D707};\end{eqnarray}$$
-
(b6)
 $|h(u)-f(u^{\prime })|<c$
for all
$|h(u)-f(u^{\prime })|<c$
for all
 $(u,u^{\prime })\in ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}}))\times ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cap \mathbb{T})$
,
$(u,u^{\prime })\in ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}}))\times ((u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cap \mathbb{T})$
,
 $j\in \mathbb{Z}_{m}$
.
$j\in \mathbb{Z}_{m}$
.

Figure 6.1. Sets in the proof of Claim 6.4.
Now, by Forstnerič and Wold [Reference Forstnerič and WoldFW09, Theorem 2.3], there is a smooth diffeomorphism
 $\unicode[STIX]{x1D719}:\overline{\mathbb{D}}\rightarrow \unicode[STIX]{x1D719}(\overline{\mathbb{D}})$
satisfying the following conditions:
$\unicode[STIX]{x1D719}:\overline{\mathbb{D}}\rightarrow \unicode[STIX]{x1D719}(\overline{\mathbb{D}})$
satisfying the following conditions:
-
(c1)
 $\unicode[STIX]{x1D719}(\overline{\mathbb{D}})\subset S+\unicode[STIX]{x1D70C}\mathbb{D}$
;
$\unicode[STIX]{x1D719}(\overline{\mathbb{D}})\subset S+\unicode[STIX]{x1D70C}\mathbb{D}$
; -
(c2)
 $\unicode[STIX]{x1D719}|_{\mathbb{D}}:\mathbb{D}\rightarrow \unicode[STIX]{x1D719}(\mathbb{D})$
is a biholomorphism;
$\unicode[STIX]{x1D719}|_{\mathbb{D}}:\mathbb{D}\rightarrow \unicode[STIX]{x1D719}(\mathbb{D})$
is a biholomorphism; -
(c3)
 $\unicode[STIX]{x1D719}$
is as close as desired to the identity map in the
$\unicode[STIX]{x1D719}$
is as close as desired to the identity map in the
 $\mathscr{C}^{1}(\overline{\mathbb{D}}\setminus \bigcup _{j\in \mathbb{Z}_{m}}(u_{j}+\unicode[STIX]{x1D706}^{\prime }\overline{\mathbb{D}}))$
-topology;
$\mathscr{C}^{1}(\overline{\mathbb{D}}\setminus \bigcup _{j\in \mathbb{Z}_{m}}(u_{j}+\unicode[STIX]{x1D706}^{\prime }\overline{\mathbb{D}}))$
-topology; -
(c4)
 $\unicode[STIX]{x1D719}(u_{j})=2u_{j}$
and
$\unicode[STIX]{x1D719}(u_{j})=2u_{j}$
and
 $\unicode[STIX]{x1D719}(\overline{\mathbb{D}}\cap (u_{j}+\unicode[STIX]{x1D706}^{\prime }\overline{\mathbb{D}}))\subset (u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})$
,
$\unicode[STIX]{x1D719}(\overline{\mathbb{D}}\cap (u_{j}+\unicode[STIX]{x1D706}^{\prime }\overline{\mathbb{D}}))\subset (u_{j}+\unicode[STIX]{x1D706}\overline{\mathbb{D}})\cup (\unicode[STIX]{x1D6FE}_{j}+\unicode[STIX]{x1D70F}\overline{\mathbb{D}})$
,
 $j\in \mathbb{Z}_{m}$
.
$j\in \mathbb{Z}_{m}$
.
If the approximation of
![]() $\widetilde{h}$
by
$\widetilde{h}$
by
![]() $h$
and the one in condition (c3) are close enough, then the Legendrian map
$h$
and the one in condition (c3) are close enough, then the Legendrian map
 $F:=h\circ \unicode[STIX]{x1D719}:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
, which may be assumed to be an embedding of class
$F:=h\circ \unicode[STIX]{x1D719}:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
, which may be assumed to be an embedding of class
![]() $\mathscr{O}(\overline{\mathbb{D}})$
by Lemmas 4.3 and 4.4, meets the conclusion of the claim. Indeed, condition (A1) clearly follows if the mentioned approximations are sufficiently close. Moreover, condition (A2) is ensured by conditions (b3) and (c4). If
$\mathscr{O}(\overline{\mathbb{D}})$
by Lemmas 4.3 and 4.4, meets the conclusion of the claim. Indeed, condition (A1) clearly follows if the mentioned approximations are sufficiently close. Moreover, condition (A2) is ensured by conditions (b3) and (c4). If
![]() $c>0$
is chosen sufficiently small, then, in view of conditions (b6) and (c4),
$c>0$
is chosen sufficiently small, then, in view of conditions (b6) and (c4),
 $G=F-\mathfrak{Y}$
is so close to
$G=F-\mathfrak{Y}$
is so close to
 $g=f-\mathfrak{Y}$
on
$g=f-\mathfrak{Y}$
on
![]() $\mathbb{T}$
that (6.2) ensures condition (A3). Likewise, if
$\mathbb{T}$
that (6.2) ensures condition (A3). Likewise, if
![]() $\unicode[STIX]{x1D6FE}\subset \mathbb{D}$
is an arc with the initial point in
$\unicode[STIX]{x1D6FE}\subset \mathbb{D}$
is an arc with the initial point in
![]() $r_{0}\overline{\mathbb{D}}$
and the final point in
$r_{0}\overline{\mathbb{D}}$
and the final point in
![]() $u_{j}$
for some
$u_{j}$
for some
![]() $j\in \mathbb{Z}_{m}$
, and if
$j\in \mathbb{Z}_{m}$
, and if
 $\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
$\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
![]() $\unicode[STIX]{x1D6FE}$
by Borel measurable subsets, then conditions (b5), (c3), and (c4) guarantee that
$\unicode[STIX]{x1D6FE}$
by Borel measurable subsets, then conditions (b5), (c3), and (c4) guarantee that
 $$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{g(u_{a})}(F(J_{a})))>2\unicode[STIX]{x1D707},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{g(u_{a})}(F(J_{a})))>2\unicode[STIX]{x1D707},\end{eqnarray}$$
and, if
![]() $c>0$
is sufficiently small,
$c>0$
is sufficiently small,
![]() $G(u_{a})$
is so close to
$G(u_{a})$
is so close to
![]() $g(u_{a})$
for all
$g(u_{a})$
for all
![]() $a\in \mathbb{Z}_{m}$
so that the above inequality gives condition (A4). This concludes the proof.◻
$a\in \mathbb{Z}_{m}$
so that the above inequality gives condition (A4). This concludes the proof.◻
Fix
![]() $\unicode[STIX]{x1D716}^{\prime }>0$
to be specified later and let
$\unicode[STIX]{x1D716}^{\prime }>0$
to be specified later and let
![]() $F$
be given by Claim 6.4. By condition (A4), there exists a number
$F$
be given by Claim 6.4. By condition (A4), there exists a number
![]() $r$
with
$r$
with
 $0<r<1-r_{0}$
enjoying the following property.
$0<r<1-r_{0}$
enjoying the following property.
-
(A5) If
 $\unicode[STIX]{x1D6FE}\subset \mathbb{D}$
is an arc with the initial point in
$\unicode[STIX]{x1D6FE}\subset \mathbb{D}$
is an arc with the initial point in
 $r_{0}\overline{\mathbb{D}}$
and the final point in
$r_{0}\overline{\mathbb{D}}$
and the final point in
 $u_{j}+r\overline{\mathbb{D}}$
for some
$u_{j}+r\overline{\mathbb{D}}$
for some
 $j\in \mathbb{Z}_{m}$
, and if
$j\in \mathbb{Z}_{m}$
, and if
 $\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
$\{J_{a}\}_{a\in \mathbb{Z}_{m}}$
is any partition of
 $\unicode[STIX]{x1D6FE}$
by Borel measurable subsets, then
$\unicode[STIX]{x1D6FE}$
by Borel measurable subsets, then $$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(F(J_{a})))>2\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(F(J_{a})))>2\unicode[STIX]{x1D707}.\end{eqnarray}$$

Figure 6.2. The sets
![]() $\unicode[STIX]{x1D6FC}_{j}^{\prime }$
and
$\unicode[STIX]{x1D6FC}_{j}^{\prime }$
and
![]() $D_{j}$
.
$D_{j}$
.
Fix another constant
![]() $\unicode[STIX]{x1D716}^{\prime \prime }>0$
to be specified later. In view of condition (A2), the continuity of
$\unicode[STIX]{x1D716}^{\prime \prime }>0$
to be specified later. In view of condition (A2), the continuity of
![]() $F$
provides numbers
$F$
provides numbers
 $0<\unicode[STIX]{x1D71A}^{\prime }<\unicode[STIX]{x1D71A}<r$
such that, setting for each
$0<\unicode[STIX]{x1D71A}^{\prime }<\unicode[STIX]{x1D71A}<r$
such that, setting for each
![]() $j\in \mathbb{Z}_{m}$
$j\in \mathbb{Z}_{m}$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{j}^{\prime } & := & \displaystyle \unicode[STIX]{x1D6FC}_{j}\setminus ((u_{j-1}+\unicode[STIX]{x1D71A}\mathbb{D})\cup (u_{j}+\unicode[STIX]{x1D71A}\mathbb{D}))\subset \unicode[STIX]{x1D6FC}_{j}\subset \mathbb{T},\nonumber\\ \displaystyle D_{j} & := & \displaystyle (\unicode[STIX]{x1D6FC}_{j}^{\prime }+\unicode[STIX]{x1D71A}^{\prime }\overline{\mathbb{D}})\cap \overline{\mathbb{D}}\subset \overline{\mathbb{D}}\setminus r_{0}\overline{\mathbb{D}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}_{j}^{\prime } & := & \displaystyle \unicode[STIX]{x1D6FC}_{j}\setminus ((u_{j-1}+\unicode[STIX]{x1D71A}\mathbb{D})\cup (u_{j}+\unicode[STIX]{x1D71A}\mathbb{D}))\subset \unicode[STIX]{x1D6FC}_{j}\subset \mathbb{T},\nonumber\\ \displaystyle D_{j} & := & \displaystyle (\unicode[STIX]{x1D6FC}_{j}^{\prime }+\unicode[STIX]{x1D71A}^{\prime }\overline{\mathbb{D}})\cap \overline{\mathbb{D}}\subset \overline{\mathbb{D}}\setminus r_{0}\overline{\mathbb{D}}\nonumber\end{eqnarray}$$
(recall that
 $r<1-r_{0}$
and see Figure 6.2), the following conditions are satisfied:
$r<1-r_{0}$
and see Figure 6.2), the following conditions are satisfied:
-
(B1)
 $|F(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
$|F(u)-f(u^{\prime })|<\unicode[STIX]{x1D716}$
and
 $|F(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
$|F(u)-\mathfrak{Y}(u^{\prime })|<\unicode[STIX]{x1D6FF}_{0}$
for all
 $(u,u^{\prime })\in D_{j}\times \unicode[STIX]{x1D6FC}_{j}$
,
$(u,u^{\prime })\in D_{j}\times \unicode[STIX]{x1D6FC}_{j}$
,
 $j\in \mathbb{Z}_{m}$
;
$j\in \mathbb{Z}_{m}$
; -
(B2)
 $|F(u/|u|)-F(u)|<\unicode[STIX]{x1D716}^{\prime \prime }$
for all
$|F(u/|u|)-F(u)|<\unicode[STIX]{x1D716}^{\prime \prime }$
for all
 $u\in D_{j}$
,
$u\in D_{j}$
,
 $j\in \mathbb{Z}_{m}$
.
$j\in \mathbb{Z}_{m}$
.
Now, for each
![]() $j\in \mathbb{Z}_{m}$
let
$j\in \mathbb{Z}_{m}$
let
 $\unicode[STIX]{x1D6F1}_{j}\subset \mathbb{C}^{3}$
denote the vectorial complex
$\unicode[STIX]{x1D6F1}_{j}\subset \mathbb{C}^{3}$
denote the vectorial complex
![]() $2$
-plane Hermitian orthogonal to the vector
$2$
-plane Hermitian orthogonal to the vector
 $$\begin{eqnarray}G(u_{j})=F(u_{j})-\mathfrak{Y}(u_{j})\in \mathbb{C}^{3}\setminus \{(x,y,z)\in \mathbb{C}^{3}:xz=0\}\end{eqnarray}$$
$$\begin{eqnarray}G(u_{j})=F(u_{j})-\mathfrak{Y}(u_{j})\in \mathbb{C}^{3}\setminus \{(x,y,z)\in \mathbb{C}^{3}:xz=0\}\end{eqnarray}$$
(see condition (A3)) as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{j} & = & \displaystyle \{(V_{1},V_{2},V_{3})\in \mathbb{C}^{3}:\overline{G_{1}(u_{j})}V_{1}+\overline{G_{2}(u_{j})}V_{2}+\overline{G_{3}(u_{j})}V_{3}=0\}\nonumber\\ \displaystyle & = & \displaystyle \{(V_{1},V_{2},V_{3})\in \mathbb{C}^{3}:\overline{G_{1}(u_{j})/G_{3}(u_{j})}V_{1}+\overline{G_{2}(u_{j})/G_{3}(u_{j})}V_{2}+V_{3}=0\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{j} & = & \displaystyle \{(V_{1},V_{2},V_{3})\in \mathbb{C}^{3}:\overline{G_{1}(u_{j})}V_{1}+\overline{G_{2}(u_{j})}V_{2}+\overline{G_{3}(u_{j})}V_{3}=0\}\nonumber\\ \displaystyle & = & \displaystyle \{(V_{1},V_{2},V_{3})\in \mathbb{C}^{3}:\overline{G_{1}(u_{j})/G_{3}(u_{j})}V_{1}+\overline{G_{2}(u_{j})/G_{3}(u_{j})}V_{2}+V_{3}=0\}.\nonumber\end{eqnarray}$$
Since
 $G_{1}(u_{j})/G_{3}(u_{j})\neq 0$
(see condition (A3)), Proposition 6.1 furnishes a continuous map
$G_{1}(u_{j})/G_{3}(u_{j})\neq 0$
(see condition (A3)), Proposition 6.1 furnishes a continuous map
 $\unicode[STIX]{x1D6F9}_{j}:(D_{j}\cap \mathbb{T})\times \mathbb{C}\rightarrow \mathbb{C}^{3}$
satisfying the following conditions for all
$\unicode[STIX]{x1D6F9}_{j}:(D_{j}\cap \mathbb{T})\times \mathbb{C}\rightarrow \mathbb{C}^{3}$
satisfying the following conditions for all
 $u\in D_{j}\cap \mathbb{T}$
:
$u\in D_{j}\cap \mathbb{T}$
:
-
–
 $\unicode[STIX]{x1D6F9}_{j}(u,0)=F(u)$
;
$\unicode[STIX]{x1D6F9}_{j}(u,0)=F(u)$
; -
–
 $\unicode[STIX]{x1D6F9}_{j}(u,\cdot ):\mathbb{C}\rightarrow \mathbb{C}^{3}$
is a proper holomorphic Legendrian embedding;
$\unicode[STIX]{x1D6F9}_{j}(u,\cdot ):\mathbb{C}\rightarrow \mathbb{C}^{3}$
is a proper holomorphic Legendrian embedding; -
–
 $\unicode[STIX]{x1D6F9}_{j}(u,\mathbb{C})\subset F(u)+\unicode[STIX]{x1D6F1}_{j}$
.
$\unicode[STIX]{x1D6F9}_{j}(u,\mathbb{C})\subset F(u)+\unicode[STIX]{x1D6F1}_{j}$
.
Thus, by the Maximum Principle, suitably shrinking and reparametrizing the curves
![]() $\unicode[STIX]{x1D6F9}_{j}(u,\cdot )$
,
$\unicode[STIX]{x1D6F9}_{j}(u,\cdot )$
,
 $u\in D_{j}\cap \mathbb{T}$
, we obtain a continuous map
$u\in D_{j}\cap \mathbb{T}$
, we obtain a continuous map
 $H_{j}:(D_{j}\cap \mathbb{T})\times \overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
enjoying the following properties:
$H_{j}:(D_{j}\cap \mathbb{T})\times \overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
enjoying the following properties:
-
(C1)
 $H_{j}(u,0)=F(u)$
for all
$H_{j}(u,0)=F(u)$
for all
 $u\in D_{j}\cap \mathbb{T}$
;
$u\in D_{j}\cap \mathbb{T}$
; -
(C2)
 $H_{j}(u,\cdot ):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
is a Legendrian disk of class
$H_{j}(u,\cdot ):\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
is a Legendrian disk of class
 $\mathscr{O}(\overline{\mathbb{D}})$
for all
$\mathscr{O}(\overline{\mathbb{D}})$
for all
 $u\in D_{j}\cap \mathbb{T}$
;
$u\in D_{j}\cap \mathbb{T}$
; -
(C3)
 $H_{j}(u,\overline{\mathbb{D}})\subset F(u)+\unicode[STIX]{x1D6F1}_{j}$
for all
$H_{j}(u,\overline{\mathbb{D}})\subset F(u)+\unicode[STIX]{x1D6F1}_{j}$
for all
 $u\in D_{j}\cap \mathbb{T}$
;
$u\in D_{j}\cap \mathbb{T}$
; -
(C4)
 $|H_{j}(u,\unicode[STIX]{x1D701})-F(u)|=\unicode[STIX]{x1D707}$
for all
$|H_{j}(u,\unicode[STIX]{x1D701})-F(u)|=\unicode[STIX]{x1D707}$
for all
 $u\in \unicode[STIX]{x1D6FC}_{j}^{\prime }$
and
$u\in \unicode[STIX]{x1D6FC}_{j}^{\prime }$
and
 $\unicode[STIX]{x1D701}\in \mathbb{T}$
;
$\unicode[STIX]{x1D701}\in \mathbb{T}$
; -
(C5)
 $|H_{j}(u,\unicode[STIX]{x1D701})-F(u)|\leqslant \unicode[STIX]{x1D707}$
for all
$|H_{j}(u,\unicode[STIX]{x1D701})-F(u)|\leqslant \unicode[STIX]{x1D707}$
for all
 $u\in D_{j}\cap \mathbb{T}$
and
$u\in D_{j}\cap \mathbb{T}$
and
 $\unicode[STIX]{x1D701}\in \overline{\mathbb{D}}$
;
$\unicode[STIX]{x1D701}\in \overline{\mathbb{D}}$
; -
(C6) if
 $u\in \mathbb{T}$
is an endpoint of the arc
$u\in \mathbb{T}$
is an endpoint of the arc
 $D_{j}\cap \mathbb{T}$
then
$D_{j}\cap \mathbb{T}$
then
 $H_{j}(u,\unicode[STIX]{x1D701})=F(u)$
for all
$H_{j}(u,\unicode[STIX]{x1D701})=F(u)$
for all
 $\unicode[STIX]{x1D701}\in \overline{\mathbb{D}}$
.
$\unicode[STIX]{x1D701}\in \overline{\mathbb{D}}$
.
Consider the continuous map
 $H:\mathbb{T}\times \overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
given by
$H:\mathbb{T}\times \overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
given by
 $$\begin{eqnarray}H(u,\unicode[STIX]{x1D701})=\left\{\begin{array}{@{}ll@{}}H_{j}(u,\unicode[STIX]{x1D701}) & \text{if }u\in D_{j}\cap \mathbb{T}\text{ for some }j\in \mathbb{Z}_{m},\\ F(u) & \text{if }u\in \mathbb{T}\setminus \mathop{\bigcup }_{j\in \mathbb{Z}_{m}}D_{j}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}H(u,\unicode[STIX]{x1D701})=\left\{\begin{array}{@{}ll@{}}H_{j}(u,\unicode[STIX]{x1D701}) & \text{if }u\in D_{j}\cap \mathbb{T}\text{ for some }j\in \mathbb{Z}_{m},\\ F(u) & \text{if }u\in \mathbb{T}\setminus \mathop{\bigcup }_{j\in \mathbb{Z}_{m}}D_{j}.\end{array}\right.\end{eqnarray}$$
Given
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
to be specified later, Lemma 3.2 furnishes a Legendrian disk
$\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
to be specified later, Lemma 3.2 furnishes a Legendrian disk
 $\widetilde{f}:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
of class
$\widetilde{f}:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{3}$
of class
![]() $\mathscr{A}^{1}(\overline{\mathbb{D}})$
such that the following conditions hold:
$\mathscr{A}^{1}(\overline{\mathbb{D}})$
such that the following conditions hold:
-
(D1)
 $\text{dist}(\widetilde{f}(u),H(u,\mathbb{T}))<\unicode[STIX]{x1D716}^{\prime \prime \prime }$
for all
$\text{dist}(\widetilde{f}(u),H(u,\mathbb{T}))<\unicode[STIX]{x1D716}^{\prime \prime \prime }$
for all
 $u\in \mathbb{T}$
;
$u\in \mathbb{T}$
; -
(D2)
 $\text{dist}(\widetilde{f}(u),H(u/|u|,\overline{\mathbb{D}}))<\unicode[STIX]{x1D716}^{\prime \prime \prime }$
for all
$\text{dist}(\widetilde{f}(u),H(u/|u|,\overline{\mathbb{D}}))<\unicode[STIX]{x1D716}^{\prime \prime \prime }$
for all
 $u\in \bigcup _{j\in \mathbb{Z}_{m}}D_{j}$
;
$u\in \bigcup _{j\in \mathbb{Z}_{m}}D_{j}$
; -
(D3)
 $\Vert \widetilde{f}-F\Vert _{1,\overline{\mathbb{D}}\setminus \bigcup _{j\in \mathbb{Z}_{m}}D_{j}}<\unicode[STIX]{x1D716}^{\prime \prime \prime }$
.
$\Vert \widetilde{f}-F\Vert _{1,\overline{\mathbb{D}}\setminus \bigcup _{j\in \mathbb{Z}_{m}}D_{j}}<\unicode[STIX]{x1D716}^{\prime \prime \prime }$
.
Moreover, by Lemmas 4.3 and 4.4, we may assume that
![]() $\widetilde{f}$
is a Legendrian embedding of class
$\widetilde{f}$
is a Legendrian embedding of class
![]() $\mathscr{O}(\overline{\mathbb{D}})$
.
$\mathscr{O}(\overline{\mathbb{D}})$
.
We claim that if the positive numbers
![]() $\unicode[STIX]{x1D716}$
,
$\unicode[STIX]{x1D716}$
,
![]() $\unicode[STIX]{x1D716}^{\prime }$
,
$\unicode[STIX]{x1D716}^{\prime }$
,
![]() $\unicode[STIX]{x1D716}^{\prime \prime }$
, and
$\unicode[STIX]{x1D716}^{\prime \prime }$
, and
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }$
are chosen sufficiently small, the Legendrian embedding
$\unicode[STIX]{x1D716}^{\prime \prime \prime }$
are chosen sufficiently small, the Legendrian embedding
![]() $\widetilde{f}$
satisfies the conclusion of the lemma. Indeed, conditions (A1), (D3), and the fact that
$\widetilde{f}$
satisfies the conclusion of the lemma. Indeed, conditions (A1), (D3), and the fact that
 $r_{0}\overline{\mathbb{D}}\subset \overline{\mathbb{D}}\setminus \bigcup _{j\in \mathbb{Z}_{m}}D_{j}$
ensure that
$r_{0}\overline{\mathbb{D}}\subset \overline{\mathbb{D}}\setminus \bigcup _{j\in \mathbb{Z}_{m}}D_{j}$
ensure that
 $\Vert \widetilde{f}-f\Vert _{1,r\overline{\mathbb{D}}}<\unicode[STIX]{x1D716}^{\prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }<\unicode[STIX]{x1D716}_{0}$
, provided that
$\Vert \widetilde{f}-f\Vert _{1,r\overline{\mathbb{D}}}<\unicode[STIX]{x1D716}^{\prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }<\unicode[STIX]{x1D716}_{0}$
, provided that
![]() $\unicode[STIX]{x1D716}^{\prime }>0$
and
$\unicode[STIX]{x1D716}^{\prime }>0$
and
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are so small to satisfy the latter inequality. To check condition (I) pick a point
$\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are so small to satisfy the latter inequality. To check condition (I) pick a point
![]() $u\in \mathbb{T}$
. Assume first that
$u\in \mathbb{T}$
. Assume first that
 $u\in \mathbb{T}\setminus \bigcup _{j\in \mathbb{Z}_{m}}D_{j}$
. Then,
$u\in \mathbb{T}\setminus \bigcup _{j\in \mathbb{Z}_{m}}D_{j}$
. Then,
 $$\begin{eqnarray}\displaystyle |\widetilde{f}(u)-\mathfrak{Y}(u)| & \stackrel{\text{(D3)}}{{<}} & \displaystyle |F(u)-\mathfrak{Y}(u)|+\unicode[STIX]{x1D716}^{\prime \prime \prime }\nonumber\\ \displaystyle & \stackrel{\text{(A2)}}{{<}} & \displaystyle |f(u)-\mathfrak{Y}(u)|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}^{\prime }\nonumber\\ \displaystyle & \stackrel{(6.3)}{{<}} & \displaystyle \unicode[STIX]{x1D6FF}_{0}+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}^{\prime }<\sqrt{\unicode[STIX]{x1D6FF}^{2}+\unicode[STIX]{x1D707}^{2}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widetilde{f}(u)-\mathfrak{Y}(u)| & \stackrel{\text{(D3)}}{{<}} & \displaystyle |F(u)-\mathfrak{Y}(u)|+\unicode[STIX]{x1D716}^{\prime \prime \prime }\nonumber\\ \displaystyle & \stackrel{\text{(A2)}}{{<}} & \displaystyle |f(u)-\mathfrak{Y}(u)|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}^{\prime }\nonumber\\ \displaystyle & \stackrel{(6.3)}{{<}} & \displaystyle \unicode[STIX]{x1D6FF}_{0}+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}^{\prime }<\sqrt{\unicode[STIX]{x1D6FF}^{2}+\unicode[STIX]{x1D707}^{2}},\nonumber\end{eqnarray}$$
where the last inequality holds provided that
![]() $\unicode[STIX]{x1D716}^{\prime }>0$
and
$\unicode[STIX]{x1D716}^{\prime }>0$
and
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are small enough. Assume that, on the contrary,
$\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are small enough. Assume that, on the contrary,
 $u\in \mathbb{T}\cap D_{j}$
for some
$u\in \mathbb{T}\cap D_{j}$
for some
![]() $j\in \mathbb{Z}_{m}$
. In this case, there exists
$j\in \mathbb{Z}_{m}$
. In this case, there exists
![]() $v_{u}\in \mathbb{T}$
and
$v_{u}\in \mathbb{T}$
and
 $w_{u}\in \unicode[STIX]{x1D6F1}_{j}$
with
$w_{u}\in \unicode[STIX]{x1D6F1}_{j}$
with
 $|w_{u}|\leqslant \unicode[STIX]{x1D707}$
such that
$|w_{u}|\leqslant \unicode[STIX]{x1D707}$
such that
 $$\begin{eqnarray}\displaystyle |\widetilde{f}(u)-\mathfrak{Y}(u)| & \stackrel{\text{(D1)},(6.4)}{{<}} & \displaystyle |H(u,v_{u})-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & = & \displaystyle |H_{j}(u,v_{u})-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(C3)},\text{(C5)}}{=} & \displaystyle |F(u)+w_{u}-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(A2)},(6.4)}{{\leqslant}} & \displaystyle |F(u_{j})+w_{u}-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+4\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(C3)}}{=} & \displaystyle \sqrt{|F(u_{j})-\mathfrak{Y}(u_{j})|^{2}+|w_{u}|^{2}}+\unicode[STIX]{x1D716}^{\prime \prime \prime }+4\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(A2)}}{{<}} & \displaystyle \sqrt{\unicode[STIX]{x1D6FF}_{0}^{2}+\unicode[STIX]{x1D707}^{2}}+\unicode[STIX]{x1D716}^{\prime \prime \prime }+4\unicode[STIX]{x1D716}\;\stackrel{(6.3)}{{<}}\;\sqrt{\unicode[STIX]{x1D6FF}^{2}+\unicode[STIX]{x1D707}^{2}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widetilde{f}(u)-\mathfrak{Y}(u)| & \stackrel{\text{(D1)},(6.4)}{{<}} & \displaystyle |H(u,v_{u})-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & = & \displaystyle |H_{j}(u,v_{u})-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(C3)},\text{(C5)}}{=} & \displaystyle |F(u)+w_{u}-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(A2)},(6.4)}{{\leqslant}} & \displaystyle |F(u_{j})+w_{u}-\mathfrak{Y}(u_{j})|+\unicode[STIX]{x1D716}^{\prime \prime \prime }+4\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(C3)}}{=} & \displaystyle \sqrt{|F(u_{j})-\mathfrak{Y}(u_{j})|^{2}+|w_{u}|^{2}}+\unicode[STIX]{x1D716}^{\prime \prime \prime }+4\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(A2)}}{{<}} & \displaystyle \sqrt{\unicode[STIX]{x1D6FF}_{0}^{2}+\unicode[STIX]{x1D707}^{2}}+\unicode[STIX]{x1D716}^{\prime \prime \prime }+4\unicode[STIX]{x1D716}\;\stackrel{(6.3)}{{<}}\;\sqrt{\unicode[STIX]{x1D6FF}^{2}+\unicode[STIX]{x1D707}^{2}},\nonumber\end{eqnarray}$$
where the last inequality holds assuming that
![]() $\unicode[STIX]{x1D716}>0$
and
$\unicode[STIX]{x1D716}>0$
and
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are sufficiently small. This proves condition (I).
$\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are sufficiently small. This proves condition (I).
Finally, let us check condition (II). If
![]() $\unicode[STIX]{x1D716}^{\prime }>0$
and
$\unicode[STIX]{x1D716}^{\prime }>0$
and
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are chosen small enough, (6.1), conditions (A1), and (D3) guarantee that
$\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are chosen small enough, (6.1), conditions (A1), and (D3) guarantee that
 $\text{dist}_{\widetilde{f}}(0,r_{0}\mathbb{T})>d_{0}>d$
, and hence it suffices to prove that
$\text{dist}_{\widetilde{f}}(0,r_{0}\mathbb{T})>d_{0}>d$
, and hence it suffices to prove that
 $\text{dist}_{\widetilde{f}}(r_{0}\mathbb{T},\mathbb{T})\geqslant \unicode[STIX]{x1D707}-(d_{0}-d)$
; equivalently,
$\text{dist}_{\widetilde{f}}(r_{0}\mathbb{T},\mathbb{T})\geqslant \unicode[STIX]{x1D707}-(d_{0}-d)$
; equivalently,
 $\text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE}))\geqslant \unicode[STIX]{x1D707}-(d_{0}-d)$
for all paths
$\text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE}))\geqslant \unicode[STIX]{x1D707}-(d_{0}-d)$
for all paths
 $\unicode[STIX]{x1D6FE}\subset \overline{\mathbb{D}}\setminus r_{0}\mathbb{D}$
with the initial point in
$\unicode[STIX]{x1D6FE}\subset \overline{\mathbb{D}}\setminus r_{0}\mathbb{D}$
with the initial point in
![]() $r_{0}\mathbb{T}$
and the final point in
$r_{0}\mathbb{T}$
and the final point in
![]() $\mathbb{T}$
. Let
$\mathbb{T}$
. Let
![]() $\unicode[STIX]{x1D6FE}$
be such a path.
$\unicode[STIX]{x1D6FE}$
be such a path.
Assume first that
 $\unicode[STIX]{x1D6FE}\cap (u_{j}+r\overline{\mathbb{D}})=\emptyset$
for all
$\unicode[STIX]{x1D6FE}\cap (u_{j}+r\overline{\mathbb{D}})=\emptyset$
for all
![]() $j\in \mathbb{Z}_{m}$
. In this case there is
$j\in \mathbb{Z}_{m}$
. In this case there is
![]() $j\in \mathbb{Z}_{m}$
and a subarc
$j\in \mathbb{Z}_{m}$
and a subarc
![]() $\widetilde{\unicode[STIX]{x1D6FE}}$
of
$\widetilde{\unicode[STIX]{x1D6FE}}$
of
![]() $\unicode[STIX]{x1D6FE}$
such that
$\unicode[STIX]{x1D6FE}$
such that
 $\widetilde{\unicode[STIX]{x1D6FE}}\subset D_{j}\setminus ((u_{j-1}+r\overline{\mathbb{D}})\cup (u_{j}+r\overline{\mathbb{D}}))$
, the initial point
$\widetilde{\unicode[STIX]{x1D6FE}}\subset D_{j}\setminus ((u_{j-1}+r\overline{\mathbb{D}})\cup (u_{j}+r\overline{\mathbb{D}}))$
, the initial point
![]() $u$
of
$u$
of
![]() $\widetilde{\unicode[STIX]{x1D6FE}}$
lies in
$\widetilde{\unicode[STIX]{x1D6FE}}$
lies in
 $(bD_{j})\cap \mathbb{D}$
and its final point
$(bD_{j})\cap \mathbb{D}$
and its final point
![]() $u^{\prime }$
lies in
$u^{\prime }$
lies in
 $\unicode[STIX]{x1D6FC}_{j}^{\prime }\subset D_{j}\cap \mathbb{T}$
. We have
$\unicode[STIX]{x1D6FC}_{j}^{\prime }\subset D_{j}\cap \mathbb{T}$
. We have
 $$\begin{eqnarray}\displaystyle \text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE})) & {>} & \displaystyle \text{length}(\widetilde{f}(\widetilde{\unicode[STIX]{x1D6FE}}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle |\widetilde{f}(u)-\widetilde{f}(u^{\prime })|\nonumber\\ \displaystyle & \stackrel{\text{(D3),\,(D1)}}{{\geqslant}} & \displaystyle |F(u)-H(u^{\prime },v_{u})|-2\unicode[STIX]{x1D716}^{\prime \prime \prime }\quad \text{for some }v_{u}\in \mathbb{T}\nonumber\\ \displaystyle & \stackrel{(6.4),\text{(A2)}}{{\geqslant}} & \displaystyle |F(u^{\prime })-H(u^{\prime },v_{u})|-2\unicode[STIX]{x1D716}^{\prime \prime \prime }-3\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(C4)}}{=} & \displaystyle \unicode[STIX]{x1D707}-2\unicode[STIX]{x1D716}^{\prime \prime \prime }-3\unicode[STIX]{x1D716}>\unicode[STIX]{x1D707}-(d_{0}-d),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE})) & {>} & \displaystyle \text{length}(\widetilde{f}(\widetilde{\unicode[STIX]{x1D6FE}}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle |\widetilde{f}(u)-\widetilde{f}(u^{\prime })|\nonumber\\ \displaystyle & \stackrel{\text{(D3),\,(D1)}}{{\geqslant}} & \displaystyle |F(u)-H(u^{\prime },v_{u})|-2\unicode[STIX]{x1D716}^{\prime \prime \prime }\quad \text{for some }v_{u}\in \mathbb{T}\nonumber\\ \displaystyle & \stackrel{(6.4),\text{(A2)}}{{\geqslant}} & \displaystyle |F(u^{\prime })-H(u^{\prime },v_{u})|-2\unicode[STIX]{x1D716}^{\prime \prime \prime }-3\unicode[STIX]{x1D716}\nonumber\\ \displaystyle & \stackrel{\text{(C4)}}{=} & \displaystyle \unicode[STIX]{x1D707}-2\unicode[STIX]{x1D716}^{\prime \prime \prime }-3\unicode[STIX]{x1D716}>\unicode[STIX]{x1D707}-(d_{0}-d),\nonumber\end{eqnarray}$$
where the last inequality holds provided that
![]() $\unicode[STIX]{x1D716}>0$
and
$\unicode[STIX]{x1D716}>0$
and
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are chosen small enough.
$\unicode[STIX]{x1D716}^{\prime \prime \prime }>0$
are chosen small enough.
Assume now that
 $\unicode[STIX]{x1D6FE}\cap (u_{j}+r^{\prime }\overline{\mathbb{D}})\neq \emptyset$
for some
$\unicode[STIX]{x1D6FE}\cap (u_{j}+r^{\prime }\overline{\mathbb{D}})\neq \emptyset$
for some
![]() $j\in \mathbb{Z}_{m}$
. Note that, since
$j\in \mathbb{Z}_{m}$
. Note that, since
![]() $\unicode[STIX]{x1D6F1}_{a}$
is perpendicular to the vector
$\unicode[STIX]{x1D6F1}_{a}$
is perpendicular to the vector
 $G(u_{a})=F(u_{a})-\mathfrak{Y}(u_{a})$
for all
$G(u_{a})=F(u_{a})-\mathfrak{Y}(u_{a})$
for all
![]() $a\in \mathbb{Z}_{m}$
, there exists for each
$a\in \mathbb{Z}_{m}$
, there exists for each
![]() $u\in D_{a}$
a point
$u\in D_{a}$
a point
 $v=v_{u}\in \overline{\mathbb{D}}$
such that
$v=v_{u}\in \overline{\mathbb{D}}$
such that
 $$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D70B}_{G(u_{a})}(\widetilde{f}(u))-\unicode[STIX]{x1D70B}_{G(u_{a})}(F(u))| & = & \displaystyle |\unicode[STIX]{x1D70B}_{G(u_{a})}(\widetilde{f}(u)-F(u))|\nonumber\\ \displaystyle & \stackrel{\text{(D2)},\text{(B2)}}{{<}} & \displaystyle \biggl|\unicode[STIX]{x1D70B}_{G(u_{a})}\biggl(H\biggl(\frac{u}{|u|},v\biggr)-F\biggl(\frac{u}{|u|}\biggr)\biggr)\biggr|+\unicode[STIX]{x1D716}^{\prime \prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }\stackrel{\text{(C3)}}{=}\unicode[STIX]{x1D716}^{\prime \prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D70B}_{G(u_{a})}(\widetilde{f}(u))-\unicode[STIX]{x1D70B}_{G(u_{a})}(F(u))| & = & \displaystyle |\unicode[STIX]{x1D70B}_{G(u_{a})}(\widetilde{f}(u)-F(u))|\nonumber\\ \displaystyle & \stackrel{\text{(D2)},\text{(B2)}}{{<}} & \displaystyle \biggl|\unicode[STIX]{x1D70B}_{G(u_{a})}\biggl(H\biggl(\frac{u}{|u|},v\biggr)-F\biggl(\frac{u}{|u|}\biggr)\biggr)\biggr|+\unicode[STIX]{x1D716}^{\prime \prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }\stackrel{\text{(C3)}}{=}\unicode[STIX]{x1D716}^{\prime \prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Then, we have
 $$\begin{eqnarray}\displaystyle \text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE})) & = & \displaystyle \text{length}\biggl(\widetilde{f}\biggl(\unicode[STIX]{x1D6FE}\bigg\backslash\mathop{\bigcup }_{a\in \mathbb{Z}_{m}}D_{a}\biggr)\biggr)+\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE}\cap D_{a}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \text{length}\biggl(\widetilde{f}\biggl(\unicode[STIX]{x1D6FE}\bigg\backslash\mathop{\bigcup }_{a\in \mathbb{Z}_{m}}D_{a}\biggr)\biggr)+\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(\widetilde{f}(\unicode[STIX]{x1D6FE}\cap D_{a}))),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE})) & = & \displaystyle \text{length}\biggl(\widetilde{f}\biggl(\unicode[STIX]{x1D6FE}\bigg\backslash\mathop{\bigcup }_{a\in \mathbb{Z}_{m}}D_{a}\biggr)\biggr)+\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE}\cap D_{a}))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \text{length}\biggl(\widetilde{f}\biggl(\unicode[STIX]{x1D6FE}\bigg\backslash\mathop{\bigcup }_{a\in \mathbb{Z}_{m}}D_{a}\biggr)\biggr)+\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(\widetilde{f}(\unicode[STIX]{x1D6FE}\cap D_{a}))),\nonumber\end{eqnarray}$$
and hence, in view of condition (D3) and (6.8), the length of
![]() $\widetilde{f}(\unicode[STIX]{x1D6FE})$
is greater or equal than
$\widetilde{f}(\unicode[STIX]{x1D6FE})$
is greater or equal than
 $$\begin{eqnarray}\text{length}\biggl(F\biggl(\unicode[STIX]{x1D6FE}\bigg\backslash\mathop{\bigcup }_{a\in \mathbb{Z}_{m}}D_{a}\biggr)\biggr)+\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(F(\unicode[STIX]{x1D6FE}\cap D_{a})))-O(\unicode[STIX]{x1D716}^{\prime \prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }).\end{eqnarray}$$
$$\begin{eqnarray}\text{length}\biggl(F\biggl(\unicode[STIX]{x1D6FE}\bigg\backslash\mathop{\bigcup }_{a\in \mathbb{Z}_{m}}D_{a}\biggr)\biggr)+\mathop{\sum }_{a\in \mathbb{Z}_{m}}\text{length}(\unicode[STIX]{x1D70B}_{G(u_{a})}(F(\unicode[STIX]{x1D6FE}\cap D_{a})))-O(\unicode[STIX]{x1D716}^{\prime \prime }+\unicode[STIX]{x1D716}^{\prime \prime \prime }).\end{eqnarray}$$
Thus, condition (A5) ensures that
 $\text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE}))>\unicode[STIX]{x1D707}$
provided that
$\text{length}(\widetilde{f}(\unicode[STIX]{x1D6FE}))>\unicode[STIX]{x1D707}$
provided that
![]() $\unicode[STIX]{x1D716}^{\prime \prime }>0$
and
$\unicode[STIX]{x1D716}^{\prime \prime }>0$
and
![]() $\unicode[STIX]{x1D716}^{\prime \prime \prime }$
are sufficiently small. This proves condition (II) and concludes the proof of Lemma 6.3.◻
$\unicode[STIX]{x1D716}^{\prime \prime \prime }$
are sufficiently small. This proves condition (II) and concludes the proof of Lemma 6.3.◻
With Lemma 6.3 in hand, one can prove the following approximation result in the same way that [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, Lemma 4.2] enables to prove [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, Lemma 4.1]. As above, although we state it just for the disk, the next lemma also holds for any compact bordered Riemann surface.
Lemma 6.5. Let
 $f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
$f:\overline{\mathbb{D}}\rightarrow \mathbb{C}^{2n+1}$
![]() $(n\in \mathbb{N})$
be a Legendrian curve of class
$(n\in \mathbb{N})$
be a Legendrian curve of class
![]() $\mathscr{A}^{1}(\overline{\mathbb{D}})$
. Given
$\mathscr{A}^{1}(\overline{\mathbb{D}})$
. Given
![]() $\unicode[STIX]{x1D706}>0$
,
$\unicode[STIX]{x1D706}>0$
,
![]() $f$
may be approximated uniformly on
$f$
may be approximated uniformly on
![]() $\overline{\mathbb{D}}$
by Legendrian embeddings
$\overline{\mathbb{D}}$
by Legendrian embeddings
 $\widetilde{f}:\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{2n+1}$
of class
$\widetilde{f}:\overline{\mathbb{D}}{\hookrightarrow}\mathbb{C}^{2n+1}$
of class
![]() $\mathscr{O}(\overline{\mathbb{D}})$
such that
$\mathscr{O}(\overline{\mathbb{D}})$
such that
 $\text{dist}_{\widetilde{f}}(0,\mathbb{T})>\unicode[STIX]{x1D706}$
.
$\text{dist}_{\widetilde{f}}(0,\mathbb{T})>\unicode[STIX]{x1D706}$
.
The main point in the proof of Lemma 6.5 is that, for any given constants
![]() $d_{0}>0$
,
$d_{0}>0$
,
![]() $\unicode[STIX]{x1D6FF}_{0}>0$
, and
$\unicode[STIX]{x1D6FF}_{0}>0$
, and
![]() $c>0$
, the sequence
$c>0$
, the sequence
 $d_{j}:=d_{j-1}+c/j$
diverges whereas the sequence
$d_{j}:=d_{j-1}+c/j$
diverges whereas the sequence
 $\unicode[STIX]{x1D6FF}_{j}:=\sqrt{\unicode[STIX]{x1D6FF}_{j-1}^{2}+c^{2}/j^{2}}$
converges as
$\unicode[STIX]{x1D6FF}_{j}:=\sqrt{\unicode[STIX]{x1D6FF}_{j-1}^{2}+c^{2}/j^{2}}$
converges as
![]() $j\in \mathbb{N}$
goes to infinity; this allows us to approximate the initial curve
$j\in \mathbb{N}$
goes to infinity; this allows us to approximate the initial curve
![]() $f$
uniformly on
$f$
uniformly on
![]() $\overline{\mathbb{D}}$
as close as desired by a Legendrian embedding
$\overline{\mathbb{D}}$
as close as desired by a Legendrian embedding
![]() $\widetilde{f}$
whose intrinsic boundary distance from
$\widetilde{f}$
whose intrinsic boundary distance from
![]() $0\in \mathbb{D}$
is as large as desired.
$0\in \mathbb{D}$
is as large as desired.
Finally, Theorem 6.2 follows from Lemma 6.5 by a standard recursive application. We refer to the proof of [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, Theorem 1.1] via [Reference Alarcón, Drinovec Drnovšek, Forstnerič and LópezADFL15b, Lemma 4.1] and leave the details to the interested reader.
Acknowledgements
The authors would like to thank Yakov Eliashberg for having provided some of the references related to Theorem A.7, and Jun-Muk Hwang for useful information regarding the results on compact Legendrian submanifolds of compact complex contact manifolds.
Appendix A Holomorphic version of Darboux’s theorems
In this appendix we collect some results concerning holomorphic contact and symplectic forms and structures. The corresponding results in the smooth case are well known and can be found in numerous sources; however, their complex (holomorphic) versions do not seem easily available in the literature. We do not claim any originality whatsoever since the proofs follow rather closely those in the smooth case. In the present paper, we strongly use Theorem A.2 (Darboux’s theorem for holomorphic contact structures) and Theorem A.6 concerning the approximation by Legendrian paths.
Theorem A.1. Let
![]() $\unicode[STIX]{x1D714}$
be a closed nondegenerate holomorphic 2-form (i.e., a holomorphic symplectic form) on a complex manifold
$\unicode[STIX]{x1D714}$
be a closed nondegenerate holomorphic 2-form (i.e., a holomorphic symplectic form) on a complex manifold
![]() $M$
of even dimension
$M$
of even dimension
![]() $2n$
. At every point
$2n$
. At every point
![]() $p\in M$
there exist local holomorphic coordinates
$p\in M$
there exist local holomorphic coordinates
 $(x_{1},y_{1},\ldots ,x_{n},y_{n})$
in which
$(x_{1},y_{1},\ldots ,x_{n},y_{n})$
in which
![]() $\unicode[STIX]{x1D714}$
equals the standard holomorphic symplectic form
$\unicode[STIX]{x1D714}$
equals the standard holomorphic symplectic form
 $\unicode[STIX]{x1D714}_{0}=dx_{1}\wedge dy_{1}+\cdots +dx_{n}\wedge dy_{n}$
.
$\unicode[STIX]{x1D714}_{0}=dx_{1}\wedge dy_{1}+\cdots +dx_{n}\wedge dy_{n}$
.
Proof. We follow Moser’s proof for the smooth case (see [Reference MoserMos65]). We may assume that
 $M=\mathbb{C}^{2n}$
with complex coordinates
$M=\mathbb{C}^{2n}$
with complex coordinates
 $z=(x_{1},y_{1},\ldots ,x_{n},y_{n})$
,
$z=(x_{1},y_{1},\ldots ,x_{n},y_{n})$
,
![]() $p=0$
, and
$p=0$
, and
 $$\begin{eqnarray}\unicode[STIX]{x1D714}|_{0}=\unicode[STIX]{x1D714}_{0}:=dx_{1}\wedge dy_{1}+\cdots +dx_{n}\wedge dy_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}|_{0}=\unicode[STIX]{x1D714}_{0}:=dx_{1}\wedge dy_{1}+\cdots +dx_{n}\wedge dy_{n}.\end{eqnarray}$$
Consider the family of holomorphic symplectic forms near
 $0\in \mathbb{C}^{2n}$
given by
$0\in \mathbb{C}^{2n}$
given by
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{t}=(1-t)\unicode[STIX]{x1D714}_{0}+t\unicode[STIX]{x1D714},\quad t\in [0,1].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{t}=(1-t)\unicode[STIX]{x1D714}_{0}+t\unicode[STIX]{x1D714},\quad t\in [0,1].\end{eqnarray}$$
We wish to find a holomorphic vector field
![]() $V_{t}$
on a neighborhood of the origin in
$V_{t}$
on a neighborhood of the origin in
![]() $\mathbb{C}^{2n}$
whose local holomorphic flow
$\mathbb{C}^{2n}$
whose local holomorphic flow
![]() $\unicode[STIX]{x1D719}_{t}$
(the solution of
$\unicode[STIX]{x1D719}_{t}$
(the solution of
 $\dot{\unicode[STIX]{x1D719}}_{t}=V_{t}\circ \unicode[STIX]{x1D719}_{t}$
,
$\dot{\unicode[STIX]{x1D719}}_{t}=V_{t}\circ \unicode[STIX]{x1D719}_{t}$
,
 $\unicode[STIX]{x1D719}_{0}(z)=z$
) satisfies
$\unicode[STIX]{x1D719}_{0}(z)=z$
) satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D714}_{t}=\unicode[STIX]{x1D714}_{0},\quad t\in [0,1]\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D714}_{t}=\unicode[STIX]{x1D714}_{0},\quad t\in [0,1]\end{eqnarray}$$
in some neighborhood of the origin. Since
![]() $\unicode[STIX]{x1D719}_{0}=\text{Id}$
, this holds at
$\unicode[STIX]{x1D719}_{0}=\text{Id}$
, this holds at
![]() $t=0$
. At time
$t=0$
. At time
![]() $t=1$
we shall then get
$t=1$
we shall then get
 $\unicode[STIX]{x1D719}_{1}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}$
which will prove the theorem.
$\unicode[STIX]{x1D719}_{1}^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{0}$
which will prove the theorem.
Let
![]() ${\mathcal{L}}_{V}$
denote the Lie derivative of a vector field
${\mathcal{L}}_{V}$
denote the Lie derivative of a vector field
![]() $V$
. We differentiate (A.1) on
$V$
. We differentiate (A.1) on
![]() $t$
:
$t$
:
 $$\begin{eqnarray}0=\frac{d}{dt}(\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D714}_{t})=\unicode[STIX]{x1D719}_{t}^{\ast }(\dot{\unicode[STIX]{x1D714}_{t}}+{\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D714}_{t})=\unicode[STIX]{x1D719}_{t}^{\ast }(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{0}+{\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D714}_{t}).\end{eqnarray}$$
$$\begin{eqnarray}0=\frac{d}{dt}(\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D714}_{t})=\unicode[STIX]{x1D719}_{t}^{\ast }(\dot{\unicode[STIX]{x1D714}_{t}}+{\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D714}_{t})=\unicode[STIX]{x1D719}_{t}^{\ast }(\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{0}+{\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D714}_{t}).\end{eqnarray}$$
Applying Cartan’s formula for the Lie derivative and noting that
![]() $d\unicode[STIX]{x1D714}_{t}=0$
gives
$d\unicode[STIX]{x1D714}_{t}=0$
gives
 $$\begin{eqnarray}{\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D714}_{t}=d(V_{t}\rfloor \unicode[STIX]{x1D714}_{t})+V_{t}\rfloor d\unicode[STIX]{x1D714}_{t}=d(V_{t}\rfloor \unicode[STIX]{x1D714}_{t}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D714}_{t}=d(V_{t}\rfloor \unicode[STIX]{x1D714}_{t})+V_{t}\rfloor d\unicode[STIX]{x1D714}_{t}=d(V_{t}\rfloor \unicode[STIX]{x1D714}_{t}).\end{eqnarray}$$
The
![]() $2$
-form
$2$
-form
![]() $\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{0}$
is closed and hence exact near the origin,
$\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{0}$
is closed and hence exact near the origin,
 $\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{0}=-d\unicode[STIX]{x1D706}$
for some holomorphic
$\unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{0}=-d\unicode[STIX]{x1D706}$
for some holomorphic
![]() $1$
-form
$1$
-form
![]() $\unicode[STIX]{x1D706}$
. Thus (A.2) is equivalent to
$\unicode[STIX]{x1D706}$
. Thus (A.2) is equivalent to
 $$\begin{eqnarray}0=d(V_{t}\rfloor \unicode[STIX]{x1D714}_{t}-\unicode[STIX]{x1D706})\quad \text{for all }t\in [0,1].\end{eqnarray}$$
$$\begin{eqnarray}0=d(V_{t}\rfloor \unicode[STIX]{x1D714}_{t}-\unicode[STIX]{x1D706})\quad \text{for all }t\in [0,1].\end{eqnarray}$$
This holds if the vector field
![]() $V_{t}$
is chosen such that
$V_{t}$
is chosen such that
 $$\begin{eqnarray}V_{t}\rfloor \unicode[STIX]{x1D714}_{t}=\unicode[STIX]{x1D706},\quad t\in [0,1].\end{eqnarray}$$
$$\begin{eqnarray}V_{t}\rfloor \unicode[STIX]{x1D714}_{t}=\unicode[STIX]{x1D706},\quad t\in [0,1].\end{eqnarray}$$
This algebraic equation for the coefficients of
![]() $V_{t}$
has a unique holomorphic solution.◻
$V_{t}$
has a unique holomorphic solution.◻
We have the following analogous result for holomorphic contact forms; see e.g. [Reference GeigesGei08, Theorem 2.5.1, p. 67] for the smooth case.
Theorem A.2. Let
![]() $\unicode[STIX]{x1D702}$
be a holomorphic contact form on a complex manifold
$\unicode[STIX]{x1D702}$
be a holomorphic contact form on a complex manifold
![]() $M^{2n+1}$
. For every point
$M^{2n+1}$
. For every point
![]() $p\in M$
there exist local holomorphic coordinates
$p\in M$
there exist local holomorphic coordinates
 $(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
on a neighborhood of
$(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
on a neighborhood of
![]() $p$
in which
$p$
in which
![]() $\unicode[STIX]{x1D702}$
agrees with the standard contact form
$\unicode[STIX]{x1D702}$
agrees with the standard contact form
 $$\begin{eqnarray}\unicode[STIX]{x1D702}_{0}=dz+\mathop{\sum }_{j=1}^{n}x_{j}dy_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{0}=dz+\mathop{\sum }_{j=1}^{n}x_{j}dy_{j}.\end{eqnarray}$$
Proof. By the same argument as in the real case (see Geiges [Reference GeigesGei08]), a holomorphic contact form
![]() $\unicode[STIX]{x1D702}$
uniquely determines a holomorphic vector field
$\unicode[STIX]{x1D702}$
uniquely determines a holomorphic vector field
![]() $R_{\unicode[STIX]{x1D702}}$
by the following two conditions:
$R_{\unicode[STIX]{x1D702}}$
by the following two conditions:
 $$\begin{eqnarray}R_{\unicode[STIX]{x1D702}}\rfloor \unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(R_{\unicode[STIX]{x1D702}})=1,\quad R_{\unicode[STIX]{x1D702}}\rfloor d\unicode[STIX]{x1D702}=0.\end{eqnarray}$$
$$\begin{eqnarray}R_{\unicode[STIX]{x1D702}}\rfloor \unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(R_{\unicode[STIX]{x1D702}})=1,\quad R_{\unicode[STIX]{x1D702}}\rfloor d\unicode[STIX]{x1D702}=0.\end{eqnarray}$$
This
![]() $R_{\unicode[STIX]{x1D702}}$
is called the Reeb vector field of
$R_{\unicode[STIX]{x1D702}}$
is called the Reeb vector field of
![]() $\unicode[STIX]{x1D702}$
. From the formula (A.3) we see that
$\unicode[STIX]{x1D702}$
. From the formula (A.3) we see that
 $$\begin{eqnarray}{\mathcal{L}}_{R_{\unicode[STIX]{x1D702}}}\unicode[STIX]{x1D702}=d(R_{\unicode[STIX]{x1D702}}\rfloor \unicode[STIX]{x1D702})+R_{\unicode[STIX]{x1D702}}\rfloor d\unicode[STIX]{x1D702}=0.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{R_{\unicode[STIX]{x1D702}}}\unicode[STIX]{x1D702}=d(R_{\unicode[STIX]{x1D702}}\rfloor \unicode[STIX]{x1D702})+R_{\unicode[STIX]{x1D702}}\rfloor d\unicode[STIX]{x1D702}=0.\end{eqnarray}$$
We may assume that
 $M=\mathbb{C}^{2n+1}$
and
$M=\mathbb{C}^{2n+1}$
and
![]() $p=0$
is the origin. By a linear algebra argument, we can choose linear complex coordinates
$p=0$
is the origin. By a linear algebra argument, we can choose linear complex coordinates
 $(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
on
$(x_{1},y_{1},\ldots ,x_{n},y_{n},z)$
on
![]() $\mathbb{C}^{2n+1}$
such that
$\mathbb{C}^{2n+1}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{0}\quad \text{and}\quad d\unicode[STIX]{x1D702}=d\unicode[STIX]{x1D702}_{0}~\text{hold on }T_{0}\mathbb{C}^{2n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{0}\quad \text{and}\quad d\unicode[STIX]{x1D702}=d\unicode[STIX]{x1D702}_{0}~\text{hold on }T_{0}\mathbb{C}^{2n+1}.\end{eqnarray}$$
It follows that
 $$\begin{eqnarray}\unicode[STIX]{x1D702}_{t}=\unicode[STIX]{x1D702}_{0}+t(\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{0}),\quad t\in [0,1],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{t}=\unicode[STIX]{x1D702}_{0}+t(\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{0}),\quad t\in [0,1],\end{eqnarray}$$
is a smooth family of holomorphic contact forms on a neighborhood of
 $0\in \mathbb{C}^{2n+1}$
such that
$0\in \mathbb{C}^{2n+1}$
such that
![]() $\dot{\unicode[STIX]{x1D702}}_{t}=0$
holds at
$\dot{\unicode[STIX]{x1D702}}_{t}=0$
holds at
 $0\in \mathbb{C}^{2n+1}$
for all
$0\in \mathbb{C}^{2n+1}$
for all
 $t\in [0,1]$
. We shall find a time-dependent holomorphic vector field
$t\in [0,1]$
. We shall find a time-dependent holomorphic vector field
![]() $V_{t}$
on a neighborhood of the origin on
$V_{t}$
on a neighborhood of the origin on
![]() $\mathbb{C}^{2n+1}$
whose flow
$\mathbb{C}^{2n+1}$
whose flow
![]() $\unicode[STIX]{x1D719}_{t}$
exists on a smaller neighborhood of
$\unicode[STIX]{x1D719}_{t}$
exists on a smaller neighborhood of
![]() $0$
for all
$0$
for all
 $t\in [0,1]$
and satisfies
$t\in [0,1]$
and satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}_{t}=\unicode[STIX]{x1D702}_{0},\quad t\in [0,1].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}_{t}=\unicode[STIX]{x1D702}_{0},\quad t\in [0,1].\end{eqnarray}$$
At time
![]() $t=1$
we shall get
$t=1$
we shall get
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{1}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{0}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{1}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{0}\end{eqnarray}$$
which will prove the theorem.
Let
![]() $R_{t}$
denote the holomorphic Reeb vector field of
$R_{t}$
denote the holomorphic Reeb vector field of
![]() $\unicode[STIX]{x1D702}_{t}$
(cf. (A.5)). We seek
$\unicode[STIX]{x1D702}_{t}$
(cf. (A.5)). We seek
![]() $V_{t}$
in the form
$V_{t}$
in the form
 $$\begin{eqnarray}V_{t}=h_{t}R_{t}+Y_{t},\quad Y_{t}\in \mathscr{L}_{t}:=\ker (\unicode[STIX]{x1D702}_{t}),\end{eqnarray}$$
$$\begin{eqnarray}V_{t}=h_{t}R_{t}+Y_{t},\quad Y_{t}\in \mathscr{L}_{t}:=\ker (\unicode[STIX]{x1D702}_{t}),\end{eqnarray}$$
where
![]() $h_{t}$
is a smooth family of holomorphic functions and
$h_{t}$
is a smooth family of holomorphic functions and
![]() $Y_{t}\in \mathscr{L}_{t}$
is a smooth family of holomorphic contact vector fields on a neighborhood of the origin. Then
$Y_{t}\in \mathscr{L}_{t}$
is a smooth family of holomorphic contact vector fields on a neighborhood of the origin. Then
 $$\begin{eqnarray}V_{t}\rfloor \unicode[STIX]{x1D702}_{t}=h_{t},\quad V_{t}\rfloor d\unicode[STIX]{x1D702}_{t}=Y_{t}\rfloor d\unicode[STIX]{x1D702}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}V_{t}\rfloor \unicode[STIX]{x1D702}_{t}=h_{t},\quad V_{t}\rfloor d\unicode[STIX]{x1D702}_{t}=Y_{t}\rfloor d\unicode[STIX]{x1D702}_{t}.\end{eqnarray}$$
Differentiating the equation (A.6) on
![]() $t$
gives
$t$
gives
 $$\begin{eqnarray}0=\dot{\unicode[STIX]{x1D702}_{t}}+d(V_{t}\rfloor \unicode[STIX]{x1D702}_{t})+V_{t}\rfloor d\unicode[STIX]{x1D702}_{t}=(\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{0}+dh_{t})+Y_{t}\rfloor d\unicode[STIX]{x1D702}_{t}.\end{eqnarray}$$
$$\begin{eqnarray}0=\dot{\unicode[STIX]{x1D702}_{t}}+d(V_{t}\rfloor \unicode[STIX]{x1D702}_{t})+V_{t}\rfloor d\unicode[STIX]{x1D702}_{t}=(\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{0}+dh_{t})+Y_{t}\rfloor d\unicode[STIX]{x1D702}_{t}.\end{eqnarray}$$
Since
![]() $d\unicode[STIX]{x1D702}_{t}$
is nondegenerate on
$d\unicode[STIX]{x1D702}_{t}$
is nondegenerate on
![]() $\mathscr{L}_{t}$
, a suitable (unique!) choice of the vector field
$\mathscr{L}_{t}$
, a suitable (unique!) choice of the vector field
![]() $Y_{t}$
tangent to
$Y_{t}$
tangent to
![]() $\mathscr{L}_{t}$
ensures that
$\mathscr{L}_{t}$
ensures that
![]() $Y_{t}\rfloor d\unicode[STIX]{x1D702}_{t}$
equals any given holomorphic
$Y_{t}\rfloor d\unicode[STIX]{x1D702}_{t}$
equals any given holomorphic
![]() $1$
-form that is annihilated by
$1$
-form that is annihilated by
![]() $R_{t}$
. Hence, it suffices to choose the function
$R_{t}$
. Hence, it suffices to choose the function
![]() $h_{t}$
such that the component of the
$h_{t}$
such that the component of the
![]() $1$
-form
$1$
-form
 $\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{0}+dh_{t}$
in the direction of
$\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{0}+dh_{t}$
in the direction of
![]() $R_{t}$
vanishes. This gives the following
$R_{t}$
vanishes. This gives the following
![]() $1$
-parameter family of quasilinear holomorphic partial differential equations for the functions
$1$
-parameter family of quasilinear holomorphic partial differential equations for the functions
![]() $h_{t}$
:
$h_{t}$
:
 $$\begin{eqnarray}R_{t}(h_{t})=R_{t}\rfloor dh_{t}=R_{t}\rfloor (\unicode[STIX]{x1D702}_{0}-\unicode[STIX]{x1D702}),\quad t\in [0,1].\end{eqnarray}$$
$$\begin{eqnarray}R_{t}(h_{t})=R_{t}\rfloor dh_{t}=R_{t}\rfloor (\unicode[STIX]{x1D702}_{0}-\unicode[STIX]{x1D702}),\quad t\in [0,1].\end{eqnarray}$$
Since
![]() $R_{t}$
is nonvanishing for all
$R_{t}$
is nonvanishing for all
![]() $t$
and the right-hand side vanishes at
$t$
and the right-hand side vanishes at
 $0\in \mathbb{C}^{2n+1}$
, this equation can be solved by the method of characteristics in a small neighborhood of
$0\in \mathbb{C}^{2n+1}$
, this equation can be solved by the method of characteristics in a small neighborhood of
![]() $0$
, and we can also choose
$0$
, and we can also choose
![]() $h_{t}$
such that
$h_{t}$
such that
 $h_{t}(0)=0$
for all
$h_{t}(0)=0$
for all
 $t\in [0,1]$
. Inserting the solution
$t\in [0,1]$
. Inserting the solution
![]() $h_{t}$
into (A.8) we then obtain a unique holomorphic vector field
$h_{t}$
into (A.8) we then obtain a unique holomorphic vector field
 $Y_{t}\in \mathscr{L}_{t}$
such that the flow of the vector field
$Y_{t}\in \mathscr{L}_{t}$
such that the flow of the vector field
![]() $V_{t}$
given by (A.7) satisfies condition (A.6).◻
$V_{t}$
given by (A.7) satisfies condition (A.6).◻
A holomorphic vector field
![]() $V$
on a complex contact manifold
$V$
on a complex contact manifold
![]() $(M,\mathscr{L})$
is said to be an infinitesimal automorphism of the contact structure
$(M,\mathscr{L})$
is said to be an infinitesimal automorphism of the contact structure
![]() $\mathscr{L}$
, or a contact holomorphic Hamiltonian, if its local holomorphic flow
$\mathscr{L}$
, or a contact holomorphic Hamiltonian, if its local holomorphic flow
![]() $\unicode[STIX]{x1D719}_{t}$
preserves
$\unicode[STIX]{x1D719}_{t}$
preserves
![]() $\mathscr{L}$
, in the sense that for all
$\mathscr{L}$
, in the sense that for all
![]() $t\in \mathbb{R}$
we have
$t\in \mathbb{R}$
we have
 $T(\unicode[STIX]{x1D719}_{t})\mathscr{L}=\mathscr{L}$
on the maximal open subset
$T(\unicode[STIX]{x1D719}_{t})\mathscr{L}=\mathscr{L}$
on the maximal open subset
 $M_{t}\subset M$
on which the flow
$M_{t}\subset M$
on which the flow
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
is defined for all
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}$
is defined for all
 $\unicode[STIX]{x1D70F}\in [0,t]$
. Assuming that
$\unicode[STIX]{x1D70F}\in [0,t]$
. Assuming that
 $\mathscr{L}=\ker (\unicode[STIX]{x1D702})$
, this is equivalent to
$\mathscr{L}=\ker (\unicode[STIX]{x1D702})$
, this is equivalent to
 $$\begin{eqnarray}{\mathcal{L}}_{V}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D702}\quad \text{for some }\unicode[STIX]{x1D706}\in \mathscr{O}(M).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{V}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D702}\quad \text{for some }\unicode[STIX]{x1D706}\in \mathscr{O}(M).\end{eqnarray}$$
The following result describes infinitesimal automorphisms of a holomorphic contact structure; see e.g. [Reference GeigesGei08, Theorem 2.3.1, p. 62] for the smooth case.
Theorem A.3. Let
![]() $(M,\unicode[STIX]{x1D702})$
be a complex contact manifold and let
$(M,\unicode[STIX]{x1D702})$
be a complex contact manifold and let
![]() $R$
be the associated Reeb vector field (A.5). There is a bijective correspondence between holomorphic functions
$R$
be the associated Reeb vector field (A.5). There is a bijective correspondence between holomorphic functions
![]() $h$
on
$h$
on
![]() $M$
and holomorphic vector fields
$M$
and holomorphic vector fields
![]() $V$
on
$V$
on
![]() $M$
which are infinitesimal holomorphic automorphisms of the contact structure
$M$
which are infinitesimal holomorphic automorphisms of the contact structure
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
. The correspondence is given by
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
. The correspondence is given by
-
–
 $V\mapsto h:=V\rfloor \unicode[STIX]{x1D702}\in \mathscr{O}(M)$
;
$V\mapsto h:=V\rfloor \unicode[STIX]{x1D702}\in \mathscr{O}(M)$
; -
–
 $\mathscr{O}(M)\ni h\mapsto V$
, where
$\mathscr{O}(M)\ni h\mapsto V$
, where
 $V=V_{h}$
is uniquely determined by the conditions (A.10)
$V=V_{h}$
is uniquely determined by the conditions (A.10) $$\begin{eqnarray}V\rfloor \unicode[STIX]{x1D702}=h,\quad V\rfloor d\unicode[STIX]{x1D702}=-dh+R(h)\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}V\rfloor \unicode[STIX]{x1D702}=h,\quad V\rfloor d\unicode[STIX]{x1D702}=-dh+R(h)\unicode[STIX]{x1D702}.\end{eqnarray}$$
In particular, if
![]() $M$
is compact then the only infinitesimal automorphisms of the contact structure
$M$
is compact then the only infinitesimal automorphisms of the contact structure
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
are the constant multiples
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
are the constant multiples
![]() $cR$
$cR$
![]() $(c\in \mathbb{C})$
of the Reeb vector field.
$(c\in \mathbb{C})$
of the Reeb vector field.
After completing our paper, we noticed that this result is already available in [Reference LeBrunLeB95, Proposition 2.1]
Proof. Assume that
![]() $V$
is a contact Hamiltonian of
$V$
is a contact Hamiltonian of
![]() $(M,\unicode[STIX]{x1D702})$
. Set
$(M,\unicode[STIX]{x1D702})$
. Set
 $h=V\rfloor \unicode[STIX]{x1D702}\in \mathscr{O}(M)$
. By the Cartan formula for the Lie derivative, condition (A.9) is equivalent to
$h=V\rfloor \unicode[STIX]{x1D702}\in \mathscr{O}(M)$
. By the Cartan formula for the Lie derivative, condition (A.9) is equivalent to
 $$\begin{eqnarray}\unicode[STIX]{x1D706}\unicode[STIX]{x1D702}={\mathcal{L}}_{V}\unicode[STIX]{x1D702}=d(V\rfloor \unicode[STIX]{x1D702})+V\rfloor d\unicode[STIX]{x1D702}=dh+V\rfloor d\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}\unicode[STIX]{x1D702}={\mathcal{L}}_{V}\unicode[STIX]{x1D702}=d(V\rfloor \unicode[STIX]{x1D702})+V\rfloor d\unicode[STIX]{x1D702}=dh+V\rfloor d\unicode[STIX]{x1D702}.\end{eqnarray}$$
Contracting this
![]() $1$
-form by the Reeb vector field
$1$
-form by the Reeb vector field
![]() $R$
for
$R$
for
![]() $\unicode[STIX]{x1D702}$
gives
$\unicode[STIX]{x1D702}$
gives
 $$\begin{eqnarray}\unicode[STIX]{x1D706}=R\rfloor dh+R\rfloor (V\rfloor d\unicode[STIX]{x1D702})=R(h)-V\rfloor (R\rfloor d\unicode[STIX]{x1D702})=R(h).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}=R\rfloor dh+R\rfloor (V\rfloor d\unicode[STIX]{x1D702})=R(h)-V\rfloor (R\rfloor d\unicode[STIX]{x1D702})=R(h).\end{eqnarray}$$
Inserting this into the previous formula shows that
![]() $V$
satisfies conditions (A.10). Conversely, given a function
$V$
satisfies conditions (A.10). Conversely, given a function
 $h\in \mathscr{O}(M)$
, the holomorphic
$h\in \mathscr{O}(M)$
, the holomorphic
![]() $1$
-form
$1$
-form
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}=-dh+R(h)\unicode[STIX]{x1D702}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}=-dh+R(h)\unicode[STIX]{x1D702}\end{eqnarray}$$
clearly satisfies
 $R\rfloor \unicode[STIX]{x1D6FC}=0$
, so
$R\rfloor \unicode[STIX]{x1D6FC}=0$
, so
![]() $\unicode[STIX]{x1D6FC}$
has no component in the direction
$\unicode[STIX]{x1D6FC}$
has no component in the direction
![]() $R$
. Since
$R$
. Since
 $\ker (d\unicode[STIX]{x1D702})=\text{span}(R)$
, there exists a unique holomorphic vector field
$\ker (d\unicode[STIX]{x1D702})=\text{span}(R)$
, there exists a unique holomorphic vector field
![]() $Y$
on
$Y$
on
![]() $M$
such that
$M$
such that
 $$\begin{eqnarray}Y\rfloor \unicode[STIX]{x1D702}=0\quad \text{and}\quad Y\rfloor d\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
$$\begin{eqnarray}Y\rfloor \unicode[STIX]{x1D702}=0\quad \text{and}\quad Y\rfloor d\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FC}.\end{eqnarray}$$
Set
 $V=hR+Y$
. Then
$V=hR+Y$
. Then
 $V\rfloor \unicode[STIX]{x1D702}=h$
and
$V\rfloor \unicode[STIX]{x1D702}=h$
and
 $V\rfloor d\unicode[STIX]{x1D702}=Y\rfloor d\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FC}$
, so
$V\rfloor d\unicode[STIX]{x1D702}=Y\rfloor d\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FC}$
, so
![]() $V$
satisfies condition (A.10). Cartan’s formula shows that
$V$
satisfies condition (A.10). Cartan’s formula shows that
 $$\begin{eqnarray}{\mathcal{L}}_{V}\unicode[STIX]{x1D702}=d(V\rfloor \unicode[STIX]{x1D702})+V\rfloor d\unicode[STIX]{x1D702}=dh+(-dh+R(h)\unicode[STIX]{x1D702})=R(h)\unicode[STIX]{x1D702}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{V}\unicode[STIX]{x1D702}=d(V\rfloor \unicode[STIX]{x1D702})+V\rfloor d\unicode[STIX]{x1D702}=dh+(-dh+R(h)\unicode[STIX]{x1D702})=R(h)\unicode[STIX]{x1D702}.\end{eqnarray}$$
Hence
![]() $V$
is an infinitesimal automorphism of the contact structure
$V$
is an infinitesimal automorphism of the contact structure
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
.◻
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
.◻
The following corollary to Theorem A.3 is analogous to [Reference GeigesGei08, Corollary 2.3.2, p. 63].
Corollary A.4. Let
![]() $(M,\unicode[STIX]{x1D702})$
be a complex contact manifold. Given a smooth family of holomorphic functions
$(M,\unicode[STIX]{x1D702})$
be a complex contact manifold. Given a smooth family of holomorphic functions
 $\{h_{t}\}_{t\in [0,1]}\subset \mathscr{O}(M)$
, let
$\{h_{t}\}_{t\in [0,1]}\subset \mathscr{O}(M)$
, let
 $\{V_{t}\}_{t\in [0,1]}$
be the corresponding family of contact Hamiltonians defined by (A.10). Assume that the flow
$\{V_{t}\}_{t\in [0,1]}$
be the corresponding family of contact Hamiltonians defined by (A.10). Assume that the flow
![]() $\unicode[STIX]{x1D719}_{t}$
of the time-dependent vector field
$\unicode[STIX]{x1D719}_{t}$
of the time-dependent vector field
![]() $V_{t}$
exists on a domain
$V_{t}$
exists on a domain
 $M_{0}\subset M$
for all
$M_{0}\subset M$
for all
 $t\in [0,1]$
. Then there is a smooth family of nonvanishing holomorphic function
$t\in [0,1]$
. Then there is a smooth family of nonvanishing holomorphic function
 $\{\unicode[STIX]{x1D706}_{t}\}_{t\in [0,1]}\subset \mathscr{O}(M_{0})$
such that
$\{\unicode[STIX]{x1D706}_{t}\}_{t\in [0,1]}\subset \mathscr{O}(M_{0})$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}_{t}\unicode[STIX]{x1D702}\quad \text{on}~M_{0},~t\in [0,1].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}_{t}\unicode[STIX]{x1D702}\quad \text{on}~M_{0},~t\in [0,1].\end{eqnarray}$$
In particular, the biholomorphic map
 $\unicode[STIX]{x1D719}_{t}:M_{0}\rightarrow \unicode[STIX]{x1D719}_{t}(M_{0})\subset M$
is a holomorphic contactomorphism of the contact structure
$\unicode[STIX]{x1D719}_{t}:M_{0}\rightarrow \unicode[STIX]{x1D719}_{t}(M_{0})\subset M$
is a holomorphic contactomorphism of the contact structure
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
for every
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
for every
 $t\in [0,1]$
.
$t\in [0,1]$
.
Proof. By the assumption we have that
 $\unicode[STIX]{x1D719}_{0}=\text{Id}_{M}$
and
$\unicode[STIX]{x1D719}_{0}=\text{Id}_{M}$
and
 $\dot{\unicode[STIX]{x1D719}_{t}}=V_{t}\circ \unicode[STIX]{x1D719}_{t}$
on
$\dot{\unicode[STIX]{x1D719}_{t}}=V_{t}\circ \unicode[STIX]{x1D719}_{t}$
on
![]() $M_{0}$
for all
$M_{0}$
for all
 $t\in [0,1]$
. Let
$t\in [0,1]$
. Let
![]() $R$
denote the Reeb vector field of
$R$
denote the Reeb vector field of
![]() $\unicode[STIX]{x1D702}$
. By (A.11) we have
$\unicode[STIX]{x1D702}$
. By (A.11) we have
 ${\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D702}=R(h_{t})\unicode[STIX]{x1D702}$
for all
${\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D702}=R(h_{t})\unicode[STIX]{x1D702}$
for all
 $t\in [0,1]$
. Hence we get the following identity on
$t\in [0,1]$
. Hence we get the following identity on
![]() $M_{0}$
:
$M_{0}$
:
 $$\begin{eqnarray}\frac{d}{dt}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D719}_{t}^{\ast }({\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D702})=\unicode[STIX]{x1D719}_{t}^{\ast }(R(h_{t})\unicode[STIX]{x1D702})=\unicode[STIX]{x1D707}_{t}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702},\quad t\in [0,1]\end{eqnarray}$$
$$\begin{eqnarray}\frac{d}{dt}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D719}_{t}^{\ast }({\mathcal{L}}_{V_{t}}\unicode[STIX]{x1D702})=\unicode[STIX]{x1D719}_{t}^{\ast }(R(h_{t})\unicode[STIX]{x1D702})=\unicode[STIX]{x1D707}_{t}\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702},\quad t\in [0,1]\end{eqnarray}$$
where
 $\unicode[STIX]{x1D707}_{t}=R(h_{t})\circ \unicode[STIX]{x1D719}_{t}\in \mathscr{O}(M_{0})$
. Since
$\unicode[STIX]{x1D707}_{t}=R(h_{t})\circ \unicode[STIX]{x1D719}_{t}\in \mathscr{O}(M_{0})$
. Since
 $\unicode[STIX]{x1D719}_{0}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}$
, it follows by integration that
$\unicode[STIX]{x1D719}_{0}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}$
, it follows by integration that
 $\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}_{t}\unicode[STIX]{x1D702}$
where
$\unicode[STIX]{x1D719}_{t}^{\ast }\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}_{t}\unicode[STIX]{x1D702}$
where
 $\unicode[STIX]{x1D706}_{t}=\exp (\int _{0}^{t}\unicode[STIX]{x1D707}_{s}ds)\in \mathscr{O}(M_{0})$
for
$\unicode[STIX]{x1D706}_{t}=\exp (\int _{0}^{t}\unicode[STIX]{x1D707}_{s}ds)\in \mathscr{O}(M_{0})$
for
 $t\in [0,1]$
.◻
$t\in [0,1]$
.◻
Example A.5. Let
 $\unicode[STIX]{x1D702}=dz+\sum _{i=1}^{n}x_{i}dy_{i}$
be the standard contact form on
$\unicode[STIX]{x1D702}=dz+\sum _{i=1}^{n}x_{i}dy_{i}$
be the standard contact form on
![]() $\mathbb{C}^{2n+1}$
. Then the correspondence in Theorem A.3 is given by
$\mathbb{C}^{2n+1}$
. Then the correspondence in Theorem A.3 is given by
 $$\begin{eqnarray}h\longmapsto V_{h}=\biggl(h-\mathop{\sum }_{j=1}^{n}x_{j}h_{x_{j}}\biggr)\unicode[STIX]{x2202}_{z}+\mathop{\sum }_{j=1}^{n}((x_{j}h_{z}-h_{y_{j}})\unicode[STIX]{x2202}_{x_{j}}+h_{x_{j}}\unicode[STIX]{x2202}_{y_{j}}).\end{eqnarray}$$
$$\begin{eqnarray}h\longmapsto V_{h}=\biggl(h-\mathop{\sum }_{j=1}^{n}x_{j}h_{x_{j}}\biggr)\unicode[STIX]{x2202}_{z}+\mathop{\sum }_{j=1}^{n}((x_{j}h_{z}-h_{y_{j}})\unicode[STIX]{x2202}_{x_{j}}+h_{x_{j}}\unicode[STIX]{x2202}_{y_{j}}).\end{eqnarray}$$
Note that for any linear function
![]() $h$
on
$h$
on
![]() $\mathbb{C}^{2n+1}$
the vector field
$\mathbb{C}^{2n+1}$
the vector field
![]() $V_{h}$
is also linear and hence completely integrable. Its flow
$V_{h}$
is also linear and hence completely integrable. Its flow
![]() $\{\unicode[STIX]{x1D719}_{t}\}_{t\in \mathbb{C}}$
is a complex
$\{\unicode[STIX]{x1D719}_{t}\}_{t\in \mathbb{C}}$
is a complex
![]() $1$
-parameter family of
$1$
-parameter family of
![]() $\mathbb{C}$
-linear contactomorphisms of the standard contact structure
$\mathbb{C}$
-linear contactomorphisms of the standard contact structure
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
on
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
on
![]() $\mathbb{C}^{2n+1}$
.
$\mathbb{C}^{2n+1}$
.
The last result that we mention concerns the possibility of approximating any smooth compact real curve in a complex contact manifold by Legendrian curves.
Theorem A.6. Let
![]() $(M,\mathscr{L})$
be a complex contact manifold. Every path
$(M,\mathscr{L})$
be a complex contact manifold. Every path
 $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
can be approximated in the
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
can be approximated in the
![]() $\mathscr{C}^{0}$
topology by smooth embeddings
$\mathscr{C}^{0}$
topology by smooth embeddings
 $\unicode[STIX]{x1D706}:[0,1]\rightarrow M$
tangential to
$\unicode[STIX]{x1D706}:[0,1]\rightarrow M$
tangential to
![]() $\mathscr{L}$
(i.e., such that
$\mathscr{L}$
(i.e., such that
 $\dot{\unicode[STIX]{x1D706}}(t)\in \mathscr{L}_{\unicode[STIX]{x1D706}(t)}$
holds for all
$\dot{\unicode[STIX]{x1D706}}(t)\in \mathscr{L}_{\unicode[STIX]{x1D706}(t)}$
holds for all
 $t\in [0,1]$
). Furthermore, assuming that the vectors
$t\in [0,1]$
). Furthermore, assuming that the vectors
![]() $\dot{\unicode[STIX]{x1D6FE}}(0)$
and
$\dot{\unicode[STIX]{x1D6FE}}(0)$
and
![]() $\dot{\unicode[STIX]{x1D6FE}}(1)$
lie in
$\dot{\unicode[STIX]{x1D6FE}}(1)$
lie in
![]() $\mathscr{L}$
at the respective points,
$\mathscr{L}$
at the respective points,
![]() $\unicode[STIX]{x1D706}$
can be chosen such that
$\unicode[STIX]{x1D706}$
can be chosen such that
 $\dot{\unicode[STIX]{x1D706}}(t)=\dot{\unicode[STIX]{x1D6FE}}(t)$
for
$\dot{\unicode[STIX]{x1D706}}(t)=\dot{\unicode[STIX]{x1D6FE}}(t)$
for
 $t\in \{0,1\}$
.
$t\in \{0,1\}$
.
Since the contact distribution
 $\mathscr{L}\subset TM$
is spanned by vector fields which, together with their commutators, span the tangent bundle
$\mathscr{L}\subset TM$
is spanned by vector fields which, together with their commutators, span the tangent bundle
![]() $TM$
at every point (see §2.1), Theorem A.6 is essentially a corollary to the following theorem of Chow [Reference ChowCho39] from 1939.
$TM$
at every point (see §2.1), Theorem A.6 is essentially a corollary to the following theorem of Chow [Reference ChowCho39] from 1939.
Theorem A.7. Let
 $V_{1},\ldots ,V_{m}$
be smooth vector fields on a connected manifold
$V_{1},\ldots ,V_{m}$
be smooth vector fields on a connected manifold
![]() $M$
such that their successive commutators span each tangent space
$M$
such that their successive commutators span each tangent space
![]() $T_{p}M$
,
$T_{p}M$
,
![]() $p\in M$
. Then every two points in
$p\in M$
. Then every two points in
![]() $M$
can be joined by a piecewise smooth path where each piece is a segment of an integral curve of one of these vector fields. Furthermore, every path
$M$
can be joined by a piecewise smooth path where each piece is a segment of an integral curve of one of these vector fields. Furthermore, every path
 $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
can be
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
can be
![]() $\mathscr{C}^{0}$
approximated by piecewise smooth paths
$\mathscr{C}^{0}$
approximated by piecewise smooth paths
 $\unicode[STIX]{x1D706}:[0,1]\rightarrow M$
of the above type such that
$\unicode[STIX]{x1D706}:[0,1]\rightarrow M$
of the above type such that
 $\unicode[STIX]{x1D706}(t)=\unicode[STIX]{x1D6FE}(t)$
for
$\unicode[STIX]{x1D706}(t)=\unicode[STIX]{x1D6FE}(t)$
for
 $t\in \{0,1\}$
.
$t\in \{0,1\}$
.
The approximation statement in Theorem A.7 is an immediate consequence of local connectivity by integral curves. Indeed, it suffices to subdivide the curve
![]() $\unicode[STIX]{x1D6FE}$
into short arcs and connect the division points by integral curves lying in small connected open sets in
$\unicode[STIX]{x1D6FE}$
into short arcs and connect the division points by integral curves lying in small connected open sets in
![]() $M$
.
$M$
.
Theorem A.7 has a complex origin. The basic case of vector fields tangent to the standard contact distribution on
![]() $\mathbb{R}^{3}$
was observed by Carathéodory (1909). The result was proved in essentially this form by Chow [Reference ChowCho39] in 1939; a similar result was obtained by Rashevski (1938). An informative historical discussion can be found in Gromov’s paper on the Carnot–Carathéodory metrics (see [Reference GromovGro96, §0.2, p. 86]); these are metrics defined by curves tangent to a distribution spanned by a collection of vector fields. Gromov gave a proof of Chow’s theorem in [Reference GromovGro96, p. 113], followed by a stronger quantitative version of it on p. 114. The proof can also be found in numerous other sources. Further, more precise results were obtained by Sussman [Reference SussmannSus73a, Reference SussmannSus73b]. These notions also appear in optimal control theory and robotics under the name of controllability; see the references in [Reference GromovGro96, §0.2, p. 86].
$\mathbb{R}^{3}$
was observed by Carathéodory (1909). The result was proved in essentially this form by Chow [Reference ChowCho39] in 1939; a similar result was obtained by Rashevski (1938). An informative historical discussion can be found in Gromov’s paper on the Carnot–Carathéodory metrics (see [Reference GromovGro96, §0.2, p. 86]); these are metrics defined by curves tangent to a distribution spanned by a collection of vector fields. Gromov gave a proof of Chow’s theorem in [Reference GromovGro96, p. 113], followed by a stronger quantitative version of it on p. 114. The proof can also be found in numerous other sources. Further, more precise results were obtained by Sussman [Reference SussmannSus73a, Reference SussmannSus73b]. These notions also appear in optimal control theory and robotics under the name of controllability; see the references in [Reference GromovGro96, §0.2, p. 86].
Proof of Theorem A.6.
By Theorem A.7,
![]() $\unicode[STIX]{x1D6FE}$
can be approximated in the
$\unicode[STIX]{x1D6FE}$
can be approximated in the
![]() $\mathscr{C}^{0}$
topology by piecewise smooth paths
$\mathscr{C}^{0}$
topology by piecewise smooth paths
 $\widetilde{\unicode[STIX]{x1D706}}:[0,1]\rightarrow M$
satisfying the conclusion of the theorem. We need to replace
$\widetilde{\unicode[STIX]{x1D706}}:[0,1]\rightarrow M$
satisfying the conclusion of the theorem. We need to replace
![]() $\widetilde{\unicode[STIX]{x1D706}}$
by a smooth embedding tangent to
$\widetilde{\unicode[STIX]{x1D706}}$
by a smooth embedding tangent to
![]() $\mathscr{L}$
and matching
$\mathscr{L}$
and matching
![]() $\unicode[STIX]{x1D6FE}$
at the endpoints.
$\unicode[STIX]{x1D6FE}$
at the endpoints.
Let us first consider the case
 $M=\mathbb{C}^{2n+1}$
and
$M=\mathbb{C}^{2n+1}$
and
 $\mathscr{L}=\ker \unicode[STIX]{x1D702}$
, where
$\mathscr{L}=\ker \unicode[STIX]{x1D702}$
, where
![]() $\unicode[STIX]{x1D702}$
is the standard holomorphic contact form given by (A.4). Let
$\unicode[STIX]{x1D702}$
is the standard holomorphic contact form given by (A.4). Let
 $\widetilde{\unicode[STIX]{x1D706}}=(\widetilde{x}_{1},\widetilde{y}_{1},\ldots ,\widetilde{x}_{n},\widetilde{y}_{n},\widetilde{z}):[0,1]\rightarrow \mathbb{C}^{2n+1}$
. By dimension reasons, a slight deformation of the map
$\widetilde{\unicode[STIX]{x1D706}}=(\widetilde{x}_{1},\widetilde{y}_{1},\ldots ,\widetilde{x}_{n},\widetilde{y}_{n},\widetilde{z}):[0,1]\rightarrow \mathbb{C}^{2n+1}$
. By dimension reasons, a slight deformation of the map
 $(\widetilde{x}_{1},\widetilde{y}_{1},\ldots ,\widetilde{x}_{n},\widetilde{y}_{n}):[0,1]\rightarrow \mathbb{C}^{2n}$
provides a smooth embedding
$(\widetilde{x}_{1},\widetilde{y}_{1},\ldots ,\widetilde{x}_{n},\widetilde{y}_{n}):[0,1]\rightarrow \mathbb{C}^{2n}$
provides a smooth embedding
 $(x_{1},y_{1},\ldots ,x_{n},y_{n}):[0,1]\rightarrow \mathbb{C}^{2n}$
such that, setting
$(x_{1},y_{1},\ldots ,x_{n},y_{n}):[0,1]\rightarrow \mathbb{C}^{2n}$
such that, setting
 $$\begin{eqnarray}z(t)=\widetilde{z}(0)-\int _{0}^{t}\mathop{\sum }_{j=1}^{n}x_{j}(s){\dot{y}}_{j}(s)ds,\quad t\in [0,1],\end{eqnarray}$$
$$\begin{eqnarray}z(t)=\widetilde{z}(0)-\int _{0}^{t}\mathop{\sum }_{j=1}^{n}x_{j}(s){\dot{y}}_{j}(s)ds,\quad t\in [0,1],\end{eqnarray}$$
we have that
-
–
 $z(t)\approx \widetilde{z}(t)$
for all
$z(t)\approx \widetilde{z}(t)$
for all
 $t\in [0,1]$
;
$t\in [0,1]$
; -
–
 $z(t)=\widetilde{z}(t)$
for all
$z(t)=\widetilde{z}(t)$
for all
 $t\in \{0,1\}$
; and
$t\in \{0,1\}$
; and -
– if
 $\dot{\unicode[STIX]{x1D6FE}}(0)$
and
$\dot{\unicode[STIX]{x1D6FE}}(0)$
and
 $\dot{\unicode[STIX]{x1D6FE}}(1)$
lie in
$\dot{\unicode[STIX]{x1D6FE}}(1)$
lie in
 $\ker \unicode[STIX]{x1D702}$
at the respective points, then
$\ker \unicode[STIX]{x1D702}$
at the respective points, then
 ${\dot{z}}(t)=\dot{\unicode[STIX]{x1D6FE}}(t)$
for
${\dot{z}}(t)=\dot{\unicode[STIX]{x1D6FE}}(t)$
for
 $t\in \{0,1\}$
.
$t\in \{0,1\}$
.
Thus, the smooth embedding
 $\unicode[STIX]{x1D706}=(x_{1},y_{1},\ldots ,x_{n},y_{n},z):I\rightarrow \mathbb{C}^{2n+1}$
satisfies the conclusion of the theorem.
$\unicode[STIX]{x1D706}=(x_{1},y_{1},\ldots ,x_{n},y_{n},z):I\rightarrow \mathbb{C}^{2n+1}$
satisfies the conclusion of the theorem.
In the general case, we choose a division
 $0=t_{0}<t_{1}<\cdots t_{k}=1$
of
$0=t_{0}<t_{1}<\cdots t_{k}=1$
of
![]() $[0,1]$
such that for every
$[0,1]$
such that for every
 $i=1,\ldots ,k$
we have
$i=1,\ldots ,k$
we have
 $\widetilde{\unicode[STIX]{x1D706}}([t_{i-1},t_{i}])\subset U_{i}$
, where
$\widetilde{\unicode[STIX]{x1D706}}([t_{i-1},t_{i}])\subset U_{i}$
, where
 $U_{i}\subset M$
is a connected coordinate neighborhood such that the restriction
$U_{i}\subset M$
is a connected coordinate neighborhood such that the restriction
![]() $\mathscr{L}|_{U_{i}}$
is given by the contact form (A.4) (cf. Theorem A.2). The above argument can then be applied within each
$\mathscr{L}|_{U_{i}}$
is given by the contact form (A.4) (cf. Theorem A.2). The above argument can then be applied within each
![]() $U_{i}$
, making sure that the embedded Legendrian curves
$U_{i}$
, making sure that the embedded Legendrian curves
 $\unicode[STIX]{x1D706}_{i}:[t_{i-1},t_{i}]\rightarrow U_{i}$
$\unicode[STIX]{x1D706}_{i}:[t_{i-1},t_{i}]\rightarrow U_{i}$
 $(i=1,\ldots ,k)$
smoothly match at the respective endpoints and do not intersect elsewhere.◻
$(i=1,\ldots ,k)$
smoothly match at the respective endpoints and do not intersect elsewhere.◻