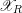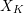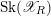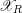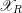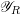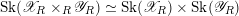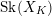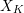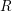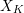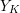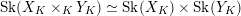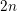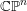1 Introduction
Let
![]() $R$
be a discrete valuation ring with quotient field
$R$
be a discrete valuation ring with quotient field
![]() $K$
and residue field
$K$
and residue field
![]() $k$
, and let
$k$
, and let
![]() $X$
be a smooth proper variety over
$X$
be a smooth proper variety over
![]() $K$
. While there may be no way to extend
$K$
. While there may be no way to extend
![]() $X$
to a smooth proper variety over
$X$
to a smooth proper variety over
![]() $R$
, in
$R$
, in
![]() $\text{char}(k)=0$
resolution of singularities guarantees that we can always produce an
$\text{char}(k)=0$
resolution of singularities guarantees that we can always produce an
![]() $R$
-model
$R$
-model
![]() $\mathscr{X}$
where the special fiber
$\mathscr{X}$
where the special fiber
![]() $\mathscr{X}_{k}$
is a strict normal crossings (snc) divisor. Given such a model, we associate the dual complex
$\mathscr{X}_{k}$
is a strict normal crossings (snc) divisor. Given such a model, we associate the dual complex
![]() ${\mathcal{D}}(\mathscr{X}_{k})$
, which is the dual intersection complex of the components of the special fiber.
${\mathcal{D}}(\mathscr{X}_{k})$
, which is the dual intersection complex of the components of the special fiber.
The dual complex of the special fiber of a such degeneration reflects the geometry of the generic fiber. If the generic fiber is rationally connected, then the dual complex of the special fiber is contractible [Reference de Fernex, Kollár and XudKX17]. For Calabi–Yau varieties, degenerations are classified by the action of monodromy on the cohomology. The principle is that the degenerations with maximally unipotent actions have the richest combinatorial structure in the dual complex. In this case, the dual complex is always a
![]() $\mathbb{Q}$
-homology sphere, and Kollár and Xu [Reference Kollár and XuKX16] show that it is a sphere if
$\mathbb{Q}$
-homology sphere, and Kollár and Xu [Reference Kollár and XuKX16] show that it is a sphere if
![]() $n\leqslant 3$
or
$n\leqslant 3$
or
![]() $n\leqslant 4$
and the special fiber of a minimal divisorially log terminal (dlt) model is snc.
$n\leqslant 4$
and the special fiber of a minimal divisorially log terminal (dlt) model is snc.
The goal of this work is to understand the dual complex of a model for the product of two smooth proper varieties over
![]() $K$
. We consider this problem from two perspectives.
$K$
. We consider this problem from two perspectives.
1.1 Skeletons of Berkovich spaces
The first is via the theory of Berkovich spaces. In this setting we assume that
![]() $K$
is complete with respect to the valuation induced by
$K$
is complete with respect to the valuation induced by
![]() $R$
, which gives rise to a non-archimedean norm on
$R$
, which gives rise to a non-archimedean norm on
![]() $K$
. In [Reference BerkovichBer90], Berkovich develops a theory of analytic geometry over
$K$
. In [Reference BerkovichBer90], Berkovich develops a theory of analytic geometry over
![]() $K$
. He associates a
$K$
. He associates a
![]() $K$
-analytic space to
$K$
-analytic space to
![]() $X$
; each point corresponds to a real valuation on the residue field of a point of
$X$
; each point corresponds to a real valuation on the residue field of a point of
![]() $X$
, extending the discrete valuation on
$X$
, extending the discrete valuation on
![]() $K$
. This space, denoted by
$K$
. This space, denoted by
![]() $X^{\text{an}}$
, is called the Berkovich space associated to
$X^{\text{an}}$
, is called the Berkovich space associated to
![]() $X$
.
$X$
.
From any snc model
![]() $\mathscr{X}$
of
$\mathscr{X}$
of
![]() $X$
one can construct a subspace of
$X$
one can construct a subspace of
![]() $X^{\text{an}}$
, called the Berkovich skeleton of
$X^{\text{an}}$
, called the Berkovich skeleton of
![]() $\mathscr{X}$
and denoted by
$\mathscr{X}$
and denoted by
![]() $\text{Sk}(\mathscr{X})$
: it is homeomorphic to the dual intersection complex of the divisor
$\text{Sk}(\mathscr{X})$
: it is homeomorphic to the dual intersection complex of the divisor
![]() $\mathscr{X}_{k}$
[Reference Mustaţă and NicaiseMN15]. The Berkovich skeletons turn out to be relevant in the study of the topology of
$\mathscr{X}_{k}$
[Reference Mustaţă and NicaiseMN15]. The Berkovich skeletons turn out to be relevant in the study of the topology of
![]() $X^{\text{an}}$
. They shape the Berkovich space, as
$X^{\text{an}}$
. They shape the Berkovich space, as
![]() $X^{\text{an}}$
is homeomorphic to the inverse limit
$X^{\text{an}}$
is homeomorphic to the inverse limit
![]() $\underset{\longleftarrow }{\lim }\,\text{Sk}(\mathscr{X})$
where
$\underset{\longleftarrow }{\lim }\,\text{Sk}(\mathscr{X})$
where
![]() $\mathscr{X}$
runs through all snc models of
$\mathscr{X}$
runs through all snc models of
![]() $X$
. Also, the homotopy type of
$X$
. Also, the homotopy type of
![]() $X^{\text{an}}$
is determined by any snc model
$X^{\text{an}}$
is determined by any snc model
![]() $\mathscr{X}$
: indeed, Berkovich and Thuillier prove that
$\mathscr{X}$
: indeed, Berkovich and Thuillier prove that
![]() $\text{Sk}(\mathscr{X})$
is a strong deformation retract of
$\text{Sk}(\mathscr{X})$
is a strong deformation retract of
![]() $X^{\text{an}}$
[Reference BerkovichBer90, Reference ThuillierThu07].
$X^{\text{an}}$
[Reference BerkovichBer90, Reference ThuillierThu07].
1.2 The dual complex of a dlt model
The other approach to the study of the dual complexes comes from birational geometry. In this setting, we consider a pair
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
over the germ of a curve. In the log general type case, running the minimal model program (MMP) distinguishes a canonical model for the degeneration
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
over the germ of a curve. In the log general type case, running the minimal model program (MMP) distinguishes a canonical model for the degeneration
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
[Reference AlexeevAle96, Reference Kollár and Shepherd-BarronKS88, Reference Hacon, McKernan and XuHMX18], at the cost of possibly introducing worse singularities. If we are willing to tolerate some ambiguity in our choice of model, we can choose instead to produce a minimal dlt model. One advantage of dlt models is that they are expected to exist for all pairs admitting a log pluricanonical form. The singularities are mild enough that it is possible to define the dual complex as the dual intersection complex of divisors of coefficient
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
[Reference AlexeevAle96, Reference Kollár and Shepherd-BarronKS88, Reference Hacon, McKernan and XuHMX18], at the cost of possibly introducing worse singularities. If we are willing to tolerate some ambiguity in our choice of model, we can choose instead to produce a minimal dlt model. One advantage of dlt models is that they are expected to exist for all pairs admitting a log pluricanonical form. The singularities are mild enough that it is possible to define the dual complex as the dual intersection complex of divisors of coefficient
![]() $1$
, denoted
$1$
, denoted
![]() ${\mathcal{D}}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. In [Reference de Fernex, Kollár and XudKX17], de Fernex, Kollár, and Xu investigate how the dual complex is affected by the operations of the MMP. They show, under mild hypotheses, that every step of the MMP induces a homotopy equivalence between dual complexes. Moreover,
${\mathcal{D}}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. In [Reference de Fernex, Kollár and XudKX17], de Fernex, Kollár, and Xu investigate how the dual complex is affected by the operations of the MMP. They show, under mild hypotheses, that every step of the MMP induces a homotopy equivalence between dual complexes. Moreover,
![]() ${\mathcal{D}}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is a piecewise linear (PL) invariant under log crepant birational maps.
${\mathcal{D}}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is a piecewise linear (PL) invariant under log crepant birational maps.
1.3 The essential skeleton
Recently there has been much interest in a synthesis of the two approaches. Kontsevich and Soibelmann [Reference Kontsevich, Soibelman, Etingof, Retakh and SingerKS06] define a version of the skeleton of a variety with trivial canonical bundle, which detects the locus of simple poles along the special fiber of the distinguished canonical form. Mustaţă and Nicaise [Reference Mustaţă and NicaiseMN15] extend their definition to any variety with non-negative Kodaira dimension. The key technical tool is the definition, for a rational pluricanonical form, of a weight function on the Berkovich space. The essential skeleton
![]() $\text{Sk}(X)$
is the union over all regular pluricanonical forms of the minimality locus of the associated weight functions.
$\text{Sk}(X)$
is the union over all regular pluricanonical forms of the minimality locus of the associated weight functions.
Thus the essential skeleton has the advantage of being intrinsic to the variety
![]() $X$
, with no dependence on a choice of model. As the weight function is closely related to the log discrepancy from birational geometry, it is natural to expect that the essential skeleton in some way encodes some of the minimal model theory of
$X$
, with no dependence on a choice of model. As the weight function is closely related to the log discrepancy from birational geometry, it is natural to expect that the essential skeleton in some way encodes some of the minimal model theory of
![]() $X$
. Nicaise and Xu [Reference Nicaise and XuNX16] show, when
$X$
. Nicaise and Xu [Reference Nicaise and XuNX16] show, when
![]() $X$
is a smooth projective variety with
$X$
is a smooth projective variety with
![]() $K_{X}$
semiample, and
$K_{X}$
semiample, and
![]() $\mathscr{X}$
is a good minimal dlt model, that the dual complex of
$\mathscr{X}$
is a good minimal dlt model, that the dual complex of
![]() $\mathscr{X}_{k}$
can be identified with the essential skeleton of
$\mathscr{X}_{k}$
can be identified with the essential skeleton of
![]() $X$
. While it is in general a difficult problem to produce good minimal dlt models, Kollár, Nicaise, and Xu [Reference Kollár, Nicaise and XuKNX17] show that for any smooth projective
$X$
. While it is in general a difficult problem to produce good minimal dlt models, Kollár, Nicaise, and Xu [Reference Kollár, Nicaise and XuKNX17] show that for any smooth projective
![]() $X$
with
$X$
with
![]() $K_{X}$
semiample,
$K_{X}$
semiample,
![]() $X$
extends to a good minimal dlt model over a finite extension of the valuation ring.
$X$
extends to a good minimal dlt model over a finite extension of the valuation ring.
1.4 Skeletons for log-regular models
To produce nice models of the product, we work in the context of logarithmic geometry. To any log-regular scheme
![]() $\mathscr{X}^{+}$
, in [Reference KatoKat94] Kato attaches a combinatorial structure
$\mathscr{X}^{+}$
, in [Reference KatoKat94] Kato attaches a combinatorial structure
![]() $F_{\mathscr{X}}$
called a fan: if we denote by
$F_{\mathscr{X}}$
called a fan: if we denote by
![]() $D_{\mathscr{X}}$
the locus where the log structure is non-trivial, then the fan
$D_{\mathscr{X}}$
the locus where the log structure is non-trivial, then the fan
![]() $F_{\mathscr{X}}$
consists of the set of the generic points of intersections of irreducible components of
$F_{\mathscr{X}}$
consists of the set of the generic points of intersections of irreducible components of
![]() $D_{\mathscr{X}}$
, equipped with a sheaf of monoids. We define a logarithmic version of the Berkovich skeleton for a log-regular model
$D_{\mathscr{X}}$
, equipped with a sheaf of monoids. We define a logarithmic version of the Berkovich skeleton for a log-regular model
![]() $\mathscr{X}^{+}$
of
$\mathscr{X}^{+}$
of
![]() $X$
over
$X$
over
![]() $R$
: it gives rise to a polyhedral complex in
$R$
: it gives rise to a polyhedral complex in
![]() $X^{\text{an}}$
whose faces correspond to the points of
$X^{\text{an}}$
whose faces correspond to the points of
![]() $F_{\mathscr{X}}$
.
$F_{\mathscr{X}}$
.
Given two log-smooth log schemes
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
over
$\mathscr{Y}^{+}$
over
![]() $R$
, their product
$R$
, their product
![]() $\mathscr{Z}^{+}$
in the category of fine and saturated log schemes is naturally log-regular, hence
$\mathscr{Z}^{+}$
in the category of fine and saturated log schemes is naturally log-regular, hence
![]() $\mathscr{Z}^{+}$
has an associated skeleton, and it is a model of the product
$\mathscr{Z}^{+}$
has an associated skeleton, and it is a model of the product
![]() $\mathscr{X}_{K}\times _{K}\mathscr{Y}_{K}$
of the generic fibers. If one of the two underlying schemes
$\mathscr{X}_{K}\times _{K}\mathscr{Y}_{K}$
of the generic fibers. If one of the two underlying schemes
![]() $\mathscr{X}$
or
$\mathscr{X}$
or
![]() $\mathscr{Y}$
is semistable, which means it has reduced special fiber, then we show that the skeleton of the product
$\mathscr{Y}$
is semistable, which means it has reduced special fiber, then we show that the skeleton of the product
![]() $\mathscr{Z}^{+}$
is the product of the skeletons, with the projection maps given by restricting the valuation to the corresponding function fields (Proposition 3.4.3).
$\mathscr{Z}^{+}$
is the product of the skeletons, with the projection maps given by restricting the valuation to the corresponding function fields (Proposition 3.4.3).
1.5 Skeletons for pairs
Working in the logarithmic setting, we may also allow a non-trivial log structure over the generic fiber. Geometrically this corresponds to adding horizontal divisors to the special fiber and yields the addition of some unbounded faces to the skeleton. In [Reference Gubler, Rabinoff and WernerGRW16] Gubler, Rabinoff, and Werner construct a skeleton for strictly semistable snc models with suitable horizontal divisors. Both constructions recover the Berkovich skeleton when there is no horizontal component and the special fiber is snc.
Pairs arise frequently in the MMP. We say that a pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is fractional snc if
$(X,\unicode[STIX]{x1D6E5}_{X})$
is fractional snc if
![]() $\unicode[STIX]{x1D6E5}_{X}$
is an effective
$\unicode[STIX]{x1D6E5}_{X}$
is an effective
![]() $\mathbb{Q}$
-divisor such that
$\mathbb{Q}$
-divisor such that
![]() $\unicode[STIX]{x1D6E5}_{X}=\sum a_{i}\unicode[STIX]{x1D6E5}_{X,i}$
with
$\unicode[STIX]{x1D6E5}_{X}=\sum a_{i}\unicode[STIX]{x1D6E5}_{X,i}$
with
![]() $0\leqslant a_{i}\leqslant 1$
and the round-up
$0\leqslant a_{i}\leqslant 1$
and the round-up
![]() $(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
is snc. Taking advantage of a construction that admits horizontal components, the definition of the essential skeleton extends to the case of a fractional snc pair
$(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
is snc. Taking advantage of a construction that admits horizontal components, the definition of the essential skeleton extends to the case of a fractional snc pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
over
$(X,\unicode[STIX]{x1D6E5}_{X})$
over
![]() $K$
, and to pluricanonical forms of some positive index
$K$
, and to pluricanonical forms of some positive index
![]() $r$
with divisor of poles no worse than
$r$
with divisor of poles no worse than
![]() $r\unicode[STIX]{x1D6E5}_{X}$
. We extend to pairs the result of Mustaţă and Nicaise [Reference Mustaţă and NicaiseMN15] on the birational invariance of the essential skeleton (Proposition 5.1.5), as well as Nicaise and Xu’s result [Reference Nicaise and XuNX16] that the essential skeleton is homeomorphic to the dual complex of a good minimal dlt model (Proposition 5.1.7). It follows from these results that we can define the notion of essential skeleton for a dlt pair.
$r\unicode[STIX]{x1D6E5}_{X}$
. We extend to pairs the result of Mustaţă and Nicaise [Reference Mustaţă and NicaiseMN15] on the birational invariance of the essential skeleton (Proposition 5.1.5), as well as Nicaise and Xu’s result [Reference Nicaise and XuNX16] that the essential skeleton is homeomorphic to the dual complex of a good minimal dlt model (Proposition 5.1.7). It follows from these results that we can define the notion of essential skeleton for a dlt pair.
1.6 Main result
Our main result establishes the behavior of essential skeletons under products.
Theorem 1.6.1. Assume that the residue field
![]() $k$
is algebraically closed. Let
$k$
is algebraically closed. Let
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
and
$(X,\unicode[STIX]{x1D6E5}_{X})$
and
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
be fractional snc pairs. Suppose that both pairs have non-negative Kodaira–Iitaka dimension and admit semistable log-regular models
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
be fractional snc pairs. Suppose that both pairs have non-negative Kodaira–Iitaka dimension and admit semistable log-regular models
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
over
$\mathscr{Y}^{+}$
over
![]() $S^{+}$
. Then the PL homeomorphism of skeletons induces a PL homeomorphism of essential skeletons
$S^{+}$
. Then the PL homeomorphism of skeletons induces a PL homeomorphism of essential skeletons
where
![]() $Z$
and
$Z$
and
![]() $\unicode[STIX]{x1D6E5}_{Z}$
are the respective products.
$\unicode[STIX]{x1D6E5}_{Z}$
are the respective products.
Semistability is a key assumption; without it the projection map might fail to be injective; see Example 3.4.4. As expected, we get a corresponding result for dual complexes of semistable good minimal dlt models (Theorem 5.3.5). Unfortunately, semistability is not well behaved under birational transformations so it seems possible that a degeneration admits a semistable good minimal dlt model but no semistable log-regular model.
1.7 Application to degenerations of hyper-Kähler varieties
As an application of Theorem 1.6.1, we study certain degenerations of hyper-Kähler varieties. One way to produce hyper-Kähler varieties is by taking the Hilbert scheme of points on a K3 surface. Another is to extend the Kummer construction to higher-dimensional abelian varieties. Aside from two other examples found by O’Grady in dimensions 6 [Reference O’GradyO’Gr03] and 10 [Reference O’GradyO’Gr99] there are no other known examples, up to deformation equivalence.
Just as for Calabi–Yau varieties, degenerations of hyper-Kähler varieties can be understood in terms of the monodromy operator on cohomology, with classification into types I, II, III. Type I is the case where the dual complex is just a single point, but types II and III have more interesting structure. Kollár, Laza, Saccà, and Voisin [Reference Kollár, Laza, Saccà and VoisinKLSV17] show that in the type II case the dual complex has the rational homology type of a point, and in the type III case of a complex projective space. Gulbrandsen, Halle, Hulek, and Zhang [Reference Gulbrandsen, Halle and HulekGHH15, Reference Gulbrandsen, Halle and HulekGHH16, Reference Gulbrandsen, Halle, Hulek and ZhangGHHZ18] use geometric invariant theory (GIT) to construct a model of the degeneration of
![]() $n$
th-order Hilbert schemes arising from some type II degenerations of K3 surfaces, and show that the dual complex is an
$n$
th-order Hilbert schemes arising from some type II degenerations of K3 surfaces, and show that the dual complex is an
![]() $n$
-simplex. There are considerations from mirror symmetry that suggest that for a type III degeneration the dual complex should be homeomorphic to
$n$
-simplex. There are considerations from mirror symmetry that suggest that for a type III degeneration the dual complex should be homeomorphic to
![]() $\mathbb{C}\mathbb{P}^{n}$
[Reference HwangHwa08, Reference Kontsevich, Soibelman, Etingof, Retakh and SingerKS06].
$\mathbb{C}\mathbb{P}^{n}$
[Reference HwangHwa08, Reference Kontsevich, Soibelman, Etingof, Retakh and SingerKS06].
Theorem 1.7.1. Assume that the residue field
![]() $k$
is algebraically closed. Let
$k$
is algebraically closed. Let
![]() $S$
be a
$S$
be a
![]() $K3$
surface over
$K3$
surface over
![]() $K$
. If
$K$
. If
![]() $S$
admits a semistable log-regular model or a semistable good minimal dlt model, then the essential skeleton of the Hilbert scheme of
$S$
admits a semistable log-regular model or a semistable good minimal dlt model, then the essential skeleton of the Hilbert scheme of
![]() $n$
points on
$n$
points on
![]() $S$
is isomorphic to the
$S$
is isomorphic to the
![]() $n$
th symmetric product of the essential skeleton of
$n$
th symmetric product of the essential skeleton of
![]() $S$
,
$S$
,
Computing these complexes gives a single point in the type I case, an
![]() $n$
-simplex in the type II case, and
$n$
-simplex in the type II case, and
![]() $\mathbb{C}\mathbb{P}^{n}$
in the type III case. The same types arise in the Kummer case.
$\mathbb{C}\mathbb{P}^{n}$
in the type III case. The same types arise in the Kummer case.
Theorem 1.7.2. Assume the residue field
![]() $k$
is algebraically closed. Let
$k$
is algebraically closed. Let
![]() $A$
be an abelian surface over
$A$
be an abelian surface over
![]() $K$
. Suppose that
$K$
. Suppose that
![]() $A$
admits a semistable log-regular model or a semistable good minimal dlt model. If the essential skeleton of
$A$
admits a semistable log-regular model or a semistable good minimal dlt model. If the essential skeleton of
![]() $A$
is homeomorphic to a point, the circle
$A$
is homeomorphic to a point, the circle
![]() $S^{1}$
or the torus
$S^{1}$
or the torus
![]() $S^{1}\times S^{1}$
, then the essential skeleton of the
$S^{1}\times S^{1}$
, then the essential skeleton of the
![]() $n$
th generalized Kummer variety
$n$
th generalized Kummer variety
![]() $K_{n}(A)$
is isomorphic to a point, the standard
$K_{n}(A)$
is isomorphic to a point, the standard
![]() $n$
-simplex or
$n$
-simplex or
![]() $\mathbb{C}\mathbb{P}^{n}$
, respectively.
$\mathbb{C}\mathbb{P}^{n}$
, respectively.
Analysis of the weight function gives a powerful yet accessible approach to controlling the skeletons of these varieties. In both cases we use Theorem 1.6.1 to establish that the skeleton of the hyper-Kähler variety is a finite quotient of the
![]() $n$
-fold product of the skeleton of the original surface under the action of a symmetric group. In the case of Hilbert schemes we can get a complete description of the action using functoriality of the projection maps, but in the Kummer case we additionally need to understand the restriction of the multiplication map to the essential skeleton of an abelian surface [Reference BerkovichBer90, Reference Halle and NicaiseHN17, Reference Temkin, Baker and PayneTem16].
$n$
-fold product of the skeleton of the original surface under the action of a symmetric group. In the case of Hilbert schemes we can get a complete description of the action using functoriality of the projection maps, but in the Kummer case we additionally need to understand the restriction of the multiplication map to the essential skeleton of an abelian surface [Reference BerkovichBer90, Reference Halle and NicaiseHN17, Reference Temkin, Baker and PayneTem16].
To our knowledge these are the first examples of type III degenerations of hyper-Kähler varieties where the PL homeomorphism type of the dual complex is known.
1.8 Structure of the paper
In § 2 we recall the Kato fan, and develop necessary background for the rest of the paper. Section 3 contains the definition and properties of the skeleton of a log-regular scheme. These first two sections require no hypothesis on the characteristic of
![]() $K$
.
$K$
.
For the remainder of the paper, we assume that
![]() $K$
has equicharacteristic
$K$
has equicharacteristic
![]() $0$
. In § 4 we introduce the weight function and essential skeleton from [Reference Mustaţă and NicaiseMN15], extending their definition to the case of a pair. In § 5 we give connections to birational geometry, along with proofs of the main theorems. We discuss an application to degenerations of hyper-Kähler varieties in § 6.
$0$
. In § 4 we introduce the weight function and essential skeleton from [Reference Mustaţă and NicaiseMN15], extending their definition to the case of a pair. In § 5 we give connections to birational geometry, along with proofs of the main theorems. We discuss an application to degenerations of hyper-Kähler varieties in § 6.
1.9 Notation
1.9.1. Let
![]() $R$
be a complete discrete valuation ring with maximal ideal
$R$
be a complete discrete valuation ring with maximal ideal
![]() $\mathfrak{m}$
, residue field
$\mathfrak{m}$
, residue field
![]() $k=R/\mathfrak{m}$
, and quotient field
$k=R/\mathfrak{m}$
, and quotient field
![]() $K$
. We assume that the valuation
$K$
. We assume that the valuation
![]() $v_{K}$
is normalized, namely
$v_{K}$
is normalized, namely
![]() $v_{K}(\unicode[STIX]{x1D70B})=1$
for any uniformizer
$v_{K}(\unicode[STIX]{x1D70B})=1$
for any uniformizer
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $R$
. We define by
$R$
. We define by
![]() $|\cdot |_{K}=\exp (-v_{K}(\cdot ))$
the absolute value on
$|\cdot |_{K}=\exp (-v_{K}(\cdot ))$
the absolute value on
![]() $K$
corresponding to
$K$
corresponding to
![]() $v_{K}$
; this turns
$v_{K}$
; this turns
![]() $K$
into a non-archimedean complete valued field.
$K$
into a non-archimedean complete valued field.
1.9.2. We write
![]() $S=\text{Spec}\,R$
and we denote by
$S=\text{Spec}\,R$
and we denote by
![]() $s$
the closed point of
$s$
the closed point of
![]() $S$
. Let
$S$
. Let
![]() $\mathscr{X}$
be an
$\mathscr{X}$
be an
![]() $R$
-scheme of finite type. We will denote by
$R$
-scheme of finite type. We will denote by
![]() $\mathscr{X}_{k}$
the special fiber of
$\mathscr{X}_{k}$
the special fiber of
![]() $\mathscr{X}$
and by
$\mathscr{X}$
and by
![]() $\mathscr{X}_{K}$
the generic fiber.
$\mathscr{X}_{K}$
the generic fiber.
1.9.3. Let
![]() $X$
be a proper
$X$
be a proper
![]() $K$
-scheme. A model for
$K$
-scheme. A model for
![]() $X$
over
$X$
over
![]() $R$
is a flat separated
$R$
is a flat separated
![]() $R$
-scheme
$R$
-scheme
![]() $\mathscr{X}$
of finite type endowed with an isomorphism of
$\mathscr{X}$
of finite type endowed with an isomorphism of
![]() $K$
-schemes
$K$
-schemes
![]() $\mathscr{X}_{K}\rightarrow X$
. If
$\mathscr{X}_{K}\rightarrow X$
. If
![]() $X$
is smooth over
$X$
is smooth over
![]() $K$
, we say that
$K$
, we say that
![]() $\mathscr{X}$
is an snc model for
$\mathscr{X}$
is an snc model for
![]() $X$
if it is regular, proper over
$X$
if it is regular, proper over
![]() $R$
, and the special fiber
$R$
, and the special fiber
![]() $\mathscr{X}_{k}$
is an snc divisor on
$\mathscr{X}_{k}$
is an snc divisor on
![]() $\mathscr{X}$
. In equicharacteristic
$\mathscr{X}$
. In equicharacteristic
![]() $0$
, such a model always exists, by Hironaka’s resolution of singularities.
$0$
, such a model always exists, by Hironaka’s resolution of singularities.
We say that a model
![]() $\mathscr{X}$
over
$\mathscr{X}$
over
![]() $R$
(not necessarily regular) is semistable if the special fiber
$R$
(not necessarily regular) is semistable if the special fiber
![]() $\mathscr{X}_{k}$
is reduced.
$\mathscr{X}_{k}$
is reduced.
1.9.4. All log schemes in this paper are fine and saturated (fs) log schemes and defined with respect to the Zariski topology. We denote a log scheme by
![]() $\mathscr{X}^{+}=(\mathscr{X},{\mathcal{M}}_{\mathscr{X}})$
, where
$\mathscr{X}^{+}=(\mathscr{X},{\mathcal{M}}_{\mathscr{X}})$
, where
![]() ${\mathcal{M}}_{\mathscr{X}}$
is the structural sheaf of monoids. The quotient sheaf
${\mathcal{M}}_{\mathscr{X}}$
is the structural sheaf of monoids. The quotient sheaf
is called the the characteristic sheaf of
![]() $\mathscr{X}^{+}$
. For every point
$\mathscr{X}^{+}$
. For every point
![]() $x$
of
$x$
of
![]() $\mathscr{X}$
, we denote by
$\mathscr{X}$
, we denote by
![]() ${\mathcal{I}}_{\mathscr{X},x}$
the ideal in
${\mathcal{I}}_{\mathscr{X},x}$
the ideal in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
generated by
${\mathcal{O}}_{\mathscr{X},x}$
generated by
If a log scheme
![]() $\mathscr{X}^{+}$
has divisorial log structure induced from a divisor
$\mathscr{X}^{+}$
has divisorial log structure induced from a divisor
![]() $D$
, we denote it by
$D$
, we denote it by
![]() $\mathscr{X}^{+}=(\mathscr{X},D)$
. In particular, we denote by
$\mathscr{X}^{+}=(\mathscr{X},D)$
. In particular, we denote by
![]() $S^{+}$
the scheme
$S^{+}$
the scheme
![]() $S$
endowed with the standard log structure (the divisorial log structure induced by
$S$
endowed with the standard log structure (the divisorial log structure induced by
![]() $s$
), namely
$s$
), namely
![]() $S^{+}=(S,s)$
.
$S^{+}=(S,s)$
.
1.9.5. A log scheme is log-regular at a point
![]() $x$
if the following two conditions are satisfied:
$x$
if the following two conditions are satisfied:
![]() ${\mathcal{O}}_{\mathscr{X},x}/{\mathcal{I}}_{\mathscr{X},x}$
is a regular local ring; and
${\mathcal{O}}_{\mathscr{X},x}/{\mathcal{I}}_{\mathscr{X},x}$
is a regular local ring; and
![]() $\dim {\mathcal{O}}_{\mathscr{X},x}=\dim {\mathcal{O}}_{\mathscr{X},x}/{\mathcal{I}}_{\mathscr{X},x}+\text{rank}\,{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
. For example, a toric variety with its toric logarithmic structure is log-regular. More generally, working over perfect fields, log-regular varieties correspond to toroidal embeddings (without self-intersections).
$\dim {\mathcal{O}}_{\mathscr{X},x}=\dim {\mathcal{O}}_{\mathscr{X},x}/{\mathcal{I}}_{\mathscr{X},x}+\text{rank}\,{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
. For example, a toric variety with its toric logarithmic structure is log-regular. More generally, working over perfect fields, log-regular varieties correspond to toroidal embeddings (without self-intersections).
If
![]() $\mathscr{X}^{+}$
is a log-regular log scheme over
$\mathscr{X}^{+}$
is a log-regular log scheme over
![]() $S^{+}$
, then the locus where the log structure is non-trivial is a divisor that we will denote by
$S^{+}$
, then the locus where the log structure is non-trivial is a divisor that we will denote by
![]() $D_{\mathscr{X}}$
. Thus, the log structure on
$D_{\mathscr{X}}$
. Thus, the log structure on
![]() $\mathscr{X}^{+}$
is the divisorial log structure induced by
$\mathscr{X}^{+}$
is the divisorial log structure induced by
![]() $D_{\mathscr{X}}$
, by [Reference KatoKat94, Theorem 11.6].
$D_{\mathscr{X}}$
, by [Reference KatoKat94, Theorem 11.6].
For a more extended dissertation of the theory of log schemes we refer to [Reference KatoKat89, Reference Gabber and RameroGR04, Reference KatoKat94].
1.9.6. Let
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
be a pair such that
$(X,\unicode[STIX]{x1D6E5}_{X})$
be a pair such that
![]() $X$
is proper over
$X$
is proper over
![]() $K$
and the round-up
$K$
and the round-up
![]() $(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
is log-regular. A log-regular log scheme
$(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
is log-regular. A log-regular log scheme
![]() $\mathscr{X}^{+}$
over
$\mathscr{X}^{+}$
over
![]() $S^{+}$
is a model for
$S^{+}$
is a model for
![]() $(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
over
$(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
over
![]() $S^{+}$
if
$S^{+}$
if
![]() $\mathscr{X}$
is a model of
$\mathscr{X}$
is a model of
![]() $X$
over
$X$
over
![]() $R$
, the closure of any component of
$R$
, the closure of any component of
![]() $\unicode[STIX]{x1D6E5}_{X}$
in
$\unicode[STIX]{x1D6E5}_{X}$
in
![]() $\mathscr{X}$
has non-empty intersection with
$\mathscr{X}$
has non-empty intersection with
![]() $\mathscr{X}_{k}$
, and
$\mathscr{X}_{k}$
, and
![]() $D_{\mathscr{X}}=\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }+\mathscr{X}_{k,\text{red}}$
.
$D_{\mathscr{X}}=\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }+\mathscr{X}_{k,\text{red}}$
.
1.9.7. We denote by
![]() $(\cdot )^{\text{an}}$
the analytification functor from the category of
$(\cdot )^{\text{an}}$
the analytification functor from the category of
![]() $K$
-schemes of finite type to Berkovich’s category of
$K$
-schemes of finite type to Berkovich’s category of
![]() $K$
-analytic spaces. For every
$K$
-analytic spaces. For every
![]() $K$
-scheme of finite type
$K$
-scheme of finite type
![]() $X$
, as a set,
$X$
, as a set,
![]() $X^{\text{an}}$
consists of the pairs
$X^{\text{an}}$
consists of the pairs
![]() $x=(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})$
where
$x=(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})$
where
![]() $\unicode[STIX]{x1D709}_{x}$
is a point of
$\unicode[STIX]{x1D709}_{x}$
is a point of
![]() $X$
and
$X$
and
![]() $|\cdot |_{x}$
is an absolute value on the residue field
$|\cdot |_{x}$
is an absolute value on the residue field
![]() $\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
of
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
of
![]() $X$
at
$X$
at
![]() $\unicode[STIX]{x1D709}_{x}$
extending the absolute value
$\unicode[STIX]{x1D709}_{x}$
extending the absolute value
![]() $|\cdot |_{K}$
on
$|\cdot |_{K}$
on
![]() $K$
. We endow
$K$
. We endow
![]() $X^{\text{an}}$
with the Berkovich topology, that is, the weakest one such that:
$X^{\text{an}}$
with the Berkovich topology, that is, the weakest one such that:
(i) the forgetful map
 $\unicode[STIX]{x1D719}:X^{\text{an}}\rightarrow X$
, defined as
$\unicode[STIX]{x1D719}:X^{\text{an}}\rightarrow X$
, defined as
 $(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})\mapsto \unicode[STIX]{x1D709}_{x}$
, is continuous;
$(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})\mapsto \unicode[STIX]{x1D709}_{x}$
, is continuous;(ii) for any Zariski open subset
 $U$
of
$U$
of
 $X$
and any regular function
$X$
and any regular function
 $f$
on
$f$
on
 $U$
the map
$U$
the map
 $|f|:\unicode[STIX]{x1D719}^{-1}(U)\rightarrow \mathbb{R}$
defined by
$|f|:\unicode[STIX]{x1D719}^{-1}(U)\rightarrow \mathbb{R}$
defined by
 $|f|(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})=|f(\unicode[STIX]{x1D709}_{x})|$
is continuous.
$|f|(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})=|f(\unicode[STIX]{x1D709}_{x})|$
is continuous.
The set
![]() $\text{Bir}(X)$
of birational points of
$\text{Bir}(X)$
of birational points of
![]() $X^{\text{an}}$
is defined as the inverse image under
$X^{\text{an}}$
is defined as the inverse image under
![]() $\unicode[STIX]{x1D719}$
of the generic point of
$\unicode[STIX]{x1D719}$
of the generic point of
![]() $X$
. By definition, it is a birational invariant of
$X$
. By definition, it is a birational invariant of
![]() $X$
.
$X$
.
1.9.8. Let
![]() $X$
be a smooth, proper
$X$
be a smooth, proper
![]() $K$
-scheme of finite type. For every point
$K$
-scheme of finite type. For every point
![]() $x\in X^{\text{an}}$
, we denote by
$x\in X^{\text{an}}$
, we denote by
![]() $\mathscr{H}(x)$
the completion of the residue field
$\mathscr{H}(x)$
the completion of the residue field
![]() $\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
with respect to the absolute value
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
with respect to the absolute value
![]() $|\cdot |_{x}$
, and by
$|\cdot |_{x}$
, and by
![]() $\mathscr{H}(x)^{\circ }$
the valuation ring of the valued field
$\mathscr{H}(x)^{\circ }$
the valuation ring of the valued field
![]() $\mathscr{H}(x)$
.
$\mathscr{H}(x)$
.
Given any snc model
![]() $\mathscr{X}$
of
$\mathscr{X}$
of
![]() $X$
, by the valuative criterion of properness, the
$X$
, by the valuative criterion of properness, the
![]() $K$
-morphism
$K$
-morphism
![]() $\text{Spec}\,(\mathscr{H}(x))\rightarrow X$
extends to an
$\text{Spec}\,(\mathscr{H}(x))\rightarrow X$
extends to an
![]() $R$
-morphism
$R$
-morphism
![]() $\text{Spec}\,(\mathscr{H}(x)^{\circ })\rightarrow \mathscr{X}$
. The image of the closed point via
$\text{Spec}\,(\mathscr{H}(x)^{\circ })\rightarrow \mathscr{X}$
. The image of the closed point via
![]() $\text{Spec}\,(\mathscr{H}(x)^{\circ })\rightarrow \mathscr{X}$
is called the center, or reduction, of
$\text{Spec}\,(\mathscr{H}(x)^{\circ })\rightarrow \mathscr{X}$
is called the center, or reduction, of
![]() $x$
on
$x$
on
![]() $\mathscr{X}$
. The map
$\mathscr{X}$
. The map
which sends
![]() $x$
to its center on
$x$
to its center on
![]() $\mathscr{X}$
, is called the reduction map with respect to
$\mathscr{X}$
, is called the reduction map with respect to
![]() $\mathscr{X}$
.
$\mathscr{X}$
.
1.9.9. We recall a few notions from birational geometry; see [Reference Kollár and MoriKM08]. Let
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
be a pair such that
$(X,\unicode[STIX]{x1D6E5}_{X})$
be a pair such that
![]() $X$
is normal,
$X$
is normal,
![]() $\unicode[STIX]{x1D6E5}_{X}$
is an effective divisor, and
$\unicode[STIX]{x1D6E5}_{X}$
is an effective divisor, and
![]() $K_{X}+\unicode[STIX]{x1D6E5}_{X}$
is
$K_{X}+\unicode[STIX]{x1D6E5}_{X}$
is
![]() $\mathbb{Q}$
-Cartier. Then we say that
$\mathbb{Q}$
-Cartier. Then we say that
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is log canonical if for every log resolution
$(X,\unicode[STIX]{x1D6E5}_{X})$
is log canonical if for every log resolution
![]() $f:Z\rightarrow X$
, in the formula
$f:Z\rightarrow X$
, in the formula
where
![]() $\unicode[STIX]{x1D6E5}_{Z}$
is the round-up of the strict transform of
$\unicode[STIX]{x1D6E5}_{Z}$
is the round-up of the strict transform of
![]() $\unicode[STIX]{x1D6E5}_{X}$
plus the reduced exceptional divisor, all the
$\unicode[STIX]{x1D6E5}_{X}$
plus the reduced exceptional divisor, all the
![]() $a_{D}$
are non-negative. The sum ranges over all components of
$a_{D}$
are non-negative. The sum ranges over all components of
![]() $\unicode[STIX]{x1D6E5}_{Z}$
. In fact the quantity
$\unicode[STIX]{x1D6E5}_{Z}$
. In fact the quantity
![]() $a_{D}$
, called the log discrepancy of
$a_{D}$
, called the log discrepancy of
![]() $D$
with respect to
$D$
with respect to
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
, depends only on the valuation corresponding to
$(X,\unicode[STIX]{x1D6E5}_{X})$
, depends only on the valuation corresponding to
![]() $D$
, and this condition need only be tested on a single log resolution.
$D$
, and this condition need only be tested on a single log resolution.
We are most interested in the case where
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
satisfies the stronger condition of being dlt. A closed subset
$(X,\unicode[STIX]{x1D6E5}_{X})$
satisfies the stronger condition of being dlt. A closed subset
![]() $Y\subset X$
is called a log canonical center if for some (equivalently any) log resolution,
$Y\subset X$
is called a log canonical center if for some (equivalently any) log resolution,
![]() $Y$
is the image of a divisor
$Y$
is the image of a divisor
![]() $D$
with
$D$
with
![]() $a_{D}=0$
. The pair
$a_{D}=0$
. The pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is said to be dlt if for every log canonical center
$(X,\unicode[STIX]{x1D6E5}_{X})$
is said to be dlt if for every log canonical center
![]() $Y$
, there is a neighborhood of the generic point of
$Y$
, there is a neighborhood of the generic point of
![]() $Y$
inside which
$Y$
inside which
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is snc. Every fractional snc pair is dlt by [Reference Kollár and MoriKM08, Corollary 2.39].
$(X,\unicode[STIX]{x1D6E5}_{X})$
is snc. Every fractional snc pair is dlt by [Reference Kollár and MoriKM08, Corollary 2.39].
We say that a pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is Kawamata log terminal (klt) if it is dlt and the coefficients of
$(X,\unicode[STIX]{x1D6E5}_{X})$
is Kawamata log terminal (klt) if it is dlt and the coefficients of
![]() $\unicode[STIX]{x1D6E5}_{X}$
are all strictly less than
$\unicode[STIX]{x1D6E5}_{X}$
are all strictly less than
![]() $1$
.
$1$
.
1.9.10. Given a morphism
![]() $f:X\rightarrow B$
, and a dlt pair
$f:X\rightarrow B$
, and a dlt pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
, we say that
$(X,\unicode[STIX]{x1D6E5}_{X})$
, we say that
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is a minimal dlt model over
$(X,\unicode[STIX]{x1D6E5}_{X})$
is a minimal dlt model over
![]() $B$
if
$B$
if
![]() $f$
is proper and
$f$
is proper and
![]() $K_{X/B}+\unicode[STIX]{x1D6E5}_{X}$
is nef. If, in addition,
$K_{X/B}+\unicode[STIX]{x1D6E5}_{X}$
is nef. If, in addition,
![]() $K_{X/B}+\unicode[STIX]{x1D6E5}_{X}$
is semiample, we say that
$K_{X/B}+\unicode[STIX]{x1D6E5}_{X}$
is semiample, we say that
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is a good minimal dlt model.
$(X,\unicode[STIX]{x1D6E5}_{X})$
is a good minimal dlt model.
Given a pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
over
$(X,\unicode[STIX]{x1D6E5}_{X})$
over
![]() $B$
, a birational map
$B$
, a birational map
![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$
is called a (good) minimal dlt model of
$\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$
is called a (good) minimal dlt model of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
if
$(X,\unicode[STIX]{x1D6E5}_{X})$
if
![]() $(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
is a (good) minimal dlt model over
$(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
is a (good) minimal dlt model over
![]() $B$
, where
$B$
, where
![]() $\unicode[STIX]{x1D6E5}_{X^{\prime }}$
is the sum of the strict transform of
$\unicode[STIX]{x1D6E5}_{X^{\prime }}$
is the sum of the strict transform of
![]() $\unicode[STIX]{x1D6E5}_{X}$
and the reduced exceptional divisor of
$\unicode[STIX]{x1D6E5}_{X}$
and the reduced exceptional divisor of
![]() $\unicode[STIX]{x1D719}^{-1}$
, the sum of all divisors of
$\unicode[STIX]{x1D719}^{-1}$
, the sum of all divisors of
![]() $X^{\prime }$
such that
$X^{\prime }$
such that
![]() $\unicode[STIX]{x1D719}^{-1}$
does not define an isomorphism along the generic point. We often suppress the map
$\unicode[STIX]{x1D719}^{-1}$
does not define an isomorphism along the generic point. We often suppress the map
![]() $\unicode[STIX]{x1D719}$
. For example, if
$\unicode[STIX]{x1D719}$
. For example, if
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is proper over
$(X,\unicode[STIX]{x1D6E5}_{X})$
is proper over
![]() $K$
, and
$K$
, and
![]() $X^{\prime }$
is proper over
$X^{\prime }$
is proper over
![]() $R$
extending
$R$
extending
![]() $X$
, then
$X$
, then
![]() $\unicode[STIX]{x1D6E5}_{X^{\prime }}$
is the sum of the strict transform of
$\unicode[STIX]{x1D6E5}_{X^{\prime }}$
is the sum of the strict transform of
![]() $\unicode[STIX]{x1D6E5}_{X}$
with the reduced special fiber of
$\unicode[STIX]{x1D6E5}_{X}$
with the reduced special fiber of
![]() $X^{\prime }$
.
$X^{\prime }$
.
2 The Kato fan of a log-regular log scheme
2.1 Definition of Kato fans
2.1.1. According to [Reference KatoKat94, Definition 9.1], a monoidal space
![]() $(T,{\mathcal{M}}_{T})$
is a topological space
$(T,{\mathcal{M}}_{T})$
is a topological space
![]() $T$
endowed with a sharp sheaf of monoids
$T$
endowed with a sharp sheaf of monoids
![]() ${\mathcal{M}}_{T}$
, where sharp means that
${\mathcal{M}}_{T}$
, where sharp means that
![]() ${\mathcal{M}}_{T,t}^{\times }=\{1\}$
for every
${\mathcal{M}}_{T,t}^{\times }=\{1\}$
for every
![]() $t\in T$
. We often denote the monoidal space simply by
$t\in T$
. We often denote the monoidal space simply by
![]() $T$
.
$T$
.
A morphism of monoidal spaces is a pair
![]() $(f,\unicode[STIX]{x1D711}):(T,{\mathcal{M}}_{T})\rightarrow (T^{\prime },{\mathcal{M}}_{T^{\prime }})$
such that
$(f,\unicode[STIX]{x1D711}):(T,{\mathcal{M}}_{T})\rightarrow (T^{\prime },{\mathcal{M}}_{T^{\prime }})$
such that
![]() $f:T\rightarrow T^{\prime }$
is a continuous function of topological spaces and
$f:T\rightarrow T^{\prime }$
is a continuous function of topological spaces and
![]() $\unicode[STIX]{x1D711}:f^{-1}({\mathcal{M}}_{T})\rightarrow {\mathcal{M}}_{T^{\prime }}$
is a sheaf homomorphism such that
$\unicode[STIX]{x1D711}:f^{-1}({\mathcal{M}}_{T})\rightarrow {\mathcal{M}}_{T^{\prime }}$
is a sheaf homomorphism such that
![]() $\unicode[STIX]{x1D711}_{t}^{-1}(\{1\})=\{1\}$
for every
$\unicode[STIX]{x1D711}_{t}^{-1}(\{1\})=\{1\}$
for every
![]() $t\in T$
.
$t\in T$
.
Example 2.1.2. If
![]() $\mathscr{X}^{+}$
is a log scheme then the Zariski topological space
$\mathscr{X}^{+}$
is a log scheme then the Zariski topological space
![]() $\mathscr{X}$
is equipped with a sheaf of sharp monoids
$\mathscr{X}$
is equipped with a sheaf of sharp monoids
![]() ${\mathcal{C}}_{\mathscr{X}}$
, namely the characteristic sheaf of
${\mathcal{C}}_{\mathscr{X}}$
, namely the characteristic sheaf of
![]() $\mathscr{X}^{+}$
. Thus
$\mathscr{X}^{+}$
. Thus
![]() $(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})$
is a monoidal space. Moreover, morphisms of log schemes induce morphisms of characteristic sheaves, hence morphisms of monoidal spaces. We therefore obtain a functor from the category of log schemes to the category of monoidal spaces.
$(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})$
is a monoidal space. Moreover, morphisms of log schemes induce morphisms of characteristic sheaves, hence morphisms of monoidal spaces. We therefore obtain a functor from the category of log schemes to the category of monoidal spaces.
Example 2.1.3. Given a monoid
![]() $P$
, we may associate to it a monoidal space called the spectrum of
$P$
, we may associate to it a monoidal space called the spectrum of
![]() $P$
. As a set,
$P$
. As a set,
![]() $\text{Spec}\,P$
is the set of all prime ideals of
$\text{Spec}\,P$
is the set of all prime ideals of
![]() $P$
. The topology is characterized by the basis open sets
$P$
. The topology is characterized by the basis open sets
![]() $D(f)=\{\mathfrak{p}\in \text{Spec}\,P|f\notin \mathfrak{p}\}$
for any
$D(f)=\{\mathfrak{p}\in \text{Spec}\,P|f\notin \mathfrak{p}\}$
for any
![]() $f\in P$
. The monoidal sheaf is defined by
$f\in P$
. The monoidal sheaf is defined by
where
![]() $S=\{f^{n}|n\geqslant 0\}$
.
$S=\{f^{n}|n\geqslant 0\}$
.
2.1.4. A monoidal space isomorphic to the monoidal space
![]() $\text{Spec}\,P$
for some monoid
$\text{Spec}\,P$
for some monoid
![]() $P$
is called an affine Kato fan. A monoidal space is called a Kato fan if it has an open covering consisting of affine Kato fans. In particular, we call a Kato fan integral, saturated, of finite type or fs if it admits a cover by the spectra of monoids with the respective properties.
$P$
is called an affine Kato fan. A monoidal space is called a Kato fan if it has an open covering consisting of affine Kato fans. In particular, we call a Kato fan integral, saturated, of finite type or fs if it admits a cover by the spectra of monoids with the respective properties.
2.1.5. A morphism of fs Kato fans
![]() $F^{\prime }\rightarrow F$
is called a subdivision if it has finite fibers and the morphism
$F^{\prime }\rightarrow F$
is called a subdivision if it has finite fibers and the morphism
is a bijection. By allowing subdivisions, a Kato fan might take the following shape.
Proposition 2.1.6 [Reference KatoKat94, Proposition 9.8].
Let
![]() $F$
be an fs Kato fan. Then there is a subdivision
$F$
be an fs Kato fan. Then there is a subdivision
![]() $F^{\prime }\rightarrow F$
such that
$F^{\prime }\rightarrow F$
such that
![]() $F^{\prime }$
has an open cover
$F^{\prime }$
has an open cover
![]() $\{U_{i}^{\prime }\}$
by affine Kato fans with
$\{U_{i}^{\prime }\}$
by affine Kato fans with
![]() $U_{i}^{\prime }\simeq \text{Spec}\,\mathbb{N}^{r_{i}}$
.
$U_{i}^{\prime }\simeq \text{Spec}\,\mathbb{N}^{r_{i}}$
.
The strategy of the proof of Proposition 2.1.6 goes back to [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMS73] and relies on a sequence of particular subdivisions of the Kato fan, the so-called star and barycentric subdivisions [Reference Abramovich, Chen, Marcus, Ulirsch, Wise, Baker and PayneACMUW16, Example 4.10].
2.2 Kato fans associated to log-regular log schemes
Theorem 2.2.1 [Reference KatoKat94, Proposition 10.2].
Let
![]() $\mathscr{X}^{+}$
be a log-regular log scheme. Then there is an initial strict morphism
$\mathscr{X}^{+}$
be a log-regular log scheme. Then there is an initial strict morphism
![]() $(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})\rightarrow F$
to a Kato fan in the category of monoidal spaces. Explicitly, there exist a Kato fan
$(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})\rightarrow F$
to a Kato fan in the category of monoidal spaces. Explicitly, there exist a Kato fan
![]() $F$
and a morphism
$F$
and a morphism
![]() $\unicode[STIX]{x1D71A}:(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})\rightarrow F$
such that
$\unicode[STIX]{x1D71A}:(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})\rightarrow F$
such that
![]() $\unicode[STIX]{x1D71A}^{-1}({\mathcal{M}}_{F})\simeq {\mathcal{C}}_{\mathscr{X}}$
and any other morphism from
$\unicode[STIX]{x1D71A}^{-1}({\mathcal{M}}_{F})\simeq {\mathcal{C}}_{\mathscr{X}}$
and any other morphism from
![]() $(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})$
to a Kato fan factors through
$(\mathscr{X},{\mathcal{C}}_{\mathscr{X}})$
to a Kato fan factors through
![]() $\unicode[STIX]{x1D71A}$
.
$\unicode[STIX]{x1D71A}$
.
The Kato fan
![]() $F$
in Theorem 2.2.1 is called the Kato fan associated to
$F$
in Theorem 2.2.1 is called the Kato fan associated to
![]() $\mathscr{X}^{+}$
. Concretely, it is the topological subspace of
$\mathscr{X}^{+}$
. Concretely, it is the topological subspace of
![]() $\mathscr{X}$
consisting of the points
$\mathscr{X}$
consisting of the points
![]() $x$
such that the maximal ideal
$x$
such that the maximal ideal
![]() $\mathfrak{m}_{x}$
of
$\mathfrak{m}_{x}$
of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
is equal to
${\mathcal{O}}_{\mathscr{X},x}$
is equal to
![]() ${\mathcal{I}}_{\mathscr{X},x}$
, and
${\mathcal{I}}_{\mathscr{X},x}$
, and
![]() ${\mathcal{M}}_{F}$
is the inverse image of
${\mathcal{M}}_{F}$
is the inverse image of
![]() ${\mathcal{C}}_{\mathscr{X}}$
on
${\mathcal{C}}_{\mathscr{X}}$
on
![]() $F$
; henceforth we write
$F$
; henceforth we write
![]() ${\mathcal{C}}_{F}$
for
${\mathcal{C}}_{F}$
for
![]() ${\mathcal{M}}_{F}$
.
${\mathcal{M}}_{F}$
.
Example 2.2.2. Assume that
![]() $\mathscr{X}$
is regular, of finite type over
$\mathscr{X}$
is regular, of finite type over
![]() $S$
, and
$S$
, and
![]() $\mathscr{X}_{k}$
is a divisor with strict normal crossings. Then
$\mathscr{X}_{k}$
is a divisor with strict normal crossings. Then
![]() $\mathscr{X}^{+}$
is log-regular and
$\mathscr{X}^{+}$
is log-regular and
![]() $F$
is the set of generic points of intersections of irreducible components of
$F$
is the set of generic points of intersections of irreducible components of
![]() $\mathscr{X}_{k}$
. For each point
$\mathscr{X}_{k}$
. For each point
![]() $x$
of
$x$
of
![]() $F$
, the stalk of
$F$
, the stalk of
![]() ${\mathcal{C}}_{F}$
is isomorphic to
${\mathcal{C}}_{F}$
is isomorphic to
![]() $(\mathbb{N}^{r},+)$
, with
$(\mathbb{N}^{r},+)$
, with
![]() $r$
the number of irreducible components of
$r$
the number of irreducible components of
![]() $\mathscr{X}_{k}$
that pass through
$\mathscr{X}_{k}$
that pass through
![]() $x$
.
$x$
.
This example admits the following partial generalization.
Lemma 2.2.3. Let
![]() $\mathscr{X}^{+}$
be a log-regular log scheme. Then the fan
$\mathscr{X}^{+}$
be a log-regular log scheme. Then the fan
![]() $F$
consists of the generic points of intersections of irreducible components of
$F$
consists of the generic points of intersections of irreducible components of
![]() $D_{\mathscr{X}}$
.
$D_{\mathscr{X}}$
.
Proof. First, we show that every such generic point is a point of
![]() $F$
. Let
$F$
. Let
![]() $E_{1},\ldots ,E_{r}$
be irreducible components of
$E_{1},\ldots ,E_{r}$
be irreducible components of
![]() $D_{\mathscr{X}}$
and let
$D_{\mathscr{X}}$
and let
![]() $x$
be a generic point of the intersection
$x$
be a generic point of the intersection
![]() $E_{1}\cap \cdots \cap E_{r}$
. We set
$E_{1}\cap \cdots \cap E_{r}$
. We set
![]() $d=\dim {\mathcal{O}}_{\mathscr{X},x}$
. Since
$d=\dim {\mathcal{O}}_{\mathscr{X},x}$
. Since
![]() $\mathscr{X}^{+}$
is log-regular, we know that
$\mathscr{X}^{+}$
is log-regular, we know that
![]() ${\mathcal{O}}_{\mathscr{X},x}/{\mathcal{I}}_{\mathscr{X},x}$
is regular and that
${\mathcal{O}}_{\mathscr{X},x}/{\mathcal{I}}_{\mathscr{X},x}$
is regular and that
We denote by
![]() $V({\mathcal{I}}_{\mathscr{X},x})$
the vanishing locus of the ideal
$V({\mathcal{I}}_{\mathscr{X},x})$
the vanishing locus of the ideal
![]() ${\mathcal{I}}_{\mathscr{X},x}$
in
${\mathcal{I}}_{\mathscr{X},x}$
in
![]() $\text{Spec}\,({\mathcal{O}}_{\mathscr{X},x})$
. We want to prove that
$\text{Spec}\,({\mathcal{O}}_{\mathscr{X},x})$
. We want to prove that
![]() ${\mathcal{I}}_{\mathscr{X},x}=\mathfrak{m}_{x}$
. We assume the contrary, hence that
${\mathcal{I}}_{\mathscr{X},x}=\mathfrak{m}_{x}$
. We assume the contrary, hence that
![]() ${\mathcal{I}}_{\mathscr{X},x}\subsetneq \mathfrak{m}_{x}$
. This assumption implies that there exists
${\mathcal{I}}_{\mathscr{X},x}\subsetneq \mathfrak{m}_{x}$
. This assumption implies that there exists
![]() $j$
such that
$j$
such that
![]() $V({\mathcal{I}}_{\mathscr{X},x})\nsubseteq E_{j}$
: indeed, if the vanishing locus is contained in each irreducible component
$V({\mathcal{I}}_{\mathscr{X},x})\nsubseteq E_{j}$
: indeed, if the vanishing locus is contained in each irreducible component
![]() $E_{i}$
, that is,
$E_{i}$
, that is,
then
![]() ${\mathcal{I}}_{\mathscr{X},x}\supseteq \mathfrak{m}_{x}$
. From the assumption of log-regularity it follows that the vanishing locus
${\mathcal{I}}_{\mathscr{X},x}\supseteq \mathfrak{m}_{x}$
. From the assumption of log-regularity it follows that the vanishing locus
![]() $V({\mathcal{I}}_{\mathscr{X},x})$
is a regular subscheme, and, moreover, that
$V({\mathcal{I}}_{\mathscr{X},x})$
is a regular subscheme, and, moreover, that
![]() $\mathscr{X}^{+}$
is Cohen–Macaulay by [Reference KatoKat94, Theorem 4.1]. Thus, there exists a regular sequence
$\mathscr{X}^{+}$
is Cohen–Macaulay by [Reference KatoKat94, Theorem 4.1]. Thus, there exists a regular sequence
![]() $(f_{1},\ldots ,f_{l})$
in
$(f_{1},\ldots ,f_{l})$
in
![]() ${\mathcal{I}}_{\mathscr{X},x}$
, where
${\mathcal{I}}_{\mathscr{X},x}$
, where
![]() $l$
is the codimension of
$l$
is the codimension of
![]() $V({\mathcal{I}}_{\mathscr{X},x})$
, that is,
$V({\mathcal{I}}_{\mathscr{X},x})$
, that is,
Moreover, by the equality (2.2.4),
![]() $\text{rank}\,{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}=l$
.
$\text{rank}\,{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}=l$
.
We claim that the residue classes of these elements
![]() $f_{i}$
in
$f_{i}$
in
![]() ${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
are linearly independent. Assume the contrary. If
${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
are linearly independent. Assume the contrary. If
![]() $l=1$
the proposition holds because
$l=1$
the proposition holds because
![]() $f_{1}$
is not a unit. Otherwise,
$f_{1}$
is not a unit. Otherwise,
![]() $l\geqslant 2$
and, up to renumbering the
$l\geqslant 2$
and, up to renumbering the
![]() $f_{i}$
, there exist an integer
$f_{i}$
, there exist an integer
![]() $e$
with
$e$
with
![]() $1<e\leqslant l$
, non-negative integers
$1<e\leqslant l$
, non-negative integers
![]() $a_{1},\ldots ,a_{l}$
, not all zero, and a unit
$a_{1},\ldots ,a_{l}$
, not all zero, and a unit
![]() $u$
in
$u$
in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
such that
${\mathcal{O}}_{\mathscr{X},x}$
such that
This contradicts the fact that
![]() $(f_{1},\ldots ,f_{l})$
is a regular sequence in
$(f_{1},\ldots ,f_{l})$
is a regular sequence in
![]() ${\mathcal{I}}_{\mathscr{X},x}$
. Thus, the classes
${\mathcal{I}}_{\mathscr{X},x}$
. Thus, the classes
![]() $\overline{f_{1}},\ldots ,\overline{f_{l}}$
are independent in
$\overline{f_{1}},\ldots ,\overline{f_{l}}$
are independent in
![]() ${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
. As we also have the equality
${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
. As we also have the equality
![]() $\text{rank}\,{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}=l$
, it follows that these classes generate
$\text{rank}\,{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}=l$
, it follows that these classes generate
![]() ${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}\otimes _{\mathbb{Z}}\mathbb{Q}$
.
${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}\otimes _{\mathbb{Z}}\mathbb{Q}$
.
Let
![]() $g_{j}$
be a non-zero element of the ideal
$g_{j}$
be a non-zero element of the ideal
![]() ${\mathcal{I}}_{\mathscr{X},x}$
that vanishes along
${\mathcal{I}}_{\mathscr{X},x}$
that vanishes along
![]() $E_{j}$
: it necessarily exists as otherwise
$E_{j}$
: it necessarily exists as otherwise
![]() $E_{j}$
is not a component of the divisor
$E_{j}$
is not a component of the divisor
![]() $D_{\mathscr{X}}$
. Then
$D_{\mathscr{X}}$
. Then
![]() $g_{j}$
satisfies
$g_{j}$
satisfies
with
![]() $b_{i}\in \mathbb{Z}$
,
$b_{i}\in \mathbb{Z}$
,
![]() $v$
is a unit in
$v$
is a unit in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
and
${\mathcal{O}}_{\mathscr{X},x}$
and
![]() $N$
is a positive integer. As
$N$
is a positive integer. As
![]() $g_{j}$
vanishes along the irreducible component
$g_{j}$
vanishes along the irreducible component
![]() $E_{j}$
, at least one of the functions
$E_{j}$
, at least one of the functions
![]() $f_{1},\ldots ,f_{l}$
has to vanish along
$f_{1},\ldots ,f_{l}$
has to vanish along
![]() $E_{j}$
: assume that it is
$E_{j}$
: assume that it is
![]() $f_{1}$
.
$f_{1}$
.
On the one hand, as
![]() $f_{1}$
is identically zero on
$f_{1}$
is identically zero on
![]() $E_{j}$
, the trace of
$E_{j}$
, the trace of
![]() $E_{j}$
on
$E_{j}$
on
![]() $V({\mathcal{I}}_{\mathscr{X},x})$
has codimension at most
$V({\mathcal{I}}_{\mathscr{X},x})$
has codimension at most
![]() $l-1$
in
$l-1$
in
![]() $E_{j}$
at the point
$E_{j}$
at the point
![]() $x$
. On the other hand, we assumed that
$x$
. On the other hand, we assumed that
![]() $V({\mathcal{I}}_{\mathscr{X},x})$
is not contained in
$V({\mathcal{I}}_{\mathscr{X},x})$
is not contained in
![]() $E_{j}$
and it has codimension
$E_{j}$
and it has codimension
![]() $l$
in
$l$
in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. Then the trace of
${\mathcal{O}}_{\mathscr{X},x}$
. Then the trace of
![]() $E_{j}$
on
$E_{j}$
on
![]() $V({\mathcal{I}}_{\mathscr{X},x})$
has codimension
$V({\mathcal{I}}_{\mathscr{X},x})$
has codimension
![]() $l$
in
$l$
in
![]() $E_{j}$
at
$E_{j}$
at
![]() $x$
. This is a contradiction. We conclude that the ideal
$x$
. This is a contradiction. We conclude that the ideal
![]() ${\mathcal{I}}_{\mathscr{X},x}$
is equal to the maximal ideal
${\mathcal{I}}_{\mathscr{X},x}$
is equal to the maximal ideal
![]() $\mathfrak{m}_{x}$
, therefore
$\mathfrak{m}_{x}$
, therefore
![]() $x$
is a point of
$x$
is a point of
![]() $F$
.
$F$
.
It remains to prove the converse implication: every point
![]() $x$
of the fan
$x$
of the fan
![]() $F$
is a generic point of an intersection of irreducible components of
$F$
is a generic point of an intersection of irreducible components of
![]() $D_{\mathscr{X}}$
. Let
$D_{\mathscr{X}}$
. Let
![]() $x$
be a point of
$x$
be a point of
![]() $F$
: by construction of Kato fan
$F$
: by construction of Kato fan
![]() $F$
, the maximal ideal of
$F$
, the maximal ideal of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
is equal to
${\mathcal{O}}_{\mathscr{X},x}$
is equal to
![]() ${\mathcal{I}}_{\mathscr{X},x}$
, thus it is generated by elements in
${\mathcal{I}}_{\mathscr{X},x}$
, thus it is generated by elements in
![]() ${\mathcal{M}}_{\mathscr{X},x}$
. The zero locus of such an element is contained in
${\mathcal{M}}_{\mathscr{X},x}$
. The zero locus of such an element is contained in
![]() $D_{\mathscr{X}}$
by definition of the logarithmic structure on
$D_{\mathscr{X}}$
by definition of the logarithmic structure on
![]() $\mathscr{X}^{+}$
. Therefore, the zero locus of a generator of
$\mathscr{X}^{+}$
. Therefore, the zero locus of a generator of
![]() $\mathfrak{m}_{x}$
in
$\mathfrak{m}_{x}$
in
![]() ${\mathcal{M}}_{\mathscr{X},x}$
is a union of irreducible components of the trace of
${\mathcal{M}}_{\mathscr{X},x}$
is a union of irreducible components of the trace of
![]() $D_{\mathscr{X}}$
on
$D_{\mathscr{X}}$
on
![]() $\text{Spec}\,{\mathcal{O}}_{\mathscr{X},x}$
and
$\text{Spec}\,{\mathcal{O}}_{\mathscr{X},x}$
and
![]() $x$
is a generic point of the intersection of all such irreducible components.◻
$x$
is a generic point of the intersection of all such irreducible components.◻
Remark 2.2.5. By convention, the generic point of the empty intersection of irreducible components is the generic point of
![]() $\mathscr{X}$
. By definition, this point is also included in the Kato fan
$\mathscr{X}$
. By definition, this point is also included in the Kato fan
![]() $F$
. Thus, for example, the Kato fan associated to
$F$
. Thus, for example, the Kato fan associated to
![]() $S^{+}$
consists of two points: the generic point of
$S^{+}$
consists of two points: the generic point of
![]() $S$
that corresponds to the empty intersection, and the closed point
$S$
that corresponds to the empty intersection, and the closed point
![]() $s$
corresponding to the unique irreducible component of the logarithmic divisorial structure.
$s$
corresponding to the unique irreducible component of the logarithmic divisorial structure.
Moreover, Example 2.2.2 also leads to the following characterization.
Proposition 2.2.6 [Reference Gabber and RameroGR04, Corollary 12.5.35].
Let
![]() $\mathscr{X}^{+}$
be a log-regular log scheme over
$\mathscr{X}^{+}$
be a log-regular log scheme over
![]() $S^{+}$
and
$S^{+}$
and
![]() $F$
its associated Kato fan. The following statements are equivalent:
$F$
its associated Kato fan. The following statements are equivalent:
(i) for every
 $x\in F$
,
$x\in F$
,
 ${\mathcal{C}}_{F,x}\simeq \mathbb{N}^{r(x)}$
,
${\mathcal{C}}_{F,x}\simeq \mathbb{N}^{r(x)}$
,(ii) the underlying scheme
 $\mathscr{X}$
is regular.
$\mathscr{X}$
is regular.
If this is the case, then the special fiber
![]() $\mathscr{X}_{k}$
is an snc divisor.
$\mathscr{X}_{k}$
is an snc divisor.
2.2.7. The construction of the Kato fan of a log scheme defines a functor from the category of log-regular log schemes to the category of Kato fans. Indeed, given a morphism of log schemes
![]() $\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
, we consider the embedding of the associated Kato fan
$\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
, we consider the embedding of the associated Kato fan
![]() $F_{\mathscr{X}}$
in
$F_{\mathscr{X}}$
in
![]() $\mathscr{X}^{+}$
and the canonical morphism
$\mathscr{X}^{+}$
and the canonical morphism
![]() $\mathscr{Y}^{+}\rightarrow F_{\mathscr{Y}}$
: the composition
$\mathscr{Y}^{+}\rightarrow F_{\mathscr{Y}}$
: the composition
functorially induces a map between associated Kato fans. Moreover, this association preserves strict morphisms [Reference UlirschUli17, Lemma 4.9].
2.3 Resolutions of log schemes via Kato fan subdivisions
Proposition 2.3.1 [Reference KatoKat94, Proposition 9.9].
Let
![]() $\mathscr{X}^{+}$
be a log-regular log scheme and let
$\mathscr{X}^{+}$
be a log-regular log scheme and let
![]() $F$
be its associated Kato fan. Let
$F$
be its associated Kato fan. Let
![]() $F^{\prime }\rightarrow F$
be a subdivision of fans. Then there exist a log scheme
$F^{\prime }\rightarrow F$
be a subdivision of fans. Then there exist a log scheme
![]() ${\mathscr{X}^{\prime }}^{+}$
, a morphism of log schemes
${\mathscr{X}^{\prime }}^{+}$
, a morphism of log schemes
![]() ${\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
, and a commutative diagram
${\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
, and a commutative diagram

such that
![]() $p^{-1}({\mathcal{M}}_{F^{\prime }})\simeq {\mathcal{C}}_{\mathscr{X}^{\prime }}$
; they define a final object in the category of such diagrams and the refinement
$p^{-1}({\mathcal{M}}_{F^{\prime }})\simeq {\mathcal{C}}_{\mathscr{X}^{\prime }}$
; they define a final object in the category of such diagrams and the refinement
![]() $F^{\prime }\rightarrow F$
is functorially induced by the morphism of log-regular log schemes
$F^{\prime }\rightarrow F$
is functorially induced by the morphism of log-regular log schemes
![]() ${\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
.
${\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
.
2.3.2. It follows that given any subdivision
![]() $F^{\prime }\rightarrow F$
of the Kato fan F associated with a log-regular log scheme
$F^{\prime }\rightarrow F$
of the Kato fan F associated with a log-regular log scheme
![]() $\mathscr{X}^{+}$
, we can construct a log scheme over
$\mathscr{X}^{+}$
, we can construct a log scheme over
![]() $\mathscr{X}^{+}$
with prescribed associated Kato fan
$\mathscr{X}^{+}$
with prescribed associated Kato fan
![]() $F^{\prime }$
. Combining this fact with Propositions 2.1.6 and 2.2.6 yields a construction of resolutions of log schemes in the following sense: for any log-regular log scheme over
$F^{\prime }$
. Combining this fact with Propositions 2.1.6 and 2.2.6 yields a construction of resolutions of log schemes in the following sense: for any log-regular log scheme over
![]() $S^{+}$
we can find a birational modification by a regular log scheme with snc special fiber. Moreover, the morphism of log schemes
$S^{+}$
we can find a birational modification by a regular log scheme with snc special fiber. Moreover, the morphism of log schemes
![]() ${\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
is obtained by a log blow-up [Reference NiziołNiz06, Theorem 5.8].
${\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
is obtained by a log blow-up [Reference NiziołNiz06, Theorem 5.8].
2.4 Fibred products and associated Kato fans
2.4.1. Given morphisms of fs log schemes
![]() $f_{1}:\mathscr{X}_{1}^{+}\rightarrow \mathscr{Y}^{+}$
and
$f_{1}:\mathscr{X}_{1}^{+}\rightarrow \mathscr{Y}^{+}$
and
![]() $f_{2}:\mathscr{X}_{2}^{+}\rightarrow \mathscr{Y}^{+}$
, their fibred product exists in the category of log schemes. It is obtained by endowing the usual fibred product of schemes
$f_{2}:\mathscr{X}_{2}^{+}\rightarrow \mathscr{Y}^{+}$
, their fibred product exists in the category of log schemes. It is obtained by endowing the usual fibred product of schemes

with the log structure associated to
![]() $p_{1}^{-1}{{\mathcal{M}}_{\mathscr{X}_{1}}\oplus }_{p_{\mathcal{Y}}^{-1}{\mathcal{M}}_{\mathcal{Y}}}p_{2}^{-1}{\mathcal{M}}_{\mathscr{X}_{2}}$
. If
$p_{1}^{-1}{{\mathcal{M}}_{\mathscr{X}_{1}}\oplus }_{p_{\mathcal{Y}}^{-1}{\mathcal{M}}_{\mathcal{Y}}}p_{2}^{-1}{\mathcal{M}}_{\mathscr{X}_{2}}$
. If
![]() $u_{1}:P\rightarrow Q_{1}$
and
$u_{1}:P\rightarrow Q_{1}$
and
![]() $u_{2}:P\rightarrow Q_{2}$
are charts for the morphisms
$u_{2}:P\rightarrow Q_{2}$
are charts for the morphisms
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
respectively, then the induced morphism
$f_{2}$
respectively, then the induced morphism
![]() $\mathscr{X}_{1}\times _{\mathscr{Y}}\mathscr{X}_{2}\rightarrow \text{Spec}\,\mathbb{Z}[{Q_{1}\oplus }_{P}Q_{2}]$
is a chart for
$\mathscr{X}_{1}\times _{\mathscr{Y}}\mathscr{X}_{2}\rightarrow \text{Spec}\,\mathbb{Z}[{Q_{1}\oplus }_{P}Q_{2}]$
is a chart for
![]() $\mathscr{X}_{1}^{+}\times _{\mathscr{Y}^{+}}\mathscr{X}_{2}^{+}$
.
$\mathscr{X}_{1}^{+}\times _{\mathscr{Y}^{+}}\mathscr{X}_{2}^{+}$
.
2.4.3. In general, the fibred product is not fs, but the category of fs log schemes also admits fibred products. Keeping the same notation, the following is a local description of the fibred product in the category of fine and saturated log schemes
in terms of the charts for
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
[Reference BultotBul15, 3.6.16]. We remark that the two fibred products above may not only have different log structures, but also the underlying schemes may differ. Nevertheless, this obviously does not occur when the monoid
$f_{2}$
[Reference BultotBul15, 3.6.16]. We remark that the two fibred products above may not only have different log structures, but also the underlying schemes may differ. Nevertheless, this obviously does not occur when the monoid
![]() ${Q_{1}\oplus }_{P}Q_{2}$
is saturated.
${Q_{1}\oplus }_{P}Q_{2}$
is saturated.
2.4.4. Log-smoothness is preserved under fs base change and composition [Reference Gabber and RameroGR04, Proposition 12.3.24]. In particular, if
![]() $f_{1}:\mathscr{X}_{1}^{+}\rightarrow \mathscr{Y}^{+}$
is log-smooth and
$f_{1}:\mathscr{X}_{1}^{+}\rightarrow \mathscr{Y}^{+}$
is log-smooth and
![]() $\mathscr{X}_{2}^{+}$
is log-regular, then
$\mathscr{X}_{2}^{+}$
is log-regular, then
![]() $\mathscr{X}_{1}^{+}\times _{\mathscr{Y}^{+}}^{\mathit{fs}}\mathscr{X}_{2}^{+}$
is log-regular, by [Reference KatoKat94, Theorem 8.2].
$\mathscr{X}_{1}^{+}\times _{\mathscr{Y}^{+}}^{\mathit{fs}}\mathscr{X}_{2}^{+}$
is log-regular, by [Reference KatoKat94, Theorem 8.2].
Consider log-smooth morphisms of fs log schemes
![]() $\mathscr{X}_{1}^{+}\rightarrow \mathscr{Y}^{+}$
and
$\mathscr{X}_{1}^{+}\rightarrow \mathscr{Y}^{+}$
and
![]() $\mathscr{X}_{2}^{+}\rightarrow \mathscr{Y}^{+}$
. The sheaves of logarithmic differentials are related by the isomorphism
$\mathscr{X}_{2}^{+}\rightarrow \mathscr{Y}^{+}$
. The sheaves of logarithmic differentials are related by the isomorphism
by [Reference Gabber and RameroGR04, Proposition 12.3.13]. Furthermore, by assumption of log-smoothness over
![]() $S^{+}$
the logarithmic differential sheaves are locally free of finite rank [Reference KatoKat94, Proposition 3.10] and we can consider their determinants; they are called log canonical bundles and denoted by
$S^{+}$
the logarithmic differential sheaves are locally free of finite rank [Reference KatoKat94, Proposition 3.10] and we can consider their determinants; they are called log canonical bundles and denoted by
![]() $\unicode[STIX]{x1D714}^{\log }$
. The following isomorphism is a direct consequence of (2.4.5):
$\unicode[STIX]{x1D714}^{\log }$
. The following isomorphism is a direct consequence of (2.4.5):
2.4.7. Similarly to the construction of fibred products of fs log schemes, the category of fs Kato fans admits fibred products: on affine Kato fans
![]() $F=\text{Spec}\,P$
and
$F=\text{Spec}\,P$
and
![]() $G=\text{Spec}\,Q$
over
$G=\text{Spec}\,Q$
over
![]() $H=\text{Spec}\,T$
,
$H=\text{Spec}\,T$
,
![]() $F\times _{H}G$
is the spectrum of the amalgamated sum
$F\times _{H}G$
is the spectrum of the amalgamated sum
![]() $(P\oplus _{T}Q)^{\text{sat}}$
in the category of fs monoids [Reference UlirschUli19, Proposition 2.4] and on the underlying topological spaces this coincides with the usual fibred product.
$(P\oplus _{T}Q)^{\text{sat}}$
in the category of fs monoids [Reference UlirschUli19, Proposition 2.4] and on the underlying topological spaces this coincides with the usual fibred product.
We seek to compare the Kato fan associated to the fibred product of log-regular log schemes with the fibred product of associated Kato fans.
Proposition 2.4.8 [Reference SaitoSai04, Lemma 2.8].
Given
![]() $\mathscr{T}^{+}$
a log-regular log scheme, let
$\mathscr{T}^{+}$
a log-regular log scheme, let
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
be log-smooth log schemes over
$\mathscr{Y}^{+}$
be log-smooth log schemes over
![]() $\mathscr{T}^{+}$
. We denote by
$\mathscr{T}^{+}$
. We denote by
![]() $\mathscr{Z}^{+}$
the fs fibred product
$\mathscr{Z}^{+}$
the fs fibred product
![]() $\mathscr{X}^{+}\times _{\mathscr{T}^{+}}^{\mathit{fs}}\mathscr{Y}^{+}$
. Then, the natural morphisms
$\mathscr{X}^{+}\times _{\mathscr{T}^{+}}^{\mathit{fs}}\mathscr{Y}^{+}$
. Then, the natural morphisms
![]() $F_{\mathscr{Z}}\rightarrow F_{\mathscr{X}}$
and
$F_{\mathscr{Z}}\rightarrow F_{\mathscr{X}}$
and
![]() $F_{\mathscr{Z}}\rightarrow F_{\mathscr{Y}}$
induce a morphism of Kato fans
$F_{\mathscr{Z}}\rightarrow F_{\mathscr{Y}}$
induce a morphism of Kato fans
that is locally an isomorphism.
2.4.10. For any pair of points
![]() $(x,y)$
in
$(x,y)$
in
![]() $F_{\mathscr{X}}\times _{F_{\mathscr{T}}}F_{\mathscr{Y}}$
, we denote by
$F_{\mathscr{X}}\times _{F_{\mathscr{T}}}F_{\mathscr{Y}}$
, we denote by
![]() $n(x,y)$
the number of preimages of
$n(x,y)$
the number of preimages of
![]() $(x,y)$
in the Kato fan of
$(x,y)$
in the Kato fan of
![]() $\mathscr{Z}^{+}$
under the local isomorphism (2.4.9).
$\mathscr{Z}^{+}$
under the local isomorphism (2.4.9).
Lemma 2.4.11. If
![]() $x^{\prime }$
is in the closure of
$x^{\prime }$
is in the closure of
![]() $x$
, and
$x$
, and
![]() $y^{\prime }$
in the closure of
$y^{\prime }$
in the closure of
![]() $y$
, then
$y$
, then
![]() $n(x^{\prime },y^{\prime })\geqslant n(x,y)$
.
$n(x^{\prime },y^{\prime })\geqslant n(x,y)$
.
Proof. Let
![]() $z^{\prime }$
be a preimage of the pair
$z^{\prime }$
be a preimage of the pair
![]() $(x^{\prime },y^{\prime })$
. By Proposition 2.4.8, there exists an open neighborhood
$(x^{\prime },y^{\prime })$
. By Proposition 2.4.8, there exists an open neighborhood
![]() $U_{z^{\prime }}$
of
$U_{z^{\prime }}$
of
![]() $z^{\prime }$
such that the restriction of
$z^{\prime }$
such that the restriction of
![]() $F_{\mathscr{Z}}\rightarrow F_{\mathscr{X}}\times _{F_{\mathscr{T}}}F_{\mathscr{Y}}$
to
$F_{\mathscr{Z}}\rightarrow F_{\mathscr{X}}\times _{F_{\mathscr{T}}}F_{\mathscr{Y}}$
to
![]() $U_{z^{\prime }}$
is an isomorphism onto its image. In particular,
$U_{z^{\prime }}$
is an isomorphism onto its image. In particular,
![]() $(x,y)$
lies in this image. Thus, there exists a unique preimage of
$(x,y)$
lies in this image. Thus, there exists a unique preimage of
![]() $(x,y)$
that is contained in
$(x,y)$
that is contained in
![]() $U_{z^{\prime }}$
. It follows that
$U_{z^{\prime }}$
. It follows that
![]() $n(x^{\prime },y^{\prime })\geqslant n(x,y)$
.◻
$n(x^{\prime },y^{\prime })\geqslant n(x,y)$
.◻
2.5 Semistability and Kato fans associated to the fibred products
2.5.1. We recall that a log-regular log scheme
![]() $\mathscr{X}^{+}$
is said to be semistable if the special fiber is reduced. We will see that semistability is a sufficient condition to establish injectivitiy of the local isomorphism (2.4.9).
$\mathscr{X}^{+}$
is said to be semistable if the special fiber is reduced. We will see that semistability is a sufficient condition to establish injectivitiy of the local isomorphism (2.4.9).
2.5.2. Given a log-regular log scheme
![]() $\mathscr{X}^{+}$
over
$\mathscr{X}^{+}$
over
![]() $S^{+}$
, the morphism
$S^{+}$
, the morphism
![]() $f:\mathscr{X}^{+}\rightarrow S^{+}$
is called saturated if for any
$f:\mathscr{X}^{+}\rightarrow S^{+}$
is called saturated if for any
![]() $x\in \mathscr{X}$
the morphism
$x\in \mathscr{X}$
the morphism
![]() ${\mathcal{C}}_{S,f(x)}\rightarrow {\mathcal{C}}_{\mathscr{X},x}$
on the stalks of the characteristic sheaves is a saturated morphism of monoids; that is, if for any
${\mathcal{C}}_{S,f(x)}\rightarrow {\mathcal{C}}_{\mathscr{X},x}$
on the stalks of the characteristic sheaves is a saturated morphism of monoids; that is, if for any
![]() $x$
and any morphism
$x$
and any morphism
![]() $u:{\mathcal{C}}_{S,f(x)}\rightarrow P$
of fs monoids, the amalgamated sum
$u:{\mathcal{C}}_{S,f(x)}\rightarrow P$
of fs monoids, the amalgamated sum
![]() ${{\mathcal{C}}_{\mathscr{X},x}\oplus }_{{\mathcal{C}}_{S,f(x)}}P$
is still a saturated monoid.
${{\mathcal{C}}_{\mathscr{X},x}\oplus }_{{\mathcal{C}}_{S,f(x)}}P$
is still a saturated monoid.
Following the work by T. Tsuji in an unpublished 1997 preprint, Vidal in [Reference Vidal, Adolphson, Baldassarri, Berthelot, Katz and LoeserVid04] defines the notion of saturation indexes for morphisms of log schemes. In the case of a log-regular log scheme
![]() $\mathscr{X}^{+}$
over
$\mathscr{X}^{+}$
over
![]() $S^{+}$
, the saturation index at a point
$S^{+}$
, the saturation index at a point
![]() $x\in \mathscr{X}_{k}$
is the least common multiple of the multiplicities in
$x\in \mathscr{X}_{k}$
is the least common multiple of the multiplicities in
![]() $\mathscr{X}_{k}$
of the prime components of
$\mathscr{X}_{k}$
of the prime components of
![]() $\mathscr{X}_{k}$
passing through
$\mathscr{X}_{k}$
passing through
![]() $x$
. The following criterion holds.
$x$
. The following criterion holds.
Lemma 2.5.3 [Reference Vidal, Adolphson, Baldassarri, Berthelot, Katz and LoeserVid04, § 1.3].
The morphism
![]() $\mathscr{X}^{+}\rightarrow S^{+}$
is saturated if and only if the saturation index at any point of
$\mathscr{X}^{+}\rightarrow S^{+}$
is saturated if and only if the saturation index at any point of
![]() $\mathscr{X}_{k}$
is equal to
$\mathscr{X}_{k}$
is equal to
![]() $1$
.
$1$
.
Proposition 2.5.4. Assume that the residue field
![]() $k$
is algebraically closed. Let
$k$
is algebraically closed. Let
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
be log-smooth log schemes over
$\mathscr{Y}^{+}$
be log-smooth log schemes over
![]() $S^{+}$
. Let
$S^{+}$
. Let
![]() $\mathscr{Z}^{+}$
be their fs fibred product. If
$\mathscr{Z}^{+}$
be their fs fibred product. If
![]() $\mathscr{X}^{+}$
is semistable, then for any pair of points
$\mathscr{X}^{+}$
is semistable, then for any pair of points
![]() $(x,y)$
in
$(x,y)$
in
![]() $F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
whose closures intersect the special fibers
$F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
whose closures intersect the special fibers
![]() $\mathscr{X}_{k}$
and
$\mathscr{X}_{k}$
and
![]() $\mathscr{Y}_{k}$
respectively, the morphism
$\mathscr{Y}_{k}$
respectively, the morphism
![]() $F_{\mathscr{Z}}\xrightarrow[{}]{}F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}},$
induced by the projections
$F_{\mathscr{Z}}\xrightarrow[{}]{}F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}},$
induced by the projections
![]() $\mathscr{Z}^{+}\rightarrow \mathscr{X}^{+}$
and
$\mathscr{Z}^{+}\rightarrow \mathscr{X}^{+}$
and
![]() $\mathscr{Z}^{+}\rightarrow \mathscr{Y}^{+}$
, is a bijection above the pair
$\mathscr{Z}^{+}\rightarrow \mathscr{Y}^{+}$
, is a bijection above the pair
![]() $(x,y)$
, namely
$(x,y)$
, namely
![]() $n(x,y)=1$
.
$n(x,y)=1$
.
Proof. Since
![]() $\mathscr{X}^{+}$
is a semistable log-regular log scheme over
$\mathscr{X}^{+}$
is a semistable log-regular log scheme over
![]() $S^{+}$
, the saturation index of
$S^{+}$
, the saturation index of
![]() $\mathscr{X}^{+}\rightarrow S^{+}$
at any point
$\mathscr{X}^{+}\rightarrow S^{+}$
at any point
![]() $x$
in
$x$
in
![]() $\mathscr{X}_{k}$
is
$\mathscr{X}_{k}$
is
![]() $1$
. Thus, by Lemma 2.5.3 the morphism
$1$
. Thus, by Lemma 2.5.3 the morphism
![]() $\mathscr{X}^{+}\rightarrow S^{+}$
is saturated, and it follows that the fibred product in the category of log schemes coincides with the fibred product in the category of fs log schemes. This fact is crucial in the sequel of the proof to describe explicitly the divisor
$\mathscr{X}^{+}\rightarrow S^{+}$
is saturated, and it follows that the fibred product in the category of log schemes coincides with the fibred product in the category of fs log schemes. This fact is crucial in the sequel of the proof to describe explicitly the divisor
![]() $D_{\mathscr{Z}}$
, and to characterize the points of
$D_{\mathscr{Z}}$
, and to characterize the points of
![]() $\mathscr{Z}_{k}$
.
$\mathscr{Z}_{k}$
.
We write
![]() $D_{\mathscr{X}}=\unicode[STIX]{x1D6E5}_{\mathscr{X}}+\mathscr{X}_{k}$
, where
$D_{\mathscr{X}}=\unicode[STIX]{x1D6E5}_{\mathscr{X}}+\mathscr{X}_{k}$
, where
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}=\sum _{i}\unicode[STIX]{x1D6E5}_{\mathscr{X},i}$
is the horizontal part and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}=\sum _{i}\unicode[STIX]{x1D6E5}_{\mathscr{X},i}$
is the horizontal part and
![]() $\mathscr{X}_{k}=\sum _{i}E_{\mathscr{X},i}$
; and
$\mathscr{X}_{k}=\sum _{i}E_{\mathscr{X},i}$
; and
![]() $D_{\mathscr{Y}}=\unicode[STIX]{x1D6E5}_{\mathscr{Y}}+\mathscr{Y}_{k,\text{red}}$
, with
$D_{\mathscr{Y}}=\unicode[STIX]{x1D6E5}_{\mathscr{Y}}+\mathscr{Y}_{k,\text{red}}$
, with
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Y}}=\sum _{j}\unicode[STIX]{x1D6E5}_{\mathscr{Y},j}$
and
$\unicode[STIX]{x1D6E5}_{\mathscr{Y}}=\sum _{j}\unicode[STIX]{x1D6E5}_{\mathscr{Y},j}$
and
![]() $\mathscr{Y}_{k,\text{red}}=\sum _{j}E_{\mathscr{Y},j}$
. The divisor
$\mathscr{Y}_{k,\text{red}}=\sum _{j}E_{\mathscr{Y},j}$
. The divisor
![]() $D_{\mathscr{Z}}$
, associated to the log structure of the fs fibred product, is given by
$D_{\mathscr{Z}}$
, associated to the log structure of the fs fibred product, is given by
![]() $D_{\mathscr{Z}}=\unicode[STIX]{x1D6E5}_{\mathscr{Z}}+\mathscr{Z}_{k,\text{red}}$
, where
$D_{\mathscr{Z}}=\unicode[STIX]{x1D6E5}_{\mathscr{Z}}+\mathscr{Z}_{k,\text{red}}$
, where
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Z}}=\unicode[STIX]{x1D6E5}_{\mathscr{X}}\times \mathscr{Y}+\mathscr{X}\times \unicode[STIX]{x1D6E5}_{\mathscr{Y}}=\sum _{l}\unicode[STIX]{x1D6E5}_{\mathscr{Z},l}$
and
$\unicode[STIX]{x1D6E5}_{\mathscr{Z}}=\unicode[STIX]{x1D6E5}_{\mathscr{X}}\times \mathscr{Y}+\mathscr{X}\times \unicode[STIX]{x1D6E5}_{\mathscr{Y}}=\sum _{l}\unicode[STIX]{x1D6E5}_{\mathscr{Z},l}$
and
![]() $\mathscr{Z}_{k,\text{red}}=\sum _{h}E_{\mathscr{Z},h}.$
As
$\mathscr{Z}_{k,\text{red}}=\sum _{h}E_{\mathscr{Z},h}.$
As
![]() $k$
is algebraically closed, the irreducible components of
$k$
is algebraically closed, the irreducible components of
![]() $\mathscr{Z}_{k}=\mathscr{X}_{k}\times _{k}\mathscr{Y}_{k}$
are given by the products of irreducible components of
$\mathscr{Z}_{k}=\mathscr{X}_{k}\times _{k}\mathscr{Y}_{k}$
are given by the products of irreducible components of
![]() $\mathscr{X}_{k}$
and
$\mathscr{X}_{k}$
and
![]() $\mathscr{Y}_{k}$
; that is, for any
$\mathscr{Y}_{k}$
; that is, for any
![]() $h$
we have
$h$
we have
![]() $E_{\mathscr{Z},h}=E_{\mathscr{X},i_{h}}\times _{k}E_{\mathscr{Y},j_{h}}$
.
$E_{\mathscr{Z},h}=E_{\mathscr{X},i_{h}}\times _{k}E_{\mathscr{Y},j_{h}}$
.
The points in the special fiber
![]() $\mathscr{Z}_{k}$
are characterized as follows:
$\mathscr{Z}_{k}$
are characterized as follows:
where
![]() $x$
and
$x$
and
![]() $y$
are points of
$y$
are points of
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
both mapped to
$\mathscr{Y}^{+}$
both mapped to
![]() $s$
, while
$s$
, while
![]() $\mathfrak{p}$
is a prime ideal of the tensor product of residue fields
$\mathfrak{p}$
is a prime ideal of the tensor product of residue fields
![]() $\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
. We assume now that
$\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
. We assume now that
![]() $z$
is a point in
$z$
is a point in
![]() $F_{\mathscr{Z}}\cap \mathscr{Z}_{k}$
, and see the restrictions on
$F_{\mathscr{Z}}\cap \mathscr{Z}_{k}$
, and see the restrictions on
![]() $x$
,
$x$
,
![]() $y$
, and
$y$
, and
![]() $\mathfrak{p}$
that follow from this assumption.
$\mathfrak{p}$
that follow from this assumption.
(i) We claim that the projections
 $x$
and
$x$
and
 $y$
are points of the respective Kato fans. By Lemma 2.2.3,
$y$
are points of the respective Kato fans. By Lemma 2.2.3,
 $z$
is a generic point of an intersection of irreducible components of
$z$
is a generic point of an intersection of irreducible components of
 $D_{\mathscr{Z}}$
.
$D_{\mathscr{Z}}$
.If every irreducible component of
 $D_{\mathscr{Z}}$
containing
$D_{\mathscr{Z}}$
containing
 $z$
is in the special fiber, then the intersection is given by The projections
$z$
is in the special fiber, then the intersection is given by The projections $$\begin{eqnarray}\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ Z},h}=\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ X},i_{h}}\times E_{\mathscr{Y},j_{h}}=\bigg(\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ X},i_{h}}\bigg)\times \bigg(\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ Y},j_{h}}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ Z},h}=\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ X},i_{h}}\times E_{\mathscr{Y},j_{h}}=\bigg(\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ X},i_{h}}\bigg)\times \bigg(\mathop{\bigcap }_{h=1}^{r}E_{\mathscr{ Y},j_{h}}\bigg).\end{eqnarray}$$
 $x$
and
$x$
and
 $y$
of
$y$
of
 $z$
are generic points of strata in
$z$
are generic points of strata in
 $\mathscr{X}_{k}$
and
$\mathscr{X}_{k}$
and
 $\mathscr{Y}_{k}$
, hence lie in the respective Kato fans.
$\mathscr{Y}_{k}$
, hence lie in the respective Kato fans.Otherwise, let
 $\unicode[STIX]{x1D6E5}_{\mathscr{Z},1},\ldots ,\unicode[STIX]{x1D6E5}_{\mathscr{Z},r^{\prime }}$
be the horizontal components of
$\unicode[STIX]{x1D6E5}_{\mathscr{Z},1},\ldots ,\unicode[STIX]{x1D6E5}_{\mathscr{Z},r^{\prime }}$
be the horizontal components of
 $D_{\mathscr{Z}}$
passing through
$D_{\mathscr{Z}}$
passing through
 $z$
. We consider the subscheme
$z$
. We consider the subscheme
 $\mathscr{D}=\bigcap _{l=1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{Z},l}$
of
$\mathscr{D}=\bigcap _{l=1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{Z},l}$
of
 $\mathscr{Z}$
, endowed with the divisorial log structure
$\mathscr{Z}$
, endowed with the divisorial log structure
 $D_{\mathscr{D}}=\mathscr{D}_{k,\text{red}}$
. Then,
$D_{\mathscr{D}}=\mathscr{D}_{k,\text{red}}$
. Then,
 $\mathscr{D}^{+}=(\mathscr{D},D_{\mathscr{D}})$
is a log-regular log scheme and
$\mathscr{D}^{+}=(\mathscr{D},D_{\mathscr{D}})$
is a log-regular log scheme and
 $z$
is a point in the Kato fan of
$z$
is a point in the Kato fan of
 $\mathscr{D}^{+}$
that corresponds to the generic point of an intersection of irreducible components of
$\mathscr{D}^{+}$
that corresponds to the generic point of an intersection of irreducible components of
 $D_{\mathscr{D}}$
, that are all contained in the special fiber. Since is itself a fibred product of log-smooth log schemes, we conclude by the previous case.
$D_{\mathscr{D}}$
, that are all contained in the special fiber. Since is itself a fibred product of log-smooth log schemes, we conclude by the previous case. $$\begin{eqnarray}\mathscr{D}=\mathop{\bigcap }_{l=1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{Z},l}=\bigg(\mathop{\bigcap }_{l=1}^{r^{\prime \prime }}\unicode[STIX]{x1D6E5}_{\mathscr{X},l}\times \mathscr{Y}\bigg)\cap \bigg(\mathop{\bigcap }_{l=r^{\prime \prime }+1}^{r^{\prime }}\mathscr{X}\times \unicode[STIX]{x1D6E5}_{\mathscr{Y},l}\bigg)=\bigg(\mathop{\bigcap }_{l=1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{X},l}\bigg)\times \bigg(\mathop{\bigcap }_{l=r^{\prime \prime }+1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{Y},l}\bigg)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{D}=\mathop{\bigcap }_{l=1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{Z},l}=\bigg(\mathop{\bigcap }_{l=1}^{r^{\prime \prime }}\unicode[STIX]{x1D6E5}_{\mathscr{X},l}\times \mathscr{Y}\bigg)\cap \bigg(\mathop{\bigcap }_{l=r^{\prime \prime }+1}^{r^{\prime }}\mathscr{X}\times \unicode[STIX]{x1D6E5}_{\mathscr{Y},l}\bigg)=\bigg(\mathop{\bigcap }_{l=1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{X},l}\bigg)\times \bigg(\mathop{\bigcap }_{l=r^{\prime \prime }+1}^{r^{\prime }}\unicode[STIX]{x1D6E5}_{\mathscr{Y},l}\bigg)\end{eqnarray}$$
(ii) We claim that the ideal
 $\mathfrak{p}$
is minimal. Since
$\mathfrak{p}$
is minimal. Since
 $z$
lies in
$z$
lies in
 $F_{\mathscr{Z}}$
, we have that
$F_{\mathscr{Z}}$
, we have that
 $\dim {\mathcal{O}}_{\mathscr{Z},z}=\text{rank}{\mathcal{C}}_{\mathscr{Z},z}^{\text{gp}}$
. At the level of characteristic sheaves holds, since the stalk at
$\dim {\mathcal{O}}_{\mathscr{Z},z}=\text{rank}{\mathcal{C}}_{\mathscr{Z},z}^{\text{gp}}$
. At the level of characteristic sheaves holds, since the stalk at $$\begin{eqnarray}\text{rank}{\mathcal{C}}_{\mathscr{Z},z}^{\text{gp}}=\text{rank}{\mathcal{C}}_{\mathscr{ X},x}^{\text{gp}}+\text{rank}{\mathcal{C}}_{\mathscr{ Y},y}^{\text{gp}}-1\end{eqnarray}$$
$$\begin{eqnarray}\text{rank}{\mathcal{C}}_{\mathscr{Z},z}^{\text{gp}}=\text{rank}{\mathcal{C}}_{\mathscr{ X},x}^{\text{gp}}+\text{rank}{\mathcal{C}}_{\mathscr{ Y},y}^{\text{gp}}-1\end{eqnarray}$$
 $z$
of the characteristic sheaf of
$z$
of the characteristic sheaf of
 $\mathscr{Z}^{+}$
is equal to
$\mathscr{Z}^{+}$
is equal to
 ${\mathcal{C}}_{\mathscr{Z},z}={{\mathcal{C}}_{\mathscr{X},x}\oplus }_{\mathbb{N}}{\mathcal{C}}_{\mathscr{Y},y}$
and the morphism
${\mathcal{C}}_{\mathscr{Z},z}={{\mathcal{C}}_{\mathscr{X},x}\oplus }_{\mathbb{N}}{\mathcal{C}}_{\mathscr{Y},y}$
and the morphism
 $\mathbb{N}\rightarrow {\mathcal{C}}_{\mathscr{X},x}$
is saturated. As
$\mathbb{N}\rightarrow {\mathcal{C}}_{\mathscr{X},x}$
is saturated. As
 $x$
and
$x$
and
 $y$
are both points in the associated Kato fans, the equality between the dimension of the local ring and the rank of the groupification of the characteristic sheaves holds for
$y$
are both points in the associated Kato fans, the equality between the dimension of the local ring and the rank of the groupification of the characteristic sheaves holds for
 $x$
and
$x$
and
 $y$
as well, and we obtain By log-regularity of
$y$
as well, and we obtain By log-regularity of $$\begin{eqnarray}\displaystyle \dim {\mathcal{O}}_{\mathscr{Z},z}=\text{rank}{\mathcal{C}}_{\mathscr{Z},z}^{\text{gp}}=\text{rank}{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}+\text{rank}{\mathcal{C}}_{\mathscr{Y},y}^{\text{gp}}-1=\dim {\mathcal{O}}_{\mathscr{X},x}+\dim {\mathcal{O}}_{\mathscr{Y},y}-1. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \dim {\mathcal{O}}_{\mathscr{Z},z}=\text{rank}{\mathcal{C}}_{\mathscr{Z},z}^{\text{gp}}=\text{rank}{\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}+\text{rank}{\mathcal{C}}_{\mathscr{Y},y}^{\text{gp}}-1=\dim {\mathcal{O}}_{\mathscr{X},x}+\dim {\mathcal{O}}_{\mathscr{Y},y}-1. & & \displaystyle \nonumber\end{eqnarray}$$
 $\mathscr{Z}^{+}$
we have the inequality
$\mathscr{Z}^{+}$
we have the inequality
 $\dim {\mathcal{O}}_{\mathscr{Z},z^{\prime }}\geqslant \text{rank}{\mathcal{C}}_{\mathscr{Z},z^{\prime }}^{\text{gp}}$
at any point
$\dim {\mathcal{O}}_{\mathscr{Z},z^{\prime }}\geqslant \text{rank}{\mathcal{C}}_{\mathscr{Z},z^{\prime }}^{\text{gp}}$
at any point
 $z^{\prime }$
, hence the equality that holds for
$z^{\prime }$
, hence the equality that holds for
 $z$
necessarily implies that
$z$
necessarily implies that
 $\mathfrak{p}$
is a minimal prime ideal of
$\mathfrak{p}$
is a minimal prime ideal of
 $\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
.
$\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
.
Let
![]() $(x,y)$
be a pair of points of
$(x,y)$
be a pair of points of
![]() $F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
that lie in the respective special fibers. In order to determine the number
$F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
that lie in the respective special fibers. In order to determine the number
![]() $n(x,y)$
of preimages of
$n(x,y)$
of preimages of
![]() $(x,y)$
in
$(x,y)$
in
![]() $F_{\mathscr{Z}}$
, we need to study the number of minimal prime ideals of the tensor product
$F_{\mathscr{Z}}$
, we need to study the number of minimal prime ideals of the tensor product
![]() $\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
. Since the residue field
$\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
. Since the residue field
![]() $k$
is an algebraically closed field, the tensor product
$k$
is an algebraically closed field, the tensor product
![]() $\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
is a domain; in particular, it has a unique minimal prime ideal, namely
$\unicode[STIX]{x1D705}(x)\otimes _{k}\unicode[STIX]{x1D705}(y)$
is a domain; in particular, it has a unique minimal prime ideal, namely
![]() $0$
. We obtain that
$0$
. We obtain that
![]() $n(x,y)=1$
.
$n(x,y)=1$
.
Let
![]() $(x,y)$
be a pair of points in
$(x,y)$
be a pair of points in
![]() $F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
whose closures intersect the special fibers, namely there exist
$F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
whose closures intersect the special fibers, namely there exist
![]() $x^{\prime }\in F_{\mathscr{X}}\cap \mathscr{X}_{k}$
and
$x^{\prime }\in F_{\mathscr{X}}\cap \mathscr{X}_{k}$
and
![]() $y^{\prime }\in F_{\mathscr{Y}}\cap \mathscr{Y}_{k}$
such that
$y^{\prime }\in F_{\mathscr{Y}}\cap \mathscr{Y}_{k}$
such that
![]() $x^{\prime }$
is in the closure of
$x^{\prime }$
is in the closure of
![]() $x$
and
$x$
and
![]() $y^{\prime }$
in the closure of
$y^{\prime }$
in the closure of
![]() $y$
. Then, by the previous part of the proof and by Lemma 2.4.11, we have
$y$
. Then, by the previous part of the proof and by Lemma 2.4.11, we have
![]() $n(x,y)\leqslant n(x^{\prime },y^{\prime })=1$
.◻
$n(x,y)\leqslant n(x^{\prime },y^{\prime })=1$
.◻
3 The skeleton of a log-regular log scheme
3.1 Construction
3.1.1. Let
![]() $\mathscr{X}^{+}$
be a log-regular log scheme over
$\mathscr{X}^{+}$
be a log-regular log scheme over
![]() $S^{+}$
. Let
$S^{+}$
. Let
![]() $x$
be a point of the associated Kato fan
$x$
be a point of the associated Kato fan
![]() $F$
. Denote by
$F$
. Denote by
![]() $F(x)$
the set of points
$F(x)$
the set of points
![]() $y$
of
$y$
of
![]() $F$
such that
$F$
such that
![]() $x$
lies in the closure of
$x$
lies in the closure of
![]() $\{y\}$
, and by
$\{y\}$
, and by
![]() ${\mathcal{C}}_{F(x)}$
the restriction of
${\mathcal{C}}_{F(x)}$
the restriction of
![]() ${\mathcal{C}}_{F}$
to
${\mathcal{C}}_{F}$
to
![]() $F(x)$
. Denote by
$F(x)$
. Denote by
![]() $\text{Spec}\,{\mathcal{C}}_{\mathscr{X},x}$
the spectrum of the monoid
$\text{Spec}\,{\mathcal{C}}_{\mathscr{X},x}$
the spectrum of the monoid
![]() ${\mathcal{C}}_{\mathscr{X},x}={\mathcal{C}}_{F,x}$
. Then there exists a canonical isomorphism of monoid spaces
${\mathcal{C}}_{\mathscr{X},x}={\mathcal{C}}_{F,x}$
. Then there exists a canonical isomorphism of monoid spaces
where the expression
![]() $s(y)=0$
means that
$s(y)=0$
means that
![]() $s^{\prime }(y)=0$
for any representative
$s^{\prime }(y)=0$
for any representative
![]() $s^{\prime }$
of
$s^{\prime }$
of
![]() $s$
in
$s$
in
![]() ${\mathcal{M}}_{\mathscr{X},x}$
. In particular, we obtain a bijective correspondence between the faces of the monoid
${\mathcal{M}}_{\mathscr{X},x}$
. In particular, we obtain a bijective correspondence between the faces of the monoid
![]() ${\mathcal{C}}_{\mathscr{X},x}$
and the points of
${\mathcal{C}}_{\mathscr{X},x}$
and the points of
![]() $F(x)$
, and for every point
$F(x)$
, and for every point
![]() $y$
of
$y$
of
![]() $F(x)$
, a surjective cospecialization morphism of monoids
$F(x)$
, a surjective cospecialization morphism of monoids
which induces an isomorphism of monoids
where
![]() $S$
denotes the monoid of elements
$S$
denotes the monoid of elements
![]() $s$
in
$s$
in
![]() ${\mathcal{C}}_{\mathscr{X},x}$
such that
${\mathcal{C}}_{\mathscr{X},x}$
such that
![]() $s(y)\neq 0$
.
$s(y)\neq 0$
.
3.1.2. For each point
![]() $x$
in
$x$
in
![]() $F$
, we denote by
$F$
, we denote by
![]() $\unicode[STIX]{x1D70E}_{x}$
the set of morphisms of monoids
$\unicode[STIX]{x1D70E}_{x}$
the set of morphisms of monoids
such that
![]() $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70B})=1$
for every uniformizer
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70B})=1$
for every uniformizer
![]() $\unicode[STIX]{x1D70B}$
in
$\unicode[STIX]{x1D70B}$
in
![]() $R$
. We endow
$R$
. We endow
![]() $\unicode[STIX]{x1D70E}_{x}$
with the topology of pointwise convergence, where
$\unicode[STIX]{x1D70E}_{x}$
with the topology of pointwise convergence, where
![]() $\mathbb{R}_{{\geqslant}0}$
carries the usual Euclidean topology. Note that
$\mathbb{R}_{{\geqslant}0}$
carries the usual Euclidean topology. Note that
![]() $\unicode[STIX]{x1D70E}_{x}$
is a polyhedron, possibly unbounded, in the real affine space
$\unicode[STIX]{x1D70E}_{x}$
is a polyhedron, possibly unbounded, in the real affine space
If
![]() $y$
is a point of
$y$
is a point of
![]() $F(x)$
, then the surjective cospecialization morphism
$F(x)$
, then the surjective cospecialization morphism
![]() $\unicode[STIX]{x1D70F}_{x,y}$
induces a topological embedding
$\unicode[STIX]{x1D70F}_{x,y}$
induces a topological embedding
![]() $\unicode[STIX]{x1D70E}_{y}\rightarrow \unicode[STIX]{x1D70E}_{x}$
that identifies
$\unicode[STIX]{x1D70E}_{y}\rightarrow \unicode[STIX]{x1D70E}_{x}$
that identifies
![]() $\unicode[STIX]{x1D70E}_{y}$
with a face of
$\unicode[STIX]{x1D70E}_{y}$
with a face of
![]() $\unicode[STIX]{x1D70E}_{x}$
.
$\unicode[STIX]{x1D70E}_{x}$
.
3.1.3. We denote by
![]() $T$
the disjoint union of the topological spaces
$T$
the disjoint union of the topological spaces
![]() $\unicode[STIX]{x1D70E}_{x}$
with
$\unicode[STIX]{x1D70E}_{x}$
with
![]() $x$
in
$x$
in
![]() $F$
. On the topological space
$F$
. On the topological space
![]() $T$
, we consider the equivalence relation
$T$
, we consider the equivalence relation
![]() ${\sim}$
generated by couples of the form
${\sim}$
generated by couples of the form
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D70F}_{x,y})$
where
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D70F}_{x,y})$
where
![]() $x$
and
$x$
and
![]() $y$
are points in
$y$
are points in
![]() $F$
such that
$F$
such that
![]() $x$
lies in the closure of
$x$
lies in the closure of
![]() $\{y\}$
and
$\{y\}$
and
![]() $\unicode[STIX]{x1D6FC}$
is a point of
$\unicode[STIX]{x1D6FC}$
is a point of
![]() $\unicode[STIX]{x1D70E}_{y}$
.
$\unicode[STIX]{x1D70E}_{y}$
.
The skeleton of
![]() $\mathscr{X}^{+}$
is defined as the quotient of the topological space
$\mathscr{X}^{+}$
is defined as the quotient of the topological space
![]() $T$
by the equivalence relation
$T$
by the equivalence relation
![]() ${\sim}$
. We denote this skeleton by
${\sim}$
. We denote this skeleton by
![]() $\text{Sk}(\mathscr{X}^{+})$
. It is clear that
$\text{Sk}(\mathscr{X}^{+})$
. It is clear that
![]() $\text{Sk}(\mathscr{X}^{+})$
has the structure of a polyhedral complex with cells
$\text{Sk}(\mathscr{X}^{+})$
has the structure of a polyhedral complex with cells
![]() $\{\unicode[STIX]{x1D70E}_{x},\,x\in F\}$
, so it comes equipped with a PL structure, and that the faces of a cell
$\{\unicode[STIX]{x1D70E}_{x},\,x\in F\}$
, so it comes equipped with a PL structure, and that the faces of a cell
![]() $\unicode[STIX]{x1D70E}_{x}$
are precisely the cells
$\unicode[STIX]{x1D70E}_{x}$
are precisely the cells
![]() $\unicode[STIX]{x1D70E}_{y}$
with
$\unicode[STIX]{x1D70E}_{y}$
with
![]() $y$
in
$y$
in
![]() $F(x)$
.
$F(x)$
.
3.1.4. We note that
![]() $\unicode[STIX]{x1D70E}_{x}$
is empty for any point
$\unicode[STIX]{x1D70E}_{x}$
is empty for any point
![]() $x$
that does not lie in the special fiber
$x$
that does not lie in the special fiber
![]() $\mathscr{X}_{k}$
: indeed, outside the special fiber any uniformizer is an invertible element, so it is trivial in
$\mathscr{X}_{k}$
: indeed, outside the special fiber any uniformizer is an invertible element, so it is trivial in
![]() ${\mathcal{C}}_{\mathscr{X},x}$
and is mapped to
${\mathcal{C}}_{\mathscr{X},x}$
and is mapped to
![]() $0$
by any morphism of monoids. Therefore, the construction of the skeleton associated to
$0$
by any morphism of monoids. Therefore, the construction of the skeleton associated to
![]() $\mathscr{X}^{+}$
only concerns the points in the Kato fan
$\mathscr{X}^{+}$
only concerns the points in the Kato fan
![]() $F$
that lie in the special fiber. Moreover, given a generic point
$F$
that lie in the special fiber. Moreover, given a generic point
![]() $x\in \mathscr{X}_{k}$
of an intersection of components of
$x\in \mathscr{X}_{k}$
of an intersection of components of
![]() $D_{\mathscr{X}}$
, where at least one component is not in the special fiber, the corresponding face
$D_{\mathscr{X}}$
, where at least one component is not in the special fiber, the corresponding face
![]() $\unicode[STIX]{x1D70E}_{x}$
is unbounded.
$\unicode[STIX]{x1D70E}_{x}$
is unbounded.
In other words, the skeleton associated to a log-regular scheme
![]() $\mathscr{X}^{+}$
, where
$\mathscr{X}^{+}$
, where
![]() $D_{\mathscr{X}}$
allows horizontal components, generalizes Berkovich’s skeletons by admitting unbounded faces in the direction of the horizontal components as well as by allowing singularities in the special fiber. It also generalizes the construction performed by Gubler, Rabinoff, and Werner in [Reference Gubler, Rabinoff and WernerGRW16] of a skeleton associated to a strictly semistable snc pair.
$D_{\mathscr{X}}$
allows horizontal components, generalizes Berkovich’s skeletons by admitting unbounded faces in the direction of the horizontal components as well as by allowing singularities in the special fiber. It also generalizes the construction performed by Gubler, Rabinoff, and Werner in [Reference Gubler, Rabinoff and WernerGRW16] of a skeleton associated to a strictly semistable snc pair.
3.2 Embedding the skeleton in the non-archimedean generic fiber
3.2.1. Let
![]() $\mathscr{X}^{+}$
be a log-regular log scheme over
$\mathscr{X}^{+}$
be a log-regular log scheme over
![]() $S^{+}$
. Let
$S^{+}$
. Let
![]() $x$
be a point of the associated Kato fan
$x$
be a point of the associated Kato fan
![]() $F$
. As the log structure on
$F$
. As the log structure on
![]() $\mathscr{X}^{+}$
is of finite type, the characteristic monoid
$\mathscr{X}^{+}$
is of finite type, the characteristic monoid
![]() ${\mathcal{C}}_{\mathscr{X},x}$
is of finite type too, and thus
${\mathcal{C}}_{\mathscr{X},x}$
is of finite type too, and thus
![]() ${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
is a free abelian group of finite rank. Hence there exists a section
${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}$
is a free abelian group of finite rank. Hence there exists a section
The section
![]() $\unicode[STIX]{x1D701}$
restricts to
$\unicode[STIX]{x1D701}$
restricts to
![]() ${\mathcal{C}}_{\mathscr{X},x}\rightarrow {\mathcal{M}}_{\mathscr{X},x}$
; indeed, if
${\mathcal{C}}_{\mathscr{X},x}\rightarrow {\mathcal{M}}_{\mathscr{X},x}$
; indeed, if
![]() $x\in {\mathcal{M}}_{\mathscr{X},x}$
then
$x\in {\mathcal{M}}_{\mathscr{X},x}$
then
![]() $\unicode[STIX]{x1D701}(\overline{x})-x\in {\mathcal{M}}_{\mathscr{X},x}^{\times }$
. Therefore we may choose a section
$\unicode[STIX]{x1D701}(\overline{x})-x\in {\mathcal{M}}_{\mathscr{X},x}^{\times }$
. Therefore we may choose a section
of the projection homomorphism
and use this section to view
![]() ${\mathcal{C}}_{\mathscr{X},x}$
as a submonoid of
${\mathcal{C}}_{\mathscr{X},x}$
as a submonoid of
![]() ${\mathcal{M}}_{\mathscr{X},x}$
. Note that
${\mathcal{M}}_{\mathscr{X},x}$
. Note that
![]() ${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
generates the ideal
${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
generates the ideal
![]() ${\mathcal{I}}_{\mathscr{X},x}$
of
${\mathcal{I}}_{\mathscr{X},x}$
of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
.
${\mathcal{O}}_{\mathscr{X},x}$
.
We propose a generalization of [Reference Mustaţă and NicaiseMN15, Lemma 2.4.4].
Lemma 3.2.3. Let
![]() $A$
be a Noetherian ring, let
$A$
be a Noetherian ring, let
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $A$
, and let
$A$
, and let
![]() $(y_{1},\ldots ,y_{m})$
be a system of generators for
$(y_{1},\ldots ,y_{m})$
be a system of generators for
![]() $I$
. We denote by
$I$
. We denote by
![]() $\hat{A}$
the
$\hat{A}$
the
![]() $I$
-adic completion of
$I$
-adic completion of
![]() $A$
. Let
$A$
. Let
![]() $B$
be a subring of
$B$
be a subring of
![]() $A$
such that the elements
$A$
such that the elements
![]() $y_{1},\ldots ,y_{m}$
belong to
$y_{1},\ldots ,y_{m}$
belong to
![]() $B$
and generate the ideal
$B$
and generate the ideal
![]() $B\cap I$
in
$B\cap I$
in
![]() $B$
. Then, in the ring
$B$
. Then, in the ring
![]() $\hat{A}$
, every element
$\hat{A}$
, every element
![]() $f$
of
$f$
of
![]() $B$
can be written as
$B$
can be written as
where the coefficients
![]() $c_{\unicode[STIX]{x1D6FD}}$
belong to
$c_{\unicode[STIX]{x1D6FD}}$
belong to
![]() $((A\setminus I)\cap B)\cup \{0\}$
.
$((A\setminus I)\cap B)\cup \{0\}$
.
Proof. Let
![]() $f$
be an element of
$f$
be an element of
![]() $B$
; we construct an expansion for
$B$
; we construct an expansion for
![]() $f$
of the form (3.2.4) by induction. If
$f$
of the form (3.2.4) by induction. If
![]() $f$
belongs to the complement of
$f$
belongs to the complement of
![]() $I$
, the conclusion trivially holds. Otherwise,
$I$
, the conclusion trivially holds. Otherwise,
![]() $f$
belongs to
$f$
belongs to
![]() $I$
and we can write
$I$
and we can write
![]() $f$
as a linear combination of the elements
$f$
as a linear combination of the elements
![]() $y_{1},\ldots ,y_{m}$
with coefficients in
$y_{1},\ldots ,y_{m}$
with coefficients in
![]() $B$
:
$B$
:
By the induction hypothesis, we suppose that
![]() $i$
is a positive integer and that we can write every
$i$
is a positive integer and that we can write every
![]() $f$
in
$f$
in
![]() $B$
as a sum of an element
$B$
as a sum of an element
![]() $f_{i}$
of the form (3.2.4) and a linear combination of degree-
$f_{i}$
of the form (3.2.4) and a linear combination of degree-
![]() $i$
monomials in the elements
$i$
monomials in the elements
![]() $y_{1},\ldots ,y_{m}$
with coefficients in
$y_{1},\ldots ,y_{m}$
with coefficients in
![]() $B$
. We apply this assumption to the coefficients
$B$
. We apply this assumption to the coefficients
![]() $b_{j}$
, hence
$b_{j}$
, hence
 $$\begin{eqnarray}b_{j}=b_{j,i}+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}\in \mathbb{Z}_{{\geqslant}0}^{m} \\ |\unicode[STIX]{x1D6FD}|=i}}b_{j,\unicode[STIX]{x1D6FD}}y^{\unicode[STIX]{x1D6FD}},\quad b_{j,\unicode[STIX]{x1D6FD}}\in B.\end{eqnarray}$$
$$\begin{eqnarray}b_{j}=b_{j,i}+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}\in \mathbb{Z}_{{\geqslant}0}^{m} \\ |\unicode[STIX]{x1D6FD}|=i}}b_{j,\unicode[STIX]{x1D6FD}}y^{\unicode[STIX]{x1D6FD}},\quad b_{j,\unicode[STIX]{x1D6FD}}\in B.\end{eqnarray}$$
Then we can write
![]() $f$
as a sum of an element
$f$
as a sum of an element
![]() $f_{i+1}$
of the form (3.2.4) and a linear combination of degree-(
$f_{i+1}$
of the form (3.2.4) and a linear combination of degree-(
![]() $i+1$
) monomials in the elements
$i+1$
) monomials in the elements
![]() $y_{1},\ldots ,y_{m}$
with coefficients in
$y_{1},\ldots ,y_{m}$
with coefficients in
![]() $B$
:
$B$
:
 $$\begin{eqnarray}f=\underbrace{\mathop{\sum }_{j=1}^{m}b_{j,i}y_{j}}_{f_{i+1}}+\mathop{\sum }_{j=1}^{m}\Bigg(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}\in \mathbb{Z}_{{\geqslant}0}^{m} \\ |\unicode[STIX]{x1D6FD}|=i}}b_{j,\unicode[STIX]{x1D6FD}}y^{\unicode[STIX]{x1D6FD}}\Bigg)y_{j}\end{eqnarray}$$
$$\begin{eqnarray}f=\underbrace{\mathop{\sum }_{j=1}^{m}b_{j,i}y_{j}}_{f_{i+1}}+\mathop{\sum }_{j=1}^{m}\Bigg(\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FD}\in \mathbb{Z}_{{\geqslant}0}^{m} \\ |\unicode[STIX]{x1D6FD}|=i}}b_{j,\unicode[STIX]{x1D6FD}}y^{\unicode[STIX]{x1D6FD}}\Bigg)y_{j}\end{eqnarray}$$
such that
![]() $f_{i}$
and
$f_{i}$
and
![]() $f_{i+1}$
have the same coefficients in degree less than or equal to
$f_{i+1}$
have the same coefficients in degree less than or equal to
![]() $i$
. Iterating this construction, we finally find an expansion of
$i$
. Iterating this construction, we finally find an expansion of
![]() $f$
of the required form.◻
$f$
of the required form.◻
3.2.5. Let
![]() $f$
be an element of
$f$
be an element of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. Considering
${\mathcal{O}}_{\mathscr{X},x}$
. Considering
![]() $A=B={\mathcal{O}}_{\mathscr{X},x}$
,
$A=B={\mathcal{O}}_{\mathscr{X},x}$
,
![]() $I=\mathfrak{m}_{x}$
, and a system of generators for
$I=\mathfrak{m}_{x}$
, and a system of generators for
![]() $\mathfrak{m}_{x}$
in
$\mathfrak{m}_{x}$
in
![]() ${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
, by Lemma 3.2.3 we can write
${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
, by Lemma 3.2.3 we can write
![]() $f$
as a formal power series
$f$
as a formal power series
in
![]() $\widehat{{\mathcal{O}}}_{\mathscr{X},x}$
, where each coefficient
$\widehat{{\mathcal{O}}}_{\mathscr{X},x}$
, where each coefficient
![]() $c_{\unicode[STIX]{x1D6FE}}$
is either zero or a unit in
$c_{\unicode[STIX]{x1D6FE}}$
is either zero or a unit in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. We call this formal series an admissible expansion of
${\mathcal{O}}_{\mathscr{X},x}$
. We call this formal series an admissible expansion of
![]() $f$
. We set
$f$
. We set
and we denote by
![]() $\unicode[STIX]{x1D6E4}_{x}(f)$
the set of elements of
$\unicode[STIX]{x1D6E4}_{x}(f)$
the set of elements of
![]() $S$
that lie on a compact face of the convex hull of
$S$
that lie on a compact face of the convex hull of
![]() $S+{\mathcal{C}}_{\mathscr{X},x}$
in
$S+{\mathcal{C}}_{\mathscr{X},x}$
in
![]() ${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}\otimes _{\mathbb{Z}}\mathbb{R}$
. We call
${\mathcal{C}}_{\mathscr{X},x}^{\text{gp}}\otimes _{\mathbb{Z}}\mathbb{R}$
. We call
![]() $\unicode[STIX]{x1D6E4}_{x}(f)$
the initial support of
$\unicode[STIX]{x1D6E4}_{x}(f)$
the initial support of
![]() $f$
at
$f$
at
![]() $x$
, notation which is justified by the next proposition.
$x$
, notation which is justified by the next proposition.
Proposition 3.2.8.
(i) The element
depends on the choice of the section (3.2.2), but not on the expansion (3.2.6). $$\begin{eqnarray}f_{x}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{x}(f)}c_{\unicode[STIX]{x1D6FE}}(x)\unicode[STIX]{x1D6FE}\in k(x)[{\mathcal{C}}_{\mathscr{X},x}]\end{eqnarray}$$
$$\begin{eqnarray}f_{x}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6E4}_{x}(f)}c_{\unicode[STIX]{x1D6FE}}(x)\unicode[STIX]{x1D6FE}\in k(x)[{\mathcal{C}}_{\mathscr{X},x}]\end{eqnarray}$$
(ii) The subset
 $\unicode[STIX]{x1D6E4}_{x}(f)$
of
$\unicode[STIX]{x1D6E4}_{x}(f)$
of
 ${\mathcal{C}}_{\mathscr{X},x}$
only depends on
${\mathcal{C}}_{\mathscr{X},x}$
only depends on
 $f$
and
$f$
and
 $x$
, and not on the choice of the section (3.2.2) or the expansion (3.2.6).
$x$
, and not on the choice of the section (3.2.2) or the expansion (3.2.6).
Proof. If we denote by
![]() $I$
the ideal of
$I$
the ideal of
![]() $k(x)[{\mathcal{C}}_{\mathscr{X},x}]$
generated by
$k(x)[{\mathcal{C}}_{\mathscr{X},x}]$
generated by
![]() ${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
, then it follows from [Reference KatoKat94] that there exists an isomorphism of
${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
, then it follows from [Reference KatoKat94] that there exists an isomorphism of
![]() $k(x)$
-algebras
$k(x)$
-algebras
Using this result and following the argument of [Reference Mustaţă and NicaiseMN15, Proposition 2.4.4], we show now that
![]() $f_{x}$
does not depend on the expansion of
$f_{x}$
does not depend on the expansion of
![]() $f$
. Let
$f$
. Let
be another admissible expansion of
![]() $f$
with associated set
$f$
with associated set
![]() $\unicode[STIX]{x1D6E4}_{x}(f)^{\prime }$
and element
$\unicode[STIX]{x1D6E4}_{x}(f)^{\prime }$
and element
![]() $f_{x}^{\prime }$
. Then
$f_{x}^{\prime }$
. Then
where the right-hand side is an admissible expansion obtained by choosing admissible expansions for the elements
![]() $c_{\unicode[STIX]{x1D6FE}}-c_{\unicode[STIX]{x1D6FE}}^{\prime }$
that do not lie in
$c_{\unicode[STIX]{x1D6FE}}-c_{\unicode[STIX]{x1D6FE}}^{\prime }$
that do not lie in
![]() ${\mathcal{O}}_{\mathscr{X},x}^{\times }\cup \{0\}$
. In particular,
${\mathcal{O}}_{\mathscr{X},x}^{\times }\cup \{0\}$
. In particular,
![]() $d_{\unicode[STIX]{x1D6FE}}(x)=c_{\unicode[STIX]{x1D6FE}}(x)-c_{\unicode[STIX]{x1D6FE}}^{\prime }(x)$
for any
$d_{\unicode[STIX]{x1D6FE}}(x)=c_{\unicode[STIX]{x1D6FE}}(x)-c_{\unicode[STIX]{x1D6FE}}^{\prime }(x)$
for any
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\unicode[STIX]{x1D6E4}_{x}(f)\cup \unicode[STIX]{x1D6E4}_{x}(f)^{\prime }$
. The isomorphism of graded algebras in (3.2.9) implies that the elements
$\unicode[STIX]{x1D6E4}_{x}(f)\cup \unicode[STIX]{x1D6E4}_{x}(f)^{\prime }$
. The isomorphism of graded algebras in (3.2.9) implies that the elements
![]() $d_{\unicode[STIX]{x1D6FE}}$
must all vanish, hence
$d_{\unicode[STIX]{x1D6FE}}$
must all vanish, hence
![]() $\unicode[STIX]{x1D6E4}_{x}(f)=\unicode[STIX]{x1D6E4}_{x}(f)^{\prime }$
and
$\unicode[STIX]{x1D6E4}_{x}(f)=\unicode[STIX]{x1D6E4}_{x}(f)^{\prime }$
and
![]() $f_{x}=f_{x}^{\prime }$
.
$f_{x}=f_{x}^{\prime }$
.
Point (ii) follows from the fact that the coefficients
![]() $c_{\unicode[STIX]{x1D6FE}}$
of
$c_{\unicode[STIX]{x1D6FE}}$
of
![]() $f_{x}$
are independent of the chosen section up to multiplication by a unit in
$f_{x}$
are independent of the chosen section up to multiplication by a unit in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
, so that the support
${\mathcal{O}}_{\mathscr{X},x}$
, so that the support
![]() $\unicode[STIX]{x1D6E4}_{x}(f)$
of
$\unicode[STIX]{x1D6E4}_{x}(f)$
of
![]() $f_{x}$
only depends on
$f_{x}$
only depends on
![]() $f$
and
$f$
and
![]() $x$
.◻
$x$
.◻
Proposition 3.2.10. Let
![]() $x$
be a point of
$x$
be a point of
![]() $F$
and let
$F$
and let
be an element of
![]() $\unicode[STIX]{x1D70E}_{x}$
.Then there exists a unique minimal real valuation
$\unicode[STIX]{x1D70E}_{x}$
.Then there exists a unique minimal real valuation
such that
![]() $v(m)=\unicode[STIX]{x1D6FC}(\overline{m})$
for each element
$v(m)=\unicode[STIX]{x1D6FC}(\overline{m})$
for each element
![]() $m$
of
$m$
of
![]() ${\mathcal{M}}_{\mathscr{X},x}$
.
${\mathcal{M}}_{\mathscr{X},x}$
.
Proof. We will prove that the map
satisfies the requirements in the statement. We fix a section
It is straightforward to check that
![]() $(f\cdot g)_{x}=f_{x}\cdot g_{x}$
for all
$(f\cdot g)_{x}=f_{x}\cdot g_{x}$
for all
![]() $f$
and
$f$
and
![]() $g$
in
$g$
in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. This implies that
${\mathcal{O}}_{\mathscr{X},x}$
. This implies that
![]() $v$
is a valuation. It is obvious that
$v$
is a valuation. It is obvious that
![]() $v(m)=\unicode[STIX]{x1D6FC}(\overline{m})$
for all
$v(m)=\unicode[STIX]{x1D6FC}(\overline{m})$
for all
![]() $m$
in
$m$
in
![]() ${\mathcal{M}}_{\mathscr{X},x}$
, since we can write
${\mathcal{M}}_{\mathscr{X},x}$
, since we can write
![]() $m$
as the product of an element of
$m$
as the product of an element of
![]() ${\mathcal{C}}_{\mathscr{X},x}$
and a unit in
${\mathcal{C}}_{\mathscr{X},x}$
and a unit in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
.
${\mathcal{O}}_{\mathscr{X},x}$
.
Now we prove minimality. Consider any real valuation
such that
![]() $w(m)=\unicode[STIX]{x1D6FC}(\overline{m})$
for each element
$w(m)=\unicode[STIX]{x1D6FC}(\overline{m})$
for each element
![]() $m$
of
$m$
of
![]() ${\mathcal{M}}_{\mathscr{X},x}$
, and let
${\mathcal{M}}_{\mathscr{X},x}$
, and let
![]() $f$
be an element of
$f$
be an element of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. We must show that
${\mathcal{O}}_{\mathscr{X},x}$
. We must show that
![]() $w(f)\geqslant v(f)$
.
$w(f)\geqslant v(f)$
.
We set
We denote by
![]() $I$
the ideal in
$I$
the ideal in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
generated by
${\mathcal{O}}_{\mathscr{X},x}$
generated by
![]() $C_{\unicode[STIX]{x1D6FC}}$
and by
$C_{\unicode[STIX]{x1D6FC}}$
and by
![]() $A$
the
$A$
the
![]() $I$
-adic completion of
$I$
-adic completion of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. By Lemma 3.2.3, we see that we can write
${\mathcal{O}}_{\mathscr{X},x}$
. By Lemma 3.2.3, we see that we can write
![]() $f$
in
$f$
in
![]() $A$
as
$A$
as
where
![]() $d_{\unicode[STIX]{x1D6FD}}$
is either zero or contained in the complement of
$d_{\unicode[STIX]{x1D6FD}}$
is either zero or contained in the complement of
![]() $I$
in
$I$
in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
.
${\mathcal{O}}_{\mathscr{X},x}$
.
Since
![]() $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FD})>0$
for every
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FD})>0$
for every
![]() $\unicode[STIX]{x1D6FD}\in C_{\unicode[STIX]{x1D6FC}}$
, we can find an integer
$\unicode[STIX]{x1D6FD}\in C_{\unicode[STIX]{x1D6FC}}$
, we can find an integer
![]() $N>0$
such that
$N>0$
such that
![]() $w(g)>w(f)$
for every element
$w(g)>w(f)$
for every element
![]() $g$
in
$g$
in
![]() $I^{N}$
. So we have
$I^{N}$
. So we have
recalling that
![]() $w(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FD})$
for all
$w(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FD})$
for all
![]() $\unicode[STIX]{x1D6FD}$
in
$\unicode[STIX]{x1D6FD}$
in
![]() ${\mathcal{C}}_{\mathscr{X},x}$
.
${\mathcal{C}}_{\mathscr{X},x}$
.
We consider the coefficients in the expansion (3.2.12) of
![]() $f$
. Applying Lemma 3.2.3 as in paragraph (3.2.5), we can write admissible expansions of these coefficients in
$f$
. Applying Lemma 3.2.3 as in paragraph (3.2.5), we can write admissible expansions of these coefficients in
![]() $\widehat{{\mathcal{O}}}_{\mathscr{X},x}$
as
$\widehat{{\mathcal{O}}}_{\mathscr{X},x}$
as
with
![]() $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})=0$
in the expansions of
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE})=0$
in the expansions of
![]() $d_{\unicode[STIX]{x1D6FD}}$
that belong to
$d_{\unicode[STIX]{x1D6FD}}$
that belong to
![]() $\mathfrak{m}_{x}\setminus I$
.
$\mathfrak{m}_{x}\setminus I$
.
Therefore we obtain an admissible expansion of
![]() $f$
$f$
and we have
![]() $v(f)=\min \{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})\,|\,c_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}\neq 0\}=\min \{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FD})\,|\,d_{\unicode[STIX]{x1D6FD}}\neq 0\}\leqslant w(f)$
.◻
$v(f)=\min \{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD})\,|\,c_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}}\neq 0\}=\min \{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FD})\,|\,d_{\unicode[STIX]{x1D6FD}}\neq 0\}\leqslant w(f)$
.◻
Remark 3.2.13. In the definition (3.2.11) of the valuation
![]() $v$
, we compute the minimum over the terms in the initial support of
$v$
, we compute the minimum over the terms in the initial support of
![]() $f$
: these elements are a finite number and they only depend on
$f$
: these elements are a finite number and they only depend on
![]() $x$
and
$x$
and
![]() $f$
by Proposition 3.2.8. Therefore, this minimum provides a well-defined function on
$f$
by Proposition 3.2.8. Therefore, this minimum provides a well-defined function on
![]() ${\mathcal{O}}_{\mathscr{X},x}\setminus \{0\}$
. Nevertheless, it is equivalent to consider the minimum over all the terms of an admissible expansion of
${\mathcal{O}}_{\mathscr{X},x}\setminus \{0\}$
. Nevertheless, it is equivalent to consider the minimum over all the terms of an admissible expansion of
![]() $f$
, that is, for any admissible expansion
$f$
, that is, for any admissible expansion
![]() $f=\sum _{\unicode[STIX]{x1D6FE}\in {\mathcal{C}}_{\mathscr{X},x}}c_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FE}$
,
$f=\sum _{\unicode[STIX]{x1D6FE}\in {\mathcal{C}}_{\mathscr{X},x}}c_{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D6FE}$
,
where
![]() $S=\{\unicode[STIX]{x1D6FE}\in {\mathcal{C}}_{\mathscr{X},x}\,|\,c_{\unicode[STIX]{x1D6FE}}\neq 0\}$
as in (3.2.7). Indeed, any element that belongs to
$S=\{\unicode[STIX]{x1D6FE}\in {\mathcal{C}}_{\mathscr{X},x}\,|\,c_{\unicode[STIX]{x1D6FE}}\neq 0\}$
as in (3.2.7). Indeed, any element that belongs to
![]() $S$
can be written as a sum of an element of the initial support of
$S$
can be written as a sum of an element of the initial support of
![]() $f$
and an element of
$f$
and an element of
![]() ${\mathcal{C}}_{\mathscr{X},x}$
. Since the morphism
${\mathcal{C}}_{\mathscr{X},x}$
. Since the morphism
![]() $\unicode[STIX]{x1D6FC}$
is additive and takes positive real values, the minimum is necessarily attained by the elements in the initial support.
$\unicode[STIX]{x1D6FC}$
is additive and takes positive real values, the minimum is necessarily attained by the elements in the initial support.
3.2.14. We will denote the valuation
![]() $v$
from Proposition 3.2.10 by
$v$
from Proposition 3.2.10 by
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
. Since
$v_{x,\unicode[STIX]{x1D6FC}}$
. Since
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
induces a real valuation on the function field of
$v_{x,\unicode[STIX]{x1D6FC}}$
induces a real valuation on the function field of
![]() $\mathscr{X}_{K}$
that extends the discrete valuation
$\mathscr{X}_{K}$
that extends the discrete valuation
![]() $v_{K}$
on
$v_{K}$
on
![]() $K$
, it defines a point of the
$K$
, it defines a point of the
![]() $K$
-analytic space
$K$
-analytic space
![]() $\mathscr{X}_{K}^{\text{an}}$
, which we will denote by the same symbol
$\mathscr{X}_{K}^{\text{an}}$
, which we will denote by the same symbol
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
. We now show that the characterization of
$v_{x,\unicode[STIX]{x1D6FC}}$
. We now show that the characterization of
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
in Proposition 3.2.10 implies that
$v_{x,\unicode[STIX]{x1D6FC}}$
in Proposition 3.2.10 implies that
for every
![]() $y$
in
$y$
in
![]() $F(x)$
and every
$F(x)$
and every
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
in
$\unicode[STIX]{x1D6FC}^{\prime }$
in
![]() $\unicode[STIX]{x1D70E}_{y}$
.
$\unicode[STIX]{x1D70E}_{y}$
.
First we note that
![]() ${\mathcal{O}}_{\mathscr{X},y}$
is the localization of
${\mathcal{O}}_{\mathscr{X},y}$
is the localization of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
with respect to the elements
${\mathcal{O}}_{\mathscr{X},x}$
with respect to the elements
![]() $m\in {\mathcal{M}}_{\mathscr{X},x}$
in the kernel of
$m\in {\mathcal{M}}_{\mathscr{X},x}$
in the kernel of
![]() $\unicode[STIX]{x1D70F}_{x,y}$
. Indeed, by construction of
$\unicode[STIX]{x1D70F}_{x,y}$
. Indeed, by construction of
![]() $\unicode[STIX]{x1D70F}_{x,y}$
, the kernel is given by
$\unicode[STIX]{x1D70F}_{x,y}$
, the kernel is given by
To obtain
![]() ${\mathcal{O}}_{\mathscr{X},y}$
from
${\mathcal{O}}_{\mathscr{X},y}$
from
![]() ${\mathcal{O}}_{\mathscr{X},x}$
, we localize by
${\mathcal{O}}_{\mathscr{X},x}$
, we localize by
Therefore we can identify the set of elements of
![]() ${\mathcal{M}}_{\mathscr{X},x}$
whose reduction is in
${\mathcal{M}}_{\mathscr{X},x}$
whose reduction is in
![]() $\ker (\unicode[STIX]{x1D70F}_{x,y})$
with the set
$\ker (\unicode[STIX]{x1D70F}_{x,y})$
with the set
![]() $S$
, recalling that, for points in the Kato fan,
$S$
, recalling that, for points in the Kato fan,
![]() ${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
generates the maximal ideal of
${\mathcal{C}}_{\mathscr{X},x}\setminus \{1\}$
generates the maximal ideal of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. Therefore we are dealing with these two morphisms:
${\mathcal{O}}_{\mathscr{X},x}$
. Therefore we are dealing with these two morphisms:
Let
![]() $f$
be an element of
$f$
be an element of
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. In the notation of Lemma 3.2.3, we apply the lemma to
${\mathcal{O}}_{\mathscr{X},x}$
. In the notation of Lemma 3.2.3, we apply the lemma to
![]() $A={\mathcal{O}}_{\mathscr{X},y}$
and
$A={\mathcal{O}}_{\mathscr{X},y}$
and
![]() $B={\mathcal{O}}_{\mathscr{X},x}$
, choosing a system of generators of
$B={\mathcal{O}}_{\mathscr{X},x}$
, choosing a system of generators of
![]() $\mathfrak{m}_{y}$
in
$\mathfrak{m}_{y}$
in
![]() ${\mathcal{C}}_{\mathscr{X},x}$
: we can find an admissible expansion of
${\mathcal{C}}_{\mathscr{X},x}$
: we can find an admissible expansion of
![]() $f$
of the form
$f$
of the form
Admissible expansions of coefficients
![]() $d_{\unicode[STIX]{x1D6FF}}$
induce an admissible expansion for
$d_{\unicode[STIX]{x1D6FF}}$
induce an admissible expansion for
![]() $f$
by
$f$
by
where
![]() $\unicode[STIX]{x1D6FE}$
runs through the set
$\unicode[STIX]{x1D6FE}$
runs through the set
![]() $S$
since
$S$
since
![]() $d_{\unicode[STIX]{x1D6FF}}\in {\mathcal{O}}_{\mathscr{X},y}^{\times }$
. Thus we have
$d_{\unicode[STIX]{x1D6FF}}\in {\mathcal{O}}_{\mathscr{X},y}^{\times }$
. Thus we have
 $$\begin{eqnarray}\displaystyle v_{y,\unicode[STIX]{x1D6FC}^{\prime }}(f) & = & \displaystyle \min \{\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D6FF})\,|\,\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E4}_{y}(f)\}\nonumber\\ \displaystyle & = & \displaystyle \min \{\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF})\,|\,\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E4}_{y}(f),\unicode[STIX]{x1D6FE}\in S\}\nonumber\\ \displaystyle & = & \displaystyle \min \{\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF})\,|\,\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E4}_{x}(f)\}\nonumber\\ \displaystyle & = & \displaystyle v_{x,\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}}(f).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{y,\unicode[STIX]{x1D6FC}^{\prime }}(f) & = & \displaystyle \min \{\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D6FF})\,|\,\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E4}_{y}(f)\}\nonumber\\ \displaystyle & = & \displaystyle \min \{\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF})\,|\,\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E4}_{y}(f),\unicode[STIX]{x1D6FE}\in S\}\nonumber\\ \displaystyle & = & \displaystyle \min \{\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF})\,|\,\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E4}_{x}(f)\}\nonumber\\ \displaystyle & = & \displaystyle v_{x,\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}}(f).\nonumber\end{eqnarray}$$
Hence, we obtain a well-defined map
by sending
![]() $\unicode[STIX]{x1D6FC}$
to
$\unicode[STIX]{x1D6FC}$
to
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
for every point
$v_{x,\unicode[STIX]{x1D6FC}}$
for every point
![]() $x$
of
$x$
of
![]() $F$
and every
$F$
and every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D70E}_{x}$
.
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D70E}_{x}$
.
Proposition 3.2.15. The map
is a topological embedding.
Proof. First, we show that
![]() $\unicode[STIX]{x1D704}$
is injective. Let
$\unicode[STIX]{x1D704}$
is injective. Let
![]() $x$
be a point of
$x$
be a point of
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D6FC}$
an element of
$\unicode[STIX]{x1D6FC}$
an element of
![]() $\unicode[STIX]{x1D70E}_{x}$
. Let
$\unicode[STIX]{x1D70E}_{x}$
. Let
![]() $y$
be the point of
$y$
be the point of
![]() $F(x)$
corresponding to the face
$F(x)$
corresponding to the face
![]() ${\mathcal{C}}_{\mathscr{X},x}\setminus \unicode[STIX]{x1D6FC}^{-1}(0)$
of
${\mathcal{C}}_{\mathscr{X},x}\setminus \unicode[STIX]{x1D6FC}^{-1}(0)$
of
![]() ${\mathcal{C}}_{\mathscr{X},x}$
. Then
${\mathcal{C}}_{\mathscr{X},x}$
. Then
![]() $\unicode[STIX]{x1D6FC}$
factors through an element
$\unicode[STIX]{x1D6FC}$
factors through an element
of
![]() $\unicode[STIX]{x1D70E}_{y}$
. Note that
$\unicode[STIX]{x1D70E}_{y}$
. Note that
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}^{\prime }$
in
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}^{\prime }$
in
![]() $\text{Sk}(\mathscr{X}^{+})$
because
$\text{Sk}(\mathscr{X}^{+})$
because
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}$
. Moreover, since
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D70F}_{x,y}$
. Moreover, since
![]() $(\unicode[STIX]{x1D6FC}^{\prime })^{-1}(0)=\{1\}$
, the center of the valuation
$(\unicode[STIX]{x1D6FC}^{\prime })^{-1}(0)=\{1\}$
, the center of the valuation
![]() $v_{y,\unicode[STIX]{x1D6FC}^{\prime }}$
is the point
$v_{y,\unicode[STIX]{x1D6FC}^{\prime }}$
is the point
![]() $y$
, so that
$y$
, so that
![]() $\text{red}_{\mathscr{X}}(v_{y,\unicode[STIX]{x1D6FC}^{\prime }})=y$
. Thus we can recover
$\text{red}_{\mathscr{X}}(v_{y,\unicode[STIX]{x1D6FC}^{\prime }})=y$
. Thus we can recover
![]() $y$
from
$y$
from
![]() $v_{y,\unicode[STIX]{x1D6FC}^{\prime }}$
. Then we can also reconstruct
$v_{y,\unicode[STIX]{x1D6FC}^{\prime }}$
. Then we can also reconstruct
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
by looking at the values of
$\unicode[STIX]{x1D6FC}^{\prime }$
by looking at the values of
![]() $v_{y,\unicode[STIX]{x1D6FC}^{\prime }}$
at the elements of
$v_{y,\unicode[STIX]{x1D6FC}^{\prime }}$
at the elements of
![]() ${\mathcal{M}}_{\mathscr{X},y}$
. We conclude that
${\mathcal{M}}_{\mathscr{X},y}$
. We conclude that
![]() $\unicode[STIX]{x1D704}$
is injective.
$\unicode[STIX]{x1D704}$
is injective.
Now, we show that
![]() $\unicode[STIX]{x1D704}$
is a homeomorphism onto its image. For any valuation
$\unicode[STIX]{x1D704}$
is a homeomorphism onto its image. For any valuation
![]() $v$
in
$v$
in
![]() $\text{Sk}(\mathscr{X}^{+})$
and any small open neighborhood
$\text{Sk}(\mathscr{X}^{+})$
and any small open neighborhood
![]() $U$
of
$U$
of
![]() $\unicode[STIX]{x1D704}(v)$
in
$\unicode[STIX]{x1D704}(v)$
in
![]() $\mathscr{X}_{K}^{\text{an}}$
, there exists a closed subset
$\mathscr{X}_{K}^{\text{an}}$
, there exists a closed subset
![]() $C$
in
$C$
in
![]() $\text{Sk}(\mathscr{X}^{+})$
such that
$\text{Sk}(\mathscr{X}^{+})$
such that
![]() $U\cap \unicode[STIX]{x1D704}(\text{Sk}(\mathscr{X}^{+}))\subseteq \unicode[STIX]{x1D704}(C)$
and, up to subdivisions, we can assume that the
$U\cap \unicode[STIX]{x1D704}(\text{Sk}(\mathscr{X}^{+}))\subseteq \unicode[STIX]{x1D704}(C)$
and, up to subdivisions, we can assume that the
![]() $C$
is a closed cell of
$C$
is a closed cell of
![]() $\text{Sk}(\mathscr{X}^{+})$
. Therefore, it suffices to prove that the restriction of
$\text{Sk}(\mathscr{X}^{+})$
. Therefore, it suffices to prove that the restriction of
![]() $\unicode[STIX]{x1D704}$
to any closed cell
$\unicode[STIX]{x1D704}$
to any closed cell
![]() $\unicode[STIX]{x1D70E}_{x}$
of
$\unicode[STIX]{x1D70E}_{x}$
of
![]() $\text{Sk}(\mathscr{X}^{+})$
is a homeomorphism. The restriction
$\text{Sk}(\mathscr{X}^{+})$
is a homeomorphism. The restriction
![]() $\unicode[STIX]{x1D704}_{|\unicode[STIX]{x1D70E}_{x}}$
is an injective map from a compact set to the Hausdorff space
$\unicode[STIX]{x1D704}_{|\unicode[STIX]{x1D70E}_{x}}$
is an injective map from a compact set to the Hausdorff space
![]() $\mathscr{X}_{K}^{\text{an}}$
, so we reduce to showing that
$\mathscr{X}_{K}^{\text{an}}$
, so we reduce to showing that
![]() $\unicode[STIX]{x1D704}_{|\unicode[STIX]{x1D70E}_{x}}$
is continuous, to conclude that
$\unicode[STIX]{x1D704}_{|\unicode[STIX]{x1D70E}_{x}}$
is continuous, to conclude that
![]() $\unicode[STIX]{x1D704}_{|\unicode[STIX]{x1D70E}_{x}}$
is a homeomorphism. By definition of the Berkovich topology, it is enough to prove that the map
$\unicode[STIX]{x1D704}_{|\unicode[STIX]{x1D70E}_{x}}$
is a homeomorphism. By definition of the Berkovich topology, it is enough to prove that the map
is continuous for every
![]() $f$
in
$f$
in
![]() ${\mathcal{O}}_{\mathscr{X},x}$
. This is obvious from the formula (3.2.11).◻
${\mathcal{O}}_{\mathscr{X},x}$
. This is obvious from the formula (3.2.11).◻
3.2.16. From now on, we will view
![]() $\text{Sk}(\mathscr{X}^{+})$
as a topological subspace of
$\text{Sk}(\mathscr{X}^{+})$
as a topological subspace of
![]() $\mathscr{X}_{K}^{\text{an}}$
by means of the embedding
$\mathscr{X}_{K}^{\text{an}}$
by means of the embedding
![]() $\unicode[STIX]{x1D704}$
in Proposition 3.2.15. If
$\unicode[STIX]{x1D704}$
in Proposition 3.2.15. If
![]() $\mathscr{X}$
is regular over
$\mathscr{X}$
is regular over
![]() $R$
and
$R$
and
![]() $\mathscr{X}_{k}$
is a divisor with strict normal crossings, the skeleton
$\mathscr{X}_{k}$
is a divisor with strict normal crossings, the skeleton
![]() $\text{Sk}(\mathscr{X}^{+})$
was described in [Reference Mustaţă and NicaiseMN15, §3.1].
$\text{Sk}(\mathscr{X}^{+})$
was described in [Reference Mustaţă and NicaiseMN15, §3.1].
3.3 Contracting the generic fiber to the skeleton
3.3.1. We denote by
![]() $D_{\mathscr{X},\text{hor}}$
the component of
$D_{\mathscr{X},\text{hor}}$
the component of
![]() $D_{\mathscr{X}}$
not contained in the special fiber
$D_{\mathscr{X}}$
not contained in the special fiber
![]() $\mathscr{X}_{k}$
. The inclusion
$\mathscr{X}_{k}$
. The inclusion
![]() $\unicode[STIX]{x1D704}:\text{Sk}(\mathscr{X}^{+})\rightarrow \mathscr{X}_{K}^{\text{an}}$
is actually an inclusion in
$\unicode[STIX]{x1D704}:\text{Sk}(\mathscr{X}^{+})\rightarrow \mathscr{X}_{K}^{\text{an}}$
is actually an inclusion in
![]() $(\mathscr{X}_{K}\setminus D_{\mathscr{X},\text{hor}})^{\text{an}}$
and it admits a continuous retraction
$(\mathscr{X}_{K}\setminus D_{\mathscr{X},\text{hor}})^{\text{an}}$
and it admits a continuous retraction
constructed as follows. Let
![]() $x$
be a point of
$x$
be a point of
![]() $(\mathscr{X}_{K}\setminus D_{\mathscr{X},\text{hor}})^{\text{an}}$
and consider the reduction map
$(\mathscr{X}_{K}\setminus D_{\mathscr{X},\text{hor}})^{\text{an}}$
and consider the reduction map
Let
![]() $E_{1},\ldots ,E_{r}$
be the irreducible components of
$E_{1},\ldots ,E_{r}$
be the irreducible components of
![]() $D_{\mathscr{X}}$
passing through the point
$D_{\mathscr{X}}$
passing through the point
![]() $\text{red}_{\mathscr{X}}(x)$
. We denote by
$\text{red}_{\mathscr{X}}(x)$
. We denote by
![]() $\unicode[STIX]{x1D709}$
the generic point of the connected component of
$\unicode[STIX]{x1D709}$
the generic point of the connected component of
![]() $E_{1}\cap \cdots \cap E_{r}$
that contains
$E_{1}\cap \cdots \cap E_{r}$
that contains
![]() $\text{red}_{\mathscr{X}}(x)$
. By Lemma 2.2.3,
$\text{red}_{\mathscr{X}}(x)$
. By Lemma 2.2.3,
![]() $\unicode[STIX]{x1D709}$
is a point in the associated Kato fan
$\unicode[STIX]{x1D709}$
is a point in the associated Kato fan
![]() $F$
. We set
$F$
. We set
![]() $\unicode[STIX]{x1D6FC}$
to be the morphism of monoids
$\unicode[STIX]{x1D6FC}$
to be the morphism of monoids
such that
![]() $\unicode[STIX]{x1D6FC}(\overline{m})=v_{x}(m)$
for any element
$\unicode[STIX]{x1D6FC}(\overline{m})=v_{x}(m)$
for any element
![]() $m$
of
$m$
of
![]() ${\mathcal{M}}_{\mathscr{X},\unicode[STIX]{x1D709}}$
. In particular,
${\mathcal{M}}_{\mathscr{X},\unicode[STIX]{x1D709}}$
. In particular,
![]() $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70B})=v_{x}(\unicode[STIX]{x1D70B})=1$
as we assumed the normalization of all valuations in the Berkovich space. Then
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70B})=v_{x}(\unicode[STIX]{x1D70B})=1$
as we assumed the normalization of all valuations in the Berkovich space. Then
![]() $\unicode[STIX]{x1D70C}_{\mathscr{X}}(x)$
is the point of
$\unicode[STIX]{x1D70C}_{\mathscr{X}}(x)$
is the point of
![]() $\text{Sk}(\mathscr{X}^{+})$
corresponding to the couple
$\text{Sk}(\mathscr{X}^{+})$
corresponding to the couple
![]() $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D6FC})$
. By construction
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D6FC})$
. By construction
![]() $\unicode[STIX]{x1D70C}_{\mathscr{X}}$
is continuous and right inverse to the inclusion
$\unicode[STIX]{x1D70C}_{\mathscr{X}}$
is continuous and right inverse to the inclusion
![]() $\unicode[STIX]{x1D704}$
.
$\unicode[STIX]{x1D704}$
.
3.3.2. Given a dominant morphism
![]() $f:\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
of integral flat separated log-regular log schemes over
$f:\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
of integral flat separated log-regular log schemes over
![]() $S$
, it induces a map between the set of birational points
$S$
, it induces a map between the set of birational points
![]() $\text{Bir}(\mathscr{X}_{K})\rightarrow \text{Bir}(\mathscr{Y}_{K})$
. As
$\text{Bir}(\mathscr{X}_{K})\rightarrow \text{Bir}(\mathscr{Y}_{K})$
. As
![]() $\text{Bir}(\mathscr{X}_{K})\subseteq (\mathscr{X}_{K}\setminus D_{\mathscr{X},\text{hor}})^{\text{an}}$
, we can employ the retraction
$\text{Bir}(\mathscr{X}_{K})\subseteq (\mathscr{X}_{K}\setminus D_{\mathscr{X},\text{hor}})^{\text{an}}$
, we can employ the retraction
![]() $\unicode[STIX]{x1D70C}$
to define a map of skeletons as follows.
$\unicode[STIX]{x1D70C}$
to define a map of skeletons as follows.

This association makes the skeleton construction
![]() $\text{Sk}(\mathscr{X}^{+})$
functorial in
$\text{Sk}(\mathscr{X}^{+})$
functorial in
![]() $\mathscr{X}^{+}$
with respect to dominant morphisms.
$\mathscr{X}^{+}$
with respect to dominant morphisms.
3.4 Skeleton of an fs fibred product
3.4.1. Let
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
be log-smooth log schemes over
$\mathscr{Y}^{+}$
be log-smooth log schemes over
![]() $S^{+}$
, and let
$S^{+}$
, and let
![]() $\mathscr{Z}^{+}$
be their fs fibred product. Let
$\mathscr{Z}^{+}$
be their fs fibred product. Let
be the continuous map of skeletons functorially associated to the projections
![]() $\text{pr}_{\mathscr{X}}:\mathscr{Z}^{+}\rightarrow \mathscr{X}^{+}$
and
$\text{pr}_{\mathscr{X}}:\mathscr{Z}^{+}\rightarrow \mathscr{X}^{+}$
and
![]() $\text{pr}_{\mathscr{Y}}:\mathscr{Z}^{+}\rightarrow \mathscr{Y}^{+}$
. We denote this map by
$\text{pr}_{\mathscr{Y}}:\mathscr{Z}^{+}\rightarrow \mathscr{Y}^{+}$
. We denote this map by
![]() $(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
and we recall that it is constructed considering the following diagram.
$(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
and we recall that it is constructed considering the following diagram.

Proposition 3.4.3. Assume that the residue field
![]() $k$
is algebraically closed. If
$k$
is algebraically closed. If
![]() $\mathscr{X}^{+}$
is semistable, then the map
$\mathscr{X}^{+}$
is semistable, then the map
![]() $(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is a PL homeomorphism.
$(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is a PL homeomorphism.
Proof. We first provide an explicit description of the map
![]() $\text{pr}_{\text{Sk}(\mathscr{X})}$
(respectively, of
$\text{pr}_{\text{Sk}(\mathscr{X})}$
(respectively, of
![]() $\text{pr}_{\text{Sk}(\mathscr{Y})}$
) in diagram (3.4.2). Then we show that the map
$\text{pr}_{\text{Sk}(\mathscr{Y})}$
) in diagram (3.4.2). Then we show that the map
![]() $(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is injective and surjective.
$(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is injective and surjective.
Let
![]() $v_{z,\unicode[STIX]{x1D700}}$
be the valuation in
$v_{z,\unicode[STIX]{x1D700}}$
be the valuation in
![]() $\text{Sk}(\mathscr{Z}^{+})$
corresponding to a couple
$\text{Sk}(\mathscr{Z}^{+})$
corresponding to a couple
![]() $(z,\unicode[STIX]{x1D700})$
with
$(z,\unicode[STIX]{x1D700})$
with
![]() $z\in F_{\mathscr{Z}}\cap \mathscr{Z}_{k}$
and
$z\in F_{\mathscr{Z}}\cap \mathscr{Z}_{k}$
and
![]() $\unicode[STIX]{x1D700}\in \unicode[STIX]{x1D70E}_{z}$
. We consider the morphism of associated Kato fans
$\unicode[STIX]{x1D700}\in \unicode[STIX]{x1D70E}_{z}$
. We consider the morphism of associated Kato fans
as established in Proposition 2.4.8. We denote respectively by
![]() $\text{pr}_{F_{\mathscr{X}}}$
and
$\text{pr}_{F_{\mathscr{X}}}$
and
![]() $\text{pr}_{F_{\mathcal{Y}}}$
the projection to the first and second factor. Then
$\text{pr}_{F_{\mathcal{Y}}}$
the projection to the first and second factor. Then
![]() $\text{pr}_{F_{\mathscr{X}}}(z)$
is a point in the associated Kato fan
$\text{pr}_{F_{\mathscr{X}}}(z)$
is a point in the associated Kato fan
![]() $F_{\mathscr{X}}$
, which we denote by
$F_{\mathscr{X}}$
, which we denote by
![]() $x$
. We consider the morphism of monoids
$x$
. We consider the morphism of monoids
and the composition
It trivially satisfies
![]() $\unicode[STIX]{x1D700}\circ i_{x}(\unicode[STIX]{x1D70B})=1$
. In order to conclude that it correctly defines a point in the skeleton
$\unicode[STIX]{x1D700}\circ i_{x}(\unicode[STIX]{x1D70B})=1$
. In order to conclude that it correctly defines a point in the skeleton
![]() $\text{Sk}(\mathscr{X}^{+})$
, we need to check the compatibility with respect to the equivalence relation
$\text{Sk}(\mathscr{X}^{+})$
, we need to check the compatibility with respect to the equivalence relation
![]() ${\sim}$
. Indeed, suppose that
${\sim}$
. Indeed, suppose that
![]() $\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}^{\prime }\circ \unicode[STIX]{x1D70F}_{z,z^{\prime }}$
for some
$\unicode[STIX]{x1D700}=\unicode[STIX]{x1D700}^{\prime }\circ \unicode[STIX]{x1D70F}_{z,z^{\prime }}$
for some
![]() $z\in \overline{\{z^{\prime }\}}$
. We denote by
$z\in \overline{\{z^{\prime }\}}$
. We denote by
![]() $x^{\prime }$
the projection of
$x^{\prime }$
the projection of
![]() $z^{\prime }$
under the local isomorphism of associated Kato fans. The diagram
$z^{\prime }$
under the local isomorphism of associated Kato fans. The diagram

is commutative as it is made up of a commutative square and a commutative triangle of arrows. Therefore, by commutativity
and this implies that
![]() $\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
defines a well-defined point
$\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
defines a well-defined point
![]() $v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
of
$v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
of
![]() $\text{Sk}(\mathscr{X}^{+})$
.
$\text{Sk}(\mathscr{X}^{+})$
.
We claim that
![]() $v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
is indeed the image of
$v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
is indeed the image of
![]() $v_{z,\unicode[STIX]{x1D700}}$
under the map
$v_{z,\unicode[STIX]{x1D700}}$
under the map
![]() $\text{pr}_{\text{Sk}(\mathscr{X})}$
. We recall that the projection
$\text{pr}_{\text{Sk}(\mathscr{X})}$
. We recall that the projection
![]() $\widehat{\text{pr}_{\mathscr{X}}}$
, in diagram (3.4.2), is such that a valuation
$\widehat{\text{pr}_{\mathscr{X}}}$
, in diagram (3.4.2), is such that a valuation
![]() $v$
on the function field
$v$
on the function field
![]() $K(\mathscr{Z}_{K})$
maps to the composition
$K(\mathscr{Z}_{K})$
maps to the composition
![]() $v\circ i$
where
$v\circ i$
where
![]() $i:K(\mathscr{X}_{K}){\hookrightarrow}K(\mathscr{Z}_{K})$
. Thus, we need to prove that the equality in the following inner diagram holds.
$i:K(\mathscr{X}_{K}){\hookrightarrow}K(\mathscr{Z}_{K})$
. Thus, we need to prove that the equality in the following inner diagram holds.

We denote
![]() $\unicode[STIX]{x1D70C}_{\mathscr{X}}(v_{z,\unicode[STIX]{x1D700}}\circ i)$
by
$\unicode[STIX]{x1D70C}_{\mathscr{X}}(v_{z,\unicode[STIX]{x1D700}}\circ i)$
by
![]() $(x,\unicode[STIX]{x1D6FC})$
as a point of
$(x,\unicode[STIX]{x1D6FC})$
as a point of
![]() $\text{Sk}(\mathscr{X}^{+})$
. By definition of the retraction
$\text{Sk}(\mathscr{X}^{+})$
. By definition of the retraction
![]() $\unicode[STIX]{x1D70C}_{\mathscr{X}}$
, the morphism
$\unicode[STIX]{x1D70C}_{\mathscr{X}}$
, the morphism
![]() $\unicode[STIX]{x1D6FC}$
is characterized by the fact that
$\unicode[STIX]{x1D6FC}$
is characterized by the fact that
![]() $\unicode[STIX]{x1D6FC}(\overline{m})=(v_{z,\unicode[STIX]{x1D700}}\circ i)(m)$
for any
$\unicode[STIX]{x1D6FC}(\overline{m})=(v_{z,\unicode[STIX]{x1D700}}\circ i)(m)$
for any
![]() $m$
in
$m$
in
![]() ${\mathcal{M}}_{\mathscr{X},x}$
and then we have
${\mathcal{M}}_{\mathscr{X},x}$
and then we have
On the other hand, for any
![]() $m$
in
$m$
in
![]() ${\mathcal{M}}_{\mathscr{X},x}$
,
${\mathcal{M}}_{\mathscr{X},x}$
,
hence we obtain that
![]() $\unicode[STIX]{x1D6FC}$
coincides with the morphism
$\unicode[STIX]{x1D6FC}$
coincides with the morphism
![]() $\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
. This means that their associated points
$\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
. This means that their associated points
![]() $\unicode[STIX]{x1D70C}_{\mathscr{X}}(v_{z,\unicode[STIX]{x1D700}}\circ i)$
and
$\unicode[STIX]{x1D70C}_{\mathscr{X}}(v_{z,\unicode[STIX]{x1D700}}\circ i)$
and
![]() $v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
coincide in
$v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
coincide in
![]() $\text{Sk}(\mathscr{X}^{+})$
.
$\text{Sk}(\mathscr{X}^{+})$
.
We now prove injectivity and surjectivity of the map
![]() $(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
. Given a pair of points in
$(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
. Given a pair of points in
![]() $\text{Sk}(\mathscr{X}^{+})\times \text{Sk}(\mathscr{Y}^{+})$
, they are of the form
$\text{Sk}(\mathscr{X}^{+})\times \text{Sk}(\mathscr{Y}^{+})$
, they are of the form
![]() $(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}}),$
with
$(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}}),$
with
![]() $x\in F_{\mathscr{X}}\cap \mathscr{X}_{k}$
,
$x\in F_{\mathscr{X}}\cap \mathscr{X}_{k}$
,
![]() $y\in F_{\mathscr{Y}}\cap \mathscr{Y}_{k}$
,
$y\in F_{\mathscr{Y}}\cap \mathscr{Y}_{k}$
,
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D70E}_{x}$
, and
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D70E}_{x}$
, and
![]() $\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D70E}_{y}$
. The assumptions of semistability of
$\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D70E}_{y}$
. The assumptions of semistability of
![]() $\mathscr{X}^{+}$
and algebraic closedness of
$\mathscr{X}^{+}$
and algebraic closedness of
![]() $k$
guarantee that there is a unique
$k$
guarantee that there is a unique
![]() $z$
in
$z$
in
![]() $F_{\mathscr{Z}}$
in the fiber of
$F_{\mathscr{Z}}$
in the fiber of
![]() $x$
and
$x$
and
![]() $y$
, by Proposition 2.5.4 and Remark 3.1.4. We claim that we can construct a unique
$y$
, by Proposition 2.5.4 and Remark 3.1.4. We claim that we can construct a unique
![]() $\unicode[STIX]{x1D700}\in \unicode[STIX]{x1D70E}_{z}$
such that
$\unicode[STIX]{x1D700}\in \unicode[STIX]{x1D70E}_{z}$
such that
![]() $(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})(v_{z,\unicode[STIX]{x1D700}})=(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}}).$
We set
$(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})(v_{z,\unicode[STIX]{x1D700}})=(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}}).$
We set

this is well defined as
![]() $\unicode[STIX]{x1D700}([\unicode[STIX]{x1D70B},1])=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70B})=1=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D700}([1,\unicode[STIX]{x1D70B}])$
. By construction, the image of
$\unicode[STIX]{x1D700}([\unicode[STIX]{x1D70B},1])=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D70B})=1=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D70B})=\unicode[STIX]{x1D700}([1,\unicode[STIX]{x1D70B}])$
. By construction, the image of
![]() $v_{z,\unicode[STIX]{x1D700}}$
is
$v_{z,\unicode[STIX]{x1D700}}$
is
![]() $(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}})$
, so the map
$(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}})$
, so the map
![]() $(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is surjective. Moreover, we can uniquely reconstruct
$(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is surjective. Moreover, we can uniquely reconstruct
![]() $\unicode[STIX]{x1D700}$
by looking at the values of
$\unicode[STIX]{x1D700}$
by looking at the values of
![]() $v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
at the elements of
$v_{x,\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})}$
at the elements of
![]() ${\mathcal{M}}_{\mathscr{X},x}$
, and of
${\mathcal{M}}_{\mathscr{X},x}$
, and of
![]() $v_{y,\text{pr}_{\mathcal{Y}}(\unicode[STIX]{x1D700})}$
at the elements of
$v_{y,\text{pr}_{\mathcal{Y}}(\unicode[STIX]{x1D700})}$
at the elements of
![]() ${\mathcal{M}}_{\mathscr{Y},y}$
. Thus
${\mathcal{M}}_{\mathscr{Y},y}$
. Thus
![]() $(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is injective.◻
$(\text{pr}_{\text{Sk}(\mathscr{X})},\text{pr}_{\text{Sk}(\mathscr{Y})})$
is injective.◻
The assumption of semistability is crucial in the result of Proposition 3.4.3. To see this, it is helpful to consider an example.
Example 3.4.4. Let
![]() $q$
be the equation of a generic quartic curve in
$q$
be the equation of a generic quartic curve in
![]() $\mathbb{P}_{\mathbb{C}((t))}^{2}$
. Then
$\mathbb{P}_{\mathbb{C}((t))}^{2}$
. Then
![]() $\mathscr{X}:tq+x^{2}y^{2}=0$
gives the equation of a family of genus-
$\mathscr{X}:tq+x^{2}y^{2}=0$
gives the equation of a family of genus-
![]() $3$
curves, degenerating to two double lines. The dual complex
$3$
curves, degenerating to two double lines. The dual complex
![]() ${\mathcal{D}}(\mathscr{X}_{\mathbb{C}})$
of the special fiber
${\mathcal{D}}(\mathscr{X}_{\mathbb{C}})$
of the special fiber
![]() $\mathscr{X}_{\mathbb{C}}$
is a line segment and
$\mathscr{X}_{\mathbb{C}}$
is a line segment and
![]() $\mathscr{X}$
has four singularities of type
$\mathscr{X}$
has four singularities of type
![]() $A_{1}$
in each component of the special fiber, corresponding to the base points of the family. In this case taking a semistable model of
$A_{1}$
in each component of the special fiber, corresponding to the base points of the family. In this case taking a semistable model of
![]() $\mathscr{X}_{\mathbb{C}((t))}$
requires an order-
$\mathscr{X}_{\mathbb{C}((t))}$
requires an order-
![]() $2$
base change
$2$
base change
![]() $R^{\prime }$
of
$R^{\prime }$
of
![]() $R=\mathbb{C}[[t]]$
, which induces coverings branched at each of these singular points (see [Reference Harris and MorrisonHM98, p. 133] for details). Let
$R=\mathbb{C}[[t]]$
, which induces coverings branched at each of these singular points (see [Reference Harris and MorrisonHM98, p. 133] for details). Let
![]() $\mathscr{Y}$
be such a semistable reduction. Thus the special fiber of
$\mathscr{Y}$
be such a semistable reduction. Thus the special fiber of
![]() $\mathscr{Y}$
consists of two elliptic curves, call them
$\mathscr{Y}$
consists of two elliptic curves, call them
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
, which intersect in two points,
$E_{2}$
, which intersect in two points,
![]() $p_{A}$
and
$p_{A}$
and
![]() $p_{B}$
, which are the preimages of the point
$p_{B}$
, which are the preimages of the point
![]() $(0:0:1)$
. The dual complex
$(0:0:1)$
. The dual complex
![]() ${\mathcal{D}}(\mathscr{Y}_{\mathbb{C}})$
of the special fiber
${\mathcal{D}}(\mathscr{Y}_{\mathbb{C}})$
of the special fiber
![]() $\mathscr{Y}_{\mathbb{C}}$
is isomorphic to
$\mathscr{Y}_{\mathbb{C}}$
is isomorphic to
![]() $S^{1}$
.
$S^{1}$
.
We will compare the dual complex of
![]() $(\mathscr{X}\times _{R}\mathscr{X})_{\mathbb{C}}$
with that of
$(\mathscr{X}\times _{R}\mathscr{X})_{\mathbb{C}}$
with that of
![]() $(\mathscr{Y}\times _{R^{\prime }}\mathscr{Y})_{\mathbb{C}}$
. The models
$(\mathscr{Y}\times _{R^{\prime }}\mathscr{Y})_{\mathbb{C}}$
. The models
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{Y}$
are not log-regular at every point, but from our perspective it is enough that they are log-regular at the generic point of each stratum. For the product with a semistable model, the dual complex is the product of the dual complexes, and
$\mathscr{Y}$
are not log-regular at every point, but from our perspective it is enough that they are log-regular at the generic point of each stratum. For the product with a semistable model, the dual complex is the product of the dual complexes, and
![]() ${\mathcal{D}}((\mathscr{Y}\times _{R^{\prime }}\mathscr{Y})_{\mathbb{C}})$
is therefore a real
${\mathcal{D}}((\mathscr{Y}\times _{R^{\prime }}\mathscr{Y})_{\mathbb{C}})$
is therefore a real
![]() $2$
-torus
$2$
-torus
![]() $S^{1}\times S^{1}$
.
$S^{1}\times S^{1}$
.
On the other hand, the dual complex of the product
![]() $(\mathscr{X}\times _{R}\mathscr{X})_{\mathbb{C}}$
is given by a quotient of
$(\mathscr{X}\times _{R}\mathscr{X})_{\mathbb{C}}$
is given by a quotient of
![]() $S^{1}\times S^{1}$
by the action of
$S^{1}\times S^{1}$
by the action of
![]() $\mathbb{Z}/2\mathbb{Z}$
.
$\mathbb{Z}/2\mathbb{Z}$
.
![]() ${\mathcal{D}}((\mathscr{Y}\times _{R^{\prime }}\mathscr{Y})_{\mathbb{C}})$
has the structure of a cell complex, whose cells correspond to ordered pairs of strata in
${\mathcal{D}}((\mathscr{Y}\times _{R^{\prime }}\mathscr{Y})_{\mathbb{C}})$
has the structure of a cell complex, whose cells correspond to ordered pairs of strata in
![]() ${\mathcal{D}}(\mathscr{Y}_{\mathbb{C}})$
, so
${\mathcal{D}}(\mathscr{Y}_{\mathbb{C}})$
, so
 $$\begin{eqnarray}\displaystyle \text{zero-dimensional strata: } & & \displaystyle \quad (E_{1},E_{2}),(E_{1},E_{1}),(E_{2},E_{1}),(E_{2},E_{2})\nonumber\\ \displaystyle \text{one-dimensional strata: } & & \displaystyle \quad (E_{1},p_{A}),(E_{1},p_{B}),(E_{2},p_{A}),(E_{2},p_{B})\nonumber\\ \displaystyle & & \displaystyle \quad (p_{A},E_{1}),(p_{B},E_{1}),(p_{A},E_{2}),(p_{B},E_{2})\nonumber\\ \displaystyle \text{two-dimensional strata: } & & \displaystyle \quad (p_{A},p_{A}),(p_{A},p_{B}),(p_{B},p_{A}),(p_{B},p_{B}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{zero-dimensional strata: } & & \displaystyle \quad (E_{1},E_{2}),(E_{1},E_{1}),(E_{2},E_{1}),(E_{2},E_{2})\nonumber\\ \displaystyle \text{one-dimensional strata: } & & \displaystyle \quad (E_{1},p_{A}),(E_{1},p_{B}),(E_{2},p_{A}),(E_{2},p_{B})\nonumber\\ \displaystyle & & \displaystyle \quad (p_{A},E_{1}),(p_{B},E_{1}),(p_{A},E_{2}),(p_{B},E_{2})\nonumber\\ \displaystyle \text{two-dimensional strata: } & & \displaystyle \quad (p_{A},p_{A}),(p_{A},p_{B}),(p_{B},p_{A}),(p_{B},p_{B}).\nonumber\end{eqnarray}$$
The action of
![]() $\mathbb{Z}/2\mathbb{Z}$
fixes
$\mathbb{Z}/2\mathbb{Z}$
fixes
![]() $E_{1}$
and
$E_{1}$
and
![]() $E_{2}$
, while switching
$E_{2}$
, while switching
![]() $p_{A}$
and
$p_{A}$
and
![]() $p_{B}$
. Therefore it fixes exactly the zero-dimensional strata while acting freely on the other points. The quotient, the complex
$p_{B}$
. Therefore it fixes exactly the zero-dimensional strata while acting freely on the other points. The quotient, the complex
![]() ${\mathcal{D}}((\mathscr{X}\times _{R}\mathscr{X})_{\mathbb{C}})$
, is piecewise linearly homeomorphic to the sphere
${\mathcal{D}}((\mathscr{X}\times _{R}\mathscr{X})_{\mathbb{C}})$
, is piecewise linearly homeomorphic to the sphere
![]() $S^{2}$
. In particular, it is not isomorphic to the product of two line segments.
$S^{2}$
. In particular, it is not isomorphic to the product of two line segments.
4 The weight function
From now on we assume
![]() $\text{char}(K)=\text{char}(k)=0$
.
$\text{char}(K)=\text{char}(k)=0$
.
4.1 Weight function associated to a logarithmic pluricanonical form
4.1.1. Let
![]() $X$
be a connected, smooth and proper
$X$
be a connected, smooth and proper
![]() $K$
-variety of dimension
$K$
-variety of dimension
![]() $n$
. We introduce the following notation: for any log-regular model
$n$
. We introduce the following notation: for any log-regular model
![]() $\mathscr{X}^{+}$
of
$\mathscr{X}^{+}$
of
![]() $X$
, for any point
$X$
, for any point
![]() $x=(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})\in X^{\text{an}}$
, and for any
$x=(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})\in X^{\text{an}}$
, and for any
![]() $\mathbb{Q}$
-Cartier divisor
$\mathbb{Q}$
-Cartier divisor
![]() $D$
on
$D$
on
![]() $\mathscr{X}^{+}$
whose support does not contain
$\mathscr{X}^{+}$
whose support does not contain
![]() $\unicode[STIX]{x1D709}_{x}$
, we set
$\unicode[STIX]{x1D709}_{x}$
, we set
where
![]() $f$
is any element of
$f$
is any element of
![]() $K(X)^{\times }$
such that
$K(X)^{\times }$
such that
![]() $mD=\text{div}(f)$
locally at
$mD=\text{div}(f)$
locally at
![]() $\text{red}_{\mathscr{X}}(x)$
, and
$\text{red}_{\mathscr{X}}(x)$
, and
![]() $m\in \mathbb{Z}_{{>}0}$
is such that
$m\in \mathbb{Z}_{{>}0}$
is such that
![]() $mD$
is Cartier.
$mD$
is Cartier.
4.1.2. Let
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
be a fractional snc pair as in § 1.5, so that
$(X,\unicode[STIX]{x1D6E5}_{X})$
be a fractional snc pair as in § 1.5, so that
![]() $\unicode[STIX]{x1D6E5}_{X}$
is an effective
$\unicode[STIX]{x1D6E5}_{X}$
is an effective
![]() $\mathbb{Q}$
-divisor such that
$\mathbb{Q}$
-divisor such that
![]() $\unicode[STIX]{x1D6E5}_{X}=\sum a_{i}\unicode[STIX]{x1D6E5}_{X,i}$
has
$\unicode[STIX]{x1D6E5}_{X}=\sum a_{i}\unicode[STIX]{x1D6E5}_{X,i}$
has
![]() $0\leqslant a_{i}\leqslant 1$
, and the round-up
$0\leqslant a_{i}\leqslant 1$
, and the round-up
![]() $X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
is snc. Let
$X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
is snc. Let
![]() $\unicode[STIX]{x1D714}$
be a regular
$\unicode[STIX]{x1D714}$
be a regular
![]() $m$
-pluricanonical form on
$m$
-pluricanonical form on
![]() $X^{+}$
with poles of order at most
$X^{+}$
with poles of order at most
![]() $ma_{i}$
along
$ma_{i}$
along
![]() $\unicode[STIX]{x1D6E5}_{X,i}$
, for some
$\unicode[STIX]{x1D6E5}_{X,i}$
, for some
![]() $m$
such that
$m$
such that
![]() $ma_{i}\in \mathbb{N}$
for any
$ma_{i}\in \mathbb{N}$
for any
![]() $i$
. Thus, such a form is a section of
$i$
. Thus, such a form is a section of
![]() ${\mathcal{O}}_{X}(m(K_{X}+\unicode[STIX]{x1D6E5}_{X}))$
, and we call it a
${\mathcal{O}}_{X}(m(K_{X}+\unicode[STIX]{x1D6E5}_{X}))$
, and we call it a
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
![]() $m$
-pluricanonical form.
$m$
-pluricanonical form.
Given a log-regular model
![]() $\mathscr{X}^{+}$
of
$\mathscr{X}^{+}$
of
![]() $X^{+}$
, where
$X^{+}$
, where
![]() $D_{\mathscr{X}}=\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }+\mathscr{X}_{k,\text{red}}$
, we can view any
$D_{\mathscr{X}}=\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }+\mathscr{X}_{k,\text{red}}$
, we can view any
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
![]() $m$
-pluricanonical forms as rational sections of the logarithmic
$m$
-pluricanonical forms as rational sections of the logarithmic
![]() $m$
-pluricanonical bundle
$m$
-pluricanonical bundle
![]() $(\unicode[STIX]{x1D714}_{\mathscr{X}^{+}/S^{+}}^{\log })^{\otimes m}$
, that is, of
$(\unicode[STIX]{x1D714}_{\mathscr{X}^{+}/S^{+}}^{\log })^{\otimes m}$
, that is, of
The form
![]() $\unicode[STIX]{x1D714}$
, viewed as a rational section of
$\unicode[STIX]{x1D714}$
, viewed as a rational section of
![]() $(\unicode[STIX]{x1D714}_{\mathscr{X}^{+}/S^{+}}^{\log })^{\otimes m}$
, defines a divisor
$(\unicode[STIX]{x1D714}_{\mathscr{X}^{+}/S^{+}}^{\log })^{\otimes m}$
, defines a divisor
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})$
on
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})$
on
![]() $\mathscr{X}^{+}$
. Note that the multiplicity in
$\mathscr{X}^{+}$
. Note that the multiplicity in
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})$
of the closure
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})$
of the closure
![]() $\overline{\unicode[STIX]{x1D6E5}_{X,i}}$
in
$\overline{\unicode[STIX]{x1D6E5}_{X,i}}$
in
![]() $\mathscr{X}$
of
$\mathscr{X}$
of
![]() $\unicode[STIX]{x1D6E5}_{X,i}$
is at least
$\unicode[STIX]{x1D6E5}_{X,i}$
is at least
![]() $m(1-a_{i})$
.
$m(1-a_{i})$
.
4.1.3. Given a
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
![]() $m$
-pluricanonical form
$m$
-pluricanonical form
![]() $\unicode[STIX]{x1D714}$
, we can consider it as a rational section of
$\unicode[STIX]{x1D714}$
, we can consider it as a rational section of
![]() $\unicode[STIX]{x1D714}_{X/K}^{\otimes m}$
. Hence, we can associate to
$\unicode[STIX]{x1D714}_{X/K}^{\otimes m}$
. Hence, we can associate to
![]() $\unicode[STIX]{x1D714}$
the weight function
$\unicode[STIX]{x1D714}$
the weight function
![]() $\text{wt}_{\unicode[STIX]{x1D714}}$
as in [Reference Mustaţă and NicaiseMN15]. The following lemma gives an interpretation of the weight function associated to
$\text{wt}_{\unicode[STIX]{x1D714}}$
as in [Reference Mustaţă and NicaiseMN15]. The following lemma gives an interpretation of the weight function associated to
![]() $\unicode[STIX]{x1D714}$
in terms of logarithmic differentials, which we will use in the sequel.
$\unicode[STIX]{x1D714}$
in terms of logarithmic differentials, which we will use in the sequel.
Lemma 4.1.4. Let
![]() $\mathscr{X}^{+}$
be a log-regular model of
$\mathscr{X}^{+}$
be a log-regular model of
![]() $X^{+}$
. Then for every point
$X^{+}$
. Then for every point
![]() $x$
of
$x$
of
![]() $\text{Sk}(\mathscr{X}^{+})$
,
$\text{Sk}(\mathscr{X}^{+})$
,
Proof. It suffices to prove the equality for the divisorial points in
![]() $\text{Sk}(\mathscr{X}^{+})$
, since they are dense in the skeleton, and both
$\text{Sk}(\mathscr{X}^{+})$
, since they are dense in the skeleton, and both
![]() $\text{wt}_{\unicode[STIX]{x1D714}}(\cdot )$
and
$\text{wt}_{\unicode[STIX]{x1D714}}(\cdot )$
and
![]() $v_{\cdot }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))$
are continuous functions on the skeleton
$v_{\cdot }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))$
are continuous functions on the skeleton
![]() $\text{Sk}(\mathscr{X}^{+})$
.
$\text{Sk}(\mathscr{X}^{+})$
.
Let
![]() $x$
be a divisorial point in
$x$
be a divisorial point in
![]() $\text{Sk}(\mathscr{X}^{+})$
. If
$\text{Sk}(\mathscr{X}^{+})$
. If
![]() $x$
corresponds to a component of the special fiber
$x$
corresponds to a component of the special fiber
![]() $\mathscr{X}_{k}$
, then the center
$\mathscr{X}_{k}$
, then the center
![]() $\text{red}_{\mathscr{X}}(x)$
of
$\text{red}_{\mathscr{X}}(x)$
of
![]() $x$
does not contain the closure of any components of
$x$
does not contain the closure of any components of
![]() $\unicode[STIX]{x1D6E5}_{X}$
. Thus, locally around
$\unicode[STIX]{x1D6E5}_{X}$
. Thus, locally around
![]() $\text{red}_{\mathscr{X}}(x)$
the log schemes
$\text{red}_{\mathscr{X}}(x)$
the log schemes
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $(\mathscr{X},\mathscr{X}_{k,\text{red}})$
are isomorphic and, in particular,
$(\mathscr{X},\mathscr{X}_{k,\text{red}})$
are isomorphic and, in particular,
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})=\text{div}_{(\mathscr{X},\mathscr{X}_{k,\text{red}})}(\unicode[STIX]{x1D714})$
. The computation in [Reference Nicaise and XuNX16, §3.2.2] shows that
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})=\text{div}_{(\mathscr{X},\mathscr{X}_{k,\text{red}})}(\unicode[STIX]{x1D714})$
. The computation in [Reference Nicaise and XuNX16, §3.2.2] shows that
![]() $\text{wt}_{\unicode[STIX]{x1D714}}(x)=v_{x}(\text{div}_{(\mathscr{X},\mathscr{X}_{k,\text{red}})}(\unicode[STIX]{x1D714}))+m$
, so we obtain the required equality.
$\text{wt}_{\unicode[STIX]{x1D714}}(x)=v_{x}(\text{div}_{(\mathscr{X},\mathscr{X}_{k,\text{red}})}(\unicode[STIX]{x1D714}))+m$
, so we obtain the required equality.
Otherwise, we consider the blow-up
![]() $h:{\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
at the closure of the center
$h:{\mathscr{X}^{\prime }}^{+}\rightarrow \mathscr{X}^{+}$
at the closure of the center
![]() $\text{red}_{\mathscr{X}}(x)$
of
$\text{red}_{\mathscr{X}}(x)$
of
![]() $x$
in
$x$
in
![]() $\mathscr{X}^{+}$
. By [Reference Kollár and MoriKM08, Lemma 2.45],Footnote
1
iterating this procedure a finite number of times, we obtain a log-regular model
$\mathscr{X}^{+}$
. By [Reference Kollár and MoriKM08, Lemma 2.45],Footnote
1
iterating this procedure a finite number of times, we obtain a log-regular model
![]() $\mathscr{Y}^{+}$
such that the
$\mathscr{Y}^{+}$
such that the
![]() $x$
corresponds to a component
$x$
corresponds to a component
![]() $E$
of the special fiber
$E$
of the special fiber
![]() $\mathscr{Y}_{k}$
. By reduction to the previous case, it is enough to check that the value
$\mathscr{Y}_{k}$
. By reduction to the previous case, it is enough to check that the value
![]() $v_{x}(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))$
does not change under such a blow-up
$v_{x}(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))$
does not change under such a blow-up
![]() $h$
.
$h$
.
The morphism
![]() $h$
is the blow-up of a stratum of the log boundary
$h$
is the blow-up of a stratum of the log boundary
![]() $\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }+\mathscr{X}_{k,\text{red}}$
, hence
$\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }+\mathscr{X}_{k,\text{red}}$
, hence
![]() $h$
is a log étale morphism. By [Reference KatoKat89, Proposition 3.12], we have
$h$
is a log étale morphism. By [Reference KatoKat89, Proposition 3.12], we have
![]() $h^{\ast }(\unicode[STIX]{x1D714}_{\mathscr{X}^{+}/S^{+}}^{\log })=\unicode[STIX]{x1D714}_{{\mathscr{ X}^{\prime }}^{+}/S^{+}}^{\log }$
. It follows that
$h^{\ast }(\unicode[STIX]{x1D714}_{\mathscr{X}^{+}/S^{+}}^{\log })=\unicode[STIX]{x1D714}_{{\mathscr{ X}^{\prime }}^{+}/S^{+}}^{\log }$
. It follows that
![]() $\text{div}_{{\mathscr{X}^{\prime }}^{+}}(\unicode[STIX]{x1D714})=h^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))$
and this concludes the proof.◻
$\text{div}_{{\mathscr{X}^{\prime }}^{+}}(\unicode[STIX]{x1D714})=h^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))$
and this concludes the proof.◻
4.1.5. We recall from [Reference Mustaţă and NicaiseMN15, § 4.7] that the Kontsevich–Soibelman skeleton
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
is the closure in
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
is the closure in
![]() $\text{Bir}(X)$
of the set of divisorial points of
$\text{Bir}(X)$
of the set of divisorial points of
![]() $X^{\text{an}}$
where the weight function
$X^{\text{an}}$
where the weight function
![]() $\text{wt}_{\unicode[STIX]{x1D714}}$
reaches its minimal weight, namely
$\text{wt}_{\unicode[STIX]{x1D714}}$
reaches its minimal weight, namely
A priori the weight function associated to a rational pluricanonical form may have minimal weight
![]() $-\infty$
, hence the corresponding Kontsevich–Soibelman skeleton would be empty. We prove that this does not occur for
$-\infty$
, hence the corresponding Kontsevich–Soibelman skeleton would be empty. We prove that this does not occur for
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic pluricanonical forms.
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic pluricanonical forms.
Proposition 4.1.6. Given a
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
![]() $m$
-pluricanonical form
$m$
-pluricanonical form
![]() $\unicode[STIX]{x1D714}$
, for any log-regular model
$\unicode[STIX]{x1D714}$
, for any log-regular model
![]() $\mathscr{X}^{+}$
of
$\mathscr{X}^{+}$
of
![]() $X^{+}$
the inclusion
$X^{+}$
the inclusion
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})\subseteq \text{Sk}(\mathscr{X}^{+})$
holds.
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})\subseteq \text{Sk}(\mathscr{X}^{+})$
holds.
Proof. Let
![]() $\mathscr{X}^{+}$
be a log-regular model of
$\mathscr{X}^{+}$
be a log-regular model of
![]() $X^{+}$
and let
$X^{+}$
and let
![]() $y$
be a divisorial point of
$y$
be a divisorial point of
![]() $X^{\text{an}}$
. It suffices to prove that
$X^{\text{an}}$
. It suffices to prove that
and that the equality holds if and only if
![]() $y$
is in
$y$
is in
![]() $\text{Sk}(\mathscr{X}^{+})$
. As in the proof of Lemma 4.1.4, we consider the blow-up of
$\text{Sk}(\mathscr{X}^{+})$
. As in the proof of Lemma 4.1.4, we consider the blow-up of
![]() $\mathscr{X}^{+}$
at the closure of
$\mathscr{X}^{+}$
at the closure of
![]() $\text{red}_{\mathscr{X}}(y)$
: iterating this procedure a finite number of times, we obtain a log-regular model
$\text{red}_{\mathscr{X}}(y)$
: iterating this procedure a finite number of times, we obtain a log-regular model
![]() $\mathscr{Y}^{+}$
such that
$\mathscr{Y}^{+}$
such that
![]() $y\in \text{Sk}(\mathscr{Y}^{+})$
.
$y\in \text{Sk}(\mathscr{Y}^{+})$
.
Let
![]() $h:\mathscr{Z}^{+}\rightarrow \mathscr{W}^{+}$
be a morphism of this sequence. If
$h:\mathscr{Z}^{+}\rightarrow \mathscr{W}^{+}$
be a morphism of this sequence. If
![]() $\overline{\{\text{red}_{\mathscr{W}}(y)\}}$
is a stratum of
$\overline{\{\text{red}_{\mathscr{W}}(y)\}}$
is a stratum of
![]() $D_{\mathscr{W}}$
, then the morphism
$D_{\mathscr{W}}$
, then the morphism
![]() $h$
induces a subdivision of the skeleton
$h$
induces a subdivision of the skeleton
![]() $\text{Sk}(\mathscr{W}^{+})$
, so
$\text{Sk}(\mathscr{W}^{+})$
, so
![]() $\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y)=\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)$
.
$\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y)=\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)$
.
Otherwise,
![]() $\overline{\{\text{red}_{\mathscr{W}}(y)\}}$
is strictly contained in a stratum
$\overline{\{\text{red}_{\mathscr{W}}(y)\}}$
is strictly contained in a stratum
![]() $V$
of
$V$
of
![]() ${\mathcal{D}}_{\mathscr{W}}$
. Let
${\mathcal{D}}_{\mathscr{W}}$
. Let
![]() $E$
be the exceptional divisor of
$E$
be the exceptional divisor of
![]() $h$
,
$h$
,
![]() $r=r_{h}+r_{v}$
be the codimension of
$r=r_{h}+r_{v}$
be the codimension of
![]() $V$
in
$V$
in
![]() $\mathscr{W}$
, where
$\mathscr{W}$
, where
![]() $r_{h}$
and
$r_{h}$
and
![]() $r_{v}$
are the number of irreducible components of
$r_{v}$
are the number of irreducible components of
![]() $\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }$
and respectively of the special fiber
$\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }$
and respectively of the special fiber
![]() $\mathscr{W}_{k}$
, containing
$\mathscr{W}_{k}$
, containing
![]() $V$
. Let
$V$
. Let
![]() $r+j$
be the codimension of
$r+j$
be the codimension of
![]() $\overline{\{\text{red}_{\mathscr{W}}(y)\}}$
, where
$\overline{\{\text{red}_{\mathscr{W}}(y)\}}$
, where
![]() $j\geqslant 1$
. We denote the projections onto
$j\geqslant 1$
. We denote the projections onto
![]() $S^{+}$
by
$S^{+}$
by
![]() $s_{\mathscr{W}}:\mathscr{W}^{+}\rightarrow S^{+}$
and
$s_{\mathscr{W}}:\mathscr{W}^{+}\rightarrow S^{+}$
and
![]() $s_{\mathscr{Z}}:\mathscr{Z}^{+}\rightarrow S^{+}$
and by
$s_{\mathscr{Z}}:\mathscr{Z}^{+}\rightarrow S^{+}$
and by
![]() $\unicode[STIX]{x1D70B}$
a uniformizer in
$\unicode[STIX]{x1D70B}$
a uniformizer in
![]() $R$
. Then we have that
$R$
. Then we have that
 $$\begin{eqnarray}\displaystyle h^{\ast }(\unicode[STIX]{x1D714}_{\mathscr{W}^{+}/S^{+}}^{\log }) & = & \displaystyle h^{\ast }(\unicode[STIX]{x1D714}_{\mathscr{ W}/R}\otimes {\mathcal{O}}_{\mathscr{W}}(\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }_{,\text{red}}+\mathscr{W}_{k,\text{red}}-s_{\mathscr{W}}^{\ast }\,\text{div}(\unicode[STIX]{x1D70B})))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}_{\mathscr{Z}/R}\otimes {\mathcal{O}}_{\mathscr{Z}}((1-r-j)E+\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }_{,\text{red}}+r_{h}E+\mathscr{Z}_{k,\text{red}}+(r_{v}-1)E-s_{\mathscr{Z}}^{\ast }\,\text{div}(\unicode[STIX]{x1D70B}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}_{\mathscr{Z}^{+}/S^{+}}^{\log }\otimes {\mathcal{O}}_{\mathscr{ Z}}(-jE).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h^{\ast }(\unicode[STIX]{x1D714}_{\mathscr{W}^{+}/S^{+}}^{\log }) & = & \displaystyle h^{\ast }(\unicode[STIX]{x1D714}_{\mathscr{ W}/R}\otimes {\mathcal{O}}_{\mathscr{W}}(\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }_{,\text{red}}+\mathscr{W}_{k,\text{red}}-s_{\mathscr{W}}^{\ast }\,\text{div}(\unicode[STIX]{x1D70B})))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}_{\mathscr{Z}/R}\otimes {\mathcal{O}}_{\mathscr{Z}}((1-r-j)E+\overline{\lceil \unicode[STIX]{x1D6E5}_{X}\rceil }_{,\text{red}}+r_{h}E+\mathscr{Z}_{k,\text{red}}+(r_{v}-1)E-s_{\mathscr{Z}}^{\ast }\,\text{div}(\unicode[STIX]{x1D70B}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}_{\mathscr{Z}^{+}/S^{+}}^{\log }\otimes {\mathcal{O}}_{\mathscr{ Z}}(-jE).\nonumber\end{eqnarray}$$
It follows that
![]() $\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714})=h^{\ast }(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714}))+mjE$
, so
$\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714})=h^{\ast }(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714}))+mjE$
, so
 $$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y)}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714})) & = & \displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y)}(h^{\ast }(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714}))+mjE)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714}))+mjv_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(E)\nonumber\\ \displaystyle & {>} & \displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y)}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714})) & = & \displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y)}(h^{\ast }(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714}))+mjE)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714}))+mjv_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(E)\nonumber\\ \displaystyle & {>} & \displaystyle v_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(\text{div}_{\mathscr{W}^{+}}(\unicode[STIX]{x1D714})),\nonumber\end{eqnarray}$$
where for the first inequality we apply [Reference Mustaţă and NicaiseMN15, Proposition 3.1.6], while the second strict inequality holds as
![]() $j>0$
and
$j>0$
and
![]() $v_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(E)>0$
since the center of the valuation
$v_{\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)}(E)>0$
since the center of the valuation
![]() $\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)$
is contained in
$\unicode[STIX]{x1D70C}_{\mathscr{W}}(y)$
is contained in
![]() $E$
. Therefore, for any such morphism
$E$
. Therefore, for any such morphism
![]() $h$
, the weight is strictly increasing, namely
$h$
, the weight is strictly increasing, namely
![]() $\text{wt}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y))>\text{wt}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D70C}_{\mathscr{W}}(y))$
. This concludes the proof.◻
$\text{wt}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D70C}_{\mathscr{Z}}(y))>\text{wt}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D70C}_{\mathscr{W}}(y))$
. This concludes the proof.◻
Only the components of
![]() $\unicode[STIX]{x1D6E5}_{X}$
with coefficient
$\unicode[STIX]{x1D6E5}_{X}$
with coefficient
![]() $a_{i}=1$
determine strata that are contained in the Kontsevich–Soibelman skeletons. The introduction of
$a_{i}=1$
determine strata that are contained in the Kontsevich–Soibelman skeletons. The introduction of
![]() $\unicode[STIX]{x1D6E5}_{X}$
-log pluricanonical forms allows us to construct non-empty Kontsevich–Soibelman skeletons even for varieties with Kodaira dimension
$\unicode[STIX]{x1D6E5}_{X}$
-log pluricanonical forms allows us to construct non-empty Kontsevich–Soibelman skeletons even for varieties with Kodaira dimension
![]() $-\infty$
, as in the following examples.
$-\infty$
, as in the following examples.
Example 4.1.7. Let
![]() $X$
be the projective line
$X$
be the projective line
![]() $\mathbb{P}_{K}^{1}$
with affine coordinates
$\mathbb{P}_{K}^{1}$
with affine coordinates
![]() $x$
and
$x$
and
![]() $y$
, and
$y$
, and
![]() $\unicode[STIX]{x1D6E5}_{X}=(0:1)+(1:0)$
. Then
$\unicode[STIX]{x1D6E5}_{X}=(0:1)+(1:0)$
. Then
![]() $a_{i}=1$
for any
$a_{i}=1$
for any
![]() $i$
and there exist
$i$
and there exist
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic canonical forms. For example, we consider
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic canonical forms. For example, we consider
Let
![]() $\mathscr{X}=\mathbb{P}_{R}^{1}$
and
$\mathscr{X}=\mathbb{P}_{R}^{1}$
and
![]() $D_{\mathscr{X}}=(0:1)+(1:0)+\mathbb{P}_{k}^{1}$
. The log scheme
$D_{\mathscr{X}}=(0:1)+(1:0)+\mathbb{P}_{k}^{1}$
. The log scheme
![]() $\mathscr{X}^{+}=(\mathscr{X},D_{\mathscr{X}})$
is a log-regular model of
$\mathscr{X}^{+}=(\mathscr{X},D_{\mathscr{X}})$
is a log-regular model of
![]() $X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and the associated skeleton
$X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and the associated skeleton
![]() $\text{Sk}(\mathscr{X}^{+})$
looks like this:
$\text{Sk}(\mathscr{X}^{+})$
looks like this:

Since
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})=0$
, the weight associated to
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})=0$
, the weight associated to
![]() $\unicode[STIX]{x1D714}$
is minimal at any point of the skeleton
$\unicode[STIX]{x1D714}$
is minimal at any point of the skeleton
![]() $\text{Sk}(\mathscr{X}^{+})$
. Thus
$\text{Sk}(\mathscr{X}^{+})$
. Thus
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})=\text{Sk}(\mathscr{X}^{+})\simeq \mathbb{R}$
.
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})=\text{Sk}(\mathscr{X}^{+})\simeq \mathbb{R}$
.
Example 4.1.8. Let
![]() $X=\mathbb{P}_{K}^{1}$
and
$X=\mathbb{P}_{K}^{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{X}=\frac{2}{3}(0:1)+\frac{2}{3}(1:0)+\frac{2}{3}(1:1)$
. So
$\unicode[STIX]{x1D6E5}_{X}=\frac{2}{3}(0:1)+\frac{2}{3}(1:0)+\frac{2}{3}(1:1)$
. So
![]() $a_{i}=\frac{2}{3}$
for any
$a_{i}=\frac{2}{3}$
for any
![]() $i$
and there exist
$i$
and there exist
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
![]() $3$
-pluricanonical forms. We set
$3$
-pluricanonical forms. We set
We consider
![]() $\mathscr{X}=\mathbb{P}_{R}^{1}$
and
$\mathscr{X}=\mathbb{P}_{R}^{1}$
and
![]() $D_{\mathscr{X}}=(0:1)+(1:0)+(1:1)+\mathbb{P}_{k}^{1}$
; then
$D_{\mathscr{X}}=(0:1)+(1:0)+(1:1)+\mathbb{P}_{k}^{1}$
; then
![]() $\mathscr{X}^{+}=(\mathscr{X},D_{\mathscr{X}})$
is a log-regular model of
$\mathscr{X}^{+}=(\mathscr{X},D_{\mathscr{X}})$
is a log-regular model of
![]() $X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and
$X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and
![]() $\text{Sk}(\mathscr{X}^{+})$
is
$\text{Sk}(\mathscr{X}^{+})$
is

Since
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})=(0:1)+(1:0)+(1:1)$
, the weight associated to
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})=(0:1)+(1:0)+(1:1)$
, the weight associated to
![]() $\unicode[STIX]{x1D714}$
is minimal at the divisorial point
$\unicode[STIX]{x1D714}$
is minimal at the divisorial point
![]() $v_{\mathbb{P}_{k}^{1}}$
corresponding to
$v_{\mathbb{P}_{k}^{1}}$
corresponding to
![]() $\mathbb{P}_{k}^{1}$
and is strictly increasing with slope
$\mathbb{P}_{k}^{1}$
and is strictly increasing with slope
![]() $1$
along the unbounded edges, when we move away from the point
$1$
along the unbounded edges, when we move away from the point
![]() $v_{\mathbb{P}_{k}^{1}}$
. Therefore,
$v_{\mathbb{P}_{k}^{1}}$
. Therefore,
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})=\{v_{\mathbb{P}_{k}^{1}}\}$
.
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})=\{v_{\mathbb{P}_{k}^{1}}\}$
.
4.2 Weight function and Kontsevich–Soibelman skeleton for products
4.2.1. Let
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
be log-regular models over
$\mathscr{Y}^{+}$
be log-regular models over
![]() $S^{+}$
of
$S^{+}$
of
![]() $X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and
$X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and
![]() $Y^{+}=(Y,\lceil \unicode[STIX]{x1D6E5}_{Y}\rceil )$
respectively. Then the fs fibred product
$Y^{+}=(Y,\lceil \unicode[STIX]{x1D6E5}_{Y}\rceil )$
respectively. Then the fs fibred product
![]() $\mathscr{Z}^{+}=\mathscr{X}^{+}\times _{S^{+}}^{\mathit{fs}}\mathscr{Y}^{+}$
is a log-regular model of
$\mathscr{Z}^{+}=\mathscr{X}^{+}\times _{S^{+}}^{\mathit{fs}}\mathscr{Y}^{+}$
is a log-regular model of
![]() $Z^{+}:=X^{+}\times _{K}^{\mathit{fs}}Y^{+}$
. Therefore, given
$Z^{+}:=X^{+}\times _{K}^{\mathit{fs}}Y^{+}$
. Therefore, given
![]() $\unicode[STIX]{x1D714}_{X^{+}}$
and
$\unicode[STIX]{x1D714}_{X^{+}}$
and
![]() $\unicode[STIX]{x1D714}_{Y^{+}}$
$\unicode[STIX]{x1D714}_{Y^{+}}$
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic and
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic and
![]() $\unicode[STIX]{x1D6E5}_{Y}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{Y}$
-logarithmic
![]() $m$
-pluricanonical forms on
$m$
-pluricanonical forms on
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
and
$(X,\unicode[STIX]{x1D6E5}_{X})$
and
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
respectively, the form
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
respectively, the form
is a
![]() $\unicode[STIX]{x1D6E5}_{Z}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{Z}$
-logarithmic
![]() $m$
-pluricanonical form on
$m$
-pluricanonical form on
![]() $(Z,\unicode[STIX]{x1D6E5}_{Z})$
, where
$(Z,\unicode[STIX]{x1D6E5}_{Z})$
, where
![]() $\unicode[STIX]{x1D6E5}_{Z}=X\times _{K}\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D6E5}_{X}\times _{K}Y$
. Viewing these forms as rational sections of logarithmic
$\unicode[STIX]{x1D6E5}_{Z}=X\times _{K}\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D6E5}_{X}\times _{K}Y$
. Viewing these forms as rational sections of logarithmic
![]() $m$
-pluricanonical bundles, we see that
$m$
-pluricanonical bundles, we see that
![]() $\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B})=\text{pr}_{\mathscr{X}^{+}}^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}}))+\text{pr}_{\mathscr{Y}^{+}}^{\ast }(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}}))$
according to (2.4.6).
$\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B})=\text{pr}_{\mathscr{X}^{+}}^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}}))+\text{pr}_{\mathscr{Y}^{+}}^{\ast }(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}}))$
according to (2.4.6).
4.2.2. Let
![]() $z$
be a point of
$z$
be a point of
![]() $F_{\mathscr{Z}}\cap \mathscr{Z}_{k}$
; as before, we denote by
$F_{\mathscr{Z}}\cap \mathscr{Z}_{k}$
; as before, we denote by
![]() $x$
and
$x$
and
![]() $y$
the images of
$y$
the images of
![]() $z$
under the local isomorphism
$z$
under the local isomorphism
![]() $F_{\mathscr{Z}}\rightarrow F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
. Any morphism
$F_{\mathscr{Z}}\rightarrow F_{\mathscr{X}}\times _{F_{S}}F_{\mathscr{Y}}$
. Any morphism
![]() $\unicode[STIX]{x1D700}\in \unicode[STIX]{x1D70E}_{z}$
defines a point
$\unicode[STIX]{x1D700}\in \unicode[STIX]{x1D70E}_{z}$
defines a point
![]() $v_{z,\unicode[STIX]{x1D700}}$
in
$v_{z,\unicode[STIX]{x1D700}}$
in
![]() $\text{Sk}(\mathscr{Z}^{+})$
. For the sake of convenience, we simply denote the valuations by the corresponding morphism and we denote
$\text{Sk}(\mathscr{Z}^{+})$
. For the sake of convenience, we simply denote the valuations by the corresponding morphism and we denote
![]() $\unicode[STIX]{x1D6FC}=\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
and
$\unicode[STIX]{x1D6FC}=\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
and
![]() $\unicode[STIX]{x1D6FD}=\text{pr}_{\mathscr{Y}}(\unicode[STIX]{x1D700})$
. We aim to relate the valuation
$\unicode[STIX]{x1D6FD}=\text{pr}_{\mathscr{Y}}(\unicode[STIX]{x1D700})$
. We aim to relate the valuation
![]() $v_{\unicode[STIX]{x1D700}}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B}))$
to the values
$v_{\unicode[STIX]{x1D700}}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B}))$
to the values
4.2.3. Let
![]() $f_{x}\in {\mathcal{O}}_{\mathscr{X},x}$
be a local equation of
$f_{x}\in {\mathcal{O}}_{\mathscr{X},x}$
be a local equation of
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}})$
around
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}})$
around
![]() $x$
. In order to evaluate
$x$
. In order to evaluate
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
on
$v_{x,\unicode[STIX]{x1D6FC}}$
on
![]() $f_{x}$
, we consider an admissible expansion of
$f_{x}$
, we consider an admissible expansion of
![]() $f_{x}$
as in (3.2.6),
$f_{x}$
as in (3.2.6),
Furthermore, this expansion also induces an expansion of
![]() $\text{pr}_{\mathscr{X}}^{\ast }(f_{x})$
by
$\text{pr}_{\mathscr{X}}^{\ast }(f_{x})$
by
as formal power series in
![]() $\widehat{{\mathcal{O}}}_{\mathscr{Z},z}$
, since the morphism of characteristic sheaves
$\widehat{{\mathcal{O}}}_{\mathscr{Z},z}$
, since the morphism of characteristic sheaves
![]() ${\mathcal{C}}_{\mathscr{X},x}{\hookrightarrow}{\mathcal{C}}_{\mathscr{Z},z}$
is injective. Following the same procedure for a local equation
${\mathcal{C}}_{\mathscr{X},x}{\hookrightarrow}{\mathcal{C}}_{\mathscr{Z},z}$
is injective. Following the same procedure for a local equation
![]() $f_{y}\in {\mathcal{O}}_{\mathscr{Y},y}$
of
$f_{y}\in {\mathcal{O}}_{\mathscr{Y},y}$
of
![]() $\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}})$
around
$\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}})$
around
![]() $y$
, we get an expansion of
$y$
, we get an expansion of
![]() $f_{y}$
that extends to
$f_{y}$
that extends to
![]() $\text{pr}_{\mathscr{Y}}^{\ast }(f_{y})$
:
$\text{pr}_{\mathscr{Y}}^{\ast }(f_{y})$
:
4.2.4. A local equation of
![]() $\unicode[STIX]{x1D71B}$
around
$\unicode[STIX]{x1D71B}$
around
![]() $z$
is determined by
$z$
is determined by
![]() $\text{pr}_{\mathscr{X}}^{\ast }(f_{x})\,\,\text{pr}_{\mathscr{Y}}^{\ast }(f_{y})$
. Thus
$\text{pr}_{\mathscr{X}}^{\ast }(f_{x})\,\,\text{pr}_{\mathscr{Y}}^{\ast }(f_{y})$
. Thus
and by multiplicativity of the valuation
![]() $v_{\unicode[STIX]{x1D700}}$
,
$v_{\unicode[STIX]{x1D700}}$
,
Recalling Remark 3.2.13, the valuation can be computed as follows:
as the elements
![]() $\unicode[STIX]{x1D6FE}$
belong to
$\unicode[STIX]{x1D6FE}$
belong to
![]() ${\mathcal{C}}_{\mathscr{X},x}$
and
${\mathcal{C}}_{\mathscr{X},x}$
and
![]() $\unicode[STIX]{x1D6FC}$
is defined to be
$\unicode[STIX]{x1D6FC}$
is defined to be
![]() $\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
, we have
$\text{pr}_{\mathscr{X}}(\unicode[STIX]{x1D700})$
, we have
Hence, we conclude that
 $$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D700}}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B})) & = & \displaystyle v_{\unicode[STIX]{x1D700}}(\text{pr}_{\mathscr{X}}^{\ast }(f_{x}))+v_{\unicode[STIX]{x1D700}}(\text{pr}_{\mathscr{Y}}^{\ast }(f_{y}))\nonumber\\ \displaystyle & = & \displaystyle v_{\unicode[STIX]{x1D6FC}}(f_{x})+v_{\unicode[STIX]{x1D6FD}}(f_{y})\nonumber\\ \displaystyle & = & \displaystyle v_{\unicode[STIX]{x1D6FC}}(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}}))+v_{\unicode[STIX]{x1D6FD}}(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}})).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D700}}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B})) & = & \displaystyle v_{\unicode[STIX]{x1D700}}(\text{pr}_{\mathscr{X}}^{\ast }(f_{x}))+v_{\unicode[STIX]{x1D700}}(\text{pr}_{\mathscr{Y}}^{\ast }(f_{y}))\nonumber\\ \displaystyle & = & \displaystyle v_{\unicode[STIX]{x1D6FC}}(f_{x})+v_{\unicode[STIX]{x1D6FD}}(f_{y})\nonumber\\ \displaystyle & = & \displaystyle v_{\unicode[STIX]{x1D6FC}}(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}}))+v_{\unicode[STIX]{x1D6FD}}(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}})).\end{eqnarray}$$
4.2.6. This result turns out to be advantageous to compute the weight function
![]() $\text{wt}_{\unicode[STIX]{x1D71B}}$
on divisorial points of
$\text{wt}_{\unicode[STIX]{x1D71B}}$
on divisorial points of
![]() $\text{Sk}(\mathscr{Z}^{+})$
:
$\text{Sk}(\mathscr{Z}^{+})$
:
 $$\begin{eqnarray}\displaystyle \text{wt}_{\unicode[STIX]{x1D71B}}(\unicode[STIX]{x1D700}) & = & \displaystyle v_{\unicode[STIX]{x1D700}}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B}))+m\nonumber\\ \displaystyle & = & \displaystyle v_{\unicode[STIX]{x1D6FC}}(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}}))+v_{\unicode[STIX]{x1D6FD}}(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}}))+m\nonumber\\ \displaystyle & = & \displaystyle \text{wt}_{\unicode[STIX]{x1D714}_{X^{+}}}(\unicode[STIX]{x1D6FC})+\text{wt}_{\unicode[STIX]{x1D714}_{Y^{+}}}(\unicode[STIX]{x1D6FD})-m.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{wt}_{\unicode[STIX]{x1D71B}}(\unicode[STIX]{x1D700}) & = & \displaystyle v_{\unicode[STIX]{x1D700}}(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D71B}))+m\nonumber\\ \displaystyle & = & \displaystyle v_{\unicode[STIX]{x1D6FC}}(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{X^{+}}))+v_{\unicode[STIX]{x1D6FD}}(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{Y^{+}}))+m\nonumber\\ \displaystyle & = & \displaystyle \text{wt}_{\unicode[STIX]{x1D714}_{X^{+}}}(\unicode[STIX]{x1D6FC})+\text{wt}_{\unicode[STIX]{x1D714}_{Y^{+}}}(\unicode[STIX]{x1D6FD})-m.\end{eqnarray}$$
4.2.8. In the notation of the previous paragraphs, our computations lead to the following result.
Theorem 4.2.9. Suppose that the residue field
![]() $k$
is algebraically closed and that
$k$
is algebraically closed and that
![]() $\mathscr{X}^{+}$
is semistable. Then, the PL homeomorphism of skeletons
$\mathscr{X}^{+}$
is semistable. Then, the PL homeomorphism of skeletons
given in Proposition 3.4.3 restricts to a PL homeomorphism of Kontsevich–Soibelman skeletons
Proof. This follows immediately from equality (4.2.7), which shows that a point in
![]() $\text{Sk}(\mathscr{Z}^{+})$
has minimal value
$\text{Sk}(\mathscr{Z}^{+})$
has minimal value
![]() $\text{wt}_{\unicode[STIX]{x1D71B}}(Z,\unicode[STIX]{x1D6E5}_{Z})$
if and only if its projections have minimal value
$\text{wt}_{\unicode[STIX]{x1D71B}}(Z,\unicode[STIX]{x1D6E5}_{Z})$
if and only if its projections have minimal value
![]() $\text{wt}_{\unicode[STIX]{x1D714}_{X^{+}}}(X,\unicode[STIX]{x1D6E5}_{X})$
and
$\text{wt}_{\unicode[STIX]{x1D714}_{X^{+}}}(X,\unicode[STIX]{x1D6E5}_{X})$
and
![]() $\text{wt}_{\unicode[STIX]{x1D714}_{Y^{+}}}(Y,\unicode[STIX]{x1D6E5}_{Y})$
.◻
$\text{wt}_{\unicode[STIX]{x1D714}_{Y^{+}}}(Y,\unicode[STIX]{x1D6E5}_{Y})$
.◻
5 The essential skeleton of a product
For this section, we assume the residue field
![]() $k$
is algebraically closed.
$k$
is algebraically closed.
5.1 Essential skeleton of a pair
5.1.1. Let
![]() $X$
be a proper variety over
$X$
be a proper variety over
![]() $K$
and
$K$
and
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
a fractional snc pair as in § 1.5. Let
$(X,\unicode[STIX]{x1D6E5}_{X})$
a fractional snc pair as in § 1.5. Let
![]() $\mathscr{X}^{+}$
be a log-regular model of
$\mathscr{X}^{+}$
be a log-regular model of
![]() $(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
over
$(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
over
![]() $S^{+}$
. Let
$S^{+}$
. Let
![]() $\unicode[STIX]{x1D714}$
be a non-zero regular
$\unicode[STIX]{x1D714}$
be a non-zero regular
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
![]() $m$
-pluricanonical form on
$m$
-pluricanonical form on
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
. There exist minimal positive integers
$(X,\unicode[STIX]{x1D6E5}_{X})$
. There exist minimal positive integers
![]() $d$
and
$d$
and
![]() $n$
such that the divisor
$n$
such that the divisor
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}^{\otimes d}\unicode[STIX]{x1D70B}^{-n})$
is effective and the multiplicity of some component of the special fiber is zero: we denote this divisor by
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}^{\otimes d}\unicode[STIX]{x1D70B}^{-n})$
is effective and the multiplicity of some component of the special fiber is zero: we denote this divisor by
![]() $D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
. It follows from the properties of the weight function (see [Reference Mustaţă and NicaiseMN15, Proposition 4.5.5]) that for any
$D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
. It follows from the properties of the weight function (see [Reference Mustaţă and NicaiseMN15, Proposition 4.5.5]) that for any
![]() $x\in \text{Sk}(\mathscr{X}^{+})$
,
$x\in \text{Sk}(\mathscr{X}^{+})$
,
Lemma 5.1.2. Let
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
be a divisorial point in
$v_{x,\unicode[STIX]{x1D6FC}}$
be a divisorial point in
![]() $\text{Sk}(\mathscr{X}^{+})$
. Then
$\text{Sk}(\mathscr{X}^{+})$
. Then
![]() $v_{x,\unicode[STIX]{x1D6FC}}\in \text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
if and only if
$v_{x,\unicode[STIX]{x1D6FC}}\in \text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
if and only if
![]() $D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
does not contain
$D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
does not contain
![]() $x$
.
$x$
.
Proof. We denote
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
simply by
$v_{x,\unicode[STIX]{x1D6FC}}$
simply by
![]() $\unicode[STIX]{x1D6FC}$
. By the above series of equalities, the weight function
$\unicode[STIX]{x1D6FC}$
. By the above series of equalities, the weight function
![]() $\text{wt}_{\unicode[STIX]{x1D714}}$
reaches its minimum at
$\text{wt}_{\unicode[STIX]{x1D714}}$
reaches its minimum at
![]() $\unicode[STIX]{x1D6FC}$
if and only if
$\unicode[STIX]{x1D6FC}$
if and only if
![]() $v_{\unicode[STIX]{x1D6FC}}(D_{\min }(\mathscr{X},\unicode[STIX]{x1D714}))$
is minimal, hence, in particular, equal to zero.
$v_{\unicode[STIX]{x1D6FC}}(D_{\min }(\mathscr{X},\unicode[STIX]{x1D714}))$
is minimal, hence, in particular, equal to zero.
Let
![]() $h:\mathscr{Y}^{+}\rightarrow \mathscr{X}^{+}$
be a sequence of blow-up morphisms of strata of
$h:\mathscr{Y}^{+}\rightarrow \mathscr{X}^{+}$
be a sequence of blow-up morphisms of strata of
![]() $D_{\mathscr{X}}$
such that
$D_{\mathscr{X}}$
such that
![]() $\unicode[STIX]{x1D6FC}$
corresponds to an irreducible component
$\unicode[STIX]{x1D6FC}$
corresponds to an irreducible component
![]() $E$
of
$E$
of
![]() $D_{\mathscr{Y}}$
. As in the proof of Proposition 4.1.6,
$D_{\mathscr{Y}}$
. As in the proof of Proposition 4.1.6,
Therefore we have that
![]() $v_{\unicode[STIX]{x1D6FC}}(D_{\min }(\mathscr{X},\unicode[STIX]{x1D714}))>0$
if and only if
$v_{\unicode[STIX]{x1D6FC}}(D_{\min }(\mathscr{X},\unicode[STIX]{x1D714}))>0$
if and only if
![]() $E\subseteq \text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}^{\otimes d}\unicode[STIX]{x1D70B}^{-n})$
, and this holds if and only if
$E\subseteq \text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}^{\otimes d}\unicode[STIX]{x1D70B}^{-n})$
, and this holds if and only if
![]() $x\in D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
.◻
$x\in D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
.◻
5.1.3. We define the essential skeleton
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
of a fractional snc pair
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
of a fractional snc pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
as the union of all Kontsevich–Soibelman skeletons
$(X,\unicode[STIX]{x1D6E5}_{X})$
as the union of all Kontsevich–Soibelman skeletons
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
, where
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
, where
![]() $\unicode[STIX]{x1D714}$
ranges over all regular
$\unicode[STIX]{x1D714}$
ranges over all regular
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic pluricanonical forms. In the case of an empty boundary, this recovers the notions introduced in [Reference Mustaţă and NicaiseMN15].
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic pluricanonical forms. In the case of an empty boundary, this recovers the notions introduced in [Reference Mustaţă and NicaiseMN15].
The further reason to define the essential skeleton this way is that it behaves nicely under birational morphisms. Let
![]() $f:X^{\prime }\rightarrow X$
be a log resolution. Then there is a
$f:X^{\prime }\rightarrow X$
be a log resolution. Then there is a
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
with snc support, and no coefficient exceeding
$\unicode[STIX]{x1D6E4}^{\prime }$
with snc support, and no coefficient exceeding
![]() $1$
, such that
$1$
, such that
![]() $K_{X^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{X})$
. Take
$K_{X^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{X})$
. Take
![]() $\unicode[STIX]{x1D6E5}_{X^{\prime }}$
to be the positive part of
$\unicode[STIX]{x1D6E5}_{X^{\prime }}$
to be the positive part of
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
and write
$\unicode[STIX]{x1D6E4}^{\prime }$
and write
For any
![]() $m$
, pullback along with multiplication by the divisor of discrepancies
$m$
, pullback along with multiplication by the divisor of discrepancies
![]() $N$
induces an isomorphism of vector spaces
$N$
induces an isomorphism of vector spaces
Let
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $\unicode[STIX]{x1D714}^{\prime }$
be corresponding forms via this isomorphism.
$\unicode[STIX]{x1D714}^{\prime }$
be corresponding forms via this isomorphism.
Proposition 5.1.5. Under the identification of the birational points of
![]() $X$
with those of
$X$
with those of
![]() $X^{\prime }$
,
$X^{\prime }$
,
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
is identified with
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
is identified with
![]() $\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
.
$\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
.
Proof. The Kontsevich–Soibelman skeleton
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
is contained in the skeleton associated to any log-regular model by Proposition 4.1.6. Thus, we choose log-regular models
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
is contained in the skeleton associated to any log-regular model by Proposition 4.1.6. Thus, we choose log-regular models
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() ${\mathscr{X}^{\prime }}^{+}$
so that
${\mathscr{X}^{\prime }}^{+}$
so that
![]() $f$
extends to a log resolution
$f$
extends to a log resolution
![]() $f_{R}:\mathscr{X}^{\prime }\rightarrow \mathscr{X}$
and the pair
$f_{R}:\mathscr{X}^{\prime }\rightarrow \mathscr{X}$
and the pair
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is fractional snc, where
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is fractional snc, where
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}=\overline{\unicode[STIX]{x1D6E5}_{X}}+\mathscr{X}_{k,\text{red}}$
. Likewise we denote
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}=\overline{\unicode[STIX]{x1D6E5}_{X}}+\mathscr{X}_{k,\text{red}}$
. Likewise we denote
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }}=\overline{\unicode[STIX]{x1D6E5}_{X^{\prime }}}+\mathscr{X}_{k,\text{red}}^{\prime }$
, and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }}=\overline{\unicode[STIX]{x1D6E5}_{X^{\prime }}}+\mathscr{X}_{k,\text{red}}^{\prime }$
, and
![]() $(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
is fractional snc as
$(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
is fractional snc as
![]() $f_{R}$
is a log resolution. It suffices to check the proposition for divisorial valuations. By Lemma 5.1.2 a divisorial valuation
$f_{R}$
is a log resolution. It suffices to check the proposition for divisorial valuations. By Lemma 5.1.2 a divisorial valuation
![]() $v$
of
$v$
of
![]() $\text{Sk}(\mathscr{X}^{+})$
is in
$\text{Sk}(\mathscr{X}^{+})$
is in
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
if and only if it is a log canonical center of
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
if and only if it is a log canonical center of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and the divisor
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and the divisor
![]() $D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
does not contain the center of
$D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
does not contain the center of
![]() $v$
.
$v$
.
Suppose
![]() $v$
is a divisorial point in
$v$
is a divisorial point in
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
. Without loss of generality, we can assume that the divisor
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
. Without loss of generality, we can assume that the divisor
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})$
in
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714})$
in
![]() $\mathscr{X}^{+}$
does not contain the center of
$\mathscr{X}^{+}$
does not contain the center of
![]() $v$
. As
$v$
. As
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is a fractional snc pair, it is dlt (1.9.9) and we have that
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is a fractional snc pair, it is dlt (1.9.9) and we have that
where
![]() $M$
is effective, thus
$M$
is effective, thus
![]() $\text{div}_{{\mathscr{X}^{\prime }}^{+}}(\unicode[STIX]{x1D714}^{\prime })=f_{R}^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))+mM$
. As
$\text{div}_{{\mathscr{X}^{\prime }}^{+}}(\unicode[STIX]{x1D714}^{\prime })=f_{R}^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}))+mM$
. As
![]() $v$
is a log canonical center of
$v$
is a log canonical center of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
,
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
,
![]() $M$
does not vanish along
$M$
does not vanish along
![]() $v$
, so neither does
$v$
, so neither does
![]() $\text{div}_{{\mathscr{X}^{\prime }}^{+}}(\unicode[STIX]{x1D714}^{\prime })$
. Likewise
$\text{div}_{{\mathscr{X}^{\prime }}^{+}}(\unicode[STIX]{x1D714}^{\prime })$
. Likewise
![]() $v$
is a log canonical center of
$v$
is a log canonical center of
![]() $(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
. It follows that
$(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
. It follows that
![]() $v\in \text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
.
$v\in \text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
.
Conversely, if
![]() $v$
is a divisorial point in
$v$
is a divisorial point in
![]() $\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
, it is a log canonical center of
$\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
, it is a log canonical center of
![]() $(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
and the divisor
$(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
and the divisor
![]() $D_{\min }(\mathscr{X}^{\prime },\unicode[STIX]{x1D714}^{\prime })$
does not contain the center of
$D_{\min }(\mathscr{X}^{\prime },\unicode[STIX]{x1D714}^{\prime })$
does not contain the center of
![]() $v$
. As a result,
$v$
. As a result,
![]() $v$
is also a log canonical center of
$v$
is also a log canonical center of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
, and the divisor
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
, and the divisor
![]() $D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
does not contain the center of
$D_{\min }(\mathscr{X},\unicode[STIX]{x1D714})$
does not contain the center of
![]() $v$
since its pullback does not.◻
$v$
since its pullback does not.◻
We define the Kontsevich–Soibelman skeleton
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
of a dlt pair
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},\unicode[STIX]{x1D714})$
of a dlt pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
as the Kontsevich–Soibelman skeleton
$(X,\unicode[STIX]{x1D6E5}_{X})$
as the Kontsevich–Soibelman skeleton
![]() $\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
where
$\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
where
![]() $(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
is any log resolution of
$(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
is any log resolution of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
, and
$(X,\unicode[STIX]{x1D6E5}_{X})$
, and
![]() $\unicode[STIX]{x1D714}^{\prime }$
is the form corresponding to
$\unicode[STIX]{x1D714}^{\prime }$
is the form corresponding to
![]() $\unicode[STIX]{x1D714}$
under the isomorphism (5.1.4): Proposition 5.1.5 guarantees that this is well defined. It follows that we can define the essential skeleton
$\unicode[STIX]{x1D714}$
under the isomorphism (5.1.4): Proposition 5.1.5 guarantees that this is well defined. It follows that we can define the essential skeleton
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
of a dlt pair
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
of a dlt pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
as the essential skeleton of any log resolution of
$(X,\unicode[STIX]{x1D6E5}_{X})$
as the essential skeleton of any log resolution of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
.
$(X,\unicode[STIX]{x1D6E5}_{X})$
.
Moreover, notice that our construction works more generally for log canonical pairs, hence the notions of Kontsevich–Soibelman skeleton and essential skeleton generalize to such pairs.
5.1.6. Suppose that
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is a proper dlt pair over
$(X,\unicode[STIX]{x1D6E5}_{X})$
is a proper dlt pair over
![]() $K$
, such that
$K$
, such that
![]() $K_{X}+\unicode[STIX]{x1D6E5}_{X}$
is semiample. Suppose also that
$K_{X}+\unicode[STIX]{x1D6E5}_{X}$
is semiample. Suppose also that
![]() $\mathscr{X}$
is a good minimal dlt model of
$\mathscr{X}$
is a good minimal dlt model of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
over
$(X,\unicode[STIX]{x1D6E5}_{X})$
over
![]() $R$
and let
$R$
and let
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}=\overline{\unicode[STIX]{x1D6E5}_{X}}+\mathscr{X}_{k,\text{red}}$
. We denote by
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}=\overline{\unicode[STIX]{x1D6E5}_{X}}+\mathscr{X}_{k,\text{red}}$
. We denote by
![]() ${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
the dual complex of the strata of the coefficient-
${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
the dual complex of the strata of the coefficient-
![]() $1$
part of
$1$
part of
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
that lie in the special fiber.
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
that lie in the special fiber.
We consider a log resolution
![]() $f:X^{\prime }\rightarrow X$
that extends to a log resolution of
$f:X^{\prime }\rightarrow X$
that extends to a log resolution of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. We write
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. We write
![]() $K_{X^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{X})$
. Let
$K_{X^{\prime }}+\unicode[STIX]{x1D6E4}^{\prime }=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{X})$
. Let
![]() $\unicode[STIX]{x1D6E5}_{X^{\prime }}$
be the positive part of
$\unicode[STIX]{x1D6E5}_{X^{\prime }}$
be the positive part of
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
. We may embed the open dual complex
$\unicode[STIX]{x1D6E4}^{\prime }$
. We may embed the open dual complex
![]() ${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
into the birational points of
${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
into the birational points of
![]() $X$
.
$X$
.
Proposition 5.1.7. This embedding identifies
![]() ${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
with
${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
with
![]() $\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
.
$\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
.
Proof. Choose a regular
![]() $R$
-model
$R$
-model
![]() $\mathscr{X}^{\prime }$
for
$\mathscr{X}^{\prime }$
for
![]() $X^{\prime }$
which is a log resolution of
$X^{\prime }$
which is a log resolution of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
extending
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
extending
![]() $f$
and let
$f$
and let
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }}=\overline{\unicode[STIX]{x1D6E5}_{X^{\prime }}}+\mathscr{X}_{k,\text{red}}^{\prime }$
, namely we have the log resolutions
$\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }}=\overline{\unicode[STIX]{x1D6E5}_{X^{\prime }}}+\mathscr{X}_{k,\text{red}}^{\prime }$
, namely we have the log resolutions
As in the previous proof, it suffices to check the proposition for divisorial valuations. Let
![]() $v$
be a divisorial valuation, and suppose
$v$
be a divisorial valuation, and suppose
![]() $v\in {\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. Then
$v\in {\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. Then
![]() $v$
is a log canonical center for
$v$
is a log canonical center for
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
, so
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
, so
![]() $v$
is also a log canonical center of
$v$
is also a log canonical center of
![]() $(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
. For a sufficiently divisible index, we may find a
$(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
. For a sufficiently divisible index, we may find a
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic pluricanonical form on
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic pluricanonical form on
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
whose associated divisor in
$(X,\unicode[STIX]{x1D6E5}_{X})$
whose associated divisor in
![]() $\mathscr{X}$
has vanishing locus
$\mathscr{X}$
has vanishing locus
![]() $C$
such that
$C$
such that
![]() $C$
is a divisor not containing the center of
$C$
is a divisor not containing the center of
![]() $v$
. After pullback, we get a
$v$
. After pullback, we get a
![]() $\unicode[STIX]{x1D6E5}_{X^{\prime }}$
-logarithmic pluricanonical form
$\unicode[STIX]{x1D6E5}_{X^{\prime }}$
-logarithmic pluricanonical form
![]() $\unicode[STIX]{x1D714}^{\prime }$
whose associated divisor in
$\unicode[STIX]{x1D714}^{\prime }$
whose associated divisor in
![]() $\mathscr{X}^{\prime }$
is supported on the strict transform of
$\mathscr{X}^{\prime }$
is supported on the strict transform of
![]() $C$
and the exceptional divisors of positive log discrepancy. But none of these contain
$C$
and the exceptional divisors of positive log discrepancy. But none of these contain
![]() $v$
. Thus,
$v$
. Thus,
![]() $v\in \text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
.
$v\in \text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }},\unicode[STIX]{x1D714}^{\prime })$
.
Conversely, if
![]() $v$
is a divisorial point in
$v$
is a divisorial point in
![]() $\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
, then
$\text{Sk}(X^{\prime },\unicode[STIX]{x1D6E5}_{X^{\prime }})$
, then
![]() $v$
is a log canonical center of
$v$
is a log canonical center of
![]() $(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
, so
$(\mathscr{X}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{X}^{\prime }})$
, so
![]() $v$
is a log canonical center of
$v$
is a log canonical center of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
, hence an element of the open dual complex
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
, hence an element of the open dual complex
![]() ${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
.◻
${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
.◻
Remark 5.1.8. Proposition 5.1.7 compares the essential skeleton of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
to the skeleton of a good minimal dlt model of
$(X,\unicode[STIX]{x1D6E5}_{X})$
to the skeleton of a good minimal dlt model of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
. Thus, the result can be restated as follows: if
$(X,\unicode[STIX]{x1D6E5}_{X})$
. Thus, the result can be restated as follows: if
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
is a dlt pair with
$(X,\unicode[STIX]{x1D6E5}_{X})$
is a dlt pair with
![]() $K_{X}+\unicode[STIX]{x1D6E5}_{X}$
semiample and
$K_{X}+\unicode[STIX]{x1D6E5}_{X}$
semiample and
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is a good minimal dlt model of
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
is a good minimal dlt model of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
over
$(X,\unicode[STIX]{x1D6E5}_{X})$
over
![]() $R$
, then
$R$
, then
![]() ${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})=\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
. This generalizes [Reference Nicaise and XuNX16, Theorem 3.3.3] to dlt pairs.
${\mathcal{D}}_{0}^{=1}(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})=\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
. This generalizes [Reference Nicaise and XuNX16, Theorem 3.3.3] to dlt pairs.
5.2 Essential skeletons and products of log-regular models
5.2.1. We say that a proper dlt pair
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
has non-negative Kodaira–Iitaka dimension if some multiple of the line bundle
$(X,\unicode[STIX]{x1D6E5}_{X})$
has non-negative Kodaira–Iitaka dimension if some multiple of the line bundle
![]() $K_{X}+\unicode[STIX]{x1D6E5}_{X}$
has a regular section. We also define products for pairs: if
$K_{X}+\unicode[STIX]{x1D6E5}_{X}$
has a regular section. We also define products for pairs: if
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
and
$(X,\unicode[STIX]{x1D6E5}_{X})$
and
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
are pairs over
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
are pairs over
![]() $K$
, then we define their product to be
$K$
, then we define their product to be
![]() $(Z,\unicode[STIX]{x1D6E5}_{Z})$
, where
$(Z,\unicode[STIX]{x1D6E5}_{Z})$
, where
![]() $Z=X\times _{K}Y$
and
$Z=X\times _{K}Y$
and
![]() $\unicode[STIX]{x1D6E5}_{Z}=\unicode[STIX]{x1D6E5}_{X}\times _{K}Y+X\times _{K}\unicode[STIX]{x1D6E5}_{Y}$
. If
$\unicode[STIX]{x1D6E5}_{Z}=\unicode[STIX]{x1D6E5}_{X}\times _{K}Y+X\times _{K}\unicode[STIX]{x1D6E5}_{Y}$
. If
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
and
$(X,\unicode[STIX]{x1D6E5}_{X})$
and
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
have semistable models
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
have semistable models
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
over
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
over
![]() $R$
, then their product is
$R$
, then their product is
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
, where
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
, where
![]() $\mathscr{Z}=\mathscr{X}\times _{R}\mathscr{Y}$
and
$\mathscr{Z}=\mathscr{X}\times _{R}\mathscr{Y}$
and
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is the sum of the strict transform of
$\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is the sum of the strict transform of
![]() $\unicode[STIX]{x1D6E5}_{Z}$
with the special fiber
$\unicode[STIX]{x1D6E5}_{Z}$
with the special fiber
![]() $\mathscr{Z}_{k}$
, which is reduced.
$\mathscr{Z}_{k}$
, which is reduced.
Theorem 5.2.2. Let
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
and
$(X,\unicode[STIX]{x1D6E5}_{X})$
and
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
be proper dlt pairs such that
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
be proper dlt pairs such that
![]() $X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and
$X^{+}=(X,\lceil \unicode[STIX]{x1D6E5}_{X}\rceil )$
and
![]() $Y^{+}=(Y,\lceil \unicode[STIX]{x1D6E5}_{Y}\rceil )$
are log-regular log schemes over
$Y^{+}=(Y,\lceil \unicode[STIX]{x1D6E5}_{Y}\rceil )$
are log-regular log schemes over
![]() $K$
. Suppose that both pairs have non-negative Kodaira–Iitaka dimension and both admit semistable log-regular models
$K$
. Suppose that both pairs have non-negative Kodaira–Iitaka dimension and both admit semistable log-regular models
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
over
$\mathscr{Y}^{+}$
over
![]() $S^{+}$
. Then the PL homeomorphism of skeletons
$S^{+}$
. Then the PL homeomorphism of skeletons
of Proposition 3.4.3 induces a PL homeomorphism of essential skeletons
where
![]() $\mathscr{Z}^{+}$
,
$\mathscr{Z}^{+}$
,
![]() $Z$
and
$Z$
and
![]() $\unicode[STIX]{x1D6E5}_{Z}$
are the respective products.
$\unicode[STIX]{x1D6E5}_{Z}$
are the respective products.
Proof. It follows immediately from Theorem 4.2.9 that we have the inclusion
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})\times \text{Sk}(Y,\unicode[STIX]{x1D6E5}_{Y})\subseteq \text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z})$
. Thus, we reduce to proving the following statement. Let
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})\times \text{Sk}(Y,\unicode[STIX]{x1D6E5}_{Y})\subseteq \text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z})$
. Thus, we reduce to proving the following statement. Let
![]() $v_{z,\unicode[STIX]{x1D700}}$
be a divisorial point in
$v_{z,\unicode[STIX]{x1D700}}$
be a divisorial point in
![]() $\text{Sk}(\mathscr{Z}^{+})$
and
$\text{Sk}(\mathscr{Z}^{+})$
and
![]() $(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}})$
be the corresponding pair in
$(v_{x,\unicode[STIX]{x1D6FC}},v_{y,\unicode[STIX]{x1D6FD}})$
be the corresponding pair in
![]() $\text{Sk}(\mathscr{X}^{+})\times \text{Sk}(\mathscr{Y}^{+})$
under the isomorphism of Proposition 3.4.3; if
$\text{Sk}(\mathscr{X}^{+})\times \text{Sk}(\mathscr{Y}^{+})$
under the isomorphism of Proposition 3.4.3; if
![]() $v_{z,\unicode[STIX]{x1D700}}$
lies in the essential skeleton
$v_{z,\unicode[STIX]{x1D700}}$
lies in the essential skeleton
![]() $\text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z})$
, then
$\text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z})$
, then
![]() $v_{x,\unicode[STIX]{x1D6FC}}$
lies in
$v_{x,\unicode[STIX]{x1D6FC}}$
lies in
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
.
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X})$
.
Assume that
![]() $v_{z,\unicode[STIX]{x1D700}}$
lies in the essential skeleton
$v_{z,\unicode[STIX]{x1D700}}$
lies in the essential skeleton
![]() $\text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z})$
. Then there exists a non-zero regular
$\text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z})$
. Then there exists a non-zero regular
![]() $\unicode[STIX]{x1D6E5}_{Z}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{Z}$
-logarithmic
![]() $m$
-pluricanonical form
$m$
-pluricanonical form
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() $Z^{+}$
, such that
$Z^{+}$
, such that
![]() $v_{z,\unicode[STIX]{x1D700}}\in \text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z},\unicode[STIX]{x1D714})$
. By Lemma 5.1.2,
$v_{z,\unicode[STIX]{x1D700}}\in \text{Sk}(Z,\unicode[STIX]{x1D6E5}_{Z},\unicode[STIX]{x1D714})$
. By Lemma 5.1.2,
![]() $D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
does not contain
$D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
does not contain
![]() $z$
.
$z$
.
Let
![]() $E$
be an irreducible component of
$E$
be an irreducible component of
![]() $\mathscr{Y}_{k}$
containing
$\mathscr{Y}_{k}$
containing
![]() $y$
and denote by
$y$
and denote by
![]() $\unicode[STIX]{x1D709}_{E}$
the generic point of
$\unicode[STIX]{x1D709}_{E}$
the generic point of
![]() $E$
. Then the point in the Kato fan of
$E$
. Then the point in the Kato fan of
![]() $\mathscr{Z}^{+}$
corresponding to
$\mathscr{Z}^{+}$
corresponding to
![]() $(x,\unicode[STIX]{x1D709}_{E})$
is not contained in
$(x,\unicode[STIX]{x1D709}_{E})$
is not contained in
![]() $D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
, as otherwise
$D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
, as otherwise
![]() $z$
would be contained in it.
$z$
would be contained in it.
As
![]() $k$
is algebraically closed, we can choose a
$k$
is algebraically closed, we can choose a
![]() $k$
-rational point
$k$
-rational point
![]() $p$
in
$p$
in
![]() $E$
such that
$E$
such that
![]() $p$
is contained in no other components of
$p$
is contained in no other components of
![]() $D_{\mathscr{Y}}$
and
$D_{\mathscr{Y}}$
and
![]() $D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
does not contain the locus
$D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
does not contain the locus
![]() $\overline{\{x\}}\times _{R}\{p\}$
. By Hensel’s lemma and the assumption of semistability,
$\overline{\{x\}}\times _{R}\{p\}$
. By Hensel’s lemma and the assumption of semistability,
![]() $p$
can be lifted to an
$p$
can be lifted to an
![]() $R$
-rational point of
$R$
-rational point of
![]() $\mathscr{Y}$
. The pullback of
$\mathscr{Y}$
. The pullback of
![]() $\mathscr{Z}^{+}$
along this
$\mathscr{Z}^{+}$
along this
![]() $R$
-rational point is an embedding
$R$
-rational point is an embedding
![]() $i:\mathscr{X}^{+}\rightarrow \mathscr{Z}^{+}$
, so we have the following diagram.
$i:\mathscr{X}^{+}\rightarrow \mathscr{Z}^{+}$
, so we have the following diagram.

Since
![]() $S$
has trivial normal bundle in
$S$
has trivial normal bundle in
![]() $\mathscr{Y}$
, we have that
$\mathscr{Y}$
, we have that
so
![]() $i^{\ast }(\unicode[STIX]{x1D714})$
is a non-zero pluricanonical form on
$i^{\ast }(\unicode[STIX]{x1D714})$
is a non-zero pluricanonical form on
![]() $X$
and, in particular, is a regular
$X$
and, in particular, is a regular
![]() $\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
$\unicode[STIX]{x1D6E5}_{X}$
-logarithmic
![]() $m$
-pluricanonical form. Moreover,
$m$
-pluricanonical form. Moreover,
![]() $D_{\min }(\mathscr{X},i^{\ast }(\unicode[STIX]{x1D714}))=i^{\ast }(D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714}))$
. Finally,
$D_{\min }(\mathscr{X},i^{\ast }(\unicode[STIX]{x1D714}))=i^{\ast }(D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714}))$
. Finally,
![]() $x$
is not contained in
$x$
is not contained in
![]() $D_{\min }(\mathscr{X},i^{\ast }(\unicode[STIX]{x1D714}))$
, as otherwise
$D_{\min }(\mathscr{X},i^{\ast }(\unicode[STIX]{x1D714}))$
, as otherwise
![]() $i(x)=\{x\}\times _{R}\{p\}$
would be contained in
$i(x)=\{x\}\times _{R}\{p\}$
would be contained in
![]() $D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
. By Lemma 5.1.2,
$D_{\min }(\mathscr{Z},\unicode[STIX]{x1D714})$
. By Lemma 5.1.2,
![]() $x$
is a point of
$x$
is a point of
![]() $\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},i^{\ast }(\unicode[STIX]{x1D714}))$
and this concludes the proof.◻
$\text{Sk}(X,\unicode[STIX]{x1D6E5}_{X},i^{\ast }(\unicode[STIX]{x1D714}))$
and this concludes the proof.◻
Remark 5.2.3. Consider the case where the line bundles
![]() $K_{X}+\unicode[STIX]{x1D6E5}_{X}$
and
$K_{X}+\unicode[STIX]{x1D6E5}_{X}$
and
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
are semiample, that is, some multiple of them is base point free. It follows from the arguments of [Reference Nicaise and XuNX16, Theorem 3.3.3] that the essential skeleton of
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
are semiample, that is, some multiple of them is base point free. It follows from the arguments of [Reference Nicaise and XuNX16, Theorem 3.3.3] that the essential skeleton of
![]() $(Z,\unicode[STIX]{x1D6E5}_{Z})$
is a finite union of Kontsevich–Soibelman skeletons where the union runs through a generating set of global sections of a sufficiently large multiple of
$(Z,\unicode[STIX]{x1D6E5}_{Z})$
is a finite union of Kontsevich–Soibelman skeletons where the union runs through a generating set of global sections of a sufficiently large multiple of
![]() $K_{Z}+\unicode[STIX]{x1D6E5}_{Z}$
. We can construct such a set from generating sets of global sections of multiples of
$K_{Z}+\unicode[STIX]{x1D6E5}_{Z}$
. We can construct such a set from generating sets of global sections of multiples of
![]() $K_{X}+\unicode[STIX]{x1D6E5}_{X}$
and
$K_{X}+\unicode[STIX]{x1D6E5}_{X}$
and
![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
respectively, via tensor product. Then, in this case, the result of Theorem 5.2.2 follows directly from Theorem 4.2.9.
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}$
respectively, via tensor product. Then, in this case, the result of Theorem 5.2.2 follows directly from Theorem 4.2.9.
5.3 Essential skeletons and products of dlt models
5.3.1. We need a combinatorial lemma to understand the formally local behavior of products of semistable dlt models.
Lemma 5.3.2. Let
![]() $M$
be the monoid generated by
$M$
be the monoid generated by
![]() $r_{1}\ldots r_{n_{1}}$
,
$r_{1}\ldots r_{n_{1}}$
,
![]() $s_{1}\ldots s_{n_{2}}$
with the single relation
$s_{1}\ldots s_{n_{2}}$
with the single relation
![]() $\sum _{i=1}^{n_{1}}r_{i}=\sum _{j=1}^{n_{2}}s_{j}$
. Then any small
$\sum _{i=1}^{n_{1}}r_{i}=\sum _{j=1}^{n_{2}}s_{j}$
. Then any small
![]() $\mathbb{Q}$
-factorialization of the affine toric variety
$\mathbb{Q}$
-factorialization of the affine toric variety
![]() $W=\text{Spec}\,(k[M])$
associated to
$W=\text{Spec}\,(k[M])$
associated to
![]() $M$
is a log resolution.
$M$
is a log resolution.
Proof. We calculate the fan of
![]() $W$
. Let
$W$
. Let
![]() $N$
be the dual lattice of
$N$
be the dual lattice of
![]() $M$
. The fan associated to
$M$
. The fan associated to
![]() $W$
is the cone of elements of
$W$
is the cone of elements of
![]() $N\,\otimes \,\mathbb{R}$
which are non-negative on
$N\,\otimes \,\mathbb{R}$
which are non-negative on
![]() $M$
. We consider these as linear functions
$M$
. We consider these as linear functions
![]() $l$
on the vector space spanned by the
$l$
on the vector space spanned by the
![]() $r_{i}$
and
$r_{i}$
and
![]() $s_{i}$
, subject to the restriction that
$s_{i}$
, subject to the restriction that
![]() $l(\sum _{i=1}^{n_{1}}r_{i})=l(\sum _{j=1}^{n_{2}}s_{j})$
. Let
$l(\sum _{i=1}^{n_{1}}r_{i})=l(\sum _{j=1}^{n_{2}}s_{j})$
. Let
![]() $x_{ij}$
be the function which is
$x_{ij}$
be the function which is
![]() $1$
on
$1$
on
![]() $r_{i}$
and
$r_{i}$
and
![]() $s_{j}$
and
$s_{j}$
and
![]() $0$
on all others. Then the fan of
$0$
on all others. Then the fan of
![]() $W$
is given by the single cone
$W$
is given by the single cone
![]() $C_{W}$
spanned by the
$C_{W}$
spanned by the
![]() $x_{ij}$
.
$x_{ij}$
.
Any
![]() $\mathbb{Q}$
-factorialization
$\mathbb{Q}$
-factorialization
![]() $\widetilde{W}$
corresponds to a simplicial subdivision of the cone
$\widetilde{W}$
corresponds to a simplicial subdivision of the cone
![]() $C_{W}$
(see [Reference FultonFul93, p. 65]). We now check that every choice of
$C_{W}$
(see [Reference FultonFul93, p. 65]). We now check that every choice of
![]() $\widetilde{W}$
is non-singular.
$\widetilde{W}$
is non-singular.
A maximal cone of
![]() $\widetilde{W}$
is spanned by
$\widetilde{W}$
is spanned by
![]() $n=n_{1}+n_{2}-1$
independent rays of
$n=n_{1}+n_{2}-1$
independent rays of
![]() $C_{W}$
. Each ray of
$C_{W}$
. Each ray of
![]() $C_{W}$
corresponds to a choice of
$C_{W}$
corresponds to a choice of
![]() $x_{ij}$
, and we can index these by edges of the complete bipartite graph
$x_{ij}$
, and we can index these by edges of the complete bipartite graph
![]() $B$
on the
$B$
on the
![]() $r_{i}$
and
$r_{i}$
and
![]() $s_{j}$
. These
$s_{j}$
. These
![]() $x_{ij}$
are independent if and only if the corresponding edges form a spanning tree. Let
$x_{ij}$
are independent if and only if the corresponding edges form a spanning tree. Let
![]() $w_{1}\ldots w_{n}$
span a maximal cone of
$w_{1}\ldots w_{n}$
span a maximal cone of
![]() $\widetilde{W}$
. On this affine chart,
$\widetilde{W}$
. On this affine chart,
![]() $\widetilde{W}$
is smooth if and only if the
$\widetilde{W}$
is smooth if and only if the
![]() $w_{i}$
generate
$w_{i}$
generate
![]() $N$
as a lattice. We have shown already that the
$N$
as a lattice. We have shown already that the
![]() $x_{ij}$
generate
$x_{ij}$
generate
![]() $N$
. But every
$N$
. But every
![]() $x_{ij}$
is either one of the
$x_{ij}$
is either one of the
![]() $w_{i}$
, or it completes a cycle in
$w_{i}$
, or it completes a cycle in
![]() $B$
, so that it is a
$B$
, so that it is a
![]() $\mathbb{Z}$
-linear combination of the
$\mathbb{Z}$
-linear combination of the
![]() $w_{i}$
.◻
$w_{i}$
.◻
Proposition 5.3.3. Let
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
be semistable projective good minimal dlt pairs over the germ of a pointed curve
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
be semistable projective good minimal dlt pairs over the germ of a pointed curve
![]() $\mathscr{C}$
, such that both
$\mathscr{C}$
, such that both
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
and
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Y}}$
contain their respective special fibers. The product
$\unicode[STIX]{x1D6E5}_{\mathscr{Y}}$
contain their respective special fibers. The product
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is a log canonical pair,
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is a log canonical pair,
![]() $K_{\mathscr{Z}}+\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is semiample, and the log canonical centers of
$K_{\mathscr{Z}}+\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is semiample, and the log canonical centers of
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
are strata of the coefficient-
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
are strata of the coefficient-
![]() $1$
part of
$1$
part of
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
.
$\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
.
Proof. We first show the product
![]() $\mathscr{Z}$
is normal. As
$\mathscr{Z}$
is normal. As
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{Y}$
are semistable, the special fibers
$\mathscr{Y}$
are semistable, the special fibers
![]() $\mathscr{X}_{k}$
and
$\mathscr{X}_{k}$
and
![]() $\mathscr{Y}_{k}$
are reduced. The dlt condition guarantees that both
$\mathscr{Y}_{k}$
are reduced. The dlt condition guarantees that both
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{Y}$
are Cohen–Macaulay, hence the Cartier divisors
$\mathscr{Y}$
are Cohen–Macaulay, hence the Cartier divisors
![]() $\mathscr{X}_{k}$
and
$\mathscr{X}_{k}$
and
![]() $\mathscr{Y}_{k}$
are Cohen–Macaulay. The special fiber
$\mathscr{Y}_{k}$
are Cohen–Macaulay. The special fiber
![]() $\mathscr{Z}_{k}$
is the product
$\mathscr{Z}_{k}$
is the product
![]() $\mathscr{X}_{k}\times _{k}\mathscr{Y}_{k}$
. Since
$\mathscr{X}_{k}\times _{k}\mathscr{Y}_{k}$
. Since
![]() $k$
is algebraically closed,
$k$
is algebraically closed,
![]() $\mathscr{Z}_{k}$
is reduced, so
$\mathscr{Z}_{k}$
is reduced, so
![]() $\mathscr{Z}$
is regular in codimension
$\mathscr{Z}$
is regular in codimension
![]() $1$
. The special fiber
$1$
. The special fiber
![]() $\mathscr{Z}_{k}$
is the product of Cohen–Macaulay varieties over a field, so it is Cohen–Macaulay by [Reference Bouchiba and KabbajBK02]. As
$\mathscr{Z}_{k}$
is the product of Cohen–Macaulay varieties over a field, so it is Cohen–Macaulay by [Reference Bouchiba and KabbajBK02]. As
![]() $\mathscr{Z}_{k}$
is a Cartier divisor in
$\mathscr{Z}_{k}$
is a Cartier divisor in
![]() $\mathscr{Z}$
,
$\mathscr{Z}$
,
![]() $\mathscr{Z}$
must be Cohen–Macaulay and, in particular, it is
$\mathscr{Z}$
must be Cohen–Macaulay and, in particular, it is
![]() $S_{2}$
.
$S_{2}$
.
The divisor
![]() $K_{\mathscr{Z}}+\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is semiample by pullback of semiample divisors. Let
$K_{\mathscr{Z}}+\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is semiample by pullback of semiample divisors. Let
![]() $(\widetilde{\mathscr{X}},\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{X}}})$
and
$(\widetilde{\mathscr{X}},\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{X}}})$
and
![]() $(\widetilde{\mathscr{Y}},\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{Y}}})$
be log resolutions of
$(\widetilde{\mathscr{Y}},\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{Y}}})$
be log resolutions of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}\mathscr{Y})$
, respectively. Then we have
$(\mathscr{Y},\unicode[STIX]{x1D6E5}\mathscr{Y})$
, respectively. Then we have
 $$\begin{eqnarray}\displaystyle & K_{\widetilde{\mathscr{X}}}+\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{X}}}=f_{\mathscr{X}}^{\ast }(K_{\mathscr{X}}+\unicode[STIX]{x1D6E5}_{\mathscr{X}})+\sum a_{i}E_{\mathscr{X},i}, & \displaystyle \nonumber\\ \displaystyle & K_{\widetilde{\mathscr{Y}}}+\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{Y}}}=f_{\mathscr{Y}}^{\ast }(K_{\mathscr{Y}}+\unicode[STIX]{x1D6E5}_{\mathscr{Y}})+\sum b_{j}E_{\mathscr{Y},j}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & K_{\widetilde{\mathscr{X}}}+\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{X}}}=f_{\mathscr{X}}^{\ast }(K_{\mathscr{X}}+\unicode[STIX]{x1D6E5}_{\mathscr{X}})+\sum a_{i}E_{\mathscr{X},i}, & \displaystyle \nonumber\\ \displaystyle & K_{\widetilde{\mathscr{Y}}}+\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{Y}}}=f_{\mathscr{Y}}^{\ast }(K_{\mathscr{Y}}+\unicode[STIX]{x1D6E5}_{\mathscr{Y}})+\sum b_{j}E_{\mathscr{Y},j}, & \displaystyle \nonumber\end{eqnarray}$$
where the coefficients
![]() $a_{i}$
and
$a_{i}$
and
![]() $b_{j}$
are non-negative. Let
$b_{j}$
are non-negative. Let
![]() $\widetilde{\mathscr{Z}}$
be a toroidal log resolution of the fs product
$\widetilde{\mathscr{Z}}$
be a toroidal log resolution of the fs product
![]() $\widetilde{\mathscr{X}}\times _{\mathscr{C}}^{\mathit{fs}}\widetilde{\mathscr{Y}}$
. In particular,
$\widetilde{\mathscr{X}}\times _{\mathscr{C}}^{\mathit{fs}}\widetilde{\mathscr{Y}}$
. In particular,
![]() $\widetilde{\mathscr{Z}}$
is a log resolution of
$\widetilde{\mathscr{Z}}$
is a log resolution of
![]() $\mathscr{Z}$
and we can write
$\mathscr{Z}$
and we can write
where
![]() $\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{Z}}}$
is effective. Over the generic fiber,
$\unicode[STIX]{x1D6E5}_{\widetilde{\mathscr{Z}}}$
is effective. Over the generic fiber,
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is dlt, so we need only compute discrepancies over the special fiber, namely study the positivity of the coefficients
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is dlt, so we need only compute discrepancies over the special fiber, namely study the positivity of the coefficients
![]() $c_{h}$
.
$c_{h}$
.
Let
![]() $\unicode[STIX]{x1D6E4}$
be a divisor of
$\unicode[STIX]{x1D6E4}$
be a divisor of
![]() $\widetilde{\mathscr{Z}}$
over the special fiber, denote by
$\widetilde{\mathscr{Z}}$
over the special fiber, denote by
![]() $v_{\unicode[STIX]{x1D6E4}}$
the corresponding divisorial valuation in
$v_{\unicode[STIX]{x1D6E4}}$
the corresponding divisorial valuation in
![]() $\text{Sk}(\widetilde{\mathscr{Z}}^{+})$
, and by
$\text{Sk}(\widetilde{\mathscr{Z}}^{+})$
, and by
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
,
$\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
,
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
, and
$\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
, and
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
its images in
$\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
its images in
![]() $\mathscr{X}$
,
$\mathscr{X}$
,
![]() $\mathscr{Y}$
, and
$\mathscr{Y}$
, and
![]() $\mathscr{Z}$
. The projections of
$\mathscr{Z}$
. The projections of
![]() $v_{\unicode[STIX]{x1D6E4}}$
in
$v_{\unicode[STIX]{x1D6E4}}$
in
![]() $\text{Sk}(\widetilde{\mathscr{X}}^{+})$
and
$\text{Sk}(\widetilde{\mathscr{X}}^{+})$
and
![]() $\text{Sk}(\widetilde{\mathscr{Y}}^{+})$
are divisorial valuations. Up to subdivisions of the skeletons, we can assume without loss of generality that the projections correspond to divisors
$\text{Sk}(\widetilde{\mathscr{Y}}^{+})$
are divisorial valuations. Up to subdivisions of the skeletons, we can assume without loss of generality that the projections correspond to divisors
![]() $\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}$
and
$\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}$
and
![]() $\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{Y}}}$
.
$\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{Y}}}$
.
Choose
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
-logarithmic and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
-logarithmic and
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Y}}$
-logarithmic pluricanonical forms
$\unicode[STIX]{x1D6E5}_{\mathscr{Y}}$
-logarithmic pluricanonical forms
![]() $\unicode[STIX]{x1D714}_{\mathscr{X}}$
on
$\unicode[STIX]{x1D714}_{\mathscr{X}}$
on
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\unicode[STIX]{x1D714}_{\mathscr{Y}}$
on
$\unicode[STIX]{x1D714}_{\mathscr{Y}}$
on
![]() $\mathscr{Y}$
respectively, such that the divisors
$\mathscr{Y}$
respectively, such that the divisors
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{X}})$
and
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{X}})$
and
![]() $\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Y}})$
do not contain
$\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Y}})$
do not contain
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
and
$\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
and
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
respectively, where
$\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
respectively, where
![]() $\mathscr{X}^{+}=(\mathscr{X},\lceil \unicode[STIX]{x1D6E5}_{\mathscr{X}}\rceil )$
and
$\mathscr{X}^{+}=(\mathscr{X},\lceil \unicode[STIX]{x1D6E5}_{\mathscr{X}}\rceil )$
and
![]() $\mathscr{Y}^{+}=(\mathscr{Y},\lceil \unicode[STIX]{x1D6E5}_{\mathscr{Y}}\rceil )$
. Then, the divisor
$\mathscr{Y}^{+}=(\mathscr{Y},\lceil \unicode[STIX]{x1D6E5}_{\mathscr{Y}}\rceil )$
. Then, the divisor
![]() $\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Z}})$
, associated to the wedge product
$\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Z}})$
, associated to the wedge product
![]() $\unicode[STIX]{x1D714}_{\mathscr{Z}}$
of the pullbacks
$\unicode[STIX]{x1D714}_{\mathscr{Z}}$
of the pullbacks
![]() $\unicode[STIX]{x1D714}_{\mathscr{X}}$
and
$\unicode[STIX]{x1D714}_{\mathscr{X}}$
and
![]() $\unicode[STIX]{x1D714}_{\mathscr{Y}}$
to
$\unicode[STIX]{x1D714}_{\mathscr{Y}}$
to
![]() $\mathscr{Z}$
, does not contain
$\mathscr{Z}$
, does not contain
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
. Denote by
$\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
. Denote by
![]() $\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}}$
,
$\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}}$
,
![]() $\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}}$
, and
$\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}}$
, and
![]() $\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}}$
the pullback of the respective forms to
$\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}}$
the pullback of the respective forms to
![]() $\widetilde{\mathscr{X}}$
,
$\widetilde{\mathscr{X}}$
,
![]() $\widetilde{\mathscr{Y}}$
, and
$\widetilde{\mathscr{Y}}$
, and
![]() $\widetilde{\mathscr{Z}}$
. Then we have
$\widetilde{\mathscr{Z}}$
. Then we have
 $$\begin{eqnarray}\displaystyle & \text{div}_{\widetilde{\mathscr{X}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}})=f_{\mathscr{X}}^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{X}}))+\sum a_{i}E_{\mathscr{X},i}, & \displaystyle \nonumber\\ \displaystyle & \text{div}_{\widetilde{\mathscr{Y}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}})=f_{\mathscr{Y}}^{\ast }(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Y}}))+\sum b_{j}E_{\mathscr{Y},j}, & \displaystyle \nonumber\\ \displaystyle & \text{div}_{\widetilde{\mathscr{Z}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}})=f_{\mathscr{Z}}^{\ast }(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Z}}))+\sum c_{h}E_{\mathscr{Z},h}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \text{div}_{\widetilde{\mathscr{X}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}})=f_{\mathscr{X}}^{\ast }(\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{X}}))+\sum a_{i}E_{\mathscr{X},i}, & \displaystyle \nonumber\\ \displaystyle & \text{div}_{\widetilde{\mathscr{Y}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}})=f_{\mathscr{Y}}^{\ast }(\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Y}}))+\sum b_{j}E_{\mathscr{Y},j}, & \displaystyle \nonumber\\ \displaystyle & \text{div}_{\widetilde{\mathscr{Z}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}})=f_{\mathscr{Z}}^{\ast }(\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Z}}))+\sum c_{h}E_{\mathscr{Z},h}. & \displaystyle \nonumber\end{eqnarray}$$
As
![]() $\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{X}})$
,
$\text{div}_{\mathscr{X}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{X}})$
,
![]() $\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Y}})$
, and
$\text{div}_{\mathscr{Y}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Y}})$
, and
![]() $\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Z}})$
do not contain
$\text{div}_{\mathscr{Z}^{+}}(\unicode[STIX]{x1D714}_{\mathscr{Z}})$
do not contain
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
,
$\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
,
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
, and
$\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
, and
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
respectively, we have
$\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
respectively, we have
 $$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}}(\text{div}_{\widetilde{\mathscr{X}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}})) & = & \displaystyle \sum a_{i}v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}}(E_{\mathscr{X},i})\geqslant 0,\nonumber\\ \displaystyle v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathcal{Y}}}}(\text{div}_{\widetilde{\mathscr{Y}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}})) & = & \displaystyle \sum b_{j}v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathcal{Y}}}}(E_{\mathscr{Y},j})\geqslant 0,\nonumber\\ \displaystyle v_{\unicode[STIX]{x1D6E4}}(\text{div}_{\widetilde{\mathscr{Z}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}})) & = & \displaystyle \sum c_{h}v_{\unicode[STIX]{x1D6E4}}(E_{\mathscr{Z},h}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}}(\text{div}_{\widetilde{\mathscr{X}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}})) & = & \displaystyle \sum a_{i}v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}}(E_{\mathscr{X},i})\geqslant 0,\nonumber\\ \displaystyle v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathcal{Y}}}}(\text{div}_{\widetilde{\mathscr{Y}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}})) & = & \displaystyle \sum b_{j}v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathcal{Y}}}}(E_{\mathscr{Y},j})\geqslant 0,\nonumber\\ \displaystyle v_{\unicode[STIX]{x1D6E4}}(\text{div}_{\widetilde{\mathscr{Z}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}})) & = & \displaystyle \sum c_{h}v_{\unicode[STIX]{x1D6E4}}(E_{\mathscr{Z},h}).\nonumber\end{eqnarray}$$
From formula (4.2.5),
![]() $v_{\unicode[STIX]{x1D6E4}}(\text{div}_{\widetilde{\mathscr{Z}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}}))=v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathcal{Y}}}}(\text{div}_{\widetilde{\mathscr{Y}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}}))+v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}}(\text{div}_{\widetilde{\mathscr{X}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}}))$
, hence we obtain that the log discrepancy of
$v_{\unicode[STIX]{x1D6E4}}(\text{div}_{\widetilde{\mathscr{Z}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Z}}}))=v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathcal{Y}}}}(\text{div}_{\widetilde{\mathscr{Y}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{Y}}}))+v_{\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}}(\text{div}_{\widetilde{\mathscr{X}}^{+}}(\unicode[STIX]{x1D714}_{\widetilde{\mathscr{X}}}))$
, hence we obtain that the log discrepancy of
![]() $\unicode[STIX]{x1D6E4}$
with respect to the pair
$\unicode[STIX]{x1D6E4}$
with respect to the pair
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is non-negative. Moreover, it is zero if and only if the log discrepancies of
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is non-negative. Moreover, it is zero if and only if the log discrepancies of
![]() $\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}$
and
$\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{X}}}$
and
![]() $\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{Y}}}$
are both zero, namely if and only if
$\unicode[STIX]{x1D6E4}_{\widetilde{\mathscr{Y}}}$
are both zero, namely if and only if
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
and
$\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
and
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
are log canonical centers of
$\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
are log canonical centers of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
, respectively. Since for dlt pairs the log canonical centers are the strata of the coefficient-
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
, respectively. Since for dlt pairs the log canonical centers are the strata of the coefficient-
![]() $1$
part of the boundary, it follows that any log canonical center of
$1$
part of the boundary, it follows that any log canonical center of
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is a product of such strata, hence a stratum of the coefficient-
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is a product of such strata, hence a stratum of the coefficient-
![]() $1$
part of
$1$
part of
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
.◻
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
.◻
5.3.4. Let
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
and
$(X,\unicode[STIX]{x1D6E5}_{X})$
and
![]() $(Y,\unicode[STIX]{x1D6E5}_{Y})$
be dlt pairs over the germ of a punctured curve
$(Y,\unicode[STIX]{x1D6E5}_{Y})$
be dlt pairs over the germ of a punctured curve
![]() $C$
, and
$C$
, and
![]() $(Z,\unicode[STIX]{x1D6E5}_{Z})$
their product, where
$(Z,\unicode[STIX]{x1D6E5}_{Z})$
their product, where
![]() $\unicode[STIX]{x1D6E5}_{Z}=X\times _{C}\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D6E5}_{X}\times _{C}Y$
. Let
$\unicode[STIX]{x1D6E5}_{Z}=X\times _{C}\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D6E5}_{X}\times _{C}Y$
. Let
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
be semistable projective good minimal dlt models over the pointed curve.
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
be semistable projective good minimal dlt models over the pointed curve.
Theorem 5.3.5. The product
![]() $(Z,\unicode[STIX]{x1D6E5}_{Z})$
has a semistable projective good minimal dlt model
$(Z,\unicode[STIX]{x1D6E5}_{Z})$
has a semistable projective good minimal dlt model
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{Z}^{\prime }})$
and
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D6E5}_{\mathscr{Z}^{\prime }})$
and
![]() ${\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D6E5}_{\mathscr{Z}^{\prime }})\simeq {\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D6E5}_{\mathscr{X}})\times {\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
.
${\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D6E5}_{\mathscr{Z}^{\prime }})\simeq {\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D6E5}_{\mathscr{X}})\times {\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
.
Proof. Let
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
be the product of
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
be the product of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
as in Proposition 5.3.3. Thus
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
as in Proposition 5.3.3. Thus
![]() $K_{\mathscr{Z}}+\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is semiample and log canonical, so any minimal dlt model over
$K_{\mathscr{Z}}+\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
is semiample and log canonical, so any minimal dlt model over
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
will also have semiample log canonical divisor.
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
will also have semiample log canonical divisor.
Let
![]() $\unicode[STIX]{x1D717}:\mathscr{W}\rightarrow \mathscr{Z}$
be a log resolution given by iterated blow-ups at centers of codimension at least
$\unicode[STIX]{x1D717}:\mathscr{W}\rightarrow \mathscr{Z}$
be a log resolution given by iterated blow-ups at centers of codimension at least
![]() $2$
. Then there exists an effective divisor
$2$
. Then there exists an effective divisor
![]() $D$
supported on all of the exceptional divisors, such that
$D$
supported on all of the exceptional divisors, such that
![]() $-D$
is
$-D$
is
![]() $\unicode[STIX]{x1D717}$
-ample.
$\unicode[STIX]{x1D717}$
-ample.
Claim. There exist
![]() $B_{\mathscr{X}}$
and
$B_{\mathscr{X}}$
and
![]() $B_{\mathscr{Y}}$
effective divisors on
$B_{\mathscr{Y}}$
effective divisors on
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{Y}$
whose respective supports contain no log canonical centers of
$\mathscr{Y}$
whose respective supports contain no log canonical centers of
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}$
and
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Y}}$
, and such that
$\unicode[STIX]{x1D6E5}_{\mathscr{Y}}$
, and such that
![]() $B_{\mathscr{X}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
$B_{\mathscr{X}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
![]() $B_{\mathscr{Y}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
are ample, for
$B_{\mathscr{Y}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
are ample, for
![]() $\unicode[STIX]{x1D716}$
small and rational.
$\unicode[STIX]{x1D716}$
small and rational.
Choose
![]() $\unicode[STIX]{x1D716}$
small and rational. Then
$\unicode[STIX]{x1D716}$
small and rational. Then
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{X}}=\unicode[STIX]{x1D6E5}_{\mathscr{X}}+B_{\mathscr{X}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
$\unicode[STIX]{x1D6E4}_{\mathscr{X}}=\unicode[STIX]{x1D6E5}_{\mathscr{X}}+B_{\mathscr{X}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Y}}=\unicode[STIX]{x1D6E5}_{\mathscr{Y}}+B_{\mathscr{Y}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
are effective, and
$\unicode[STIX]{x1D6E4}_{\mathscr{Y}}=\unicode[STIX]{x1D6E5}_{\mathscr{Y}}+B_{\mathscr{Y}}-\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
are effective, and
![]() $(\mathscr{X},\unicode[STIX]{x1D6E4}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E4}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E4}_{\mathscr{Y}})$
are klt. Let
$(\mathscr{Y},\unicode[STIX]{x1D6E4}_{\mathscr{Y}})$
are klt. Let
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{W}}^{\prime }$
be the log pullback to
$\unicode[STIX]{x1D6E4}_{\mathscr{W}}^{\prime }$
be the log pullback to
![]() $\mathscr{W}$
of the product
$\mathscr{W}$
of the product
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
of
$\unicode[STIX]{x1D6E4}_{\mathscr{Z}}$
of
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
and
$\unicode[STIX]{x1D6E4}_{\mathscr{X}}$
and
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
, namely
$\unicode[STIX]{x1D6E4}_{\mathscr{Y}}$
, namely
![]() $K_{\mathscr{W}}+\unicode[STIX]{x1D6E4}_{\mathscr{W}}^{\prime }=\unicode[STIX]{x1D717}^{\ast }(K_{\mathscr{Z}}+\unicode[STIX]{x1D6E4}_{\mathscr{Z}})$
; we denote by
$K_{\mathscr{W}}+\unicode[STIX]{x1D6E4}_{\mathscr{W}}^{\prime }=\unicode[STIX]{x1D717}^{\ast }(K_{\mathscr{Z}}+\unicode[STIX]{x1D6E4}_{\mathscr{Z}})$
; we denote by
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{W}}$
the positive part of
$\unicode[STIX]{x1D6E4}_{\mathscr{W}}$
the positive part of
![]() $\unicode[STIX]{x1D6E4}_{\mathscr{W}}^{\prime }$
. Since
$\unicode[STIX]{x1D6E4}_{\mathscr{W}}^{\prime }$
. Since
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E4}_{\mathscr{Z}})$
was klt, so is
$(\mathscr{Z},\unicode[STIX]{x1D6E4}_{\mathscr{Z}})$
was klt, so is
![]() $(\mathscr{W},\unicode[STIX]{x1D6E4}_{\mathscr{W}})$
. For sufficiently small
$(\mathscr{W},\unicode[STIX]{x1D6E4}_{\mathscr{W}})$
. For sufficiently small
![]() $\unicode[STIX]{x1D6FF}$
,
$\unicode[STIX]{x1D6FF}$
,
![]() $(\mathscr{W},\unicode[STIX]{x1D6E4}_{\mathscr{W}}+\unicode[STIX]{x1D6FF}D)$
is still klt.
$(\mathscr{W},\unicode[STIX]{x1D6E4}_{\mathscr{W}}+\unicode[STIX]{x1D6FF}D)$
is still klt.
Let
![]() $\unicode[STIX]{x1D6FC}_{i}$
be arbitrary small rational coefficients, one for each divisor
$\unicode[STIX]{x1D6FC}_{i}$
be arbitrary small rational coefficients, one for each divisor
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}$
of
$\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}$
of
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
with coefficient
$\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
with coefficient
![]() $1$
and in the special fiber. We will recover the requested dlt model by running an MMP with scaling on the pair
$1$
and in the special fiber. We will recover the requested dlt model by running an MMP with scaling on the pair
![]() $(\mathscr{W},\unicode[STIX]{x1D6E4}_{\mathscr{W}}+\unicode[STIX]{x1D6FF}D-\sum \unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1})$
, scaling with respect to an ample divisor
$(\mathscr{W},\unicode[STIX]{x1D6E4}_{\mathscr{W}}+\unicode[STIX]{x1D6FF}D-\sum \unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1})$
, scaling with respect to an ample divisor
![]() $A$
equivalent to
$A$
equivalent to
![]() $-D$
. By [Reference Birkar, Cascini, Hacon and McKernanBCHM10] this MMP terminates in a log terminal model
$-D$
. By [Reference Birkar, Cascini, Hacon and McKernanBCHM10] this MMP terminates in a log terminal model
![]() $\unicode[STIX]{x1D719}:\mathscr{W}{\dashrightarrow}\mathscr{Z}^{\prime }$
. Moreover, as long as the
$\unicode[STIX]{x1D719}:\mathscr{W}{\dashrightarrow}\mathscr{Z}^{\prime }$
. Moreover, as long as the
![]() $\unicode[STIX]{x1D6FC}_{i}$
are small relative to
$\unicode[STIX]{x1D6FC}_{i}$
are small relative to
![]() $\unicode[STIX]{x1D6FF}$
, when the MMP terminates it must be the case that every exceptional divisor is contracted. As running MMP induces birational contractions, the morphism
$\unicode[STIX]{x1D6FF}$
, when the MMP terminates it must be the case that every exceptional divisor is contracted. As running MMP induces birational contractions, the morphism
![]() $\unicode[STIX]{x1D713}:\mathscr{Z}^{\prime }\rightarrow \mathscr{Z}$
is small. Hence
$\unicode[STIX]{x1D713}:\mathscr{Z}^{\prime }\rightarrow \mathscr{Z}$
is small. Hence
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is log canonical, and every log canonical center dominates a stratum of the coefficient-
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is log canonical, and every log canonical center dominates a stratum of the coefficient-
![]() $1$
part of
$1$
part of
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
.
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
.
By construction of
![]() $\mathscr{Z}^{\prime }$
, the divisor
$\mathscr{Z}^{\prime }$
, the divisor
![]() $-\sum \,\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D719}_{\ast }A$
is
$-\sum \,\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D719}_{\ast }A$
is
![]() $\unicode[STIX]{x1D713}$
-ample, where
$\unicode[STIX]{x1D713}$
-ample, where
![]() $\unicode[STIX]{x1D707}$
is arbitrarily small. But for
$\unicode[STIX]{x1D707}$
is arbitrarily small. But for
![]() $\unicode[STIX]{x1D707}$
small enough, we can absorb
$\unicode[STIX]{x1D707}$
small enough, we can absorb
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D719}_{\ast }A$
into the term
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D719}_{\ast }A$
into the term
![]() $\unicode[STIX]{x1D6FF}D$
. Thus in fact
$\unicode[STIX]{x1D6FF}D$
. Thus in fact
![]() $-\sum \,\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}$
is
$-\sum \,\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}$
is
![]() $\unicode[STIX]{x1D713}$
-ample. As a result we can represent
$\unicode[STIX]{x1D713}$
-ample. As a result we can represent
At this point we may take an arbitrarily large Veronese subring and assume the
![]() $\unicode[STIX]{x1D6FC}_{i}$
are all integers.
$\unicode[STIX]{x1D6FC}_{i}$
are all integers.
Now we show that
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is a dlt pair by looking at a formal toric model. Indeed, by Proposition 5.3.3,
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is a dlt pair by looking at a formal toric model. Indeed, by Proposition 5.3.3,
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is formally locally toric at the log canonical centers, and the condition of being dlt is a formally local property. Moreover, we reduce to checking this property at the log canonical centers of
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is formally locally toric at the log canonical centers, and the condition of being dlt is a formally local property. Moreover, we reduce to checking this property at the log canonical centers of
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
that lie in the special fiber, as the generic fibers of
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
that lie in the special fiber, as the generic fibers of
![]() $\mathscr{Z}^{\prime }$
and
$\mathscr{Z}^{\prime }$
and
![]() $\mathscr{Z}$
are isomorphic and the latter is dlt.
$\mathscr{Z}$
are isomorphic and the latter is dlt.
Let
![]() $z$
be the generic point of the image in
$z$
be the generic point of the image in
![]() $\mathscr{Z}$
of a log canonical center of
$\mathscr{Z}$
of a log canonical center of
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
, hence
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
, hence
![]() $z$
is the generic point of a log canonical center of
$z$
is the generic point of a log canonical center of
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
and by Proposition 5.3.3 it is a stratum of the coefficient-
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
and by Proposition 5.3.3 it is a stratum of the coefficient-
![]() $1$
part of
$1$
part of
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
. Let
$\unicode[STIX]{x1D6E5}_{\mathscr{Z}}$
. Let
![]() $x$
and
$x$
and
![]() $y$
be the generic points of the corresponding strata of
$y$
be the generic points of the corresponding strata of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
. Let
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
. Let
![]() $E_{x}$
and
$E_{x}$
and
![]() $E_{y}$
be the monoids of effective Cartier divisors supported on the strata near
$E_{y}$
be the monoids of effective Cartier divisors supported on the strata near
![]() $x$
and
$x$
and
![]() $y$
, respectively. Then the corresponding monoid for
$y$
, respectively. Then the corresponding monoid for
![]() $z$
is
$z$
is
![]() $\langle E_{x}\oplus E_{y}\rangle /(t_{x}=t_{y})$
, where
$\langle E_{x}\oplus E_{y}\rangle /(t_{x}=t_{y})$
, where
![]() $t_{x}$
and
$t_{x}$
and
![]() $t_{y}$
are the respective sums of local equations of strata in the special fibers. This monoid has the form
$t_{y}$
are the respective sums of local equations of strata in the special fibers. This monoid has the form
![]() $M\oplus \mathbb{N}^{l}$
, where
$M\oplus \mathbb{N}^{l}$
, where
![]() $l$
is the number of horizontal divisors containing
$l$
is the number of horizontal divisors containing
![]() $z$
, and
$z$
, and
![]() $M$
is a monoid of the type considered in Lemma 5.3.2. The toric variety
$M$
is a monoid of the type considered in Lemma 5.3.2. The toric variety
![]() $T_{M,k}=\text{Spec}\,k[M\oplus \mathbb{N}^{l}]$
is a formal local model for
$T_{M,k}=\text{Spec}\,k[M\oplus \mathbb{N}^{l}]$
is a formal local model for
![]() $\mathscr{Z}$
near
$\mathscr{Z}$
near
![]() $z$
, so it suffices to consider
$z$
, so it suffices to consider
where the divisors
![]() $\unicode[STIX]{x1D6E5}_{T,i}$
range over the torus invariant Weil divisors corresponding to the
$\unicode[STIX]{x1D6E5}_{T,i}$
range over the torus invariant Weil divisors corresponding to the
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}$
.
$\unicode[STIX]{x1D6E5}_{\mathscr{Z},i}^{=1}$
.
The divisors corresponding to the
![]() $l$
generators of
$l$
generators of
![]() $\mathbb{N}^{l}$
are Cartier, so their contribution to
$\mathbb{N}^{l}$
are Cartier, so their contribution to
![]() $T$
is trivial and we can reduce to the case
$T$
is trivial and we can reduce to the case
![]() $l=0$
. For sufficiently general choices for the
$l=0$
. For sufficiently general choices for the
![]() $\unicode[STIX]{x1D6FC}_{i}$
, the toric variety
$\unicode[STIX]{x1D6FC}_{i}$
, the toric variety
![]() $T^{\prime }$
is simplicial, its fan being induced by the simplicial subdivision of the fan of
$T^{\prime }$
is simplicial, its fan being induced by the simplicial subdivision of the fan of
![]() $T_{M,k}$
such that the
$T_{M,k}$
such that the
![]() $\unicode[STIX]{x1D6FC}_{i}$
induce a strictly convex PL function. Thus,
$\unicode[STIX]{x1D6FC}_{i}$
induce a strictly convex PL function. Thus,
![]() $T^{\prime }$
is a small
$T^{\prime }$
is a small
![]() $\mathbb{Q}$
-factorialization of
$\mathbb{Q}$
-factorialization of
![]() $T_{M,k}$
. By Lemma 5.3.2, for any such model,
$T_{M,k}$
. By Lemma 5.3.2, for any such model,
![]() $T^{\prime }$
is a smooth toric variety, hence its invariant divisors are snc. Thus
$T^{\prime }$
is a smooth toric variety, hence its invariant divisors are snc. Thus
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is dlt.
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is dlt.
Finally, we compute the dual complex of the coefficient-
![]() $1$
part of
$1$
part of
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
by looking at formal toric models again. Locally at the generic points of the log canonical centers,
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
by looking at formal toric models again. Locally at the generic points of the log canonical centers,
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
are snc, hence log-regular, and are also semistable. By Proposition 2.5.4 there is a bijective correspondence between pairs of points in the Kato fans of
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
are snc, hence log-regular, and are also semistable. By Proposition 2.5.4 there is a bijective correspondence between pairs of points in the Kato fans of
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{Y}$
locally around the log canonical centers and the points in the Kato fan of their product. This induces, by Proposition 3.4.3, a PL homeomorphism between the product of skeletons around the log canonical centers and the skeleton of their product, namely a bijective correspondence between pairs of points in the dual complexes
$\mathscr{Y}$
locally around the log canonical centers and the points in the Kato fan of their product. This induces, by Proposition 3.4.3, a PL homeomorphism between the product of skeletons around the log canonical centers and the skeleton of their product, namely a bijective correspondence between pairs of points in the dual complexes
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
, and points in the skeleton of
$\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
, and points in the skeleton of
![]() $(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
whose projections map to
$(\mathscr{Z},\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
whose projections map to
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
. A face
$\unicode[STIX]{x1D6E5}_{\mathscr{Y}}^{=1}$
. A face
![]() $\unicode[STIX]{x1D70E}_{z}$
of the skeleton of
$\unicode[STIX]{x1D70E}_{z}$
of the skeleton of
![]() $\mathscr{Z}$
, where
$\mathscr{Z}$
, where
![]() $z$
is a log canonical center corresponding to
$z$
is a log canonical center corresponding to
![]() $(x,y)$
, corresponds to a prime ideal of the monoid
$(x,y)$
, corresponds to a prime ideal of the monoid
![]() $E_{z}=\langle E_{x}\oplus E_{y}\rangle /(t_{x}=t_{y})$
. Thus, we may reduce to considering such faces in the formal toric model
$E_{z}=\langle E_{x}\oplus E_{y}\rangle /(t_{x}=t_{y})$
. Thus, we may reduce to considering such faces in the formal toric model
![]() $T_{M,k}$
, and to studying the dual complex of the coefficient-
$T_{M,k}$
, and to studying the dual complex of the coefficient-
![]() $1$
part of
$1$
part of
![]() $(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
in the formal model
$(\mathscr{Z}^{\prime },\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
in the formal model
![]() $T^{\prime }$
. But
$T^{\prime }$
. But
![]() $T^{\prime }$
is obtained by a simplicial subdivision of
$T^{\prime }$
is obtained by a simplicial subdivision of
![]() $T$
. Thus, we conclude that the dual complex
$T$
. Thus, we conclude that the dual complex
![]() ${\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is identified with the product of the dual complexes of the coefficient-
${\mathcal{D}}_{0}^{=1}(\unicode[STIX]{x1D713}^{\ast }\unicode[STIX]{x1D6E5}_{\mathscr{Z}})$
is identified with the product of the dual complexes of the coefficient-
![]() $1$
part of
$1$
part of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
and
![]() $(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
.◻
$(\mathscr{Y},\unicode[STIX]{x1D6E5}_{\mathscr{Y}})$
.◻
Proof of Claim.
Let
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
be a good projective minimal dlt model of
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
be a good projective minimal dlt model of
![]() $(X,\unicode[STIX]{x1D6E5}_{X})$
and let
$(X,\unicode[STIX]{x1D6E5}_{X})$
and let
![]() $A_{\mathscr{X}}$
be an ample divisor on
$A_{\mathscr{X}}$
be an ample divisor on
![]() $\mathscr{X}$
. Let
$\mathscr{X}$
. Let
![]() ${\mathcal{J}}$
be the ideal sheaf of
${\mathcal{J}}$
be the ideal sheaf of
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and let
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and let
be the blow-up of
![]() $\mathscr{X}$
with respect to
$\mathscr{X}$
with respect to
![]() ${\mathcal{J}}$
. Then the transform
${\mathcal{J}}$
. Then the transform
![]() $-((\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1})^{\prime }+E)$
is a
$-((\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1})^{\prime }+E)$
is a
![]() $\unicode[STIX]{x1D712}$
-ample Cartier divisor, where
$\unicode[STIX]{x1D712}$
-ample Cartier divisor, where
![]() $(\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1})^{\prime }$
denotes the strict transform of
$(\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1})^{\prime }$
denotes the strict transform of
![]() $\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
$\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
and
![]() $E$
an effective divisor supported on the exceptional divisor of
$E$
an effective divisor supported on the exceptional divisor of
![]() $\unicode[STIX]{x1D712}$
. For small positive rational
$\unicode[STIX]{x1D712}$
. For small positive rational
![]() $\unicode[STIX]{x1D700}$
,
$\unicode[STIX]{x1D700}$
,
![]() $\unicode[STIX]{x1D712}^{\ast }(A_{\mathscr{X}})-\unicode[STIX]{x1D700}((\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1})^{\prime }+E)$
is ample. We choose such an
$\unicode[STIX]{x1D712}^{\ast }(A_{\mathscr{X}})-\unicode[STIX]{x1D700}((\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1})^{\prime }+E)$
is ample. We choose such an
![]() $\unicode[STIX]{x1D700}$
. For a sufficiently large integer
$\unicode[STIX]{x1D700}$
. For a sufficiently large integer
![]() $n$
, we can find
$n$
, we can find
such that
![]() $G_{\mathscr{X}^{\prime }}$
is effective and contains no log canonical centers. Then the pushforward
$G_{\mathscr{X}^{\prime }}$
is effective and contains no log canonical centers. Then the pushforward
![]() $G_{\mathscr{X}}\sim nA_{\mathscr{X}}-n\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
of
$G_{\mathscr{X}}\sim nA_{\mathscr{X}}-n\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}_{\mathscr{X}}^{=1}$
of
![]() $G_{\mathscr{X}^{\prime }}$
is effective and contains no log canonical centers of
$G_{\mathscr{X}^{\prime }}$
is effective and contains no log canonical centers of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. In particular,
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. In particular,
![]() $G_{\mathscr{X}}$
is Cartier at the log canonical centers of
$G_{\mathscr{X}}$
is Cartier at the log canonical centers of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
.
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
.
We can run the same construction for the ideal sheaf of the divisor
![]() $G_{\mathscr{X}}$
. Notice that the blow-up with respect to
$G_{\mathscr{X}}$
. Notice that the blow-up with respect to
![]() $G_{\mathscr{X}}$
is an isomorphism at the log canonical centers of
$G_{\mathscr{X}}$
is an isomorphism at the log canonical centers of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
as there
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
as there
![]() $G_{\mathscr{X}}$
is Cartier. We obtain that, for sufficiently small positive rationals
$G_{\mathscr{X}}$
is Cartier. We obtain that, for sufficiently small positive rationals
![]() $\unicode[STIX]{x1D6FF}$
and then sufficiently large integers
$\unicode[STIX]{x1D6FF}$
and then sufficiently large integers
![]() $m$
, we can find
$m$
, we can find
![]() $H_{\mathscr{X}}\sim mA_{\mathscr{X}}-m\unicode[STIX]{x1D6FF}G_{\mathscr{X}}$
such that it is effective and does not contain any log canonical center of
$H_{\mathscr{X}}\sim mA_{\mathscr{X}}-m\unicode[STIX]{x1D6FF}G_{\mathscr{X}}$
such that it is effective and does not contain any log canonical center of
![]() $(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. Then
$(\mathscr{X},\unicode[STIX]{x1D6E5}_{\mathscr{X}})$
. Then
implies that
For
![]() $\unicode[STIX]{x1D6FF}$
sufficiently small the term
$\unicode[STIX]{x1D6FF}$
sufficiently small the term
![]() $(1/\unicode[STIX]{x1D6FF}-n)$
is positive, and then for
$(1/\unicode[STIX]{x1D6FF}-n)$
is positive, and then for
![]() $m$
sufficiently large
$m$
sufficiently large
![]() $B_{\mathscr{X}}=(1/m\unicode[STIX]{x1D6FF})H_{\mathscr{X}}$
, which concludes the proof.◻
$B_{\mathscr{X}}=(1/m\unicode[STIX]{x1D6FF})H_{\mathscr{X}}$
, which concludes the proof.◻
6 Applications
6.1 Weight functions and skeletons for finite quotients
6.1.1. Let
![]() $X$
be a connected, smooth and proper
$X$
be a connected, smooth and proper
![]() $K$
-variety and let
$K$
-variety and let
![]() $G$
be a finite group acting on
$G$
be a finite group acting on
![]() $X$
. Let
$X$
. Let
![]() $X^{\text{an}}$
be the analytification of
$X^{\text{an}}$
be the analytification of
![]() $X$
. We recall that any point of
$X$
. We recall that any point of
![]() $X^{\text{an}}$
is a pair
$X^{\text{an}}$
is a pair
![]() $x=(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})$
with
$x=(\unicode[STIX]{x1D709}_{x},|\cdot |_{x})$
with
![]() $\unicode[STIX]{x1D709}_{x}\in X$
and
$\unicode[STIX]{x1D709}_{x}\in X$
and
![]() $|\cdot |_{x}$
an absolute value on the residue field
$|\cdot |_{x}$
an absolute value on the residue field
![]() $\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
that extends the absolute value on
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
that extends the absolute value on
![]() $K$
. For any point
$K$
. For any point
![]() $\unicode[STIX]{x1D709}_{x}$
of
$\unicode[STIX]{x1D709}_{x}$
of
![]() $X$
, an element
$X$
, an element
![]() $g$
of the group
$g$
of the group
![]() $G$
induces an isomorphism between the residue fields
$G$
induces an isomorphism between the residue fields
![]() $\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
and
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D709}_{x})$
and
![]() $\unicode[STIX]{x1D705}(g.\unicode[STIX]{x1D709}_{x})$
, which we still denote by
$\unicode[STIX]{x1D705}(g.\unicode[STIX]{x1D709}_{x})$
, which we still denote by
![]() $g$
. Then the action of
$g$
. Then the action of
![]() $G$
extends to
$G$
extends to
![]() $X^{\text{an}}$
in the following way:
$X^{\text{an}}$
in the following way:
In particular, the action preserves the sets of divisorial and birational points of
![]() $X$
.
$X$
.
Let
![]() $f:X\rightarrow Y=X/G$
be the quotient map of
$f:X\rightarrow Y=X/G$
be the quotient map of
![]() $K$
-schemes, let
$K$
-schemes, let
![]() $f^{\text{an}}:X^{\text{an}}\rightarrow Y^{\text{an}}$
be the map of Berkovich spaces induced by functoriality and let
$f^{\text{an}}:X^{\text{an}}\rightarrow Y^{\text{an}}$
be the map of Berkovich spaces induced by functoriality and let
![]() $\tilde{f}:X^{\text{an}}\rightarrow X^{\text{an}}/G$
be the quotient map of topological spaces.
$\tilde{f}:X^{\text{an}}\rightarrow X^{\text{an}}/G$
be the quotient map of topological spaces.
Proposition 6.1.2 [Reference BerkovichBer95, Corollary 5].
In the above notation, there is a canonical homeomorphism between
![]() $X^{\text{an}}/G$
and
$X^{\text{an}}/G$
and
![]() $Y^{\text{an}}$
such that
$Y^{\text{an}}$
such that
![]() $\tilde{f}$
and
$\tilde{f}$
and
![]() $f^{\text{an}}$
are identified.
$f^{\text{an}}$
are identified.
Lemma 6.1.3. Let
![]() $\unicode[STIX]{x1D714}$
be an
$\unicode[STIX]{x1D714}$
be an
![]() $m$
-pluricanonical rational form on
$m$
-pluricanonical rational form on
![]() $X$
. If
$X$
. If
![]() $\unicode[STIX]{x1D714}$
is
$\unicode[STIX]{x1D714}$
is
![]() $G$
-invariant, then the weight function associated to
$G$
-invariant, then the weight function associated to
![]() $\unicode[STIX]{x1D714}$
on the set of birational points is stable under the action of
$\unicode[STIX]{x1D714}$
on the set of birational points is stable under the action of
![]() $G$
.
$G$
.
Proof. Let
![]() $x$
be a birational point of
$x$
be a birational point of
![]() $X$
and
$X$
and
![]() $g$
an element of
$g$
an element of
![]() $G$
. There exist snc models
$G$
. There exist snc models
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{X}^{\prime }$
over
$\mathscr{X}^{\prime }$
over
![]() $R$
such that
$R$
such that
![]() $x\in \text{Sk}(\mathscr{X})$
and
$x\in \text{Sk}(\mathscr{X})$
and
![]() $g.x\in \text{Sk}(\mathscr{X}^{\prime })$
. By replacing them by an snc model
$g.x\in \text{Sk}(\mathscr{X}^{\prime })$
. By replacing them by an snc model
![]() $\mathscr{Y}$
that dominates both
$\mathscr{Y}$
that dominates both
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $\mathscr{X}^{\prime }$
, we can assume that both points lies in
$\mathscr{X}^{\prime }$
, we can assume that both points lies in
![]() $\text{Sk}(\mathscr{Y})$
. The weights of
$\text{Sk}(\mathscr{Y})$
. The weights of
![]() $\unicode[STIX]{x1D714}$
at
$\unicode[STIX]{x1D714}$
at
![]() $x$
and
$x$
and
![]() $g.x$
are such that
$g.x$
are such that
as
![]() $\unicode[STIX]{x1D714}$
is a
$\unicode[STIX]{x1D714}$
is a
![]() $G$
-invariant form. Thus we see that birational points in the same
$G$
-invariant form. Thus we see that birational points in the same
![]() $G$
-orbit have the same weight with respect to
$G$
-orbit have the same weight with respect to
![]() $\unicode[STIX]{x1D714}$
.◻
$\unicode[STIX]{x1D714}$
.◻
Corollary 6.1.4. Let
![]() $\unicode[STIX]{x1D714}$
be a
$\unicode[STIX]{x1D714}$
be a
![]() $G$
-invariant pluricanonical rational form on
$G$
-invariant pluricanonical rational form on
![]() $X$
. Then the Kontsevich–Soibelman skeleton
$X$
. Then the Kontsevich–Soibelman skeleton
![]() $\text{Sk}(X,\unicode[STIX]{x1D714})$
is stable under the action of
$\text{Sk}(X,\unicode[STIX]{x1D714})$
is stable under the action of
![]() $G$
.
$G$
.
Proof. This follows immediately from Lemma 6.1.3.◻
6.1.5. Let
![]() $y$
be a divisorial point of
$y$
be a divisorial point of
![]() $Y^{\text{an}}$
and consider a normal
$Y^{\text{an}}$
and consider a normal
![]() $R$
-model
$R$
-model
![]() $\mathscr{Y}$
of
$\mathscr{Y}$
of
![]() $Y$
adapted to
$Y$
adapted to
![]() $y$
; this means that
$y$
; this means that
![]() $y$
is the divisorial valuation associated to
$y$
is the divisorial valuation associated to
![]() $(\mathscr{Y},E)$
for some irreducible component
$(\mathscr{Y},E)$
for some irreducible component
![]() $E$
of
$E$
of
![]() $\mathscr{Y}_{k}$
, and the model
$\mathscr{Y}_{k}$
, and the model
![]() $\mathscr{Y}$
is regular in a neighborhood of the generic point of
$\mathscr{Y}$
is regular in a neighborhood of the generic point of
![]() $E$
. We denote by
$E$
. We denote by
![]() $\mathscr{X}$
the normalization of
$\mathscr{X}$
the normalization of
![]() $\mathscr{Y}$
inside
$\mathscr{Y}$
inside
![]() $K(X)$
, where
$K(X)$
, where
![]() $K(\mathscr{Y})=K(Y)=K(X)^{G}{\hookrightarrow}K(X)$
. As
$K(\mathscr{Y})=K(Y)=K(X)^{G}{\hookrightarrow}K(X)$
. As
![]() $X$
is normal and the quotient map
$X$
is normal and the quotient map
![]() $f:X\rightarrow Y$
is finite, we obtain that
$f:X\rightarrow Y$
is finite, we obtain that
![]() $\mathscr{X}$
is an
$\mathscr{X}$
is an
![]() $R$
-model of
$R$
-model of
![]() $X$
. Moreover, by normality
$X$
. Moreover, by normality
![]() $\mathscr{X}$
is regular at the generic points of the special fiber
$\mathscr{X}$
is regular at the generic points of the special fiber
![]() $\mathscr{X}_{k}$
.
$\mathscr{X}_{k}$
.
6.1.6. We assume
![]() $\text{char}(k)=0$
. We denote respectively by
$\text{char}(k)=0$
. We denote respectively by
![]() $R$
and by
$R$
and by
![]() $B$
the codimension-
$B$
the codimension-
![]() $1$
components of the ramification locus and of the branch locus of
$1$
components of the ramification locus and of the branch locus of
![]() $f:X\rightarrow Y$
. We set
$f:X\rightarrow Y$
. We set
![]() $X^{+}=(X,R_{\text{red}})$
and
$X^{+}=(X,R_{\text{red}})$
and
![]() $Y^{+}=(Y,B_{\text{red}})$
. Then
$Y^{+}=(Y,B_{\text{red}})$
. Then
![]() $f$
extends to a morphism of log schemes
$f$
extends to a morphism of log schemes
![]() $f^{+}:X^{+}\rightarrow Y^{+}$
.
$f^{+}:X^{+}\rightarrow Y^{+}$
.
Lemma 6.1.7. The reflexive sheaves
![]() $\unicode[STIX]{x1D714}_{X^{+}/K}^{\log }$
and
$\unicode[STIX]{x1D714}_{X^{+}/K}^{\log }$
and
![]() $\unicode[STIX]{x1D714}_{Y^{+}/K}^{\log }$
are identified via the pullback
$\unicode[STIX]{x1D714}_{Y^{+}/K}^{\log }$
are identified via the pullback
![]() $(f^{+})^{\ast }$
along the smooth locus of
$(f^{+})^{\ast }$
along the smooth locus of
![]() $Y$
.
$Y$
.
Proof. From a generalization of [Reference HartshorneHar77, Proposition IV.2.3] to higher dimension, we have that
![]() $\unicode[STIX]{x1D714}_{X/K}=f^{\ast }(\unicode[STIX]{x1D714}_{Y/K})\,\otimes \,{\mathcal{O}}_{X}(R)$
along the smooth locus of
$\unicode[STIX]{x1D714}_{X/K}=f^{\ast }(\unicode[STIX]{x1D714}_{Y/K})\,\otimes \,{\mathcal{O}}_{X}(R)$
along the smooth locus of
![]() $Y$
. It follows that
$Y$
. It follows that
In order to study the divisor
![]() $R+R_{\text{red}}$
, we consider one irreducible component of
$R+R_{\text{red}}$
, we consider one irreducible component of
![]() $B$
. Let
$B$
. Let
![]() $D_{B}$
be an irreducible component of
$D_{B}$
be an irreducible component of
![]() $B$
, denote by
$B$
, denote by
![]() $e$
the ramification index of
$e$
the ramification index of
![]() $f$
at
$f$
at
![]() $D_{B}$
, and by
$D_{B}$
, and by
![]() $D_{R}$
the support of the preimage of
$D_{R}$
the support of the preimage of
![]() $D_{B}$
. As
$D_{B}$
. As
![]() $\text{mult}_{D_{R}}(R)=e-1$
,
$\text{mult}_{D_{R}}(R)=e-1$
,
![]() $\text{mult}_{D_{R}}(f^{\ast }(D_{B}))=e$
, and
$\text{mult}_{D_{R}}(f^{\ast }(D_{B}))=e$
, and
![]() $\text{mult}_{D_{R}}(R_{\text{red}})=1$
, we conclude that
$\text{mult}_{D_{R}}(R_{\text{red}})=1$
, we conclude that
![]() $R+R_{\text{red}}=f^{\ast }(B)$
, and finally
$R+R_{\text{red}}=f^{\ast }(B)$
, and finally
![]() $\unicode[STIX]{x1D714}_{X^{+}/K}^{\log }=(f^{+})^{\ast }(\unicode[STIX]{x1D714}_{Y^{+}/K}^{\log })$
.◻
$\unicode[STIX]{x1D714}_{X^{+}/K}^{\log }=(f^{+})^{\ast }(\unicode[STIX]{x1D714}_{Y^{+}/K}^{\log })$
.◻
In particular, Lemma 6.1.7 implies that
![]() $G$
-equivariant logarithmic pluricanonical forms on
$G$
-equivariant logarithmic pluricanonical forms on
![]() $X$
correspond to logarithmic pluricanonical forms on
$X$
correspond to logarithmic pluricanonical forms on
![]() $Y$
via pullback.
$Y$
via pullback.
Proposition 6.1.8. Let
![]() $\unicode[STIX]{x1D714}$
be a
$\unicode[STIX]{x1D714}$
be a
![]() $G$
-invariant
$G$
-invariant
![]() $R_{\text{red}}$
-logarithmic
$R_{\text{red}}$
-logarithmic
![]() $m$
-pluricanonical form on
$m$
-pluricanonical form on
![]() $X^{+}$
and let
$X^{+}$
and let
![]() $\overline{\unicode[STIX]{x1D714}}$
be the corresponding
$\overline{\unicode[STIX]{x1D714}}$
be the corresponding
![]() $B_{\text{red}}$
-logarithmic form on
$B_{\text{red}}$
-logarithmic form on
![]() $Y^{+}$
via pullback. Let
$Y^{+}$
via pullback. Let
![]() $y$
be a divisorial point of
$y$
be a divisorial point of
![]() $Y^{\text{an}}$
. Then, for any divisorial point
$Y^{\text{an}}$
. Then, for any divisorial point
![]() $x\in (f^{\text{an}})^{-1}(y)$
, the weights of
$x\in (f^{\text{an}})^{-1}(y)$
, the weights of
![]() $\unicode[STIX]{x1D714}$
at
$\unicode[STIX]{x1D714}$
at
![]() $x$
and of
$x$
and of
![]() $\overline{\unicode[STIX]{x1D714}}$
at
$\overline{\unicode[STIX]{x1D714}}$
at
![]() $y$
coincide.
$y$
coincide.
Proof. Let
![]() $\mathscr{Y}$
be a model of
$\mathscr{Y}$
be a model of
![]() $Y$
over
$Y$
over
![]() $R$
such that
$R$
such that
![]() $y$
has divisorial representation
$y$
has divisorial representation
![]() $(\mathscr{Y},E)$
and the model is regular at the generic point of
$(\mathscr{Y},E)$
and the model is regular at the generic point of
![]() $E$
. Let
$E$
. Let
![]() $\mathscr{X}$
be the normalization of
$\mathscr{X}$
be the normalization of
![]() $\mathscr{Y}$
in
$\mathscr{Y}$
in
![]() $K(X)$
: as we observed in paragraph 6.1.5, it is a model of
$K(X)$
: as we observed in paragraph 6.1.5, it is a model of
![]() $X$
, regular at generic points of the special fiber
$X$
, regular at generic points of the special fiber
![]() $\mathscr{X}_{k}$
. We denote as well by
$\mathscr{X}_{k}$
. We denote as well by
![]() $f:\mathscr{X}\rightarrow \mathscr{Y}$
the extension of
$f:\mathscr{X}\rightarrow \mathscr{Y}$
the extension of
![]() $f$
. The preimage of
$f$
. The preimage of
![]() $E$
coincides with the pullback of the Cartier divisor
$E$
coincides with the pullback of the Cartier divisor
![]() $E$
on
$E$
on
![]() $\mathscr{X}$
, hence
$\mathscr{X}$
, hence
![]() $f^{-1}(E)$
still defines a codimension-
$f^{-1}(E)$
still defines a codimension-
![]() $1$
subset on
$1$
subset on
![]() $\mathscr{X}$
. We denote by
$\mathscr{X}$
. We denote by
![]() $F_{i}$
the irreducible components of
$F_{i}$
the irreducible components of
![]() $f^{-1}(E)$
and we associate to the
$f^{-1}(E)$
and we associate to the
![]() $F_{i}$
their corresponding divisorial valuations
$F_{i}$
their corresponding divisorial valuations
![]() $x_{i}=(\mathscr{X},F_{i})$
. By Lemma 6.1.3, it is enough to prove the result for one of the
$x_{i}=(\mathscr{X},F_{i})$
. By Lemma 6.1.3, it is enough to prove the result for one of the
![]() $x_{i}$
. We denote it by
$x_{i}$
. We denote it by
![]() $x=(\mathscr{X},F)$
and we compare the weights at
$x=(\mathscr{X},F)$
and we compare the weights at
![]() $y$
and
$y$
and
![]() $x$
.
$x$
.
We recall that for log étale morphisms the sheaves of logarithmic differentials are stable under pullback [Reference KatoKat89, Proposition 3.12]. Furthermore, it suffices to check that, locally around the generic point of
![]() $F,$
the morphism
$F,$
the morphism
![]() $\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
is a log étale morphism of divisorial log structures, to conclude that the weights coincide. For this purpose, we will apply Kato’s criterion for log étaleness [Reference KatoKat89, Theorem 3.5] to log schemes with respect to the étale topology.
$\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
is a log étale morphism of divisorial log structures, to conclude that the weights coincide. For this purpose, we will apply Kato’s criterion for log étaleness [Reference KatoKat89, Theorem 3.5] to log schemes with respect to the étale topology.
We denote by
![]() $\unicode[STIX]{x1D709}_{F}$
the generic point of
$\unicode[STIX]{x1D709}_{F}$
the generic point of
![]() $F$
and by
$F$
and by
![]() $\unicode[STIX]{x1D709}_{E}$
the generic point of
$\unicode[STIX]{x1D709}_{E}$
the generic point of
![]() $E$
. The divisorial log structures on
$E$
. The divisorial log structures on
![]() $\mathscr{X}^{+}$
and
$\mathscr{X}^{+}$
and
![]() $\mathscr{Y}^{+}$
have charts
$\mathscr{Y}^{+}$
have charts
![]() $\mathbb{N}$
at
$\mathbb{N}$
at
![]() $\unicode[STIX]{x1D709}_{F}$
and
$\unicode[STIX]{x1D709}_{F}$
and
![]() $\unicode[STIX]{x1D709}_{E}$
. In the étale topology, the normalization morphism
$\unicode[STIX]{x1D709}_{E}$
. In the étale topology, the normalization morphism
![]() $\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
admits a chart induced by
$\mathscr{X}^{+}\rightarrow \mathscr{Y}^{+}$
admits a chart induced by
![]() $u:\mathbb{N}\rightarrow \mathbb{N}$
, where
$u:\mathbb{N}\rightarrow \mathbb{N}$
, where
![]() $1\mapsto m$
for some positive integer
$1\mapsto m$
for some positive integer
![]() $m$
as follows.
$m$
as follows.

Firstly, by the universal property of the fiber product, we have a morphism
and it corresponds to
This is a morphism of finite type with finite fibers between regular rings and by [Reference LiuLiu02, Lemma 4.3.20] and [Reference NowakNow97] it is flat and unramified, hence étale. One of the two conditions in Kato’s criterion for log étaleness is then fulfilled. Secondly, the chart
![]() $u:\mathbb{N}\mapsto \mathbb{N}$
induces a group homomorphism
$u:\mathbb{N}\mapsto \mathbb{N}$
induces a group homomorphism
![]() $u^{\text{gp}}:\mathbb{Z}\mapsto \mathbb{Z}$
; in particular, it is injective and it has finite cokernel. Then
$u^{\text{gp}}:\mathbb{Z}\mapsto \mathbb{Z}$
; in particular, it is injective and it has finite cokernel. Then
![]() $u$
satisfies the second condition of Kato’s criterion for log étaleness. Therefore we conclude that
$u$
satisfies the second condition of Kato’s criterion for log étaleness. Therefore we conclude that
![]() $\text{wt}_{\overline{\unicode[STIX]{x1D714}}}(y)=\text{wt}_{\unicode[STIX]{x1D714}}(x)$
.◻
$\text{wt}_{\overline{\unicode[STIX]{x1D714}}}(y)=\text{wt}_{\unicode[STIX]{x1D714}}(x)$
.◻
Proposition 6.1.9. Let
![]() $\unicode[STIX]{x1D714}$
be a
$\unicode[STIX]{x1D714}$
be a
![]() $G$
-invariant
$G$
-invariant
![]() $R_{\text{red}}$
-logarithmic pluricanonical form on
$R_{\text{red}}$
-logarithmic pluricanonical form on
![]() $X$
and let
$X$
and let
![]() $\overline{\unicode[STIX]{x1D714}}$
be the corresponding
$\overline{\unicode[STIX]{x1D714}}$
be the corresponding
![]() $B_{\text{red}}$
-logarithmic form. Then the canonical homeomorphism between
$B_{\text{red}}$
-logarithmic form. Then the canonical homeomorphism between
![]() $X^{\text{an}}/G$
and
$X^{\text{an}}/G$
and
![]() $Y^{\text{an}}$
of Proposition 6.1.2 induces the homeomorphism
$Y^{\text{an}}$
of Proposition 6.1.2 induces the homeomorphism
6.1.10. Let
![]() $X$
be a smooth
$X$
be a smooth
![]() $K$
-variety and let
$K$
-variety and let
![]() $\unicode[STIX]{x1D714}_{X}$
be a pluricanonical form on
$\unicode[STIX]{x1D714}_{X}$
be a pluricanonical form on
![]() $X$
. Let
$X$
. Let
![]() $\text{pr}_{j}:X^{n}\rightarrow X$
be the
$\text{pr}_{j}:X^{n}\rightarrow X$
be the
![]() $j$
th canonical projection. Then
$j$
th canonical projection. Then
is a pluricanonical form on
![]() $X^{n}$
and, moreover, it is invariant under the action of
$X^{n}$
and, moreover, it is invariant under the action of
![]() $\mathfrak{S}_{n}$
. We denote by
$\mathfrak{S}_{n}$
. We denote by
![]() $\overline{\unicode[STIX]{x1D714}}$
the corresponding form on the quotient
$\overline{\unicode[STIX]{x1D714}}$
the corresponding form on the quotient
![]() $X^{n}/\mathfrak{S}_{n}$
as in Lemma 6.1.7.
$X^{n}/\mathfrak{S}_{n}$
as in Lemma 6.1.7.
Proposition 6.1.11. Assume that the residue field
![]() $k$
is algebraically closed. If
$k$
is algebraically closed. If
![]() $X$
admits a semistable log-regular model or a semistable good minimal dlt model, then the Kontsevich–Soibelman skeleton of the
$X$
admits a semistable log-regular model or a semistable good minimal dlt model, then the Kontsevich–Soibelman skeleton of the
![]() $n$
th symmetric product of
$n$
th symmetric product of
![]() $X$
associated to
$X$
associated to
![]() $\overline{\unicode[STIX]{x1D714}}$
is PL homeomorphic to the
$\overline{\unicode[STIX]{x1D714}}$
is PL homeomorphic to the
![]() $n$
th symmetric product of the Kontsevich–Soibelman skeleton of
$n$
th symmetric product of the Kontsevich–Soibelman skeleton of
![]() $X$
associated to
$X$
associated to
![]() $\unicode[STIX]{x1D714}_{X}$
.
$\unicode[STIX]{x1D714}_{X}$
.
Proof. Iterating the result of Theorems 5.2.2 and 5.3.5, we have that the projection map defines a PL homeomorphism of Kontsevich–Soibelman skeletons
Thus, applying Proposition 6.1.9 with the group
![]() $\mathfrak{S}_{n}$
acting on the product
$\mathfrak{S}_{n}$
acting on the product
![]() $X^{n}$
, we obtain that
$X^{n}$
, we obtain that
Since the action on the Kontsevich–Soibelman skeleton
![]() $\text{Sk}(X^{n},\unicode[STIX]{x1D714})$
is induced from the symmetric action on
$\text{Sk}(X^{n},\unicode[STIX]{x1D714})$
is induced from the symmetric action on
![]() $X^{n}$
, and the projections
$X^{n}$
, and the projections
![]() $\text{pr}_{j}:X^{n}\rightarrow X$
functorially induce the projections
$\text{pr}_{j}:X^{n}\rightarrow X$
functorially induce the projections
![]() $\overline{\text{pr}_{j}}:\text{Sk}(X,\unicode[STIX]{x1D714}_{X})^{n}\rightarrow \text{Sk}(X,\unicode[STIX]{x1D714})$
, the action of
$\overline{\text{pr}_{j}}:\text{Sk}(X,\unicode[STIX]{x1D714}_{X})^{n}\rightarrow \text{Sk}(X,\unicode[STIX]{x1D714})$
, the action of
![]() $\mathfrak{S}_{n}$
on
$\mathfrak{S}_{n}$
on
![]() $\text{Sk}(X,\unicode[STIX]{x1D714})^{n}$
is exactly by permutations of the components. Thus,
$\text{Sk}(X,\unicode[STIX]{x1D714})^{n}$
is exactly by permutations of the components. Thus,
6.2 The essential skeleton of Hilbert schemes of a
 $\text{K3}$
surface
$\text{K3}$
surface
6.2.1. Let
![]() $S$
be an irreducible regular surface. We consider
$S$
be an irreducible regular surface. We consider
![]() $\text{Hilb}^{n}(S)$
the Hilbert scheme of
$\text{Hilb}^{n}(S)$
the Hilbert scheme of
![]() $n$
points on
$n$
points on
![]() $S$
: by [Reference FogartyFog68] it is an irreducible regular variety of dimension
$S$
: by [Reference FogartyFog68] it is an irreducible regular variety of dimension
![]() $2n$
. Moreover, the morphism
$2n$
. Moreover, the morphism
that sends a zero-dimensional scheme
![]() $Z\subseteq S$
to its associated zero-cycle
$Z\subseteq S$
to its associated zero-cycle
![]() $[Z]$
is a birational morphism, called the Hilbert–Chow morphism.
$[Z]$
is a birational morphism, called the Hilbert–Chow morphism.
6.2.2. Let
![]() $S$
be a
$S$
be a
![]() $K3$
surface over
$K3$
surface over
![]() $K$
, namely
$K$
, namely
![]() $S$
is a complete non-singular variety of dimension
$S$
is a complete non-singular variety of dimension
![]() $2$
such that
$2$
such that
![]() $\unicode[STIX]{x1D6FA}_{S/K}^{2}\simeq {\mathcal{O}}_{S}\text{ and }H^{1}(S,{\mathcal{O}}_{S})=0$
. In particular,
$\unicode[STIX]{x1D6FA}_{S/K}^{2}\simeq {\mathcal{O}}_{S}\text{ and }H^{1}(S,{\mathcal{O}}_{S})=0$
. In particular,
![]() $S$
is a variety with trivial canonical line bundle.
$S$
is a variety with trivial canonical line bundle.
Corollary 6.2.3. Assume that the residue field
![]() $k$
is algebraically closed. Suppose that
$k$
is algebraically closed. Suppose that
![]() $S$
admits a semistable log-regular model or a semistable good minimal dlt model. Then the essential skeleton of the Hilbert scheme of
$S$
admits a semistable log-regular model or a semistable good minimal dlt model. Then the essential skeleton of the Hilbert scheme of
![]() $n$
points on
$n$
points on
![]() $S$
is PL homeomorphic to the
$S$
is PL homeomorphic to the
![]() $n$
th symmetric product of the essential skeleton of
$n$
th symmetric product of the essential skeleton of
![]() $S$
,
$S$
,
Proof. This follows immediately from Corollary 6.1.11 and the birational invariance of the essential skeleton [Reference Mustaţă and NicaiseMN15, Proposition 4.10.1].◻
Proposition 6.2.4. If the essential skeleton of
![]() $S$
is PL homeomorphic to a point, a closed interval or the two-dimensional sphere, then the essential skeleton of
$S$
is PL homeomorphic to a point, a closed interval or the two-dimensional sphere, then the essential skeleton of
![]() $\text{Hilb}^{n}(S)$
is PL homeomorphic to a point, the standard
$\text{Hilb}^{n}(S)$
is PL homeomorphic to a point, the standard
![]() $n$
-simplex or
$n$
-simplex or
![]() $\mathbb{C}\mathbb{P}^{n}$
, respectively.
$\mathbb{C}\mathbb{P}^{n}$
, respectively.
Proof. Applying Corollary 6.2.3, we reduce to the computation of the symmetric product of a point, a closed interval or the sphere
![]() $S^{2}$
. Then, the result is trivially true in the first two cases, and follows from [Reference HatcherHat02, §4K] in the third case.◻
$S^{2}$
. Then, the result is trivially true in the first two cases, and follows from [Reference HatcherHat02, §4K] in the third case.◻
6.3 The essential skeleton of generalized Kummer varieties
6.3.1. Let
![]() $A$
be an abelian surface over
$A$
be an abelian surface over
![]() $K$
, namely a complete non-singular, connected group variety of dimension
$K$
, namely a complete non-singular, connected group variety of dimension
![]() $2$
. Since
$2$
. Since
![]() $A$
is a group variety, the canonical line bundle is trivial and the group structure provides a multiplication morphism
$A$
is a group variety, the canonical line bundle is trivial and the group structure provides a multiplication morphism
![]() $m_{n+1}:A\times A\times \cdots \times A\rightarrow A$
that is invariant under the permutation action of
$m_{n+1}:A\times A\times \cdots \times A\rightarrow A$
that is invariant under the permutation action of
![]() $\mathfrak{S}_{n+1}$
, hence it induces a morphism
$\mathfrak{S}_{n+1}$
, hence it induces a morphism
by composition with the Hilbert–Chow morphism. Then
![]() $K_{n}(A)=\unicode[STIX]{x1D6F4}_{n+1}^{-1}(1)$
is called the
$K_{n}(A)=\unicode[STIX]{x1D6F4}_{n+1}^{-1}(1)$
is called the
![]() $n$
th generalized Kummer variety and is a hyper-Kähler manifold of dimension
$n$
th generalized Kummer variety and is a hyper-Kähler manifold of dimension
![]() $2n$
[Reference BeauvilleBea83].
$2n$
[Reference BeauvilleBea83].
6.3.2. In [Reference Halle and NicaiseHN17, Proposition 4.3.2], Halle and Nicaise, using Temkin’s generalization of the weight function [Reference Temkin, Baker and PayneTem16], prove that the essential skeleton of an abelian variety
![]() $A$
over
$A$
over
![]() $K$
coincides with the construction of a skeleton of
$K$
coincides with the construction of a skeleton of
![]() $A$
done by Berkovich in [Reference BerkovichBer90, Paragraph 6.5]. It follows from this identification and [Reference BerkovichBer90, Theorem 6.5.1] that the essential skeleton of
$A$
done by Berkovich in [Reference BerkovichBer90, Paragraph 6.5]. It follows from this identification and [Reference BerkovichBer90, Theorem 6.5.1] that the essential skeleton of
![]() $A$
has a group structure, compatible with the group structure on
$A$
has a group structure, compatible with the group structure on
![]() $A^{\text{an}}$
under the retraction
$A^{\text{an}}$
under the retraction
![]() $\unicode[STIX]{x1D70C}_{A}$
of
$\unicode[STIX]{x1D70C}_{A}$
of
![]() $A^{\text{an}}$
onto the essential skeleton, so the diagram
$A^{\text{an}}$
onto the essential skeleton, so the diagram

commutes, where
![]() $\unicode[STIX]{x1D707}$
denotes the multiplication of
$\unicode[STIX]{x1D707}$
denotes the multiplication of
![]() $\text{Sk}(A)$
.
$\text{Sk}(A)$
.
Proposition 6.3.3. Assume that the residue field
![]() $k$
is algebraically closed. Suppose that
$k$
is algebraically closed. Suppose that
![]() $A$
admits a semistable log-regular model or a semistable good minimal dlt model. Then the essential skeleton of the
$A$
admits a semistable log-regular model or a semistable good minimal dlt model. Then the essential skeleton of the
![]() $n$
th generalized Kummer variety is PL homeomorphic to the symmetric quotient of the kernel of the morphism
$n$
th generalized Kummer variety is PL homeomorphic to the symmetric quotient of the kernel of the morphism
![]() $\unicode[STIX]{x1D707}$
, namely,
$\unicode[STIX]{x1D707}$
, namely,
Proof. The first homeomorphism follows from the birational invariance of the essential skeleton [Reference Mustaţă and NicaiseMN15, Proposition 4.10.1]. We write
For any choice of an
![]() $\mathfrak{S}_{n+1}$
-invariant generating canonical form on
$\mathfrak{S}_{n+1}$
-invariant generating canonical form on
![]() $L$
, it follows from Proposition 6.1.9 that
$L$
, it follows from Proposition 6.1.9 that
![]() $\text{Sk}(L/\mathfrak{S}_{n+1})\simeq \text{Sk}(L)/\mathfrak{S}_{n+1}$
. We reduce to studying the quotients
$\text{Sk}(L/\mathfrak{S}_{n+1})\simeq \text{Sk}(L)/\mathfrak{S}_{n+1}$
. We reduce to studying the quotients
![]() $\text{Sk}(L)/\mathfrak{S}_{n+1}$
and
$\text{Sk}(L)/\mathfrak{S}_{n+1}$
and
![]() $\unicode[STIX]{x1D6EC}/\mathfrak{S}_{n+1}$
.
$\unicode[STIX]{x1D6EC}/\mathfrak{S}_{n+1}$
.
Let
![]() $\mathfrak{S}_{n}^{\prime }$
and
$\mathfrak{S}_{n}^{\prime }$
and
![]() $\mathfrak{S}_{n}^{\prime \prime }$
be the subgroups of
$\mathfrak{S}_{n}^{\prime \prime }$
be the subgroups of
![]() $\mathfrak{S}_{n+1}$
of the permutations that fix
$\mathfrak{S}_{n+1}$
of the permutations that fix
![]() $n$
and
$n$
and
![]() $n+1$
, respectively. Then
$n+1$
, respectively. Then
![]() $\mathfrak{S}_{n+1}$
is generated by the two subgroups, so its action on
$\mathfrak{S}_{n+1}$
is generated by the two subgroups, so its action on
![]() $\text{Sk}(L)$
and
$\text{Sk}(L)$
and
![]() $\unicode[STIX]{x1D6EC}$
is completely determined by the actions of these subgroups. We consider the isomorphisms
$\unicode[STIX]{x1D6EC}$
is completely determined by the actions of these subgroups. We consider the isomorphisms
Then
![]() $f_{n}$
is
$f_{n}$
is
![]() $\mathfrak{S}_{n}^{\prime }$
-equivariant,
$\mathfrak{S}_{n}^{\prime }$
-equivariant,
![]() $f_{n+1}$
is
$f_{n+1}$
is
![]() $\mathfrak{S}_{n}^{\prime \prime }$
-equivariant and the morphism
$\mathfrak{S}_{n}^{\prime \prime }$
-equivariant and the morphism
![]() $\unicode[STIX]{x1D713}$
$\unicode[STIX]{x1D713}$

is equivariant with respect to the action of
![]() $\mathfrak{S}_{n}^{\prime \prime }$
on the source and of
$\mathfrak{S}_{n}^{\prime \prime }$
on the source and of
![]() $\mathfrak{S}_{n}^{\prime }$
on the target. Hence, we obtain a commutative diagram of equivariant isomorphisms. We denote by
$\mathfrak{S}_{n}^{\prime }$
on the target. Hence, we obtain a commutative diagram of equivariant isomorphisms. We denote by
![]() $\overline{f}_{n}$
,
$\overline{f}_{n}$
,
![]() $\overline{f}_{n+1}$
and
$\overline{f}_{n+1}$
and
![]() $\overline{\unicode[STIX]{x1D713}}$
the isomorphisms induced on the essential skeletons. By Theorems 5.2.2 and 5.3.5 we can identify
$\overline{\unicode[STIX]{x1D713}}$
the isomorphisms induced on the essential skeletons. By Theorems 5.2.2 and 5.3.5 we can identify
![]() $\text{Sk}(A^{n})$
with
$\text{Sk}(A^{n})$
with
![]() $\text{Sk}(A)^{n}$
. Thus, we have the following commutative diagram.
$\text{Sk}(A)^{n}$
. Thus, we have the following commutative diagram.

Then the action of
![]() $\mathfrak{S}_{n+1}$
on
$\mathfrak{S}_{n+1}$
on
![]() $\text{Sk}(L)$
is induced by the isomorphisms
$\text{Sk}(L)$
is induced by the isomorphisms
![]() $\overline{f}_{n}$
and
$\overline{f}_{n}$
and
![]() $\overline{f}_{n+1}$
from the actions of
$\overline{f}_{n+1}$
from the actions of
![]() $\mathfrak{S}_{n}^{\prime \prime }$
and
$\mathfrak{S}_{n}^{\prime \prime }$
and
![]() $\mathfrak{S}_{n}^{\prime }$
on
$\mathfrak{S}_{n}^{\prime }$
on
![]() $\text{Sk}(A)^{n}$
and these actions are compatible as
$\text{Sk}(A)^{n}$
and these actions are compatible as
![]() $\overline{\unicode[STIX]{x1D713}}$
is equivariant.
$\overline{\unicode[STIX]{x1D713}}$
is equivariant.
In a similar way,
![]() $\unicode[STIX]{x1D6EC}$
is isomorphic to
$\unicode[STIX]{x1D6EC}$
is isomorphic to
![]() $n$
copies of
$n$
copies of
![]() $\text{Sk}(A)$
and comes equipped with an action of
$\text{Sk}(A)$
and comes equipped with an action of
![]() $\mathfrak{S}_{n+1}$
. So we have equivariant projections
$\mathfrak{S}_{n+1}$
. So we have equivariant projections
![]() $g_{n}$
and
$g_{n}$
and
![]() $g_{n+1}$
with respect to
$g_{n+1}$
with respect to
![]() $\mathfrak{S}_{n}^{\prime }$
and
$\mathfrak{S}_{n}^{\prime }$
and
![]() $\mathfrak{S}_{n}^{\prime \prime }$
. The equivariant morphism that completes and makes the diagram commutative is
$\mathfrak{S}_{n}^{\prime \prime }$
. The equivariant morphism that completes and makes the diagram commutative is
![]() $\overline{\unicode[STIX]{x1D713}}$
. Finally, we have the equivariant commutative diagram
$\overline{\unicode[STIX]{x1D713}}$
. Finally, we have the equivariant commutative diagram

and we conclude that the quotients
![]() $\text{Sk}(L)/\mathfrak{S}_{n+1}$
and
$\text{Sk}(L)/\mathfrak{S}_{n+1}$
and
![]() $\unicode[STIX]{x1D6EC}/\mathfrak{S}_{n+1}$
are homeomorphic.◻
$\unicode[STIX]{x1D6EC}/\mathfrak{S}_{n+1}$
are homeomorphic.◻
Proposition 6.3.4. If the essential skeleton of
![]() $A$
is PL homeomorphic to a point, the circle
$A$
is PL homeomorphic to a point, the circle
![]() $S^{1}$
or the torus
$S^{1}$
or the torus
![]() $S^{1}\times S^{1}$
, then the essential skeleton of
$S^{1}\times S^{1}$
, then the essential skeleton of
![]() $K_{n}(A)$
is PL homeomorphic to a point, the standard
$K_{n}(A)$
is PL homeomorphic to a point, the standard
![]() $n$
-simplex or
$n$
-simplex or
![]() $\mathbb{C}\mathbb{P}^{n}$
, respectively.
$\mathbb{C}\mathbb{P}^{n}$
, respectively.
Proof. The case of the point is trivial. For the circle
![]() $S^{1}$
, it follows directly from [Reference MortonMor67, Theorem]. To prove the result for the torus
$S^{1}$
, it follows directly from [Reference MortonMor67, Theorem]. To prove the result for the torus
![]() $S^{1}\times S^{1}$
, we apply [Reference LooijengaLoo76/77, Theorem 3.4]: the action of the symmetric group corresponds to the root system of
$S^{1}\times S^{1}$
, we apply [Reference LooijengaLoo76/77, Theorem 3.4]: the action of the symmetric group corresponds to the root system of
![]() $A_{n}$
, the highest root is the sum of the simple roots, each with coefficient
$A_{n}$
, the highest root is the sum of the simple roots, each with coefficient
![]() $1$
, and so the quotient is the complex projective space of dimension
$1$
, and so the quotient is the complex projective space of dimension
![]() $n$
.◻
$n$
.◻
6.4 Remarks on hyper-Kähler varieties
6.4.1. The cases we consider in Propositions 6.2.4 and 6.3.4 are motivated by the work of Kulikov, Persson, and Pinkham. In [Reference KulikovKul77] and [Reference Persson and PinkhamPP81], they consider degenerations over the unit complex disk, of surfaces such that some power of the canonical bundle is trivial. They prove that, after base change and birational transformations, any such degeneration can be arranged to be semistable with trivial canonical bundle, namely a Kulikov degeneration. Then they classify the possible special fibers of Kulikov degenerations according to the type of degeneration.
We recall that the monodromy operator
![]() $T$
on
$T$
on
![]() $\text{H}^{2}(X_{t},\mathbb{Q})$
of the fibers
$\text{H}^{2}(X_{t},\mathbb{Q})$
of the fibers
![]() $X_{t}$
of a Kulikov degeneration is unipotent, so we denote by
$X_{t}$
of a Kulikov degeneration is unipotent, so we denote by
![]() $\unicode[STIX]{x1D708}$
the nilpotency index of
$\unicode[STIX]{x1D708}$
the nilpotency index of
![]() $\log (T)$
, namely the positive integer such that
$\log (T)$
, namely the positive integer such that
![]() $\log (T)^{\unicode[STIX]{x1D708}}=0$
and
$\log (T)^{\unicode[STIX]{x1D708}}=0$
and
![]() $\log (T)^{(\unicode[STIX]{x1D708}-1)}\neq 0$
. The type of the Kulikov degeneration is defined as the nilpotency index
$\log (T)^{(\unicode[STIX]{x1D708}-1)}\neq 0$
. The type of the Kulikov degeneration is defined as the nilpotency index
![]() $\unicode[STIX]{x1D708}$
and called type I, II or III accordingly.
$\unicode[STIX]{x1D708}$
and called type I, II or III accordingly.
It follows from [Reference KulikovKul77, Theorem II], that the dual complex of the special fiber of a Kulikov degeneration of a
![]() $K3$
surface is a point, a closed interval or the sphere
$K3$
surface is a point, a closed interval or the sphere
![]() $S^{2}$
according to the respective type. For a degeneration of abelian surfaces, the dual complex of the special fiber is homeomorphic to a point, the circle
$S^{2}$
according to the respective type. For a degeneration of abelian surfaces, the dual complex of the special fiber is homeomorphic to a point, the circle
![]() $S^{1}$
or the torus
$S^{1}$
or the torus
![]() $S^{1}\times S^{1}$
according to the three types (see an overview of these results in [Reference Friedman and MorrisonFM83]). In all cases, the dimension of the dual complex is equal
$S^{1}\times S^{1}$
according to the three types (see an overview of these results in [Reference Friedman and MorrisonFM83]). In all cases, the dimension of the dual complex is equal
![]() $\unicode[STIX]{x1D708}-1$
, hence determined by the type.
$\unicode[STIX]{x1D708}-1$
, hence determined by the type.
6.4.2. Hilbert schemes of
![]() $K3$
surfaces and generalized Kummer varieties represent two families of examples of hyper-Kähler varieties. For a semistable degeneration of hyper-Kähler manifolds over the unit disk, it is possible to define the type as the nilpotency index of the monodromy operator on the second cohomology group. It naturally extends the definition for Kulikov degenerations.
$K3$
surfaces and generalized Kummer varieties represent two families of examples of hyper-Kähler varieties. For a semistable degeneration of hyper-Kähler manifolds over the unit disk, it is possible to define the type as the nilpotency index of the monodromy operator on the second cohomology group. It naturally extends the definition for Kulikov degenerations.
In [Reference Kollár, Laza, Saccà and VoisinKLSV17], Kollár, Laza, Saccà, and Voisin study the essential skeleton of a degeneration of hyper-Kähler manifolds in terms of the type. More precisely, in their Theorem 0.10, given a minimal dlt degeneration of
![]() $2n$
-dimensional hyper-Kähler manifolds, firstly they prove that the dual complex of the special fiber has dimension
$2n$
-dimensional hyper-Kähler manifolds, firstly they prove that the dual complex of the special fiber has dimension
![]() $(\unicode[STIX]{x1D708}-1)n$
, where
$(\unicode[STIX]{x1D708}-1)n$
, where
![]() $\unicode[STIX]{x1D708}$
denotes the type of the degeneration. Secondly, they prove that, in the type III case, the dual complex is a simply connected closed pseudo-manifold with the rational homology of
$\unicode[STIX]{x1D708}$
denotes the type of the degeneration. Secondly, they prove that, in the type III case, the dual complex is a simply connected closed pseudo-manifold with the rational homology of
![]() $\mathbb{C}\mathbb{P}^{n}$
.
$\mathbb{C}\mathbb{P}^{n}$
.
From this perspective, Propositions 6.2.4 and 6.3.4 confirm and strengthen their result for the specific cases of Hilbert schemes and generalized Kummer varieties. In particular, we turn the rational cohomological description of the essential skeleton (Theorem 0.10(ii)) into a topological characterization.
For Hilbert schemes associated to some type II degenerations of
![]() $K3$
surfaces, a complementary proof of our result is due to Gulbrandsen, Halle, Hulek, and Zhang; see [Reference Gulbrandsen, Halle and HulekGHH16, Reference Gulbrandsen, Halle, Hulek and ZhangGHHZ18]. Their approach is based on the method of expanded degenerations, which first appeared in [Reference LiLi01], and on the construction of suitable GIT quotients, in order to obtain an explicit minimal dlt degeneration for the associated family of Hilbert schemes.
$K3$
surfaces, a complementary proof of our result is due to Gulbrandsen, Halle, Hulek, and Zhang; see [Reference Gulbrandsen, Halle and HulekGHH16, Reference Gulbrandsen, Halle, Hulek and ZhangGHHZ18]. Their approach is based on the method of expanded degenerations, which first appeared in [Reference LiLi01], and on the construction of suitable GIT quotients, in order to obtain an explicit minimal dlt degeneration for the associated family of Hilbert schemes.
6.4.3. The structure of the essential skeleton of a degeneration of hyper-Kähler manifolds is relevant in the context of mirror symmetry and in view of the work of Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS01, Reference Kontsevich, Soibelman, Etingof, Retakh and SingerKS06]. The Strominger–Yau–Zaslow (SYZ) fibration [Reference Strominger, Yau and ZaslowSYZ96] is a conjectural geometric explanation for the phenomenon of mirror symmetry and, roughly speaking, asserts the existence of a special Lagrangian fibration, such that mirror pairs of manifolds with trivial canonical bundle should admit fiberwise dual special Lagrangian fibrations. Moreover, the expectation is that, for type III degenerations of
![]() $2n$
-dimensional hyper-Kähler manifolds, the base of the SYZ fibration is
$2n$
-dimensional hyper-Kähler manifolds, the base of the SYZ fibration is
![]() $\mathbb{C}\mathbb{P}^{n}$
(see, for instance, [Reference HwangHwa08]).
$\mathbb{C}\mathbb{P}^{n}$
(see, for instance, [Reference HwangHwa08]).
The most relevant fact from our perspective is that Kontsevich and Soibelman predict that the base of the Lagrangian fibration of a type III degeneration is homeomorphic to the essential skeleton. So, the outcomes on the topology of the essential skeleton we obtain in Propositions 6.2.4 and 6.3.4 match the predictions of mirror symmetry about the occurrence of
![]() $\mathbb{C}\mathbb{P}^{n}$
in the type III case.
$\mathbb{C}\mathbb{P}^{n}$
in the type III case.
Acknowledgements
The authors would like to thank Drew Armstrong, Lorenzo Fantini, Phillip Griffiths, Lars Halvard Halle, Sean Keel, Janos Kollár, Mirko Mauri, Johannes Nicaise, Giulia Saccà, Chenyang Xu, and David Zureick-Brown for helpful conversations, comments, and suggestions. The authors thank the anonymous referee for helpful comments and corrections. The authors are especially grateful to Johannes Nicaise, Mazzon’s advisor, both for suggesting this project and for putting the authors in contact. Mazzon is grateful to the University of Miami for hosting her visit during the completion of this project. Brown was supported by the Simons Foundation Collaboration Grant 524003. Mazzon was partially supported by the ERC Starting Grant MOTZETA (project 306610) of the European Research Council (PI: Johannes Nicaise), and by the Engineering and Physical Sciences Research Council [EP/L015234/1]. The EPSRC Centre for Doctoral Training in Geometry and Number Theory (The London School of Geometry and Number Theory), University College London.