Hostname: page-component-5c6d5d7d68-tdptf Total loading time: 0 Render date: 2024-08-15T14:30:45.548Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodicity for infinite periodic translation surfaces

Published online by Cambridge University Press:  03 June 2013

Pascal Hubert  and
Barak Weiss
Pascal Hubert
Affiliation:
LATP, Case Cour A, Faculté des sciences de Saint Jérôme, Avenue Escadrille Normandie-Niemen, 13397 Marseille Cedex 20, France email hubert@cmi.univ-mrs.fr
Barak Weiss
Affiliation:
Ben Gurion University, Be’er Sheva, 84105, Israel email barakw@math.bgu.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

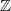For a $ \mathbb{Z} $-cover 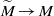$\widetilde {M} \rightarrow M$ of a translation surface, which is a lattice surface, and which admits infinite strips, we prove that almost every direction for the straightline flow is ergodic.

Keywords

ergodicityinfiniteperiodictranslation surfaces

MSC classification

Secondary: 57S25: Groups acting on specific manifolds
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 8 , August 2013 , pp. 1364 - 1380
Copyright
© The Author(s) 2013 

References

Aaronson, J., Nakada, H., Sarig, O. and Solomyak, R., Invariant measures and asymptotics for some skew products, Israel J. Math. 128 (2002), 93–134.Google Scholar
Conze, J.-P., Equirépartition et ergodicité de transformations cylindriques, in Séminaire de Probabilité de Rennes (UER de Mathématiques et Informatique, 1976), 1–21.Google Scholar
Conze, J.-P. and Fraczek, K., Cocycles over interval exchange transformations and multivalued Hamiltonian flows, Preprint (2010), http://arxiv.org/abs/1003.1808.Google Scholar
Einsiedler, M., Kadyrov, S. and Pohl, A., Escape of mass and entropy for diagonal flows in real rank one situations, Preprint (2011), http://arxiv.org/abs/1110.0910.Google Scholar
Fraczek, K. and Ulcigrai, C., Non-ergodic $ \mathbb{Z} $-periodic billiards and infinite translation surfaces, Preprint (2011), http://arxiv.org/abs/1109.4584.Google Scholar
Hooper, P., Dynamics on an infinite staircase with the lattice property, Preprint (2008), http://arxiv.org/abs/0802.0189.Google Scholar
Hooper, P., The invariant measures of some infinite interval exchange maps, Preprint (2010), http://arxiv.org/abs/1005.1902.Google Scholar
Hooper, W. P., Hubert, P. and Weiss, B., Dynamics on the infinite staircase surface, Preprint (2008), http://www.math.bgu.ac.il/~barakw/staircase.pdf.Google Scholar
Hooper, W. P. and Weiss, B., Generalized staircases: recurrence and symmetry, Ann. Inst. Fourier 62 (2012), 1581–1600.CrossRefGoogle Scholar
Hubert, P. and Schmithuesen, G., Infinite translation surfaces with infinitely generated Veech group, J. Mod. Dyn. 4 (2010), 715–732.Google Scholar
Katok, S., Fuchsian groups, Chicago Lectures in Mathematics (University of Chicago Press, 1992).Google Scholar
Kesten, H., On a conjecture of Erdős and Szüsz related to uniform distribution mod $1$, Acta Arith. 12 (1966/1967), 193–212.Google Scholar
Kleinbock, D. and Weiss, B., Modified Schmidt games and a conjecture of Margulis, Preprint (2011).Google Scholar
König, D. and Szücs, A., Mouvement d’un point abandonné à l’interieur d’un cube, Rend. Circ. Mat. Palermo 36 (1913), 79–90.Google Scholar
Masur, H., Hausdorff dimension of the set of nonergodic foliations of a quadratic differential, Duke Math. J. 66 (1992), 387–442.CrossRefGoogle Scholar
Masur, H. and Tabachnikov, S., Rational billiards and flat structures, in Handbook of dynamical systems, Vol. 1A (North-Holland, Amsterdam, 2002), 1015–1089.Google Scholar
Monteil, T., A homological condition for a dynamical and illuminatory classification of torus branched coverings, Preprint (2006), http://arxiv.org/abs/math/0603352.Google Scholar
Panov, D., Foliations with unbounded deviation on ${ \mathbb{T} }^{2} $, J. Mod. Dyn. 3 (2009), 589–594.Google Scholar
Patterson, S. J., Diophantine approximation in Fuchsian groups, Phil. Trans. Roy. Soc. Lond. 282 (1976), 527–563.Google Scholar
Petersen, K., On a series of cosecants related to a problem in ergodic theory, Compositio Math. 26 (1973), 313–317.Google Scholar
Ralston, D., $1/ 2$-heavy sequences driven by rotations, Preprint (2011), http://arxiv.org/abs/1106.0577.Google Scholar
Schmidt, K., Cocycles of ergodic transformation groups, Chicago Lectures in Mathematics (MacMillan, India, 1977), available at http://www.mat.univie.ac.at/~kschmidt.Google Scholar
Veech, W. A., Teichmüller curves in moduli space, Eisenstein series and an application to triangular billiards, Invent. Math. 97 (1989), 553–583.Google Scholar
Viana, M., Dynamics of interval exchange maps and Teichmüller flows, Lecture notes of graduate courses taught at IMPA in 2005 and 2007. Working preliminary manuscript, http://w3.impa.br/~viana/out/ietf.pdf.Google Scholar
Zorich, A., Flat surfaces, Frontiers in number theory, physics, and geometry I (Springer, Berlin, 2006), 437–583.Google Scholar