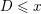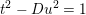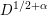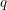1 Introduction and main results
Let
![]() $D$
be a non-square positive integer. The Pell equation is usually referred to as
$D$
be a non-square positive integer. The Pell equation is usually referred to as
to which the solution can be written in the usual form
The classical Dirichlet’s unit theorem asserts that the set of solutions to (1.1) is non-trivial and has the form
where
![]() $\unicode[STIX]{x1D700}_{D}$
is called the fundamental solution of (1.1) and is given by
$\unicode[STIX]{x1D700}_{D}$
is called the fundamental solution of (1.1) and is given by
Writing
![]() $\unicode[STIX]{x1D700}_{D}:=t_{0}+u_{0}\sqrt{D}$
, we have
$\unicode[STIX]{x1D700}_{D}:=t_{0}+u_{0}\sqrt{D}$
, we have
![]() $t_{0},u_{0}\geqslant 1$
, from which we deduce that
$t_{0},u_{0}\geqslant 1$
, from which we deduce that
![]() $t_{0}=\sqrt{1+u_{0}^{2}D}>\sqrt{D}$
and finally
$t_{0}=\sqrt{1+u_{0}^{2}D}>\sqrt{D}$
and finally
We are interested in counting the integers
![]() $D$
for which
$D$
for which
![]() $\unicode[STIX]{x1D700}_{D}$
or
$\unicode[STIX]{x1D700}_{D}$
or
![]() $\unicode[STIX]{x1D702}_{D}$
is less than a fixed power of
$\unicode[STIX]{x1D702}_{D}$
is less than a fixed power of
![]() $D$
.
$D$
.
For
![]() $\unicode[STIX]{x1D6FC}>0$
and
$\unicode[STIX]{x1D6FC}>0$
and
![]() $x\geqslant 2$
, define
$x\geqslant 2$
, define
In his pioneer work, Hooley [Reference HooleyHoo84] proved the following theorem.
Theorem A (Hooley).
Let
![]() $\unicode[STIX]{x1D700}_{0}$
satisfy
$\unicode[STIX]{x1D700}_{0}$
satisfy
![]() $0<\unicode[STIX]{x1D700}_{0}<\frac{1}{2}$
. As
$0<\unicode[STIX]{x1D700}_{0}<\frac{1}{2}$
. As
![]() $x\rightarrow +\infty$
, one has
$x\rightarrow +\infty$
, one has
uniformly for
![]() $\unicode[STIX]{x1D700}_{0}\leqslant \unicode[STIX]{x1D6FC}\leqslant \frac{1}{2}.$
$\unicode[STIX]{x1D700}_{0}\leqslant \unicode[STIX]{x1D6FC}\leqslant \frac{1}{2}.$
In the same paper, Hooley [Reference HooleyHoo84, p. 110] also made the following conjecture.
Conjecture 1.1 (Hooley).
For any given
![]() $\unicode[STIX]{x1D6FC}>\frac{1}{2}$
, we have
$\unicode[STIX]{x1D6FC}>\frac{1}{2}$
, we have
where
 $$\begin{eqnarray}C(\unicode[STIX]{x1D6FC})=\left\{\begin{array}{@{}ll@{}}0,\quad & \unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},1],\\ \frac{1}{18}(\unicode[STIX]{x1D6FC}-1)^{2},\quad & \unicode[STIX]{x1D6FC}\in \, ]\!1,\frac{5}{2} ],\\ \frac{1}{24}(4\unicode[STIX]{x1D6FC}-7),\quad & \unicode[STIX]{x1D6FC}\in \, ]\!\frac{5}{2},+\infty \![.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}C(\unicode[STIX]{x1D6FC})=\left\{\begin{array}{@{}ll@{}}0,\quad & \unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},1],\\ \frac{1}{18}(\unicode[STIX]{x1D6FC}-1)^{2},\quad & \unicode[STIX]{x1D6FC}\in \, ]\!1,\frac{5}{2} ],\\ \frac{1}{24}(4\unicode[STIX]{x1D6FC}-7),\quad & \unicode[STIX]{x1D6FC}\in \, ]\!\frac{5}{2},+\infty \![.\end{array}\right.\end{eqnarray}$$
Fouvry [Reference FouvryFou16] made a first significant step towards Hooley’s conjecture in the case
![]() $\unicode[STIX]{x1D6FC}\in ]\!\frac{1}{2},1\!]\!.$
In fact, he proved the following theorem.
$\unicode[STIX]{x1D6FC}\in ]\!\frac{1}{2},1\!]\!.$
In fact, he proved the following theorem.
Theorem B (Fouvry).
As
![]() $x\rightarrow +\infty$
, one has
$x\rightarrow +\infty$
, one has
and
uniformly for
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
Moreover, Fouvry [Reference FouvryFou16] considered a conjectural estimation for short exponential sums.
Conjecture 1.2. There exists an absolute
![]() $\unicode[STIX]{x1D717}\in \! [\frac{1}{2},1\![$
, such that for any integer
$\unicode[STIX]{x1D717}\in \! [\frac{1}{2},1\![$
, such that for any integer
![]() $k\geqslant 0,$
one has the inequality
$k\geqslant 0,$
one has the inequality
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ N<n\leqslant N_{1} \\ m\equiv a\,(\operatorname{mod}4^{k}),(m,n)=1}}e\bigg(\frac{h\overline{n}^{2}}{m^{2}}\bigg)\ll _{k}(h,m^{2})^{1/2}N^{\unicode[STIX]{x1D717}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ N<n\leqslant N_{1} \\ m\equiv a\,(\operatorname{mod}4^{k}),(m,n)=1}}e\bigg(\frac{h\overline{n}^{2}}{m^{2}}\bigg)\ll _{k}(h,m^{2})^{1/2}N^{\unicode[STIX]{x1D717}}\end{eqnarray}$$
uniformly for any integers
![]() $a,h,m$
satisfying
$a,h,m$
satisfying
![]() $h\neq 0,m\geqslant 1$
and
$h\neq 0,m\geqslant 1$
and
![]() $2\nmid am$
, for any real number
$2\nmid am$
, for any real number
![]() $N$
satisfying
$N$
satisfying
![]() $m\leqslant N\leqslant m^{2}$
and
$m\leqslant N\leqslant m^{2}$
and
![]() $N<N_{1}\leqslant 2N.$
$N<N_{1}\leqslant 2N.$
Assuming Conjecture 1.2, Fouvry [Reference FouvryFou16] derived the following stronger lower bounds.
Theorem C (Fouvry).
Assume that Conjecture 1.2 is true for some
![]() $\unicode[STIX]{x1D717}\in \! [\!\frac{1}{2},1\![$
. As
$\unicode[STIX]{x1D717}\in \! [\!\frac{1}{2},1\![$
. As
![]() $x\rightarrow +\infty$
, one has
$x\rightarrow +\infty$
, one has
and
uniformly for
![]() $\unicode[STIX]{x1D6FC}\in [{\textstyle \frac{1}{2}},{\textstyle \frac{1}{1+\unicode[STIX]{x1D717}}}].$
$\unicode[STIX]{x1D6FC}\in [{\textstyle \frac{1}{2}},{\textstyle \frac{1}{1+\unicode[STIX]{x1D717}}}].$
The first inequality coincides with Hooley’s Conjecture 1.1 when
![]() $\unicode[STIX]{x1D6FC}$
is slightly larger than
$\unicode[STIX]{x1D6FC}$
is slightly larger than
![]() $\frac{1}{2}.$
On the other hand, Bourgain [Reference BourgainBou15] considered Conjecture 1.2 itself. In particular, he succeeded in saving a power of
$\frac{1}{2}.$
On the other hand, Bourgain [Reference BourgainBou15] considered Conjecture 1.2 itself. In particular, he succeeded in saving a power of
![]() $\log N$
in the trivial bound for the sum involved. This allows him to improve the lower bound (1.2) by replacing the term
$\log N$
in the trivial bound for the sum involved. This allows him to improve the lower bound (1.2) by replacing the term
![]() $-4(\unicode[STIX]{x1D6FC}-\frac{1}{2})^{2}$
with the term
$-4(\unicode[STIX]{x1D6FC}-\frac{1}{2})^{2}$
with the term
![]() $O((\unicode[STIX]{x1D6FC}-\frac{1}{2})^{2+c})$
, where
$O((\unicode[STIX]{x1D6FC}-\frac{1}{2})^{2+c})$
, where
![]() $c$
is some positive constant.
$c$
is some positive constant.
Bourgain’s improvement is of interest only if
![]() $\unicode[STIX]{x1D6FC}$
is quite close to
$\unicode[STIX]{x1D6FC}$
is quite close to
![]() $\frac{1}{2}$
and one should pay much more attention if every parameter is to be made effective. The aim of this paper is to give another improvement to Theorem B towards Conjecture 1.1.
$\frac{1}{2}$
and one should pay much more attention if every parameter is to be made effective. The aim of this paper is to give another improvement to Theorem B towards Conjecture 1.1.
Theorem 1.1. Let
![]() $x\rightarrow +\infty$
. For any fixed
$x\rightarrow +\infty$
. For any fixed
![]() $\unicode[STIX]{x1D703}\in \, ]\!0,\frac{1}{2}\! [,$
we have
$\unicode[STIX]{x1D703}\in \, ]\!0,\frac{1}{2}\! [,$
we have
and
uniformly in
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1]$
, where
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1]$
, where
![]() $\unicode[STIX]{x1D70C}$
is the Dickman function given by (A.1) and
$\unicode[STIX]{x1D70C}$
is the Dickman function given by (A.1) and
Fix
![]() $\unicode[STIX]{x1D703}\in \, ]\!0,\frac{1}{2}\! [$
. One may check that
$\unicode[STIX]{x1D703}\in \, ]\!0,\frac{1}{2}\! [$
. One may check that
![]() $F_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FC})$
is always positive for
$F_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D6FC})$
is always positive for
![]() $\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},1]$
and monotonically increasing in
$\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},1]$
and monotonically increasing in
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},{\textstyle \frac{6}{11+2\unicode[STIX]{x1D703}}}]$
. In particular, for
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},{\textstyle \frac{6}{11+2\unicode[STIX]{x1D703}}}]$
. In particular, for
![]() $\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},\frac{6}{11}\! [,$
we take
$\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},\frac{6}{11}\! [,$
we take
![]() $\unicode[STIX]{x1D703}=3/\unicode[STIX]{x1D6FC}-\frac{11}{2}$
such that
$\unicode[STIX]{x1D703}=3/\unicode[STIX]{x1D6FC}-\frac{11}{2}$
such that
![]() $\unicode[STIX]{x1D6FC}={\textstyle \frac{6}{11+2\unicode[STIX]{x1D703}}}$
and
$\unicode[STIX]{x1D6FC}={\textstyle \frac{6}{11+2\unicode[STIX]{x1D703}}}$
and
Moreover,
![]() $\unicode[STIX]{x1D70C}(2\unicode[STIX]{x1D6FC}/(6-11\unicode[STIX]{x1D6FC}))/\unicode[STIX]{x1D6FC}>0.3008$
for
$\unicode[STIX]{x1D70C}(2\unicode[STIX]{x1D6FC}/(6-11\unicode[STIX]{x1D6FC}))/\unicode[STIX]{x1D6FC}>0.3008$
for
![]() $\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},\frac{35}{69} ].$
Hence we may conclude the following consequence.
$\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},\frac{35}{69} ].$
Hence we may conclude the following consequence.
Corollary 1.1. Let
![]() $x\rightarrow +\infty$
. Uniformly for
$x\rightarrow +\infty$
. Uniformly for
![]() $\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},\frac{35}{69}\! ],$
we have
$\unicode[STIX]{x1D6FC}\in \, ]\!\frac{1}{2},\frac{35}{69}\! ],$
we have
and
The framework of the proof is based on [Reference FouvryFou16]. To make the paper clear, we will present the proof as complete as possible, but also with omitting some details that are not quite essential to understand the underlying ideas.
The key point of proving Theorem 1.1 is a variant of Conjecture 1.2 that can be proved unconditionally. More precisely, if one allows the moduli
![]() $m^{2}$
to be smooth numbers (integers free of large prime factors), it is possible to prove the existence of
$m^{2}$
to be smooth numbers (integers free of large prime factors), it is possible to prove the existence of
![]() $\unicode[STIX]{x1D717}$
in Conjecture 1.2 as long as
$\unicode[STIX]{x1D717}$
in Conjecture 1.2 as long as
![]() $N$
is not too small. The details can be referred to Theorem 3.1 and § 4. We will adopt the
$N$
is not too small. The details can be referred to Theorem 3.1 and § 4. We will adopt the
![]() $q$
-analogue of van der Corput method, which can be at least dated back to Heath-Brown [Reference Heath-BrownHea78] on the proof of Weyl-type subconvex bounds for Dirichlet
$q$
-analogue of van der Corput method, which can be at least dated back to Heath-Brown [Reference Heath-BrownHea78] on the proof of Weyl-type subconvex bounds for Dirichlet
![]() $L$
-functions to well-factorable moduli. Instead of the
$L$
-functions to well-factorable moduli. Instead of the
![]() $AB$
-process in [Reference Heath-BrownHea78], we apply the
$AB$
-process in [Reference Heath-BrownHea78], we apply the
![]() $BAB$
-process by introducing a completion in the initial step. It is expected that one can do better on the exponential sums in Conjecture 1.2 if better factorizations of the moduli are imposed; see [Reference Wu and XiWX16] for instance in the case of squarefree moduli. However, the improvements to Theorem 1.1 would be rather slight, since the density of smooth numbers decays rapidly when the size of their prime factors decreases.
$BAB$
-process by introducing a completion in the initial step. It is expected that one can do better on the exponential sums in Conjecture 1.2 if better factorizations of the moduli are imposed; see [Reference Wu and XiWX16] for instance in the case of squarefree moduli. However, the improvements to Theorem 1.1 would be rather slight, since the density of smooth numbers decays rapidly when the size of their prime factors decreases.
As an extension to Theorem 1.1, one may consider
for
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FD}\geqslant 0.$
Conjecture 1.1 would yield asymptotics for
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FD}\geqslant 0.$
Conjecture 1.1 would yield asymptotics for
![]() $S(x;\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
while
$S(x;\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
while
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
are of different prescribed sizes. A weaker statement would assert that, for any
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
are of different prescribed sizes. A weaker statement would assert that, for any
![]() $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FD}\geqslant 0,$
there exists a positive constant
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FD}\geqslant 0,$
there exists a positive constant
![]() $c=c(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, such that
$c=c(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
, such that
for all large
![]() $x>x_{0}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
. This weaker statement was made unconditionally by Fouvry and Jouve [Reference Fouvry and JouveFJ12] whenever
$x>x_{0}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
. This weaker statement was made unconditionally by Fouvry and Jouve [Reference Fouvry and JouveFJ12] whenever
![]() $\unicode[STIX]{x1D6FD}<\frac{3}{2}$
. It is expected that the arguments in this paper can enlarge the admissible range of
$\unicode[STIX]{x1D6FD}<\frac{3}{2}$
. It is expected that the arguments in this paper can enlarge the admissible range of
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
Notation and convention
As usual,
![]() $e(x)=e^{2\unicode[STIX]{x1D70B}ix}$
,
$e(x)=e^{2\unicode[STIX]{x1D70B}ix}$
,
![]() $\unicode[STIX]{x1D711}$
denotes the Euler function and
$\unicode[STIX]{x1D711}$
denotes the Euler function and
![]() $\unicode[STIX]{x1D714}(q)$
counts the number of distinct prime factors of
$\unicode[STIX]{x1D714}(q)$
counts the number of distinct prime factors of
![]() $q$
. The variable
$q$
. The variable
![]() $p$
is reserved for prime numbers. Denote by
$p$
is reserved for prime numbers. Denote by
![]() $q^{\flat }$
and
$q^{\flat }$
and
![]() $q^{\sharp }$
the squarefree and squarefull parts of
$q^{\sharp }$
the squarefree and squarefull parts of
![]() $q$
, respectively; namely,
$q$
, respectively; namely,
For a real number
![]() $x,$
denote by
$x,$
denote by
![]() $[x]$
its integral part and
$[x]$
its integral part and
![]() $\Vert x\Vert =\min _{n\in \mathbf{Z}}|x-n|$
. From time to time, we use
$\Vert x\Vert =\min _{n\in \mathbf{Z}}|x-n|$
. From time to time, we use
![]() $(m,n)$
to denote the greatest common divisor of
$(m,n)$
to denote the greatest common divisor of
![]() $m,n$
, and also to denote a tuple given by two coordinates; these will not cause confusions as one will see later. The symbol
$m,n$
, and also to denote a tuple given by two coordinates; these will not cause confusions as one will see later. The symbol
![]() $\ast$
in summation reminds us to sum over primitive elements such that poles of the summand are avoided. For a function
$\ast$
in summation reminds us to sum over primitive elements such that poles of the summand are avoided. For a function
![]() $f\in L^{1}(\mathbf{R})$
, its Fourier transform is defined as
$f\in L^{1}(\mathbf{R})$
, its Fourier transform is defined as
We use
![]() $\unicode[STIX]{x1D700}$
to denote a very small positive number, which might be different at each occurrence; we also write
$\unicode[STIX]{x1D700}$
to denote a very small positive number, which might be different at each occurrence; we also write
![]() $X^{\unicode[STIX]{x1D700}}\log X\ll X^{\unicode[STIX]{x1D700}}.$
The convention
$X^{\unicode[STIX]{x1D700}}\log X\ll X^{\unicode[STIX]{x1D700}}.$
The convention
![]() $n\sim N$
means
$n\sim N$
means
![]() $N<n\leqslant 2N$
.
$N<n\leqslant 2N$
.
2 Fundamental transformations: after Hooley and Fouvry
We first make some fundamental transformations following the arguments of Hooley and Fouvry. For some conclusions, we omit the proof and the detailed arguments can be found in [Reference HooleyHoo84] and [Reference FouvryFou16].
2.1 An initial transformation
First, we write
 $$\begin{eqnarray}S(x,\unicode[STIX]{x1D6FC})=\sum _{\substack{ t^{2}-Du^{2}=1 \\ 1<t+u\sqrt{D}\leqslant D^{1/2+\unicode[STIX]{x1D6FC}}}}1=\mathop{\sum }_{1\leqslant u\leqslant X_{\unicode[STIX]{x1D6FC}}}\,\mathop{\sum }_{\substack{ Y_{2}(u,\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(u) \\ Du^{2}=t^{2}-1}}1,\end{eqnarray}$$
$$\begin{eqnarray}S(x,\unicode[STIX]{x1D6FC})=\sum _{\substack{ t^{2}-Du^{2}=1 \\ 1<t+u\sqrt{D}\leqslant D^{1/2+\unicode[STIX]{x1D6FC}}}}1=\mathop{\sum }_{1\leqslant u\leqslant X_{\unicode[STIX]{x1D6FC}}}\,\mathop{\sum }_{\substack{ Y_{2}(u,\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(u) \\ Du^{2}=t^{2}-1}}1,\end{eqnarray}$$
where
Here,
![]() $Y_{1}(u,\unicode[STIX]{x1D6FC})$
is a function in
$Y_{1}(u,\unicode[STIX]{x1D6FC})$
is a function in
![]() $u$
, implicitly defined by the equation
$u$
, implicitly defined by the equation
We have the following asymptotic characterization for
![]() $Y_{2}(u,\unicode[STIX]{x1D6FC}).$
The proof can be found in [Reference FouvryFou16, Lemma 2.1] and the subsequent remark.
$Y_{2}(u,\unicode[STIX]{x1D6FC}).$
The proof can be found in [Reference FouvryFou16, Lemma 2.1] and the subsequent remark.
Lemma 2.1. Let
![]() $\unicode[STIX]{x1D6FC}>0.$
The function
$\unicode[STIX]{x1D6FC}>0.$
The function
![]() $u\mapsto Y_{2}(u,\unicode[STIX]{x1D6FC})$
is of
$u\mapsto Y_{2}(u,\unicode[STIX]{x1D6FC})$
is of
![]() $\mathscr{C}^{\infty }$
-class and satisfies the inequalities
$\mathscr{C}^{\infty }$
-class and satisfies the inequalities
and
as
![]() $u\rightarrow +\infty .$
$u\rightarrow +\infty .$
2.2 A first dissection of
 $S(x,\unicode[STIX]{x1D6FC})$
$S(x,\unicode[STIX]{x1D6FC})$
We truncate the
![]() $u$
-sum in (2.1) at
$u$
-sum in (2.1) at
![]() $X_{1/2}$
, and the contributions from
$X_{1/2}$
, and the contributions from
![]() $u\leqslant X_{1/2}$
and
$u\leqslant X_{1/2}$
and
![]() $u>X_{1/2}$
are respectively denoted by
$u>X_{1/2}$
are respectively denoted by
![]() $A(x,\unicode[STIX]{x1D6FC})$
and
$A(x,\unicode[STIX]{x1D6FC})$
and
![]() $B(x,\unicode[STIX]{x1D6FC}).$
Therefore,
$B(x,\unicode[STIX]{x1D6FC}).$
Therefore,
Accordingly, we may define
![]() $A^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
and
$A^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
and
![]() $B^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
by introducing the extra restriction
$B^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
by introducing the extra restriction
![]() $t+u\sqrt{D}=\unicode[STIX]{x1D700}_{D}$
to the equation
$t+u\sqrt{D}=\unicode[STIX]{x1D700}_{D}$
to the equation
![]() $t^{2}-Du^{2}=1.$
$t^{2}-Du^{2}=1.$
As stated by Fouvry [Reference FouvryFou16, Formula (4.5)], we have the following.
Lemma 2.2. Let
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
As
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
As
![]() $x\rightarrow +\infty ,$
we have
$x\rightarrow +\infty ,$
we have
Our task thus reduces to proving a lower bound for
![]() $B(x,\unicode[STIX]{x1D6FC}).$
Put
$B(x,\unicode[STIX]{x1D6FC}).$
Put
![]() ${\mathcal{R}}(u):=\{\unicode[STIX]{x1D6FA}\,(\operatorname{mod}u^{2}):\unicode[STIX]{x1D6FA}^{2}\equiv 1\,(\operatorname{mod}u^{2})\}.$
We then have
${\mathcal{R}}(u):=\{\unicode[STIX]{x1D6FA}\,(\operatorname{mod}u^{2}):\unicode[STIX]{x1D6FA}^{2}\equiv 1\,(\operatorname{mod}u^{2})\}.$
We then have
 $$\begin{eqnarray}B(x,\unicode[STIX]{x1D6FC})=\mathop{\sum }_{X_{1/2}<u\leqslant X_{\unicode[STIX]{x1D6FC}}}\,\mathop{\sum }_{\unicode[STIX]{x1D6FA}\in {\mathcal{R}}(u)}\,\mathop{\sum }_{\substack{ Y_{2}(u,\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(u) \\ t\equiv \unicode[STIX]{x1D6FA}\,(\operatorname{mod}u^{2})}}1.\end{eqnarray}$$
$$\begin{eqnarray}B(x,\unicode[STIX]{x1D6FC})=\mathop{\sum }_{X_{1/2}<u\leqslant X_{\unicode[STIX]{x1D6FC}}}\,\mathop{\sum }_{\unicode[STIX]{x1D6FA}\in {\mathcal{R}}(u)}\,\mathop{\sum }_{\substack{ Y_{2}(u,\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(u) \\ t\equiv \unicode[STIX]{x1D6FA}\,(\operatorname{mod}u^{2})}}1.\end{eqnarray}$$
Put
![]() $\unicode[STIX]{x1D6FE}(u)=|{\mathcal{R}}(u)|$
. Thus
$\unicode[STIX]{x1D6FE}(u)=|{\mathcal{R}}(u)|$
. Thus
![]() $u\mapsto \unicode[STIX]{x1D6FE}(u)$
is multiplicative and satisfies
$u\mapsto \unicode[STIX]{x1D6FE}(u)$
is multiplicative and satisfies
2.3 Analysis of
 ${\mathcal{R}}(u)$
${\mathcal{R}}(u)$
For
![]() $u\geqslant 1$
, write
$u\geqslant 1$
, write
![]() $u=2^{k}u_{0}$
, where
$u=2^{k}u_{0}$
, where
![]() $u_{0}$
is an odd integer. The choice of
$u_{0}$
is an odd integer. The choice of
![]() $(k,u_{0})$
is unique for each
$(k,u_{0})$
is unique for each
![]() $u\geqslant 1$
. The Chinese remainder theorem implies
$u\geqslant 1$
. The Chinese remainder theorem implies
In this way, one can establish a bijection between
![]() ${\mathcal{R}}(u)$
and
${\mathcal{R}}(u)$
and
![]() ${\mathcal{R}}(2^{k})\times {\mathcal{R}}(u_{0}).$
Starting from (2.9), we decompose
${\mathcal{R}}(2^{k})\times {\mathcal{R}}(u_{0}).$
Starting from (2.9), we decompose
![]() $B(x,\unicode[STIX]{x1D6FC})$
by
$B(x,\unicode[STIX]{x1D6FC})$
by
where
 $$\begin{eqnarray}B(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)=\mathop{\sum }_{\substack{ 2^{-k}X_{1/2}<u\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}} \\ 2\nmid u}}~\mathop{\sum }_{\unicode[STIX]{x1D6FA}\in {\mathcal{R}}(u)}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u,\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u) \\ t\equiv \unicode[STIX]{x1D6FA}\,(\operatorname{mod}u^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1.\end{eqnarray}$$
$$\begin{eqnarray}B(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)=\mathop{\sum }_{\substack{ 2^{-k}X_{1/2}<u\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}} \\ 2\nmid u}}~\mathop{\sum }_{\unicode[STIX]{x1D6FA}\in {\mathcal{R}}(u)}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u,\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u) \\ t\equiv \unicode[STIX]{x1D6FA}\,(\operatorname{mod}u^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1.\end{eqnarray}$$
The task will be evaluating
![]() $B(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
for all
$B(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
for all
![]() $k\geqslant 0$
and
$k\geqslant 0$
and
![]() $\unicode[STIX]{x1D709}\in {\mathcal{R}}(2^{k}).$
This would require the following description of
$\unicode[STIX]{x1D709}\in {\mathcal{R}}(2^{k}).$
This would require the following description of
![]() ${\mathcal{R}}(u)$
that allows us to create one more variable. This is Lemma 4.1 in [Reference FouvryFou16].
${\mathcal{R}}(u)$
that allows us to create one more variable. This is Lemma 4.1 in [Reference FouvryFou16].
Lemma 2.3. Let
![]() $u$
be a positive odd integer. Then there is a bijection
$u$
be a positive odd integer. Then there is a bijection
![]() $\unicode[STIX]{x1D6F7}$
between the set of coprime decompositions of
$\unicode[STIX]{x1D6F7}$
between the set of coprime decompositions of
![]() $u$
$u$
and the set of roots of congruence
Such a bijection can be defined by
![]() $\unicode[STIX]{x1D6F7}(u_{1},u_{2})\,=\,\unicode[STIX]{x1D6FA}$
, where
$\unicode[STIX]{x1D6F7}(u_{1},u_{2})\,=\,\unicode[STIX]{x1D6FA}$
, where
![]() $\unicode[STIX]{x1D6FA}$
is uniquely determined by the congruences
$\unicode[STIX]{x1D6FA}$
is uniquely determined by the congruences
![]() $\unicode[STIX]{x1D6FA}\equiv 1\,(\operatorname{mod}u_{1}^{2})$
and
$\unicode[STIX]{x1D6FA}\equiv 1\,(\operatorname{mod}u_{1}^{2})$
and
![]() $\unicode[STIX]{x1D6FA}\equiv -1\,(\operatorname{mod}u_{2}^{2})$
. In an equivalent manner, we have the congruence
$\unicode[STIX]{x1D6FA}\equiv -1\,(\operatorname{mod}u_{2}^{2})$
. In an equivalent manner, we have the congruence
Here
![]() $\overline{u}_{1}u_{1}\equiv 1\,(\operatorname{mod}u_{2})$
and
$\overline{u}_{1}u_{1}\equiv 1\,(\operatorname{mod}u_{2})$
and
![]() $\overline{u}_{2}u_{2}\equiv 1\,(\operatorname{mod}u_{1})$
.
$\overline{u}_{2}u_{2}\equiv 1\,(\operatorname{mod}u_{1})$
.
With the help of Lemma 2.3, we may rewrite
![]() $B(x,\unicode[STIX]{x1D6FC};k,\unicode[STIX]{x1D709})$
as
$B(x,\unicode[STIX]{x1D6FC};k,\unicode[STIX]{x1D709})$
as
 $$\begin{eqnarray}\displaystyle B(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k) & = & \displaystyle \sum _{\substack{ 2^{-k}X_{1/2}<u_{1}u_{2}\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2}) \\ t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1\nonumber\\ \displaystyle & =: & \displaystyle B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)+B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k) & = & \displaystyle \sum _{\substack{ 2^{-k}X_{1/2}<u_{1}u_{2}\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2}) \\ t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1\nonumber\\ \displaystyle & =: & \displaystyle B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)+B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k),\nonumber\end{eqnarray}$$
where
![]() $B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
and
$B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
and
![]() $B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
correspond to the restrictions
$B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
correspond to the restrictions
![]() $u_{1}>u_{2}$
and
$u_{1}>u_{2}$
and
![]() $u_{1}<u_{2}$
, respectively. Since the treatments of
$u_{1}<u_{2}$
, respectively. Since the treatments of
![]() $B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
and
$B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
and
![]() $B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
are similar, it suffices to study
$B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
are similar, it suffices to study
![]() $B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
as presented in the next section.
$B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
as presented in the next section.
We close this section with the trivial equality
which is a consequence of the equivalence
This allows us to transfer between
![]() $S^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
and
$S^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
and
![]() $S(x,\unicode[STIX]{x1D6FC})$
.
$S(x,\unicode[STIX]{x1D6FC})$
.
3 Lower bound for
 $B(x,\unicode[STIX]{x1D6FC})$
$B(x,\unicode[STIX]{x1D6FC})$
In order to conclude the lower bound for
![]() $B(x,\unicode[STIX]{x1D6FC})$
, we now start the study of
$B(x,\unicode[STIX]{x1D6FC})$
, we now start the study of
![]() $B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
. Recall that
$B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
. Recall that
 $$\begin{eqnarray}B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)=\sum _{\substack{ 2^{-k}X_{1/2}<u_{1}u_{2}\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}} \\ u_{1}<u_{2} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2}) \\ t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1.\end{eqnarray}$$
$$\begin{eqnarray}B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)=\sum _{\substack{ 2^{-k}X_{1/2}<u_{1}u_{2}\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}} \\ u_{1}<u_{2} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2}) \\ t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1.\end{eqnarray}$$
We would like to drop the multiplicative constraints
![]() $2^{-k}X_{1/2}<u_{1}u_{2}\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}}$
and sum over
$2^{-k}X_{1/2}<u_{1}u_{2}\leqslant 2^{-k}X_{\unicode[STIX]{x1D6FC}}$
and sum over
![]() $u_{1},u_{2}$
separately. To do so, we may introduce the following inequality
$u_{1},u_{2}$
separately. To do so, we may introduce the following inequality
where we have the following.
∙ The summation is over all
 $\mathbf{U}=(U_{1},U_{2})$
satisfying and
$\mathbf{U}=(U_{1},U_{2})$
satisfying and $$\begin{eqnarray}U_{1}<U_{2},\quad X_{1/2}<2^{k}U_{1}U_{2}\leqslant \frac{X_{\unicode[STIX]{x1D6FC}}}{8},\end{eqnarray}$$
$$\begin{eqnarray}U_{1}<U_{2},\quad X_{1/2}<2^{k}U_{1}U_{2}\leqslant \frac{X_{\unicode[STIX]{x1D6FC}}}{8},\end{eqnarray}$$
 $U_{1},U_{2}$
being powers of
$U_{1},U_{2}$
being powers of
 $2$
.
$2$
.∙ The summation is over all
 $\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k})$
satisfying
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k})$
satisfying
 $(\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2},4^{k})=1$
.
$(\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2},4^{k})=1$
.∙ We have defined
 $$\begin{eqnarray}B(x,\unicode[STIX]{x1D6FC};\boldsymbol{ U},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},k):=\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2}) \\ t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1.\end{eqnarray}$$
$$\begin{eqnarray}B(x,\unicode[STIX]{x1D6FC};\boldsymbol{ U},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},k):=\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2}) \\ t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}) \\ t\equiv \unicode[STIX]{x1D709}\,(\operatorname{mod}4^{k})}}1.\end{eqnarray}$$
Of course the condition
![]() $(2,u_{1}u_{2})=1$
can be dropped when
$(2,u_{1}u_{2})=1$
can be dropped when
![]() $k\geqslant 1$
. The parameter
$k\geqslant 1$
. The parameter
![]() $\unicode[STIX]{x1D6FC}$
is supposed to be fixed and the congruence conditions modulo
$\unicode[STIX]{x1D6FC}$
is supposed to be fixed and the congruence conditions modulo
![]() $4^{k}$
are harmless. So to shorten the notation, we write
$4^{k}$
are harmless. So to shorten the notation, we write
![]() $B(x,\mathbf{U}):=B(x,\unicode[STIX]{x1D6FC};\mathbf{U},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},k)$
. Finally we shall not make precise the dependence on
$B(x,\mathbf{U}):=B(x,\unicode[STIX]{x1D6FC};\mathbf{U},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},k)$
. Finally we shall not make precise the dependence on
![]() $k$
of some
$k$
of some
![]() $O$
-symbols, since we shall work with a finite number of values of
$O$
-symbols, since we shall work with a finite number of values of
![]() $k$
. The case
$k$
. The case
![]() $k=0$
is typical and really reflects the difficulties of the method.
$k=0$
is typical and really reflects the difficulties of the method.
3.1 Reduction to exponential sums: after Fouvry
The congruence condition
![]() $t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2})$
implies that
$t\equiv \unicode[STIX]{x1D6F7}(u_{1},u_{2})\,(\operatorname{mod}u_{1}^{2}u_{2}^{2})$
implies that
![]() $t\equiv -1\,(\operatorname{mod}u_{2}^{2})$
, i.e.,
$t\equiv -1\,(\operatorname{mod}u_{2}^{2})$
, i.e.,
![]() $t=-1+\ell u_{2}^{2}$
for some
$t=-1+\ell u_{2}^{2}$
for some
![]() $\ell \in \mathbf{Z}.$
Since
$\ell \in \mathbf{Z}.$
Since
![]() $Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2})$
, then there is no such
$Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})\leqslant t\leqslant Y_{3}(2^{k}u_{1}u_{2})$
, then there is no such
![]() $t$
if
$t$
if
![]() $u_{2}$
is too large, for instance when
$u_{2}$
is too large, for instance when
Hence we can suppose
otherwise
![]() $B(x,\mathbf{U})=0.$
$B(x,\mathbf{U})=0.$
Since
![]() $u_{1}u_{2}$
is odd, we deduce from (2.13) the equivalence
$u_{1}u_{2}$
is odd, we deduce from (2.13) the equivalence
with
where
![]() $u_{1}^{2}u_{2}^{2}\cdot \overline{(u_{1}^{2}u_{2}^{2})}\equiv 1\,(\operatorname{mod}4^{k}),u_{2}^{2}\overline{u_{2}^{2}}\equiv 1\,(\operatorname{mod}u_{1}^{2})$
and
$u_{1}^{2}u_{2}^{2}\cdot \overline{(u_{1}^{2}u_{2}^{2})}\equiv 1\,(\operatorname{mod}4^{k}),u_{2}^{2}\overline{u_{2}^{2}}\equiv 1\,(\operatorname{mod}u_{1}^{2})$
and
![]() $4^{k}\overline{4^{k}}\equiv 1\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}).$
It follows that
$4^{k}\overline{4^{k}}\equiv 1\,(\operatorname{mod}u_{1}^{2}u_{2}^{2}).$
It follows that
with
![]() $\unicode[STIX]{x1D705}:=(\unicode[STIX]{x1D709}+1)\overline{\unicode[STIX]{x1D709}_{1}^{2}\unicode[STIX]{x1D709}_{2}^{2}}/4^{k}.$
The three terms on the right-hand side have completely different structures: the first one is constant, the second one changes very slowly when
$\unicode[STIX]{x1D705}:=(\unicode[STIX]{x1D709}+1)\overline{\unicode[STIX]{x1D709}_{1}^{2}\unicode[STIX]{x1D709}_{2}^{2}}/4^{k}.$
The three terms on the right-hand side have completely different structures: the first one is constant, the second one changes very slowly when
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
vary, the third one oscillates a lot when
$u_{2}$
vary, the third one oscillates a lot when
![]() $u_{2}$
varies with
$u_{2}$
varies with
![]() $u_{1}$
fixed.
$u_{1}$
fixed.
For each fixed
![]() $k$
, we rewrite the sum
$k$
, we rewrite the sum
![]() $B(x,\mathbf{U})$
as
$B(x,\mathbf{U})$
as
 $$\begin{eqnarray}B(x,\boldsymbol{ U})=B(x,\unicode[STIX]{x1D6FC};\boldsymbol{ U},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},k)=\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}\leqslant t\leqslant Y_{3} \\ t\equiv t_{0}\,(\operatorname{mod}4^{k}u_{1}^{2}u_{2}^{2})}}1,\end{eqnarray}$$
$$\begin{eqnarray}B(x,\boldsymbol{ U})=B(x,\unicode[STIX]{x1D6FC};\boldsymbol{ U},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},k)=\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ Y_{2}\leqslant t\leqslant Y_{3} \\ t\equiv t_{0}\,(\operatorname{mod}4^{k}u_{1}^{2}u_{2}^{2})}}1,\end{eqnarray}$$
where
![]() $Y_{2}:=Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})$
and
$Y_{2}:=Y_{2}(2^{k}u_{1}u_{2},\unicode[STIX]{x1D6FC})$
and
![]() $Y_{3}:=Y_{3}(2^{k}u_{1}u_{2})$
. As in [Reference FouvryFou16], we smooth the
$Y_{3}:=Y_{3}(2^{k}u_{1}u_{2})$
. As in [Reference FouvryFou16], we smooth the
![]() $t$
-sum via the following lemma.
$t$
-sum via the following lemma.
Lemma 3.1. For every
![]() $\unicode[STIX]{x1D6FF}>0$
there exists a smooth function
$\unicode[STIX]{x1D6FF}>0$
there exists a smooth function
![]() $g:\mathbf{R}\rightarrow \mathbf{R}$
which has the two properties
$g:\mathbf{R}\rightarrow \mathbf{R}$
which has the two properties
and
Let
![]() $g$
be a smooth function given as in Lemma 3.1. Hence
$g$
be a smooth function given as in Lemma 3.1. Hence
 $$\begin{eqnarray}B(x,\boldsymbol{ U})\geqslant \sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ t\in \mathbf{Z} \\ t\equiv t_{0}\,(\operatorname{mod}4^{k}u_{1}^{2}u_{2}^{2})}}g\bigg(\frac{t-(Y_{2}+Y_{3})/2}{Y_{3}-Y_{2}}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}B(x,\boldsymbol{ U})\geqslant \sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}~\mathop{\sum }_{\substack{ t\in \mathbf{Z} \\ t\equiv t_{0}\,(\operatorname{mod}4^{k}u_{1}^{2}u_{2}^{2})}}g\bigg(\frac{t-(Y_{2}+Y_{3})/2}{Y_{3}-Y_{2}}\bigg).\end{eqnarray}$$
By Poisson summation, the
![]() $t$
-sum becomes
$t$
-sum becomes
From integration by parts, we have
![]() $\widehat{g}(y)\ll (1+|y|)^{-A}$
for any
$\widehat{g}(y)\ll (1+|y|)^{-A}$
for any
![]() $A\geqslant 0$
. Note that
$A\geqslant 0$
. Note that
The above sum over
![]() $h$
can be truncated to
$h$
can be truncated to
![]() $0\leqslant |h|\leqslant H$
with
$0\leqslant |h|\leqslant H$
with
![]() $H=U_{1}U_{2}x^{-1/2+\unicode[STIX]{x1D700}}$
, and the remaining contribution is at most
$H=U_{1}U_{2}x^{-1/2+\unicode[STIX]{x1D700}}$
, and the remaining contribution is at most
![]() $O(x^{-2017}).$
Therefore,
$O(x^{-2017}).$
Therefore,
 $$\begin{eqnarray}\displaystyle B(x,\mathbf{U}) & {\geqslant} & \displaystyle \sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}\mathop{\sum }_{0\leqslant |h|\leqslant H}\widehat{g}\bigg(\frac{h(Y_{3}-Y_{2})}{4^{k}u_{1}^{2}u_{2}^{2}}\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg(h\unicode[STIX]{x1D705}+2h\frac{\overline{4^{k}u_{2}^{2}}}{u_{1}^{2}}-\frac{h(2+Y_{2}+Y_{3})}{2\cdot 4^{k}u_{1}^{2}u_{2}^{2}}\bigg)+O(x^{-1949})\nonumber\\ \displaystyle & = & \displaystyle B_{1}(x,\mathbf{U})+B_{2}(x,\mathbf{U})+O(x^{-1949}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(x,\mathbf{U}) & {\geqslant} & \displaystyle \sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}\mathop{\sum }_{0\leqslant |h|\leqslant H}\widehat{g}\bigg(\frac{h(Y_{3}-Y_{2})}{4^{k}u_{1}^{2}u_{2}^{2}}\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,e\bigg(h\unicode[STIX]{x1D705}+2h\frac{\overline{4^{k}u_{2}^{2}}}{u_{1}^{2}}-\frac{h(2+Y_{2}+Y_{3})}{2\cdot 4^{k}u_{1}^{2}u_{2}^{2}}\bigg)+O(x^{-1949})\nonumber\\ \displaystyle & = & \displaystyle B_{1}(x,\mathbf{U})+B_{2}(x,\mathbf{U})+O(x^{-1949}),\nonumber\end{eqnarray}$$
where
![]() $B_{1}(x,\mathbf{U})$
and
$B_{1}(x,\mathbf{U})$
and
![]() $B_{2}(x,\mathbf{U})$
are used to denote contributions from
$B_{2}(x,\mathbf{U})$
are used to denote contributions from
![]() $h=0$
and
$h=0$
and
![]() $h\neq 0$
, respectively.
$h\neq 0$
, respectively.
First,
 $$\begin{eqnarray}B_{1}(x,\mathbf{U})=(1-\unicode[STIX]{x1D6FF})\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}},\end{eqnarray}$$
$$\begin{eqnarray}B_{1}(x,\mathbf{U})=(1-\unicode[STIX]{x1D6FF})\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}},\end{eqnarray}$$
which is
![]() $\asymp \sqrt{x}$
. It is also desirable to show that
$\asymp \sqrt{x}$
. It is also desirable to show that
for some
![]() $\unicode[STIX]{x1D700}_{0}>0$
. By standard tools from analysis (see [Reference FouvryFou16] for details), it suffices to prove that
$\unicode[STIX]{x1D700}_{0}>0$
. By standard tools from analysis (see [Reference FouvryFou16] for details), it suffices to prove that
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ h\leqslant H \\ h\equiv h_{0}\,(\operatorname{mod}4^{k})}}\sum _{\substack{ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}e\bigg(2h\frac{\overline{4^{k}u_{2}^{2}}}{u_{1}^{2}}\bigg)\ll U_{1}U_{2}x^{-\unicode[STIX]{x1D700}_{0}},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ h\leqslant H \\ h\equiv h_{0}\,(\operatorname{mod}4^{k})}}\sum _{\substack{ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}e\bigg(2h\frac{\overline{4^{k}u_{2}^{2}}}{u_{1}^{2}}\bigg)\ll U_{1}U_{2}x^{-\unicode[STIX]{x1D700}_{0}},\end{eqnarray}$$
where
![]() $U_{j}<U_{j}^{\ast }\leqslant 2U_{j}$
,
$U_{j}<U_{j}^{\ast }\leqslant 2U_{j}$
,
![]() $j=1,2$
. After transforming the
$j=1,2$
. After transforming the
![]() $u_{2}$
-sum to a complete sum
$u_{2}$
-sum to a complete sum
![]() $T(\cdot ,u_{1}^{2})$
, where
$T(\cdot ,u_{1}^{2})$
, where
Fouvry [Reference FouvryFou16] evaluated
![]() $T(\cdot ,u_{1}^{2})$
in terms of classical Gauss sums and Jacobi symbols. He then arrived at a bilinear form involving Jacobi symbols, for which a celebrated estimate due to Heath-Brown [Reference Heath-BrownHea95] was applied. Amongst some other delicate arguments, Fouvry was able to prove (3.4) under the conditions
$T(\cdot ,u_{1}^{2})$
in terms of classical Gauss sums and Jacobi symbols. He then arrived at a bilinear form involving Jacobi symbols, for which a celebrated estimate due to Heath-Brown [Reference Heath-BrownHea95] was applied. Amongst some other delicate arguments, Fouvry was able to prove (3.4) under the conditions
in which case he obtained the lower bound
 $$\begin{eqnarray}B(x,\mathbf{U})\geqslant (1-\unicode[STIX]{x1D6FF})\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}+O(x^{1/2-\unicode[STIX]{x1D700}_{0}}).\end{eqnarray}$$
$$\begin{eqnarray}B(x,\mathbf{U})\geqslant (1-\unicode[STIX]{x1D6FF})\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}+O(x^{1/2-\unicode[STIX]{x1D700}_{0}}).\end{eqnarray}$$
To obtain a better lower bound for
![]() $B(x,\unicode[STIX]{x1D6FC})$
and thus for
$B(x,\unicode[STIX]{x1D6FC})$
and thus for
![]() $S(x,\unicode[STIX]{x1D6FC})$
, it is natural to expect that (3.4) and (3.7) can hold in larger ranges of
$S(x,\unicode[STIX]{x1D6FC})$
, it is natural to expect that (3.4) and (3.7) can hold in larger ranges of
![]() $U_{1},U_{2}$
. However, it seems rather difficult when
$U_{1},U_{2}$
. However, it seems rather difficult when
![]() $U_{1}$
is quite close to
$U_{1}$
is quite close to
![]() $U_{2}$
since the
$U_{2}$
since the
![]() $u_{2}$
-sum is too short in the sense of the Pólya–Vinogradov barrier. In fact, Bourgain [Reference BourgainBou15] managed to control the left-hand side in (3.5), but with a saving of a small power of
$u_{2}$
-sum is too short in the sense of the Pólya–Vinogradov barrier. In fact, Bourgain [Reference BourgainBou15] managed to control the left-hand side in (3.5), but with a saving of a small power of
![]() $\log x$
rather than that of
$\log x$
rather than that of
![]() $x$
. This allows him to improve upon Fouvry when
$x$
. This allows him to improve upon Fouvry when
![]() $\unicode[STIX]{x1D6FC}$
is rather close to
$\unicode[STIX]{x1D6FC}$
is rather close to
![]() $\frac{1}{2}$
in Theorem B.
$\frac{1}{2}$
in Theorem B.
In our subsequent argument, we will specialize
![]() $u_{1}$
with special structures in the original sum (3.3) before Poisson summation. More precisely, we will consider those
$u_{1}$
with special structures in the original sum (3.3) before Poisson summation. More precisely, we will consider those
![]() $u_{1}$
consisting of only small prime factors, so that
$u_{1}$
consisting of only small prime factors, so that
![]() $u_{1}$
has good factorizations, which enable us to control the exponential sums in (3.5) even though
$u_{1}$
has good factorizations, which enable us to control the exponential sums in (3.5) even though
![]() $U_{1}$
is quite close to
$U_{1}$
is quite close to
![]() $U_{2}$
.
$U_{2}$
.
3.2 Lower bound of
 $B(x,\mathbf{U})$
: smooth approach
$B(x,\mathbf{U})$
: smooth approach
A positive integer
![]() $n$
is said to be
$n$
is said to be
![]() $y$
-smooth (or friable) if all prime factors of
$y$
-smooth (or friable) if all prime factors of
![]() $n$
do not exceed
$n$
do not exceed
![]() $y$
. Let
$y$
. Let
![]() $\unicode[STIX]{x1D703}\in \, ]\!0,\frac{1}{2}\! [$
be a fixed number. If
$\unicode[STIX]{x1D703}\in \, ]\!0,\frac{1}{2}\! [$
be a fixed number. If
![]() $n$
is
$n$
is
![]() $n^{\unicode[STIX]{x1D703}}$
-smooth, the inclusion–exclusion principle yields the existence of the divisor
$n^{\unicode[STIX]{x1D703}}$
-smooth, the inclusion–exclusion principle yields the existence of the divisor
![]() $d\mid n$
such that
$d\mid n$
such that
![]() $n^{\unicode[STIX]{x1D703}_{0}}\leqslant d\leqslant n^{\unicode[STIX]{x1D703}_{0}+\unicode[STIX]{x1D703}}$
for any
$n^{\unicode[STIX]{x1D703}_{0}}\leqslant d\leqslant n^{\unicode[STIX]{x1D703}_{0}+\unicode[STIX]{x1D703}}$
for any
![]() $\unicode[STIX]{x1D703}_{0}\in [0,1-\unicode[STIX]{x1D703}].$
$\unicode[STIX]{x1D703}_{0}\in [0,1-\unicode[STIX]{x1D703}].$
We now restrict these
![]() $u_{1}$
in the right-hand side of (3.3) to
$u_{1}$
in the right-hand side of (3.3) to
![]() $U_{1}^{\unicode[STIX]{x1D703}}$
-smooth numbers and put
$U_{1}^{\unicode[STIX]{x1D703}}$
-smooth numbers and put
 $$\begin{eqnarray}B^{\ast }(x,\boldsymbol{ U})=\sum _{\substack{ u_{1}\sim U_{1},u_{2}\geqslant 1 \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)\mathop{\sum }_{\substack{ t\in \mathbf{Z} \\ t\equiv t_{0}\,(\operatorname{mod}4^{k}u_{1}^{2}u_{2}^{2})}}g\bigg(\frac{t-(Y_{2}+Y_{3})/2}{Y_{3}-Y_{2}}\bigg),\end{eqnarray}$$
$$\begin{eqnarray}B^{\ast }(x,\boldsymbol{ U})=\sum _{\substack{ u_{1}\sim U_{1},u_{2}\geqslant 1 \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)\mathop{\sum }_{\substack{ t\in \mathbf{Z} \\ t\equiv t_{0}\,(\operatorname{mod}4^{k}u_{1}^{2}u_{2}^{2})}}g\bigg(\frac{t-(Y_{2}+Y_{3})/2}{Y_{3}-Y_{2}}\bigg),\end{eqnarray}$$
where
![]() $g_{1}(y)=g(y-\frac{3}{2})$
with
$g_{1}(y)=g(y-\frac{3}{2})$
with
![]() $g$
given as in Lemma 3.1. Following the similar arguments of Fouvry, we may derive that
$g$
given as in Lemma 3.1. Following the similar arguments of Fouvry, we may derive that
where
 $$\begin{eqnarray}\displaystyle B_{1}^{\ast }(x,\mathbf{U}) & = & \displaystyle (1-\unicode[STIX]{x1D6FF})\sum _{\substack{ u_{1}\sim U_{1},u_{2}\geqslant 1 \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (1-\unicode[STIX]{x1D6FF})^{2}\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{1}^{\ast }(x,\mathbf{U}) & = & \displaystyle (1-\unicode[STIX]{x1D6FF})\sum _{\substack{ u_{1}\sim U_{1},u_{2}\geqslant 1 \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (1-\unicode[STIX]{x1D6FF})^{2}\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}},\nonumber\end{eqnarray}$$
and we expect to show that
for some
![]() $\unicode[STIX]{x1D700}_{0}>0$
, for which it suffices to prove, for all
$\unicode[STIX]{x1D700}_{0}>0$
, for which it suffices to prove, for all
![]() $U_{1}^{\ast }\in \, ]\!U_{1},2U_{1} ]$
, that
$U_{1}^{\ast }\in \, ]\!U_{1},2U_{1} ]$
, that
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ h\leqslant H \\ h\equiv h_{0}\,(\operatorname{mod}4^{k})}}~\sum _{\substack{ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)e\bigg(2h\frac{\overline{4^{k}u_{2}^{2}}}{u_{1}^{2}}\bigg)\ll U_{1}U_{2}x^{-\unicode[STIX]{x1D700}_{0}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ h\leqslant H \\ h\equiv h_{0}\,(\operatorname{mod}4^{k})}}~\sum _{\substack{ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)e\bigg(2h\frac{\overline{4^{k}u_{2}^{2}}}{u_{1}^{2}}\bigg)\ll U_{1}U_{2}x^{-\unicode[STIX]{x1D700}_{0}}.\end{eqnarray}$$
We will prove the following.
Theorem 3.1. There exists some
![]() $\unicode[STIX]{x1D700}_{0}\in \, ]\!0,10^{-2017}\! [$
such that (3.10) holds, provided that
$\unicode[STIX]{x1D700}_{0}\in \, ]\!0,10^{-2017}\! [$
such that (3.10) holds, provided that
Put
![]() $U_{1}=x^{\unicode[STIX]{x1D6FE}_{1}}$
and
$U_{1}=x^{\unicode[STIX]{x1D6FE}_{1}}$
and
![]() $U_{2}=x^{\unicode[STIX]{x1D6FE}_{2}}$
. In addition to the restrictions
$U_{2}=x^{\unicode[STIX]{x1D6FE}_{2}}$
. In addition to the restrictions
![]() $\unicode[STIX]{x1D6FE}_{2}<\unicode[STIX]{x1D6FE}_{1}+\frac{1}{2},\frac{1}{2}<\unicode[STIX]{x1D6FE}_{1}+\unicode[STIX]{x1D6FE}_{2}<\unicode[STIX]{x1D6FC}$
, (3.6) requires
$\unicode[STIX]{x1D6FE}_{2}<\unicode[STIX]{x1D6FE}_{1}+\frac{1}{2},\frac{1}{2}<\unicode[STIX]{x1D6FE}_{1}+\unicode[STIX]{x1D6FE}_{2}<\unicode[STIX]{x1D6FC}$
, (3.6) requires
![]() $\unicode[STIX]{x1D6FE}_{1}<\frac{1}{4}$
, and we require
$\unicode[STIX]{x1D6FE}_{1}<\frac{1}{4}$
, and we require
![]() $\unicode[STIX]{x1D6FE}_{2}<1-\frac{26}{9}\unicode[STIX]{x1D6FE}_{1}$
in the particular case
$\unicode[STIX]{x1D6FE}_{2}<1-\frac{26}{9}\unicode[STIX]{x1D6FE}_{1}$
in the particular case
![]() $\unicode[STIX]{x1D703}=\frac{1}{36}$
. In Figure 1, the shaded area shows what we can gain more than the previous approach (we are gaining relatively more as
$\unicode[STIX]{x1D703}=\frac{1}{36}$
. In Figure 1, the shaded area shows what we can gain more than the previous approach (we are gaining relatively more as
![]() $\unicode[STIX]{x1D6FC}$
becomes closer to
$\unicode[STIX]{x1D6FC}$
becomes closer to
![]() $\frac{1}{2}$
).
$\frac{1}{2}$
).

Figure 1. Admissible values of
![]() $(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
.
$(\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2})$
.
The proof of Theorem 3.1 will be given in the next section. To see the advantage of our approach, one may consider the particular case
![]() $U_{1}=U_{2}$
, and our first restriction will reduce to
$U_{1}=U_{2}$
, and our first restriction will reduce to
![]() $U_{1}\leqslant x^{3/(11+2\unicode[STIX]{x1D703})-\unicode[STIX]{x1D700}_{0}}$
; however, the stronger restriction
$U_{1}\leqslant x^{3/(11+2\unicode[STIX]{x1D703})-\unicode[STIX]{x1D700}_{0}}$
; however, the stronger restriction
![]() $U_{1}\leqslant x^{1/4-5\unicode[STIX]{x1D700}_{0}}$
in (3.6) is required.
$U_{1}\leqslant x^{1/4-5\unicode[STIX]{x1D700}_{0}}$
in (3.6) is required.
Therefore, we may obtain the lower bound
 $$\begin{eqnarray}B(x,\mathbf{U})\geqslant (1-\unicode[STIX]{x1D6FF})^{2}\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}+O(x^{1/2-\unicode[STIX]{x1D700}_{0}})\end{eqnarray}$$
$$\begin{eqnarray}B(x,\mathbf{U})\geqslant (1-\unicode[STIX]{x1D6FF})^{2}\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}+O(x^{1/2-\unicode[STIX]{x1D700}_{0}})\end{eqnarray}$$
subject to the restrictions in (3.11).
3.3 A weakened form of Theorem 1.1
Up to now, we have two lower bounds for
![]() $B(x,\mathbf{U})$
, i.e., (3.7) and (3.12), subject to the restrictions in (3.6) and (3.11), respectively. In what follows, we will take into account all such admissible tuples
$B(x,\mathbf{U})$
, i.e., (3.7) and (3.12), subject to the restrictions in (3.6) and (3.11), respectively. In what follows, we will take into account all such admissible tuples
![]() $(k,\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},U_{1},U_{2})$
, for which we appeal to (3.7) if (3.6) is satisfied, and appeal to (3.12) if (3.6) is not satisfied but (3.11) is valid. To this end, we define two sets of tuples
$(k,\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},U_{1},U_{2})$
, for which we appeal to (3.7) if (3.6) is satisfied, and appeal to (3.12) if (3.6) is not satisfied but (3.11) is valid. To this end, we define two sets of tuples
and
where
![]() $\unicode[STIX]{x1D702}$
is a sufficiently small positive number.
$\unicode[STIX]{x1D702}$
is a sufficiently small positive number.
First, we may derive a lower bound for
![]() $B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
by inserting the inequality (3.7) or (3.12) into (3.1). A similar lower bound also holds for
$B^{{<}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
by inserting the inequality (3.7) or (3.12) into (3.1). A similar lower bound also holds for
![]() $B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
by symmetry. Therefore, we have
$B^{{>}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D709},k)$
by symmetry. Therefore, we have
 $$\begin{eqnarray}\displaystyle B(x,\unicode[STIX]{x1D6FC}) & {\geqslant} & \displaystyle 2(1-\unicode[STIX]{x1D6FF})\mathop{\sum }_{k=0}^{k_{0}}~\mathop{\sum }_{\unicode[STIX]{x1D709}\in {\mathcal{R}}(2^{k})}~\mathop{\sum }_{\mathbf{U}\in \mathscr{U}_{1}}~\sum _{\substack{ \unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ 2\nmid \unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}}~\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,2(1-2\unicode[STIX]{x1D6FF})\mathop{\sum }_{k=0}^{k_{0}}~\mathop{\sum }_{\unicode[STIX]{x1D709}\in {\mathcal{R}}(2^{k})}~\mathop{\sum }_{\mathbf{U}\in \mathscr{U}_{2}}~\sum _{\substack{ \unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ 2\nmid \unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}}\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}+O(x^{1/2}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(x,\unicode[STIX]{x1D6FC}) & {\geqslant} & \displaystyle 2(1-\unicode[STIX]{x1D6FF})\mathop{\sum }_{k=0}^{k_{0}}~\mathop{\sum }_{\unicode[STIX]{x1D709}\in {\mathcal{R}}(2^{k})}~\mathop{\sum }_{\mathbf{U}\in \mathscr{U}_{1}}~\sum _{\substack{ \unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ 2\nmid \unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}}~\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}\nonumber\\ \displaystyle & & \displaystyle +\,2(1-2\unicode[STIX]{x1D6FF})\mathop{\sum }_{k=0}^{k_{0}}~\mathop{\sum }_{\unicode[STIX]{x1D709}\in {\mathcal{R}}(2^{k})}~\mathop{\sum }_{\mathbf{U}\in \mathscr{U}_{2}}~\sum _{\substack{ \unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ 2\nmid \unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}}}\sum _{\substack{ u_{1}\sim U_{1},u_{2}\sim U_{2} \\ u_{1}\equiv \unicode[STIX]{x1D709}_{1},u_{2}\equiv \unicode[STIX]{x1D709}_{2}\,(\operatorname{mod}4^{k}) \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{Y_{3}-Y_{2}}{4^{k}u_{1}^{2}u_{2}^{2}}+O(x^{1/2}),\nonumber\end{eqnarray}$$
where
![]() $U_{1},U_{2}$
are also restricted to be powers of 2. Recall that
$U_{1},U_{2}$
are also restricted to be powers of 2. Recall that
We then obtain the lower bound
 $$\begin{eqnarray}\displaystyle B(x,\unicode[STIX]{x1D6FC}) & {\geqslant} & \displaystyle 2(1-2\unicode[STIX]{x1D6FF})\bigg(\mathop{\sum }_{k=0}^{k_{0}}\frac{\unicode[STIX]{x1D6FE}(2^{k})}{2^{k}}\bigg)\bigg\{\sum _{\substack{ (u_{1},u_{2})\in \mathscr{V}_{1} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{1}{u_{1}u_{2}}+\sum _{\substack{ (u_{1},u_{2})\in \mathscr{V}_{2} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{1}{u_{1}u_{2}}\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,O(x^{1/2}\log x),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B(x,\unicode[STIX]{x1D6FC}) & {\geqslant} & \displaystyle 2(1-2\unicode[STIX]{x1D6FF})\bigg(\mathop{\sum }_{k=0}^{k_{0}}\frac{\unicode[STIX]{x1D6FE}(2^{k})}{2^{k}}\bigg)\bigg\{\sum _{\substack{ (u_{1},u_{2})\in \mathscr{V}_{1} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1}}\frac{1}{u_{1}u_{2}}+\sum _{\substack{ (u_{1},u_{2})\in \mathscr{V}_{2} \\ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{1}{u_{1}u_{2}}\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,O(x^{1/2}\log x),\nonumber\end{eqnarray}$$
where
and
Taking
![]() $k_{0}=k_{0}(\unicode[STIX]{x1D6FF})$
very large,
$k_{0}=k_{0}(\unicode[STIX]{x1D6FF})$
very large,
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FF})$
very small, and letting
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FF})$
very small, and letting
![]() $\unicode[STIX]{x1D6FF}$
tend to zero, we conclude from Lemma A.1 that
$\unicode[STIX]{x1D6FF}$
tend to zero, we conclude from Lemma A.1 that
uniformly for
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1],$
where
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1],$
where
 $$\begin{eqnarray}B^{\prime }(x,\unicode[STIX]{x1D6FC})=4\sqrt{x}\mathop{\sum }_{\substack{ x^{1/4}<u_{1}\leqslant x^{\min \{\unicode[STIX]{x1D6FC}/2,3/(11+2\unicode[STIX]{x1D703})\}} \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth} \\ 2\nmid u_{1}}}\frac{\unicode[STIX]{x1D711}(u_{1})}{u_{1}^{2}}\log (\sqrt{x}u_{1}^{-(5+2\unicode[STIX]{x1D703})/3}).\end{eqnarray}$$
$$\begin{eqnarray}B^{\prime }(x,\unicode[STIX]{x1D6FC})=4\sqrt{x}\mathop{\sum }_{\substack{ x^{1/4}<u_{1}\leqslant x^{\min \{\unicode[STIX]{x1D6FC}/2,3/(11+2\unicode[STIX]{x1D703})\}} \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth} \\ 2\nmid u_{1}}}\frac{\unicode[STIX]{x1D711}(u_{1})}{u_{1}^{2}}\log (\sqrt{x}u_{1}^{-(5+2\unicode[STIX]{x1D703})/3}).\end{eqnarray}$$
Note that
![]() $B^{\prime }(x,\unicode[STIX]{x1D6FC})$
is what we have gained more than Fouvry [Reference FouvryFou16]. From Lemma A.3, we arrive at
$B^{\prime }(x,\unicode[STIX]{x1D6FC})$
is what we have gained more than Fouvry [Reference FouvryFou16]. From Lemma A.3, we arrive at
with
One may check that
as given in Theorem 1.1. Combining this asymptotic evaluation for
![]() $B^{\prime }(x,\unicode[STIX]{x1D6FC})$
with (3.13), we may conclude a lower bound for
$B^{\prime }(x,\unicode[STIX]{x1D6FC})$
with (3.13), we may conclude a lower bound for
![]() $B(x,\unicode[STIX]{x1D6FC})$
, from which and (2.8), (2.7), we get
$B(x,\unicode[STIX]{x1D6FC})$
, from which and (2.8), (2.7), we get
uniformly for
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
3.4 Concluding Theorem 1.1
To pass from a lower bound of
![]() $S(x,\unicode[STIX]{x1D6FC})$
to that of
$S(x,\unicode[STIX]{x1D6FC})$
to that of
![]() $S^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
, it is natural to invoke the identity (2.14) and Theorem A. In fact, one can do a bit better following the arguments of Fouvry [Reference FouvryFou16] and show that the above lower bound (3.14) also hold for
$S^{\text{f}}(x,\unicode[STIX]{x1D6FC})$
, it is natural to invoke the identity (2.14) and Theorem A. In fact, one can do a bit better following the arguments of Fouvry [Reference FouvryFou16] and show that the above lower bound (3.14) also hold for
![]() $S^{\text{f}}(x,\unicode[STIX]{x1D6FC}).$
This will depend on a more elaborate study of the contribution from non-fundamental solutions. In other words, we would like to show that the non-fundamental solutions create negligible contributions to
$S^{\text{f}}(x,\unicode[STIX]{x1D6FC}).$
This will depend on a more elaborate study of the contribution from non-fundamental solutions. In other words, we would like to show that the non-fundamental solutions create negligible contributions to
![]() $A(x,\unicode[STIX]{x1D6FC})$
and
$A(x,\unicode[STIX]{x1D6FC})$
and
![]() $B(x,\unicode[STIX]{x1D6FC}).$
$B(x,\unicode[STIX]{x1D6FC}).$
The following lemma is borrowed directly from [Reference FouvryFou16, Lemma 9.1].
Lemma 3.2. Uniformly for
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1]$
and
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1]$
and
![]() $x\geqslant 2$
, one has
$x\geqslant 2$
, one has
To deal with the contribution of the non-fundamental solutions to
![]() $B(x,\unicode[STIX]{x1D6FC})$
, we also follow Fouvry. The above arguments which lead to (3.14) are essentially counting the number
$B(x,\unicode[STIX]{x1D6FC})$
, we also follow Fouvry. The above arguments which lead to (3.14) are essentially counting the number
![]() $\mathscr{N}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})$
of 5-tuples of integers
$\mathscr{N}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})$
of 5-tuples of integers
![]() $(k,t,u_{1},u_{2},D)$
satisfying
$(k,t,u_{1},u_{2},D)$
satisfying
 $$\begin{eqnarray}\displaystyle & \displaystyle 2\nmid u_{1}u_{2},\quad (u_{1},u_{2})=1,\quad 0\leqslant k\leqslant k_{0},\quad D\leqslant x, & \displaystyle \nonumber\\ \displaystyle & \displaystyle X_{1/2}\leqslant 2^{k}u_{1}u_{2}\leqslant X_{\unicode[STIX]{x1D6FC}},\quad t+2^{k}u_{1}u_{2}\sqrt{D}\leqslant D^{1/2+\unicode[STIX]{x1D6FC}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle t^{2}\equiv 1\quad (\operatorname{mod}4^{k}),\quad t\equiv 1\quad (\operatorname{mod}u_{1}^{2}),\quad t\equiv -1\quad (\operatorname{mod}u_{2}^{2}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 2\nmid u_{1}u_{2},\quad (u_{1},u_{2})=1,\quad 0\leqslant k\leqslant k_{0},\quad D\leqslant x, & \displaystyle \nonumber\\ \displaystyle & \displaystyle X_{1/2}\leqslant 2^{k}u_{1}u_{2}\leqslant X_{\unicode[STIX]{x1D6FC}},\quad t+2^{k}u_{1}u_{2}\sqrt{D}\leqslant D^{1/2+\unicode[STIX]{x1D6FC}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle t^{2}\equiv 1\quad (\operatorname{mod}4^{k}),\quad t\equiv 1\quad (\operatorname{mod}u_{1}^{2}),\quad t\equiv -1\quad (\operatorname{mod}u_{2}^{2}), & \displaystyle \nonumber\end{eqnarray}$$
as well as one of the following restrictions:
∙
 $u_{1}\leqslant u_{2}\leqslant u_{1}x^{1/2-\unicode[STIX]{x1D702}},~u_{1}\leqslant x^{1/4-\unicode[STIX]{x1D702}}$
;
$u_{1}\leqslant u_{2}\leqslant u_{1}x^{1/2-\unicode[STIX]{x1D702}},~u_{1}\leqslant x^{1/4-\unicode[STIX]{x1D702}}$
;∙
 $u_{2}\leqslant u_{1}\leqslant u_{2}x^{1/2-\unicode[STIX]{x1D702}},~u_{2}\leqslant x^{1/4-\unicode[STIX]{x1D702}}$
;
$u_{2}\leqslant u_{1}\leqslant u_{2}x^{1/2-\unicode[STIX]{x1D702}},~u_{2}\leqslant x^{1/4-\unicode[STIX]{x1D702}}$
;∙
 $u_{1}\leqslant u_{2}\leqslant u_{1}x^{1/2-\unicode[STIX]{x1D702}},~u_{1}^{(8+2\unicode[STIX]{x1D703})/3}u_{2}\leqslant x^{1-\unicode[STIX]{x1D702}}$
;
$u_{1}\leqslant u_{2}\leqslant u_{1}x^{1/2-\unicode[STIX]{x1D702}},~u_{1}^{(8+2\unicode[STIX]{x1D703})/3}u_{2}\leqslant x^{1-\unicode[STIX]{x1D702}}$
;∙
 $u_{2}\leqslant u_{1}\leqslant u_{2}x^{1/2-\unicode[STIX]{x1D702}},~u_{1}u_{2}^{(8+2\unicode[STIX]{x1D703})/3}\leqslant x^{1-\unicode[STIX]{x1D702}}$
.
$u_{2}\leqslant u_{1}\leqslant u_{2}x^{1/2-\unicode[STIX]{x1D702}},~u_{1}u_{2}^{(8+2\unicode[STIX]{x1D703})/3}\leqslant x^{1-\unicode[STIX]{x1D702}}$
.
By introducing the extra constraint
![]() $t+2^{k}u_{1}u_{2}\sqrt{D}=\unicode[STIX]{x1D700}_{D}$
, we may also define
$t+2^{k}u_{1}u_{2}\sqrt{D}=\unicode[STIX]{x1D700}_{D}$
, we may also define
![]() $\mathscr{N}^{\text{f}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})$
. In fact, the above arguments yield
$\mathscr{N}^{\text{f}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})$
. In fact, the above arguments yield
which are true for every positive
![]() $\unicode[STIX]{x1D700}>0$
and for every
$\unicode[STIX]{x1D700}>0$
and for every
![]() $k_{0}\geqslant 0.$
More precisely, we have proved for every
$k_{0}\geqslant 0.$
More precisely, we have proved for every
![]() $\unicode[STIX]{x1D6FF}$
,
$\unicode[STIX]{x1D6FF}$
,
![]() $0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{0}(\unicode[STIX]{x1D6FF}),k_{0}>k_{0}(\unicode[STIX]{x1D6FF})$
and
$0<\unicode[STIX]{x1D700}<\unicode[STIX]{x1D700}_{0}(\unicode[STIX]{x1D6FF}),k_{0}>k_{0}(\unicode[STIX]{x1D6FF})$
and
![]() $x>x_{0}(\unicode[STIX]{x1D6FF})$
that
$x>x_{0}(\unicode[STIX]{x1D6FF})$
that
with
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1].$
Following the approach of Fouvry [Reference FouvryFou16], we can state the following without proof.
Lemma 3.3. For every
![]() $k_{0}\geqslant 0$
and every
$k_{0}\geqslant 0$
and every
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
uniformly for
![]() $\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1]$
and
$\unicode[STIX]{x1D6FC}\in [\frac{1}{2},1]$
and
![]() $x\geqslant 2.$
$x\geqslant 2.$
We are now ready to complete the proof of Theorem 1.1. In view of (3.15), we may write
 $$\begin{eqnarray}\displaystyle S^{\text{f}}(x,\unicode[STIX]{x1D6FC}) & = & \displaystyle A^{\text{f}}(x,\unicode[STIX]{x1D6FC})+B^{\text{f}}(x,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle A^{\text{f}}(x,\unicode[STIX]{x1D6FC})+\mathscr{N}^{\text{f}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})\nonumber\\ \displaystyle & = & \displaystyle A(x,\unicode[STIX]{x1D6FC})+\mathscr{N}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})+\{A^{\text{f}}(x,\unicode[STIX]{x1D6FC})-A(x,\unicode[STIX]{x1D6FC})\}\nonumber\\ \displaystyle & & \displaystyle +\,\{\mathscr{N}^{\text{f}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})-\mathscr{N}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S^{\text{f}}(x,\unicode[STIX]{x1D6FC}) & = & \displaystyle A^{\text{f}}(x,\unicode[STIX]{x1D6FC})+B^{\text{f}}(x,\unicode[STIX]{x1D6FC})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle A^{\text{f}}(x,\unicode[STIX]{x1D6FC})+\mathscr{N}^{\text{f}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})\nonumber\\ \displaystyle & = & \displaystyle A(x,\unicode[STIX]{x1D6FC})+\mathscr{N}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})+\{A^{\text{f}}(x,\unicode[STIX]{x1D6FC})-A(x,\unicode[STIX]{x1D6FC})\}\nonumber\\ \displaystyle & & \displaystyle +\,\{\mathscr{N}^{\text{f}}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})-\mathscr{N}(x,\unicode[STIX]{x1D6FC};\unicode[STIX]{x1D700},k_{0})\},\nonumber\end{eqnarray}$$
which are true for every
![]() $\unicode[STIX]{x1D700}>0$
and
$\unicode[STIX]{x1D700}>0$
and
![]() $k_{0}\geqslant 0$
. From Lemmas 3.2 and 3.3, we obtain
$k_{0}\geqslant 0$
. From Lemmas 3.2 and 3.3, we obtain
By (2.8), (3.16), and by choosing
![]() $k_{0}=k_{0}(\unicode[STIX]{x1D6FF})$
sufficiently large,
$k_{0}=k_{0}(\unicode[STIX]{x1D6FF})$
sufficiently large,
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FF})$
sufficiently small, and letting
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D6FF})$
sufficiently small, and letting
![]() $\unicode[STIX]{x1D6FF}$
tend to zero, we find the lower bound (3.14) holds definitely for
$\unicode[STIX]{x1D6FF}$
tend to zero, we find the lower bound (3.14) holds definitely for
![]() $S^{\text{f}}(x,\unicode[STIX]{x1D6FC}).$
This establishes (1.4).
$S^{\text{f}}(x,\unicode[STIX]{x1D6FC}).$
This establishes (1.4).
The lower bounds for
![]() $S(x,\unicode[STIX]{x1D6FC})$
in Theorem 1.1 can be deduced from (1.2) by adding the contribution of the non-fundamental solutions, as it is shown by (2.14).
$S(x,\unicode[STIX]{x1D6FC})$
in Theorem 1.1 can be deduced from (1.2) by adding the contribution of the non-fundamental solutions, as it is shown by (2.14).
4 Estimate for triple exponential sums
We now prove Theorem 3.1. For the economy of the presentation, we only focus on the case
![]() $k=0$
and define
$k=0$
and define
 $$\begin{eqnarray}\mathfrak{S}(U_{1},U_{2},H):=\mathop{\sum }_{h\leqslant H}\sum _{\substack{ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)e\bigg(\frac{h\overline{u_{2}^{2}}}{u_{1}^{2}}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}(U_{1},U_{2},H):=\mathop{\sum }_{h\leqslant H}\sum _{\substack{ (2,u_{1}u_{2})=(u_{1},u_{2})=1 \\ u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}g_{1}\bigg(\frac{u_{2}}{U_{2}}\bigg)e\bigg(\frac{h\overline{u_{2}^{2}}}{u_{1}^{2}}\bigg).\end{eqnarray}$$
We would like to show that
for some
![]() $\unicode[STIX]{x1D700}_{0}\in \, ]\!0,10^{-2017}\! [$
while
$\unicode[STIX]{x1D700}_{0}\in \, ]\!0,10^{-2017}\! [$
while
![]() $U_{1},U_{2}$
fall into the ranges in (3.11).
$U_{1},U_{2}$
fall into the ranges in (3.11).
By Poisson summation, the
![]() $u_{2}$
-sum in (4.1) becomes
$u_{2}$
-sum in (4.1) becomes
 $$\begin{eqnarray}\mathop{\sum }_{u_{2}}=\frac{U_{2}}{2u_{1}^{2}}\mathop{\sum }_{r\in \mathbf{Z}}\widehat{g_{1}}\bigg(\frac{rU_{2}}{2u_{1}^{2}}\bigg)\mathop{\sum }_{\substack{ z\,(\operatorname{mod}2u_{1}^{2}) \\ (z,2u_{1})=1}}e\bigg(\frac{h\overline{z^{2}}}{u_{1}^{2}}+\frac{rz}{2u_{1}^{2}}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{u_{2}}=\frac{U_{2}}{2u_{1}^{2}}\mathop{\sum }_{r\in \mathbf{Z}}\widehat{g_{1}}\bigg(\frac{rU_{2}}{2u_{1}^{2}}\bigg)\mathop{\sum }_{\substack{ z\,(\operatorname{mod}2u_{1}^{2}) \\ (z,2u_{1})=1}}e\bigg(\frac{h\overline{z^{2}}}{u_{1}^{2}}+\frac{rz}{2u_{1}^{2}}\bigg).\end{eqnarray}$$
From the Chinese remainder theorem, the sum over
![]() $z$
can be rewritten as
$z$
can be rewritten as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ z_{1}\,(\operatorname{mod}u_{1}^{2}) \\ (z_{1},u_{1})=1}}\mathop{\sum }_{\substack{ z_{2}\,(\operatorname{mod}2) \\ (z,2)=1}}e\bigg(\frac{h\overline{(2z_{1}+u_{1}^{2}z_{2})^{2}}}{u_{1}^{2}}+\frac{r(2z_{1}+u_{1}^{2}z_{2})}{2u_{1}^{2}}\bigg)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ z_{1}\,(\operatorname{mod}u_{1}^{2}) \\ (z_{1},u_{1})=1}}\mathop{\sum }_{\substack{ z_{2}\,(\operatorname{mod}2) \\ (z,2)=1}}e\bigg(\frac{h\overline{(2z_{1})^{2}}}{u_{1}^{2}}+\frac{rz_{1}}{u_{1}^{2}}+\frac{rz_{2}}{2}\bigg)=(-1)^{r}K(r,\overline{4}h;u_{1}^{2}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{\substack{ z_{1}\,(\operatorname{mod}u_{1}^{2}) \\ (z_{1},u_{1})=1}}\mathop{\sum }_{\substack{ z_{2}\,(\operatorname{mod}2) \\ (z,2)=1}}e\bigg(\frac{h\overline{(2z_{1}+u_{1}^{2}z_{2})^{2}}}{u_{1}^{2}}+\frac{r(2z_{1}+u_{1}^{2}z_{2})}{2u_{1}^{2}}\bigg)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\substack{ z_{1}\,(\operatorname{mod}u_{1}^{2}) \\ (z_{1},u_{1})=1}}\mathop{\sum }_{\substack{ z_{2}\,(\operatorname{mod}2) \\ (z,2)=1}}e\bigg(\frac{h\overline{(2z_{1})^{2}}}{u_{1}^{2}}+\frac{rz_{1}}{u_{1}^{2}}+\frac{rz_{2}}{2}\bigg)=(-1)^{r}K(r,\overline{4}h;u_{1}^{2}),\nonumber\end{eqnarray}$$
where
![]() $K$
is an analogue of Kloosterman sums:
$K$
is an analogue of Kloosterman sums:
Hence we may conclude that
Note that
![]() $K(0,h;q)=T(h,q)$
and if
$K(0,h;q)=T(h,q)$
and if
![]() $q$
is odd, we have
$q$
is odd, we have
![]() $T(\overline{4}h,q)=T(h,q)$
. According to
$T(\overline{4}h,q)=T(h,q)$
. According to
![]() $r=0$
and
$r=0$
and
![]() $r\neq 0$
, we split
$r\neq 0$
, we split
![]() $\mathfrak{S}(U_{1},U_{2},H)$
by
$\mathfrak{S}(U_{1},U_{2},H)$
by
where
 $$\begin{eqnarray}\mathfrak{S}_{1}(U_{1},U_{2},H)=\frac{U_{2}(1-\unicode[STIX]{x1D6FF})}{2}\mathop{\sum }_{h\leqslant H}\mathop{\sum }_{\substack{ u_{1}\in \, ]\!U_{1},U_{1}^{\ast }] \\ 2\nmid u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{T(h,u_{1}^{2})}{u_{1}^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{1}(U_{1},U_{2},H)=\frac{U_{2}(1-\unicode[STIX]{x1D6FF})}{2}\mathop{\sum }_{h\leqslant H}\mathop{\sum }_{\substack{ u_{1}\in \, ]\!U_{1},U_{1}^{\ast }] \\ 2\nmid u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{T(h,u_{1}^{2})}{u_{1}^{2}}\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathfrak{S}_{2}(U_{1},U_{2},H)=\frac{U_{2}}{2}\mathop{\sum }_{h\leqslant H}\mathop{\sum }_{\substack{ u_{1}\in \, ]\!U_{1},U_{1}^{\ast }] \\ 2\nmid u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{1}{u_{1}^{2}}\mathop{\sum }_{0\neq r\in \mathbf{Z}}(-1)^{r}\widehat{g}_{1}\bigg(\frac{rU_{2}}{2u_{1}^{2}}\bigg)K(r,\overline{4}h;u_{1}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{2}(U_{1},U_{2},H)=\frac{U_{2}}{2}\mathop{\sum }_{h\leqslant H}\mathop{\sum }_{\substack{ u_{1}\in \, ]\!U_{1},U_{1}^{\ast }] \\ 2\nmid u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{1}{u_{1}^{2}}\mathop{\sum }_{0\neq r\in \mathbf{Z}}(-1)^{r}\widehat{g}_{1}\bigg(\frac{rU_{2}}{2u_{1}^{2}}\bigg)K(r,\overline{4}h;u_{1}^{2}).\end{eqnarray}$$
Following the approach of Fouvry, one may express
![]() $T(h,u_{1}^{2})$
in terms of Jacobi symbols (see [Reference FouvryFou16, Lemma 6.2]) and then appeal to the bilinear estimate of Heath-Brown [Reference Heath-BrownHea95], getting
$T(h,u_{1}^{2})$
in terms of Jacobi symbols (see [Reference FouvryFou16, Lemma 6.2]) and then appeal to the bilinear estimate of Heath-Brown [Reference Heath-BrownHea95], getting
which produces the second restriction in (3.6). Moreover, Fouvry proved that
which produces the first restriction in (3.6).
Our task will be proving a stronger estimate for
![]() $\mathfrak{S}_{2}(U_{1},U_{2},H)$
by virtue of the special structure of
$\mathfrak{S}_{2}(U_{1},U_{2},H)$
by virtue of the special structure of
![]() $u_{1}$
. More precisely, we shall prove that
$u_{1}$
. More precisely, we shall prove that
where
![]() $Q$
will be chosen at our demand. This would at least require the following inequality as proved by Fouvry [Reference FouvryFou16]. In fact, Fouvry only considered those
$Q$
will be chosen at our demand. This would at least require the following inequality as proved by Fouvry [Reference FouvryFou16]. In fact, Fouvry only considered those
![]() $q$
that are perfect squares, and his argument also applies to more general
$q$
that are perfect squares, and his argument also applies to more general
![]() $q$
.
$q$
.
Lemma 4.1. Let
![]() $q$
be an odd positive integer. Then we have
$q$
be an odd positive integer. Then we have
As an extension to
![]() $K(m,n;q)$
, we define another exponential sum
$K(m,n;q)$
, we define another exponential sum
where
![]() $\ast$
in summation reminds us to sum over primitive elements, i.e.,
$\ast$
in summation reminds us to sum over primitive elements, i.e.,
![]() $(a(a+u),q)=1.$
We will need the following inequality.
$(a(a+u),q)=1.$
We will need the following inequality.
Lemma 4.2. For each odd
![]() $q\geqslant 1$
, we have
$q\geqslant 1$
, we have
where
The proof of Lemma 4.2 will be given in Appendix B.
We now start to prove Theorem 3.1. Due to the decay of
![]() $\widehat{g}_{1}$
, we may truncate the
$\widehat{g}_{1}$
, we may truncate the
![]() $r$
-sum in
$r$
-sum in
![]() $\mathfrak{S}_{2}(U_{1},U_{2},H)$
by
$\mathfrak{S}_{2}(U_{1},U_{2},H)$
by
![]() $R=U_{1}^{2+\unicode[STIX]{x1D700}}U_{2}^{-1},$
so that
$R=U_{1}^{2+\unicode[STIX]{x1D700}}U_{2}^{-1},$
so that
 $$\begin{eqnarray}\displaystyle \mathfrak{S}_{2}(U_{1},U_{2},H) & = & \displaystyle \frac{U_{2}}{2}\mathop{\sum }_{h\leqslant H}\mathop{\sum }_{\substack{ u_{1}\in \, ]\!U_{1},U_{1}^{\ast }] \\ 2\nmid u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{1}{u_{1}^{2}}\mathop{\sum }_{1\leqslant |r|\leqslant R}(-1)^{r}\widehat{g}_{1}\bigg(\frac{rU_{2}}{2u_{1}^{2}}\bigg)K(r,\overline{4}h;u_{1}^{2})\nonumber\\ \displaystyle & & \displaystyle +\,O((U_{1}U_{2}H)^{-2017}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{2}(U_{1},U_{2},H) & = & \displaystyle \frac{U_{2}}{2}\mathop{\sum }_{h\leqslant H}\mathop{\sum }_{\substack{ u_{1}\in \, ]\!U_{1},U_{1}^{\ast }] \\ 2\nmid u_{1}\text{ is }U_{1}^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{1}{u_{1}^{2}}\mathop{\sum }_{1\leqslant |r|\leqslant R}(-1)^{r}\widehat{g}_{1}\bigg(\frac{rU_{2}}{2u_{1}^{2}}\bigg)K(r,\overline{4}h;u_{1}^{2})\nonumber\\ \displaystyle & & \displaystyle +\,O((U_{1}U_{2}H)^{-2017}).\end{eqnarray}$$
Our project will be controlling the cancellations while summing over
![]() $r$
with
$r$
with
![]() $1\leqslant |r|\leqslant R$
. More precisely, we would like to estimate
$1\leqslant |r|\leqslant R$
. More precisely, we would like to estimate
The contributions from negative
![]() $r$
and positive
$r$
and positive
![]() $r$
can be treated similarly, it thus suffices to consider
$r$
can be treated similarly, it thus suffices to consider
which can be rewritten as
Clearly,
![]() $K(2r,\overline{4}h;u_{1}^{2})=K(r,h;u_{1}^{2})$
. By partial summation, it suffices to consider
$K(2r,\overline{4}h;u_{1}^{2})=K(r,h;u_{1}^{2})$
. By partial summation, it suffices to consider
For each
![]() $u_{0}\mid u_{1}$
, we define
$u_{0}\mid u_{1}$
, we define
![]() $d,q_{1},q_{2}$
by
$d,q_{1},q_{2}$
by
It follows that
![]() $u_{1}^{2}=q_{1}q_{2}$
and
$u_{1}^{2}=q_{1}q_{2}$
and
![]() $(q_{1},q_{2})=1$
. By virtue of the
$(q_{1},q_{2})=1$
. By virtue of the
![]() $q$
-analogue of van der Corput method, we will prove the following.
$q$
-analogue of van der Corput method, we will prove the following.
Lemma 4.3. With the above notation, we have
Proof. Lemma 4.3 is a trivial consequence of Lemma 4.1 if
![]() $R\leqslant u_{0}^{2}.$
We now assume
$R\leqslant u_{0}^{2}.$
We now assume
![]() $R>u_{0}^{2}.$
Denote by
$R>u_{0}^{2}.$
Denote by
![]() $I_{R}$
the characteristic function of the interval
$I_{R}$
the characteristic function of the interval
![]() $[1,R].$
Thus,
$[1,R].$
Thus,
for any
![]() $\ell \in \mathbf{Z}.$
From the Chinese remainder theorem, we may write
$\ell \in \mathbf{Z}.$
From the Chinese remainder theorem, we may write
where we have used the fact that
![]() $q_{1}\mid u_{0}^{2}.$
$q_{1}\mid u_{0}^{2}.$
For
![]() $L=[R/u_{0}^{2}]$
, we sum over
$L=[R/u_{0}^{2}]$
, we sum over
![]() $\ell$
, getting
$\ell$
, getting
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}(R,u_{1}^{2};h) & = & \displaystyle \frac{1}{L}\mathop{\sum }_{\ell \leqslant L}\mathop{\sum }_{r\in \mathbf{Z}}I_{R}(r+u_{0}^{2}\ell )K(r+u_{0}^{2}\ell ,h;u_{1}^{2})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{L}\mathop{\sum }_{r\in \mathbf{Z}}|K(r,h\overline{q}_{2}^{3};q_{1})|\bigg|\mathop{\sum }_{\ell \leqslant L}I_{R}(r+u_{0}^{2}\ell )K(r+u_{0}^{2}\ell ,h\overline{q}_{1}^{3};q_{2})\bigg|.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}(R,u_{1}^{2};h) & = & \displaystyle \frac{1}{L}\mathop{\sum }_{\ell \leqslant L}\mathop{\sum }_{r\in \mathbf{Z}}I_{R}(r+u_{0}^{2}\ell )K(r+u_{0}^{2}\ell ,h;u_{1}^{2})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{L}\mathop{\sum }_{r\in \mathbf{Z}}|K(r,h\overline{q}_{2}^{3};q_{1})|\bigg|\mathop{\sum }_{\ell \leqslant L}I_{R}(r+u_{0}^{2}\ell )K(r+u_{0}^{2}\ell ,h\overline{q}_{1}^{3};q_{2})\bigg|.\nonumber\end{eqnarray}$$
From Lemma 4.1 we find
In view of the support of
![]() $I_{R}$
, the sum over
$I_{R}$
, the sum over
![]() $r$
is in fact restricted to
$r$
is in fact restricted to
![]() $[-R,R].$
By Cauchy inequality, we derive that
$[-R,R].$
By Cauchy inequality, we derive that
Squaring out and switching summations, we get
where
![]() $I_{\ell }$
is an interval, depending on
$I_{\ell }$
is an interval, depending on
![]() $\ell$
, of length at most
$\ell$
, of length at most
![]() $R$
. For
$R$
. For
![]() $\ell =0$
, we appeal to Lemma 4.1 to estimate the
$\ell =0$
, we appeal to Lemma 4.1 to estimate the
![]() $r$
-sum trivially. For
$r$
-sum trivially. For
![]() $1\leqslant |\ell |\leqslant L$
, reasonable cancellations in the
$1\leqslant |\ell |\leqslant L$
, reasonable cancellations in the
![]() $r$
-sum are expected. In fact, by completion, we have
$r$
-sum are expected. In fact, by completion, we have
where
and
Firstly,
Opening each
![]() $K$
by definition, the orthogonality of additive characters gives
$K$
by definition, the orthogonality of additive characters gives
 $$\begin{eqnarray}\displaystyle \widehat{K}(y,q_{2};h,q_{1},u_{0},\ell ) & = & \displaystyle e\bigg(\frac{-u_{0}^{2}\ell y}{q_{2}}\bigg)\sum ^{\ast }_{a\,(\operatorname{mod}q_{2})}e\bigg(\frac{h\overline{q}_{1}^{3}(\overline{a^{2}}-\overline{(a+y)^{2}})-u_{0}^{2}\ell a}{q_{2}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle e\bigg(\frac{-u_{0}^{2}\ell y}{q_{2}}\bigg)\mathscr{B}(h\overline{q}_{1}^{3},-h\overline{q}_{1}^{3},-u_{0}^{2}\ell ,y;q_{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widehat{K}(y,q_{2};h,q_{1},u_{0},\ell ) & = & \displaystyle e\bigg(\frac{-u_{0}^{2}\ell y}{q_{2}}\bigg)\sum ^{\ast }_{a\,(\operatorname{mod}q_{2})}e\bigg(\frac{h\overline{q}_{1}^{3}(\overline{a^{2}}-\overline{(a+y)^{2}})-u_{0}^{2}\ell a}{q_{2}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle e\bigg(\frac{-u_{0}^{2}\ell y}{q_{2}}\bigg)\mathscr{B}(h\overline{q}_{1}^{3},-h\overline{q}_{1}^{3},-u_{0}^{2}\ell ,y;q_{2}).\nonumber\end{eqnarray}$$
For
![]() $y=0$
, we have
$y=0$
, we have
For
![]() $y\neq 0$
, we would like to appeal to Lemma 4.2. To do so, we first derive from Lemma 4.2 that (we have
$y\neq 0$
, we would like to appeal to Lemma 4.2. To do so, we first derive from Lemma 4.2 that (we have
![]() $q_{2}^{\flat }=1$
since
$q_{2}^{\flat }=1$
since
![]() $q_{2}$
is a perfect square)
$q_{2}$
is a perfect square)
This yields
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{r\in I_{\ell }}[\cdots \,] & \ll & \displaystyle R(u_{0}^{2}\ell ,q_{2})+q_{2}^{1/2+\unicode[STIX]{x1D700}}(h,u_{0}^{2}\ell ,q_{2}^{\ddagger })\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2}\mathop{\sum }_{1\leqslant |y|\leqslant q_{2}/2}\min \bigg\{R,\frac{q_{2}}{y}\bigg\}(y,u_{0}^{2}\ell ,q_{2}^{\ddagger })\nonumber\\ \displaystyle & \ll & \displaystyle R(u_{0}^{2}\ell ,q_{2})+q_{2}^{3/2+\unicode[STIX]{x1D700}}(h,u_{0}^{2}\ell ,q_{2}^{\ddagger })\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{r\in I_{\ell }}[\cdots \,] & \ll & \displaystyle R(u_{0}^{2}\ell ,q_{2})+q_{2}^{1/2+\unicode[STIX]{x1D700}}(h,u_{0}^{2}\ell ,q_{2}^{\ddagger })\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2}\mathop{\sum }_{1\leqslant |y|\leqslant q_{2}/2}\min \bigg\{R,\frac{q_{2}}{y}\bigg\}(y,u_{0}^{2}\ell ,q_{2}^{\ddagger })\nonumber\\ \displaystyle & \ll & \displaystyle R(u_{0}^{2}\ell ,q_{2})+q_{2}^{3/2+\unicode[STIX]{x1D700}}(h,u_{0}^{2}\ell ,q_{2}^{\ddagger })\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2},\nonumber\end{eqnarray}$$
from which and (4.6) we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}(R,u_{1}^{2};h)^{2} & \ll & \displaystyle \frac{u_{1}^{\unicode[STIX]{x1D700}}q_{1}R}{L}\big\{Rq_{2}(h,q_{2})+LR(u_{0}^{2},q_{2})+Lq_{2}^{3/2}(h,u_{0}^{2},q_{2}^{\ddagger })\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2}\big\}\nonumber\\ \displaystyle & \ll & \displaystyle u_{1}^{\unicode[STIX]{x1D700}}R\big\{(u_{0}u_{1})^{2}+q_{1}R(u_{0}^{2},q_{2})+u_{1}^{2}q_{2}^{1/2}(h,u_{0}^{2})\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2}\big\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}(R,u_{1}^{2};h)^{2} & \ll & \displaystyle \frac{u_{1}^{\unicode[STIX]{x1D700}}q_{1}R}{L}\big\{Rq_{2}(h,q_{2})+LR(u_{0}^{2},q_{2})+Lq_{2}^{3/2}(h,u_{0}^{2},q_{2}^{\ddagger })\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2}\big\}\nonumber\\ \displaystyle & \ll & \displaystyle u_{1}^{\unicode[STIX]{x1D700}}R\big\{(u_{0}u_{1})^{2}+q_{1}R(u_{0}^{2},q_{2})+u_{1}^{2}q_{2}^{1/2}(h,u_{0}^{2})\cdot \unicode[STIX]{x1D6EF}(q_{2})^{1/2}\big\}.\nonumber\end{eqnarray}$$
Note that
![]() $q_{2}=(u_{1}d/u_{0})^{2}=\{u_{1}(u_{0},(u_{1}/u_{0})^{\infty })/u_{0}\}^{2}.$
Thus,
$q_{2}=(u_{1}d/u_{0})^{2}=\{u_{1}(u_{0},(u_{1}/u_{0})^{\infty })/u_{0}\}^{2}.$
Thus,
We then conclude that
which gives Lemma 4.3 immediately. ◻
In view of Lemma 4.3 and the discussions before it, we may derive from (4.5) that
where
![]() $U_{1}^{\unicode[STIX]{x1D703}_{0}}\leqslant Q\leqslant U_{1}^{\unicode[STIX]{x1D703}_{0}+\unicode[STIX]{x1D703}}$
. In view of the choice
$U_{1}^{\unicode[STIX]{x1D703}_{0}}\leqslant Q\leqslant U_{1}^{\unicode[STIX]{x1D703}_{0}+\unicode[STIX]{x1D703}}$
. In view of the choice
![]() $R=U_{1}^{2+\unicode[STIX]{x1D700}}U_{2}^{-1}$
, Lemma A.5 yields
$R=U_{1}^{2+\unicode[STIX]{x1D700}}U_{2}^{-1}$
, Lemma A.5 yields
from which and (4.3) we conclude that
Choosing
![]() $\unicode[STIX]{x1D703}_{0}=(1-2\unicode[STIX]{x1D703})/3$
, we then have
$\unicode[STIX]{x1D703}_{0}=(1-2\unicode[STIX]{x1D703})/3$
, we then have
![]() $U_{1}^{(1-2\unicode[STIX]{x1D703})/3}\leqslant Q\leqslant U_{1}^{(1+\unicode[STIX]{x1D703})/3}$
. Recalling the choice of
$U_{1}^{(1-2\unicode[STIX]{x1D703})/3}\leqslant Q\leqslant U_{1}^{(1+\unicode[STIX]{x1D703})/3}$
. Recalling the choice of
![]() $H$
, we then arrive at the expected estimate (4.2), provided that (3.11) holds.
$H$
, we then arrive at the expected estimate (4.2), provided that (3.11) holds.
Acknowledgements
I am very grateful to the referee for the valuable comments and suggestions. The work is supported in part by NSFC (No. 11601413) and NSBRP (No. 2017JQ1016) of Shaanxi Province.
Appendix A Mean values of arithmetic functions
A.1 Some basic asymptotics
The first part of the appendix is devoted to state several basic asymptotics.
Recall that
![]() $\unicode[STIX]{x1D6FE}(u)$
denotes the number of solutions to the congruence equation
$\unicode[STIX]{x1D6FE}(u)$
denotes the number of solutions to the congruence equation
![]() $x^{2}\equiv 1\,(\operatorname{mod}u^{2}).$
As a multiplicative function,
$x^{2}\equiv 1\,(\operatorname{mod}u^{2}).$
As a multiplicative function,
![]() $\unicode[STIX]{x1D6FE}$
satisfies the evaluation (2.10). We are now ready to state the following averages.
$\unicode[STIX]{x1D6FE}$
satisfies the evaluation (2.10). We are now ready to state the following averages.
Lemma A.1. As
![]() $N\rightarrow +\infty$
, we have
$N\rightarrow +\infty$
, we have
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant N \\ (n,q)=1}}\frac{1}{n}=\frac{\unicode[STIX]{x1D711}(q)}{q}\log N+O\bigg(1+\mathop{\sum }_{d|q}\frac{\log d}{d}\bigg),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant N \\ (n,q)=1}}\frac{1}{n}=\frac{\unicode[STIX]{x1D711}(q)}{q}\log N+O\bigg(1+\mathop{\sum }_{d|q}\frac{\log d}{d}\bigg),\end{eqnarray}$$
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant N \\ (n,2)=1}}\frac{\unicode[STIX]{x1D711}(n)}{n^{2}}\sim \frac{4}{\unicode[STIX]{x1D70B}^{2}}\log N,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant N \\ (n,2)=1}}\frac{\unicode[STIX]{x1D711}(n)}{n^{2}}\sim \frac{4}{\unicode[STIX]{x1D70B}^{2}}\log N,\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant N \\ (n,2)=1}}\frac{\unicode[STIX]{x1D711}(n)\log n}{n^{2}}\sim \frac{2}{\unicode[STIX]{x1D70B}^{2}}\log ^{2}N.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ n\leqslant N \\ (n,2)=1}}\frac{\unicode[STIX]{x1D711}(n)\log n}{n^{2}}\sim \frac{2}{\unicode[STIX]{x1D70B}^{2}}\log ^{2}N.\end{eqnarray}$$
Proof. The first one can be derived from the evaluations of
![]() $\unicode[STIX]{x1D6FE}(2^{n})$
as given in (2.10). The other three asymptotics can be found in Fouvry [Reference FouvryFou16, Lemma 8.1, Lemma 8.2].◻
$\unicode[STIX]{x1D6FE}(2^{n})$
as given in (2.10). The other three asymptotics can be found in Fouvry [Reference FouvryFou16, Lemma 8.1, Lemma 8.2].◻
A.2 Smooth numbers
Denote by
![]() ${\mathcal{S}}(x,y)$
the set of
${\mathcal{S}}(x,y)$
the set of
![]() $y$
-smooth numbers not exceeding
$y$
-smooth numbers not exceeding
![]() $x$
. Write
$x$
. Write
![]() $\unicode[STIX]{x1D6F9}(x,y)=|{\mathcal{S}}(x,y)|.$
We now introduce the Dickman function
$\unicode[STIX]{x1D6F9}(x,y)=|{\mathcal{S}}(x,y)|.$
We now introduce the Dickman function
![]() $\unicode[STIX]{x1D70C}(u)$
by
$\unicode[STIX]{x1D70C}(u)$
by
In the first several intervals, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(u) & = & \displaystyle 1-\log u,\quad u\in \, ]\!1,2],\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(u) & = & \displaystyle 1-\log u+\int _{2}^{u}\frac{\log (t-1)}{t}\,dt,\quad u\in \, ]\!2,3],\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(u) & = & \displaystyle 1-\log u+\int _{2}^{u}\frac{\log (t-1)}{t}\,dt-\int _{3}^{u}\frac{dt}{t}\int _{2}^{t-1}\frac{\log (s-1)}{s}\,ds,\quad u\in \, ]\!3,4].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}(u) & = & \displaystyle 1-\log u,\quad u\in \, ]\!1,2],\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(u) & = & \displaystyle 1-\log u+\int _{2}^{u}\frac{\log (t-1)}{t}\,dt,\quad u\in \, ]\!2,3],\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}(u) & = & \displaystyle 1-\log u+\int _{2}^{u}\frac{\log (t-1)}{t}\,dt-\int _{3}^{u}\frac{dt}{t}\int _{2}^{t-1}\frac{\log (s-1)}{s}\,ds,\quad u\in \, ]\!3,4].\nonumber\end{eqnarray}$$
The following lemma is classical and shows
![]() $\unicode[STIX]{x1D70C}$
is the density function of smooth numbers.
$\unicode[STIX]{x1D70C}$
is the density function of smooth numbers.
Lemma A.2. Uniformly for
![]() $x\geqslant y\geqslant 2$
, we have
$x\geqslant y\geqslant 2$
, we have
Proof. See [Reference TenenbaumTen95, p. 367, Theorem 6]. ◻
Lemma A.3. Let
![]() $\unicode[STIX]{x1D703}\in \, ]\!0,1\![$
be fixed. As
$\unicode[STIX]{x1D703}\in \, ]\!0,1\![$
be fixed. As
![]() $N\rightarrow +\infty$
, we have
$N\rightarrow +\infty$
, we have
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ 2\nmid n\leqslant N \\ n\text{ is }n^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{\unicode[STIX]{x1D711}(n)}{n^{2}}\sim \frac{4}{\unicode[STIX]{x1D70B}^{2}}\unicode[STIX]{x1D70C}\bigg(\frac{1}{\unicode[STIX]{x1D703}}\bigg)\log N,\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ 2\nmid n\leqslant N \\ n\text{ is }n^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{\unicode[STIX]{x1D711}(n)}{n^{2}}\sim \frac{4}{\unicode[STIX]{x1D70B}^{2}}\unicode[STIX]{x1D70C}\bigg(\frac{1}{\unicode[STIX]{x1D703}}\bigg)\log N,\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ 2\nmid n\leqslant N \\ n\text{ is }n^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{\unicode[STIX]{x1D711}(n)\log n}{n^{2}}\sim \frac{2}{\unicode[STIX]{x1D70B}^{2}}\unicode[STIX]{x1D70C}\bigg(\frac{1}{\unicode[STIX]{x1D703}}\bigg)\log ^{2}N.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ 2\nmid n\leqslant N \\ n\text{ is }n^{\unicode[STIX]{x1D703}}\text{-}\text{smooth}}}\frac{\unicode[STIX]{x1D711}(n)\log n}{n^{2}}\sim \frac{2}{\unicode[STIX]{x1D70B}^{2}}\unicode[STIX]{x1D70C}\bigg(\frac{1}{\unicode[STIX]{x1D703}}\bigg)\log ^{2}N.\end{eqnarray}$$
Proof. One can refer to [Reference Tenenbaum and WuTW03], for instance, for some general theorems on the mean values of multiplicative functions over smooth numbers. In particular, one has
 $$\begin{eqnarray}\mathop{\sum }_{\substack{ 2\nmid n\leqslant N \\ n\text{ is }n\unicode[STIX]{x1D703}\text{-}\text{smooth}}}\frac{\unicode[STIX]{x1D711}(n)}{n}=\frac{4}{\unicode[STIX]{x1D70B}^{2}}\unicode[STIX]{x1D70C}\bigg(\frac{1}{\unicode[STIX]{x1D703}}\bigg)N+O\bigg(\frac{N}{\log N}\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\substack{ 2\nmid n\leqslant N \\ n\text{ is }n\unicode[STIX]{x1D703}\text{-}\text{smooth}}}\frac{\unicode[STIX]{x1D711}(n)}{n}=\frac{4}{\unicode[STIX]{x1D70B}^{2}}\unicode[STIX]{x1D70C}\bigg(\frac{1}{\unicode[STIX]{x1D703}}\bigg)N+O\bigg(\frac{N}{\log N}\bigg).\end{eqnarray}$$
The lemma then follows from the partial summation. ◻
Lemma A.4. For all
![]() $q\geqslant 1$
, we have
$q\geqslant 1$
, we have
Proof. Note that
![]() $n\mapsto (n^{\sharp })^{1/4}(n,q)^{1/2}$
is multiplicative. For
$n\mapsto (n^{\sharp })^{1/4}(n,q)^{1/2}$
is multiplicative. For
![]() $\Re s>1$
, we consider the Dirichlet series
$\Re s>1$
, we consider the Dirichlet series
By the Euler product formula, we have
 $$\begin{eqnarray}\displaystyle \mathscr{D}(s) & = & \displaystyle \mathop{\prod }_{p}\bigg(\mathop{\sum }_{k\geqslant 0}\frac{((p^{k})^{\sharp })^{1/4}(p^{k},q)^{1/2}}{p^{ks}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p}\bigg(1+\frac{(p,q)^{1/2}}{p^{s}}+\mathop{\sum }_{k\geqslant 2}\frac{(p^{k},q)^{1/2}}{p^{k(s-1/4)}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p\nmid q}\bigg(1+\frac{1}{p^{s}}+\mathop{\sum }_{k\geqslant 2}\frac{1}{p^{k(s-1/4)}}\bigg)\cdot \mathop{\prod }_{p\mid q}\bigg(1+\frac{1}{p^{s-1/2}}+\mathop{\sum }_{k\geqslant 2}\frac{(p^{k},q)^{1/2}}{p^{k(s-1/4)}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D701}(s)\mathscr{D}_{1}(s)\mathscr{D}_{2}(s,q),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{D}(s) & = & \displaystyle \mathop{\prod }_{p}\bigg(\mathop{\sum }_{k\geqslant 0}\frac{((p^{k})^{\sharp })^{1/4}(p^{k},q)^{1/2}}{p^{ks}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p}\bigg(1+\frac{(p,q)^{1/2}}{p^{s}}+\mathop{\sum }_{k\geqslant 2}\frac{(p^{k},q)^{1/2}}{p^{k(s-1/4)}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{p\nmid q}\bigg(1+\frac{1}{p^{s}}+\mathop{\sum }_{k\geqslant 2}\frac{1}{p^{k(s-1/4)}}\bigg)\cdot \mathop{\prod }_{p\mid q}\bigg(1+\frac{1}{p^{s-1/2}}+\mathop{\sum }_{k\geqslant 2}\frac{(p^{k},q)^{1/2}}{p^{k(s-1/4)}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D701}(s)\mathscr{D}_{1}(s)\mathscr{D}_{2}(s,q),\nonumber\end{eqnarray}$$
where
![]() $\mathscr{D}_{1}(s)$
is holomorphic for
$\mathscr{D}_{1}(s)$
is holomorphic for
![]() $\Re s>3/4$
and
$\Re s>3/4$
and
The lemma then follows from a routine application of Perron’s formula. ◻
The following inequality is a consequence of Rankin’s method, which is a stronger version of [Reference FouvryFou16, Lemma 7.2].
Lemma A.5. For any
![]() $\unicode[STIX]{x1D700}>0$
, one has
$\unicode[STIX]{x1D700}>0$
, one has
Proof. Denote by
![]() $S$
the sum in question. First, we have
$S$
the sum in question. First, we have
 $$\begin{eqnarray}S\ll \mathop{\sum }_{n\leqslant N}\mathop{\sum }_{d\mid n^{\infty }}d^{1/2}\mathop{\sum }_{\substack{ m\leqslant N/n \\ d\mid m}}((mn)^{\sharp })^{1/4}=\mathop{\sum }_{n\leqslant N}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{1/2}\mathop{\sum }_{\substack{ m\leqslant N/(nd)}}((mnd)^{\sharp })^{1/4}.\end{eqnarray}$$
$$\begin{eqnarray}S\ll \mathop{\sum }_{n\leqslant N}\mathop{\sum }_{d\mid n^{\infty }}d^{1/2}\mathop{\sum }_{\substack{ m\leqslant N/n \\ d\mid m}}((mn)^{\sharp })^{1/4}=\mathop{\sum }_{n\leqslant N}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{1/2}\mathop{\sum }_{\substack{ m\leqslant N/(nd)}}((mnd)^{\sharp })^{1/4}.\end{eqnarray}$$
Note that
giving
from which and Lemma A.4 it follows that
 $$\begin{eqnarray}\displaystyle S & \ll & \displaystyle \mathop{\sum }_{n\leqslant N}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{1/2}((nd)^{\sharp })^{1/4}\mathop{\sum }_{\substack{ m\leqslant N/(nd)}}(m^{\sharp })^{1/4}(m,nd)^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle N^{1+\unicode[STIX]{x1D700}}\mathop{\sum }_{n\leqslant N}\frac{1}{n}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{-1/2}((nd)^{\sharp })^{1/4}\nonumber\\ \displaystyle & \ll & \displaystyle N^{1+\unicode[STIX]{x1D700}}\mathop{\sum }_{n\leqslant N}\frac{(n^{\sharp })^{1/4}}{n}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{-1/2}(d^{\sharp })^{1/4}((n,d)^{\flat })^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S & \ll & \displaystyle \mathop{\sum }_{n\leqslant N}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{1/2}((nd)^{\sharp })^{1/4}\mathop{\sum }_{\substack{ m\leqslant N/(nd)}}(m^{\sharp })^{1/4}(m,nd)^{1/2}\nonumber\\ \displaystyle & \ll & \displaystyle N^{1+\unicode[STIX]{x1D700}}\mathop{\sum }_{n\leqslant N}\frac{1}{n}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{-1/2}((nd)^{\sharp })^{1/4}\nonumber\\ \displaystyle & \ll & \displaystyle N^{1+\unicode[STIX]{x1D700}}\mathop{\sum }_{n\leqslant N}\frac{(n^{\sharp })^{1/4}}{n}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{-1/2}(d^{\sharp })^{1/4}((n,d)^{\flat })^{1/2}.\nonumber\end{eqnarray}$$
By Rankin’s method, the last sum over
![]() $d$
is, for any
$d$
is, for any
![]() $\unicode[STIX]{x1D700}>0$
,
$\unicode[STIX]{x1D700}>0$
,
 $$\begin{eqnarray}\displaystyle & {\leqslant} & \displaystyle N^{\unicode[STIX]{x1D700}}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{-1/2-\unicode[STIX]{x1D700}}(d^{\sharp })^{1/4}((n,d)^{\flat })^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle N^{\unicode[STIX]{x1D700}}\mathop{\prod }_{p\mid n}\bigg(1+\mathop{\sum }_{k\geqslant 1}\frac{((p^{k})^{\sharp })^{1/4}((n,p^{k})^{\flat })^{1/2}}{p^{k(1/2+\unicode[STIX]{x1D700})}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle N^{\unicode[STIX]{x1D700}}\mathop{\prod }_{p\mid n}\bigg(1+\frac{2}{p^{\unicode[STIX]{x1D700}}}+\mathop{\sum }_{k\geqslant 3}\frac{1}{p^{k(1/4+\unicode[STIX]{x1D700})-1/2}}\bigg)\nonumber\\ \displaystyle & \ll & \displaystyle (nN)^{\unicode[STIX]{x1D700}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\leqslant} & \displaystyle N^{\unicode[STIX]{x1D700}}\mathop{\sum }_{\substack{ d\leqslant N \\ d\mid n^{\infty }}}d^{-1/2-\unicode[STIX]{x1D700}}(d^{\sharp })^{1/4}((n,d)^{\flat })^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle N^{\unicode[STIX]{x1D700}}\mathop{\prod }_{p\mid n}\bigg(1+\mathop{\sum }_{k\geqslant 1}\frac{((p^{k})^{\sharp })^{1/4}((n,p^{k})^{\flat })^{1/2}}{p^{k(1/2+\unicode[STIX]{x1D700})}}\bigg)\nonumber\\ \displaystyle & = & \displaystyle N^{\unicode[STIX]{x1D700}}\mathop{\prod }_{p\mid n}\bigg(1+\frac{2}{p^{\unicode[STIX]{x1D700}}}+\mathop{\sum }_{k\geqslant 3}\frac{1}{p^{k(1/4+\unicode[STIX]{x1D700})-1/2}}\bigg)\nonumber\\ \displaystyle & \ll & \displaystyle (nN)^{\unicode[STIX]{x1D700}}\nonumber\end{eqnarray}$$
by re-defining
![]() $\unicode[STIX]{x1D700}$
. We now get
$\unicode[STIX]{x1D700}$
. We now get
where the last step follows from Lemma A.4 together with partial summation and taking
![]() $q=1$
therein.◻
$q=1$
therein.◻
Appendix B Estimate for
 $\mathscr{B}(m,n,\ell ,u;q)$
$\mathscr{B}(m,n,\ell ,u;q)$
While invoking the ideas of the
![]() $q$
-analogue of the van der Corput method, we have transformed the original algebraic exponential sum
$q$
-analogue of the van der Corput method, we have transformed the original algebraic exponential sum
![]() $K(m,n,q)$
to a new sum
$K(m,n,q)$
to a new sum
![]() $\mathscr{B}(m,n,\ell ,u;q)$
as given by (4.4). This appendix will be devoted to present an estimation for
$\mathscr{B}(m,n,\ell ,u;q)$
as given by (4.4). This appendix will be devoted to present an estimation for
![]() $\mathscr{B}(m,n,\ell ,u;q)$
that suits well in our applications to Theorem 1.1. In fact, the job can be done for the general complete exponential sum
$\mathscr{B}(m,n,\ell ,u;q)$
that suits well in our applications to Theorem 1.1. In fact, the job can be done for the general complete exponential sum
Here
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D706}_{2}$
with
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D706}_{2}$
with
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \mathbf{Z}[X]$
and
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in \mathbf{Z}[X]$
and
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
being coprime in
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
being coprime in
![]() $\mathbf{Z}[X]$
. The values of
$\mathbf{Z}[X]$
. The values of
![]() $a$
such that
$a$
such that
![]() $(\unicode[STIX]{x1D706}_{2}(a),q)\neq 1$
are excluded from summation. We define the degree of
$(\unicode[STIX]{x1D706}_{2}(a),q)\neq 1$
are excluded from summation. We define the degree of
![]() $\unicode[STIX]{x1D706}$
by
$\unicode[STIX]{x1D706}$
by
If
we then adopt the convention that
for all
![]() $c\mid q.$
$c\mid q.$
There are many known estimates for complete exponential sums in the literature. In [Reference Wu and XiWX16, Theorem B.1], we obtained the following estimate for
![]() $\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D706},q)$
.
$\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D706},q)$
.
Theorem B.1. Let
![]() $d=d(\unicode[STIX]{x1D706})\geqslant 1.$
For
$d=d(\unicode[STIX]{x1D706})\geqslant 1.$
For
![]() $q\geqslant 1,$
we have
$q\geqslant 1,$
we have
where
![]() $q^{\ddagger }$
and
$q^{\ddagger }$
and
![]() $\unicode[STIX]{x1D6EF}(q)$
are given as in Lemma 4.2.
$\unicode[STIX]{x1D6EF}(q)$
are given as in Lemma 4.2.
In fact, the case of
![]() $q$
being a prime is essentially due to Weil [Reference WeilWei48], and one can refer to [Reference BombieriBom66] for a complete proof that suits quite well in our situation. Thanks to the Chinese remainder theorem, the evaluation of
$q$
being a prime is essentially due to Weil [Reference WeilWei48], and one can refer to [Reference BombieriBom66] for a complete proof that suits quite well in our situation. Thanks to the Chinese remainder theorem, the evaluation of
![]() $\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D706},q)$
can be reduced to the case of prime power moduli
$\unicode[STIX]{x1D6F4}(\unicode[STIX]{x1D706},q)$
can be reduced to the case of prime power moduli
![]() $p^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6FC}\geqslant 2)$
, which can usually be treated following an elementary device; see [Reference Iwaniec and KowalskiIK04, §12.3] for details. This is in fact the line of the proof in [Reference Wu and XiWX16].
$p^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D6FC}\geqslant 2)$
, which can usually be treated following an elementary device; see [Reference Iwaniec and KowalskiIK04, §12.3] for details. This is in fact the line of the proof in [Reference Wu and XiWX16].
The upper bound in Theorem B.1 is complicated at first glance and it even gives a worse bound than the trivial one if
![]() $\unicode[STIX]{x1D706}$
is a constant function modulo
$\unicode[STIX]{x1D706}$
is a constant function modulo
![]() $q$
. However, it provides an essentially optimal bound if we have an extra average over
$q$
. However, it provides an essentially optimal bound if we have an extra average over
![]() $q$
, since
$q$
, since
![]() $(\unicode[STIX]{x1D706},q^{\flat })^{1/2}(\unicode[STIX]{x1D706},q^{\flat })_{\ast }^{1/2}(\unicode[STIX]{x1D706}^{\prime },q^{\ddagger })\unicode[STIX]{x1D6EF}(q)^{1/2}$
does not oscillate too much on average.
$(\unicode[STIX]{x1D706},q^{\flat })^{1/2}(\unicode[STIX]{x1D706},q^{\flat })_{\ast }^{1/2}(\unicode[STIX]{x1D706}^{\prime },q^{\ddagger })\unicode[STIX]{x1D6EF}(q)^{1/2}$
does not oscillate too much on average.
Given
![]() $m,n,u,\ell \in \mathbf{Z},$
we take
$m,n,u,\ell \in \mathbf{Z},$
we take
with
Moreover, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D706}_{1}^{\prime }\unicode[STIX]{x1D706}_{2}-\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}^{\prime })(x)\nonumber\\ \displaystyle & & \displaystyle \quad =(5\ell x^{4}+8\ell ux^{3}+3\ell u^{2}x^{2}+2(m+n)x+2mu)x^{2}(x+u)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(4x^{3}+6ux^{2}+2u^{2}x)(\ell x^{5}+2\ell ux^{4}+\ell u^{2}x^{3}+(m+n)x^{2}+2mux+mu^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =5\ell x^{8}+8\ell ux^{7}+3\ell u^{2}x^{6}+2(m+n)x^{5}+2mux^{4}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,10\ell ux^{7}+16\ell u^{2}x^{6}+6\ell u^{3}x^{5}+4(m+n)ux^{4}+4mu^{2}x^{3}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,5\ell u^{2}x^{6}+8\ell u^{3}x^{5}+3\ell u^{4}x^{4}+2(m+n)u^{2}x^{3}+2mu^{3}x^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(4\ell x^{8}+8\ell ux^{7}+4\ell u^{2}x^{6}+4(m+n)x^{5}+8mux^{4}+4mu^{2}x^{3})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(6\ell ux^{7}+12\ell u^{2}x^{6}+6\ell u^{3}x^{5}+6(m+n)ux^{4}+12mu^{2}x^{3}+6mu^{3}x^{2})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(2\ell u^{2}x^{6}+4\ell u^{3}x^{5}+2\ell u^{4}x^{4}+4mu^{3}x^{2}+2mu^{4}x)\nonumber\\ \displaystyle & & \displaystyle \quad =\ell x^{8}+4\ell ux^{7}-6\ell u^{2}x^{6}-(2m+2n-4\ell u^{3})x^{5}+(\ell u^{4}-2nu-8mu)x^{4}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(2n-10m)u^{2}x^{3}-8mu^{3}x^{2}-2mu^{4}x.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D706}_{1}^{\prime }\unicode[STIX]{x1D706}_{2}-\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}^{\prime })(x)\nonumber\\ \displaystyle & & \displaystyle \quad =(5\ell x^{4}+8\ell ux^{3}+3\ell u^{2}x^{2}+2(m+n)x+2mu)x^{2}(x+u)^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(4x^{3}+6ux^{2}+2u^{2}x)(\ell x^{5}+2\ell ux^{4}+\ell u^{2}x^{3}+(m+n)x^{2}+2mux+mu^{2})\nonumber\\ \displaystyle & & \displaystyle \quad =5\ell x^{8}+8\ell ux^{7}+3\ell u^{2}x^{6}+2(m+n)x^{5}+2mux^{4}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,10\ell ux^{7}+16\ell u^{2}x^{6}+6\ell u^{3}x^{5}+4(m+n)ux^{4}+4mu^{2}x^{3}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,5\ell u^{2}x^{6}+8\ell u^{3}x^{5}+3\ell u^{4}x^{4}+2(m+n)u^{2}x^{3}+2mu^{3}x^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(4\ell x^{8}+8\ell ux^{7}+4\ell u^{2}x^{6}+4(m+n)x^{5}+8mux^{4}+4mu^{2}x^{3})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(6\ell ux^{7}+12\ell u^{2}x^{6}+6\ell u^{3}x^{5}+6(m+n)ux^{4}+12mu^{2}x^{3}+6mu^{3}x^{2})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,(2\ell u^{2}x^{6}+4\ell u^{3}x^{5}+2\ell u^{4}x^{4}+4mu^{3}x^{2}+2mu^{4}x)\nonumber\\ \displaystyle & & \displaystyle \quad =\ell x^{8}+4\ell ux^{7}-6\ell u^{2}x^{6}-(2m+2n-4\ell u^{3})x^{5}+(\ell u^{4}-2nu-8mu)x^{4}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(2n-10m)u^{2}x^{3}-8mu^{3}x^{2}-2mu^{4}x.\nonumber\end{eqnarray}$$
Thus, for odd
![]() $c\mid q$
, we have
$c\mid q$
, we have
and
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D706}^{\prime },c) & = & \displaystyle (\ell ,4\ell u,6\ell u^{2},2m+2n-4\ell u^{3},\ell u^{4}-2nu-8mu,(2n-10m)u^{2},8mu^{3},2mu^{4},c)\nonumber\\ \displaystyle & = & \displaystyle (\ell ,m+n,(4m+n)u,(5m-n)u^{2},mu^{3},c)\nonumber\\ \displaystyle & = & \displaystyle (\ell ,m+n,3mu,6mu^{2},mu^{3},c)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 3(\ell ,m+n,mu,c)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 3(\ell ,m,n,c)(\ell ,m+n,u,c).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D706}^{\prime },c) & = & \displaystyle (\ell ,4\ell u,6\ell u^{2},2m+2n-4\ell u^{3},\ell u^{4}-2nu-8mu,(2n-10m)u^{2},8mu^{3},2mu^{4},c)\nonumber\\ \displaystyle & = & \displaystyle (\ell ,m+n,(4m+n)u,(5m-n)u^{2},mu^{3},c)\nonumber\\ \displaystyle & = & \displaystyle (\ell ,m+n,3mu,6mu^{2},mu^{3},c)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 3(\ell ,m+n,mu,c)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 3(\ell ,m,n,c)(\ell ,m+n,u,c).\nonumber\end{eqnarray}$$
Note that
![]() $d(\unicode[STIX]{x1D706})=\deg (\unicode[STIX]{x1D706}_{1})+\deg (\unicode[STIX]{x1D706}_{2})=5+4=9.$
$d(\unicode[STIX]{x1D706})=\deg (\unicode[STIX]{x1D706}_{1})+\deg (\unicode[STIX]{x1D706}_{2})=5+4=9.$
From Theorem B.1, we may conclude the following estimate as given in Lemma 4.2.
Theorem B.2. For each odd
![]() $q\geqslant 1$
, we have
$q\geqslant 1$
, we have