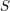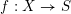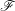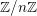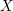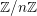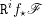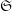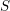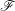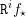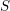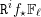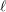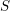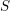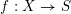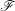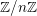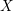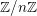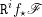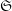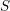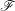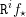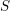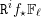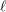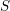Introduction
0.1
Soient
![]() $S$
un schéma et
$S$
un schéma et
![]() $f:X\rightarrow S$
un morphisme propre de présentation finie. D’après un théorème de finitude classique, dû à Michael Artin et Alexander Grothendieck [SGA 4 XIV, 1.1], pour tout faisceau constructible
$f:X\rightarrow S$
un morphisme propre de présentation finie. D’après un théorème de finitude classique, dû à Michael Artin et Alexander Grothendieck [SGA 4 XIV, 1.1], pour tout faisceau constructible
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X$
, les faisceaux de
$X$
, les faisceaux de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules
$\mathbb{Z}/n\mathbb{Z}$
-modules
![]() $\mathtt{R}^{i}f_{\star }\mathscr{F}$
, obtenus par image directe, sont également constructibles : (lorsque
$\mathtt{R}^{i}f_{\star }\mathscr{F}$
, obtenus par image directe, sont également constructibles : (lorsque
![]() $S$
est cohérent, par exemple nœthérien) il existe une stratification
$S$
est cohérent, par exemple nœthérien) il existe une stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S$
telle que les faisceaux
$S$
telle que les faisceaux
![]() $\mathtt{R}^{i}f_{\star }\mathscr{F}$
soient localement constants et de présentation finie sur les strates. (Ils sont également nuls pour
$\mathtt{R}^{i}f_{\star }\mathscr{F}$
soient localement constants et de présentation finie sur les strates. (Ils sont également nuls pour
![]() $i\gg 0$
indépendamment de
$i\gg 0$
indépendamment de
![]() $\mathscr{F}$
.)
$\mathscr{F}$
.)
À
![]() $f$
fixé, il est naturel de s’interroger sur la dépendance de
$f$
fixé, il est naturel de s’interroger sur la dépendance de
![]() $\mathfrak{S}$
en
$\mathfrak{S}$
en
![]() $\mathscr{F}$
, notamment sous la forme suivante, qui n’est qu’un cas particulier des questions que l’on souhaite aborder ici
:
$\mathscr{F}$
, notamment sous la forme suivante, qui n’est qu’un cas particulier des questions que l’on souhaite aborder ici
:
Existe-t-il une stratification
![]() $\mathfrak{S}$
qui convienne pour tous les faisceaux
$\mathfrak{S}$
qui convienne pour tous les faisceaux
![]() $\mathtt{R}^{i}f_{\star }\mathbb{Z}/n\mathbb{Z}$
, où
$\mathtt{R}^{i}f_{\star }\mathbb{Z}/n\mathbb{Z}$
, où
![]() $n$
parcourt les entiers inversibles sur
$n$
parcourt les entiers inversibles sur
![]() $S$
?
$S$
?
(Notons que si l’entier
![]() $n$
parcourt les puissances d’un même nombre premier
$n$
parcourt les puissances d’un même nombre premier
![]() $\ell$
, comme cela est naturel du point de vue de la cohomologie
$\ell$
, comme cela est naturel du point de vue de la cohomologie
![]() $\ell$
-adique, la réponse à la question précédente est trivialement « oui ».)
$\ell$
-adique, la réponse à la question précédente est trivialement « oui ».)
0.2
Si
![]() $S$
est de type fini sur le corps
$S$
est de type fini sur le corps
![]() $\mathbb{C}$
des nombres complexes, l’existence d’une telle stratification est bien connue en vertu du résultat analogue pour le morphisme d’espaces topologiques
$\mathbb{C}$
des nombres complexes, l’existence d’une telle stratification est bien connue en vertu du résultat analogue pour le morphisme d’espaces topologiques
![]() $X(\mathbb{C})\rightarrow S(\mathbb{C})$
— cf. par exemple [Reference BorelBor84, V.10.16] ou [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, p. 153, premier paragraphe] — et du théorème de comparaison entre cohomologie de Betti et cohomologie étale de M. Artin et A. Grothendieck [SGA 4 XVI, 4.1].
$X(\mathbb{C})\rightarrow S(\mathbb{C})$
— cf. par exemple [Reference BorelBor84, V.10.16] ou [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, p. 153, premier paragraphe] — et du théorème de comparaison entre cohomologie de Betti et cohomologie étale de M. Artin et A. Grothendieck [SGA 4 XVI, 4.1].
0.3
Bien entendu, tant pour les applications que pour les démonstrations, il est utile de ne pas se restreindre à des faisceaux constants mais de considérer des faisceaux — et même des complexes — constructibles le long d’une stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $X$
(au sens évident rappelé en 1.1.3). Cependant, en cohomologie étale, des phénomènes de ramification sauvage font que l’on ne peut s’attendre à ce que, donnés un morphisme propre
$X$
(au sens évident rappelé en 1.1.3). Cependant, en cohomologie étale, des phénomènes de ramification sauvage font que l’on ne peut s’attendre à ce que, donnés un morphisme propre
![]() $f:X\rightarrow S$
et
$f:X\rightarrow S$
et
![]() $\mathfrak{X}$
une stratification de
$\mathfrak{X}$
une stratification de
![]() $X$
, il existe une stratification
$X$
, il existe une stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S$
telle que les images directes supérieures par
$S$
telle que les images directes supérieures par
![]() $f$
de faisceaux sur
$f$
de faisceaux sur
![]() $X$
constructibles le long de
$X$
constructibles le long de
![]() $\mathfrak{X}$
soient constructibles le long de
$\mathfrak{X}$
soient constructibles le long de
![]() $\mathfrak{S}$
. En effet, si par exemple
$\mathfrak{S}$
. En effet, si par exemple
![]() $\ell$
est un nombre premier fixé,
$\ell$
est un nombre premier fixé,
![]() $k$
un corps algébriquement clos de caractéristique
$k$
un corps algébriquement clos de caractéristique
![]() $p>0$
divisant
$p>0$
divisant
![]() $\ell -1$
et
$\ell -1$
et
![]() $\unicode[STIX]{x1D713}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{F}_{\ell }^{\times }$
un caractère non-trivial, les
$\unicode[STIX]{x1D713}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{F}_{\ell }^{\times }$
un caractère non-trivial, les
![]() $\mathbb{F}_{\ell }$
-faisceaux d’Artin–Schreier
$\mathbb{F}_{\ell }$
-faisceaux d’Artin–Schreier
![]() $\mathscr{L}_{\unicode[STIX]{x1D706}}:=\mathscr{L}_{\unicode[STIX]{x1D713}}((x-\unicode[STIX]{x1D706})y)$
sur
$\mathscr{L}_{\unicode[STIX]{x1D706}}:=\mathscr{L}_{\unicode[STIX]{x1D713}}((x-\unicode[STIX]{x1D706})y)$
sur
![]() $\mathbf{A}_{x/\mathbb{F}_{p}}^{1}\times \mathbf{A}_{y/\mathbb{F}_{p}}^{1}$
sont lisses pour chaque
$\mathbf{A}_{x/\mathbb{F}_{p}}^{1}\times \mathbf{A}_{y/\mathbb{F}_{p}}^{1}$
sont lisses pour chaque
![]() $\unicode[STIX]{x1D706}\in k$
mais les faisceaux image directe exceptionnelle
$\unicode[STIX]{x1D706}\in k$
mais les faisceaux image directe exceptionnelle
![]() $\mathtt{R}^{2}\;\text{pr}_{1!}\mathscr{L}_{\unicode[STIX]{x1D706}}$
ne sont pas constructibles le long d’une même stratification de
$\mathtt{R}^{2}\;\text{pr}_{1!}\mathscr{L}_{\unicode[STIX]{x1D706}}$
ne sont pas constructibles le long d’une même stratification de
![]() $\mathbf{A}_{x/\mathbb{F}_{p}}^{1}$
, indépendante de
$\mathbf{A}_{x/\mathbb{F}_{p}}^{1}$
, indépendante de
![]() $\unicode[STIX]{x1D706}$
: le faisceau
$\unicode[STIX]{x1D706}$
: le faisceau
![]() $\mathtt{R}^{2}\text{pr}_{1!}\mathscr{L}_{\unicode[STIX]{x1D706}}$
est non nul et à support dans
$\mathtt{R}^{2}\text{pr}_{1!}\mathscr{L}_{\unicode[STIX]{x1D706}}$
est non nul et à support dans
![]() $\{\unicode[STIX]{x1D706}\}$
. (Voir [Reference LaumonLau87, 1.2.2.2] pour l’analogue
$\{\unicode[STIX]{x1D706}\}$
. (Voir [Reference LaumonLau87, 1.2.2.2] pour l’analogue
![]() $\ell$
-adique et [Reference OrgogozoOrg03, p. 139–140] pour une discussion du même phénomène dans une autre perspective.) La flèche
$\ell$
-adique et [Reference OrgogozoOrg03, p. 139–140] pour une discussion du même phénomène dans une autre perspective.) La flèche
![]() $\mathtt{R}^{2}\text{pr}_{1!}\mathscr{L}_{\unicode[STIX]{x1D706}}\rightarrow \mathtt{R}^{2}\text{pr}_{1\star }\mathscr{L}_{\unicode[STIX]{x1D706}}$
d’oubli des supports étant un isomorphisme [Reference LaumonLau87, 1.3.1.1], on voit également que l’on ne dispose pas d’un analogue uniforme « naïf » du théorème [Th. finitude, 1.9 (ii)] de commutation au changement de base générique : en tout point au voisinage duquel
$\mathtt{R}^{2}\text{pr}_{1!}\mathscr{L}_{\unicode[STIX]{x1D706}}\rightarrow \mathtt{R}^{2}\text{pr}_{1\star }\mathscr{L}_{\unicode[STIX]{x1D706}}$
d’oubli des supports étant un isomorphisme [Reference LaumonLau87, 1.3.1.1], on voit également que l’on ne dispose pas d’un analogue uniforme « naïf » du théorème [Th. finitude, 1.9 (ii)] de commutation au changement de base générique : en tout point au voisinage duquel
![]() $\mathtt{R}^{2}\text{pr}_{1\star }\mathscr{L}_{\unicode[STIX]{x1D706}}$
commute au changement de base, sa fibre est nécessairement nulle. Cependant, comme l’a démontré Luc Illusie — motivé par une question de Jean-Pierre Serre –, la situation est aussi bonne que possible si l’on considère des coefficients constants (voir [Reference IllusieIll10]).
$\mathtt{R}^{2}\text{pr}_{1\star }\mathscr{L}_{\unicode[STIX]{x1D706}}$
commute au changement de base, sa fibre est nécessairement nulle. Cependant, comme l’a démontré Luc Illusie — motivé par une question de Jean-Pierre Serre –, la situation est aussi bonne que possible si l’on considère des coefficients constants (voir [Reference IllusieIll10]).
La formule de Grothendieck–Ogg–Šafarevič [SGA 5 X, 7.2] montre également que l’on ne peut obtenir de bornes uniformes sur les nombres de Betti, comme celles rappelées au paragraphe suivant, sans hypothèse de modération.
0.4
Dans [Reference Katz and LaumonKL85, § 3] (voir aussi par exemple [Reference Fouvry and KatzFK01, § 2] et [Reference KatzKat90, § 13]) sont établis des résultats intermédiaires entre l’énoncé topologique rappelé ci-dessus et des énoncés, à démontrer, tenant compte de la ramification sauvage. Nicholas Katz et Gérard Laumon établissent notamment le résultat suivant, sous l’hypothèse technique supplémentaire que
![]() $S$
est de type fini sur un schéma nœthérien régulier de dimension inférieure ou égale à
$S$
est de type fini sur un schéma nœthérien régulier de dimension inférieure ou égale à
![]() $1$
[Reference Katz and LaumonKL85, 3.1.2] : il existe un entier
$1$
[Reference Katz and LaumonKL85, 3.1.2] : il existe un entier
![]() $N\geqslant 1$
et une stratification
$N\geqslant 1$
et une stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S$
tels que pour chaque nombre premier
$S$
tels que pour chaque nombre premier
![]() $\ell$
, chaque
$\ell$
, chaque
![]() $\mathscr{K}\in \text{Ob}\;\mathtt{D}_{c}^{b}(X[1/N\ell ],\mathbb{Q}_{\ell })$
constructible le long de
$\mathscr{K}\in \text{Ob}\;\mathtt{D}_{c}^{b}(X[1/N\ell ],\mathbb{Q}_{\ell })$
constructible le long de
![]() $\mathfrak{X}[1/N\ell ]$
, le complexe
$\mathfrak{X}[1/N\ell ]$
, le complexe
![]() $\mathtt{R}f_{\star }\mathscr{K}\in \text{Ob}\;\mathtt{D}_{c}^{b}(S[1/N\ell ],\mathbb{Q}_{\ell })$
est constructible le long de
$\mathtt{R}f_{\star }\mathscr{K}\in \text{Ob}\;\mathtt{D}_{c}^{b}(S[1/N\ell ],\mathbb{Q}_{\ell })$
est constructible le long de
![]() $\mathfrak{S}[1/N\ell ]$
. (« Constructible le long de … » : voir 1.1.3.) De plus, les auteurs majorent uniformément la taille des images directes : il existe une constante
$\mathfrak{S}[1/N\ell ]$
. (« Constructible le long de … » : voir 1.1.3.) De plus, les auteurs majorent uniformément la taille des images directes : il existe une constante
![]() $C$
telle que pour chaque
$C$
telle que pour chaque
![]() $s\in S[1/N\ell ]$
on ait l’inégalité
$s\in S[1/N\ell ]$
on ait l’inégalité
où
![]() $\Vert \mathscr{K}\Vert (x):=\sum _{i}\dim _{\mathbb{Q}_{\ell }}\mathtt{H}^{i}(\mathscr{K})_{\overline{x}}$
pour un choix arbitraire de point géométrique
$\Vert \mathscr{K}\Vert (x):=\sum _{i}\dim _{\mathbb{Q}_{\ell }}\mathtt{H}^{i}(\mathscr{K})_{\overline{x}}$
pour un choix arbitraire de point géométrique
![]() $\overline{x}$
au-dessus de
$\overline{x}$
au-dessus de
![]() $x\in X$
.
$x\in X$
.
Ce résultat s’appuie sur la résolution des singularités d’Hironaka et n’est intéressant que si la caractéristique générique de
![]() $S$
est nulle. Cette hypothèse permet également, grâce au lemme d’Abhyankar relatif (cf. [Reference Katz and LaumonKL85, § 3.4.2] et [SGA 1 XIII, 5.5]), d’ignorer la ramification sauvage.
$S$
est nulle. Cette hypothèse permet également, grâce au lemme d’Abhyankar relatif (cf. [Reference Katz and LaumonKL85, § 3.4.2] et [SGA 1 XIII, 5.5]), d’ignorer la ramification sauvage.
0.5
L’objectif de ce texte est de s’affranchir de ces restrictions : les « fibrations élémentaires » [SGA 4 XI, § 3] utilisées dans [Reference Katz and LaumonKL85] sont remplacées par des courbes nodales, dont l’ubiquité a été démontrée par Aise Johan de Jong [Reference de JongdeJ96, Reference de JongdeJ97]. Armé de cet outil et familier des techniques de dévissages en cohomologie étale, on est confronté à la difficulté suivante : trouver un énoncé de stabilité de familles « (uniformément) constructibles et modérées ». On le doit à Ofer Gabber, dont la contribution à cet article ne s’arrête pas là. Un point clef est que « uniformément » doit être interprété localement pour la topologie propre — engendrée par la prétopologie dont les morphismes couvrants sont les morphismes propres et surjectifs — (ou la topologie
![]() $h$
), idée que l’on trouve déjà dans une lettre de Richard Pink à N. Katz [Reference PinkPin95], pourtant antérieure aux travaux de A. J. de Jong. (L’insuffisance d’une localisation pour la topologie finie est expliquée en 3.2.)
$h$
), idée que l’on trouve déjà dans une lettre de Richard Pink à N. Katz [Reference PinkPin95], pourtant antérieure aux travaux de A. J. de Jong. (L’insuffisance d’une localisation pour la topologie finie est expliquée en 3.2.)
Les méthodes employées ici font que la plupart des résultats de cet article sont de démonstration plus simple dans le cas particulier des schémas de type fini sur un anneau de Dedekind mais nous les énonçons pour des schémas quasi-excellents, quitte à en donner la démonstration en deux temps. Il est apparu que l’hypothèse d’excellence n’était pas toujours nécessaire, notamment pour le théorème d’uniformité propre ; pour ne pas retarder à nouveau la publication de ce texte, nous avons préféré nous contenter d’esquisser les modifications à apporter (voir par exemple 3.5.5). Nous espérons que le lecteur nous pardonnera ce choix.
0.6
Le résultat principal de cet article est le théorème 3.1.1, qui apporte une réponse positive à la question formulée en 0.1, pour des faisceaux non nécessairement constants dont on borne uniformément, en un sens grossier, la ramification sauvage. Plus précisément, on montre que pour tout morphisme
![]() $f:X\rightarrow S$
entre schémas nœthériens excellents et toute stratification
$f:X\rightarrow S$
entre schémas nœthériens excellents et toute stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $X$
, il existe une stratification
$X$
, il existe une stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S$
telle que les images directes supérieures d’un
$S$
telle que les images directes supérieures d’un
![]() $X$
-faisceau étale de torsion inversible sur
$X$
-faisceau étale de torsion inversible sur
![]() $X$
, constructible le long de
$X$
, constructible le long de
![]() $\mathfrak{X}$
, et modéré au sens de 1.3.1, soient constructibles le long de
$\mathfrak{X}$
, et modéré au sens de 1.3.1, soient constructibles le long de
![]() $\mathfrak{S}$
. De plus, il existe une altération commune
$\mathfrak{S}$
. De plus, il existe une altération commune
![]() $S^{\prime }\rightarrow S$
qui les modère.
$S^{\prime }\rightarrow S$
qui les modère.
Comme expliqué en 6.2, un tel résultat peut être considéré comme une variante relative de la finitude des ultraproduits des groupes de cohomologie
![]() $\mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
pour
$\mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
pour
![]() $\ell$
variable, où
$\ell$
variable, où
![]() $X$
est propre sur un corps séparablement clos. Finitude qui, rappelons-le, entraîne le théorème [Reference GabberGab83] sur la torsion dans la cohomologie
$X$
est propre sur un corps séparablement clos. Finitude qui, rappelons-le, entraîne le théorème [Reference GabberGab83] sur la torsion dans la cohomologie
![]() $\ell$
-adique d’une variété et pose naturellement la question d’adapter [Reference DeligneDel80] à ces théories cohomologiques. Une variante unipotente de nos résultats permet également de retrouver un des principaux ingrédients de [Reference Böckle, Gajda and PetersenBGP18] : il s’agit d’une généralisation, uniforme en
$\ell$
-adique d’une variété et pose naturellement la question d’adapter [Reference DeligneDel80] à ces théories cohomologiques. Une variante unipotente de nos résultats permet également de retrouver un des principaux ingrédients de [Reference Böckle, Gajda and PetersenBGP18] : il s’agit d’une généralisation, uniforme en
![]() $\ell$
, du théorème de quasi-unipotence de Grothendieck sur une base de dimension arbitraire. (En dimension
$\ell$
, du théorème de quasi-unipotence de Grothendieck sur une base de dimension arbitraire. (En dimension
![]() $1$
, ce résultat est dû à P. Deligne ; voir 6.1 pour notre énoncé.) L’article [Reference Böckle, Gajda and PetersenBGP18] fait suite à un article de J.-P. Serre sur la presque indépendance de représentations
$1$
, ce résultat est dû à P. Deligne ; voir 6.1 pour notre énoncé.) L’article [Reference Böckle, Gajda and PetersenBGP18] fait suite à un article de J.-P. Serre sur la presque indépendance de représentations
![]() $\ell$
-adiques d’origine géométrique.
$\ell$
-adiques d’origine géométrique.
0.7
Signalons maintenant quelques limites de la méthode. Tout d’abord, on aimerait des résultats d’indépendance de
![]() $\ell$
, beaucoup plus forts, mais qui semblent malheureusement hors de portée : la descente cohomologique — utilisée de façon répétée — fait naturellement apparaître des différentielles dans la suite spectrale correspondante ; on ignore si elles sont « motiviques » (cf. [Reference de JongdeJ96, introduction]). D’autre part, comme expliqué ci-dessus, on obtient notamment des majorations de nombres de Betti : peut-on calculer explicitement une borne et les nombres de Betti d’un schéma donné pour chaque
$\ell$
, beaucoup plus forts, mais qui semblent malheureusement hors de portée : la descente cohomologique — utilisée de façon répétée — fait naturellement apparaître des différentielles dans la suite spectrale correspondante ; on ignore si elles sont « motiviques » (cf. [Reference de JongdeJ96, introduction]). D’autre part, comme expliqué ci-dessus, on obtient notamment des majorations de nombres de Betti : peut-on calculer explicitement une borne et les nombres de Betti d’un schéma donné pour chaque
![]() $\ell$
donné ? Les techniques de cet article ne permettent pas de répondre à cette question (voir cependant [Reference Madore and OrgogozoMO15] pour le calcul des nombres de Betti). Enfin, nous ne considérons des situations sauvages que de façon superficielle : on se ramène immédiatement à des cas modérés pour lesquels les techniques classiques — voir par exemple [SGA 7 XIII, 2.1.9-11] — s’appliquent. Il serait intéressant de reprendre les résultats de cet article à la lumière des travaux plus récents sur la ramification sauvage (voir par exemple [Reference Kato and SaitoKS13]).
$\ell$
donné ? Les techniques de cet article ne permettent pas de répondre à cette question (voir cependant [Reference Madore and OrgogozoMO15] pour le calcul des nombres de Betti). Enfin, nous ne considérons des situations sauvages que de façon superficielle : on se ramène immédiatement à des cas modérés pour lesquels les techniques classiques — voir par exemple [SGA 7 XIII, 2.1.9-11] — s’appliquent. Il serait intéressant de reprendre les résultats de cet article à la lumière des travaux plus récents sur la ramification sauvage (voir par exemple [Reference Kato and SaitoKS13]).
1 Définitions, sorites et préliminaires topologiques
1.1 Constructibilité
1.1.1
Soit
![]() $X$
un schéma nœthérien. Une stratification de
$X$
un schéma nœthérien. Une stratification de
![]() $X$
est une partition finie (ensembliste)
$X$
est une partition finie (ensembliste)
![]() $\mathfrak{X}$
en sous-schémas réduits localement fermés (non vides), appelés strates. Si pour toute strate
$\mathfrak{X}$
en sous-schémas réduits localement fermés (non vides), appelés strates. Si pour toute strate
![]() $S$
le bord
$S$
le bord
![]() $\unicode[STIX]{x2202}S=\overline{S}-S$
est réunion de strates, on dit que
$\unicode[STIX]{x2202}S=\overline{S}-S$
est réunion de strates, on dit que
![]() $\mathfrak{X}$
est une bonne stratification. Un schéma stratifié est un schéma muni d’une stratification. Enfin, une stratification
$\mathfrak{X}$
est une bonne stratification. Un schéma stratifié est un schéma muni d’une stratification. Enfin, une stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $X$
est adaptée à une partie
$X$
est adaptée à une partie
![]() $Z\subseteq X$
si chaque strate de
$Z\subseteq X$
si chaque strate de
![]() $\mathfrak{X}$
est contenue dans
$\mathfrak{X}$
est contenue dans
![]() $Z$
ou
$Z$
ou
![]() $X-Z$
.
$X-Z$
.
Faisons les observations suivantes :
(1) toute stratification se raffine en une bonne stratification [Sta, lemme 09Y5].
Et dans le cas d’une bonne stratification :
(2) toute strate, étant localement fermée, est ouverte dans son adhérence ;
(3) tout strate
 $S$
maximale pour la relation d’ordre partiel «
$S$
maximale pour la relation d’ordre partiel «
 $x\leqslant y$
si et seulement si
$x\leqslant y$
si et seulement si
 $x\subseteq \overline{y}$
» est ouverte :
$x\subseteq \overline{y}$
» est ouverte : 
Si
![]() $f:Y\rightarrow X$
est un morphisme, on note
$f:Y\rightarrow X$
est un morphisme, on note
![]() $\mathfrak{X}_{Y}$
ou
$\mathfrak{X}_{Y}$
ou
![]() $f^{\star }\mathfrak{X}$
la stratification de
$f^{\star }\mathfrak{X}$
la stratification de
![]() $Y$
déduite de
$Y$
déduite de
![]() $\mathfrak{X}$
par image inverse (réduite) des strates.
$\mathfrak{X}$
par image inverse (réduite) des strates.
1.1.2 Mise en garde
Notons que l’image inverse d’une bonne stratification par un morphisme
![]() $f:Y\rightarrow X$
n’est pas nécessairement bonne : si
$f:Y\rightarrow X$
n’est pas nécessairement bonne : si
![]() $S$
est une partie localement fermée, l’inclusion
$S$
est une partie localement fermée, l’inclusion
![]() $\overline{f^{-1}(S)}\subseteq f^{-1}(\overline{S})$
peut être stricte. De même, si
$\overline{f^{-1}(S)}\subseteq f^{-1}(\overline{S})$
peut être stricte. De même, si
![]() $U$
est un ouvert d’un schéma nœthérien
$U$
est un ouvert d’un schéma nœthérien
![]() $X$
, il n’est en général pas vrai que la stratification
$X$
, il n’est en général pas vrai que la stratification
![]() $\{U,X\setminus U\}$
soit bonne.
$\{U,X\setminus U\}$
soit bonne.
Compte tenu de (1) ci-dessus, ces observations n’ont pas de conséquence fâcheuse.
1.1.3
Soient
![]() $X$
un schéma et
$X$
un schéma et
![]() $(X^{\prime },\mathfrak{X}^{\prime })$
un
$(X^{\prime },\mathfrak{X}^{\prime })$
un
![]() $X$
-schéma stratifié nœthérien. On dit qu’un faisceau étale sur
$X$
-schéma stratifié nœthérien. On dit qu’un faisceau étale sur
![]() $X$
est constructible le long de
$X$
est constructible le long de
![]() $\mathfrak{X}^{\prime }$
(ou
$\mathfrak{X}^{\prime }$
(ou
![]() $\mathfrak{X}^{\prime }$
-constructible) si son image inverse sur
$\mathfrak{X}^{\prime }$
-constructible) si son image inverse sur
![]() $X^{\prime }$
est (ensemblistement) constructible et localement constante sur chacune des strates de
$X^{\prime }$
est (ensemblistement) constructible et localement constante sur chacune des strates de
![]() $\mathfrak{X}^{\prime }$
. Lorsque
$\mathfrak{X}^{\prime }$
. Lorsque
![]() $X^{\prime }=X$
, on retrouve la définition de [Reference Katz and LaumonKL85, § 3.0].
$X^{\prime }=X$
, on retrouve la définition de [Reference Katz and LaumonKL85, § 3.0].
Dans cet article on dira souvent « lisse » pour « localement constant (ensemblistement) constructible » et, assez systématiquement, « faisceau » pour « faisceau étale ».
À des fins de dévissage, le résultat suivant — obtenu en utilisant (3) supra Footnote 1 et procédant par récurrence — est particulièrement utile. (C’est principalement ce fait qui motive l’usage de bonnes stratifications.)
Proposition 1.1.4 [SGA 4 IX, 2.5].
Soient
![]() $(X,\mathfrak{X})$
un schéma nœthérien stratifié et
$(X,\mathfrak{X})$
un schéma nœthérien stratifié et
![]() $\mathscr{F}$
un faisceau abélien constructible le long de
$\mathscr{F}$
un faisceau abélien constructible le long de
![]() $\mathfrak{X}$
. Si
$\mathfrak{X}$
. Si
![]() $\mathfrak{X}$
est
$\mathfrak{X}$
est
![]() $\text{bonne}$
, il existe une filtration finie sur
$\text{bonne}$
, il existe une filtration finie sur
![]() $\mathscr{F}$
de gradué isomorphe à une somme directe de faisceaux du type
$\mathscr{F}$
de gradué isomorphe à une somme directe de faisceaux du type
![]() $i_{\star }j_{!}\mathscr{L}$
, où
$i_{\star }j_{!}\mathscr{L}$
, où
![]() $j:S{\hookrightarrow}\overline{S}$
est l’immersion ouverte d’une strate de
$j:S{\hookrightarrow}\overline{S}$
est l’immersion ouverte d’une strate de
![]() $\mathfrak{X}$
dans son adhérence,
$\mathfrak{X}$
dans son adhérence,
![]() $i$
l’immersion fermée de
$i$
l’immersion fermée de
![]() $\overline{S}$
dans
$\overline{S}$
dans
![]() $X$
et
$X$
et
![]() $\mathscr{L}$
est un faisceau abélien
$\mathscr{L}$
est un faisceau abélien
![]() $\text{lisse}$
sur
$\text{lisse}$
sur
![]() $S$
. De plus, il existe une telle filtration de longueur majorée par un entier ne dépendant que de
$S$
. De plus, il existe une telle filtration de longueur majorée par un entier ne dépendant que de
![]() $\mathfrak{X}$
(et pas de
$\mathfrak{X}$
(et pas de
![]() $\mathscr{F}$
).
$\mathscr{F}$
).
L’énoncé ci-dessus est une variante de celui de [SGA 4 IX], dans lequel on se donne une partition de
![]() $X$
.
$X$
.
1.2 Unipotence
1.2.1
Soient
![]() $X$
un schéma et
$X$
un schéma et
![]() $(X^{\prime },\mathfrak{X}^{\prime })$
un
$(X^{\prime },\mathfrak{X}^{\prime })$
un
![]() $X$
-schéma stratifié nœthérien. On dit qu’un faisceau étale abélien sur
$X$
-schéma stratifié nœthérien. On dit qu’un faisceau étale abélien sur
![]() $X$
est unipotent le long de
$X$
est unipotent le long de
![]() $\mathfrak{X}^{\prime }$
(ou
$\mathfrak{X}^{\prime }$
(ou
![]() $\mathfrak{X}^{\prime }$
-unipotent) si ses tirés en arrière aux strates de
$\mathfrak{X}^{\prime }$
-unipotent) si ses tirés en arrière aux strates de
![]() $\mathfrak{X}^{\prime }$
sont extensions de faisceaux constants. Il est dit localement unipotent le long de
$\mathfrak{X}^{\prime }$
sont extensions de faisceaux constants. Il est dit localement unipotent le long de
![]() $\mathfrak{X}^{\prime }$
(ou
$\mathfrak{X}^{\prime }$
(ou
![]() $\mathfrak{X}^{\prime }$
-localement unipotent) si pour tout hensélisé strict
$\mathfrak{X}^{\prime }$
-localement unipotent) si pour tout hensélisé strict
![]() $T$
de
$T$
de
![]() $X^{\prime }$
— ou de façon équivalente tout
$X^{\prime }$
— ou de façon équivalente tout
![]() $X^{\prime }$
-schéma strictement local
$X^{\prime }$
-schéma strictement local
![]() $T$
—, son image inverse sur le schéma
$T$
—, son image inverse sur le schéma
![]() $T$
est unipotent le long de
$T$
est unipotent le long de
![]() $\mathfrak{X}_{T}^{\prime }$
. Par exemple, un faisceau lisse est localement unipotent (le long de toute stratification).
$\mathfrak{X}_{T}^{\prime }$
. Par exemple, un faisceau lisse est localement unipotent (le long de toute stratification).
(À la formulation près, cette définition se trouve dans [Reference PinkPin95].Footnote 2 )
1.2.2
Notons qu’un faisceau abélien constructible qui est localement unipotent le long de
![]() $\mathfrak{X}$
est automatiquement constructible le long de
$\mathfrak{X}$
est automatiquement constructible le long de
![]() $\mathfrak{X}$
: une extension de faisceaux lisses est lisse [SGA 4 IX, 2.1 (iii)] et la lissité se teste sur les hensélisés stricts (cf. [SGA 4 IX, 2.13 (i)]).
$\mathfrak{X}$
: une extension de faisceaux lisses est lisse [SGA 4 IX, 2.1 (iii)] et la lissité se teste sur les hensélisés stricts (cf. [SGA 4 IX, 2.13 (i)]).
1.2.3
Si
![]() $\mathscr{L}$
est un faisceau lisse sur un ouvert dense
$\mathscr{L}$
est un faisceau lisse sur un ouvert dense
![]() $U$
normal connexe d’un schéma
$U$
normal connexe d’un schéma
![]() $X$
et
$X$
et
![]() $\mathfrak{X}$
est une stratification adaptée à
$\mathfrak{X}$
est une stratification adaptée à
![]() $U$
, le faisceau constructible
$U$
, le faisceau constructible
![]() $j_{!}\mathscr{L}$
est localement unipotent le long de
$j_{!}\mathscr{L}$
est localement unipotent le long de
![]() $\mathfrak{X}$
si et seulement si il l’est le long de la stratification
$\mathfrak{X}$
si et seulement si il l’est le long de la stratification
![]() $\{U,X\setminus U\}$
: sur un schéma normal, l’unipotence d’un faisceau lisse se teste en les points maximaux.
$\{U,X\setminus U\}$
: sur un schéma normal, l’unipotence d’un faisceau lisse se teste en les points maximaux.
Lemme. Soient
![]() $X$
un schéma nœthérien normal intègre de point générique
$X$
un schéma nœthérien normal intègre de point générique
![]() $\unicode[STIX]{x1D702}$
. Un faisceau étale abélien lisse sur
$\unicode[STIX]{x1D702}$
. Un faisceau étale abélien lisse sur
![]() $X$
est unipotent, c’est-à-dire extension de faisceaux constants, si et seulement si sa restriction à
$X$
est unipotent, c’est-à-dire extension de faisceaux constants, si et seulement si sa restriction à
![]() $\unicode[STIX]{x1D702}$
l’est.
$\unicode[STIX]{x1D702}$
l’est.
1.2.4
Soient
![]() $G$
un groupe et
$G$
un groupe et
![]() $\mathscr{F}$
un
$\mathscr{F}$
un
![]() $X$
-faisceau étale abélien muni d’une action de
$X$
-faisceau étale abélien muni d’une action de
![]() $G$
, c’est-à-dire d’un morphisme
$G$
, c’est-à-dire d’un morphisme
![]() $G\rightarrow \mathtt{Aut}(\mathscr{F})$
. Nous dirons que
$G\rightarrow \mathtt{Aut}(\mathscr{F})$
. Nous dirons que
![]() $\mathscr{F}$
est
$\mathscr{F}$
est
![]() $G$
-unipotent s’il existe une filtration finie croissante par des sous-faisceaux
$G$
-unipotent s’il existe une filtration finie croissante par des sous-faisceaux
![]() $G$
-stables
$G$
-stables
![]() $\mathscr{F}_{i}$
telle que
$\mathscr{F}_{i}$
telle que
![]() $G$
agisse trivialement sur les quotients
$G$
agisse trivialement sur les quotients
![]() $\mathscr{F}_{i+1}/\mathscr{F}_{i}$
.
$\mathscr{F}_{i+1}/\mathscr{F}_{i}$
.
Lemme 1.2.5. Un
![]() $G$
-faisceau abélien constructible
$G$
-faisceau abélien constructible
![]() $\mathscr{F}$
sur un schéma nœthérien
$\mathscr{F}$
sur un schéma nœthérien
![]() $X$
est
$X$
est
![]() $G$
-unipotent si et seulement si pour tout point géométrique
$G$
-unipotent si et seulement si pour tout point géométrique
![]() $\overline{x}\rightarrow X$
, la fibre
$\overline{x}\rightarrow X$
, la fibre
![]() $\mathscr{F}_{\overline{x}}$
est
$\mathscr{F}_{\overline{x}}$
est
![]() $G$
-unipotente.
$G$
-unipotente.
Démonstration.
La condition sur les fibres géométriques est évidemment nécessaire. Considérons la réciproque. Les deux conditions étant stables par extension, restriction à un ouvert (resp. fermé) et application des endofoncteurs
![]() $j_{!}j^{\ast }$
et
$j_{!}j^{\ast }$
et
![]() $i_{\star }i^{\star }$
, un dévissage immédiat nous ramène au cas particulier où
$i_{\star }i^{\star }$
, un dévissage immédiat nous ramène au cas particulier où
![]() $\mathscr{F}$
est de la forme
$\mathscr{F}$
est de la forme
![]() $j_{!}\mathscr{L}$
, où
$j_{!}\mathscr{L}$
, où
![]() $\mathscr{L}$
est un faisceau abélien lisse et
$\mathscr{L}$
est un faisceau abélien lisse et
![]() $j$
une immersion ouverte. Le prolongement par zéro préservant la
$j$
une immersion ouverte. Le prolongement par zéro préservant la
![]() $G$
-unipotence, on peut supposer que
$G$
-unipotence, on peut supposer que
![]() $\mathscr{F}$
est un faisceau lisse. On peut supposer
$\mathscr{F}$
est un faisceau lisse. On peut supposer
![]() $X$
connexe et voir
$X$
connexe et voir
![]() $\mathscr{L}$
comme un
$\mathscr{L}$
comme un
![]() $\unicode[STIX]{x1D70B}_{1}(X,\overline{x})$
-module
$\unicode[STIX]{x1D70B}_{1}(X,\overline{x})$
-module
![]() $M$
, où
$M$
, où
![]() $\overline{x}\rightarrow X$
est un point géométrique de
$\overline{x}\rightarrow X$
est un point géométrique de
![]() $X$
. On est donc ramené à montrer que si
$X$
. On est donc ramené à montrer que si
![]() $M$
est un groupe abélien fini muni d’une action continue d’un groupe profini
$M$
est un groupe abélien fini muni d’une action continue d’un groupe profini
![]() $\unicode[STIX]{x1D70B}$
et de l’action d’un groupe
$\unicode[STIX]{x1D70B}$
et de l’action d’un groupe
![]() $G$
commutant à l’action de
$G$
commutant à l’action de
![]() $\unicode[STIX]{x1D70B}$
, le groupe
$\unicode[STIX]{x1D70B}$
, le groupe
![]() $M$
est
$M$
est
![]() $G$
-unipotent en tant que
$G$
-unipotent en tant que
![]() $\unicode[STIX]{x1D70B}$
-module continu si et seulement si il l’est en tant que groupe abélien. Or, si
$\unicode[STIX]{x1D70B}$
-module continu si et seulement si il l’est en tant que groupe abélien. Or, si
![]() $v\in M-\{0\}$
est un point fixe de
$v\in M-\{0\}$
est un point fixe de
![]() $G$
, le sous-
$G$
, le sous-
![]() $\unicode[STIX]{x1D70B}$
-module
$\unicode[STIX]{x1D70B}$
-module
![]() $N$
de
$N$
de
![]() $M$
engendré par
$M$
engendré par
![]() $v$
est muni d’une action triviale de
$v$
est muni d’une action triviale de
![]() $G$
et la suite exacte
$G$
et la suite exacte
![]() $0\rightarrow N\rightarrow M\rightarrow M/N\rightarrow 0$
permet de conclure par récurrence.◻
$0\rightarrow N\rightarrow M\rightarrow M/N\rightarrow 0$
permet de conclure par récurrence.◻
1.3 Modération
1.3.1
Un faisceau
![]() $\mathscr{F}$
sur un schéma nœthérien
$\mathscr{F}$
sur un schéma nœthérien
![]() $X$
est dit modéré si pour tout hensélisé strict
$X$
est dit modéré si pour tout hensélisé strict
![]() $T$
de
$T$
de
![]() $X$
— ou de façon équivalente tout
$X$
— ou de façon équivalente tout
![]() $X$
-schéma strictement local
$X$
-schéma strictement local
![]() $T$
—, de point fermé
$T$
—, de point fermé
![]() $t$
, tout point
$t$
, tout point
![]() $u$
de
$u$
de
![]() $T$
et tout point géométrique
$T$
et tout point géométrique
![]() $\overline{u}$
localisé en
$\overline{u}$
localisé en
![]() $u$
, l’action de
$u$
, l’action de
![]() $\unicode[STIX]{x1D70B}_{1}(u,\overline{u})$
sur la fibre
$\unicode[STIX]{x1D70B}_{1}(u,\overline{u})$
sur la fibre
![]() $\mathscr{F}_{\overline{u}}$
en
$\mathscr{F}_{\overline{u}}$
en
![]() $\overline{u}$
se factorise à travers un quotient d’ordre premier à l’exposant caractéristique du corps résiduel
$\overline{u}$
se factorise à travers un quotient d’ordre premier à l’exposant caractéristique du corps résiduel
![]() $\unicode[STIX]{x1D705}(t)$
.
$\unicode[STIX]{x1D705}(t)$
.
1.3.2
Cette définition, due à O. Gabber, satisfait les deux compatibilités suivantes :
(1) un faisceau localement constant est modéré ;
(2) un faisceau sur un trait est modéré au sens ci-dessus si et seulement si sa restriction au point générique est modérée au sens usuel [SGA 1 XIII, 2.1.1].
1.3.3
Un faisceau abélien de torsion inversible sur
![]() $X$
et localement unipotent est modéré : pour tout
$X$
et localement unipotent est modéré : pour tout
![]() $p$
-groupe fini
$p$
-groupe fini
![]() $P$
et tout entier
$P$
et tout entier
![]() $n\bot p$
,Footnote
3
une extension de
$n\bot p$
,Footnote
3
une extension de
![]() $\mathbb{Z}/n\mathbb{Z}[P]$
-modules triviaux est triviale.
$\mathbb{Z}/n\mathbb{Z}[P]$
-modules triviaux est triviale.
1.4 Sorites
Soit
![]() $X$
un schéma nœthérien. La propriété, pour un faisceau abélien
$X$
un schéma nœthérien. La propriété, pour un faisceau abélien
![]() $\mathscr{F}$
sur
$\mathscr{F}$
sur
![]() $X$
, d’être constructible (resp. modéré, localement unipotent) le long d’une stratification
$X$
, d’être constructible (resp. modéré, localement unipotent) le long d’une stratification
![]() $\mathfrak{X}$
est stable par
:
$\mathfrak{X}$
est stable par
:
1.4.1
raffinement de la stratification :
![]() $\mathfrak{X}^{\prime }=\{X_{j}^{\prime }\}$
raffine
$\mathfrak{X}^{\prime }=\{X_{j}^{\prime }\}$
raffine
![]() $\mathfrak{X}=\{X_{i}\}$
s’il existe pour chaque
$\mathfrak{X}=\{X_{i}\}$
s’il existe pour chaque
![]() $j$
un indice
$j$
un indice
![]() $i$
tel que
$i$
tel que
![]() $X_{j}^{\prime }\subseteq X_{i}$
;
$X_{j}^{\prime }\subseteq X_{i}$
;
1.4.2
image inverse du faisceau et de la stratification ;
1.4.3
prolongement par zéro depuis un fermé : si
![]() $\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de
$\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de
![]() $\mathfrak{X}$
et
$\mathfrak{X}$
et
![]() $i:X{\hookrightarrow}Y$
est une immersion fermée, le faisceau
$i:X{\hookrightarrow}Y$
est une immersion fermée, le faisceau
![]() $i_{\star }\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de la stratification de
$i_{\star }\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de la stratification de
![]() $\mathfrak{Y}$
déduite de
$\mathfrak{Y}$
déduite de
![]() $\mathfrak{X}$
par ajout de la partie
$\mathfrak{X}$
par ajout de la partie
![]() $Y\setminus X\subseteq Y$
. Quitte à raffiner cette stratification
$Y\setminus X\subseteq Y$
. Quitte à raffiner cette stratification
![]() $i_{\star }\mathfrak{X}$
, il existe une bonne stratification de
$i_{\star }\mathfrak{X}$
, il existe une bonne stratification de
![]() $Y$
, indépendante de
$Y$
, indépendante de
![]() $\mathscr{F}$
, le long de laquelle le faisceau est constructible (resp. modéré, localement unipotent).
$\mathscr{F}$
, le long de laquelle le faisceau est constructible (resp. modéré, localement unipotent).
(Signalons que la stratification ci-dessus est bonne par exemple si
![]() $X$
n’est nulle part dense dans
$X$
n’est nulle part dense dans
![]() $Y$
.)
$Y$
.)
1.4.4
De plus, si l’on considère des faisceaux abéliens de torsion inversible sur
![]() $X$
, on a également stabilité par extension du faisceau. C’est tautologique, sans l’hypothèse sur la torsion, pour l’unipotence locale. Cela résulte de la semi-simplicité de l’action des sous-groupes de Sylow pour la modération (cf. 1.3.3).
$X$
, on a également stabilité par extension du faisceau. C’est tautologique, sans l’hypothèse sur la torsion, pour l’unipotence locale. Cela résulte de la semi-simplicité de l’action des sous-groupes de Sylow pour la modération (cf. 1.3.3).
Remarque 1.4.5. Signalons une fois pour toutes que la condition de modération est particulière en ce sens qu’elle ne fait pas intervenir de stratification. Il nous a semblé préférable, ici et par la suite, de ne pas l’isoler pour autant des deux autres conditions (constructibilité et locale unipotence, le long d’une stratification). Prendre garde au fait que c’est la seule des trois propriétés qui soit stable par sous-quotient quelconque ; on a cependant le substitut ci-dessous.
1.4.6
Soit
![]() $k:Z{\hookrightarrow}X$
une immersion ouverte ou fermée. Si
$k:Z{\hookrightarrow}X$
une immersion ouverte ou fermée. Si
![]() $\mathscr{F}$
est un faisceau sur
$\mathscr{F}$
est un faisceau sur
![]() $X$
constructible (resp. localement unipotent) le long d’une stratification
$X$
constructible (resp. localement unipotent) le long d’une stratification
![]() $\mathfrak{X}$
adaptée à
$\mathfrak{X}$
adaptée à
![]() $Z$
(au sens de 1.1.1), alors le sous-quotient
$Z$
(au sens de 1.1.1), alors le sous-quotient
![]() $k_{!}k^{\star }\mathscr{F}$
du faisceau
$k_{!}k^{\star }\mathscr{F}$
du faisceau
![]() $\mathscr{F}$
est constructible (resp. localement unipotent) le long de
$\mathscr{F}$
est constructible (resp. localement unipotent) le long de
![]() $\mathfrak{X}$
. (Amplification : dans la proposition 1.1.4, le gradué est également constructible (resp. localement unipotent) le long de
$\mathfrak{X}$
. (Amplification : dans la proposition 1.1.4, le gradué est également constructible (resp. localement unipotent) le long de
![]() $\mathfrak{X}$
.)
$\mathfrak{X}$
.)
De plus, il existe pour toute stratification
![]() $\mathfrak{X}$
une stratification la raffinant adaptée à
$\mathfrak{X}$
une stratification la raffinant adaptée à
![]() $Z$
: intersecter les strates avec
$Z$
: intersecter les strates avec
![]() $Z$
et son complémentaire. Elle est bonne si
$Z$
et son complémentaire. Elle est bonne si
![]() $\mathfrak{X}$
l’est.
$\mathfrak{X}$
l’est.
Signalons également le fait suivant, de vérification immédiate.
1.4.7
Soient
![]() $\mathfrak{X}_{\unicode[STIX]{x1D6FC}}$
des stratifications des composantes irréductibles
$\mathfrak{X}_{\unicode[STIX]{x1D6FC}}$
des stratifications des composantes irréductibles
![]() $X_{\unicode[STIX]{x1D6FC}}$
de
$X_{\unicode[STIX]{x1D6FC}}$
de
![]() $X$
. Il existe une stratification
$X$
. Il existe une stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $X$
satisfaisant la propriété suivante : tout faisceau
$X$
satisfaisant la propriété suivante : tout faisceau
![]() $\mathscr{F}$
sur
$\mathscr{F}$
sur
![]() $X$
dont les restrictions aux
$X$
dont les restrictions aux
![]() $X_{\unicode[STIX]{x1D6FC}}$
sont constructibles (resp. modérées, localement unipotentes) le long de
$X_{\unicode[STIX]{x1D6FC}}$
sont constructibles (resp. modérées, localement unipotentes) le long de
![]() $\mathfrak{X}_{\unicode[STIX]{x1D6FC}}$
est également constructible (resp. modéré, localement unipotent) le long de
$\mathfrak{X}_{\unicode[STIX]{x1D6FC}}$
est également constructible (resp. modéré, localement unipotent) le long de
![]() $\mathfrak{X}$
. (Voir la proposition 1.5.4 pour une généralisation.)
$\mathfrak{X}$
. (Voir la proposition 1.5.4 pour une généralisation.)
1.4.8
Enfin, ces conditions sont locales pour la topologie de Zariski (et même étale) : si
![]() $U_{i}\rightarrow X$
est un recouvrement de
$U_{i}\rightarrow X$
est un recouvrement de
![]() $X$
par des ouverts de Zariski, le faisceau
$X$
par des ouverts de Zariski, le faisceau
![]() $\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de la stratification
$\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de la stratification
![]() $\mathfrak{X}$
si et seulement si, pour chaque
$\mathfrak{X}$
si et seulement si, pour chaque
![]() $i$
, le faisceau
$i$
, le faisceau
![]() $\mathscr{F}_{|U_{i}}$
l’est, le long de la stratification
$\mathscr{F}_{|U_{i}}$
l’est, le long de la stratification
![]() $\mathfrak{X}_{U_{i}}$
de
$\mathfrak{X}_{U_{i}}$
de
![]() $U_{i}$
.
$U_{i}$
.
1.4.9 Mise en garde
Il n’est par contre pas vrai qu’un faisceau à la fois modéré sur un ouvert et sur son complémentaire est nécessairement modéré : il faut que le prolongement par zéro de l’ouvert à l’espace entier soit modéré. Plus précisément, si
![]() $j:U{\hookrightarrow}X$
est une immersion ouverte,
$j:U{\hookrightarrow}X$
est une immersion ouverte,
![]() $i:F{\hookrightarrow}X$
l’immersion fermée du complémentaire et
$i:F{\hookrightarrow}X$
l’immersion fermée du complémentaire et
![]() $\mathscr{F}$
un faisceau de torsion inversible sur
$\mathscr{F}$
un faisceau de torsion inversible sur
![]() $X$
tel que
$X$
tel que
![]() $j_{!}j^{\star }\mathscr{F}$
et
$j_{!}j^{\star }\mathscr{F}$
et
![]() $i_{\star }i^{\star }\mathscr{F}$
— ou, de façon équivalente,
$i_{\star }i^{\star }\mathscr{F}$
— ou, de façon équivalente,
![]() $i^{\star }\mathscr{F}$
— soient modérés, alors
$i^{\star }\mathscr{F}$
— soient modérés, alors
![]() $\mathscr{F}$
est modéré : cela résulte de la suite exacte
$\mathscr{F}$
est modéré : cela résulte de la suite exacte
(Notons que les supports des faisceaux étant disjoints, l’extension est modérée sans hypothèse sur les coefficients ; cf. 1.4.4.) Même résultat dans le cas constructible (resp. localement unipotent) le long d’une stratification adaptée à
![]() $U$
.
$U$
.
Signalons cependant que cette subtilité — qui aura son importance en 4.4 — n’apparaît pas dans le cas constructible (ou globalement unipotent) : si
![]() $\mathscr{F}$
est un faisceau,
$\mathscr{F}$
est un faisceau,
![]() $U$
un ouvert de complémentaire
$U$
un ouvert de complémentaire
![]() $F$
et
$F$
et
![]() $\mathfrak{X}$
une stratification adaptée à
$\mathfrak{X}$
une stratification adaptée à
![]() $U$
, alors
$U$
, alors
![]() $\mathscr{F}$
est constructible (ou globalement unipotent) le long de
$\mathscr{F}$
est constructible (ou globalement unipotent) le long de
![]() $\mathfrak{X}$
dès que
$\mathfrak{X}$
dès que
![]() $\mathscr{F}_{|U}$
et
$\mathscr{F}_{|U}$
et
![]() $\mathscr{F}_{|F}$
sont constructibles (resp. globalement unipotents) le long de
$\mathscr{F}_{|F}$
sont constructibles (resp. globalement unipotents) le long de
![]() $\mathfrak{X}_{U}$
et
$\mathfrak{X}_{U}$
et
![]() $\mathfrak{X}_{F}$
respectivement.
$\mathfrak{X}_{F}$
respectivement.
Pour référence ultérieure, signalons la variante suivante (dont on omettra avec raison la lecture).
1.4.10
Amplification. Soient
![]() $j:U{\hookrightarrow}X$
et
$j:U{\hookrightarrow}X$
et
![]() $k:F^{\circ }{\hookrightarrow}F:=X\setminus U$
deux immersions ouvertes et
$k:F^{\circ }{\hookrightarrow}F:=X\setminus U$
deux immersions ouvertes et
![]() $\mathfrak{X}$
une stratification de
$\mathfrak{X}$
une stratification de
![]() $X$
adaptée à
$X$
adaptée à
![]() $U$
et
$U$
et
![]() $F^{\circ }$
. Notons
$F^{\circ }$
. Notons
![]() $j^{\prime }$
l’immersion ouverte de
$j^{\prime }$
l’immersion ouverte de
![]() $U^{\prime }:=U\cup F^{\circ }$
dans
$U^{\prime }:=U\cup F^{\circ }$
dans
![]() $X$
. Alors, si
$X$
. Alors, si
![]() $j_{!}j^{\star }\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de
$j_{!}j^{\star }\mathscr{F}$
est constructible (resp. modéré, localement unipotent) le long de
![]() $\mathfrak{X}$
et
$\mathfrak{X}$
et
![]() $k_{!}k^{\star }(\mathscr{F}_{|F})$
est constructible (resp. modéré, localement unipotent) le long de
$k_{!}k^{\star }(\mathscr{F}_{|F})$
est constructible (resp. modéré, localement unipotent) le long de
![]() $\mathfrak{X}_{F}$
, alors le faisceau
$\mathfrak{X}_{F}$
, alors le faisceau
![]() $j_{!}^{\prime }{j^{\prime }}^{\star }\mathscr{F}$
est également constructible (resp. modéré, localement unipotent) le long de
$j_{!}^{\prime }{j^{\prime }}^{\star }\mathscr{F}$
est également constructible (resp. modéré, localement unipotent) le long de
![]() $\mathfrak{X}$
.
$\mathfrak{X}$
.
1.5 Constructibilité, modération et unipotence uniformes
Soient
![]() $X$
un schéma nœthérien,
$X$
un schéma nœthérien,
![]() $\mathtt{T}$
une topologie sur la catégorie des
$\mathtt{T}$
une topologie sur la catégorie des
![]() $X$
-schémas de type fini et
$X$
-schémas de type fini et
![]() $\mathbb{F}=(\mathscr{F}_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
une famille de faisceaux étales abéliens sur
$\mathbb{F}=(\mathscr{F}_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
une famille de faisceaux étales abéliens sur
![]() $X$
(ou plus généralement sur des ouverts
$X$
(ou plus généralement sur des ouverts
![]() $U_{\unicode[STIX]{x1D706}}$
de
$U_{\unicode[STIX]{x1D706}}$
de
![]() $X$
; voir 1.5.2).
$X$
; voir 1.5.2).
1.5.1
La famille
![]() $\mathbb{F}$
est dite constructible (resp. modérée, localement unipotente) pour la topologie
$\mathbb{F}$
est dite constructible (resp. modérée, localement unipotente) pour la topologie
![]() $\mathtt{T}$
s’il existe une famille couvrante
$\mathtt{T}$
s’il existe une famille couvrante
![]() $(q_{i}:X_{i}\rightarrow X)_{i\in I}$
pour la topologie
$(q_{i}:X_{i}\rightarrow X)_{i\in I}$
pour la topologie
![]() $\mathtt{T}$
et des stratifications
$\mathtt{T}$
et des stratifications
![]() $\mathfrak{X}_{i}$
des
$\mathfrak{X}_{i}$
des
![]() $X_{i}$
telles que les faisceaux
$X_{i}$
telles que les faisceaux
![]() $q_{i}^{\star }\mathscr{F}_{\unicode[STIX]{x1D706}}$
,
$q_{i}^{\star }\mathscr{F}_{\unicode[STIX]{x1D706}}$
,
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, soient tous constructibles (resp. modérés, localement unipotents) le long des
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
, soient tous constructibles (resp. modérés, localement unipotents) le long des
![]() $\mathfrak{X}_{i}$
(1.1.3). Si l’on souhaite être plus précis, on dit également les faisceaux
$\mathfrak{X}_{i}$
(1.1.3). Si l’on souhaite être plus précis, on dit également les faisceaux
![]() $\mathscr{F}_{\unicode[STIX]{x1D706}}$
sont modérés (resp. rendus localement unipotents) par les
$\mathscr{F}_{\unicode[STIX]{x1D706}}$
sont modérés (resp. rendus localement unipotents) par les
![]() $q_{i},\mathfrak{X}_{i}$
(ou simplement par les
$q_{i},\mathfrak{X}_{i}$
(ou simplement par les
![]() $q_{i}$
). Pour insister sur le fait que l’on considère une famille de faisceaux et non un seul faisceau, on dira parfois que la famille est « uniformément » constructible (resp. modérée, localement unipotente).
$q_{i}$
). Pour insister sur le fait que l’on considère une famille de faisceaux et non un seul faisceau, on dira parfois que la famille est « uniformément » constructible (resp. modérée, localement unipotente).
Lorsque
![]() $\mathtt{T}$
est la topologie grossière, on dit simplement qu’une famille est « constructible (resp. modérée, localement unipotente) sur
$\mathtt{T}$
est la topologie grossière, on dit simplement qu’une famille est « constructible (resp. modérée, localement unipotente) sur
![]() $X$
».
$X$
».
Signalons que la définition précédente, et l’introduction du terme de « famille » de faisceaux, n’est qu’une commodité de langage dont on pourrait se passer (comparer avec [Reference Katz and LaumonKL85, § 3]).
1.5.2 Convention
Pour tout entier
![]() $n$
, on note «
$n$
, on note «
![]() $-\mapsto -[1/n]$
» le foncteur de changement de base de
$-\mapsto -[1/n]$
» le foncteur de changement de base de
![]() $\text{Spec}(\mathbb{Z})$
à
$\text{Spec}(\mathbb{Z})$
à
![]() $\text{Spec}(\mathbb{Z}[1/n])$
. Par exemple, si
$\text{Spec}(\mathbb{Z}[1/n])$
. Par exemple, si
![]() $X$
est un schéma, on note
$X$
est un schéma, on note
![]() $X[1/n]$
le produit fibré
$X[1/n]$
le produit fibré
![]() $X\times _{\text{Spec}(\mathbb{Z})}\text{Spec}(\mathbb{Z}[1/n])$
. De même pour un morphisme de schémas ou une stratification par exemple. Si cela ne semble pas prêter à confusion, nous noterons parfois «
$X\times _{\text{Spec}(\mathbb{Z})}\text{Spec}(\mathbb{Z}[1/n])$
. De même pour un morphisme de schémas ou une stratification par exemple. Si cela ne semble pas prêter à confusion, nous noterons parfois «
![]() $-\mapsto -^{\dagger }$
» ce foncteur, l’entier
$-\mapsto -^{\dagger }$
» ce foncteur, l’entier
![]() $n$
étant alors sous-entendu.
$n$
étant alors sous-entendu.
Pour éviter certaines lourdeurs, nous omettrons parfois la mention de ces foncteurs. Par exemple, étant donné un schéma nœthérien
![]() $X$
, on dira de manière abusive qu’une famille de faisceaux
$X$
, on dira de manière abusive qu’une famille de faisceaux
![]() $\mathscr{F}_{\unicode[STIX]{x1D706}}$
de
$\mathscr{F}_{\unicode[STIX]{x1D706}}$
de
![]() $\mathbb{Z}/n_{\unicode[STIX]{x1D706}}\mathbb{Z}$
-modules sur
$\mathbb{Z}/n_{\unicode[STIX]{x1D706}}\mathbb{Z}$
-modules sur
![]() $X[1/n_{\unicode[STIX]{x1D706}}]$
est « constructible sur
$X[1/n_{\unicode[STIX]{x1D706}}]$
est « constructible sur
![]() $X$
» s’il existe une stratification
$X$
» s’il existe une stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $X$
telle que les
$X$
telle que les
![]() $\mathscr{F}_{\unicode[STIX]{x1D706}}$
soient constructibles le long de
$\mathscr{F}_{\unicode[STIX]{x1D706}}$
soient constructibles le long de
![]() $\mathfrak{X}[1/n_{\unicode[STIX]{x1D706}}]$
.
$\mathfrak{X}[1/n_{\unicode[STIX]{x1D706}}]$
.
1.5.3
Une famille est constructible (resp. modérée, localement unipotente) pour la topologie étale si et seulement si elle l’est pour la topologie grossière (c’est-à-dire sur
![]() $X$
).
$X$
).
La proposition suivante — dont nous ne ferons pas usage dans cet article — limite sérieusement l’intérêt de la définition 1.5.1 dans le cas constructible. (Voir également la proposition 1.6.7
infra pour un énoncé de modération « automatique » pour une famille à un élément.) Elle renforce le résultat bien connu selon lequel un faisceau
![]() $\mathscr{F}$
sur
$\mathscr{F}$
sur
![]() $X$
est constructible si et seulement si son image inverse par un morphisme surjectif de présentation finie l’est ([SGA 4 IX, 2.8] ; voir aussi [Reference OrgogozoOrg06, § 9.1, 10.5]).
$X$
est constructible si et seulement si son image inverse par un morphisme surjectif de présentation finie l’est ([SGA 4 IX, 2.8] ; voir aussi [Reference OrgogozoOrg06, § 9.1, 10.5]).
Proposition 1.5.4. Soient
![]() $X$
un schéma nœthérien et
$X$
un schéma nœthérien et
![]() $(X^{\prime },\mathfrak{X}^{\prime })$
un
$(X^{\prime },\mathfrak{X}^{\prime })$
un
![]() $X$
-schéma surjectif de type fini, stratifié. Il existe une stratification
$X$
-schéma surjectif de type fini, stratifié. Il existe une stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $X$
telle que tout faisceau
$X$
telle que tout faisceau
![]() $\mathscr{F}$
sur
$\mathscr{F}$
sur
![]() $X$
constructible le long de
$X$
constructible le long de
![]() $\mathfrak{X}^{\prime }$
soit constructible le long de
$\mathfrak{X}^{\prime }$
soit constructible le long de
![]() $\mathfrak{X}$
.
$\mathfrak{X}$
.
Une famille constructible localement pour les topologies considérées dans cette article (topologie
![]() $h$
, topologie des altérations) est donc même constructible pour la topologie grossière.
$h$
, topologie des altérations) est donc même constructible pour la topologie grossière.
Démonstration.
Supposons
![]() $X$
irréductible pour simplifier (cf. 1.4.7). Il existe un ouvert
$X$
irréductible pour simplifier (cf. 1.4.7). Il existe un ouvert
![]() $V\subseteq X^{\prime }$
d’une strate de
$V\subseteq X^{\prime }$
d’une strate de
![]() $\mathfrak{X}^{\prime }$
tel que
$\mathfrak{X}^{\prime }$
tel que
![]() $U:=f(V)$
contienne le point générique de
$U:=f(V)$
contienne le point générique de
![]() $X$
. Quitte à rétrécir
$X$
. Quitte à rétrécir
![]() $V$
, on peut supposer
$V$
, on peut supposer
![]() $U$
ouvert et le faisceau constructible
$U$
ouvert et le faisceau constructible
![]() $\unicode[STIX]{x1D6F1}:=(V\rightarrow U)_{\star }\mathbb{Z}/2\mathbb{Z}$
lisse, de formation compatible au changement de base.
$\unicode[STIX]{x1D6F1}:=(V\rightarrow U)_{\star }\mathbb{Z}/2\mathbb{Z}$
lisse, de formation compatible au changement de base.
Montrons que sous ces hypothèses tout faisceau
![]() $\mathscr{F}$
sur
$\mathscr{F}$
sur
![]() $X$
lisse sur
$X$
lisse sur
![]() $V\subseteq X^{\prime }$
est également lisse sur
$V\subseteq X^{\prime }$
est également lisse sur
![]() $U\subseteq X$
; ceci permet de conclure par récurrence nœthérienne. Le schéma
$U\subseteq X$
; ceci permet de conclure par récurrence nœthérienne. Le schéma
![]() $U$
étant nœthérien donc localement connexe par arcs [SGA 4 IX, 2.12], il suffit de vérifier que pour chaque morphisme
$U$
étant nœthérien donc localement connexe par arcs [SGA 4 IX, 2.12], il suffit de vérifier que pour chaque morphisme
![]() $\overline{y}{\rightsquigarrow}\overline{x}$
de points géométriques de
$\overline{y}{\rightsquigarrow}\overline{x}$
de points géométriques de
![]() $U$
, le morphisme de spécialisation
$U$
, le morphisme de spécialisation
![]() $\mathscr{F}_{\overline{x}}\rightarrow \mathscr{F}_{\overline{y}}$
est un isomorphisme [SGA 4 IX, 2.13]. Par hypothèse sur le faisceau
$\mathscr{F}_{\overline{x}}\rightarrow \mathscr{F}_{\overline{y}}$
est un isomorphisme [SGA 4 IX, 2.13]. Par hypothèse sur le faisceau
![]() $\unicode[STIX]{x1D6F1}$
, les flèches
$\unicode[STIX]{x1D6F1}$
, les flèches
![]() $\unicode[STIX]{x1D70B}_{0}(V_{\overline{y}})\rightarrow \unicode[STIX]{x1D70B}_{0}(V\times _{U}U_{(\overline{x})})\leftarrow \unicode[STIX]{x1D70B}_{0}(V_{\overline{x}})$
sont des isomorphismes de sorte que toute composante connexe
$\unicode[STIX]{x1D70B}_{0}(V_{\overline{y}})\rightarrow \unicode[STIX]{x1D70B}_{0}(V\times _{U}U_{(\overline{x})})\leftarrow \unicode[STIX]{x1D70B}_{0}(V_{\overline{x}})$
sont des isomorphismes de sorte que toute composante connexe
![]() $W$
de
$W$
de
![]() $V\times _{U}U_{(\overline{x})}$
rencontre
$V\times _{U}U_{(\overline{x})}$
rencontre
![]() $V_{\overline{y}}$
et
$V_{\overline{y}}$
et
![]() $V_{\overline{x}}$
. Ainsi, le morphisme
$V_{\overline{x}}$
. Ainsi, le morphisme
![]() $\overline{y}{\rightsquigarrow}\overline{x}$
se relève dans
$\overline{y}{\rightsquigarrow}\overline{x}$
se relève dans
![]() $W$
en une chaîne de spécialisations-générisations ; la conclusion résulte alors de la lissité de
$W$
en une chaîne de spécialisations-générisations ; la conclusion résulte alors de la lissité de
![]() $\mathscr{F}$
sur
$\mathscr{F}$
sur
![]() $W$
.◻
$W$
.◻
1.6 Un « lemme » d’Ofer Gabber
1.6.1 Motivations
Comme signalé dans l’introduction, nous utiliserons principalement dans cet article la topologie propre ou — compte tenu du caractère Zariski (et même étale) local de nos conditions — la topologie
![]() $h$
. (Voir aussi 1.6.5
infra.) Les dévissages, de nature géométrique ou faisceautique (cf. la proposition 1.1.4), et le formalisme des six opérations font jouer un rôle clef aux immersions fermées. Le résultat suivant de O. Gabber a pour conséquence que tout se passe dans cet article comme si tout
$h$
. (Voir aussi 1.6.5
infra.) Les dévissages, de nature géométrique ou faisceautique (cf. la proposition 1.1.4), et le formalisme des six opérations font jouer un rôle clef aux immersions fermées. Le résultat suivant de O. Gabber a pour conséquence que tout se passe dans cet article comme si tout
![]() $h$
-recouvrement d’un fermé est trace d’un
$h$
-recouvrement d’un fermé est trace d’un
![]() $h$
-recouvrement de l’espace ambiant.
$h$
-recouvrement de l’espace ambiant.
Proposition 1.6.2 (O. Gabber).
Soient
![]() $X$
un schéma nœthérien,
$X$
un schéma nœthérien,
![]() $i:F{\hookrightarrow}X$
une immersion fermée et
$i:F{\hookrightarrow}X$
une immersion fermée et
![]() $f:F^{\prime }\rightarrow F$
un morphisme fini (resp. propre) et surjectif. Il existe un morphisme fini surjectif (resp. une altération)
$f:F^{\prime }\rightarrow F$
un morphisme fini (resp. propre) et surjectif. Il existe un morphisme fini surjectif (resp. une altération)
![]() $X^{\prime }\rightarrow X$
tel que toute composante irréductible
$X^{\prime }\rightarrow X$
tel que toute composante irréductible
![]() $T$
de
$T$
de
![]() $F\times _{X}X^{\prime }$
, munie de la structure réduite, soit la source d’un
$F\times _{X}X^{\prime }$
, munie de la structure réduite, soit la source d’un
![]() $F$
-morphisme vers
$F$
-morphisme vers
![]() $F^{\prime }$
.
$F^{\prime }$
.

La suite de cette section 1.6 est consacrée à la démonstration de cette proposition et quelques conséquences.
1.6.3 Cas propre
Il résulte de [Reference OrgogozoOrg06, lemme 4.3] (également dû à O. Gabber) que le cas propre se ramène au cas fini, traité ci-dessous. Pour la commodité du lecteur, nous rappelons brièvement l’argument. Comme expliqué dans [Reference OrgogozoOrg06], il résulte du théorème de platification par éclatement qu’il existe pour tout sous-schéma fermé intègre
![]() $Z$
de
$Z$
de
![]() $F$
un éclatement
$F$
un éclatement
![]() $\widetilde{Z}\rightarrow Z$
et un diagramme commutatif
$\widetilde{Z}\rightarrow Z$
et un diagramme commutatif

Par compacité de
![]() $F^{\text{cons}}$
[ÉGA I, 7.2.11–13], il existe un nombre fini de fermés intègres
$F^{\text{cons}}$
[ÉGA I, 7.2.11–13], il existe un nombre fini de fermés intègres
![]() $Z_{i}$
tels que
$Z_{i}$
tels que
![]() $F$
soit la réunion des ouverts
$F$
soit la réunion des ouverts
![]() $Z_{i}-R_{i}$
, où
$Z_{i}-R_{i}$
, où
![]() $R_{i}$
est le centre de l’éclatement
$R_{i}$
est le centre de l’éclatement
![]() $\widetilde{Z}_{i}\rightarrow Z_{i}$
.
$\widetilde{Z}_{i}\rightarrow Z_{i}$
.
Soit
![]() $\widetilde{X}$
l’éclatement dominant les éclatés de
$\widetilde{X}$
l’éclatement dominant les éclatés de
![]() $X$
le long des
$X$
le long des
![]() $R_{i}$
et notons
$R_{i}$
et notons
![]() $T_{\unicode[STIX]{x1D6FC}}$
les composantes irréductibles du produit fibré
$T_{\unicode[STIX]{x1D6FC}}$
les composantes irréductibles du produit fibré
![]() $F_{\widetilde{X}}:=F\times _{X}\widetilde{X}$
. Par construction, chaque
$F_{\widetilde{X}}:=F\times _{X}\widetilde{X}$
. Par construction, chaque
![]() $T_{\unicode[STIX]{x1D6FC}}$
s’envoie sur un
$T_{\unicode[STIX]{x1D6FC}}$
s’envoie sur un
![]() $\widetilde{Z_{i}}$
. Le schéma
$\widetilde{Z_{i}}$
. Le schéma
![]() $T^{\prime }=\coprod _{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}^{\prime }$
, obtenu par changement de base comme dans le diagramme ci-dessous, est alors fini surjectif sur
$T^{\prime }=\coprod _{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}^{\prime }$
, obtenu par changement de base comme dans le diagramme ci-dessous, est alors fini surjectif sur
![]() $F_{\widetilde{X}}$
et il existe un
$F_{\widetilde{X}}$
et il existe un
![]() $F$
-morphisme de
$F$
-morphisme de
![]() $T^{\prime }$
vers
$T^{\prime }$
vers
![]() $F^{\prime }$
. Comme annoncé, ceci nous ramène au cas où le morphisme
$F^{\prime }$
. Comme annoncé, ceci nous ramène au cas où le morphisme
![]() $F^{\prime }{\twoheadrightarrow}F$
est fini (surjectif).
$F^{\prime }{\twoheadrightarrow}F$
est fini (surjectif).

1.6.4 Cas fini
On commence par supposer
![]() $X$
affine pour simplifier.
$X$
affine pour simplifier.
1.6.4.1
Rappelons ([BourbA, VI, § 6, n°5], [Reference Lombardi and QuittéLQ11, III.§ 4, VII.§ 4] ; voir aussi [Reference Bhargava and SatrianoBS14, § 6]) que si
![]() $A$
est un anneau et
$A$
est un anneau et
![]() $f\in A[t]$
est un polynôme unitaire, on peut définir l’algèbre de décomposition universelle
$f\in A[t]$
est un polynôme unitaire, on peut définir l’algèbre de décomposition universelle
![]() $\text{Adu}_{A}(f)$
de
$\text{Adu}_{A}(f)$
de
![]() $f$
, quotient de l’anneau
$f$
, quotient de l’anneau
![]() $A[y_{i},1\leqslant i\leqslant \deg (f)]$
par les relations obtenues en imposant l’égalité
$A[y_{i},1\leqslant i\leqslant \deg (f)]$
par les relations obtenues en imposant l’égalité
![]() $\prod _{i}(t-y_{i})=f(t)$
. Si
$\prod _{i}(t-y_{i})=f(t)$
. Si
![]() $P$
est une famille finie de polynôme unitaires, on note
$P$
est une famille finie de polynôme unitaires, on note
![]() $\text{Adu}_{A}(P)$
le produit tensoriel des
$\text{Adu}_{A}(P)$
le produit tensoriel des
![]() $\text{Adu}_{A}(f)$
, pour
$\text{Adu}_{A}(f)$
, pour
![]() $f\in P$
, au-dessus de
$f\in P$
, au-dessus de
![]() $A$
. Lorsque
$A$
. Lorsque
![]() $X=\text{Spec}(A)$
, on note
$X=\text{Spec}(A)$
, on note
![]() $\text{Sdu}_{X}(P)$
le schéma de décomposition universel, spectre de cette algèbre. Par construction, pour tout point
$\text{Sdu}_{X}(P)$
le schéma de décomposition universel, spectre de cette algèbre. Par construction, pour tout point
![]() $x^{\prime }$
de
$x^{\prime }$
de
![]() $\text{Sdu}_{X}(P)$
d’image
$\text{Sdu}_{X}(P)$
d’image
![]() $x$
dans
$x$
dans
![]() $X$
, l’extension
$X$
, l’extension
![]() $\unicode[STIX]{x1D705}(x^{\prime })/\unicode[STIX]{x1D705}(x)$
est finie quasi-galoisienne (
$\unicode[STIX]{x1D705}(x^{\prime })/\unicode[STIX]{x1D705}(x)$
est finie quasi-galoisienne (
![]() $=$
normale).
$=$
normale).
1.6.4.2
Lorsque dans la proposition 1.6.2 le schéma
![]() $X$
est affine, le morphisme fini
$X$
est affine, le morphisme fini
![]() $F^{\prime }\rightarrow F$
correspond à un morphisme fini
$F^{\prime }\rightarrow F$
correspond à un morphisme fini
![]() $\mathscr{O}(F)\rightarrow \mathscr{O}(F^{\prime })$
de
$\mathscr{O}(F)\rightarrow \mathscr{O}(F^{\prime })$
de
![]() $\mathscr{O}(X)$
-algèbres. Choisissons arbitrairement des générateurs
$\mathscr{O}(X)$
-algèbres. Choisissons arbitrairement des générateurs
![]() $a_{1},\ldots ,a_{n}$
de
$a_{1},\ldots ,a_{n}$
de
![]() $\mathscr{O}(F^{\prime })$
sur
$\mathscr{O}(F^{\prime })$
sur
![]() $\mathscr{O}(F)$
satisfaisant des équations unitaires
$\mathscr{O}(F)$
satisfaisant des équations unitaires
![]() $q_{i}\in Q\subseteq \mathscr{O}(F)[t]$
, que l’on relève (arbitrairement) en des équations unitaires
$q_{i}\in Q\subseteq \mathscr{O}(F)[t]$
, que l’on relève (arbitrairement) en des équations unitaires
![]() $p_{i}\in P\subseteq \mathscr{O}(X)[t]$
. Soit
$p_{i}\in P\subseteq \mathscr{O}(X)[t]$
. Soit
![]() $X^{\prime }:=\text{Sdu}_{X}(P)$
le schéma de décomposition universel associé ; le produit fibré
$X^{\prime }:=\text{Sdu}_{X}(P)$
le schéma de décomposition universel associé ; le produit fibré
![]() $F_{X^{\prime }}:=F\times _{X}X^{\prime }$
est alors
$F_{X^{\prime }}:=F\times _{X}X^{\prime }$
est alors
![]() $\text{Sdu}_{F}(Q)$
.
$\text{Sdu}_{F}(Q)$
.
Soit
![]() $x^{\prime }$
un point de
$x^{\prime }$
un point de
![]() $X^{\prime }$
d’image
$X^{\prime }$
d’image
![]() $x\in F$
dans
$x\in F$
dans
![]() $X$
. Pour tout point
$X$
. Pour tout point
![]() $f^{\prime }$
de
$f^{\prime }$
de
![]() $F^{\prime }$
au-dessus de
$F^{\prime }$
au-dessus de
![]() $x$
, il existe par construction un
$x$
, il existe par construction un
![]() $x$
-morphisme
$x$
-morphisme
![]() $x^{\prime }\rightarrow f^{\prime }$
.
$x^{\prime }\rightarrow f^{\prime }$
.

Appliquant ceci aux points maximaux de
![]() $F_{X^{\prime }}$
, on observe que pour toute composante irréductible
$F_{X^{\prime }}$
, on observe que pour toute composante irréductible
![]() $T_{\unicode[STIX]{x1D6FC}}$
de
$T_{\unicode[STIX]{x1D6FC}}$
de
![]() $F_{X^{\prime }}$
il existe un
$F_{X^{\prime }}$
il existe un
![]() $F$
-morphisme de son point générique vers
$F$
-morphisme de son point générique vers
![]() $F^{\prime }$
. Par construction également, ce morphisme s’étend, de façon unique, à la composante irréductible
$F^{\prime }$
. Par construction également, ce morphisme s’étend, de façon unique, à la composante irréductible
![]() $T_{\unicode[STIX]{x1D6FC}}$
tout entière (munie de la structure réduite). En effet, tout diagramme commutatif comme-ci dessous, où
$T_{\unicode[STIX]{x1D6FC}}$
tout entière (munie de la structure réduite). En effet, tout diagramme commutatif comme-ci dessous, où
![]() $K,K^{\prime }$
et
$K,K^{\prime }$
et
![]() $K^{\prime \prime }$
sont les corps des fractions d’anneaux intègres
$K^{\prime \prime }$
sont les corps des fractions d’anneaux intègres
![]() $R,R^{\prime }$
et
$R,R^{\prime }$
et
![]() $R^{\prime \prime }$
, se complète par un
$R^{\prime \prime }$
, se complète par un
![]() $R$
-morphisme
$R$
-morphisme
![]() $R^{\prime }\rightarrow R^{\prime \prime }$
.
$R^{\prime }\rightarrow R^{\prime \prime }$
.

1.6.4.3
Cas général : on ne suppose plus
![]() $X$
affine, mais on se donne un recouvrement fini par des ouverts affines
$X$
affine, mais on se donne un recouvrement fini par des ouverts affines
![]() $U_{i}$
. Posons
$U_{i}$
. Posons
![]() $F_{i}:=F\times _{X}U_{i}$
.
$F_{i}:=F\times _{X}U_{i}$
.
Lorsque
![]() $F_{i}$
est non vide, on considère un schéma de décomposition universel
$F_{i}$
est non vide, on considère un schéma de décomposition universel
![]() $U_{i}^{\prime }{\twoheadrightarrow}U_{i}$
associé (non canoniquement) comme ci-dessus au diagramme
$U_{i}^{\prime }{\twoheadrightarrow}U_{i}$
associé (non canoniquement) comme ci-dessus au diagramme
![]() $F_{i}^{\prime }{\twoheadrightarrow}F_{i}{\hookrightarrow}U_{i}$
(où
$F_{i}^{\prime }{\twoheadrightarrow}F_{i}{\hookrightarrow}U_{i}$
(où
![]() $F_{i}^{\prime }:=F^{\prime }\times _{F}F_{i}$
). Le morphisme
$F_{i}^{\prime }:=F^{\prime }\times _{F}F_{i}$
). Le morphisme
![]() $U_{i}^{\prime }\rightarrow U_{i}$
s’étend en un morphisme fini
$U_{i}^{\prime }\rightarrow U_{i}$
s’étend en un morphisme fini
![]() $X_{i}^{\prime }{\twoheadrightarrow}X$
: considérer le coproduit de
$X_{i}^{\prime }{\twoheadrightarrow}X$
: considérer le coproduit de
![]() $X\setminus U_{i}$
avec une approximation de la normalisation de
$X\setminus U_{i}$
avec une approximation de la normalisation de
![]() $X$
dans
$X$
dans
![]() $U_{i}^{\prime }$
, qui coïncide avec
$U_{i}^{\prime }$
, qui coïncide avec
![]() $U_{i}^{\prime }$
sur
$U_{i}^{\prime }$
sur
![]() $U_{i}$
. (Écrire la normalisation comme une limite de
$U_{i}$
. (Écrire la normalisation comme une limite de
![]() $X$
-schémas finis.)
$X$
-schémas finis.)
Lorsque
![]() $F_{i}=\varnothing$
(c’est-à-dire
$F_{i}=\varnothing$
(c’est-à-dire
![]() $F\cap U_{i}=\varnothing$
), on pose
$F\cap U_{i}=\varnothing$
), on pose
![]() $X_{i}^{\prime }:=X$
.
$X_{i}^{\prime }:=X$
.
Soit
![]() $X^{\prime }$
le produit fibré sur
$X^{\prime }$
le produit fibré sur
![]() $X$
des
$X$
des
![]() $X_{i}^{\prime }$
. La démonstration du paragraphe précédent s’applique mutatis mutandis, l’unicité susmentionnée des prolongements nous permettant de se restreindre aux schémas affines
$X_{i}^{\prime }$
. La démonstration du paragraphe précédent s’applique mutatis mutandis, l’unicité susmentionnée des prolongements nous permettant de se restreindre aux schémas affines
![]() $U_{i}$
.
$U_{i}$
.
1.6.5
La proposition 1.6.2, dans le cas particulier où
![]() $F=X$
, entraîne qu’une famille constructible et modérée (resp. constructible et localement unipotente) pour la topologie
$F=X$
, entraîne qu’une famille constructible et modérée (resp. constructible et localement unipotente) pour la topologie
![]() $h$
l’est aussi pour la topologie des altérations. (On rappelle que ces topologies sont engendrées par les recouvrements de Zariski et les morphismes surjectifs propres, génériquement finis dans le second cas.)
$h$
l’est aussi pour la topologie des altérations. (On rappelle que ces topologies sont engendrées par les recouvrements de Zariski et les morphismes surjectifs propres, génériquement finis dans le second cas.)
Remarque 1.6.6 (O. Gabber).
Bien que nous n’en ferons pas usage, observons que si une famille est « modérée » (ou rendue localement unipotente) par une altération, elle l’est aussi par une altération génériquement étale. Cela résulte de l’invariance du topos étale par homéomorphisme universel [SGA 4 VIII, § 1] et du fait que toute altération
![]() $X^{\prime }\rightarrow X$
se décompose en
$X^{\prime }\rightarrow X$
se décompose en
![]() $X^{\prime }\rightarrow X^{\prime \prime }\rightarrow X$
, où
$X^{\prime }\rightarrow X^{\prime \prime }\rightarrow X$
, où
![]() $X^{\prime \prime }\rightarrow X$
est une altération génériquement étale et
$X^{\prime \prime }\rightarrow X$
est une altération génériquement étale et
![]() $X^{\prime }\rightarrow X^{\prime \prime }$
est un morphisme fini radiciel. En effet, si
$X^{\prime }\rightarrow X^{\prime \prime }$
est un morphisme fini radiciel. En effet, si
![]() $X^{\prime }\rightarrow X$
est localement défini par une injection d’anneaux
$X^{\prime }\rightarrow X$
est localement défini par une injection d’anneaux
![]() $A{\hookrightarrow}B$
, avec
$A{\hookrightarrow}B$
, avec
![]() $A$
et
$A$
et
![]() $B$
intègres, on peut factoriser cette injection en
$B$
intègres, on peut factoriser cette injection en
![]() $A{\hookrightarrow}A[B^{p^{n}}]{\hookrightarrow}B$
; cette construction se recolle et, pour
$A{\hookrightarrow}A[B^{p^{n}}]{\hookrightarrow}B$
; cette construction se recolle et, pour
![]() $n$
grand, l’extension
$n$
grand, l’extension
![]() $\text{Frac}(A[B^{p^{n}}])\,/\,\text{Frac}(A)$
ainsi obtenue est étale (cf. p. ex. [BourbA, V § 7 n°7, cor. 2 (démonstration)]).
$\text{Frac}(A[B^{p^{n}}])\,/\,\text{Frac}(A)$
ainsi obtenue est étale (cf. p. ex. [BourbA, V § 7 n°7, cor. 2 (démonstration)]).
Terminons par une application, qui est une conséquence immédiate du lemme de Gabber précédent et de la possibilité de trivialiser un faisceau lisse par un morphisme fini étale.
Proposition 1.6.7. Tout faisceau constructible sur un schéma nœthérien est modéré par un morphisme
![]() $\text{fini}$
surjectif.
$\text{fini}$
surjectif.
Démonstration.
Quitte à plonger le faisceau,
![]() $\mathscr{F}$
, dans
$\mathscr{F}$
, dans
![]() $\mathbb{Z}/n\mathbb{Z}[\mathscr{F}]$
pour un entier
$\mathbb{Z}/n\mathbb{Z}[\mathscr{F}]$
pour un entier
![]() $n>1$
, on peut supposer le faisceau abélien. (On utilise le fait que
$n>1$
, on peut supposer le faisceau abélien. (On utilise le fait que
![]() $\mathscr{F}\mapsto \mathbb{Z}/n\mathbb{Z}[\mathscr{F}]$
commute aux fibres.) Par passage à la limite — utiliser par exemple [Reference Thomason and TrobaughTT90, C.9] et [SGA 4 IX, 2.7.4] — et stabilité par image inverse, on peut supposer le schéma nœthérien excellent. Par dévissage (triangle
$\mathscr{F}\mapsto \mathbb{Z}/n\mathbb{Z}[\mathscr{F}]$
commute aux fibres.) Par passage à la limite — utiliser par exemple [Reference Thomason and TrobaughTT90, C.9] et [SGA 4 IX, 2.7.4] — et stabilité par image inverse, on peut supposer le schéma nœthérien excellent. Par dévissage (triangle
![]() $j_{!}j^{\star }\rightarrow \text{Id}\rightarrow i_{\star }i^{\star }\stackrel{+1}{\rightarrow }$
) et la proposition 1.6.2, on se ramène par récurrence nœthérienne sur
$j_{!}j^{\star }\rightarrow \text{Id}\rightarrow i_{\star }i^{\star }\stackrel{+1}{\rightarrow }$
) et la proposition 1.6.2, on se ramène par récurrence nœthérienne sur
![]() $X$
au cas d’un faisceau de la forme
$X$
au cas d’un faisceau de la forme
![]() $j_{!}\mathscr{L}$
, où
$j_{!}\mathscr{L}$
, où
![]() $j:U{\hookrightarrow}X$
est une immersion ouverte d’image dense et
$j:U{\hookrightarrow}X$
est une immersion ouverte d’image dense et
![]() $\mathscr{L}$
est un faisceau lisse. Soit
$\mathscr{L}$
est un faisceau lisse. Soit
![]() $U^{\prime }\rightarrow U$
un revêtement étale trivialisant
$U^{\prime }\rightarrow U$
un revêtement étale trivialisant
![]() $\mathscr{L}$
et considérons le normalisé
$\mathscr{L}$
et considérons le normalisé
![]() $X^{\prime }\rightarrow X$
de
$X^{\prime }\rightarrow X$
de
![]() $X$
dans
$X$
dans
![]() $U^{\prime }$
. Le faisceau
$U^{\prime }$
. Le faisceau
![]() $(X^{\prime }\rightarrow X)^{\star }(j_{!}\mathscr{L})$
est modéré.◻
$(X^{\prime }\rightarrow X)^{\star }(j_{!}\mathscr{L})$
est modéré.◻
1.7 Extensions ponctuelles
1.7.1
Soient
![]() $f:X\rightarrow Y$
un morphisme de schémas, munis de la topologie étale,
$f:X\rightarrow Y$
un morphisme de schémas, munis de la topologie étale,
![]() $\{{\mathscr{F}_{\unicode[STIX]{x1D706}}\}}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
des faisceaux abéliens sur
$\{{\mathscr{F}_{\unicode[STIX]{x1D706}}\}}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
des faisceaux abéliens sur
![]() $X$
et
$X$
et
![]() $N\geqslant 0$
un entier. On dit qu’un faisceau abélien
$N\geqslant 0$
un entier. On dit qu’un faisceau abélien
![]() $\mathscr{G}$
sur
$\mathscr{G}$
sur
![]() $Y$
est
$Y$
est
![]() $N$
-extension ponctuelle de sous-quotients des
$N$
-extension ponctuelle de sous-quotients des
![]() $\mathscr{F}_{\unicode[STIX]{x1D706}}$
(resp. relativement à
$\mathscr{F}_{\unicode[STIX]{x1D706}}$
(resp. relativement à
![]() $f$
) s’il existe pour chaque point géométrique
$f$
) s’il existe pour chaque point géométrique
![]() $y$
de
$y$
de
![]() $Y$
une filtration à
$Y$
une filtration à
![]() $N$
crans de la fibre
$N$
crans de la fibre
![]() $\mathscr{G}_{y}$
dont les quotients successifs sont des sous-quotients de fibres des
$\mathscr{G}_{y}$
dont les quotients successifs sont des sous-quotients de fibres des
![]() $\mathscr{F}_{\unicode[STIX]{x1D706}}$
en des points géométriques de
$\mathscr{F}_{\unicode[STIX]{x1D706}}$
en des points géométriques de
![]() $X$
(resp. au-dessus de
$X$
(resp. au-dessus de
![]() $y$
).
$y$
).
1.7.2 Sorites
Les faits suivants sont de vérification immédiate.
(i) Soient
 $f:X\rightarrow Y$
un morphisme,
$f:X\rightarrow Y$
un morphisme,
 $\mathscr{F}$
un faisceau abélien sur
$\mathscr{F}$
un faisceau abélien sur
 $X$
, un morphisme
$X$
, un morphisme
 $\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
et
$\unicode[STIX]{x1D70B}:X^{\prime }\rightarrow X$
et
 $f^{\prime }:X^{\prime }\rightarrow Y$
le composé
$f^{\prime }:X^{\prime }\rightarrow Y$
le composé
 $f\circ \unicode[STIX]{x1D70B}$
. Si un faisceau
$f\circ \unicode[STIX]{x1D70B}$
. Si un faisceau
 $\mathscr{G}$
sur
$\mathscr{G}$
sur
 $Y$
est
$Y$
est
 $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}^{\prime }:=\unicode[STIX]{x1D70B}^{\star }\mathscr{F}$
relativement à
$\mathscr{F}^{\prime }:=\unicode[STIX]{x1D70B}^{\star }\mathscr{F}$
relativement à
 $f^{\prime }$
, il est également
$f^{\prime }$
, il est également
 $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
 $f$
.
$f$
.(ii) Soient
 $f:X\rightarrow Y$
un morphisme,
$f:X\rightarrow Y$
un morphisme,
 $k:Z{\hookrightarrow}X$
une immersion, et
$k:Z{\hookrightarrow}X$
une immersion, et
 $\mathscr{F}$
un faisceau abélien sur
$\mathscr{F}$
un faisceau abélien sur
 $Z$
. Un faisceau
$Z$
. Un faisceau
 $\mathscr{G}$
sur
$\mathscr{G}$
sur
 $Y$
est
$Y$
est
 $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
relativement au composé
$\mathscr{F}$
relativement au composé
 $g:=f\circ k$
si et seulement si il est
$g:=f\circ k$
si et seulement si il est
 $N$
-extension ponctuelle de
$N$
-extension ponctuelle de
 $k_{!}\mathscr{F}$
relativement à
$k_{!}\mathscr{F}$
relativement à
 $f$
.
$f$
.(iii) Soient
 $f:X\rightarrow Y$
un morphisme,
$f:X\rightarrow Y$
un morphisme,
 $\mathscr{F}$
un faisceau sur
$\mathscr{F}$
un faisceau sur
 $X$
, un triangle distingué de complexes sur
$X$
, un triangle distingué de complexes sur $$\begin{eqnarray}\mathscr{K}_{1}\rightarrow \mathscr{K}\rightarrow \mathscr{K}_{2}\stackrel{+1}{\rightarrow }\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{K}_{1}\rightarrow \mathscr{K}\rightarrow \mathscr{K}_{2}\stackrel{+1}{\rightarrow }\end{eqnarray}$$
 $Y$
et
$Y$
et
 $q$
un entier. Si chaque
$q$
un entier. Si chaque
 $\mathtt{H}^{q}(\mathscr{K}_{\unicode[STIX]{x1D706}})$
,
$\mathtt{H}^{q}(\mathscr{K}_{\unicode[STIX]{x1D706}})$
,
 $\unicode[STIX]{x1D706}\in \{1,2\}$
, est
$\unicode[STIX]{x1D706}\in \{1,2\}$
, est
 $N_{\unicode[STIX]{x1D706}}$
-extension ponctuelle de sous-quotients de
$N_{\unicode[STIX]{x1D706}}$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
 $f$
, le faisceau
$f$
, le faisceau
 $\mathtt{H}^{q}\mathscr{K}$
est
$\mathtt{H}^{q}\mathscr{K}$
est
 $(N_{1}+N_{2})$
-extension ponctuelle de sous-quotients de
$(N_{1}+N_{2})$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
 $f$
.
$f$
.(On appliquera ceci au cas particulier où les deux complexes
 $\mathscr{K}_{\unicode[STIX]{x1D706}}$
sont obtenus par application du foncteur
$\mathscr{K}_{\unicode[STIX]{x1D706}}$
sont obtenus par application du foncteur
 $\mathtt{R}f_{\star }$
à une suite exacte
$\mathtt{R}f_{\star }$
à une suite exacte
 $0\rightarrow \mathscr{F}_{1}\rightarrow \mathscr{F}\rightarrow \mathscr{F}_{2}\rightarrow 0$
de faisceaux sur
$0\rightarrow \mathscr{F}_{1}\rightarrow \mathscr{F}\rightarrow \mathscr{F}_{2}\rightarrow 0$
de faisceaux sur
 $X$
.)
$X$
.)(iv) Soient
 $f:X\rightarrow Z=(g:Y\rightarrow Z)\circ (h:X\rightarrow Y)$
un morphisme,
$f:X\rightarrow Z=(g:Y\rightarrow Z)\circ (h:X\rightarrow Y)$
un morphisme,
 $\mathscr{F}$
un faisceau sur
$\mathscr{F}$
un faisceau sur
 $X$
,
$X$
,
 $\mathscr{G}$
un faisceau sur
$\mathscr{G}$
un faisceau sur
 $Y$
et
$Y$
et
 $\mathscr{H}$
un faisceau sur
$\mathscr{H}$
un faisceau sur
 $Z$
. Si
$Z$
. Si
 $\mathscr{G}$
est
$\mathscr{G}$
est
 $N_{1}$
-extension ponctuelle de sous-quotients de
$N_{1}$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
(relativement à
$\mathscr{F}$
(relativement à
 $h$
) et
$h$
) et
 $\mathscr{H}$
est
$\mathscr{H}$
est
 $N_{2}$
-extension ponctuelle de sous-quotients de
$N_{2}$
-extension ponctuelle de sous-quotients de
 $\mathscr{G}$
(relativement à
$\mathscr{G}$
(relativement à
 $g$
), alors
$g$
), alors
 $\mathscr{H}$
est
$\mathscr{H}$
est
 $(N_{1}\times N_{2})$
-extension ponctuelle de sous-quotients de
$(N_{1}\times N_{2})$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
(relativement à
$\mathscr{F}$
(relativement à
 $f$
).
$f$
).(On appliquera ceci au cas particulier où
 $\mathscr{G}:=\mathtt{R}^{i}h_{\star }\mathscr{F}$
et
$\mathscr{G}:=\mathtt{R}^{i}h_{\star }\mathscr{F}$
et
 $\mathscr{H}:=\mathtt{R}^{j}g_{\star }\mathscr{G}$
.)
$\mathscr{H}:=\mathtt{R}^{j}g_{\star }\mathscr{G}$
.)(v) Soient
un carré cartésien avec
 $g$
surjectif et
$g$
surjectif et
 $\mathscr{F}$
(resp.
$\mathscr{F}$
(resp.
 $\mathscr{G}$
) un faisceau abélien sur
$\mathscr{G}$
) un faisceau abélien sur
 $X$
(resp.
$X$
(resp.
 $Y$
). Pour tout entier
$Y$
). Pour tout entier
 $N\geqslant 0$
, le faisceau
$N\geqslant 0$
, le faisceau
 $\mathscr{G}$
est
$\mathscr{G}$
est
 $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
 $f$
si et seulement si le faisceau
$f$
si et seulement si le faisceau
 $g^{\star }\mathscr{G}$
est
$g^{\star }\mathscr{G}$
est
 $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
 ${g^{\prime }}^{\star }\mathscr{F}$
relativement à
${g^{\prime }}^{\star }\mathscr{F}$
relativement à
 $f^{\prime }$
.
$f^{\prime }$
.(On appliquera ceci au cas particulier où
 $f$
est un morphisme propre,
$f$
est un morphisme propre,
 $\mathscr{G}:=\mathtt{R}^{q}f_{\star }\mathscr{F}$
, et
$\mathscr{G}:=\mathtt{R}^{q}f_{\star }\mathscr{F}$
, et
 $g^{\star }\mathscr{G}=\mathtt{R}^{q}f_{\star }^{\prime }\mathscr{F}$
.)
$g^{\star }\mathscr{G}=\mathtt{R}^{q}f_{\star }^{\prime }\mathscr{F}$
.)
2 Lemmes d’Abhyankar et courbes nodales
2.1 Paires toriques et courbes nodales : rappels
2.1.1
Rappelons que si
![]() $X$
est un schéma et
$X$
est un schéma et
![]() $j:U{\hookrightarrow}X$
est un ouvert dense, la paire
$j:U{\hookrightarrow}X$
est un ouvert dense, la paire
![]() $(X,U)$
est dite torique [Reference MochizukiMoc99, 1.2] ou log-régulière [STG VI, 1.4] si le schéma
$(X,U)$
est dite torique [Reference MochizukiMoc99, 1.2] ou log-régulière [STG VI, 1.4] si le schéma
![]() $X$
muni de la log-structureFootnote
4
image directe
$X$
muni de la log-structureFootnote
4
image directe
![]() $\mathscr{O}_{X}\,\cap \,j_{\star }\mathscr{O}_{U}^{\times }{\hookrightarrow}\mathscr{O}_{X}$
est log-régulier et
$\mathscr{O}_{X}\,\cap \,j_{\star }\mathscr{O}_{U}^{\times }{\hookrightarrow}\mathscr{O}_{X}$
est log-régulier et
![]() $U$
est l’ouvert de trivialité de cette log-structure. (Par définition, un log-schéma log-régulier est fin et saturé [fs].) Tout log-schéma
$U$
est l’ouvert de trivialité de cette log-structure. (Par définition, un log-schéma log-régulier est fin et saturé [fs].) Tout log-schéma
![]() $(X,M_{X})$
log-régulier est de ce type ; cf. p. ex. [Reference Gabber and RameroGR16, 10.5.53]. L’exemple typique d’une paire torique est constitué d’un schéma régulier
$(X,M_{X})$
log-régulier est de ce type ; cf. p. ex. [Reference Gabber and RameroGR16, 10.5.53]. L’exemple typique d’une paire torique est constitué d’un schéma régulier
![]() $X$
et du complémentaire
$X$
et du complémentaire
![]() $U$
du support d’un diviseur à croisements normaux (resp. à croisements normaux strict). Une telle paire est dite régulière (resp. strictement régulière). Réciproquement, toute paire torique
$U$
du support d’un diviseur à croisements normaux (resp. à croisements normaux strict). Une telle paire est dite régulière (resp. strictement régulière). Réciproquement, toute paire torique
![]() $(X,U)$
avec
$(X,U)$
avec
![]() $X$
régulier est une paire régulière au sens précédent. Nous commettrons l’abus de notation suivant : si
$X$
régulier est une paire régulière au sens précédent. Nous commettrons l’abus de notation suivant : si
![]() $(X,U)$
est torique, on désignera également par
$(X,U)$
est torique, on désignera également par
![]() $(X,U)$
le log-schéma muni de la log-structure introduite ci-dessus.
$(X,U)$
le log-schéma muni de la log-structure introduite ci-dessus.
2.1.2
Soit maintenant
![]() $X$
un schéma nœthérien. Rappelons qu’un
$X$
un schéma nœthérien. Rappelons qu’un
![]() $X$
-schéma
$X$
-schéma
![]() $Y$
est une courbe nodale si le morphisme structural
$Y$
est une courbe nodale si le morphisme structural
![]() $h:Y\rightarrow X$
est projectif, plat, à fibres géométriques des courbes connexes ayant au pire des singularités quadratiques ordinaires. Nous dirons d’une courbe nodale
$h:Y\rightarrow X$
est projectif, plat, à fibres géométriques des courbes connexes ayant au pire des singularités quadratiques ordinaires. Nous dirons d’une courbe nodale
![]() $h:Y\rightarrow X$
qu’elle est adaptée à une paire
$h:Y\rightarrow X$
qu’elle est adaptée à une paire
![]() $(Y^{\circ },X^{\circ })$
, où
$(Y^{\circ },X^{\circ })$
, où
![]() $Y^{\circ }$
(resp.
$Y^{\circ }$
(resp.
![]() $X^{\circ }$
) est un ouvert dense de
$X^{\circ }$
) est un ouvert dense de
![]() $Y$
(resp.
$Y$
(resp.
![]() $X$
) lorsque les conditions suivantes sont satisfaites
:
$X$
) lorsque les conditions suivantes sont satisfaites
:
– le morphisme
 $h$
est lisse au-dessus de
$h$
est lisse au-dessus de
 $X^{\circ }$
;
$X^{\circ }$
;– il existe un diviseur
 $D$
étale sur
$D$
étale sur
 $X$
contenu dans le lieu lisse de
$X$
contenu dans le lieu lisse de
 $h$
tel que
$h$
tel que
 $Y^{\circ }=h^{-1}(X^{\circ })\cap (Y-D)$
.
$Y^{\circ }=h^{-1}(X^{\circ })\cap (Y-D)$
.

Un lien avec la géométrie logarithmique est donné par la proposition bien connue suivante ([STG VI, 1.9], [Reference MochizukiMoc99, 4.2] ou [Reference SaitoSai04, 1.12]).
Proposition 2.1.3. Soit
![]() $h:Y\rightarrow X$
une courbe nodale adaptée à une paire d’ouverts denses
$h:Y\rightarrow X$
une courbe nodale adaptée à une paire d’ouverts denses
![]() $(Y^{\circ },X^{\circ })$
telle que
$(Y^{\circ },X^{\circ })$
telle que
![]() $(X,X^{\circ })$
soit
$(X,X^{\circ })$
soit
![]() $\text{torique}$
. Alors le morphisme
$\text{torique}$
. Alors le morphisme
![]() $(Y,Y^{\circ })\rightarrow (X,X^{\circ })$
est
$(Y,Y^{\circ })\rightarrow (X,X^{\circ })$
est
![]() $\text{log-lisse}$
et la paire
$\text{log-lisse}$
et la paire
![]() $(Y,Y^{\circ })$
est torique.
$(Y,Y^{\circ })$
est torique.
(Voir aussi 2.3.6.)
2.2 Pureté
2.2.1
Soient
![]() $X$
un schéma régulier connexe,
$X$
un schéma régulier connexe,
![]() $D$
un diviseur à croisements normaux et
$D$
un diviseur à croisements normaux et
![]() $U=X\setminus D$
. Pour tout faisceau
$U=X\setminus D$
. Pour tout faisceau
![]() $\mathscr{L}$
lisse sur
$\mathscr{L}$
lisse sur
![]() $U$
il est équivalent de demander que le prolongement par zéro
$U$
il est équivalent de demander que le prolongement par zéro
![]() $j_{!}\mathscr{L}$
soit modéré au sens de 1.3.1 ou bien que
$j_{!}\mathscr{L}$
soit modéré au sens de 1.3.1 ou bien que
![]() $\mathscr{L}$
soit modéré le long de
$\mathscr{L}$
soit modéré le long de
![]() $D$
au sens usuel (c’est-à-dire : pour tout point maximal
$D$
au sens usuel (c’est-à-dire : pour tout point maximal
![]() $d$
de
$d$
de
![]() $D$
, l’inertie sauvage du corps discrètement valué
$D$
, l’inertie sauvage du corps discrètement valué
![]() $\text{Frac}(\mathscr{O}_{X,d})$
agit trivialement). Seule une implication est non triviale ; elle résulte immédiatement du lemme d’Abhyankar usuel [SGA 1 XIII, 5.2].
$\text{Frac}(\mathscr{O}_{X,d})$
agit trivialement). Seule une implication est non triviale ; elle résulte immédiatement du lemme d’Abhyankar usuel [SGA 1 XIII, 5.2].
2.2.2
Considérons maintenant une variante logarithmique du critère de modération précédent s’appuyant sur un théorème de pureté logarithmique (Katô K., cf. p. ex. [Reference MochizukiMoc99, 3.3]). On ne suppose plus la paire
![]() $(X,U)$
régulière mais seulement torique. La condition de modération en les points maximaux du diviseur
$(X,U)$
régulière mais seulement torique. La condition de modération en les points maximaux du diviseur
![]() $D$
garde un sens, car
$D$
garde un sens, car
![]() $X$
est normal ([Reference KatoKat94, 4.1] ou [Reference Gabber and RameroGR16, 10.5.29]). Si un faisceau abélien
$X$
est normal ([Reference KatoKat94, 4.1] ou [Reference Gabber and RameroGR16, 10.5.29]). Si un faisceau abélien
![]() $\mathscr{L}$
de
$\mathscr{L}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules, lisse sur
$\mathbb{Z}/n\mathbb{Z}$
-modules, lisse sur
![]() $U$
, satisfait cette condition, il existe un revêtement étale
$U$
, satisfait cette condition, il existe un revêtement étale
![]() $U^{\prime }\rightarrow U$
, modéré le long de
$U^{\prime }\rightarrow U$
, modéré le long de
![]() $D$
(au sens usuel, [Reference Gabber and RameroGR16, 11.3.16], [Reference IllusieIll81, 2.6]) trivialisant
$D$
(au sens usuel, [Reference Gabber and RameroGR16, 11.3.16], [Reference IllusieIll81, 2.6]) trivialisant
![]() $\mathscr{L}$
. Soit
$\mathscr{L}$
. Soit
![]() $X^{\prime }$
le normalisé de
$X^{\prime }$
le normalisé de
![]() $X$
dans
$X$
dans
![]() $U^{\prime }$
; le morphisme
$U^{\prime }$
; le morphisme
![]() $X^{\prime }\rightarrow X$
est fini et surjectif. D’après [Reference Gabber and RameroGR16, 11.3.43], la paire
$X^{\prime }\rightarrow X$
est fini et surjectif. D’après [Reference Gabber and RameroGR16, 11.3.43], la paire
![]() $(X^{\prime },U^{\prime })$
est torique et le morphisme de log-schémas
$(X^{\prime },U^{\prime })$
est torique et le morphisme de log-schémas
![]() $(X^{\prime },U^{\prime })\rightarrow (X,U)$
est un revêtement log-étale, au sens de [Reference Gabber and RameroGR16, 11.3.13]. Lorsque
$(X^{\prime },U^{\prime })\rightarrow (X,U)$
est un revêtement log-étale, au sens de [Reference Gabber and RameroGR16, 11.3.13]. Lorsque
![]() $X$
est strictement local d’exposant caractéristique résiduel
$X$
est strictement local d’exposant caractéristique résiduel
![]() $p$
, le groupe fondamental logarithmique de la paire
$p$
, le groupe fondamental logarithmique de la paire
![]() $(X,U)$
est abélien d’ordre profini premier à
$(X,U)$
est abélien d’ordre profini premier à
![]() $p$
[Reference Gabber and RameroGR16, 11.3.41]. Il en résulte formellement que le faisceau
$p$
[Reference Gabber and RameroGR16, 11.3.41]. Il en résulte formellement que le faisceau
![]() $j_{!}\mathscr{L}$
est modéré. Résumons ces observations sous la forme d’un lemme.
$j_{!}\mathscr{L}$
est modéré. Résumons ces observations sous la forme d’un lemme.
Lemme 2.2.3. Soient
![]() $(X,U)$
une paire
$(X,U)$
une paire
![]() $\text{torique}$
,
$\text{torique}$
,
![]() $j:U{\hookrightarrow}X$
l’immersion ouverte et
$j:U{\hookrightarrow}X$
l’immersion ouverte et
![]() $\mathscr{L}$
un faisceau abélien lisse sur
$\mathscr{L}$
un faisceau abélien lisse sur
![]() $U$
de
$U$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules (
$\mathbb{Z}/n\mathbb{Z}$
-modules (
![]() $n\geqslant 1$
). Les conditions suivantes sont équivalentes
:
$n\geqslant 1$
). Les conditions suivantes sont équivalentes
:
(i) le prolongement par zéro
 $j_{!}\mathscr{L}$
est modéré (au sens de 1.3.1) ;
$j_{!}\mathscr{L}$
est modéré (au sens de 1.3.1) ;(ii)
 $\mathscr{L}$
est
$\mathscr{L}$
est
 $\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}~\text{le long de}$
$\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}~\text{le long de}$
 $D$
: pour tout point maximal
$D$
: pour tout point maximal
 $d$
de
$d$
de
 $D$
, l’inertie sauvage du corps discrètement valué
$D$
, l’inertie sauvage du corps discrètement valué
 $\text{Frac}(\mathscr{O}_{X,d})$
agit trivialement sur la fibre de
$\text{Frac}(\mathscr{O}_{X,d})$
agit trivialement sur la fibre de
 $\mathscr{L}$
en un point géométrique au-dessus de
$\mathscr{L}$
en un point géométrique au-dessus de
 $d$
;
$d$
;(iii) il existe un revêtement log-étale
 $(X^{\prime },U^{\prime })\rightarrow (X,U)$
tel que
$(X^{\prime },U^{\prime })\rightarrow (X,U)$
tel que
 $\mathscr{L}_{|U^{\prime }}$
soit trivial.
$\mathscr{L}_{|U^{\prime }}$
soit trivial.
Remarque 2.2.4. L’analogue de ce lemme pour l’unipotence est faux : il existe par exemple une paire torique
![]() $(X,U)$
avec
$(X,U)$
avec
![]() $X$
strictement local de dimension
$X$
strictement local de dimension
![]() $2$
et un faisceau
$2$
et un faisceau
![]() $\mathscr{L}$
lisse sur
$\mathscr{L}$
lisse sur
![]() $U$
qui n’est pas unipotent (sur
$U$
qui n’est pas unipotent (sur
![]() $U$
) mais localement unipotent en les points maximaux de
$U$
) mais localement unipotent en les points maximaux de
![]() $X-U$
. En effet, comme expliqué en [Reference Gabber and RameroGR16, 11.3.52-55], on peut calculer le groupe fondamental du spectre épointé
$X-U$
. En effet, comme expliqué en [Reference Gabber and RameroGR16, 11.3.52-55], on peut calculer le groupe fondamental du spectre épointé
![]() $X^{\star }:=X-\{x\}$
(pour
$X^{\star }:=X-\{x\}$
(pour
![]() $X$
de dimension quelconque) et en particulier [Reference Gabber and RameroGR16, 11.3.57] construire une paire comme ci-dessus telle que
$X$
de dimension quelconque) et en particulier [Reference Gabber and RameroGR16, 11.3.57] construire une paire comme ci-dessus telle que
![]() $\unicode[STIX]{x1D70B}_{1}(X^{\star })=\mathbb{Z}/2\mathbb{Z}$
.
$\unicode[STIX]{x1D70B}_{1}(X^{\star })=\mathbb{Z}/2\mathbb{Z}$
.
2.3 Image directe : courbe nodale
Faute de référence adéquate, ce paragraphe est consacré à la démonstration de la proposition suivante. (Signalons cependant que, dans le cas localement unipotent, cet énoncé et une esquisse de preuve — différente — figurent dans [Reference PinkPin95].)
Proposition 2.3.1. Soient
![]() $X$
un schéma nœthérien,
$X$
un schéma nœthérien,
![]() $h:Y\rightarrow X$
une courbe nodale adaptée à une paire d’ouverts denses
$h:Y\rightarrow X$
une courbe nodale adaptée à une paire d’ouverts denses
![]() $(Y^{\circ },X^{\circ })$
, avec
$(Y^{\circ },X^{\circ })$
, avec
![]() $X^{\circ }$
normal, et
$X^{\circ }$
normal, et
![]() $\mathscr{L}$
un faisceau lisse de
$\mathscr{L}$
un faisceau lisse de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $Y^{\circ }$
, où
$Y^{\circ }$
, où
![]() $n$
est un entier inversible sur
$n$
est un entier inversible sur
![]() $X$
, tel que
$X$
, tel que
![]() $j_{!}\mathscr{L}$
soit
$j_{!}\mathscr{L}$
soit
![]() $\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}$
(resp. localement unipotent le long de la stratification
$\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}$
(resp. localement unipotent le long de la stratification
![]() $\mathfrak{Y}:=\{Y^{\circ },Y\setminus Y^{\circ }\}$
de
$\mathfrak{Y}:=\{Y^{\circ },Y\setminus Y^{\circ }\}$
de
![]() $Y$
), où
$Y$
), où
![]() $j$
désigne l’immersion ouverte
$j$
désigne l’immersion ouverte
![]() $Y^{\circ }{\hookrightarrow}Y$
. Alors, les faisceaux
$Y^{\circ }{\hookrightarrow}Y$
. Alors, les faisceaux
![]() $\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
(
$\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
(
![]() $0\leqslant i\leqslant 2$
) sont constructibles et modérés (resp. localement unipotents) le long de la stratification
$0\leqslant i\leqslant 2$
) sont constructibles et modérés (resp. localement unipotents) le long de la stratification
![]() $\mathfrak{X}:=\{X^{\circ },X\setminus X^{\circ }\}$
de
$\mathfrak{X}:=\{X^{\circ },X\setminus X^{\circ }\}$
de
![]() $X$
.
$X$
.
Nous traitons d’abord le cas où la paire
![]() $(X,X^{\circ })$
est torique : cela est suffisant pour établir le théorème de constructibilité uniforme pour les morphismes propres dans le cas des schémas quasi-excellents. Le cas des schémas nœthériens généraux est ensuite esquissé.
$(X,X^{\circ })$
est torique : cela est suffisant pour établir le théorème de constructibilité uniforme pour les morphismes propres dans le cas des schémas quasi-excellents. Le cas des schémas nœthériens généraux est ensuite esquissé.
Fixons un entier
![]() $i\in \{0,1,2\}$
.
$i\in \{0,1,2\}$
.
2.3.2 Constructibilité
Le faisceau
![]() $\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
est nul sur le fermé
$\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
est nul sur le fermé
![]() $X\setminus X^{\circ }$
: cela résulte du théorème de changement de base propre et du fait que l’ouvert
$X\setminus X^{\circ }$
: cela résulte du théorème de changement de base propre et du fait que l’ouvert
![]() $Y^{\circ }$
ne rencontre pas le fermé
$Y^{\circ }$
ne rencontre pas le fermé
![]() $h^{-1}(X\setminus X^{\circ })$
. Montrons maintenant que
$h^{-1}(X\setminus X^{\circ })$
. Montrons maintenant que
![]() $\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
est lisse sur l’ouvert
$\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
est lisse sur l’ouvert
![]() $X^{\circ }$
. On peut supposer
$X^{\circ }$
. On peut supposer
![]() $X=X^{\circ }$
. Le lemme bien connu ci-dessous et la propreté de
$X=X^{\circ }$
. Le lemme bien connu ci-dessous et la propreté de
![]() $h$
nous ramènent au cas où
$h$
nous ramènent au cas où
![]() $X$
est un trait hensélien, qui résulte de [SGA 7 XIII, 2.1.11].
$X$
est un trait hensélien, qui résulte de [SGA 7 XIII, 2.1.11].
(Le même argument se trouve dans [Reference PinkPin95, théorème 4].)
Lemme. Soient
![]() $X$
un schéma nœthérien,
$X$
un schéma nœthérien,
![]() $(f:Y\rightarrow X,\mathscr{F})$
une paire cohomologiquement propre et
$(f:Y\rightarrow X,\mathscr{F})$
une paire cohomologiquement propre et
![]() $c\geqslant 0$
un entier tel que
$c\geqslant 0$
un entier tel que
![]() $\mathscr{H}:=\mathtt{R}^{c}f_{\star }\mathscr{F}$
soit constructible. Alors,
$\mathscr{H}:=\mathtt{R}^{c}f_{\star }\mathscr{F}$
soit constructible. Alors,
![]() $\mathscr{H}$
est
$\mathscr{H}$
est
![]() $\text{lisse}$
si et seulement si pour tout
$\text{lisse}$
si et seulement si pour tout
![]() $X$
-trait strictement hensélien
$X$
-trait strictement hensélien
![]() $T$
, le faisceau
$T$
, le faisceau
![]() $\mathtt{R}^{c}f_{T\star }\mathscr{F}_{|Y_{T}}$
est lisse sur
$\mathtt{R}^{c}f_{T\star }\mathscr{F}_{|Y_{T}}$
est lisse sur
![]() $T$
.
$T$
.
Démonstration.
Par propreté cohomologique, il s’agit de montrer que le faisceau constructible
![]() $\mathscr{H}$
est lisse si ses tirés en arrière sur tout
$\mathscr{H}$
est lisse si ses tirés en arrière sur tout
![]() $X$
-trait strictement hensélien le sont. Or, d’après [SGA 4 IX, 2.13 (i)]), il faut montrer que pour toute spécialisation
$X$
-trait strictement hensélien le sont. Or, d’après [SGA 4 IX, 2.13 (i)]), il faut montrer que pour toute spécialisation
![]() $b{\rightsquigarrow}a$
de points géométriques de
$b{\rightsquigarrow}a$
de points géométriques de
![]() $X$
, le morphisme
$X$
, le morphisme
![]() $\mathscr{H}_{a}\rightarrow \mathscr{H}_{b}$
est un isomorphisme. D’après [ÉGA II, 7.1.9], il existe un morphisme local
$\mathscr{H}_{a}\rightarrow \mathscr{H}_{b}$
est un isomorphisme. D’après [ÉGA II, 7.1.9], il existe un morphisme local
![]() $T\rightarrow X_{(a)}$
, induisant un isomorphisme sur les corps résiduels en les points fermés et envoyant le point générique de
$T\rightarrow X_{(a)}$
, induisant un isomorphisme sur les corps résiduels en les points fermés et envoyant le point générique de
![]() $T$
sur (l’image de)
$T$
sur (l’image de)
![]() $b$
. Ceci suffit pour conclure.◻
$b$
. Ceci suffit pour conclure.◻
2.3.3 Modération : cas où la paire
 $(X,X^{\circ })$
est torique
$(X,X^{\circ })$
est torique
Soit
![]() $\unicode[STIX]{x1D70B}:(Y^{\prime },Y^{\prime \circ })\rightarrow (Y,Y^{\circ })$
un revêtement log-étale tel que
$\unicode[STIX]{x1D70B}:(Y^{\prime },Y^{\prime \circ })\rightarrow (Y,Y^{\circ })$
un revêtement log-étale tel que
![]() $\mathscr{L}_{|Y^{\prime \circ }}:=\unicode[STIX]{x1D70B}^{\circ \star }\mathscr{L}$
soit constant (2.2.3). La transitivité des images directes et un dévissage classique (cf. par exemple [Th. finitude, A, 1.3.3]), reposant sur le fait que le prolongement par zéro du conoyau de la flèche
$\mathscr{L}_{|Y^{\prime \circ }}:=\unicode[STIX]{x1D70B}^{\circ \star }\mathscr{L}$
soit constant (2.2.3). La transitivité des images directes et un dévissage classique (cf. par exemple [Th. finitude, A, 1.3.3]), reposant sur le fait que le prolongement par zéro du conoyau de la flèche
![]() $\mathscr{L}{\hookrightarrow}\unicode[STIX]{x1D70B}_{\star }^{\circ }\unicode[STIX]{x1D70B}^{\circ \star }\mathscr{L}$
est également modéré, nous ramènent à montrer que pour tout revêtement log-étale
$\mathscr{L}{\hookrightarrow}\unicode[STIX]{x1D70B}_{\star }^{\circ }\unicode[STIX]{x1D70B}^{\circ \star }\mathscr{L}$
est également modéré, nous ramènent à montrer que pour tout revêtement log-étale
![]() $\unicode[STIX]{x1D70F}:(Y^{\prime },Y^{\prime \circ })\rightarrow (Y,Y^{\circ })$
, le faisceau
$\unicode[STIX]{x1D70F}:(Y^{\prime },Y^{\prime \circ })\rightarrow (Y,Y^{\circ })$
, le faisceau
![]() $\mathtt{R}^{i}(h\circ \unicode[STIX]{x1D70F})_{\star }(j_{!}^{\prime }\mathbb{Z}/n\mathbb{Z})$
est modéré. (On note
$\mathtt{R}^{i}(h\circ \unicode[STIX]{x1D70F})_{\star }(j_{!}^{\prime }\mathbb{Z}/n\mathbb{Z})$
est modéré. (On note
![]() $j^{\prime }$
le changement de base
$j^{\prime }$
le changement de base
![]() $j\times _{Y}Y^{\prime }$
.) D’après les résultats rappelés au paragraphe précédent, ce faisceau est le prolongement par zéro d’un faisceau lisse sur
$j\times _{Y}Y^{\prime }$
.) D’après les résultats rappelés au paragraphe précédent, ce faisceau est le prolongement par zéro d’un faisceau lisse sur
![]() $X^{\circ }$
. Le lemme d’Abhyankar logarithmique (2.2.3), nous permet de supposer dans le cas torique que
$X^{\circ }$
. Le lemme d’Abhyankar logarithmique (2.2.3), nous permet de supposer dans le cas torique que
![]() $X$
est un trait strictement hensélien, dont nous notons
$X$
est un trait strictement hensélien, dont nous notons
![]() $\unicode[STIX]{x1D702}$
le point générique de sorte que
$\unicode[STIX]{x1D702}$
le point générique de sorte que
![]() $X^{\circ }=\{\unicode[STIX]{x1D702}\}$
, sans quoi
$X^{\circ }=\{\unicode[STIX]{x1D702}\}$
, sans quoi
![]() $X=X^{\circ }$
et il n’y a rien à démontrer. Soit
$X=X^{\circ }$
et il n’y a rien à démontrer. Soit
![]() $\overline{\unicode[STIX]{x1D702}}$
un point géométrique au-dessus de
$\overline{\unicode[STIX]{x1D702}}$
un point géométrique au-dessus de
![]() $\unicode[STIX]{x1D702}$
; on veut montrer que l’action de
$\unicode[STIX]{x1D702}$
; on veut montrer que l’action de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
![]() $H_{c}^{i}(Y_{\overline{\unicode[STIX]{x1D702}}}^{\prime \circ },\mathbb{Z}/n\mathbb{Z})$
est modérée. Par lissité de
$H_{c}^{i}(Y_{\overline{\unicode[STIX]{x1D702}}}^{\prime \circ },\mathbb{Z}/n\mathbb{Z})$
est modérée. Par lissité de
![]() $Y_{\unicode[STIX]{x1D702}}^{\prime \circ }$
sur
$Y_{\unicode[STIX]{x1D702}}^{\prime \circ }$
sur
![]() $\unicode[STIX]{x1D702}$
et dualité de Poincaré, il suffit de démontrer la modération de la cohomologie sans support (en degré cohomologique
$\unicode[STIX]{x1D702}$
et dualité de Poincaré, il suffit de démontrer la modération de la cohomologie sans support (en degré cohomologique
![]() $2-i$
). Ceci est un cas particulier du résultat suivant [Reference IllusieIll02, 8.4.3] :
$2-i$
). Ceci est un cas particulier du résultat suivant [Reference IllusieIll02, 8.4.3] :
Soient
![]() $(W,\mathscr{M}_{W})$
un log-schéma fin et saturé, propre et log-lisse sur
$(W,\mathscr{M}_{W})$
un log-schéma fin et saturé, propre et log-lisse sur
![]() $(X,\unicode[STIX]{x1D702})$
d’ouvert de trivialité
$(X,\unicode[STIX]{x1D702})$
d’ouvert de trivialité
![]() $W^{\circ }$
contenu dans
$W^{\circ }$
contenu dans
![]() $W_{\unicode[STIX]{x1D702}}$
, et
$W_{\unicode[STIX]{x1D702}}$
, et
![]() $n$
un entier inversible sur
$n$
un entier inversible sur
![]() $X$
. Alors l’action de
$X$
. Alors l’action de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur chaque
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur chaque
![]() $\mathtt{H}^{j}(W_{\overline{\unicode[STIX]{x1D702}}}^{\circ },\mathbb{Z}/n\mathbb{Z})$
est modérée.
$\mathtt{H}^{j}(W_{\overline{\unicode[STIX]{x1D702}}}^{\circ },\mathbb{Z}/n\mathbb{Z})$
est modérée.
2.3.4 Unipotence : cas d’un trait
Commençons par le cas où
![]() $X$
est un trait strictement hensélien et
$X$
est un trait strictement hensélien et
![]() $X^{\circ }=\{\unicode[STIX]{x1D702}\}$
. Notons
$X^{\circ }=\{\unicode[STIX]{x1D702}\}$
. Notons
![]() $s$
le point fermé de
$s$
le point fermé de
![]() $X$
et
$X$
et
![]() $\overline{\unicode[STIX]{x1D702}}$
un point géométrique au-dessus de
$\overline{\unicode[STIX]{x1D702}}$
un point géométrique au-dessus de
![]() $\unicode[STIX]{x1D702}$
. On veut montrer que l’action de
$\unicode[STIX]{x1D702}$
. On veut montrer que l’action de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
![]() $\mathtt{H}_{c}^{i}(Y_{\overline{\unicode[STIX]{x1D702}}}^{\circ },\mathscr{L})=\mathtt{H}^{i}(Y_{s},\unicode[STIX]{x1D6F9}_{h}j_{\unicode[STIX]{x1D702}!}\mathscr{L})$
est unipotente. Il suffit de montrer que pour chaque
$\mathtt{H}_{c}^{i}(Y_{\overline{\unicode[STIX]{x1D702}}}^{\circ },\mathscr{L})=\mathtt{H}^{i}(Y_{s},\unicode[STIX]{x1D6F9}_{h}j_{\unicode[STIX]{x1D702}!}\mathscr{L})$
est unipotente. Il suffit de montrer que pour chaque
![]() $\unicode[STIX]{x1D6FC}$
, l’action de
$\unicode[STIX]{x1D6FC}$
, l’action de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
![]() $\unicode[STIX]{x1D6F9}_{h}^{\unicode[STIX]{x1D6FC}}(j_{\unicode[STIX]{x1D702}!}\mathscr{L})$
est unipotente, c’est-à-dire (1.2.4) qu’il existe une filtration de ce faisceau à gradué muni de l’action triviale. D’après le lemme 1.2.5, le problème est local (pour la topologie étale) sur
$\unicode[STIX]{x1D6F9}_{h}^{\unicode[STIX]{x1D6FC}}(j_{\unicode[STIX]{x1D702}!}\mathscr{L})$
est unipotente, c’est-à-dire (1.2.4) qu’il existe une filtration de ce faisceau à gradué muni de l’action triviale. D’après le lemme 1.2.5, le problème est local (pour la topologie étale) sur
![]() $Y_{s}$
(donc sur
$Y_{s}$
(donc sur
![]() $Y$
) et on peut alors supposer, par dévissage, que le faisceau localement unipotent
$Y$
) et on peut alors supposer, par dévissage, que le faisceau localement unipotent
![]() $\mathscr{L}$
est constant, de valeur
$\mathscr{L}$
est constant, de valeur
![]() $\mathbb{Z}/n\mathbb{Z}$
pour un entier
$\mathbb{Z}/n\mathbb{Z}$
pour un entier
![]() $n$
inversible sur
$n$
inversible sur
![]() $X$
. Le triangle
$X$
. Le triangle
où
![]() $i$
est l’immersion fermée du diviseur
$i$
est l’immersion fermée du diviseur
![]() $D$
dans
$D$
dans
![]() $Y$
(et l’égalité résulte de [SGA 7 XIII, 1.3.6.1]), nous ramène à démontrer l’unipotence des faisceaux
$Y$
(et l’égalité résulte de [SGA 7 XIII, 1.3.6.1]), nous ramène à démontrer l’unipotence des faisceaux
![]() $\unicode[STIX]{x1D6F9}_{h}^{\unicode[STIX]{x1D6FC}}(\mathbb{Z}/n\mathbb{Z})$
. Or, il est bien connu que l’action de l’inertie sur ces faisceaux est triviale (voir par exemple [Reference IllusieIll04, § 3.3] et [SGA 7 I, 3.3]).
$\unicode[STIX]{x1D6F9}_{h}^{\unicode[STIX]{x1D6FC}}(\mathbb{Z}/n\mathbb{Z})$
. Or, il est bien connu que l’action de l’inertie sur ces faisceaux est triviale (voir par exemple [Reference IllusieIll04, § 3.3] et [SGA 7 I, 3.3]).
2.3.5 Unipotence : cas général
On procède par réduction au cas précédent. Le théorème de changement de base propre nous permet d’une part de supposer le schéma de base
![]() $X$
strictement local intègre, de point fermé
$X$
strictement local intègre, de point fermé
![]() $x$
et de point générique
$x$
et de point générique
![]() $\unicode[STIX]{x1D702}\in X^{\circ }$
— dont on note
$\unicode[STIX]{x1D702}\in X^{\circ }$
— dont on note
![]() $\overline{\unicode[STIX]{x1D702}}\rightarrow \unicode[STIX]{x1D702}$
un point générique géométrique — et d’autre part d’exprimer la cohomologie
$\overline{\unicode[STIX]{x1D702}}\rightarrow \unicode[STIX]{x1D702}$
un point générique géométrique — et d’autre part d’exprimer la cohomologie
![]() $\mathtt{R}\unicode[STIX]{x1D6E4}(Y_{\overline{\unicode[STIX]{x1D702}}},j_{!}\mathscr{L})$
de la fibre générique géométrique comme la cohomologie
$\mathtt{R}\unicode[STIX]{x1D6E4}(Y_{\overline{\unicode[STIX]{x1D702}}},j_{!}\mathscr{L})$
de la fibre générique géométrique comme la cohomologie
![]() $\mathtt{R}\unicode[STIX]{x1D6E4}(Y_{x},\unicode[STIX]{x1D6F9}_{x,\overline{\unicode[STIX]{x1D702}}}(j_{!}\mathscr{L}))$
de la fibre spéciale
$\mathtt{R}\unicode[STIX]{x1D6E4}(Y_{x},\unicode[STIX]{x1D6F9}_{x,\overline{\unicode[STIX]{x1D702}}}(j_{!}\mathscr{L}))$
de la fibre spéciale
![]() $Y_{x}$
à coefficients dans un complexe naturellement muni d’une action de
$Y_{x}$
à coefficients dans un complexe naturellement muni d’une action de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
, calculant la cohomologie des fibres de Milnor :
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
, calculant la cohomologie des fibres de Milnor :
(Sur la théorie de P. Deligne des cycles évanescents en dimension
![]() ${\geqslant}1$
, voir par exemple [Reference LaumonLau83].) D’après 1.2.3 et la normalité de
${\geqslant}1$
, voir par exemple [Reference LaumonLau83].) D’après 1.2.3 et la normalité de
![]() $X^{\circ }$
, il suffit de montrer que l’action du groupe de Galois
$X^{\circ }$
, il suffit de montrer que l’action du groupe de Galois
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur chaque
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur chaque
![]() $\mathtt{H}_{c}^{i}(Y_{\overline{\unicode[STIX]{x1D702}}}^{\circ },\mathscr{L})$
est unipotente. La description précédente et le critère 1.2.5 nous ramènent à démontrer l’énoncé local suivant : pour tout entier
$\mathtt{H}_{c}^{i}(Y_{\overline{\unicode[STIX]{x1D702}}}^{\circ },\mathscr{L})$
est unipotente. La description précédente et le critère 1.2.5 nous ramènent à démontrer l’énoncé local suivant : pour tout entier
![]() $0\leqslant \unicode[STIX]{x1D6FC}\leqslant 2$
et tout point géométrique
$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 2$
et tout point géométrique
![]() $\overline{y}$
de
$\overline{y}$
de
![]() $Y$
localisé en
$Y$
localisé en
![]() $y\in (Y\setminus Y^{\circ })_{x}$
, l’action du groupe de Galois
$y\in (Y\setminus Y^{\circ })_{x}$
, l’action du groupe de Galois
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur le groupe de cohomologie
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur le groupe de cohomologie
![]() $\mathtt{H}^{\unicode[STIX]{x1D6FC}}(\overline{V},j_{!}\mathscr{L})=\unicode[STIX]{x1D6F9}_{x,\overline{\unicode[STIX]{x1D702}}}^{\unicode[STIX]{x1D6FC}}(j_{!}\mathscr{L})_{\overline{y}}$
de la fibre de Milnor
$\mathtt{H}^{\unicode[STIX]{x1D6FC}}(\overline{V},j_{!}\mathscr{L})=\unicode[STIX]{x1D6F9}_{x,\overline{\unicode[STIX]{x1D702}}}^{\unicode[STIX]{x1D6FC}}(j_{!}\mathscr{L})_{\overline{y}}$
de la fibre de Milnor
![]() $\overline{V}:=Y_{(\overline{y})}\times _{X}\overline{\unicode[STIX]{x1D702}}$
est unipotente. (Rappelons que
$\overline{V}:=Y_{(\overline{y})}\times _{X}\overline{\unicode[STIX]{x1D702}}$
est unipotente. (Rappelons que
![]() $j$
est l’immersion ouverte
$j$
est l’immersion ouverte
![]() $Y^{\circ }{\hookrightarrow}Y$
.) Par hypothèse, la restriction du faisceau
$Y^{\circ }{\hookrightarrow}Y$
.) Par hypothèse, la restriction du faisceau
![]() $\mathscr{L}$
à
$\mathscr{L}$
à
![]() $V:=Y_{(\overline{y})}\times _{X}\unicode[STIX]{x1D702}$
est unipotente ; par dévissage, on peut donc supposer le faisceau
$V:=Y_{(\overline{y})}\times _{X}\unicode[STIX]{x1D702}$
est unipotente ; par dévissage, on peut donc supposer le faisceau
![]() $\mathscr{L}$
constant de valeur
$\mathscr{L}$
constant de valeur
![]() $L$
. Le triangle
$L$
. Le triangle
![]() $j_{!}L\rightarrow L\rightarrow i_{\star }L\stackrel{+1}{\rightarrow }$
sur
$j_{!}L\rightarrow L\rightarrow i_{\star }L\stackrel{+1}{\rightarrow }$
sur
![]() $Y_{\unicode[STIX]{x1D702}}$
nous ramène à montrer que l’action de
$Y_{\unicode[STIX]{x1D702}}$
nous ramène à montrer que l’action de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
![]() $\mathtt{H}^{\unicode[STIX]{x1D6FC}}(\overline{V},L)$
et
$\mathtt{H}^{\unicode[STIX]{x1D6FC}}(\overline{V},L)$
et
![]() $\mathtt{H}^{\unicode[STIX]{x1D6FC}-1}(\overline{V}\times _{Y}D,L)$
est unipotente, où
$\mathtt{H}^{\unicode[STIX]{x1D6FC}-1}(\overline{V}\times _{Y}D,L)$
est unipotente, où
![]() $D$
est le fermé de
$D$
est le fermé de
![]() $Y$
constitué des diviseurs horizontaux. Par locale acyclicité des morphismes lisses seul est à considérer le premier groupe, dans le cas particulier où
$Y$
constitué des diviseurs horizontaux. Par locale acyclicité des morphismes lisses seul est à considérer le premier groupe, dans le cas particulier où
![]() $y$
est un point singulier du morphisme
$y$
est un point singulier du morphisme
![]() $h$
. Notons que le lieu singulier du morphisme
$h$
. Notons que le lieu singulier du morphisme
![]() $h$
est fini sur la base : la proposition [ÉGA II, 7.1.7] nous permet comme dans le lemme ci-dessus (et [Reference OrgogozoOrg06, § 7.1]) de supposer que
$h$
est fini sur la base : la proposition [ÉGA II, 7.1.7] nous permet comme dans le lemme ci-dessus (et [Reference OrgogozoOrg06, § 7.1]) de supposer que
![]() $X$
est un trait, par comparaison avec la théorie classique des cycles évanescents de Grothendieck. (On utilise ici un théorème de P. Deligne de commutation au changement de base, rappelé en [Reference OrgogozoOrg06, prop. 6.1].)
$X$
est un trait, par comparaison avec la théorie classique des cycles évanescents de Grothendieck. (On utilise ici un théorème de P. Deligne de commutation au changement de base, rappelé en [Reference OrgogozoOrg06, prop. 6.1].)
2.3.6 Modération : cas général (esquisse)
Comme dans le paragraphe précédent, on se ramene à démontrer l’énoncé local suivant (pour
![]() $X$
strictement local, de point fermé
$X$
strictement local, de point fermé
![]() $x$
) : pour tout point géométrique
$x$
) : pour tout point géométrique
![]() $\overline{y}$
de
$\overline{y}$
de
![]() $Y$
localisé en
$Y$
localisé en
![]() $y\in (Y\setminus Y^{\circ })_{x}$
, l’action du groupe de Galois
$y\in (Y\setminus Y^{\circ })_{x}$
, l’action du groupe de Galois
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur les groupes de cohomologie
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur les groupes de cohomologie
![]() $\mathtt{H}^{\unicode[STIX]{x1D6FC}}(\overline{V},j_{!}\mathscr{L})$
de la fibre de Milnor
$\mathtt{H}^{\unicode[STIX]{x1D6FC}}(\overline{V},j_{!}\mathscr{L})$
de la fibre de Milnor
![]() $\overline{V}:=Y_{(\overline{y})}\times _{X}\overline{\unicode[STIX]{x1D702}}$
est d’ordre premier à l’exposant caractéristique
$\overline{V}:=Y_{(\overline{y})}\times _{X}\overline{\unicode[STIX]{x1D702}}$
est d’ordre premier à l’exposant caractéristique
![]() $p$
de
$p$
de
![]() $x$
. Nous traitons ici le cas où
$x$
. Nous traitons ici le cas où
![]() $Y\rightarrow X$
n’est pas lisse en
$Y\rightarrow X$
n’est pas lisse en
![]() $y$
, l’autre cas étant semblable et plus élémentaire. D’après [Reference KatoKat00, § 2, p. 227]Footnote
5
(voir aussi [Reference MochizukiMoc95, § 3]), le morphisme
$y$
, l’autre cas étant semblable et plus élémentaire. D’après [Reference KatoKat00, § 2, p. 227]Footnote
5
(voir aussi [Reference MochizukiMoc95, § 3]), le morphisme
![]() $h:Y\rightarrow X$
est sous-jacent à un morphisme log-lisse saturé
$h:Y\rightarrow X$
est sous-jacent à un morphisme log-lisse saturé
![]() $(Y,\mathscr{N})\rightarrow (X,\mathscr{M})$
entre log-schémas fins et saturés (fs) tel que le lieu de trivialité de
$(Y,\mathscr{N})\rightarrow (X,\mathscr{M})$
entre log-schémas fins et saturés (fs) tel que le lieu de trivialité de
![]() $(Y,\mathscr{N})$
(resp. de
$(Y,\mathscr{N})$
(resp. de
![]() $(X,\mathscr{M})$
) contienne la fibre
$(X,\mathscr{M})$
) contienne la fibre
![]() $Y_{\unicode[STIX]{x1D702}}$
(resp.
$Y_{\unicode[STIX]{x1D702}}$
(resp.
![]() $\unicode[STIX]{x1D702}$
). Notons
$\unicode[STIX]{x1D702}$
). Notons
![]() $V$
la fibre
$V$
la fibre
![]() $Y_{(\overline{y})}\times _{X}\unicode[STIX]{x1D702}$
, normale par [Reference Gabber and RameroGR16, 10.7.17 (i)] ; la restriction à
$Y_{(\overline{y})}\times _{X}\unicode[STIX]{x1D702}$
, normale par [Reference Gabber and RameroGR16, 10.7.17 (i)] ; la restriction à
![]() $V$
du faisceau
$V$
du faisceau
![]() $\mathscr{L}$
correspond à une représentation de
$\mathscr{L}$
correspond à une représentation de
![]() $\unicode[STIX]{x1D70B}_{1}(V)$
, qui — par hypothèse de modération — se factorise à travers son plus grand quotient
$\unicode[STIX]{x1D70B}_{1}(V)$
, qui — par hypothèse de modération — se factorise à travers son plus grand quotient
![]() $\unicode[STIX]{x1D70B}_{1}(V)_{\bot p}$
premier à
$\unicode[STIX]{x1D70B}_{1}(V)_{\bot p}$
premier à
![]() $p$
: le groupe fondamental du schéma
$p$
: le groupe fondamental du schéma
![]() $V$
est un quotient du groupe de Galois du point générique
$V$
est un quotient du groupe de Galois du point générique
![]() $v$
de
$v$
de
![]() $V$
et l’action de ce dernier se factorise par hypothèse à travers un quotient premier à
$V$
et l’action de ce dernier se factorise par hypothèse à travers un quotient premier à
![]() $p$
. Les revêtements d’ordre premier à
$p$
. Les revêtements d’ordre premier à
![]() $p$
de
$p$
de
![]() $\overline{V}$
étant modérés, ils proviennent de la log-structure d’après le théorème [Reference Gabber and RameroGR16, 11.4.39] d’acyclicité des morphismes log-lisses : il existe donc un morphisme Kummer-étale
$\overline{V}$
étant modérés, ils proviennent de la log-structure d’après le théorème [Reference Gabber and RameroGR16, 11.4.39] d’acyclicité des morphismes log-lisses : il existe donc un morphisme Kummer-étale
![]() $(Y^{\prime },\mathscr{N}^{\prime })\rightarrow (Y,\mathscr{N})$
tel que la restriction de
$(Y^{\prime },\mathscr{N}^{\prime })\rightarrow (Y,\mathscr{N})$
tel que la restriction de
![]() $\mathscr{L}$
à la fibre
$\mathscr{L}$
à la fibre
![]() $V^{\prime }=Y_{(\overline{y})}^{\prime }\times _{X}\unicode[STIX]{x1D702}$
correspondante soit l’image inverse d’un faisceau sur
$V^{\prime }=Y_{(\overline{y})}^{\prime }\times _{X}\unicode[STIX]{x1D702}$
correspondante soit l’image inverse d’un faisceau sur
![]() $\unicode[STIX]{x1D702}$
, de monodromie première à
$\unicode[STIX]{x1D702}$
, de monodromie première à
![]() $p$
. (On utilise ici le fait que le groupe fondamental de
$p$
. (On utilise ici le fait que le groupe fondamental de
![]() $V$
est extension de
$V$
est extension de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
par le groupe fondamental de
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
par le groupe fondamental de
![]() $\overline{V}$
.) Ceci nous ramène à démontrer la modération dans le cas particulier où
$\overline{V}$
.) Ceci nous ramène à démontrer la modération dans le cas particulier où
![]() $\mathscr{L}$
est un faisceau constant. Par commutation des cycles proches aux changements de base dans ce cas (rappelée en 2.3.5
supra), on peut supposer que
$\mathscr{L}$
est un faisceau constant. Par commutation des cycles proches aux changements de base dans ce cas (rappelée en 2.3.5
supra), on peut supposer que
![]() $X$
est un trait, de corps des fractions
$X$
est un trait, de corps des fractions
![]() $\unicode[STIX]{x1D705}(\unicode[STIX]{x1D702})$
. La modération est connue dans ce cas (2.3.3).
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D702})$
. La modération est connue dans ce cas (2.3.3).
2.4 Image directe : immersion ouverte régulière
Ce paragraphe est consacré à la démonstration de la proposition suivante, dont on trouvera une variante en [Reference Gabber and LoeserGL96, lemme 4.3.2], et notamment d’un complément sur la taille des images directes.
Proposition 2.4.1. Soient
![]() $j:X^{\circ }{\hookrightarrow}X$
une immersion ouverte telle que la paire
$j:X^{\circ }{\hookrightarrow}X$
une immersion ouverte telle que la paire
![]() $(X,X^{\circ })$
soit strictement régulière (2.1.1) et
$(X,X^{\circ })$
soit strictement régulière (2.1.1) et
![]() $\mathscr{L}$
un faisceau lisse de
$\mathscr{L}$
un faisceau lisse de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X^{\circ }$
, où
$X^{\circ }$
, où
![]() $n$
est un entier inversible sur
$n$
est un entier inversible sur
![]() $X$
, tel que
$X$
, tel que
![]() $j_{!}\mathscr{L}$
soit
$j_{!}\mathscr{L}$
soit
![]() $\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}$
(resp. localement unipotent le long de
$\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}$
(resp. localement unipotent le long de
![]() $\{X^{\circ },X\setminus X^{\circ }\}$
). Soit
$\{X^{\circ },X\setminus X^{\circ }\}$
). Soit
![]() $\mathfrak{D}$
la stratification de
$\mathfrak{D}$
la stratification de
![]() $X$
définie par la fonction semi-continue supérieurement associant à un point le nombre de branches de
$X$
définie par la fonction semi-continue supérieurement associant à un point le nombre de branches de
![]() $D:=X\setminus X^{\circ }$
y passant. Alors, les faisceaux
$D:=X\setminus X^{\circ }$
y passant. Alors, les faisceaux
![]() $\mathtt{R}^{c}j_{\star }\mathscr{L}$
(
$\mathtt{R}^{c}j_{\star }\mathscr{L}$
(
![]() $c\in \mathbb{N}$
) sont constructibles et modérés (resp. localement unipotents) le long de la stratification
$c\in \mathbb{N}$
) sont constructibles et modérés (resp. localement unipotents) le long de la stratification
![]() $\mathfrak{D}$
.
$\mathfrak{D}$
.
De plus :
(i) si
 $X$
est lisse sur un schéma
$X$
est lisse sur un schéma
 $S$
et
$S$
et
 $D=X\setminus X^{\circ }$
est le complémentaire d’un diviseur à croisements normaux relativement à
$D=X\setminus X^{\circ }$
est le complémentaire d’un diviseur à croisements normaux relativement à
 $S$
, la formation de
$S$
, la formation de
 $\mathtt{R}^{c}j_{\star }\mathscr{L}$
commute aux changements de bases
$\mathtt{R}^{c}j_{\star }\mathscr{L}$
commute aux changements de bases
 $S^{\prime }\rightarrow S$
;
$S^{\prime }\rightarrow S$
;(ii) si
 $k:X{\hookrightarrow}\overline{X}$
est une immersion ouverte et
$k:X{\hookrightarrow}\overline{X}$
est une immersion ouverte et
 $k_{!}j_{!}\mathscr{L}$
modéré (resp. localement unipotent le long de la stratification
$k_{!}j_{!}\mathscr{L}$
modéré (resp. localement unipotent le long de la stratification
 $\{X^{\circ },\overline{X}\setminus X^{\circ }\}$
de
$\{X^{\circ },\overline{X}\setminus X^{\circ }\}$
de
 $\overline{X}$
), le complexe
$\overline{X}$
), le complexe
 $k_{!}\mathtt{R}j_{\star }\mathscr{L}$
est à cohomologie modérée (resp. localement unipotente le long de la stratification définie par
$k_{!}\mathtt{R}j_{\star }\mathscr{L}$
est à cohomologie modérée (resp. localement unipotente le long de la stratification définie par
 $\mathfrak{D}$
, et le fermé
$\mathfrak{D}$
, et le fermé
 $F=\overline{X}\setminus X$
).
$F=\overline{X}\setminus X$
).
« Nombre de branches » : c’est le rang des fibres de
![]() $\mathtt{R}^{1}j_{\star }\mathbb{F}_{\ell }$
, pour
$\mathtt{R}^{1}j_{\star }\mathbb{F}_{\ell }$
, pour
![]() $\ell$
inversible sur
$\ell$
inversible sur
![]() $X$
, ou encore le rang de la log-structure naturellement associée à
$X$
, ou encore le rang de la log-structure naturellement associée à
![]() $(X,X^{\circ })$
— de sorte que
$(X,X^{\circ })$
— de sorte que
![]() $\mathfrak{D}$
est la stratification canonique [STG VI, 1.5] — : on choisit donc
$\mathfrak{D}$
est la stratification canonique [STG VI, 1.5] — : on choisit donc
![]() $\mathfrak{D}$
de sorte que la proposition soit automatiquement vraie pour les faisceaux constants.
$\mathfrak{D}$
de sorte que la proposition soit automatiquement vraie pour les faisceaux constants.
Traitons tout d’abord l’assertion principale dans le cas constructible modéré ; la commutation au changement de base (i) est établie en 2.4.3 et le léger renforcement (ii) en 2.4.4. Le cas unipotent, plus facile, est traité en 2.4.5, directement sous la forme forte (ii).
2.4.2 Cas modéré
L’énoncé étant local pour la topologie étale, on peut supposer
![]() $X$
strictement local. Le diviseur
$X$
strictement local. Le diviseur
![]() $D$
est donc réunion transverse de diviseurs réguliers
$D$
est donc réunion transverse de diviseurs réguliers
![]() $D_{i}=\text{div}(t_{i})$
, où les
$D_{i}=\text{div}(t_{i})$
, où les
![]() $t_{1},\ldots ,t_{b}$
sont des éléments de
$t_{1},\ldots ,t_{b}$
sont des éléments de
![]() $\unicode[STIX]{x1D6E4}(X,\mathscr{O}_{X})$
. Comme dans [Reference DeligneDel80, § 1.7.8], posons
$\unicode[STIX]{x1D6E4}(X,\mathscr{O}_{X})$
. Comme dans [Reference DeligneDel80, § 1.7.8], posons
![]() $X_{r}:=X[(t_{i})^{1/r}:1\leqslant i\leqslant b]$
pour chaque entier
$X_{r}:=X[(t_{i})^{1/r}:1\leqslant i\leqslant b]$
pour chaque entier
![]() $r\geqslant 1$
. C’est un schéma régulier [SGA 1 XIII, 4.1] et
$r\geqslant 1$
. C’est un schéma régulier [SGA 1 XIII, 4.1] et
![]() $X_{r}^{\circ }:=X^{\circ }\times _{X}X_{r}$
est le complémentaire d’un diviseur strictement à croisements normaux
$X_{r}^{\circ }:=X^{\circ }\times _{X}X_{r}$
est le complémentaire d’un diviseur strictement à croisements normaux
![]() $D_{r}$
. Notons
$D_{r}$
. Notons
![]() $\unicode[STIX]{x1D70B}_{r}$
le morphisme fini
$\unicode[STIX]{x1D70B}_{r}$
le morphisme fini
![]() $X_{r}\rightarrow X$
,
$X_{r}\rightarrow X$
,
![]() $\unicode[STIX]{x1D70B}_{r}^{\circ }:X_{r}^{\circ }\rightarrow X^{\circ }$
le morphisme étale qui s’en déduit par restriction à l’ouvert
$\unicode[STIX]{x1D70B}_{r}^{\circ }:X_{r}^{\circ }\rightarrow X^{\circ }$
le morphisme étale qui s’en déduit par restriction à l’ouvert
![]() $X^{\circ }$
et
$X^{\circ }$
et
![]() $j_{r}:X_{r}^{\circ }{\hookrightarrow}X_{r}$
l’immersion ouverte. L’hypothèse de modération assure que pour chaque
$j_{r}:X_{r}^{\circ }{\hookrightarrow}X_{r}$
l’immersion ouverte. L’hypothèse de modération assure que pour chaque
![]() $\mathscr{L}$
comme dans l’énoncé il existe un entier
$\mathscr{L}$
comme dans l’énoncé il existe un entier
![]() $r$
, premier à la caractéristique résiduelle de
$r$
, premier à la caractéristique résiduelle de
![]() $X$
, tel que
$X$
, tel que
![]() $\mathscr{L}_{r}:=\unicode[STIX]{x1D70B}_{r}^{\circ \star }\mathscr{L}$
soit un faisceau constant sur
$\mathscr{L}_{r}:=\unicode[STIX]{x1D70B}_{r}^{\circ \star }\mathscr{L}$
soit un faisceau constant sur
![]() $X_{r}^{\circ }$
, de fibre que nous notons
$X_{r}^{\circ }$
, de fibre que nous notons
![]() $L$
(droit).
$L$
(droit).

Le morphisme d’adjonction
![]() $\mathscr{L}\rightarrow \mathscr{L}^{\prime }:=\unicode[STIX]{x1D70B}_{r_{\star }}^{\circ }\mathscr{L}_{r}$
étant injectif de conoyau lisse et modéré le long de
$\mathscr{L}\rightarrow \mathscr{L}^{\prime }:=\unicode[STIX]{x1D70B}_{r_{\star }}^{\circ }\mathscr{L}_{r}$
étant injectif de conoyau lisse et modéré le long de
![]() $D$
, il suffit — par récurrence sur le degré cohomologique — d’établir la proposition pour le faisceau
$D$
, il suffit — par récurrence sur le degré cohomologique — d’établir la proposition pour le faisceau
![]() $\mathscr{L}^{\prime }$
. (Comparer avec [Th. finitude, A, 1.3.3] et 2.3.3.) Par transitivité des images directes, on a
$\mathscr{L}^{\prime }$
. (Comparer avec [Th. finitude, A, 1.3.3] et 2.3.3.) Par transitivité des images directes, on a
![]() $\mathtt{R}j_{\star }\mathscr{L}^{\prime }={\unicode[STIX]{x1D70B}_{r}}_{\star }\mathtt{R}{j_{r}}_{\star }\mathscr{L}_{r}$
. Puisque l’image directe par
$\mathtt{R}j_{\star }\mathscr{L}^{\prime }={\unicode[STIX]{x1D70B}_{r}}_{\star }\mathtt{R}{j_{r}}_{\star }\mathscr{L}_{r}$
. Puisque l’image directe par
![]() $\unicode[STIX]{x1D70B}_{r}$
transforme un faisceau constructible modéré le long de
$\unicode[STIX]{x1D70B}_{r}$
transforme un faisceau constructible modéré le long de
![]() $\mathfrak{D}_{r}$
en un faisceau constructible modéré le long de
$\mathfrak{D}_{r}$
en un faisceau constructible modéré le long de
![]() $\mathfrak{D}$
, il suffit de traiter le cas
$\mathfrak{D}$
, il suffit de traiter le cas
![]() $r=1$
, c’est-à-dire
$r=1$
, c’est-à-dire
![]() $\mathscr{L}$
constant. Cela résulte de la pureté cohomologique absolue, démontrée par O. Gabber (voir par exemple [STG XVI, 3.1.4]).
$\mathscr{L}$
constant. Cela résulte de la pureté cohomologique absolue, démontrée par O. Gabber (voir par exemple [STG XVI, 3.1.4]).
2.4.3 (i) : commutation au changement de base
La propreté cohomologique du morphisme fini
![]() ${\unicode[STIX]{x1D70B}_{r}}_{\star }$
nous permet, comme dans le paragraphe précédent, de nous ramener au cas particulier où le faisceau
${\unicode[STIX]{x1D70B}_{r}}_{\star }$
nous permet, comme dans le paragraphe précédent, de nous ramener au cas particulier où le faisceau
![]() $\mathscr{L}$
est constant : on veut montrer que le faisceau
$\mathscr{L}$
est constant : on veut montrer que le faisceau
![]() $\mathtt{R}^{c}j_{\star }L$
commute aux changements de base
$\mathtt{R}^{c}j_{\star }L$
commute aux changements de base
![]() $S^{\prime }\rightarrow S$
lorsque
$S^{\prime }\rightarrow S$
lorsque
![]() $L$
est constant, fini, de torsion inversible sur
$L$
est constant, fini, de torsion inversible sur
![]() $S$
. Cela résulte de [Th. finitude, A, 1.3.3 (i)].
$S$
. Cela résulte de [Th. finitude, A, 1.3.3 (i)].
2.4.4 (ii) : étude à l’infini, cas modéré
On démontre maintenant l’énoncé 2.4.1(ii) dans le cas modéré, en « passant à la limite sur
![]() $r$
». (Cette présentation, plus élégante que l’originale, nous a été proposée par O. Gabber.Footnote
6
)
$r$
». (Cette présentation, plus élégante que l’originale, nous a été proposée par O. Gabber.Footnote
6
)
Fixons un entier
![]() $c\geqslant 0$
. Le problème étant à nouveau local pour la topologie étale, on peut supposer
$c\geqslant 0$
. Le problème étant à nouveau local pour la topologie étale, on peut supposer
![]() $\overline{X}$
strictement local, d’exposant caractéristique
$\overline{X}$
strictement local, d’exposant caractéristique
![]() $p\geqslant 1$
. Soit
$p\geqslant 1$
. Soit
![]() $\overline{d}$
un point géométrique localisé en
$\overline{d}$
un point géométrique localisé en
![]() $d\in D:=X\setminus X^{\circ }$
, d’exposant caractéristique
$d\in D:=X\setminus X^{\circ }$
, d’exposant caractéristique
![]() $p_{d}$
divisant
$p_{d}$
divisant
![]() $p$
. (L’énoncé à démontrer est trivial si on se place en un point de
$p$
. (L’énoncé à démontrer est trivial si on se place en un point de
![]() $\overline{X}\setminus X$
ou de
$\overline{X}\setminus X$
ou de
![]() $X^{\circ }$
.) On veut montrer que l’action du groupe de Galois
$X^{\circ }$
.) On veut montrer que l’action du groupe de Galois
![]() $\unicode[STIX]{x1D70B}_{1}(d,\overline{d})$
sur
$\unicode[STIX]{x1D70B}_{1}(d,\overline{d})$
sur
![]() $\mathtt{H}^{c}(X_{(\overline{d})}^{\circ },\mathscr{L})$
— où
$\mathtt{H}^{c}(X_{(\overline{d})}^{\circ },\mathscr{L})$
— où
![]() $X_{(\overline{d})}^{\circ }$
est l’ouvert normal
$X_{(\overline{d})}^{\circ }$
est l’ouvert normal
![]() $X^{\circ }\times _{X}X_{(\overline{d})}$
de l’hensélisé strict en
$X^{\circ }\times _{X}X_{(\overline{d})}$
de l’hensélisé strict en
![]() $\overline{d}$
— se factorise à travers un quotient premier à
$\overline{d}$
— se factorise à travers un quotient premier à
![]() $p$
. Par pureté, les dévissages du paragraphe précédent montrent que ce groupe de cohomologie est isomorphe à
$p$
. Par pureté, les dévissages du paragraphe précédent montrent que ce groupe de cohomologie est isomorphe à
![]() $\mathtt{H}^{c}(\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ },\overline{\unicode[STIX]{x1D702}}),L)$
, où
$\mathtt{H}^{c}(\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ },\overline{\unicode[STIX]{x1D702}}),L)$
, où
![]() $L$
est la fibre de
$L$
est la fibre de
![]() $\mathscr{L}$
en un point générique géométrique
$\mathscr{L}$
en un point générique géométrique
![]() $\overline{\unicode[STIX]{x1D702}}$
de
$\overline{\unicode[STIX]{x1D702}}$
de
![]() $X_{(\overline{d})}^{\circ }$
localisé en un point
$X_{(\overline{d})}^{\circ }$
localisé en un point
![]() $\unicode[STIX]{x1D702}$
de
$\unicode[STIX]{x1D702}$
de
![]() $X_{(\overline{d})}^{\circ }$
, et
$X_{(\overline{d})}^{\circ }$
, et
![]() $\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ },\overline{\unicode[STIX]{x1D702}})$
est (non canoniquement) isomorphe à
$\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ },\overline{\unicode[STIX]{x1D702}})$
est (non canoniquement) isomorphe à
![]() $\widehat{\mathbb{Z}}^{(p_{d}^{\prime })}(1)^{b}$
, où
$\widehat{\mathbb{Z}}^{(p_{d}^{\prime })}(1)^{b}$
, où
![]() $b$
est le nombre de branches de
$b$
est le nombre de branches de
![]() $D$
en
$D$
en
![]() $\overline{d}$
. Le faisceau
$\overline{d}$
. Le faisceau
![]() $\mathscr{L}$
étant modéré sur
$\mathscr{L}$
étant modéré sur
![]() $\overline{X}$
, l’action du quotient
$\overline{X}$
, l’action du quotient
![]() $\unicode[STIX]{x1D70B}_{1}(X_{(d)}^{\circ },\overline{\unicode[STIX]{x1D702}})$
de
$\unicode[STIX]{x1D70B}_{1}(X_{(d)}^{\circ },\overline{\unicode[STIX]{x1D702}})$
de
![]() $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D702},\overline{\unicode[STIX]{x1D702}})$
sur
![]() $L$
se fait à travers un quotient d’ordre premier à
$L$
se fait à travers un quotient d’ordre premier à
![]() $p$
. La conclusion résulte alors du lemme ci-dessous, appliqué à la suite exacte déduite de
$p$
. La conclusion résulte alors du lemme ci-dessous, appliqué à la suite exacte déduite de
![]() $1\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{(\overline{d})}^{\circ })\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{(d)}^{\circ })\rightarrow \unicode[STIX]{x1D70B}_{1}(d,\overline{d})\rightarrow 1$
par le quotient caractéristique
$1\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{(\overline{d})}^{\circ })\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{(d)}^{\circ })\rightarrow \unicode[STIX]{x1D70B}_{1}(d,\overline{d})\rightarrow 1$
par le quotient caractéristique
![]() $\unicode[STIX]{x1D70B}_{1}(X^{\circ }(\overline{d})){\twoheadrightarrow}\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ })=\unicode[STIX]{x1D70B}_{1}(X_{(\overline{d})}^{\circ })/N$
, où
$\unicode[STIX]{x1D70B}_{1}(X^{\circ }(\overline{d})){\twoheadrightarrow}\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ })=\unicode[STIX]{x1D70B}_{1}(X_{(\overline{d})}^{\circ })/N$
, où
![]() $G$
est le groupe de Galois,
$G$
est le groupe de Galois,
![]() $A$
le groupe fondamental modéré
$A$
le groupe fondamental modéré
![]() $\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ })$
et enfin
$\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(X_{(\overline{d})}^{\circ })$
et enfin
![]() $\unicode[STIX]{x1D70B}$
le quotient
$\unicode[STIX]{x1D70B}$
le quotient
![]() $\unicode[STIX]{x1D70B}_{1}(X_{(d)}^{\circ })/N$
. Notons que les groupes d’inertie modérés en les points maximaux de
$\unicode[STIX]{x1D70B}_{1}(X_{(d)}^{\circ })/N$
. Notons que les groupes d’inertie modérés en les points maximaux de
![]() $D$
engendrent
$D$
engendrent
![]() $A$
et sont stables sous l’action naturelle de
$A$
et sont stables sous l’action naturelle de
![]() $G$
car les branches sont définies sur l’hensélisé (non strict)
$G$
car les branches sont définies sur l’hensélisé (non strict)
![]() $X_{(d)}^{\circ }$
.
$X_{(d)}^{\circ }$
.
Lemme. Soient
![]() $p$
un nombre premier,
$p$
un nombre premier,
![]() $n\bot p$
un entier,
$n\bot p$
un entier,
![]() $1\rightarrow A\rightarrow \unicode[STIX]{x1D70B}\rightarrow G\rightarrow 1$
une suite exacte de groupes profinis et
$1\rightarrow A\rightarrow \unicode[STIX]{x1D70B}\rightarrow G\rightarrow 1$
une suite exacte de groupes profinis et
![]() $L$
un
$L$
un
![]() $\mathbb{Z}/n\mathbb{Z}$
-module fini muni d’une action continue de
$\mathbb{Z}/n\mathbb{Z}$
-module fini muni d’une action continue de
![]() $\unicode[STIX]{x1D70B}$
se factorisant à travers un quotient premier à
$\unicode[STIX]{x1D70B}$
se factorisant à travers un quotient premier à
![]() $p$
. On suppose de plus le groupe
$p$
. On suppose de plus le groupe
![]() $A$
$A$
![]() $\text{ab}\acute{\text{e}}\text{lien}$
et produit fini, comme
$\text{ab}\acute{\text{e}}\text{lien}$
et produit fini, comme
![]() $G$
-module, de groupes procycliques sans torsion d’ordre premier à
$G$
-module, de groupes procycliques sans torsion d’ordre premier à
![]() $p$
. Alors, pour tout entier
$p$
. Alors, pour tout entier
![]() $c\geqslant 0$
, l’action de
$c\geqslant 0$
, l’action de
![]() $G$
sur
$G$
sur
![]() $\mathtt{H}^{c}(A,L)$
se factorise à travers
$\mathtt{H}^{c}(A,L)$
se factorise à travers
![]() $G_{\bot p}$
.
$G_{\bot p}$
.
Démonstration.
La décomposition
![]() $G$
-équivariante de
$G$
-équivariante de
![]() $A$
en produit, la suite spectrale de Hochschild-Serre et l’hypothèse
$A$
en produit, la suite spectrale de Hochschild-Serre et l’hypothèse
![]() $n\bot p$
— garantissant la stabilité par extension de la propriété à démontrer — nous ramènent immédiatement au cas particulier où
$n\bot p$
— garantissant la stabilité par extension de la propriété à démontrer — nous ramènent immédiatement au cas particulier où
![]() $A$
est procyclique ; géométriquement, cela revient à supposer qu’il n’y a qu’une branche (
$A$
est procyclique ; géométriquement, cela revient à supposer qu’il n’y a qu’une branche (
![]() $b=1$
avec les notations précédentes). Pour un tel
$b=1$
avec les notations précédentes). Pour un tel
![]() $A$
, il est bien connu que la cohomologie de
$A$
, il est bien connu que la cohomologie de
![]() $L$
est concentrée en degrés
$L$
est concentrée en degrés
![]() $\{0,1\}$
et
$\{0,1\}$
et
![]() $\mathtt{H}^{0}(A,L)$
(resp.
$\mathtt{H}^{0}(A,L)$
(resp.
![]() $\mathtt{H}^{1}(A,L(1))$
) sont respectivement les invariants et coïnvariants de
$\mathtt{H}^{1}(A,L(1))$
) sont respectivement les invariants et coïnvariants de ![]() . (Voir par exemple [STG XVII, § 1.2] pour une discussion de ces isomorphismes, indépendants du choix d’un progénérateur.) L’action de
. (Voir par exemple [STG XVII, § 1.2] pour une discussion de ces isomorphismes, indépendants du choix d’un progénérateur.) L’action de
![]() $\unicode[STIX]{x1D70B}$
sur
$\unicode[STIX]{x1D70B}$
sur
![]() $L$
se factorisant par un quotient d’ordre premier à
$L$
se factorisant par un quotient d’ordre premier à
![]() $p$
, il en est de même de l’action de
$p$
, il en est de même de l’action de
![]() $G$
sur les sous-quotients
$G$
sur les sous-quotients
![]() $\mathtt{H}^{0}(A,L)$
et
$\mathtt{H}^{0}(A,L)$
et
![]() $\mathtt{H}^{1}(A,L)$
de
$\mathtt{H}^{1}(A,L)$
de
![]() $L$
.◻
$L$
.◻
2.4.5 (ii) : cas unipotent
Comme précédemment, on peut supposer
![]() $\overline{X}$
strictement local et, par hypothèse,
$\overline{X}$
strictement local et, par hypothèse,
![]() $\mathscr{L}$
extension de faisceaux constants sur
$\mathscr{L}$
extension de faisceaux constants sur
![]() $X^{\circ }$
puis, par dévissage immédiat, constant et même isomorphe à
$X^{\circ }$
puis, par dévissage immédiat, constant et même isomorphe à
![]() $\mathbb{Z}/n\mathbb{Z}$
quitte à remplacer
$\mathbb{Z}/n\mathbb{Z}$
quitte à remplacer
![]() $n$
par un diviseur. Il s’agit donc de montrer la locale unipotence des faisceaux
$n$
par un diviseur. Il s’agit donc de montrer la locale unipotence des faisceaux
![]() $k_{!}\mathtt{R}^{c}j_{\star }\mathbb{Z}/n\mathbb{Z}$
, pour
$k_{!}\mathtt{R}^{c}j_{\star }\mathbb{Z}/n\mathbb{Z}$
, pour
![]() $n$
inversible sur
$n$
inversible sur
![]() $\overline{X}$
. Cela résulte immédiatement de la pureté cohomologique absolue [STG XVI, 3.1.4].
$\overline{X}$
. Cela résulte immédiatement de la pureté cohomologique absolue [STG XVI, 3.1.4].
Ceci achève la démonstration de la proposition 2.4.1. Nous souhaitons maintenant borner la taille des images directes par l’immersion ouverte
![]() $j$
. (L’étude des fibres de
$j$
. (L’étude des fibres de
![]() $k_{!}\mathtt{R}j_{\star }$
s’y ramène immédiatement.)
$k_{!}\mathtt{R}j_{\star }$
s’y ramène immédiatement.)
Proposition 2.4.6. Soit
![]() $c\geqslant 0$
un entier. Il existe une fonction
$c\geqslant 0$
un entier. Il existe une fonction
![]() $\unicode[STIX]{x1D711}_{c}:\mathbb{N}\rightarrow \mathbb{N}$
telle que pour toute paire régulière et strictement locale
$\unicode[STIX]{x1D711}_{c}:\mathbb{N}\rightarrow \mathbb{N}$
telle que pour toute paire régulière et strictement locale
![]() $(X,X^{\circ })$
, tout entier
$(X,X^{\circ })$
, tout entier
![]() $n\geqslant 1$
inversible sur
$n\geqslant 1$
inversible sur
![]() $X$
et tout faisceau lisse
$X$
et tout faisceau lisse
![]() $\mathscr{L}$
de
$\mathscr{L}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X^{\circ }$
constructible et modéré le long de
$X^{\circ }$
constructible et modéré le long de
![]() $X\setminus X^{\circ }=\sum _{i=1}^{b}D_{i}$
le groupe de cohomologie
$X\setminus X^{\circ }=\sum _{i=1}^{b}D_{i}$
le groupe de cohomologie
![]() $\mathtt{H}^{c}(X^{\circ },\mathscr{L})$
soit
$\mathtt{H}^{c}(X^{\circ },\mathscr{L})$
soit
![]() $\unicode[STIX]{x1D711}_{c}(b)$
-extension ponctuelle de sous-quotients de
$\unicode[STIX]{x1D711}_{c}(b)$
-extension ponctuelle de sous-quotients de
![]() $\mathscr{L}$
, où
$\mathscr{L}$
, où
![]() $b$
désigne le nombre de branches de
$b$
désigne le nombre de branches de
![]() $D:=X\setminus X^{\circ }$
.
$D:=X\setminus X^{\circ }$
.
« extension ponctuelle » : cf. 1.7.
Démonstration.
Reprenons les notations du paragraphe 2.4.2. Soient
![]() $r$
tel que
$r$
tel que
![]() $\unicode[STIX]{x1D70B}_{r}^{\circ \star }\mathscr{L}$
soit constant, de fibre
$\unicode[STIX]{x1D70B}_{r}^{\circ \star }\mathscr{L}$
soit constant, de fibre
![]() $L$
, et
$L$
, et
![]() $\boldsymbol{\unicode[STIX]{x1D707}}_{r,X}$
le groupe cyclique d’ordre
$\boldsymbol{\unicode[STIX]{x1D707}}_{r,X}$
le groupe cyclique d’ordre
![]() $r$
des racines de l’unité d’ordre divisant
$r$
des racines de l’unité d’ordre divisant
![]() $r$
dans
$r$
dans
![]() $\unicode[STIX]{x1D6E4}(X,\mathscr{O}_{X})$
. Le revêtement
$\unicode[STIX]{x1D6E4}(X,\mathscr{O}_{X})$
. Le revêtement
![]() $X_{r}^{\circ }\rightarrow X^{\circ }$
étant galoisien de groupe
$X_{r}^{\circ }\rightarrow X^{\circ }$
étant galoisien de groupe
![]() $\boldsymbol{\unicode[STIX]{x1D707}}_{r,X}^{b}$
, le complexe
$\boldsymbol{\unicode[STIX]{x1D707}}_{r,X}^{b}$
, le complexe
![]() $\mathtt{R}\unicode[STIX]{x1D6E4}(X^{\circ },\mathscr{L})$
se réécrit
$\mathtt{R}\unicode[STIX]{x1D6E4}(X^{\circ },\mathscr{L})$
se réécrit
![]() $\mathtt{R}\unicode[STIX]{x1D6E4}(\boldsymbol{\unicode[STIX]{x1D707}}_{r,X}^{b},\mathtt{R}\unicode[STIX]{x1D6E4}(X_{r}^{\circ },L))$
. Rappelons [Reference SerreSer68, VIII.§ 4] que si
$\mathtt{R}\unicode[STIX]{x1D6E4}(\boldsymbol{\unicode[STIX]{x1D707}}_{r,X}^{b},\mathtt{R}\unicode[STIX]{x1D6E4}(X_{r}^{\circ },L))$
. Rappelons [Reference SerreSer68, VIII.§ 4] que si
![]() $G=\langle \unicode[STIX]{x1D70E}\rangle$
est un groupe cyclique et
$G=\langle \unicode[STIX]{x1D70E}\rangle$
est un groupe cyclique et
![]() $M$
un
$M$
un
![]() $G$
-module, la cohomologie de
$G$
-module, la cohomologie de
![]() $G$
à valeurs dans
$G$
à valeurs dans
![]() $M$
est représentée par le complexe périodique
$M$
est représentée par le complexe périodique
où
![]() $t=\sum _{g\in G}g$
, et le premier
$t=\sum _{g\in G}g$
, et le premier
![]() $M$
est placé en degré
$M$
est placé en degré
![]() $0$
. Cette description, uniforme en
$0$
. Cette description, uniforme en
![]() $r$
, nous ramène au cas particulier où
$r$
, nous ramène au cas particulier où
![]() $r=1$
, c’est-à-dire où
$r=1$
, c’est-à-dire où
![]() $\mathscr{L}$
est constant, que l’on peut alors supposer isomorphe à
$\mathscr{L}$
est constant, que l’on peut alors supposer isomorphe à
![]() $\mathbb{Z}/n\mathbb{Z}$
. Dans ce cas, la conclusion résulte de la pureté :
$\mathbb{Z}/n\mathbb{Z}$
. Dans ce cas, la conclusion résulte de la pureté :
![]() $\displaystyle \mathtt{H}^{c}(X^{\circ },\mathbb{Z}/n\mathbb{Z})=\bigwedge ^{c}(\mathbb{Z}^{b}/n\mathbb{Z}^{b})$
.
$\displaystyle \mathtt{H}^{c}(X^{\circ },\mathbb{Z}/n\mathbb{Z})=\bigwedge ^{c}(\mathbb{Z}^{b}/n\mathbb{Z}^{b})$
.
Alternativement, on aurait pu passer à la limite sur
![]() $r$
et utiliser la description de
$r$
et utiliser la description de
![]() $\mathtt{H}^{c}(A,L)$
faite en 2.4.4. Ceci permet d’ailleurs d’établir immédiatement l’annulation
$\mathtt{H}^{c}(A,L)$
faite en 2.4.4. Ceci permet d’ailleurs d’établir immédiatement l’annulation
![]() $\mathtt{H}^{c}(X^{\circ },\mathscr{L})=0$
pour
$\mathtt{H}^{c}(X^{\circ },\mathscr{L})=0$
pour
![]() $c>b$
.◻
$c>b$
.◻
3 Image directe par un morphisme propre
Nous allons montrer que la propriété d’une famille d’être constructible et modérée (resp. localement unipotente) pour la topologie des altérations (1.6.5, [STG II, 2.3.3]) est stable par image directe propre. Cette stabilité est mise en défaut si l’on considère la topologie finie au lieu de la topologie des altérations (voir 3.2).
Ces résultats sont connus de longue date d’Ofer Gabber.
3.1 Énoncés
Théorème 3.1.1. (d’uniformité propre). Soient
![]() $S$
un schéma nœthérien quasi-excellent,
$S$
un schéma nœthérien quasi-excellent,
![]() $f:X\rightarrow S$
un morphisme
$f:X\rightarrow S$
un morphisme
![]() $\text{propre}$
,
$\text{propre}$
,
![]() $\unicode[STIX]{x1D6FC}:X^{\prime }{\twoheadrightarrow}X$
une altération et
$\unicode[STIX]{x1D6FC}:X^{\prime }{\twoheadrightarrow}X$
une altération et
![]() $\mathfrak{X}$
une stratification de
$\mathfrak{X}$
une stratification de
![]() $X^{\prime }$
. Il existe une altération
$X^{\prime }$
. Il existe une altération
![]() $\unicode[STIX]{x1D6FD}:S^{\prime }{\twoheadrightarrow}S$
et une stratification
$\unicode[STIX]{x1D6FD}:S^{\prime }{\twoheadrightarrow}S$
et une stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S^{\prime }$
telles que pour tout entier
$S^{\prime }$
telles que pour tout entier
![]() $n\geqslant 1$
, tout
$n\geqslant 1$
, tout
![]() $i\geqslant 0$
et tout faisceau
$i\geqslant 0$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X[1/n]$
dont l’image inverse
$X[1/n]$
dont l’image inverse
![]() $\unicode[STIX]{x1D6FC}[1/n]^{\star }\mathscr{F}$
est constructible et modérée (resp. constructible et localement unipotente) le long de
$\unicode[STIX]{x1D6FC}[1/n]^{\star }\mathscr{F}$
est constructible et modérée (resp. constructible et localement unipotente) le long de
![]() $\mathfrak{X}[1/n]$
(au sens de 1.1.3, 1.3.1, 1.2.1) alors chaque
$\mathfrak{X}[1/n]$
(au sens de 1.1.3, 1.3.1, 1.2.1) alors chaque
![]() $\unicode[STIX]{x1D6FD}[1/n]^{\star }\mathtt{R}^{i}f[1/n]_{\star }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
$\unicode[STIX]{x1D6FD}[1/n]^{\star }\mathtt{R}^{i}f[1/n]_{\star }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{S}[1/n]$
.
$\mathfrak{S}[1/n]$
.

De plus, il existe un entier
![]() $N$
, dépendant uniquement du triplet
$N$
, dépendant uniquement du triplet
![]() $(f,\unicode[STIX]{x1D6FC},\mathfrak{X})$
, tel que chaque
$(f,\unicode[STIX]{x1D6FC},\mathfrak{X})$
, tel que chaque
![]() $\mathtt{R}^{i}f[1/n]_{\star }\mathscr{F}$
comme ci-dessus soit
$\mathtt{R}^{i}f[1/n]_{\star }\mathscr{F}$
comme ci-dessus soit
![]() $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
![]() $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
![]() $f$
(au sens de 1.7).
$f$
(au sens de 1.7).
3.1.2
Tout faisceau abélien constructible sur un schéma nœthérien étant modéré par un morphisme fini surjectif (cf. 1.6.7), on peut voir l’énoncé 3.1.1 comme une amélioration du théorème classique de constructibilité des images directes par un morphisme propre [SGA 4 XIV, 1.1], du moins lorsque l’on suppose la base nœthérienne quasi-excellente. (L’hypothèse d’excellence est d’ailleurs superflue ; voir 3.5.5 pour une esquisse d’argument, dont les détails sont laissés au lecteur.)
Il est également naturel d’exprimer le théorème précédent sous forme « dérivée ».
3.1.3
Soient
![]() $\unicode[STIX]{x1D6FC},\mathfrak{X}$
comme ci-dessus et
$\unicode[STIX]{x1D6FC},\mathfrak{X}$
comme ci-dessus et
![]() $n$
inversible sur
$n$
inversible sur
![]() $X$
. Notons
$X$
. Notons
![]() $D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/n\mathbb{Z})$
la sous-catégorie pleine triangulée de
$D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/n\mathbb{Z})$
la sous-catégorie pleine triangulée de
![]() $D_{c}^{b}(X,\mathbb{Z}/n\mathbb{Z})$
des complexes à cohomologie constructible le long de
$D_{c}^{b}(X,\mathbb{Z}/n\mathbb{Z})$
des complexes à cohomologie constructible le long de
![]() $\mathfrak{X}$
et modérée par
$\mathfrak{X}$
et modérée par
![]() $\unicode[STIX]{x1D6FC}$
. Il existe
$\unicode[STIX]{x1D6FC}$
. Il existe
![]() $\unicode[STIX]{x1D6FD},\mathfrak{S}$
tels que
$\unicode[STIX]{x1D6FD},\mathfrak{S}$
tels que
![]() $\mathtt{R}f_{\star }:D_{c}^{b}(X,\mathbb{Z}/n\mathbb{Z})\rightarrow D_{c}^{b}(S,\mathbb{Z}/n\mathbb{Z})$
induise un foncteur entre les sous-catégories
$\mathtt{R}f_{\star }:D_{c}^{b}(X,\mathbb{Z}/n\mathbb{Z})\rightarrow D_{c}^{b}(S,\mathbb{Z}/n\mathbb{Z})$
induise un foncteur entre les sous-catégories
![]() $D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/n\mathbb{Z})\rightarrow D_{\unicode[STIX]{x1D6FD},\mathfrak{S}}^{b\;\text{mod}}(S,\mathbb{Z}/n\mathbb{Z})$
. (Comparer avec [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, § 2.2.10–17].) Soit maintenant
$D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/n\mathbb{Z})\rightarrow D_{\unicode[STIX]{x1D6FD},\mathfrak{S}}^{b\;\text{mod}}(S,\mathbb{Z}/n\mathbb{Z})$
. (Comparer avec [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, § 2.2.10–17].) Soit maintenant
![]() $\text{}\underline{n}=(n_{i})_{i\in I}$
une famille d’entiers. Notons
$\text{}\underline{n}=(n_{i})_{i\in I}$
une famille d’entiers. Notons
![]() $D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})$
la catégorie triangulée produit
$D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})$
la catégorie triangulée produit
![]() $\prod _{i}D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X[1/n_{i}],\mathbb{Z}/n_{i}\mathbb{Z})$
et
$\prod _{i}D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X[1/n_{i}],\mathbb{Z}/n_{i}\mathbb{Z})$
et
![]() $D_{c}^{b\;\text{mod}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})_{h}$
la colimite sur
$D_{c}^{b\;\text{mod}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})_{h}$
la colimite sur
![]() $(\unicode[STIX]{x1D6FC},\mathfrak{X})$
des catégories triangulées
$(\unicode[STIX]{x1D6FC},\mathfrak{X})$
des catégories triangulées
![]() $D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})$
.
$D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{mod}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})$
.
Si
![]() $f:X\rightarrow S$
est un morphisme propre, le théorème ci-dessus affirme que les foncteurs
$f:X\rightarrow S$
est un morphisme propre, le théorème ci-dessus affirme que les foncteurs
![]() $\mathtt{R}f_{\star }:D_{c}^{b}(X[1/n_{i}],\mathbb{Z}/n_{i}\mathbb{Z})\rightarrow D_{c}^{b}(S[1/n_{i}],\mathbb{Z}/n_{i}\mathbb{Z})$
induisent un foncteur
$\mathtt{R}f_{\star }:D_{c}^{b}(X[1/n_{i}],\mathbb{Z}/n_{i}\mathbb{Z})\rightarrow D_{c}^{b}(S[1/n_{i}],\mathbb{Z}/n_{i}\mathbb{Z})$
induisent un foncteur
Mêmes énoncés pour les catégories
![]() $D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{unip}}(X,\mathbb{Z}/n\mathbb{Z})$
et
$D_{\unicode[STIX]{x1D6FC},\mathfrak{X}}^{b\;\text{unip}}(X,\mathbb{Z}/n\mathbb{Z})$
et
![]() $D_{c}^{b\;\text{unip}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})_{h}$
, définies de manière évidente.
$D_{c}^{b\;\text{unip}}(X,\mathbb{Z}/\text{}\underline{n}\mathbb{Z})_{h}$
, définies de manière évidente.
Ces énoncés sont non triviaux même lorsque tous les
![]() $n_{i}$
sont égaux : si l’on ne considère par exemple que des
$n_{i}$
sont égaux : si l’on ne considère par exemple que des
![]() $\mathbb{F}_{\ell }$
-faisceaux dans le théorème 3.1.1 (pour un
$\mathbb{F}_{\ell }$
-faisceaux dans le théorème 3.1.1 (pour un
![]() $\ell$
fixé), la conclusion ne résulte pas directement, pour
$\ell$
fixé), la conclusion ne résulte pas directement, pour
![]() $I$
de cardinal
$I$
de cardinal
![]() ${>}1$
, du théorème de constructibilité usuel et fixer un
${>}1$
, du théorème de constructibilité usuel et fixer un
![]() $\ell$
ne semble d’ailleurs pas simplifier la démonstration. Notons cependant que si les entiers
$\ell$
ne semble d’ailleurs pas simplifier la démonstration. Notons cependant que si les entiers
![]() $n_{i}$
sont des puissances d’un même nombre premier
$n_{i}$
sont des puissances d’un même nombre premier
![]() $\ell$
, la généralité apportée par l’ensemble d’indices
$\ell$
, la généralité apportée par l’ensemble d’indices
![]() $I$
est illusoire : un
$I$
est illusoire : un
![]() $\mathbb{Z}/\ell ^{r}\mathbb{Z}$
-faisceau constructible
$\mathbb{Z}/\ell ^{r}\mathbb{Z}$
-faisceau constructible
![]() $\mathscr{F}$
est muni d’une filtration
$\mathscr{F}$
est muni d’une filtration
![]() $\mathscr{F}_{\unicode[STIX]{x1D6FC}}:=\ell ^{\unicode[STIX]{x1D6FC}}\mathscr{F}$
de gradués des
$\mathscr{F}_{\unicode[STIX]{x1D6FC}}:=\ell ^{\unicode[STIX]{x1D6FC}}\mathscr{F}$
de gradués des
![]() $\mathbb{F}_{\ell }$
-faisceaux constructibles, lisses (resp. modérés, localement unipotents) si et seulement si il en est ainsi de
$\mathbb{F}_{\ell }$
-faisceaux constructibles, lisses (resp. modérés, localement unipotents) si et seulement si il en est ainsi de
![]() $\mathscr{F}$
. (Si
$\mathscr{F}$
. (Si
![]() $\mathscr{F}$
est même plat, les gradués non nuls sont isomorphes à
$\mathscr{F}$
est même plat, les gradués non nuls sont isomorphes à
![]() $\mathscr{F}/\ell \mathscr{F}$
.)
$\mathscr{F}/\ell \mathscr{F}$
.)
Remarque 3.1.4. Soient
![]() $X$
un schéma propre et lisse sur un corps algébriquement clos
$X$
un schéma propre et lisse sur un corps algébriquement clos
![]() $k$
de caractéristique
$k$
de caractéristique
![]() $p\geqslant 0$
,
$p\geqslant 0$
,
![]() $D$
un diviseur à croisements normaux et
$D$
un diviseur à croisements normaux et
![]() $U$
l’ouvert complémentaire. Il résulte du théorème précédent qu’il existe une constante
$U$
l’ouvert complémentaire. Il résulte du théorème précédent qu’il existe une constante
![]() $C_{X,D}$
telle que pour tout
$C_{X,D}$
telle que pour tout
![]() $\ell \neq p$
et tout
$\ell \neq p$
et tout
![]() $\mathbb{F}_{\ell }$
-faisceau lisse
$\mathbb{F}_{\ell }$
-faisceau lisse
![]() $\mathscr{L}$
sur
$\mathscr{L}$
sur
![]() $U$
, modéré le long de
$U$
, modéré le long de
![]() $D$
, on ait
$D$
, on ait
![]() $h_{c}^{i}(U,\mathscr{L})\leqslant C_{X,D}\cdot \text{rang}(\mathscr{L})$
. Comme l’a expliqué Claude Sabbah à l’auteur, on peut en donner la démonstration suivante lorsque
$h_{c}^{i}(U,\mathscr{L})\leqslant C_{X,D}\cdot \text{rang}(\mathscr{L})$
. Comme l’a expliqué Claude Sabbah à l’auteur, on peut en donner la démonstration suivante lorsque
![]() $k$
est le corps
$k$
est le corps
![]() $\mathbb{C}$
de nombres complexes. Soit
$\mathbb{C}$
de nombres complexes. Soit
![]() $T$
un voisinage tubulaire ouvert de
$T$
un voisinage tubulaire ouvert de
![]() $D(\mathbb{C})$
tel que l’inclusion du compact
$D(\mathbb{C})$
tel que l’inclusion du compact
![]() $K=X(\mathbb{C})-T$
dans
$K=X(\mathbb{C})-T$
dans
![]() $U(\mathbb{C})$
soit une équivalence d’homotopie ; le groupe de cohomologie
$U(\mathbb{C})$
soit une équivalence d’homotopie ; le groupe de cohomologie
![]() $\mathtt{H}_{\text{Betti},c}^{i}(U(\mathbb{C}),\mathscr{L})$
est donc isomorphe à
$\mathtt{H}_{\text{Betti},c}^{i}(U(\mathbb{C}),\mathscr{L})$
est donc isomorphe à
![]() $\mathtt{H}_{\text{Betti},c}^{i}(K,\mathscr{L})$
. Par compacité, il existe un recouvrement fini
$\mathtt{H}_{\text{Betti},c}^{i}(K,\mathscr{L})$
. Par compacité, il existe un recouvrement fini
![]() $V_{i}$
de
$V_{i}$
de
![]() $K$
par des ouverts simplement connexes. Il en résulte que la cohomologie de
$K$
par des ouverts simplement connexes. Il en résulte que la cohomologie de
![]() $U(\mathbb{C})$
à valeurs dans
$U(\mathbb{C})$
à valeurs dans
![]() $\mathscr{L}$
est l’aboutissement d’une suite spectrale dont les objets de la première « page » ne dépendent que des
$\mathscr{L}$
est l’aboutissement d’une suite spectrale dont les objets de la première « page » ne dépendent que des
![]() $V_{i}$
et du rang de
$V_{i}$
et du rang de
![]() $\mathscr{L}$
. On conclut par le théorème de comparaison Betti-étale d’Artin–Grothendieck. Il serait sans doute intéressant d’adapter cet argument au cas d’un corps quelconque à l’aide d’un voisinage tubulaire adéquat.
$\mathscr{L}$
. On conclut par le théorème de comparaison Betti-étale d’Artin–Grothendieck. Il serait sans doute intéressant d’adapter cet argument au cas d’un corps quelconque à l’aide d’un voisinage tubulaire adéquat.
3.2 Un exemple
L’objet de cette section est de montrer que l’image directe d’une famille de faisceaux constants constructibles (donc, a fortiori, constructible et modérée pour la topologie grossière) n’est pas nécessairement modérée pour la topologie finie. Il est pour cela nécessaire de considérer une base de dimension
![]() ${>}1$
. On commence par rappeler une construction exprimant un groupe de monodromie locale, en dimension
${>}1$
. On commence par rappeler une construction exprimant un groupe de monodromie locale, en dimension
![]() $2$
, comme un groupe de monodromie globale en dimension
$2$
, comme un groupe de monodromie globale en dimension
![]() $1$
. (Ce résultat est bien connu ; cf. par exemple [Reference Kato and SaitoKS13, 2.6.3.1].) On rappelle ensuite un résultat de Igusa garantissant l’existence de familles à un paramètre à grosse monodromie.
$1$
. (Ce résultat est bien connu ; cf. par exemple [Reference Kato and SaitoKS13, 2.6.3.1].) On rappelle ensuite un résultat de Igusa garantissant l’existence de familles à un paramètre à grosse monodromie.
3.2.1
Soient
![]() $k$
un corps algébriquement clos,
$k$
un corps algébriquement clos,
![]() $U_{0}$
un ouvert de
$U_{0}$
un ouvert de
![]() $X_{0}=\mathbf{P}_{k}^{1}$
et
$X_{0}=\mathbf{P}_{k}^{1}$
et
![]() $X=\mathbf{A}_{k}^{2}$
. On considère l’application rationnelle
$X=\mathbf{A}_{k}^{2}$
. On considère l’application rationnelle
![]() $X{\dashrightarrow}X_{0}$
,
$X{\dashrightarrow}X_{0}$
,
![]() $(u,v)\mapsto t=u/v$
et l’on note
$(u,v)\mapsto t=u/v$
et l’on note
![]() $U\subseteq X$
l’ouvert complémentaire des droites
$U\subseteq X$
l’ouvert complémentaire des droites
![]() $u=\unicode[STIX]{x1D706}v$
pour
$u=\unicode[STIX]{x1D706}v$
pour
![]() $\unicode[STIX]{x1D706}\in X_{0}-U_{0}$
. Notons
$\unicode[STIX]{x1D706}\in X_{0}-U_{0}$
. Notons
![]() $O\in X$
l’origine,
$O\in X$
l’origine,
![]() $X_{(O)}$
l’hensélisé (strict) et
$X_{(O)}$
l’hensélisé (strict) et
![]() $U_{(O)}$
le produit fibré
$U_{(O)}$
le produit fibré
![]() $X_{(O)}\times _{X}U$
. Le morphisme
$X_{(O)}\times _{X}U$
. Le morphisme
![]() $U\rightarrow U_{0}$
induit un morphisme entre les groupes fondamentaux, de même que
$U\rightarrow U_{0}$
induit un morphisme entre les groupes fondamentaux, de même que
![]() $U_{(O)}\rightarrow U$
. Par composition, on en déduit un morphisme
$U_{(O)}\rightarrow U$
. Par composition, on en déduit un morphisme
![]() $\unicode[STIX]{x1D70B}_{1}(U_{(O)})\rightarrow \unicode[STIX]{x1D70B}_{1}(U_{0})$
; nous allons voir que ce dernier morphisme est surjectif. (La surjectivité de
$\unicode[STIX]{x1D70B}_{1}(U_{(O)})\rightarrow \unicode[STIX]{x1D70B}_{1}(U_{0})$
; nous allons voir que ce dernier morphisme est surjectif. (La surjectivité de
![]() $\unicode[STIX]{x1D70B}_{1}(U)\rightarrow \unicode[STIX]{x1D70B}_{1}(U_{0})$
est quant à elle triviale,
$\unicode[STIX]{x1D70B}_{1}(U)\rightarrow \unicode[STIX]{x1D70B}_{1}(U_{0})$
est quant à elle triviale,
![]() $U\rightarrow U_{0}$
ayant une section.)
$U\rightarrow U_{0}$
ayant une section.)
Soit
![]() $V_{0}$
un revêtement fini étale connexe de
$V_{0}$
un revêtement fini étale connexe de
![]() $U_{0}$
; on veut montrer que le produit fibré
$U_{0}$
; on veut montrer que le produit fibré
![]() $V_{0}\times _{U_{0}}U_{(O)}$
est également connexe. Notons
$V_{0}\times _{U_{0}}U_{(O)}$
est également connexe. Notons
![]() $Y_{0}$
la normalisation de
$Y_{0}$
la normalisation de
![]() $X_{0}$
dans
$X_{0}$
dans
![]() $V_{0}$
et
$V_{0}$
et
![]() $Y$
celle de
$Y$
celle de
![]() $X$
dans l’image inverse
$X$
dans l’image inverse
![]() $V:=V_{0}\times _{U_{0}}U$
. Montrons que la fibre de
$V:=V_{0}\times _{U_{0}}U$
. Montrons que la fibre de
![]() $Y\rightarrow X$
au-dessus de l’origine
$Y\rightarrow X$
au-dessus de l’origine
![]() $O$
est connexe, c’est-à-dire est un point. Soit
$O$
est connexe, c’est-à-dire est un point. Soit
![]() $X^{\prime }$
l’éclatement de
$X^{\prime }$
l’éclatement de
![]() $X$
en l’origine ; c’est un fibré en
$X$
en l’origine ; c’est un fibré en
![]() $\mathbf{A}^{1}$
sur
$\mathbf{A}^{1}$
sur
![]() $X_{0}$
. Il en est donc de même du produit fibré
$X_{0}$
. Il en est donc de même du produit fibré
![]() $Y^{\prime }:=X^{\prime }\times _{X_{0}}Y_{0}$
sur
$Y^{\prime }:=X^{\prime }\times _{X_{0}}Y_{0}$
sur
![]() $Y_{0}$
. De la normalité de
$Y_{0}$
. De la normalité de
![]() $Y^{\prime }$
, donc de
$Y^{\prime }$
, donc de
![]() $\mathscr{O}(Y^{\prime })$
, et de l’égalité
$\mathscr{O}(Y^{\prime })$
, et de l’égalité
![]() $Y_{U}^{\prime }=V$
, on tire que le morphisme
$Y_{U}^{\prime }=V$
, on tire que le morphisme
![]() $Y\rightarrow X$
est la factorisation de Stein du morphisme
$Y\rightarrow X$
est la factorisation de Stein du morphisme
![]() $Y^{\prime }\rightarrow X$
. La fibre de
$Y^{\prime }\rightarrow X$
. La fibre de
![]() $Y^{\prime }\rightarrow X$
au-dessus de l’origine étant
$Y^{\prime }\rightarrow X$
au-dessus de l’origine étant
![]() $Y_{0}$
, donc connexe, il en est de même de celle de
$Y_{0}$
, donc connexe, il en est de même de celle de
![]() $Y\rightarrow X$
.Footnote
7
$Y\rightarrow X$
.Footnote
7

3.2.2
Soient maintenant
![]() $p$
un nombre premier impair,
$p$
un nombre premier impair,
![]() $k=\mathbb{F}_{p}$
,
$k=\mathbb{F}_{p}$
,
![]() $g\geqslant 1$
et
$g\geqslant 1$
et
![]() $f\in k[x]$
un polynôme de degré
$f\in k[x]$
un polynôme de degré
![]() $2g$
sans facteur carré. Notons
$2g$
sans facteur carré. Notons
![]() $U_{0}$
l’ouvert
$U_{0}$
l’ouvert
![]() $\text{Spec}(k[t][f(t)^{-1}])$
de
$\text{Spec}(k[t][f(t)^{-1}])$
de
![]() $\mathbf{A}_{k}^{1}$
et
$\mathbf{A}_{k}^{1}$
et
![]() $\unicode[STIX]{x1D70B}_{U_{0}}:\mathscr{C}\rightarrow U_{0}$
la courbe projective lisse d’équation affine
$\unicode[STIX]{x1D70B}_{U_{0}}:\mathscr{C}\rightarrow U_{0}$
la courbe projective lisse d’équation affine
![]() $y^{2}=f(x)(t-x)$
. Pour chaque nombre premier impair
$y^{2}=f(x)(t-x)$
. Pour chaque nombre premier impair
![]() $\ell \neq p$
, notons
$\ell \neq p$
, notons
![]() $\mathscr{F}_{\ell }$
le
$\mathscr{F}_{\ell }$
le
![]() $\mathbb{F}_{\ell }$
-faisceau lisse
$\mathbb{F}_{\ell }$
-faisceau lisse
![]() $\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{U_{0}\star }\mathbb{F}_{\ell }$
sur
$\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{U_{0}\star }\mathbb{F}_{\ell }$
sur
![]() $U_{0}$
. D’après [Reference IgusaIgu59] lorsque
$U_{0}$
. D’après [Reference IgusaIgu59] lorsque
![]() $g=1$
et [Reference YuYu95] en général, le groupe de monodromie géométrique de
$g=1$
et [Reference YuYu95] en général, le groupe de monodromie géométrique de
![]() $\mathscr{F}_{\ell }$
est tout le groupe symplectique
$\mathscr{F}_{\ell }$
est tout le groupe symplectique
![]() $\text{Sp}(2g,\mathbb{F}_{\ell })$
. Rappelons rapidement un argument possible : le prolongement par zéro de
$\text{Sp}(2g,\mathbb{F}_{\ell })$
. Rappelons rapidement un argument possible : le prolongement par zéro de
![]() $\mathscr{F}_{\ell }$
à
$\mathscr{F}_{\ell }$
à
![]() $\mathbf{A}_{k}^{1}$
étant convolution additive de deux faisceaux de Kummer (quadratiques) explicites (voir [Reference Katz and SarnakKS99, 10.1.17]), les résultats généraux de [Reference KatzKat88, ch. 8] entraînent que le faisceau
$\mathbf{A}_{k}^{1}$
étant convolution additive de deux faisceaux de Kummer (quadratiques) explicites (voir [Reference Katz and SarnakKS99, 10.1.17]), les résultats généraux de [Reference KatzKat88, ch. 8] entraînent que le faisceau
![]() $\mathscr{F}_{\ell }$
est « Fourier-irréductible » au sens d’op. cit. La conclusion résulte alors de la théorie de Picard–Lefschetz — la monodromie est engendrée par des transvections — et d’un théorème de théorie des groupes [Reference Zalesskiĭ and SerëžkinZS76]. (Voir aussi [Reference Katz and SarnakKS99, p. 293–300] ainsi que [Reference DeligneDel74a, 5.11] pour des variantes
$\mathscr{F}_{\ell }$
est « Fourier-irréductible » au sens d’op. cit. La conclusion résulte alors de la théorie de Picard–Lefschetz — la monodromie est engendrée par des transvections — et d’un théorème de théorie des groupes [Reference Zalesskiĭ and SerëžkinZS76]. (Voir aussi [Reference Katz and SarnakKS99, p. 293–300] ainsi que [Reference DeligneDel74a, 5.11] pour des variantes
![]() $\ell$
-adiques.)
$\ell$
-adiques.)
3.2.3
Soit
![]() $U$
l’ouvert de
$U$
l’ouvert de
![]() $X=\mathbf{A}_{k}^{2}$
défini à partir de
$X=\mathbf{A}_{k}^{2}$
défini à partir de
![]() $U_{0}$
comme en 3.2.1. On étend la courbe
$U_{0}$
comme en 3.2.1. On étend la courbe
![]() $\unicode[STIX]{x1D70B}_{U}:=\unicode[STIX]{x1D70B}_{U_{0}}\times _{U_{0}}U$
en une courbe propre
$\unicode[STIX]{x1D70B}_{U}:=\unicode[STIX]{x1D70B}_{U_{0}}\times _{U_{0}}U$
en une courbe propre
![]() $\unicode[STIX]{x1D70B}_{X}$
au-dessus de
$\unicode[STIX]{x1D70B}_{X}$
au-dessus de
![]() $X$
par normalisation, en voyant
$X$
par normalisation, en voyant
![]() $\mathscr{C}\times _{U_{0}}U$
comme un revêtement double de
$\mathscr{C}\times _{U_{0}}U$
comme un revêtement double de
![]() $\mathbf{P}_{U}^{1}$
. Pour chaque
$\mathbf{P}_{U}^{1}$
. Pour chaque
![]() $\ell \neq p$
impair, la monodromie locale en l’origine
$\ell \neq p$
impair, la monodromie locale en l’origine
![]() $O\in X$
du faisceau lisse
$O\in X$
du faisceau lisse
![]() $\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{U\star }\mathbb{F}_{\ell }$
sur
$\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{U\star }\mathbb{F}_{\ell }$
sur
![]() $U$
est, d’après les résultats des deux paragraphes précédents, le groupe
$U$
est, d’après les résultats des deux paragraphes précédents, le groupe
![]() $\text{Sp}(2g,\mathbb{F}_{\ell })$
. RappelonsFootnote
8
que son cardinal est le produit
$\text{Sp}(2g,\mathbb{F}_{\ell })$
. RappelonsFootnote
8
que son cardinal est le produit
![]() $\ell ^{g^{2}}\prod _{1}^{g}(\ell ^{2i}-1)$
. Il en résulte que lorsqu’une puissance
$\ell ^{g^{2}}\prod _{1}^{g}(\ell ^{2i}-1)$
. Il en résulte que lorsqu’une puissance
![]() $p^{r}$
de
$p^{r}$
de
![]() $p$
divise
$p$
divise
![]() $\ell -1$
— ce qui se produit pour une infinité de nombres premiers
$\ell -1$
— ce qui se produit pour une infinité de nombres premiers
![]() $\ell$
— les
$\ell$
— les
![]() $p$
-Sylow de la monodromie locale en l’origine sont de cardinal au moins
$p$
-Sylow de la monodromie locale en l’origine sont de cardinal au moins
![]() $p^{r}$
.
$p^{r}$
.
Ceci a pour conséquence qu’il n’existe pas de
![]() $X$
-morphisme fini surjectif modérant simultanément tous les faisceaux
$X$
-morphisme fini surjectif modérant simultanément tous les faisceaux
![]() $\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{X\star }\mathbb{F}_{\ell }$
, pour
$\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{X\star }\mathbb{F}_{\ell }$
, pour
![]() $\ell \neq p$
impair. Par contre, l’éclatement
$\ell \neq p$
impair. Par contre, l’éclatement
![]() $X^{\prime }\rightarrow X$
convient car chaque
$X^{\prime }\rightarrow X$
convient car chaque
![]() $\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{X_{0}\star }\mathbb{F}_{\ell }$
est modéré sur
$\mathtt{R}^{1}\unicode[STIX]{x1D70B}_{X_{0}\star }\mathbb{F}_{\ell }$
est modéré sur
![]() $X_{0}$
, de même que son tiré en arrière par
$X_{0}$
, de même que son tiré en arrière par
![]() $X^{\prime }\rightarrow X_{0}$
.
$X^{\prime }\rightarrow X_{0}$
.
3.3 Premières réductions
Nous commençons la démonstration du théorème 3.1.1 — dont nous reprenons les notations — par des réductions diverses. Le complément sur la majoration des fibres est traité en 3.6.
3.3.1 Réduction au cas où
 $X^{\prime }=X$
$X^{\prime }=X$
Nous vérifions ici que le théorème d’uniformité propre découle du cas particulier où l’altération
![]() $\unicode[STIX]{x1D6FC}:X^{\prime }\rightarrow X$
de la source est l’identité. Soit
$\unicode[STIX]{x1D6FC}:X^{\prime }\rightarrow X$
de la source est l’identité. Soit
![]() $X_{\bullet }$
le cosquelette de
$X_{\bullet }$
le cosquelette de
![]() $\unicode[STIX]{x1D6FC}$
— c’est un hyperrecouvrement propre de
$\unicode[STIX]{x1D6FC}$
— c’est un hyperrecouvrement propre de
![]() $X$
([SGA 4 Vbis], [Reference DeligneDel74b, 5.3.8]) — et notons
$X$
([SGA 4 Vbis], [Reference DeligneDel74b, 5.3.8]) — et notons
![]() $\mathfrak{X}_{j}$
(
$\mathfrak{X}_{j}$
(
![]() $j\geqslant 0$
) les stratifications déduites de
$j\geqslant 0$
) les stratifications déduites de
![]() $\mathfrak{X}$
sur
$\mathfrak{X}$
sur
![]() $X^{\prime }=X_{0}$
par image inverse sur chaque
$X^{\prime }=X_{0}$
par image inverse sur chaque
![]() $X_{j}$
. Pour tout faisceau
$X_{j}$
. Pour tout faisceau
![]() $\mathscr{F}$
sur
$\mathscr{F}$
sur
![]() $X[1/n]$
comme dans l’énoncé, on a
$X[1/n]$
comme dans l’énoncé, on a
![]() $\mathtt{R}f[1/n]_{\star }\mathscr{F}=\mathtt{R}f_{\bullet }[1/n]_{\star }\mathscr{F}_{\bullet }$
, où
$\mathtt{R}f[1/n]_{\star }\mathscr{F}=\mathtt{R}f_{\bullet }[1/n]_{\star }\mathscr{F}_{\bullet }$
, où
![]() $f_{\bullet }$
est le morphisme
$f_{\bullet }$
est le morphisme
![]() $X_{\bullet }\rightarrow S$
et
$X_{\bullet }\rightarrow S$
et
![]() $\mathscr{F}_{\bullet }$
le tiré en arrière de
$\mathscr{F}_{\bullet }$
le tiré en arrière de
![]() $\mathscr{F}$
sur (le topos total du schéma simplicial)
$\mathscr{F}$
sur (le topos total du schéma simplicial)
![]() $X_{\bullet }[1/n]$
.
$X_{\bullet }[1/n]$
.
Si
![]() $\mathscr{F}$
est constructible et localement unipotent le long de
$\mathscr{F}$
est constructible et localement unipotent le long de
![]() $\mathfrak{X}[1/n]$
, il en est de même de chaque
$\mathfrak{X}[1/n]$
, il en est de même de chaque
![]() $\mathscr{F}_{j}$
le long des
$\mathscr{F}_{j}$
le long des
![]() $\mathfrak{X}_{j}[1/n]$
(1.4). De même, si
$\mathfrak{X}_{j}[1/n]$
(1.4). De même, si
![]() $\mathscr{F}$
est modéré par
$\mathscr{F}$
est modéré par
![]() $\unicode[STIX]{x1D6FC}[1/n]$
, chaque faisceau
$\unicode[STIX]{x1D6FC}[1/n]$
, chaque faisceau
![]() $\mathscr{F}_{j}$
sur
$\mathscr{F}_{j}$
sur
![]() $X_{j}[1/n]$
est modéré.
$X_{j}[1/n]$
est modéré.
Soit
![]() $d$
un majorant de la dimension des fibres de
$d$
un majorant de la dimension des fibres de
![]() $f$
. Supposons que pour chaque
$f$
. Supposons que pour chaque
![]() $j\leqslant 2d$
, le théorème soit démontré pour le morphisme propre
$j\leqslant 2d$
, le théorème soit démontré pour le morphisme propre
![]() $f_{j}:X_{j}\rightarrow S$
, l’altération identité et la stratification
$f_{j}:X_{j}\rightarrow S$
, l’altération identité et la stratification
![]() $\mathfrak{X}_{j}$
de
$\mathfrak{X}_{j}$
de
![]() $X_{j}$
. Notons
$X_{j}$
. Notons
![]() $\unicode[STIX]{x1D6FD}_{j}$
,
$\unicode[STIX]{x1D6FD}_{j}$
,
![]() $\mathfrak{S}_{j}$
et
$\mathfrak{S}_{j}$
et
![]() $N_{j}$
respectivement les altérations de
$N_{j}$
respectivement les altérations de
![]() $S$
, stratifications et entiers associés.
$S$
, stratifications et entiers associés.

Par stabilité par image inverse des propriétés considérées on peut supposer les morphismes
![]() $\unicode[STIX]{x1D6FD}_{j}$
tous égaux à un même morphisme
$\unicode[STIX]{x1D6FD}_{j}$
tous égaux à un même morphisme
![]() $\unicode[STIX]{x1D6FD}:S^{\prime }\rightarrow S$
. (L’ensemble partiellement ordonné des altérations de
$\unicode[STIX]{x1D6FD}:S^{\prime }\rightarrow S$
. (L’ensemble partiellement ordonné des altérations de
![]() $S$
est filtrant [à droite].) Quitte à raffiner les stratifications
$S$
est filtrant [à droite].) Quitte à raffiner les stratifications
![]() $\mathfrak{S}_{j}$
, on peut également supposer qu’elles sont toutes égales à une même stratification
$\mathfrak{S}_{j}$
, on peut également supposer qu’elles sont toutes égales à une même stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S^{\prime }$
. (Même argument.) D’après la suite spectrale de descente ([Reference DeligneDel74b, 5.2.7.1], [SGA 4 Vbis, 3.3.3])
$S^{\prime }$
. (Même argument.) D’après la suite spectrale de descente ([Reference DeligneDel74b, 5.2.7.1], [SGA 4 Vbis, 3.3.3])
chaque
![]() $\mathtt{R}^{k}f[1/n]_{\star }\mathscr{F}$
est extension itérée de sous-quotients des
$\mathtt{R}^{k}f[1/n]_{\star }\mathscr{F}$
est extension itérée de sous-quotients des
![]() $\mathtt{R}^{i}f_{j}[1/n]_{\star }\mathscr{F}_{j}$
pour
$\mathtt{R}^{i}f_{j}[1/n]_{\star }\mathscr{F}_{j}$
pour
![]() $i+j=k$
et, par hypothèse, nul pour
$i+j=k$
et, par hypothèse, nul pour
![]() $k>2d$
. La constructibilité et locale unipotence (resp. modération) le long de
$k>2d$
. La constructibilité et locale unipotence (resp. modération) le long de
![]() $\mathfrak{S}$
des images directes par
$\mathfrak{S}$
des images directes par
![]() $f$
d’un faisceau comme dans l’énoncé sont alors conséquence de l’hypothèse sur
$f$
d’un faisceau comme dans l’énoncé sont alors conséquence de l’hypothèse sur
![]() $(\unicode[STIX]{x1D6FD},\mathfrak{S})$
relativement aux
$(\unicode[STIX]{x1D6FD},\mathfrak{S})$
relativement aux
![]() $f_{j}$
et de la stabilité par extension de ces propriétés.
$f_{j}$
et de la stabilité par extension de ces propriétés.
3.3.2 Réduction au cas où la base
 $S$
est intègre
$S$
est intègre
Les réductions au cas connexe et réduit sont immédiates. On peut également supposer
![]() $S$
intègre car le coproduit de ses composantes irréductibles en est une altération.
$S$
intègre car le coproduit de ses composantes irréductibles en est une altération.
3.3.3 Réduction au cas où les faisceaux sont le prolongement par zéro de faisceaux lisses sur une même strate dense
Soient
![]() $n\geqslant 1$
un entier,
$n\geqslant 1$
un entier,
![]() $\mathscr{F}$
un faisceau de
$\mathscr{F}$
un faisceau de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X^{\dagger }:=X[1/n]$
(notation de 1.5.2) et
$X^{\dagger }:=X[1/n]$
(notation de 1.5.2) et
![]() $\mathfrak{X}$
une stratification de
$\mathfrak{X}$
une stratification de
![]() $X=X^{\prime }$
, comme on peut le supposer d’après 3.3.1. Si
$X=X^{\prime }$
, comme on peut le supposer d’après 3.3.1. Si
![]() $\mathscr{F}$
est constructible le long de la stratification
$\mathscr{F}$
est constructible le long de la stratification
![]() $\mathfrak{X}^{\dagger }$
— que l’on peut supposer bonne, quitte à la raffiner —, il est d’après la proposition 1.1.4 extension successive de faisceaux
$\mathfrak{X}^{\dagger }$
— que l’on peut supposer bonne, quitte à la raffiner —, il est d’après la proposition 1.1.4 extension successive de faisceaux
![]() $i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
, où
:
$i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
, où
:
–
 $j$
est l’immersion ouverte d’une strate
$j$
est l’immersion ouverte d’une strate
 $W$
de
$W$
de
 $\mathfrak{X}$
dans son adhérence
$\mathfrak{X}$
dans son adhérence
 $Y:=\overline{W}$
;
$Y:=\overline{W}$
;–
 $i$
est l’immersion fermée de
$i$
est l’immersion fermée de
 $Y$
dans
$Y$
dans
 $X$
;
$X$
;–
 $\mathscr{L}$
est un faisceau abélien lisse de
$\mathscr{L}$
est un faisceau abélien lisse de
 $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
 $W^{\dagger }$
.
$W^{\dagger }$
.

Les faisceaux
![]() $i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
sont constructibles (resp. modérés, localement unipotents) le long de
$i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
sont constructibles (resp. modérés, localement unipotents) le long de
![]() $\mathfrak{X}^{\dagger }$
.
$\mathfrak{X}^{\dagger }$
.
Réciproquement, la stabilité par extension de ces mêmes propriétés et la suite exacte longue de cohomologie associée à une extension de faisceaux nous ramènent à démontrer le théorème pour les faisceaux
![]() $\mathscr{F}=i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
comme ci-dessus. Par finitude du nombre de strates et la propriété des altérations d’être filtrantes à droite (cf. 3.3.1), on peut supposer les immersions
$\mathscr{F}=i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
comme ci-dessus. Par finitude du nombre de strates et la propriété des altérations d’être filtrantes à droite (cf. 3.3.1), on peut supposer les immersions
![]() $i$
et
$i$
et
![]() $j$
fixées. Posons
$j$
fixées. Posons
![]() $\mathfrak{Y}:=\mathfrak{X}_{Y}$
, la stratification déduite de
$\mathfrak{Y}:=\mathfrak{X}_{Y}$
, la stratification déduite de
![]() $\mathfrak{X}$
par restriction au fermé
$\mathfrak{X}$
par restriction au fermé
![]() $Y$
, et
$Y$
, et
![]() $g:=f\circ i:Y\rightarrow S$
le morphisme composé. Le faisceau
$g:=f\circ i:Y\rightarrow S$
le morphisme composé. Le faisceau
![]() $j_{!}^{\dagger }\mathscr{L}=i^{\dagger \star }i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
étant modéré (resp. localement unipotent) le long de
$j_{!}^{\dagger }\mathscr{L}=i^{\dagger \star }i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
étant modéré (resp. localement unipotent) le long de
![]() $\mathfrak{Y}^{\dagger }$
si
$\mathfrak{Y}^{\dagger }$
si
![]() $i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
l’est le long de
$i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L}$
l’est le long de
![]() $\mathfrak{X}^{\dagger }$
, il résulte de la formule
$\mathfrak{X}^{\dagger }$
, il résulte de la formule
![]() $\mathtt{R}g_{\star }^{\dagger }(j_{!}^{\dagger }\mathscr{L})=\mathtt{R}f_{\star }^{\dagger }(i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L})$
, que l’on peut faire l’hypothèse supplémentaire que
$\mathtt{R}g_{\star }^{\dagger }(j_{!}^{\dagger }\mathscr{L})=\mathtt{R}f_{\star }^{\dagger }(i_{\star }^{\dagger }j_{!}^{\dagger }\mathscr{L})$
, que l’on peut faire l’hypothèse supplémentaire que
![]() $Y=X$
, c’est-à-dire que
$Y=X$
, c’est-à-dire que
![]() $\mathscr{F}$
est de la forme
$\mathscr{F}$
est de la forme
![]() $j_{!}^{\dagger }\mathscr{L}$
.
$j_{!}^{\dagger }\mathscr{L}$
.
3.4 Énoncé de la récurrence nœthérienne
Nous introduisons ici deux énoncés,
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
et
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
et
![]() $\mathtt{Unip}(S,\unicode[STIX]{x1D70C},d)$
, pour
$\mathtt{Unip}(S,\unicode[STIX]{x1D70C},d)$
, pour
![]() $S$
nœthérien intègre quasi-excellent, et
$S$
nœthérien intègre quasi-excellent, et
![]() $\unicode[STIX]{x1D70C},d\geqslant -1$
des entiers. Il résulte des dévissages 3.3.1 et 3.3.2, ainsi que de la nullité des
$\unicode[STIX]{x1D70C},d\geqslant -1$
des entiers. Il résulte des dévissages 3.3.1 et 3.3.2, ainsi que de la nullité des
![]() $\mathtt{R}^{i}f_{\star }$
pour
$\mathtt{R}^{i}f_{\star }$
pour
![]() $i$
grand que la conjonction de ces énoncés entraîne le théorème d’uniformité propre 3.1.1. La suite de cette section 3 sera donc consacrée à la démonstration par récurrence de ces énoncés.
$i$
grand que la conjonction de ces énoncés entraîne le théorème d’uniformité propre 3.1.1. La suite de cette section 3 sera donc consacrée à la démonstration par récurrence de ces énoncés.
3.4.1
Pour chaque triplet
![]() $(S,\unicode[STIX]{x1D70C},d)$
, où
$(S,\unicode[STIX]{x1D70C},d)$
, où
![]() $S$
est un schéma nœthérien quasi-excellent intègre ou vide et
$S$
est un schéma nœthérien quasi-excellent intègre ou vide et
![]() $\unicode[STIX]{x1D70C}\geqslant -1$
,
$\unicode[STIX]{x1D70C}\geqslant -1$
,
![]() $d\geqslant -1$
sont des entiers, on considère les deux énoncés suivants
:
$d\geqslant -1$
sont des entiers, on considère les deux énoncés suivants
:
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
: pour toute altération intègre
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
: pour toute altération intègre
![]() $T$
de
$T$
de
![]() $S$
, tout
$S$
, tout
![]() $T$
-schéma propre
$T$
-schéma propre
![]() $f:Y\rightarrow T$
de fibre générique de dimension au plus
$f:Y\rightarrow T$
de fibre générique de dimension au plus
![]() $d$
et toute stratification
$d$
et toute stratification
![]() $\mathfrak{Y}$
de
$\mathfrak{Y}$
de
![]() $Y$
, il existe une altération
$Y$
, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:T^{\prime }\rightarrow T$
, une stratification
$\unicode[STIX]{x1D6FD}:T^{\prime }\rightarrow T$
, une stratification
![]() $\mathfrak{T}$
de
$\mathfrak{T}$
de
![]() $T$
et un entier
$T$
et un entier
![]() $N$
tels que pour tout entier
$N$
tels que pour tout entier
![]() $n\geqslant 1$
et tout faisceau
$n\geqslant 1$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $Y[1/n]$
constructible le long de
$Y[1/n]$
constructible le long de
![]() $\mathfrak{Y}[1/n]$
et modéré, chaque image directe
$\mathfrak{Y}[1/n]$
et modéré, chaque image directe
![]() $\mathtt{R}^{k}f[1/n]_{\star }\mathscr{F}$
est, pour
$\mathtt{R}^{k}f[1/n]_{\star }\mathscr{F}$
est, pour
![]() $k\leqslant \unicode[STIX]{x1D70C}$
, constructible le long de
$k\leqslant \unicode[STIX]{x1D70C}$
, constructible le long de
![]() $\mathfrak{T}[1/n]$
, modérée par
$\mathfrak{T}[1/n]$
, modérée par
![]() $\unicode[STIX]{x1D6FD}[1/n]$
et
$\unicode[STIX]{x1D6FD}[1/n]$
et
![]() $N$
-extension ponctuelle de
$N$
-extension ponctuelle de
![]() $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
![]() $f[1/n]$
;
$f[1/n]$
;
et
![]() $\mathtt{Unip}(S,\unicode[STIX]{x1D70C},d)$
: pour toute altération intègre
$\mathtt{Unip}(S,\unicode[STIX]{x1D70C},d)$
: pour toute altération intègre
![]() $T$
de
$T$
de
![]() $S$
, tout
$S$
, tout
![]() $T$
-schéma propre
$T$
-schéma propre
![]() $f:Y\rightarrow T$
de fibre générique de dimension au plus
$f:Y\rightarrow T$
de fibre générique de dimension au plus
![]() $d$
et toute stratification
$d$
et toute stratification
![]() $\mathfrak{Y}$
de
$\mathfrak{Y}$
de
![]() $Y$
, il existe une altération
$Y$
, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:T^{\prime }\rightarrow T$
et une stratification
$\unicode[STIX]{x1D6FD}:T^{\prime }\rightarrow T$
et une stratification
![]() $\mathfrak{T}$
de
$\mathfrak{T}$
de
![]() $T^{\prime }$
telles que pour tout entier
$T^{\prime }$
telles que pour tout entier
![]() $n\geqslant 1$
et tout faisceau
$n\geqslant 1$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $Y[1/n]$
constructible et localement unipotent le long de
$Y[1/n]$
constructible et localement unipotent le long de
![]() $\mathfrak{Y}[1/n]$
, chaque image directe
$\mathfrak{Y}[1/n]$
, chaque image directe
![]() $\mathtt{R}^{k}f[1/n]_{\star }\mathscr{F}$
est, pour
$\mathtt{R}^{k}f[1/n]_{\star }\mathscr{F}$
est, pour
![]() $k\leqslant \unicode[STIX]{x1D70C}$
, constructible et localement unipotente le long de
$k\leqslant \unicode[STIX]{x1D70C}$
, constructible et localement unipotente le long de
![]() $\mathfrak{T}[1/n]$
.
$\mathfrak{T}[1/n]$
.

Commençons par quelques remarques sur ces énoncés.
3.4.2
Le premier énoncé (
![]() $\mathtt{Mod}$
) affirme l’existence d’une stratification de
$\mathtt{Mod}$
) affirme l’existence d’une stratification de
![]() $T$
et non de
$T$
et non de
![]() $T^{\prime }$
: cela revient au même d’après le résultat de descente de stratification 1.5.4. Dans
$T^{\prime }$
: cela revient au même d’après le résultat de descente de stratification 1.5.4. Dans
![]() $\mathtt{Unip}$
, le complément sur les extensions ponctuelles n’est pas inclus ; d’après l’observation 1.3.3, cela résulte du cas modéré.
$\mathtt{Unip}$
, le complément sur les extensions ponctuelles n’est pas inclus ; d’après l’observation 1.3.3, cela résulte du cas modéré.
Si
![]() $T$
est une altération intègre d’un schéma
$T$
est une altération intègre d’un schéma
![]() $S$
comme ci-dessus, les propriétés
$S$
comme ci-dessus, les propriétés
![]() $\mathtt{Mod}(T,\unicode[STIX]{x1D70C},d)$
et
$\mathtt{Mod}(T,\unicode[STIX]{x1D70C},d)$
et
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
sont équivalentes ; de même pour la variante (localement) unipotente : on démontre une propriété de l’espace de Zariski–Riemann.
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
sont équivalentes ; de même pour la variante (localement) unipotente : on démontre une propriété de l’espace de Zariski–Riemann.
Enfin, notons que ces énoncés sont trivialement vrais pour
![]() $S=\varnothing$
ou
$S=\varnothing$
ou
![]() $\unicode[STIX]{x1D70C}=-1$
; ce n’est pas le cas pour
$\unicode[STIX]{x1D70C}=-1$
; ce n’est pas le cas pour
![]() $d=-1$
(morphisme non dominant).
$d=-1$
(morphisme non dominant).
3.4.3
Fixons
![]() $(S,\unicode[STIX]{x1D70C},d)$
et précisons la différence entre l’énoncé
$(S,\unicode[STIX]{x1D70C},d)$
et précisons la différence entre l’énoncé
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
ci-dessus et l’énoncé analogue où l’on considère plus généralement des faisceaux
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
ci-dessus et l’énoncé analogue où l’on considère plus généralement des faisceaux
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules constructibles modérés le long d’une stratification non pas de
$\mathbb{Z}/n\mathbb{Z}$
-modules constructibles modérés le long d’une stratification non pas de
![]() $Y$
mais d’une (même) altération
$Y$
mais d’une (même) altération
![]() $\unicode[STIX]{x1D6FC}:Y^{\prime }\rightarrow Y$
. La formule de descente cohomologique
$\unicode[STIX]{x1D6FC}:Y^{\prime }\rightarrow Y$
. La formule de descente cohomologique
![]() $\mathtt{R}f_{\star }^{\dagger }\mathscr{F}=\mathtt{R}f_{\bullet \star }^{\dagger }\mathscr{F}_{\bullet }$
, où la source de
$\mathtt{R}f_{\star }^{\dagger }\mathscr{F}=\mathtt{R}f_{\bullet \star }^{\dagger }\mathscr{F}_{\bullet }$
, où la source de
![]() $f_{\bullet }$
est le
$f_{\bullet }$
est le
![]() $0$
-cosquelette de
$0$
-cosquelette de
![]() $\unicode[STIX]{x1D6FC}$
, ramène (comme en 3.3.1) cet énoncé a priori plus général à la conjonction de
$\unicode[STIX]{x1D6FC}$
, ramène (comme en 3.3.1) cet énoncé a priori plus général à la conjonction de
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
et de
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
et de
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C}-1,\ast )$
c’est-à-dire des
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C}-1,\ast )$
c’est-à-dire des
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C}-1,d^{\prime })$
pour
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C}-1,d^{\prime })$
pour
![]() $d^{\prime }\geqslant -1$
.
$d^{\prime }\geqslant -1$
.
Même résultat pour
![]() $\mathtt{Unip}$
, mutatis mutandis.
$\mathtt{Unip}$
, mutatis mutandis.
3.4.4
Nous allons démontrer le théorème 3.1.1 par récurrence nœthérienne en considérant la relation bien fondée (
![]() $=$
nœthérienne)
$=$
nœthérienne)
![]() $\prec$
sur les triplets
$\prec$
sur les triplets
![]() $(S,\unicode[STIX]{x1D70C},d)$
lexicographiquement déduite des relations d’ordre usuelles sur les entiers
$(S,\unicode[STIX]{x1D70C},d)$
lexicographiquement déduite des relations d’ordre usuelles sur les entiers
![]() $\unicode[STIX]{x1D70C}$
et
$\unicode[STIX]{x1D70C}$
et
![]() $d$
et de la relation binaire :
$d$
et de la relation binaire :
![]() $S^{\prime }\prec S$
si et seulement si
$S^{\prime }\prec S$
si et seulement si
![]() $S^{\prime }$
est (isomorphe à) un fermé strict d’une altération intègre de
$S^{\prime }$
est (isomorphe à) un fermé strict d’une altération intègre de
![]() $S$
.
$S$
.
Notons tout de suite qu’il résulte du « lemme de Gabber » (1.6.2) que la propriété
![]() $\mathtt{Mod}$
ou
$\mathtt{Mod}$
ou
![]() $\mathtt{Unip}$
d’un triplet
$\mathtt{Unip}$
d’un triplet
![]() $(S,\unicode[STIX]{x1D70C},-1)$
est conséquence de cette même propriété pour les triplets
$(S,\unicode[STIX]{x1D70C},-1)$
est conséquence de cette même propriété pour les triplets
![]() $(\ast \prec S,\unicode[STIX]{x1D70C},\ast )$
.
$(\ast \prec S,\unicode[STIX]{x1D70C},\ast )$
.
Lemme. La relation
![]() $S^{\prime }\prec S$
précédente est bien fondée : il n’existe pas de suite
$S^{\prime }\prec S$
précédente est bien fondée : il n’existe pas de suite
![]() $\text{infinie}$
$\text{infinie}$
![]() $(S_{n})$
de schémas nœthériens intègres telle que
$(S_{n})$
de schémas nœthériens intègres telle que
![]() $S_{n+1}$
soit un fermé strict d’une altération
$S_{n+1}$
soit un fermé strict d’une altération
![]() $S_{n}^{\prime }$
de
$S_{n}^{\prime }$
de
![]() $S_{n}$
.
$S_{n}$
.

Démonstration.
On raisonne par l’absurde, en supposant qu’il existe une suite infinie
![]() $\cdots \rightarrow S_{n+1}{\hookrightarrow}S_{n}^{\prime }\rightarrow S_{n}{\hookrightarrow}\cdots \,$
(
$\cdots \rightarrow S_{n+1}{\hookrightarrow}S_{n}^{\prime }\rightarrow S_{n}{\hookrightarrow}\cdots \,$
(
![]() $n\geqslant 0$
), où chaque
$n\geqslant 0$
), où chaque
![]() $S_{n}^{\prime }\rightarrow S_{n}$
est une altération et chaque
$S_{n}^{\prime }\rightarrow S_{n}$
est une altération et chaque
![]() $S_{n+1}{\hookrightarrow}S_{n}^{\prime }$
est une immersion fermée stricte. Les images
$S_{n+1}{\hookrightarrow}S_{n}^{\prime }$
est une immersion fermée stricte. Les images
![]() $F_{n}$
des
$F_{n}$
des
![]() $S_{n}$
dans
$S_{n}$
dans
![]() $S:=S_{0}$
forment une suite décroissante, donc stationnaire, de fermés de
$S:=S_{0}$
forment une suite décroissante, donc stationnaire, de fermés de
![]() $S$
. Il existe donc un entier
$S$
. Il existe donc un entier
![]() $N$
tel que les points génériques des schémas
$N$
tel que les points génériques des schémas
![]() $S_{n}$
, pour
$S_{n}$
, pour
![]() $n\geqslant N$
, soient tous d’image un même point
$n\geqslant N$
, soient tous d’image un même point
![]() $\unicode[STIX]{x1D70F}\in S$
. Pour chaque tel
$\unicode[STIX]{x1D70F}\in S$
. Pour chaque tel
![]() $n$
, la restriction de
$n$
, la restriction de
![]() $S_{n}^{\prime }\rightarrow S_{n}$
(resp.
$S_{n}^{\prime }\rightarrow S_{n}$
(resp.
![]() $S_{n+1}{\hookrightarrow}S_{n}^{\prime }$
) aux fibres au-dessus de
$S_{n+1}{\hookrightarrow}S_{n}^{\prime }$
) aux fibres au-dessus de
![]() $\unicode[STIX]{x1D70F}$
est encore une altération (resp. une immersion fermée stricte). Ceci nous ramène au cas particulier où les
$\unicode[STIX]{x1D70F}$
est encore une altération (resp. une immersion fermée stricte). Ceci nous ramène au cas particulier où les
![]() $S_{n}$
sont des schémas algébriques sur un corps, auquel cas la conclusion résulte des inégalités
$S_{n}$
sont des schémas algébriques sur un corps, auquel cas la conclusion résulte des inégalités
![]() $\dim (S_{n+1})<\dim (S_{n})<+\infty$
pour chaque
$\dim (S_{n+1})<\dim (S_{n})<+\infty$
pour chaque
![]() $n\geqslant 0$
.◻
$n\geqslant 0$
.◻
3.5 Réduction au cas des courbes
3.5.1 Morphismes plurinodaux [Reference de JongdeJ97, 5.8] : définitions et ubiquité
Soit
![]() $f:Y\rightarrow T$
un morphisme entre schémas intègres et soit
$f:Y\rightarrow T$
un morphisme entre schémas intègres et soit
![]() $Y^{\circ }$
(resp.
$Y^{\circ }$
(resp.
![]() $T^{\circ }$
) un ouvert dense de
$T^{\circ }$
) un ouvert dense de
![]() $Y$
(resp.
$Y$
(resp.
![]() $T$
). On dit que
$T$
). On dit que
![]() $f$
est plurinodal adapté à
$f$
est plurinodal adapté à
![]() $(Y^{\circ },T^{\circ })$
s’il existe
:
$(Y^{\circ },T^{\circ })$
s’il existe
:
– une factorisation
où $$\begin{eqnarray}f=(f_{d}:Y_{d}\rightarrow Y_{d-1})\circ \cdots \circ (f_{1}:Y_{1}\rightarrow Y_{0}),\end{eqnarray}$$
$$\begin{eqnarray}f=(f_{d}:Y_{d}\rightarrow Y_{d-1})\circ \cdots \circ (f_{1}:Y_{1}\rightarrow Y_{0}),\end{eqnarray}$$
 $Y_{0}=T$
et
$Y_{0}=T$
et
 $Y_{d}=Y$
,
$Y_{d}=Y$
,
 $d\in \mathbb{N}$
;
$d\in \mathbb{N}$
;– des ouverts denses
 $Y_{i}^{\circ }\subseteq Y_{i}$
, où
$Y_{i}^{\circ }\subseteq Y_{i}$
, où
 $Y_{0}^{\circ }=T^{\circ }$
et
$Y_{0}^{\circ }=T^{\circ }$
et
 $Y_{d}^{\circ }=Y^{\circ }$
,
$Y_{d}^{\circ }=Y^{\circ }$
,
tels que chaque
![]() $f_{i}$
soit une courbe nodale adaptée à
$f_{i}$
soit une courbe nodale adaptée à
![]() $(Y_{i}^{\circ },Y_{i-1}^{\circ })$
au sens de 2.1.2.
$(Y_{i}^{\circ },Y_{i-1}^{\circ })$
au sens de 2.1.2.
Un morphisme
![]() $f:Y\rightarrow T$
est plurinodal (resp. plurinodal adapté à un ouvert dense
$f:Y\rightarrow T$
est plurinodal (resp. plurinodal adapté à un ouvert dense
![]() $Y^{\circ }$
de
$Y^{\circ }$
de
![]() $Y$
) s’il existe des ouverts denses
$Y$
) s’il existe des ouverts denses
![]() $Y^{\circ }$
et
$Y^{\circ }$
et
![]() $T^{\circ }$
(resp. un ouvert dense
$T^{\circ }$
(resp. un ouvert dense
![]() $T^{\circ }$
) de sorte que
$T^{\circ }$
) de sorte que
![]() $f$
soit adapté à
$f$
soit adapté à
![]() $(Y^{\circ },T^{\circ })$
.
$(Y^{\circ },T^{\circ })$
.
Un morphisme non nécessairement dominant
![]() $f:Y\rightarrow T$
est dit presque plurinodal (resp. presque plurinodal adapté à un ouvert dense
$f:Y\rightarrow T$
est dit presque plurinodal (resp. presque plurinodal adapté à un ouvert dense
![]() $Y^{\circ }$
de
$Y^{\circ }$
de
![]() $Y$
) s’il est somme de morphismes plurinodaux entre schémas intègres et d’un morphisme non dominant (resp. et si pour chaque composante connexe
$Y$
) s’il est somme de morphismes plurinodaux entre schémas intègres et d’un morphisme non dominant (resp. et si pour chaque composante connexe
![]() $Z$
de
$Z$
de
![]() $Y$
dominant
$Y$
dominant
![]() $T$
, le morphisme composé
$T$
, le morphisme composé
![]() $Z\rightarrow T$
est plurinodal adapté à
$Z\rightarrow T$
est plurinodal adapté à
![]() $Z^{\circ }:=Y^{\circ }\cap Z$
).
$Z^{\circ }:=Y^{\circ }\cap Z$
).
L’ubiquité de ces morphismes est assurée par le théorème suivant [Reference de JongdeJ97, corollaire 5.10].
Théorème. [de Jong] Soient
![]() $f:Y\rightarrow T$
un morphisme propre, où
$f:Y\rightarrow T$
un morphisme propre, où
![]() $T$
est un schéma intègre nœthérien quasi-excellent, et
$T$
est un schéma intègre nœthérien quasi-excellent, et
![]() $Y^{\circ }$
un ouvert dense de
$Y^{\circ }$
un ouvert dense de
![]() $Y$
. Il existe une altération
$Y$
. Il existe une altération
![]() $T^{\prime }\rightarrow T$
et un hyperrecouvrement propre
$T^{\prime }\rightarrow T$
et un hyperrecouvrement propre
![]() $Y_{\bullet }^{\prime }\rightarrow Y\times _{T}T^{\prime }$
tel que
$Y_{\bullet }^{\prime }\rightarrow Y\times _{T}T^{\prime }$
tel que
![]() $Y_{0}^{\prime }\rightarrow T^{\prime }$
soit
$Y_{0}^{\prime }\rightarrow T^{\prime }$
soit
![]() $\text{presque plurinodal}$
adapté à un ouvert
$\text{presque plurinodal}$
adapté à un ouvert
![]() $Y_{0}^{\prime \circ \circ }$
contenu dans
$Y_{0}^{\prime \circ \circ }$
contenu dans
![]() $Y_{0}^{\prime \circ }:=Y^{\circ }\times _{Y}Y_{0}^{\prime }$
.
$Y_{0}^{\prime \circ }:=Y^{\circ }\times _{Y}Y_{0}^{\prime }$
.
(L’énoncé original est légèrement différent ; voir [Reference OrgogozoOrg06, § 4.3] si nécessaire pour une discussion.)
Comme expliqué en [Reference de JongdeJ97, 5.16], l’hypothèse d’excellence n’est pas nécessaire : on peut s’en affranchir par passage à la limite.
3.5.2
Revenons à la démonstration par récurrence des énoncés 3.4.1. À cet effet, on fixe un schéma nœthérien
![]() $S$
, des entiers
$S$
, des entiers
![]() $\unicode[STIX]{x1D70C}\geqslant -1,d\geqslant -1$
— que l’on peut supposer
$\unicode[STIX]{x1D70C}\geqslant -1,d\geqslant -1$
— que l’on peut supposer
![]() ${\geqslant}0$
par récurrence et le lemme de Gabber — et on considère une altération intègre
${\geqslant}0$
par récurrence et le lemme de Gabber — et on considère une altération intègre
![]() $T$
de
$T$
de
![]() $S$
, un morphisme propre (dominant)
$S$
, un morphisme propre (dominant)
![]() $f:Y\rightarrow T$
de fibre générique de dimension au plus
$f:Y\rightarrow T$
de fibre générique de dimension au plus
![]() $d$
et une stratification
$d$
et une stratification
![]() $\mathfrak{Y}$
de
$\mathfrak{Y}$
de
![]() $Y$
. D’après 3.3.3 (démonstration), on peut supposer que chaque faisceau test
$Y$
. D’après 3.3.3 (démonstration), on peut supposer que chaque faisceau test
![]() $\mathscr{F}$
des énoncés
$\mathscr{F}$
des énoncés
![]() $\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
et
$\mathtt{Mod}(S,\unicode[STIX]{x1D70C},d)$
et
![]() $\mathtt{Unip}(S,\unicode[STIX]{x1D70C},d)$
est le prolongement par zéro d’un faisceau lisse de
$\mathtt{Unip}(S,\unicode[STIX]{x1D70C},d)$
est le prolongement par zéro d’un faisceau lisse de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur la strate ouverte dense
$\mathbb{Z}/n\mathbb{Z}$
-modules sur la strate ouverte dense
![]() $Y^{\circ }[1/n]$
de
$Y^{\circ }[1/n]$
de
![]() $\mathfrak{Y}[1/n]$
, pour un entier
$\mathfrak{Y}[1/n]$
, pour un entier
![]() $n\geqslant 1$
(dépendant du faisceau).
$n\geqslant 1$
(dépendant du faisceau).
Montrons maintenant que l’on peut supposer le morphisme
![]() $f:Y\rightarrow T$
plurinodal adapté à la strate dense. On peut supposer que l’altération
$f:Y\rightarrow T$
plurinodal adapté à la strate dense. On peut supposer que l’altération
![]() $T^{\prime }\rightarrow T$
du théorème précédent est l’identité car l’énoncé que l’on souhaite démontrer est local en bas pour la topologie des altérations ; il est même local en haut pour cette topologie, de façon compatible à la récurrence, cf. 3.4.3. La descente cohomologique (cf. 3.3.1) et l’hypothèse de récurrence pour les triplets
$T^{\prime }\rightarrow T$
du théorème précédent est l’identité car l’énoncé que l’on souhaite démontrer est local en bas pour la topologie des altérations ; il est même local en haut pour cette topologie, de façon compatible à la récurrence, cf. 3.4.3. La descente cohomologique (cf. 3.3.1) et l’hypothèse de récurrence pour les triplets
![]() $(S,\unicode[STIX]{x1D70C}-1,\ast )$
nous permettent alors de supposer de plus le morphisme
$(S,\unicode[STIX]{x1D70C}-1,\ast )$
nous permettent alors de supposer de plus le morphisme
![]() $f$
presque plurinodal :
$f$
presque plurinodal :
![]() $f=f_{+}\coprod f_{-}$
, où
$f=f_{+}\coprod f_{-}$
, où
![]() $f_{+}$
est plurinodal adapté à un ouvert
$f_{+}$
est plurinodal adapté à un ouvert
![]() $Y^{\circ \circ }$
de la strate dense
$Y^{\circ \circ }$
de la strate dense
![]() $Y^{\circ }\subseteq Y$
et
$Y^{\circ }\subseteq Y$
et
![]() $f_{-}$
est un morphisme propre non surjectif, d’image
$f_{-}$
est un morphisme propre non surjectif, d’image
![]() $F\subseteq T$
. Il résulte de l’hypothèse de récurrence pour les triplets
$F\subseteq T$
. Il résulte de l’hypothèse de récurrence pour les triplets
![]() $(F,\unicode[STIX]{x1D70C},\ast )$
— avec
$(F,\unicode[STIX]{x1D70C},\ast )$
— avec
![]() $F\prec S$
— et du lemme de Gabber 1.6.2 que l’on peut supposer
$F\prec S$
— et du lemme de Gabber 1.6.2 que l’on peut supposer
![]() $f=f_{+}$
.
$f=f_{+}$
.
Notons resp.
![]() $j^{\circ }$
et
$j^{\circ }$
et
![]() $j^{\circ \circ }$
les immersions ouvertes de
$j^{\circ \circ }$
les immersions ouvertes de
![]() $Y^{\circ }$
et
$Y^{\circ }$
et
![]() $Y^{\circ \circ }$
dans
$Y^{\circ \circ }$
dans
![]() $Y$
, et fixons un entier
$Y$
, et fixons un entier
![]() $n\geqslant 1$
. Pour tout faisceau test
$n\geqslant 1$
. Pour tout faisceau test
![]() $\mathscr{F}={j^{\circ }}_{!}^{\dagger }\mathscr{L}^{\circ }$
, où
$\mathscr{F}={j^{\circ }}_{!}^{\dagger }\mathscr{L}^{\circ }$
, où
![]() $\mathscr{L}^{\circ }$
est un faisceau lisse de
$\mathscr{L}^{\circ }$
est un faisceau lisse de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() ${Y^{\circ }}^{\dagger }$
, on a une suite exacte
${Y^{\circ }}^{\dagger }$
, on a une suite exacte
où
![]() $\mathscr{L}^{\circ \circ }:=\mathscr{L}_{|{Y^{\circ \circ }}^{\dagger }}^{\circ }$
, et le conoyau
$\mathscr{L}^{\circ \circ }:=\mathscr{L}_{|{Y^{\circ \circ }}^{\dagger }}^{\circ }$
, et le conoyau
![]() $\overline{\mathscr{L}}$
est un faisceau constructible à support dans le fermé strict
$\overline{\mathscr{L}}$
est un faisceau constructible à support dans le fermé strict
![]() $Z^{\dagger }:=(Y-Y^{\circ \circ })^{\dagger }$
de
$Z^{\dagger }:=(Y-Y^{\circ \circ })^{\dagger }$
de
![]() $Y$
. Pour
$Y$
. Pour
![]() $\mathscr{L}^{\circ }$
variable — mais astreint aux conditions déduites de celles sur
$\mathscr{L}^{\circ }$
variable — mais astreint aux conditions déduites de celles sur
![]() $\mathscr{F}$
comme ci-dessus —, les
$\mathscr{F}$
comme ci-dessus —, les
![]() $\overline{\mathscr{L}}$
forment une famille (uniformément) constructible (quitte à raffiner
$\overline{\mathscr{L}}$
forment une famille (uniformément) constructible (quitte à raffiner
![]() $\mathfrak{Y}$
) ; modérée (resp. localement unipotente) si la famille des faisceaux
$\mathfrak{Y}$
) ; modérée (resp. localement unipotente) si la famille des faisceaux
![]() ${j^{\circ }}_{!}^{\dagger }\mathscr{L}^{\circ }$
l’est : cela résulte de la stabilité par quotient (cf. 1.4). La suite exacte longue de cohomologie associée à la suite exacte précédente et la stabilité par extension, maintes fois utilisée, nous ramènent à considérer des faisceaux test de la forme
${j^{\circ }}_{!}^{\dagger }\mathscr{L}^{\circ }$
l’est : cela résulte de la stabilité par quotient (cf. 1.4). La suite exacte longue de cohomologie associée à la suite exacte précédente et la stabilité par extension, maintes fois utilisée, nous ramènent à considérer des faisceaux test de la forme
![]() ${j^{\circ \circ }}_{!}^{\dagger }\mathscr{L}^{\circ \circ }$
ou bien
${j^{\circ \circ }}_{!}^{\dagger }\mathscr{L}^{\circ \circ }$
ou bien
![]() $\overline{\mathscr{L}}$
. Dans ce dernier cas, on peut utiliser l’hypothèse de récurrence pour le triplet
$\overline{\mathscr{L}}$
. Dans ce dernier cas, on peut utiliser l’hypothèse de récurrence pour le triplet
![]() $(S,\unicode[STIX]{x1D70C},d-1)$
car la dimension de la fibre générique de
$(S,\unicode[STIX]{x1D70C},d-1)$
car la dimension de la fibre générique de
![]() $Z$
sur
$Z$
sur
![]() $T$
est strictement inférieure à celle de
$T$
est strictement inférieure à celle de
![]() $Y$
. (On rappelle que l’on a supposé
$Y$
. (On rappelle que l’on a supposé
![]() $d\geqslant 0$
, c’est-à-dire
$d\geqslant 0$
, c’est-à-dire
![]() $f$
dominant.)
$f$
dominant.)
Comme annoncé, on peut donc supposer — quitte à raffiner
![]() $\mathfrak{Y}$
à nouveau — que l’on a l’égalité
$\mathfrak{Y}$
à nouveau — que l’on a l’égalité
![]() $Y^{\circ \circ }=Y^{\circ }$
, c’est-à-dire que le morphisme
$Y^{\circ \circ }=Y^{\circ }$
, c’est-à-dire que le morphisme
![]() $f$
est plurinodal adapté à une strate dense
$f$
est plurinodal adapté à une strate dense
![]() $Y^{\circ }$
de
$Y^{\circ }$
de
![]() $\mathfrak{Y}$
. On peut également supposer
$\mathfrak{Y}$
. On peut également supposer
![]() $Y$
intègre.
$Y$
intègre.
3.5.3
Sous les hypothèses en vigueur, on peut factoriser le morphisme
![]() $f:Y\rightarrow T$
en
$f:Y\rightarrow T$
en
![]() $f=g\,\circ \,h$
, où
$f=g\,\circ \,h$
, où
![]() $h:(Y,Y^{\circ })\rightarrow (X,X^{\circ })$
est une courbe nodale adaptée et
$h:(Y,Y^{\circ })\rightarrow (X,X^{\circ })$
est une courbe nodale adaptée et
![]() $g:(X,X^{\circ })\rightarrow (T,T^{\circ })$
est un morphisme plurinodal adapté.
$g:(X,X^{\circ })\rightarrow (T,T^{\circ })$
est un morphisme plurinodal adapté.

D’après le théorème de résolution par altération des singularités des schémas quasi-excellents d’O. Gabber (voir [STG VII, 1.1] et [STG II, 3.2.1]), il existe des diagrammes commutatifs indicés par
![]() $i$
$i$

où
![]() $\widetilde{T}$
est une même altération de
$\widetilde{T}$
est une même altération de
![]() $T$
, les
$T$
, les
![]() $T_{i}^{\prime }$
forment un recouvrement fini de Zariski de
$T_{i}^{\prime }$
forment un recouvrement fini de Zariski de
![]() $\widetilde{T}$
, et la paire
$\widetilde{T}$
, et la paire
![]() $(T^{\prime },T^{\prime \circ }:=T^{\prime }\times _{T}T^{\circ })$
est régulière (2.1). D’après la proposition 2.3.1, appliqué au morphisme
$(T^{\prime },T^{\prime \circ }:=T^{\prime }\times _{T}T^{\circ })$
est régulière (2.1). D’après la proposition 2.3.1, appliqué au morphisme
![]() $h^{\prime }:=h\times _{T}T^{\prime }:Y^{\prime }\rightarrow X^{\prime }$
et aux ouverts
$h^{\prime }:=h\times _{T}T^{\prime }:Y^{\prime }\rightarrow X^{\prime }$
et aux ouverts
![]() $Y^{\prime \circ }:=Y^{\circ }\times _{T}T^{\prime }$
,
$Y^{\prime \circ }:=Y^{\circ }\times _{T}T^{\prime }$
,
![]() $X^{\prime \circ }:=X^{\circ }\times _{T}T^{\prime }$
, pour chaque
$X^{\prime \circ }:=X^{\circ }\times _{T}T^{\prime }$
, pour chaque
![]() $k\in \{0,1,2\}$
la famille des
$k\in \{0,1,2\}$
la famille des
![]() $\mathtt{R}^{k}{h^{\prime }}_{\star }^{\dagger }(\mathscr{F}^{\prime })$
est constructible et modérée (resp. localement unipotente) sur
$\mathtt{R}^{k}{h^{\prime }}_{\star }^{\dagger }(\mathscr{F}^{\prime })$
est constructible et modérée (resp. localement unipotente) sur
![]() $X^{\prime }$
, lorsque
$X^{\prime }$
, lorsque
![]() $\mathscr{F}$
parcourt les faisceaux test du type considéré : prolongement par zéro d’un faisceau lisse, modéré (resp. localement unipotent). (Notons que par hypothèse sur
$\mathscr{F}$
parcourt les faisceaux test du type considéré : prolongement par zéro d’un faisceau lisse, modéré (resp. localement unipotent). (Notons que par hypothèse sur
![]() $g$
et d’après la proposition 2.1.3 la paire
$g$
et d’après la proposition 2.1.3 la paire
![]() $(X^{\prime },X^{\prime \circ })$
est torique.)
$(X^{\prime },X^{\prime \circ })$
est torique.)

Par stabilité par image inverse et théorème de changement de base propre, il en est de même des
![]() $\mathtt{R}^{k}{h_{i}^{\prime }}_{\star }^{\dagger }(\mathscr{F}_{i}^{\prime })$
. Enfin, la propriété d’une famille d’être constructible et modérée (resp. localement unipotente) étant Zariski locale, on a constructibilité et modération (resp. locale unipotence) des
$\mathtt{R}^{k}{h_{i}^{\prime }}_{\star }^{\dagger }(\mathscr{F}_{i}^{\prime })$
. Enfin, la propriété d’une famille d’être constructible et modérée (resp. localement unipotente) étant Zariski locale, on a constructibilité et modération (resp. locale unipotence) des
![]() $\mathtt{R}^{k}\widetilde{h}_{\star }^{\dagger }(\widetilde{\mathscr{F}})$
.
$\mathtt{R}^{k}\widetilde{h}_{\star }^{\dagger }(\widetilde{\mathscr{F}})$
.
Quitte à remplacer
![]() $T$
par
$T$
par
![]() $\widetilde{T}$
, on peut donc supposer la famille des
$\widetilde{T}$
, on peut donc supposer la famille des
![]() $\mathtt{R}^{k}h_{\star }^{\dagger }\mathscr{F}$
constructible et modérée (resp. localement unipotente) sur
$\mathtt{R}^{k}h_{\star }^{\dagger }\mathscr{F}$
constructible et modérée (resp. localement unipotente) sur
![]() $X$
. (Notons que cela est plus fort que de supposer le résultat après altération de
$X$
. (Notons que cela est plus fort que de supposer le résultat après altération de
![]() $X$
.) La formule
$X$
.) La formule
![]() $\mathtt{R}f_{\star }=\mathtt{R}g_{\star }\circ \mathtt{R}h_{\star }$
(et ses variantes au-dessus des ouverts
$\mathtt{R}f_{\star }=\mathtt{R}g_{\star }\circ \mathtt{R}h_{\star }$
(et ses variantes au-dessus des ouverts
![]() $T^{\dagger }=T[1/n]$
) nous permet, via la suite spectrale associée, d’utiliser l’hypothèse de récurrence pour le triplet
$T^{\dagger }=T[1/n]$
) nous permet, via la suite spectrale associée, d’utiliser l’hypothèse de récurrence pour le triplet
![]() $(S,\unicode[STIX]{x1D70C},d-1)$
: la dimension de la fibre générique de
$(S,\unicode[STIX]{x1D70C},d-1)$
: la dimension de la fibre générique de
![]() $g$
est strictement inférieure à celle de
$g$
est strictement inférieure à celle de
![]() $f$
.
$f$
.
Ceci achève la démonstration du théorème 3.1.1, excepté le complément sur la majoration des fibres : on a montré que les énoncés pour les triplets
![]() $(S,\unicode[STIX]{x1D70C},d-1)$
,
$(S,\unicode[STIX]{x1D70C},d-1)$
,
![]() $(S,\unicode[STIX]{x1D70C},-1,\ast )$
,
$(S,\unicode[STIX]{x1D70C},-1,\ast )$
,
![]() $(\ast \prec S,\unicode[STIX]{x1D70C},\ast )$
entraînent l’énoncé correspondant de modération ou locale unipotence pour le triplet
$(\ast \prec S,\unicode[STIX]{x1D70C},\ast )$
entraînent l’énoncé correspondant de modération ou locale unipotence pour le triplet
![]() $(S,\unicode[STIX]{x1D70C},d)$
. On peut donc conclure par récurrence grâce au lemme du paragraphe 3.4.4. Initialisation : on rappelle que les énoncés sont trivialement vrais pour
$(S,\unicode[STIX]{x1D70C},d)$
. On peut donc conclure par récurrence grâce au lemme du paragraphe 3.4.4. Initialisation : on rappelle que les énoncés sont trivialement vrais pour
![]() $S=\varnothing$
ou
$S=\varnothing$
ou
![]() $\unicode[STIX]{x1D70C}=-1$
et que l’énoncé pour un triplet
$\unicode[STIX]{x1D70C}=-1$
et que l’énoncé pour un triplet
![]() $(S^{\prime },\unicode[STIX]{x1D70C}^{\prime },-1)$
est également conséquence des
$(S^{\prime },\unicode[STIX]{x1D70C}^{\prime },-1)$
est également conséquence des
![]() $(\ast \prec S^{\prime },\unicode[STIX]{x1D70C}^{\prime },\ast )$
.
$(\ast \prec S^{\prime },\unicode[STIX]{x1D70C}^{\prime },\ast )$
.
3.5.4
Notons que la démonstration du théorème 3.1.1 donne plus : pour tout changement de base lisse
![]() $R\rightarrow S$
, la paire
$R\rightarrow S$
, la paire
![]() $(\unicode[STIX]{x1D6FD}:S^{\prime }{\twoheadrightarrow}S,\mathfrak{S})\times _{S}R$
— obtenue en prenant l’image inverse des données obtenues par la démonstration que nous avons suivie — convient pour le triplet
$(\unicode[STIX]{x1D6FD}:S^{\prime }{\twoheadrightarrow}S,\mathfrak{S})\times _{S}R$
— obtenue en prenant l’image inverse des données obtenues par la démonstration que nous avons suivie — convient pour le triplet
![]() $(f,\unicode[STIX]{x1D6FC},\mathfrak{X})\times _{S}R$
. Ceci résulte de la récurrence et du fait que si
$(f,\unicode[STIX]{x1D6FC},\mathfrak{X})\times _{S}R$
. Ceci résulte de la récurrence et du fait que si
![]() $(T,T^{\circ })$
est une paire régulière et
$(T,T^{\circ })$
est une paire régulière et
![]() $Q\rightarrow T$
lisse, la paire
$Q\rightarrow T$
lisse, la paire
![]() $(Q,Q^{\circ }:=T^{\circ }\times _{T}Q)$
est encore régulière.
$(Q,Q^{\circ }:=T^{\circ }\times _{T}Q)$
est encore régulière.
3.5.5
Mieux : la proposition 2.3.1 sous la forme la plus générale, dont la démonstration a été seulement esquissée en 2.3.6 dans le cas d’une base non nécessairement torique, permet d’établir le théorème d’uniformité propre dans le cas où
![]() $S$
est seulement nœthérien (et pas nécessairement quasi-excellent), et ce de façon compatible à tout changement de base (et pas seulement aux changements de base lisses). Ce raffinement sur les changements de base autorisés nous permet par descente des objets (morphismes, faisceaux, et stratifications) de supposer la base de type fini sur
$S$
est seulement nœthérien (et pas nécessairement quasi-excellent), et ce de façon compatible à tout changement de base (et pas seulement aux changements de base lisses). Ce raffinement sur les changements de base autorisés nous permet par descente des objets (morphismes, faisceaux, et stratifications) de supposer la base de type fini sur
![]() $\text{Spec}(\mathbb{Z})$
donc en particulier excellente. Par normalisation (finie), on peut également la supposer normale. Les dévissages précédents s’appliquent sans changement et nous ramènent à la proposition susmentionnée pour les courbes nodales, sans utiliser le théorème de résolution par altération des singularités d’O. Gabber mais seulement le théorème de A. J. de Jong. (La récurrence 3.5.3 devient alors significativement plus simple : il s’agit seulement d’une récurrence sur la dimension relative dans le cas plurinodal.)
$\text{Spec}(\mathbb{Z})$
donc en particulier excellente. Par normalisation (finie), on peut également la supposer normale. Les dévissages précédents s’appliquent sans changement et nous ramènent à la proposition susmentionnée pour les courbes nodales, sans utiliser le théorème de résolution par altération des singularités d’O. Gabber mais seulement le théorème de A. J. de Jong. (La récurrence 3.5.3 devient alors significativement plus simple : il s’agit seulement d’une récurrence sur la dimension relative dans le cas plurinodal.)
3.6 Majoration des fibres
Signalons rapidement en quoi la méthode suivie entraîne le complément, énoncé en 3.1.1, sur la « majoration » uniforme des fibres des images directes propres.
3.6.1
Réduction au cas
![]() $\unicode[STIX]{x1D6FC}=\text{Id}$
(
$\unicode[STIX]{x1D6FC}=\text{Id}$
(
![]() $\leftrightarrow$
3.3.1) : observer que si chaque
$\leftrightarrow$
3.3.1) : observer que si chaque
![]() $\mathtt{R}^{i}f_{j\star }^{\dagger }\mathscr{F}_{j}$
est
$\mathtt{R}^{i}f_{j\star }^{\dagger }\mathscr{F}_{j}$
est
![]() $N_{j}$
-extension ponctuelle de
$N_{j}$
-extension ponctuelle de
![]() $\mathscr{F}_{j}$
relativement à
$\mathscr{F}_{j}$
relativement à
![]() $f_{j}^{\dagger }$
, le faisceau
$f_{j}^{\dagger }$
, le faisceau
![]() $\mathtt{R}^{k}f_{\star }^{\dagger }\mathscr{F}$
est
$\mathtt{R}^{k}f_{\star }^{\dagger }\mathscr{F}$
est
![]() $N$
-extension ponctuelle de
$N$
-extension ponctuelle de
![]() $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
![]() $f^{\dagger }$
pour
$f^{\dagger }$
pour
![]() $N:=(k+1)\times \max _{0\leqslant j\leqslant 2d+1}N_{j}$
.
$N:=(k+1)\times \max _{0\leqslant j\leqslant 2d+1}N_{j}$
.
3.6.2
Réduction au cas
![]() $\mathscr{F}=j_{!}^{\dagger }\mathscr{L}$
(
$\mathscr{F}=j_{!}^{\dagger }\mathscr{L}$
(
![]() $\leftrightarrow$
3.3.3) : d’une part, d’après la proposition 1.1.4, on a une borne a priori sur la longueur d’une filtration à gradués des prolongements par zéro de lisses et, d’autre part, la réduction au cas d’une strate ouverte est licite d’après 1.7.2(ii).
$\leftrightarrow$
3.3.3) : d’une part, d’après la proposition 1.1.4, on a une borne a priori sur la longueur d’une filtration à gradués des prolongements par zéro de lisses et, d’autre part, la réduction au cas d’une strate ouverte est licite d’après 1.7.2(ii).
3.6.3
Réduction au cas plurinodal (
![]() $\leftrightarrow$
3.5.2) : utiliser (la récurrence et) la stabilité par extension, 1.7.2(iii).
$\leftrightarrow$
3.5.2) : utiliser (la récurrence et) la stabilité par extension, 1.7.2(iii).
3.6.4
Réduction au cas nodal (
![]() $\leftrightarrow$
3.5.3) : la propriété à démontrer est Zariski locale sur la source, stable par changement de base d’après 1.7.2(v), et compatible à la factorisation
$\leftrightarrow$
3.5.3) : la propriété à démontrer est Zariski locale sur la source, stable par changement de base d’après 1.7.2(v), et compatible à la factorisation
![]() $f=g\circ h$
au sens de 1.7.2(iv).
$f=g\circ h$
au sens de 1.7.2(iv).
3.6.5
Il reste à montrer que sous les hypothèses de la proposition 2.3.1, les faisceaux
![]() $\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
(
$\mathtt{R}^{i}h_{\star }(j_{!}\mathscr{L})$
(
![]() $0\leqslant i\leqslant 2$
) sont
$0\leqslant i\leqslant 2$
) sont
![]() $N$
-extensions ponctuelles de sous-quotients de
$N$
-extensions ponctuelles de sous-quotients de
![]() $\mathscr{L}$
pour un entier
$\mathscr{L}$
pour un entier
![]() $N$
ne dépendant que du morphisme
$N$
ne dépendant que du morphisme
![]() $h:Y\rightarrow X$
et de l’immersion ouverte
$h:Y\rightarrow X$
et de l’immersion ouverte
![]() $j:Y^{\circ }{\hookrightarrow}Y$
. Il suffit pour cela de vérifier que si
$j:Y^{\circ }{\hookrightarrow}Y$
. Il suffit pour cela de vérifier que si
![]() $U$
est un ouvert d’une courbe projective lisse connexe
$U$
est un ouvert d’une courbe projective lisse connexe
![]() $C$
sur un corps algébriquement clos, et
$C$
sur un corps algébriquement clos, et
![]() $\mathscr{L}$
abélien lisse (de torsion inversible sur
$\mathscr{L}$
abélien lisse (de torsion inversible sur
![]() $C$
) et modéré sur
$C$
) et modéré sur
![]() $U$
, les groupes
$U$
, les groupes
![]() $\mathtt{H}_{c}^{i}(U,\mathscr{L})$
sont
$\mathtt{H}_{c}^{i}(U,\mathscr{L})$
sont
![]() $N$
-extensions ponctuelles de sous-quotients de
$N$
-extensions ponctuelles de sous-quotients de
![]() $\mathscr{L}$
pour un entier
$\mathscr{L}$
pour un entier
![]() $N$
ne dépendant que du genre de
$N$
ne dépendant que du genre de
![]() $C$
et du cardinal de
$C$
et du cardinal de
![]() $C-U$
, qui varient l’un comme l’autre de façon constructible en famille. C’est évident pour
$C-U$
, qui varient l’un comme l’autre de façon constructible en famille. C’est évident pour
![]() $i=0$
, également vrai pour
$i=0$
, également vrai pour
![]() $i=2$
par dualité et conséquence de la formule de Grothendieck–Ogg–Šafarevič [SGA 5 X, 7.1] pour
$i=2$
par dualité et conséquence de la formule de Grothendieck–Ogg–Šafarevič [SGA 5 X, 7.1] pour
![]() $i=1$
. (Noter que l’on utilise cette formule dans le cas modéré, bien plus élémentaire ; cf. [Reference OggOgg62, prop. 6, p. 199] ou [Reference ŠafarevičŠaf61, th. 3, p. 337].)
$i=1$
. (Noter que l’on utilise cette formule dans le cas modéré, bien plus élémentaire ; cf. [Reference OggOgg62, prop. 6, p. 199] ou [Reference ŠafarevičŠaf61, th. 3, p. 337].)
4 Image directe par une immersion ouverte
4.1 Énoncé et stratégie
Le but de cette section est d’établir le théorème suivant.
Théorème 4.1.1. Soient
![]() $X$
un schéma nœthérien quasi-excellent et
$X$
un schéma nœthérien quasi-excellent et
![]() $j:U{\hookrightarrow}X$
une immersion ouverte. La propriété d’une famille
$j:U{\hookrightarrow}X$
une immersion ouverte. La propriété d’une famille
![]() $\mathbb{F}$
de faisceaux sur
$\mathbb{F}$
de faisceaux sur
![]() $X$
d’être constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations est préservée par le foncteur
$X$
d’être constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations est préservée par le foncteur
![]() $\mathtt{R}j_{\star }j^{\star }$
.
$\mathtt{R}j_{\star }j^{\star }$
.
En d’autres termes, et plus précisément, pour tout entier
![]() $c\geqslant -1$
, toute altération
$c\geqslant -1$
, toute altération
![]() $\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
et toute stratification
$\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
et toute stratification
![]() $\mathfrak{X}_{1}$
de
$\mathfrak{X}_{1}$
de
![]() $X_{1}$
, il existe une altération
$X_{1}$
, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:X_{2}\rightarrow X$
et une stratification
$\unicode[STIX]{x1D6FD}:X_{2}\rightarrow X$
et une stratification
![]() $\mathfrak{X}_{2}$
de
$\mathfrak{X}_{2}$
de
![]() $X_{2}$
telles que pour tout entier
$X_{2}$
telles que pour tout entier
![]() $n\geqslant 1$
et tout faisceau
$n\geqslant 1$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X^{\dagger }=X[1/n]$
constructible et modéré (resp. constructible et localement unipotent) le long de
$X^{\dagger }=X[1/n]$
constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{X}_{1}^{\dagger }$
alors
$\mathfrak{X}_{1}^{\dagger }$
alors
![]() $\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
$\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{X}_{2}^{\dagger }$
.
$\mathfrak{X}_{2}^{\dagger }$
.
De plus :
(a) il existe un entier
 $N$
, dépendant uniquement du quadruplet
$N$
, dépendant uniquement du quadruplet
 $(j,\unicode[STIX]{x1D6FC},\mathfrak{X}_{1},c)$
, tel que chaque
$(j,\unicode[STIX]{x1D6FC},\mathfrak{X}_{1},c)$
, tel que chaque
 $\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
comme ci-dessus soit
$\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
comme ci-dessus soit
 $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
au sens de 1.7 ;
$\mathscr{F}$
au sens de 1.7 ;(b) si
 $X$
est de type fini sur un schéma
$X$
est de type fini sur un schéma
 $S$
, il existe un ouvert dense
$S$
, il existe un ouvert dense
 $S^{\circ }$
de
$S^{\circ }$
de
 $S$
tel que la formation de chaque
$S$
tel que la formation de chaque
 $\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
comme ci-dessus commute aux changements de base
$\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
comme ci-dessus commute aux changements de base
 $S^{\prime }\rightarrow S^{\circ }$
.
$S^{\prime }\rightarrow S^{\circ }$
.
Remarques 4.1.2.
(i) Si
 $X$
est de dimension finie, il résulte de [Reference IllusieSTG XVIIIA
, 1.1] qu’il existe un entier
$X$
est de dimension finie, il résulte de [Reference IllusieSTG XVIIIA
, 1.1] qu’il existe un entier
 $C$
tel que les
$C$
tel que les
 $\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
comme ci-dessus soient nuls pour chaque
$\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
comme ci-dessus soient nuls pour chaque
 $c\geqslant C$
. On peut donc trouver des données
$c\geqslant C$
. On peut donc trouver des données
 $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
 $\mathfrak{X}_{2}$
et
$\mathfrak{X}_{2}$
et
 $N$
qui conviennent pour tout
$N$
qui conviennent pour tout
 $c$
. Il est vraisemblable qu’en adaptant la méthode de [STG XV], on puisse s’affranchir de cette hypothèse supplémentaire sur
$c$
. Il est vraisemblable qu’en adaptant la méthode de [STG XV], on puisse s’affranchir de cette hypothèse supplémentaire sur
 $X$
. (Un point de départ possible est l’observation que [STG XV, 2.1.7] est valable plus généralement pour des coefficients lisses modérés.)
$X$
. (Un point de départ possible est l’observation que [STG XV, 2.1.7] est valable plus généralement pour des coefficients lisses modérés.)(ii) A priori, même si
 $\unicode[STIX]{x1D6FC}=\text{Id}$
, on ne peut pas nécessairement prendre
$\unicode[STIX]{x1D6FC}=\text{Id}$
, on ne peut pas nécessairement prendre
 $\unicode[STIX]{x1D6FD}=\text{Id}$
.
$\unicode[STIX]{x1D6FD}=\text{Id}$
.
4.1.3 Stratégie
On procède par récurrence sur l’entier
![]() $c$
. La première des deux méthodes d’O. Gabber, exposée en [STG XIII, § 2], s’adapte sans difficulté particulière si ce n’est qu’il nous faut établir un analogue du théorème de constructibilité générique [Th. finitude, 1.9 (i)] de P. Deligne sous une forme légèrement renforcée. (Voir la mise en garde 1.4.9, et 4.5
infra pour l’énoncé précis.)
$c$
. La première des deux méthodes d’O. Gabber, exposée en [STG XIII, § 2], s’adapte sans difficulté particulière si ce n’est qu’il nous faut établir un analogue du théorème de constructibilité générique [Th. finitude, 1.9 (i)] de P. Deligne sous une forme légèrement renforcée. (Voir la mise en garde 1.4.9, et 4.5
infra pour l’énoncé précis.)
4.2 Dévissages
4.2.1
Pour alléger l’exposition, on ne fera en général pas mention des entiers
![]() $n\geqslant 1$
, et on omet les foncteurs
$n\geqslant 1$
, et on omet les foncteurs
![]() $-[1/n]=-^{\dagger }$
: on note
$-[1/n]=-^{\dagger }$
: on note
![]() $j$
pour
$j$
pour
![]() $j^{\dagger }=j[1/n]$
, etc., et
$j^{\dagger }=j[1/n]$
, etc., et
![]() $\unicode[STIX]{x1D6EC}$
pour
$\unicode[STIX]{x1D6EC}$
pour
![]() $\mathbb{Z}/n\mathbb{Z}$
.
$\mathbb{Z}/n\mathbb{Z}$
.
Rappelons que l’on procède par récurrence sur le degré cohomologique
![]() ${\leqslant}c$
, où
${\leqslant}c$
, où
![]() $c$
est un entier
$c$
est un entier
![]() ${\geqslant}-1$
, en s’autorisant à changer
${\geqslant}-1$
, en s’autorisant à changer
![]() $X$
. Le cas
$X$
. Le cas
![]() $c=-1$
est tautologiquement vrai.
$c=-1$
est tautologiquement vrai.
4.2.2 (Réduction au cas
 $X_{1}=X$
)
$X_{1}=X$
)
Cela résulte du théorème d’uniformité propre (3.1.1) et de la descente cohomologique, sous la forme
![]() $\mathtt{R}j_{\star }j^{\star }=\mathtt{R}\unicode[STIX]{x1D700}_{\star }\mathtt{R}j_{\bullet \star }j_{\bullet }^{\star }$
, où
$\mathtt{R}j_{\star }j^{\star }=\mathtt{R}\unicode[STIX]{x1D700}_{\star }\mathtt{R}j_{\bullet \star }j_{\bullet }^{\star }$
, où
![]() $\unicode[STIX]{x1D700}:X_{\bullet }\rightarrow X$
est le
$\unicode[STIX]{x1D700}:X_{\bullet }\rightarrow X$
est le
![]() $0$
-cosquelette de l’altération
$0$
-cosquelette de l’altération
![]() $\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
et
$\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
et
![]() $j_{\bullet }:U_{\bullet }{\hookrightarrow}X_{\bullet }$
est le morphisme déduit de
$j_{\bullet }:U_{\bullet }{\hookrightarrow}X_{\bullet }$
est le morphisme déduit de
![]() $j$
par changement de base
$j$
par changement de base
![]() $X_{\bullet }\rightarrow X$
(cf. 3.3.1),
$X_{\bullet }\rightarrow X$
(cf. 3.3.1),
Ce même argument nous permet de supposer que
![]() $X$
est un coproduit fini de schémas intègres et, finalement, que
$X$
est un coproduit fini de schémas intègres et, finalement, que
![]() $X$
est intègre (cf. 3.3.2).
$X$
est intègre (cf. 3.3.2).
4.2.3 (Réduction au cas où les faisceaux sont des prolongements par zéro de faisceaux lisses sur la strate ouverte
 $V\in \mathfrak{X}_{1}$
de
$V\in \mathfrak{X}_{1}$
de
 $X$
)
$X$
)
Elle est entièrement semblable à la réduction effectuée en 3.3.3, une fois constaté que si
![]() $i:F{\hookrightarrow}X$
est une immersion fermée, on a
$i:F{\hookrightarrow}X$
est une immersion fermée, on a
![]() $\mathtt{R}j_{\star }j^{\star }\circ i_{\star }=i_{\star }\circ \mathtt{R}(j\times _{X}i)_{\star }(j\times _{X}i)^{\star }$
.
$\mathtt{R}j_{\star }j^{\star }\circ i_{\star }=i_{\star }\circ \mathtt{R}(j\times _{X}i)_{\star }(j\times _{X}i)^{\star }$
.
4.2.4 (Réduction au cas où la strate ouverte
 $V$
est contenue dans
$V$
est contenue dans
 $U$
)
$U$
)
D’après la réduction précédente, on peut supposer le faisceau
![]() $\mathscr{F}$
de la forme
$\mathscr{F}$
de la forme
![]() $h_{!}\mathscr{L}$
où
$h_{!}\mathscr{L}$
où
![]() $h$
est l’immersion ouverte de la strate ouverte
$h$
est l’immersion ouverte de la strate ouverte
![]() $V$
dans
$V$
dans
![]() $X$
et
$X$
et
![]() $\mathscr{L}$
est un faisceau lisse sur
$\mathscr{L}$
est un faisceau lisse sur
![]() $V$
de
$V$
de
![]() $\unicode[STIX]{x1D6EC}$
-modules. Notons
$\unicode[STIX]{x1D6EC}$
-modules. Notons
![]() $U^{\circ }$
l’ouvert
$U^{\circ }$
l’ouvert
![]() $V\cap U$
.
$V\cap U$
.

Le complexe
![]() $\mathtt{R}j_{\star }j^{\star }(h_{!}\mathscr{L})=\mathtt{R}j_{\star }(h_{!}^{\circ }\mathscr{L}^{\circ })$
se réécrit
$\mathtt{R}j_{\star }j^{\star }(h_{!}\mathscr{L})=\mathtt{R}j_{\star }(h_{!}^{\circ }\mathscr{L}^{\circ })$
se réécrit
![]() $\mathtt{R}j_{\star }j^{\star }(j_{!}h_{!}^{\circ }\mathscr{L}^{\circ })$
. Quitte à raffiner la stratification, le sous-faisceau
$\mathtt{R}j_{\star }j^{\star }(j_{!}h_{!}^{\circ }\mathscr{L}^{\circ })$
. Quitte à raffiner la stratification, le sous-faisceau
![]() $j_{!}h_{!}^{\circ }\mathscr{L}^{\circ }$
de
$j_{!}h_{!}^{\circ }\mathscr{L}^{\circ }$
de
![]() $h_{!}\mathscr{L}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
$h_{!}\mathscr{L}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{X}_{1}$
; on peut donc supposer
$\mathfrak{X}_{1}$
; on peut donc supposer
![]() $V\subseteq U$
, c’est-à-dire
$V\subseteq U$
, c’est-à-dire
![]() $V=U^{\circ }$
.
$V=U^{\circ }$
.
4.2.5 (Réduction au cas où
 $j^{\star }\mathscr{F}$
est lisse, c’est-à-dire
$j^{\star }\mathscr{F}$
est lisse, c’est-à-dire
 $V=U$
)
$V=U$
)
Sous l’hypothèse précédente, le morphisme
![]() $h$
se factorise à travers
$h$
se factorise à travers
![]() $j$
selon le diagramme suivant :
$j$
selon le diagramme suivant :

On veut montrer que, sous nos hypothèses, les faisceaux
![]() $\mathtt{R}^{c}j_{\star }(h_{!}^{\circ }\mathscr{L})$
sont uniformément constructibles et modérés (resp. constructibles et localement unipotents) pour la topologie des altérations. Soient
$\mathtt{R}^{c}j_{\star }(h_{!}^{\circ }\mathscr{L})$
sont uniformément constructibles et modérés (resp. constructibles et localement unipotents) pour la topologie des altérations. Soient
![]() $F$
le fermé
$F$
le fermé
![]() $U-U^{\circ }$
de
$U-U^{\circ }$
de
![]() $U$
,
$U$
,
![]() $i:F{\hookrightarrow}U$
l’immersion fermée et considérons l’adhérence
$i:F{\hookrightarrow}U$
l’immersion fermée et considérons l’adhérence
![]() $\overline{F}$
de
$\overline{F}$
de
![]() $F$
dans
$F$
dans
![]() $X$
,
$X$
,
![]() $j_{F}:F{\hookrightarrow}\overline{F}$
l’immersion ouverte correspondante et enfin
$j_{F}:F{\hookrightarrow}\overline{F}$
l’immersion ouverte correspondante et enfin
![]() $\overline{i}$
l’immersion fermée de
$\overline{i}$
l’immersion fermée de
![]() $\overline{F}$
dans
$\overline{F}$
dans
![]() $X$
.
$X$
.

Le triangle distingué
(déduit par application de
![]() $\mathtt{R}j_{\star }$
au triangle
$\mathtt{R}j_{\star }$
au triangle
![]() $h_{!}^{\circ }h^{\circ \star }\rightarrow \text{Id}\rightarrow i_{\star }i^{\star }$
évalué en
$h_{!}^{\circ }h^{\circ \star }\rightarrow \text{Id}\rightarrow i_{\star }i^{\star }$
évalué en
![]() $\mathtt{R}h_{\star }^{\circ }\mathscr{L}=j^{\star }\mathtt{R}h_{\star }\mathscr{L}$
) nous ramène à montrer l’uniformité (resp. la commutation générique aux changements de base) en degré
$\mathtt{R}h_{\star }^{\circ }\mathscr{L}=j^{\star }\mathtt{R}h_{\star }\mathscr{L}$
) nous ramène à montrer l’uniformité (resp. la commutation générique aux changements de base) en degré
![]() $c$
du second terme et en degré
$c$
du second terme et en degré
![]() $c-1$
du troisième. Par récurrence sur
$c-1$
du troisième. Par récurrence sur
![]() $c$
, il suffit d’étudier le seul terme central : on peut donc dorénavant supposer que
$c$
, il suffit d’étudier le seul terme central : on peut donc dorénavant supposer que
![]() $j=h$
, c’est-à-dire que
$j=h$
, c’est-à-dire que
![]() $j^{\star }\mathscr{F}$
est égal au faisceau
$j^{\star }\mathscr{F}$
est égal au faisceau
![]() $\mathscr{L}$
, lisse sur
$\mathscr{L}$
, lisse sur
![]() $U^{\circ }=U$
.
$U^{\circ }=U$
.
4.3 Cas d’un « bon » schéma
Dans le cas particulier, souvent suffisant en pratique, où
![]() $X$
est de type fini sur un corps ou un schéma de Dedekind, la démonstration du théorème 4.1.1 est immédiate à partir de ce qui précède, et ne fait donc pas appel aux résultats génériques des paragraphes suivants. (On ne considère pas les compléments dans l’esquisse qui suit et renvoyons le lecteur à la démonstration donnée dans le cas général.)
$X$
est de type fini sur un corps ou un schéma de Dedekind, la démonstration du théorème 4.1.1 est immédiate à partir de ce qui précède, et ne fait donc pas appel aux résultats génériques des paragraphes suivants. (On ne considère pas les compléments dans l’esquisse qui suit et renvoyons le lecteur à la démonstration donnée dans le cas général.)
En effet, d’après [Reference de JongdeJ96, 4.1 et 8.2], il existe pour un tel
![]() $X$
un hyperrecouvrement propre
$X$
un hyperrecouvrement propre
![]() $X_{\bullet }\rightarrow X$
tel que la paire
$X_{\bullet }\rightarrow X$
tel que la paire
![]() $(X_{\bullet },U_{\bullet })$
soit régulière, étage par étage. La descente cohomologique et le théorème d’uniformité dans le cas propre nous permettent donc de supposer la paire
$(X_{\bullet },U_{\bullet })$
soit régulière, étage par étage. La descente cohomologique et le théorème d’uniformité dans le cas propre nous permettent donc de supposer la paire
![]() $(X,U)$
régulière. Or, il résulte de la proposition 2.4.1 que
$(X,U)$
régulière. Or, il résulte de la proposition 2.4.1 que
![]() $\mathtt{R}j_{\star }\mathscr{L}$
est à cohomologie uniformément constructible et modérée (resp. constructible et localement unipotente) sur
$\mathtt{R}j_{\star }\mathscr{L}$
est à cohomologie uniformément constructible et modérée (resp. constructible et localement unipotente) sur
![]() $X$
. (Noter qu’il n’est pas nécessaire d’avoir recourt à une altération du but.)
$X$
. (Noter qu’il n’est pas nécessaire d’avoir recourt à une altération du but.)
4.4 Cas général : réduction à l’uniformité générique
Traitons maintenant le cas modéré, sans supposer le schéma
![]() $X$
de type fini sur un corps ou un schéma de Dedekind. Le cas localement unipotent est semblable et laissé au lecteur ; la majoration des fibres sera brièvement traitée ci-après (4.5.7). Quant à la propreté cohomologique générique, elle résulte immédiatement du théorème de changement de base propre et du corollaire 4.5.3(ii).
$X$
de type fini sur un corps ou un schéma de Dedekind. Le cas localement unipotent est semblable et laissé au lecteur ; la majoration des fibres sera brièvement traitée ci-après (4.5.7). Quant à la propreté cohomologique générique, elle résulte immédiatement du théorème de changement de base propre et du corollaire 4.5.3(ii).
Une récurrence nœthérienne sur (les fermés de)
![]() $X$
, le lemme de Gabber 1.6.2 et l’observation 1.4.10 appliquée aux faisceaux
$X$
, le lemme de Gabber 1.6.2 et l’observation 1.4.10 appliquée aux faisceaux
![]() $\mathscr{K}:=\mathtt{R}^{c}j_{\star }\mathscr{L}$
(pour
$\mathscr{K}:=\mathtt{R}^{c}j_{\star }\mathscr{L}$
(pour
![]() $\mathscr{L}$
lisse sur
$\mathscr{L}$
lisse sur
![]() $U$
comme précédemment) nous ramènent à montrer que si
$U$
comme précédemment) nous ramènent à montrer que si
![]() $i:F{\hookrightarrow}X$
est un fermé contenu dans
$i:F{\hookrightarrow}X$
est un fermé contenu dans
![]() $X\setminus U$
, il existe une immersion ouverte
$X\setminus U$
, il existe une immersion ouverte
![]() $k:F^{\circ }{\hookrightarrow}F$
d’image dense, une altération
$k:F^{\circ }{\hookrightarrow}F$
d’image dense, une altération
![]() $a:F^{\prime }\rightarrow F$
et enfin une stratification
$a:F^{\prime }\rightarrow F$
et enfin une stratification
![]() $\mathfrak{F}$
de
$\mathfrak{F}$
de
![]() $F$
telles que les faisceaux
$F$
telles que les faisceaux
![]() $k_{!}k^{\star }(\mathscr{K}_{|F})$
soient constructibles et modérés le long de
$k_{!}k^{\star }(\mathscr{K}_{|F})$
soient constructibles et modérés le long de
![]() $\mathfrak{F}$
. D’après le théorème de résolution des singularités d’O. Gabber [STG VII, 1.1], il existe un hyperrecouvrement
$\mathfrak{F}$
. D’après le théorème de résolution des singularités d’O. Gabber [STG VII, 1.1], il existe un hyperrecouvrement
![]() $\unicode[STIX]{x1D700}_{X}:X_{\bullet }\rightarrow X$
pour la topologie
$\unicode[STIX]{x1D700}_{X}:X_{\bullet }\rightarrow X$
pour la topologie
![]() $h$
tel qu’à chaque étage
$h$
tel qu’à chaque étage
![]() $n$
, le schéma
$n$
, le schéma
![]() $X_{n}$
soit régulier,
$X_{n}$
soit régulier,
![]() $F_{n}:=F\times _{X}X_{n}$
un diviseur à croisements normaux strict et
$F_{n}:=F\times _{X}X_{n}$
un diviseur à croisements normaux strict et
![]() $U_{n}:=U\times _{X}X_{n}$
le complémentaire d’un tel diviseur. D’après la formule d’hyper-changement de base ([STG XIIA
, 2.2.5], [STG XIIB
]) d’O. Gabber, le morphisme
$U_{n}:=U\times _{X}X_{n}$
le complémentaire d’un tel diviseur. D’après la formule d’hyper-changement de base ([STG XIIA
, 2.2.5], [STG XIIB
]) d’O. Gabber, le morphisme
est un isomorphisme. Les morphismes
![]() $\unicode[STIX]{x1D700}_{F,n}:F_{n}\rightarrow F$
n’étant pas nécessairement propres, on ne peut appliquer directement le théorème d’uniformité propre. Cependant, la proposition 4.5.1 ci-dessous, appliquée pour
$\unicode[STIX]{x1D700}_{F,n}:F_{n}\rightarrow F$
n’étant pas nécessairement propres, on ne peut appliquer directement le théorème d’uniformité propre. Cependant, la proposition 4.5.1 ci-dessous, appliquée pour
![]() $n$
variable aux morphismes
$n$
variable aux morphismes
![]() $f:=\unicode[STIX]{x1D700}_{F,n}$
(dans le cas particulier
$f:=\unicode[STIX]{x1D700}_{F,n}$
(dans le cas particulier
![]() $S=Y$
), nous ramène à démontrer le fait suivant, lorsque
$S=Y$
), nous ramène à démontrer le fait suivant, lorsque
![]() $X^{\prime }=X_{n}$
,
$X^{\prime }=X_{n}$
,
![]() $F^{\prime }=F_{n}$
, et
$F^{\prime }=F_{n}$
, et
![]() $U^{\prime }=U_{n}$
.
$U^{\prime }=U_{n}$
.
Lemme. Soient

un diagramme commutatif à carrés cartésiens et traits pleins, où :
–
 $X^{\prime }$
est régulier, séparé de type fini sur
$X^{\prime }$
est régulier, séparé de type fini sur
 $X$
;
$X$
;–
 $F^{\prime }$
est un diviseur à croisements normaux strict ;
$F^{\prime }$
est un diviseur à croisements normaux strict ;–
 $U^{\prime }$
est le complémentaire d’un tel diviseur.
$U^{\prime }$
est le complémentaire d’un tel diviseur.
Alors, il existe une
![]() $F$
-compactification
$F$
-compactification
![]() $k^{\prime }:F^{\prime }{\hookrightarrow}\overline{F}^{\prime }$
de
$k^{\prime }:F^{\prime }{\hookrightarrow}\overline{F}^{\prime }$
de
![]() $F^{\prime }$
telle que pour tout faisceau lisse
$F^{\prime }$
telle que pour tout faisceau lisse
![]() $\mathscr{L}$
de
$\mathscr{L}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $U$
tel que
$U$
tel que
![]() $j_{!}\mathscr{L}$
soit modéré (resp. localement unipotents) et
$j_{!}\mathscr{L}$
soit modéré (resp. localement unipotents) et
![]() $n\geqslant 1$
inversible sur
$n\geqslant 1$
inversible sur
![]() $X$
, les faisceaux
$X$
, les faisceaux
![]() $k_{!}^{\prime }{i^{\prime }}^{\star }\mathtt{R}^{c^{\prime }}j_{\star }^{\prime }\mathscr{L}$
, pour
$k_{!}^{\prime }{i^{\prime }}^{\star }\mathtt{R}^{c^{\prime }}j_{\star }^{\prime }\mathscr{L}$
, pour
![]() $c^{\prime }\leqslant c$
, sont modérés et constructibles (resp. localement unipotents) le long d’une stratification de
$c^{\prime }\leqslant c$
, sont modérés et constructibles (resp. localement unipotents) le long d’une stratification de
![]() $\overline{F}^{\prime }$
.
$\overline{F}^{\prime }$
.
Démonstration du lemme.
Il suffit de considérer une compactification de
![]() $X^{\prime }\rightarrow X$
— à l’infini de laquelle le faisceau
$X^{\prime }\rightarrow X$
— à l’infini de laquelle le faisceau
![]() $j_{!}^{\prime }\mathscr{L}$
est automatiquement modéré car
$j_{!}^{\prime }\mathscr{L}$
est automatiquement modéré car
![]() $j_{!}\mathscr{L}$
l’est sur
$j_{!}\mathscr{L}$
l’est sur
![]() $X$
— et la compactification induite de
$X$
— et la compactification induite de
![]() $F^{\prime }$
par changement de base
$F^{\prime }$
par changement de base
![]() $F{\hookrightarrow}X$
. La conclusion résulte de la proposition 2.4.1(ii).◻
$F{\hookrightarrow}X$
. La conclusion résulte de la proposition 2.4.1(ii).◻
4.5 Énoncés génériques
Le but de ce paragraphe est d’établir la proposition suivante et d’achever ainsi la démonstration du théorème 4.1.1 (excepté le (a), traité ultérieurement). Pour alléger les énoncés, on fixe l’entier
![]() $c$
et le schéma nœthérien quasi-excellent
$c$
et le schéma nœthérien quasi-excellent
![]() $S$
.
$S$
.
Proposition 4.5.1. Soient
![]() $f:X\rightarrow Y$
un morphisme séparé de type fini entre
$f:X\rightarrow Y$
un morphisme séparé de type fini entre
![]() $S$
-schémas de type fini et
$S$
-schémas de type fini et
![]() $j:X{\hookrightarrow}\overline{X}$
une
$j:X{\hookrightarrow}\overline{X}$
une
![]() $Y$
-compactification de
$Y$
-compactification de
![]() $f$
. Alors, si
$f$
. Alors, si
![]() $\mathbb{F}$
est une famille sur
$\mathbb{F}$
est une famille sur
![]() $X$
telle que
$X$
telle que
![]() $j_{!}\mathbb{F}$
soit constructible modérée (resp. localement unipotente) sur
$j_{!}\mathbb{F}$
soit constructible modérée (resp. localement unipotente) sur
![]() $\overline{X}$
, il existe une immersion ouverte dominante
$\overline{X}$
, il existe une immersion ouverte dominante
![]() $k_{S}:S^{\circ }{\hookrightarrow}S$
telle que
$k_{S}:S^{\circ }{\hookrightarrow}S$
telle que
![]() $k_{Y!}\mathtt{R}^{c}f_{\star }^{\circ }\mathbb{F}$
soit constructible modérée (resp. localement unipotente) pour la topologie des altérations sur
$k_{Y!}\mathtt{R}^{c}f_{\star }^{\circ }\mathbb{F}$
soit constructible modérée (resp. localement unipotente) pour la topologie des altérations sur
![]() $S$
, où
$S$
, où
![]() $f^{\circ }:=f\times _{S}S^{\circ }$
et
$f^{\circ }:=f\times _{S}S^{\circ }$
et
![]() $k_{Y}:=k\times _{S}Y$
.
$k_{Y}:=k\times _{S}Y$
.
Plus précisément, pour toute stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $\overline{X}$
, il existe une altération
$\overline{X}$
, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:Y^{\prime }\rightarrow Y$
et une stratification
$\unicode[STIX]{x1D6FD}:Y^{\prime }\rightarrow Y$
et une stratification
![]() $\mathfrak{Y}$
de
$\mathfrak{Y}$
de
![]() $Y^{\prime }$
telles que pour tout entier
$Y^{\prime }$
telles que pour tout entier
![]() $n\geqslant 1$
et tout faisceau
$n\geqslant 1$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X^{\dagger }=X[1/n]$
tel que
$X^{\dagger }=X[1/n]$
tel que
![]() $j_{!}^{\dagger }\mathscr{F}$
soit constructible et modéré (resp. constructible et localement unipotent) le long de
$j_{!}^{\dagger }\mathscr{F}$
soit constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{X}^{\dagger }$
alors chaque
$\mathfrak{X}^{\dagger }$
alors chaque
![]() $\unicode[STIX]{x1D6FD}^{\dagger \star }k_{Y!}^{\dagger }\mathtt{R}^{c}{f_{\star }^{\circ }}^{\dagger }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
$\unicode[STIX]{x1D6FD}^{\dagger \star }k_{Y!}^{\dagger }\mathtt{R}^{c}{f_{\star }^{\circ }}^{\dagger }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{Y}^{\dagger }$
. (On note abusivement
$\mathfrak{Y}^{\dagger }$
. (On note abusivement
![]() $\mathscr{F}$
pour sa restriction à
$\mathscr{F}$
pour sa restriction à
![]() ${X^{\circ }}^{\dagger }$
.)
${X^{\circ }}^{\dagger }$
.)
De plus, la formation de
![]() $\mathtt{R}^{c}{f_{\star }^{\circ }}^{\dagger }\mathscr{F}$
commute aux changements de base
$\mathtt{R}^{c}{f_{\star }^{\circ }}^{\dagger }\mathscr{F}$
commute aux changements de base
![]() $S^{\prime }\rightarrow S^{\circ }$
.
$S^{\prime }\rightarrow S^{\circ }$
.
Remarques 4.5.2.
(a) L’énoncé ne dit pas que si
 $\mathbb{F}$
est une famille constructible modérée (resp. localement unipotente) sur
$\mathbb{F}$
est une famille constructible modérée (resp. localement unipotente) sur
 $X$
, il existe une immersion ouverte dominante
$X$
, il existe une immersion ouverte dominante
 $Y^{\circ }{\hookrightarrow}Y$
provenant de
$Y^{\circ }{\hookrightarrow}Y$
provenant de
 $S$
telle que
$S$
telle que
 $\mathtt{R}f_{\star }^{\circ }\mathbb{F}$
soit constructible modérée (resp. localement unipotente) sur
$\mathtt{R}f_{\star }^{\circ }\mathbb{F}$
soit constructible modérée (resp. localement unipotente) sur
 $S^{\circ }$
: on fait une hypothèse à l’infini (relativement à
$S^{\circ }$
: on fait une hypothèse à l’infini (relativement à
 $Y$
). (Voir 0.3 pour un contre-exemple à un tel énoncé.)
$Y$
). (Voir 0.3 pour un contre-exemple à un tel énoncé.)(b) Insistons sur le fait que cet énoncé est un corollaire du théorème 4.1.1, d’après lequel on peut prendre
 $S^{\circ }=S$
(c’est-à-dire
$S^{\circ }=S$
(c’est-à-dire
 $k=\text{Id}$
).
$k=\text{Id}$
).
En particulier :
Corollaire 4.5.3. Soient
![]() $X$
un
$X$
un
![]() $S$
-schéma de type fini et
$S$
-schéma de type fini et
![]() $j:U{\hookrightarrow}X$
une immersion ouverte. Pour toute stratification
$j:U{\hookrightarrow}X$
une immersion ouverte. Pour toute stratification
![]() $\mathfrak{X}_{1}$
de
$\mathfrak{X}_{1}$
de
![]() $X$
, il existe une altération
$X$
, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:X_{2}\rightarrow X$
, une stratification
$\unicode[STIX]{x1D6FD}:X_{2}\rightarrow X$
, une stratification
![]() $\mathfrak{X}_{2}$
de
$\mathfrak{X}_{2}$
de
![]() $X_{2}$
et une immersion ouverte dominante
$X_{2}$
et une immersion ouverte dominante
![]() $k_{S}:S^{\circ }{\hookrightarrow}S$
telles que pour tout entier
$k_{S}:S^{\circ }{\hookrightarrow}S$
telles que pour tout entier
![]() $n\geqslant 1$
et tout faisceau
$n\geqslant 1$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X^{\dagger }=X[1/n]$
constructible et modéré (resp. constructible et localement unipotent) le long de
$X^{\dagger }=X[1/n]$
constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{X}_{1}^{\dagger }$
alors
:
$\mathfrak{X}_{1}^{\dagger }$
alors
:
(i) chaque
 $k_{X!}^{\dagger }k_{X}^{\dagger \star }\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
$k_{X!}^{\dagger }k_{X}^{\dagger \star }\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
 $\mathfrak{X}_{2}^{\dagger }$
, où
$\mathfrak{X}_{2}^{\dagger }$
, où
 $k_{X}$
est l’immersion ouverte
$k_{X}$
est l’immersion ouverte
 $k_{S}\times _{S}X$
;
$k_{S}\times _{S}X$
;(ii) la formation de chaque
 $\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
commute aux changements de base
$\mathtt{R}^{c}j_{\star }^{\dagger }j^{\dagger \star }\mathscr{F}$
commute aux changements de base
 $S^{\prime }\rightarrow S^{\circ }$
.
$S^{\prime }\rightarrow S^{\circ }$
.
4.5.4
Montrons que, réciproquement, le cas particulier d’une immersion ouverte entraîne la proposition 4.5.1, dont nous reprenons les notations. Soit
![]() $k_{S}:S^{\circ }{\hookrightarrow}S$
une immersion ouverte comme en 4.5.3 associée à l’immersion ouverte
$k_{S}:S^{\circ }{\hookrightarrow}S$
une immersion ouverte comme en 4.5.3 associée à l’immersion ouverte
![]() $j:X{\hookrightarrow}\overline{X}$
. Par changement de base, on obtient la moitié droite du diagramme commutatif ci-dessous.
$j:X{\hookrightarrow}\overline{X}$
. Par changement de base, on obtient la moitié droite du diagramme commutatif ci-dessous.

On s’intéresse au foncteur
![]() $k_{Y!}f_{\star }^{\circ }k_{X}^{\star }$
(où l’on omet les
$k_{Y!}f_{\star }^{\circ }k_{X}^{\star }$
(où l’on omet les
![]() $\mathtt{R}$
). Compte tenu des isomorphismes
$\mathtt{R}$
). Compte tenu des isomorphismes
![]() $f_{\star }^{\circ }=\overline{f}_{\star }^{\circ }j_{\star }^{\circ }$
(transitivité),
$f_{\star }^{\circ }=\overline{f}_{\star }^{\circ }j_{\star }^{\circ }$
(transitivité),
![]() $k_{Y!}\overline{f}_{\star }^{\circ }=\overline{f}_{\star }k_{\overline{X}!}$
(propreté de
$k_{Y!}\overline{f}_{\star }^{\circ }=\overline{f}_{\star }k_{\overline{X}!}$
(propreté de
![]() $\overline{f}$
) et
$\overline{f}$
) et
![]() $k_{\overline{X}}^{\star }j_{\star }=j_{\star }^{\circ }k_{X}^{\star }$
(changement de base trivial), on a donc
$k_{\overline{X}}^{\star }j_{\star }=j_{\star }^{\circ }k_{X}^{\star }$
(changement de base trivial), on a donc
La conclusion résulte aussitôt de l’hypothèse sur
![]() $k_{\overline{X}!}k_{\overline{X}}^{\star }j_{\star }$
et du théorème d’uniformité propre (3.1.1).
$k_{\overline{X}!}k_{\overline{X}}^{\star }j_{\star }$
et du théorème d’uniformité propre (3.1.1).
La commutation aux changements de base de
![]() $f_{\star }^{\circ }=\overline{f}_{\star }^{\circ }j_{\star }^{\circ }$
résulte du théorème de changement de base propre pour
$f_{\star }^{\circ }=\overline{f}_{\star }^{\circ }j_{\star }^{\circ }$
résulte du théorème de changement de base propre pour
![]() $\overline{f}^{\circ }$
et de la propreté cohomologique de
$\overline{f}^{\circ }$
et de la propreté cohomologique de
![]() $j^{\circ }$
(relativement aux faisceaux considérés).
$j^{\circ }$
(relativement aux faisceaux considérés).
La suite de ce 4.5 est donc consacrée à la démonstration du corollaire 4.5.3.
4.5.5 Dévissages
Mutatis mutandis, les réductions suivant 4.2.2 s’appliquent dans ce cadre générique. Pour la dernière, au cas du prolongement par zéro d’un faisceau lisse sur la strate dense, on utilise l’hypothèse de récurrence selon laquelle l’énoncé 4.1.1 est vrai pour l’entier
![]() $c-1$
.
$c-1$
.
(On aurait pu faire intervenir dans l’énoncé du corollaire une altération
![]() $\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
non nécessairement identité ; la réduction au cas
$\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
non nécessairement identité ; la réduction au cas
![]() $\unicode[STIX]{x1D6FC}=\text{Id}$
aurait alors été possible par commutation de
$\unicode[STIX]{x1D6FC}=\text{Id}$
aurait alors été possible par commutation de
![]() $k_{!}k^{\star }$
aux images directes propres.)
$k_{!}k^{\star }$
aux images directes propres.)
4.5.6
4.5.6.1
Démontrons le corollaire 4.5.3, dans le cas particulier — suffisant d’après ce qui précède — où les faisceaux test
![]() $\mathscr{F}$
sont de la forme
$\mathscr{F}$
sont de la forme
![]() $j_{!}\mathscr{L}$
, avec
$j_{!}\mathscr{L}$
, avec
![]() $\mathscr{L}$
lisse sur
$\mathscr{L}$
lisse sur
![]() $U$
(ou plus précisément
$U$
(ou plus précisément
![]() $U^{\dagger }$
). Nous allons faire un usage relatif de [Reference de JongdeJ96] nous permettant — à l’instar de [Reference IllusieIll10, § 3] et [Reference OrgogozoOrg03, § 2] — de supposer que
$U^{\dagger }$
). Nous allons faire un usage relatif de [Reference de JongdeJ96] nous permettant — à l’instar de [Reference IllusieIll10, § 3] et [Reference OrgogozoOrg03, § 2] — de supposer que
![]() $U$
est génériquement le complémentaire d’un diviseur à croisements normaux (relatif) dans un
$U$
est génériquement le complémentaire d’un diviseur à croisements normaux (relatif) dans un
![]() $S$
-schéma lisse, comme nous allons maintenant l’expliquer. Commençons par observer que le problème étant local sur
$S$
-schéma lisse, comme nous allons maintenant l’expliquer. Commençons par observer que le problème étant local sur
![]() $X$
et
$X$
et
![]() $S$
, on peut supposer le morphisme de type fini
$S$
, on peut supposer le morphisme de type fini
![]() $X\rightarrow S$
séparé, et
$X\rightarrow S$
séparé, et
![]() $S=\text{Spec}(A)$
intègre, de point générique
$S=\text{Spec}(A)$
intègre, de point générique
![]() $\unicode[STIX]{x1D702}=\text{Spec}(K)$
. Comme expliqué dans les deux références ci-dessus, on contourne la difficulté due au fait que
$\unicode[STIX]{x1D702}=\text{Spec}(K)$
. Comme expliqué dans les deux références ci-dessus, on contourne la difficulté due au fait que
![]() $K$
n’est pas parfait par passage à la limite. Soit la perfection « générique »
$K$
n’est pas parfait par passage à la limite. Soit la perfection « générique »
![]() $T$
de
$T$
de
![]() $S$
: si
$S$
: si
![]() $\text{car}.\,(K)=p>0$
, c’est le spectre de la
$\text{car}.\,(K)=p>0$
, c’est le spectre de la
![]() $\mathbb{F}_{p}$
-algèbre
$\mathbb{F}_{p}$
-algèbre
![]() $A^{\text{parf}}=\text{colim}_{a\mapsto a^{p}}A$
parfaite,Footnote
9
ainsi que ses localisés ; sinon,
$A^{\text{parf}}=\text{colim}_{a\mapsto a^{p}}A$
parfaite,Footnote
9
ainsi que ses localisés ; sinon,
![]() $T:=S$
. Les constructions géométriques (en nombre fini) suivantes, a priori faites sur
$T:=S$
. Les constructions géométriques (en nombre fini) suivantes, a priori faites sur
![]() $T$
pour pouvoir appliquer le théorème de résolution des singularités de A. J. de Jong [Reference de JongdeJ96, 4.1–2] au-dessus de son point générique parfait, se descendent à un schéma
$T$
pour pouvoir appliquer le théorème de résolution des singularités de A. J. de Jong [Reference de JongdeJ96, 4.1–2] au-dessus de son point générique parfait, se descendent à un schéma
![]() $S^{\prime }=\text{Spec}(B)$
universellement homéomorphe à
$S^{\prime }=\text{Spec}(B)$
universellement homéomorphe à
![]() $S$
. Un tel morphisme est innocent ; on peut donc supposer abusivement que
$S$
. Un tel morphisme est innocent ; on peut donc supposer abusivement que
![]() $S=T$
(et en particulier
$S=T$
(et en particulier
![]() $K=K^{\text{parf}}$
) pour simplifier les notations.
$K=K^{\text{parf}}$
) pour simplifier les notations.
4.5.6.2
La technique de [Reference IllusieIll10] et [Reference OrgogozoOrg03] conduit pour chaque entier
![]() $N$
à un « bon » hyperrecouvrement propre (tronqué)
$N$
à un « bon » hyperrecouvrement propre (tronqué)
![]() $X_{\bullet \leqslant N}^{\circ }\rightarrow X^{\circ }:=X\times _{S}S^{\circ }$
au-dessus d’un ouvert dense
$X_{\bullet \leqslant N}^{\circ }\rightarrow X^{\circ }:=X\times _{S}S^{\circ }$
au-dessus d’un ouvert dense
![]() $S^{\circ }$
de
$S^{\circ }$
de
![]() $S$
. « Bon » signifie ici : lisse sur
$S$
. « Bon » signifie ici : lisse sur
![]() $S^{\circ }$
, étage par étage, et tel que les
$S^{\circ }$
, étage par étage, et tel que les
![]() $U_{n}^{\circ }:=U\times _{X}X_{n}^{\circ }$
soient complémentaires d’un diviseur à croisements normaux strict relativement à
$U_{n}^{\circ }:=U\times _{X}X_{n}^{\circ }$
soient complémentaires d’un diviseur à croisements normaux strict relativement à
![]() $S^{\circ }$
. On souhaite ici un hyperrecouvrement propre
$S^{\circ }$
. On souhaite ici un hyperrecouvrement propre
![]() $X_{\bullet \leqslant N}\rightarrow X$
induisant sur un ouvert dense
$X_{\bullet \leqslant N}\rightarrow X$
induisant sur un ouvert dense
![]() $S^{\circ }$
un hyperrecouvrement du type précédent. Commençons par énoncer un lemme, conséquence immédiate du théorème [Reference de JongdeJ96, 4.1] susmentionné.
$S^{\circ }$
un hyperrecouvrement du type précédent. Commençons par énoncer un lemme, conséquence immédiate du théorème [Reference de JongdeJ96, 4.1] susmentionné.
Lemme. Soit le diagramme cartésien à traits pleins ci-dessous.

Il existe un morphisme propre et surjectif
![]() $Z\rightarrow Y$
induisant les carrés cartésiens supérieurs tel que
$Z\rightarrow Y$
induisant les carrés cartésiens supérieurs tel que
![]() $Z_{\unicode[STIX]{x1D702}}$
soit lisse sur
$Z_{\unicode[STIX]{x1D702}}$
soit lisse sur
![]() $\unicode[STIX]{x1D702}$
et que l’ouvert
$\unicode[STIX]{x1D702}$
et que l’ouvert
![]() $W_{\unicode[STIX]{x1D702}}\subseteq Z_{\unicode[STIX]{x1D702}}$
en soit le complémentaire d’un diviseur à croisements normaux strict.
$W_{\unicode[STIX]{x1D702}}\subseteq Z_{\unicode[STIX]{x1D702}}$
en soit le complémentaire d’un diviseur à croisements normaux strict.
(Prendre pour
![]() $Z$
une
$Z$
une
![]() $Y$
-compactification d’une résolution de
$Y$
-compactification d’une résolution de
![]() $Y_{\unicode[STIX]{x1D702}}$
adaptée à l’ouvert
$Y_{\unicode[STIX]{x1D702}}$
adaptée à l’ouvert
![]() $V_{\unicode[STIX]{x1D702}}$
.)
$V_{\unicode[STIX]{x1D702}}$
.)
Les techniques classiques de construction d’hyperrecouvrements — voir aussi [Reference Gillet and SouléGS09, § 2.4] pour un problème semblable — nous permettent de déduire de ce lemme une construction étage par étage d’un hyperrecouvrement propre tronqué
![]() $X_{\bullet \leqslant N}\rightarrow X$
tel que les paires
$X_{\bullet \leqslant N}\rightarrow X$
tel que les paires
![]() $(X_{n},U_{n})$
soient génériquement régulières :
$(X_{n},U_{n})$
soient génériquement régulières :
![]() $X_{\bullet \leqslant n}$
étant construit, on pose
$X_{\bullet \leqslant n}$
étant construit, on pose
![]() $Y:=\text{cosq}(X_{\bullet \leqslant n})_{n+1}$
et
$Y:=\text{cosq}(X_{\bullet \leqslant n})_{n+1}$
et
![]() $X_{n+1}$
est alors le
$X_{n+1}$
est alors le
![]() $Y$
-schéma propre
$Y$
-schéma propre
![]() $Z$
fourni par le lemme. La lissité au-dessus de
$Z$
fourni par le lemme. La lissité au-dessus de
![]() $\unicode[STIX]{x1D702}$
des schémas
$\unicode[STIX]{x1D702}$
des schémas
![]() $X_{n}$
et des branches des diviseurs
$X_{n}$
et des branches des diviseurs
![]() $X_{n}\setminus U_{n}$
ainsi construits pour
$X_{n}\setminus U_{n}$
ainsi construits pour
![]() $n\leqslant N$
s’étend à un ouvert dense
$n\leqslant N$
s’étend à un ouvert dense
![]() $S^{\circ }$
de
$S^{\circ }$
de
![]() $S$
.
$S$
.
4.5.6.3
En omettant les troncations, on a donc un diagramme commutatif à carrés cartésiens

Par descente cohomologique, on peut réécrire le foncteur étudié :
où l’on omet à nouveau les
![]() $\mathtt{R}$
. Or, il résulte de 2.4.1(ii) que pour
$\mathtt{R}$
. Or, il résulte de 2.4.1(ii) que pour
![]() $\mathscr{L}$
lisse sur
$\mathscr{L}$
lisse sur
![]() $U$
tel que
$U$
tel que
![]() $j_{!}\mathscr{L}$
soit modéré (resp. localement unipotent), les faisceaux
$j_{!}\mathscr{L}$
soit modéré (resp. localement unipotent), les faisceaux
![]() $k_{X_{n}!}\mathtt{R}^{c}j_{\star }^{\circ }\mathscr{L}^{\circ }$
le sont également. L’énoncé 4.5.3(i) résulte alors du théorème d’uniformité propre pour les
$k_{X_{n}!}\mathtt{R}^{c}j_{\star }^{\circ }\mathscr{L}^{\circ }$
le sont également. L’énoncé 4.5.3(i) résulte alors du théorème d’uniformité propre pour les
![]() $\unicode[STIX]{x1D700}_{n}$
,
$\unicode[STIX]{x1D700}_{n}$
,
![]() $n\leqslant c<N$
. Enfin, la propreté cohomologique des
$n\leqslant c<N$
. Enfin, la propreté cohomologique des
![]() $j_{n}^{\circ }$
relativement à
$j_{n}^{\circ }$
relativement à
![]() $S^{\circ }$
ayant été établie en 2.4.1 (cf. 2.4.3), l’énoncé 4.5.3(ii) résulte du théorème de changement de base propre (pour les
$S^{\circ }$
ayant été établie en 2.4.1 (cf. 2.4.3), l’énoncé 4.5.3(ii) résulte du théorème de changement de base propre (pour les
![]() $\unicode[STIX]{x1D700}_{n}^{\circ }$
).
$\unicode[STIX]{x1D700}_{n}^{\circ }$
).
4.5.7 Majoration des fibres
Pour établir 4.1.1(a), la démonstration précédente nous ramène sans difficulté à la proposition 2.4.6, déjà établie et à l’énoncé dans le cas propre. Dans le cas « absolu », passant par les énoncés génériques, on procède à nouveau par récurrence sur les fermés de
![]() $X\setminus U$
; la mise en garde 1.4.9 sur la nécessité de considérer des prolongements par zéro n’a par contre trivialement pas lieu d’être.
$X\setminus U$
; la mise en garde 1.4.9 sur la nécessité de considérer des prolongements par zéro n’a par contre trivialement pas lieu d’être.
5 Six opérations
5.1 Image directe par un morphisme non nécessairement propre
Le théorème suivant résulte immédiatement, par composition, des énoncés 3.1.1 (cas d’un morphisme propre) et 4.1.1 (cas d’une immersion ouverte).
Théorème. Soient
![]() $S$
un schéma nœthérien quasi-excellent,
$S$
un schéma nœthérien quasi-excellent,
![]() $f:X\rightarrow S$
un morphisme de type fini,
$f:X\rightarrow S$
un morphisme de type fini,
![]() $j:X{\hookrightarrow}\overline{X}$
une
$j:X{\hookrightarrow}\overline{X}$
une
![]() $S$
-compactification de
$S$
-compactification de
![]() $X$
et
$X$
et
![]() $\mathbb{F}$
une famille de faisceaux sur
$\mathbb{F}$
une famille de faisceaux sur
![]() $X$
telle que la famille
$X$
telle que la famille
![]() $j_{!}\mathbb{F}$
soit constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations. Alors, la famille des complexes
$j_{!}\mathbb{F}$
soit constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations. Alors, la famille des complexes
![]() $\mathtt{R}f_{\star }\mathbb{F}$
sur
$\mathtt{R}f_{\star }\mathbb{F}$
sur
![]() $S$
est constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations.
$S$
est constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations.

En d’autres termes, et plus précisément, pour tout entier
![]() $c\geqslant 0$
, toute altération
$c\geqslant 0$
, toute altération
![]() $\unicode[STIX]{x1D6FC}:\overline{X}^{\prime }\rightarrow \overline{X}$
et toute stratification
$\unicode[STIX]{x1D6FC}:\overline{X}^{\prime }\rightarrow \overline{X}$
et toute stratification
![]() $\overline{\mathfrak{X}}$
de
$\overline{\mathfrak{X}}$
de
![]() $\overline{X}^{\prime }$
, il existe une altération
$\overline{X}^{\prime }$
, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:S^{\prime }\rightarrow S$
et une stratification
$\unicode[STIX]{x1D6FD}:S^{\prime }\rightarrow S$
et une stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S^{\prime }$
telles que pour tout entier
$S^{\prime }$
telles que pour tout entier
![]() $n\geqslant 1$
et tout faisceau
$n\geqslant 1$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $X^{\dagger }=X[1/n]$
tel que
$X^{\dagger }=X[1/n]$
tel que
![]() $\unicode[STIX]{x1D6FC}^{\dagger \star }j_{!}^{\dagger }\mathscr{F}$
soit constructible et modérée (resp. constructible et localement unipotent) le long de
$\unicode[STIX]{x1D6FC}^{\dagger \star }j_{!}^{\dagger }\mathscr{F}$
soit constructible et modérée (resp. constructible et localement unipotent) le long de
![]() $\overline{\mathfrak{X}}^{\dagger }$
alors chaque
$\overline{\mathfrak{X}}^{\dagger }$
alors chaque
![]() $\unicode[STIX]{x1D6FD}^{\dagger \star }\mathtt{R}^{c}f_{\star }^{\dagger }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
$\unicode[STIX]{x1D6FD}^{\dagger \star }\mathtt{R}^{c}f_{\star }^{\dagger }\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{S}^{\dagger }$
.
$\mathfrak{S}^{\dagger }$
.
De plus, il existe un entier
![]() $N$
et un ouvert dense
$N$
et un ouvert dense
![]() $S^{\circ }\subseteq S$
, dépendant uniquement du quadruplet
$S^{\circ }\subseteq S$
, dépendant uniquement du quadruplet
![]() $(f,\unicode[STIX]{x1D6FC},\overline{\mathfrak{X}},c)$
, tels que chaque
$(f,\unicode[STIX]{x1D6FC},\overline{\mathfrak{X}},c)$
, tels que chaque
![]() $\mathtt{R}^{c}f_{\star }^{\dagger }\mathscr{F}$
comme ci-dessus
$\mathtt{R}^{c}f_{\star }^{\dagger }\mathscr{F}$
comme ci-dessus
(i) soit
 $N$
-extension ponctuelle de sous-quotients de
$N$
-extension ponctuelle de sous-quotients de
 $\mathscr{F}$
;
$\mathscr{F}$
;(ii) commute aux changements de base
 $T\rightarrow S^{\circ }$
.
$T\rightarrow S^{\circ }$
.
Remarques.
(a) L’hypothèse d’excellence est ici essentielle.
(b) Pour la dépendance en
 $c$
, voir la remarque 4.1.2(i).
$c$
, voir la remarque 4.1.2(i).(c) On ne dit pas que
 $\mathtt{R}^{c}f_{\star }^{\dagger }\mathscr{F}$
est
$\mathtt{R}^{c}f_{\star }^{\dagger }\mathscr{F}$
est
 $N$
-extension ponctuelle de
$N$
-extension ponctuelle de
 $\mathscr{F}$
relativement à
$\mathscr{F}$
relativement à
 $f$
(au sens de 1.7) : c’est trivialement faux lorsque
$f$
(au sens de 1.7) : c’est trivialement faux lorsque
 $f=j\neq \text{Id}$
par exemple.
$f=j\neq \text{Id}$
par exemple.
5.2 Autres opérations
5.2.1
Nous avons établi un résultat de stabilité par
![]() $f_{\star }$
, en faisant une hypothèse — dont on ne peut totalement s’affranchir — sur le comportement des faisceaux à l’infini d’une même compactification.
$f_{\star }$
, en faisant une hypothèse — dont on ne peut totalement s’affranchir — sur le comportement des faisceaux à l’infini d’une même compactification.
5.2.2
Cette même hypothèse rend tautologique la stabilité par
![]() $f_{!}$
à partir du théorème d’uniformité propre.
$f_{!}$
à partir du théorème d’uniformité propre.
Considérons maintenant brièvement les
![]() $4$
des
$4$
des
![]() $6$
-opérations restantes.
$6$
-opérations restantes.
5.2.3
La stabilité par
![]() $f^{\star }$
est tautologique.
$f^{\star }$
est tautologique.
5.2.4
Comme expliqué en [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, p. 151] ou [Th. finitude, 1.5], la stabilité par
![]() $f^{!}$
se ramène à la stabilité par
$f^{!}$
se ramène à la stabilité par
![]() $\mathtt{R}j_{\star }j^{\star }$
, déjà établie : le théorème ci-dessous résulte des faits suivants
:
$\mathtt{R}j_{\star }j^{\star }$
, déjà établie : le théorème ci-dessous résulte des faits suivants
:
– la propriété à démontrer est locale pour la topologie de Zariski (en haut et en bas) ;
– un morphisme affine est lissifiable ;
– si
 $S^{\prime }\rightarrow S$
est une altération, il en est de même de
$S^{\prime }\rightarrow S$
est une altération, il en est de même de
 $\mathbf{A}_{S^{\prime }}^{d}\rightarrow \mathbf{A}_{S}^{d}$
;
$\mathbf{A}_{S^{\prime }}^{d}\rightarrow \mathbf{A}_{S}^{d}$
;– dualité de Poincaré et innocuité de la torsion à la Tate ;
– existence d’un triangle distingué
 $i_{\star }i^{!}\rightarrow \text{Id}\rightarrow \mathtt{R}j_{\star }j^{\star }\stackrel{+1}{\rightarrow }$
.
$i_{\star }i^{!}\rightarrow \text{Id}\rightarrow \mathtt{R}j_{\star }j^{\star }\stackrel{+1}{\rightarrow }$
.
Théorème. Soient
![]() $S$
un schéma nœthérien quasi-excellent et
$S$
un schéma nœthérien quasi-excellent et
![]() $f:X\rightarrow S$
un morphisme séparé de type fini. La propriété d’une famille
$f:X\rightarrow S$
un morphisme séparé de type fini. La propriété d’une famille
![]() $\mathbb{F}$
de faisceaux (sur
$\mathbb{F}$
de faisceaux (sur
![]() $S$
) d’être constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations est préservée par le foncteur
$S$
) d’être constructible et modérée (resp. constructible et localement unipotente) pour la topologie des altérations est préservée par le foncteur
![]() $f^{!}$
.
$f^{!}$
.
En d’autres termes, et plus précisément, pour tout entier
![]() $c\geqslant 0$
, toute altération
$c\geqslant 0$
, toute altération
![]() $\unicode[STIX]{x1D6FC}:S^{\prime }\rightarrow S$
et toute stratification
$\unicode[STIX]{x1D6FC}:S^{\prime }\rightarrow S$
et toute stratification
![]() $\mathfrak{S}$
de
$\mathfrak{S}$
de
![]() $S^{\prime }$
, il existe une altération
$S^{\prime }$
, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:X^{\prime }\rightarrow X$
et une stratification
$\unicode[STIX]{x1D6FD}:X^{\prime }\rightarrow X$
et une stratification
![]() $\mathfrak{X}$
de
$\mathfrak{X}$
de
![]() $X^{\prime }$
telles que pour tout entier
$X^{\prime }$
telles que pour tout entier
![]() $n\geqslant 1$
et tout faisceau
$n\geqslant 1$
et tout faisceau
![]() $\mathscr{F}$
de
$\mathscr{F}$
de
![]() $\mathbb{Z}/n\mathbb{Z}$
-modules sur
$\mathbb{Z}/n\mathbb{Z}$
-modules sur
![]() $S^{\dagger }=S[1/n]$
tel que
$S^{\dagger }=S[1/n]$
tel que
![]() $\unicode[STIX]{x1D6FC}^{\dagger \star }\mathscr{F}$
soit constructible et modérée (resp. constructible et localement unipotent) le long de
$\unicode[STIX]{x1D6FC}^{\dagger \star }\mathscr{F}$
soit constructible et modérée (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{S}^{\dagger }$
, chaque
$\mathfrak{S}^{\dagger }$
, chaque
![]() $\unicode[STIX]{x1D6FD}^{\dagger \star }\mathtt{R}^{c}f^{\dagger !}\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
$\unicode[STIX]{x1D6FD}^{\dagger \star }\mathtt{R}^{c}f^{\dagger !}\mathscr{F}$
est constructible et modéré (resp. constructible et localement unipotent) le long de
![]() $\mathfrak{X}^{\dagger }$
.
$\mathfrak{X}^{\dagger }$
.

5.2.5
Stabilité par
![]() $\otimes ^{\mathbb{L}}$
. On souhaite montrer que si
$\otimes ^{\mathbb{L}}$
. On souhaite montrer que si
![]() $(X,\mathfrak{X})$
est un schéma nœthérien stratifié alors pour tout
$(X,\mathfrak{X})$
est un schéma nœthérien stratifié alors pour tout
![]() $n\geqslant 1$
et toute paire
$n\geqslant 1$
et toute paire
![]() $\mathscr{A},\mathscr{B}\in \text{Ob}\;D_{\mathfrak{X}}^{-\;\text{mod}}(X[1/n],\mathbb{Z}/n\mathbb{Z})$
(variante évidente de la notation introduite en 3.1.3) le produit tensoriel
$\mathscr{A},\mathscr{B}\in \text{Ob}\;D_{\mathfrak{X}}^{-\;\text{mod}}(X[1/n],\mathbb{Z}/n\mathbb{Z})$
(variante évidente de la notation introduite en 3.1.3) le produit tensoriel
![]() $\mathscr{A}\otimes _{\mathbb{Z}/n\mathbb{Z}}^{\mathbb{L}}\mathscr{B}$
appartient également à
$\mathscr{A}\otimes _{\mathbb{Z}/n\mathbb{Z}}^{\mathbb{L}}\mathscr{B}$
appartient également à
![]() $D_{\mathfrak{X}}^{-\;\text{mod}}(X[1/n],\mathbb{Z}/n\mathbb{Z})$
Footnote
10
et de même pour les complexes à cohomologie localement unipotente le long de
$D_{\mathfrak{X}}^{-\;\text{mod}}(X[1/n],\mathbb{Z}/n\mathbb{Z})$
Footnote
10
et de même pour les complexes à cohomologie localement unipotente le long de
![]() $\mathfrak{X}$
.
$\mathfrak{X}$
.
Par dévissage des complexes, on peut supposer que
![]() $\mathscr{A}$
et
$\mathscr{A}$
et
![]() $\mathscr{B}$
sont des faisceaux placés en degré nul. Par dévissage (1.1.4) des faisceaux constructibles le long de
$\mathscr{B}$
sont des faisceaux placés en degré nul. Par dévissage (1.1.4) des faisceaux constructibles le long de
![]() $\mathfrak{X}$
— ou plutôt
$\mathfrak{X}$
— ou plutôt
![]() $\mathfrak{X}^{\dagger }=\mathfrak{X}[1/n]$
mais nous ignorons cette subtilité pour simplifier les notations —, de l’entier
$\mathfrak{X}^{\dagger }=\mathfrak{X}[1/n]$
mais nous ignorons cette subtilité pour simplifier les notations —, de l’entier
![]() $n$
(voir par exemple [Th. finitude, A, 2.2 b)] ou [STG XVII, 7.4.6] pour un raffinement), et grâce à la formule de projection triviale (pour une immersion ouverte ou fermée), on se ramène à l’étude des produits tensoriels
$n$
(voir par exemple [Th. finitude, A, 2.2 b)] ou [STG XVII, 7.4.6] pour un raffinement), et grâce à la formule de projection triviale (pour une immersion ouverte ou fermée), on se ramène à l’étude des produits tensoriels
![]() $j_{!}(\mathscr{L}\otimes _{\mathbb{Z}/\ell ^{r}\mathbb{Z}}^{\mathbb{L}}\mathscr{M})$
, où
$j_{!}(\mathscr{L}\otimes _{\mathbb{Z}/\ell ^{r}\mathbb{Z}}^{\mathbb{L}}\mathscr{M})$
, où
![]() $\mathscr{L},\mathscr{M}$
sont des faisceaux lisses de
$\mathscr{L},\mathscr{M}$
sont des faisceaux lisses de
![]() $\mathbb{F}_{\ell }$
-espaces vectoriels sur une même strate ouverte dense
$\mathbb{F}_{\ell }$
-espaces vectoriels sur une même strate ouverte dense
![]() $U\subseteq X=X[1/\ell ]$
. (Cette réduction n’utilise pas le théorème d’uniformité propre pour une immersion fermée — c’est-à-dire essentiellement le lemme de Gabber — car il n’est pas nécessaire d’avoir recours à une altération.)
$U\subseteq X=X[1/\ell ]$
. (Cette réduction n’utilise pas le théorème d’uniformité propre pour une immersion fermée — c’est-à-dire essentiellement le lemme de Gabber — car il n’est pas nécessaire d’avoir recours à une altération.)
Comme d’autre part
![]() $\mathscr{L}\otimes _{\mathbb{Z}/\ell ^{r}\mathbb{Z}}^{\mathbb{L}}\mathscr{M}=(\mathscr{L}\otimes _{\mathbb{Z}/\ell ^{r}\mathbb{Z}}^{\mathbb{L}}\mathbb{F}_{\ell })\otimes _{\mathbb{F}_{\ell }}^{\mathbb{L}}\mathscr{M}$
est représenté (pour
$\mathscr{L}\otimes _{\mathbb{Z}/\ell ^{r}\mathbb{Z}}^{\mathbb{L}}\mathscr{M}=(\mathscr{L}\otimes _{\mathbb{Z}/\ell ^{r}\mathbb{Z}}^{\mathbb{L}}\mathbb{F}_{\ell })\otimes _{\mathbb{F}_{\ell }}^{\mathbb{L}}\mathscr{M}$
est représenté (pour
![]() $r>1$
) par le complexe (concentré en degrés
$r>1$
) par le complexe (concentré en degrés
![]() ${\leqslant}0$
)
${\leqslant}0$
)
il suffit d’observer que si
![]() $j_{!}\mathscr{L}$
et
$j_{!}\mathscr{L}$
et
![]() $j_{!}\mathscr{M}$
sont modérés (resp. localement unipotents le long d’une stratification
$j_{!}\mathscr{M}$
sont modérés (resp. localement unipotents le long d’une stratification
![]() $\mathfrak{X}$
), il en est de même de
$\mathfrak{X}$
), il en est de même de
![]() $j_{!}(\mathscr{L}\otimes _{\mathbb{F}_{\ell }}\mathscr{M})$
.
$j_{!}(\mathscr{L}\otimes _{\mathbb{F}_{\ell }}\mathscr{M})$
.
5.2.6
Stabilité par
![]() $\mathbf{RHom}$
. On suppose
$\mathbf{RHom}$
. On suppose
![]() $X$
de dimension finie, pour éviter d’avoir a priori besoin de tronquer (cf. 4.1.2). Soient
$X$
de dimension finie, pour éviter d’avoir a priori besoin de tronquer (cf. 4.1.2). Soient
![]() $\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
une altération et
$\unicode[STIX]{x1D6FC}:X_{1}\rightarrow X$
une altération et
![]() $\mathfrak{X}_{1}$
une stratification de
$\mathfrak{X}_{1}$
une stratification de
![]() $X_{1}$
. On veut montrer qu’il existe une altération
$X_{1}$
. On veut montrer qu’il existe une altération
![]() $\unicode[STIX]{x1D6FD}:X_{2}\rightarrow X$
et une stratification
$\unicode[STIX]{x1D6FD}:X_{2}\rightarrow X$
et une stratification
![]() $\mathfrak{X}_{2}$
de
$\mathfrak{X}_{2}$
de
![]() $X_{2}$
telles que pour chaque
$X_{2}$
telles que pour chaque
![]() $n$
, le foncteur
$n$
, le foncteur
![]() $\mathbf{RHom}:D(X[1/n],\mathbb{Z}/n\mathbb{Z})^{\text{op}}\times D(X[1/n],\mathbb{Z}/n\mathbb{Z})\rightarrow D(X[1/n],\mathbb{Z}/n\mathbb{Z})$
induise un foncteur
$\mathbf{RHom}:D(X[1/n],\mathbb{Z}/n\mathbb{Z})^{\text{op}}\times D(X[1/n],\mathbb{Z}/n\mathbb{Z})\rightarrow D(X[1/n],\mathbb{Z}/n\mathbb{Z})$
induise un foncteur
On procède à nouveau comme dans [Reference Beilinson, Bernstein, Deligne and GabberBBDG82, 6.1.2, p. 151]. (Voir aussi [Th. finitude, A, 1.6], [SGA 5 I, § 3.3] ou [STG XVII, § 7.6].) La formule
pour une immersion
![]() $f$
nous ramène par dévissages et stabilité par
$f$
nous ramène par dévissages et stabilité par
![]() $\mathtt{R}j_{\star }$
(4.1.1) — nécessitant peut-être de grossir
$\mathtt{R}j_{\star }$
(4.1.1) — nécessitant peut-être de grossir
![]() $X_{1}$
et raffiner
$X_{1}$
et raffiner
![]() $\mathfrak{X}_{1}$
— à montrer que si
$\mathfrak{X}_{1}$
— à montrer que si
![]() $\mathscr{L}$
est un faisceau lisse sur un ouvert dense
$\mathscr{L}$
est un faisceau lisse sur un ouvert dense
![]() $j:U{\hookrightarrow}X$
tel que
$j:U{\hookrightarrow}X$
tel que
![]() $j_{!}\mathscr{L}$
soit modéré (resp. localement unipotent) le long de
$j_{!}\mathscr{L}$
soit modéré (resp. localement unipotent) le long de
![]() $\mathfrak{X}_{1}$
, et
$\mathfrak{X}_{1}$
, et
![]() $\mathscr{G}$
est également constructible et modéré (resp. localement unipotent) le long de
$\mathscr{G}$
est également constructible et modéré (resp. localement unipotent) le long de
![]() $\mathfrak{X}_{1}$
, alors il en est de même des faisceaux
$\mathfrak{X}_{1}$
, alors il en est de même des faisceaux
![]() $j_{!}\mathbf{Ext}^{i}(\mathscr{L},j^{\star }\mathscr{G})$
(
$j_{!}\mathbf{Ext}^{i}(\mathscr{L},j^{\star }\mathscr{G})$
(
![]() $i\geqslant 0$
). Or, sous l’hypothèse faite sur
$i\geqslant 0$
). Or, sous l’hypothèse faite sur
![]() $\mathscr{L}$
, il existe un carré cartésien
$\mathscr{L}$
, il existe un carré cartésien

avec
![]() $X^{\prime }\rightarrow X$
fini surjectif,
$X^{\prime }\rightarrow X$
fini surjectif,
![]() $U^{\prime }\rightarrow U$
fini étale tel que
$U^{\prime }\rightarrow U$
fini étale tel que
![]() $\mathscr{L}_{|U^{\prime }}$
soit trivial et si
$\mathscr{L}_{|U^{\prime }}$
soit trivial et si
![]() $\mathscr{H}$
est un faisceau sur
$\mathscr{H}$
est un faisceau sur
![]() $U_{1}:=U\times _{X}X_{1}$
, la constructibilité et modération (resp. locale unipotence) de
$U_{1}:=U\times _{X}X_{1}$
, la constructibilité et modération (resp. locale unipotence) de
![]() $j_{1!}^{\prime }\mathscr{H}_{1}^{\prime }$
(sur
$j_{1!}^{\prime }\mathscr{H}_{1}^{\prime }$
(sur
![]() $X_{1}^{\prime }:=X_{1}\times _{X}X^{\prime }$
) le long de
$X_{1}^{\prime }:=X_{1}\times _{X}X^{\prime }$
) le long de
![]() $\mathfrak{X}_{1}^{\prime }$
entraîne la constructibilité et modération (resp. locale unipotence) de
$\mathfrak{X}_{1}^{\prime }$
entraîne la constructibilité et modération (resp. locale unipotence) de
![]() $j_{1!}\mathscr{H}_{1}$
le long de
$j_{1!}\mathscr{H}_{1}$
le long de
![]() $\mathfrak{X}_{1}$
. (Dans le cas unipotent, on utilise le fait que si un groupe
$\mathfrak{X}_{1}$
. (Dans le cas unipotent, on utilise le fait que si un groupe
![]() $G$
agit sur un
$G$
agit sur un
![]() $\mathbb{F}_{\ell }$
-module
$\mathbb{F}_{\ell }$
-module
![]() $M$
de sorte que la restriction à
$M$
de sorte que la restriction à
![]() $H\lhd G$
soit unipotente alors l’action de
$H\lhd G$
soit unipotente alors l’action de
![]() $G$
est également unipotente si le quotient
$G$
est également unipotente si le quotient
![]() $G/H$
est un
$G/H$
est un
![]() $\ell$
-groupe.Footnote
11
) Écrivant
$\ell$
-groupe.Footnote
11
) Écrivant
![]() $\mathscr{L}$
comme un quotient de
$\mathscr{L}$
comme un quotient de
![]() $(U^{\prime }\rightarrow U)_{\star }(U^{\prime }\rightarrow U)^{\star }\mathscr{L}$
et utilisant la formule d’adjonction rappelée ci-dessus (pour
$(U^{\prime }\rightarrow U)_{\star }(U^{\prime }\rightarrow U)^{\star }\mathscr{L}$
et utilisant la formule d’adjonction rappelée ci-dessus (pour
![]() $f$
le morphisme étale
$f$
le morphisme étale
![]() $U^{\prime }\rightarrow U$
), ceci nous ramène au cas particulier où
$U^{\prime }\rightarrow U$
), ceci nous ramène au cas particulier où
![]() $\mathscr{L}$
est même trivial, puis par résolution projective au cas
$\mathscr{L}$
est même trivial, puis par résolution projective au cas
![]() $\mathscr{L}=\unicode[STIX]{x1D6EC}$
. Pour conclure, il ne reste plus qu’à utiliser le fait que
$\mathscr{L}=\unicode[STIX]{x1D6EC}$
. Pour conclure, il ne reste plus qu’à utiliser le fait que
![]() $\mathbf{RHom}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6EC},j^{\star }\mathscr{G})=j^{\star }\mathscr{G}$
.
$\mathbf{RHom}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6EC},j^{\star }\mathscr{G})=j^{\star }\mathscr{G}$
.
6 Applications
6.1 Représentations
 $\ell$
-adiques
$\ell$
-adiques
Dans [Reference Böckle, Gajda and PetersenBGP18], les auteurs démontrent une conjecture de presque indépendance des représentations
![]() $\ell$
-adiques associées à un schéma algébrique, due à J.-P. Serre en caractéristique nulle [Reference SerreSer13, § 3.2]. Un des ingrédients de leur démonstration est le fait suivant [Reference Böckle, Gajda and PetersenBGP18, 6.3, 7.4], que les auteurs démontrent par réduction au cas des courbes (à la Wiesend) et en utilisant [Reference DeligneDel73, 9.8] :
$\ell$
-adiques associées à un schéma algébrique, due à J.-P. Serre en caractéristique nulle [Reference SerreSer13, § 3.2]. Un des ingrédients de leur démonstration est le fait suivant [Reference Böckle, Gajda and PetersenBGP18, 6.3, 7.4], que les auteurs démontrent par réduction au cas des courbes (à la Wiesend) et en utilisant [Reference DeligneDel73, 9.8] :
Proposition. Soit
![]() $k$
un corps parfait,
$k$
un corps parfait,
![]() $K/k$
une extension de type fini et
$K/k$
une extension de type fini et
![]() $X_{K}$
un
$X_{K}$
un
![]() $K$
-schéma algébrique. Il existe une extension finie étale
$K$
-schéma algébrique. Il existe une extension finie étale
![]() $L/K$
, un
$L/K$
, un
![]() $k$
-schéma propre et lisse
$k$
-schéma propre et lisse
![]() $T$
de corps des fractions
$T$
de corps des fractions
![]() $L$
et un diviseur à croisements normaux
$L$
et un diviseur à croisements normaux
![]() $D$
dans
$D$
dans
![]() $T$
tels que
$T$
tels que
![]() $\text{pour chaque nombre premier}$
$\text{pour chaque nombre premier}$
![]() $\ell$
inversible sur
$\ell$
inversible sur
![]() $k$
,
$k$
,
(i) l’action du groupe de Galois
 $G_{L}$
sur
$G_{L}$
sur
 $\mathtt{H}^{\star }(X_{\overline{K}},\mathbb{Q}_{\ell })$
se factorise à travers le groupe fondamental
$\mathtt{H}^{\star }(X_{\overline{K}},\mathbb{Q}_{\ell })$
se factorise à travers le groupe fondamental
 $\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}$
$\text{mod}\acute{\text{e}}\text{r}\acute{\text{e}}$
 $\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(T,D)$
;
$\unicode[STIX]{x1D70B}_{1}^{\text{mod}}(T,D)$
;(ii) pour chaque point maximal
 $d$
de
$d$
de
 $D$
, l’action sur
$D$
, l’action sur
 $\mathtt{H}^{\star }(X_{\overline{K}},\mathbb{Q}_{\ell })$
du groupe d’inertie correspondant soit
$\mathtt{H}^{\star }(X_{\overline{K}},\mathbb{Q}_{\ell })$
du groupe d’inertie correspondant soit
 $\text{unipotente}$
.
$\text{unipotente}$
.
C’est également un corollaire immédiat de nos résultats.
Démonstration.
Par déploiement, il existe un
![]() $k$
-schéma de type fini
$k$
-schéma de type fini
![]() $U$
de corps des fractions
$U$
de corps des fractions
![]() $K$
, et un morphisme de type fini
$K$
, et un morphisme de type fini
![]() $X\rightarrow U$
de fibre générique
$X\rightarrow U$
de fibre générique
![]() $X_{K}$
. Soit
$X_{K}$
. Soit
![]() $S$
une
$S$
une
![]() $k$
-compactification de
$k$
-compactification de
![]() $U$
et notons
$U$
et notons
![]() $f:X\rightarrow S$
le morphisme composé. D’après 5.1, il existe une altération
$f:X\rightarrow S$
le morphisme composé. D’après 5.1, il existe une altération
![]() $\unicode[STIX]{x1D6FD}:T\rightarrow S$
et une stratification
$\unicode[STIX]{x1D6FD}:T\rightarrow S$
et une stratification
![]() $\mathfrak{T}$
de
$\mathfrak{T}$
de
![]() $T$
telle que les faisceaux
$T$
telle que les faisceaux
![]() $\unicode[STIX]{x1D6FD}^{\ast }\mathtt{R}^{i}f_{\star }\mathbb{Q}_{\ell }$
, pour
$\unicode[STIX]{x1D6FD}^{\ast }\mathtt{R}^{i}f_{\star }\mathbb{Q}_{\ell }$
, pour
![]() $\ell \neq \text{car}.\,(k)$
et
$\ell \neq \text{car}.\,(k)$
et
![]() $i\in \mathbb{N}$
, soient constructibles, modérés et localement unipotents le long de
$i\in \mathbb{N}$
, soient constructibles, modérés et localement unipotents le long de
![]() $\mathfrak{T}$
. Quitte à rétrécir
$\mathfrak{T}$
. Quitte à rétrécir
![]() $U$
, on peut supposer ces faisceaux lisses sur cet ouvert et que
$U$
, on peut supposer ces faisceaux lisses sur cet ouvert et que
![]() $V:=\unicode[STIX]{x1D6FD}^{-1}(W)$
est la strate ouverte dense de
$V:=\unicode[STIX]{x1D6FD}^{-1}(W)$
est la strate ouverte dense de
![]() $T$
. Comme remarqué en 1.6.6, on peut supposer l’altération
$T$
. Comme remarqué en 1.6.6, on peut supposer l’altération
![]() $\unicode[STIX]{x1D6FD}$
génériquement étale. D’après [Reference de JongdeJ96, 4.1], on peut également supposer le morphisme
$\unicode[STIX]{x1D6FD}$
génériquement étale. D’après [Reference de JongdeJ96, 4.1], on peut également supposer le morphisme
![]() $T\rightarrow \text{Spec}(k)$
lisse et l’ouvert
$T\rightarrow \text{Spec}(k)$
lisse et l’ouvert
![]() $V$
être le complémentaire d’un diviseur à croisements normaux
$V$
être le complémentaire d’un diviseur à croisements normaux
![]() $D$
.◻
$D$
.◻
Remarque.
Le résultat de P. Deligne [Reference BerthelotBer97, 6.3.2] d’indépendance de
![]() $\ell$
dans le théorème de monodromie de Grothendieck est également un corollaire immédiat de 5.1, du moins pour un trait excellent. Pour des précisions numériques dans cette direction, voir [Reference UmezakiUme16].
$\ell$
dans le théorème de monodromie de Grothendieck est également un corollaire immédiat de 5.1, du moins pour un trait excellent. Pour des précisions numériques dans cette direction, voir [Reference UmezakiUme16].
6.2 Lien avec la torsion
Soient
![]() $k$
un corps algébriquement clos d’exposant caractéristique
$k$
un corps algébriquement clos d’exposant caractéristique
![]() $p\geqslant 1$
et
$p\geqslant 1$
et
![]() $X$
un schéma projectif et lisse sur
$X$
un schéma projectif et lisse sur
![]() $k$
. Pour chaque nombre premier
$k$
. Pour chaque nombre premier
![]() $\ell$
différent de
$\ell$
différent de
![]() $p$
et chaque entier
$p$
et chaque entier
![]() $i\geqslant 0$
les
$i\geqslant 0$
les
![]() $\mathbb{Z}_{\ell }$
-modules
$\mathbb{Z}_{\ell }$
-modules
![]() $\mathtt{H}^{i}(X,\mathbb{Z}_{\ell }):=\lim _{n}\mathtt{H}^{i}(X,\mathbb{Z}/\ell ^{n})$
sont de type fini [SGA 5 VI, 2.2]. D’après [Reference GabberGab83, théorème], ils sont sans torsion pour presque tout
$\mathtt{H}^{i}(X,\mathbb{Z}_{\ell }):=\lim _{n}\mathtt{H}^{i}(X,\mathbb{Z}/\ell ^{n})$
sont de type fini [SGA 5 VI, 2.2]. D’après [Reference GabberGab83, théorème], ils sont sans torsion pour presque tout
![]() $\ell$
. Si
$\ell$
. Si
![]() $k$
est de caractéristique nulle, cela résulte du théorème de comparaison Betti-étale d’Artin–Grothendieck [SGA 4 XI, 4.4] ; si
$k$
est de caractéristique nulle, cela résulte du théorème de comparaison Betti-étale d’Artin–Grothendieck [SGA 4 XI, 4.4] ; si
![]() $p>1$
, un ingrédient clef de sa démonstration est le théorème du pgcd [Reference DeligneDel80, § 4.5].
$p>1$
, un ingrédient clef de sa démonstration est le théorème du pgcd [Reference DeligneDel80, § 4.5].
L’objet de ce paragraphe est d’expliquer une approche alternative — qui nous a été communiquée par N. Katz — au théorème susmentionné d’O. Gabber (6.2.2). Signalons cependant qu’elle repose aussi, quoique indirectement, sur le théorème du pgcd.
6.2.1
Soient
![]() $\mathfrak{L}$
un ultrafiltre non principal sur l’ensemble des nombres premiers différents de
$\mathfrak{L}$
un ultrafiltre non principal sur l’ensemble des nombres premiers différents de
![]() $p$
[BourbTG, I.§ 4],
$p$
[BourbTG, I.§ 4],
![]() $\mathfrak{m}_{\mathfrak{L}}=\{a=(a_{\ell }),\{\ell :a_{\ell }=0\}\in \mathfrak{L}\}$
l’idéal maximal de l’anneau
$\mathfrak{m}_{\mathfrak{L}}=\{a=(a_{\ell }),\{\ell :a_{\ell }=0\}\in \mathfrak{L}\}$
l’idéal maximal de l’anneau
![]() $A=\prod _{\ell \neq p}\mathbb{F}_{\ell }$
associé et
$A=\prod _{\ell \neq p}\mathbb{F}_{\ell }$
associé et
![]() $\mathbb{F}_{\mathfrak{L}}=A/\mathfrak{m}_{\mathfrak{L}}$
son corps résiduel, de caractéristique nulle. Supposons
$\mathbb{F}_{\mathfrak{L}}=A/\mathfrak{m}_{\mathfrak{L}}$
son corps résiduel, de caractéristique nulle. Supposons
![]() $k$
algébrique sur un corps fini — c’est le cas crucial — et admettons un instant (voir le théorème 6.2.3) que le foncteur
$k$
algébrique sur un corps fini — c’est le cas crucial — et admettons un instant (voir le théorème 6.2.3) que le foncteur
![]() $X\mapsto \mathtt{H}^{\star }(X,\mathbb{F}_{\mathfrak{L}}):=(\prod _{\ell \neq p}\mathtt{H}^{\star }(X,\mathbb{F}_{\ell }))\otimes _{A}\mathbb{F}_{\mathfrak{L}}$
définisse une cohomologie de Weil [Reference KleimanKle68, § 1.2] ; pour notre propos, finitude, dualité de Poincaré, théorème de Lefschetz faible pour les sections hyperplanes lisses et interprétation cohomologique de la fonction
$X\mapsto \mathtt{H}^{\star }(X,\mathbb{F}_{\mathfrak{L}}):=(\prod _{\ell \neq p}\mathtt{H}^{\star }(X,\mathbb{F}_{\ell }))\otimes _{A}\mathbb{F}_{\mathfrak{L}}$
définisse une cohomologie de Weil [Reference KleimanKle68, § 1.2] ; pour notre propos, finitude, dualité de Poincaré, théorème de Lefschetz faible pour les sections hyperplanes lisses et interprétation cohomologique de la fonction
![]() $\unicode[STIX]{x1D701}$
suffisent. Comme démontré dans [Reference Katz and MessingKM74, II, corollaire 1], il résulte alors de [Reference DeligneDel80] que l’on a pour chaque
$\unicode[STIX]{x1D701}$
suffisent. Comme démontré dans [Reference Katz and MessingKM74, II, corollaire 1], il résulte alors de [Reference DeligneDel80] que l’on a pour chaque
![]() $i\geqslant 0$
l’égalité
$i\geqslant 0$
l’égalité
où
![]() $b^{i}(X)$
est le
$b^{i}(X)$
est le
![]() $i$
-ème nombre de Betti de
$i$
-ème nombre de Betti de
![]() $X$
, nombre que l’on lit par exemple sur la fonction zêta d’un « modèle » de
$X$
, nombre que l’on lit par exemple sur la fonction zêta d’un « modèle » de
![]() $X$
sur un corps fini. Le groupe de cohomologie
$X$
sur un corps fini. Le groupe de cohomologie
![]() $\mathtt{H}^{i}(X,\mathbb{F}_{\mathfrak{L}})$
étant un ultraproduit des
$\mathtt{H}^{i}(X,\mathbb{F}_{\mathfrak{L}})$
étant un ultraproduit des
![]() $\mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
sa dimension est la limite, suivant l’ultrafiltre
$\mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
sa dimension est la limite, suivant l’ultrafiltre
![]() $\mathfrak{L}$
, de la fonction
$\mathfrak{L}$
, de la fonction
![]() $\ell \mapsto h^{i}(X,\mathbb{F}_{\ell }):=\dim _{\mathbb{F}_{\ell }}\mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
, bornée d’après le théorème d’uniformité propre 3.1.1. (Voir aussi infra pour un argument plus direct dans ce cas particulier.) En symboles :
$\ell \mapsto h^{i}(X,\mathbb{F}_{\ell }):=\dim _{\mathbb{F}_{\ell }}\mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
, bornée d’après le théorème d’uniformité propre 3.1.1. (Voir aussi infra pour un argument plus direct dans ce cas particulier.) En symboles :
Le résultat précédent étant vrai pour tout ultrafiltre non principal
![]() $\mathfrak{L}$
, on en déduit l’égalité
$\mathfrak{L}$
, on en déduit l’égalité
![]() $h^{i}(X,\mathbb{F}_{\ell })=b^{i}(X)$
pour tous les
$h^{i}(X,\mathbb{F}_{\ell })=b^{i}(X)$
pour tous les
![]() $\ell$
sauf au plus un nombre fini d’entre eux. D’autre part, on a l’égalité
$\ell$
sauf au plus un nombre fini d’entre eux. D’autre part, on a l’égalité
pour tout
![]() $\ell \neq p$
, de sorte que l’on a finalement
$\ell \neq p$
, de sorte que l’on a finalement
![]() $h^{i}(X,\mathbb{F}_{\ell })=h^{i}(X,\mathbb{Q}_{\ell })$
pour presque tout
$h^{i}(X,\mathbb{F}_{\ell })=h^{i}(X,\mathbb{Q}_{\ell })$
pour presque tout
![]() $\ell$
. La suite exacte des coefficients universels,
$\ell$
. La suite exacte des coefficients universels,
permet alors de conclure, c’est-à-dire de retrouver le théorème d’O. Gabber sur l’absence de torsion pour presque tout
![]() $\ell$
. (L’injectivité de
$\ell$
. (L’injectivité de
![]() $\mathtt{H}^{i}(X,\mathbb{Z}_{\ell })\otimes \mathbb{F}_{\ell }\rightarrow \mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
suffirait.)
$\mathtt{H}^{i}(X,\mathbb{Z}_{\ell })\otimes \mathbb{F}_{\ell }\rightarrow \mathtt{H}^{i}(X,\mathbb{F}_{\ell })$
suffirait.)
Théorème 6.2.2. (O. Gabber ; J. Suh). Soit
![]() $X$
un schéma propre et lisse sur un corps algébriquement clos. Alors pour presque tout nombre premier
$X$
un schéma propre et lisse sur un corps algébriquement clos. Alors pour presque tout nombre premier
![]() $\ell$
, les groupes
$\ell$
, les groupes
![]() $\mathtt{H}^{i}(X,\mathbb{Z}_{\ell })$
sont sans torsion.
$\mathtt{H}^{i}(X,\mathbb{Z}_{\ell })$
sont sans torsion.
Le cas projectif est bien connu [Reference GabberGab83, théorème] ; comme l’ont indépendamment observé O. Gabber et J. Suh [Reference SuhSuh12, § 1], le cas propre s’y ramène.
Démonstration (esquisse).
Cas projectif. Comme expliqué ci-dessus, cela résulte immédiatement des théorèmes de Katz–Messing et d’uniformité, ce dernier sous la forme faible présentée dans le paragraphe 6.2.4 ci-dessous.
Réduction du cas propre au cas projectif. D’après [Reference de JongdeJ96, 4.1], il existe une altération génériquement étale
![]() $a:X^{\prime }\rightarrow X$
de degré
$a:X^{\prime }\rightarrow X$
de degré
![]() $d$
avec
$d$
avec
![]() $X^{\prime }$
projectif et lisse sur le corps de base. Fixons un entier
$X^{\prime }$
projectif et lisse sur le corps de base. Fixons un entier
![]() $n$
inversible sur
$n$
inversible sur
![]() $X$
et notons
$X$
et notons
![]() $\unicode[STIX]{x1D6EC}=\mathbb{Z}/n\mathbb{Z}$
. Le morphisme
$\unicode[STIX]{x1D6EC}=\mathbb{Z}/n\mathbb{Z}$
. Le morphisme
![]() $a$
est d’intersection complète car
$a$
est d’intersection complète car
![]() $X$
et
$X$
et
![]() $X^{\prime }$
sont réguliers ; on peut donc construire un morphisme
$X^{\prime }$
sont réguliers ; on peut donc construire un morphisme
![]() $\unicode[STIX]{x1D6EC}\rightarrow a^{!}\unicode[STIX]{x1D6EC}$
dans la catégorie dérivée positive des faisceaux de
$\unicode[STIX]{x1D6EC}\rightarrow a^{!}\unicode[STIX]{x1D6EC}$
dans la catégorie dérivée positive des faisceaux de
![]() $\unicode[STIX]{x1D6EC}$
-modules, défini par la classe de Gysin [STG XVI, 2.5.11]. Il induit par adjonction un morphisme
$\unicode[STIX]{x1D6EC}$
-modules, défini par la classe de Gysin [STG XVI, 2.5.11]. Il induit par adjonction un morphisme
![]() $a_{\star }a^{\star }\unicode[STIX]{x1D6EC}=a_{!}a^{\star }\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}$
et le composé
$a_{\star }a^{\star }\unicode[STIX]{x1D6EC}=a_{!}a^{\star }\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}$
et le composé
![]() $\unicode[STIX]{x1D6EC}\rightarrow a_{\star }a^{\star }\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}$
est la multiplication par le degré
$\unicode[STIX]{x1D6EC}\rightarrow a_{\star }a^{\star }\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}$
est la multiplication par le degré
![]() $d$
: comme expliqué en [STG XVI, 3.5.9, démonstration], on se ramène par restriction à un ouvert dense au cas particulier élémentaire où
$d$
: comme expliqué en [STG XVI, 3.5.9, démonstration], on se ramène par restriction à un ouvert dense au cas particulier élémentaire où
![]() $a$
est fini étale.
$a$
est fini étale.
Passant à la limite sur
![]() $n=\ell ^{r}$
, on en déduit qu’il existe pour chaque
$n=\ell ^{r}$
, on en déduit qu’il existe pour chaque
![]() $\ell$
un morphisme trace
$\ell$
un morphisme trace
![]() $\mathtt{R}a_{\star }\mathbb{Z}_{\ell }\rightarrow \mathbb{Z}_{\ell }$
tel que les morphismes composés
$\mathtt{R}a_{\star }\mathbb{Z}_{\ell }\rightarrow \mathbb{Z}_{\ell }$
tel que les morphismes composés
coïncident avec la multiplication par
![]() $d$
pour chaque
$d$
pour chaque
![]() $i$
. En particulier, si
$i$
. En particulier, si
![]() $\mathtt{H}^{i}(X^{\prime },\mathbb{Z}_{\ell })$
est sans torsion et
$\mathtt{H}^{i}(X^{\prime },\mathbb{Z}_{\ell })$
est sans torsion et
![]() $\ell \bot d$
, il en est de même de
$\ell \bot d$
, il en est de même de
![]() $\mathtt{H}^{i}(X,\mathbb{Z}_{\ell })$
. Ceci nous ramène au cas projectif.◻
$\mathtt{H}^{i}(X,\mathbb{Z}_{\ell })$
. Ceci nous ramène au cas projectif.◻
D’après [Reference Madore and OrgogozoMO15, 0.8], on peut en principe vérifier si un
![]() $\ell$
donné est exceptionnel. Il serait intéressant de savoir borner a priori leur nombre.
$\ell$
donné est exceptionnel. Il serait intéressant de savoir borner a priori leur nombre.
6.2.3
Vérifions maintenant brièvement que la « cohomologie modulo
![]() $\mathfrak{L}$
»,
$\mathfrak{L}$
»,
![]() $\mathtt{H}^{\star }(-,\mathbb{F}_{\mathfrak{L}})$
, est une cohomologie de Weil. Ceci est expliqué par Ivan Tomašić dans [Reference TomašićTom04] ; on constate que le seul point ne résultant pas immédiatement des énoncés classiques sur la cohomologie modulo
$\mathtt{H}^{\star }(-,\mathbb{F}_{\mathfrak{L}})$
, est une cohomologie de Weil. Ceci est expliqué par Ivan Tomašić dans [Reference TomašićTom04] ; on constate que le seul point ne résultant pas immédiatement des énoncés classiques sur la cohomologie modulo
![]() $\ell$
est la finitude de ces espaces vectoriels sur
$\ell$
est la finitude de ces espaces vectoriels sur
![]() $\mathbb{F}_{\mathfrak{L}}$
. Dans [Reference TomašićTom04, 3.2 (i), démonstration], ceci est présenté comme un corollaire du théorème d’O. Gabber, ce qui rendrait l’argument précédent circulaire. Cependant, notre théorème 3.1.1 en donne une démonstration indépendante.
$\mathbb{F}_{\mathfrak{L}}$
. Dans [Reference TomašićTom04, 3.2 (i), démonstration], ceci est présenté comme un corollaire du théorème d’O. Gabber, ce qui rendrait l’argument précédent circulaire. Cependant, notre théorème 3.1.1 en donne une démonstration indépendante.
6.2.4
Signalons qu’il n’est pas difficile de majorer uniformément en
![]() $\ell$
les nombres de Betti (avec ou sans support) d’un schéma algébrique sur un corps algébriquement clos
$\ell$
les nombres de Betti (avec ou sans support) d’un schéma algébrique sur un corps algébriquement clos
![]() $k$
(sans utiliser le théorème sur l’absence de torsion), par des arguments proches de ceux de [Reference KatzKat01]. (Comparer également avec [Reference IllusieIll10, § 1].)
$k$
(sans utiliser le théorème sur l’absence de torsion), par des arguments proches de ceux de [Reference KatzKat01]. (Comparer également avec [Reference IllusieIll10, § 1].)
Esquissons un argument.
(i) On souhaite montrer que si
 $X$
est un
$X$
est un
 $k$
-schéma propre, il existe une constante
$k$
-schéma propre, il existe une constante
 $C_{X}$
telle que pour tout nombre premier
$C_{X}$
telle que pour tout nombre premier
 $\ell \neq p$
et tout
$\ell \neq p$
et tout
 $\mathbb{F}_{\ell }$
-faisceau lisse
$\mathbb{F}_{\ell }$
-faisceau lisse
 $\mathscr{L}$
sur
$\mathscr{L}$
sur
 $X$
, on ait
$X$
, on ait
 $\dim _{\mathbb{F}_{\ell }}\mathtt{H}^{i}(X,\mathscr{L})\leqslant C_{X}\cdot \text{rang}(\mathscr{L})$
.
$\dim _{\mathbb{F}_{\ell }}\mathtt{H}^{i}(X,\mathscr{L})\leqslant C_{X}\cdot \text{rang}(\mathscr{L})$
.On se ramène par [Reference de JongdeJ96] et descente cohomologique au cas projectif lisse et on procède ensuite par récurrence. La dualité de Poincaré et le théorème de Lefschetz nous ramènent, par l’hypothèse de récurrence, à l’étude de la cohomologie en degré médian. Ou, de façon équivalente, à la majoration uniforme des caractéristiques d’Euler–Poincaré
 $\unicode[STIX]{x1D712}(X,\mathscr{L})$
.
$\unicode[STIX]{x1D712}(X,\mathscr{L})$
.(ii) On montre alors que si
 $X$
un
$X$
un
 $k$
-schéma projectif et lisse, il existe une constante
$k$
-schéma projectif et lisse, il existe une constante
 $C_{X}^{\prime }$
telle que
$C_{X}^{\prime }$
telle que
 $|\unicode[STIX]{x1D712}(X,\mathscr{L})|\leqslant C_{X}^{\prime }\cdot \text{rang}(\mathscr{L})$
pour tout nombre premier
$|\unicode[STIX]{x1D712}(X,\mathscr{L})|\leqslant C_{X}^{\prime }\cdot \text{rang}(\mathscr{L})$
pour tout nombre premier
 $\ell \neq p$
et tout
$\ell \neq p$
et tout
 $\mathbb{F}_{\ell }$
-faisceau lisse
$\mathbb{F}_{\ell }$
-faisceau lisse
 $\mathscr{L}$
.
$\mathscr{L}$
.On procède à nouveau par récurrence sur
 $\dim (X)$
. Pour une courbe, c’est un corollaire de l’égalité
$\dim (X)$
. Pour une courbe, c’est un corollaire de l’égalité
 $\unicode[STIX]{x1D712}(X,\mathscr{L})=\text{rang}(\mathscr{L})\cdot \unicode[STIX]{x1D712}(X)$
. En général, considérons un diagramme
$\unicode[STIX]{x1D712}(X,\mathscr{L})=\text{rang}(\mathscr{L})\cdot \unicode[STIX]{x1D712}(X)$
. En général, considérons un diagramme
 $\mathbf{P}_{k}^{1}\leftarrow X^{\prime }\rightarrow X$
où
$\mathbf{P}_{k}^{1}\leftarrow X^{\prime }\rightarrow X$
où
 $X^{\prime }\rightarrow X$
est birationnel et
$X^{\prime }\rightarrow X$
est birationnel et
 $X^{\prime }\rightarrow \mathbf{P}_{k}^{1}$
est un pinceau de Lefschetz. Par récurrence, il suffit de démontrer le résultat pour
$X^{\prime }\rightarrow \mathbf{P}_{k}^{1}$
est un pinceau de Lefschetz. Par récurrence, il suffit de démontrer le résultat pour
 $X^{\prime }$
car si
$X^{\prime }$
car si
 $F$
est un fermé de
$F$
est un fermé de
 $X$
, on a
$X$
, on a
 $\unicode[STIX]{x1D712}(X,\mathscr{L})=\unicode[STIX]{x1D712}_{c}(U,\mathscr{L})+\unicode[STIX]{x1D712}(F,\mathscr{L})$
et de même pour
$\unicode[STIX]{x1D712}(X,\mathscr{L})=\unicode[STIX]{x1D712}_{c}(U,\mathscr{L})+\unicode[STIX]{x1D712}(F,\mathscr{L})$
et de même pour
 $X^{\prime }$
. On peut donc supposer
$X^{\prime }$
. On peut donc supposer
 $X=X^{\prime }$
. D’après la formule de Grothendieck–Ogg–Šafarevič sur
$X=X^{\prime }$
. D’après la formule de Grothendieck–Ogg–Šafarevič sur
 $\mathbf{P}_{k}^{1}$
et l’égalité
$\mathbf{P}_{k}^{1}$
et l’égalité
 $\unicode[STIX]{x1D712}(X,\mathscr{L})=\unicode[STIX]{x1D712}(\mathbf{P}_{k}^{1},\mathtt{R}f_{\star }\mathscr{L})$
, il suffit de démontrer que les
$\unicode[STIX]{x1D712}(X,\mathscr{L})=\unicode[STIX]{x1D712}(\mathbf{P}_{k}^{1},\mathtt{R}f_{\star }\mathscr{L})$
, il suffit de démontrer que les
 $\mathtt{R}^{i}f_{\ast }\mathscr{L}$
sont modérés (Picard–Lefschetz), de rangs génériques uniformément bornés par une fonction linéaire en le rang (récurrence) et qu’il en est de même du rang
$\mathtt{R}^{i}f_{\ast }\mathscr{L}$
sont modérés (Picard–Lefschetz), de rangs génériques uniformément bornés par une fonction linéaire en le rang (récurrence) et qu’il en est de même du rang
 $h^{i}(X_{t},\mathscr{L})$
des fibres en les points singuliers
$h^{i}(X_{t},\mathscr{L})$
des fibres en les points singuliers
 $t\in \mathbf{P}_{k}^{1}$
. Ceci résulte du fait que l’écart avec le rang générique est contrôlé par les cycles évanescents (de nature locale) : les fibres des
$t\in \mathbf{P}_{k}^{1}$
. Ceci résulte du fait que l’écart avec le rang générique est contrôlé par les cycles évanescents (de nature locale) : les fibres des
 $\unicode[STIX]{x1D6F9}_{f}^{i}(\mathbb{F}_{\ell })$
sont de rang au plus
$\unicode[STIX]{x1D6F9}_{f}^{i}(\mathbb{F}_{\ell })$
sont de rang au plus
 $1$
et
$1$
et
 $\mathscr{L}\simeq \mathbb{F}_{\ell }^{r}$
sur les hensélisés stricts.
$\mathscr{L}\simeq \mathbb{F}_{\ell }^{r}$
sur les hensélisés stricts.(iii) Montrons maintenant que si
 $X$
un
$X$
un
 $k$
-schéma algébrique, il existe une constante
$k$
-schéma algébrique, il existe une constante
 $C_{X}^{\prime \prime }$
telle que pour tout nombre premier
$C_{X}^{\prime \prime }$
telle que pour tout nombre premier
 $\ell \neq p$
et tout entier
$\ell \neq p$
et tout entier
 $i$
on ait où
$i$
on ait où $$\begin{eqnarray}\dim _{\mathbb{F}_{\ell }}\mathtt{H}_{?}^{i}(X,\mathbb{F}_{\ell })\leqslant C_{X}^{\prime \prime },\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbb{F}_{\ell }}\mathtt{H}_{?}^{i}(X,\mathbb{F}_{\ell })\leqslant C_{X}^{\prime \prime },\end{eqnarray}$$
 $?\in \{\varnothing ,c\}$
.
$?\in \{\varnothing ,c\}$
.Par altération et descente cohomologique, on peut supposer que
 $X$
est le complémentaire d’un diviseur à croisements normaux dans un schéma lisse. Le cas de la cohomologie à support compact d’un tel
$X$
est le complémentaire d’un diviseur à croisements normaux dans un schéma lisse. Le cas de la cohomologie à support compact d’un tel
 $X$
se ramène, par récurrence sur la dimension, au cas propre et lisse déjà traité. Le cas de la cohomologie usuelle d’un schéma lisse se ramène au cas précédent par dualité de Poincaré.
$X$
se ramène, par récurrence sur la dimension, au cas propre et lisse déjà traité. Le cas de la cohomologie usuelle d’un schéma lisse se ramène au cas précédent par dualité de Poincaré.
Remarque 6.2.5. Signalons que par comparaison à la caractéristique nulle le théorème d’uniformité propre — sous la forme déjà établie dans [Reference Katz and LaumonKL85] — entraîne également des résultats d’indépendance de
![]() $\ell$
en grande caractéristique. À titre d’exemple, voici un énoncé dont on trouvera une autre démonstration dans [Reference Brünjes and SerpéBS08, 3.4].
$\ell$
en grande caractéristique. À titre d’exemple, voici un énoncé dont on trouvera une autre démonstration dans [Reference Brünjes and SerpéBS08, 3.4].
Proposition. Soient
![]() $n$
et
$n$
et
![]() $d$
des entiers. Il existe une constante
$d$
des entiers. Il existe une constante
![]() $C_{n,d}$
telle que pour tout corps algébriquement clos
$C_{n,d}$
telle que pour tout corps algébriquement clos
![]() $k$
de caractéristique
$k$
de caractéristique
![]() $p>C_{n,d}$
et toute hypersurface
$p>C_{n,d}$
et toute hypersurface
![]() $H$
de degré
$H$
de degré
![]() $d$
de
$d$
de
![]() $\mathbf{P}_{k}^{n}$
, on ait l’égalité des nombres de Betti
$\mathbf{P}_{k}^{n}$
, on ait l’égalité des nombres de Betti
![]() $b_{i}(H,\mathbb{Q}_{\ell })=b_{i}(H,\mathbb{Q}_{\ell ^{\prime }})$
pour tout entier
$b_{i}(H,\mathbb{Q}_{\ell })=b_{i}(H,\mathbb{Q}_{\ell ^{\prime }})$
pour tout entier
![]() $i$
et toute paire de nombres premiers
$i$
et toute paire de nombres premiers
![]() $\ell$
et
$\ell$
et
![]() $\ell ^{\prime }$
distincts de
$\ell ^{\prime }$
distincts de
![]() $p$
.
$p$
.
Il serait intéressant de savoir si l’on peut, ne serait-ce qu’en principe, calculer une telle constante
![]() $C_{n,d}$
.
$C_{n,d}$
.
Remerciements
C’est avec un grand plaisir que j’exprime mes sincères remerciements à Ahmed Abbes, Nick Katz, Arthur Ogus, Joël Riou, Jean-Pierre Serre, Zheng Weizhe et tout particulièrement Saito Takeshi pour avoir relevé une erreur dans une version antérieure de ce texte ainsi qu’Ofer Gabber et Luc Illusie pour leur aide cruciale et leurs encouragements.