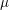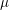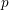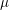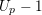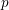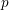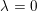1 Introduction
1.1 Setting the stage
Let
![]() $(p,k)$
be an irregular pair – that is,
$(p,k)$
be an irregular pair – that is,
![]() $p$
is an irregular prime such that
$p$
is an irregular prime such that
![]() $p$
divides the numerator of
$p$
divides the numerator of
![]() $B_{k}$
, the
$B_{k}$
, the
![]() $k$
th Bernoulli number. In [Reference RibetRib76], Ribet proved the converse of Herbrand’s theorem which predicts the non-triviality of a particular eigenspace of the
$k$
th Bernoulli number. In [Reference RibetRib76], Ribet proved the converse of Herbrand’s theorem which predicts the non-triviality of a particular eigenspace of the
![]() $p$
-part of the class group of
$p$
-part of the class group of
![]() $\mathbb{Q}(\unicode[STIX]{x1D707}_{p})$
under the action of
$\mathbb{Q}(\unicode[STIX]{x1D707}_{p})$
under the action of
![]() $\operatorname{Gal}(\mathbb{Q}(\unicode[STIX]{x1D707}_{p})/\mathbb{Q})$
. His method exploited a congruence between an Eisenstein series and a cuspform. Ribet worked in weight 2 at level
$\operatorname{Gal}(\mathbb{Q}(\unicode[STIX]{x1D707}_{p})/\mathbb{Q})$
. His method exploited a congruence between an Eisenstein series and a cuspform. Ribet worked in weight 2 at level
![]() $p$
, but we describe the idea here in weight
$p$
, but we describe the idea here in weight
![]() $k$
and level
$k$
and level
![]() $1$
; namely, let
$1$
; namely, let
denote the Eisenstein series of weight
![]() $k>2$
on
$k>2$
on
![]() $\operatorname{SL}_{2}(\mathbb{Z})$
. Under the assumption that
$\operatorname{SL}_{2}(\mathbb{Z})$
. Under the assumption that
![]() $(p,k)$
is an irregular pair, the constant term of
$(p,k)$
is an irregular pair, the constant term of
![]() $E_{k}$
vanishes mod
$E_{k}$
vanishes mod
![]() $p$
, and thus
$p$
, and thus
![]() $E_{k}$
‘looks like’ a cuspform modulo
$E_{k}$
‘looks like’ a cuspform modulo
![]() $p$
. One can make this idea precise and prove the existence of a cuspidal eigenform
$p$
. One can make this idea precise and prove the existence of a cuspidal eigenform
![]() $g_{k}$
of weight
$g_{k}$
of weight
![]() $k$
and level 1 which is congruent to the Eisenstein series
$k$
and level 1 which is congruent to the Eisenstein series
![]() $E_{k}$
. The mod
$E_{k}$
. The mod
![]() $p$
Galois representation of
$p$
Galois representation of
![]() $g_{k}$
is then reducible, and from this Galois representation one can extract the desired unramified extension of
$g_{k}$
is then reducible, and from this Galois representation one can extract the desired unramified extension of
![]() $\mathbb{Q}(\unicode[STIX]{x1D707}_{p})$
.
$\mathbb{Q}(\unicode[STIX]{x1D707}_{p})$
.
Wiles in [Reference WilesWil90] pushed this argument further by looking at the whole Hida family of the
![]() $g_{k}$
as
$g_{k}$
as
![]() $k$
varies
$k$
varies
![]() $p$
-adically. By analyzing the intersection of the Eisenstein and cuspidal branches of this Hida family (in the Hilbert modular case), Wiles proved the main conjecture over totally real fields.
$p$
-adically. By analyzing the intersection of the Eisenstein and cuspidal branches of this Hida family (in the Hilbert modular case), Wiles proved the main conjecture over totally real fields.
In this paper, rather than looking at the Iwasawa theory of class groups, we will instead focus on the Iwasawa theory of these famous cuspforms
![]() $g_{k}$
in their own right. Namely, we will examine the
$g_{k}$
in their own right. Namely, we will examine the
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions and Selmer groups of the
$L$
-functions and Selmer groups of the
![]() $g_{k}$
as
$g_{k}$
as
![]() $k$
varies
$k$
varies
![]() $p$
-adically. In fact, within the paper, we will study a larger collection of cuspforms with reducible residual representations by allowing for congruences with Eisenstein series with characters. However, to keep things simple, for the remainder of the introduction we will continue to work with tame level
$p$
-adically. In fact, within the paper, we will study a larger collection of cuspforms with reducible residual representations by allowing for congruences with Eisenstein series with characters. However, to keep things simple, for the remainder of the introduction we will continue to work with tame level
![]() $N=1$
.
$N=1$
.
To further set the stage, let us recall the Hida theoretic picture of congruences between Eisenstein series and cuspforms. Namely, to put the
![]() $E_{k}$
in a
$E_{k}$
in a
![]() $p$
-adic family, we must consider
$p$
-adic family, we must consider
![]() $E_{k}^{\operatorname{ord}}:=E_{k}(z)-p^{k-1}E_{k}(pz)$
, the ordinary
$E_{k}^{\operatorname{ord}}:=E_{k}(z)-p^{k-1}E_{k}(pz)$
, the ordinary
![]() $p$
-stabilization to
$p$
-stabilization to
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
. Explicitly, we have
$\unicode[STIX]{x1D6E4}_{0}(p)$
. Explicitly, we have
where
![]() $\unicode[STIX]{x1D70E}_{k-1}^{(p)}(n)$
is the sum of the
$\unicode[STIX]{x1D70E}_{k-1}^{(p)}(n)$
is the sum of the
![]() $(k-1)$
th powers of the prime-to-
$(k-1)$
th powers of the prime-to-
![]() $p$
divisors of
$p$
divisors of
![]() $n$
. Since
$n$
. Since
![]() $d^{k}$
is a
$d^{k}$
is a
![]() $p$
-adically continuous function in
$p$
-adically continuous function in
![]() $k$
as long as
$k$
as long as
![]() $(d,p)=1$
, we see that the functions
$(d,p)=1$
, we see that the functions
![]() $\unicode[STIX]{x1D70E}_{k-1}^{(p)}(n)$
satisfy nice
$\unicode[STIX]{x1D70E}_{k-1}^{(p)}(n)$
satisfy nice
![]() $p$
-adic properties.
$p$
-adic properties.
Specifically, let
![]() ${\mathcal{W}}=\operatorname{Hom}_{\operatorname{cont}}(\mathbb{Z}_{p}^{\times },\mathbb{C}_{p}^{\times })$
denote weight space which is isomorphic to
${\mathcal{W}}=\operatorname{Hom}_{\operatorname{cont}}(\mathbb{Z}_{p}^{\times },\mathbb{C}_{p}^{\times })$
denote weight space which is isomorphic to
![]() $p-1$
copies of the open unit disc of
$p-1$
copies of the open unit disc of
![]() $\mathbb{C}_{p}$
. Let
$\mathbb{C}_{p}$
. Let
![]() ${\mathcal{W}}_{j}$
denote the disc of weights with tame character
${\mathcal{W}}_{j}$
denote the disc of weights with tame character
![]() $\unicode[STIX]{x1D714}^{j}$
where
$\unicode[STIX]{x1D714}^{j}$
where
![]() $\unicode[STIX]{x1D714}$
is the mod
$\unicode[STIX]{x1D714}$
is the mod
![]() $p$
cyclotomic character. We view
$p$
cyclotomic character. We view
![]() $\mathbb{Z}{\hookrightarrow}{\mathcal{W}}$
by identifying
$\mathbb{Z}{\hookrightarrow}{\mathcal{W}}$
by identifying
![]() $k$
with the character
$k$
with the character
![]() $z\mapsto z^{k}$
. Then there exist rigid analytic functions
$z\mapsto z^{k}$
. Then there exist rigid analytic functions
![]() $A_{n}$
on
$A_{n}$
on
![]() ${\mathcal{W}}$
such that
${\mathcal{W}}$
such that
![]() $A_{n}(k)=\unicode[STIX]{x1D70E}_{k-1}^{(p)}(n)$
for each
$A_{n}(k)=\unicode[STIX]{x1D70E}_{k-1}^{(p)}(n)$
for each
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
The constant term of
![]() $E_{k}^{\operatorname{ord}}$
also enjoys nice
$E_{k}^{\operatorname{ord}}$
also enjoys nice
![]() $p$
-adic properties. For
$p$
-adic properties. For
![]() $k>2$
even, we have
$k>2$
even, we have
![]() $-(1-p^{k-1})(B_{k}/2k)=\frac{1}{2}\unicode[STIX]{x1D701}_{p}(k)$
where
$-(1-p^{k-1})(B_{k}/2k)=\frac{1}{2}\unicode[STIX]{x1D701}_{p}(k)$
where
![]() $\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
is the
$\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
is the
![]() $p$
-adic
$p$
-adic
![]() $\unicode[STIX]{x1D701}$
-function as in [Reference ColmezCol00, Reference Bellaïche and DasguptaBD15]. In particular, the formal
$\unicode[STIX]{x1D701}$
-function as in [Reference ColmezCol00, Reference Bellaïche and DasguptaBD15]. In particular, the formal
![]() $q$
-expansion
$q$
-expansion
defines the
![]() $p$
-adic Eisenstein family in the weight variable
$p$
-adic Eisenstein family in the weight variable
![]() $\unicode[STIX]{x1D705}$
over all even components of weight space.
$\unicode[STIX]{x1D705}$
over all even components of weight space.
Note further that if
![]() $\unicode[STIX]{x1D705}_{0}$
is a zero of
$\unicode[STIX]{x1D705}_{0}$
is a zero of
![]() $\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
(which necessarily cannot be a classical weight), then the weight
$\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
(which necessarily cannot be a classical weight), then the weight
![]() $\unicode[STIX]{x1D705}_{0}$
Eisenstein series
$\unicode[STIX]{x1D705}_{0}$
Eisenstein series
![]() ${\mathcal{E}}_{\unicode[STIX]{x1D705}_{0}}$
‘looks cuspidal’. In the spirit of Ribet’s proof of the converse to Herbrand’s theorem, one can show that there is a cuspidal Hida family which specializes at weight
${\mathcal{E}}_{\unicode[STIX]{x1D705}_{0}}$
‘looks cuspidal’. In the spirit of Ribet’s proof of the converse to Herbrand’s theorem, one can show that there is a cuspidal Hida family which specializes at weight
![]() $\unicode[STIX]{x1D705}_{0}$
to an Eisenstein series. That is, the weights of the crossing points of the cuspidal and Eisenstein branches of the Hida family occur precisely at the zeros of
$\unicode[STIX]{x1D705}_{0}$
to an Eisenstein series. That is, the weights of the crossing points of the cuspidal and Eisenstein branches of the Hida family occur precisely at the zeros of
![]() $\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
.
$\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
.
We set some notation. Let
![]() $\mathbb{T}$
denote the universal ordinary Hecke algebra of tame level
$\mathbb{T}$
denote the universal ordinary Hecke algebra of tame level
![]() $N=1$
acting on ordinary modular forms of all weights (as in [Reference HidaHid86]) which is a
$N=1$
acting on ordinary modular forms of all weights (as in [Reference HidaHid86]) which is a
![]() $\unicode[STIX]{x1D6EC}$
-module where
$\unicode[STIX]{x1D6EC}$
-module where
![]() $\unicode[STIX]{x1D6EC}=\mathbb{Z}_{p}[[1+p\mathbb{Z}_{p}]]$
. Let
$\unicode[STIX]{x1D6EC}=\mathbb{Z}_{p}[[1+p\mathbb{Z}_{p}]]$
. Let
![]() $\mathbb{T}^{c}$
denote the quotient of
$\mathbb{T}^{c}$
denote the quotient of
![]() $\mathbb{T}$
corresponding to the cuspidal Hecke algebra, and let
$\mathbb{T}$
corresponding to the cuspidal Hecke algebra, and let
![]() $\mathfrak{m}^{c}\subseteq \mathbb{T}^{c}$
denote some maximal ideal containing the cuspidal Eisenstein ideal. Note that the choice of such an ideal implicitly chooses some disc
$\mathfrak{m}^{c}\subseteq \mathbb{T}^{c}$
denote some maximal ideal containing the cuspidal Eisenstein ideal. Note that the choice of such an ideal implicitly chooses some disc
![]() ${\mathcal{W}}_{j}$
of weight space over which our Hida family sits and for which
${\mathcal{W}}_{j}$
of weight space over which our Hida family sits and for which
![]() $(p,j)$
is an irregular pair.
$(p,j)$
is an irregular pair.
For simplicity and concreteness, we begin by imposing the hypothesis
so that the geometry of the Hida family is as simple as possible. We note that this condition is equivalent to there being a unique cuspidal eigenform
![]() $f_{k}$
in weight
$f_{k}$
in weight
![]() $k$
congruent to
$k$
congruent to
![]() $E_{k}^{\operatorname{ord}}$
for one (equivalently any)
$E_{k}^{\operatorname{ord}}$
for one (equivalently any)
![]() $k\equiv j\;(\text{mod}\,p-1)$
. The condition (Cuspidal rank one) certainly does not hold for all irregular pairs
$k\equiv j\;(\text{mod}\,p-1)$
. The condition (Cuspidal rank one) certainly does not hold for all irregular pairs
![]() $(p,k)$
. But we checked that it does hold for all irregular pairs
$(p,k)$
. But we checked that it does hold for all irregular pairs
![]() $(p,k)$
with
$(p,k)$
with
![]() $p<10^{5}$
with the exception of
$p<10^{5}$
with the exception of
![]() $p=547$
and
$p=547$
and
![]() $k=486$
. In this case,
$k=486$
. In this case,
![]() $\dim _{\mathbb{Z}_{p}}\mathbb{T}_{\mathfrak{m}^{c}}^{c}=2$
.
$\dim _{\mathbb{Z}_{p}}\mathbb{T}_{\mathfrak{m}^{c}}^{c}=2$
.
1.2
 $p$
-adic
$p$
-adic
 $L$
-functions and mod
$L$
-functions and mod
 $p$
multiplicity one
$p$
multiplicity one
Each of the cuspforms
![]() $f_{k}$
have an associated
$f_{k}$
have an associated
![]() $p$
-adic
$p$
-adic
![]() $L$
-function
$L$
-function
![]() $L_{p}^{+}(f_{k})$
, which can equivalently be viewed as a
$L_{p}^{+}(f_{k})$
, which can equivalently be viewed as a
![]() $\mathbb{Z}_{p}$
-valued measure on
$\mathbb{Z}_{p}$
-valued measure on
![]() $\mathbb{Z}_{p}^{\times }$
or as an element in the completed group algebra
$\mathbb{Z}_{p}^{\times }$
or as an element in the completed group algebra
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
. The
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
. The
![]() $+$
superscript here indicates that this is the
$+$
superscript here indicates that this is the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function supported only on even characters. Moreover, these
$L$
-function supported only on even characters. Moreover, these
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions vary
$L$
-functions vary
![]() $p$
-adic analytically in
$p$
-adic analytically in
![]() $k$
, yielding a two-variable
$k$
, yielding a two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function as in [Reference KitagawaKit94, Reference Greenberg and StevensGS93].
$L$
-function as in [Reference KitagawaKit94, Reference Greenberg and StevensGS93].
Under (Cuspidal rank one), we can view the two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function
$L$
-function
![]() $L_{p}^{+}(\unicode[STIX]{x1D705})$
as an element in
$L_{p}^{+}(\unicode[STIX]{x1D705})$
as an element in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
where
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
where
![]() $\unicode[STIX]{x1D6E4}_{w,j}=1+p\mathbb{Z}_{p}$
. Here, we think of
$\unicode[STIX]{x1D6E4}_{w,j}=1+p\mathbb{Z}_{p}$
. Here, we think of
![]() $\unicode[STIX]{x1D705}$
as ranging over weights in
$\unicode[STIX]{x1D705}$
as ranging over weights in
![]() ${\mathcal{W}}_{j}$
. That is, under this assumption, we can conflate a parameter of the Hida family with a parameter of
${\mathcal{W}}_{j}$
. That is, under this assumption, we can conflate a parameter of the Hida family with a parameter of
![]() ${\mathcal{W}}_{j}$
. At each classical weight in
${\mathcal{W}}_{j}$
. At each classical weight in
![]() ${\mathcal{W}}_{j}$
, the two-variable
${\mathcal{W}}_{j}$
, the two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function specializes to a one-variable
$L$
-function specializes to a one-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function. That is, for
$L$
-function. That is, for
![]() $k\in \mathbb{Z}^{{\geqslant}2}\cap {\mathcal{W}}_{j}$
we have
$k\in \mathbb{Z}^{{\geqslant}2}\cap {\mathcal{W}}_{j}$
we have
One can also naturally attach
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions to Eisenstein series (e.g. via overconvergent modular symbols as in [Reference Greenberg and StevensGS93]), and somewhat surprisingly the result is simply the zero distribution (see Theorem 2.3).Footnote
1
$L$
-functions to Eisenstein series (e.g. via overconvergent modular symbols as in [Reference Greenberg and StevensGS93]), and somewhat surprisingly the result is simply the zero distribution (see Theorem 2.3).Footnote
1
The key idea of this paper is to use the vanishing of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions on the Eisenstein branch and the intersection points of the Eisenstein and cuspidal branches to make deductions about the cuspidal
$L$
-functions on the Eisenstein branch and the intersection points of the Eisenstein and cuspidal branches to make deductions about the cuspidal
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions. Indeed, if there were a two-variable
$L$
-functions. Indeed, if there were a two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function defined simultaneously over both the Eisenstein and cuspidal branches, the vanishing of the
$L$
-function defined simultaneously over both the Eisenstein and cuspidal branches, the vanishing of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function on the Eisenstein branch would imply the vanishing of the
$L$
-function on the Eisenstein branch would imply the vanishing of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions at the crossing points of the branches. This in turn would mean that
$L$
-functions at the crossing points of the branches. This in turn would mean that
![]() $L_{p}^{+}(f_{k})$
becomes more and more divisible by
$L_{p}^{+}(f_{k})$
becomes more and more divisible by
![]() $p$
as
$p$
as
![]() $k$
moves close to one of these crossing points – i.e. to one of the zeros of
$k$
moves close to one of these crossing points – i.e. to one of the zeros of
![]() $\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
. In the language of Iwasawa theory, this means that the
$\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
. In the language of Iwasawa theory, this means that the
![]() $\unicode[STIX]{x1D707}$
-invariants in the Hida family blow up as you approach these zeros!
$\unicode[STIX]{x1D707}$
-invariants in the Hida family blow up as you approach these zeros!
We now set some further notation and introduce a mod
![]() $p$
multiplicity-one condition which helps explain this phenomenon. Let
$p$
multiplicity-one condition which helps explain this phenomenon. Let
![]() $\mathbb{T}_{k}$
(respectively,
$\mathbb{T}_{k}$
(respectively,
![]() $\mathbb{T}_{k}^{c}$
) denote the full Hecke algebra over
$\mathbb{T}_{k}^{c}$
) denote the full Hecke algebra over
![]() $\mathbb{Z}_{p}$
which acts faithfully on
$\mathbb{Z}_{p}$
which acts faithfully on
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
(respectively,
$M_{k}(\unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
(respectively,
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
). Let
$S_{k}(\unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
). Let
![]() $\mathfrak{m}_{k}$
denote the maximal ideal of
$\mathfrak{m}_{k}$
denote the maximal ideal of
![]() $\mathbb{T}_{k}$
corresponding to
$\mathbb{T}_{k}$
corresponding to
![]() $E_{k}^{\operatorname{ord}}$
, and let
$E_{k}^{\operatorname{ord}}$
, and let
![]() $\mathfrak{m}_{k}^{c}$
denote the image of
$\mathfrak{m}_{k}^{c}$
denote the image of
![]() $\mathfrak{m}_{k}$
in
$\mathfrak{m}_{k}$
in
![]() $\mathbb{T}_{k}^{c}$
. Let
$\mathbb{T}_{k}^{c}$
. Let
![]() $(p,k)$
be an irregular pair, in which case
$(p,k)$
be an irregular pair, in which case
![]() $\mathfrak{m}_{k}^{c}$
is a maximal ideal (i.e. it is a proper ideal). We consider the condition
$\mathfrak{m}_{k}^{c}$
is a maximal ideal (i.e. it is a proper ideal). We consider the condition
where
![]() ${\mathcal{P}}_{g}$
is the collection of
${\mathcal{P}}_{g}$
is the collection of
![]() $\mathbb{Q}_{p}$
-polynomials of degree less than or equal to
$\mathbb{Q}_{p}$
-polynomials of degree less than or equal to
![]() $g$
which preserve
$g$
which preserve
![]() $\mathbb{Z}_{p}$
. We will see that (Mult One) holds for one irregular pair
$\mathbb{Z}_{p}$
. We will see that (Mult One) holds for one irregular pair
![]() $(p,k)$
if and only if it holds for all irregular pairs
$(p,k)$
if and only if it holds for all irregular pairs
![]() $(p,k)$
as
$(p,k)$
as
![]() $k$
runs over a fixed residue class mod
$k$
runs over a fixed residue class mod
![]() $p-1$
(Theorem 3.9).
$p-1$
(Theorem 3.9).
To see the relevance of condition (Mult One), a weaker version of the argument on
![]() $\unicode[STIX]{x1D707}$
-invariants given above would be to simply say that since
$\unicode[STIX]{x1D707}$
-invariants given above would be to simply say that since
![]() $f_{k}$
and
$f_{k}$
and
![]() $E_{k}^{\operatorname{ord}}$
satisfy a congruence modulo
$E_{k}^{\operatorname{ord}}$
satisfy a congruence modulo
![]() $p$
, one would hope for their
$p$
, one would hope for their
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions to also satisfy a congruence. Since the
$L$
-functions to also satisfy a congruence. Since the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function of
$L$
-function of
![]() $E_{k}^{\operatorname{ord}}$
is 0, we would then deduce that the
$E_{k}^{\operatorname{ord}}$
is 0, we would then deduce that the
![]() $\unicode[STIX]{x1D707}(f_{k})>0$
. However, the implication that a congruence of forms leads to a congruence of
$\unicode[STIX]{x1D707}(f_{k})>0$
. However, the implication that a congruence of forms leads to a congruence of
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions is a subtle one which is typically proven via a congruence between their associated modular symbols – that is, via (Mult One). Mod
$L$
-functions is a subtle one which is typically proven via a congruence between their associated modular symbols – that is, via (Mult One). Mod
![]() $p$
multiplicity one is now well established in the residually irreducible case (e.g. [Reference WilesWil95]), but is more subtle in the residually reducible case, and not always true for tame level greater than 1. But we do note that (Cuspidal rank one) implies (Mult One) (see Lemma 3.24 and Theorem 3.11).
$p$
multiplicity one is now well established in the residually irreducible case (e.g. [Reference WilesWil95]), but is more subtle in the residually reducible case, and not always true for tame level greater than 1. But we do note that (Cuspidal rank one) implies (Mult One) (see Lemma 3.24 and Theorem 3.11).
We now state a precise theorem relating the
![]() $\unicode[STIX]{x1D707}$
-invariants of the
$\unicode[STIX]{x1D707}$
-invariants of the
![]() $f_{k}$
with the
$f_{k}$
with the
![]() $p$
-adic
$p$
-adic
![]() $\unicode[STIX]{x1D701}$
-function. For
$\unicode[STIX]{x1D701}$
-function. For
![]() $a$
even, we write
$a$
even, we write
![]() $\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{a})$
for the
$\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{a})$
for the
![]() $\unicode[STIX]{x1D707}$
-invariant of the projection of
$\unicode[STIX]{x1D707}$
-invariant of the projection of
![]() $L_{p}^{+}(f)$
to the
$L_{p}^{+}(f)$
to the
![]() $\unicode[STIX]{x1D714}^{a}$
-component of the semi-local ring
$\unicode[STIX]{x1D714}^{a}$
-component of the semi-local ring
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
.
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
.
Theorem 1.1. Fix an irregular pair
![]() $(p,j)$
and assume that (Cuspidal rank one) holds for this pair. Then
$(p,j)$
and assume that (Cuspidal rank one) holds for this pair. Then
in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
. In particular,
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
. In particular,
for each even
![]() $a$
with
$a$
with
![]() $0\leqslant a\leqslant p-1$
and for classical
$0\leqslant a\leqslant p-1$
and for classical
![]() $k\equiv j\;(\text{mod}\,p-1)$
.
$k\equiv j\;(\text{mod}\,p-1)$
.
Note that this theorem makes precise the previous claim that the
![]() $\unicode[STIX]{x1D707}$
-invariants blow up as one approaches the zeros of the
$\unicode[STIX]{x1D707}$
-invariants blow up as one approaches the zeros of the
![]() $p$
-adic
$p$
-adic
![]() $\unicode[STIX]{x1D701}$
-function as the above lower bound blows up as one approaches these zeros.
$\unicode[STIX]{x1D701}$
-function as the above lower bound blows up as one approaches these zeros.
Our method of proof of this theorem is to build a two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function on the full Hida family (i.e. on both the cuspidal and Eisenstein branches). We follow the construction of Greenberg and Stevens, but keep careful track over the integrality of all of the objects. Then (Mult One) implies that some large space of overconvergent modular symbols is free as a Hecke module. This freeness allows us to build a two-variable
$L$
-function on the full Hida family (i.e. on both the cuspidal and Eisenstein branches). We follow the construction of Greenberg and Stevens, but keep careful track over the integrality of all of the objects. Then (Mult One) implies that some large space of overconvergent modular symbols is free as a Hecke module. This freeness allows us to build a two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function over the full Hida algebra.
$L$
-function over the full Hida algebra.
With this two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function in hand, the vanishing of the
$L$
-function in hand, the vanishing of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions of the Eisenstein series implies the divisibility of Theorem 1.1. We note that the last claim of the theorem follows immediately from this divisibility. Indeed, when one specializes
$L$
-functions of the Eisenstein series implies the divisibility of Theorem 1.1. We note that the last claim of the theorem follows immediately from this divisibility. Indeed, when one specializes
![]() $\unicode[STIX]{x1D705}$
to some classical weight
$\unicode[STIX]{x1D705}$
to some classical weight
![]() $k$
, one gets that the number
$k$
, one gets that the number
![]() $\unicode[STIX]{x1D701}_{p}(k)$
divides
$\unicode[STIX]{x1D701}_{p}(k)$
divides
![]() $L_{p}^{+}(f_{k})$
in
$L_{p}^{+}(f_{k})$
in
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
– which exactly gives the above lower bound on the
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
– which exactly gives the above lower bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant.
$\unicode[STIX]{x1D707}$
-invariant.
We now give an upper bound on
![]() $\unicode[STIX]{x1D707}$
-invariants which holds even without our (Cuspidal rank one) assumption. In what follows, we write
$\unicode[STIX]{x1D707}$
-invariants which holds even without our (Cuspidal rank one) assumption. In what follows, we write
![]() $\unicode[STIX]{x1D707}(f)$
for
$\unicode[STIX]{x1D707}(f)$
for
![]() $\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{0})$
.
$\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{0})$
.
Theorem 1.2. Fix an irregular pair
![]() $(p,j)$
and assume that (Mult One) holds for this pair. Then
$(p,j)$
and assume that (Mult One) holds for this pair. Then
for all classical
![]() $k\equiv j\;(\text{mod}\,p-1)$
.
$k\equiv j\;(\text{mod}\,p-1)$
.
We sketch the simple proof of this theorem. Assuming (Mult One), one shows that
![]() $L(f_{k},1)/\unicode[STIX]{x1D6FA}_{f}^{+}$
is a
$L(f_{k},1)/\unicode[STIX]{x1D6FA}_{f}^{+}$
is a
![]() $p$
-adic unit (as one knows that the plus modular symbol attached to
$p$
-adic unit (as one knows that the plus modular symbol attached to
![]() $f$
is congruent to a boundary symbol mod
$f$
is congruent to a boundary symbol mod
![]() $p$
). The interpolation formula for the
$p$
). The interpolation formula for the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function thus gives that
$L$
-function thus gives that
![]() $L_{p}(f_{k},\mathbf{1})$
has valuation
$L_{p}(f_{k},\mathbf{1})$
has valuation
![]() $\operatorname{ord}_{p}(a_{p}(k)-1)$
which in turns gives our upper bound on
$\operatorname{ord}_{p}(a_{p}(k)-1)$
which in turns gives our upper bound on
![]() $\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D707}$
.
Thus under (Cuspidal rank one) (which implies (Mult One)), we get the string of inequalities
We note that since
![]() $a_{p}(E_{\unicode[STIX]{x1D705}}^{\operatorname{ord}})=1$
for all
$a_{p}(E_{\unicode[STIX]{x1D705}}^{\operatorname{ord}})=1$
for all
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}$
, we have that
$\unicode[STIX]{x1D705}\in {\mathcal{W}}$
, we have that
![]() $\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
divides
$\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
divides
![]() $a_{p}(f_{\unicode[STIX]{x1D705}})-1$
in
$a_{p}(f_{\unicode[STIX]{x1D705}})-1$
in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w}]]$
which is consistent with the above inequalities.
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w}]]$
which is consistent with the above inequalities.
Given the philosophy that
![]() $\unicode[STIX]{x1D707}$
-invariants are ‘as small as they can be’, it is tempting to make the following conjecture. We will also further justify this conjecture after analyzing the algebraic side of the situation.
$\unicode[STIX]{x1D707}$
-invariants are ‘as small as they can be’, it is tempting to make the following conjecture. We will also further justify this conjecture after analyzing the algebraic side of the situation.
Conjecture 1.3. For an irregular pair
![]() $(p,j)$
satisfying (Cuspidal rank one) we have
$(p,j)$
satisfying (Cuspidal rank one) we have
for
![]() $a$
even and for any classical
$a$
even and for any classical
![]() $k\equiv j\;(\text{mod}\,p-1)$
.
$k\equiv j\;(\text{mod}\,p-1)$
.
Besides giving an elegant formula for
![]() $\unicode[STIX]{x1D707}$
-invariants in a Hida family, the above conjecture has an appealing philosophical feel. Namely, the non-trivial
$\unicode[STIX]{x1D707}$
-invariants in a Hida family, the above conjecture has an appealing philosophical feel. Namely, the non-trivial
![]() $\unicode[STIX]{x1D707}$
-invariant is explained away through
$\unicode[STIX]{x1D707}$
-invariant is explained away through
![]() $p$
-adic variation. For an isolated form, a non-trivial
$p$
-adic variation. For an isolated form, a non-trivial
![]() $\unicode[STIX]{x1D707}$
-invariant almost feels like an error in the choice of the complex period. However, in the family, one sees these
$\unicode[STIX]{x1D707}$
-invariant almost feels like an error in the choice of the complex period. However, in the family, one sees these
![]() $\unicode[STIX]{x1D707}$
-invariants explicitly arising from the special values of some interesting analytic function. Further, by Ferrero and Washington [Reference Ferrero and WashingtonFW79], the
$\unicode[STIX]{x1D707}$
-invariants explicitly arising from the special values of some interesting analytic function. Further, by Ferrero and Washington [Reference Ferrero and WashingtonFW79], the
![]() $\unicode[STIX]{x1D707}$
-invariant of
$\unicode[STIX]{x1D707}$
-invariant of
![]() $\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
is 0, and so all divisibility by a power of
$\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
is 0, and so all divisibility by a power of
![]() $p$
vanishes in the family. We further note that Conjecture 1.3 implies the weaker statement that the two-variable
$p$
vanishes in the family. We further note that Conjecture 1.3 implies the weaker statement that the two-variable
![]() $\unicode[STIX]{x1D707}$
-invariant of
$\unicode[STIX]{x1D707}$
-invariant of
![]() $L_{p}^{+}(\unicode[STIX]{x1D705})$
vanishes.
$L_{p}^{+}(\unicode[STIX]{x1D705})$
vanishes.
We note that this conjecture holds for
![]() $a=0$
for all irregular pairs
$a=0$
for all irregular pairs
![]() $(p,k)$
with
$(p,k)$
with
![]() $p<2000$
. Unfortunately, this provides scant evidence for the conjecture as in this range,
$p<2000$
. Unfortunately, this provides scant evidence for the conjecture as in this range,
![]() $\operatorname{ord}_{p}(a_{p}(f_{k})-1)=1$
, and thus the lower bound equals the upper bound in the inequalities in (1), forcing Conjecture 1.3 to hold.
$\operatorname{ord}_{p}(a_{p}(f_{k})-1)=1$
, and thus the lower bound equals the upper bound in the inequalities in (1), forcing Conjecture 1.3 to hold.
However, when
![]() $a>0$
, we have no a priori upper bound on the
$a>0$
, we have no a priori upper bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant (i.e. Theorem 1.2 does not apply) and thus we must instead compute
$\unicode[STIX]{x1D707}$
-invariant (i.e. Theorem 1.2 does not apply) and thus we must instead compute
![]() $\unicode[STIX]{x1D707}$
-invariants of
$\unicode[STIX]{x1D707}$
-invariants of
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions to verify that our conjecture holds. In this case, we verified that our conjecture holds for
$L$
-functions to verify that our conjecture holds. In this case, we verified that our conjecture holds for
![]() $p<750$
(for all even
$p<750$
(for all even
![]() $a$
). For details, see § 3.9 where we describe the extensive computation we did using the algorithms in [Reference Pollack and StevensPS11] on overconvergent modular symbols.
$a$
). For details, see § 3.9 where we describe the extensive computation we did using the algorithms in [Reference Pollack and StevensPS11] on overconvergent modular symbols.
Returning to the case of trivial tame character (i.e.
![]() $a=0$
), when the lower and upper bounds of (1) meet, the
$a=0$
), when the lower and upper bounds of (1) meet, the
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions of the
$L$
-functions of the
![]() $f_{k}$
turn out to be very simple. In what follows,
$f_{k}$
turn out to be very simple. In what follows,
![]() $L_{p}^{+}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D714}^{a})$
denotes the projection of
$L_{p}^{+}(\unicode[STIX]{x1D705},\unicode[STIX]{x1D714}^{a})$
denotes the projection of
![]() $L_{p}^{+}(\unicode[STIX]{x1D705})$
to the
$L_{p}^{+}(\unicode[STIX]{x1D705})$
to the
![]() $\unicode[STIX]{x1D714}^{a}$
-component of
$\unicode[STIX]{x1D714}^{a}$
-component of
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
.
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
.
Theorem 1.4. Fix an irregular pair
![]() $(p,j)$
satisfying (Cuspidal rank one) and for which
$(p,j)$
satisfying (Cuspidal rank one) and for which
Then
where
![]() $U$
is a unit in
$U$
is a unit in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times (1+p\mathbb{Z}_{p})]]$
. In particular, for every classical
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times (1+p\mathbb{Z}_{p})]]$
. In particular, for every classical
![]() $k\equiv j\;(\text{mod}\,p-1)$
, we have that
$k\equiv j\;(\text{mod}\,p-1)$
, we have that
That is, up to a unit,
![]() $L_{p}^{+}(f_{k},\unicode[STIX]{x1D714}^{0})$
is simply a power of
$L_{p}^{+}(f_{k},\unicode[STIX]{x1D714}^{0})$
is simply a power of
![]() $p$
.
$p$
.
We sketch the proof here. For our fixed
![]() $j$
, our assumption combined with (1) tells us the value of the
$j$
, our assumption combined with (1) tells us the value of the
![]() $\unicode[STIX]{x1D707}$
-invariant exactly:
$\unicode[STIX]{x1D707}$
-invariant exactly:
But, as argued above, we know that the value of
![]() $L_{p}^{+}(f_{j})$
at the trivial character has
$L_{p}^{+}(f_{j})$
at the trivial character has
![]() $p$
-adic valuation equal to
$p$
-adic valuation equal to
![]() $\operatorname{ord}_{p}(a_{p}(j)-1)$
. Since this valuation equals the
$\operatorname{ord}_{p}(a_{p}(j)-1)$
. Since this valuation equals the
![]() $\unicode[STIX]{x1D707}$
-invariant, we get that
$\unicode[STIX]{x1D707}$
-invariant, we get that
![]() $\unicode[STIX]{x1D706}(f_{j})=0$
. Then the divisibility of Theorem 3.26 tells us that the projection of
$\unicode[STIX]{x1D706}(f_{j})=0$
. Then the divisibility of Theorem 3.26 tells us that the projection of
to
![]() $\mathbb{Z}_{p}[[1+p\mathbb{Z}_{p}]]$
has vanishing
$\mathbb{Z}_{p}[[1+p\mathbb{Z}_{p}]]$
has vanishing
![]() $\unicode[STIX]{x1D707}$
- and
$\unicode[STIX]{x1D707}$
- and
![]() $\unicode[STIX]{x1D706}$
-invariants since
$\unicode[STIX]{x1D706}$
-invariants since
![]() $\unicode[STIX]{x1D707}(f_{j})=\operatorname{ord}_{p}(\unicode[STIX]{x1D701}_{p}(j))$
, and is thus a unit. Since
$\unicode[STIX]{x1D707}(f_{j})=\operatorname{ord}_{p}(\unicode[STIX]{x1D701}_{p}(j))$
, and is thus a unit. Since
![]() $L_{p}^{+}(\unicode[STIX]{x1D705})/\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
specializes to a unit at one weight, it must itself be a unit, as desired.
$L_{p}^{+}(\unicode[STIX]{x1D705})/\unicode[STIX]{x1D701}_{p}(\unicode[STIX]{x1D705})$
specializes to a unit at one weight, it must itself be a unit, as desired.
We note that it appears reasonable to believe that the case where the upper and lower bounds of (1) meet is the ‘generic’ case. Indeed, if
![]() $e=\operatorname{ord}_{p}(\unicode[STIX]{x1D701}_{p}(k))$
, then
$e=\operatorname{ord}_{p}(\unicode[STIX]{x1D701}_{p}(k))$
, then
![]() $p^{e}$
necessarily divides
$p^{e}$
necessarily divides
![]() $a_{p}(f_{k})-1$
, and one might imagine that
$a_{p}(f_{k})-1$
, and one might imagine that
![]() $(a_{p}(f_{k})-1)/p^{e}$
is a random number modulo
$(a_{p}(f_{k})-1)/p^{e}$
is a random number modulo
![]() $p$
. If this is the case, then for any given
$p$
. If this is the case, then for any given
![]() $p$
, the probability is
$p$
, the probability is
![]() $1/p$
for these bounds not to meet. One then expects there to be infinitely many
$1/p$
for these bounds not to meet. One then expects there to be infinitely many
![]() $p$
such that the bounds in (1) fail to meet, but, given how slowly
$p$
such that the bounds in (1) fail to meet, but, given how slowly
![]() $\sum _{p}(1/p)$
diverges, such examples will be extremely rare.
$\sum _{p}(1/p)$
diverges, such examples will be extremely rare.
1.3 A more general picture
We now discuss the more general case where (Cuspidal rank one) is no longer assumed to hold, but for this introduction we retain the tame level
![]() $N=1$
. In trying to repeat the arguments from earlier in the introduction without assuming (Cuspidal rank one), several new difficulties emerge. First, we no longer have that (Mult One) is automatically satisfied, which is key to our construction of a two-variable
$N=1$
. In trying to repeat the arguments from earlier in the introduction without assuming (Cuspidal rank one), several new difficulties emerge. First, we no longer have that (Mult One) is automatically satisfied, which is key to our construction of a two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function over both the cuspidal and Eisenstein families. Second, the intersections of the cuspidal branches and the Eisenstein branch are no longer controlled solely by the
$L$
-function over both the cuspidal and Eisenstein families. Second, the intersections of the cuspidal branches and the Eisenstein branch are no longer controlled solely by the
![]() $p$
-adic
$p$
-adic
![]() $\unicode[STIX]{x1D701}$
-function. Indeed, if there are multiple branches of the cuspidal family, some of them may not even intersect the Eisenstein family.
$\unicode[STIX]{x1D701}$
-function. Indeed, if there are multiple branches of the cuspidal family, some of them may not even intersect the Eisenstein family.
To remedy the first of these problems, we introduce a Gorenstein hypothesis,
where
![]() $(p,k)$
is some irregular pair. We note that (Goren) holds for one irregular pair
$(p,k)$
is some irregular pair. We note that (Goren) holds for one irregular pair
![]() $(p,k)$
if and only if it holds for all
$(p,k)$
if and only if it holds for all
![]() $(p,k)$
as
$(p,k)$
as
![]() $k$
varies over a fixed residue class mod
$k$
varies over a fixed residue class mod
![]() $p-1$
if and only if
$p-1$
if and only if
![]() $\mathbb{T}_{\mathfrak{m}}$
is Gorenstein where
$\mathbb{T}_{\mathfrak{m}}$
is Gorenstein where
![]() $\mathfrak{m}\subseteq \mathbb{T}$
is the maximal ideal attached to
$\mathfrak{m}\subseteq \mathbb{T}$
is the maximal ideal attached to
![]() $E_{k}$
.
$E_{k}$
.
The connection between Gorenstein hypotheses and mod
![]() $p$
multiplicity one in the residually irreducible case has been understood for a while now as in [Reference MazurMaz78, Reference TilouineTil97, Reference WilesWil95]. In our residually reducible case, we have that (Goren) implies (Mult One) which follows from work by Ohta [Reference OhtaOht99, Reference OhtaOht00] and Sharifi [Reference SharifiSha11] (see Theorem 3.11).
$p$
multiplicity one in the residually irreducible case has been understood for a while now as in [Reference MazurMaz78, Reference TilouineTil97, Reference WilesWil95]. In our residually reducible case, we have that (Goren) implies (Mult One) which follows from work by Ohta [Reference OhtaOht99, Reference OhtaOht00] and Sharifi [Reference SharifiSha11] (see Theorem 3.11).
We also note that in this more general setting we cannot consider our cuspidal two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function as an elements in
$L$
-function as an elements in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
since we are not able to conflate the Hida family with weight space. Instead, we will consider the two-variable
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
since we are not able to conflate the Hida family with weight space. Instead, we will consider the two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function as an element
$L$
-function as an element
![]() $L_{p}^{+}(\mathfrak{m}^{c})$
in
$L_{p}^{+}(\mathfrak{m}^{c})$
in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
. The weight variable of
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
. The weight variable of
![]() $L_{p}^{+}(\mathfrak{m})$
then varies over the spectrum of
$L_{p}^{+}(\mathfrak{m})$
then varies over the spectrum of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
; that is, for
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
; that is, for
![]() $\mathfrak{p}$
a height-one prime of
$\mathfrak{p}$
a height-one prime of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
of residual characteristic 0, we can ‘evaluate’
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
of residual characteristic 0, we can ‘evaluate’
![]() $L_{p}^{+}(\mathfrak{m}^{c})$
at
$L_{p}^{+}(\mathfrak{m}^{c})$
at
![]() $\mathfrak{p}$
by looking at its image in
$\mathfrak{p}$
by looking at its image in
![]() $(\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p})[[\mathbb{Z}_{p}^{\times }]]$
. Here
$(\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p})[[\mathbb{Z}_{p}^{\times }]]$
. Here
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}$
is a finite extension of
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}$
is a finite extension of
![]() $\mathbb{Z}_{p}$
. Moreover, if
$\mathbb{Z}_{p}$
. Moreover, if
![]() $\mathfrak{p}_{f}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is the prime ideal associated with a classical ordinary eigenform
$\mathfrak{p}_{f}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is the prime ideal associated with a classical ordinary eigenform
![]() $f$
, then the image of
$f$
, then the image of
![]() $L_{p}^{+}(\mathfrak{m}^{c})$
in
$L_{p}^{+}(\mathfrak{m}^{c})$
in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}[[\mathbb{Z}_{p}^{\times }]]$
recovers the single variable
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}[[\mathbb{Z}_{p}^{\times }]]$
recovers the single variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function
$L$
-function
![]() $L_{p}^{+}(f)$
.
$L_{p}^{+}(f)$
.
For the second problem, to find a replacement for the
![]() $p$
-adic
$p$
-adic
![]() $\unicode[STIX]{x1D701}$
-function to control the intersection of the Eisenstein and cuspidal branches, we seek a single element in the cuspidal Hecke algebra
$\unicode[STIX]{x1D701}$
-function to control the intersection of the Eisenstein and cuspidal branches, we seek a single element in the cuspidal Hecke algebra
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
which measures congruences between Eisenstein series and cuspforms. Essentially, by definition, we can simply use a generator, if one exists, of the cuspidal Eisenstein ideal in
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
which measures congruences between Eisenstein series and cuspforms. Essentially, by definition, we can simply use a generator, if one exists, of the cuspidal Eisenstein ideal in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. That is, assume the Eisenstein ideal of
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. That is, assume the Eisenstein ideal of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is principal, generated by, say,
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is principal, generated by, say,
![]() $L_{\operatorname{eis}}$
. Fix a weight-
$L_{\operatorname{eis}}$
. Fix a weight-
![]() $k$
cuspidal eigenform
$k$
cuspidal eigenform
![]() $f$
congruent to
$f$
congruent to
![]() $E_{k}^{\operatorname{ord}}$
and let
$E_{k}^{\operatorname{ord}}$
and let
![]() $\mathfrak{p}_{f}\subseteq \mathbb{T}^{c}$
denote the corresponding prime ideal. Then
$\mathfrak{p}_{f}\subseteq \mathbb{T}^{c}$
denote the corresponding prime ideal. Then
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}$
is some finite extension of
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}$
is some finite extension of
![]() $\mathbb{Z}_{p}$
. Write
$\mathbb{Z}_{p}$
. Write
![]() ${\mathcal{O}}_{f}$
for the ring of integers in the field of fractions of
${\mathcal{O}}_{f}$
for the ring of integers in the field of fractions of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}$
, and write
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}$
, and write
![]() $L_{\operatorname{eis}}(\mathfrak{p}_{f})$
to denote the image of
$L_{\operatorname{eis}}(\mathfrak{p}_{f})$
to denote the image of
![]() $L_{\operatorname{eis}}$
in
$L_{\operatorname{eis}}$
in
![]() ${\mathcal{O}}_{f}$
. We then have that
${\mathcal{O}}_{f}$
. We then have that
![]() $E_{k}^{\operatorname{ord}}$
is congruent to
$E_{k}^{\operatorname{ord}}$
is congruent to
![]() $f$
modulo
$f$
modulo
![]() $L_{\operatorname{eis}}(\mathfrak{p}_{f}){\mathcal{O}}_{f}$
.
$L_{\operatorname{eis}}(\mathfrak{p}_{f}){\mathcal{O}}_{f}$
.
Unfortunately, there is no a priori reason why the Eisenstein ideal is principal. To ensure the principality of this ideal we introduce another Gorenstein condition,
where
![]() $(p,k)$
is some irregular pair. Again, by Hida theory, (Cusp Goren) holds for one irregular pair
$(p,k)$
is some irregular pair. Again, by Hida theory, (Cusp Goren) holds for one irregular pair
![]() $(p,k)$
if and only if it holds for all
$(p,k)$
if and only if it holds for all
![]() $(p,k)$
as
$(p,k)$
as
![]() $k$
varies over a fixed residue class mod
$k$
varies over a fixed residue class mod
![]() $p-1$
if and only if
$p-1$
if and only if
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is Gorenstein.
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is Gorenstein.
Now, by work by Ohta [Reference OhtaOht05], we have that (Goren) and (Cusp Goren) hold if and only if the Eisenstein ideal is principal (see Theorem 3.5). We also note that Vandiver’s conjecture implies that both (Goren) and (Cusp Goren) hold (see Proposition 3.7), and so we can offer no examples where these hypotheses fail when
![]() $N=1$
. However, when
$N=1$
. However, when
![]() $N>1$
one does not expect these hypotheses to hold generally (see [Reference WakeWak15, Corollary 1.4]).
$N>1$
one does not expect these hypotheses to hold generally (see [Reference WakeWak15, Corollary 1.4]).
The following is our generalization of Theorem 1.1. Let
![]() $\unicode[STIX]{x1D71B}$
denote a uniformizer of
$\unicode[STIX]{x1D71B}$
denote a uniformizer of
![]() ${\mathcal{O}}_{f}$
.
${\mathcal{O}}_{f}$
.
Theorem 1.5. Fix an irregular pair
![]() $(p,j)$
and assume that (Goren) and (Cusp Goren) hold for this pair, and let
$(p,j)$
and assume that (Goren) and (Cusp Goren) hold for this pair, and let
![]() $\mathfrak{m}^{c}$
denote the corresponding maximal ideal of
$\mathfrak{m}^{c}$
denote the corresponding maximal ideal of
![]() $\mathbb{T}^{c}$
. Let
$\mathbb{T}^{c}$
. Let
![]() $L_{\operatorname{eis}}$
denote a generator of the cuspidal Eisenstein ideal of
$L_{\operatorname{eis}}$
denote a generator of the cuspidal Eisenstein ideal of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. Then
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. Then
in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
. In particular,
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
. In particular,
for all even
![]() $a$
with
$a$
with
![]() $0\leqslant a\leqslant p-2$
, and all
$0\leqslant a\leqslant p-2$
, and all
![]() $f$
in the Hida family corresponding to
$f$
in the Hida family corresponding to
![]() $\mathfrak{m}^{c}$
.
$\mathfrak{m}^{c}$
.
We again conjecture that the above inequality is in fact an equality (see Conjecture 3.16). Further, this lower bound meets the upper bound of Theorem 1.2 if and only if the cuspidal Eisenstein ideal is generated by
![]() $U_{p}-1$
. In this case, our Gorenstein hypotheses are automatically satisfied and we have the following generalization of Theorem 1.4 which asserts that the Iwasawa theory in this case is as simple as it can be.
$U_{p}-1$
. In this case, our Gorenstein hypotheses are automatically satisfied and we have the following generalization of Theorem 1.4 which asserts that the Iwasawa theory in this case is as simple as it can be.
Theorem 1.6. For an irregular pair
![]() $(p,j)$
for which
$(p,j)$
for which
![]() $U_{p}-1$
generates the cuspidal Eisenstein ideal of
$U_{p}-1$
generates the cuspidal Eisenstein ideal of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
, we have
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
, we have
for all
![]() $f$
in the corresponding Hida family.
$f$
in the corresponding Hida family.
1.4 Selmer groups
We return to the situation where
![]() $(p,j)$
is an irregular pair which satisfies (Goren) and (Cusp Goren) and let
$(p,j)$
is an irregular pair which satisfies (Goren) and (Cusp Goren) and let
![]() $L_{\operatorname{eis}}$
denote a generator of the associated cuspidal Eisenstein ideal. Let
$L_{\operatorname{eis}}$
denote a generator of the associated cuspidal Eisenstein ideal. Let
![]() $f$
denote some classical form which belongs to the corresponding Hida family.
$f$
denote some classical form which belongs to the corresponding Hida family.
On the algebraic side, we note that there is not a well-defined Selmer group attached to
![]() $f$
. Indeed, within the Galois representation
$f$
. Indeed, within the Galois representation
![]() $\unicode[STIX]{x1D70C}_{f}:G_{\mathbb{Q}}\rightarrow \operatorname{Aut}(V_{f})$
, one must choose a Galois stable lattice
$\unicode[STIX]{x1D70C}_{f}:G_{\mathbb{Q}}\rightarrow \operatorname{Aut}(V_{f})$
, one must choose a Galois stable lattice
![]() $T\subseteq V_{f}$
. One then attaches a Selmer group to
$T\subseteq V_{f}$
. One then attaches a Selmer group to
![]() $V_{f}/T$
; we denote this Selmer group by
$V_{f}/T$
; we denote this Selmer group by
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },V_{f}/T)\subseteq H^{1}(\mathbb{Q}_{\infty },V_{f}/T)$
, where
$\operatorname{Sel}(\mathbb{Q}_{\infty },V_{f}/T)\subseteq H^{1}(\mathbb{Q}_{\infty },V_{f}/T)$
, where
![]() $\mathbb{Q}_{\infty }$
is the cyclotomic
$\mathbb{Q}_{\infty }$
is the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension. Changing the lattice
$\mathbb{Z}_{p}$
-extension. Changing the lattice
![]() $T$
can change the
$T$
can change the
![]() $\unicode[STIX]{x1D707}$
-invariant of the corresponding Selmer group.
$\unicode[STIX]{x1D707}$
-invariant of the corresponding Selmer group.
In this setting we have the following collection of lower bounds on the possible algebraic
![]() $\unicode[STIX]{x1D707}$
-invariants that can occur.
$\unicode[STIX]{x1D707}$
-invariants that can occur.
Theorem 1.7. Let
![]() $(p,j)$
denote an irregular pair satisfying (Goren) and (Cusp Goren) and let
$(p,j)$
denote an irregular pair satisfying (Goren) and (Cusp Goren) and let
![]() $f$
denote a classical eigenform in the corresponding Hida family. Then there exists a chain of lattice
$f$
denote a classical eigenform in the corresponding Hida family. Then there exists a chain of lattice
![]() $T_{0}\subseteq T_{1}\subseteq \cdots \subseteq T_{m}$
in
$T_{0}\subseteq T_{1}\subseteq \cdots \subseteq T_{m}$
in
![]() $V_{f}$
with
$V_{f}$
with
![]() $m=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis}}(\mathfrak{p}_{f}))$
such that
$m=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis}}(\mathfrak{p}_{f}))$
such that
for
![]() $0\leqslant r\leqslant m$
.
$0\leqslant r\leqslant m$
.
This theorem is proven as follows. For each
![]() $r$
in the above range, there is a lattice
$r$
in the above range, there is a lattice
![]() $T_{r}$
such that
$T_{r}$
such that
![]() $T_{r}/p^{r}T_{r}$
is a reducible representation with a cyclic submodule of size
$T_{r}/p^{r}T_{r}$
is a reducible representation with a cyclic submodule of size
![]() $p^{r}$
which is odd and ramified at
$p^{r}$
which is odd and ramified at
![]() $p$
. Using Greenberg’s methods as in [Reference GreenbergGre99, Proposition 5.7], the lower bound on
$p$
. Using Greenberg’s methods as in [Reference GreenbergGre99, Proposition 5.7], the lower bound on
![]() $\unicode[STIX]{x1D707}$
follows.
$\unicode[STIX]{x1D707}$
follows.
Greenberg, in the case of elliptic curves, would then conjecture that this lower bound on
![]() $\unicode[STIX]{x1D707}$
is actually an equality (see [Reference GreenbergGre99, Conjecture 1.11 and p. 70]). Combining this conjecture with Theorem 1.1, we see that if there is any main conjecture defined over
$\unicode[STIX]{x1D707}$
is actually an equality (see [Reference GreenbergGre99, Conjecture 1.11 and p. 70]). Combining this conjecture with Theorem 1.1, we see that if there is any main conjecture defined over
![]() $\mathbb{Z}_{p}$
for
$\mathbb{Z}_{p}$
for
![]() $f$
, we must be using the lattice
$f$
, we must be using the lattice
![]() $T_{r}$
with maximal
$T_{r}$
with maximal
![]() $\unicode[STIX]{x1D707}$
-invariant. Set
$\unicode[STIX]{x1D707}$
-invariant. Set
![]() $T$
equal to such a lattice and let
$T$
equal to such a lattice and let
![]() $A_{f}=V_{f}/T$
.
$A_{f}=V_{f}/T$
.
We now state an upper bound for the algebraic
![]() $\unicode[STIX]{x1D707}$
-invariant. To do so, we need to invoke Vandiver’s conjecture. For
$\unicode[STIX]{x1D707}$
-invariant. To do so, we need to invoke Vandiver’s conjecture. For
![]() $r$
even, we write the
$r$
even, we write the
![]() $\unicode[STIX]{x1D714}^{r}$
-part of Vandiver’s conjecture as follows:
$\unicode[STIX]{x1D714}^{r}$
-part of Vandiver’s conjecture as follows:
Theorem 1.8. Let
![]() $(p,j)$
be an irregular pair for which
$(p,j)$
be an irregular pair for which
![]() $(\text{Vand}\;\unicode[STIX]{x1D714}^{2-j})$
holds. For
$(\text{Vand}\;\unicode[STIX]{x1D714}^{2-j})$
holds. For
![]() $f$
a classical form in the corresponding Hida family, we have
$f$
a classical form in the corresponding Hida family, we have
Our method of proof is analogous to the proof of Theorem 1.2. There we bounded the
![]() $\unicode[STIX]{x1D707}$
-invariant of the
$\unicode[STIX]{x1D707}$
-invariant of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function by computing the
$L$
-function by computing the
![]() $p$
-adic valuation of its special value at the trivial character. Here we instead look at
$p$
-adic valuation of its special value at the trivial character. Here we instead look at
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}$
and by bounding its size we get a bound on the
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}$
and by bounding its size we get a bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant (see Lemma 5.7). To bound the size of
$\unicode[STIX]{x1D707}$
-invariant (see Lemma 5.7). To bound the size of
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}$
, we use a control theorem to compare this group with
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}$
, we use a control theorem to compare this group with
![]() $\operatorname{Sel}(\mathbb{Q},A_{f})$
which we in turn control via Vandiver’s conjecture.
$\operatorname{Sel}(\mathbb{Q},A_{f})$
which we in turn control via Vandiver’s conjecture.
We now state the algebraic analogue of Conjecture 1.3 for our chosen lattice, and note that this is essentially Greenberg’s conjecture on
![]() $\unicode[STIX]{x1D707}$
-invariants in this special case.
$\unicode[STIX]{x1D707}$
-invariants in this special case.
Conjecture 1.9. For an irregular pair
![]() $(p,j)$
satisfying (Goren) and (Cusp Goren) and
$(p,j)$
satisfying (Goren) and (Cusp Goren) and
![]() $f$
a classical form in the corresponding Hida family, we have
$f$
a classical form in the corresponding Hida family, we have
Finally, we state a theorem in the case where the lower and upper bounds meet.
Theorem 1.10. For an irregular pair
![]() $(p,j)$
such that
$(p,j)$
such that
![]() $U_{p}-1$
generates the corresponding cuspidal Eisenstein ideal, we have
$U_{p}-1$
generates the corresponding cuspidal Eisenstein ideal, we have
for each classical
![]() $f$
in the corresponding Hida family. In particular,
$f$
in the corresponding Hida family. In particular,
We note that we do not need to assume Vandiver’s conjecture for the above theorem as our assumption that
![]() $U_{p}-1$
generates the cuspidal Eisenstein ideal implies that the relevant class group vanishes by the results in [Reference WakeWak15].
$U_{p}-1$
generates the cuspidal Eisenstein ideal implies that the relevant class group vanishes by the results in [Reference WakeWak15].
Combining Theorems 1.4 and 1.10 yields the following result.
Corollary 1.11 (The main conjecture).
For an irregular pair
![]() $(p,j)$
satisfying
$(p,j)$
satisfying
![]() $(\text{Vand}\;\unicode[STIX]{x1D714}^{2-j})$
and such that
$(\text{Vand}\;\unicode[STIX]{x1D714}^{2-j})$
and such that
![]() $U_{p}-1$
generates the corresponding cuspidal Eisenstein ideal, we have
$U_{p}-1$
generates the corresponding cuspidal Eisenstein ideal, we have
for each classical
![]() $f$
in the corresponding Hida family.
$f$
in the corresponding Hida family.
We note that the above main conjecture over
![]() $\unicode[STIX]{x1D6EC}[1/p]$
follows from Kato’s work [Reference KatoKat04, Theorem 17.4.2] as the
$\unicode[STIX]{x1D6EC}[1/p]$
follows from Kato’s work [Reference KatoKat04, Theorem 17.4.2] as the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function is a unit up to a power of
$L$
-function is a unit up to a power of
![]() $p$
. However, neither [Reference KatoKat04] nor [Reference Skinner and UrbanSU14] control what happens with the algebraic and analytic
$p$
. However, neither [Reference KatoKat04] nor [Reference Skinner and UrbanSU14] control what happens with the algebraic and analytic
![]() $\unicode[STIX]{x1D707}$
-invariants in the residually reducible case.
$\unicode[STIX]{x1D707}$
-invariants in the residually reducible case.
This paper is organized as follows. In the following section we recall Stevens’ theory of overconvergent modular symbols and its connection to
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions. The heavy lifting of constructing two-variable
$L$
-functions. The heavy lifting of constructing two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions is relegated to Appendix A. In the third section we carry out our analysis of analytic
$L$
-functions is relegated to Appendix A. In the third section we carry out our analysis of analytic
![]() $\unicode[STIX]{x1D707}$
-invariants sketched in the introduction. In the fourth section we recall the basic definitions and facts about Selmer groups. In the fifth section we carry out our analysis of algebraic
$\unicode[STIX]{x1D707}$
-invariants sketched in the introduction. In the fourth section we recall the basic definitions and facts about Selmer groups. In the fifth section we carry out our analysis of algebraic
![]() $\unicode[STIX]{x1D707}$
-invariants.
$\unicode[STIX]{x1D707}$
-invariants.
2 Overconvergent modular symbols and
 $p$
-adic
$p$
-adic
 $L$
-functions
$L$
-functions
In this section we recall Glenn Stevens’ theory of overconvergent modular symbols and its connection to
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions (see [Reference StevensSte94] as well as [Reference Pollack and StevensPS11]).
$L$
-functions (see [Reference StevensSte94] as well as [Reference Pollack and StevensPS11]).
2.1 Modular symbols
Let
![]() $\unicode[STIX]{x1D6E5}_{0}$
denote the space of degree-zero divisors on
$\unicode[STIX]{x1D6E5}_{0}$
denote the space of degree-zero divisors on
![]() $\mathbb{P}^{1}(\mathbb{Q})$
, and let
$\mathbb{P}^{1}(\mathbb{Q})$
, and let
![]() $V$
be some right
$V$
be some right
![]() $\mathbb{Z}[\unicode[STIX]{x1D6E4}]$
-module where
$\mathbb{Z}[\unicode[STIX]{x1D6E4}]$
-module where
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{1}(N)$
. We define the space of
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{1}(N)$
. We define the space of
![]() $V$
-valued modular symbols of level
$V$
-valued modular symbols of level
![]() $\unicode[STIX]{x1D6E4}$
to be the collection of additive maps
$\unicode[STIX]{x1D6E4}$
to be the collection of additive maps
Here
![]() $\unicode[STIX]{x1D6E4}$
acts on
$\unicode[STIX]{x1D6E4}$
acts on
![]() $\unicode[STIX]{x1D6E5}_{0}$
on the left via linear fractional transformations
$\unicode[STIX]{x1D6E5}_{0}$
on the left via linear fractional transformations
![]() $\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\cdot z=(az+b)/(cz+d)$
.
$\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\cdot z=(az+b)/(cz+d)$
.
We will also be interested in a subspace of boundary modular symbols:
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D6E5},V)$
where
$\operatorname{Hom}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D6E5},V)$
where
![]() $\unicode[STIX]{x1D6E5}=\operatorname{Div}(\mathbb{P}^{1}(\mathbb{Q}))$
. Note that these boundary symbols naturally map to
$\unicode[STIX]{x1D6E5}=\operatorname{Div}(\mathbb{P}^{1}(\mathbb{Q}))$
. Note that these boundary symbols naturally map to
![]() $V$
-valued modular symbols of level
$V$
-valued modular symbols of level
![]() $\unicode[STIX]{x1D6E4}$
by restriction to
$\unicode[STIX]{x1D6E4}$
by restriction to
![]() $\unicode[STIX]{x1D6E5}_{0}$
.
$\unicode[STIX]{x1D6E5}_{0}$
.
If
![]() $V$
is endowed with an action of a larger collection of matrices, one can define a natural Hecke action on these spaces of modular symbols. For instance, for a prime
$V$
is endowed with an action of a larger collection of matrices, one can define a natural Hecke action on these spaces of modular symbols. For instance, for a prime
![]() $p$
, consider the semi-group
$p$
, consider the semi-group
If
![]() $V$
is a
$V$
is a
![]() $\mathbb{Z}[S_{0}(p)]$
-module, then
$\mathbb{Z}[S_{0}(p)]$
-module, then
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D6E5}_{0},V)$
is naturally a Hecke module.
$\operatorname{Hom}_{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D6E5}_{0},V)$
is naturally a Hecke module.
If the order of every torsion element of
![]() $\unicode[STIX]{x1D6E4}$
acts invertibly on
$\unicode[STIX]{x1D6E4}$
acts invertibly on
![]() $V$
, then [Reference Ash and StevensAS86, Proposition 4.2] yields a canonical isomorphism
$V$
, then [Reference Ash and StevensAS86, Proposition 4.2] yields a canonical isomorphism
Further, this map is Hecke equivariant when Hecke operators are defined on these spaces. In what follows, we will often tacitly identify spaces of modular symbols with compactly supported cohomology groups.
For
![]() $F$
a field and
$F$
a field and
![]() $g\geqslant 0$
, let
$g\geqslant 0$
, let
![]() ${\mathcal{P}}_{g}(F)\subseteq F[z]$
denote the subset of polynomials with degree less than or equal to
${\mathcal{P}}_{g}(F)\subseteq F[z]$
denote the subset of polynomials with degree less than or equal to
![]() $g$
. Set
$g$
. Set
![]() ${\mathcal{P}}_{g}^{\vee }(F)=\operatorname{Hom}({\mathcal{P}}_{g}(F),F)$
. We endow
${\mathcal{P}}_{g}^{\vee }(F)=\operatorname{Hom}({\mathcal{P}}_{g}(F),F)$
. We endow
![]() ${\mathcal{P}}_{g}(F)$
with a left action of
${\mathcal{P}}_{g}(F)$
with a left action of
![]() $S_{0}(p)$
by
$S_{0}(p)$
by
for
![]() $P\in {\mathcal{P}}_{g}(F)$
and
$P\in {\mathcal{P}}_{g}(F)$
and
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{2}(\mathbb{Q})$
, and equip
$\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{2}(\mathbb{Q})$
, and equip
![]() ${\mathcal{P}}_{g}^{\vee }(F)$
with a right action by
${\mathcal{P}}_{g}^{\vee }(F)$
with a right action by
for
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{P}}_{g}^{\vee }(F)$
.
$\unicode[STIX]{x1D6FC}\in {\mathcal{P}}_{g}^{\vee }(F)$
.
One can associate to each eigenform
![]() $f$
in
$f$
in
![]() $S_{k}(\unicode[STIX]{x1D6E4},\mathbb{C})$
a
$S_{k}(\unicode[STIX]{x1D6E4},\mathbb{C})$
a
![]() ${\mathcal{P}}_{k-2}^{\vee }(\mathbb{C})$
-valued modular symbol
${\mathcal{P}}_{k-2}^{\vee }(\mathbb{C})$
-valued modular symbol
![]() $\unicode[STIX]{x1D709}_{f}$
of level
$\unicode[STIX]{x1D709}_{f}$
of level
![]() $\unicode[STIX]{x1D6E4}$
defined by
$\unicode[STIX]{x1D6E4}$
defined by
where
![]() $r,s\in \mathbb{P}^{1}(\mathbb{Q})$
; here we write
$r,s\in \mathbb{P}^{1}(\mathbb{Q})$
; here we write
![]() $\{r\}$
for the divisor associated to
$\{r\}$
for the divisor associated to
![]() $r\in \mathbb{Q}$
. The symbol
$r\in \mathbb{Q}$
. The symbol
![]() $\unicode[STIX]{x1D709}_{f}$
is a Hecke eigensymbol with the same Hecke eigenvalues as
$\unicode[STIX]{x1D709}_{f}$
is a Hecke eigensymbol with the same Hecke eigenvalues as
![]() $f$
.
$f$
.
Since the matrix
![]() $\unicode[STIX]{x1D704}:=\big(\!\begin{smallmatrix}-1 & 0\\ 0 & 1\end{smallmatrix}\!\big)$
normalizes
$\unicode[STIX]{x1D704}:=\big(\!\begin{smallmatrix}-1 & 0\\ 0 & 1\end{smallmatrix}\!\big)$
normalizes
![]() $\unicode[STIX]{x1D6E4}$
, it acts as an involution on these spaces of modular symbols. Thus
$\unicode[STIX]{x1D6E4}$
, it acts as an involution on these spaces of modular symbols. Thus
![]() $\unicode[STIX]{x1D709}_{f}$
can be uniquely written as
$\unicode[STIX]{x1D709}_{f}$
can be uniquely written as
![]() $\unicode[STIX]{x1D709}_{f}^{+}+\unicode[STIX]{x1D709}_{f}^{-}$
, with
$\unicode[STIX]{x1D709}_{f}^{+}+\unicode[STIX]{x1D709}_{f}^{-}$
, with
![]() $\unicode[STIX]{x1D709}_{f}^{\pm }$
in the
$\unicode[STIX]{x1D709}_{f}^{\pm }$
in the
![]() $\pm 1$
-eigenspace of
$\pm 1$
-eigenspace of
![]() $\unicode[STIX]{x1D704}$
. By a theorem of Shimura [Reference ShimuraShi76], there exist complex numbers
$\unicode[STIX]{x1D704}$
. By a theorem of Shimura [Reference ShimuraShi76], there exist complex numbers
![]() $\unicode[STIX]{x1D6FA}_{f}^{\pm }$
and a number field
$\unicode[STIX]{x1D6FA}_{f}^{\pm }$
and a number field
![]() $K$
such that for each
$K$
such that for each
![]() $D\in \unicode[STIX]{x1D6E5}_{0}$
,
$D\in \unicode[STIX]{x1D6E5}_{0}$
,
![]() $\unicode[STIX]{x1D709}_{f}^{\pm }(D)$
takes values in
$\unicode[STIX]{x1D709}_{f}^{\pm }(D)$
takes values in
![]() $K\unicode[STIX]{x1D6FA}_{f}^{\pm }$
. We can thus view
$K\unicode[STIX]{x1D6FA}_{f}^{\pm }$
. We can thus view
![]() $\unicode[STIX]{x1D711}_{f}^{\pm }:=\unicode[STIX]{x1D709}_{f}^{\pm }/\unicode[STIX]{x1D6FA}_{f}^{\pm }$
as taking values in
$\unicode[STIX]{x1D711}_{f}^{\pm }:=\unicode[STIX]{x1D709}_{f}^{\pm }/\unicode[STIX]{x1D6FA}_{f}^{\pm }$
as taking values in
![]() ${\mathcal{P}}_{k-2}^{\vee }(K)$
, and, for a fixed embedding
${\mathcal{P}}_{k-2}^{\vee }(K)$
, and, for a fixed embedding
![]() $\overline{\mathbb{Q}}{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
, we can view
$\overline{\mathbb{Q}}{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
, we can view
![]() $\unicode[STIX]{x1D711}_{f}^{\pm }$
as taking values in
$\unicode[STIX]{x1D711}_{f}^{\pm }$
as taking values in
![]() ${\mathcal{P}}_{k-2}^{\vee }(\overline{\mathbb{Q}}_{p})$
.
${\mathcal{P}}_{k-2}^{\vee }(\overline{\mathbb{Q}}_{p})$
.
As we are interested in
![]() $\unicode[STIX]{x1D707}$
-invariants in this paper, we must carefully normalize our choice of periods. To this end, we will choose
$\unicode[STIX]{x1D707}$
-invariants in this paper, we must carefully normalize our choice of periods. To this end, we will choose
![]() $\unicode[STIX]{x1D6FA}_{f}^{\pm }$
so that for all
$\unicode[STIX]{x1D6FA}_{f}^{\pm }$
so that for all
![]() $D\in \unicode[STIX]{x1D6E5}_{0}$
, all values of
$D\in \unicode[STIX]{x1D6E5}_{0}$
, all values of
![]() $\unicode[STIX]{x1D711}_{f}^{\pm }(D)\in {\mathcal{P}}_{k-2}^{\vee }(\overline{\mathbb{Q}}_{p})$
are
$\unicode[STIX]{x1D711}_{f}^{\pm }(D)\in {\mathcal{P}}_{k-2}^{\vee }(\overline{\mathbb{Q}}_{p})$
are
![]() $p$
-adic integers. Further, we insist that there is at least one divisor
$p$
-adic integers. Further, we insist that there is at least one divisor
![]() $D$
so that
$D$
so that
![]() $\unicode[STIX]{x1D711}_{f}^{\pm }(D)$
takes on at least one value which is a
$\unicode[STIX]{x1D711}_{f}^{\pm }(D)$
takes on at least one value which is a
![]() $p$
-adic unit. Periods
$p$
-adic unit. Periods
![]() $\unicode[STIX]{x1D6FA}_{f}^{\pm }$
which achieve this normalization we will call canonical periods.
$\unicode[STIX]{x1D6FA}_{f}^{\pm }$
which achieve this normalization we will call canonical periods.
Remark 2.1. We note that this definition differs slightly from the one given in [Reference VatsalVat99], where parabolic cohomology is used rather than compactly supported cohomology.
2.2 Measures and
 $p$
-adic
$p$
-adic
 $L$
-functions
$L$
-functions
Let
![]() $G$
denote a
$G$
denote a
![]() $p$
-adic Lie group which for this paper we will be taking to be
$p$
-adic Lie group which for this paper we will be taking to be
![]() $\mathbb{Z}_{p}$
,
$\mathbb{Z}_{p}$
,
![]() $\mathbb{Z}_{p}^{\times }$
or
$\mathbb{Z}_{p}^{\times }$
or
![]() $\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}$
. Let
$\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}$
. Let
![]() $\operatorname{Cont}(G)$
denote the space of continuous maps from
$\operatorname{Cont}(G)$
denote the space of continuous maps from
![]() $G$
to
$G$
to
![]() $\mathbb{Z}_{p}$
, and let
$\mathbb{Z}_{p}$
, and let
![]() $\operatorname{Meas}(G)$
denote the continuous
$\operatorname{Meas}(G)$
denote the continuous
![]() $\mathbb{Z}_{p}$
-dual of
$\mathbb{Z}_{p}$
-dual of
![]() $\operatorname{Cont}(G)$
which we regard as the space of
$\operatorname{Cont}(G)$
which we regard as the space of
![]() $\mathbb{Z}_{p}$
-valued measures on
$\mathbb{Z}_{p}$
-valued measures on
![]() $G$
.
$G$
.
For
![]() $\unicode[STIX]{x1D707}\in \operatorname{Meas}(G)$
and
$\unicode[STIX]{x1D707}\in \operatorname{Meas}(G)$
and
![]() $U$
a compact open of
$U$
a compact open of
![]() $G$
, we write
$G$
, we write
![]() $\unicode[STIX]{x1D707}(U)$
for
$\unicode[STIX]{x1D707}(U)$
for
![]() $\unicode[STIX]{x1D707}(\mathbf{1}_{U})$
where
$\unicode[STIX]{x1D707}(\mathbf{1}_{U})$
where
![]() $\mathbf{1}_{U}$
is the characteristic function of
$\mathbf{1}_{U}$
is the characteristic function of
![]() $U$
. Since the
$U$
. Since the
![]() $\mathbb{Z}_{p}$
-span of these characteristic functions is dense in
$\mathbb{Z}_{p}$
-span of these characteristic functions is dense in
![]() $\operatorname{Cont}(G)$
, a measure is uniquely determined by its values on the compact opens of
$\operatorname{Cont}(G)$
, a measure is uniquely determined by its values on the compact opens of
![]() $G$
. We further note that there is a natural isomorphism
$G$
. We further note that there is a natural isomorphism
![]() $\operatorname{Meas}(G)\cong \mathbb{Z}_{p}[[G]]$
which sends the Dirac measure
$\operatorname{Meas}(G)\cong \mathbb{Z}_{p}[[G]]$
which sends the Dirac measure
![]() $\unicode[STIX]{x1D6FF}_{g}$
supported at
$\unicode[STIX]{x1D6FF}_{g}$
supported at
![]() $g\in G$
to the group-like element
$g\in G$
to the group-like element
![]() $[g]$
in
$[g]$
in
![]() $\mathbb{Z}_{p}[[G]]$
.
$\mathbb{Z}_{p}[[G]]$
.
Set
![]() $\unicode[STIX]{x1D6E4}_{0}=\unicode[STIX]{x1D6E4}_{0}(p)\cap \unicode[STIX]{x1D6E4}_{1}(N)$
, and let
$\unicode[STIX]{x1D6E4}_{0}=\unicode[STIX]{x1D6E4}_{0}(p)\cap \unicode[STIX]{x1D6E4}_{1}(N)$
, and let
![]() $f$
be a
$f$
be a
![]() $p$
-ordinary eigenform in
$p$
-ordinary eigenform in
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{0},\overline{\mathbb{Q}}_{p})$
; that is, if
$S_{k}(\unicode[STIX]{x1D6E4}_{0},\overline{\mathbb{Q}}_{p})$
; that is, if
![]() $a_{p}(f)$
is the
$a_{p}(f)$
is the
![]() $p$
th Fourier coefficient of
$p$
th Fourier coefficient of
![]() $f$
, then
$f$
, then
![]() $a_{p}(f)$
is a
$a_{p}(f)$
is a
![]() $p$
-adic unit. Then
$p$
-adic unit. Then
![]() $L_{p}(f)$
, the
$L_{p}(f)$
, the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function of
$L$
-function of
![]() $f$
, is an element of
$f$
, is an element of
![]() $\operatorname{Meas}(\mathbb{Z}_{p}^{\times })\,\otimes \,{\mathcal{O}}$
where
$\operatorname{Meas}(\mathbb{Z}_{p}^{\times })\,\otimes \,{\mathcal{O}}$
where
![]() ${\mathcal{O}}:={\mathcal{O}}_{f}$
is the subring of
${\mathcal{O}}:={\mathcal{O}}_{f}$
is the subring of
![]() $\overline{\mathbb{Q}}_{p}$
generated over
$\overline{\mathbb{Q}}_{p}$
generated over
![]() $\mathbb{Z}_{p}$
by the Hecke eigenvalues of
$\mathbb{Z}_{p}$
by the Hecke eigenvalues of
![]() $f$
. Explicitly, we define
$f$
. Explicitly, we define
![]() $L_{p}(f)$
via the formula
$L_{p}(f)$
via the formula
and
![]() $L_{p}(f)=L_{p}^{+}(f)+L_{p}^{-}(f)$
. The fact that this formula for
$L_{p}(f)=L_{p}^{+}(f)+L_{p}^{-}(f)$
. The fact that this formula for
![]() $L_{p}(f)$
defines a measure follows from the fact that
$L_{p}(f)$
defines a measure follows from the fact that
![]() $\unicode[STIX]{x1D711}_{f}^{\pm }$
is a
$\unicode[STIX]{x1D711}_{f}^{\pm }$
is a
![]() $U_{p}$
-eigensymbol with eigenvalue
$U_{p}$
-eigensymbol with eigenvalue
![]() $a_{p}(f)$
.Footnote
2
$a_{p}(f)$
.Footnote
2
If
![]() $\unicode[STIX]{x1D712}$
denotes a Dirichlet character of conductor
$\unicode[STIX]{x1D712}$
denotes a Dirichlet character of conductor
![]() $p^{n}$
, then the
$p^{n}$
, then the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function satisfies the interpolation property:
$L$
-function satisfies the interpolation property:
 $$\begin{eqnarray}\int _{\mathbb{Z}_{p}^{\times }}\unicode[STIX]{x1D712}\,dL_{p}(f)=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{a_{p}(f)^{n}}\cdot \frac{p^{n}}{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}^{-1})}\cdot \frac{L(f,\unicode[STIX]{x1D712}^{-1},1)}{\unicode[STIX]{x1D6FA}_{f}^{\unicode[STIX]{x1D700}}}\quad & n>0,\\ \displaystyle \biggl(1-\frac{1}{a_{p}(f)}\biggr)\frac{L(f,1)}{\unicode[STIX]{x1D6FA}_{f}^{+}}\quad & n=0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{Z}_{p}^{\times }}\unicode[STIX]{x1D712}\,dL_{p}(f)=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{a_{p}(f)^{n}}\cdot \frac{p^{n}}{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}^{-1})}\cdot \frac{L(f,\unicode[STIX]{x1D712}^{-1},1)}{\unicode[STIX]{x1D6FA}_{f}^{\unicode[STIX]{x1D700}}}\quad & n>0,\\ \displaystyle \biggl(1-\frac{1}{a_{p}(f)}\biggr)\frac{L(f,1)}{\unicode[STIX]{x1D6FA}_{f}^{+}}\quad & n=0,\end{array}\right.\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D700}$
equals the sign of
$\unicode[STIX]{x1D700}$
equals the sign of
![]() $\unicode[STIX]{x1D712}(-1)$
.
$\unicode[STIX]{x1D712}(-1)$
.
2.3 Overconvergent modular symbols and
 $p$
-adic
$p$
-adic
 $L$
-functions
$L$
-functions
We endow the space
![]() $\operatorname{Meas}(\mathbb{Z}_{p})$
with a weight-
$\operatorname{Meas}(\mathbb{Z}_{p})$
with a weight-
![]() $g$
action of
$g$
action of
![]() $S_{0}(p)$
via the formula
$S_{0}(p)$
via the formula
where
![]() $\unicode[STIX]{x1D6FE}=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)$
and
$\unicode[STIX]{x1D6FE}=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)$
and
![]() $f$
is a continuous function on
$f$
is a continuous function on
![]() $\mathbb{Z}_{p}$
. When equipped with this action, we denote this space of measures by
$\mathbb{Z}_{p}$
. When equipped with this action, we denote this space of measures by
![]() $\operatorname{Meas}_{g}(\mathbb{Z}_{p})$
.
$\operatorname{Meas}_{g}(\mathbb{Z}_{p})$
.
Let
![]() ${\mathcal{P}}_{g}:={\mathcal{P}}_{g}(\mathbb{Z}_{p})\subset {\mathcal{P}}_{g}(\mathbb{Q}_{p})$
denote the continuous
${\mathcal{P}}_{g}:={\mathcal{P}}_{g}(\mathbb{Z}_{p})\subset {\mathcal{P}}_{g}(\mathbb{Q}_{p})$
denote the continuous
![]() $\mathbb{Z}_{p}$
-valued functions on
$\mathbb{Z}_{p}$
-valued functions on
![]() $\mathbb{Z}_{p}$
which are given by
$\mathbb{Z}_{p}$
which are given by
![]() $\mathbb{Q}_{p}$
-polynomials of degree less than or equal to
$\mathbb{Q}_{p}$
-polynomials of degree less than or equal to
![]() $k$
. This space is generated over
$k$
. This space is generated over
![]() $\mathbb{Z}_{p}$
by the binomial coefficients
$\mathbb{Z}_{p}$
by the binomial coefficients
![]() $\binom{z}{j}$
for
$\binom{z}{j}$
for
![]() $0\leqslant j\leqslant k$
(see Theorem A.2). Set
$0\leqslant j\leqslant k$
(see Theorem A.2). Set
![]() ${\mathcal{P}}_{g}^{\vee }=\operatorname{Hom}({\mathcal{P}}_{g},\mathbb{Z}_{p})$
.
${\mathcal{P}}_{g}^{\vee }=\operatorname{Hom}({\mathcal{P}}_{g},\mathbb{Z}_{p})$
.
As
![]() ${\mathcal{P}}_{g}$
naturally sits inside
${\mathcal{P}}_{g}$
naturally sits inside
![]() $\operatorname{Cont}(\mathbb{Z}_{p})$
, restriction yields an
$\operatorname{Cont}(\mathbb{Z}_{p})$
, restriction yields an
![]() $S_{0}(p)$
-equivariant map
$S_{0}(p)$
-equivariant map
and thus a map
We refer to both of these maps as specializations.
If
![]() $X$
is a Hecke module with an action of
$X$
is a Hecke module with an action of
![]() $U_{p}$
, we define
$U_{p}$
, we define
![]() $X^{\operatorname{ord}}$
to be the intersection of the image of all powers of
$X^{\operatorname{ord}}$
to be the intersection of the image of all powers of
![]() $U_{p}$
. The following is Stevens’ control theorem in the ordinary case (see [Reference StevensSte94, Reference Pollack and StevensPS11, Reference Pollack and StevensPS13]).
$U_{p}$
. The following is Stevens’ control theorem in the ordinary case (see [Reference StevensSte94, Reference Pollack and StevensPS11, Reference Pollack and StevensPS13]).
Theorem 2.2 (Stevens).
For
![]() $g\geqslant 0$
, specialization induces the isomorphism
$g\geqslant 0$
, specialization induces the isomorphism
Moreover, if
![]() $\unicode[STIX]{x1D6F7}^{\pm }\in H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},\operatorname{Meas}_{k-2}(\mathbb{Z}_{p}))\,\otimes \,\overline{\mathbb{Q}}_{p}$
is the unique lift of
$\unicode[STIX]{x1D6F7}^{\pm }\in H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},\operatorname{Meas}_{k-2}(\mathbb{Z}_{p}))\,\otimes \,\overline{\mathbb{Q}}_{p}$
is the unique lift of
![]() $\unicode[STIX]{x1D711}_{f}^{\pm }$
, then
$\unicode[STIX]{x1D711}_{f}^{\pm }$
, then
is the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function of
$L$
-function of
![]() $f$
; that is, it satisfies the interpolation property in (2) for some choice of canonical periods
$f$
; that is, it satisfies the interpolation property in (2) for some choice of canonical periods
![]() $\unicode[STIX]{x1D6FA}_{f}^{\pm }$
.
$\unicode[STIX]{x1D6FA}_{f}^{\pm }$
.
2.4
 $p$
-adic
$p$
-adic
 $L$
-functions of ordinary Eisenstein series
$L$
-functions of ordinary Eisenstein series
Fix a primitive character
![]() $\unicode[STIX]{x1D713}:(\mathbb{Z}/N\mathbb{Z})^{\times }\rightarrow \mathbb{C}^{\times }$
and consider the Eisenstein series
$\unicode[STIX]{x1D713}:(\mathbb{Z}/N\mathbb{Z})^{\times }\rightarrow \mathbb{C}^{\times }$
and consider the Eisenstein series
The following theorem describes overconvergent modular symbols with the same system of Hecke eigenvalues as
![]() $E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
.
$E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
.
Theorem 2.3. Let
![]() $\unicode[STIX]{x1D6F7}$
be any element of
$\unicode[STIX]{x1D6F7}$
be any element of
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},\operatorname{Meas}_{k-2}(\mathbb{Z}_{p}))$
satisfying
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},\operatorname{Meas}_{k-2}(\mathbb{Z}_{p}))$
satisfying
and
for
![]() $\unicode[STIX]{x1D713}$
a Dirichlet character of conductor
$\unicode[STIX]{x1D713}$
a Dirichlet character of conductor
![]() $N$
. Then:
$N$
. Then:
(1)
 $\unicode[STIX]{x1D6F7}$
is a boundary symbol;
$\unicode[STIX]{x1D6F7}$
is a boundary symbol;(2)
 $\unicode[STIX]{x1D6F7}$
is in the plus subspace (i.e.
$\unicode[STIX]{x1D6F7}$
is in the plus subspace (i.e.
 $\unicode[STIX]{x1D6F7}|\unicode[STIX]{x1D704}=\unicode[STIX]{x1D6F7}$
);
$\unicode[STIX]{x1D6F7}|\unicode[STIX]{x1D704}=\unicode[STIX]{x1D6F7}$
);(3)
 $\unicode[STIX]{x1D6F7}(\{\infty \}-\{0\})$
is a constant multiple of
$\unicode[STIX]{x1D6F7}(\{\infty \}-\{0\})$
is a constant multiple of
 $\unicode[STIX]{x1D6FF}_{0}$
, the Dirac distribution at
$\unicode[STIX]{x1D6FF}_{0}$
, the Dirac distribution at
 $0$
.
$0$
.
Proof. Our proof relies heavily on [Reference Bellaïche and DasguptaBD15]. Let
![]() $\unicode[STIX]{x1D719}$
denote the specialization of
$\unicode[STIX]{x1D719}$
denote the specialization of
![]() $\unicode[STIX]{x1D6F7}$
to
$\unicode[STIX]{x1D6F7}$
to
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee })^{\operatorname{ord}}$
. Since
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee })^{\operatorname{ord}}$
. Since
![]() $\unicode[STIX]{x1D719}$
is an Eisenstein symbol, standard descriptions of classical spaces of modular symbols (as in [Reference Bellaïche and DasguptaBD15, Proposition 2.5]) show that
$\unicode[STIX]{x1D719}$
is an Eisenstein symbol, standard descriptions of classical spaces of modular symbols (as in [Reference Bellaïche and DasguptaBD15, Proposition 2.5]) show that
![]() $\unicode[STIX]{x1D719}$
is a boundary symbol while [Reference Bellaïche and DasguptaBD15, Proposition 2.9] shows that
$\unicode[STIX]{x1D719}$
is a boundary symbol while [Reference Bellaïche and DasguptaBD15, Proposition 2.9] shows that
![]() $\unicode[STIX]{x1D719}$
is in the plus subspace. Then [Reference Bellaïche and DasguptaBD15, Proposition 5.7] shows that
$\unicode[STIX]{x1D719}$
is in the plus subspace. Then [Reference Bellaïche and DasguptaBD15, Proposition 5.7] shows that
![]() $\unicode[STIX]{x1D6F7}$
itself must have been a boundary symbol in the plus subspace. Finally, [Reference Bellaïche and DasguptaBD15, Lemma 5.1] shows that
$\unicode[STIX]{x1D6F7}$
itself must have been a boundary symbol in the plus subspace. Finally, [Reference Bellaïche and DasguptaBD15, Lemma 5.1] shows that
![]() $\unicode[STIX]{x1D6F7}(\{\infty \})=0$
, while [Reference Bellaïche and DasguptaBD15, Proposition 5.2] shows that
$\unicode[STIX]{x1D6F7}(\{\infty \})=0$
, while [Reference Bellaïche and DasguptaBD15, Proposition 5.2] shows that
![]() $\unicode[STIX]{x1D6F7}(\{0\})$
is a constant multiple of
$\unicode[STIX]{x1D6F7}(\{0\})$
is a constant multiple of
![]() $\unicode[STIX]{x1D6FF}_{0}$
.◻
$\unicode[STIX]{x1D6FF}_{0}$
.◻
Remark 2.4. (1) One can explicitly write down such Eisenstein symbols. This is done in great detail in [Reference Bellaïche and DasguptaBD15, § 5.2].
(2) In light of Theorems 2.2 and 2.3, the natural
![]() $p$
-adic
$p$
-adic
![]() $L$
-function to attach to
$L$
-function to attach to
![]() $E_{k,\unicode[STIX]{x1D713}}^{(p)}$
on even components of weight space is simply 0 as the restriction of
$E_{k,\unicode[STIX]{x1D713}}^{(p)}$
on even components of weight space is simply 0 as the restriction of
![]() $\unicode[STIX]{x1D6FF}_{0}$
to
$\unicode[STIX]{x1D6FF}_{0}$
to
![]() $\mathbb{Z}_{p}^{\times }$
vanishes.
$\mathbb{Z}_{p}^{\times }$
vanishes.
(3) On odd components of weight space, the above approach does not suggest what
![]() $p$
-adic
$p$
-adic
![]() $L$
-function to attach to this Eisenstein series as there is no overconvergent modular symbol with these Eisenstein eigenvalues in the minus subspace. However, in [Reference Bellaïche and DasguptaBD15], a partial overconvergent modular symbol with the correct eigenvalues was constructed in the minus subspace and its associated
$L$
-function to attach to this Eisenstein series as there is no overconvergent modular symbol with these Eisenstein eigenvalues in the minus subspace. However, in [Reference Bellaïche and DasguptaBD15], a partial overconvergent modular symbol with the correct eigenvalues was constructed in the minus subspace and its associated
![]() $p$
-adic
$p$
-adic
![]() $L$
-function is (naturally enough) a product of
$L$
-function is (naturally enough) a product of
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions of characters.
$L$
-functions of characters.
3 Analytic results
3.1 Basic set-up
Fix a prime
![]() $p\geqslant 5$
and a tame level
$p\geqslant 5$
and a tame level
![]() $N$
. We assume for the remainder of the paper that
$N$
. We assume for the remainder of the paper that
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
. Let
$p\nmid \unicode[STIX]{x1D711}(N)$
. Let
![]() $\mathbb{T}$
denote the universal ordinary Hecke algebra of tame level
$\mathbb{T}$
denote the universal ordinary Hecke algebra of tame level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
, and let
$\unicode[STIX]{x1D6E4}_{1}(N)$
, and let
![]() $\mathbb{T}^{c}$
denote its cuspidal quotient. Both
$\mathbb{T}^{c}$
denote its cuspidal quotient. Both
![]() $\mathbb{T}$
and
$\mathbb{T}$
and
![]() $\mathbb{T}^{c}$
are modules over
$\mathbb{T}^{c}$
are modules over
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times (\mathbb{Z}/N\mathbb{Z})^{\times }]]$
via the diamond operators. For
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times (\mathbb{Z}/N\mathbb{Z})^{\times }]]$
via the diamond operators. For
![]() $a\in \mathbb{Z}_{p}^{\times }$
, we write
$a\in \mathbb{Z}_{p}^{\times }$
, we write
![]() $\langle a\rangle$
to denote the corresponding group-like element of
$\langle a\rangle$
to denote the corresponding group-like element of
![]() $(a,a)$
in
$(a,a)$
in
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times (\mathbb{Z}/N\mathbb{Z})^{\times }]]$
. Further, let
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times (\mathbb{Z}/N\mathbb{Z})^{\times }]]$
. Further, let
![]() $\mathbb{T}_{k}$
(respectively,
$\mathbb{T}_{k}$
(respectively,
![]() $\mathbb{T}_{k}^{c}$
) denote the full Hecke algebra over
$\mathbb{T}_{k}^{c}$
) denote the full Hecke algebra over
![]() $\mathbb{Z}_{p}$
which acts faithfully on
$\mathbb{Z}_{p}$
which acts faithfully on
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
(respectively,
$M_{k}(\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
(respectively,
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
).
$S_{k}(\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p))^{\operatorname{ord}}$
).
Set
![]() ${\mathcal{I}}$
equal to the Eisenstein ideal of
${\mathcal{I}}$
equal to the Eisenstein ideal of
![]() $\mathbb{T}$
; that is, the ideal generated by
$\mathbb{T}$
; that is, the ideal generated by
![]() $T_{\ell }-(1+\langle \ell \rangle \ell ^{-1})$
for
$T_{\ell }-(1+\langle \ell \rangle \ell ^{-1})$
for
![]() $\ell \nmid Np$
and by
$\ell \nmid Np$
and by
![]() $U_{q}-1$
for
$U_{q}-1$
for
![]() $q\mid Np$
. Let
$q\mid Np$
. Let
![]() ${\mathcal{I}}^{c}$
denote the image of
${\mathcal{I}}^{c}$
denote the image of
![]() ${\mathcal{I}}$
in
${\mathcal{I}}$
in
![]() $\mathbb{T}^{c}$
which we will call the cuspidal Eisenstein ideal. We also denote by
$\mathbb{T}^{c}$
which we will call the cuspidal Eisenstein ideal. We also denote by
![]() ${\mathcal{I}}_{k}$
(respectively,
${\mathcal{I}}_{k}$
(respectively,
![]() ${\mathcal{I}}_{k}^{c}$
) the image of
${\mathcal{I}}_{k}^{c}$
) the image of
![]() ${\mathcal{I}}$
in
${\mathcal{I}}$
in
![]() $\mathbb{T}_{k}$
(respectively,
$\mathbb{T}_{k}$
(respectively,
![]() $\mathbb{T}_{k}^{c}$
).
$\mathbb{T}_{k}^{c}$
).
Let
![]() $\mathfrak{m}^{c}\subseteq \mathbb{T}^{c}$
be a maximal ideal and write
$\mathfrak{m}^{c}\subseteq \mathbb{T}^{c}$
be a maximal ideal and write
![]() $\mathfrak{m}$
for its pre-image in
$\mathfrak{m}$
for its pre-image in
![]() $\mathbb{T}$
. We note that a choice of a maximal ideal
$\mathbb{T}$
. We note that a choice of a maximal ideal
![]() $\mathfrak{m}$
of
$\mathfrak{m}$
of
![]() $\mathbb{T}$
distinguishes an even character of
$\mathbb{T}$
distinguishes an even character of
![]() $(\mathbb{Z}/Np\mathbb{Z})^{\times }$
in the following way. The components of the semi-local ring
$(\mathbb{Z}/Np\mathbb{Z})^{\times }$
in the following way. The components of the semi-local ring
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times (\mathbb{Z}/N\mathbb{Z})^{\times }]]$
are indexed by the characters of
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times (\mathbb{Z}/N\mathbb{Z})^{\times }]]$
are indexed by the characters of
![]() $(\mathbb{Z}/pN\mathbb{Z})^{\times }$
since
$(\mathbb{Z}/pN\mathbb{Z})^{\times }$
since
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
, and the restriction of
$p\nmid \unicode[STIX]{x1D711}(N)$
, and the restriction of
![]() $\mathfrak{m}$
to this ring is a maximal ideal which cuts out one of these components. Write
$\mathfrak{m}$
to this ring is a maximal ideal which cuts out one of these components. Write
![]() $\unicode[STIX]{x1D703}:=\unicode[STIX]{x1D703}_{\mathfrak{m}}$
for the corresponding character of
$\unicode[STIX]{x1D703}:=\unicode[STIX]{x1D703}_{\mathfrak{m}}$
for the corresponding character of
![]() $(\mathbb{Z}/pN\mathbb{Z})^{\times }$
and write
$(\mathbb{Z}/pN\mathbb{Z})^{\times }$
and write
![]() $\unicode[STIX]{x1D703}_{\mathfrak{m}}=\unicode[STIX]{x1D714}^{j(\mathfrak{m})}\unicode[STIX]{x1D713}_{\mathfrak{m}}$
with
$\unicode[STIX]{x1D703}_{\mathfrak{m}}=\unicode[STIX]{x1D714}^{j(\mathfrak{m})}\unicode[STIX]{x1D713}_{\mathfrak{m}}$
with
![]() $0\leqslant j(\mathfrak{m})<p-1$
and
$0\leqslant j(\mathfrak{m})<p-1$
and
![]() $\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D713}_{\mathfrak{m}}$
a character on
$\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D713}_{\mathfrak{m}}$
a character on
![]() $(\mathbb{Z}/N\mathbb{Z})^{\times }$
. Note that
$(\mathbb{Z}/N\mathbb{Z})^{\times }$
. Note that
![]() $(-1)^{j(\mathfrak{m})}=\unicode[STIX]{x1D713}(-1)$
and that
$(-1)^{j(\mathfrak{m})}=\unicode[STIX]{x1D713}(-1)$
and that
![]() $\unicode[STIX]{x1D703}$
is an even character.
$\unicode[STIX]{x1D703}$
is an even character.
Write
![]() $\mathfrak{m}_{k}$
and
$\mathfrak{m}_{k}$
and
![]() $\mathfrak{m}_{k}^{c}$
for the image of
$\mathfrak{m}_{k}^{c}$
for the image of
![]() $\mathfrak{m}$
in
$\mathfrak{m}$
in
![]() $\mathbb{T}_{k}$
and
$\mathbb{T}_{k}$
and
![]() $\mathbb{T}_{k}^{c}$
, respectively. These images are maximal as long as
$\mathbb{T}_{k}^{c}$
, respectively. These images are maximal as long as
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
. We say that these ideals,
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
. We say that these ideals,
![]() $\mathfrak{m}$
,
$\mathfrak{m}$
,
![]() $\mathfrak{m}^{c}$
,
$\mathfrak{m}^{c}$
,
![]() $\mathfrak{m}_{k}$
,
$\mathfrak{m}_{k}$
,
![]() $\mathfrak{m}_{k}^{c}$
, are Eisenstein if
$\mathfrak{m}_{k}^{c}$
, are Eisenstein if
![]() $\mathfrak{m}\supseteq {\mathcal{I}}$
(equivalently,
$\mathfrak{m}\supseteq {\mathcal{I}}$
(equivalently,
![]() $\mathfrak{m}^{c}\supseteq {\mathcal{I}}^{c}$
). We note that the existence of a maximal ideal
$\mathfrak{m}^{c}\supseteq {\mathcal{I}}^{c}$
). We note that the existence of a maximal ideal
![]() $\mathfrak{m}\supseteq {\mathcal{I}}$
is equivalent to
$\mathfrak{m}\supseteq {\mathcal{I}}$
is equivalent to
![]() $\operatorname{ord}_{p}(B_{j(\mathfrak{m}),\unicode[STIX]{x1D713}_{\mathfrak{m}}})>0$
.
$\operatorname{ord}_{p}(B_{j(\mathfrak{m}),\unicode[STIX]{x1D713}_{\mathfrak{m}}})>0$
.
Consider the following conditions:
∙
 $\unicode[STIX]{x1D713}_{\mathfrak{m}}$
is a primitive character of conductor
$\unicode[STIX]{x1D713}_{\mathfrak{m}}$
is a primitive character of conductor
 $N$
;
$N$
;∙
 $j(\mathfrak{m})=1\;\Longrightarrow \;\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)\neq 1$
.
$j(\mathfrak{m})=1\;\Longrightarrow \;\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)\neq 1$
.
We say that
![]() $\mathfrak{m}$
satisfies (Good Eisen) if it is Eisenstein and the above two conditions hold. The main reason for these conditions (along with
$\mathfrak{m}$
satisfies (Good Eisen) if it is Eisenstein and the above two conditions hold. The main reason for these conditions (along with
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
) is that they ensure that there is a unique Eisenstein component in the families we are considering. This is verified in the following lemma.
$p\nmid \unicode[STIX]{x1D711}(N)$
) is that they ensure that there is a unique Eisenstein component in the families we are considering. This is verified in the following lemma.
Lemma 3.1. If
![]() $\mathfrak{m}\subseteq \mathbb{T}$
is an maximal ideal satisfying (Good Eisen), then the subspace of Eisenstein series in
$\mathfrak{m}\subseteq \mathbb{T}$
is an maximal ideal satisfying (Good Eisen), then the subspace of Eisenstein series in
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}}^{\operatorname{ord}}$
is one-dimensional for
$M_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}}^{\operatorname{ord}}$
is one-dimensional for
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
Proof. Clearly
![]() $E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}^{\operatorname{ord}}$
is in this space. Assume there is another Eisenstein series
$E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}^{\operatorname{ord}}$
is in this space. Assume there is another Eisenstein series
![]() $E$
in this space which is an eigenform. Then there exist characters
$E$
in this space which is an eigenform. Then there exist characters
![]() $\unicode[STIX]{x1D712}_{1}$
and
$\unicode[STIX]{x1D712}_{1}$
and
![]() $\unicode[STIX]{x1D712}_{2}$
with conductors
$\unicode[STIX]{x1D712}_{2}$
with conductors
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
such that
$f_{2}$
such that
![]() $f_{1}f_{2}\mid Np$
and
$f_{1}f_{2}\mid Np$
and
![]() $E$
has eigenvalues
$E$
has eigenvalues
![]() $\unicode[STIX]{x1D712}_{1}(\ell )+\unicode[STIX]{x1D712}_{2}(\ell )\ell ^{k-1}$
for
$\unicode[STIX]{x1D712}_{1}(\ell )+\unicode[STIX]{x1D712}_{2}(\ell )\ell ^{k-1}$
for
![]() $\ell \nmid (Np/f_{1}f_{2})$
. For each such
$\ell \nmid (Np/f_{1}f_{2})$
. For each such
![]() $\ell$
, we then have congruences
$\ell$
, we then have congruences
where
![]() $\mathfrak{p}$
is the maximal ideal of
$\mathfrak{p}$
is the maximal ideal of
![]() $\mathbb{Z}_{p}[\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D711}(N)}]$
. Thus the linear independence of characters and the fact that
$\mathbb{Z}_{p}[\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D711}(N)}]$
. Thus the linear independence of characters and the fact that
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
yield that either (a)
$p\nmid \unicode[STIX]{x1D711}(N)$
yield that either (a)
![]() $\unicode[STIX]{x1D712}_{1}=1$
and
$\unicode[STIX]{x1D712}_{1}=1$
and
![]() $\unicode[STIX]{x1D712}_{2}=\unicode[STIX]{x1D713}_{\mathfrak{m}}$
, or (b)
$\unicode[STIX]{x1D712}_{2}=\unicode[STIX]{x1D713}_{\mathfrak{m}}$
, or (b)
![]() $\unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D713}_{\mathfrak{m}}\unicode[STIX]{x1D714}^{k-1}$
and
$\unicode[STIX]{x1D712}_{1}=\unicode[STIX]{x1D713}_{\mathfrak{m}}\unicode[STIX]{x1D714}^{k-1}$
and
![]() $\unicode[STIX]{x1D712}_{2}=\unicode[STIX]{x1D714}^{1-k}$
.
$\unicode[STIX]{x1D712}_{2}=\unicode[STIX]{x1D714}^{1-k}$
.
In case (a), we see that
![]() $f_{1}=1$
while
$f_{1}=1$
while
![]() $f_{2}=N$
since
$f_{2}=N$
since
![]() $\unicode[STIX]{x1D713}_{\mathfrak{m}}$
is primitive. Thus
$\unicode[STIX]{x1D713}_{\mathfrak{m}}$
is primitive. Thus
![]() $E$
and
$E$
and
![]() $E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}^{\operatorname{ord}}$
have the same eigenvalues at all primes
$E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}^{\operatorname{ord}}$
have the same eigenvalues at all primes
![]() $\ell$
except possibly for
$\ell$
except possibly for
![]() $\ell =p$
. But since
$\ell =p$
. But since
![]() $E$
is ordinary, this forces its
$E$
is ordinary, this forces its
![]() $U_{p}$
-eigenvalue to be
$U_{p}$
-eigenvalue to be
![]() $\unicode[STIX]{x1D712}_{1}(p)=1$
and
$\unicode[STIX]{x1D712}_{1}(p)=1$
and
![]() $E$
and
$E$
and
![]() $E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}^{\operatorname{ord}}$
have the same eigenvalues at all primes.
$E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}^{\operatorname{ord}}$
have the same eigenvalues at all primes.
In case (b), since
![]() $f_{1}f_{2}\mid Np$
, we must have that
$f_{1}f_{2}\mid Np$
, we must have that
![]() $k\equiv 1\;(\text{mod}\,p-1)$
, in which case
$k\equiv 1\;(\text{mod}\,p-1)$
, in which case
![]() $j(\mathfrak{m})=1$
,
$j(\mathfrak{m})=1$
,
![]() $f_{1}=N$
and
$f_{1}=N$
and
![]() $f_{2}=1$
. Again since
$f_{2}=1$
. Again since
![]() $E$
is ordinary we must have that its
$E$
is ordinary we must have that its
![]() $U_{p}$
-eigenvalue is
$U_{p}$
-eigenvalue is
![]() $\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)$
and that
$\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)$
and that
![]() $\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)\equiv 1\;(\text{mod}\,\mathfrak{p})$
. But since
$\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)\equiv 1\;(\text{mod}\,\mathfrak{p})$
. But since
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
, this implies that
$p\nmid \unicode[STIX]{x1D711}(N)$
, this implies that
![]() $\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)=1$
which contradicts
$\unicode[STIX]{x1D713}_{\mathfrak{m}}(p)=1$
which contradicts
![]() $\mathfrak{m}$
satisfying (Good Eisen).◻
$\mathfrak{m}$
satisfying (Good Eisen).◻
To conform to the notation of the introduction, we note that if
![]() $N=1$
and
$N=1$
and
![]() $(p,j)$
is an irregular pair, then there is a unique maximal ideal
$(p,j)$
is an irregular pair, then there is a unique maximal ideal
![]() $\mathfrak{m}$
containing
$\mathfrak{m}$
containing
![]() ${\mathcal{I}}$
with
${\mathcal{I}}$
with
![]() $j(\mathfrak{m})\equiv j\;(\text{mod}\,p-1)$
. Moreover, (Good Eisen) is vacuous in this case.
$j(\mathfrak{m})\equiv j\;(\text{mod}\,p-1)$
. Moreover, (Good Eisen) is vacuous in this case.
3.2 Gorenstein conditions and the principality of the Eisenstein ideal
We continue to use the notation of § 3.1. We thank Wake for his help with many of the proofs in this section.
Proposition 3.2. Fix a maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
. The following statements are equivalent:
$\mathfrak{m}\subseteq \mathbb{T}$
. The following statements are equivalent:
(1)
 $\mathbb{T}_{k,\mathfrak{m}_{k}}$
(respectively,
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
(respectively,
 $\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
) is Gorenstein for some
$\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
) is Gorenstein for some
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
 $k\geqslant 2$
;
$k\geqslant 2$
;(2)
 $\mathbb{T}_{k,\mathfrak{m}_{k}}$
(respectively,
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
(respectively,
 $\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
) is Gorenstein for all
$\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
) is Gorenstein for all
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
 $k\geqslant 2$
;
$k\geqslant 2$
;(3)
 $\mathbb{T}_{\mathfrak{m}}$
(respectively,
$\mathbb{T}_{\mathfrak{m}}$
(respectively,
 $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
) is Gorenstein.
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
) is Gorenstein.
Proof. Let
![]() $\mathfrak{p}_{k}$
denote the principal ideal of
$\mathfrak{p}_{k}$
denote the principal ideal of
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
generated by
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
generated by
![]() $[\unicode[STIX]{x1D6FE}]-\unicode[STIX]{x1D6FE}^{k}$
where
$[\unicode[STIX]{x1D6FE}]-\unicode[STIX]{x1D6FE}^{k}$
where
![]() $\unicode[STIX]{x1D6FE}$
is a topological generator of
$\unicode[STIX]{x1D6FE}$
is a topological generator of
![]() $\mathbb{Z}_{p}^{\times }$
. By Hida’s control theorem [Reference HidaHid86, Corollary 3.2], we have
$\mathbb{Z}_{p}^{\times }$
. By Hida’s control theorem [Reference HidaHid86, Corollary 3.2], we have
![]() $\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{k}\mathbb{T}_{\mathfrak{m}}\cong \mathbb{T}_{k,\mathfrak{m}_{k}}$
. Thus
$\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{k}\mathbb{T}_{\mathfrak{m}}\cong \mathbb{T}_{k,\mathfrak{m}_{k}}$
. Thus
![]() $\mathbb{T}_{\mathfrak{m}}$
is Gorenstein if and only if
$\mathbb{T}_{\mathfrak{m}}$
is Gorenstein if and only if
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}$
is Gorenstein. The same argument also applies to the cuspidal Hecke algebras.◻
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
is Gorenstein. The same argument also applies to the cuspidal Hecke algebras.◻
Definition 3.3. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
denote a maximal ideal. We say that
$\mathfrak{m}\subseteq \mathbb{T}$
denote a maximal ideal. We say that
![]() $\mathfrak{m}$
(respectively,
$\mathfrak{m}$
(respectively,
![]() $\mathfrak{m}^{c}$
) satisfies (Goren) (respectively, (Cusp Goren)) if any of the equivalent conditions of Proposition 3.2 hold for
$\mathfrak{m}^{c}$
) satisfies (Goren) (respectively, (Cusp Goren)) if any of the equivalent conditions of Proposition 3.2 hold for
![]() $\mathbb{T}_{\mathfrak{m}}$
(respectively,
$\mathbb{T}_{\mathfrak{m}}$
(respectively,
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
).
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
).
Lemma 3.4. If
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Good Eisen), we have
$\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Good Eisen), we have
![]() ${\mathcal{I}}_{\mathfrak{m}}\cong {\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
as
${\mathcal{I}}_{\mathfrak{m}}\cong {\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
as
![]() $\mathbb{T}_{\mathfrak{m}}$
-modules and
$\mathbb{T}_{\mathfrak{m}}$
-modules and
![]() ${\mathcal{I}}_{k,\mathfrak{m}}\cong {\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
as
${\mathcal{I}}_{k,\mathfrak{m}}\cong {\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
as
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}$
-modules.
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
-modules.
Proof. Let
![]() $K$
be the kernel of the natural surjection
$K$
be the kernel of the natural surjection
![]() ${\mathcal{I}}_{k,\mathfrak{m}}{\twoheadrightarrow}{\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
. By definition
${\mathcal{I}}_{k,\mathfrak{m}}{\twoheadrightarrow}{\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
. By definition
![]() $K$
annihilates
$K$
annihilates
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}_{k}}$
. Further, by Lemma 3.1,
$S_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}_{k}}$
. Further, by Lemma 3.1,
![]() ${\mathcal{I}}_{k,\mathfrak{m}}$
annihilates all Eisenstein series in
${\mathcal{I}}_{k,\mathfrak{m}}$
annihilates all Eisenstein series in
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}_{k}}$
. Thus
$M_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}_{k}}$
. Thus
![]() $K$
annihilates all cuspforms and Eisenstein series, and hence
$K$
annihilates all cuspforms and Eisenstein series, and hence
![]() $K=0$
. Then
$K=0$
. Then
![]() ${\mathcal{I}}_{k,\mathfrak{m}}\cong {\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
for all classical
${\mathcal{I}}_{k,\mathfrak{m}}\cong {\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
for all classical
![]() $k$
immediately implies that the natural map
$k$
immediately implies that the natural map
![]() ${\mathcal{I}}_{\mathfrak{m}}{\twoheadrightarrow}{\mathcal{I}}_{\mathfrak{m}}^{c}$
is an isomorphism as well.◻
${\mathcal{I}}_{\mathfrak{m}}{\twoheadrightarrow}{\mathcal{I}}_{\mathfrak{m}}^{c}$
is an isomorphism as well.◻
Theorem 3.5. Let
![]() $\mathfrak{m}$
denote an Eisenstein maximal ideal of
$\mathfrak{m}$
denote an Eisenstein maximal ideal of
![]() $\mathbb{T}$
. The following statements are equivalent:
$\mathbb{T}$
. The following statements are equivalent:
(1)
 $\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Goren) and (Cusp Goren);
$\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Goren) and (Cusp Goren);(2)
 $\mathbb{T}_{\mathfrak{m}}$
and
$\mathbb{T}_{\mathfrak{m}}$
and
 $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
are complete intersections;
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
are complete intersections;(3)
 ${\mathcal{I}}_{\mathfrak{m}}$
is principal;
${\mathcal{I}}_{\mathfrak{m}}$
is principal;(4)
 ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is principal;
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is principal;(5)
 ${\mathcal{I}}_{k,\mathfrak{m}_{k}}$
is principal for some
${\mathcal{I}}_{k,\mathfrak{m}_{k}}$
is principal for some
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
;
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
;(6)
 ${\mathcal{I}}_{k,\mathfrak{m}_{k}^{c}}^{c}$
is principal for some
${\mathcal{I}}_{k,\mathfrak{m}_{k}^{c}}^{c}$
is principal for some
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
Proof. By Lemma 3.4, we have (3)
![]() $\;\Longleftrightarrow \;$
(4) and (5)
$\;\Longleftrightarrow \;$
(4) and (5)
![]() $\;\Longleftrightarrow \;$
(6). Also, (3)
$\;\Longleftrightarrow \;$
(6). Also, (3)
![]() $\;\Longrightarrow \;$
(5) is clear and (2)
$\;\Longrightarrow \;$
(5) is clear and (2)
![]() $\;\Longrightarrow \;$
(1) is clear. Further, it is a theorem of Ohta [Reference OhtaOht05, Theorem 2] that (1)
$\;\Longrightarrow \;$
(1) is clear. Further, it is a theorem of Ohta [Reference OhtaOht05, Theorem 2] that (1)
![]() $\;\Longrightarrow \;$
(3).
$\;\Longrightarrow \;$
(3).
Thus, it suffices to check that (6)
![]() $\;\Longrightarrow \;$
(2). To this end, first note that
$\;\Longrightarrow \;$
(2). To this end, first note that
![]() $\mathbb{T}_{\mathfrak{m}}$
is a complete intersection if and only if
$\mathbb{T}_{\mathfrak{m}}$
is a complete intersection if and only if
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a complete intersection if and only if
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a complete intersection if and only if
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a complete intersection. Further, since
$\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a complete intersection. Further, since
![]() $\mathfrak{m}_{k}={\mathcal{I}}_{k,\mathfrak{m}_{k}}+p\mathbb{T}_{k,\mathfrak{m}_{k}}$
and
$\mathfrak{m}_{k}={\mathcal{I}}_{k,\mathfrak{m}_{k}}+p\mathbb{T}_{k,\mathfrak{m}_{k}}$
and
![]() ${\mathcal{I}}_{k,\mathfrak{m}_{k}}$
is principal by Lemma 3.4, we have that the maximal ideal of
${\mathcal{I}}_{k,\mathfrak{m}_{k}}$
is principal by Lemma 3.4, we have that the maximal ideal of
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}$
is principal. But then
$\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}$
is principal. But then
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a finite-dimensional local
$\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a finite-dimensional local
![]() $\mathbb{F}_{p}$
-algebra with principal maximal ideal. We must then have that
$\mathbb{F}_{p}$
-algebra with principal maximal ideal. We must then have that
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}\cong \mathbb{F}_{p}[x]/(x^{r})$
for some
$\mathbb{T}_{k,\mathfrak{m}_{k}}/p\mathbb{T}_{k,\mathfrak{m}_{k}}\cong \mathbb{F}_{p}[x]/(x^{r})$
for some
![]() $r\geqslant 0$
, and is thus a complete intersection. An identical argument works for
$r\geqslant 0$
, and is thus a complete intersection. An identical argument works for
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
as well.◻
$\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
as well.◻
The conditions (Goren) and (Cusp Goren) do not hold generally. See [Reference WakeWak15, Corollary 1.4] for an example where (Goren) fails. However, there are no known counter-examples to (Goren) or (Cusp Goren) when the tame level
![]() $N=1$
. Indeed, we will verify that these two conditions follow from Vandiver’s conjecture in this case.
$N=1$
. Indeed, we will verify that these two conditions follow from Vandiver’s conjecture in this case.
Definition 3.6. For
![]() $k$
even, we say that
$k$
even, we say that
![]() $(p,k)$
satisfies
$(p,k)$
satisfies
![]() $(\text{Vand}\;\unicode[STIX]{x1D714}^{k})$
if
$(\text{Vand}\;\unicode[STIX]{x1D714}^{k})$
if
Proposition 3.7. Let
![]() $N=1$
and let
$N=1$
and let
![]() $(p,k)$
denote an irregular pair with corresponding maximal ideal
$(p,k)$
denote an irregular pair with corresponding maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
. Then
$\mathfrak{m}\subseteq \mathbb{T}$
. Then
![]() $(\text{Vand}\;\unicode[STIX]{x1D714}^{k})$
and
$(\text{Vand}\;\unicode[STIX]{x1D714}^{k})$
and
![]() $(\text{Vand}\;\unicode[STIX]{x1D714}^{2-k})$
imply that
$(\text{Vand}\;\unicode[STIX]{x1D714}^{2-k})$
imply that
![]() $\mathfrak{m}$
satisfies (Goren) and (Cusp Goren).
$\mathfrak{m}$
satisfies (Goren) and (Cusp Goren).
Proof. By [Reference KuriharaKur93, Theorem 0.4],
![]() $(\text{Vand}\;\unicode[STIX]{x1D714}^{k})$
and
$(\text{Vand}\;\unicode[STIX]{x1D714}^{k})$
and
![]() $(\text{Vand}\;\unicode[STIX]{x1D714}^{2-k})$
together imply that
$(\text{Vand}\;\unicode[STIX]{x1D714}^{2-k})$
together imply that
![]() ${\mathcal{I}}_{k,\mathfrak{m}_{k}^{c}}^{c}\subseteq \mathbb{T}_{k}^{c}$
is principal. Then, by Theorem 3.5, we have that
${\mathcal{I}}_{k,\mathfrak{m}_{k}^{c}}^{c}\subseteq \mathbb{T}_{k}^{c}$
is principal. Then, by Theorem 3.5, we have that
![]() $\mathbb{T}_{\mathfrak{m}}$
and
$\mathbb{T}_{\mathfrak{m}}$
and
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
are Gorenstein.◻
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
are Gorenstein.◻
Remark 3.8. We remind the reader that Vandiver’s conjecture is known to hold for
![]() $p<2^{31}$
[Reference Hart, Harvey and OngHHO17], and so (Goren) and (Cusp Goren) hold in these cases as well when
$p<2^{31}$
[Reference Hart, Harvey and OngHHO17], and so (Goren) and (Cusp Goren) hold in these cases as well when
![]() $N=1$
.
$N=1$
.
3.3 Freeness of spaces of modular symbols
Let
![]() $\tilde{\unicode[STIX]{x1D6EC}}=\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
,
$\tilde{\unicode[STIX]{x1D6EC}}=\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
,
![]() ${\mathcal{M}}=\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
and consider
${\mathcal{M}}=\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
and consider
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})$
. The following theorem is proven in Appendix A.
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})$
. The following theorem is proven in Appendix A.
Theorem 3.9. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (Good Eisen). The following conditions are equivalent:
$\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (Good Eisen). The following conditions are equivalent:
(1) for some (equivalently, for all)
 $j>2$
with
$j>2$
with
 $j\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
, we have
$j\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
, we have  $$\begin{eqnarray}\dim _{\mathbb{F}_{p}}(H_{c}^{1}(\unicode[STIX]{x1D6E4},{\mathcal{P}}_{j-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}[\mathfrak{m}_{j}])=1;\end{eqnarray}$$
$$\begin{eqnarray}\dim _{\mathbb{F}_{p}}(H_{c}^{1}(\unicode[STIX]{x1D6E4},{\mathcal{P}}_{j-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}[\mathfrak{m}_{j}])=1;\end{eqnarray}$$
(2)
 $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}})$
is free over
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}})$
is free over
 $\mathbb{T}_{\mathfrak{m}}$
.
$\mathbb{T}_{\mathfrak{m}}$
.
Proof. First note that (Good Eisen) implies the condition (Eisen
![]() $^{+}$
) from Appendix A. Indeed, (Good Eisen) implies by Lemma 3.1 that
$^{+}$
) from Appendix A. Indeed, (Good Eisen) implies by Lemma 3.1 that
![]() $E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}$
spans the Eisenstein subspace of
$E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}$
spans the Eisenstein subspace of
![]() $M_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}_{k}}$
. Since the boundary symbol associated to
$M_{k}(\unicode[STIX]{x1D6E4}_{0},\unicode[STIX]{x1D713}_{\mathfrak{m}})_{\mathfrak{m}_{k}}$
. Since the boundary symbol associated to
![]() $E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}$
is in the plus subspace (see [Reference Bellaïche and DasguptaBD15, Proposition 2.9]), (Eisen
$E_{k,\unicode[STIX]{x1D713}_{\mathfrak{m}}}$
is in the plus subspace (see [Reference Bellaïche and DasguptaBD15, Proposition 2.9]), (Eisen
![]() $^{+}$
) follows. Thus, this theorem follows immediately from Theorem A.16 after we note that it is fine to replace
$^{+}$
) follows. Thus, this theorem follows immediately from Theorem A.16 after we note that it is fine to replace
![]() $\unicode[STIX]{x1D6E4}_{0}$
with
$\unicode[STIX]{x1D6E4}_{0}$
with
![]() $\unicode[STIX]{x1D6E4}$
since there are no ordinary
$\unicode[STIX]{x1D6E4}$
since there are no ordinary
![]() $p$
-new forms in weights greater than 2.◻
$p$
-new forms in weights greater than 2.◻
If
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfies either of the above conditions, we say that
$\mathfrak{m}\subseteq \mathbb{T}$
satisfies either of the above conditions, we say that
![]() $\mathfrak{m}$
satisfies (Mult One). Now let
$\mathfrak{m}$
satisfies (Mult One). Now let
as in [Reference Fukaya and KatoFK12, 1.5–1.6].
Proposition 3.10. We have
as Hecke modules where
![]() $M_{\unicode[STIX]{x1D6EC}}$
is the space of
$M_{\unicode[STIX]{x1D6EC}}$
is the space of
![]() $\unicode[STIX]{x1D6EC}$
-adic modular forms of tame level
$\unicode[STIX]{x1D6EC}$
-adic modular forms of tame level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
.
$\unicode[STIX]{x1D6E4}_{1}(N)$
.
Proof. By [Reference OhtaOht03, Remark 3.5.10], we have an identification between
![]() $\tilde{H}_{c}^{1}(N)^{\pm }$
and
$\tilde{H}_{c}^{1}(N)^{\pm }$
and
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4},\operatorname{Meas}({\mathcal{D}}))^{\pm }$
where
$H_{c}^{1}(\unicode[STIX]{x1D6E4},\operatorname{Meas}({\mathcal{D}}))^{\pm }$
where
![]() ${\mathcal{D}}=\{(x,y)\in \mathbb{Z}_{p}^{2}\mid (x,y)=1\}$
. Since
${\mathcal{D}}=\{(x,y)\in \mathbb{Z}_{p}^{2}\mid (x,y)=1\}$
. Since
![]() $\operatorname{Meas}({\mathcal{D}})\cong \operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{0}}^{\unicode[STIX]{x1D6E4}}({\mathcal{M}})$
, by Shapiro’s lemma, we then have
$\operatorname{Meas}({\mathcal{D}})\cong \operatorname{Ind}_{\unicode[STIX]{x1D6E4}_{0}}^{\unicode[STIX]{x1D6E4}}({\mathcal{M}})$
, by Shapiro’s lemma, we then have
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})\cong \tilde{H}_{c}^{1}(N)$
. Then the pairing in [Reference Fukaya and KatoFK12, (1.6.7)] yields
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})\cong \tilde{H}_{c}^{1}(N)$
. Then the pairing in [Reference Fukaya and KatoFK12, (1.6.7)] yields
![]() $\tilde{H}_{c}^{1}(N)^{\pm }\cong \operatorname{Hom}_{\mathbb{T}}(\tilde{H}^{1}(N)^{\mp },M_{\unicode[STIX]{x1D6EC}})$
as desired.◻
$\tilde{H}_{c}^{1}(N)^{\pm }\cong \operatorname{Hom}_{\mathbb{T}}(\tilde{H}^{1}(N)^{\mp },M_{\unicode[STIX]{x1D6EC}})$
as desired.◻
Theorem 3.11. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (Good Eisen) and (Goren). Then (Mult One) holds for
$\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (Good Eisen) and (Goren). Then (Mult One) holds for
![]() $\mathfrak{m}$
.
$\mathfrak{m}$
.
Proof. By [Reference Fukaya and KatoFK12, Proposition 6.3.5 and (1.7.13)],
![]() $\tilde{H}^{1}(N)_{\mathfrak{m}}^{-}$
is a dualizing module for
$\tilde{H}^{1}(N)_{\mathfrak{m}}^{-}$
is a dualizing module for
![]() $\mathbb{T}_{\mathfrak{m}}$
and is thus free over
$\mathbb{T}_{\mathfrak{m}}$
and is thus free over
![]() $\mathbb{T}_{\mathfrak{m}}$
, assuming (Goren). As
$\mathbb{T}_{\mathfrak{m}}$
, assuming (Goren). As
![]() $(M_{\unicode[STIX]{x1D6EC}})_{\mathfrak{m}}\cong \mathbb{T}_{\mathfrak{m}}$
when
$(M_{\unicode[STIX]{x1D6EC}})_{\mathfrak{m}}\cong \mathbb{T}_{\mathfrak{m}}$
when
![]() $\mathbb{T}_{\mathfrak{m}}$
is Gorenstein, by Proposition 3.10, we have that
$\mathbb{T}_{\mathfrak{m}}$
is Gorenstein, by Proposition 3.10, we have that
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})_{\mathfrak{m}}^{+}$
is free over
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})_{\mathfrak{m}}^{+}$
is free over
![]() $\mathbb{T}_{\mathfrak{m}}$
. Again since
$\mathbb{T}_{\mathfrak{m}}$
. Again since
![]() $\mathbb{T}_{\mathfrak{m}}$
is Gorenstein, we have
$\mathbb{T}_{\mathfrak{m}}$
is Gorenstein, we have
![]() $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}})$
is free over
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}})$
is free over
![]() $\mathbb{T}_{\mathfrak{m}}$
as desired.◻
$\mathbb{T}_{\mathfrak{m}}$
as desired.◻
3.4 Lower bounds
Fix a maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and (Goren). Then, by Theorem 3.11, (Mult One) holds for
$\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and (Goren). Then, by Theorem 3.11, (Mult One) holds for
![]() $\mathfrak{m}$
, and thus the construction in Appendix A.6 yields a two-variable
$\mathfrak{m}$
, and thus the construction in Appendix A.6 yields a two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function
$L$
-function
![]() $L_{p}^{+}(\mathfrak{m})$
in
$L_{p}^{+}(\mathfrak{m})$
in
![]() $\mathbb{T}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
defined over the full Hecke algebra. We now check that
$\mathbb{T}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
defined over the full Hecke algebra. We now check that
![]() $L_{p}^{+}(\mathfrak{m})\in \mathbb{T}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
vanishes along the Eisenstein component.
$L_{p}^{+}(\mathfrak{m})\in \mathbb{T}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
vanishes along the Eisenstein component.
Theorem 3.12. If
![]() $\mathfrak{m}\subseteq \mathbb{T}$
is an Eisenstein maximal ideal satisfying (Good Eisen) and (Goren), then
$\mathfrak{m}\subseteq \mathbb{T}$
is an Eisenstein maximal ideal satisfying (Good Eisen) and (Goren), then
where
![]() ${\mathcal{I}}$
is the Eisenstein ideal of
${\mathcal{I}}$
is the Eisenstein ideal of
![]() $\mathbb{T}$
.
$\mathbb{T}$
.
Proof. To prove this corollary, it suffices to see that the image of
![]() $L_{p}^{+}(\mathfrak{m})$
vanishes in
$L_{p}^{+}(\mathfrak{m})$
vanishes in
![]() $\mathbb{T}_{\mathfrak{m}}/{\mathcal{I}}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
. To see this, let
$\mathbb{T}_{\mathfrak{m}}/{\mathcal{I}}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
. To see this, let
![]() $\mathfrak{p}_{\operatorname{eis},k}\subseteq \mathfrak{m}$
denote the ideal generated by
$\mathfrak{p}_{\operatorname{eis},k}\subseteq \mathfrak{m}$
denote the ideal generated by
![]() $T_{\ell }-(1+\unicode[STIX]{x1D713}(\ell )\ell ^{k-1})$
for
$T_{\ell }-(1+\unicode[STIX]{x1D713}(\ell )\ell ^{k-1})$
for
![]() $\ell \nmid Np$
and by
$\ell \nmid Np$
and by
![]() $U_{q}-1$
for
$U_{q}-1$
for
![]() $q\mid Np$
. It suffices to see that the image of
$q\mid Np$
. It suffices to see that the image of
![]() $L_{p}^{+}(\mathfrak{m})$
vanishes in
$L_{p}^{+}(\mathfrak{m})$
vanishes in
![]() $\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{\operatorname{eis},k}[[\mathbb{Z}_{p}^{\times }]]$
for all classical
$\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{\operatorname{eis},k}[[\mathbb{Z}_{p}^{\times }]]$
for all classical
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
. But, by construction, the image of
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
. But, by construction, the image of
![]() $L_{p}^{+}(\mathfrak{m})$
in
$L_{p}^{+}(\mathfrak{m})$
in
![]() $\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{\operatorname{eis},k}[[\mathbb{Z}_{p}^{\times }]]$
equals
$\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{\operatorname{eis},k}[[\mathbb{Z}_{p}^{\times }]]$
equals
![]() $\unicode[STIX]{x1D6F7}(\{\infty \}-\{0\})|_{\mathbb{Z}_{p}^{\times }}$
for some eigensymbol
$\unicode[STIX]{x1D6F7}(\{\infty \}-\{0\})|_{\mathbb{Z}_{p}^{\times }}$
for some eigensymbol
![]() $\unicode[STIX]{x1D6F7}$
in
$\unicode[STIX]{x1D6F7}$
in
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},\operatorname{Meas}_{k}(\mathbb{Z}_{p}))^{+}$
annihilated by
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},\operatorname{Meas}_{k}(\mathbb{Z}_{p}))^{+}$
annihilated by
![]() $\mathfrak{p}_{\operatorname{eis},k}$
. Thus, by Theorem 2.3,
$\mathfrak{p}_{\operatorname{eis},k}$
. Thus, by Theorem 2.3,
![]() $\unicode[STIX]{x1D6F7}(\{\infty \}-\{0\})|_{\mathbb{Z}_{p}^{\times }}=0$
as desired.◻
$\unicode[STIX]{x1D6F7}(\{\infty \}-\{0\})|_{\mathbb{Z}_{p}^{\times }}=0$
as desired.◻
Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (Good Eisen). Set
$\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (Good Eisen). Set
![]() $L_{p}^{+}(\mathfrak{m}^{c})$
equal to the image of
$L_{p}^{+}(\mathfrak{m}^{c})$
equal to the image of
![]() $L_{p}^{+}(\mathfrak{m})$
in
$L_{p}^{+}(\mathfrak{m})$
in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
which is the cuspidal two-variable
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
which is the cuspidal two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function. If we further assume that both (Goren) and (Cusp Goren) hold, by Theorem 3.5, the cuspidal Eisenstein ideal
$L$
-function. If we further assume that both (Goren) and (Cusp Goren) hold, by Theorem 3.5, the cuspidal Eisenstein ideal
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is principal, generated by, say,
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is principal, generated by, say,
![]() $L_{\operatorname{eis},\mathfrak{m}}$
. The following theorem gives a lower bound on the
$L_{\operatorname{eis},\mathfrak{m}}$
. The following theorem gives a lower bound on the
![]() $\unicode[STIX]{x1D707}$
-invariants of the forms in the Hida family parameterized by
$\unicode[STIX]{x1D707}$
-invariants of the forms in the Hida family parameterized by
![]() $\mathfrak{m}^{c}$
in terms of
$\mathfrak{m}^{c}$
in terms of
![]() $L_{\operatorname{eis},\mathfrak{m}}$
. As we will be imposing the following three hypotheses in much of what follows, let us say that
$L_{\operatorname{eis},\mathfrak{m}}$
. As we will be imposing the following three hypotheses in much of what follows, let us say that
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfies (
$\mathfrak{m}\subseteq \mathbb{T}$
satisfies (
![]() $\star$
) if
$\star$
) if
![]() $\mathfrak{m}$
satisfies (Good Eisen), (Goren) and (Cusp Goren).
$\mathfrak{m}$
satisfies (Good Eisen), (Goren) and (Cusp Goren).
Before stating our theorem on
![]() $\unicode[STIX]{x1D707}$
-invariants, we first define how these invariants are normalized.
$\unicode[STIX]{x1D707}$
-invariants, we first define how these invariants are normalized.
Definition 3.13. Let
![]() ${\mathcal{O}}$
be a finite extension of
${\mathcal{O}}$
be a finite extension of
![]() $\mathbb{Z}_{p}$
and let
$\mathbb{Z}_{p}$
and let
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}={\mathcal{O}}[[1+p\mathbb{Z}_{p}]]$
. Let
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}={\mathcal{O}}[[1+p\mathbb{Z}_{p}]]$
. Let
![]() $\unicode[STIX]{x1D71B}$
be a uniformizer of the integral closure of
$\unicode[STIX]{x1D71B}$
be a uniformizer of the integral closure of
![]() ${\mathcal{O}}$
. For a non-zero element
${\mathcal{O}}$
. For a non-zero element
![]() $h\in \unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
, we define
$h\in \unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
, we define
![]() $\unicode[STIX]{x1D707}(f)$
to be
$\unicode[STIX]{x1D707}(f)$
to be
![]() $n$
, where
$n$
, where
![]() $n$
is the largest integer such that
$n$
is the largest integer such that
![]() $h\in \unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}-\unicode[STIX]{x1D71B}^{n+1}\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
.
$h\in \unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}-\unicode[STIX]{x1D71B}^{n+1}\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
.
Let
![]() $\mathfrak{p}_{f}$
be a classical height-one prime of
$\mathfrak{p}_{f}$
be a classical height-one prime of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
associated to some ordinary cuspidal eigenform
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
associated to some ordinary cuspidal eigenform
![]() $f$
in the Hida family corresponding to
$f$
in the Hida family corresponding to
![]() $\mathfrak{m}^{c}$
. Write
$\mathfrak{m}^{c}$
. Write
![]() ${\mathcal{O}}:={\mathcal{O}}_{f}$
for the finite extension of
${\mathcal{O}}:={\mathcal{O}}_{f}$
for the finite extension of
![]() $\mathbb{Z}_{p}$
equal to the integral closure of
$\mathbb{Z}_{p}$
equal to the integral closure of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}$
, and write
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}$
, and write
![]() $\unicode[STIX]{x1D71B}$
for a uniformizer of
$\unicode[STIX]{x1D71B}$
for a uniformizer of
![]() ${\mathcal{O}}$
. We write
${\mathcal{O}}$
. We write
![]() $L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f})$
for the image of
$L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f})$
for the image of
![]() $L_{\operatorname{eis},\mathfrak{m}}$
in
$L_{\operatorname{eis},\mathfrak{m}}$
in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}\subseteq {\mathcal{O}}$
.
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{f}\subseteq {\mathcal{O}}$
.
For each
![]() $a$
with
$a$
with
![]() $0\leqslant a<p-1$
and
$0\leqslant a<p-1$
and
![]() $R$
any ring, we have a map
$R$
any ring, we have a map
![]() $R[[\mathbb{Z}_{p}^{\times }]]\rightarrow R[[1+p\mathbb{Z}_{p}]]$
given by
$R[[\mathbb{Z}_{p}^{\times }]]\rightarrow R[[1+p\mathbb{Z}_{p}]]$
given by
![]() $[x]\mapsto \unicode[STIX]{x1D714}^{a}(x)[x/\unicode[STIX]{x1D714}(x)]$
where
$[x]\mapsto \unicode[STIX]{x1D714}^{a}(x)[x/\unicode[STIX]{x1D714}(x)]$
where
![]() $x\in \mathbb{Z}_{p}^{\times }$
. We write
$x\in \mathbb{Z}_{p}^{\times }$
. We write
![]() $L_{p}^{+}(f,\unicode[STIX]{x1D714}^{a})$
and
$L_{p}^{+}(f,\unicode[STIX]{x1D714}^{a})$
and
![]() $L_{p}^{+}(\mathfrak{m},\unicode[STIX]{x1D714}^{a})$
for the respective images of
$L_{p}^{+}(\mathfrak{m},\unicode[STIX]{x1D714}^{a})$
for the respective images of
![]() $L_{p}^{+}(f)$
and
$L_{p}^{+}(f)$
and
![]() $L_{p}^{+}(\mathfrak{m})$
under the corresponding maps. Further, we write
$L_{p}^{+}(\mathfrak{m})$
under the corresponding maps. Further, we write
![]() $\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{a})$
for
$\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{a})$
for
![]() $\unicode[STIX]{x1D707}(L_{p}^{+}(f,\unicode[STIX]{x1D714}^{a}))$
.
$\unicode[STIX]{x1D707}(L_{p}^{+}(f,\unicode[STIX]{x1D714}^{a}))$
.
Theorem 3.14. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (
$\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal satisfying (
![]() $\star$
). Let
$\star$
). Let
![]() $L_{\operatorname{eis},\mathfrak{m}}$
denote a generator of the Eisenstein ideal
$L_{\operatorname{eis},\mathfrak{m}}$
denote a generator of the Eisenstein ideal
![]() ${\mathcal{I}}^{c}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. Then
${\mathcal{I}}^{c}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. Then
in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
. In particular,
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
. In particular,
for all even
![]() $a$
with
$a$
with
![]() $0\leqslant a\leqslant p-2$
, and all
$0\leqslant a\leqslant p-2$
, and all
![]() $f$
in the Hida family corresponding to
$f$
in the Hida family corresponding to
![]() $\mathfrak{m}^{c}$
.
$\mathfrak{m}^{c}$
.
Proof. By Theorem 3.12,
![]() $L_{p}^{+}(\mathfrak{m})\in {\mathcal{I}}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
. Projecting to
$L_{p}^{+}(\mathfrak{m})\in {\mathcal{I}}_{\mathfrak{m}}[[\mathbb{Z}_{p}^{\times }]]$
. Projecting to
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
implies that
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
implies that
![]() $L_{p}^{+}(\mathfrak{m}^{c})\in {\mathcal{I}}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
, and is thus divisible by
$L_{p}^{+}(\mathfrak{m}^{c})\in {\mathcal{I}}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]$
, and is thus divisible by
![]() $L_{\operatorname{eis},\mathfrak{m}}$
as desired.
$L_{\operatorname{eis},\mathfrak{m}}$
as desired.
The second assertion is immediate from the first as
![]() $L_{p}^{+}(\mathfrak{m}^{c})$
specializes to
$L_{p}^{+}(\mathfrak{m}^{c})$
specializes to
![]() $L_{p}^{+}(f)$
at the prime
$L_{p}^{+}(f)$
at the prime
![]() $\mathfrak{p}_{f}$
while
$\mathfrak{p}_{f}$
while
![]() $L_{\operatorname{eis},\mathfrak{m}}$
specializes to the number
$L_{\operatorname{eis},\mathfrak{m}}$
specializes to the number
![]() $L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f})\in {\mathcal{O}}$
and thus contributes to the
$L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f})\in {\mathcal{O}}$
and thus contributes to the
![]() $\unicode[STIX]{x1D707}$
-invariant.◻
$\unicode[STIX]{x1D707}$
-invariant.◻
3.5 Upper bounds
We now establish an upper bound on
![]() $\unicode[STIX]{x1D707}$
-invariants of these residually reducible forms under the hypothesis (Mult One).
$\unicode[STIX]{x1D707}$
-invariants of these residually reducible forms under the hypothesis (Mult One).
Theorem 3.15. Fix an Eisenstein maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Mult One). Let
$\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Mult One). Let
![]() $f$
be a classical cuspidal eigenform in the Hida family for
$f$
be a classical cuspidal eigenform in the Hida family for
![]() $\mathfrak{m}^{c}$
. Then
$\mathfrak{m}^{c}$
. Then
Proof. To prove this theorem, we simply check that the valuation of
![]() $L_{p}^{+}(f)$
evaluated at the trivial character is bounded by
$L_{p}^{+}(f)$
evaluated at the trivial character is bounded by
![]() $\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
as this immediately gives the desired bound on the
$\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
as this immediately gives the desired bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant. By the interpolation property of
$\unicode[STIX]{x1D707}$
-invariant. By the interpolation property of
![]() $L_{p}^{+}(f)$
, we have
$L_{p}^{+}(f)$
, we have
We claim that
![]() $\unicode[STIX]{x1D711}_{f}^{+}(\{\infty \}-\{0\})(1)$
is a
$\unicode[STIX]{x1D711}_{f}^{+}(\{\infty \}-\{0\})(1)$
is a
![]() $p$
-adic unit, which clearly implies the theorem.
$p$
-adic unit, which clearly implies the theorem.
To see this, let
![]() $k$
denote the weight of
$k$
denote the weight of
![]() $f$
. Then, by [Reference Bellaïche and DasguptaBD15, Proposition 2.5(iii)], there is a unique (up to scaling) boundary eigensymbol
$f$
. Then, by [Reference Bellaïche and DasguptaBD15, Proposition 2.5(iii)], there is a unique (up to scaling) boundary eigensymbol
![]() $\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
in
$\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
in
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee })^{+}$
with the same system of Hecke eigenvalues as
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee })^{+}$
with the same system of Hecke eigenvalues as
![]() $E_{k,\unicode[STIX]{x1D713}}^{(p)}$
. We fix
$E_{k,\unicode[STIX]{x1D713}}^{(p)}$
. We fix
![]() $\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
to be as defined in [Reference Bellaïche and DasguptaBD15, (22)] which is normalized so that its image in
$\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
to be as defined in [Reference Bellaïche and DasguptaBD15, (22)] which is normalized so that its image in
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}$
is non-zero.
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}$
is non-zero.
Since
![]() $\unicode[STIX]{x1D711}_{f}^{+}$
and
$\unicode[STIX]{x1D711}_{f}^{+}$
and
![]() $\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
have congruent systems of Hecke eigenvalues, by (Mult One), we have that the images of these symbols in
$\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
have congruent systems of Hecke eigenvalues, by (Mult One), we have that the images of these symbols in
![]() $H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}$
are non-zero multiples of one another. Moreover, the explicit description of
$H_{c}^{1}(\unicode[STIX]{x1D6E4}_{0},{\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}$
are non-zero multiples of one another. Moreover, the explicit description of
![]() $\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
in [Reference Bellaïche and DasguptaBD15, (22)], tells use that
$\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
in [Reference Bellaïche and DasguptaBD15, (22)], tells use that
![]() $\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
is not supported on the
$\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}$
is not supported on the
![]() $\infty$
cusp while
$\infty$
cusp while
![]() $\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}(\{0\})$
is the functional
$\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D713}}(\{0\})$
is the functional
![]() $P(z)\mapsto P(0)$
. Thus,
$P(z)\mapsto P(0)$
. Thus,
and thus
![]() $\unicode[STIX]{x1D711}_{f}^{+}(\{\infty \}-\{0\})(1)$
is a
$\unicode[STIX]{x1D711}_{f}^{+}(\{\infty \}-\{0\})(1)$
is a
![]() $p$
-adic unit as desired.◻
$p$
-adic unit as desired.◻
3.6 Conjecture on
 $\unicode[STIX]{x1D707}$
-invariants
$\unicode[STIX]{x1D707}$
-invariants
Under the assumption (
![]() $\star$
) (which implies (Mult One)), Theorems 3.14 and 3.15 imply the following string of inequalities:Footnote
3
$\star$
) (which implies (Mult One)), Theorems 3.14 and 3.15 imply the following string of inequalities:Footnote
3
Given the philosophy that
![]() $\unicode[STIX]{x1D707}$
-invariants are ‘as small as they can be’, it is tempting to make the following conjecture.
$\unicode[STIX]{x1D707}$
-invariants are ‘as small as they can be’, it is tempting to make the following conjecture.
Conjecture 3.16. Fix a maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfying (
$\mathfrak{m}\subseteq \mathbb{T}$
satisfying (
![]() $\star$
) and let
$\star$
) and let
![]() $L_{\operatorname{eis},\mathfrak{m}}$
denote a generator of
$L_{\operatorname{eis},\mathfrak{m}}$
denote a generator of
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
. Then
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
. Then
for all even
![]() $a$
and all classical
$a$
and all classical
![]() $\mathfrak{p}_{f}$
contained in
$\mathfrak{p}_{f}$
contained in
![]() $\mathfrak{m}^{c}$
.
$\mathfrak{m}^{c}$
.
The following proposition shows that to check this conjecture it suffices to check that (4) holds for a single form
![]() $f$
in the family.
$f$
in the family.
Proposition 3.17. Assume
![]() $\mathfrak{m}\subseteq \mathbb{T}$
is a maximal ideal satisfying (
$\mathfrak{m}\subseteq \mathbb{T}$
is a maximal ideal satisfying (
![]() $\star$
). For each fixed even number
$\star$
). For each fixed even number
![]() $a$
, we have that
$a$
, we have that
![]() $\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{a})=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f}))$
holds for one classical
$\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{a})=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f}))$
holds for one classical
![]() $\mathfrak{p}_{f}\subseteq \mathfrak{m}^{c}$
if and only if this equation holds for all such
$\mathfrak{p}_{f}\subseteq \mathfrak{m}^{c}$
if and only if this equation holds for all such
![]() $\mathfrak{p}_{f}$
.
$\mathfrak{p}_{f}$
.
Proof. By Theorem 3.14,
![]() $L_{p}^{+}(\mathfrak{m}^{c},\unicode[STIX]{x1D714}^{a})/L_{\operatorname{eis},\mathfrak{m}}$
is integral, and by assumption, this power series has at least one specialization with vanishing
$L_{p}^{+}(\mathfrak{m}^{c},\unicode[STIX]{x1D714}^{a})/L_{\operatorname{eis},\mathfrak{m}}$
is integral, and by assumption, this power series has at least one specialization with vanishing
![]() $\unicode[STIX]{x1D707}$
-invariant. Thus, by [Reference Emerton, Pollack and WestonEPW06, Proposition 3.7.3], every specialization has vanishing
$\unicode[STIX]{x1D707}$
-invariant. Thus, by [Reference Emerton, Pollack and WestonEPW06, Proposition 3.7.3], every specialization has vanishing
![]() $\unicode[STIX]{x1D707}$
-invariant, proving the proposition.◻
$\unicode[STIX]{x1D707}$
-invariant, proving the proposition.◻
3.7 When the bounds meet
In the case when the lower and upper bounds of (3) meet (e.g. when
![]() $U_{p}-1$
generates
$U_{p}-1$
generates
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
), the Iwasawa theory of our situation becomes much simpler. We begin with a lemma.
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
), the Iwasawa theory of our situation becomes much simpler. We begin with a lemma.
Proposition 3.18. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be an Eisenstein maximal ideal. The following statements are equivalent:
$\mathfrak{m}\subseteq \mathbb{T}$
be an Eisenstein maximal ideal. The following statements are equivalent:
(1)
 ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is generated by
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is generated by
 $U_{p}-1$
;
$U_{p}-1$
;(2)
 ${\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
is generated by
${\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
is generated by
 $U_{p}-1$
for every
$U_{p}-1$
for every
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
 $k\geqslant 2$
;
$k\geqslant 2$
;(3)
 ${\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
is generated by
${\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
is generated by
 $U_{p}-1$
for some
$U_{p}-1$
for some
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
 $k\geqslant 2$
.
$k\geqslant 2$
.
Proof. We check that (3) implies (1). Since
![]() ${\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
is principal, by Theorem 3.5, we have that
${\mathcal{I}}_{k,\mathfrak{m}^{c}}^{c}$
is principal, by Theorem 3.5, we have that
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is principal, generated by, say,
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is principal, generated by, say,
![]() $L_{\operatorname{eis},\mathfrak{m}}$
. Consider now
$L_{\operatorname{eis},\mathfrak{m}}$
. Consider now
![]() $(U_{p}-1)/L_{\operatorname{eis},\mathfrak{m}}\in \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. This element specializes to a unit in weight
$(U_{p}-1)/L_{\operatorname{eis},\mathfrak{m}}\in \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. This element specializes to a unit in weight
![]() $k$
, and is thus itself a unit. Hence,
$k$
, and is thus itself a unit. Hence,
![]() $L_{\operatorname{eis},\mathfrak{m}}$
differs from
$L_{\operatorname{eis},\mathfrak{m}}$
differs from
![]() $U_{p}-1$
by a unit, and thus
$U_{p}-1$
by a unit, and thus
![]() $U_{p}-1$
generates
$U_{p}-1$
generates
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
.◻
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
.◻
Definition 3.19. An Eisenstein maximal ideal
![]() $\mathfrak{m}$
of
$\mathfrak{m}$
of
![]() $\mathbb{T}$
satisfies
$\mathbb{T}$
satisfies
![]() $(U_{p}-1\;\text{gens})$
if any of the equivalent conditions of Proposition 3.18 hold.
$(U_{p}-1\;\text{gens})$
if any of the equivalent conditions of Proposition 3.18 hold.
Lemma 3.20.
![]() $(U_{p}-1\;\text{gens})$
implies (Goren) and (Cusp Goren).
$(U_{p}-1\;\text{gens})$
implies (Goren) and (Cusp Goren).
Proof. This claim follows immediately from Theorem 3.5. ◻
In what follows, we write
![]() $\unicode[STIX]{x1D706}(f)$
for
$\unicode[STIX]{x1D706}(f)$
for
![]() $\unicode[STIX]{x1D706}(f,\unicode[STIX]{x1D714}^{0})$
and
$\unicode[STIX]{x1D706}(f,\unicode[STIX]{x1D714}^{0})$
and
![]() $\unicode[STIX]{x1D707}(f)$
for
$\unicode[STIX]{x1D707}(f)$
for
![]() $\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{0})$
.
$\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{0})$
.
Theorem 3.21. For an Eisenstein maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and
$\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and
![]() $(U_{p}-1\;\text{gens})$
, we have
$(U_{p}-1\;\text{gens})$
, we have
where
![]() $U$
is a unit in
$U$
is a unit in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[1+p\mathbb{Z}_{p}]]$
. In particular, for every
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[1+p\mathbb{Z}_{p}]]$
. In particular, for every
![]() $f$
in the Hida family of
$f$
in the Hida family of
![]() $\mathfrak{m}^{c}$
, we have
$\mathfrak{m}^{c}$
, we have
That is,
![]() $L_{p}(f,\unicode[STIX]{x1D714}^{0})$
is simply a power of
$L_{p}(f,\unicode[STIX]{x1D714}^{0})$
is simply a power of
![]() $p$
, up to a unit.
$p$
, up to a unit.
Proof. By Lemma 3.20, (Goren) and (Cusp Goren) hold automatically. Further, for
![]() $\mathfrak{p}_{f}\subseteq \mathfrak{m}^{c}$
,
$\mathfrak{p}_{f}\subseteq \mathfrak{m}^{c}$
,
![]() $(U_{p}-1\;\text{gens})$
and the inequalities in (3) tell us the value of the
$(U_{p}-1\;\text{gens})$
and the inequalities in (3) tell us the value of the
![]() $\unicode[STIX]{x1D707}$
-invariant exactly:
$\unicode[STIX]{x1D707}$
-invariant exactly:
But, as in the proof of Theorem 3.15, we know that
![]() $L_{p}^{+}(f)$
evaluated at
$L_{p}^{+}(f)$
evaluated at
![]() $\mathbf{1}$
has
$\mathbf{1}$
has
![]() $p$
-adic valuation equal to
$p$
-adic valuation equal to
![]() $\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
. Since this valuation also equals the
$\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
. Since this valuation also equals the
![]() $\unicode[STIX]{x1D707}$
-invariant, we get that
$\unicode[STIX]{x1D707}$
-invariant, we get that
![]() $\unicode[STIX]{x1D706}(f)=0$
.
$\unicode[STIX]{x1D706}(f)=0$
.
By Theorem 3.14, the quotient
![]() $L_{p}(\mathfrak{m}^{c},\unicode[STIX]{x1D714}^{0})/L_{\operatorname{eis},\mathfrak{m}}$
is integral. Further,
$L_{p}(\mathfrak{m}^{c},\unicode[STIX]{x1D714}^{0})/L_{\operatorname{eis},\mathfrak{m}}$
is integral. Further,
has vanishing
![]() $\unicode[STIX]{x1D707}$
- and
$\unicode[STIX]{x1D707}$
- and
![]() $\unicode[STIX]{x1D706}$
-invariants (since
$\unicode[STIX]{x1D706}$
-invariants (since
![]() $\unicode[STIX]{x1D707}(f)=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f}))$
), and is thus a unit. But then
$\unicode[STIX]{x1D707}(f)=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f}))$
), and is thus a unit. But then
![]() $L_{p}(\mathfrak{m}^{c},\unicode[STIX]{x1D714}^{0})/L_{\operatorname{eis},\mathfrak{m}}$
has a unit specialization, and it must itself be a unit.◻
$L_{p}(\mathfrak{m}^{c},\unicode[STIX]{x1D714}^{0})/L_{\operatorname{eis},\mathfrak{m}}$
has a unit specialization, and it must itself be a unit.◻
3.8 The special case of (Cuspidal rank one)
In the special case where (Cuspidal rank one) of the introduction holds, the results of the previous sections both become more concrete (with
![]() $L_{\operatorname{eis},\mathfrak{m}}$
being replaced by a
$L_{\operatorname{eis},\mathfrak{m}}$
being replaced by a
![]() $p$
-adic
$p$
-adic
![]() $L$
-function) and no longer require any Gorenstein hypotheses (as they are automatically satisfied). We have the following proposition.
$L$
-function) and no longer require any Gorenstein hypotheses (as they are automatically satisfied). We have the following proposition.
Proposition 3.22. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal. The following statements are equivalent:
$\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal. The following statements are equivalent:
(1)
 $\dim _{\unicode[STIX]{x1D6EC}}\mathbb{T}_{\mathfrak{m}^{c}}^{c}=1$
;
$\dim _{\unicode[STIX]{x1D6EC}}\mathbb{T}_{\mathfrak{m}^{c}}^{c}=1$
;(2)
 $\dim _{\mathbb{Z}_{p}}\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}=1$
for some
$\dim _{\mathbb{Z}_{p}}\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}=1$
for some
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
 $k\geqslant 2$
;
$k\geqslant 2$
;(3)
 $\dim _{\mathbb{Z}_{p}}\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}=1$
for all
$\dim _{\mathbb{Z}_{p}}\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}=1$
for all
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
,
 $k\geqslant 2$
.
$k\geqslant 2$
.
Proof. This proposition follows from Hida’s control theorem:
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{k}\mathbb{T}_{\mathfrak{m}^{c}}^{c}\cong \mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
.◻
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}/\mathfrak{p}_{k}\mathbb{T}_{\mathfrak{m}^{c}}^{c}\cong \mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
.◻
Definition 3.23. For a maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
, we say that
$\mathfrak{m}\subseteq \mathbb{T}$
, we say that
![]() $\mathfrak{m}$
satisfies (Cuspidal rank one) if any of the equivalent conditions of Proposition 3.22 hold.
$\mathfrak{m}$
satisfies (Cuspidal rank one) if any of the equivalent conditions of Proposition 3.22 hold.
Lemma 3.24. If an Eisenstein maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Good Eisen) and (Cuspidal rank one), then it also satisfies (Goren) and (Cusp Goren).
$\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Good Eisen) and (Cuspidal rank one), then it also satisfies (Goren) and (Cusp Goren).
Proof. If
![]() $(p,j)$
satisfies (Cuspidal rank one), then
$(p,j)$
satisfies (Cuspidal rank one), then
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
has rank 1 over
$\mathbb{T}_{k,\mathfrak{m}_{k}^{c}}^{c}$
has rank 1 over
![]() $\mathbb{Z}_{p}$
and clearly (Cusp Goren) holds. Further, by Lemma 3.1, (Good Eisen) implies that
$\mathbb{Z}_{p}$
and clearly (Cusp Goren) holds. Further, by Lemma 3.1, (Good Eisen) implies that
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}$
has rank 2 over
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
has rank 2 over
![]() $\mathbb{Z}_{p}$
. This in turn implies that
$\mathbb{Z}_{p}$
. This in turn implies that
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}$
is generated by a single element over
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
is generated by a single element over
![]() $\mathbb{Z}_{p}$
. In particular,
$\mathbb{Z}_{p}$
. In particular,
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a complete intersection and thus (Goren) holds.◻
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
is a complete intersection and thus (Goren) holds.◻
By the above lemma and Theorem 3.5, we know that
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is principal when (Cuspidal rank one) holds. In this case, work by Wiles and Ohta [Reference WilesWil90, Reference OhtaOht03] implies that this generator can be taken to be a
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is principal when (Cuspidal rank one) holds. In this case, work by Wiles and Ohta [Reference WilesWil90, Reference OhtaOht03] implies that this generator can be taken to be a
![]() $p$
-adic
$p$
-adic
![]() $L$
-function. More precisely, let
$L$
-function. More precisely, let
![]() $L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})$
be defined as in [Reference Bellaïche and DasguptaBD15]. Here we view
$L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})$
be defined as in [Reference Bellaïche and DasguptaBD15]. Here we view
![]() $L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})$
as a function on weight space and we have
$L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})$
as a function on weight space and we have
for
![]() $k\geqslant 1$
with
$k\geqslant 1$
with
![]() $(-1)^{k}=\unicode[STIX]{x1D713}(-1)$
. Set
$(-1)^{k}=\unicode[STIX]{x1D713}(-1)$
. Set
![]() $\unicode[STIX]{x1D6E4}_{w,j}=1+p\mathbb{Z}_{p}$
and view
$\unicode[STIX]{x1D6E4}_{w,j}=1+p\mathbb{Z}_{p}$
and view
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}]]$
as Iwasawa functions on
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}]]$
as Iwasawa functions on
![]() ${\mathcal{W}}_{j}$
. Then
${\mathcal{W}}_{j}$
. Then
![]() $L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})|_{{\mathcal{W}}_{j}}$
is in
$L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})|_{{\mathcal{W}}_{j}}$
is in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}]]$
as long as either
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}]]$
as long as either
![]() $\unicode[STIX]{x1D713}$
is non-trivial or
$\unicode[STIX]{x1D713}$
is non-trivial or
![]() $j\neq 0$
.
$j\neq 0$
.
Note that under (Cuspidal rank one) we can identify
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
with
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
with
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}]]$
and we can and will view
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}]]$
and we can and will view
![]() $L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})|_{{\mathcal{W}}_{j}}$
as an element of
$L_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D705})|_{{\mathcal{W}}_{j}}$
as an element of
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
.
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
.
Theorem 3.25. If
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Cuspidal rank one), then
$\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Cuspidal rank one), then
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is generated by
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}$
is generated by
![]() $L_{p}(\unicode[STIX]{x1D713}_{\mathfrak{m}}^{-1},\unicode[STIX]{x1D705})|_{{\mathcal{W}}_{j(\mathfrak{m})}}$
.
$L_{p}(\unicode[STIX]{x1D713}_{\mathfrak{m}}^{-1},\unicode[STIX]{x1D705})|_{{\mathcal{W}}_{j(\mathfrak{m})}}$
.
Proof. This theorem is simply [Reference OhtaOht03, Proposition 3.1.9] in the special case when (Cuspidal rank one) holds. ◻
Under (Cuspidal rank one), we can consider
![]() $L_{p}^{+}(\mathfrak{m}^{c})$
in
$L_{p}^{+}(\mathfrak{m}^{c})$
in
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]\cong \mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
, and we write
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}[[\mathbb{Z}_{p}^{\times }]]\cong \mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
, and we write
![]() $L_{p}^{+}(\mathfrak{m}^{c})$
as
$L_{p}^{+}(\mathfrak{m}^{c})$
as
![]() $L_{p}^{+}(\unicode[STIX]{x1D705})$
where
$L_{p}^{+}(\unicode[STIX]{x1D705})$
where
![]() $\unicode[STIX]{x1D705}$
is thought to range over weights in
$\unicode[STIX]{x1D705}$
is thought to range over weights in
![]() ${\mathcal{W}}_{j}$
.
${\mathcal{W}}_{j}$
.
The following theorem is the simplified version of Theorem 3.14 when (Cuspidal rank one) holds. We denote by
![]() $f_{k}$
the unique normalized cuspidal eigenform of weight
$f_{k}$
the unique normalized cuspidal eigenform of weight
![]() $k$
and level
$k$
and level
![]() $\unicode[STIX]{x1D6E4}_{0}$
congruent to
$\unicode[STIX]{x1D6E4}_{0}$
congruent to
![]() $E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
.
$E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
.
Theorem 3.26. Fix an Eisenstein maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and (Cuspidal rank one). Then
$\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and (Cuspidal rank one). Then
in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
. In particular,
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times \mathbb{Z}_{p}^{\times }]]$
. In particular,
for each even
![]() $a$
with
$a$
with
![]() $0\leqslant a\leqslant p-1$
and for all
$0\leqslant a\leqslant p-1$
and for all
![]() $k\geqslant 2$
with
$k\geqslant 2$
with
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
Proof. This theorem follows immediately from Theorems 3.14 and 3.25, noting that Lemma 3.24 gives us that (Goren) and (Cusp Goren) hold. ◻
We can likewise deduce the analogue of Theorem 1.4 of the introduction from Theorem 3.21.
Theorem 3.27. Fix an Eisenstein maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and (Cuspidal rank one) and for which
$\mathfrak{m}\subseteq \mathbb{T}$
satisfying (Good Eisen) and (Cuspidal rank one) and for which
for some
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
. Then
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
. Then
where
![]() $U$
is a unit in
$U$
is a unit in
![]() $\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times (1+p\mathbb{Z}_{p})]]$
. In particular, for every
$\mathbb{Z}_{p}[[\unicode[STIX]{x1D6E4}_{w,j}\times (1+p\mathbb{Z}_{p})]]$
. In particular, for every
![]() $k\geqslant 2$
with
$k\geqslant 2$
with
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
, we have that
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
, we have that
That is,
![]() $L_{p}^{+}(f_{k},\unicode[STIX]{x1D714}^{0})$
is simply a power of
$L_{p}^{+}(f_{k},\unicode[STIX]{x1D714}^{0})$
is simply a power of
![]() $p$
, up to a unit.
$p$
, up to a unit.
3.9 Numerical verification of Conjecture 3.16
Using Proposition 3.17, we numerically verified that the
![]() $a=0$
case of this conjecture holds for
$a=0$
case of this conjecture holds for
![]() $N=1$
and all irregular pairs
$N=1$
and all irregular pairs
![]() $(p,k)$
with
$(p,k)$
with
![]() $p<2000$
. However, in every such case,
$p<2000$
. However, in every such case,
![]() $\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f}))=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
, and thus the inequalities in (3) automatically imply the conjecture holds. Thus these checks do not yield much evidence for the conjecture.
$\operatorname{ord}_{\unicode[STIX]{x1D71B}}(L_{\operatorname{eis},\mathfrak{m}}(\mathfrak{p}_{f}))=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
, and thus the inequalities in (3) automatically imply the conjecture holds. Thus these checks do not yield much evidence for the conjecture.
However, when
![]() $a\not \equiv 0\;(\text{mod}\,p-1)$
, the upper bound in (3) does not a priori hold and we instead directly computed the relevant
$a\not \equiv 0\;(\text{mod}\,p-1)$
, the upper bound in (3) does not a priori hold and we instead directly computed the relevant
![]() $\unicode[STIX]{x1D707}$
-invariant to verify this conjecture. Namely, we verified that Conjecture 3.16 holds when
$\unicode[STIX]{x1D707}$
-invariant to verify this conjecture. Namely, we verified that Conjecture 3.16 holds when
![]() $N=1$
and
$N=1$
and
![]() $p<750$
for all even values of
$p<750$
for all even values of
![]() $a$
(except when
$a$
(except when
![]() $p=547$
and
$p=547$
and
![]() $k=486$
when (Cuspidal rank one) does not hold). Further, for
$k=486$
when (Cuspidal rank one) does not hold). Further, for
![]() $N$
prime, let
$N$
prime, let
![]() $\unicode[STIX]{x1D712}_{N}$
denote the unique quadratic character of conductor
$\unicode[STIX]{x1D712}_{N}$
denote the unique quadratic character of conductor
![]() $N$
. We verified this conjecture for
$N$
. We verified this conjecture for
![]() $\unicode[STIX]{x1D712}_{N}$
for
$\unicode[STIX]{x1D712}_{N}$
for
![]() $N=3,5,7$
and
$N=3,5,7$
and
![]() $p<500,400,300$
respectively, again for all even values of
$p<500,400,300$
respectively, again for all even values of
![]() $a$
. These computations included approximately 100 distinct eigenforms and in all of these examples the above-mentioned exception was the only time (Cuspidal rank one) failed.
$a$
. These computations included approximately 100 distinct eigenforms and in all of these examples the above-mentioned exception was the only time (Cuspidal rank one) failed.
We further mention that in all of these tests there was a single example where the
![]() $a=0$
case of the conjecture did not immediately follow from the bounds in (3), namely,
$a=0$
case of the conjecture did not immediately follow from the bounds in (3), namely,
![]() $\operatorname{ord}_{19}(B_{8,\unicode[STIX]{x1D712}_{5}})=2$
. In this case there is a unique cuspidal eigenform
$\operatorname{ord}_{19}(B_{8,\unicode[STIX]{x1D712}_{5}})=2$
. In this case there is a unique cuspidal eigenform
![]() $f\in S_{8}(\unicode[STIX]{x1D6E4}_{1}(5),\unicode[STIX]{x1D712}_{5},\mathbb{Z}_{19})$
congruent to
$f\in S_{8}(\unicode[STIX]{x1D6E4}_{1}(5),\unicode[STIX]{x1D712}_{5},\mathbb{Z}_{19})$
congruent to
![]() $E_{8,\unicode[STIX]{x1D712}_{5}}$
, and as expected from the Bernoulli divisibility, these forms are congruent modulo
$E_{8,\unicode[STIX]{x1D712}_{5}}$
, and as expected from the Bernoulli divisibility, these forms are congruent modulo
![]() $19^{2}$
. Moreover,
$19^{2}$
. Moreover,
![]() $\operatorname{ord}_{19}(a_{19}(f)-1)=3$
and thus the bounds in (3) do not meet. In this case, we computed that
$\operatorname{ord}_{19}(a_{19}(f)-1)=3$
and thus the bounds in (3) do not meet. In this case, we computed that
![]() $\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{0})=2$
, which verifies Conjecture 3.16. We further computed that
$\unicode[STIX]{x1D707}(f,\unicode[STIX]{x1D714}^{0})=2$
, which verifies Conjecture 3.16. We further computed that
![]() $\unicode[STIX]{x1D706}(f,\unicode[STIX]{x1D714}^{0})=1$
in contrast to the behavior of these invariants described by Theorem 3.21 when the bounds of (3) do meet.
$\unicode[STIX]{x1D706}(f,\unicode[STIX]{x1D714}^{0})=1$
in contrast to the behavior of these invariants described by Theorem 3.21 when the bounds of (3) do meet.
We briefly mention here the method used to compute the relevant
![]() $\unicode[STIX]{x1D707}$
-invariants as it was a bit novel and explain why (Cuspidal rank one) was needed. Fix
$\unicode[STIX]{x1D707}$
-invariants as it was a bit novel and explain why (Cuspidal rank one) was needed. Fix
![]() $N$
,
$N$
,
![]() $\unicode[STIX]{x1D713}$
and a pair
$\unicode[STIX]{x1D713}$
and a pair
![]() $(p,k)$
such that
$(p,k)$
such that
![]() $p\mid B_{k,\unicode[STIX]{x1D713}}$
. We formed a random overconvergent modular symbol
$p\mid B_{k,\unicode[STIX]{x1D713}}$
. We formed a random overconvergent modular symbol
![]() $\unicode[STIX]{x1D6F7}$
of level
$\unicode[STIX]{x1D6F7}$
of level
![]() $Np$
, weight
$Np$
, weight
![]() $k$
, and nebentype
$k$
, and nebentype
![]() $\unicode[STIX]{x1D713}$
as in [Reference Pollack and StevensPS11]. Working modulo a low accuracy (around modulo
$\unicode[STIX]{x1D713}$
as in [Reference Pollack and StevensPS11]. Working modulo a low accuracy (around modulo
![]() $p^{4}$
), we projected
$p^{4}$
), we projected
![]() $\unicode[STIX]{x1D6F7}$
to the ordinary subspace (i.e. computed
$\unicode[STIX]{x1D6F7}$
to the ordinary subspace (i.e. computed
![]() $\unicode[STIX]{x1D6F7}\mid U_{p}^{4}$
), and then used the other Hecke operators to form a (non-boundary) eigensymbol whose
$\unicode[STIX]{x1D6F7}\mid U_{p}^{4}$
), and then used the other Hecke operators to form a (non-boundary) eigensymbol whose
![]() $\ell$
th eigenvalue was congruent to
$\ell$
th eigenvalue was congruent to
![]() $1+\unicode[STIX]{x1D712}(\ell )\ell ^{k-1}$
. When (Cuspidal rank one) holds, there is a unique such symbol and thus this symbol must be the one associated to the cuspidal eigenform we are considering. Evaluating the resulting symbol at
$1+\unicode[STIX]{x1D712}(\ell )\ell ^{k-1}$
. When (Cuspidal rank one) holds, there is a unique such symbol and thus this symbol must be the one associated to the cuspidal eigenform we are considering. Evaluating the resulting symbol at
![]() $\{\infty \}-\{0\}$
then gives the relevant
$\{\infty \}-\{0\}$
then gives the relevant
![]() $p$
-adic
$p$
-adic
![]() $L$
-function (modulo
$L$
-function (modulo
![]() $p^{4}$
) from which an upper bound for the
$p^{4}$
) from which an upper bound for the
![]() $\unicode[STIX]{x1D707}$
-invariant can be obtained. In every case, this upper bound matched our proven lower bound, verifying the conjecture.
$\unicode[STIX]{x1D707}$
-invariant can be obtained. In every case, this upper bound matched our proven lower bound, verifying the conjecture.
4 Selmer groups
Let
![]() $f=\sum _{n}a_{n}q^{n}$
be a normalized eigenform in
$f=\sum _{n}a_{n}q^{n}$
be a normalized eigenform in
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{1}(N),\unicode[STIX]{x1D713},\overline{\mathbb{Q}}_{p})$
. We further assume that
$S_{k}(\unicode[STIX]{x1D6E4}_{1}(N),\unicode[STIX]{x1D713},\overline{\mathbb{Q}}_{p})$
. We further assume that
![]() $f$
is
$f$
is
![]() $p$
-ordinary, that is,
$p$
-ordinary, that is,
![]() $\operatorname{ord}_{p}(a_{p})=1$
. Attached to
$\operatorname{ord}_{p}(a_{p})=1$
. Attached to
![]() $f$
we have its (homological) Galois representation
$f$
we have its (homological) Galois representation
![]() $\unicode[STIX]{x1D70C}_{f}:G_{\mathbb{Q}}\rightarrow \operatorname{Aut}(V_{f})$
where
$\unicode[STIX]{x1D70C}_{f}:G_{\mathbb{Q}}\rightarrow \operatorname{Aut}(V_{f})$
where
![]() $V_{f}$
is a two-dimensional vector space over
$V_{f}$
is a two-dimensional vector space over
![]() $K=\mathbb{Q}_{p}(\{{a_{n}\}}_{n})$
. We note that
$K=\mathbb{Q}_{p}(\{{a_{n}\}}_{n})$
. We note that
![]() $\det (\unicode[STIX]{x1D70C}_{f})=\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{k-1}$
where
$\det (\unicode[STIX]{x1D70C}_{f})=\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{k-1}$
where
![]() $\unicode[STIX]{x1D700}$
is the
$\unicode[STIX]{x1D700}$
is the
![]() $p$
-adic cyclotomic character. Set
$p$
-adic cyclotomic character. Set
![]() ${\mathcal{O}}$
equal to the ring of integers of
${\mathcal{O}}$
equal to the ring of integers of
![]() $K$
, and choose a Galois stable
$K$
, and choose a Galois stable
![]() ${\mathcal{O}}$
-lattice
${\mathcal{O}}$
-lattice
![]() $T_{f}\subseteq V_{f}$
.
$T_{f}\subseteq V_{f}$
.
Since
![]() $f$
is
$f$
is
![]() $p$
-ordinary, the representation
$p$
-ordinary, the representation
![]() $\unicode[STIX]{x1D70C}_{f}$
is locally reducible at
$\unicode[STIX]{x1D70C}_{f}$
is locally reducible at
![]() $p$
[Reference HidaHid12, Theorem 4.2.7(2)], and we have an exact sequence of
$p$
[Reference HidaHid12, Theorem 4.2.7(2)], and we have an exact sequence of
![]() $G_{\mathbb{Q}_{p}}$
-representations
$G_{\mathbb{Q}_{p}}$
-representations
where
![]() $\unicode[STIX]{x1D702}$
is an unramified character which sends
$\unicode[STIX]{x1D702}$
is an unramified character which sends
![]() $\operatorname{Frob}_{p}$
to
$\operatorname{Frob}_{p}$
to
![]() $\unicode[STIX]{x1D6FC}_{p}$
, the unit root of
$\unicode[STIX]{x1D6FC}_{p}$
, the unit root of
![]() $x^{2}-a_{p}x+\unicode[STIX]{x1D713}(p)p^{k-1}$
.
$x^{2}-a_{p}x+\unicode[STIX]{x1D713}(p)p^{k-1}$
.
Further, set
![]() $A_{f}=V_{f}/T_{f}$
which is isomorphic to
$A_{f}=V_{f}/T_{f}$
which is isomorphic to
![]() $(K/{\mathcal{O}})^{2}$
and endowed with an action of
$(K/{\mathcal{O}})^{2}$
and endowed with an action of
![]() $G_{\mathbb{Q}}$
. We then have an exact sequence of
$G_{\mathbb{Q}}$
. We then have an exact sequence of
![]() $G_{\mathbb{Q}_{p}}$
-representations
$G_{\mathbb{Q}_{p}}$
-representations
and
where
![]() $\unicode[STIX]{x1D71B}$
is a uniformizer of
$\unicode[STIX]{x1D71B}$
is a uniformizer of
![]() ${\mathcal{O}}$
. Finally, set
${\mathcal{O}}$
. Finally, set
![]() $\mathbb{F}={\mathcal{O}}/\unicode[STIX]{x1D71B}{\mathcal{O}}$
.
$\mathbb{F}={\mathcal{O}}/\unicode[STIX]{x1D71B}{\mathcal{O}}$
.
4.1 Definitions of Selmer groups
Let
![]() $\mathbb{Q}_{\infty }$
denote the cyclotomic
$\mathbb{Q}_{\infty }$
denote the cyclotomic
![]() $\mathbb{Z}_{p}$
-extension of
$\mathbb{Z}_{p}$
-extension of
![]() $\mathbb{Q}$
and set
$\mathbb{Q}$
and set
![]() $\unicode[STIX]{x1D6E4}:=\operatorname{Gal}(\mathbb{Q}_{\infty }/\mathbb{Q})$
. Following Greenberg [Reference GreenbergGre89], we define the Selmer group
$\unicode[STIX]{x1D6E4}:=\operatorname{Gal}(\mathbb{Q}_{\infty }/\mathbb{Q})$
. Following Greenberg [Reference GreenbergGre89], we define the Selmer group
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})$
as the collection of classes
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})$
as the collection of classes
![]() $\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D70E}$
in
![]() $H^{1}(\mathbb{Q}_{\infty },A_{f})$
such that: (1) for
$H^{1}(\mathbb{Q}_{\infty },A_{f})$
such that: (1) for
![]() $v$
a place of
$v$
a place of
![]() $\mathbb{Q}_{\infty }$
not over
$\mathbb{Q}_{\infty }$
not over
![]() $p$
,
$p$
,
![]() $\operatorname{res}_{v}(\unicode[STIX]{x1D70E})$
is unramified, that is,
$\operatorname{res}_{v}(\unicode[STIX]{x1D70E})$
is unramified, that is,
![]() $\unicode[STIX]{x1D70E}$
is in the kernel of
$\unicode[STIX]{x1D70E}$
is in the kernel of
where
![]() $I_{v}$
is a choice of the inertia group at
$I_{v}$
is a choice of the inertia group at
![]() $v$
; and (2)
$v$
; and (2)
![]() $\unicode[STIX]{x1D70E}$
lies in the kernel of
$\unicode[STIX]{x1D70E}$
lies in the kernel of
where the final map is induced by (5) and
![]() $I_{p,\infty }$
is a choice of an inertia group at the unique prime of
$I_{p,\infty }$
is a choice of an inertia group at the unique prime of
![]() $\mathbb{Q}_{\infty }$
over
$\mathbb{Q}_{\infty }$
over
![]() $p$
.
$p$
.
One can also analogously define these Selmer groups over
![]() $\mathbb{Q}$
or over
$\mathbb{Q}$
or over
![]() $\mathbb{Q}(\unicode[STIX]{x1D707}_{p^{\infty }})$
. We can define Selmer groups of
$\mathbb{Q}(\unicode[STIX]{x1D707}_{p^{\infty }})$
. We can define Selmer groups of
![]() $A_{f,j}:=A_{f}\,\otimes \,\unicode[STIX]{x1D714}^{j}$
by simply twisting (5) and using this new sequence to define the local condition at
$A_{f,j}:=A_{f}\,\otimes \,\unicode[STIX]{x1D714}^{j}$
by simply twisting (5) and using this new sequence to define the local condition at
![]() $p$
. Since
$p$
. Since
![]() $\mathbb{Q}(\unicode[STIX]{x1D707}_{p})/\mathbb{Q}$
has degree prime to
$\mathbb{Q}(\unicode[STIX]{x1D707}_{p})/\mathbb{Q}$
has degree prime to
![]() $p$
, we have the following relationship between these Selmer groups:
$p$
, we have the following relationship between these Selmer groups:
Remark 4.1. We note that if
![]() $f$
arises from some elliptic curve
$f$
arises from some elliptic curve
![]() $E/\mathbb{Q}$
, then
$E/\mathbb{Q}$
, then
![]() $\operatorname{Sel}(\mathbb{Q},A_{f})$
defined above may not equal the
$\operatorname{Sel}(\mathbb{Q},A_{f})$
defined above may not equal the
![]() $p$
-adic Selmer group of
$p$
-adic Selmer group of
![]() $E$
,
$E$
,
![]() $\operatorname{Sel}(\mathbb{Q},E[p^{\infty }])$
, whose local conditions are defined by the Kummer map. Indeed, for
$\operatorname{Sel}(\mathbb{Q},E[p^{\infty }])$
, whose local conditions are defined by the Kummer map. Indeed, for
![]() $\ell \neq p$
, the image of the Kummer map vanishes while there can be unramified cocyles at
$\ell \neq p$
, the image of the Kummer map vanishes while there can be unramified cocyles at
![]() $\ell$
for primes of bad reduction. As a result,
$\ell$
for primes of bad reduction. As a result,
![]() $\operatorname{Sel}(\mathbb{Q},A_{f})$
can be larger than
$\operatorname{Sel}(\mathbb{Q},A_{f})$
can be larger than
![]() $\operatorname{Sel}(\mathbb{Q},E[p^{\infty }])$
and we will see that control theorems (see Proposition 4.4) work better for these larger Selmer groups.
$\operatorname{Sel}(\mathbb{Q},E[p^{\infty }])$
and we will see that control theorems (see Proposition 4.4) work better for these larger Selmer groups.
The definition of the local condition at
![]() $p$
in all of these Selmer groups is given by restriction to the inertia group at
$p$
in all of these Selmer groups is given by restriction to the inertia group at
![]() $p$
. However, as proven in the following lemma, restricting to the decomposition at
$p$
. However, as proven in the following lemma, restricting to the decomposition at
![]() $p$
instead does not change the definition of these Selmer groups. (In the language of Greenberg [Reference GreenbergGre89], the strict Selmer group matches the full Selmer group in our case.)
$p$
instead does not change the definition of these Selmer groups. (In the language of Greenberg [Reference GreenbergGre89], the strict Selmer group matches the full Selmer group in our case.)
Lemma 4.2. Let
![]() $D_{p,\infty }\supset I_{p,\infty }$
be a choice of decomposition and inertia groups at the unique prime of
$D_{p,\infty }\supset I_{p,\infty }$
be a choice of decomposition and inertia groups at the unique prime of
![]() $\mathbb{Q}_{\infty }$
over
$\mathbb{Q}_{\infty }$
over
![]() $p$
, and likewise define
$p$
, and likewise define
![]() $D_{p}\supset I_{p}$
as decomposition and inertia groups at
$D_{p}\supset I_{p}$
as decomposition and inertia groups at
![]() $p$
. Then the following maps are injective:
$p$
. Then the following maps are injective:
and
Proof. We check the injectivity of the first map as the argument for the second is identical. The kernel of this map is
![]() $H^{1}(\mathbb{Q}_{p}^{\operatorname{un}}/\mathbb{Q}_{p},(K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))^{I_{p}})$
where
$H^{1}(\mathbb{Q}_{p}^{\operatorname{un}}/\mathbb{Q}_{p},(K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))^{I_{p}})$
where
![]() $\mathbb{Q}_{p}^{\operatorname{un}}$
is the maximal unramified extension of
$\mathbb{Q}_{p}^{\operatorname{un}}$
is the maximal unramified extension of
![]() $\mathbb{Q}_{p}$
. If
$\mathbb{Q}_{p}$
. If
![]() $j\not \equiv 0\;(\text{mod}\,p-1)$
, then
$j\not \equiv 0\;(\text{mod}\,p-1)$
, then
![]() $(K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))^{I_{p}}=0$
and we are done.
$(K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))^{I_{p}}=0$
and we are done.
Otherwise, since
![]() $\operatorname{Gal}(\mathbb{Q}_{p}^{\operatorname{un}}/\mathbb{Q}_{p})$
is topologically cyclic generated by
$\operatorname{Gal}(\mathbb{Q}_{p}^{\operatorname{un}}/\mathbb{Q}_{p})$
is topologically cyclic generated by
![]() $\operatorname{Frob}_{p}$
, we have that
$\operatorname{Frob}_{p}$
, we have that
![]() $H^{1}(\mathbb{Q}_{p}^{\operatorname{un}}/\mathbb{Q}_{p},K/{\mathcal{O}}(\unicode[STIX]{x1D702}))$
is given by the cokernel of
$H^{1}(\mathbb{Q}_{p}^{\operatorname{un}}/\mathbb{Q}_{p},K/{\mathcal{O}}(\unicode[STIX]{x1D702}))$
is given by the cokernel of
As long as
![]() $\operatorname{Frob}_{p}-1$
is not identically zero on
$\operatorname{Frob}_{p}-1$
is not identically zero on
![]() $K/{\mathcal{O}}(\unicode[STIX]{x1D702})$
we are done since
$K/{\mathcal{O}}(\unicode[STIX]{x1D702})$
we are done since
![]() $K/{\mathcal{O}}$
is divisible. Since
$K/{\mathcal{O}}$
is divisible. Since
![]() $\unicode[STIX]{x1D702}(\operatorname{Frob}_{p})=\unicode[STIX]{x1D6FC}_{p}$
, the unit root of
$\unicode[STIX]{x1D702}(\operatorname{Frob}_{p})=\unicode[STIX]{x1D6FC}_{p}$
, the unit root of
![]() $x^{2}-a_{p}x+\unicode[STIX]{x1D713}(p)p^{k-1}$
, we simply need to check then that
$x^{2}-a_{p}x+\unicode[STIX]{x1D713}(p)p^{k-1}$
, we simply need to check then that
![]() $\unicode[STIX]{x1D6FC}_{p}\neq 1$
. But if
$\unicode[STIX]{x1D6FC}_{p}\neq 1$
. But if
![]() $\unicode[STIX]{x1D6FC}_{p}=1$
, then the other root of this quadratic would be
$\unicode[STIX]{x1D6FC}_{p}=1$
, then the other root of this quadratic would be
![]() $\unicode[STIX]{x1D713}(p)p^{k-1}$
. Hence
$\unicode[STIX]{x1D713}(p)p^{k-1}$
. Hence
![]() $a_{p}=1+\unicode[STIX]{x1D713}(p)p^{k-1}$
, which violates the Weil bounds.◻
$a_{p}=1+\unicode[STIX]{x1D713}(p)p^{k-1}$
, which violates the Weil bounds.◻
We will need to consider one last kind of Selmer group; namely, we will define the Selmer group of the finite Galois module
![]() $A_{f}[\unicode[STIX]{x1D71B}^{n}]$
. We follow the method of [Reference Emerton, Pollack and WestonEPW06, § 4.2] and note that these Selmer groups depend not just on
$A_{f}[\unicode[STIX]{x1D71B}^{n}]$
. We follow the method of [Reference Emerton, Pollack and WestonEPW06, § 4.2] and note that these Selmer groups depend not just on
![]() $A_{f}[\unicode[STIX]{x1D71B}^{n}]$
, but on the modular form
$A_{f}[\unicode[STIX]{x1D71B}^{n}]$
, but on the modular form
![]() $f$
itself. Namely, if we are working over
$f$
itself. Namely, if we are working over
![]() $\mathbb{Q}_{\infty }$
, then our local condition at
$\mathbb{Q}_{\infty }$
, then our local condition at
![]() $v\nmid p$
is given by the image of
$v\nmid p$
is given by the image of
![]() $A_{f}^{G_{v}}/\unicode[STIX]{x1D71B}^{n}$
in
$A_{f}^{G_{v}}/\unicode[STIX]{x1D71B}^{n}$
in
![]() $H^{1}(\mathbb{Q}_{\infty ,v},A_{f}[\unicode[STIX]{x1D71B}^{n}])$
where
$H^{1}(\mathbb{Q}_{\infty ,v},A_{f}[\unicode[STIX]{x1D71B}^{n}])$
where
![]() $G_{v}=G_{\mathbb{Q}_{\infty ,v}}$
. At
$G_{v}=G_{\mathbb{Q}_{\infty ,v}}$
. At
![]() $p$
, we use (6) to define our local condition just as in the case of characteristic 0. As before, we can also define these objects over
$p$
, we use (6) to define our local condition just as in the case of characteristic 0. As before, we can also define these objects over
![]() $\mathbb{Q}$
or
$\mathbb{Q}$
or
![]() $\mathbb{Q}(\unicode[STIX]{x1D707}_{p^{\infty }})$
and we can analogously define Selmer groups of
$\mathbb{Q}(\unicode[STIX]{x1D707}_{p^{\infty }})$
and we can analogously define Selmer groups of
![]() $A_{f,j}[\unicode[STIX]{x1D71B}^{n}]$
.
$A_{f,j}[\unicode[STIX]{x1D71B}^{n}]$
.
The reason for the above definition of the local condition at
![]() $v\nmid p$
is that it is exactly the condition needed to make the following lemma true.
$v\nmid p$
is that it is exactly the condition needed to make the following lemma true.
Lemma 4.3. There are natural maps
which are surjective and have respective kernels
![]() $H^{0}(\mathbb{Q},A_{f,j})/p^{r}H^{0}(\mathbb{Q},A_{f,j})$
and
$H^{0}(\mathbb{Q},A_{f,j})/p^{r}H^{0}(\mathbb{Q},A_{f,j})$
and
![]() $H^{0}(\mathbb{Q}_{\infty },A_{f,j})/p^{r}H^{0}(\mathbb{Q}_{\infty },A_{f,j})$
.
$H^{0}(\mathbb{Q}_{\infty },A_{f,j})/p^{r}H^{0}(\mathbb{Q}_{\infty },A_{f,j})$
.
Proof. Verifying this lemma is just a diagram chase. ◻
4.2 The control theorem
We now state a key control theorem for these Selmer groups, closely following [Reference GreenbergGre99].
Proposition 4.4. If
![]() $H^{0}(\mathbb{Q},A_{f,j}[\unicode[STIX]{x1D71B}])=0$
, then the natural map
$H^{0}(\mathbb{Q},A_{f,j}[\unicode[STIX]{x1D71B}])=0$
, then the natural map
is injective and has cokernel bounded by the size of
![]() ${\mathcal{O}}/(\unicode[STIX]{x1D6FC}_{p}-1){\mathcal{O}}$
. Moreover, the map is surjective if
${\mathcal{O}}/(\unicode[STIX]{x1D6FC}_{p}-1){\mathcal{O}}$
. Moreover, the map is surjective if
![]() $j\not \equiv 0\;(\text{mod}\,p-1)$
.
$j\not \equiv 0\;(\text{mod}\,p-1)$
.
Proof. By Lemma 4.2, we have a commutative diagram:

where
![]() ${\mathcal{H}}_{\operatorname{loc}}^{(p)}:=\bigoplus _{\ell \mid N}H^{1}(I_{\ell },A_{f})$
and
${\mathcal{H}}_{\operatorname{loc}}^{(p)}:=\bigoplus _{\ell \mid N}H^{1}(I_{\ell },A_{f})$
and
![]() ${\mathcal{H}}_{\infty ,\operatorname{loc}}^{(p)}:=\bigoplus _{v\mid N}H^{1}(I_{v},A_{f})$
where
${\mathcal{H}}_{\infty ,\operatorname{loc}}^{(p)}:=\bigoplus _{v\mid N}H^{1}(I_{v},A_{f})$
where
![]() $v$
runs over primes of
$v$
runs over primes of
![]() $\mathbb{Q}_{\infty }$
. We seek to apply the snake lemma and thus we must analyze the kernel and cokernel of
$\mathbb{Q}_{\infty }$
. We seek to apply the snake lemma and thus we must analyze the kernel and cokernel of
![]() $h$
and the kernel of
$h$
and the kernel of
![]() $r$
.
$r$
.
The cokernel of
![]() $h$
maps to
$h$
maps to
![]() $H^{2}(\unicode[STIX]{x1D6E4},H^{0}(\mathbb{Q}_{\infty },A_{f,j}))$
which vanishes since
$H^{2}(\unicode[STIX]{x1D6E4},H^{0}(\mathbb{Q}_{\infty },A_{f,j}))$
which vanishes since
![]() $\unicode[STIX]{x1D6E4}\cong \mathbb{Z}_{p}$
has cohomological dimension 1. The kernel of
$\unicode[STIX]{x1D6E4}\cong \mathbb{Z}_{p}$
has cohomological dimension 1. The kernel of
![]() $h$
equals
$h$
equals
![]() $H^{1}(\unicode[STIX]{x1D6E4},H^{0}(\mathbb{Q}_{\infty },A_{f,j}))$
. To see that this group vanishes, it suffices to see that
$H^{1}(\unicode[STIX]{x1D6E4},H^{0}(\mathbb{Q}_{\infty },A_{f,j}))$
. To see that this group vanishes, it suffices to see that
![]() $H^{0}(\mathbb{Q}_{\infty },A_{f,j})$
vanishes. But by assumption
$H^{0}(\mathbb{Q}_{\infty },A_{f,j})$
vanishes. But by assumption
![]() $H^{0}(\mathbb{Q},A_{f,j}[\unicode[STIX]{x1D71B}])=0$
which implies
$H^{0}(\mathbb{Q},A_{f,j}[\unicode[STIX]{x1D71B}])=0$
which implies
![]() $H^{0}(\mathbb{Q},A_{f,j})=0$
which in turn implies
$H^{0}(\mathbb{Q},A_{f,j})=0$
which in turn implies
![]() $H^{0}(\mathbb{Q}_{\infty },A_{f,j})=0$
as
$H^{0}(\mathbb{Q}_{\infty },A_{f,j})=0$
as
![]() $\operatorname{Gal}(\mathbb{Q}_{\infty }/\mathbb{Q})$
is pro-
$\operatorname{Gal}(\mathbb{Q}_{\infty }/\mathbb{Q})$
is pro-
![]() $p$
. Thus,
$p$
. Thus,
![]() $h$
is an isomorphism.
$h$
is an isomorphism.
To determine the kernel of
![]() $r$
, we first note that
$r$
, we first note that
![]() $I_{\ell }\cong I_{v}$
if
$I_{\ell }\cong I_{v}$
if
![]() $v\mid \ell \neq p$
as
$v\mid \ell \neq p$
as
![]() $\mathbb{Q}_{\infty }/\mathbb{Q}$
is unramified at
$\mathbb{Q}_{\infty }/\mathbb{Q}$
is unramified at
![]() $\ell$
. Thus
$\ell$
. Thus
![]() ${\mathcal{H}}_{\operatorname{loc}}^{(p)}$
injects into
${\mathcal{H}}_{\operatorname{loc}}^{(p)}$
injects into
![]() ${\mathcal{H}}_{\infty ,\operatorname{loc}}^{(p)}$
, and
${\mathcal{H}}_{\infty ,\operatorname{loc}}^{(p)}$
, and
![]() $\ker (r)$
equals the kernel of
$\ker (r)$
equals the kernel of
![]() $H^{1}(D_{p},K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))\rightarrow H^{1}(D_{p,\infty },K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))$
which in turn is isomorphic to
$H^{1}(D_{p},K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))\rightarrow H^{1}(D_{p,\infty },K/{\mathcal{O}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}^{j}))$
which in turn is isomorphic to
If
![]() $j\not \equiv 0\;(\text{mod}\,p-1)$
, then the above
$j\not \equiv 0\;(\text{mod}\,p-1)$
, then the above
![]() $H^{0}$
-term vanishes and
$H^{0}$
-term vanishes and
![]() $\ker (r)=0$
. Otherwise, since
$\ker (r)=0$
. Otherwise, since
![]() $\operatorname{Gal}(\mathbb{Q}_{\infty ,p}/\mathbb{Q}_{p})$
is topologically cyclic, we have
$\operatorname{Gal}(\mathbb{Q}_{\infty ,p}/\mathbb{Q}_{p})$
is topologically cyclic, we have
![]() $\ker (r)$
is given by the
$\ker (r)$
is given by the
![]() $\operatorname{Gal}(\mathbb{Q}_{\infty ,p}/\mathbb{Q}_{p})$
-coinvariants of
$\operatorname{Gal}(\mathbb{Q}_{\infty ,p}/\mathbb{Q}_{p})$
-coinvariants of
![]() $H^{0}(\mathbb{Q}_{\infty ,p},K/{\mathcal{O}}(\unicode[STIX]{x1D702}))$
. Since
$H^{0}(\mathbb{Q}_{\infty ,p},K/{\mathcal{O}}(\unicode[STIX]{x1D702}))$
. Since
![]() $\unicode[STIX]{x1D702}$
is the unramified character sending
$\unicode[STIX]{x1D702}$
is the unramified character sending
![]() $\operatorname{Frob}_{p}$
to
$\operatorname{Frob}_{p}$
to
![]() $\unicode[STIX]{x1D6FC}_{p}$
, we have
$\unicode[STIX]{x1D6FC}_{p}$
, we have
But then
The proposition then follows, in either case, from the snake lemma. ◻
4.3 The main conjecture
Let
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}:={\mathcal{O}}[[1+p\mathbb{Z}_{p}]]\cong {\mathcal{O}}[[\operatorname{Gal}(\mathbb{Q}_{\infty }/\mathbb{Q})]]$
. The following main conjecture relates these Selmer group over
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}:={\mathcal{O}}[[1+p\mathbb{Z}_{p}]]\cong {\mathcal{O}}[[\operatorname{Gal}(\mathbb{Q}_{\infty }/\mathbb{Q})]]$
. The following main conjecture relates these Selmer group over
![]() $\mathbb{Q}_{\infty }$
to
$\mathbb{Q}_{\infty }$
to
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions.
$L$
-functions.
Conjecture 4.5 (Main conjecture).
We have that
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j})^{\vee }$
is a finitely generated torsion
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j})^{\vee }$
is a finitely generated torsion
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module, and
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module, and
At this level of generality, where the Galois representation of
![]() $f$
is not assumed to be residually irreducible, we can only state a main conjecture with
$f$
is not assumed to be residually irreducible, we can only state a main conjecture with
![]() $p$
inverted. The reason for this is that
$p$
inverted. The reason for this is that
![]() $L_{p}(f)$
only depends upon the modular form
$L_{p}(f)$
only depends upon the modular form
![]() $f$
, while
$f$
, while
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j})$
depends on a choice of a lattice in the Galois representation
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j})$
depends on a choice of a lattice in the Galois representation
![]() $V_{f}$
. The choice of a lattice can change the left-hand side by powers of
$V_{f}$
. The choice of a lattice can change the left-hand side by powers of
![]() $\unicode[STIX]{x1D71B}$
. The issue of which lattice to pick to correctly match the
$\unicode[STIX]{x1D71B}$
. The issue of which lattice to pick to correctly match the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function will be further discussed in the next section.
$L$
-function will be further discussed in the next section.
The following is a deep theorem of Kato which proves half of the main conjecture.
Theorem 4.6 (Kato).
We have that
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j})^{\vee }$
is a finitely generated torsion
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j})^{\vee }$
is a finitely generated torsion
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module, and
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module, and
in
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}[1/p]$
.
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}[1/p]$
.
Proof. See [Reference KatoKat04, Theorems 17.4.1 and 17.4.2]. Note that the hypothesis that
![]() $\overline{\unicode[STIX]{x1D70C}}_{f}$
has large image is not used in this part of Kato’s work.◻
$\overline{\unicode[STIX]{x1D70C}}_{f}$
has large image is not used in this part of Kato’s work.◻
5 Algebraic results
We continue with the notation of the previous section so that
![]() $f$
is a normalized cuspidal eigenform in
$f$
is a normalized cuspidal eigenform in
![]() $S_{k}(\unicode[STIX]{x1D6E4}_{1}(N),\unicode[STIX]{x1D713},\overline{\mathbb{Q}}_{p})$
where
$S_{k}(\unicode[STIX]{x1D6E4}_{1}(N),\unicode[STIX]{x1D713},\overline{\mathbb{Q}}_{p})$
where
![]() $p\nmid N$
and
$p\nmid N$
and
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
.
$p\nmid \unicode[STIX]{x1D711}(N)$
.
Definition 5.1. Let
![]() $\operatorname{eis}(f)$
denote the largest integer
$\operatorname{eis}(f)$
denote the largest integer
![]() $n\geqslant 0$
such that
$n\geqslant 0$
such that
![]() $f\equiv E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}\;(\text{mod}\,\unicode[STIX]{x1D71B}^{n})$
where this congruence occurs in
$f\equiv E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}\;(\text{mod}\,\unicode[STIX]{x1D71B}^{n})$
where this congruence occurs in
![]() ${\mathcal{O}}/\unicode[STIX]{x1D71B}^{n}{\mathcal{O}}[[q]]$
.
${\mathcal{O}}/\unicode[STIX]{x1D71B}^{n}{\mathcal{O}}[[q]]$
.
Throughout this section we assume that
![]() $\operatorname{eis}(f)>0$
. In particular,
$\operatorname{eis}(f)>0$
. In particular,
![]() $f$
is ordinary and let
$f$
is ordinary and let
![]() $\mathfrak{m}=\mathfrak{m}_{f}$
denote the maximal ideal in
$\mathfrak{m}=\mathfrak{m}_{f}$
denote the maximal ideal in
![]() $\mathbb{T}$
corresponding to
$\mathbb{T}$
corresponding to
![]() $f$
. Note then that
$f$
. Note then that
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{\mathfrak{m}}$
. We further assume that
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{\mathfrak{m}}$
. We further assume that
![]() $\mathfrak{m}$
satisfies (Good Eisen).
$\mathfrak{m}$
satisfies (Good Eisen).
We note again that there is not a unique lattice (up to homothety) in the Galois representation
![]() $V_{f}$
. The following lemma describes the situation more precisely.
$V_{f}$
. The following lemma describes the situation more precisely.
Lemma 5.2. If
![]() $\mathfrak{m}_{f}$
satisfies (Good Eisen), then in
$\mathfrak{m}_{f}$
satisfies (Good Eisen), then in
![]() $V_{f}$
there exists a sequence of Galois stable lattices
$V_{f}$
there exists a sequence of Galois stable lattices
no two of which are homothetic, such that the following statements hold.
(1)
 $T_{i}/T_{i-1}$
is isomorphic to
$T_{i}/T_{i-1}$
is isomorphic to
 $\mathbb{F}$
.
$\mathbb{F}$
.(2) For
 $i\neq 0,\operatorname{eis}(f)$
, we have that
$i\neq 0,\operatorname{eis}(f)$
, we have that
 $T_{i}/\unicode[STIX]{x1D71B}T_{i}$
is a split extension of
$T_{i}/\unicode[STIX]{x1D71B}T_{i}$
is a split extension of
 $\mathbb{F}$
and
$\mathbb{F}$
and
 $\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})$
.
$\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})$
.(3) For
 $i=\operatorname{eis}(f)$
, we have a non-split extension
$i=\operatorname{eis}(f)$
, we have a non-split extension  $$\begin{eqnarray}0\rightarrow \mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})\rightarrow T_{\operatorname{ eis}(f)}/\unicode[STIX]{x1D71B}T_{\operatorname{eis}(f)}\rightarrow \mathbb{F}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})\rightarrow T_{\operatorname{ eis}(f)}/\unicode[STIX]{x1D71B}T_{\operatorname{eis}(f)}\rightarrow \mathbb{F}\rightarrow 0.\end{eqnarray}$$
(4) For
 $i=0$
, we have a non-split extension
$i=0$
, we have a non-split extension  $$\begin{eqnarray}0\rightarrow \mathbb{F}\rightarrow T_{0}/\unicode[STIX]{x1D71B}T_{0}\rightarrow \mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathbb{F}\rightarrow T_{0}/\unicode[STIX]{x1D71B}T_{0}\rightarrow \mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})\rightarrow 0.\end{eqnarray}$$
(5)
 $T_{i}/\unicode[STIX]{x1D71B}^{i}T_{i}$
contains a submodule isomorphic to
$T_{i}/\unicode[STIX]{x1D71B}^{i}T_{i}$
contains a submodule isomorphic to
 ${\mathcal{O}}/\unicode[STIX]{x1D71B}^{i}{\mathcal{O}}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{k-1})$
.
${\mathcal{O}}/\unicode[STIX]{x1D71B}^{i}{\mathcal{O}}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{k-1})$
.
Proof. As
![]() $f$
admits a congruence to
$f$
admits a congruence to
![]() $E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
modulo
$E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
modulo
![]() $\unicode[STIX]{x1D71B}^{\operatorname{eis}(f)}$
, the existence of such a chain of lattices is standard as in [Reference BellaïcheBel09, § 1.2]. If a longer chain existed, then
$\unicode[STIX]{x1D71B}^{\operatorname{eis}(f)}$
, the existence of such a chain of lattices is standard as in [Reference BellaïcheBel09, § 1.2]. If a longer chain existed, then
![]() $f$
would admit a congruence modulo
$f$
would admit a congruence modulo
![]() $\unicode[STIX]{x1D71B}^{m}$
with
$\unicode[STIX]{x1D71B}^{m}$
with
![]() $m>\operatorname{eis}(f)$
to some Eisenstein series (necessarily not
$m>\operatorname{eis}(f)$
to some Eisenstein series (necessarily not
![]() $E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
). However, (Good Eisen) and Lemma 3.1 prevent this possibility.◻
$E_{k,\unicode[STIX]{x1D713}}^{\operatorname{ord}}$
). However, (Good Eisen) and Lemma 3.1 prevent this possibility.◻
We will see that the choice of lattice in
![]() $V_{f}$
will affect the value of the
$V_{f}$
will affect the value of the
![]() $\unicode[STIX]{x1D707}$
-invariant of the corresponding Selmer group.
$\unicode[STIX]{x1D707}$
-invariant of the corresponding Selmer group.
5.1 Lower bounds
Set
![]() $A_{f,j}^{(r)}:=V_{f}/T_{r}\,\otimes \,\unicode[STIX]{x1D714}^{j}$
for
$A_{f,j}^{(r)}:=V_{f}/T_{r}\,\otimes \,\unicode[STIX]{x1D714}^{j}$
for
![]() $0\leqslant r\leqslant \operatorname{eis}(f)$
. By Theorem 4.6, the Selmer group
$0\leqslant r\leqslant \operatorname{eis}(f)$
. By Theorem 4.6, the Selmer group
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j}^{(r)})$
is a cotorsion
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f,j}^{(r)})$
is a cotorsion
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module and thus has associated
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module and thus has associated
![]() $\unicode[STIX]{x1D707}$
- and
$\unicode[STIX]{x1D707}$
- and
![]() $\unicode[STIX]{x1D706}$
-invariants. Following Greenberg, we now give lower bounds on these
$\unicode[STIX]{x1D706}$
-invariants. Following Greenberg, we now give lower bounds on these
![]() $\unicode[STIX]{x1D707}$
-invariants which grow as
$\unicode[STIX]{x1D707}$
-invariants which grow as
![]() $r$
grows.
$r$
grows.
Theorem 5.3. For
![]() $0\leqslant r\leqslant \operatorname{eis}(f)$
and for
$0\leqslant r\leqslant \operatorname{eis}(f)$
and for
![]() $j$
even, we have
$j$
even, we have
Proof. By Lemma 5.2, we have that
![]() $A_{f,j}^{(r)}$
contains a submodule isomorphic to
$A_{f,j}^{(r)}$
contains a submodule isomorphic to
![]() ${\mathcal{O}}/\unicode[STIX]{x1D71B}^{r}{\mathcal{O}}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{k-1}\unicode[STIX]{x1D714}^{j})$
which is cyclic, odd, and ramified at
${\mathcal{O}}/\unicode[STIX]{x1D71B}^{r}{\mathcal{O}}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D700}^{k-1}\unicode[STIX]{x1D714}^{j})$
which is cyclic, odd, and ramified at
![]() $p$
. Our theorem then follows exactly as in [Reference GreenbergGre99, Proposition 5.7] where an analogous statement is proven in the case of elliptic curves.◻
$p$
. Our theorem then follows exactly as in [Reference GreenbergGre99, Proposition 5.7] where an analogous statement is proven in the case of elliptic curves.◻
To relate this discussion to the our bounds on analytic
![]() $\unicode[STIX]{x1D707}$
-invariants, especially Theorem 3.14, we have the following lemma.
$\unicode[STIX]{x1D707}$
-invariants, especially Theorem 3.14, we have the following lemma.
Lemma 5.4. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal and assume that the cuspidal Eisenstein ideal
$\mathfrak{m}\subseteq \mathbb{T}$
be a maximal ideal and assume that the cuspidal Eisenstein ideal
![]() ${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is principal with generator
${\mathcal{I}}_{\mathfrak{m}^{c}}^{c}\subseteq \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
is principal with generator
![]() $L_{\operatorname{eis},\mathfrak{m}}$
. Then for
$L_{\operatorname{eis},\mathfrak{m}}$
. Then for
![]() $\mathfrak{p}_{f}\subseteq \mathfrak{m}^{c}$
, we have
$\mathfrak{p}_{f}\subseteq \mathfrak{m}^{c}$
, we have
Proof. This lemma follows simply from the definition of
![]() ${\mathcal{I}}$
.◻
${\mathcal{I}}$
.◻
5.2 Upper bounds
Let
![]() $\mathfrak{m}$
be a maximal ideal of
$\mathfrak{m}$
be a maximal ideal of
![]() $\mathbb{T}$
, and let
$\mathbb{T}$
, and let
![]() $f$
be a classical eigenform in the Hida family for
$f$
be a classical eigenform in the Hida family for
![]() $\mathfrak{m}^{c}$
. Set
$\mathfrak{m}^{c}$
. Set
![]() $T=T_{\operatorname{eis}(f)}$
as in Lemma 5.2, and
$T=T_{\operatorname{eis}(f)}$
as in Lemma 5.2, and
![]() $A_{f}:=V_{f}/T$
. This is the choice of lattice which maximizes our lower bound on the
$A_{f}:=V_{f}/T$
. This is the choice of lattice which maximizes our lower bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant. This subsection is devoted to proving an upper bound on the
$\unicode[STIX]{x1D707}$
-invariant. This subsection is devoted to proving an upper bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant of
$\unicode[STIX]{x1D707}$
-invariant of
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\vee }$
. Compare with Theorem 3.15 on the analytic side.
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\vee }$
. Compare with Theorem 3.15 on the analytic side.
Consider now our nebentype character
![]() $\unicode[STIX]{x1D713}:(\mathbb{Z}/N\mathbb{Z})^{\times }\rightarrow \overline{\mathbb{Q}}_{p}$
as a Galois character, and let
$\unicode[STIX]{x1D713}:(\mathbb{Z}/N\mathbb{Z})^{\times }\rightarrow \overline{\mathbb{Q}}_{p}$
as a Galois character, and let
![]() $K_{\unicode[STIX]{x1D713}}\subseteq \mathbb{Q}(\unicode[STIX]{x1D707}_{N})$
be the smallest field which trivializes
$K_{\unicode[STIX]{x1D713}}\subseteq \mathbb{Q}(\unicode[STIX]{x1D707}_{N})$
be the smallest field which trivializes
![]() $\unicode[STIX]{x1D713}$
. We note that
$\unicode[STIX]{x1D713}$
. We note that
![]() $K_{\unicode[STIX]{x1D713}}$
is disjoint from
$K_{\unicode[STIX]{x1D713}}$
is disjoint from
![]() $\mathbb{Q}(\unicode[STIX]{x1D707}_{p})$
, and thus
$\mathbb{Q}(\unicode[STIX]{x1D707}_{p})$
, and thus
![]() $\operatorname{Gal}(K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})/K_{\unicode[STIX]{x1D713}})\cong \unicode[STIX]{x1D6E5}$
. In particular, we can discuss the
$\operatorname{Gal}(K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})/K_{\unicode[STIX]{x1D713}})\cong \unicode[STIX]{x1D6E5}$
. In particular, we can discuss the
![]() $\unicode[STIX]{x1D714}^{j}$
-eigenspaces in
$\unicode[STIX]{x1D714}^{j}$
-eigenspaces in
![]() $\operatorname{Cl}(K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p}))$
. We need a Vandiver-type hypothesis to achieve an upper bound on the
$\operatorname{Cl}(K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p}))$
. We need a Vandiver-type hypothesis to achieve an upper bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant, namely,
$\unicode[STIX]{x1D707}$
-invariant, namely,
Remark 5.5. We note that this condition does not hold generally when
![]() $N>1$
. See [Reference WakeWak15, Corollary 1.4] for explicit counter-examples and the relation of these counter-examples to
$N>1$
. See [Reference WakeWak15, Corollary 1.4] for explicit counter-examples and the relation of these counter-examples to
![]() $\mathbb{T}_{\mathfrak{m}}$
being Gorenstein.
$\mathbb{T}_{\mathfrak{m}}$
being Gorenstein.
Theorem 5.6. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be an maximal ideal satisfying:
$\mathfrak{m}\subseteq \mathbb{T}$
be an maximal ideal satisfying:
(i) (Good Eisen);
(ii)
 $(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-j(\mathfrak{m})})$
;
$(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-j(\mathfrak{m})})$
;(iii)
 $j(\mathfrak{m})=2\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
$j(\mathfrak{m})=2\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
Then for
![]() $f$
a classical eigenform in the Hida family for
$f$
a classical eigenform in the Hida family for
![]() $\mathfrak{m}^{c}$
, we have
$\mathfrak{m}^{c}$
, we have
We begin with a simple lemma which gives an upper bound on the
![]() $\unicode[STIX]{x1D707}$
-invariant of a
$\unicode[STIX]{x1D707}$
-invariant of a
![]() $\unicode[STIX]{x1D6EC}$
-module in terms the module’s
$\unicode[STIX]{x1D6EC}$
-module in terms the module’s
![]() $\unicode[STIX]{x1D6E4}$
-coinvariants.
$\unicode[STIX]{x1D6E4}$
-coinvariants.
Lemma 5.7. Let
![]() $X$
be a finitely generated torsion
$X$
be a finitely generated torsion
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module with no finite submodules. If
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module with no finite submodules. If
![]() $X_{\unicode[STIX]{x1D6E4}}$
is finite with size bounded by
$X_{\unicode[STIX]{x1D6E4}}$
is finite with size bounded by
![]() $M$
, then
$M$
, then
![]() $q^{\unicode[STIX]{x1D707}(X)}\leqslant M$
.
$q^{\unicode[STIX]{x1D707}(X)}\leqslant M$
.
Proof. Using the structure theorem of finitely generated
![]() $\unicode[STIX]{x1D6EC}$
-modules, we know that we have a map
$\unicode[STIX]{x1D6EC}$
-modules, we know that we have a map
with finite kernel and cokernel where
![]() $Y=\bigoplus _{i}\unicode[STIX]{x1D6EC}/f_{i}^{n_{i}}\unicode[STIX]{x1D6EC}$
and the
$Y=\bigoplus _{i}\unicode[STIX]{x1D6EC}/f_{i}^{n_{i}}\unicode[STIX]{x1D6EC}$
and the
![]() $f_{i}$
are irreducible. Since
$f_{i}$
are irreducible. Since
![]() $X$
has no finite submodule, we get an exact sequence
$X$
has no finite submodule, we get an exact sequence
with
![]() $K$
finite. Thus,
$K$
finite. Thus,
Since we are assuming that
![]() $X_{\unicode[STIX]{x1D6E4}}$
is finite, we have
$X_{\unicode[STIX]{x1D6E4}}$
is finite, we have
![]() $f_{i}(0)\neq 0$
for all
$f_{i}(0)\neq 0$
for all
![]() $i$
, and thus
$i$
, and thus
![]() $Y^{\unicode[STIX]{x1D6E4}}=0$
. Our exact sequence is then just
$Y^{\unicode[STIX]{x1D6E4}}=0$
. Our exact sequence is then just
and we deduce that
![]() $|X_{\unicode[STIX]{x1D6E4}}|=|Y_{\unicode[STIX]{x1D6E4}}|$
since
$|X_{\unicode[STIX]{x1D6E4}}|=|Y_{\unicode[STIX]{x1D6E4}}|$
since
![]() $|K^{\unicode[STIX]{x1D6E4}}|=|K_{\unicode[STIX]{x1D6E4}}|$
. Finally, since
$|K^{\unicode[STIX]{x1D6E4}}|=|K_{\unicode[STIX]{x1D6E4}}|$
. Finally, since
![]() $(\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}/\unicode[STIX]{x1D71B}^{r}\unicode[STIX]{x1D6EC}_{{\mathcal{O}}})_{\unicode[STIX]{x1D6E4}}$
has size
$(\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}/\unicode[STIX]{x1D71B}^{r}\unicode[STIX]{x1D6EC}_{{\mathcal{O}}})_{\unicode[STIX]{x1D6E4}}$
has size
![]() $q^{r}$
, we have
$q^{r}$
, we have
![]() $|Y_{\unicode[STIX]{x1D6E4}}|\geqslant q^{\unicode[STIX]{x1D707}(X)}$
. Thus
$|Y_{\unicode[STIX]{x1D6E4}}|\geqslant q^{\unicode[STIX]{x1D707}(X)}$
. Thus
as desired. ◻
In light of Lemma 5.7, we need to bound the size of
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}$
. By Proposition 4.4, we thus need to control the size of
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}$
. By Proposition 4.4, we thus need to control the size of
![]() $\operatorname{Sel}(\mathbb{Q},A_{f})$
. This is done in the following lemma.
$\operatorname{Sel}(\mathbb{Q},A_{f})$
. This is done in the following lemma.
Proposition 5.8. Under the hypotheses of Theorem 5.6, we have
![]() $\operatorname{Sel}(\mathbb{Q},A_{f})=0$
.
$\operatorname{Sel}(\mathbb{Q},A_{f})=0$
.
Proof. By definition of
![]() $T:=T_{\operatorname{eis}(f)}$
, there exists a non-split short exact sequence
$T:=T_{\operatorname{eis}(f)}$
, there exists a non-split short exact sequence
In particular,
![]() $H^{0}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])=H^{0}(\mathbb{Q},\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}))=0$
as
$H^{0}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])=H^{0}(\mathbb{Q},\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}))=0$
as
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}$
is odd. Thus, by Lemma 4.3, to prove this proposition it suffices to check that
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}$
is odd. Thus, by Lemma 4.3, to prove this proposition it suffices to check that
![]() $\operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])=0$
.
$\operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])=0$
.
The above short exact sequence yields
We claim that the image of
![]() $H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}))$
in
$H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}))$
in
![]() $H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
contains
$H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
contains
![]() $\operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
.
$\operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
.
To this end, take
![]() $\unicode[STIX]{x1D719}\in \operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
and let
$\unicode[STIX]{x1D719}\in \operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
and let
![]() $\operatorname{im}(\unicode[STIX]{x1D719})$
denote the image of
$\operatorname{im}(\unicode[STIX]{x1D719})$
denote the image of
![]() $\unicode[STIX]{x1D719}$
in
$\unicode[STIX]{x1D719}$
in
![]() $H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F})=\operatorname{Hom}(\operatorname{Gal}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q}),\mathbb{F})$
, and we will check that
$H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F})=\operatorname{Hom}(\operatorname{Gal}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q}),\mathbb{F})$
, and we will check that
![]() $\operatorname{im}(\unicode[STIX]{x1D719})$
vanishes. Since
$\operatorname{im}(\unicode[STIX]{x1D719})$
vanishes. Since
![]() $\unicode[STIX]{x1D719}$
is a Selmer class,
$\unicode[STIX]{x1D719}$
is a Selmer class,
![]() $\unicode[STIX]{x1D719}$
is unramified outside
$\unicode[STIX]{x1D719}$
is unramified outside
![]() $p$
. Further, the very definition of the local condition at
$p$
. Further, the very definition of the local condition at
![]() $p$
tells us that
$p$
tells us that
![]() $\operatorname{im}(\unicode[STIX]{x1D719})$
is unramified at
$\operatorname{im}(\unicode[STIX]{x1D719})$
is unramified at
![]() $p$
. In particular,
$p$
. In particular,
![]() $\operatorname{im}(\unicode[STIX]{x1D719})$
is unramified everywhere and hence zero as desired.
$\operatorname{im}(\unicode[STIX]{x1D719})$
is unramified everywhere and hence zero as desired.
Thus
with the
![]() $-1$
coming from
$-1$
coming from
![]() $H^{0}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F})\cong \mathbb{F}$
. Lemma 5.9 below, whose hypotheses are satisfied by (Good Eisen) and our running assumption that
$H^{0}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F})\cong \mathbb{F}$
. Lemma 5.9 below, whose hypotheses are satisfied by (Good Eisen) and our running assumption that
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
, then gives
$p\nmid \unicode[STIX]{x1D711}(N)$
, then gives
which is 0 by
![]() $(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})$
.◻
$(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})$
.◻
Lemma 5.9. Let
![]() $\unicode[STIX]{x1D713}$
be a character of conductor
$\unicode[STIX]{x1D713}$
be a character of conductor
![]() $N$
and let
$N$
and let
![]() $\unicode[STIX]{x1D6F4}$
denote the set of primes dividing
$\unicode[STIX]{x1D6F4}$
denote the set of primes dividing
![]() $pN$
. Assume that:
$pN$
. Assume that:
(1)
 $p\nmid \unicode[STIX]{x1D711}(N)$
;
$p\nmid \unicode[STIX]{x1D711}(N)$
;(2)
 $(-1)^{k}=\unicode[STIX]{x1D713}(-1)$
;
$(-1)^{k}=\unicode[STIX]{x1D713}(-1)$
;(3)
 $k\equiv 2\;(\text{mod}\,p-1)\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
$k\equiv 2\;(\text{mod}\,p-1)\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
Then
Proof. Let
![]() $X=\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})$
and
$X=\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1})$
and
![]() $X^{\ast }=\mathbb{F}(\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})$
. Set
$X^{\ast }=\mathbb{F}(\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})$
. Set
![]() $H_{f}^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
equal to the subcollection of classes in
$H_{f}^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
equal to the subcollection of classes in
![]() $H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
which are locally trivial at all places in
$H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
which are locally trivial at all places in
![]() $\unicode[STIX]{x1D6F4}$
. Then, by [Reference WilesWil95, Proposition 1.6], we have
$\unicode[STIX]{x1D6F4}$
. Then, by [Reference WilesWil95, Proposition 1.6], we have
where
We analyze each term individually. First note that
![]() $H^{0}(\mathbb{Q},X)=0$
as
$H^{0}(\mathbb{Q},X)=0$
as
![]() $\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}$
is non-trivial (being odd) and
$\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}$
is non-trivial (being odd) and
![]() $H^{0}(\mathbb{Q},X^{\ast })=0$
as we have assumed that
$H^{0}(\mathbb{Q},X^{\ast })=0$
as we have assumed that
![]() $\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k}$
is non-trivial. Further,
$\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k}$
is non-trivial. Further,
![]() $\#H^{0}(\mathbb{R},X^{\ast })=q$
as
$\#H^{0}(\mathbb{R},X^{\ast })=q$
as
![]() $\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k}$
is an even character. Now, for
$\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k}$
is an even character. Now, for
![]() $\ell \in \unicode[STIX]{x1D6F4}-\{p\}$
, clearly
$\ell \in \unicode[STIX]{x1D6F4}-\{p\}$
, clearly
![]() $H^{0}(\mathbb{Q}_{\ell },X)=0$
as
$H^{0}(\mathbb{Q}_{\ell },X)=0$
as
![]() $\unicode[STIX]{x1D713}$
is ramified at
$\unicode[STIX]{x1D713}$
is ramified at
![]() $\ell$
. Finally,
$\ell$
. Finally,
![]() $H^{0}(\mathbb{Q}_{p},X^{\ast })=0$
as either
$H^{0}(\mathbb{Q}_{p},X^{\ast })=0$
as either
![]() $k\not \equiv 2\;(\text{mod}\,p-1)$
or
$k\not \equiv 2\;(\text{mod}\,p-1)$
or
![]() $\unicode[STIX]{x1D713}(p)\neq 1$
by assumption.
$\unicode[STIX]{x1D713}(p)\neq 1$
by assumption.
Thus,
![]() $h_{\infty }=q$
,
$h_{\infty }=q$
,
![]() $h_{\ell }=1$
for all
$h_{\ell }=1$
for all
![]() $\ell \in \unicode[STIX]{x1D6F4}$
, and
$\ell \in \unicode[STIX]{x1D6F4}$
, and
Let
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D713}}=\operatorname{Gal}(K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})/\mathbb{Q})$
, which has size prime to
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D713}}=\operatorname{Gal}(K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})/\mathbb{Q})$
, which has size prime to
![]() $p$
as we are assuming that
$p$
as we are assuming that
![]() $p\nmid \unicode[STIX]{x1D711}(N)$
. Thus we have
$p\nmid \unicode[STIX]{x1D711}(N)$
. Thus we have
 $$\begin{eqnarray}\displaystyle H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast }) & \stackrel{{\sim}}{\rightarrow } & \displaystyle H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p}),X^{\ast })^{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D713}}}\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D713}}}(\operatorname{Gal}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})),X^{\ast })\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(\operatorname{Gal}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p}))^{(\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})},\mathbb{F}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast }) & \stackrel{{\sim}}{\rightarrow } & \displaystyle H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p}),X^{\ast })^{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D713}}}\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D713}}}(\operatorname{Gal}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})),X^{\ast })\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(\operatorname{Gal}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p}))^{(\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})},\mathbb{F}).\nonumber\end{eqnarray}$$
The image of
![]() $H_{f}^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
in
$H_{f}^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
in
![]() $H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
thus lands in
$H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},X^{\ast })$
thus lands in
where
![]() $H_{\unicode[STIX]{x1D713}}$
denotes the Hilbert class field of
$H_{\unicode[STIX]{x1D713}}$
denotes the Hilbert class field of
![]() $K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})$
. Hence,
$K_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D707}_{p})$
. Hence,
which proves the lemma. ◻
Proof of Theorem 5.6.
By Proposition 5.8,
![]() $(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})$
implies
$(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-k})$
implies
![]() $\operatorname{Sel}(\mathbb{Q},A_{f})=0$
. Thus, by Proposition 4.4, we have that
$\operatorname{Sel}(\mathbb{Q},A_{f})=0$
. Thus, by Proposition 4.4, we have that
![]() $|\text{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}|\leqslant q^{\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)}$
. We note that, by our choice of
$|\text{Sel}(\mathbb{Q}_{\infty },A_{f})^{\unicode[STIX]{x1D6E4}}|\leqslant q^{\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)}$
. We note that, by our choice of
![]() $T$
, we have
$T$
, we have
![]() $H^{0}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])=0$
, which is needed to invoke Proposition 4.4. Finally, by [Reference Greenberg and VatsalGV00, Proposition 2.5],
$H^{0}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])=0$
, which is needed to invoke Proposition 4.4. Finally, by [Reference Greenberg and VatsalGV00, Proposition 2.5],
![]() $\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\vee }$
has no non-zero finite submodules; thus
$\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\vee }$
has no non-zero finite submodules; thus
![]() $\unicode[STIX]{x1D707}(\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\vee })\leqslant \operatorname{ord}_{p}(a_{p}(f)-1)$
by Lemma 5.7.◻
$\unicode[STIX]{x1D707}(\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})^{\vee })\leqslant \operatorname{ord}_{p}(a_{p}(f)-1)$
by Lemma 5.7.◻
Remark 5.10. We note that if
![]() $j(\mathfrak{m})=2$
and
$j(\mathfrak{m})=2$
and
![]() $\unicode[STIX]{x1D713}(p)=1$
, then Proposition 5.8 does not hold. Indeed, in this case Lemma 5.9 gives that the image of
$\unicode[STIX]{x1D713}(p)=1$
, then Proposition 5.8 does not hold. Indeed, in this case Lemma 5.9 gives that the image of
![]() $H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}))$
in
$H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},\mathbb{F}(\unicode[STIX]{x1D713}\unicode[STIX]{x1D714}^{k-1}))$
in
![]() $H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
yields a non-trivial class in
$H^{1}(\mathbb{Q}_{\unicode[STIX]{x1D6F4}}/\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
yields a non-trivial class in
![]() $\operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
. Nonetheless Theorem 5.6 likely holds in this case even if our method of proof fails.
$\operatorname{Sel}(\mathbb{Q},A_{f}[\unicode[STIX]{x1D71B}])$
. Nonetheless Theorem 5.6 likely holds in this case even if our method of proof fails.
5.3 Conjecture
We continue with the notation and assumptions of the previous section so that
![]() $A_{f}=V_{f}/T_{\operatorname{eis}(f)}$
. Theorems 5.3 and 5.6 give the following string of inequalities:
$A_{f}=V_{f}/T_{\operatorname{eis}(f)}$
. Theorems 5.3 and 5.6 give the following string of inequalities:
Greenberg has formulated precise conjectures on
![]() $\unicode[STIX]{x1D707}$
-invariants of Selmer groups of an elliptic curve in terms of the Galois module structure of
$\unicode[STIX]{x1D707}$
-invariants of Selmer groups of an elliptic curve in terms of the Galois module structure of
![]() $E[p^{n}]$
for
$E[p^{n}]$
for
![]() $n$
large enough [Reference GreenbergGre99, Conjecture 1.11 and p. 70]. These conjectures readily generalize to the case of modular forms and in this context predict that the lower bound gives the true value of the
$n$
large enough [Reference GreenbergGre99, Conjecture 1.11 and p. 70]. These conjectures readily generalize to the case of modular forms and in this context predict that the lower bound gives the true value of the
![]() $\unicode[STIX]{x1D707}$
-invariant.
$\unicode[STIX]{x1D707}$
-invariant.
Conjecture 5.11. We have
5.4 When the bounds meet
As on the analytic side, when the upper and lower bound in (7) meet, the Iwasawa theory becomes very simple. In this section, we will prove the following theorem which establishes that the Selmer group is entirely given by the
![]() $\unicode[STIX]{x1D707}$
-invariant in this situation (compare with Theorem 3.21 on the analytic side).
$\unicode[STIX]{x1D707}$
-invariant in this situation (compare with Theorem 3.21 on the analytic side).
Theorem 5.12. Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be an maximal ideal satisfying:
$\mathfrak{m}\subseteq \mathbb{T}$
be an maximal ideal satisfying:
∙ (Good Eisen);
∙
 $(U_{p}-1\;\text{gens})$
;
$(U_{p}-1\;\text{gens})$
;∙
 $j(\mathfrak{m})=2\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
$j(\mathfrak{m})=2\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
Then for
![]() $f$
a classical eigenform in the Hida family for
$f$
a classical eigenform in the Hida family for
![]() $\mathfrak{m}^{c}$
, we have
$\mathfrak{m}^{c}$
, we have
Proof. To ease notation, let
![]() $S=\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})$
. First note that by Theorem 3.5 we know that
$S=\operatorname{Sel}(\mathbb{Q}_{\infty },A_{f})$
. First note that by Theorem 3.5 we know that
![]() $\mathbb{T}$
is Gorenstein as
$\mathbb{T}$
is Gorenstein as
![]() $(U_{p}-1\;\text{gens})$
holds. Then by [Reference WakeWak15, Theorem 1.2], we have that
$(U_{p}-1\;\text{gens})$
holds. Then by [Reference WakeWak15, Theorem 1.2], we have that
![]() $(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-j(\mathfrak{m})})$
holds. Hence, by Theorems 5.3 and 5.6,
$(\text{Vand}\;\unicode[STIX]{x1D713}^{-1}\unicode[STIX]{x1D714}^{2-j(\mathfrak{m})})$
holds. Hence, by Theorems 5.3 and 5.6,
Further, by Lemma 5.4,
![]() $(U_{p}-1\;\text{gens})$
implies that
$(U_{p}-1\;\text{gens})$
implies that
![]() $\operatorname{eis}(f)=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
, and thus
$\operatorname{eis}(f)=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
, and thus
![]() $\unicode[STIX]{x1D707}(S^{\vee })=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
.
$\unicode[STIX]{x1D707}(S^{\vee })=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
.
Let
![]() $h\in \unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
denote the characteristic power series of
$h\in \unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
denote the characteristic power series of
![]() $S^{\vee }$
. Then, by [Reference GreenbergGre99, Lemma 4.2], we have
$S^{\vee }$
. Then, by [Reference GreenbergGre99, Lemma 4.2], we have
Clearly,
![]() $\operatorname{ord}_{\unicode[STIX]{x1D71B}}h(0)\geqslant \unicode[STIX]{x1D707}(S^{\vee })=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
. Further, in the course of the proof of Proposition 4.4, the exact sequence
$\operatorname{ord}_{\unicode[STIX]{x1D71B}}h(0)\geqslant \unicode[STIX]{x1D707}(S^{\vee })=\operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
. Further, in the course of the proof of Proposition 4.4, the exact sequence
and the surjection
![]() ${\mathcal{O}}/(a_{p}(f)-1){\mathcal{O}}{\twoheadrightarrow}\ker (r)$
were derived. By Proposition 5.8, we have
${\mathcal{O}}/(a_{p}(f)-1){\mathcal{O}}{\twoheadrightarrow}\ker (r)$
were derived. By Proposition 5.8, we have
![]() $\operatorname{Sel}(\mathbb{Q},A_{f})=0$
, and thus
$\operatorname{Sel}(\mathbb{Q},A_{f})=0$
, and thus
![]() $\operatorname{ord}_{q}|S^{\unicode[STIX]{x1D6E4}}|\leqslant \operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
. Thus, we must have that
$\operatorname{ord}_{q}|S^{\unicode[STIX]{x1D6E4}}|\leqslant \operatorname{ord}_{\unicode[STIX]{x1D71B}}(a_{p}(f)-1)$
. Thus, we must have that
But now
![]() $\unicode[STIX]{x1D707}(h)=\operatorname{ord}_{\unicode[STIX]{x1D71B}}h(0)$
, and hence
$\unicode[STIX]{x1D707}(h)=\operatorname{ord}_{\unicode[STIX]{x1D71B}}h(0)$
, and hence
![]() $\unicode[STIX]{x1D706}(h)=0$
(as in the proof of Theorem 3.21).
$\unicode[STIX]{x1D706}(h)=0$
(as in the proof of Theorem 3.21).
We now know that
![]() $\unicode[STIX]{x1D707}(S^{\vee })=\operatorname{eis}(f)$
and
$\unicode[STIX]{x1D707}(S^{\vee })=\operatorname{eis}(f)$
and
![]() $\unicode[STIX]{x1D706}(S^{\vee })=0$
, and thus to prove our theorem it suffices to check that
$\unicode[STIX]{x1D706}(S^{\vee })=0$
, and thus to prove our theorem it suffices to check that
![]() $S^{\vee }$
is a cyclic
$S^{\vee }$
is a cyclic
![]() $\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module. By Nakayama’s lemma, it suffices to check that
$\unicode[STIX]{x1D6EC}_{{\mathcal{O}}}$
-module. By Nakayama’s lemma, it suffices to check that
![]() $(S^{\vee })_{\unicode[STIX]{x1D6E4}}$
is a cyclic
$(S^{\vee })_{\unicode[STIX]{x1D6E4}}$
is a cyclic
![]() ${\mathcal{O}}$
-module, or equivalently that
${\mathcal{O}}$
-module, or equivalently that
![]() $S^{\unicode[STIX]{x1D6E4}}$
is a cyclic
$S^{\unicode[STIX]{x1D6E4}}$
is a cyclic
![]() ${\mathcal{O}}$
-module. Returning to (8), we can now deduce that
${\mathcal{O}}$
-module. Returning to (8), we can now deduce that
![]() $S^{\unicode[STIX]{x1D6E4}}\cong \ker (r)\cong {\mathcal{O}}/(a_{p}(f)-1){\mathcal{O}}$
as all of these modules have the same size. Thus,
$S^{\unicode[STIX]{x1D6E4}}\cong \ker (r)\cong {\mathcal{O}}/(a_{p}(f)-1){\mathcal{O}}$
as all of these modules have the same size. Thus,
![]() $S^{\unicode[STIX]{x1D6E4}}$
is
$S^{\unicode[STIX]{x1D6E4}}$
is
![]() ${\mathcal{O}}$
-cyclic, which concludes the proof.◻
${\mathcal{O}}$
-cyclic, which concludes the proof.◻
Corollary 5.13 (Main conjecture).
Let
![]() $\mathfrak{m}\subseteq \mathbb{T}$
be an maximal ideal satisfying:
$\mathfrak{m}\subseteq \mathbb{T}$
be an maximal ideal satisfying:
∙ (Good Eisen);
∙
 $(U_{p}-1\;\text{gens})$
;
$(U_{p}-1\;\text{gens})$
;∙
 $j(\mathfrak{m})=2\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
$j(\mathfrak{m})=2\;\Longrightarrow \;\unicode[STIX]{x1D713}(p)\neq 1$
.
Then, for
![]() $f$
a classical eigenform in the Hida family for
$f$
a classical eigenform in the Hida family for
![]() $\mathfrak{m}^{c}$
, we have
$\mathfrak{m}^{c}$
, we have
Acknowledgements
We heartily thank Preston Wake for his help and advice throughout this project, especially for his extensive help with the arguments involving the Gorenstein properties of Hecke algebras. The second author thanks the Max Planck Institute for Mathematics in Bonn for the wonderful environment provided during his extended visit there. The first author was supported by NSF grant DMS-1405993. The second author was supported by NSF grants DMS-1303302 and DMS-1702178 as well as a fellowship from the Simons Foundation.
Appendix A Two-variable
 $p$
-adic
$p$
-adic
 $L$
-functions
$L$
-functions
Let
![]() $\mathbb{T}$
denote the universal ordinary Hecke algebra of tame level
$\mathbb{T}$
denote the universal ordinary Hecke algebra of tame level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
acting on modular forms (not just cuspforms), and let
$\unicode[STIX]{x1D6E4}_{1}(N)$
acting on modular forms (not just cuspforms), and let
![]() $\mathfrak{m}$
denote a maximal ideal of
$\mathfrak{m}$
denote a maximal ideal of
![]() $\mathbb{T}$
. We aim to construct a two-variable
$\mathbb{T}$
. We aim to construct a two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function over
$L$
-function over
![]() $\mathbb{T}_{\mathfrak{m}}$
, assuming the maximal ideal
$\mathbb{T}_{\mathfrak{m}}$
, assuming the maximal ideal
![]() $\mathfrak{m}$
satisfies (Mult One). Specifically, we construct elementsFootnote
4
$\mathfrak{m}$
satisfies (Mult One). Specifically, we construct elementsFootnote
4
such that for any classical height-one prime
![]() $\mathfrak{p}_{f}\subseteq \mathbb{T}_{\mathfrak{m}}$
of residue characteristic
$\mathfrak{p}_{f}\subseteq \mathbb{T}_{\mathfrak{m}}$
of residue characteristic
![]() $0$
, the image of
$0$
, the image of
![]() $L_{p}^{+}(\mathfrak{m})$
in
$L_{p}^{+}(\mathfrak{m})$
in
![]() $\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{f}\,\otimes \,\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
yields the
$\mathbb{T}_{\mathfrak{m}}/\mathfrak{p}_{f}\,\otimes \,\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
yields the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function
$L$
-function
![]() $L_{p}^{+}(f)$
, and similarly for
$L_{p}^{+}(f)$
, and similarly for
![]() $L_{p}^{-}(\mathfrak{m})$
.
$L_{p}^{-}(\mathfrak{m})$
.
A.1 Integral control theorems
Recall the definition of
![]() ${\mathcal{P}}_{g}$
for
${\mathcal{P}}_{g}$
for
![]() $g\geqslant 0$
as well as the specialization map
$g\geqslant 0$
as well as the specialization map
![]() $\operatorname{Meas}_{g}(\mathbb{Z}_{p})\rightarrow {\mathcal{P}}_{g}^{\vee }$
from § 2.3. In this section we aim to prove the following integral version of the control theorem in Theorem 2.2. In what follows, we write
$\operatorname{Meas}_{g}(\mathbb{Z}_{p})\rightarrow {\mathcal{P}}_{g}^{\vee }$
from § 2.3. In this section we aim to prove the following integral version of the control theorem in Theorem 2.2. In what follows, we write
![]() $H_{c}^{i}(X)$
for
$H_{c}^{i}(X)$
for
![]() $H_{c}^{i}(\unicode[STIX]{x1D6E4}_{0},X)$
.
$H_{c}^{i}(\unicode[STIX]{x1D6E4}_{0},X)$
.
Theorem A.1. Specialization induces an isomorphism
Towards proving Theorem A.1, we recall the following famous result of Mahler.
Theorem A.2. Any continuous function
![]() $f:\mathbb{Z}_{p}\rightarrow \mathbb{Q}_{p}$
can be written uniquely in the form
$f:\mathbb{Z}_{p}\rightarrow \mathbb{Q}_{p}$
can be written uniquely in the form
![]() $f(x)=\sum _{j=0}^{\infty }c_{j}\binom{x}{j}$
with
$f(x)=\sum _{j=0}^{\infty }c_{j}\binom{x}{j}$
with
![]() $\{c_{j}\}$
a sequence in
$\{c_{j}\}$
a sequence in
![]() $\mathbb{Q}_{p}$
tending to
$\mathbb{Q}_{p}$
tending to
![]() $0$
. Moreover,
$0$
. Moreover,
In particular, if
![]() $f$
takes values in
$f$
takes values in
![]() $\mathbb{Z}_{p}$
, then all of the
$\mathbb{Z}_{p}$
, then all of the
![]() $c_{j}$
are integral.
$c_{j}$
are integral.
Proof. See [Reference MahlerMah58]. ◻
Corollary A.3. The map which associates
![]() $\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p})$
to the sequence
$\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p})$
to the sequence
![]() $\{\unicode[STIX]{x1D707}(\binom{x}{j})\}_{j=0}^{\infty }$
establishes a bijection between
$\{\unicode[STIX]{x1D707}(\binom{x}{j})\}_{j=0}^{\infty }$
establishes a bijection between
![]() $\operatorname{Meas}(\mathbb{Z}_{p})$
and the collection of sequences in
$\operatorname{Meas}(\mathbb{Z}_{p})$
and the collection of sequences in
![]() $\mathbb{Z}_{p}$
.
$\mathbb{Z}_{p}$
.
Proof. This corollary follows immediately from Theorem A.2. ◻
Lemma A.4. The specialization map
![]() $\operatorname{Meas}_{g}(\mathbb{Z}_{p})\rightarrow {\mathcal{P}}_{g}^{\vee }$
is surjective.
$\operatorname{Meas}_{g}(\mathbb{Z}_{p})\rightarrow {\mathcal{P}}_{g}^{\vee }$
is surjective.
Proof. By Theorem A.2,
![]() ${\mathcal{P}}_{g}$
is generated over
${\mathcal{P}}_{g}$
is generated over
![]() $\mathbb{Z}_{p}$
by the binomial coefficients
$\mathbb{Z}_{p}$
by the binomial coefficients
![]() $\binom{x}{j}$
for
$\binom{x}{j}$
for
![]() $0\leqslant j\leqslant k$
. Thus this lemma follows directly from Corollary A.3.◻
$0\leqslant j\leqslant k$
. Thus this lemma follows directly from Corollary A.3.◻
Proof of Theorem A.1.
By Lemma A.4, we have an exact sequence
where
![]() $K$
is the subspace of measures which vanish on polynomials of degree less than or equal to
$K$
is the subspace of measures which vanish on polynomials of degree less than or equal to
![]() $k$
. The long exact sequence for cohomology then gives
$k$
. The long exact sequence for cohomology then gives
We first show
![]() $H_{c}^{1}(K)^{\operatorname{ord}}=0$
. To this end, take
$H_{c}^{1}(K)^{\operatorname{ord}}=0$
. To this end, take
![]() $\unicode[STIX]{x1D6F7}\in H_{c}^{1}(K)^{\operatorname{ord}}$
, and for any
$\unicode[STIX]{x1D6F7}\in H_{c}^{1}(K)^{\operatorname{ord}}$
, and for any
![]() $n$
we can write
$n$
we can write
![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F9}\mid U_{p}^{n}$
with
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F9}\mid U_{p}^{n}$
with
![]() $\unicode[STIX]{x1D6F9}\in H_{c}^{1}(K)^{\operatorname{ord}}$
. Then
$\unicode[STIX]{x1D6F9}\in H_{c}^{1}(K)^{\operatorname{ord}}$
. Then
Since all values of
![]() $\unicode[STIX]{x1D6F9}$
are in
$\unicode[STIX]{x1D6F9}$
are in
![]() $K$
, we have in particular that
$K$
, we have in particular that
Thus, by Lemma A.5 below, we have
![]() $\unicode[STIX]{x1D6F7}(D)(a+p^{n}\mathbb{Z}_{p})=0$
for all
$\unicode[STIX]{x1D6F7}(D)(a+p^{n}\mathbb{Z}_{p})=0$
for all
![]() $a$
. But since
$a$
. But since
![]() $n$
was chosen arbitrarily, we have that
$n$
was chosen arbitrarily, we have that
![]() $\unicode[STIX]{x1D6F7}(D)$
and thus
$\unicode[STIX]{x1D6F7}(D)$
and thus
![]() $\unicode[STIX]{x1D6F7}$
is identically zero.
$\unicode[STIX]{x1D6F7}$
is identically zero.
To see
![]() $H_{c}^{2}(K)^{\operatorname{ord}}=0$
, note that
$H_{c}^{2}(K)^{\operatorname{ord}}=0$
, note that
Here we are computing
![]() $K^{\operatorname{ord}}$
with respect to the
$K^{\operatorname{ord}}$
with respect to the
![]() $U_{p}$
-operator
$U_{p}$
-operator
![]() $\sum _{a=0}^{p-1}\big(\!\begin{smallmatrix}1 & a\\ 0 & p\end{smallmatrix}\!\big)$
. It thus suffices to show that
$\sum _{a=0}^{p-1}\big(\!\begin{smallmatrix}1 & a\\ 0 & p\end{smallmatrix}\!\big)$
. It thus suffices to show that
![]() $K^{\operatorname{ord}}=0$
. But this follows from Lemma A.6 below.◻
$K^{\operatorname{ord}}=0$
. But this follows from Lemma A.6 below.◻
Lemma A.5. If
![]() $\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p})$
such that
$\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p})$
such that
![]() $\unicode[STIX]{x1D707}(\mathbb{Z}_{p})=0$
, then
$\unicode[STIX]{x1D707}(\mathbb{Z}_{p})=0$
, then
for all
![]() $b\in \mathbb{Z}_{p}$
.
$b\in \mathbb{Z}_{p}$
.
Proof. We have
When
![]() $a\not \equiv b\;(\text{mod}\,p^{n})$
, the function
$a\not \equiv b\;(\text{mod}\,p^{n})$
, the function
![]() $\mathbf{1}_{b+p^{n}\mathbb{Z}_{p}}(a+p^{n}z)$
is identically zero. When
$\mathbf{1}_{b+p^{n}\mathbb{Z}_{p}}(a+p^{n}z)$
is identically zero. When
![]() $a\equiv b\;(\text{mod}\,p^{n})$
, we have
$a\equiv b\;(\text{mod}\,p^{n})$
, we have
by assumption. ◻
Define an action of
![]() $U_{p}$
on
$U_{p}$
on
![]() $\operatorname{Meas}(\mathbb{Z}_{p})$
simply by the action of
$\operatorname{Meas}(\mathbb{Z}_{p})$
simply by the action of
![]() $\sum _{a=0}^{p-1}\big(\!\begin{smallmatrix}1 & a\\ 0 & p\end{smallmatrix}\!\big)$
.
$\sum _{a=0}^{p-1}\big(\!\begin{smallmatrix}1 & a\\ 0 & p\end{smallmatrix}\!\big)$
.
Lemma A.6. We have
![]() $\operatorname{Meas}(\mathbb{Z}_{p})^{\operatorname{ord}}=0$
.
$\operatorname{Meas}(\mathbb{Z}_{p})^{\operatorname{ord}}=0$
.
Proof. For
![]() $\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p})^{\operatorname{ord}}$
, write
$\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p})^{\operatorname{ord}}$
, write
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{n}\mid U_{p}^{n}$
for each
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{n}\mid U_{p}^{n}$
for each
![]() $n\geqslant 0$
. Then
$n\geqslant 0$
. Then
which is independent of
![]() $b$
. But this clearly forces
$b$
. But this clearly forces
![]() $\unicode[STIX]{x1D707}$
to vanish.◻
$\unicode[STIX]{x1D707}$
to vanish.◻
We end this section with a ‘mod
![]() $p$
’ control theorem.
$p$
’ control theorem.
Lemma A.7. We have
Proof. Starting with the short exact sequence
gives
As before, we have
Since
![]() $\operatorname{Meas}_{g}(\mathbb{Z}_{p}^{\times }){\twoheadrightarrow}{\mathcal{P}}_{g}^{\vee }$
(Lemma A.4) and
$\operatorname{Meas}_{g}(\mathbb{Z}_{p}^{\times }){\twoheadrightarrow}{\mathcal{P}}_{g}^{\vee }$
(Lemma A.4) and
![]() $\operatorname{Meas}_{g}(\mathbb{Z}_{p}^{\times })^{\operatorname{ord}}=0$
(Lemma A.6), we get
$\operatorname{Meas}_{g}(\mathbb{Z}_{p}^{\times })^{\operatorname{ord}}=0$
(Lemma A.6), we get
![]() $({\mathcal{P}}_{g}^{\vee })^{\operatorname{ord}}=0$
and thus
$({\mathcal{P}}_{g}^{\vee })^{\operatorname{ord}}=0$
and thus
![]() $H_{c}^{2}({\mathcal{P}}_{g}^{\vee })^{\operatorname{ord}}=0$
.◻
$H_{c}^{2}({\mathcal{P}}_{g}^{\vee })^{\operatorname{ord}}=0$
.◻
A.2 Two-variable measures and specialization
Recall the natural isomorphism
which sends the Dirac measure
![]() $\unicode[STIX]{x1D6FF}_{x}$
supported at
$\unicode[STIX]{x1D6FF}_{x}$
supported at
![]() $x\in \mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}$
to the group-like element
$x\in \mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}$
to the group-like element
![]() $[x]$
in
$[x]$
in
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
. We endow
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
. We endow
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
with the
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
with the
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-action arising from the embedding
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-action arising from the embedding
The factor of
![]() $a^{2}$
here is related to the fact that weight-
$a^{2}$
here is related to the fact that weight-
![]() $k$
modular forms correspond to
$k$
modular forms correspond to
![]() $\operatorname{Sym}^{k-2}$
-valued modular symbols. In terms of measures, the corresponding action of
$\operatorname{Sym}^{k-2}$
-valued modular symbols. In terms of measures, the corresponding action of
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
on
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
on
![]() $\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
is given by
$\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
is given by
for
![]() $a\in \mathbb{Z}_{p}^{\times }$
and
$a\in \mathbb{Z}_{p}^{\times }$
and
![]() $\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
.
$\unicode[STIX]{x1D707}\in \operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
.
The space
![]() $\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
also admits an action of
$\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
also admits an action of
![]() $\unicode[STIX]{x1D6F4}_{0}(p)$
defined by
$\unicode[STIX]{x1D6F4}_{0}(p)$
defined by
The specialization to weight
![]() $g$
is then the following
$g$
is then the following
![]() $\unicode[STIX]{x1D6F4}_{0}(p)$
-equivariant map:
$\unicode[STIX]{x1D6F4}_{0}(p)$
-equivariant map:
 $$\begin{eqnarray}\displaystyle \operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}) & \longrightarrow & \displaystyle \operatorname{Meas}_{g}(\mathbb{Z}_{p})\nonumber\\ \displaystyle \unicode[STIX]{x1D707} & \mapsto & \displaystyle \biggl(f\mapsto \int _{\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}}x^{g}f(y/x)\,d\unicode[STIX]{x1D707}(x,y)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}) & \longrightarrow & \displaystyle \operatorname{Meas}_{g}(\mathbb{Z}_{p})\nonumber\\ \displaystyle \unicode[STIX]{x1D707} & \mapsto & \displaystyle \biggl(f\mapsto \int _{\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}}x^{g}f(y/x)\,d\unicode[STIX]{x1D707}(x,y)\biggr).\nonumber\end{eqnarray}$$
Let
![]() $\mathfrak{p}_{k}\subseteq \mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
denote the ideal generated by elements of the form
$\mathfrak{p}_{k}\subseteq \mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
denote the ideal generated by elements of the form
![]() $[a]-a^{k}$
. We note that
$[a]-a^{k}$
. We note that
![]() $\mathfrak{p}_{k}$
is a principal ideal with generator
$\mathfrak{p}_{k}$
is a principal ideal with generator
![]() $\unicode[STIX]{x1D70B}_{k}=[\unicode[STIX]{x1D6FE}]-\unicode[STIX]{x1D6FE}^{k}$
where
$\unicode[STIX]{x1D70B}_{k}=[\unicode[STIX]{x1D6FE}]-\unicode[STIX]{x1D6FE}^{k}$
where
![]() $\unicode[STIX]{x1D6FE}$
is a topological generator of
$\unicode[STIX]{x1D6FE}$
is a topological generator of
![]() $\mathbb{Z}_{p}^{\times }$
.
$\mathbb{Z}_{p}^{\times }$
.
Lemma A.8. The specialization map
![]() $\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})\rightarrow \operatorname{Meas}_{g}(\mathbb{Z}_{p})$
sits in the exact sequence
$\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})\rightarrow \operatorname{Meas}_{g}(\mathbb{Z}_{p})$
sits in the exact sequence
where
![]() $\unicode[STIX]{x1D70B}_{k}$
is any generator of the ideal
$\unicode[STIX]{x1D70B}_{k}$
is any generator of the ideal
![]() $\mathfrak{p}_{k}$
.
$\mathfrak{p}_{k}$
.
Proof. To prove this lemma, we will work with the interpretation of these measure spaces as group algebras. Specialization is then the map
which sends the group-like element
![]() $[(a,b)]$
to
$[(a,b)]$
to
![]() $a^{k-2}[b/a]$
. We immediately see then that specialization is surjective as
$a^{k-2}[b/a]$
. We immediately see then that specialization is surjective as
![]() $[(1,b)]$
maps to
$[(1,b)]$
maps to
![]() $[b]$
.
$[b]$
.
To see that multiplication by
![]() $\unicode[STIX]{x1D70B}_{k}$
is injective, note that
$\unicode[STIX]{x1D70B}_{k}$
is injective, note that
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
is isomorphic to a direct sum of
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
is isomorphic to a direct sum of
![]() $p-1$
copies of
$p-1$
copies of
![]() $\mathbb{Z}_{p}[[(1+p\mathbb{Z}_{p})\times \mathbb{Z}_{p}]]$
with projections induced by the characters of
$\mathbb{Z}_{p}[[(1+p\mathbb{Z}_{p})\times \mathbb{Z}_{p}]]$
with projections induced by the characters of
![]() $(\mathbb{Z}/p\mathbb{Z})^{\times }$
. Since
$(\mathbb{Z}/p\mathbb{Z})^{\times }$
. Since
![]() $\mathbb{Z}_{p}[[(1+p\mathbb{Z}_{p})\times \mathbb{Z}_{p}]]$
is a domain, it suffices to see that no projection of
$\mathbb{Z}_{p}[[(1+p\mathbb{Z}_{p})\times \mathbb{Z}_{p}]]$
is a domain, it suffices to see that no projection of
![]() $\unicode[STIX]{x1D70B}_{k}$
is 0, which is true by inspection.
$\unicode[STIX]{x1D70B}_{k}$
is 0, which is true by inspection.
Finally, to compute the kernel of specialization, we will make a change of variables on
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
. Namely, consider the group isomorphism
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
. Namely, consider the group isomorphism
which induces a ring isomorphism
The map
![]() $\unicode[STIX]{x1D6FC}$
is
$\unicode[STIX]{x1D6FC}$
is
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-linear if we endow the target with the same
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-linear if we endow the target with the same
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-action as before, but we endow the source with the
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-action as before, but we endow the source with the
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-action arising from embedding
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
-action arising from embedding
By precomposing by
![]() $\unicode[STIX]{x1D6FC}$
, it suffices to compute the kernel of
$\unicode[STIX]{x1D6FC}$
, it suffices to compute the kernel of
![]() $\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]\rightarrow \mathbb{Z}_{p}[[\mathbb{Z}_{p}]]$
where the group-like element
$\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]\rightarrow \mathbb{Z}_{p}[[\mathbb{Z}_{p}]]$
where the group-like element
![]() $[(a,b)]$
simply maps to
$[(a,b)]$
simply maps to
![]() $a^{k-2}[b]$
. This kernel is visibly equal to
$a^{k-2}[b]$
. This kernel is visibly equal to
![]() $\mathfrak{p}_{k}\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
as desired.◻
$\mathfrak{p}_{k}\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]$
as desired.◻
A.3 Two-variable control theorem
For ease of notation we write
![]() ${\mathcal{M}}$
for
${\mathcal{M}}$
for
![]() $\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
and
$\operatorname{Meas}(\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p})$
and
![]() ${\mathcal{M}}_{g}$
for
${\mathcal{M}}_{g}$
for
![]() $\operatorname{Meas}_{g}(\mathbb{Z}_{p})$
.
$\operatorname{Meas}_{g}(\mathbb{Z}_{p})$
.
Theorem A.9. Specialization induces the isomorphism
Proof. Taking the long exact sequence corresponding to the exact sequence from Lemma A.8 and passing to ordinary parts gives
We have
which one can see vanishes just as in the proof of the Lemma A.6, completing the proof of the theorem. ◻
Corollary A.10. For
![]() $k\geqslant 2$
, we have
$k\geqslant 2$
, we have
A.4 Control theorems on the dual side
For a maximal ideal
![]() $\mathfrak{m}\subseteq \mathbb{T}$
, the space
$\mathfrak{m}\subseteq \mathbb{T}$
, the space
![]() $H_{c}^{1}({\mathcal{P}}_{g}^{\vee }\,\otimes \,\mathbb{F}_{p})[\mathfrak{m}_{k}]$
is more directly related to
$H_{c}^{1}({\mathcal{P}}_{g}^{\vee }\,\otimes \,\mathbb{F}_{p})[\mathfrak{m}_{k}]$
is more directly related to
![]() $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})$
than to
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})$
than to
![]() $H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}$
, where
$H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}$
, where
![]() $\tilde{\unicode[STIX]{x1D6EC}}:=\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
. For this reason, we now prove a control theorem on the dual side. We begin with a few lemmas.
$\tilde{\unicode[STIX]{x1D6EC}}:=\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }]]$
. For this reason, we now prove a control theorem on the dual side. We begin with a few lemmas.
Lemma A.11. Let
![]() $K$
be a field,
$K$
be a field,
![]() $R$
a finitely generated
$R$
a finitely generated
![]() $K$
-algebra, and
$K$
-algebra, and
![]() $M$
a finitely generated
$M$
a finitely generated
![]() $R$
-module. For any ideal
$R$
-module. For any ideal
![]() $I\subseteq R$
, we have:
$I\subseteq R$
, we have:
(1)
 $M[I]^{\vee }\cong M^{\vee }/IM^{\vee }$
;
$M[I]^{\vee }\cong M^{\vee }/IM^{\vee }$
;(2)
 $(M/IM)^{\vee }\cong M^{\vee }[I]$
.
$(M/IM)^{\vee }\cong M^{\vee }[I]$
.
Here
![]() $X^{\vee }=\operatorname{Hom}_{K}(X,K)$
.
$X^{\vee }=\operatorname{Hom}_{K}(X,K)$
.
Proof. First note that the second isomorphism implies the first. Indeed, applying the second isomorphism to
![]() $M^{\vee }$
gives
$M^{\vee }$
gives
and thus
To see the second isomorphism, there is a natural map
which is clearly injective. Moreover, the image of this map lands in
![]() $M^{\vee }[I]$
since if
$M^{\vee }[I]$
since if
![]() $a\in I$
and
$a\in I$
and
![]() $\unicode[STIX]{x1D719}:M\rightarrow M/IM\rightarrow K$
is in the image, then
$\unicode[STIX]{x1D719}:M\rightarrow M/IM\rightarrow K$
is in the image, then
![]() $(a\cdot \unicode[STIX]{x1D719})(m)=\unicode[STIX]{x1D719}(am)=0$
for all
$(a\cdot \unicode[STIX]{x1D719})(m)=\unicode[STIX]{x1D719}(am)=0$
for all
![]() $m\in M$
.
$m\in M$
.
Finally, to get surjectivity, take
![]() $\unicode[STIX]{x1D719}\in M^{\vee }[I]$
. So
$\unicode[STIX]{x1D719}\in M^{\vee }[I]$
. So
![]() $\unicode[STIX]{x1D719}:M\rightarrow K$
and
$\unicode[STIX]{x1D719}:M\rightarrow K$
and
![]() $a\cdot \unicode[STIX]{x1D719}=0$
for all
$a\cdot \unicode[STIX]{x1D719}=0$
for all
![]() $a\in I$
. To prove surjectivity, we simply need to see that
$a\in I$
. To prove surjectivity, we simply need to see that
![]() $\unicode[STIX]{x1D719}(IM)=0$
. But this follows since for
$\unicode[STIX]{x1D719}(IM)=0$
. But this follows since for
![]() $a\in I$
,
$a\in I$
,
![]() $\unicode[STIX]{x1D719}(am)=(a\cdot \unicode[STIX]{x1D719})(m)=0$
.◻
$\unicode[STIX]{x1D719}(am)=(a\cdot \unicode[STIX]{x1D719})(m)=0$
.◻
Lemma A.12. Let
![]() $M$
be a projective
$M$
be a projective
![]() $R$
-module and
$R$
-module and
![]() $I=aR$
a principal ideal of
$I=aR$
a principal ideal of
![]() $R$
where
$R$
where
![]() $a$
is not a zero-divisor. Then
$a$
is not a zero-divisor. Then
Proof. Since
![]() $a$
is not a zero-divisor, we have
$a$
is not a zero-divisor, we have
and thus
This last Ext group vanishes as
![]() $M$
is projective over
$M$
is projective over
![]() $R$
, which proves the lemma.◻
$R$
, which proves the lemma.◻
The following lemma gives control theorems for
![]() $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})$
.
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})$
.
Lemma A.13. For
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
and
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
and
![]() $g=k-2\geqslant 0$
, we have
$g=k-2\geqslant 0$
, we have
and
Proof. Set
![]() $X=H_{c}^{1}({\mathcal{M}})^{\operatorname{ord}}$
. Then for the first part we have
$X=H_{c}^{1}({\mathcal{M}})^{\operatorname{ord}}$
. Then for the first part we have
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})\,\otimes _{\tilde{\unicode[STIX]{x1D6EC}}}\,\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k} & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}}/\mathfrak{p}_{k}X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k})\quad (\text{Lemma A.12})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}((X/\mathfrak{p}_{k}X)_{\mathfrak{m}_{k}},\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee })_{\mathfrak{m}_{k}},\mathbb{Z}_{p})\quad (\text{Corollary A.10}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})\,\otimes _{\tilde{\unicode[STIX]{x1D6EC}}}\,\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k} & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}}/\mathfrak{p}_{k}X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k})\quad (\text{Lemma A.12})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}((X/\mathfrak{p}_{k}X)_{\mathfrak{m}_{k}},\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee })_{\mathfrak{m}_{k}},\mathbb{Z}_{p})\quad (\text{Corollary A.10}).\nonumber\end{eqnarray}$$
For the second part, we have
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m} & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})\,\otimes _{\tilde{\unicode[STIX]{x1D6EC}}}\,(\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee })_{\mathfrak{m}_{k}},\mathbb{Z}_{p})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\quad (\text{part 1 above})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee })_{\mathfrak{m}_{k}}\,\otimes _{\mathbb{Z}_{p}}\,\mathbb{F}_{p},\mathbb{F}_{p})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\quad (\text{Lemma A.12})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee }\,\otimes \,\mathbb{F}_{p})_{\mathfrak{m}_{k}},\mathbb{F}_{p})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\quad (\text{Lemma A.7})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee }\,\otimes \,\mathbb{F}_{p})[\mathfrak{m}_{k}],\mathbb{F}_{p})\quad (\text{Lemma A.11}).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m} & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(X_{\mathfrak{m}},\tilde{\unicode[STIX]{x1D6EC}})\,\otimes _{\tilde{\unicode[STIX]{x1D6EC}}}\,(\tilde{\unicode[STIX]{x1D6EC}}/\mathfrak{p}_{k})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee })_{\mathfrak{m}_{k}},\mathbb{Z}_{p})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\quad (\text{part 1 above})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee })_{\mathfrak{m}_{k}}\,\otimes _{\mathbb{Z}_{p}}\,\mathbb{F}_{p},\mathbb{F}_{p})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\quad (\text{Lemma A.12})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee }\,\otimes \,\mathbb{F}_{p})_{\mathfrak{m}_{k}},\mathbb{F}_{p})\,\otimes _{\mathbb{T}}\,\mathbb{T}/\mathfrak{m}\quad (\text{Lemma A.7})\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{g}^{\vee }\,\otimes \,\mathbb{F}_{p})[\mathfrak{m}_{k}],\mathbb{F}_{p})\quad (\text{Lemma A.11}).\Box \nonumber\end{eqnarray}$$
A.5 Freeness over the Hecke algebra
For
![]() $\mathfrak{m}\subseteq \mathbb{T}$
maximal, we aim to show that
$\mathfrak{m}\subseteq \mathbb{T}$
maximal, we aim to show that
![]() $\mathfrak{m}$
satisfies a mod
$\mathfrak{m}$
satisfies a mod
![]() $p$
multiplicity-one assumption if and only if
$p$
multiplicity-one assumption if and only if
![]() $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})$
is free over
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})$
is free over
![]() $\mathbb{T}_{\mathfrak{m}}$
for
$\mathbb{T}_{\mathfrak{m}}$
for
![]() $\unicode[STIX]{x1D700}=+$
and free over
$\unicode[STIX]{x1D700}=+$
and free over
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
if
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
if
![]() $\unicode[STIX]{x1D700}=-$
. However, such a result cannot hold unconditionally as the Eisenstein Hecke eigensystems do not always all occur in the plus subspace. We thus introduce the following hypothesis on
$\unicode[STIX]{x1D700}=-$
. However, such a result cannot hold unconditionally as the Eisenstein Hecke eigensystems do not always all occur in the plus subspace. We thus introduce the following hypothesis on
![]() $\mathfrak{m}$
to force this condition to hold.
$\mathfrak{m}$
to force this condition to hold.
Definition A.14. We say that
![]() $\mathfrak{m}\subset \mathbb{T}$
satisfies (Eisen
$\mathfrak{m}\subset \mathbb{T}$
satisfies (Eisen
![]() $^{+}$
) if
$^{+}$
) if
![]() $\operatorname{Hom}_{\unicode[STIX]{x1D6E4}_{0}}(\unicode[STIX]{x1D6E5},{\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{-}=0$
for all (equivalently, for one) classical
$\operatorname{Hom}_{\unicode[STIX]{x1D6E4}_{0}}(\unicode[STIX]{x1D6E5},{\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{-}=0$
for all (equivalently, for one) classical
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
Note that (Eisen
![]() $^{+}$
) is automatically satisfied if
$^{+}$
) is automatically satisfied if
![]() $\mathfrak{m}$
is not an Eisenstein maximal ideal. It is also automatically satisfied if
$\mathfrak{m}$
is not an Eisenstein maximal ideal. It is also automatically satisfied if
![]() $N$
is square-free. But it fails, for instance, when
$N$
is square-free. But it fails, for instance, when
![]() $N=9$
as the boundary symbol attached to
$N=9$
as the boundary symbol attached to
![]() $E_{k,\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}$
lies in the minus subspace where
$E_{k,\unicode[STIX]{x1D712},\unicode[STIX]{x1D712}}$
lies in the minus subspace where
![]() $\unicode[STIX]{x1D712}$
is the non-trivial (odd) character of order 3.
$\unicode[STIX]{x1D712}$
is the non-trivial (odd) character of order 3.
Lemma A.15. If
![]() $\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Eisen
$\mathfrak{m}\subseteq \mathbb{T}$
satisfies (Eisen
![]() $^{+}$
), for
$^{+}$
), for
![]() $k\geqslant 2$
,
$k\geqslant 2$
,
![]() $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
, we have
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
, we have
and
as Hecke modules.
Proof. The lemma follows immediately from [Reference BellaïcheBel12, Proposition 3.15]. ◻
Theorem A.16. Let
![]() $\mathfrak{m}$
be a maximal ideal of
$\mathfrak{m}$
be a maximal ideal of
![]() $\mathbb{T}$
satisfying (Eisen
$\mathbb{T}$
satisfying (Eisen
![]() $^{+}$
). The following statements are equivalent:
$^{+}$
). The following statements are equivalent:
(1)
 $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}}),$
is a free
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}}),$
is a free
 $\mathbb{T}_{\mathfrak{m}}$
-module of rank
$\mathbb{T}_{\mathfrak{m}}$
-module of rank
 $1$
;
$1$
;(2)
 $\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}[\overline{\mathfrak{m}}_{k}]=1$
for all
$\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}[\overline{\mathfrak{m}}_{k}]=1$
for all
 $k\geqslant 2$
,
$k\geqslant 2$
,
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
;
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
;(3)
 $\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}[\overline{\mathfrak{m}}_{k}]=1$
for some
$\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{+}[\overline{\mathfrak{m}}_{k}]=1$
for some
 $k\geqslant 2$
,
$k\geqslant 2$
,
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
Proof. Lemma A.13 gives that (1) implies (2). The implication (2) implies (3) is clear. So we just need to show that (3) implies (1). To this end, by Lemma A.13 and Nakayama’s lemma, (3) implies that
![]() $Y^{+}:=\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}})$
is a cyclic
$Y^{+}:=\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{+},\tilde{\unicode[STIX]{x1D6EC}})$
is a cyclic
![]() $\mathbb{T}_{\mathfrak{m}}$
-module. We then have an exact sequence
$\mathbb{T}_{\mathfrak{m}}$
-module. We then have an exact sequence
and thus
as
![]() $Y^{+}$
is
$Y^{+}$
is
![]() $\tilde{\unicode[STIX]{x1D6EC}}$
-torsion-free. Note that if we show for a single
$\tilde{\unicode[STIX]{x1D6EC}}$
-torsion-free. Note that if we show for a single
![]() $k$
that
$k$
that
![]() $K/\mathfrak{p}_{k}K=0$
, then, by Nakayama’s lemma,
$K/\mathfrak{p}_{k}K=0$
, then, by Nakayama’s lemma,
![]() $K=0$
, and
$K=0$
, and
![]() $Y^{+}$
is free of rank 1 over
$Y^{+}$
is free of rank 1 over
![]() $\mathbb{T}$
.
$\mathbb{T}$
.
To this end, recall that
![]() $\mathbb{T}/\mathfrak{p}_{k}\mathbb{T}\cong \mathbb{T}_{k}$
which is a torsion-free
$\mathbb{T}/\mathfrak{p}_{k}\mathbb{T}\cong \mathbb{T}_{k}$
which is a torsion-free
![]() $\mathbb{Z}_{p}$
-module. Also,
$\mathbb{Z}_{p}$
-module. Also,
![]() $Y^{+}/\mathfrak{p}_{k}Y^{+}\cong \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{+},\mathbb{Z}_{p})$
by Lemma A.13 which is also torsion-free. Thus, it suffices to see that the
$Y^{+}/\mathfrak{p}_{k}Y^{+}\cong \operatorname{Hom}(H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{+},\mathbb{Z}_{p})$
by Lemma A.13 which is also torsion-free. Thus, it suffices to see that the
![]() $\mathbb{Z}_{p}$
-ranks of
$\mathbb{Z}_{p}$
-ranks of
![]() $\mathbb{T}_{k,\mathfrak{m}_{k}}$
and
$\mathbb{T}_{k,\mathfrak{m}_{k}}$
and
![]() $H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{+}$
match. But this follows immediately from Lemma A.15.◻
$H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{+}$
match. But this follows immediately from Lemma A.15.◻
Theorem A.17. Let
![]() $\mathfrak{m}^{c}$
be a maximal ideal of
$\mathfrak{m}^{c}$
be a maximal ideal of
![]() $\mathbb{T}^{c}$
satisfying (Eisen
$\mathbb{T}^{c}$
satisfying (Eisen
![]() $^{+}$
). The following statements are equivalent:
$^{+}$
). The following statements are equivalent:
(1)
 $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}^{c}}^{-},\tilde{\unicode[STIX]{x1D6EC}}),$
is a free
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}^{c}}^{-},\tilde{\unicode[STIX]{x1D6EC}}),$
is a free
 $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
-module of rank
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
-module of rank
 $1$
;
$1$
;(2)
 $\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{-}[\overline{\mathfrak{m}}_{k}]=1$
for all
$\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{-}[\overline{\mathfrak{m}}_{k}]=1$
for all
 $k\geqslant 2$
,
$k\geqslant 2$
,
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
;
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
;(3)
 $\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{-}[\overline{\mathfrak{m}}_{k}]=1$
for some
$\dim _{\mathbb{T}/\mathfrak{m}}H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee }\,\otimes \,\mathbb{F}_{p})^{-}[\overline{\mathfrak{m}}_{k}]=1$
for some
 $k\geqslant 2$
,
$k\geqslant 2$
,
 $k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
$k\equiv j(\mathfrak{m})\;(\text{mod}\,p-1)$
.
Proof. We first need to justify why
![]() $X^{-}:=H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{-}$
is even a module over
$X^{-}:=H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{-}$
is even a module over
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. To this end, take
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. To this end, take
![]() $h$
in the kernel of
$h$
in the kernel of
![]() $\mathbb{T}_{\mathfrak{m}}\rightarrow \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
, and we will show that
$\mathbb{T}_{\mathfrak{m}}\rightarrow \mathbb{T}_{\mathfrak{m}^{c}}^{c}$
, and we will show that
![]() $h$
kills
$h$
kills
![]() $X^{-}$
. For
$X^{-}$
. For
![]() $x\in X^{-}$
, consider the image of
$x\in X^{-}$
, consider the image of
![]() $hx$
in
$hx$
in
Further, by Lemma A.15, we have
![]() $H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{-}{\hookrightarrow}S_{k}(\unicode[STIX]{x1D6E4}_{0},\overline{\mathbb{Q}}_{p})$
. Thus, the image of
$H_{c}^{1}({\mathcal{P}}_{k-2}^{\vee })_{\mathfrak{m}_{k}}^{-}{\hookrightarrow}S_{k}(\unicode[STIX]{x1D6E4}_{0},\overline{\mathbb{Q}}_{p})$
. Thus, the image of
![]() $hx$
in
$hx$
in
![]() $X^{-}/\mathfrak{p}_{k}X^{-}$
vanishes. Since this is true for all
$X^{-}/\mathfrak{p}_{k}X^{-}$
vanishes. Since this is true for all
![]() $k\geqslant 2$
, we deduce that
$k\geqslant 2$
, we deduce that
![]() $hx=0$
and that
$hx=0$
and that
![]() $X^{-}$
is a
$X^{-}$
is a
![]() $\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
-module. The remainder of the proof follows exactly as in the proof of Theorem A.16.◻
$\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
-module. The remainder of the proof follows exactly as in the proof of Theorem A.16.◻
A.6 Two-variable
 $p$
-adic
$p$
-adic
 $L$
-functions
$L$
-functions
In this section, we assume that
so that we know that
![]() $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})$
is a free
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})$
is a free
![]() $\mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}$
-module, where
$\mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}$
-module, where
![]() $\mathbb{T}_{\mathfrak{m}}^{+}:=\mathbb{T}_{\mathfrak{m}}$
and
$\mathbb{T}_{\mathfrak{m}}^{+}:=\mathbb{T}_{\mathfrak{m}}$
and
![]() $\mathbb{T}_{\mathfrak{m}}^{-}:=\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. Moreover, we now fix an isomorphism
$\mathbb{T}_{\mathfrak{m}}^{-}:=\mathbb{T}_{\mathfrak{m}^{c}}^{c}$
. Moreover, we now fix an isomorphism
![]() $\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\cong \mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}$
.
$\operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})_{\mathfrak{m}}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\cong \mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}$
.
Consider the
![]() $\tilde{\unicode[STIX]{x1D6EC}}$
-linear map
$\tilde{\unicode[STIX]{x1D6EC}}$
-linear map
Let
![]() $L_{p}^{\unicode[STIX]{x1D700}}$
denote the corresponding element of
$L_{p}^{\unicode[STIX]{x1D700}}$
denote the corresponding element of
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},{\mathcal{M}}) & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\,\hat{\otimes }_{\tilde{\unicode[STIX]{x1D6EC}}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\,\hat{\otimes }_{\tilde{\unicode[STIX]{x1D6EC}}}\,(\tilde{\unicode[STIX]{x1D6EC}}\,\hat{\otimes }_{\mathbb{Z}_{p}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}]])\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\,\hat{\otimes }_{\mathbb{Z}_{p}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}]].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},{\mathcal{M}}) & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\,\hat{\otimes }_{\tilde{\unicode[STIX]{x1D6EC}}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}^{\times }\times \mathbb{Z}_{p}]]\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\,\hat{\otimes }_{\tilde{\unicode[STIX]{x1D6EC}}}\,(\tilde{\unicode[STIX]{x1D6EC}}\,\hat{\otimes }_{\mathbb{Z}_{p}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}]])\nonumber\\ \displaystyle & \cong & \displaystyle \operatorname{Hom}_{\tilde{\unicode[STIX]{x1D6EC}}}(H_{c}^{1}({\mathcal{M}})^{\operatorname{ord},\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D6EC}})\,\hat{\otimes }_{\mathbb{Z}_{p}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}]].\nonumber\end{eqnarray}$$
Here the second isomorphism arises from
where
![]() $\tilde{\unicode[STIX]{x1D6EC}}$
acts on
$\tilde{\unicode[STIX]{x1D6EC}}$
acts on
![]() $\tilde{\unicode[STIX]{x1D6EC}}\,\hat{\otimes }_{\mathbb{Z}_{p}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}]]$
simply by acting on the first coordinate.
$\tilde{\unicode[STIX]{x1D6EC}}\,\hat{\otimes }_{\mathbb{Z}_{p}}\,\mathbb{Z}_{p}[[\mathbb{Z}_{p}]]$
simply by acting on the first coordinate.
Let
![]() $L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m})$
denote the image of
$L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m})$
denote the image of
![]() $L_{p}^{\unicode[STIX]{x1D700}}$
in
$L_{p}^{\unicode[STIX]{x1D700}}$
in
For
![]() $\mathfrak{p}$
a height-one prime ideal of
$\mathfrak{p}$
a height-one prime ideal of
![]() $\mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}$
with
$\mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}$
with
![]() ${\mathcal{O}}:=\mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}/\mathfrak{p}$
, we write
${\mathcal{O}}:=\mathbb{T}_{\mathfrak{m}}^{\unicode[STIX]{x1D700}}/\mathfrak{p}$
, we write
![]() $\mathfrak{p}(L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m}))$
for the image of
$\mathfrak{p}(L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m}))$
for the image of
![]() $L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m})$
under the map
$L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m})$
under the map
We call
![]() $L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m})$
the two-variable
$L_{p}^{\unicode[STIX]{x1D700}}(\mathfrak{m})$
the two-variable
![]() $p$
-adic
$p$
-adic
![]() $L$
-function attached to
$L$
-function attached to
![]() $\mathfrak{m}$
as it has the following interpolation property.
$\mathfrak{m}$
as it has the following interpolation property.
Proposition A.18. Let
![]() $\mathfrak{m}$
be a maximal ideal of
$\mathfrak{m}$
be a maximal ideal of
![]() $\mathbb{T}$
, and let
$\mathbb{T}$
, and let
![]() $\mathfrak{p}_{f}$
be a classical height-one prime of
$\mathfrak{p}_{f}$
be a classical height-one prime of
![]() $\mathbb{T}$
corresponding to an eigenform
$\mathbb{T}$
corresponding to an eigenform
![]() $f$
. Let
$f$
. Let
![]() ${\mathcal{O}}$
denote the subring of
${\mathcal{O}}$
denote the subring of
![]() $\overline{\mathbb{Q}}_{p}$
generated by the Hecke eigenvalues of
$\overline{\mathbb{Q}}_{p}$
generated by the Hecke eigenvalues of
![]() $f$
. Then
$f$
. Then
as
![]() ${\mathcal{O}}$
-valued measures on
${\mathcal{O}}$
-valued measures on
![]() $\mathbb{Z}_{p}^{\times }$
(for some choice of canonical period
$\mathbb{Z}_{p}^{\times }$
(for some choice of canonical period
![]() $\unicode[STIX]{x1D6FA}_{f}^{\unicode[STIX]{x1D700}}$
).
$\unicode[STIX]{x1D6FA}_{f}^{\unicode[STIX]{x1D700}}$
).
Proof. Given the control theorems proven in this appendix, the proof of this theorem is just a diagram chase. ◻