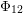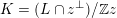1 Introduction
The singular theta correspondence (see [Reference BorcherdsBor98] and also [Reference BruinierBru02]) is a map from modular forms for the Weil representation of
![]() $\text{SL}_{2}(\mathbb{Z})$
to automorphic forms on orthogonal groups. More precisely, let
$\text{SL}_{2}(\mathbb{Z})$
to automorphic forms on orthogonal groups. More precisely, let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $n>2$
and even with discriminant form
$n>2$
and even with discriminant form
![]() $D$
and
$D$
and
![]() $F$
a modular form for the Weil representation of
$F$
a modular form for the Weil representation of
![]() $\text{SL}_{2}(\mathbb{Z})$
on
$\text{SL}_{2}(\mathbb{Z})$
on
![]() $\mathbb{C}[D]$
of weight
$\mathbb{C}[D]$
of weight
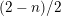 $(2-n)/2$
, which is holomorphic on the upper halfplane and has integral principal part. Then Borcherds associates an automorphic form
$(2-n)/2$
, which is holomorphic on the upper halfplane and has integral principal part. Then Borcherds associates an automorphic form
![]() $\unicode[STIX]{x1D6F9}(F)$
of weight
$\unicode[STIX]{x1D6F9}(F)$
of weight
![]() $c_{0}(0)/2$
for
$c_{0}(0)/2$
for
![]() $O(L)$
to
$O(L)$
to
![]() $F$
where
$F$
where
![]() $c_{0}(0)$
denotes the constant coefficient in the Fourier expansion of
$c_{0}(0)$
denotes the constant coefficient in the Fourier expansion of
![]() $F_{0}$
. The function
$F_{0}$
. The function
![]() $\unicode[STIX]{x1D6F9}(F)$
has nice product expansions at the rational
$\unicode[STIX]{x1D6F9}(F)$
has nice product expansions at the rational
![]() $0$
-dimensional cusps and is called the automorphic product associated to
$0$
-dimensional cusps and is called the automorphic product associated to
![]() $L$
and
$L$
and
![]() $F$
. The divisor of
$F$
. The divisor of
![]() $\unicode[STIX]{x1D6F9}(F)$
is a linear combination of rational quadratic divisors whose orders are determined by the principal part of
$\unicode[STIX]{x1D6F9}(F)$
is a linear combination of rational quadratic divisors whose orders are determined by the principal part of
![]() $F$
. Bruinier [Reference BruinierBru14] has shown that if
$F$
. Bruinier [Reference BruinierBru14] has shown that if
![]() $L$
splits two hyperbolic planes, then every automorphic form for
$L$
splits two hyperbolic planes, then every automorphic form for
![]() $O(L)$
whose divisor is a linear combination of rational quadratic divisors is an automorphic product.
$O(L)$
whose divisor is a linear combination of rational quadratic divisors is an automorphic product.
The smallest possible weight of a non-constant holomorphic automorphic form on
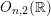 $O_{n,2}(\mathbb{R})$
is given by
$O_{n,2}(\mathbb{R})$
is given by
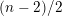 $(n-2)/2$
. Forms of this so-called singular weight are particularly interesting because their Fourier coefficients are supported only on isotropic vectors. Holomorphic automorphic products of singular weight seem to be very rare. The few known examples are all related to infinite-dimensional Lie superalgebras, i.e. given by the denominator functions of generalised Kac–Moody superalgebras. One of the main open problems in the theory of automorphic forms on orthogonal groups is to classify holomorphic automorphic products of singular weight [Reference BorcherdsBor95]. In this paper, we prove some new results in this direction.
$(n-2)/2$
. Forms of this so-called singular weight are particularly interesting because their Fourier coefficients are supported only on isotropic vectors. Holomorphic automorphic products of singular weight seem to be very rare. The few known examples are all related to infinite-dimensional Lie superalgebras, i.e. given by the denominator functions of generalised Kac–Moody superalgebras. One of the main open problems in the theory of automorphic forms on orthogonal groups is to classify holomorphic automorphic products of singular weight [Reference BorcherdsBor95]. In this paper, we prove some new results in this direction.
The simplest holomorphic automorphic product of singular weight is the function
![]() $\unicode[STIX]{x1D6F7}_{12}$
. It is the theta lift of the inverse of the Dedekind function
$\unicode[STIX]{x1D6F7}_{12}$
. It is the theta lift of the inverse of the Dedekind function
![]() $\unicode[STIX]{x1D6E5}$
on the unimodular lattice
$\unicode[STIX]{x1D6E5}$
on the unimodular lattice
![]() $\mathit{II}_{26,2}$
. The product expansion of
$\mathit{II}_{26,2}$
. The product expansion of
![]() $\unicode[STIX]{x1D6F7}_{12}$
at a cusp is given by
$\unicode[STIX]{x1D6F7}_{12}$
at a cusp is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{12}(Z)=e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \mathit{II}_{25,1}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[1/\unicode[STIX]{x1D6E5}](-\unicode[STIX]{x1D6FC}^{2}/2)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{12}(Z)=e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \mathit{II}_{25,1}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[1/\unicode[STIX]{x1D6E5}](-\unicode[STIX]{x1D6FC}^{2}/2)},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70C}$
is a primitive norm
$\unicode[STIX]{x1D70C}$
is a primitive norm
![]() $0$
vector in
$0$
vector in
![]() $\mathit{II}_{25,1}$
corresponding to the Leech lattice. The function
$\mathit{II}_{25,1}$
corresponding to the Leech lattice. The function
![]() $\unicode[STIX]{x1D6F7}_{12}$
is holomorphic and has zeros of order
$\unicode[STIX]{x1D6F7}_{12}$
is holomorphic and has zeros of order
![]() $1$
orthogonal to the roots of
$1$
orthogonal to the roots of
![]() $\mathit{II}_{26,2}$
. Since
$\mathit{II}_{26,2}$
. Since
![]() $\unicode[STIX]{x1D6F7}_{12}$
has weight 12, i.e. singular weight, its Fourier coefficients are supported only on norm
$\unicode[STIX]{x1D6F7}_{12}$
has weight 12, i.e. singular weight, its Fourier coefficients are supported only on norm
![]() $0$
vectors. This can be used to show that it has the sum expansion
$0$
vectors. This can be used to show that it has the sum expansion
 $$\begin{eqnarray}\displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \mathit{II}_{25,1}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[1/\unicode[STIX]{x1D6E5}](-\unicode[STIX]{x1D6FC}^{2}/2)}=\mathop{\sum }_{w\in W}\det (w)e((w\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{n=1}^{\infty }(1-e((nw\unicode[STIX]{x1D70C},Z)))^{24}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \mathit{II}_{25,1}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[1/\unicode[STIX]{x1D6E5}](-\unicode[STIX]{x1D6FC}^{2}/2)}=\mathop{\sum }_{w\in W}\det (w)e((w\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{n=1}^{\infty }(1-e((nw\unicode[STIX]{x1D70C},Z)))^{24}. & & \displaystyle \nonumber\end{eqnarray}$$
Here
![]() $W$
is the reflection group of
$W$
is the reflection group of
![]() $\mathit{II}_{25,1}$
.
$\mathit{II}_{25,1}$
.
This identity is the denominator identity of an infinite-dimensional Lie algebra describing the physical states of a bosonic string moving on the torus
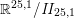 $\mathbb{R}^{25,1}/\mathit{II}_{25,1}$
called the fake monster algebra [Reference BorcherdsBor90].
$\mathbb{R}^{25,1}/\mathit{II}_{25,1}$
called the fake monster algebra [Reference BorcherdsBor90].
The function
![]() $\unicode[STIX]{x1D6F7}_{12}$
also has some nice geometric applications. In [Reference Gritsenko, Hulek and SankaranGHS07], the authors show that the moduli space of polarised K3 surfaces of degree
$\unicode[STIX]{x1D6F7}_{12}$
also has some nice geometric applications. In [Reference Gritsenko, Hulek and SankaranGHS07], the authors show that the moduli space of polarised K3 surfaces of degree
![]() $d$
is of general type for
$d$
is of general type for
![]() $d>61$
using quasi-pullbacks of
$d>61$
using quasi-pullbacks of
![]() $\unicode[STIX]{x1D6F7}_{12}$
.
$\unicode[STIX]{x1D6F7}_{12}$
.
The first main result of this paper is the following characterisation (see Theorem 4.5).
The function
![]() $\unicode[STIX]{x1D6F7}_{12}$
is the only holomorphic automorphic product of singular weight on a unimodular lattice.
$\unicode[STIX]{x1D6F7}_{12}$
is the only holomorphic automorphic product of singular weight on a unimodular lattice.
Next, we consider lattices of prime level. We show that for a given discriminant form
![]() $D$
of prime level, the number of lattices with dual quotient isomorphic to
$D$
of prime level, the number of lattices with dual quotient isomorphic to
![]() $D$
carrying a holomorphic automorphic product of singular weight is finite and we give an explicit bound for the signature. The precise statement is as follows (see Theorems 5.7 and 5.12).
$D$
carrying a holomorphic automorphic product of singular weight is finite and we give an explicit bound for the signature. The precise statement is as follows (see Theorems 5.7 and 5.12).
Let
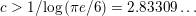 $c>1/\text{log}\,(\unicode[STIX]{x1D70B}e/6)=2.83309\ldots \,$
. Then there exists a constant
$c>1/\text{log}\,(\unicode[STIX]{x1D70B}e/6)=2.83309\ldots \,$
. Then there exists a constant
![]() $d$
with the following property: let
$d$
with the following property: let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $n>2$
and prime level splitting a hyperbolic plane
$n>2$
and prime level splitting a hyperbolic plane
![]() $\mathit{II}_{1,1}$
. Let
$\mathit{II}_{1,1}$
. Let
![]() $D$
be the discriminant form of
$D$
be the discriminant form of
![]() $L$
. Suppose
$L$
. Suppose
![]() $L$
carries a holomorphic automorphic product of singular weight. Then
$L$
carries a holomorphic automorphic product of singular weight. Then
 $$\begin{eqnarray}n\leqslant c\log |D|+d.\end{eqnarray}$$
$$\begin{eqnarray}n\leqslant c\log |D|+d.\end{eqnarray}$$
The constant
![]() $d$
does not depend on the level, but only on
$d$
does not depend on the level, but only on
![]() $c$
. The proof is constructive. We can take, for example,
$c$
. The proof is constructive. We can take, for example,
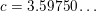 $c=3.59750\ldots$
and
$c=3.59750\ldots$
and
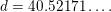 $d=40.52171\ldots .$
Given a discriminant form
$d=40.52171\ldots .$
Given a discriminant form
![]() $D$
of prime level, the theorem allows us to determine all holomorphic automorphic products of singular weight on lattices with dual quotient isomorphic to
$D$
of prime level, the theorem allows us to determine all holomorphic automorphic products of singular weight on lattices with dual quotient isomorphic to
![]() $D$
by working out the obstruction theory in the possible signatures.
$D$
by working out the obstruction theory in the possible signatures.
We sketch the proofs of the first two main results. To obtain a restriction on the signature in the prime level case, we pair the vector valued modular form
![]() $F$
associated to the automorphic product
$F$
associated to the automorphic product
![]() $\unicode[STIX]{x1D6F9}$
with an Eisenstein series for the dual Weil representation. We obtain a relation between the signature and a sum over the principal part of
$\unicode[STIX]{x1D6F9}$
with an Eisenstein series for the dual Weil representation. We obtain a relation between the signature and a sum over the principal part of
![]() $F$
. We expand this sum in the degrees of the divisors which are non-negative by the holomorphicity of
$F$
. We expand this sum in the degrees of the divisors which are non-negative by the holomorphicity of
![]() $\unicode[STIX]{x1D6F9}$
. Then we apply the Riemann–Roch theorem to
$\unicode[STIX]{x1D6F9}$
. Then we apply the Riemann–Roch theorem to
![]() $F$
to derive the bound. In the unimodular case, a similar argument gives the uniqueness.
$F$
to derive the bound. In the unimodular case, a similar argument gives the uniqueness.
The expansion of an automorphic form on
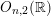 $O_{n,2}(\mathbb{R})$
at a cusp is sometimes the denominator function of an infinite-dimensional Lie superalgebra. In that case, the divisor of the automorphic form is locally the sum of rational quadratic divisors
$O_{n,2}(\mathbb{R})$
at a cusp is sometimes the denominator function of an infinite-dimensional Lie superalgebra. In that case, the divisor of the automorphic form is locally the sum of rational quadratic divisors
![]() $\unicode[STIX]{x1D6FC}^{\bot }$
of order
$\unicode[STIX]{x1D6FC}^{\bot }$
of order
![]() $1$
where
$1$
where
![]() $\unicode[STIX]{x1D6FC}$
is a root. An automorphic form on
$\unicode[STIX]{x1D6FC}$
is a root. An automorphic form on
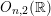 $O_{n,2}(\mathbb{R})$
is called reflective if this condition holds globally (see also [Reference BorcherdsBor99, Reference Gritsenko and NikulinGN02]). So far, all known examples of holomorphic automorphic products of singular weight are reflective.
$O_{n,2}(\mathbb{R})$
is called reflective if this condition holds globally (see also [Reference BorcherdsBor99, Reference Gritsenko and NikulinGN02]). So far, all known examples of holomorphic automorphic products of singular weight are reflective.
In [Reference ScheithauerSch06], certain reflective automorphic products of singular weight on lattices of prime level are classified. The assumptions are that the underlying lattice
![]() $L$
does not have maximal
$L$
does not have maximal
![]() $p$
-rank and that all roots of a fixed norm give zeros, i.e. the corresponding vector valued modular form is invariant under the orthogonal group of the discriminant form of
$p$
-rank and that all roots of a fixed norm give zeros, i.e. the corresponding vector valued modular form is invariant under the orthogonal group of the discriminant form of
![]() $L$
. The second condition is quite restrictive. Surprisingly we find only three additional cases when we remove these assumptions. This is the third main result of this paper (see Theorem 6.28).
$L$
. The second condition is quite restrictive. Surprisingly we find only three additional cases when we remove these assumptions. This is the third main result of this paper (see Theorem 6.28).
Let
![]() $L$
be a lattice of prime level and signature
$L$
be a lattice of prime level and signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n>2$
and
$n>2$
and
![]() $\unicode[STIX]{x1D6F9}$
a reflective automorphic product of singular weight on
$\unicode[STIX]{x1D6F9}$
a reflective automorphic product of singular weight on
![]() $L$
. Then, as a function on the corresponding Hermitian symmetric domain,
$L$
. Then, as a function on the corresponding Hermitian symmetric domain,
![]() $\unicode[STIX]{x1D6F9}$
is the theta lift of one of the following modular forms.
$\unicode[STIX]{x1D6F9}$
is the theta lift of one of the following modular forms.

With three exceptions, all of these functions come from symmetric modular forms. At a suitable cusp
![]() $\unicode[STIX]{x1D6F9}$
is the twisted denominator function of the fake monster algebra by the indicated element in Conway’s group.
$\unicode[STIX]{x1D6F9}$
is the twisted denominator function of the fake monster algebra by the indicated element in Conway’s group.
Conversely, all the given modular forms lift to reflective automorphic products of singular weight on the respective lattices.
The cases not coming from symmetric modular forms are those corresponding to the elements of order
![]() $4$
and
$4$
and
![]() $9$
in Conway’s group.
$9$
in Conway’s group.
The sum expansion of the theta lift of
 $F_{(1/4)\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}},M^{+}}$
gives a new infinite product identity (see Proposition 6.23).
$F_{(1/4)\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}},M^{+}}$
gives a new infinite product identity (see Proposition 6.23).
The above result can be used to classify generalised Kac–Moody superalgebras whose denominator functions are reflective automorphic products of singular weight on lattices of prime level.
We describe the proof of the theorem. Reflective automorphic products of singular weight associated to symmetric forms can be classified by the Eisenstein condition [Reference ScheithauerSch06]. It turns out that in the non-symmetric case the Riemann–Roch theorem imposes strong restrictions (see Theorem 6.5). In the remaining cases we work out the obstruction theory and determine the possible reflective modular forms. Many of them lift to the same function leaving us with the above list.
The paper is organised as follows. In § 2, we summarise some results on modular forms for the Weil representation. Then we recall Borcherds’ singular theta correspondence and define reflective forms. In § 4, we prove that the only holomorphic automorphic product of singular weight on a unimodular lattice is the theta lift of
![]() $1/\unicode[STIX]{x1D6E5}$
on
$1/\unicode[STIX]{x1D6E5}$
on
![]() $\mathit{II}_{26,2}$
. Next, we show that holomorphic automorphic products of singular weight on lattices of prime level exist only in small signatures. Finally, we give a complete classification of reflective automorphic products of singular weight on lattices of prime level.
$\mathit{II}_{26,2}$
. Next, we show that holomorphic automorphic products of singular weight on lattices of prime level exist only in small signatures. Finally, we give a complete classification of reflective automorphic products of singular weight on lattices of prime level.
2 Modular forms for the Weil representation
In this section, we recall some results on modular forms for the Weil representation from [Reference ScheithauerSch09, Reference ScheithauerSch15].
Let
![]() $D$
be a discriminant form with quadratic form
$D$
be a discriminant form with quadratic form
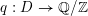 $q:D\rightarrow \mathbb{Q}/\mathbb{Z}$
and associated bilinear form
$q:D\rightarrow \mathbb{Q}/\mathbb{Z}$
and associated bilinear form
![]() $(\,,\,)$
(see [Reference ScheithauerSch09, Reference NikulinNik79] and [Reference Conway and SloaneCS99, ch. 15]). We assume that
$(\,,\,)$
(see [Reference ScheithauerSch09, Reference NikulinNik79] and [Reference Conway and SloaneCS99, ch. 15]). We assume that
![]() $D$
has even signature. The level of
$D$
has even signature. The level of
![]() $D$
is the smallest positive integer
$D$
is the smallest positive integer
![]() $N$
such that
$N$
such that
 $Nq(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
for all
$Nq(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
for all
![]() $\unicode[STIX]{x1D6FE}\in D$
. We define a scalar product on the group ring
$\unicode[STIX]{x1D6FE}\in D$
. We define a scalar product on the group ring
![]() $\mathbb{C}[D]$
which is linear in the first and antilinear in the second variable by
$\mathbb{C}[D]$
which is linear in the first and antilinear in the second variable by
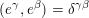 $(e^{\unicode[STIX]{x1D6FE}},e^{\unicode[STIX]{x1D6FD}})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}$
. Then there is a unitary action of the group
$(e^{\unicode[STIX]{x1D6FE}},e^{\unicode[STIX]{x1D6FD}})=\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}}$
. Then there is a unitary action of the group
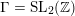 $\unicode[STIX]{x1D6E4}=\text{SL}_{2}(\mathbb{Z})$
on
$\unicode[STIX]{x1D6E4}=\text{SL}_{2}(\mathbb{Z})$
on
![]() $\mathbb{C}[D]$
satisfying
$\mathbb{C}[D]$
satisfying
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{D}(T)e^{\unicode[STIX]{x1D6FE}} & = & \displaystyle e(-q(\unicode[STIX]{x1D6FE}))e^{\unicode[STIX]{x1D6FE}},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{D}(S)e^{\unicode[STIX]{x1D6FE}} & = & \displaystyle \frac{e(\operatorname{sign}(D)/8)}{\sqrt{|D|}}\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in D}e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}))e^{\unicode[STIX]{x1D6FD}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{D}(T)e^{\unicode[STIX]{x1D6FE}} & = & \displaystyle e(-q(\unicode[STIX]{x1D6FE}))e^{\unicode[STIX]{x1D6FE}},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{D}(S)e^{\unicode[STIX]{x1D6FE}} & = & \displaystyle \frac{e(\operatorname{sign}(D)/8)}{\sqrt{|D|}}\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in D}e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}))e^{\unicode[STIX]{x1D6FD}},\nonumber\end{eqnarray}$$
where
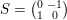 $S=\big(\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!\big)$
and
$S=\big(\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!\big)$
and
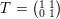 $T=\big(\!\begin{smallmatrix}1 & 1\\ 0 & 1\end{smallmatrix}\!\big)$
are the standard generators of
$T=\big(\!\begin{smallmatrix}1 & 1\\ 0 & 1\end{smallmatrix}\!\big)$
are the standard generators of
![]() $\unicode[STIX]{x1D6E4}$
. This representation is called the Weil representation of
$\unicode[STIX]{x1D6E4}$
. This representation is called the Weil representation of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\mathbb{C}[D]$
. It commutes with the orthogonal group
$\mathbb{C}[D]$
. It commutes with the orthogonal group
![]() $O(D)$
of
$O(D)$
of
![]() $D$
. Suppose the level of
$D$
. Suppose the level of
![]() $D$
divides
$D$
divides
![]() $N$
and let
$N$
and let
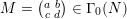 $M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}_{0}(N)$
. Then
$M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}_{0}(N)$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{D}(M)e^{\unicode[STIX]{x1D6FE}}=\biggl(\frac{a}{|D|}\biggr)e((a-1)\operatorname{oddity}(D)/8)e(-bdq(\unicode[STIX]{x1D6FE}))e^{d\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{D}(M)e^{\unicode[STIX]{x1D6FE}}=\biggl(\frac{a}{|D|}\biggr)e((a-1)\operatorname{oddity}(D)/8)e(-bdq(\unicode[STIX]{x1D6FE}))e^{d\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
A general formula for the action of
![]() $\unicode[STIX]{x1D70C}_{D}$
is given in [Reference ScheithauerSch09, Theorem 4.7].
$\unicode[STIX]{x1D70C}_{D}$
is given in [Reference ScheithauerSch09, Theorem 4.7].
Let
 $$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
be a holomorphic function on the complex upper halfplane
![]() ${\mathcal{H}}$
with values in
${\mathcal{H}}$
with values in
![]() $\mathbb{C}[D]$
and
$\mathbb{C}[D]$
and
![]() $k$
an integer. Then
$k$
an integer. Then
![]() $F$
is a modular form for
$F$
is a modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
of weight
$\unicode[STIX]{x1D70C}_{D}$
of weight
![]() $k$
if
$k$
if
 $$\begin{eqnarray}F(M\unicode[STIX]{x1D70F})=(c\unicode[STIX]{x1D70F}+d)^{k}\unicode[STIX]{x1D70C}_{D}(M)F(\unicode[STIX]{x1D70F})\end{eqnarray}$$
$$\begin{eqnarray}F(M\unicode[STIX]{x1D70F})=(c\unicode[STIX]{x1D70F}+d)^{k}\unicode[STIX]{x1D70C}_{D}(M)F(\unicode[STIX]{x1D70F})\end{eqnarray}$$
for all
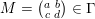 $M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}$
and
$M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}$
and
![]() $F$
is meromorphic at
$F$
is meromorphic at
![]() $\infty$
. We say that
$\infty$
. We say that
![]() $F$
is symmetric if it is invariant under the action of
$F$
is symmetric if it is invariant under the action of
![]() $O(D)$
.
$O(D)$
.
Classical examples of modular forms for the dual Weil representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
are theta functions. Let
$\overline{\unicode[STIX]{x1D70C}}_{D}$
are theta functions. Let
![]() $L$
be a positive-definite even lattice of even rank
$L$
be a positive-definite even lattice of even rank
![]() $2k$
with discriminant form
$2k$
with discriminant form
![]() $D$
. For
$D$
. For
![]() $\unicode[STIX]{x1D6FE}\in D$
define
$\unicode[STIX]{x1D6FE}\in D$
define
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FE}+L}q^{\unicode[STIX]{x1D6FC}^{2}/2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6FE}+L}q^{\unicode[STIX]{x1D6FC}^{2}/2},\end{eqnarray}$$
where
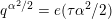 $q^{\unicode[STIX]{x1D6FC}^{2}/2}=e(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FC}^{2}/2)$
. Then
$q^{\unicode[STIX]{x1D6FC}^{2}/2}=e(\unicode[STIX]{x1D70F}\unicode[STIX]{x1D6FC}^{2}/2)$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D703}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
is a modular form for the dual Weil representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
of weight
$\overline{\unicode[STIX]{x1D70C}}_{D}$
of weight
![]() $k$
which is holomorphic at
$k$
which is holomorphic at
![]() $\infty$
.
$\infty$
.
Let
![]() $f$
be a complex function on
$f$
be a complex function on
![]() ${\mathcal{H}}$
and
${\mathcal{H}}$
and
![]() $k$
an integer. For
$k$
an integer. For
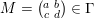 $M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}$
we define the function
$M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}$
we define the function
![]() $f|_{k,M}$
on
$f|_{k,M}$
on
![]() ${\mathcal{H}}$
by
${\mathcal{H}}$
by
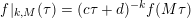 $f|_{k,M}(\unicode[STIX]{x1D70F})=(c\unicode[STIX]{x1D70F}+d)^{-k}f(M\unicode[STIX]{x1D70F})$
.
$f|_{k,M}(\unicode[STIX]{x1D70F})=(c\unicode[STIX]{x1D70F}+d)^{-k}f(M\unicode[STIX]{x1D70F})$
.
We can easily construct modular forms for the Weil representation by symmetrising scalar-valued modular forms on congruence subgroups (see [Reference ScheithauerSch15, Theorem 3.1]).
Theorem 2.1. Let
![]() $D$
be a discriminant form of even signature and level dividing
$D$
be a discriminant form of even signature and level dividing
![]() $N$
.
$N$
.
Let
![]() $f$
be a scalar-valued modular form on
$f$
be a scalar-valued modular form on
![]() $\unicode[STIX]{x1D6E4}_{0}(N)$
of weight
$\unicode[STIX]{x1D6E4}_{0}(N)$
of weight
![]() $k$
and character
$k$
and character
![]() $\unicode[STIX]{x1D712}_{D}$
and
$\unicode[STIX]{x1D712}_{D}$
and
![]() $H$
an isotropic subset of
$H$
an isotropic subset of
![]() $D$
that is invariant under
$D$
that is invariant under
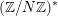 $(\mathbb{Z}/N\mathbb{Z})^{\ast }$
. Then
$(\mathbb{Z}/N\mathbb{Z})^{\ast }$
. Then
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D6E4}_{0}(N),f,H}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{0}(N)\setminus \unicode[STIX]{x1D6E4}}\,\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H}f|_{k,M}\unicode[STIX]{x1D70C}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6E4}_{0}(N),f,H}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{0}(N)\setminus \unicode[STIX]{x1D6E4}}\,\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H}f|_{k,M}\unicode[STIX]{x1D70C}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
is a modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
of weight
$\unicode[STIX]{x1D70C}_{D}$
of weight
![]() $k$
.
$k$
.
Let
![]() $\unicode[STIX]{x1D6FE}\in D$
and
$\unicode[STIX]{x1D6FE}\in D$
and
![]() $f$
a scalar-valued modular form on
$f$
a scalar-valued modular form on
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
of weight
$\unicode[STIX]{x1D6E4}_{1}(N)$
of weight
![]() $k$
and character
$k$
and character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}$
. Then
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE}}$
. Then
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D6E4}_{1}(N),f,\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{1}(N)\setminus \unicode[STIX]{x1D6E4}}f|_{k,M}\unicode[STIX]{x1D70C}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6E4}_{1}(N),f,\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{1}(N)\setminus \unicode[STIX]{x1D6E4}}f|_{k,M}\unicode[STIX]{x1D70C}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
is a modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
of weight
$\unicode[STIX]{x1D70C}_{D}$
of weight
![]() $k$
.
$k$
.
Let
![]() $f$
be a scalar-valued modular form on
$f$
be a scalar-valued modular form on
![]() $\unicode[STIX]{x1D6E4}(N)$
of weight
$\unicode[STIX]{x1D6E4}(N)$
of weight
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FE}\in D$
. Then
$\unicode[STIX]{x1D6FE}\in D$
. Then
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D6E4}(N),f,\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}(N)\setminus \unicode[STIX]{x1D6E4}}f|_{k,M}\unicode[STIX]{x1D70C}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6E4}(N),f,\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}(N)\setminus \unicode[STIX]{x1D6E4}}f|_{k,M}\unicode[STIX]{x1D70C}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
is a modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
of weight
$\unicode[STIX]{x1D70C}_{D}$
of weight
![]() $k$
.
$k$
.
Every modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
can be written as a linear combination of liftings from
$\unicode[STIX]{x1D70C}_{D}$
can be written as a linear combination of liftings from
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
or
$\unicode[STIX]{x1D6E4}_{1}(N)$
or
![]() $\unicode[STIX]{x1D6E4}(N)$
.
$\unicode[STIX]{x1D6E4}(N)$
.
Explicit formulas for these function are given in [Reference ScheithauerSch15, § 3].
We also have the following proposition.
Proposition 2.2. Let
![]() $D$
be a discriminant form of even signature and
$D$
be a discriminant form of even signature and
![]() $H$
an isotropic subgroup of
$H$
an isotropic subgroup of
![]() $D$
. Then
$D$
. Then
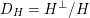 $D_{H}=H^{\bot }/H$
is a discriminant form of the same signature as
$D_{H}=H^{\bot }/H$
is a discriminant form of the same signature as
![]() $D$
.
$D$
.
Let
![]() $F_{D}$
be a modular form for
$F_{D}$
be a modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
. For
$\unicode[STIX]{x1D70C}_{D}$
. For
 $\unicode[STIX]{x1D6FE}\in H^{\bot }$
define
$\unicode[STIX]{x1D6FE}\in H^{\bot }$
define
 $$\begin{eqnarray}F_{D_{H},\unicode[STIX]{x1D6FE}+H}=\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6FE}+H}F_{D,\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{D_{H},\unicode[STIX]{x1D6FE}+H}=\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \unicode[STIX]{x1D6FE}+H}F_{D,\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
Then
![]() $F_{D_{H}}$
is a modular form for
$F_{D_{H}}$
is a modular form for
![]() $\unicode[STIX]{x1D70C}_{D_{H}}$
.
$\unicode[STIX]{x1D70C}_{D_{H}}$
.
Conversely, let
![]() $F_{D_{H}}$
be a modular form for the Weil representation of
$F_{D_{H}}$
be a modular form for the Weil representation of
![]() $D_{H}$
. Define
$D_{H}$
. Define
 $$\begin{eqnarray}F_{D,\unicode[STIX]{x1D6FE}}=F_{D_{H},\unicode[STIX]{x1D6FE}+H}\end{eqnarray}$$
$$\begin{eqnarray}F_{D,\unicode[STIX]{x1D6FE}}=F_{D_{H},\unicode[STIX]{x1D6FE}+H}\end{eqnarray}$$
if
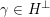 $\unicode[STIX]{x1D6FE}\in H^{\bot }$
and
$\unicode[STIX]{x1D6FE}\in H^{\bot }$
and
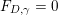 $F_{D,\unicode[STIX]{x1D6FE}}=0$
otherwise. Then
$F_{D,\unicode[STIX]{x1D6FE}}=0$
otherwise. Then
![]() $F_{D}$
is a modular form for
$F_{D}$
is a modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
.
$\unicode[STIX]{x1D70C}_{D}$
.
We will need the Eisenstein series for the dual Weil representation. They can be constructed as follows. Let
![]() $D$
be a discriminant form of even signature and level dividing
$D$
be a discriminant form of even signature and level dividing
![]() $N$
. Let
$N$
. Let
 $\unicode[STIX]{x1D6E4}_{\infty }^{+}=\{T^{n}\mid n\in \mathbb{Z}\}$
. Then
$\unicode[STIX]{x1D6E4}_{\infty }^{+}=\{T^{n}\mid n\in \mathbb{Z}\}$
. Then
 $$\begin{eqnarray}E_{k}=\frac{1}{2}\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{\infty }^{+}\setminus \unicode[STIX]{x1D6E4}_{1}(N)}1|_{k,M}\end{eqnarray}$$
$$\begin{eqnarray}E_{k}=\frac{1}{2}\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{\infty }^{+}\setminus \unicode[STIX]{x1D6E4}_{1}(N)}1|_{k,M}\end{eqnarray}$$
is an Eisenstein series for
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
of weight
$\unicode[STIX]{x1D6E4}_{1}(N)$
of weight
![]() $k$
. Let
$k$
. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be isotropic. Then
$\unicode[STIX]{x1D6FE}\in D$
be isotropic. Then
 $$\begin{eqnarray}E_{\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{1}(N)\setminus \unicode[STIX]{x1D6E4}}E_{k}|_{k,M}\overline{\unicode[STIX]{x1D70C}}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}E_{\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{1}(N)\setminus \unicode[STIX]{x1D6E4}}E_{k}|_{k,M}\overline{\unicode[STIX]{x1D70C}}_{D}(M^{-1})e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
is an Eisenstein series for the dual Weil representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
. It is easy to see that
$\overline{\unicode[STIX]{x1D70C}}_{D}$
. It is easy to see that
![]() $E_{\unicode[STIX]{x1D6FE}}$
gives the Eisenstein series defined in [Reference BruinierBru02]. For
$E_{\unicode[STIX]{x1D6FE}}$
gives the Eisenstein series defined in [Reference BruinierBru02]. For
![]() $\unicode[STIX]{x1D6FE}=0$
we have
$\unicode[STIX]{x1D6FE}=0$
we have
 $$\begin{eqnarray}E_{0}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{0}(N)\setminus \unicode[STIX]{x1D6E4}}E_{k,\unicode[STIX]{x1D712}}|_{k,M}\overline{\unicode[STIX]{x1D70C}}_{D}(M^{-1})e^{0},\end{eqnarray}$$
$$\begin{eqnarray}E_{0}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{0}(N)\setminus \unicode[STIX]{x1D6E4}}E_{k,\unicode[STIX]{x1D712}}|_{k,M}\overline{\unicode[STIX]{x1D70C}}_{D}(M^{-1})e^{0},\end{eqnarray}$$
where
 $$\begin{eqnarray}E_{k,\unicode[STIX]{x1D712}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{1}(N)\setminus \unicode[STIX]{x1D6E4}_{0}(N)}\unicode[STIX]{x1D712}(M)E_{k}|_{k,M}\end{eqnarray}$$
$$\begin{eqnarray}E_{k,\unicode[STIX]{x1D712}}=\mathop{\sum }_{M\in \unicode[STIX]{x1D6E4}_{1}(N)\setminus \unicode[STIX]{x1D6E4}_{0}(N)}\unicode[STIX]{x1D712}(M)E_{k}|_{k,M}\end{eqnarray}$$
is an Eisenstein series for
![]() $\unicode[STIX]{x1D6E4}_{0}(N)$
of weight
$\unicode[STIX]{x1D6E4}_{0}(N)$
of weight
![]() $k$
and character
$k$
and character
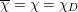 $\overline{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{D}$
. We will write
$\overline{\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{D}$
. We will write
![]() $E$
for the Eisenstein series
$E$
for the Eisenstein series
![]() $E_{0}$
.
$E_{0}$
.
The dimension of the space of holomorphic modular forms for the Weil representation can be worked out using the Riemann–Roch theorem [Reference FreitagFre12] or the Selberg trace formula [Reference Eholzer and SkoruppaES95, Reference BorcherdsBor00].
The residue theorem implies the following result.
Proposition 2.3. Let
![]() $D$
be a discriminant form of even signature and
$D$
be a discriminant form of even signature and
![]() $F$
a modular form for
$F$
a modular form for
![]() $\unicode[STIX]{x1D70C}_{D}$
of weight
$\unicode[STIX]{x1D70C}_{D}$
of weight
![]() $2-k$
with
$2-k$
with
![]() $k\geqslant 3$
. Let
$k\geqslant 3$
. Let
![]() $G$
be a modular form for
$G$
be a modular form for
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
of weight
$\overline{\unicode[STIX]{x1D70C}}_{D}$
of weight
![]() $k$
. Then the constant coefficient of
$k$
. Then the constant coefficient of
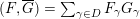 $(F,\overline{G})=\sum _{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}G_{\unicode[STIX]{x1D6FE}}$
vanishes.
$(F,\overline{G})=\sum _{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}G_{\unicode[STIX]{x1D6FE}}$
vanishes.
More generally we have (see [Reference BorcherdsBor99, Theorem 3.1] and [Reference BruinierBru02, Theorem 1.17]) the following theorem.
Theorem 2.4. Let
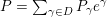 $P=\sum _{\unicode[STIX]{x1D6FE}\in D}P_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}$
, where
$P=\sum _{\unicode[STIX]{x1D6FE}\in D}P_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}$
, where
 $$\begin{eqnarray}P_{\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{\substack{ n\in \mathbb{Z}-q(\unicode[STIX]{x1D6FE}) \\ n<0}}c_{\unicode[STIX]{x1D6FE}}(n)q^{n}\end{eqnarray}$$
$$\begin{eqnarray}P_{\unicode[STIX]{x1D6FE}}=\mathop{\sum }_{\substack{ n\in \mathbb{Z}-q(\unicode[STIX]{x1D6FE}) \\ n<0}}c_{\unicode[STIX]{x1D6FE}}(n)q^{n}\end{eqnarray}$$
is a finite Fourier polynomial with complex coefficients. Then
![]() $P$
is the principal part of a modular form of weight
$P$
is the principal part of a modular form of weight
![]() $2-k$
,
$2-k$
,
![]() $k\geqslant 3$
, for
$k\geqslant 3$
, for
![]() $\unicode[STIX]{x1D70C}_{D}$
if and only if the linear map
$\unicode[STIX]{x1D70C}_{D}$
if and only if the linear map
 $$\begin{eqnarray}\begin{array}{@{}cccl@{}}\unicode[STIX]{x1D719}_{P}: & S_{\overline{\unicode[STIX]{x1D70C}}_{D},k} & \longrightarrow & \mathbb{C}\\ & G & \longmapsto & \text{constant coefficient of }(P,\overline{G})\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cccl@{}}\unicode[STIX]{x1D719}_{P}: & S_{\overline{\unicode[STIX]{x1D70C}}_{D},k} & \longrightarrow & \mathbb{C}\\ & G & \longmapsto & \text{constant coefficient of }(P,\overline{G})\end{array}\end{eqnarray}$$
vanishes on
![]() $S_{\overline{\unicode[STIX]{x1D70C}}_{D},k}$
.
$S_{\overline{\unicode[STIX]{x1D70C}}_{D},k}$
.
We will use Theorem 2.1 to work out the obstruction spaces
![]() $S_{\overline{\unicode[STIX]{x1D70C}}_{D},k}$
in several cases in § 6.
$S_{\overline{\unicode[STIX]{x1D70C}}_{D},k}$
in several cases in § 6.
3 Automorphic products
We describe some properties of automorphic products [Reference BorcherdsBor98] and define reflective automorphic products.
Let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $n>2$
even,
$n>2$
even,
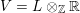 $V=L\otimes _{\mathbb{Z}}\mathbb{R}$
and
$V=L\otimes _{\mathbb{Z}}\mathbb{R}$
and
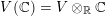 $V(\mathbb{C})=V\otimes _{\mathbb{R}}\mathbb{C}$
. Then
$V(\mathbb{C})=V\otimes _{\mathbb{R}}\mathbb{C}$
. Then
 $$\begin{eqnarray}{\mathcal{K}}=\{Z\in V(\mathbb{C})\mid (Z,Z)=0,(Z,\overline{Z})<0\}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}=\{Z\in V(\mathbb{C})\mid (Z,Z)=0,(Z,\overline{Z})<0\}\end{eqnarray}$$
is a complex manifold with two connected components that are exchanged by the map
![]() $Z\mapsto \overline{Z}$
. We choose one of the components and denote it by
$Z\mapsto \overline{Z}$
. We choose one of the components and denote it by
![]() ${\mathcal{H}}$
. There is a subgroup
${\mathcal{H}}$
. There is a subgroup
![]() $O(V)^{+}$
of index 2 in the orthogonal group
$O(V)^{+}$
of index 2 in the orthogonal group
![]() $O(V)$
, which preserves the two connected components of
$O(V)$
, which preserves the two connected components of
![]() ${\mathcal{K}}$
. This group acts holomorphically on
${\mathcal{K}}$
. This group acts holomorphically on
![]() ${\mathcal{H}}$
.
${\mathcal{H}}$
.
Let
![]() $\unicode[STIX]{x1D6E4}$
be a finite index subgroup of
$\unicode[STIX]{x1D6E4}$
be a finite index subgroup of
![]() $O(L)^{+}$
and
$O(L)^{+}$
and
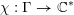 $\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{C}^{\ast }$
a unitary character. Since the abelianisation of
$\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow \mathbb{C}^{\ast }$
a unitary character. Since the abelianisation of
![]() $\unicode[STIX]{x1D6E4}$
is finite,
$\unicode[STIX]{x1D6E4}$
is finite,
![]() $\unicode[STIX]{x1D712}$
has finite order. Let
$\unicode[STIX]{x1D712}$
has finite order. Let
![]() $k$
be an integer. A meromorphic function
$k$
be an integer. A meromorphic function
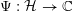 $\unicode[STIX]{x1D6F9}:{\mathcal{H}}\rightarrow \mathbb{C}$
is called an automorphic form of weight
$\unicode[STIX]{x1D6F9}:{\mathcal{H}}\rightarrow \mathbb{C}$
is called an automorphic form of weight
![]() $k$
for
$k$
for
![]() $\unicode[STIX]{x1D6E4}$
with character
$\unicode[STIX]{x1D6E4}$
with character
![]() $\unicode[STIX]{x1D712}$
if
$\unicode[STIX]{x1D712}$
if
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(MZ) & = & \displaystyle \unicode[STIX]{x1D712}(M)\unicode[STIX]{x1D6F9}(Z),\nonumber\\ \displaystyle \unicode[STIX]{x1D6F9}(tZ) & = & \displaystyle t^{-k}\unicode[STIX]{x1D6F9}(Z)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(MZ) & = & \displaystyle \unicode[STIX]{x1D712}(M)\unicode[STIX]{x1D6F9}(Z),\nonumber\\ \displaystyle \unicode[STIX]{x1D6F9}(tZ) & = & \displaystyle t^{-k}\unicode[STIX]{x1D6F9}(Z)\nonumber\end{eqnarray}$$
for all
![]() $M\in \unicode[STIX]{x1D6E4}$
and
$M\in \unicode[STIX]{x1D6E4}$
and
![]() $t\in \mathbb{C}^{\ast }$
.
$t\in \mathbb{C}^{\ast }$
.
The weight of a holomorphic automorphic form is bounded below (see [Reference BorcherdsBor95, Corollary 3.3]).
Proposition 3.1. Let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $n>2$
even and rational Witt rank
$n>2$
even and rational Witt rank
![]() $2$
. Let
$2$
. Let
![]() $\unicode[STIX]{x1D6F9}$
be a non-constant holomorphic automorphic form of weight
$\unicode[STIX]{x1D6F9}$
be a non-constant holomorphic automorphic form of weight
![]() $k$
for the discriminant kernel of
$k$
for the discriminant kernel of
![]() $O(L)^{+}$
. Then,
$O(L)^{+}$
. Then,
 $k\geqslant (n-2)/2$
. If
$k\geqslant (n-2)/2$
. If
![]() $\unicode[STIX]{x1D6F9}$
has weight
$\unicode[STIX]{x1D6F9}$
has weight
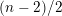 $(n-2)/2$
, then the non-vanishing Fourier coefficients correspond to isotropic vectors.
$(n-2)/2$
, then the non-vanishing Fourier coefficients correspond to isotropic vectors.
The weight
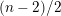 $(n-2)/2$
is called the singular weight.
$(n-2)/2$
is called the singular weight.
Let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $n>2$
even with discriminant form
$n>2$
even with discriminant form
![]() $D$
. Let
$D$
. Let
![]() $F$
be a modular form for the Weil representation of
$F$
be a modular form for the Weil representation of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\mathbb{C}[D]$
of weight
$\mathbb{C}[D]$
of weight
![]() $1-n/2$
with integral principal part. We denote the Fourier coefficients of
$1-n/2$
with integral principal part. We denote the Fourier coefficients of
![]() $F$
by
$F$
by
![]() $c_{\unicode[STIX]{x1D6FE}}(n)$
and assume that
$c_{\unicode[STIX]{x1D6FE}}(n)$
and assume that
![]() $c_{0}(0)$
is even. Then Borcherds’ singular theta correspondence [Reference BorcherdsBor98, Theorem 13.3] associates an automorphic form
$c_{0}(0)$
is even. Then Borcherds’ singular theta correspondence [Reference BorcherdsBor98, Theorem 13.3] associates an automorphic form
![]() $\unicode[STIX]{x1D6F9}$
to
$\unicode[STIX]{x1D6F9}$
to
![]() $F$
.
$F$
.
Theorem 3.2. There is a meromorphic function
 $\unicode[STIX]{x1D6F9}:{\mathcal{H}}\rightarrow \mathbb{C}$
with the following properties.
$\unicode[STIX]{x1D6F9}:{\mathcal{H}}\rightarrow \mathbb{C}$
with the following properties.
-
(1) The function
 $\unicode[STIX]{x1D6F9}$
is an automorphic form of weight
$\unicode[STIX]{x1D6F9}$
is an automorphic form of weight
 $c_{0}(0)/2$
for the group
$c_{0}(0)/2$
for the group
 $O(L,F)^{+}$
.
$O(L,F)^{+}$
. -
(2) The only zeros or poles of
 $\unicode[STIX]{x1D6F9}$
lie on rational quadratic divisors
$\unicode[STIX]{x1D6F9}$
lie on rational quadratic divisors
 $\unicode[STIX]{x1D6FE}^{\bot }$
where
$\unicode[STIX]{x1D6FE}^{\bot }$
where
 $\unicode[STIX]{x1D6FE}$
is a primitive vector of positive norm in
$\unicode[STIX]{x1D6FE}$
is a primitive vector of positive norm in
 $L^{\prime }$
. The divisor
$L^{\prime }$
. The divisor
 $\unicode[STIX]{x1D6FE}^{\bot }$
has order
$\unicode[STIX]{x1D6FE}^{\bot }$
has order  $$\begin{eqnarray}\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2).\end{eqnarray}$$
-
(3) For each primitive isotropic vector
 $z$
in
$z$
in
 $L$
and for each Weyl chamber
$L$
and for each Weyl chamber
 $W$
of
$W$
of
 $K=(L\cap z^{\bot })/\mathbb{Z}z$
the restriction
$K=(L\cap z^{\bot })/\mathbb{Z}z$
the restriction
 $\unicode[STIX]{x1D6F9}_{z}$
has an infinite product expansion converging in a neighbourhood of the cusp corresponding to
$\unicode[STIX]{x1D6F9}_{z}$
has an infinite product expansion converging in a neighbourhood of the cusp corresponding to
 $z$
that is up to a constant
$z$
that is up to a constant  $$\begin{eqnarray}e((Z,\unicode[STIX]{x1D70C}))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}\,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FE}\in L^{\prime }/L \\ \unicode[STIX]{x1D6FE}|_{(L\cap z^{\bot })}=\unicode[STIX]{x1D6FC}}}(1-e((\unicode[STIX]{x1D6FE},z^{\prime })+(\unicode[STIX]{x1D6FC},Z)))^{c_{\unicode[STIX]{x1D6FE}}(-\unicode[STIX]{x1D6FC}^{2}/2)}.\end{eqnarray}$$
$$\begin{eqnarray}e((Z,\unicode[STIX]{x1D70C}))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}\,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FE}\in L^{\prime }/L \\ \unicode[STIX]{x1D6FE}|_{(L\cap z^{\bot })}=\unicode[STIX]{x1D6FC}}}(1-e((\unicode[STIX]{x1D6FE},z^{\prime })+(\unicode[STIX]{x1D6FC},Z)))^{c_{\unicode[STIX]{x1D6FE}}(-\unicode[STIX]{x1D6FC}^{2}/2)}.\end{eqnarray}$$
The function
![]() $\unicode[STIX]{x1D6F9}$
is called the automorphic product corresponding to
$\unicode[STIX]{x1D6F9}$
is called the automorphic product corresponding to
![]() $F$
.
$F$
.
Bruinier proved the following converse theorem [Reference BruinierBru14, Theorem 1.2].
Theorem 3.3. Let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $n>2$
and even and
$n>2$
and even and
![]() $\unicode[STIX]{x1D6F9}$
an automorphic form for the discriminant kernel of
$\unicode[STIX]{x1D6F9}$
an automorphic form for the discriminant kernel of
![]() $O(L)^{+}$
whose divisor is a linear combination of rational quadratic divisors. If
$O(L)^{+}$
whose divisor is a linear combination of rational quadratic divisors. If
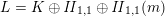 $L=K\oplus \mathit{II}_{1,1}\oplus \mathit{II}_{1,1}(m)$
for some positive integer
$L=K\oplus \mathit{II}_{1,1}\oplus \mathit{II}_{1,1}(m)$
for some positive integer
![]() $m$
, then up to a constant factor the function
$m$
, then up to a constant factor the function
![]() $\unicode[STIX]{x1D6F9}$
is the theta lift of a modular form for the Weil representation of
$\unicode[STIX]{x1D6F9}$
is the theta lift of a modular form for the Weil representation of
![]() $L$
.
$L$
.
Let
![]() $L$
and
$L$
and
![]() $F_{L}$
be as above. Suppose
$F_{L}$
be as above. Suppose
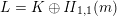 $L=K\oplus \mathit{II}_{1,1}(m)$
for some positive integer
$L=K\oplus \mathit{II}_{1,1}(m)$
for some positive integer
![]() $m$
. Let
$m$
. Let
![]() $M$
be a finite index sublattice of
$M$
be a finite index sublattice of
![]() $K$
. Then
$K$
. Then
 $H=K/M\subset K^{\prime }/M\subset M^{\prime }/M$
is an isotropic subgroup of the discriminant form of
$H=K/M\subset K^{\prime }/M\subset M^{\prime }/M$
is an isotropic subgroup of the discriminant form of
![]() $M$
with orthogonal complement
$M$
with orthogonal complement
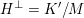 $H^{\bot }=K^{\prime }/M$
. Note that
$H^{\bot }=K^{\prime }/M$
. Note that
![]() $H^{\bot }/H$
is naturally isomorphic to
$H^{\bot }/H$
is naturally isomorphic to
![]() $K^{\prime }/K$
. The function
$K^{\prime }/K$
. The function
![]() $F_{L}$
induces a modular form
$F_{L}$
induces a modular form
![]() $F_{N}$
on
$F_{N}$
on
 $N=M\oplus \mathit{II}_{1,1}(m)$
. The embedding
$N=M\oplus \mathit{II}_{1,1}(m)$
. The embedding
![]() $N\rightarrow L$
gives an identification of the domains
$N\rightarrow L$
gives an identification of the domains
![]() ${\mathcal{H}}_{N}$
and
${\mathcal{H}}_{N}$
and
![]() ${\mathcal{H}}_{L}$
.
${\mathcal{H}}_{L}$
.
Proposition 3.4. Under this identification, the automorphic products
![]() $\unicode[STIX]{x1D6F9}(F_{L})$
and
$\unicode[STIX]{x1D6F9}(F_{L})$
and
![]() $\unicode[STIX]{x1D6F9}(F_{N})$
coincide as functions on
$\unicode[STIX]{x1D6F9}(F_{N})$
coincide as functions on
![]() ${\mathcal{H}}_{L}$
.
${\mathcal{H}}_{L}$
.
Proof. We choose a primitive norm
![]() $0$
vector
$0$
vector
![]() $z$
in
$z$
in
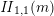 $\mathit{II}_{1,1}(m)$
. Then, the product expansion of
$\mathit{II}_{1,1}(m)$
. Then, the product expansion of
![]() $\unicode[STIX]{x1D6F9}(F_{N})$
at the cusp corresponding to
$\unicode[STIX]{x1D6F9}(F_{N})$
at the cusp corresponding to
![]() $z$
is given by
$z$
is given by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(F_{N})_{z}(Z)=c_{N}e((\unicode[STIX]{x1D70C}_{N},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {M^{\prime }}^{+}}\mathop{\prod }_{j\in \mathbb{Z}/m\mathbb{Z}}(1-e(j/m)e((\unicode[STIX]{x1D6FC},Z)))^{c_{N,\unicode[STIX]{x1D6FC}+jz/m}(-\unicode[STIX]{x1D6FC}^{2}/2)}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(F_{N})_{z}(Z)=c_{N}e((\unicode[STIX]{x1D70C}_{N},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {M^{\prime }}^{+}}\mathop{\prod }_{j\in \mathbb{Z}/m\mathbb{Z}}(1-e(j/m)e((\unicode[STIX]{x1D6FC},Z)))^{c_{N,\unicode[STIX]{x1D6FC}+jz/m}(-\unicode[STIX]{x1D6FC}^{2}/2)}. & & \displaystyle \nonumber\end{eqnarray}$$
The components
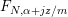 $F_{N,\unicode[STIX]{x1D6FC}+jz/m}$
of
$F_{N,\unicode[STIX]{x1D6FC}+jz/m}$
of
![]() $F_{N}$
vanish unless
$F_{N}$
vanish unless
 $\unicode[STIX]{x1D6FC}\in H^{\bot }$
and
$\unicode[STIX]{x1D6FC}\in H^{\bot }$
and
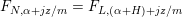 $F_{N,\unicode[STIX]{x1D6FC}+jz/m}=F_{L,(\unicode[STIX]{x1D6FC}+H)+jz/m}$
in that case. It follows
$F_{N,\unicode[STIX]{x1D6FC}+jz/m}=F_{L,(\unicode[STIX]{x1D6FC}+H)+jz/m}$
in that case. It follows
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(F_{N})_{z}(Z)=c_{N}e((\unicode[STIX]{x1D70C}_{N},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}\mathop{\prod }_{j\in \mathbb{Z}/m\mathbb{Z}}(1-e(j/m)e((\unicode[STIX]{x1D6FC},Z)))^{c_{L,\unicode[STIX]{x1D6FC}+jz/m}(-\unicode[STIX]{x1D6FC}^{2}/2)}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F9}(F_{N})_{z}(Z)=c_{N}e((\unicode[STIX]{x1D70C}_{N},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}\mathop{\prod }_{j\in \mathbb{Z}/m\mathbb{Z}}(1-e(j/m)e((\unicode[STIX]{x1D6FC},Z)))^{c_{L,\unicode[STIX]{x1D6FC}+jz/m}(-\unicode[STIX]{x1D6FC}^{2}/2)}. & & \displaystyle \nonumber\end{eqnarray}$$
This implies
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(F_{N})_{z}(Z)=\frac{c_{N}}{c_{L}}\unicode[STIX]{x1D6F9}(F_{L})_{z}(Z).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(F_{N})_{z}(Z)=\frac{c_{N}}{c_{L}}\unicode[STIX]{x1D6F9}(F_{L})_{z}(Z).\end{eqnarray}$$
It is not difficult to see that
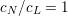 $c_{N}/c_{L}=1$
. Hence,
$c_{N}/c_{L}=1$
. Hence,
![]() $\unicode[STIX]{x1D6F9}(F_{N})$
and
$\unicode[STIX]{x1D6F9}(F_{N})$
and
![]() $\unicode[STIX]{x1D6F9}(F_{L})$
coincide in a neighbourhood of the cusp
$\unicode[STIX]{x1D6F9}(F_{L})$
coincide in a neighbourhood of the cusp
![]() $z$
and, therefore, coincide on
$z$
and, therefore, coincide on
![]() ${\mathcal{H}}_{L}$
.◻
${\mathcal{H}}_{L}$
.◻
Let
![]() $L$
be an even lattice of signature
$L$
be an even lattice of signature
![]() $(n,2)$
,
$(n,2)$
,
![]() $n>2$
even with discriminant form
$n>2$
even with discriminant form
![]() $D$
. A root of
$D$
. A root of
![]() $L$
is a primitive vector
$L$
is a primitive vector
![]() $\unicode[STIX]{x1D6FC}$
of positive norm in
$\unicode[STIX]{x1D6FC}$
of positive norm in
![]() $L$
such that the reflection
$L$
such that the reflection
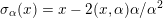 $\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}(x)=x-2(x,\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FC}^{2}$
is in
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D6FC}}(x)=x-2(x,\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D6FC}/\unicode[STIX]{x1D6FC}^{2}$
is in
![]() $O(L)$
. Let
$O(L)$
. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
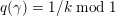 $q(\unicode[STIX]{x1D6FE})=1/k\;\text{mod}\;1$
for some positive integer
$q(\unicode[STIX]{x1D6FE})=1/k\;\text{mod}\;1$
for some positive integer
![]() $k$
. We say that
$k$
. We say that
![]() $\unicode[STIX]{x1D6FE}$
corresponds to roots if the order of
$\unicode[STIX]{x1D6FE}$
corresponds to roots if the order of
![]() $\unicode[STIX]{x1D6FE}$
divides
$\unicode[STIX]{x1D6FE}$
divides
![]() $k$
and if there is a vector
$k$
and if there is a vector
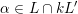 $\unicode[STIX]{x1D6FC}\in L\cap kL^{\prime }$
of norm
$\unicode[STIX]{x1D6FC}\in L\cap kL^{\prime }$
of norm
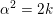 $\unicode[STIX]{x1D6FC}^{2}=2k$
with
$\unicode[STIX]{x1D6FC}^{2}=2k$
with
 $\unicode[STIX]{x1D6FC}/k=\unicode[STIX]{x1D6FE}\;\text{mod}\;L$
then
$\unicode[STIX]{x1D6FC}/k=\unicode[STIX]{x1D6FE}\;\text{mod}\;L$
then
![]() $\unicode[STIX]{x1D6FC}$
is a root. Let
$\unicode[STIX]{x1D6FC}$
is a root. Let
![]() $F$
be a modular form for the Weil representation of
$F$
be a modular form for the Weil representation of
![]() $L$
. The function
$L$
. The function
![]() $F$
is called reflective if
$F$
is called reflective if
![]() $F$
has weight
$F$
has weight
 $1-n/2$
and the only singular terms of
$1-n/2$
and the only singular terms of
![]() $F$
come from components
$F$
come from components
![]() $F_{\unicode[STIX]{x1D6FE}}$
with
$F_{\unicode[STIX]{x1D6FE}}$
with
![]() $\unicode[STIX]{x1D6FE}$
corresponding to roots of
$\unicode[STIX]{x1D6FE}$
corresponding to roots of
![]() $L$
and are of the form
$L$
and are of the form
![]() $q^{-1/k}$
. An automorphic product
$q^{-1/k}$
. An automorphic product
![]() $\unicode[STIX]{x1D6F9}$
on
$\unicode[STIX]{x1D6F9}$
on
![]() $L$
is called reflective if it is the theta lift of a reflective modular form
$L$
is called reflective if it is the theta lift of a reflective modular form
![]() $F$
. The divisor of
$F$
. The divisor of
![]() $\unicode[STIX]{x1D6F9}$
has a nice geometric description in this case (see [Reference ScheithauerSch06, § 9]).
$\unicode[STIX]{x1D6F9}$
has a nice geometric description in this case (see [Reference ScheithauerSch06, § 9]).
Proposition 3.5. Let
![]() $\unicode[STIX]{x1D6F9}$
be a reflective automorphic product on
$\unicode[STIX]{x1D6F9}$
be a reflective automorphic product on
![]() $L$
. Then,
$L$
. Then,
![]() $\unicode[STIX]{x1D6F9}$
is holomorphic and its zeros are zeros of order
$\unicode[STIX]{x1D6F9}$
is holomorphic and its zeros are zeros of order
![]() $1$
at the rational quadratic divisors
$1$
at the rational quadratic divisors
![]() $\unicode[STIX]{x1D6FC}^{\bot }$
where
$\unicode[STIX]{x1D6FC}^{\bot }$
where
![]() $\unicode[STIX]{x1D6FC}$
is a root of
$\unicode[STIX]{x1D6FC}$
is a root of
![]() $L$
with
$L$
with
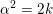 $\unicode[STIX]{x1D6FC}^{2}=2k$
and
$\unicode[STIX]{x1D6FC}^{2}=2k$
and
 $c_{\unicode[STIX]{x1D6FC}/k}(-1/k)=1$
.
$c_{\unicode[STIX]{x1D6FC}/k}(-1/k)=1$
.
4 Singular weight forms on unimodular lattices
In this section, we show that the function
![]() $\unicode[STIX]{x1D6F7}_{12}$
is the only holomorphic automorphic product of singular weight on a unimodular lattice.
$\unicode[STIX]{x1D6F7}_{12}$
is the only holomorphic automorphic product of singular weight on a unimodular lattice.
Let
![]() $L$
be an even unimodular lattice of signature
$L$
be an even unimodular lattice of signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n>2$
and let
$n>2$
and let
![]() $\unicode[STIX]{x1D6F9}(F)$
be a holomorphic automorphic product of singular weight on
$\unicode[STIX]{x1D6F9}(F)$
be a holomorphic automorphic product of singular weight on
![]() $L$
.
$L$
.
Since
![]() $L$
is unimodular, we have that
$L$
is unimodular, we have that
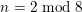 $n=2\;\text{mod}\;8$
. By assumption the modular form
$n=2\;\text{mod}\;8$
. By assumption the modular form
![]() $F$
has weight
$F$
has weight
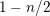 $1-n/2$
, is holomorphic on
$1-n/2$
, is holomorphic on
![]() ${\mathcal{H}}$
and has a finite order pole at
${\mathcal{H}}$
and has a finite order pole at
![]() $\infty$
. We write
$\infty$
. We write
 $$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}}c(m)q^{m}\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}}c(m)q^{m}\end{eqnarray}$$
with
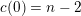 $c(0)=n-2$
and define
$c(0)=n-2$
and define
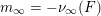 $m_{\infty }=-\unicode[STIX]{x1D708}_{\infty }(F)$
, i.e.
$m_{\infty }=-\unicode[STIX]{x1D708}_{\infty }(F)$
, i.e.
![]() $m_{\infty }$
is the largest integer such that
$m_{\infty }$
is the largest integer such that
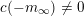 $c(-m_{\infty })\neq 0$
. The coefficients
$c(-m_{\infty })\neq 0$
. The coefficients
![]() $c(-m)$
,
$c(-m)$
,
![]() $m>0$
of the principal part of
$m>0$
of the principal part of
![]() $F$
are integral.
$F$
are integral.
Let
 $$\begin{eqnarray}E_{k}(\unicode[STIX]{x1D70F})=1-\frac{2k}{B_{k}}\mathop{\sum }_{m>0}\unicode[STIX]{x1D70E}_{k-1}(m)q^{m}\end{eqnarray}$$
$$\begin{eqnarray}E_{k}(\unicode[STIX]{x1D70F})=1-\frac{2k}{B_{k}}\mathop{\sum }_{m>0}\unicode[STIX]{x1D70E}_{k-1}(m)q^{m}\end{eqnarray}$$
be the Eisenstein series of weight
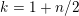 $k=1+n/2$
for
$k=1+n/2$
for
![]() $\unicode[STIX]{x1D6E4}$
. Pairing
$\unicode[STIX]{x1D6E4}$
. Pairing
![]() $F$
with
$F$
with
![]() $E_{k}$
(see Proposition 2.3) we obtain the following result.
$E_{k}$
(see Proposition 2.3) we obtain the following result.
Proposition 4.1. The principal part of
![]() $F$
satisfies
$F$
satisfies
 $$\begin{eqnarray}2(k-2)-\frac{2k}{B_{k}}\mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m)=0.\end{eqnarray}$$
$$\begin{eqnarray}2(k-2)-\frac{2k}{B_{k}}\mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m)=0.\end{eqnarray}$$
This result restricts the possible values of
![]() $k$
.
$k$
.
Proposition 4.2. We have
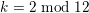 $k=2\;\text{mod}\;12$
.
$k=2\;\text{mod}\;12$
.
Proof. The previous proposition implies
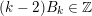 $(k-2)B_{k}\in \mathbb{Z}$
. The von Staudt–Clausen theorem states that
$(k-2)B_{k}\in \mathbb{Z}$
. The von Staudt–Clausen theorem states that
 $$\begin{eqnarray}B_{k}+\mathop{\sum }_{(p-1)|k}\frac{1}{p}\in \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}B_{k}+\mathop{\sum }_{(p-1)|k}\frac{1}{p}\in \mathbb{Z}.\end{eqnarray}$$
Hence,
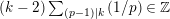 $(k-2)\sum _{(p-1)|k}(1/p)\in \mathbb{Z}$
and
$(k-2)\sum _{(p-1)|k}(1/p)\in \mathbb{Z}$
and
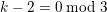 $k-2=0\;\text{mod}\;3$
. The assertion now follows from the condition on
$k-2=0\;\text{mod}\;3$
. The assertion now follows from the condition on
![]() $n$
.◻
$n$
.◻
The modular form
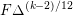 $F\unicode[STIX]{x1D6E5}^{(k-2)/12}$
has weight
$F\unicode[STIX]{x1D6E5}^{(k-2)/12}$
has weight
![]() $0$
, is holomorphic on
$0$
, is holomorphic on
![]() $H$
and possibly has a pole at
$H$
and possibly has a pole at
![]() $\infty$
. Hence,
$\infty$
. Hence,
 $$\begin{eqnarray}m_{\infty }\geqslant \frac{k-2}{12}.\end{eqnarray}$$
$$\begin{eqnarray}m_{\infty }\geqslant \frac{k-2}{12}.\end{eqnarray}$$
The divisor of
![]() $\unicode[STIX]{x1D6F9}(F)$
is a linear combination of rational quadratic divisors
$\unicode[STIX]{x1D6F9}(F)$
is a linear combination of rational quadratic divisors
![]() $\unicode[STIX]{x1D6FE}^{\bot }$
where
$\unicode[STIX]{x1D6FE}^{\bot }$
where
![]() $\unicode[STIX]{x1D6FE}$
is a primitive vector of positive norm in
$\unicode[STIX]{x1D6FE}$
is a primitive vector of positive norm in
![]() $L$
. The order of
$L$
. The order of
![]() $\unicode[STIX]{x1D6FE}^{\bot }$
is
$\unicode[STIX]{x1D6FE}^{\bot }$
is
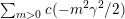 $\sum _{m>0}c(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2)$
. The holomorphicity of
$\sum _{m>0}c(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2)$
. The holomorphicity of
![]() $\unicode[STIX]{x1D6F9}(F)$
does not imply that the coefficients of the principal part of
$\unicode[STIX]{x1D6F9}(F)$
does not imply that the coefficients of the principal part of
![]() $F$
are non-negative. However, the function
$F$
are non-negative. However, the function
![]() $g$
on the positive integers defined by
$g$
on the positive integers defined by
 $$\begin{eqnarray}g(d)=\mathop{\sum }_{m>0}c(-dm^{2})\end{eqnarray}$$
$$\begin{eqnarray}g(d)=\mathop{\sum }_{m>0}c(-dm^{2})\end{eqnarray}$$
is non-negative because the lattice
![]() $L$
splits a hyperbolic plane
$L$
splits a hyperbolic plane
![]() $\mathit{II}_{1,1}$
and therefore contains primitive vectors of arbitrary norm.
$\mathit{II}_{1,1}$
and therefore contains primitive vectors of arbitrary norm.
Theorem 4.3. The principal part of
![]() $F$
satisfies the inequality
$F$
satisfies the inequality
 $$\begin{eqnarray}\mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m)\geqslant m_{\infty }^{k-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m)\geqslant m_{\infty }^{k-1}.\end{eqnarray}$$
Proof. We have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m) & = & \displaystyle \mathop{\sum }_{m>0}c(-m)\mathop{\sum }_{d\mid m}d^{k-1}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{d\mid m}c(-m)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{t>0}c(-td)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{\substack{ m>0 \\ t\;\text{squarefree}}}c(-m^{2}td)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{t\;\text{squarefree}}g(td)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m>0}g(m)\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree}}}d^{k-1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m) & = & \displaystyle \mathop{\sum }_{m>0}c(-m)\mathop{\sum }_{d\mid m}d^{k-1}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{d\mid m}c(-m)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{t>0}c(-td)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{\substack{ m>0 \\ t\;\text{squarefree}}}c(-m^{2}td)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{t\;\text{squarefree}}g(td)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m>0}g(m)\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree}}}d^{k-1}\nonumber\end{eqnarray}$$
so that
 $$\begin{eqnarray}\mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m)\geqslant g(m_{\infty })m_{\infty }^{k-1}=c(-m_{\infty })m_{\infty }^{k-1}\geqslant m_{\infty }^{k-1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m>0}c(-m)\unicode[STIX]{x1D70E}_{k-1}(m)\geqslant g(m_{\infty })m_{\infty }^{k-1}=c(-m_{\infty })m_{\infty }^{k-1}\geqslant m_{\infty }^{k-1}.\end{eqnarray}$$
This proves the theorem. ◻
We obtain the inequalities
 $$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant m_{\infty }^{k-1}\leqslant \frac{k-2}{k}B_{k}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant m_{\infty }^{k-1}\leqslant \frac{k-2}{k}B_{k}.\end{eqnarray}$$
Note that
 $k=2\;\text{mod}\;4$
implies that the Bernoulli numbers
$k=2\;\text{mod}\;4$
implies that the Bernoulli numbers
![]() $B_{k}$
are positive.
$B_{k}$
are positive.
Proposition 4.4. The only solution of the inequality
 $$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant \frac{k-2}{k}B_{k}\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant \frac{k-2}{k}B_{k}\end{eqnarray}$$
with
![]() $k>2$
and
$k>2$
and
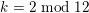 $k=2\;\text{mod}\;12$
is
$k=2\;\text{mod}\;12$
is
![]() $k=14$
. In this case, equality holds.
$k=14$
. In this case, equality holds.
Proof. We can write the inequality as
 $$\begin{eqnarray}1\leqslant \frac{(k-2)^{2}}{12k}\biggl(\frac{12}{k-2}\biggr)^{k}B_{k}.\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant \frac{(k-2)^{2}}{12k}\biggl(\frac{12}{k-2}\biggr)^{k}B_{k}.\end{eqnarray}$$
For
![]() $k\rightarrow \infty$
we have
$k\rightarrow \infty$
we have
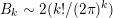 $B_{k}\sim 2(k!/(2\unicode[STIX]{x1D70B})^{k})$
and
$B_{k}\sim 2(k!/(2\unicode[STIX]{x1D70B})^{k})$
and
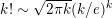 $k!\sim \sqrt{2\unicode[STIX]{x1D70B}k}(k/e)^{k}$
so that
$k!\sim \sqrt{2\unicode[STIX]{x1D70B}k}(k/e)^{k}$
so that
 $$\begin{eqnarray}\displaystyle \frac{(k-2)^{2}}{12k}\biggl(\frac{12}{k-2}\biggr)^{k}B_{k} & {\sim} & \displaystyle 2\sqrt{2\unicode[STIX]{x1D70B}k}\frac{(k-2)^{2}}{12k}\biggl(\frac{k}{k-2}\biggr)^{k}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{1}{6}\sqrt{2\unicode[STIX]{x1D70B}}e^{2}k^{3/2}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{(k-2)^{2}}{12k}\biggl(\frac{12}{k-2}\biggr)^{k}B_{k} & {\sim} & \displaystyle 2\sqrt{2\unicode[STIX]{x1D70B}k}\frac{(k-2)^{2}}{12k}\biggl(\frac{k}{k-2}\biggr)^{k}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}\nonumber\\ \displaystyle & {\sim} & \displaystyle \frac{1}{6}\sqrt{2\unicode[STIX]{x1D70B}}e^{2}k^{3/2}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}.\nonumber\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D70B}e>6$
, the last expression tends to
$\unicode[STIX]{x1D70B}e>6$
, the last expression tends to
![]() $0$
as
$0$
as
![]() $k\rightarrow \infty$
. Hence, the inequality has only finitely many solutions. It is easy to verify that
$k\rightarrow \infty$
. Hence, the inequality has only finitely many solutions. It is easy to verify that
![]() $k=14$
is the only solution.◻
$k=14$
is the only solution.◻
Now, the classification result follows.
Theorem 4.5. Let
![]() $L$
be an even unimodular lattice of signature
$L$
be an even unimodular lattice of signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n>2$
and let
$n>2$
and let
![]() $\unicode[STIX]{x1D6F9}(F)$
be a holomorphic automorphic product of singular weight on
$\unicode[STIX]{x1D6F9}(F)$
be a holomorphic automorphic product of singular weight on
![]() $L$
. Then
$L$
. Then
![]() $n=26$
and
$n=26$
and
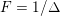 $F=1/\unicode[STIX]{x1D6E5}$
. The expansion of
$F=1/\unicode[STIX]{x1D6E5}$
. The expansion of
![]() $\unicode[STIX]{x1D6F9}$
at a cusp is given by
$\unicode[STIX]{x1D6F9}$
at a cusp is given by
 $$\begin{eqnarray}e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \mathit{II}_{25,1}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[1/\unicode[STIX]{x1D6E5}](-\unicode[STIX]{x1D6FC}^{2}/2)}=\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D6E5}((w\unicode[STIX]{x1D70C},Z)).\end{eqnarray}$$
$$\begin{eqnarray}e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in \mathit{II}_{25,1}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[1/\unicode[STIX]{x1D6E5}](-\unicode[STIX]{x1D6FC}^{2}/2)}=\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D6E5}((w\unicode[STIX]{x1D70C},Z)).\end{eqnarray}$$
Proof. We have
![]() $k=14$
and
$k=14$
and
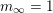 $m_{\infty }=1$
. Hence,
$m_{\infty }=1$
. Hence,
 $$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=q^{-1}+24+\cdots\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=q^{-1}+24+\cdots\end{eqnarray}$$
by Proposition 4.1. Since
![]() $F$
is holomorphic on
$F$
is holomorphic on
![]() ${\mathcal{H}}$
we obtain
${\mathcal{H}}$
we obtain
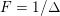 $F=1/\unicode[STIX]{x1D6E5}$
.◻
$F=1/\unicode[STIX]{x1D6E5}$
.◻
We conclude this section with some examples.
Let
 $$\begin{eqnarray}j(\unicode[STIX]{x1D70F})=q^{-1}+744+196884q+21493760q^{2}+\cdots\end{eqnarray}$$
$$\begin{eqnarray}j(\unicode[STIX]{x1D70F})=q^{-1}+744+196884q+21493760q^{2}+\cdots\end{eqnarray}$$
be the modular invariant. Then the function
 $$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D70F}) & = & \displaystyle (j(\unicode[STIX]{x1D70F})^{3}-2256j(\unicode[STIX]{x1D70F})^{2}+1105920j(\unicode[STIX]{x1D70F})-40890369)/\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle q^{-4}-q^{-1}+1610809344+11828339932860q+\cdots \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m\in \mathbb{Z}}c(m)q^{m}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D70F}) & = & \displaystyle (j(\unicode[STIX]{x1D70F})^{3}-2256j(\unicode[STIX]{x1D70F})^{2}+1105920j(\unicode[STIX]{x1D70F})-40890369)/\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70F})\nonumber\\ \displaystyle & = & \displaystyle q^{-4}-q^{-1}+1610809344+11828339932860q+\cdots \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{m\in \mathbb{Z}}c(m)q^{m}\nonumber\end{eqnarray}$$
is a modular form of weight
![]() $-12$
for
$-12$
for
![]() $\unicode[STIX]{x1D6E4}$
, holomorphic on
$\unicode[STIX]{x1D6E4}$
, holomorphic on
![]() ${\mathcal{H}}$
with a pole of order
${\mathcal{H}}$
with a pole of order
![]() $4$
at
$4$
at
![]() $\infty$
. Note that the coefficient
$\infty$
. Note that the coefficient
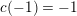 $c(-1)=-1$
of the principal part of
$c(-1)=-1$
of the principal part of
![]() $F$
is negative. Let
$F$
is negative. Let
![]() $L$
be an even unimodular lattice of signature
$L$
be an even unimodular lattice of signature
![]() $(26,2)$
and
$(26,2)$
and
![]() $\unicode[STIX]{x1D6F9}(F)$
the automorphic product corresponding to
$\unicode[STIX]{x1D6F9}(F)$
the automorphic product corresponding to
![]() $F$
on
$F$
on
![]() $L$
. Then
$L$
. Then
![]() $\unicode[STIX]{x1D6F9}(F)$
is a holomorphic automorphic form of weight
$\unicode[STIX]{x1D6F9}(F)$
is a holomorphic automorphic form of weight
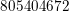 $805404672$
whose zeros are zeros of order
$805404672$
whose zeros are zeros of order
![]() $1$
at the divisors
$1$
at the divisors
![]() $\unicode[STIX]{x1D6FE}^{\bot }$
where
$\unicode[STIX]{x1D6FE}^{\bot }$
where
![]() $\unicode[STIX]{x1D6FE}$
is a primitive vector of norm
$\unicode[STIX]{x1D6FE}$
is a primitive vector of norm
![]() $\unicode[STIX]{x1D6FE}^{2}=8$
in
$\unicode[STIX]{x1D6FE}^{2}=8$
in
![]() $L$
. If
$L$
. If
![]() $\unicode[STIX]{x1D6FE}$
is a vector of norm
$\unicode[STIX]{x1D6FE}$
is a vector of norm
![]() $\unicode[STIX]{x1D6FE}^{2}=2$
in
$\unicode[STIX]{x1D6FE}^{2}=2$
in
![]() $L$
, then the divisor
$L$
, then the divisor
![]() $\unicode[STIX]{x1D6FE}^{\bot }$
has order
$\unicode[STIX]{x1D6FE}^{\bot }$
has order
 $c(-4)+c(-1)=0$
.
$c(-4)+c(-1)=0$
.
Next, we consider non-holomorphic automorphic products.
Proposition 4.6. Let
![]() $L$
be an even unimodular lattice of signature
$L$
be an even unimodular lattice of signature
![]() $(n,2)$
with
$(n,2)$
with
 $$\begin{eqnarray}n=26,50,74,122,146,170\text{ or }194.\end{eqnarray}$$
$$\begin{eqnarray}n=26,50,74,122,146,170\text{ or }194.\end{eqnarray}$$
Then,
![]() $L$
carries infinitely many meromorphic automorphic products of weight
$L$
carries infinitely many meromorphic automorphic products of weight
![]() $12$
.
$12$
.
Proof. First, we consider the case
![]() $n=26$
. Let
$n=26$
. Let
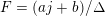 $F=(aj+b)/\unicode[STIX]{x1D6E5}$
with
$F=(aj+b)/\unicode[STIX]{x1D6E5}$
with
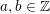 $a,b\in \mathbb{Z}$
. Then
$a,b\in \mathbb{Z}$
. Then
 $$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=aq^{-2}+(768a+b)q^{-1}+(215064a+24b)+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=aq^{-2}+(768a+b)q^{-1}+(215064a+24b)+\cdots \,.\end{eqnarray}$$
Since
 $(215064,24)=24$
there are infinitely many choices for
$(215064,24)=24$
there are infinitely many choices for
![]() $a$
and
$a$
and
![]() $b$
such that
$b$
such that
![]() $F$
has constant coefficient
$F$
has constant coefficient
![]() $24$
. This implies that there are infinitely many meromorphic automorphic products of weight
$24$
. This implies that there are infinitely many meromorphic automorphic products of weight
![]() $12$
on
$12$
on
![]() $L$
. In the general case, write
$L$
. In the general case, write
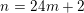 $n=24m+2$
and let
$n=24m+2$
and let
 $$\begin{eqnarray}F=(a_{m}j^{m}+\cdots +a_{1}j+a_{0})/\unicode[STIX]{x1D6E5}^{m}.\end{eqnarray}$$
$$\begin{eqnarray}F=(a_{m}j^{m}+\cdots +a_{1}j+a_{0})/\unicode[STIX]{x1D6E5}^{m}.\end{eqnarray}$$
Then there are infinitely many
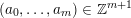 $(a_{0},\ldots ,a_{m})\in \mathbb{Z}^{m+1}$
such that
$(a_{0},\ldots ,a_{m})\in \mathbb{Z}^{m+1}$
such that
![]() $F$
has constant coefficient
$F$
has constant coefficient
![]() $24$
.◻
$24$
.◻
We explain the exception at
![]() $n=98$
. Let
$n=98$
. Let
 $$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}}c(m)q^{m}\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}}c(m)q^{m}\end{eqnarray}$$
be a modular form of weight
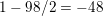 $1-98/2=-48$
for
$1-98/2=-48$
for
![]() $\unicode[STIX]{x1D6E4}$
, holomorphic on
$\unicode[STIX]{x1D6E4}$
, holomorphic on
![]() ${\mathcal{H}}$
with a pole at
${\mathcal{H}}$
with a pole at
![]() $\infty$
. Suppose
$\infty$
. Suppose
![]() $F$
has integral principal part. Since the Eisenstein series
$F$
has integral principal part. Since the Eisenstein series
![]() $E_{10}$
has Fourier expansion
$E_{10}$
has Fourier expansion
 $$\begin{eqnarray}E_{10}(\unicode[STIX]{x1D70F})=1-264\mathop{\sum }_{m>0}\unicode[STIX]{x1D70E}_{9}(m)q^{m}\end{eqnarray}$$
$$\begin{eqnarray}E_{10}(\unicode[STIX]{x1D70F})=1-264\mathop{\sum }_{m>0}\unicode[STIX]{x1D70E}_{9}(m)q^{m}\end{eqnarray}$$
the constant coefficient of
![]() $FE_{10}^{5}$
is given by
$FE_{10}^{5}$
is given by
 $c(0)+264(\cdots \,)$
. This coefficient has to vanish so that
$c(0)+264(\cdots \,)$
. This coefficient has to vanish so that
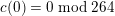 $c(0)=0\;\text{mod}\;264$
. This implies that the weight of a meromorphic automorphic product on a unimodular lattice of signature
$c(0)=0\;\text{mod}\;264$
. This implies that the weight of a meromorphic automorphic product on a unimodular lattice of signature
![]() $(98,2)$
is divisible by
$(98,2)$
is divisible by
![]() $132$
.
$132$
.
Finally, we remark that lifting constants with Gritsenko’s additive lift [Reference GritsenkoGri91] (see also [Reference BorcherdsBor98, Theorem 14.3]) shows that holomorphic automorphic forms of singular weight exist on any unimodular lattice of signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n>2$
. By Theorem 3.3, the divisor of such a function is not a linear combination of rational quadratic divisors.
$n>2$
. By Theorem 3.3, the divisor of such a function is not a linear combination of rational quadratic divisors.
5 The prime level case
Let
![]() $L$
be an even lattice of prime level carrying a holomorphic automorphic product of singular weight. We derive an explicit bound for the signature of
$L$
be an even lattice of prime level carrying a holomorphic automorphic product of singular weight. We derive an explicit bound for the signature of
![]() $L$
.
$L$
.
We consider the cases of even and odd
![]() $p$
-ranks separately.
$p$
-ranks separately.
5.1 Even
 $p$
-rank
$p$
-rank
Let
![]() $L$
be an even lattice of prime level
$L$
be an even lattice of prime level
![]() $p$
and genus
$p$
and genus
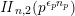 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
![]() $n>2$
and
$n>2$
and
![]() $n_{p}$
even carrying a holomorphic automorphic product
$n_{p}$
even carrying a holomorphic automorphic product
![]() $\unicode[STIX]{x1D6F9}(F)$
of singular weight.
$\unicode[STIX]{x1D6F9}(F)$
of singular weight.
Let
![]() $D$
be the discriminant form of
$D$
be the discriminant form of
![]() $L$
. The oddity formula (see [Reference Conway and SloaneCS99, ch. 15, § 7.7])
$L$
. The oddity formula (see [Reference Conway and SloaneCS99, ch. 15, § 7.7])
 $$\begin{eqnarray}e(\operatorname{sign}(D)/8)=\unicode[STIX]{x1D6FE}_{p}(D)\end{eqnarray}$$
$$\begin{eqnarray}e(\operatorname{sign}(D)/8)=\unicode[STIX]{x1D6FE}_{p}(D)\end{eqnarray}$$
implies
 $$\begin{eqnarray}e((n-2)/8)=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}.\end{eqnarray}$$
$$\begin{eqnarray}e((n-2)/8)=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}.\end{eqnarray}$$
Hence,
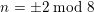 $n=\pm 2\;\text{mod}\;8$
and
$n=\pm 2\;\text{mod}\;8$
and
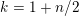 $k=1+n/2$
is an even integer. Note that
$k=1+n/2$
is an even integer. Note that
![]() $k\geqslant 4$
. Define
$k\geqslant 4$
. Define
 $$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}=-(-1)^{k/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}=-(-1)^{k/2}.\end{eqnarray}$$
Let
![]() $E$
be the Eisenstein series of weight
$E$
be the Eisenstein series of weight
![]() $k$
for
$k$
for
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
corresponding to
$\overline{\unicode[STIX]{x1D70C}}_{D}$
corresponding to
![]() $0$
. Write
$0$
. Write
 $$\begin{eqnarray}E=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}E_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}E=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}E_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
with
 $$\begin{eqnarray}E_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}+q(\unicode[STIX]{x1D6FE})}a_{\unicode[STIX]{x1D6FE}}(m)q^{m}.\end{eqnarray}$$
$$\begin{eqnarray}E_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}+q(\unicode[STIX]{x1D6FE})}a_{\unicode[STIX]{x1D6FE}}(m)q^{m}.\end{eqnarray}$$
Define
 $$\begin{eqnarray}c_{k,p,n_{p}}=\unicode[STIX]{x1D709}\frac{2k}{B_{k}}\frac{1}{p^{k}-1}\frac{1}{p^{(n_{p}-2)/2}}.\end{eqnarray}$$
$$\begin{eqnarray}c_{k,p,n_{p}}=\unicode[STIX]{x1D709}\frac{2k}{B_{k}}\frac{1}{p^{k}-1}\frac{1}{p^{(n_{p}-2)/2}}.\end{eqnarray}$$
Note that
![]() $c_{k,p,n_{p}}$
is positive. By explicit calculation we can derive the following formulas for the Fourier coefficients
$c_{k,p,n_{p}}$
is positive. By explicit calculation we can derive the following formulas for the Fourier coefficients
![]() $a_{\unicode[STIX]{x1D6FE}}(m)$
(see also [Reference ScheithauerSch06, Theorem 7.1]).
$a_{\unicode[STIX]{x1D6FE}}(m)$
(see also [Reference ScheithauerSch06, Theorem 7.1]).
Proposition 5.1. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
and
$\unicode[STIX]{x1D6FE}\in D$
and
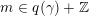 $m\in q(\unicode[STIX]{x1D6FE})+\mathbb{Z}$
,
$m\in q(\unicode[STIX]{x1D6FE})+\mathbb{Z}$
,
![]() $m>0$
.
$m>0$
.
If
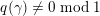 $q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
, then
$q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
, then
 $$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}\unicode[STIX]{x1D70E}_{k-1}(pm).\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}\unicode[STIX]{x1D70E}_{k-1}(pm).\end{eqnarray}$$
Suppose
 $q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
. Write
$q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
. Write
 $m=p^{\unicode[STIX]{x1D708}}a$
with
$m=p^{\unicode[STIX]{x1D708}}a$
with
 $(a,p)=1$
. Then
$(a,p)=1$
. Then
 $$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1}(a)\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1}(a)\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D6FE}\neq 0$
and
$\unicode[STIX]{x1D6FE}\neq 0$
and
 $$\begin{eqnarray}\displaystyle a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1}(a)+\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\unicode[STIX]{x1D70E}_{k-1}(a)-\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\unicode[STIX]{x1D70E}_{k-1}(m) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1}(a)+\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\unicode[STIX]{x1D70E}_{k-1}(a)-\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\unicode[STIX]{x1D70E}_{k-1}(m) & & \displaystyle \nonumber\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D6FE}=0$
.
$\unicode[STIX]{x1D6FE}=0$
.
Write
 $$\begin{eqnarray}F=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
with
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}-q(\unicode[STIX]{x1D6FE})}c_{\unicode[STIX]{x1D6FE}}(m)q^{m}.\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=\mathop{\sum }_{m\in \mathbb{Z}-q(\unicode[STIX]{x1D6FE})}c_{\unicode[STIX]{x1D6FE}}(m)q^{m}.\end{eqnarray}$$
Pairing
![]() $F$
with the Eisenstein series
$F$
with the Eisenstein series
![]() $E$
(see Proposition 2.3) we obtain
$E$
(see Proposition 2.3) we obtain
 $$\begin{eqnarray}2(k-2)+\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)=0.\end{eqnarray}$$
$$\begin{eqnarray}2(k-2)+\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)=0.\end{eqnarray}$$
In the following, we will often need that
![]() $L$
splits a hyperbolic plane
$L$
splits a hyperbolic plane
![]() $\mathit{II}_{1,1}$
. We give a criterion for this.
$\mathit{II}_{1,1}$
. We give a criterion for this.
Proposition 5.2. The lattice
![]() $L$
splits a hyperbolic plane
$L$
splits a hyperbolic plane
![]() $\mathit{II}_{1,1}$
if and only if
$\mathit{II}_{1,1}$
if and only if
 $$\begin{eqnarray}n_{p}=n\quad \text{and}\quad \unicode[STIX]{x1D709}=+1\end{eqnarray}$$
$$\begin{eqnarray}n_{p}=n\quad \text{and}\quad \unicode[STIX]{x1D709}=+1\end{eqnarray}$$
or
 $$\begin{eqnarray}n_{p}\leqslant n-2.\end{eqnarray}$$
$$\begin{eqnarray}n_{p}\leqslant n-2.\end{eqnarray}$$
Proof. Suppose
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
, i.e.
$\mathit{II}_{1,1}$
, i.e.
 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})=\mathit{II}_{n-1,1}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})\oplus \mathit{II}_{1,1}$
. If
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})=\mathit{II}_{n-1,1}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})\oplus \mathit{II}_{1,1}$
. If
 $n_{p}\leqslant n-2$
, this gives no restriction on
$n_{p}\leqslant n-2$
, this gives no restriction on
![]() $\unicode[STIX]{x1D716}_{p}$
. If
$\unicode[STIX]{x1D716}_{p}$
. If
![]() $n_{p}=n$
, then the sign rule (see [Reference Conway and SloaneCS99, ch. 15, § 7.7]) applied to
$n_{p}=n$
, then the sign rule (see [Reference Conway and SloaneCS99, ch. 15, § 7.7]) applied to
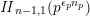 $\mathit{II}_{n-1,1}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
implies
$\mathit{II}_{n-1,1}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
implies
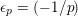 $\unicode[STIX]{x1D716}_{p}=(-1/p)$
so that
$\unicode[STIX]{x1D716}_{p}=(-1/p)$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}=\biggl(\frac{-1}{p}\biggr)^{1+n/2}=+1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}=\biggl(\frac{-1}{p}\biggr)^{1+n/2}=+1.\end{eqnarray}$$
The converse is now clear. ◻
Let
![]() $d$
be a positive rational number such that
$d$
be a positive rational number such that
![]() $pd$
is integral. We define functions
$pd$
is integral. We define functions
 $$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}d),\end{eqnarray}$$
$$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}d),\end{eqnarray}$$
where we assume
![]() $m$
to be integral. We have
$m$
to be integral. We have
 $$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=g_{0}(p^{2}d)+\mathop{\sum }_{(m,p)=1}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}d).\end{eqnarray}$$
$$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=g_{0}(p^{2}d)+\mathop{\sum }_{(m,p)=1}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}d).\end{eqnarray}$$
This implies
 $$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=g_{0}(p^{2}d)\end{eqnarray}$$
$$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=g_{0}(p^{2}d)\end{eqnarray}$$
if
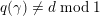 $q(\unicode[STIX]{x1D6FE})\neq d\;\text{mod}\;1$
.
$q(\unicode[STIX]{x1D6FE})\neq d\;\text{mod}\;1$
.
The divisor of
![]() $\unicode[STIX]{x1D6F9}(F)$
is a linear combination of rational quadratic divisors
$\unicode[STIX]{x1D6F9}(F)$
is a linear combination of rational quadratic divisors
![]() $\unicode[STIX]{x1D6FE}^{\bot }$
, where
$\unicode[STIX]{x1D6FE}^{\bot }$
, where
![]() $\unicode[STIX]{x1D6FE}$
is a primitive vector of positive norm in
$\unicode[STIX]{x1D6FE}$
is a primitive vector of positive norm in
![]() $L$
. The divisor
$L$
. The divisor
![]() $\unicode[STIX]{x1D6FE}^{\bot }$
has order
$\unicode[STIX]{x1D6FE}^{\bot }$
has order
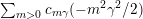 $\sum _{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2)$
. Since
$\sum _{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2)$
. Since
![]() $\unicode[STIX]{x1D6F9}(F)$
is holomorphic this is a non-negative integer.
$\unicode[STIX]{x1D6F9}(F)$
is holomorphic this is a non-negative integer.
Proposition 5.3. Suppose
![]() $L$
splits a hyperbolic plane
$L$
splits a hyperbolic plane
![]() $\mathit{II}_{1,1}$
. Then
$\mathit{II}_{1,1}$
. Then
 $$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)\geqslant 0\end{eqnarray}$$
$$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)\geqslant 0\end{eqnarray}$$
for all
![]() $\unicode[STIX]{x1D6FE}\in D$
.
$\unicode[STIX]{x1D6FE}\in D$
.
Proof. By the above remark we can assume that
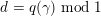 $d=q(\unicode[STIX]{x1D6FE})\;\text{mod}\;1$
. Write
$d=q(\unicode[STIX]{x1D6FE})\;\text{mod}\;1$
. Write
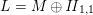 $L=M\oplus \mathit{II}_{1,1}$
. Choose a representative of
$L=M\oplus \mathit{II}_{1,1}$
. Choose a representative of
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $M^{\prime }$
. By adding a primitive element of suitable norm in
$M^{\prime }$
. By adding a primitive element of suitable norm in
![]() $\mathit{II}_{1,1}$
we obtain a primitive element
$\mathit{II}_{1,1}$
we obtain a primitive element
![]() $\unicode[STIX]{x1D6FE}\in L^{\prime }$
of norm
$\unicode[STIX]{x1D6FE}\in L^{\prime }$
of norm
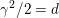 $\unicode[STIX]{x1D6FE}^{2}/2=d$
. The holomorphicity of
$\unicode[STIX]{x1D6FE}^{2}/2=d$
. The holomorphicity of
![]() $\unicode[STIX]{x1D6F9}(F)$
implies that
$\unicode[STIX]{x1D6F9}(F)$
implies that
 $$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}d)=\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2)\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}g_{\unicode[STIX]{x1D6FE}}(d)=\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}d)=\mathop{\sum }_{m>0}c_{m\unicode[STIX]{x1D6FE}}(-m^{2}\unicode[STIX]{x1D6FE}^{2}/2)\geqslant 0.\end{eqnarray}$$
This proves the proposition. ◻
We also define the multiplicative function
 $$\begin{eqnarray}h(m)=\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree} \\ (m/d,p)=1}}d^{k-1}.\end{eqnarray}$$
$$\begin{eqnarray}h(m)=\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree} \\ (m/d,p)=1}}d^{k-1}.\end{eqnarray}$$
Now we expand the sum
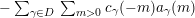 $-\sum _{\unicode[STIX]{x1D6FE}\in D}\,\sum _{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)$
in terms of the non-negative divisor degrees
$-\sum _{\unicode[STIX]{x1D6FE}\in D}\,\sum _{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)$
in terms of the non-negative divisor degrees
![]() $g_{\unicode[STIX]{x1D6FE}}$
.
$g_{\unicode[STIX]{x1D6FE}}$
.
Theorem 5.4. Suppose
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
. Let
$\mathit{II}_{1,1}$
. Let
 $c_{p}=1-1/p$
. Then
$c_{p}=1-1/p$
. Then
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & {\geqslant} & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{p}c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}g_{0}(m)h(m).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & {\geqslant} & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{p}c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}g_{0}(m)h(m).\nonumber\end{eqnarray}$$
Proof. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
with
$\unicode[STIX]{x1D6FE}\in D$
with
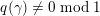 $q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
. Then
$q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
. Then
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{(m,p)=1}c_{j\unicode[STIX]{x1D6FE}}(-m/p)\mathop{\sum }_{d\mid m}d^{k-1}\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{(t,p)=1}c_{j\unicode[STIX]{x1D6FE}}(-td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}\,\mathop{\sum }_{(m,p)=1}c_{j\unicode[STIX]{x1D6FE}}(-m^{2}td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{l=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}\,\mathop{\sum }_{m=l\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{j\unicode[STIX]{x1D6FE}}(-m^{2}td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{l=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}\,\mathop{\sum }_{m=l\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{lj\unicode[STIX]{x1D6FE}}(-m^{2}td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{j\unicode[STIX]{x1D6FE}}(td/p)-g_{0}(tdp))\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{(m,p)=1}(g_{j\unicode[STIX]{x1D6FE}}(m/p)-g_{0}(mp))\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree}}}d^{k-1}\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m/p=q(j\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}(g_{j\unicode[STIX]{x1D6FE}}(m/p)-g_{0}(mp))h(m).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{(m,p)=1}c_{j\unicode[STIX]{x1D6FE}}(-m/p)\mathop{\sum }_{d\mid m}d^{k-1}\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{(t,p)=1}c_{j\unicode[STIX]{x1D6FE}}(-td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}\,\mathop{\sum }_{(m,p)=1}c_{j\unicode[STIX]{x1D6FE}}(-m^{2}td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{l=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}\,\mathop{\sum }_{m=l\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{j\unicode[STIX]{x1D6FE}}(-m^{2}td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{l=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}\,\mathop{\sum }_{m=l\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{lj\unicode[STIX]{x1D6FE}}(-m^{2}td/p)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{(d,p)=1}d^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{j\unicode[STIX]{x1D6FE}}(td/p)-g_{0}(tdp))\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{(m,p)=1}(g_{j\unicode[STIX]{x1D6FE}}(m/p)-g_{0}(mp))\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree}}}d^{k-1}\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m/p=q(j\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}(g_{j\unicode[STIX]{x1D6FE}}(m/p)-g_{0}(mp))h(m).\nonumber\end{eqnarray}$$
For
 $\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
with
$\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
with
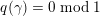 $q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
we find analogously
$q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
we find analogously
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m)=c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}(g_{j\unicode[STIX]{x1D6FE}}(m)-g_{0}(mp^{2}))h(m). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m)=c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}(g_{j\unicode[STIX]{x1D6FE}}(m)-g_{0}(mp^{2}))h(m). & & \displaystyle \nonumber\end{eqnarray}$$
For
![]() $\unicode[STIX]{x1D6FE}=0$
, we have
$\unicode[STIX]{x1D6FE}=0$
, we have
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{d>0}d^{k-1}\,\mathop{\sum }_{(t,p)=1}c_{0}(-td)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\mathop{\sum }_{(d,p)=1}d^{k-1}\,\mathop{\sum }_{t>0}c_{0}(-td)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{t>0}c_{0}(-td)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{d>0}d^{k-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{0}(td)-g_{0}(tdp^{2}))\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\mathop{\sum }_{(d,p)=1}d^{k-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{0}(td)+g_{0}(tdp))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\mathop{\sum }_{d>0}d^{k-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{0}(td)+g_{0}(tdp))\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}(g_{0}(m)-g_{0}(mp^{2}))h(m)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\mathop{\sum }_{(m,p)=1}(g_{0}(m)+g_{0}(mp))h(m)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\mathop{\sum }_{m>0}(g_{0}(m)+g_{0}(mp))h(m).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{d>0}d^{k-1}\,\mathop{\sum }_{(t,p)=1}c_{0}(-td)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\mathop{\sum }_{(d,p)=1}d^{k-1}\,\mathop{\sum }_{t>0}c_{0}(-td)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\mathop{\sum }_{d>0}d^{k-1}\mathop{\sum }_{t>0}c_{0}(-td)\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{d>0}d^{k-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{0}(td)-g_{0}(tdp^{2}))\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\mathop{\sum }_{(d,p)=1}d^{k-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{0}(td)+g_{0}(tdp))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\mathop{\sum }_{d>0}d^{k-1}\,\mathop{\sum }_{\substack{ t\;\text{squarefree} \\ (t,p)=1}}(g_{0}(td)+g_{0}(tdp))\nonumber\\ \displaystyle & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}(g_{0}(m)-g_{0}(mp^{2}))h(m)\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{n_{p}/2}\mathop{\sum }_{(m,p)=1}(g_{0}(m)+g_{0}(mp))h(m)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-2)/2}(p-1)\mathop{\sum }_{m>0}(g_{0}(m)+g_{0}(mp))h(m).\nonumber\end{eqnarray}$$
Using
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{m>0}g_{0}(m)h(m) & = & \displaystyle \mathop{\sum }_{(m,p)=1}g_{0}(m)h(m)+p^{k-1}\mathop{\sum }_{(m,p)=1}g_{0}(mp)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,p^{2(k-1)}\mathop{\sum }_{m>0}g_{0}(mp^{2})h(m)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{m>0}g_{0}(m)h(m) & = & \displaystyle \mathop{\sum }_{(m,p)=1}g_{0}(m)h(m)+p^{k-1}\mathop{\sum }_{(m,p)=1}g_{0}(mp)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,p^{2(k-1)}\mathop{\sum }_{m>0}g_{0}(mp^{2})h(m)\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathop{\sum }_{m>0}g_{0}(mp)h(m)=\mathop{\sum }_{(m,p)=1}g_{0}(mp)h(m)+p^{k-1}\mathop{\sum }_{m>0}g_{0}(mp^{2})h(m),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{m>0}g_{0}(mp)h(m)=\mathop{\sum }_{(m,p)=1}g_{0}(mp)h(m)+p^{k-1}\mathop{\sum }_{m>0}g_{0}(mp^{2})h(m),\end{eqnarray}$$
we find
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}c_{k,p,n_{p}}^{0}\mathop{\sum }_{(m,p)=1}g_{0}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}c_{k,n_{p},j}^{1}\mathop{\sum }_{m=j\hspace{0.2em}{\rm mod}\hspace{0.2em}p}g_{0}(mp)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}c_{k,p,n_{p}}^{{\geqslant}2}\mathop{\sum }_{m>0}g_{0}(mp^{2})h(m)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}c_{k,p,n_{p}}^{0}\mathop{\sum }_{(m,p)=1}g_{0}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}c_{k,n_{p},j}^{1}\mathop{\sum }_{m=j\hspace{0.2em}{\rm mod}\hspace{0.2em}p}g_{0}(mp)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}c_{k,p,n_{p}}^{{\geqslant}2}\mathop{\sum }_{m>0}g_{0}(mp^{2})h(m)\nonumber\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle c_{k,p,n_{p}}^{0} & = & \displaystyle p^{k-1}-\unicode[STIX]{x1D709}p^{(n_{p}-2)/2},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & = & \displaystyle p^{n}-a_{k,p,n_{p},j}+\unicode[STIX]{x1D709}p^{(n_{p}-2)/2}((p-1)p^{k-1}-1),\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & = & \displaystyle p^{k-1}(p^{n}-a_{k,p,n_{p},0}+\unicode[STIX]{x1D709}p^{(n_{p}-2)/2}(p-1)(p^{k-1}+1)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{k,p,n_{p}}^{0} & = & \displaystyle p^{k-1}-\unicode[STIX]{x1D709}p^{(n_{p}-2)/2},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & = & \displaystyle p^{n}-a_{k,p,n_{p},j}+\unicode[STIX]{x1D709}p^{(n_{p}-2)/2}((p-1)p^{k-1}-1),\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & = & \displaystyle p^{k-1}(p^{n}-a_{k,p,n_{p},0}+\unicode[STIX]{x1D709}p^{(n_{p}-2)/2}(p-1)(p^{k-1}+1)),\nonumber\end{eqnarray}$$
where
![]() $a_{k,p,n_{p},j}$
denotes the number of elements
$a_{k,p,n_{p},j}$
denotes the number of elements
![]() $\unicode[STIX]{x1D6FE}\in D$
of norm
$\unicode[STIX]{x1D6FE}\in D$
of norm
 $q(\unicode[STIX]{x1D6FE})=j/p\;\text{mod}\;1$
. For
$q(\unicode[STIX]{x1D6FE})=j/p\;\text{mod}\;1$
. For
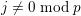 $j\neq 0\;\text{mod}\;p$
we have
$j\neq 0\;\text{mod}\;p$
we have
 $$\begin{eqnarray}a_{k,p,n_{p},j}=p^{n_{p}-1}-\unicode[STIX]{x1D709}p^{(n_{p}-2)/2}\end{eqnarray}$$
$$\begin{eqnarray}a_{k,p,n_{p},j}=p^{n_{p}-1}-\unicode[STIX]{x1D709}p^{(n_{p}-2)/2}\end{eqnarray}$$
(see [Reference ScheithauerSch06, Proposition 3.2]) so that
 $$\begin{eqnarray}\displaystyle c_{k,p,n_{p},j}^{1} & = & \displaystyle p^{n}-p^{n_{p}-1}+\unicode[STIX]{x1D709}p^{(n+n_{p}-2)/2}(p-1),\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & = & \displaystyle p^{k-1}(p^{n}-p^{n_{p}-1}+\unicode[STIX]{x1D709}p^{(n+n_{p}-2)/2}(p-1)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{k,p,n_{p},j}^{1} & = & \displaystyle p^{n}-p^{n_{p}-1}+\unicode[STIX]{x1D709}p^{(n+n_{p}-2)/2}(p-1),\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & = & \displaystyle p^{k-1}(p^{n}-p^{n_{p}-1}+\unicode[STIX]{x1D709}p^{(n+n_{p}-2)/2}(p-1)).\nonumber\end{eqnarray}$$
Since
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
, we obtain the following bounds
$\mathit{II}_{1,1}$
, we obtain the following bounds
 $$\begin{eqnarray}\displaystyle c_{k,p,n_{p}}^{0} & {\geqslant} & \displaystyle (1-1/p)p^{k-1},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & {\geqslant} & \displaystyle (1-1/p)p^{2(k-1)},\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & {\geqslant} & \displaystyle (1-1/p)p^{3(k-1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{k,p,n_{p}}^{0} & {\geqslant} & \displaystyle (1-1/p)p^{k-1},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & {\geqslant} & \displaystyle (1-1/p)p^{2(k-1)},\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & {\geqslant} & \displaystyle (1-1/p)p^{3(k-1)}.\nonumber\end{eqnarray}$$
Applying the above formula for
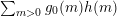 $\sum _{m>0}g_{0}(m)h(m)$
once more, we obtain
$\sum _{m>0}g_{0}(m)h(m)$
once more, we obtain
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & {\geqslant} & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{p}c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}g_{0}(m)h(m).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & {\geqslant} & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{p}c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}g_{0}(m)h(m).\nonumber\end{eqnarray}$$
This proves the theorem. ◻
Define
 $m_{\infty }=\max _{\unicode[STIX]{x1D6FE}\in D}(-\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}}))$
. Note that
$m_{\infty }=\max _{\unicode[STIX]{x1D6FE}\in D}(-\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}}))$
. Note that
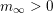 $m_{\infty }>0$
.
$m_{\infty }>0$
.
Proposition 5.5. Suppose
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
. Then
$\mathit{II}_{1,1}$
. Then
 $$\begin{eqnarray}m_{\infty }\geqslant \frac{k-2}{12}.\end{eqnarray}$$
$$\begin{eqnarray}m_{\infty }\geqslant \frac{k-2}{12}.\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D6FE}\in D$
such that
$\unicode[STIX]{x1D6FE}\in D$
such that
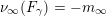 $\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})=-m_{\infty }$
. Then
$\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})=-m_{\infty }$
. Then
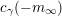 $c_{\unicode[STIX]{x1D6FE}}(-m_{\infty })$
is a positive integer.
$c_{\unicode[STIX]{x1D6FE}}(-m_{\infty })$
is a positive integer.
Proof. The function
![]() $F_{0}$
is a non-zero modular form for
$F_{0}$
is a non-zero modular form for
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
of weight
$\unicode[STIX]{x1D6E4}_{0}(p)$
of weight
![]() $2-k$
. Applying the Riemann–Roch theorem to
$2-k$
. Applying the Riemann–Roch theorem to
![]() $F_{0}$
we obtain
$F_{0}$
we obtain
 $$\begin{eqnarray}p\unicode[STIX]{x1D708}_{0}(F_{0})+\unicode[STIX]{x1D708}_{\infty }(F_{0})\leqslant -\frac{k-2}{12}(p+1)\end{eqnarray}$$
$$\begin{eqnarray}p\unicode[STIX]{x1D708}_{0}(F_{0})+\unicode[STIX]{x1D708}_{\infty }(F_{0})\leqslant -\frac{k-2}{12}(p+1)\end{eqnarray}$$
(see [Reference Hirzebruch, Berger and JungHBJ94, Theorem 4.1]). The formula for the
![]() $S$
-transformation (see § 2) implies
$S$
-transformation (see § 2) implies
 $$\begin{eqnarray}\unicode[STIX]{x1D708}_{0}(F_{0})=\unicode[STIX]{x1D708}_{\infty }\biggl(\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{0}(F_{0})=\unicode[STIX]{x1D708}_{\infty }\biggl(\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}\biggr).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D6FE}\in D$
such that
$\unicode[STIX]{x1D6FE}\in D$
such that
![]() $\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})$
is minimal. Since
$\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})$
is minimal. Since
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
, there is a primitive vector
$\mathit{II}_{1,1}$
, there is a primitive vector
![]() $\unicode[STIX]{x1D707}$
in
$\unicode[STIX]{x1D707}$
in
![]() $L^{\prime }$
with
$L^{\prime }$
with
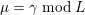 $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FE}\;\text{mod}\;L$
and
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6FE}\;\text{mod}\;L$
and
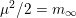 $\unicode[STIX]{x1D707}^{2}/2=m_{\infty }$
. Then, the divisor
$\unicode[STIX]{x1D707}^{2}/2=m_{\infty }$
. Then, the divisor
![]() $\unicode[STIX]{x1D707}^{\bot }$
has order
$\unicode[STIX]{x1D707}^{\bot }$
has order
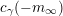 $c_{\unicode[STIX]{x1D6FE}}(-m_{\infty })$
which is a positive integer by the holomorphicity of
$c_{\unicode[STIX]{x1D6FE}}(-m_{\infty })$
which is a positive integer by the holomorphicity of
![]() $\unicode[STIX]{x1D6F9}(F)$
. Hence,
$\unicode[STIX]{x1D6F9}(F)$
. Hence,
 $$\begin{eqnarray}\unicode[STIX]{x1D708}_{\infty }\biggl(\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}\biggr)=\min _{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\infty }\biggl(\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}\biggr)=\min _{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
It follows
 $$\begin{eqnarray}p\min _{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})+\min _{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})\leqslant -\frac{k-2}{12}(p+1).\end{eqnarray}$$
$$\begin{eqnarray}p\min _{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})+\min _{\unicode[STIX]{x1D6FE}\in D}\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})\leqslant -\frac{k-2}{12}(p+1).\end{eqnarray}$$
This completes the proof. ◻
We obtain the following inequalities.
Proposition 5.6. Suppose
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
. Then
$\mathit{II}_{1,1}$
. Then
 $$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant m_{\infty }^{k-1}\leqslant \unicode[STIX]{x1D709}\frac{p^{n_{p}/2}}{c_{p}}\frac{k-2}{k}B_{k}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant m_{\infty }^{k-1}\leqslant \unicode[STIX]{x1D709}\frac{p^{n_{p}/2}}{c_{p}}\frac{k-2}{k}B_{k}.\end{eqnarray}$$
Proof. Suppose
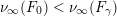 $\unicode[STIX]{x1D708}_{\infty }(F_{0})<\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})$
for all
$\unicode[STIX]{x1D708}_{\infty }(F_{0})<\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})$
for all
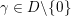 $\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
. Then the Eisenstein condition and the estimate in Theorem 5.4 give
$\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
. Then the Eisenstein condition and the estimate in Theorem 5.4 give
 $$\begin{eqnarray}\displaystyle 2(k-2) & = & \displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle c_{p}c_{k,p,n_{p}}p^{k-1}g_{0}(m_{\infty })h(m_{\infty })\nonumber\\ \displaystyle & {\geqslant} & \displaystyle c_{p}c_{k,p,n_{p}}p^{k-1}m_{\infty }^{k-1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2(k-2) & = & \displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle c_{p}c_{k,p,n_{p}}p^{k-1}g_{0}(m_{\infty })h(m_{\infty })\nonumber\\ \displaystyle & {\geqslant} & \displaystyle c_{p}c_{k,p,n_{p}}p^{k-1}m_{\infty }^{k-1}\nonumber\end{eqnarray}$$
so that
 $$\begin{eqnarray}m_{\infty }^{k-1}\leqslant \unicode[STIX]{x1D709}\frac{p^{n_{p}/2}}{c_{p}}\frac{k-2}{k}B_{k}.\end{eqnarray}$$
$$\begin{eqnarray}m_{\infty }^{k-1}\leqslant \unicode[STIX]{x1D709}\frac{p^{n_{p}/2}}{c_{p}}\frac{k-2}{k}B_{k}.\end{eqnarray}$$
The assertion now follows from Proposition 5.5. Suppose
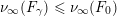 $\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})\leqslant \unicode[STIX]{x1D708}_{\infty }(F_{0})$
for some
$\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})\leqslant \unicode[STIX]{x1D708}_{\infty }(F_{0})$
for some
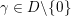 $\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
. Choose
$\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
. Choose
![]() $\unicode[STIX]{x1D6FE}\neq 0$
such that
$\unicode[STIX]{x1D6FE}\neq 0$
such that
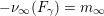 $-\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})=m_{\infty }$
. Then,
$-\unicode[STIX]{x1D708}_{\infty }(F_{\unicode[STIX]{x1D6FE}})=m_{\infty }$
. Then,
 $$\begin{eqnarray}-\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)\geqslant c_{k,p,n_{p}}p^{k-1}m_{\infty }^{k-1}\end{eqnarray}$$
$$\begin{eqnarray}-\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m)\geqslant c_{k,p,n_{p}}p^{k-1}m_{\infty }^{k-1}\end{eqnarray}$$
and the statement follows analogously. ◻
We remark that the first inequality in the proposition is a consequence of the Riemann–Roch theorem and the second is a consequence of the Eisenstein condition.
Theorem 5.7. Let
![]() $L$
be an even lattice of level
$L$
be an even lattice of level
![]() $p$
and genus
$p$
and genus
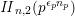 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
![]() $n>2$
and
$n>2$
and
![]() $n_{p}$
even splitting a hyperbolic plane
$n_{p}$
even splitting a hyperbolic plane
![]() $\mathit{II}_{1,1}$
. Suppose
$\mathit{II}_{1,1}$
. Suppose
![]() $L$
carries a holomorphic automorphic product of singular weight. Then for each
$L$
carries a holomorphic automorphic product of singular weight. Then for each
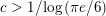 $c>1/\text{log}\,(\unicode[STIX]{x1D70B}e/6)$
there exists a constant
$c>1/\text{log}\,(\unicode[STIX]{x1D70B}e/6)$
there exists a constant
![]() $d$
depending only on
$d$
depending only on
![]() $c$
such that
$c$
such that
 $$\begin{eqnarray}n\leqslant cn_{p}\log (p)+d.\end{eqnarray}$$
$$\begin{eqnarray}n\leqslant cn_{p}\log (p)+d.\end{eqnarray}$$
Proof. Recall that
![]() $k\geqslant 4$
. Using
$k\geqslant 4$
. Using
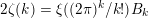 $2\unicode[STIX]{x1D701}(k)=\unicode[STIX]{x1D709}((2\unicode[STIX]{x1D70B})^{k}/k!)B_{k}$
and
$2\unicode[STIX]{x1D701}(k)=\unicode[STIX]{x1D709}((2\unicode[STIX]{x1D70B})^{k}/k!)B_{k}$
and
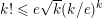 $k!\leqslant e\sqrt{k}(k/e)^{k}$
we derive from Proposition 5.6 the inequality
$k!\leqslant e\sqrt{k}(k/e)^{k}$
we derive from Proposition 5.6 the inequality
 $$\begin{eqnarray}1\leqslant e^{2}p^{n_{p}/2}k^{3/2}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant e^{2}p^{n_{p}/2}k^{3/2}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}\end{eqnarray}$$
respectively
 $$\begin{eqnarray}0\leqslant 2+\frac{n_{p}}{2}\log (p)+\frac{3}{2}\log (k)-k\log \biggl(\frac{\unicode[STIX]{x1D70B}e}{6}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant 2+\frac{n_{p}}{2}\log (p)+\frac{3}{2}\log (k)-k\log \biggl(\frac{\unicode[STIX]{x1D70B}e}{6}\biggr).\end{eqnarray}$$
If
![]() $t$
is a tangent of the real logarithm then
$t$
is a tangent of the real logarithm then
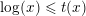 $\log (x)\leqslant t(x)$
for all
$\log (x)\leqslant t(x)$
for all
![]() $x>0$
. Thus,
$x>0$
. Thus,
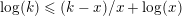 $\log (k)\leqslant (k-x)/x+\log (x)$
for all
$\log (k)\leqslant (k-x)/x+\log (x)$
for all
![]() $x>0$
. It follows
$x>0$
. It follows
 $$\begin{eqnarray}0\leqslant -\biggl(\log \biggl(\frac{\unicode[STIX]{x1D70B}e}{6}\biggr)-\frac{3}{2x}\biggr)k+\frac{n_{p}}{2}\log (p)+\frac{3}{2}(\log (x)-1)+2\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant -\biggl(\log \biggl(\frac{\unicode[STIX]{x1D70B}e}{6}\biggr)-\frac{3}{2x}\biggr)k+\frac{n_{p}}{2}\log (p)+\frac{3}{2}(\log (x)-1)+2\end{eqnarray}$$
for all
![]() $x>0$
. If
$x>0$
. If
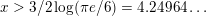 $x>3/2\log (\unicode[STIX]{x1D70B}e/6)=4.24964\ldots$
this gives an upper bound on
$x>3/2\log (\unicode[STIX]{x1D70B}e/6)=4.24964\ldots$
this gives an upper bound on
![]() $k$
and on
$k$
and on
![]() $n$
, i.e.
$n$
, i.e.
 $$\begin{eqnarray}n\leqslant c(x)n_{p}\log (p)+d(x)\end{eqnarray}$$
$$\begin{eqnarray}n\leqslant c(x)n_{p}\log (p)+d(x)\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle c(x) & = & \displaystyle \frac{2}{2\log (\unicode[STIX]{x1D70B}e/6)-3/x}\nonumber\\ \displaystyle d(x) & = & \displaystyle (3\log (x)+1)c(x)-2\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c(x) & = & \displaystyle \frac{2}{2\log (\unicode[STIX]{x1D70B}e/6)-3/x}\nonumber\\ \displaystyle d(x) & = & \displaystyle (3\log (x)+1)c(x)-2\nonumber\end{eqnarray}$$
in this case. ◻
Note that the proof is constructive. For example, taking
![]() $x=20$
gives the bounds
$x=20$
gives the bounds
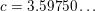 $c=3.59750\ldots$
and
$c=3.59750\ldots$
and
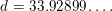 $d=33.92899\ldots .$
$d=33.92899\ldots .$
5.2 Odd
 $p$
-rank
$p$
-rank
Now let
![]() $L$
be an even lattice of prime level
$L$
be an even lattice of prime level
![]() $p$
and genus
$p$
and genus
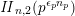 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
![]() $n>2$
and
$n>2$
and
![]() $n_{p}$
odd. Suppose
$n_{p}$
odd. Suppose
![]() $\unicode[STIX]{x1D6F9}(F)$
is a holomorphic automorphic product of singular weight on
$\unicode[STIX]{x1D6F9}(F)$
is a holomorphic automorphic product of singular weight on
![]() $L$
.
$L$
.
Since
![]() $n_{p}$
is odd, it follows that
$n_{p}$
is odd, it follows that
![]() $p$
is odd as well.
$p$
is odd as well.
The oddity formula implies
 $$\begin{eqnarray}e((n-2)/8)=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D716}_{p}\biggl({\displaystyle \frac{2}{p}}\biggr)\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ \displaystyle \unicode[STIX]{x1D716}_{p}\biggl({\displaystyle \frac{2}{p}}\biggr)(-1)^{(n_{p}-1)/2}e(1/4)\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}e((n-2)/8)=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D716}_{p}\biggl({\displaystyle \frac{2}{p}}\biggr)\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ \displaystyle \unicode[STIX]{x1D716}_{p}\biggl({\displaystyle \frac{2}{p}}\biggr)(-1)^{(n_{p}-1)/2}e(1/4)\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\end{array}\right.\end{eqnarray}$$
so that
 $$\begin{eqnarray}n=\left\{\begin{array}{@{}ll@{}}\displaystyle \pm 2\hspace{0.2em}{\rm mod}\hspace{0.2em}8\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ \displaystyle 0\hspace{0.2em}{\rm mod}\hspace{0.2em}4\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}n=\left\{\begin{array}{@{}ll@{}}\displaystyle \pm 2\hspace{0.2em}{\rm mod}\hspace{0.2em}8\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ \displaystyle 0\hspace{0.2em}{\rm mod}\hspace{0.2em}4\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4.\end{array}\right.\end{eqnarray}$$
Define
 $k=1+n/2$
and
$k=1+n/2$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D716}_{p}\biggl(\frac{2}{p}\biggr)\biggl(\frac{-1}{p}\biggr)^{(n_{p}-1)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D716}_{p}\biggl(\frac{2}{p}\biggr)\biggl(\frac{-1}{p}\biggr)^{(n_{p}-1)/2}.\end{eqnarray}$$
Then
 $$\begin{eqnarray}\unicode[STIX]{x1D709}=\left\{\begin{array}{@{}ll@{}}\displaystyle -(-1)^{k/2}\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ -(-1)^{(k-1)/2}\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\left\{\begin{array}{@{}ll@{}}\displaystyle -(-1)^{k/2}\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ -(-1)^{(k-1)/2}\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4.\end{array}\right.\end{eqnarray}$$
Let
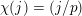 $\unicode[STIX]{x1D712}(j)=(j/p)$
. Define the twisted divisor sum
$\unicode[STIX]{x1D712}(j)=(j/p)$
. Define the twisted divisor sum
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{l,\unicode[STIX]{x1D712}}(m)=\mathop{\sum }_{d\mid m}\unicode[STIX]{x1D712}(m/d)d^{l}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{l,\unicode[STIX]{x1D712}}(m)=\mathop{\sum }_{d\mid m}\unicode[STIX]{x1D712}(m/d)d^{l}\end{eqnarray}$$
and the generalised Bernoulli numbers
![]() $B_{m,\unicode[STIX]{x1D712}}$
by
$B_{m,\unicode[STIX]{x1D712}}$
by
 $$\begin{eqnarray}\mathop{\sum }_{j=1}^{p}\frac{\unicode[STIX]{x1D712}(j)xe^{jx}}{e^{px}-1}=\mathop{\sum }_{m\geqslant 0}B_{m,\unicode[STIX]{x1D712}}\frac{x^{m}}{m!}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{p}\frac{\unicode[STIX]{x1D712}(j)xe^{jx}}{e^{px}-1}=\mathop{\sum }_{m\geqslant 0}B_{m,\unicode[STIX]{x1D712}}\frac{x^{m}}{m!}\end{eqnarray}$$
(see [Reference IwasawaIwa72]). Let
 $$\begin{eqnarray}c_{k,p,n_{p}}=\unicode[STIX]{x1D709}\frac{2k}{B_{k,\unicode[STIX]{x1D712}}}\frac{1}{p^{(n_{p}-1)/2}}.\end{eqnarray}$$
$$\begin{eqnarray}c_{k,p,n_{p}}=\unicode[STIX]{x1D709}\frac{2k}{B_{k,\unicode[STIX]{x1D712}}}\frac{1}{p^{(n_{p}-1)/2}}.\end{eqnarray}$$
The positivity of
![]() $L(k,\unicode[STIX]{x1D712})$
implies that
$L(k,\unicode[STIX]{x1D712})$
implies that
![]() $c_{k,p,n_{p}}$
is positive. We describe the Fourier coefficients
$c_{k,p,n_{p}}$
is positive. We describe the Fourier coefficients
![]() $a_{\unicode[STIX]{x1D6FE}}(m)$
of the Eisenstein series
$a_{\unicode[STIX]{x1D6FE}}(m)$
of the Eisenstein series
![]() $E$
.
$E$
.
Proposition 5.8. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
and
$\unicode[STIX]{x1D6FE}\in D$
and
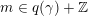 $m\in q(\unicode[STIX]{x1D6FE})+\mathbb{Z}$
,
$m\in q(\unicode[STIX]{x1D6FE})+\mathbb{Z}$
,
![]() $m>0$
.
$m>0$
.
If
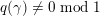 $q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
, then
$q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
, then
 $$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(pm).\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(pm).\end{eqnarray}$$
Suppose
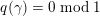 $q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
. Write
$q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
. Write
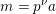 $m=p^{\unicode[STIX]{x1D708}}a$
with
$m=p^{\unicode[STIX]{x1D708}}a$
with
 $(a,p)=1$
. Then
$(a,p)=1$
. Then
 $$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(a)\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(a)\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D6FE}\neq 0$
and
$\unicode[STIX]{x1D6FE}\neq 0$
and
 $$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(a)-\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-1)/2}\unicode[STIX]{x1D712}(a)\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(a)\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D6FE}}(m)=-c_{k,p,n_{p}}p^{(\unicode[STIX]{x1D708}+1)(k-1)}\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(a)-\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-1)/2}\unicode[STIX]{x1D712}(a)\unicode[STIX]{x1D70E}_{k-1,\unicode[STIX]{x1D712}}(a)\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D6FE}=0$
.
$\unicode[STIX]{x1D6FE}=0$
.
We have the following result.
Proposition 5.9. The lattice
![]() $L$
splits a hyperbolic plane
$L$
splits a hyperbolic plane
![]() $\mathit{II}_{1,1}$
if and only if
$\mathit{II}_{1,1}$
if and only if
 $$\begin{eqnarray}n_{p}\leqslant n-1.\end{eqnarray}$$
$$\begin{eqnarray}n_{p}\leqslant n-1.\end{eqnarray}$$
As above, we denote the Fourier coefficients of
![]() $F$
by
$F$
by
![]() $c_{\unicode[STIX]{x1D6FE}}$
and define the functions
$c_{\unicode[STIX]{x1D6FE}}$
and define the functions
![]() $g_{\unicode[STIX]{x1D6FE}}$
. We also define
$g_{\unicode[STIX]{x1D6FE}}$
. We also define
 $$\begin{eqnarray}h_{\unicode[STIX]{x1D712}}(m)=\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree}}}\unicode[STIX]{x1D712}(m/d)d^{k-1}.\end{eqnarray}$$
$$\begin{eqnarray}h_{\unicode[STIX]{x1D712}}(m)=\mathop{\sum }_{\substack{ d\mid m \\ m/d\;\text{squarefree}}}\unicode[STIX]{x1D712}(m/d)d^{k-1}.\end{eqnarray}$$
The function
![]() $h_{\unicode[STIX]{x1D712}}$
is bounded below by
$h_{\unicode[STIX]{x1D712}}$
is bounded below by
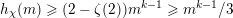 $h_{\unicode[STIX]{x1D712}}(m)\geqslant (2-\unicode[STIX]{x1D701}(2))m^{k-1}\geqslant m^{k-1}/3$
.
$h_{\unicode[STIX]{x1D712}}(m)\geqslant (2-\unicode[STIX]{x1D701}(2))m^{k-1}\geqslant m^{k-1}/3$
.
Theorem 5.10. Suppose
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
. Let
$\mathit{II}_{1,1}$
. Let
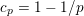 $c_{p}=1-1/p$
. Then
$c_{p}=1-1/p$
. Then
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & {\geqslant} & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{p}c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & {\geqslant} & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\,\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{p}c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m).\nonumber\end{eqnarray}$$
Proof. The argument is analogous to the proof of Theorem 5.4. We describe the necessary modifications.
Let
![]() $\unicode[STIX]{x1D6FE}\in D$
with
$\unicode[STIX]{x1D6FE}\in D$
with
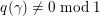 $q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
. Then
$q(\unicode[STIX]{x1D6FE})\neq 0\;\text{mod}\;1$
. Then
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m)=c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m/p=q(j\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}(g_{j\unicode[STIX]{x1D6FE}}(m/p)-g_{0}(mp))h_{\unicode[STIX]{x1D712}}(m). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m)=c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m/p=q(j\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}(g_{j\unicode[STIX]{x1D6FE}}(m/p)-g_{0}(mp))h_{\unicode[STIX]{x1D712}}(m). & & \displaystyle \nonumber\end{eqnarray}$$
For
 $\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
with
$\unicode[STIX]{x1D6FE}\in D\setminus \{0\}$
with
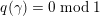 $q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
we find
$q(\unicode[STIX]{x1D6FE})=0\;\text{mod}\;1$
we find
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m)=c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}(g_{j\unicode[STIX]{x1D6FE}}(m)-g_{0}(mp^{2}))h_{\unicode[STIX]{x1D712}}(m). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}c_{j\unicode[STIX]{x1D6FE}}(-m)a_{j\unicode[STIX]{x1D6FE}}(m)=c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m>0}(g_{j\unicode[STIX]{x1D6FE}}(m)-g_{0}(mp^{2}))h_{\unicode[STIX]{x1D712}}(m). & & \displaystyle \nonumber\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D6FE}=0$
, then
$\unicode[STIX]{x1D6FE}=0$
, then
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}(g_{0}(m)-g_{0}(mp^{2}))h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-1)/2}\mathop{\sum }_{(m,p)=1}(g_{0}(m)+g_{0}(mp))\unicode[STIX]{x1D712}(m)h_{\unicode[STIX]{x1D712}}(m).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{m>0}(g_{0}(m)-g_{0}(mp^{2}))h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D709}c_{k,p,n_{p}}p^{(n_{p}-1)/2}\mathop{\sum }_{(m,p)=1}(g_{0}(m)+g_{0}(mp))\unicode[STIX]{x1D712}(m)h_{\unicode[STIX]{x1D712}}(m).\nonumber\end{eqnarray}$$
Using
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{m>0}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m) & = & \displaystyle \mathop{\sum }_{(m,p)=1}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m)+p^{k-1}\mathop{\sum }_{(m,p)=1}g_{0}(mp)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,p^{2(k-1)}\mathop{\sum }_{m>0}g_{0}(mp^{2})h_{\unicode[STIX]{x1D712}}(m),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{m>0}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m) & = & \displaystyle \mathop{\sum }_{(m,p)=1}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m)+p^{k-1}\mathop{\sum }_{(m,p)=1}g_{0}(mp)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,p^{2(k-1)}\mathop{\sum }_{m>0}g_{0}(mp^{2})h_{\unicode[STIX]{x1D712}}(m),\nonumber\end{eqnarray}$$
we obtain
 $$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m=j\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{k,p,n_{p},j}^{0}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m=j\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{k,p,n_{p},j}^{1}g_{0}(mp)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}c_{k,p,n_{p}}^{{\geqslant}2}\mathop{\sum }_{m>0}g_{0}(mp^{2})h_{\unicode[STIX]{x1D712}}(m)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}\,\mathop{\sum }_{m>0}c_{\unicode[STIX]{x1D6FE}}(-m)a_{\unicode[STIX]{x1D6FE}}(m) & = & \displaystyle c_{k,p,n_{p}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D \\ q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m/p=q(\unicode[STIX]{x1D6FE})\hspace{0.2em}{\rm mod}\hspace{0.2em}1}g_{\unicode[STIX]{x1D6FE}}(m/p)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}p^{k-1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FE}\in D\setminus \{0\} \\ q(\unicode[STIX]{x1D6FE})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}\mathop{\sum }_{m>0}g_{\unicode[STIX]{x1D6FE}}(m)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m=j\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{k,p,n_{p},j}^{0}g_{0}(m)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}\mathop{\sum }_{j=1}^{p-1}\,\mathop{\sum }_{m=j\hspace{0.2em}{\rm mod}\hspace{0.2em}p}c_{k,p,n_{p},j}^{1}g_{0}(mp)h_{\unicode[STIX]{x1D712}}(m)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k,p,n_{p}}c_{k,p,n_{p}}^{{\geqslant}2}\mathop{\sum }_{m>0}g_{0}(mp^{2})h_{\unicode[STIX]{x1D712}}(m)\nonumber\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle c_{k,p,n_{p},j}^{0} & = & \displaystyle p^{k-1}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}(j)p^{(n_{p}-1)/2},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & = & \displaystyle p^{2(k-1)}-a_{k,p,n_{p},j}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}(j)p^{(n_{p}-1)/2},\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & = & \displaystyle p^{3(k-1)}-p^{k-1}a_{k,p,n_{p},0},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{k,p,n_{p},j}^{0} & = & \displaystyle p^{k-1}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}(j)p^{(n_{p}-1)/2},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & = & \displaystyle p^{2(k-1)}-a_{k,p,n_{p},j}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D712}(j)p^{(n_{p}-1)/2},\nonumber\\ \displaystyle c_{k,p,n_{p}}^{{\geqslant}2} & = & \displaystyle p^{3(k-1)}-p^{k-1}a_{k,p,n_{p},0},\nonumber\end{eqnarray}$$
where
![]() $a_{k,p,n_{p},j}$
denotes the number of elements
$a_{k,p,n_{p},j}$
denotes the number of elements
![]() $\unicode[STIX]{x1D6FE}\in D$
of norm
$\unicode[STIX]{x1D6FE}\in D$
of norm
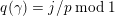 $q(\unicode[STIX]{x1D6FE})=j/p\;\text{mod}\;1$
. Since
$q(\unicode[STIX]{x1D6FE})=j/p\;\text{mod}\;1$
. Since
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
we have
$\mathit{II}_{1,1}$
we have
 $$\begin{eqnarray}\displaystyle c_{k,p,n_{p},j}^{0} & {\geqslant} & \displaystyle (1-1/p)p^{k-1},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & {\geqslant} & \displaystyle (1-1/p^{2})p^{2(k-1)},\nonumber\\ \displaystyle c_{k,p,n_{p},m}^{{\geqslant}2} & {\geqslant} & \displaystyle (1-1/p^{2})p^{3(k-1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{k,p,n_{p},j}^{0} & {\geqslant} & \displaystyle (1-1/p)p^{k-1},\nonumber\\ \displaystyle c_{k,p,n_{p},j}^{1} & {\geqslant} & \displaystyle (1-1/p^{2})p^{2(k-1)},\nonumber\\ \displaystyle c_{k,p,n_{p},m}^{{\geqslant}2} & {\geqslant} & \displaystyle (1-1/p^{2})p^{3(k-1)}.\nonumber\end{eqnarray}$$
This implies the assertion. ◻
Pairing
![]() $F$
with the Eisenstein series
$F$
with the Eisenstein series
![]() $E$
and applying the Riemann–Roch theorem to
$E$
and applying the Riemann–Roch theorem to
![]() $F_{0}$
, we obtain the following result.
$F_{0}$
, we obtain the following result.
Proposition 5.11. Suppose
![]() $L$
splits
$L$
splits
![]() $\mathit{II}_{1,1}$
. Then
$\mathit{II}_{1,1}$
. Then
 $$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant m_{\infty }^{k-1}\leqslant 3\unicode[STIX]{x1D709}\frac{p^{(n_{p}+1)/2}}{c_{p}}\frac{k-2}{k}\frac{B_{k,\unicode[STIX]{x1D712}}}{p^{k}}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{k-2}{12}\biggr)^{k-1}\leqslant m_{\infty }^{k-1}\leqslant 3\unicode[STIX]{x1D709}\frac{p^{(n_{p}+1)/2}}{c_{p}}\frac{k-2}{k}\frac{B_{k,\unicode[STIX]{x1D712}}}{p^{k}}.\end{eqnarray}$$
We can now derive a bound on
![]() $n$
.
$n$
.
Theorem 5.12. Let
![]() $L$
be an even lattice of level
$L$
be an even lattice of level
![]() $p$
and genus
$p$
and genus
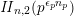 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
![]() $n>2$
and
$n>2$
and
![]() $n_{p}$
odd splitting a hyperbolic plane
$n_{p}$
odd splitting a hyperbolic plane
![]() $\mathit{II}_{1,1}$
. Suppose
$\mathit{II}_{1,1}$
. Suppose
![]() $L$
carries a holomorphic automorphic product of singular weight. Then for each
$L$
carries a holomorphic automorphic product of singular weight. Then for each
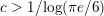 $c>1/\text{log}(\unicode[STIX]{x1D70B}e/6)$
there exists a constant
$c>1/\text{log}(\unicode[STIX]{x1D70B}e/6)$
there exists a constant
![]() $d$
depending only on
$d$
depending only on
![]() $c$
such that
$c$
such that
 $$\begin{eqnarray}n\leqslant cn_{p}\log (p)+d.\end{eqnarray}$$
$$\begin{eqnarray}n\leqslant cn_{p}\log (p)+d.\end{eqnarray}$$
Proof. Here we use
 $2L(k,\unicode[STIX]{x1D712})=\unicode[STIX]{x1D709}\sqrt{p}((2\unicode[STIX]{x1D70B})^{k}/k!)(B_{k,\unicode[STIX]{x1D712}}/p^{k})$
and
$2L(k,\unicode[STIX]{x1D712})=\unicode[STIX]{x1D709}\sqrt{p}((2\unicode[STIX]{x1D70B})^{k}/k!)(B_{k,\unicode[STIX]{x1D712}}/p^{k})$
and
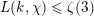 $L(k,\unicode[STIX]{x1D712})\leqslant \unicode[STIX]{x1D701}(3)$
to obtain
$L(k,\unicode[STIX]{x1D712})\leqslant \unicode[STIX]{x1D701}(3)$
to obtain
 $$\begin{eqnarray}1\leqslant \frac{5}{2}e^{2}p^{n_{p}/2}k^{3/2}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}.\end{eqnarray}$$
$$\begin{eqnarray}1\leqslant \frac{5}{2}e^{2}p^{n_{p}/2}k^{3/2}\biggl(\frac{6}{\unicode[STIX]{x1D70B}e}\biggr)^{k}.\end{eqnarray}$$
As above, this implies
 $$\begin{eqnarray}n\leqslant c(x)n_{p}\log (p)+d(x)\end{eqnarray}$$
$$\begin{eqnarray}n\leqslant c(x)n_{p}\log (p)+d(x)\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle c(x) & = & \displaystyle \frac{2}{2\log (\unicode[STIX]{x1D70B}e/6)-3/x},\nonumber\\ \displaystyle d(x) & = & \displaystyle (3\log (x)+1+2\log (5/2))c(x)-2\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c(x) & = & \displaystyle \frac{2}{2\log (\unicode[STIX]{x1D70B}e/6)-3/x},\nonumber\\ \displaystyle d(x) & = & \displaystyle (3\log (x)+1+2\log (5/2))c(x)-2\nonumber\end{eqnarray}$$
for
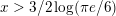 $x>3/2\log (\unicode[STIX]{x1D70B}e/6)$
.◻
$x>3/2\log (\unicode[STIX]{x1D70B}e/6)$
.◻
Note that the constant
![]() $d$
is slightly larger here than in Theorem 5.7. Taking
$d$
is slightly larger here than in Theorem 5.7. Taking
![]() $x=20$
we obtain the bounds
$x=20$
we obtain the bounds
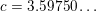 $c=3.59750\ldots$
and
$c=3.59750\ldots$
and
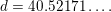 $d=40.52171\ldots .$
$d=40.52171\ldots .$
5.3 An example
Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
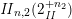 $\mathit{II}_{n,2}(2_{\mathit{II}}^{+n_{2}})$
with
$\mathit{II}_{n,2}(2_{\mathit{II}}^{+n_{2}})$
with
![]() $n>2$
and
$n>2$
and
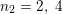 $n_{2}=2,~4$
or
$n_{2}=2,~4$
or
![]() $6$
carrying a holomorphic automorphic product of singular weight. Then
$6$
carrying a holomorphic automorphic product of singular weight. Then
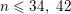 $n\leqslant 34,~42$
respectively
$n\leqslant 34,~42$
respectively
![]() $42$
and
$42$
and
 $$\begin{eqnarray}\frac{k-2}{12}\leqslant m_{\infty }\leqslant \biggl(2^{(n_{2}+2)/2}\frac{k-2}{k}B_{k}\biggr)^{1/(k-1)}\end{eqnarray}$$
$$\begin{eqnarray}\frac{k-2}{12}\leqslant m_{\infty }\leqslant \biggl(2^{(n_{2}+2)/2}\frac{k-2}{k}B_{k}\biggr)^{1/(k-1)}\end{eqnarray}$$
by Theorem 5.7 and Proposition 5.6. The values of the bounds are given in the following table.

Since
![]() $m_{\infty }$
is half-integral we obtain the following theorem.
$m_{\infty }$
is half-integral we obtain the following theorem.
Theorem 5.13. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
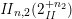 $\mathit{II}_{n,2}(2_{\mathit{II}}^{+n_{2}})$
with
$\mathit{II}_{n,2}(2_{\mathit{II}}^{+n_{2}})$
with
![]() $n>2$
and
$n>2$
and
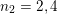 $n_{2}=2,4$
or
$n_{2}=2,4$
or
![]() $6$
carrying a holomorphic automorphic product of singular weight. Then
$6$
carrying a holomorphic automorphic product of singular weight. Then
![]() $n=10$
or
$n=10$
or
![]() $26$
.
$26$
.
6 Reflective forms
In this section, we remove the hypotheses made in [Reference ScheithauerSch06] and give a complete classification of reflective automorphic products of singular weight on lattices of prime level.
6.1 General results
We derive some general bounds and formulate the Eisenstein condition for reflective modular forms.
Let
![]() $L$
be an even lattice of prime level
$L$
be an even lattice of prime level
![]() $p$
and genus
$p$
and genus
 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
![]() $n>2$
. Let
$n>2$
. Let
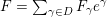 $F=\sum _{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}$
be a non-zero reflective modular form on
$F=\sum _{\unicode[STIX]{x1D6FE}\in D}F_{\unicode[STIX]{x1D6FE}}e^{\unicode[STIX]{x1D6FE}}$
be a non-zero reflective modular form on
![]() $L$
(see § 3). Then
$L$
(see § 3). Then
![]() $F$
has weight
$F$
has weight
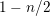 $1-n/2$
,
$1-n/2$
,
 $$\begin{eqnarray}F_{0}(\unicode[STIX]{x1D70F})=c_{0}(-1)q^{-1}+\mathop{\sum }_{\substack{ m\in \mathbb{Z} \\ m\geqslant 0}}c_{0}(m)q^{m}\end{eqnarray}$$
$$\begin{eqnarray}F_{0}(\unicode[STIX]{x1D70F})=c_{0}(-1)q^{-1}+\mathop{\sum }_{\substack{ m\in \mathbb{Z} \\ m\geqslant 0}}c_{0}(m)q^{m}\end{eqnarray}$$
with
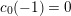 $c_{0}(-1)=0$
or
$c_{0}(-1)=0$
or
![]() $1$
,
$1$
,
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=c_{\unicode[STIX]{x1D6FE}}(-1/p)q^{-1/p}+\mathop{\sum }_{\substack{ m\in \mathbb{Z}-1/p \\ m>0}}c_{\unicode[STIX]{x1D6FE}}(m)q^{m}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D70F})=c_{\unicode[STIX]{x1D6FE}}(-1/p)q^{-1/p}+\mathop{\sum }_{\substack{ m\in \mathbb{Z}-1/p \\ m>0}}c_{\unicode[STIX]{x1D6FE}}(m)q^{m}\end{eqnarray}$$
with
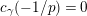 $c_{\unicode[STIX]{x1D6FE}}(-1/p)=0$
or
$c_{\unicode[STIX]{x1D6FE}}(-1/p)=0$
or
![]() $1$
if
$1$
if
 $q(\unicode[STIX]{x1D6FE})=1/p\;\text{mod}\;1$
and the other components
$q(\unicode[STIX]{x1D6FE})=1/p\;\text{mod}\;1$
and the other components
![]() $F_{\unicode[STIX]{x1D6FE}}$
of
$F_{\unicode[STIX]{x1D6FE}}$
of
![]() $F$
are holomorphic at
$F$
are holomorphic at
![]() $\infty$
. We define integers
$\infty$
. We define integers
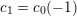 $c_{1}=c_{0}(-1)$
and
$c_{1}=c_{0}(-1)$
and
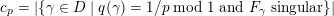 $c_{p}=|\{\unicode[STIX]{x1D6FE}\in D\mid q(\unicode[STIX]{x1D6FE})=1/p\;\text{mod}\;1\text{ and }F_{\unicode[STIX]{x1D6FE}}\text{ singular}\}|$
.
$c_{p}=|\{\unicode[STIX]{x1D6FE}\in D\mid q(\unicode[STIX]{x1D6FE})=1/p\;\text{mod}\;1\text{ and }F_{\unicode[STIX]{x1D6FE}}\text{ singular}\}|$
.
Proposition 6.1. We have
![]() $n<26$
. If
$n<26$
. If
![]() $c_{1}=0$
, then
$c_{1}=0$
, then
 $n\leqslant 2+24/(p+1)$
.
$n\leqslant 2+24/(p+1)$
.
Proof. The conditions imply
![]() $F_{0}\neq 0$
. Since
$F_{0}\neq 0$
. Since
![]() $F$
is reflective, the product
$F$
is reflective, the product
![]() $F_{0}\unicode[STIX]{x1D6E5}$
is a modular form for
$F_{0}\unicode[STIX]{x1D6E5}$
is a modular form for
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
of weight
$\unicode[STIX]{x1D6E4}_{0}(p)$
of weight
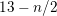 $13-n/2$
which is holomorphic on the upper halfplane and at the cusps. Hence,
$13-n/2$
which is holomorphic on the upper halfplane and at the cusps. Hence,
![]() $n\leqslant 26$
. If
$n\leqslant 26$
. If
![]() $n=26$
the function
$n=26$
the function
![]() $F_{0}$
must be
$F_{0}$
must be
![]() $1/\unicode[STIX]{x1D6E5}$
. However, as a result,
$1/\unicode[STIX]{x1D6E5}$
. However, as a result,
![]() $F$
does not transform correctly under
$F$
does not transform correctly under
![]() $S$
. This proves the first statement. If
$S$
. This proves the first statement. If
![]() $c_{1}=0$
the Riemann–Roch theorem applied to
$c_{1}=0$
the Riemann–Roch theorem applied to
![]() $F_{0}$
gives
$F_{0}$
gives
 $$\begin{eqnarray}-1\leqslant p\unicode[STIX]{x1D708}_{0}(F_{0})+\unicode[STIX]{x1D708}_{\infty }(F_{0})\leqslant \frac{m}{12}(p+1),\end{eqnarray}$$
$$\begin{eqnarray}-1\leqslant p\unicode[STIX]{x1D708}_{0}(F_{0})+\unicode[STIX]{x1D708}_{\infty }(F_{0})\leqslant \frac{m}{12}(p+1),\end{eqnarray}$$
where
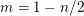 $m=1-n/2$
is the weight of
$m=1-n/2$
is the weight of
![]() $F_{0}$
. This implies the second statement.◻
$F_{0}$
. This implies the second statement.◻
Pairing
![]() $F$
with the Eisenstein series
$F$
with the Eisenstein series
![]() $E$
of weight
$E$
of weight
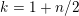 $k=1+n/2$
we obtain (see Propositions 5.1 and 5.8) the following result.
$k=1+n/2$
we obtain (see Propositions 5.1 and 5.8) the following result.
Proposition 6.2. Suppose
![]() $F_{0}$
has constant coefficient
$F_{0}$
has constant coefficient
![]() $n-2$
. Then
$n-2$
. Then
 $$\begin{eqnarray}\frac{k-2}{k}B_{k}(p^{k}-1)=\unicode[STIX]{x1D709}_{\text{even}}(p^{k-n_{p}/2}c_{1}+p^{1-n_{p}/2}c_{p})-c_{1}\end{eqnarray}$$
$$\begin{eqnarray}\frac{k-2}{k}B_{k}(p^{k}-1)=\unicode[STIX]{x1D709}_{\text{even}}(p^{k-n_{p}/2}c_{1}+p^{1-n_{p}/2}c_{p})-c_{1}\end{eqnarray}$$
with
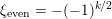 $\unicode[STIX]{x1D709}_{\text{even}}=-(-1)^{k/2}$
if
$\unicode[STIX]{x1D709}_{\text{even}}=-(-1)^{k/2}$
if
![]() $n_{p}$
is even and
$n_{p}$
is even and
 $$\begin{eqnarray}\frac{k-2}{k}B_{k,\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D709}_{\text{odd}}(p^{k-(n_{p}+1)/2}c_{1}+p^{(1-n_{p})/2}c_{p})+c_{1}\end{eqnarray}$$
$$\begin{eqnarray}\frac{k-2}{k}B_{k,\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D709}_{\text{odd}}(p^{k-(n_{p}+1)/2}c_{1}+p^{(1-n_{p})/2}c_{p})+c_{1}\end{eqnarray}$$
with
 $$\begin{eqnarray}\unicode[STIX]{x1D709}_{\text{odd}}=\left\{\begin{array}{@{}ll@{}}\displaystyle -(-1)^{k/2}\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ \displaystyle -(-1)^{(k-1)/2}\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{\text{odd}}=\left\{\begin{array}{@{}ll@{}}\displaystyle -(-1)^{k/2}\quad & \displaystyle \text{if }p=1\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\\ \displaystyle -(-1)^{(k-1)/2}\quad & \displaystyle \text{if }p=3\hspace{0.2em}{\rm mod}\hspace{0.2em}4,\end{array}\right.\end{eqnarray}$$
if
![]() $n_{p}$
is odd.
$n_{p}$
is odd.
We will also need the following result.
Proposition 6.3. If
 $n_{p}=n+2$
, then
$n_{p}=n+2$
, then
 $n-2=0\;\text{mod}\;8$
and
$n-2=0\;\text{mod}\;8$
and
![]() $L$
is a rescaling of
$L$
is a rescaling of
![]() $\mathit{II}_{n,2}$
by
$\mathit{II}_{n,2}$
by
![]() $p$
.
$p$
.
Proof. Since
![]() $\unicode[STIX]{x1D6FE}_{p}(D)$
is a fourth root of unity the oddity formula
$\unicode[STIX]{x1D6FE}_{p}(D)$
is a fourth root of unity the oddity formula
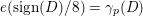 $e(\operatorname{sign}(D)/8)=\unicode[STIX]{x1D6FE}_{p}(D)$
implies that
$e(\operatorname{sign}(D)/8)=\unicode[STIX]{x1D6FE}_{p}(D)$
implies that
![]() $n$
is even. Then
$n$
is even. Then
![]() $n_{p}$
is also even and
$n_{p}$
is also even and
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{p}(D)=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{p}(D)=\unicode[STIX]{x1D716}_{p}\biggl(\frac{-1}{p}\biggr)^{n_{p}/2}.\end{eqnarray}$$
Hence,
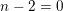 $n-2=0$
or
$n-2=0$
or
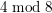 $4\;\text{mod}\;8$
and
$4\;\text{mod}\;8$
and
 $\unicode[STIX]{x1D6FE}_{p}(D)=\unicode[STIX]{x1D716}_{p}$
. The lattice
$\unicode[STIX]{x1D6FE}_{p}(D)=\unicode[STIX]{x1D716}_{p}$
. The lattice
![]() $L$
has determinant
$L$
has determinant
![]() $p^{n+2}$
so that
$p^{n+2}$
so that
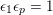 $\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{p}=1$
by the sign rule. Now
$\unicode[STIX]{x1D716}_{1}\unicode[STIX]{x1D716}_{p}=1$
by the sign rule. Now
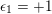 $\unicode[STIX]{x1D716}_{1}=+1$
because
$\unicode[STIX]{x1D716}_{1}=+1$
because
![]() $L$
has maximal
$L$
has maximal
![]() $p$
-rank and therefore
$p$
-rank and therefore
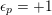 $\unicode[STIX]{x1D716}_{p}=+1$
. Applying the oddity formula again, we obtain
$\unicode[STIX]{x1D716}_{p}=+1$
. Applying the oddity formula again, we obtain
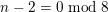 $n-2=0\;\text{mod}\;8$
. The second statement follows from the fact that there is only one class in the genus
$n-2=0\;\text{mod}\;8$
. The second statement follows from the fact that there is only one class in the genus
 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
under the given conditions.◻
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
under the given conditions.◻
6.2 Symmetric forms
Here we classify reflective modular forms that are invariant under
![]() $O(D)$
.
$O(D)$
.
Let
![]() $L$
be an even lattice of prime level
$L$
be an even lattice of prime level
![]() $p$
and genus
$p$
and genus
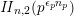 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
![]() $n>2$
. Then the number of elements
$n>2$
. Then the number of elements
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $D$
of order
$D$
of order
![]() $p$
and norm
$p$
and norm
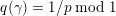 $q(\unicode[STIX]{x1D6FE})=1/p\;\text{mod}\;1$
is given by
$q(\unicode[STIX]{x1D6FE})=1/p\;\text{mod}\;1$
is given by
 $$\begin{eqnarray}p^{n_{p}-1}-\unicode[STIX]{x1D709}_{\text{even}}p^{(n_{p}-2)/2}\end{eqnarray}$$
$$\begin{eqnarray}p^{n_{p}-1}-\unicode[STIX]{x1D709}_{\text{even}}p^{(n_{p}-2)/2}\end{eqnarray}$$
if
![]() $n_{p}$
is even and by
$n_{p}$
is even and by
 $$\begin{eqnarray}p^{n_{p}-1}+\unicode[STIX]{x1D709}_{\text{odd}}p^{(n_{p}-1)/2}\end{eqnarray}$$
$$\begin{eqnarray}p^{n_{p}-1}+\unicode[STIX]{x1D709}_{\text{odd}}p^{(n_{p}-1)/2}\end{eqnarray}$$
if
![]() $n_{p}$
is odd (see [Reference ScheithauerSch06, Proposition 3.2]). Suppose
$n_{p}$
is odd (see [Reference ScheithauerSch06, Proposition 3.2]). Suppose
![]() $L$
carries a symmetric reflective modular form
$L$
carries a symmetric reflective modular form
![]() $F$
with
$F$
with
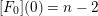 $[F_{0}](0)=n-2$
. Then the Eisenstein condition takes the form
$[F_{0}](0)=n-2$
. Then the Eisenstein condition takes the form
 $$\begin{eqnarray}\frac{k-2}{k}B_{k}(p^{k}-1)=\unicode[STIX]{x1D709}_{\text{even}}(p^{k-n_{p}/2}d_{1}+p^{n_{p}/2}d_{p})-d_{1}-d_{p}\end{eqnarray}$$
$$\begin{eqnarray}\frac{k-2}{k}B_{k}(p^{k}-1)=\unicode[STIX]{x1D709}_{\text{even}}(p^{k-n_{p}/2}d_{1}+p^{n_{p}/2}d_{p})-d_{1}-d_{p}\end{eqnarray}$$
if
![]() $n_{p}$
is even and
$n_{p}$
is even and
 $$\begin{eqnarray}\frac{k-2}{k}B_{k,\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D709}_{\text{odd}}(p^{k-(n_{p}+1)/2}d_{1}+p^{(n_{p}-1)/2}d_{p})+d_{1}+d_{p}\end{eqnarray}$$
$$\begin{eqnarray}\frac{k-2}{k}B_{k,\unicode[STIX]{x1D712}}=\unicode[STIX]{x1D709}_{\text{odd}}(p^{k-(n_{p}+1)/2}d_{1}+p^{(n_{p}-1)/2}d_{p})+d_{1}+d_{p}\end{eqnarray}$$
if
![]() $n_{p}$
is odd. Here
$n_{p}$
is odd. Here
![]() $d_{1}$
and
$d_{1}$
and
![]() $d_{p}$
can be
$d_{p}$
can be
![]() $0$
or
$0$
or
![]() $1$
. In the case
$1$
. In the case
 $n_{p}<n+2$
, the solutions of these equations have been determined in [Reference ScheithauerSch06].
$n_{p}<n+2$
, the solutions of these equations have been determined in [Reference ScheithauerSch06].
Theorem 6.4. Let
![]() $L$
be an even lattice of prime level
$L$
be an even lattice of prime level
![]() $p$
and genus
$p$
and genus
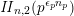 $\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
$\mathit{II}_{n,2}(p^{\unicode[STIX]{x1D716}_{p}n_{p}})$
with
![]() $n>2$
carrying a symmetric reflective modular form
$n>2$
carrying a symmetric reflective modular form
![]() $F$
. Suppose
$F$
. Suppose
![]() $F_{0}$
has constant coefficient
$F_{0}$
has constant coefficient
![]() $n-2$
. Then
$n-2$
. Then
![]() $L$
and
$L$
and
![]() $F$
are given in the following table.
$F$
are given in the following table.

The
![]() $\unicode[STIX]{x1D702}$
-product in the last column is a modular form for
$\unicode[STIX]{x1D702}$
-product in the last column is a modular form for
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
whose lift on
$\unicode[STIX]{x1D6E4}_{0}(p)$
whose lift on
![]() $0$
gives
$0$
gives
![]() $F$
.
$F$
.
Conversely, each of these functions is a reflective modular form on
![]() $L$
with the above stated properties.
$L$
with the above stated properties.
Proof. We only have to consider the case
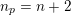 $n_{p}=n+2$
. Then
$n_{p}=n+2$
. Then
![]() $n=10$
or
$n=10$
or
![]() $18$
and
$18$
and
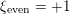 $\unicode[STIX]{x1D709}_{\text{even}}=+1$
by Propositions 6.3 and 6.1. The Eisenstein condition simplifies to
$\unicode[STIX]{x1D709}_{\text{even}}=+1$
by Propositions 6.3 and 6.1. The Eisenstein condition simplifies to
 $$\begin{eqnarray}\frac{k-2}{k}B_{k}=d_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{k-2}{k}B_{k}=d_{p}.\end{eqnarray}$$
Now the left-hand side is
![]() $1/63$
for
$1/63$
for
![]() $k=6$
and
$k=6$
and
![]() $2/33$
for
$2/33$
for
![]() $k=10$
. Hence, there are no reflective forms if
$k=10$
. Hence, there are no reflective forms if
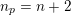 $n_{p}=n+2$
.◻
$n_{p}=n+2$
.◻
6.3 Bounds in the non-symmetric case
In this section, we derive bounds on the signature for reflective modular forms which are not invariant under
![]() $O(D)$
.
$O(D)$
.
First, we recall the Riemann–Roch theorem for
![]() $\unicode[STIX]{x1D6E4}_{1}(p)$
.
$\unicode[STIX]{x1D6E4}_{1}(p)$
.
Let
![]() $p$
be prime. For
$p$
be prime. For
![]() $p\geqslant 3$
, the group
$p\geqslant 3$
, the group
![]() $\unicode[STIX]{x1D6E4}_{1}(p)$
has
$\unicode[STIX]{x1D6E4}_{1}(p)$
has
![]() $p-1$
classes of cusps which can be represented by
$p-1$
classes of cusps which can be represented by
![]() $1/c$
with
$1/c$
with
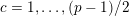 $c=1,\ldots ,(p-1)/2$
of width
$c=1,\ldots ,(p-1)/2$
of width
![]() $p$
and
$p$
and
![]() $a/p$
with
$a/p$
with
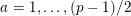 $a=1,\ldots ,(p-1)/2$
of width
$a=1,\ldots ,(p-1)/2$
of width
![]() $1$
. The cusps of
$1$
. The cusps of
![]() $\unicode[STIX]{x1D6E4}_{1}(2)$
can be represented by
$\unicode[STIX]{x1D6E4}_{1}(2)$
can be represented by
![]() $1/2$
of width
$1/2$
of width
![]() $1$
and
$1$
and
![]() $1/1$
of width
$1/1$
of width
![]() $2$
. Let
$2$
. Let
![]() $f\neq 0$
be a meromorphic modular form on
$f\neq 0$
be a meromorphic modular form on
![]() $\unicode[STIX]{x1D6E4}_{1}(p)$
of weight
$\unicode[STIX]{x1D6E4}_{1}(p)$
of weight
![]() $m$
and finite-order character. For
$m$
and finite-order character. For
![]() $p\geqslant 5$
, there are no torsion points and the Riemann–Roch theorem states
$p\geqslant 5$
, there are no torsion points and the Riemann–Roch theorem states
 $$\begin{eqnarray}\mathop{\sum }_{c=1}^{(p-1)/2}p\unicode[STIX]{x1D708}_{1/c}(f)+\mathop{\sum }_{a=1}^{(p-1)/2}\unicode[STIX]{x1D708}_{a/p}(f)+\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{1}(p)\setminus H}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70F}}(f)=\frac{m}{24}(p^{2}-1).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{c=1}^{(p-1)/2}p\unicode[STIX]{x1D708}_{1/c}(f)+\mathop{\sum }_{a=1}^{(p-1)/2}\unicode[STIX]{x1D708}_{a/p}(f)+\mathop{\sum }_{\unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{1}(p)\setminus H}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70F}}(f)=\frac{m}{24}(p^{2}-1).\end{eqnarray}$$
For
![]() $p=3$
, we have
$p=3$
, we have
 $$\begin{eqnarray}3\unicode[STIX]{x1D708}_{1/1}(f)+\unicode[STIX]{x1D708}_{1/3}(f)+\frac{1}{3}\unicode[STIX]{x1D708}_{e_{3}}(f)+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{1}(3)\setminus H \\ \unicode[STIX]{x1D70F}\neq e_{3}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E4}_{1}(3)}}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70F}}(f)=\frac{m}{3}\end{eqnarray}$$
$$\begin{eqnarray}3\unicode[STIX]{x1D708}_{1/1}(f)+\unicode[STIX]{x1D708}_{1/3}(f)+\frac{1}{3}\unicode[STIX]{x1D708}_{e_{3}}(f)+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{1}(3)\setminus H \\ \unicode[STIX]{x1D70F}\neq e_{3}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E4}_{1}(3)}}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70F}}(f)=\frac{m}{3}\end{eqnarray}$$
with
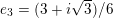 $e_{3}=(3+i\sqrt{3})/6$
and
$e_{3}=(3+i\sqrt{3})/6$
and
 $$\begin{eqnarray}2\unicode[STIX]{x1D708}_{1/1}(f)+\unicode[STIX]{x1D708}_{1/2}(f)+\frac{1}{2}\unicode[STIX]{x1D708}_{e_{2}}(f)+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{1}(2)\setminus H \\ \unicode[STIX]{x1D70F}\neq e_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E4}_{1}(2)}}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70F}}(f)=\frac{m}{4}\end{eqnarray}$$
$$\begin{eqnarray}2\unicode[STIX]{x1D708}_{1/1}(f)+\unicode[STIX]{x1D708}_{1/2}(f)+\frac{1}{2}\unicode[STIX]{x1D708}_{e_{2}}(f)+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D70F}\in \unicode[STIX]{x1D6E4}_{1}(2)\setminus H \\ \unicode[STIX]{x1D70F}\neq e_{2}\hspace{0.2em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6E4}_{1}(2)}}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70F}}(f)=\frac{m}{4}\end{eqnarray}$$
with
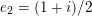 $e_{2}=(1+i)/2$
if
$e_{2}=(1+i)/2$
if
![]() $p=2$
.
$p=2$
.
Theorem 6.5. Let
![]() $L$
be an even lattice of prime level
$L$
be an even lattice of prime level
![]() $p$
and signature
$p$
and signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n>2$
carrying a non-symmetric reflective modular form
$n>2$
carrying a non-symmetric reflective modular form
![]() $F$
. Then
$F$
. Then
![]() $p\leqslant 11$
and
$p\leqslant 11$
and
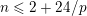 $n\leqslant 2+24/p$
.
$n\leqslant 2+24/p$
.
Proof. Since
![]() $F$
is non-symmetric there are
$F$
is non-symmetric there are
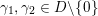 $\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\in D\setminus \{0\}$
of the same norm such that
$\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2}\in D\setminus \{0\}$
of the same norm such that
 $$\begin{eqnarray}f=F_{\unicode[STIX]{x1D6FE}_{1}}-F_{\unicode[STIX]{x1D6FE}_{2}}\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}f=F_{\unicode[STIX]{x1D6FE}_{1}}-F_{\unicode[STIX]{x1D6FE}_{2}}\neq 0.\end{eqnarray}$$
The function
![]() $f$
is a modular form on
$f$
is a modular form on
![]() $\unicode[STIX]{x1D6E4}_{1}(p)$
of weight
$\unicode[STIX]{x1D6E4}_{1}(p)$
of weight
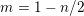 $m=1-n/2$
and finite-order character.
$m=1-n/2$
and finite-order character.
Let
![]() $\unicode[STIX]{x1D6FE}\in D$
and
$\unicode[STIX]{x1D6FE}\in D$
and
 $M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}$
. Then
$M=\big(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!\big)\in \unicode[STIX]{x1D6E4}$
. Then
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D6FE}}|_{m,M}=\biggl(\frac{a}{|D|}\biggr)e(-abq(\unicode[STIX]{x1D6FE}))F_{a\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D6FE}}|_{m,M}=\biggl(\frac{a}{|D|}\biggr)e(-abq(\unicode[STIX]{x1D6FE}))F_{a\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
if
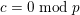 $c=0\;\text{mod}\;p$
and
$c=0\;\text{mod}\;p$
and
 $$\begin{eqnarray}\displaystyle F_{\unicode[STIX]{x1D6FE}}|_{m,M}=\frac{e(-\text{sign}(D)/8)}{\sqrt{|D|}}\biggl(\frac{-c}{|D|}\biggr)\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e(-c^{-1}dq(\unicode[STIX]{x1D707}))e(-b(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}))e(-abq(\unicode[STIX]{x1D6FE}))F_{a\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{\unicode[STIX]{x1D6FE}}|_{m,M}=\frac{e(-\text{sign}(D)/8)}{\sqrt{|D|}}\biggl(\frac{-c}{|D|}\biggr)\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e(-c^{-1}dq(\unicode[STIX]{x1D707}))e(-b(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}))e(-abq(\unicode[STIX]{x1D6FE}))F_{a\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}} & & \displaystyle \nonumber\end{eqnarray}$$
if
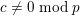 $c\neq 0\;\text{mod}\;p$
. The coefficient at
$c\neq 0\;\text{mod}\;p$
. The coefficient at
![]() $F_{0}$
in this sum is
$F_{0}$
in this sum is
 $$\begin{eqnarray}e(-c^{-1}dq(\unicode[STIX]{x1D707}))e(-b(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}))e(-abq(\unicode[STIX]{x1D6FE}))=e(-c^{-1}aq(\unicode[STIX]{x1D6FE})),\end{eqnarray}$$
$$\begin{eqnarray}e(-c^{-1}dq(\unicode[STIX]{x1D707}))e(-b(\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}))e(-abq(\unicode[STIX]{x1D6FE}))=e(-c^{-1}aq(\unicode[STIX]{x1D6FE})),\end{eqnarray}$$
i.e. only depends on the norm of
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.
This implies that for all
![]() $M\in \unicode[STIX]{x1D6E4}$
, the function
$M\in \unicode[STIX]{x1D6E4}$
, the function
![]() $f|_{m,M}$
is a linear combination of functions
$f|_{m,M}$
is a linear combination of functions
![]() $F_{\unicode[STIX]{x1D6FE}}$
with
$F_{\unicode[STIX]{x1D6FE}}$
with
![]() $\unicode[STIX]{x1D6FE}\neq 0$
. Hence,
$\unicode[STIX]{x1D6FE}\neq 0$
. Hence,
 $$\begin{eqnarray}\unicode[STIX]{x1D708}_{s}(f)\geqslant -1/p\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{s}(f)\geqslant -1/p\end{eqnarray}$$
for all cusps
![]() $s$
of
$s$
of
![]() $\unicode[STIX]{x1D6E4}_{1}(p)$
. It follows that
$\unicode[STIX]{x1D6E4}_{1}(p)$
. It follows that
 $$\begin{eqnarray}-\frac{p-1}{2}\biggl(1+\frac{1}{p}\biggr)\leqslant \frac{m}{24}(p^{2}-1).\end{eqnarray}$$
$$\begin{eqnarray}-\frac{p-1}{2}\biggl(1+\frac{1}{p}\biggr)\leqslant \frac{m}{24}(p^{2}-1).\end{eqnarray}$$
This proves the theorem. ◻
Note that the bounds do not hold in the symmetric case.
Using Theorem 6.5, we can determine the non-symmetric forms on lattices of prime level by analysing the obstructions in a finite number of cases. For
![]() $p=3$
, which is the most complicated case, we describe this explicitly in the next section. The other cases are analogous.
$p=3$
, which is the most complicated case, we describe this explicitly in the next section. The other cases are analogous.
6.4 Level
 $3$
$3$
In this section we determine the reflective forms on lattices of level
![]() $3$
and signature
$3$
and signature
![]() $(n,2)$
where
$(n,2)$
where
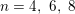 $n=4,~6,~8$
or
$n=4,~6,~8$
or
![]() $10$
.
$10$
.
Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
 $\mathit{II}_{10,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
$\mathit{II}_{10,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
![]() $F$
a reflective form on
$F$
a reflective form on
![]() $L$
. Suppose
$L$
. Suppose
![]() $F_{0}$
has constant coefficient
$F_{0}$
has constant coefficient
 $[F_{0}](0)=8$
. Then
$[F_{0}](0)=8$
. Then
![]() $c_{1}=1$
(see Proposition 6.1) and the Eisenstein condition gives the following value for
$c_{1}=1$
(see Proposition 6.1) and the Eisenstein condition gives the following value for
![]() $c_{3}$
(see Proposition 6.2).
$c_{3}$
(see Proposition 6.2).


Since
![]() $c_{3}$
should be a non-negative integer, this already excludes the first three cases.
$c_{3}$
should be a non-negative integer, this already excludes the first three cases.
The space
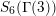 $S_{6}(\unicode[STIX]{x1D6E4}(3))$
has dimension
$S_{6}(\unicode[STIX]{x1D6E4}(3))$
has dimension
![]() $3$
and is spanned by the functions
$3$
and is spanned by the functions
![]() $\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}^{2}$
,
$\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}^{2}$
,
 $\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}$
and
$\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}$
and
![]() $\unicode[STIX]{x1D702}_{1^{6}3^{6}}$
. The liftings of these functions generate the obstruction space
$\unicode[STIX]{x1D702}_{1^{6}3^{6}}$
. The liftings of these functions generate the obstruction space
![]() $S_{\overline{\unicode[STIX]{x1D70C}}_{D},6}$
.
$S_{\overline{\unicode[STIX]{x1D70C}}_{D},6}$
.
Pairing
![]() $F$
with the lift
$F$
with the lift
![]() $F_{\unicode[STIX]{x1D702}_{1^{6}3^{6}},0}$
of the
$F_{\unicode[STIX]{x1D702}_{1^{6}3^{6}},0}$
of the
![]() $\unicode[STIX]{x1D702}$
-product
$\unicode[STIX]{x1D702}$
-product
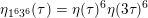 $\unicode[STIX]{x1D702}_{1^{6}3^{6}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{6}$
we obtain
$\unicode[STIX]{x1D702}_{1^{6}3^{6}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{6}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{6}$
we obtain
 $$\begin{eqnarray}1-\frac{1}{3^{n_{3}/2}}-\frac{c_{3}}{3^{(n_{3}+4)/2}}=0.\end{eqnarray}$$
$$\begin{eqnarray}1-\frac{1}{3^{n_{3}/2}}-\frac{c_{3}}{3^{(n_{3}+4)/2}}=0.\end{eqnarray}$$
Proposition 6.6. There are no reflective modular forms with constant coefficient
![]() $8$
on lattices of genus
$8$
on lattices of genus
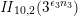 $\mathit{II}_{10,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
.
$\mathit{II}_{10,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
.
Next, we consider the case
![]() $n=8$
. Let
$n=8$
. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
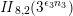 $\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
$\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
![]() $F$
a reflective modular form on
$F$
a reflective modular form on
![]() $L$
with
$L$
with
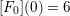 $[F_{0}](0)=6$
. Then we obtain the following for
$[F_{0}](0)=6$
. Then we obtain the following for
![]() $c_{3}$
.
$c_{3}$
.

The discriminant form of type
![]() $3^{+1}$
contains no elements
$3^{+1}$
contains no elements
![]() $\unicode[STIX]{x1D6FE}$
of norm
$\unicode[STIX]{x1D6FE}$
of norm
 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Hence, this case can be excluded.
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Hence, this case can be excluded.
The space
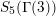 $S_{5}(\unicode[STIX]{x1D6E4}(3))$
has dimension
$S_{5}(\unicode[STIX]{x1D6E4}(3))$
has dimension
![]() $2$
and is spanned by the functions
$2$
and is spanned by the functions
![]() $\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}$
and
$\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}$
and
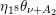 $\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}$
. The liftings of these functions generate the obstruction space
$\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}$
. The liftings of these functions generate the obstruction space
![]() $S_{\overline{\unicode[STIX]{x1D70C}}_{D},5}$
.
$S_{\overline{\unicode[STIX]{x1D70C}}_{D},5}$
.
The lattice
![]() $A_{2}$
has genus
$A_{2}$
has genus
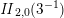 $\mathit{II}_{2,0}(3^{-1})$
and is isomorphic to its rescaled dual
$\mathit{II}_{2,0}(3^{-1})$
and is isomorphic to its rescaled dual
![]() $A_{2}^{\prime }(3)$
. The theta functions of
$A_{2}^{\prime }(3)$
. The theta functions of
![]() $A_{2}$
can be written as
$A_{2}$
can be written as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{A_{2}} & = & \displaystyle \frac{\unicode[STIX]{x1D702}_{1^{3}}+9\unicode[STIX]{x1D702}_{9^{3}}}{\unicode[STIX]{x1D702}_{3^{1}}},\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}} & = & \displaystyle {\textstyle \frac{1}{2}}(\unicode[STIX]{x1D703}_{A_{2}^{\prime }}-\unicode[STIX]{x1D703}_{A_{2}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{A_{2}} & = & \displaystyle \frac{\unicode[STIX]{x1D702}_{1^{3}}+9\unicode[STIX]{x1D702}_{9^{3}}}{\unicode[STIX]{x1D702}_{3^{1}}},\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}} & = & \displaystyle {\textstyle \frac{1}{2}}(\unicode[STIX]{x1D703}_{A_{2}^{\prime }}-\unicode[STIX]{x1D703}_{A_{2}}).\nonumber\end{eqnarray}$$
They transform under
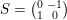 $S=\big(\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!\big)$
as
$S=\big(\!\begin{smallmatrix}0 & -1\\ 1 & 0\end{smallmatrix}\!\big)$
as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{A_{2}}|_{1,S} & = & \displaystyle \frac{e(-1/4)}{\sqrt{3}}(\unicode[STIX]{x1D703}_{A_{2}}+2\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}})=\frac{e(-1/4)}{\sqrt{3}}\unicode[STIX]{x1D703}_{A_{2}^{\prime }},\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}|_{1,S} & = & \displaystyle \frac{e(-1/4)}{\sqrt{3}}(\unicode[STIX]{x1D703}_{A_{2}}-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}_{A_{2}}|_{1,S} & = & \displaystyle \frac{e(-1/4)}{\sqrt{3}}(\unicode[STIX]{x1D703}_{A_{2}}+2\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}})=\frac{e(-1/4)}{\sqrt{3}}\unicode[STIX]{x1D703}_{A_{2}^{\prime }},\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}|_{1,S} & = & \displaystyle \frac{e(-1/4)}{\sqrt{3}}(\unicode[STIX]{x1D703}_{A_{2}}-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}).\nonumber\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
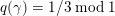 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then the lift of
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then the lift of
![]() $\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}$
with respect to the dual Weil representation
$\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}$
with respect to the dual Weil representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
on
$\overline{\unicode[STIX]{x1D70C}}_{D}$
on
![]() $\unicode[STIX]{x1D6FE}$
is given by
$\unicode[STIX]{x1D6FE}$
is given by
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
with
 $$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
$$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
and
 $$\begin{eqnarray}F_{1/1}=-\frac{1}{3^{(n_{3}-1)/2}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}}),\end{eqnarray}$$
$$\begin{eqnarray}F_{1/1}=-\frac{1}{3^{(n_{3}-1)/2}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}}),\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D702}_{1^{8}}(\unicode[STIX]{x1D703}_{A_{2}}+2\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}})=g_{0}+g_{1}+g_{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{1^{8}}(\unicode[STIX]{x1D703}_{A_{2}}+2\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}})=g_{0}+g_{1}+g_{2}\end{eqnarray}$$
and
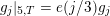 $g_{j}|_{5,T}=e(j/3)g_{j}$
. Note that
$g_{j}|_{5,T}=e(j/3)g_{j}$
. Note that
![]() $g_{0}=0$
. We obtain an analogous result for the lift of
$g_{0}=0$
. We obtain an analogous result for the lift of
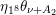 $\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}$
with respect to
$\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}}$
with respect to
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
on an element
$\overline{\unicode[STIX]{x1D70C}}_{D}$
on an element
![]() $\unicode[STIX]{x1D6FE}\in D$
of norm
$\unicode[STIX]{x1D6FE}\in D$
of norm
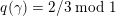 $q(\unicode[STIX]{x1D6FE})=2/3\;\text{mod}\;1$
.
$q(\unicode[STIX]{x1D6FE})=2/3\;\text{mod}\;1$
.
Let
 $$\begin{eqnarray}M=\{\unicode[STIX]{x1D6FE}\in D\mid q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1\text{ and }F_{\unicode[STIX]{x1D6FE}}\text{ singular}\}.\end{eqnarray}$$
$$\begin{eqnarray}M=\{\unicode[STIX]{x1D6FE}\in D\mid q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1\text{ and }F_{\unicode[STIX]{x1D6FE}}\text{ singular}\}.\end{eqnarray}$$
We assume now that
![]() $M$
is non-empty. Then
$M$
is non-empty. Then
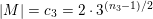 $|M|=c_{3}=2\cdot 3^{(n_{3}-1)/2}$
and
$|M|=c_{3}=2\cdot 3^{(n_{3}-1)/2}$
and
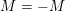 $M=-M$
because
$M=-M$
because
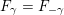 $F_{\unicode[STIX]{x1D6FE}}=F_{-\unicode[STIX]{x1D6FE}}$
. The crucial result to determine the structure of
$F_{\unicode[STIX]{x1D6FE}}=F_{-\unicode[STIX]{x1D6FE}}$
. The crucial result to determine the structure of
![]() $M$
is the following proposition.
$M$
is the following proposition.
Proposition 6.7. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
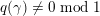 $q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
. Then
$q(\unicode[STIX]{x1D6FE})\neq 0\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
. Then
 $$\begin{eqnarray}|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=\left\{\begin{array}{@{}ll@{}}2|M|/3\quad & \text{if }\unicode[STIX]{x1D6FE}\in M,\\ |M|/3\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=\left\{\begin{array}{@{}ll@{}}2|M|/3\quad & \text{if }\unicode[STIX]{x1D6FE}\in M,\\ |M|/3\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Proof. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
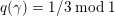 $q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
. Suppose
$q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
. Suppose
![]() $\unicode[STIX]{x1D6FE}\in M$
. Then pairing
$\unicode[STIX]{x1D6FE}\in M$
. Then pairing
![]() $F$
with
$F$
with
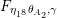 $F_{\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}},\unicode[STIX]{x1D6FE}}$
gives
$F_{\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{A_{2}},\unicode[STIX]{x1D6FE}}$
gives
 $$\begin{eqnarray}2-\frac{1}{3^{(n_{3}-1)/2}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in M}(e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))+e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})))=0\end{eqnarray}$$
$$\begin{eqnarray}2-\frac{1}{3^{(n_{3}-1)/2}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in M}(e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))+e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})))=0\end{eqnarray}$$
so that
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D707}\in M}(e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))+e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})))=|M|.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D707}\in M}(e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))+e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})))=|M|.\end{eqnarray}$$
This implies
 $$\begin{eqnarray}|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=2|M|/3.\end{eqnarray}$$
$$\begin{eqnarray}|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=2|M|/3.\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D6FE}\notin M$
the same argument shows
$\unicode[STIX]{x1D6FE}\notin M$
the same argument shows
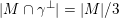 $|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=|M|/3$
. In case
$|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=|M|/3$
. In case
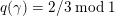 $q(\unicode[STIX]{x1D6FE})=2/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
the statement follows from pairing
$q(\unicode[STIX]{x1D6FE})=2/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
the statement follows from pairing
![]() $F$
with
$F$
with
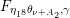 $F_{\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}},\unicode[STIX]{x1D6FE}}$
.◻
$F_{\unicode[STIX]{x1D702}_{1^{8}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D708}+A_{2}},\unicode[STIX]{x1D6FE}}$
.◻
The proposition implies that
![]() $M^{\bot }$
is an isotropic subgroup of
$M^{\bot }$
is an isotropic subgroup of
![]() $D$
. Let
$D$
. Let
![]() $\unicode[STIX]{x1D6FE}\in M$
and
$\unicode[STIX]{x1D6FE}\in M$
and
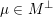 $\unicode[STIX]{x1D707}\in M^{\bot }$
. Then
$\unicode[STIX]{x1D707}\in M^{\bot }$
. Then
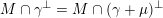 $M\cap \unicode[STIX]{x1D6FE}^{\bot }=M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }$
. Hence, the group
$M\cap \unicode[STIX]{x1D6FE}^{\bot }=M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }$
. Hence, the group
![]() $M^{\bot }$
acts on
$M^{\bot }$
acts on
![]() $M$
by translations.
$M$
by translations.
Proposition 6.8. Let
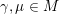 $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
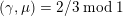 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=2/3\;\text{mod}\;1$
. Then
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=2/3\;\text{mod}\;1$
. Then
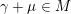 $\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}\in M$
.
$\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}\in M$
.
Proof. The sets
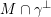 $M\cap \unicode[STIX]{x1D6FE}^{\bot }$
and
$M\cap \unicode[STIX]{x1D6FE}^{\bot }$
and
 $M\cap \unicode[STIX]{x1D707}^{\bot }$
are both subsets of
$M\cap \unicode[STIX]{x1D707}^{\bot }$
are both subsets of
 $M\setminus \{\pm \unicode[STIX]{x1D6FE}\}$
. Hence,
$M\setminus \{\pm \unicode[STIX]{x1D6FE}\}$
. Hence,
 $$\begin{eqnarray}|(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })|\geqslant 4|M|/3-(|M|-2)=|M|/3+2.\end{eqnarray}$$
$$\begin{eqnarray}|(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })|\geqslant 4|M|/3-(|M|-2)=|M|/3+2.\end{eqnarray}$$
Since
 $(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })\subset (M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot })$
this implies
$(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })\subset (M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot })$
this implies
 $|M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }|=2|M|/3$
and
$|M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }|=2|M|/3$
and
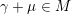 $\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}\in M$
.◻
$\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}\in M$
.◻
Proposition 6.9. Let
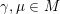 $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=0\;\text{mod}\;1$
. Then
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=0\;\text{mod}\;1$
. Then
 $$\begin{eqnarray}(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })=M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }.\end{eqnarray}$$
$$\begin{eqnarray}(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })=M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }.\end{eqnarray}$$
Proof. We have
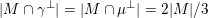 $|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=|M\cap \unicode[STIX]{x1D707}^{\bot }|=2|M|/3$
so that
$|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=|M\cap \unicode[STIX]{x1D707}^{\bot }|=2|M|/3$
so that
 $$\begin{eqnarray}|(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })|\geqslant 4|M|/3-|M|=|M|/3.\end{eqnarray}$$
$$\begin{eqnarray}|(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })|\geqslant 4|M|/3-|M|=|M|/3.\end{eqnarray}$$
On the other hand,
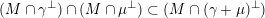 $(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })\subset (M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot })$
and
$(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D707}^{\bot })\subset (M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot })$
and
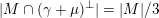 $|M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }|=|M|/3$
because
$|M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot }|=|M|/3$
because
 $q(\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})=2/3\;\text{mod}\;1$
. This implies the statement.◻
$q(\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})=2/3\;\text{mod}\;1$
. This implies the statement.◻
Proposition 6.10. Let
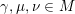 $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}\in M$
such that
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}\in M$
such that
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=(\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})=2/3\quad \text{mod}\;1.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=(\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})=2/3\quad \text{mod}\;1.\end{eqnarray}$$
Then
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\quad \text{mod}\;1.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\quad \text{mod}\;1.\end{eqnarray}$$
Proof. First suppose
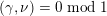 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Define
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Define
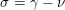 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D708}$
. Then
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D708}$
. Then
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D707})=0$
. However, this contradicts
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D707})=0$
. However, this contradicts
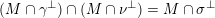 $(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D708}^{\bot })=M\cap \unicode[STIX]{x1D70E}^{\bot }$
. Next we assume
$(M\cap \unicode[STIX]{x1D6FE}^{\bot })\cap (M\cap \unicode[STIX]{x1D708}^{\bot })=M\cap \unicode[STIX]{x1D70E}^{\bot }$
. Next we assume
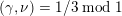 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=1/3\;\text{mod}\;1$
. Here we define
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=1/3\;\text{mod}\;1$
. Here we define
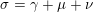 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}+\unicode[STIX]{x1D708}$
. Note that
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}+\unicode[STIX]{x1D708}$
. Note that
![]() $\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}$
is in
$\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707}$
is in
![]() $M$
and
$M$
and
 $(\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Then
$(\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Then
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D707})=0\;\text{mod}\;1$
. This contradicts
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D707})=0\;\text{mod}\;1$
. This contradicts
 $(M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot })\cap (M\cap \unicode[STIX]{x1D708}^{\bot })=M\cap \unicode[STIX]{x1D70E}^{\bot }$
. Hence,
$(M\cap (\unicode[STIX]{x1D6FE}+\unicode[STIX]{x1D707})^{\bot })\cap (M\cap \unicode[STIX]{x1D708}^{\bot })=M\cap \unicode[STIX]{x1D70E}^{\bot }$
. Hence,
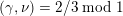 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\;\text{mod}\;1$
.◻
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\;\text{mod}\;1$
.◻
A consequence of this result is the following proposition.
Proposition 6.11. Let
 $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
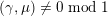 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})\neq 0\;\text{mod}\;1$
. Then
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})\neq 0\;\text{mod}\;1$
. Then
 $$\begin{eqnarray}M\cap \unicode[STIX]{x1D6FE}^{\bot }=M\cap \unicode[STIX]{x1D707}^{\bot }.\end{eqnarray}$$
$$\begin{eqnarray}M\cap \unicode[STIX]{x1D6FE}^{\bot }=M\cap \unicode[STIX]{x1D707}^{\bot }.\end{eqnarray}$$
Proposition 6.12. Let
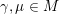 $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}\in M$
such that
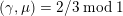 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=2/3\;\text{mod}\;1$
. Then
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=2/3\;\text{mod}\;1$
. Then
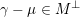 $\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D707}\in M^{\bot }$
.
$\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D707}\in M^{\bot }$
.
Proof. Define
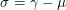 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D707}$
. Then
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D707}$
. Then
 $M\cap \unicode[STIX]{x1D6FE}^{\bot }=M\cap \unicode[STIX]{x1D707}^{\bot }$
implies
$M\cap \unicode[STIX]{x1D6FE}^{\bot }=M\cap \unicode[STIX]{x1D707}^{\bot }$
implies
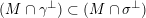 $(M\cap \unicode[STIX]{x1D6FE}^{\bot })\subset (M\cap \unicode[STIX]{x1D70E}^{\bot })$
. Let
$(M\cap \unicode[STIX]{x1D6FE}^{\bot })\subset (M\cap \unicode[STIX]{x1D70E}^{\bot })$
. Let
![]() $\unicode[STIX]{x1D708}\in M$
such that
$\unicode[STIX]{x1D708}\in M$
such that
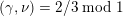 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\;\text{mod}\;1$
. Then
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\;\text{mod}\;1$
. Then
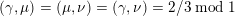 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=(\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})=(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\;\text{mod}\;1$
by the above transitivity result. Hence,
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})=(\unicode[STIX]{x1D707},\unicode[STIX]{x1D708})=(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=2/3\;\text{mod}\;1$
by the above transitivity result. Hence,
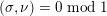 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Similarly, if
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Similarly, if
![]() $\unicode[STIX]{x1D708}\in M$
such that
$\unicode[STIX]{x1D708}\in M$
such that
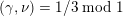 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=1/3\;\text{mod}\;1$
, then
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D708})=1/3\;\text{mod}\;1$
, then
 $(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Hence, all elements in
$(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D708})=0\;\text{mod}\;1$
. Hence, all elements in
![]() $M$
are orthogonal to
$M$
are orthogonal to
![]() $\unicode[STIX]{x1D70E}$
.◻
$\unicode[STIX]{x1D70E}$
.◻
Proposition 6.13. The group
![]() $M^{\bot }$
is an isotropic subgroup of
$M^{\bot }$
is an isotropic subgroup of
![]() $D$
order
$D$
order
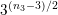 $3^{(n_{3}-3)/2}$
.
$3^{(n_{3}-3)/2}$
.
Proof. Let
![]() $\unicode[STIX]{x1D6FE}\in M$
. Then the elements
$\unicode[STIX]{x1D6FE}\in M$
. Then the elements
![]() $\unicode[STIX]{x1D707}\in M$
with
$\unicode[STIX]{x1D707}\in M$
with
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})\neq 0\;\text{mod}\;1$
are in
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707})\neq 0\;\text{mod}\;1$
are in
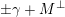 $\pm \unicode[STIX]{x1D6FE}+M^{\bot }$
. Hence,
$\pm \unicode[STIX]{x1D6FE}+M^{\bot }$
. Hence,
![]() $M$
decomposes as
$M$
decomposes as
 $$\begin{eqnarray}M=(\unicode[STIX]{x1D6FE}+M^{\bot })\cup (-\unicode[STIX]{x1D6FE}+M^{\bot })\cup (M\cap \unicode[STIX]{x1D6FE}^{\bot })\end{eqnarray}$$
$$\begin{eqnarray}M=(\unicode[STIX]{x1D6FE}+M^{\bot })\cup (-\unicode[STIX]{x1D6FE}+M^{\bot })\cup (M\cap \unicode[STIX]{x1D6FE}^{\bot })\end{eqnarray}$$
so that
 $$\begin{eqnarray}|M|=2|M^{\bot }|+2|M|/3.\end{eqnarray}$$
$$\begin{eqnarray}|M|=2|M^{\bot }|+2|M|/3.\end{eqnarray}$$
This implies the statement. ◻
Proposition 6.14. The set
![]() $M$
is of the form
$M$
is of the form
 $$\begin{eqnarray}M=\mathop{\bigcup }_{i=1}^{3}(\unicode[STIX]{x1D6FE}_{i}+M^{\bot })\cup \mathop{\bigcup }_{i=1}^{3}(-\unicode[STIX]{x1D6FE}_{i}+M^{\bot })\end{eqnarray}$$
$$\begin{eqnarray}M=\mathop{\bigcup }_{i=1}^{3}(\unicode[STIX]{x1D6FE}_{i}+M^{\bot })\cup \mathop{\bigcup }_{i=1}^{3}(-\unicode[STIX]{x1D6FE}_{i}+M^{\bot })\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D6FE}_{i}\in M$
and
$\unicode[STIX]{x1D6FE}_{i}\in M$
and
 $(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
for
$(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\hspace{0.2em}{\rm mod}\hspace{0.2em}1$
for
![]() $i\neq j$
.
$i\neq j$
.
Let
![]() $H$
be an isotropic subgroup of
$H$
be an isotropic subgroup of
![]() $D$
of order
$D$
of order
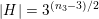 $|H|=3^{(n_{3}-3)/2}$
. Then the lift of
$|H|=3^{(n_{3}-3)/2}$
. Then the lift of
![]() $9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}$
, with respect to
$9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}$
, with respect to
![]() $\unicode[STIX]{x1D70C}_{D}$
on
$\unicode[STIX]{x1D70C}_{D}$
on
![]() $H$
, is given by
$H$
, is given by
 $$\begin{eqnarray}F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}=F_{1/3}+F_{1/1}\end{eqnarray}$$
$$\begin{eqnarray}F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}=F_{1/3}+F_{1/1}\end{eqnarray}$$
with
 $$\begin{eqnarray}F_{1/3}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H}9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F_{1/3}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H}9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
and
 $$\begin{eqnarray}F_{1/1}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H^{\bot }}g_{j_{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}F_{1/1}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in H^{\bot }}g_{j_{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
where
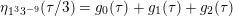 $\unicode[STIX]{x1D702}_{1^{3}3^{-9}}(\unicode[STIX]{x1D70F}/3)=g_{0}(\unicode[STIX]{x1D70F})+g_{1}(\unicode[STIX]{x1D70F})+g_{2}(\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D702}_{1^{3}3^{-9}}(\unicode[STIX]{x1D70F}/3)=g_{0}(\unicode[STIX]{x1D70F})+g_{1}(\unicode[STIX]{x1D70F})+g_{2}(\unicode[STIX]{x1D70F})$
and
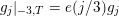 $g_{j}|_{-3,T}=e(j/3)g_{j}$
. Note that
$g_{j}|_{-3,T}=e(j/3)g_{j}$
. Note that
 $$\begin{eqnarray}\displaystyle g_{0} & = & \displaystyle -3\unicode[STIX]{x1D702}_{1^{-9}3^{3}},\nonumber\\ \displaystyle g_{1} & = & \displaystyle 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{0} & = & \displaystyle -3\unicode[STIX]{x1D702}_{1^{-9}3^{3}},\nonumber\\ \displaystyle g_{1} & = & \displaystyle 0.\nonumber\end{eqnarray}$$
The function
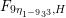 $F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}$
has
$F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}$
has
![]() $0$
-component
$0$
-component
 $F_{0}=6\unicode[STIX]{x1D702}_{1^{-9}3^{3}}$
and is reflective. The singular components are the
$F_{0}=6\unicode[STIX]{x1D702}_{1^{-9}3^{3}}$
and is reflective. The singular components are the
![]() $F_{\unicode[STIX]{x1D6FE}}$
with
$F_{\unicode[STIX]{x1D6FE}}$
with
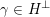 $\unicode[STIX]{x1D6FE}\in H^{\bot }$
and
$\unicode[STIX]{x1D6FE}\in H^{\bot }$
and
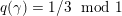 $q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.6em}{\rm mod}\hspace{0.2em}1$
. The discriminant form
$q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.6em}{\rm mod}\hspace{0.2em}1$
. The discriminant form
![]() $H^{\bot }/H$
is of type
$H^{\bot }/H$
is of type
![]() $3^{-3}$
. It is generated by elements
$3^{-3}$
. It is generated by elements
 $\{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE}_{3}\}$
with
$\{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE}_{3}\}$
with
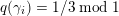 $q(\unicode[STIX]{x1D6FE}_{i})=1/3\;\text{mod}\;1$
and
$q(\unicode[STIX]{x1D6FE}_{i})=1/3\;\text{mod}\;1$
and
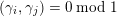 $(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\;\text{mod}\;1$
for
$(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\;\text{mod}\;1$
for
![]() $i\neq j$
. We obtain the following result (see Theorem 2.1 and Proposition 2.2).
$i\neq j$
. We obtain the following result (see Theorem 2.1 and Proposition 2.2).
Proposition 6.15. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
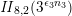 $\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
carrying a reflective modular form. Suppose
$\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
carrying a reflective modular form. Suppose
![]() $F_{0}$
is holomorphic at
$F_{0}$
is holomorphic at
![]() $\infty$
and has constant coefficient
$\infty$
and has constant coefficient
![]() $6$
. Then
$6$
. Then
![]() $n_{3}\geqslant 3$
and
$n_{3}\geqslant 3$
and
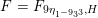 $F=F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}$
for some isotropic subgroup
$F=F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}$
for some isotropic subgroup
![]() $H$
of
$H$
of
![]() $D$
of order
$D$
of order
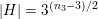 $|H|=3^{(n_{3}-3)/2}$
. In this case, the overlattice
$|H|=3^{(n_{3}-3)/2}$
. In this case, the overlattice
![]() $L_{H}$
of
$L_{H}$
of
![]() $L$
corresponding to
$L$
corresponding to
![]() $H$
has genus
$H$
has genus
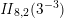 $\mathit{II}_{8,2}(3^{-3})$
and the function
$\mathit{II}_{8,2}(3^{-3})$
and the function
![]() $F$
can also be induced from the symmetric form
$F$
can also be induced from the symmetric form
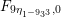 $F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
on
$F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
on
![]() $L_{H}$
.
$L_{H}$
.
We can decompose
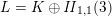 $L=K\oplus \mathit{II}_{1,1}(3)$
, where
$L=K\oplus \mathit{II}_{1,1}(3)$
, where
![]() $K$
has genus
$K$
has genus
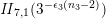 $\mathit{II}_{7,1}(3^{-\unicode[STIX]{x1D716}_{3}(n_{3}-2)})$
and assume that
$\mathit{II}_{7,1}(3^{-\unicode[STIX]{x1D716}_{3}(n_{3}-2)})$
and assume that
![]() $H$
is a maximal isotropic subgroup of the discriminant form of
$H$
is a maximal isotropic subgroup of the discriminant form of
![]() $K$
. Then the embedding
$K$
. Then the embedding
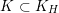 $K\subset K_{H}$
gives an embedding
$K\subset K_{H}$
gives an embedding
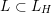 $L\subset L_{H}$
and identifies the corresponding domains
$L\subset L_{H}$
and identifies the corresponding domains
![]() ${\mathcal{H}}_{L}$
and
${\mathcal{H}}_{L}$
and
![]() ${\mathcal{H}}_{L_{H}}$
. Proposition 3.4 implies the following proposition.
${\mathcal{H}}_{L_{H}}$
. Proposition 3.4 implies the following proposition.
Proposition 6.16. The theta lifts of
![]() $F$
and
$F$
and
 $F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
coincide as functions under this identification.
$F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
coincide as functions under this identification.
We calculate the product expansions of the automorphic product
![]() $\unicode[STIX]{x1D6F9}$
corresponding to
$\unicode[STIX]{x1D6F9}$
corresponding to
 $F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
on
$F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
on
![]() $L$
of genus
$L$
of genus
 $\mathit{II}_{8,2}(3^{-3})$
.
$\mathit{II}_{8,2}(3^{-3})$
.
First, we decompose
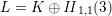 $L=K\oplus \mathit{II}_{1,1}(3)$
. Then
$L=K\oplus \mathit{II}_{1,1}(3)$
. Then
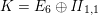 $K=E_{6}\oplus \mathit{II}_{1,1}$
. We choose a primitive norm
$K=E_{6}\oplus \mathit{II}_{1,1}$
. We choose a primitive norm
![]() $0$
vector
$0$
vector
![]() $z$
in
$z$
in
![]() $\mathit{II}_{1,1}(3)$
.
$\mathit{II}_{1,1}(3)$
.
Proposition 6.17. The expansion of
![]() $\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
$\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
![]() $z$
is given by
$z$
is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in (3K^{\prime })^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[-3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/6)}\nonumber\\ \displaystyle & & \displaystyle \quad =1+\sum c(\unicode[STIX]{x1D706})e((\unicode[STIX]{x1D706},Z))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in (3K^{\prime })^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[-3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/6)}\nonumber\\ \displaystyle & & \displaystyle \quad =1+\sum c(\unicode[STIX]{x1D706})e((\unicode[STIX]{x1D706},Z))\nonumber\end{eqnarray}$$
where
![]() $c(\unicode[STIX]{x1D706})$
is the coefficient at
$c(\unicode[STIX]{x1D706})$
is the coefficient at
![]() $q^{n}$
in
$q^{n}$
in
![]() $\unicode[STIX]{x1D702}_{1^{9}3^{-3}}$
if
$\unicode[STIX]{x1D702}_{1^{9}3^{-3}}$
if
![]() $\unicode[STIX]{x1D706}$
is
$\unicode[STIX]{x1D706}$
is
![]() $n$
times a primitive norm
$n$
times a primitive norm
![]() $0$
vector in
$0$
vector in
![]() $K^{+}$
and
$K^{+}$
and
![]() $0$
otherwise.
$0$
otherwise.
Proof. The product expansion of
![]() $\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
$\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
![]() $z$
is
$z$
is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[F_{\unicode[STIX]{x1D6FC}}](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e(1/3)e((\unicode[STIX]{x1D6FC},Z)))^{[F_{\unicode[STIX]{x1D6FC}+z/3}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(1-e(2/3)e((\unicode[STIX]{x1D6FC},Z)))^{[F_{\unicode[STIX]{x1D6FC}+2z/3}](-\unicode[STIX]{x1D6FC}^{2}/2)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[F_{\unicode[STIX]{x1D6FC}}](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e(1/3)e((\unicode[STIX]{x1D6FC},Z)))^{[F_{\unicode[STIX]{x1D6FC}+z/3}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,(1-e(2/3)e((\unicode[STIX]{x1D6FC},Z)))^{[F_{\unicode[STIX]{x1D6FC}+2z/3}](-\unicode[STIX]{x1D6FC}^{2}/2)}.\nonumber\end{eqnarray}$$
By the above formulas for the components of
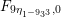 $F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
, this product is equal to
$F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},0}$
, this product is equal to
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in (3K^{\prime })^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[-3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/6)}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in (3K^{\prime })^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[-3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/6)}. & & \displaystyle \nonumber\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D6F9}$
has singular weight, the Fourier expansion of
$\unicode[STIX]{x1D6F9}$
has singular weight, the Fourier expansion of
![]() $\unicode[STIX]{x1D6F9}_{z}$
is supported only on norm
$\unicode[STIX]{x1D6F9}_{z}$
is supported only on norm
![]() $0$
vectors of
$0$
vectors of
![]() $K^{\prime }$
. Hence,
$K^{\prime }$
. Hence,
![]() $\unicode[STIX]{x1D6F9}_{z}$
has the stated sum expansion.◻
$\unicode[STIX]{x1D6F9}_{z}$
has the stated sum expansion.◻
This is the twisted denominator identity of the fake monster superalgebra [Reference ScheithauerSch00] corresponding to an element of class
![]() $3A$
in
$3A$
in
![]() $O(E_{8})$
(see [Reference ScheithauerSch01, Proposition 6.1]).
$O(E_{8})$
(see [Reference ScheithauerSch01, Proposition 6.1]).
Now, we decompose
 $L=K\oplus \mathit{II}_{1,1}$
with
$L=K\oplus \mathit{II}_{1,1}$
with
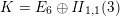 $K=E_{6}\oplus \mathit{II}_{1,1}(3)$
and choose a primitive norm
$K=E_{6}\oplus \mathit{II}_{1,1}(3)$
and choose a primitive norm
![]() $0$
vector
$0$
vector
![]() $z$
in
$z$
in
![]() $\mathit{II}_{1,1}$
. Then we have the following result.
$\mathit{II}_{1,1}$
. Then we have the following result.
Proposition 6.18. The expansion of
![]() $\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
$\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
![]() $z$
is given by
$z$
is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D702}_{1^{-3}3^{9}}((w\unicode[STIX]{x1D70C},Z)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[9\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D702}_{1^{-3}3^{9}}((w\unicode[STIX]{x1D70C},Z)),\nonumber\end{eqnarray}$$
where
![]() $W$
is the reflection group of
$W$
is the reflection group of
![]() $K^{\prime }$
generated by the roots of norm
$K^{\prime }$
generated by the roots of norm
 $\unicode[STIX]{x1D6FC}^{2}=2/3$
.
$\unicode[STIX]{x1D6FC}^{2}=2/3$
.
This is the twisted denominator identity of the fake monster algebra corresponding to an element of class
![]() $3C$
in
$3C$
in
![]() $\mathit{Co}_{0}$
(see [Reference ScheithauerSch04, Proposition 10.7]).
$\mathit{Co}_{0}$
(see [Reference ScheithauerSch04, Proposition 10.7]).
Again, let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
 $\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
carrying a reflective modular form
$\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
carrying a reflective modular form
![]() $F$
.
$F$
.
The lift of
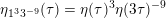 $\unicode[STIX]{x1D702}_{1^{3}3^{-9}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{-9}$
with respect to
$\unicode[STIX]{x1D702}_{1^{3}3^{-9}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{3}\unicode[STIX]{x1D702}(3\unicode[STIX]{x1D70F})^{-9}$
with respect to
![]() $\unicode[STIX]{x1D70C}_{D}$
on
$\unicode[STIX]{x1D70C}_{D}$
on
![]() $0$
is given by
$0$
is given by
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}=F_{1/3}+F_{1/1}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}=F_{1/3}+F_{1/1}\end{eqnarray}$$
with
 $$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{3}3^{-9}}e^{0}\end{eqnarray}$$
$$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{3}3^{-9}}e^{0}\end{eqnarray}$$
and
 $$\begin{eqnarray}F_{1/1}=3^{(11-n_{3})/2}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}g_{j_{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
$$\begin{eqnarray}F_{1/1}=3^{(11-n_{3})/2}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in D}g_{j_{\unicode[STIX]{x1D6FE}}}e^{\unicode[STIX]{x1D6FE}},\end{eqnarray}$$
where
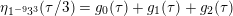 $\unicode[STIX]{x1D702}_{1^{-9}3^{3}}(\unicode[STIX]{x1D70F}/3)=g_{0}(\unicode[STIX]{x1D70F})+g_{1}(\unicode[STIX]{x1D70F})+g_{2}(\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D702}_{1^{-9}3^{3}}(\unicode[STIX]{x1D70F}/3)=g_{0}(\unicode[STIX]{x1D70F})+g_{1}(\unicode[STIX]{x1D70F})+g_{2}(\unicode[STIX]{x1D70F})$
and
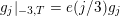 $g_{j}|_{-3,T}=e(j/3)g_{j}$
. The modular form
$g_{j}|_{-3,T}=e(j/3)g_{j}$
. The modular form
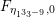 $F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
is reflective and has
$F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
is reflective and has
![]() $0$
-component
$0$
-component
 $$\begin{eqnarray}F_{0}(\unicode[STIX]{x1D70F})=q^{-1}+(3^{(11-n_{3})/2}-3)+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}F_{0}(\unicode[STIX]{x1D70F})=q^{-1}+(3^{(11-n_{3})/2}-3)+\cdots \,.\end{eqnarray}$$
Proposition 6.19. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
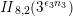 $\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and let
$\mathit{II}_{8,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and let
![]() $F$
be a reflective modular form on
$F$
be a reflective modular form on
![]() $L$
with
$L$
with
![]() $c_{1}=1$
and
$c_{1}=1$
and
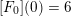 $[F_{0}](0)=6$
. Then,
$[F_{0}](0)=6$
. Then,
![]() $n_{3}=7$
and
$n_{3}=7$
and
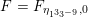 $F=F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
or
$F=F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
or
![]() $n_{3}=9$
and
$n_{3}=9$
and
 $F=F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}+F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}$
for some isotropic subgroup
$F=F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}+F_{9\unicode[STIX]{x1D702}_{1^{-9}3^{3}},H}$
for some isotropic subgroup
![]() $H$
of order
$H$
of order
![]() $27$
.
$27$
.
Suppose
![]() $L$
has genus
$L$
has genus
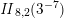 $\mathit{II}_{8,2}(3^{-7})$
. Then the level
$\mathit{II}_{8,2}(3^{-7})$
. Then the level
![]() $1$
expansion of the theta lift of
$1$
expansion of the theta lift of
 $F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
on
$F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
on
![]() $L$
is the twisted denominator identity of the fake monster superalgebra corresponding to an element in
$L$
is the twisted denominator identity of the fake monster superalgebra corresponding to an element in
![]() $O(E_{8})$
of class
$O(E_{8})$
of class
![]() $3A$
and the level
$3A$
and the level
![]() $3$
expansion gives the twisted denominator identity of the fake monster algebra corresponding to an element in
$3$
expansion gives the twisted denominator identity of the fake monster algebra corresponding to an element in
![]() $\mathit{Co}_{0}$
of class
$\mathit{Co}_{0}$
of class
![]() $3C$
.
$3C$
.
The case
![]() $n_{3}=9$
has already been described above because we have the following result.
$n_{3}=9$
has already been described above because we have the following result.
Proposition 6.20. Let
![]() $L$
be of genus
$L$
be of genus
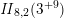 $\mathit{II}_{8,2}(3^{+9})$
. Then the theta lift of
$\mathit{II}_{8,2}(3^{+9})$
. Then the theta lift of
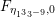 $F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
on
$F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
on
![]() $L$
is constant.
$L$
is constant.
Proof. We decompose
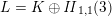 $L=K\oplus \mathit{II}_{1,1}(3)$
, where
$L=K\oplus \mathit{II}_{1,1}(3)$
, where
![]() $K$
has genus
$K$
has genus
 $\mathit{II}_{7,1}(3^{-7})$
and choose a primitive norm
$\mathit{II}_{7,1}(3^{-7})$
and choose a primitive norm
![]() $0$
vector
$0$
vector
![]() $z$
in
$z$
in
![]() $\mathit{II}_{1,1}(3)$
. Then the product expansion of the theta lift
$\mathit{II}_{1,1}(3)$
. Then the product expansion of the theta lift
![]() $\unicode[STIX]{x1D6F9}$
of
$\unicode[STIX]{x1D6F9}$
of
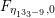 $F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
at the cusp corresponding to
$F_{\unicode[STIX]{x1D702}_{1^{3}3^{-9}},0}$
at the cusp corresponding to
![]() $z$
is given by
$z$
is given by
 $$\begin{eqnarray}\displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in (3K^{\prime })^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/6)}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in K^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in (3K^{\prime })^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](-\unicode[STIX]{x1D6FC}^{2}/6)}. & & \displaystyle \nonumber\end{eqnarray}$$
The Fourier coefficients
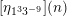 $[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](n)$
vanish for
$[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](n)$
vanish for
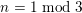 $n=1\;\text{mod}\;3$
and
$n=1\;\text{mod}\;3$
and
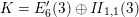 $K=E_{6}^{\prime }(3)\oplus \mathit{II}_{1,1}(3)$
contains no elements
$K=E_{6}^{\prime }(3)\oplus \mathit{II}_{1,1}(3)$
contains no elements
![]() $\unicode[STIX]{x1D6FC}$
of norm
$\unicode[STIX]{x1D6FC}$
of norm
 $-\unicode[STIX]{x1D6FC}^{2}/2=2\;\text{mod}\;3$
. This implies that the first product extends only over the elements
$-\unicode[STIX]{x1D6FC}^{2}/2=2\;\text{mod}\;3$
. This implies that the first product extends only over the elements
![]() $\unicode[STIX]{x1D6FC}\in K$
satisfying
$\unicode[STIX]{x1D6FC}\in K$
satisfying
 $\unicode[STIX]{x1D6FC}^{2}/2=0\;\text{mod}\;3$
, i.e.,
$\unicode[STIX]{x1D6FC}^{2}/2=0\;\text{mod}\;3$
, i.e.,
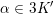 $\unicode[STIX]{x1D6FC}\in 3K^{\prime }$
. Now,
$\unicode[STIX]{x1D6FC}\in 3K^{\prime }$
. Now,
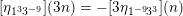 $[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](3n)=-[3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](n)$
so that the product is constant. This finishes the proof.◻
$[\unicode[STIX]{x1D702}_{1^{3}3^{-9}}](3n)=-[3\unicode[STIX]{x1D702}_{1^{-9}3^{3}}](n)$
so that the product is constant. This finishes the proof.◻
Now we consider the case
![]() $n=6$
. Let
$n=6$
. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
 $\mathit{II}_{6,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
$\mathit{II}_{6,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
![]() $F$
a reflective form on
$F$
a reflective form on
![]() $L$
with
$L$
with
 $[F_{0}](0)=4$
. We find the following value for
$[F_{0}](0)=4$
. We find the following value for
![]() $c_{3}$
.
$c_{3}$
.

Hence, we can assume that
![]() $F_{0}$
is holomorphic at
$F_{0}$
is holomorphic at
![]() $\infty$
and
$\infty$
and
![]() $n_{3}=4$
or
$n_{3}=4$
or
![]() $6$
.
$6$
.
The space
 $S_{4}(\unicode[STIX]{x1D6E4}(3))$
has dimension
$S_{4}(\unicode[STIX]{x1D6E4}(3))$
has dimension
![]() $1$
and is spanned by the function
$1$
and is spanned by the function
![]() $\unicode[STIX]{x1D702}_{1^{8}}$
. The liftings of this function generate the obstruction space
$\unicode[STIX]{x1D702}_{1^{8}}$
. The liftings of this function generate the obstruction space
![]() $S_{\overline{\unicode[STIX]{x1D70C}}_{D},4}$
.
$S_{\overline{\unicode[STIX]{x1D70C}}_{D},4}$
.
Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then the lift of
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then the lift of
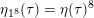 $\unicode[STIX]{x1D702}_{1^{8}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{8}$
with respect to the dual Weil representation
$\unicode[STIX]{x1D702}_{1^{8}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}(\unicode[STIX]{x1D70F})^{8}$
with respect to the dual Weil representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{D}$
on
$\overline{\unicode[STIX]{x1D70C}}_{D}$
on
![]() $\unicode[STIX]{x1D6FE}$
is given by
$\unicode[STIX]{x1D6FE}$
is given by
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
with
 $$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{8}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
$$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{8}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
and
 $$\begin{eqnarray}F_{1/1}=-\frac{1}{3^{(n_{3}-2)/2}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D707}\in D \\ q(\unicode[STIX]{x1D707})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}e((\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}))\unicode[STIX]{x1D702}_{1^{8}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}}).\end{eqnarray}$$
$$\begin{eqnarray}F_{1/1}=-\frac{1}{3^{(n_{3}-2)/2}}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D707}\in D \\ q(\unicode[STIX]{x1D707})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1}}e((\unicode[STIX]{x1D707},\unicode[STIX]{x1D6FE}))\unicode[STIX]{x1D702}_{1^{8}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}}).\end{eqnarray}$$
As above, we define
 $$\begin{eqnarray}M=\{\unicode[STIX]{x1D6FE}\in D\mid q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1\text{ and }F_{\unicode[STIX]{x1D6FE}}\text{ singular}\}.\end{eqnarray}$$
$$\begin{eqnarray}M=\{\unicode[STIX]{x1D6FE}\in D\mid q(\unicode[STIX]{x1D6FE})=1/3\hspace{0.2em}{\rm mod}\hspace{0.2em}1\text{ and }F_{\unicode[STIX]{x1D6FE}}\text{ singular}\}.\end{eqnarray}$$
Then
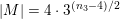 $|M|=4\cdot 3^{(n_{3}-4)/2}$
and
$|M|=4\cdot 3^{(n_{3}-4)/2}$
and
 $M=-M$
. Pairing
$M=-M$
. Pairing
![]() $F$
with
$F$
with
![]() $F_{\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}$
we obtain the following result.
$F_{\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}$
we obtain the following result.
Proposition 6.21. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then
 $$\begin{eqnarray}|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=\left\{\begin{array}{@{}ll@{}}\displaystyle 5|M|/6\quad & \displaystyle \text{if }\unicode[STIX]{x1D6FE}\in M,\\ \displaystyle |M|/3\quad & \displaystyle \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=\left\{\begin{array}{@{}ll@{}}\displaystyle 5|M|/6\quad & \displaystyle \text{if }\unicode[STIX]{x1D6FE}\in M,\\ \displaystyle |M|/3\quad & \displaystyle \text{otherwise.}\end{array}\right.\end{eqnarray}$$
This excludes the case
![]() $n_{3}=4$
. We assume now that
$n_{3}=4$
. We assume now that
![]() $n_{3}=6$
. Then the proposition shows that
$n_{3}=6$
. Then the proposition shows that
![]() $M$
must be of the form
$M$
must be of the form
 $$\begin{eqnarray}M=\{\pm \unicode[STIX]{x1D6FE}_{1},\ldots ,\pm \unicode[STIX]{x1D6FE}_{6}\}\end{eqnarray}$$
$$\begin{eqnarray}M=\{\pm \unicode[STIX]{x1D6FE}_{1},\ldots ,\pm \unicode[STIX]{x1D6FE}_{6}\}\end{eqnarray}$$
with
 $(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\;\text{mod}\;1$
for
$(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\;\text{mod}\;1$
for
![]() $i\neq j$
. In particular,
$i\neq j$
. In particular,
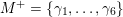 $M^{+}=\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{6}\}$
is a basis of
$M^{+}=\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{6}\}$
is a basis of
![]() $D$
. Let
$D$
. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
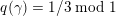 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
with
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
with
![]() $\unicode[STIX]{x1D6FE}\notin M$
. Then
$\unicode[STIX]{x1D6FE}\notin M$
. Then
![]() $\unicode[STIX]{x1D6FE}$
is a linear combination of four of the
$\unicode[STIX]{x1D6FE}$
is a linear combination of four of the
![]() $\unicode[STIX]{x1D6FE}_{i}$
so that
$\unicode[STIX]{x1D6FE}_{i}$
so that
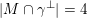 $|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=4$
. Hence, the principal part of
$|M\cap \unicode[STIX]{x1D6FE}^{\bot }|=4$
. Hence, the principal part of
![]() $F$
satisfies all obstructions coming from
$F$
satisfies all obstructions coming from
![]() $S_{\overline{\unicode[STIX]{x1D70C}}_{D},4}$
. This implies that a reflective modular form with constant coefficient
$S_{\overline{\unicode[STIX]{x1D70C}}_{D},4}$
. This implies that a reflective modular form with constant coefficient
![]() $4$
on
$4$
on
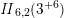 $\mathit{II}_{6,2}(3^{+6})$
exists.
$\mathit{II}_{6,2}(3^{+6})$
exists.
We give an explicit construction. Let
![]() $\unicode[STIX]{x1D6FE}\in D$
be of norm
$\unicode[STIX]{x1D6FE}\in D$
be of norm
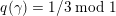 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then the lift of
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then the lift of
![]() $\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}}$
on
$\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}}$
on
![]() $\unicode[STIX]{x1D6FE}$
with respect to
$\unicode[STIX]{x1D6FE}$
with respect to
![]() $\unicode[STIX]{x1D70C}_{D}$
is given by
$\unicode[STIX]{x1D70C}_{D}$
is given by
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
with
 $$\begin{eqnarray}F_{1/3}=\frac{\unicode[STIX]{x1D703}_{A_{2}}^{2}}{\unicode[STIX]{x1D702}_{1^{8}}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
$$\begin{eqnarray}F_{1/3}=\frac{\unicode[STIX]{x1D703}_{A_{2}}^{2}}{\unicode[STIX]{x1D702}_{1^{8}}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
and
 $$\begin{eqnarray}F_{1/1}=\frac{1}{3^{3}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}})\end{eqnarray}$$
$$\begin{eqnarray}F_{1/1}=\frac{1}{3^{3}}\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}})\end{eqnarray}$$
where
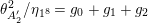 $\unicode[STIX]{x1D703}_{A_{2}^{\prime }}^{2}/\unicode[STIX]{x1D702}_{1^{8}}=g_{0}+g_{1}+g_{2}$
and
$\unicode[STIX]{x1D703}_{A_{2}^{\prime }}^{2}/\unicode[STIX]{x1D702}_{1^{8}}=g_{0}+g_{1}+g_{2}$
and
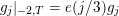 $g_{j}|_{-2,T}=e(j/3)g_{j}$
. Note that
$g_{j}|_{-2,T}=e(j/3)g_{j}$
. Note that
 $g_{2}=\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}}$
.
$g_{2}=\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}}$
.
The function
 $\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}_{1^{-3}3^{2}9^{-3}}(\unicode[STIX]{x1D70F}/3)$
is a modular form for
$\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D702}_{1^{-3}3^{2}9^{-3}}(\unicode[STIX]{x1D70F}/3)$
is a modular form for
![]() $\unicode[STIX]{x1D6E4}(3)$
of weight
$\unicode[STIX]{x1D6E4}(3)$
of weight
![]() $-2$
. If we decompose
$-2$
. If we decompose
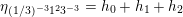 $\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}}=h_{0}+h_{1}+h_{2}$
with
$\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}}=h_{0}+h_{1}+h_{2}$
with
 $h_{j}|_{-2,T}=e(j/3)h_{j}$
, then
$h_{j}|_{-2,T}=e(j/3)h_{j}$
, then
![]() $g_{2}=h_{2}$
,
$g_{2}=h_{2}$
,
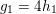 $g_{1}=4h_{1}$
and
$g_{1}=4h_{1}$
and
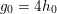 $g_{0}=4h_{0}$
. It follows
$g_{0}=4h_{0}$
. It follows
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}={\textstyle \frac{1}{3}}F_{\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}},\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}}={\textstyle \frac{1}{3}}F_{\unicode[STIX]{x1D702}_{(1/3)^{-3}1^{2}3^{-3}},\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
Now let
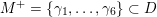 $M^{+}=\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{6}\}\subset D$
such that
$M^{+}=\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{6}\}\subset D$
such that
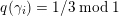 $q(\unicode[STIX]{x1D6FE}_{i})=1/3\;\text{mod}\;1$
,
$q(\unicode[STIX]{x1D6FE}_{i})=1/3\;\text{mod}\;1$
,
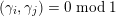 $(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\;\text{mod}\;1$
for
$(\unicode[STIX]{x1D6FE}_{i},\unicode[STIX]{x1D6FE}_{j})=0\;\text{mod}\;1$
for
![]() $i\neq j$
and
$i\neq j$
and
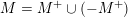 $M=M^{+}\cup (-M^{+})$
. Define
$M=M^{+}\cup (-M^{+})$
. Define
 $$\begin{eqnarray}F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}=\frac{3}{4}\mathop{\sum }_{i=1}^{6}F_{\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}=\frac{3}{4}\mathop{\sum }_{i=1}^{6}F_{\unicode[STIX]{x1D703}_{A_{2}}^{2}/\unicode[STIX]{x1D702}_{1^{8}},\unicode[STIX]{x1D6FE}_{i}}.\end{eqnarray}$$
The components of
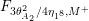 $F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}$
can be described as follows. Write
$F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}$
can be described as follows. Write
![]() $\unicode[STIX]{x1D707}\in D$
as
$\unicode[STIX]{x1D707}\in D$
as
 $\unicode[STIX]{x1D707}=\sum _{i=1}^{6}c_{i}\unicode[STIX]{x1D6FE}_{i}$
and let
$\unicode[STIX]{x1D707}=\sum _{i=1}^{6}c_{i}\unicode[STIX]{x1D6FE}_{i}$
and let
![]() $\operatorname{wt}(\unicode[STIX]{x1D707})$
denote the number of non-zero
$\operatorname{wt}(\unicode[STIX]{x1D707})$
denote the number of non-zero
![]() $c_{i}$
. Then
$c_{i}$
. Then
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})=g_{2}(\unicode[STIX]{x1D70F})=q^{-1/3}+20q^{2/3}+176q^{5/3}+1020q^{8/3}+4794q^{11/3}+\cdots\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70F})=g_{2}(\unicode[STIX]{x1D70F})=q^{-1/3}+20q^{2/3}+176q^{5/3}+1020q^{8/3}+4794q^{11/3}+\cdots\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D707}\in M$
and
$\unicode[STIX]{x1D707}\in M$
and
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D707}}={\textstyle \frac{1}{12}}(4-\operatorname{wt}(\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D707}}={\textstyle \frac{1}{12}}(4-\operatorname{wt}(\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}\end{eqnarray}$$
with
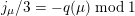 $j_{\unicode[STIX]{x1D707}}/3=-q(\unicode[STIX]{x1D707})\;\text{mod}\;1$
otherwise. In particular,
$j_{\unicode[STIX]{x1D707}}/3=-q(\unicode[STIX]{x1D707})\;\text{mod}\;1$
otherwise. In particular,
 $$\begin{eqnarray}F_{0}(\unicode[STIX]{x1D70F})={\textstyle \frac{1}{3}}g_{0}(\unicode[STIX]{x1D70F})=4+60q+432q^{2}+2328q^{3}+10320q^{4}+40068q^{5}+\cdots\end{eqnarray}$$
$$\begin{eqnarray}F_{0}(\unicode[STIX]{x1D70F})={\textstyle \frac{1}{3}}g_{0}(\unicode[STIX]{x1D70F})=4+60q+432q^{2}+2328q^{3}+10320q^{4}+40068q^{5}+\cdots\end{eqnarray}$$
and
![]() $F_{\unicode[STIX]{x1D707}}=0$
if
$F_{\unicode[STIX]{x1D707}}=0$
if
 $q(\unicode[STIX]{x1D707})=1/3\;\text{mod}\;1$
and
$q(\unicode[STIX]{x1D707})=1/3\;\text{mod}\;1$
and
![]() $\unicode[STIX]{x1D707}\notin M$
. Hence,
$\unicode[STIX]{x1D707}\notin M$
. Hence,
![]() $F$
is reflective. Conversely, we have the following proposition.
$F$
is reflective. Conversely, we have the following proposition.
Proposition 6.22. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
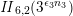 $\mathit{II}_{6,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
$\mathit{II}_{6,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
![]() $F$
a reflective form on
$F$
a reflective form on
![]() $L$
with
$L$
with
![]() $[F_{0}](0)$
$[F_{0}](0)$
![]() $=4$
. Then
$=4$
. Then
![]() $n_{3}=6$
and
$n_{3}=6$
and
 $F=F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}$
for some
$F=F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}$
for some
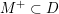 $M^{+}\subset D$
as above.
$M^{+}\subset D$
as above.
Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
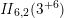 $\mathit{II}_{6,2}(3^{+6})$
. We can decompose
$\mathit{II}_{6,2}(3^{+6})$
. We can decompose
![]() $L$
as
$L$
as
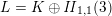 $L=K\oplus \mathit{II}_{1,1}(3)$
with
$L=K\oplus \mathit{II}_{1,1}(3)$
with
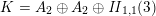 $K=A_{2}\oplus A_{2}\oplus \mathit{II}_{1,1}(3)$
. Then
$K=A_{2}\oplus A_{2}\oplus \mathit{II}_{1,1}(3)$
. Then
![]() $K$
has genus
$K$
has genus
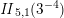 $\mathit{II}_{5,1}(3^{-4})$
. We choose an orthogonal basis
$\mathit{II}_{5,1}(3^{-4})$
. We choose an orthogonal basis
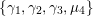 $\{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE}_{3},\unicode[STIX]{x1D707}_{4}\}$
of the discriminant form of
$\{\unicode[STIX]{x1D6FE}_{1},\unicode[STIX]{x1D6FE}_{2},\unicode[STIX]{x1D6FE}_{3},\unicode[STIX]{x1D707}_{4}\}$
of the discriminant form of
![]() $K$
satisfying
$K$
satisfying
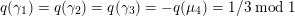 $q(\unicode[STIX]{x1D6FE}_{1})=q(\unicode[STIX]{x1D6FE}_{2})=q(\unicode[STIX]{x1D6FE}_{3})=-q(\unicode[STIX]{x1D707}_{4})=1/3\;\text{mod}\;1$
and an orthogonal basis
$q(\unicode[STIX]{x1D6FE}_{1})=q(\unicode[STIX]{x1D6FE}_{2})=q(\unicode[STIX]{x1D6FE}_{3})=-q(\unicode[STIX]{x1D707}_{4})=1/3\;\text{mod}\;1$
and an orthogonal basis
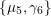 $\{\unicode[STIX]{x1D707}_{5},\unicode[STIX]{x1D6FE}_{6}\}$
of the discriminant form of
$\{\unicode[STIX]{x1D707}_{5},\unicode[STIX]{x1D6FE}_{6}\}$
of the discriminant form of
![]() $\mathit{II}_{1,1}(3)$
satisfying
$\mathit{II}_{1,1}(3)$
satisfying
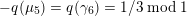 $-q(\unicode[STIX]{x1D707}_{5})=q(\unicode[STIX]{x1D6FE}_{6})=1/3\;\text{mod}\;1$
. We define
$-q(\unicode[STIX]{x1D707}_{5})=q(\unicode[STIX]{x1D6FE}_{6})=1/3\;\text{mod}\;1$
. We define
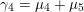 $\unicode[STIX]{x1D6FE}_{4}=\unicode[STIX]{x1D707}_{4}+\unicode[STIX]{x1D707}_{5}$
,
$\unicode[STIX]{x1D6FE}_{4}=\unicode[STIX]{x1D707}_{4}+\unicode[STIX]{x1D707}_{5}$
,
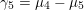 $\unicode[STIX]{x1D6FE}_{5}=\unicode[STIX]{x1D707}_{4}-\unicode[STIX]{x1D707}_{5}$
and
$\unicode[STIX]{x1D6FE}_{5}=\unicode[STIX]{x1D707}_{4}-\unicode[STIX]{x1D707}_{5}$
and
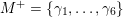 $M^{+}=\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{6}\}$
. Let
$M^{+}=\{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{6}\}$
. Let
![]() $\unicode[STIX]{x1D6F9}$
be the theta lift of
$\unicode[STIX]{x1D6F9}$
be the theta lift of
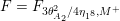 $F=F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}$
on
$F=F_{3\unicode[STIX]{x1D703}_{A_{2}}^{2}/4\unicode[STIX]{x1D702}_{1^{8}},M^{+}}$
on
![]() $L$
. We choose a primitive norm
$L$
. We choose a primitive norm
![]() $0$
vector
$0$
vector
![]() $z$
in
$z$
in
![]() $\mathit{II}_{1,1}(3)$
. Then
$\mathit{II}_{1,1}(3)$
. Then
![]() $z$
has level
$z$
has level
![]() $3$
and
$3$
and
 $\operatorname{wt}(z/3)=3$
.
$\operatorname{wt}(z/3)=3$
.
Proposition 6.23. The expansion of
![]() $\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
$\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
![]() $z$
is given by
$z$
is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=0}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/4](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=3 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=3}}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=3 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=6}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/4](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[-g_{0}/6](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=2 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=2}}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[g_{1}/6](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=2 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=5}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{1}/4](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[-g_{1}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=5}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[-g_{1}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=1}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{2}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D702}_{1^{3}3^{-2}9^{3}}((w\unicode[STIX]{x1D70C},Z)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=0}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/4](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=3 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=3}}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=3 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=6}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{0}/4](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[-g_{0}/6](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=2 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=2}}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[g_{1}/6](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=2 \\ \operatorname{wt}(\unicode[STIX]{x1D6FC}\pm z/3)=5}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{1}/4](-\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[-g_{1}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=5}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[-g_{1}/12](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \operatorname{wt}(\unicode[STIX]{x1D6FC})=1}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[g_{2}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D702}_{1^{3}3^{-2}9^{3}}((w\unicode[STIX]{x1D70C},Z)),\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70C}$
is a primitive norm
$\unicode[STIX]{x1D70C}$
is a primitive norm
![]() $0$
vector in
$0$
vector in
![]() $K^{\prime }$
with
$K^{\prime }$
with
 $\operatorname{wt}(\unicode[STIX]{x1D70C})=3$
and
$\operatorname{wt}(\unicode[STIX]{x1D70C})=3$
and
 $\operatorname{wt}(\unicode[STIX]{x1D70C}\pm z/3)=6$
and
$\operatorname{wt}(\unicode[STIX]{x1D70C}\pm z/3)=6$
and
![]() $W$
is the reflection group of
$W$
is the reflection group of
![]() $K^{\prime }$
generated by the roots
$K^{\prime }$
generated by the roots
![]() $\unicode[STIX]{x1D6FC}\in K^{\prime }$
of norm
$\unicode[STIX]{x1D6FC}\in K^{\prime }$
of norm
 $\unicode[STIX]{x1D6FC}^{2}=2/3$
and weight
$\unicode[STIX]{x1D6FC}^{2}=2/3$
and weight
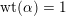 $\operatorname{wt}(\unicode[STIX]{x1D6FC})=1$
.
$\operatorname{wt}(\unicode[STIX]{x1D6FC})=1$
.
This identity is a new infinite product identity. One can show that it can also be obtained by twisting the denominator identity of the fake monster algebra by an element of class
![]() $9C$
in
$9C$
in
![]() $\mathit{Co}_{0}$
.
$\mathit{Co}_{0}$
.
Finally, we consider the case
![]() $n=4$
. Let
$n=4$
. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
 $\mathit{II}_{4,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
$\mathit{II}_{4,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
![]() $F$
a reflective form on
$F$
a reflective form on
![]() $L$
with
$L$
with
 $[F_{0}](0)=2$
. Then, the Eisenstein condition gives the following value for
$[F_{0}](0)=2$
. Then, the Eisenstein condition gives the following value for
![]() $c_{3}$
.
$c_{3}$
.

Since
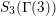 $S_{3}(\unicode[STIX]{x1D6E4}(3))$
is trivial, the obstruction space
$S_{3}(\unicode[STIX]{x1D6E4}(3))$
is trivial, the obstruction space
![]() $S_{\overline{\unicode[STIX]{x1D70C}}_{D},3}$
vanishes. Hence,
$S_{\overline{\unicode[STIX]{x1D70C}}_{D},3}$
vanishes. Hence,
![]() $L$
carries a reflective form with constant coefficient
$L$
carries a reflective form with constant coefficient
![]() $2$
if and only if it has genus
$2$
if and only if it has genus
 $\mathit{II}_{4,2}(3^{-5})$
.
$\mathit{II}_{4,2}(3^{-5})$
.
Let
![]() $D$
be a discriminant form of type
$D$
be a discriminant form of type
![]() $3^{-5}$
and
$3^{-5}$
and
![]() $\unicode[STIX]{x1D6FE}\in D$
of norm
$\unicode[STIX]{x1D6FE}\in D$
of norm
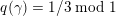 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then, the lift of
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Then, the lift of
![]() $\unicode[STIX]{x1D702}_{1^{1}3^{-3}}$
on
$\unicode[STIX]{x1D702}_{1^{1}3^{-3}}$
on
![]() $\unicode[STIX]{x1D6FE}$
with respect to the Weil representation
$\unicode[STIX]{x1D6FE}$
with respect to the Weil representation
![]() $\unicode[STIX]{x1D70C}_{D}$
is given by
$\unicode[STIX]{x1D70C}_{D}$
is given by
 $$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
$$\begin{eqnarray}F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}=F_{1/3}+F_{1/1}\end{eqnarray}$$
with
 $$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{1}3^{-3}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
$$\begin{eqnarray}F_{1/3}=\unicode[STIX]{x1D702}_{1^{1}3^{-3}}(e^{\unicode[STIX]{x1D6FE}}+e^{-\unicode[STIX]{x1D6FE}})\end{eqnarray}$$
and
 $$\begin{eqnarray}F_{1/1}=\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}}),\end{eqnarray}$$
$$\begin{eqnarray}F_{1/1}=\mathop{\sum }_{\unicode[STIX]{x1D707}\in D}e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D707}))g_{j_{\unicode[STIX]{x1D707}}}(e^{\unicode[STIX]{x1D707}}+e^{-\unicode[STIX]{x1D707}}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D702}_{1^{-3}3^{1}}(\unicode[STIX]{x1D70F}/3)=g_{0}(\unicode[STIX]{x1D70F})+g_{1}(\unicode[STIX]{x1D70F})+g_{2}(\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D702}_{1^{-3}3^{1}}(\unicode[STIX]{x1D70F}/3)=g_{0}(\unicode[STIX]{x1D70F})+g_{1}(\unicode[STIX]{x1D70F})+g_{2}(\unicode[STIX]{x1D70F})$
and
 $g_{j}|_{-1,T}=e(j/3)g_{j}$
. Note that
$g_{j}|_{-1,T}=e(j/3)g_{j}$
. Note that
 $F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}$
is reflective and
$F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}$
is reflective and
![]() $F_{0}$
has constant coefficient
$F_{0}$
has constant coefficient
![]() $2$
.
$2$
.
Proposition 6.24. Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
 $\mathit{II}_{4,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
$\mathit{II}_{4,2}(3^{\unicode[STIX]{x1D716}_{3}n_{3}})$
and
![]() $F$
a reflective form on
$F$
a reflective form on
![]() $L$
with
$L$
with
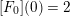 $[F_{0}](0)=2$
. Then
$[F_{0}](0)=2$
. Then
![]() $L$
has genus
$L$
has genus
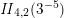 $\mathit{II}_{4,2}(3^{-5})$
and
$\mathit{II}_{4,2}(3^{-5})$
and
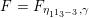 $F=F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}$
for some element
$F=F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}$
for some element
![]() $\unicode[STIX]{x1D6FE}\in D$
of norm
$\unicode[STIX]{x1D6FE}\in D$
of norm
 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
.
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
.
Let
![]() $L$
be a lattice of genus
$L$
be a lattice of genus
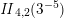 $\mathit{II}_{4,2}(3^{-5})$
. We choose an element
$\mathit{II}_{4,2}(3^{-5})$
. We choose an element
![]() $\unicode[STIX]{x1D6FE}\in D$
of norm
$\unicode[STIX]{x1D6FE}\in D$
of norm
 $q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Let
$q(\unicode[STIX]{x1D6FE})=1/3\;\text{mod}\;1$
. Let
![]() $\unicode[STIX]{x1D6F9}$
be the automorphic product corresponding to
$\unicode[STIX]{x1D6F9}$
be the automorphic product corresponding to
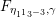 $F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}$
on
$F_{\unicode[STIX]{x1D702}_{1^{1}3^{-3}},\unicode[STIX]{x1D6FE}}$
on
![]() $L$
.
$L$
.
We decompose
 $L=K\oplus \mathit{II}_{1,1}(3)$
such that
$L=K\oplus \mathit{II}_{1,1}(3)$
such that
![]() $\unicode[STIX]{x1D6FE}$
is in the discriminant form of
$\unicode[STIX]{x1D6FE}$
is in the discriminant form of
![]() $\mathit{II}_{1,1}(3)$
and choose a primitive norm
$\mathit{II}_{1,1}(3)$
and choose a primitive norm
![]() $0$
vector
$0$
vector
![]() $z$
in
$z$
in
![]() $\mathit{II}_{1,1}(3)$
. Then
$\mathit{II}_{1,1}(3)$
. Then
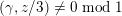 $(\unicode[STIX]{x1D6FE},z/3)\neq 0\;\text{mod}\;1$
. Note that
$(\unicode[STIX]{x1D6FE},z/3)\neq 0\;\text{mod}\;1$
. Note that
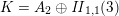 $K=A_{2}\oplus \mathit{II}_{1,1}(3)$
.
$K=A_{2}\oplus \mathit{II}_{1,1}(3)$
.
Proposition 6.25. The expansion of
![]() $\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
$\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
![]() $z$
is given by
$z$
is given by
 $$\begin{eqnarray}\displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[3\unicode[STIX]{x1D702}_{1^{-3}3^{1}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[-\unicode[STIX]{x1D702}_{1^{-3}3^{1}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}=1+\sum c(\unicode[STIX]{x1D706})e((\unicode[STIX]{x1D706},Z)) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[3\unicode[STIX]{x1D702}_{1^{-3}3^{1}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[-\unicode[STIX]{x1D702}_{1^{-3}3^{1}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}=1+\sum c(\unicode[STIX]{x1D706})e((\unicode[STIX]{x1D706},Z)) & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $c(\unicode[STIX]{x1D706})$
is the coefficient at
$c(\unicode[STIX]{x1D706})$
is the coefficient at
![]() $q^{n}$
in
$q^{n}$
in
![]() $\unicode[STIX]{x1D702}_{1^{3}3^{-1}}$
if
$\unicode[STIX]{x1D702}_{1^{3}3^{-1}}$
if
![]() $\unicode[STIX]{x1D706}$
is
$\unicode[STIX]{x1D706}$
is
![]() $n$
times a primitive norm
$n$
times a primitive norm
![]() $0$
vector in
$0$
vector in
![]() ${K^{\prime }}^{+}$
and
${K^{\prime }}^{+}$
and
![]() $0$
otherwise.
$0$
otherwise.
This is the twisted denominator identity of the fake monster superalgebra corresponding to an element of class
![]() $9A$
.
$9A$
.
We can also decompose
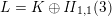 $L=K\oplus \mathit{II}_{1,1}(3)$
such that
$L=K\oplus \mathit{II}_{1,1}(3)$
such that
![]() $\unicode[STIX]{x1D6FE}$
is in the discriminant form of
$\unicode[STIX]{x1D6FE}$
is in the discriminant form of
![]() $K$
. Again we choose a primitive norm
$K$
. Again we choose a primitive norm
![]() $0$
vector
$0$
vector
![]() $z$
in
$z$
in
![]() $\mathit{II}_{1,1}(3)$
. Then we have the following result.
$\mathit{II}_{1,1}(3)$
. Then we have the following result.
Proposition 6.26. The expansion of
![]() $\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
$\unicode[STIX]{x1D6F9}$
at the cusp corresponding to
![]() $z$
is given by
$z$
is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[(e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}))+e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC})))\unicode[STIX]{x1D702}_{1^{-3}3^{1}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \unicode[STIX]{x1D6FC}=\pm \unicode[STIX]{x1D6FE}\hspace{0.2em}{\rm mod}\hspace{0.2em}K}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[\unicode[STIX]{x1D702}_{1^{1}3^{-3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D702}_{3^{-1}9^{3}}((w\unicode[STIX]{x1D70C},Z)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle e((\unicode[STIX]{x1D70C},Z))\mathop{\prod }_{\unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+}}(1-e((3\unicode[STIX]{x1D6FC},Z)))^{[(e((\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}))+e(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC})))\unicode[STIX]{x1D702}_{1^{-3}3^{1}}](-3\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{\substack{ \unicode[STIX]{x1D6FC}\in {K^{\prime }}^{+} \\ \unicode[STIX]{x1D6FC}=\pm \unicode[STIX]{x1D6FE}\hspace{0.2em}{\rm mod}\hspace{0.2em}K}}(1-e((\unicode[STIX]{x1D6FC},Z)))^{[\unicode[STIX]{x1D702}_{1^{1}3^{-3}}](-\unicode[STIX]{x1D6FC}^{2}/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{w\in W}\det (w)\unicode[STIX]{x1D702}_{3^{-1}9^{3}}((w\unicode[STIX]{x1D70C},Z)),\nonumber\end{eqnarray}$$
where
![]() $W$
is the reflection group of
$W$
is the reflection group of
![]() $K^{\prime }$
generated by the vectors
$K^{\prime }$
generated by the vectors
![]() $\unicode[STIX]{x1D6FC}\in K^{\prime }$
of norm
$\unicode[STIX]{x1D6FC}\in K^{\prime }$
of norm
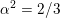 $\unicode[STIX]{x1D6FC}^{2}=2/3$
satisfying
$\unicode[STIX]{x1D6FC}^{2}=2/3$
satisfying
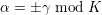 $\unicode[STIX]{x1D6FC}=\pm \unicode[STIX]{x1D6FE}\;\text{mod}\;K$
.
$\unicode[STIX]{x1D6FC}=\pm \unicode[STIX]{x1D6FE}\;\text{mod}\;K$
.
This is the twisted denominator identity of the fake monster algebra corresponding to an element in
![]() $\mathit{Co}_{0}$
of class
$\mathit{Co}_{0}$
of class
![]() $9B$
.
$9B$
.
The automorphic product
![]() $\unicode[STIX]{x1D6F9}$
was first described in [Reference Dittmann, Hagemeier and SchwagenscheidtDHS15].
$\unicode[STIX]{x1D6F9}$
was first described in [Reference Dittmann, Hagemeier and SchwagenscheidtDHS15].
6.5 Classification
In this section, we formulate the classification theorems for reflective forms.
First, we list the reflective modular forms on lattices of prime level.
Theorem 6.27. Let
![]() $L$
be a lattice of prime level and signature
$L$
be a lattice of prime level and signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n>2$
carrying a reflective modular form
$n>2$
carrying a reflective modular form
![]() $F$
. Suppose
$F$
. Suppose
![]() $F_{0}$
has constant coefficient
$F_{0}$
has constant coefficient
![]() $n-2$
. Then
$n-2$
. Then
![]() $L$
and
$L$
and
![]() $F$
are given in the following table.
$F$
are given in the following table.

Conversely each of the functions
![]() $F$
is a reflective modular form on
$F$
is a reflective modular form on
![]() $L$
with constant coefficient
$L$
with constant coefficient
 $[F_{0}](0)=n-2$
.
$[F_{0}](0)=n-2$
.
We have seen that many of these forms give the same function under the singular theta correspondence.
Theorem 6.28. Let
![]() $L$
be a lattice of prime level and signature
$L$
be a lattice of prime level and signature
![]() $(n,2)$
with
$(n,2)$
with
![]() $n>2$
and let
$n>2$
and let
![]() $\unicode[STIX]{x1D6F9}$
be a reflective automorphic product of singular weight on
$\unicode[STIX]{x1D6F9}$
be a reflective automorphic product of singular weight on
![]() $L$
. Then, as a function on the corresponding Hermitian symmetric domain, the automorphic product
$L$
. Then, as a function on the corresponding Hermitian symmetric domain, the automorphic product
![]() $\unicode[STIX]{x1D6F9}$
is the theta lift of one of the following modular forms.
$\unicode[STIX]{x1D6F9}$
is the theta lift of one of the following modular forms.

Hence, with three exceptions, all these functions come from symmetric modular forms. Moreover, at a suitable cusp
![]() $\unicode[STIX]{x1D6F9}$
is the twisted denominator identity of the fake monster algebra by the indicated element in Conway’s group.
$\unicode[STIX]{x1D6F9}$
is the twisted denominator identity of the fake monster algebra by the indicated element in Conway’s group.
Conversely all the given modular forms lift to reflective automorphic products of singular weight on the corresponding lattices.
Acknowledgements
The author thanks R. E. Borcherds, J. H. Bruinier, M. Dittmann, E. Freitag, V. A. Gritsenko, G. Harder, S. Möller and M. Rössler for stimulating discussions and the referee for helpful comments.