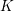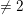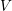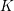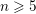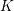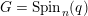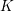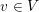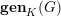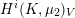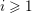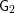1 Introduction
Let
![]() $K$
be a field. The purpose of this paper is to present new results in the framework of the following general problem:
$K$
be a field. The purpose of this paper is to present new results in the framework of the following general problem:
(
) (When) can one equip
 $K$
with a natural set
$K$
with a natural set
 $V$
of discrete valuations such that for a given absolutely almost simple simply connected algebraic
$V$
of discrete valuations such that for a given absolutely almost simple simply connected algebraic
 $K$
-group
$K$
-group
 $G$
, the set of
$G$
, the set of
 $K$
-isomorphism classes of (inner)
$K$
-isomorphism classes of (inner)
 $K$
-forms of
$K$
-forms of
 $G$
having good reduction at all
$G$
having good reduction at all
 $v\in V$
(respectively, at all
$v\in V$
(respectively, at all
 $v\in V\setminus S$
, where
$v\in V\setminus S$
, where
 $S\subset V$
is an arbitrary finite subset) is finite?
$S\subset V$
is an arbitrary finite subset) is finite?
(We refer to the subsection Notation and conventions below for the definition of good reduction.)
Although the analysis of Abelian varieties defined over a global field and having good reduction at a given set of places of the field has been one of the central topics in arithmetic geometry for a long time, particularly since the work of Faltings [Reference FaltingsFal83], similar questions in various situations involving linear algebraic groups have received less attention so far. Thus, before formulating our results, we would like to include a brief account of the previous work in this direction and discuss connections between (

Historically, the consideration of forms of linear algebraic groups with good reduction can be traced back to the work of Harder [Reference HarderHar67], Colliot-Thélène and Sansuc [Reference Colliot-Thélène and SansucCS79] and Gross [Reference GrossGro96]. We note that in [Reference HarderHar67], the focus was primarily on a number field
![]() $K$
. In this case, combining well-known results about the properness of the global-to-local map for the Galois cohomology of algebraic groups [Reference SerreSer97, ch. III, 4.6] with the fact that an absolutely almost simple algebraic group with good reduction over a
$K$
. In this case, combining well-known results about the properness of the global-to-local map for the Galois cohomology of algebraic groups [Reference SerreSer97, ch. III, 4.6] with the fact that an absolutely almost simple algebraic group with good reduction over a
![]() $p$
-adic field is necessarily quasi-split, one can see that a set
$p$
-adic field is necessarily quasi-split, one can see that a set
![]() $V$
consisting of almost all nonarchimedean places of
$V$
consisting of almost all nonarchimedean places of
![]() $K$
satisfies
$K$
satisfies
![]() $(\ast )$
; see [Reference GrossGro96, Reference ConradCon15] for more precise results over
$(\ast )$
; see [Reference GrossGro96, Reference ConradCon15] for more precise results over
![]() $K=\mathbb{Q}$
, and also [Reference Javanpeykar and LoughranJL15].
$K=\mathbb{Q}$
, and also [Reference Javanpeykar and LoughranJL15].
The case where
![]() $K=k(x)$
is the field of rational functions in one variable over a field
$K=k(x)$
is the field of rational functions in one variable over a field
![]() $k$
and
$k$
and
![]() $V$
consists of the discrete valuations
$V$
consists of the discrete valuations
![]() $v_{p(x)}$
corresponding to all irreducible polynomials
$v_{p(x)}$
corresponding to all irreducible polynomials
![]() $p(x)\in k[x]$
was considered by Raghunathan and Ramanathan [Reference Raghunathan and RamanathanRR84] (see also [Reference Chernousov, Gille and PianzolaCGP12, Theorem 2.1]): their result implies that if
$p(x)\in k[x]$
was considered by Raghunathan and Ramanathan [Reference Raghunathan and RamanathanRR84] (see also [Reference Chernousov, Gille and PianzolaCGP12, Theorem 2.1]): their result implies that if
![]() $G_{0}$
is a (connected) semi-simple group over
$G_{0}$
is a (connected) semi-simple group over
![]() $k$
and
$k$
and
![]() $G$
is obtained from
$G$
is obtained from
![]() $G_{0}$
by the base change
$G_{0}$
by the base change
![]() $K/k$
, then any
$K/k$
, then any
![]() $K$
-form
$K$
-form
![]() $G$
that splits over
$G$
that splits over
![]() $\bar{k}(x)$
(where
$\bar{k}(x)$
(where
![]() $\bar{k}$
is a separable closure of
$\bar{k}$
is a separable closure of
![]() $k$
) and has good reduction at all
$k$
) and has good reduction at all
![]() $v\in V$
is obtained by base change from a certain
$v\in V$
is obtained by base change from a certain
![]() $k$
-form of
$k$
-form of
![]() $G_{0}$
. In the same notation, a description of the
$G_{0}$
. In the same notation, a description of the
![]() $K$
-forms of
$K$
-forms of
![]() $G$
that (split over
$G$
that (split over
![]() $\bar{k}(x)$
and) have good reduction at all
$\bar{k}(x)$
and) have good reduction at all
![]() $v\in V\setminus \{v_{x}\}$
was obtained by Chernousov, Gille and Pianzola [Reference Chernousov, Gille and PianzolaCGP12], which played a crucial role in the proof of the conjugacy of the analogues of Cartan subalgebras in certain infinite-dimensional Lie algebras [Reference Chernousov, Neher, Pianzola and YahorauCNPY16]. (We note that if
$v\in V\setminus \{v_{x}\}$
was obtained by Chernousov, Gille and Pianzola [Reference Chernousov, Gille and PianzolaCGP12], which played a crucial role in the proof of the conjugacy of the analogues of Cartan subalgebras in certain infinite-dimensional Lie algebras [Reference Chernousov, Neher, Pianzola and YahorauCNPY16]. (We note that if
![]() $k$
has characteristic zero, then every semi-simple
$k$
has characteristic zero, then every semi-simple
![]() $K$
-group
$K$
-group
![]() $G$
becomes quasi-split over
$G$
becomes quasi-split over
![]() $\bar{k}(x)$
, which implies that those
$\bar{k}(x)$
, which implies that those
![]() $G$
that have good reduction at all
$G$
that have good reduction at all
![]() $v\in V\setminus \{v_{x}\}$
automatically split over
$v\in V\setminus \{v_{x}\}$
automatically split over
![]() $\bar{k}(x)$
.)
$\bar{k}(x)$
.)
In all these instances,
![]() $K$
was the fraction field of a certain Dedekind ring and
$K$
was the fraction field of a certain Dedekind ring and
![]() $V$
was the set of discrete valuations associated with the nonzero prime ideals of this ring, making the situation ‘one-dimensional’. Although the finiteness questions have not been fully answered yet even in the one-dimensional case (cf. Theorem 1.4 below and subsequent remarks), the current work on the following problems necessitate the analysis of (
$V$
was the set of discrete valuations associated with the nonzero prime ideals of this ring, making the situation ‘one-dimensional’. Although the finiteness questions have not been fully answered yet even in the one-dimensional case (cf. Theorem 1.4 below and subsequent remarks), the current work on the following problems necessitate the analysis of (
• The genus problem. Given an absolutely almost simple simply connected algebraic
![]() $K$
-group
$K$
-group
![]() $G$
, its genus
$G$
, its genus
![]() $\mathbf{gen}_{K}(G)$
is defined to be the set of
$\mathbf{gen}_{K}(G)$
is defined to be the set of
![]() $K$
-isomorphism classes of
$K$
-isomorphism classes of
![]() $K$
-forms
$K$
-forms
![]() $G^{\prime }$
of
$G^{\prime }$
of
![]() $G$
that have the same isomorphism classes of maximal
$G$
that have the same isomorphism classes of maximal
![]() $K$
-tori as
$K$
-tori as
![]() $G$
(the latter means that every maximal
$G$
(the latter means that every maximal
![]() $K$
-torus
$K$
-torus
![]() $T$
of
$T$
of
![]() $G$
is
$G$
is
![]() $K$
-isomorphic to some maximal
$K$
-isomorphic to some maximal
![]() $K$
-torus
$K$
-torus
![]() $T^{\prime }$
of
$T^{\prime }$
of
![]() $G^{\prime }$
, and vice versa). One expects
$G^{\prime }$
, and vice versa). One expects
![]() $\mathbf{gen}_{K}(G)$
to be finite for any
$\mathbf{gen}_{K}(G)$
to be finite for any
![]() $G$
over an arbitrary finitely generated field
$G$
over an arbitrary finitely generated field
![]() $K$
. This has been proven for groups of all types when
$K$
. This has been proven for groups of all types when
![]() $K$
is a number field [Reference Prasad and RapinchukPR09, Theorem 7.5], and for inner forms of type
$K$
is a number field [Reference Prasad and RapinchukPR09, Theorem 7.5], and for inner forms of type
![]() $\mathsf{A}_{\ell }$
over arbitrary finitely generated fields, cf. [Reference Chernousov, Rapinchuk and RapinchukCRR13, Reference Chernousov, Rapinchuk and RapinchukCRR16a, Reference Chernousov, Rapinchuk and RapinchukCRR1]. The connection between the genus and good reduction described in [Reference Chernousov, Rapinchuk and RapinchukCRR16b, Theorem 5] and [Reference Chernousov, Rapinchuk and RapinchukCRR2] implies that (under minor additional technical assumptions) the fact that
$\mathsf{A}_{\ell }$
over arbitrary finitely generated fields, cf. [Reference Chernousov, Rapinchuk and RapinchukCRR13, Reference Chernousov, Rapinchuk and RapinchukCRR16a, Reference Chernousov, Rapinchuk and RapinchukCRR1]. The connection between the genus and good reduction described in [Reference Chernousov, Rapinchuk and RapinchukCRR16b, Theorem 5] and [Reference Chernousov, Rapinchuk and RapinchukCRR2] implies that (under minor additional technical assumptions) the fact that
![]() $K$
possesses a set
$K$
possesses a set
![]() $V$
of discrete valuations such that (
$V$
of discrete valuations such that (
![]() $G$
implies that
$G$
implies that
![]() $\mathbf{gen}_{K}(G)$
is finite. Thus, (
$\mathbf{gen}_{K}(G)$
is finite. Thus, (
• The Hasse principle. For a given algebraic
![]() $K$
-group
$K$
-group
![]() $G$
and a given set
$G$
and a given set
![]() $V$
of valuations of
$V$
of valuations of
![]() $K$
, one considers the global-to-local map in Galois cohomology:
$K$
, one considers the global-to-local map in Galois cohomology:
(where
![]() $K_{v}$
is the completion of
$K_{v}$
is the completion of
![]() $K$
with respect to
$K$
with respect to
![]() $v$
), and one says that the Hasse principle holds for
$v$
), and one says that the Hasse principle holds for
![]() $G$
with respect to
$G$
with respect to
![]() $V$
if
$V$
if
![]() $\unicode[STIX]{x1D703}_{G,V}$
is injective (cf. [Reference SerreSer97, ch. III, § 4.7]). Although the Hasse principle does hold in many important situations over a number field
$\unicode[STIX]{x1D703}_{G,V}$
is injective (cf. [Reference SerreSer97, ch. III, § 4.7]). Although the Hasse principle does hold in many important situations over a number field
![]() $K$
(in which case, one takes for
$K$
(in which case, one takes for
![]() $V$
the set of all valuations of
$V$
the set of all valuations of
![]() $K$
, including archimedean ones; see [Reference Platonov and RapinchukPR94, ch. VI]), it may fail for general semi-simple groups [Reference SerreSer97, 4.7], but for any algebraic group
$K$
, including archimedean ones; see [Reference Platonov and RapinchukPR94, ch. VI]), it may fail for general semi-simple groups [Reference SerreSer97, 4.7], but for any algebraic group
![]() $G$
over a number field
$G$
over a number field
![]() $K$
, the map
$K$
, the map
![]() $\unicode[STIX]{x1D703}_{G,V}$
is proper (in other words, the deviation from the Hasse principle is always finite). It is important to point out that the affirmative answer to (
$\unicode[STIX]{x1D703}_{G,V}$
is proper (in other words, the deviation from the Hasse principle is always finite). It is important to point out that the affirmative answer to (

![]() $K$
,
$K$
,
![]() $V$
and
$V$
and
![]() $G$
, then for the corresponding adjoint group
$G$
, then for the corresponding adjoint group
![]() $\overline{G}$
the map
$\overline{G}$
the map
![]() $\unicode[STIX]{x1D703}_{\overline{G},V}$
is proper (cf. § 5.2). See Conjecture B and its discussion below for more concrete statements/results.
$\unicode[STIX]{x1D703}_{\overline{G},V}$
is proper (cf. § 5.2). See Conjecture B and its discussion below for more concrete statements/results.
• Eigenvalue rigidity. Let
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
be two semi-simple algebraic groups over a field
$G_{2}$
be two semi-simple algebraic groups over a field
![]() $F$
of characteristic zero and let
$F$
of characteristic zero and let
![]() $\unicode[STIX]{x1D6E4}_{i}\subset G_{i}(F)$
be a Zariski-dense subgroup for
$\unicode[STIX]{x1D6E4}_{i}\subset G_{i}(F)$
be a Zariski-dense subgroup for
![]() $i=1,2$
. In [Reference Prasad and RapinchukPR09], the notion of weak commensurability of
$i=1,2$
. In [Reference Prasad and RapinchukPR09], the notion of weak commensurability of
![]() $\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{1}$
and
![]() $\unicode[STIX]{x1D6E4}_{2}$
, based on the consideration of eigenvalues of semi-simple elements of those subgroups, was introduced and developed. A detailed analysis of weakly commensurable arithmetic groups was used in [Reference Prasad and RapinchukPR09] to derive geometric consequences. It is currently expected that certain results allowing one to (almost) recover some characteristics of an arithmetic group from the information about the eigenvalues of its elements should be valid for arbitrary finitely generated Zariski-dense subgroups; this phenomenon is called eigenvalue rigidity [Reference RapinchukRap14]. Central to it is the following finiteness conjecture [Reference Prasad and RapinchukPR15, Reference RapinchukRap14]: let
$\unicode[STIX]{x1D6E4}_{2}$
, based on the consideration of eigenvalues of semi-simple elements of those subgroups, was introduced and developed. A detailed analysis of weakly commensurable arithmetic groups was used in [Reference Prasad and RapinchukPR09] to derive geometric consequences. It is currently expected that certain results allowing one to (almost) recover some characteristics of an arithmetic group from the information about the eigenvalues of its elements should be valid for arbitrary finitely generated Zariski-dense subgroups; this phenomenon is called eigenvalue rigidity [Reference RapinchukRap14]. Central to it is the following finiteness conjecture [Reference Prasad and RapinchukPR15, Reference RapinchukRap14]: let
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
be absolutely simple (adjoint) algebraic groups over a field
$G_{2}$
be absolutely simple (adjoint) algebraic groups over a field
![]() $F$
of characteristic zero, and let
$F$
of characteristic zero, and let
![]() $\unicode[STIX]{x1D6E4}_{1}\subset G_{1}(F)$
be a finitely generated Zariski-dense subgroup with trace fieldFootnote
1
$\unicode[STIX]{x1D6E4}_{1}\subset G_{1}(F)$
be a finitely generated Zariski-dense subgroup with trace fieldFootnote
1
![]() $K=K_{\unicode[STIX]{x1D6E4}_{1}}$
. Then there are only finitely many
$K=K_{\unicode[STIX]{x1D6E4}_{1}}$
. Then there are only finitely many
![]() $F/K$
-forms
$F/K$
-forms
![]() $\mathscr{G}_{2}^{(1)},\ldots ,\mathscr{G}_{2}^{(r)}$
of
$\mathscr{G}_{2}^{(1)},\ldots ,\mathscr{G}_{2}^{(r)}$
of
![]() $G_{2}$
such that any finitely generated Zariski-dense subgroup
$G_{2}$
such that any finitely generated Zariski-dense subgroup
![]() $\unicode[STIX]{x1D6E4}_{2}\subset G_{2}(F)$
that is weakly commensurable to
$\unicode[STIX]{x1D6E4}_{2}\subset G_{2}(F)$
that is weakly commensurable to
![]() $\unicode[STIX]{x1D6E4}_{1}$
is
$\unicode[STIX]{x1D6E4}_{1}$
is
![]() $G_{2}(F)$
-conjugate to a subgroup of
$G_{2}(F)$
-conjugate to a subgroup of
![]() $\mathscr{G}_{2}^{(j)}(K)\subset G_{2}(F)$
for some
$\mathscr{G}_{2}^{(j)}(K)\subset G_{2}(F)$
for some
![]() $j=1,\ldots ,r$
. Note that the field
$j=1,\ldots ,r$
. Note that the field
![]() $K$
is finitely generated, hence admits a divisorial set of places
$K$
is finitely generated, hence admits a divisorial set of places
![]() $V$
(see below). Then if (
$V$
(see below). Then if (
![]() $K$
,
$K$
,
![]() $V$
and an absolutely almost simple simply connected group
$V$
and an absolutely almost simple simply connected group
![]() $G$
of the same type as
$G$
of the same type as
![]() $G_{2}$
, the above finiteness conjecture is valid, cf. [Reference Chernousov, Rapinchuk and RapinchukCRR2].
$G_{2}$
, the above finiteness conjecture is valid, cf. [Reference Chernousov, Rapinchuk and RapinchukCRR2].
While various forms of the Hasse principle (including the cohomological form cited above) have been studied extensively for a long time, the genus problem and eigenvalue rigidity emerged relatively recently as an extension of the research carried out in [Reference Prasad and RapinchukPR09] in connection with some geometric problems for isospectral and length-commensurable locally symmetric spaces. Thus, the fact that (

To make (
![]() $K$
or restrict the type of an absolutely almost simple algebraic
$K$
or restrict the type of an absolutely almost simple algebraic
![]() $K$
-group
$K$
-group
![]() $G$
in its statement (or do both). It is most interesting to investigate (
$G$
in its statement (or do both). It is most interesting to investigate (
![]() $K$
. In this case,
$K$
. In this case,
![]() $K$
possesses natural sets of discrete valuations called divisorial. More precisely, let
$K$
possesses natural sets of discrete valuations called divisorial. More precisely, let
![]() $\mathfrak{X}$
be a normal irreducible scheme of finite type over
$\mathfrak{X}$
be a normal irreducible scheme of finite type over
![]() $\mathbb{Z}$
(if
$\mathbb{Z}$
(if
![]() $\operatorname{char}K=0$
) or over a finite field (if
$\operatorname{char}K=0$
) or over a finite field (if
![]() $\operatorname{char}K>0$
) such that
$\operatorname{char}K>0$
) such that
![]() $K$
is the field of rational functions on
$K$
is the field of rational functions on
![]() $\mathfrak{X}$
(we will refer to
$\mathfrak{X}$
(we will refer to
![]() $\mathfrak{X}$
as a model of
$\mathfrak{X}$
as a model of
![]() $K$
). It is well-known that to every prime divisor
$K$
). It is well-known that to every prime divisor
![]() $\mathfrak{Z}$
of
$\mathfrak{Z}$
of
![]() $\mathfrak{X}$
there corresponds a discrete valuation
$\mathfrak{X}$
there corresponds a discrete valuation
![]() $v_{\mathfrak{Z}}$
on
$v_{\mathfrak{Z}}$
on
![]() $K$
(cf. [Reference CutkoskyCut18, 12.3] and [Reference HartshorneHar77, ch. II, § 6]). Then
$K$
(cf. [Reference CutkoskyCut18, 12.3] and [Reference HartshorneHar77, ch. II, § 6]). Then
is called the divisorial set of places of
![]() $K$
corresponding to the model
$K$
corresponding to the model
![]() $\mathfrak{X}$
. Any set of places
$\mathfrak{X}$
. Any set of places
![]() $V$
of
$V$
of
![]() $K$
of this form (for some model
$K$
of this form (for some model
![]() $\mathfrak{X}$
) will be simply called divisorial. Note that any two divisorial sets
$\mathfrak{X}$
) will be simply called divisorial. Note that any two divisorial sets
![]() $V_{1}$
and
$V_{1}$
and
![]() $V_{2}$
are commensurable, i.e.
$V_{2}$
are commensurable, i.e.
![]() $V_{i}\setminus (V_{1}\,\cap \,V_{2})$
is finite for
$V_{i}\setminus (V_{1}\,\cap \,V_{2})$
is finite for
![]() $i=1,2$
, and for any finite subset
$i=1,2$
, and for any finite subset
![]() $S$
of a divisorial set
$S$
of a divisorial set
![]() $V$
the set
$V$
the set
![]() $V\setminus S$
contains a divisorial set. We then can formulate the following more precise version of (
$V\setminus S$
contains a divisorial set. We then can formulate the following more precise version of (
Conjecture A. Let
![]() $K$
be a finitely generated field and let
$K$
be a finitely generated field and let
![]() $V$
be a divisorial set of places. Then for a given absolutely almost simple algebraic
$V$
be a divisorial set of places. Then for a given absolutely almost simple algebraic
![]() $K$
-group
$K$
-group
![]() $G$
, the set of
$G$
, the set of
![]() $K$
-isomorphism classes of (inner)
$K$
-isomorphism classes of (inner)
![]() $K$
-forms of
$K$
-forms of
![]() $G$
that have good reduction at all
$G$
that have good reduction at all
![]() $v\in V$
is finite.
$v\in V$
is finite.
Rapoport suggested that a finiteness statement of such nature is likely to be true for arbitrary reductive
![]() $K$
-groups, namely the number of
$K$
-groups, namely the number of
![]() $K$
-isomorphisms classes of reductive
$K$
-isomorphisms classes of reductive
![]() $K$
-groups of bounded dimension (or rank) that have good reduction at all
$K$
-groups of bounded dimension (or rank) that have good reduction at all
![]() $v\in V$
should be finite. At this point, Conjecture A is known over arbitrary finitely generated only for inner forms of type
$v\in V$
should be finite. At this point, Conjecture A is known over arbitrary finitely generated only for inner forms of type
![]() $\mathsf{A}_{\ell +1}$
with
$\mathsf{A}_{\ell +1}$
with
![]() $(\ell +1)$
prime to
$(\ell +1)$
prime to
![]() $\operatorname{char}K$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Reference Chernousov, Rapinchuk and RapinchukCRR16b]). In fact, before the current paper Conjecture A was not known for any other type over fields other than global.
$\operatorname{char}K$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Reference Chernousov, Rapinchuk and RapinchukCRR16b]). In fact, before the current paper Conjecture A was not known for any other type over fields other than global.
One of the goals of the paper is to prove Conjecture A for the spinor groups of quadratic forms, and also some unitary groups and groups of type
![]() $\mathsf{G}_{2}$
, over two-dimensional global fields of characteristic
$\mathsf{G}_{2}$
, over two-dimensional global fields of characteristic
![]() $\neq \,2$
. Following Kato [Reference KatoKat86], by a two-dimensional global field, we mean either the function field
$\neq \,2$
. Following Kato [Reference KatoKat86], by a two-dimensional global field, we mean either the function field
![]() $K=k(C)$
of a smooth geometrically integral curve
$K=k(C)$
of a smooth geometrically integral curve
![]() $C$
over a number field
$C$
over a number field
![]() $k$
, or the function field
$k$
, or the function field
![]() $K=k(S)$
of a smooth geometrically integral surface
$K=k(S)$
of a smooth geometrically integral surface
![]() $S$
over a finite field
$S$
over a finite field
![]() $k$
.
$k$
.
Theorem 1.1. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $V$
be a divisorial set of places of
$V$
be a divisorial set of places of
![]() $K$
. Fix an integer
$K$
. Fix an integer
![]() $n\geqslant 5$
. Then the set of
$n\geqslant 5$
. Then the set of
![]() $K$
-isomorphism classes of spinor groups
$K$
-isomorphism classes of spinor groups
![]() $G=\operatorname{Spin}_{n}(q)$
of nondegenerate quadratic forms in
$G=\operatorname{Spin}_{n}(q)$
of nondegenerate quadratic forms in
![]() $n$
variables over
$n$
variables over
![]() $K$
that have good reduction at all
$K$
that have good reduction at all
![]() $v\in V$
is finite.
$v\in V$
is finite.
We will now indicate some consequences of this result for two of the three problems discussed above. First, we have the following finiteness result for the genus of spinor groups over two-dimensional global fields.
Theorem 1.2. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $G=\operatorname{Spin}_{n}(q)$
, where
$G=\operatorname{Spin}_{n}(q)$
, where
![]() $q$
is an
$q$
is an
![]() $n$
-dimensional nondegenerate quadratic form over
$n$
-dimensional nondegenerate quadratic form over
![]() $K$
. If either
$K$
. If either
![]() $n\geqslant 5$
is odd or
$n\geqslant 5$
is odd or
![]() $n\geqslant 10$
is even and
$n\geqslant 10$
is even and
![]() $q$
is
$q$
is
![]() $K$
-isotropic, then
$K$
-isotropic, then
![]() $\mathbf{gen}_{K}(G)$
is finite.
$\mathbf{gen}_{K}(G)$
is finite.
(In fact, we prove that the number of
![]() $K$
-isomorphism classes of spinor groups
$K$
-isomorphism classes of spinor groups
![]() $G^{\prime }=\operatorname{Spin}_{n}(q^{\prime })$
of nondegenerate
$G^{\prime }=\operatorname{Spin}_{n}(q^{\prime })$
of nondegenerate
![]() $n$
-dimensional quadratic forms
$n$
-dimensional quadratic forms
![]() $q^{\prime }$
over
$q^{\prime }$
over
![]() $K$
that have the same isomorphism classes of maximal
$K$
that have the same isomorphism classes of maximal
![]() $K$
-tori as
$K$
-tori as
![]() $G$
is finite for any
$G$
is finite for any
![]() $n\geqslant 5$
; see Theorem 5.1.)
$n\geqslant 5$
; see Theorem 5.1.)
Another application deals with the global-to-local map in Galois cohomology. Namely, the techniques developed to prove Theorem 1.1 also yield the following.
Theorem 1.3. With notation as in Theorem 1.1, for
![]() $G=\operatorname{SO}_{n}(q)$
the map
$G=\operatorname{SO}_{n}(q)$
the map
is proper, i.e. the pre-image of a finite set is finite.
Moreover, our techniques in fact yield similar results for some groups
![]() $G$
of the form
$G$
of the form
![]() $\operatorname{SL}_{1,D}$
(cf. Theorem 5.7), some unitary groups and groups of type
$\operatorname{SL}_{1,D}$
(cf. Theorem 5.7), some unitary groups and groups of type
![]() $\mathsf{G}_{2}$
(cf. §§ 8–9), and a partial result for some spinor groups (cf. Proposition 5.8). Based on these results, we propose the following conjecture.
$\mathsf{G}_{2}$
(cf. §§ 8–9), and a partial result for some spinor groups (cf. Proposition 5.8). Based on these results, we propose the following conjecture.
Conjecture B. Let
![]() $K$
be a two-dimensional global field and let
$K$
be a two-dimensional global field and let
![]() $V$
be a divisorial set of places of
$V$
be a divisorial set of places of
![]() $K$
. Then for any absolutely almost simple (or even semi-simple) algebraic group
$K$
. Then for any absolutely almost simple (or even semi-simple) algebraic group
![]() $G$
, the natural map
$G$
, the natural map
is proper. In particular,
is finite.
(We note that the use of twisting shows that proving the finiteness of
![]() $\unicode[STIX]{x0428}(G,V)$
is the most essential part of Conjecture B.)
$\unicode[STIX]{x0428}(G,V)$
is the most essential part of Conjecture B.)
Of course, it would be quite tempting to extend this conjecture to all finitely generated fields, but for this more evidence needs to be developed. At this point, the only result that goes beyond two-dimensional global fields is that for any finitely generated field
![]() $K$
, its divisorial set of places
$K$
, its divisorial set of places
![]() $V$
, and any
$V$
, and any
![]() $n$
prime to
$n$
prime to
![]() $\operatorname{char}K$
, the map
$\operatorname{char}K$
, the map
![]() $H^{1}(K,G)\rightarrow \prod _{v\in V}H^{1}(K_{v},G)$
is proper for
$H^{1}(K,G)\rightarrow \prod _{v\in V}H^{1}(K_{v},G)$
is proper for
![]() $G=\operatorname{PGL}_{n}$
, which follows from the finiteness of the unramified Brauer group
$G=\operatorname{PGL}_{n}$
, which follows from the finiteness of the unramified Brauer group
![]() $_{n\!}\operatorname{Br}(K)_{V}$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Reference Chernousov, Rapinchuk and RapinchukCRR16b]).
$_{n\!}\operatorname{Br}(K)_{V}$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Reference Chernousov, Rapinchuk and RapinchukCRR16b]).
Applications to weakly commensurable Zariski-dense subgroups will be given in [Reference Chernousov, Rapinchuk and RapinchukCRR2].
Theorem 1.1 will be derived from a more general Theorem 2.1 (see § 3) that (potentially) enables one to answer (
![]() $\mathsf{G}_{2}$
, with good reduction over a class of fields that are not finitely generated. This class includes the function fields of
$\mathsf{G}_{2}$
, with good reduction over a class of fields that are not finitely generated. This class includes the function fields of
![]() $p$
-adic curves that have received a great deal of attention in recent years (we refer the reader to [Reference BrusselBru10, Reference Colliot-Thélène, Parimala and SureshCPS12, Reference ParimalaPar14, Reference Parimala and SureshPS98] and references therein for various results involving division algebras, quadratic forms and algebraic groups over those fields), but is in fact much larger. We will formulate our results using a generalization of Serre’s condition
$p$
-adic curves that have received a great deal of attention in recent years (we refer the reader to [Reference BrusselBru10, Reference Colliot-Thélène, Parimala and SureshCPS12, Reference ParimalaPar14, Reference Parimala and SureshPS98] and references therein for various results involving division algebras, quadratic forms and algebraic groups over those fields), but is in fact much larger. We will formulate our results using a generalization of Serre’s condition
![]() $(\text{F})$
(see [Reference SerreSer97, ch. III, § 4]) offered in [Reference RapinchukRap18]. Let
$(\text{F})$
(see [Reference SerreSer97, ch. III, § 4]) offered in [Reference RapinchukRap18]. Let
![]() $K$
be a field and let
$K$
be a field and let
![]() $m\geqslant 1$
an integer prime to
$m\geqslant 1$
an integer prime to
![]() $\operatorname{char}K$
. We then introduce the following condition on
$\operatorname{char}K$
. We then introduce the following condition on
![]() $K$
:
$K$
:
-
 $(\text{F}_{m}^{\prime })$
$(\text{F}_{m}^{\prime })$
For every finite separable extension
 $L/K$
, the quotient
$L/K$
, the quotient
 $L^{\times }/{L^{\times }}^{m}$
is finite.
$L^{\times }/{L^{\times }}^{m}$
is finite.
(Note that if
![]() $L^{\times }/{L^{\times }}^{m}$
is finite for every finite separable extension
$L^{\times }/{L^{\times }}^{m}$
is finite for every finite separable extension
![]() $L/K$
, then it is finite for any finite extension of
$L/K$
, then it is finite for any finite extension of
![]() $K$
; see [Reference RapinchukRap18, Lemma 2.8]). Combining Theorem 2.1 with the results on the finiteness of unramified cohomology with
$K$
; see [Reference RapinchukRap18, Lemma 2.8]). Combining Theorem 2.1 with the results on the finiteness of unramified cohomology with
![]() $\unicode[STIX]{x1D707}_{m}$
-coefficients over fields satisfying
$\unicode[STIX]{x1D707}_{m}$
-coefficients over fields satisfying
![]() $(\text{F}_{m}^{\prime })$
(see [Reference RapinchukRap18]), we obtain the following.
$(\text{F}_{m}^{\prime })$
(see [Reference RapinchukRap18]), we obtain the following.
Theorem 1.4. Let
![]() $C$
be a smooth geometrically integral curve over a field
$C$
be a smooth geometrically integral curve over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
that satisfies condition
$\neq 2$
that satisfies condition
![]() $(\text{F}_{2}^{\prime })$
and let
$(\text{F}_{2}^{\prime })$
and let
![]() $K=k(C)$
be its function field. Denote by
$K=k(C)$
be its function field. Denote by
![]() $V$
the set of discrete valuations of
$V$
the set of discrete valuations of
![]() $K$
corresponding to the closed points of
$K$
corresponding to the closed points of
![]() $C$
. Then the number of
$C$
. Then the number of
![]() $K$
-isomorphism classes of spinor groups
$K$
-isomorphism classes of spinor groups
![]() $G=\operatorname{Spin}_{n}(q)$
of nondegenerate quadratic forms
$G=\operatorname{Spin}_{n}(q)$
of nondegenerate quadratic forms
![]() $q$
over
$q$
over
![]() $K$
in
$K$
in
![]() $n\geqslant 5$
variables that have good reduction at all
$n\geqslant 5$
variables that have good reduction at all
![]() $v\in V$
is finite.
$v\in V$
is finite.
Theorem 1.4 is likely to extend to absolutely almost simple simply connected groups of all types over the function fields of curves defined over a field that satisfies condition
![]() $(\text{F})$
; see Conjecture 7.3. In this regard, we observe that in §§ 8–9 we extend the above results for spinor groups to the special unitary groups of Hermitian forms over quadratic extensions of the base field and to groups of type
$(\text{F})$
; see Conjecture 7.3. In this regard, we observe that in §§ 8–9 we extend the above results for spinor groups to the special unitary groups of Hermitian forms over quadratic extensions of the base field and to groups of type
![]() $\mathsf{G}_{2}$
(for the same fields
$\mathsf{G}_{2}$
(for the same fields
![]() $K$
and the same sets of valuations
$K$
and the same sets of valuations
![]() $V$
).
$V$
).
The paper is organized as follows. In § 2, we develop some formalism involving the Picard group associated with a set of discrete valuations and then use it to formulate a general result (Theorem 2.1) that reduces the proof of the finiteness of the set of isomorphism classes of spinor groups having good reduction to the finiteness of certain unramified cohomology groups. We prove Theorem 2.1 in § 3, where we also give an application of our method to the properness of the global-to-local map in Galois cohomology (Theorem 3.4). In § 4, we combine Theorem 2.1 with the finiteness results for unramified cohomology of two-dimensional global fields to prove Theorem 1.1. It should be pointed out that these finiteness results are known in degrees
![]() ${\leqslant}2$
and easily follow from the theorems of Poitou–Tate in degrees
${\leqslant}2$
and easily follow from the theorems of Poitou–Tate in degrees
![]() ${\geqslant}4$
, but have not appeared in the literature in degree three. We derive the required fact in degree three (Corollary 6.2) from the more general Theorem 6.1. For several reasons (see the discussion in § 4.1), we give two proofs of the characteristic zero case of Theorem 6.1: that given in § 6 is based on the referee’s suggestions, whereas that in Appendix A is our original argument. The positive characteristic case of Theorem 6.1 is treated in § 7, along with the finiteness results involving fields of type
${\geqslant}4$
, but have not appeared in the literature in degree three. We derive the required fact in degree three (Corollary 6.2) from the more general Theorem 6.1. For several reasons (see the discussion in § 4.1), we give two proofs of the characteristic zero case of Theorem 6.1: that given in § 6 is based on the referee’s suggestions, whereas that in Appendix A is our original argument. The positive characteristic case of Theorem 6.1 is treated in § 7, along with the finiteness results involving fields of type
![]() $(\text{F}_{m}^{\prime })$
and the proof of Theorem 1.4. Theorems 1.2 and 1.3 are proved in § 5. Finally, in §§ 8–9, we present finiteness results for special unitary groups and groups of type
$(\text{F}_{m}^{\prime })$
and the proof of Theorem 1.4. Theorems 1.2 and 1.3 are proved in § 5. Finally, in §§ 8–9, we present finiteness results for special unitary groups and groups of type
![]() $\mathsf{G}_{2}$
.
$\mathsf{G}_{2}$
.
Notation and conventions. For a field
![]() $k$
, we will denote by
$k$
, we will denote by
![]() $\bar{k}$
a fixed separable closure. Given a discrete valuation
$\bar{k}$
a fixed separable closure. Given a discrete valuation
![]() $v$
of
$v$
of
![]() $k$
, we let
$k$
, we let
![]() $k_{v}$
and
$k_{v}$
and
![]() $k^{(v)}$
denote the completion and the residue field of
$k^{(v)}$
denote the completion and the residue field of
![]() $k$
at
$k$
at
![]() $v$
, respectively. We recall that a
$v$
, respectively. We recall that a
![]() $\operatorname{Gal}(\bar{k}/k)$
-module
$\operatorname{Gal}(\bar{k}/k)$
-module
![]() $M$
is said to be unramified at
$M$
is said to be unramified at
![]() $v$
if for some (equivalently, any) extension
$v$
if for some (equivalently, any) extension
![]() $w$
of
$w$
of
![]() $v$
to
$v$
to
![]() $\bar{k}$
, the inertia subgroup of the decomposition group
$\bar{k}$
, the inertia subgroup of the decomposition group
![]() $\operatorname{Dec}_{w}\subset \operatorname{Gal}(\bar{k}/k)$
acts trivially on
$\operatorname{Dec}_{w}\subset \operatorname{Gal}(\bar{k}/k)$
acts trivially on
![]() $M$
. In addition, if
$M$
. In addition, if
![]() $G$
is an absolutely almost simple linear algebraic group defined over
$G$
is an absolutely almost simple linear algebraic group defined over
![]() $k$
, we will say that
$k$
, we will say that
![]() $G$
has good reduction at
$G$
has good reduction at
![]() $v$
if there exists a reductive group scheme
$v$
if there exists a reductive group scheme
![]() $\mathscr{G}$
over the valuation ring
$\mathscr{G}$
over the valuation ring
![]() ${\mathcal{O}}_{v}$
of
${\mathcal{O}}_{v}$
of
![]() $k_{v}$
whose generic fiber
$k_{v}$
whose generic fiber
![]() $\mathscr{G}\otimes _{{\mathcal{O}}_{v}}k_{v}$
is isomorphic to
$\mathscr{G}\otimes _{{\mathcal{O}}_{v}}k_{v}$
is isomorphic to
![]() $G\otimes _{k}k_{v}$
(this definition, involving completions, is convenient for applications to the Hasse principle).
$G\otimes _{k}k_{v}$
(this definition, involving completions, is convenient for applications to the Hasse principle).
We will follow the conventions outlined in [Reference Garibaldi, Merkurjev and SerreGMS03, ch. II, § 7.8] regarding Tate twists of Galois modules. Namely, suppose
![]() $v$
is a discrete valuation of
$v$
is a discrete valuation of
![]() $k$
,
$k$
,
![]() $n$
an integer prime to
$n$
an integer prime to
![]() $\operatorname{char}k^{(v)}$
and
$\operatorname{char}k^{(v)}$
and
![]() $M$
a finite
$M$
a finite
![]() $\operatorname{Gal}(\bar{k}/k)$
-module satisfying
$\operatorname{Gal}(\bar{k}/k)$
-module satisfying
![]() $nM=0$
. For an integer
$nM=0$
. For an integer
![]() $d$
, one defines
$d$
, one defines
![]() $M(d)$
to be
$M(d)$
to be
![]() $\unicode[STIX]{x1D707}_{n}^{\otimes d}\otimes M$
if
$\unicode[STIX]{x1D707}_{n}^{\otimes d}\otimes M$
if
![]() $d\geqslant 0$
and
$d\geqslant 0$
and
![]() $\operatorname{Hom}(\unicode[STIX]{x1D707}_{n}^{\otimes (-d)},M)$
if
$\operatorname{Hom}(\unicode[STIX]{x1D707}_{n}^{\otimes (-d)},M)$
if
![]() $d<0$
. In particular,
$d<0$
. In particular,
![]() $M(-1)=\operatorname{Hom}(\unicode[STIX]{x1D707}_{n},M)$
. In the case where
$M(-1)=\operatorname{Hom}(\unicode[STIX]{x1D707}_{n},M)$
. In the case where
![]() $M$
is torsion (but not necessarily finite) without any elements of order equal to the residue characteristic, one writes
$M$
is torsion (but not necessarily finite) without any elements of order equal to the residue characteristic, one writes
![]() $M=\underset{\longrightarrow }{\lim }M^{\prime }$
, where
$M=\underset{\longrightarrow }{\lim }M^{\prime }$
, where
![]() $M^{\prime }$
are the finite submodules of
$M^{\prime }$
are the finite submodules of
![]() $M$
, and sets
$M$
, and sets
![]() $M(d)=\underset{\longrightarrow }{\lim }M^{\prime }(d)$
. As usual, we will use
$M(d)=\underset{\longrightarrow }{\lim }M^{\prime }(d)$
. As usual, we will use
![]() $\unicode[STIX]{x1D707}_{n}^{\otimes d}$
to denote
$\unicode[STIX]{x1D707}_{n}^{\otimes d}$
to denote
![]() $\mathbb{Z}/n\mathbb{Z}(d)$
for all
$\mathbb{Z}/n\mathbb{Z}(d)$
for all
![]() $d$
.
$d$
.
Finally, we recall that if
![]() $n$
is an integer prime to
$n$
is an integer prime to
![]() $\operatorname{char}k$
, then isomorphism
$\operatorname{char}k$
, then isomorphism
![]() $k^{\times }/{k^{\times }}^{n}\simeq H^{1}(k,\unicode[STIX]{x1D707}_{n})$
from Kummer theory is induced by sending an element
$k^{\times }/{k^{\times }}^{n}\simeq H^{1}(k,\unicode[STIX]{x1D707}_{n})$
from Kummer theory is induced by sending an element
![]() $a\in k^{\times }$
to the cohomology class of the 1-cocycle
$a\in k^{\times }$
to the cohomology class of the 1-cocycle
When
![]() $n=2$
, we will denote this cocycle simply by
$n=2$
, we will denote this cocycle simply by
![]() $\unicode[STIX]{x1D712}_{a}.$
$\unicode[STIX]{x1D712}_{a}.$
2 The Picard group associated with a set of discrete valuations
Suppose that a field
![]() $K$
is equipped with a set
$K$
is equipped with a set
![]() $V$
of discrete valuations that satisfies the following condition:
$V$
of discrete valuations that satisfies the following condition:
(A) For any
 $a\in K^{\times }$
, the set
$a\in K^{\times }$
, the set
 $V(a):=\{v\in V\mid v(a)\neq 0\}$
is finite.
$V(a):=\{v\in V\mid v(a)\neq 0\}$
is finite.
(It is worth noting that
![]() $(\text{A})$
automatically holds for a divisorial set of valuations
$(\text{A})$
automatically holds for a divisorial set of valuations
![]() $V$
of a finitely generated field
$V$
of a finitely generated field
![]() $K$
.) We now let
$K$
.) We now let
![]() $\operatorname{Div}(V)$
denote the free Abelian group on the set
$\operatorname{Div}(V)$
denote the free Abelian group on the set
![]() $V$
, the elements of which will be called ‘divisors’. The fact that
$V$
, the elements of which will be called ‘divisors’. The fact that
![]() $V$
satisfies
$V$
satisfies
![]() $(\text{A})$
enables one to associate to any
$(\text{A})$
enables one to associate to any
![]() $a\in K^{\times }$
the corresponding ‘principal divisor’
$a\in K^{\times }$
the corresponding ‘principal divisor’
Let
![]() $\text{P}(V)$
denote the subgroup of
$\text{P}(V)$
denote the subgroup of
![]() $\operatorname{Div}(V)$
formed by all principal divisors. We call the quotient
$\operatorname{Div}(V)$
formed by all principal divisors. We call the quotient
![]() $\operatorname{Div}(V)/\text{P}(V)$
the Picard group of
$\operatorname{Div}(V)/\text{P}(V)$
the Picard group of
![]() $V$
and denote it by
$V$
and denote it by
![]() $\operatorname{Pic}(V)$
.
$\operatorname{Pic}(V)$
.
Next, we recall (cf. [Reference Garibaldi, Merkurjev and SerreGMS03, ch. II]) that for a discrete valuation
![]() $v$
of a field
$v$
of a field
![]() $K$
and a finite Galois module
$K$
and a finite Galois module
![]() $M$
that is unramified at
$M$
that is unramified at
![]() $v$
and order of which is prime to
$v$
and order of which is prime to
![]() $\operatorname{char}K^{(v)}$
, one has a residue map
$\operatorname{char}K^{(v)}$
, one has a residue map
In particular, for every
![]() $n$
prime to
$n$
prime to
![]() $\operatorname{char}K^{(v)}$
and every
$\operatorname{char}K^{(v)}$
and every
![]() $d$
we have the residue map
$d$
we have the residue map
An element of
![]() $H^{i}(K,M)$
(in particular, of
$H^{i}(K,M)$
(in particular, of
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes d})$
) is said to be unramified if it lies in the kernel of the relevant residue map.
$H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes d})$
) is said to be unramified if it lies in the kernel of the relevant residue map.
In this section, we only consider cohomology with coefficients in
![]() $\unicode[STIX]{x1D707}_{2}=\{\pm 1\}$
. Then for a discrete valuation
$\unicode[STIX]{x1D707}_{2}=\{\pm 1\}$
. Then for a discrete valuation
![]() $v$
of
$v$
of
![]() $K$
, the corresponding residue map is defined whenever
$K$
, the corresponding residue map is defined whenever
![]() $\operatorname{char}K^{(v)}\neq 2$
and will be denoted by
$\operatorname{char}K^{(v)}\neq 2$
and will be denoted by
We now make the following assumption:
(B)
 $\operatorname{char}K^{(v)}\neq 2$
for all
$\operatorname{char}K^{(v)}\neq 2$
for all
 $v\in V$
.
$v\in V$
.
We then define the
![]() $i$
th unramified cohomology group of
$i$
th unramified cohomology group of
![]() $K$
with respect to
$K$
with respect to
![]() $V$
by
$V$
by
With this notation, we have the following result.
Theorem 2.1. Let
![]() $K$
be a field equipped with a set
$K$
be a field equipped with a set
![]() $V$
of discrete valuations satisfying conditions
$V$
of discrete valuations satisfying conditions
![]() $(\text{A})$
and
$(\text{A})$
and
![]() $(\text{B})$
and let
$(\text{B})$
and let
![]() $n\geqslant 5$
be an integer. Assume that:
$n\geqslant 5$
be an integer. Assume that:
(1) the quotient
 $\operatorname{Pic}(V)/2\cdot \operatorname{Pic}(V)$
is finite; and
$\operatorname{Pic}(V)/2\cdot \operatorname{Pic}(V)$
is finite; and(2) the unramified cohomology groups
 $H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
are finite for all
$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
are finite for all
 $i=1,\ldots ,\ell :=[\log _{2}n]+1$
.
$i=1,\ldots ,\ell :=[\log _{2}n]+1$
.
Then the number of
![]() $K$
-isomorphism classes of spinor groups
$K$
-isomorphism classes of spinor groups
![]() $G=\operatorname{Spin}_{n}(q)$
of nondegenerate quadratic forms
$G=\operatorname{Spin}_{n}(q)$
of nondegenerate quadratic forms
![]() $q$
over
$q$
over
![]() $K$
in
$K$
in
![]() $n$
variables that have good reduction at all
$n$
variables that have good reduction at all
![]() $v\in V$
is
$v\in V$
is
(in particular, finite).
We postpone the proof of Theorem 2.1 until the next section, and recall now the connection between
![]() $\operatorname{Pic}(V)$
and the idèles, which is well-known in the classical setting (cf. [Reference Cassels and FröhlichCF10, ch. II, §17]). Given a field
$\operatorname{Pic}(V)$
and the idèles, which is well-known in the classical setting (cf. [Reference Cassels and FröhlichCF10, ch. II, §17]). Given a field
![]() $K$
endowed with a set
$K$
endowed with a set
![]() $V$
of discrete valuations that satisfies (A), we define the group of idèles
$V$
of discrete valuations that satisfies (A), we define the group of idèles
![]() $\mathbb{I}(K,V)$
as the restricted direct product of the multiplicative groups
$\mathbb{I}(K,V)$
as the restricted direct product of the multiplicative groups
![]() $K_{v}^{\times }$
for
$K_{v}^{\times }$
for
![]() $v\in V$
with respect to the groups of units
$v\in V$
with respect to the groups of units
![]() $U_{v}={\mathcal{O}}_{v}^{\times }$
:
$U_{v}={\mathcal{O}}_{v}^{\times }$
:
Furthermore, we let
be the subgroup of integral idèles. As
![]() $V$
satisfies (A), one can consider the diagonal embedding
$V$
satisfies (A), one can consider the diagonal embedding
![]() $K^{\times }{\hookrightarrow}\mathbb{I}(K,V)$
, the image of which will be called the group of principal idèles and denoted also by
$K^{\times }{\hookrightarrow}\mathbb{I}(K,V)$
, the image of which will be called the group of principal idèles and denoted also by
![]() $K^{\times }$
. Then
$K^{\times }$
. Then
is a surjective group homomorphism with kernel
![]() $\ker \unicode[STIX]{x1D708}=\mathbb{I}_{0}(K,V)$
. Thus, we obtain the following.
$\ker \unicode[STIX]{x1D708}=\mathbb{I}_{0}(K,V)$
. Thus, we obtain the following.
Lemma 2.2. The map
![]() $\unicode[STIX]{x1D708}$
induces a natural identification of the quotient
$\unicode[STIX]{x1D708}$
induces a natural identification of the quotient
![]() $\mathbb{I}(K,V)/\mathbb{I}_{0}(K,V)K^{\times }$
with
$\mathbb{I}(K,V)/\mathbb{I}_{0}(K,V)K^{\times }$
with
![]() $\operatorname{Pic}(V)$
.
$\operatorname{Pic}(V)$
.
3 Proof of Theorem 2.1 and its variations
3.1 Two facts about the Witt ring
Let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $\neq 2$
. We let
$\neq 2$
. We let
![]() $W(F)$
and
$W(F)$
and
![]() $I(F)$
denote the Witt ring of
$I(F)$
denote the Witt ring of
![]() $F$
and its fundamental ideal, respectively. For a nondegenerate quadratic form
$F$
and its fundamental ideal, respectively. For a nondegenerate quadratic form
![]() $q$
over
$q$
over
![]() $F$
,
$F$
,
![]() $[q]$
denotes the corresponding class in
$[q]$
denotes the corresponding class in
![]() $W(F)$
. As usual, the quadratic form
$W(F)$
. As usual, the quadratic form
![]() $a_{1}x_{1}^{2}+\cdots +a_{n}x_{n}^{2}$
with
$a_{1}x_{1}^{2}+\cdots +a_{n}x_{n}^{2}$
with
![]() $a_{i}\in F^{\times }$
will be denoted by
$a_{i}\in F^{\times }$
will be denoted by
![]() $\langle a_{1},\ldots ,a_{n}\rangle$
, whereas
$\langle a_{1},\ldots ,a_{n}\rangle$
, whereas
![]() $\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
will be used to denote the
$\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
will be used to denote the
![]() $d$
-fold Pfister form
$d$
-fold Pfister form
![]() $\langle 1,-a_{1}\rangle \otimes \cdots \otimes \langle 1,-a_{d}\rangle$
. Clearly, for any
$\langle 1,-a_{1}\rangle \otimes \cdots \otimes \langle 1,-a_{d}\rangle$
. Clearly, for any
![]() $d\geqslant 1$
, the
$d\geqslant 1$
, the
![]() $d$
th power
$d$
th power
![]() $I(F)^{d}$
is additively generated by the classes of
$I(F)^{d}$
is additively generated by the classes of
![]() $d$
-fold Pfister forms.
$d$
-fold Pfister forms.
Lemma 3.1. Let
![]() $q$
be a nondegenerate quadratic form over
$q$
be a nondegenerate quadratic form over
![]() $F$
such that
$F$
such that
![]() $[q]\in I(F)^{d}$
for some
$[q]\in I(F)^{d}$
for some
![]() $d\geqslant 1$
. Then for any
$d\geqslant 1$
. Then for any
![]() $\unicode[STIX]{x1D706}\in F^{\times }$
, we have
$\unicode[STIX]{x1D706}\in F^{\times }$
, we have
![]() $[\unicode[STIX]{x1D706}q]\in I(F)^{d}$
and
$[\unicode[STIX]{x1D706}q]\in I(F)^{d}$
and
![]() $[\unicode[STIX]{x1D706}q]+I(F)^{d+1}=[q]+I(F)^{d+1}$
.
$[\unicode[STIX]{x1D706}q]+I(F)^{d+1}=[q]+I(F)^{d+1}$
.
Proof. The fact that
![]() $[\unicode[STIX]{x1D706}q]\in I(F)^{d}$
is obvious. Furthermore, we have
$[\unicode[STIX]{x1D706}q]\in I(F)^{d}$
is obvious. Furthermore, we have
as required. ◻
Now, let
![]() $F$
be a field complete with respect to a discrete valuation
$F$
be a field complete with respect to a discrete valuation
![]() $v$
such that the characteristic of the residue field
$v$
such that the characteristic of the residue field
![]() $F^{(v)}$
is
$F^{(v)}$
is
![]() $\neq 2$
. We let
$\neq 2$
. We let
![]() $U(F)$
denote the group of units in
$U(F)$
denote the group of units in
![]() $F$
, and fix a uniformizer
$F$
, and fix a uniformizer
![]() $\unicode[STIX]{x1D70B}$
. Then one can define the first and second residue maps
$\unicode[STIX]{x1D70B}$
. Then one can define the first and second residue maps
which are homomorphisms of additive groups uniquely characterized by the conditions
for any
![]() $u\in U(F)$
(where
$u\in U(F)$
(where
![]() $\bar{u}$
denote the image of
$\bar{u}$
denote the image of
![]() $u$
in
$u$
in
![]() $F^{(v)}$
) (see [Reference LamLam05, ch. VI, § 1] or [Reference MilnorMil70, § 5] for the details). Let
$F^{(v)}$
) (see [Reference LamLam05, ch. VI, § 1] or [Reference MilnorMil70, § 5] for the details). Let
![]() $W_{0}(F)$
be the subring of
$W_{0}(F)$
be the subring of
![]() $W(F)$
generated by the classes of
$W(F)$
generated by the classes of
![]() $\langle u\rangle$
for
$\langle u\rangle$
for
![]() $u\in U(F)$
. Then
$u\in U(F)$
. Then
![]() $W_{0}(F)=\operatorname{Ker}\unicode[STIX]{x2202}_{2}$
, whereas
$W_{0}(F)=\operatorname{Ker}\unicode[STIX]{x2202}_{2}$
, whereas
![]() $\unicode[STIX]{x2202}_{1}$
yields an isomorphism between
$\unicode[STIX]{x2202}_{1}$
yields an isomorphism between
![]() $W_{0}(F)$
and
$W_{0}(F)$
and
![]() $W(F^{(v)})$
. Thus, we have the following split exact sequence
$W(F^{(v)})$
. Thus, we have the following split exact sequence
Let
![]() $I_{0}(F)=W_{0}(F)\,\cap \,I(F)$
. Milnor [Reference MilnorMil70, § 5] shows that for any
$I_{0}(F)=W_{0}(F)\,\cap \,I(F)$
. Milnor [Reference MilnorMil70, § 5] shows that for any
![]() $d\geqslant 1$
, the restriction of
$d\geqslant 1$
, the restriction of
![]() $\unicode[STIX]{x2202}_{2}$
to
$\unicode[STIX]{x2202}_{2}$
to
![]() $I^{d}(F)$
(the
$I^{d}(F)$
(the
![]() $d$
th power of
$d$
th power of
![]() $I(F)$
) yields the exact sequence
$I(F)$
) yields the exact sequence
This, in particular, gives the following result.
Lemma 3.2. For any
![]() $d\geqslant 1$
, we have
$d\geqslant 1$
, we have
![]() $I(F)^{d}\,\cap \,W_{0}(F)=I_{0}(F)^{d}$
.
$I(F)^{d}\,\cap \,W_{0}(F)=I_{0}(F)^{d}$
.
3.2 The Milnor isomorphism and unramified classes
Again let
![]() $F$
be a field of characteristic
$F$
be a field of characteristic
![]() $\neq 2$
. It is a consequence of Voevodsky’s proof of the Milnor conjecture (see [Reference Orlov, Vishik and VoevodskyOVV07, Reference VoevodskyVoe03, Reference VoevodskyVoe11]) that for
$\neq 2$
. It is a consequence of Voevodsky’s proof of the Milnor conjecture (see [Reference Orlov, Vishik and VoevodskyOVV07, Reference VoevodskyVoe03, Reference VoevodskyVoe11]) that for
![]() $d\geqslant 1$
, there are natural isomorphisms of Abelian groups
$d\geqslant 1$
, there are natural isomorphisms of Abelian groups
Explicitly,
![]() $\unicode[STIX]{x1D6FE}_{F,d}$
is defined by sending the class of the Pfister form
$\unicode[STIX]{x1D6FE}_{F,d}$
is defined by sending the class of the Pfister form
![]() $\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
to the cup-product
$\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
to the cup-product
![]() $\unicode[STIX]{x1D712}_{a_{1}}\,\cup \,\cdots \,\cup \,\unicode[STIX]{x1D712}_{a_{d}}$
, where for
$\unicode[STIX]{x1D712}_{a_{1}}\,\cup \,\cdots \,\cup \,\unicode[STIX]{x1D712}_{a_{d}}$
, where for
![]() $a\in F^{\times }$
, we let
$a\in F^{\times }$
, we let
![]() $\unicode[STIX]{x1D712}_{a}$
be the corresponding 1-cocycle given by Kummer theory.
$\unicode[STIX]{x1D712}_{a}$
be the corresponding 1-cocycle given by Kummer theory.
Lemma 3.3. Let
![]() $F$
be a field complete with respect to a discrete valuation
$F$
be a field complete with respect to a discrete valuation
![]() $v$
such that
$v$
such that
![]() $\operatorname{char}F^{(v)}\neq 2$
and let
$\operatorname{char}F^{(v)}\neq 2$
and let
![]() $d\geqslant 1$
. If
$d\geqslant 1$
. If
![]() $q$
is a nondegenerate quadratic form over
$q$
is a nondegenerate quadratic form over
![]() $F$
such that
$F$
such that
![]() $[\unicode[STIX]{x1D706}q]\in I(F)^{d}\,\cap \,W_{0}(F)$
for some
$[\unicode[STIX]{x1D706}q]\in I(F)^{d}\,\cap \,W_{0}(F)$
for some
![]() $\unicode[STIX]{x1D706}\in F^{\times }$
(notation as in the previous subsection), then
$\unicode[STIX]{x1D706}\in F^{\times }$
(notation as in the previous subsection), then
![]() $[q]\in I(F)^{d}$
and the cohomology class
$[q]\in I(F)^{d}$
and the cohomology class
![]() $\unicode[STIX]{x1D6FE}_{F,d}([q])\in H^{d}(F,\unicode[STIX]{x1D707}_{2})$
is unramified at
$\unicode[STIX]{x1D6FE}_{F,d}([q])\in H^{d}(F,\unicode[STIX]{x1D707}_{2})$
is unramified at
![]() $v$
.
$v$
.
Proof. It immediately follows from Lemma 3.1 that
![]() $[q]\in I(F)^{d}$
and
$[q]\in I(F)^{d}$
and
![]() $\unicode[STIX]{x1D6FE}_{F,d}([q])=\unicode[STIX]{x1D6FE}_{F,d}([\unicode[STIX]{x1D706}q])$
. Thus, it is enough to show that if
$\unicode[STIX]{x1D6FE}_{F,d}([q])=\unicode[STIX]{x1D6FE}_{F,d}([\unicode[STIX]{x1D706}q])$
. Thus, it is enough to show that if
![]() $[q]\in I(F)^{d}\,\cap \,W_{0}(F)$
, then
$[q]\in I(F)^{d}\,\cap \,W_{0}(F)$
, then
![]() $\unicode[STIX]{x1D6FE}_{F,d}([q])$
is unramified at
$\unicode[STIX]{x1D6FE}_{F,d}([q])$
is unramified at
![]() $v$
. According to Lemma 3.2, we have
$v$
. According to Lemma 3.2, we have
![]() $I(F)^{d}\,\cap \,W_{0}(F)=I_{0}(F)^{d}$
, which is additively generated by the classes of Pfister forms
$I(F)^{d}\,\cap \,W_{0}(F)=I_{0}(F)^{d}$
, which is additively generated by the classes of Pfister forms
![]() $\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
with
$\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
with
![]() $a_{i}\in U(F)$
. However, for any such form, the corresponding class
$a_{i}\in U(F)$
. However, for any such form, the corresponding class
is clearly unramified, and our claim follows. ◻
3.3 Proof of Theorem 2.1
Let
![]() $\{q_{i}\}\text{}_{i\in I}$
be a family of
$\{q_{i}\}\text{}_{i\in I}$
be a family of
![]() $n$
-dimensional nondegenerate quadratic forms over
$n$
-dimensional nondegenerate quadratic forms over
![]() $K$
such that:
$K$
such that:
∙ for each
 $i\in I$
, the spinor group
$i\in I$
, the spinor group
 $G_{i}=\operatorname{Spin}_{n}(q_{i})$
has good reduction at all
$G_{i}=\operatorname{Spin}_{n}(q_{i})$
has good reduction at all
 $v\in V$
; and
$v\in V$
; and∙ for
 $i,j\in I$
,
$i,j\in I$
,
 $i\neq j$
, the forms
$i\neq j$
, the forms
 $q_{i}$
and
$q_{i}$
and
 $q_{j}$
are not similar (i.e.
$q_{j}$
are not similar (i.e.
 $q_{i}$
is not equivalent to any nonzero scalar multiple of
$q_{i}$
is not equivalent to any nonzero scalar multiple of
 $q_{j}$
).
$q_{j}$
).
We wish to show that
![]() $I$
is finite and
$I$
is finite and
where
We begin by observing that the first of the above conditions implies that for each
![]() $i\in I$
and any
$i\in I$
and any
![]() $v\in V$
, there exists
$v\in V$
, there exists
![]() $\unicode[STIX]{x1D706}_{v}^{(i)}\in K_{v}^{\times }$
such that the form
$\unicode[STIX]{x1D706}_{v}^{(i)}\in K_{v}^{\times }$
such that the form
![]() $\unicode[STIX]{x1D706}_{v}^{(i)}q_{i}\in W_{0}(K_{v})$
in the above notation. In addition, we may assume without loss of generality that for each
$\unicode[STIX]{x1D706}_{v}^{(i)}q_{i}\in W_{0}(K_{v})$
in the above notation. In addition, we may assume without loss of generality that for each
![]() $i\in I$
, we have
$i\in I$
, we have
![]() $\unicode[STIX]{x1D706}_{v}^{(i)}=1$
for almost all
$\unicode[STIX]{x1D706}_{v}^{(i)}=1$
for almost all
![]() $v$
; then
$v$
; then
![]() $\unicode[STIX]{x1D706}^{(i)}:=(\unicode[STIX]{x1D706}_{v}^{(i)})_{v\in V}\in \mathbb{I}(K,V)$
. Using Lemma 2.2, we see that
$\unicode[STIX]{x1D706}^{(i)}:=(\unicode[STIX]{x1D706}_{v}^{(i)})_{v\in V}\in \mathbb{I}(K,V)$
. Using Lemma 2.2, we see that
Thus, there exists a subset
![]() $J_{0}\subset I$
of size
$J_{0}\subset I$
of size
![]() ${\geqslant}|I|/d_{0}$
(if
${\geqslant}|I|/d_{0}$
(if
![]() $I$
is infinite then this simply means that
$I$
is infinite then this simply means that
![]() $J_{0}$
is also infinite) such that all
$J_{0}$
is also infinite) such that all
![]() $\unicode[STIX]{x1D706}^{(i)}$
for
$\unicode[STIX]{x1D706}^{(i)}$
for
![]() $i\in J_{0}$
have the same image in
$i\in J_{0}$
have the same image in
![]() $\mathbb{I}(K,V)/\mathbb{I}(K,V)^{2}\mathbb{I}_{0}(K,V)K^{\times }$
. Now, fix
$\mathbb{I}(K,V)/\mathbb{I}(K,V)^{2}\mathbb{I}_{0}(K,V)K^{\times }$
. Now, fix
![]() $j_{0}\in J_{0}$
. For any
$j_{0}\in J_{0}$
. For any
![]() $j\in J_{0}$
, we can write
$j\in J_{0}$
, we can write
(assuming that the elements
![]() $\unicode[STIX]{x1D6FC}^{(j_{0})}$
,
$\unicode[STIX]{x1D6FC}^{(j_{0})}$
,
![]() $\unicode[STIX]{x1D6FD}^{(j_{0})}$
and
$\unicode[STIX]{x1D6FD}^{(j_{0})}$
and
![]() $\unicode[STIX]{x1D6FF}^{(j_{0})}$
are all trivial), and then set
$\unicode[STIX]{x1D6FF}^{(j_{0})}$
are all trivial), and then set
We note that the forms
![]() $\tilde{q}_{j}$
for
$\tilde{q}_{j}$
for
![]() $j\in J_{0}$
remain pairwise nonsimilar, in particular, inequivalent. Furthermore, for any
$j\in J_{0}$
remain pairwise nonsimilar, in particular, inequivalent. Furthermore, for any
![]() $v\in V$
we have
$v\in V$
we have
![]() $\tilde{\unicode[STIX]{x1D706}}_{v}^{(j)}\tilde{q}_{j}=\unicode[STIX]{x1D706}_{v}^{(j)}q_{j}$
, hence
$\tilde{\unicode[STIX]{x1D706}}_{v}^{(j)}\tilde{q}_{j}=\unicode[STIX]{x1D706}_{v}^{(j)}q_{j}$
, hence
![]() $[\tilde{\unicode[STIX]{x1D706}}_{v}^{(j)}\tilde{q}_{j}]\in W_{0}(K_{v})$
, and
$[\tilde{\unicode[STIX]{x1D706}}_{v}^{(j)}\tilde{q}_{j}]\in W_{0}(K_{v})$
, and
Then for any
![]() $v\in V$
, the form
$v\in V$
, the form
is equivalent to
As
![]() $\unicode[STIX]{x1D6FD}_{v}^{(j)}\in U(K_{v})$
, we see that
$\unicode[STIX]{x1D6FD}_{v}^{(j)}\in U(K_{v})$
, we see that
![]() $[q(j,v)]\in W_{0}(K_{v})\,\cap \,I(K_{v})$
. Now, invoking Lemma 3.3 with
$[q(j,v)]\in W_{0}(K_{v})\,\cap \,I(K_{v})$
. Now, invoking Lemma 3.3 with
![]() $d=1$
, we obtain that
$d=1$
, we obtain that
![]() $\unicode[STIX]{x1D6FE}_{K_{v},1}([\tilde{q}_{j}]-[\tilde{q}_{j_{0}}])\in H^{1}(K_{v},\unicode[STIX]{x1D707}_{2})$
is unramified at
$\unicode[STIX]{x1D6FE}_{K_{v},1}([\tilde{q}_{j}]-[\tilde{q}_{j_{0}}])\in H^{1}(K_{v},\unicode[STIX]{x1D707}_{2})$
is unramified at
![]() $v$
. This being true for all
$v$
. This being true for all
![]() $v\in V$
, we conclude that
$v\in V$
, we conclude that
Then one can find a subset
![]() $J_{1}\subset J_{0}$
of size
$J_{1}\subset J_{0}$
of size
(again, if
![]() $I$
is infinite this simply means that
$I$
is infinite this simply means that
![]() $J_{1}$
is also infinite) such that the elements
$J_{1}$
is also infinite) such that the elements
![]() $[\tilde{q}_{j}]-[\tilde{q}_{j_{0}}]\in I(K)$
for
$[\tilde{q}_{j}]-[\tilde{q}_{j_{0}}]\in I(K)$
for
![]() $j\in J_{1}$
have the same image under
$j\in J_{1}$
have the same image under
![]() $\unicode[STIX]{x1D6FE}_{K,1}$
. Fix
$\unicode[STIX]{x1D6FE}_{K,1}$
. Fix
![]() $j_{1}\in J_{1}$
. Then for any
$j_{1}\in J_{1}$
. Then for any
![]() $j\in J_{1}$
we have
$j\in J_{1}$
we have
implying that
![]() $[\tilde{q}_{j}]-[\tilde{q}_{j_{1}}]\in I(K)^{2}$
. Furthermore, we observe that
$[\tilde{q}_{j}]-[\tilde{q}_{j_{1}}]\in I(K)^{2}$
. Furthermore, we observe that
using which one shows that for each
![]() $v\in V$
the class of the form
$v\in V$
the class of the form
![]() $\tilde{\unicode[STIX]{x1D706}}_{v}^{(j_{1})}(\tilde{q}_{j}\bot (-\tilde{q}_{j_{1}}))$
lies in
$\tilde{\unicode[STIX]{x1D706}}_{v}^{(j_{1})}(\tilde{q}_{j}\bot (-\tilde{q}_{j_{1}}))$
lies in
![]() $W_{0}(K_{v})\,\cap \,I(K_{v})^{2}$
. Now, Lemma 3.3 with
$W_{0}(K_{v})\,\cap \,I(K_{v})^{2}$
. Now, Lemma 3.3 with
![]() $d=2$
yields that
$d=2$
yields that
Then there exists a subset
![]() $J_{2}\subset J_{1}$
of size
$J_{2}\subset J_{1}$
of size
![]() ${\geqslant}|I|/(d_{0}d_{1}d_{2})$
such that the elements
${\geqslant}|I|/(d_{0}d_{1}d_{2})$
such that the elements
![]() $[\tilde{q}_{j}]-[\tilde{q}_{j_{1}}]$
for
$[\tilde{q}_{j}]-[\tilde{q}_{j_{1}}]$
for
![]() $j\in J_{2}$
have the same image under
$j\in J_{2}$
have the same image under
![]() $\unicode[STIX]{x1D6FE}_{K,2}$
. Consequently, fixing
$\unicode[STIX]{x1D6FE}_{K,2}$
. Consequently, fixing
![]() $j_{2}\in J_{2}$
, we will have
$j_{2}\in J_{2}$
, we will have
![]() $[\tilde{q}_{j}]-[\tilde{q}_{j_{2}}]\in I(K)^{3}$
for all
$[\tilde{q}_{j}]-[\tilde{q}_{j_{2}}]\in I(K)^{3}$
for all
![]() $j\in J_{2}$
. Proceeding inductively, we construct a nested sequence of subsets
$j\in J_{2}$
. Proceeding inductively, we construct a nested sequence of subsets
such that:
(a)
 $|J_{m}|\geqslant |I|/(d_{0}d_{1}\cdots d_{m})$
; and
$|J_{m}|\geqslant |I|/(d_{0}d_{1}\cdots d_{m})$
; and(b) fixing
 $j_{m}\in J_{m}$
, we will have
$j_{m}\in J_{m}$
, we will have
 $[\tilde{q}_{j}]-[\tilde{q}_{j_{m}}]\in I(K)^{m+1}$
for all
$[\tilde{q}_{j}]-[\tilde{q}_{j_{m}}]\in I(K)^{m+1}$
for all
 $j\in J_{m}$
,
$j\in J_{m}$
,
for any
![]() $m=1,\ldots ,\ell$
. However, according to [Reference LamLam05, ch. X, Hauptsatz 5.1], the dimension of any positive-dimensional anisotropic form in
$m=1,\ldots ,\ell$
. However, according to [Reference LamLam05, ch. X, Hauptsatz 5.1], the dimension of any positive-dimensional anisotropic form in
![]() $I(K)^{\ell +1}$
is
$I(K)^{\ell +1}$
is
![]() ${\geqslant}2^{\ell +1}>2^{\log _{2}n+1}=2n$
. Thus, the fact that
${\geqslant}2^{\ell +1}>2^{\log _{2}n+1}=2n$
. Thus, the fact that
implies that the form
![]() $\tilde{q}_{j}\bot (-\tilde{q}_{j_{\ell }})$
is hyperbolic, and consequently
$\tilde{q}_{j}\bot (-\tilde{q}_{j_{\ell }})$
is hyperbolic, and consequently
![]() $\tilde{q}_{j}$
and
$\tilde{q}_{j}$
and
![]() $\tilde{q}_{j_{\ell }}$
are equivalent. As
$\tilde{q}_{j_{\ell }}$
are equivalent. As
![]() $j\in J_{\ell }$
was arbitrary and the forms
$j\in J_{\ell }$
was arbitrary and the forms
![]() $\tilde{q}_{j}$
for
$\tilde{q}_{j}$
for
![]() $j\in J_{\ell }$
are pairwise inequivalent, we see that
$j\in J_{\ell }$
are pairwise inequivalent, we see that
![]() $J_{\ell }$
actually reduces to a single element. Then the inequality in part (a) yields the required estimation (1).◻
$J_{\ell }$
actually reduces to a single element. Then the inequality in part (a) yields the required estimation (1).◻
3.4 Another application of the method
The method developed to prove Theorem 2.1 can be used in various situations. Here we would like to indicate one application to the analysis of the global-to-local map in Galois cohomology.
Theorem 3.4. Let
![]() $K$
be a field equipped with a set
$K$
be a field equipped with a set
![]() $V$
of discrete valuations satisfying conditions
$V$
of discrete valuations satisfying conditions
![]() $(\text{A})$
and
$(\text{A})$
and
![]() $(\text{B})$
and let
$(\text{B})$
and let
![]() $n\geqslant 5$
be an integer. Assume that:
$n\geqslant 5$
be an integer. Assume that:
-
 $(\bullet )$
$(\bullet )$
for each
 $i=1,\ldots ,[\log _{2}n]+1=\ell$
, the kernel
$i=1,\ldots ,[\log _{2}n]+1=\ell$
, the kernel
 $\unicode[STIX]{x1D6FA}_{i}$
of the diagonal map
$\unicode[STIX]{x1D6FA}_{i}$
of the diagonal map  $$\begin{eqnarray}H^{i}(K,\unicode[STIX]{x1D707}_{2})\longrightarrow \mathop{\prod }_{v\in V}H^{i}(K_{v},\unicode[STIX]{x1D707}_{2})\end{eqnarray}$$
$$\begin{eqnarray}H^{i}(K,\unicode[STIX]{x1D707}_{2})\longrightarrow \mathop{\prod }_{v\in V}H^{i}(K_{v},\unicode[STIX]{x1D707}_{2})\end{eqnarray}$$
is finite of order
 $\unicode[STIX]{x1D714}_{i}$
.
$\unicode[STIX]{x1D714}_{i}$
.
Then for a nondegenerate
![]() $n$
-dimensional quadratic form
$n$
-dimensional quadratic form
![]() $q$
over
$q$
over
![]() $K$
and the diagonal map
$K$
and the diagonal map
the set
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70B}(h))$
is finite of size
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70B}(h))$
is finite of size
![]() ${\leqslant}\unicode[STIX]{x1D714}_{1}\cdots \unicode[STIX]{x1D714}_{\ell }$
for any
${\leqslant}\unicode[STIX]{x1D714}_{1}\cdots \unicode[STIX]{x1D714}_{\ell }$
for any
![]() $h\in H^{1}(K,\operatorname{SO}_{n}(q))$
. In particular,
$h\in H^{1}(K,\operatorname{SO}_{n}(q))$
. In particular,
![]() $\unicode[STIX]{x1D70B}$
is a proper map.
$\unicode[STIX]{x1D70B}$
is a proper map.
Proof. Let
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70B}(h))=\{h_{i}\}\text{}_{i\in I}$
and let
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70B}(h))=\{h_{i}\}\text{}_{i\in I}$
and let
![]() $q_{i}$
be the quadratic form obtained from
$q_{i}$
be the quadratic form obtained from
![]() $q$
by twisting using
$q$
by twisting using
![]() $h_{i}$
. It is well-known that the
$h_{i}$
. It is well-known that the
![]() $K$
-equivalence classes of nondegenerate
$K$
-equivalence classes of nondegenerate
![]() $n$
-dimensional quadratic forms over
$n$
-dimensional quadratic forms over
![]() $K$
are in a natural bijective correspondence with the elements of
$K$
are in a natural bijective correspondence with the elements of
![]() $H^{1}(K,\text{O}_{n}(q))$
. As the map
$H^{1}(K,\text{O}_{n}(q))$
. As the map
![]() $H^{1}(K,\operatorname{SO}_{n}(q))\rightarrow H^{1}(K,\text{O}_{n}(q))$
is injective (cf. [Reference Platonov and RapinchukPR94, § 6.6]), the forms
$H^{1}(K,\operatorname{SO}_{n}(q))\rightarrow H^{1}(K,\text{O}_{n}(q))$
is injective (cf. [Reference Platonov and RapinchukPR94, § 6.6]), the forms
![]() $q_{i}$
for
$q_{i}$
for
![]() $i\in I$
are pairwise inequivalent. On the other hand, by our construction, the form
$i\in I$
are pairwise inequivalent. On the other hand, by our construction, the form
![]() $q_{i}$
for any
$q_{i}$
for any
![]() $i\in I$
is equivalent over
$i\in I$
is equivalent over
![]() $K_{v}$
to the form
$K_{v}$
to the form
![]() $q_{0}$
obtained from
$q_{0}$
obtained from
![]() $q$
by twisting using
$q$
by twisting using
![]() $h$
, for any
$h$
, for any
![]() $v\in V$
. Thus, for any
$v\in V$
. Thus, for any
![]() $i,j\in I$
, the class
$i,j\in I$
, the class
![]() $[q_{i}]-[q_{j}]$
is trivial in
$[q_{i}]-[q_{j}]$
is trivial in
![]() $W(K_{v})$
for any
$W(K_{v})$
for any
![]() $v\in V$
. Thus, using the compatibility of the map
$v\in V$
. Thus, using the compatibility of the map
![]() $\unicode[STIX]{x1D6FE}_{F,d}$
with base change, we conclude that if
$\unicode[STIX]{x1D6FE}_{F,d}$
with base change, we conclude that if
![]() $[q_{i}]-[q_{j}]\in I(K)^{d}$
, then
$[q_{i}]-[q_{j}]\in I(K)^{d}$
, then
![]() $\unicode[STIX]{x1D6FE}_{K,d}([q_{i}]-[q_{j}])\in \unicode[STIX]{x1D6FA}_{d}$
.
$\unicode[STIX]{x1D6FE}_{K,d}([q_{i}]-[q_{j}])\in \unicode[STIX]{x1D6FA}_{d}$
.
We now proceed as in the proof of Theorem 2.1. Fix
![]() $j_{0}\in I$
. Then there exists a subset
$j_{0}\in I$
. Then there exists a subset
![]() $J_{1}\subset I$
of size
$J_{1}\subset I$
of size
![]() ${\geqslant}|I|/\unicode[STIX]{x1D714}_{1}$
such that all elements
${\geqslant}|I|/\unicode[STIX]{x1D714}_{1}$
such that all elements
![]() $[q_{j}]-[q_{j_{0}}]\in I(K)$
for
$[q_{j}]-[q_{j_{0}}]\in I(K)$
for
![]() $j\in J_{1}$
have the same image under
$j\in J_{1}$
have the same image under
![]() $\unicode[STIX]{x1D6FE}_{K,1}$
. Fix
$\unicode[STIX]{x1D6FE}_{K,1}$
. Fix
![]() $j_{1}\in J_{1}$
. Then for any
$j_{1}\in J_{1}$
. Then for any
![]() $j\in J_{1}$
we have
$j\in J_{1}$
we have
which means that
![]() $[q_{j}]-[q_{j_{1}}]\in I(K)^{2}$
. Inductively, we construct a sequence of subsets
$[q_{j}]-[q_{j_{1}}]\in I(K)^{2}$
. Inductively, we construct a sequence of subsets
![]() $I\supset J_{1}\supset J_{2}\supset \cdots \supset J_{\ell }$
such that:
$I\supset J_{1}\supset J_{2}\supset \cdots \supset J_{\ell }$
such that:
-
 $(\text{a}^{\prime })$
$(\text{a}^{\prime })$
 $|J_{m}|\geqslant |I|/\unicode[STIX]{x1D714}_{1}\cdots \unicode[STIX]{x1D714}_{m}$
;
$|J_{m}|\geqslant |I|/\unicode[STIX]{x1D714}_{1}\cdots \unicode[STIX]{x1D714}_{m}$
;-
 $(\text{b}^{\prime })$
$(\text{b}^{\prime })$
fixing
 $j_{m}\in J_{m}$
, we will have
$j_{m}\in J_{m}$
, we will have
 $[q_{j}]-[q_{j_{m}}]\in I(K)^{m+1}$
for all
$[q_{j}]-[q_{j_{m}}]\in I(K)^{m+1}$
for all
 $j\in J_{m}$
,
$j\in J_{m}$
,
for any
![]() $m=1,\ldots ,\ell$
. As in the proof of Theorem 2.1, we see that the fact that
$m=1,\ldots ,\ell$
. As in the proof of Theorem 2.1, we see that the fact that
![]() $[q_{j}]\,-\,[q_{j_{\ell }}]\in I(K)^{\ell +1}$
implies that
$[q_{j}]\,-\,[q_{j_{\ell }}]\in I(K)^{\ell +1}$
implies that
![]() $q_{j}$
and
$q_{j}$
and
![]() $q_{j_{\ell }}$
are actually equivalent. This means that
$q_{j_{\ell }}$
are actually equivalent. This means that
![]() $J_{\ell }$
reduces to a single element, and then the inequality in
$J_{\ell }$
reduces to a single element, and then the inequality in
![]() $(\text{a}^{\prime })$
yields the required estimation.◻
$(\text{a}^{\prime })$
yields the required estimation.◻
We observe that for any
![]() $i$
, we have the inclusion
$i$
, we have the inclusion
![]() $\unicode[STIX]{x1D6FA}_{i}\subset H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
in the above notation. In particular, the finiteness of
$\unicode[STIX]{x1D6FA}_{i}\subset H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
in the above notation. In particular, the finiteness of
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
implies that of
$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
implies that of
![]() $\unicode[STIX]{x1D6FA}_{i}$
, which enables us to apply Theorem 3.4.
$\unicode[STIX]{x1D6FA}_{i}$
, which enables us to apply Theorem 3.4.
4 Proof of Theorem 1.1
4.1 The proof
Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $V$
be any divisorial set of places of
$V$
be any divisorial set of places of
![]() $K$
associated with a (normal) model
$K$
associated with a (normal) model
![]() $\mathfrak{X}$
of finite type on which
$\mathfrak{X}$
of finite type on which
![]() $2$
is invertible (thus,
$2$
is invertible (thus,
![]() $\operatorname{char}K^{(v)}\neq 2$
for all
$\operatorname{char}K^{(v)}\neq 2$
for all
![]() $v\in V$
). According to Theorem 2.1, it is enough to establish the finiteness of the quotient
$v\in V$
). According to Theorem 2.1, it is enough to establish the finiteness of the quotient
![]() $\operatorname{Pic}(V)/2\cdot \operatorname{Pic}(V)$
and of the unramified cohomology groups
$\operatorname{Pic}(V)/2\cdot \operatorname{Pic}(V)$
and of the unramified cohomology groups
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
for all
$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
for all
![]() $i\geqslant 1$
. However, it easily follows from the definitions that the group
$i\geqslant 1$
. However, it easily follows from the definitions that the group
![]() $\operatorname{Pic}(V)$
coincides with the usual Picard group
$\operatorname{Pic}(V)$
coincides with the usual Picard group
![]() $\operatorname{Pic}(\mathfrak{X})$
of the scheme
$\operatorname{Pic}(\mathfrak{X})$
of the scheme
![]() $\mathfrak{X}$
. Thus, the finiteness of
$\mathfrak{X}$
. Thus, the finiteness of
![]() $\operatorname{Pic}(V)/2\cdot \operatorname{Pic}(V)$
is a consequence of the following well-known statement.
$\operatorname{Pic}(V)/2\cdot \operatorname{Pic}(V)$
is a consequence of the following well-known statement.
Proposition 4.1. Let
![]() $\mathfrak{X}$
be an irreducible normal scheme of finite type over
$\mathfrak{X}$
be an irreducible normal scheme of finite type over
![]() $\mathbb{Z}$
or a finite field and let
$\mathbb{Z}$
or a finite field and let
![]() $n\geqslant 2$
be an integer that is invertible on
$n\geqslant 2$
be an integer that is invertible on
![]() $\mathfrak{X}$
. Then the quotient
$\mathfrak{X}$
. Then the quotient
![]() $\operatorname{Pic}(\mathfrak{X})/n\cdot \operatorname{Pic}(\mathfrak{X})$
and the
$\operatorname{Pic}(\mathfrak{X})/n\cdot \operatorname{Pic}(\mathfrak{X})$
and the
![]() $n$
-torsion
$n$
-torsion
![]() $_{n\!}\operatorname{Pic}(\mathfrak{X})$
are finite groups.
$_{n\!}\operatorname{Pic}(\mathfrak{X})$
are finite groups.
Sketch of proof.
As
![]() $n$
is invertible on
$n$
is invertible on
![]() $\mathfrak{X}$
, we have the following Kummer sequence of étale sheaves on
$\mathfrak{X}$
, we have the following Kummer sequence of étale sheaves on
![]() $\mathfrak{X}$
$\mathfrak{X}$
which gives rise to the long exact sequence
in étale cohomology. As
![]() $\operatorname{Pic}(\mathfrak{X})=H^{1}(\mathfrak{X},\mathbb{G}_{m,\mathfrak{X}})$
(cf. [Reference MilneMil80, ch. III, Proposition 4.9]), we have a surjection
$\operatorname{Pic}(\mathfrak{X})=H^{1}(\mathfrak{X},\mathbb{G}_{m,\mathfrak{X}})$
(cf. [Reference MilneMil80, ch. III, Proposition 4.9]), we have a surjection
![]() $H^{1}(\mathfrak{X},\unicode[STIX]{x1D707}_{n,\mathfrak{X}}){\twoheadrightarrow}_{n\!}\operatorname{Pic}(\mathfrak{X})$
and an injection
$H^{1}(\mathfrak{X},\unicode[STIX]{x1D707}_{n,\mathfrak{X}}){\twoheadrightarrow}_{n\!}\operatorname{Pic}(\mathfrak{X})$
and an injection
![]() $\operatorname{Pic}(\mathfrak{X})/n\cdot \operatorname{Pic}(\mathfrak{X}){\hookrightarrow}H^{2}(\mathfrak{X},\unicode[STIX]{x1D707}_{n,\mathfrak{X}})$
. Thus, it is enough to prove the finiteness of
$\operatorname{Pic}(\mathfrak{X})/n\cdot \operatorname{Pic}(\mathfrak{X}){\hookrightarrow}H^{2}(\mathfrak{X},\unicode[STIX]{x1D707}_{n,\mathfrak{X}})$
. Thus, it is enough to prove the finiteness of
![]() $H^{i}(\mathfrak{X},\unicode[STIX]{x1D707}_{n,\mathfrak{X}})$
for
$H^{i}(\mathfrak{X},\unicode[STIX]{x1D707}_{n,\mathfrak{X}})$
for
![]() $i=1,2$
. In fact, these groups are finite for all
$i=1,2$
. In fact, these groups are finite for all
![]() $i$
. For
$i$
. For
![]() $\mathfrak{X}$
of finite type over a finite field, this is a consequence of [Reference DeligneSGA4½, Théorème 1.1 in ‘Théorèmes de finitude’] and the Leray spectral sequence [Reference MilneMil80, ch. III, Theorem 1.18] in general and is [Reference MilneMil80, ch. VI, Corollary 5.5] for
$\mathfrak{X}$
of finite type over a finite field, this is a consequence of [Reference DeligneSGA4½, Théorème 1.1 in ‘Théorèmes de finitude’] and the Leray spectral sequence [Reference MilneMil80, ch. III, Theorem 1.18] in general and is [Reference MilneMil80, ch. VI, Corollary 5.5] for
![]() $\mathfrak{X}$
smooth. For
$\mathfrak{X}$
smooth. For
![]() $\mathfrak{X}$
of finite type over
$\mathfrak{X}$
of finite type over
![]() $\mathbb{Z}$
, this is [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Theorem 10.2].◻
$\mathbb{Z}$
, this is [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Theorem 10.2].◻
It should be noted that Kahn [Reference KahnKah06] in fact showed that the group
![]() $\operatorname{Pic}(\mathfrak{X})$
is finitely generated.
$\operatorname{Pic}(\mathfrak{X})$
is finitely generated.
Combining the finiteness of
![]() $_{2\!}\operatorname{Pic}(V)$
with the fact that the group of
$_{2\!}\operatorname{Pic}(V)$
with the fact that the group of
![]() $V$
-units
$V$
-units
is finitely generated (cf. [Reference SamuelSam66]) and applying [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Proposition 5.1(a)], we obtain that
![]() $H^{1}(K,\unicode[STIX]{x1D707}_{2})_{V}$
is finite. The finiteness of
$H^{1}(K,\unicode[STIX]{x1D707}_{2})_{V}$
is finite. The finiteness of
![]() $H^{2}(K,\unicode[STIX]{x1D707}_{2})_{V}=_{2\!}\operatorname{Br}(K)_{V}$
was established in [Reference Chernousov, Rapinchuk and RapinchukCRR16a, § 10]. The finiteness of
$H^{2}(K,\unicode[STIX]{x1D707}_{2})_{V}=_{2\!}\operatorname{Br}(K)_{V}$
was established in [Reference Chernousov, Rapinchuk and RapinchukCRR16a, § 10]. The finiteness of
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
is a new result (see Corollary 6.2 of the more general Theorem 6.1) whose proof requires separate arguments in the characteristic zero and positive characteristic cases. The proof for the characteristic zero case that is given in § 6 was suggested by one of the referees; it uses several powerful results, first and foremost, those of Kato [Reference KatoKat86] on cohomological Hasse principles. We have included our original proof of Theorem 6.1 in Appendix A. It uses considerably less input; in particular, it does not rely on Kato’s local–global principle but is based instead on a modification of Jannsen’s [Reference JannsenJan89–90] proof of the latter. The reason we decided to keep this argument in the paper is that it appears to be more amenable to generalizations in the spirit of Jannsen’s proof [Reference JannsenJan16] of Kato’s local–global principle for higher-dimensional varieties that generalized his original argument [Reference JannsenJan89–90]. The finiteness of
$H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
is a new result (see Corollary 6.2 of the more general Theorem 6.1) whose proof requires separate arguments in the characteristic zero and positive characteristic cases. The proof for the characteristic zero case that is given in § 6 was suggested by one of the referees; it uses several powerful results, first and foremost, those of Kato [Reference KatoKat86] on cohomological Hasse principles. We have included our original proof of Theorem 6.1 in Appendix A. It uses considerably less input; in particular, it does not rely on Kato’s local–global principle but is based instead on a modification of Jannsen’s [Reference JannsenJan89–90] proof of the latter. The reason we decided to keep this argument in the paper is that it appears to be more amenable to generalizations in the spirit of Jannsen’s proof [Reference JannsenJan16] of Kato’s local–global principle for higher-dimensional varieties that generalized his original argument [Reference JannsenJan89–90]. The finiteness of
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
for two-dimensional global fields of positive characteristic will be established in § 7 (we note that this result is implicitly contained in [Reference RapinchukRap18, Proposition 4.4 and Remark 4.5]).
$H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
for two-dimensional global fields of positive characteristic will be established in § 7 (we note that this result is implicitly contained in [Reference RapinchukRap18, Proposition 4.4 and Remark 4.5]).
As the cohomological dimension of a two-dimensional global field of positive characteristic is
![]() ${\leqslant}3$
(cf. [Reference SerreSer97, ch. II, 4.2]), the groups
${\leqslant}3$
(cf. [Reference SerreSer97, ch. II, 4.2]), the groups
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{2})$
vanish for all
$H^{i}(K,\unicode[STIX]{x1D707}_{2})$
vanish for all
![]() $i\geqslant 4$
. We will now show that in characteristic zero, the finiteness of
$i\geqslant 4$
. We will now show that in characteristic zero, the finiteness of
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
for
$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
for
![]() $i\geqslant 4$
easily follows from the results of Poitou–Tate (cf. [Reference SerreSer97, ch. II, 6.3]), which will complete the proof of Theorem 1.1.
$i\geqslant 4$
easily follows from the results of Poitou–Tate (cf. [Reference SerreSer97, ch. II, 6.3]), which will complete the proof of Theorem 1.1.
Proposition 4.2. Let
![]() $C$
be a smooth (but not necessarily projective) geometrically integral curve over a number field
$C$
be a smooth (but not necessarily projective) geometrically integral curve over a number field
![]() $k$
, and
$k$
, and
![]() $K=k(C)$
. Then for
$K=k(C)$
. Then for
![]() $i\geqslant 4$
, the groups
$i\geqslant 4$
, the groups
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V_{0}}$
, where
$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V_{0}}$
, where
![]() $V_{0}$
is the set of geometric places of
$V_{0}$
is the set of geometric places of
![]() $K$
associated with the closed points of
$K$
associated with the closed points of
![]() $C$
, are finite.
$C$
, are finite.
To apply the proposition in our situation, we observe that given a divisorial set of places
![]() $V$
of a two-dimensional global field
$V$
of a two-dimensional global field
![]() $K$
of characteristic zero, there exists a smooth geometrically connected curve
$K$
of characteristic zero, there exists a smooth geometrically connected curve
![]() $C$
defined over a number field
$C$
defined over a number field
![]() $k$
such that
$k$
such that
![]() $K=k(C)$
and for the set of geometric places
$K=k(C)$
and for the set of geometric places
![]() $V_{0}$
of
$V_{0}$
of
![]() $K$
associated with the closed points of
$K$
associated with the closed points of
![]() $C$
, we have the inclusion
$C$
, we have the inclusion
For the proof of the proposition, we first need to review the exact sequence for the étale cohomology of a curve, which will also be used in Appendix A.
4.2 The fundamental exact sequence
Let
![]() $C$
be a geometrically integral smooth affine curve over an arbitrary field
$C$
be a geometrically integral smooth affine curve over an arbitrary field
![]() $k$
and let
$k$
and let
![]() $n\geqslant 2$
be an integer prime to
$n\geqslant 2$
be an integer prime to
![]() $\operatorname{char}k$
. Then for any integer
$\operatorname{char}k$
. Then for any integer
![]() $d$
, we consider the Hochschild–Serre spectral sequence in étale cohomology
$d$
, we consider the Hochschild–Serre spectral sequence in étale cohomology
As
![]() $C$
is affine, we have
$C$
is affine, we have
![]() $H^{p}(C\otimes _{k}\bar{k},\unicode[STIX]{x1D707}_{n}^{\otimes d})=0$
for
$H^{p}(C\otimes _{k}\bar{k},\unicode[STIX]{x1D707}_{n}^{\otimes d})=0$
for
![]() $p\geqslant 2$
(cf. [Stacks19, Lemma 65.3], [Reference MilneMil80, ch. V, § 2]). Thus, for each
$p\geqslant 2$
(cf. [Stacks19, Lemma 65.3], [Reference MilneMil80, ch. V, § 2]). Thus, for each
![]() $\ell \geqslant 1$
, the spectral sequence yields the following short exact sequence:
$\ell \geqslant 1$
, the spectral sequence yields the following short exact sequence:
Furthermore, let
![]() $V_{0}$
denote the set of places of
$V_{0}$
denote the set of places of
![]() $K=k(C)$
associated with the closed points of
$K=k(C)$
associated with the closed points of
![]() $C$
. Then, because
$C$
. Then, because
![]() $n$
is prime to
$n$
is prime to
![]() $\operatorname{char}k$
, it follows from the Bloch–Ogus spectral sequence (see [Reference Bloch and OgusBO74, Reference Colliot-Thélène, Hoobler and KahnCHK97, Reference Jannsen, Sato and SaitoJSS14]) that for each
$\operatorname{char}k$
, it follows from the Bloch–Ogus spectral sequence (see [Reference Bloch and OgusBO74, Reference Colliot-Thélène, Hoobler and KahnCHK97, Reference Jannsen, Sato and SaitoJSS14]) that for each
![]() $\ell \geqslant 1$
, the natural map
$\ell \geqslant 1$
, the natural map
![]() $H^{\ell }(C,\unicode[STIX]{x1D707}_{n}^{\otimes d})\rightarrow H^{\ell }(K,\unicode[STIX]{x1D707}_{n}^{\otimes d})_{V_{0}}$
is surjective. (This is a consequence of the fact that the
$H^{\ell }(C,\unicode[STIX]{x1D707}_{n}^{\otimes d})\rightarrow H^{\ell }(K,\unicode[STIX]{x1D707}_{n}^{\otimes d})_{V_{0}}$
is surjective. (This is a consequence of the fact that the
![]() $E_{2}$
-terms in the Bloch–Ogus spectral sequence satisfy
$E_{2}$
-terms in the Bloch–Ogus spectral sequence satisfy
![]() $E_{2}^{p,q}=0$
for all
$E_{2}^{p,q}=0$
for all
![]() $p>\dim C=1$
and all
$p>\dim C=1$
and all
![]() $q$
, whereas
$q$
, whereas
![]() $E_{2}^{0,q}=H^{q}(K,\unicode[STIX]{x1D707}_{n}^{\otimes d})_{V_{0}}$
.)
$E_{2}^{0,q}=H^{q}(K,\unicode[STIX]{x1D707}_{n}^{\otimes d})_{V_{0}}$
.)
Let
Equivalently,
It follows that we have the following equality for the Tate twist
4.3 Proof of Proposition 4.2
We may assume that
![]() $C$
is affine, and it is enough to show that
$C$
is affine, and it is enough to show that
![]() $H^{i}(C,\unicode[STIX]{x1D707}_{n}^{\otimes d})$
is finite for all
$H^{i}(C,\unicode[STIX]{x1D707}_{n}^{\otimes d})$
is finite for all
![]() $i\geqslant 4$
. According to Poitou–Tate, for a number field
$i\geqslant 4$
. According to Poitou–Tate, for a number field
![]() $k$
and any finite Galois module
$k$
and any finite Galois module
![]() $M$
, the natural homomorphism
$M$
, the natural homomorphism
where
![]() $V_{\infty }^{k}$
is the set of all real places of
$V_{\infty }^{k}$
is the set of all real places of
![]() $k$
, is an isomorphism for any
$k$
, is an isomorphism for any
![]() $i\geqslant 3$
(see [Reference SerreSer97, ch. II, 6.3, Theorem B]); in particular, the group
$i\geqslant 3$
(see [Reference SerreSer97, ch. II, 6.3, Theorem B]); in particular, the group
![]() $H^{i}(k,M)$
is finite. As
$H^{i}(k,M)$
is finite. As
![]() $H^{1}(C\otimes _{k}\bar{k},\unicode[STIX]{x1D707}_{n}^{\otimes d})$
is finite by [Reference Artin, Deligne, Grothendieck and VerdierSGA4, Exposé XVI, Théorème 5.2], it follows that the left-most and the right-most terms in the exact sequence (2) are finite. Thus, the middle term is also finite for all
$H^{1}(C\otimes _{k}\bar{k},\unicode[STIX]{x1D707}_{n}^{\otimes d})$
is finite by [Reference Artin, Deligne, Grothendieck and VerdierSGA4, Exposé XVI, Théorème 5.2], it follows that the left-most and the right-most terms in the exact sequence (2) are finite. Thus, the middle term is also finite for all
![]() $i\geqslant 4$
, as required.◻
$i\geqslant 4$
, as required.◻
5 Proof of Theorems 1.2 and 1.3.
5.1 The finiteness of genus
Theorem 1.2 will be derived from the following result.
Theorem 5.1. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $G=\operatorname{Spin}_{n}(q)$
, where
$G=\operatorname{Spin}_{n}(q)$
, where
![]() $q$
is a nondegenerate quadratic form over
$q$
is a nondegenerate quadratic form over
![]() $K$
of dimension
$K$
of dimension
![]() $n\geqslant 5$
. Then the number of
$n\geqslant 5$
. Then the number of
![]() $K$
-isomorphism classes of the spinor groups
$K$
-isomorphism classes of the spinor groups
![]() $G^{\prime }=\operatorname{Spin}_{n}(q^{\prime })$
of nondegenerate
$G^{\prime }=\operatorname{Spin}_{n}(q^{\prime })$
of nondegenerate
![]() $n$
-dimensional quadratic forms
$n$
-dimensional quadratic forms
![]() $q^{\prime }$
over
$q^{\prime }$
over
![]() $K$
that have the same isomorphism classes of maximal
$K$
that have the same isomorphism classes of maximal
![]() $K$
-tori as
$K$
-tori as
![]() $G$
, is finite.
$G$
, is finite.
To prove Theorem 5.1, we need the following general statement.
Theorem 5.2 [Reference Chernousov, Rapinchuk and RapinchukCRR16b, Theorem 5].
Let
![]() $G$
be an absolutely almost simple simply connected algebraic group over a field
$G$
be an absolutely almost simple simply connected algebraic group over a field
![]() $K$
and let
$K$
and let
![]() $v$
be a discrete valuation of
$v$
be a discrete valuation of
![]() $K$
. Assume that the residue field
$K$
. Assume that the residue field
![]() $K^{(v)}$
is finitely generated and that
$K^{(v)}$
is finitely generated and that
![]() $G$
has good reduction at
$G$
has good reduction at
![]() $v$
. Then any
$v$
. Then any
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
also has good reduction at
$G^{\prime }\in \mathbf{gen}_{K}(G)$
also has good reduction at
![]() $v$
. Moreover, the reduction
$v$
. Moreover, the reduction
![]() ${\text{}\underline{G}^{\prime }}^{(v)}$
lies in the genus
${\text{}\underline{G}^{\prime }}^{(v)}$
lies in the genus
![]() $\mathbf{gen}_{K^{(v)}}(\text{}\underline{G}^{(v)})$
of the reduction
$\mathbf{gen}_{K^{(v)}}(\text{}\underline{G}^{(v)})$
of the reduction
![]() $\text{}\underline{G}^{(v)}$
.
$\text{}\underline{G}^{(v)}$
.
Let
![]() $V$
be a divisorial set of places of our two-dimensional global field
$V$
be a divisorial set of places of our two-dimensional global field
![]() $K$
of characteristic
$K$
of characteristic
![]() $\neq \,2$
. Using the fact that
$\neq \,2$
. Using the fact that
![]() $V$
satisfies condition (A), it is not difficult to see that the set
$V$
satisfies condition (A), it is not difficult to see that the set
![]() $v\in V$
where
$v\in V$
where
![]() $G=\operatorname{Spin}_{n}(q)$
does not have good reduction, is finite. Picking a divisorial set of places in the complement of this finite set, we may assume without loss of generality that
$G=\operatorname{Spin}_{n}(q)$
does not have good reduction, is finite. Picking a divisorial set of places in the complement of this finite set, we may assume without loss of generality that
![]() $G$
has good reduction at all
$G$
has good reduction at all
![]() $v\in V$
. Then according to Theorem 5.2, every
$v\in V$
. Then according to Theorem 5.2, every
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
has good reduction at all
$G^{\prime }\in \mathbf{gen}_{K}(G)$
has good reduction at all
![]() $v\in V$
. Thus, Theorem 1.1 yields the finiteness of the number of
$v\in V$
. Thus, Theorem 1.1 yields the finiteness of the number of
![]() $K$
-isomorphism classes of the spinor groups
$K$
-isomorphism classes of the spinor groups
![]() $G^{\prime }=\operatorname{Spin}_{n}(q^{\prime })$
lying in
$G^{\prime }=\operatorname{Spin}_{n}(q^{\prime })$
lying in
![]() $\mathbf{gen}_{K}(G)$
, which is precisely the assertion of Theorem 5.1.
$\mathbf{gen}_{K}(G)$
, which is precisely the assertion of Theorem 5.1.
Now, Theorem 1.2 for quadratic forms of odd dimension immediately follows from Theorem 5.1. To consider the case of isotropic quadratic forms
![]() $q$
of even dimension, we need to combine the latter with part (a) of the following proposition, which implies that every group in
$q$
of even dimension, we need to combine the latter with part (a) of the following proposition, which implies that every group in
![]() $\mathbf{gen}_{K}(G)$
is of the form
$\mathbf{gen}_{K}(G)$
is of the form
![]() $\operatorname{Spin}_{n}(q^{\prime })$
.
$\operatorname{Spin}_{n}(q^{\prime })$
.
Proposition 5.3. Let
![]() $K$
be an infinite finitely generated field of characteristic
$K$
be an infinite finitely generated field of characteristic
![]() $\neq 2$
, let
$\neq 2$
, let
![]() $G=\operatorname{Spin}_{n}(q)$
where
$G=\operatorname{Spin}_{n}(q)$
where
![]() $q$
is a nondegenerate quadratic form over
$q$
is a nondegenerate quadratic form over
![]() $K$
of even dimension
$K$
of even dimension
![]() $n\geqslant 10$
and let
$n\geqslant 10$
and let
![]() $H=\widetilde{\operatorname{SU}}_{m}(D,h)$
(universal cover) where
$H=\widetilde{\operatorname{SU}}_{m}(D,h)$
(universal cover) where
![]() $D$
is a central division algebra over
$D$
is a central division algebra over
![]() $K$
of degree
$K$
of degree
![]() $d\geqslant 1$
with an orthogonal involution
$d\geqslant 1$
with an orthogonal involution
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $h$
is a nondegenerate
$h$
is a nondegenerate
![]() $m$
-dimensional
$m$
-dimensional
![]() $\unicode[STIX]{x1D70F}$
-Hermitian form.
$\unicode[STIX]{x1D70F}$
-Hermitian form.
(a) If
 $d>1$
and
$d>1$
and
 $q$
is
$q$
is
 $K$
-isotropic, then
$K$
-isotropic, then
 $H\notin \mathbf{gen}_{K}(G)$
.
$H\notin \mathbf{gen}_{K}(G)$
.(b) If
 $d>2$
, then
$d>2$
, then
 $H\notin \mathbf{gen}_{K}(G)$
for any
$H\notin \mathbf{gen}_{K}(G)$
for any
 $q$
.
$q$
.
(Note that
![]() $d$
is a power of
$d$
is a power of
![]() $2$
.)
$2$
.)
We will first establish one general fact that involves the notion of generic tori, which we now recall for the reader’s convenience. Let
![]() $\mathscr{G}$
be a semi-simple algebraic group over a field
$\mathscr{G}$
be a semi-simple algebraic group over a field
![]() $\mathscr{K}$
. Fix a maximal
$\mathscr{K}$
. Fix a maximal
![]() $\mathscr{K}$
-torus
$\mathscr{K}$
-torus
![]() $\mathscr{T}$
of
$\mathscr{T}$
of
![]() $\mathscr{G}$
, and let
$\mathscr{G}$
, and let
![]() $\unicode[STIX]{x1D6F7}(\mathscr{G},\mathscr{T})$
and
$\unicode[STIX]{x1D6F7}(\mathscr{G},\mathscr{T})$
and
![]() $W(\mathscr{G},\mathscr{T})$
denote the corresponding root system and the Weyl group. The natural action of the absolute Galois group
$W(\mathscr{G},\mathscr{T})$
denote the corresponding root system and the Weyl group. The natural action of the absolute Galois group
![]() $\operatorname{Gal}(\mathscr{K}^{\text{sep}}/\mathscr{K})$
, where
$\operatorname{Gal}(\mathscr{K}^{\text{sep}}/\mathscr{K})$
, where
![]() $\mathscr{K}^{\text{sep}}$
is a fixed separable closure of
$\mathscr{K}^{\text{sep}}$
is a fixed separable closure of
![]() $\mathscr{K}$
, on the character group
$\mathscr{K}$
, on the character group
![]() $X(\mathscr{T})$
of
$X(\mathscr{T})$
of
![]() $\mathscr{T}$
gives rise to a group homomorphism
$\mathscr{T}$
gives rise to a group homomorphism
that factors through the Galois group
![]() $\operatorname{Gal}(\mathscr{K}_{\mathscr{T}}/\mathscr{K})$
of the minimal splitting field of
$\operatorname{Gal}(\mathscr{K}_{\mathscr{T}}/\mathscr{K})$
of the minimal splitting field of
![]() $\mathscr{T}$
in
$\mathscr{T}$
in
![]() $\mathscr{K}^{\text{sep}}$
inducing an injective homomorphism
$\mathscr{K}^{\text{sep}}$
inducing an injective homomorphism
![]() $\bar{\unicode[STIX]{x1D703}}_{\mathscr{T}}:\operatorname{Gal}(\mathscr{K}_{\mathscr{T}}/\mathscr{K})\rightarrow \operatorname{Aut}(\unicode[STIX]{x1D6F7}(\mathscr{G},\mathscr{T}))$
. We say that
$\bar{\unicode[STIX]{x1D703}}_{\mathscr{T}}:\operatorname{Gal}(\mathscr{K}_{\mathscr{T}}/\mathscr{K})\rightarrow \operatorname{Aut}(\unicode[STIX]{x1D6F7}(\mathscr{G},\mathscr{T}))$
. We say that
![]() $\mathscr{T}$
is generic over
$\mathscr{T}$
is generic over
![]() $\mathscr{K}$
if
$\mathscr{K}$
if
![]() $\unicode[STIX]{x1D703}_{\mathscr{T}}(\operatorname{Gal}(\mathscr{K}^{\text{sep}}/\mathscr{K}))\supset W(\mathscr{T},\mathscr{G})$
.
$\unicode[STIX]{x1D703}_{\mathscr{T}}(\operatorname{Gal}(\mathscr{K}^{\text{sep}}/\mathscr{K}))\supset W(\mathscr{T},\mathscr{G})$
.
Proposition 5.4. Let
![]() $\mathscr{D}$
be a central division algebra of degree
$\mathscr{D}$
be a central division algebra of degree
![]() $d>1$
over a field
$d>1$
over a field
![]() $\mathscr{K}$
of characteristic
$\mathscr{K}$
of characteristic
![]() $\neq 2$
with an orthogonal involution
$\neq 2$
with an orthogonal involution
![]() $\unicode[STIX]{x1D70F}$
, and let
$\unicode[STIX]{x1D70F}$
, and let
![]() $h$
be a nondegenerate
$h$
be a nondegenerate
![]() $m$
-dimensional
$m$
-dimensional
![]() $\unicode[STIX]{x1D70F}$
-Hermitian form. Then
$\unicode[STIX]{x1D70F}$
-Hermitian form. Then
![]() $\mathscr{H}=\operatorname{SU}_{m}(\mathscr{D},h)$
does not contain a maximal
$\mathscr{H}=\operatorname{SU}_{m}(\mathscr{D},h)$
does not contain a maximal
![]() $\mathscr{K}$
-torus of the form
$\mathscr{K}$
-torus of the form
![]() $\mathscr{T}=\mathscr{T}_{1}\mathscr{T}_{2}$
(almost direct product over
$\mathscr{T}=\mathscr{T}_{1}\mathscr{T}_{2}$
(almost direct product over
![]() $\mathscr{K}$
) where
$\mathscr{K}$
) where
![]() $\mathscr{T}_{1}=\mathbb{G}_{m}$
and
$\mathscr{T}_{1}=\mathbb{G}_{m}$
and
![]() $\mathscr{T}_{2}$
is isomorphic to a generic torus in a
$\mathscr{T}_{2}$
is isomorphic to a generic torus in a
![]() $\mathscr{K}$
-group of type
$\mathscr{K}$
-group of type
![]() $\mathsf{D}_{n/2-1}$
with
$\mathsf{D}_{n/2-1}$
with
![]() $n=dm$
.
$n=dm$
.
Proof. We begin with the following lemma.
Lemma 5.5. Notations as in Proposition 5.4, let
![]() $r$
denote the Witt index of
$r$
denote the Witt index of
![]() $h$
. Then for any nontrivial
$h$
. Then for any nontrivial
![]() $\mathscr{K}$
-split torus
$\mathscr{K}$
-split torus
![]() $\mathscr{S}$
of
$\mathscr{S}$
of
![]() $\mathscr{H}$
, the centralizer
$\mathscr{H}$
, the centralizer
![]() $C_{\mathscr{H}}(\mathscr{S})$
is an almost direct product
$C_{\mathscr{H}}(\mathscr{S})$
is an almost direct product
![]() $\mathscr{S}_{0}\mathscr{H}_{1}\cdots \mathscr{H}_{s}$
over
$\mathscr{S}_{0}\mathscr{H}_{1}\cdots \mathscr{H}_{s}$
over
![]() $\mathscr{K}$
, where
$\mathscr{K}$
, where
![]() $\mathscr{S}_{0}$
is the central torus of
$\mathscr{S}_{0}$
is the central torus of
![]() $C_{\mathscr{H}}(\mathscr{S})$
and each
$C_{\mathscr{H}}(\mathscr{S})$
and each
![]() $\mathscr{H}_{i}$
is a semi-simple
$\mathscr{H}_{i}$
is a semi-simple
![]() $\mathscr{K}$
-group either of inner type
$\mathscr{K}$
-group either of inner type
![]() $\mathsf{A}_{\ell -1}$
with
$\mathsf{A}_{\ell -1}$
with
![]() $\ell \leqslant dr$
or of type
$\ell \leqslant dr$
or of type
![]() $\mathsf{D}_{\ell }$
with
$\mathsf{D}_{\ell }$
with
![]() $\ell \leqslant d(m-2)/2$
(and not a triality form when
$\ell \leqslant d(m-2)/2$
(and not a triality form when
![]() $\ell =4$
).
$\ell =4$
).
Proof. Let
![]() $\unicode[STIX]{x1D712}_{0}=1,\unicode[STIX]{x1D712}_{1},-\unicode[STIX]{x1D712}_{1},\ldots ,\unicode[STIX]{x1D712}_{t},-\unicode[STIX]{x1D712}_{t}$
be all the weights for the action of
$\unicode[STIX]{x1D712}_{0}=1,\unicode[STIX]{x1D712}_{1},-\unicode[STIX]{x1D712}_{1},\ldots ,\unicode[STIX]{x1D712}_{t},-\unicode[STIX]{x1D712}_{t}$
be all the weights for the action of
![]() $\mathscr{S}(\mathscr{K})$
on
$\mathscr{S}(\mathscr{K})$
on
![]() $W=\mathscr{D}^{m}$
, and denote by
$W=\mathscr{D}^{m}$
, and denote by
![]() $W_{\unicode[STIX]{x1D712}}$
the weight subspace corresponding to the character
$W_{\unicode[STIX]{x1D712}}$
the weight subspace corresponding to the character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $\mathscr{S}$
. Set
$\mathscr{S}$
. Set
Then
![]() $W$
has the following orthogonal decomposition
$W$
has the following orthogonal decomposition
Let
so that
![]() $m_{i}\leqslant r\leqslant m/2$
and
$m_{i}\leqslant r\leqslant m/2$
and
![]() $\dim _{\mathscr{D}}W_{i}=2m_{i}$
. Then
$\dim _{\mathscr{D}}W_{i}=2m_{i}$
. Then
where
![]() $\mathscr{F}_{0}=\operatorname{SU}_{m_{0}}(\mathscr{D},h|W_{0})$
and
$\mathscr{F}_{0}=\operatorname{SU}_{m_{0}}(\mathscr{D},h|W_{0})$
and
![]() $\mathscr{F}_{i}$
for
$\mathscr{F}_{i}$
for
![]() $i>0$
is the stabilizer of the subspaces
$i>0$
is the stabilizer of the subspaces
![]() $W_{\unicode[STIX]{x1D712}_{i}}$
and
$W_{\unicode[STIX]{x1D712}_{i}}$
and
![]() $W_{-\unicode[STIX]{x1D712}_{i}}$
in
$W_{-\unicode[STIX]{x1D712}_{i}}$
in
![]() $\operatorname{SU}_{2m_{i}}(\mathscr{D},h|W_{i})$
. As
$\operatorname{SU}_{2m_{i}}(\mathscr{D},h|W_{i})$
. As
![]() $m_{i}\geqslant 1$
and
$m_{i}\geqslant 1$
and
![]() $t>0$
as
$t>0$
as
![]() $\mathscr{S}$
is nontrivial, we see that
$\mathscr{S}$
is nontrivial, we see that
![]() $m_{0}\leqslant m-2$
, and therefore
$m_{0}\leqslant m-2$
, and therefore
![]() $\mathscr{F}_{0}$
is of type
$\mathscr{F}_{0}$
is of type
![]() $\mathsf{D}_{\ell }$
with
$\mathsf{D}_{\ell }$
with
(obviously, not a triality form). Furthermore, for
![]() $i>0$
, the group
$i>0$
, the group
![]() $\mathscr{F}_{i}$
is isomorphic to
$\mathscr{F}_{i}$
is isomorphic to
![]() $\operatorname{GL}(W_{\unicode[STIX]{x1D712}_{i}})$
(or
$\operatorname{GL}(W_{\unicode[STIX]{x1D712}_{i}})$
(or
![]() $\operatorname{GL}(W_{-\unicode[STIX]{x1D712}_{i}})$
). Thus, its semi-simple part is
$\operatorname{GL}(W_{-\unicode[STIX]{x1D712}_{i}})$
). Thus, its semi-simple part is
![]() $\operatorname{SL}(W_{\unicode[STIX]{x1D712}_{i}})$
, which is an inner form of type
$\operatorname{SL}(W_{\unicode[STIX]{x1D712}_{i}})$
, which is an inner form of type
![]() $\mathsf{A}_{\ell -1}$
with
$\mathsf{A}_{\ell -1}$
with
We will now complete the proof of Proposition 5.4. Assume the contrary, i.e.
![]() $\mathscr{H}$
contains a maximal
$\mathscr{H}$
contains a maximal
![]() $\mathscr{K}$
-torus
$\mathscr{K}$
-torus
![]() $\mathscr{T}=\mathscr{T}_{1}\mathscr{T}_{2}$
as in the proposition. Applying the lemma to
$\mathscr{T}=\mathscr{T}_{1}\mathscr{T}_{2}$
as in the proposition. Applying the lemma to
![]() $\mathscr{S}=\mathscr{T}_{1}$
, we obtain that
$\mathscr{S}=\mathscr{T}_{1}$
, we obtain that
where
![]() $\mathscr{S}_{0}$
is the central torus of
$\mathscr{S}_{0}$
is the central torus of
![]() $C_{\mathscr{H}}(\mathscr{T}_{1})$
and the
$C_{\mathscr{H}}(\mathscr{T}_{1})$
and the
![]() $\mathscr{H}_{i}$
are semisimple
$\mathscr{H}_{i}$
are semisimple
![]() $\mathscr{K}$
-groups of the types specified in the lemma. Clearly,
$\mathscr{K}$
-groups of the types specified in the lemma. Clearly,
![]() $\mathscr{T}\not \subset \mathscr{S}_{0}$
as otherwise
$\mathscr{T}\not \subset \mathscr{S}_{0}$
as otherwise
![]() $\mathscr{H}$
would be quasi-split over
$\mathscr{H}$
would be quasi-split over
![]() $\mathscr{K}$
, which it is not because
$\mathscr{K}$
, which it is not because
![]() $d>1$
. As
$d>1$
. As
![]() $\mathscr{T}_{1}\subset \mathscr{S}_{0}$
, we conclude that
$\mathscr{T}_{1}\subset \mathscr{S}_{0}$
, we conclude that
![]() $\mathscr{T}_{2}\not \subset \mathscr{S}_{0}$
. It follows that there exists
$\mathscr{T}_{2}\not \subset \mathscr{S}_{0}$
. It follows that there exists
![]() $i\in \{1,\ldots ,s\}$
such that
$i\in \{1,\ldots ,s\}$
such that
This means that for the quotient map
![]() $\unicode[STIX]{x1D70B}_{i}:C_{\mathscr{H}}(\mathscr{T}_{1})\rightarrow C_{\mathscr{H}}(\mathscr{T}_{1})/\hat{\mathscr{H}}_{i}=:\bar{\mathscr{H}}_{i}$
, we have
$\unicode[STIX]{x1D70B}_{i}:C_{\mathscr{H}}(\mathscr{T}_{1})\rightarrow C_{\mathscr{H}}(\mathscr{T}_{1})/\hat{\mathscr{H}}_{i}=:\bar{\mathscr{H}}_{i}$
, we have
![]() $\unicode[STIX]{x1D70B}_{i}(\mathscr{T}_{2})\neq \{e\}$
. Being generic over
$\unicode[STIX]{x1D70B}_{i}(\mathscr{T}_{2})\neq \{e\}$
. Being generic over
![]() $\mathscr{K}$
, the torus
$\mathscr{K}$
, the torus
![]() $\mathscr{T}_{2}$
is
$\mathscr{T}_{2}$
is
![]() $\mathscr{K}$
-irreducible, i.e. contains no proper
$\mathscr{K}$
-irreducible, i.e. contains no proper
![]() $\mathscr{K}$
-defined subtori. Thus, the restriction of
$\mathscr{K}$
-defined subtori. Thus, the restriction of
![]() $\unicode[STIX]{x1D70B}_{i}$
gives an isogeny of
$\unicode[STIX]{x1D70B}_{i}$
gives an isogeny of
![]() $\mathscr{T}_{2}$
onto a
$\mathscr{T}_{2}$
onto a
![]() $\mathscr{K}$
-subtorus
$\mathscr{K}$
-subtorus
![]() $\bar{\mathscr{T}}_{i}$
of
$\bar{\mathscr{T}}_{i}$
of
![]() $\bar{\mathscr{H}}_{i}$
. Moreover, because
$\bar{\mathscr{H}}_{i}$
. Moreover, because
![]() $\dim \mathscr{T}_{2}=\operatorname{rk}\mathscr{H}-1$
and
$\dim \mathscr{T}_{2}=\operatorname{rk}\mathscr{H}-1$
and
![]() $\operatorname{rk}\bar{\mathscr{H}}_{i}\leqslant \operatorname{rk}\mathscr{H}-1$
, we see that
$\operatorname{rk}\bar{\mathscr{H}}_{i}\leqslant \operatorname{rk}\mathscr{H}-1$
, we see that
![]() $\bar{\mathscr{T}}_{i}$
is actually a maximal
$\bar{\mathscr{T}}_{i}$
is actually a maximal
![]() $\mathscr{K}$
-torus of
$\mathscr{K}$
-torus of
![]() $\bar{\mathscr{H}}_{i}$
. Let
$\bar{\mathscr{H}}_{i}$
. Let
![]() $\mathscr{L}$
be the common minimal splitting field of
$\mathscr{L}$
be the common minimal splitting field of
![]() $\mathscr{T}_{2}$
and
$\mathscr{T}_{2}$
and
![]() $\bar{\mathscr{T}}_{i}$
. As
$\bar{\mathscr{T}}_{i}$
. As
![]() $\mathscr{T}_{2}$
is
$\mathscr{T}_{2}$
is
![]() $\mathscr{K}$
-generic in a group of type
$\mathscr{K}$
-generic in a group of type
![]() $\mathsf{D}_{n/2-1}$
where
$\mathsf{D}_{n/2-1}$
where
![]() $n=dm$
, we have
$n=dm$
, we have
Now, assume that
![]() $\mathscr{H}_{i}$
is an inner form of type
$\mathscr{H}_{i}$
is an inner form of type
![]() $\mathsf{A}_{\ell -1}$
with
$\mathsf{A}_{\ell -1}$
with
![]() $\ell \leqslant dr$
. As
$\ell \leqslant dr$
. As
![]() $r\leqslant m/2$
, we obtain
$r\leqslant m/2$
, we obtain
Comparing with (4), we obtain the inequality
which fails for all
![]() $n\geqslant 10$
.
$n\geqslant 10$
.
Next, let
![]() $\mathscr{H}_{i}$
be of type
$\mathscr{H}_{i}$
be of type
![]() $\mathsf{D}_{\ell }$
with
$\mathsf{D}_{\ell }$
with
![]() $\ell \leqslant d(m-2)/2\leqslant n/2-2$
as
$\ell \leqslant d(m-2)/2\leqslant n/2-2$
as
![]() $d\geqslant 2$
. As it is not a triality form when
$d\geqslant 2$
. As it is not a triality form when
![]() $\ell =4$
, we have
$\ell =4$
, we have
Thus, comparing with (4), we obtain the inequality
which never holds for
![]() $n\geqslant 6$
.
$n\geqslant 6$
.
Thus, the assumption that
![]() $\mathscr{H}$
contains a maximal
$\mathscr{H}$
contains a maximal
![]() $\mathscr{K}$
-torus
$\mathscr{K}$
-torus
![]() $\mathscr{T}=\mathscr{T}_{1}\mathscr{T}_{2}$
leads to a contradiction in both cases, proving our claim.◻
$\mathscr{T}=\mathscr{T}_{1}\mathscr{T}_{2}$
leads to a contradiction in both cases, proving our claim.◻
Proof of Proposition 5.3.
(a) Write
![]() $q=q_{1}\bot q_{2}$
, where
$q=q_{1}\bot q_{2}$
, where
![]() $q_{1}$
is a two-dimensional hyperbolic form. Then
$q_{1}$
is a two-dimensional hyperbolic form. Then
![]() $T_{1}=\operatorname{Spin}_{2}(q_{1})$
is a one-dimensional split torus
$T_{1}=\operatorname{Spin}_{2}(q_{1})$
is a one-dimensional split torus
![]() $\mathbb{G}_{m}$
. As
$\mathbb{G}_{m}$
. As
![]() $K$
is infinite and finitely generated, we can find a maximal
$K$
is infinite and finitely generated, we can find a maximal
![]() $K$
-torus
$K$
-torus
![]() $T_{2}$
of
$T_{2}$
of
![]() $\operatorname{Spin}_{n-2}(q_{2})$
that is generic over
$\operatorname{Spin}_{n-2}(q_{2})$
that is generic over
![]() $K$
(cf. [Reference Prasad and RapinchukPR03, Reference Prasad and RapinchukPR17]). Consider the maximal
$K$
(cf. [Reference Prasad and RapinchukPR03, Reference Prasad and RapinchukPR17]). Consider the maximal
![]() $K$
-torus
$K$
-torus
![]() $T=T_{1}T_{2}$
of
$T=T_{1}T_{2}$
of
![]() $G$
. Then it follows from Proposition 5.4 that
$G$
. Then it follows from Proposition 5.4 that
![]() $T$
is not isomorphic to a maximal
$T$
is not isomorphic to a maximal
![]() $K$
-torus of
$K$
-torus of
![]() $H$
, hence
$H$
, hence
![]() $H\notin \mathbf{gen}_{K}(G)$
.
$H\notin \mathbf{gen}_{K}(G)$
.
(b) Again, write
![]() $q=q_{1}\bot q_{2}$
where
$q=q_{1}\bot q_{2}$
where
![]() $q_{1}=\langle a_{1},a_{2}\rangle$
is a binary form. Set
$q_{1}=\langle a_{1},a_{2}\rangle$
is a binary form. Set
![]() $L=K(\sqrt{-a_{1}a_{2}})$
. If
$L=K(\sqrt{-a_{1}a_{2}})$
. If
![]() $L=K$
, then our claim follows from part (a). Thus, we may assume that
$L=K$
, then our claim follows from part (a). Thus, we may assume that
![]() $L$
is a quadratic extension of
$L$
is a quadratic extension of
![]() $K$
. Then
$K$
. Then
![]() $T_{1}=\operatorname{Spin}_{2}(q_{1})$
is the one-dimensional norm torus
$T_{1}=\operatorname{Spin}_{2}(q_{1})$
is the one-dimensional norm torus
![]() $\text{R}_{L/K}^{(1)}(\mathbb{G}_{m})$
. Furthermore, let
$\text{R}_{L/K}^{(1)}(\mathbb{G}_{m})$
. Furthermore, let
![]() $T_{2}$
be a maximal
$T_{2}$
be a maximal
![]() $K$
-torus of
$K$
-torus of
![]() $\operatorname{Spin}_{n-2}(q_{2})$
that is generic over
$\operatorname{Spin}_{n-2}(q_{2})$
that is generic over
![]() $L$
(cf. [Reference Prasad and RapinchukPR03, Reference Prasad and RapinchukPR17]). Then the maximal
$L$
(cf. [Reference Prasad and RapinchukPR03, Reference Prasad and RapinchukPR17]). Then the maximal
![]() $K$
-torus
$K$
-torus
![]() $T=T_{1}T_{2}$
is not isomorphic to a maximal
$T=T_{1}T_{2}$
is not isomorphic to a maximal
![]() $K$
-torus of
$K$
-torus of
![]() $H$
. Indeed, assume the contrary, i.e.
$H$
. Indeed, assume the contrary, i.e.
![]() $T\subset H$
. Note that over
$T\subset H$
. Note that over
![]() $L$
, the torus
$L$
, the torus
![]() $T$
is an almost direct product
$T$
is an almost direct product
![]() $T_{1}^{\prime }T_{2}^{\prime }$
where
$T_{1}^{\prime }T_{2}^{\prime }$
where
![]() $T_{1}^{\prime }$
is a one-dimensional split torus and
$T_{1}^{\prime }$
is a one-dimensional split torus and
![]() $T_{2}^{\prime }$
is isomorphic to a generic torus in a group of type
$T_{2}^{\prime }$
is isomorphic to a generic torus in a group of type
![]() $\mathsf{D}_{n/2-1}$
. At the same time, since
$\mathsf{D}_{n/2-1}$
. At the same time, since
![]() $d>2$
, the group
$d>2$
, the group
![]() $H$
is
$H$
is
![]() $L$
-isomorphic to
$L$
-isomorphic to
![]() $\widetilde{\text{SU}}_{m^{\prime }}(\mathscr{D},h^{\prime })$
where
$\widetilde{\text{SU}}_{m^{\prime }}(\mathscr{D},h^{\prime })$
where
![]() $\mathscr{D}$
is a central division algebra over
$\mathscr{D}$
is a central division algebra over
![]() $\mathscr{K}=L$
of degree
$\mathscr{K}=L$
of degree
![]() $d^{\prime }>1$
and
$d^{\prime }>1$
and
![]() $h^{\prime }$
is an
$h^{\prime }$
is an
![]() $m^{\prime }$
-dimensional Hermitian form (note that
$m^{\prime }$
-dimensional Hermitian form (note that
![]() $d^{\prime }m^{\prime }=dm$
). However, this contradicts Proposition 5.4. Thus, again
$d^{\prime }m^{\prime }=dm$
). However, this contradicts Proposition 5.4. Thus, again
![]() $H\notin \mathbf{gen}_{K}(G)$
.◻
$H\notin \mathbf{gen}_{K}(G)$
.◻
Remark 5.6. It follows from Proposition 5.3(b) that to complete the proof of Theorem 1.2 for all even-dimensional form, it would be sufficient to demonstrate that
![]() $\mathbf{gen}_{K}(G)$
cannot contain a group of the form
$\mathbf{gen}_{K}(G)$
cannot contain a group of the form
![]() $H=\widetilde{\operatorname{SU}}_{m}(D,h)$
where
$H=\widetilde{\operatorname{SU}}_{m}(D,h)$
where
![]() $D$
is a central quaternion division algebra over
$D$
is a central quaternion division algebra over
![]() $K$
. The proof of Proposition 5.3(b) given above shows that this boils down to proving that for any quaternion division algebra
$K$
. The proof of Proposition 5.3(b) given above shows that this boils down to proving that for any quaternion division algebra
![]() $D$
over
$D$
over
![]() $K$
, the given quadratic form
$K$
, the given quadratic form
![]() $q$
contains a binary subform
$q$
contains a binary subform
![]() $q_{1}=\langle a_{1},a_{2}\rangle$
such that the field
$q_{1}=\langle a_{1},a_{2}\rangle$
such that the field
![]() $K(\sqrt{-a_{1}a_{2}})$
does not split
$K(\sqrt{-a_{1}a_{2}})$
does not split
![]() $D$
, which seems very likely at least when the dimension of
$D$
, which seems very likely at least when the dimension of
![]() $q$
is sufficiently large (note that those
$q$
is sufficiently large (note that those
![]() $d\in K^{\times }\setminus {K^{\times }}^{2}$
for which
$d\in K^{\times }\setminus {K^{\times }}^{2}$
for which
![]() $K(\sqrt{d}){\hookrightarrow}D$
must be represented by the ternary quadratic form associated with
$K(\sqrt{d}){\hookrightarrow}D$
must be represented by the ternary quadratic form associated with
![]() $D$
).
$D$
).
5.2 Properness of the global-to-local map
Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $V$
be a divisorial set of places. As we already mentioned, for each
$V$
be a divisorial set of places. As we already mentioned, for each
![]() $i\geqslant 1$
, the kernel
$i\geqslant 1$
, the kernel
is contained in
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
, hence is finiteFootnote
2
(cf. § 4.1). Applying now Theorem 3.4, we conclude that for
$H^{i}(K,\unicode[STIX]{x1D707}_{2})_{V}$
, hence is finiteFootnote
2
(cf. § 4.1). Applying now Theorem 3.4, we conclude that for
![]() $q$
a nondegenerate quadratic form in
$q$
a nondegenerate quadratic form in
![]() $n\geqslant 5$
variables and
$n\geqslant 5$
variables and
![]() $G=\operatorname{SO}_{n}(q)$
, the map
$G=\operatorname{SO}_{n}(q)$
, the map
is proper, which is precisely the assertion of Theorem 1.3.
To put this result in a more general context, we recall the following general observation [Reference Chernousov, Rapinchuk and RapinchukCRR15, Reference RapinchukRap14]: Let
![]() $G$
be an absolutely almost simple simply connected algebraic group over a field
$G$
be an absolutely almost simple simply connected algebraic group over a field
![]() $K$
, and let
$K$
, and let
![]() $V$
be a set of discrete valuations of
$V$
be a set of discrete valuations of
![]() $K$
that satisfies condition (A). Assume that for any finite subset
$K$
that satisfies condition (A). Assume that for any finite subset
![]() $S\subset V$
, the set of
$S\subset V$
, the set of
![]() $K$
-isomorphism classes of inner
$K$
-isomorphism classes of inner
![]() $K$
-forms of
$K$
-forms of
![]() $G$
having good reduction at all
$G$
having good reduction at all
![]() $v\in V\setminus S$
is finite. Then for the corresponding adjoint group
$v\in V\setminus S$
is finite. Then for the corresponding adjoint group
![]() $\overline{G}$
, the map
$\overline{G}$
, the map
is proper. This means, in particular, that for
![]() $n$
odd, Theorem 1.3
directly follows from Theorem 1.1. On the other hand, for
$n$
odd, Theorem 1.3
directly follows from Theorem 1.1. On the other hand, for
![]() $n$
even, the latter implies neither Theorem 1.3 nor the corresponding fact for the simply connected and adjoint groups
$n$
even, the latter implies neither Theorem 1.3 nor the corresponding fact for the simply connected and adjoint groups
![]() $\widetilde{G}=\operatorname{Spin}_{n}(q)$
and
$\widetilde{G}=\operatorname{Spin}_{n}(q)$
and
![]() $\overline{G}=\operatorname{PSO}_{n}(q)$
(thus, in this case Theorem 1.3 is an independent result). Later, we will see that the analogues of Theorem 1.3 are valid for special unitary groups of Hermitian forms over a quadratic extension of the base (two-dimensional global) field and for the group of type
$\overline{G}=\operatorname{PSO}_{n}(q)$
(thus, in this case Theorem 1.3 is an independent result). Later, we will see that the analogues of Theorem 1.3 are valid for special unitary groups of Hermitian forms over a quadratic extension of the base (two-dimensional global) field and for the group of type
![]() $\mathsf{G}_{2}$
over such a field (note that all these groups are simply connected); see Theorems 8.4 and 9.1(iii). We close this subsection with some additional results on the properness of the global-to-local map for simply connected groups.
$\mathsf{G}_{2}$
over such a field (note that all these groups are simply connected); see Theorems 8.4 and 9.1(iii). We close this subsection with some additional results on the properness of the global-to-local map for simply connected groups.
Theorem 5.7. Let
![]() $K$
be a two-dimensional global field, let
$K$
be a two-dimensional global field, let
![]() $V$
be its divisorial set of places and let
$V$
be its divisorial set of places and let
![]() $m$
be a square-free integer prime to
$m$
be a square-free integer prime to
![]() $\operatorname{char}K$
. Then for a central simple
$\operatorname{char}K$
. Then for a central simple
![]() $K$
-algebra
$K$
-algebra
![]() $A$
of degree
$A$
of degree
![]() $m$
and
$m$
and
![]() $G=\operatorname{SL}_{1,A}$
, the map
$G=\operatorname{SL}_{1,A}$
, the map
is proper.
Proof. We may assume without loss of generality that
![]() $\operatorname{char}K^{(v)}$
is prime to
$\operatorname{char}K^{(v)}$
is prime to
![]() $m$
for all
$m$
for all
![]() $v\in V$
. It is well-known (cf. [Reference Knus, Merkurjev, Rost and TignolKMRT98, 29.4]) that for any extension
$v\in V$
. It is well-known (cf. [Reference Knus, Merkurjev, Rost and TignolKMRT98, 29.4]) that for any extension
![]() $F/K$
there is a bijection
$F/K$
there is a bijection
and this bijection is functorial in
![]() $F$
. Thus, letting
$F$
. Thus, letting
![]() $A_{v}=A_{K_{v}}$
for
$A_{v}=A_{K_{v}}$
for
![]() $v\in V$
, we need to show that the map
$v\in V$
, we need to show that the map
has finite kernel. For any field extension
![]() $F/K$
, we have a homomorphism
$F/K$
, we have a homomorphism
where
![]() $[A_{F}]$
is the class of
$[A_{F}]$
is the class of
![]() $A_{F}$
in
$A_{F}$
in
![]() $_{m}\operatorname{Br}(F)=H^{2}(F,\unicode[STIX]{x1D707}_{m})$
. As
$_{m}\operatorname{Br}(F)=H^{2}(F,\unicode[STIX]{x1D707}_{m})$
. As
![]() $m$
is square-free, according to [Reference Merkurjev and SuslinMS82, Theorem 12.2], the kernel of this map coincides with
$m$
is square-free, according to [Reference Merkurjev and SuslinMS82, Theorem 12.2], the kernel of this map coincides with
![]() $\operatorname{Nrd}_{A_{F}/F}(A_{F}^{\times })$
, so we have an injective homomorphism
$\operatorname{Nrd}_{A_{F}/F}(A_{F}^{\times })$
, so we have an injective homomorphism
Then we have the following commutative diagram

where
![]() $\unicode[STIX]{x1D6E5}_{V}=\prod _{v\in V}\unicode[STIX]{x1D6FF}_{K_{v}}$
. The fact that the unramified cohomology group
$\unicode[STIX]{x1D6E5}_{V}=\prod _{v\in V}\unicode[STIX]{x1D6FF}_{K_{v}}$
. The fact that the unramified cohomology group
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{m}^{\otimes 2})_{V}$
is finite (Theorem 6.1) implies that
$H^{3}(K,\unicode[STIX]{x1D707}_{m}^{\otimes 2})_{V}$
is finite (Theorem 6.1) implies that
![]() $\ker \unicode[STIX]{x1D702}$
is finite. Then using the injectivity of
$\ker \unicode[STIX]{x1D702}$
is finite. Then using the injectivity of
![]() $\unicode[STIX]{x1D6FF}_{K}$
, we conclude that
$\unicode[STIX]{x1D6FF}_{K}$
, we conclude that
![]() $\ker \unicode[STIX]{x1D704}$
is finite as well, as needed.◻
$\ker \unicode[STIX]{x1D704}$
is finite as well, as needed.◻
We now turn to spinor groups. Let
![]() $q$
be a nondegenerate quadratic form of dimension at least three over a field
$q$
be a nondegenerate quadratic form of dimension at least three over a field
![]() $K$
of characteristic
$K$
of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $\unicode[STIX]{x1D70B}:\operatorname{Spin}_{n}(q)\rightarrow \operatorname{SO}_{n}(q)$
be the canonical
$\unicode[STIX]{x1D70B}:\operatorname{Spin}_{n}(q)\rightarrow \operatorname{SO}_{n}(q)$
be the canonical
![]() $K$
-isogeny. For a field extension
$K$
-isogeny. For a field extension
![]() $F/K$
, we let
$F/K$
, we let
be the map induced by
![]() $\unicode[STIX]{x1D70B}$
. Assume now that
$\unicode[STIX]{x1D70B}$
. Assume now that
![]() $K$
is equipped with a set
$K$
is equipped with a set
![]() $V$
of discrete valuations such that the map
$V$
of discrete valuations such that the map
![]() $\unicode[STIX]{x1D703}:H^{1}(K,\operatorname{SO}_{n}(q))\rightarrow \prod _{v\in V}H^{1}(K_{v},\operatorname{SO}_{n}(q))$
is proper. Then, analyzing the commutative diagram
$\unicode[STIX]{x1D703}:H^{1}(K,\operatorname{SO}_{n}(q))\rightarrow \prod _{v\in V}H^{1}(K_{v},\operatorname{SO}_{n}(q))$
is proper. Then, analyzing the commutative diagram

where
![]() $\unicode[STIX]{x1D6F1}=\prod _{v\in V}\unicode[STIX]{x1D70B}_{K_{v}}$
, and using twisting, we see that in order to prove that
$\unicode[STIX]{x1D6F1}=\prod _{v\in V}\unicode[STIX]{x1D70B}_{K_{v}}$
, and using twisting, we see that in order to prove that
![]() $\tilde{\unicode[STIX]{x1D703}}$
is proper, it is enough to prove that for any nondegenerate
$\tilde{\unicode[STIX]{x1D703}}$
is proper, it is enough to prove that for any nondegenerate
![]() $n$
-dimensional quadratic form
$n$
-dimensional quadratic form
![]() $q^{\prime }$
over
$q^{\prime }$
over
![]() $K$
, the set
$K$
, the set
(where
![]() $\unicode[STIX]{x1D70B}_{K}^{\prime }$
is the map analogous to
$\unicode[STIX]{x1D70B}_{K}^{\prime }$
is the map analogous to
![]() $\unicode[STIX]{x1D70B}_{K}$
for the quadratic form
$\unicode[STIX]{x1D70B}_{K}$
for the quadratic form
![]() $q^{\prime }$
) is finite. For a field extension
$q^{\prime }$
) is finite. For a field extension
![]() $F/K$
, combining the standard exact sequence of cohomology corresponding to the exact sequence
$F/K$
, combining the standard exact sequence of cohomology corresponding to the exact sequence
with the description of the spinor norm (cf. [Reference Knus, Merkurjev, Rost and TignolKMRT98, 13.30, 13.31]), one easily obtains a (functorial) identification of
![]() $\ker \unicode[STIX]{x1D70B}_{F}^{\prime }$
with the quotient
$\ker \unicode[STIX]{x1D70B}_{F}^{\prime }$
with the quotient
![]() $F^{\times }/\operatorname{Sn}(q^{\prime },F)$
, where
$F^{\times }/\operatorname{Sn}(q^{\prime },F)$
, where
![]() $\operatorname{Sn}(q^{\prime },F)$
denotes the image of the spinor norm
$\operatorname{Sn}(q^{\prime },F)$
denotes the image of the spinor norm
![]() $\operatorname{SO}_{n}(q^{\prime })_{F}$
. Furthermore, one observes that this identification induces an injection of the set (5) into the kernel of the map
$\operatorname{SO}_{n}(q^{\prime })_{F}$
. Furthermore, one observes that this identification induces an injection of the set (5) into the kernel of the map
Thus, if
![]() $\unicode[STIX]{x1D703}$
is known to be proper, then to establish the properness of
$\unicode[STIX]{x1D703}$
is known to be proper, then to establish the properness of
![]() $\tilde{\unicode[STIX]{x1D703}}$
, it is sufficient to prove that the kernel of
$\tilde{\unicode[STIX]{x1D703}}$
, it is sufficient to prove that the kernel of
![]() $\unicode[STIX]{x1D708}_{q^{\prime },V}$
is finite for all nondegenerate
$\unicode[STIX]{x1D708}_{q^{\prime },V}$
is finite for all nondegenerate
![]() $n$
-dimensional quadratic forms
$n$
-dimensional quadratic forms
![]() $q^{\prime }$
over
$q^{\prime }$
over
![]() $K$
. (Of course,
$K$
. (Of course,
![]() $\ker \unicode[STIX]{x1D708}_{q^{\prime },V}$
is automatically trivial if
$\ker \unicode[STIX]{x1D708}_{q^{\prime },V}$
is automatically trivial if
![]() $q^{\prime }$
is
$q^{\prime }$
is
![]() $K$
-isotropic, so the properness of
$K$
-isotropic, so the properness of
![]() $\unicode[STIX]{x1D703}$
immediately implies that of
$\unicode[STIX]{x1D703}$
immediately implies that of
![]() $\tilde{\unicode[STIX]{x1D703}}$
if every
$\tilde{\unicode[STIX]{x1D703}}$
if every
![]() $n$
-dimensional quadratic form over
$n$
-dimensional quadratic form over
![]() $K$
is isotropic, i.e.
$K$
is isotropic, i.e.
![]() $n$
is greater than the
$n$
is greater than the
![]() $u$
-invariant of
$u$
-invariant of
![]() $K$
.)
$K$
.)
Here we would like to point out the following partial result on the finiteness of the set (5).
Proposition 5.8. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $V$
be its divisorial set of places. If
$V$
be its divisorial set of places. If
![]() $q$
is a quadratic Pfister form over
$q$
is a quadratic Pfister form over
![]() $K$
of dimension
$K$
of dimension
![]() $n=2^{d}$
, then the intersection
$n=2^{d}$
, then the intersection
is finite.
Proof. According to the discussion prior to the statement of the proposition, it is enough to show that the map
has finite kernel. By our assumption,
![]() $q$
is a Pfister form
$q$
is a Pfister form
![]() $\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
for some
$\langle \!\langle a_{1},\ldots ,a_{d}\rangle \!\rangle$
for some
![]() $a_{1},\ldots ,a_{d}\in K^{\times }$
. For any field extension
$a_{1},\ldots ,a_{d}\in K^{\times }$
. For any field extension
![]() $F/K$
, using the fact that the nonzero values of
$F/K$
, using the fact that the nonzero values of
![]() $q$
over
$q$
over
![]() $F$
form a subgroup of
$F$
form a subgroup of
![]() $F^{\times }$
(see [Reference LamLam05, ch. X, Theorem 1.8]), it is easy to see that
$F^{\times }$
(see [Reference LamLam05, ch. X, Theorem 1.8]), it is easy to see that
![]() $a\in F^{\times }$
belongs to
$a\in F^{\times }$
belongs to
![]() $\operatorname{Sn}(q,F)$
if and only if the Pfister form
$\operatorname{Sn}(q,F)$
if and only if the Pfister form
![]() $q\bot (-aq)=\langle \!\langle a_{1},\ldots ,a_{d},a\rangle \!\rangle$
is isotropic, hence hyperbolic (cf. [Reference LamLam05, ch. X, Theorem 1.7]). The latter is equivalent to the symbol
$q\bot (-aq)=\langle \!\langle a_{1},\ldots ,a_{d},a\rangle \!\rangle$
is isotropic, hence hyperbolic (cf. [Reference LamLam05, ch. X, Theorem 1.7]). The latter is equivalent to the symbol
or the cup-product
being trivial. Thus, the map
gives rise to an injective map
We then have the following commutative diagram

where
![]() $\unicode[STIX]{x1D6E5}_{V}=\prod _{v\in V}\unicode[STIX]{x1D6FF}_{K_{v}}$
. As we already mentioned several times, the finiteness of the unramified cohomology group
$\unicode[STIX]{x1D6E5}_{V}=\prod _{v\in V}\unicode[STIX]{x1D6FF}_{K_{v}}$
. As we already mentioned several times, the finiteness of the unramified cohomology group
![]() $H^{d+1}(K,\unicode[STIX]{x1D707}_{2})_{V}$
(see § 4.1), implies the finiteness of
$H^{d+1}(K,\unicode[STIX]{x1D707}_{2})_{V}$
(see § 4.1), implies the finiteness of
![]() $\ker \unicode[STIX]{x1D704}_{d+1}$
. Thus, the injectivity of
$\ker \unicode[STIX]{x1D704}_{d+1}$
. Thus, the injectivity of
![]() $\unicode[STIX]{x1D6FF}_{K}$
yields the finiteness of
$\unicode[STIX]{x1D6FF}_{K}$
yields the finiteness of
![]() $\ker \unicode[STIX]{x1D702}_{q,V}$
, as required.◻
$\ker \unicode[STIX]{x1D702}_{q,V}$
, as required.◻
6 The finiteness of unramified
 $H^{3}$
for two-dimensional global fields: characteristic zero case
$H^{3}$
for two-dimensional global fields: characteristic zero case
To complete the proof of Theorem 1.1 and its consequences, we need to prove the following.
Theorem 6.1. Let
![]() $K$
be a two-dimensional global field, let
$K$
be a two-dimensional global field, let
![]() $n\geqslant 1$
be an integer prime to
$n\geqslant 1$
be an integer prime to
![]() $\operatorname{char}K$
and let
$\operatorname{char}K$
and let
![]() $V$
be a divisorial set of places such that
$V$
be a divisorial set of places such that
![]() $\operatorname{char}K^{(v)}$
is prime to
$\operatorname{char}K^{(v)}$
is prime to
![]() $n$
for all
$n$
for all
![]() $v\in V$
. Then the unramified cohomology group
$v\in V$
. Then the unramified cohomology group
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V}$
is finite.
$H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V}$
is finite.
Corollary 6.2. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $V$
be a divisorial set of places such that
$V$
be a divisorial set of places such that
![]() $\operatorname{char}K^{(v)}\neq 2$
for all
$\operatorname{char}K^{(v)}\neq 2$
for all
![]() $v\in V$
. Then the unramified cohomology group
$v\in V$
. Then the unramified cohomology group
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
is finite.
$H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
is finite.
In the current section, we treat the characteristic zero case, where
![]() $K$
is the function field of a smooth geometrically integral curve
$K$
is the function field of a smooth geometrically integral curve
![]() $C$
over a number field
$C$
over a number field
![]() $k$
, following the referee’s suggestions; the positive characteristic case is handled at the end of § 7. We begin by considering the case of a projective curve. Thus, let
$k$
, following the referee’s suggestions; the positive characteristic case is handled at the end of § 7. We begin by considering the case of a projective curve. Thus, let
![]() $\widetilde{C}$
be a smooth projective geometrically integral curve over a number field
$\widetilde{C}$
be a smooth projective geometrically integral curve over a number field
![]() $k$
with function field
$k$
with function field
![]() $K=k(\widetilde{C})$
, and let
$K=k(\widetilde{C})$
, and let
![]() $V_{0}(\widetilde{C})$
be the set of geometric places of
$V_{0}(\widetilde{C})$
be the set of geometric places of
![]() $K$
corresponding to the closed points of
$K$
corresponding to the closed points of
![]() $\widetilde{C}$
. It was observed by Colliot-Thélène [Reference Colliot-ThélèneCol96, proof of Theorem 6.2] and (independently) by Berhuy [Reference BerhuyBer07, Example 6] that Kato’s cohomological Hasse principle [Reference KatoKat86] implies the following finiteness result.
$\widetilde{C}$
. It was observed by Colliot-Thélène [Reference Colliot-ThélèneCol96, proof of Theorem 6.2] and (independently) by Berhuy [Reference BerhuyBer07, Example 6] that Kato’s cohomological Hasse principle [Reference KatoKat86] implies the following finiteness result.
Theorem 6.3. In the above notation, the unramified cohomology group
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V_{0}(\widetilde{C})}$
is finite, for any
$H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V_{0}(\widetilde{C})}$
is finite, for any
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
Proof. Let
![]() $V^{k}$
be the set of (the equivalence classes of) all valuations of
$V^{k}$
be the set of (the equivalence classes of) all valuations of
![]() $k$
. Then according to [Reference KatoKat86, Theorem 0.8], the map
$k$
. Then according to [Reference KatoKat86, Theorem 0.8], the map
where
![]() $\widetilde{C}_{v}=\widetilde{C}\times _{k}k_{v}$
, is injective. Clearly, for
$\widetilde{C}_{v}=\widetilde{C}\times _{k}k_{v}$
, is injective. Clearly, for
![]() $v\in V^{k}$
, the restriction map takes
$v\in V^{k}$
, the restriction map takes
![]() $H^{3}(k(\widetilde{C}),\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V_{0}(\widetilde{C})}$
into
$H^{3}(k(\widetilde{C}),\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V_{0}(\widetilde{C})}$
into
![]() $H^{3}(k_{v}(\widetilde{C}),\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V_{0}(\widetilde{C}_{v})}$
. However, it was shown in [Reference KatoKat86, Corollary 2.9] that the latter group is finite for all
$H^{3}(k_{v}(\widetilde{C}),\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V_{0}(\widetilde{C}_{v})}$
. However, it was shown in [Reference KatoKat86, Corollary 2.9] that the latter group is finite for all
![]() $v$
(see also Theorem 7.1 below), and is in fact trivial if
$v$
(see also Theorem 7.1 below), and is in fact trivial if
![]() $v$
is nonarchimedean and
$v$
is nonarchimedean and
![]() $\widetilde{C}_{v}$
has good reduction at
$\widetilde{C}_{v}$
has good reduction at
![]() $v$
. As
$v$
. As
![]() $\widetilde{C}$
has good reduction at almost all
$\widetilde{C}$
has good reduction at almost all
![]() $v\in V^{k}$
, the required finiteness follows.◻
$v\in V^{k}$
, the required finiteness follows.◻
Now, given an arbitrary smooth geometrically integral curve
![]() $C$
over a number field
$C$
over a number field
![]() $k$
, we let
$k$
, we let
![]() $\widetilde{C}$
denote the (unique) smooth geometrically integral projective curve over
$\widetilde{C}$
denote the (unique) smooth geometrically integral projective curve over
![]() $k$
containing
$k$
containing
![]() $C$
as an open subset. Then Theorem 6.3 immediately gives the finiteness of the unramified cohomology group
$C$
as an open subset. Then Theorem 6.3 immediately gives the finiteness of the unramified cohomology group
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})$
for any divisorial set of places
$H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})$
for any divisorial set of places
![]() $V$
of
$V$
of
![]() $K=k(C)=k(\widetilde{C})$
that contains
$K=k(C)=k(\widetilde{C})$
that contains
![]() $V_{0}(\widetilde{C})$
. To establish the finiteness for any divisorial set, we need to describe the relationship between the unramified cohomology of a scheme and that of the complement of a closed subscheme of codimension one. This relationship, which essentially follows from the construction of Kato’s complex in [Reference KatoKat86], was first observed by Colliot-Thélène [Reference Colliot-ThélèneCol96, § 2].
$V_{0}(\widetilde{C})$
. To establish the finiteness for any divisorial set, we need to describe the relationship between the unramified cohomology of a scheme and that of the complement of a closed subscheme of codimension one. This relationship, which essentially follows from the construction of Kato’s complex in [Reference KatoKat86], was first observed by Colliot-Thélène [Reference Colliot-ThélèneCol96, § 2].
Let
![]() $X$
be an excellent Noetherian scheme and
$X$
be an excellent Noetherian scheme and
![]() $n$
an integer invertible on
$n$
an integer invertible on
![]() $X$
. For a point
$X$
. For a point
![]() $x\in X$
, we let
$x\in X$
, we let
![]() $\unicode[STIX]{x1D705}(x)$
denote its residue field, and let
$\unicode[STIX]{x1D705}(x)$
denote its residue field, and let
![]() $X_{p}$
be the set of points of dimension
$X_{p}$
be the set of points of dimension
![]() $p$
. For any integers
$p$
. For any integers
![]() $i,j$
, Kato [Reference KatoKat86] constructs a homological complex
$i,j$
, Kato [Reference KatoKat86] constructs a homological complex
![]() $C_{n}^{i,j}(X)$
$C_{n}^{i,j}(X)$
where the term
![]() $\bigoplus _{x\in X_{p}}H^{p+i}(\unicode[STIX]{x1D705}(x),\unicode[STIX]{x1D707}_{n}^{\otimes (p+j)})$
is placed in degree
$\bigoplus _{x\in X_{p}}H^{p+i}(\unicode[STIX]{x1D705}(x),\unicode[STIX]{x1D707}_{n}^{\otimes (p+j)})$
is placed in degree
![]() $p$
. The differentials
$p$
. The differentials
are defined as follows. Let
![]() $x\in X_{p}$
and set
$x\in X_{p}$
and set
![]() $Z_{x}=\overline{\{x\}}$
to be the closure of
$Z_{x}=\overline{\{x\}}$
to be the closure of
![]() $x$
in
$x$
in
![]() $X$
. Then each point
$X$
. Then each point
![]() $y$
of codimension one on
$y$
of codimension one on
![]() $Z_{x}$
corresponds to a point in
$Z_{x}$
corresponds to a point in
![]() $X_{p-1}$
. Let
$X_{p-1}$
. Let
![]() $y_{1},\ldots ,y_{s}$
be the points on the normalization
$y_{1},\ldots ,y_{s}$
be the points on the normalization
![]() $\tilde{Z}_{x}$
lying above
$\tilde{Z}_{x}$
lying above
![]() $y$
. The local ring at each
$y$
. The local ring at each
![]() $y_{k}$
is a discrete valuation ring, yielding a discrete valuation on the function field
$y_{k}$
is a discrete valuation ring, yielding a discrete valuation on the function field
![]() $\unicode[STIX]{x1D705}(x)$
of
$\unicode[STIX]{x1D705}(x)$
of
![]() $\tilde{Z}_{x}$
. Let
$\tilde{Z}_{x}$
. Let
be the corresponding residue map. One then defines
where
![]() $\operatorname{Cor}$
is the corestriction map. The differential
$\operatorname{Cor}$
is the corestriction map. The differential
![]() $\unicode[STIX]{x2202}_{p}$
is the direct sum of all such maps. In [Reference KatoKat86, Proposition 1.7], Kato verified that this construction produces a complex. Note that if
$\unicode[STIX]{x2202}_{p}$
is the direct sum of all such maps. In [Reference KatoKat86, Proposition 1.7], Kato verified that this construction produces a complex. Note that if
![]() $X$
is a Noetherian integral normal scheme of dimension
$X$
is a Noetherian integral normal scheme of dimension
![]() $d$
with function field
$d$
with function field
![]() $K$
, then the construction of the differentials implies that the degree
$K$
, then the construction of the differentials implies that the degree
![]() $d$
homology
$d$
homology
![]() $H_{d}(C_{n}^{i,j}(X))$
of
$H_{d}(C_{n}^{i,j}(X))$
of
![]() $C_{n}^{i,j}(X)$
is precisely the unramified cohomology
$C_{n}^{i,j}(X)$
is precisely the unramified cohomology
![]() $H^{d+j}(K,\unicode[STIX]{x1D707}_{n}^{\otimes (d+j)})_{V(X)}$
, where
$H^{d+j}(K,\unicode[STIX]{x1D707}_{n}^{\otimes (d+j)})_{V(X)}$
, where
![]() $V(X)$
is the set of discrete valuations of
$V(X)$
is the set of discrete valuations of
![]() $K$
corresponding to the prime divisors of
$K$
corresponding to the prime divisors of
![]() $X$
.
$X$
.
Suppose now that
![]() $X$
is an excellent integral Noetherian normal scheme with function field
$X$
is an excellent integral Noetherian normal scheme with function field
![]() $K$
and
$K$
and
![]() $Y\subset X$
is a normal closed subscheme of pure codimension one. Thus, if
$Y\subset X$
is a normal closed subscheme of pure codimension one. Thus, if
![]() $Y=\bigcup _{j\in J}Y_{j}$
is the decomposition into irreducible components, then each
$Y=\bigcup _{j\in J}Y_{j}$
is the decomposition into irreducible components, then each
![]() $Y_{j}$
has codimension one in
$Y_{j}$
has codimension one in
![]() $X$
, and we let
$X$
, and we let
![]() $\unicode[STIX]{x1D705}_{j}$
denote the function field of
$\unicode[STIX]{x1D705}_{j}$
denote the function field of
![]() $Y_{j}$
. Set
$Y_{j}$
. Set
![]() $U=X\setminus Y$
, and let
$U=X\setminus Y$
, and let
![]() $n$
be a positive integer invertible on
$n$
be a positive integer invertible on
![]() $X$
. Then, for any
$X$
. Then, for any
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
![]() $\ell$
, we have a canonical embedding
$\ell$
, we have a canonical embedding
On the other hand, for each
![]() $j\in J$
, one has the residue map
$j\in J$
, one has the residue map
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes \ell })\rightarrow H^{i-1}(\unicode[STIX]{x1D705}_{j},\unicode[STIX]{x1D707}_{n}^{\otimes (\ell -1)})$
, and we let
$H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes \ell })\rightarrow H^{i-1}(\unicode[STIX]{x1D705}_{j},\unicode[STIX]{x1D707}_{n}^{\otimes (\ell -1)})$
, and we let
denote the direct sum of the residue maps.
Proposition 6.4. The above maps
![]() $r$
and
$r$
and
![]() $s$
give the following exact sequence of unramified cohomology groups
$s$
give the following exact sequence of unramified cohomology groups
Proof. Let
![]() $d=\dim X$
. The initial segment of the Kato complex for
$d=\dim X$
. The initial segment of the Kato complex for
![]() $X$
is
$X$
is
and for
![]() $U$
it is
$U$
it is
As noted above, the normality of
![]() $X$
implies that
$X$
implies that
At the next stage of the Kato complex for
![]() $X$
, there are residue maps
$X$
, there are residue maps
for all
![]() $j\in J$
, where
$j\in J$
, where
![]() $c=\dim Y_{j}=d-1$
, and the assumption that
$c=\dim Y_{j}=d-1$
, and the assumption that
![]() $Y$
is normal gives
$Y$
is normal gives
Now, the fact that we have a complex implies that the map
![]() $r$
takes
$r$
takes
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes \ell })_{V(U)}$
into
$H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes \ell })_{V(U)}$
into
and the exactness of (6) then follows easily from the construction. ◻
Proof of Theorem 6.1.
First, let
![]() $C$
be any smooth geometrically integral curve over
$C$
be any smooth geometrically integral curve over
![]() $k$
such that
$k$
such that
![]() $K=k(C)$
, and let
$K=k(C)$
, and let
![]() $\widetilde{C}$
be a smooth projective geometrically integral curve over
$\widetilde{C}$
be a smooth projective geometrically integral curve over
![]() $k$
containing
$k$
containing
![]() $C$
. Suppose that we are given smooth models
$C$
. Suppose that we are given smooth models
![]() ${\mathcal{C}}\subset \widetilde{{\mathcal{C}}}$
of
${\mathcal{C}}\subset \widetilde{{\mathcal{C}}}$
of
![]() $C$
and
$C$
and
![]() $\tilde{C}$
, respectively, over a suitable open subsect
$\tilde{C}$
, respectively, over a suitable open subsect
![]() $T\subset \operatorname{Spec}(\mathbb{Z})$
such that
$T\subset \operatorname{Spec}(\mathbb{Z})$
such that
![]() $\tilde{{\mathcal{C}}}\setminus {\mathcal{C}}$
is of pure codimension one. The inclusion
$\tilde{{\mathcal{C}}}\setminus {\mathcal{C}}$
is of pure codimension one. The inclusion
in conjunction with Theorem 6.3 implies that
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V(\widetilde{{\mathcal{C}}})}$
is finite.
$H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V(\widetilde{{\mathcal{C}}})}$
is finite.
Now, let
be the decomposition into irreducible components, and let
![]() $\unicode[STIX]{x1D705}_{j}$
be the function field of
$\unicode[STIX]{x1D705}_{j}$
be the function field of
![]() $Y_{j}$
. By construction, each
$Y_{j}$
. By construction, each
![]() $\unicode[STIX]{x1D705}_{j}$
is a number field and
$\unicode[STIX]{x1D705}_{j}$
is a number field and
![]() $Y_{j}$
is the spectrum of the ring of
$Y_{j}$
is the spectrum of the ring of
![]() $S_{j}$
-integers in
$S_{j}$
-integers in
![]() $\unicode[STIX]{x1D705}_{j}$
for some finite subset
$\unicode[STIX]{x1D705}_{j}$
for some finite subset
![]() $S_{j}\subset V^{\unicode[STIX]{x1D705}_{j}}$
containing
$S_{j}\subset V^{\unicode[STIX]{x1D705}_{j}}$
containing
![]() $V_{\infty }^{\unicode[STIX]{x1D705}_{j}}$
. Set
$V_{\infty }^{\unicode[STIX]{x1D705}_{j}}$
. Set
![]() $T_{j}=V^{\unicode[STIX]{x1D705}_{j}}\setminus S_{j}$
. Then
$T_{j}=V^{\unicode[STIX]{x1D705}_{j}}\setminus S_{j}$
. Then
![]() $H^{2}(\unicode[STIX]{x1D705}_{j},\unicode[STIX]{x1D707}_{n})_{V(Y_{j})}$
coincides with the unramified Brauer group
$H^{2}(\unicode[STIX]{x1D705}_{j},\unicode[STIX]{x1D707}_{n})_{V(Y_{j})}$
coincides with the unramified Brauer group
![]() $_{n\!}\operatorname{Br}(\unicode[STIX]{x1D705}_{j})$
, the finiteness of which easily follows from the Artin–Hasse–Brauer–Noether theorem (cf. [Reference Chernousov, Rapinchuk and RapinchukCRR13, 3.6] and [Reference Chernousov, Rapinchuk and RapinchukCRR16a, 3.5]). Let us consider now the exact sequence of Proposition 6.4 for
$_{n\!}\operatorname{Br}(\unicode[STIX]{x1D705}_{j})$
, the finiteness of which easily follows from the Artin–Hasse–Brauer–Noether theorem (cf. [Reference Chernousov, Rapinchuk and RapinchukCRR13, 3.6] and [Reference Chernousov, Rapinchuk and RapinchukCRR16a, 3.5]). Let us consider now the exact sequence of Proposition 6.4 for
![]() $X=\widetilde{{\mathcal{C}}}$
and
$X=\widetilde{{\mathcal{C}}}$
and
![]() $U={\mathcal{C}}$
for
$U={\mathcal{C}}$
for
![]() $i=3$
and
$i=3$
and
![]() $\ell =2$
. As the finiteness of
$\ell =2$
. As the finiteness of
has already been established, we obtain the finiteness of
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V({\mathcal{C}})}$
. This proves the Theorem for the divisorial set
$H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V({\mathcal{C}})}$
. This proves the Theorem for the divisorial set
![]() $V=V({\mathcal{C}})$
. However, it is easy to see that any divisorial set of valuations
$V=V({\mathcal{C}})$
. However, it is easy to see that any divisorial set of valuations
![]() $V$
of
$V$
of
![]() $K$
contains a set of the form
$K$
contains a set of the form
![]() $V({\mathcal{C}})$
for a suitable curve
$V({\mathcal{C}})$
for a suitable curve
![]() $C$
over
$C$
over
![]() $k$
and its model
$k$
and its model
![]() ${\mathcal{C}}$
as above, completing the argument in the general case.◻
${\mathcal{C}}$
as above, completing the argument in the general case.◻
As we have already mentioned, in Appendix A we give an alternative (in fact, our initial) proof of Theorem 6.1 in characteristic zero, which does not use Kato’s cohomological Hasse principle, but rather is inspired by Jannsen’s [Reference JannsenJan89–90] approach to the latter.
7 Proofs of Theorem 1.4 and of Theorem 6.1 in positive characteristic
The reason we treat these two results in the same section is that both arguments ultimately depend on the same techniques, namely finiteness theorems in étale cohomology and Bloch–Ogus theory. We begin with the proof of Theorem 1.4, which relies on the following.
Theorem 7.1 [Reference RapinchukRap18, Theorem 1.3(a)].
Let
![]() $C$
be a smooth geometrically integral curve over a field
$C$
be a smooth geometrically integral curve over a field
![]() $k$
, let
$k$
, let
![]() $V_{0}$
be the set of places of
$V_{0}$
be the set of places of
![]() $K=k(C)$
associated with the closed points of
$K=k(C)$
associated with the closed points of
![]() $C$
and let
$C$
and let
![]() $m\geqslant 1$
be an integer prime to
$m\geqslant 1$
be an integer prime to
![]() $\operatorname{char}k$
. If
$\operatorname{char}k$
. If
![]() $k$
satisfies condition
$k$
satisfies condition
![]() $(\text{F}_{m}^{\prime })$
(see § 1), then for any
$(\text{F}_{m}^{\prime })$
(see § 1), then for any
![]() $i\geqslant 1$
and any
$i\geqslant 1$
and any
![]() $j$
, the unramified cohomology group
$j$
, the unramified cohomology group
![]() $H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes j})_{V_{0}}$
is finite.
$H^{i}(K,\unicode[STIX]{x1D707}_{n}^{\otimes j})_{V_{0}}$
is finite.
We refer the reader to [Reference RapinchukRap18] for a discussion of properties and examples of fields satisfying condition
![]() $(\text{F}_{m}^{\prime })$
. A sketch of the proof of Theorem 7.1 will be given below after briefly recalling some facts from Bloch–Ogus theory that are also needed for the proof of Theorem 6.1 in positive characteristic. Here we only mention that the proof of Theorem 7.1 makes use of the following statement, which is of independent interest and which we will also need in the proof of Theorem 1.4.
$(\text{F}_{m}^{\prime })$
. A sketch of the proof of Theorem 7.1 will be given below after briefly recalling some facts from Bloch–Ogus theory that are also needed for the proof of Theorem 6.1 in positive characteristic. Here we only mention that the proof of Theorem 7.1 makes use of the following statement, which is of independent interest and which we will also need in the proof of Theorem 1.4.
Proposition 7.2 [Reference RapinchukRap18, Theorem 1.1].
Let
![]() $K$
be a field and
$K$
be a field and
![]() $m\geqslant 1$
be an integer prime to
$m\geqslant 1$
be an integer prime to
![]() $\operatorname{char}K$
. Assume that
$\operatorname{char}K$
. Assume that
![]() $K$
satisfies
$K$
satisfies
![]() $(\text{F}_{m}^{\prime })$
. Then for any finite Galois module
$(\text{F}_{m}^{\prime })$
. Then for any finite Galois module
![]() $A$
over
$A$
over
![]() $K$
such that
$K$
such that
![]() $mA=0$
, the groups
$mA=0$
, the groups
![]() $H^{i}(K,A)$
are finite for all
$H^{i}(K,A)$
are finite for all
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
Proof of Theorem 1.4.
We need to check the conditions of Theorem 2.1 for
![]() $V=V_{0}$
. Condition (2) follows immediately from Theorem 7.1. To verify (1), we observe that the argument given in the proof of Proposition 4.1 shows that there exists an embedding
$V=V_{0}$
. Condition (2) follows immediately from Theorem 7.1. To verify (1), we observe that the argument given in the proof of Proposition 4.1 shows that there exists an embedding
Then, because the group
![]() $H^{2}(C\otimes _{k}\bar{k},\unicode[STIX]{x1D707}_{2})$
is finite and of exponent 2 (see [Reference Artin, Deligne, Grothendieck and VerdierSGA4, Exposé XVI, Théorème 5.2]), the finiteness of
$H^{2}(C\otimes _{k}\bar{k},\unicode[STIX]{x1D707}_{2})$
is finite and of exponent 2 (see [Reference Artin, Deligne, Grothendieck and VerdierSGA4, Exposé XVI, Théorème 5.2]), the finiteness of
![]() $H^{2}(C,\unicode[STIX]{x1D707}_{2})$
follows easily from Proposition 7.2 (with condition
$H^{2}(C,\unicode[STIX]{x1D707}_{2})$
follows easily from Proposition 7.2 (with condition
![]() $(\text{F}_{2}^{\prime })$
) and the Hochschild–Serre spectral sequence
$(\text{F}_{2}^{\prime })$
) and the Hochschild–Serre spectral sequence
Alternatively, note that we may assume that
![]() $C$
is affine, in which case the fundamental sequence (2) yields the following exact sequence
$C$
is affine, in which case the fundamental sequence (2) yields the following exact sequence
The extreme terms are finite in view of condition
![]() $(\text{F}_{2}^{\prime })$
and Proposition 7.2, so the middle term is also finite, as required.◻
$(\text{F}_{2}^{\prime })$
and Proposition 7.2, so the middle term is also finite, as required.◻
We expect a suitable analogue of Theorem 1.4 to be valid for all types, and would like to propose the following conjecture.
Conjecture 7.3. Let
![]() $K=k(C)$
be the function field of a smooth affine geometrically integral curve over a field
$K=k(C)$
be the function field of a smooth affine geometrically integral curve over a field
![]() $k$
and let
$k$
and let
![]() $V_{0}$
be the set of discrete valuations associated with the closed points of
$V_{0}$
be the set of discrete valuations associated with the closed points of
![]() $C$
. Furthermore, let
$C$
. Furthermore, let
![]() $G$
be an absolutely almost simple simply connected algebraic
$G$
be an absolutely almost simple simply connected algebraic
![]() $K$
-group and let
$K$
-group and let
![]() $m$
be the order of the automorphism group of its root system. Assume that
$m$
be the order of the automorphism group of its root system. Assume that
![]() $\operatorname{char}k$
is prime to
$\operatorname{char}k$
is prime to
![]() $m$
and that
$m$
and that
![]() $k$
satisfies
$k$
satisfies
![]() $(\text{F}_{m}^{\prime })$
. Then the set of
$(\text{F}_{m}^{\prime })$
. Then the set of
![]() $K$
-isomorphism classes of
$K$
-isomorphism classes of
![]() $K$
-forms of
$K$
-forms of
![]() $G$
that have good reduction at all
$G$
that have good reduction at all
![]() $v\in V_{0}$
is finite.
$v\in V_{0}$
is finite.
It is likely that the conclusion should be true under more lax assumptions, e.g. it is probably enough to require condition
![]() $(\text{F}_{p}^{\prime })$
for all primes
$(\text{F}_{p}^{\prime })$
for all primes
![]() $p\mid m$
or even a certain subset of the set of such primes.
$p\mid m$
or even a certain subset of the set of such primes.
Applying Theorem 3.4 in conjunction with Theorem 7.1, we obtain the following.
Theorem 7.4. Let
![]() $C$
be a smooth geometrically integral curve over a field
$C$
be a smooth geometrically integral curve over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
that satisfies condition
$\neq 2$
that satisfies condition
![]() $(\text{F}_{2}^{\prime })$
, and let
$(\text{F}_{2}^{\prime })$
, and let
![]() $K=k(C)$
be its function field. Denote by
$K=k(C)$
be its function field. Denote by
![]() $V_{0}$
the set of discrete valuations of
$V_{0}$
the set of discrete valuations of
![]() $K$
associated with the closed points of
$K$
associated with the closed points of
![]() $C$
. Then for a nondegenerate quadratic form
$C$
. Then for a nondegenerate quadratic form
![]() $q$
of dimension
$q$
of dimension
![]() $n\geqslant 5$
over
$n\geqslant 5$
over
![]() $K$
and
$K$
and
![]() $G=\operatorname{SO}_{n}(q)$
, the map
$G=\operatorname{SO}_{n}(q)$
, the map
is proper.
We expect that the conclusion of the theorem should be true for any absolutely almost simple group under the assumptions made in Conjecture 7.3. Here is one result for spinor groups in a more specialized situation. Keep the above notations but now assume that
![]() $k$
is a finite extension of the
$k$
is a finite extension of the
![]() $p$
-adic field
$p$
-adic field
![]() $\mathbb{Q}_{p}$
. Recall that
$\mathbb{Q}_{p}$
. Recall that
![]() $k$
satisfies Serre’s condition
$k$
satisfies Serre’s condition
![]() $(\text{F})$
(cf. [Reference SerreSer97, ch. III, § 4]), hence condition
$(\text{F})$
(cf. [Reference SerreSer97, ch. III, § 4]), hence condition
![]() $(\text{F}_{m}^{\prime })$
for all
$(\text{F}_{m}^{\prime })$
for all
![]() $m$
. Furthermore, Parimala and Suresh [Reference Parimala and SureshPS10] showed that the
$m$
. Furthermore, Parimala and Suresh [Reference Parimala and SureshPS10] showed that the
![]() $u$
-invariant of
$u$
-invariant of
![]() $K$
is
$K$
is
![]() $8$
, i.e. any quadratic form over
$8$
, i.e. any quadratic form over
![]() $K$
of dimension
$K$
of dimension
![]() ${\geqslant}9$
is isotropic. Thus, combining Theorem 7.4 with the discussion preceding Proposition 5.8, we obtain the following.
${\geqslant}9$
is isotropic. Thus, combining Theorem 7.4 with the discussion preceding Proposition 5.8, we obtain the following.
Corollary 7.5. In the above notation, for any quadratic form
![]() $q$
over
$q$
over
![]() $K$
in
$K$
in
![]() $n\geqslant 9$
variables and
$n\geqslant 9$
variables and
![]() $\tilde{G}=\operatorname{Spin}_{n}(q)$
, the map
$\tilde{G}=\operatorname{Spin}_{n}(q)$
, the map
![]() $\unicode[STIX]{x1D703}_{\tilde{G},V_{0}}$
is proper.
$\unicode[STIX]{x1D703}_{\tilde{G},V_{0}}$
is proper.
We now recall several results from Bloch–Ogus theory. For any smooth algebraic variety
![]() $X$
over an arbitrary field
$X$
over an arbitrary field
![]() $F$
, Bloch and Ogus [Reference Bloch and OgusBO74] established the existence of the following cohomological first quadrant spectral sequence
$F$
, Bloch and Ogus [Reference Bloch and OgusBO74] established the existence of the following cohomological first quadrant spectral sequence
where
![]() $X^{(p)}$
denotes the set of points of
$X^{(p)}$
denotes the set of points of
![]() $X$
of codimension
$X$
of codimension
![]() $p$
and the summands are the Galois cohomology groups of the residue fields
$p$
and the summands are the Galois cohomology groups of the residue fields
![]() $\unicode[STIX]{x1D705}(x)$
(the original statement of Bloch–Ogus was actually given in terms of étale homology, with the above version obtained via absolute purity; we refer the reader to [Reference Colliot-Thélène, Hoobler and KahnCHK97] for a derivation of this spectral sequence that avoids the use of étale homology, as well as to [Reference Colliot-ThélèneCol95] for an extensive discussion of applications of this spectral sequence to the Gersten conjecture). The spectral sequence yields a complex
$\unicode[STIX]{x1D705}(x)$
(the original statement of Bloch–Ogus was actually given in terms of étale homology, with the above version obtained via absolute purity; we refer the reader to [Reference Colliot-Thélène, Hoobler and KahnCHK97] for a derivation of this spectral sequence that avoids the use of étale homology, as well as to [Reference Colliot-ThélèneCol95] for an extensive discussion of applications of this spectral sequence to the Gersten conjecture). The spectral sequence yields a complex
and it is well-known (see, e.g., [Reference Jannsen, Sato and SaitoJSS14, Remark 2.5.5]) that the differentials in (8) coincide up to sign with the differentials in Kato’s complex that was recalled in § 5. The fundamental result of Bloch and Ogus was the calculation of the
![]() $E_{2}$
-term of (7): they showed that
$E_{2}$
-term of (7): they showed that
where
![]() ${\mathcal{H}}^{q}(\unicode[STIX]{x1D707}_{m}^{\otimes j})$
denotes the Zariski sheaf on
${\mathcal{H}}^{q}(\unicode[STIX]{x1D707}_{m}^{\otimes j})$
denotes the Zariski sheaf on
![]() $X$
associated to the presheaf that assigns to an open
$X$
associated to the presheaf that assigns to an open
![]() $U\subset X$
the cohomology group
$U\subset X$
the cohomology group
![]() $H^{i}(U,\unicode[STIX]{x1D707}_{m}^{\otimes j}).$
The resulting (first quadrant) spectral sequence
$H^{i}(U,\unicode[STIX]{x1D707}_{m}^{\otimes j}).$
The resulting (first quadrant) spectral sequence
is usually referred to as the Bloch–Ogus spectral sequence and has the following key properties:
(a)
 $E_{2}^{p,q}=0$
for
$E_{2}^{p,q}=0$
for
 $p>\dim X$
and all
$p>\dim X$
and all
 $q$
;
$q$
;(b)
 $E_{2}^{p,q}=0$
for
$E_{2}^{p,q}=0$
for
 $p>q$
; and
$p>q$
; and(c)
 $E_{2}^{0,q}=H^{0}(X,{\mathcal{H}}^{q}(\unicode[STIX]{x1D707}_{m}^{\otimes b}))$
coincides with the unramified cohomology
$E_{2}^{0,q}=H^{0}(X,{\mathcal{H}}^{q}(\unicode[STIX]{x1D707}_{m}^{\otimes b}))$
coincides with the unramified cohomology
 $H^{q}(F(X),\unicode[STIX]{x1D707}_{m}^{\otimes b})_{V_{0}}$
with respect to the geometric places (associated with the prime divisors of
$H^{q}(F(X),\unicode[STIX]{x1D707}_{m}^{\otimes b})_{V_{0}}$
with respect to the geometric places (associated with the prime divisors of
 $X$
) of the function field
$X$
) of the function field
 $F(X)$
.
$F(X)$
.
For our applications, we now state the following proposition, whose proof combines Proposition 7.2 with the Hochschild–Serre spectral sequence.
Proposition 7.6 [Reference RapinchukRap18, Corollary 3.2].
Suppose
![]() $K$
is a field and
$K$
is a field and
![]() $m\geqslant 1$
is integer prime to
$m\geqslant 1$
is integer prime to
![]() $\operatorname{char}K$
. If
$\operatorname{char}K$
. If
![]() $K$
is of type
$K$
is of type
![]() $(F_{m}^{\prime })$
, then for any smooth geometrically integral algebraic variety
$(F_{m}^{\prime })$
, then for any smooth geometrically integral algebraic variety
![]() $X$
over
$X$
over
![]() $K$
, the étale cohomology groups
$K$
, the étale cohomology groups
![]() $H^{i}(X,\unicode[STIX]{x1D707}_{m}^{\otimes j})$
are finite for all
$H^{i}(X,\unicode[STIX]{x1D707}_{m}^{\otimes j})$
are finite for all
![]() $i\geqslant 0$
and all
$i\geqslant 0$
and all
![]() $j$
.
$j$
.
Sketch of proof of Theorem 7.1.
As
![]() $\dim C=1$
, property (a) of the Bloch–Ogus spectral sequence gives surjective edge maps
$\dim C=1$
, property (a) of the Bloch–Ogus spectral sequence gives surjective edge maps
![]() $E^{i}\rightarrow E_{2}^{0,i}$
for all
$E^{i}\rightarrow E_{2}^{0,i}$
for all
![]() $i\geqslant 1$
. Thus, in view of property (c), we obtain surjections
$i\geqslant 1$
. Thus, in view of property (c), we obtain surjections
for all
![]() $i\geqslant 1$
. The finiteness of the unramified cohomology groups then follows from Proposition 7.6.
$i\geqslant 1$
. The finiteness of the unramified cohomology groups then follows from Proposition 7.6.
Proof of Theorem 6.1 in positive characteristic.
Here
![]() $K$
is the function field
$K$
is the function field
![]() $k(X)$
of a smooth geometrically integral surface
$k(X)$
of a smooth geometrically integral surface
![]() $X$
over a finite field
$X$
over a finite field
![]() $k$
. Property (b) of the Bloch–Ogus spectral sequence yields an exact sequence
$k$
. Property (b) of the Bloch–Ogus spectral sequence yields an exact sequence
Hence, using the well-known isomorphism
where
![]() $CH^{2}(X)$
is the Chow group of codimension-two cycles on
$CH^{2}(X)$
is the Chow group of codimension-two cycles on
![]() $X$
(see, e.g. the proof of [Reference Bloch and OgusBO74, Theorem 7.7]), together with property (c) above, we obtain the exact sequence
$X$
(see, e.g. the proof of [Reference Bloch and OgusBO74, Theorem 7.7]), together with property (c) above, we obtain the exact sequence
The left-most term is finite by Proposition 7.6. On the other hand, because
![]() $X$
is a smooth surface over a finite field, the group
$X$
is a smooth surface over a finite field, the group
![]() $CH^{2}(X)$
is finitely generated (see [Reference Colliot-Thélène, Sansuc and SouléCSS83, Proposition 4 and Corollaire 7]). It follows that
$CH^{2}(X)$
is finitely generated (see [Reference Colliot-Thélène, Sansuc and SouléCSS83, Proposition 4 and Corollaire 7]). It follows that
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{m}^{\otimes 2})_{V_{0}}$
is finite, as needed.◻
$H^{3}(K,\unicode[STIX]{x1D707}_{m}^{\otimes 2})_{V_{0}}$
is finite, as needed.◻
8 Special unitary groups of Hermitian forms over quadratic extensions
Let
![]() $K$
be a field of characteristic
$K$
be a field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $L/K$
be a quadratic field extension with nontrivial automorphism
$L/K$
be a quadratic field extension with nontrivial automorphism
![]() $\unicode[STIX]{x1D70F}$
. A choice of a basis of
$\unicode[STIX]{x1D70F}$
. A choice of a basis of
![]() $L$
over
$L$
over
![]() $K$
enables us to identify
$K$
enables us to identify
![]() $L$
with
$L$
with
![]() $K^{2}$
. Then for any
$K^{2}$
. Then for any
![]() $n\geqslant 1$
the space
$n\geqslant 1$
the space
![]() $L^{n}$
gets identified with
$L^{n}$
gets identified with
![]() $K^{2n}$
, and under this identification, to any
$K^{2n}$
, and under this identification, to any
![]() $\unicode[STIX]{x1D70F}$
-Hermitian form
$\unicode[STIX]{x1D70F}$
-Hermitian form
![]() $h$
on
$h$
on
![]() $L^{n}$
, there naturally corresponds a quadratic form
$L^{n}$
, there naturally corresponds a quadratic form
![]() $q=q_{h}$
on
$q=q_{h}$
on
![]() $K^{2n}$
given by
$K^{2n}$
given by
![]() $q_{h}(x)=h(x)$
for
$q_{h}(x)=h(x)$
for
![]() $x\in K^{2n}=L^{n}$
. Recall that if
$x\in K^{2n}=L^{n}$
. Recall that if
![]() $s(x,y)$
is the sesquilinear form on
$s(x,y)$
is the sesquilinear form on
![]() $L^{n}\times L^{n}$
that gives
$L^{n}\times L^{n}$
that gives
![]() $h$
(i.e.
$h$
(i.e.
![]() $h(x)=s(x,x)$
), then the bilinear form
$h(x)=s(x,x)$
), then the bilinear form
![]() $b$
on
$b$
on
![]() $K^{2n}\times K^{2n}$
associated with
$K^{2n}\times K^{2n}$
associated with
![]() $q_{h}$
is given by
$q_{h}$
is given by
The following result, attributed in [Reference GersteinGer08, § 2.9] to Jacobson, is well-known and easy to prove: two
![]() $n$
-dimensional Hermitian forms
$n$
-dimensional Hermitian forms
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
are equivalent if and only if the corresponding
$h_{2}$
are equivalent if and only if the corresponding
![]() $2n$
-dimensional quadratic forms
$2n$
-dimensional quadratic forms
![]() $q_{h_{1}}$
and
$q_{h_{1}}$
and
![]() $q_{h_{2}}$
are equivalent. In terms of Galois cohomology, this means that the natural map
$q_{h_{2}}$
are equivalent. In terms of Galois cohomology, this means that the natural map
is injective. On the other hand, it is well-known that the map
is also injective (the proof repeats verbatim the argument for the injectivity of the map
cf. [Reference BerhuyBer10, proof of Corollary IV.11.3] or [Reference Knus, Merkurjev, Rost and TignolKMRT98, 29.E]). It follows that the map
is injective (in fact, it remains injective also over any extension of
![]() $K$
). In this section, we use these facts to prove the analogues of Theorems 1.1–1.4 for the special unitary groups
$K$
). In this section, we use these facts to prove the analogues of Theorems 1.1–1.4 for the special unitary groups
![]() $\operatorname{SU}_{n}(L/K,h)$
of nondegenerate
$\operatorname{SU}_{n}(L/K,h)$
of nondegenerate
![]() $n$
-dimensional Hermitian forms
$n$
-dimensional Hermitian forms
![]() $(n\geqslant 2)$
.
$(n\geqslant 2)$
.
First, let
![]() $G=\operatorname{SU}_{n}(L/K,h)$
in the above notation and let
$G=\operatorname{SU}_{n}(L/K,h)$
in the above notation and let
![]() $v$
be a discrete valuation of
$v$
be a discrete valuation of
![]() $K$
. There are two cases.
$K$
. There are two cases.
Case 1:
![]() $v$
splits in
$v$
splits in
![]() $L$
(i.e.
$L$
(i.e.
![]() $L\,\otimes _{K}\,K_{v}\simeq K_{v}\oplus K_{v}$
). In this case
$L\,\otimes _{K}\,K_{v}\simeq K_{v}\oplus K_{v}$
). In this case
![]() $G$
is
$G$
is
![]() $K_{v}$
-isomorphic to
$K_{v}$
-isomorphic to
![]() $\operatorname{SL}_{n}$
, hence has good reduction at
$\operatorname{SL}_{n}$
, hence has good reduction at
![]() $v$
. At the same time, the corresponding quadratic form
$v$
. At the same time, the corresponding quadratic form
![]() $q_{h}$
becomes hyperbolic over
$q_{h}$
becomes hyperbolic over
![]() $K_{v}$
and therefore (trivially)
$K_{v}$
and therefore (trivially)
![]() $[q_{h}]\in W_{0}(K_{v})$
in the notation of § 3.
$[q_{h}]\in W_{0}(K_{v})$
in the notation of § 3.
Case 2:
![]() $v$
does not split in
$v$
does not split in
![]() $L$
(i.e.
$L$
(i.e.
![]() $L_{v}:=L\,\otimes _{K}\,K_{v}$
is a quadratic field extension of
$L_{v}:=L\,\otimes _{K}\,K_{v}$
is a quadratic field extension of
![]() $K_{v}$
). Then
$K_{v}$
). Then
![]() $G$
has good reduction at
$G$
has good reduction at
![]() $v$
if and only if
$v$
if and only if
![]() $L_{v}/K_{v}$
is unramified at
$L_{v}/K_{v}$
is unramified at
![]() $v$
and there exists
$v$
and there exists
![]() $\unicode[STIX]{x1D706}\in K_{v}^{\times }$
such that the Hermitian
$\unicode[STIX]{x1D706}\in K_{v}^{\times }$
such that the Hermitian
![]() $L_{v}/K_{v}$
-form
$L_{v}/K_{v}$
-form
![]() $\unicode[STIX]{x1D706}h$
is equivalent to a Hermitian form given by
$\unicode[STIX]{x1D706}h$
is equivalent to a Hermitian form given by
with
![]() $a_{i}\in U(K_{v})$
. Then again
$a_{i}\in U(K_{v})$
. Then again
![]() $[\unicode[STIX]{x1D706}q_{h}]\in W_{0}(K_{v})$
.
$[\unicode[STIX]{x1D706}q_{h}]\in W_{0}(K_{v})$
.
Thus, in all cases, the fact that
![]() $G$
has a good reduction at
$G$
has a good reduction at
![]() $v$
implies that there exists
$v$
implies that there exists
![]() $\unicode[STIX]{x1D706}\in K_{v}^{\times }$
such that
$\unicode[STIX]{x1D706}\in K_{v}^{\times }$
such that
![]() $[\unicode[STIX]{x1D706}q_{h}]\in W_{0}(K_{v})$
, or equivalently the group
$[\unicode[STIX]{x1D706}q_{h}]\in W_{0}(K_{v})$
, or equivalently the group
![]() $H=\operatorname{Spin}_{2n}(q_{h})$
has a good reduction at
$H=\operatorname{Spin}_{2n}(q_{h})$
has a good reduction at
![]() $v$
. It is now easy to derive a unitary analogue of Theorem 1.1.
$v$
. It is now easy to derive a unitary analogue of Theorem 1.1.
Theorem 8.1. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $V$
be a divisorial set of places. Fix a quadratic extension
$V$
be a divisorial set of places. Fix a quadratic extension
![]() $L/K$
, and let
$L/K$
, and let
![]() $n\geqslant 2$
. Then the number of
$n\geqslant 2$
. Then the number of
![]() $K$
-isomorphism classes of special unitary groups
$K$
-isomorphism classes of special unitary groups
![]() $G=\operatorname{SU}_{n}(L/K,h)$
of nondegenerate Hermitian
$G=\operatorname{SU}_{n}(L/K,h)$
of nondegenerate Hermitian
![]() $L/K$
-forms in
$L/K$
-forms in
![]() $n$
variables that have good reduction at all
$n$
variables that have good reduction at all
![]() $v\in V$
is finite.
$v\in V$
is finite.
Indeed, let
![]() $G_{i}=\operatorname{SU}_{n}(L/K,h_{i})$
$G_{i}=\operatorname{SU}_{n}(L/K,h_{i})$
![]() $(i\in I)$
be an infinite family of pairwise nonisomorphic special unitary groups associated with the quadratic extension
$(i\in I)$
be an infinite family of pairwise nonisomorphic special unitary groups associated with the quadratic extension
![]() $L/K$
such that each
$L/K$
such that each
![]() $G_{i}$
has a good reduction at every
$G_{i}$
has a good reduction at every
![]() $v\in V$
. Then
$v\in V$
. Then
![]() $H_{i}=\operatorname{Spin}_{2n}(q_{h_{i}})$
$H_{i}=\operatorname{Spin}_{2n}(q_{h_{i}})$
![]() $(i\in I)$
is a family of spinor groups each having good reduction at all
$(i\in I)$
is a family of spinor groups each having good reduction at all
![]() $v\in V$
. Applying Theorem 1.1, we conclude that the groups
$v\in V$
. Applying Theorem 1.1, we conclude that the groups
![]() $H_{i}$
and
$H_{i}$
and
![]() $H_{j}$
are
$H_{j}$
are
![]() $K$
-isomorphic for some
$K$
-isomorphic for some
![]() $i,j\in I$
,
$i,j\in I$
,
![]() $i\neq j$
. Then for some
$i\neq j$
. Then for some
![]() $\unicode[STIX]{x1D706}\in K^{\times }$
, the quadratic forms
$\unicode[STIX]{x1D706}\in K^{\times }$
, the quadratic forms
![]() $q_{h_{i}}$
and
$q_{h_{i}}$
and
![]() $\unicode[STIX]{x1D706}q_{h_{j}}$
are equivalent. It now follows from Jacobson’s theorem that the Hermitian forms
$\unicode[STIX]{x1D706}q_{h_{j}}$
are equivalent. It now follows from Jacobson’s theorem that the Hermitian forms
![]() $h_{i}$
and
$h_{i}$
and
![]() $\unicode[STIX]{x1D706}h_{j}$
are equivalent, hence the groups
$\unicode[STIX]{x1D706}h_{j}$
are equivalent, hence the groups
![]() $G_{i}$
and
$G_{i}$
and
![]() $G_{j}$
are isomorphic, a contradiction.
$G_{j}$
are isomorphic, a contradiction.
Remark 8.2. It follows, for example, from [Reference Chernousov, Rapinchuk and RapinchukCRR16a, Proposition 5.1] that
![]() $K$
has only finitely many quadratic extensions
$K$
has only finitely many quadratic extensions
![]() $L/K$
that are unramified at all
$L/K$
that are unramified at all
![]() $v\in V$
(note that this conclusion remains valid for any finitely generated field
$v\in V$
(note that this conclusion remains valid for any finitely generated field
![]() $K$
and a divisorial set of places
$K$
and a divisorial set of places
![]() $V$
). Thus, in effect, Theorem 8.1 yields the finiteness of the set of
$V$
). Thus, in effect, Theorem 8.1 yields the finiteness of the set of
![]() $K$
-isomorphic classes of the special unitary groups with good reduction at all
$K$
-isomorphic classes of the special unitary groups with good reduction at all
![]() $v\in V$
of
$v\in V$
of
![]() $n$
-dimensional nondegenerate Hermitian forms associated with all quadratic extensions
$n$
-dimensional nondegenerate Hermitian forms associated with all quadratic extensions
![]() $L/K$
.
$L/K$
.
Turning now to the genus of
![]() $G=\operatorname{SU}_{n}(L/K,h)$
, we observe that any
$G=\operatorname{SU}_{n}(L/K,h)$
, we observe that any
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
is of the form
$G^{\prime }\in \mathbf{gen}_{K}(G)$
is of the form
![]() $G^{\prime }=\operatorname{SU}_{n}(L/K,h^{\prime })$
. This is clear for
$G^{\prime }=\operatorname{SU}_{n}(L/K,h^{\prime })$
. This is clear for
![]() $n=2$
, so we assume that
$n=2$
, so we assume that
![]() $n\geqslant 3$
. The group
$n\geqslant 3$
. The group
![]() $G$
possesses a maximal
$G$
possesses a maximal
![]() $K$
-torus
$K$
-torus
![]() $T$
of the form
$T$
of the form
![]() $\text{R}_{L/K}(\mathbb{G}_{m})^{n-1}$
, so the group
$\text{R}_{L/K}(\mathbb{G}_{m})^{n-1}$
, so the group
![]() $G^{\prime }$
also has such a maximal
$G^{\prime }$
also has such a maximal
![]() $K$
-torus. Note that the nontrivial automorphism
$K$
-torus. Note that the nontrivial automorphism
![]() $\unicode[STIX]{x1D70F}\in \operatorname{Gal}(L/K)$
acts on the character group
$\unicode[STIX]{x1D70F}\in \operatorname{Gal}(L/K)$
acts on the character group
![]() $X(T)$
as multiplication by
$X(T)$
as multiplication by
![]() $(-1)$
, and because
$(-1)$
, and because
![]() $-\text{id}$
is not in the Weyl group of the root system of type
$-\text{id}$
is not in the Weyl group of the root system of type
![]() $A_{n-1}$
$A_{n-1}$
![]() $(n\geqslant 3)$
, we see that
$(n\geqslant 3)$
, we see that
![]() $G^{\prime }$
is an outer form of the split group of this type and
$G^{\prime }$
is an outer form of the split group of this type and
![]() $L$
is the minimal extension of
$L$
is the minimal extension of
![]() $K$
over which it becomes an inner form. Furthermore, because
$K$
over which it becomes an inner form. Furthermore, because
![]() $G^{\prime }$
splits over
$G^{\prime }$
splits over
![]() $L$
, it cannot involve any noncommutative division
$L$
, it cannot involve any noncommutative division
![]() $L$
-algebra in its description, and therefore it must be of the form
$L$
-algebra in its description, and therefore it must be of the form
![]() $\operatorname{SU}_{n}(L/K,h^{\prime })$
(cf. [Reference Platonov and RapinchukPR94, 2.3]). Now, arguing as in the proof of Theorem 1.2 (cf. § 4.4) on the basis of Theorem 8.1, we obtain the following statement, which is even more complete (in the sense that it has no exceptions) than Theorem 1.2.
$\operatorname{SU}_{n}(L/K,h^{\prime })$
(cf. [Reference Platonov and RapinchukPR94, 2.3]). Now, arguing as in the proof of Theorem 1.2 (cf. § 4.4) on the basis of Theorem 8.1, we obtain the following statement, which is even more complete (in the sense that it has no exceptions) than Theorem 1.2.
Theorem 8.3. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $G=\operatorname{SU}_{n}(L/K,h)$
, where
$G=\operatorname{SU}_{n}(L/K,h)$
, where
![]() $L/K$
is a quadratic extension and
$L/K$
is a quadratic extension and
![]() $h$
is a nondegenerate Hermitian form of dimension
$h$
is a nondegenerate Hermitian form of dimension
![]() $n\geqslant 2$
associated with
$n\geqslant 2$
associated with
![]() $L/K$
. Then the genus
$L/K$
. Then the genus
![]() $\mathbf{gen}_{K}(G)$
is finite.
$\mathbf{gen}_{K}(G)$
is finite.
Next, we have the following cohomological statement, which is analogous to Theorem 1.3.
Theorem 8.4. Notation as in Theorem 8.1, for
![]() $G=\operatorname{SU}_{n}(L/K,h)$
the map
$G=\operatorname{SU}_{n}(L/K,h)$
the map
is proper.
Indeed, let
![]() $H=\operatorname{SO}_{2n}(q_{h})$
. Then we have the following commutative diagram.
$H=\operatorname{SO}_{2n}(q_{h})$
. Then we have the following commutative diagram.

According to Theorem 1.3, the map
![]() $\unicode[STIX]{x1D6FF}$
is proper. On the other hand, as we pointed out earlier in this section, the map
$\unicode[STIX]{x1D6FF}$
is proper. On the other hand, as we pointed out earlier in this section, the map
![]() $\unicode[STIX]{x1D6FD}$
is injective, and the properness of
$\unicode[STIX]{x1D6FD}$
is injective, and the properness of
![]() $\unicode[STIX]{x1D6FC}$
follows.
$\unicode[STIX]{x1D6FC}$
follows.
Finally, we have the following result for special unitary groups over function fields of curves over fields satisfying
![]() $(\text{F}_{2}^{\prime })$
, which is analogous to Theorem 1.4 and which is actually derived from it just like Theorem 8.1 was derived from Theorem 1.1.
$(\text{F}_{2}^{\prime })$
, which is analogous to Theorem 1.4 and which is actually derived from it just like Theorem 8.1 was derived from Theorem 1.1.
Theorem 8.5. Let
![]() $C$
be a smooth geometrically integral curve over a field
$C$
be a smooth geometrically integral curve over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
that satisfies condition
$\neq 2$
that satisfies condition
![]() $(\text{F}_{2}^{\prime })$
and let
$(\text{F}_{2}^{\prime })$
and let
![]() $K=k(C)$
. Denote by
$K=k(C)$
. Denote by
![]() $V$
the set of discrete valuations of
$V$
the set of discrete valuations of
![]() $K$
corresponding to the closed points of
$K$
corresponding to the closed points of
![]() $C$
. Let
$C$
. Let
![]() $L/K$
be a quadratic extension. Then the number of
$L/K$
be a quadratic extension. Then the number of
![]() $K$
-isomorphism classes of special unitary groups
$K$
-isomorphism classes of special unitary groups
![]() $G=\operatorname{SU}_{n}(L/K,h)$
of nondegenerate Hermitian
$G=\operatorname{SU}_{n}(L/K,h)$
of nondegenerate Hermitian
![]() $L/K$
-forms
$L/K$
-forms
![]() $h$
in
$h$
in
![]() $n\geqslant 2$
variables that have good reduction at all
$n\geqslant 2$
variables that have good reduction at all
![]() $v\in V$
is finite.
$v\in V$
is finite.
Remark 8.6. A similar approach can be used to obtain the analogues of Theorems 8.1 and 8.3–8.5 for the (special) unitary groups
![]() $G=\operatorname{SU}_{n}(D,h)$
of nondegenerate Hermitian forms
$G=\operatorname{SU}_{n}(D,h)$
of nondegenerate Hermitian forms
![]() $h$
of dimension
$h$
of dimension
![]() $n\geqslant 2$
over a quaternion division algebra
$n\geqslant 2$
over a quaternion division algebra
![]() $D$
with center
$D$
with center
![]() $K$
with the canonical involution. (We note that these are precisely the absolutely almost simple simply connected groups of type
$K$
with the canonical involution. (We note that these are precisely the absolutely almost simple simply connected groups of type
![]() $\mathsf{C}_{n}$
that split over a quadratic extension of the base field.) More precisely, let us first fix a central quaternion division algebra
$\mathsf{C}_{n}$
that split over a quadratic extension of the base field.) More precisely, let us first fix a central quaternion division algebra
![]() $D$
over
$D$
over
![]() $K$
. Then fixing a basis of
$K$
. Then fixing a basis of
![]() $D$
over
$D$
over
![]() $K$
enables us to identify
$K$
enables us to identify
![]() $D^{n}$
with
$D^{n}$
with
![]() $K^{4n}$
, and in terms of this identification, the Hermitian form
$K^{4n}$
, and in terms of this identification, the Hermitian form
![]() $h$
corresponds to a quadratic form
$h$
corresponds to a quadratic form
![]() $q_{h}$
on
$q_{h}$
on
![]() $K^{4n}$
. Furthermore, one has an analogue of Jacobson’s theorem: two nondegenerate
$K^{4n}$
. Furthermore, one has an analogue of Jacobson’s theorem: two nondegenerate
![]() $n$
-dimensional Hermitian forms
$n$
-dimensional Hermitian forms
![]() $h_{1}$
and
$h_{1}$
and
![]() $h_{2}$
over
$h_{2}$
over
![]() $D$
if and only if the corresponding
$D$
if and only if the corresponding
![]() $4n$
-dimensional quadratic forms
$4n$
-dimensional quadratic forms
![]() $q_{h_{1}}$
and
$q_{h_{1}}$
and
![]() $q_{h_{2}}$
are equivalent. Next, if
$q_{h_{2}}$
are equivalent. Next, if
![]() $G=\operatorname{SU}_{n}(D,h)$
has good reduction at a discrete valuation
$G=\operatorname{SU}_{n}(D,h)$
has good reduction at a discrete valuation
![]() $v$
of
$v$
of
![]() $K$
, then
$K$
, then
![]() $D$
is unramified at
$D$
is unramified at
![]() $v$
and
$v$
and
![]() $H=\operatorname{Spin}_{4n}(b_{h})$
has good reduction at
$H=\operatorname{Spin}_{4n}(b_{h})$
has good reduction at
![]() $v$
. Using these remarks, one can repeat the above arguments almost verbatim to establish the analogues of the theorems of the current section in this situation over the same two classes of fields, i.e. over two-dimensional global fields
$v$
. Using these remarks, one can repeat the above arguments almost verbatim to establish the analogues of the theorems of the current section in this situation over the same two classes of fields, i.e. over two-dimensional global fields
![]() $K$
of characteristic
$K$
of characteristic
![]() $\neq 2$
equipped with a divisorial set of places
$\neq 2$
equipped with a divisorial set of places
![]() $V$
and over the function fields
$V$
and over the function fields
![]() $K=k(C)$
of smooth geometrically integral curves
$K=k(C)$
of smooth geometrically integral curves
![]() $C$
over a field
$C$
over a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
satisfying condition
$\neq 2$
satisfying condition
![]() $(\text{F}_{2}^{\prime })$
equipped with the set
$(\text{F}_{2}^{\prime })$
equipped with the set
![]() $V$
of geometric places associated with the closed points of
$V$
of geometric places associated with the closed points of
![]() $C$
. Details will be published elsewhere. We now recall that for both classes,
$C$
. Details will be published elsewhere. We now recall that for both classes,
![]() $_{2\!}\operatorname{Br}(K)_{V}$
is known to be finite, implying that the number of isomorphism classes of central quaternion division
$_{2\!}\operatorname{Br}(K)_{V}$
is known to be finite, implying that the number of isomorphism classes of central quaternion division
![]() $K$
-algebras
$K$
-algebras
![]() $D$
such that there exists a nondegenerate
$D$
such that there exists a nondegenerate
![]() $n$
-dimensional Hermitian form
$n$
-dimensional Hermitian form
![]() $h$
for which
$h$
for which
![]() $G=\operatorname{SU}_{n}(D,h)$
has good reduction at all
$G=\operatorname{SU}_{n}(D,h)$
has good reduction at all
![]() $v\in V$
is finite. Eventually, this shows that the set of
$v\in V$
is finite. Eventually, this shows that the set of
![]() $K$
-isomorphism classes of absolutely almost simple simply connected
$K$
-isomorphism classes of absolutely almost simple simply connected
![]() $K$
-groups of type
$K$
-groups of type
![]() $\mathsf{C}_{n}$
that split over a quadratic extension of the base field and have good reduction at all
$\mathsf{C}_{n}$
that split over a quadratic extension of the base field and have good reduction at all
![]() $v\in V$
is finite (for
$v\in V$
is finite (for
![]() $K$
and
$K$
and
![]() $V$
as above). Observe that Remark 8.2 yields a similar statement for type
$V$
as above). Observe that Remark 8.2 yields a similar statement for type
![]() $\mathsf{A}_{n}$
, and the results of §9 do so for groups of type
$\mathsf{A}_{n}$
, and the results of §9 do so for groups of type
![]() $\mathsf{G}_{2}$
. Thus, it would be interesting to see whether this statement in fact extends to forms of all types that split over a quadratic extension of the base field – this would be an important test for the general problem (
$\mathsf{G}_{2}$
. Thus, it would be interesting to see whether this statement in fact extends to forms of all types that split over a quadratic extension of the base field – this would be an important test for the general problem (
9 Groups of type
 $\mathsf{G}_{2}$
$\mathsf{G}_{2}$
Let
![]() $G_{0}$
be the split group of type
$G_{0}$
be the split group of type
![]() $\mathsf{G}_{2}$
over a field
$\mathsf{G}_{2}$
over a field
![]() $K$
of characteristic
$K$
of characteristic
![]() $\neq 2$
. Then the
$\neq 2$
. Then the
![]() $K$
-isomorphism classes of
$K$
-isomorphism classes of
![]() $K$
-groups of type
$K$
-groups of type
![]() $\mathsf{G}_{2}$
are in a natural one-to-one correspondence with the elements of the (pointed) set
$\mathsf{G}_{2}$
are in a natural one-to-one correspondence with the elements of the (pointed) set
![]() $H^{1}(K,G_{0})$
. Furthermore, there is a natural map
$H^{1}(K,G_{0})$
. Furthermore, there is a natural map
that has the following explicit description: if
![]() $\unicode[STIX]{x1D709}\in H^{1}(K,G_{0})$
and the twisted group
$\unicode[STIX]{x1D709}\in H^{1}(K,G_{0})$
and the twisted group
![]() $G=_{\unicode[STIX]{x1D709}}G_{0}$
is the automorphism group of the octonion algebra
$G=_{\unicode[STIX]{x1D709}}G_{0}$
is the automorphism group of the octonion algebra
![]() $\mathbb{O}=\mathbb{O}(a,b,c)$
corresponding to a triple
$\mathbb{O}=\mathbb{O}(a,b,c)$
corresponding to a triple
![]() $(a,b,c)\in (K^{\times })^{3}$
, then
$(a,b,c)\in (K^{\times })^{3}$
, then
where for
![]() $t\in K^{\times }$
we let
$t\in K^{\times }$
we let
![]() $\unicode[STIX]{x1D712}_{t}\in H^{1}(K,\unicode[STIX]{x1D707}_{2})$
denote, by abuse of notation, the cohomology class of the usual 1-cocycle
$\unicode[STIX]{x1D712}_{t}\in H^{1}(K,\unicode[STIX]{x1D707}_{2})$
denote, by abuse of notation, the cohomology class of the usual 1-cocycle
![]() $\unicode[STIX]{x1D712}_{t}$
coming from Kummer theory. It is well-known that
$\unicode[STIX]{x1D712}_{t}$
coming from Kummer theory. It is well-known that
![]() $\unicode[STIX]{x1D706}_{K}$
is injective (cf. [Reference SerreSer97, ch. III, Appendix 2, 3.3]).
$\unicode[STIX]{x1D706}_{K}$
is injective (cf. [Reference SerreSer97, ch. III, Appendix 2, 3.3]).
Now, suppose that
![]() $K$
is equipped with a discrete valuation
$K$
is equipped with a discrete valuation
![]() $v$
such that
$v$
such that
![]() $\operatorname{char}K^{(v)}\neq 2$
. Then the automorphism group
$\operatorname{char}K^{(v)}\neq 2$
. Then the automorphism group
![]() $G$
of an octonian algebra
$G$
of an octonian algebra
![]() $\mathbb{O}$
has good reduction at
$\mathbb{O}$
has good reduction at
![]() $v$
if and only if
$v$
if and only if
![]() $\mathbb{O}$
can be represented by a triple
$\mathbb{O}$
can be represented by a triple
![]() $(a,b,c)\in (K^{\times })^{3}$
such that
$(a,b,c)\in (K^{\times })^{3}$
such that
It follows that if
![]() $G=_{\unicode[STIX]{x1D709}}G_{0}$
has good reduction at
$G=_{\unicode[STIX]{x1D709}}G_{0}$
has good reduction at
![]() $v$
, then the cocycle
$v$
, then the cocycle
![]() $\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709})\in H^{3}(K,\unicode[STIX]{x1D707}_{2})$
is unramified at
$\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709})\in H^{3}(K,\unicode[STIX]{x1D707}_{2})$
is unramified at
![]() $v$
. Now, using Corollary 6.2, we obtain the following.
$v$
. Now, using Corollary 6.2, we obtain the following.
Theorem 9.1. Let
![]() $K$
be a two-dimensional global field of characteristic
$K$
be a two-dimensional global field of characteristic
![]() $\neq 2$
, let
$\neq 2$
, let
![]() $V$
be a divisorial set of places and let
$V$
be a divisorial set of places and let
![]() $G$
be a simple algebraic
$G$
be a simple algebraic
![]() $K$
-group of type
$K$
-group of type
![]() $\mathsf{G}_{2}$
.
$\mathsf{G}_{2}$
.
(i) The number of
 $K$
-isomorphism classes of
$K$
-isomorphism classes of
 $K$
-forms
$K$
-forms
 $G^{\prime }$
having good reduction at all
$G^{\prime }$
having good reduction at all
 $v\in V$
is finite.
$v\in V$
is finite.(ii) The genus
 $\mathbf{gen}_{K}(G)$
is finite.
$\mathbf{gen}_{K}(G)$
is finite.(iii) The map
 $\unicode[STIX]{x1D703}_{G,V}:H^{1}(K,G)\longrightarrow \prod _{v\in V}H^{1}(K_{v},G)$
is proper.
$\unicode[STIX]{x1D703}_{G,V}:H^{1}(K,G)\longrightarrow \prod _{v\in V}H^{1}(K_{v},G)$
is proper.
Proof. Part (i) immediately follows from the remarks preceding the statement of the theorem and Corollary 6.2. Part (ii) is derived from part (i) and Theorem 5.2 just like Theorem 1.2 was derived from Theorem 1.1. Finally, part (iii) is derived from part (i) and the observation mentioned in § 5.2. (Alternatively, one can use the injectivity of
![]() $\unicode[STIX]{x1D706}_{K}$
and the fact that the kernel
$\unicode[STIX]{x1D706}_{K}$
and the fact that the kernel
![]() $\unicode[STIX]{x1D6FA}_{3}$
of the map
$\unicode[STIX]{x1D6FA}_{3}$
of the map
is finite, which immediately follows from the finiteness of
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
.)◻
$H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
.)◻
Next, we describe the analogues for groups of type
![]() $\mathsf{G}_{2}$
of the results of § 7.
$\mathsf{G}_{2}$
of the results of § 7.
Theorem 9.2. Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $\neq 2$
that satisfies condition
$\neq 2$
that satisfies condition
![]() $(\text{F}_{2}^{\prime })$
, let
$(\text{F}_{2}^{\prime })$
, let
![]() $K=k(C)$
be the function field of a smooth affine geometrically integral curve
$K=k(C)$
be the function field of a smooth affine geometrically integral curve
![]() $C$
over
$C$
over
![]() $k$
and let
$k$
and let
![]() $V_{0}$
be the set of places of
$V_{0}$
be the set of places of
![]() $K$
corresponding to the closed points of
$K$
corresponding to the closed points of
![]() $C$
. If
$C$
. If
![]() $G$
is a simple algebraic
$G$
is a simple algebraic
![]() $K$
-group of type
$K$
-group of type
![]() $\mathsf{G}_{2}$
, then:
$\mathsf{G}_{2}$
, then:
(i) the number of
 $K$
-isomorphism classes of
$K$
-isomorphism classes of
 $K$
-forms
$K$
-forms
 $G^{\prime }$
having good reduction at all
$G^{\prime }$
having good reduction at all
 $v\in V_{0}$
is finite;
$v\in V_{0}$
is finite;(ii) the map
 $\unicode[STIX]{x1D703}_{G,V_{0}}:H^{1}(K,G)\longrightarrow \prod _{v\in V_{0}}H^{1}(K_{v},G)$
is proper.
$\unicode[STIX]{x1D703}_{G,V_{0}}:H^{1}(K,G)\longrightarrow \prod _{v\in V_{0}}H^{1}(K_{v},G)$
is proper.
Proof. Again, part (i) follows from the discussion preceding the statement of Theorems 9.1 and 7.1. Then part (ii) follows from (i) and the observation made in [Reference Chernousov, Rapinchuk and RapinchukCRR15, Reference RapinchukRap14] that we discussed at the beginning of § 5.2. (As in the proof of Theorem 9.1, one can alternatively use the injectivity of
![]() $\unicode[STIX]{x1D706}_{K}$
in conjunction with the fact that the homomorphism
$\unicode[STIX]{x1D706}_{K}$
in conjunction with the fact that the homomorphism
has finite kernel, which is a consequence of the finiteness of
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V_{0}}$
.)◻
$H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V_{0}}$
.)◻
We now turn to a result that provides information about the genus of a group of type
![]() $\mathsf{G}_{2}$
over the fields of rational functions over global fields.
$\mathsf{G}_{2}$
over the fields of rational functions over global fields.
Theorem 9.3. Let
![]() $K=k(x_{1},\ldots ,x_{r})$
the field of rational functions in
$K=k(x_{1},\ldots ,x_{r})$
the field of rational functions in
![]() $r$
variables over a global field
$r$
variables over a global field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
![]() $G$
be a simple
$G$
be a simple
![]() $K$
-group of type
$K$
-group of type
![]() $\mathsf{G}_{2}$
.
$\mathsf{G}_{2}$
.
(i) If
 $r=1$
, then the genus
$r=1$
, then the genus
 $\mathbf{gen}_{K}(G)$
reduces to a single element.
$\mathbf{gen}_{K}(G)$
reduces to a single element.(ii) The genus
 $\mathbf{gen}_{K}(G)$
is finite for any
$\mathbf{gen}_{K}(G)$
is finite for any
 $r$
.
$r$
.
The proof requires more detailed information about the ‘residues’ of groups of type
![]() $\mathsf{G}_{2}$
at places of bad reduction. Thus, let
$\mathsf{G}_{2}$
at places of bad reduction. Thus, let
![]() $K$
be a field with a discrete valuation
$K$
be a field with a discrete valuation
![]() $v$
such that the residue field
$v$
such that the residue field
![]() $\mathscr{K}=K^{(v)}$
is of characteristic
$\mathscr{K}=K^{(v)}$
is of characteristic
![]() $\neq 2$
and let
$\neq 2$
and let
be the corresponding residue map. It is well-known (cf. [Reference Gille and SzamuelyGS06, §§ 7.1 and 7.5]) that any ‘decomposable’ element
![]() $\unicode[STIX]{x1D712}_{a}\,\cup \,\unicode[STIX]{x1D712}_{b}\,\cup \,\unicode[STIX]{x1D712}_{c}$
, where
$\unicode[STIX]{x1D712}_{a}\,\cup \,\unicode[STIX]{x1D712}_{b}\,\cup \,\unicode[STIX]{x1D712}_{c}$
, where
![]() $a,b,c\in K^{\times }$
(and by the Bloch–Kato conjecture such elements generate
$a,b,c\in K^{\times }$
(and by the Bloch–Kato conjecture such elements generate
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})$
) can be written in the form
$H^{3}(K,\unicode[STIX]{x1D707}_{2})$
) can be written in the form
![]() $\unicode[STIX]{x1D712}_{a^{\prime }}\,\cup \,\unicode[STIX]{x1D712}_{b^{\prime }}\,\cup \,\unicode[STIX]{x1D712}_{c^{\prime }}$
with
$\unicode[STIX]{x1D712}_{a^{\prime }}\,\cup \,\unicode[STIX]{x1D712}_{b^{\prime }}\,\cup \,\unicode[STIX]{x1D712}_{c^{\prime }}$
with
![]() $v(a^{\prime })=v(b^{\prime })=0$
and
$v(a^{\prime })=v(b^{\prime })=0$
and
![]() $v(c^{\prime })=0$
or
$v(c^{\prime })=0$
or
![]() $1$
, and that on elements of this form the residue map is given by
$1$
, and that on elements of this form the residue map is given by
where
![]() $\bar{a},\bar{b}$
are the images of
$\bar{a},\bar{b}$
are the images of
![]() $a,b$
in
$a,b$
in
![]() $\mathscr{K}^{\times }$
. We define the quaternion algebra corresponding to the residue of such an element to be the matrix algebra
$\mathscr{K}^{\times }$
. We define the quaternion algebra corresponding to the residue of such an element to be the matrix algebra
![]() $M_{2}(\mathscr{K})$
in the first case and the standard quaternion algebra
$M_{2}(\mathscr{K})$
in the first case and the standard quaternion algebra
![]() $((\bar{a},\bar{b})/\mathscr{K})$
in the second. We will assume henceforth that
$((\bar{a},\bar{b})/\mathscr{K})$
in the second. We will assume henceforth that
![]() $\mathscr{K}$
is finitely generated.
$\mathscr{K}$
is finitely generated.
Lemma 9.4. Given
![]() $\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in H^{1}(K,G_{0})$
, we denote by
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in H^{1}(K,G_{0})$
, we denote by
![]() $G_{i}=_{\unicode[STIX]{x1D709}_{i}}G_{0}$
the corresponding group and set
$G_{i}=_{\unicode[STIX]{x1D709}_{i}}G_{0}$
the corresponding group and set
![]() $\mathscr{D}_{i}$
to be the quaternion algebra over
$\mathscr{D}_{i}$
to be the quaternion algebra over
![]() $\mathscr{K}$
corresponding to the residue
$\mathscr{K}$
corresponding to the residue
![]() $\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{i}))$
for
$\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{i}))$
for
![]() $i=1,2$
. If
$i=1,2$
. If
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
have the same isomorphism classes of maximal
$G_{2}$
have the same isomorphism classes of maximal
![]() $K$
-tori, then
$K$
-tori, then
![]() $\mathscr{D}_{1}$
and
$\mathscr{D}_{1}$
and
![]() $\mathscr{D}_{2}$
have the same isomorphism classes of maximal étale
$\mathscr{D}_{2}$
have the same isomorphism classes of maximal étale
![]() $\mathscr{K}$
-subalgebras.
$\mathscr{K}$
-subalgebras.
Proof. Let
![]() $\mathbb{O}_{i}$
be an octonian
$\mathbb{O}_{i}$
be an octonian
![]() $K$
-algebra such that
$K$
-algebra such that
![]() $G_{i}=\operatorname{Aut}(\mathbb{O}_{i})$
for
$G_{i}=\operatorname{Aut}(\mathbb{O}_{i})$
for
![]() $i=1,2$
. Suppose
$i=1,2$
. Suppose
![]() $\mathbb{O}_{i}$
can be represented by a triple
$\mathbb{O}_{i}$
can be represented by a triple
![]() $(a_{i},b_{i},c_{i})\in (K^{\times })^{3}$
such that
$(a_{i},b_{i},c_{i})\in (K^{\times })^{3}$
such that
![]() $v(a_{i})=v(b_{i})=v(c_{i})=0$
. Then
$v(a_{i})=v(b_{i})=v(c_{i})=0$
. Then
![]() $G_{i}$
has a good reduction at
$G_{i}$
has a good reduction at
![]() $v$
. As
$v$
. As
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
have the same isomorphism classes of maximal
$G_{2}$
have the same isomorphism classes of maximal
![]() $K$
-tori, by Theorem 5.2 the group
$K$
-tori, by Theorem 5.2 the group
![]() $G_{3-i}$
also has good reduction at
$G_{3-i}$
also has good reduction at
![]() $v$
. This means that
$v$
. This means that
![]() $\mathbb{O}_{3-i}$
can also be represented by a triple
$\mathbb{O}_{3-i}$
can also be represented by a triple
![]() $(a_{3-i},b_{3-i},c_{3-i})\in (K^{\times })^{3}$
such that
$(a_{3-i},b_{3-i},c_{3-i})\in (K^{\times })^{3}$
such that
![]() $v(a_{3-i})=v(b_{3-i})=v(c_{3-i})=0$
. In this case, both residues
$v(a_{3-i})=v(b_{3-i})=v(c_{3-i})=0$
. In this case, both residues
![]() $\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{1}))$
and
$\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{1}))$
and
![]() $\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{2}))$
are trivial, so our claim is obvious. It remains to consider the case where
$\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{2}))$
are trivial, so our claim is obvious. It remains to consider the case where
![]() $\mathbb{O}_{i}$
is represented by a triple
$\mathbb{O}_{i}$
is represented by a triple
![]() $(a_{i},b_{i},c_{i})\in (K^{\times })^{3}$
satisfying
$(a_{i},b_{i},c_{i})\in (K^{\times })^{3}$
satisfying
for
![]() $i=1,2$
. Then
$i=1,2$
. Then
![]() $\mathscr{D}_{i}$
is the quaternion algebra
$\mathscr{D}_{i}$
is the quaternion algebra
![]() $((\bar{a}_{i},\bar{b}_{i})/\mathscr{K})$
where
$((\bar{a}_{i},\bar{b}_{i})/\mathscr{K})$
where
![]() $\bar{a}_{i},\bar{b}_{i}$
are the images of
$\bar{a}_{i},\bar{b}_{i}$
are the images of
![]() $a_{i},b_{i}$
in
$a_{i},b_{i}$
in
![]() $\mathscr{K}^{\times }$
. To prove that
$\mathscr{K}^{\times }$
. To prove that
![]() $\mathscr{D}_{1}$
and
$\mathscr{D}_{1}$
and
![]() $\mathscr{D}_{2}$
have the same maximal étale subalgebras, it suffices to prove the following:
$\mathscr{D}_{2}$
have the same maximal étale subalgebras, it suffices to prove the following:
Let
![]() $\mathscr{L}$
be an extension of
$\mathscr{L}$
be an extension of
![]() $\mathscr{K}$
of degree
$\mathscr{K}$
of degree
![]() ${\leqslant}2$
. Then
${\leqslant}2$
. Then
![]() $\mathscr{L}$
splits
$\mathscr{L}$
splits
![]() $\mathscr{D}_{1}$
if and only if it splits
$\mathscr{D}_{1}$
if and only if it splits
![]() $\mathscr{D}_{2}$
.
$\mathscr{D}_{2}$
.
Let
![]() $L$
be the unramified extension of
$L$
be the unramified extension of
![]() $K_{v}$
with the residue field
$K_{v}$
with the residue field
![]() $\mathscr{L}$
. We have
$\mathscr{L}$
. We have
where
![]() $\hat{\unicode[STIX]{x2202}}_{v}:H^{3}(K_{v},\unicode[STIX]{x1D707}_{2})\rightarrow H^{2}(\mathscr{K},\unicode[STIX]{x1D707}_{2})$
is the residue map and
$\hat{\unicode[STIX]{x2202}}_{v}:H^{3}(K_{v},\unicode[STIX]{x1D707}_{2})\rightarrow H^{2}(\mathscr{K},\unicode[STIX]{x1D707}_{2})$
is the residue map and
![]() $\hat{\unicode[STIX]{x1D709}}_{i}$
is the image of
$\hat{\unicode[STIX]{x1D709}}_{i}$
is the image of
![]() $\unicode[STIX]{x1D709}_{i}$
under the restriction map
$\unicode[STIX]{x1D709}_{i}$
under the restriction map
![]() $H^{1}(K,G_{0})\rightarrow H^{1}(K_{v},G_{0})$
. As residue maps commute with restriction maps for unramified extensions, we further obtain
$H^{1}(K,G_{0})\rightarrow H^{1}(K_{v},G_{0})$
. As residue maps commute with restriction maps for unramified extensions, we further obtain
where
![]() $\hat{\unicode[STIX]{x2202}}_{v}^{L}:H^{3}(L,\unicode[STIX]{x1D707}_{2})\rightarrow H^{2}(\mathscr{L},\unicode[STIX]{x1D707}_{2})$
is the residue map for
$\hat{\unicode[STIX]{x2202}}_{v}^{L}:H^{3}(L,\unicode[STIX]{x1D707}_{2})\rightarrow H^{2}(\mathscr{L},\unicode[STIX]{x1D707}_{2})$
is the residue map for
![]() $L$
(see [Reference Colliot-ThélèneCol95, Proposition 3.3.1]).
$L$
(see [Reference Colliot-ThélèneCol95, Proposition 3.3.1]).
Now, suppose that
![]() $\mathscr{L}$
splits
$\mathscr{L}$
splits
![]() $\mathscr{D}_{i}$
, i.e. the quaternion algebra
$\mathscr{D}_{i}$
, i.e. the quaternion algebra
![]() $((\bar{a}_{i},\bar{b}_{i})/\mathscr{L})$
is trivial. Then it follows from Hensel’s lemma that the quaternion algebra
$((\bar{a}_{i},\bar{b}_{i})/\mathscr{L})$
is trivial. Then it follows from Hensel’s lemma that the quaternion algebra
![]() $((a_{i},b_{i})/L)$
is also trivial, and therefore the group
$((a_{i},b_{i})/L)$
is also trivial, and therefore the group
![]() $G_{i}$
becomes split over
$G_{i}$
becomes split over
![]() $L$
. Define a two-dimensional
$L$
. Define a two-dimensional
![]() $K_{v}$
-torus
$K_{v}$
-torus
![]() $T$
to be
$T$
to be
(where, as usual,
![]() $\text{R}_{L/K_{v}}^{(1)}(\mathbb{G}_{m})$
denotes the corresponding norm torus). Then
$\text{R}_{L/K_{v}}^{(1)}(\mathbb{G}_{m})$
denotes the corresponding norm torus). Then
![]() $T$
is isomorphic to a maximal
$T$
is isomorphic to a maximal
![]() $K_{v}$
-torus of
$K_{v}$
-torus of
![]() $G_{i}$
. As
$G_{i}$
. As
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
have the same isomorphism classes of maximal
$G_{2}$
have the same isomorphism classes of maximal
![]() $K$
-tori, they also have the same isomorphism classes of maximal
$K$
-tori, they also have the same isomorphism classes of maximal
![]() $K_{v}$
-tori (see [Reference Rapinchuk and RapinchukRR10, Remark 2.2]). Thus,
$K_{v}$
-tori (see [Reference Rapinchuk and RapinchukRR10, Remark 2.2]). Thus,
![]() $T$
is isomorphic to a maximal
$T$
is isomorphic to a maximal
![]() $K_{v}$
-torus of
$K_{v}$
-torus of
![]() $G_{3-i}$
as well. Then the cocycle
$G_{3-i}$
as well. Then the cocycle
![]() $\operatorname{Res}_{L/K_{v}}(\hat{\unicode[STIX]{x1D709}}_{3-i})$
is trivial, so applying (10) with
$\operatorname{Res}_{L/K_{v}}(\hat{\unicode[STIX]{x1D709}}_{3-i})$
is trivial, so applying (10) with
![]() $i$
replaced by
$i$
replaced by
![]() $3-i$
, we obtain that
$3-i$
, we obtain that
![]() $\operatorname{Res}_{\mathscr{L}/\mathscr{K}}(\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{3-i})))$
is trivial, i.e.
$\operatorname{Res}_{\mathscr{L}/\mathscr{K}}(\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{3-i})))$
is trivial, i.e.
![]() $\mathscr{L}$
splits
$\mathscr{L}$
splits
![]() $\mathscr{L}_{3-i}$
, as required.◻
$\mathscr{L}_{3-i}$
, as required.◻
Corollary 9.5. Assume that the residue field
![]() $\mathscr{K}=K^{(v)}$
is finitely generated and has the following property:
$\mathscr{K}=K^{(v)}$
is finitely generated and has the following property:
-
 $(\star )$
$(\star )$
If
 $D_{1}$
and
$D_{1}$
and
 $D_{2}$
are central quaternion algebras over
$D_{2}$
are central quaternion algebras over
 $\mathscr{K}$
that have the same maximal étale subalgebras, then
$\mathscr{K}$
that have the same maximal étale subalgebras, then
 $D_{1}\simeq D_{2}$
.
$D_{1}\simeq D_{2}$
.
If
![]() $\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in H^{1}(K,G_{0})$
are such that the corresponding groups
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in H^{1}(K,G_{0})$
are such that the corresponding groups
![]() $G_{i}=_{\unicode[STIX]{x1D709}_{i}}G_{0}$
for
$G_{i}=_{\unicode[STIX]{x1D709}_{i}}G_{0}$
for
![]() $i=1,2$
have the same isomorphism classes of maximal
$i=1,2$
have the same isomorphism classes of maximal
![]() $K$
-tori, then
$K$
-tori, then
![]() $\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{1}))=\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{2}))$
.
$\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{1}))=\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}_{2}))$
.
Proof of Theorem 9.3(i).
We will prove a more general result. To formulate it, in addition to property
![]() $(\star )$
of a field
$(\star )$
of a field
![]() $\mathscr{K}$
from Corollary 9.5, we need to introduce the following property of a field
$\mathscr{K}$
from Corollary 9.5, we need to introduce the following property of a field
![]() $k$
.
$k$
.
-
 $(\star \star )$
$(\star \star )$
If
 $G_{1}$
and
$G_{1}$
and
 $G_{2}$
are two
$G_{2}$
are two
 $k$
-groups of type
$k$
-groups of type
 $\mathsf{G}_{2}$
having the same maximal tori, then
$\mathsf{G}_{2}$
having the same maximal tori, then  $$\begin{eqnarray}G_{1}\simeq G_{2}\quad \text{over }k.\end{eqnarray}$$
$$\begin{eqnarray}G_{1}\simeq G_{2}\quad \text{over }k.\end{eqnarray}$$
Theorem 9.6. Assume that a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq 2$
satisfies
$\neq 2$
satisfies
![]() $(\star \star )$
and that any finite extension
$(\star \star )$
and that any finite extension
![]() $\ell$
of
$\ell$
of
![]() $k$
satisfies
$k$
satisfies
![]() $(\star )$
. Then the field of rational functions
$(\star )$
. Then the field of rational functions
![]() $K=k(x)$
satisfies
$K=k(x)$
satisfies
![]() $(\star \star )$
.
$(\star \star )$
.
We note that the mere fact that
![]() $k$
satisfies
$k$
satisfies
![]() $(\star )$
implies that
$(\star )$
implies that
![]() $K=k(x)$
also satisfies
$K=k(x)$
also satisfies
![]() $(\star )$
; see [Reference Rapinchuk and RapinchukRR10, Theorem A]. Furthermore, it is well-known that global fields satisfy both conditions
$(\star )$
; see [Reference Rapinchuk and RapinchukRR10, Theorem A]. Furthermore, it is well-known that global fields satisfy both conditions
![]() $(\star )$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR13, 3.6]) and
$(\star )$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR13, 3.6]) and
![]() $(\star \star )$
(cf. [Reference Prasad and RapinchukPR09, Theorem 7.5]), so Theorem 9.6 immediately yields the assertion of Theorem 9.3(i).
$(\star \star )$
(cf. [Reference Prasad and RapinchukPR09, Theorem 7.5]), so Theorem 9.6 immediately yields the assertion of Theorem 9.3(i).
To prove Theorem 9.6, we let
![]() $V$
denote the set of all places of
$V$
denote the set of all places of
![]() $K=k(x)$
that are trivial on
$K=k(x)$
that are trivial on
![]() $k$
(these of course correspond to the closed points of
$k$
(these of course correspond to the closed points of
![]() $\mathbb{P}_{k}^{1}$
). It follows from the above remarks that we may assume the field
$\mathbb{P}_{k}^{1}$
). It follows from the above remarks that we may assume the field
![]() $k$
to be infinite. Now, let
$k$
to be infinite. Now, let
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
, and let
$G^{\prime }\in \mathbf{gen}_{K}(G)$
, and let
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }\in H^{1}(K,G_{0})$
be the corresponding cocycles (so that
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime }\in H^{1}(K,G_{0})$
be the corresponding cocycles (so that
![]() $G=_{\unicode[STIX]{x1D709}}G_{0}$
and
$G=_{\unicode[STIX]{x1D709}}G_{0}$
and
![]() $G^{\prime }=_{\unicode[STIX]{x1D709}^{\prime }}G_{0}$
). For any
$G^{\prime }=_{\unicode[STIX]{x1D709}^{\prime }}G_{0}$
). For any
![]() $v\in V$
, since the residue field
$v\in V$
, since the residue field
![]() $K^{(v)}$
is a finite extension of
$K^{(v)}$
is a finite extension of
![]() $k$
, hence satisfies
$k$
, hence satisfies
![]() $(\star )$
by our assumption, we conclude from Corollary 9.5 that
$(\star )$
by our assumption, we conclude from Corollary 9.5 that
Thus,
However, according to Faddeev’s sequence (cf. [Reference Garibaldi, Merkurjev and SerreGMS03, ch. III, § 9] and [Reference Gille and SzamuelyGS06, 6.9]), the natural (inflation) map
![]() $\unicode[STIX]{x1D704}:H^{3}(k,\unicode[STIX]{x1D707}_{2})\rightarrow H^{3}(K,\unicode[STIX]{x1D707}_{2})$
identifies
$\unicode[STIX]{x1D704}:H^{3}(k,\unicode[STIX]{x1D707}_{2})\rightarrow H^{3}(K,\unicode[STIX]{x1D707}_{2})$
identifies
![]() $H^{3}(k,\unicode[STIX]{x1D707}_{2})$
with the unramified group
$H^{3}(k,\unicode[STIX]{x1D707}_{2})$
with the unramified group
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
. Then in terms of this identification,
$H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}$
. Then in terms of this identification,
![]() $\unicode[STIX]{x1D701}$
in (11) belongs to
$\unicode[STIX]{x1D701}$
in (11) belongs to
![]() $H^{3}(k,\unicode[STIX]{x1D707}_{2})$
. We would like to show that actually
$H^{3}(k,\unicode[STIX]{x1D707}_{2})$
. We would like to show that actually
![]() $\unicode[STIX]{x1D701}=1$
, which will imply that
$\unicode[STIX]{x1D701}=1$
, which will imply that
![]() $G^{\prime }\simeq G$
.
$G^{\prime }\simeq G$
.
As
![]() $k$
is infinite, we can pick
$k$
is infinite, we can pick
![]() $v\in V$
so that
$v\in V$
so that
![]() $K^{(v)}=k$
and
$K^{(v)}=k$
and
![]() $G$
and
$G$
and
![]() $G^{\prime }$
have smooth reductions
$G^{\prime }$
have smooth reductions
![]() $\text{}\underline{G}^{(v)}$
and
$\text{}\underline{G}^{(v)}$
and
![]() ${\text{}\underline{G}^{\prime }}^{(v)}$
at
${\text{}\underline{G}^{\prime }}^{(v)}$
at
![]() $v$
. We have the natural map
$v$
. We have the natural map
(defined on the
![]() $v$
-unramified part) such that
$v$
-unramified part) such that
![]() $\unicode[STIX]{x1D716}_{v}\circ \unicode[STIX]{x1D704}=\operatorname{id}$
. Clearly, the images under
$\unicode[STIX]{x1D716}_{v}\circ \unicode[STIX]{x1D704}=\operatorname{id}$
. Clearly, the images under
![]() $\unicode[STIX]{x1D706}_{k}$
of the cocycles that correspond to
$\unicode[STIX]{x1D706}_{k}$
of the cocycles that correspond to
![]() $\text{}\underline{G}^{(v)}$
and
$\text{}\underline{G}^{(v)}$
and
![]() ${\text{}\underline{G}^{\prime }}^{(v)}$
coincide with
${\text{}\underline{G}^{\prime }}^{(v)}$
coincide with
![]() $\unicode[STIX]{x1D716}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}))$
and
$\unicode[STIX]{x1D716}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}))$
and
![]() $\unicode[STIX]{x1D716}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}^{\prime }))$
, respectively. Now, by the last assertion of Theorem 5.2, the groups
$\unicode[STIX]{x1D716}_{v}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}^{\prime }))$
, respectively. Now, by the last assertion of Theorem 5.2, the groups
![]() $\text{}\underline{G}^{(v)}$
and
$\text{}\underline{G}^{(v)}$
and
![]() ${\text{}\underline{G}^{\prime }}^{(v)}$
have the same isomorphism classes of maximal
${\text{}\underline{G}^{\prime }}^{(v)}$
have the same isomorphism classes of maximal
![]() $k$
-tori, so because
$k$
-tori, so because
![]() $k$
is assumed to satisfy
$k$
is assumed to satisfy
![]() $(\star \star )$
, we conclude that
$(\star \star )$
, we conclude that
![]() $\text{}\underline{G}^{(v)}\simeq {\text{}\underline{G}^{\prime }}^{(v)}$
. This means that
$\text{}\underline{G}^{(v)}\simeq {\text{}\underline{G}^{\prime }}^{(v)}$
. This means that
Applying
![]() $\unicode[STIX]{x1D716}_{v}$
to (11) and comparing the result with (12), we obtain that
$\unicode[STIX]{x1D716}_{v}$
to (11) and comparing the result with (12), we obtain that
![]() $\unicode[STIX]{x1D716}_{v}(\unicode[STIX]{x1D701})=1$
, and consequently
$\unicode[STIX]{x1D716}_{v}(\unicode[STIX]{x1D701})=1$
, and consequently
![]() $\unicode[STIX]{x1D701}=1$
, as required.◻
$\unicode[STIX]{x1D701}=1$
, as required.◻
Proof of Theorem 9.3(ii).
We view
![]() $K$
as the field of rational functions on
$K$
as the field of rational functions on
![]() $\mathbb{P}_{k}^{r}$
, and let
$\mathbb{P}_{k}^{r}$
, and let
![]() $V$
be the set of discrete valuations on
$V$
be the set of discrete valuations on
![]() $K$
associated with the prime divisors. Pick a finite subset
$K$
associated with the prime divisors. Pick a finite subset
![]() $V_{0}=\{v_{1},\ldots ,v_{d}\}$
of
$V_{0}=\{v_{1},\ldots ,v_{d}\}$
of
![]() $V$
so that
$V$
so that
![]() $G$
has a good reduction at all
$G$
has a good reduction at all
![]() $v\in V\setminus V_{0}$
. For each
$v\in V\setminus V_{0}$
. For each
![]() $i=1,\ldots ,d$
, we let
$i=1,\ldots ,d$
, we let
![]() $\mathscr{D}_{i}$
denote the quaternion algebra over the residue field
$\mathscr{D}_{i}$
denote the quaternion algebra over the residue field
![]() $\mathscr{K}_{i}=K^{(v_{i})}$
that corresponds to the residue
$\mathscr{K}_{i}=K^{(v_{i})}$
that corresponds to the residue
![]() $\unicode[STIX]{x2202}_{v_{i}}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}))$
, where
$\unicode[STIX]{x2202}_{v_{i}}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}))$
, where
![]() $\unicode[STIX]{x1D709}\in H^{1}(K,G_{0})$
is such that
$\unicode[STIX]{x1D709}\in H^{1}(K,G_{0})$
is such that
![]() $G=_{\unicode[STIX]{x1D709}}G_{0}$
. Given any other
$G=_{\unicode[STIX]{x1D709}}G_{0}$
. Given any other
![]() $K$
-group
$K$
-group
![]() $G^{\prime }$
of type
$G^{\prime }$
of type
![]() $\mathsf{G}_{2}$
, we set
$\mathsf{G}_{2}$
, we set
![]() $\unicode[STIX]{x1D709}^{\prime }=\unicode[STIX]{x1D709}(G^{\prime })$
to be the cohomology class in
$\unicode[STIX]{x1D709}^{\prime }=\unicode[STIX]{x1D709}(G^{\prime })$
to be the cohomology class in
![]() $H^{1}(K,G_{0})$
such that
$H^{1}(K,G_{0})$
such that
![]() $G^{\prime }=_{\unicode[STIX]{x1D709}^{\prime }}G_{0}$
, and for
$G^{\prime }=_{\unicode[STIX]{x1D709}^{\prime }}G_{0}$
, and for
![]() $i=1,\ldots ,d,$
denote by
$i=1,\ldots ,d,$
denote by
![]() $\mathscr{D}_{i}^{\prime }=\mathscr{D}_{i}(G^{\prime })$
the quaternion algebra corresponding to the residue
$\mathscr{D}_{i}^{\prime }=\mathscr{D}_{i}(G^{\prime })$
the quaternion algebra corresponding to the residue
![]() $\unicode[STIX]{x2202}_{v_{i}}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}^{\prime }))$
. Then Lemma 9.4 tells us that the correspondence
$\unicode[STIX]{x2202}_{v_{i}}(\unicode[STIX]{x1D706}_{K}(\unicode[STIX]{x1D709}^{\prime }))$
. Then Lemma 9.4 tells us that the correspondence
![]() $G^{\prime }\mapsto (\mathscr{D}_{i}^{\prime })$
gives a map
$G^{\prime }\mapsto (\mathscr{D}_{i}^{\prime })$
gives a map
where the genus
![]() $\mathbf{gen}_{\mathscr{K}}(\mathscr{D})$
of a central quaternion algebra
$\mathbf{gen}_{\mathscr{K}}(\mathscr{D})$
of a central quaternion algebra
![]() $\mathscr{D}$
over a field
$\mathscr{D}$
over a field
![]() $\mathscr{K}$
(of characteristic
$\mathscr{K}$
(of characteristic
![]() $\neq 2$
) is defined to be the set of the Brauer classes
$\neq 2$
) is defined to be the set of the Brauer classes
![]() $[\mathscr{D}^{\prime }]$
of central quaternion
$[\mathscr{D}^{\prime }]$
of central quaternion
![]() $\mathscr{K}$
-algebras
$\mathscr{K}$
-algebras
![]() $\mathscr{D}^{\prime }$
having the same maximal étale subalgebras as
$\mathscr{D}^{\prime }$
having the same maximal étale subalgebras as
![]() $\mathscr{D}$
; see [Reference Chernousov, Rapinchuk and RapinchukCRR15, Reference Chernousov, Rapinchuk and RapinchukCRR16a] for the details. As each genus
$\mathscr{D}$
; see [Reference Chernousov, Rapinchuk and RapinchukCRR15, Reference Chernousov, Rapinchuk and RapinchukCRR16a] for the details. As each genus
![]() $\mathbf{gen}_{\mathscr{K}_{i}}(\mathscr{D}_{i})$
is finite [Reference Chernousov, Rapinchuk and RapinchukCRR15], to prove that
$\mathbf{gen}_{\mathscr{K}_{i}}(\mathscr{D}_{i})$
is finite [Reference Chernousov, Rapinchuk and RapinchukCRR15], to prove that
![]() $\mathbf{gen}_{K}(G)$
is finite, it suffices to show that each fiber
$\mathbf{gen}_{K}(G)$
is finite, it suffices to show that each fiber
![]() $\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G^{\prime }))$
for
$\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G^{\prime }))$
for
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
is finite. For this we note that Theorem 5.2 implies that for any
$G^{\prime }\in \mathbf{gen}_{K}(G)$
is finite. For this we note that Theorem 5.2 implies that for any
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
and any
$G^{\prime }\in \mathbf{gen}_{K}(G)$
and any
![]() $v\in V\setminus V_{0}$
, the residue
$v\in V\setminus V_{0}$
, the residue
![]() $\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(G^{\prime }))$
is trivial. Consequently, for any
$\unicode[STIX]{x2202}_{v}(\unicode[STIX]{x1D706}_{K}(G^{\prime }))$
is trivial. Consequently, for any
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
, any
$G^{\prime }\in \mathbf{gen}_{K}(G)$
, any
![]() $G^{\prime \prime }\in \unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G^{\prime }))$
, and corresponding cocycles
$G^{\prime \prime }\in \unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G^{\prime }))$
, and corresponding cocycles
![]() $\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709}^{\prime \prime }$
, we have
$\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709}^{\prime \prime }$
, we have
However, from Faddeev’s sequence, we again see that in our situation
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}=H^{3}(k,\unicode[STIX]{x1D707}_{2})$
(cf. [Reference Garibaldi, Merkurjev and SerreGMS03, Theorem 10.1]). As
$H^{3}(K,\unicode[STIX]{x1D707}_{2})_{V}=H^{3}(k,\unicode[STIX]{x1D707}_{2})$
(cf. [Reference Garibaldi, Merkurjev and SerreGMS03, Theorem 10.1]). As
![]() $k$
is a global field, the latter group is finite by Poitou–Tate, so, from the injectivity of
$k$
is a global field, the latter group is finite by Poitou–Tate, so, from the injectivity of
![]() $\unicode[STIX]{x1D706}_{K}$
, we obtain the finiteness of the fibers
$\unicode[STIX]{x1D706}_{K}$
, we obtain the finiteness of the fibers
![]() $\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G^{\prime }))$
for
$\unicode[STIX]{x1D70C}^{-1}(\unicode[STIX]{x1D70C}(G^{\prime }))$
for
![]() $G^{\prime }\in \mathbf{gen}_{K}(G)$
, and hence the finiteness of
$G^{\prime }\in \mathbf{gen}_{K}(G)$
, and hence the finiteness of
![]() $\mathbf{gen}_{K}(G)$
.◻
$\mathbf{gen}_{K}(G)$
.◻
Appendix A An alternative proof of Theorem 6.1 in characteristic zero
Let
![]() $K$
be a two-dimensional global field of characteristic zero. Take any smooth geometrically integral affine curve
$K$
be a two-dimensional global field of characteristic zero. Take any smooth geometrically integral affine curve
![]() $C$
over a number field
$C$
over a number field
![]() $k$
such that
$k$
such that
![]() $K=k(C)$
, and let
$K=k(C)$
, and let
![]() $V_{0}$
denote the set of discrete valuations of
$V_{0}$
denote the set of discrete valuations of
![]() $K$
corresponding to the closed points of
$K$
corresponding to the closed points of
![]() $C$
. Furthermore, we can pick a finite subset
$C$
. Furthermore, we can pick a finite subset
![]() $S\subset V^{k}$
containing all archimedean places so that there exists a model
$S\subset V^{k}$
containing all archimedean places so that there exists a model
![]() ${\mathcal{C}}$
of
${\mathcal{C}}$
of
![]() $C$
over the ring of
$C$
over the ring of
![]() $S$
-integers
$S$
-integers
![]() ${\mathcal{O}}_{k,S}$
that has good reduction at all
${\mathcal{O}}_{k,S}$
that has good reduction at all
![]() $v\in V^{k}\setminus S$
. Then every such
$v\in V^{k}\setminus S$
. Then every such
![]() $v$
has a canonical extension
$v$
has a canonical extension
![]() $\tilde{v}$
to
$\tilde{v}$
to
![]() $K$
defined by
$K$
defined by
![]() ${\mathcal{C}}$
, and we let
${\mathcal{C}}$
, and we let
![]() $V_{1}=\{\tilde{v}\mid v\in V^{k}\setminus S\}$
. It is easy to see that any divisorial set of places of
$V_{1}=\{\tilde{v}\mid v\in V^{k}\setminus S\}$
. It is easy to see that any divisorial set of places of
![]() $K$
contains
$K$
contains
![]() $V_{0}\cup V_{1}$
for a suitable choice of
$V_{0}\cup V_{1}$
for a suitable choice of
![]() $C$
,
$C$
,
![]() $S$
and
$S$
and
![]() ${\mathcal{C}}$
. Thus, it is enough to prove the following.
${\mathcal{C}}$
. Thus, it is enough to prove the following.
Theorem A.1. Set
![]() $V=V_{0}\cup V_{1}$
in the above notation. Let
$V=V_{0}\cup V_{1}$
in the above notation. Let
![]() $n\geqslant 1$
be an integer such that
$n\geqslant 1$
be an integer such that
![]() $S$
contains all divisors of
$S$
contains all divisors of
![]() $n$
, so that
$n$
, so that
![]() $\operatorname{char}K^{(v)}$
is prime to
$\operatorname{char}K^{(v)}$
is prime to
![]() $n$
for all
$n$
for all
![]() $v\in V$
. Then the unramified cohomology group
$v\in V$
. Then the unramified cohomology group
![]() $H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V}$
is finite.
$H^{3}(K,\unicode[STIX]{x1D707}_{n}^{\otimes 2})_{V}$
is finite.
We begin by developing some formalism that applies in a more general situation.
A.1 Two injectivity results
Let
![]() $C$
be a smooth geometrically integral curve over an arbitrary field
$C$
be a smooth geometrically integral curve over an arbitrary field
![]() $k$
and let
$k$
and let
![]() $p$
be a prime
$p$
be a prime
![]() $\neq \operatorname{char}k$
. Then for any
$\neq \operatorname{char}k$
. Then for any
![]() $n\geqslant m$
, we have the following commutative diagram of étale sheaves on
$n\geqslant m$
, we have the following commutative diagram of étale sheaves on
![]() $C$
$C$

where
![]() $[p^{\ell }]$
denotes the morphism
$[p^{\ell }]$
denotes the morphism
![]() $x\mapsto x^{p^{\ell }}$
. Passing to cohomology, we obtain the following commutative diagram
$x\mapsto x^{p^{\ell }}$
. Passing to cohomology, we obtain the following commutative diagram

where
![]() $[p^{\ell }]$
denotes multiplication by
$[p^{\ell }]$
denotes multiplication by
![]() $p^{\ell }$
. We now use the following elementary statement.
$p^{\ell }$
. We now use the following elementary statement.
Lemma A.2. Let
![]() $A$
be an Abelian group and let
$A$
be an Abelian group and let
![]() $p$
be a prime. Consider the family of Abelian groups
$p$
be a prime. Consider the family of Abelian groups
![]() $A/p^{n}A$
for
$A/p^{n}A$
for
![]() $n\geqslant 1$
with morphisms
$n\geqslant 1$
with morphisms
![]() $\unicode[STIX]{x1D70B}_{n}^{m}:A/p^{m}A\rightarrow A/p^{n}A$
for
$\unicode[STIX]{x1D70B}_{n}^{m}:A/p^{m}A\rightarrow A/p^{n}A$
for
![]() $n\geqslant m$
given by
$n\geqslant m$
given by
Then the direct limit
![]() $\underset{\longrightarrow }{\lim }(A/p^{n}A,\unicode[STIX]{x1D70B}_{n}^{m})$
can be naturally identified with
$\underset{\longrightarrow }{\lim }(A/p^{n}A,\unicode[STIX]{x1D70B}_{n}^{m})$
can be naturally identified with
![]() $A\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
.
$A\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
.
Proof. For
![]() $n\geqslant 1$
, define
$n\geqslant 1$
, define
![]() $\unicode[STIX]{x1D706}_{n}:A/p^{n}A\rightarrow A\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
by
$\unicode[STIX]{x1D706}_{n}:A/p^{n}A\rightarrow A\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
by
![]() $a+p^{n}A\mapsto a\otimes (p^{-n}+\mathbb{Z}_{p})$
. As
$a+p^{n}A\mapsto a\otimes (p^{-n}+\mathbb{Z}_{p})$
. As
this map is well-defined. Furthermore, for
![]() $n\geqslant m$
we have
$n\geqslant m$
we have
so the
![]() $\unicode[STIX]{x1D706}_{m}$
assemble into a (surjective) homomorphism
$\unicode[STIX]{x1D706}_{m}$
assemble into a (surjective) homomorphism
To construct the inverse map, we start with a map
and check that this map is well-defined and bilinear. This yields a homomorphism
which is easily seen to be the inverse of
![]() $\unicode[STIX]{x1D706}$
.◻
$\unicode[STIX]{x1D706}$
.◻
As usual, for an Abelian group
![]() $A$
and
$A$
and
![]() $n\in \mathbb{N}$
, we write
$n\in \mathbb{N}$
, we write
![]() $_{n}A=\{a\in A\mid na=0\}$
. Furthermore, for a prime
$_{n}A=\{a\in A\mid na=0\}$
. Furthermore, for a prime
![]() $p$
, we write
$p$
, we write
![]() $_{p^{\infty }}A=\{a\in A\mid p^{n}a=0\text{ for some }n\geqslant 1\}$
. If
$_{p^{\infty }}A=\{a\in A\mid p^{n}a=0\text{ for some }n\geqslant 1\}$
. If
![]() $p\neq \operatorname{char}k$
, then we set
$p\neq \operatorname{char}k$
, then we set
Taking the direct limits of the diagrams (A.1) over all
![]() $n\geqslant m$
and using Lemma A.2, we obtain the following exact sequence
$n\geqslant m$
and using Lemma A.2, we obtain the following exact sequence
which leads to our first injectivity result.
Lemma A.3. For a prime
![]() $p\neq \operatorname{char}k$
, if
$p\neq \operatorname{char}k$
, if
![]() $\operatorname{Pic}(C)\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
(in particular, if
$\operatorname{Pic}(C)\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
(in particular, if
![]() $\operatorname{Pic}(C)$
is torsion), then the canonical map
$\operatorname{Pic}(C)$
is torsion), then the canonical map
![]() $H^{2}(C,\mathbb{Q}_{p}/\mathbb{Z}_{p}(1))\longrightarrow _{p^{\infty }}\operatorname{Br}(C)$
is an isomorphism.
$H^{2}(C,\mathbb{Q}_{p}/\mathbb{Z}_{p}(1))\longrightarrow _{p^{\infty }}\operatorname{Br}(C)$
is an isomorphism.
In particular, if
![]() $k$
is a finite field and
$k$
is a finite field and
![]() $C$
is affine, then
$C$
is affine, then
![]() $\operatorname{Pic}(C)$
is finite, and we obtain the following.
$\operatorname{Pic}(C)$
is finite, and we obtain the following.
Corollary A.4. If
![]() $k$
is a finite field and
$k$
is a finite field and
![]() $C$
is affine, then for any prime
$C$
is affine, then for any prime
![]() $p\neq \operatorname{char}k$
, the canonical map
$p\neq \operatorname{char}k$
, the canonical map
is injective.
The second injectivity result that we need is the following well-known consequence of the truth of the Bloch–Kato conjecture (cf. [Reference JannsenJan16, p. 3]).
Lemma A.5. Let
![]() $p$
be a prime
$p$
be a prime
![]() $\neq \operatorname{char}k$
. Then for all
$\neq \operatorname{char}k$
. Then for all
![]() $n\geqslant 1$
, the map
$n\geqslant 1$
, the map
induced by the natural embedding
![]() $\unicode[STIX]{x1D707}_{p^{n}}^{\otimes (\ell -1)}{\hookrightarrow}\mathbb{Q}_{p}/\mathbb{Z}_{p}(\ell -1)$
is injective for any
$\unicode[STIX]{x1D707}_{p^{n}}^{\otimes (\ell -1)}{\hookrightarrow}\mathbb{Q}_{p}/\mathbb{Z}_{p}(\ell -1)$
is injective for any
![]() $\ell \geqslant 2$
.
$\ell \geqslant 2$
.
A.2 The fundamental sequence and unramified cohomology
Let
![]() $k$
be a field equipped with a discrete valuation
$k$
be a field equipped with a discrete valuation
![]() $v$
, with valuation ring
$v$
, with valuation ring
![]() ${\mathcal{O}}_{v}$
and residue field
${\mathcal{O}}_{v}$
and residue field
![]() $k^{(v)}$
. Fix a prime
$k^{(v)}$
. Fix a prime
![]() $p\neq \operatorname{char}k^{(v)}$
. Given a smooth geometrically integral affine curve
$p\neq \operatorname{char}k^{(v)}$
. Given a smooth geometrically integral affine curve
![]() $C$
over
$C$
over
![]() $k$
, we let
$k$
, we let
![]() $\widetilde{C}$
denote the smooth geometrically integral projective curve over
$\widetilde{C}$
denote the smooth geometrically integral projective curve over
![]() $k$
that contains
$k$
that contains
![]() $C$
as an open subset. We will assume there exist models
$C$
as an open subset. We will assume there exist models
![]() ${\mathcal{C}}\subset \widetilde{{\mathcal{C}}}$
of these curves over
${\mathcal{C}}\subset \widetilde{{\mathcal{C}}}$
of these curves over
![]() ${\mathcal{O}}_{v}$
such that the associated reductions
${\mathcal{O}}_{v}$
such that the associated reductions
![]() $\text{}\underline{C}^{(v)}\subset \text{}\underline{\widetilde{C}}^{(v)}$
are smooth, geometrically integral and satisfy
$\text{}\underline{C}^{(v)}\subset \text{}\underline{\widetilde{C}}^{(v)}$
are smooth, geometrically integral and satisfy
Then the specialization map defines an isomorphism of the maximal pro-
![]() $p$
quotients of the fundamental groups:
$p$
quotients of the fundamental groups:
(with a compatible choice of base points); see [SGA1, ch. XIII].
As in our previous discussion, let
![]() $\tilde{v}$
be the extension of
$\tilde{v}$
be the extension of
![]() $v$
to
$v$
to
![]() $K=k(C)$
defined by
$K=k(C)$
defined by
![]() ${\mathcal{C}}$
. We say that an element of
${\mathcal{C}}$
. We say that an element of
![]() $H^{\ell }(C,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes d})$
is unramified at
$H^{\ell }(C,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes d})$
is unramified at
![]() $v$
if its image in
$v$
if its image in
![]() $H^{\ell }(K,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes d})$
is unramified at
$H^{\ell }(K,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes d})$
is unramified at
![]() $\tilde{v}$
in the usual sense.
$\tilde{v}$
in the usual sense.
Now, set
Considering the fundamental sequences (2) in § 4 for
![]() $d=2$
,
$d=2$
,
![]() $\ell =3$
and
$\ell =3$
and
![]() $n=p^{m}$
$n=p^{m}$
![]() $(m\geqslant 1)$
and taking their direct limit, we obtain a map
$(m\geqslant 1)$
and taking their direct limit, we obtain a map
Similarly, we obtain a map
The isomorphism (A.3) enables us to identify
with
![]() $\operatorname{Hom}(\unicode[STIX]{x1D70B}_{1}(C\otimes _{k}\bar{k}),\mathbb{Q}_{p}/\mathbb{Z}_{p}(1))$
, which in turn, according to (3), can be identified with the twist
$\operatorname{Hom}(\unicode[STIX]{x1D70B}_{1}(C\otimes _{k}\bar{k}),\mathbb{Q}_{p}/\mathbb{Z}_{p}(1))$
, which in turn, according to (3), can be identified with the twist
![]() $M(p)(-1)$
. In the sequel (in particular, in the proof of Proposition A.6), we will routinely use the identification of
$M(p)(-1)$
. In the sequel (in particular, in the proof of Proposition A.6), we will routinely use the identification of
![]() $M(p)(-1)$
with
$M(p)(-1)$
with
![]() $M^{(v)}(p)$
as Galois modules compatible with the canonical identification of the decomposition group of
$M^{(v)}(p)$
as Galois modules compatible with the canonical identification of the decomposition group of
![]() $v$
with the absolute Galois group of
$v$
with the absolute Galois group of
![]() $k^{(v)}$
. Furthermore, in view of the isomorphism (A.3), the inertia group of
$k^{(v)}$
. Furthermore, in view of the isomorphism (A.3), the inertia group of
![]() $v$
acts trivially on
$v$
acts trivially on
![]() $M_{m}(p)$
, hence on
$M_{m}(p)$
, hence on
![]() $M(p)$
. We thus have the residue map
$M(p)$
. We thus have the residue map
(obtained by taking the direct limit of the residue maps for all
![]() $M_{m}(p)$
). Our goal in this subsection is to prove that
$M_{m}(p)$
). Our goal in this subsection is to prove that
![]() $\unicode[STIX]{x1D714}_{k}^{2,3}(p)$
takes unramified classes to unramified ones. More precisely, we have the following.
$\unicode[STIX]{x1D714}_{k}^{2,3}(p)$
takes unramified classes to unramified ones. More precisely, we have the following.
Proposition A.6. Let
![]() $p$
be a prime
$p$
be a prime
![]() $\neq \operatorname{char}k^{(v)}$
and assume that
$\neq \operatorname{char}k^{(v)}$
and assume that
![]() $\operatorname{Pic}(\text{}\underline{C}^{(v)})\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
. If
$\operatorname{Pic}(\text{}\underline{C}^{(v)})\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
. If
![]() $x\in H^{3}(C,\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
is unramified at
$x\in H^{3}(C,\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
is unramified at
![]() $v$
in the sense specified above, then
$v$
in the sense specified above, then
![]() $\unicode[STIX]{x1D714}_{k}^{2,3}(p)(x)$
is also unramified at
$\unicode[STIX]{x1D714}_{k}^{2,3}(p)(x)$
is also unramified at
![]() $v$
(i.e.
$v$
(i.e.
![]() $\unicode[STIX]{x2202}_{v}^{M(p)}(\unicode[STIX]{x1D714}_{k}^{2,3}(p)(x))=0$
).
$\unicode[STIX]{x2202}_{v}^{M(p)}(\unicode[STIX]{x1D714}_{k}^{2,3}(p)(x))=0$
).
The proof critically depends on the existence of certain analogues of residue maps with nice properties in the étale cohomology of curves. Namely, let
![]() $n$
be an integer that is invertible in
$n$
be an integer that is invertible in
![]() ${\mathcal{O}}_{v}$
. Combining the localization sequence with absolute purity, one obtains the following ‘residue map’:
${\mathcal{O}}_{v}$
. Combining the localization sequence with absolute purity, one obtains the following ‘residue map’:
(see [Reference Colliot-ThélèneCol95, § 3.2] and [Reference RapinchukRap19] for the details). It should be noted that this approach in fact enables one to recover the usual residue maps in Galois cohomology, at least up to sign (cf. [Reference Jannsen, Sato and SaitoJSS14]). We need the following properties of the above maps.
Theorem A.7 [Reference RapinchukRap19].
For every
![]() $\ell \geqslant 2$
, we have commutative diagrams
$\ell \geqslant 2$
, we have commutative diagrams

and

where
![]() $\unicode[STIX]{x1D708}_{k}^{b,\ell }$
and
$\unicode[STIX]{x1D708}_{k}^{b,\ell }$
and
![]() $\unicode[STIX]{x1D708}_{k^{(v)}}^{b-1,\ell -1}$
are the natural maps induced by passage to the generic point, and the maps
$\unicode[STIX]{x1D708}_{k^{(v)}}^{b-1,\ell -1}$
are the natural maps induced by passage to the generic point, and the maps
![]() $\unicode[STIX]{x2202}_{v}^{\ell -1}$
and
$\unicode[STIX]{x2202}_{v}^{\ell -1}$
and
![]() $\unicode[STIX]{x1D6FF}_{v}^{\ell }$
coincide up to sign with the usual residue maps in Galois cohomology.
$\unicode[STIX]{x1D6FF}_{v}^{\ell }$
coincide up to sign with the usual residue maps in Galois cohomology.
Proof of Proposition A.6.
Taking the direct limits of diagrams (A.4) and (A.5) above, we obtain the following commutative diagrams

(here we use the identification of
![]() $M^{(v)}(p)$
with
$M^{(v)}(p)$
with
![]() $M(p)(-1)$
mentioned earlier), and
$M(p)(-1)$
mentioned earlier), and

where, up to sign,
![]() $\unicode[STIX]{x2202}_{v}^{2}(p)$
coincides with
$\unicode[STIX]{x2202}_{v}^{2}(p)$
coincides with
![]() $\unicode[STIX]{x2202}_{v}^{M(p)}$
, and
$\unicode[STIX]{x2202}_{v}^{M(p)}$
, and
![]() $\unicode[STIX]{x1D6FF}_{v}^{3}(p)$
with the residue map in Galois cohomology. As
$\unicode[STIX]{x1D6FF}_{v}^{3}(p)$
with the residue map in Galois cohomology. As
![]() $\text{}\underline{C}^{(v)}$
is smooth (so that
$\text{}\underline{C}^{(v)}$
is smooth (so that
![]() $\operatorname{Br}(\text{}\underline{C}^{(v)})$
injects into
$\operatorname{Br}(\text{}\underline{C}^{(v)})$
injects into
![]() $\operatorname{Br}(k^{(v)}(\text{}\underline{C}^{(v)}))$
), Lemma A.3 and our assumption that
$\operatorname{Br}(k^{(v)}(\text{}\underline{C}^{(v)}))$
), Lemma A.3 and our assumption that
![]() $\operatorname{Pic}(\text{}\underline{C}^{(v)})\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
imply that
$\operatorname{Pic}(\text{}\underline{C}^{(v)})\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
imply that
![]() $\unicode[STIX]{x1D708}_{k^{(v)}}^{1}(p)$
is injective. On the other hand, because
$\unicode[STIX]{x1D708}_{k^{(v)}}^{1}(p)$
is injective. On the other hand, because
![]() $x$
is unramified at
$x$
is unramified at
![]() $v$
, using the commutativity of (A.7), we obtain
$v$
, using the commutativity of (A.7), we obtain
Thus, we conclude that
![]() $\unicode[STIX]{x1D70C}_{v}(p)(x)=0$
. The commutativity of (A.6) then implies
$\unicode[STIX]{x1D70C}_{v}(p)(x)=0$
. The commutativity of (A.6) then implies
and the required fact follows. ◻
A.3 The unramified cohomology of
 $M(p)$
$M(p)$
Now let
![]() $k$
be a number field and let
$k$
be a number field and let
![]() $V\subset V_{f}^{k}$
be a cofinite set of (finite) places that does not contain any places lying above
$V\subset V_{f}^{k}$
be a cofinite set of (finite) places that does not contain any places lying above
![]() $p$
and such that
$p$
and such that
![]() $C$
has good reduction at all
$C$
has good reduction at all
![]() $v\in V$
. Then, as we discussed above, for every
$v\in V$
. Then, as we discussed above, for every
![]() $v\in V$
one has the residue map
$v\in V$
one has the residue map
We then define the (second) unramified cohomology of
![]() $M(p)$
by
$M(p)$
by
The following proposition is crucial for the proof of Theorem A.1.
Proposition A.8. For any
![]() $m\geqslant 1$
, the group
$m\geqslant 1$
, the group
![]() $_{p^{m}}H^{2}(k,M(p))_{V}$
is finite.
$_{p^{m}}H^{2}(k,M(p))_{V}$
is finite.
We begin with the following elementary statement.
Lemma A.9. Let
![]() $T$
be a torus over an arbitrary field
$T$
be a torus over an arbitrary field
![]() $k$
and
$k$
and
![]() $p$
be a prime
$p$
be a prime
![]() $\neq \operatorname{char}k$
. Then:
$\neq \operatorname{char}k$
. Then:
(1) for any
 $i\geqslant 2$
, the natural map
$i\geqslant 2$
, the natural map
 $H^{i}(k,_{p^{\infty }}T(\bar{k}))\rightarrow _{p^{\infty }}H^{i}(k,T)$
is an isomorphism;
$H^{i}(k,_{p^{\infty }}T(\bar{k}))\rightarrow _{p^{\infty }}H^{i}(k,T)$
is an isomorphism;(2) for
 $i=1$
, we have an exact sequence
$i=1$
, we have an exact sequence  $$\begin{eqnarray}0\rightarrow T(k)\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}\longrightarrow H^{1}(k,_{p^{\infty }}T(\bar{k}))\longrightarrow _{p^{\infty }}H^{1}(k,T)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T(k)\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}\longrightarrow H^{1}(k,_{p^{\infty }}T(\bar{k}))\longrightarrow _{p^{\infty }}H^{1}(k,T)\rightarrow 0.\end{eqnarray}$$
Proof. Let
![]() $T(p)=_{p^{\infty }}T(\bar{k})$
. The exact sequence
$T(p)=_{p^{\infty }}T(\bar{k})$
. The exact sequence
for any
![]() $i\geqslant 1$
gives rise to the following exact sequence
$i\geqslant 1$
gives rise to the following exact sequence
On the other hand, the quotient
![]() $T(\bar{k})/T(p)$
is a uniquely
$T(\bar{k})/T(p)$
is a uniquely
![]() $p$
-divisible group, implying that
$p$
-divisible group, implying that
and our claim for
![]() $i\geqslant 2$
follows. To consider the case
$i\geqslant 2$
follows. To consider the case
![]() $i=1$
, we need to show that the cokernel of the map
$i=1$
, we need to show that the cokernel of the map
is isomorphic to
![]() $T(k)\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. It is easy to see that
$T(k)\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. It is easy to see that
![]() $H^{0}(k,T(\bar{k})/T(p))=T(p)_{0}/T(p)$
, where
$H^{0}(k,T(\bar{k})/T(p))=T(p)_{0}/T(p)$
, where
Thus,
![]() $\operatorname{Coker}\unicode[STIX]{x1D6FC}\simeq T(p)_{0}/T(p)T(k)$
. However, the map
$\operatorname{Coker}\unicode[STIX]{x1D6FC}\simeq T(p)_{0}/T(p)T(k)$
. However, the map
extends to an isomorphism
![]() $T(k)\otimes _{\mathbb{Z}}\mathbb{Z}[1/p]/\mathbb{Z}\simeq T(p)_{0}/T(p)T(k)$
, and assertion (2) follows.◻
$T(k)\otimes _{\mathbb{Z}}\mathbb{Z}[1/p]/\mathbb{Z}\simeq T(p)_{0}/T(p)T(k)$
, and assertion (2) follows.◻
We now describe the structure of
![]() $M(p)$
. Let
$M(p)$
. Let
![]() $\widetilde{C}$
be the smooth projective curve over
$\widetilde{C}$
be the smooth projective curve over
![]() $k$
that contains
$k$
that contains
![]() $C$
as an open subset. We then have the following localization sequence (cf. [Reference JannsenJan89–90, p. 126]):
$C$
as an open subset. We then have the following localization sequence (cf. [Reference JannsenJan89–90, p. 126]):
 $$\begin{eqnarray}\displaystyle & & \displaystyle 0\longrightarrow H^{1}(\widetilde{C}\otimes _{k}\bar{k},\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))\longrightarrow H^{1}(C\otimes _{k}\bar{k},\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))\longrightarrow \nonumber\\ \displaystyle & & \displaystyle \quad \bigoplus _{x\in \widetilde{C}\setminus C}\operatorname{Ind}_{k(x)}^{k}(\mathbb{Q}_{p}/\mathbb{Z}_{p}(1))\stackrel{\text{tr}}{\longrightarrow }\mathbb{Q}_{p}/\mathbb{Z}_{p}(1)\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 0\longrightarrow H^{1}(\widetilde{C}\otimes _{k}\bar{k},\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))\longrightarrow H^{1}(C\otimes _{k}\bar{k},\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))\longrightarrow \nonumber\\ \displaystyle & & \displaystyle \quad \bigoplus _{x\in \widetilde{C}\setminus C}\operatorname{Ind}_{k(x)}^{k}(\mathbb{Q}_{p}/\mathbb{Z}_{p}(1))\stackrel{\text{tr}}{\longrightarrow }\mathbb{Q}_{p}/\mathbb{Z}_{p}(1)\longrightarrow 0.\end{eqnarray}$$
Let us recall that given a finite collection
![]() $\ell _{1},\ldots ,\ell _{d}$
of finite separable extensions of an arbitrary field
$\ell _{1},\ldots ,\ell _{d}$
of finite separable extensions of an arbitrary field
![]() $k$
, the
$k$
, the
![]() $k$
-torus
$k$
-torus
where
![]() $N$
is the product of the norm maps
$N$
is the product of the norm maps
![]() $N_{\ell _{i}/k}$
for the extensions
$N_{\ell _{i}/k}$
for the extensions
![]() $\ell _{i}/k$
,
$\ell _{i}/k$
,
![]() $i=1,\ldots ,d$
, is called the multi-norm torus associated with
$i=1,\ldots ,d$
, is called the multi-norm torus associated with
![]() $\ell _{1},\ldots ,\ell _{d}$
. Henceforth, we assume that for each
$\ell _{1},\ldots ,\ell _{d}$
. Henceforth, we assume that for each
![]() $x\in \widetilde{C}\setminus C$
, the residue field
$x\in \widetilde{C}\setminus C$
, the residue field
![]() $k(x)$
is a separable extension of
$k(x)$
is a separable extension of
![]() $k$
, which of course is automatically true if
$k$
, which of course is automatically true if
![]() $k$
is perfect (recall that in Theorem A.1,
$k$
is perfect (recall that in Theorem A.1,
![]() $k$
is a number field). Then (A.8) gives rise to the following exact sequence of Galois modules
$k$
is a number field). Then (A.8) gives rise to the following exact sequence of Galois modules
where
![]() $A(p)=H^{1}(\widetilde{C}\otimes _{k}\bar{k},\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
and
$A(p)=H^{1}(\widetilde{C}\otimes _{k}\bar{k},\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
and
![]() $T(p)=_{p^{\infty }}T(\bar{k})$
, with
$T(p)=_{p^{\infty }}T(\bar{k})$
, with
![]() $T$
being the multi-norm torus associated with the field extensions
$T$
being the multi-norm torus associated with the field extensions
![]() $k(x)/k$
for
$k(x)/k$
for
![]() $x\in \widetilde{C}\setminus C$
.
$x\in \widetilde{C}\setminus C$
.
Let
![]() $T$
be a torus over a field
$T$
be a torus over a field
![]() $\mathscr{K}$
that is complete with respect to a discrete valuation
$\mathscr{K}$
that is complete with respect to a discrete valuation
![]() $v$
. We call an element
$v$
. We call an element
![]() $x\in H^{i}(\mathscr{K},T)$
unramified if it lies in the image of the inflation map
$x\in H^{i}(\mathscr{K},T)$
unramified if it lies in the image of the inflation map
where
![]() $\mathscr{K}^{\text{ur}}$
is the maximal unramified extension of
$\mathscr{K}^{\text{ur}}$
is the maximal unramified extension of
![]() $\mathscr{K}$
with the valuation ring
$\mathscr{K}$
with the valuation ring
![]() $\mathscr{O}(\mathscr{K}^{\text{ur}})$
, and
$\mathscr{O}(\mathscr{K}^{\text{ur}})$
, and
![]() $T(\mathscr{O}(\mathscr{K}^{\text{ur}}))$
is the (unique) maximal bounded subgroup of
$T(\mathscr{O}(\mathscr{K}^{\text{ur}}))$
is the (unique) maximal bounded subgroup of
![]() $T(\mathscr{K}^{\text{ur}})$
. It follows from [Reference Garibaldi, Merkurjev and SerreGMS03, ch. II, § 7] that for a finite unramified
$T(\mathscr{K}^{\text{ur}})$
. It follows from [Reference Garibaldi, Merkurjev and SerreGMS03, ch. II, § 7] that for a finite unramified
![]() $\operatorname{Gal}(\overline{\mathscr{K}}/\mathscr{K})$
-module
$\operatorname{Gal}(\overline{\mathscr{K}}/\mathscr{K})$
-module
![]() $\mathscr{M}$
whose order is prime to the residue characteristic
$\mathscr{M}$
whose order is prime to the residue characteristic
![]() $\operatorname{char}\mathscr{K}^{(v)}$
, an element
$\operatorname{char}\mathscr{K}^{(v)}$
, an element
![]() $x\in H^{i}(\mathscr{K},\mathscr{M})$
is unramified as defined in § 2 if and only if it lies in the image of the inflation map
$x\in H^{i}(\mathscr{K},\mathscr{M})$
is unramified as defined in § 2 if and only if it lies in the image of the inflation map
![]() $H^{i}(\mathscr{K}^{\text{ur}}/\mathscr{K},\mathscr{M})\longrightarrow H^{i}(\mathscr{K},\mathscr{M})$
. Thus, for a finite Galois submodule
$H^{i}(\mathscr{K}^{\text{ur}}/\mathscr{K},\mathscr{M})\longrightarrow H^{i}(\mathscr{K},\mathscr{M})$
. Thus, for a finite Galois submodule
![]() $\mathscr{M}\subset T(\mathscr{K}^{\text{ur}})$
of order prime to
$\mathscr{M}\subset T(\mathscr{K}^{\text{ur}})$
of order prime to
![]() $\operatorname{char}\mathscr{K}^{(v)}$
, the natural map
$\operatorname{char}\mathscr{K}^{(v)}$
, the natural map
![]() $H^{i}(\mathscr{K},\mathscr{M})\rightarrow H^{i}(\mathscr{K},T)$
takes unramified classes to unramified ones. In addition, if the splitting field of
$H^{i}(\mathscr{K},\mathscr{M})\rightarrow H^{i}(\mathscr{K},T)$
takes unramified classes to unramified ones. In addition, if the splitting field of
![]() $T$
is unramified over
$T$
is unramified over
![]() $\mathscr{K}$
, then any finite subgroup
$\mathscr{K}$
, then any finite subgroup
![]() $\mathscr{M}\subset T(\overline{\mathscr{K}})$
of order prime to
$\mathscr{M}\subset T(\overline{\mathscr{K}})$
of order prime to
![]() $\operatorname{char}\mathscr{K}^{(v)}$
is automatically contained in
$\operatorname{char}\mathscr{K}^{(v)}$
is automatically contained in
![]() $T(\mathscr{O}(\mathscr{K}^{\text{ur}}))$
. More generally, for a torsion Galois submodule
$T(\mathscr{O}(\mathscr{K}^{\text{ur}}))$
. More generally, for a torsion Galois submodule
![]() $\mathscr{M}$
of
$\mathscr{M}$
of
![]() $T(\mathscr{O}(\mathscr{K}^{\text{ur}}))$
that does not contain elements of order divisible by the residue characteristic, an element
$T(\mathscr{O}(\mathscr{K}^{\text{ur}}))$
that does not contain elements of order divisible by the residue characteristic, an element
![]() $x\in H^{i}(\mathscr{K},\mathscr{M})$
is unramified if it comes from an unramified element in
$x\in H^{i}(\mathscr{K},\mathscr{M})$
is unramified if it comes from an unramified element in
![]() $H^{i}(\mathscr{K},\mathscr{M}^{\prime })$
for some finite Galois submodule
$H^{i}(\mathscr{K},\mathscr{M}^{\prime })$
for some finite Galois submodule
![]() $\mathscr{M}^{\prime }$
of
$\mathscr{M}^{\prime }$
of
![]() $\mathscr{M}$
.
$\mathscr{M}$
.
Now, if
![]() $T$
is a torus defined over an arbitrary field
$T$
is a torus defined over an arbitrary field
![]() $k$
with a discrete valuation
$k$
with a discrete valuation
![]() $v$
, then
$v$
, then
![]() $x\in H^{i}(k,T)$
is defined to be unramified at
$x\in H^{i}(k,T)$
is defined to be unramified at
![]() $v$
if its image in
$v$
if its image in
![]() $H^{i}(k_{v},T)$
is unramified in the sense specified above. Furthermore, for a set
$H^{i}(k_{v},T)$
is unramified in the sense specified above. Furthermore, for a set
![]() $V$
of discrete valuations of
$V$
of discrete valuations of
![]() $k$
, we let
$k$
, we let
![]() $H^{i}(k,T)_{V}$
denote the subgroup of
$H^{i}(k,T)_{V}$
denote the subgroup of
![]() $H^{i}(k,T)$
consisting of elements that are unramified at all
$H^{i}(k,T)$
consisting of elements that are unramified at all
![]() $v\in V$
. We will use these remarks to prove the following.
$v\in V$
. We will use these remarks to prove the following.
Lemma A.10. Let
![]() $k$
be a number field, let
$k$
be a number field, let
![]() $\ell _{1},\ldots ,\ell _{d}$
be finite extensions of
$\ell _{1},\ldots ,\ell _{d}$
be finite extensions of
![]() $k$
and let
$k$
and let
![]() $T$
be the multi-norm torus associated with these extensions. Suppose
$T$
be the multi-norm torus associated with these extensions. Suppose
![]() $p$
is a prime and let
$p$
is a prime and let
![]() $V\subset V_{f}^{k}$
be a cofinite set of places such that
$V\subset V_{f}^{k}$
be a cofinite set of places such that
![]() $\operatorname{char}k^{(v)}$
is prime to
$\operatorname{char}k^{(v)}$
is prime to
![]() $p$
for all
$p$
for all
![]() $v\in V$
. Then for any
$v\in V$
. Then for any
![]() $m\geqslant 1$
, the group
$m\geqslant 1$
, the group
is finite.
Proof. By shrinking
![]() $V$
if necessary, we may assume that the extensions
$V$
if necessary, we may assume that the extensions
![]() $\ell _{1},\ldots ,\ell _{d}$
are unramified at all
$\ell _{1},\ldots ,\ell _{d}$
are unramified at all
![]() $v\in V$
. Then it follows from the above discussion that the map
$v\in V$
. Then it follows from the above discussion that the map
![]() $H^{2}(k,T(p))\rightarrow H^{2}(k,T)$
takes unramified classes at
$H^{2}(k,T(p))\rightarrow H^{2}(k,T)$
takes unramified classes at
![]() $v\in V$
to unramified ones. In addition, according to Lemma A.9, this map is injective. Thus, it is enough to show that for any
$v\in V$
to unramified ones. In addition, according to Lemma A.9, this map is injective. Thus, it is enough to show that for any
![]() $n\geqslant 1$
, the group
$n\geqslant 1$
, the group
![]() $_{n}H^{2}(k,T)_{V}$
is finite. We have an exact sequence of
$_{n}H^{2}(k,T)_{V}$
is finite. We have an exact sequence of
![]() $k$
-tori
$k$
-tori
As
![]() $H^{1}(k,\mathbb{G}_{m})=1$
by Hilbert’s Satz 90, the cohomological sequence associated with (A.10) shows that the natural map
$H^{1}(k,\mathbb{G}_{m})=1$
by Hilbert’s Satz 90, the cohomological sequence associated with (A.10) shows that the natural map
![]() $H^{2}(k,T)\rightarrow H^{2}(k,T_{0})$
is injective. Thus, it is enough to establish the finiteness of
$H^{2}(k,T)\rightarrow H^{2}(k,T_{0})$
is injective. Thus, it is enough to establish the finiteness of
![]() $_{n}H^{2}(k,T_{0})_{V}$
, for which we only need to consider the case of
$_{n}H^{2}(k,T_{0})_{V}$
, for which we only need to consider the case of
![]() $T_{0}=\text{R}_{\ell /k}(\mathbb{G}_{m})$
for some finite (separable) extension
$T_{0}=\text{R}_{\ell /k}(\mathbb{G}_{m})$
for some finite (separable) extension
![]() $\ell /k$
. As above, we may assume that every
$\ell /k$
. As above, we may assume that every
![]() $v\in V$
is unramified in
$v\in V$
is unramified in
![]() $\ell /k$
. Let
$\ell /k$
. Let
![]() $V^{\prime }$
be the set of all extensions to
$V^{\prime }$
be the set of all extensions to
![]() $\ell$
of places in
$\ell$
of places in
![]() $V$
. Then the restriction of the isomorphism
$V$
. Then the restriction of the isomorphism
![]() $H^{2}(k,T_{0})\simeq H^{2}(\ell ,\mathbb{G}_{m})$
yields an isomorphism
$H^{2}(k,T_{0})\simeq H^{2}(\ell ,\mathbb{G}_{m})$
yields an isomorphism
![]() $H^{2}(k,T_{0})_{V}\simeq H^{2}(\ell ,\mathbb{G}_{m})_{V^{\prime }}$
. Thus,
$H^{2}(k,T_{0})_{V}\simeq H^{2}(\ell ,\mathbb{G}_{m})_{V^{\prime }}$
. Thus,
the
![]() $V^{\prime }$
-unramified part of the
$V^{\prime }$
-unramified part of the
![]() $n$
-torsion in the Brauer group of
$n$
-torsion in the Brauer group of
![]() $\ell$
, which is known to be finite (cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a, 3.5]).◻
$\ell$
, which is known to be finite (cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a, 3.5]).◻
Remark A.11. Using the fact that the unramified Brauer group
![]() $_{n\!}\operatorname{Br}(k)_{V}$
is finite for any finitely generated field
$_{n\!}\operatorname{Br}(k)_{V}$
is finite for any finitely generated field
![]() $k$
of characteristic prime to
$k$
of characteristic prime to
![]() $n$
and a divisorial set of places
$n$
and a divisorial set of places
![]() $V$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a]), one easily generalizes Lemma A.10 to any finitely generated field
$V$
(cf. [Reference Chernousov, Rapinchuk and RapinchukCRR16a]), one easily generalizes Lemma A.10 to any finitely generated field
![]() $k$
of characteristic
$k$
of characteristic
![]() $\neq p$
.
$\neq p$
.
Proof of Proposition A.8.
The exact sequence (A.9) gives rise to the following exact sequence of cohomology groups
Clearly,
![]() $\unicode[STIX]{x1D6FE}(\text{}_{p^{m}}H^{2}(k,M(p))_{V})\subset _{p^{m}}H^{2}(k,T(p))_{V}$
, and the latter is finite by Lemma A.10. Thus, it remains to show that the intersection
$\unicode[STIX]{x1D6FE}(\text{}_{p^{m}}H^{2}(k,M(p))_{V})\subset _{p^{m}}H^{2}(k,T(p))_{V}$
, and the latter is finite by Lemma A.10. Thus, it remains to show that the intersection
is finite. Pick
![]() $m_{0}\geqslant 0$
so that
$m_{0}\geqslant 0$
so that
![]() $p^{m_{0}}$
annihilates
$p^{m_{0}}$
annihilates
![]() $_{p^{\infty }}H^{1}(k,T)$
; note that the latter has finite exponent dividing the degree
$_{p^{\infty }}H^{1}(k,T)$
; note that the latter has finite exponent dividing the degree
![]() $[\ell :k]$
, where
$[\ell :k]$
, where
![]() $\ell$
is the minimal splitting field of
$\ell$
is the minimal splitting field of
![]() $T$
. It follows from the exact sequence in Lemma A.9(2) that then the group
$T$
. It follows from the exact sequence in Lemma A.9(2) that then the group
![]() $p^{m_{0}}\cdot H^{1}(k,T(p))$
is
$p^{m_{0}}\cdot H^{1}(k,T(p))$
is
![]() $p$
-divisible.
$p$
-divisible.
Now, let
![]() $x\in H^{2}(k,A(p))$
be such that
$x\in H^{2}(k,A(p))$
be such that
![]() $p^{m}\cdot \unicode[STIX]{x1D6FD}(x)=0$
. Then
$p^{m}\cdot \unicode[STIX]{x1D6FD}(x)=0$
. Then
![]() $p^{m}x=\unicode[STIX]{x1D6FC}(y)$
for some
$p^{m}x=\unicode[STIX]{x1D6FC}(y)$
for some
![]() $y\in H^{1}(k,T(p))$
, and consequently letting
$y\in H^{1}(k,T(p))$
, and consequently letting
![]() $d=m\,+\,m_{0}$
we have
$d=m\,+\,m_{0}$
we have
![]() $p^{d}x=\unicode[STIX]{x1D6FC}(p^{m_{0}}y)$
. The divisibility of
$p^{d}x=\unicode[STIX]{x1D6FC}(p^{m_{0}}y)$
. The divisibility of
![]() $p^{m_{0}}\cdot H^{1}(k,T(p))$
implies that one can find
$p^{m_{0}}\cdot H^{1}(k,T(p))$
implies that one can find
![]() $z\in H^{1}(k,T(p))$
satisfying
$z\in H^{1}(k,T(p))$
satisfying
Then
This proves the inclusion
and it remains to show that
![]() $_{p^{d}}H^{2}(k,A(p))$
is finite. However, according to statement (1) on [Reference JannsenJan89–90, p. 127], the map
$_{p^{d}}H^{2}(k,A(p))$
is finite. However, according to statement (1) on [Reference JannsenJan89–90, p. 127], the map
is an isomorphism. On the other hand,
![]() $H^{2}(k_{v},A(p))=0$
for any
$H^{2}(k_{v},A(p))=0$
for any
![]() $v\notin S^{\prime }=S\cup V_{\infty }^{k}$
, where
$v\notin S^{\prime }=S\cup V_{\infty }^{k}$
, where
![]() $S$
is the set of points of bad reduction for
$S$
is the set of points of bad reduction for
![]() $\widetilde{C}$
(see [Reference JannsenJan89–90, statement (5) on p. 131]). Thus,
$\widetilde{C}$
(see [Reference JannsenJan89–90, statement (5) on p. 131]). Thus,
However, for any
![]() $v$
, the group
$v$
, the group
![]() $_{p^{d}}H^{2}(k_{v},A(p))$
is a quotient of
$_{p^{d}}H^{2}(k_{v},A(p))$
is a quotient of
![]() $H^{2}(k_{v},_{p^{d}}A(p))$
, which is finite because
$H^{2}(k_{v},_{p^{d}}A(p))$
, which is finite because
![]() $_{p^{d}}A(p)$
is finite and
$_{p^{d}}A(p)$
is finite and
![]() $k_{v}$
is a finite extension of
$k_{v}$
is a finite extension of
![]() $\mathbb{Q}_{q}$
for some
$\mathbb{Q}_{q}$
for some
![]() $q$
(cf. [Reference SerreSer97, ch. II, § 5, Proposition 14]), completing the argument.◻
$q$
(cf. [Reference SerreSer97, ch. II, § 5, Proposition 14]), completing the argument.◻
(Note that while we actually prove the finiteness of
![]() $\operatorname{Im}\unicode[STIX]{x1D6FD}\,\cap \,_{p^{m}}H^{2}(k,M(p))$
, for the proof of Proposition A.8 it would be sufficient to prove the finiteness of
$\operatorname{Im}\unicode[STIX]{x1D6FD}\,\cap \,_{p^{m}}H^{2}(k,M(p))$
, for the proof of Proposition A.8 it would be sufficient to prove the finiteness of
![]() $\operatorname{Im}\unicode[STIX]{x1D6FD}\,\cap \,_{p^{m}}H^{2}(k,M(p))_{V}$
.)
$\operatorname{Im}\unicode[STIX]{x1D6FD}\,\cap \,_{p^{m}}H^{2}(k,M(p))_{V}$
.)
A.4 Proof of Theorem A.1
First, it is enough to consider the case where
![]() $n=p^{m}$
with
$n=p^{m}$
with
![]() $p$
a prime and
$p$
a prime and
![]() $m\geqslant 1$
. Second, deleting a finite number of places from
$m\geqslant 1$
. Second, deleting a finite number of places from
![]() $V_{1}$
if necessary, we may assume that any
$V_{1}$
if necessary, we may assume that any
![]() $v\in V_{1}$
satisfies the assumptions made in the beginning of § A.2 (recall that
$v\in V_{1}$
satisfies the assumptions made in the beginning of § A.2 (recall that
![]() $\operatorname{char}k^{(v)}$
is prime to
$\operatorname{char}k^{(v)}$
is prime to
![]() $p$
by the assumptions made in the statement of the theorem). Consider the following commutative diagram
$p$
by the assumptions made in the statement of the theorem). Consider the following commutative diagram

As
![]() $\unicode[STIX]{x1D6FE}$
is injective (Lemma A.5), it is enough to establish the finiteness of
$\unicode[STIX]{x1D6FE}$
is injective (Lemma A.5), it is enough to establish the finiteness of
![]() $\unicode[STIX]{x1D6FE}(H^{3}(k(C),\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})_{V})$
. As we pointed out in § 4.2, the natural map
$\unicode[STIX]{x1D6FE}(H^{3}(k(C),\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})_{V})$
. As we pointed out in § 4.2, the natural map
![]() $H^{3}(C,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})\rightarrow H^{3}(k(C),\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})_{V_{0}}$
is surjective, implying that
$H^{3}(C,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})\rightarrow H^{3}(k(C),\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})_{V_{0}}$
is surjective, implying that
![]() $\unicode[STIX]{x1D6FD}$
in (A.11) is also surjective. Thus,
$\unicode[STIX]{x1D6FD}$
in (A.11) is also surjective. Thus,
and it is enough to prove the following.
Proposition A.12. The image of
![]() $\unicode[STIX]{x1D6FC}:H^{3}(C,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})_{V}\longrightarrow H^{3}(C,\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
is finite.
$\unicode[STIX]{x1D6FC}:H^{3}(C,\unicode[STIX]{x1D707}_{p^{m}}^{\otimes 2})_{V}\longrightarrow H^{3}(C,\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
is finite.
Proof. We will use the following exact sequence
obtained by taking the direct limit of the sequences (2) from §4.2. By Poitou–Tate (cf. [Reference SerreSer97, ch. II, 6.3]), for any
![]() $n\geqslant 1$
, the natural map
$n\geqslant 1$
, the natural map
where
![]() $V_{\text{real}}^{k}$
is the set of all real places of
$V_{\text{real}}^{k}$
is the set of all real places of
![]() $k$
, is an isomorphism. Complex conjugation acts on
$k$
, is an isomorphism. Complex conjugation acts on
![]() $\unicode[STIX]{x1D707}_{n}$
by inversion, hence acts trivially on
$\unicode[STIX]{x1D707}_{n}$
by inversion, hence acts trivially on
![]() $\unicode[STIX]{x1D707}_{n}^{\otimes 2}$
. It follows that
$\unicode[STIX]{x1D707}_{n}^{\otimes 2}$
. It follows that
![]() $H^{3}(k_{v},\unicode[STIX]{x1D707}_{n}^{\otimes 2})$
is trivial if
$H^{3}(k_{v},\unicode[STIX]{x1D707}_{n}^{\otimes 2})$
is trivial if
![]() $n$
is odd, and
$n$
is odd, and
for any
![]() $v\in V_{\text{real}}^{k}$
. Thus,
$v\in V_{\text{real}}^{k}$
. Thus,
![]() $H^{3}(k,\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
is trivial if
$H^{3}(k,\mathbb{Q}_{p}/\mathbb{Z}_{p}(2))$
is trivial if
![]() $p>2$
and isomorphic to
$p>2$
and isomorphic to
![]() $(\mathbb{Z}/2\mathbb{Z})^{r}$
for
$(\mathbb{Z}/2\mathbb{Z})^{r}$
for
![]() $p=2$
, where
$p=2$
, where
![]() $r=|V_{\text{real}}^{k}|$
. In any case, it is finite. Thus, to prove that
$r=|V_{\text{real}}^{k}|$
. In any case, it is finite. Thus, to prove that
![]() $\unicode[STIX]{x1D6FC}$
has finite image, it is enough to show that
$\unicode[STIX]{x1D6FC}$
has finite image, it is enough to show that
is finite. Clearly,
![]() $\unicode[STIX]{x1D6E5}\subset _{p^{m}}H^{2}(k,M(p))$
. Now, because the residue field
$\unicode[STIX]{x1D6E5}\subset _{p^{m}}H^{2}(k,M(p))$
. Now, because the residue field
![]() $k^{(v)}$
is finite and the curve
$k^{(v)}$
is finite and the curve
![]() $C$
is affine, we have
$C$
is affine, we have
![]() $\operatorname{Pic}\text{}\underline{C}^{(v)}\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
(Corollary A.4). Thus, applying Proposition A.6, we obtain that
$\operatorname{Pic}\text{}\underline{C}^{(v)}\otimes _{\mathbb{Z}}\mathbb{Q}_{p}/\mathbb{Z}_{p}=0$
(Corollary A.4). Thus, applying Proposition A.6, we obtain that
![]() $\unicode[STIX]{x1D6E5}$
is contained in
$\unicode[STIX]{x1D6E5}$
is contained in
![]() $H^{2}(k,M(p))_{V}$
, and therefore in fact
$H^{2}(k,M(p))_{V}$
, and therefore in fact
![]() $\unicode[STIX]{x1D6E5}\subset _{p^{m}}H^{2}(k,M(p))_{V}$
. As the latter is finite by Proposition A.8, the required fact follows.◻
$\unicode[STIX]{x1D6E5}\subset _{p^{m}}H^{2}(k,M(p))_{V}$
. As the latter is finite by Proposition A.8, the required fact follows.◻