Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marrakchi, Amine
2017.
Solidity of Type III Bernoulli Crossed Products.
Communications in Mathematical Physics,
Vol. 350,
Issue. 3,
p.
897.
Houdayer, Cyril
and
Isono, Yusuke
2017.
Unique prime factorization and bicentralizer problem for a class of type III factors.
Advances in Mathematics,
Vol. 305,
Issue. ,
p.
402.
Chifan, Ionuţ
and
Ioana, Adrian
2018.
Amalgamated free product rigidity for group von Neumann algebras.
Advances in Mathematics,
Vol. 329,
Issue. ,
p.
819.
Houdayer, Cyril
Marrakchi, Amine
and
Verraedt, Peter
2019.
Fullness and Connes' τ invariant of type III tensor product factors.
Journal de Mathématiques Pures et Appliquées,
Vol. 121,
Issue. ,
p.
113.
Isono, Yusuke
2019.
Unique prime factorization for infinite tensor product factors.
Journal of Functional Analysis,
Vol. 276,
Issue. 7,
p.
2245.
Houdayer, Cyril
and
Isono, Yusuke
2020.
Factoriality, Connes' type III invariants and fullness of amalgamated free product von Neumann algebras.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 150,
Issue. 3,
p.
1495.
Isono, Yusuke
2020.
ON FUNDAMENTAL GROUPS OF TENSOR PRODUCT FACTORS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 19,
Issue. 4,
p.
1121.
Chifan, Ionut
and
Udrea, Bogdan Teodor
2020.
Some rigidity results for II1 factors arising from wreath products of property (T) groups.
Journal of Functional Analysis,
Vol. 278,
Issue. 7,
p.
108419.
Houdayer, Cyril
and
Trom, Benjamin
2021.
Structure of extensions of free Araki–Woods factors.
Annales de l'Institut Fourier,
Vol. 71,
Issue. 2,
p.
473.
Drimbe, Daniel
2021.
Product Rigidity in Von Neumann and C$$^*$$-Algebras Via S-Malleable Deformations.
Communications in Mathematical Physics,
Vol. 388,
Issue. 1,
p.
329.
Ioana, Adrian
and
Spaas, Pieter
2021.
II1 FACTORS WITH EXOTIC CENTRAL SEQUENCE ALGEBRAS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 20,
Issue. 5,
p.
1671.
Popa, Sorin
and
Vaes, Stefaan
2022.
W$$^*$$-Rigidity Paradigms for Embeddings of $$\hbox {II}_1$$ Factors.
Communications in Mathematical Physics,
Vol. 395,
Issue. 2,
p.
907.
Drimbe, Daniel
2022.
Solid Ergodicity and Orbit Equivalence Rigidity for Coinduced Actions.
International Mathematics Research Notices,
Vol. 2022,
Issue. 11,
p.
8251.
Hasegawa, Kei
Isono, Yusuke
and
Kanda, Tomohiro
2022.
Boundary and Rigidity of Nonsingular Bernoulli Actions.
Communications in Mathematical Physics,
Vol. 389,
Issue. 2,
p.
977.
Drimbe, Daniel
2023.
Measure equivalence rigidity via s-malleable deformations.
Compositio Mathematica,
Vol. 159,
Issue. 10,
p.
2023.
Boutonnet, Rémi
Drimbe, Daniel
Ioana, Adrian
and
Popa, Sorin
2024.
Non-isomorphism of A∗n,2≤n≤∞, for a non-separable abelian von Neumann algebra A.
Geometric and Functional Analysis,
Vol. 34,
Issue. 2,
p.
393.
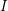 $I$ be any nonempty set and let
$I$ be any nonempty set and let 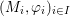 $(M_{i},\unicode[STIX]{x1D711}_{i})_{i\in I}$ be any family of nonamenable factors, endowed with arbitrary faithful normal states, that belong to a large class
$(M_{i},\unicode[STIX]{x1D711}_{i})_{i\in I}$ be any family of nonamenable factors, endowed with arbitrary faithful normal states, that belong to a large class 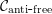 ${\mathcal{C}}_{\text{anti}\text{-}\text{free}}$ of (possibly type
${\mathcal{C}}_{\text{anti}\text{-}\text{free}}$ of (possibly type 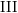 $\text{III}$) von Neumann algebras including all nonprime factors, all nonfull factors and all factors possessing Cartan subalgebras. For the free product
$\text{III}$) von Neumann algebras including all nonprime factors, all nonfull factors and all factors possessing Cartan subalgebras. For the free product 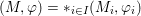 $(M,\unicode[STIX]{x1D711})=\ast _{i\in I}(M_{i},\unicode[STIX]{x1D711}_{i})$, we show that the free product von Neumann algebra
$(M,\unicode[STIX]{x1D711})=\ast _{i\in I}(M_{i},\unicode[STIX]{x1D711}_{i})$, we show that the free product von Neumann algebra 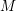 $M$ retains the cardinality
$M$ retains the cardinality  $|I|$ and each nonamenable factor
$|I|$ and each nonamenable factor 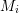 $M_{i}$ up to stably inner conjugacy, after permutation of the indices. Our main theorem unifies all previous Kurosh-type rigidity results for free product type
$M_{i}$ up to stably inner conjugacy, after permutation of the indices. Our main theorem unifies all previous Kurosh-type rigidity results for free product type 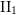 $\text{II}_{1}$ factors and is new for free product type
$\text{II}_{1}$ factors and is new for free product type  $\text{III}$ factors. It moreover provides new rigidity phenomena for type
$\text{III}$ factors. It moreover provides new rigidity phenomena for type 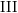 $\text{III}$ factors.
$\text{III}$ factors.



