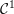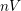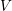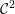1 Introduction
Differentiable structures on Cantor sets have first been considered by Sullivan in [Reference SullivanSul88]. Our aim is to consider groups of diffeomorphisms of Cantor sets, mapping class groups of Cantor punctured spheres and their relations with Thompson-like groups. In particular, the usual Thompson groups (see [Reference Cannon, Floyd and ParryCFP96]) can be retrieved as diffeomorphism groups of Cantor subsets of suitable spaces (a line, a circle or a 2-sphere).
Let
![]() $M$
be a compact manifold and
$M$
be a compact manifold and
![]() $C\;\subset \;M$
be a Cantor set, namely a compact totally disconnected subset without isolated points. Any two Cantor sets are homeomorphic as topological spaces. But if
$C\;\subset \;M$
be a Cantor set, namely a compact totally disconnected subset without isolated points. Any two Cantor sets are homeomorphic as topological spaces. But if
![]() $M$
has dimension
$M$
has dimension
![]() $m\geqslant 3$
there exist Cantor sets
$m\geqslant 3$
there exist Cantor sets
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
embedded into
$C_{2}$
embedded into
![]() $M$
so that there is no ambient homeomorphism of
$M$
so that there is no ambient homeomorphism of
![]() $M$
carrying
$M$
carrying
![]() $C_{1}$
into
$C_{1}$
into
![]() $C_{2}$
. One says that
$C_{2}$
. One says that
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
are not topologically equivalent Cantor set embeddings.
$C_{2}$
are not topologically equivalent Cantor set embeddings.
A Cantor subset of
![]() $\mathbb{R}^{m}$
is tame if there is a homeomorphism of
$\mathbb{R}^{m}$
is tame if there is a homeomorphism of
![]() $\mathbb{R}^{m}$
which sends it within a coordinates axis. All Cantor sets in
$\mathbb{R}^{m}$
which sends it within a coordinates axis. All Cantor sets in
![]() $\mathbb{R}^{m}$
, for
$\mathbb{R}^{m}$
, for
![]() $m\leqslant 2$
are tame, but there exist uncountably many wild (i.e. not tame) Cantor sets in
$m\leqslant 2$
are tame, but there exist uncountably many wild (i.e. not tame) Cantor sets in
![]() $\mathbb{R}^{m}$
, for every
$\mathbb{R}^{m}$
, for every
![]() $m\geqslant 3$
(see [Reference BlankenshipBla51]).
$m\geqslant 3$
(see [Reference BlankenshipBla51]).
One defines similarly smooth equivalence and smoothly tame Cantor sets. The analogous story for diffeomorphisms is already interesting for
![]() $m=1$
, as Cantor subsets of
$m=1$
, as Cantor subsets of
![]() $\mathbb{R}$
might be differentiably non-equivalent. Our main concern is the image of the group of diffeomorphisms of
$\mathbb{R}$
might be differentiably non-equivalent. Our main concern is the image of the group of diffeomorphisms of
![]() $M$
which preserve a Cantor set
$M$
which preserve a Cantor set
![]() $C$
into the automorphisms group of
$C$
into the automorphisms group of
![]() $C$
. Under fairly general conditions we are able to prove that this is a countable group, thereby providing an interesting class of discrete groups. For Cantor sets obtained from a topological iterated function system the associated groups are non-trivial, while for many self-similar Cantor sets these are versions of Thompson’s groups.
$C$
. Under fairly general conditions we are able to prove that this is a countable group, thereby providing an interesting class of discrete groups. For Cantor sets obtained from a topological iterated function system the associated groups are non-trivial, while for many self-similar Cantor sets these are versions of Thompson’s groups.
A. General countability statements
1.1 Pure mapping class groups
Definition 1. Let
![]() $M$
be a compact orientable manifold and
$M$
be a compact orientable manifold and
![]() $C\;\subset \;M$
a Cantor subset. We denote by
$C\;\subset \;M$
a Cantor subset. We denote by
 $\text{Diff}^{k}(M,C)$
the group of diffeomorphisms of class
$\text{Diff}^{k}(M,C)$
the group of diffeomorphisms of class
![]() ${\mathcal{C}}^{k}$
of
${\mathcal{C}}^{k}$
of
![]() $M$
sending
$M$
sending
![]() $C$
to itself, by
$C$
to itself, by
 $\text{Diff}^{k,+}(M,C)$
the subgroup of orientation preserving diffeomorphisms and by
$\text{Diff}^{k,+}(M,C)$
the subgroup of orientation preserving diffeomorphisms and by
 $P\text{Diff}^{k,+}(M,C)$
the subgroup of pure orientation preserving diffeomorphisms, i.e. pointwise preserving
$P\text{Diff}^{k,+}(M,C)$
the subgroup of pure orientation preserving diffeomorphisms, i.e. pointwise preserving
![]() $C$
.
$C$
.
The
![]() ${\mathcal{C}}^{k}$
-mapping class group
${\mathcal{C}}^{k}$
-mapping class group
 ${\mathcal{M}}^{k,+}(M,C)$
is the group
${\mathcal{M}}^{k,+}(M,C)$
is the group
 $\unicode[STIX]{x1D70B}_{0}(\text{Diff}^{k,+}(M,C))$
of
$\unicode[STIX]{x1D70B}_{0}(\text{Diff}^{k,+}(M,C))$
of
![]() ${\mathcal{C}}^{k}$
-isotopy classes of orientation preserving diffeomorphisms rel
${\mathcal{C}}^{k}$
-isotopy classes of orientation preserving diffeomorphisms rel
![]() $C$
(i.e. which are the identity on
$C$
(i.e. which are the identity on
![]() $C$
) of class
$C$
) of class
![]() ${\mathcal{C}}^{k}$
. The pure
${\mathcal{C}}^{k}$
. The pure
![]() ${\mathcal{C}}^{k}$
-mapping class group
${\mathcal{C}}^{k}$
-mapping class group
 $P{\mathcal{M}}^{k,+}(M,C)$
is the group
$P{\mathcal{M}}^{k,+}(M,C)$
is the group
 $\unicode[STIX]{x1D70B}_{0}(P\text{Diff}^{k,+}(M,C))$
of
$\unicode[STIX]{x1D70B}_{0}(P\text{Diff}^{k,+}(M,C))$
of
![]() ${\mathcal{C}}^{k}$
-isotopy classes of pure orientation preserving
${\mathcal{C}}^{k}$
-isotopy classes of pure orientation preserving
![]() ${\mathcal{C}}^{k}$
-diffeomorphisms rel
${\mathcal{C}}^{k}$
-diffeomorphisms rel
![]() $C$
.
$C$
.
In a similar vein but a different context, the group of homeomorphisms
 $\text{Diff}^{0}(M,A)$
associated to a manifold
$\text{Diff}^{0}(M,A)$
associated to a manifold
![]() $M$
and a countable dense set
$M$
and a countable dense set
![]() $A\;\subset \;M$
was studied recently in [Reference Dijkstra and van MillDM10]. The authors proved there that
$A\;\subset \;M$
was studied recently in [Reference Dijkstra and van MillDM10]. The authors proved there that
 $\text{Diff}^{0}(M,A)$
is either isomorphic to a countably infinite product of copies of
$\text{Diff}^{0}(M,A)$
is either isomorphic to a countably infinite product of copies of
![]() $\mathbb{Q}$
, when
$\mathbb{Q}$
, when
![]() $M$
is 1-dimensional, or the Erdös subgroup of
$M$
is 1-dimensional, or the Erdös subgroup of
![]() $l^{2}$
elements, otherwise. In the present setting, when
$l^{2}$
elements, otherwise. In the present setting, when
![]() $A$
is closed and the smoothness is at least
$A$
is closed and the smoothness is at least
![]() ${\mathcal{C}}^{1}$
the situation is fundamentally different.
${\mathcal{C}}^{1}$
the situation is fundamentally different.
If we write
 $C=\bigcap _{j=1}^{\infty }C_{j}$
, where each
$C=\bigcap _{j=1}^{\infty }C_{j}$
, where each
![]() $C_{j}$
is a compact submanifold of
$C_{j}$
is a compact submanifold of
![]() $M$
and
$M$
and
 $C_{j+1}\;\subset \;\text{int}(C_{j})$
for all
$C_{j+1}\;\subset \;\text{int}(C_{j})$
for all
![]() $j$
, then the sequence
$j$
, then the sequence
![]() $\{C_{j}\}$
is called a defining sequence for
$\{C_{j}\}$
is called a defining sequence for
![]() $C$
. It is known that
$C$
. It is known that
![]() $C$
is a tame Cantor set if and only if we can choose
$C$
is a tame Cantor set if and only if we can choose
![]() $C_{j}$
to be finite unions of disjoint disks.
$C_{j}$
to be finite unions of disjoint disks.
Definition 2. The class of
![]() $\unicode[STIX]{x1D711}$
in
$\unicode[STIX]{x1D711}$
in
 $P{\mathcal{M}}^{k,+}(M,C)$
is compactly supported if there exists some defining sequence
$P{\mathcal{M}}^{k,+}(M,C)$
is compactly supported if there exists some defining sequence
![]() $\{C_{j}\}$
of
$\{C_{j}\}$
of
![]() $C$
and some
$C$
and some
![]() $n$
for which the restriction of
$n$
for which the restriction of
![]() $\unicode[STIX]{x1D711}$
to
$\unicode[STIX]{x1D711}$
to
![]() $C_{n}$
is
$C_{n}$
is
![]() ${\mathcal{C}}^{k}$
-isotopic to identity rel
${\mathcal{C}}^{k}$
-isotopic to identity rel
![]() $C$
.
$C$
.
Note that the property of being compactly supported is independent of the choice of the defining sequence.
Our first result is as follows.
Theorem 1. Let
![]() $C$
be a
$C$
be a
![]() ${\mathcal{C}}^{k}$
-tame Cantor set, namely a Cantor subset of a closed interval
${\mathcal{C}}^{k}$
-tame Cantor set, namely a Cantor subset of a closed interval
![]() ${\mathcal{C}}^{k}$
-embedded in a compact orientable manifold
${\mathcal{C}}^{k}$
-embedded in a compact orientable manifold
![]() $M$
of dimension at least
$M$
of dimension at least
![]() $2$
. If
$2$
. If
![]() $k\geqslant 2$
, then all classes in the group
$k\geqslant 2$
, then all classes in the group
 $P{\mathcal{M}}^{k,+}(M,C)$
are compactly supported. In particular, the group
$P{\mathcal{M}}^{k,+}(M,C)$
are compactly supported. In particular, the group
 $P{\mathcal{M}}^{k,+}(M,C)$
is countable.
$P{\mathcal{M}}^{k,+}(M,C)$
is countable.
In contrast, the topological mapping class group
 $P{\mathcal{M}}^{0,+}(S^{2},C)$
is uncountable. We might expect
$P{\mathcal{M}}^{0,+}(S^{2},C)$
is uncountable. We might expect
 $P{\mathcal{M}}^{k,+}(M,C)$
to be countable for
$P{\mathcal{M}}^{k,+}(M,C)$
to be countable for
![]() $k\geqslant 2$
even when
$k\geqslant 2$
even when
![]() $C$
is only a
$C$
is only a
![]() ${\mathcal{C}}^{0}$
-tame Cantor subset of
${\mathcal{C}}^{0}$
-tame Cantor subset of
![]() $M$
.
$M$
.
The following precises the second statement in Theorem 1.
Corollary 1. Let
![]() $C$
be a
$C$
be a
![]() ${\mathcal{C}}^{k}$
-tame Cantor subset of a compact orientable surface
${\mathcal{C}}^{k}$
-tame Cantor subset of a compact orientable surface
![]() $M$
and
$M$
and
![]() $\{C_{j}\}$
be a defining sequence for
$\{C_{j}\}$
be a defining sequence for
![]() $C$
consisting of finite unions of disjoint disks. If
$C$
consisting of finite unions of disjoint disks. If
![]() $k\geqslant 2$
, then
$k\geqslant 2$
, then
 $P{\mathcal{M}}^{k,+}(M,C)$
coincides with the inductive limit
$P{\mathcal{M}}^{k,+}(M,C)$
coincides with the inductive limit
 $\lim _{j\rightarrow \infty }P{\mathcal{M}}^{k,+}(M-\text{int}(C_{j}))$
of pure mapping class groups of compact subsurfaces.
$\lim _{j\rightarrow \infty }P{\mathcal{M}}^{k,+}(M-\text{int}(C_{j}))$
of pure mapping class groups of compact subsurfaces.
Note that, when
![]() $N$
is a compact surface the isomorphism type of
$N$
is a compact surface the isomorphism type of
 $P{\mathcal{M}}^{k,+}(N)$
is independent of
$P{\mathcal{M}}^{k,+}(N)$
is independent of
![]() $k$
.
$k$
.
1.2
 ${\mathcal{C}}^{1}$
-diffeomorphism groups of Cantor sets
${\mathcal{C}}^{1}$
-diffeomorphism groups of Cantor sets
We now turn to the full mapping class groups. Several groups which arose recently in the literature could be thought to play the role of the mapping class groups for some infinite type surfaces, for instance the group
![]() ${\mathcal{B}}$
from [Reference Funar and KapoudjianFK04] and its version
${\mathcal{B}}$
from [Reference Funar and KapoudjianFK04] and its version
![]() $BV$
, which was defined by Brin [Reference BrinBri07] and Dehornoy [Reference DehornoyDeh06], independently. These two groups are braidings of the Thompson group
$BV$
, which was defined by Brin [Reference BrinBri07] and Dehornoy [Reference DehornoyDeh06], independently. These two groups are braidings of the Thompson group
![]() $V$
(see [Reference Cannon, Floyd and ParryCFP96]). Geometric constructions of the same sort permitted the authors of [Reference Funar and KapoudjianFK08] to derive two braidings
$V$
(see [Reference Cannon, Floyd and ParryCFP96]). Geometric constructions of the same sort permitted the authors of [Reference Funar and KapoudjianFK08] to derive two braidings
![]() $T^{\ast }$
and
$T^{\ast }$
and
![]() $T^{\sharp }$
of the Thompson group
$T^{\sharp }$
of the Thompson group
![]() $T$
.
$T$
.
Our next goal is to show that these groups are indeed smooth mapping class groups in the usual sense and that most (if not all) smooth mapping class groups of Cantor sets are related to some Thompson-like groups.
Assume for the moment that
![]() $C\;\subset \;M$
is smoothly tame. Set then
$C\;\subset \;M$
is smoothly tame. Set then
 $\mathfrak{diff}_{M}^{k}(C)$
and
$\mathfrak{diff}_{M}^{k}(C)$
and
 $\mathfrak{diff}_{M}^{k,+}(C)$
for the groups of induced transformations of
$\mathfrak{diff}_{M}^{k,+}(C)$
for the groups of induced transformations of
![]() $C$
arising as restrictions of elements of
$C$
arising as restrictions of elements of
 $\text{Diff}^{k}(M,C)$
and
$\text{Diff}^{k}(M,C)$
and
 $\text{Diff}^{k,+}(M,C)$
, respectively. The
$\text{Diff}^{k,+}(M,C)$
, respectively. The
![]() ${\mathcal{C}}^{k}$
topology on
${\mathcal{C}}^{k}$
topology on
 $\text{Diff}^{k}(M,C)$
induces a topology on
$\text{Diff}^{k}(M,C)$
induces a topology on
 $\mathfrak{diff}_{M}^{k}(C)$
.
$\mathfrak{diff}_{M}^{k}(C)$
.
Notice now that we have the exact sequence:
 $$\begin{eqnarray}1\rightarrow P{\mathcal{M}}^{k,+}(M,C)\rightarrow {\mathcal{M}}^{k,+}(M,C)\rightarrow \mathfrak{diff}_{M}^{k,+}(C)\rightarrow 1.\end{eqnarray}$$
$$\begin{eqnarray}1\rightarrow P{\mathcal{M}}^{k,+}(M,C)\rightarrow {\mathcal{M}}^{k,+}(M,C)\rightarrow \mathfrak{diff}_{M}^{k,+}(C)\rightarrow 1.\end{eqnarray}$$
By Theorem 1 the group
 ${\mathcal{M}}^{k,+}(M,C)$
is discrete countable if and only if
${\mathcal{M}}^{k,+}(M,C)$
is discrete countable if and only if
 $\mathfrak{diff}_{M}^{k,+}(C)$
does, when
$\mathfrak{diff}_{M}^{k,+}(C)$
does, when
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $M$
is compact (or the interior of a compact manifold).
$M$
is compact (or the interior of a compact manifold).
Classical Thompson groups can be realized as groups of dyadic piecewise linear homeomorphisms (or bijections) of an interval, circle or a Cantor set (see [Reference Cannon, Floyd and ParryCFP96, Reference Ghys and SergiescuGS87]) or as groups of automorphisms at infinity of graphs (respecting or not the planarity), as in [Reference NeretinNer92]. Notice that the more involved construction from [Reference Ghys and SergiescuGS87] provides embeddings of Thompson groups into the group of diffeomorphisms of the circle, admitting invariant minimal Cantor sets. In particular, Ghys and Sergiescu obtained embeddings as discrete subgroups of the group of diffeomorphisms (see [Reference Ghys and SergiescuGS87, Theorem 2.3]).
In our setting we see that whenever it is discrete and countable the group
 ${\mathcal{M}}^{k,+}(M,C)$
is the braiding of
${\mathcal{M}}^{k,+}(M,C)$
is the braiding of
 $\mathfrak{diff}_{M}^{k,+}(C)$
according to Corollary 1, as in the cases studied in [Reference BrinBri07, Reference DehornoyDeh06, Reference Funar and KapoudjianFK04, Reference Funar and KapoudjianFK08]. This raises the question whether
$\mathfrak{diff}_{M}^{k,+}(C)$
according to Corollary 1, as in the cases studied in [Reference BrinBri07, Reference DehornoyDeh06, Reference Funar and KapoudjianFK04, Reference Funar and KapoudjianFK08]. This raises the question whether
 $\mathfrak{diff}_{M}^{k,+}(C)$
is a Thompson-like group, in general. We were not able to solve this question in full generality and actually when
$\mathfrak{diff}_{M}^{k,+}(C)$
is a Thompson-like group, in general. We were not able to solve this question in full generality and actually when
![]() $C$
is a generic Cantor set of the interval we expect the group
$C$
is a generic Cantor set of the interval we expect the group
 $\mathfrak{diff}_{M}^{k,+}(C)$
be trivial. To this purpose we introduce the following property of Cantor sets.
$\mathfrak{diff}_{M}^{k,+}(C)$
be trivial. To this purpose we introduce the following property of Cantor sets.
Definition 3. The Cantor subset
![]() $C$
of an interval is
$C$
of an interval is
![]() $\unicode[STIX]{x1D70E}$
-sparse if, for any
$\unicode[STIX]{x1D70E}$
-sparse if, for any
 $a,b\in C$
, there is a complementary interval
$a,b\in C$
, there is a complementary interval
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\;\subset \;(a,b)\;\cap \;\mathbb{R}\setminus C$
such that
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\;\subset \;(a,b)\;\cap \;\mathbb{R}\setminus C$
such that
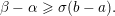 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D70E}(b-a).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D70E}(b-a).\end{eqnarray}$$
Moreover
![]() $C$
is sparse if it is
$C$
is sparse if it is
![]() $\unicode[STIX]{x1D70E}$
-sparse for some
$\unicode[STIX]{x1D70E}$
-sparse for some
![]() $\unicode[STIX]{x1D70E}>0$
.
$\unicode[STIX]{x1D70E}>0$
.
Set
 $\mathfrak{diff}^{k}(C)=\mathfrak{diff}_{\mathbb{R}}^{k}(C)$
,
$\mathfrak{diff}^{k}(C)=\mathfrak{diff}_{\mathbb{R}}^{k}(C)$
,
 $\mathfrak{diff}^{k,+}(C)=\mathfrak{diff}_{\mathbb{R}}^{k,+}(C)$
for the sake of notational simplicity.
$\mathfrak{diff}^{k,+}(C)=\mathfrak{diff}_{\mathbb{R}}^{k,+}(C)$
for the sake of notational simplicity.
Theorem 2. If
![]() $C$
is a sparse Cantor subset of
$C$
is a sparse Cantor subset of
![]() $\mathbb{R}$
, then the group
$\mathbb{R}$
, then the group
 $\mathfrak{diff}^{1}(C)$
is countable. If
$\mathfrak{diff}^{1}(C)$
is countable. If
![]() $C$
is a sparse Cantor set in
$C$
is a sparse Cantor set in
 $S^{1}=\mathbb{R}/\mathbb{Z}$
, then
$S^{1}=\mathbb{R}/\mathbb{Z}$
, then
 $\mathfrak{diff}_{S^{1}}^{1}(C)$
is countable.
$\mathfrak{diff}_{S^{1}}^{1}(C)$
is countable.
Theorem 2 cannot be extended to all Cantor sets
![]() $C$
, without additional assumptions, as we can see from the examples given in § 5.
$C$
, without additional assumptions, as we can see from the examples given in § 5.
We have the following more general version of the previous result.
Theorem 3. If
![]() $C$
is a sparse Cantor subset of an interval
$C$
is a sparse Cantor subset of an interval
![]() ${\mathcal{C}}^{1}$
-embedded into a compact orientable manifold
${\mathcal{C}}^{1}$
-embedded into a compact orientable manifold
![]() $M$
, then the group
$M$
, then the group
 $\mathfrak{diff}_{M}^{1}(C)$
is countable and discrete.
$\mathfrak{diff}_{M}^{1}(C)$
is countable and discrete.
Although we only considered smoothly tame Cantor subsets above, there is a large supply of topologically tame Cantor subsets in any dimensions for which we can prove the countability.
Theorem 4. Let
![]() $C_{i}$
be sparse Cantor sets in
$C_{i}$
be sparse Cantor sets in
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
 $C=C_{1}\times C_{2}\times \cdots \times C_{n}\;\subset \;\mathbb{R}^{n}$
. Then the group
$C=C_{1}\times C_{2}\times \cdots \times C_{n}\;\subset \;\mathbb{R}^{n}$
. Then the group
 $\mathfrak{diff}_{\mathbb{R}^{n}}^{1}(C)$
is countable.
$\mathfrak{diff}_{\mathbb{R}^{n}}^{1}(C)$
is countable.
Observe that the Lebesgue measure of a sparse Cantor set is zero. In this direction, notice that Deroin, Kleptsyn and Navas recently proved that invariant Cantor sets of groups of real-analytic circle diffeomorphisms have zero Lebesgue measure (see [Reference Deroin, Kleptsyn and NavasDKN13, Corollary 1.17]). The result cannot be extended to
![]() ${\mathcal{C}}^{1}$
-diffeomorphisms, due to the Denjoy counterexamples, but it might hold more generally for all
${\mathcal{C}}^{1}$
-diffeomorphisms, due to the Denjoy counterexamples, but it might hold more generally for all
![]() ${\mathcal{C}}^{2}$
-diffeomorphisms of the circle according to a conjecture of Hector (see the discussion in [Reference Deroin, Kleptsyn and NavasDKN13] and [Reference Deroin, Kleptsyn and NavasDKN09, Conjecture 1.11]).
${\mathcal{C}}^{2}$
-diffeomorphisms of the circle according to a conjecture of Hector (see the discussion in [Reference Deroin, Kleptsyn and NavasDKN13] and [Reference Deroin, Kleptsyn and NavasDKN09, Conjecture 1.11]).
The key point is to show that the stabilizer of a point in this group is a finitely generated abelian group (see Lemma 7, Proposition 1). The discreteness of the stabilizers seems to be the counterpart to the following unpublished theorem of G. Hector (see [Reference NavasNav06]): If the subgroup
![]() $G$
of the group
$G$
of the group
 $\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
of analytic diffeomorphisms of the circle has an exceptional minimal set, then the stabilizer
$\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
of analytic diffeomorphisms of the circle has an exceptional minimal set, then the stabilizer
![]() $G_{a}$
of any point
$G_{a}$
of any point
![]() $a$
of the circle in
$a$
of the circle in
![]() $G$
is either trivial or
$G$
is either trivial or
![]() $\mathbb{Z}$
. As a corollary every subgroup of
$\mathbb{Z}$
. As a corollary every subgroup of
 $\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
having a minimal Cantor set is countable. This is, of course, not true for subgroups of
$\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
having a minimal Cantor set is countable. This is, of course, not true for subgroups of
 $\text{Diff}^{\infty }(S^{1})$
. Nevertheless, the stabilizer
$\text{Diff}^{\infty }(S^{1})$
. Nevertheless, the stabilizer
![]() $G_{a}$
of a subgroup
$G_{a}$
of a subgroup
 $G\;\subset \;\text{Diff}^{2}(S^{1})$
with an exceptional minimal set cannot contain two germs whose logarithm of their derivatives are rationally independent, according to a classical result of Sacksteder [Reference SackstederSac65, Theorem 2]. Sacksteder’s result cannot be extended to
$G\;\subset \;\text{Diff}^{2}(S^{1})$
with an exceptional minimal set cannot contain two germs whose logarithm of their derivatives are rationally independent, according to a classical result of Sacksteder [Reference SackstederSac65, Theorem 2]. Sacksteder’s result cannot be extended to
![]() ${\mathcal{C}}^{1}$
-diffeomorphisms. The proof of our key result is related to Thurston’s generalization of Reeb’s stability theorem from [Reference ThurstonThu74] and uses in an essential way the fact that the Cantor set is sparse while allowing only
${\mathcal{C}}^{1}$
-diffeomorphisms. The proof of our key result is related to Thurston’s generalization of Reeb’s stability theorem from [Reference ThurstonThu74] and uses in an essential way the fact that the Cantor set is sparse while allowing only
![]() ${\mathcal{C}}^{1}$
-smoothness of the diffeomorphisms.
${\mathcal{C}}^{1}$
-smoothness of the diffeomorphisms.
Remark 1. Note that mapping class groups
 ${\mathcal{M}}^{1}(M,C)$
depend essentially on the ambient manifold
${\mathcal{M}}^{1}(M,C)$
depend essentially on the ambient manifold
![]() $M$
(see [Reference Aramayona and FunarAF17]). On the contrary, if
$M$
(see [Reference Aramayona and FunarAF17]). On the contrary, if
 $C\;\subset \;\text{int}(D^{n})$
is fixed, then for any embedding of the disk
$C\;\subset \;\text{int}(D^{n})$
is fixed, then for any embedding of the disk
![]() $D^{n}$
in the interior of some orientable
$D^{n}$
in the interior of some orientable
![]() $n$
-manifold
$n$
-manifold
![]() $M^{n}$
the groups
$M^{n}$
the groups
 $\mathfrak{diff}_{M}^{1}(C)$
are isomorphic. Moreover, these groups stabilize with respect to the standard embeddings
$\mathfrak{diff}_{M}^{1}(C)$
are isomorphic. Moreover, these groups stabilize with respect to the standard embeddings
 $D^{n}\;\subset \;D^{n+k}$
, for large enough
$D^{n}\;\subset \;D^{n+k}$
, for large enough
![]() $k$
. One could however vary the groups
$k$
. One could however vary the groups
 $\mathfrak{diff}_{M}^{1}(C)$
by allowing
$\mathfrak{diff}_{M}^{1}(C)$
by allowing
![]() $C$
to intersect the boundary of
$C$
to intersect the boundary of
![]() $M$
in different patterns (isolated points, Cantor subsets etc.).
$M$
in different patterns (isolated points, Cantor subsets etc.).
B. Specific families of Cantor sets
1.3 Iterated functions systems
Definition 4. A contractive iterated function system (abbreviated contractive IFS) is a finite family
 $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
of contractive maps
$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
of contractive maps
 $\unicode[STIX]{x1D719}_{j}:\mathbb{R}^{d}\rightarrow \mathbb{R}^{d}$
. Recall that a map
$\unicode[STIX]{x1D719}_{j}:\mathbb{R}^{d}\rightarrow \mathbb{R}^{d}$
. Recall that a map
![]() $\unicode[STIX]{x1D719}$
is contractive if its Lipschitz constant is smaller than unity, namely:
$\unicode[STIX]{x1D719}$
is contractive if its Lipschitz constant is smaller than unity, namely:
 $$\begin{eqnarray}\sup _{x,y\in \mathbb{R}^{d}}\frac{d(\unicode[STIX]{x1D719}(x),\unicode[STIX]{x1D719}(y))}{d(x,y)}<1.\end{eqnarray}$$
$$\begin{eqnarray}\sup _{x,y\in \mathbb{R}^{d}}\frac{d(\unicode[STIX]{x1D719}(x),\unicode[STIX]{x1D719}(y))}{d(x,y)}<1.\end{eqnarray}$$
According to Hutchinson (see [Reference HutchinsonHut81]) there exists a unique non-empty compact
 $C=C_{\unicode[STIX]{x1D6F7}}\;\subset \;\mathbb{R}^{d}$
, called the attractor of the contractive IFS
$C=C_{\unicode[STIX]{x1D6F7}}\;\subset \;\mathbb{R}^{d}$
, called the attractor of the contractive IFS
![]() $\unicode[STIX]{x1D6F7}$
, such that
$\unicode[STIX]{x1D6F7}$
, such that
 $C=\bigcup _{j=0}^{n}\unicode[STIX]{x1D719}_{j}(C)$
.
$C=\bigcup _{j=0}^{n}\unicode[STIX]{x1D719}_{j}(C)$
.
Example 1. The central Cantor set
![]() $C_{\unicode[STIX]{x1D706}}$
, with
$C_{\unicode[STIX]{x1D706}}$
, with
![]() $\unicode[STIX]{x1D706}>2$
, is the attractor of the IFS
$\unicode[STIX]{x1D706}>2$
, is the attractor of the IFS
 $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1})$
on
$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1})$
on
![]() $\mathbb{R}$
given by
$\mathbb{R}$
given by
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}(x)=\frac{1}{\unicode[STIX]{x1D706}}x,\quad \unicode[STIX]{x1D719}_{1}(x)=\frac{1}{\unicode[STIX]{x1D706}}x+\frac{\unicode[STIX]{x1D706}-1}{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}(x)=\frac{1}{\unicode[STIX]{x1D706}}x,\quad \unicode[STIX]{x1D719}_{1}(x)=\frac{1}{\unicode[STIX]{x1D706}}x+\frac{\unicode[STIX]{x1D706}-1}{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
Although the IFS makes sense also when
 $1<\unicode[STIX]{x1D706}\leqslant 2$
, in this case the attractor is not a Cantor set but the whole interval
$1<\unicode[STIX]{x1D706}\leqslant 2$
, in this case the attractor is not a Cantor set but the whole interval
![]() $[0,1]$
.
$[0,1]$
.
Consider now the following type of IFS of topological nature.
Definition 5. Let
![]() $U$
be an orientable manifold (possibly non-compact) and
$U$
be an orientable manifold (possibly non-compact) and
 $\unicode[STIX]{x1D719}_{j}:U\rightarrow U$
be finitely many orientation preserving homeomorphisms on their image. We say that
$\unicode[STIX]{x1D719}_{j}:U\rightarrow U$
be finitely many orientation preserving homeomorphisms on their image. We say that
 $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
has a strict attractive basin
$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
has a strict attractive basin
![]() $M$
if
$M$
if
![]() $M$
is a compact orientable submanifold
$M$
is a compact orientable submanifold
![]() $M\;\subset \;U$
with the following properties:
$M\;\subset \;U$
with the following properties:
(i)
 $\unicode[STIX]{x1D719}_{j}(M)\;\subset \;\text{int}(M)$
, for all
$\unicode[STIX]{x1D719}_{j}(M)\;\subset \;\text{int}(M)$
, for all
 $j\in \{0,1,\ldots ,n\}$
;
$j\in \{0,1,\ldots ,n\}$
;(ii)
 $\unicode[STIX]{x1D719}_{i}(M)\;\cap \;\unicode[STIX]{x1D719}_{j}(M)=\emptyset$
, for any
$\unicode[STIX]{x1D719}_{i}(M)\;\cap \;\unicode[STIX]{x1D719}_{j}(M)=\emptyset$
, for any
 $j\neq i\in \{0,1,\ldots ,n\}$
.
$j\neq i\in \{0,1,\ldots ,n\}$
.
We say that the pair
![]() $(\unicode[STIX]{x1D6F7},M)$
is an invertible IFS if
$(\unicode[STIX]{x1D6F7},M)$
is an invertible IFS if
![]() $M$
is a strict attractive basin for
$M$
is a strict attractive basin for
![]() $\unicode[STIX]{x1D6F7}$
. If moreover,
$\unicode[STIX]{x1D6F7}$
. If moreover,
![]() $\unicode[STIX]{x1D719}_{j}$
are
$\unicode[STIX]{x1D719}_{j}$
are
![]() ${\mathcal{C}}^{k}$
-diffeomorphisms on their image, then we say that the IFS is of class
${\mathcal{C}}^{k}$
-diffeomorphisms on their image, then we say that the IFS is of class
![]() ${\mathcal{C}}^{k}$
.
${\mathcal{C}}^{k}$
.
The existence of an attractive basin is a topological version of uniform contractivity of
![]() $\unicode[STIX]{x1D719}_{j}$
. There exists then a unique invariant non-empty compact
$\unicode[STIX]{x1D719}_{j}$
. There exists then a unique invariant non-empty compact
 $C_{\unicode[STIX]{x1D6F7}}\;\subset \;M$
with the property that
$C_{\unicode[STIX]{x1D6F7}}\;\subset \;M$
with the property that
 $C_{\unicode[STIX]{x1D6F7}}=\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{i}(C_{\unicode[STIX]{x1D6F7}})$
.
$C_{\unicode[STIX]{x1D6F7}}=\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{i}(C_{\unicode[STIX]{x1D6F7}})$
.
Theorem 5. Consider a
![]() ${\mathcal{C}}^{1}$
contractive invertible IFS
${\mathcal{C}}^{1}$
contractive invertible IFS
![]() $(\unicode[STIX]{x1D6F7},M)$
,
$(\unicode[STIX]{x1D6F7},M)$
,
 $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
, whose strict attractive basin
$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
, whose strict attractive basin
![]() $M$
is diffeomorphic to a
$M$
is diffeomorphic to a
![]() $d$
-dimensional ball. Then, the group
$d$
-dimensional ball. Then, the group
 $\mathfrak{diff}_{M}^{1}(C_{\unicode[STIX]{x1D6F7}})$
contains the Thompson group
$\mathfrak{diff}_{M}^{1}(C_{\unicode[STIX]{x1D6F7}})$
contains the Thompson group
![]() $F_{n+1}$
, when
$F_{n+1}$
, when
![]() $M$
is of dimension
$M$
is of dimension
![]() $d=1$
and the Thompson group
$d=1$
and the Thompson group
![]() $V_{n+1}$
, when
$V_{n+1}$
, when
![]() $d\geqslant 2$
, respectively.
$d\geqslant 2$
, respectively.
In particular, the groups
 $\mathfrak{diff}_{M}^{1}(C_{\unicode[STIX]{x1D6F7}})$
are (highly) non-trivial.
$\mathfrak{diff}_{M}^{1}(C_{\unicode[STIX]{x1D6F7}})$
are (highly) non-trivial.
For a clear introduction to the classical Thompson groups
![]() $F,T,V$
we refer to [Reference Cannon, Floyd and ParryCFP96]. The generalized versions
$F,T,V$
we refer to [Reference Cannon, Floyd and ParryCFP96]. The generalized versions
 $F_{n},T_{n},V_{n}$
were considered by Higman ([Reference HigmanHig74] and further extended and studied by Brown and Stein (see [Reference SteinSte92]), Bieri and Strebel (see [Reference Bieri and StrebelBS16]) and Laget [Reference LagetLag04]. We will recall their definitions in § 2.
$F_{n},T_{n},V_{n}$
were considered by Higman ([Reference HigmanHig74] and further extended and studied by Brown and Stein (see [Reference SteinSte92]), Bieri and Strebel (see [Reference Bieri and StrebelBS16]) and Laget [Reference LagetLag04]. We will recall their definitions in § 2.
The result of the theorem does not hold when the attractive basin
![]() $M$
is not a ball. For instance, when
$M$
is not a ball. For instance, when
![]() $M$
is a 3-dimensional solid torus, by taking non-trivial (linked) embeddings
$M$
is a 3-dimensional solid torus, by taking non-trivial (linked) embeddings
 $\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{i}(M)\;\subset \;M$
we can provide examples of wild Cantor sets, some of them being topologically rigid, in which case the group
$\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{i}(M)\;\subset \;M$
we can provide examples of wild Cantor sets, some of them being topologically rigid, in which case the group
 $\mathfrak{diff}_{M}^{1}(C)$
is trivial (see [Reference ShilepskyShi74, Reference WrightWri86]).
$\mathfrak{diff}_{M}^{1}(C)$
is trivial (see [Reference ShilepskyShi74, Reference WrightWri86]).
1.4 Self-similar Cantor subsets of the line
The second part of this paper is devoted to concrete examples of groups arising from these constructions, for particular choices of Cantor sets. We will be concerned in this section with self-similar Cantor sets, namely attractors of IFS which consist only of similitudes. The typical example is the central ternary Cantor set
 $C_{\unicode[STIX]{x1D706}}\;\subset \;[0,1]$
of parameter
$C_{\unicode[STIX]{x1D706}}\;\subset \;[0,1]$
of parameter
![]() $\unicode[STIX]{x1D706}>2$
from Example 1.
$\unicode[STIX]{x1D706}>2$
from Example 1.
Let
 $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
be an IFS of affine transformations of
$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
be an IFS of affine transformations of
![]() $[0,1]$
, given by
$[0,1]$
, given by
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{j}(x)=\unicode[STIX]{x1D706}_{j}x+a_{j},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{j}(x)=\unicode[STIX]{x1D706}_{j}x+a_{j},\end{eqnarray}$$
where
 $$\begin{eqnarray}0=a_{0}<\unicode[STIX]{x1D706}_{0}<a_{1}<\unicode[STIX]{x1D706}_{1}+a_{1}<a_{2}<\cdots <\unicode[STIX]{x1D706}_{n-1}+a_{n-1}<a_{n}<\unicode[STIX]{x1D706}_{n}+a_{n}=1.\end{eqnarray}$$
$$\begin{eqnarray}0=a_{0}<\unicode[STIX]{x1D706}_{0}<a_{1}<\unicode[STIX]{x1D706}_{1}+a_{1}<a_{2}<\cdots <\unicode[STIX]{x1D706}_{n-1}+a_{n-1}<a_{n}<\unicode[STIX]{x1D706}_{n}+a_{n}=1.\end{eqnarray}$$
The last condition means that the segments
 $\unicode[STIX]{x1D719}_{j}([0,1])$
are mutually disjoint, so that the attractor
$\unicode[STIX]{x1D719}_{j}([0,1])$
are mutually disjoint, so that the attractor
 $C=C_{\unicode[STIX]{x1D6F7}}$
is a sparse Cantor subset of
$C=C_{\unicode[STIX]{x1D6F7}}$
is a sparse Cantor subset of
![]() $[0,1]$
. The positive reals
$[0,1]$
. The positive reals
 $g_{j}=a_{j+1}-\unicode[STIX]{x1D706}_{j}-a_{j}$
are the initial gaps as they represent the distance between consecutive intervals
$g_{j}=a_{j+1}-\unicode[STIX]{x1D706}_{j}-a_{j}$
are the initial gaps as they represent the distance between consecutive intervals
 $\unicode[STIX]{x1D719}_{j}([0,1])$
and
$\unicode[STIX]{x1D719}_{j}([0,1])$
and
 $\unicode[STIX]{x1D719}_{j+1}([0,1])$
. The image of
$\unicode[STIX]{x1D719}_{j+1}([0,1])$
. The image of
![]() $[0,1]$
by the elements of the monoid generated by
$[0,1]$
by the elements of the monoid generated by
![]() $\unicode[STIX]{x1D6F7}$
are called standard intervals.
$\unicode[STIX]{x1D6F7}$
are called standard intervals.
We consider the groups
![]() $F_{C}$
and
$F_{C}$
and
![]() $T_{C}$
defined as follows. Let
$T_{C}$
defined as follows. Let
 $PL(\mathbb{R},C)$
and
$PL(\mathbb{R},C)$
and
 $PL(S^{1},C)$
be the groups of orientation preserving piecewise linear homeomorphisms of
$PL(S^{1},C)$
be the groups of orientation preserving piecewise linear homeomorphisms of
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
 $S^{1}=\mathbb{R}/\mathbb{Z}$
respectively, keeping invariant
$S^{1}=\mathbb{R}/\mathbb{Z}$
respectively, keeping invariant
![]() $C$
, i.e. of those homeomorphisms
$C$
, i.e. of those homeomorphisms
![]() $\unicode[STIX]{x1D711}$
for which there exists a finite covering of
$\unicode[STIX]{x1D711}$
for which there exists a finite covering of
![]() $C$
by standard disjoint intervals
$C$
by standard disjoint intervals
![]() $\{I_{j}\}$
,
$\{I_{j}\}$
,
 $\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
$\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
 $a_{j},b_{j}\in C$
, such that
$a_{j},b_{j}\in C$
, such that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=b_{j}+\unicode[STIX]{x1D6EC}_{\mathbf{k}_{j}}(x-a_{j})\quad \text{for any }x\in I_{j},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=b_{j}+\unicode[STIX]{x1D6EC}_{\mathbf{k}_{j}}(x-a_{j})\quad \text{for any }x\in I_{j},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6EC}_{\mathbf{k}}=\prod _{i=0}^{n}\unicode[STIX]{x1D706}_{i}^{k_{i}}$
, for each multi-index
$\unicode[STIX]{x1D6EC}_{\mathbf{k}}=\prod _{i=0}^{n}\unicode[STIX]{x1D706}_{i}^{k_{i}}$
, for each multi-index
 $\mathbf{k}=(k_{0},k_{1},\ldots ,k_{n})\in \mathbb{Z}^{n+1}$
. Eventually
$\mathbf{k}=(k_{0},k_{1},\ldots ,k_{n})\in \mathbb{Z}^{n+1}$
. Eventually
![]() $F_{C}$
and
$F_{C}$
and
![]() $T_{C}$
are the images of
$T_{C}$
are the images of
 $PL(\mathbb{R},C)$
and
$PL(\mathbb{R},C)$
and
 $PL(S^{1},C)$
, respectively, in the group of homeomorphisms of
$PL(S^{1},C)$
, respectively, in the group of homeomorphisms of
![]() $C$
. Similarly we have the group of piecewise affine exchanges
$C$
. Similarly we have the group of piecewise affine exchanges
![]() $PE(C)$
which are (not necessarily orientation preserving) left continuous bijections of
$PE(C)$
which are (not necessarily orientation preserving) left continuous bijections of
![]() $S^{1}$
preserving
$S^{1}$
preserving
![]() $C$
, i.e. of those (not necessarily continuous) maps
$C$
, i.e. of those (not necessarily continuous) maps
![]() $\unicode[STIX]{x1D711}$
for which there exists a finite covering of
$\unicode[STIX]{x1D711}$
for which there exists a finite covering of
![]() $C$
by standard disjoint intervals
$C$
by standard disjoint intervals
![]() $\{I_{j}\}$
,
$\{I_{j}\}$
,
 $\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
$\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
 $a_{j},b_{j}\in C$
, such that
$a_{j},b_{j}\in C$
, such that
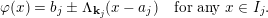 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=b_{j}\pm \unicode[STIX]{x1D6EC}_{\mathbf{k}_{j}}(x-a_{j})\quad \text{for any }x\in I_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=b_{j}\pm \unicode[STIX]{x1D6EC}_{\mathbf{k}_{j}}(x-a_{j})\quad \text{for any }x\in I_{j}.\end{eqnarray}$$
We denote by
![]() $V_{C}^{\pm }$
its image into the group of homeomorphisms of
$V_{C}^{\pm }$
its image into the group of homeomorphisms of
![]() $C$
. We denote by
$C$
. We denote by
 $V_{C}\;\subset \;V_{C}^{\pm }$
the subgroup obtained by requiring the restrictions of
$V_{C}\;\subset \;V_{C}^{\pm }$
the subgroup obtained by requiring the restrictions of
![]() $\unicode[STIX]{x1D711}$
to each standard interval
$\unicode[STIX]{x1D711}$
to each standard interval
![]() $I_{j}$
be orientation-preserving, as in (3).
$I_{j}$
be orientation-preserving, as in (3).
Definition 6. The self-similar Cantor set
 $C\;\subset \;[0,1]$
satisfies the genericity condition
$C\;\subset \;[0,1]$
satisfies the genericity condition
![]() $(C)$
if
$(C)$
if
(i) either all homothety ratios
 $\unicode[STIX]{x1D706}_{i}$
are equal and all initial generation gaps
$\unicode[STIX]{x1D706}_{i}$
are equal and all initial generation gaps
 $g_{\unicode[STIX]{x1D6FC}}$
are equal;
$g_{\unicode[STIX]{x1D6FC}}$
are equal;(ii) or the factors
 $\unicode[STIX]{x1D706}_{i}$
and the gaps
$\unicode[STIX]{x1D706}_{i}$
and the gaps
 $g_{\unicode[STIX]{x1D6FC}}$
are incommensurable, in the following sense:
$g_{\unicode[STIX]{x1D6FC}}$
are incommensurable, in the following sense:(a)
 $\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}=g_{\unicode[STIX]{x1D6FD}}$
implies that
$\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}=g_{\unicode[STIX]{x1D6FD}}$
implies that
 $\mathbf{k}=0$
and
$\mathbf{k}=0$
and
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$
;
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$
;(b) there exists no permutation
 $\unicode[STIX]{x1D70E}$
different from identity and
$\unicode[STIX]{x1D70E}$
different from identity and
 $\mathbf{k},\mathbf{k}_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{+}^{n+1}$
such that for all
$\mathbf{k},\mathbf{k}_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{+}^{n+1}$
such that for all
 $\unicode[STIX]{x1D6FD}$
we have:
$\unicode[STIX]{x1D6FD}$
we have:  $$\begin{eqnarray}\frac{g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})}}{g_{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D6EC}_{-\mathbf{k}_{\unicode[STIX]{x1D6FD}}+(1/n)\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}\mathbf{k}_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})}}{g_{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D6EC}_{-\mathbf{k}_{\unicode[STIX]{x1D6FD}}+(1/n)\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}\mathbf{k}_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
Theorem 6. Let
 $C\;\subset \;[0,1]$
be a self-similar Cantor set satisfying the genericity condition
$C\;\subset \;[0,1]$
be a self-similar Cantor set satisfying the genericity condition
![]() $(C)$
. Then for every
$(C)$
. Then for every
 $\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C)$
we can find a covering of
$\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C)$
we can find a covering of
![]() $C$
by a finite collection of disjoint standard intervals
$C$
by a finite collection of disjoint standard intervals
![]() $\{I_{j}\}$
, whose images are also standard intervals, integers
$\{I_{j}\}$
, whose images are also standard intervals, integers
 $\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
$\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
 $a_{j},b_{j}\in C$
, such that the restriction of the map
$a_{j},b_{j}\in C$
, such that the restriction of the map
![]() $\unicode[STIX]{x1D711}$
has the form
$\unicode[STIX]{x1D711}$
has the form
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=b_{j}+\unicode[STIX]{x1D6EC}_{\mathbf{k}_{j}}(x-a_{j})\quad \text{for any }x\in I_{j}\;\cap \;C.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=b_{j}+\unicode[STIX]{x1D6EC}_{\mathbf{k}_{j}}(x-a_{j})\quad \text{for any }x\in I_{j}\;\cap \;C.\end{eqnarray}$$
In particular,
 $\mathfrak{diff}^{1,+}(C)$
is isomorphic to
$\mathfrak{diff}^{1,+}(C)$
is isomorphic to
![]() $F_{C}$
,
$F_{C}$
,
 $\mathfrak{diff}_{S^{1}}^{1,+}(C)$
is isomorphic to
$\mathfrak{diff}_{S^{1}}^{1,+}(C)$
is isomorphic to
![]() $T_{C}$
and
$T_{C}$
and
 $\mathfrak{diff}_{S^{2}}^{1,+}(C)$
is isomorphic to
$\mathfrak{diff}_{S^{2}}^{1,+}(C)$
is isomorphic to
![]() $V_{C}^{\pm }$
. Moreover, these are isomorphic to the Thompson groups
$V_{C}^{\pm }$
. Moreover, these are isomorphic to the Thompson groups
 $F_{n+1},T_{n+1}$
and the signed Thompson group
$F_{n+1},T_{n+1}$
and the signed Thompson group
![]() $V_{n+1}^{\pm }$
, respectively.
$V_{n+1}^{\pm }$
, respectively.
The main points in the statement of the theorem are the finiteness of the covering and the fact that the intervals are standard.
Remark 2. If the self-similar Cantor set does not satisfy the genericity condition
![]() $(C)$
, then the same proof provides for every
$(C)$
, then the same proof provides for every
 $\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C)$
a covering of
$\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C)$
a covering of
![]() $C$
by a finite collection of disjoint intervals
$C$
by a finite collection of disjoint intervals
![]() $\{I_{j}\}$
, integers
$\{I_{j}\}$
, integers
 $\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
$\mathbf{k}_{j}\in \mathbb{Z}^{n+1}$
and
 $a_{j},b_{j}\in C$
, such that the restriction of the map
$a_{j},b_{j}\in C$
, such that the restriction of the map
![]() $\unicode[STIX]{x1D711}$
is given by the formula (39), a slight generalization of (5) above. However, it is not clear that one could assume that the images of
$\unicode[STIX]{x1D711}$
is given by the formula (39), a slight generalization of (5) above. However, it is not clear that one could assume that the images of
![]() $\{I_{j}\}$
are standard intervals and, in particular, that
$\{I_{j}\}$
are standard intervals and, in particular, that
 $\mathfrak{diff}^{1,+}(C)$
is isomorphic to some Thompson group.
$\mathfrak{diff}^{1,+}(C)$
is isomorphic to some Thompson group.
We derive easily now the interpretation for the Thompson groups and their braided versions as follows.
Corollary 2.
(i) Let
 $C$
be the image of the standard ternary Cantor subset into the equatorial circle of the sphere
$C$
be the image of the standard ternary Cantor subset into the equatorial circle of the sphere
 $S^{2}$
and
$S^{2}$
and
 $k\geqslant 2$
.
$k\geqslant 2$
.(a) The smooth mapping class group
 ${\mathcal{M}}^{k,+}(D_{+}^{2},C)$
is the Thompson group
${\mathcal{M}}^{k,+}(D_{+}^{2},C)$
is the Thompson group
 $T$
, where
$T$
, where
 $D_{+}^{2}$
denotes the upper hemisphere.
$D_{+}^{2}$
denotes the upper hemisphere.(b) The smooth mapping class group
 ${\mathcal{M}}^{k,+}(S^{2},C)$
is the group of half-twists
${\mathcal{M}}^{k,+}(S^{2},C)$
is the group of half-twists
 ${\mathcal{B}}^{1/2}$
from [Reference Funar and NguyenFN16].
${\mathcal{B}}^{1/2}$
from [Reference Funar and NguyenFN16].
(ii) Let
 $C$
be the standard ternary Cantor subset of an interval contained in the interior of a 2-disk
$C$
be the standard ternary Cantor subset of an interval contained in the interior of a 2-disk
 $D^{2}$
and
$D^{2}$
and
 $k\geqslant 2$
. Then
$k\geqslant 2$
. Then
 ${\mathcal{M}}^{k,+}(D^{2},C)$
is the group of half-twists of the punctured disk (see [Reference Aramayona and FunarAF17]).
${\mathcal{M}}^{k,+}(D^{2},C)$
is the group of half-twists of the punctured disk (see [Reference Aramayona and FunarAF17]).
Remark 3. The group of half twists
![]() ${\mathcal{B}}^{1/2}$
is an extension of the signed Thompson group
${\mathcal{B}}^{1/2}$
is an extension of the signed Thompson group
![]() $V^{\pm }$
by the compactly supported pure mapping class group of
$V^{\pm }$
by the compactly supported pure mapping class group of
![]() $S^{2}-C$
. It is similar to the braided Thompson group
$S^{2}-C$
. It is similar to the braided Thompson group
![]() ${\mathcal{B}}$
from [Reference Funar and KapoudjianFK04] (see § 2.5), which is an extension of
${\mathcal{B}}$
from [Reference Funar and KapoudjianFK04] (see § 2.5), which is an extension of
![]() $V$
by the same pure mapping class group, in particular it is also finitely presented (see [Reference Aramayona and FunarAF17]).
$V$
by the same pure mapping class group, in particular it is also finitely presented (see [Reference Aramayona and FunarAF17]).
Remark 4. The central ternary Cantor sets
![]() $C_{\unicode[STIX]{x1D706}}$
are pairwise non-diffeomorphic, i.e. there is no
$C_{\unicode[STIX]{x1D706}}$
are pairwise non-diffeomorphic, i.e. there is no
![]() ${\mathcal{C}}^{1}$
diffeomorphism of
${\mathcal{C}}^{1}$
diffeomorphism of
![]() $\mathbb{R}$
sending
$\mathbb{R}$
sending
![]() $C_{\unicode[STIX]{x1D706}}$
into
$C_{\unicode[STIX]{x1D706}}$
into
![]() $C_{\unicode[STIX]{x1D706}^{\prime }}$
for
$C_{\unicode[STIX]{x1D706}^{\prime }}$
for
![]() $\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D706}^{\prime }$
. Indeed, if it were such a diffeomorphism then the Hausdorff dimensions of the two Cantor sets would agree, while the Hausdorff dimension of
$\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D706}^{\prime }$
. Indeed, if it were such a diffeomorphism then the Hausdorff dimensions of the two Cantor sets would agree, while the Hausdorff dimension of
![]() $C_{\unicode[STIX]{x1D706}}$
is
$C_{\unicode[STIX]{x1D706}}$
is
 $\log 2/\text{log}\,\unicode[STIX]{x1D706}$
(see [Reference FalconerFal03], Theorem 1.14). Nevertheless, the groups
$\log 2/\text{log}\,\unicode[STIX]{x1D706}$
(see [Reference FalconerFal03], Theorem 1.14). Nevertheless, the groups
 $\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
are all isomorphic, for
$\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
are all isomorphic, for
![]() $\unicode[STIX]{x1D706}>2$
, according to Theorem 6.
$\unicode[STIX]{x1D706}>2$
, according to Theorem 6.
We notice that a weaker version of our Theorem 6 concerning the form of
![]() ${\mathcal{C}}^{1}$
-diffeomorphisms of the central Cantor sets
${\mathcal{C}}^{1}$
-diffeomorphisms of the central Cantor sets
![]() $C_{\unicode[STIX]{x1D706}}$
, was already obtained in [Reference Bamón, Moreira, Plaza and VeraBMPV97, Proposition 1].
$C_{\unicode[STIX]{x1D706}}$
, was already obtained in [Reference Bamón, Moreira, Plaza and VeraBMPV97, Proposition 1].
A case which attracted considerable interest is that of bi-Lipschitz homeomorphisms of Cantor sets (see [Reference Cooper and PignataroCP88, Reference Falconer and MarshFM92] and the recent [Reference Rao, Ruan and YangRRY12, Reference Xi and XiongXX13]). In particular, the results of Falconer and Marsh [Reference Falconer and MarshFM92] imply that every bi-Lipschitz homeomorphism of a Cantor set is given by a pair of possibly infinite coverings of the Cantor set by disjoint intervals and affine homeomorphisms between the corresponding intervals. Notice that any countable subgroup of
 $\text{Diff}^{0}(S^{1})$
(or
$\text{Diff}^{0}(S^{1})$
(or
 $\text{Diff}^{0}([0,1])$
can be conjugated (by a homeomorphism) into the corresponding group of bi-Lipschitz homeomorphisms (see [Reference Deroin, Kleptsyn and NavasDKN07, Theorem D]).
$\text{Diff}^{0}([0,1])$
can be conjugated (by a homeomorphism) into the corresponding group of bi-Lipschitz homeomorphisms (see [Reference Deroin, Kleptsyn and NavasDKN07, Theorem D]).
1.5 Self-similar Cantor dusts
The next step is to go to higher dimensions. Examples of Blankenship (see [Reference BlankenshipBla51]) show that there exist wild Cantor sets in
![]() $\mathbb{R}^{n}$
, for every
$\mathbb{R}^{n}$
, for every
![]() $n\geqslant 3$
. A Cantor set
$n\geqslant 3$
. A Cantor set
![]() $C$
is tame if and only if for every
$C$
is tame if and only if for every
![]() $\unicode[STIX]{x1D700}>0$
there exist finitely many disjoint piecewise linear cells of diameter smaller than
$\unicode[STIX]{x1D700}>0$
there exist finitely many disjoint piecewise linear cells of diameter smaller than
![]() $\unicode[STIX]{x1D700}$
whose interiors cover
$\unicode[STIX]{x1D700}$
whose interiors cover
![]() $C$
. In particular, products of tame Cantor sets are tame. More generally, the product of a Cantor subset of
$C$
. In particular, products of tame Cantor sets are tame. More generally, the product of a Cantor subset of
![]() $\mathbb{R}^{n}$
with any compact
$\mathbb{R}^{n}$
with any compact
![]() $0$
-dimensional subset
$0$
-dimensional subset
 $Z\;\subset \;\mathbb{R}^{m}$
is a tame Cantor subset of
$Z\;\subset \;\mathbb{R}^{m}$
is a tame Cantor subset of
![]() $\mathbb{R}^{m+n}$
(see [Reference McMillanMcm64, Corollary 2]).
$\mathbb{R}^{m+n}$
(see [Reference McMillanMcm64, Corollary 2]).
In order to emphasize the role of the embedding we will consider now the simplest Cantor subsets, which although tame they are not smoothly tame. Let
 $C_{\unicode[STIX]{x1D706}}^{n}\;\subset \;\mathbb{R}^{n}$
be the Cartesian product of
$C_{\unicode[STIX]{x1D706}}^{n}\;\subset \;\mathbb{R}^{n}$
be the Cartesian product of
![]() $n$
copies of
$n$
copies of
![]() $C_{\unicode[STIX]{x1D706}}$
, where
$C_{\unicode[STIX]{x1D706}}$
, where
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $\unicode[STIX]{x1D706}>2$
, which is itself a Cantor set.
$\unicode[STIX]{x1D706}>2$
, which is itself a Cantor set.
Theorem 7. Let
 $\unicode[STIX]{x1D711}\in \mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C_{\unicode[STIX]{x1D706}}^{n})$
, where
$\unicode[STIX]{x1D711}\in \mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C_{\unicode[STIX]{x1D706}}^{n})$
, where
![]() $\unicode[STIX]{x1D706}>2$
. Then there is a covering of
$\unicode[STIX]{x1D706}>2$
. Then there is a covering of
![]() $C_{\unicode[STIX]{x1D706}}^{n}$
by a finite collection of disjoint standard parallelepipeds
$C_{\unicode[STIX]{x1D706}}^{n}$
by a finite collection of disjoint standard parallelepipeds
![]() $\{I_{j}\}$
, integers
$\{I_{j}\}$
, integers
![]() $k_{j,i}\in \mathbb{Z}$
and
$k_{j,i}\in \mathbb{Z}$
and
 $a_{j,i},b_{j,i}\in C_{\unicode[STIX]{x1D706}}$
, such that
$a_{j,i},b_{j,i}\in C_{\unicode[STIX]{x1D706}}$
, such that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=(b_{j,i}+\unicode[STIX]{x1D706}^{k_{j}}(x_{i}-a_{j,i}))_{i=1,n}\circ S_{j}\quad \text{for any }x\in I_{j}\;\cap \;C_{\unicode[STIX]{x1D706}}^{n},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=(b_{j,i}+\unicode[STIX]{x1D706}^{k_{j}}(x_{i}-a_{j,i}))_{i=1,n}\circ S_{j}\quad \text{for any }x\in I_{j}\;\cap \;C_{\unicode[STIX]{x1D706}}^{n},\end{eqnarray}$$
where
![]() $S_{j}$
is an orientation preserving symmetry of the cube. In particular,
$S_{j}$
is an orientation preserving symmetry of the cube. In particular,
 $\mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C_{\unicode[STIX]{x1D706}}^{n})$
is isomorphic to the
$\mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C_{\unicode[STIX]{x1D706}}^{n})$
is isomorphic to the
![]() $n$
-dimensional Brin group
$n$
-dimensional Brin group
![]() $nV^{\text{sym}}$
decorated by the group
$nV^{\text{sym}}$
decorated by the group
![]() $D_{n}$
of positive symmetries of the cube (see § 2).
$D_{n}$
of positive symmetries of the cube (see § 2).
Notice that in a series of papers (see [Reference BrinBri04, Reference BrinBri10, Reference Bleak and LanoueBL10, Reference Hennig and MatucciHM12]) by Brin, Bleak and Lanoue, Hennig and Matucci the authors proved that the higher-dimensional Thompson groups
![]() $nV$
defined by Brin are pairwise non-isomorphic finitely presented simple groups (see also [Reference RubinRub96, Reference RubinRub89]).
$nV$
defined by Brin are pairwise non-isomorphic finitely presented simple groups (see also [Reference RubinRub96, Reference RubinRub89]).
Remark 5. Note that the group
 $\mathfrak{diff}_{[0,1]^{n}}^{1}(C_{\unicode[STIX]{x1D706}}^{n})$
is a proper subgroup of
$\mathfrak{diff}_{[0,1]^{n}}^{1}(C_{\unicode[STIX]{x1D706}}^{n})$
is a proper subgroup of
 $\mathfrak{diff}_{\mathbb{R}^{n}}^{1}(C_{\unicode[STIX]{x1D706}}^{n})$
.
$\mathfrak{diff}_{\mathbb{R}^{n}}^{1}(C_{\unicode[STIX]{x1D706}}^{n})$
.
2 Definition of Thompson-like groups
The standard reference for the classical Thompson groups is [Reference Cannon, Floyd and ParryCFP96]. For the sake of completeness we provide here the basic definitions from several different perspectives, which lead naturally to the generalizations considered by Brown and Stein and further to the high dimensional Brin groups.
2.1 Groups of piecewise affine homeomorphisms/bijections
Thompson’s group
![]() $F$
is the group of piecewise dyadic affine homeomorphisms of the interval
$F$
is the group of piecewise dyadic affine homeomorphisms of the interval
![]() $[0,1]$
. Namely, for each
$[0,1]$
. Namely, for each
![]() $f\in F$
, there exist two dyadic subdivisions of
$f\in F$
, there exist two dyadic subdivisions of
![]() $[0,1]$
,
$[0,1]$
,
 $a_{0}=0<a_{1}<\cdots <a_{n}=1$
and
$a_{0}=0<a_{1}<\cdots <a_{n}=1$
and
 $b_{0}=0<b_{1}\cdots <b_{n}$
, with
$b_{0}=0<b_{1}\cdots <b_{n}$
, with
![]() $n\in \mathbb{N}^{\ast }$
, such that
$n\in \mathbb{N}^{\ast }$
, such that
 $a_{i+1}-a_{i}$
and
$a_{i+1}-a_{i}$
and
 $b_{i+1}-b_{i}$
belong to
$b_{i+1}-b_{i}$
belong to
 $\{n/2^{k},\;n,k\in \mathbb{N}\}$
, so that the restriction of
$\{n/2^{k},\;n,k\in \mathbb{N}\}$
, so that the restriction of
![]() $f$
to
$f$
to
 $[a_{i},a_{i+1}]$
is the unique increasing affine map onto
$[a_{i},a_{i+1}]$
is the unique increasing affine map onto
 $[b_{i},b_{i+1}]$
.
$[b_{i},b_{i+1}]$
.
Therefore, an element of
![]() $F$
is completely determined by the data of two dyadic subdivisions of
$F$
is completely determined by the data of two dyadic subdivisions of
![]() $[0,1]$
having the same cardinality.
$[0,1]$
having the same cardinality.
Let us identify the circle to the quotient space
 $[0,1]/0\sim 1$
. Thompson’s group
$[0,1]/0\sim 1$
. Thompson’s group
![]() $T$
is the group of piecewise dyadic affine orientation preserving homeomorphisms of the circle. In other words, for each
$T$
is the group of piecewise dyadic affine orientation preserving homeomorphisms of the circle. In other words, for each
![]() $g\in T$
, there exist two dyadic subdivisions of
$g\in T$
, there exist two dyadic subdivisions of
![]() $[0,1]$
,
$[0,1]$
,
 $a_{0}=0<a_{1}<\cdots <a_{n}=1$
and
$a_{0}=0<a_{1}<\cdots <a_{n}=1$
and
 $b_{0}=0<b_{1}\cdots <b_{n}$
, with
$b_{0}=0<b_{1}\cdots <b_{n}$
, with
![]() $n\in \mathbb{N}^{\ast }$
, and
$n\in \mathbb{N}^{\ast }$
, and
 $i_{0}\in \{1,\ldots ,n\}$
, such that, for each
$i_{0}\in \{1,\ldots ,n\}$
, such that, for each
 $i\in \{0,\ldots ,n-1\}$
, the restriction of
$i\in \{0,\ldots ,n-1\}$
, the restriction of
![]() $g$
to
$g$
to
 $[a_{i},a_{i+1}]$
is the unique increasing map onto
$[a_{i},a_{i+1}]$
is the unique increasing map onto
 $[b_{i+i_{0}},b_{i+i_{0}+1}]$
. The indices must be understood modulo
$[b_{i+i_{0}},b_{i+i_{0}+1}]$
. The indices must be understood modulo
![]() $n$
.
$n$
.
Therefore, an element of
![]() $T$
is completely determined by the data of two dyadic subdivisions of
$T$
is completely determined by the data of two dyadic subdivisions of
![]() $[0,1]$
having the same cardinality, say
$[0,1]$
having the same cardinality, say
![]() $n\in \mathbb{N}^{\ast }$
, plus an integer
$n\in \mathbb{N}^{\ast }$
, plus an integer
![]() $i_{0}$
mod
$i_{0}$
mod
![]() $n$
.
$n$
.
Finally, Thompson’s group
![]() $V$
is the group of bijections of
$V$
is the group of bijections of
![]() $[\!0,1\![$
, which are right-continuous at each point, piecewise non-decreasing and dyadic affine. In other words, for each
$[\!0,1\![$
, which are right-continuous at each point, piecewise non-decreasing and dyadic affine. In other words, for each
![]() $h\in V$
, there exist two dyadic subdivisions of
$h\in V$
, there exist two dyadic subdivisions of
![]() $[0,1]$
,
$[0,1]$
,
 $a_{0}=0<a_{1}<\cdots <a_{n}=1$
and
$a_{0}=0<a_{1}<\cdots <a_{n}=1$
and
 $b_{0}=0<b_{1}\cdots <b_{n}$
, with
$b_{0}=0<b_{1}\cdots <b_{n}$
, with
![]() $n\in \mathbb{N}^{\ast }$
, and a permutation
$n\in \mathbb{N}^{\ast }$
, and a permutation
![]() $\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
, such that, for each
$\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
, such that, for each
 $i\in \{1,\ldots ,n\}$
, the restriction of
$i\in \{1,\ldots ,n\}$
, the restriction of
![]() $h$
to
$h$
to
 $[\!a_{i-1},a_{i}\! [$
is the unique non-decreasing affine map onto
$[\!a_{i-1},a_{i}\! [$
is the unique non-decreasing affine map onto
 $[\!b_{\unicode[STIX]{x1D70E}(i)-1},b_{\unicode[STIX]{x1D70E}(i)}\! [$
. It follows that an element
$[\!b_{\unicode[STIX]{x1D70E}(i)-1},b_{\unicode[STIX]{x1D70E}(i)}\! [$
. It follows that an element
![]() $h$
of
$h$
of
![]() $V$
is completely determined by the data of two dyadic subdivisions of
$V$
is completely determined by the data of two dyadic subdivisions of
![]() $[0,1]$
having the same cardinality, say
$[0,1]$
having the same cardinality, say
![]() $n\in \mathbb{N}^{\ast }$
, plus a permutation
$n\in \mathbb{N}^{\ast }$
, plus a permutation
![]() $\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
. Denoting
$\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
. Denoting
 $I_{i}=[a_{i-1},a_{i}]$
and
$I_{i}=[a_{i-1},a_{i}]$
and
 $J_{i}=[b_{i-1},b_{i}]$
, these data can be summarized into a triple
$J_{i}=[b_{i-1},b_{i}]$
, these data can be summarized into a triple
 $((J_{i})_{1\leqslant i\leqslant n},(I_{i})_{1\leqslant i\leqslant n},\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n})$
.
$((J_{i})_{1\leqslant i\leqslant n},(I_{i})_{1\leqslant i\leqslant n},\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n})$
.
The signed Thompson group
![]() $V^{\pm }$
is the group of right-continuous bijections of the unit circle that map the set of dyadic rationals to itself, are differentiable except at finitely many points, and such that, on every interval of differentiability, they are affine maps whose derivatives are (positive or negative) powers of
$V^{\pm }$
is the group of right-continuous bijections of the unit circle that map the set of dyadic rationals to itself, are differentiable except at finitely many points, and such that, on every interval of differentiability, they are affine maps whose derivatives are (positive or negative) powers of
![]() $2$
.
$2$
.
We have obvious inclusions
 $F\;\subset \;T\;\subset \;V\;\subset \;V^{\pm }$
. R.J. Thompson proved in 1965 that
$F\;\subset \;T\;\subset \;V\;\subset \;V^{\pm }$
. R.J. Thompson proved in 1965 that
![]() $F,T$
and
$F,T$
and
![]() $V$
are finitely presented groups and that
$V$
are finitely presented groups and that
![]() $T$
and
$T$
and
![]() $V$
are simple (cf. [Reference Cannon, Floyd and ParryCFP96]). The group
$V$
are simple (cf. [Reference Cannon, Floyd and ParryCFP96]). The group
![]() $V^{\pm }$
is also finitely presented and simple (see [Reference Aramayona and FunarAF17]). The group
$V^{\pm }$
is also finitely presented and simple (see [Reference Aramayona and FunarAF17]). The group
![]() $F$
is not perfect, as
$F$
is not perfect, as
 $F/[F,F]$
is isomorphic to
$F/[F,F]$
is isomorphic to
![]() $\mathbb{Z}^{2}$
, but
$\mathbb{Z}^{2}$
, but
 $F^{\prime }=[F,F]$
is simple. However,
$F^{\prime }=[F,F]$
is simple. However,
![]() $F^{\prime }$
is not finitely generated (this is related to the fact that an element
$F^{\prime }$
is not finitely generated (this is related to the fact that an element
![]() $f$
of
$f$
of
![]() $F$
lies in
$F$
lies in
![]() $F^{\prime }$
if and only if its support is included in
$F^{\prime }$
if and only if its support is included in
![]() $]\!0,1\!\,\![$
).
$]\!0,1\!\,\![$
).
2.2 Groups of diagrams of finite binary trees
A finite binary rooted planar tree is a finite planar tree having a unique 2-valent vertex, called the root, a set of monovalent vertices called the leaves, and whose other vertices are 3-valent. The planarity of the tree provides a canonical labelling of its leaves, in the following way. Assuming that the plane is oriented, the leaves are labelled from 1 to
![]() $n$
, from left to right, the root being at the top and the leaves at the bottom.
$n$
, from left to right, the root being at the top and the leaves at the bottom.
There exists a bijection between the set of dyadic subdivisions of
![]() $[0,1]$
and the set of finite binary rooted planar trees. Indeed, given such a tree, one may label its vertices by dyadic intervals in the following way. First, the root is labelled by
$[0,1]$
and the set of finite binary rooted planar trees. Indeed, given such a tree, one may label its vertices by dyadic intervals in the following way. First, the root is labelled by
![]() $[0,1]$
. Suppose that a vertex is labelled by
$[0,1]$
. Suppose that a vertex is labelled by
 $I=[k/2^{n},(k+1)/2^{n}]$
, then its two descendant vertices are labelled by the two halves
$I=[k/2^{n},(k+1)/2^{n}]$
, then its two descendant vertices are labelled by the two halves
![]() $I$
:
$I$
:
 $[k/2^{n},(2k+1)/2^{n+1}]$
for the left one and
$[k/2^{n},(2k+1)/2^{n+1}]$
for the left one and
 $[(2k+1)/(2^{n+1}),(k+1)/2^{n}]$
for the right one. Finally, the dyadic subdivision associated to the tree is the sequence of intervals which label its leaves.
$[(2k+1)/(2^{n+1}),(k+1)/2^{n}]$
for the right one. Finally, the dyadic subdivision associated to the tree is the sequence of intervals which label its leaves.
Thus, an element
![]() $h$
of
$h$
of
![]() $V$
is represented by a triple
$V$
is represented by a triple
 $(\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E})$
, where
$(\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E})$
, where
![]() $\unicode[STIX]{x1D70F}_{0}$
and
$\unicode[STIX]{x1D70F}_{0}$
and
![]() $\unicode[STIX]{x1D70F}_{1}$
have the same number of leaves
$\unicode[STIX]{x1D70F}_{1}$
have the same number of leaves
![]() $n\in \mathbb{N}^{\ast }$
, and
$n\in \mathbb{N}^{\ast }$
, and
![]() $\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
. Such a triple will be called a symbol for
$\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
. Such a triple will be called a symbol for
![]() $h$
. It is convenient to interpret the permutation
$h$
. It is convenient to interpret the permutation
![]() $\unicode[STIX]{x1D70E}$
as the bijection
$\unicode[STIX]{x1D70E}$
as the bijection
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
which maps the
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D70E}}$
which maps the
![]() $i$
th leaf of the source tree
$i$
th leaf of the source tree
![]() $\unicode[STIX]{x1D70F}_{0}$
to the
$\unicode[STIX]{x1D70F}_{0}$
to the
![]() $\unicode[STIX]{x1D70E}(i)$
th leaf of the target tree
$\unicode[STIX]{x1D70E}(i)$
th leaf of the target tree
![]() $\unicode[STIX]{x1D70F}_{1}$
. When
$\unicode[STIX]{x1D70F}_{1}$
. When
![]() $h$
belongs to
$h$
belongs to
![]() $F$
, the permutation
$F$
, the permutation
![]() $\unicode[STIX]{x1D70E}$
is identity and the symbol reduces to a pair of trees
$\unicode[STIX]{x1D70E}$
is identity and the symbol reduces to a pair of trees
![]() $(\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0})$
.
$(\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0})$
.
Now, two symbols are equivalent if they represent the same element of
![]() $V$
and one denotes by
$V$
and one denotes by
 $[\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}]$
the equivalence class. The composition law of piecewise dyadic affine bijections is pushed out on the set of equivalence classes of symbols in the following way. In order to define
$[\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}]$
the equivalence class. The composition law of piecewise dyadic affine bijections is pushed out on the set of equivalence classes of symbols in the following way. In order to define
 $[\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{0}^{\prime },\unicode[STIX]{x1D70E}^{\prime }]\cdot [\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}]$
, one may suppose, at the price of refining both symbols, that the tree
$[\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{0}^{\prime },\unicode[STIX]{x1D70E}^{\prime }]\cdot [\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}]$
, one may suppose, at the price of refining both symbols, that the tree
![]() $\unicode[STIX]{x1D70F}_{1}$
coincides with the tree
$\unicode[STIX]{x1D70F}_{1}$
coincides with the tree
![]() $\unicode[STIX]{x1D70F}_{0}^{\prime }$
. Then the product of the two symbols is
$\unicode[STIX]{x1D70F}_{0}^{\prime }$
. Then the product of the two symbols is
 $$\begin{eqnarray}[\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70E}^{\prime }]\cdot [\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}]=[\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}^{\prime }\circ \unicode[STIX]{x1D70E}].\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70E}^{\prime }]\cdot [\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}]=[\unicode[STIX]{x1D70F}_{1}^{\prime },\unicode[STIX]{x1D70F}_{0},\unicode[STIX]{x1D70E}^{\prime }\circ \unicode[STIX]{x1D70E}].\end{eqnarray}$$
It follows that
![]() $V$
is isomorphic to the group of equivalence classes of symbols endowed with this internal law. Now, every element of
$V$
is isomorphic to the group of equivalence classes of symbols endowed with this internal law. Now, every element of
![]() $V^{\pm }$
is encoded by an enhanced symbol
$V^{\pm }$
is encoded by an enhanced symbol
 $(T,T^{\prime },\unicode[STIX]{x1D70E},\unicode[STIX]{x1D700})$
, where
$(T,T^{\prime },\unicode[STIX]{x1D70E},\unicode[STIX]{x1D700})$
, where
![]() $T,T^{\prime }$
are admissible trees,
$T,T^{\prime }$
are admissible trees,
 $\unicode[STIX]{x1D70E}:\unicode[STIX]{x2202}T\rightarrow \unicode[STIX]{x2202}T^{\prime }$
is a bijection and
$\unicode[STIX]{x1D70E}:\unicode[STIX]{x2202}T\rightarrow \unicode[STIX]{x2202}T^{\prime }$
is a bijection and
 $\unicode[STIX]{x1D700}\in (\mathbb{Z}/2\mathbb{Z})^{\unicode[STIX]{x2202}T^{\prime }}$
, up to equivalence.
$\unicode[STIX]{x1D700}\in (\mathbb{Z}/2\mathbb{Z})^{\unicode[STIX]{x2202}T^{\prime }}$
, up to equivalence.
2.3 Partial automorphisms of trees
The beginning of the article [Reference Greenberg and SergiescuGS91] formalizes a change of point of view, consisting in considering, not the finite binary trees, but their complements in the infinite binary tree.
Let
![]() ${\mathcal{T}}_{2}$
be the infinite binary rooted planar tree (all its vertices other than the root are 3-valent). Each finite binary rooted planar tree
${\mathcal{T}}_{2}$
be the infinite binary rooted planar tree (all its vertices other than the root are 3-valent). Each finite binary rooted planar tree
![]() $\unicode[STIX]{x1D70F}$
can be embedded in a unique way into
$\unicode[STIX]{x1D70F}$
can be embedded in a unique way into
![]() ${\mathcal{T}}_{2}$
, assuming that the embedding maps the root of
${\mathcal{T}}_{2}$
, assuming that the embedding maps the root of
![]() $\unicode[STIX]{x1D70F}$
onto the root of
$\unicode[STIX]{x1D70F}$
onto the root of
![]() ${\mathcal{T}}_{2}$
, and respects the orientation. Therefore,
${\mathcal{T}}_{2}$
, and respects the orientation. Therefore,
![]() $\unicode[STIX]{x1D70F}$
may be identified with a subtree of
$\unicode[STIX]{x1D70F}$
may be identified with a subtree of
![]() ${\mathcal{T}}_{2}$
, whose root coincides with that of
${\mathcal{T}}_{2}$
, whose root coincides with that of
![]() ${\mathcal{T}}_{2}$
.
${\mathcal{T}}_{2}$
.
Definition 7 (Cf. [Reference Kapoudjian and SergiescuKS05]).
A partial isomorphism of
![]() ${\mathcal{T}}_{2}$
consists of the data of two finite binary rooted subtrees
${\mathcal{T}}_{2}$
consists of the data of two finite binary rooted subtrees
![]() $\unicode[STIX]{x1D70F}_{0}$
and
$\unicode[STIX]{x1D70F}_{0}$
and
![]() $\unicode[STIX]{x1D70F}_{1}$
of
$\unicode[STIX]{x1D70F}_{1}$
of
![]() ${\mathcal{T}}_{2}$
having the same number of leaves
${\mathcal{T}}_{2}$
having the same number of leaves
![]() $n\in \mathbb{N}^{\ast }$
, and an isomorphism
$n\in \mathbb{N}^{\ast }$
, and an isomorphism
 $q:{\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{0}\rightarrow {\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{1}$
. The complements of
$q:{\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{0}\rightarrow {\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{1}$
. The complements of
![]() $\unicode[STIX]{x1D70F}_{0}$
and
$\unicode[STIX]{x1D70F}_{0}$
and
![]() $\unicode[STIX]{x1D70F}_{1}$
have
$\unicode[STIX]{x1D70F}_{1}$
have
![]() $n$
components, each one isomorphic to
$n$
components, each one isomorphic to
![]() ${\mathcal{T}}_{2}$
, which are enumerated from 1 to
${\mathcal{T}}_{2}$
, which are enumerated from 1 to
![]() $n$
according to the labeling of the leaves of the trees
$n$
according to the labeling of the leaves of the trees
![]() $\unicode[STIX]{x1D70F}_{0}$
and
$\unicode[STIX]{x1D70F}_{0}$
and
![]() $\unicode[STIX]{x1D70F}_{1}$
. Thus,
$\unicode[STIX]{x1D70F}_{1}$
. Thus,
 ${\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{0}=T_{0}^{1}\;\cup \;\cdots \;\cup \;T_{0}^{n}$
and
${\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{0}=T_{0}^{1}\;\cup \;\cdots \;\cup \;T_{0}^{n}$
and
 ${\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{1}=T_{1}^{1}\;\cup \;\cdots \;\cup \;T_{1}^{n}$
where the
${\mathcal{T}}_{2}\setminus \unicode[STIX]{x1D70F}_{1}=T_{1}^{1}\;\cup \;\cdots \;\cup \;T_{1}^{n}$
where the
![]() $T_{j}^{i}$
are the connected components. Equivalently, the partial isomorphism of
$T_{j}^{i}$
are the connected components. Equivalently, the partial isomorphism of
![]() ${\mathcal{T}}_{2}$
is given by a permutation
${\mathcal{T}}_{2}$
is given by a permutation
![]() $\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
and, for
$\unicode[STIX]{x1D70E}\in \mathfrak{S}_{n}$
and, for
 $i=1,\ldots ,n$
, an isomorphism
$i=1,\ldots ,n$
, an isomorphism
 $q_{i}:T_{0}^{i}\rightarrow T_{1}^{\unicode[STIX]{x1D70E}(i)}$
.
$q_{i}:T_{0}^{i}\rightarrow T_{1}^{\unicode[STIX]{x1D70E}(i)}$
.
Two partial automorphisms
![]() $q$
and
$q$
and
![]() $r$
can be composed if and only if the target of
$r$
can be composed if and only if the target of
![]() $r$
coincides with the source of
$r$
coincides with the source of
![]() $r$
. One gets the partial automorphism
$r$
. One gets the partial automorphism
![]() $q\circ r$
. The composition provides a structure of inverse monoid on the set of partial automorphisms.
$q\circ r$
. The composition provides a structure of inverse monoid on the set of partial automorphisms.
Let
![]() $\unicode[STIX]{x2202}{\mathcal{T}}_{2}$
be the boundary of
$\unicode[STIX]{x2202}{\mathcal{T}}_{2}$
be the boundary of
![]() ${\mathcal{T}}_{2}$
(also called the set of ‘ends’ of
${\mathcal{T}}_{2}$
(also called the set of ‘ends’ of
![]() ${\mathcal{T}}_{2}$
) endowed with its usual topology, for which it is a Cantor set. Although a partial automorphism does not act (globally) on the tree, it does act on its boundary. One has therefore a morphism from the monoid of partial isomorphism into the homeomorphisms of
${\mathcal{T}}_{2}$
) endowed with its usual topology, for which it is a Cantor set. Although a partial automorphism does not act (globally) on the tree, it does act on its boundary. One has therefore a morphism from the monoid of partial isomorphism into the homeomorphisms of
![]() $\unicode[STIX]{x2202}{\mathcal{T}}_{2}$
, whose image
$\unicode[STIX]{x2202}{\mathcal{T}}_{2}$
, whose image
![]() $N$
is the spheromorphisms group of Neretin (see [Reference NeretinNer92]).
$N$
is the spheromorphisms group of Neretin (see [Reference NeretinNer92]).
Thompson’s group
![]() $V$
can be viewed as the subgroup of
$V$
can be viewed as the subgroup of
![]() $N$
which is the image of those partial automorphisms which respect the local orientation of the edges.
$N$
which is the image of those partial automorphisms which respect the local orientation of the edges.
2.4 Generalizations following Brown and Stein, Bieri and Strebel
Brown considered in [Reference BrownBro87] similar groups
 $F_{n,r}\;\subset \;T_{n,r}\;\subset \;V_{n,r}$
(extending the previous work of Higman), which were defined as in the last two constructions above but using instead of binary trees forests of
$F_{n,r}\;\subset \;T_{n,r}\;\subset \;V_{n,r}$
(extending the previous work of Higman), which were defined as in the last two constructions above but using instead of binary trees forests of
![]() $r$
copies of
$r$
copies of
![]() $n$
-ary trees so that
$n$
-ary trees so that
![]() $F,T,V$
correspond to
$F,T,V$
correspond to
![]() $n=2$
and
$n=2$
and
![]() $r=1$
. The isomorphism type of
$r=1$
. The isomorphism type of
![]() $V_{n,r}$
and
$V_{n,r}$
and
![]() $T_{n,r}$
only depends on
$T_{n,r}$
only depends on
![]() $r$
(mod
$r$
(mod
![]() $n$
) while
$n$
) while
![]() $F_{n,r}$
depends only on
$F_{n,r}$
depends only on
![]() $n$
. We drop the subscript
$n$
. We drop the subscript
![]() $r$
when
$r$
when
![]() $r=1$
. These groups are finitely presented and of type
$r=1$
. These groups are finitely presented and of type
![]() $FP_{\infty }$
according to [Reference Brown and GeogheganBG84] for the case of
$FP_{\infty }$
according to [Reference Brown and GeogheganBG84] for the case of
![]() $F$
and
$F$
and
![]() $T$
and then [Reference BrownBro87, Theorem 4.17] for its extension to all other groups from this family. Moreover, Higman has proved (see [Reference HigmanHig74]) that
$T$
and then [Reference BrownBro87, Theorem 4.17] for its extension to all other groups from this family. Moreover, Higman has proved (see [Reference HigmanHig74]) that
![]() $V_{n,r}$
has a simple subgroup of index
$V_{n,r}$
has a simple subgroup of index
 $\text{g.c.d}(2,n-1)$
, and this was extended by Brown who showed that
$\text{g.c.d}(2,n-1)$
, and this was extended by Brown who showed that
![]() $F_{n}$
have simple commutator and
$F_{n}$
have simple commutator and
![]() $T_{n,r}$
have simple double commutator groups (see [Reference BrownBro87] for more details and refinements).
$T_{n,r}$
have simple double commutator groups (see [Reference BrownBro87] for more details and refinements).
One can obtain these groups also by considering
![]() $n$
-adic piecewise affine homeomorphisms (or bijections) of
$n$
-adic piecewise affine homeomorphisms (or bijections) of
![]() $[0,r]$
(with identified endpoints for
$[0,r]$
(with identified endpoints for
![]() $T_{n,r}$
) i.e. having singularities in
$T_{n,r}$
) i.e. having singularities in
![]() $\mathbb{Z}[1/n]$
and derivatives in
$\mathbb{Z}[1/n]$
and derivatives in
 $\{n^{a},a\in \mathbb{Z}\}$
. This point of view was taken further by Bieri, Strebel and Stein in [Reference Bieri and StrebelBS16, Reference SteinSte92]. Specifically, given a multiplicative subgroup
$\{n^{a},a\in \mathbb{Z}\}$
. This point of view was taken further by Bieri, Strebel and Stein in [Reference Bieri and StrebelBS16, Reference SteinSte92]. Specifically, given a multiplicative subgroup
![]() $P\;\subset \;\mathbb{R}$
, a
$P\;\subset \;\mathbb{R}$
, a
![]() $\mathbb{Z}[P]$
-submodule
$\mathbb{Z}[P]$
-submodule
![]() $A\;\subset \;\mathbb{R}$
satisfying
$A\;\subset \;\mathbb{R}$
satisfying
 $P\cdot A=A$
, and a positive
$P\cdot A=A$
, and a positive
![]() $r\in A$
, one can consider the group
$r\in A$
, one can consider the group
![]() $F_{A,P,r}$
of those
$F_{A,P,r}$
of those
![]() $\text{PL}$
homeomorphisms of
$\text{PL}$
homeomorphisms of
![]() $[0,r]$
with finite singular set in
$[0,r]$
with finite singular set in
![]() $A$
and all slopes in
$A$
and all slopes in
![]() $P$
. There are similar families
$P$
. There are similar families
![]() $T_{A,P,r}$
and
$T_{A,P,r}$
and
![]() $V_{A,P,r}$
. Brown and Stein proved that
$V_{A,P,r}$
. Brown and Stein proved that
 $F_{\mathbb{Z}[1/(n_{1}n_{2}\cdots n_{k})],\langle n_{1},n_{2},\ldots ,n_{k}\rangle ,r}$
is finitely presented of
$F_{\mathbb{Z}[1/(n_{1}n_{2}\cdots n_{k})],\langle n_{1},n_{2},\ldots ,n_{k}\rangle ,r}$
is finitely presented of
![]() $FP_{\infty }$
type. Furthermore
$FP_{\infty }$
type. Furthermore
![]() $F_{A,P,r}$
and
$F_{A,P,r}$
and
![]() $V_{A,P,r}$
have simple commutator subgroups, while
$V_{A,P,r}$
have simple commutator subgroups, while
![]() $T_{A,P,r}$
have simple second commutator subgroups.
$T_{A,P,r}$
have simple second commutator subgroups.
The signed version
![]() $V_{n,r}^{\pm }$
of
$V_{n,r}^{\pm }$
of
![]() $V_{n,r}$
is defined as above, by allowing both orientation preserving and orientation reversing piecewise affine homeomorphisms.
$V_{n,r}$
is defined as above, by allowing both orientation preserving and orientation reversing piecewise affine homeomorphisms.
2.5 Mapping class groups of infinite surfaces and braided Thompson groups
Let
![]() $\mathscr{S}_{0,\infty }$
be the oriented surface of genus zero, which is the following inductive limit of compact oriented genus zero surfaces with boundary
$\mathscr{S}_{0,\infty }$
be the oriented surface of genus zero, which is the following inductive limit of compact oriented genus zero surfaces with boundary
![]() $\mathscr{S}_{n}$
. Starting with a cylinder
$\mathscr{S}_{n}$
. Starting with a cylinder
![]() $\mathscr{S}_{1}$
, one gets
$\mathscr{S}_{1}$
, one gets
![]() $\mathscr{S}_{n+1}$
from
$\mathscr{S}_{n+1}$
from
![]() $\mathscr{S}_{n}$
by gluing a pair of pants (i.e. a three-holed sphere) along each boundary circle of
$\mathscr{S}_{n}$
by gluing a pair of pants (i.e. a three-holed sphere) along each boundary circle of
![]() $\mathscr{S}_{n}$
. This construction yields, for each
$\mathscr{S}_{n}$
. This construction yields, for each
![]() $n\geqslant 1$
, an embedding
$n\geqslant 1$
, an embedding
 $\mathscr{S}_{n}{\hookrightarrow}\mathscr{S}_{n+1}$
, with an orientation on
$\mathscr{S}_{n}{\hookrightarrow}\mathscr{S}_{n+1}$
, with an orientation on
![]() $\mathscr{S}_{n+1}$
compatible with that of
$\mathscr{S}_{n+1}$
compatible with that of
![]() $\mathscr{S}_{n}$
. The resulting inductive limit (in the topological category) of the
$\mathscr{S}_{n}$
. The resulting inductive limit (in the topological category) of the
![]() $\mathscr{S}_{n}$
is the surface
$\mathscr{S}_{n}$
is the surface
 $\mathscr{S}_{0,\infty }=\lim _{\stackrel{\rightarrow }{n}}\mathscr{S}_{n}$
.
$\mathscr{S}_{0,\infty }=\lim _{\stackrel{\rightarrow }{n}}\mathscr{S}_{n}$
.
By the above construction, the surface
![]() $\mathscr{S}_{0,\infty }$
is the union of a cylinder and of countably many pairs of pants. This topological decomposition of
$\mathscr{S}_{0,\infty }$
is the union of a cylinder and of countably many pairs of pants. This topological decomposition of
![]() $\mathscr{S}_{0,\infty }$
will be called the canonical pair of pants decomposition.
$\mathscr{S}_{0,\infty }$
will be called the canonical pair of pants decomposition.
The set of isotopy classes of orientation-preserving homeomorphisms of
![]() $\mathscr{S}_{0,\infty }$
is an uncountable group. By restricting to a certain type of homeomorphism (called asymptotically rigid), we shall obtain countable subgroups (see [Reference Funar and KapoudjianFK04, Reference Funar and KapoudjianFK08]).
$\mathscr{S}_{0,\infty }$
is an uncountable group. By restricting to a certain type of homeomorphism (called asymptotically rigid), we shall obtain countable subgroups (see [Reference Funar and KapoudjianFK04, Reference Funar and KapoudjianFK08]).
Any connected and compact subsurface of
![]() $\mathscr{S}_{0,\infty }$
which is the union of the cylinder and finitely many pairs of pants of the canonical decomposition will be called an admissible subsurface of
$\mathscr{S}_{0,\infty }$
which is the union of the cylinder and finitely many pairs of pants of the canonical decomposition will be called an admissible subsurface of
![]() $\mathscr{S}_{0,\infty }$
. The type of such a subsurface
$\mathscr{S}_{0,\infty }$
. The type of such a subsurface
![]() $S$
is the number of connected components in its boundary.
$S$
is the number of connected components in its boundary.
A rigid structure on
![]() $\mathscr{S}_{0,\infty }$
is given by a pants decomposition together with a set of disjoint proper arcs joining distinct ends such that each pair of pants intersects essentially only three arcs which join different boundary circles. One component of complement of the union of arcs is called the visible side. We fix a rigid structure on the surface underlying the canonical pants decomposition.
$\mathscr{S}_{0,\infty }$
is given by a pants decomposition together with a set of disjoint proper arcs joining distinct ends such that each pair of pants intersects essentially only three arcs which join different boundary circles. One component of complement of the union of arcs is called the visible side. We fix a rigid structure on the surface underlying the canonical pants decomposition.
Definition 8 (Following [Reference Kapoudjian and SergiescuKS05, Reference Funar and KapoudjianFK04]).
A homeomorphism
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
![]() $\mathscr{S}_{0,\infty }$
is asymptotically rigid if there exist two admissible subsurfaces
$\mathscr{S}_{0,\infty }$
is asymptotically rigid if there exist two admissible subsurfaces
![]() $S_{0}$
and
$S_{0}$
and
![]() $S_{1}$
having the same type, such that
$S_{1}$
having the same type, such that
 $\unicode[STIX]{x1D711}(S_{0})=S_{1}$
and whose restriction
$\unicode[STIX]{x1D711}(S_{0})=S_{1}$
and whose restriction
 $\mathscr{S}_{0,\infty }\setminus S_{0}\rightarrow \mathscr{S}_{0,\infty }\setminus S_{1}$
is rigid, meaning that it maps each pair of pants (of the canonical pants decomposition) onto a pair of pants and the visible side onto the visible side. If we drop the last requirement we say that the homeomorphism
$\mathscr{S}_{0,\infty }\setminus S_{0}\rightarrow \mathscr{S}_{0,\infty }\setminus S_{1}$
is rigid, meaning that it maps each pair of pants (of the canonical pants decomposition) onto a pair of pants and the visible side onto the visible side. If we drop the last requirement we say that the homeomorphism
![]() $\unicode[STIX]{x1D711}$
is asymptotically quasi-rigid.
$\unicode[STIX]{x1D711}$
is asymptotically quasi-rigid.
The asymptotically rigid and quasi-rigid mapping class groups of
![]() $\mathscr{S}_{0,\infty }$
are the groups of isotopy classes of asymptotically rigid and quasi-rigid homeomorphisms, respectively.
$\mathscr{S}_{0,\infty }$
are the groups of isotopy classes of asymptotically rigid and quasi-rigid homeomorphisms, respectively.
The asymptotically rigid mapping class group
![]() ${\mathcal{B}}$
and the quasi-rigid mapping class group
${\mathcal{B}}$
and the quasi-rigid mapping class group
![]() ${\mathcal{B}}^{1/2}$
of
${\mathcal{B}}^{1/2}$
of
![]() $\mathscr{S}_{0,\infty }$
are finitely presented groups (see [Reference Funar and KapoudjianFK04, Reference Aramayona and FunarAF17]) which fit into the exact sequences:
$\mathscr{S}_{0,\infty }$
are finitely presented groups (see [Reference Funar and KapoudjianFK04, Reference Aramayona and FunarAF17]) which fit into the exact sequences:
 $$\begin{eqnarray}\displaystyle & \displaystyle 1\rightarrow P{\mathcal{M}}(\mathscr{S}_{0,\infty })\rightarrow {\mathcal{B}}\rightarrow V\rightarrow 1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle 1\rightarrow P{\mathcal{M}}(\mathscr{S}_{0,\infty })\rightarrow {\mathcal{B}}^{1/2}\rightarrow V^{\pm }\rightarrow 1. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 1\rightarrow P{\mathcal{M}}(\mathscr{S}_{0,\infty })\rightarrow {\mathcal{B}}\rightarrow V\rightarrow 1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle 1\rightarrow P{\mathcal{M}}(\mathscr{S}_{0,\infty })\rightarrow {\mathcal{B}}^{1/2}\rightarrow V^{\pm }\rightarrow 1. & \displaystyle \nonumber\end{eqnarray}$$
Some very similar versions of the same group (using a Cantor disk instead of a Cantor sphere or a more combinatorial framework) were obtained independently by Brin [Reference BrinBri07] and Dehornoy [Reference DehornoyDeh06]. We will call any version of them braided Thompson groups.
2.6 Brin’s groups
 $nV$
and their decorated versions
$nV$
and their decorated versions
A rather different direction was taken in the seminal paper [Reference BrinBri04] of Brin, where the author constructed a family of countable groups
![]() $nV$
acting as homeomorphisms of the product of
$nV$
acting as homeomorphisms of the product of
![]() $n$
-copies of the standard triadic Cantor, generalizing the group
$n$
-copies of the standard triadic Cantor, generalizing the group
![]() $V$
which occurs for
$V$
which occurs for
![]() $n=1$
.
$n=1$
.
Let
 $I^{n}\;\subset \;\mathbb{R}^{n}$
denote the unit cube. A numbered pattern is a finite dyadic partition of
$I^{n}\;\subset \;\mathbb{R}^{n}$
denote the unit cube. A numbered pattern is a finite dyadic partition of
![]() $I^{n}$
into parallelepipeds along with a numbering. A dyadic partition is obtained from the cube by dividing at each step of the process one parallelepiped into two equal halves by a cutting hyperplane parallel to one of the coordinates’ hyperplane.
$I^{n}$
into parallelepipeds along with a numbering. A dyadic partition is obtained from the cube by dividing at each step of the process one parallelepiped into two equal halves by a cutting hyperplane parallel to one of the coordinates’ hyperplane.
One definition of
![]() $nV$
is the group of piecewise affine (not continuous!) transformations associated to pairs of numbered patterns. Given the numbered patterns
$nV$
is the group of piecewise affine (not continuous!) transformations associated to pairs of numbered patterns. Given the numbered patterns
 $P=(L_{1},L_{2},\ldots ,L_{n})$
and
$P=(L_{1},L_{2},\ldots ,L_{n})$
and
 $Q=(R_{1},R_{2},\ldots ,R_{n})$
, we set
$Q=(R_{1},R_{2},\ldots ,R_{n})$
, we set
![]() $\unicode[STIX]{x1D711}_{P,Q}$
for the unique piecewise affine transformation of the cube sending affinely each
$\unicode[STIX]{x1D711}_{P,Q}$
for the unique piecewise affine transformation of the cube sending affinely each
![]() $L_{i}$
into
$L_{i}$
into
![]() $R_{i}$
and preserving the coordinates’ hyperplanes. Thus
$R_{i}$
and preserving the coordinates’ hyperplanes. Thus
![]() $nV$
is the group of piecewise affine transformations of the form
$nV$
is the group of piecewise affine transformations of the form
![]() $\unicode[STIX]{x1D711}_{P,Q}$
, with
$\unicode[STIX]{x1D711}_{P,Q}$
, with
![]() $P,Q$
running over the set of all possible dyadic partitions.
$P,Q$
running over the set of all possible dyadic partitions.
Another description is as a group of homeomorphisms of the product
![]() $C^{n}$
of the standard triadic Cantor set
$C^{n}$
of the standard triadic Cantor set
![]() $C$
. Parallelepipeds in a dyadic partition correspond to closed and open (clopen) subsets of
$C$
. Parallelepipeds in a dyadic partition correspond to closed and open (clopen) subsets of
![]() $C^{n}$
. Every dyadic cutting hyperplane
$C^{n}$
. Every dyadic cutting hyperplane
![]() $H$
subdividing some parallelepiped
$H$
subdividing some parallelepiped
![]() $R$
into two halves determines a parallel shadow (open) parallelepiped in
$R$
into two halves determines a parallel shadow (open) parallelepiped in
![]() $R$
whose width is one third of the width of
$R$
whose width is one third of the width of
![]() $R$
in the direction orthogonal to
$R$
in the direction orthogonal to
![]() $H$
. Notice then that the complement of the union of all shadow parallelepipeds is
$H$
. Notice then that the complement of the union of all shadow parallelepipeds is
![]() $C^{n}$
. Every pattern
$C^{n}$
. Every pattern
 $P=(R_{1},R_{2},\ldots ,R_{n})$
determines a numbered collection of parallelepipeds
$P=(R_{1},R_{2},\ldots ,R_{n})$
determines a numbered collection of parallelepipeds
 $X_{P}=(X(R_{1}),X(R_{2}),\ldots ,X(R_{n}))$
whose complementary is the set of shadow parallelepipeds of those cutting hyperplanes used to build
$X_{P}=(X(R_{1}),X(R_{2}),\ldots ,X(R_{n}))$
whose complementary is the set of shadow parallelepipeds of those cutting hyperplanes used to build
![]() $P$
. Then
$P$
. Then
 $A(R_{i})=X(R_{i})\;\cap \;C^{n}$
form a clopen partition of
$A(R_{i})=X(R_{i})\;\cap \;C^{n}$
form a clopen partition of
![]() $C^{n}$
. For a pair of patterns
$C^{n}$
. For a pair of patterns
![]() $P,Q$
we define the homeomorphism
$P,Q$
we define the homeomorphism
![]() $h_{P,Q}$
of
$h_{P,Q}$
of
![]() $C^{n}$
as the unique homeomorphism which sends affinely
$C^{n}$
as the unique homeomorphism which sends affinely
![]() $A(L_{i})$
into
$A(L_{i})$
into
![]() $A(R_{i})$
and preserves the orientation in each coordinate. This amounts to say that
$A(R_{i})$
and preserves the orientation in each coordinate. This amounts to say that
![]() $h_{P,Q}$
is the restriction to
$h_{P,Q}$
is the restriction to
![]() $C^{n}$
of the piecewise affine transformation sending affinely
$C^{n}$
of the piecewise affine transformation sending affinely
![]() $X(L_{i})$
into
$X(L_{i})$
into
![]() $X(R_{i})$
and preserving the coordinates’ hyperplanes.
$X(R_{i})$
and preserving the coordinates’ hyperplanes.
The groups
![]() $nV$
are simple (see e.g. [Reference BrinBri04, Reference BrinBri10]) and finitely presented (see [Reference Hennig and MatucciHM12]). The stabilizer at some
$nV$
are simple (see e.g. [Reference BrinBri04, Reference BrinBri10]) and finitely presented (see [Reference Hennig and MatucciHM12]). The stabilizer at some
![]() $a\in C^{n}$
of the (germs of) homeomorphisms in
$a\in C^{n}$
of the (germs of) homeomorphisms in
![]() $nV$
is isomorphic to
$nV$
is isomorphic to
![]() $\mathbb{Z}^{r(a)}$
, where
$\mathbb{Z}^{r(a)}$
, where
![]() $r(a)$
is the number of rational coordinates of
$r(a)$
is the number of rational coordinates of
![]() $a$
. This implies that the groups
$a$
. This implies that the groups
![]() $nV$
are pairwise non-isomorphic (see [Reference Bleak and LanoueBL10] for details).
$nV$
are pairwise non-isomorphic (see [Reference Bleak and LanoueBL10] for details).
We could of course extend this construction to arbitrary products of central Cantor sets
![]() $C_{\unicode[STIX]{x1D706}}$
in the spirit of Brown and Stein, Bieri and Strebel as above.
$C_{\unicode[STIX]{x1D706}}$
in the spirit of Brown and Stein, Bieri and Strebel as above.
As in the case of groups
![]() $V_{n,r}$
there exists a decorated version
$V_{n,r}$
there exists a decorated version
![]() $nV^{\text{sym}}$
of
$nV^{\text{sym}}$
of
![]() $nV$
by allowing piecewise affine transformations
$nV$
by allowing piecewise affine transformations
![]() $h_{P,Q}$
to be arbitrary affine isomorphisms between
$h_{P,Q}$
to be arbitrary affine isomorphisms between
![]() $A(L_{i})$
into
$A(L_{i})$
into
![]() $A(R_{i})$
, not necessarily preserving each coordinate’s hyperplane. We will say that
$A(R_{i})$
, not necessarily preserving each coordinate’s hyperplane. We will say that
![]() $nV^{\text{sym}}$
is the
$nV^{\text{sym}}$
is the
![]() $n$
-dimensional Brin group decorated by
$n$
-dimensional Brin group decorated by
![]() $D_{n}$
, where
$D_{n}$
, where
![]() $D_{n}$
denotes the group of orientation preserving symmetries of the cube. Its elements correspond to numbered patterns
$D_{n}$
denotes the group of orientation preserving symmetries of the cube. Its elements correspond to numbered patterns
 $P=(L_{1},L_{2},\ldots ,L_{n})$
and
$P=(L_{1},L_{2},\ldots ,L_{n})$
and
 $Q=(R_{1},R_{2},\ldots ,R_{n})$
, along with a
$Q=(R_{1},R_{2},\ldots ,R_{n})$
, along with a
![]() $n$
-tuple
$n$
-tuple
 $\unicode[STIX]{x1D6F4}=(\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\ldots ,\unicode[STIX]{x1D70E}_{n})$
of orientation preserving symmetries of the
$\unicode[STIX]{x1D6F4}=(\unicode[STIX]{x1D70E}_{1},\unicode[STIX]{x1D70E}_{2},\ldots ,\unicode[STIX]{x1D70E}_{n})$
of orientation preserving symmetries of the
![]() $n$
-cube. The map
$n$
-cube. The map
![]() $\unicode[STIX]{x1D711}_{P,Q,\unicode[STIX]{x1D6F4}}$
consists of the unique piecewise affine transformation sending
$\unicode[STIX]{x1D711}_{P,Q,\unicode[STIX]{x1D6F4}}$
consists of the unique piecewise affine transformation sending
![]() $\unicode[STIX]{x1D70E}_{i}(L_{i})$
into
$\unicode[STIX]{x1D70E}_{i}(L_{i})$
into
![]() $R_{i}$
. Recall that
$R_{i}$
. Recall that
![]() $D_{n}$
is the group of orthogonal
$D_{n}$
is the group of orthogonal
![]() $n\times n$
matrices with integer entries and unit determinant. One defines in the same way the
$n\times n$
matrices with integer entries and unit determinant. One defines in the same way the
![]() $n$
-dimensional Brin group
$n$
-dimensional Brin group
 $nV^{\pm \text{sym}}$
decorated by
$nV^{\pm \text{sym}}$
decorated by
![]() $O_{n}$
, where
$O_{n}$
, where
![]() $O_{n}$
denotes the hyperoctahedral group of all symmetries of the cube, which is the higher-dimensional generalization of
$O_{n}$
denotes the hyperoctahedral group of all symmetries of the cube, which is the higher-dimensional generalization of
![]() $V^{\pm }$
.
$V^{\pm }$
.
3 Proof of general countability statements
3.1 Proof of Theorem 1
We parameterize the interval
![]() $E$
containing the Cantor set
$E$
containing the Cantor set
![]() $C$
by the
$C$
by the
![]() ${\mathcal{C}}^{k}$
-curve
${\mathcal{C}}^{k}$
-curve
 $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
and denote by
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow M$
and denote by
 $A\;\subset \;[0,1]$
the preimage of
$A\;\subset \;[0,1]$
the preimage of
![]() $C$
, which is still a Cantor set. We may assume that
$C$
, which is still a Cantor set. We may assume that
 $\{0,1\}\;\subset \;A$
. For the sake of simplicity we suppose that the interval
$\{0,1\}\;\subset \;A$
. For the sake of simplicity we suppose that the interval
![]() $E$
lies in the interior of
$E$
lies in the interior of
![]() $M$
. The proof works in general, with only minor modifications. Let
$M$
. The proof works in general, with only minor modifications. Let
 $\unicode[STIX]{x1D711}\in \text{Diff}^{k,+}(M,C)$
and denote by
$\unicode[STIX]{x1D711}\in \text{Diff}^{k,+}(M,C)$
and denote by
 $\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FE}(t)$
. Consider a
$\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D6FE}(t)$
. Consider a
![]() ${\mathcal{C}}^{k}$
-coordinates chart
${\mathcal{C}}^{k}$
-coordinates chart
![]() $U\;\subset \;M$
containing
$U\;\subset \;M$
containing
![]() $E$
, such that
$E$
, such that
![]() $U$
is identified with an open disk, while
$U$
is identified with an open disk, while
![]() $\unicode[STIX]{x1D6FE}$
is now linear and parameterized by arc length, namely that
$\unicode[STIX]{x1D6FE}$
is now linear and parameterized by arc length, namely that
 $\Vert \dot{\unicode[STIX]{x1D6FE}}\Vert =1$
and
$\Vert \dot{\unicode[STIX]{x1D6FE}}\Vert =1$
and
![]() $\ddot{\unicode[STIX]{x1D6FE}}=0$
. The norm
$\ddot{\unicode[STIX]{x1D6FE}}=0$
. The norm
![]() $\Vert \cdot \Vert$
is associated to the standard scalar product
$\Vert \cdot \Vert$
is associated to the standard scalar product
![]() $\langle \,,\rangle$
on
$\langle \,,\rangle$
on
![]() $U$
induced from
$U$
induced from
![]() $\mathbb{R}^{n}$
.
$\mathbb{R}^{n}$
.
The strategy of the proof is as follows. We define a subset
 $I_{\unicode[STIX]{x1D700}}\;\subset \;[0,1]$
consisting of finitely many intervals which contains
$I_{\unicode[STIX]{x1D700}}\;\subset \;[0,1]$
consisting of finitely many intervals which contains
![]() $A$
. At first one straightens out
$A$
. At first one straightens out
![]() $\unicode[STIX]{x1D709}$
in the complementary of
$\unicode[STIX]{x1D709}$
in the complementary of
![]() $I_{\unicode[STIX]{x1D700}}$
. To this purpose we modify
$I_{\unicode[STIX]{x1D700}}$
. To this purpose we modify
![]() $\unicode[STIX]{x1D711}$
by composing with a convenient compactly supported diffeomorphism. Further we show that there is an isotopy rel
$\unicode[STIX]{x1D711}$
by composing with a convenient compactly supported diffeomorphism. Further we show that there is an isotopy rel
![]() $A$
which straightens out the remaining arcs of
$A$
which straightens out the remaining arcs of
![]() $\unicode[STIX]{x1D709}$
. Eventually, one proves that a diffeomorphism preserving the orientation of the surface which fixes the arc
$\unicode[STIX]{x1D709}$
. Eventually, one proves that a diffeomorphism preserving the orientation of the surface which fixes the arc
![]() $E$
is, up to isotopy, supported outside a disk neighborhood of
$E$
is, up to isotopy, supported outside a disk neighborhood of
![]() $E$
. This will show that
$E$
. This will show that
![]() $\unicode[STIX]{x1D711}$
has a compactly supported class.
$\unicode[STIX]{x1D711}$
has a compactly supported class.
Assume for the moment that
![]() $A$
is just an infinite set without isolated points. The set of those
$A$
is just an infinite set without isolated points. The set of those
![]() $t$
for which
$t$
for which
 $\unicode[STIX]{x1D6FE}(t)=\unicode[STIX]{x1D709}(t)$
is a closed subset of
$\unicode[STIX]{x1D6FE}(t)=\unicode[STIX]{x1D709}(t)$
is a closed subset of
![]() $[0,1]$
containing
$[0,1]$
containing
![]() $A$
and hence its closure
$A$
and hence its closure
![]() $\overline{A}$
. Now let
$\overline{A}$
. Now let
![]() $t_{0}\in \overline{A}$
. Then, since
$t_{0}\in \overline{A}$
. Then, since
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D709}$
are differentiable at
$\unicode[STIX]{x1D709}$
are differentiable at
![]() $t_{0}$
we have
$t_{0}$
we have
 $$\begin{eqnarray}\dot{\unicode[STIX]{x1D6FE}}(t_{0})=\lim _{t\in A,t\rightarrow t_{0}}\frac{\unicode[STIX]{x1D6FE}(t)-\unicode[STIX]{x1D6FE}(t_{0})}{t-t_{0}}=\lim _{t\in A,t\rightarrow t_{0}}\frac{\unicode[STIX]{x1D709}(t)-\unicode[STIX]{x1D709}(t_{0})}{t-t_{0}}=\dot{\unicode[STIX]{x1D709}}(t_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\dot{\unicode[STIX]{x1D6FE}}(t_{0})=\lim _{t\in A,t\rightarrow t_{0}}\frac{\unicode[STIX]{x1D6FE}(t)-\unicode[STIX]{x1D6FE}(t_{0})}{t-t_{0}}=\lim _{t\in A,t\rightarrow t_{0}}\frac{\unicode[STIX]{x1D709}(t)-\unicode[STIX]{x1D709}(t_{0})}{t-t_{0}}=\dot{\unicode[STIX]{x1D709}}(t_{0}).\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D711}$
is twice differentiable then the same argument shows that
$\unicode[STIX]{x1D711}$
is twice differentiable then the same argument shows that
 $$\begin{eqnarray}\ddot{\unicode[STIX]{x1D6FE}}(t_{0})=\ddot{\unicode[STIX]{x1D709}}(t_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\ddot{\unicode[STIX]{x1D6FE}}(t_{0})=\ddot{\unicode[STIX]{x1D709}}(t_{0}).\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D711}$
is of class
$\unicode[STIX]{x1D711}$
is of class
![]() ${\mathcal{C}}^{2}$
, for every
${\mathcal{C}}^{2}$
, for every
![]() $\unicode[STIX]{x1D700}>0$
, there exists
$\unicode[STIX]{x1D700}>0$
, there exists
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})>0$
such that whenever
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})>0$
such that whenever
 $s_{1},s_{2}\in A$
, with
$s_{1},s_{2}\in A$
, with
 $|s_{1}-s_{2}|<\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})$
we have
$|s_{1}-s_{2}|<\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})$
we have
 $$\begin{eqnarray}\displaystyle & \displaystyle 1-\unicode[STIX]{x1D700}<\langle \dot{\unicode[STIX]{x1D6FE}}(t),\dot{\unicode[STIX]{x1D709}}(t)\rangle \leqslant 1\quad \text{for all }t\in [s_{1},s_{2}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 1-\unicode[STIX]{x1D700}<\langle \dot{\unicode[STIX]{x1D6FE}}(t),\dot{\unicode[STIX]{x1D709}}(t)\rangle \leqslant 1\quad \text{for all }t\in [s_{1},s_{2}], & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle |\ddot{\unicode[STIX]{x1D709}}(t)|<\unicode[STIX]{x1D700}\quad \text{for all }t\in [s_{1},s_{2}]. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle |\ddot{\unicode[STIX]{x1D709}}(t)|<\unicode[STIX]{x1D700}\quad \text{for all }t\in [s_{1},s_{2}]. & \displaystyle\end{eqnarray}$$
We assume now that
 $A=\bigcap _{j=1}^{\infty }A_{j}$
is the infinite nested intersection of the closed finite unions of intervals
$A=\bigcap _{j=1}^{\infty }A_{j}$
is the infinite nested intersection of the closed finite unions of intervals
 $A_{j}\supset A_{j+1}\supset \cdots \,$
.
$A_{j}\supset A_{j+1}\supset \cdots \,$
.
We denote
 $I_{\unicode[STIX]{x1D700}}=\bigcup _{s_{1},s_{2}\in A;|s_{1}-s_{2}|\leqslant (\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})/2)}[s_{1},s_{2}]\;\subset \;[0,1]$
. We choose
$I_{\unicode[STIX]{x1D700}}=\bigcup _{s_{1},s_{2}\in A;|s_{1}-s_{2}|\leqslant (\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})/2)}[s_{1},s_{2}]\;\subset \;[0,1]$
. We choose
![]() $\unicode[STIX]{x1D700}>0$
small enough such that the image of
$\unicode[STIX]{x1D700}>0$
small enough such that the image of
![]() $\unicode[STIX]{x1D709}|_{I_{\unicode[STIX]{x1D700}}}$
is contained within the coordinates disk
$\unicode[STIX]{x1D709}|_{I_{\unicode[STIX]{x1D700}}}$
is contained within the coordinates disk
![]() $U$
.
$U$
.
Set further
 $\unicode[STIX]{x1D6FE}_{s}(t)=(1-s)\unicode[STIX]{x1D6FE}(t)+s\;\unicode[STIX]{x1D709}(t)$
, for
$\unicode[STIX]{x1D6FE}_{s}(t)=(1-s)\unicode[STIX]{x1D6FE}(t)+s\;\unicode[STIX]{x1D709}(t)$
, for
 $t\in [s_{1},s_{2}]\;\subset \;I_{\unicode[STIX]{x1D700}}$
and
$t\in [s_{1},s_{2}]\;\subset \;I_{\unicode[STIX]{x1D700}}$
and
 $s\in [0,1]$
.
$s\in [0,1]$
.
Lemma 1. Fix
![]() $\unicode[STIX]{x1D700}<1$
as above. Let
$\unicode[STIX]{x1D700}<1$
as above. Let
 $s_{1},s_{2}\in A$
, such that
$s_{1},s_{2}\in A$
, such that
 $|s_{1}-s_{2}|\leqslant \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})/2$
. Then
$|s_{1}-s_{2}|\leqslant \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})/2$
. Then
![]() $\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
provides a
$\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
provides a
![]() ${\mathcal{C}}^{k}$
-isotopy between the restrictions
${\mathcal{C}}^{k}$
-isotopy between the restrictions
![]() $\unicode[STIX]{x1D6FE}|_{[s_{1},s_{2}]}$
and
$\unicode[STIX]{x1D6FE}|_{[s_{1},s_{2}]}$
and
![]() $\unicode[STIX]{x1D709}|_{[s_{1},s_{2}]}$
to the interval
$\unicode[STIX]{x1D709}|_{[s_{1},s_{2}]}$
to the interval
![]() $[s_{1},s_{2}]$
. In particular, the image
$[s_{1},s_{2}]$
. In particular, the image
![]() $\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
is contained within the union of orthogonal strips
$\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
is contained within the union of orthogonal strips
 $(\unicode[STIX]{x1D6FE}(I_{\unicode[STIX]{x1D700}})\times \mathbb{R})\;\cap \;U$
.
$(\unicode[STIX]{x1D6FE}(I_{\unicode[STIX]{x1D700}})\times \mathbb{R})\;\cap \;U$
.
Proof. We have to prove that for any
 $s\in [0,1]$
the curve
$s\in [0,1]$
the curve
![]() $\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
is simple. This follows immediately from the fact that whenever
$\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
is simple. This follows immediately from the fact that whenever
![]() $\unicode[STIX]{x1D700}<1$
we have
$\unicode[STIX]{x1D700}<1$
we have
 $$\begin{eqnarray}\langle \dot{\unicode[STIX]{x1D6FE}}_{s}(t),\dot{\unicode[STIX]{x1D6FE}}(t)\rangle \geqslant 1-s+s\langle \dot{\unicode[STIX]{x1D709}}(t),\dot{\unicode[STIX]{x1D6FE}}(t)\rangle \geqslant 1-\unicode[STIX]{x1D700}s>0\end{eqnarray}$$
$$\begin{eqnarray}\langle \dot{\unicode[STIX]{x1D6FE}}_{s}(t),\dot{\unicode[STIX]{x1D6FE}}(t)\rangle \geqslant 1-s+s\langle \dot{\unicode[STIX]{x1D709}}(t),\dot{\unicode[STIX]{x1D6FE}}(t)\rangle \geqslant 1-\unicode[STIX]{x1D700}s>0\end{eqnarray}$$
for any
 $t\in [0,1]$
,
$t\in [0,1]$
,
 $s\in [0,1]$
. Further, note that the curve
$s\in [0,1]$
. Further, note that the curve
![]() $\unicode[STIX]{x1D6FE}_{s}(t)$
, for
$\unicode[STIX]{x1D6FE}_{s}(t)$
, for
 $s\in [0,1]$
and fixed
$s\in [0,1]$
and fixed
![]() $t\in I_{\unicode[STIX]{x1D700}}$
is a segment joining
$t\in I_{\unicode[STIX]{x1D700}}$
is a segment joining
![]() $\unicode[STIX]{x1D709}(t)$
with its orthogonal projection onto
$\unicode[STIX]{x1D709}(t)$
with its orthogonal projection onto
![]() $\unicode[STIX]{x1D6FE}(I_{\unicode[STIX]{x1D700}})$
.◻
$\unicode[STIX]{x1D6FE}(I_{\unicode[STIX]{x1D700}})$
.◻
We set
 $$\begin{eqnarray}\unicode[STIX]{x1D702}(t)=\left\{\begin{array}{@{}cc@{}}\unicode[STIX]{x1D709}(t) & \text{ if }t\in I_{\unicode[STIX]{x1D700}},\\ \unicode[STIX]{x1D6FE}(t) & \text{if }t\not \in I_{\unicode[STIX]{x1D700}}.\\ \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}(t)=\left\{\begin{array}{@{}cc@{}}\unicode[STIX]{x1D709}(t) & \text{ if }t\in I_{\unicode[STIX]{x1D700}},\\ \unicode[STIX]{x1D6FE}(t) & \text{if }t\not \in I_{\unicode[STIX]{x1D700}}.\\ \end{array}\right.\end{eqnarray}$$
Lemma 2. There exists a compactly supported diffeomorphism
 $\unicode[STIX]{x1D713}\in P\text{Diff}^{k,+}(M,C)$
such that
$\unicode[STIX]{x1D713}\in P\text{Diff}^{k,+}(M,C)$
such that
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709})$
and
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709})$
and
![]() $\unicode[STIX]{x1D702}$
are isotopic rel
$\unicode[STIX]{x1D702}$
are isotopic rel
![]() $A$
.
$A$
.
Proof. Lemma 1 shows that the image of
![]() $\unicode[STIX]{x1D702}$
is a simple curve, as
$\unicode[STIX]{x1D702}$
is a simple curve, as
![]() $\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
is contained within the union of orthogonal strips
$\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
is contained within the union of orthogonal strips
 $(\unicode[STIX]{x1D6FE}(I_{\unicode[STIX]{x1D700}})\times \mathbb{R})\;\cap \;U$
, and thus it cannot intersect
$(\unicode[STIX]{x1D6FE}(I_{\unicode[STIX]{x1D700}})\times \mathbb{R})\;\cap \;U$
, and thus it cannot intersect
 $\unicode[STIX]{x1D6FE}([0,1]\setminus I_{\unicode[STIX]{x1D700}})$
.
$\unicode[STIX]{x1D6FE}([0,1]\setminus I_{\unicode[STIX]{x1D700}})$
.
Note that
![]() $A\;\subset \;I_{\unicode[STIX]{x1D700}}$
, since
$A\;\subset \;I_{\unicode[STIX]{x1D700}}$
, since
![]() $A$
has no isolated points. The endpoints of a maximal complementary interval should belong to
$A$
has no isolated points. The endpoints of a maximal complementary interval should belong to
![]() $A$
, by maximality. In particular, its length should be greater than
$A$
, by maximality. In particular, its length should be greater than
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})/2$
, and hence there are only finitely many maximal complementary intervals say
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D700})/2$
, and hence there are only finitely many maximal complementary intervals say
 $J_{1},J_{2},\ldots ,J_{p}$
. Then
$J_{1},J_{2},\ldots ,J_{p}$
. Then
![]() $\unicode[STIX]{x1D709}(J_{i})$
are pairwise disjoint smooth arcs whose interiors are
$\unicode[STIX]{x1D709}(J_{i})$
are pairwise disjoint smooth arcs whose interiors are
 $\unicode[STIX]{x1D709}(\text{int}(J_{i}))\;\subset \;M-C$
, each such arc joining two distinct points of
$\unicode[STIX]{x1D709}(\text{int}(J_{i}))\;\subset \;M-C$
, each such arc joining two distinct points of
![]() $C$
. Moreover, as
$C$
. Moreover, as
 $\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D6FE}(t)$
, for
$\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D6FE}(t)$
, for
 $t\in \bigcup _{i=1}^{p}\unicode[STIX]{x2202}J_{i}$
, we can straighten out the half-arcs of
$t\in \bigcup _{i=1}^{p}\unicode[STIX]{x2202}J_{i}$
, we can straighten out the half-arcs of
![]() $\unicode[STIX]{x1D709}$
around these points. Namely, there exists a small neighborhood
$\unicode[STIX]{x1D709}$
around these points. Namely, there exists a small neighborhood
![]() $N(I_{\unicode[STIX]{x1D700}})$
of
$N(I_{\unicode[STIX]{x1D700}})$
of
![]() $I_{\unicode[STIX]{x1D700}}$
within
$I_{\unicode[STIX]{x1D700}}$
within
![]() $[0,1]$
such that after perturbing
$[0,1]$
such that after perturbing
![]() $\unicode[STIX]{x1D709}$
by an isotopy supported in
$\unicode[STIX]{x1D709}$
by an isotopy supported in
 $N(I_{\unicode[STIX]{x1D700}})\;\cap \;(\bigcup _{i=1}^{p}J_{i})$
we have
$N(I_{\unicode[STIX]{x1D700}})\;\cap \;(\bigcup _{i=1}^{p}J_{i})$
we have
 $\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D6FE}(t)$
, for
$\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D6FE}(t)$
, for
 $t\in N(I_{\unicode[STIX]{x1D700}})\;\cap \;(\bigcup _{i=1}^{p}J_{i})$
.
$t\in N(I_{\unicode[STIX]{x1D700}})\;\cap \;(\bigcup _{i=1}^{p}J_{i})$
.
Now the arcs
![]() $\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
are disjoint both from
$\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
are disjoint both from
 $\unicode[STIX]{x1D709}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
and
$\unicode[STIX]{x1D709}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
and
 $\unicode[STIX]{x1D6FE}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
. There exists then a small enough open neighborhood
$\unicode[STIX]{x1D6FE}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
. There exists then a small enough open neighborhood
![]() $V$
of
$V$
of
![]() $\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
within
$\unicode[STIX]{x1D709}(I_{\unicode[STIX]{x1D700}})$
within
![]() $U$
which is disjoint from both
$U$
which is disjoint from both
 $\unicode[STIX]{x1D709}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
and
$\unicode[STIX]{x1D709}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
and
 $\unicode[STIX]{x1D6FE}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
. Therefore there exists an orientation preserving diffeomorphism
$\unicode[STIX]{x1D6FE}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
. Therefore there exists an orientation preserving diffeomorphism
![]() $\unicode[STIX]{x1D713}$
supported on
$\unicode[STIX]{x1D713}$
supported on
![]() $M-V$
, thus compactly supported, such that
$M-V$
, thus compactly supported, such that
 $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}})))=\unicode[STIX]{x1D6FE}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
, and hence
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}})))=\unicode[STIX]{x1D6FE}(J_{i}\setminus N(I_{\unicode[STIX]{x1D700}}))$
, and hence
 $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}(J_{i}))=\unicode[STIX]{x1D702}(J_{i})$
. Thus
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709}(J_{i}))=\unicode[STIX]{x1D702}(J_{i})$
. Thus
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709})$
and
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709})$
and
![]() $\unicode[STIX]{x1D702}$
are isotopic rel
$\unicode[STIX]{x1D702}$
are isotopic rel
![]() $A$
, as claimed.◻
$A$
, as claimed.◻
Lemma 3. The curves
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D702}$
are isotopic rel
$\unicode[STIX]{x1D702}$
are isotopic rel
![]() $A$
.
$A$
.
Proof. We will prove that the family
 $$\begin{eqnarray}\unicode[STIX]{x1D702}_{s}(t)=\left\{\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FE}_{s}(t) & \text{ if }t\in I_{\unicode[STIX]{x1D700}},\\ \unicode[STIX]{x1D6FE}(t) & \text{ if }t\not \in I_{\unicode[STIX]{x1D700}},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{s}(t)=\left\{\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FE}_{s}(t) & \text{ if }t\in I_{\unicode[STIX]{x1D700}},\\ \unicode[STIX]{x1D6FE}(t) & \text{ if }t\not \in I_{\unicode[STIX]{x1D700}},\end{array}\right.\end{eqnarray}$$
is the desired isotopy. From Lemma 1 it suffices to show that there are not intersections between the segments of curves
 $\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
and
$\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
and
![]() $\unicode[STIX]{x1D6FE}_{s}|_{[s_{3},s_{4}]}$
, when
$\unicode[STIX]{x1D6FE}_{s}|_{[s_{3},s_{4}]}$
, when
![]() $s_{i}\in A$
and
$s_{i}\in A$
and
 $[s_{1},s_{2}],[s_{3},s_{4}]\;\subset \;I_{\unicode[STIX]{x1D700}}$
are disjoint.
$[s_{1},s_{2}],[s_{3},s_{4}]\;\subset \;I_{\unicode[STIX]{x1D700}}$
are disjoint.
Let
 $p=\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}(t_{0})$
be a point on the first curve segment. We want to estimate the angle
$p=\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}(t_{0})$
be a point on the first curve segment. We want to estimate the angle
![]() $\unicode[STIX]{x1D6FD}$
of the Euclidean triangle with vertices
$\unicode[STIX]{x1D6FD}$
of the Euclidean triangle with vertices
 $p,\unicode[STIX]{x1D6FE}(s_{1}),\unicode[STIX]{x1D6FE}(s_{2})$
at
$p,\unicode[STIX]{x1D6FE}(s_{1}),\unicode[STIX]{x1D6FE}(s_{2})$
at
![]() $\unicode[STIX]{x1D6FE}_{s}(s_{1})$
. We can write then
$\unicode[STIX]{x1D6FE}_{s}(s_{1})$
. We can write then
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1}),\dot{\unicode[STIX]{x1D6FE}}(0)\rangle =\int _{0}^{t_{0}-s_{1}}\langle \dot{\unicode[STIX]{x1D6FE}}_{s}(s_{1}+x),\quad \dot{\unicode[STIX]{x1D6FE}}(0)\rangle \,dx=\int _{0}^{t_{0}-s_{1}}1-s+s\langle \dot{\unicode[STIX]{x1D709}}(s_{1}+x),\dot{\unicode[STIX]{x1D6FE}}(0)\rangle \,dx.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1}),\dot{\unicode[STIX]{x1D6FE}}(0)\rangle =\int _{0}^{t_{0}-s_{1}}\langle \dot{\unicode[STIX]{x1D6FE}}_{s}(s_{1}+x),\quad \dot{\unicode[STIX]{x1D6FE}}(0)\rangle \,dx=\int _{0}^{t_{0}-s_{1}}1-s+s\langle \dot{\unicode[STIX]{x1D709}}(s_{1}+x),\dot{\unicode[STIX]{x1D6FE}}(0)\rangle \,dx.\end{eqnarray}$$
Then (9) implies
 $$\begin{eqnarray}\Vert \!\unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1})\!\!\Vert \!\cos (\unicode[STIX]{x1D6FD})=\langle \unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1}),\quad \dot{\unicode[STIX]{x1D6FE}}(0)\rangle \geqslant (t_{0}-s_{1})(1-s\unicode[STIX]{x1D700}).\end{eqnarray}$$
$$\begin{eqnarray}\Vert \!\unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1})\!\!\Vert \!\cos (\unicode[STIX]{x1D6FD})=\langle \unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1}),\quad \dot{\unicode[STIX]{x1D6FE}}(0)\rangle \geqslant (t_{0}-s_{1})(1-s\unicode[STIX]{x1D700}).\end{eqnarray}$$
On the other hand from (10) we derive
 $$\begin{eqnarray}\Vert \dot{\unicode[STIX]{x1D709}}(x)-\dot{\unicode[STIX]{x1D709}}(s_{1})\Vert \leqslant \unicode[STIX]{x1D700}(x-s_{1}),\end{eqnarray}$$
$$\begin{eqnarray}\Vert \dot{\unicode[STIX]{x1D709}}(x)-\dot{\unicode[STIX]{x1D709}}(s_{1})\Vert \leqslant \unicode[STIX]{x1D700}(x-s_{1}),\end{eqnarray}$$
and then
 $$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1})\Vert \leqslant \int _{0}^{t_{0}-s_{1}}\Vert \!\dot{\unicode[STIX]{x1D6FE}}_{s}(x)\!\!\Vert dx\leqslant \int _{0}^{t_{0}-s_{1}}(s\Vert \!\dot{\unicode[STIX]{x1D709}}(x)\!\!\Vert +(1-s))\,dx\leqslant t_{0}-s_{1}+\frac{\unicode[STIX]{x1D700}}{2}(t_{0}-s_{1})^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert \unicode[STIX]{x1D6FE}_{s}(t_{0})-\unicode[STIX]{x1D6FE}_{s}(s_{1})\Vert \leqslant \int _{0}^{t_{0}-s_{1}}\Vert \!\dot{\unicode[STIX]{x1D6FE}}_{s}(x)\!\!\Vert dx\leqslant \int _{0}^{t_{0}-s_{1}}(s\Vert \!\dot{\unicode[STIX]{x1D709}}(x)\!\!\Vert +(1-s))\,dx\leqslant t_{0}-s_{1}+\frac{\unicode[STIX]{x1D700}}{2}(t_{0}-s_{1})^{2}.\end{eqnarray}$$
From (15) we obtain
 $$\begin{eqnarray}\cos (\unicode[STIX]{x1D6FD})\geqslant \frac{1-s\unicode[STIX]{x1D700}}{1+(\unicode[STIX]{x1D700}/2)(t_{0}+s_{1})}\geqslant \frac{1-\unicode[STIX]{x1D700}}{1+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}\cos (\unicode[STIX]{x1D6FD})\geqslant \frac{1-s\unicode[STIX]{x1D700}}{1+(\unicode[STIX]{x1D700}/2)(t_{0}+s_{1})}\geqslant \frac{1-\unicode[STIX]{x1D700}}{1+\unicode[STIX]{x1D700}}.\end{eqnarray}$$
If we choose
![]() $\unicode[STIX]{x1D700}\leqslant {\textstyle \frac{1}{3}}$
then
$\unicode[STIX]{x1D700}\leqslant {\textstyle \frac{1}{3}}$
then
 $\unicode[STIX]{x1D6FD}\in [-\unicode[STIX]{x1D70B}/3,\unicode[STIX]{x1D70B}/3]$
.
$\unicode[STIX]{x1D6FD}\in [-\unicode[STIX]{x1D70B}/3,\unicode[STIX]{x1D70B}/3]$
.
Assume now the contrary of our claim, namely that there exists some intersection point
![]() $p$
between
$p$
between
![]() $\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
and
$\unicode[STIX]{x1D6FE}_{s}|_{[s_{1},s_{2}]}$
and
 $\unicode[STIX]{x1D6FE}_{s}|_{[s_{3},s_{4}]}$
. Up to a symmetry of indices we can assume that the Euclidean triangle with vertices at
$\unicode[STIX]{x1D6FE}_{s}|_{[s_{3},s_{4}]}$
. Up to a symmetry of indices we can assume that the Euclidean triangle with vertices at
![]() $p$
,
$p$
,
![]() $\unicode[STIX]{x1D6FE}_{s}(s_{1})$
and
$\unicode[STIX]{x1D6FE}_{s}(s_{1})$
and
![]() $\unicode[STIX]{x1D6FE}_{s}(s_{2})$
has the angle
$\unicode[STIX]{x1D6FE}_{s}(s_{2})$
has the angle
![]() $\unicode[STIX]{x1D6FD}$
at
$\unicode[STIX]{x1D6FD}$
at
![]() $\unicode[STIX]{x1D6FE}_{s}(s_{1})$
within the interval
$\unicode[STIX]{x1D6FE}_{s}(s_{1})$
within the interval
![]() $[\unicode[STIX]{x1D70B}/2,\unicode[STIX]{x1D70B})$
. This contradicts our estimates (18) for
$[\unicode[STIX]{x1D70B}/2,\unicode[STIX]{x1D70B})$
. This contradicts our estimates (18) for
![]() $\unicode[STIX]{x1D6FD}$
.◻
$\unicode[STIX]{x1D6FD}$
.◻
The last ingredient of the proof of Theorem 1 is as follows.
Lemma 4. Assume that there exists an isotopy of class
![]() ${\mathcal{C}}^{k}$
between
${\mathcal{C}}^{k}$
between
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
 $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE}))$
rel
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE}))$
rel
![]() $A$
. Then
$A$
. Then
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() ${\mathcal{C}}^{k}$
-isotopic to a compactly supported diffeomorphism from
${\mathcal{C}}^{k}$
-isotopic to a compactly supported diffeomorphism from
 $P\text{Diff}^{k,+}(M,C)$
.
$P\text{Diff}^{k,+}(M,C)$
.
Proof. We can assume that the disk
![]() $D$
of diameter
$D$
of diameter
![]() $E$
is contained in
$E$
is contained in
![]() $U$
.
$U$
.
If the dimension of
![]() $M$
is 2, the endpoints of
$M$
is 2, the endpoints of
![]() $E$
separate the circle
$E$
separate the circle
![]() $\unicode[STIX]{x2202}D$
into two arcs, say
$\unicode[STIX]{x2202}D$
into two arcs, say
![]() $F^{+}$
and
$F^{+}$
and
![]() $F^{-}$
. The circular order of the three arcs
$F^{-}$
. The circular order of the three arcs
 $F^{+},E,F^{-}$
around an endpoint of
$F^{+},E,F^{-}$
around an endpoint of
![]() $E$
is preserved by
$E$
is preserved by
 $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}\in \text{Diff}^{k,+}(M,C)$
. Note that
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}\in \text{Diff}^{k,+}(M,C)$
. Note that
![]() $E$
is fixed by
$E$
is fixed by
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}$
. Thus there exists a
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}$
. Thus there exists a
![]() ${\mathcal{C}}^{k}$
-isotopy which is identity on
${\mathcal{C}}^{k}$
-isotopy which is identity on
![]() $E$
, sends
$E$
, sends
 $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(F^{+}))$
to
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(F^{+}))$
to
![]() $F^{+}$
and
$F^{+}$
and
 $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(F^{-}))$
to
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(F^{-}))$
to
![]() $F^{-}$
. Therefore
$F^{-}$
. Therefore
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}$
is isotopic to a diffeomorphism supported on the complement of
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}$
is isotopic to a diffeomorphism supported on the complement of
![]() $D$
and hence its class is compactly supported. The claim follows now, because
$D$
and hence its class is compactly supported. The claim follows now, because
![]() $\unicode[STIX]{x1D713}$
is equally compactly supported.
$\unicode[STIX]{x1D713}$
is equally compactly supported.
If the dimension of
![]() $M$
is at least 3, there exists an isotopy of
$M$
is at least 3, there exists an isotopy of
![]() $M$
sending
$M$
sending
 $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}D))$
to
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}D))$
to
![]() $\unicode[STIX]{x2202}D$
, which is identity on
$\unicode[STIX]{x2202}D$
, which is identity on
![]() $E$
, because
$E$
, because
 $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}\in P\text{Diff}^{k,+}(M,C)$
and we conclude as above.◻
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D711}\in P\text{Diff}^{k,+}(M,C)$
and we conclude as above.◻
3.2 Sparse sets and proofs of Theorems 2, 3 and 4
3.2.1 Preliminaries
Let
![]() ${\mathcal{N}}_{\unicode[STIX]{x1D700}}(a)$
denote the
${\mathcal{N}}_{\unicode[STIX]{x1D700}}(a)$
denote the
![]() $\unicode[STIX]{x1D700}$
-neighborhood
$\unicode[STIX]{x1D700}$
-neighborhood
 $|x-a|<\unicode[STIX]{x1D700}$
of
$|x-a|<\unicode[STIX]{x1D700}$
of
![]() $a$
in
$a$
in
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
![]() ${\mathcal{N}}_{\unicode[STIX]{x1D700}}^{\pm }(a)$
the punctured right and left semi-neighborhoods of
${\mathcal{N}}_{\unicode[STIX]{x1D700}}^{\pm }(a)$
the punctured right and left semi-neighborhoods of
![]() $a$
, i.e.,
$a$
, i.e.,
 $a<x<a+\unicode[STIX]{x1D700}$
and
$a<x<a+\unicode[STIX]{x1D700}$
and
 $a-\unicode[STIX]{x1D700}<x<a$
, respectively.
$a-\unicode[STIX]{x1D700}<x<a$
, respectively.
We say that
![]() $a\in C$
is a left point of
$a\in C$
is a left point of
![]() $C$
if there is a left semi-neighborhood
$C$
if there is a left semi-neighborhood
![]() ${\mathcal{N}}^{-}(a)$
such that
${\mathcal{N}}^{-}(a)$
such that
 ${\mathcal{N}}^{-}(a)\;\cap \;C=\varnothing$
. In the same way we define right points.
${\mathcal{N}}^{-}(a)\;\cap \;C=\varnothing$
. In the same way we define right points.
For
![]() $a\in C$
denote by
$a\in C$
denote by
![]() $\text{Diff}_{a}^{k}$
the stabilizer of
$\text{Diff}_{a}^{k}$
the stabilizer of
![]() $a$
in
$a$
in
 $\text{Diff}^{k}(\mathbb{R},C)$
, and by
$\text{Diff}^{k}(\mathbb{R},C)$
, and by
![]() $\mathfrak{diff}_{a}^{k}$
the group of
$\mathfrak{diff}_{a}^{k}$
the group of
![]() $k$
-germs of elements of the stabilizer of
$k$
-germs of elements of the stabilizer of
![]() $a$
in
$a$
in
 $\mathfrak{diff}^{k}(C)$
. The superscript
$\mathfrak{diff}^{k}(C)$
. The superscript
![]() $+$
in
$+$
in
![]() $\text{Diff}_{a}^{k,+}$
and
$\text{Diff}_{a}^{k,+}$
and
![]() $\mathfrak{diff}_{a}^{k,+}$
means that we only consider those diffeomorphisms that preserve the orientation of the interval, i.e. increasing.
$\mathfrak{diff}_{a}^{k,+}$
means that we only consider those diffeomorphisms that preserve the orientation of the interval, i.e. increasing.
Let
![]() $\unicode[STIX]{x1D711}$
be a diffeomorphism with
$\unicode[STIX]{x1D711}$
be a diffeomorphism with
 $\unicode[STIX]{x1D711}(a)=a$
. We say that
$\unicode[STIX]{x1D711}(a)=a$
. We say that
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() $N$
-flat at
$N$
-flat at
![]() $a$
if
$a$
if
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)-x=o((x-a)^{N})\quad \text{as }x\rightarrow a.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)-x=o((x-a)^{N})\quad \text{as }x\rightarrow a.\end{eqnarray}$$
Lemma 5. Assume that
![]() $C$
is a
$C$
is a
![]() $\unicode[STIX]{x1D70E}$
-sparse subset of
$\unicode[STIX]{x1D70E}$
-sparse subset of
![]() $\mathbb{R}$
. Let
$\mathbb{R}$
. Let
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}$
be 1-flat at
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}$
be 1-flat at
![]() $a\in C$
. Then
$a\in C$
. Then
![]() $\unicode[STIX]{x1D711}|_{C}$
is identity in a small neighborhood of
$\unicode[STIX]{x1D711}|_{C}$
is identity in a small neighborhood of
![]() $a$
.
$a$
.
Proof. Observe first that
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
, since
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
, since
 $\unicode[STIX]{x1D711}^{\prime }(a)=1$
and hence
$\unicode[STIX]{x1D711}^{\prime }(a)=1$
and hence
![]() $\unicode[STIX]{x1D711}$
must be increasing. We can assume without loss of generality that
$\unicode[STIX]{x1D711}$
must be increasing. We can assume without loss of generality that
![]() $a$
is not a right point of
$a$
is not a right point of
![]() $C$
. Suppose that
$C$
. Suppose that
![]() $\unicode[STIX]{x1D711}$
is non-trivial on
$\unicode[STIX]{x1D711}$
is non-trivial on
 ${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)\;\cap \;C$
for any
${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)\;\cap \;C$
for any
![]() $\unicode[STIX]{x1D6FF}>0$
.
$\unicode[STIX]{x1D6FF}>0$
.
We first claim that fixed points of
![]() $\unicode[STIX]{x1D711}$
accumulate from the right to
$\unicode[STIX]{x1D711}$
accumulate from the right to
![]() $a$
. Otherwise, there exists some
$a$
. Otherwise, there exists some
![]() $\unicode[STIX]{x1D6FF}$
such that
$\unicode[STIX]{x1D6FF}$
such that
 $\unicode[STIX]{x1D711}(x)-x$
keeps a constant sign for all
$\unicode[STIX]{x1D711}(x)-x$
keeps a constant sign for all
 $x\in {\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)$
. Assume that this sign is positive and choose
$x\in {\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)$
. Assume that this sign is positive and choose
 $b\in {\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)\;\cap \;C$
. Let
$b\in {\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)\;\cap \;C$
. Let
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\,\;\subset \;\,(a,b)$
be a maximal complementary interval of length at least
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\,\;\subset \;\,(a,b)$
be a maximal complementary interval of length at least
 $\unicode[STIX]{x1D70E}(b-a)$
. By maximality
$\unicode[STIX]{x1D70E}(b-a)$
. By maximality
![]() $\unicode[STIX]{x1D6FC}\in C$
. Since
$\unicode[STIX]{x1D6FC}\in C$
. Since
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})\in C$
and
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})\in C$
and
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})>\unicode[STIX]{x1D6FC}$
we have
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})>\unicode[STIX]{x1D6FC}$
we have
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})\geqslant \unicode[STIX]{x1D6FD}$
, so that
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})\geqslant \unicode[STIX]{x1D6FD}$
, so that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-a}{\unicode[STIX]{x1D6FC}-a}=\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}+1\geqslant \frac{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}+1\geqslant \frac{\unicode[STIX]{x1D70E}(b-a)}{\unicode[STIX]{x1D6FC}-a}+1\geqslant 1+\unicode[STIX]{x1D70E}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-a}{\unicode[STIX]{x1D6FC}-a}=\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}+1\geqslant \frac{\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}+1\geqslant \frac{\unicode[STIX]{x1D70E}(b-a)}{\unicode[STIX]{x1D6FC}-a}+1\geqslant 1+\unicode[STIX]{x1D70E}.\end{eqnarray}$$
By the mean value theorem there exists
 $\unicode[STIX]{x1D709}\in (a,\unicode[STIX]{x1D6FC})$
such that:
$\unicode[STIX]{x1D709}\in (a,\unicode[STIX]{x1D6FC})$
such that:
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709})=\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-a}{\unicode[STIX]{x1D6FC}-a}\geqslant 1+\unicode[STIX]{x1D70E}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709})=\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-a}{\unicode[STIX]{x1D6FC}-a}\geqslant 1+\unicode[STIX]{x1D70E}.\end{eqnarray}$$
But this inequality contradicts the 1-flatness condition for small
![]() $\unicode[STIX]{x1D6FF}$
, as taking the limit when
$\unicode[STIX]{x1D6FF}$
, as taking the limit when
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
we would obtain
$\unicode[STIX]{x1D6FF}\rightarrow 0$
we would obtain
 $\unicode[STIX]{x1D711}^{\prime }(a)\geqslant 1+\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D711}^{\prime }(a)\geqslant 1+\unicode[STIX]{x1D70E}$
.
When the sign of
 $\unicode[STIX]{x1D711}(x)-x$
is negative we reach the same conclusion by considering
$\unicode[STIX]{x1D711}(x)-x$
is negative we reach the same conclusion by considering
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FD})-\unicode[STIX]{x1D6FD}$
. This proves the claim.
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FD})-\unicode[STIX]{x1D6FD}$
. This proves the claim.
Therefore there is a decreasing sequence
![]() $u_{k}$
accumulating at
$u_{k}$
accumulating at
![]() $a$
, such that
$a$
, such that
 $\unicode[STIX]{x1D711}(u_{k})=u_{k}$
. As
$\unicode[STIX]{x1D711}(u_{k})=u_{k}$
. As
 $\unicode[STIX]{x1D711}|_{C\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)}$
is not identity for any
$\unicode[STIX]{x1D711}|_{C\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)}$
is not identity for any
![]() $\unicode[STIX]{x1D6FF}>0$
there exists a decreasing sequence
$\unicode[STIX]{x1D6FF}>0$
there exists a decreasing sequence
![]() $v_{k}\in C$
accumulating on
$v_{k}\in C$
accumulating on
![]() $a$
, such that all
$a$
, such that all
 $\unicode[STIX]{x1D711}(v_{k})-v_{k}$
are of the same sign, say positive. Therefore, up to passing to a subsequence, we obtain a sequence of disjoint intervals
$\unicode[STIX]{x1D711}(v_{k})-v_{k}$
are of the same sign, say positive. Therefore, up to passing to a subsequence, we obtain a sequence of disjoint intervals
![]() $(\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j})$
such that
$(\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j})$
such that
 $\unicode[STIX]{x1D6FD}_{j+1}\leqslant \unicode[STIX]{x1D6FC}_{j}$
,
$\unicode[STIX]{x1D6FD}_{j+1}\leqslant \unicode[STIX]{x1D6FC}_{j}$
,
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{j})=\unicode[STIX]{x1D6FC}_{j}$
,
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{j})=\unicode[STIX]{x1D6FC}_{j}$
,
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FD}_{j})=\unicode[STIX]{x1D6FD}_{j}$
, and
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FD}_{j})=\unicode[STIX]{x1D6FD}_{j}$
, and
 $v_{j}\in (\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j})$
.
$v_{j}\in (\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j})$
.
Since
![]() $\unicode[STIX]{x1D711}$
is monotone, it has to be monotone increasing, by above. Thus
$\unicode[STIX]{x1D711}$
is monotone, it has to be monotone increasing, by above. Thus
 $\unicode[STIX]{x1D711}^{k}(v_{j})\in [\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}]$
, for any
$\unicode[STIX]{x1D711}^{k}(v_{j})\in [\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}]$
, for any
![]() $k\in \mathbb{Z}$
, where
$k\in \mathbb{Z}$
, where
![]() $\unicode[STIX]{x1D711}^{k}$
denotes the
$\unicode[STIX]{x1D711}^{k}$
denotes the
![]() $k$
th iterate of
$k$
th iterate of
![]() $\unicode[STIX]{x1D711}$
. The bi-infinite sequence
$\unicode[STIX]{x1D711}$
. The bi-infinite sequence
![]() $\unicode[STIX]{x1D711}^{k}(v_{j})$
is increasing and so
$\unicode[STIX]{x1D711}^{k}(v_{j})$
is increasing and so
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{j}\leqslant \lim _{k\rightarrow -\infty }\unicode[STIX]{x1D711}^{k}(v_{j})<\lim _{k\rightarrow \infty }\unicode[STIX]{x1D711}^{k}(v_{j})\leqslant \unicode[STIX]{x1D6FD}_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{j}\leqslant \lim _{k\rightarrow -\infty }\unicode[STIX]{x1D711}^{k}(v_{j})<\lim _{k\rightarrow \infty }\unicode[STIX]{x1D711}^{k}(v_{j})\leqslant \unicode[STIX]{x1D6FD}_{j}.\end{eqnarray}$$
Now
 $\lim _{k\rightarrow -\infty }\unicode[STIX]{x1D711}^{k}(v_{j})$
and
$\lim _{k\rightarrow -\infty }\unicode[STIX]{x1D711}^{k}(v_{j})$
and
 $\lim _{k\rightarrow \infty }\unicode[STIX]{x1D711}^{k}(v_{j})$
are fixed points of
$\lim _{k\rightarrow \infty }\unicode[STIX]{x1D711}^{k}(v_{j})$
are fixed points of
![]() $\unicode[STIX]{x1D711}$
and we can assume, without loss of generality that our choice of intervals is such that
$\unicode[STIX]{x1D711}$
and we can assume, without loss of generality that our choice of intervals is such that
 $\unicode[STIX]{x1D6FC}_{j}=\lim _{k\rightarrow -\infty }\unicode[STIX]{x1D711}^{k}(v_{j})$
,
$\unicode[STIX]{x1D6FC}_{j}=\lim _{k\rightarrow -\infty }\unicode[STIX]{x1D711}^{k}(v_{j})$
,
 $\lim _{k\rightarrow \infty }\unicode[STIX]{x1D711}^{k}(v_{j})=\unicode[STIX]{x1D6FD}_{j}$
. In particular
$\lim _{k\rightarrow \infty }\unicode[STIX]{x1D711}^{k}(v_{j})=\unicode[STIX]{x1D6FD}_{j}$
. In particular
 $\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}\in C$
.
$\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}\in C$
.
As
![]() $C$
is
$C$
is
![]() $\unicode[STIX]{x1D70E}$
-sparse there is a complementary interval
$\unicode[STIX]{x1D70E}$
-sparse there is a complementary interval
 $(\unicode[STIX]{x1D6FE}_{j},\unicode[STIX]{x1D6FF}_{j})\;\subset \;(\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j})$
of length at least
$(\unicode[STIX]{x1D6FE}_{j},\unicode[STIX]{x1D6FF}_{j})\;\subset \;(\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j})$
of length at least
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FC}_{j})$
. The interval
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FC}_{j})$
. The interval
![]() $(\unicode[STIX]{x1D6FE}_{j},\unicode[STIX]{x1D6FF}_{j})$
cannot contain any point
$(\unicode[STIX]{x1D6FE}_{j},\unicode[STIX]{x1D6FF}_{j})$
cannot contain any point
![]() $\unicode[STIX]{x1D711}^{k}(v_{j})$
and thus there exists some
$\unicode[STIX]{x1D711}^{k}(v_{j})$
and thus there exists some
![]() $k_{j}\in \mathbb{Z}$
such that
$k_{j}\in \mathbb{Z}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{k_{j}}(v_{j})\leqslant \unicode[STIX]{x1D6FE}_{j}<\unicode[STIX]{x1D6FF}_{j}\leqslant \unicode[STIX]{x1D711}^{k_{j}+1}(v_{j}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{k_{j}}(v_{j})\leqslant \unicode[STIX]{x1D6FE}_{j}<\unicode[STIX]{x1D6FF}_{j}\leqslant \unicode[STIX]{x1D711}^{k_{j}+1}(v_{j}).\end{eqnarray}$$
Denote
 $\unicode[STIX]{x1D711}^{k_{j}}(v_{j})=\unicode[STIX]{x1D702}_{j}$
. We have then
$\unicode[STIX]{x1D711}^{k_{j}}(v_{j})=\unicode[STIX]{x1D702}_{j}$
. We have then
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702}_{j})-\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{j})}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}-1=\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702}_{j})-\unicode[STIX]{x1D702}_{j}}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}\geqslant \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FC}_{j})}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}\geqslant \unicode[STIX]{x1D70E}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702}_{j})-\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{j})}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}-1=\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702}_{j})-\unicode[STIX]{x1D702}_{j}}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}\geqslant \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FC}_{j})}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}\geqslant \unicode[STIX]{x1D70E}.\end{eqnarray}$$
By the mean value theorem there exists
 $\unicode[STIX]{x1D709}_{j}\in (\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D702}_{j})$
such that
$\unicode[STIX]{x1D709}_{j}\in (\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D702}_{j})$
such that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702}_{j})-\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{j})}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}=\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709}_{j}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D702}_{j})-\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{j})}{\unicode[STIX]{x1D702}_{j}-\unicode[STIX]{x1D6FC}_{j}}=\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709}_{j}),\end{eqnarray}$$
and thus such that
 $\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709}_{j})\geqslant 1+\unicode[STIX]{x1D70E}$
. As
$\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709}_{j})\geqslant 1+\unicode[STIX]{x1D70E}$
. As
![]() $\unicode[STIX]{x1D711}^{\prime }$
is continuous at
$\unicode[STIX]{x1D711}^{\prime }$
is continuous at
![]() $a$
, by letting
$a$
, by letting
![]() $j$
go to infinity we derive
$j$
go to infinity we derive
 $\unicode[STIX]{x1D711}^{\prime }(a)\geqslant 1+\unicode[STIX]{x1D70E}$
which contradicts the 1-flatness.◻
$\unicode[STIX]{x1D711}^{\prime }(a)\geqslant 1+\unicode[STIX]{x1D70E}$
which contradicts the 1-flatness.◻
Lemma 6. If
![]() $C$
is
$C$
is
![]() $\unicode[STIX]{x1D70E}$
-sparse and
$\unicode[STIX]{x1D70E}$
-sparse and
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}$
is not 1-flat then
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}$
is not 1-flat then
 $$\begin{eqnarray}|\unicode[STIX]{x1D711}^{\prime }(a)-1|\geqslant \unicode[STIX]{x1D70E}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D711}^{\prime }(a)-1|\geqslant \unicode[STIX]{x1D70E}.\end{eqnarray}$$
Proof. Let
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}$
not 1-flat, so that
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}$
not 1-flat, so that
 $\unicode[STIX]{x1D711}^{\prime }(a)\neq 1$
. Let us further suppose that
$\unicode[STIX]{x1D711}^{\prime }(a)\neq 1$
. Let us further suppose that
 $\unicode[STIX]{x1D711}^{\prime }(a)>1$
, the other situation being similar. For any
$\unicode[STIX]{x1D711}^{\prime }(a)>1$
, the other situation being similar. For any
![]() $\unicode[STIX]{x1D6FF}>0$
we can choose
$\unicode[STIX]{x1D6FF}>0$
we can choose
 $b\in {\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)\;\cap \;C$
. There is then a maximal complementary interval
$b\in {\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(a)\;\cap \;C$
. There is then a maximal complementary interval
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\;\subset \;(a,b)$
of length at least
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\;\subset \;(a,b)$
of length at least
 $\unicode[STIX]{x1D70E}(b-a)$
. By maximality
$\unicode[STIX]{x1D70E}(b-a)$
. By maximality
![]() $\unicode[STIX]{x1D6FC}\in C$
.
$\unicode[STIX]{x1D6FC}\in C$
.
We claim that for small enough
![]() $\unicode[STIX]{x1D6FF}$
we have
$\unicode[STIX]{x1D6FF}$
we have
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})>\unicode[STIX]{x1D6FC}$
. Assume the contrary. By the mean value theorem there exists
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})>\unicode[STIX]{x1D6FC}$
. Assume the contrary. By the mean value theorem there exists
 $\unicode[STIX]{x1D709}\in (a,\unicode[STIX]{x1D6FC})\;\subset \;(a,b)$
such that
$\unicode[STIX]{x1D709}\in (a,\unicode[STIX]{x1D6FC})\;\subset \;(a,b)$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709})=1+\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}\leqslant 1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709})=1+\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}\leqslant 1\end{eqnarray}$$
and letting
![]() $\unicode[STIX]{x1D6FF}$
go to
$\unicode[STIX]{x1D6FF}$
go to
![]() $0$
we would obtain
$0$
we would obtain
 $\unicode[STIX]{x1D711}^{\prime }(a)\leqslant 1$
, contradicting our assumptions. Thus
$\unicode[STIX]{x1D711}^{\prime }(a)\leqslant 1$
, contradicting our assumptions. Thus
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})>\unicode[STIX]{x1D6FC}$
, and hence
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})>\unicode[STIX]{x1D6FC}$
, and hence
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})\geqslant \unicode[STIX]{x1D6FD}$
. As above, the mean value theorem provides us
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})\geqslant \unicode[STIX]{x1D6FD}$
. As above, the mean value theorem provides us
 $\unicode[STIX]{x1D709}\in (a,\unicode[STIX]{x1D6FC})$
so that
$\unicode[STIX]{x1D709}\in (a,\unicode[STIX]{x1D6FC})$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709})=1+\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}\geqslant 1+\unicode[STIX]{x1D70E}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{\prime }(\unicode[STIX]{x1D709})=1+\frac{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D6FC}}{\unicode[STIX]{x1D6FC}-a}\geqslant 1+\unicode[STIX]{x1D70E}.\end{eqnarray}$$
Letting
![]() $\unicode[STIX]{x1D6FF}$
go to zero we obtain
$\unicode[STIX]{x1D6FF}$
go to zero we obtain
 $\unicode[STIX]{x1D711}^{\prime }(a)\geqslant 1+\unicode[STIX]{x1D70E}$
. When
$\unicode[STIX]{x1D711}^{\prime }(a)\geqslant 1+\unicode[STIX]{x1D70E}$
. When
 $\unicode[STIX]{x1D711}^{\prime }(a)<1$
we can use similar methods or pass to
$\unicode[STIX]{x1D711}^{\prime }(a)<1$
we can use similar methods or pass to
![]() $\unicode[STIX]{x1D711}^{-1}$
in order to obtain
$\unicode[STIX]{x1D711}^{-1}$
in order to obtain
 $\unicode[STIX]{x1D711}^{\prime }(a)\leqslant 1-\unicode[STIX]{x1D70E}$
.◻
$\unicode[STIX]{x1D711}^{\prime }(a)\leqslant 1-\unicode[STIX]{x1D70E}$
.◻
Lemma 7. Let
![]() $C$
sparse and
$C$
sparse and
![]() $a\in C$
. Then one of the following holds:
$a\in C$
. Then one of the following holds:
(i) either for any
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
, the restriction
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
, the restriction
 $\unicode[STIX]{x1D711}|_{C}$
is identity in a small neighborhood of
$\unicode[STIX]{x1D711}|_{C}$
is identity in a small neighborhood of
 $a$
, so that
$a$
, so that
 $\mathfrak{diff}_{a}^{1,+}=1$
;
$\mathfrak{diff}_{a}^{1,+}=1$
;(ii) or else, there is
 $\unicode[STIX]{x1D713}_{a}\in \text{Diff}_{a}^{1,+}$
such that for any
$\unicode[STIX]{x1D713}_{a}\in \text{Diff}_{a}^{1,+}$
such that for any
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
the restriction of
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
the restriction of
 $\unicode[STIX]{x1D711}$
to a small neighborhood
$\unicode[STIX]{x1D711}$
to a small neighborhood
 ${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)\;\cap \;C$
coincides with the iterate
${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)\;\cap \;C$
coincides with the iterate
 $\unicode[STIX]{x1D713}_{a}^{k}|_{C}$
for some
$\unicode[STIX]{x1D713}_{a}^{k}|_{C}$
for some
 $k\in \mathbb{Z}\setminus \{0\}$
. Moreover, any such
$k\in \mathbb{Z}\setminus \{0\}$
. Moreover, any such
 $\unicode[STIX]{x1D713}_{a}$
is of the form (28)where
$\unicode[STIX]{x1D713}_{a}$
is of the form (28)where $$\begin{eqnarray}\unicode[STIX]{x1D713}_{a}(x)=a+p(x-a)+o(x-a)\quad \text{as }x\rightarrow a,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{a}(x)=a+p(x-a)+o(x-a)\quad \text{as }x\rightarrow a,\end{eqnarray}$$
 $|p-1|\geqslant \unicode[STIX]{x1D70E}$
. Thus
$|p-1|\geqslant \unicode[STIX]{x1D70E}$
. Thus
 $\mathfrak{diff}_{a}^{1,+}=\mathbb{Z}$
.
$\mathfrak{diff}_{a}^{1,+}=\mathbb{Z}$
.
Proof. If the first alternative doesn’t hold, by Lemma 5 we can assume that there exists some
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
which is not 1-flat.
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
which is not 1-flat.
The map
 $\unicode[STIX]{x1D712}:\text{Diff}_{a}^{1}\rightarrow \mathbb{R}^{\ast }$
given by
$\unicode[STIX]{x1D712}:\text{Diff}_{a}^{1}\rightarrow \mathbb{R}^{\ast }$
given by
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}^{\prime }(a)$
is easily seen to be a group homomorphism. By Lemma 6 the subgroup
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}^{\prime }(a)$
is easily seen to be a group homomorphism. By Lemma 6 the subgroup
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+})$
of
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+})$
of
![]() $\mathbb{R}_{+}^{\ast }$
is discrete and non-trivial and thus it is isomorphic to
$\mathbb{R}_{+}^{\ast }$
is discrete and non-trivial and thus it is isomorphic to
![]() $\mathbb{Z}$
. Let
$\mathbb{Z}$
. Let
 $\unicode[STIX]{x1D713}_{a}\in \text{Diff}_{a}^{1,+}$
be a germ whose image
$\unicode[STIX]{x1D713}_{a}\in \text{Diff}_{a}^{1,+}$
be a germ whose image
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D713}_{a})$
is a generator of
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D713}_{a})$
is a generator of
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+})$
. Then
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+})$
. Then
![]() $\unicode[STIX]{x1D713}_{a}$
is not 1-flat and thus, by Lemma 6, it satisfies (28).
$\unicode[STIX]{x1D713}_{a}$
is not 1-flat and thus, by Lemma 6, it satisfies (28).
If
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
, then we can write
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1,+}$
, then we can write
 $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}_{a}^{k}\unicode[STIX]{x1D703}$
, for some
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}_{a}^{k}\unicode[STIX]{x1D703}$
, for some
 $k\in \mathbb{Z}\setminus \{0\}$
and
$k\in \mathbb{Z}\setminus \{0\}$
and
 $\unicode[STIX]{x1D703}\in \ker \unicode[STIX]{x1D712}$
. But the kernel of
$\unicode[STIX]{x1D703}\in \ker \unicode[STIX]{x1D712}$
. But the kernel of
![]() $\unicode[STIX]{x1D712}$
consists of those
$\unicode[STIX]{x1D712}$
consists of those
 $\unicode[STIX]{x1D703}\in \text{Diff}_{a}^{1,+}$
which are 1-flat. By Lemma 5 the restriction of
$\unicode[STIX]{x1D703}\in \text{Diff}_{a}^{1,+}$
which are 1-flat. By Lemma 5 the restriction of
![]() $\unicode[STIX]{x1D703}$
to some neighborhood
$\unicode[STIX]{x1D703}$
to some neighborhood
 ${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)\;\cap \;C$
is identity. This proves that
${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)\;\cap \;C$
is identity. This proves that
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}_{a}^{k}$
in a neighborhood
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}_{a}^{k}$
in a neighborhood
 ${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)\;\cap \;C$
, as claimed.◻
${\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)\;\cap \;C$
, as claimed.◻
Remark 6. If
 $C=C_{\unicode[STIX]{x1D706}}$
is the ternary central Cantor set in
$C=C_{\unicode[STIX]{x1D706}}$
is the ternary central Cantor set in
![]() $\mathbb{R}$
, then
$\mathbb{R}$
, then
 $\mathfrak{diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
is not always
$\mathfrak{diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
is not always
![]() $\mathbb{Z}$
. An element
$\mathbb{Z}$
. An element
![]() $a$
of
$a$
of
![]() $C_{\unicode[STIX]{x1D706}}$
is called
$C_{\unicode[STIX]{x1D706}}$
is called
![]() $\unicode[STIX]{x1D706}$
-rational if it has an eventually periodic development
$\unicode[STIX]{x1D706}$
-rational if it has an eventually periodic development
 $$\begin{eqnarray}a=\mathop{\sum }_{i=1}^{\infty }a_{i}\unicode[STIX]{x1D706}^{i},\end{eqnarray}$$
$$\begin{eqnarray}a=\mathop{\sum }_{i=1}^{\infty }a_{i}\unicode[STIX]{x1D706}^{i},\end{eqnarray}$$
where
 $a_{i}\in \{0,\unicode[STIX]{x1D706}-1\}$
. Therefore
$a_{i}\in \{0,\unicode[STIX]{x1D706}-1\}$
. Therefore
 $\mathfrak{diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
is
$\mathfrak{diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
is
![]() $\mathbb{Z}$
if and only if
$\mathbb{Z}$
if and only if
![]() $a$
is
$a$
is
![]() $\unicode[STIX]{x1D706}$
-rational and trivial, otherwise.
$\unicode[STIX]{x1D706}$
-rational and trivial, otherwise.
Remark 7. Since the subgroup
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1})\;\subset \;\mathbb{R}^{\ast }$
is discrete there exists
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1})\;\subset \;\mathbb{R}^{\ast }$
is discrete there exists
![]() $\unicode[STIX]{x1D706}\geqslant 1$
such that
$\unicode[STIX]{x1D706}\geqslant 1$
such that
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1})$
is of the form
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1})$
is of the form
![]() $\langle \unicode[STIX]{x1D706}\rangle$
,
$\langle \unicode[STIX]{x1D706}\rangle$
,
![]() $\langle -\unicode[STIX]{x1D706}\rangle$
or
$\langle -\unicode[STIX]{x1D706}\rangle$
or
![]() $\langle \pm \unicode[STIX]{x1D706}\rangle$
. Here
$\langle \pm \unicode[STIX]{x1D706}\rangle$
. Here
![]() $\langle x\rangle$
denotes the subgroup of
$\langle x\rangle$
denotes the subgroup of
![]() $\mathbb{R}^{\ast }$
generated by
$\mathbb{R}^{\ast }$
generated by
![]() $x$
. In particular
$x$
. In particular
![]() $\mathfrak{diff}_{a}^{1}$
is isomorphic to either
$\mathfrak{diff}_{a}^{1}$
is isomorphic to either
![]() $1$
,
$1$
,
![]() $\mathbb{Z}/2\mathbb{Z}$
,
$\mathbb{Z}/2\mathbb{Z}$
,
![]() $\mathbb{Z}$
, or else
$\mathbb{Z}$
, or else
 $\mathbb{Z}\oplus \mathbb{Z}/2\mathbb{Z}$
.
$\mathbb{Z}\oplus \mathbb{Z}/2\mathbb{Z}$
.
However, if
![]() $a$
is a left (or right) point of
$a$
is a left (or right) point of
![]() $C$
then there is no decreasing homeomorphism of
$C$
then there is no decreasing homeomorphism of
![]() $(\mathbb{R},C)$
fixing
$(\mathbb{R},C)$
fixing
![]() $a$
. Thus
$a$
. Thus
 $\text{Diff}_{a}^{1}=\text{Diff}_{a}^{1,+}$
, and the result of Lemma 28 holds more generally for
$\text{Diff}_{a}^{1}=\text{Diff}_{a}^{1,+}$
, and the result of Lemma 28 holds more generally for
![]() $\text{Diff}_{a}^{1}$
.
$\text{Diff}_{a}^{1}$
.
3.2.2 Proof of Theorem 2
We need to show that the identity is an isolated point of the group
 $\mathfrak{diff}^{1}(C)$
, if
$\mathfrak{diff}^{1}(C)$
, if
![]() $C$
is
$C$
is
![]() $\unicode[STIX]{x1D70E}$
-sparse. To this purpose consider an element
$\unicode[STIX]{x1D70E}$
-sparse. To this purpose consider an element
 $\mathfrak{diff}^{1}(C)$
having a representative
$\mathfrak{diff}^{1}(C)$
having a representative
 $\unicode[STIX]{x1D713}\in \text{Diff}^{1}(\mathbb{R},C)$
such that
$\unicode[STIX]{x1D713}\in \text{Diff}^{1}(\mathbb{R},C)$
such that
 $$\begin{eqnarray}1-\unicode[STIX]{x1D70E}<\unicode[STIX]{x1D713}^{\prime }(x)<1+\unicode[STIX]{x1D70E}\quad \text{for any }x\in C.\end{eqnarray}$$
$$\begin{eqnarray}1-\unicode[STIX]{x1D70E}<\unicode[STIX]{x1D713}^{\prime }(x)<1+\unicode[STIX]{x1D70E}\quad \text{for any }x\in C.\end{eqnarray}$$
There is no loss of generality in assuming that
 $\unicode[STIX]{x1D713}\in \text{Diff}^{1,+}(\mathbb{R},C)$
, i.e. that
$\unicode[STIX]{x1D713}\in \text{Diff}^{1,+}(\mathbb{R},C)$
, i.e. that
![]() $\unicode[STIX]{x1D713}$
is monotone increasing. The minimal element
$\unicode[STIX]{x1D713}$
is monotone increasing. The minimal element
![]() $\min C$
of
$\min C$
of
![]() $C$
should therefore be fixed by any element of
$C$
should therefore be fixed by any element of
 $\text{Diff}^{1,+}(\mathbb{R},C)$
, in particular by
$\text{Diff}^{1,+}(\mathbb{R},C)$
, in particular by
![]() $\unicode[STIX]{x1D713}$
. By Lemma 6,
$\unicode[STIX]{x1D713}$
. By Lemma 6,
 $\unicode[STIX]{x1D713}\in \text{Diff}_{\min C}^{1}(\mathbb{R},C)$
must be 1-flat at
$\unicode[STIX]{x1D713}\in \text{Diff}_{\min C}^{1}(\mathbb{R},C)$
must be 1-flat at
![]() $\min C$
.
$\min C$
.
Consider the set
 $$\begin{eqnarray}U=\{x\in C;\unicode[STIX]{x1D713}(z)=z\text{ for any }z\in C\;\cap \;(-\infty ,x]\}.\end{eqnarray}$$
$$\begin{eqnarray}U=\{x\in C;\unicode[STIX]{x1D713}(z)=z\text{ for any }z\in C\;\cap \;(-\infty ,x]\}.\end{eqnarray}$$
The set
![]() $U$
is non-empty, as
$U$
is non-empty, as
 $\min C\in U$
. Let
$\min C\in U$
. Let
 $\unicode[STIX]{x1D709}=\sup U$
.
$\unicode[STIX]{x1D709}=\sup U$
.
Assume first that
![]() $\unicode[STIX]{x1D709}$
is not a right point of
$\unicode[STIX]{x1D709}$
is not a right point of
![]() $C$
. Since
$C$
. Since
![]() $\unicode[STIX]{x1D713}$
is continuous,
$\unicode[STIX]{x1D713}$
is continuous,
![]() $\unicode[STIX]{x1D709}\in U$
so that
$\unicode[STIX]{x1D709}\in U$
so that
 $\unicode[STIX]{x1D713}\in \text{Diff}_{\unicode[STIX]{x1D709}}^{1}$
. From Lemma 6
$\unicode[STIX]{x1D713}\in \text{Diff}_{\unicode[STIX]{x1D709}}^{1}$
. From Lemma 6
 $\unicode[STIX]{x1D713}^{\prime }(\unicode[STIX]{x1D709})=1$
and
$\unicode[STIX]{x1D713}^{\prime }(\unicode[STIX]{x1D709})=1$
and
![]() $\unicode[STIX]{x1D713}$
is 1-flat at
$\unicode[STIX]{x1D713}$
is 1-flat at
![]() $\unicode[STIX]{x1D709}$
. According to Lemma 5 there is some
$\unicode[STIX]{x1D709}$
. According to Lemma 5 there is some
![]() $\unicode[STIX]{x1D6FF}>0$
such that the restriction
$\unicode[STIX]{x1D6FF}>0$
such that the restriction
 $\unicode[STIX]{x1D713}|_{C\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(\unicode[STIX]{x1D709})}$
is identity, which contradicts the maximality of
$\unicode[STIX]{x1D713}|_{C\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}^{+}(\unicode[STIX]{x1D709})}$
is identity, which contradicts the maximality of
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
If
![]() $\unicode[STIX]{x1D709}$
is a right point of
$\unicode[STIX]{x1D709}$
is a right point of
![]() $C$
, then there is some maximal complementary interval
$C$
, then there is some maximal complementary interval
 $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\;\subset \;\mathbb{R}\setminus C$
. Since
$(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\;\subset \;\mathbb{R}\setminus C$
. Since
 $\unicode[STIX]{x1D713}|_{C\;\cap \;[\min C,\unicode[STIX]{x1D709}]}$
is identity it follows that
$\unicode[STIX]{x1D713}|_{C\;\cap \;[\min C,\unicode[STIX]{x1D709}]}$
is identity it follows that
 $\unicode[STIX]{x1D713}(C\;\cap \;[\unicode[STIX]{x1D709},\infty ))\;\subset \;C\;\cap \;[\unicode[STIX]{x1D709},\infty )$
. As
$\unicode[STIX]{x1D713}(C\;\cap \;[\unicode[STIX]{x1D709},\infty ))\;\subset \;C\;\cap \;[\unicode[STIX]{x1D709},\infty )$
. As
![]() $\unicode[STIX]{x1D702}$
is the minimal element of
$\unicode[STIX]{x1D702}$
is the minimal element of
 $C\;\cap \;(\unicode[STIX]{x1D709},\infty )$
it should be a fixed point of
$C\;\cap \;(\unicode[STIX]{x1D709},\infty )$
it should be a fixed point of
![]() $\unicode[STIX]{x1D713}|_{[\unicode[STIX]{x1D709},\infty )}$
and so
$\unicode[STIX]{x1D713}|_{[\unicode[STIX]{x1D709},\infty )}$
and so
![]() $\unicode[STIX]{x1D702}\in U$
. This contradicts the maximality of
$\unicode[STIX]{x1D702}\in U$
. This contradicts the maximality of
![]() $\unicode[STIX]{x1D709}$
. Hence
$\unicode[STIX]{x1D709}$
. Hence
![]() $\unicode[STIX]{x1D713}$
is identity on
$\unicode[STIX]{x1D713}$
is identity on
![]() $C$
.
$C$
.
Remark 8. The same arguments show that if
 $C\;\subset \;[0,1]$
is a sparse Cantor set and
$C\;\subset \;[0,1]$
is a sparse Cantor set and
 $\mathfrak{diff}_{0}^{1,+}(C)=1$
, then
$\mathfrak{diff}_{0}^{1,+}(C)=1$
, then
 $\mathfrak{diff}^{1,+}(C)=1$
.
$\mathfrak{diff}^{1,+}(C)=1$
.
For the second claim of the theorem let
![]() $V_{\unicode[STIX]{x1D6FF}}$
be the set of those elements in
$V_{\unicode[STIX]{x1D6FF}}$
be the set of those elements in
 $\mathfrak{diff}_{S^{1}}^{1}(C)$
having a representative
$\mathfrak{diff}_{S^{1}}^{1}(C)$
having a representative
 $\unicode[STIX]{x1D713}\in \text{Diff}^{1}(S^{1},C)$
such that
$\unicode[STIX]{x1D713}\in \text{Diff}^{1}(S^{1},C)$
such that
 $$\begin{eqnarray}1-\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D713}^{\prime }(x)<1+\unicode[STIX]{x1D6FF}\quad \text{for any }x\in C.\end{eqnarray}$$
$$\begin{eqnarray}1-\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D713}^{\prime }(x)<1+\unicode[STIX]{x1D6FF}\quad \text{for any }x\in C.\end{eqnarray}$$
Here elements of
 $\text{Diff}^{1}(S^{1})$
are identified with real periodic functions on
$\text{Diff}^{1}(S^{1})$
are identified with real periodic functions on
![]() $\mathbb{R}$
. We choose
$\mathbb{R}$
. We choose
 $\unicode[STIX]{x1D6FF}<\min (\unicode[STIX]{x1D70E},0.3)$
. It is enough to prove that
$\unicode[STIX]{x1D6FF}<\min (\unicode[STIX]{x1D70E},0.3)$
. It is enough to prove that
![]() $V_{\unicode[STIX]{x1D6FF}}$
is finite.
$V_{\unicode[STIX]{x1D6FF}}$
is finite.
Consider a complementary interval
 $J\;\subset \;S^{1}-C$
of maximal possible length, say
$J\;\subset \;S^{1}-C$
of maximal possible length, say
![]() $|J|$
. Consider its right end
$|J|$
. Consider its right end
![]() $\unicode[STIX]{x1D702}$
, with respect to the cyclic orientation. If
$\unicode[STIX]{x1D702}$
, with respect to the cyclic orientation. If
![]() $\unicode[STIX]{x1D713}\in V_{\unicode[STIX]{x1D6FF}}$
is such that
$\unicode[STIX]{x1D713}\in V_{\unicode[STIX]{x1D6FF}}$
is such that
 $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D702})=\unicode[STIX]{x1D702}$
, then the arguments from the proof of Theorem 2 show that
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D702})=\unicode[STIX]{x1D702}$
, then the arguments from the proof of Theorem 2 show that
 $\unicode[STIX]{x1D713}(x)=x$
when
$\unicode[STIX]{x1D713}(x)=x$
when
![]() $x\in C$
.
$x\in C$
.
We claim that the set of intervals of the form
![]() $\unicode[STIX]{x1D713}(J)$
, for
$\unicode[STIX]{x1D713}(J)$
, for
![]() $\unicode[STIX]{x1D713}\in V_{\unicode[STIX]{x1D6FF}}$
is finite. Each
$\unicode[STIX]{x1D713}\in V_{\unicode[STIX]{x1D6FF}}$
is finite. Each
![]() $\unicode[STIX]{x1D713}(J)$
is a maximal complementary interval, because if it were contained in a larger interval
$\unicode[STIX]{x1D713}(J)$
is a maximal complementary interval, because if it were contained in a larger interval
![]() $J^{\prime }$
, then
$J^{\prime }$
, then
![]() $\unicode[STIX]{x1D713}^{-1}(J)$
would be a complementary interval strictly larger than
$\unicode[STIX]{x1D713}^{-1}(J)$
would be a complementary interval strictly larger than
![]() $J$
. This shows that any two such intervals
$J$
. This shows that any two such intervals
![]() $\unicode[STIX]{x1D713}(J)$
and
$\unicode[STIX]{x1D713}(J)$
and
![]() $\unicode[STIX]{x1D711}(J)$
are either disjoint or they coincide, for otherwise their union would contradict their maximality. Further, each
$\unicode[STIX]{x1D711}(J)$
are either disjoint or they coincide, for otherwise their union would contradict their maximality. Further, each
![]() $\unicode[STIX]{x1D713}(J)$
has length at least
$\unicode[STIX]{x1D713}(J)$
has length at least
 $(1-\unicode[STIX]{x1D6FF})|J|$
. This shows that the set of intervals is a finite set
$(1-\unicode[STIX]{x1D6FF})|J|$
. This shows that the set of intervals is a finite set
 $\{J_{1},J_{2},\ldots ,J_{k}\}$
.
$\{J_{1},J_{2},\ldots ,J_{k}\}$
.
Assume that
 $\unicode[STIX]{x1D713}(J)=\unicode[STIX]{x1D711}(J)$
and both
$\unicode[STIX]{x1D713}(J)=\unicode[STIX]{x1D711}(J)$
and both
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D711}$
preserve the orientation of the circle. If the right end of
$\unicode[STIX]{x1D711}$
preserve the orientation of the circle. If the right end of
![]() $J$
is
$J$
is
![]() $\unicode[STIX]{x1D702}$
, with respect to the cyclic orientation, then
$\unicode[STIX]{x1D702}$
, with respect to the cyclic orientation, then
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}$
sends
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}$
sends
![]() $J$
to
$J$
to
![]() $J$
and hence fixes
$J$
and hence fixes
![]() $\unicode[STIX]{x1D702}$
. Then the arguments from the proof of Theorem 2 show that
$\unicode[STIX]{x1D702}$
. Then the arguments from the proof of Theorem 2 show that
 $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}(x)=x$
when
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}(x)=x$
when
![]() $x\in C$
. It follows that there are at most
$x\in C$
. It follows that there are at most
![]() $2k$
elements in
$2k$
elements in
![]() $V_{\unicode[STIX]{x1D6FF}}$
, finishing the proof of the first part.
$V_{\unicode[STIX]{x1D6FF}}$
, finishing the proof of the first part.
3.2.3 Proof of Theorem 3
Let
![]() $C$
be a Cantor set contained within a
$C$
be a Cantor set contained within a
![]() ${\mathcal{C}}^{1}$
-embedded simple closed curve
${\mathcal{C}}^{1}$
-embedded simple closed curve
![]() $L$
on the orientable manifold
$L$
on the orientable manifold
![]() $M$
. For the sake of simplicity we will suppose from now on that
$M$
. For the sake of simplicity we will suppose from now on that
![]() $M$
is a surface, but the proof goes on without essential modifications in higher dimensions. Let
$M$
is a surface, but the proof goes on without essential modifications in higher dimensions. Let
![]() $\unicode[STIX]{x1D711}$
be a diffeomorphism of
$\unicode[STIX]{x1D711}$
be a diffeomorphism of
![]() $M$
sending
$M$
sending
![]() $C$
into
$C$
into
![]() $C$
. Fix a parameterization of a collar
$C$
. Fix a parameterization of a collar
![]() $N$
such that
$N$
such that
![]() $(N,L)$
is identified with
$(N,L)$
is identified with
 $(L\times [-1,1],L\times \{0\})$
. Denote by
$(L\times [-1,1],L\times \{0\})$
. Denote by
 $\unicode[STIX]{x1D70B}:N\rightarrow L$
the projection on the first factor and by
$\unicode[STIX]{x1D70B}:N\rightarrow L$
the projection on the first factor and by
 $h:N\rightarrow [-1,1]$
the projection on the second factor.
$h:N\rightarrow [-1,1]$
the projection on the second factor.
There exists an open neighborhood
![]() $U$
of
$U$
of
![]() $C$
in
$C$
in
![]() $L$
so that
$L$
so that
 $\unicode[STIX]{x1D711}(U)\;\subset \;N$
. In particular, the closure
$\unicode[STIX]{x1D711}(U)\;\subset \;N$
. In particular, the closure
![]() $\overline{U}$
is a finite union of closed intervals. The map
$\overline{U}$
is a finite union of closed intervals. The map
 $\unicode[STIX]{x1D711}:\overline{U}\rightarrow N=L\times [-1,1]$
has the property
$\unicode[STIX]{x1D711}:\overline{U}\rightarrow N=L\times [-1,1]$
has the property
 $h\circ \unicode[STIX]{x1D711}(a)=0$
, for each
$h\circ \unicode[STIX]{x1D711}(a)=0$
, for each
![]() $a\in C$
. Therefore the differential
$a\in C$
. Therefore the differential
 $D_{a}\,(h\circ \unicode[STIX]{x1D711})=0$
, for each
$D_{a}\,(h\circ \unicode[STIX]{x1D711})=0$
, for each
![]() $a\in C$
. Since
$a\in C$
. Since
![]() $\unicode[STIX]{x1D711}$
is a diffeomorphism
$\unicode[STIX]{x1D711}$
is a diffeomorphism
 $D_{a}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})\neq 0$
, for every
$D_{a}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})\neq 0$
, for every
![]() $a\in C$
.
$a\in C$
.
For each
![]() $a\in C$
consider an open interval neighborhood
$a\in C$
consider an open interval neighborhood
![]() $U_{a}$
within
$U_{a}$
within
![]() $L$
, so that
$L$
, so that
 $D_{x}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})\neq 0$
and
$D_{x}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})\neq 0$
and
 $\Vert \!D_{x}\,(h\circ \unicode[STIX]{x1D711})\!\!\Vert <1$
, for every
$\Vert \!D_{x}\,(h\circ \unicode[STIX]{x1D711})\!\!\Vert <1$
, for every
![]() $x\in \overline{U_{a}}$
. We obtain an open covering
$x\in \overline{U_{a}}$
. We obtain an open covering
 $\{U_{a};a\in C\}$
of
$\{U_{a};a\in C\}$
of
![]() $C$
. As
$C$
. As
![]() $C$
is compact there exists a finite subcovering by intervals
$C$
is compact there exists a finite subcovering by intervals
 $\{U_{1},U_{2},\ldots ,U_{n}\}$
. Without loss of generality one can suppose that
$\{U_{1},U_{2},\ldots ,U_{n}\}$
. Without loss of generality one can suppose that
![]() $U_{j}\;\subset \;U$
, for all
$U_{j}\;\subset \;U$
, for all
![]() $j$
. We consider such a covering having the minimal number of elements. This implies that
$j$
. We consider such a covering having the minimal number of elements. This implies that
![]() $\overline{U_{j}}$
are disjoint intervals.
$\overline{U_{j}}$
are disjoint intervals.
For every
![]() $j$
the map
$j$
the map
 $\unicode[STIX]{x1D70B}|_{\unicode[STIX]{x1D711}(\overline{U_{j}})}:\unicode[STIX]{x1D711}(\overline{U_{j}})\rightarrow \unicode[STIX]{x1D70B}(\unicode[STIX]{x1D711}(\overline{U_{j}}))\;\subset \;L$
is a diffeomorphism on its image, since
$\unicode[STIX]{x1D70B}|_{\unicode[STIX]{x1D711}(\overline{U_{j}})}:\unicode[STIX]{x1D711}(\overline{U_{j}})\rightarrow \unicode[STIX]{x1D70B}(\unicode[STIX]{x1D711}(\overline{U_{j}}))\;\subset \;L$
is a diffeomorphism on its image, since
![]() $\unicode[STIX]{x1D711}(\overline{U_{j}})$
is connected and
$\unicode[STIX]{x1D711}(\overline{U_{j}})$
is connected and
 $D_{x}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})\neq 0$
, for any
$D_{x}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})\neq 0$
, for any
![]() $x\in \overline{U_{j}}$
.
$x\in \overline{U_{j}}$
.
Consider a slightly smaller closed interval
![]() $I_{j}\;\subset \;U_{j}$
such that
$I_{j}\;\subset \;U_{j}$
such that
 $I_{j}\;\cap \;C=U_{j}\;\cap \;C$
.
$I_{j}\;\cap \;C=U_{j}\;\cap \;C$
.
Let
![]() $\unicode[STIX]{x1D707}$
be a positive smooth function on
$\unicode[STIX]{x1D707}$
be a positive smooth function on
 $\bigsqcup _{j=1}^{n}\overline{U_{j}}$
such
$\bigsqcup _{j=1}^{n}\overline{U_{j}}$
such
![]() $\unicode[STIX]{x1D707}(t)$
equals 1 near the boundary points and vanishes on
$\unicode[STIX]{x1D707}(t)$
equals 1 near the boundary points and vanishes on
![]() $\bigsqcup _{j=1}^{n}I_{j}$
. Define
$\bigsqcup _{j=1}^{n}I_{j}$
. Define
 $\unicode[STIX]{x1D719}_{s}:\bigsqcup _{j=1}^{n}\overline{U_{j}}\rightarrow N$
by
$\unicode[STIX]{x1D719}_{s}:\bigsqcup _{j=1}^{n}\overline{U_{j}}\rightarrow N$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{s}(x)=(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711}(x),(s\unicode[STIX]{x1D707}(x)+1-s)\cdot h\circ \unicode[STIX]{x1D711}(x)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{s}(x)=(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711}(x),(s\unicode[STIX]{x1D707}(x)+1-s)\cdot h\circ \unicode[STIX]{x1D711}(x)).\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D719}_{0}(x)=\unicode[STIX]{x1D711}(x)$
and for each
$\unicode[STIX]{x1D719}_{0}(x)=\unicode[STIX]{x1D711}(x)$
and for each
 $s\in [0,1]$
we have
$s\in [0,1]$
we have
 $\unicode[STIX]{x1D719}_{s}(x)=\unicode[STIX]{x1D711}(x)$
, for
$\unicode[STIX]{x1D719}_{s}(x)=\unicode[STIX]{x1D711}(x)$
, for
![]() $x$
near the boundary points of
$x$
near the boundary points of
 $\bigsqcup _{j=1}^{n}\overline{U_{j}}$
. Furthermore
$\bigsqcup _{j=1}^{n}\overline{U_{j}}$
. Furthermore
 $\unicode[STIX]{x1D719}_{1}(x)=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711}(x)\in L$
, when
$\unicode[STIX]{x1D719}_{1}(x)=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711}(x)\in L$
, when
 $x\in \bigsqcup _{j=1}^{n}I_{j}$
. One should also notice that
$x\in \bigsqcup _{j=1}^{n}I_{j}$
. One should also notice that
 $\unicode[STIX]{x1D719}_{s}(x)=\unicode[STIX]{x1D711}(x)$
, for each
$\unicode[STIX]{x1D719}_{s}(x)=\unicode[STIX]{x1D711}(x)$
, for each
![]() $x\in C$
and
$x\in C$
and
 $s\in [0,1]$
.
$s\in [0,1]$
.
Now denote
 $J_{j}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711}(I_{j})$
. It is clear that
$J_{j}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711}(I_{j})$
. It is clear that
 $C=\unicode[STIX]{x1D711}(C)\;\subset \;\bigcup _{j=1}^{n}J_{j}$
. We claim that we can assume that
$C=\unicode[STIX]{x1D711}(C)\;\subset \;\bigcup _{j=1}^{n}J_{j}$
. We claim that we can assume that
![]() $J_{j}$
are disjoint. Indeed, since
$J_{j}$
are disjoint. Indeed, since
![]() $\unicode[STIX]{x1D711}$
is bijective we have
$\unicode[STIX]{x1D711}$
is bijective we have
 $\unicode[STIX]{x1D711}(I_{j}\;\cap \;C)\;\cap \;\unicode[STIX]{x1D711}(I_{k}\;\cap \;C)=\emptyset$
, for any
$\unicode[STIX]{x1D711}(I_{j}\;\cap \;C)\;\cap \;\unicode[STIX]{x1D711}(I_{k}\;\cap \;C)=\emptyset$
, for any
![]() $j\neq k$
. Since
$j\neq k$
. Since
 $\unicode[STIX]{x1D711}(I_{j}\;\cap \;C)$
are closed subsets of
$\unicode[STIX]{x1D711}(I_{j}\;\cap \;C)$
are closed subsets of
![]() $L$
there exists
$L$
there exists
![]() $\unicode[STIX]{x1D700}>0$
so that
$\unicode[STIX]{x1D700}>0$
so that
 $d(\unicode[STIX]{x1D711}(I_{j}\;\cap \;C),\unicode[STIX]{x1D711}(I_{k}\;\cap \;C))\geqslant \unicode[STIX]{x1D700}$
, for
$d(\unicode[STIX]{x1D711}(I_{j}\;\cap \;C),\unicode[STIX]{x1D711}(I_{k}\;\cap \;C))\geqslant \unicode[STIX]{x1D700}$
, for
![]() $j\neq k$
, where
$j\neq k$
, where
![]() $d$
is a metric on
$d$
is a metric on
![]() $L$
. Since
$L$
. Since
 $\unicode[STIX]{x1D719}_{1}(I_{j}\;\cap \;C)=\unicode[STIX]{x1D711}(I_{j}\;\cap \;C)$
, we have
$\unicode[STIX]{x1D719}_{1}(I_{j}\;\cap \;C)=\unicode[STIX]{x1D711}(I_{j}\;\cap \;C)$
, we have
 $d(\unicode[STIX]{x1D719}_{1}(I_{j}\;\cap \;C),\unicode[STIX]{x1D719}_{1}(I_{k}\;\cap \;C))\geqslant \unicode[STIX]{x1D700}$
, for
$d(\unicode[STIX]{x1D719}_{1}(I_{j}\;\cap \;C),\unicode[STIX]{x1D719}_{1}(I_{k}\;\cap \;C))\geqslant \unicode[STIX]{x1D700}$
, for
![]() $j\neq k$
. Thus there exist some open neighborhoods
$j\neq k$
. Thus there exist some open neighborhoods
![]() $J_{j}^{\prime }$
of
$J_{j}^{\prime }$
of
 $\unicode[STIX]{x1D719}_{1}(I_{j}\;\cap \;C)$
within
$\unicode[STIX]{x1D719}_{1}(I_{j}\;\cap \;C)$
within
![]() $L$
so that
$L$
so that
 $d(J_{j}^{\prime },J_{k}^{\prime })\geqslant {\textstyle \frac{1}{2}}\unicode[STIX]{x1D700}$
, for all
$d(J_{j}^{\prime },J_{k}^{\prime })\geqslant {\textstyle \frac{1}{2}}\unicode[STIX]{x1D700}$
, for all
![]() $j\neq k$
. As
$j\neq k$
. As
![]() $\unicode[STIX]{x1D719}_{1}$
is a diffeomorphism there exist open neighborhoods
$\unicode[STIX]{x1D719}_{1}$
is a diffeomorphism there exist open neighborhoods
![]() $I_{j}^{\prime }$
of
$I_{j}^{\prime }$
of
![]() $I_{j}\;\cap \;C$
with the property that
$I_{j}\;\cap \;C$
with the property that
 $\unicode[STIX]{x1D719}_{1}(I_{j}^{\prime })\;\subset \;J_{j}^{\prime }$
, for all
$\unicode[STIX]{x1D719}_{1}(I_{j}^{\prime })\;\subset \;J_{j}^{\prime }$
, for all
![]() $j$
. Now
$j$
. Now
![]() $I_{j}^{\prime }$
and
$I_{j}^{\prime }$
and
![]() $J_{j}^{\prime }$
are finite unions of open intervals. We can replace them by closed intervals with the same intersection with
$J_{j}^{\prime }$
are finite unions of open intervals. We can replace them by closed intervals with the same intersection with
![]() $C$
. This produces two new families of disjoint closed intervals related by
$C$
. This produces two new families of disjoint closed intervals related by
![]() $\unicode[STIX]{x1D719}_{1}$
, as the initial situation. This proves the claim.
$\unicode[STIX]{x1D719}_{1}$
, as the initial situation. This proves the claim.
We obtained that there exist two coverings
 $\{I_{1},I_{2},\ldots ,I_{n}\}$
and
$\{I_{1},I_{2},\ldots ,I_{n}\}$
and
 $\{J_{1},J_{2},\ldots ,J_{n}\}$
of
$\{J_{1},J_{2},\ldots ,J_{n}\}$
of
![]() $C$
by disjoint closed intervals and a diffeomorphism
$C$
by disjoint closed intervals and a diffeomorphism
 $\unicode[STIX]{x1D719}_{1}:\bigsqcup _{j=1}^{n}I_{j}\rightarrow \bigsqcup _{j=1}^{n}J_{j}$
such that
$\unicode[STIX]{x1D719}_{1}:\bigsqcup _{j=1}^{n}I_{j}\rightarrow \bigsqcup _{j=1}^{n}J_{j}$
such that
 $\unicode[STIX]{x1D719}_{1}(x)=\unicode[STIX]{x1D711}(x)$
, for any
$\unicode[STIX]{x1D719}_{1}(x)=\unicode[STIX]{x1D711}(x)$
, for any
![]() $x\in C$
.
$x\in C$
.
Notice that the sign of
 $D_{a}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})$
might not be the same for all intervals.
$D_{a}(\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D711})$
might not be the same for all intervals.
Every partition of
![]() $C$
induced by a covering
$C$
induced by a covering
 $\{I_{1},I_{2},\ldots ,I_{n}\}$
as above is determined by the choice of complementary intervals, namely the
$\{I_{1},I_{2},\ldots ,I_{n}\}$
as above is determined by the choice of complementary intervals, namely the
![]() $n-1$
connected components of
$n-1$
connected components of
 $L\setminus \bigcup _{j=1}^{n}I_{j}$
. It follows that there are only countably many finite partitions of
$L\setminus \bigcup _{j=1}^{n}I_{j}$
. It follows that there are only countably many finite partitions of
![]() $C$
of the type considered here. Next, the set of those elements of
$C$
of the type considered here. Next, the set of those elements of
 $\mathfrak{diff}_{M}^{1}(C)$
which arise from partitions induced by the coverings
$\mathfrak{diff}_{M}^{1}(C)$
which arise from partitions induced by the coverings
 $\{I_{1},I_{2},\ldots ,I_{n}\}$
and
$\{I_{1},I_{2},\ldots ,I_{n}\}$
and
 $\{J_{1},J_{2},\ldots ,J_{n}\}$
of
$\{J_{1},J_{2},\ldots ,J_{n}\}$
of
![]() $C$
is acted upon transitively by the stabilizer of one partition. The stabilizer of one partition embeds into the product of
$C$
is acted upon transitively by the stabilizer of one partition. The stabilizer of one partition embeds into the product of
 $\mathfrak{diff}_{I_{j}}^{1}(C\;\cap \;I_{j})$
. Theorem 2 then implies that
$\mathfrak{diff}_{I_{j}}^{1}(C\;\cap \;I_{j})$
. Theorem 2 then implies that
 $\mathfrak{diff}_{M}^{1}(C)$
is countable.
$\mathfrak{diff}_{M}^{1}(C)$
is countable.
3.2.4 Proof of Theorem 4
Before proceeding, we need some preparatory material. Let
 $A\;\subset \;\mathbb{R}^{n}$
be a set without isolated points. Let
$A\;\subset \;\mathbb{R}^{n}$
be a set without isolated points. Let
![]() $T_{p}\mathbb{R}^{n}$
denote the tangent space at
$T_{p}\mathbb{R}^{n}$
denote the tangent space at
![]() $p$
on
$p$
on
![]() $\mathbb{R}^{n}$
and
$\mathbb{R}^{n}$
and
 $UT_{p}\mathbb{R}^{n}\;\subset \;T_{p}\mathbb{R}^{n}$
the sphere of unit vectors. For any
$UT_{p}\mathbb{R}^{n}\;\subset \;T_{p}\mathbb{R}^{n}$
the sphere of unit vectors. For any
![]() $p\in A$
one defines the unit tangent spread
$p\in A$
one defines the unit tangent spread
 $UT_{p}A\;\subset \;UT_{p}\mathbb{R}^{n}$
at
$UT_{p}A\;\subset \;UT_{p}\mathbb{R}^{n}$
at
![]() $p$
as the set of vectors
$p$
as the set of vectors
 $v\in UT_{p}\mathbb{R}^{n}$
for which there exists a sequence of points
$v\in UT_{p}\mathbb{R}^{n}$
for which there exists a sequence of points
![]() $a_{i}\in A$
with
$a_{i}\in A$
with
 $\lim _{i\rightarrow \infty }a_{i}=p$
and
$\lim _{i\rightarrow \infty }a_{i}=p$
and
 $$\begin{eqnarray}\lim _{i\rightarrow \infty }\frac{a_{i}-p}{\Vert \!a_{i}-p\Vert }=v.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{i\rightarrow \infty }\frac{a_{i}-p}{\Vert \!a_{i}-p\Vert }=v.\end{eqnarray}$$
Vectors in
![]() $UT_{p}A$
will also be called (unit) tangent vectors at
$UT_{p}A$
will also be called (unit) tangent vectors at
![]() $p$
to
$p$
to
![]() $A$
. We also set
$A$
. We also set
 $T_{p}A=\mathbb{R}_{+}\cdot UT_{p}A\;\subset \;T_{p}\mathbb{R}^{n}$
for the tangent spread at
$T_{p}A=\mathbb{R}_{+}\cdot UT_{p}A\;\subset \;T_{p}\mathbb{R}^{n}$
for the tangent spread at
![]() $p$
.
$p$
.
A differentiable map
 $\unicode[STIX]{x1D711}:(\mathbb{R}^{n},A)\rightarrow (\mathbb{R}^{n},B)$
induces a tangent map
$\unicode[STIX]{x1D711}:(\mathbb{R}^{n},A)\rightarrow (\mathbb{R}^{n},B)$
induces a tangent map
 $T_{p}\unicode[STIX]{x1D711}:T_{p}A\rightarrow T_{\unicode[STIX]{x1D711}(p)}B$
. Specifically, let
$T_{p}\unicode[STIX]{x1D711}:T_{p}A\rightarrow T_{\unicode[STIX]{x1D711}(p)}B$
. Specifically, let
 $D_{p}\unicode[STIX]{x1D711}:T_{p}\mathbb{R}^{n}\rightarrow T_{\unicode[STIX]{x1D711}(p)}\mathbb{R}^{n}$
be the differential of
$D_{p}\unicode[STIX]{x1D711}:T_{p}\mathbb{R}^{n}\rightarrow T_{\unicode[STIX]{x1D711}(p)}\mathbb{R}^{n}$
be the differential of
![]() $\unicode[STIX]{x1D711}$
; then we have
$\unicode[STIX]{x1D711}$
; then we have
 $$\begin{eqnarray}T_{p}\unicode[STIX]{x1D711}=U(D_{p}\unicode[STIX]{x1D711}),\end{eqnarray}$$
$$\begin{eqnarray}T_{p}\unicode[STIX]{x1D711}=U(D_{p}\unicode[STIX]{x1D711}),\end{eqnarray}$$
where for a linear map
 $L:V\rightarrow W$
between vector spaces we denoted by
$L:V\rightarrow W$
between vector spaces we denoted by
 $U(L):U(V)\rightarrow U(W)$
the map induced on the unit spheres, namely
$U(L):U(V)\rightarrow U(W)$
the map induced on the unit spheres, namely
 $$\begin{eqnarray}U(L)v=\frac{L(v)}{\Vert \!L(v)\!\!\Vert }.\end{eqnarray}$$
$$\begin{eqnarray}U(L)v=\frac{L(v)}{\Vert \!L(v)\!\!\Vert }.\end{eqnarray}$$
As the unit tangent spread
![]() $UT_{p}A$
is a subset of the unit sphere, it inherits the spherical geometry and metric. In particular, it makes sense to consider the convex hull
$UT_{p}A$
is a subset of the unit sphere, it inherits the spherical geometry and metric. In particular, it makes sense to consider the convex hull
 $\text{Hull}(UT_{p}A)\;\subset \;UT_{p}\mathbb{R}^{n}$
in the sphere.
$\text{Hull}(UT_{p}A)\;\subset \;UT_{p}\mathbb{R}^{n}$
in the sphere.
Although tangent spreads to product Cantor sets might depend on the particular factors, their convex hulls have a simple description. Let
 $C=C_{1}\times C_{2}\times \cdots \times C_{n}\;\subset \;\mathbb{R}^{n}$
be a product of Cantor sets
$C=C_{1}\times C_{2}\times \cdots \times C_{n}\;\subset \;\mathbb{R}^{n}$
be a product of Cantor sets
![]() $C_{i}\;\subset \;\mathbb{R}$
. The usual cubical complex underlying the
$C_{i}\;\subset \;\mathbb{R}$
. The usual cubical complex underlying the
![]() $n$
-dimensional cube
$n$
-dimensional cube
![]() $[0,1]^{n}$
will be denoted by
$[0,1]^{n}$
will be denoted by
![]() $\Box ^{n}$
. Then denote by
$\Box ^{n}$
. Then denote by
![]() $Lk(p)$
the spherical link of
$Lk(p)$
the spherical link of
![]() $p\in \Box ^{n}$
. If
$p\in \Box ^{n}$
. If
![]() $p$
belongs to a
$p$
belongs to a
![]() $k$
-dimensional cube but not to a
$k$
-dimensional cube but not to a
![]() $(k+1)$
-dimensional cube of
$(k+1)$
-dimensional cube of
![]() $\Box ^{n}$
then
$\Box ^{n}$
then
![]() $Lk(p)$
is isometric to the link
$Lk(p)$
is isometric to the link
![]() ${\mathcal{L}}_{k,n}$
of the origin in
${\mathcal{L}}_{k,n}$
of the origin in
 $\mathbb{R}^{k}\times \mathbb{R}_{+}^{n-k}$
. Thus there are precisely
$\mathbb{R}^{k}\times \mathbb{R}_{+}^{n-k}$
. Thus there are precisely
![]() $n+1$
different isometry types of links of points.
$n+1$
different isometry types of links of points.
Now a direct inspection shows that for each
![]() $p\in C$
there exists some
$p\in C$
there exists some
![]() $k$
so that the convex hull
$k$
so that the convex hull
 $\text{Hull}(UT_{p}A)$
is isometric to
$\text{Hull}(UT_{p}A)$
is isometric to
![]() ${\mathcal{L}}_{k,n}$
.
${\mathcal{L}}_{k,n}$
.
When the diffeomorphism
 $\unicode[STIX]{x1D711}:(\mathbb{R}^{n},C)\rightarrow (\mathbb{R}^{n},C)$
is also conformal, then the tangent maps are isometries between the unit tangent spreads, because the spherical distance is given by angles between the corresponding vectors. However this is not true for general diffeomorphisms.
$\unicode[STIX]{x1D711}:(\mathbb{R}^{n},C)\rightarrow (\mathbb{R}^{n},C)$
is also conformal, then the tangent maps are isometries between the unit tangent spreads, because the spherical distance is given by angles between the corresponding vectors. However this is not true for general diffeomorphisms.
Nevertheless the spherical links
![]() ${\mathcal{L}}_{k,n}$
are quite particular. There exist
${\mathcal{L}}_{k,n}$
are quite particular. There exist
![]() $n+k$
vectors along the coordinates’ axes which are extremal points of
$n+k$
vectors along the coordinates’ axes which are extremal points of
![]() $UT_{p}C$
, such that their convex hull is
$UT_{p}C$
, such that their convex hull is
 $\text{Hull}(UT_{p}C)$
, so isometric to
$\text{Hull}(UT_{p}C)$
, so isometric to
![]() ${\mathcal{L}}_{k,n}$
. These are vectors of the form
${\mathcal{L}}_{k,n}$
. These are vectors of the form
 $e_{i},-e_{i},e_{j}$
, where
$e_{i},-e_{i},e_{j}$
, where
![]() $e_{i}$
correspond to the coordinates’ axes in
$e_{i}$
correspond to the coordinates’ axes in
![]() $\mathbb{R}^{k}$
and
$\mathbb{R}^{k}$
and
![]() $e_{j}$
to those in
$e_{j}$
to those in
![]() $\mathbb{R}^{n-k}$
. Now, any diffeomorphism
$\mathbb{R}^{n-k}$
. Now, any diffeomorphism
 $\unicode[STIX]{x1D711}:(\mathbb{R}^{n},C)\rightarrow (\mathbb{R}^{n},C)$
should send a unit tangent spread of type
$\unicode[STIX]{x1D711}:(\mathbb{R}^{n},C)\rightarrow (\mathbb{R}^{n},C)$
should send a unit tangent spread of type
![]() ${\mathcal{L}}_{k,n}$
into one of the same type, since
${\mathcal{L}}_{k,n}$
into one of the same type, since
![]() ${\mathcal{L}}_{k,n}$
is not affinely equivalent to
${\mathcal{L}}_{k,n}$
is not affinely equivalent to
![]() ${\mathcal{L}}_{k^{\prime },n}$
, for
${\mathcal{L}}_{k^{\prime },n}$
, for
![]() $k\neq k^{\prime }$
. Moreover, the extremal vectors are sent into extremal vectors of the same type.
$k\neq k^{\prime }$
. Moreover, the extremal vectors are sent into extremal vectors of the same type.
Further, let
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{n},C)$
such that
$\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{n},C)$
such that
 $\Vert D_{a}\unicode[STIX]{x1D711}-\mathbf{1}\Vert \leqslant \unicode[STIX]{x1D700}$
for all
$\Vert D_{a}\unicode[STIX]{x1D711}-\mathbf{1}\Vert \leqslant \unicode[STIX]{x1D700}$
for all
![]() $a\in C$
. Assume now that the unit tangent spread
$a\in C$
. Assume now that the unit tangent spread
![]() $UT_{a}C$
is isometric to
$UT_{a}C$
is isometric to
![]() ${\mathcal{L}}_{0,n}$
, namely it is of corner type. In this case
${\mathcal{L}}_{0,n}$
, namely it is of corner type. In this case
 $U(D_{a}\unicode[STIX]{x1D711})$
should permute the
$U(D_{a}\unicode[STIX]{x1D711})$
should permute the
![]() $n$
coordinate vectors, which are the extremal vectors of
$n$
coordinate vectors, which are the extremal vectors of
![]() ${\mathcal{L}}_{0,n}$
. Therefore either
${\mathcal{L}}_{0,n}$
. Therefore either
 $U(D_{a}\unicode[STIX]{x1D711})=\mathbf{1}$
, or else
$U(D_{a}\unicode[STIX]{x1D711})=\mathbf{1}$
, or else
 $$\begin{eqnarray}\Vert U(D_{a}\unicode[STIX]{x1D711})-\mathbf{1}\Vert \geqslant \sqrt{2},\end{eqnarray}$$
$$\begin{eqnarray}\Vert U(D_{a}\unicode[STIX]{x1D711})-\mathbf{1}\Vert \geqslant \sqrt{2},\end{eqnarray}$$
which yields
 $$\begin{eqnarray}\Vert D_{a}\unicode[STIX]{x1D711}-\mathbf{1}\Vert \geqslant \sqrt{2}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert D_{a}\unicode[STIX]{x1D711}-\mathbf{1}\Vert \geqslant \sqrt{2}.\end{eqnarray}$$
In other words, taking
![]() $\unicode[STIX]{x1D700}<\sqrt{2}$
any diffeomorphism
$\unicode[STIX]{x1D700}<\sqrt{2}$
any diffeomorphism
![]() $\unicode[STIX]{x1D711}$
as above should satisfy
$\unicode[STIX]{x1D711}$
as above should satisfy
 $U(D_{a}\unicode[STIX]{x1D711})=\mathbf{1}$
. Now, if
$U(D_{a}\unicode[STIX]{x1D711})=\mathbf{1}$
. Now, if
![]() $\unicode[STIX]{x1D711}$
is of class
$\unicode[STIX]{x1D711}$
is of class
![]() ${\mathcal{C}}^{1}$
then
${\mathcal{C}}^{1}$
then
 $U(D_{a}\unicode[STIX]{x1D711})$
is continuous. Since the set of corner points is dense in
$U(D_{a}\unicode[STIX]{x1D711})$
is continuous. Since the set of corner points is dense in
![]() $C$
we derive
$C$
we derive
 $U(D_{a}\unicode[STIX]{x1D711})=\mathbf{1}$
, for any
$U(D_{a}\unicode[STIX]{x1D711})=\mathbf{1}$
, for any
![]() $a\in C$
. This is the same as saying that for any
$a\in C$
. This is the same as saying that for any
![]() $a\in C$
the linear map
$a\in C$
the linear map
![]() $D_{a}\unicode[STIX]{x1D711}$
is represented by a diagonal matrix, with respect to the standard coordinate system of
$D_{a}\unicode[STIX]{x1D711}$
is represented by a diagonal matrix, with respect to the standard coordinate system of
![]() $\mathbb{R}^{n}$
.
$\mathbb{R}^{n}$
.
Proposition 1. Let
![]() $a\in C$
be a corner point. The map
$a\in C$
be a corner point. The map
 $\unicode[STIX]{x1D712}:\mathfrak{diff}_{\mathbb{R}^{n},a}^{1}(C)\rightarrow (\mathbb{R}^{\ast })^{n}$
, which associates to the germ
$\unicode[STIX]{x1D712}:\mathfrak{diff}_{\mathbb{R}^{n},a}^{1}(C)\rightarrow (\mathbb{R}^{\ast })^{n}$
, which associates to the germ
![]() $\unicode[STIX]{x1D711}$
the eigenvalues of
$\unicode[STIX]{x1D711}$
the eigenvalues of
![]() $D_{a}\unicode[STIX]{x1D711}$
is an isomorphism onto a discrete subgroup of
$D_{a}\unicode[STIX]{x1D711}$
is an isomorphism onto a discrete subgroup of
![]() $(\mathbb{R}^{\ast })^{n}$
.
$(\mathbb{R}^{\ast })^{n}$
.
Proof. Let
 $\{x_{1},x_{2},\ldots ,x_{n}\}$
be the standard coordinate functions on
$\{x_{1},x_{2},\ldots ,x_{n}\}$
be the standard coordinate functions on
![]() $\mathbb{R}^{n}$
and
$\mathbb{R}^{n}$
and
 $\unicode[STIX]{x1D70B}_{j}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n-1}$
denote the projection onto the hyperplane
$\unicode[STIX]{x1D70B}_{j}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n-1}$
denote the projection onto the hyperplane
 $H_{j}=\{x_{j}=0\}$
. For the sake of simplicity we assume that
$H_{j}=\{x_{j}=0\}$
. For the sake of simplicity we assume that
 $a=(0,0,\ldots ,0)$
, and that the convex hull of the unit tangent spread is the union of the sets
$a=(0,0,\ldots ,0)$
, and that the convex hull of the unit tangent spread is the union of the sets
 $H_{j}^{+}=H_{j}\;\cap \;\{x_{i}\geqslant 0,i=1,\ldots ,n\}$
. We will use induction on
$H_{j}^{+}=H_{j}\;\cap \;\{x_{i}\geqslant 0,i=1,\ldots ,n\}$
. We will use induction on
![]() $n$
. The claim was proved in Lemma 7 for
$n$
. The claim was proved in Lemma 7 for
![]() $n=1$
. Assume it holds for all dimensions at most
$n=1$
. Assume it holds for all dimensions at most
![]() $n-1$
.
$n-1$
.
Let
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{n},C)$
such that
$\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{n},C)$
such that
 $\unicode[STIX]{x1D711}(a)=a$
. Assume that
$\unicode[STIX]{x1D711}(a)=a$
. Assume that
 $\Vert D_{x}\unicode[STIX]{x1D711}-\mathbf{1}\Vert <{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70E}<{\textstyle \frac{1}{2}}$
for all
$\Vert D_{x}\unicode[STIX]{x1D711}-\mathbf{1}\Vert <{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70E}<{\textstyle \frac{1}{2}}$
for all
![]() $x$
in a neighborhood
$x$
in a neighborhood
![]() $V$
of
$V$
of
![]() $a$
in
$a$
in
![]() $\mathbb{R}^{n}$
. We will prove that
$\mathbb{R}^{n}$
. We will prove that
![]() $\unicode[STIX]{x1D711}|_{C}$
is a trivial germ at
$\unicode[STIX]{x1D711}|_{C}$
is a trivial germ at
![]() $a$
. This shows that the image of
$a$
. This shows that the image of
![]() $\unicode[STIX]{x1D712}$
is a discrete subgroup of
$\unicode[STIX]{x1D712}$
is a discrete subgroup of
![]() $(\mathbb{R}^{\ast })^{n}$
and the kernel of
$(\mathbb{R}^{\ast })^{n}$
and the kernel of
![]() $\unicode[STIX]{x1D712}$
is trivial.
$\unicode[STIX]{x1D712}$
is trivial.
Consider the maps
 $\unicode[STIX]{x1D711}_{j}:H_{j}\rightarrow H_{j}$
given by
$\unicode[STIX]{x1D711}_{j}:H_{j}\rightarrow H_{j}$
given by
 $\unicode[STIX]{x1D711}_{j}(x)=\unicode[STIX]{x1D70B}_{j}\circ \unicode[STIX]{x1D711}(x)$
. The determinant of
$\unicode[STIX]{x1D711}_{j}(x)=\unicode[STIX]{x1D70B}_{j}\circ \unicode[STIX]{x1D711}(x)$
. The determinant of
![]() $D_{a}\unicode[STIX]{x1D711}_{j}$
is the product of all eigenvalues of
$D_{a}\unicode[STIX]{x1D711}_{j}$
is the product of all eigenvalues of
![]() $D_{a}\unicode[STIX]{x1D711}$
but the
$D_{a}\unicode[STIX]{x1D711}$
but the
![]() $j$
th eigenvalue, and hence it is non-zero. Moreover, we have
$j$
th eigenvalue, and hence it is non-zero. Moreover, we have
 $\Vert D_{a}\unicode[STIX]{x1D711}_{j}-\mathbf{1}\Vert <{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70E}$
.
$\Vert D_{a}\unicode[STIX]{x1D711}_{j}-\mathbf{1}\Vert <{\textstyle \frac{1}{2}}\unicode[STIX]{x1D70E}$
.
We claim the following.
Lemma 8. The map
 $\unicode[STIX]{x1D711}_{j}:H_{j}\;\cap \;V\rightarrow H_{j}$
is injective.
$\unicode[STIX]{x1D711}_{j}:H_{j}\;\cap \;V\rightarrow H_{j}$
is injective.
Proof. Assume the contrary, namely that there exist two points
 $p,q\in H_{j}\,\cap \,V$
such that
$p,q\in H_{j}\,\cap \,V$
such that
 $\unicode[STIX]{x1D70B}_{j}(\unicode[STIX]{x1D711}(p))=\unicode[STIX]{x1D70B}_{j}(\unicode[STIX]{x1D711}(q))$
. Consider the first non-trivial case
$\unicode[STIX]{x1D70B}_{j}(\unicode[STIX]{x1D711}(p))=\unicode[STIX]{x1D70B}_{j}(\unicode[STIX]{x1D711}(q))$
. Consider the first non-trivial case
![]() $n=2$
, when
$n=2$
, when
![]() $H_{j}^{+}$
are half-lines issued from
$H_{j}^{+}$
are half-lines issued from
![]() $a$
. The mean value theorem and the previous equality prove that there exists some
$a$
. The mean value theorem and the previous equality prove that there exists some
 $\unicode[STIX]{x1D709}\in H_{j}^{+}\;\cap \;V$
between
$\unicode[STIX]{x1D709}\in H_{j}^{+}\;\cap \;V$
between
![]() $p$
and
$p$
and
![]() $q$
so that
$q$
so that
 $(\unicode[STIX]{x1D70B}_{j}\circ \unicode[STIX]{x1D711})^{\prime }(\unicode[STIX]{x1D709})=0$
. This amounts to the fact that the image of
$(\unicode[STIX]{x1D70B}_{j}\circ \unicode[STIX]{x1D711})^{\prime }(\unicode[STIX]{x1D709})=0$
. This amounts to the fact that the image of
![]() $D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}$
is contained in the kernel of
$D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}$
is contained in the kernel of
 $D_{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})}\unicode[STIX]{x1D70B}_{j}$
, namely that
$D_{\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709})}\unicode[STIX]{x1D70B}_{j}$
, namely that
 $$\begin{eqnarray}\langle D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}(v_{j}),v_{j}\rangle =0,\end{eqnarray}$$
$$\begin{eqnarray}\langle D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}(v_{j}),v_{j}\rangle =0,\end{eqnarray}$$
where
![]() $v_{j}$
is a unit tangent vector to
$v_{j}$
is a unit tangent vector to
![]() $H_{j}^{+}$
at
$H_{j}^{+}$
at
![]() $\unicode[STIX]{x1D709}$
. We derive
$\unicode[STIX]{x1D709}$
. We derive
 $\Vert D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}_{j}-\mathbf{1}\Vert \geqslant 1$
, contradicting our assumptions.
$\Vert D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}_{j}-\mathbf{1}\Vert \geqslant 1$
, contradicting our assumptions.
In the general case
![]() $n>2$
we will use a trick to reduce ourselves to
$n>2$
we will use a trick to reduce ourselves to
![]() $n=2$
, because we lack a multidimensional mean value theorem. Let
$n=2$
, because we lack a multidimensional mean value theorem. Let
![]() $P$
be a generic affine 2-dimensional half-plane whose boundary line passes through
$P$
be a generic affine 2-dimensional half-plane whose boundary line passes through
![]() $p$
and
$p$
and
![]() $q$
. We can find arbitrarily small
$q$
. We can find arbitrarily small
![]() ${\mathcal{C}}^{1}$
-isotopy deformations
${\mathcal{C}}^{1}$
-isotopy deformations
![]() $\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D713}$
of
![]() $\unicode[STIX]{x1D711}_{j}$
so that
$\unicode[STIX]{x1D711}_{j}$
so that
![]() $\unicode[STIX]{x1D713}(H_{j})$
is transversal to
$\unicode[STIX]{x1D713}(H_{j})$
is transversal to
![]() $P$
and
$P$
and
 $\Vert D_{a}\unicode[STIX]{x1D713}-\mathbf{1}\Vert <\unicode[STIX]{x1D70E}$
. It follows that
$\Vert D_{a}\unicode[STIX]{x1D713}-\mathbf{1}\Vert <\unicode[STIX]{x1D70E}$
. It follows that
 $\unicode[STIX]{x1D713}(H_{j})\;\cap \;P$
is a 1-dimensional manifold
$\unicode[STIX]{x1D713}(H_{j})\;\cap \;P$
is a 1-dimensional manifold
![]() $Z$
with a boundary containing both
$Z$
with a boundary containing both
![]() $p$
and
$p$
and
![]() $q$
. Now either there exist two distinct points of the boundary
$q$
. Now either there exist two distinct points of the boundary
![]() $\unicode[STIX]{x2202}Z$
joined by an arc within
$\unicode[STIX]{x2202}Z$
joined by an arc within
![]() $Z$
, or else there is an arc of
$Z$
, or else there is an arc of
![]() $Z$
issued from
$Z$
issued from
![]() $p$
which returns to
$p$
which returns to
![]() $p$
, contradicting the transversality of the intersection
$p$
, contradicting the transversality of the intersection
 $\unicode[STIX]{x1D713}(H_{j})\;\cap \;P$
. In any case the mean value argument above shows that a point
$\unicode[STIX]{x1D713}(H_{j})\;\cap \;P$
. In any case the mean value argument above shows that a point
![]() $\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709})$
of
$\unicode[STIX]{x1D713}(\unicode[STIX]{x1D709})$
of
![]() $Z$
should exist for which the tangent vector
$Z$
should exist for which the tangent vector
![]() $v$
is orthogonal to
$v$
is orthogonal to
![]() $H_{j}$
. We can write
$H_{j}$
. We can write
 $v=D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D713}(w)$
, for some tangent vector
$v=D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D713}(w)$
, for some tangent vector
![]() $w\in H_{j}$
at
$w\in H_{j}$
at
![]() $\unicode[STIX]{x1D709}$
. It follows that
$\unicode[STIX]{x1D709}$
. It follows that
 $$\begin{eqnarray}\langle D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D713}(w),w\rangle =0,\end{eqnarray}$$
$$\begin{eqnarray}\langle D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D713}(w),w\rangle =0,\end{eqnarray}$$
which implies
 $\Vert D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D713}-\mathbf{1}\Vert \geqslant 1$
, contradicting our assumptions.◻
$\Vert D_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D713}-\mathbf{1}\Vert \geqslant 1$
, contradicting our assumptions.◻
It follows that
 $\unicode[STIX]{x1D711}_{j}:H_{j}\;\cap \;V\rightarrow H_{j}$
is an injective map of maximal rank in a neighborhood
$\unicode[STIX]{x1D711}_{j}:H_{j}\;\cap \;V\rightarrow H_{j}$
is an injective map of maximal rank in a neighborhood
![]() $V$
of
$V$
of
![]() $a$
, and hence a diffeomorphism on its image. The projection
$a$
, and hence a diffeomorphism on its image. The projection
![]() $\unicode[STIX]{x1D70B}_{j}$
sends
$\unicode[STIX]{x1D70B}_{j}$
sends
![]() $C$
into
$C$
into
![]() $C\;\cap \;H_{j}$
, so that
$C\;\cap \;H_{j}$
, so that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{j}(C\;\cap \;H_{j}\;\cap \;V)\;\subset \;C\;\cap \;\unicode[STIX]{x1D711}(H_{j}\;\cap \;V)\;\subset \;C\;\cap \;H_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{j}(C\;\cap \;H_{j}\;\cap \;V)\;\subset \;C\;\cap \;\unicode[STIX]{x1D711}(H_{j}\;\cap \;V)\;\subset \;C\;\cap \;H_{j}.\end{eqnarray}$$
Our aim is to use the induction hypothesis for
![]() $\unicode[STIX]{x1D711}_{j}$
. In order to do that we need to show that the class of
$\unicode[STIX]{x1D711}_{j}$
. In order to do that we need to show that the class of
![]() $\unicode[STIX]{x1D711}_{j}$
defines indeed an element of
$\unicode[STIX]{x1D711}_{j}$
defines indeed an element of
 $\mathfrak{diff}_{\mathbb{R}^{n-1},a}^{1}(C)$
, where we identified
$\mathfrak{diff}_{\mathbb{R}^{n-1},a}^{1}(C)$
, where we identified
![]() $H_{j}$
with
$H_{j}$
with
![]() $\mathbb{R}^{n-1}$
.
$\mathbb{R}^{n-1}$
.
We assume from now on that the neighborhood
![]() $V$
is a parallelepiped, all whose vertices being corner points. Its boundary
$V$
is a parallelepiped, all whose vertices being corner points. Its boundary
![]() $\unicode[STIX]{x2202}V$
will then consist of the union of the faces
$\unicode[STIX]{x2202}V$
will then consist of the union of the faces
 $V_{j}=\unicode[STIX]{x2202}V\;\cap \;H_{j}^{+}$
with their respective parallel faces
$V_{j}=\unicode[STIX]{x2202}V\;\cap \;H_{j}^{+}$
with their respective parallel faces
![]() $V_{j}^{\prime }$
. The parallelepiped
$V_{j}^{\prime }$
. The parallelepiped
![]() $V$
is surrounded by gaps, whose smaller width is some
$V$
is surrounded by gaps, whose smaller width is some
![]() $\unicode[STIX]{x1D6FF}>0$
. Let
$\unicode[STIX]{x1D6FF}>0$
. Let
![]() $V^{\unicode[STIX]{x1D6FF}}$
be the
$V^{\unicode[STIX]{x1D6FF}}$
be the
![]() $\unicode[STIX]{x1D6FF}$
-neighborhood of
$\unicode[STIX]{x1D6FF}$
-neighborhood of
![]() $V$
. If
$V$
. If
![]() $\unicode[STIX]{x1D711}$
is Lipschitz with Lipschitz constant
$\unicode[STIX]{x1D711}$
is Lipschitz with Lipschitz constant
![]() $1+\unicode[STIX]{x1D700}$
and
$1+\unicode[STIX]{x1D700}$
and
 $$\begin{eqnarray}(1+\unicode[STIX]{x1D700})l_{i}<\unicode[STIX]{x1D6FF}+l_{i}\end{eqnarray}$$
$$\begin{eqnarray}(1+\unicode[STIX]{x1D700})l_{i}<\unicode[STIX]{x1D6FF}+l_{i}\end{eqnarray}$$
where
![]() $l_{i}$
are the edge lengths of
$l_{i}$
are the edge lengths of
![]() $V$
then the image
$V$
then the image
![]() $\unicode[STIX]{x1D711}(V)$
is contained in
$\unicode[STIX]{x1D711}(V)$
is contained in
![]() $V^{\unicode[STIX]{x1D6FF}}$
, so that
$V^{\unicode[STIX]{x1D6FF}}$
, so that
 $\unicode[STIX]{x1D711}_{j}(V_{j})\;\subset \;V^{\unicode[STIX]{x1D6FF}}\;\cap \;H_{j}$
.
$\unicode[STIX]{x1D711}_{j}(V_{j})\;\subset \;V^{\unicode[STIX]{x1D6FF}}\;\cap \;H_{j}$
.
Further
 $\unicode[STIX]{x1D711}_{j}(\unicode[STIX]{x2202}V_{j})$
bounds
$\unicode[STIX]{x1D711}_{j}(\unicode[STIX]{x2202}V_{j})$
bounds
![]() $\unicode[STIX]{x1D711}_{j}(V_{j})$
and thus there are no points of
$\unicode[STIX]{x1D711}_{j}(V_{j})$
and thus there are no points of
![]() $C\;\cap \;H_{j}$
accumulating on
$C\;\cap \;H_{j}$
accumulating on
![]() $\unicode[STIX]{x1D711}_{j}(V_{j})$
, as their unit tangent spread cannot be of the type
$\unicode[STIX]{x1D711}_{j}(V_{j})$
, as their unit tangent spread cannot be of the type
 ${\mathcal{L}}_{n-1,n-1}$
. Thus
${\mathcal{L}}_{n-1,n-1}$
. Thus
 $C-\unicode[STIX]{x1D711}_{j}(V_{j})$
is a closed subset of
$C-\unicode[STIX]{x1D711}_{j}(V_{j})$
is a closed subset of
![]() $C$
and hence its distance to
$C$
and hence its distance to
![]() $\unicode[STIX]{x1D711}_{j}(V_{j})$
is strictly positive. There exists then an open set
$\unicode[STIX]{x1D711}_{j}(V_{j})$
is strictly positive. There exists then an open set
![]() $U\;\subset \;V^{\unicode[STIX]{x1D6FF}}$
which contains
$U\;\subset \;V^{\unicode[STIX]{x1D6FF}}$
which contains
![]() $\unicode[STIX]{x1D711}_{j}(V_{j})$
such that
$\unicode[STIX]{x1D711}_{j}(V_{j})$
such that
 $U\;\cap \;(C-\unicode[STIX]{x1D711}_{j}(V_{j}))=\emptyset$
. It follows that there exists an extension of
$U\;\cap \;(C-\unicode[STIX]{x1D711}_{j}(V_{j}))=\emptyset$
. It follows that there exists an extension of
![]() $\unicode[STIX]{x1D711}_{j}$
to a diffeomorphism
$\unicode[STIX]{x1D711}_{j}$
to a diffeomorphism
![]() $\unicode[STIX]{x1D6F7}_{j}$
of
$\unicode[STIX]{x1D6F7}_{j}$
of
![]() $(H_{j},C)$
which is identity outside
$(H_{j},C)$
which is identity outside
![]() $U$
, and hence on
$U$
, and hence on
 $(V_{\unicode[STIX]{x1D6FF}}\;\cap \;H_{j})\;\cup \;(C-\unicode[STIX]{x1D711}(V_{j}))$
.
$(V_{\unicode[STIX]{x1D6FF}}\;\cap \;H_{j})\;\cup \;(C-\unicode[STIX]{x1D711}(V_{j}))$
.
It only remains to check that
![]() $\unicode[STIX]{x1D6F7}_{j}^{-1}(C)$
is also contained in
$\unicode[STIX]{x1D6F7}_{j}^{-1}(C)$
is also contained in
![]() $C$
, as needed for
$C$
, as needed for
 $\unicode[STIX]{x1D6F7}_{j}\in \text{Diff}^{1}(\mathbb{R}^{n-1},C)$
. This follows as shown below.
$\unicode[STIX]{x1D6F7}_{j}\in \text{Diff}^{1}(\mathbb{R}^{n-1},C)$
. This follows as shown below.
Lemma 9. The map
![]() $\unicode[STIX]{x1D711}_{j}$
has the property
$\unicode[STIX]{x1D711}_{j}$
has the property
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{j}(C\;\cap \;V_{j})=C\;\cap \;\unicode[STIX]{x1D711}(V_{j}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{j}(C\;\cap \;V_{j})=C\;\cap \;\unicode[STIX]{x1D711}(V_{j}).\end{eqnarray}$$
Proof. Assume that there exists some point
![]() $p$
in
$p$
in
 $\unicode[STIX]{x1D711}(V_{j})\;\cap \;C$
which does not belong to
$\unicode[STIX]{x1D711}(V_{j})\;\cap \;C$
which does not belong to
![]() $V_{j}$
. Then the line issued from
$V_{j}$
. Then the line issued from
![]() $p$
which is orthogonal to
$p$
which is orthogonal to
![]() $V_{j}$
intersects
$V_{j}$
intersects
![]() $\unicode[STIX]{x1D711}(V_{j})$
only once, from Lemma 8. On the other hand there are points of
$\unicode[STIX]{x1D711}(V_{j})$
only once, from Lemma 8. On the other hand there are points of
![]() $C$
on this line, as
$C$
on this line, as
![]() $C$
is a product and
$C$
is a product and
![]() $p\not \in V_{j}$
. By Jordan’s theorem there exist points of
$p\not \in V_{j}$
. By Jordan’s theorem there exist points of
![]() $C$
which belong to different components of
$C$
which belong to different components of
 $R^{n}-\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
which contradicts the fact that
$R^{n}-\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
which contradicts the fact that
![]() $\unicode[STIX]{x1D711}$
is surjective on
$\unicode[STIX]{x1D711}$
is surjective on
![]() $C$
.
$C$
.
Thus
 $\unicode[STIX]{x1D711}(C\;\cap \;V_{j})\;\subset \;C\;\cap \;V_{j}$
. The same argument for
$\unicode[STIX]{x1D711}(C\;\cap \;V_{j})\;\subset \;C\;\cap \;V_{j}$
. The same argument for
![]() $\unicode[STIX]{x1D711}^{-1}$
yields the opposite inclusion and hence
$\unicode[STIX]{x1D711}^{-1}$
yields the opposite inclusion and hence
 $\unicode[STIX]{x1D711}(C\;\cap \;V_{j})=C\;\cap \;V_{j}$
. Our claim follows.◻
$\unicode[STIX]{x1D711}(C\;\cap \;V_{j})=C\;\cap \;V_{j}$
. Our claim follows.◻
Lemma 9 tells us that
![]() $\unicode[STIX]{x1D711}_{j}$
defines a germ in
$\unicode[STIX]{x1D711}_{j}$
defines a germ in
 $\mathfrak{diff}_{H_{j},a}^{1}(C\;\cap \;H_{j})$
, namely both
$\mathfrak{diff}_{H_{j},a}^{1}(C\;\cap \;H_{j})$
, namely both
![]() $\unicode[STIX]{x1D711}_{j}$
and
$\unicode[STIX]{x1D711}_{j}$
and
![]() $\unicode[STIX]{x1D711}_{j}^{-1}$
sends
$\unicode[STIX]{x1D711}_{j}^{-1}$
sends
![]() $C\;\cap \;H_{j}$
into itself. By the induction hypothesis
$C\;\cap \;H_{j}$
into itself. By the induction hypothesis
 $\unicode[STIX]{x1D711}_{j}|_{C\;\cap \;H_{j}}$
must be identity in a neighborhood of
$\unicode[STIX]{x1D711}_{j}|_{C\;\cap \;H_{j}}$
must be identity in a neighborhood of
![]() $a$
within
$a$
within
![]() $H_{j}$
.
$H_{j}$
.
Notice that this implies already that
 $D_{a}\unicode[STIX]{x1D711}=\mathbf{1}$
, and hence establishing the first claim of Proposition 1.
$D_{a}\unicode[STIX]{x1D711}=\mathbf{1}$
, and hence establishing the first claim of Proposition 1.
For the second claim we consider the distance
 $d(C-V,V)=\unicode[STIX]{x1D707}>0$
, as
$d(C-V,V)=\unicode[STIX]{x1D707}>0$
, as
![]() $V$
is surrounded by gaps. We suppose further that
$V$
is surrounded by gaps. We suppose further that
 $$\begin{eqnarray}\Vert D_{x}\unicode[STIX]{x1D711}-\mathbf{1}\Vert <\min \biggl(\frac{\unicode[STIX]{x1D70E}}{2},\frac{\unicode[STIX]{x1D707}}{1+\unicode[STIX]{x1D70E}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\Vert D_{x}\unicode[STIX]{x1D711}-\mathbf{1}\Vert <\min \biggl(\frac{\unicode[STIX]{x1D70E}}{2},\frac{\unicode[STIX]{x1D707}}{1+\unicode[STIX]{x1D70E}}\biggr).\end{eqnarray}$$
We know that
 $\unicode[STIX]{x1D711}(y,0)=(y,u(y))$
, for
$\unicode[STIX]{x1D711}(y,0)=(y,u(y))$
, for
 $y\in C\;\cap \;V\;\cap \;H_{n}$
and some function
$y\in C\;\cap \;V\;\cap \;H_{n}$
and some function
![]() $u\geqslant 0$
. The next step is to show that
$u\geqslant 0$
. The next step is to show that
 $u|_{C\;\cap \;V\;\cap \;H_{n}}=0$
.
$u|_{C\;\cap \;V\;\cap \;H_{n}}=0$
.
Assume that there exists some
 $x\in C\;\cap \;V\;\cap \;H_{n}$
so that
$x\in C\;\cap \;V\;\cap \;H_{n}$
so that
 $u(x)>0$
. Observe that
$u(x)>0$
. Observe that
 $u(x)\in C_{n}$
, since
$u(x)\in C_{n}$
, since
 $\unicode[STIX]{x1D711}(C)\;\subset \;C$
. Since points of
$\unicode[STIX]{x1D711}(C)\;\subset \;C$
. Since points of
![]() $C_{n}$
which are not endpoints are dense in
$C_{n}$
which are not endpoints are dense in
![]() $C_{n}$
there should exist
$C_{n}$
there should exist
![]() $x\in C$
for which
$x\in C$
for which
![]() $u(x)$
is not an endpoint of
$u(x)$
is not an endpoint of
![]() $C_{n}$
. Set
$C_{n}$
. Set
 $z=(x,u(x))\in C$
.
$z=(x,u(x))\in C$
.
Then for each
![]() $\unicode[STIX]{x1D708}>0$
there exist points
$\unicode[STIX]{x1D708}>0$
there exist points
 $z_{+},z_{-}\in C$
with
$z_{+},z_{-}\in C$
with
 $\unicode[STIX]{x1D70B}_{n}(z_{+})=\unicode[STIX]{x1D70B}_{n}(z_{-})=x$
, so that the distances
$\unicode[STIX]{x1D70B}_{n}(z_{+})=\unicode[STIX]{x1D70B}_{n}(z_{-})=x$
, so that the distances
 $d(z_{+},z),d(z_{-},z)<\unicode[STIX]{x1D708}$
.
$d(z_{+},z),d(z_{-},z)<\unicode[STIX]{x1D708}$
.
Observe that the segment
![]() $z_{+}z_{-}$
intersects just once
$z_{+}z_{-}$
intersects just once
![]() $\unicode[STIX]{x1D711}(H_{n}^{+})$
, namely at
$\unicode[STIX]{x1D711}(H_{n}^{+})$
, namely at
![]() $z$
. One might expect to use Jordan’s theorem in order to derive that
$z$
. One might expect to use Jordan’s theorem in order to derive that
![]() $z_{+}\in C$
and
$z_{+}\in C$
and
![]() $z_{-}\in C$
could not belong to the same connected component of
$z_{-}\in C$
could not belong to the same connected component of
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
. This is not exactly true, as the segment
$\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
. This is not exactly true, as the segment
![]() $z_{+}z_{-}$
could possibly intersect other sheets like
$z_{+}z_{-}$
could possibly intersect other sheets like
![]() $\unicode[STIX]{x1D711}(H_{j}^{+})$
which are part of
$\unicode[STIX]{x1D711}(H_{j}^{+})$
which are part of
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
.
$\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
.
Set
![]() $r$
for the distance between
$r$
for the distance between
 $x\in H_{n}^{+}$
and the union of the other
$x\in H_{n}^{+}$
and the union of the other
![]() $2n-1$
faces of
$2n-1$
faces of
![]() $\unicode[STIX]{x2202}V$
. By the induction hypothesis we can assume that
$\unicode[STIX]{x2202}V$
. By the induction hypothesis we can assume that
![]() $r>0$
. Choose now
$r>0$
. Choose now
![]() $\unicode[STIX]{x1D708}$
so that
$\unicode[STIX]{x1D708}$
so that
 $\unicode[STIX]{x1D708}<\min ((1-\unicode[STIX]{x1D70E})r/2,\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D70E})/2)$
.
$\unicode[STIX]{x1D708}<\min ((1-\unicode[STIX]{x1D70E})r/2,\unicode[STIX]{x1D707}(1-\unicode[STIX]{x1D70E})/2)$
.
Suppose that there exist
 $x_{+},x_{-}\in C\;\cap \;V$
such that
$x_{+},x_{-}\in C\;\cap \;V$
such that
 $\unicode[STIX]{x1D711}(x_{+})=z_{+}$
and
$\unicode[STIX]{x1D711}(x_{+})=z_{+}$
and
 $\unicode[STIX]{x1D711}(x_{-})=z_{-}$
. By Jordan’s theorem the segment
$\unicode[STIX]{x1D711}(x_{-})=z_{-}$
. By Jordan’s theorem the segment
![]() $z_{+}z_{-}$
intersects at least once
$z_{+}z_{-}$
intersects at least once
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V-H_{n}^{+})$
, say in a point
$\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V-H_{n}^{+})$
, say in a point
 $\tilde{z}=\unicode[STIX]{x1D711}(\tilde{x})$
.
$\tilde{z}=\unicode[STIX]{x1D711}(\tilde{x})$
.
We have then
 $d(x,\tilde{x})\geqslant r$
, while
$d(x,\tilde{x})\geqslant r$
, while
 $$\begin{eqnarray}d(\unicode[STIX]{x1D711}(x),\unicode[STIX]{x1D711}(\tilde{x}))\leqslant d(z_{+},z_{-})\leqslant 2\unicode[STIX]{x1D708}.\end{eqnarray}$$
$$\begin{eqnarray}d(\unicode[STIX]{x1D711}(x),\unicode[STIX]{x1D711}(\tilde{x}))\leqslant d(z_{+},z_{-})\leqslant 2\unicode[STIX]{x1D708}.\end{eqnarray}$$
On the other hand the
![]() ${\mathcal{C}}^{1}$
-diffeomorphism
${\mathcal{C}}^{1}$
-diffeomorphism
![]() $\unicode[STIX]{x1D711}^{-1}$
is Lipschitz with Lipschitz constant bounded by
$\unicode[STIX]{x1D711}^{-1}$
is Lipschitz with Lipschitz constant bounded by
 $\sup _{x\in V}\Vert D_{x}\unicode[STIX]{x1D711}^{-1}\Vert$
. Now, by standard functional calculus we have:
$\sup _{x\in V}\Vert D_{x}\unicode[STIX]{x1D711}^{-1}\Vert$
. Now, by standard functional calculus we have:
 $$\begin{eqnarray}\Vert D_{x}\unicode[STIX]{x1D711}^{-1}\Vert \leqslant \mathop{\sum }_{k=0}^{\infty }\Vert \mathbf{1}-D_{x}\unicode[STIX]{x1D711}\Vert ^{k}<\frac{1}{1-\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert D_{x}\unicode[STIX]{x1D711}^{-1}\Vert \leqslant \mathop{\sum }_{k=0}^{\infty }\Vert \mathbf{1}-D_{x}\unicode[STIX]{x1D711}\Vert ^{k}<\frac{1}{1-\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
Therefore the Lipschitz constant of
![]() $\unicode[STIX]{x1D711}^{-1}$
is bounded above by
$\unicode[STIX]{x1D711}^{-1}$
is bounded above by
 $1/(1-\unicode[STIX]{x1D70E})$
so that
$1/(1-\unicode[STIX]{x1D70E})$
so that
 $$\begin{eqnarray}d(x,\tilde{x})\leqslant \frac{1}{1-\unicode[STIX]{x1D70E}}d(\unicode[STIX]{x1D711}(x),\unicode[STIX]{x1D711}(\tilde{x}))\leqslant \frac{2\unicode[STIX]{x1D708}}{1-\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
$$\begin{eqnarray}d(x,\tilde{x})\leqslant \frac{1}{1-\unicode[STIX]{x1D70E}}d(\unicode[STIX]{x1D711}(x),\unicode[STIX]{x1D711}(\tilde{x}))\leqslant \frac{2\unicode[STIX]{x1D708}}{1-\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
This contradicts our choice of
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
Furthermore if one of
![]() $x_{+},x_{-}$
, say
$x_{+},x_{-}$
, say
![]() $x_{+}$
belongs to
$x_{+}$
belongs to
![]() $C-V$
then we have
$C-V$
then we have
 $d(x,x_{+})\geqslant \unicode[STIX]{x1D707}$
while
$d(x,x_{+})\geqslant \unicode[STIX]{x1D707}$
while
 $$\begin{eqnarray}d(\unicode[STIX]{x1D711}(x),\unicode[STIX]{x1D711}(x_{+}))\leqslant \unicode[STIX]{x1D708}\end{eqnarray}$$
$$\begin{eqnarray}d(\unicode[STIX]{x1D711}(x),\unicode[STIX]{x1D711}(x_{+}))\leqslant \unicode[STIX]{x1D708}\end{eqnarray}$$
and the argument above still leads to a contradiction.
This shows that
![]() $\unicode[STIX]{x1D711}$
cannot be surjective on
$\unicode[STIX]{x1D711}$
cannot be surjective on
![]() $C$
. On the other hand a diffeomorphism of
$C$
. On the other hand a diffeomorphism of
![]() $\mathbb{R}^{n}$
which preserves
$\mathbb{R}^{n}$
which preserves
![]() $C$
restricts to a bijection on
$C$
restricts to a bijection on
![]() $C$
. If it were not surjective then its inverse would send points of
$C$
. If it were not surjective then its inverse would send points of
![]() $C$
outside.
$C$
outside.
In particular
 $u(x)|_{C\;\cap \;H_{n}^{+}}=0$
and so
$u(x)|_{C\;\cap \;H_{n}^{+}}=0$
and so
 $\unicode[STIX]{x1D711}|_{C\;\cap \;H_{n}^{+}}$
is identity. The same proof shows that
$\unicode[STIX]{x1D711}|_{C\;\cap \;H_{n}^{+}}$
is identity. The same proof shows that
 $\unicode[STIX]{x1D711}|_{C\;\cap \;H_{j}^{+}}$
is identity, for all
$\unicode[STIX]{x1D711}|_{C\;\cap \;H_{j}^{+}}$
is identity, for all
![]() $j$
.
$j$
.
By using the same argument when
![]() $a$
runs over the points of
$a$
runs over the points of
 $V\;\cap \;C\;\cap \;\bigcup _{j=1}^{n}H_{j}^{+}$
we derive that
$V\;\cap \;C\;\cap \;\bigcup _{j=1}^{n}H_{j}^{+}$
we derive that
![]() $\unicode[STIX]{x1D711}|_{C\;\cap \;V}$
is identity, as claimed.◻
$\unicode[STIX]{x1D711}|_{C\;\cap \;V}$
is identity, as claimed.◻
End of the proof of theorem 4
. The proof is by induction on
![]() $n$
. For
$n$
. For
![]() $n=1$
this was already proved above. Let
$n=1$
this was already proved above. Let
![]() $V$
denote now the smallest parallelepiped containing
$V$
denote now the smallest parallelepiped containing
![]() $C$
, in order to match previous notations and constructions. Suppose that
$C$
, in order to match previous notations and constructions. Suppose that
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{n},C)$
is such that
$\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{n},C)$
is such that
 $\Vert D_{x}\unicode[STIX]{x1D711}-\mathbf{1}\Vert <\unicode[STIX]{x1D700}$
, for all
$\Vert D_{x}\unicode[STIX]{x1D711}-\mathbf{1}\Vert <\unicode[STIX]{x1D700}$
, for all
![]() $x\in V^{\unicode[STIX]{x1D6FF}}$
. Then
$x\in V^{\unicode[STIX]{x1D6FF}}$
. Then
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
surrounds
$\unicode[STIX]{x1D711}(\unicode[STIX]{x2202}V)$
surrounds
![]() $C$
and the proof of Lemma 9 gives us
$C$
and the proof of Lemma 9 gives us
 $\unicode[STIX]{x1D711}(C\;\cap \;\unicode[STIX]{x2202}V)=C\;\cap \;\unicode[STIX]{x2202}V$
. Moreover, each
$\unicode[STIX]{x1D711}(C\;\cap \;\unicode[STIX]{x2202}V)=C\;\cap \;\unicode[STIX]{x2202}V$
. Moreover, each
![]() $\unicode[STIX]{x1D711}_{j}$
preserves the associated face
$\unicode[STIX]{x1D711}_{j}$
preserves the associated face
![]() $V_{j}$
. By the induction hypothesis
$V_{j}$
. By the induction hypothesis
![]() $\unicode[STIX]{x1D711}_{j}$
is the identity. It follows that
$\unicode[STIX]{x1D711}_{j}$
is the identity. It follows that
 $\unicode[STIX]{x1D711}|_{C\;\cap \;\unicode[STIX]{x2202}V}$
is the identity. We can therefore use Proposition 1 to derive that around every corner point of
$\unicode[STIX]{x1D711}|_{C\;\cap \;\unicode[STIX]{x2202}V}$
is the identity. We can therefore use Proposition 1 to derive that around every corner point of
 $C\;\cap \;\unicode[STIX]{x2202}V$
the map
$C\;\cap \;\unicode[STIX]{x2202}V$
the map
![]() $\unicode[STIX]{x1D711}|_{C}$
is identity. The same argument works for all corner points of
$\unicode[STIX]{x1D711}|_{C}$
is identity. The same argument works for all corner points of
![]() $V$
.
$V$
.
Remark 9. If
 $C=C_{\unicode[STIX]{x1D706}}^{n}$
, then
$C=C_{\unicode[STIX]{x1D706}}^{n}$
, then
 $\mathfrak{diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
is isomorphic to
$\mathfrak{diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
is isomorphic to
![]() $\mathbb{Z}^{r(a)}$
, where
$\mathbb{Z}^{r(a)}$
, where
![]() $r(a)$
is the number of coordinates of
$r(a)$
is the number of coordinates of
![]() $a$
which are
$a$
which are
![]() $\unicode[STIX]{x1D706}$
-rational (compare with [Reference Bleak and LanoueBL10]).
$\unicode[STIX]{x1D706}$
-rational (compare with [Reference Bleak and LanoueBL10]).
4 Diffeomorphism groups of specific Cantor sets
4.1 Proof of Theorem 5
Observe first that
![]() $C_{\unicode[STIX]{x1D6F7}}$
is a Cantor set. Indeed the contractivity assumption implies that an infinite intersection
$C_{\unicode[STIX]{x1D6F7}}$
is a Cantor set. Indeed the contractivity assumption implies that an infinite intersection
 $\lim _{p\rightarrow \infty }\unicode[STIX]{x1D719}_{i_{1}}\unicode[STIX]{x1D719}_{i_{2}}\cdots \unicode[STIX]{x1D719}_{i_{p}}(M)$
cannot contain but a single point. Two such points which are distinct are separated by some smoothly embedded sphere, which is the image of
$\lim _{p\rightarrow \infty }\unicode[STIX]{x1D719}_{i_{1}}\unicode[STIX]{x1D719}_{i_{2}}\cdots \unicode[STIX]{x1D719}_{i_{p}}(M)$
cannot contain but a single point. Two such points which are distinct are separated by some smoothly embedded sphere, which is the image of
![]() $\unicode[STIX]{x2202}M$
by an element of the semigroup generated by
$\unicode[STIX]{x2202}M$
by an element of the semigroup generated by
![]() $\unicode[STIX]{x1D6F7}$
, so that the set
$\unicode[STIX]{x1D6F7}$
, so that the set
![]() $C_{\unicode[STIX]{x1D6F7}}$
is totally disconnected. The perfectness follows the same way.
$C_{\unicode[STIX]{x1D6F7}}$
is totally disconnected. The perfectness follows the same way.
We will draw a rooted
![]() $(n+2)$
-valent tree
$(n+2)$
-valent tree
![]() ${\mathcal{T}}$
with edges directed downwards. When
${\mathcal{T}}$
with edges directed downwards. When
 $M=[0,1]$
there is an extra structure on
$M=[0,1]$
there is an extra structure on
![]() ${\mathcal{T}}$
, as all edges issued from a vertex are enumerated from left to right.
${\mathcal{T}}$
, as all edges issued from a vertex are enumerated from left to right.
There is a one-to-one correspondence between the points of the boundary at infinity of the tree and the points of the Cantor set
 $C=C_{\unicode[STIX]{x1D6F7}}$
associated to the invertible IFS
$C=C_{\unicode[STIX]{x1D6F7}}$
associated to the invertible IFS
![]() $(\unicode[STIX]{x1D6F7},M)$
. To each point
$(\unicode[STIX]{x1D6F7},M)$
. To each point
![]() $\unicode[STIX]{x1D709}\in C$
we can assign an infinite sequence
$\unicode[STIX]{x1D709}\in C$
we can assign an infinite sequence
 $I=i_{1}i_{2}\cdots i_{p}\cdots \,,$
so that
$I=i_{1}i_{2}\cdots i_{p}\cdots \,,$
so that
 $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}(I)$
where we denoted:
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}(I)$
where we denoted:
 $$\begin{eqnarray}\unicode[STIX]{x1D709}(I)=\mathop{\bigcap }_{p=1}^{\infty }\unicode[STIX]{x1D719}_{i_{1}}\unicode[STIX]{x1D719}_{i_{2}}\cdots \unicode[STIX]{x1D719}_{i_{p}}(M).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}(I)=\mathop{\bigcap }_{p=1}^{\infty }\unicode[STIX]{x1D719}_{i_{1}}\unicode[STIX]{x1D719}_{i_{2}}\cdots \unicode[STIX]{x1D719}_{i_{p}}(M).\end{eqnarray}$$
The vertices of the tree are endowed with a compatible labeling by means of finite multi-indices
![]() $I$
, where the root has associated the empty index and the vertex
$I$
, where the root has associated the empty index and the vertex
![]() $v_{I}$
is the one reached after traveling along the edges labeled
$v_{I}$
is the one reached after traveling along the edges labeled
 $i_{1},i_{2},\ldots ,i_{p}$
. We also put
$i_{1},i_{2},\ldots ,i_{p}$
. We also put
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{I}(x)=\unicode[STIX]{x1D719}_{i_{1}}\unicode[STIX]{x1D719}_{i_{2}}\cdots \unicode[STIX]{x1D719}_{i_{p}}(x)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{I}(x)=\unicode[STIX]{x1D719}_{i_{1}}\unicode[STIX]{x1D719}_{i_{2}}\cdots \unicode[STIX]{x1D719}_{i_{p}}(x)\end{eqnarray}$$
for finite
![]() $I$
. This extends obviously to the case of infinite multi-indices
$I$
. This extends obviously to the case of infinite multi-indices
![]() $I$
.
$I$
.
We further need to introduce a special class of germs, as follows.
Definition 9. The standard germ associated with the finite multi-indices
![]() $I$
and
$I$
and
![]() $J$
is the diffeomorphism
$J$
is the diffeomorphism
 $\unicode[STIX]{x1D719}_{I/J}:\unicode[STIX]{x1D719}_{I}(M)\rightarrow \unicode[STIX]{x1D719}_{J}(M)$
given by
$\unicode[STIX]{x1D719}_{I/J}:\unicode[STIX]{x1D719}_{I}(M)\rightarrow \unicode[STIX]{x1D719}_{J}(M)$
given by
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{I/J}(\unicode[STIX]{x1D719}_{I}(x))=\unicode[STIX]{x1D719}_{J}(x).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{I/J}(\unicode[STIX]{x1D719}_{I}(x))=\unicode[STIX]{x1D719}_{J}(x).\end{eqnarray}$$
Standard germs preserve the Cantor set
![]() $C$
as germs, namely
$C$
as germs, namely
 $\unicode[STIX]{x1D719}_{I/J}(C\;\cap \;\unicode[STIX]{x1D719}_{I}(M))\;\subset \;C\;\cap \;\unicode[STIX]{x1D719}_{J}(M)$
. In fact if
$\unicode[STIX]{x1D719}_{I/J}(C\;\cap \;\unicode[STIX]{x1D719}_{I}(M))\;\subset \;C\;\cap \;\unicode[STIX]{x1D719}_{J}(M)$
. In fact if
![]() $S$
is an infinite multi-index then
$S$
is an infinite multi-index then
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{I/J}(\unicode[STIX]{x1D709}(IS))=\unicode[STIX]{x1D709}(JS).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{I/J}(\unicode[STIX]{x1D709}(IS))=\unicode[STIX]{x1D709}(JS).\end{eqnarray}$$
Graphically we can realize this map as a partial isomorphism of the tree
![]() ${\mathcal{T}}$
which maps the subtree hanging at
${\mathcal{T}}$
which maps the subtree hanging at
![]() $v_{I}$
onto the subtree hanging at
$v_{I}$
onto the subtree hanging at
![]() $v_{J}$
.
$v_{J}$
.
Consider a pair
![]() $(t_{1},t_{2})$
of finite labeled subtrees of the same degree of
$(t_{1},t_{2})$
of finite labeled subtrees of the same degree of
![]() ${\mathcal{T}}$
both containing the root, and whose leaves are enumerated
${\mathcal{T}}$
both containing the root, and whose leaves are enumerated
 $v_{I_{1}},v_{I_{2}},\ldots ,v_{I_{p}}$
and
$v_{I_{1}},v_{I_{2}},\ldots ,v_{I_{p}}$
and
 $v_{J_{1}},v_{J_{2}},\ldots ,v_{J_{p}}$
.
$v_{J_{1}},v_{J_{2}},\ldots ,v_{J_{p}}$
.
Lemma 10. Assume that
![]() $\unicode[STIX]{x1D719}_{j}$
are orientation preserving diffeomorphisms of
$\unicode[STIX]{x1D719}_{j}$
are orientation preserving diffeomorphisms of
![]() $M$
. Then the map
$M$
. Then the map
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D719}_{I_{k}/J_{k}}(x)\quad \text{if }x\in \unicode[STIX]{x1D719}_{I_{k}}(C)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(x)=\unicode[STIX]{x1D719}_{I_{k}/J_{k}}(x)\quad \text{if }x\in \unicode[STIX]{x1D719}_{I_{k}}(C)\end{eqnarray}$$
defines an element
 $\unicode[STIX]{x1D719}_{(t_{1},t_{2})}\in \mathfrak{diff}^{1,+}(C)$
.
$\unicode[STIX]{x1D719}_{(t_{1},t_{2})}\in \mathfrak{diff}^{1,+}(C)$
.
Proof. We know that
 $C=\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{i}(C)$
, since
$C=\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{i}(C)$
, since
![]() $C$
is the attractor of
$C$
is the attractor of
![]() $\unicode[STIX]{x1D6F7}$
. By recurrence on the number of leaves we show that
$\unicode[STIX]{x1D6F7}$
. By recurrence on the number of leaves we show that
 $$\begin{eqnarray}C=\mathop{\bigcup }_{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(C)\end{eqnarray}$$
$$\begin{eqnarray}C=\mathop{\bigcup }_{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(C)\end{eqnarray}$$
for any finite subtree
![]() $t$
of
$t$
of
![]() ${\mathcal{T}}$
containing the root and having leaves
${\mathcal{T}}$
containing the root and having leaves
![]() $v_{I_{i}}$
,
$v_{I_{i}}$
,
![]() $i=0,n$
. Now
$i=0,n$
. Now
![]() $\unicode[STIX]{x1D719}$
is a smooth orientation preserving map defined on
$\unicode[STIX]{x1D719}$
is a smooth orientation preserving map defined on
 $\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(M)$
, and so its domain of definition contains
$\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(M)$
, and so its domain of definition contains
![]() $C$
.
$C$
.
When the dimension
![]() $d=1$
, the complementary
$d=1$
, the complementary
 $M\setminus \bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(M)$
is the union of finitely many intervals, which we call gaps and there exists by orientability assumption an extension of
$M\setminus \bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(M)$
is the union of finitely many intervals, which we call gaps and there exists by orientability assumption an extension of
![]() $\unicode[STIX]{x1D719}$
to a diffeomorphism of
$\unicode[STIX]{x1D719}$
to a diffeomorphism of
 $M=[0,1]$
sending gaps into gaps.
$M=[0,1]$
sending gaps into gaps.
When the dimension
![]() $d>1$
, the complementary gap
$d>1$
, the complementary gap
 $M\setminus \bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(M)$
is now connected and diffeomorphic to the standard disk with
$M\setminus \bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(M)$
is now connected and diffeomorphic to the standard disk with
![]() $(n+1)$
holes. Moreover, the restriction of
$(n+1)$
holes. Moreover, the restriction of
![]() $\unicode[STIX]{x1D719}$
to every sphere
$\unicode[STIX]{x1D719}$
to every sphere
 $\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{I_{i}}(M)$
is isotopic to identity since it is orientation preserving and it admits an extension to the ball. Taking a suitable smoothing at the singular vertex of the conical extension of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{I_{i}}(M)$
is isotopic to identity since it is orientation preserving and it admits an extension to the ball. Taking a suitable smoothing at the singular vertex of the conical extension of
 $\unicode[STIX]{x1D719}|_{\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(\unicode[STIX]{x2202}M)}$
we obtain an extension of
$\unicode[STIX]{x1D719}|_{\bigcup _{i=0}^{n}\unicode[STIX]{x1D719}_{I_{i}}(\unicode[STIX]{x2202}M)}$
we obtain an extension of
![]() $\unicode[STIX]{x1D719}$
to a diffeomorphism of the ball
$\unicode[STIX]{x1D719}$
to a diffeomorphism of the ball
![]() $M$
, possibly non-trivial on
$M$
, possibly non-trivial on
![]() $\unicode[STIX]{x2202}M$
.
$\unicode[STIX]{x2202}M$
.
This extension preserves
![]() $C$
invariant as gaps are disjoint from
$C$
invariant as gaps are disjoint from
![]() $C$
and therefore defines an element
$C$
and therefore defines an element
 $\unicode[STIX]{x1D719}_{(t_{1},t_{2})}\in \mathfrak{diff}^{1,+}(C)$
.◻
$\unicode[STIX]{x1D719}_{(t_{1},t_{2})}\in \mathfrak{diff}^{1,+}(C)$
.◻
End of the proof of Theorem 5
. Let us stabilize the pair of trees
![]() $(t_{1},t_{2})$
to a pair
$(t_{1},t_{2})$
to a pair
![]() $(t_{1}^{\prime },t_{2}^{\prime })$
, where
$(t_{1}^{\prime },t_{2}^{\prime })$
, where
![]() $t_{j}^{\prime }$
is obtained from
$t_{j}^{\prime }$
is obtained from
![]() $t_{j}$
by adding the first descendants at vertex
$t_{j}$
by adding the first descendants at vertex
![]() $v_{I_{s}}$
, for
$v_{I_{s}}$
, for
![]() $j=1$
and
$j=1$
and
![]() $v_{J_{s}}$
, when
$v_{J_{s}}$
, when
![]() $j=2$
. The new vertices come with a compatible labeling. Moreover, an orientation preserving diffeomorphism of
$j=2$
. The new vertices come with a compatible labeling. Moreover, an orientation preserving diffeomorphism of
![]() $C$
induces a monotone map of the boundary of the tree, when
$C$
induces a monotone map of the boundary of the tree, when
![]() $d=1$
.
$d=1$
.
By direct inspection using the explicit form of
![]() $\unicode[STIX]{x1D719}$
we find that:
$\unicode[STIX]{x1D719}$
we find that:
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{(t_{1},t_{2})}=\unicode[STIX]{x1D719}_{(t_{1}^{\prime },t_{2}^{\prime })}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{(t_{1},t_{2})}=\unicode[STIX]{x1D719}_{(t_{1}^{\prime },t_{2}^{\prime })}.\end{eqnarray}$$
Thus the map which associates to the pair
![]() $(t_{1},t_{2})$
of labeled trees the element
$(t_{1},t_{2})$
of labeled trees the element
![]() $\unicode[STIX]{x1D719}_{(t_{1},t_{2})}$
factors through a map
$\unicode[STIX]{x1D719}_{(t_{1},t_{2})}$
factors through a map
 $F_{n+1}\rightarrow \mathfrak{diff}^{1,+}(C)$
, for
$F_{n+1}\rightarrow \mathfrak{diff}^{1,+}(C)$
, for
![]() $d=1$
, and
$d=1$
, and
 $V_{n+1}\rightarrow \mathfrak{diff}^{1,+}(C)$
, for
$V_{n+1}\rightarrow \mathfrak{diff}^{1,+}(C)$
, for
![]() $d=2$
, respectively. This is easily seen to be a homomorphism. When
$d=2$
, respectively. This is easily seen to be a homomorphism. When
![]() $I\neq J$
the map
$I\neq J$
the map
![]() $\unicode[STIX]{x1D711}_{I/J}|_{C}$
is not identity since
$\unicode[STIX]{x1D711}_{I/J}|_{C}$
is not identity since
 $\unicode[STIX]{x1D711}_{I}(M)\;\cap \;\unicode[STIX]{x1D711}_{J}(M)=\emptyset$
. This proves that the homomorphism defined above is injective, thereby ending the proof of Theorem 5.
$\unicode[STIX]{x1D711}_{I}(M)\;\cap \;\unicode[STIX]{x1D711}_{J}(M)=\emptyset$
. This proves that the homomorphism defined above is injective, thereby ending the proof of Theorem 5.
Remark 10. There is a more general setting in which we allow basins to have boundary fixed points. We say that the compact submanifold
![]() $M$
is an attractive basin for
$M$
is an attractive basin for
 $\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
if, for all
$\unicode[STIX]{x1D6F7}=(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1},\ldots ,\unicode[STIX]{x1D719}_{n})$
if, for all
 $j\in \{0,1,\ldots ,n\}$
we have
$j\in \{0,1,\ldots ,n\}$
we have
(i)
 $\unicode[STIX]{x1D719}_{j}(\text{int}(M))\;\subset \;\text{int}(M)$
;
$\unicode[STIX]{x1D719}_{j}(\text{int}(M))\;\subset \;\text{int}(M)$
;(ii)
 $\text{int}(\unicode[STIX]{x1D719}_{j}^{-1}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M))\supset \text{int}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M)$
;
$\text{int}(\unicode[STIX]{x1D719}_{j}^{-1}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M))\supset \text{int}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M)$
;(iii)
 $\unicode[STIX]{x1D719}_{i}(M)\;\cap \;\unicode[STIX]{x1D719}_{j}(M)=\emptyset$
, for any
$\unicode[STIX]{x1D719}_{i}(M)\;\cap \;\unicode[STIX]{x1D719}_{j}(M)=\emptyset$
, for any
 $i\neq j\in \{0,1,\ldots ,n\}$
;
$i\neq j\in \{0,1,\ldots ,n\}$
;(iv)
 $\text{int}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M)\;\subset \;\text{int}(\unicode[STIX]{x1D719}_{j}^{-1}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M))$
.
$\text{int}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M)\;\subset \;\text{int}(\unicode[STIX]{x1D719}_{j}^{-1}(\unicode[STIX]{x1D719}_{j}(\unicode[STIX]{x2202}M)\;\cap \;\unicode[STIX]{x2202}M))$
.
Using similar arguments one can show that
 $\mathfrak{diff}^{1}(C_{\unicode[STIX]{x1D6F7}})$
contains
$\mathfrak{diff}^{1}(C_{\unicode[STIX]{x1D6F7}})$
contains
![]() $F_{n+1}$
whenever
$F_{n+1}$
whenever
![]() $\unicode[STIX]{x1D6F7}$
has an attractive basin.
$\unicode[STIX]{x1D6F7}$
has an attractive basin.
Remark 11. If the Cantor set
![]() $C$
is invertible, namely there exists an orientation reversing diffeomorphism
$C$
is invertible, namely there exists an orientation reversing diffeomorphism
![]() $\unicode[STIX]{x1D719}$
of
$\unicode[STIX]{x1D719}$
of
![]() $M$
preserving
$M$
preserving
![]() $C$
, then we can replace the homeomorphisms
$C$
, then we can replace the homeomorphisms
![]() $\unicode[STIX]{x1D719}_{j}$
which reverse the orientation by
$\unicode[STIX]{x1D719}_{j}$
which reverse the orientation by
![]() $\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D719}_{j}$
. However, there exist non-invertible Cantor subsets, for instance the union of two copies
$\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D719}_{j}$
. However, there exist non-invertible Cantor subsets, for instance the union of two copies
 $C_{\unicode[STIX]{x1D706}}\;\cup \;(1+C_{\unicode[STIX]{x1D707}})$
, for
$C_{\unicode[STIX]{x1D706}}\;\cup \;(1+C_{\unicode[STIX]{x1D707}})$
, for
![]() $\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D707}$
.
4.2 Proof of Theorem 6 for
 $C=C_{\unicode[STIX]{x1D706}}$
$C=C_{\unicode[STIX]{x1D706}}$
Our strategy is to give first a detailed proof of Theorem 6 in the case when
 $C=C_{\unicode[STIX]{x1D706}}$
and then to explain the necessary changes needed to achieve the general case in the next section.
$C=C_{\unicode[STIX]{x1D706}}$
and then to explain the necessary changes needed to achieve the general case in the next section.
We first need the following lemma.
Lemma 11. If
![]() $a$
is a left (or right) point of
$a$
is a left (or right) point of
![]() $C_{\unicode[STIX]{x1D706}}$
, then
$C_{\unicode[STIX]{x1D706}}$
, then
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1})$
is the subgroup
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1})$
is the subgroup
 $\langle \unicode[STIX]{x1D706}\rangle \;\subset \;\mathbb{R}^{\ast }$
.
$\langle \unicode[STIX]{x1D706}\rangle \;\subset \;\mathbb{R}^{\ast }$
.
Proof. Recall from Remark 7 that
 $\text{Diff}_{a}^{1}(C_{\unicode[STIX]{x1D706}})=\text{Diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
. The set
$\text{Diff}_{a}^{1}(C_{\unicode[STIX]{x1D706}})=\text{Diff}_{a}^{1,+}(C_{\unicode[STIX]{x1D706}})$
. The set
![]() $L(C_{\unicode[STIX]{x1D706}})$
of left points of
$L(C_{\unicode[STIX]{x1D706}})$
of left points of
![]() $C_{\unicode[STIX]{x1D706}}$
is affinely locally homogeneous, namely for any two left points
$C_{\unicode[STIX]{x1D706}}$
is affinely locally homogeneous, namely for any two left points
![]() $a$
and
$a$
and
![]() $b$
there exists an affine germ sending a neighborhood of
$b$
there exists an affine germ sending a neighborhood of
![]() $a$
in
$a$
in
![]() $C_{\unicode[STIX]{x1D706}}$
into a neighborhood of
$C_{\unicode[STIX]{x1D706}}$
into a neighborhood of
![]() $b$
in
$b$
in
![]() $C_{\unicode[STIX]{x1D706}}$
. Therefore it suffices to analyze
$C_{\unicode[STIX]{x1D706}}$
. Therefore it suffices to analyze
 $\text{Diff}_{0}^{1,+}(C_{\unicode[STIX]{x1D706}})$
. Moreover,
$\text{Diff}_{0}^{1,+}(C_{\unicode[STIX]{x1D706}})$
. Moreover,
![]() $0$
is the minimal element of
$0$
is the minimal element of
![]() $C_{\unicode[STIX]{x1D706}}$
and therefore it should be fixed by any element of
$C_{\unicode[STIX]{x1D706}}$
and therefore it should be fixed by any element of
 $\text{Diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
.
$\text{Diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
.
Elements of
![]() $L(C_{\unicode[STIX]{x1D706}})$
can be described explicitly, as
$L(C_{\unicode[STIX]{x1D706}})$
can be described explicitly, as
 $$\begin{eqnarray}L(C_{\unicode[STIX]{x1D706}})=\mathop{\bigcup }_{n=1}^{\infty }\biggl\{x\in [0,1];x=\mathop{\sum }_{j=1}^{n}a_{j}\unicode[STIX]{x1D706}^{-j},\text{ where }a_{j}\in \{0,\unicode[STIX]{x1D706}-1\}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}L(C_{\unicode[STIX]{x1D706}})=\mathop{\bigcup }_{n=1}^{\infty }\biggl\{x\in [0,1];x=\mathop{\sum }_{j=1}^{n}a_{j}\unicode[STIX]{x1D706}^{-j},\text{ where }a_{j}\in \{0,\unicode[STIX]{x1D706}-1\}\biggr\}.\end{eqnarray}$$
Therefore there exists
![]() $\unicode[STIX]{x1D6FF}$
such that the multiplication by
$\unicode[STIX]{x1D6FF}$
such that the multiplication by
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
sends
$\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
sends
 $C_{\unicode[STIX]{x1D706}}\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(0)$
into
$C_{\unicode[STIX]{x1D706}}\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(0)$
into
![]() $C_{\unicode[STIX]{x1D706}}$
. This easily implies that
$C_{\unicode[STIX]{x1D706}}$
. This easily implies that
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+})$
contains the subgroup
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+})$
contains the subgroup
![]() $\langle \unicode[STIX]{x1D706}\rangle$
.
$\langle \unicode[STIX]{x1D706}\rangle$
.
For the reverse inclusion we need a sharpening of Lemma 6. Note first that the set of lengths of gaps in
![]() $C_{\unicode[STIX]{x1D706}}$
is
$C_{\unicode[STIX]{x1D706}}$
is
 $\{(\unicode[STIX]{x1D706}-2)\unicode[STIX]{x1D706}^{-n},n\in \mathbb{Z}_{+}\setminus \{0\}\}$
. In particular, the quotients of the lengths of any two gaps belong to
$\{(\unicode[STIX]{x1D706}-2)\unicode[STIX]{x1D706}^{-n},n\in \mathbb{Z}_{+}\setminus \{0\}\}$
. In particular, the quotients of the lengths of any two gaps belong to
![]() $\langle \unicode[STIX]{x1D706}\rangle$
.
$\langle \unicode[STIX]{x1D706}\rangle$
.
Let
![]() $\unicode[STIX]{x1D6FC}>1$
be a minimal element occurring in
$\unicode[STIX]{x1D6FC}>1$
be a minimal element occurring in
 $\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1,+}(C_{\unicode[STIX]{x1D706}}))\;\subset \;\mathbb{R}_{+}^{\ast }$
. By Lemma 7 there exists
$\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1,+}(C_{\unicode[STIX]{x1D706}}))\;\subset \;\mathbb{R}_{+}^{\ast }$
. By Lemma 7 there exists
![]() $k\in \mathbb{Z}_{+}$
such that
$k\in \mathbb{Z}_{+}$
such that
 $\unicode[STIX]{x1D706}^{-1}=\unicode[STIX]{x1D6FC}^{k}$
. Let
$\unicode[STIX]{x1D706}^{-1}=\unicode[STIX]{x1D6FC}^{k}$
. Let
 $\unicode[STIX]{x1D711}\in \text{Diff}_{0}^{1,+}$
be such that
$\unicode[STIX]{x1D711}\in \text{Diff}_{0}^{1,+}$
be such that
 $\unicode[STIX]{x1D711}^{\prime }(0)=\unicode[STIX]{x1D706}^{-1/k}$
.
$\unicode[STIX]{x1D711}^{\prime }(0)=\unicode[STIX]{x1D706}^{-1/k}$
.
For every gap
![]() $I$
, the image
$I$
, the image
 $J=\unicode[STIX]{x1D711}(I)$
is another gap and the ratio
$J=\unicode[STIX]{x1D711}(I)$
is another gap and the ratio
![]() $|J|/|I|$
is an element in
$|J|/|I|$
is an element in
![]() $\langle \unicode[STIX]{x1D706}\rangle$
, hence of the form
$\langle \unicode[STIX]{x1D706}\rangle$
, hence of the form
![]() $\unicode[STIX]{x1D706}^{i(I)}$
, for some integer
$\unicode[STIX]{x1D706}^{i(I)}$
, for some integer
![]() $i(I)$
. Further, there is a point
$i(I)$
. Further, there is a point
![]() $x_{I}\in I$
for which
$x_{I}\in I$
for which
 $\unicode[STIX]{x1D711}^{\prime }(x_{I})=\unicode[STIX]{x1D706}^{i(I)}$
. Letting
$\unicode[STIX]{x1D711}^{\prime }(x_{I})=\unicode[STIX]{x1D706}^{i(I)}$
. Letting
![]() $I_{n}$
be a sequence of gaps converging to the origin, we have that
$I_{n}$
be a sequence of gaps converging to the origin, we have that
![]() $\unicode[STIX]{x1D711}^{\prime }(x_{I_{n}})$
converges to
$\unicode[STIX]{x1D711}^{\prime }(x_{I_{n}})$
converges to
 $\unicode[STIX]{x1D711}^{\prime }(0)=\unicode[STIX]{x1D706}^{-1/k}$
. The sequence of integers
$\unicode[STIX]{x1D711}^{\prime }(0)=\unicode[STIX]{x1D706}^{-1/k}$
. The sequence of integers
![]() $i(I_{n})$
hence converges to
$i(I_{n})$
hence converges to
![]() $-1/k$
, which forces
$-1/k$
, which forces
![]() $k=1$
.◻
$k=1$
.◻
We next observe that for each left point
![]() $a$
of
$a$
of
![]() $C_{\unicode[STIX]{x1D706}}$
there exists a small neighborhood
$C_{\unicode[STIX]{x1D706}}$
there exists a small neighborhood
![]() $U_{a}$
of
$U_{a}$
of
![]() $a$
such that the affine map
$a$
such that the affine map
 $\unicode[STIX]{x1D713}_{a}=a+\unicode[STIX]{x1D706}(x-a)$
sends
$\unicode[STIX]{x1D713}_{a}=a+\unicode[STIX]{x1D706}(x-a)$
sends
 $U_{a}\;\cap \;C_{\unicode[STIX]{x1D706}}$
into
$U_{a}\;\cap \;C_{\unicode[STIX]{x1D706}}$
into
![]() $C_{\unicode[STIX]{x1D706}}$
, defining therefore a germ in
$C_{\unicode[STIX]{x1D706}}$
, defining therefore a germ in
![]() $\mathfrak{diff}_{a}^{1,+}$
. Then Lemmas 11 and 7 imply together that
$\mathfrak{diff}_{a}^{1,+}$
. Then Lemmas 11 and 7 imply together that
![]() $\mathfrak{diff}_{a}^{1,+}$
is generated by
$\mathfrak{diff}_{a}^{1,+}$
is generated by
 $\unicode[STIX]{x1D713}_{a}=a+\unicode[STIX]{x1D706}(x-a)$
.
$\unicode[STIX]{x1D713}_{a}=a+\unicode[STIX]{x1D706}(x-a)$
.
Let
![]() $a$
and
$a$
and
![]() $b$
be two left points of
$b$
be two left points of
![]() $C_{\unicode[STIX]{x1D706}}$
. Denote by
$C_{\unicode[STIX]{x1D706}}$
. Denote by
![]() $D(a,b)$
the set of germs at
$D(a,b)$
the set of germs at
![]() $a$
of classes of local diffeomorphisms
$a$
of classes of local diffeomorphisms
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
![]() $(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
such that
$(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
such that
 $\unicode[STIX]{x1D711}(a)=b$
. Then
$\unicode[STIX]{x1D711}(a)=b$
. Then
![]() $D(a,b)$
is acted upon transitively by
$D(a,b)$
is acted upon transitively by
![]() $\mathfrak{diff}_{a}^{1,+}$
. Using an argument similar to the one from above concerning stabilizers,
$\mathfrak{diff}_{a}^{1,+}$
. Using an argument similar to the one from above concerning stabilizers,
![]() $D(a,b)$
consists of germs of maps of the form
$D(a,b)$
consists of germs of maps of the form
 $\unicode[STIX]{x1D713}_{a,b,k}=b+\unicode[STIX]{x1D706}^{k}(x-a)$
, with
$\unicode[STIX]{x1D713}_{a,b,k}=b+\unicode[STIX]{x1D706}^{k}(x-a)$
, with
![]() $k\in \mathbb{Z}$
.
$k\in \mathbb{Z}$
.
Now let
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
such that
$\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
such that
 $\unicode[STIX]{x1D711}(a)=b$
. From above there exists
$\unicode[STIX]{x1D711}(a)=b$
. From above there exists
![]() $\unicode[STIX]{x1D6FF}>0$
such that
$\unicode[STIX]{x1D6FF}>0$
such that
 $\unicode[STIX]{x1D711}|_{C_{\unicode[STIX]{x1D706}}\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)}$
coincides with
$\unicode[STIX]{x1D711}|_{C_{\unicode[STIX]{x1D706}}\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)}$
coincides with
 $\unicode[STIX]{x1D713}_{a,b,k}|_{C_{\unicode[STIX]{x1D706}}\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)}$
and hence
$\unicode[STIX]{x1D713}_{a,b,k}|_{C_{\unicode[STIX]{x1D706}}\;\cap \;{\mathcal{N}}_{\unicode[STIX]{x1D6FF}}(a)}$
and hence
 $\unicode[STIX]{x1D711}^{\prime }(a)\in \langle \unicode[STIX]{x1D706}\rangle$
. Therefore, for any left point
$\unicode[STIX]{x1D711}^{\prime }(a)\in \langle \unicode[STIX]{x1D706}\rangle$
. Therefore, for any left point
![]() $a\in C_{\unicode[STIX]{x1D706}}$
we have
$a\in C_{\unicode[STIX]{x1D706}}$
we have
 $\unicode[STIX]{x1D711}^{\prime }(a)\in \langle \unicode[STIX]{x1D706}\rangle$
. Now, left points of
$\unicode[STIX]{x1D711}^{\prime }(a)\in \langle \unicode[STIX]{x1D706}\rangle$
. Now, left points of
![]() $C_{\unicode[STIX]{x1D706}}$
are dense in
$C_{\unicode[STIX]{x1D706}}$
are dense in
![]() $C_{\unicode[STIX]{x1D706}}$
,
$C_{\unicode[STIX]{x1D706}}$
,
![]() $\unicode[STIX]{x1D711}^{\prime }$
is continuous and
$\unicode[STIX]{x1D711}^{\prime }$
is continuous and
![]() $\langle \unicode[STIX]{x1D706}\rangle$
has no other accumulation points in
$\langle \unicode[STIX]{x1D706}\rangle$
has no other accumulation points in
![]() $\mathbb{R}^{\ast }$
. It follows that
$\mathbb{R}^{\ast }$
. It follows that
 $\unicode[STIX]{x1D711}^{\prime }(a)\in \langle \unicode[STIX]{x1D706}\rangle$
, for any
$\unicode[STIX]{x1D711}^{\prime }(a)\in \langle \unicode[STIX]{x1D706}\rangle$
, for any
![]() $a\in C_{\unicode[STIX]{x1D706}}$
and any
$a\in C_{\unicode[STIX]{x1D706}}$
and any
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
.
$\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
.
For a given
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
its derivative
$\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C_{\unicode[STIX]{x1D706}})$
its derivative
![]() $\unicode[STIX]{x1D711}^{\prime }$
is continuous on the whole interval
$\unicode[STIX]{x1D711}^{\prime }$
is continuous on the whole interval
![]() $[0,1]$
and hence is bounded. Moreover, the same argument for
$[0,1]$
and hence is bounded. Moreover, the same argument for
![]() $\unicode[STIX]{x1D711}^{-1}$
shows that
$\unicode[STIX]{x1D711}^{-1}$
shows that
![]() $\unicode[STIX]{x1D711}^{\prime }$
is also bounded from below away from
$\unicode[STIX]{x1D711}^{\prime }$
is also bounded from below away from
![]() $0$
, so that
$0$
, so that
![]() $\unicode[STIX]{x1D711}^{\prime }|_{C_{\unicode[STIX]{x1D706}}}$
can only take finitely many values of the form
$\unicode[STIX]{x1D711}^{\prime }|_{C_{\unicode[STIX]{x1D706}}}$
can only take finitely many values of the form
![]() $\unicode[STIX]{x1D706}^{n}$
,
$\unicode[STIX]{x1D706}^{n}$
,
![]() $n\in \mathbb{Z}$
.
$n\in \mathbb{Z}$
.
The following is a key ingredient in the description of the group
 $\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
.
$\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
.
Lemma 12. Let
 $\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
. There is a covering of
$\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})$
. There is a covering of
![]() $C_{\unicode[STIX]{x1D706}}$
by a finite collection of disjoint closed intervals
$C_{\unicode[STIX]{x1D706}}$
by a finite collection of disjoint closed intervals
![]() $I_{k}$
, such that
$I_{k}$
, such that
 $\unicode[STIX]{x1D711}|_{C_{\unicode[STIX]{x1D706}}\;\cap \;I_{k}}$
is the restriction of an affine function to
$\unicode[STIX]{x1D711}|_{C_{\unicode[STIX]{x1D706}}\;\cap \;I_{k}}$
is the restriction of an affine function to
 $I_{k}\;\cap \;C_{\unicode[STIX]{x1D706}}$
. Specifically,
$I_{k}\;\cap \;C_{\unicode[STIX]{x1D706}}$
. Specifically,
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D711}(c_{k})+\unicode[STIX]{x1D706}^{j_{k}}(x-c_{k})\quad \text{for }x\in I_{k}\;\cap \;C_{\unicode[STIX]{x1D706}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D711}(c_{k})+\unicode[STIX]{x1D706}^{j_{k}}(x-c_{k})\quad \text{for }x\in I_{k}\;\cap \;C_{\unicode[STIX]{x1D706}},\end{eqnarray}$$
where
![]() $c_{k}$
is a left point of
$c_{k}$
is a left point of
 $C_{\unicode[STIX]{x1D706}}\;\cap \;I_{k}$
.
$C_{\unicode[STIX]{x1D706}}\;\cap \;I_{k}$
.
Proof. For
![]() $c\in C_{\unicode[STIX]{x1D706}}$
there is some
$c\in C_{\unicode[STIX]{x1D706}}$
there is some
![]() $m\in \mathbb{Z}$
such that
$m\in \mathbb{Z}$
such that
 $\unicode[STIX]{x1D711}^{\prime }(c)=\unicode[STIX]{x1D706}^{m}$
. We want to prove that there exists an open neighborhood
$\unicode[STIX]{x1D711}^{\prime }(c)=\unicode[STIX]{x1D706}^{m}$
. We want to prove that there exists an open neighborhood
![]() $U$
of
$U$
of
![]() $c$
such that
$c$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D711}(c)+\unicode[STIX]{x1D706}^{j_{k}}(x-c)\quad \text{for }x\in U\;\cap \;C_{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D711}(c)+\unicode[STIX]{x1D706}^{j_{k}}(x-c)\quad \text{for }x\in U\;\cap \;C_{\unicode[STIX]{x1D706}}.\end{eqnarray}$$
Then such neighborhoods will cover
![]() $C_{\unicode[STIX]{x1D706}}$
and we can extract a finite subcovering by clopen (closed and open) subsets with the same property.
$C_{\unicode[STIX]{x1D706}}$
and we can extract a finite subcovering by clopen (closed and open) subsets with the same property.
This claim is true for any left (and by similar arguments for right) end points
![]() $c$
of
$c$
of
![]() $C_{\unicode[STIX]{x1D706}}$
. It is then sufficient to prove that whenever we have a sequence of left points
$C_{\unicode[STIX]{x1D706}}$
. It is then sufficient to prove that whenever we have a sequence of left points
 $a_{n}\rightarrow a_{\infty }$
contained in a closed interval
$a_{n}\rightarrow a_{\infty }$
contained in a closed interval
 $U\;\subset \;[0,1]$
and a
$U\;\subset \;[0,1]$
and a
![]() ${\mathcal{C}}^{1}$
-diffeomorphism
${\mathcal{C}}^{1}$
-diffeomorphism
 $\unicode[STIX]{x1D711}:U\rightarrow \unicode[STIX]{x1D711}(U)\;\subset \;[0,1]$
with
$\unicode[STIX]{x1D711}:U\rightarrow \unicode[STIX]{x1D711}(U)\;\subset \;[0,1]$
with
 $\unicode[STIX]{x1D711}(C\;\cap \;U)\;\subset \;C$
, there exists a neighborhood
$\unicode[STIX]{x1D711}(C\;\cap \;U)\;\subset \;C$
, there exists a neighborhood
![]() $U_{a_{\infty }}$
of
$U_{a_{\infty }}$
of
![]() $a_{\infty }$
and an affine function
$a_{\infty }$
and an affine function
![]() $\unicode[STIX]{x1D713}$
such that for large enough
$\unicode[STIX]{x1D713}$
such that for large enough
![]() $n$
the following holds:
$n$
the following holds:
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{\infty }}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{\infty }}.\end{eqnarray}$$
Around each left point
![]() $a_{n}$
there are affine maps
$a_{n}$
there are affine maps
 $\unicode[STIX]{x1D713}_{a_{n},k_{n}}:U_{a_{n},k_{n}}\rightarrow [0,1]$
defining germs in
$\unicode[STIX]{x1D713}_{a_{n},k_{n}}:U_{a_{n},k_{n}}\rightarrow [0,1]$
defining germs in
 $D(a_{n},c_{n})$
, where
$D(a_{n},c_{n})$
, where
 $c_{n}=\unicode[STIX]{x1D711}(a_{n})$
, such that
$c_{n}=\unicode[STIX]{x1D711}(a_{n})$
, such that
![]() $c_{n}$
converge to
$c_{n}$
converge to
 $c_{\infty }=\unicode[STIX]{x1D711}(a_{\infty })$
and
$c_{\infty }=\unicode[STIX]{x1D711}(a_{\infty })$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}_{a_{n},k_{n}}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{n},k_{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}_{a_{n},k_{n}}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{n},k_{n}}.\end{eqnarray}$$
We can further assume that
 $U_{a_{n},k_{n}}\;\cap \;C_{\unicode[STIX]{x1D706}}$
are clopen sets and we can take
$U_{a_{n},k_{n}}\;\cap \;C_{\unicode[STIX]{x1D706}}$
are clopen sets and we can take
 $U_{a_{n},k_{n}}=[a_{n},b_{n}]$
where
$U_{a_{n},k_{n}}=[a_{n},b_{n}]$
where
![]() $b_{n}$
are right points of
$b_{n}$
are right points of
![]() $C_{\unicode[STIX]{x1D706}}$
, and the sequence
$C_{\unicode[STIX]{x1D706}}$
, and the sequence
![]() $a_{n}$
is monotone, say increasing.
$a_{n}$
is monotone, say increasing.
There is no loss of generality to assume that
 $\unicode[STIX]{x1D713}_{a_{n},k_{n}}^{\prime }|_{C\;\cap \;U_{a_{n},k_{n}}}$
is independent on
$\unicode[STIX]{x1D713}_{a_{n},k_{n}}^{\prime }|_{C\;\cap \;U_{a_{n},k_{n}}}$
is independent on
![]() $n$
, say it equals
$n$
, say it equals
![]() $\unicode[STIX]{x1D706}^{m}$
, namely
$\unicode[STIX]{x1D706}^{m}$
, namely
![]() $k_{n}=m$
. Replacing
$k_{n}=m$
. Replacing
![]() $\unicode[STIX]{x1D711}$
by its inverse
$\unicode[STIX]{x1D711}$
by its inverse
![]() $\unicode[STIX]{x1D711}^{-1}$
we can also assume that
$\unicode[STIX]{x1D711}^{-1}$
we can also assume that
![]() $m\leqslant 0$
. Since
$m\leqslant 0$
. Since
![]() $C_{\unicode[STIX]{x1D706}}$
is invariant by the homothety of factor
$C_{\unicode[STIX]{x1D706}}$
is invariant by the homothety of factor
![]() $\unicode[STIX]{x1D706}$
and center
$\unicode[STIX]{x1D706}$
and center
![]() $0$
, we can further reduce the problem to the case where
$0$
, we can further reduce the problem to the case where
![]() $m=0$
. We have then
$m=0$
. We have then
 $\unicode[STIX]{x1D711}^{\prime }(a_{\infty })=1$
, by continuity.
$\unicode[STIX]{x1D711}^{\prime }(a_{\infty })=1$
, by continuity.
Choose
![]() $n$
large enough so that
$n$
large enough so that
 $|\unicode[STIX]{x1D711}^{\prime }(x)-1|<\unicode[STIX]{x1D700}$
, for any
$|\unicode[STIX]{x1D711}^{\prime }(x)-1|<\unicode[STIX]{x1D700}$
, for any
 $x\in [a_{n},a_{\infty }]$
, where the exact value of
$x\in [a_{n},a_{\infty }]$
, where the exact value of
![]() $\unicode[STIX]{x1D700}$
will be chosen later. Now consider the maximal interval of the form
$\unicode[STIX]{x1D700}$
will be chosen later. Now consider the maximal interval of the form
![]() $[a_{n},b]$
to which we can extend
$[a_{n},b]$
to which we can extend
![]() $\unicode[STIX]{x1D713}_{a_{n},0}$
to an affine function which coincides with
$\unicode[STIX]{x1D713}_{a_{n},0}$
to an affine function which coincides with
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
 $C\;\cap \;[a_{n},b]$
.
$C\;\cap \;[a_{n},b]$
.
If
![]() $b=a_{\infty }$
, then the Lemma follows. Otherwise, it is no loss of generality in assuming that
$b=a_{\infty }$
, then the Lemma follows. Otherwise, it is no loss of generality in assuming that
![]() $b=b_{n}$
and thus
$b=b_{n}$
and thus
![]() $b$
is a right point of
$b$
is a right point of
![]() $C_{\unicode[STIX]{x1D706}}$
. Then
$C_{\unicode[STIX]{x1D706}}$
. Then
![]() $b_{n}$
is adjacent to some gap
$b_{n}$
is adjacent to some gap
![]() $(b_{n},d)$
. Since
$(b_{n},d)$
. Since
![]() $d$
is a left point of
$d$
is a left point of
![]() $C_{\unicode[STIX]{x1D706}}$
and
$C_{\unicode[STIX]{x1D706}}$
and
 $\unicode[STIX]{x1D711}^{\prime }(d)=1$
, we can suppose that
$\unicode[STIX]{x1D711}^{\prime }(d)=1$
, we can suppose that
 $d=a_{n+1}$
.
$d=a_{n+1}$
.
Since
![]() $\unicode[STIX]{x1D711}$
preserves
$\unicode[STIX]{x1D711}$
preserves
![]() $C\;\cap \;U$
, it should send the gap
$C\;\cap \;U$
, it should send the gap
 $(b_{n},a_{n+1})$
into some gap contained into
$(b_{n},a_{n+1})$
into some gap contained into
 $[\unicode[STIX]{x1D711}(a_{n}),\unicode[STIX]{x1D711}(b_{n+1})]$
. Recall from above that the ratios of lengths of gaps of
$[\unicode[STIX]{x1D711}(a_{n}),\unicode[STIX]{x1D711}(b_{n+1})]$
. Recall from above that the ratios of lengths of gaps of
![]() $C_{\unicode[STIX]{x1D706}}$
is the discrete subset
$C_{\unicode[STIX]{x1D706}}$
is the discrete subset
 $\langle \unicode[STIX]{x1D706}\rangle \;\subset \;\mathbb{R}^{\ast }$
. When
$\langle \unicode[STIX]{x1D706}\rangle \;\subset \;\mathbb{R}^{\ast }$
. When
 $|\unicode[STIX]{x1D711}^{\prime }(x)-1|<\unicode[STIX]{x1D700}$
, we derive that the ratio of the lengths of the gaps
$|\unicode[STIX]{x1D711}^{\prime }(x)-1|<\unicode[STIX]{x1D700}$
, we derive that the ratio of the lengths of the gaps
 $\unicode[STIX]{x1D711}(b_{n},a_{n+1})$
and
$\unicode[STIX]{x1D711}(b_{n},a_{n+1})$
and
 $(b_{n},a_{n+1})$
is bounded by
$(b_{n},a_{n+1})$
is bounded by
![]() $1+\unicode[STIX]{x1D700}$
. By taking
$1+\unicode[STIX]{x1D700}$
. By taking
 $\unicode[STIX]{x1D700}<1-\unicode[STIX]{x1D706}$
we see that the only possibility is that the lengths of these two gaps coincide, namely that
$\unicode[STIX]{x1D700}<1-\unicode[STIX]{x1D706}$
we see that the only possibility is that the lengths of these two gaps coincide, namely that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(a_{n+1})=\unicode[STIX]{x1D711}(b_{n})+a_{n+1}-b_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(a_{n+1})=\unicode[STIX]{x1D711}(b_{n})+a_{n+1}-b_{n}.\end{eqnarray}$$
This implies that there is a smooth extension of
![]() $\unicode[STIX]{x1D713}_{a_{n},0}$
to an affine function on
$\unicode[STIX]{x1D713}_{a_{n},0}$
to an affine function on
 $[a_{n},b_{n+1}]$
which coincides with
$[a_{n},b_{n+1}]$
which coincides with
![]() $\unicode[STIX]{x1D711}$
on points of
$\unicode[STIX]{x1D711}$
on points of
![]() $C_{\unicode[STIX]{x1D706}}$
, contradicting the maximality of
$C_{\unicode[STIX]{x1D706}}$
, contradicting the maximality of
![]() $b=b_{n}$
. This proves that
$b=b_{n}$
. This proves that
![]() $b=a_{\infty }$
, proving the claim.
$b=a_{\infty }$
, proving the claim.
When
![]() $a_{\infty }$
is not a right point we also have an affine extension of
$a_{\infty }$
is not a right point we also have an affine extension of
![]() $\unicode[STIX]{x1D711}$
to a right neighborhood of
$\unicode[STIX]{x1D711}$
to a right neighborhood of
![]() $a_{\infty }$
, by the same argument.◻
$a_{\infty }$
, by the same argument.◻
Consider the rooted binary tree
![]() ${\mathcal{T}}$
embedded in the plane so that its ends abut on the interval
${\mathcal{T}}$
embedded in the plane so that its ends abut on the interval
![]() $[0,1]$
. We label each edge
$[0,1]$
. We label each edge
![]() $e$
by
$e$
by
 $l(e)\in \{0,\unicode[STIX]{x1D706}-1\}$
, such that the leftmost edge is always labeled
$l(e)\in \{0,\unicode[STIX]{x1D706}-1\}$
, such that the leftmost edge is always labeled
![]() $0$
. Let
$0$
. Let
![]() $v$
be a vertex of
$v$
be a vertex of
![]() ${\mathcal{T}}$
and
${\mathcal{T}}$
and
 $e_{1},e_{2},\ldots ,e_{n}$
the sequence of edges representing the geodesic which joins the root to
$e_{1},e_{2},\ldots ,e_{n}$
the sequence of edges representing the geodesic which joins the root to
![]() $v$
. To the vertex
$v$
. To the vertex
![]() $v$
one associates then the number
$v$
one associates then the number
 $$\begin{eqnarray}r(v)=\mathop{\sum }_{j=1}^{n}l(e_{j})\unicode[STIX]{x1D706}^{-j}.\end{eqnarray}$$
$$\begin{eqnarray}r(v)=\mathop{\sum }_{j=1}^{n}l(e_{j})\unicode[STIX]{x1D706}^{-j}.\end{eqnarray}$$
Denote by
![]() $D(v)$
the set of all descendants of the vertex
$D(v)$
the set of all descendants of the vertex
![]() $v$
. If
$v$
. If
![]() $I$
is a closed interval in
$I$
is a closed interval in
![]() $[0,1]$
we claim that
$[0,1]$
we claim that
 $L(C_{\unicode[STIX]{x1D706}})\;\cap \;I$
coincides with the set
$L(C_{\unicode[STIX]{x1D706}})\;\cap \;I$
coincides with the set
 $r(D(v_{I}))$
, for some unique vertex
$r(D(v_{I}))$
, for some unique vertex
![]() $v_{I}\in {\mathcal{T}}$
. Furthermore, if
$v_{I}\in {\mathcal{T}}$
. Furthermore, if
 $I_{1},I_{2},\ldots ,I_{k}$
is a set of disjoint standard intervals covering
$I_{1},I_{2},\ldots ,I_{k}$
is a set of disjoint standard intervals covering
![]() $C_{\unicode[STIX]{x1D706}}$
then
$C_{\unicode[STIX]{x1D706}}$
then
 $v_{I_{1}},v_{I_{2}},\ldots ,v_{I_{k}}$
are the leaves of a finite binary subtree
$v_{I_{1}},v_{I_{2}},\ldots ,v_{I_{k}}$
are the leaves of a finite binary subtree
 $T(I_{1},I_{2},\ldots ,I_{k})$
of
$T(I_{1},I_{2},\ldots ,I_{k})$
of
![]() ${\mathcal{T}}$
containing the root. In particular, if
${\mathcal{T}}$
containing the root. In particular, if
 $J_{1},J_{2},\ldots ,J_{k}$
is another covering of
$J_{1},J_{2},\ldots ,J_{k}$
is another covering of
![]() $C_{\unicode[STIX]{x1D706}}$
by standard intervals then we have two finite trees
$C_{\unicode[STIX]{x1D706}}$
by standard intervals then we have two finite trees
 $T(I_{1},I_{2},\ldots ,I_{k})$
and
$T(I_{1},I_{2},\ldots ,I_{k})$
and
 $T(J_{1},J_{2},\ldots ,J_{k})$
. Further, we also have affine bijections
$T(J_{1},J_{2},\ldots ,J_{k})$
. Further, we also have affine bijections
 $\unicode[STIX]{x1D711}_{j}:I_{j}\rightarrow J_{j}$
which are of the form
$\unicode[STIX]{x1D711}_{j}:I_{j}\rightarrow J_{j}$
which are of the form
 $\unicode[STIX]{x1D711}_{j}(x)=b_{j}+\unicode[STIX]{x1D706}^{k_{j}}(x-a_{j})$
, where
$\unicode[STIX]{x1D711}_{j}(x)=b_{j}+\unicode[STIX]{x1D706}^{k_{j}}(x-a_{j})$
, where
 $a_{j},b_{j}\in L(C_{\unicode[STIX]{x1D706}})$
. It is clear that
$a_{j},b_{j}\in L(C_{\unicode[STIX]{x1D706}})$
. It is clear that
 $\unicode[STIX]{x1D711}_{j}(I_{j}\;\cap \;L(C_{\unicode[STIX]{x1D706}}))=J_{j}\;\cap \;L(C_{\unicode[STIX]{x1D706}})$
. The explicit form of
$\unicode[STIX]{x1D711}_{j}(I_{j}\;\cap \;L(C_{\unicode[STIX]{x1D706}}))=J_{j}\;\cap \;L(C_{\unicode[STIX]{x1D706}})$
. The explicit form of
 $\unicode[STIX]{x1D711}_{j}|_{I_{j}\;\cap \;L(C_{\unicode[STIX]{x1D706}})}$
actually can be interpreted in terms of
$\unicode[STIX]{x1D711}_{j}|_{I_{j}\;\cap \;L(C_{\unicode[STIX]{x1D706}})}$
actually can be interpreted in terms of
![]() $r(v_{I_{j}})$
, as follows. Let
$r(v_{I_{j}})$
, as follows. Let
![]() ${\mathcal{D}}(v)$
be the planar rooted subtree of
${\mathcal{D}}(v)$
be the planar rooted subtree of
![]() ${\mathcal{T}}$
of vertices
${\mathcal{T}}$
of vertices
![]() $D(v)$
and root
$D(v)$
and root
![]() $v$
. There is a natural identification
$v$
. There is a natural identification
![]() $\unicode[STIX]{x1D704}_{v,w}$
of the planar binary rooted trees
$\unicode[STIX]{x1D704}_{v,w}$
of the planar binary rooted trees
![]() $D(v)$
and
$D(v)$
and
![]() $D(w)$
, for any
$D(w)$
, for any
 $v,w\in {\mathcal{T}}$
. When we further identify
$v,w\in {\mathcal{T}}$
. When we further identify
 $L(C_{\unicode[STIX]{x1D706}})\;\cap \;I_{j}$
with the set
$L(C_{\unicode[STIX]{x1D706}})\;\cap \;I_{j}$
with the set
 $r(D(v_{I_{j}}))$
the induced action of
$r(D(v_{I_{j}}))$
the induced action of
![]() $\unicode[STIX]{x1D711}_{j}$
on
$\unicode[STIX]{x1D711}_{j}$
on
 $w\in D(v_{I_{j}})$
coincides with
$w\in D(v_{I_{j}})$
coincides with
![]() $\unicode[STIX]{x1D704}_{v_{I_{j}},v_{J_{j}}}$
.
$\unicode[STIX]{x1D704}_{v_{I_{j}},v_{J_{j}}}$
.
Consider now the operation of replacing an interval
![]() $I_{j}$
by two disjoint intervals
$I_{j}$
by two disjoint intervals
![]() $I_{j}^{\prime }$
and
$I_{j}^{\prime }$
and
![]() $I_{j}^{\prime \prime }$
whose union is disjoint from the other intervals
$I_{j}^{\prime \prime }$
whose union is disjoint from the other intervals
![]() $I_{k}$
. Correspondingly we replace
$I_{k}$
. Correspondingly we replace
![]() $J_{j}$
by the couple
$J_{j}$
by the couple
 $\{J_{j}^{\prime },J_{j}^{\prime \prime }\}=\{\unicode[STIX]{x1D711}_{j}(I_{j}^{\prime }),\unicode[STIX]{x1D711}_{j}(I_{j}^{\prime \prime })\}$
and
$\{J_{j}^{\prime },J_{j}^{\prime \prime }\}=\{\unicode[STIX]{x1D711}_{j}(I_{j}^{\prime }),\unicode[STIX]{x1D711}_{j}(I_{j}^{\prime \prime })\}$
and
![]() $\unicode[STIX]{x1D711}_{j}$
by its restrictions to these smaller intervals. This operation does not change the element in
$\unicode[STIX]{x1D711}_{j}$
by its restrictions to these smaller intervals. This operation does not change the element in
 $\mathfrak{diff}^{1}(C_{\unicode[STIX]{x1D706}})$
. The immediate consequence of the description of
$\mathfrak{diff}^{1}(C_{\unicode[STIX]{x1D706}})$
. The immediate consequence of the description of
![]() $\unicode[STIX]{x1D711}_{j}$
is that the pairs of trees
$\unicode[STIX]{x1D711}_{j}$
is that the pairs of trees
 $T(I_{1},\ldots ,I_{j}^{\prime },I_{j}^{\prime \prime },\ldots ,I_{k})$
and
$T(I_{1},\ldots ,I_{j}^{\prime },I_{j}^{\prime \prime },\ldots ,I_{k})$
and
 $T(J_{1},\ldots ,J_{j}^{\prime },J_{j}^{\prime \prime },\ldots ,J_{k})$
are both obtained from
$T(J_{1},\ldots ,J_{j}^{\prime },J_{j}^{\prime \prime },\ldots ,J_{k})$
are both obtained from
 $T(I_{1},I_{2},\ldots ,I_{k})$
and
$T(I_{1},I_{2},\ldots ,I_{k})$
and
 $T(J_{1},J_{2},\ldots ,J_{k})$
by adding one caret at the
$T(J_{1},J_{2},\ldots ,J_{k})$
by adding one caret at the
![]() $j$
th leaf. This proves that this pair of trees is a well-defined element of the standard Thompson group
$j$
th leaf. This proves that this pair of trees is a well-defined element of the standard Thompson group
![]() $F$
. It is rather clear that the map defined this way
$F$
. It is rather clear that the map defined this way
 $\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})\rightarrow F$
is an isomorphism.
$\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})\rightarrow F$
is an isomorphism.
In a similar way we define an isomorphism
 $\mathfrak{diff}_{S^{1}}^{1,+}(C_{\unicode[STIX]{x1D706}})\rightarrow T$
, when we work with the infinite unrooted binary tree
$\mathfrak{diff}_{S^{1}}^{1,+}(C_{\unicode[STIX]{x1D706}})\rightarrow T$
, when we work with the infinite unrooted binary tree
![]() ${\mathcal{T}}$
embedded in the plane so that its ends abut to
${\mathcal{T}}$
embedded in the plane so that its ends abut to
![]() $S^{1}$
.
$S^{1}$
.
In the case of
 $\mathfrak{diff}_{S^{2}}^{1}(C_{\unicode[STIX]{x1D706}})$
we use the proof of Theorem 3 and the infinite unrooted binary tree
$\mathfrak{diff}_{S^{2}}^{1}(C_{\unicode[STIX]{x1D706}})$
we use the proof of Theorem 3 and the infinite unrooted binary tree
![]() ${\mathcal{T}}$
without any planar structure. The only difference is that the restrictions
${\mathcal{T}}$
without any planar structure. The only difference is that the restrictions
![]() $\unicode[STIX]{x1D711}|_{I_{j}}$
are not having anymore a coherent orientation. Some of them might be orientation preserving while the others may not. This explains the isomorphism between
$\unicode[STIX]{x1D711}|_{I_{j}}$
are not having anymore a coherent orientation. Some of them might be orientation preserving while the others may not. This explains the isomorphism between
 $\mathfrak{diff}_{S^{2}}^{1}(C_{\unicode[STIX]{x1D706}})$
and the signed Thompson group
$\mathfrak{diff}_{S^{2}}^{1}(C_{\unicode[STIX]{x1D706}})$
and the signed Thompson group
![]() $V^{\pm }$
. This ends the proof of Theorem 6 in the case of
$V^{\pm }$
. This ends the proof of Theorem 6 in the case of
 $C=C_{\unicode[STIX]{x1D706}}$
.
$C=C_{\unicode[STIX]{x1D706}}$
.
4.3 Proof of the general case of Theorem 6
The only missing ingredient is the result generalizing Lemma 12 to the more general self-similar sets considered here, as follows.
Lemma 13. Let
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C)$
, where
$\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C)$
, where
 $C=C_{\unicode[STIX]{x1D6F7}}$
is a self-similar Cantor set satisfying the genericity condition
$C=C_{\unicode[STIX]{x1D6F7}}$
is a self-similar Cantor set satisfying the genericity condition
![]() $(C)$
. Then there is a covering of
$(C)$
. Then there is a covering of
![]() $C$
by a finite collection of disjoint intervals
$C$
by a finite collection of disjoint intervals
![]() $I_{k}$
, such that
$I_{k}$
, such that
![]() $\unicode[STIX]{x1D711}|_{C\;\cap \;I_{k}}$
is the restriction of an affine function to
$\unicode[STIX]{x1D711}|_{C\;\cap \;I_{k}}$
is the restriction of an affine function to
![]() $I_{k}\;\cap \;C$
.
$I_{k}\;\cap \;C$
.
The proof of this lemma for incommensurable parameters will occupy § 4.3.1. In the case when gaps and homothety factors are respectively equal the proof given above extends word by word.
Now, any
![]() $\unicode[STIX]{x1D711}$
in the group
$\unicode[STIX]{x1D711}$
in the group
 $\mathfrak{diff}^{1,+}(C)$
corresponds to a pair of coverings of
$\mathfrak{diff}^{1,+}(C)$
corresponds to a pair of coverings of
![]() $C$
by intervals
$C$
by intervals
 $(I_{1},I_{2},\ldots ,I_{k})$
and
$(I_{1},I_{2},\ldots ,I_{k})$
and
 $(J_{1},J_{2},\ldots ,J_{k})$
so that
$(J_{1},J_{2},\ldots ,J_{k})$
so that
![]() $\unicode[STIX]{x1D711}$
sends affinely
$\unicode[STIX]{x1D711}$
sends affinely
![]() $I_{j}$
into
$I_{j}$
into
![]() $J_{j}$
, for all
$J_{j}$
, for all
![]() $j$
. These intervals could be chosen to be of the form
$j$
. These intervals could be chosen to be of the form
![]() $[a,b]$
, where
$[a,b]$
, where
![]() $a$
is a left point of
$a$
is a left point of
![]() $C$
and
$C$
and
![]() $b$
is a right point of
$b$
is a right point of
![]() $C$
. We call them clopen intervals.
$C$
. We call them clopen intervals.
Particular examples of clopen intervals are the images of
![]() $[0,1]$
by the semigroup generated by
$[0,1]$
by the semigroup generated by
![]() $\unicode[STIX]{x1D6F7}$
, which will be called standard (clopen) intervals. Each standard clopen interval corresponds to a finite geodesic path descending from the root in the (regular rooted) tree of valence
$\unicode[STIX]{x1D6F7}$
, which will be called standard (clopen) intervals. Each standard clopen interval corresponds to a finite geodesic path descending from the root in the (regular rooted) tree of valence
![]() $n+2$
associated to
$n+2$
associated to
![]() $\unicode[STIX]{x1D6F7}$
. Thus standard intervals are associated to vertices of the
$\unicode[STIX]{x1D6F7}$
. Thus standard intervals are associated to vertices of the
![]() $(n+2)$
-valent tree, and one says that they belong to the
$(n+2)$
-valent tree, and one says that they belong to the
![]() $k$
th generation of standard intervals if the associated vertex is at distance
$k$
th generation of standard intervals if the associated vertex is at distance
![]() $k$
from the root. The complementary intervals to the union of all
$k$
from the root. The complementary intervals to the union of all
![]() $k$
th generation of standard intervals will be the
$k$
th generation of standard intervals will be the
![]() $k$
th generation of gaps. Moreover, given a standard interval
$k$
th generation of gaps. Moreover, given a standard interval
![]() $I$
of the
$I$
of the
![]() $k$
th generation, the gaps of the
$k$
th generation, the gaps of the
![]() $(k+1)$
th generation lying in
$(k+1)$
th generation lying in
![]() $I$
will also be called the first generation of gaps in
$I$
will also be called the first generation of gaps in
![]() $I$
. Notice that, conversely, every gap is a first generation gap for some uniquely determined standard interval, to be called its antecedent standard interval.
$I$
. Notice that, conversely, every gap is a first generation gap for some uniquely determined standard interval, to be called its antecedent standard interval.
Note that the intervals obtained in the previous lemma were not necessarily standard intervals. It then remains to prove the following enhancement of Lemma 13.
Lemma 14. We assume that
 $C=C_{\unicode[STIX]{x1D6F7}}$
, where
$C=C_{\unicode[STIX]{x1D6F7}}$
, where
![]() $\unicode[STIX]{x1D6F7}$
verifies the genericity condition
$\unicode[STIX]{x1D6F7}$
verifies the genericity condition
![]() $(C)$
from Definition 6. Then any
$(C)$
from Definition 6. Then any
 $\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C)$
corresponds to a pair of coverings of
$\unicode[STIX]{x1D711}\in \mathfrak{diff}^{1,+}(C)$
corresponds to a pair of coverings of
![]() $C$
by standard intervals
$C$
by standard intervals
 $(I_{1},I_{2},\ldots ,I_{k})$
and
$(I_{1},I_{2},\ldots ,I_{k})$
and
 $(J_{1},J_{2},\ldots ,J_{k})$
so that
$(J_{1},J_{2},\ldots ,J_{k})$
so that
![]() $\unicode[STIX]{x1D711}$
sends affinely
$\unicode[STIX]{x1D711}$
sends affinely
![]() $I_{j}$
into
$I_{j}$
into
![]() $J_{j}$
, for all
$J_{j}$
, for all
![]() $j$
.
$j$
.
Proof. Every clopen interval is the disjoint union of finitely many standard intervals and open gaps. We can therefore suppose that all
![]() $I_{j}$
are standard intervals.
$I_{j}$
are standard intervals.
Note that for any two standard intervals
 $I,J\;\subset \;[0,1]$
there exists an affine bijection
$I,J\;\subset \;[0,1]$
there exists an affine bijection
 $(I,I\;\cap \;C)\rightarrow (J,J\;\cap \;C)$
, because this holds when
$(I,I\;\cap \;C)\rightarrow (J,J\;\cap \;C)$
, because this holds when
 $I=[0,1]$
.
$I=[0,1]$
.
We now claim that, conversely, if there exists an affine bijection
 $\unicode[STIX]{x1D711}:(I,I\;\cap \;C)\rightarrow (J,J\;\cap \;C)$
and
$\unicode[STIX]{x1D711}:(I,I\;\cap \;C)\rightarrow (J,J\;\cap \;C)$
and
![]() $I$
is standard then its image
$I$
is standard then its image
![]() $J$
is also a standard interval. This will prove Lemma 14.
$J$
is also a standard interval. This will prove Lemma 14.
Consider a maximal standard interval
![]() $I^{\prime }\;\subset \;J$
. Composing
$I^{\prime }\;\subset \;J$
. Composing
![]() $\unicode[STIX]{x1D711}$
with the affine map in
$\unicode[STIX]{x1D711}$
with the affine map in
 $\mathfrak{diff}^{1,+}(C)$
sending bijectively
$\mathfrak{diff}^{1,+}(C)$
sending bijectively
 $(I^{\prime },I^{\prime }\;\cap \;C)$
onto
$(I^{\prime },I^{\prime }\;\cap \;C)$
onto
 $(I,I\;\cap \;C)$
we can assume that
$(I,I\;\cap \;C)$
we can assume that
![]() $I=I^{\prime }$
. In particular, the homothety factor
$I=I^{\prime }$
. In particular, the homothety factor
![]() $\unicode[STIX]{x1D707}$
of the affine map
$\unicode[STIX]{x1D707}$
of the affine map
 $\unicode[STIX]{x1D711}:I\rightarrow J$
is at least
$\unicode[STIX]{x1D711}:I\rightarrow J$
is at least
![]() $1$
.
$1$
.
Assume first that all homothety ratios are equal to
![]() $\unicode[STIX]{x1D706}$
and all initial gaps have the same length
$\unicode[STIX]{x1D706}$
and all initial gaps have the same length
![]() $g$
, as in Definition 6(i). Observe that all gaps will have sizes of the form
$g$
, as in Definition 6(i). Observe that all gaps will have sizes of the form
![]() $\unicode[STIX]{x1D706}^{m}g$
, for some
$\unicode[STIX]{x1D706}^{m}g$
, for some
 $m\in \mathbb{Z}_{+}$
. Moreover, if
$m\in \mathbb{Z}_{+}$
. Moreover, if
![]() $I$
is a standard interval of the
$I$
is a standard interval of the
![]() $k$
th generation, then the set of largest gaps in
$k$
th generation, then the set of largest gaps in
![]() $I$
consists of
$I$
consists of
![]() $n$
equidistant gaps of size
$n$
equidistant gaps of size
![]() $\unicode[STIX]{x1D706}^{k}g$
. Their image by the affine map
$\unicode[STIX]{x1D706}^{k}g$
. Their image by the affine map
![]() $\unicode[STIX]{x1D711}$
is the set of largest gaps in
$\unicode[STIX]{x1D711}$
is the set of largest gaps in
![]() $J$
, so that the latter are also
$J$
, so that the latter are also
![]() $n$
equidistant equal gaps in
$n$
equidistant equal gaps in
![]() $J$
, necessarily of size
$J$
, necessarily of size
![]() $\unicode[STIX]{x1D706}^{n+k}g$
, for some
$\unicode[STIX]{x1D706}^{n+k}g$
, for some
![]() $n\in \mathbb{Z}_{-}$
. In particular the homothety factor is
$n\in \mathbb{Z}_{-}$
. In particular the homothety factor is
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D706}^{n}$
.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D706}^{n}$
.
We now consider the antecedent standard intervals associated to the largest gaps of
![]() $J$
. If such a gap had size
$J$
. If such a gap had size
![]() $\unicode[STIX]{x1D706}^{n+k}g$
, its antecedent interval would have size
$\unicode[STIX]{x1D706}^{n+k}g$
, its antecedent interval would have size
![]() $\unicode[STIX]{x1D706}^{n+k}$
. If two of the largest gaps in
$\unicode[STIX]{x1D706}^{n+k}$
. If two of the largest gaps in
![]() $J$
have distinct antecedent intervals, then they would be separated by another gap of size
$J$
have distinct antecedent intervals, then they would be separated by another gap of size
 $\unicode[STIX]{x1D706}^{n-1+k}g$
, contradicting their maximality in
$\unicode[STIX]{x1D706}^{n-1+k}g$
, contradicting their maximality in
![]() $J$
. Therefore all but possibly the leftmost and rightmost intervals of the complement of these
$J$
. Therefore all but possibly the leftmost and rightmost intervals of the complement of these
![]() $n$
gaps in
$n$
gaps in
![]() $J$
are standard.
$J$
are standard.
Now, the interval between two consecutive gaps in
![]() $I$
is a standard interval of length
$I$
is a standard interval of length
![]() $\unicode[STIX]{x1D706}^{k+1}$
, whose image by the affine map
$\unicode[STIX]{x1D706}^{k+1}$
, whose image by the affine map
![]() $\unicode[STIX]{x1D711}$
has length
$\unicode[STIX]{x1D711}$
has length
![]() $\unicode[STIX]{x1D706}^{n+k+1}$
. This shows that the leftmost and the rightmost intervals also should be standard intervals, as they have the same size as the remaining
$\unicode[STIX]{x1D706}^{n+k+1}$
. This shows that the leftmost and the rightmost intervals also should be standard intervals, as they have the same size as the remaining
![]() $(n-1)$
standard intervals between consecutive image gaps. This proves that
$(n-1)$
standard intervals between consecutive image gaps. This proves that
![]() $J$
is a standard interval.
$J$
is a standard interval.
Consider now the case when homothety factors and gap lengths are incommensurable, as in Definition 6(ii). The set of gaps of the same generation is totally ordered from the leftmost gap towards the right. The sequence of lengths of
![]() $(k+1)$
th generation gaps within a standard interval of the
$(k+1)$
th generation gaps within a standard interval of the
![]() $k$
th generation is of the form
$k$
th generation is of the form
 $(\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{1},\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{2},\ldots ,\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{n})$
, for some
$(\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{1},\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{2},\ldots ,\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{n})$
, for some
![]() $\mathbf{k}$
. Consider now a gap of the first generation, say
$\mathbf{k}$
. Consider now a gap of the first generation, say
![]() $\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}$
, of
$\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}$
, of
![]() $I$
. Its image by an affine map should be a gap of
$I$
. Its image by an affine map should be a gap of
![]() $J$
. It follows that there exists some
$J$
. It follows that there exists some
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})\in \{1,2,\ldots ,n\}$
and
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})\in \{1,2,\ldots ,n\}$
and
 $\mathbf{k}_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{+}^{n+1}$
, so that:
$\mathbf{k}_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{+}^{n+1}$
, so that:
 $$\begin{eqnarray}\unicode[STIX]{x1D707}\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}}g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}}g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}$
is the homothety factor of the map
$\unicode[STIX]{x1D707}$
is the homothety factor of the map
![]() $\unicode[STIX]{x1D711}$
. Conversely, any gap of
$\unicode[STIX]{x1D711}$
. Conversely, any gap of
![]() $I\;\subset \;J$
is the image by
$I\;\subset \;J$
is the image by
![]() $\unicode[STIX]{x1D711}$
of some gap of
$\unicode[STIX]{x1D711}$
of some gap of
![]() $I$
, and hence there exists some
$I$
, and hence there exists some
 $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})\in \{1,2,\ldots ,n\}$
and
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})\in \{1,2,\ldots ,n\}$
and
 $\mathbf{l}_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{+}^{n+1}$
, so that:
$\mathbf{l}_{\unicode[STIX]{x1D6FC}}\in \mathbb{Z}_{+}^{n+1}$
, so that:
 $$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6EC}_{\mathbf{l}_{\unicode[STIX]{x1D6FC}}}g_{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D6EC}_{\mathbf{k}}g_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6EC}_{\mathbf{l}_{\unicode[STIX]{x1D6FC}}}g_{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})}.\end{eqnarray}$$
Getting rid of
![]() $\unicode[STIX]{x1D707}$
in the two equalities above we obtain the following identities, for all
$\unicode[STIX]{x1D707}$
in the two equalities above we obtain the following identities, for all
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
:
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
:
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}+\mathbf{l}_{\unicode[STIX]{x1D6FD}}-2\mathbf{k}}\quad g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}g_{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD})}=g_{\unicode[STIX]{x1D6FC}}g_{\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}+\mathbf{l}_{\unicode[STIX]{x1D6FD}}-2\mathbf{k}}\quad g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}g_{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD})}=g_{\unicode[STIX]{x1D6FC}}g_{\unicode[STIX]{x1D6FD}}.\end{eqnarray}$$
By taking
 $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})$
we derive:
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})$
we derive:
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}+\mathbf{l}_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}-2\mathbf{k}}\;g_{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))}=g_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}+\mathbf{l}_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}-2\mathbf{k}}\;g_{\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))}=g_{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
If
![]() $g_{\unicode[STIX]{x1D6FC}}$
and
$g_{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D706}_{j}$
satisfy the genericity condition
$\unicode[STIX]{x1D706}_{j}$
satisfy the genericity condition
![]() $(C)$
the last equality implies
$(C)$
the last equality implies
 $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))=\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC}))=\unicode[STIX]{x1D6FC}$
and
 $\mathbf{k}_{\unicode[STIX]{x1D6FC}}+\mathbf{l}_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}=2\mathbf{k}$
, for every
$\mathbf{k}_{\unicode[STIX]{x1D6FC}}+\mathbf{l}_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}=2\mathbf{k}$
, for every
![]() $\unicode[STIX]{x1D6FC}$
. A symmetric argument yields
$\unicode[STIX]{x1D6FC}$
. A symmetric argument yields
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC}))=\unicode[STIX]{x1D6FC}$
, so that
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC}))=\unicode[STIX]{x1D6FC}$
, so that
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70F}$
are bijections inverse to each other. Furthermore we derive:
$\unicode[STIX]{x1D70F}$
are bijections inverse to each other. Furthermore we derive:
 $$\begin{eqnarray}\unicode[STIX]{x1D707}^{n}=\mathop{\prod }_{\unicode[STIX]{x1D6FC}=1}^{n}\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}-\mathbf{k}}\frac{g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}}{g_{\unicode[STIX]{x1D6FC}}}=\unicode[STIX]{x1D6EC}_{\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}(\mathbf{k}_{\unicode[STIX]{x1D6FC}}-\mathbf{k})},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}^{n}=\mathop{\prod }_{\unicode[STIX]{x1D6FC}=1}^{n}\unicode[STIX]{x1D6EC}_{\mathbf{k}_{\unicode[STIX]{x1D6FC}}-\mathbf{k}}\frac{g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FC})}}{g_{\unicode[STIX]{x1D6FC}}}=\unicode[STIX]{x1D6EC}_{\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}(\mathbf{k}_{\unicode[STIX]{x1D6FC}}-\mathbf{k})},\end{eqnarray}$$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6EC}_{-\mathbf{k}+(1/n)\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}\mathbf{k}_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6EC}_{-\mathbf{k}+(1/n)\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}\mathbf{k}_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
Therefore, for each
![]() $\unicode[STIX]{x1D6FD}$
we have:
$\unicode[STIX]{x1D6FD}$
we have:
 $$\begin{eqnarray}\frac{g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})}}{g_{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D6EC}_{-\mathbf{k}_{\unicode[STIX]{x1D6FD}}+(1/n)\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}\mathbf{k}_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{g_{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FD})}}{g_{\unicode[STIX]{x1D6FD}}}=\unicode[STIX]{x1D6EC}_{-\mathbf{k}_{\unicode[STIX]{x1D6FD}}+(1/n)\mathop{\sum }_{\unicode[STIX]{x1D6FC}=1}^{n}\mathbf{k}_{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$
Then our assumptions of genericity imply that
![]() $\unicode[STIX]{x1D70E}$
must be identity. It turns out that all
$\unicode[STIX]{x1D70E}$
must be identity. It turns out that all
![]() $\mathbf{k}_{\unicode[STIX]{x1D6FC}}$
are equal to some
$\mathbf{k}_{\unicode[STIX]{x1D6FC}}$
are equal to some
![]() $\overline{\mathbf{k}}$
and hence
$\overline{\mathbf{k}}$
and hence
 $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6EC}_{\overline{\mathbf{k}}-\mathbf{k}}$
.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D6EC}_{\overline{\mathbf{k}}-\mathbf{k}}$
.
Observe that there exists a standard interval
![]() $J^{\prime }$
and an affine bijection
$J^{\prime }$
and an affine bijection
 $\unicode[STIX]{x1D713}:(I,I\;\cap \;C)\rightarrow (J^{\prime },J^{\prime }\;\cap \;C)$
with homothety factor
$\unicode[STIX]{x1D713}:(I,I\;\cap \;C)\rightarrow (J^{\prime },J^{\prime }\;\cap \;C)$
with homothety factor
![]() $\unicode[STIX]{x1D6EC}_{\overline{\mathbf{k}}-\mathbf{k}}$
. Therefore
$\unicode[STIX]{x1D6EC}_{\overline{\mathbf{k}}-\mathbf{k}}$
. Therefore
 $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}:J^{\prime }\rightarrow J$
is a translation. Moreover, as
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}:J^{\prime }\rightarrow J$
is a translation. Moreover, as
![]() $\unicode[STIX]{x1D70E}$
was identity the sequence of first generation gaps in
$\unicode[STIX]{x1D70E}$
was identity the sequence of first generation gaps in
![]() $J^{\prime }$
is sent by
$J^{\prime }$
is sent by
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}$
into the sequence of first generation gaps of some standard interval
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}$
into the sequence of first generation gaps of some standard interval
![]() $J^{\prime \prime }$
. By induction, the ordered sequence of the
$J^{\prime \prime }$
. By induction, the ordered sequence of the
![]() $k$
th generation of gaps in
$k$
th generation of gaps in
![]() $J^{\prime }$
is sent by
$J^{\prime }$
is sent by
![]() $\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}$
into the sequence of the
$\unicode[STIX]{x1D711}\circ \unicode[STIX]{x1D713}^{-1}$
into the sequence of the
![]() $k$
th generation gaps of
$k$
th generation gaps of
![]() $J^{\prime \prime }$
. Since
$J^{\prime \prime }$
. Since
![]() $J$
and
$J$
and
![]() $J^{\prime \prime }$
have the same length it follows that
$J^{\prime \prime }$
have the same length it follows that
![]() $J=J^{\prime \prime }$
and hence
$J=J^{\prime \prime }$
and hence
![]() $J$
is a standard interval, as claimed.◻
$J$
is a standard interval, as claimed.◻
Now, it is immediate that
 $\langle \unicode[STIX]{x1D706}_{0}\rangle \;\subset \;\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1,+})$
, and by Lemma 7 there exists some
$\langle \unicode[STIX]{x1D706}_{0}\rangle \;\subset \;\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1,+})$
, and by Lemma 7 there exists some
 $N\in \mathbb{Z}_{+}$
so that
$N\in \mathbb{Z}_{+}$
so that
 $\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1,+})=\langle \unicode[STIX]{x1D706}_{1}^{1/N}\rangle$
. Since
$\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1,+})=\langle \unicode[STIX]{x1D706}_{1}^{1/N}\rangle$
. Since
![]() $L(C)$
is affinely locally homogeneous this holds for any left point
$L(C)$
is affinely locally homogeneous this holds for any left point
![]() $a$
of
$a$
of
![]() $C$
.
$C$
.
Then, the general form of an affine germ locally preserving
![]() $C$
around a left point
$C$
around a left point
 $c_{k}\in C\;\cap \;I_{k}$
is
$c_{k}\in C\;\cap \;I_{k}$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D711}(c_{k})+\unicode[STIX]{x1D6EC}_{\mathbf{j}_{k},N}(x-c_{k})\quad \text{for }x\in I_{k}\;\cap \;C,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D711}(c_{k})+\unicode[STIX]{x1D6EC}_{\mathbf{j}_{k},N}(x-c_{k})\quad \text{for }x\in I_{k}\;\cap \;C,\end{eqnarray}$$
where, for each multi-index
 $\mathbf{k}=(k_{0},k_{1},\ldots ,k_{n})$
we put
$\mathbf{k}=(k_{0},k_{1},\ldots ,k_{n})$
we put
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{k},N}=\unicode[STIX]{x1D706}_{0}^{k_{0}/N}\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D706}_{i}^{k_{i}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{\mathbf{k},N}=\unicode[STIX]{x1D706}_{0}^{k_{0}/N}\mathop{\prod }_{i=1}^{n}\unicode[STIX]{x1D706}_{i}^{k_{i}}.\end{eqnarray}$$
Furthermore, we can modify any germ in
![]() $\text{Diff}_{0}^{1,+}$
by using homotheties of ratios
$\text{Diff}_{0}^{1,+}$
by using homotheties of ratios
![]() $\unicode[STIX]{x1D706}_{0}^{k}$
,
$\unicode[STIX]{x1D706}_{0}^{k}$
,
![]() $k\in \mathbb{Z}$
in order to obtain a diffeomorphism
$k\in \mathbb{Z}$
in order to obtain a diffeomorphism
 $\unicode[STIX]{x1D711}:[0,1]\rightarrow [0,r]$
sending
$\unicode[STIX]{x1D711}:[0,1]\rightarrow [0,r]$
sending
![]() $C$
into
$C$
into
![]() $C$
. By Lemma 13 we can assume that
$C$
. By Lemma 13 we can assume that
![]() $\unicode[STIX]{x1D711}$
is an affine map, and by Lemma 14
$\unicode[STIX]{x1D711}$
is an affine map, and by Lemma 14
![]() $[0,r]$
must be a standard interval. It follows that the homothety factor of
$[0,r]$
must be a standard interval. It follows that the homothety factor of
![]() $\unicode[STIX]{x1D711}$
is a power of
$\unicode[STIX]{x1D711}$
is a power of
![]() $\unicode[STIX]{x1D706}_{0}$
. This implies that
$\unicode[STIX]{x1D706}_{0}$
. This implies that
![]() $N=1$
.
$N=1$
.
Pairs of coverings by standard clopen intervals of
![]() $C$
correspond to pairs of finite rooted subtrees. Subdividing the covering by standard subintervals is then equivalent to stabilizing the trees. This provides isomorphisms with the Thompson groups
$C$
correspond to pairs of finite rooted subtrees. Subdividing the covering by standard subintervals is then equivalent to stabilizing the trees. This provides isomorphisms with the Thompson groups
![]() $F_{n+1}$
,
$F_{n+1}$
,
![]() $T_{n+1}$
and the signed Thompson group
$T_{n+1}$
and the signed Thompson group
![]() $V_{n+1}^{\pm }$
, respectively, ending the proof of Theorem 6.
$V_{n+1}^{\pm }$
, respectively, ending the proof of Theorem 6.
4.3.1 Proof of Lemma 13 for incommensurable parameters
We will use a much weaker restriction than the total incommensurability, see the conditions used below.
Recall from § 4.1 that the rooted
![]() $(n+2)$
-valent tree associated to the IFS has the edges issued from a vertex labeled by integers from
$(n+2)$
-valent tree associated to the IFS has the edges issued from a vertex labeled by integers from
![]() $0$
to
$0$
to
![]() $n$
(from left to right). Then left points of
$n$
(from left to right). Then left points of
![]() $C$
correspond to sequences which eventually end in
$C$
correspond to sequences which eventually end in
![]() $0$
, namely of the form
$0$
, namely of the form
 $$\begin{eqnarray}L(i_{1}\cdots i_{p})=i_{1}i_{2}\cdots i_{p}000000\cdots \,,\end{eqnarray}$$
$$\begin{eqnarray}L(i_{1}\cdots i_{p})=i_{1}i_{2}\cdots i_{p}000000\cdots \,,\end{eqnarray}$$
while right points correspond to sequences which eventually end in
![]() $n$
:
$n$
:
 $$\begin{eqnarray}R(i_{1}\cdots i_{p})=i_{1}\cdots i_{p}nnnnnn\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}R(i_{1}\cdots i_{p})=i_{1}\cdots i_{p}nnnnnn\cdots \,.\end{eqnarray}$$
Consider two finite multi-indices
 $I=i_{1}\cdots i_{p}$
and
$I=i_{1}\cdots i_{p}$
and
 $J=j_{1}\cdots j_{q}$
and set
$J=j_{1}\cdots j_{q}$
and set
 $a=L(i_{1}\cdots i_{p})$
,
$a=L(i_{1}\cdots i_{p})$
,
 $b=R(i_{1}\cdots i_{p})$
,
$b=R(i_{1}\cdots i_{p})$
,
 $\unicode[STIX]{x1D6FC}=L(j_{1}\cdots j_{q})$
,
$\unicode[STIX]{x1D6FC}=L(j_{1}\cdots j_{q})$
,
 $\unicode[STIX]{x1D6FD}=R(j_{1}\cdots j_{q})$
. Following Definition 9 the standard germ
$\unicode[STIX]{x1D6FD}=R(j_{1}\cdots j_{q})$
. Following Definition 9 the standard germ
![]() $\unicode[STIX]{x1D713}_{I,J}$
is the affine map
$\unicode[STIX]{x1D713}_{I,J}$
is the affine map
 $\unicode[STIX]{x1D713}_{I,J}:[a,b]\rightarrow [\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}]$
given by the formula:
$\unicode[STIX]{x1D713}_{I,J}:[a,b]\rightarrow [\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}]$
given by the formula:
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{I,J}(x)=a+\biggl(\frac{\mathop{\prod }_{m=1}^{q}\unicode[STIX]{x1D706}_{j_{m}}}{\mathop{\prod }_{k=1}^{p}\unicode[STIX]{x1D706}_{i_{k}}^{-1}}\biggr)(x-a).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{I,J}(x)=a+\biggl(\frac{\mathop{\prod }_{m=1}^{q}\unicode[STIX]{x1D706}_{j_{m}}}{\mathop{\prod }_{k=1}^{p}\unicode[STIX]{x1D706}_{i_{k}}^{-1}}\biggr)(x-a).\end{eqnarray}$$
Each multi-index
![]() $I$
determines a vertex
$I$
determines a vertex
![]() $v_{I}$
of the tree, which is the endpoint of the geodesic issued from the root which travels along the edges labeled
$v_{I}$
of the tree, which is the endpoint of the geodesic issued from the root which travels along the edges labeled
 $i_{1},i_{2},\ldots ,i_{p}$
. Then, at the level of trees a standard germ corresponds to a combinatorial map sending the subtree hanging at the vertex
$i_{1},i_{2},\ldots ,i_{p}$
. Then, at the level of trees a standard germ corresponds to a combinatorial map sending the subtree hanging at the vertex
![]() $v_{I}$
onto the subtree issued from the vertex
$v_{I}$
onto the subtree issued from the vertex
![]() $v_{J}$
, as in the figure below:
$v_{J}$
, as in the figure below:

An extension of the standard germ
 $\unicode[STIX]{x1D713}:[a,b]\rightarrow [\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}]$
is a standard germ defined on
$\unicode[STIX]{x1D713}:[a,b]\rightarrow [\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}]$
is a standard germ defined on
 $[c,d]\supset [a,b]$
whose restriction to
$[c,d]\supset [a,b]$
whose restriction to
![]() $[a,b]$
coincides with
$[a,b]$
coincides with
![]() $\unicode[STIX]{x1D713}$
such that
$\unicode[STIX]{x1D713}$
such that
![]() $[c,d]$
corresponds to a vertex
$[c,d]$
corresponds to a vertex
![]() $v_{I^{\prime }}$
of the tree whose multi-index
$v_{I^{\prime }}$
of the tree whose multi-index
![]() $I^{\prime }$
is a prefix of
$I^{\prime }$
is a prefix of
![]() $I$
, namely
$I$
, namely
 $I^{\prime }=i_{1}i_{2}\cdots i_{r}$
with
$I^{\prime }=i_{1}i_{2}\cdots i_{r}$
with
![]() $r\leqslant p$
. Note that a non-trivial extension of
$r\leqslant p$
. Note that a non-trivial extension of
![]() $\unicode[STIX]{x1D713}$
exists only if
$\unicode[STIX]{x1D713}$
exists only if
![]() $i_{p}=j_{q}$
.
$i_{p}=j_{q}$
.
A multi-germ is a finite collection of standard germs
 $\unicode[STIX]{x1D713}_{j}:[a_{j},b_{j}]\rightarrow [\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}]$
such that:
$\unicode[STIX]{x1D713}_{j}:[a_{j},b_{j}]\rightarrow [\unicode[STIX]{x1D6FC}_{j},\unicode[STIX]{x1D6FD}_{j}]$
such that:
 $$\begin{eqnarray}a_{1}<b_{1}<a_{2}<b_{2}<c<\cdots <a_{k}<b_{k},\quad \unicode[STIX]{x1D6FC}_{1}<\unicode[STIX]{x1D6FD}_{1}<\unicode[STIX]{x1D6FC}_{2}<\unicode[STIX]{x1D6FD}_{2}<\cdots <\unicode[STIX]{x1D6FC}_{k}<\unicode[STIX]{x1D6FD}_{k}\end{eqnarray}$$
$$\begin{eqnarray}a_{1}<b_{1}<a_{2}<b_{2}<c<\cdots <a_{k}<b_{k},\quad \unicode[STIX]{x1D6FC}_{1}<\unicode[STIX]{x1D6FD}_{1}<\unicode[STIX]{x1D6FC}_{2}<\unicode[STIX]{x1D6FD}_{2}<\cdots <\unicode[STIX]{x1D6FC}_{k}<\unicode[STIX]{x1D6FD}_{k}\end{eqnarray}$$
and
 $[b_{j},a_{j+1}]$
and
$[b_{j},a_{j+1}]$
and
 $[\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FC}_{j+1}]$
are gaps of
$[\unicode[STIX]{x1D6FD}_{j},\unicode[STIX]{x1D6FC}_{j+1}]$
are gaps of
![]() $C$
, for all
$C$
, for all
![]() $j$
.
$j$
.
Eventually an extension of a multi-germ
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,k}$
is a multi-germ
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,k}$
is a multi-germ
 $\{\unicode[STIX]{x1D703}_{j}\}_{j=1,m}$
such that every standard germ
$\{\unicode[STIX]{x1D703}_{j}\}_{j=1,m}$
such that every standard germ
![]() $\unicode[STIX]{x1D713}_{j}$
is extended by some
$\unicode[STIX]{x1D713}_{j}$
is extended by some
![]() $\unicode[STIX]{x1D703}_{i}$
. Notice that several elements of the multi-germ
$\unicode[STIX]{x1D703}_{i}$
. Notice that several elements of the multi-germ
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,k}$
might have the same extension
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,k}$
might have the same extension
![]() $\unicode[STIX]{x1D703}_{i}$
.
$\unicode[STIX]{x1D703}_{i}$
.
Lemma 15. Let
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
be a multi-germ with the property that there exist constants
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
be a multi-germ with the property that there exist constants
 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}>0$
satisfying
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}>0$
satisfying
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}}{\unicode[STIX]{x1D708}}>\frac{1}{\max (\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{n})},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D707}}{\unicode[STIX]{x1D708}}>\frac{1}{\max (\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\ldots ,\unicode[STIX]{x1D706}_{n})},\end{eqnarray}$$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D713}_{j}^{\prime }(x)\leqslant \unicode[STIX]{x1D708}\quad \text{for every }x.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}\leqslant \unicode[STIX]{x1D713}_{j}^{\prime }(x)\leqslant \unicode[STIX]{x1D708}\quad \text{for every }x.\end{eqnarray}$$
If one standard germ
![]() $\unicode[STIX]{x1D713}_{i}$
, for some
$\unicode[STIX]{x1D713}_{i}$
, for some
 $i\in \{1,2,\ldots ,m\}$
, admits an extension
$i\in \{1,2,\ldots ,m\}$
, admits an extension
![]() $\unicode[STIX]{x1D712}$
, then there exists an extension of the multi-germ
$\unicode[STIX]{x1D712}$
, then there exists an extension of the multi-germ
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
containing the standard germ
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
containing the standard germ
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
Moreover, if a diffeomorphism
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R},C)$
whose derivative
$\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R},C)$
whose derivative
![]() $\unicode[STIX]{x1D711}^{\prime }$
verifies the condition for derivative (41) coincides with the multi-germ
$\unicode[STIX]{x1D711}^{\prime }$
verifies the condition for derivative (41) coincides with the multi-germ
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
on
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
on
![]() $[a_{1},b_{m}]$
, then it coincides with
$[a_{1},b_{m}]$
, then it coincides with
![]() $\unicode[STIX]{x1D712}$
on its domain of definition.
$\unicode[STIX]{x1D712}$
on its domain of definition.
Proof. The standard germ
![]() $\unicode[STIX]{x1D713}_{j}$
is of the form
$\unicode[STIX]{x1D713}_{j}$
is of the form
 $\unicode[STIX]{x1D713}_{j}=\unicode[STIX]{x1D713}_{I,J}$
, with
$\unicode[STIX]{x1D713}_{j}=\unicode[STIX]{x1D713}_{I,J}$
, with
 $i_{p}=j_{q}=k$
. We want to construct an increasing function extending the standard germ
$i_{p}=j_{q}=k$
. We want to construct an increasing function extending the standard germ
![]() $\unicode[STIX]{x1D713}_{I,J}$
which satisfies the condition (41) for the derivative. Such a function will be called a continuation of
$\unicode[STIX]{x1D713}_{I,J}$
which satisfies the condition (41) for the derivative. Such a function will be called a continuation of
![]() $\unicode[STIX]{x1D713}_{j}$
. Moving one step upward on the tree (i.e. the ancestor vertices) we arrive at the vertices
$\unicode[STIX]{x1D713}_{j}$
. Moving one step upward on the tree (i.e. the ancestor vertices) we arrive at the vertices
![]() $v_{I^{\prime }}$
and
$v_{I^{\prime }}$
and
![]() $v_{J^{\prime }}$
, where
$v_{J^{\prime }}$
, where
![]() $I=I^{\prime }k$
,
$I=I^{\prime }k$
,
 $J=J^{\prime }k$
.
$J=J^{\prime }k$
.
Consider first
![]() $k<n$
and seek for a continuation on the right side of the interval on which
$k<n$
and seek for a continuation on the right side of the interval on which
![]() $\unicode[STIX]{x1D713}_{I,J}$
is defined. Therefore the continuation must have the form drawn below, where points marked by squares correspond to each other:
$\unicode[STIX]{x1D713}_{I,J}$
is defined. Therefore the continuation must have the form drawn below, where points marked by squares correspond to each other:

Since the ratio of the derivatives is uniformly bounded, the vertices corresponding to squares should be on the same level, namely at equal distance from the vertices
![]() $v_{I^{\prime }}$
and
$v_{I^{\prime }}$
and
![]() $v_{J^{\prime }}$
, respectively. Consider the highest possible level of such squares for which the extended map is compatible with the standard germ
$v_{J^{\prime }}$
, respectively. Consider the highest possible level of such squares for which the extended map is compatible with the standard germ
![]() $\unicode[STIX]{x1D713}_{j+1}$
. We claim that this continuation has the following form, namely that squares sit on the vertices
$\unicode[STIX]{x1D713}_{j+1}$
. We claim that this continuation has the following form, namely that squares sit on the vertices
![]() $v_{I^{\prime }k+1}$
and
$v_{I^{\prime }k+1}$
and
![]() $v_{J^{\prime }k+1}$
:
$v_{J^{\prime }k+1}$
:

Assume the contrary holds, namely that the squares sit on lower levels, as in the figure below:

Consider further continuation to the right of this increasing function. We label points on the next branch issued from the ancestor of square vertices by triangles and further by hexagons etc. Consider further the highest levels for which continuation is compatible. Then the picture

is impossible, since the ancestor of the square vertex also should have been labeled by a square. Therefore we must continue along an infinite path down to a boundary point of the tree, as in the following figure:

The boundary point corresponds to an infinite multi-index
![]() $I$
. Then
$I$
. Then
 $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}(I)\in [0,1]$
cannot be a right point of the Cantor set, since this would give a continuation to a whole subtree issued from
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}(I)\in [0,1]$
cannot be a right point of the Cantor set, since this would give a continuation to a whole subtree issued from
![]() $v_{I^{\prime }}$
, contradicting the form of our path.
$v_{I^{\prime }}$
, contradicting the form of our path.
Now our continuation coincides with the multi-germ
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
for values
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
for values
 $x\in [a_{j},\unicode[STIX]{x1D709}]$
. Since
$x\in [a_{j},\unicode[STIX]{x1D709}]$
. Since
![]() $\unicode[STIX]{x1D709}$
is not a right point, they coincide in a right semi-neighborhood of
$\unicode[STIX]{x1D709}$
is not a right point, they coincide in a right semi-neighborhood of
![]() $\unicode[STIX]{x1D709}$
and this contradicts the choice of our infinite path.
$\unicode[STIX]{x1D709}$
and this contradicts the choice of our infinite path.
We summarize the discussion above as follows. Let
![]() $k_{r}<n$
; then the only possible right continuation (which satisfies the condition (41)) of
$k_{r}<n$
; then the only possible right continuation (which satisfies the condition (41)) of
 $\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r},Jk_{1}\cdots k_{r}}$
is by the germ
$\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r},Jk_{1}\cdots k_{r}}$
is by the germ
 $\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r-1}k_{r}+1,Jk_{1}\cdots k_{r-1}k_{r}+1}$
. A similar argument shows that whenever
$\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r-1}k_{r}+1,Jk_{1}\cdots k_{r-1}k_{r}+1}$
. A similar argument shows that whenever
![]() $k_{r}>0$
the only possible left continuation (which satisfies the condition (41)) of
$k_{r}>0$
the only possible left continuation (which satisfies the condition (41)) of
 $\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r},Jk_{1}\cdots k_{r}}$
is by the germ
$\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r},Jk_{1}\cdots k_{r}}$
is by the germ
 $\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r-1}k_{r}-1,Jk_{1}\cdots k_{r-1}k_{r}-1}$
.
$\unicode[STIX]{x1D713}_{Ik_{1}\cdots k_{r-1}k_{r}-1,Jk_{1}\cdots k_{r-1}k_{r}-1}$
.
Repeating the same argument, we get the desired statement. ◻
Lemma 16. There exists
![]() $\unicode[STIX]{x1D700}>0$
with the following property. Consider a standard germ
$\unicode[STIX]{x1D700}>0$
with the following property. Consider a standard germ
![]() $\unicode[STIX]{x1D713}_{I,J}$
with
$\unicode[STIX]{x1D713}_{I,J}$
with
![]() $i_{p}\neq j_{q}$
and
$i_{p}\neq j_{q}$
and
 $j_{q}\neq n\neq i_{p}$
.
$j_{q}\neq n\neq i_{p}$
.
Then any continuation of
![]() $\unicode[STIX]{x1D713}_{I,J}$
to a standard germ
$\unicode[STIX]{x1D713}_{I,J}$
to a standard germ
![]() $\unicode[STIX]{x1D703}$
sending
$\unicode[STIX]{x1D703}$
sending
 $L(i_{1}i_{2}\cdots i_{p-1}i_{p}+1)$
to
$L(i_{1}i_{2}\cdots i_{p-1}i_{p}+1)$
to
 $L(j_{1}j_{2}\cdots j_{q-1}j_{q}+1)$
which is defined in a right semi-neighborhood of
$L(j_{1}j_{2}\cdots j_{q-1}j_{q}+1)$
which is defined in a right semi-neighborhood of
 $L(i_{1}i_{2}\cdots i_{p-1}i_{p}+1)$
is either an extension of the standard germ
$L(i_{1}i_{2}\cdots i_{p-1}i_{p}+1)$
is either an extension of the standard germ
![]() $\unicode[STIX]{x1D713}_{I,J}$
, or else it verifies:
$\unicode[STIX]{x1D713}_{I,J}$
, or else it verifies:
 $$\begin{eqnarray}\biggl|\frac{\unicode[STIX]{x1D713}_{I,J}^{\prime }}{\unicode[STIX]{x1D703}^{\prime }}-1\biggr|>\unicode[STIX]{x1D700}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\frac{\unicode[STIX]{x1D713}_{I,J}^{\prime }}{\unicode[STIX]{x1D703}^{\prime }}-1\biggr|>\unicode[STIX]{x1D700}.\end{eqnarray}$$
Notice that
![]() $\unicode[STIX]{x1D703}$
is locally affine and hence we don’t need to specify the point (of the corresponding domain of definition) in which we consider the derivative.
$\unicode[STIX]{x1D703}$
is locally affine and hence we don’t need to specify the point (of the corresponding domain of definition) in which we consider the derivative.
Proof. The ratio of the derivatives of the standard germs
![]() $\unicode[STIX]{x1D713}_{I,J}$
and
$\unicode[STIX]{x1D713}_{I,J}$
and
 $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D713}_{i_{1}i_{2}\cdots i_{p-1}i_{p}+1,\;j_{1}j_{2}\cdots j_{q-1}j_{q}+1}$
is given by
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D713}_{i_{1}i_{2}\cdots i_{p-1}i_{p}+1,\;j_{1}j_{2}\cdots j_{q-1}j_{q}+1}$
is given by
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D713}^{\prime }}{\unicode[STIX]{x1D703}^{\prime }}=\frac{\unicode[STIX]{x1D706}_{i_{p}}^{-1}\unicode[STIX]{x1D706}_{i_{q}}}{\unicode[STIX]{x1D706}_{i_{p}+1}^{-1}\unicode[STIX]{x1D706}_{i_{q}+1}}\unicode[STIX]{x1D706}_{1}^{m},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D713}^{\prime }}{\unicode[STIX]{x1D703}^{\prime }}=\frac{\unicode[STIX]{x1D706}_{i_{p}}^{-1}\unicode[STIX]{x1D706}_{i_{q}}}{\unicode[STIX]{x1D706}_{i_{p}+1}^{-1}\unicode[STIX]{x1D706}_{i_{q}+1}}\unicode[STIX]{x1D706}_{1}^{m},\end{eqnarray}$$
where
![]() $m\in \mathbb{Z}$
. This is a discrete subset of
$m\in \mathbb{Z}$
. This is a discrete subset of
![]() $\mathbb{R}^{\ast }$
and hence the claim.◻
$\mathbb{R}^{\ast }$
and hence the claim.◻
We can apply the same arguments when
 $i_{p}\neq 0\neq j_{q}$
. Specifically, we have the following lemma.
$i_{p}\neq 0\neq j_{q}$
. Specifically, we have the following lemma.
Lemma 17. Let
![]() $n\geqslant 2$
. Then there exists
$n\geqslant 2$
. Then there exists
![]() $\unicode[STIX]{x1D700}>0$
such that any multi-germ
$\unicode[STIX]{x1D700}>0$
such that any multi-germ
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
with the property:
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
with the property:
 $$\begin{eqnarray}\biggl|\frac{\unicode[STIX]{x1D713}_{i}^{\prime }}{\unicode[STIX]{x1D713}_{j}^{\prime }}-1\biggr|<\unicode[STIX]{x1D700}\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\frac{\unicode[STIX]{x1D713}_{i}^{\prime }}{\unicode[STIX]{x1D713}_{j}^{\prime }}-1\biggr|<\unicode[STIX]{x1D700}\end{eqnarray}$$
admits an extension containing with at most two elements.
Proof. It remains to examine the standard germs
![]() $\unicode[STIX]{x1D713}_{I,J}$
in following two cases:
$\unicode[STIX]{x1D713}_{I,J}$
in following two cases:
 $$\begin{eqnarray}(I,J)\in \{(i_{1}\cdots i_{p-1}0,\;J=j_{1}\cdots j_{q-1}n),\;(i_{1}\cdots i_{p-1}n,\;j_{1}\cdots j_{q-1}0)\}.\end{eqnarray}$$
$$\begin{eqnarray}(I,J)\in \{(i_{1}\cdots i_{p-1}0,\;J=j_{1}\cdots j_{q-1}n),\;(i_{1}\cdots i_{p-1}n,\;j_{1}\cdots j_{q-1}0)\}.\end{eqnarray}$$
The corresponding picture depends on the number
![]() $s$
of occurrences of
$s$
of occurrences of
![]() $n$
in the tail of
$n$
in the tail of
 $j_{1}\cdots j_{q-1}n$
and the positions of the the square vertices (having
$j_{1}\cdots j_{q-1}n$
and the positions of the the square vertices (having
![]() $r$
and
$r$
and
![]() $m$
respectively ancestors labeled
$m$
respectively ancestors labeled
![]() $0$
) as below:
$0$
) as below:

The ratio of derivatives is
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D706}_{n}^{s}\unicode[STIX]{x1D706}_{k}\unicode[STIX]{x1D706}_{k+1}^{-1}\unicode[STIX]{x1D706}_{0}^{-r}}{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{1}^{-1}\unicode[STIX]{x1D706}_{0}^{-m}}=\frac{\unicode[STIX]{x1D706}_{k}\unicode[STIX]{x1D706}_{1}}{\unicode[STIX]{x1D706}_{k+1}}\cdot \frac{\unicode[STIX]{x1D706}_{n}^{s}}{\unicode[STIX]{x1D706}_{0}^{r-m+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D706}_{n}^{s}\unicode[STIX]{x1D706}_{k}\unicode[STIX]{x1D706}_{k+1}^{-1}\unicode[STIX]{x1D706}_{0}^{-r}}{\unicode[STIX]{x1D706}_{0}\unicode[STIX]{x1D706}_{1}^{-1}\unicode[STIX]{x1D706}_{0}^{-m}}=\frac{\unicode[STIX]{x1D706}_{k}\unicode[STIX]{x1D706}_{1}}{\unicode[STIX]{x1D706}_{k+1}}\cdot \frac{\unicode[STIX]{x1D706}_{n}^{s}}{\unicode[STIX]{x1D706}_{0}^{r-m+1}}.\end{eqnarray}$$
Letting
![]() $s$
and
$s$
and
 $\unicode[STIX]{x1D707}=r-m+1$
be large enough we can insure that
$\unicode[STIX]{x1D707}=r-m+1$
be large enough we can insure that
![]() $\unicode[STIX]{x1D706}_{n}^{s}/\unicode[STIX]{x1D706}_{0}^{\unicode[STIX]{x1D707}}$
is arbitrarily close to
$\unicode[STIX]{x1D706}_{n}^{s}/\unicode[STIX]{x1D706}_{0}^{\unicode[STIX]{x1D707}}$
is arbitrarily close to
 $\unicode[STIX]{x1D706}_{k+1}/\unicode[STIX]{x1D706}_{k}\unicode[STIX]{x1D706}_{1}$
. In this case
$\unicode[STIX]{x1D706}_{k+1}/\unicode[STIX]{x1D706}_{k}\unicode[STIX]{x1D706}_{1}$
. In this case
![]() $\unicode[STIX]{x1D707}>0$
, so that we can automatically extend the new standard germ obtained this way and get the figure below, where the position of the squared vertex is the highest possible:
$\unicode[STIX]{x1D707}>0$
, so that we can automatically extend the new standard germ obtained this way and get the figure below, where the position of the squared vertex is the highest possible:

Now, as
![]() $n\geqslant 2$
we cannot find a non-trivial extension of the two standard germs corresponding to the labeled vertices. This means that there is an extension with at most two elements, thereby proving our statement.◻
$n\geqslant 2$
we cannot find a non-trivial extension of the two standard germs corresponding to the labeled vertices. This means that there is an extension with at most two elements, thereby proving our statement.◻
Lemma 18. Let
![]() $n=1$
. Then there exists
$n=1$
. Then there exists
![]() $\unicode[STIX]{x1D700}>0$
such that any multi-germ
$\unicode[STIX]{x1D700}>0$
such that any multi-germ
 $\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
verifying the condition:
$\{\unicode[STIX]{x1D713}_{j}\}_{j=1,m}$
verifying the condition:
 $$\begin{eqnarray}\biggl|\frac{\unicode[STIX]{x1D713}_{i}^{\prime }}{\unicode[STIX]{x1D713}_{j}^{\prime }}-1\biggr|<1+\unicode[STIX]{x1D700}\end{eqnarray}$$
$$\begin{eqnarray}\biggl|\frac{\unicode[STIX]{x1D713}_{i}^{\prime }}{\unicode[STIX]{x1D713}_{j}^{\prime }}-1\biggr|<1+\unicode[STIX]{x1D700}\end{eqnarray}$$
admits an extension containing at most
![]() $4$
elements.
$4$
elements.
Proof. The only possible situation is that pictured below:

Consider a right continuation as follows:

In the left-hand side picture we have
![]() $r+1$
ancestors of the fat dotted vertex which are labeled
$r+1$
ancestors of the fat dotted vertex which are labeled
![]() $1$
and
$1$
and
![]() $s$
ancestors of the square vertex labeled
$s$
ancestors of the square vertex labeled
![]() $0$
, while in the right-hand picture there are
$0$
, while in the right-hand picture there are
![]() $v$
ancestors of the square vertex labeled
$v$
ancestors of the square vertex labeled
![]() $0$
. Then the ratio of derivatives of the two standard germs is:
$0$
. Then the ratio of derivatives of the two standard germs is:
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D706}_{1}^{-r-1}\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{0}^{s}}{\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{0}^{v}}=\frac{\unicode[STIX]{x1D706}_{0}^{s-v}}{\unicode[STIX]{x1D706}_{1}^{r+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D706}_{1}^{-r-1}\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{0}^{s}}{\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{0}^{v}}=\frac{\unicode[STIX]{x1D706}_{0}^{s-v}}{\unicode[STIX]{x1D706}_{1}^{r+1}}.\end{eqnarray}$$
We can approximate arbitrarily close
![]() $1$
by
$1$
by
 $\unicode[STIX]{x1D706}_{0}^{s-v}/\unicode[STIX]{x1D706}_{1}^{r+1}$
, but then
$\unicode[STIX]{x1D706}_{0}^{s-v}/\unicode[STIX]{x1D706}_{1}^{r+1}$
, but then
![]() $s-v$
must be large, and in particular positive. This implies that we can automatically extend this to a standard germ as follows:
$s-v$
must be large, and in particular positive. This implies that we can automatically extend this to a standard germ as follows:

or, after removing non-essential information:

And we now see that a right continuation is impossible. Thus we get our claim. ◻
4.3.2 Cantor sets with commensurable parameters
The genericity condition
![]() $(C)$
could be extended to include also the case when all homothety factors
$(C)$
could be extended to include also the case when all homothety factors
![]() $\unicode[STIX]{x1D706}_{i}$
are commensurable. We skip the details and present instead an example of an asymmetric Cantor set
$\unicode[STIX]{x1D706}_{i}$
are commensurable. We skip the details and present instead an example of an asymmetric Cantor set
![]() $AC$
which is the attractor of the IFS:
$AC$
which is the attractor of the IFS:
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}(x)={\textstyle \frac{1}{4}}x,\quad \unicode[STIX]{x1D719}_{1}(x)={\textstyle \frac{1}{2}}x+{\textstyle \frac{1}{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{0}(x)={\textstyle \frac{1}{4}}x,\quad \unicode[STIX]{x1D719}_{1}(x)={\textstyle \frac{1}{2}}x+{\textstyle \frac{1}{2}}.\end{eqnarray}$$
For each finite multi-index
 $I=i_{1}i_{2}\cdots i_{k}$
, with
$I=i_{1}i_{2}\cdots i_{k}$
, with
 $i_{j}\in \{0,1\}$
we set
$i_{j}\in \{0,1\}$
we set
![]() $l_{\emptyset }=0$
and define by induction:
$l_{\emptyset }=0$
and define by induction:
 $$\begin{eqnarray}l_{0I}={\textstyle \frac{1}{4}}l_{I},\quad l_{1I}={\textstyle \frac{1}{2}}l_{I}+{\textstyle \frac{1}{2}}.\end{eqnarray}$$
$$\begin{eqnarray}l_{0I}={\textstyle \frac{1}{4}}l_{I},\quad l_{1I}={\textstyle \frac{1}{2}}l_{I}+{\textstyle \frac{1}{2}}.\end{eqnarray}$$
Then
 $L(AC)=\{l_{I};I\text{ finite and admissible}\}$
, where
$L(AC)=\{l_{I};I\text{ finite and admissible}\}$
, where
 $I=i_{1}i_{2}\cdots i_{k}$
is admissible if it is either empty or else
$I=i_{1}i_{2}\cdots i_{k}$
is admissible if it is either empty or else
![]() $i_{k}=1$
. If we set
$i_{k}=1$
. If we set
 $l_{I}=\lim _{k\rightarrow \infty }l_{i_{1}i_{2}\ldots i_{k}}$
for infinite
$l_{I}=\lim _{k\rightarrow \infty }l_{i_{1}i_{2}\ldots i_{k}}$
for infinite
![]() $I$
, then
$I$
, then
![]() $AC$
is the union of
$AC$
is the union of
![]() $L(AC)$
and the set of
$L(AC)$
and the set of
![]() $l_{I}$
, with infinite
$l_{I}$
, with infinite
![]() $I$
. Further,
$I$
. Further,
![]() $L(AC)$
is identified with the set of those
$L(AC)$
is identified with the set of those
![]() $l_{I}$
for which
$l_{I}$
for which
![]() $I$
is infinite and eventually
$I$
is infinite and eventually
![]() $0$
. It follows as in the case of
$0$
. It follows as in the case of
![]() $C_{\unicode[STIX]{x1D706}}$
that
$C_{\unicode[STIX]{x1D706}}$
that
 $\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1}(AC))=\langle 4\rangle$
. Further, for
$\unicode[STIX]{x1D712}(\text{Diff}_{0}^{1}(AC))=\langle 4\rangle$
. Further, for
 $a,b\in L(AC)$
, we obtain
$a,b\in L(AC)$
, we obtain
 $$\begin{eqnarray}D(a,b)=\biggl\{\unicode[STIX]{x1D713}_{a,b,k}=b+\frac{1}{2^{n(a,b)}}4^{-k}(x-a),k\in \mathbb{Z}\biggr\},\end{eqnarray}$$
$$\begin{eqnarray}D(a,b)=\biggl\{\unicode[STIX]{x1D713}_{a,b,k}=b+\frac{1}{2^{n(a,b)}}4^{-k}(x-a),k\in \mathbb{Z}\biggr\},\end{eqnarray}$$
where
 $n(a,b)\in \{0,1\}$
is the parity of the length of the geodesic joining
$n(a,b)\in \{0,1\}$
is the parity of the length of the geodesic joining
![]() $a$
to
$a$
to
![]() $b$
in the reduced binary tree associated to the IFS.
$b$
in the reduced binary tree associated to the IFS.
The previous arguments show that any element
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
 $\mathfrak{diff}^{1,+}(AC)$
determines a finite covering of
$\mathfrak{diff}^{1,+}(AC)$
determines a finite covering of
![]() $AC$
by intervals
$AC$
by intervals
![]() $I_{j}$
on which
$I_{j}$
on which
![]() $\unicode[STIX]{x1D711}|_{I_{j}}$
is of the form
$\unicode[STIX]{x1D711}|_{I_{j}}$
is of the form
![]() $\unicode[STIX]{x1D713}_{a_{j},b_{j},k_{j}}$
, for some
$\unicode[STIX]{x1D713}_{a_{j},b_{j},k_{j}}$
, for some
 $a_{j}\in L(AC)$
. Moreover
$a_{j}\in L(AC)$
. Moreover
 $\mathfrak{diff}^{1,+}(AC)$
is isomorphic to the Thompson group
$\mathfrak{diff}^{1,+}(AC)$
is isomorphic to the Thompson group
![]() $F$
.
$F$
.
4.4 Proof of Theorem 7
Let
 $\text{Diff}_{a}^{1}(\mathbb{R}^{n},C)$
denote the stabilizer of
$\text{Diff}_{a}^{1}(\mathbb{R}^{n},C)$
denote the stabilizer of
![]() $a\in C$
in the group
$a\in C$
in the group
 $\text{Diff}^{1}(\mathbb{R}^{n},C)$
. We verify immediately that the map
$\text{Diff}^{1}(\mathbb{R}^{n},C)$
. We verify immediately that the map
 $\unicode[STIX]{x1D712}:\text{Diff}_{a}^{1}(\mathbb{R}^{n},C)\rightarrow \text{GL}(n,\mathbb{R})$
, given by
$\unicode[STIX]{x1D712}:\text{Diff}_{a}^{1}(\mathbb{R}^{n},C)\rightarrow \text{GL}(n,\mathbb{R})$
, given by
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711})=D_{a}\unicode[STIX]{x1D711}$
is a homomorphism. In the case when
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711})=D_{a}\unicode[STIX]{x1D711}$
is a homomorphism. In the case when
![]() $C$
is a product we can describe explicitly
$C$
is a product we can describe explicitly
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1}(\mathbb{R}^{n},C))$
. For the sake of simplicity we restrict ourselves to the case
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1}(\mathbb{R}^{n},C))$
. For the sake of simplicity we restrict ourselves to the case
![]() $n=2$
. Consider
$n=2$
. Consider
 $C=C_{\unicode[STIX]{x1D706}_{1}}\times C_{\unicode[STIX]{x1D706}_{2}}$
. We say that
$C=C_{\unicode[STIX]{x1D706}_{1}}\times C_{\unicode[STIX]{x1D706}_{2}}$
. We say that
 $a=(a_{1},a_{2})\in C$
is an end point of
$a=(a_{1},a_{2})\in C$
is an end point of
![]() $C$
if both
$C$
if both
![]() $a_{i}$
are endpoints of
$a_{i}$
are endpoints of
![]() $C_{\unicode[STIX]{x1D706}_{i}}$
.
$C_{\unicode[STIX]{x1D706}_{i}}$
.
Lemma 19. Suppose that
![]() $\unicode[STIX]{x1D706}_{i}>2$
and
$\unicode[STIX]{x1D706}_{i}>2$
and
![]() $a$
is an end point of
$a$
is an end point of
![]() $C$
.
$C$
.
(i) If
 $\unicode[STIX]{x1D706}_{1}\neq \unicode[STIX]{x1D706}_{2}$
then (43)
$\unicode[STIX]{x1D706}_{1}\neq \unicode[STIX]{x1D706}_{2}$
then (43) $$\begin{eqnarray}\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1}(\mathbb{R}^{2},C))=\langle \unicode[STIX]{x1D706}_{1}\rangle \oplus \langle \unicode[STIX]{x1D706}_{2}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1}(\mathbb{R}^{2},C))=\langle \unicode[STIX]{x1D706}_{1}\rangle \oplus \langle \unicode[STIX]{x1D706}_{2}\rangle .\end{eqnarray}$$
(ii) If
 $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}=\unicode[STIX]{x1D706}$
then (44)
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}=\unicode[STIX]{x1D706}$
then (44) $$\begin{eqnarray}\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+}(\mathbb{R}^{2},C))=\langle \unicode[STIX]{x1D706}\rangle \oplus \langle \unicode[STIX]{x1D706}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1,+}(\mathbb{R}^{2},C))=\langle \unicode[STIX]{x1D706}\rangle \oplus \langle \unicode[STIX]{x1D706}\rangle .\end{eqnarray}$$
Proof. From the first part of the proof of Theorem 4 we infer that whenever
![]() $C$
is a product and
$C$
is a product and
![]() $a\in C$
is fixed by
$a\in C$
is fixed by
![]() $\unicode[STIX]{x1D711},$
its differential
$\unicode[STIX]{x1D711},$
its differential
![]() $D_{a}\unicode[STIX]{x1D711}$
must send both horizontal and vertical vectors into horizontal or vertical vectors.
$D_{a}\unicode[STIX]{x1D711}$
must send both horizontal and vertical vectors into horizontal or vertical vectors.
Moreover, when
![]() $\unicode[STIX]{x1D706}_{i}$
are distinct, the horizontality/verticality of the segment should be preserved. Otherwise
$\unicode[STIX]{x1D706}_{i}$
are distinct, the horizontality/verticality of the segment should be preserved. Otherwise
![]() $\unicode[STIX]{x1D711}$
would induce a germ of
$\unicode[STIX]{x1D711}$
would induce a germ of
![]() ${\mathcal{C}}^{1}$
-diffeomorphism
${\mathcal{C}}^{1}$
-diffeomorphism
 $\unicode[STIX]{x1D719}:(\mathbb{R},C_{\unicode[STIX]{x1D706}_{1}})\rightarrow (\mathbb{R},C_{\unicode[STIX]{x1D706}_{2}})$
. By Remark 4 we need
$\unicode[STIX]{x1D719}:(\mathbb{R},C_{\unicode[STIX]{x1D706}_{1}})\rightarrow (\mathbb{R},C_{\unicode[STIX]{x1D706}_{2}})$
. By Remark 4 we need
 $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
.
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
.
Therefore
![]() $\unicode[STIX]{x1D711}$
restricts to germs of diffeomorphisms
$\unicode[STIX]{x1D711}$
restricts to germs of diffeomorphisms
 $\unicode[STIX]{x1D719}_{i}\in \text{Diff}_{a_{i}}^{1}(\mathbb{R},C_{\unicode[STIX]{x1D706}_{i}})$
. By Lemma 11 and Remark 7
$\unicode[STIX]{x1D719}_{i}\in \text{Diff}_{a_{i}}^{1}(\mathbb{R},C_{\unicode[STIX]{x1D706}_{i}})$
. By Lemma 11 and Remark 7
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D719}_{i})=\langle \unicode[STIX]{x1D706}_{i}\rangle$
. This proves the first item.
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D719}_{i})=\langle \unicode[STIX]{x1D706}_{i}\rangle$
. This proves the first item.
On the other hand when
 $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
we can locally identify
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
we can locally identify
 $(C_{\unicode[STIX]{x1D706}_{1}},a_{1})$
and
$(C_{\unicode[STIX]{x1D706}_{1}},a_{1})$
and
 $(C_{\unicode[STIX]{x1D706}_{2}},a_{2})$
by an affine germ. The linear map
$(C_{\unicode[STIX]{x1D706}_{2}},a_{2})$
by an affine germ. The linear map
 $R_{a}=(\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!)$
which exchanges the two orthogonal axes meeting at
$R_{a}=(\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!)$
which exchanges the two orthogonal axes meeting at
![]() $a\in C$
belongs to
$a\in C$
belongs to
 $\text{Diff}_{a}^{1}(\mathbb{R}^{2},C)$
. We can compose
$\text{Diff}_{a}^{1}(\mathbb{R}^{2},C)$
. We can compose
![]() $\unicode[STIX]{x1D711}$
with
$\unicode[STIX]{x1D711}$
with
![]() $R_{a}$
, if needed, in order to have
$R_{a}$
, if needed, in order to have
![]() $D_{a}\unicode[STIX]{x1D711}$
diagonal. Thus
$D_{a}\unicode[STIX]{x1D711}$
diagonal. Thus
 $\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1}(\mathbb{R}^{2},C))=\langle \langle \unicode[STIX]{x1D706}\rangle \oplus \langle \unicode[STIX]{x1D706}\rangle ,R_{a}\rangle$
. Taking into account that
$\unicode[STIX]{x1D712}(\text{Diff}_{a}^{1}(\mathbb{R}^{2},C))=\langle \langle \unicode[STIX]{x1D706}\rangle \oplus \langle \unicode[STIX]{x1D706}\rangle ,R_{a}\rangle$
. Taking into account that
 $\det (R_{a})=-1$
, so
$\det (R_{a})=-1$
, so
![]() $R_{a}$
is orientation reversing, we obtain the claim.
$R_{a}$
is orientation reversing, we obtain the claim.
Observe that
 $\mathfrak{diff}_{a,\mathbb{R}^{2}}^{1}(C)$
is either isomorphic to
$\mathfrak{diff}_{a,\mathbb{R}^{2}}^{1}(C)$
is either isomorphic to
![]() $\mathbb{Z}^{2}$
, when
$\mathbb{Z}^{2}$
, when
![]() $\unicode[STIX]{x1D706}_{i}$
are distinct, or an extension of
$\unicode[STIX]{x1D706}_{i}$
are distinct, or an extension of
![]() $\mathbb{Z}^{2}$
by
$\mathbb{Z}^{2}$
by
![]() $\mathbb{Z}/2\mathbb{Z}$
, otherwise.◻
$\mathbb{Z}/2\mathbb{Z}$
, otherwise.◻
Consider now that
 $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
. Now let
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
. Now let
![]() $a$
and
$a$
and
![]() $b$
be two end points of
$b$
be two end points of
![]() $C$
. Denote by
$C$
. Denote by
![]() $D(a,b)$
the set of germs at
$D(a,b)$
the set of germs at
![]() $a$
of classes in
$a$
of classes in
 $\mathfrak{diff}_{\mathbb{R}^{2}}^{1}(C)$
having representatives
$\mathfrak{diff}_{\mathbb{R}^{2}}^{1}(C)$
having representatives
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{2},C)$
such that
$\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{2},C)$
such that
 $\unicode[STIX]{x1D711}(a)=b$
. This set is acted upon transitively by
$\unicode[STIX]{x1D711}(a)=b$
. This set is acted upon transitively by
 $\mathfrak{diff}_{a,\mathbb{R}^{2}}^{1,+}(C)$
, so that
$\mathfrak{diff}_{a,\mathbb{R}^{2}}^{1,+}(C)$
, so that
![]() $D(a,b)$
consists of maps of the form
$D(a,b)$
consists of maps of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{a,b,\mathbf{k},n}(x)=(b_{j,i}+\unicode[STIX]{x1D706}^{k_{j}}(x_{i}-a_{j,i}))_{i=1,2}\circ S_{a}^{n_{b}}\quad \text{for any }x\in I_{j}\;\cap \;C.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{a,b,\mathbf{k},n}(x)=(b_{j,i}+\unicode[STIX]{x1D706}^{k_{j}}(x_{i}-a_{j,i}))_{i=1,2}\circ S_{a}^{n_{b}}\quad \text{for any }x\in I_{j}\;\cap \;C.\end{eqnarray}$$
where
![]() $S_{a}^{n_{b}}$
is an element of the group
$S_{a}^{n_{b}}$
is an element of the group
![]() $D_{2}$
of orientation preserving symmetries of the square, namely
$D_{2}$
of orientation preserving symmetries of the square, namely
![]() $S_{a}$
is a rotation of order
$S_{a}$
is a rotation of order
![]() $4$
fixing
$4$
fixing
![]() $a$
and
$a$
and
 $n_{b}\in \{0,1,2,3\}$
.
$n_{b}\in \{0,1,2,3\}$
.
Now the set of endpoints of
![]() $C$
is kept invariant by any
$C$
is kept invariant by any
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{2},C)$
. Therefore, for any endpoint
$\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R}^{2},C)$
. Therefore, for any endpoint
![]() $a\in C$
there exists some
$a\in C$
there exists some
![]() $k_{i},n$
depending on
$k_{i},n$
depending on
![]() $a$
such that
$a$
such that
 $D_{a}\unicode[STIX]{x1D711}=(\unicode[STIX]{x1D706}^{k_{1}}\oplus \unicode[STIX]{x1D706}^{k_{2}})\circ S_{a}^{n}$
. The set of possible values of
$D_{a}\unicode[STIX]{x1D711}=(\unicode[STIX]{x1D706}^{k_{1}}\oplus \unicode[STIX]{x1D706}^{k_{2}})\circ S_{a}^{n}$
. The set of possible values of
![]() $D_{a}\unicode[STIX]{x1D711}$
is then a discrete subset of
$D_{a}\unicode[STIX]{x1D711}$
is then a discrete subset of
 $\text{GL}(2,\mathbb{R})$
. Since endpoints of
$\text{GL}(2,\mathbb{R})$
. Since endpoints of
![]() $C$
are dense in
$C$
are dense in
![]() $C$
and
$C$
and
![]() $D\unicode[STIX]{x1D711}$
is continuous we have
$D\unicode[STIX]{x1D711}$
is continuous we have
![]() $D_{a}\unicode[STIX]{x1D711}$
is of the form
$D_{a}\unicode[STIX]{x1D711}$
is of the form
 $(\unicode[STIX]{x1D706}^{k_{1}}\oplus \unicode[STIX]{x1D706}^{k_{2}})\circ S_{a}^{n}$
, for any
$(\unicode[STIX]{x1D706}^{k_{1}}\oplus \unicode[STIX]{x1D706}^{k_{2}})\circ S_{a}^{n}$
, for any
![]() $a\in C$
and any
$a\in C$
and any
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C)$
.
$\unicode[STIX]{x1D711}\in \text{Diff}^{1,+}(\mathbb{R},C)$
.
For a given
![]() $\unicode[STIX]{x1D711}$
both the norm
$\unicode[STIX]{x1D711}$
both the norm
![]() $\Vert D\unicode[STIX]{x1D711}\Vert$
and the determinant
$\Vert D\unicode[STIX]{x1D711}\Vert$
and the determinant
 $\det (D\unicode[STIX]{x1D711})$
of its differential are continuous on
$\det (D\unicode[STIX]{x1D711})$
of its differential are continuous on
 $[0,1]\times [0,1]$
and hence they are bounded. Moreover, the same argument for
$[0,1]\times [0,1]$
and hence they are bounded. Moreover, the same argument for
![]() $\unicode[STIX]{x1D711}^{-1}$
shows that these quantities are also bounded from below away from
$\unicode[STIX]{x1D711}^{-1}$
shows that these quantities are also bounded from below away from
![]() $0$
, so that
$0$
, so that
![]() $D\unicode[STIX]{x1D711}|_{C}$
can only take finitely many values. The next point is the analogue of Lemma 12 to this situation.
$D\unicode[STIX]{x1D711}|_{C}$
can only take finitely many values. The next point is the analogue of Lemma 12 to this situation.
Lemma 20. There is a covering of
![]() $C$
by a finite collection of disjoint standard rectangles
$C$
by a finite collection of disjoint standard rectangles
![]() $I_{k}$
whose images are standard rectangles such that
$I_{k}$
whose images are standard rectangles such that
![]() $\unicode[STIX]{x1D711}|_{C\;\cap \;I_{k}}$
is the restriction of an affine function and more precisely we have
$\unicode[STIX]{x1D711}|_{C\;\cap \;I_{k}}$
is the restriction of an affine function and more precisely we have
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=(\unicode[STIX]{x1D706}^{j_{k,1}}\oplus \unicode[STIX]{x1D706}^{j_{k,2}})\circ S_{b_{k}}^{m_{k}}(x-(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}))+\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\quad \text{for }x\in I_{k}\;\cap \;C,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=(\unicode[STIX]{x1D706}^{j_{k,1}}\oplus \unicode[STIX]{x1D706}^{j_{k,2}})\circ S_{b_{k}}^{m_{k}}(x-(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}))+\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\quad \text{for }x\in I_{k}\;\cap \;C,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FC}_{i}$
are left points of
$\unicode[STIX]{x1D6FC}_{i}$
are left points of
![]() $C_{i}$
.
$C_{i}$
.
Proof. We can choose both
![]() $I_{k}$
and their images to be standard rectangles, as in the case of central Cantor sets
$I_{k}$
and their images to be standard rectangles, as in the case of central Cantor sets
![]() $C_{\unicode[STIX]{x1D706}}$
.
$C_{\unicode[STIX]{x1D706}}$
.
Let
![]() $c\in C$
. Then
$c\in C$
. Then
 $D_{c}\unicode[STIX]{x1D711}=(\unicode[STIX]{x1D706}^{j_{k,1}}\oplus \unicode[STIX]{x1D706}^{j_{k,2}})\circ S_{b_{k}}^{m_{k}}$
, which we denote by
$D_{c}\unicode[STIX]{x1D711}=(\unicode[STIX]{x1D706}^{j_{k,1}}\oplus \unicode[STIX]{x1D706}^{j_{k,2}})\circ S_{b_{k}}^{m_{k}}$
, which we denote by
![]() $A$
for simplicity in the proof. We have to prove that there exists a neighborhood
$A$
for simplicity in the proof. We have to prove that there exists a neighborhood
![]() $U$
of
$U$
of
![]() $c$
such that
$c$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=A(x-(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}))+\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\quad \text{for }x\in U\;\cap \;C.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=A(x-(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}))+\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})\quad \text{for }x\in U\;\cap \;C.\end{eqnarray}$$
Such neighborhoods will cover
![]() $C$
and we can extract a finite subcovering by clopen sets to get the statement.
$C$
and we can extract a finite subcovering by clopen sets to get the statement.
This claim is true for endpoints
 $a=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})$
of
$a=(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})$
of
![]() $C$
. It is then sufficient to prove that whenever we have a sequence of endpoints
$C$
. It is then sufficient to prove that whenever we have a sequence of endpoints
 $a_{n}\rightarrow a_{\infty }$
contained in a closed rectangle
$a_{n}\rightarrow a_{\infty }$
contained in a closed rectangle
 $U\;\subset \;[0,1]$
and a
$U\;\subset \;[0,1]$
and a
![]() ${\mathcal{C}}^{1}$
-diffeomorphism
${\mathcal{C}}^{1}$
-diffeomorphism
 $\unicode[STIX]{x1D711}:U\rightarrow \unicode[STIX]{x1D711}(U)\;\subset \;[0,1]$
with
$\unicode[STIX]{x1D711}:U\rightarrow \unicode[STIX]{x1D711}(U)\;\subset \;[0,1]$
with
 $\unicode[STIX]{x1D711}(C\;\cap \;U)\;\subset \;C$
, there exists a neighborhood
$\unicode[STIX]{x1D711}(C\;\cap \;U)\;\subset \;C$
, there exists a neighborhood
![]() $U_{a_{\infty }}$
of
$U_{a_{\infty }}$
of
![]() $a_{\infty }$
and an affine function
$a_{\infty }$
and an affine function
![]() $\unicode[STIX]{x1D713}$
such that for large enough
$\unicode[STIX]{x1D713}$
such that for large enough
![]() $n$
the following holds:
$n$
the following holds:
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{\infty }}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{\infty }}.\end{eqnarray}$$
Around each left point
![]() $a_{n}$
there are affine maps
$a_{n}$
there are affine maps
 $\unicode[STIX]{x1D713}_{a_{n}}:U_{a_{n},k_{n}}\rightarrow [0,1]$
defining germs in
$\unicode[STIX]{x1D713}_{a_{n}}:U_{a_{n},k_{n}}\rightarrow [0,1]$
defining germs in
 $D(a_{n},c_{n})$
, where
$D(a_{n},c_{n})$
, where
 $c_{n}=\unicode[STIX]{x1D711}(a_{n})$
, such that
$c_{n}=\unicode[STIX]{x1D711}(a_{n})$
, such that
![]() $c_{n}$
converge to
$c_{n}$
converge to
 $c_{\infty }=\unicode[STIX]{x1D711}(a_{\infty })$
and
$c_{\infty }=\unicode[STIX]{x1D711}(a_{\infty })$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}_{a_{n}}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{n},k_{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(x)=\unicode[STIX]{x1D713}_{a_{n}}(x)\quad \text{for }x\in C_{\unicode[STIX]{x1D706}}\;\cap \;U_{a_{n},k_{n}}.\end{eqnarray}$$
We can further assume that
 $U_{a_{n}}\;\cap \;C_{\unicode[STIX]{x1D706}}$
are clopen sets and we can take
$U_{a_{n}}\;\cap \;C_{\unicode[STIX]{x1D706}}$
are clopen sets and we can take
![]() $U_{a_{n}}$
to be standard rectangles
$U_{a_{n}}$
to be standard rectangles
 $[\unicode[STIX]{x1D6FC}_{n,1},\unicode[STIX]{x1D6FD}_{n,1}]\times [\unicode[STIX]{x1D6FC}_{n,2},\unicode[STIX]{x1D6FD}_{n,2}]$
where
$[\unicode[STIX]{x1D6FC}_{n,1},\unicode[STIX]{x1D6FD}_{n,1}]\times [\unicode[STIX]{x1D6FC}_{n,2},\unicode[STIX]{x1D6FD}_{n,2}]$
where
![]() $\unicode[STIX]{x1D6FD}_{n,i}$
are right points of
$\unicode[STIX]{x1D6FD}_{n,i}$
are right points of
![]() $C_{i}$
.
$C_{i}$
.
There is no loss of generality to assume that
 $D\unicode[STIX]{x1D713}_{a_{n}}|_{C\;\cap \;U_{a_{n}}}$
is independent on
$D\unicode[STIX]{x1D713}_{a_{n}}|_{C\;\cap \;U_{a_{n}}}$
is independent on
![]() $n$
, say it equals
$n$
, say it equals
 $(\unicode[STIX]{x1D706}^{m_{1}}\oplus \unicode[STIX]{x1D706}^{m_{2}})S^{j}$
. Replacing
$(\unicode[STIX]{x1D706}^{m_{1}}\oplus \unicode[STIX]{x1D706}^{m_{2}})S^{j}$
. Replacing
![]() $\unicode[STIX]{x1D711}$
by its inverse
$\unicode[STIX]{x1D711}$
by its inverse
![]() $\unicode[STIX]{x1D711}^{-1}$
we can also assume that
$\unicode[STIX]{x1D711}^{-1}$
we can also assume that
![]() $m_{1}\leqslant 0$
. Since
$m_{1}\leqslant 0$
. Since
![]() $C_{1}$
is invariant by the homothety of factor
$C_{1}$
is invariant by the homothety of factor
![]() $\unicode[STIX]{x1D706}$
and center
$\unicode[STIX]{x1D706}$
and center
![]() $0$
, we can further reduce the problem to the case where
$0$
, we can further reduce the problem to the case where
![]() $m_{1}=0$
. We can further assume that
$m_{1}=0$
. We can further assume that
![]() $m_{2}\leqslant 0$
by the same trick and finally get rid of the second diagonal component of the differential. Then, by continuity, we have
$m_{2}\leqslant 0$
by the same trick and finally get rid of the second diagonal component of the differential. Then, by continuity, we have
 $D_{a_{\infty }}\unicode[STIX]{x1D711}=S^{j}$
.
$D_{a_{\infty }}\unicode[STIX]{x1D711}=S^{j}$
.
Choose
![]() $n$
large enough so that
$n$
large enough so that
 $\Vert D_{x}\unicode[STIX]{x1D711}(x)-\mathbf{1}\Vert <\unicode[STIX]{x1D700}$
, for any
$\Vert D_{x}\unicode[STIX]{x1D711}(x)-\mathbf{1}\Vert <\unicode[STIX]{x1D700}$
, for any
![]() $x$
in a square centered at
$x$
in a square centered at
![]() $a_{\infty }$
and containing all
$a_{\infty }$
and containing all
![]() $U_{a_{n}}$
, with
$U_{a_{n}}$
, with
![]() $n$
large enough, where the exact value of
$n$
large enough, where the exact value of
![]() $\unicode[STIX]{x1D700}$
will be chosen later.
$\unicode[STIX]{x1D700}$
will be chosen later.
Now consider the maximal standard rectangle of the form
 $U^{\prime }=[\unicode[STIX]{x1D6FC}_{n,1},\unicode[STIX]{x1D6FD}_{1}]\times [\unicode[STIX]{x1D6FC}_{n,2},\unicode[STIX]{x1D6FD}_{2}]$
to which we can extend
$U^{\prime }=[\unicode[STIX]{x1D6FC}_{n,1},\unicode[STIX]{x1D6FD}_{1}]\times [\unicode[STIX]{x1D6FC}_{n,2},\unicode[STIX]{x1D6FD}_{2}]$
to which we can extend
![]() $\unicode[STIX]{x1D713}_{a_{n}}$
to an affine function which coincides with
$\unicode[STIX]{x1D713}_{a_{n}}$
to an affine function which coincides with
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $C\;\cap \;U^{\prime }$
.
$C\;\cap \;U^{\prime }$
.
The endpoint
![]() $(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2})$
belongs to the closure of three maximal rectangular gaps: the rectangle
$(\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2})$
belongs to the closure of three maximal rectangular gaps: the rectangle
![]() $Q$
which is opposite to
$Q$
which is opposite to
![]() $U^{\prime }$
is a product of two gaps, while the other two
$U^{\prime }$
is a product of two gaps, while the other two
![]() $Q_{v}$
and
$Q_{v}$
and
![]() $Q_{h}$
are products of gaps with one (vertical or horizontal) side of
$Q_{h}$
are products of gaps with one (vertical or horizontal) side of
![]() $U^{\prime }$
. Since
$U^{\prime }$
. Since
![]() $D_{x}\unicode[STIX]{x1D711}$
is close to identity the image of the rectangular gaps are closed to rectangular gaps of approximatively the same sizes. Now, the images by
$D_{x}\unicode[STIX]{x1D711}$
is close to identity the image of the rectangular gaps are closed to rectangular gaps of approximatively the same sizes. Now, the images by
![]() $\unicode[STIX]{x1D711}$
of the vertices of
$\unicode[STIX]{x1D711}$
of the vertices of
![]() $Q$
are points of
$Q$
are points of
![]() $C$
forming a rectangle, which is itself the product of two gaps. Thus the sizes of this rectangle belong to the set
$C$
forming a rectangle, which is itself the product of two gaps. Thus the sizes of this rectangle belong to the set
 $\{(\unicode[STIX]{x1D706}-2)\unicode[STIX]{x1D706}^{-n};n\in \mathbb{Z}_{+}\}\times \{(\unicode[STIX]{x1D706}-2)\unicode[STIX]{x1D706}^{-n};n\in \mathbb{Z}_{+}\}$
. Since the ratios of two different lengths form a discrete set and
$\{(\unicode[STIX]{x1D706}-2)\unicode[STIX]{x1D706}^{-n};n\in \mathbb{Z}_{+}\}\times \{(\unicode[STIX]{x1D706}-2)\unicode[STIX]{x1D706}^{-n};n\in \mathbb{Z}_{+}\}$
. Since the ratios of two different lengths form a discrete set and
![]() $D_{x}\unicode[STIX]{x1D711}$
is close to identity, the four points in the image form a rectangle congruent to
$D_{x}\unicode[STIX]{x1D711}$
is close to identity, the four points in the image form a rectangle congruent to
![]() $Q$
. A similar argument holds now for the rectangles
$Q$
. A similar argument holds now for the rectangles
![]() $Q_{v}$
and
$Q_{v}$
and
![]() $Q_{h}$
. This implies that
$Q_{h}$
. This implies that
![]() $\unicode[STIX]{x1D713}_{a_{n}}$
can be extended to an affine function on a strictly larger rectangle, contradicting our assumptions. This proves the claim.◻
$\unicode[STIX]{x1D713}_{a_{n}}$
can be extended to an affine function on a strictly larger rectangle, contradicting our assumptions. This proves the claim.◻
This description shows that
 $\mathfrak{diff}_{\mathbb{R}^{2}}^{1,+}(C)$
is isomorphic to
$\mathfrak{diff}_{\mathbb{R}^{2}}^{1,+}(C)$
is isomorphic to
![]() $2V^{\text{sym}}$
, namely the Brin’s group decorated by
$2V^{\text{sym}}$
, namely the Brin’s group decorated by
![]() $D_{2}$
(see [Reference BrinBri04] for the non-decorated case). Here
$D_{2}$
(see [Reference BrinBri04] for the non-decorated case). Here
![]() $D_{2}$
is the group of the orientation preserving symmetries of the cube, namely the group of orthogonal matrices with integral entries and unit determinant.
$D_{2}$
is the group of the orientation preserving symmetries of the cube, namely the group of orthogonal matrices with integral entries and unit determinant.
Remark 12. We can obtain smaller decoration by choosing self-similar Cantor sets with fewer symmetries. For instance,
 $\mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C)$
is isomorphic to Brin’s group decorated by the positive isometry group of a rectangular parallelepiped with edges of different sizes, if
$\mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C)$
is isomorphic to Brin’s group decorated by the positive isometry group of a rectangular parallelepiped with edges of different sizes, if
 $C=C_{\unicode[STIX]{x1D706}_{1}}\times C_{\unicode[STIX]{x1D706}_{2}}\times \cdots C_{\unicode[STIX]{x1D706}_{n}}$
, where
$C=C_{\unicode[STIX]{x1D706}_{1}}\times C_{\unicode[STIX]{x1D706}_{2}}\times \cdots C_{\unicode[STIX]{x1D706}_{n}}$
, where
![]() $\unicode[STIX]{x1D706}_{i}$
are pairwise distinct but commensurable, namely there exists
$\unicode[STIX]{x1D706}_{i}$
are pairwise distinct but commensurable, namely there exists
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{R}_{+}^{\ast }$
and
$\unicode[STIX]{x1D6FC}\in \mathbb{R}_{+}^{\ast }$
and
![]() $k_{i}\in \mathbb{Z}$
such that
$k_{i}\in \mathbb{Z}$
such that
 $\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D6FC}^{k_{i}}$
, for all
$\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D6FC}^{k_{i}}$
, for all
![]() $i$
. We expect a similar result when
$i$
. We expect a similar result when
![]() $\unicode[STIX]{x1D706}_{i}$
are incommensurable. Moreover, by replacing each
$\unicode[STIX]{x1D706}_{i}$
are incommensurable. Moreover, by replacing each
![]() $C_{\unicode[STIX]{x1D706}_{i}}$
by some non-invertible self-similar Cantor set, the corresponding group
$C_{\unicode[STIX]{x1D706}_{i}}$
by some non-invertible self-similar Cantor set, the corresponding group
 $\mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C)$
is isomorphic to Brin’s group
$\mathfrak{diff}_{\mathbb{R}^{n}}^{1,+}(C)$
is isomorphic to Brin’s group
![]() $nV$
.
$nV$
.
Remark 13. Following the arguments in the proof of Theorem 3 one shows that
 $\mathfrak{diff}_{\mathbb{R}^{n+k}}^{1,+}(C)$
, for
$\mathfrak{diff}_{\mathbb{R}^{n+k}}^{1,+}(C)$
, for
![]() $k\geqslant 1$
, is Brin’s group
$k\geqslant 1$
, is Brin’s group
 $nV^{\pm \text{sym}}$
decorated by the hyperoctahedral group
$nV^{\pm \text{sym}}$
decorated by the hyperoctahedral group
![]() $O_{n}$
, namely the group of symmetries of the cube (possibly reversing the orientation).
$O_{n}$
, namely the group of symmetries of the cube (possibly reversing the orientation).
5 Examples and counterexamples
5.1 Non-sparse Cantor sets with uncountable diffeomorphism group
Let
 $h:\mathbb{R}_{+}\rightarrow \mathbb{R}$
be a
$h:\mathbb{R}_{+}\rightarrow \mathbb{R}$
be a
![]() $C^{\infty }$
-function satisfying the following conditions:
$C^{\infty }$
-function satisfying the following conditions:
 $$\begin{eqnarray}\displaystyle h(x) & = & \displaystyle 0\quad \text{for }0\leqslant x\leqslant 1,x\geqslant 2,\nonumber\\ \displaystyle h(x) & {>} & \displaystyle 0\quad \text{for }1<x<2,\nonumber\\ \displaystyle h^{\prime }(x) & {>} & \displaystyle -1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(x) & = & \displaystyle 0\quad \text{for }0\leqslant x\leqslant 1,x\geqslant 2,\nonumber\\ \displaystyle h(x) & {>} & \displaystyle 0\quad \text{for }1<x<2,\nonumber\\ \displaystyle h^{\prime }(x) & {>} & \displaystyle -1.\nonumber\end{eqnarray}$$
Since the maps
 $g_{j}:[0,1]\rightarrow [0,1]$
given by
$g_{j}:[0,1]\rightarrow [0,1]$
given by
 $$\begin{eqnarray}g_{j}(x)=x+2^{-2^{j}}h(2^{j}x),\quad j\in \mathbb{Z}_{+}^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}g_{j}(x)=x+2^{-2^{j}}h(2^{j}x),\quad j\in \mathbb{Z}_{+}^{\ast },\end{eqnarray}$$
are strictly increasing, they are smooth diffeomorphisms of the interval. The support of
![]() $g_{j}$
is
$g_{j}$
is
 $[2^{-j},2^{-j+1}]$
and hence the diffeomorphisms
$[2^{-j},2^{-j+1}]$
and hence the diffeomorphisms
![]() $g_{j}$
pairwise commute. Their derivatives are of the form:
$g_{j}$
pairwise commute. Their derivatives are of the form:
 $$\begin{eqnarray}g_{j}^{\prime }(x)=1+2^{j-2^{j}}h^{\prime }(2^{j}x),\end{eqnarray}$$
$$\begin{eqnarray}g_{j}^{\prime }(x)=1+2^{j-2^{j}}h^{\prime }(2^{j}x),\end{eqnarray}$$
and respectively
 $$\begin{eqnarray}g_{j}^{(k)}(x)=2^{kj-2^{j}}h^{(k)}(2^{j}x)\quad \text{for }k\geqslant 2.\end{eqnarray}$$
$$\begin{eqnarray}g_{j}^{(k)}(x)=2^{kj-2^{j}}h^{(k)}(2^{j}x)\quad \text{for }k\geqslant 2.\end{eqnarray}$$
Consider the group
![]() $R$
consisting of bounded infinite sequences
$R$
consisting of bounded infinite sequences
 $\mathbf{m}=m_{1},m_{2},\ldots$
of integers, endowed with the term-wise addition.
$\mathbf{m}=m_{1},m_{2},\ldots$
of integers, endowed with the term-wise addition.
There is a map
 $\unicode[STIX]{x1D6E9}:R\rightarrow \text{Diff}^{0}([0,1])$
given by
$\unicode[STIX]{x1D6E9}:R\rightarrow \text{Diff}^{0}([0,1])$
given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}(\mathbf{m})=\lim _{n\rightarrow \infty }g_{1}^{m_{1}}\circ g_{2}^{m_{2}}\circ \cdots \circ g_{n}^{m_{n}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(\mathbf{m})=\lim _{n\rightarrow \infty }g_{1}^{m_{1}}\circ g_{2}^{m_{2}}\circ \cdots \circ g_{n}^{m_{n}},\end{eqnarray}$$
where
![]() $g_{j}^{m}$
is the
$g_{j}^{m}$
is the
![]() $m$
-fold composition of
$m$
-fold composition of
![]() $g_{j}$
. The order in the previous definition does not matter, as the maps commute. The limit map
$g_{j}$
. The order in the previous definition does not matter, as the maps commute. The limit map
![]() $\unicode[STIX]{x1D6E9}(m)$
is immediately seen to be a homeomorphism of
$\unicode[STIX]{x1D6E9}(m)$
is immediately seen to be a homeomorphism of
![]() $[0,1]$
which is a diffeomorphism outside
$[0,1]$
which is a diffeomorphism outside
![]() $0$
.
$0$
.
Let us first consider only those
![]() $\mathbf{m}$
where
$\mathbf{m}$
where
 $m_{j}\in \{0,1\}$
. Then we can compute first
$m_{j}\in \{0,1\}$
. Then we can compute first
 $$\begin{eqnarray}\lim _{x\rightarrow 0}\unicode[STIX]{x1D6E9}(\mathbf{m})^{\prime }(x)=1,\end{eqnarray}$$
$$\begin{eqnarray}\lim _{x\rightarrow 0}\unicode[STIX]{x1D6E9}(\mathbf{m})^{\prime }(x)=1,\end{eqnarray}$$
and then
 $$\begin{eqnarray}\lim _{x\rightarrow 0}\unicode[STIX]{x1D6E9}(\mathbf{m})^{(k)}(x)=1\quad \text{for }k\geqslant 2.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{x\rightarrow 0}\unicode[STIX]{x1D6E9}(\mathbf{m})^{(k)}(x)=1\quad \text{for }k\geqslant 2.\end{eqnarray}$$
Therefore
![]() $\unicode[STIX]{x1D6E9}(\mathbf{m})$
is a
$\unicode[STIX]{x1D6E9}(\mathbf{m})$
is a
![]() ${\mathcal{C}}^{\infty }$
diffeomorphism of
${\mathcal{C}}^{\infty }$
diffeomorphism of
![]() $[0,1]$
.
$[0,1]$
.
Moreover any element of
![]() $R$
can be represented as a product of
$R$
can be represented as a product of
![]() $\unicode[STIX]{x1D6E9}(\mathbf{m})$
, with
$\unicode[STIX]{x1D6E9}(\mathbf{m})$
, with
![]() $\mathbf{m}$
of having only
$\mathbf{m}$
of having only
![]() $0$
or
$0$
or
![]() $1$
entries. This implies that
$1$
entries. This implies that
 $\unicode[STIX]{x1D6E9}(R)\;\subset \;\text{Diff}^{\infty }([0,1])$
. Furthermore it is clear that
$\unicode[STIX]{x1D6E9}(R)\;\subset \;\text{Diff}^{\infty }([0,1])$
. Furthermore it is clear that
![]() $\unicode[STIX]{x1D6E9}$
is injective, by looking at the factor corresponding to the first place where two sequences disagree. This implies that
$\unicode[STIX]{x1D6E9}$
is injective, by looking at the factor corresponding to the first place where two sequences disagree. This implies that
![]() $\unicode[STIX]{x1D6E9}$
provides a faithful
$\unicode[STIX]{x1D6E9}$
provides a faithful
![]() ${\mathcal{C}}^{\infty }$
action of
${\mathcal{C}}^{\infty }$
action of
![]() $R$
by
$R$
by
![]() ${\mathcal{C}}^{\infty }$
diffeomorphisms on
${\mathcal{C}}^{\infty }$
diffeomorphisms on
![]() $[0,1]$
.
$[0,1]$
.
The dynamics of each
![]() $g_{j}$
on its support
$g_{j}$
on its support
 $[2^{-j},2^{-j+1}]$
is of type north-south with repelling and attracting fixed points on the boundary. Pick up some
$[2^{-j},2^{-j+1}]$
is of type north-south with repelling and attracting fixed points on the boundary. Pick up some
 $a_{j}\in (2^{-j},2^{-j+1})$
, so that
$a_{j}\in (2^{-j},2^{-j+1})$
, so that
 $b_{j}=g_{j}(a_{j})>a_{j}$
. Then the intervals
$b_{j}=g_{j}(a_{j})>a_{j}$
. Then the intervals
 $g_{j}^{n}((a_{j},b_{j}))$
are all pairwise disjoint. If
$g_{j}^{n}((a_{j},b_{j}))$
are all pairwise disjoint. If
 $C_{j}^{0}\;\subset \;[a_{j},b_{j}]$
is some Cantor set, then the closure of its orbit, namely
$C_{j}^{0}\;\subset \;[a_{j},b_{j}]$
is some Cantor set, then the closure of its orbit, namely
 $C_{j}=\bigcup _{k=-\infty }^{\infty }g_{j}^{k}(C_{j}^{0})\;\cup \;\{2^{-j},2^{-j+1}\}$
is a
$C_{j}=\bigcup _{k=-\infty }^{\infty }g_{j}^{k}(C_{j}^{0})\;\cup \;\{2^{-j},2^{-j+1}\}$
is a
![]() $g_{j}$
-invariant Cantor subset of
$g_{j}$
-invariant Cantor subset of
 $[2^{-j},2^{-j+1}]$
. Moreover, for any
$[2^{-j},2^{-j+1}]$
. Moreover, for any
![]() $n\neq 0$
the restriction
$n\neq 0$
the restriction
![]() $g_{j}^{n}|_{C_{j}}$
cannot be identity, since
$g_{j}^{n}|_{C_{j}}$
cannot be identity, since
![]() $g_{j}^{n}$
is strictly increasing.
$g_{j}^{n}$
is strictly increasing.
Then their union
 $C=\bigcup _{j=1}^{\infty }C_{j}$
is a Cantor subset of
$C=\bigcup _{j=1}^{\infty }C_{j}$
is a Cantor subset of
![]() $[0,1]$
and for
$[0,1]$
and for
![]() $\mathbf{m}$
not identically
$\mathbf{m}$
not identically
![]() $0$
we also have
$0$
we also have
 $\unicode[STIX]{x1D6E9}(\mathbf{m})|_{C}$
is not identity. This shows that the diffeomorphism group
$\unicode[STIX]{x1D6E9}(\mathbf{m})|_{C}$
is not identity. This shows that the diffeomorphism group
 $\mathfrak{diff}^{\infty }(C)$
contains
$\mathfrak{diff}^{\infty }(C)$
contains
![]() $R$
. In particular,
$R$
. In particular,
 $\mathfrak{diff}^{\infty }(C)$
is uncountable.
$\mathfrak{diff}^{\infty }(C)$
is uncountable.
This technique of construction is close to that involved in other classical constructions in the field, as in [Reference TsuboiTsu95, Reference NavasNav08, Reference JorqueraJor12]. In particular, such a group arises as the group of fragmentations of elements of the Grigorchuk–Maki group of intermediate growth acting by
![]() ${\mathcal{C}}^{1}$
-diffeomorphisms of the interval from [Reference NavasNav08].
${\mathcal{C}}^{1}$
-diffeomorphisms of the interval from [Reference NavasNav08].
5.2 Non-sparse Cantor set with trivial diffeomorphism group
Let
![]() $X$
be obtained by removing a sequence of intervals, as follows. At the first step we remove from
$X$
be obtained by removing a sequence of intervals, as follows. At the first step we remove from
![]() $[0,1]$
the central interval of length
$[0,1]$
the central interval of length
![]() $1/4$
. At the
$1/4$
. At the
![]() $m$
th step we have
$m$
th step we have
![]() $2^{m}$
intervals which we label, starting from the leftmost to the rightmost as
$2^{m}$
intervals which we label, starting from the leftmost to the rightmost as
 $I_{1}^{(m)},I_{2}^{(m)},\ldots ,I_{2^{m}}^{(m)}$
. We remove then from
$I_{1}^{(m)},I_{2}^{(m)},\ldots ,I_{2^{m}}^{(m)}$
. We remove then from
![]() $I_{j}^{(m)}$
the central interval of length
$I_{j}^{(m)}$
the central interval of length
 $2^{-2^{2^{m-1}-1+j}}$
. The result of this procedure is a Cantor set
$2^{-2^{2^{m-1}-1+j}}$
. The result of this procedure is a Cantor set
![]() $X$
which is not sparse.
$X$
which is not sparse.
Let
 $\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R},X)$
. Suppose first that there exists a sequence
$\unicode[STIX]{x1D711}\in \text{Diff}^{1}(\mathbb{R},X)$
. Suppose first that there exists a sequence
![]() $I_{n}$
of gaps approaching
$I_{n}$
of gaps approaching
![]() $0$
from the right side with the property that for every
$0$
from the right side with the property that for every
![]() $n$
we have
$n$
we have
 $J_{n}=\unicode[STIX]{x1D711}(I_{n})\neq I_{n}$
. Then there exists points
$J_{n}=\unicode[STIX]{x1D711}(I_{n})\neq I_{n}$
. Then there exists points
 $x_{I_{n}}\in I_{n}$
such that
$x_{I_{n}}\in I_{n}$
such that
 $\unicode[STIX]{x1D711}^{\prime }(x_{I_{n}})=|J_{n}|/|I_{n}|$
. The sequence
$\unicode[STIX]{x1D711}^{\prime }(x_{I_{n}})=|J_{n}|/|I_{n}|$
. The sequence
![]() $x_{I_{n}}$
converges to
$x_{I_{n}}$
converges to
![]() $0$
. Now lengths of gaps belong to the discrete set
$0$
. Now lengths of gaps belong to the discrete set
 $\{2^{-2^{n}},n\in \mathbb{Z}_{+}\}$
and there are not two gaps of the same length. Therefore any infinite sequence of lengths
$\{2^{-2^{n}},n\in \mathbb{Z}_{+}\}$
and there are not two gaps of the same length. Therefore any infinite sequence of lengths
 $|J_{n}|/|I_{n}|\neq 1$
has a subsequence which either converges to
$|J_{n}|/|I_{n}|\neq 1$
has a subsequence which either converges to
![]() $0$
or is unbounded. This implies that
$0$
or is unbounded. This implies that
![]() $\unicode[STIX]{x1D711}^{\prime }(0)$
is either
$\unicode[STIX]{x1D711}^{\prime }(0)$
is either
![]() $0$
or infinite, which contradicts the fact that
$0$
or infinite, which contradicts the fact that
![]() $\unicode[STIX]{x1D711}$
was a diffeomorphism.
$\unicode[STIX]{x1D711}$
was a diffeomorphism.
It follows that for any sequence
![]() $I_{n}$
as above and large enough
$I_{n}$
as above and large enough
![]() $n$
we have
$n$
we have
 $\unicode[STIX]{x1D711}(I_{n})=I_{n}$
. In particular
$\unicode[STIX]{x1D711}(I_{n})=I_{n}$
. In particular
 $\unicode[STIX]{x1D711}(0)=0$
. This holds for any left point of
$\unicode[STIX]{x1D711}(0)=0$
. This holds for any left point of
![]() $X$
and hence
$X$
and hence
 $\mathfrak{diff}^{1}(X)=1$
.
$\mathfrak{diff}^{1}(X)=1$
.
Now let
 $I,J\;\subset \;[0,1]$
be closed intervals intersecting
$I,J\;\subset \;[0,1]$
be closed intervals intersecting
![]() $X$
intersecting along Cantor sets. The arguments above also show that there exists a diffeomorphism
$X$
intersecting along Cantor sets. The arguments above also show that there exists a diffeomorphism
 $\unicode[STIX]{x1D711}:(I,X\;\cap \;I)\rightarrow (J,X\;\cap \;J)$
if and only if
$\unicode[STIX]{x1D711}:(I,X\;\cap \;I)\rightarrow (J,X\;\cap \;J)$
if and only if
![]() $I=J$
and
$I=J$
and
![]() $\unicode[STIX]{x1D711}|_{X\;\cap \;I}$
is the identity. From the proof of Theorem 3 (see § 3.2.3) we deduce that
$\unicode[STIX]{x1D711}|_{X\;\cap \;I}$
is the identity. From the proof of Theorem 3 (see § 3.2.3) we deduce that
 $\mathfrak{diff}_{M}^{1}(X)=1$
for any manifold
$\mathfrak{diff}_{M}^{1}(X)=1$
for any manifold
![]() $M$
containing the
$M$
containing the
![]() ${\mathcal{C}}^{1}$
-interval
${\mathcal{C}}^{1}$
-interval
![]() $[0,1]$
.
$[0,1]$
.
5.3 Sparse Cantor set with trivial diffeomorphism group
Start from the interval
 $I^{(0)}=[0,1]$
by removing a central gap
$I^{(0)}=[0,1]$
by removing a central gap
![]() $J_{1}^{(1)}$
of size
$J_{1}^{(1)}$
of size
![]() $(1-\unicode[STIX]{x1D700})$
. By recurrence at the
$(1-\unicode[STIX]{x1D700})$
. By recurrence at the
![]() $n$
th step we have
$n$
th step we have
![]() $2^{n}$
intervals
$2^{n}$
intervals
![]() $I_{j}^{(n)}$
,
$I_{j}^{(n)}$
,
 $j=1,\ldots ,2^{n}$
, numbered from the left to the right. To go further we remove a central gap
$j=1,\ldots ,2^{n}$
, numbered from the left to the right. To go further we remove a central gap
![]() $J_{j}^{(n+1)}$
from
$J_{j}^{(n+1)}$
from
![]() $I_{j}^{(n)}$
of length
$I_{j}^{(n)}$
of length
 $|J_{j}^{(n+1)}|=(1-\unicode[STIX]{x1D700}^{n})|I_{j}^{(n)}|$
. The set so obtained is obviously a sparse Cantor set
$|J_{j}^{(n+1)}|=(1-\unicode[STIX]{x1D700}^{n})|I_{j}^{(n)}|$
. The set so obtained is obviously a sparse Cantor set
![]() $C_{0}$
.
$C_{0}$
.
Let
![]() $a\in C_{0}$
. Let
$a\in C_{0}$
. Let
![]() $b_{n}$
be the right endpoint of the interval
$b_{n}$
be the right endpoint of the interval
![]() $I_{j_{n}}^{(n)}$
to which
$I_{j_{n}}^{(n)}$
to which
![]() $a$
belongs. Then set
$a$
belongs. Then set
![]() $(x_{n},y_{n})$
for the gap
$(x_{n},y_{n})$
for the gap
 $J_{j_{n}}^{(n+1)}\;\subset \;I_{j_{n}}^{(n)}$
. There is no loss of generality of assuming that
$J_{j_{n}}^{(n+1)}\;\subset \;I_{j_{n}}^{(n)}$
. There is no loss of generality of assuming that
 $a<x_{n}<y_{n}<b_{n}$
. Given
$a<x_{n}<y_{n}<b_{n}$
. Given
 $\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}(\mathbb{R},C_{0})$
, with
$\unicode[STIX]{x1D711}\in \text{Diff}_{a}^{1}(\mathbb{R},C_{0})$
, with
 $\unicode[STIX]{x1D711}^{\prime }(a)\neq 1$
, there are infinitely many
$\unicode[STIX]{x1D711}^{\prime }(a)\neq 1$
, there are infinitely many
![]() $n$
for which the gap
$n$
for which the gap
![]() $J_{j_{n}}^{(n)}$
is not fixed by
$J_{j_{n}}^{(n)}$
is not fixed by
![]() $\unicode[STIX]{x1D711}$
. It follows that either
$\unicode[STIX]{x1D711}$
. It follows that either
 $\unicode[STIX]{x1D711}(y_{n})<x_{n}$
, or
$\unicode[STIX]{x1D711}(y_{n})<x_{n}$
, or
 $\unicode[STIX]{x1D711}(x_{n})>y_{n}$
, for infinitely many
$\unicode[STIX]{x1D711}(x_{n})>y_{n}$
, for infinitely many
![]() $n$
. By symmetry we can assume that the second alternative holds. Then
$n$
. By symmetry we can assume that the second alternative holds. Then
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(x_{n})-x_{n}}{x_{n}-a}\geqslant \frac{|y_{n}-x_{n}|}{|x_{n}-a|}\geqslant \frac{(1-\unicode[STIX]{x1D700}^{n})|b_{n}-a|}{|x_{n}-a|}\geqslant \frac{(1-\unicode[STIX]{x1D700}^{n})|b_{n}-a|}{\unicode[STIX]{x1D700}^{n}|b_{n}-a|}=\frac{1-\unicode[STIX]{x1D700}^{n}}{\unicode[STIX]{x1D700}^{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D711}(x_{n})-x_{n}}{x_{n}-a}\geqslant \frac{|y_{n}-x_{n}|}{|x_{n}-a|}\geqslant \frac{(1-\unicode[STIX]{x1D700}^{n})|b_{n}-a|}{|x_{n}-a|}\geqslant \frac{(1-\unicode[STIX]{x1D700}^{n})|b_{n}-a|}{\unicode[STIX]{x1D700}^{n}|b_{n}-a|}=\frac{1-\unicode[STIX]{x1D700}^{n}}{\unicode[STIX]{x1D700}^{n}}.\end{eqnarray}$$
Letting
![]() $n\rightarrow \infty$
we obtain that
$n\rightarrow \infty$
we obtain that
 $\unicode[STIX]{x1D711}^{\prime }(a)=\infty$
, contradiction. This proves that
$\unicode[STIX]{x1D711}^{\prime }(a)=\infty$
, contradiction. This proves that
 $\mathfrak{diff}_{a}^{1,+}(C_{0})=1$
.
$\mathfrak{diff}_{a}^{1,+}(C_{0})=1$
.
From Remark 8 we have
 $\mathfrak{diff}^{1,+}(C_{0})=1$
. Moreover, the proof of Theorem 3 implies that
$\mathfrak{diff}^{1,+}(C_{0})=1$
. Moreover, the proof of Theorem 3 implies that
 $\mathfrak{diff}_{M}^{1,+}(C_{0})=1$
for any manifold
$\mathfrak{diff}_{M}^{1,+}(C_{0})=1$
for any manifold
![]() $M$
containing the
$M$
containing the
![]() ${\mathcal{C}}^{1}$
-interval
${\mathcal{C}}^{1}$
-interval
![]() $[0,1]$
.
$[0,1]$
.
Another potential example. In order to convert the non-sparse example above
![]() $X$
into a sparse Cantor set with the same properties, we have to mix ordinary gaps and very small gaps. Start as above from the interval
$X$
into a sparse Cantor set with the same properties, we have to mix ordinary gaps and very small gaps. Start as above from the interval
 $I^{(0)}=[0,1]$
by removing a central gap
$I^{(0)}=[0,1]$
by removing a central gap
![]() $LG^{(1)}$
of size
$LG^{(1)}$
of size
![]() ${\textstyle \frac{1}{3}}$
and two very small gaps each one centered within an interval component of
${\textstyle \frac{1}{3}}$
and two very small gaps each one centered within an interval component of
 $I^{(0)}-LG^{(1)}$
, namely
$I^{(0)}-LG^{(1)}$
, namely
![]() $SG_{1}^{(1)}$
and
$SG_{1}^{(1)}$
and
![]() $SG_{2}^{(1)}$
of lengths
$SG_{2}^{(1)}$
of lengths
![]() $2^{-2^{\unicode[STIX]{x1D6FC}}}$
and
$2^{-2^{\unicode[STIX]{x1D6FC}}}$
and
![]() $2^{-2^{\unicode[STIX]{x1D6FC}+1}}$
, respectively. Here
$2^{-2^{\unicode[STIX]{x1D6FC}+1}}$
, respectively. Here
![]() $\unicode[STIX]{x1D6FC}$
is chosen so that
$\unicode[STIX]{x1D6FC}$
is chosen so that
 $$\begin{eqnarray}{\textstyle \frac{1}{3}}-2^{-2^{\unicode[STIX]{x1D6FC}}}>{\textstyle \frac{1}{6}}.\end{eqnarray}$$
$$\begin{eqnarray}{\textstyle \frac{1}{3}}-2^{-2^{\unicode[STIX]{x1D6FC}}}>{\textstyle \frac{1}{6}}.\end{eqnarray}$$
We obtain at the next stage four intervals
 $I_{1}^{(1)},I_{2}^{(1)},I_{3}^{(1)},I_{4}^{(1)}$
, labeled from the left to the right.
$I_{1}^{(1)},I_{2}^{(1)},I_{3}^{(1)},I_{4}^{(1)}$
, labeled from the left to the right.
By recurrence at the
![]() $n$
th step we have
$n$
th step we have
![]() $4^{n}$
intervals
$4^{n}$
intervals
![]() $I_{j}^{(n)}$
,
$I_{j}^{(n)}$
,
 $j=1,\ldots ,4^{n}$
. To go further we remove first a central gap
$j=1,\ldots ,4^{n}$
. To go further we remove first a central gap
 $LG_{j}^{(n+1)}$
from
$LG_{j}^{(n+1)}$
from
![]() $I_{j}^{(n)}$
of length
$I_{j}^{(n)}$
of length
 $|LG_{j}^{(n+1)}|={\textstyle \frac{1}{3}}|I_{j}^{(n)}|$
. Further we remove two very small gaps each one centered within an interval component of
$|LG_{j}^{(n+1)}|={\textstyle \frac{1}{3}}|I_{j}^{(n)}|$
. Further we remove two very small gaps each one centered within an interval component of
 $I_{j}^{(n)}-LG_{j}^{(n)}$
, namely
$I_{j}^{(n)}-LG_{j}^{(n)}$
, namely
![]() $SG_{2j+1}^{(n)}$
and
$SG_{2j+1}^{(n)}$
and
![]() $SG_{2j+2}^{(n)}$
of lengths
$SG_{2j+2}^{(n)}$
of lengths
 $2^{-2^{\unicode[STIX]{x1D6FC}+j+4^{n}}}$
and
$2^{-2^{\unicode[STIX]{x1D6FC}+j+4^{n}}}$
and
 $2^{-2^{\unicode[STIX]{x1D6FC}+j+1+4^{n}}}$
. Letting
$2^{-2^{\unicode[STIX]{x1D6FC}+j+1+4^{n}}}$
. Letting
![]() $n$
go to
$n$
go to
![]() $\infty$
we obtain a
$\infty$
we obtain a
![]() ${\textstyle \frac{1}{3}}$
-sparse Cantor set
${\textstyle \frac{1}{3}}$
-sparse Cantor set
![]() $MC$
. We believe that
$MC$
. We believe that
 $\mathfrak{diff}^{1,+}(MC)=1$
.
$\mathfrak{diff}^{1,+}(MC)=1$
.
5.4 Split Cantor sets
Two Cantor sets
 $C_{i}\;\subset \;\mathbb{R}^{n}$
are locally smoothly non-equivalent if for any
$C_{i}\;\subset \;\mathbb{R}^{n}$
are locally smoothly non-equivalent if for any
![]() $p_{i}\;\subset \;C_{i}$
there is no
$p_{i}\;\subset \;C_{i}$
there is no
![]() ${\mathcal{C}}^{1}$
-diffeomorphism germ
${\mathcal{C}}^{1}$
-diffeomorphism germ
 $(\mathbb{R}^{n},C_{1},p_{1})\rightarrow (\mathbb{R}^{n},C_{2},p_{2})$
.
$(\mathbb{R}^{n},C_{1},p_{1})\rightarrow (\mathbb{R}^{n},C_{2},p_{2})$
.
A Cantor set in
 $C\;\subset \;\mathbb{R}^{n}$
is said to be smoothly split if we can write
$C\;\subset \;\mathbb{R}^{n}$
is said to be smoothly split if we can write
 $C=C_{1}\;\cup \;C_{2}$
as a union of two Cantor sets with
$C=C_{1}\;\cup \;C_{2}$
as a union of two Cantor sets with
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
locally smoothly non-equivalent and contained in disjoint intervals.
$C_{2}$
locally smoothly non-equivalent and contained in disjoint intervals.
We have the following proposition.
Proposition 2. Let
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
 $C\;\subset \;\mathbb{R}^{n}$
be a Cantor set which is smoothly split as
$C\;\subset \;\mathbb{R}^{n}$
be a Cantor set which is smoothly split as
 $C_{1}\;\cup \;C_{2}$
. Then
$C_{1}\;\cup \;C_{2}$
. Then
 $\mathfrak{diff}^{1,+}(C)=\mathfrak{diff}^{1,+}(C_{1})\times \mathfrak{diff}^{1,+}(C_{2})$
.
$\mathfrak{diff}^{1,+}(C)=\mathfrak{diff}^{1,+}(C_{1})\times \mathfrak{diff}^{1,+}(C_{2})$
.
Proof. In this situation,
![]() $C_{i}$
are contained into disjoint intervals
$C_{i}$
are contained into disjoint intervals
![]() $U_{i}$
. Then diffeomorphisms preserving
$U_{i}$
. Then diffeomorphisms preserving
![]() $C$
should also send each
$C$
should also send each
![]() $C_{i}$
into itself. Furthermore all elements from
$C_{i}$
into itself. Furthermore all elements from
 $\mathfrak{diff}^{1,+}(C_{1})\times \mathfrak{diff}^{1,+}(C_{2})$
can be realized as classes of pairs of commuting diffeomorphisms supported in
$\mathfrak{diff}^{1,+}(C_{1})\times \mathfrak{diff}^{1,+}(C_{2})$
can be realized as classes of pairs of commuting diffeomorphisms supported in
![]() $U_{i}$
.◻
$U_{i}$
.◻
According to Remark 4 the central Cantor sets
![]() $C_{\unicode[STIX]{x1D706}}$
are pairwise locally smoothly non-equivalent. In particular the union
$C_{\unicode[STIX]{x1D706}}$
are pairwise locally smoothly non-equivalent. In particular the union
 $C_{\unicode[STIX]{x1D706}}\;\cup \;2+C_{\unicode[STIX]{x1D707}}$
of two distinct Cantor sets, one of which is translated by
$C_{\unicode[STIX]{x1D706}}\;\cup \;2+C_{\unicode[STIX]{x1D707}}$
of two distinct Cantor sets, one of which is translated by
![]() $2$
is a split Cantor set. It follows that
$2$
is a split Cantor set. It follows that
 $$\begin{eqnarray}\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}}\;\cup \;2+C_{\unicode[STIX]{x1D707}})=\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})\times \mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D707}})\cong F\times F,\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}}\;\cup \;2+C_{\unicode[STIX]{x1D707}})=\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}})\times \mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D707}})\cong F\times F,\end{eqnarray}$$
for distinct
![]() $\unicode[STIX]{x1D706}$
and
$\unicode[STIX]{x1D706}$
and
![]() $\unicode[STIX]{x1D707}$
. It is not clear what would be
$\unicode[STIX]{x1D707}$
. It is not clear what would be
 $\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}}\;\cup \;C_{\unicode[STIX]{x1D707}})$
or
$\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}}\;\cup \;C_{\unicode[STIX]{x1D707}})$
or
 $\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}}+C_{\unicode[STIX]{x1D707}})$
(for those parameters for which the sum is still a Cantor set).
$\mathfrak{diff}^{1,+}(C_{\unicode[STIX]{x1D706}}+C_{\unicode[STIX]{x1D707}})$
(for those parameters for which the sum is still a Cantor set).
5.5 Questions
The countability of
 $\mathfrak{diff}_{M}^{1}(C)$
relies on the description of the group of germs of the stabilizer
$\mathfrak{diff}_{M}^{1}(C)$
relies on the description of the group of germs of the stabilizer
![]() $G_{a}$
of a point
$G_{a}$
of a point
![]() $a\in C$
for a finitely generated group
$a\in C$
for a finitely generated group
 $G\;\subset \;\text{Diff}^{1}(M,C)$
: it is cyclic when
$G\;\subset \;\text{Diff}^{1}(M,C)$
: it is cyclic when
 $\dim M=1$
and
$\dim M=1$
and
![]() $C$
is sparse and (a finite extension of) a subgroup of
$C$
is sparse and (a finite extension of) a subgroup of
![]() $\mathbb{Z}^{n}$
if
$\mathbb{Z}^{n}$
if
 $\dim M=n$
and
$\dim M=n$
and
![]() $C$
is a product of
$C$
is a product of
![]() $n$
sparse Cantor subsets of the line. We think that a similar result holds for any sparse enough Cantor subset of
$n$
sparse Cantor subsets of the line. We think that a similar result holds for any sparse enough Cantor subset of
![]() $M$
in higher dimensions, not necessarily a product. One should note that if the action of a group
$M$
in higher dimensions, not necessarily a product. One should note that if the action of a group
 $G\;\subset \;\text{Diff}^{2}(S^{1})$
admits a Markov partition (see [Reference Deroin, Kleptsyn and NavasDKN09, Reference Deroin, Kleptsyn and NavasDKN13]) and an exceptional minimal set
$G\;\subset \;\text{Diff}^{2}(S^{1})$
admits a Markov partition (see [Reference Deroin, Kleptsyn and NavasDKN09, Reference Deroin, Kleptsyn and NavasDKN13]) and an exceptional minimal set
![]() $C$
then
$C$
then
![]() $C$
must indeed be sparse.
$C$
must indeed be sparse.
It seems presently unknown whether for any
![]() ${\mathcal{C}}^{1}$
-locally discrete group
${\mathcal{C}}^{1}$
-locally discrete group
![]() $G$
of
$G$
of
 $\text{Diff}^{2}(S^{1})$
with an exceptional minimal set every point stabilizer should have a cyclic group of germs. Recall that a group
$\text{Diff}^{2}(S^{1})$
with an exceptional minimal set every point stabilizer should have a cyclic group of germs. Recall that a group
 $G\;\subset \;\text{Diff}^{2}(S^{1})$
is
$G\;\subset \;\text{Diff}^{2}(S^{1})$
is
![]() ${\mathcal{C}}^{1}$
-locally discrete if the restriction of the identity to any interval intersecting its minimal set is isolated in the
${\mathcal{C}}^{1}$
-locally discrete if the restriction of the identity to any interval intersecting its minimal set is isolated in the
![]() ${\mathcal{C}}^{1}$
-topology among the restrictions of elements of
${\mathcal{C}}^{1}$
-topology among the restrictions of elements of
![]() $G$
. In particular groups
$G$
. In particular groups
 $G\;\subset \;\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
with an exceptional minimal set are
$G\;\subset \;\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
with an exceptional minimal set are
![]() ${\mathcal{C}}^{1}$
-locally discrete, as well as Fuchsian groups. One believes that the action of every
${\mathcal{C}}^{1}$
-locally discrete, as well as Fuchsian groups. One believes that the action of every
![]() ${\mathcal{C}}^{1}$
-locally discrete subgroup of
${\mathcal{C}}^{1}$
-locally discrete subgroup of
 $\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
has a Markov partition (see [Reference Alvarez, Filimonov, Kleptsyn, Malicet, Cotón, Navas and TriestinoAFKM+15, Main Conjecture]).
$\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
has a Markov partition (see [Reference Alvarez, Filimonov, Kleptsyn, Malicet, Cotón, Navas and TriestinoAFKM+15, Main Conjecture]).
A well-known conjecture of Dippolito (see [Reference DippolitoDip78, pp. 448–449]) states that for a finitely generated group
 $G\;\subset \;\text{Diff}^{2}(S^{1})$
with a minimal exceptional
$G\;\subset \;\text{Diff}^{2}(S^{1})$
with a minimal exceptional
![]() $C$
such that the groups of germs of stabilizers are cyclic the Radon–Nikodym derivative of every element of
$C$
such that the groups of germs of stabilizers are cyclic the Radon–Nikodym derivative of every element of
![]() $G$
(with respect to an invariant measure) should be locally constant. This suggests that our results describing the elements of
$G$
(with respect to an invariant measure) should be locally constant. This suggests that our results describing the elements of
 $\mathfrak{diff}_{M}^{1}(C)$
for Cantor sets associated to generic affine IFS might be extended to more general Cantor sets. For instance, when
$\mathfrak{diff}_{M}^{1}(C)$
for Cantor sets associated to generic affine IFS might be extended to more general Cantor sets. For instance, when
 $C=\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6E4}\;\subset \;S^{1}$
is the limit set of a second kind Fuchsian group
$C=\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D6E4}\;\subset \;S^{1}$
is the limit set of a second kind Fuchsian group
![]() $\unicode[STIX]{x1D6E4}$
then
$\unicode[STIX]{x1D6E4}$
then
 $\mathfrak{diff}_{M}^{1,+}(C)$
should also be isomorphic to one of the Greenberg generalizations
$\mathfrak{diff}_{M}^{1,+}(C)$
should also be isomorphic to one of the Greenberg generalizations
![]() $T_{\unicode[STIX]{x1D6E4}}$
or
$T_{\unicode[STIX]{x1D6E4}}$
or
![]() $V_{\unicode[STIX]{x1D6E4}}^{\pm }$
of the Thompson groups associated to
$V_{\unicode[STIX]{x1D6E4}}^{\pm }$
of the Thompson groups associated to
![]() $\unicode[STIX]{x1D6E4}$
(see [Reference GreenbergGre91]). More generally, if
$\unicode[STIX]{x1D6E4}$
(see [Reference GreenbergGre91]). More generally, if
 $\unicode[STIX]{x1D6E4}\;\subset \;\text{Diff}^{1}(M)$
is a finitely generated group having an exceptional minimal set
$\unicode[STIX]{x1D6E4}\;\subset \;\text{Diff}^{1}(M)$
is a finitely generated group having an exceptional minimal set
![]() $C$
, the group
$C$
, the group
 $\mathfrak{diff}_{M}^{1}(C)$
is closely related to the group of piecewise-
$\mathfrak{diff}_{M}^{1}(C)$
is closely related to the group of piecewise-
![]() $\unicode[STIX]{x1D6E4}$
homeomorphisms of
$\unicode[STIX]{x1D6E4}$
homeomorphisms of
![]() $(M,C)$
. Note that an exceptional minimal set of a Denjoy
$(M,C)$
. Note that an exceptional minimal set of a Denjoy
![]() ${\mathcal{C}}^{1}$
-diffeomorphism (i.e. without periodic points and whose derivative has bounded variation) of the circle is not generic in our sense, as the spectrum of ratios of lengths of gaps contains
${\mathcal{C}}^{1}$
-diffeomorphism (i.e. without periodic points and whose derivative has bounded variation) of the circle is not generic in our sense, as the spectrum of ratios of lengths of gaps contains
![]() $1$
in its closure (see [Reference McDuffMcd81, Reference PortelaPor09]). On the other hand Triestino conjectured that any finitely generated
$1$
in its closure (see [Reference McDuffMcd81, Reference PortelaPor09]). On the other hand Triestino conjectured that any finitely generated
![]() ${\mathcal{C}}^{1}$
-locally discrete subgroup of
${\mathcal{C}}^{1}$
-locally discrete subgroup of
 $\text{Diff}^{2}(S^{1})$
is
$\text{Diff}^{2}(S^{1})$
is
![]() ${\mathcal{C}}^{1}$
-semi-conjugate to a subgroup of a generalized subgroup
${\mathcal{C}}^{1}$
-semi-conjugate to a subgroup of a generalized subgroup
![]() $T_{\unicode[STIX]{x1D6E4}}$
, where now
$T_{\unicode[STIX]{x1D6E4}}$
, where now
 $\unicode[STIX]{x1D6E4}\;\subset \;\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
is Gromov-hyperbolic and
$\unicode[STIX]{x1D6E4}\;\subset \;\text{Diff}^{\unicode[STIX]{x1D714}}(S^{1})$
is Gromov-hyperbolic and
![]() ${\mathcal{C}}^{1}$
-locally discrete. Similar questions arise for
${\mathcal{C}}^{1}$
-locally discrete. Similar questions arise for
![]() ${\mathcal{C}}^{1}$
-locally discrete subgroups of
${\mathcal{C}}^{1}$
-locally discrete subgroups of
 $\text{Diff}^{2}(M,C)$
in relation to the generalized groups
$\text{Diff}^{2}(M,C)$
in relation to the generalized groups
![]() $V_{\unicode[STIX]{x1D6E4}}^{\pm }$
, associated to
$V_{\unicode[STIX]{x1D6E4}}^{\pm }$
, associated to
 $\unicode[STIX]{x1D6E4}\;\subset \;\text{Diff}^{\unicode[STIX]{x1D714}}(M,C)$
.
$\unicode[STIX]{x1D6E4}\;\subset \;\text{Diff}^{\unicode[STIX]{x1D714}}(M,C)$
.
Every couple of Cantor sets which are attractors of IFS arising from
![]() ${\mathcal{C}}^{1}$
-diffeomorphisms of the line have arbitrarily small perturbations in the
${\mathcal{C}}^{1}$
-diffeomorphisms of the line have arbitrarily small perturbations in the
![]() ${\mathcal{C}}^{1}$
-topology which makes them disjoint and generically their arithmetic difference is still a Cantor set, according to a remarkable result of Moreira [Reference MoreiraMor11]. We don’t know how the group
${\mathcal{C}}^{1}$
-topology which makes them disjoint and generically their arithmetic difference is still a Cantor set, according to a remarkable result of Moreira [Reference MoreiraMor11]. We don’t know how the group
 $\mathfrak{diff}_{M}^{1}(C)$
varies under a
$\mathfrak{diff}_{M}^{1}(C)$
varies under a
![]() ${\mathcal{C}}^{1}$
-perturbation of the IFS and in particular whether it might be larger than the Thompson-type group associated to the IFS.
${\mathcal{C}}^{1}$
-perturbation of the IFS and in particular whether it might be larger than the Thompson-type group associated to the IFS.
The validity of some version of the Tits alternative for diffeomorphism groups has its counterpart both for
 $\mathfrak{diff}_{M}^{1}(C)$
and the smooth mapping class groups: does any finitely generated subgroup contains a free subgroup on two generators or else it has a finite orbit on the Cantor set
$\mathfrak{diff}_{M}^{1}(C)$
and the smooth mapping class groups: does any finitely generated subgroup contains a free subgroup on two generators or else it has a finite orbit on the Cantor set
![]() $C$
? This was recently settled in the affirmative by Hurtado and Militon (see [Reference Hurtado and MilitonHM15]) for
$C$
? This was recently settled in the affirmative by Hurtado and Militon (see [Reference Hurtado and MilitonHM15]) for
 ${\mathcal{M}}^{1}(M,C_{\unicode[STIX]{x1D706}})$
where
${\mathcal{M}}^{1}(M,C_{\unicode[STIX]{x1D706}})$
where
![]() $C_{\unicode[STIX]{x1D706}}$
is the standard ternary Cantor set. Whether a strong Tits alternative could hold for the groups associated to some Cantor sets comprises the question on finding the solvable subgroups of
$C_{\unicode[STIX]{x1D706}}$
is the standard ternary Cantor set. Whether a strong Tits alternative could hold for the groups associated to some Cantor sets comprises the question on finding the solvable subgroups of
 $\mathfrak{diff}_{M}^{1}(C)$
, which started to be investigated in [Reference Bonatti, Monteverde, Navas and RivasBMNR17]. Recall that the Thompson group
$\mathfrak{diff}_{M}^{1}(C)$
, which started to be investigated in [Reference Bonatti, Monteverde, Navas and RivasBMNR17]. Recall that the Thompson group
![]() $F$
does not contain any free non-abelian group though is not virtually solvable. Notice that, by slightly extending [Reference Castro, Jorquera and NavasCJN14], every finitely-generated torsion-free nilpotent group can be made act on the interval with an invariant Cantor set, but we do not know whether there exists a non-virtually-abelian, nilpotent group of
$F$
does not contain any free non-abelian group though is not virtually solvable. Notice that, by slightly extending [Reference Castro, Jorquera and NavasCJN14], every finitely-generated torsion-free nilpotent group can be made act on the interval with an invariant Cantor set, but we do not know whether there exists a non-virtually-abelian, nilpotent group of
![]() ${\mathcal{C}}^{1}$
-diffeomorphisms of a generic Cantor set.
${\mathcal{C}}^{1}$
-diffeomorphisms of a generic Cantor set.
Acknowledgements
The authors are grateful to B. Deroin, L. Guillou, P. Haissinsky, S.Hurtado, I. Liousse, V. Sergiescu and M. Triestino for useful discussions and to the referees for having thoroughly read this paper, for their corrections and comments. The first author was supported by the ANR 2011 BS 01 020 01 ModGroup and the second author by the FWF grant P25142. Part of this work was done during the authors’ visit to the Erwin Schrödinger Institute, whose hospitality and support are acknowledged.