Article contents
On the Construction of Well-Conditioned Hierarchical Bases for 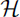 (div)-Conforming ℝn Simplicial Elements
(div)-Conforming ℝn Simplicial Elements
Published online by Cambridge University Press: 03 June 2015
Abstract
Hierarchical bases of arbitrary order for 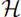 (div)-conforming triangular and tetrahedral elements are constructed with the goal of improving the conditioning of the mass and stiffness matrices. For the basis with the triangular element, it is found numerically that the conditioning is acceptable up to the approximation of order four, and is better than a corresponding basis in the dissertation by Sabine Zaglmayr [High Order Finite Element Methods for Electromagnetic Field Computation, Johannes Kepler Universität, Linz, 2006]. The sparsity of the mass matrices from the newly constructed basis and from the one by Zaglmayr is similar for approximations up to order four. The stiffness matrix with the new basis is much sparser than that with the basis by Zaglmayr for approximations up to order four. For the tetrahedral element, it is identified numerically that the conditioning is acceptable only up to the approximation of order three. Compared with the newly constructed basis for the triangular element, the sparsity of the mass matrices from the basis for the tetrahedral element is relatively sparser.
(div)-conforming triangular and tetrahedral elements are constructed with the goal of improving the conditioning of the mass and stiffness matrices. For the basis with the triangular element, it is found numerically that the conditioning is acceptable up to the approximation of order four, and is better than a corresponding basis in the dissertation by Sabine Zaglmayr [High Order Finite Element Methods for Electromagnetic Field Computation, Johannes Kepler Universität, Linz, 2006]. The sparsity of the mass matrices from the newly constructed basis and from the one by Zaglmayr is similar for approximations up to order four. The stiffness matrix with the new basis is much sparser than that with the basis by Zaglmayr for approximations up to order four. For the tetrahedral element, it is identified numerically that the conditioning is acceptable only up to the approximation of order three. Compared with the newly constructed basis for the triangular element, the sparsity of the mass matrices from the basis for the tetrahedral element is relatively sparser.
- Type
- Research Article
- Information
- Copyright
- Copyright © Global Science Press Limited 2013
References
- 6
- Cited by


