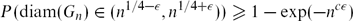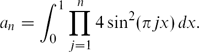Honouring the Memory of Philippe Flajolet - Part 3
Paper
Formulae and Asymptotics for Coefficients of Algebraic Functions
-
- Published online by Cambridge University Press:
- 11 December 2014, pp. 1-53
-
- Article
- Export citation
Gaussian Distribution of Trie Depth for Strongly Tame Sources
-
- Published online by Cambridge University Press:
- 11 December 2014, pp. 54-103
-
- Article
- Export citation
Towards a Realistic Analysis of Some Popular Sorting Algorithms
-
- Published online by Cambridge University Press:
- 11 December 2014, pp. 104-144
-
- Article
- Export citation
On the Diameter of Random Planar Graphs
-
- Published online by Cambridge University Press:
- 18 September 2014, pp. 145-178
-
- Article
- Export citation
Loose Hamilton Cycles in Regular Hypergraphs
-
- Published online by Cambridge University Press:
- 24 September 2014, pp. 179-194
-
- Article
- Export citation
Resolution of T. Ward's Question and the Israel–Finch Conjecture: Precise Analysis of an Integer Sequence Arising in Dynamics
-
- Published online by Cambridge University Press:
- 02 October 2014, pp. 195-215
-
- Article
- Export citation
Asymptotics of Symmetric Compound Poisson Population Models
-
- Published online by Cambridge University Press:
- 08 September 2014, pp. 216-253
-
- Article
- Export citation
Longest Increasing Subsequences of Randomly Chosen Multi-Row Arrays
-
- Published online by Cambridge University Press:
- 02 October 2014, pp. 254-293
-
- Article
- Export citation
Counting Decomposable Univariate Polynomials
-
- Published online by Cambridge University Press:
- 05 September 2014, pp. 294-328
-
- Article
- Export citation
Central Limit Theorems for Additive Tree Parameters with Small Toll Functions
-
- Published online by Cambridge University Press:
- 08 September 2014, pp. 329-353
-
- Article
- Export citation
Diagonal Asymptotics for Products of Combinatorial Classes
-
- Published online by Cambridge University Press:
- 10 October 2014, pp. 354-372
-
- Article
- Export citation
Corrigendum
‘The Asymptotic Number of Connected d-Uniform Hypergraphs’ — CORRIGENDUM
-
- Published online by Cambridge University Press:
- 14 October 2014, pp. 373-375
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
CPC volume 24 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 08 April 2017, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
CPC volume 24 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 08 April 2017, pp. b1-b3
-
- Article
-
- You have access
- Export citation