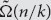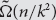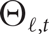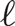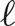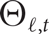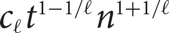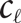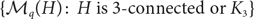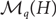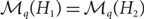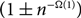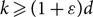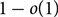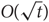In this paper we propose a polynomial-time deterministic algorithm for approximately counting the k-colourings of the random graph G(n, d/n), for constant d>0. In particular, our algorithm computes in polynomial time a 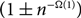 $(1\pm n^{-\Omega(1)})$
-approximation of the so-called ‘free energy’ of the k-colourings of G(n, d/n), for
$(1\pm n^{-\Omega(1)})$
-approximation of the so-called ‘free energy’ of the k-colourings of G(n, d/n), for 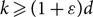 $k\geq (1+\varepsilon) d$
with probability
$k\geq (1+\varepsilon) d$
with probability 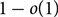 $1-o(1)$
over the graph instances.
$1-o(1)$
over the graph instances.
Our algorithm uses spatial correlation decay to compute numerically estimates of marginals of the Gibbs distribution. Spatial correlation decay has been used in different counting schemes for deterministic counting. So far algorithms have exploited a certain kind of set-to-point correlation decay, e.g. the so-called Gibbs uniqueness. Here we deviate from this setting and exploit a point-to-point correlation decay. The spatial mixing requirement is that for a pair of vertices the correlation between their corresponding configurations becomes weaker with their distance.
Furthermore, our approach generalizes in that it allows us to compute the Gibbs marginals for small sets of nearby vertices. Also, we establish a connection between the fluctuations of the number of colourings of G(n, d/n) and the fluctuations of the number of short cycles and edges in the graph.