Article contents
Surprise Probabilities in Markov Chains
Published online by Cambridge University Press: 16 March 2017
Abstract
In a Markov chain started at a state x, the hitting time τ(y) is the first time that the chain reaches another state y. We study the probability 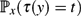 $\mathbb{P}_x(\tau(y) = t)$ that the first visit to y occurs precisely at a given time t. Informally speaking, the event that a new state is visited at a large time t may be considered a ‘surprise’. We prove the following three bounds.
$\mathbb{P}_x(\tau(y) = t)$ that the first visit to y occurs precisely at a given time t. Informally speaking, the event that a new state is visited at a large time t may be considered a ‘surprise’. We prove the following three bounds.
• In any Markov chain with n states,
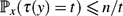 $\mathbb{P}_x(\tau(y) = t) \le {n}/{t}$.
$\mathbb{P}_x(\tau(y) = t) \le {n}/{t}$.• In a reversible chain with n states,
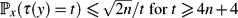 $\mathbb{P}_x(\tau(y) = t) \le {\sqrt{2n}}/{t}$ for $t \ge 4n + 4$.
$\mathbb{P}_x(\tau(y) = t) \le {\sqrt{2n}}/{t}$ for $t \ge 4n + 4$.• For random walk on a simple graph with n ≥ 2 vertices,
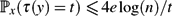 $\mathbb{P}_x(\tau(y) = t) \le 4e \log(n)/t$.
$\mathbb{P}_x(\tau(y) = t) \le 4e \log(n)/t$.
To prove the bound for random walk on graphs, we establish the following estimate conjectured by Aldous, Ding and Oveis-Gharan (private communication): for random walk on an n-vertex graph, for every initial vertex x,
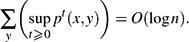 $$
\sum_y \biggl( \sup_{t \ge 0} p^t(x, y) \biggr) = O(\log n).
$$
$$
\sum_y \biggl( \sup_{t \ge 0} p^t(x, y) \biggr) = O(\log n).
$$
MSC classification
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2017
References
- 2
- Cited by




