Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kontoyiannis, Ioannis
and
Madiman, Mokshay
2012.
Sumset inequalities for differential entropy and mutual information.
p.
1261.
Madiman, Mokshay
Marcus, Adam W.
and
Tetali, Prasad
2012.
Entropy and set cardinality inequalities for partition‐determined functions.
Random Structures & Algorithms,
Vol. 40,
Issue. 4,
p.
399.
Kontoyiannis, Ioannis
and
Madiman, Mokshay
2013.
The entropy of sums and Rusza's divergence on abelian groups.
p.
1.
Bibak, Khodakhast
2013.
Number Theory and Related Fields.
Vol. 43,
Issue. ,
p.
99.
Haghighatshoar, Saeid
Abbe, Emmanuel
and
Telatar, Emre
2013.
A new entropy power inequality for integer-valued random variables.
p.
589.
Fritz, Tobias
and
Chaves, Rafael
2013.
Entropic Inequalities and Marginal Problems.
IEEE Transactions on Information Theory,
Vol. 59,
Issue. 2,
p.
803.
Haghighatshoar, Saeid
Abbe, Emmanuel
and
Telatar, I. Emre
2014.
A New Entropy Power Inequality for Integer-Valued Random Variables.
IEEE Transactions on Information Theory,
Vol. 60,
Issue. 7,
p.
3787.
Lecouvey, Cédric
2014.
Plünnecke and Kneser type theorems for dimension estimates.
Combinatorica,
Vol. 34,
Issue. 3,
p.
331.
Wang, Liyao
Woo, Jae Oh
and
Madiman, Mokshay
2014.
A lower bound on the Rényi entropy of convolutions in the integers.
p.
2829.
Hochman, Michael
2014.
On self-similar sets with overlaps and inverse theorems for entropy.
Annals of Mathematics,
Vol. 180,
Issue. 2,
p.
773.
Kontoyiannis, Ioannis
and
Madiman, Mokshay
2014.
Sumset and Inverse Sumset Inequalities for Differential Entropy and Mutual Information.
IEEE Transactions on Information Theory,
Vol. 60,
Issue. 8,
p.
4503.
Jog, Varun
and
Anantharam, Venkat
2014.
The Entropy Power Inequality and Mrs. Gerber's Lemma for Groups of Order <inline-formula> <tex-math notation="TeX">${2^{n}}$ </tex-math></inline-formula>.
IEEE Transactions on Information Theory,
Vol. 60,
Issue. 7,
p.
3773.
Hochman, Michael
2014.
Geometry and Analysis of Fractals.
Vol. 88,
Issue. ,
p.
225.
Woo, Jae Oh
and
Madiman, Mokshay
2015.
A discrete entropy power inequality for uniform distributions.
p.
1625.
Wu, Yihong
Shamai Shitz, Shlomo
and
Verdu, Sergio
2015.
Information Dimension and the Degrees of Freedom of the Interference Channel.
IEEE Transactions on Information Theory,
Vol. 61,
Issue. 1,
p.
256.
Fahs, Jihad
and
Abou-Faycal, Ibrahim
2015.
A New Tight Upper Bound on the Entropy of Sums.
Entropy,
Vol. 17,
Issue. 12,
p.
8312.
Stotz, David
and
Bolcskei, Helmut
2016.
Characterizing Degrees of Freedom Through Additive Combinatorics.
IEEE Transactions on Information Theory,
Vol. 62,
Issue. 11,
p.
6423.
Makkuva, Ashok Vardhan
and
Wu, Yihong
2016.
On additive-combinatorial affine inequalities for Shannon entropy and differential entropy.
p.
1053.
Zhu, Jingge
and
Gastpar, Michael
2016.
Typical sumsets of linear codes.
p.
46.
Zhu, Jingge
and
Gastpar, Michael
2016.
Typical sumsets of lattice points.
p.
1816.
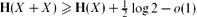 , where o(1) goes to zero as H(X) → ∞.
, where o(1) goes to zero as H(X) → ∞.



