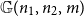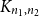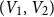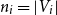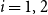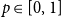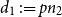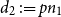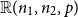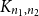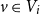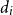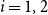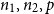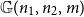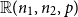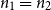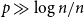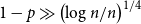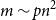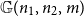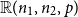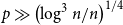1. Introduction
1.1. History and motivation
The Sandwich Conjecture of Kim and Vu [Reference Kim and Vu6] claims that if
![]() $d \gg \log n$
, then for some sequences
$d \gg \log n$
, then for some sequences
![]() $p_1 = p_1(n) \sim d/n$
and
$p_1 = p_1(n) \sim d/n$
and
![]() $p_2 = p_2(n) \sim d/n$
there is a joint distribution of a random d-regular graph
$p_2 = p_2(n) \sim d/n$
there is a joint distribution of a random d-regular graph
![]() $\mathbb{R}(n,d)$
and two binomial random graphs
$\mathbb{R}(n,d)$
and two binomial random graphs
![]() $\mathbb{G}(n,p_1)$
and
$\mathbb{G}(n,p_1)$
and
![]() $\mathbb{G}(n,p_2)$
such that with probability tending to 1
$\mathbb{G}(n,p_2)$
such that with probability tending to 1
If true, the Sandwich Conjecture would essentially reduce the study of any monotone graph property of the random graph
![]() $\mathbb{R}(n,d)$
in the regime
$\mathbb{R}(n,d)$
in the regime
![]() $d \gg \log n$
to the more manageable
$d \gg \log n$
to the more manageable
![]() $\mathbb{G}(n,p)$
.
$\mathbb{G}(n,p)$
.
For
![]() $\log n \ll d \ll n^{1/3}(\log n)^{-2}$
, Kim and Vu proved the embedding
$\log n \ll d \ll n^{1/3}(\log n)^{-2}$
, Kim and Vu proved the embedding
![]() $\mathbb{G}(n,p_1) \subseteq \mathbb{R}(n,d)$
as well as an imperfect embedding
$\mathbb{G}(n,p_1) \subseteq \mathbb{R}(n,d)$
as well as an imperfect embedding
![]() $\mathbb{R}(n,d) \setminus H \subseteq \mathbb{G}(n,p_2)$
, where H is some pretty sparse subgraph of
$\mathbb{R}(n,d) \setminus H \subseteq \mathbb{G}(n,p_2)$
, where H is some pretty sparse subgraph of
![]() $\mathbb{R}(n,d)$
. In [Reference Dudek, Frieze, Ruciński and Šileikis2] the lower embedding was extended to
$\mathbb{R}(n,d)$
. In [Reference Dudek, Frieze, Ruciński and Šileikis2] the lower embedding was extended to
![]() $d \ll n$
(and, in fact, to uniform hypergraph counterparts of the models
$d \ll n$
(and, in fact, to uniform hypergraph counterparts of the models
![]() $\mathbb{G}(n,p)$
and
$\mathbb{G}(n,p)$
and
![]() $\mathbb{R}(n,d)$
). Recently, Gao, Isaev and McKay [Reference Gao, Isaev and McKay4] came up with a result which confirms the conjecture for
$\mathbb{R}(n,d)$
). Recently, Gao, Isaev and McKay [Reference Gao, Isaev and McKay4] came up with a result which confirms the conjecture for
![]() $d \gg n/\sqrt{\log n}$
([Reference Gao, Isaev and McKay4] is the first paper that gives the (perfect) embedding
$d \gg n/\sqrt{\log n}$
([Reference Gao, Isaev and McKay4] is the first paper that gives the (perfect) embedding
![]() $\mathbb{R}(n,d) \subseteq \mathbb{G}(n,p_2)$
for some range of d) and, subsequently, Gao [Reference Gao3] widely extended this range to
$\mathbb{R}(n,d) \subseteq \mathbb{G}(n,p_2)$
for some range of d) and, subsequently, Gao [Reference Gao3] widely extended this range to
![]() $d=\Omega(\log^7n)$
.
$d=\Omega(\log^7n)$
.
Initially motivated by a paper of Perarnau and Petridis [Reference Perarnau and Petridis12] (see Section 9), we consider sandwiching for bipartite graphs, in which the natural counterparts of
![]() $\mathbb{G}(n,p)$
and
$\mathbb{G}(n,p)$
and
![]() $\mathbb{R}(n,d)$
are random subgraphs of the complete bipartite graph
$\mathbb{R}(n,d)$
are random subgraphs of the complete bipartite graph
![]() ${K_{n_1,n_2}}$
rather than of
${K_{n_1,n_2}}$
rather than of
![]() $K_n$
.
$K_n$
.
1.2. New results
We consider three models of random subgraphs of
![]() ${K_{n_1,n_2}}$
, the complete bipartite graph with bipartition
${K_{n_1,n_2}}$
, the complete bipartite graph with bipartition
![]() $(V_1, V_2)$
, where
$(V_1, V_2)$
, where
![]() $|V_1| = n_1, |V_2| = n_2$
. Given an integer
$|V_1| = n_1, |V_2| = n_2$
. Given an integer
![]() $m \in [0, n_1n_2]$
, let
$m \in [0, n_1n_2]$
, let
![]() ${\mathbb{G}(n_1,n_2,m)}$
be an m-edge subgraph of
${\mathbb{G}(n_1,n_2,m)}$
be an m-edge subgraph of
![]() ${K_{n_1,n_2}}$
chosen uniformly at random (the bipartite Erdős–Rényi model). Given a number
${K_{n_1,n_2}}$
chosen uniformly at random (the bipartite Erdős–Rényi model). Given a number
![]() $p \in [0,1]$
, let
$p \in [0,1]$
, let
![]() ${\mathbb{G}(n_1,n_2,p)}$
be the binomial bipartite random graph where each edge of
${\mathbb{G}(n_1,n_2,p)}$
be the binomial bipartite random graph where each edge of
![]() ${K_{n_1,n_2}}$
is included independently with probability p. Note that in the latter model,
${K_{n_1,n_2}}$
is included independently with probability p. Note that in the latter model,
![]() $pn_{3-i}$
is the expected degree of each vertex in
$pn_{3-i}$
is the expected degree of each vertex in
![]() $V_i$
,
$V_i$
,
![]() $i=1,2$
. If, in addition,
$i=1,2$
. If, in addition,
are integers (we shall always make this implicit assumption), we let
![]() ${{\mathcal{R}}(n_1,n_2,p)}$
be the class of subgraphs of
${{\mathcal{R}}(n_1,n_2,p)}$
be the class of subgraphs of
![]() ${K_{n_1,n_2}}$
such that every
${K_{n_1,n_2}}$
such that every
![]() $v \in V_i$
has degree
$v \in V_i$
has degree
![]() $d_i$
, for
$d_i$
, for
![]() $i = 1, 2$
(it is an easy exercise to show that
$i = 1, 2$
(it is an easy exercise to show that
![]() ${{\mathcal{R}}(n_1,n_2,p)}$
is non-empty). We call such graphs p-biregular. Let
${{\mathcal{R}}(n_1,n_2,p)}$
is non-empty). We call such graphs p-biregular. Let
![]() $\mathbb{R}(n_1,n_2,p)$
be a random graph chosen uniformly from
$\mathbb{R}(n_1,n_2,p)$
be a random graph chosen uniformly from
![]() ${{\mathcal{R}}(n_1,n_2,p)}$
.
${{\mathcal{R}}(n_1,n_2,p)}$
.
In this paper we establish an embedding of
![]() $\mathbb{G}(n_1,n_2,m)$
into
$\mathbb{G}(n_1,n_2,m)$
into
![]() $\mathbb{R}(n_1,n_2,p)$
. This easily implies an embedding of
$\mathbb{R}(n_1,n_2,p)$
. This easily implies an embedding of
![]() ${\mathbb{G}(n_1,n_2,p)}$
into
${\mathbb{G}(n_1,n_2,p)}$
into
![]() $\mathbb{R}(n_1,n_2,p)$
. Moreover, by taking complements, our result translates immediately to the opposite embedding of
$\mathbb{R}(n_1,n_2,p)$
. Moreover, by taking complements, our result translates immediately to the opposite embedding of
![]() $\mathbb{R}(n_1,n_2,p)$
into
$\mathbb{R}(n_1,n_2,p)$
into
![]() $\mathbb{G}(n_1,n_2,m)$
(and thus into
$\mathbb{G}(n_1,n_2,m)$
(and thus into
![]() ${\mathbb{G}(n_1,n_2,p)}$
). This idea was first used in [Reference Gao, Isaev and McKay4] to prove
${\mathbb{G}(n_1,n_2,p)}$
). This idea was first used in [Reference Gao, Isaev and McKay4] to prove
![]() $\mathbb{R}(n,d) \subseteq \mathbb{G}(n,p)$
for
$\mathbb{R}(n,d) \subseteq \mathbb{G}(n,p)$
for
![]() $p \gg \frac{1}{\sqrt{\log n}}$
. In particular, in the balanced case (
$p \gg \frac{1}{\sqrt{\log n}}$
. In particular, in the balanced case (
![]() $n_1=n_2\,{:\!=}\,n$
), we prove this opposite embedding for
$n_1=n_2\,{:\!=}\,n$
), we prove this opposite embedding for
![]() $p \gg \left( \log^3 n / n \right)^{1/4}$
.
$p \gg \left( \log^3 n / n \right)^{1/4}$
.
The proof is far from a straightforward adaptation of the proof in [Reference Dudek, Frieze, Ruciński and Šileikis2]. The common aspect shared by the proofs is that the edges of
![]() $\mathbb{R}(n_1,n_2,p)$
are revealed in a random order, giving a graph process which turns out to be, for most of the time, similar to the basic Erdős–Rényi process that generates
$\mathbb{R}(n_1,n_2,p)$
are revealed in a random order, giving a graph process which turns out to be, for most of the time, similar to the basic Erdős–Rényi process that generates
![]() ${\mathbb{G}(n_1,n_2,m)}$
. The rest of the current proof is different in that it avoids using the configuration model. Instead, we focus on showing that both
${\mathbb{G}(n_1,n_2,m)}$
. The rest of the current proof is different in that it avoids using the configuration model. Instead, we focus on showing that both
![]() $\mathbb{R}(n_1,n_2,p)$
and its random t-edge subgraphs are pseudorandom. We achieve this by applying the switching method (when
$\mathbb{R}(n_1,n_2,p)$
and its random t-edge subgraphs are pseudorandom. We achieve this by applying the switching method (when
![]() $\min \left\{ p, 1-p \right\}$
is small) and otherwise via asymptotic enumeration of bipartite graphs with a given degree sequence proved in [Reference Canfield, Greenhill and McKay1] (see Theorem 5).
$\min \left\{ p, 1-p \right\}$
is small) and otherwise via asymptotic enumeration of bipartite graphs with a given degree sequence proved in [Reference Canfield, Greenhill and McKay1] (see Theorem 5).
In addition, for
![]() $p > 0.49$
, we rely on a non-probabilistic result about the existence of alternating cycles in 2-edge-coloured pseudorandom graphs (Lemma 20), which might be of separate interest.
$p > 0.49$
, we rely on a non-probabilistic result about the existence of alternating cycles in 2-edge-coloured pseudorandom graphs (Lemma 20), which might be of separate interest.
Throughout the paper we assume that the underlying complete bipartite graph
![]() ${K_{n_1,n_2}}$
grows on both sides, that is,
${K_{n_1,n_2}}$
grows on both sides, that is,
![]() $\min\{n_1,n_2\} \to \infty$
, and any parameters (e.g., p, m), events, random variables, etc., are allowed to depend on
$\min\{n_1,n_2\} \to \infty$
, and any parameters (e.g., p, m), events, random variables, etc., are allowed to depend on
![]() $(n_1,n_2)$
. In most cases we will make the dependence on
$(n_1,n_2)$
. In most cases we will make the dependence on
![]() $(n_1,n_2)$
implicit, with all limits and asymptotic notation like
$(n_1,n_2)$
implicit, with all limits and asymptotic notation like
![]() $O, \Omega, \sim$
considered with respect to
$O, \Omega, \sim$
considered with respect to
![]() $\min\{n_1,n_2\} \to \infty$
. We say that an event
$\min\{n_1,n_2\} \to \infty$
. We say that an event
![]() $\mathcal E = \mathcal E(n_1,n_2)$
holds asymptotically almost surely (a.a.s.) if
$\mathcal E = \mathcal E(n_1,n_2)$
holds asymptotically almost surely (a.a.s.) if
![]() $\mathbb{P}\left(\mathcal E\right) \to 1$
.
$\mathbb{P}\left(\mathcal E\right) \to 1$
.
Our main results are Theorem 2 below and its immediate Corollary 3. For a gentle start we first state an abridged version of both in the balanced case
![]() $n_1 = n_2 = n$
. Note that
$n_1 = n_2 = n$
. Note that
![]() $pn^2$
is the number of edges in
$pn^2$
is the number of edges in
![]() $\mathbb{R}(n,n,p)$
.
$\mathbb{R}(n,n,p)$
.
Theorem 1. If
![]() $p\gg\frac{\log n}{n}$
and
$p\gg\frac{\log n}{n}$
and
![]() $1 - p \gg \left( \frac{\log n}{n} \right)^{1/4}$
, then for some
$1 - p \gg \left( \frac{\log n}{n} \right)^{1/4}$
, then for some
![]() $m \sim pn^2$
there is a joint distribution of random graphs
$m \sim pn^2$
there is a joint distribution of random graphs
![]() $\mathbb{G}(n,n,m)$
and
$\mathbb{G}(n,n,m)$
and
![]() $\mathbb{R}(n,n,p)$
such that
$\mathbb{R}(n,n,p)$
such that
If
![]() $p\gg\left(\frac{\log^3 n}{n}\right)^{1/4}$
, then for some
$p\gg\left(\frac{\log^3 n}{n}\right)^{1/4}$
, then for some
![]() $m \sim pn^2$
there is a joint distribution of random graphs
$m \sim pn^2$
there is a joint distribution of random graphs
![]() $\mathbb{G}(n,n,m)$
and
$\mathbb{G}(n,n,m)$
and
![]() $\mathbb{R}(n,n,p)$
such that
$\mathbb{R}(n,n,p)$
such that
Moreover, in (1) and (2) one can replace
![]() $\mathbb{G}(n,n,m)$
by the binomial random graph
$\mathbb{G}(n,n,m)$
by the binomial random graph
![]() $\mathbb{G}(n,n,p')$
, for some
$\mathbb{G}(n,n,p')$
, for some
![]() $p' \sim p$
.
$p' \sim p$
.
The condition
![]() $p \gg (\log n)/n$
is necessary for (1) to hold with
$p \gg (\log n)/n$
is necessary for (1) to hold with
![]() $m \sim pn^2$
(see Remark 26), since otherwise the maximum degree of
$m \sim pn^2$
(see Remark 26), since otherwise the maximum degree of
![]() $\mathbb{G}(n,n,m)$
is no longer
$\mathbb{G}(n,n,m)$
is no longer
![]() $pn(1+o(1))$
a.a.s. We guess that the maximum degree is, vaguely speaking, the only obstacle for embedding
$pn(1+o(1))$
a.a.s. We guess that the maximum degree is, vaguely speaking, the only obstacle for embedding
![]() $\mathbb{G}(n,n,m)$
(or
$\mathbb{G}(n,n,m)$
(or
![]() $\mathbb{G}(n,n,p')$
) into
$\mathbb{G}(n,n,p')$
) into
![]() $\mathbb{R}(n_1,n_2,p)$
, see Conjecture 1 in Section 10.
$\mathbb{R}(n_1,n_2,p)$
, see Conjecture 1 in Section 10.
We further write
![]() $N \,{:\!=}\, n_1n_2$
,
$N \,{:\!=}\, n_1n_2$
,
![]() $q \,{:\!=}\, 1 - p$
,
$q \,{:\!=}\, 1 - p$
,
![]() $\hat n \,{:\!=}\, \min \left\{ n_1, n_2 \right\}$
,
$\hat n \,{:\!=}\, \min \left\{ n_1, n_2 \right\}$
,
![]() $\hat p \,{:\!=}\, \min \{p, q\}$
, and let
$\hat p \,{:\!=}\, \min \{p, q\}$
, and let
 \begin{equation} \mathbb{I} \,{:\!=}\,\mathbb{I}(n_1,n_2,p)= \begin{cases} 1, & \hat p < 2\dfrac{n_1n_2^{-1} + n_1^{-1}n_2}{\log N}\\ \\[-8pt] 0, & \hat p \ge 2\dfrac{n_1n_2^{-1} + n_1^{-1}n_2}{\log N}. \end{cases}\end{equation}
\begin{equation} \mathbb{I} \,{:\!=}\,\mathbb{I}(n_1,n_2,p)= \begin{cases} 1, & \hat p < 2\dfrac{n_1n_2^{-1} + n_1^{-1}n_2}{\log N}\\ \\[-8pt] 0, & \hat p \ge 2\dfrac{n_1n_2^{-1} + n_1^{-1}n_2}{\log N}. \end{cases}\end{equation}
Note that
![]() $\mathbb{I}=0$
entails that the vertex classes are rather balanced: the ratio of their sizes cannot exceed
$\mathbb{I}=0$
entails that the vertex classes are rather balanced: the ratio of their sizes cannot exceed
![]() $\tfrac 1 4 \log N$
. Moreover,
$\tfrac 1 4 \log N$
. Moreover,
![]() $\mathbb{I}=0$
implies that
$\mathbb{I}=0$
implies that
![]() $\hat p \ge 4/\log N$
.
$\hat p \ge 4/\log N$
.
Theorem 2. For every constant
![]() $C > 0$
, there is a constant
$C > 0$
, there is a constant
![]() $C^*$
such that whenever the parameter
$C^*$
such that whenever the parameter
![]() $p \in [0,1]$
satisfies
$p \in [0,1]$
satisfies
and
 \begin{equation}1\ge\gamma \,{:\!=}\, \begin{cases} C^* \left( p^2 \mathbb{I} + \sqrt{\frac{\log N}{p\hat n }}\right), \quad & p \le 0.49 \\ \\[-8pt] C^* \left( q^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n} \right)^{1/4} + \frac1q\sqrt{\frac{\log N}{\hat n}} \log \frac{\hat n}{\log N}\right), \quad & p > 0.49, \end{cases}\end{equation}
\begin{equation}1\ge\gamma \,{:\!=}\, \begin{cases} C^* \left( p^2 \mathbb{I} + \sqrt{\frac{\log N}{p\hat n }}\right), \quad & p \le 0.49 \\ \\[-8pt] C^* \left( q^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n} \right)^{1/4} + \frac1q\sqrt{\frac{\log N}{\hat n}} \log \frac{\hat n}{\log N}\right), \quad & p > 0.49, \end{cases}\end{equation}
there is, for
![]() $m \,{:\!=}\, \lceil(1-\gamma)pN\rceil$
, a joint distribution of random graphs
$m \,{:\!=}\, \lceil(1-\gamma)pN\rceil$
, a joint distribution of random graphs
![]() ${\mathbb{G}(n_1,n_2,m)}$
and
${\mathbb{G}(n_1,n_2,m)}$
and
![]() $\mathbb{R}(n_1,n_2,p)$
such that
$\mathbb{R}(n_1,n_2,p)$
such that
If, in addition
![]() $\gamma \le 1/2$
, then for
$\gamma \le 1/2$
, then for
![]() $p' \,{:\!=}\, (1 - 2\gamma)p$
, there is a joint distribution of
$p' \,{:\!=}\, (1 - 2\gamma)p$
, there is a joint distribution of
![]() $\mathbb{G}(n_1,n_2,p')$
and
$\mathbb{G}(n_1,n_2,p')$
and
![]() $\mathbb{R}(n_1,n_2,p)$
such that
$\mathbb{R}(n_1,n_2,p)$
such that
By inflating
![]() $C^*$
, the constant
$C^*$
, the constant
![]() $0.49$
in (5) can be replaced by any constant smaller than
$0.49$
in (5) can be replaced by any constant smaller than
![]() $1/2$
. It can be shown (see Remark 27 in Section 10) that if
$1/2$
. It can be shown (see Remark 27 in Section 10) that if
![]() $p \le 1/4$
and
$p \le 1/4$
and
![]() $\gamma = \Theta\left( \sqrt{\frac{\log N}{p\hat n }} \right)$
, then
$\gamma = \Theta\left( \sqrt{\frac{\log N}{p\hat n }} \right)$
, then
![]() $\gamma$
has optimal order of magnitude. For more remarks about the conditions of Theorem 2 and the role of the indicator
$\gamma$
has optimal order of magnitude. For more remarks about the conditions of Theorem 2 and the role of the indicator
![]() $\mathbb{I}$
, see Section 10.
$\mathbb{I}$
, see Section 10.
By taking the complements of
![]() $\mathbb{R}(n_1,n_2,p)$
and
$\mathbb{R}(n_1,n_2,p)$
and
![]() $\mathbb{G}(n_1,n_2,m)$
and swapping p and q, we immediately obtain the following consequence of Theorem 2 which provides the opposite embedding.
$\mathbb{G}(n_1,n_2,m)$
and swapping p and q, we immediately obtain the following consequence of Theorem 2 which provides the opposite embedding.
Corollary 3. For every constant
![]() $C > 0$
there is a constant
$C > 0$
there is a constant
![]() $C^*$
such that whenever the parameter
$C^*$
such that whenever the parameter
![]() $p \in [0,1]$
satisfies
$p \in [0,1]$
satisfies
and
 \begin{equation*} 1 \ge \bar\gamma\,{:\!=}\, \begin{cases} C^*\left( p^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n} \right)^{1/4} + \frac 1p\sqrt{\frac{\log N}{\hat n}} \log \frac{\hat n}{\log N}\right), \quad p < 0.51, \\ \\[-9pt] C^*\left( q^2 \mathbb{I} + \sqrt{\frac{\log N}{q\hat n}}\right), \quad p \ge 0.51, \end{cases} \end{equation*}
\begin{equation*} 1 \ge \bar\gamma\,{:\!=}\, \begin{cases} C^*\left( p^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n} \right)^{1/4} + \frac 1p\sqrt{\frac{\log N}{\hat n}} \log \frac{\hat n}{\log N}\right), \quad p < 0.51, \\ \\[-9pt] C^*\left( q^2 \mathbb{I} + \sqrt{\frac{\log N}{q\hat n}}\right), \quad p \ge 0.51, \end{cases} \end{equation*}
there is, for
![]() $\bar m=\lfloor(p+\bar\gamma q)N\rfloor$
, a joint distribution of random graphs
$\bar m=\lfloor(p+\bar\gamma q)N\rfloor$
, a joint distribution of random graphs
![]() $\mathbb{G}(n_1,n_2,\bar m)$
and
$\mathbb{G}(n_1,n_2,\bar m)$
and
![]() $\mathbb{R}(n_1,n_2,p)$
such that
$\mathbb{R}(n_1,n_2,p)$
such that
If, in addition,
![]() $\bar \gamma \le 1/2$
, then for
$\bar \gamma \le 1/2$
, then for
![]() $p'' \,{:\!=}\, (p + 2\bar{\gamma} q)N$
there is a joint distribution of
$p'' \,{:\!=}\, (p + 2\bar{\gamma} q)N$
there is a joint distribution of
![]() $\mathbb{G}(n_1,n_2,p'')$
and
$\mathbb{G}(n_1,n_2,p'')$
and
![]() $\mathbb{R}(n_1,n_2,p)$
such that
$\mathbb{R}(n_1,n_2,p)$
such that
Proof. The assumptions of Corollary 3 yield the assumptions of Theorem 2 with
![]() $\gamma=\bar\gamma$
and with p and q swapped. Note also that
$\gamma=\bar\gamma$
and with p and q swapped. Note also that
Thus, by Theorem 2, with probability
![]() $1 - O(N^{-C})$
we have
$1 - O(N^{-C})$
we have
![]() $\mathbb{G}(n_1,n_2,N - \bar m) \subseteq \mathbb{R}(n_1,n_2,q)$
, which, by taking complements, translates into (9). Similarly
$\mathbb{G}(n_1,n_2,N - \bar m) \subseteq \mathbb{R}(n_1,n_2,q)$
, which, by taking complements, translates into (9). Similarly
Thus, by Theorem 2, with probability
![]() $1 - O(N^{-C})$
we have
$1 - O(N^{-C})$
we have
![]() $\mathbb{G}(n_1,n_2,N-p''N) \subseteq \mathbb{R}(n_1,n_2,q)$
, which, by taking complements yields embedding (10).
$\mathbb{G}(n_1,n_2,N-p''N) \subseteq \mathbb{R}(n_1,n_2,q)$
, which, by taking complements yields embedding (10).
Proof of Theorem 1. We apply Theorem 2 and Corollary 3 with
![]() $C=1$
and the corresponding
$C=1$
and the corresponding
![]() $C^*$
. Note that for
$C^*$
. Note that for
![]() $n_1=n_2=n$
, the ratio in (3) equals
$n_1=n_2=n$
, the ratio in (3) equals
![]() $4/\log N = 2/\log n$
, so
$4/\log N = 2/\log n$
, so
To prove (1), assume
![]() $p\gg\log n/n$
and
$p\gg\log n/n$
and
![]() $q \gg \left( \log n/n \right)^{1/4}$
and apply Theorem 2. Note that condition (4) holds and it is straightforward to check that, regardless of whether
$q \gg \left( \log n/n \right)^{1/4}$
and apply Theorem 2. Note that condition (4) holds and it is straightforward to check that, regardless of whether
![]() $p \le 0.49$
or
$p \le 0.49$
or
![]() $p > 0.49$
,
$p > 0.49$
,
![]() $\gamma \to 0$
. In particular,
$\gamma \to 0$
. In particular,
![]() $\gamma \le 1/2$
. We conclude that, indeed, embedding (1) holds with
$\gamma \le 1/2$
. We conclude that, indeed, embedding (1) holds with
![]() $m = \lceil (1 - \gamma)p N \rceil \sim pn^2$
and (1) still holds if we replace
$m = \lceil (1 - \gamma)p N \rceil \sim pn^2$
and (1) still holds if we replace
![]() $\mathbb{G}(n,n,m)$
by
$\mathbb{G}(n,n,m)$
by
![]() $\mathbb{G}(n,n,p')$
with
$\mathbb{G}(n,n,p')$
with
![]() $p' = (1 - 2\gamma)p \sim p$
.
$p' = (1 - 2\gamma)p \sim p$
.
For (2) first note that when
![]() $p \to 1$
, embedding (2) holds trivially with
$p \to 1$
, embedding (2) holds trivially with
![]() $m = n^2$
(even though a nontrivial embedding follows in this case under an additional assumption
$m = n^2$
(even though a nontrivial embedding follows in this case under an additional assumption
![]() $q \gg \log n/n$
. Hence, we further assume
$q \gg \log n/n$
. Hence, we further assume
![]() $q = \Omega(1)$
,
$q = \Omega(1)$
,
![]() $p\gg\left(\log^3 n / n\right)^{1/4}$
and apply Corollary 1.2. Note that condition (8) holds. It is routine to check, taking into account (11), that
$p\gg\left(\log^3 n / n\right)^{1/4}$
and apply Corollary 1.2. Note that condition (8) holds. It is routine to check, taking into account (11), that
![]() $\bar\gamma\le 1/2$
and, moreover,
$\bar\gamma\le 1/2$
and, moreover,
![]() $\bar\gamma q = o(p)$
. We conclude that (2) holds with
$\bar\gamma q = o(p)$
. We conclude that (2) holds with
![]() $m = \lfloor(p + \bar\gamma q)N \rfloor \sim Np = n^2p$
and (2) still holds if
$m = \lfloor(p + \bar\gamma q)N \rfloor \sim Np = n^2p$
and (2) still holds if
![]() $\mathbb{G}(n,n,m)$
is replaced by
$\mathbb{G}(n,n,m)$
is replaced by
![]() $\mathbb{G}(n,n,p')$
with
$\mathbb{G}(n,n,p')$
with
![]() $p' = p + 2 \bar \gamma q \sim p$
.
$p' = p + 2 \bar \gamma q \sim p$
.
1.3. A note on the second version of the manuscript
This project was initially aimed at extending the result in [Reference Dudek, Frieze, Ruciński and Šileikis2] to bipartite graphs and, thus, limited to the lower embedding
![]() $\mathbb{G}(n,n,p_1) \subseteq \mathbb{R}(n,n,p)$
only. While it was in progress, Gao, Isaev and McKay [Reference Gao, Isaev and McKay4] made an improvement on the Sandwich Conjecture by using a surprisingly fruitful idea of taking complements to obtain the upper embedding
$\mathbb{G}(n,n,p_1) \subseteq \mathbb{R}(n,n,p)$
only. While it was in progress, Gao, Isaev and McKay [Reference Gao, Isaev and McKay4] made an improvement on the Sandwich Conjecture by using a surprisingly fruitful idea of taking complements to obtain the upper embedding
![]() $\mathbb{R}(n,d) \subseteq \mathbb{G}(n,p_2)$
directly from the lower embedding
$\mathbb{R}(n,d) \subseteq \mathbb{G}(n,p_2)$
directly from the lower embedding
![]() $\mathbb{G}(n,p_1) \subseteq \mathbb{R}(n,d)$
. We then decided to borrow this idea (but nothing else) and strengthen some of our lemmas to get a significantly broader range of p for which the upper embedding (i.e. Corollary 1.2) holds. It turned out that our approach works for non-bipartite regular graphs, too. Therefore, prompted by the recent substantial progress of Gao [Reference Gao3] on the Sandwich Conjecture (which appeared on arXiv after the first version of this manuscript), in the current version of the manuscript we added Section 7, which outlines how to modify our proofs to get a corresponding sandwiching for non-bipartite graphs. This improves upon the results in [Reference Gao, Isaev and McKay4] (for regular graphs), but is now superseded by [Reference Gao3].
$\mathbb{G}(n,p_1) \subseteq \mathbb{R}(n,d)$
. We then decided to borrow this idea (but nothing else) and strengthen some of our lemmas to get a significantly broader range of p for which the upper embedding (i.e. Corollary 1.2) holds. It turned out that our approach works for non-bipartite regular graphs, too. Therefore, prompted by the recent substantial progress of Gao [Reference Gao3] on the Sandwich Conjecture (which appeared on arXiv after the first version of this manuscript), in the current version of the manuscript we added Section 7, which outlines how to modify our proofs to get a corresponding sandwiching for non-bipartite graphs. This improves upon the results in [Reference Gao, Isaev and McKay4] (for regular graphs), but is now superseded by [Reference Gao3].
1.4. Organisation
In Section 2 we introduce the notation and tools used throughout the paper: the switching technique, probabilistic inequalities and an enumeration result for bipartite graphs with a given degree sequence. In Section 3 we state a crucial Lemma 6 and show how it implies Theorem 2.
In Section 4 we give a proof of Lemma 6 based on two technical lemmas, one about the concentration of a degree-related parameter (Lemma 9), the other (Lemma 10) facilitating the switching technique used in the proof of Lemma 6. Lemma 9 is proved in Section 5, after giving some auxiliary results establishing the concentration of degrees and co-degrees in
![]() $\mathbb{R}(n_1,n_2,p)$
as well as in its conditional versions. In Section 6, we present a proof of Lemma 10, preceded by a purely deterministic result about alternating cycles in 2-edge-coloured pseudorandom graphs. We defer some technical but straightforward results and their proofs (e.g., the proof of Claim 7) to Section 8. A flowchart of the results ultimately leading to the proof of Theorem 2 is presented in Figure 1.
$\mathbb{R}(n_1,n_2,p)$
as well as in its conditional versions. In Section 6, we present a proof of Lemma 10, preceded by a purely deterministic result about alternating cycles in 2-edge-coloured pseudorandom graphs. We defer some technical but straightforward results and their proofs (e.g., the proof of Claim 7) to Section 8. A flowchart of the results ultimately leading to the proof of Theorem 2 is presented in Figure 1.

Figure 1. The structure of the proof of Theorem 2. An arrow from statement A to statement B means that A is used in the proof of B. The numbers in the brackets point to the section where a statement is formulated and where it is proved (unless the proof follows the statement immediately); external results have instead an article reference in square brackets.
The contents of Section 7 were already described (see Subsection 1.3 above). Section 9 contains an application of our main Theorem 2, which was part of the motivation for our research. In Section 10 we present some concluding remarks and our version of the (bipartite) sandwiching conjecture.
2. Preliminaries
2.1. Notation
Recall that
are the degrees of vertices in a p-biregular graph, and thus, the number of edges in any p-biregular graph
![]() $H \in {{\mathcal{R}}(n_1,n_2,p)}$
is
$H \in {{\mathcal{R}}(n_1,n_2,p)}$
is
Throughout the proofs we also use shorthand notation
and
![]() $[n] \,{:\!=}\, \left\{ 1, \dots, n \right\}$
. All logarithms appearing in this paper are natural.
$[n] \,{:\!=}\, \left\{ 1, \dots, n \right\}$
. All logarithms appearing in this paper are natural.
By
![]() $\Gamma_{G}(v)$
we denote the set of neighbours of a vertex v in a graph G.
$\Gamma_{G}(v)$
we denote the set of neighbours of a vertex v in a graph G.
2.2. Switchings
The switching technique is used to compare the size of two classes of graphs, say
![]() ${\mathcal{R}}$
and
${\mathcal{R}}$
and
![]() ${\mathcal{R}}'$
, by defining an auxiliary bipartite graph
${\mathcal{R}}'$
, by defining an auxiliary bipartite graph
![]() $B\,{:\!=}\,B({\mathcal{R}},{\mathcal{R}}')$
, in which two graphs
$B\,{:\!=}\,B({\mathcal{R}},{\mathcal{R}}')$
, in which two graphs
![]() $H \in {\mathcal{R}}$
,
$H \in {\mathcal{R}}$
,
![]() $H' \in {\mathcal{R}}'$
are connected by an edge whenever H can be transformed into H
′ by some operation (a forward switching) that deletes and/or creates some edges of H. By counting the number of edges of
$H' \in {\mathcal{R}}'$
are connected by an edge whenever H can be transformed into H
′ by some operation (a forward switching) that deletes and/or creates some edges of H. By counting the number of edges of
![]() $B({\mathcal{R}},{\mathcal{R}}')$
in two ways, we see that
$B({\mathcal{R}},{\mathcal{R}}')$
in two ways, we see that
which easily implies that
The reverse operation mapping
![]() $H' \in {\mathcal{R}}'$
to its neighbours in graph B, is called a backward switching. Usually, one defines the forward switching in such a way that the backward switching can be easily described.
$H' \in {\mathcal{R}}'$
to its neighbours in graph B, is called a backward switching. Usually, one defines the forward switching in such a way that the backward switching can be easily described.
All switchings used in this paper follow the same pattern. For a fixed graph
![]() $G \subseteq K$
(possibly empty), where
$G \subseteq K$
(possibly empty), where
![]() $K \,{:\!=}\, {K_{n_1,n_2}}$
, the families
$K \,{:\!=}\, {K_{n_1,n_2}}$
, the families
![]() ${\mathcal{R}}, {\mathcal{R}}'$
will be subsets of
${\mathcal{R}}, {\mathcal{R}}'$
will be subsets of
Every
![]() $H \in {\mathcal{R}}_G$
will be interpreted as a blue-red colouring of the edges of
$H \in {\mathcal{R}}_G$
will be interpreted as a blue-red colouring of the edges of
![]() $K\setminus G$
: those in
$K\setminus G$
: those in
![]() $H\setminus G$
will be coloured blue and those in
$H\setminus G$
will be coloured blue and those in
![]() $K \setminus H$
— red. Given
$K \setminus H$
— red. Given
![]() $H\in{\mathcal{R}}$
, consider a subset S of the edges of
$H\in{\mathcal{R}}$
, consider a subset S of the edges of
![]() $K\setminus G$
in which for every vertex
$K\setminus G$
in which for every vertex
![]() $v \in V_1 \cup V_2$
the blue degree equals the red degree, i.e.,
$v \in V_1 \cup V_2$
the blue degree equals the red degree, i.e.,
![]() $\deg_{(H\setminus G)\cap S}(v)=\deg_{(K\setminus H)\cap S}(v)$
. Then switching the colours within S produces another graph
$\deg_{(H\setminus G)\cap S}(v)=\deg_{(K\setminus H)\cap S}(v)$
. Then switching the colours within S produces another graph
![]() $H' \in {\mathcal{R}}_G$
. Formally, E(H
′) is the symmetric difference
$H' \in {\mathcal{R}}_G$
. Formally, E(H
′) is the symmetric difference
![]() $E(H) \triangle S$
. In each application of the switching technique, we will restrict the choices of S to make sure that
$E(H) \triangle S$
. In each application of the switching technique, we will restrict the choices of S to make sure that
![]() $H' \in {\mathcal{R}}'$
.
$H' \in {\mathcal{R}}'$
.
As an elementary illustration of this technique, which nevertheless turns out to be useful in Section 6, we prove here the following result. A cycle in
![]() $K\setminus G$
is alternating if it is a union of a blue matching and a red matching. Note that the definition depends on H. We will omit mentioning this dependence, as H will always be clear from the context. Given
$K\setminus G$
is alternating if it is a union of a blue matching and a red matching. Note that the definition depends on H. We will omit mentioning this dependence, as H will always be clear from the context. Given
![]() $e \in K\setminus G$
, set
$e \in K\setminus G$
, set
Proposition 4. Let a graph
![]() $G\subseteq K$
be such that
$G\subseteq K$
be such that
![]() ${\mathcal{R}}_G\neq\emptyset$
and let
${\mathcal{R}}_G\neq\emptyset$
and let
![]() $e\in K\setminus G$
. Assume that for some number
$e\in K\setminus G$
. Assume that for some number
![]() $D > 0$
and every
$D > 0$
and every
![]() $H\in {\mathcal{R}}_{G}$
the edge e is contained in an alternating cycle of length at most 2D. Then
$H\in {\mathcal{R}}_{G}$
the edge e is contained in an alternating cycle of length at most 2D. Then
![]() ${\mathcal{R}}_{G,\neg e}\neq\emptyset$
,
${\mathcal{R}}_{G,\neg e}\neq\emptyset$
,
![]() ${\mathcal{R}}_{G, e}\neq\emptyset$
, and
${\mathcal{R}}_{G, e}\neq\emptyset$
, and
Proof. Let
![]() $B = B({\mathcal{R}}_{G,e}, {\mathcal{R}}_{G,\neg e})$
be the switching graph corresponding to the following forward switching: choose an alternating cycle S of length at most 2D containing e and switch the colours of edges within S. Note that the backward switching does precisely the same. Note that by the assumption, the minimum degree
$B = B({\mathcal{R}}_{G,e}, {\mathcal{R}}_{G,\neg e})$
be the switching graph corresponding to the following forward switching: choose an alternating cycle S of length at most 2D containing e and switch the colours of edges within S. Note that the backward switching does precisely the same. Note that by the assumption, the minimum degree
![]() $\delta(B)$
is at least 1.
$\delta(B)$
is at least 1.
Since
![]() ${\mathcal{R}}_G={\mathcal{R}}_{G, e}\cup{\mathcal{R}}_{G, \neg e} \neq \emptyset$
, one of the classes
${\mathcal{R}}_G={\mathcal{R}}_{G, e}\cup{\mathcal{R}}_{G, \neg e} \neq \emptyset$
, one of the classes
![]() ${\mathcal{R}}_{G, e}$
and
${\mathcal{R}}_{G, e}$
and
![]() ${\mathcal{R}}_{G, \neg e}$
is non-empty and, in view of
${\mathcal{R}}_{G, \neg e}$
is non-empty and, in view of
![]() $\delta(B) \ge 1$
, the other one is non-empty as well. For
$\delta(B) \ge 1$
, the other one is non-empty as well. For
![]() $\ell = 2, \dots, D$
, the number of cycles of length
$\ell = 2, \dots, D$
, the number of cycles of length
![]() $2\ell$
containing e is, crudely, at most
$2\ell$
containing e is, crudely, at most
![]() $n_1^{\ell - 1} n_2^{\ell - 1} = N^{\ell - 1}$
, hence the maximum degree is
$n_1^{\ell - 1} n_2^{\ell - 1} = N^{\ell - 1}$
, hence the maximum degree is
Thus, by (14), we obtain the claimed bounds.
2.3. Probabilistic inequalities
We first state a few basic concentration inequalities that we apply in our proofs. For a sum X of independent Bernoulli (not necessarily identically distributed) random variables, writing
![]() $\mu = \operatorname{\mathbb{E}} X$
, we have (see Theorem 2.8, (2.5), (2.6), and (2.11) in [Reference Janson, Łuczak and Rucinski5]) that
$\mu = \operatorname{\mathbb{E}} X$
, we have (see Theorem 2.8, (2.5), (2.6), and (2.11) in [Reference Janson, Łuczak and Rucinski5]) that
Let
![]() $\Gamma$
be a set of size
$\Gamma$
be a set of size
![]() $|\Gamma|=g$
and let
$|\Gamma|=g$
and let
![]() $A \subseteq \Gamma$
,
$A \subseteq \Gamma$
,
![]() $|A|=a \ge1$
. For an integer
$|A|=a \ge1$
. For an integer
![]() $r \in [0,g]$
, choose uniformly at random a subset
$r \in [0,g]$
, choose uniformly at random a subset
![]() $R \subseteq \Gamma$
of size
$R \subseteq \Gamma$
of size
![]() $|R|=r$
. The random variable
$|R|=r$
. The random variable
![]() $Y = |A \cap R|$
has then the hypergeometric distribution
$Y = |A \cap R|$
has then the hypergeometric distribution
![]() $\operatorname{Hyp}(g, a, r)$
with expectation
$\operatorname{Hyp}(g, a, r)$
with expectation
![]() $\mu \,{:\!=}\, \operatorname{\mathbb{E}} Y = ar/g$
. By Theorem 2.10 in [Reference Janson, Łuczak and Rucinski5], inequalities (17) and (18) hold for Y, too.
$\mu \,{:\!=}\, \operatorname{\mathbb{E}} Y = ar/g$
. By Theorem 2.10 in [Reference Janson, Łuczak and Rucinski5], inequalities (17) and (18) hold for Y, too.
Moreover, by Remark 2.6 in [Reference Janson, Łuczak and Rucinski5], inequalities (17) and (18) also hold for a random variable Z which has Poisson distribution
![]() $\operatorname{Po}(\mu)$
with expectation
$\operatorname{Po}(\mu)$
with expectation
![]() $\mu$
. In this case, we also have the following simple fact. For
$\mu$
. In this case, we also have the following simple fact. For
![]() $k\ge0$
, set
$k\ge0$
, set
![]() $q_k=\mathbb{P}\left(Z=k\right)$
. Then
$q_k=\mathbb{P}\left(Z=k\right)$
. Then
![]() $q_k/q_{k-1}=\mu/k$
, and hence
$q_k/q_{k-1}=\mu/k$
, and hence
![]() $k = \lfloor\mu\rfloor$
maximises
$k = \lfloor\mu\rfloor$
maximises
![]() $q_k$
(we say that such k is a mode of Z). Since
$q_k$
(we say that such k is a mode of Z). Since
![]() $\operatorname{Var} Z = \mu$
, by Chebyshev’s inequality,
$\operatorname{Var} Z = \mu$
, by Chebyshev’s inequality,
![]() $\mathbb{P}\left(|Z-\mu|<\sqrt{2\mu}\right)\ge1/2$
. Moreover, the interval
$\mathbb{P}\left(|Z-\mu|<\sqrt{2\mu}\right)\ge1/2$
. Moreover, the interval
![]() $(\mu - \sqrt{2 \mu}, \mu + \sqrt{2 \mu})$
contains at most
$(\mu - \sqrt{2 \mu}, \mu + \sqrt{2 \mu})$
contains at most
![]() $\lceil \sqrt{8\mu}\:\rceil$
integers, hence it follows that
$\lceil \sqrt{8\mu}\:\rceil$
integers, hence it follows that
2.4. Asymptotic enumeration of dense bipartite graphs
To estimate co-degrees of
![]() $\mathbb{R}(n,n,p)$
we will use the following asymptotic formula by Canfield, Greenhill and McKay [Reference Canfield, Greenhill and McKay1]. We reformulate it slightly for our convenience.
$\mathbb{R}(n,n,p)$
we will use the following asymptotic formula by Canfield, Greenhill and McKay [Reference Canfield, Greenhill and McKay1]. We reformulate it slightly for our convenience.
Given two vectors
![]() ${\mathbf{d}}_1 = (d_{1,v}, v \in V_1)$
and
${\mathbf{d}}_1 = (d_{1,v}, v \in V_1)$
and
![]() ${\mathbf{d}}_2 = (d_{2,v}, v \in V_2)$
of positive integers such that
${\mathbf{d}}_2 = (d_{2,v}, v \in V_2)$
of positive integers such that
![]() $\sum_{v \in V_1} d_{1, v} = \sum_{v \in V_2} d_{2,v}$
, let
$\sum_{v \in V_1} d_{1, v} = \sum_{v \in V_2} d_{2,v}$
, let
![]() ${{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)}$
be the class of bipartite graphs on
${{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)}$
be the class of bipartite graphs on
![]() $(V_1, V_2)$
with vertex degrees
$(V_1, V_2)$
with vertex degrees
![]() $\deg(v) = d_{i,v}, v \in V_i, i = 1,2$
. Let
$\deg(v) = d_{i,v}, v \in V_i, i = 1,2$
. Let
![]() $|V_i| = n_i$
and write
$|V_i| = n_i$
and write
![]() $\bar d_i = {n_i}^{-1}\sum_{v \in V_i} d_{i,v}$
,
$\bar d_i = {n_i}^{-1}\sum_{v \in V_i} d_{i,v}$
,
![]() $D_i = \sum_{v \in V_i} (d_{i,v} - \bar d_i)^2$
,
$D_i = \sum_{v \in V_i} (d_{i,v} - \bar d_i)^2$
,
![]() $p = \bar d_1/n_2 = \bar d_2/n_1$
, and
$p = \bar d_1/n_2 = \bar d_2/n_1$
, and
![]() $q = 1 - p$
.
$q = 1 - p$
.
Theorem 5. ([Reference Canfield, Greenhill and McKay1]) Given any positive constants a, b, C such that
![]() $a+b < 1/2$
, there exists a constant
$a+b < 1/2$
, there exists a constant
![]() $\epsilon > 0$
so that the following holds. Consider the set of degree sequences
$\epsilon > 0$
so that the following holds. Consider the set of degree sequences
![]() ${\mathbf{d}}_1,{\mathbf{d}}_2$
satisfying
${\mathbf{d}}_1,{\mathbf{d}}_2$
satisfying
-
i.
 $\max_{v \in V_1}|d_{1,v} - \bar d_1| \le Cn_2^{1/2 + \epsilon}$
,
$\max_{v \in V_1}|d_{1,v} - \bar d_1| \le Cn_2^{1/2 + \epsilon}$
,
 $\max_{v \in V_2} |d_{2,v} - \bar d_2| \le Cn_1^{1/2 + \epsilon}$
$\max_{v \in V_2} |d_{2,v} - \bar d_2| \le Cn_1^{1/2 + \epsilon}$
-
ii.
 $\max \{n_1, n_2\} \le C(pq)^2(\min \left\{ n_1, n_2 \right\})^{1 + \epsilon}$
$\max \{n_1, n_2\} \le C(pq)^2(\min \left\{ n_1, n_2 \right\})^{1 + \epsilon}$
-
iii.
 $ \frac{(1 - 2p)^2}{4pq} \left( 1 + \frac{5n_1}{6n_2} + \frac{5n_2}{6n_1} \right) \le a \log \max \left\{ n_1, n_2 \right\}$
.
$ \frac{(1 - 2p)^2}{4pq} \left( 1 + \frac{5n_1}{6n_2} + \frac{5n_2}{6n_1} \right) \le a \log \max \left\{ n_1, n_2 \right\}$
.
If
![]() $\min\{n_1, n_2\} \to \infty$
, then uniformly for all such
$\min\{n_1, n_2\} \to \infty$
, then uniformly for all such
![]() ${\mathbf{d}}_1,{\mathbf{d}}_2$
${\mathbf{d}}_1,{\mathbf{d}}_2$
 \begin{align} |{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)| &= \binom{n_1n_2}{p n_1n_2}^{-1} \prod_{v \in V_1}\binom {n_2}{d_{1,v}} \prod_{v \in V_2}\binom {n_1}{d_{2,v}} \times \nonumber\\&\quad \times \exp \left[ -\frac{1}{2}\left( 1- \frac{D_1}{pqn_1n_2} \right)\left(1- \frac{D_2}{pqn_1n_2} \right) + O\left((\max\left\{ n_1,n_2 \right\})^{-b}\right) \right],\end{align}
\begin{align} |{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)| &= \binom{n_1n_2}{p n_1n_2}^{-1} \prod_{v \in V_1}\binom {n_2}{d_{1,v}} \prod_{v \in V_2}\binom {n_1}{d_{2,v}} \times \nonumber\\&\quad \times \exp \left[ -\frac{1}{2}\left( 1- \frac{D_1}{pqn_1n_2} \right)\left(1- \frac{D_2}{pqn_1n_2} \right) + O\left((\max\left\{ n_1,n_2 \right\})^{-b}\right) \right],\end{align}
where the constants implicit in the error term may depend on a,b,C.
Note that condition (ii) of Theorem 5 implies the corresponding condition in [Reference Canfield, Greenhill and McKay1] after adjusting
![]() $\epsilon$
. Also, the uniformity of the bound is not explicitly stated in [Reference Canfield, Greenhill and McKay1], but, given
$\epsilon$
. Also, the uniformity of the bound is not explicitly stated in [Reference Canfield, Greenhill and McKay1], but, given
![]() $n_1, n_2$
, one should take
$n_1, n_2$
, one should take
![]() ${\mathbf{d}}_1, {\mathbf{d}}_2$
with the worst error and apply the result in [Reference Canfield, Greenhill and McKay1].
${\mathbf{d}}_1, {\mathbf{d}}_2$
with the worst error and apply the result in [Reference Canfield, Greenhill and McKay1].
3. A crucial lemma
3.1. The set-up
Recall that
![]() $K = {K_{n_1,n_2}}$
has
$K = {K_{n_1,n_2}}$
has
![]() $N = n_1n_2$
edges. Consider a sequence of graphs
$N = n_1n_2$
edges. Consider a sequence of graphs
![]() $\mathbb{G}(t) \subseteq K$
for
$\mathbb{G}(t) \subseteq K$
for
![]() $t = 0, \dots , N$
, where
$t = 0, \dots , N$
, where
![]() $\mathbb{G}(0)$
is empty and, for
$\mathbb{G}(0)$
is empty and, for
![]() $t < N$
,
$t < N$
,
![]() $\mathbb{G}(t + 1)$
is obtained from
$\mathbb{G}(t + 1)$
is obtained from
![]() $\mathbb{G}(t)$
by adding an edge
$\mathbb{G}(t)$
by adding an edge
![]() $\varepsilon_{t + 1}$
chosen from
$\varepsilon_{t + 1}$
chosen from
![]() $K \setminus \mathbb{G}(t)$
uniformly at random, that is, for every graph
$K \setminus \mathbb{G}(t)$
uniformly at random, that is, for every graph
![]() $G \subseteq K$
of size t and every edge
$G \subseteq K$
of size t and every edge
![]() $e \in K \setminus G$
$e \in K \setminus G$
Of course,
![]() $(\varepsilon_1, \dots, \varepsilon_N)$
is just a uniformly random ordering of the edges of K.
$(\varepsilon_1, \dots, \varepsilon_N)$
is just a uniformly random ordering of the edges of K.
Our approach to proving Theorem 2 is to represent the random regular graph
![]() $\mathbb{R}(n_1,n_2,p)$
as the outcome of a random process which behaves similarly to
$\mathbb{R}(n_1,n_2,p)$
as the outcome of a random process which behaves similarly to
![]() $(\mathbb{G}(t))_t$
. Recalling that a p-biregular graph has
$(\mathbb{G}(t))_t$
. Recalling that a p-biregular graph has
![]() $M = pN$
edges, let
$M = pN$
edges, let
be a uniformly random ordering of the edges of
![]() $\mathbb{R}(n_1,n_2,p)$
. By taking the initial segments, we obtain a sequence of random graphs
$\mathbb{R}(n_1,n_2,p)$
. By taking the initial segments, we obtain a sequence of random graphs
For convenience, we shorten
Let us mention here that for a fixed
![]() $H \in {{\mathcal{R}}(n_1,n_2,p)}$
, conditioning on
$H \in {{\mathcal{R}}(n_1,n_2,p)}$
, conditioning on
![]() $\mathbb{R} = H$
, the edge set of the random subgraph
$\mathbb{R} = H$
, the edge set of the random subgraph
![]() $\mathbb{R}(t)$
is a uniformly random t-element subset of the edge set of H. This observation often leads to a hypergeometric distribution and will be utilised several times in our proofs.
$\mathbb{R}(t)$
is a uniformly random t-element subset of the edge set of H. This observation often leads to a hypergeometric distribution and will be utilised several times in our proofs.
We say that a graph G with t edges is admissible, if the family
![]() ${\mathcal{R}}_G$
(see definition (15)) is non-empty, or, equivalently,
${\mathcal{R}}_G$
(see definition (15)) is non-empty, or, equivalently,
For an admissible graph G with t edges and any edge
![]() $ e \in K \setminus G$
, let
$ e \in K \setminus G$
, let
The conditional space underlying (22) can be described as first extending G uniformly at random to an element of
![]() ${\mathcal{R}}_G$
and then randomly permuting the new
${\mathcal{R}}_G$
and then randomly permuting the new
![]() $M-t$
edges.
$M-t$
edges.
The main idea behind the proof of Theorem 2 is that the conditional probabilities in (22) behave similarly to those in (21). Observe that
![]() $p_{t+1}(e,\mathbb{R}(t)) = \mathbb{P}\left({\eta_{t+1} = e}\,|\,{\mathbb{R}(t)}\right)$
. Given a real number
$p_{t+1}(e,\mathbb{R}(t)) = \mathbb{P}\left({\eta_{t+1} = e}\,|\,{\mathbb{R}(t)}\right)$
. Given a real number
![]() $\chi \ge 0$
and
$\chi \ge 0$
and
![]() $t \in \{0, \dots, M - 1\}$
, we define an
$t \in \{0, \dots, M - 1\}$
, we define an
![]() $\mathbb{R}(t)$
-measurable event
$\mathbb{R}(t)$
-measurable event
In the crucial lemma below, we are going to show that for suitably chosen
![]() $\gamma_0, \gamma_1, \dots$
, a.a.s. the events
$\gamma_0, \gamma_1, \dots$
, a.a.s. the events
![]() ${\mathcal{A}}(t,\gamma_t)$
occur simultaneously for all
${\mathcal{A}}(t,\gamma_t)$
occur simultaneously for all
![]() $t = 0,\dots,t_0-1$
where
$t = 0,\dots,t_0-1$
where
![]() $t_0$
is quite close to M. Postponing the choice of
$t_0$
is quite close to M. Postponing the choice of
![]() $\gamma_t$
and
$\gamma_t$
and
![]() $t_0$
, we define an event
$t_0$
, we define an event
 \begin{equation} {\mathcal{A}} \,{:\!=}\, \bigcap_{t = 0}^{ t_0 - 1}{\mathcal{A}}(t, \gamma_t).\end{equation}
\begin{equation} {\mathcal{A}} \,{:\!=}\, \bigcap_{t = 0}^{ t_0 - 1}{\mathcal{A}}(t, \gamma_t).\end{equation}
Intuitively, the event
![]() ${\mathcal{A}}$
asserts that up to time
${\mathcal{A}}$
asserts that up to time
![]() $t_0$
the process
$t_0$
the process
![]() $\mathbb{R}(t)$
stays ‘almost uniform’, which will enable us to embed
$\mathbb{R}(t)$
stays ‘almost uniform’, which will enable us to embed
![]() ${\mathbb{G}(n_1,n_2,m)}$
into
${\mathbb{G}(n_1,n_2,m)}$
into
![]() $\mathbb{R}(t_0)$
.
$\mathbb{R}(t_0)$
.
To define time
![]() $t_0$
, it is convenient to parametrise the time by the proportion of edges of
$t_0$
, it is convenient to parametrise the time by the proportion of edges of
![]() $\mathbb{R}$
‘not yet revealed’ after t steps. For this, we define by
$\mathbb{R}$
‘not yet revealed’ after t steps. For this, we define by
Given a constant
![]() $C > 0$
and, we define (recalling the notation in (12)) the ‘final’ value
$C > 0$
and, we define (recalling the notation in (12)) the ‘final’ value
![]() $\tau_0$
of
$\tau_0$
of
![]() $\tau$
as
$\tau$
as
 \begin{equation} \tau_0 \,{:\!=}\, \begin{cases} \dfrac{3 \cdot 3240^2(C + 4)\log N}{p \hat n}, \quad & p \le 0.49, \\ \\[-9pt] 700(3(C + 4))^{1/4} \left( q^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n}\right)^{1/4}\right), \quad & p > 0.49. \end{cases}\end{equation}
\begin{equation} \tau_0 \,{:\!=}\, \begin{cases} \dfrac{3 \cdot 3240^2(C + 4)\log N}{p \hat n}, \quad & p \le 0.49, \\ \\[-9pt] 700(3(C + 4))^{1/4} \left( q^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n}\right)^{1/4}\right), \quad & p > 0.49. \end{cases}\end{equation}
(Some of the constants appearing here and below are sharp or almost sharp, but others have room to spare as we round them up to the nearest ‘nice’ number.)
Consider the following assumptions on p (which we will later show to follow from the assumptions of Theorem 2):
and
At the end of this subsection we show that these three assumptions imply
so that
is a non-negative integer. Further, for
![]() $t = 0, \dots, M - 1$
, define
$t = 0, \dots, M - 1$
, define
 \begin{equation} \gamma_t \,{:\!=}\, 1080 \hat p^2 \mathbb{I} + \begin{cases} 3240 \sqrt{\dfrac{2(C + 3)\log N}{\tau p \hat n}}, \quad & p \le 0.49, \\ \\[-9pt] 25,000 \sqrt{\dfrac{(C + 3)\log N}{ \tau^2q^2 \hat n}} , \quad & p > 0.49. \end{cases}\end{equation}
\begin{equation} \gamma_t \,{:\!=}\, 1080 \hat p^2 \mathbb{I} + \begin{cases} 3240 \sqrt{\dfrac{2(C + 3)\log N}{\tau p \hat n}}, \quad & p \le 0.49, \\ \\[-9pt] 25,000 \sqrt{\dfrac{(C + 3)\log N}{ \tau^2q^2 \hat n}} , \quad & p > 0.49. \end{cases}\end{equation}
Taking (29) for granted, we now state our crucial lemma, which is proved in Section 4.
Lemma 6. For every constant
![]() $C > 0$
, if assumptions (26), (27) and (28) hold, then
$C > 0$
, if assumptions (26), (27) and (28) hold, then
where the constant implicit in the O-term in (31) may also depend on C.
It remains to show (29). When
![]() $p \le 0.49$
, inequality (29) is equivalent to (26). For
$p \le 0.49$
, inequality (29) is equivalent to (26). For
![]() $p > 0.49$
, we have
$p > 0.49$
, we have
![]() $q \le 51\hat p/49$
, which together with assumptions (27) and (28) implies that
$q \le 51\hat p/49$
, which together with assumptions (27) and (28) implies that
3.2. Proof of Theorem 2
From Lemma 6 we are going to deduce Theorem 2 using a coupling argument similar to the one which was employed by Dudek, Frieze, Ruciński and Šileikis [Reference Dudek, Frieze, Ruciński and Šileikis2], but with an extra tweak (inspired by Kim and Vu [Reference Kim and Vu6]) of letting the probabilities
![]() $\gamma_t$
of Bernoulli random variables depend on t, which reduces the error
$\gamma_t$
of Bernoulli random variables depend on t, which reduces the error
![]() $\gamma$
in (5).
$\gamma$
in (5).
It is easy to check that the assumptions of Lemma 6 follow from the assumptions of Theorem 2. Indeed, (28) coincides with assumption (4), while (26) and (27) follow from the assumption
![]() $\gamma \le 1$
(see (5)) for sufficiently large
$\gamma \le 1$
(see (5)) for sufficiently large
![]() $C^*$
.
$C^*$
.
Our aim is to couple
![]() $(\mathbb{G}(t))_t$
and
$(\mathbb{G}(t))_t$
and
![]() $(\mathbb{R}(t))_t$
on the event
$(\mathbb{R}(t))_t$
on the event
![]() ${\mathcal{A}}$
defined in (23). For this we will define a graph process
${\mathcal{A}}$
defined in (23). For this we will define a graph process
![]() $\mathbb{R}'(t) \,{:\!=}\, \{\eta^{\prime}_1, \dots, \eta^{\prime}_t\}, t = 0, \dots, t_0$
so that for every admissible graph G with
$\mathbb{R}'(t) \,{:\!=}\, \{\eta^{\prime}_1, \dots, \eta^{\prime}_t\}, t = 0, \dots, t_0$
so that for every admissible graph G with
![]() $t \in [0, M -1]$
edges and every
$t \in [0, M -1]$
edges and every
![]() $e \in K \setminus G$
$e \in K \setminus G$
where
![]() $p_{t+1}(e, G)$
was defined in (22). Note that
$p_{t+1}(e, G)$
was defined in (22). Note that
![]() $\mathbb{R}'(0)$
is an empty graph. Since the distribution of the process
$\mathbb{R}'(0)$
is an empty graph. Since the distribution of the process
![]() $(\mathbb{R}(t))_t$
is determined by the conditional probabilities (22), in view of (32), the distribution of
$(\mathbb{R}(t))_t$
is determined by the conditional probabilities (22), in view of (32), the distribution of
![]() $\mathbb{R}'(t_0)$
is the same as that of
$\mathbb{R}'(t_0)$
is the same as that of
![]() $\mathbb{R}(t_0)$
and therefore we will identify
$\mathbb{R}(t_0)$
and therefore we will identify
![]() $\mathbb{R}'(t_0)$
with
$\mathbb{R}'(t_0)$
with
![]() $\mathbb{R}(t_0)$
. As the second step, we will show that a.a.s.
$\mathbb{R}(t_0)$
. As the second step, we will show that a.a.s.
![]() ${\mathbb{G}(n_1,n_2,m)}$
can be sampled from
${\mathbb{G}(n_1,n_2,m)}$
can be sampled from
![]() $\mathbb{R}'(t_0) = \mathbb{R}(t_0)$
.
$\mathbb{R}'(t_0) = \mathbb{R}(t_0)$
.
Proceeding with the definition, set
![]() $\mathbb{R}'(0)$
to be the empty graph and define graphs
$\mathbb{R}'(0)$
to be the empty graph and define graphs
![]() $\mathbb{R}'(t)$
,
$\mathbb{R}'(t)$
,
![]() $t = 1, \dots, t_0$
, inductively, as follows. Hence, let us further fix
$t = 1, \dots, t_0$
, inductively, as follows. Hence, let us further fix
![]() $t \in [0, t_0-1]$
and suppose that
$t \in [0, t_0-1]$
and suppose that
have been already chosen. Our immediate goal is to select a random pair of edges
![]() $\varepsilon_{t+1}$
and
$\varepsilon_{t+1}$
and
![]() $\eta_{t+1}^{\prime}$
, according to, resp., (21) and (32), in such a way that the event
$\eta_{t+1}^{\prime}$
, according to, resp., (21) and (32), in such a way that the event
![]() $\varepsilon_{t+1}\in \mathbb{R}'(t+1)$
is quite likely.
$\varepsilon_{t+1}\in \mathbb{R}'(t+1)$
is quite likely.
To this end, draw
![]() $\varepsilon_{t + 1}$
uniformly at random from
$\varepsilon_{t + 1}$
uniformly at random from
![]() $K \setminus G_t$
and, independently, generate a Bernoulli random variable
$K \setminus G_t$
and, independently, generate a Bernoulli random variable
![]() $\xi_{t+1}$
with the probability of success
$\xi_{t+1}$
with the probability of success
![]() $1 - \gamma_t$
(which is in [0,1] by (146)). If event
$1 - \gamma_t$
(which is in [0,1] by (146)). If event
![]() ${\mathcal{A}}(t, \gamma_t)$
has occurred, that is, if
${\mathcal{A}}(t, \gamma_t)$
has occurred, that is, if
then draw a random edge
![]() $\zeta_{t+1} \in K \setminus R_t$
according to the distribution
$\zeta_{t+1} \in K \setminus R_t$
according to the distribution
where the inequality holds by (33). Observe also that
so
![]() $\zeta_{t+1}$
has a properly defined distribution. Finally, fix an arbitrary bijection
$\zeta_{t+1}$
has a properly defined distribution. Finally, fix an arbitrary bijection
between the sets of edges and define
 \begin{equation*}\eta^{\prime}_{t+1} = \begin{cases}\varepsilon_{t+1}, &\text{ if } \xi_{t + 1} = 1, \varepsilon_{t+1} \in K \setminus R_t,\\ \\[-9pt] f_{R_t, G_t}(\varepsilon_{t+1}), &\text{ if } \xi_{t + 1} = 1, \varepsilon_{t+1} \in R_t,\\ \\[-9pt] \zeta_{t+1}, &\text{ if } \xi_{t + 1} = 0. \\\end{cases}\end{equation*}
\begin{equation*}\eta^{\prime}_{t+1} = \begin{cases}\varepsilon_{t+1}, &\text{ if } \xi_{t + 1} = 1, \varepsilon_{t+1} \in K \setminus R_t,\\ \\[-9pt] f_{R_t, G_t}(\varepsilon_{t+1}), &\text{ if } \xi_{t + 1} = 1, \varepsilon_{t+1} \in R_t,\\ \\[-9pt] \zeta_{t+1}, &\text{ if } \xi_{t + 1} = 0. \\\end{cases}\end{equation*}
On the other hand, if event
![]() ${\mathcal{A}}(t, \gamma_t)$
has failed, then
${\mathcal{A}}(t, \gamma_t)$
has failed, then
![]() $\eta^{\prime}_{t+1}$
is sampled directly (without defining
$\eta^{\prime}_{t+1}$
is sampled directly (without defining
![]() $\zeta_{t+1}$
) according to the distribution (32). With this definition of
$\zeta_{t+1}$
) according to the distribution (32). With this definition of
![]() $(\mathbb{R}'(t))_{t= 0}^{t_0}$
, it is easy to check that for
$(\mathbb{R}'(t))_{t= 0}^{t_0}$
, it is easy to check that for
![]() $\eta^{\prime}_{t+1}$
defined above, (32) indeed holds, so from now on we drop the prime
$\eta^{\prime}_{t+1}$
defined above, (32) indeed holds, so from now on we drop the prime
![]() $^{\prime}$
and identify
$^{\prime}$
and identify
![]() $\mathbb{R}'(t)$
with
$\mathbb{R}'(t)$
with
![]() $\mathbb{R}(t)$
, which is a subset of
$\mathbb{R}(t)$
, which is a subset of
![]() $\mathbb{R}(n_1,n_2,p)$
.
$\mathbb{R}(n_1,n_2,p)$
.
Most importantly, we conclude that, for
![]() $t = 0, \cdots, t_0 - 1$
$t = 0, \cdots, t_0 - 1$
In view of this, define
and recall that
![]() $m=\lceil (1-\gamma)M\rceil$
. If
$m=\lceil (1-\gamma)M\rceil$
. If
![]() $|S| \ge m$
, define
$|S| \ge m$
, define
![]() ${\mathbb{G}(n_1,n_2,m)}$
as, say, the edges indexed by the smallest m elements of S (note that since the vectors
${\mathbb{G}(n_1,n_2,m)}$
as, say, the edges indexed by the smallest m elements of S (note that since the vectors
![]() $(\xi_i)$
and
$(\xi_i)$
and
![]() $(\varepsilon_i)$
are independent, after conditioning on S, these m edges are uniformly distributed), and if
$(\varepsilon_i)$
are independent, after conditioning on S, these m edges are uniformly distributed), and if
![]() $|S| < m$
, then define
$|S| < m$
, then define
![]() ${\mathbb{G}(n_1,n_2,m)}$
as, say, the graph with edges
${\mathbb{G}(n_1,n_2,m)}$
as, say, the graph with edges
![]() $\{\varepsilon_1, \dots, \varepsilon_m\}$
. Recalling the definition (23) of the event
$\{\varepsilon_1, \dots, \varepsilon_m\}$
. Recalling the definition (23) of the event
![]() ${\mathcal{A}}$
, by (34) we observe that
${\mathcal{A}}$
, by (34) we observe that
![]() ${\mathcal{A}}$
implies the inclusion
${\mathcal{A}}$
implies the inclusion
![]() $\left\{ \varepsilon_t\ \, :\, \ t \in S \right\} \subseteq \mathbb{R}(t_0) \subset \mathbb{R}(M) = \mathbb{R}(n_1,n_2,p)$
. On the other hand
$\left\{ \varepsilon_t\ \, :\, \ t \in S \right\} \subseteq \mathbb{R}(t_0) \subset \mathbb{R}(M) = \mathbb{R}(n_1,n_2,p)$
. On the other hand
![]() $|S| \ge m$
implies
$|S| \ge m$
implies
![]() ${\mathbb{G}(n_1,n_2,m)} \subseteq \left\{ \varepsilon_t\ \, :\, \ t \in S \right\}$
, so
${\mathbb{G}(n_1,n_2,m)} \subseteq \left\{ \varepsilon_t\ \, :\, \ t \in S \right\}$
, so
Since, by Lemma 6, event
![]() ${\mathcal{A}}$
holds with probability
${\mathcal{A}}$
holds with probability
![]() $1 - O(N^{-C})$
, to complete the proof of (6) it suffices to show that also
$1 - O(N^{-C})$
, to complete the proof of (6) it suffices to show that also
For this we need the following claim whose technical proof is deferred to Section 8.
Claim 7. We have
where
 \begin{equation*} \theta \,{:\!=}\, 1080 \hat p^2 \mathbb{I} + \begin{cases} 6480\sqrt{\dfrac{2(C + 3)\log N}{p\hat n}}, &\quad p \le 0.49, \\ \\[-9pt] 6250\sqrt{\dfrac{(C + 3)\log N}{q^2\hat n } }\log \frac{\hat n}{\log N}, &\quad p > 0.49, \end{cases}\end{equation*}
\begin{equation*} \theta \,{:\!=}\, 1080 \hat p^2 \mathbb{I} + \begin{cases} 6480\sqrt{\dfrac{2(C + 3)\log N}{p\hat n}}, &\quad p \le 0.49, \\ \\[-9pt] 6250\sqrt{\dfrac{(C + 3)\log N}{q^2\hat n } }\log \frac{\hat n}{\log N}, &\quad p > 0.49, \end{cases}\end{equation*}
and, with
![]() $\gamma$
as in (5),
$\gamma$
as in (5),
Recalling that
![]() $t_0 = \lfloor (1 - \tau_0)M \rfloor$
and
$t_0 = \lfloor (1 - \tau_0)M \rfloor$
and
![]() $m = \lceil(1-\gamma)M\rceil$
, we have
$m = \lceil(1-\gamma)M\rceil$
, we have
 \begin{equation} \begin{split} t_0 - \theta M - m &\ge (1-\tau_0)M - 1 - \theta M - (1-\gamma)M - 1 \\[3pt] &= (\gamma - \tau_0 - \theta)M - 2 \overset{\mbox{(36)}}{\ge} \sqrt{2C M \log N}. \end{split} \end{equation}
\begin{equation} \begin{split} t_0 - \theta M - m &\ge (1-\tau_0)M - 1 - \theta M - (1-\gamma)M - 1 \\[3pt] &= (\gamma - \tau_0 - \theta)M - 2 \overset{\mbox{(36)}}{\ge} \sqrt{2C M \log N}. \end{split} \end{equation}
Since
![]() $|S|$
is a sum of independent Bernoulli random variables,
$|S|$
is a sum of independent Bernoulli random variables,
 \begin{align*} \mathbb{P}\left(|S| < m\right) &= \mathbb{P}\left(|S| < \operatorname{\mathbb{E}}|S|- (\operatorname{\mathbb{E}}|S| - m) \right) \overset{\mbox{(35)}}{\le} \mathbb{P}\left(|S| < \operatorname{\mathbb{E}}|S| -(t_0 - \theta M - m)\right) \\ \fbox{(18), $\operatorname{\mathbb{E}} |S| \le M$}\quad &\overset{\mbox{}}{\le} \exp \left( -\frac{(t_0 - \theta M - m)^2}{2M} \right) \overset{\mbox{(38)}}{\le} \exp \left( - C \log N \right) = N^{-C},\end{align*}
\begin{align*} \mathbb{P}\left(|S| < m\right) &= \mathbb{P}\left(|S| < \operatorname{\mathbb{E}}|S|- (\operatorname{\mathbb{E}}|S| - m) \right) \overset{\mbox{(35)}}{\le} \mathbb{P}\left(|S| < \operatorname{\mathbb{E}}|S| -(t_0 - \theta M - m)\right) \\ \fbox{(18), $\operatorname{\mathbb{E}} |S| \le M$}\quad &\overset{\mbox{}}{\le} \exp \left( -\frac{(t_0 - \theta M - m)^2}{2M} \right) \overset{\mbox{(38)}}{\le} \exp \left( - C \log N \right) = N^{-C},\end{align*}
which as mentioned above, implies (6).
Finally, we prove (7) by coupling
![]() $\mathbb{G}(n_1, n_2, p')$
with
$\mathbb{G}(n_1, n_2, p')$
with
![]() $\mathbb{G}(n_1,n_2, m)$
so that the former is a subset of the latter with probability
$\mathbb{G}(n_1,n_2, m)$
so that the former is a subset of the latter with probability
![]() $1 - O(N^{-C})$
. Denote by
$1 - O(N^{-C})$
. Denote by
![]() $X \,{:\!=}\, e(\mathbb{G}(n_1,n_2,p'))$
the number of edges of
$X \,{:\!=}\, e(\mathbb{G}(n_1,n_2,p'))$
the number of edges of
![]() $\mathbb{G}(n_1,n_2, p')$
. Whenever
$\mathbb{G}(n_1,n_2, p')$
. Whenever
![]() $X \le m$
, choose X edges of
$X \le m$
, choose X edges of
![]() $\mathbb{G}(n_1,n_2,m)$
at random and declare them to be a copy of
$\mathbb{G}(n_1,n_2,m)$
at random and declare them to be a copy of
![]() $\mathbb{G}(n_1,n_2,p')$
. Otherwise sample
$\mathbb{G}(n_1,n_2,p')$
. Otherwise sample
![]() $\mathbb{G}(n_1,n_2,p')$
independently from
$\mathbb{G}(n_1,n_2,p')$
independently from
![]() $\mathbb{G}(n_1,n_2,m)$
. Hence it remains to show that
$\mathbb{G}(n_1,n_2,m)$
. Hence it remains to show that
![]() $\mathbb{P}\left(X > m\right) = O(N^{-C})$
.
$\mathbb{P}\left(X > m\right) = O(N^{-C})$
.
Recalling that
![]() $m = \lceil{{(1-\gamma)}}\rceil pN$
and
$m = \lceil{{(1-\gamma)}}\rceil pN$
and
![]() $p' = (1 - 2\gamma)p$
, we have
$p' = (1 - 2\gamma)p$
, we have
![]() $m/N \ge (1 - \gamma)p = p' + \gamma p$
. Since
$m/N \ge (1 - \gamma)p = p' + \gamma p$
. Since
![]() $X \sim \operatorname{Bin}(N,p')$
, Chernoff’s bound (17) implies that
$X \sim \operatorname{Bin}(N,p')$
, Chernoff’s bound (17) implies that
Choosing
![]() $C^*$
sufficiently large, the definition (5) implies
$C^*$
sufficiently large, the definition (5) implies
![]() $\gamma \ge \sqrt{\frac{2C\log N}{p N}}$
with a lot of room (to see this easier in the case
$\gamma \ge \sqrt{\frac{2C\log N}{p N}}$
with a lot of room (to see this easier in the case
![]() $p > 0.49$
, note that (4) implies
$p > 0.49$
, note that (4) implies
![]() $\log(\hat n/\log N) \ge 1$
, say). So (38) implies
$\log(\hat n/\log N) \ge 1$
, say). So (38) implies
![]() $\mathbb{P}\left(X > m\right) \le N^{-C}$
.
$\mathbb{P}\left(X > m\right) \le N^{-C}$
.
4. Proof of Lemma 6
4.1. Preparations
Recall our notation
![]() $K = {K_{n_1,n_2}}$
, and
$K = {K_{n_1,n_2}}$
, and
![]() ${\mathcal{R}}_G$
defined in (15). Fix an integer
${\mathcal{R}}_G$
defined in (15). Fix an integer
![]() $t \in [0, t_0)$
. For a graph G with t edges and
$t \in [0, t_0)$
. For a graph G with t edges and
![]() $e, f \in K\setminus G$
, define
$e, f \in K\setminus G$
, define
By skipping a few technical steps, we will see that the essence of the proof of Lemma 6 is to show that the ratio
![]() ${|{\mathcal{R}}_{G,e,\neg f}|} / {|{\mathcal{R}}_{G,f,\neg e}|}$
is approximately 1 for any pair of edges e,f, where G is a ‘typical’ instance of
${|{\mathcal{R}}_{G,e,\neg f}|} / {|{\mathcal{R}}_{G,f,\neg e}|}$
is approximately 1 for any pair of edges e,f, where G is a ‘typical’ instance of
![]() $\mathbb{R}(t)$
.
$\mathbb{R}(t)$
.
Recalling our generic definition of switchings from Subsection 2.2, let us treat the graphs in
![]() ${\mathcal{R}} \,{:\!=}\, {\mathcal{R}}_{G,e,\neg f}$
and
${\mathcal{R}} \,{:\!=}\, {\mathcal{R}}_{G,e,\neg f}$
and
![]() ${\mathcal{R}}' \,{:\!=}\, {\mathcal{R}}_{G,f,\neg e}$
as blue-red edge colourings of the graph
${\mathcal{R}}' \,{:\!=}\, {\mathcal{R}}_{G,f,\neg e}$
as blue-red edge colourings of the graph
![]() $K \setminus G$
. Recall that a path or a cycle in
$K \setminus G$
. Recall that a path or a cycle in
![]() $K \setminus G$
is alternating if no two consecutive edges have the same colour.
$K \setminus G$
is alternating if no two consecutive edges have the same colour.
When edges e, f are disjoint, we define the switching graph
![]() $B = B({\mathcal{R}},{\mathcal{R}}')$
by putting an edge between
$B = B({\mathcal{R}},{\mathcal{R}}')$
by putting an edge between
![]() $H \in {\mathcal{R}}$
and
$H \in {\mathcal{R}}$
and
![]() $H' \in {\mathcal{R}}'$
whenever there is an alternating 6-cycle containing e and f in H such that switching the colours in the cycle gives H
$H' \in {\mathcal{R}}'$
whenever there is an alternating 6-cycle containing e and f in H such that switching the colours in the cycle gives H
![]() $^{\prime}$
(see Figure 2). If e and f share a vertex, instead of 6-cycles we use alternating 4-cycles containing e and f.
$^{\prime}$
(see Figure 2). If e and f share a vertex, instead of 6-cycles we use alternating 4-cycles containing e and f.

Figure 2. Switching between H and H
![]() $^{\prime}$
when e and f are disjoint: solid edges are in
$^{\prime}$
when e and f are disjoint: solid edges are in
![]() $H \setminus G$
(or
$H \setminus G$
(or
![]() $H' \setminus G$
) and the dashed ones in
$H' \setminus G$
) and the dashed ones in
![]() $K \setminus H$
(or
$K \setminus H$
(or
![]() $K \setminus H'$
).
$K \setminus H'$
).
It is easy to describe the vertex degrees in B. For distinct
![]() $u,v\in V_i$
, let
$u,v\in V_i$
, let
![]() $\theta_{G,H}(u,v)$
be the number of (alternating) paths uxv such that ux is blue and xv is red. Note that
$\theta_{G,H}(u,v)$
be the number of (alternating) paths uxv such that ux is blue and xv is red. Note that
![]() $\theta_{G,H}(u,v) = |\Gamma_{H\setminus G}(u)\cap\Gamma_{K\setminus H}(v)|$
. Then, setting
$\theta_{G,H}(u,v) = |\Gamma_{H\setminus G}(u)\cap\Gamma_{K\setminus H}(v)|$
. Then, setting
![]() $f = u_1u_2$
and
$f = u_1u_2$
and
![]() $e = v_1v_2$
, where
$e = v_1v_2$
, where
![]() $u_i,v_i\in V_i$
,
$u_i,v_i\in V_i$
,
![]() $i = 1,2$
,
$i = 1,2$
,
and
Note that equation (13) is equivalent to
 \begin{equation} \frac{|{\mathcal{R}}|}{|{\mathcal{R}}'|} = \frac{\frac1{|{\mathcal{R}}'|}\sum_{H'\in{\mathcal{R}}'}\deg_B(H')}{\frac1{|{\mathcal{R}}|}\sum_{H\in{\mathcal{R}}}\deg_B(H)}.\end{equation}
\begin{equation} \frac{|{\mathcal{R}}|}{|{\mathcal{R}}'|} = \frac{\frac1{|{\mathcal{R}}'|}\sum_{H'\in{\mathcal{R}}'}\deg_B(H')}{\frac1{|{\mathcal{R}}|}\sum_{H\in{\mathcal{R}}}\deg_B(H)}.\end{equation}
In view of (39) and (40), the denominator of the RHS above is the (conditional) expectation of the random variable
![]() $\prod_{i : u_i \neq v_i} \theta_{G,\mathbb{R}}(u_i,v_i)$
, given that
$\prod_{i : u_i \neq v_i} \theta_{G,\mathbb{R}}(u_i,v_i)$
, given that
![]() $\mathbb{R}$
contains G and e, but not f (and similarly for the numerator).
$\mathbb{R}$
contains G and e, but not f (and similarly for the numerator).
To get an idea of how large that expectation could be, let us focus on one factor, say,
![]() $\theta_{G,\mathbb{R}}(u_1,v_1)$
, assuming
$\theta_{G,\mathbb{R}}(u_1,v_1)$
, assuming
![]() $u_1 \neq v_1$
. Clearly, the red degree of
$u_1 \neq v_1$
. Clearly, the red degree of
![]() $v_1$
equals
$v_1$
equals
![]() $|\Gamma_{K\setminus\mathbb{R}}(v_1)| = n_2 - d_2 = qn_2$
. Since
$|\Gamma_{K\setminus\mathbb{R}}(v_1)| = n_2 - d_2 = qn_2$
. Since
![]() $|\Gamma_{\mathbb{R}}(v_1)| = pn_2$
, viewing
$|\Gamma_{\mathbb{R}}(v_1)| = pn_2$
, viewing
![]() $\mathbb{R} \setminus G$
as a
$\mathbb{R} \setminus G$
as a
![]() $\tau$
-dense subgraph of
$\tau$
-dense subgraph of
![]() $\mathbb{R}$
(see (24)) we expect that the blue neighbourhood
$\mathbb{R}$
(see (24)) we expect that the blue neighbourhood
![]() $|\Gamma_{\mathbb{R}\setminus G}(u_1)|$
is approximately
$|\Gamma_{\mathbb{R}\setminus G}(u_1)|$
is approximately
![]() $\tau p n_2$
. It is reasonable to expect that for typical G and
$\tau p n_2$
. It is reasonable to expect that for typical G and
![]() $\mathbb{R}$
the red and blue neighbourhoods intersect proportionally, that is, on a set of size about
$\mathbb{R}$
the red and blue neighbourhoods intersect proportionally, that is, on a set of size about
![]() $q \cdot \tau p \cdot n_2 = \tau qd_1$
.
$q \cdot \tau p \cdot n_2 = \tau qd_1$
.
Inspired by this heuristic, we say that, for
![]() $\delta > 0$
, an admissible graph G with t edges is
$\delta > 0$
, an admissible graph G with t edges is
![]() $\delta$
-typical if
$\delta$
-typical if
where the outer maximum is taken over distinct pairs of edges. (The bound
![]() $\tau^2 \delta$
has hardly any intuition, but it is simple and sufficient for our purposes.)
$\tau^2 \delta$
has hardly any intuition, but it is simple and sufficient for our purposes.)
Lemma 6 is a relatively easy consequence of the upcoming Lemma 8, which states that for a suitably chosen function
![]() $\delta(t)$
it is very likely that the initial segments of
$\delta(t)$
it is very likely that the initial segments of
![]() $\mathbb{R}$
are
$\mathbb{R}$
are
![]() $\delta(t)$
-typical.
$\delta(t)$
-typical.
For each
![]() $t = 0, \dots, t_0 - 1$
, define
$t = 0, \dots, t_0 - 1$
, define
 \begin{equation} \delta(t) \,{:\!=}\, 120\hat p^2 \mathbb{I} + 360 \sqrt{\frac{(C + 3)\lambda(t)}{6\tau pq\hat n }} ,\end{equation}
\begin{equation} \delta(t) \,{:\!=}\, 120\hat p^2 \mathbb{I} + 360 \sqrt{\frac{(C + 3)\lambda(t)}{6\tau pq\hat n }} ,\end{equation}
where
 \begin{equation} \lambda(t) \,{:\!=}\,\begin{cases} 6 \log N, \quad &p \le 0.49, \\ \\[-9pt] 6\log N + \dfrac{64\log N}{\tau p q}, \quad &p > 0.49.\end{cases}\end{equation}
\begin{equation} \lambda(t) \,{:\!=}\,\begin{cases} 6 \log N, \quad &p \le 0.49, \\ \\[-9pt] 6\log N + \dfrac{64\log N}{\tau p q}, \quad &p > 0.49.\end{cases}\end{equation}
For future reference, note that
Indeed, recalling (30), for
![]() $p\le0.49$
,
$p\le0.49$
,
 \begin{equation*} 9\delta(t) \le 1080\hat p^2 \mathbb{I} + 3240 \sqrt{\frac{2(C + 3)\log N}{\tau p\hat n }} =\gamma_t,\end{equation*}
\begin{equation*} 9\delta(t) \le 1080\hat p^2 \mathbb{I} + 3240 \sqrt{\frac{2(C + 3)\log N}{\tau p\hat n }} =\gamma_t,\end{equation*}
while, for
![]() $p > 0.49$
, noting that
$p > 0.49$
, noting that
![]() $\lambda(t)\le 70\log N/(\tau pq)$
, we have
$\lambda(t)\le 70\log N/(\tau pq)$
, we have
 \begin{equation*}9\delta(t) \le 1080\hat p^2 \mathbb{I} + 3240 \sqrt{\frac{70(C + 3)\log N}{0.49^2 \cdot 6\tau^2q^2\hat n}} \le \gamma_t.\end{equation*}
\begin{equation*}9\delta(t) \le 1080\hat p^2 \mathbb{I} + 3240 \sqrt{\frac{70(C + 3)\log N}{0.49^2 \cdot 6\tau^2q^2\hat n}} \le \gamma_t.\end{equation*}
Lemma 8. For every constant
![]() $C > 0$
, under the conditions of Lemma 6,
$C > 0$
, under the conditions of Lemma 6,
Note that the LHS of (42) is a function of graph G, say f(G). Hence, Lemma 8 asserts that, with high probability,
![]() $f(\mathbb{R}(t))$
is small for all
$f(\mathbb{R}(t))$
is small for all
![]() $t < t_0$
. The main idea of the proof of Lemma 8, which we defer to Subsection 4.3, is to bound
$t < t_0$
. The main idea of the proof of Lemma 8, which we defer to Subsection 4.3, is to bound
![]() $f(\mathbb{R}(t))$
by a ratio of two simpler functions (again conditional probabilities) of
$f(\mathbb{R}(t))$
by a ratio of two simpler functions (again conditional probabilities) of
![]() $\mathbb{R}(t)$
. Lemmas 9 and 10 below bound each of these conditional probabilities separately.
$\mathbb{R}(t)$
. Lemmas 9 and 10 below bound each of these conditional probabilities separately.
For any
![]() $t = 0, \dots, M$
and distinct
$t = 0, \dots, M$
and distinct
![]() $u_i, v_i \in V_i$
,
$u_i, v_i \in V_i$
,
![]() $i = 1,2$
, set
$i = 1,2$
, set
where
![]() $\theta_{G,H}(u_i,v_i) = |\Gamma_{H\setminus G}(u_i)\cap\Gamma_{K\setminus H}(v_i)|$
was introduced earlier in this subsection.
$\theta_{G,H}(u_i,v_i) = |\Gamma_{H\setminus G}(u_i)\cap\Gamma_{K\setminus H}(v_i)|$
was introduced earlier in this subsection.
Lemma 9. For every constant
![]() $C>0$
, under the conditions of Lemma 6, for
$C>0$
, under the conditions of Lemma 6, for
![]() $i \in [2]$
we have that with probability
$i \in [2]$
we have that with probability
![]() $1 - O(N^{-C})$
,
$1 - O(N^{-C})$
,
Lemma 10. For every constant
![]() $C > 0$
, under the conditions of Lemma 6, with probability
$C > 0$
, under the conditions of Lemma 6, with probability
![]() $1 - O(N^{-C})$
$1 - O(N^{-C})$
4.2. Proof of Lemma 6
In view of Lemma 8, it suffices to show that if
![]() $t < t_0$
, and a t-edge graph G is
$t < t_0$
, and a t-edge graph G is
![]() $\delta(t)$
-typical, then
$\delta(t)$
-typical, then
Fix
![]() $f \in K \setminus G$
which maximises
$f \in K \setminus G$
which maximises
![]() $p_{t+1}(f,G)$
. Since the average of
$p_{t+1}(f,G)$
. Since the average of
![]() $p_{t+1}(e,G)$
over
$p_{t+1}(e,G)$
over
![]() $e \in K \setminus G$
is exactly
$e \in K \setminus G$
is exactly
![]() $\frac{1}{N - t}$
, we have
$\frac{1}{N - t}$
, we have
![]() $p_{t+1}(f,G) \ge \frac{1}{N - t}$
and therefore it is enough to prove that, for every
$p_{t+1}(f,G) \ge \frac{1}{N - t}$
and therefore it is enough to prove that, for every
![]() $e \in K \setminus (G \cup \{f\})$
,
$e \in K \setminus (G \cup \{f\})$
,
Recall the definitions of
![]() ${\mathcal{R}}_G$
in (15),
${\mathcal{R}}_G$
in (15),
![]() ${\mathcal{R}}_{G,e}, {\mathcal{R}}_{G, \neg e}$
in (16), and
${\mathcal{R}}_{G,e}, {\mathcal{R}}_{G, \neg e}$
in (16), and
![]() ${\mathcal{R}} = {\mathcal{R}}_{G,e,\neg f}$
and
${\mathcal{R}} = {\mathcal{R}}_{G,e,\neg f}$
and
![]() ${\mathcal{R}}' = {\mathcal{R}}_{G, f, \neg e}$
from Subsection 4.1 and observe that
${\mathcal{R}}' = {\mathcal{R}}_{G, f, \neg e}$
from Subsection 4.1 and observe that
![]() ${\mathcal{R}} = {\mathcal{R}}_{G\cup \{e\},\neg f}$
too. In view of the remark immediately following (22),
${\mathcal{R}} = {\mathcal{R}}_{G\cup \{e\},\neg f}$
too. In view of the remark immediately following (22),
Therefore,
Write
![]() $e = v_1v_2$
and
$e = v_1v_2$
and
![]() $f = u_1u_2$
and for simplicity assume that both
$f = u_1u_2$
and for simplicity assume that both
![]() $u_1 \neq v_1$
and
$u_1 \neq v_1$
and
![]() $u_2 \neq v_2$
(otherwise the proof goes mutatis mutandis and is, in fact, a bit simpler). By (39), (40), and (41),
$u_2 \neq v_2$
(otherwise the proof goes mutatis mutandis and is, in fact, a bit simpler). By (39), (40), and (41),
where
and
Since G is
![]() $\delta$
-typical with
$\delta$
-typical with
![]() $\delta = \delta(t)$
, denoting the LHS of (42) as
$\delta = \delta(t)$
, denoting the LHS of (42) as
![]() $p_*$
, we have
$p_*$
, we have
![]() $p_* \le \tau^2 \delta$
, so
$p_* \le \tau^2 \delta$
, so
Moreover, since, deterministically,
using (42) again, we infer that
 \begin{align} \operatorname{\mathbb{E}}_{\text{bottom}} \notag &\le (1 + \delta) \tau qd_1 \cdot (1 + \delta)\tau qd_2 \cdot (1 - p_*) + 4p^2q^2N \cdot p_*\\[3pt] &\le (1 + \delta)^2\tau^2p^2q^2N + 4p^2q^2N \cdot \tau^2\delta \le (1 + 6\delta + \delta^2)\tau^2p^2q^2N .\end{align}
\begin{align} \operatorname{\mathbb{E}}_{\text{bottom}} \notag &\le (1 + \delta) \tau qd_1 \cdot (1 + \delta)\tau qd_2 \cdot (1 - p_*) + 4p^2q^2N \cdot p_*\\[3pt] &\le (1 + \delta)^2\tau^2p^2q^2N + 4p^2q^2N \cdot \tau^2\delta \le (1 + 6\delta + \delta^2)\tau^2p^2q^2N .\end{align}
Finally, combining the bounds on
![]() $\operatorname{\mathbb{E}}_{\text{top}}$
and
$\operatorname{\mathbb{E}}_{\text{top}}$
and
![]() $\operatorname{\mathbb{E}}_{\text{bottom}}$
and using (45), we conclude that
$\operatorname{\mathbb{E}}_{\text{bottom}}$
and using (45), we conclude that
and the proof of Lemma 6 is complete.
4.3. Proof of Lemma 8
By Lemmas 9 and 10 the events (47) (for each
![]() $i \in [2]$
) and (48) hold simultaneously with probability
$i \in [2]$
) and (48) hold simultaneously with probability
![]() $1 - O(N^{-C})$
. Hence it suffices to fix an arbitrary integer
$1 - O(N^{-C})$
. Hence it suffices to fix an arbitrary integer
![]() $t < t_0$
and a realisation of
$t < t_0$
and a realisation of
![]() $\mathbb{R}(t)$
, say
$\mathbb{R}(t)$
, say
![]() $\mathbb{R}(t) = G$
satisfying inequalities (47) (for each
$\mathbb{R}(t) = G$
satisfying inequalities (47) (for each
![]() $i \in [2]$
) and (48) and to prove that G is
$i \in [2]$
) and (48) and to prove that G is
![]() $\delta(t)$
-typical. Fix any such G and define events
$\delta(t)$
-typical. Fix any such G and define events
 \begin{equation*} {\mathcal{E}} \,{:\!=}\, \bigcup_{i \in [2]} \left\{ \max_{u,v \in V_i, u \neq v}\left|\frac{\theta_{G,\mathbb{R}}(u,v)}{\tau qd_i } - 1\right| > \delta(t) \right\} \quad\text{and}\quad {\mathcal{F}}_{e,f} \,{:\!=}\, \{ e\in \mathbb{R}, f \notin \mathbb{R} \}.\end{equation*}
\begin{equation*} {\mathcal{E}} \,{:\!=}\, \bigcup_{i \in [2]} \left\{ \max_{u,v \in V_i, u \neq v}\left|\frac{\theta_{G,\mathbb{R}}(u,v)}{\tau qd_i } - 1\right| > \delta(t) \right\} \quad\text{and}\quad {\mathcal{F}}_{e,f} \,{:\!=}\, \{ e\in \mathbb{R}, f \notin \mathbb{R} \}.\end{equation*}
Since, conditioning on the event
![]() $\mathbb{R}(t) = G$
, we have
$\mathbb{R}(t) = G$
, we have
![]() $\theta_{G,\mathbb{R}}(u_i,v_i) = \theta_t(u_i,v_i)$
, by the choice of G we have
$\theta_{G,\mathbb{R}}(u_i,v_i) = \theta_t(u_i,v_i)$
, by the choice of G we have
and
Note that the probability on the LHS of (42) does not change if we replace
![]() $G \subseteq \mathbb{R}$
by
$G \subseteq \mathbb{R}$
by
![]() $\mathbb{R}(t) = G$
, since conditioning on either event makes
$\mathbb{R}(t) = G$
, since conditioning on either event makes
![]() $\mathbb{R}$
uniformly distributed over
$\mathbb{R}$
uniformly distributed over
![]() ${\mathcal{R}}_G$
(i.e., biregular graphs containing G) and the random variables
${\mathcal{R}}_G$
(i.e., biregular graphs containing G) and the random variables
![]() $\theta_{G,\mathbb{R}}(u_i,v_i)$
do not depend on the random ordering of the edges of
$\theta_{G,\mathbb{R}}(u_i,v_i)$
do not depend on the random ordering of the edges of
![]() $\mathbb{R}$
. Hence it remains to prove that (52) and (53) imply, for any distinct edges
$\mathbb{R}$
. Hence it remains to prove that (52) and (53) imply, for any distinct edges
![]() $e = v_1v_2,$
$e = v_1v_2,$
![]() $f = u_1u_2 \in K \setminus G$
, that
$f = u_1u_2 \in K \setminus G$
, that
The probability on the LHS of (54) is at most
![]() $\mathbb{P}\left({{\mathcal{E}}}\,|\,{\mathbb{R}(t) = G, {\mathcal{F}}_{e,f}}\right)$
. Inequalities (52) and (53) imply that
$\mathbb{P}\left({{\mathcal{E}}}\,|\,{\mathbb{R}(t) = G, {\mathcal{F}}_{e,f}}\right)$
. Inequalities (52) and (53) imply that
Finally, even a quick glance at the definitions of
![]() $\delta(t)$
and
$\delta(t)$
and
![]() $\tau_0$
(see (43) and (25)) reveals that
$\tau_0$
(see (43) and (25)) reveals that
![]() $\min \{ \tau_0,\delta(t) \} \ge 1/\hat n$
. Thus, we get, with a huge margin,
$\min \{ \tau_0,\delta(t) \} \ge 1/\hat n$
. Thus, we get, with a huge margin,
5. Degrees and co-degrees
In this section we prove facts about the neighbourhood structure of
![]() $\mathbb{R}(t)$
, one of which will be enough to deduce Lemma 9, while the other two will be used in the proof of Lemma 10 in Section 6. We start, in Subsection 5.1, with a tail bound for the co-degrees in
$\mathbb{R}(t)$
, one of which will be enough to deduce Lemma 9, while the other two will be used in the proof of Lemma 10 in Section 6. We start, in Subsection 5.1, with a tail bound for the co-degrees in
![]() $\mathbb{R} = \mathbb{R}(n_1,n_2,p)$
(Lemma 11). In Subsection 5.2 we analyse the process
$\mathbb{R} = \mathbb{R}(n_1,n_2,p)$
(Lemma 11). In Subsection 5.2 we analyse the process
![]() $(\mathbb{R}(t))_t$
. First, we show that the vertex degrees in the process grow proportionally until almost the very end (Lemma 13). Then, conditioning on
$(\mathbb{R}(t))_t$
. First, we show that the vertex degrees in the process grow proportionally until almost the very end (Lemma 13). Then, conditioning on
![]() $\mathbb{R}$
having concentrated co-degrees, we prove that the co-degrees in
$\mathbb{R}$
having concentrated co-degrees, we prove that the co-degrees in
![]() $\mathbb{R}(t)$
do not exceed their expectation too much (Lemma 14). Finally, in Subsection 5.3, we present a proof of Lemma 9 based on Lemma 11.
$\mathbb{R}(t)$
do not exceed their expectation too much (Lemma 14). Finally, in Subsection 5.3, we present a proof of Lemma 9 based on Lemma 11.
5.1. Co-degrees in the random biregular graph
Recall that
![]() $\Gamma_F(v)$
is the set of neighbours of a vertex v in a graph F. We define the co-degree of two distinct vertices u, v as
$\Gamma_F(v)$
is the set of neighbours of a vertex v in a graph F. We define the co-degree of two distinct vertices u, v as
A few times we will use the following simple observation: for
![]() $F \subseteq K$
and distinct
$F \subseteq K$
and distinct
![]() $u,v\in V_1$
,
$u,v\in V_1$
,
 \begin{equation} \begin{split} \operatorname{cod}_{F}(u, v) &= |\Gamma_{F}(u)| + |\Gamma_{F}(v)| - |\Gamma_{F}(u) \cup \Gamma_{F}(v)| \\[3pt] &= \deg_F(u) + \deg_F(v) - \left( n_2 - \operatorname{cod}_{K \setminus F}(u,v) \right), \end{split}\end{equation}
\begin{equation} \begin{split} \operatorname{cod}_{F}(u, v) &= |\Gamma_{F}(u)| + |\Gamma_{F}(v)| - |\Gamma_{F}(u) \cup \Gamma_{F}(v)| \\[3pt] &= \deg_F(u) + \deg_F(v) - \left( n_2 - \operatorname{cod}_{K \setminus F}(u,v) \right), \end{split}\end{equation}
where, recall,
![]() $K = {K_{n_1,n_2}}$
is the complete bipartite graph.
$K = {K_{n_1,n_2}}$
is the complete bipartite graph.
Due to symmetry, we prove the following concentration result for pairs of vertices on one side of the bipartition only.
Lemma 11. Suppose that
![]() $\hat p\hat n \to \infty$
and let
$\hat p\hat n \to \infty$
and let
![]() $\lambda = \lambda(n_1,n_2)$
be such that
$\lambda = \lambda(n_1,n_2)$
be such that
![]() $\lambda \to \infty$
. Then, for any distinct
$\lambda \to \infty$
. Then, for any distinct
![]() $u_1, v_1 \in V_1$
,
$u_1, v_1 \in V_1$
,
where
![]() $\mathbb{I}$
is defined in (3).
$\mathbb{I}$
is defined in (3).
Proof. We first claim that it is sufficient to assume
![]() $p \le 1/2$
and prove that for any distinct
$p \le 1/2$
and prove that for any distinct
![]() $u_1, v_1 \in V_1$
$u_1, v_1 \in V_1$
To see this, note that by (56), recalling
![]() $q = 1 - p$
,
$q = 1 - p$
,
Further,
![]() $K \setminus \mathbb{R} = K \setminus \mathbb{R}(n_1,n_2,p)$
has the same distribution as
$K \setminus \mathbb{R} = K \setminus \mathbb{R}(n_1,n_2,p)$
has the same distribution as
![]() $\mathbb{R}(n_1,n_2,q)$
. So, if
$\mathbb{R}(n_1,n_2,q)$
. So, if
![]() $p > 1/2$
, the lemma follows by applying (57) with q instead of p.
$p > 1/2$
, the lemma follows by applying (57) with q instead of p.
The crude proof idea comes from our anticipation that
![]() $\operatorname{cod}_\mathbb{R}(u_1,v_1)$
behaves similarly to
$\operatorname{cod}_\mathbb{R}(u_1,v_1)$
behaves similarly to
![]() $\operatorname{cod}_{{\mathbb{G}(n_1,n_2,p)}}(u_1,v_1)$
, which is distributed as
$\operatorname{cod}_{{\mathbb{G}(n_1,n_2,p)}}(u_1,v_1)$
, which is distributed as
![]() $\operatorname{Bin}(n_2, p^2)$
or, approximately, as
$\operatorname{Bin}(n_2, p^2)$
or, approximately, as
![]() $\operatorname{Po}(p^2n_2)$
. We will show that each tail of
$\operatorname{Po}(p^2n_2)$
. We will show that each tail of
![]() $\operatorname{cod}_\mathbb{R}(u_1,u_2)$
is comparable to the tail of
$\operatorname{cod}_\mathbb{R}(u_1,u_2)$
is comparable to the tail of
![]() $\operatorname{Po}(\mu)$
with expectation
$\operatorname{Po}(\mu)$
with expectation
![]() $\mu$
fairly close to
$\mu$
fairly close to
![]() $p^2n_2$
and then apply the Chernoff bounds (this is packaged in Claim 12 below). Further we consider the cases
$p^2n_2$
and then apply the Chernoff bounds (this is packaged in Claim 12 below). Further we consider the cases
![]() $\mathbb{I} = 1$
and
$\mathbb{I} = 1$
and
![]() $\mathbb{I} = 0$
and apply Claim 12 analogously to the proof of Theorem 2.1 in [Reference Krivelevich, Sudakov, Vu and Wormald7]: in the case
$\mathbb{I} = 0$
and apply Claim 12 analogously to the proof of Theorem 2.1 in [Reference Krivelevich, Sudakov, Vu and Wormald7]: in the case
![]() $\mathbb{I} = 1$
we use switchings and in the case
$\mathbb{I} = 1$
we use switchings and in the case
![]() $\mathbb{I} = 0$
we use asymptotic enumeration (Theorem 5).
$\mathbb{I} = 0$
we use asymptotic enumeration (Theorem 5).
Fix distinct
![]() $u_1, v_1 \in V_1$
and set
$u_1, v_1 \in V_1$
and set
![]() $X(u_1,v_1): = \operatorname{cod}_{\mathbb{R}}(u_1,v_1)$
. Further, recall that
$X(u_1,v_1): = \operatorname{cod}_{\mathbb{R}}(u_1,v_1)$
. Further, recall that
![]() ${{\mathcal{R}}(n_1,n_2,p)}$
is the class of subgraphs of
${{\mathcal{R}}(n_1,n_2,p)}$
is the class of subgraphs of
![]() ${K_{n_1,n_2}}$
such that every
${K_{n_1,n_2}}$
such that every
![]() $v \in V_i$
has degree
$v \in V_i$
has degree
![]() $d_i$
, for
$d_i$
, for
![]() $i = 1, 2$
, and let
$i = 1, 2$
, and let
Claim 12. Fix two vertices
![]() $u_1,v_1\in V_1$
. Suppose that positive numbers
$u_1,v_1\in V_1$
. Suppose that positive numbers
![]() $r_k, k = 0, \dots, d_1,$
are such that
$r_k, k = 0, \dots, d_1,$
are such that
and there exist numbers
![]() $0 \le \mu_- \le \mu_+ \le N$
such that
$0 \le \mu_- \le \mu_+ \le N$
such that
If
![]() $x \ge \sqrt{2\mu_+ \lambda} + \lambda$
, then
$x \ge \sqrt{2\mu_+ \lambda} + \lambda$
, then
Proof. Note that if
![]() $Z_+ \sim \operatorname{Po}(\mu_+)$
, then
$Z_+ \sim \operatorname{Po}(\mu_+)$
, then
![]() $\mu_+/k = \mathbb{P}\left(Z_+ = k\right)/\mathbb{P}\left(Z_+ = k - 1\right)$
. Setting
$\mu_+/k = \mathbb{P}\left(Z_+ = k\right)/\mathbb{P}\left(Z_+ = k - 1\right)$
. Setting
![]() $m = \lfloor \mu_+ \rfloor$
, for any integer
$m = \lfloor \mu_+ \rfloor$
, for any integer
![]() $i\in\{m,\dots,d_1\}$
, and abbreviating
$i\in\{m,\dots,d_1\}$
, and abbreviating
![]() $X\,{:\!=}\,X(u_1,v_1)$
and
$X\,{:\!=}\,X(u_1,v_1)$
and
![]() ${\mathcal{R}}_j\,{:\!=}\,{\mathcal{R}}_j(u_1,v_1)$
, we have
${\mathcal{R}}_j\,{:\!=}\,{\mathcal{R}}_j(u_1,v_1)$
, we have
 \begin{align*} \mathbb{P}\left(X \ge i\right) &= \frac{\sum_{j \ge i}|{\mathcal{R}}_j| }{|{{\mathcal{R}}(n_1,n_2,p)}|}\le \sum_{j \ge i} \frac{|{\mathcal{R}}_j|}{|{\mathcal{R}}_{m}|} \sim \sum_{j \ge i} \frac{r_j}{r_m} = \sum_{j \ge i} \prod_{k = m + 1}^{j} \frac{r_k}{r_{k-1}} \le \sum_{j \ge i} \prod_{k = m + 1}^{j} \frac{\mu_+}{k}\\ &= \sum_{j \ge i} \prod_{k = m + 1}^{j}\frac{\mathbb{P}\left(Z_+ = k\right)}{\mathbb{P}\left(Z_+ = k-1\right)} = \sum_{j \ge i} \frac{\mathbb{P}\left(Z_+ = j\right)}{\mathbb{P}\left(Z_+ = m\right)} = \frac{\mathbb{P}\left(Z_+ \ge i\right)}{\mathbb{P}\left(Z_+ = m\right)}. \end{align*}
\begin{align*} \mathbb{P}\left(X \ge i\right) &= \frac{\sum_{j \ge i}|{\mathcal{R}}_j| }{|{{\mathcal{R}}(n_1,n_2,p)}|}\le \sum_{j \ge i} \frac{|{\mathcal{R}}_j|}{|{\mathcal{R}}_{m}|} \sim \sum_{j \ge i} \frac{r_j}{r_m} = \sum_{j \ge i} \prod_{k = m + 1}^{j} \frac{r_k}{r_{k-1}} \le \sum_{j \ge i} \prod_{k = m + 1}^{j} \frac{\mu_+}{k}\\ &= \sum_{j \ge i} \prod_{k = m + 1}^{j}\frac{\mathbb{P}\left(Z_+ = k\right)}{\mathbb{P}\left(Z_+ = k-1\right)} = \sum_{j \ge i} \frac{\mathbb{P}\left(Z_+ = j\right)}{\mathbb{P}\left(Z_+ = m\right)} = \frac{\mathbb{P}\left(Z_+ \ge i\right)}{\mathbb{P}\left(Z_+ = m\right)}. \end{align*}
Since
![]() $\mu_+ \le N$
, by (19) we have
$\mu_+ \le N$
, by (19) we have
![]() $\mathbb{P}\left(Z_+ = m\right) = \Omega(1/\sqrt{\mu_+}) = \Omega(1/\sqrt{N})$
, and conclude that
$\mathbb{P}\left(Z_+ = m\right) = \Omega(1/\sqrt{\mu_+}) = \Omega(1/\sqrt{N})$
, and conclude that
Similarly, if
![]() $Z_- \sim \operatorname{Po}(\mu_-)$
, then for
$Z_- \sim \operatorname{Po}(\mu_-)$
, then for
![]() $i\le m \,{:\!=}\, \lfloor \mu_- \rfloor$
, using
$i\le m \,{:\!=}\, \lfloor \mu_- \rfloor$
, using
![]() $k/\mu_- = \mathbb{P}\left(Z_- = k-1\right)/\mathbb{P}\left(Z_- = k\right)$
,
$k/\mu_- = \mathbb{P}\left(Z_- = k-1\right)/\mathbb{P}\left(Z_- = k\right)$
,
 \begin{equation*} \mathbb{P}\left(X \le i\right)\le \sum_{j \le i} \frac{|{\mathcal{R}}_j|}{|{\mathcal{R}}_{m}|} \sim \sum_{j \le i}\prod_{k = j + 1}^{ m} \frac{r_{k-1}}{r_{k}} \le \sum_{j \le i}\prod_{k = j + 1}^{ m} \frac{\mathbb{P}\left(Z_- = k-1\right)}{\mathbb{P}\left(Z_- = k\right)} = \frac{\mathbb{P}\left(Z_- \le i\right)}{\mathbb{P}\left(Z_- = m\right)}, \end{equation*}
\begin{equation*} \mathbb{P}\left(X \le i\right)\le \sum_{j \le i} \frac{|{\mathcal{R}}_j|}{|{\mathcal{R}}_{m}|} \sim \sum_{j \le i}\prod_{k = j + 1}^{ m} \frac{r_{k-1}}{r_{k}} \le \sum_{j \le i}\prod_{k = j + 1}^{ m} \frac{\mathbb{P}\left(Z_- = k-1\right)}{\mathbb{P}\left(Z_- = k\right)} = \frac{\mathbb{P}\left(Z_- \le i\right)}{\mathbb{P}\left(Z_- = m\right)}, \end{equation*}
and therefore, again using (19),
Since the RHS of (58) does not depend on x, we can assume the equality:
![]() $x = \sqrt{2\mu_+\lambda} + \lambda$
. Inequalities (17) and (18) imply
$x = \sqrt{2\mu_+\lambda} + \lambda$
. Inequalities (17) and (18) imply
 \begin{equation*} \begin{split} \mathbb{P}\left(Z_+ \ge \mu_+ + x\right) &+ \mathbb{P}\left(Z_- \le \mu_- - x\right) \le \exp \left( - \frac{x^2}{2(\mu_+ + x/3)} \right) + \exp \left( -\frac{x^2}{2\mu_-} \right) \\[3pt] \fbox{$\mu_- \le \mu_+, x > 0$}\quad &\le 2 \exp \left( -\frac{x^2}{2(\mu_+ + x/3)} \right) \\[3pt] \fbox{$x = \sqrt{2 \mu_+ \lambda} + \lambda$}\quad &= 2 \exp \left( -\frac{\lambda(2\mu_+ + 2\sqrt{2\mu_+ \lambda} + \lambda)}{2\mu_+ + \sqrt{2\mu_+ \lambda}/3 + \lambda/3} \right) \le 2e^{-\lambda}. \end{split}\end{equation*}
\begin{equation*} \begin{split} \mathbb{P}\left(Z_+ \ge \mu_+ + x\right) &+ \mathbb{P}\left(Z_- \le \mu_- - x\right) \le \exp \left( - \frac{x^2}{2(\mu_+ + x/3)} \right) + \exp \left( -\frac{x^2}{2\mu_-} \right) \\[3pt] \fbox{$\mu_- \le \mu_+, x > 0$}\quad &\le 2 \exp \left( -\frac{x^2}{2(\mu_+ + x/3)} \right) \\[3pt] \fbox{$x = \sqrt{2 \mu_+ \lambda} + \lambda$}\quad &= 2 \exp \left( -\frac{\lambda(2\mu_+ + 2\sqrt{2\mu_+ \lambda} + \lambda)}{2\mu_+ + \sqrt{2\mu_+ \lambda}/3 + \lambda/3} \right) \le 2e^{-\lambda}. \end{split}\end{equation*}
It remains to prove (57). We consider separately the cases
![]() $\mathbb{I} = 1$
and
$\mathbb{I} = 1$
and
![]() $\mathbb{I} = 0$
.
$\mathbb{I} = 0$
.
Case
![]() $\mathbb{I} = 1$
. If
$\mathbb{I} = 1$
. If
![]() $p \ge 1/5$
, then deterministically
$p \ge 1/5$
, then deterministically
![]() $\operatorname{cod}_\mathbb{R}(u_1,u_2) \le pn_2\le 5p^2n_2 \le p^2 n_2 + 20 p^3 n_2$
and
$\operatorname{cod}_\mathbb{R}(u_1,u_2) \le pn_2\le 5p^2n_2 \le p^2 n_2 + 20 p^3 n_2$
and
![]() $\operatorname{cod}_\mathbb{R}(u_1, u_2) - p^2 n_2 \ge - p^2 n_2 \ge -5p^3 n_2$
, and hence (57) holds trivially. So we further assume
$\operatorname{cod}_\mathbb{R}(u_1, u_2) - p^2 n_2 \ge - p^2 n_2 \ge -5p^3 n_2$
, and hence (57) holds trivially. So we further assume
![]() $p < 1/5$
.
$p < 1/5$
.
Setting
![]() $r_k = |{\mathcal{R}}_k|$
, we are going to prove bounds on
$r_k = |{\mathcal{R}}_k|$
, we are going to prove bounds on
![]() $r_k/r_{k-1}$
,
$r_k/r_{k-1}$
,
![]() $k\ge 1$
, using a switching between
$k\ge 1$
, using a switching between
![]() ${\mathcal{R}} = {\mathcal{R}}_k$
and
${\mathcal{R}} = {\mathcal{R}}_k$
and
![]() ${\mathcal{R}}' = {\mathcal{R}}_{k-1}$
. To this end, recall our terminology from Subsection 2.2 (with
${\mathcal{R}}' = {\mathcal{R}}_{k-1}$
. To this end, recall our terminology from Subsection 2.2 (with
![]() $G = \emptyset$
): any graph
$G = \emptyset$
): any graph
![]() $H \subseteq K$
is interpreted as a colouring of the edges of K, with the edges in H blue and the rest red. We define a forward switching as follows: pick a common blue neighbour
$H \subseteq K$
is interpreted as a colouring of the edges of K, with the edges in H blue and the rest red. We define a forward switching as follows: pick a common blue neighbour
![]() $w_2 \in \Gamma_H(u_1) \cap \Gamma_H(v_1)$
and find two alternating 4-cycles
$w_2 \in \Gamma_H(u_1) \cap \Gamma_H(v_1)$
and find two alternating 4-cycles
![]() $u_1w_2x_1x_2$
and
$u_1w_2x_1x_2$
and
![]() $v_1w_2y_1y_2$
so that
$v_1w_2y_1y_2$
so that
![]() $x_1 \neq y_1$
,
$x_1 \neq y_1$
,
![]() $x_2 \neq y_2$
. Moreover, we restrict the choice of the cycles to those for which
$x_2 \neq y_2$
. Moreover, we restrict the choice of the cycles to those for which
![]() $v_1x_2$
and
$v_1x_2$
and
![]() $u_1y_2$
are red; this is to make sure that swapping of the colours on each of the two cycles (but keeping the colour of
$u_1y_2$
are red; this is to make sure that swapping of the colours on each of the two cycles (but keeping the colour of
![]() $v_1x_2,u_1y_2$
red) indeed decreases
$v_1x_2,u_1y_2$
red) indeed decreases
![]() $\operatorname{cod}_{\mathbb{R}}(u_1,v_1)$
by one, thus mapping
$\operatorname{cod}_{\mathbb{R}}(u_1,v_1)$
by one, thus mapping
![]() $H \in {\mathcal{R}}_k$
to
$H \in {\mathcal{R}}_k$
to
![]() $H' \in {\mathcal{R}}_{k-1}$
(see Figure 3).
$H' \in {\mathcal{R}}_{k-1}$
(see Figure 3).

Figure 3. Switching between
![]() $H \in {\mathcal{R}}_k(u_1,v_1)$
and
$H \in {\mathcal{R}}_k(u_1,v_1)$
and
![]() $H' \in {\mathcal{R}}_{k-1}(u_1,v_1)$
: solid edges are in H and H
$H' \in {\mathcal{R}}_{k-1}(u_1,v_1)$
: solid edges are in H and H
![]() $^{\prime}$
and the dashed ones in
$^{\prime}$
and the dashed ones in
![]() $K \setminus H$
and
$K \setminus H$
and
![]() $K \setminus H'$
, respectively.
$K \setminus H'$
, respectively.
Let
![]() $B_k \,{:\!=}\, B({\mathcal{R}}_k, {\mathcal{R}}_{k-1})$
be the auxiliary graph corresponding to the described switching. Since the number of choices of
$B_k \,{:\!=}\, B({\mathcal{R}}_k, {\mathcal{R}}_{k-1})$
be the auxiliary graph corresponding to the described switching. Since the number of choices of
![]() $w_2$
is k for any
$w_2$
is k for any
![]() $H \in {\mathcal{R}}_k$
, we will show upper and lower bounds on
$H \in {\mathcal{R}}_k$
, we will show upper and lower bounds on
![]() $\deg_{B_k}(H)/k$
by fixing
$\deg_{B_k}(H)/k$
by fixing
![]() $w_2$
and proving upper and lower bounds on the possible choices of
$w_2$
and proving upper and lower bounds on the possible choices of
![]() $(x_1, x_2, y_1, y_2)$
.
$(x_1, x_2, y_1, y_2)$
.
For the upper bound, since there are
![]() $n_2 - 2d_1 + k$
common red neighbours of
$n_2 - 2d_1 + k$
common red neighbours of
![]() $u_1$
and
$u_1$
and
![]() $v_1$
(one can use (56) for this), the number of choices of distinct
$v_1$
(one can use (56) for this), the number of choices of distinct
![]() $x_2, y_2$
is exactly
$x_2, y_2$
is exactly
![]() $(n_2 - 2d_1 + k)_2$
, while the number of choices of
$(n_2 - 2d_1 + k)_2$
, while the number of choices of
![]() $x_1$
and
$x_1$
and
![]() $y_1$
, as blue neighbours of, resp.,
$y_1$
, as blue neighbours of, resp.,
![]() $x_2$
and
$x_2$
and
![]() $y_2$
, is at most
$y_2$
, is at most
![]() $d_2^2$
. Ignoring the requirements that
$d_2^2$
. Ignoring the requirements that
![]() $x_1\neq y_1$
and that both
$x_1\neq y_1$
and that both
![]() $x_1w_2$
and
$x_1w_2$
and
![]() $y_1w_2$
should be red), we have shown
$y_1w_2$
should be red), we have shown
For the lower bound, we subtract from the upper bound (61) the number of choices of
![]() $(x_1, x_2, y_1, y_2)$
for which either
$(x_1, x_2, y_1, y_2)$
for which either
![]() $x_1 = y_1$
or at least one of
$x_1 = y_1$
or at least one of
![]() $x_1w_2$
and
$x_1w_2$
and
![]() $y_1w_2$
is blue (the assumption
$y_1w_2$
is blue (the assumption
![]() $x_2 \neq y_2$
was taken into account in the upper bound). The number of choices with
$x_2 \neq y_2$
was taken into account in the upper bound). The number of choices with
![]() $x_1 = y_1$
is at most
$x_1 = y_1$
is at most
![]() $n_1d_1^2$
, and those with, say,
$n_1d_1^2$
, and those with, say,
![]() $x_1w_2$
blue, is at most
$x_1w_2$
blue, is at most
![]() $d_2d_1 \cdot (n_2 - 2d_1 + k)d_2 $
. Indeed, there are
$d_2d_1 \cdot (n_2 - 2d_1 + k)d_2 $
. Indeed, there are
![]() $\deg_H(w_2) \le d_2$
candidates for
$\deg_H(w_2) \le d_2$
candidates for
![]() $x_1$
and, then, at most
$x_1$
and, then, at most
![]() $d_1$
candidates for
$d_1$
candidates for
![]() $x_2$
,
$x_2$
,
![]() $\operatorname{cod}_{K \setminus H}(u_1,u_2) = n_2 - 2d_1 + k$
candidates for
$\operatorname{cod}_{K \setminus H}(u_1,u_2) = n_2 - 2d_1 + k$
candidates for
![]() $y_2$
, and then
$y_2$
, and then
![]() $d_2$
choices of
$d_2$
choices of
![]() $y_1$
. Therefore
$y_1$
. Therefore
 \begin{align*} \deg_{B_k}(H)/k &\ge (n_2 - 2d_1 + k)_2d_2^2 - n_1d_1^2 - 2(n_2 - 2d_1 + k)d_1d_2^2 \\[3pt]&= (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \frac{n_1d_1^2}{(n_2 - 2d_1 + k)_2 d_2^2} - \frac{2d_1}{n_2 - 2d_1 + k - 1}\right) \\[3pt]\fbox{$d_1 = n_2p, d_2 = n_1p, k \ge 1$}\quad& \ge (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \frac{n_2^2}{(n_2 - 2pn_2)^2 n_1} - \frac{2pn_2}{n_2 - 2pn_2}\right) \\[3pt]&= (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \frac{1}{(1 - 2p)^2n_1} - \frac{2p}{1 - 2p}\right) \\[3pt]\fbox{$p\le1/5$}\quad &\ge (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \left( \frac{25}{9pn_1} + \frac{10}{3} \right) p \right) \\[3pt]\fbox{$\hat p \hat n \to \infty$}\quad &\ge (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - 4p \right).\end{align*}
\begin{align*} \deg_{B_k}(H)/k &\ge (n_2 - 2d_1 + k)_2d_2^2 - n_1d_1^2 - 2(n_2 - 2d_1 + k)d_1d_2^2 \\[3pt]&= (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \frac{n_1d_1^2}{(n_2 - 2d_1 + k)_2 d_2^2} - \frac{2d_1}{n_2 - 2d_1 + k - 1}\right) \\[3pt]\fbox{$d_1 = n_2p, d_2 = n_1p, k \ge 1$}\quad& \ge (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \frac{n_2^2}{(n_2 - 2pn_2)^2 n_1} - \frac{2pn_2}{n_2 - 2pn_2}\right) \\[3pt]&= (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \frac{1}{(1 - 2p)^2n_1} - \frac{2p}{1 - 2p}\right) \\[3pt]\fbox{$p\le1/5$}\quad &\ge (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - \left( \frac{25}{9pn_1} + \frac{10}{3} \right) p \right) \\[3pt]\fbox{$\hat p \hat n \to \infty$}\quad &\ge (n_2 - 2d_1 + k)_2 d_2^2 \left( 1 - 4p \right).\end{align*}
A moment of thought (and a glance at Figure 3) reveals that the backward switching corresponds to choosing a common red neighbour
![]() $w_2$
of
$w_2$
of
![]() $u_1$
and
$u_1$
and
![]() $v_1$
, choosing alternating cycles
$v_1$
, choosing alternating cycles
![]() $u_1w_2x_1x_2$
and
$u_1w_2x_1x_2$
and
![]() $v_1w_2y_1y_2$
such that
$v_1w_2y_1y_2$
such that
![]() $x_1 \neq y_1$
and the edges
$x_1 \neq y_1$
and the edges
![]() $v_1x_2$
and
$v_1x_2$
and
![]() $u_1y_2$
are red (note that these assumptions imply
$u_1y_2$
are red (note that these assumptions imply
![]() $x_2 \neq y_2$
), and swapping the colours along the cycles.
$x_2 \neq y_2$
), and swapping the colours along the cycles.
Since for every
![]() $H' \in {\mathcal{R}}_{k-1}$
the number of choices of
$H' \in {\mathcal{R}}_{k-1}$
the number of choices of
![]() $x_2 \in \Gamma_{H'}(u_1) \setminus \Gamma_{H'}(v_1)$
and
$x_2 \in \Gamma_{H'}(u_1) \setminus \Gamma_{H'}(v_1)$
and
![]() $ y_2 \in \Gamma_{H'}(v_1) \setminus \Gamma_{H'}(u_1)$
is exactly
$ y_2 \in \Gamma_{H'}(v_1) \setminus \Gamma_{H'}(u_1)$
is exactly
![]() $(d_1 - k + 1)^2$
, we will bound
$(d_1 - k + 1)^2$
, we will bound
![]() $\deg_{B_k}(H')/(d_1 - k + 1)^2$
from above and below by fixing
$\deg_{B_k}(H')/(d_1 - k + 1)^2$
from above and below by fixing
![]() $x_2, y_2$
and estimating the number of possible triplets
$x_2, y_2$
and estimating the number of possible triplets
![]() $(w_2, x_1,y_1)$
. For the upper bound, we can choose
$(w_2, x_1,y_1)$
. For the upper bound, we can choose
![]() $w_2$
in exactly
$w_2$
in exactly
![]() $\operatorname{cod}_{K \setminus H'}(u_1,u_2) = n_2 - 2d_1 + k - 1$
ways, and a pair
$\operatorname{cod}_{K \setminus H'}(u_1,u_2) = n_2 - 2d_1 + k - 1$
ways, and a pair
![]() $x_1, y_1$
of distinct blue neighbours of
$x_1, y_1$
of distinct blue neighbours of
![]() $w_2$
in at most
$w_2$
in at most
![]() $(d_2)_2$
ways (we ignore the requirement that
$(d_2)_2$
ways (we ignore the requirement that
![]() $x_1x_2$
and
$x_1x_2$
and
![]() $y_1y_2$
are red). Thus,
$y_1y_2$
are red). Thus,
For the lower bound, given
![]() $x_2, y_2$
, we need to subtract from the upper bound (62) the number of choices of
$x_2, y_2$
, we need to subtract from the upper bound (62) the number of choices of
![]() $w_2, x_1, y_1$
for which
$w_2, x_1, y_1$
for which
![]() $x_1x_2$
or
$x_1x_2$
or
![]() $y_1y_2$
is blue. In the former case, ignoring other constraints, there are at most
$y_1y_2$
is blue. In the former case, ignoring other constraints, there are at most
![]() $d_2$
choices of a blue neighbour
$d_2$
choices of a blue neighbour
![]() $x_1$
of
$x_1$
of
![]() $x_2$
, at most
$x_2$
, at most
![]() $d_1$
choices of a blue neighbour
$d_1$
choices of a blue neighbour
![]() $w_2$
of
$w_2$
of
![]() $x_1$
, and at most
$x_1$
, and at most
![]() $d_2$
choices of a blue neighbour
$d_2$
choices of a blue neighbour
![]() $y_1$
of
$y_1$
of
![]() $w_2$
. By symmetry, the total number of bad choices is at most
$w_2$
. By symmetry, the total number of bad choices is at most
![]() $2d_1d_2^2$
, whence
$2d_1d_2^2$
, whence
 \begin{align*} \deg_{B_k}(H')/(d_1 - k + 1)^2 &\ge (n_2 - 2d_1 + k - 1)(d_2)_2 - 2d_1d_2^2 \\[3pt] \fbox{$k \ge 1$}\quad &\ge (n_2 - 2d_1 + k - 1)d_2^2\left( 1 - \frac{1}{d_2} - \frac{2d_1}{n_2 - 2d_1} \right) \\[3pt] \fbox{$d_1 = n_2p, p \le 1/5$}\quad &\ge (n_2 - 2d_1 + k - 1)d_2^2\left( 1- d_2^{-1} - 4p \right).\end{align*}
\begin{align*} \deg_{B_k}(H')/(d_1 - k + 1)^2 &\ge (n_2 - 2d_1 + k - 1)(d_2)_2 - 2d_1d_2^2 \\[3pt] \fbox{$k \ge 1$}\quad &\ge (n_2 - 2d_1 + k - 1)d_2^2\left( 1 - \frac{1}{d_2} - \frac{2d_1}{n_2 - 2d_1} \right) \\[3pt] \fbox{$d_1 = n_2p, p \le 1/5$}\quad &\ge (n_2 - 2d_1 + k - 1)d_2^2\left( 1- d_2^{-1} - 4p \right).\end{align*}
Since, by our assumptions,
![]() $d_2 \ge \hat p\hat n \to \infty$
and
$d_2 \ge \hat p\hat n \to \infty$
and
![]() $p \le 1/5$
, it follows that the graphs
$p \le 1/5$
, it follows that the graphs
![]() $B_k$
for
$B_k$
for
![]() $k = 1, \dots, d_1$
have minimum degrees at least 1. In particular, this means that starting with any p-biregular graph, by applying a certain number of switchings, we can obtain a p-biregular graph with arbitrary co-degree. Since we implicitly assume
$k = 1, \dots, d_1$
have minimum degrees at least 1. In particular, this means that starting with any p-biregular graph, by applying a certain number of switchings, we can obtain a p-biregular graph with arbitrary co-degree. Since we implicitly assume
![]() ${{\mathcal{R}}(n_1,n_2,p)}$
is non-empty, this implies that all classes
${{\mathcal{R}}(n_1,n_2,p)}$
is non-empty, this implies that all classes
![]() ${\mathcal{R}}_k, k = 0, \dots, d_1,$
are non-empty, i.e., the numbers
${\mathcal{R}}_k, k = 0, \dots, d_1,$
are non-empty, i.e., the numbers
![]() $r_k = |{\mathcal{R}}_k|$
are all positive, satisfying one of the conditions of Claim 12.
$r_k = |{\mathcal{R}}_k|$
are all positive, satisfying one of the conditions of Claim 12.
Using (14) and bounds on the degrees in
![]() $B_k$
, for
$B_k$
, for
![]() $k = 1, \dots, d_1,$
we have
$k = 1, \dots, d_1,$
we have
 \begin{align} \notag \frac{r_k}{r_{k-1}} \le \frac{\max_{H' \in {\mathcal{R}}' }\deg_{B_k}(H')}{\min_{H \in {\mathcal{R}}} \deg_{B_k}(H)} &\le \frac{(d_1 - k + 1)^2}{k(n_2 - 2d_1 + k)}\cdot\frac{1}{1 - 4p} \\ &\le \frac{(d_1 - k + 1)^2}{k(n_2 - 2d_1 + k)} \cdot \left( 1 + 20p \right),\end{align}
\begin{align} \notag \frac{r_k}{r_{k-1}} \le \frac{\max_{H' \in {\mathcal{R}}' }\deg_{B_k}(H')}{\min_{H \in {\mathcal{R}}} \deg_{B_k}(H)} &\le \frac{(d_1 - k + 1)^2}{k(n_2 - 2d_1 + k)}\cdot\frac{1}{1 - 4p} \\ &\le \frac{(d_1 - k + 1)^2}{k(n_2 - 2d_1 + k)} \cdot \left( 1 + 20p \right),\end{align}
(where the last inequality holds because
![]() $p \le 1/5$
implies
$p \le 1/5$
implies
![]() $\frac{1}{1 - 4p} = 1 + \frac{4p}{1 - 4p} \le 1 + 20p$
), and
$\frac{1}{1 - 4p} = 1 + \frac{4p}{1 - 4p} \le 1 + 20p$
), and
Let
![]() $\mu$
be a real number such that
$\mu$
be a real number such that
After solving for
![]() $\mu$
, we have
$\mu$
, we have
Define
From (63), (65), and (67), for
![]() $\mu \le k \le d_1$
, we have
$\mu \le k \le d_1$
, we have
On the other hand, from (64), (65), and (67) that, for
![]() $1\le k \le \mu$
, we have
$1\le k \le \mu$
, we have
Note that, since
![]() $\min\{d_1,d_2\} = p\hat n \to \infty$
and
$\min\{d_1,d_2\} = p\hat n \to \infty$
and
![]() $p\le1/5$
, it follows by (66), and (67) that
$p\le1/5$
, it follows by (66), and (67) that
Therefore,
Consequently, setting
we have, by (69)
Noting that the last inequality in (68) implies
![]() $x \ge \sqrt{\mu_+n_2} + \lambda $
, using Claim 12 we obtain (57), completing the proof in the case
$x \ge \sqrt{\mu_+n_2} + \lambda $
, using Claim 12 we obtain (57), completing the proof in the case
![]() $\mathbb{I} = 1$
.
$\mathbb{I} = 1$
.
Case
![]() $\mathbb{I} = 0$
. For the switching argument used in the previous case it was crucial that p was small, as otherwise several estimates would be negative and so meaningless. Therefore, it cannot be used now. Fortunately, in this case we are in a position to apply an asymptotic enumeration approach based on Theorem 5 and analogous to the proof of Theorem 2.1 in [Reference Krivelevich, Sudakov, Vu and Wormald7].
$\mathbb{I} = 0$
. For the switching argument used in the previous case it was crucial that p was small, as otherwise several estimates would be negative and so meaningless. Therefore, it cannot be used now. Fortunately, in this case we are in a position to apply an asymptotic enumeration approach based on Theorem 5 and analogous to the proof of Theorem 2.1 in [Reference Krivelevich, Sudakov, Vu and Wormald7].
Recall the notation
![]() ${{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)}$
defined before Theorem 5. Writing
${{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)}$
defined before Theorem 5. Writing
![]() $A = \Gamma_H(u_1)$
and
$A = \Gamma_H(u_1)$
and
![]() $B = \Gamma_H(v_1)$
, we note that every graph in
$B = \Gamma_H(v_1)$
, we note that every graph in
![]() ${\mathcal{R}}_k$
induces an ordered partition of
${\mathcal{R}}_k$
induces an ordered partition of
![]() $V_2$
into four sets
$V_2$
into four sets
![]() $A \cap B$
,
$A \cap B$
,
![]() $A \setminus B$
,
$A \setminus B$
,
![]() $B \setminus A$
and
$B \setminus A$
and
![]() $V_2 \setminus (A \cup B)$
, of sizes, respectively,
$V_2 \setminus (A \cup B)$
, of sizes, respectively,
![]() $k, d_1 - k, d_1 - k$
, and
$k, d_1 - k, d_1 - k$
, and
![]() $n_2 - 2d_1 + k$
. There are exactly
$n_2 - 2d_1 + k$
. There are exactly
such partitions. After removing vertices
![]() $u_1$
and
$u_1$
and
![]() $v_1$
, we obtain a graph
$v_1$
, we obtain a graph
![]() $H^* \in {{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)}$
on
$H^* \in {{\mathcal{R}}({\mathbf{d}}_1,{\mathbf{d}}_2)}$
on
![]() $(V_1\setminus\{u_1,v_1\}, V_2)$
, with
$(V_1\setminus\{u_1,v_1\}, V_2)$
, with
![]() ${\mathbf{d}}_1$
having all its
${\mathbf{d}}_1$
having all its
![]() $n_1 - 2$
entries equal to
$n_1 - 2$
entries equal to
![]() $d_1$
, and entries of
$d_1$
, and entries of
![]() ${\mathbf{d}}_2$
determined by the partition: entries equal to
${\mathbf{d}}_2$
determined by the partition: entries equal to
![]() $d_2 - 2$
on
$d_2 - 2$
on
![]() $A \cap B$
, to
$A \cap B$
, to
![]() $d_2 - 1$
on
$d_2 - 1$
on
![]() $A \triangle B$
and the remaining ones equal to
$A \triangle B$
and the remaining ones equal to
![]() $d_2$
. Since
$d_2$
. Since
![]() $H^*$
together with the ordered partition uniquely determines H, we have
$H^*$
together with the ordered partition uniquely determines H, we have
Let us check that the three assumptions (i)–(iii) of Theorem 5 are satisfied. When doing so, we should remember that we have
![]() $n_1 - 2$
instead of
$n_1 - 2$
instead of
![]() $n_1$
, but that the parameter
$n_1$
, but that the parameter
![]() $p = d_1/n_2$
remains intact. With foresight, choose
$p = d_1/n_2$
remains intact. With foresight, choose
![]() $a = 0.35$
and, say,
$a = 0.35$
and, say,
![]() $b = 0.1$
, and, for convenience
$b = 0.1$
, and, for convenience
![]() $C = 1$
, which determine, via Theorem 5, an
$C = 1$
, which determine, via Theorem 5, an
![]() $\epsilon > 0$
.
$\epsilon > 0$
.
Note that
![]() $\mathbb{I} = 0$
implies
$\mathbb{I} = 0$
implies
As the degrees on one side are all equal and on the other side they differ from each other by at most 2, assumption (i) holds true with a big margin. Using
![]() $q \ge 1/2$
and the first inequality in (71), we get
$q \ge 1/2$
and the first inequality in (71), we get
 \begin{equation*} (pq)^2\min\{n_1 - 2,n_2\}^{1 + \epsilon} \ge \frac{p^2\hat n^{1 + \epsilon}}{4}(1 + o(1)) = \Omega \left( \frac{ \left(\max \left\{ n_1, n_2 \right\}\right)^{1 + \epsilon}}{(\log N)^{3 + \epsilon}} \right) \gg \max \left\{ n_1, n_2 \right\},\end{equation*}
\begin{equation*} (pq)^2\min\{n_1 - 2,n_2\}^{1 + \epsilon} \ge \frac{p^2\hat n^{1 + \epsilon}}{4}(1 + o(1)) = \Omega \left( \frac{ \left(\max \left\{ n_1, n_2 \right\}\right)^{1 + \epsilon}}{(\log N)^{3 + \epsilon}} \right) \gg \max \left\{ n_1, n_2 \right\},\end{equation*}
which implies assumption (ii) for large
![]() $\hat n$
. Finally, using elementary inequalities
$\hat n$
. Finally, using elementary inequalities
![]() $(1 - 2p)^2 \le q$
(since
$(1 - 2p)^2 \le q$
(since
![]() $p \le 1/2$
),
$p \le 1/2$
),
![]() $1 \le \left( n_1/n_2 + n_2/n_1 \right)/2$
, and the second inequality in (71), we obtain
$1 \le \left( n_1/n_2 + n_2/n_1 \right)/2$
, and the second inequality in (71), we obtain
 \begin{align*} \frac{(1 - 2p)^2}{4pq} &\left(1 + \frac{5(n_1 - 2)}{6n_2} + \frac{5n_2}{6(n_1 - 1)}\right) \le \frac{1}{4p}\left( \frac{1}{2} + \frac{5}{6} \right)\left(\frac{n_1}{n_2} + \frac{n_2}{n_1}\right) (1 + o(1)) \\ &\le \frac{1}{3}\log \max \left\{ n_1, n_2 \right\} (1 + o(1)) \ll 0.35 \cdot \log \max \left\{ n_1 - 2, n_2 \right\},\end{align*}
\begin{align*} \frac{(1 - 2p)^2}{4pq} &\left(1 + \frac{5(n_1 - 2)}{6n_2} + \frac{5n_2}{6(n_1 - 1)}\right) \le \frac{1}{4p}\left( \frac{1}{2} + \frac{5}{6} \right)\left(\frac{n_1}{n_2} + \frac{n_2}{n_1}\right) (1 + o(1)) \\ &\le \frac{1}{3}\log \max \left\{ n_1, n_2 \right\} (1 + o(1)) \ll 0.35 \cdot \log \max \left\{ n_1 - 2, n_2 \right\},\end{align*}
which for large
![]() $\hat n$
implies assumption (iii) with
$\hat n$
implies assumption (iii) with
![]() $a = 0.35$
.
$a = 0.35$
.
Note that in (20) we have
![]() $D_1 = 0$
, while
$D_1 = 0$
, while
![]() $D_2 \le 4n_2 \ll pq n_1n_2$
, by the assumption
$D_2 \le 4n_2 \ll pq n_1n_2$
, by the assumption
![]() $\hat p\hat n\to\infty$
. Thus, uniformly over k, the exponent in (20) is
$\hat p\hat n\to\infty$
. Thus, uniformly over k, the exponent in (20) is
![]() $-1/2 + o(1)$
and, by Theorem 5,
$-1/2 + o(1)$
and, by Theorem 5,
 \begin{equation*} |{\mathcal{R}}_k| \sim \frac {e^{-1/2}n_2!\binom {n_2}{d_1}^{n_1 - 2} \binom {n_1 - 2}{d_{2} - 2}^{k}\binom {n_1 - 2}{d_{2} - 1}^{2d_1 - 2k}\binom {n_1 - 2}{d_{2}}^{n_1 - 2d_1 + k}} {k!(d_1 - k)!^2(n_2 - 2d_1 + k)!\binom{(n_1 - 2)n_2}{(n_1 - 2)d_1}} =: r_k.\end{equation*}
\begin{equation*} |{\mathcal{R}}_k| \sim \frac {e^{-1/2}n_2!\binom {n_2}{d_1}^{n_1 - 2} \binom {n_1 - 2}{d_{2} - 2}^{k}\binom {n_1 - 2}{d_{2} - 1}^{2d_1 - 2k}\binom {n_1 - 2}{d_{2}}^{n_1 - 2d_1 + k}} {k!(d_1 - k)!^2(n_2 - 2d_1 + k)!\binom{(n_1 - 2)n_2}{(n_1 - 2)d_1}} =: r_k.\end{equation*}
Straightforward calculations yield
and, because
![]() $d_2/n_1 = p\le1/2$
,
$d_2/n_1 = p\le1/2$
,
(Compare with (63) and (64) to note the absence of
![]() $\Theta(p)$
error terms.) With
$\Theta(p)$
error terms.) With
![]() $\mu$
as in (66), we redefine
$\mu$
as in (66), we redefine
From (66) and (72) it follows that
and
From (73) it follows
![]() $\mu_+ \le 6p^2n_2$
, which implies that x defined in (70) satisfies
$\mu_+ \le 6p^2n_2$
, which implies that x defined in (70) satisfies
![]() $x \ge \sqrt{2\mu_+\lambda} + \lambda$
. Consequently, using (73), (74) and Claim 12 we infer
$x \ge \sqrt{2\mu_+\lambda} + \lambda$
. Consequently, using (73), (74) and Claim 12 we infer
We have obtained (57) in the case
![]() $\mathbb{I} = 0$
.
$\mathbb{I} = 0$
.
5.2. Degrees and co-degrees in
 $\mathbb{R}(t)$
$\mathbb{R}(t)$
For convenience, having fixed
![]() $H\in{{\mathcal{R}}(n_1,n_2,p)}$
, we will denote by
$H\in{{\mathcal{R}}(n_1,n_2,p)}$
, we will denote by
![]() $\mathbb{P}_H$
and
$\mathbb{P}_H$
and
![]() $\operatorname{\mathbb{E}}_H$
the conditional probability and expectation with respect to the event
$\operatorname{\mathbb{E}}_H$
the conditional probability and expectation with respect to the event
![]() $\mathbb{R} = H$
. In the conditional space defined by such an event,
$\mathbb{R} = H$
. In the conditional space defined by such an event,
![]() $(\eta_1, \dots, \eta_M)$
is just a uniformly random permutation of the edges of H and therefore
$(\eta_1, \dots, \eta_M)$
is just a uniformly random permutation of the edges of H and therefore
![]() $\mathbb{R}(t)$
is a uniformly random t-subset of edges of H.
$\mathbb{R}(t)$
is a uniformly random t-subset of edges of H.
We first show that the degrees of vertices in the process
![]() $\mathbb{R}(t)$
grow proportionally almost until the end. Recall that
$\mathbb{R}(t)$
grow proportionally almost until the end. Recall that
![]() $d_1 = pn_2,\; d_2 = pn_1$
, while
$d_1 = pn_2,\; d_2 = pn_1$
, while
![]() $\tau=\tau(t)$
and
$\tau=\tau(t)$
and
![]() $\tau_0$
are defined, respectively, in (24) and (25).
$\tau_0$
are defined, respectively, in (24) and (25).
Lemma 13. If
![]() $\lambda = \lambda(n_1,n_2) \le \tau_0 p \hat n$
, then for
$\lambda = \lambda(n_1,n_2) \le \tau_0 p \hat n$
, then for
![]() $i = 1, 2$
, with probability
$i = 1, 2$
, with probability
![]() $1 - O(N^2e^{-9\lambda/4})$
$1 - O(N^2e^{-9\lambda/4})$
Proof. Fix
![]() $t < t_0$
and
$t < t_0$
and
![]() $v\in V_i$
and set
$v\in V_i$
and set
![]() $X_t(v) \,{:\!=}\, \deg_{\mathbb{R} \setminus \mathbb{R}(t)}(v)$
. For any
$X_t(v) \,{:\!=}\, \deg_{\mathbb{R} \setminus \mathbb{R}(t)}(v)$
. For any
![]() $H \in {{\mathcal{R}}(n_1,n_2,p)}$
, conditioning on
$H \in {{\mathcal{R}}(n_1,n_2,p)}$
, conditioning on
![]() $\mathbb{R} = H$
, the random variable
$\mathbb{R} = H$
, the random variable
![]() $X_t(v) \sim \operatorname{Hyp}(M, d_i, M - t)$
has a hypergeometric distribution. Since the distribution does not depend on H,
$X_t(v) \sim \operatorname{Hyp}(M, d_i, M - t)$
has a hypergeometric distribution. Since the distribution does not depend on H,
![]() $X_t(v)$
has the same distribution unconditionally. In view of (24),
$X_t(v)$
has the same distribution unconditionally. In view of (24),
![]() $\operatorname{\mathbb{E}} X_t(v) = \tau d_i$
, therefore combining (17) and (18), for all
$\operatorname{\mathbb{E}} X_t(v) = \tau d_i$
, therefore combining (17) and (18), for all
![]() $x > 0$
,
$x > 0$
,
 \begin{align}\mathbb{P}\left(|X_t(v) - \tau d_i| \ge x\right)\le 2 \exp \left\{ - \frac{x^2}{2\left(\tau d_i + x/3 \right)} \right\}= 2 \exp \left\{ - \frac{x^2}{2\tau d_i\left(1 + x/(3\tau d_i) \right)} \right\}.\end{align}
\begin{align}\mathbb{P}\left(|X_t(v) - \tau d_i| \ge x\right)\le 2 \exp \left\{ - \frac{x^2}{2\left(\tau d_i + x/3 \right)} \right\}= 2 \exp \left\{ - \frac{x^2}{2\tau d_i\left(1 + x/(3\tau d_i) \right)} \right\}.\end{align}
Let
![]() $x \,{:\!=}\, 3\sqrt{\lambda\tau d_i}$
. Since
$x \,{:\!=}\, 3\sqrt{\lambda\tau d_i}$
. Since
![]() $\tau \ge \tau_0$
, by the assumption
$\tau \ge \tau_0$
, by the assumption
![]() $\lambda\le \tau_0 p\hat n $
,
$\lambda\le \tau_0 p\hat n $
,
Consequently, taking the union bound over all
![]() $(1 - \tau_0)Mn_i \le N^2$
choices of t and v and using (76) and (77), we conclude that (75) fails with probability at most
$(1 - \tau_0)Mn_i \le N^2$
choices of t and v and using (76) and (77), we conclude that (75) fails with probability at most
 \begin{equation*}2N^2\exp \left\{ - \frac{x^2}{2\tau d_i\left(1 + x/(3\tau d_i) \right)} \right\}\le 2N^2\exp \left\{ -\frac{9 \tau d_i \lambda}{4\tau d_i} \right\} = 2N^2e^{-9\lambda/4}.\end{equation*}
\begin{equation*}2N^2\exp \left\{ - \frac{x^2}{2\tau d_i\left(1 + x/(3\tau d_i) \right)} \right\}\le 2N^2\exp \left\{ -\frac{9 \tau d_i \lambda}{4\tau d_i} \right\} = 2N^2e^{-9\lambda/4}.\end{equation*}
In the proof of Lemma 10, to have a pseudorandom-like property of
![]() $\mathbb{R} \setminus \mathbb{R}(t)$
for
$\mathbb{R} \setminus \mathbb{R}(t)$
for
![]() $p > 0.49$
, we will need a bound on the upper tail of co-degrees in
$p > 0.49$
, we will need a bound on the upper tail of co-degrees in
![]() $\mathbb{R}(t)$
. Recall the definition of co-degree from (55).
$\mathbb{R}(t)$
. Recall the definition of co-degree from (55).
Lemma 14. Assume that
![]() $n_1 \ge n_2$
and
$n_1 \ge n_2$
and
![]() $p > 0.49$
. If
$p > 0.49$
. If
![]() $\lambda = \lambda(n_1,n_2) \ge \log N$
, then, with probability
$\lambda = \lambda(n_1,n_2) \ge \log N$
, then, with probability
![]() $1 - O(N^3e^{-\lambda/3 })$
,
$1 - O(N^3e^{-\lambda/3 })$
,
Proof. If
![]() $\lambda \ge n_2$
, inequality (78) holds trivially, so let us assume
$\lambda \ge n_2$
, inequality (78) holds trivially, so let us assume
![]() $\lambda < n_2$
. We can condition on
$\lambda < n_2$
. We can condition on
![]() $\mathbb{R} = H$
satisfying
$\mathbb{R} = H$
satisfying
 \begin{align} \notag \forall u_1,v_1 \in V_1 \quad\operatorname{cod}_{H}(u_1,v_1) & \le p^2n_2+ 20\left(\hat p^3n_2\mathbb{I} + n_2\hat p/\hat n + \sqrt{\hat p^2\lambda n_2}\right) + \lambda\\[3pt] \notag \fbox{$\hat p \le \min \{q, 0.5\}, n_2 = \hat n$}\quad&\le p^2n_2+ 20\left(q^3n_2\mathbb{I} + 0.5 + 0.5\sqrt{\lambda n_2}\right) + \lambda\\[3pt] \fbox{$1 \ll \lambda < n_2$}\quad &\le p^2n_2 + 20q^3n_2 \mathbb{I} + 12\sqrt{\lambda n_2}.\end{align}
\begin{align} \notag \forall u_1,v_1 \in V_1 \quad\operatorname{cod}_{H}(u_1,v_1) & \le p^2n_2+ 20\left(\hat p^3n_2\mathbb{I} + n_2\hat p/\hat n + \sqrt{\hat p^2\lambda n_2}\right) + \lambda\\[3pt] \notag \fbox{$\hat p \le \min \{q, 0.5\}, n_2 = \hat n$}\quad&\le p^2n_2+ 20\left(q^3n_2\mathbb{I} + 0.5 + 0.5\sqrt{\lambda n_2}\right) + \lambda\\[3pt] \fbox{$1 \ll \lambda < n_2$}\quad &\le p^2n_2 + 20q^3n_2 \mathbb{I} + 12\sqrt{\lambda n_2}.\end{align}
Indeed, the probability of the opposite event can be bounded, by Lemma 11 and the union bound, by
![]() $O\left(n_1^2\sqrt Ne^{-\lambda}\right) \ll N^3e^{-\lambda}$
. Taking this bound into account, it thus suffices to show that if H satisfies (79), then for any distinct
$O\left(n_1^2\sqrt Ne^{-\lambda}\right) \ll N^3e^{-\lambda}$
. Taking this bound into account, it thus suffices to show that if H satisfies (79), then for any distinct
![]() $u_1, v_1\in V_1$
and
$u_1, v_1\in V_1$
and
![]() $t \le M$
$t \le M$
since then the proof is completed by a union bound over
![]() $O(N^3)$
choices of
$O(N^3)$
choices of
![]() $t, u_1, v_1$
.
$t, u_1, v_1$
.
Fix
![]() $t \le M, u_1 \neq v_1$
and let
$t \le M, u_1 \neq v_1$
and let
![]() $Y \,{:\!=}\, \left| \Gamma_{\mathbb{R}(t)}(u_1) \cap \Gamma_{H}(v_1)\right|$
and
$Y \,{:\!=}\, \left| \Gamma_{\mathbb{R}(t)}(u_1) \cap \Gamma_{H}(v_1)\right|$
and
![]() $\operatorname{cod}_H \,{:\!=}\, \operatorname{cod}_H(u_1, v_1)$
. The distribution of Y conditioned on
$\operatorname{cod}_H \,{:\!=}\, \operatorname{cod}_H(u_1, v_1)$
. The distribution of Y conditioned on
![]() $\mathbb{R} = H$
is hypergeometric
$\mathbb{R} = H$
is hypergeometric
![]() $\operatorname{Hyp}(M, \operatorname{cod}_H, t)$
, and hence, by (79),
$\operatorname{Hyp}(M, \operatorname{cod}_H, t)$
, and hence, by (79),
Using (17), a trivial bound
![]() $\mu_Y \le n_2$
, and our assumption
$\mu_Y \le n_2$
, and our assumption
![]() $\lambda < n_2$
,
$\lambda < n_2$
,
Since also trivially
![]() $Y \le \min\{d_1, t\}$
, we have shown that given
$Y \le \min\{d_1, t\}$
, we have shown that given
![]() $\mathbb{R} = H$
, with probability at least
$\mathbb{R} = H$
, with probability at least
![]() $1 - e^{-\lambda/3}$
,
$1 - e^{-\lambda/3}$
,
Let
![]() ${\mathcal{E}}_{(80)}$
be the event that the inequality in (80) holds. By the law of total probability,
${\mathcal{E}}_{(80)}$
be the event that the inequality in (80) holds. By the law of total probability,
 \begin{align*} \mathbb{P}_H\left({{\mathcal{E}}_{(80)}}\right) &= \sum_y \mathbb{P}_H\left({{\mathcal{E}}_{(80)}}\,|\,{Y = y}\right)\mathbb{P}_H\left({Y = y}\right) \\[3pt] \fbox{(81)}\quad &\le \sum_{y \le y_0}\mathbb{P}_H\left({{\mathcal{E}}_{(80)}}\,|\,{Y = y}\right)\mathbb{P}_H\left({Y = y}\right) + e^{-\lambda/3}.\end{align*}
\begin{align*} \mathbb{P}_H\left({{\mathcal{E}}_{(80)}}\right) &= \sum_y \mathbb{P}_H\left({{\mathcal{E}}_{(80)}}\,|\,{Y = y}\right)\mathbb{P}_H\left({Y = y}\right) \\[3pt] \fbox{(81)}\quad &\le \sum_{y \le y_0}\mathbb{P}_H\left({{\mathcal{E}}_{(80)}}\,|\,{Y = y}\right)\mathbb{P}_H\left({Y = y}\right) + e^{-\lambda/3}.\end{align*}
Hence, to prove (80), it suffices to show that, for any
![]() $ y = 0, \dots, y_0$
,
$ y = 0, \dots, y_0$
,
Fix an integer
![]() $y \in [0, y_0]$
and a set
$y \in [0, y_0]$
and a set
![]() $S\subseteq V_2$
of size
$S\subseteq V_2$
of size
![]() $|S| = y \le y_0$
. Under an additional conditioning
$|S| = y \le y_0$
. Under an additional conditioning
![]() $\Gamma_{\mathbb{R}(t)}(u_1)\cap \Gamma_H(v_1) = S$
, set
$\Gamma_{\mathbb{R}(t)}(u_1)\cap \Gamma_H(v_1) = S$
, set
![]() $\mathbb{R}(t)$
is the union of a fixed y-element set
$\mathbb{R}(t)$
is the union of a fixed y-element set
![]() $\{u_1w\,\ :\,\ w \in S\}$
and a random
$\{u_1w\,\ :\,\ w \in S\}$
and a random
![]() $(t - y)$
-element subset of
$(t - y)$
-element subset of
![]() $E(H) \setminus \{u_1w\,\ :\,\ w \in \Gamma_H(u_1)\cap \Gamma_H(v_1)\}$
. Thus, in this conditional space,
$E(H) \setminus \{u_1w\,\ :\,\ w \in \Gamma_H(u_1)\cap \Gamma_H(v_1)\}$
. Thus, in this conditional space,
![]() $X \,{:\!=}\, \operatorname{cod}_{\mathbb{R}(t)}(u_1,v_1)$
counts how many of these
$X \,{:\!=}\, \operatorname{cod}_{\mathbb{R}(t)}(u_1,v_1)$
counts how many of these
![]() $t-y$
random edges fall into the set
$t-y$
random edges fall into the set
![]() $\{v_1w\,\ :\,\ w \in S\}$
and therefore
$\{v_1w\,\ :\,\ w \in S\}$
and therefore
![]() $X \sim \operatorname{Hyp}(M - \operatorname{cod}_H, y, t - y)$
. Moreover, the distribution of X is the same for all S of size y, so X has the same distribution when conditioned on
$X \sim \operatorname{Hyp}(M - \operatorname{cod}_H, y, t - y)$
. Moreover, the distribution of X is the same for all S of size y, so X has the same distribution when conditioned on
![]() $Y = y$
. In particular,
$Y = y$
. In particular,
 \begin{align*} \mu_X \,{:\!=}\, \operatorname{\mathbb{E}}_H\left({X}\,|\,{Y = y}\right) &= \frac{y(t-y)}{M-\operatorname{cod}_H} \\[3pt] \fbox{$y \ge 0$}\quad &\le \frac{yt}{M} \left(1 + \frac{\operatorname{cod}_H}{M - \operatorname{cod}_H}\right) \\[3pt] \fbox{$M = pn_1n_2, \operatorname{cod}_H \le pn_2$}\quad &\le (1-\tau) y \left(1 + \frac{1}{n_1 - 1}\right) \\[3pt] \fbox{$y \le y_0$ and (81)}\quad &\le (1-\tau)^2p^2n_2 + 20q^3n_2 \mathbb{I} + 13 \sqrt{\lambda n_2} + \frac{n_2}{n_1 - 1}. \\[3pt] \fbox{$n_1 \ge n_2$}\quad &\le (1-\tau)^2p^2n_2 + 20q^3n_2 \mathbb{I} + 14 \sqrt{\lambda n_2}. \end{align*}
\begin{align*} \mu_X \,{:\!=}\, \operatorname{\mathbb{E}}_H\left({X}\,|\,{Y = y}\right) &= \frac{y(t-y)}{M-\operatorname{cod}_H} \\[3pt] \fbox{$y \ge 0$}\quad &\le \frac{yt}{M} \left(1 + \frac{\operatorname{cod}_H}{M - \operatorname{cod}_H}\right) \\[3pt] \fbox{$M = pn_1n_2, \operatorname{cod}_H \le pn_2$}\quad &\le (1-\tau) y \left(1 + \frac{1}{n_1 - 1}\right) \\[3pt] \fbox{$y \le y_0$ and (81)}\quad &\le (1-\tau)^2p^2n_2 + 20q^3n_2 \mathbb{I} + 13 \sqrt{\lambda n_2} + \frac{n_2}{n_1 - 1}. \\[3pt] \fbox{$n_1 \ge n_2$}\quad &\le (1-\tau)^2p^2n_2 + 20q^3n_2 \mathbb{I} + 14 \sqrt{\lambda n_2}. \end{align*}
Using again (17) as well as inequalities
![]() $\mu_X \le n_2$
and
$\mu_X \le n_2$
and
![]() $\lambda \le n_2$
, we infer that
$\lambda \le n_2$
, we infer that
which, together with the above upper bound on
![]() $\mu_X$
, implies (82). This completes the proof of Lemma 14.
$\mu_X$
, implies (82). This completes the proof of Lemma 14.
5.3. Proof of Lemma 9
Recall the definitions of
![]() $\tau=\tau(t)$
in (24),
$\tau=\tau(t)$
in (24),
![]() $\delta(t)$
in (43), and
$\delta(t)$
in (43), and
![]() $\lambda(t)$
in (44). In this proof we utilise some technical bounds on
$\lambda(t)$
in (44). In this proof we utilise some technical bounds on
![]() $\tau\,{:\!=}\,\tau(t)$
and
$\tau\,{:\!=}\,\tau(t)$
and
![]() $\gamma_t$
proved in Section 8 (see Proposition 23). In particular, the bound (146) on
$\gamma_t$
proved in Section 8 (see Proposition 23). In particular, the bound (146) on
![]() $\gamma_t$
, together with (45), implies that
$\gamma_t$
, together with (45), implies that
(We do not even need to remember what
![]() $\gamma_t$
is to see that.)
$\gamma_t$
is to see that.)
We now derive an upper bound on
![]() $\lambda(t)$
. By (147), with a huge margin,
$\lambda(t)$
. By (147), with a huge margin,
On the other hand, for
![]() $p > 0.49$
, squaring and rearranging the inequality (145) implies
$p > 0.49$
, squaring and rearranging the inequality (145) implies
Summing up, for any p,
Without loss of generality, we assume that
![]() $i = 1$
. Let
$i = 1$
. Let
![]() ${\mathcal{F}}_t$
be the family of graphs H satisfying, for any distinct
${\mathcal{F}}_t$
be the family of graphs H satisfying, for any distinct
![]() $u_1, v_1 \in V_1$
,
$u_1, v_1 \in V_1$
,
 \begin{equation} |d_1 - \operatorname{cod}_H(u_1, v_1) - pqn_2| \le 20\hat p n_{2} \left(\hat p^2\mathbb{I} + \frac{1}{\hat n} + \sqrt{\frac{(C+3)\lambda(t)}{n_{2}}} + \frac{(C+3)\lambda(t)}{20\hat pn_2}\right).\end{equation}
\begin{equation} |d_1 - \operatorname{cod}_H(u_1, v_1) - pqn_2| \le 20\hat p n_{2} \left(\hat p^2\mathbb{I} + \frac{1}{\hat n} + \sqrt{\frac{(C+3)\lambda(t)}{n_{2}}} + \frac{(C+3)\lambda(t)}{20\hat pn_2}\right).\end{equation}
Lemma 11 with
![]() $\lambda = (C+3)\lambda(t)$
and a union bound over the
$\lambda = (C+3)\lambda(t)$
and a union bound over the
![]() $O(N^2)$
choices of
$O(N^2)$
choices of
![]() $u_1, v_1$
imply
$u_1, v_1$
imply
Writing
![]() $\delta_* = \sqrt{\frac{(C+3)\lambda(t)}{\tau p q \hat n}}$
and noting that (84) implies
$\delta_* = \sqrt{\frac{(C+3)\lambda(t)}{\tau p q \hat n}}$
and noting that (84) implies
![]() $\delta_* \le 1/2$
, the sum of the last three terms in the parentheses in (85) is at most
$\delta_* \le 1/2$
, the sum of the last three terms in the parentheses in (85) is at most
In addition, the factor in front of the brackets is at most
![]() $40pq n_2$
. Thus, (85) implies
$40pq n_2$
. Thus, (85) implies
We claim that for
![]() $t = 0, \dots, t_0 - 1$
$t = 0, \dots, t_0 - 1$
and deferring its proof to the end we first show how (86) and (88) imply the lemma.
Inequalities (86) and (88) imply
 \begin{align} \notag \mathbb{P}\left(\max_{u_1 \ne v_1} \left|\frac{\theta_t(u_1,v_1)}{\tau pqn_2 } - 1\right| \ge \delta(t)\right) &\le 2N^2e^{-(C+3)\lambda(t)} + \mathbb{P}\left(\mathbb{R} \notin {\mathcal{F}}_t\right) \\[3pt] &= O(N^{-(C+1)}e^{-2\lambda(t))}).\end{align}
\begin{align} \notag \mathbb{P}\left(\max_{u_1 \ne v_1} \left|\frac{\theta_t(u_1,v_1)}{\tau pqn_2 } - 1\right| \ge \delta(t)\right) &\le 2N^2e^{-(C+3)\lambda(t)} + \mathbb{P}\left(\mathbb{R} \notin {\mathcal{F}}_t\right) \\[3pt] &= O(N^{-(C+1)}e^{-2\lambda(t))}).\end{align}
Consider random variables, for
![]() $t = 0, \dots, t_0 - 1$
,
$t = 0, \dots, t_0 - 1$
,
Using Markov’s inequality and (89), we infer that
which, taking the union bound over the O(N) choices of t, implies that (47) holds with the desired probability, completing the proof of lemma.
Returning to the proof of (88), fix
![]() $t < t_0, H \in {\mathcal{F}}_t$
and two distinct vertices
$t < t_0, H \in {\mathcal{F}}_t$
and two distinct vertices
![]() $u_1,v_1\in V_1$
. Conditioning on
$u_1,v_1\in V_1$
. Conditioning on
![]() $\mathbb{R} = H$
, note that, recalling (46), random variable
$\mathbb{R} = H$
, note that, recalling (46), random variable
![]() $X \,{:\!=}\, \theta_t(u_1,v_1) = |\Gamma_{H \setminus \mathbb{R}(t)}(u_i)\cap\Gamma_{K\setminus H}(v_i)|$
counts elements in the intersection of two subsets of E(H): a fixed set
$X \,{:\!=}\, \theta_t(u_1,v_1) = |\Gamma_{H \setminus \mathbb{R}(t)}(u_i)\cap\Gamma_{K\setminus H}(v_i)|$
counts elements in the intersection of two subsets of E(H): a fixed set
![]() $ \left\{ (u_i,w)\ \, :\ \, w \in \Gamma_H(u_i) \cap \Gamma_{K \setminus H}(v_i) \right\}$
of size
$ \left\{ (u_i,w)\ \, :\ \, w \in \Gamma_H(u_i) \cap \Gamma_{K \setminus H}(v_i) \right\}$
of size
![]() $d_1 - \operatorname{cod}_H(u_1, v_1)$
and a random set
$d_1 - \operatorname{cod}_H(u_1, v_1)$
and a random set
![]() $H \setminus \mathbb{R}(t)$
of size
$H \setminus \mathbb{R}(t)$
of size
![]() $M - t$
. Hence
$M - t$
. Hence
![]() $X \sim \operatorname{Hyp}(M, d_1 - \operatorname{cod}_H(u_1,v_1), M -t)$
has the hypergeometric distribution with expectation
$X \sim \operatorname{Hyp}(M, d_1 - \operatorname{cod}_H(u_1,v_1), M -t)$
has the hypergeometric distribution with expectation
Note that by (87),
Let
![]() $\lambda^* \,{:\!=}\, (3C + 9)\lambda(t)$
. From (90), (83), and (84) it follows that
$\lambda^* \,{:\!=}\, (3C + 9)\lambda(t)$
. From (90), (83), and (84) it follows that
Note that (43) implies
 \begin{equation*} \begin{split} \mathbb{P}_H\left({|X - \mu_X| \ge \sqrt{\mu_X \lambda^*} }\right) &\le 2 \exp \left\{ - \frac{\lambda^*}{2\left(1 + \frac{1}{3}\sqrt{\lambda^*/\mu_X } \right)} \right\} \\[3pt] &\le 2 e^{-3\lambda^*/8}\le 2 e^{-\lambda^*/3} = 2e^{-(C + 3)\lambda(t)}. \end{split}\end{equation*}
\begin{equation*} \begin{split} \mathbb{P}_H\left({|X - \mu_X| \ge \sqrt{\mu_X \lambda^*} }\right) &\le 2 \exp \left\{ - \frac{\lambda^*}{2\left(1 + \frac{1}{3}\sqrt{\lambda^*/\mu_X } \right)} \right\} \\[3pt] &\le 2 e^{-3\lambda^*/8}\le 2 e^{-\lambda^*/3} = 2e^{-(C + 3)\lambda(t)}. \end{split}\end{equation*}
Thus, with probability
![]() $1 - 2e^{-(C+3)\lambda(t)}$
$1 - 2e^{-(C+3)\lambda(t)}$
 \begin{align*} |\theta_t(u_1,v_1) - \tau p q n_2| &\le |X - \mu_X| + |\mu_X - \tau p q n_2| \\[4pt] &\le \sqrt{\mu_X \lambda^*} + |\mu_X - \tau p q n_2| \\[4pt] \fbox{(90), (92)}\quad &\le \sqrt{\left( 1 + \delta(t)/3 \right)\tau p q n_2 \cdot \delta^2(t)\tau p q n_2 / 10} + (\delta(t)/3) \tau p q n_2\\[4pt] \fbox{(83)}\quad &\le \delta(t)\tau pqn_2 (\sqrt{(1 + 1/27)/10} + 1/3) \\[4pt] &\le \delta(t)\tau pqn_2.\end{align*}
\begin{align*} |\theta_t(u_1,v_1) - \tau p q n_2| &\le |X - \mu_X| + |\mu_X - \tau p q n_2| \\[4pt] &\le \sqrt{\mu_X \lambda^*} + |\mu_X - \tau p q n_2| \\[4pt] \fbox{(90), (92)}\quad &\le \sqrt{\left( 1 + \delta(t)/3 \right)\tau p q n_2 \cdot \delta^2(t)\tau p q n_2 / 10} + (\delta(t)/3) \tau p q n_2\\[4pt] \fbox{(83)}\quad &\le \delta(t)\tau pqn_2 (\sqrt{(1 + 1/27)/10} + 1/3) \\[4pt] &\le \delta(t)\tau pqn_2.\end{align*}
Hence, applying also the union bound over all
![]() $n_1^2 \le N^2$
choices of
$n_1^2 \le N^2$
choices of
![]() $u_1,v_1$
, we infer (88).
$u_1,v_1$
, we infer (88).
6. Alternating cycles in regularly 2-edge-coloured jumbled graphs
The ultimate goal of this section is to prove Lemma 10. While for
![]() $p\le0.49$
the proof follows relatively easily from Lemma 13 by a standard switching technique, the case
$p\le0.49$
the proof follows relatively easily from Lemma 13 by a standard switching technique, the case
![]() $p > 0.49$
is much more involved. To cope with it, we first study the existence of alternating walks and cycles in a class of 2-edge-coloured pseudorandom graphs.
$p > 0.49$
is much more involved. To cope with it, we first study the existence of alternating walks and cycles in a class of 2-edge-coloured pseudorandom graphs.
In Subsection 6.1, we define an appropriate notion of pseudorandom bipartite graphs (jumbledness), inspired by a similar notion introduced implicitly by Thomason in [Reference Thomason14]. We show that for
![]() $p > 0.49$
and suitably chosen parameters, the random graph
$p > 0.49$
and suitably chosen parameters, the random graph
![]() $K\setminus \mathbb{R}(t)$
is jumbled with high probability (Lemma 17).
$K\setminus \mathbb{R}(t)$
is jumbled with high probability (Lemma 17).
The next two subsections are devoted to 2-edge-coloured jumbled graphs which are almost regular in each colour. After proving a technical Lemma 18 in Subsection 6.2, in Subsection 6.3 we show the existence of alternating short walks between any two vertices of almost regular 2-edge-coloured jumbled graphs (Lemma 19).
An immediate consequence of Lemma 19 is Lemma 20, which states that every edge belongs to an alternating short cycle. The latter result together with a standard switching argument (Proposition 4) will be used in the proof of Lemma 10 for
![]() $p > 0.49$
. That proof, for both cases
$p > 0.49$
. That proof, for both cases
![]() $p\le 0.49$
and
$p\le 0.49$
and
![]() $p > 0.49$
, is presented in Subsection 6.4.
$p > 0.49$
, is presented in Subsection 6.4.
6.1. Jumbled graphs
Let
![]() $K\,{:\!=}\, {K_{n_1,n_2}}$
be the complete bipartite graph with partition classes
$K\,{:\!=}\, {K_{n_1,n_2}}$
be the complete bipartite graph with partition classes
![]() $V_1$
and
$V_1$
and
![]() $V_2$
, where
$V_2$
, where
![]() $|V_i| = n_i$
. Given a bipartite graph
$|V_i| = n_i$
. Given a bipartite graph
![]() $F \subseteq K$
and two subsets
$F \subseteq K$
and two subsets
![]() $A \subseteq V_1$
,
$A \subseteq V_1$
,
![]() $B \subseteq V_2$
, denote by
$B \subseteq V_2$
, denote by
![]() $e_F(A,B)$
the number of edges of F between A and B. Recall that
$e_F(A,B)$
the number of edges of F between A and B. Recall that
![]() $N = n_1n_2$
and
$N = n_1n_2$
and
![]() $M = pN$
.
$M = pN$
.
Given real numbers
![]() $\pi,\delta\in(0,1)$
, we say that a graph
$\pi,\delta\in(0,1)$
, we say that a graph
![]() $F \subseteq K$
is
$F \subseteq K$
is
![]() $(\pi, \delta)$
-jumbled if for every
$(\pi, \delta)$
-jumbled if for every
![]() $A \subseteq V_1$
and
$A \subseteq V_1$
and
![]() $B \subseteq V_2$
$B \subseteq V_2$
The following result of Thomason [14, Theorem 2], which quantifies a variant of jumbledness in terms of the degrees and co-degrees of a graph, will turn out to be crucial for us.
Theorem 15 ([Reference Thomason14]). Let
![]() $F \subseteq K$
be a bipartite graph and
$F \subseteq K$
be a bipartite graph and
![]() $\rho \in (0,1)$
and
$\rho \in (0,1)$
and
![]() $\mu \ge 0$
be given. If
$\mu \ge 0$
be given. If
then, for all
![]() $A \subseteq V_1$
and
$A \subseteq V_1$
and
![]() $B \subseteq V_2$
,
$B \subseteq V_2$
,
Remark 16. The proof in [Reference Thomason14] is given only in the case
![]() $n_1 = n_2 = n$
. However, it carries over in this more general setting, as in [Reference Thomason14] n always refers to
$n_1 = n_2 = n$
. However, it carries over in this more general setting, as in [Reference Thomason14] n always refers to
![]() $|V_2|$
.
$|V_2|$
.
Recall that
![]() $K\setminus \mathbb{R}(t)$
has precisely
$K\setminus \mathbb{R}(t)$
has precisely
![]() $N - t = N - (1-\tau)M = (\tau p + q)N$
edges. The following technical result states that, under the conditions of Lemma 6, with high probability,
$N - t = N - (1-\tau)M = (\tau p + q)N$
edges. The following technical result states that, under the conditions of Lemma 6, with high probability,
![]() $K\setminus \mathbb{R}(t)$
is jumbled for parameters which are tailored for Lemma 20.
$K\setminus \mathbb{R}(t)$
is jumbled for parameters which are tailored for Lemma 20.
Lemma 17. Let
![]() $\alpha = \min \{ \tau p, q \}$
and
$\alpha = \min \{ \tau p, q \}$
and
![]() $\pi \,{:\!=}\, \tau p + q$
. For every constant
$\pi \,{:\!=}\, \tau p + q$
. For every constant
![]() $C > 0$
and
$C > 0$
and
![]() $p > 0.49$
, if assumptions (27) and (28) hold, then, with probability
$p > 0.49$
, if assumptions (27) and (28) hold, then, with probability
![]() $1 - O(N^{-C })$
, for all
$1 - O(N^{-C })$
, for all
![]() $t < t_0$
$t < t_0$
and for any
![]() $e \in K \setminus \mathbb{R}(t)$
$e \in K \setminus \mathbb{R}(t)$
Proof. W.l.o.g., we assume that
![]() $n_1\ge n_2$
. Let
$n_1\ge n_2$
. Let
![]() $\lambda \,{:\!=}\, 3(C + 4)\log N$
, and
$\lambda \,{:\!=}\, 3(C + 4)\log N$
, and
The plan is to show that
and that with the correct probability,
![]() $K \setminus \mathbb{R}(t)$
and
$K \setminus \mathbb{R}(t)$
and
![]() $K \setminus \mathbb{R}(t) \cup \{e\}$
are in fact
$K \setminus \mathbb{R}(t) \cup \{e\}$
are in fact
![]() $(\pi, \delta)$
-jumbled.
$(\pi, \delta)$
-jumbled.
We start with the proof of (95). Notice that, by (28),
Since
![]() $\hat p > \tfrac{49}{51}q$
, condition (27) implies that
$\hat p > \tfrac{49}{51}q$
, condition (27) implies that
![]() $1/320 \ge q^{1/2} \mathbb{I}$
. After multiplying both sides by 10q, we get
$1/320 \ge q^{1/2} \mathbb{I}$
. After multiplying both sides by 10q, we get
which together with the second inequality in (96) implies
On the other hand, using
![]() $p > 0.49$
,
$p > 0.49$
,
![]() $\tau \ge \tau_0$
and the definition (25) of
$\tau \ge \tau_0$
and the definition (25) of
![]() $\tau_0$
, we infer that
$\tau_0$
, we infer that
 \begin{align*} \frac{\tau p}{16} &\ge \frac{0.49 \cdot \tau_0}{16} = \frac{0.49 \cdot 700\cdot (3(C + 4))^{1/4}}{16} \left( \left(\frac{\log N}{n_2}\right)^{1/4} + q^{3/2} \mathbb{I}\right) \\ &\ge 20 \left( \lambda/{n_2} \right)^{1/4} + 10q^{3/2} \mathbb{I} = \delta.\end{align*}
\begin{align*} \frac{\tau p}{16} &\ge \frac{0.49 \cdot \tau_0}{16} = \frac{0.49 \cdot 700\cdot (3(C + 4))^{1/4}}{16} \left( \left(\frac{\log N}{n_2}\right)^{1/4} + q^{3/2} \mathbb{I}\right) \\ &\ge 20 \left( \lambda/{n_2} \right)^{1/4} + 10q^{3/2} \mathbb{I} = \delta.\end{align*}
Hence
![]() $\alpha/16 = \min \left\{ \tau p/16, q/16 \right\} \ge \delta$
, implying (95).
$\alpha/16 = \min \left\{ \tau p/16, q/16 \right\} \ge \delta$
, implying (95).
We now prove the jumbledness, first focusing on
![]() $K \setminus \mathbb{R}(t)$
and then indicating the tiny change in calculation for
$K \setminus \mathbb{R}(t)$
and then indicating the tiny change in calculation for
![]() $K \setminus (\mathbb{R}(t) \cup \{e\})$
. Fixing an arbitrary
$K \setminus (\mathbb{R}(t) \cup \{e\})$
. Fixing an arbitrary
![]() $t < t_0$
, we will first show that, with probability
$t < t_0$
, we will first show that, with probability
![]() $1 - O(N^{-C -1})$
, conditions (93) of Theorem 15 are satisfied by
$1 - O(N^{-C -1})$
, conditions (93) of Theorem 15 are satisfied by
![]() $F = K \setminus \mathbb{R}(t)$
and
$F = K \setminus \mathbb{R}(t)$
and
![]() $F = K \setminus (\mathbb{R}(t) \cup \{e\})$
for suitably chosen
$F = K \setminus (\mathbb{R}(t) \cup \{e\})$
for suitably chosen
![]() $\rho$
and
$\rho$
and
![]() $\mu$
. Then we will apply Theorem 15 to deduce that
$\mu$
. Then we will apply Theorem 15 to deduce that
![]() $K \setminus \mathbb{R}(t)$
is
$K \setminus \mathbb{R}(t)$
is
![]() $(\pi, \delta)$
-jumbled. Lemma 17 will follow by applying the union bound over all (at most
$(\pi, \delta)$
-jumbled. Lemma 17 will follow by applying the union bound over all (at most
![]() $t_0\le M\le N$
) choices of t.
$t_0\le M\le N$
) choices of t.
By (147),
![]() $\lambda \le \tau_0 p \hat n$
with a big room to spare. Note that
$\lambda \le \tau_0 p \hat n$
with a big room to spare. Note that
which implies that
![]() $|\deg_{K \setminus \mathbb{R}(t)}(v) - \pi n_2|=|\deg_{\mathbb{R}(t)}(v) - (1-\tau)d_1|$
. Hence, by Lemma 13, with probability
$|\deg_{K \setminus \mathbb{R}(t)}(v) - \pi n_2|=|\deg_{\mathbb{R}(t)}(v) - (1-\tau)d_1|$
. Hence, by Lemma 13, with probability
![]() $1 - O(N^2e^{-\lambda})$
,
$1 - O(N^2e^{-\lambda})$
,
Moreover, recalling that
![]() $n_1\ge n_2$
and, again using (97), Lemma 14 implies that, with probability
$n_1\ge n_2$
and, again using (97), Lemma 14 implies that, with probability
![]() $1 - O(N^3e^{-\lambda/3})$
,
$1 - O(N^3e^{-\lambda/3})$
,
Since
![]() $\lambda = 3(C + 4)\log N$
, the intersection of events (98) and (99) holds with probability
$\lambda = 3(C + 4)\log N$
, the intersection of events (98) and (99) holds with probability
![]() $1 - O(N^3e^{-\lambda/3}) = 1 - O(N^{-C - 1})$
.
$1 - O(N^3e^{-\lambda/3}) = 1 - O(N^{-C - 1})$
.
Note that for distinct
![]() $u, v \in V_1$
, by (56) and (98)
$u, v \in V_1$
, by (56) and (98)
which, by (99), implies that
Set
and note that by the inequality
![]() $\pi\le1$
and by (96), we have
$\pi\le1$
and by (96), we have
![]() $0 < \rho < 1$
. Furthermore,
$0 < \rho < 1$
. Furthermore,
![]() $\rho^2\ge\pi^2-6\sqrt{\lambda/ n_2}$
. Hence, (98) and (101) imply the assumptions (93) for
$\rho^2\ge\pi^2-6\sqrt{\lambda/ n_2}$
. Hence, (98) and (101) imply the assumptions (93) for
![]() $F = K \setminus \mathbb{R}(t)$
with the above
$F = K \setminus \mathbb{R}(t)$
with the above
![]() $\rho$
and
$\rho$
and
![]() $\mu$
. Consequently, by Theorem 15 (using
$\mu$
. Consequently, by Theorem 15 (using
![]() $a \le n_1$
and
$a \le n_1$
and
![]() $\rho\le\pi$
),
$\rho\le\pi$
),
Further, since
![]() $N=n_1n_2$
,
$N=n_1n_2$
,
![]() $n_1\ge n_2 \ge b$
and
$n_1\ge n_2 \ge b$
and
![]() $a,\lambda \ge 1$
, we have, with a big margin,
$a,\lambda \ge 1$
, we have, with a big margin,
It follows, applying the inequality
![]() $\sqrt{x + y} \le \sqrt x+ \sqrt y$
as well as (94), that
$\sqrt{x + y} \le \sqrt x+ \sqrt y$
as well as (94), that
Moreover, note that using
![]() $ab \le n_1n_2 = N$
and the first inequality in (96),
$ab \le n_1n_2 = N$
and the first inequality in (96),
meaning that
![]() $K \setminus \mathbb{R}(t)$
is
$K \setminus \mathbb{R}(t)$
is
![]() $(\pi, \delta)$
-jumbled.
$(\pi, \delta)$
-jumbled.
If above we replace
![]() $K \setminus \mathbb{R}(t)$
by
$K \setminus \mathbb{R}(t)$
by
![]() $K \setminus (\mathbb{R}(t) \cup \left\{ e \right\})$
, the upper bound in (98) and the bound in (101) still hold trivially, while the lower bound
$K \setminus (\mathbb{R}(t) \cup \left\{ e \right\})$
, the upper bound in (98) and the bound in (101) still hold trivially, while the lower bound
![]() $\pi n_2 - 3 \sqrt{\lambda n_2}$
in (98) remains correct, since
$\pi n_2 - 3 \sqrt{\lambda n_2}$
in (98) remains correct, since
![]() $\deg_{K \setminus (\mathbb{R}(t) \cup \{e\})}(v) \ge \deg_{K \setminus \mathbb{R}(t)}(v) - 1$
and we have plenty of room in (98). Hence Theorem 15 applies with the same
$\deg_{K \setminus (\mathbb{R}(t) \cup \{e\})}(v) \ge \deg_{K \setminus \mathbb{R}(t)}(v) - 1$
and we have plenty of room in (98). Hence Theorem 15 applies with the same
![]() $\rho$
and
$\rho$
and
![]() $\mu$
, implying that
$\mu$
, implying that
![]() $K \setminus (\mathbb{R}(t) \cup \{e\})$
is also
$K \setminus (\mathbb{R}(t) \cup \{e\})$
is also
![]() $(\pi, \delta)$
-jumbled.
$(\pi, \delta)$
-jumbled.
6.2. A technical inequality for blue-red graphs
We find it convenient to introduce relative counterparts of basic graph quantities. Below
![]() $i\in\{1,2\}$
. As before, let
$i\in\{1,2\}$
. As before, let
![]() $K\,{:\!=}\, {K_{n_1,n_2}}$
be the complete bipartite graph with partition classes
$K\,{:\!=}\, {K_{n_1,n_2}}$
be the complete bipartite graph with partition classes
![]() $V_1$
and
$V_1$
and
![]() $V_2$
, where
$V_2$
, where
![]() $|V_i| = n_i$
. The relative size of a subset of vertices
$|V_i| = n_i$
. The relative size of a subset of vertices
![]() $S\subseteq V_i$
is
$S\subseteq V_i$
is
Further, for
![]() $X\subseteq V_1$
and
$X\subseteq V_1$
and
![]() $Y\subseteq V_{2}$
and a subgraph
$Y\subseteq V_{2}$
and a subgraph
![]() $F \subseteq K$
, we define the relative edge count
$F \subseteq K$
, we define the relative edge count
Moreover, for
![]() $v\in V_i$
and
$v\in V_i$
and
![]() $Y\subseteq V_{3-i}$
, we define the relative degree
$Y\subseteq V_{3-i}$
, we define the relative degree
If
![]() $Y = V_{3-i}$
, we shorten
$Y = V_{3-i}$
, we shorten
![]() $d_F(v,Y)$
to
$d_F(v,Y)$
to
![]() $d_F(v)$
.
$d_F(v)$
.
In this notation, a graph F is
![]() $(\pi,\delta)$
-jumbled if for every
$(\pi,\delta)$
-jumbled if for every
![]() $X \subseteq V_1$
,
$X \subseteq V_1$
,
![]() $Y \subseteq V_2$
$Y \subseteq V_2$
Now, let the edges of a graph F be 2-coloured by blue and red, and let B and R be the subgraphs of F induced by the edges of colour, resp., blue and red. We then call
![]() $F = B \cup R$
a blue-red graph. Note that
$F = B \cup R$
a blue-red graph. Note that
We say that a blue-red graph F is
![]() $(r,b,\delta)$
-regular, if
$(r,b,\delta)$
-regular, if
If F is at the same time
![]() $(r+b, \delta)$
-jumbled and
$(r+b, \delta)$
-jumbled and
![]() $(r,b,\delta)$
-regular, as in the technical lemma below, we will sometimes loosely refer to such a graph as regularly jumbled.
$(r,b,\delta)$
-regular, as in the technical lemma below, we will sometimes loosely refer to such a graph as regularly jumbled.
Finally, for every
![]() $S\subseteq V_i$
,
$S\subseteq V_i$
,
![]() $i = 1,2$
, set
$i = 1,2$
, set
![]() $\overline{S}\,{:\!=}\,V_i\setminus S$
.
$\overline{S}\,{:\!=}\,V_i\setminus S$
.
Lemma 18. Let
![]() $r, b \in (0,1)$
be real numbers and define
$r, b \in (0,1)$
be real numbers and define
![]() $\alpha \,{:\!=}\, \min \{r,b\}$
. Let
$\alpha \,{:\!=}\, \min \{r,b\}$
. Let
![]() $\nu<\alpha/16$
and
$\nu<\alpha/16$
and
![]() $\delta \leq \alpha/16$
be positive reals and let
$\delta \leq \alpha/16$
be positive reals and let
![]() $F \subseteq K$
be a
$F \subseteq K$
be a
![]() $(r, b, \delta)$
-regular,
$(r, b, \delta)$
-regular,
![]() $(b + r, \delta)$
-jumbled bipartite blue-red graph. If sets
$(b + r, \delta)$
-jumbled bipartite blue-red graph. If sets
![]() $X \subseteq V_i$
,
$X \subseteq V_i$
,
![]() $Y \subseteq V_{3-i}$
satisfy
$Y \subseteq V_{3-i}$
satisfy
and
then
Proof. Since
from (105) we have
and, similarly,
By summing (106), (109) and (110), we infer that
On the other hand, by (105),
and
Hence, by (104) with
![]() $\pi = b + r$
,
$\pi = b + r$
,
 \begin{align*} \varepsilon_F(X,Y) + \varepsilon_F(X,\overline{Y}) + \varepsilon_F(\overline{X},Y) &\geq (b + r - 2\delta) (s(X) + s(Y)) - \varepsilon_F(X, Y) \\[3pt] & \ge (b + r - 2\delta) (s(X) + s(Y)) - (b + r)s(X)s(Y) - \delta \sqrt{s(X)s(Y)}. \end{align*}
\begin{align*} \varepsilon_F(X,Y) + \varepsilon_F(X,\overline{Y}) + \varepsilon_F(\overline{X},Y) &\geq (b + r - 2\delta) (s(X) + s(Y)) - \varepsilon_F(X, Y) \\[3pt] & \ge (b + r - 2\delta) (s(X) + s(Y)) - (b + r)s(X)s(Y) - \delta \sqrt{s(X)s(Y)}. \end{align*}
Comparing with (111), we obtain the inequality
Denoting
![]() $x \,{:\!=}\, bs(X)$
and
$x \,{:\!=}\, bs(X)$
and
![]() $y \,{:\!=}\, rs(Y)$
and
$y \,{:\!=}\, rs(Y)$
and
![]() $h \,{:\!=}\, rb/(b + r)$
, this becomes
$h \,{:\!=}\, rb/(b + r)$
, this becomes
Trivially, by the definitions of s(X) and
![]() $\alpha$
, and by our assumptions on
$\alpha$
, and by our assumptions on
![]() $\nu$
and
$\nu$
and
![]() $\delta$
, we have
$\delta$
, we have
Since our goal—inequality (108)—now reads as
to complete the proof it is enough to assume, without loss of generality, that
![]() $\max \{x, y\} = y$
and show, equivalently, that
$\max \{x, y\} = y$
and show, equivalently, that
By (107) we have
![]() $x = \min\{x,y\} \le h$
. Note that
$x = \min\{x,y\} \le h$
. Note that
![]() $x = h$
cannot hold, since then the LHS of (112) would equal h, contradicting the fact that
$x = h$
cannot hold, since then the LHS of (112) would equal h, contradicting the fact that
![]() $\psi < h$
. Hence, we have
$\psi < h$
. Hence, we have
![]() $x < h$
, which, together with
$x < h$
, which, together with
![]() $\psi < h$
and (112), implies that
$\psi < h$
and (112), implies that
and (113) is proved.
6.3. Alternating walks and cycles
A cycle in a blue-red bipartite graph is said to be alternating if it is a union of a red matching and a blue matching, that is, every other edge is blue and the remaining edges are red. The ultimate goal of this subsection is to show that for every edge in a regularly jumbled blue-red bipartite graph, there is an alternating cycle of bounded length containing that edge. We are going to achieve it by utilising walks.
Given
![]() $x,y\in V_1\cup V_2$
, an alternating walk from x to y in a blue-red graph F is a sequence of (not necessarily distinct) vertices
$x,y\in V_1\cup V_2$
, an alternating walk from x to y in a blue-red graph F is a sequence of (not necessarily distinct) vertices
![]() $(v_1 = x,\dots,v_s = y)$
such that for each
$(v_1 = x,\dots,v_s = y)$
such that for each
![]() $i = 1,\dots,s-1$
,
$i = 1,\dots,s-1$
,
![]() $v_iv_{i+1}\in F$
, every other edge is blue and the remaining edges are red. There is no restriction on the colour of the initial edge
$v_iv_{i+1}\in F$
, every other edge is blue and the remaining edges are red. There is no restriction on the colour of the initial edge
![]() $v_1v_2$
. The length of a walk is defined as the number of edges, or
$v_1v_2$
. The length of a walk is defined as the number of edges, or
![]() $s-1$
.
$s-1$
.
If the vertices
![]() $v_1,\dots,v_s$
are all distinct, an alternating walk is called an alternating path. Note also that if F is bipartite,
$v_1,\dots,v_s$
are all distinct, an alternating walk is called an alternating path. Note also that if F is bipartite,
![]() $x\in V_1,\;y\in V_2$
, and the edge xy is, say, blue, then every alternating path from x to y which begins (and thus ends) with a red edge together with xy forms an alternating cycle containing xy.
$x\in V_1,\;y\in V_2$
, and the edge xy is, say, blue, then every alternating path from x to y which begins (and thus ends) with a red edge together with xy forms an alternating cycle containing xy.
The first result of this section asserts that regularly jumbled blue-red bipartite graphs have a short alternating walk between any pair of vertices.
Lemma 19. Given
![]() $r, b \in (0,1)$
such that
$r, b \in (0,1)$
such that
![]() $\alpha \,{:\!=}\, \min \{r,b\}$
, let
$\alpha \,{:\!=}\, \min \{r,b\}$
, let
![]() $\delta \in (0,\alpha/16]$
and let
$\delta \in (0,\alpha/16]$
and let
![]() $F \subseteq K$
be an
$F \subseteq K$
be an
![]() $(r, b, \delta)$
-regular,
$(r, b, \delta)$
-regular,
![]() $(b + r, \delta)$
-jumbled blue-red graph. Let
$(b + r, \delta)$
-jumbled blue-red graph. Let
![]() $L = 4\lceil 16/rb \rceil + 1$
. For any
$L = 4\lceil 16/rb \rceil + 1$
. For any
![]() $x\in V_i$
and
$x\in V_i$
and
![]() $y\in V_{3-i}$
there exist at least two alternating walks from x to y of length at most L, one starting with a blue edge and another starting with a red edge.
$y\in V_{3-i}$
there exist at least two alternating walks from x to y of length at most L, one starting with a blue edge and another starting with a red edge.
Proof. For
![]() $w \in V_1 \cup V_2$
and an integer
$w \in V_1 \cup V_2$
and an integer
![]() $k \ge 1$
, define
$k \ge 1$
, define
![]() $R^w_k$
and
$R^w_k$
and
![]() $B^w_k$
as the sets of vertices
$B^w_k$
as the sets of vertices
![]() $v\in V(F)$
such that there is an alternating walk from v to w of length
$v\in V(F)$
such that there is an alternating walk from v to w of length
![]() $\ell \le k$
,
$\ell \le k$
,
![]() $\ell\equiv k \pmod{2}$
, starting with, respectively, a red edge and a blue edge. (Note that these definitions concern walks ending with w.)
$\ell\equiv k \pmod{2}$
, starting with, respectively, a red edge and a blue edge. (Note that these definitions concern walks ending with w.)
Clearly, for every
![]() $k\ge3$
,
$k\ge3$
,
![]() $B^w_{k-2}\subseteq B^w_k$
and
$B^w_{k-2}\subseteq B^w_k$
and
![]() $R^w_{k-2}\subseteq R^w_k$
. Observe also that for any
$R^w_{k-2}\subseteq R^w_k$
. Observe also that for any
![]() $k \geq 2$
, by definition the sets
$k \geq 2$
, by definition the sets
![]() $R^w_{k-1}$
and
$R^w_{k-1}$
and
![]() $B^w_k$
are contained in opposite sides of the bipartition
$B^w_k$
are contained in opposite sides of the bipartition
![]() $(V_1,V_2)$
and, moreover,
$(V_1,V_2)$
and, moreover,
By symmetry,
![]() $B_{k-1}^w$
and
$B_{k-1}^w$
and
![]() $R_k^w$
are contained in opposite sides of
$R_k^w$
are contained in opposite sides of
![]() $(V_1,V_2)$
and
$(V_1,V_2)$
and
Set
![]() $\nu = rb/16$
and note that, since
$\nu = rb/16$
and note that, since
![]() $r,b < 1$
, we have
$r,b < 1$
, we have
![]() $\nu < \alpha/16$
. There exists an integer
$\nu < \alpha/16$
. There exists an integer
![]() $t\leq T \,{:\!=}\, \lceil 1/\nu \rceil = \lceil 16/rb \rceil$
such that
$t\leq T \,{:\!=}\, \lceil 1/\nu \rceil = \lceil 16/rb \rceil$
such that
since otherwise
![]() $1 \ge s({R^w_{2T + 1}}) \ge \sum_{i = 1}^{T} s({R^w_{2i+1} \setminus R^w_{2i-1}}) > \nu T \ge 1$
, which is a contradiction.
$1 \ge s({R^w_{2T + 1}}) \ge \sum_{i = 1}^{T} s({R^w_{2i+1} \setminus R^w_{2i-1}}) > \nu T \ge 1$
, which is a contradiction.
Combining (115) for
![]() $k = 2t + 1$
and (117), we get
$k = 2t + 1$
and (117), we get
Set
![]() $X = R^w_{2t + 1}, Y = B^w_{2t}$
, for convenience. We claim that
$X = R^w_{2t + 1}, Y = B^w_{2t}$
, for convenience. We claim that
Assuming the contrary, we have
which, together with (118), constitute the assumptions of Lemma 18. Applying it, we get
where the second inequality follows by our assumption
![]() $\delta \le \alpha/16$
.
$\delta \le \alpha/16$
.
On the other hand, since X contains the set
![]() $R^w_1 = \Gamma_R(w)$
of red neighbours of w, by
$R^w_1 = \Gamma_R(w)$
of red neighbours of w, by
![]() $(r, b, \delta)$
-regularity of F we have
$(r, b, \delta)$
-regularity of F we have
![]() $s(X) \ge r - \delta \ge \frac{15}{16}r$
, a contradiction with (120). Hence, we have shown (119). Since
$s(X) \ge r - \delta \ge \frac{15}{16}r$
, a contradiction with (120). Hence, we have shown (119). Since
![]() $X = R^w_{2t + 1}\subseteq R^w_{2T + 1}$
and
$X = R^w_{2t + 1}\subseteq R^w_{2T + 1}$
and
![]() $Y = B^w_{2t}\subseteq B^w_{2T}$
, we also have
$Y = B^w_{2t}\subseteq B^w_{2T}$
, we also have
Since we chose w arbitrarily, (121) holds for
![]() $w \in \left\{ x,y \right\}$
, implying
$w \in \left\{ x,y \right\}$
, implying
Let us assume, without loss of generality, that
![]() $x \in V_1$
and
$x \in V_1$
and
![]() $y \in V_2$
. Then,
$y \in V_2$
. Then,
![]() $B^x_{2T}, R^y_{2T + 1}\subseteq V_1$
and, in particular, for every vertex
$B^x_{2T}, R^y_{2T + 1}\subseteq V_1$
and, in particular, for every vertex
![]() $v\in B^x_{2T}$
there is a walk (of even length at most 2T) from v to x starting with a blue and thus ending with a red edge. By (122),
$v\in B^x_{2T}$
there is a walk (of even length at most 2T) from v to x starting with a blue and thus ending with a red edge. By (122),
![]() $s({B^x_{2T}}) + s({R^y_{2T + 1}}) > 1$
, so there exists
$s({B^x_{2T}}) + s({R^y_{2T + 1}}) > 1$
, so there exists
![]() $v \in B^x_{2T} \cap R^y_{2T + 1}$
. This means that there is an alternating walk of length at most
$v \in B^x_{2T} \cap R^y_{2T + 1}$
. This means that there is an alternating walk of length at most
![]() $2T + (2T + 1)= 4\lceil 16/rb \rceil + 1 = L$
from x to y (through v) that starts with a red edge.
$2T + (2T + 1)= 4\lceil 16/rb \rceil + 1 = L$
from x to y (through v) that starts with a red edge.
By an analogous reasoning with the roles of the colours red and blue swapped,
![]() $R^x_{2T}\cap B^y_{2T + 1}\neq \emptyset$
, and thus there is an alternating walk of length at most
$R^x_{2T}\cap B^y_{2T + 1}\neq \emptyset$
, and thus there is an alternating walk of length at most
![]() $2T + (2T + 1) = L $
from x to y which starts with a blue edge.
$2T + (2T + 1) = L $
from x to y which starts with a blue edge.
The following result is an easy consequence of Lemma 19.
Lemma 20. Let
![]() $r, b \in (0,1)$
,
$r, b \in (0,1)$
,
![]() $\alpha \,{:\!=}\, \min \{r,b\}$
, and
$\alpha \,{:\!=}\, \min \{r,b\}$
, and
![]() $\delta\in (0,\alpha/16]$
. If
$\delta\in (0,\alpha/16]$
. If
![]() $F \subseteq K$
is an
$F \subseteq K$
is an
![]() $(r, b, \delta)$
-regular,
$(r, b, \delta)$
-regular,
![]() $(r + b, \delta)$
-jumbled blue-red bipartite graph, then every edge of F belongs to an alternating cycle of length at most 2D, where
$(r + b, \delta)$
-jumbled blue-red bipartite graph, then every edge of F belongs to an alternating cycle of length at most 2D, where
![]() $D = 2\lceil 16/rb \rceil + 1$
.
$D = 2\lceil 16/rb \rceil + 1$
.
Proof. Let xy be an edge with
![]() $x\in V_1$
,
$x\in V_1$
,
![]() $y\in V_2$
. Without loss of generality, we assume that xy is blue. Then, by Lemma 19, there exists at least one alternating walk from x to y of length at most
$y\in V_2$
. Without loss of generality, we assume that xy is blue. Then, by Lemma 19, there exists at least one alternating walk from x to y of length at most
![]() $4\lceil 16/rb \rceil + 1 = 2D - 1$
starting with a red edge. Consider a shortest such walk W. We claim W is a path. Indeed, assume that W is not a path and let w be the first repeated vertex on W. If we remove the whole segment of the walk between the first two occurrences of w, what remains is still an alternating walk from x to y starting with a red edge (since this segment has an even number of edges), contradicting the minimality of W. The path W is not just a single edge xy (since xy is blue) and therefore W and xy form an alternating cycle of length at most 2D.
$4\lceil 16/rb \rceil + 1 = 2D - 1$
starting with a red edge. Consider a shortest such walk W. We claim W is a path. Indeed, assume that W is not a path and let w be the first repeated vertex on W. If we remove the whole segment of the walk between the first two occurrences of w, what remains is still an alternating walk from x to y starting with a red edge (since this segment has an even number of edges), contradicting the minimality of W. The path W is not just a single edge xy (since xy is blue) and therefore W and xy form an alternating cycle of length at most 2D.
6.4. Proof of Lemma 10
Let
![]() $\alpha = \min \left\{ \tau p, q \right\}$
. Applying Lemma 13 with
$\alpha = \min \left\{ \tau p, q \right\}$
. Applying Lemma 13 with
![]() $\lambda = (C + 1)\log N$
(note that the condition
$\lambda = (C + 1)\log N$
(note that the condition
![]() $\lambda \le \tau_0p\hat n$
follows generously from (147)) we have that, with probability
$\lambda \le \tau_0p\hat n$
follows generously from (147)) we have that, with probability
![]() $1 - O(N^{-C})$
, for every
$1 - O(N^{-C})$
, for every
![]() $t < t_0$
$t < t_0$
where
Whenever
![]() $p > 0.49$
, by Lemma 17, with probability
$p > 0.49$
, by Lemma 17, with probability
![]() $1 - O(N^{-C})$
for every
$1 - O(N^{-C})$
for every
![]() $t < t_0$
we have that
$t < t_0$
we have that
Fix
![]() $\mathbb{R}(t) = G$
satisfying (123) and (124). It remains to prove that for every pair of distinct edges
$\mathbb{R}(t) = G$
satisfying (123) and (124). It remains to prove that for every pair of distinct edges
![]() $e, f \in K \setminus G$
$e, f \in K \setminus G$
where
![]() $D = 3$
if
$D = 3$
if
![]() $p \le 0.49$
and
$p \le 0.49$
and
![]() $D = 32/\tau p q + 3$
, if
$D = 32/\tau p q + 3$
, if
![]() $p > 0.49$
. For this, fix distinct edges
$p > 0.49$
. For this, fix distinct edges
![]() $e,f\in K\setminus G$
. Aiming to apply Proposition 4, we need to verify the assumption on the existence of alternating cycles containing a given edge.
$e,f\in K\setminus G$
. Aiming to apply Proposition 4, we need to verify the assumption on the existence of alternating cycles containing a given edge.
Given a graph G′ and
![]() $H\in{\mathcal{R}}_{G'}$
, recall our convention to call the edges of
$H\in{\mathcal{R}}_{G'}$
, recall our convention to call the edges of
![]() $H\setminus G'$
blue and the edges of
$H\setminus G'$
blue and the edges of
![]() $K\setminus H$
red.
$K\setminus H$
red.
Claim 21. Let
![]() $G'\in\{ G,\;G\cup \{e\}\}$
. For every
$G'\in\{ G,\;G\cup \{e\}\}$
. For every
![]() $H \in {\mathcal{R}}_{G'}$
, every edge
$H \in {\mathcal{R}}_{G'}$
, every edge
![]() $g \in K \setminus G'$
is contained in an alternating cycle of length at most 2D.
$g \in K \setminus G'$
is contained in an alternating cycle of length at most 2D.
From Claim 21 we complete the proof of (125) as follows. Since G is admissible, we have
![]() ${\mathcal{R}}_G \ne \emptyset$
. Therefore Proposition 4 implies
${\mathcal{R}}_G \ne \emptyset$
. Therefore Proposition 4 implies
Since (126) implies
![]() ${\mathcal{R}}_{G \cup \left\{ e \right\}} = {\mathcal{R}}_{G, e} \ne \emptyset$
, Proposition 4, applied to graph
${\mathcal{R}}_{G \cup \left\{ e \right\}} = {\mathcal{R}}_{G, e} \ne \emptyset$
, Proposition 4, applied to graph
![]() $G \cup \left\{ e \right\}$
and edge f, implies
$G \cup \left\{ e \right\}$
and edge f, implies
Using (126) and (127), we infer
 \begin{align*} \notag &\frac{1}{\mathbb{P}\left({e \in \mathbb{R}, f \notin \mathbb{R}}\,|\,{\mathbb{R}(t) = G}\right)} = \frac{|{\mathcal{R}}_G|}{|{\mathcal{R}}_{G,e,\neg f}|} = \frac{|{\mathcal{R}}_G|}{|{\mathcal{R}}_{G,e}|} \cdot \frac{|{\mathcal{R}}_{G,e}|}{|{\mathcal{R}}_{G,e,\neg f}|} \\[3pt] &= \left( 1 + \frac{|{\mathcal{R}}_{G,\neg e}|}{|{\mathcal{R}}_{G,e}|} \right) \cdot \left( 1 + \frac{|{\mathcal{R}}_{G,e,f}|}{|{\mathcal{R}}_{G,e,\neg f}|} \right) \\[3pt] &= \left( 1 + \frac{|{\mathcal{R}}_{G,\neg e}|}{|{\mathcal{R}}_{G,e}|} \right) \cdot \left( 1 + \frac{|{\mathcal{R}}_{G \cup\{e\},f}|}{|{\mathcal{R}}_{G \cup \{e\},\neg f}|} \right) \le N^{2D},\end{align*}
\begin{align*} \notag &\frac{1}{\mathbb{P}\left({e \in \mathbb{R}, f \notin \mathbb{R}}\,|\,{\mathbb{R}(t) = G}\right)} = \frac{|{\mathcal{R}}_G|}{|{\mathcal{R}}_{G,e,\neg f}|} = \frac{|{\mathcal{R}}_G|}{|{\mathcal{R}}_{G,e}|} \cdot \frac{|{\mathcal{R}}_{G,e}|}{|{\mathcal{R}}_{G,e,\neg f}|} \\[3pt] &= \left( 1 + \frac{|{\mathcal{R}}_{G,\neg e}|}{|{\mathcal{R}}_{G,e}|} \right) \cdot \left( 1 + \frac{|{\mathcal{R}}_{G,e,f}|}{|{\mathcal{R}}_{G,e,\neg f}|} \right) \\[3pt] &= \left( 1 + \frac{|{\mathcal{R}}_{G,\neg e}|}{|{\mathcal{R}}_{G,e}|} \right) \cdot \left( 1 + \frac{|{\mathcal{R}}_{G \cup\{e\},f}|}{|{\mathcal{R}}_{G \cup \{e\},\neg f}|} \right) \le N^{2D},\end{align*}
which implies (125).
It remains to prove Claim 21. As a preparation, we derive bounds on the vertex degrees in
![]() $G\cup\{e\}$
. Note that the inequality (147) implies
$G\cup\{e\}$
. Note that the inequality (147) implies
and
The latter, together with (123), implies that, for an arbitrary
![]() $e \in K \setminus G$
,
$e \in K \setminus G$
,
We consider two cases with respect to p.
Case
![]() $\mathbf{p \le 0.49}$
. We first claim that for any two vertices
$\mathbf{p \le 0.49}$
. We first claim that for any two vertices
![]() $x_i \in V_i, i = 1,2$
, there is an alternating path
$x_i \in V_i, i = 1,2$
, there is an alternating path
![]() $x_1y_2y_1x_2$
such that
$x_1y_2y_1x_2$
such that
![]() $x_1y_2$
is red (and thus
$x_1y_2$
is red (and thus
![]() $y_1y_2$
is blue and
$y_1y_2$
is blue and
![]() $y_1x_2$
is red). The number of ways to choose a blue edge
$y_1x_2$
is red). The number of ways to choose a blue edge
![]() $y_1y_2$
is
$y_1y_2$
is
We bound the bad choices of
![]() $y_1y_2$
which do not give a desired alternating path. These correspond to the walks (we must permit
$y_1y_2$
which do not give a desired alternating path. These correspond to the walks (we must permit
![]() $y_1 = x_1$
and
$y_1 = x_1$
and
![]() $y_2 = x_2$
)
$y_2 = x_2$
)
![]() $x_1y_2y_1$
and
$x_1y_2y_1$
and
![]() $x_2y_1y_2$
whose first edge in non-red, i.e., it belongs to H, while the second one is blue, i.e., it belongs to
$x_2y_1y_2$
whose first edge in non-red, i.e., it belongs to H, while the second one is blue, i.e., it belongs to
![]() $H\setminus G'$
. By second inequalities in (123) and in (130), there are at most
$H\setminus G'$
. By second inequalities in (123) and in (130), there are at most
![]() $d_1 \cdot\tau(1 + \delta)d_2$
choices of such
$d_1 \cdot\tau(1 + \delta)d_2$
choices of such
![]() $x_1y_2y_1$
and at most
$x_1y_2y_1$
and at most
![]() $d_2 \cdot \tau(1 + \delta)d_1$
choices of such
$d_2 \cdot \tau(1 + \delta)d_1$
choices of such
![]() $x_2y_1y_2$
, so altogether there are at most
$x_2y_1y_2$
, so altogether there are at most
bad choices of
![]() $y_1y_2$
. Thus, noting that
$y_1y_2$
. Thus, noting that
![]() $1/\tau p N \le \delta\le 0.001$
(cf. (129) and (128)), the number of good choices of
$1/\tau p N \le \delta\le 0.001$
(cf. (129) and (128)), the number of good choices of
![]() $y_1y_2$
is
$y_1y_2$
is
implying that there exists a desired path
![]() $x_1y_2y_1x_2$
.
$x_1y_2y_1x_2$
.
This immediately implies that if
![]() $g = x_1x_2$
is blue, then g is contained in an alternating 4-cycle. If
$g = x_1x_2$
is blue, then g is contained in an alternating 4-cycle. If
![]() $g = u_1u_2$
is red, then we choose blue neighbours
$g = u_1u_2$
is red, then we choose blue neighbours
![]() $x_1 \in \Gamma_{H\setminus G'}(u_2)$
and
$x_1 \in \Gamma_{H\setminus G'}(u_2)$
and
![]() $x_2 \in \Gamma_{H \setminus G'}(u_1)$
(which exist due to the lower bounds in (123) and (130) being positive). Since there exists an alternating path
$x_2 \in \Gamma_{H \setminus G'}(u_1)$
(which exist due to the lower bounds in (123) and (130) being positive). Since there exists an alternating path
![]() $x_1y_2y_1x_2$
starting with a red edge, we obtain an alternating 6-cycle containing g. This proves Claim 6.4 in the case
$x_1y_2y_1x_2$
starting with a red edge, we obtain an alternating 6-cycle containing g. This proves Claim 6.4 in the case
![]() $p \le 0.49$
.
$p \le 0.49$
.
Case
![]() $\mathbf{p > 0.49}$
. We aim to apply Lemma 20. We first verify that, for
$\mathbf{p > 0.49}$
. We aim to apply Lemma 20. We first verify that, for
![]() $G'\in\{G, G\cup\{e\}\}$
and every
$G'\in\{G, G\cup\{e\}\}$
and every
![]() $H\in{\mathcal{R}}_{G'}$
, blue-red graph
$H\in{\mathcal{R}}_{G'}$
, blue-red graph
![]() $K\setminus G'$
is
$K\setminus G'$
is
![]() $(q, \tau p, \alpha/16)$
-regular. This assumption is trivial for the red graph
$(q, \tau p, \alpha/16)$
-regular. This assumption is trivial for the red graph
![]() $K\setminus H$
, which is q-biregular regardless of G
′. In view of (123) and (130), the relative degrees
$K\setminus H$
, which is q-biregular regardless of G
′. In view of (123) and (130), the relative degrees
![]() $d_{H\setminus G'}(v)$
in the blue graph lie in the interval
$d_{H\setminus G'}(v)$
in the blue graph lie in the interval
![]() $[\tau p - 2\delta \tau p, \tau p + 2\delta \tau p]$
. Since (28) implies
$[\tau p - 2\delta \tau p, \tau p + 2\delta \tau p]$
. Since (28) implies
and (128) implies
![]() $\delta \tau p \le \tau p / 32$
, we obtain
$\delta \tau p \le \tau p / 32$
, we obtain
![]() $2 \delta \tau p \le \alpha/16$
. Hence, indeed,
$2 \delta \tau p \le \alpha/16$
. Hence, indeed,
![]() $K\setminus G'$
is
$K\setminus G'$
is
![]() $(q, \tau p, \alpha/16)$
-regular.
$(q, \tau p, \alpha/16)$
-regular.
On the other hand, by (124)
![]() $K \setminus G$
is also
$K \setminus G$
is also
![]() $(\tau p + q, \alpha/16)$
-jumbled. Hence, by Lemma 20 with
$(\tau p + q, \alpha/16)$
-jumbled. Hence, by Lemma 20 with
![]() $F = K\setminus G'$
,
$F = K\setminus G'$
,
![]() $r = q$
and
$r = q$
and
![]() $b = \tau p$
, the edge g belongs to an alternating cycle of length at most 2D with
$b = \tau p$
, the edge g belongs to an alternating cycle of length at most 2D with
![]() $D = 2\lceil 16/\tau pq \rceil + 1 \le 32/\tau pq + 3$
. Claim 21 is proven.
$D = 2\lceil 16/\tau pq \rceil + 1 \le 32/\tau pq + 3$
. Claim 21 is proven.
7. Extension to non-bipartite graphs
Given integers n and d,
![]() $0\le d\le n-1$
such that nd is even, define the random regular graph
$0\le d\le n-1$
such that nd is even, define the random regular graph
![]() $\mathbb{R}(n,d)$
as a graph selected uniformly at random from the family
$\mathbb{R}(n,d)$
as a graph selected uniformly at random from the family
![]() ${\mathcal{R}}(n,d)$
of all d-regular graphs on an n-vertex set V. To make the comparison with the binomial model
${\mathcal{R}}(n,d)$
of all d-regular graphs on an n-vertex set V. To make the comparison with the binomial model
![]() $\mathbb{G}(n,p)$
easier, similarly as in the bipartite case, we set
$\mathbb{G}(n,p)$
easier, similarly as in the bipartite case, we set
![]() $p=\tfrac d{n-1}$
and define
$p=\tfrac d{n-1}$
and define
![]() $\mathbb{R}(n,p)\,{:\!=}\,\mathbb{R}(n,d)$
. In what follows, we often suppress the parameter d and instead just assume that
$\mathbb{R}(n,p)\,{:\!=}\,\mathbb{R}(n,d)$
. In what follows, we often suppress the parameter d and instead just assume that
![]() $0\le p\le 1$
,
$0\le p\le 1$
,
![]() $p(n-1)$
is an integer, and
$p(n-1)$
is an integer, and
![]() $p(n-1)n$
is even.
$p(n-1)n$
is even.
As described below, our proof of Theorem 2 can be adjusted to yield its non-bipartite version and, consequently, also a non-bipartite version of Corollary 3. Instead of formulating these two quite technical results, we limit ourselves to just stating their abridged version, analogous to Theorem 1. It confirms the Sandwich Conjecture of Kim and Vu [Reference Kim and Vu6] whenever
![]() $d \gg \left( n\log n \right)^{3/4}$
and
$d \gg \left( n\log n \right)^{3/4}$
and
![]() $n - d \gg n^{3/4} (\log n)^{1/4} $
.
$n - d \gg n^{3/4} (\log n)^{1/4} $
.
Theorem 1′. If
then for some
![]() $m \sim p\binom n2$
, there is a joint distribution of random graphs
$m \sim p\binom n2$
, there is a joint distribution of random graphs
![]() $\mathbb{G}(n,m)$
and
$\mathbb{G}(n,m)$
and
![]() $\mathbb{R}(n,p)$
such that
$\mathbb{R}(n,p)$
such that
If
 \begin{equation*} p\gg\left(\frac{\log^3 n}{n}\right)^{1/4}, \end{equation*}
\begin{equation*} p\gg\left(\frac{\log^3 n}{n}\right)^{1/4}, \end{equation*}
then for some
![]() $m \sim p\binom n2$
, there is a joint distribution of random graphs
$m \sim p\binom n2$
, there is a joint distribution of random graphs
![]() $\mathbb{G}(n,m)$
and
$\mathbb{G}(n,m)$
and
![]() $\mathbb{R}(n,p)$
such that
$\mathbb{R}(n,p)$
such that
Moreover, in both inclusions, one can replace
![]() $\mathbb{G}(n,m)$
by the binomial random graph
$\mathbb{G}(n,m)$
by the binomial random graph
![]() $\mathbb{G}(n,p')$
, for some
$\mathbb{G}(n,p')$
, for some
![]() $p' \sim p$
.
$p' \sim p$
.
To obtain a proof of Theorem 1
![]() $^{\prime}$
, one would modify the proof of Theorem 2 and its prerequisites fixing, say,
$^{\prime}$
, one would modify the proof of Theorem 2 and its prerequisites fixing, say,
![]() $C = 1$
. For the bulk of the proof (see Sections 3–6) the changes are straightforward and consist mainly of replacing
$C = 1$
. For the bulk of the proof (see Sections 3–6) the changes are straightforward and consist mainly of replacing
![]() $K = K_{n_1, n_2}$
by
$K = K_{n_1, n_2}$
by
![]() $K_n$
, both
$K_n$
, both
![]() $n_1$
and
$n_1$
and
![]() $n_2$
by n,
$n_2$
by n,
![]() $N = n_1 n_2$
by
$N = n_1 n_2$
by
![]() $\binom{n}{2}$
, both
$\binom{n}{2}$
, both
![]() $d_1$
and
$d_1$
and
![]() $d_2$
by
$d_2$
by
![]() $p(n-1)$
, as well as of setting
$p(n-1)$
, as well as of setting
![]() $\mathbb{I} = 0$
. In particular, we redefine (cf. (25))
$\mathbb{I} = 0$
. In particular, we redefine (cf. (25))
 \begin{equation} \tau_0 \,{:\!=}\, C_1\begin{cases} \dfrac{\log n}{p n}, \quad & p \le 0.49, \\ \\[-9pt] \left(\dfrac{\log n}{n}\right)^{1/4}, \quad & p > 0.49, \end{cases}\end{equation}
\begin{equation} \tau_0 \,{:\!=}\, C_1\begin{cases} \dfrac{\log n}{p n}, \quad & p \le 0.49, \\ \\[-9pt] \left(\dfrac{\log n}{n}\right)^{1/4}, \quad & p > 0.49, \end{cases}\end{equation}
 \begin{equation*} \gamma_t = C_2 \begin{cases} \sqrt{\dfrac{\log n}{\tau p n}}, \quad & p \le 0.49, \\ \\[-9pt] \sqrt{\dfrac{\log n}{\tau^2 q^2 n}}, \quad & p > 0.49, \end{cases}\end{equation*}
\begin{equation*} \gamma_t = C_2 \begin{cases} \sqrt{\dfrac{\log n}{\tau p n}}, \quad & p \le 0.49, \\ \\[-9pt] \sqrt{\dfrac{\log n}{\tau^2 q^2 n}}, \quad & p > 0.49, \end{cases}\end{equation*}
and
 \begin{equation*} \gamma \,{:\!=}\, C_3 \begin{cases} \sqrt{\dfrac{\log n}{p n}}, \quad & p \le 0.49, \\ \\[-9pt] \left(\dfrac{\log n}{n}\right)^{1/4}, \quad & p > 0.49, \end{cases}\end{equation*}
\begin{equation*} \gamma \,{:\!=}\, C_3 \begin{cases} \sqrt{\dfrac{\log n}{p n}}, \quad & p \le 0.49, \\ \\[-9pt] \left(\dfrac{\log n}{n}\right)^{1/4}, \quad & p > 0.49, \end{cases}\end{equation*}
for some appropriately chosen constants
![]() $C_1, C_2, C_3 > 0$
and replace assumptions (26)–(28) by conditions (131). Some other constants appearing in various definitions, might need to be updated, too.
$C_1, C_2, C_3 > 0$
and replace assumptions (26)–(28) by conditions (131). Some other constants appearing in various definitions, might need to be updated, too.
The proofs of non-bipartite versions of Theorem 2, Claim 7, Lemmas 8, 9, 13, and 14 follow the bipartite ones in a straightforward way.
The proof of Lemma 6 is modified also in a straightforward way except for one technical change. In the switching graph B we consider 6-circuits rather than 6-cycles (that is, we allow the vertices
![]() $x_1$
and
$x_1$
and
![]() $x_2$
in Figure 2 coincide). With this definition the degrees in the switching graph B (cf. (39)–(40)) are now as follows. If edges
$x_2$
in Figure 2 coincide). With this definition the degrees in the switching graph B (cf. (39)–(40)) are now as follows. If edges
![]() $f = u_1u_2$
and
$f = u_1u_2$
and
![]() $e = v_1v_2$
are disjoint, then
$e = v_1v_2$
are disjoint, then
and
If e and f share a vertex (without loss of generality,
![]() $u_1 = v_1$
), then
$u_1 = v_1$
), then
We modify the definition (42) of a
![]() $\delta$
-typical graph by taking the maximum over all pairs
$\delta$
-typical graph by taking the maximum over all pairs
![]() $(u, v) \in f \times e$
of distinct vertices. Since we now have two terms in (133) and (134), the bounds in (49) and (50) get some extra factors 2, which cancel out, leading to a bound similar to (51), but with constant 9 inflated.
$(u, v) \in f \times e$
of distinct vertices. Since we now have two terms in (133) and (134), the bounds in (49) and (50) get some extra factors 2, which cancel out, leading to a bound similar to (51), but with constant 9 inflated.
There is also a little inconvenience related to the analog of formula (56). Namely, now
so, the formula gets an extra factor O(1), which turns out to be negligible.
Set
![]() $\mathbb{R}\,{:\!=}\,\mathbb{R}(n,p)$
. More substantial modifications needed to prove Theorem 1
$\mathbb{R}\,{:\!=}\,\mathbb{R}(n,p)$
. More substantial modifications needed to prove Theorem 1
![]() $^{\prime}$
(which we discuss in detail below) are the following.
$^{\prime}$
(which we discuss in detail below) are the following.
Lemma 11 (only the case
 $\mathbb{I}=0$
left). Instead of using the asymptotic enumeration formula of Canfield, Greenhill and McKay (Theorem 5), we apply the one of Liebenau and Wormald [Reference Liebenau and Wormald8].
$\mathbb{I}=0$
left). Instead of using the asymptotic enumeration formula of Canfield, Greenhill and McKay (Theorem 5), we apply the one of Liebenau and Wormald [Reference Liebenau and Wormald8].Lemma 10 in the case
 $p > 0.49$
. Instead of directly showing the existence of short alternating cycles in
$p > 0.49$
. Instead of directly showing the existence of short alternating cycles in
 $K_n\setminus \mathbb{R}(t)=(K_n\setminus\mathbb{R})\cup(\mathbb{R}\setminus \mathbb{R}(t))$
, we create a blue-red auxiliary bipartite graph from
$K_n\setminus \mathbb{R}(t)=(K_n\setminus\mathbb{R})\cup(\mathbb{R}\setminus \mathbb{R}(t))$
, we create a blue-red auxiliary bipartite graph from
 $K_n \setminus \mathbb{R}(t)$
and apply unchanged Lemma 20 to it.
$K_n \setminus \mathbb{R}(t)$
and apply unchanged Lemma 20 to it.
7.1. Sketch of co-degree concentration for regular graphs
The non-bipartite version of Lemma 11 below is obtained by just setting
![]() $\mathbb{I}=0$
and replacing
$\mathbb{I}=0$
and replacing
![]() $\hat n$
by n (the resulting term
$\hat n$
by n (the resulting term
![]() $\hat p$
is swallowed by
$\hat p$
is swallowed by
![]() $\lambda$
).
$\lambda$
).
Lemma 11′. Suppose that
![]() $\hat p n \to \infty$
and
$\hat p n \to \infty$
and
![]() $\lambda = \lambda(n)\to \infty$
. Then, for any distinct
$\lambda = \lambda(n)\to \infty$
. Then, for any distinct
![]() $u, v \in [n]$
,
$u, v \in [n]$
,
As before, it is sufficient to assume that
![]() $p \le 1/2$
and thus replace
$p \le 1/2$
and thus replace
![]() $\hat p$
by p in (136). Indeed, by (135) and the identity
$\hat p$
by p in (136). Indeed, by (135) and the identity
![]() $2p-1=p^2-q^2$
,
$2p-1=p^2-q^2$
,
This allows, for
![]() $p>1/2$
, to replace p by q, as explained in the proof of Lemma 11 (the error O(1) is absorbed by the term
$p>1/2$
, to replace p by q, as explained in the proof of Lemma 11 (the error O(1) is absorbed by the term
![]() $\lambda$
).
$\lambda$
).
The proof of (136) for
![]() $p \le 1/2$
is based on the following enumeration result by Liebenau and Wormald [Reference Liebenau and Wormald8] (see Cor. 1.5 and Conj. 1.2 therein), proved for some ranges of d already by McKay and Wormald [Reference McKay and Wormald10,Reference McKay and Wormald11].
$p \le 1/2$
is based on the following enumeration result by Liebenau and Wormald [Reference Liebenau and Wormald8] (see Cor. 1.5 and Conj. 1.2 therein), proved for some ranges of d already by McKay and Wormald [Reference McKay and Wormald10,Reference McKay and Wormald11].
Given a sequence
![]() $\mathbf{d}=(d_1,\dots,d_n)$
, let
$\mathbf{d}=(d_1,\dots,d_n)$
, let
![]() $g(\mathbf{d})$
denote the number of graphs G on the vertex set
$g(\mathbf{d})$
denote the number of graphs G on the vertex set
![]() $V=(v_1,\dots,v_n)$
whose degree sequence is
$V=(v_1,\dots,v_n)$
whose degree sequence is
![]() $\mathbf{d}$
, that is,
$\mathbf{d}$
, that is,
![]() $\deg_G(v_i)=d_i$
,
$\deg_G(v_i)=d_i$
,
![]() $i=1,\dots,n$
. Further, let
$i=1,\dots,n$
. Further, let
Theorem 22 ([Reference Liebenau and Wormald8]). For some absolute constant
![]() $\varepsilon > 0$
, if
$\varepsilon > 0$
, if
![]() $\mathbf{d}=\mathbf{d}(n)$
satisfies
$\mathbf{d}=\mathbf{d}(n)$
satisfies
![]() $\max_i|d_i-\bar d|=o(n^\varepsilon\hat d)$
,
$\max_i|d_i-\bar d|=o(n^\varepsilon\hat d)$
,
![]() $n\hat d\to\infty$
, as
$n\hat d\to\infty$
, as
![]() $n\to\infty$
, and
$n\to\infty$
, and
![]() $\sum_{i=1}^nd_i$
is even, then
$\sum_{i=1}^nd_i$
is even, then
 \begin{equation*} g(\mathbf{d})\sim\sqrt2\exp\left(-\frac14-\frac{\gamma_2^2}{4\mu^2(1-\mu)^2}\right)\left(\mu^\mu(1-\mu)^{1-\mu}\right)^{\binom n2}\prod_{i=1}^n\binom{n-1}{d_i}.\end{equation*}
\begin{equation*} g(\mathbf{d})\sim\sqrt2\exp\left(-\frac14-\frac{\gamma_2^2}{4\mu^2(1-\mu)^2}\right)\left(\mu^\mu(1-\mu)^{1-\mu}\right)^{\binom n2}\prod_{i=1}^n\binom{n-1}{d_i}.\end{equation*}
The proof of Lemma 11
![]() $^{\prime}$
follows the lines of the proof of Lemma 11 in the case
$^{\prime}$
follows the lines of the proof of Lemma 11 in the case
![]() $\mathbb{I}=0$
. For fixed distinct
$\mathbb{I}=0$
. For fixed distinct
![]() $u,v\in V$
we define, as before,
$u,v\in V$
we define, as before,
![]() ${\mathcal{R}}_k = \{ G \in {\mathcal{R}}(n,d)\,\ :\,\ \operatorname{cod}_G(u,v) = k \}$
,
${\mathcal{R}}_k = \{ G \in {\mathcal{R}}(n,d)\,\ :\,\ \operatorname{cod}_G(u,v) = k \}$
,
![]() $0\le k\le d$
. Using Theorem 22, it is tedious but straightforward to find a sequence
$0\le k\le d$
. Using Theorem 22, it is tedious but straightforward to find a sequence
![]() $r_k\,{:\!=}\,r_k(n,d)$
such that
$r_k\,{:\!=}\,r_k(n,d)$
such that
![]() $|{\mathcal{R}}_k|\sim r_k$
. We have
$|{\mathcal{R}}_k|\sim r_k$
. We have
![]() $r_k = r_k^0 + r_k^1$
, as the formula for
$r_k = r_k^0 + r_k^1$
, as the formula for
![]() $|{\mathcal{R}}_k|$
breaks into two, according to whether uv is an edge (
$|{\mathcal{R}}_k|$
breaks into two, according to whether uv is an edge (
![]() $r_k^1)$
or not (
$r_k^1)$
or not (
![]() $r_k^0$
). It can be checked that
$r_k^0$
). It can be checked that
![]() $r_0, \dots, r_d > 0$
and, for
$r_0, \dots, r_d > 0$
and, for
![]() $1\le k\le d$
,
$1\le k\le d$
,
as well as
Let
![]() $\mu^0 \,{:\!=}\, (d+1)^2/n$
and
$\mu^0 \,{:\!=}\, (d+1)^2/n$
and
![]() $\mu^1 \,{:\!=}\, d^2/n$
. For
$\mu^1 \,{:\!=}\, d^2/n$
. For
![]() $\mu^0\le k\le d$
and, respectively, for
$\mu^0\le k\le d$
and, respectively, for
![]() $\mu^1\le k\le d$
,
$\mu^1\le k\le d$
,
Thus, for
![]() $\mu^0\le k\le d$
,
$\mu^0\le k\le d$
,
Similarly, setting
![]() $\rho=\left(1-\frac1d\right)\left(1-\frac1{n-1-d}\right)$
, for
$\rho=\left(1-\frac1d\right)\left(1-\frac1{n-1-d}\right)$
, for
![]() $1\le k\le\mu^0$
and, respectively,
$1\le k\le\mu^0$
and, respectively,
![]() $1\le k\le\mu^1$
,
$1\le k\le\mu^1$
,
So, for
![]() $1\le k\le\mu^1$
,
$1\le k\le\mu^1$
,
Setting conveniently
![]() $\mu_+\,{:\!=}\,\mu^0$
and
$\mu_+\,{:\!=}\,\mu^0$
and
![]() $\mu_-\,{:\!=}\,\mu^1\rho$
, we may now apply Claim 12, which extends straighforwardly to the non-bipartite setting.
$\mu_-\,{:\!=}\,\mu^1\rho$
, we may now apply Claim 12, which extends straighforwardly to the non-bipartite setting.
We have, using that
![]() $d \ge 1$
,
$d \ge 1$
,
Also, using
![]() $p \le 1/2$
,
$p \le 1/2$
,
whence, setting
![]() $X = \operatorname{cod}_{\mathbb{R}}(u_1,v_1)$
, and
$X = \operatorname{cod}_{\mathbb{R}}(u_1,v_1)$
, and
![]() $x = 20\sqrt{p^2 n \lambda} + \lambda - 2$
,
$x = 20\sqrt{p^2 n \lambda} + \lambda - 2$
,
We now bound the RHS of (138) using Claim 12 with
![]() $\lambda - 2$
instead of
$\lambda - 2$
instead of
![]() $\lambda$
. Noting that (137) implies
$\lambda$
. Noting that (137) implies
![]() $x \ge \sqrt{2 \mu_+ (\lambda - 2)} + (\lambda - 2)$
, we have
$x \ge \sqrt{2 \mu_+ (\lambda - 2)} + (\lambda - 2)$
, we have
Since
![]() $\sqrt{N} e^{-(\lambda -2)} = \Theta(n e^{-\lambda})$
, this completes the proof of Lemma 11
$\sqrt{N} e^{-(\lambda -2)} = \Theta(n e^{-\lambda})$
, this completes the proof of Lemma 11
![]() $^{\prime}$
.
$^{\prime}$
.
7.2. Sketch of the proof of new Lemma 10, case
 $p > 0.49$
$p > 0.49$
For completeness, we state here the non-bipartite counterpart of Lemma 10 which on the surface looks almost identical.
Lemma 10′. Assuming (131), we have, a.a.s.,
Looking at the diagram in Figure 1, we see that the proof of Lemma 10 relies on several other results, most notably Lemmas 17 and 20. It would be, however, a very tedious task to come up with non-bipartite counterpart of Lemma 20, and, consequently, ones of Lemmas 19 and 18. Instead, we rather convert the non-bipartite case into the bipartite one by a standard probabilistic construction and use Lemmas 17 and 20 practically unchanged.
Given a blue-red graph
![]() $H \subseteq K_n$
, let
$H \subseteq K_n$
, let
![]() $\operatorname{bip}\!(H)$
be a random blue-red bipartite graph with bipartition
$\operatorname{bip}\!(H)$
be a random blue-red bipartite graph with bipartition
![]() $V_1 = \left\{ u_1, \dots, u_n \right\}, V_2 = \left\{ v_1, \dots, v_n \right\}$
, such that for each edge
$V_1 = \left\{ u_1, \dots, u_n \right\}, V_2 = \left\{ v_1, \dots, v_n \right\}$
, such that for each edge
![]() $ij \in E(H)$
we flip a fair coin and include into
$ij \in E(H)$
we flip a fair coin and include into
![]() $\operatorname{bip}\!(H)$
either
$\operatorname{bip}\!(H)$
either
![]() $u_iv_j$
or
$u_iv_j$
or
![]() $u_jv_i$
(coloured the same colour as ij), with the flips being independent. In particular,
$u_jv_i$
(coloured the same colour as ij), with the flips being independent. In particular,
![]() $|E(\operatorname{bip}\!(H))| = |E(H)|$
, so the density of
$|E(\operatorname{bip}\!(H))| = |E(H)|$
, so the density of
![]() $\operatorname{bip}\!(H)$
is exactly half of that of H, while, if the densities of the blue and red subgraphs of H are b and r, then the expected densities of the blue and red subgraphs of
$\operatorname{bip}\!(H)$
is exactly half of that of H, while, if the densities of the blue and red subgraphs of H are b and r, then the expected densities of the blue and red subgraphs of
![]() $\operatorname{bip}\!(H)$
are
$\operatorname{bip}\!(H)$
are
![]() $b/2$
and
$b/2$
and
![]() $r/2$
.
$r/2$
.
Note that if there is an instance of
![]() $\operatorname{bip}\!(H)$
in which an edge
$\operatorname{bip}\!(H)$
in which an edge
![]() $u_iv_j$
is contained in an alternating cycle of length at most D, then ij is contained in an alternating circuit of the same length. It is not, in general, a cycle, since some vertices can be repeated, but edges are not, as the edges of
$u_iv_j$
is contained in an alternating cycle of length at most D, then ij is contained in an alternating circuit of the same length. It is not, in general, a cycle, since some vertices can be repeated, but edges are not, as the edges of
![]() $\operatorname{bip}\!(H)$
correspond to different edges of H. Luckily, Proposition 4 actually works for alternating circuits too, since in a circuit the blue and red degrees of each vertex equal each other (see the paragraph following equation (15)) and, similarly as for cycles, in
$\operatorname{bip}\!(H)$
correspond to different edges of H. Luckily, Proposition 4 actually works for alternating circuits too, since in a circuit the blue and red degrees of each vertex equal each other (see the paragraph following equation (15)) and, similarly as for cycles, in
![]() $K_n$
there are at most
$K_n$
there are at most
![]() $n^{2\ell-2}$
circuits of length
$n^{2\ell-2}$
circuits of length
![]() $\ell$
containing a given edge e. Defining
$\ell$
containing a given edge e. Defining
![]() ${\mathcal{R}}_G$
,
${\mathcal{R}}_G$
,
![]() ${\mathcal{R}}_{G,e}$
, and
${\mathcal{R}}_{G,e}$
, and
![]() $ {\mathcal{R}}_{G,\neg e}$
analogously to the bipartite case (cf. (15) and (16)), and making obvious modifications of the proof of Proposition 4, we obtain the following.
$ {\mathcal{R}}_{G,\neg e}$
analogously to the bipartite case (cf. (15) and (16)), and making obvious modifications of the proof of Proposition 4, we obtain the following.
Proposition 4′. Let a graph
![]() $G\subseteq K_n$
be such that
$G\subseteq K_n$
be such that
![]() ${\mathcal{R}}_G\neq\emptyset$
and let
${\mathcal{R}}_G\neq\emptyset$
and let
![]() $e\in K_n\setminus G$
. Assume that for some number
$e\in K_n\setminus G$
. Assume that for some number
![]() $D > 0$
and every
$D > 0$
and every
![]() $H\in {\mathcal{R}}_{G}$
the edge e is contained in an alternating circuit of length at most 2D. Then
$H\in {\mathcal{R}}_{G}$
the edge e is contained in an alternating circuit of length at most 2D. Then
![]() ${\mathcal{R}}_{G,\neg e}\neq\emptyset$
,
${\mathcal{R}}_{G,\neg e}\neq\emptyset$
,
![]() ${\mathcal{R}}_{G, e}\neq\emptyset$
, and
${\mathcal{R}}_{G, e}\neq\emptyset$
, and
The plan to adapt the proof of Lemma 10 is to condition on
![]() $K_n\setminus\mathbb{R}(t)$
having its degrees and co-degrees concentrated (using the non-bipartite counterparts of Lemmas 13 and 14) and then show that there is an instance F of
$K_n\setminus\mathbb{R}(t)$
having its degrees and co-degrees concentrated (using the non-bipartite counterparts of Lemmas 13 and 14) and then show that there is an instance F of
![]() $\operatorname{bip}\!(K_n \setminus \mathbb{R}(t))$
in which the degrees and co-degrees are similarly concentrated, with just a negligibly larger error.
$\operatorname{bip}\!(K_n \setminus \mathbb{R}(t))$
in which the degrees and co-degrees are similarly concentrated, with just a negligibly larger error.
In particular, such an F is
![]() $(q/2,\tau p/2,\alpha/32)$
-regular (as before, we denote
$(q/2,\tau p/2,\alpha/32)$
-regular (as before, we denote
![]() $\alpha = \min \left\{ \tau p, q \right\}$
). Then, applying Theorem 15 along the lines of the proof of Lemma 17, we show that F is also
$\alpha = \min \left\{ \tau p, q \right\}$
). Then, applying Theorem 15 along the lines of the proof of Lemma 17, we show that F is also
![]() $(\pi/2, \alpha/32)$
-jumbled, where, as before,
$(\pi/2, \alpha/32)$
-jumbled, where, as before,
![]() $\pi = \tau p + q$
. Hence, we are in position to apply Lemma 20, obtaining for every edge of F an alternating cycle of length
$\pi = \tau p + q$
. Hence, we are in position to apply Lemma 20, obtaining for every edge of F an alternating cycle of length
![]() $O\left( 1/(\tau p q) \right)$
in F. As explained above, this implies alternating circuits in
$O\left( 1/(\tau p q) \right)$
in F. As explained above, this implies alternating circuits in
![]() $K_n \setminus \mathbb{R}(t)$
of the same length, and so we may complete the proof of Lemma 10
$K_n \setminus \mathbb{R}(t)$
of the same length, and so we may complete the proof of Lemma 10
![]() $^{\prime}$
, based on Proposition 4
$^{\prime}$
, based on Proposition 4
![]() $^{\prime}$
, in the way we did it in the bipartite case.
$^{\prime}$
, in the way we did it in the bipartite case.
Let us now present some more details. We condition on
![]() $\mathbb{R}(t) = G$
such that (cf. (75) and (78))
$\mathbb{R}(t) = G$
such that (cf. (75) and (78))
and
Fix an arbitrary
![]() $H \in {\mathcal{R}}_G$
. Since the red graph
$H \in {\mathcal{R}}_G$
. Since the red graph
![]() $K_n \setminus H$
is
$K_n \setminus H$
is
![]() $q(n-1)$
-regular, we have
$q(n-1)$
-regular, we have
![]() $\deg_{\operatorname{bip}\!(K_n \setminus H)} (v) \sim \operatorname{Bin}(q(n-1), 1/2)$
. Thus, by a routine application of the Chernoff bound a.a.s.
$\deg_{\operatorname{bip}\!(K_n \setminus H)} (v) \sim \operatorname{Bin}(q(n-1), 1/2)$
. Thus, by a routine application of the Chernoff bound a.a.s.
By (139), the blue graph
![]() $H \setminus G$
has degrees
$H \setminus G$
has degrees
![]() $pn - (1 - \tau)pn + O\left( \delta \tau p n \right) = \tau p n + O\left( \sqrt{n \log n} \right)$
, so the Chernoff bound implies that (using
$pn - (1 - \tau)pn + O\left( \delta \tau p n \right) = \tau p n + O\left( \sqrt{n \log n} \right)$
, so the Chernoff bound implies that (using
![]() $p > 0.49$
) a.a.s.
$p > 0.49$
) a.a.s.
By (131) and (132), since
![]() $p>0.49$
and
$p>0.49$
and
![]() $\tau\ge \tau_0$
,
$\tau\ge \tau_0$
,
Consequently,
![]() $\sqrt{n\log n} \ll \alpha n$
and, with a big margin, we conclude that a.a.s.
$\sqrt{n\log n} \ll \alpha n$
and, with a big margin, we conclude that a.a.s.
![]() $\operatorname{bip}\!(K_n \setminus G)$
is
$\operatorname{bip}\!(K_n \setminus G)$
is
![]() $(q/2, \tau p/2, \alpha/32)$
-regular.
$(q/2, \tau p/2, \alpha/32)$
-regular.
Next, we check that
![]() $\operatorname{bip}\!(K_n \setminus G)$
is
$\operatorname{bip}\!(K_n \setminus G)$
is
![]() $(\pi/2, \alpha/32)$
-jumbled. Inequalities (141) and (142) imply
$(\pi/2, \alpha/32)$
-jumbled. Inequalities (141) and (142) imply
Further, by (135), (139), and (140), we have that (cf. (100))
 \begin{align*} \max_{u \ne v}\operatorname{cod}_{K_n \setminus G}(u, v) &\le 2\max_{v \in [n]} \deg_{K_n \setminus G}(v) - (n - 2 - \operatorname{cod}_{G}(u,v))\\[3pt] &=(2 \pi - 1)n + (1 - \pi)^2 n + O(\sqrt{n\log n}) = \pi^2 n + O\left( \sqrt{n\log n} \right). \end{align*}
\begin{align*} \max_{u \ne v}\operatorname{cod}_{K_n \setminus G}(u, v) &\le 2\max_{v \in [n]} \deg_{K_n \setminus G}(v) - (n - 2 - \operatorname{cod}_{G}(u,v))\\[3pt] &=(2 \pi - 1)n + (1 - \pi)^2 n + O(\sqrt{n\log n}) = \pi^2 n + O\left( \sqrt{n\log n} \right). \end{align*}
Since for every
![]() $u, v \in [n], u \ne v$
,
$u, v \in [n], u \ne v$
,
![]() $ \operatorname{cod}_{\operatorname{bip}\!(K_n \setminus G)}(u,v) \sim \operatorname{Bin}( \operatorname{cod}_{K_n \setminus G}(u,v), \tfrac{1}{4})$
, by a simple application of Chernoff’s inequality and the union bound we show that a.a.s.
$ \operatorname{cod}_{\operatorname{bip}\!(K_n \setminus G)}(u,v) \sim \operatorname{Bin}( \operatorname{cod}_{K_n \setminus G}(u,v), \tfrac{1}{4})$
, by a simple application of Chernoff’s inequality and the union bound we show that a.a.s.
Now, fix an instance F of the graph
![]() $\operatorname{bip}\!(K_n \setminus G)$
for which (141), (142) and (144) hold.
$\operatorname{bip}\!(K_n \setminus G)$
for which (141), (142) and (144) hold.
Applying Theorem 15, by calculations similar to those in the proof of Lemma 17, from (143) and (144) we deduce that F is
![]() $( \pi/2, \alpha/32)$
-jumbled. Since we earlier showed that F is
$( \pi/2, \alpha/32)$
-jumbled. Since we earlier showed that F is
![]() $(q/2, \tau p/2, \alpha/32)$
-regular, Lemma 20 implies that in F every edge is contained in an alternating cycle of length
$(q/2, \tau p/2, \alpha/32)$
-regular, Lemma 20 implies that in F every edge is contained in an alternating cycle of length
![]() $O\left( 1/(\tau p q) \right)$
and therefore in
$O\left( 1/(\tau p q) \right)$
and therefore in
![]() $K_n \setminus G$
every edge is contained in an alternating circuit of the same length. The same argument implies alternating cycles in
$K_n \setminus G$
every edge is contained in an alternating circuit of the same length. The same argument implies alternating cycles in
![]() $K_n \setminus (G \cup \{e\})$
for an arbitrary edge e, since only the lower bound in (139) has to be decreased by a negligible quantity 1.
$K_n \setminus (G \cup \{e\})$
for an arbitrary edge e, since only the lower bound in (139) has to be decreased by a negligible quantity 1.
The rest of the proof of Lemma 10
![]() $^{\prime}$
in the case
$^{\prime}$
in the case
![]() $p > 0.49$
follows along similar lines.
$p > 0.49$
follows along similar lines.
8. Technical facts
Here we collect a few technical or very plausible facts with their easy proofs. Most of them have been already utilised in the paper. An exception is Proposition 24 to be used only in Remark 26, Section 10.
We begin with convenient consequences of the assumptions of Lemma 6.
Proposition 23. For
![]() $t = 0, \dots, t_0 - 1$
, the conditions of Lemma 6, namely, (26), (27), and (28), imply that
$t = 0, \dots, t_0 - 1$
, the conditions of Lemma 6, namely, (26), (27), and (28), imply that
and
Proof. Since
![]() $\tau = \tau(t) \ge \tau(t_0) \ge \tau_0$
and
$\tau = \tau(t) \ge \tau(t_0) \ge \tau_0$
and
![]() $\gamma_t$
is increasing in t, the first inequalities in (145)–(147) are immediate and it is enough to prove the second inequalities.
$\gamma_t$
is increasing in t, the first inequalities in (145)–(147) are immediate and it is enough to prove the second inequalities.
Inequality (145) follows from the definition (25) of
![]() $\tau_0$
and (28).
$\tau_0$
and (28).
To show (146), for
![]() $p\le0.49$
, using the definition of
$p\le0.49$
, using the definition of
![]() $\tau_0$
(see (25)) and (27), we get
$\tau_0$
(see (25)) and (27), we get
while for
![]() $p > 0.49$
$p > 0.49$
To see (147) first note that for
![]() $p \le 0.49$
it is straightforward from the definition of
$p \le 0.49$
it is straightforward from the definition of
![]() $\tau_0$
in (25). For
$\tau_0$
in (25). For
![]() $p > 0.49$
, observing that (26) implies
$p > 0.49$
, observing that (26) implies
![]() $\sqrt{\tfrac{3(C+4)\log N}{\hat{n}}} \le \sqrt{\hat p /3240} \le 1/3240$
, we argue that
$\sqrt{\tfrac{3(C+4)\log N}{\hat{n}}} \le \sqrt{\hat p /3240} \le 1/3240$
, we argue that
whence (147) follows.
Next, we give a proof of Claim 7 which was instrumental in deducing Theorem 2 from Lemma 6 in Section 3.2.
Proof of Claim 7. Writing
![]() $X = t_0 - |S|$
, we have
$X = t_0 - |S|$
, we have
![]() $\operatorname{\mathbb{E}} X = \sum_{t=0}^{t_0 - 1} \gamma_t$
. Denoting
$\operatorname{\mathbb{E}} X = \sum_{t=0}^{t_0 - 1} \gamma_t$
. Denoting
![]() $\alpha \,{:\!=}\, 1080\hat p^2 \mathbb{I}$
and
$\alpha \,{:\!=}\, 1080\hat p^2 \mathbb{I}$
and
 \begin{equation*} \beta \,{:\!=}\, \begin{cases} 3240\sqrt{\dfrac{2(C + 3)\log N}{p\hat n}}, \quad & p \le 0.49, \\ \\[-9pt] 25,000 \sqrt{\dfrac{(C + 3)\log N}{q^2\hat n } } , \quad & p > 0.49, \end{cases} \end{equation*}
\begin{equation*} \beta \,{:\!=}\, \begin{cases} 3240\sqrt{\dfrac{2(C + 3)\log N}{p\hat n}}, \quad & p \le 0.49, \\ \\[-9pt] 25,000 \sqrt{\dfrac{(C + 3)\log N}{q^2\hat n } } , \quad & p > 0.49, \end{cases} \end{equation*}
we have
 \begin{equation*} \gamma_t = \alpha + \begin{cases} \beta \tau^{-1/2}, \quad & p \le 0.49, \\ \\[-9pt] \beta \tau^{-1}, \quad & p > 0.49. \end{cases} \end{equation*}
\begin{equation*} \gamma_t = \alpha + \begin{cases} \beta \tau^{-1/2}, \quad & p \le 0.49, \\ \\[-9pt] \beta \tau^{-1}, \quad & p > 0.49. \end{cases} \end{equation*}
Since, trivially,
![]() $\sum_{t = 0}^{t_0 - 1} \alpha = \alpha t_0 \le \alpha M = 1080\hat p^2 \mathbb{I} \cdot M$
, to prove (35), it suffices to show that
$\sum_{t = 0}^{t_0 - 1} \alpha = \alpha t_0 \le \alpha M = 1080\hat p^2 \mathbb{I} \cdot M$
, to prove (35), it suffices to show that
 \begin{equation} \sum_{t = 0}^{t_0 - 1} \tau^{-1/2} \le 2M, \quad \text{and} \quad \sum_{t = 0}^{t_0 - 1} \tau^{-1} \le \frac{M}{4}\log \frac{\hat n}{\log N}. \end{equation}
\begin{equation} \sum_{t = 0}^{t_0 - 1} \tau^{-1/2} \le 2M, \quad \text{and} \quad \sum_{t = 0}^{t_0 - 1} \tau^{-1} \le \frac{M}{4}\log \frac{\hat n}{\log N}. \end{equation}
Since
![]() $\tau = \tau(t) = 1 - t/M$
is positive and decreasing on [0,M),
$\tau = \tau(t) = 1 - t/M$
is positive and decreasing on [0,M),
 \begin{equation*} \sum_{t = 0}^{t_0 - 1} \tau^{-1/2} \le \sum_{t = 0}^{M - 1} \tau^{-1/2} \le \int_0^M \tau^{-1/2} dt = M \int_0^{1} \tau^{-1/2} d\tau = 2M,\end{equation*}
\begin{equation*} \sum_{t = 0}^{t_0 - 1} \tau^{-1/2} \le \sum_{t = 0}^{M - 1} \tau^{-1/2} \le \int_0^M \tau^{-1/2} dt = M \int_0^{1} \tau^{-1/2} d\tau = 2M,\end{equation*}
implying the first inequality in (148). On the other hand, recalling
![]() $t_0 = \lfloor (1-\tau_0)M \rfloor$
,
$t_0 = \lfloor (1-\tau_0)M \rfloor$
,
 \begin{equation*} \sum_{t = 0}^{t_0 - 1} \tau^{-1} \le \int_0^{t_0} \tau^{-1} dt \le \int_0^{(1-\tau_0)M} \tau^{-1} dt \le M \int_{\tau_0}^{1} \tau^{-1} d\tau = M \log \frac{1}{\tau_0} \le \frac{M}{4} \log \frac{\hat n}{\log N},\end{equation*}
\begin{equation*} \sum_{t = 0}^{t_0 - 1} \tau^{-1} \le \int_0^{t_0} \tau^{-1} dt \le \int_0^{(1-\tau_0)M} \tau^{-1} dt \le M \int_{\tau_0}^{1} \tau^{-1} d\tau = M \log \frac{1}{\tau_0} \le \frac{M}{4} \log \frac{\hat n}{\log N},\end{equation*}
which implies the second inequality in (148).
Checking (36) is a dull inspection of definitions using conditions (28)–(29), which the readers might prefer to do themselves. We nevertheless spell out the details starting with the case
![]() $p\le 0.49$
. Choosing
$p\le 0.49$
. Choosing
![]() $C^*$
large enough,
$C^*$
large enough,
 \begin{align*} \gamma &= C^*\left( p^2 \mathbb{I} + \sqrt{\frac{\log N}{p\hat n }}\right) \\[3pt] &\ge 1080 p^2 \mathbb{I} + 6480 \sqrt{\frac{(C + 3)\log N}{p\hat n }} + 3240\sqrt{\frac{3(C + 4)\log N}{p\hat n}} + \sqrt{\frac{\log N}{p\hat n}} + \sqrt{\frac{2C\log N}{p\hat n}}\\[3pt] &\ge \theta + \sqrt{\tau_0} + 2\sqrt{1/M} + \sqrt{\frac{2C\log N}{M}} \overset{\mbox{(29)}}{\ge} \theta + \tau_0 + 2/M + \sqrt{\frac{2C\log N}{M}}.\end{align*}
\begin{align*} \gamma &= C^*\left( p^2 \mathbb{I} + \sqrt{\frac{\log N}{p\hat n }}\right) \\[3pt] &\ge 1080 p^2 \mathbb{I} + 6480 \sqrt{\frac{(C + 3)\log N}{p\hat n }} + 3240\sqrt{\frac{3(C + 4)\log N}{p\hat n}} + \sqrt{\frac{\log N}{p\hat n}} + \sqrt{\frac{2C\log N}{p\hat n}}\\[3pt] &\ge \theta + \sqrt{\tau_0} + 2\sqrt{1/M} + \sqrt{\frac{2C\log N}{M}} \overset{\mbox{(29)}}{\ge} \theta + \tau_0 + 2/M + \sqrt{\frac{2C\log N}{M}}.\end{align*}
In the case
![]() $p > 0.49$
, note that
$p > 0.49$
, note that
![]() $q^{3/2}\ge q^2\ge \hat p^2$
. Therefore, assuming
$q^{3/2}\ge q^2\ge \hat p^2$
. Therefore, assuming
![]() $C^*$
is large enough,
$C^*$
is large enough,
 \begin{equation*} \gamma/3 \ge 700\left(3(C+4)\right)^{1/4} \left( q^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n}\right)^{1/4}\right) = \tau_0,\end{equation*}
\begin{equation*} \gamma/3 \ge 700\left(3(C+4)\right)^{1/4} \left( q^{3/2}\mathbb{I} + \left(\frac{\log N}{\hat n}\right)^{1/4}\right) = \tau_0,\end{equation*}
and
 \begin{equation*}\gamma/3 \ge 1080q^{3/2}\mathbb{I} + 6250\sqrt{\frac{(C + 3)\log N}{q^2\hat n}}\log\frac{\hat n}{\log N} \ge \theta.\end{equation*}
\begin{equation*}\gamma/3 \ge 1080q^{3/2}\mathbb{I} + 6250\sqrt{\frac{(C + 3)\log N}{q^2\hat n}}\log\frac{\hat n}{\log N} \ge \theta.\end{equation*}
Finally, because (28) implies
![]() $\hat n / (\log N) \ge 1$
and
$\hat n / (\log N) \ge 1$
and
![]() $d_1, d_2 \ge 1$
implies
$d_1, d_2 \ge 1$
implies
![]() $M \ge \hat n$
, for large enough
$M \ge \hat n$
, for large enough
![]() $C^*$
,
$C^*$
,
 \begin{align*} \gamma/3 \ge \frac{C^*}{3}\left( \frac{\log N}{\hat n} \right)^{1/4} &\ge \frac{\log N}{\hat n} + \sqrt{\frac{2C\log N}{\hat n}} \\[3pt] \fbox{$p > 0.49$, $M \ge \hat n$}\quad & \ge \frac{2}{M} + \sqrt{\frac{2C\log N}{M}},\end{align*}
\begin{align*} \gamma/3 \ge \frac{C^*}{3}\left( \frac{\log N}{\hat n} \right)^{1/4} &\ge \frac{\log N}{\hat n} + \sqrt{\frac{2C\log N}{\hat n}} \\[3pt] \fbox{$p > 0.49$, $M \ge \hat n$}\quad & \ge \frac{2}{M} + \sqrt{\frac{2C\log N}{M}},\end{align*}
which, with the previous two inequalities, implies (36).
We conclude this technical section with a lower bound on the maximum degree in a binomial random graph.
Proposition 24. If
![]() $p' \le 1/4$
and
$p' \le 1/4$
and
![]() $n_2 \le n_1$
, then a.a.s. the maximum degree of
$n_2 \le n_1$
, then a.a.s. the maximum degree of
![]() $\mathbb{G}(n_1,n_2,p')$
in
$\mathbb{G}(n_1,n_2,p')$
in
![]() $V_1$
is at least
$V_1$
is at least
![]() $\kappa \,{:\!=}\, \min \{ \lceil{{p'n_2 + \sqrt{p'(1-p')n_2\log n_1}}}\rceil, n_2 \}$
.
$\kappa \,{:\!=}\, \min \{ \lceil{{p'n_2 + \sqrt{p'(1-p')n_2\log n_1}}}\rceil, n_2 \}$
.
Proof. Writing
![]() $Z \sim \mathcal{N}(n_2p', n_2p'(1- p'))$
, by Slud’s inequality [Reference Slud13, Theorem 2.1] we have
$Z \sim \mathcal{N}(n_2p', n_2p'(1- p'))$
, by Slud’s inequality [Reference Slud13, Theorem 2.1] we have
hence by a standard approximation of the normal tail we obtain
Therefore, the probability that all vertices in
![]() $V_1$
have degrees smaller than
$V_1$
have degrees smaller than
![]() $\kappa$
is
$\kappa$
is
proving the proposition.
9. Application: perfect matchings between subsets of vertices
Perarnau and Petridis in [Reference Perarnau and Petridis12], in connection with a problem of Plünnecke, studied the existence of perfect matchings between fixed subsets of vertices in random biregular graphs. In particular, they proved the following result (which we state in our notation to make it easier to apply Theorem 2).
Theorem 25. (Theorem 2 in [Reference Perarnau and Petridis12]) Let
![]() $k>0$
be a constant, and assume
$k>0$
be a constant, and assume
![]() $n_2 = kn_1$
and
$n_2 = kn_1$
and
![]() $pn_2 \le n_1$
. Take subsets
$pn_2 \le n_1$
. Take subsets
![]() $A\subseteq V_1$
and
$A\subseteq V_1$
and
![]() $B\subseteq V_2$
of size
$B\subseteq V_2$
of size
![]() $pn_2$
and let
$pn_2$
and let
![]() $\mathcal M_{A,B}$
denote the event that the subgraph of
$\mathcal M_{A,B}$
denote the event that the subgraph of
![]() $\mathbb{R}(n_1, n_2, p)$
induced by A and B contains a perfect matching. As
$\mathbb{R}(n_1, n_2, p)$
induced by A and B contains a perfect matching. As
![]() $\hat n \to \infty$
, we have
$\hat n \to \infty$
, we have
and
Perarnau and Petridis [Reference Perarnau and Petridis12] speculated that if the bipartite version of the Sandwich Conjecture was true, then Theorem 25 would follow straightforwardly from the classical result of Erdős and Rényi on perfect matchings in the random bipartite graph (see Theorem 4.1 in [Reference Janson, Łuczak and Rucinski5]). That result, in particular, implies that the bipartite binomial random graph
![]() $\mathbb{G}(n',n',p')$
contains a perfect matching a.a.s. whenever
$\mathbb{G}(n',n',p')$
contains a perfect matching a.a.s. whenever
![]() $p'n'-\log n'\to\infty$
as
$p'n'-\log n'\to\infty$
as
![]() $n'\to\infty$
. We show how this, together with Theorem 2, implies the 1-statement in (149), provided that condition (4) of Theorem 2 is satisfied, which in particular implies
$n'\to\infty$
. We show how this, together with Theorem 2, implies the 1-statement in (149), provided that condition (4) of Theorem 2 is satisfied, which in particular implies
By Theorem 2, the random graph
![]() $\mathbb{R}(n_1,n_2,p)$
a.a.s. contains a random graph
$\mathbb{R}(n_1,n_2,p)$
a.a.s. contains a random graph
![]() $\mathbb{G}(n_1,n_2,p')$
with
$\mathbb{G}(n_1,n_2,p')$
with
where
![]() $\gamma$
is defined in (5). In particular, the subgraph of
$\gamma$
is defined in (5). In particular, the subgraph of
![]() $\mathbb{R}(n_1,n_2,p)$
induced by A and B contains a random graph
$\mathbb{R}(n_1,n_2,p)$
induced by A and B contains a random graph
![]() $\mathbb{G}(pn_2, pn_2, p')$
. To see that the latter random graph contains a perfect matching a.a.s., let us verify the Erdős–Rényi condition
$\mathbb{G}(pn_2, pn_2, p')$
. To see that the latter random graph contains a perfect matching a.a.s., let us verify the Erdős–Rényi condition
From the assumption in (149) it follows that
For our purposes, it is sufficient to check that
since then
which together with the condition in (149) imply
To see that (152) holds, first note that
![]() $\mathbb{I} = 1$
implies
$\mathbb{I} = 1$
implies
![]() $p = O( (\log N)^{-1})$
for
$p = O( (\log N)^{-1})$
for
![]() $p \le 0.49$
and
$p \le 0.49$
and
![]() $q = O( (\log N)^{-1})$
for
$q = O( (\log N)^{-1})$
for
![]() $p > 0.49$
; hence, regardless of p, the first term in the definition of
$p > 0.49$
; hence, regardless of p, the first term in the definition of
![]() $\gamma$
is
$\gamma$
is
![]() $o\left( (\log N)^{-1} \right)$
. The remaining terms are much smaller: for
$o\left( (\log N)^{-1} \right)$
. The remaining terms are much smaller: for
![]() $p \le 0.49$
inequality (151) implies that the second term in the definition of
$p \le 0.49$
inequality (151) implies that the second term in the definition of
![]() $\gamma$
is
$\gamma$
is
![]() $O\left( (\log N)^{1/2}\hat n^{-1/4} \right) \ll (\log N)^{-1}$
, while in the case
$O\left( (\log N)^{1/2}\hat n^{-1/4} \right) \ll (\log N)^{-1}$
, while in the case
![]() $p > 0.49$
assumption (150) implies that the last two terms in the definition of
$p > 0.49$
assumption (150) implies that the last two terms in the definition of
![]() $\gamma$
are at most
$\gamma$
are at most
![]() $(\log N)^{O(1)}\hat n^{-1/4} \ll (\log N)^{-1}$
.
$(\log N)^{O(1)}\hat n^{-1/4} \ll (\log N)^{-1}$
.
10. Concluding remarks
Remark 26. Assume
![]() $p \le 1/4$
. If a.a.s.
$p \le 1/4$
. If a.a.s.
![]() $\mathbb{G}(n_1, n_2, p') \subseteq \mathbb{R}(n_1,n_2,p)$
, then we must have
$\mathbb{G}(n_1, n_2, p') \subseteq \mathbb{R}(n_1,n_2,p)$
, then we must have
To see this, assume, without loss of generality, that
![]() $n_2 \le n_1$
, and note that by Proposition 24 we must have
$n_2 \le n_1$
, and note that by Proposition 24 we must have
![]() $p'n_2 + \sqrt{p'(1 - p')n_2\log n_1} \le pn_2$
, and therefore
$p'n_2 + \sqrt{p'(1 - p')n_2\log n_1} \le pn_2$
, and therefore
![]() $p/p' \ge 1 + \sqrt{\frac{(1 - p')\log n_1}{p'n_2}} $
. Since
$p/p' \ge 1 + \sqrt{\frac{(1 - p')\log n_1}{p'n_2}} $
. Since
![]() $p' \le p \le 1/4$
and
$p' \le p \le 1/4$
and
![]() $n_2 \le n_1$
, we have
$n_2 \le n_1$
, we have
![]() $p/p' = 1 + \Omega\left( \sqrt{\tfrac{\log N}{p\hat n }} \right)$
, whence (153) follows.
$p/p' = 1 + \Omega\left( \sqrt{\tfrac{\log N}{p\hat n }} \right)$
, whence (153) follows.
Remark 27. In view of Remark 26, the error
![]() $\gamma$
in Theorem 2 has optimal order of magnitude, whenever
$\gamma$
in Theorem 2 has optimal order of magnitude, whenever
![]() $p \le 1/4$
, provided that also
$p \le 1/4$
, provided that also
![]() $p^2 \mathbb{I} = O\left( \sqrt{\log N / p \hat n} \right)$
(that is, if either
$p^2 \mathbb{I} = O\left( \sqrt{\log N / p \hat n} \right)$
(that is, if either
![]() $p = O\left( \left( (\log N)/\hat n \right)^{1/5}\right)$
or
$p = O\left( \left( (\log N)/\hat n \right)^{1/5}\right)$
or
![]() $\mathbb{I} = 0$
).
$\mathbb{I} = 0$
).
From Remark 26 it also follows that we cannot have
![]() $\gamma = o(1)$
for
$\gamma = o(1)$
for
![]() $\log N = \Omega(p\hat n )$
. Theorem 2 does not apply to the case
$\log N = \Omega(p\hat n )$
. Theorem 2 does not apply to the case
![]() $\log N \ge p\hat n /(C^*)^2$
, but we think it would be interesting to find the largest p
′ for which one can a.a.s. embed
$\log N \ge p\hat n /(C^*)^2$
, but we think it would be interesting to find the largest p
′ for which one can a.a.s. embed
![]() $\mathbb{G}(n_1,n_2,p')$
into
$\mathbb{G}(n_1,n_2,p')$
into
![]() $\mathbb{R}(n_1,n_2,p)$
even in this case. The tightest embedding one can expect is the one permitted by the maximum degree. We conjecture that such an embedding is possible.
$\mathbb{R}(n_1,n_2,p)$
even in this case. The tightest embedding one can expect is the one permitted by the maximum degree. We conjecture that such an embedding is possible.
Conjecture 1. Suppose that a sequence of parameters
![]() $(n_1, n_2, p, p')$
is such that a.a.s. in
$(n_1, n_2, p, p')$
is such that a.a.s. in
![]() $\mathbb{G}(n_1, n_2, p')$
the maximum degree over
$\mathbb{G}(n_1, n_2, p')$
the maximum degree over
![]() $V_1$
is at most
$V_1$
is at most
![]() $d_1 = n_2p$
and the maximum degree over
$d_1 = n_2p$
and the maximum degree over
![]() $V_2$
is at most
$V_2$
is at most
![]() $d_2 = n_1p$
. There is a joint distribution of
$d_2 = n_1p$
. There is a joint distribution of
![]() $\mathbb{G}(n_1, n_2, p')$
and
$\mathbb{G}(n_1, n_2, p')$
and
![]() $\mathbb{R}(n_1,n_2,p)$
such that
$\mathbb{R}(n_1,n_2,p)$
such that
Note that if Conjecture 1 is true, then by taking complements we also have the tightest embedding
![]() $\mathbb{R}(n_1,n_2,p) \subseteq \mathbb{G}(n_1,n_2,p'')$
that the minimum degrees of
$\mathbb{R}(n_1,n_2,p) \subseteq \mathbb{G}(n_1,n_2,p'')$
that the minimum degrees of
![]() $\mathbb{G}(n_1,n_2,p'')$
permit.
$\mathbb{G}(n_1,n_2,p'')$
permit.
We also propose the following strengthening of the Kim–Vu Sandwich Conjecture.
Conjecture 2. Suppose that a sequence of parameters (n, p, p
′) is such that a.a.s. in
![]() $\mathbb{G}(n, p')$
the maximum degree is at most
$\mathbb{G}(n, p')$
the maximum degree is at most
![]() $d = (n-1)p$
. There is a joint distribution of
$d = (n-1)p$
. There is a joint distribution of
![]() $\mathbb{G}(n, p')$
and
$\mathbb{G}(n, p')$
and
![]() $\mathbb{R}(n,p)$
such that
$\mathbb{R}(n,p)$
such that
Remark 28. For constant p, to obtain
![]() $\gamma = o(1)$
in Theorem 2, we need to assume
$\gamma = o(1)$
in Theorem 2, we need to assume
![]() $\mathbb{I} = 0$
, which requires a rather restricted ratio
$\mathbb{I} = 0$
, which requires a rather restricted ratio
![]() $n_1/n_2$
. For example, one cannot afford
$n_1/n_2$
. For example, one cannot afford
![]() $n_1 = n_2^{1+\delta}$
for any constant
$n_1 = n_2^{1+\delta}$
for any constant
![]() $\delta > 0$
. This restriction comes from an enumeration result we use in the proof, namely, Theorem 5 (see condition (iii) therein). Should enumeration be proven with a relaxed condition, it would automatically improve our Theorem 2.
$\delta > 0$
. This restriction comes from an enumeration result we use in the proof, namely, Theorem 5 (see condition (iii) therein). Should enumeration be proven with a relaxed condition, it would automatically improve our Theorem 2.
Remark 29. The terms
![]() $ p^2\mathbb{I}$
and
$ p^2\mathbb{I}$
and
![]() $q^{3/2}\mathbb{I}$
in (5) are artifacts of the application of switchings in Lemma 11. In the sparse case (
$q^{3/2}\mathbb{I}$
in (5) are artifacts of the application of switchings in Lemma 11. In the sparse case (
![]() $\hat p \to 0$
) it is plausible that the condition
$\hat p \to 0$
) it is plausible that the condition
![]() $\mathbb{I} = 0$
can be made much milder by using a very recent enumeration result of Liebenau and Wormald [Reference Liebenau and Wormald9] instead of Theorem 5. Due to the schedule of this manuscript, we did not check what this would imply, but readers seeking smaller errors in (5) are encouraged to do so.
$\mathbb{I} = 0$
can be made much milder by using a very recent enumeration result of Liebenau and Wormald [Reference Liebenau and Wormald9] instead of Theorem 5. Due to the schedule of this manuscript, we did not check what this would imply, but readers seeking smaller errors in (5) are encouraged to do so.
Acknowledgement
We thank Noga Alon and Benny Sudakov who, at the conference Random Structures & Algorithms 2019, suggested a way to show the existence of alternating paths in non-bipartite graphs. We are also thankful to the anonymous referee for useful remarks.