Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-25T05:55:24.668Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Random Satisfiable Process

Published online by Cambridge University Press:  01 September 2009

MICHAEL KRIVELEVICH ,
BENNY SUDAKOV  and
DAN VILENCHIK
MICHAEL KRIVELEVICH
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv, Israel (e-mail: krivelev@post.tau.ac.il)
BENNY SUDAKOV
Affiliation:
Department of Mathematics, UCLA, Los Angeles, USA (e-mail: bsudakov@math.ucla.edu)
DAN VILENCHIK
Affiliation:
Department of Mathematics, UCLA, Los Angeles, USA (e-mail: danny.vilenchik@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work we suggest a new model for generating random satisfiable k-CNF formulas. To generate such formulas. randomly permute all 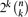possible clauses over the variables x1,. . .,xn, and starting from the empty formula, go over the clauses one by one, including each new clause as you go along if, after its addition, the formula remains satisfiable. We study the evolution of this process, namely the distribution over formulas obtained after scanning through the first m clauses (in the random permutation's order).

Random processes with conditioning on a certain property being respected are widely studied in the context of graph properties. This study was pioneered by Ruciński and Wormald in 1992 for graphs with a fixed degree sequence, and also by Erdős, Suen and Winkler in 1995 for triangle-free and bipartite graphs. Since then many other graph properties have been studied, such as planarity and H-freeness. Thus our model is a natural extension of this approach to the satisfiability setting.

Our main contribution is as follows. For m ≥ cn, c = c(k) a sufficiently large constant, we are able to characterize the structure of the solution space of a typical formula in this distribution. Specifically, we show that typically all satisfying assignments are essentially clustered in one cluster, and all but e−Ω(m/n)n of the variables take the same value in all satisfying assignments. We also describe a polynomial-time algorithm that finds w.h.p. a satisfying assignment for such formulas.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 18 , Issue 5: New Directions in Algorithms, Combinatorics and Optimization , September 2009 , pp. 775 - 801
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Achlioptas, D. and Coja-Oghlan, A. (2008) Algorithmic barriers from phase transitions. In Proc. 49th Annual IEEE Symposium on Foundations of Computer Science, pp. 793–802.CrossRefGoogle Scholar
[2]Achlioptas, D. and Ricci-Tersenghi, F. (2006) On the solution-space geometry of random constraint satisfaction problems. In Proc. 38th ACM Symposium on Theory of Computing, pp. 130–139.CrossRefGoogle Scholar
[3]Alon, N. and Kahale, N. (1997) A spectral technique for coloring random 3-colorable graphs. SIAM J. Comput. 26 1733–1748.CrossRefGoogle Scholar
[4]Alon, N. and Spencer, J. (2000) The Probabilistic Method, 2nd edn, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley-Interscience, New York.CrossRefGoogle Scholar
[5]Ben-Sasson, E., Bilu, Y. and Gutfreund, D. (2002) Finding a randomly planted assignment in a random 3CNF. Manuscript.Google Scholar
[6]Bohman, T., Frieze, A., Martin, R., Ruszinko, M. and Smyth, C. (2007) Randomly generated intersecting hypergraphs II. Random Struct. Alg. 30 17–34.CrossRefGoogle Scholar
[7]Chen, H. (2004) An algorithm for SAT above the threshold. In Theory and Applications of Satisfiability Testing: 6th International Conference (SAT 2003), Vol. 2919 of Lecture Notes in Computer Science, Springer, pp. 14–24.CrossRefGoogle Scholar
[8]Coja-Oghlan, A., Krivelevich, M. and Vilenchik, D. (2007) Why almost all k-colorable graphs are easy. In Proc. 24th Symposium on Theoretical Aspects of Computer Science, Vol. 4393 of Lecture Notes in Computer Science, Springer, pp. 121–132.Google Scholar
[9]Coja-Oghlan, A., Krivelevich, M. and Vilenchik, D. (2007) Why almost all satisfiable k-CNF formulas are easy. In 13th Conference on Analysis of Algorithms: DMTCS Proceedings, pp. 89–102.CrossRefGoogle Scholar
[10]Cook, S. (1971) The complexity of theorem-proving procedures. In Proc. 3rd ACM Symposium on Theory of Computing, pp. 151–158.CrossRefGoogle Scholar
[11]Erdős, P., Suen, S. and Winkler, P. (1995) On the size of a random maximal graph. Random Struct. Alg. 6 309–318.CrossRefGoogle Scholar
[12]Feige, U., Mossel, E. and Vilenchik, D. (2006) Complete convergence of message passing algorithms for some satisfiability problems. In Approximation, Randomization, and Combinatorial Optimization: Algorithms and Techniques (Proc. RANDOM 2006), Vol. 4110 of Lecture Notes in Computer Science, Springer, pp. 339–350.CrossRefGoogle Scholar
[13]Feige, U. and Vilenchik, D. (2004) A local search algorithm for 3SAT. Technical report, The Weizmann Institute of Science.Google Scholar
[14]Flaxman, A. (2003) A spectral technique for random satisfiable 3CNF formulas. In Proc. 14th ACM–SIAM Symposium on Discrete Algorithms, pp. 357–363.Google Scholar
[15]Friedgut, E. (1999) Sharp thresholds of graph properties, and the k-sat problem. J. Amer. Math. Soc. 12 1017–1054.CrossRefGoogle Scholar
[16]Gallager, R. (1963) Low-Density Parity-Check Codes, MIT Press, Cambridge.CrossRefGoogle Scholar
[17]Gerke, S., Schlatter, D., Steger, A. and Taraz, A. (2008) The random planar graph process. Random Struct. Alg. 32 236–261.CrossRefGoogle Scholar
[18]Håstad, J. (2001) Some optimal inapproximability results. J. Assoc. Comput. Mach. 48 798–859.CrossRefGoogle Scholar
[19]Krivelevich, M. and Vilenchik, D. (2006) Solving random satisfiable 3CNF formulas in expected polynomial time. In Proc. 17th ACM–SIAM Symposium on Discrete Algorithms, pp. 454–463.CrossRefGoogle Scholar
[20]Kučera, L. (1977) Expected behavior of graph coloring algorithms. In Proc. Fundamentals of Computation Theory, Vol. 56 of Lecture Notes in Computer Science, Springer, Berlin, pp. 447–451.CrossRefGoogle Scholar
[21]Lovász, L. (1993) Combinatorial Problems and Exercises, 2nd edn, Elsevier, Amsterdam.Google Scholar
[22]Mezard, M., Mora, T. and Zecchina, R. (2005) Clustering of solutions in the random satisfiability problem. Phys. Review Letters 94 197–205.CrossRefGoogle ScholarPubMed
[23]Osthus, D. and Taraz, A. (2001) Random maximal H-free graphs. Random Struct. Alg. 18 61–82.3.0.CO;2-T>CrossRefGoogle Scholar
[24]Pearl, J. (1988) Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, Morgan Kaufmann, San Francisco, CA, USA.Google Scholar
[25]Ruciński, A. and Wormald, N. (1992) Random graph processes with degree restrictions. Combin. Probab. Comput. 1 169–180.CrossRefGoogle Scholar