Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T14:09:46.751Z Has data issue: false hasContentIssue false
  • English
  • Français

On the peel number and the leaf-height of Galton–Watson trees

Part of: Markov processes

Published online by Cambridge University Press:  09 June 2022

Luc Devroye ,
Marcel K. Goh  and
Rosie Y. Zhao
Luc Devroye
Affiliation:
School of Computer Science, McGill University, Montreal, QC, Canada
Marcel K. Goh*
Affiliation:
School of Computer Science, McGill University, Montreal, QC, Canada
Rosie Y. Zhao
Affiliation:
School of Computer Science, McGill University, Montreal, QC, Canada
*
*Corresponding author. Email: marcel.goh@mail.mcgill.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We study several parameters of a random Bienaymé–Galton–Watson tree 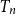$T_n$ of size $n$ defined in terms of an offspring distribution 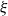$\xi$ with mean 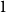$1$ and nonzero finite variance 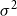$\sigma ^2$ . Let 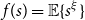$f(s)=\mathbb{E}\{s^\xi \}$ be the generating function of the random variable $\xi$ . We show that the independence number is in probability asymptotic to 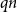$qn$ , where 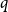$q$ is the unique solution to 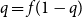$q = f(1-q)$ . One of the many algorithms for finding the largest independent set of nodes uses a notion of repeated peeling away of all leaves and their parents. 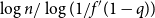The number of rounds of peeling is shown to be in probability asymptotic to $\log n/\log (1/f'(1-q))$ . Finally, we study a related parameter which we call the leaf-height. Also sometimes called the protection number, this is the maximal shortest path length between any node and a leaf in its subtree. 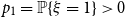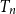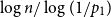If $p_1 = \mathbb{P}\{\xi =1\}\gt 0$ , then we show that the maximum leaf-height over all nodes in $T_n$ is in probability asymptotic to $\log n/\log (1/p_1)$ . If 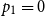$p_1 = 0$ and $\kappa$ is the first integer 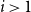$i\gt 1$ with 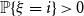$\mathbb{P}\{\xi =i\}\gt 0$ , then the leaf-height is in probability asymptotic to 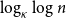$\log _\kappa \log n$ .

Keywords

Independence numberBienaymé–Galton–Watson treesprotection number

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 1 , January 2023 , pp. 68 - 90
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. (1991) Asymptotic fringe distributions for general families of random trees. Ann. Appl. Probab. 1 228–266.CrossRefGoogle Scholar
Alsmeyer, G. (2008) Galton–Watson Processes. Course notes at the University of Münster.Google Scholar
Athreya, K. and Ney, P. (1972) Branching Processes. Springer Verlag.CrossRefGoogle Scholar
Banderier, C., Kuba, M. and Panholzer, A. (2009) Analysis of three graph parameters for random trees. Random Struct. Algorithms 35 42–69.CrossRefGoogle Scholar
Bóna, M. (2014) $k$ -protected vertices in binary search trees. Adv. Appl. Math. 53 1–11.CrossRefGoogle Scholar
Brešar, B., Jakovac, M., Katrenič, J., Semanišin, G. and Taranenko, A. (2013) On the vertex $k$ -path cover. Discrete Appl. Math. 161 1943–1949.CrossRefGoogle Scholar
Broutin, N., Devroye, L. and Fraiman, N. (2020) Recursive functions on conditional Galton–Watson trees. Random Struct. Algorithms 57 304–316.CrossRefGoogle Scholar
Cheon, G.-S. and Shapiro, L. W. (2008) Protected points in ordered trees. Appl. Math. Lett. 21 516–520.CrossRefGoogle Scholar
Copenhaver, K. (2017) $k$ -protected vertices in unlabeled rooted plane trees. Graph Combinator. 33 347–355.CrossRefGoogle Scholar
Du, R. R. X. and Prodinger, H. (2012) On protected nodes in digital search trees. Appl. Math. Lett. 25 1025–1028.CrossRefGoogle Scholar
Dwass, M. (1969) The total progeny in a branching process. J. Appl. Probab. 6 682–686.CrossRefGoogle Scholar
Flajolet, P. and Odlyzko, A. (1982) The average height of binary trees and other simple trees. J. Comput. Syst. Sci. 25 171–213.CrossRefGoogle Scholar
Fuchs, M., Holmgren, C., Mitsche, D. and Neininger, R. (2021) A note on the independence number, domination number and related parameters of random binary search trees and random recursive trees. Discrete Appl. Math. 292(1) 64–71.CrossRefGoogle Scholar
Gittenberger, B., Gołȩbiewski, Z., Larcher, I. and Sulkowska, M.. “Protection numbers in simply generated trees and Pólya trees,”. arXiv preprint 1904. 03519, 2019.Google Scholar
Janson, S. (2012) Simply generated trees, conditioned Galton–Watson trees, random allocations and condensation. Probab. Surv. 9(none) 103–252.CrossRefGoogle Scholar
Janson, S. (2016) Asymptotic normality of fringe subtrees and additive functionals in conditioned Galton–Watson trees. Random Struct. Algorithms 48(1) 57–101.CrossRefGoogle Scholar
Kersting, G.. “On the height profile of a conditioned Galton–Watson tree,”. arXiv preprint 1101. 3656, 1998.Google Scholar
Kesten, Harry (1986) Subdiffusive behavior of a random walk on a random cluster. Ann. l’Inst. Henri Poincaré 22 425–487.Google Scholar
Kolchin, V. F. (1986) Random Mappings. Optimisation Software Inc.Google Scholar
Lyons, R. and Peres, Y. (2017) Probability on Trees and Networks. Cambridge University Press.Google Scholar
Mahmoud, H. M. and Ward, M. D. (2012) Asymptotic distribution of two-protected nodes in random binary search trees. Appl. Math. Lett. 25(12) 2218–2222.CrossRefGoogle Scholar
Mahmoud, H. M. and Ward, M. D. (2015) Asymptotic properties of protected nodes in random recursive trees. J. Appl. Probab. 52 290–297.CrossRefGoogle Scholar
Mansour, T. (2011) Protected points in $k$ -ary trees. Appl. Math. Lett. 24 478–480.CrossRefGoogle Scholar
Rogozin, B. A. (1961) On an estimate of the concentration function. Theor. Probab. Appl. 6 94–97.CrossRefGoogle Scholar
Stufler, B. (2019) Local limits of large Galton–Watson trees rerooted at a random vertex. Ann. l’Inst. Henri Poincaré Probab. Stat. 55 155–183.Google Scholar