Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Boche, Holger
Schaefer, Rafael F.
and
Poor, H. Vincent
2017.
Characterization of super-additivity and discontinuity behavior of the capacity of arbitrarily varying channels under list decoding.
p.
2820.
Boche, Holger
and
Deppe, Christian
2017.
Robust and secure identification.
p.
1539.
Boche, H.
Schaefer, R. F.
and
Poor, H. V.
2018.
Analytical Properties of Shannon’s Capacity of Arbitrarily Varying Channels under List Decoding: Super-Additivity and Discontinuity Behavior.
Problems of Information Transmission,
Vol. 54,
Issue. 3,
p.
199.
Boche, Holger
and
Deppe, Christian
2018.
Secure Identification for Wiretap Channels; Robustness, Super-Additivity and Continuity.
IEEE Transactions on Information Forensics and Security,
Vol. 13,
Issue. 7,
p.
1641.
Ahlswede, Rudolf
2019.
Probabilistic Methods and Distributed Information.
Vol. 15,
Issue. ,
p.
175.
Boche, Holger
and
Deppe, Christian
2019.
Secure Identification Under Passive Eavesdroppers and Active Jamming Attacks.
IEEE Transactions on Information Forensics and Security,
Vol. 14,
Issue. 2,
p.
472.
Boche, Holger
Schaefer, Rafael F.
and
Poor, H. Vincent
2020.
Identification Capacity of Channels With Feedback: Discontinuity Behavior, Super-Activation, and Turing Computability.
IEEE Transactions on Information Theory,
Vol. 66,
Issue. 10,
p.
6184.
Sason, Igal
2024.
Observations on graph invariants with the Lovász $ \vartheta $-function.
AIMS Mathematics,
Vol. 9,
Issue. 6,
p.
15385.
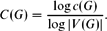 $$C(G) = \ffrac {\log c(G)}{\log |V(G)|}.$$
$$C(G) = \ffrac {\log c(G)}{\log |V(G)|}.$$

