Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T13:52:32.274Z Has data issue: false hasContentIssue false
  • English
  • Français

On Erdős–Ko–Rado for Random Hypergraphs II

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  18 October 2018

A. HAMM  and
J. KAHN
A. HAMM
Affiliation:
Department of Mathematics, Winthrop University, Rock Hill, SC 29733, USA (e-mail: hamma@winthrop.edu)
J. KAHN
Affiliation:
Department of Mathematics, Rutgers University, Piscataway, NJ 08854, USA (e-mail: jkahn@math.rutgers.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Denote by 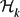${\mathcal H}_k$(n, p) the random k-graph in which each k-subset of {1,. . .,n} is present with probability p, independent of other choices. More or less answering a question of Balogh, Bohman and Mubayi, we show: there is a fixed ε > 0 such that if n = 2k + 1 and p > 1 - ε, then w.h.p. (that is, with probability tending to 1 as k → ∞), 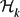${\mathcal H}_k$(n, p) has the ‘Erdős–Ko–Rado property’. We also mention a similar random version of Sperner's theorem.

MSC classification

Primary: 05D40: Probabilistic methods
Secondary: 05D05: Extremal set theory 05C65: Hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 1 , January 2019 , pp. 61 - 80
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported by NSF grant DMS1201337.

References

[1] Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, Wiley.Google Scholar
[2] Babai, L., Simonovits, M. and Spencer, J. (1990) Extremal subgraphs of random graphs. J. Graph Theory 14 599–622.Google Scholar
[3] Balogh, J. (2014) On the applications of counting independent sets in hypergraphs. In Workshop on Probabilistic and Extremal Combinatorics, IMA.Google Scholar
[4] Balogh, J., Bohman, T. and Mubayi, D. (2009) Erdős–Ko–Rado in random hypergraphs. Combin. Probab. Comput. 18 629–646.Google Scholar
[5] Balogh, J., Morris, R. and Samotij, W. (2015) Independent sets in hypergraphs. J. Amer. Math. Soc. 28 669–709.Google Scholar
[6] Balogh, J., Mycroft, R. and Treglown, A. (2014) A random version of Sperner's theorem. J. Combin. Theory Ser. A 128 104–110.Google Scholar
[7] Bollobás, B. (1986) Combinatorics, Cambridge University Press.Google Scholar
[8] Collares~Neto, M. and Morris, R. (2016) Maximum-size antichains in random set-systems. Random Struct. Alg. 49 308–321.Google Scholar
[9] Conlon, D. and Gowers, T. (2016) Combinatorial theorems in sparse random sets. Ann. Math. 184 367–454.Google Scholar
[10] DeMarco, R. and Turán's, Kahn, J. Theorem for random graphs. arXiv1501.01340v1Google Scholar
[11] Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. Oxford Ser. (2) 12 313–320.Google Scholar
[12] Frankl, P. (1987) Erdős–Ko–Rado theorem with conditions on the maximal degree. J. Combin. Theory Ser. A 46 252–263.Google Scholar
[13] Frankl, P. and Rödl, V. (1986) Large triangle-free subgraphs in graphs without K 4. Graphs Combin. 2 135–144.Google Scholar
[14] Hamm, A. and Kahn, J. On Erdős–Ko–Rado for random hypergraphs I. arXiv1412.5085v1Google Scholar
[15] Hilton, A. J. W. and Milner, E. C. (1967) Some intersection theorems for systems of finite sets. Quart. J. Math. Oxford Ser. (2) 18 369–384.Google Scholar
[16] Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.Google Scholar
[17] Katona, G. O. H. (1966) A theorem on finite sets. In Theory of Graphs: Proc. Colloq. Tihany, Akademiai Kiado / Academic Press, pp. 187–207.Google Scholar
[18] Knuth, D. E. (1969) The Art of Computer Programming, Vol. I, Addison Wesley.Google Scholar
[19] Kohayakawa, Y., Łuczak, T. and Rödl, V. (1997) On K 4-free subgraphs of random graphs. Combinatorica 17 173–213.Google Scholar
[20] Kruskal, J. B. (1963) The number of simplices in a complex. In Mathematical Optimization Techniques (Bellman, R., ed.), University of California Press, pp. 251–278.Google Scholar
[21] Lovász, L. (1993) Combinatorial Problems and Exercises, American Mathematical Society.Google Scholar
[22] Osthus, D. (2000) Maximum antichains in random subsets of a finite set. J. Combin. Theory Ser. A 90 336–346.Google Scholar
[23] Ramsey, F. B. (1930) On a problem of formal logic. Proc. London Math. Soc. 30 264–286.Google Scholar
[24] Rödl, V. and Ruciński, A. (1995) Threshold functions for Ramsey properties. J. Amer. Math. Soc. 8 917–942.Google Scholar
[25] Rödl, V. and Schacht, M. (2013) Extremal results in random graphs. In Erdős Centennial (Lovász, L. et al. eds), Vol. 25 of Bolyai Society Mathematical Studies, János Bolyai Mathematical Society, pp. 535–583.Google Scholar
[26] Sapozhenko, A. A. (1987) On the number of connected subsets with given cardinality of the boundary in bipartite graphs (in Russian). Metody Diskret. Analiz. 45 42–70.Google Scholar
[27] Saxton, D. and Thomason, A. (2015) Hypergraph containers. Inventio Math. 201 925–992.Google Scholar
[28] Schacht, M. (2016) Extremal results for random discrete structures. Ann. of Math. 184 333–365.Google Scholar
[29] Sperner, E. (1928) Ein Satz über Untermengen einer endlichen Menge. Math. Z. 27 544–548.Google Scholar
[30] Szemerédi, E. (1975) On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 199–245.Google Scholar
[31] Turán, P. (1941) Eine Extremalaufgabe aus der Graphentheorie. Mat. Fiz Lapook 48 436–452.Google Scholar