Article contents
A natural barrier in random greedy hypergraph matching
Published online by Cambridge University Press: 27 June 2019
Abstract
Let r ⩾ 2 be a fixed constant and let 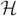 $ {\cal H} $ be an r-uniform, D-regular hypergraph on N vertices. Assume further that D → ∞ as N → ∞ and that degrees of pairs of vertices in
$ {\cal H} $ be an r-uniform, D-regular hypergraph on N vertices. Assume further that D → ∞ as N → ∞ and that degrees of pairs of vertices in 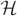 $ {\cal H} $ are at most L where L = D/( log N)ω(1). We consider the random greedy algorithm for forming a matching in
$ {\cal H} $ are at most L where L = D/( log N)ω(1). We consider the random greedy algorithm for forming a matching in 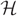 $ {\cal H} $. We choose a matching at random by iteratively choosing edges uniformly at random to be in the matching and deleting all edges that share at least one vertex with a chosen edge before moving on to the next choice. This process terminates when there are no edges remaining in the graph. We show that with high probability the proportion of vertices of
$ {\cal H} $. We choose a matching at random by iteratively choosing edges uniformly at random to be in the matching and deleting all edges that share at least one vertex with a chosen edge before moving on to the next choice. This process terminates when there are no edges remaining in the graph. We show that with high probability the proportion of vertices of 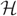 $ {\cal H} $ that are not saturated by the final matching is at most (L/D)(1/(2(r−1)))+o(1). This point is a natural barrier in the analysis of the random greedy hypergraph matching process.
$ {\cal H} $ that are not saturated by the final matching is at most (L/D)(1/(2(r−1)))+o(1). This point is a natural barrier in the analysis of the random greedy hypergraph matching process.
MSC classification
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
Research supported in part by NSF grant DMS-1001638 and Simons Foundation grant #426894.
Research supported in part by NSF grants DMS-1001638 and DMS-1100215.
References
- 2
- Cited by


