Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T22:22:30.999Z Has data issue: false hasContentIssue false
  • English
  • Français

A natural barrier in random greedy hypergraph matching

Part of: Extremal combinatorics Theory of computing Combinatorial probability

Published online by Cambridge University Press:  27 June 2019

Patrick Bennett  and
Tom Bohman
Patrick Bennett
Affiliation:
Mathematics Department, Western Michigan University, Kalamazoo, MI 49008, USA, Email: patrick.bennett@wmich.edu
Tom Bohman*
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA
*
*Corresponding author. Email: tbohman@math.cmu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let r ⩾ 2 be a fixed constant and let 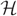$ {\cal H} $ be an r-uniform, D-regular hypergraph on N vertices. Assume further that D → ∞ as N → ∞ and that degrees of pairs of vertices in 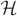$ {\cal H} $ are at most L where L = D/( log N)ω(1). We consider the random greedy algorithm for forming a matching in 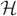$ {\cal H} $. We choose a matching at random by iteratively choosing edges uniformly at random to be in the matching and deleting all edges that share at least one vertex with a chosen edge before moving on to the next choice. This process terminates when there are no edges remaining in the graph. We show that with high probability the proportion of vertices of 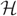$ {\cal H} $ that are not saturated by the final matching is at most (L/D)(1/(2(r−1)))+o(1). This point is a natural barrier in the analysis of the random greedy hypergraph matching process.

MSC classification

Primary: 05D40: Probabilistic methods
Secondary: 60C05: Combinatorial probability 68Q87: Probability in computer science (algorithm analysis, random structures, phase transitions, etc.)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 6 , November 2019 , pp. 816 - 825
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by NSF grant DMS-1001638 and Simons Foundation grant #426894.

‡

Research supported in part by NSF grants DMS-1001638 and DMS-1100215.

References

Alon, N., Kim, J. and Spencer, J. (1997) Nearly perfect matchings in regular simple hypergraphs. Israel J. Math. 100 171–187.CrossRefGoogle Scholar
Bohman, T. (2009) The triangle-free process. Adv. Math. 221 1653–1677.CrossRefGoogle Scholar
Bohman, T., Frieze, A. and Lubetzky, E. (2010) A note on the random greedy triangle packing algorithm. J. Combin. 1 477–488.CrossRefGoogle Scholar
Bohman, T., Frieze, A. and Lubetzky, E. (2015) Random triangle removal. Adv. Math. 280 379–438.CrossRefGoogle Scholar
Bohman, T. and Picollelli, M. (2012) Evolution of SIR epidemics on random graphs with a fixed degree sequence. Random Struct. Alg. 41 179–214.CrossRefGoogle Scholar
Erd˝os, P. and Hanani, H. (1963) On a limit theorem in combinatorial analysis. Publ. Math. Debrecen 10 10–13.Google Scholar
Grable, D. (1997) On random greedy triangle packing. Electron. J. Combin. 4 R11.Google Scholar
Kostochka, A. and Rödl, V. (1998) Partial Steiner systems and matchings in hypergraphs. Random Struct. Alg. 13 335–347.3.0.CO;2-W>CrossRefGoogle Scholar
Pippenger, N. and Spencer, J. (1989) Asymptotic behavior of the chromatic index for hypergraphs. J. Combin. Theory Ser. A 51 24–42.CrossRefGoogle Scholar
Rödl, V. (1985) On a packing and covering problem. European J. Combin. 6 69–78.CrossRefGoogle Scholar
Rödl, V. and Thoma, L. (1996) Asymptotic packing and the random greedy algorithm. Random Struct. Alg. 8 161–177.3.0.CO;2-W>CrossRefGoogle Scholar
Spencer, J. (1995) Asymptotic packing via a branching process. Random Struct. Alg. 7 167–172.CrossRefGoogle Scholar
Telcs, A., Wormald, N. and Zhou, S. (2007) Hamiltonicity of random graphs produced by 2-processes. Random Struct. Alg. 31 450–481.CrossRefGoogle Scholar
Vu, V. (2000) New bounds on nearly perfect matchings in hypergraphs: Higher codegrees do help. Random Struct. Alg. 17 29–63.3.0.CO;2-W>CrossRefGoogle Scholar
Wormald, N. (1999) The differential equation method for random graph processes and greedy algorithms. In Lectures on Approximation and Randomized Algorithms (Karonski, M. and Prömel, H. J., eds), PWN, pp. 73–155.Google Scholar