Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-24T02:37:31.567Z Has data issue: false hasContentIssue false
  • English
  • Français

Large Unavoidable Subtournaments

Part of: Extremal combinatorics Graph theory

Published online by Cambridge University Press:  21 June 2016

EOIN LONG
EOIN LONG*
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv 69978, Israel (e-mail: eoinlong@post.tau.ac.il)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Dk denote the tournament on 3k vertices consisting of three disjoint vertex classes V1, V2 and V3 of size k, each oriented as a transitive subtournament, and with edges directed from V1 to V2, from V2 to V3 and from V3 to V1. Fox and Sudakov proved that given a natural number k and ε > 0, there is n0(k, ε) such that every tournament of order n ⩾ n0(k,ε) which is ε-far from being transitive contains Dk as a subtournament. Their proof showed that 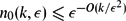$n_0(k,\epsilon ) \leq \epsilon ^{-O(k/\epsilon ^2)}$ and they conjectured that this could be reduced to n0(k, ε) ⩽ ε−O(k). Here we prove this conjecture.

MSC classification

Primary: 05D10: Ramsey theory
Secondary: 05C20: Directed graphs (digraphs), tournaments
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 1 , January 2017 , pp. 68 - 77
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Agarwal, P. and Pach, J. (1995) Combinatorial Geometry, Wiley.Google Scholar
[2] Alon, N. and Spencer, J. (2008) The Probabilistic Method, third edition, Wiley.CrossRefGoogle Scholar
[3] Berger, E., Choromanski, K., Chudnovksy, M., Fox, J., Loebl, M., Scott, A., Seymour, P. and Thomassé, S. (2013) Tournaments and colouring. J. Combin. Theory Ser. B 103 1–20.CrossRefGoogle Scholar
[4] Conlon, D. (2009) A new upper bound for diagonal Ramsey numbers. Ann. of Math. 170 941–960.CrossRefGoogle Scholar
[5] Cutler, J. and Montágh, B. (2008) Unavoidable subgraphs of colored graphs. Discrete Math. 308 4396–4413.Google Scholar
[6] Erdős, P. (1947) Some remarks on the theory of graphs. Bull. Amer. Math. Soc. 53 292–294.CrossRefGoogle Scholar
[7] Erdős, P. and Moser, L. (1964) On the representation of directed graphs as unions of orderings. Publ. Math. Inst. Hungar. Acad. Sci. 9 125–132.Google Scholar
[8] Erdős, P. and Szekeres, G. (1935) A combinatorial problem in geometry. Compositio Mathematica 2 463–470.Google Scholar
[9] Fox, J. and Sudakov, B. (2008) Unavoidable patterns. J. Combin. Theory Ser. A 115 1561–1569.Google Scholar
[10] Fox, J. and Sudakov, B. (2011) Dependent random choice. Random Struct. Alg. 38 68–99.CrossRefGoogle Scholar
[11] Furstenberg, H. (1981) Recurrence in Ergodic Theory and Combinatorial Number Theory, Princeton University Press.Google Scholar
[12] Kövari, T., Sós, V. T. and Turán, P. (1954) On a problem of K. Zarankiewicz. Colloq. Math. 3 50–57.CrossRefGoogle Scholar
[13] Graham, R. L., Rothschild, B. L. and Spencer, J. H. (1990) Ramsey Theory, second edition, Wiley.Google Scholar
[14] Ramsey, F. P. (1930) On a problem of formal logic. Proc. London Math. Soc. 30 264–286.Google Scholar
[15] Shapira, A. and Yuster, R. (2016) Unavoidable tournaments. J. Combin. Theory Ser. B, 116 191–207.Google Scholar
[16] Spencer, J. (1975) Ramsey's theorem: A new lower bound. J. Combin. Theory Ser. A 18 108–115.Google Scholar
[17] Zarankiewicz, K. (1951) Problem P 101. Colloq. Math. 2 301.Google Scholar