Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-07-07T03:52:22.718Z Has data issue: false hasContentIssue false
  • English
  • Français

Enumerating Contingency Tables via Random Permanents

Published online by Cambridge University Press:  01 January 2008

ALEXANDER BARVINOK
ALEXANDER BARVINOK*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109-1043, USA (e-mail: barvinok@umich.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Given m positive integers R = (ri), n positive integers C = (cj) such that Σri = Σcj = N, and mn non-negative weights W=(wij), we consider the total weight T=T(R, C; W) of non-negative integer matrices D=(dij) with the row sums ri, column sums cj, and the weight of D equal to 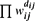. For different choices of R, C, and W, the quantity T(R,C; W) specializes to the permanent of a matrix, the number of contingency tables with prescribed margins, and the number of integer feasible flows in a network. We present a randomized algorithm whose complexity is polynomial in N and which computes a number T′=T′(R,C;W) such that T′ ≤ T ≤ α(R,C)T′ where 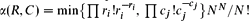. In many cases, ln T′ provides an asymptotically accurate estimate of ln T. The idea of the algorithm is to express T as the expectation of the permanent of an N × N random matrix with exponentially distributed entries and approximate the expectation by the integral T′ of an efficiently computable log-concave function on ℝmn.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 1 , January 2008 , pp. 1 - 19
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. and Spencer, J. (2000) The Probabilistic Method, 2nd edn, Wiley–Interscience.CrossRefGoogle Scholar
[2]Applegate, D. and Kannan, R. (1991) Sampling and integration of log-concave functions. In Proc. Twenty-Third Annual ACM Symposium on Theory of Computing, ACM Press, pp. 156–163.CrossRefGoogle Scholar
[3]Baldoni-Silva, W., De Loera, J. A. and Vergne, M. (2004) Counting integer flows in networks. Found. Comput. Math. 4 277–314.CrossRefGoogle Scholar
[4]Barvinok, A. (2005) Low rank approximations of symmetric polynomials and asymptotic counting of contingency tables. Preprint: arXiv math.CO/0503170.Google Scholar
[5]Barvinok, A. and Pommersheim, J. E. (1999) An algorithmic theory of lattice points in polyhedra. In New Perspectives in Algebraic Combinatorics (Berkeley, CA, 1996–97), Vol. 38 of Math. Sci. Res. Inst. Publ., Cambridge University Press, pp. 91–147.Google Scholar
[6]Bregman, L. M. (1973) Certain properties of nonnegative matrices and their permanents. Dokl. Akad. Nauk SSSR 211 27–30.Google Scholar
[7]Cryan, M. and Dyer, M. (2003) A polynomial-time algorithm to approximately count contingency tables when the number of rows is constant. J. Comput. System Sci. 67 291–310.CrossRefGoogle Scholar
[8]Cryan, M., Dyer, M. and Randall, D. (2005) Approximately counting integral flows and cell-bounded contingency tables. In STOC'05: Proc. 37th Annual ACM Symposium on Theory of Computing, ACM Press, pp. 413–422.CrossRefGoogle Scholar
[9]Diaconis, P. and Gamburd, A. (2004) Random matrices, magic squares and matching polynomials. Electron. J. Combin. 11 # 2.CrossRefGoogle Scholar
[10]Diaconis, P. and Gangolli, A. (1995) Rectangular arrays with fixed margins. In Discrete Probability and Algorithms (Minneapolis, MN, 1993), Vol. 72 of IMA Vol. Math. Appl., Springer, pp. 15–41.CrossRefGoogle Scholar
[11]Diaconis, P. and Sturmfels, B. (1998) Algebraic algorithms for sampling from conditional distributions. Annals Statist. 26 363–397.CrossRefGoogle Scholar
[12]Dyer, M., Kannan, R. and Mount, J. (1997) Sampling contingency tables. Random Struct. Alg. 10 487–506.3.0.CO;2-Q>CrossRefGoogle Scholar
[13]Egorychev, G. P. (1981) The solution of van der Waerden's problem for permanents. Adv. in Math. 42 299–305.CrossRefGoogle Scholar
[14]Falikman, D. I. (1981) Proof of the van der Waerden conjecture on the permanent of a doubly stochastic matrix. Mat. Zametki 29 931–938.Google Scholar
[15]Frieze, A. and Kannan, R. (1999) Log-Sobolev inequalities and sampling from log-concave distributions. Ann. Appl. Probab. 9 14–26.CrossRefGoogle Scholar
[16]Frieze, A., Kannan, R. and Polson, N. (1994) Sampling from log-concave distributions. Ann. Appl. Probab. 4 812–837; correction, p. 1255.Google Scholar
[17]Gurvits, L. (2006) The van der Waerden conjecture for mixed discriminants. Adv. Math. 200 435–454.CrossRefGoogle Scholar
[18]Gurvits, L. and Samorodnitsky, A. (2002) A deterministic algorithm for approximating the mixed discriminant and mixed volume, and a combinatorial corollary. Discrete Comput. Geom. 27 531–550.CrossRefGoogle Scholar
[19]Jerrum, M., Sinclair, A. and Vigoda, E. (2004) A polynomial-time approximation algorithm for the permanent of a matrix with nonnegative entries. J. Assoc. Comput. Mach. 51 671–697.CrossRefGoogle Scholar
[20]Kalantari, B. and Khachiyan, L. (1996) On the complexity of nonnegative-matrix scaling. Linear Algebra Appl. 240 87–103.CrossRefGoogle Scholar
[21]Linial, N., Samorodnitsky, A. and Wigderson, A. (2000) A deterministic strongly polynomial algorithm for matrix scaling and approximate permanents. Combinatorica 20 545–568.CrossRefGoogle Scholar
[22]van Lint, J. H. and Wilson, R. M. (2001) A Course in Combinatorics, 2nd edn, Cambridge University Press.CrossRefGoogle Scholar
[23]London, D. (1971) On matrices with a doubly stochastic pattern. J. Math. Anal. Appl. 34 648–652.CrossRefGoogle Scholar
[24]Lovász, L. and Vempala, S. (2006) Fast algorithms for logconcave functions: Sampling, rounding, integration and optimization. In Proc. 47th Annual IEEE Symposium on Foundations of Computer Science, IEEE Press, pp. 57–68.Google Scholar
[25]Minc, H. (1978) Permanents, Addison-Wesley.Google Scholar
[26]Morris, B. J. (2002) Improved bounds for sampling contingency tables. Random Struct. Alg. 21 135–146.CrossRefGoogle Scholar
[27]Nemirovski, A. and Rothblum, U. (1999) On complexity of matrix scaling. Linear Algebra Appl. 302/303 435–460.CrossRefGoogle Scholar
[28]Samorodnitsky, A. (2006) Personal communication.Google Scholar
[29]Sinkhorn, R. (1964) A relationship between arbitrary positive matrices and doubly stochastic matrices. Ann. Math. Statist. 35 876–879.CrossRefGoogle Scholar
[30]Soules, G. W. (2003) New permanental upper bounds for nonnegative matrices. Linear Multilinear Algebra 51 319–337.CrossRefGoogle Scholar
[31]Stanley, R. P. (1997) Enumerative Combinatorics, Vol. 1. Corrected reprint of the 1986 original, Cambridge University Press.CrossRefGoogle Scholar
[32]Vempala, S. (2005) Geometric random walks: A survey. In Combinatorial and Computational Geometry, Vol. 52 of Mathematical Sciences Research Institute Publications, Cambridge University Press, pp. 577–616.Google Scholar
[33]Yong, A. (2006) Contingency table and magic square enumeration. Available at: http://www.math.umn.edu/~ayong/contingency.htmlGoogle Scholar