Article contents
A non-increasing tree growth process for recursive trees and applications
Published online by Cambridge University Press: 19 October 2020
Abstract
We introduce a non-increasing tree growth process 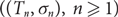 $((T_n,{\sigma}_n),\, n\ge 1)$
, where Tn is a rooted labelled tree on n vertices and σn is a permutation of the vertex labels. The construction of (Tn, σn) from (Tn−1, σn−1) involves rewiring a random (possibly empty) subset of edges in Tn−1 towards the newly added vertex; as a consequence Tn−1 ⊄ Tn with positive probability. The key feature of the process is that the shape of Tn has the same law as that of a random recursive tree, while the degree distribution of any given vertex is not monotone in the process.
$((T_n,{\sigma}_n),\, n\ge 1)$
, where Tn is a rooted labelled tree on n vertices and σn is a permutation of the vertex labels. The construction of (Tn, σn) from (Tn−1, σn−1) involves rewiring a random (possibly empty) subset of edges in Tn−1 towards the newly added vertex; as a consequence Tn−1 ⊄ Tn with positive probability. The key feature of the process is that the shape of Tn has the same law as that of a random recursive tree, while the degree distribution of any given vertex is not monotone in the process.
We present two applications. First, while couplings between Kingman’s coalescent and random recursive trees were known for any fixed n, this new process provides a non-standard coupling of all finite Kingman’s coalescents. Second, we use the new process and the Chen–Stein method to extend the well-understood properties of degree distribution of random recursive trees to extremal-range cases. Namely, we obtain convergence rates on the number of vertices with degree at least 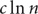 $c\ln n$
, c ∈ (1, 2), in trees with n vertices. Further avenues of research are discussed.
$c\ln n$
, c ∈ (1, 2), in trees with n vertices. Further avenues of research are discussed.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 2
- Cited by



