Article contents
Graph Colouring with No Large Monochromatic Components
Published online by Cambridge University Press: 01 July 2008
Abstract
For a graph G and an integer t we let mcct(G) be the smallest m such that there exists a colouring of the vertices of G by t colours with no monochromatic connected subgraph having more than m vertices. Let 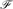 be any non-trivial minor-closed family of graphs. We show that mcc2(G) = O(n2/3) for any n-vertex graph G ∈
be any non-trivial minor-closed family of graphs. We show that mcc2(G) = O(n2/3) for any n-vertex graph G ∈ 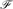 . This bound is asymptotically optimal and it is attained for planar graphs. More generally, for every such
. This bound is asymptotically optimal and it is attained for planar graphs. More generally, for every such 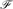 , and every fixed t we show that mcct(G)=O(n2/(t+1)). On the other hand, we have examples of graphs G with no Kt+3 minor and with mcct(G)=Ω(n2/(2t−1)).
, and every fixed t we show that mcct(G)=O(n2/(t+1)). On the other hand, we have examples of graphs G with no Kt+3 minor and with mcct(G)=Ω(n2/(2t−1)).
It is also interesting to consider graphs of bounded degrees. Haxell, Szabó and Tardos proved mcc2(G) ≤ 20000 for every graph G of maximum degree 5. We show that there are n-vertex 7-regular graphs G with mcc2(G)=Ω(n), and more sharply, for every ϵ > 0 there exists cϵ > 0 and n-vertex graphs of maximum degree 7, average degree at most 6 + ϵ for all subgraphs, and with mcc2(G) ≥ cϵn. For 6-regular graphs it is known only that the maximum order of magnitude of mcc2 is between 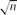 and n.
and n.
We also offer a Ramsey-theoretic perspective of the quantity mcct(G).
- Type
- Paper
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
- 15
- Cited by


