Article contents
Frozen (Δ + 1)-colourings of bounded degree graphs
Published online by Cambridge University Press: 19 October 2020
Abstract
Let G be a graph on n vertices and with maximum degree Δ, and let k be an integer. The k-recolouring graph of G is the graph whose vertices are k-colourings of G and where two k-colourings are adjacent if they differ at exactly one vertex. It is well known that the k-recolouring graph is connected for 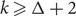 $k\geq \Delta+2$
. Feghali, Johnson and Paulusma (J. Graph Theory83 (2016) 340–358) showed that the (Δ + 1)-recolouring graph is composed by a unique connected component of size at least 2 and (possibly many) isolated vertices.
$k\geq \Delta+2$
. Feghali, Johnson and Paulusma (J. Graph Theory83 (2016) 340–358) showed that the (Δ + 1)-recolouring graph is composed by a unique connected component of size at least 2 and (possibly many) isolated vertices.
In this paper, we study the proportion of isolated vertices (also called frozen colourings) in the (Δ + 1)-recolouring graph. Our first contribution is to show that if G is connected, the proportion of frozen colourings of G is exponentially smaller in n than the total number of colourings. This motivates the use of the Glauber dynamics to approximate the number of (Δ + 1)-colourings of a graph. In contrast to the conjectured mixing time of O(nlog n) for 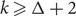 $k\geq \Delta+2$
colours, we show that the mixing time of the Glauber dynamics for (Δ + 1)-colourings restricted to non-frozen colourings can be Ω(n2). Finally, we prove some results about the existence of graphs with large girth and frozen colourings, and study frozen colourings in random regular graphs.
$k\geq \Delta+2$
colours, we show that the mixing time of the Glauber dynamics for (Δ + 1)-colourings restricted to non-frozen colourings can be Ω(n2). Finally, we prove some results about the existence of graphs with large girth and frozen colourings, and study frozen colourings in random regular graphs.
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 2
- Cited by



