Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-18T07:41:01.626Z Has data issue: false hasContentIssue false
  • English
  • Français

Expected Maximum Block Size in Critical Random Graphs

Part of: Discrete mathematics in relation to computer science Graph theory

Published online by Cambridge University Press:  25 July 2019

V. Rasendrahasina ,
A. Rasoanaivo  and
V. Ravelomanana
V. Rasendrahasina*
Affiliation:
ENS – Université d’ Antananarivo, 101 Antananarivo, Madagascar
A. Rasoanaivo
Affiliation:
LIMA – Université d’ Antananarivo, 101 Antananarivo, Madagascar
V. Ravelomanana
Affiliation:
IRIF UMR CNRS 8243 – Universite Denis Diderot, 75013 Paris, France
*
*Corresponding author. Email: vlad@irif.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G(n,M) be a uniform random graph with n vertices and M edges. Let 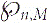${\wp_{n,m}}$ be the maximum block size of G(n,M), that is, the maximum size of its maximal 2-connected induced subgraphs. We determine the expectation of 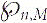${\wp_{n,m}}$ near the critical point M = n/2. When n − 2M ≫ n2/3, we find a constant c1 such that

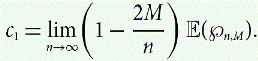$$c_1 = \lim_{n \rightarrow \infty} \left({1 - \frac{2M}{n}} \right) \,\E({\wp_{n,m}}).$$
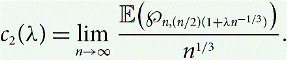Inside the window of transition of G(n,M) with M = (n/2)(1 + λn−1/3), where λ is any real number, we find an exact analytic expression for
$$c_2(\lambda) = \lim_{n \rightarrow \infty} \frac{\E{\left({\wp_{n,{{(n/2)}({1+\lambda n^{-1/3}})}}}\right)}}{n^{1/3}}.$$
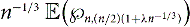 This study relies on the symbolic method and analytic tools from generating function theory, which enable us to describe the evolution of $n^{-1/3}\,\E{\left({\wp_{n,{{(n/2)}({1+\lambda n^{-1/3}})}}}\right)}$ as a function of λ.

MSC classification

Primary: 68R05: Combinatorics
Secondary: 05C30: Enumeration in graph theory 05C80: Random graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Special Issue 4: Analysis of Algorithms , July 2019 , pp. 638 - 655
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banderier, C., Flajolet, P., Schaeffer, G. and Soria, M. (2001) Random maps, coalescing saddles, singularity analysis, and Airy phenomena. Random Struct. Alg. 19 194–246.CrossRefGoogle Scholar
Bollobás, B. (2001) Random Graphs, second edition. Cambridge University Press.CrossRefGoogle Scholar
Chae, G. B., Palmer, E. M. and Robinson, R.W. (2007) Counting labeled general cubic graphs. Discrete Math. 307 2979–2992.CrossRefGoogle Scholar
Daudé, H. and Ravelomanana, V. (2009) Random 2-XORSAT phase transition. Algorithmica 59 48–65.Google Scholar
Dembo, A. and Montanari, A. (2008) Finite size scaling for the core of large random hypergraphs. Ann. Appl. Probab. 18 1993–2040.CrossRefGoogle Scholar
Ding, J., Kim, J. H., Lubetzky, E. and Peres, Y. (2011) Anatomy of a young giant component in the random graph. Random Struct. Alg. 39 139–178.CrossRefGoogle Scholar
Drmota, M. and Noy, M. (2013) Extremal parameters in sub-critical graph classes. In 10th Meeting on Analytic Algorithmics and Combinatorics (ANALCO), pp. 1–7.CrossRefGoogle Scholar
Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5 17–61.Google Scholar
Finch, S. R. (2003) Mathematical Constants. Cambridge University Press.Google Scholar
Flajolet, P., Knuth, D. E. and Pittel, B. (1989) The first cycles in an evolving graph. Discrete Math. 75 167–215.CrossRefGoogle Scholar
Flajolet, P. and Odlyzko, A. (1990) Random mapping statistics. In Advances in Cryptology (EUROCRYPT), Vol. 434 of Lecture Notes in Computer Science, Springer, pp. 329–354.CrossRefGoogle Scholar
Flajolet, P. and Sedgewick, B. (2009) Analytic Combinatorics. Cambridge University Press.CrossRefGoogle Scholar
Frieze, A. M. and McDiarmid, C. (1997). Algorithmic theory of random graphs. Random Struct. Alg. 10 5–42.3.0.CO;2-Z>CrossRefGoogle Scholar
Gao, Z. and Wormald, N. C. (1999) The size of the largest components in random planar maps. SIAM J. Discrete Math. 12 217–228.CrossRefGoogle Scholar
Gilbert, E. (1959) Random graphs. Ann. Math. Statist. 30 1141–1144.CrossRefGoogle Scholar
Giménez, O., Noy, M. and Rué, J. J. (2013) Graph classes with given 3-connected components: Asymptotic enumeration and random graphs. Random Struct. Alg. 42 438–479.CrossRefGoogle Scholar
Goulden, I. P. and Jackson, D. M. (1983) Combinatorial Enumeration. Wiley.Google Scholar
Harary, F. and Palmer, E. (1973) Graphical Enumeration. Academic Press.Google Scholar
Janson, S., Knuth, D. E., Łuczak, T. and Pittel, B. (1993) The birth of the giant component. Random Struct. Alg. 4 233–358.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs. Wiley-Interscience.CrossRefGoogle Scholar
Matoušek, J. and Nešetřil, J. (2008) An Invitation to Discrete Mathematics, second edition. Oxford University Press.Google Scholar
Noy, M., Ravelomanana, V. and Rué, J. J. (2015) On the probability of planarity of a random graph near the critical point. Proc. Amer. Math. Soc. 143 925–936.CrossRefGoogle Scholar
Panagiotou, K. (2009) Blocks in constrained random graphs with fixed average degree. In 21st International Conference on Formal Power Series and Algebraic Combinatorics.Google Scholar
Panagiotou, K. and Steger, A. (2010) Maximal biconnected subgraphs of random planar graphs. ACM Trans. Alg. 6 31.Google Scholar
Pittel, B. (1988) A random graph with a sub-critical number of edges. Trans. Amer. Math. Soc. 309 51–75.CrossRefGoogle Scholar
Wright, E. M. (1977) The number of connected sparsely edged graphs. J. Graph Theory 1 317–330.CrossRefGoogle Scholar
Wright, E. M. (1980) The number of connected sparsely edged graphs III: Asymptotic results. J. Graph Theory 4 393–407.CrossRefGoogle Scholar