Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T09:07:51.943Z Has data issue: false hasContentIssue false
  • English
  • Français

Clustered 3-colouring graphs of bounded degree

Part of: Graph theory

Published online by Cambridge University Press:  18 June 2021

Vida Dujmović ,
Louis Esperet ,
Pat Morin ,
Bartosz Walczak  and
David R. Wood
Vida Dujmović
Affiliation:
School of Computer Science and Electrical Engineering, University of Ottawa, Ottawa, Canada
Louis Esperet
Affiliation:
Laboratoire G-SCOP (CNRS, Univ. Grenoble Alpes), Grenoble, France
Pat Morin
Affiliation:
School of Computer Science, Carleton University, Ottawa, Canada
Bartosz Walczak
Affiliation:
Department of Theoretical Computer Science, Faculty of Mathematics and Computer Science, Jagiellonian University, Kraków, Poland
David R. Wood*
Affiliation:
School of Mathematics, Monash University, Melbourne, Australia
*
*Corresponding author. Email: david.wood@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A (not necessarily proper) vertex colouring of a graph has clustering c if every monochromatic component has at most c vertices. We prove that planar graphs with maximum degree 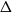$\Delta$ are 3-colourable with clustering 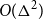$O(\Delta^2)$. The previous best bound was 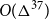$O(\Delta^{37})$. This result for planar graphs generalises to graphs that can be drawn on a surface of bounded Euler genus with a bounded number of crossings per edge. We then prove that graphs with maximum degree 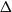$\Delta$ that exclude a fixed minor are 3-colourable with clustering 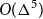$O(\Delta^5)$. The best previous bound for this result was exponential in 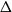$\Delta$.

Keywords

clustered colouringplanar graphsgraph minors

MSC classification

Primary: 05C10: Planar graphs; geometric and topological aspects of graph theory
Secondary: 05C15: Coloring of graphs and hypergraphs 05C83: Graph minors
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 123 - 135
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research is supported by NSERC.

†

Partially supported by ANR Projects GATO (anr-16-CE40-0009-01) and GrR (anr-18-CE40-0032).

§

Research is supported by NSERC.

Research is partially supported by the National Science Centre of Poland grant 2015/17/D/ST1/00585.

∥

Research is supported by the Australian Research Council.

References

Alon, N., Ding, G., Oporowski, B. and Vertigan, D. (2003) Partitioning into graphs with only small components. J. Combin. Theory Ser. B 87(2) 231–243.CrossRefGoogle Scholar
Alon, N., Seymour, P. and Thomas, R. (1990) A separator theorem for nonplanar graphs. J. Amer. Math. Soc. 3(4) 801–808.CrossRefGoogle Scholar
Appel, K. and Haken, W. (1989) Every Planar Map is Four Colorable, Vol. 98 of Contemporary Mathematics, American Mathematical Society.Google Scholar
Baker, B. S. (1994) Approximation algorithms for NP-complete problems on planar graphs. J. ACM 41(1) 153–180.CrossRefGoogle Scholar
Bannister, M. J., Devanny, W. E., Dujmović, V., Eppstein, D. and Wood, D. R. (2019) Track layouts, layered path decompositions, and leveled planarity. Algorithmica 81(4) 1561–1583.CrossRefGoogle Scholar
Bodlaender, H. L. (1998) A partial k-arboretum of graphs with bounded treewidth. Theoret. Comput. Sci. 209(1–2) 1–45.CrossRefGoogle Scholar
Bonamy, M., Gavoille, C. and Pilipczuk, M. (2020) Shorter labeling schemes for planar graphs. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms (SODA’20) (Chawla, S., ed.), pp. 446–462.CrossRefGoogle Scholar
Chen, Z.-Z., Grigni, M. and Papadimitriou, C. H. (2002) Map graphs. J. ACM 49(2) 127–138.CrossRefGoogle Scholar
Choi, I. and Esperet, L. (2019) Improper coloring of graphs on surfaces. J. Graph Theory 91(1) 16–34.CrossRefGoogle Scholar
Debski, M., Felsner, S., Micek, P. and Schröder, F. (2020) Improved bounds for centered colorings. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms (SODA’20) (Chawla, S., ed.), pp. 2212–2226.CrossRefGoogle Scholar
Diestel, R. and Kühn, D. (2005) Graph minor hierarchies. Discrete Appl. Math. 145(2) 167–182.CrossRefGoogle Scholar
Ding, G. and Oporowski, B. (1995) Some results on tree decomposition of graphs. J. Graph Theory 20(4) 481–499.CrossRefGoogle Scholar
Dujmović, V., Eppstein, D., Joret, G., Morin, P. and Wood, D. R. (2020) Minor-closed graph classes with bounded layered pathwidth. SIAM J. Disc. Math. 34(3) 1693–1709.CrossRefGoogle Scholar
Dujmović, V., Eppstein, D. and Wood, D. R. (2017) Structure of graphs with locally restricted crossings. SIAM J. Discrete Math. 31(2) 805–824.CrossRefGoogle Scholar
Dujmović, V., Esperet, L., Joret, G., Gavoille, C., Micek, P. and Morin, P. (to appear) Adjacency labelling for planar graphs (and beyond). J. ACM. arXiv:2003.04280.Google Scholar
Dujmović, V., Esperet, L., Joret, G., Walczak, B. and Wood, D. R. (2020 a) Planar graphs have bounded nonrepetitive chromatic number. Adv. Comb. 5.CrossRefGoogle Scholar
Dujmović, V. and Frati, F. (2018) Stack and queue layouts via layered separators. J. Graph Algorithms Appl. 22(1) 89–99.CrossRefGoogle Scholar
Dujmović, V., Joret, G., Micek, P., Morin, P., Ueckerdt, T. and Wood, D. R. (2020 b) Planar graphs have bounded queue-number. J. ACM 67(4) 22.Google Scholar
Dujmović, V., Morin, P. and Wood, D. R. (2017) Layered separators in minor-closed graph classes with applications. J. Combin. Theory Ser. B 127 111–147.CrossRefGoogle Scholar
Dujmović, V., Morin, P. and Wood, D. R. (2019) Graph product structure for non-minor-closed classes. arXiv:1907.05168.Google Scholar
Dvořák, Z. and Norin, S. (2017) Islands in minor-closed classes. I. Bounded treewidth and separators. arXiv:1710.02727.Google Scholar
Edwards, K., Kang, D. Y., Kim, J., Oum, S.-i. and Seymour, P. (2015) A relative of Hadwiger’s conjecture. SIAM J. Discrete Math. 29(4) 2385–2388.CrossRefGoogle Scholar
Eppstein, D. (2000) Diameter and treewidth in minor-closed graph families. Algorithmica 27(3–4) 275–291.CrossRefGoogle Scholar
Esperet, L. and Joret, G. (2014) Colouring planar graphs with three colours and no large monochromatic components. Comb. Prob. Comput. 23(4) 551–570.CrossRefGoogle Scholar
Esperet, L., Joret, G. and Morin, P. (2020) Sparse universal graphs for planarity. arXiv:2010.05779.Google Scholar
Esperet, L. and Ochem, P. (2016) Islands in graphs on surfaces. SIAM J. Discrete Math. 30(1) 206–219.CrossRefGoogle Scholar
Fomin, F. V., Lokshtanov, D. and Saurabh, S. (2012) Bidimensionality and geometric graphs. In Proceedings of the 23rd Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1563–1575.CrossRefGoogle Scholar
Gale, D. (1979) The game of Hex and the Brouwer fixed-point theorem. Amer. Math. Monthly 86(10) 818–827.CrossRefGoogle Scholar
Halin, R. (1976) S-functions for graphs. J. Geometry 8(1–2) 171–186.CrossRefGoogle Scholar
Harvey, D. J. and Wood, D. R. (2017) Parameters tied to treewidth. J. Graph Theory 84(4) 364–385.CrossRefGoogle Scholar
Haxell, P., Szabó, T. and Tardos, G. (2003) Bounded size components—partitions and transversals. J. Combin. Theory Ser. B 88(2) 281–297.CrossRefGoogle Scholar
Hendrey, K. and Wood, D. R. (2019) Defective and clustered colouring of sparse graphs. Comb. Probab. Comput. 28(5) 791–810.CrossRefGoogle Scholar
Kang, D. Y. and Oum, S.-i. (2019) Improper coloring of graphs with no odd clique minor. Comb. Prob. Comput. 28(5) 740–754.CrossRefGoogle Scholar
Kleinberg, J. M., Motwani, R., Raghavan, P. and Venkatasubramanian, S. (1997) Storage management for evolving databases. In 38th Annual Symposium on Foundations of Computer Science (FOCS’97), IEEE, pp. 353–362.CrossRefGoogle Scholar
Linial, N., Matoušek, J., Sheffet, O. and Tardos, G. (2008) Graph colouring with no large monochromatic components. Comb. Prob. Comput. 17(4) 577–589.CrossRefGoogle Scholar
Lipton, R. J. and Tarjan, R. E. (1979) A separator theorem for planar graphs. SIAM J. Appl. Math. 36(2) 177–189.CrossRefGoogle Scholar
Liu, C.-H. and Oum, S.-i. (2018) Partitioning H-minor free graphs into three subgraphs with no large components. J. Comb. Theory Ser. B 128 114–133.CrossRefGoogle Scholar
Liu, C.-H. and Wood, D. R. (2019 a) Clustered coloring of graphs excluding a subgraph and a minor. arXiv:1905.09495.Google Scholar
Liu, C.-H. and Wood, D. R. (2019 b) Clustered graph coloring and layered treewidth. arXiv:1905.08969.Google Scholar
Liu, C.-H. and Wood, D. R. (2019 c) Clustered variants of Hajós’ conjecture. arXiv:1908.05597.Google Scholar
Matoušek, J. and Přívětivý, A. (2008) Large monochromatic components in two-colored grids. SIAM J. Discrete Math. 22(1) 295–311.CrossRefGoogle Scholar
Mohar, B., Reed, B. and Wood, D. R. (2017) Colourings with bounded monochromatic components in graphs of given circumference. Australas. J. Combin. 69(2) 236–242.Google Scholar
Mohar, B. and Thomassen, C. (2001) Graphs on Surfaces, Johns Hopkins University Press.Google Scholar
Norin, S., Scott, A., Seymour, P. and Wood, D. R. (2019) Clustered colouring in minor-closed classes. Combinatorica 39(6) 1387–1412.CrossRefGoogle Scholar
Norin, S., Scott, A. and Wood, D. R. (2020) Clustered colouring of graph classes with bounded treedepth or pathwidth, arXiv:2012.05554.Google Scholar
Reed, B. A. (1997) Tree width and tangles: a new connectivity measure and some applications. In Surveys in Combinatorics, Vol. 241 of London Mathematical Society Lecture Note Series (R. A. Editor Bailey, ed.), Cambridge University Press, pp. 87–162.CrossRefGoogle Scholar
Robertson, N., Sanders, D. P., Seymour, P. and Thomas, R. (1997) The four-colour theorem. J. Combin. Theory Ser. B 70(1) 2–44.CrossRefGoogle Scholar
Robertson, N. and Seymour, P. (1984) Graph minors. III. Planar tree-width. J. Combin. Theory Ser. B 36(1) 49–64.CrossRefGoogle Scholar
Robertson, N. and Seymour, P. (1986) Graph minors. II. Algorithmic aspects of tree-width. J. Algorithms 7(3) 309–322.CrossRefGoogle Scholar
Robertson, N. and Seymour, P. (2003) Graph minors. XVI. Excluding a non-planar graph. J. Combin. Theory Ser. B 89(1) 43–76.CrossRefGoogle Scholar
Scott, A. and Wood, D. R. (2020) Better bounds for poset dimension and boxicity. Trans. Am. Math. Soc. 373(3) 2157–2172.CrossRefGoogle Scholar
Shahrokhi, F. (2013) New representation results for planar graphs. In Proceedings of the 29th European Workshop on Computational Geometry (EuroCG 2013), pp. 177–180. arXiv:1502.06175.Google Scholar
van den Heuvel, J. and Wood, D. R. (2018) Improper colourings inspired by Hadwiger’s conjecture. J. London Math. Soc. 98 129–148.CrossRefGoogle Scholar
Wood, D. R. (2009) On tree-partition-width. Eur. J. Comb. 30(5) 1245–1253.CrossRefGoogle Scholar
Wood, D. R. (2018) Defective and clustered graph colouring. Electron. J. Comb. DS23. Version 1.CrossRefGoogle Scholar