Research Article
On Mennicke Groups of Deficiency Zero II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 289-293
-
- Article
-
- You have access
- Export citation
Correction
Notice of Retraction
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 294
-
- Article
-
- You have access
- Export citation
Research Article
On Rings With Engel Cycles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 295-300
-
- Article
-
- You have access
- Export citation
A Question of Valdivia on Quasinormable Fréchet Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 301-304
-
- Article
-
- You have access
- Export citation
Variations on Müntz's Theme
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 305-310
-
- Article
-
- You have access
- Export citation
The Behaviour of Homology in the Localization of Finite Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 311-320
-
- Article
-
- You have access
- Export citation
The Hilbert Problem—A Distributional Approach
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-328
-
- Article
-
- You have access
- Export citation
A New Approach to Operator Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 329-337
-
- Article
-
- You have access
- Export citation
Poorly Approximated ℤ2-Cocycles For Transformations With Rational Discrete Spectrum
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 338-342
-
- Article
-
- You have access
- Export citation
Simultaneous Monotone Lp Approximation, p → ∞
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 343-350
-
- Article
-
- You have access
- Export citation
Two Continua Having A Property of J. L. Kelley
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 351-356
-
- Article
-
- You have access
- Export citation
Topological Properties of Legendrian Singularities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 357-363
-
- Article
-
- You have access
- Export citation
Special Principal Ideal Rings and Absolute Subretracts
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 364-367
-
- Article
-
- You have access
- Export citation
An Order-Theoretical Characterization of Varieties of Bands
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 368-374
-
- Article
-
- You have access
- Export citation
Elliptic Curves and Modular Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 375-384
-
- Article
-
- You have access
- Export citation
A Limit Theorem for Brownian Motion in a Random Scenery
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-391
-
- Article
-
- You have access
- Export citation
Correction
lp-Norms of Some Generalized Hausdorff Matrices: Corrections
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 392
-
- Article
-
- You have access
- Export citation
Research Article
Δ-Moves On Links and Jones Polynomial Evaluations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 393-400
-
- Article
-
- You have access
- Export citation
On Sierpinski's Conjecture Concerning the Euler Totient
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 401-404
-
- Article
-
- You have access
- Export citation
The Converse of the Dominated Ergodic Theorem in Hurewicz Setting
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 405-411
-
- Article
-
- You have access
- Export citation



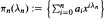 then the collection of spaces
then the collection of spaces 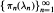 is dense in C[0,1] if and only if lim sup(log
is dense in C[0,1] if and only if lim sup(log 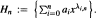 The derivations of these results require an examination of the location of the zeros of the associated Chebyshev polynomials.
The derivations of these results require an examination of the location of the zeros of the associated Chebyshev polynomials.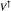 of an operator space
of an operator space 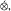 , which satisfies the expected functorial properties. As is the case for Banach spaces, given an operator space
, which satisfies the expected functorial properties. As is the case for Banach spaces, given an operator space 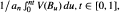 , where {B
, where {B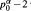 where p
where p