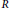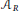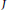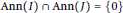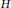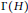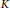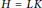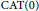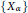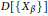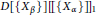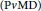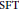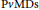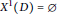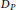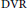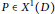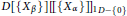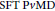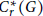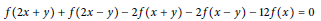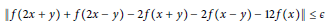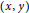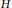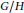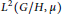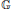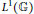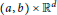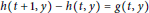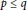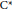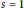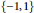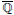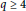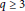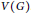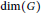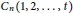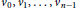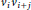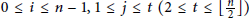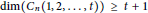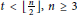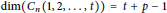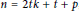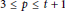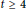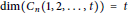Research Article
The Co-annihilating-ideal Graphs of Commutative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-11
-
- Article
-
- You have access
- Export citation
Co-maximal Graphs of Subgroups of Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 12-25
-
- Article
-
- You have access
- Export citation
Self 2-distance Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 26-42
-
- Article
-
- You have access
- Export citation
On the Dual König Property of the Order-interval Hypergraph of Two Classes of N-free Posets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 43-53
-
- Article
-
- You have access
- Export citation
Tubular Free by Cyclic Groups Act Freely on CAT(0) Cube Complexes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-62
-
- Article
-
- You have access
- Export citation
Power Series Rings Over Prüfer v-multiplication Domains. II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-76
-
- Article
-
- You have access
- Export citation
Nilpotent Group C*-algebras as Compact Quantum Metric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 77-94
-
- Article
-
- You have access
- Export citation
Cubic Functional Equations on Restricted Domains of Lebesgue Measure Zero
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-103
-
- Article
-
- You have access
- Export citation
An Extension of Nikishin’s Factorization Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 104-110
-
- Article
-
- You have access
- Export citation
Abstract Plancherel (Trace) Formulas over Homogeneous Spaces of Compact Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 111-121
-
- Article
-
- You have access
- Export citation
A Homological Property and Arens Regularity of Locally Compact Quantum Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-130
-
- Article
-
- You have access
- Export citation
Some Estimates for Generalized Commutators of Rough Fractional Maximal and Integral Operators on Generalized Weighted Morrey Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 131-145
-
- Article
-
- You have access
- Export citation
The Dirichlet Problem for the Slab with Entire Data and a Difference Equation for Harmonic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 146-153
-
- Article
-
- You have access
- Export citation
On Chromatic Functors and Stable Partitions of Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 154-164
-
- Article
-
- You have access
- Export citation
Cokernels of Homomorphisms from Burnside Rings to Inverse Limits
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 165-172
-
- Article
-
- You have access
- Export citation
On Ulam Stability of a Functional Equation in Banach Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 173-183
-
- Article
-
- You have access
- Export citation
On a Conjecture of Livingston
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-195
-
- Article
-
- You have access
- Export citation
Correction
Corrigendum to “Generalized Cesàro Matrices”
-
- Published online by Cambridge University Press:
- 20 November 2018, p. 196
-
- Article
-
- You have access
- Export citation
Research Article
Degree Kirchhoff Index of Bicyclic Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 197-205
-
- Article
-
- You have access
- Export citation
The Metric Dimension of Circulant Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 206-216
-
- Article
-
- You have access
- Export citation