Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Adamczak, Radosław
Guédon, Olivier
Latała, Rafał
Litvak, Alexander
Oleszkiewicz, Krzysztof
Pajor, Alain
and
Tomczak-Jaegermann, Nicole
2012.
Moment estimates for convex measures.
Electronic Journal of Probability,
Vol. 17,
Issue. none,
Latała, Rafał
2014.
Geometric Aspects of Functional Analysis.
Vol. 2116,
Issue. ,
p.
293.
Vershynin, Roman
2015.
Sampling Theory, a Renaissance.
p.
3.
Bogachev, Vladimir Igorevich
2016.
Распределения многочленов на многомерных и бесконечномерных пространствах с мерами.
Успехи математических наук,
Vol. 71,
Issue. 4(430),
p.
107.
Alonso-Gutiérrez, David
Litvak, Alexander E.
and
Tomczak-Jaegermann, Nicole
2016.
On the Isotropic Constant of Random Polytopes.
The Journal of Geometric Analysis,
Vol. 26,
Issue. 1,
p.
645.
Latała, Rafał
and
Strzelecka, Marta
2016.
Weak and strong moments of ℓᵣ-norms of log-concave vectors.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 8,
p.
3597.
Strzelecka, Marta
Strzelecki, Michal
and
Tkocz, Tomasz
2017.
On the convex infimum convolution inequality
with optimal cost function
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 14,
Issue. 1,
p.
903.
Anatolyev, Stanislav
and
Yaskov, Pavel
2017.
ASYMPTOTICS OF DIAGONAL ELEMENTS OF PROJECTION MATRICES UNDER MANY INSTRUMENTS/REGRESSORS.
Econometric Theory,
Vol. 33,
Issue. 3,
p.
717.
Latała, Rafał
2017.
Convexity and Concentration.
Vol. 161,
Issue. ,
p.
525.
Chafaï, Djalil
and
Tikhomirov, Konstantin
2018.
On the convergence of the extremal eigenvalues of empirical covariance matrices with dependence.
Probability Theory and Related Fields,
Vol. 170,
Issue. 3-4,
p.
847.
Latała, Rafał
and
Strzelecka, Marta
2018.
COMPARISON OF WEAK AND STRONG MOMENTS FOR VECTORS WITH INDEPENDENT COORDINATES.
Mathematika,
Vol. 64,
Issue. 1,
p.
211.
Saumard, Adrien
and
Wellner, Jon A.
2019.
On the isoperimetric constant, covariance inequalities and $L_{p}$-Poincaré inequalities in dimension one.
Bernoulli,
Vol. 25,
Issue. 3,
Kabán, Ata
2020.
Sufficient ensemble size for random matrix theory-based handling of singular covariance matrices.
Analysis and Applications,
Vol. 18,
Issue. 05,
p.
929.
Latała, Rafał
and
Nayar, Piotr
2020.
Hadamard products and moments of random vectors.
Advances in Mathematics,
Vol. 375,
Issue. ,
p.
107414.
Barbier, Jean
Panchenko, Dmitry
and
Sáenz, Manuel
2022.
Strong replica symmetry for high-dimensional disordered log-concave Gibbs measures.
Information and Inference: A Journal of the IMA,
Vol. 11,
Issue. 3,
p.
1079.
Klartag, B.
and
Milman, V.
2022.
Analysis at Large.
p.
203.
Narayanan, Hariharan
Sheffield, Scott
and
Tao, Terence
2023.
Sums of GUE matrices and concentration of hives from correlation decay of eigengaps.
Probability Theory and Related Fields,
Zhivotovskiy, Nikita
2024.
Dimension-free bounds for sums of independent matrices and simple tensors via the variational principle.
Electronic Journal of Probability,
Vol. 29,
Issue. none,
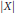 $\left| X \right|$ of an isotropic log-concave random vector
$\left| X \right|$ of an isotropic log-concave random vector 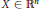 $X\,\in \,{{\mathbb{R}}^{n}},$ stating that for every
$X\,\in \,{{\mathbb{R}}^{n}},$ stating that for every 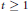 $t\,\ge \,1$,
$t\,\ge \,1$,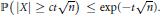 $$\mathbb{P}\left( \left| X \right|\,\ge \,ct\sqrt{n} \right)\,\le \,\exp (-t\sqrt{n}).$$
$$\mathbb{P}\left( \left| X \right|\,\ge \,ct\sqrt{n} \right)\,\le \,\exp (-t\sqrt{n}).$$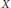 $X$ and any
$X$ and any 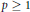 $p\,\ge \,1$,
$p\,\ge \,1$, $${{(\mathbb{E}{{\left| X \right|}^{p}})}^{1/p}}\,\sim \,\mathbb{E}\left| X \right|\,+\,\underset{z\in {{S}^{n-1}}}{\mathop{\sup }}\,\,{{(\mathbb{E}{{\left| \left\langle z,\,X \right\rangle \right|}^{p}})}^{1/p}}.$$
$${{(\mathbb{E}{{\left| X \right|}^{p}})}^{1/p}}\,\sim \,\mathbb{E}\left| X \right|\,+\,\underset{z\in {{S}^{n-1}}}{\mathop{\sup }}\,\,{{(\mathbb{E}{{\left| \left\langle z,\,X \right\rangle \right|}^{p}})}^{1/p}}.$$



