Article contents
A Remark on a Weighted Landau Inequality of Kwong and Zettl
Published online by Cambridge University Press: 20 November 2018
Abstract
In this note we extend a theorem of Kwong and Zettl concerning the inequality
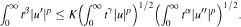
The Kwong-Zettl result holds for 1 ≤ p < ∞ and real numbers α, β, γ such that the conditions (i) β = (α + γ)/2, (ii) β > - 1 , and (iii) γ - 1 - p hold. Here the inequality is proved with β satisfying (i) for all α, γ except p — 1,-1 — p. In this case the inequality is false; however u is shown to satisfy the inequality
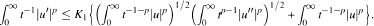
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1995
References
- 1
- Cited by


