Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-19T08:57:48.750Z Has data issue: false hasContentIssue false
  • English
  • Français

Real Hypersurfaces in Complex Two-Plane Grassmannians with Reeb Parallel Structure Jacobi Operator

Published online by Cambridge University Press:  20 November 2018

Imsoon Jeong ,
Seonhui Kim  and
Young Jin Suh
Imsoon Jeong
Affiliation:
Department of Mathematics, Kyungpook National University, Taegu, 702-701, KOREA e-mail: imsoon.jeong@gmail.comkimsh0123@hanmail.netyjsuh@knu.ac.kr
Seonhui Kim
Affiliation:
Department of Mathematics, Kyungpook National University, Taegu, 702-701, KOREA e-mail: imsoon.jeong@gmail.comkimsh0123@hanmail.netyjsuh@knu.ac.kr
Young Jin Suh
Affiliation:
Department of Mathematics, Kyungpook National University, Taegu, 702-701, KOREA e-mail: imsoon.jeong@gmail.comkimsh0123@hanmail.netyjsuh@knu.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give a characterization of a real hypersurface of Type 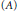$\left( A \right)$ in complex two-plane Grassmannians 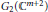${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$, which means a tube over a totally geodesic 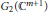${{G}_{2}}\left( {{\mathbb{C}}^{m+1}} \right)$ in 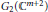${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$, by means of the Reeb parallel structure Jacobi operator 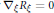${{\nabla }_{\xi }}{{R}_{\xi }}\,=\,0$.

Keywords

53C4053C15real hypersurfacescomplex two-plane GrassmanniansHopf hypersurfaceReeb parallelstructure Jacobi operator
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 821 - 833
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Ahn, S.-S., Lee, S.-B., and Suh, Y. J., On ruled real hypersurfaces in a complex space form.Tsukuba J. Math. 17 (1993), no. 2, 311–322.Google Scholar
[2] Berndt, J., Real hypersurfaces with constant principal curvatures in complex hyperbolic space. J. Reine Angew. Math. 395 (1989), 132–141.Google Scholar
[3] Berndt, J., Real hypersurfaces in quaternionic space forms.J. Reine Angew. Math. 419 (1991), 9–26.Google Scholar
[4] Berndt, J., Riemannian geometry of complex two-plane Grassmannian.Rend. Sem. Mat. Univ. Politec. Torino 55 (1997), no. 1, 19–83.Google Scholar
[5] Berndt, J. and Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians.Monatsh. Math. 127 (1999), no. 1, 1–14. http://dx.doi.org/10.1007/s006050050018 Google Scholar
[6] Berndt, J. and Suh, Y. J., Isometric flows on real hypersurfaces in complex two-plane Grassmannians Monatsh. Math. 137 (2002), no. 2, 87–98. http://dx.doi.org/10.1007/s00605-001-0494-4 Google Scholar
[7] Choi, Y. S. and Suh, Y. J., Real hypersurfaces with-parallel shape operator in complex two-plane Grassmannians. Bull. Austral. Math. Soc. 75 (2007), no. 1, 1–16. http://dx.doi.org/10.1017/S0004972700038934 Google Scholar
[8] Jeong, I., Kimura, M., Lee, H., and Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with Reeb parallel shape operator. Monatsh. Math., to appear. http://dx.doi.org/10.1007/s00605-013-0475-4 Google Scholar
[9] Jeong, I., Machado, C. J., J. D. Pérez, and Suh, Y. J., Real hypersurface in complex two-plane Grassmannians with D?-parallel structure Jacobi operator. Internat. J. Math. 22 (2011), no. 5, 655–673. http://dx.doi.org/10.1142/S0129167X11006957 Google Scholar
[10] Jeong, I., Pérez, J. D., and Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with parallel structure Jacobi operator. Acta Math. Hungar. 112 (2009), no. 1–2, 173–186. http://dx.doi.org/10.1007/s10474-008-8004-y Google Scholar
[11] Ki, U-H., Pérez, J. D., Santos, F. G., and Suh, Y. J., Real hypersurfaces in complex space forms with-parallel Ricci tensor and structure Jacobi operator. J. Korean Math. Soc. 44 (2007), no. 2, 307–326. http://dx.doi.org/10.4134/JKMS.2007.44.2.307 Google Scholar
[12] Kimura, M., Real hypersurfaces and complex submanifolds in complex projective space.Trans. Amer. Math. Soc. 296 (1986), no. 1, 137–149. http://dx.doi.org/10.1090/S0002-9947-1986-0837803-2 Google Scholar
[13] Kimura, M., Sectional curvatures of holomorphic planes on a real hypersurface in Pn(C). Math. Ann. 276 (1987), no. 3, 487–497. http://dx.doi.org/10.1007/BF01450843 Google Scholar
[14] Lee, H. and Suh, Y. J., Real hypersurfaces of type B in complex two-plane Grassmannians related to the Reeb vector.Bull. Korean Math. Soc. 47 (2010), no. 3, 551–561. http://dx.doi.org/10.4134/BKMS.2010.47.3.551 Google Scholar
[15] Martinez, A. and Pérez, J. D., Real hypersurfaces in quaternionic projective space. Ann. Math. Pura Appl. 145 (1986), 355–384. http://dx.doi.org/10.1007/BF01790548 Google Scholar
[16] Machado, C. J. and J. D. Pérez, Real hypersurfaces in complex two-plane Grassmannians whose Jacobi operators are -invariant. Internat. J. Math. 23 (2012), no. 3, 1250002. http://dx.doi.org/10.1142/S0129167X1100746X Google Scholar
[17] Pérez, J. D. and Suh, Y. J., Real hypersurfaces of quaternionic projective space satisfying r_i R = 0. Differential Geom. Appl. 7 (1997), no. 3, 211–217. http://dx.doi.org/10.1016/S0926-2245(97)00003-X Google Scholar
[18] Pérez, J. D. and Suh, Y. J., The Ricci tensor of real hypersurfaces in complex two-plane Grassmannians.J. Korean Math. Soc. 44 (2007), no. 1, 211–235. http://dx.doi.org/10.4134/JKMS.2007.44.1.211 Google Scholar
[19] Pérez, J. D., Santos, F. G., and Suh, Y. J., Real hypersurfaces in complex projective space whose structure Jacobi operator is Lie-parallel. Differential Geom. Appl. 22 (2005), no. 2. 181–188. http://dx.doi.org/10.1016/j.difgeo.2004.10.005 Google Scholar
[20] Pérez, J. D., Santos, F. G., and Suh, Y. J., Real hypersurfaces in complex projective space whose structure Jacobi operator is D-parallel. Bull. Belg. Math. Soc. Simon Stevin 13 (2006), no. 3, 459–469.Google Scholar