Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-23T19:21:04.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Integer Invariants of Regular Cyclic Actions

Published online by Cambridge University Press:  20 November 2018

Robert D. Little
Robert D. Little*
Affiliation:
Department of Mathematics University of Hawaii at Manoa 2565 The Mall Honolulu, HI 96822 USA, e-mail: little@math.hawaii.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 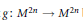$g:\,{{M}^{2n}}\,\to \,{{M}^{2n}}$ be a smooth map of period 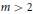$m\,>\,2$ which preserves orientation. Suppose that the cyclic action defined by 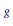$g$ is regular and that the normal bundle of the fixed point set 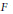$F$ has a 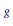$g$-equivariant complex structure. Let 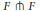$F\,\pitchfork \,F$ be the transverse self-intersection of 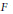$F$ with itself. If the 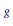$g$-signature 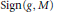$\text{Sign(g,}\,\text{M)}$ is a rational integer and 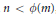$n\,<\,\phi (m)$, then there exists a choice of orientations such that 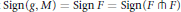$\text{Sign}\,\text{(g,}\,\text{M)}\,\text{=}\,\text{Sign}\,\text{F}\,\text{=}\,\text{Sign}(F\,\pitchfork \,F)$.

Keywords

57S17
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 1 , 01 March 2004 , pp. 60 - 72
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Alexander, J. P., Hamrick, G. C. and Vick, J. W., The signature of the fixed set of odd period. Proc. Amer.Math. Soc. 57 (1976), 327–331.Google Scholar
[2] Atiyah, M. F. and Singer, I. M., The index of elliptic operators III. Ann. of Math. 87 (1968), 546–604.Google Scholar
[3] Berend, D. and Katz, G., Separating number theory and topology in the Atiyah-Singer g-signature formula. Duke J. Math. 61 (1990), 939–971.Google Scholar
[4] Bredon, G. E., Introduction to Compact Transformation Groups. Academic Press, London, 1972.Google Scholar
[5] Dovermann, K. H., Rigid cyclic group actions on cohomology complex projective space. Math. Proc. Cambridge Philos. Soc. 101 (1987), 487–507.Google Scholar
[6] Dovermann, K. H. and Little, R. D., Involutions of cohomology complex projective space with codimension-two fixed points. Indiana J. Math. 41 (1992), 197–211.Google Scholar
[7] Hirzebruch, F., Involutionen auf Mannigfaltigkeiten. Proc. Conf. on Trans. Groups, New Orleans, Springer Verlag, 1967, 148–167.Google Scholar
[8] J¨anich, K. and Ossa, E., On the signature of an involution. Topology 8 (1969), 27–30.Google Scholar
[9] Kawakubo, K., The index and generalized Todd genus of Zp actions. Amer. J. Math. 97 (1975), 182–204.Google Scholar
[10] Little, R. D., Self-intersection of fixed manifolds and relations for the multisignature.Math. Scand. 69 (1991), 167–178.Google Scholar
[11] Little, R. D., The stable signature of a regular cyclic action. Proc. Amer. Math. Soc. 130 (2002), 259–266.Google Scholar
[12] Royster, D. C., An analogue of the stabilization map for regular Zp actions. Rocky Mountain J. Math. 24 (1994), 689–708.Google Scholar