Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-22T12:10:14.437Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Pontrjagin Algebra of a Certain Class of Flags of Foliations

Published online by Cambridge University Press:  20 November 2018

F. J. Carreras  and
A. M. Naveira
F. J. Carreras
Affiliation:
Departamento de Geometría y Topologia Facultad de Matemáticas Universidad de Valencia Burjasot (Valencia), Spain
A. M. Naveira
Affiliation:
Departamento de Geometría y Topologia Facultad de Matemáticas Universidad de Valencia Burjasot (Valencia), Spain
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

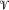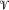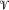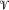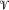Let (𝓜,g) be a Riemannian manifold and let 1, 2, 3 be mutually orthogonal distributions on 𝓜 of dimensions p1, p2,P3 such that p1 + p2 + p3 = dim 𝓜. We assume that , and 1, ⊕ 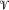2 are integrable and that all the geodesies of 𝓜 with initial tangent vector in 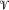2 remain tangent to 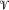2. Then, we prove that Pontk(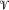2, ⊕ 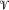3) = 0 for k > p2 + 2p3, where Pontk(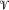2, ⊕ 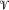3) is the subspace of the Pontrjagin algebra of 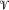2 ⊕ 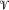3 generated by forms of degree k.

Keywords

53C15flag manifoldsbundle-like metricsPontrjagin algebra of a vector bundle
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 28 , Issue 1 , 01 March 1985 , pp. 77 - 83
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Bott, R., Lectures on characteristic classes and foliations, Lecture Notes in Mathematics, Springer-Verlag, 279(1972), pp. 1–80.Google Scholar
2. Cordero, L.A. and Masa, X., Characteristic classes of subfoliations, Ann. Inst. Fourier, Grenoble 31, 2 (1981), pp. 61–86.Google Scholar
3. Gil-Medrano, O., On the geometric properties of some classes of almost-product structures, Rend. Circ. Mat. Palermo 32 (1983), 315-329.Google Scholar
4. Kobayashi, S. and Nomizu, K., Foundations of Differential Geometry, Vol. I and II, Interscience, 1963, 1969.Google Scholar
5. Miquel, V., Some examples of Riemannian almost-product manifolds, Pac. J. Math. III (1984), 163–178.Google Scholar
6. Naveira, A.M., A classification of Riemannian almost-product manifolds, Rendiconti di Matematica, 3 (1983), 577-592.Google Scholar
7. Pasternack, J.S., Foliations and compact Lie group actions, Comm. Math. Helv. 46 (1971), pp. 467–477.Google Scholar
8. Reinhart, B., Foliated manifolds with bundle-like metrics, Ann. of Math. 69 (1959), pp. 119–131.Google Scholar
9. Vaisman, I., Almost-multifoliate Riemannian manifolds, Ann. St. Univ. “Al. I. Cuza”, XVI (1970), pp. 97–104.Google Scholar