No CrossRef data available.
Article contents
On Carleman Integral Operators
Published online by Cambridge University Press: 20 November 2018
Extract
L2(a, b)
1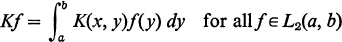
with the property
2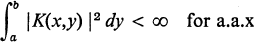
were originally defined by T. Carleman [4]. Here he imposed on the kernel the conditions of measurability and hermiticity,
3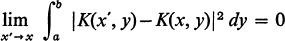
for all x with the exception of a countable set with a finite number of limit points and
4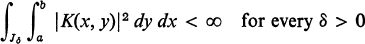
where Jδ denotes the interval [a, b] with the exception of subintervals |x - ξv| < δ; here ξv represents a finite set of points for which (3) fails to hold.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1970


