Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-21T14:26:00.164Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-extendable Zero Sets of Harmonic and Holomorphic Functions

Published online by Cambridge University Press:  20 November 2018

P. M. Gauthier
P. M. Gauthier*
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, Montréal, Que., H3C 3J7 e-mail: gauthier@dms.umontreal.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the zero sets of harmonic functions on open sets in 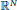${{\mathbb{R}}^{N}}$ and holomorphic functions on open sets in 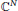${{\mathbb{C}}^{N}}$. We show that the non-extendability of such zero sets is a generic phenomenon.

Keywords

31B2532A4032A6032D15boundary behaviourharmonicholomorphiczero sets
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 303 - 310
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Bernal-Gonzâlezand, L. Ordonez Cabrera, M., Lineability criteria, with applications.J. Funct. Anal. 266(2014), no. 6, 3997–4025.http://dx.doi.org/10.1016/j.jfa.2O13.11.014 Google Scholar
[2] Gardiner, S. J., Harmonic approximation.London Math. Soc. Lecture Notes Series, 221, Cambridge University Press, Cambridge, 1995.Google Scholar
[3] Manne, P. E., E. E Wold, and N. 0vrelid, Holomorphic convexity and Carleman approximation by entire functions on Stein manifolds. Math. Ann. 351(2011), 571–585. http://dx.doi.org/!0.1007/s00208-010-0605-4 Google Scholar