Hostname: page-component-84b7d79bbc-rnpqb Total loading time: 0 Render date: 2024-07-29T16:50:07.187Z Has data issue: false hasContentIssue false
  • English
  • Français

New Characterizations of the Reflexivity in Terms of the Set of Norm Attaining Functionals

Published online by Cambridge University Press:  20 November 2018

Mariá D. Acosta  and
Manuel Ruiz Galán
Mariá D. Acosta
Affiliation:
Departamento de Análisis Matemático Facultad de Ciencias Universidad de Granada 18071 Granada Spain, e-mail: dacosta@goliat.ugr.es
Manuel Ruiz Galán
Affiliation:
Departamento de Matemática Aplicada E.U. Arquitectura Técnica Universidad de Granada 18071 Granada Spain, e-mail: mruizg@goliat.ugr.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

As a consequence of results due to Bourgain and Stegall, on a separable Banach space whose unit ball is not dentable, the set of norm attaining functionals has empty interior (in the norm topology). First we show that any Banach space can be renormed to fail this property. Then, our main positive result can be stated as follows: if a separable Banach space 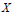$X$ is very smooth or its bidual satisfies the 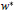${{\mathcal{w}}^{*}}$-Mazur intersection property, then either 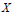$X$ is reflexive or the set of norm attaining functionals has empty interior, hence the same result holds if 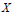$X$ has the Mazur intersection property and so, if the norm of 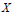$X$ is Fréchet differentiable. However, we prove that smoothness is not a sufficient condition for the same conclusion.

Keywords

46B0446B1046B20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 3 , 01 September 1998 , pp. 279 - 289
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Acosta, M. D., Aguirre, F. J. and Payá, R., A space by W. Gowers and new results on norm and numerical radius attaining operators. Acta Univ. Carolin. Math. Phys. 33 (1992), 5–14.Google Scholar
2. Bonsall, F. F. and Duncan, J., Numerical Ranges II. London Math. Soc. Lecture Note Ser. 10, Cambridge University Press, 1973.Google Scholar
3. Bourgin, R. D., Geometric aspects of convex sets with the Radon-Nikodym property. Lecture Notes in Math. 993, Springer-Verlag, Berlin, 1983.Google Scholar
4. Debs, G., Godefroy, G. and Saint Raymond, J., Topological properties of the set of norm-attaining linear functionals. Canad. J. Math. 47 (1995), 318–329.Google Scholar
5. Deville, R., Godefroy, G. and Zizler, V., Smoothness and renormings in Banach spaces. Pitman Monographs Surveys Pure Appl. Math. 64, Longman Sci. Tech., New York, 1993.Google Scholar
6. Diestel, J. and Faires, B., On vector measures. Trans. Amer.Math. Soc. 198 (1974), 253–271.Google Scholar
7. Dunford, N. and Schwarz, J. T., Linear Operators Part I: General theory. Interscience Publishers, New York, 1958.Google Scholar
8. Garling, D. J. H., On symmetric sequence spaces. Proc. London Math. Soc. 16 (1966), 85–106.Google Scholar
9. Giles, J. R., Gregory, D. A. and Sims, B., Geometrical implications of upper semi-continuity of the duality mapping on a Banach space. Pacific J. Math. 79 (1978), 99–109.Google Scholar
10. Giles, J. R., Gregory, D. A. and Sims, B., Characterisation of normed linear spaces with Mazur's intersection property. Bull. Austral. Math. Soc. 18 (1978), 105–123.Google Scholar
11. Godefroy, G., Metric characterization of first Baire class linear forms and octahedral norms. Studia Math. 95 (1989), 1–15.Google Scholar
12. Godefroy, G., Some applications of Simons’ inequality. Murcia Seminar on Functional Analysis II (to appear).Google Scholar
13. Haydon, R., A counterexample to several questions about scattered compact spaces. Bull. London Math. Soc. 22 (1990), 261–268.Google Scholar
14. Harmand, P., Werner, D. and Werner, W., M-ideals in Banach spaces and Banach algebras. Lecture Notes in Math. 1547, Springer-Verlag, Berlin, 1993.Google Scholar
15. James, R. C., Weak compactness and reflexivity. Israel J. Math. 2 (1964), 101–119.Google Scholar
16. Jiménez Sevilla, M. and Moreno, J. P., Renorming Banach spaces with the Mazur intersection property. J. Funct. Anal. 144 (1997), 486–504.Google Scholar
17. Jiménez Sevilla, M. and Moreno, J. P., A note on norm attaining functionals. Proc. Amer. Math. Soc. (to appear).Google Scholar
18. Kenderov, P. S. and Giles, J. R., On the structure of Banach spaces with Mazur's intersection property. Math. Ann. 291 (1991), 463–473.Google Scholar
19. Mazur, S., Über konvexe Mengen in linearen normierten Räumen. Studia Math. 4 (1933), 70–84.Google Scholar
20. Mazur, S., Über schwache Konvergentz in den Räumen lp . Studia Math. 4 (1933), 128–133.Google Scholar
21. Phelps, R. R., A representation theorem for bounded convex sets. Proc. Amer. Math. Soc. 11 (1960), 976–983.Google Scholar
22. Sargent, W. L. C., Some sequence spaces related to the lp spaces. J. London Math. Soc. 35 (1960), 161–171.Google Scholar
23. Simons, S., A convergence theorem with boundary. Pacific J. Math. 40 (1972), 703–708.Google Scholar
24. Simons, S., Maximinimax, minimax, and antiminimax theorems and a result of R. C. James. Pacific J.Math. 40 (1972), 709–718.Google Scholar
25. Sullivan, F., Dentability, smoothability and stronger properties in Banach spaces. Indiana Math. J. 26 (1977), 545–553.Google Scholar
26. Werner, D., New classes of Banach spaces which are M-ideals in their biduals. Math. Proc. Cambridge Philos. Soc. 111 (1992), 337–354.Google Scholar