Article contents
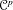 $\mathscr{C}^{p}$-parametrization in O-minimal Structures
$\mathscr{C}^{p}$-parametrization in O-minimal Structures
Part of:
Model theory
Published online by Cambridge University Press: 09 January 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We give a geometric and elementary proof of the uniform 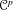 $\mathscr{C}^{p}$-parametrization theorem of Yomdin and Gromov in arbitrary o-minimal structures.
$\mathscr{C}^{p}$-parametrization theorem of Yomdin and Gromov in arbitrary o-minimal structures.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
Burguet, D.,
A proof of Yomdin-Gromov’s algebraic lemma
. Israel J. Math.
168(2008), 291–316. https://doi.org/10.1007/s11856-008-1069-z.Google Scholar
Cluckers, R., Comte, G., and Loeser, F., Non-archimedean Yomdin-Gromov parametrization and points of bounded height. 2014. arxiv:1404.1952.Google Scholar
Cluckers, R., Pila, J., and Wilkie, A., Uniform parametrization of subanalytic sets and diophantine applications. 2018. arxiv:1605.05916.Google Scholar
Coste, M., An introduction to O-minimal geometry, Dottorato di Ricerca in Matematica, Edizioni ETS, Pisa, 2000.Google Scholar
Gromov, M.,
Entropy, homology and semialgebraic geometry
. Séminaire Bourbaki, 1985/86, Astérisque
145–146(1987), 5, 225–240.Google Scholar
Hironaka, H., Introduction to real analytic sets and real analytic maps. Dottorato di Ricerca in Matematica, Edizioni ETS, Pisa, 2009.Google Scholar
Kocel-Cynk, B., Pawłucki, W., and Valette, A.,
Short geometric proof that Hausdorff limits are definable in any o-minimal structure
. Adv. Geom.
14(2014), no. 1, 49–58. https://doi.org/10.1515/advgeom-2013-0028.Google Scholar
Kurdyka, K. and Pawłucki, W.,
Subanalytic version of Whitney’s extension theorem
. Studia Math.
124(1997), no. 3, 269–280.Google Scholar
Łojasiewicz, S., Ensembles semi-analytiques. Institut des Hautes Études Scientifiques, Bures-sur-Yvette, 1965.Google Scholar
Pawłucki, W.,
Le théorème de Puiseux pour une application sous-analytique
. Bull. Polish Acad. Sci. Math.
32(1984), no. 9–10, 555–560.Google Scholar
Pawłucki, W.,
Lipschitz cell decomposition in o-minimal structures. I
. Illinois J. Math.
52(2008), 1045–1063.Google Scholar
Pila, J. and Wilkie, A. J.,
The rational points of a definable set
. Duke Math. J.
133(2006), no. 3, 591–616. https://doi.org/10.1215/S0012-7094-06-13336-7.Google Scholar
van den Dries, L., Tame topology and o-minimal structures. London Mathematical Society Lecture Note Series, 248, Cambridge University Press, Cambridge, 1998. https://doi.org/10.1017/CBO9780511525919.Google Scholar
Yomdin, Y.,
Volume growth and entropy
. Israel J. Math.
57(1987), 285–300. https://doi.org/10.1007/BF02766215.Google Scholar
Yomdin, Y.,
C
k
-resolution of semialgebraic mappings. Addendum to: “Volume growth and entropy”
. Israel J. Math.
57(1987), 301–317. https://doi.org/10.1007/BF02766216.Google Scholar
Yomdin, Y.,
Analytic reparametrization of semialgebraic sets
. J. Complexity
24(2008), no. 1, 54–76. https://doi.org/10.1016/j.jco.2007.03.009.Google Scholar
Yomdin, Y.,
Smooth parametrizations in dynamics, analysis, diophantine and computational geometry
. Jpn. J. Ind. Appl. Math.
32(2015), no. 2, 411–435. https://doi.org/10.1007/s13160-015-0176-6.Google Scholar
- 2
- Cited by


